Studia podyplomowe INŻYNIERIA MATERIAŁÓW POLIMEROWYCH Edycja II marzec - listopad 2014
|
|
|
- Seweryn Baranowski
- 7 lat temu
- Przeglądów:
Transkrypt
1 Studia podyplomowe IŻYIERIA MATERIAŁÓW POLIMEROWYCH Edycja II marzec - listopad 2014 Organizacja i realizacja studiów oraz opracowanie materiałów dydaktycznych są współfinansowane ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego jako zadanie projektu Rozszerzenie i wzbogacenie oferty edukacyjnej oraz poprawa jakości kształcenia na Wydziale Chemicznym Politechniki Rzeszowskiej realizowanego w Programie Operacyjnym Kapitał Ludzki, umowa nr UDA POKL /09-01 Politechnika Rzeszowska im. I. Łukasiewicza, Wydział Chemiczny
2 Fizykochemia i właściwości fizyczne polimerów Wykład 2
3 Treść wykładu Giętkość makrocząsteczek Wymiary pojedynczej cząsteczki: odległość końców łańcucha, promień bezwładności Rzeczywiste wymiary kłębków typowych polimerów Cząsteczki sztywne. Długość persystentna, długość konturu Wymiary makrocząsteczek nieliniowych Parametr długości segmentu b. Pojęcie objętości wyłączonej, punkt i temperatura Θ (theta). Roztwory rozcieńczone, semirozcieńczone i stężone. Wykres pseudofazowy roztworów polimerów. Wymiary makrocząsteczek w roztworach, współczynnik ekspansji kłębka. Koncepcja blobów.
4 Wymiary makrocząsteczek makrocząsteczka typ M długość/ mm 1 mm = 10 6 nm średnica nm polietylen zwykły ultra ,001 0,03 ~0,2 ~0,2 DA Escherichia coli (pałeczka okrężnicy) genom ludzki ? 1, ~2,0 j. wyżej (1,5 m = 1, nm) Gdyby średnica makrocząsteczki stanowiącej genom ludzki była równa 1 mm, wtedy jej długość byłaby równa kilkuset kilometrom
5 Wymiary makrocząsteczek Model makrocząsteczki polietylenu o masie cząsteczkowej 10 5 Rzeczywista długość: 0,001 mm (dla M = 10 5 ): powiększenie 10 7 x 10 m, Ø= ~1 mm
6 Wymiary i cechy (bio)makrocząsteczek 1. Bardzo duży stosunek l/d l d (f) Wielkość (długość) (bio)makrocząsteczek ewoluowała dla osiągnięcia pewnych cech użytkowych (albo: konieczność osiągnięcia pewnych cech użytkowych doprowadziła do utworzenia <stworzenia> biomakrocząsteczek) - zawartość informacji (olbrzymia) - właściwości fizyczne 1) Splątania 2) Konformacje 3) Struktury 4) Objętość wyłączona Główne cechy syntezy: 1) Selektywność: 10 5 x ta sama reakcja (99.999%) 2) Historia syntezy - błędy pozostają w produkcie makrocząsteczce
7 Splątania makrocząsteczek wpływ na właściwości fizyczne deformacja Splątania (entanglements) są odpowiedzialne za większość najważniejszych właściwości polimerów (wydłużenie, wytrzymałość, twardość dowolny rodzaj deformacji w stanie skondensowanym polimerów amorficznych. Kształt kłębka polimeru ma także związek ze splątaniami.
8 Izomeria cis-trans. Mikrostruktura polidienów CH 2 CH CH CH 2 CH 2 CH polibutadien-1,4 CH CH 2 polibutadien-1,2 CH 2 CH CH CH 2 CH 2 CH CH cis-polibutadien-1,4 CH 3 C CH H 2 C CH 2 CH 2 trans-polibutadien-1,4 cis-poliizopren-1,4
9 Taktyczność makrocząsteczek liniowych R C H H C R CH 2 CH 2 R HR HH RR HH RH R R HR HR HR HR HR H R HH RR HH RR HH R polimer ataktyczny izotaktyczny syndiotaktyczny
10 Konformacja makrocząsteczek - Definicje konformacja (konfiguracja) chwilowe rozmieszczenie elementów budowy makrocząsteczki w przestrzeni kłębek statystyczny pręt, helisa
11 MODELE Makrocząsteczki liniowa rozgałęziona polimer usieciowany atomowy łańcuch główny łańcuch wiązań łańcuch wygładzony
12 Modele makrocząsteczek liniowych kulka-wiązanie (bead and stick) łańcuch swobodnie związany kulka-sprężynka (bead and spring) sznur pereł (pearl necklace) modele 2D i 3D ciągłe modele 2D i 3D dyskretne
13 Dyskretne modele łańcuchów polimeru. Typy krat (siatek) Także modele 3D!
14 Oddziaływania dalekiego zasięgu: Objętość wyłączona
15 Oddziaływania dalekiego zasięgu (ilustracja dla modelu dyskretnego) Z RW z Z ( z 1) RRW Random Walk on-return Random Walk z: liczba koordynacyjna kraty (tutaj 4)
16 Oddziaływania dalekiego zasięgu (ilustracja), cd. lim Z z SAW eff z 1 1 z eff Self-Avoiding Walk
17 H 3 C H 3 C H H H H C H 3 H H H H C H 3 C H 3 H H H H C H 3 Giętkość makrocząsteczek (-) gauche (G ) trans (T) (+) gauche (G + ) E gauche E trans E k B T- cząsteczka giętka k B - stała Boltzmanna E - miara giętkości k B T energia ruchów termicznych: RT na 1 mol, w 25 2,73 kj/mol
18 Makrokonformacje makrocząsteczek w fazie krystalicznej (górny szereg) i w rozcieńczonym roztworze (dolny szereg) Podwójna helisa sztywny pręt Łańcuch w pełni rozprostowany Helisa sztywny pręt Podwójna helisa łańcuch persystentny Kłębek bezładny Konformacja mieszana - helisa/kłębek Helisa łańcuch persystentny
19 Mikrokonformacje łańcucha (stan krystaliczny) zygzakowata: (...TTTT...) = [T] n helikalna: (... G ± G ± G ± G ±...) = [G ± ] n, lub (...TG ± TG ± TG ±...) = [TG ± ] n, lub... Przykłady: [T] n [G ] n lub [G + ] n
20 [G ± ] n [TG ] n lub [TG + ] n
21 Schemat helikalnej struktury izotaktycznego poli(propylenu) wraz z rzutem na płaszczyznę prostopadłą do osi helisy [ - atomy węgla łańcucha głównego (CH 2 i CH), - atomy węgla grupy CH 3 ; atomy wodoru pominięto dla uproszczenia]. polichloral przykład polimeru o jednokierunkowym skręceniu helisy. Polimer nierozpuszczalny.
22 C H 3 C H 3 ( C H 2 ) n ( C H ) ( C H C H 2 O n C H 2 O C H 2 C O ) n ( P E O ) ( i - P P O ) ( i - P L A ) O [TTG ± ] n [T] n [TTG ± ] n H O C H 2 C C H 2 C H 2 C H 2 C H 2 C H 2 C H 2 C C H 2 C H 2 C H 2 C H 2 C C H 2 O H H O O H C H 2 C C H 2 C H 2 C H 2 C H 2 C H 2 C H 2 C C H 2 C H 2 C H 2 C H 2 C C H 2 O H H O O H C H 2 C C H 2 C H 2 C H 2 C H 2 C H 2 C H 2 C C H 2 C H 2 C H 2 C H 2 C C H 2 O H Warstwowa struktura poliamidu 66 O
23 Statystyka giętkiej makrocząsteczki liniowej R - miara wielkości kłębka Model łańcucha swobodnie związanego wektorów-wiązań r o jednakowej długości pominięcie szczegółów budowy chemicznej wszystkie kąty między wiązaniami są jednakowo prawdopodobne brak oddziaływań dalekiego zasięgu stan niezaburzony (niezakłócony)
24 Statystyka giętkiej makrocząsteczki liniowej R = 0 1 R 2 = R R = r i r j i=1 j=1 = r r i r j i=1 j>i r i r j = r 2 cos θ ij R 2 = r 2 P R = Funkcja rozkładu Gaussa 3 2π R 2 3/2 exp 3R R 2 R 2
25 (2) θ 2 (1) θ 1 φ 2 r 2 r 3 φ 3 (3) r 4 r 5 (4) ( 2) r 1 φ 1 (0) (5) r 1 r θ 1 ( 1) Łańcuch swobodnie związany ze stałymi kątami, złożony z wiązań. Kąty θ i są kątami dopełniającymi. ()
26 Dla stałych kątów walencyjnych: r i r j = r 2 cos j i θ 1 R 2 = r cos j i θ r cos θ 1 cos θ 2r2 cos θ 1 cos θ 1 cos θ 2 dla, pamiętając, że kąt pomiędzy wiązaniami wynosi π θ < 90 : R 2 = r cos θ 1 cos θ Jeżeli kąt θ jest kątem dopełniającym kąta wiązań skierowanych do 1+cos θ naroży tetraedru, wtedy = 2. 1 cos θ i=1 j>i =
27 Statystyka giętkiej makrocząsteczki liniowej C C C r C C C C C C C C segment zastępczy P r = 3 2π r 2 3/2 Model gaussowski exp 3r r 2 r 2 konturowa długość łańcucha: L = b stosunek charakterystyczny: C = R2 0 b 2 zasada skalowania: b = r 2 1/2 b 2 = r 2
28 Gaussowski model makrocząsteczki. Łańcuch kulka-sprężynka r r 2 1/2 = b
29 Statystyka giętkiej makrocząsteczki liniowej polimer C = R2 0 b 2 polietylen (polimetylen) 6,6-6,8 polistyren ataktyczny 9,9-10,2 polipropylen ataktyczny 5,3-7,0 polimer C = R2 0 b 2 poli(metakrylan metylu) ataktyczny 6,9±0,5 poli(tlenek etylenu) 4,0 polidimetylosiloksan 6,2-7,6 poliizobutylen 6,6 poliamid 6,6 5,9 poli(octan winylu) ataktyczny 8,9-9,2 L-polipeptydy 8,5-9,5
30 r Statystyka giętkiej makrocząsteczki liniowej r 1 s 1 s s i Promień bezwładności: R G = 1 i=1 s i s i 1 2 s 3 s 1 r 2 Średni promień bezwładności: R G Wartość średnia: dla pojedynczej cząsteczki w czasie dla wielu identycznych cząsteczek r 1
31 Parametry charakteryzujące wielkość makrocząsteczki r 1 R 2 1/2 r r i Odległość końców łańcucha Średni promień bezwładności R G 2 = 1 6 R2
32 Statystyka giętkiej makrocząsteczki liniowej Stan niezaburzony: roztwór w rozpuszczalniku (theta) w polimerze stopionym lub w stanie skondensowanym dane w [nm(mol/g) 1/2 ] lub [nm/mer 1/2 ] R G / M w 10 2 R G / P w 10 2 R G / M w 10 2 R G / P w 10 2 polimer stan skondensowany roztwór theta polistyren polietylen poli(chlorek winylu) poli(tereftalan etylu) poli(metakrylan metylu) ataktyczny syndiotaktyczny izotaktyczny polibutadien szkliwo stop stop szkliwo stop szkliwo szkliwo szkliwo stop 2,65-2,8 2,75 4,5-4,6 4,0 3,9 2,5-2,7 2,9 3,0 3, , ,9-24,2 31,6 54, ,6 2,7-2,8 2,7-2,8 4,5 3,7 4,2 2,5 2,4 2,8 3,4-4, , ,6 23,9 29,2 58, ,8
33 Makrocząsteczki sztywne poli(1,4-fenylenowinylen) (PPV), poli(amid 1,4-benzoesowy) (PBA) poli(1,4-fenylenoamid tereftalowy) (PTA) (Kevlar ), poli(1,4-fenyleno-2,6-benzobistiazol) (PBT)
34 Helisa makrocząsteczka o regularnej budowie Cyfry P/q w symbolu helisa P/q oznaczają liczbę merów w jednym okresie helisy i liczbę obrotów na jeden okres Helisa 1/3 Helisa 7/2 Helisa 4/1
35 Konformacja białek R * a n * Białka są poliamidami, a ściślej poli(a-l-aminokwasami) Wiązanie amidowe ma charakter wiązania podwójnego: Konfrmacja trans jest o ok. 10 kj/mol korzystniejsza energetycznie od cis
36 Konformacja białek, cd. Z rentgenografii wynika, że drugorzędowa struktura białek ma postać:...g G TG G T)... [(T - trans) wynika ze sztywnego kąta dwuściennego]. Taka makrokonformacja nosi nazwę a-helisy. Schemat a-helisy łańcucha polipeptydowego. Linia przerywana oznacza wewnątrzcząsteczkowe wiązania wodorowe stabilizujące helisę.
37 ( C H 2 H C O O H C P O C H O O C H ) n R B ' B ', B " = z a s a d y p u r y n o w e [ c y t o z y n a ( C ), t y m i n a ( T ) ] l u b p i r y m i d y n o w e [ a d e n i n a ( A ), g u a n i n a ( G ) ] B " C H C H R O ( O O C H P C H O O C H 2 ) n H H O H O ( A ) ( T ) C H 3 H H O H O H H ( C ) ( G ) Struktura podwójnej helisy kwasu dezoksyrybonukleinowego
38 s-ps Zmiana konformacji wskutek działania rozpuszczalnika Rozpuszczalnik PEI Kłębek bezładny Domeny krystaliczne - długie helisy HO 2 Krótkie fragmenty helikalne Schematyczna ilustracja zmian konformacyjnych w syndiotaktycznym poli(styrenie) (s-ps) i poli(etylenoiminie) (PEI) [-CH 2 -CH 2 --] pod wpływem par rozpuszczalników.
39 Statystyka łańcucha polimeru sztywnego, długość persystentna persistent (ang.) aktywny wbrew przeciwnościom, uparty, trwały, regularnie powtarzający się,...
40 Współczynniki sztywności polimerów Polimer a/l 0 Poli(tlenek etylenu) 2.5 Poli(propylen) 3 Poli(etylen) 3.5 Poli(metakrylan metylu) 4 Poli(styren) 5 Dioctan celulozy 26 Poli(p-benzamid) 200 DA (podwójna helisa) 300 Poli(L-glutaminian benzylu) (a-helisa) 500 a długość persystentna, l 0 długość konturowa/stopień polimeryzacji (~ L/)
41 Statystyka łańcucha polimeru sztywnego, model łańcucha dżdżownicy (worm-like chain) Funkcja rozkładu: Porod-Kratky lim R2 = 2ab 4a 2 1 exp b a Wartości asymptotyczne: łańcuch giętki: b/a sztywny pręt: b/a małe, a ~ lim (b/a) R2 = ab lim (b/a) 1 R2 ~ 2 R G 2 = ba 3 a2 + 2 a3 b 1 + a b 1 exp b a
42 Wymiary sztywnych cząsteczek (a) Mikrofotografia SF cząsteczek DA osadzonych na mice z roztworu fizjologicznego. (b) <R 2 > jako funkcja długości konturowej mierzonej w różnych buforach. Linia ciągła wyliczona ze wzoru Poroda-Kratky ego dla długości persystentnej równej 53 nm. S.S. Sheiko, M. Möller, Chem. Rev, 2001, 101(12),
43 Wymiary makrocząsteczek nieliniowych (model gaussowski) K = R G 2 = r 2 Tr K + łańcuch liniowy 1 6 r2 cząsteczka cykliczna 1 12 r2 f-ramienna gwiazda ( = 1 + fm) 1 12 m r f
44 Makrocząsteczki nieliniowe a: gwiazda b: grzebień c: z długimi rozgałęzieniami d: z krótkimi rozgałęzieniami Parametr rozgałęzienia: 2 g g = R G,rozg 2 R G,lin
45 Giętka makrocząsteczka polimeru liniowego w stanie niezaburzonym: R 2 1/2 ~b 1/2 R G ~b 1/2 zasada skalowania: b = b 2 1/2 b 2 = b 2 b segment łańcucha (wymiar liniowy) b 3 objętość segmentu 1/b 3 stężenie segmentów
46 Przykład dane w [nm(mol/g) 1/2 ] R G / M w 10 2 R G / P w 10 2 polietylen stopiony 4,5-4,6 23,9-24,2 polietylen o M w = 10 5 R G = 0, /2 = 14 nm; objętość kuli opisywanej przez kłębek: (4π/3) 14 3 = nm 3 gęstość polietylenu 1g/cm 3 = g/nm 3 = 6, /14 43 grupy metylenowe/nm 3. Ale w obrębie kłębka mamy grup CH 2 wobec 10 5 / własnych grup CH 2 makrocząsteczki / W obrębie kłębka na 1 grupę CH 2 makro- cząsteczki przypada 70 grup należących do innych makro- cząsteczek.
47 Łańcuch polimeru wypełnia w przybliżeniu kulę o promieniu R G R G pojedynczy segment zajmuje objętość ~b 3
48 ~2R G cx () cx () cx () c- x x x Schematyczna ilustracja fluktuacji stężenia segmentów makrocząsteczek w roztworze rozcieńczonym, semirozcieńczonym i semistężonym. (c stężenie wyrażone w liczbie segmentów w jednostce objętości)
49 stężenie, począwszy od którego kłębki zaczynają się przenikać: c ~ R G 3 Objętość wyłączona segmenty mają skończoną (niezerową) objętość izolowany kłębek nie przenika się z innymi kłębkami (w roztworze rozcieńczonym)
50 Objętość wyłączona
51 Oddziaływania dalekiego zasięgu (ilustracja) RW 12 RRW 11 Z RW z Z ( z 1) RRW Random Walk on-return Random Walk
52 Oddziaływania dalekiego zasięgu (ilustracja), cd SAW lim Z z SAW eff z 1 1 z eff Wersja 3D Self-Avoiding Walk
53 Zasięg oddziaływania oddziaływanie bliskiego zasięgu oddziaływanie dalekiego zasięgu
54 Typy krat (siatek)
55 R G /b Self avoiding walk Wyniki symulacji promienia bezwładności dla samounikających się ścieżek (self avoiding walks) na kracie kubicznej. Prosta opisana jest równaniem: R G = 0,4205 b 0,5934 M. M. Green,. C. Peterson, T. Sato, A. Teramoto, R. Cook, Science 268, 1860 (1995).
56 R G /nm Promień bezwładności roztworów polimeru w dobrym rozpuszczalniku M /g/mol Promienie bezwładności polistyrenu w benzenie i toluenie. Prostą opisuje wzór: R G = 0,01234 M 0,5936 J. des Cloizeaux, G. Jannink, Polymers in Solution: Their Modelling and Structure, Oxford Univ. Press: Clarendon (1990).
57 Współczynnik ekspansji kłębka α 2 = R2 R 2 0 metodami perturbacyjnymi określono: α 5 α 3 = f(z) dla 3/2 v 1/2 z = 3 2π b 3 np.: α 5 α 3 = 2,6z najdokładniejszy wynik: R 2 = b 2 (1 + 4/3z 2,075z 2 + 6,279z 3 25,057z ,135z 5 594,717z 6 + ) metodą grup renormalizacyjnych: R G ~b 0,588±0,015 Doi M., Edwards S.F.: The theory of polymer dynamics, Clarendon Press, Oxford 1986.
58 Parametr ilościowy (współczynnik oddziaływania polimer rozpuszczalnik) ε pp ε ss Wskutek wymieszania oddziaływania segmentów zmieniają się. Energia czterech oddziaływań ε pp ( polimer-polimer) i czterech ε ss ( rozpuszczalnik-rozpuszczalnik) może się zmienić w cztery oddziaływania ε ps (polimer-rozpuszczalnik) i po dwa ε pp i ε ss. 4ε pp + 4ε ss 4ε ps + 2ε pp + 2ε ss Różnica wynosi: 4ε ps 2ε pp 2ε ss Formalnie, parametr oddziaływania jest zatem równy (na jeden segment): χ = Z ε ps (ε pp ε ss )/2 /k B T ε ps
59 Parametr ilościowy (współczynnik oddziaływania polimer rozpuszczalnik) χ < 0 χ > 0 preferowane kontakty p s preferowane kontakty p p i s s χ 0; dla dobrych rozpuszczalników, tj. rozpuszczalników wykazujących duże powinowactwo do segmentów (równość zachodzi dla rozpuszczalników atermicznych), χ = ½; dla słabych rozpuszczalników, których oddziaływanie z segmentami równoważy jedynie wzajemne przyciąganie segmentów i zaledwie utrzymuje makrocząsteczki w roztworze, χ > ½; dla złych rozpuszczalników.
60 Parametr objętości wyłączonej v Ma on wymiar objętości i charakteryzuje zmianę objętości pojedynczego segmentu wywołaną obecnością rozpuszczalnika. Związek pomiędzy χ a v jest następujący: v~b χ Temperatura θ: temperatura, w której oddziaływania polimer polimer są równoważone oddziaływaniami polimer rozpuszczalnik. W temperaturze θ: v = 0; χ = 1/2
61 Wymiary kłębka w dobrym rozpuszczalniku W stanie niezaburzonym: P R = 3 2πb 2 3/2 exp 3R R R entropia łańcucha: S~k B ln P R ~ k 2 B ~ k b 2 B R zmiana wymiarów: ds~ k G B dr b 2 G; T S = T człon entalpowy (oddziaływania): k B Tv R 3 ; G 2b 2 R G 2 b 2 R G 0 Energia swobodna związana ze zmianami wymiarów kłębka: 2 R ds~k G B b 2 A = k B T v2 R G 3 + R 2 G b 2
62 Wymiary kłębka w dobrym rozpuszczalniku, cd. A = k B T v2 R G 3 + R 2 G b 2 różniczkowanie ΔA wzgl. R G daje wymiar przy minimum energii: d A dr G = k B T 3 v2 R G 4 R G 5 = 3 2 vb R G b 2 = 0 R G ~ v b 3 1/5 b 3/5
63 a zatem: gdyż: Wymiary kłębka w dobrym rozpuszczalniku, cd. R G ~ v b 3 1/5 b 3/5 v R G ~b 3/5 b 3 = 1 2 χ 1 2 Podsumowanie: Liniowy wymiar kłębka giętkiej makrocząsteczki w rozcieńczonym roztworze polimeru jest proporcjonalny do stopnia polimeryzacji w potędze (ν gr. ni, nie v): ν = 1/2 dla rozpuszczalnika theta, ν = 3/5 dla dobrego rozpuszczalnika.
64 Udział objętościowy segmentów w kłębku polimeru Objętość pojedynczego segmentu można oszacować jako ~b 3. Udział objętościowy segmentów polimeru w kłębku wynosi zatem: b 3 3 R b3 G ν b 3 = 1 3ν Wykładnik 1 3ν ma wartość od 1/2 dla idealnego łańcucha (bez oddziaływań netto; ν = 1/2) do 4/5 dla łańcucha w dobrym rozpuszczalniku (ν = 3/5) lub 0,77 dla ν = 0,59. Im lepszy rozpuszczalnik, tym udział ten jest mniejszy. Ten udział jest b. mały i dla rzeczywistej makrocząsteczki wynosi ok. 3% dla = 100 i ok. 0,5% dla = 1000.
65 Udział objętościowy segmentów w kłębku polimeru W rozcieńczonych roztworach kłębki się nie przenikają (objętość wyłączona). W miarę zwiększania stężenia roztworu, wyrażonego, np. w g/dm 3, muszą one zacząć się przenikać. Początek przenikania ma miejsce dla stężenia oznaczonego jako c ~ 1 3ν i oszacowanego równaniami: c 4 3 πr G 3 = M A c 2R G 3 = M A lub c η = 1 A oznacza liczbę Avogadro, a η, graniczną liczbę lepkościową. Rozcieńczony roztwór polimeru: c < c
66 Stężenie cząsteczek sztywnych Sztywne makrocząsteczki o długości konturowej L tworzą roztwór rozcieńczony, kiedy pojedyncza cząsteczka ma do dyspozycji objętość ~L 3. Stężenie początku przenikania kłębków wynosi zatem: c L 3 = M A i jest znacznie mniejsze, niż dla łańcucha giętkiego.
67 Zależność wymiarów kłębka od stężenia c(r) - gęstość segmentów w pojedynczym kłębku warunki brzegowe operacji skalowania (ν = 1/2... 3/5) ~ R 1 G ν ; dn = c r 4πr 2 dr; = 4π r 2 c r dr~ R G b b funkcja c r musi mieć wymiar odwrotności objętości oraz postać: 1 ν Zatem: c r ~ 1 b 3 c(r)~ 1 b b 3 r b r c r ~ 1 b ν 4/3 dla ν = 3/5 oraz b r dla ν = 1/2
68 Zależność wymiarów kłębka od stężenia cr () cr () 4/3-4/3 1 b R G b x promień ekranowania ξ R G
69 Koncepcja blobów W obrębie kuli o promieniu ξ segmenty oddziaływają ze sobą tak jak w izolowanym kłębku. Wskutek obecności segmentów pochodzących od innych makrocząsteczek (ekranowanie) segmenty nie oddziaływają poza tą odległością z innymi segmentami własnej cząsteczki Makrocząsteczka tworzy łańcuch złożony z g spęcznionych segmentów o wymiarze liniowym ξ i niezaburzonym charakterze.
70 Łańcuch blobów Zgodnie z zasadami skalowania, w dobrym rozpuszczalniku: ξ~bg 3/5 ξ - promień ekranowania g liczba segmentów w blobie, a zatem R G ~ξ g 1/2 ~b 1/2 g 3/5 1/2 = b 1/2 g 1/10
71 Zależność R G od stężenia φ = cb 3 (φ ułamek objętościowy polimeru w roztworze. Metodą skalowania poszukujemy relacji typu: φ m ξ ξ φ = R G φ (φ* ułamek objętościowy odpowiadający c*) Wykładnik m ξ dobieramy eliminując zależność R G i φ* od Z uwagi, że: R G = b ν φ ~ b3 R G 3 ~1 3ν a zatem m ξ musi mieć wartość: ν/(1 3ν). Dla dobrego rozpuszczalnika (ν = 3/5): m ξ = 3/4 (Dla rozpuszczalnika theta (ν = 1/2): m ξ = 1).
72 Zależność R G od stężenia Poszukiwana relacja ma zatem postać: ξ φ = bφ 3/4 a więc: Stąd: g = ξ b 5/3 = φ 3/4 5/3 = φ 5/4 R G ~b 1/2 φ 5/4 1/10 = b 1/2 φ 1/8 Właściwości asymptotyczne: c ~ c*: R G ~b 1/2 4/5 1/8 = b 1/2+1/10 = b 3/5 φ 1: R G ~b 1/2 φ 1/8 = R G ~b 1/2
73 T T θ M θ Pseudofazowy wykres fazowy 1/ 2 M1/ I roztworów polimerów c* I' II III c** cm 1/2 cm 1/2 c * * ~ T IV -c**
74 Relacje w obszarach wykresu pseudofazowego Obszar R G 2 ξ 2 I I II III 6/5 v 2/5 φ 1/4 v 1/4 - - φ 3/2 v 1/2 φ 2
75 Przemiana kłębek-globuła W obszarze IV mamy do czynienia z podziałem fazy roztwór (stop polimerów) rozdziela się na roztwory o większym i mniejszym stężeniu. W miarę pogorszenia się jakości rozpuszczalnika kontakty polimer-rozpuszczalnik stają się coraz słabsze i kłębek zmniejsza swoje wymiary, aż do przemiany w globułę, gdzie występuje znacznie mniej kontaktów polimer-rozpuszczalnik na rzecz kontaktów polimer-polimer. W stanie pełnego upakowania segmentów liniowe wymiary makrocząsteczki stają się proporcjonalne do 1/3.
76 Przemiana kłębek-globuła Jeżeli jest wielkością wystarczająco dużą przemiana: R G ~b 1/2 do R G ~b 1/3 staje się dość gwałtowna R G /nm i jest nazywane przemianą kłębek-globuła. (ang. coin-globule) Przemiana kłębek globuła dla poli(-izopropyloakrylamidu) w roztworze wodnym chłodzenie ogrzewanie
Wykład 3. Makrocząsteczki w roztworze i w stanie skondensowanym.
 Wykład 3 Makrocząsteczki w roztworze i w stanie skondensowanym. Roztwory polimerów Zakresy stężeń: a) odległości pomiędzy środkami masy kłębków większe niż średnice kłębków b) odległości
Wykład 3 Makrocząsteczki w roztworze i w stanie skondensowanym. Roztwory polimerów Zakresy stężeń: a) odległości pomiędzy środkami masy kłębków większe niż średnice kłębków b) odległości
POLIMERY DO WTRYSKIWANIA Polimery termoplastyczne. Fizyczne właściwości polimerów. 1. prof. dr hab. inż. Henryk Galina
 POLIMERY DO WTRYSKIWANIA Polimery termoplastyczne Fizyczne właściwości polimerów. 1 prof. dr hab. inż. Henryk Galina Pojęcia podstawowe polimer makrocząsteczka jednostka monomeryczna, konstytucyjna mer
POLIMERY DO WTRYSKIWANIA Polimery termoplastyczne Fizyczne właściwości polimerów. 1 prof. dr hab. inż. Henryk Galina Pojęcia podstawowe polimer makrocząsteczka jednostka monomeryczna, konstytucyjna mer
Fizyczne właściwości polimerów Cz. 2
 POLIMERY DO WTRYSKIWANIA Polimery termoplastyczne Fizyczne właściwości polimerów Cz. 2 prof. dr hab. inż. Henryk Galina Łańcuch pojedynczej makrocząsteczki w sieci innych łańcuchów Zależność modułu od
POLIMERY DO WTRYSKIWANIA Polimery termoplastyczne Fizyczne właściwości polimerów Cz. 2 prof. dr hab. inż. Henryk Galina Łańcuch pojedynczej makrocząsteczki w sieci innych łańcuchów Zależność modułu od
Wykład 3. Termodynamika i kinetyka procesowa - wykład 2. Anna Ptaszek. 24 kwietnia Katedra Inżynierii i Aparatury Przemysłu Spożywczego
 Wykład 3 wykład 2 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 24 kwietnia 2018 1 / 1 Konformacje łańcuchów Budowa amylozy i amylopektyny http://polysac3db.cermav.cnrs.fr/home.html 2 / 1 Konformacje
Wykład 3 wykład 2 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 24 kwietnia 2018 1 / 1 Konformacje łańcuchów Budowa amylozy i amylopektyny http://polysac3db.cermav.cnrs.fr/home.html 2 / 1 Konformacje
Wykład 6. Anna Ptaszek. 8 września Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Fizykochemia biopolimerów - wykład 6.
 Wykład 6 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 8 września 2016 1 / 27 Konformacje łańcuchów Budowa amylozy i amylopektyny http://polysac3db.cermav.cnrs.fr/home.html 2 / 27 Konformacje łańcuchów
Wykład 6 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 8 września 2016 1 / 27 Konformacje łańcuchów Budowa amylozy i amylopektyny http://polysac3db.cermav.cnrs.fr/home.html 2 / 27 Konformacje łańcuchów
dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG
 3. POLIMERY AMORFICZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego
3. POLIMERY AMORFICZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego
dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG
 4. POLIMERY KRYSTALICZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego
4. POLIMERY KRYSTALICZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego
relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
 1 STECHIOMETRIA INTERPRETACJA ILOŚCIOWA ZJAWISK CHEMICZNYCH relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
1 STECHIOMETRIA INTERPRETACJA ILOŚCIOWA ZJAWISK CHEMICZNYCH relacje ilościowe ( masowe,objętościowe i molowe ) dotyczące połączeń 1. pierwiastków w związkach chemicznych 2. związków chemicznych w reakcjach
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego
 Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
Wykład 5 Widmo rotacyjne dwuatomowego rotatora sztywnego W5. Energia molekuł Przemieszczanie się całych molekuł w przestrzeni - Ruch translacyjny - Odbywa się w fazie gazowej i ciekłej, w fazie stałej
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne
 Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Równowaga. równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) równowaga stabilna (pełna) brak równowagi rozpraszanie energii
 Równowaga równowaga stabilna (pełna) równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) brak równowagi rozpraszanie energii energia swobodna Co jest warunkiem równowagi? temperatura W
Równowaga równowaga stabilna (pełna) równowaga metastabilna (niepełna) równowaga niestabilna (nietrwała) brak równowagi rozpraszanie energii energia swobodna Co jest warunkiem równowagi? temperatura W
Modelowanie konformacji giętkich łańcuchów polimerowych
 Waldemar Nowicki ĆWICZENIE 4 Modelowanie konformacji giętkich łańcuchów polimerowych Podstawowe pojęcia: konformacja makrocząsteczki, błądzenie przypadkowe, nieprzecinające się błądzenie przypadkowe, kłębek
Waldemar Nowicki ĆWICZENIE 4 Modelowanie konformacji giętkich łańcuchów polimerowych Podstawowe pojęcia: konformacja makrocząsteczki, błądzenie przypadkowe, nieprzecinające się błądzenie przypadkowe, kłębek
Wykład 27/28 stycznia 2005; pytania z wykładów 1-3.
 Wykład 4 Makrocząsteczki i polimery w stanie skondensowanym (stałym) c.d. 1. Polimery amorficzne. Właściwości. 2. Polimery krystaliczne. Micele. Sferolity. 3. Polimery ciekłokrystaliczne. Wykład 27/28
Wykład 4 Makrocząsteczki i polimery w stanie skondensowanym (stałym) c.d. 1. Polimery amorficzne. Właściwości. 2. Polimery krystaliczne. Micele. Sferolity. 3. Polimery ciekłokrystaliczne. Wykład 27/28
Repetytorium z wybranych zagadnień z chemii
 Repetytorium z wybranych zagadnień z chemii Mol jest to liczebność materii występująca, gdy liczba cząstek (elementów) układu jest równa liczbie atomów zawartych w masie 12 g węgla 12 C (równa liczbie
Repetytorium z wybranych zagadnień z chemii Mol jest to liczebność materii występująca, gdy liczba cząstek (elementów) układu jest równa liczbie atomów zawartych w masie 12 g węgla 12 C (równa liczbie
Podstawowe prawa opisujące właściwości gazów zostały wyprowadzone dla gazu modelowego, nazywanego gazem doskonałym (idealnym).
 Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
Spis treści 1 Stan gazowy 2 Gaz doskonały 21 Definicja mikroskopowa 22 Definicja makroskopowa (termodynamiczna) 3 Prawa gazowe 31 Prawo Boyle a-mariotte a 32 Prawo Gay-Lussaca 33 Prawo Charlesa 34 Prawo
dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG
 2. METODY WYZNACZANIA MASY MOLOWEJ POLIMERÓW dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej
2. METODY WYZNACZANIA MASY MOLOWEJ POLIMERÓW dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej
Wykład 2. (godz. 2 - ) Masy cząsteczkowe, masy molowe, rozkład mas cząsteczkowych (molowych), mikrostruktura makrocząsteczek.
 Wykład 2. (godz. 2 - ) Masy cząsteczkowe, masy molowe, rozkład mas cząsteczkowych (molowych), mikrostruktura makrocząsteczek. CEMIA MAKCZĄSTECZEK (PLIMEÓW) Masa cząsteczkowa (Mc) jest masą określonej cząsteczki,
Wykład 2. (godz. 2 - ) Masy cząsteczkowe, masy molowe, rozkład mas cząsteczkowych (molowych), mikrostruktura makrocząsteczek. CEMIA MAKCZĄSTECZEK (PLIMEÓW) Masa cząsteczkowa (Mc) jest masą określonej cząsteczki,
dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG
 1. POLIMERY A TWORZYWA SZTUCZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach
1. POLIMERY A TWORZYWA SZTUCZNE dr hab. inż. Józef Haponiuk Katedra Technologii Polimerów Wydział Chemiczny PG Politechnika Gdaoska, 2011 r. Publikacja współfinansowana ze środków Unii Europejskiej w ramach
Elektrolity polimerowe. 1. Modele transportu jonów 2. Rodzaje elektrolitów polimerowych 3. Zastosowania elektrolitów polimerowych
 Elektrolity polimerowe 1. Modele transportu jonów 2. Rodzaje elektrolitów polimerowych 3. Zastosowania elektrolitów polimerowych Zalety - Giętkie, otrzymywane w postaci folii - Lekkie (wysoka gęstość energii/kg)
Elektrolity polimerowe 1. Modele transportu jonów 2. Rodzaje elektrolitów polimerowych 3. Zastosowania elektrolitów polimerowych Zalety - Giętkie, otrzymywane w postaci folii - Lekkie (wysoka gęstość energii/kg)
CHEMIA MAKROCZĄSTECZEK (POLIMERÓW)
 CHEMIA MAKROCZĄSTECZEK (POLIMERÓW) Model makrocząsteczki polietylenu o masie cząsteczkowej 100 000 Rzeczywista długość makrocząsteczki 0.001 mm. Powiększenie: x 10 7 (0.001 mm 10 m) ARCHITEKTURA MAKROCZĄSTECZEK
CHEMIA MAKROCZĄSTECZEK (POLIMERÓW) Model makrocząsteczki polietylenu o masie cząsteczkowej 100 000 Rzeczywista długość makrocząsteczki 0.001 mm. Powiększenie: x 10 7 (0.001 mm 10 m) ARCHITEKTURA MAKROCZĄSTECZEK
Szkło. T g szkła używanego w oknach katedr wynosi ok. 600 C, a czas relaksacji sięga lat. FIZYKA 3 MICHAŁ MARZANTOWICZ
 Szkło Przechłodzona ciecz, w której ruchy uległy zamrożeniu Tzw. przejście szkliste: czas potrzebny na zmianę konfiguracji cząsteczek (czas relaksacji) jest rzędu minut lub dłuższy T g szkła używanego
Szkło Przechłodzona ciecz, w której ruchy uległy zamrożeniu Tzw. przejście szkliste: czas potrzebny na zmianę konfiguracji cząsteczek (czas relaksacji) jest rzędu minut lub dłuższy T g szkła używanego
Zestaw pytań egzaminu inŝynierskiego przeprowadzanego w Katedrze Fizykochemii i Technologii Polimerów dla kierunku CHEMIA
 Zestaw pytań egzaminu inŝynierskiego przeprowadzanego w Katedrze Fizykochemii i Technologii Polimerów dla kierunku CHEMIA 1. Metody miareczkowania w analizie chemicznej, wyjaśnić działanie wskaźników 2.
Zestaw pytań egzaminu inŝynierskiego przeprowadzanego w Katedrze Fizykochemii i Technologii Polimerów dla kierunku CHEMIA 1. Metody miareczkowania w analizie chemicznej, wyjaśnić działanie wskaźników 2.
Masy cząsteczkowe, rozkład mas cząsteczkowych, mikrostruktura. Wykład 2 i 3
 Masy cząsteczkowe, rozkład mas cząsteczkowych, mikrostruktura Wykład 2 i 3 CEMIA MAKCZĄSTECZEK (PLIMEÓW) Masa cząsteczkowa (Mc) jest masą określonej cząsteczki, wyrażoną w atomowych jednostkach masy, gramach
Masy cząsteczkowe, rozkład mas cząsteczkowych, mikrostruktura Wykład 2 i 3 CEMIA MAKCZĄSTECZEK (PLIMEÓW) Masa cząsteczkowa (Mc) jest masą określonej cząsteczki, wyrażoną w atomowych jednostkach masy, gramach
Kopolimery statystyczne. Kopolimery blokowe. kopolimerów w blokowych. Sonochemiczna synteza -A-A-A-A-A-A-A-B-B-B-B-B-B-B-B-B-B- Typowe metody syntezy:
 1 Sonochemiczna synteza kopolimerów w blokowych Kopolimery statystyczne -A-B-A-A-B-A-B-B-A-B-A-B-A-A-B-B-A- Kopolimery blokowe -A-A-A-A-A-A-A-B-B-B-B-B-B-B-B-B-B- Typowe metody syntezy: Polimeryzacja żyjąca
1 Sonochemiczna synteza kopolimerów w blokowych Kopolimery statystyczne -A-B-A-A-B-A-B-B-A-B-A-B-A-A-B-B-A- Kopolimery blokowe -A-A-A-A-A-A-A-B-B-B-B-B-B-B-B-B-B- Typowe metody syntezy: Polimeryzacja żyjąca
S ścianki naczynia w jednostce czasu przekazywany
 FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
Krystalizacja Polimerów Istotny Aspekt Procesu Przetwórstwa
 Krystalizacja Polimerów Istotny Aspekt Procesu Przetwórstwa dr hab. inż. Przemysław Postawa, prof. PCz Zakład Przetwórstwa Polimerów Politechniki Częstochowskiej Zakład Przetwórstwa Polimerów Politechnika
Krystalizacja Polimerów Istotny Aspekt Procesu Przetwórstwa dr hab. inż. Przemysław Postawa, prof. PCz Zakład Przetwórstwa Polimerów Politechniki Częstochowskiej Zakład Przetwórstwa Polimerów Politechnika
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ
 OZNACZANIE ŚREDNIEJ MASY CZĄSTECZKOWEJ POLIMERU WSTĘP Lepkość roztworu polimeru jest z reguły większa od lepkości rozpuszczalnika. Dla polimeru lepkość graniczna [η ] określa zmianę lepkości roztworu przypadającą
OZNACZANIE ŚREDNIEJ MASY CZĄSTECZKOWEJ POLIMERU WSTĘP Lepkość roztworu polimeru jest z reguły większa od lepkości rozpuszczalnika. Dla polimeru lepkość graniczna [η ] określa zmianę lepkości roztworu przypadającą
Program MC. Obliczyć radialną funkcję korelacji. Zrobić jej wykres. Odczytać z wykresu wartość radialnej funkcji korelacji w punkcie r=
 Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
Wykład 8. Równowaga fazowa Roztwory rzeczywiste
 Wykład 8 Równowaga fazowa Roztwory rzeczywiste Roztwory doskonałe Porównanie roztworów doskonałych i Roztwory Doskonałe rzeczywistych Roztwory Rzeczywiste Spełniają prawo Raoulta Mieszanie w warunkach
Wykład 8 Równowaga fazowa Roztwory rzeczywiste Roztwory doskonałe Porównanie roztworów doskonałych i Roztwory Doskonałe rzeczywistych Roztwory Rzeczywiste Spełniają prawo Raoulta Mieszanie w warunkach
1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej?
 Tematy opisowe 1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej? 2. Omów pomiar potencjału na granicy faz elektroda/roztwór elektrolitu. Podaj przykład, omów skale potencjału i elektrody
Tematy opisowe 1. Od czego i w jaki sposób zależy szybkość reakcji chemicznej? 2. Omów pomiar potencjału na granicy faz elektroda/roztwór elektrolitu. Podaj przykład, omów skale potencjału i elektrody
Krystalografia. Analiza wyników rentgenowskiej analizy strukturalnej i sposób ich prezentacji
 Krystalografia Analiza wyników rentgenowskiej analizy strukturalnej i sposób ich prezentacji Opis geometrii Symetria: kryształu: grupa przestrzenna cząsteczki: grupa punktowa Parametry geometryczne współrzędne
Krystalografia Analiza wyników rentgenowskiej analizy strukturalnej i sposób ich prezentacji Opis geometrii Symetria: kryształu: grupa przestrzenna cząsteczki: grupa punktowa Parametry geometryczne współrzędne
Podstawowe pojęcia i prawa chemiczne
 Podstawowe pojęcia i prawa chemiczne Pierwiastki, nazewnictwo i symbole. Budowa atomu, izotopy. Przemiany promieniotwórcze, okres półtrwania. Układ okresowy. Właściwości pierwiastków a ich położenie w
Podstawowe pojęcia i prawa chemiczne Pierwiastki, nazewnictwo i symbole. Budowa atomu, izotopy. Przemiany promieniotwórcze, okres półtrwania. Układ okresowy. Właściwości pierwiastków a ich położenie w
Formularz opisu przedmiotu (formularz sylabusa) dotyczy studiów I i II stopnia. Fizykochemia polimerów. Wydział Chemii/Zakład Technologii Chemicznej
 Załącznik nr 1 do zarządzenia nr 11 Rektora UW z dnia 19 lutego 2010 r. w sprawie opisu przedmiotu w Uniwersyteckim Katalogu Przedmiotów zamieszczonym w Uniwersyteckim Systemie Obsługi Studiów (USOS) i
Załącznik nr 1 do zarządzenia nr 11 Rektora UW z dnia 19 lutego 2010 r. w sprawie opisu przedmiotu w Uniwersyteckim Katalogu Przedmiotów zamieszczonym w Uniwersyteckim Systemie Obsługi Studiów (USOS) i
CHARAKTERYSTYKA TWORZYW POLIMEROWYCH Z UWZGLĘDNIENIEM M.IN. POZIOMU WSKAŹNIKÓW WYTRZYMAŁOŚCIOWYCH, ODPORNOŚCI NA KOROZJĘ, CENY.
 Temat 5: CHARAKTERYSTYKA TWORZYW POLIMEROWYCH Z UWZGLĘDNIENIEM M.IN. POZIOMU WSKAŹNIKÓW WYTRZYMAŁOŚCIOWYCH, ODPORNOŚCI NA KOROZJĘ, CENY. Wykład 2.5h 1) Istota budowy chemicznej i fizycznej polimerów; jej
Temat 5: CHARAKTERYSTYKA TWORZYW POLIMEROWYCH Z UWZGLĘDNIENIEM M.IN. POZIOMU WSKAŹNIKÓW WYTRZYMAŁOŚCIOWYCH, ODPORNOŚCI NA KOROZJĘ, CENY. Wykład 2.5h 1) Istota budowy chemicznej i fizycznej polimerów; jej
Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. u = 0, (6.1) jest operatorem Laplace a. (x,y)
 Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
Wykład 6 Funkcje harmoniczne Ważną rolę odgrywają tzw. funkcje harmoniczne. Przyjmujemy następującą definicję. e f i n i c j a Funkcję u (x 1, x 2,..., x n ) nazywamy harmoniczną w obszarze R n wtedy i
imię i nazwisko, nazwa szkoły, miejscowość Zadania I etapu Konkursu Chemicznego Trzech Wydziałów PŁ V edycja
 Zadanie 1 (2 pkt.) Zmieszano 80 cm 3 roztworu CH3COOH o stężeniu 5% wag. i gęstości 1,006 g/cm 3 oraz 70 cm 3 roztworu CH3COOK o stężeniu 0,5 mol/dm 3. Obliczyć ph powstałego roztworu. Jak zmieni się ph
Zadanie 1 (2 pkt.) Zmieszano 80 cm 3 roztworu CH3COOH o stężeniu 5% wag. i gęstości 1,006 g/cm 3 oraz 70 cm 3 roztworu CH3COOK o stężeniu 0,5 mol/dm 3. Obliczyć ph powstałego roztworu. Jak zmieni się ph
STRUKTURA STOPÓW CHARAKTERYSTYKA FAZ. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 STRUKTURA STOPÓW CHARAKTERYSTYKA FAZ Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Stop tworzywo składające się z metalu stanowiącego osnowę, do którego
STRUKTURA STOPÓW CHARAKTERYSTYKA FAZ Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Stop tworzywo składające się z metalu stanowiącego osnowę, do którego
1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru
 1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru Wzór związku chemicznego podaje jakościowy jego skład z jakich pierwiastków jest zbudowany oraz liczbę atomów poszczególnych pierwiastków
1. Stechiometria 1.1. Obliczenia składu substancji na podstawie wzoru Wzór związku chemicznego podaje jakościowy jego skład z jakich pierwiastków jest zbudowany oraz liczbę atomów poszczególnych pierwiastków
Kryteria oceniania z chemii kl VII
 Kryteria oceniania z chemii kl VII Ocena dopuszczająca -stosuje zasady BHP w pracowni -nazywa sprzęt laboratoryjny i szkło oraz określa ich przeznaczenie -opisuje właściwości substancji używanych na co
Kryteria oceniania z chemii kl VII Ocena dopuszczająca -stosuje zasady BHP w pracowni -nazywa sprzęt laboratoryjny i szkło oraz określa ich przeznaczenie -opisuje właściwości substancji używanych na co
Za poprawną metodę Za poprawne obliczenia wraz z podaniem zmiany ph
 Zadanie 1 ( pkt.) Zmieszano 80 cm roztworu CHCH o stężeniu 5% wag. i gęstości 1,006 g/cm oraz 70 cm roztworu CHCK o stężeniu 0,5 mol/dm. bliczyć ph powstałego roztworu. Jak zmieni się ph roztworu po wprowadzeniu
Zadanie 1 ( pkt.) Zmieszano 80 cm roztworu CHCH o stężeniu 5% wag. i gęstości 1,006 g/cm oraz 70 cm roztworu CHCK o stężeniu 0,5 mol/dm. bliczyć ph powstałego roztworu. Jak zmieni się ph roztworu po wprowadzeniu
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Nauka o Materiałach. Wykład VIII. Odkształcenie materiałów właściwości sprężyste. Jerzy Lis
 Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Transport jonów: kryształy jonowe
 Transport jonów: kryształy jonowe Jodek srebra AgI W 420 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie Frenkla podsieci anionowej, klastry
Transport jonów: kryształy jonowe Jodek srebra AgI W 420 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie Frenkla podsieci anionowej, klastry
11.Chemia organiczna. Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu)
 11.Chemia organiczna. Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Związki organiczne CHEMIA ORGANICZNA Def. 1. (Gmelin 1848, Kekule 1851 ) chemia
11.Chemia organiczna. Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Związki organiczne CHEMIA ORGANICZNA Def. 1. (Gmelin 1848, Kekule 1851 ) chemia
Czym się różni ciecz od ciała stałego?
 Szkła Czym się różni ciecz od ciała stałego? gęstość Czy szkło to ciecz czy ciało stałe? Szkło powstaje w procesie chłodzenia cieczy. Czy szkło to ciecz przechłodzona? kryształ szkło ciecz przechłodzona
Szkła Czym się różni ciecz od ciała stałego? gęstość Czy szkło to ciecz czy ciało stałe? Szkło powstaje w procesie chłodzenia cieczy. Czy szkło to ciecz przechłodzona? kryształ szkło ciecz przechłodzona
CHEMIA MAKROCZĄSTECZEK (POLIMERÓW) Uniwersytet Jagielloński Kraków,
 Wykład 1 CEMIA MAKROCZĄSTECZEK (POLIMERÓW) Uniwersytet Jagielloński Kraków, 2003-2004 Stanisław Penczek Polska Akademia Nauk Centrum Badań Molekularnych i Makromolekularnych, Łódź CEMIA MAKROCZĄSTECZEK
Wykład 1 CEMIA MAKROCZĄSTECZEK (POLIMERÓW) Uniwersytet Jagielloński Kraków, 2003-2004 Stanisław Penczek Polska Akademia Nauk Centrum Badań Molekularnych i Makromolekularnych, Łódź CEMIA MAKROCZĄSTECZEK
Atomy wieloelektronowe
 Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Wiązania atomowe Atomy wieloelektronowe, obsadzanie stanów elektronowych, układ poziomów energii. Przykładowe konfiguracje elektronów, gazy szlachetne, litowce, chlorowce, układ okresowy pierwiastków,
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii
 Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Wykład 2. Termodynamika i kinetyka procesowa- wykład. Anna Ptaszek. 13 marca Katedra Inżynierii i Aparatury Przemysłu Spożywczego
 Wykład i kinetyka procesowa- wykład Katedra Inżynierii i Aparatury Przemysłu Spożywczego 13 marca 014 1/30 Czym są biopolimery? To polimery pochodzenia naturalnego. Należą do nich polisacharydy i białka.
Wykład i kinetyka procesowa- wykład Katedra Inżynierii i Aparatury Przemysłu Spożywczego 13 marca 014 1/30 Czym są biopolimery? To polimery pochodzenia naturalnego. Należą do nich polisacharydy i białka.
Wykład 12. Anna Ptaszek. 16 września Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Fizykochemia biopolimerów - wykład 12.
 Wykład 12 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 16 września 2016 1 / 23 Pomiar lepkości wiskozymetry (lepkościomierze) 2 / 23 Pomiar lepkości reometry rotacyjne 3 / 23 Pomiar lepkości reometry
Wykład 12 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 16 września 2016 1 / 23 Pomiar lepkości wiskozymetry (lepkościomierze) 2 / 23 Pomiar lepkości reometry rotacyjne 3 / 23 Pomiar lepkości reometry
CHEMIA. Wymagania szczegółowe. Wymagania ogólne
 CHEMIA Wymagania ogólne Wymagania szczegółowe Uczeń: zapisuje konfiguracje elektronowe atomów pierwiastków do Z = 36 i jonów o podanym ładunku, uwzględniając rozmieszczenie elektronów na podpowłokach [
CHEMIA Wymagania ogólne Wymagania szczegółowe Uczeń: zapisuje konfiguracje elektronowe atomów pierwiastków do Z = 36 i jonów o podanym ładunku, uwzględniając rozmieszczenie elektronów na podpowłokach [
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
3. Przejścia fazowe pomiędzy trzema stanami skupienia materii:
 Temat: Zmiany stanu skupienia. 1. Energia sieci krystalicznej- wielkość dzięki której można oszacować siły przyciągania w krysztale 2. Energia wiązania sieci krystalicznej- ilość energii potrzebnej do
Temat: Zmiany stanu skupienia. 1. Energia sieci krystalicznej- wielkość dzięki której można oszacować siły przyciągania w krysztale 2. Energia wiązania sieci krystalicznej- ilość energii potrzebnej do
FIZYKA STATYSTYCZNA. d dp. jest sumaryczną zmianą pędu cząsteczek zachodzącą na powierzchni S w
 FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej
 Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
Materiały pomocnicze do laboratorium z przedmiotu Metody i Narzędzia Symulacji Komputerowej w Systemach Technicznych Symulacja prosta dyszy pomiarowej Bendemanna Opracował: dr inż. Andrzej J. Zmysłowski
PODSTAWY CHEMII INŻYNIERIA BIOMEDYCZNA. Wykład 2
 PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Statyka Cieczy i Gazów. Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał
 Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
III Podkarpacki Konkurs Chemiczny 2010/2011. ETAP I r. Godz Zadanie 1
 III Podkarpacki Konkurs Chemiczny 2010/2011 KOPKCh ETAP I 22.10.2010 r. Godz. 10.00-12.00 Zadanie 1 1. Jon Al 3+ zbudowany jest z 14 neutronów oraz z: a) 16 protonów i 13 elektronów b) 10 protonów i 13
III Podkarpacki Konkurs Chemiczny 2010/2011 KOPKCh ETAP I 22.10.2010 r. Godz. 10.00-12.00 Zadanie 1 1. Jon Al 3+ zbudowany jest z 14 neutronów oraz z: a) 16 protonów i 13 elektronów b) 10 protonów i 13
MATERIAŁY POMOCNICZE DO ĆWICZEŃ LABORATORYJNYCH Materiałoznawstwo III. Właściwości mechaniczne tworzyw polimerowych
 MATERIAŁY POMOCNICZE DO ĆWICZEŃ LABORATORYJNYCH Materiałoznawstwo III Właściwości mechaniczne tworzyw polimerowych Właściwości mechaniczne to zespół cech fizycznych opisujących wytrzymałość materiału na
MATERIAŁY POMOCNICZE DO ĆWICZEŃ LABORATORYJNYCH Materiałoznawstwo III Właściwości mechaniczne tworzyw polimerowych Właściwości mechaniczne to zespół cech fizycznych opisujących wytrzymałość materiału na
Zagadnienia. Budowa atomu a. rozmieszczenie elektronów na orbitalach Z = 1-40; I
 Nr zajęć Data Zagadnienia Budowa atomu a. rozmieszczenie elektronów na orbitalach Z = 1-40; I 9.10.2012. b. określenie liczby cząstek elementarnych na podstawie zapisu A z E, również dla jonów; c. określenie
Nr zajęć Data Zagadnienia Budowa atomu a. rozmieszczenie elektronów na orbitalach Z = 1-40; I 9.10.2012. b. określenie liczby cząstek elementarnych na podstawie zapisu A z E, również dla jonów; c. określenie
ANALIZA WYNIKÓW MATURY 2017 Z CHEMII
 ANALIZA WYNIKÓW MATURY 2017 Z CHEMII Wrocław, 30 listopada 2017 r. Jolanta Baldy Okręgowa Komisja Egzaminacyjna we Wrocławiu Matura 2017 z chemii w liczbach Średni wynik procentowy Okręg 38% Kraj 41% Okręg
ANALIZA WYNIKÓW MATURY 2017 Z CHEMII Wrocław, 30 listopada 2017 r. Jolanta Baldy Okręgowa Komisja Egzaminacyjna we Wrocławiu Matura 2017 z chemii w liczbach Średni wynik procentowy Okręg 38% Kraj 41% Okręg
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12
 Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
Podstawowe pojęcia Masa atomowa (cząsteczkowa) - to stosunek masy atomu danego pierwiastka chemicznego (cząsteczki związku chemicznego) do masy 1/12 atomu węgla 12 C. Mol - jest taką ilością danej substancji,
Bryła sztywna. Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka
 Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Stefan Połowiński CHEMIA FIZYCZNA POLIMERÓW
 Stefan Połowiński HEMIA FIZYZNA PLIMERÓW Spis treści Przedmowa 1.Wstęp. harakterystyka fizykochemiczna makrocząsteczek.1 Pojęcia podstawowe. Konfiguracje makroczasteczki.3 Rozmiary i kształt makrocząsteczki.4
Stefan Połowiński HEMIA FIZYZNA PLIMERÓW Spis treści Przedmowa 1.Wstęp. harakterystyka fizykochemiczna makrocząsteczek.1 Pojęcia podstawowe. Konfiguracje makroczasteczki.3 Rozmiary i kształt makrocząsteczki.4
Wstęp. Krystalografia geometryczna
 Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Energetyka konwencjonalna odnawialna i jądrowa
 Energetyka konwencjonalna odnawialna i jądrowa Wykład 8-27.XI.2018 Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Wykład 8 Energia atomowa i jądrowa
Energetyka konwencjonalna odnawialna i jądrowa Wykład 8-27.XI.2018 Zygmunt Szefliński Środowiskowe Laboratorium Ciężkich Jonów szef@fuw.edu.pl http://www.fuw.edu.pl/~szef/ Wykład 8 Energia atomowa i jądrowa
Surface settlement due to tunnelling. Marek Cała Katedra Geomechaniki, Budownictwa i Geotechniki
 urface settlement due to tunnelling Projektowanie i wykonawstwo budowli podziemnych pod zagospodarowana powierzchnią terenu wymaga oszacowania wielkości deformacji wewnątrz górotworu, a szczególnie powierzchni
urface settlement due to tunnelling Projektowanie i wykonawstwo budowli podziemnych pod zagospodarowana powierzchnią terenu wymaga oszacowania wielkości deformacji wewnątrz górotworu, a szczególnie powierzchni
Węglowodory poziom podstawowy
 Węglowodory poziom podstawowy Zadanie 1. (2 pkt) Źródło: CKE 2010 (PP), zad. 19. W wyniku całkowitego spalenia 1 mola cząsteczek węglowodoru X powstały 2 mole cząsteczek wody i 3 mole cząsteczek tlenku
Węglowodory poziom podstawowy Zadanie 1. (2 pkt) Źródło: CKE 2010 (PP), zad. 19. W wyniku całkowitego spalenia 1 mola cząsteczek węglowodoru X powstały 2 mole cząsteczek wody i 3 mole cząsteczek tlenku
WYZNACZANIE ROZMIARÓW
 POLITECHNIKA ŁÓDZKA INSTRUKCJA Z LABORATORIUM W ZAKŁADZIE BIOFIZYKI Ćwiczenie 6 WYZNACZANIE ROZMIARÓW MAKROCZĄSTECZEK I. WSTĘP TEORETYCZNY Procesy zachodzące między atomami lub cząsteczkami w skali molekularnej
POLITECHNIKA ŁÓDZKA INSTRUKCJA Z LABORATORIUM W ZAKŁADZIE BIOFIZYKI Ćwiczenie 6 WYZNACZANIE ROZMIARÓW MAKROCZĄSTECZEK I. WSTĘP TEORETYCZNY Procesy zachodzące między atomami lub cząsteczkami w skali molekularnej
Rozcieńczanie, zatężanie i mieszanie roztworów, przeliczanie stężeń
 Rozcieńczanie, zatężanie i mieszanie roztworów, przeliczanie stężeń Materiały pomocnicze do zajęć wspomagających z chemii opracował: dr Błażej Gierczyk Wydział Chemii UAM Rozcieńczanie i zatężanie roztworów
Rozcieńczanie, zatężanie i mieszanie roztworów, przeliczanie stężeń Materiały pomocnicze do zajęć wspomagających z chemii opracował: dr Błażej Gierczyk Wydział Chemii UAM Rozcieńczanie i zatężanie roztworów
POLIMERYZACJA KOORDYNACYJNA
 POLIMEYZAJA KOODYNAYJNA Proces katalityczny: - tworzą się związki koordynacyjne pomiędzy katalizatorem a monomerem - tworzą się polimery taktyczne - stereoregularne Polimeryzacji koordynacyjnej ulegają:
POLIMEYZAJA KOODYNAYJNA Proces katalityczny: - tworzą się związki koordynacyjne pomiędzy katalizatorem a monomerem - tworzą się polimery taktyczne - stereoregularne Polimeryzacji koordynacyjnej ulegają:
Wykład 4. Fizykochemia biopolimerów- wykład 4. Anna Ptaszek. 5 listopada Katedra Inżynierii i Aparatury Przemysłu Spożywczego
 Wykład 4 - wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 listopada 2013 1/30 Czym są biopolimery? To polimery pochodzenia naturalnego. Należą do nich polisacharydy i białka. 2/30 Polisacharydy
Wykład 4 - wykład 4 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 listopada 2013 1/30 Czym są biopolimery? To polimery pochodzenia naturalnego. Należą do nich polisacharydy i białka. 2/30 Polisacharydy
STATYCZNA PRÓBA SKRĘCANIA
 Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie STATYCZNA PRÓBA SKRĘCANIA Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Skręcanie pręta występuje w przypadku
Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie STATYCZNA PRÓBA SKRĘCANIA Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Skręcanie pręta występuje w przypadku
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II
 TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II Czas trwania testu 120 minut Informacje 1. Proszę sprawdzić czy arkusz zawiera 10 stron. Ewentualny brak należy zgłosić nauczycielowi. 2. Proszę rozwiązać
TEST PRZYROSTU KOMPETENCJI Z CHEMII DLA KLAS II Czas trwania testu 120 minut Informacje 1. Proszę sprawdzić czy arkusz zawiera 10 stron. Ewentualny brak należy zgłosić nauczycielowi. 2. Proszę rozwiązać
Blok I: Wyrażenia algebraiczne. dla xy = 1. (( 7) x ) 2 ( 7) 11 7 x c) x ( x 2) 4 (x 3 ) 3 dla x 0 d)
 Blok I: Wyrażenia algebraiczne I. Obliczyć a) 9 9 9 9 ) 7 y y dla y = z, jeśli = 0 4, y = 0 0.7 i z = y 64 7) ) 7) 7 7 I. Uprościć wyrażenia a) 48 6 4 dla 0 5) 4 dla 0 ) 4 ) dla 0 45 4 y ) dla yz 0 I.
Blok I: Wyrażenia algebraiczne I. Obliczyć a) 9 9 9 9 ) 7 y y dla y = z, jeśli = 0 4, y = 0 0.7 i z = y 64 7) ) 7) 7 7 I. Uprościć wyrażenia a) 48 6 4 dla 0 5) 4 dla 0 ) 4 ) dla 0 45 4 y ) dla yz 0 I.
NARZĘDZIA DO PRZETWÓRSTWA POLIMERÓW
 NARZĘDZIA DO PRZETWÓRSTWA POLIMERÓW STUDIA PODYPLOMOWE MATERIAŁY i TECHNOLOGIE PRZETWÓRSTWA TWORZYW SZTUCZNYCH Zakład Przetwórstwa Polimerów Politechnika Częstochowska Dr inż. Tomasz JARUGA Z a k ł a d
NARZĘDZIA DO PRZETWÓRSTWA POLIMERÓW STUDIA PODYPLOMOWE MATERIAŁY i TECHNOLOGIE PRZETWÓRSTWA TWORZYW SZTUCZNYCH Zakład Przetwórstwa Polimerów Politechnika Częstochowska Dr inż. Tomasz JARUGA Z a k ł a d
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
A4.06 Instrukcja wykonania ćwiczenia
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.06 Instrukcja wykonania ćwiczenia Lepkościowo średnia masa cząsteczkowa polimeru Zakres zagadnień obowiązujących do ćwiczenia 1. Związki wielkocząsteczkowe
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.06 Instrukcja wykonania ćwiczenia Lepkościowo średnia masa cząsteczkowa polimeru Zakres zagadnień obowiązujących do ćwiczenia 1. Związki wielkocząsteczkowe
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ. Zmiany makroskopowe. Zmiany makroskopowe
 WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
1. Jaką funkcję w procesach polimeryzacji wolnorodnikowej pełnią niŝej wymienione związki?: (5 pkt.)
 Imię i nazwisko:... Suma punktów:...na 89 moŝliwych 1. Jaką funkcję w procesach polimeryzacji wolnorodnikowej pełnią niŝej wymienione związki?: (5 pkt.) O...... O O O O O... N 2... H O O... 2. Jakie 3
Imię i nazwisko:... Suma punktów:...na 89 moŝliwych 1. Jaką funkcję w procesach polimeryzacji wolnorodnikowej pełnią niŝej wymienione związki?: (5 pkt.) O...... O O O O O... N 2... H O O... 2. Jakie 3
Fizyka statystyczna Zwyrodniały gaz Fermiego. P. F. Góra
 Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
Fizyka statystyczna Zwyrodniały gaz Fermiego P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2016 Fermiony w niskich temperaturach Wychodzimy ze znanego już wtrażenia na wielka sumę statystyczna: Ξ = i=0
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY
 WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
STABILNOŚĆ TERMICZNA TWORZYW SZTUCZNYCH
 KATERA TELGII PLIMERÓW IŻYIERIA PLIMERÓW LABRATRIUM: STABILŚĆ TERMIZA TWRZYW SZTUZY pracował: dr inż. T. Łazarewicz 1 1. WPRWAZEIE TERETYZE Temperatura w której rozpoczyna się rozkład związków stanowi
KATERA TELGII PLIMERÓW IŻYIERIA PLIMERÓW LABRATRIUM: STABILŚĆ TERMIZA TWRZYW SZTUZY pracował: dr inż. T. Łazarewicz 1 1. WPRWAZEIE TERETYZE Temperatura w której rozpoczyna się rozkład związków stanowi
Część I ZADANIA PROBLEMOWE (26 punktów)
 Zadanie 1 (0 6 punktów) Część I ZADANIA PROBLEMOWE (26 punktów) W podanym niżej tekście w miejsce kropek wpisz: - kwas solny - kwas mlekowy - kwas octowy - zjełczałe masło - woda sodowa - pokrzywa - zsiadłe
Zadanie 1 (0 6 punktów) Część I ZADANIA PROBLEMOWE (26 punktów) W podanym niżej tekście w miejsce kropek wpisz: - kwas solny - kwas mlekowy - kwas octowy - zjełczałe masło - woda sodowa - pokrzywa - zsiadłe
1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych.
 Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Studia podyplomowe INŻYNIERIA MATERIAŁÓW POLIMEROWYCH Edycja II marzec - listopad 2014
 Studia podyplomowe INŻYNIERIA MATERIAŁÓW POLIMEROWYCH Edycja II marzec - listopad 2014 Organizacja i realizacja studiów oraz opracowanie materiałów dydaktycznych są współfinansowane ze środków Unii Europejskiej
Studia podyplomowe INŻYNIERIA MATERIAŁÓW POLIMEROWYCH Edycja II marzec - listopad 2014 Organizacja i realizacja studiów oraz opracowanie materiałów dydaktycznych są współfinansowane ze środków Unii Europejskiej
Wymagania programowe: Gimnazjum chemia kl. II
 Wymagania programowe: Gimnazjum chemia kl. II Dział: Wewnętrzna budowa materii Ocena dopuszczająca [1] posługuje się symbolami odróżnia wzór sumaryczny od wzoru strukturalnego zapisuje wzory sumaryczne
Wymagania programowe: Gimnazjum chemia kl. II Dział: Wewnętrzna budowa materii Ocena dopuszczająca [1] posługuje się symbolami odróżnia wzór sumaryczny od wzoru strukturalnego zapisuje wzory sumaryczne
Ligand to cząsteczka albo jon, który związany jest z jonem albo atomem centralnym.
 138 Poznanie struktury cząsteczek jest niezwykle ważnym przedsięwzięciem w chemii, ponieważ pozwala nam zrozumieć zachowanie się materii, ale także daje podstawy do praktycznego wykorzystania zdobytej
138 Poznanie struktury cząsteczek jest niezwykle ważnym przedsięwzięciem w chemii, ponieważ pozwala nam zrozumieć zachowanie się materii, ale także daje podstawy do praktycznego wykorzystania zdobytej
KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW
 POUFNE Pieczątka szkoły 16 styczeń 2010 r. Kod ucznia Wpisuje uczeń po otrzymaniu zadań Imię Wpisać po rozkodowaniu pracy Czas pracy 90 minut Nazwisko KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY
POUFNE Pieczątka szkoły 16 styczeń 2010 r. Kod ucznia Wpisuje uczeń po otrzymaniu zadań Imię Wpisać po rozkodowaniu pracy Czas pracy 90 minut Nazwisko KONKURS CHEMICZNY DLA UCZNIÓW GIMNAZJÓW ROK SZKOLNY
Nauka o Materiałach. Wykład IX. Odkształcenie materiałów właściwości plastyczne. Jerzy Lis
 Nauka o Materiałach Wykład IX Odkształcenie materiałów właściwości plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Odkształcenie plastyczne 2. Parametry makroskopowe 3. Granica plastyczności
Nauka o Materiałach Wykład IX Odkształcenie materiałów właściwości plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Odkształcenie plastyczne 2. Parametry makroskopowe 3. Granica plastyczności
WYKŁAD 3 CZĄSTECZKI WIELOATOMOWE ZWIĄZKI WĘGLA
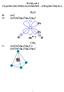 WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
WYKŁAD 3 ZĄSTEZKI WIELOATOMOWE ZWIĄZKI WĘGLA O : (s) O: (s) (s) (p z ) (p x ) (p y ) px py s 90 o? s 4 : (s) (s) (p x ) (p y ) (s) (s) (p x ) (p y ) (p z ) s pz px py s so : (s) s s.orbital MOLEKULARNY
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 13 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
Wstęp do astrofizyki I Wykład 13 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
Materiały Reaktorowe. Właściwości mechaniczne
 Materiały Reaktorowe Właściwości mechaniczne Naprężenie i odkształcenie F A 0 l i l 0 l 0 l l 0 a. naprężenie rozciągające b. naprężenie ściskające c. naprężenie ścinające d. Naprężenie torsyjne Naprężenie
Materiały Reaktorowe Właściwości mechaniczne Naprężenie i odkształcenie F A 0 l i l 0 l 0 l l 0 a. naprężenie rozciągające b. naprężenie ściskające c. naprężenie ścinające d. Naprężenie torsyjne Naprężenie
Bryła sztywna. Wstęp do Fizyki I (B+C) Wykład XIX: Prawa ruchu Moment bezwładności Energia ruchu obrotowego
 Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XIX: Prawa ruchu Moment bezwładności Energia ruchu obrotowego Obrót wokół ustalonej osi Prawa ruchu Dla bryły sztywnej obracajacej się wokół ostalonej osi mement
Bryła sztywna Wstęp do Fizyki I (B+C) Wykład XIX: Prawa ruchu Moment bezwładności Energia ruchu obrotowego Obrót wokół ustalonej osi Prawa ruchu Dla bryły sztywnej obracajacej się wokół ostalonej osi mement
VI Podkarpacki Konkurs Chemiczny 2013/2014
 VI Podkarpacki Konkurs Chemiczny 01/01 ETAP I 1.11.01 r. Godz. 10.00-1.00 KOPKCh Uwaga! Masy molowe pierwiastków podano na końcu zestawu. Zadanie 1 1. Znając liczbę masową pierwiastka można określić liczbę:
VI Podkarpacki Konkurs Chemiczny 01/01 ETAP I 1.11.01 r. Godz. 10.00-1.00 KOPKCh Uwaga! Masy molowe pierwiastków podano na końcu zestawu. Zadanie 1 1. Znając liczbę masową pierwiastka można określić liczbę:
