WYKORZYSTANIE WIEDZY POZNANEJ Z PLIKÓW B.ZESZYT.001.N. I B.ZESZYT.O.
|
|
|
- Agnieszka Karpińska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Rys.1. WYKRZYSTANIE WIEDZY PZNANEJ Z PLIKÓW B.ZESZYT.001.N. I B.ZESZYT ; str.1 a=r=100 b= φ φ1= ATAN(a/b) = 1, [rad] φ1= 74, [ ] φ1= 4992 [] Rys ; a=r=100 ĆWIARTKA I ELIPSY(o) α = 15 [ ] b= α α α α α 4 3 α (-)X (-)Y (+)Y (+)X dot.: Poszukiwania zależności analitycznyc Koszalin dnia r
2 Rys.3. WYKRZYSTANIE WIEDZY PZNANEJ Z PLIKÓW B.ZESZYT.001.N. I B.ZESZYT ; str.2 (-)X (-)Y Z12=X6. Z6=X12 Z11=X5. Z5=X11 Z10=X4. Z4=X10 (+)Y (+)X a=r=100 Z9=X3. Z3=X9 Z8=X2. Z2=X8 α = 15 [ ] Z7=X1. Z1=X7 Z22 Z23 Z24 Z0. X0=Z0 b= 27 Z Z19 Z20 φ Z2 Z1 Z0 Z18 Z5 Z4 Z3 α Z18 α Z6=Z18=0 Z17 PRZYKŁAD "TURB" Z16 Z15 Z14 Z13 α α α α Z12=X6 ĆWIARTKA IV ELIPSY(o) Dane: a= 100,00 j. PÓŁCIĘCIW KRĘGU I ELIPSY(o) b= 27,00 j. Z12/Z0=Z11/Z1=Z10/Z2=Z9/Z3= PSTAĆ KANNICZNA Z8/Z4=Z7/Z5=Z5/Z7=Z4/Z8=Z3/Z9= ELIPSY : na płaszczyźnie (XZ) Z2/Z10=Z1/Z11. (X^2/a^2)+(z^2/b^2)=1 φ1= ATAN(a/b) = 1, [rad] W tym wzorze niezmienne są wielkości: półosie elipsy φ1= 74, [ ] φ1= 4992 [] a i b, które decydują o wielkościac narysowanyc na rzutni płaszczyzny pionowej. Jest to bezwątpienia elipsa(o) pocodząca od odcylonego okręgu, koła (o)k od pionu o kąt (24). Czyli o kąt: *360 /24 = 74, [ ] tj. 1, [rad] DYGRESJA. Kiedy w pracy, na budowie przyszło mi wykreślić profil dennicy wypukłej do zbiornika, próbowałem wykonać tę czynność wykonać ręcznie, przy użyciu dratwy. Niestety, dratwa się rozciągała. Potem użyłem drut miedziany. Efekt był ten sam. Więc, postanowiłem wykonać profil półdennicy metodą analityczną. Potem dostrzegłem b.ważny szczegół. Cięciwy od 18 w prawo, tj. w kierunku 19 należy zagęścić, by uzyskać dokładniejszy łuk elipsy. W miarę zbliżania się do 24 cięciwy można stawiać rzadziej. WZÓR P PRZEKSZTAŁCENIU: Ze = ± (b^2*(1-(x^2))/a^2)^0,5 j. a = 100^2= ,00 j.^2 Kolejne i ostateczne przekształcenie wzoru wygląda następująco: 27^2= 729,00 j.^2 b = Ze = ± (b^2-(b/a)^2*x^2)^0,5 elipsa(o) W tym przypadku będę korzystał z tarczy zegara (24) Taraz wystarczy w miejsce "X" wstawiać dowolne wielkości =< od b. 0 Z0 = ± (729,00-(27,00/100,00)^2*X0^2)^0,5= 27 j. X0= a*sin(radiany(0))= 0 j. 0 [ ] 1 Z1 = ± (729,00-(27,00/100,00)^2*X1^2)^0,5= 26, j. X1= a*sin(radiany(1*α))= 25, j. 15 [ ] 2 Z2 = ± (729,00-(27,00/100,00)^2*X2^2)^0,5= 23, j. X2= a*sin(radiany(2*α))= 50 j. 30 [ ] 3 Z3 = ± (729,00-(27,00/100,00)^2*X3^2)^0,5= 19, j. X3= a*sin(radiany(3*α))= 70, j. 45 [ ] 4 Z4 = ± (729,00-(27,00/100,00)^2*X4^2)^0,5= 13,5 j. X4= a*sin(radiany(4*α))= 86, j. 60 [ ] 5 Z5 = ± (729,00-(27,00/100,00)^2*X5^2)^0,5= 6, j. X5= a*sin(radiany(5*α))= 96, j. 75 [ ] 6 Z6 = ± (729,00-(27,00/100,00)^2*X6^2)^0,5= dąży do 0 j. X6= a*sin(radiany(6*α))= 100 j. 90 [ ] 7 Z7 = ± (729,00-(27,00/100,00)^2*X7^2)^0,5= 6, j. X7= a*sin(radiany(7*α))= 96, j. 105 [ ] 8 Z8 = ± (729,00-(27,00/100,00)^2*X8^2)^0,5= 13,5 j. X8= a*sin(radiany(8*α))= 86, j. 120 [ ] 9 Z9 = ± (729,00-(27,00/100,00)^2*X9^2)^0,5= 19, j. X9= a*sin(radiany(9*α))= 70, j. 135 [ ] Z10= ± (729,00-(27,00/100,00)^2*X10^2)^0,5= 23, j. X10= a*sin(radiany(10*α))= 50 Z11= ± (729,00-(27,00/100,00)^2*X11^2)^0,5= 26, j. X11= a*sin(radiany(11*α))= 25, Z12= ± (729,00-(27,00/100,00)^2*X12^2)^0,5= 27 j. X12= a*sin(radiany(12*α))= 0 10 j. 150 [ ] 11 j. 165 [ ] 12 j. 180 [ ] PRPRCJNALNŚĆ Jest coś, na co nie zwracałem Państwa uwagę. Przy TAN(a/b) kąta φ1, tj. wyznaczaniu (kierunkowej; kierunkowej), nie wskazywałem wielkości, przy któryc funkcja traci sens liczbowy np. gdy wielkość b=0. Na tarczy zegara (24) są to godziny 6 i 18. W związku z tym należy zapisać: dąży do 0 Na WSI w Koszalinie uczono mnie, by stosować zastrzeżenia, że wielkość b 0. Być może brak odpowiednic zapisów i zastrzeżeń matematycznyc obecnie wymaganyc, powoduje, że moje prace nie są aprobowane, ponieważ przy aśle na Google: "B.Zeszyt.001" pisze słowo USUŃ. Jeszcze jedno. Na różnyc blogac związanyc z matematyką pytają ludzie cyt. Czy elipsa jest okręgiem? W mojej geometrii kulowej opisałem w sposób oczywisty jak pojmuję to zagadnienie. Dlatego powtórzę jeszcze raz ten problem na kolejnej stronie. dot.: Poszukiwania zależności analitycznyc Koszalin dnia r
3 str.3 Zacznę od przedstawienia układu przestrzennego (XYZ). Grube strzałki wskazują płaszczyzny o wielkościac (-)X (-)Y dodatnic. Cienkie, przerywane linie wskazują płaszczyzny o wielkościac ujemnyc. Na każdej płaszczyźnie rysuję punkt centralny "" (w środku). Najwygodniej jest mi pokazywanie płaszczyzny pionowej (XZ). Wtedy po prawej stronie mam wielkości (+) osi X od pktu, a (-) po lewej stronie osi X. Podobnie jest z wysokością. (+)Y (+)X d pktu w górę mam wartości dodatnie, a w dół od pktu mam wartości ujemne. Tak przedstawiłem pł. (XZ). Teraz odwrócę się całą swoją sylwetką o kąt 90 w lewo. W tym momencie postąpiłem wbrew zasadzie: zawsze w prawo, po to, by pokazać bezpośrednio płaszczyznę (YZ), na której widoczny jest ruc południkowy. Płaszczyzna (YZ) jest także pionowa, lecz bywa tak, że pokazuję ją w pozycji leżącej. Wtedy na rysunku umieszczam małego ludzika który ręką wskazuje godz. 0 na tarczy zegara np. (24) lub piszę słowa: nogi, głowa. Kolor wysokości Z jest jasno-zółty. Warto na to zwrócić uwagę. Po wstępie, przystępuję do odpowiedzi na pytanie: Czy elipsa jest okręgiem? Na płaszczyźnie (XZ) Rys.3 narysowałem okrąg, a właściwie koło. Jest w pozycji stojącej. Potem narysowałem to samo koło, gdy odcyliło się od pionu rucem równoleżnikowym, na godzinę: r(o)(24). dpowiada to kątowi:~ *360 /24 = 74, [ ]. Co z tego wynika? dpowiedź jest następująca: Mam cały czas doczynienie z kołem, to po pierwsze. Wymiary rzutu prostokątnego odcylonego koła od pionuna na płaszczyznę (XZ) spełniają warunki jakie stawia się ELIPSIE. Dlatego zapisuję przy elipsie taki znak (o). Znak ten mówi, że ta elipsa pocodzi od koła odcylonego ELIPSA(o). tym temacie mówi mój plik B.Zeszyt.032.A. z uwzględnieniem pocodzenia elipsy: ELIPSA(o) i odcylone koło(o) od pionu w rzucie prostokątnym poziomym na płaszczyznę pionową, różni się tylko nazwą. Stąd najważniejsze jest tu pocodzenie elipsy(o). Uwzględniając ten aspekt można wykluczyć postać koła, czy okręgu jako elipsy. Dodatkowym argumentem jest fakt, iż przy wartościac półosi: a=b mimośród i ogniskowa nie istnieją, ponieważ mają wartości zerowe!!! A, przypisywanie ELIPSIE cec (szczególnego przypadku) jest pojęciem błędnym. Powiem tak. Nawet mikroskopijne odcylenie okręgu, koła od pionu skutkuje powstaniem ELIPSY(o), obserując ten ruc na płaszczyźnie pionowej w rzucie poziomym prostokątnym. I to jest PRAWDĄ. Na czyimś blogu wyczytałem postawione pytanie: Czy elipsa jest okręgiem i (odwrotnie). dpowiedź udzielono następującą. 1. krąg jest elipsą (szczególnym przypadkiem). Elipsa oczywiście nie musi być okręgiem. 2. Tak jak kwadrat jest prostokątem, ale nie każdy prostokąt jest kwadratem. Powiem szczerze, nie da się tego pojąć, ani zrozumieć, o co autorowi codziło pisząc takie rzeczy, jako odpowiedź? Zacznę od końca. To, że dwóc facetów ma takie same nazwisko wcale nie oznacza, że są z tej samej rodziny. Proszę Państwa. Uważam, iż autorowi codziło o stwierdzenie, że kwadrat spełnia warunki stawiane prostokątowi, a to wielka różnica, bo nie da się postawić znaku równości między kwadratem i prostokątem. Może być tyko tak: (kwadrat prostokąt). Dalej pisze cyt."ale nie każdy prostokąt jest kwadratem". Zgadzam się z tą częścią odpowiedzi. Człowiek złośliwy, który by cciał Państwu namieszać w głowac powiedziałny, że nie zgadza się z tą częścią odpowiedzi, opisując czynności jakie wykonał. Prostokąt ma wymiar: a i b. brócę ten prostokąt o 90, tak żeby podstawa prostokąta miała mniejszy wymiar tj.b. Teraz na płaszczyźnie pionowej (XZ) układu (XYZ) dokonam odcylenie prostokąta, w którym wymiar a w rzucie prostokątnym poziomym przyjmie wartość b. Wystarczy kąt o odpowiednim odcyleniu prostokąta. Tak by prostokąt na płaszczyźnie pionowej miał wymiary w rzucie ( b*b). Wtedy będzie kwadratem każdy prostokąt, bez wyjątków. Taki sposób myślenia jest "naginaniem prawdy". Krótko mówiąc - byłoby kłamstwem. Uznaję ELIPSĘ, która nie pocodzi z odcylonego okręgu, koła. W układzie (XYZ), na płaszczyźnie (XZ) występuje w pozycji pionowej. Została skonstrułowana po obliczeniac wymiarów: a i b. Ma więc wielkości: e - mimośrodu; F1F2 - ogniskowej: c itp. Ta ELIPSA podobnie jak każda inna figura płaska, podlega także odcyleniu kołowemu (o). Jeżeli na płaszczyźnie (XZ) następuje ruc równoleżnikowy, to na płaszczyźnie (YZ) jest zawsze śladem i tu występuje problem, bo ślad dotyczy osi b. W przypadku następnego rucu południkowego. Następuje ruc na odcinku przestrzeni (pasma) o wymiarze szerokości b. To byłoby na tyle. TURB BLICZENIE DŁUGŚCI PRMIENI WYCHDZĄCYCH ZE ŚRDKA ELIPSY(o) Z (0:12) = ± X (0:12) = ± Pomienie elipsy(±) W kolumnie (k:n) są obliczone półcięciwy skośne przecodzące półcięciwy elipsy półcięciwy skośne przez pkt centralny elipsy(o). Można obliczyć każdą inną cięciwę (24) pionowe i poziome ((c:f)^2+(g:j)^2)^0,5 skośną nie przecodzącą przez centralny pkt elipsy(o). Można (a:b) (c:f) (g:j) (k:n) każdą inną cięciwę narysować i obliczyć, bez problemu. Cięciwa nie musi przecodzić przez pkt. Ktoś zecce zapytać po co jest 1 26, , , potrzebna cięciwa? dpowiadam. Każdy łuk oparty jest na cięciwie 2 23, , W przypadku łuku elipsy(o), mamy doczynienie z łukiem(o). 3 19, , , Tak, z łukiem kołowym, odcylonym od pionu. Wiemy też, że ten 4 13,5 86, , kąt φ1 ma obliczoną lub wyznaczoną swoją wielkość. A każda 5 6, , , elipsa(o) podobnie jak koło, może mieć swoje wycinki i odcinki Na razie niewiele się o tym nie mówi, bo nikt nie wie jak trzeba się 7-6, , , za to zabrać. Skoro udało mi się obliczyć metodą przybliżoną w 8-13,5-86, , tabeli pliku B.Zeszyt.001.M. czwartą część obwodu elipsy, to tą 9-19, , , metodą potrafię obliczyć każdy łuk(o) oparty na cięciwie elipsy(o) , , Czekało by mnie mnóstwo pracy, lecz cęć poznania bierze górę, 11-26, , , nad wysiłkiem. Inaczej, człowiek nie dojdzie do żadnego celu Można również pojść inną drogą, rozpatrując stopień zagęszczenia punktów. W przypadku cięciw poziomyc elipsa(o) na połosiac (-)X: i :(+)X zacowuję wymiary w rucu równoleżnikowym. Natomiast w przypadku półosi : i : następuje zagęszczenie punktów. Im bliżej godziny 24;0 i 12 gęstość jest największa. Ten program komputerowy z trudem podąża ze zgraniem pikseli. Byłoby dobrze, gdyby piksele były rozłożone w górę i w bok jako kwadraty. Kiedy przeuwam linię pionową np. w prawo przy 400% dot.:do rozwiązywania zadań okrąg - elipsa(o) linia skacze mi zbyt daleko. Warto zagęścić piksele, już jako kwadraty. Koszalin dnia r
4 ZADANIA D RZWIĄZANIA Z RYSUNKAMI. MATERIAŁ DTYCZĄCY PLIKÓW: B.Zeszyt.001.: M; N;. ZADANIE Nr ;0 2 Rys krąg w wyniku rucu równoleżnikowego został odcylony od 2, pionu na godz. 4, Poza tym,na godz. 2,72941 jest punkt stanowiący początek półcięciwy 4,55555 okręgu. Promień okręgu r = 100 j. r = 100 j. 3).bliczyć: b - półoś małą elipsy(o); 4).bliczyć: e - mimośród; 5). bliczyć: F1F2 - ogniskową elipsy(o) 5).Udział powierzcni elipsy(o) do powierzcni koła tego okręgu U str ZADANIE Nr ; Rys.2. krąg w wyniku rucu równoleżnikowego 19 został odcylony od pionu na godz. 7, Poza tym,na godz. 4,59963 jest punkt stanowiący początek półcięciwy 4,59963 okręgu. Promień okręgu r = 100 j. 3).bliczyć: b - półoś małą elipsy(o); r= 100j. 4).bliczyć: e - mimośród; 5). 7,39982 bliczyć:(f1f2) - ogniskową elipsy(o) 5).Udział powierzcni elipsy(o) do powierzcni koła tego okręgu U ZADANIE Nr ; Rys.3. krąg w wyniku rucu równoleżnikowego 19 został odcylony od pionu na godz. 13,7889. Poza tym,na godz. 7,87773 jest punkt stanowiący początek półcięciwy okręgu. Promień okręgu r = 100 j. 3).bliczyć: b - półoś małą elipsy(o); 4).bliczyć: e - mimośród; 5). r = 100j. bliczyć: F1F2 - ogniskową elipsy(o) 7, ).Udział powierzcni elipsy(o) do powierzcni koła tego okręgu U 17 13, RZWIĄZANIA TYCH TRZECH ZADAŃ SĄ NA STR.5. dot.: Zadania do rozwiązania okrąg - elipsa(o) Koszalin dnia r
5 str ; RZWIĄZANIE ZADANIA Nr 1. 1).Kierunkowa równoleżnikowa 19 wyznacza kąt odcylenia okręgu od pionu. Najlepiej to przesta- Rys.4. pkt 2,72941 wić w formie godz.na określonej tarczy zegara:r(o)4,55555(24). bliczam kąt φ1,który ukazuje odcylenie okręgu od pionu (YZ): & 4,55555*360 /24 = 68, [ ] Nie ma płaszczyzny(yz) & 4,55555 na rysunku.temu tematowi poświęciłem tyle miejsca, że byłoby r =Zo= 100 j. śmieszne powtarzać kolejny raz. Na Rys.4 jest płaszcz.(xz). Ze kierunkowa bliczam półcięciwę elipsy(o)ze,z narysow.trójkąta, mając: r; φ1. φ1 Z'e Ze= r*cos(φ1) = 100*cos(radiany(68,33325)) = 36, j. bliczam półcięciwę okręgu Z'o w pkt. 2, ,72941*360 /24 = 40, [ ] tj. 0, [rad] Z'o= r*cos(&) = 100*cos(0, )= 75, j. r = Zo Z'o bliczam półcięciwę elipsy(o) Z'e, korzystając z proporcji: Zo Zo/Ze=Z'o/Z'e dla pkt.2,72941 okręgu półcięciwa wynosi: Z'e= Ze*Z'o/Zo= 27, j. bliczam mimośród e: a=100j. b= Ze= 36, j. bliczam wg wzoru: e=(a^2-b^2)/a^2 17 e = 0, bliczam ogniskową: (F1F2) c=± (a^2-b^2)^0, c = ± 92, j. U= 0, To wszystko ).Kierunkowa równoleżnikowa 19 Rys.4. wyznacza kąt odcylenia okręgu od pionu. Najlepiej to przestawić w formie godz.na określonej tarczy zegara:r(o)7,399824(24). bliczam kąt φ1,który ukazuje odcylenie okręgu od pionu (YZ): 7,399824*360 /24 = 110, [ ] Nie ma płaszczyzny(yz) & pkt 4,59963 na rysunku.temu tematowi poświęciłem tyle miejsca, że byłoby & śmieszne powtarzać kolejny raz. Na Rys.4 jest płaszcz.(xz). Ze kierunkowa bliczam półcięciwę elipsy(o)ze,z narysow.trójkąta, mając: r; φ1. φ1 Z'e Ze= r*cos(φ2) = 100*cos(radiany( ,997360)) = 35, j. r= Zo=100j. bliczam półcięciwę okręgu Z'o w pkt. 4, φ2= 180 -φ1 Z'o 4,59963*360 /24 = 68, [ ] tj. 1, [rad] 7,39982 Z'o= r*cos(&) = 100*cos(1, )= 35, j. r = Zo Zo bliczam półcięciwę elipsy(o) Z'e, korzystając z proporcji: Zo/Ze=Z'o/Z'e dla pkt.4,59963 okręgu półcięciwa wynosi: Z'e= Ze*Z'o/Zo= 12, j. bliczam mimośród e: a=100j. b= Ze= 35, j. bliczam wg wzoru: e=(a^2-b^2)/a^2 17 e = 0, bliczam ogniskową: (F1F2) c=± (a^2-b^2)^0, c = ± 93, j. U= 0, To wszystko ;0 2 RZWIĄZANIE ZADANIA Nr ).Kierunkowa równoleżnikowa 19 Rys.4. wyznacza kąt odcylenia okręgu od pionu. Najlepiej to przestawić w formie godz.na określonej tarczy zegara:r(o)7,399824(24). bliczam kąt φ1,który ukazuje odcylenie okręgu od pionu (YZ): 13,7889*360 /24 = 206, [ ] Nie ma płaszczyzny (YZ) na rysunku.temu tematowi poświęciłem tyle miejsca, że byłoby niezręcznie powtarzać to kolejny raz. Na Rys.4 jest płaszcz.(xz). Ze & Z'e bliczam półcięciwę elipsy(o)ze, z narys.trójkąta, mając: r; φ1. φ1 Ze= r*cos(φ2) = 100*cos(radiany( ,83350)) = 89, j. bliczam półcięciwę okręgu Z'o w pkt. 7, &1=180 -& ;0 2 RZWIĄZANIE ZADANIA Nr 2. Z'o 7,87773*360 /24 = 118,1660 [ ] tj. &1= 61,8341 [ ] tj. 1,07921 [rad] φ2=180 -φ1 Z'o= r*cos(&1) = 100*cos(1, )= 54, j. r = Zo Zo &1 pkt 7,87773 bliczam półcięciwę elipsy(o) Z'e, korzystając z proporcji: Zo/Ze=Z'o/Z'e dla pkt.7,87773 okręgu półcięciwa wynosi: &1=180 -& Z'e= Ze*Z'o/Zo= 48, j. bliczam mimośród e: a=100j. 13,7889 b= Ze= 89, j. bliczam wg wzoru: e=(a^2-b^2)/a^2 17 e = 0, bliczam ogniskową: (F1F2) c=± (a^2-b^2)^0, c = ± 45, j. U= 0, To wszystko. Nie przedstawiłem zadania w ćwiartce II okręgu, bo zabrakło mi miejsca na stronie 4. Wszystkie zadania niezależnie w której są ćwiartce okręgu należy rozwiązywać identycznie, jak wyżej. dot.: Rozwiązywanie zadań okrąg - elipsa(o) Koszalin dnia r
TABELA PRZELICZENIOWA
 Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował: inż. Kazimierz arski Romana - imię
Rys.5a. Grot stożka widziany jako trójkąt równoram. Dwa rysunki w jednym. W' 1h na kole Pkt W najbardziej. 23h na kole w4 2h na kole Ø3
 BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
BRÓT KÓŁ SI (Z) GRTA STŻKEG SKRĘTNEG Z PLIKU SKRYPT (R).009.N NA GDZINIE (24h). Grot turbiny stożkowo-skrętny, ośmiołukowy.rys.powiększony 2*.Ruch obrotowy równoleżnikowy grota wokół osi (X) Rys.6a Rys.5a
MAGAZYN WIEDZY NR 1 O GEOMETRII KULOWEJ. PROJEKT TWÓRCY (gk). PRZYPOMINA POMNIK. WALEC TRAPEZOWY Z KORYTEM KOŁO. Nr2 6h(48h) ELIPSA pionowa O
 MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
MAGAZYN WIEDZY NR 1 GEMETRII KULWEJ. PRJEKT TWÓRCY (). PRZYPMINA PMNIK. str.1 Rys.1 Widziane KŁ Nr3 Widziana ELIPSA przy kierunku patrzenia 90 na jej centrum. Nr2 6h() ELIPSA pionowa WALEC TRAPEZWY Z KRYTEM
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1
 PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
PLANIMETRIA CZYLI GEOMETRIA PŁASZCZYZNY CZ. 1 Planimetria to dział geometrii, w którym przedmiotem badań są własności figur geometrycznych leżących na płaszczyźnie (patrz określenie płaszczyzny). Pojęcia
gk T GEOMETRIA WYKREŚLNA PRZESTRZENNA T (GK) W PRAKTYCE. SZTUKA TRASOWANIA CZ.1. Rys.3. Rys.4. Rysunek jest zbyt duży, zmniejszę go na str.2.
 GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
GEOMERIA WYKREŚLNA PRZESRZENNA (GK) W PRAKYCE. SZUKA RASOWANIA CZ.1. str.1 Kiedyś od jakiegoś gościa otrzymałem emaila. Pytał mnie jakie należy stosować linie i jakie grubości tych linii. W końcu zapytał
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
PODSTAWY > Figury płaskie (1) KĄTY. Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach:
 PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
PODSTAWY > Figury płaskie (1) KĄTY Kąt składa się z ramion i wierzchołka. Jego wielkość jest mierzona w stopniach: Kąt możemy opisać wpisując w łuk jego miarę (gdy jest znana). Gdy nie znamy miary kąta,
Rys.1. str.1. 48h;0h 18h 19h 20h 21h 22h 46h. 44h r1 4h. 10h. 38h. 34h 14h. 32h 16h. 24h jest linią do przenoszenia szablonów
 Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
Moje własne opracowanie torusa na przyrządach: tarczy zegara (48h); szablonu listwowego A. en rysunek ORUSA, będzie miał ostatecznie 48 promieni. str.1 Rys.1 N 48h;0h 18h 19h 20h 21h 22h 46h 2h 4h 6h 8h
FUNKCJA LINIOWA - WYKRES
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (Postać kierunkowa) Funkcja liniowa jest podstawowym typem funkcji. Jest to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości
400% Rys.2a Negatyw *** ZASADA *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na OPIS WYKONYWANYCH CZYNNOŚCI.
 Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
Szkic 1. `````2 2 str.1 PWIĘKSZ! 00% Rys.2a *** ZSD *** Rys.1a Pozytyw pł.(yz) Zabawa "włosem" musi być oparta na 0h() 12 dwóch rzutach prostokątnych, na dwie 12 płaszczyzny tj. MPĘ (XY) i pł.(yz). Powyższe
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM
 WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
WYMAGANIA EDUKACYJNE Z MATEMATYKI DLA KLASY TRZECIEJ NA ROK SZKOLNY 2011/2012 DO PROGRAMU MATEMATYKA Z PLUSEM LICZBY, WYRAŻENIA ALGEBRAICZNE umie obliczyć potęgę o wykładniku naturalnym; umie obliczyć
FUNKCJA LINIOWA - WYKRES. y = ax + b. a i b to współczynniki funkcji, które mają wartości liczbowe
 FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
FUNKCJA LINIOWA - WYKRES Wzór funkcji liniowej (postać kierunkowa) Funkcja liniowa to funkcja o wzorze: y = ax + b a i b to współczynniki funkcji, które mają wartości liczbowe Szczególnie ważny w postaci
Zad.3. Jakub Trojgo i Jakub Wieczorek. 14 grudnia 2013
 Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
Zad.3 Jakub Trojgo i Jakub Wieczorek 14 grudnia 2013 W pierwszej części naszej pracy będziemy chcieli zbadać ciągłość funkcji f(x, y) w przypadku gdy płaszczyzna wyposażona jest w jedną z topologii: a)
TWORZENIE OBIEKTÓW GRAFICZNYCH
 R O Z D Z I A Ł 2 TWORZENIE OBIEKTÓW GRAFICZNYCH Rozdział ten poświęcony będzie dokładnemu wyjaśnieniu, w jaki sposób działają polecenia służące do rysowania różnych obiektów oraz jak z nich korzystać.
R O Z D Z I A Ł 2 TWORZENIE OBIEKTÓW GRAFICZNYCH Rozdział ten poświęcony będzie dokładnemu wyjaśnieniu, w jaki sposób działają polecenia służące do rysowania różnych obiektów oraz jak z nich korzystać.
Definicja obrotu: Definicja elementów obrotu:
 5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
5. Obroty i kłady Definicja obrotu: Obrotem punktu A dookoła prostej l nazywamy ruch punktu A po okręgu k zawartym w płaszczyźnie prostopadłej do prostej l w kierunku zgodnym lub przeciwnym do ruchu wskazówek
gk T Rozwiązanie Zadania nr1 - uzupełnienie
 TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
TRÓJKĄT LGICZNY - W NAWIĄZANIU D PLIKU: Skrypt (R).009.02. str.1 SZKIC RIENTACJI Rys.1 pł.(xz) PRZYKŁAD Nr 1 PRZESTRZENNEJ Moim celem jest pokazanie Państwu w jaki sposó zmienię położenie odcylone stożka
Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM
 Zespól Szkół Ogólnokształcących i Zawodowych w Ciechanowcu 23 czerwca 2017r. Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM Strona 1 z 9 1. Geometria płaska trójkąty zna
Zespól Szkół Ogólnokształcących i Zawodowych w Ciechanowcu 23 czerwca 2017r. Wymagania na egzamin poprawkowy z matematyki z zakresu klasy drugiej TECHNIKUM Strona 1 z 9 1. Geometria płaska trójkąty zna
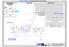
gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii
![gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii gk T Rys.5 pionowa oś WYDRĄŻONE KORYTO Rys.6 symetrii Ł łuk kąta 90 &1k &1p pionowa oś Cięciwa=2* 3= 83, [mm] symetrii](/thumbs/103/159774468.jpg) Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
Należy się Państwu wyjaśnienie dotyczące znaku: literki C w kółeczku. Jest to znak certyfikatu. Na ten znak zapracowałem od momentu, gdy ponownie, tym razem ja, odkryłem KOŁO. Na początku była to nowa
gk T Okrąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 Rys.2
 krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
krąg z punktami wg tarczy zegara (24h), przerobiony na turbinę obrotową. Uruchomienie fantazji. Rys.1 23h 1h 22h 2h str.1 21h 3h 20h 4h 19h 5h 18h 6h 17h 7h 16h 8h 15h 9h 14h 10h 13h 11h Rys.2 Szablon
Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas
 Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas klasa I 1)Działania na liczbach: dopuszczający: uczeń potrafi poprawnie wykonać cztery podstawowe działania na ułamkach
Wymagania edukacyjne z matematyki do programu pracy z podręcznikiem Matematyka wokół nas klasa I 1)Działania na liczbach: dopuszczający: uczeń potrafi poprawnie wykonać cztery podstawowe działania na ułamkach
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE
 Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
Umiejętności opracowanie: Maria Lampert LISTA MOICH OSIĄGNIĘĆ FIGURY I PRZEKSZTAŁCENIA GEOMETRYCZNE Co powinienem umieć Umiejętności znam podstawowe przekształcenia geometryczne: symetria osiowa i środkowa,
OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV
 OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV LICZBY NATURALNE - umie dodawać i odejmować pamięciowo w zakresie 100 bez przekraczania progu dziesiątkowego, - zna tabliczkę mnożenia i dzielenia w zakresie 100,
OGÓLNE KRYTERIA OCENIANIA DLA KLASY IV LICZBY NATURALNE - umie dodawać i odejmować pamięciowo w zakresie 100 bez przekraczania progu dziesiątkowego, - zna tabliczkę mnożenia i dzielenia w zakresie 100,
wymagania programowe z matematyki kl. II gimnazjum
 wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
wymagania programowe z matematyki kl. II gimnazjum Umie obliczyć potęgę liczby wymiernej o wykładniku naturalnym. 1. Arytmetyka występują potęgi o wykładniku naturalnym. Umie zapisać i porównać duże liczby
LUBELSKA PRÓBA PRZED MATURĄ POZIOM PODSTAWOWY Klasa 1 Klasa 1
 Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
Klasa III technikum Egzamin poprawkowy z matematyki sierpień I. CIĄGI LICZBOWE 1. Pojęcie ciągu liczbowego. b) a n =
 /9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
/9 Narysuj wykres ciągu (a n ) o wyrazie ogólnym: I. CIĄGI LICZBOWE. Pojęcie ciągu liczbowego. a) a n =5n dla n
TABELA PRZELICZENIOWA
 Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Romana - imię mojej małżonki Nr 18h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. str.1 GK Pierwsze kroki w geometrii (). Motto: Patrzymy na to samo, widzimy coś innego. T opracował:
Internetowe Ko³o M a t e m a t yc z n e
 Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0, C. 0. D. 0 5% 6 II sposób: x nieznana liczba
GEOMETRIA ELEMENTARNA
 Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
Bardo, 7 11 XII A. D. 2016 I Uniwersytecki Obóz Olimpiady Matematycznej GEOMETRIA ELEMENTARNA materiały przygotował Antoni Kamiński na podstawie zbiorów zadań: Przygotowanie do olimpiad matematycznych
RZUTOWANIE PROSTOKĄTNE
 RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
RZUTOWANIE PROSTOKĄTNE wg PN-EN ISO 5456-2 rzutowanie prostokątne (przedstawienie prostokątne) stanowi odwzorowanie geometrycznej postaci konstrukcji w postaci rysunków dwuwymiarowych. Jest to taki rodzaj
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 b BS Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
METODA RZUTÓW MONGE A (II CZ.)
 RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
RZUT PUNKTU NA TRZECIĄ RZUTNIĘ METODA RZUTÓW MONGE A (II CZ.) Dodanie trzeciej rzutni pozwala na dostrzeżenie ważnej, ogólnej zależności. Jeżeli trzecia rzutnia została postawiona na drugiej - pionowej,
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TLog Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność rozwiązywania
Tra r n a s n fo f rm r a m c a ja a na n p a rę r ż ę eń e pomi m ę i d ę zy y uk u ł k a ł d a am a i m i obr b ó r cony n m y i m
 Wytrzymałość materiałów Naprężenia główne na przykładzie płaskiego stanu naprężeń 1 Tensor naprężeń Naprężenia w stanie przestrzennym: τ τxz τ yx τ yz τzx τzy zz Układ współrzędnych jest zwykle wybrany
Wytrzymałość materiałów Naprężenia główne na przykładzie płaskiego stanu naprężeń 1 Tensor naprężeń Naprężenia w stanie przestrzennym: τ τxz τ yx τ yz τzx τzy zz Układ współrzędnych jest zwykle wybrany
Przekształcanie wykresów.
 Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
Sławomir Jemielity Przekształcanie wykresów. Pokażemy tu, jak zmiana we wzorze funkcji wpływa na wygląd jej wykresu. A. Mamy wykres funkcji f(). Jak będzie wyglądał wykres f ( ) + a, a stała? ( ) f ( )
PRÓBNA MATURA ZADANIA PRZYKŁADOWE
 ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
ZESPÓŁ SZKÓŁ HOTELARSKO TURYSTYCZNO GASTRONOMICZNYCH NR UL. KRASNOŁĘCKA 3, WARSZAWA Z A D AN I A Z A M K N I Ę T E ) Liczba, której 5% jest równe 6, to : A. 0,3 C. 30. D. 0 5% 6 II sposób: x nieznana liczba
PODSTAWY RYSUNKU TECHNICZNEGO formaty arkuszy
 Format PODSTAWY RYSUNKU TECHNICZNEGO formaty arkuszy Wymiary arkusza (mm) A0 841 x 1189 A1 594 x 841 A2 420 x 594 A3 297 x 420 A4 210 x 297 Rysunki wykonujemy na formacie A4, muszą one mieć obramowanie
Format PODSTAWY RYSUNKU TECHNICZNEGO formaty arkuszy Wymiary arkusza (mm) A0 841 x 1189 A1 594 x 841 A2 420 x 594 A3 297 x 420 A4 210 x 297 Rysunki wykonujemy na formacie A4, muszą one mieć obramowanie
WYMAGANIA NA OCENĘ 12. Równania kwadratowe Uczeń demonstruje opanowanie umiejętności ogólnych rozwiązując zadania, w których:
 str. 1 / 1. Równania kwadratowe sprawdza, czy liczba jest pierwiastkiem równania, po uporządkowaniu równania określa jego rodzaj (zupełne, niezupełne), rozwiązuje proste uporządkowane równania zupełne
str. 1 / 1. Równania kwadratowe sprawdza, czy liczba jest pierwiastkiem równania, po uporządkowaniu równania określa jego rodzaj (zupełne, niezupełne), rozwiązuje proste uporządkowane równania zupełne
Wymagania edukacyjne z matematyki na poszczególne śródroczne oceny klasyfikacyjne dla klasy IV w roku 2019/2020.
 Wymagania edukacyjne z matematyki na poszczególne śródroczne oceny klasyfikacyjne dla klasy IV w roku 2019/2020. Ocenę niedostateczną otrzymuje uczeń, który nie spełnia wymagań edukacyjnych niezbędynych
Wymagania edukacyjne z matematyki na poszczególne śródroczne oceny klasyfikacyjne dla klasy IV w roku 2019/2020. Ocenę niedostateczną otrzymuje uczeń, który nie spełnia wymagań edukacyjnych niezbędynych
ZESPÓŁ SZKÓŁ W OBRZYCKU
 Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
1.. FUNKCJE TRYGONOMETRYCZNE Poziom (K) lub (P)
 Wymagania edukacyjne dla klasy IIIc technik informatyk 1.. FUNKCJE TRYGONOMETRYCZNE rok szkolny 2014/2015 zaznacza kąt w układzie współrzędnych, wskazuje jego ramię początkowe i końcowe wyznacza wartości
Wymagania edukacyjne dla klasy IIIc technik informatyk 1.. FUNKCJE TRYGONOMETRYCZNE rok szkolny 2014/2015 zaznacza kąt w układzie współrzędnych, wskazuje jego ramię początkowe i końcowe wyznacza wartości
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI
 WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATURĄ MAJ 2015 1. Sprawdź, czy arkusz egzaminacyjny zawiera 22 strony ( zadania 1 19). Ewentualny brak zgłoś przewodniczącemu
WPISUJE ZDAJĄCY KOD PESEL PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY PRZED MATURĄ MAJ 2015 1. Sprawdź, czy arkusz egzaminacyjny zawiera 22 strony ( zadania 1 19). Ewentualny brak zgłoś przewodniczącemu
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2018/2019 klasa 1 TŻiUG Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego. Umiejętność
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, , tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Rozwiązanie:
 Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum
 Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
FUNKCJE. Kurs ZDAJ MATURĘ Z MATEMATYKI MODUŁ 5 Teoria funkcje cz.1. Definicja funkcji i wiadomości podstawowe
 1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
1 FUNKCJE Definicja funkcji i wiadomości podstawowe Jeżeli mamy dwa zbiory: zbiór X i zbiór Y, i jeżeli każdemu elementowi ze zbioru X przyporządkujemy dokładnie jeden element ze zbioru Y, to takie przyporządkowanie
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ
 KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
; B = Wykonaj poniższe obliczenia: Mnożenia, transpozycje etc wykonuję programem i przepisuję wyniki. Mam nadzieję, że umiesz mnożyć macierze...
 Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks.
 1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
1 Projekt połowicznej, prostej endoprotezy stawu biodrowego w programie SOLIDWorks. Rysunek. Widok projektowanej endoprotezy według normy z wymiarami charakterystycznymi. 2 3 Rysunek. Ilustracje pomocnicze
LUBELSKA PRÓBA PRZED MATURĄ POZIOM PODSTAWOWY Klasa 1 Klasa 1
 Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
Klasa 1 POZIOM PODSTAWOWY Czas pracy 170 minut Instrukcja dla piszącego 1. Sprawdź, czy arkusz zawiera 18 stron. 2. Rozwiązania zadań i odpowiedzi zamieść w miejscu na to przeznaczonym. 3. W zadaniach
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE II GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 2015/16)
 Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania na egzamin poprawkowy z matematyki dla klasy I A LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania edukacyjne, kontrola i ocena. w nauczaniu matematyki w zakresie. podstawowym dla uczniów technikum. część II
 Wymagania edukacyjne, kontrola i ocena w nauczaniu matematyki w zakresie podstawowym dla uczniów technikum część II Figury na płaszczyźnie kartezjańskiej L.p. Temat lekcji Uczeń demonstruje opanowanie
Wymagania edukacyjne, kontrola i ocena w nauczaniu matematyki w zakresie podstawowym dla uczniów technikum część II Figury na płaszczyźnie kartezjańskiej L.p. Temat lekcji Uczeń demonstruje opanowanie
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
1/4(koła; okrągu) A A' P'(x)
 skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
skrypt Romany (R) 18h gk dla wszystkich ludzi świata Romana - imię mojej małżonki Nr 19h 17h Pierwsze kroki stawiane w geometrii kulowej (sferycznej) w praktyce. Motto: Patrzymy na to samo, widzimy coś
1. LICZBY (1) 2. LICZBY (2) DZIAŁ Z PODRĘCZNIKA L.P. NaCoBeZu kryteria sukcesu w języku ucznia
 L.P. DZIAŁ Z PODRĘCZNIKA NaCoBeZu kryteria sukcesu w języku ucznia 1. LICZBY (1) 2. LICZBY (2) 1. Znam pojęcie liczby naturalne, całkowite, wymierne, dodatnie, ujemne, niedodatnie, odwrotne, przeciwne.
L.P. DZIAŁ Z PODRĘCZNIKA NaCoBeZu kryteria sukcesu w języku ucznia 1. LICZBY (1) 2. LICZBY (2) 1. Znam pojęcie liczby naturalne, całkowite, wymierne, dodatnie, ujemne, niedodatnie, odwrotne, przeciwne.
Geometria analityczna - przykłady
 Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Geometria wykreślna. 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław. Politechnika Gdańska, Wydział Architektury
 Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Geometria wykreślna 5. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Architektura, semestr I 1 5. Obroty i
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7
 Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
Dydaktyka matematyki (III etap edukacyjny) IV rok matematyki Semestr letni 2017/2018 Ćwiczenia nr 7 Lang: Pole powierzchni kuli Nierówność dla objętości skorupki: (pow. małej kuli) h objętość skorupki
Matematyka z plusem Klasa IV
 Matematyka z plusem Klasa IV KLASA IV SZCZEGÓŁOWE CELE EDUKACYJNE KSZTAŁCENIE Rozwijanie sprawności rachunkowej Wykonywanie jednodziałaniowych obliczeń pamięciowych na liczbach naturalnych. Stosowanie
Matematyka z plusem Klasa IV KLASA IV SZCZEGÓŁOWE CELE EDUKACYJNE KSZTAŁCENIE Rozwijanie sprawności rachunkowej Wykonywanie jednodziałaniowych obliczeń pamięciowych na liczbach naturalnych. Stosowanie
G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm
![G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm G T. Przyrząd graficzny o średnicy [KS] 48h w (gks). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. ϕ 7,00 cm ϕ 5,00 cm ϕ 3,00 cm](/thumbs/71/64805542.jpg) Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Przyrząd graficzny o średnicy [KS] 48h w (). Dokładniejsze graficzne wyznaczanie kątów. Perspektywa. Rys.1 Nie określona płaszczyzna rzutu Kuli [K]. 354,375 358,125 1,875 5,625 356,25 48h ; 0h 3,75 Format
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2017/2018 klasa pierwsza Branżowa Szkoła
 Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2017/2018 klasa pierwsza Branżowa Szkoła Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego.
Wymagania na egzamin poprawkowy z matematyki w roku szkolnym 2017/2018 klasa pierwsza Branżowa Szkoła Podstawowa wiedza zawiera się w pisemnych sprawdzianach które odbyły się w ciągu całego roku szkolnego.
Odcinki, proste, kąty, okręgi i skala
 Odcinki, proste, kąty, okręgi i skala str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Na którym rysunku przedstawiono odcinek? 2. Połącz figurę z jej nazwą. odcinek łamana prosta półprosta
Odcinki, proste, kąty, okręgi i skala str. 1/5...... imię i nazwisko lp. w dzienniku...... klasa data 1. Na którym rysunku przedstawiono odcinek? 2. Połącz figurę z jej nazwą. odcinek łamana prosta półprosta
PRÓBNY EGZAMIN MATURALNY Z MATEMATYKI poziom rozszerzony
 Próbny egzamin maturalny z matematyki. Poziom rozszerzony 1 PRÓNY EGZMIN MTURLNY Z MTEMTYKI poziom rozszerzony ZNI ZMKNIĘTE W każdym z zadań 1.. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0
Próbny egzamin maturalny z matematyki. Poziom rozszerzony 1 PRÓNY EGZMIN MTURLNY Z MTEMTYKI poziom rozszerzony ZNI ZMKNIĘTE W każdym z zadań 1.. wybierz i zaznacz jedną poprawną odpowiedź. Zadanie 1. (0
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 2015/16) Wykaz zakładanych osiągnięć ucznia klasy I liceum
 Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
Wymagania na egzamin poprawkowy z matematyki dla klasy I C LO (Rok szkolny 05/6) Wykaz zakładanych osiągnięć ucznia klasy I liceum (osiągnięcia ucznia w zakresie podstawowym) I. Liczby rzeczywiste. Język
PYTANIA TEORETYCZNE Z MATEMATYKI
 Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
Zbiory liczbowe: 1. Wymień znane Ci zbiory liczbowe. 2. Co to są liczby rzeczywiste? 3. Co to są liczby naturalne? 4. Co to są liczby całkowite? 5. Co to są liczby wymierne? 6. Co to są liczby niewymierne?
gk T Zadania nr 2. opracował: inż. Kazimierz Barski dla wszystkich ludzi świata TECHNIKA Koszalin dnia r
 ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
ZNI O ROZWIĄZ. Z WOM UKŁMI PLNT, W KTÓRYH 7 ZY 8 PLNT KRĄŻY WOKÓŁ WÓH WIZ W WÓH PŁSZZYZNH. str.1 PYTNI Z INORMJMI: 1). dzie należy umieścić dwie gwiazdy, by odróżnić oba układy planetarne? 2). Pokazane
SCENARIUSZ LEKCJI MATEMATYKI W LICEUM OGÓLNOKSZTAŁCĄCYM. Powtórzenie i utrwalenie wiadomości dotyczących geometrii figur płaskich.
 Katarzyna Gawinkowska Hanna Małecka VI L.O im J. Korczaka w ZSO nr 2 w Sosnowcu SCENARIUSZ LEKCJI MATEMATYKI W LICEUM OGÓLNOKSZTAŁCĄCYM Temat: Powtórzenie i utrwalenie wiadomości dotyczących geometrii
Katarzyna Gawinkowska Hanna Małecka VI L.O im J. Korczaka w ZSO nr 2 w Sosnowcu SCENARIUSZ LEKCJI MATEMATYKI W LICEUM OGÓLNOKSZTAŁCĄCYM Temat: Powtórzenie i utrwalenie wiadomości dotyczących geometrii
WYMAGANIA EDUKACYJNE
 GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
GIMNAZJUM NR 2 W RYCZOWIE WYMAGANIA EDUKACYJNE niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z MATEMATYKI w klasie II gimnazjum str. 1 Wymagania edukacyjne niezbędne
SZa 98 strona 1 Rysunek techniczny
 Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
Wstęp Wymiarowanie Rodzaje linii rysunkowych i ich przeznaczenie 1. linia ciągła cienka linie pomocnicze, kreskowanie przekrojów, linie wymiarowe, 2. linia ciągła gruba krawędzie widoczne 3. linia kreskowa
CIĄGI wiadomości podstawowe
 1 CIĄGI wiadomości podstawowe Jak głosi definicja ciąg liczbowy to funkcja, której dziedziną są liczby naturalne dodatnie (w zadaniach oznacza się to najczęściej n 1) a wartościami tej funkcji są wszystkie
1 CIĄGI wiadomości podstawowe Jak głosi definicja ciąg liczbowy to funkcja, której dziedziną są liczby naturalne dodatnie (w zadaniach oznacza się to najczęściej n 1) a wartościami tej funkcji są wszystkie
Wymagania na poszczególne oceny w klasie II gimnazjum do programu nauczania MATEMATYKA NA CZASIE
 Wymagania na poszczególne oceny w klasie II gimnazjum do programu nauczania MATEMATYKA NA CZASIE Wymagania konieczne K dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je
Wymagania na poszczególne oceny w klasie II gimnazjum do programu nauczania MATEMATYKA NA CZASIE Wymagania konieczne K dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je
ROK SZKOLNY 2017/2018 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY:
 ROK SZKOLNY 2017/2018 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY: KLASA II GIMNAZJUM Wymagania konieczne K dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je zatem opanować
ROK SZKOLNY 2017/2018 WYMAGANIA EDUKACYJNE NA POSZCZEGÓLNE OCENY: KLASA II GIMNAZJUM Wymagania konieczne K dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je zatem opanować
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 11 Teoria planimetria
 1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
1 Pomimo, że ten dział, to typowa geometria wydawałoby się trudny dział to paradoksalnie troszkę tu odpoczniemy, jeśli chodzi o teorię. Dlaczego? Otóż jak zapewne doskonale wiesz, na maturze otrzymasz
Tik Z wiadomości wstępne
 Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
Tik Z wiadomości wstępne Zofia Walczak 17 lutego 2014 1 Co należy wiedzieć na początku Aby rozpocząć pracę z TikZ -em należy w preambule dokumentu wczytać pakiet używając polecenia \usepackage{tikz}. Tik
Kształcenie w zakresie podstawowym. Klasa 3
 Kształcenie w zakresie podstawowym. Klasa 3 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
Kształcenie w zakresie podstawowym. Klasa 3 Poniżej podajemy umiejętności, jakie powinien zdobyć uczeń z każdego działu, aby uzyskać poszczególne stopnie. Na ocenę dopuszczającą uczeń powinien opanować
MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE
 MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE - pojęcie liczby naturalnej, całkowitej, wymiernej, niewymiernej, - sposób i potrzebę zaokrąglania liczb, - pojęcie wartości bezwzględnej,
MATEMATYKA KLASY III gimnazjum LICZBY I WYRAŻENIA ALGEBRAICZNE - pojęcie liczby naturalnej, całkowitej, wymiernej, niewymiernej, - sposób i potrzebę zaokrąglania liczb, - pojęcie wartości bezwzględnej,
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Planimetria VII. Wymagania egzaminacyjne:
 Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
Wymagania egzaminacyjne: a) korzysta ze związków między kątem środkowym, kątem wpisanym i kątem między styczną a cięciwą okręgu, b) wykorzystuje własności figur podobnych w zadaniach, w tym umieszczonych
11. Znajdż równanie prostej prostopadłej do prostej k i przechodzącej przez punkt A = (2;2).
 1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
1. Narysuj poniższe figury: a), b), c) 2. Punkty A = (0;1) oraz B = (-1;0) należą do okręgu którego środek należy do prostej o równaniu x-2 = 0. Podaj równanie okręgu. 3. Znaleźć równanie okręgu przechodzącego
ZBIÓR ZADAŃ Z MATEMATYKI DLA KLASY II GIMNAZJUM W ZAKRESIE WYMAGAŃ KONIECZNYCH I PODSTAWOWYCH
 ZBIÓR ZADAŃ Z MATEMATYKI DLA KLASY II GIMNAZJUM W ZAKRESIE WYMAGAŃ KONIECZNYCH I PODSTAWOWYCH Opracowała: nauczyciel matematyki mgr Małgorzata Drejka Legionowo 007 SPIS TREŚCI ALGEBRA potęgi i pierwiastki
ZBIÓR ZADAŃ Z MATEMATYKI DLA KLASY II GIMNAZJUM W ZAKRESIE WYMAGAŃ KONIECZNYCH I PODSTAWOWYCH Opracowała: nauczyciel matematyki mgr Małgorzata Drejka Legionowo 007 SPIS TREŚCI ALGEBRA potęgi i pierwiastki
XII Olimpiada Matematyczna Juniorów Zawody stopnia pierwszego część korespondencyjna (1 września 2016 r. 17 października 2016 r.)
 XII Olimpiada Matematyczna Juniorów Zawody stopnia pierwszego część korespondencyjna ( września 06 r. 7 października 06 r.) Szkice rozwiązań zadań konkursowych. Liczby wymierne a, b, c spełniają równanie
XII Olimpiada Matematyczna Juniorów Zawody stopnia pierwszego część korespondencyjna ( września 06 r. 7 października 06 r.) Szkice rozwiązań zadań konkursowych. Liczby wymierne a, b, c spełniają równanie
Wymagania edukacyjne z matematyki
 Wymagania edukacyjne z matematyki Poziom podstawowy Klasa IIIb r.szk. 2014/2015 PLANIMETRIA(1) rozróżnia trójkąty: ostrokątne, prostokątne, rozwartokątne stosuje twierdzenie o sumie miar kątów w trójkącie
Wymagania edukacyjne z matematyki Poziom podstawowy Klasa IIIb r.szk. 2014/2015 PLANIMETRIA(1) rozróżnia trójkąty: ostrokątne, prostokątne, rozwartokątne stosuje twierdzenie o sumie miar kątów w trójkącie
WYMIAROWANIE. Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych.
 WYMIAROWANIE Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych. Zasady wymiarowania podlegają oczywiście normalizacji. W Polsce obowiązującą
WYMIAROWANIE Wymiarowanie jest to podawanie wymiarów przedmiotów na rysunkach technicznych za pomocą linii, liczb i znaków wymiarowych. Zasady wymiarowania podlegają oczywiście normalizacji. W Polsce obowiązującą
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy w roku szkolnym 2018/2019 w CKZiU nr 3 Ekonomik w Zielonej Górze KLASA III fl POZIOM PODSTAWOWY I. Funkcja kwadratowa narysować wykres funkcji
Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego)
 Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego) Ocena DOPUSZCZAJĄCY DOSTATECZNY DOBRY BARDZO DOBRY CELUJĄCY Uczeń: Uczeń:
Kryteria oceniania osiągnięć uczniów z matematyki w kl. III gimnazjum. (Program Matematyka z plusem dla III etapu edukacyjnego) Ocena DOPUSZCZAJĄCY DOSTATECZNY DOBRY BARDZO DOBRY CELUJĄCY Uczeń: Uczeń:
PLAN WYNIKOWY Z MATEMATYKI DLA II KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem. PODSTAWOWE Uczeń zna: POTĘGI I PIERWIASTKI
 Ewa Koralewska LP..... 5... OGÓLNA PODSTA- WA PROGRA- MOWA PLAN WYNIKOWY Z MATEMATYKI DLA II KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem TEMATYKA LEKCJI LICZBA GODZIN Lekcja organizacyjna. Potęga
Ewa Koralewska LP..... 5... OGÓLNA PODSTA- WA PROGRA- MOWA PLAN WYNIKOWY Z MATEMATYKI DLA II KL. GIMNAZJUM do podręcznika GWO Matematyka z plusem TEMATYKA LEKCJI LICZBA GODZIN Lekcja organizacyjna. Potęga
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM
 WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
WYMAGANIA EDUKACYJNE NIEZBĘDNE DO UZYSKANIA ŚRÓDROCZNYCH I ROCZNYCH OCEN KLASYFIKACYJNYCH Z MATEMATYKI W KLASIE III GIMNAZJUM OCENA ŚRÓDROCZNA: NIEDOSTATECZNY ocenę niedostateczny otrzymuje uczeń, który
I. Funkcja kwadratowa
 Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
Pojęcia, wymagania i przykładowe zadania na egzamin poprawkowy dla klas III w roku szkolnym 2017/2018 w Zespole Szkół Ekonomicznych w Zielonej Górze Dla każdej klasy 3 obowiązuje taka ilość poniższego
KONKURS ZOSTAŃ PITAGORASEM MUM. Podstawowe własności figur geometrycznych na płaszczyźnie
 KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
KONKURS ZOSTAŃ PITAGORASEM MUM ETAP I TEST II Podstawowe własności figur geometrycznych na płaszczyźnie 1. A. Stosunek pola koła wpisanego w kwadrat o boku długości 6 do pola koła opisanego na tym kwadracie
Wymagania edukacyjne z matematyki w XVIII Liceum Ogólnokształcącym w Krakowie, zakres podstawowy. Klasa druga.
 Wymagania edukacyjne z matematyki w XVIII Liceum Ogólnokształcącym w Krakowie, zakres podstawowy. Klasa druga. Funkcja liniowa. Uczeń otrzymuje ocenę dopuszczającą, jeśli: - rozpoznaje funkcję liniową
Wymagania edukacyjne z matematyki w XVIII Liceum Ogólnokształcącym w Krakowie, zakres podstawowy. Klasa druga. Funkcja liniowa. Uczeń otrzymuje ocenę dopuszczającą, jeśli: - rozpoznaje funkcję liniową
SZCZEGÓŁOWE WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI KLASA II 2016/2017
 SZCZEGÓŁOWE WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI KLASA II 2016/2017 Ocenę dopuszczającą otrzymuje uczeń, który: (Symetrie) zna pojęcie punktów symetrycznych względem prostej, umie rozpoznawać figury
SZCZEGÓŁOWE WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI KLASA II 2016/2017 Ocenę dopuszczającą otrzymuje uczeń, który: (Symetrie) zna pojęcie punktów symetrycznych względem prostej, umie rozpoznawać figury
Powtórzenie wiadomości o figurach na płaszczyźnie
 Literka.pl Powtórzenie wiadomości o figurach na płaszczyźnie Data dodania: 2009-06-13 16:49:26 Autor: Sylwia Tillack Konspekt opracowany na podstawie podręcznika i ćwiczeń Matematyka z Plusem wydawnictwa
Literka.pl Powtórzenie wiadomości o figurach na płaszczyźnie Data dodania: 2009-06-13 16:49:26 Autor: Sylwia Tillack Konspekt opracowany na podstawie podręcznika i ćwiczeń Matematyka z Plusem wydawnictwa
Wymagania z matematyki na poszczególne stopnie szkolne w klasie trzeciej gimnazjum
 Wymagania z matematyki na poszczególne stopnie szkolne w klasie trzeciej gimnazjum I LICZBY I WYRAŻENIA ALGEBRAICZNE podawanie przykładów liczb naturalnych, całkowitych, wymiernych i niewymiernych; porównywanie
Wymagania z matematyki na poszczególne stopnie szkolne w klasie trzeciej gimnazjum I LICZBY I WYRAŻENIA ALGEBRAICZNE podawanie przykładów liczb naturalnych, całkowitych, wymiernych i niewymiernych; porównywanie
Układ scalony UL 1111
 1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
1 Układ scalony UL 1111 Punkty lutownicze prostokątne najczęściej wykorzystujemy do projektowania punktów lutowniczych na płytce drukowanej służące najczęściej do wlutowywania podstawek lub układów scalonych
Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny)
 edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
edukacyjne niezbędne do uzyskania poszczególnych śródrocznych ocen klasyfikacyjnych z matematyki klasa 2 (oddział gimnazjalny) Stopień Rozdział 1. Potęgi i pierwiastki zapisuje w postaci potęgi iloczyn
EGZAMIN W KLASIE TRZECIEJ GIMNAZJUM W ROKU SZKOLNYM 2014/2015
 EGZAMIN W KLASIE TRZEIEJ GIMNAZJUM W ROKU SZKOLNYM 2014/2015 ZĘŚĆ 2. MATEMATYKA ZASADY OENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ GM-M7 KWIEIEŃ 2015 Zadanie 1. (0 1) I. Wykorzystanie i tworzenie informacji. Umiejętność
EGZAMIN W KLASIE TRZEIEJ GIMNAZJUM W ROKU SZKOLNYM 2014/2015 ZĘŚĆ 2. MATEMATYKA ZASADY OENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ GM-M7 KWIEIEŃ 2015 Zadanie 1. (0 1) I. Wykorzystanie i tworzenie informacji. Umiejętność
