Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Wyznaczanie stałej dysocjacji kwasu mlekowego metodą potencjometryczną
|
|
|
- Antonina Monika Owczarek
- 8 lat temu
- Przeglądów:
Transkrypt
1 Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Wyzncznie stłej dysocjcji kwsu mlekowego metodą potencjometryczną opiekun ćwiczeni: dr K. Kublczyk ćwiczenie nr 12 Zkres zgdnień obowiązujących do ćwiczeni 1. Definicj kwsów i zsd. 2. Równowgi kwsowo-zsdowe. 3. Rol rozpuszczlnik w procesie dysocjcji. 4. Pomir ph roztworu. 5. Budow i zsd dziłni elektrod odwrclnych względem jonów wodorowych orz elektrod odniesieni. Litertur 1. Prc zbiorow pod red. Woźnickiej J. i Piekrskiego H. Ćwiczeni lbortoryjne z chemii fizycznej, Wydwnictwo UŁ, Łódź Libuś W., Libuś Z., Elektrochemi, PWN, Wrszw Prc zbiorow pod red. Bielńskiego A., Chemi fizyczn, PWN, Wrszw Sobczyk L., Kisz A., Gtner K., Koll A., Eksperymentln chemi fizyczn, PWN, Wrszw Sobczyk L., Kisz A., Chemi fizyczn dl przyrodników, PWN, Wrszw Kisz A., Elektrochemi I, WNT, Wrszw Atkins P. W., Chemi fizyczn, Wydwnictwo Nukowe PWN, Wrszw Minczewski J., Mrczenko Z., Chemi nlityczn, t. 3, PWN, Wrszw Oprcownie ćwiczeni: dr A. Piekrsk
2 Celem ćwiczeni jest wyznczenie stłej dysocjcji kwsu mlekowego metodą potencjometryczną Ukłd pomirowy Do pomiru ph bdnego roztworu stosowny jest pehmetr typu N 5170E, zoptrzony w elektrodę kombinowną typu OSH orz czujnik tempertury. Odczynniki chemiczne i sprzęt lbortoryjny: kws mlekowy (0,01 mol dm -3 ), NOH (0,05 mol dm -3 ), bufor (N 2 HPO 4 C 6 H 8 O 7 H 2 O) o ph = 3,00±0,05, biuret utomtyczn, 2 zlewki (100 cm 3 ) i (150 cm 3 ), mieszdło mgnetyczne, pipet (25 cm 3 ), gruszk gumow, tryskwk z wodą destylowną. Wykonnie ćwiczeni i przedstwienie wyników pomirów 1. Włączyć pehmetr do sieci. 2. Zlewkę o pojemności 100 cm 3 npełnić roztworem buforowym o wrtości ph = Elektrodę pomirową wyjąć ze zlewki z wodą destylowną, osuszyć z pomocą bibuły, nstępnie znurzyć w zlewce z buforem. 4. Uruchomić pehmetr wyłącznikiem znjdującym się n prwej bocznej ścince przyrządu. Ustwić przełącznik zkresu pomirowego n pomir ph Pokrętłem klibrcj ustwić n skli przyrządu wrtość ph odpowidjącą wrtości ph roztworu buforowego, czyli ph = Do zlewki o pojemności 150 cm 3 odmierzyć dokłdnie z pomocą pipety 75 cm 3 roztworu kwsu mlekowego o stężeniu 0,01 mol dm Przenieść elektrodę pomirową do zlewki z roztworem kwsu mlekowego. Mireczkownie wstępne 8. Wykonć mireczkownie wstępne bdnego roztworu. W tym celu roztwór kwsu mlekowego mireczkowć roztworem NOH o stężeniu c = 0,05 mol dm -3, dodjąc kżdorzowo po 1,0 cm 3 zsdy. Po dokłdnym wymieszniu roztworu odczytć wrtość jego ph n skli pehmetru. Mireczkownie zkończyć, gdy ph roztworu osiągnie wrtość 11,5. N podstwie uzysknych dnych lub wykonnego odręcznie wykresu, ocenić zkres ph w pobliżu punktu równowżnikowego. 2
3 Mireczkownie dokłdne 9. Mireczkownie kwsu wykonć ponownie w tki sposób, by uzyskć duże zgęszczenie pomirów n łukch krzywej mireczkowni orz w pobliżu punktu równowżnikowego. W tym celu roztwór NOH nleży początkowo dodwć po 0,5cm 3, w pobliżu punktu końcowego mireczkowni po 0,1cm Po zkończeniu ćwiczeni przemywć elektrodę wodą destylowną ż do osiągnięci wrtości ph = 7, nstępnie umieścić ją w zlewce z wodą destylowną. Tbel wyników V NOH [cm 3 ] 0 0,5 1 1,5 ph ph V [cm 3 ] ph/ V [cm -3 ] Oprcownie i dyskusj wyników pomirów Metod grficzn uzyskni stłej dysocjcji kwsu mlekowego ( p K ) grf 1. Sporządzić wykres zleżności ph = f(v NOH ) krzyw cłkow. 2. Wyznczyć punkt końcowy mireczkowni metodą pierwszej pochodnej, tzn. wykreślić funkcję ph/ V = f(v NOH ) (krzyw różniczkow). Wykres sporządzić w zkresie 9 16 cm 3 dodwnej zsdy. Otrzymne wrtości pochodnych ph/ V odkłd się w funkcji objętości w środku odcink osi V odpowidjącego dodnej porcji odczynnik. 3. Odczytć dokłdną wrtość objętości zsdy NOH, któr odpowid mksimum n krzywej różniczkowej. Mksimum krzywej ph/ V = f(v) rzutowne n oś odciętych wyzncz objętość odczynnik (NOH) odpowidjącą punktowi końcowemu mireczkowni. Obliczyć rzeczywiste stężenie kwsu mlekowego wziętego do mireczkowni (c 0 HA ). 4. Odczytć z wykresu ph = f(v NOH ) wrtość ph roztworu kwsu, gdy zostł on w połowie zmireczkowny ( c HA c ). W tych wrunkch równnie Henderson Hsselblch, w którym A p K ozncz stłą dysocjcji słbego kwsu, cha stężenie kwsu w roztworze po dodniu określonej ilości zsdy, c A stężenie sprzężonej z kwsem zsdy: 3
4 cha p K = ph+ lg (1) c A przyjmuje postć: p K = ph tym smym odczytn przez ns wrtość ph jest równ poszukiwnej wrtości ( p K ) grf. Oblicznie stłej dysocjcji kwsu mlekowego n podstwie krzywej mireczkowni 1. Korzystjąc ze wzoru Henderson Hsselblch (1) obliczyć p K kwsu mlekowego dl poszczególnych pomirów. Do obliczeń nleży brć pod uwgę wrtości ph z początkowego zkresu mireczkowni (obszr prostoliniowy). Wyznczyć wrtość średnią p K. 2. Obliczyć średni błąd kwdrtowy średniej wrtości p K wg wzoru: S p K = n ν i= 1 2 i n( n 1) gdzie: ν = p K i p K, n liczb pomirów. 3. Porównć uzyskne dwiem metodmi wrtości p K kwsu mlekowego ( p K ) grf i ( p K ) num z wrtością literturową ( p K ) lit. Zinterpretowć otrzymne wyniki. 4. Do sprwozdni dołączyć wykresy wykonne n ppierze milimetrowym. Tbel wyników obliczeń Objętość dodnego NOH [cm 3 ] ph Stężenie kwsu c HA [mol dm -3 ] Stężenie zsdy c A - [mol dm -3 ] p K p K ν 2 i ν i S p K 0,5 1 1,5. Zestwienie wrtości stłych kwsowych kwsu mlekowego ( p K ) grf p K ( p K ) lit 4
5 Pomir ph Pomiru wrtości ph (zgodnie z definicją ph = lg + ) dokonuje się poprzez wyznczenie ktywności jonów wodorowych znjdujących się w roztworze. Aktywność H 3 O + możn uzyskć n podstwie pomiru siły elektromotorycznej (SEM) ogniw zbudownego z elektrody odwrclnej względem jonów wodorowych orz elektrody odniesieni. Do elektrod odwrclnych względem jonów wodorowych nleżą nstępujące elektrody: wodorow (H + /H 2,1br,Pt), ntymonow (H + /Sb 2 O 3,Sb) orz chinhydronow (H + /Q,QH 2 /Pt). Potencjł kżdej z nich opisuje tk sm zleżność: E = E 0 + RT F ln H + 3 O Wrtości potencjłów poszczególnych elektrod różnią się jednk między sobą z powodu różnych wrtości potencjłów stndrdowych E 0. Potencjł stndrdowy elektrody wodorowej jest równy zeru, podczs gdy elektrody ntymonowej i chinhydronowej przybierją określone wrtości chrkterystyczne dl kżdej z nich. Jko elektrody odniesieni zwykle używ się elektrody II rodzju odwrclnej względem nionu. Zzwyczj są to elektrody klomelow (Cl - /Hg 2 Cl 2,Hg) lub chlorosrebrow (Cl - /AgCl,Ag), których potencjły w dnych wrunkch ciśnieni i tempertury zleżą wyłącznie od ktywności jonów chlorkowych obecnych w roztworze. W celu uzyskni stłej wrtości potencjłu elektrody odniesieni w dnych wrunkch, niezleżnej od stężeni jonów chlorkowych stosuje się elektrody nsycone, w których stężenie jonów chlorkowych zleży wyłącznie od rozpuszczlności elektrolitu w dnej temperturze. Sił elektromotoryczn ogniw zbudownego z elektrody odwrclnej względem jonów wodorowych i elektrody odniesieni o stłym i znnym potencjle pozwl obliczyć ph roztworu. N przykłd, znjąc SEM ogniw zbudownego z elektrody wodorowej i nsyconej elektrody klomelowej możn obliczyć ph roztworu z równni: 0,2444 ph = E 0,0591 gdzie: 0,2444V wrtość potencjłu nsyconej elektrody klomelowej, 0,0591 wrtość ilorzu 2,303RT/F w temperturze 298K. H 5
6 Kżd z wyżej przedstwionych elektrod odwrclnych względem jonów wodorowych m pewne ogrniczeni. Elektrody wodorowej nie możn używć w roztworch zwierjących substncje dezktywujące powierzchnię pltyny, zś elektrody chinhydronowej w roztworch o ph > 8. W prktyce, zmist wymienionych wyżej elektrod stosuje się elektrodę szklną. Elektrod szkln nie jest elektrodą odwrclną względem jonów wodorowych, chociż doświdczlnie stwierdzono, że zchowuje się tk, jk omówione wyżej elektrody tego typu. Stnowi ją rurk szkln zkończon cienkościenną bnieczką wykonną ze specjlnego szkł o ściśle określonym skłdzie chemicznym. Bnieczk wypełnion jest roztworem o stłej wrtości ph, zwierjącym jony Cl (np. HCl o stężeniu 0,1 mol dm -3 ). W roztworze tym umieszczon jest elektrod chlorosrebrn, któr spełni tutj tylko rolę niepolryzowlnego kontktu elektrycznego. Bnieczk szkln stnowi membrnę, któr oddziel bdny roztwór o nieznnym ph od wewnętrznego roztworu, o stłej wrtości ph. Rekcj elektrody szklnej n zminę ktywności jonów wodorowych jest wynikiem złożonego procesu zchodzącego pomiędzy powierzchnią membrny, roztwormi po obu jej stronch. Potencjł elektrody szklnej zleży od stosunku stężeni jonów wodorowych w roztworze wewnętrznym i zewnętrznym. Jk wcześniej wspomnino, wewnątrz bnieczki utrzymywne jest stłe stężenie jonów wodorowych, ztem potencjł elektrody zleży od ktywności jonów wodorowych znjdujących się w roztworze zewnętrznym, w którym elektrod jest znurzon. Zleżność tę wyzncz się przez klibrcję elektrody w roztworch buforowych o znnej wrtości ph. Przyjmuje się, że potencjł elektrody szklnej jest równy zeru (E = 0), gdy ph roztworu jest równe 7. Często elektrodę szklną łączy się z elektrodą chlorosrebrną jko elektrodą odniesieni w jednej obudowie. Elektrod tk nosi nzwę elektrody kombinownej, chociż fktycznie jest ogniwem pomirowym, przeznczonym do pomirów ph roztworów wodnych. Siłę elektromotoryczną ogniw, którego jedną z elektrod jest elektrod szkln mierzy się przy pomocy mikrowoltomierzy, które ze względu n brdzo duży opór bnieczki szklnej muszą zwierć ukłdy wzmcnijące. Przyrządy tkie nzwne zostły pehmetrmi i dją możliwość odczytu zrówno SEM, jk i ph. Wrtość ph roztworu możn bezpośrednio odczytć ze skli pehmetru po uprzedniej klibrcji elektrody. 6
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Energia aktywacji jodowania acetonu. opracowała dr B. Nowicka, aktualizacja D.
 Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
Wyznaczanie stałych kwasowości p-nitrofenolu i glicyny metodą pehametryczną
 Wyzncznie stłych kwsowości p-nitrofenolu i glicyny metodą pehmetryczną 1 Wyzncznie stłych kwsowości p-nitrofenolu i glicyny metodą pehmetryczną 1. Cel ćwiczeni Celem pomirów jest ilościowe schrkteryzownie
Wyzncznie stłych kwsowości p-nitrofenolu i glicyny metodą pehmetryczną 1 Wyzncznie stłych kwsowości p-nitrofenolu i glicyny metodą pehmetryczną 1. Cel ćwiczeni Celem pomirów jest ilościowe schrkteryzownie
Ćwiczenie Nr 5A: WYZNACZANIE LICZB PRZENOSZENIA Z POMIARÓW SIŁY ELEKTROMOTORYCZNEJ OGNIW STĘŻENIOWYCH
 Ćwiczenie Nr 5A: WYZNACZANIE LICZB PRZENOSZENIA Z POMIARÓW SIŁY ELEKTROMOTORYCZNEJ OGNIW STĘŻENIOWYCH Ogniw stężeniowe zbudowne są z dwóch identycznych elektrod, znurzonych w roztworch tego smego elektrolitu,
Ćwiczenie Nr 5A: WYZNACZANIE LICZB PRZENOSZENIA Z POMIARÓW SIŁY ELEKTROMOTORYCZNEJ OGNIW STĘŻENIOWYCH Ogniw stężeniowe zbudowne są z dwóch identycznych elektrod, znurzonych w roztworch tego smego elektrolitu,
ZASTOSOWANIE POMIARU SEM OGNIW GALWANICZNYCH DO WYZNACZANIA WIELKOŚCI FIZYKOCHEMICZNYCH
 Ćwiczenie nr 6 ZASTOSOWANIE POMIARU SEM OGNIW GALWANICZNYCH DO WYZNACZANIA WIELKOŚCI IZYKOCHEMICZNYCH I. Cel ćwiczeni Celem ćwiczeni jest: wyznczenie iloczynu rozpuszczlności soli trudno rozpuszczlnych
Ćwiczenie nr 6 ZASTOSOWANIE POMIARU SEM OGNIW GALWANICZNYCH DO WYZNACZANIA WIELKOŚCI IZYKOCHEMICZNYCH I. Cel ćwiczeni Celem ćwiczeni jest: wyznczenie iloczynu rozpuszczlności soli trudno rozpuszczlnych
A4.05 Instrukcja wykonania ćwiczenia
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.05 nstrukcja wykonania ćwiczenia Wyznaczanie współczynników aktywności soli trudno rozpuszczalnej metodą pomiaru rozpuszczalności Zakres zagadnień obowiązujących
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.05 nstrukcja wykonania ćwiczenia Wyznaczanie współczynników aktywności soli trudno rozpuszczalnej metodą pomiaru rozpuszczalności Zakres zagadnień obowiązujących
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
2. Tensometria mechaniczna
 . Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
. Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
Obliczenia z wykorzystaniem równowagi w roztworach
 Obliczeni z wykorzystniem równowgi w roztworch Obliczeni w roztworch Jkie są skłdniki roztworu? tóre rekcje dysocjcji przebiegją cłkowicie (1% dysocjcji)? tóre rekcje osiągją stn równowgi? tóre z rekcji
Obliczeni z wykorzystniem równowgi w roztworch Obliczeni w roztworch Jkie są skłdniki roztworu? tóre rekcje dysocjcji przebiegją cłkowicie (1% dysocjcji)? tóre rekcje osiągją stn równowgi? tóre z rekcji
Q = a 3. równ. równ. N 2 (g) + 3H 2 (g) 2 NH 3 (g) θ H
 ĆWICZENIE 4. Wyzncznie stłych dysocjcji kwsów metodą potencjometryczną. Bdnie wpływu podstwników n równowgę dysocjcji kwsów krboksylowych. STATYKA CEMICZNA. Stł równowgi oszukiwnie wyrżeni opisującego
ĆWICZENIE 4. Wyzncznie stłych dysocjcji kwsów metodą potencjometryczną. Bdnie wpływu podstwników n równowgę dysocjcji kwsów krboksylowych. STATYKA CEMICZNA. Stł równowgi oszukiwnie wyrżeni opisującego
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
ĆWICZENIE 2 KONDUKTOMETRIA
 ĆWICZENIE 2 KONDUKTOMETRIA 1. Oznaczanie słabych kwasów w sokach i syropach owocowych metodą miareczkowania konduktometrycznego Celem ćwiczenia jest ilościowe oznaczenie zawartości słabych kwasów w sokach
ĆWICZENIE 2 KONDUKTOMETRIA 1. Oznaczanie słabych kwasów w sokach i syropach owocowych metodą miareczkowania konduktometrycznego Celem ćwiczenia jest ilościowe oznaczenie zawartości słabych kwasów w sokach
WYZNACZANIE STAŁEJ RÓWNOWAGI KWASOWO ZASADOWEJ W ROZTWORACH WODNYCH
 Politehni Śląs WYDZIŁ CHEMICZNY KTEDR FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNCZNIE STŁEJ RÓWNOWGI KWSOWO ZSDOWEJ W ROZTWORCH WODNYCH Opieun: Miejse ćwizeni: Ktrzyn Kruiewiz Ktedr Fizyohemii i Tehnoii
Politehni Śląs WYDZIŁ CHEMICZNY KTEDR FIZYKOCHEMII I TECHNOLOGII POLIMERÓW WYZNCZNIE STŁEJ RÓWNOWGI KWSOWO ZSDOWEJ W ROZTWORCH WODNYCH Opieun: Miejse ćwizeni: Ktrzyn Kruiewiz Ktedr Fizyohemii i Tehnoii
ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GRANULOMETRYCZNEJ SUROWCÓW I PRODUKTÓW
 1 ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GANULOMETYCZNEJ SUOWCÓW I PODUKTÓW 1. Cel zkres ćwczen Celem ćwczen jest opnowne przez studentów metody oceny mterłu sypkego pod względem loścowej zwrtośc frkcj
1 ĆWICZENIE ANALIZA SITOWA I PODSTAWY OCENY GANULOMETYCZNEJ SUOWCÓW I PODUKTÓW 1. Cel zkres ćwczen Celem ćwczen jest opnowne przez studentów metody oceny mterłu sypkego pod względem loścowej zwrtośc frkcj
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Ć W I C Z E N I E N R E-14
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
STYLE. TWORZENIE SPISÓW TREŚCI
 STYLE. TWORZENIE SPISÓW TREŚCI Ćwiczenie 1 Tworzenie nowego stylu n bzie istniejącego 1. Formtujemy jeden kpit tekstu i zznczmy go (stnowi on wzorzec). 2. Wybiermy Nrzędzi główne, rozwijmy okno Style (lub
STYLE. TWORZENIE SPISÓW TREŚCI Ćwiczenie 1 Tworzenie nowego stylu n bzie istniejącego 1. Formtujemy jeden kpit tekstu i zznczmy go (stnowi on wzorzec). 2. Wybiermy Nrzędzi główne, rozwijmy okno Style (lub
Ćwiczenie 8 (studenci biotechnologii) Potencjometria Potencjometryczne wyznaczanie PK miareczkowania słabego kwasu
 Ćwiczenie 8 (studenci biotechnologii) Potencjometria Potencjometryczne wyznaczanie PK miareczkowania słabego kwasu Potencjometria Klasyczne miareczkowanie od miareczkowania potencjometrycznego różni się
Ćwiczenie 8 (studenci biotechnologii) Potencjometria Potencjometryczne wyznaczanie PK miareczkowania słabego kwasu Potencjometria Klasyczne miareczkowanie od miareczkowania potencjometrycznego różni się
Wektor kolumnowy m wymiarowy macierz prostokątna o wymiarze n=1 Wektor wierszowy n wymiarowy macierz prostokątna o wymiarze m=1
 Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Struktura energetyczna ciał stałych-cd. Fizyka II dla Elektroniki, lato
 Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Struktur energetyczn cił stłych-cd Fizyk II dl Elektroniki, lto 011 1 Fizyk II dl Elektroniki, lto 011 Przybliżenie periodycznego potencjłu sieci krystlicznej model Kronig- Penney potencjł rzeczywisty
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Adsorpcja kwasu octowego na węglu aktywnym. opracowała dr hab. Małgorzata Jóźwiak
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Adsorpcja kwasu octowego na węglu aktywnym opracowała dr hab. Małgorzata Jóźwiak ćwiczenie nr Zakres zagadnień obowiązujących do ćwiczenia 1. Charakterystyka
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Adsorpcja kwasu octowego na węglu aktywnym opracowała dr hab. Małgorzata Jóźwiak ćwiczenie nr Zakres zagadnień obowiązujących do ćwiczenia 1. Charakterystyka
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
Miareczkowanie potencjometryczne
 Miareczkowanie potencjometryczne Miareczkowanie potencjometryczne polega na mierzeniu za pomocą pehametru zmian ph zachodzących w badanym roztworze pod wpływem dodawania do niego mol ściśle odmierzonych
Miareczkowanie potencjometryczne Miareczkowanie potencjometryczne polega na mierzeniu za pomocą pehametru zmian ph zachodzących w badanym roztworze pod wpływem dodawania do niego mol ściśle odmierzonych
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Wpływ stężenia kwasu na szybkość hydrolizy estru
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wpływ stężenia kwasu na szybkość hydrolizy estru ćwiczenie nr 25 opracowała dr B. Nowicka, aktualizacja D. Waliszewski Zakres zagadnień obowiązujących do
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wpływ stężenia kwasu na szybkość hydrolizy estru ćwiczenie nr 25 opracowała dr B. Nowicka, aktualizacja D. Waliszewski Zakres zagadnień obowiązujących do
Ćwiczenie 42 Wyznaczanie ogniskowych soczewek
 Ćwiczenie 4 Wyzncznie ogniskowych soczewek Wstęp teoretyczny: Krzyszto Rębils. utorem ćwiczeni w Prcowni izycznej Zkłdu izyki Uniwersytetu Rolniczego w Krkowie jest Józe Zpłotny. ZJWISK ZŁMNI ŚWITŁ Świtło,
Ćwiczenie 4 Wyzncznie ogniskowych soczewek Wstęp teoretyczny: Krzyszto Rębils. utorem ćwiczeni w Prcowni izycznej Zkłdu izyki Uniwersytetu Rolniczego w Krkowie jest Józe Zpłotny. ZJWISK ZŁMNI ŚWITŁ Świtło,
Materiały pomocnicze do ćwiczeń z przedmiotu: Ogrzewnictwo, wentylacja i klimatyzacja II. Klimatyzacja
 Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Izoterma rozpuszczalności w układzie trójskładnikowym
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Izoterma rozpuszczalności w układzie trójskładnikowym ćwiczenie nr 28 Zakres zagadnień obowiązujących do ćwiczenia 1. Stan równowagi układu i rodzaje równowag
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Izoterma rozpuszczalności w układzie trójskładnikowym ćwiczenie nr 28 Zakres zagadnień obowiązujących do ćwiczenia 1. Stan równowagi układu i rodzaje równowag
WYZNACZANIE STAŁEJ DYSOCJACJI SŁABEGO KWASU ORGANICZNEGO
 10 WYZNACZANIE STAŁEJ DYSOCJACJI SŁABEGO KWASU ORGANICZNEGO CEL ĆWICZENIA Poznanie podstawowych zagadnień teorii dysocjacji elektrolitycznej i problemów związanych z właściwościami kwasów i zasad oraz
10 WYZNACZANIE STAŁEJ DYSOCJACJI SŁABEGO KWASU ORGANICZNEGO CEL ĆWICZENIA Poznanie podstawowych zagadnień teorii dysocjacji elektrolitycznej i problemów związanych z właściwościami kwasów i zasad oraz
1 Ćwiczenie Reakcje utleniania - redukcji wstęp teoretyczny. RT nf Procesy utleniania-redukcji
 Ćwiczenie 5. Rekcje utlenini - redukcji wstęp teoretyczny.. Procesy utlenini-redukcji Rekcjmi utlenini-redukcji nzywmy procesy chemiczne, którym towrzyszy zmin stopni utlenieni. Procesem utlenieni nzywmy
Ćwiczenie 5. Rekcje utlenini - redukcji wstęp teoretyczny.. Procesy utlenini-redukcji Rekcjmi utlenini-redukcji nzywmy procesy chemiczne, którym towrzyszy zmin stopni utlenieni. Procesem utlenieni nzywmy
Aparatura sterująca i sygnalizacyjna Czujniki indukcyjne zbliżeniowe LSI
 Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Algebra macierzowa. Akademia Morska w Gdyni Katedra Automatyki Okrętowej Teoria sterowania. Mirosław Tomera 1. ELEMENTARNA TEORIA MACIERZOWA
 kdemi Morsk w Gdyni Ktedr utomtyki Okrętowej Teori sterowni lger mcierzow Mirosłw Tomer. ELEMENTRN TEORI MCIERZOW W nowoczesnej teorii sterowni rdzo często istnieje potrze zstosowni notcji mcierzowej uprszczjącej
kdemi Morsk w Gdyni Ktedr utomtyki Okrętowej Teori sterowni lger mcierzow Mirosłw Tomer. ELEMENTRN TEORI MCIERZOW W nowoczesnej teorii sterowni rdzo często istnieje potrze zstosowni notcji mcierzowej uprszczjącej
ph ROZTWORÓW WODNYCH
 ph ROZTWORÓW WODNYCH ph roztworów monyh kwsów i zsd H O H O A α 00 % MeOH Me OH MeOH α 00 % np.: HCl, r, HI, HNO, HClO i HClO NOH, OH, CsOH i ROH [H O [OH MeOH ph - log poh - log MeOH Mone kwsy dwuprotonowe,
ph ROZTWORÓW WODNYCH ph roztworów monyh kwsów i zsd H O H O A α 00 % MeOH Me OH MeOH α 00 % np.: HCl, r, HI, HNO, HClO i HClO NOH, OH, CsOH i ROH [H O [OH MeOH ph - log poh - log MeOH Mone kwsy dwuprotonowe,
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
2. Funktory TTL cz.2
 2. Funktory TTL z.2 1.2 Funktory z otwrtym kolektorem (O.. open olletor) ysunek poniżej przedstwi odnośny frgment płyty zołowej modelu. Shemt wewnętrzny pojedynzej rmki NAND z otwrtym kolektorem (O..)
2. Funktory TTL z.2 1.2 Funktory z otwrtym kolektorem (O.. open olletor) ysunek poniżej przedstwi odnośny frgment płyty zołowej modelu. Shemt wewnętrzny pojedynzej rmki NAND z otwrtym kolektorem (O..)
Wymagania kl. 2. Uczeń:
 Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
Wymgni kl. 2 Zkres podstwowy Temt lekcji Zkres treści Osiągnięci uczni. SUMY ALGEBRAICZNE. Sumy lgebriczne definicj jednominu pojęcie współczynnik jednominu porządkuje jednominy pojęcie sumy lgebricznej
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
Porównanie precyzji i dokładności dwóch metod oznaczania stężenia HCl
 Porównanie precyzji i dokładności dwóch metod oznaczania stężenia HCl Metoda 1: Oznaczanie stężenia HCl metodą miareczkowania potencjometrycznego (strąceniowe) Wyposażenie: - miernik potencjału 1 szt.
Porównanie precyzji i dokładności dwóch metod oznaczania stężenia HCl Metoda 1: Oznaczanie stężenia HCl metodą miareczkowania potencjometrycznego (strąceniowe) Wyposażenie: - miernik potencjału 1 szt.
Wykład 2. Pojęcie całki niewłaściwej do rachunku prawdopodobieństwa
 Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Hydroliza i bufory. Hydroliza soli Bufory Krzywe miareczkowania Wskaźniki ph
 Hydroliz i bufory Hydroliz oli Bufory rzywe mirezkowni Wkźniki ph 1 Hydroliz Proe rozkłdu jkiejś ubtnji ntępująy pod wpływem wody Hydroliz oli - rekje nionów lub ktionów z zątezkmi wody ole łbyh kwów i
Hydroliz i bufory Hydroliz oli Bufory rzywe mirezkowni Wkźniki ph 1 Hydroliz Proe rozkłdu jkiejś ubtnji ntępująy pod wpływem wody Hydroliz oli - rekje nionów lub ktionów z zątezkmi wody ole łbyh kwów i
BADANIE ZALEŻNOŚCI PRZENIKALNOŚCI MAGNETYCZNEJ
 ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
INSTRUKCJA. - Jak rozwiązywać zadania wysoko punktowane?
 INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
f(x)dx (1.7) b f(x)dx = F (x) = F (b) F (a) (1.2)
 Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Równania i nierówności kwadratowe z jedną niewiadomą
 50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
RÓWNOWAGI REAKCJI KOMPLEKSOWANIA
 POLITECHNIK POZNŃSK ZKŁD CHEMII FIZYCZNEJ ĆWICZENI PRCOWNI CHEMII FIZYCZNEJ RÓWNOWGI REKCJI KOMPLEKSOWNI WSTĘP Ważną grupę reakcji chemicznych wykorzystywanych w chemii fizycznej i analitycznej stanowią
POLITECHNIK POZNŃSK ZKŁD CHEMII FIZYCZNEJ ĆWICZENI PRCOWNI CHEMII FIZYCZNEJ RÓWNOWGI REKCJI KOMPLEKSOWNI WSTĘP Ważną grupę reakcji chemicznych wykorzystywanych w chemii fizycznej i analitycznej stanowią
MATeMAtyka 3 inf. Przedmiotowy system oceniania wraz z określeniem wymagań edukacyjnych. Zakres podstawowy i rozszerzony. Dorota Ponczek, Karolina Wej
 Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Dorot Ponczek, Krolin Wej MATeMAtyk 3 inf Przedmiotowy system ocenini wrz z określeniem wymgń edukcyjnych Zkres podstwowy i rozszerzony Wyróżnione zostły nstępujące wymgni progrmowe: konieczne (K), podstwowe
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
cz. 2 dr inż. Zbigniew Szklarski
 Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Wykłd 11: Elektrosttyk cz. 2 dr inż. Zbigniew Szklrski szkl@gh.edu.pl http://lyer.uci.gh.edu.pl/z.szklrski/ Pole elektryczne przewodnik N powierzchni metlicznej (przewodzącej) cły łdunek gromdzi się n
Rachunek prawdopodobieństwa i statystyka matematyczna.
 Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Metody Badań Składu Chemicznego
 Metody Badań Składu Chemicznego Wydział Inżynierii Materiałowej i Ceramiki Kierunek: Inżynieria Materiałowa (NIESTACJONARNE) Ćwiczenie 5: Pomiary SEM ogniwa - miareczkowanie potencjometryczne. Pomiary
Metody Badań Składu Chemicznego Wydział Inżynierii Materiałowej i Ceramiki Kierunek: Inżynieria Materiałowa (NIESTACJONARNE) Ćwiczenie 5: Pomiary SEM ogniwa - miareczkowanie potencjometryczne. Pomiary
Komisja Egzaminacyjna dla Aktuariuszy LII Egzamin dla Aktuariuszy z 15 marca 2010 r. Część I Matematyka finansowa
 Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Ćwiczenia laboratoryjne z przedmiotu : Napędy Hydrauliczne i Pneumatyczne
 Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Wymagania na ocenę dopuszczającą z matematyki klasa II Matematyka - Babiański, Chańko-Nowa Era nr prog. DKOS 4015-99/02
 Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Wymgni n ocenę dopuszczjącą z mtemtyki kls II Mtemtyk - Bbiński, Chńko-Now Er nr prog. DKOS 4015-99/02 Temt lekcji Zkres treści Osiągnięci uczni WIELOMIANY 1. Stopień i współczynniki wielominu 2. Dodwnie
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Modelowanie 3 D na podstawie fotografii amatorskich
 Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
ĆWICZENIE 13. ANALIZA INSTRUMENTALNA Miareczkowanie Potencjometryczne
 ĆWICZENIE 13 ANALIZA INSTRUMENTALNA Miareczkowanie Potencjometryczne Oznaczanie kwasu ortofosforowego w Coca-Coli za pomocą miareczkowania potencjometrycznego roztworem wodorotlenku sodu DZIAŁ: Potencjometria
ĆWICZENIE 13 ANALIZA INSTRUMENTALNA Miareczkowanie Potencjometryczne Oznaczanie kwasu ortofosforowego w Coca-Coli za pomocą miareczkowania potencjometrycznego roztworem wodorotlenku sodu DZIAŁ: Potencjometria
Fizyka. Kurs przygotowawczy. na studia inżynierskie. mgr Kamila Haule
 Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Szczegółowe wymagania edukacyjne z matematyki, klasa 2C, poziom podstawowy
 Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Szczegółowe wymgni edukcyjne z mtemtyki, kls 2C, poziom podstwowy Wymgni konieczne () dotyczą zgdnieo elementrnych, stnowiących swego rodzju podstwę, ztem powinny byd opnowne przez kżdego uczni. Wymgni
Macierz. Wyznacznik macierzy. Układ równań liniowych
 Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Temt wykłdu: Mcierz. Wyzncznik mcierzy. Ukłd równń liniowych Kody kolorów: żółty nowe pojęcie pomrńczowy uwg kursyw komentrz * mterił ndobowiązkowy Ann Rjfur, Mtemtyk Zgdnieni. Pojęci. Dziłni n mcierzch.
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Wyznaczanie ciepła właściwego cieczy metodą kalorymetryczną
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wyznaczanie ciepła właściwego cieczy metodą kalorymetryczną opracowanie ćwiczenia: dr J. Woźnicka, dr S. Belica ćwiczenie nr 38 Zakres zagadnień obowiązujących
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego Wyznaczanie ciepła właściwego cieczy metodą kalorymetryczną opracowanie ćwiczenia: dr J. Woźnicka, dr S. Belica ćwiczenie nr 38 Zakres zagadnień obowiązujących
Wspomaganie obliczeń za pomocą programu MathCad
 Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Zadanie 5. Kratownica statycznie wyznaczalna.
 dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II TAK
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
Praca, potencjał i pojemność
 Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
Prc, potencjł i pojemność Mciej J. Mrowiński 1 listopd 2010 Zdnie PPP1 h Wyzncz wrtość potencjłu elektrycznego w punkcie oddlonym o h od cienkiego, jednorodnie nłdownego łdunkiem Q pierścieni o promieniu.
Od lewej: piramida Chefrena, Wielki Sfinks, piramida Cheopsa.
 1. Pirmidiotologi. W obfitej literturze przedmiotu podje się, że pirmid Ceops, lub też z ngielsk Wielk Pirmid (te Gret Pyrmid), zwier w swej konstrukcji pełną i szczegółową istorię rodzju ludzkiego od
1. Pirmidiotologi. W obfitej literturze przedmiotu podje się, że pirmid Ceops, lub też z ngielsk Wielk Pirmid (te Gret Pyrmid), zwier w swej konstrukcji pełną i szczegółową istorię rodzju ludzkiego od
Spis treści. Wstęp. Roztwory elektrolitów
 Spis treści 1 Wstęp 1.1 Roztwory elektrolitów 1.2 Aktywność elektrolitów 1.3 Teorie kwasów i zasad 1.3.1 Teoria Arrheniusa 1.3.2 Teoria Lowry ego-brönsteda 1.3.3 Teoria Lewisa 1.4 Roztwory buforowe 1.5
Spis treści 1 Wstęp 1.1 Roztwory elektrolitów 1.2 Aktywność elektrolitów 1.3 Teorie kwasów i zasad 1.3.1 Teoria Arrheniusa 1.3.2 Teoria Lowry ego-brönsteda 1.3.3 Teoria Lewisa 1.4 Roztwory buforowe 1.5
2. PODSTAWY STATYKI NA PŁASZCZYŹNIE
 M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
M. DSTY STTYKI N ŁSZZYŹNIE. DSTY STTYKI N ŁSZZYŹNIE.. Zsdy dynmiki Newton Siłą nzywmy wektorową wielkość, któr jest mirą mechnicznego oddziływni n ciło ze strony innych cił. dlszej części ędziemy rozptrywć
Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną CZĘŚĆ DOŚWIADCZALNA. Tabela wyników pomiaru
 Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną Cel ćwiczenia Celem ćwiczenia jest wyznaczenie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną. Zakres wymaganych
Wyznaczanie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną Cel ćwiczenia Celem ćwiczenia jest wyznaczenie stałej dysocjacji pk a słabego kwasu metodą konduktometryczną. Zakres wymaganych
Ćwiczenie 6 Wpływ dawki kwasu acetylosalicylowego na jego farmakokinetykę
 Ćwiczenie 6 Wpływ dwki kws cetyloslicylowego n jego frmkokinetykę Celem ćwiczeni jest zbdnie wpływ dwki kws cetyloslicylowego n jego frmkokinetykę. Wprowdzenie: Ćwiczenie poleg n oznczeni ilości slicylnów
Ćwiczenie 6 Wpływ dwki kws cetyloslicylowego n jego frmkokinetykę Celem ćwiczeni jest zbdnie wpływ dwki kws cetyloslicylowego n jego frmkokinetykę. Wprowdzenie: Ćwiczenie poleg n oznczeni ilości slicylnów
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Układ elektrohydrauliczny do badania siłowników teleskopowych i tłokowych
 TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
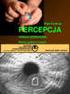 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
A4.04 Instrukcja wykonania ćwiczenia
 Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.04 Instrukcja wykonania ćwiczenia Wyznaczanie cząstkowych molowych objętości wody i alkoholu Zakres zagadnień obowiązujących do ćwiczenia 1. Znajomość
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego A4.04 Instrukcja wykonania ćwiczenia Wyznaczanie cząstkowych molowych objętości wody i alkoholu Zakres zagadnień obowiązujących do ćwiczenia 1. Znajomość
Uszczelnienie przepływowe w maszyn przepływowych oraz sposób diagnozowania uszczelnienia przepływowego zwłaszcza w maszyn przepływowych
 Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
DZIAŁ 2. Figury geometryczne
 1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
1 kl. 6, Scenriusz lekcji Pole powierzchni bryły DZAŁ 2. Figury geometryczne Temt w podręczniku: Pole powierzchni bryły Temt jest przeznczony do relizcji podczs 2 godzin lekcyjnych. Zostł zplnowny jko
Zadania. I. Podzielność liczb całkowitych
 Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Katalog wymagań programowych na poszczególne stopnie szkolne. Matematyka. Poznać, zrozumieć
 Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
Ktlog wymgń progrmowych n poszczególne stopnie szkolne Mtemtyk. Poznć, zrozumieć Ksztłcenie w zkresie podstwowym. Kls 2 Poniżej podjemy umiejętności, jkie powinien zdobyć uczeń z kżdego dziłu, by uzyskć
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU
 POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
POMIAR MODUŁU SPRĘŻYSTOŚCI STALI PRZEZ POMIAR WYDŁUŻENIA DRUTU I. Cel ćwiczeni: zpoznnie z teorią odksztłceń sprężystych cił stłych orz z prwem Hooke.Wyzncznie modułu sprężystości (modułu Young) metodą
Potencjometryczna metoda oznaczania chlorków w wodach i ściekach z zastosowaniem elektrody jonoselektywnej
 Potencjometryczna metoda oznaczania chlorków w wodach i ściekach z zastosowaniem elektrody jonoselektywnej opracowanie: dr Jadwiga Zawada Cel ćwiczenia: poznanie podstaw teoretycznych i praktycznych metody
Potencjometryczna metoda oznaczania chlorków w wodach i ściekach z zastosowaniem elektrody jonoselektywnej opracowanie: dr Jadwiga Zawada Cel ćwiczenia: poznanie podstaw teoretycznych i praktycznych metody
Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych
 CHEMI FIZYCZN Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych W ćwiczeniu przeprowadzana jest reakcja utleniania jonów tiosiarczanowych za pomocą jonów żelaza(iii). Przebieg
CHEMI FIZYCZN Ćwiczenie 8 Wyznaczanie stałej szybkości reakcji utleniania jonów tiosiarczanowych W ćwiczeniu przeprowadzana jest reakcja utleniania jonów tiosiarczanowych za pomocą jonów żelaza(iii). Przebieg
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Technikum Nr 2 im. gen. Mieczysłw Smorwińskiego w Zespole Szkół Ekonomicznych w Kliszu Wymgni edukcyjne niezbędne do uzyskni poszczególnych śródrocznych i rocznych ocen klsyfikcyjnych z obowiązkowych zjęć
Ćwiczenie 19 Wyznaczanie molowego współczynnika absorpcji. Ilościowe oznaczanie p-nitrofenolu. Zależność molowego współczynnika absorpcji od ph.
 Ćwiczenie 19 Wyzncznie molowego współczynnik bsorpcji. Ilościowe ozncznie p-nitrofenolu. Zleżność molowego współczynnik bsorpcji od ph. Część teoretyczn: Spektroskopi obejmuje szereg metod bdni mterii
Ćwiczenie 19 Wyzncznie molowego współczynnik bsorpcji. Ilościowe ozncznie p-nitrofenolu. Zleżność molowego współczynnik bsorpcji od ph. Część teoretyczn: Spektroskopi obejmuje szereg metod bdni mterii
ZADANIA ZAMKNIĘTE. Zadanie 1 (1p). Ile wynosi 0,5% kwoty 120 mln zł? A. 6 mln zł B. 6 tys. zł C. 600 tys. zł D. 60 tys. zł
 TRZECI SEMESTR LICEUM OGÓLNOKSZTAŁCĄCEGO DLA DOROSŁYCH PRACA KONTROLNA Z MATEMATYKI ROZSZERZONEJ O TEMACIE: Liczby rzeczywiste i wyrżeni lgebriczne Niniejsz prc kontroln skłd się z zdń zmkniętych ( zdń)
TRZECI SEMESTR LICEUM OGÓLNOKSZTAŁCĄCEGO DLA DOROSŁYCH PRACA KONTROLNA Z MATEMATYKI ROZSZERZONEJ O TEMACIE: Liczby rzeczywiste i wyrżeni lgebriczne Niniejsz prc kontroln skłd się z zdń zmkniętych ( zdń)
Zaokrąglanie i zapisywanie wyników obliczeń przybliżonych
 Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
Pierwiastek z liczby zespolonej
 Pierwistek z liczby zespolonej Twierdzenie: Istnieje dokłdnie n różnych pierwistków n-tego stopni z kżdej liczby zespolonej różnej od zer, tzn. rozwiązń równni w n z i wszystkie te pierwistki dją się zpisć
Pierwistek z liczby zespolonej Twierdzenie: Istnieje dokłdnie n różnych pierwistków n-tego stopni z kżdej liczby zespolonej różnej od zer, tzn. rozwiązń równni w n z i wszystkie te pierwistki dją się zpisć
5.4.1. Ruch unoszenia, względny i bezwzględny
 5.4.1. Ruch unozeni, zględny i bezzględny Przy ominiu ruchu punktu lub bryły zkłdliśmy, że punkt lub brył poruzły ię zględem ukłdu odnieieni x, y, z użnego z nieruchomy. Możn rozptrzyć tki z przypdek,
5.4.1. Ruch unozeni, zględny i bezzględny Przy ominiu ruchu punktu lub bryły zkłdliśmy, że punkt lub brył poruzły ię zględem ukłdu odnieieni x, y, z użnego z nieruchomy. Możn rozptrzyć tki z przypdek,
Obliczenia w roztworach
 Oblizeni z wykorzystniem równowgi w roztworh Oblizeni w roztworh Jkie są skłdniki roztworu? tóre rekje dysojji przebiegją łkowiie (% dysojji)? tóre rekje osiągją stn równowgi? tóre z rekji równowgowyh
Oblizeni z wykorzystniem równowgi w roztworh Oblizeni w roztworh Jkie są skłdniki roztworu? tóre rekje dysojji przebiegją łkowiie (% dysojji)? tóre rekje osiągją stn równowgi? tóre z rekji równowgowyh
Wyznacznikiem macierzy kwadratowej A stopnia n nazywamy liczbę det A określoną następująco:
 Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
Def.8. Wyzncznikiem mcierzy kwdrtowej stopni n nzywmy liczbę det określoną nstępująco:.det.det dl n n det det n det n, gdzie i j ozncz mcierz, którą otrzymujemy z mcierzy przez skreślenie i- tego wiersz
METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO
 MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
Kodowanie liczb. Kodowanie stałopozycyjne liczb całkowitych. Niech liczba całkowita a ma w systemie dwójkowym postać: Kod prosty
 Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II LO
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II LO 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
Oznaczanie kwasu fosforowego w Coca-Coli
 Oznaczanie kwasu fosforowego w Coca-Coli Instrukcja do ćwiczeń opracowana w Katedrze Chemii Środowiska Uniwersytetu Łódzkiego. Miareczkowanie jest jedną z podstawowych czynności laboratoryjnych. Polega
Oznaczanie kwasu fosforowego w Coca-Coli Instrukcja do ćwiczeń opracowana w Katedrze Chemii Środowiska Uniwersytetu Łódzkiego. Miareczkowanie jest jedną z podstawowych czynności laboratoryjnych. Polega
