Transmisja światła i struktura fotoniczna supersieci optycznych
|
|
|
- Nadzieja Sikorska
- 8 lat temu
- Przeglądów:
Transkrypt
1 Transmisja światła i struktura fotoniczna supersieci optycznych Włodzimierz Salejda Instytut Fizyki Seminarium Instytutu Fizyki, 15 stycznia 2007
2 Skład zespołu 1.Dr inŝ. Agnieszka Klauzer-Kruszyna 2.Dr inŝ. Michał Hugo Tyc 3.Karol Tarnowski, student V r. WPPT
3 Plan seminarium 1. Wprowadzenie Motywacja; typy supersieci, model supersieci optycznej 2. Transmisja światła spolaryzowanego Macierz charakterystyczna (MCh); odwzorowania śladów i antyśladów MCh; transmitancja,wybrane wyniki analityczne i numeryczne 3. Struktura fotoniczna supersieci optycznych Zagadnienie własne Maxwella; problemy otwarte; wybrane wyniki 4. Podsumowanie 5. Dodatek popularno-naukowy
4 Wprowadzenie motywacja Wielowarstwowe układy optyczne, zwane dalej supersieciami optycznymi, to przedmiot trwającego zainteresowania z powodów aplikacyjnych oraz poznawczych. Filtry i rezonatory, zwierciadła Bragga to urządzenia odgrywające istotną rolę m.in. w optyce, optoelektronice, elektronice kwantowej, fotonice, gdzie działanie wielu urządzeń oparte jest o właściwości transmisji/odbicia FEM przez sieci optyczne. Zainteresowania supersieciami optycznymi stymulowało odkrycie: kwazikryształów, metamateriałów wykazujących zjawisko ujemnego załamania FEM, kryształów fotonicznych, rozwój technologii materiałowych.
5 Wprowadzenie cele badań Wyznaczenie i zbadanie właściwości: transmisji światła spolaryzowanego w supersieciach optycznych, struktury fotonicznej supersieci optycznych.
6 Wprowadzenie binarne supersieci optyczne; definicje Binarna supersieć optyczna jest zbudowana z dwóch dielektrycznych warstw A, B o ustalonych parametrach: współczynników załamania n A, n B, grubości d A, d B, µ A, ε A oraz µ B, ε B.
7 Wprowadzenie model SO Supersieć optyczna umieszczona pomiędzy ośrodkami dielektrycznymi
8 Wprowadzenie binarne supersieci optyczne; definicje. Supersieci: periodyczna i prosta Fibonacciego Supersieć periodyczna S 0 = A, S 1 = B, S N = S 0 S 1 S 0 S 1... S 0 S 1 = (S 0 S 1 ) L, gdzie L = 1, 2,... ; symbol oznacza konkatenację. Prosta supersieć Fibonacciego S 0 = B, S 1 = A, S 2 = (S 1 S 0 ), S 3 = (S 2 S 1 ),..., S L+1 = (S L S L-1 ), gdzie L = 1, 2,... nr pokolenia; symbol oznacza konkatenację. Reguła podstawiania: Konstrukcja rekurencyjna:
9 Wprowadzenie binarne supersieci optyczne; definicje Uogólnione supersieci Fibonacciego S 0 = B, S 1 = A, S 2 = (S 1 ) M (S 0 ) N, S 3 = (S 2 ) M (S 1 ) N,..., S L+1 = (S L ) M (S L-1 ) N, gdzie L = 1, 2,... nr pokolenia; symbol oznacza konkatenację, M i N parametry konkatenacji; oznaczenia SF(M, N). W tabeli kolejno: S(M=1, N=1) S(M=2, N=1) S(M=1, N=2) Całkowita liczba warstw w supersieci Całkowita długość supersieci
10 Wprowadzenie binarne supersieci optyczne; definicje Supersieć podwojonego okresu S 0 = B, S 1 = B A, S 2 = S 1 (S 0 ) 2, S 3 = S 2 (S 1 ) 2,..., S L+1 = S L (S L-1 ) 2, gdzie L = 1, 2,... nr pokolenia; symbol oznacza konkatenację;
11 Wprowadzenie binarne supersieci optyczne; definicje Prosta i uogólnione supersieci Thue Morse a gdzie L = 1, 2,... nr pokolenia; prostą sieć przedstawia tabela po lewej stronie. Sadkjsahdkjashds
12 Wprowadzenie binarne supersieci optyczne; definicje Prosta i uogólnione supersieci Thue Morse a (USTM) gdzie L = 1, 2,... nr pokolenia; uogólnioną sieć przedstawia górna część poniŝszej tabeli. N i M to parametry konkatenacji; tabela poniŝej przedstawia przykład USTM z N=2 i M=1.
13 Wprowadzenie binarne supersieci optyczne; definicje Supersieci typu Rudin Shapiro Konstrukcja w oparciu o czteroelementowy alfabet Sieć binarną generują podstawienia
14 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej
15 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej Macierz charakterystyczna Γ Macierz propagacji w j-tej warstwie Macierz transmisji przez granicę warstw
16 Wektory natęŝenia pola elektrycznego i magnetycznego FEM na granicy ośrodków dla polaryzacji s (TE) oraz polaryzacji p (TM) 2. Transmisja światła spolaryzowanego; typy polaryzacji
17 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej, gdzie Współczynniki amplitudowe Fresnela transmisji i odbicia
18 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej Transmitancja i reflektancja supersieci optycznej
19 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej Transmitancja i w formalizmie odwzorowań śladów i antyśladów macierzy charakterystycznej Γ ślad diagonalny Γ antyślad diagonalny Γ
20 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej Transmitancja i w formalizmie odwzorowań śladów i antyśladów macierzy charakterystycznej Γ wielkości pomocnicze symetryczny ślad diagonalny Γ antysymetryczny antyślad diagonalny Γ antysymetryczny antyślad niediagonalny Γ symetryczny antyślad niediagonalny Γ η = Γ + Γ 12 Γ 21
21 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej 1. Transmitancja supersieci optycznej umieszczonej w ośrodku A Macierz charakterystyczna Transmitancja supersieci optycznej
22 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej 1. Transmitancja supersieci optycznej umieszczonej w ośrodku A Transmitancja supersieci optycznej,
23 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej 1. Transmitancja uogólnionej supersieci optycznej Fibonacciego umieszczonej w ośrodku A Transmitancja supersieci optycznej Zmodyfikowane wielomiany Czebyszewa, m nieujemna liczba całkowita Wielomiany Czebyszewa I i II rodzaju
24 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej 2. Transmitancja uogólnionej supersieci optycznej Fibonacciego umieszczonej w dowolnym ośrodku Transmitancja supersieci optycznej,
25 2. Transmisja światła spolaryzowanego Formalizm dynamicznych odwzorowańśladów i antyśladów macierzy charakterystycznej 3. Transmitancja uogólnionej supersieci optycznej Fibonacciego umieszczonej między dwoma róŝnymi ośrodkami Transmitancja supersieci optycznej,
26 , Pełny układ nieliniowych odwzorowań śladów i antyśladów dla uogólnionych supersieci optycznych Fibonacciego; znajomość ich wartości dla 3 początkowych pokoleń ( L=0, 1,2) pozwala wyznaczyć wartości śladów i antyśladów dla L 2 oraz transmitancję supersieci optycznej.
27 2. Transmisja światła spolaryzowanego Transmitancja w formalizmie odwzorowań śladów i antyśladów Pełny układ nieliniowych odwzorowań śladów i antyśladów + 1 = σ L L 1 L-2 L L 1 L 2 = F ( τ,τ,τ,ς,ς ),,ς L+ 1 ς L L 1 L-2 L L 1 L 2 został wyprowadzony analitycznie dla wymienionych wcześniej supersieci optycznych typu: Thue-Morse, Rudin-Shapiro, podwojonego okresu. ( τ,τ ) τ,τ L = F + 1 τ L L 1 L-2 ( τ,τ,τ,σ,σ ) σ L F,σ ς ( τ,τ,τ,η,η ) ηl F,η + 1 = η L L 1 L-2 L L 1 L 2 Wyniki nieopublikowane symetryczny ślad diagonalny antysymetryczny antyślad diagonalny antysymetryczny antyślad niediagonalny symetryczny antyślad niediagonalny η = Γ + Γ 12 Γ 21
28 2. Transmisja światła spolaryzowanego Transmitancja w formalizmie odwzorowań śladów i antyśladów Znajomość analitycznych nieliniowych odwzorowań śladów i antyśladów ( ) τ,τ L = F τ,τ + 1 τ L L 1 L-2 ( ), + 1 = Fσ τ L,τ L 1,τ L-2,σ L,σ L 1 L 2 σ L,σ ς F τ,τ,τ,ς,ς,ς L 1 ς L L 1 L-2 L L 1 ηl Fη τ L,τ L 1,τ L-2,ηL,ηL 1,η ( ) 2 ( ) + = L + 1 = L 2 symetryczny ślad diagonalny antysymetryczny antyślad diagonalny antysymetryczny antyślad niediagonalny symetryczny antyślad niediagonalny pozwoliła zbadać numerycznie właściwości transmitancji rozpatrywanych supersieci optycznych w funkcji parametrów modelu.
29 2. Transmisja światła spolaryzowanego Transmitancja w formalizmie odwzorowań śladów i antyśladów Uogólniono analityczny formalizm nieliniowych odwzorowań śladów i antyśladów na przypadek tunelowania światła Transmitancję wyznaczono dla supersieci optycznych zbudowanych: z materiałów prawoskrętnych (n>0), z metamateriałów [materiałów lewoskrętnych (n<0)] i prawoskrętnych (n>0), z uwzględnieniem zjawiska tunelowania światła. Wyniki nieopublikowane,
30 2. Transmisja światła spolaryzowanego Transmitancja w formalizmie odwzorowań śladów i antyśladów Zaproponowane podejście pozwala na zbadanie właściwości transmitancji supersieci optycznych zaleŝnych od: Typów polaryzacji Długości fali Kątów padania Grubości warstw (z uwzględnieniem tunelowania) Współczynników załamania: materiałów warstw (prawoi lewoskrętnych), ośrodków zewnętrznych Typów supersieci z uwzględnieniem: rodzaju supersieci (L numer pokolenia, parametry konkatenacji N i M), materiałów warstw Dyspersji,
31 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Przedstawiamy kilka wyników ilustrujących zaleŝności transmitancji od wybranych parametrów modelu Rezultaty obliczeń prezentujemy w postaci map szarości Na następnym slajdzie transmitancje supersieci optycznych: periodycznych i prostych Fibonacciego
32
33 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i uogólnionych Fibonacciego typu (2,1)
34
35 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i uogólnionych Fibonacciego typu (1,2)
36
37 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i prostej Thue-Morse a Wyniki nieopublikowane
38
39 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i uogólnionych Thue-Morse a (1,2) Wyniki nieopublikowane
40
41 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i uogólnionych Thue-Morse a (2,1) Wyniki nieopublikowane
42
43 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i Rudin-Shapiro Wyniki nieopublikowane
44
45 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i prostej Fibonaciego; grubość warstwy B mniejsza i równa 50 nm Wyniki nieopublikowane
46
47 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje supersieci optycznych: periodycznych i prostych Fibonacciego dla róŝnych wartości współczynników ośrodka zewnętrznego
48
49 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancje prostych supersieci optycznych Fibonacciego dla róŝnych wartości współczynników ośrodka zewnętrznego
50
51 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Tunelowanie światła w supersieciach: periodycznych, z podwojonym okresem, Rudin- Shapiro, prostych i uogólnionych Fibonacciego Wyniki nieopublikowane
52
53 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Tunelowanie światła w supersieciach mieszanych zawierających metamateriały wykazujących ujemne załamanie światła Wyniki nieopublikowane
54 Transmitancja w formalizmie odwzorowań śladów i antyśladów: mieszane SO
55 Transmitancja w formalizmie odwzorowań śladów i antyśladów: mieszane SO
56 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancja supersieci mieszanych zawierających metamateriały wykazujących ujemne załamanie światła. Przypadek bezdyspersyjny. Supersieci periodyczne Wyniki nieopublikowane
57
58 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancja supersieci mieszanych zawierających metamateriały wykazujących ujemne załamanie światła. Przypadek bezdyspersyjny. Supersieci periodyczne i proste Fibonacciego Wyniki nieopublikowane
59
60 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancja supersieci mieszanych zawierających metamateriały wykazujących ujemne załamanie światła. Przypadek bezdyspersyjny. Uogólnione supersieci prawoskrętne i lewoskrętne typu Fibonacciego Wyniki nieopublikowane
61
62 2. Transmisja światła spolaryzowanego Wybrane wyniki obliczeń Transmitancja supersieci mieszanych zawierających metamateriały wykazujących ujemne załamanie światła. Uwzględniono silną dyspersję metamateriału. Supersieci periodyczne i proste Fibonacciego Wyniki nieopublikowane
63
64 2. Transmisja światła spolaryzowanego Podsumowanie i najwaŝniejsze wnioski 1. Wyprowadzono analitycznie odwzorowania śladów i antyśladów macierzy charakterystycznych dla wybranych SO. 2. WyraŜono transmitancję jako funkcję śladów i antyśladów macierzy charakterystycznych SO oraz parametrów modelu. 3. Zaprojektowano i zaprogramowano środowisko programowe do wyznaczania transmitancji SO. 4. Zbadano szczegółowo właściwości transmitancji rozpatrywanych SO. 5. Wykazano w oparciu o wyniki numeryczne, Ŝe transmitancja SO 1. Transmitancja supersieci optycznych zaleŝy silnie od przestrzennego rozkładu zaleŝy silnie od: warstw; właściwości transmisji supersieci modyfikuje dodatkowy stopień swobody: rozkład warstw. przestrzennego rozkładu warstw, współczynników załamania ośrodków zewnętrznych.
65 Transmisja światła i struktura fotoniczna supersieci optycznych Włodzimierz Salejda Instytut Fizyki Seminarium Instytutu Fizyki, 15 stycznia 2007
66 Plan seminarium 1. Wprowadzenie Motywacja; model supersieci optycznej; supersieci periodyczne i aperiodyczne 2. Transmisja światła a spolaryzowanego Macierz charakterystyczna (MCh( MCh); odwzorowania śladów w i antyślad ladów MCh; ; transmitancja,wybrane wyniki analityczne i numeryczne 3. Struktura fotoniczna supersieci optycznych Zagadnienie własne Maxwella; wybrane wyniki; otwarte problemy; 4. Podsumowanie
67 Kryształy fotoniczne Kryształy fotoniczne to periodyczne lub aperiodyczne dielektryczne lub metaliczne struktury zaprojektowane i wykonane w celu kontrolowania propagacji światła. Wykonuje się je głównie dwoma metodami tworząc: sieć uporządkowanych przestrzennie powietrznych dziur w materiale dielektrycznym (zwanym dielektryczną matrycą) sieć wtrąceń materiałowych o wysokim współczynniku załamania w ośrodku o mniejszym współczynniku. Propagujące się w krysztale fotonicznym FEM odddziaływuje ze zmiennym polem potencjalnym współczynnika załamania. Prowadzi to w rezultacie do struktury fotonicznej złoŝonej z pasm przewodzenia i pasm wzbronionych dla FEM
68 Kryształy fotoniczne
69 Kryształy fotoniczne Electromagnetic Theory and Applications for Photonic Crystals, Ed. K. Yasumoto, CRC Press Taylor and Francis Group, 2006
70 Kwazijednowymiarowy kryształ fotoniczny Graficzna ilustracja układu
71 Kwazijednowymiarowy kryształ fotoniczny Zagadnienie własne Maxwella (stacjonarne równania falowe)
72 Kwazijednowymiarowy kryształ fotoniczny Zagadnienie własne Maxwella (stacjonarne równania falowe) Periodyczne aproksymanty, periodyczne warunki brzegowe Strefa Brillouina Rozwiązanie stacjonarnych równań falowych Fotoniczna struktura pasmowa ω(q)
73 Kwazijednowymiarowy kryształ fotoniczny Zagadnienie własne Maxwella (stacjonarne równania falowe) Periodyczne aproksymanty, periodyczne warunki brzegowe, metoda róŝnic skończonych zastosowanie metod i algorytmów przedstawionych w ksiąŝce W. Salejda, M.H. Tyc, M. Just, Algebraiczne metody rozwiązywania równania Schrödingera, PWN, Warszawa 2002 Numeryczne rozwiązania stacjonarnych równań falowych pozwala wyznaczyć zaleŝności dyspersyjne ω(q) oraz G ( ω ) ( ω) G = D L πv g
74 Kwazijednowymiarowy kryształ fotoniczny Zagadnienie własne Maxwella (stacjonarne równania falowe) Periodyczne aproksymanty, periodyczne warunki brzegowe Numeryczne rozwiązania stacjonarnych równań falowych Dyskretna siatka punktów Algebraiczne zagadnienia własne s p
75 Kwazijednowymiarowy kryształ fotoniczny Zagadnienie własne Maxwella (stacjonarne równanie falowe) Periodyczne aproksymanty, periodyczne warunki brzegowe Jawne postacie algebraicznych zagadnień własnych hermitowskie uogólnione zagadnienie własne
76 Kwazijednowymiarowy kryształ fotoniczny Jawne postacie algebraicznych zagadnień własnych hermitowskie zagadnienie własne
77 Kwazijednowymiarowy kryształ fotoniczny Wybrane wyniki numeryczne (nieopublikowane); przypadek bezdyspersyjny
78 Kwazijednowymiarowy kryształ fotoniczny Wybrane wyniki numeryczne (nieopublikowane); przypadek bezdyspersyjny
79 Kwazijednowymiarowy kryształ fotoniczny Wybrane wyniki numeryczne (nieopublikowane); przypadek silnie dyspersyjny b
80 Kwazijednowymiarowy kryształ fotoniczny Wybrane wyniki numeryczne (nieopublikowane) Metoda obliczeń oparta o formalizm macierzy przejścia Γ; tr ( Γ ), w przypadku periodycznych warunków brzegowych, przyjmuje wartości z przedziału < 2, +2>; zaleŝności dyspersyjne wyznaczano rozwiązując równanie ( qd ) = tr[ Γ( ω) ], gdzie d = D. 2cos L
81 Kwazijednowymiarowy kryształ fotoniczny Wybrane wyniki numeryczne (nieopublikowane)
82 Podsumowanie cz Sformułowano zagadnienia własne Maxwella dla obu typów polaryzacji światła w przypadku wielowarstwowego kryształu fotonicznego (kwazijednowymiarowy kryształ fotoniczny) 2. Zastosowano metody i algorytmy rozwinięte dla przypadku rozwiązywania jednowymiarowego, jednocząstkowego równania Schrödingera przedstawione obszernie w ksiąŝce W. Salejda, M.H. Tyc, M. Just, Algebraiczne metody rozwiązywania równania Schrödingera, PWN, Warszawa Wstępne wyniki obliczeń numerycznych wskazują na przydatność i poprawność zaproponowanego podejścia do wyznaczania i badania właściwości fotonicznej struktury pasmowej kwazijednowymiarowych kryształów fotonicznych.
83 Publikacje, komunikaty konferencyjne 1. A. Klauzer-Kruszyna, W. Salejda, M.H. Tyc, Polarized light transmission through quasi-one-dimensional aperiodic photonic structures, XXXIIth International School on Physics of Semiconducting Compounds "Jaszowiec 2003", Ustroń-Jaszowiec, maj/czerwiec A. Klauzer-Kruszyna, W. Salejda, M.H. Tyc, Polarized light transmission through generalized Fibonacci multilayers. 1. Dynamical maps approach, Optik (Stuttg.), vol. 115, nr 6, strony , 2004 r. 3. A. Klauzer-Kruszyna, W. Salejda, M.H. Tyc, Polarized light transmission through generalized Fibonacci multilayers. 2. Numerical results, Optik (Stuttg.) vol. 115, nr 6, strony , 2004 r. 4. W. Salejda, M.H. Tyc, A. Klauzer-Kruszyna, K. Tarnowski, Photonic band structure of the quasi-one-dimensional photonic quasicrystals, w materiałach Photonic crystals and fibers, SPIE International Congress on Optics and Optoelectronics, Warsaw, 31 August 1 September 2005, Edytorzy: W. Urbańczyk, B. Jaskórzyńska, P. St. J. Russell (eds),, Bellingham, Wash., SPIE, The International Society for Optical Engineering, cop. 2005, strony 59501R R-7, SPIE Proceedings Series, ISSN X; vol
84 Publikacje, komunikaty konferencyjne 5. W. Salejda, A. Klauzer-Kruszyna, M.H. Tyc, K. Tarnowski Karol, Electromagnetic wave propagation through aperiodic superlattices composed of left- and right-handed materials, SPIE International Congress on Optics and Optoelectronics, Warsaw, 31 August 1 September 2005, Ed. T. Szoplik [i in.], Metamaterials, Bellingham, Wash., SPIE, The International Society for Optical Engineering, cop. 2005, strony , SPIE Proceedings Series, ISSN X; vol M.H. Tyc, W. Salejda, A. Klauzer-Kruszyna, K. Tarnowski Karol, Photonic band structure of quasi-one-dimensional photonic quasicrystals composed of right- and left-handed materials, Symposium on Photonics Technologies for the 7th Framework Programme "OPERA-2015", Wrocław, X A. Klauzer-Kruszyna Agnieszka, W. Salejda, M.H. Tyc, W. Burbo, Środowisko obliczeniowedo symulacji propagacji światła spolaryzowanego w strukturach wielowarstwowych, w materiałach konferencyjnych Nauczanie fizyki w wyŝszych szkołach technicznych. XIV Konferencja, Bydgoszcz, czerwca 2004}, strony , Bydgoszcz, Wydaw. Uczel. Akademii Techniczno-Rolniczej 2004 r. A. Klauzer-Kruszyna, Propagacja światła spolaryzowanego w wybranych supersieciach aperiodycznych, praca doktorska, Wrocław 2005; dostępna na stronie Milena Dziębaj, Metody otrzymywania i właściwości optyczne materiałów z ujemnym współczynnikiem załamania, praca magisterska, Wrocław 2006;
85 Cytowania w 2005 r
86 Cytowania w 2006 r
87 Problemy, zagadnienia otwarte 1. Propagacja światła spolaryzowanego w supersieciach optycznych z metamateriałami z uwzględnieniem absorpcji FEM (słaba i silna dyspersja, zespolony współczynnik załamania) wymaga to zastosowania nowych metod odmiennych od dotychczas opracowanych i zastosowanych. 2. Wyznaczenie struktury fotonicznej supersieci optycznych z metamateriałami, tj. rozwiązanie stacjonarnych równań falowych (zagadnień własnych Maxwella) dla obu polaryzacji przy zaniedbaniu absorpcji FEM.
88 Dziękuję za: uwagę, obecność, cierpliwe wysłuchanie!
89 Dodatek popularnonaukowy Część przygotowana i dedykowana studentom uczestnikom seminarium Instytutu Fizyki PWr pt. Transmisja światła i struktura fotoniczna supersieci optycznych Włodzimierz Salejda Instytut Fizyki, Politechniki Wrocławskiej 15 stycznia 2007 r
90 Zjawisko ujemnego załamania światła
91 Zjawisko ujemnego załamania światła David Smith, Department of Physics, University of California, San Diego, USA publikuje w Physics World, maj 2003 ( artykuł pt. The reality of negative refraction, w którym stawia następującą tezę: Recent experiments that demonstrate the negative refraction of light could bring a heated scientific debate to a close, and give negativeindex materials a positive future.
92 Zjawisko ujemnego załamania światła Doświadczalne potwierdzenie zjawiska ujemnego załamania światła Andrew Houck ze współpracownikami z Massachusetts Institute of Technology (MIT) wykonali doświadczenie nad transmisją mikrofal przez próbki z materiałów (o kształcie prostokątnego trapezu) prawo- i lewoskrętnych (A. Houck, J. Brock, I. Chuang, Experimental Observations of Left-Handed Materials That Obeys Snell Law, Phys. Rev. Lett. 90, (2003)). Jako prawoskrętnego ośrodka referencyjnego uŝyto teflonu (rysunek górny po prawej stronie.
93 Zjawisko ujemnego załamania światła Claudio Parazzoli, Kin Li ze współpracownikami z działu Phantom Works korporacji Boeinga skonstruowali próbkę w kształcie klina (zdjęcie obok). Eksperyment potwierdził istnienie zjawiska ujemnego załamania światła w zakresie mikrofal; Phys. Rev. Lett Grupa ta obliczyła współczynnik załamania dla próbki metamateriału i porównała z danymi doświadczalnymi. Teoria i doświadczenie były w bardzo dobrej zgodności (w zakresie zastosowanych częstości).
94
95 Czapka niewidka! MoŜe być w zasadzie skonstruowana z wykorzystaniem właściwości metamateriałów, ale póki co tylko w obszarze mikrofalowym widma elektromagnetycznego
96
97
98 Literatura popularnonaukowa 1. John B. Pendry (teoretyk, profesor w Imperial College London), David R. Smith (eksperymentator, profesor elektroniki i informatyki w Duke University), Metamorfoza soczewki, Świat Nauki, nr 8, sierpień John B. Pendry, David R. Smith, Reversing Light with Negative Refraction, Physics Today, vol. 57, nr 6, (2004)
99 John B. Pendry, David R. Smith, Metamorfoza soczewki, Świat Nauki, nr 8, sierpień 2006.
100 John B. Pendry, David R. Smith, Metamorfoza soczewki, Świat Nauki, nr 8, sierpień 2006.
101 John B. Pendry, David R. Smith, Metamorfoza soczewki, Świat Nauki, nr 8, sierpień 2006.
102 Zjawisko ujemnego załamania światła
103 John B. Pendry, David R. Smith, Metamorfoza soczewki, Świat Nauki, nr 8, sierpień 2006.
104 John B. Pendry, David R. Smith, Metamorfoza soczewki, Świat Nauki, nr 8, sierpień 2006.
105
106
107 Równania Maxwella: analiza V. Veselago Analiza V. Veselago równań Maxwella r. falowe MoŜliwe związki
108 Równania Maxwella: analiza V. Veselago Analiza V. Veselago r. falowe równań Maxwella Analiza równań Maxwella dla płaskiej FEM
109 Równania Maxwella: analiza V. Veselago Dla płaskiej FEM Analiza V. Veselago równań Maxwella Układ równań Maxwella przyjmuje postać MoŜliwe związki
110 Równania Maxwella: analiza V. Veselago Dla płaskiej FEM Analiza V. Veselago równań Maxwella Układ równań Maxwella przyjmuje postać gdzie, MoŜliwe związki
111 Równania Maxwella: analiza V. Veselago Analiza V. Veselago równań Maxwella Dla płaskiej FEM Dopuszczalne r. Maxwella związki
112 Ośrodki lewoskrętne (LHM) i prawoskrętne (RHM) Wnioski końcowe analizy V. Veselago równań Maxwella Dopuszczalne r. Maxwella związki Ośrodki prawoskrętne E H v g k vf Wektor Poytinga E H nie zaleŝy od rodzaju ośrodka v f k Ośrodki lewoskrętne E H v g Wektory prędkości fazowej v f i grupowej v g są równoległe Wektory prędkości fazowej v f i grupowej v g są antyrównoległe
113 Literatura 1. Negative-Refraction Metamaterials, Fundamental Pronciples and Aplications, Eds. George V. Eleftheriades and Keith G. Balman, Wiley-Interscience, Institute of Electric and Electronics Engineers (IEEE), Wiley and Sons, Electromagnetic Metamaterials. Transmission Line Theory and Microwave Applications. The Engineering Approach, Wiley-Interscience, Institute of Electric and Electronics Engineers (IEEE), Wiley and Sons, 2006
Lp Temat Opis Opiekun
 Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Lp Temat Opis Opiekun
 Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Fizyka - mgr Lp Temat Opis Opiekun 1 Międzypowierzchniowe plazmony właściwości fizyczne i zastosowania Cele pracy: 1) zdobycie wiedzy nt. oddziaływania fal elektromagnetycznych z materią oraz fizyki plazmonów;
Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional
 Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Fotonika Wykłady 10: Kryształy fotoniczne, fale Blocha, fotoniczna przerwa wzbroniona, zwierciadła Bragga i odbicie omnidirectional Plan: Jednowymiarowe kryształy fotoniczne Fale Blocha, fotoniczna struktura
Fotonika kurs magisterski grupa R41 semestr VII Specjalność: Inżynieria fotoniczna. Egzamin ustny: trzy zagadnienia do objaśnienia
 Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Dr inż. Tomasz Kozacki Prof. dr hab.inż. Romuald Jóźwicki Zakład Techniki Optycznej Instytut Mikromechaniki i Fotoniki pokój 513a ogłoszenia na tablicach V-tego piętra kurs magisterski grupa R41 semestr
Motywacja Podstawy. Historia Teoria 2D PhC Podsumowanie. Szymon Lis Photonics Group szymon.lis@pwr.wroc.pl C-2 p.305. Motywacja.
 Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
Politechnika Wrocławska Plan wykładu 1. 2D Kryształy Fotoniczne opis teoretyczny 2. Podstawowe informacje 3. Rys historyczny 4. Opis teoretyczny - optyka vs. elektronika - równania Maxwella Wydział Elektroniki
PRACA DYPLOMOWA MAGISTERSKA
 Wydział Podstawowych Problemów Techniki PRACA DYPLOMOWA MAGISTERSKA Analiza numeryczna rozkładu i propagacji pola elektromagnetycznego w metamateriałach metodą FDTD Karol Lech Tarnowski Opiekun: dr hab.
Wydział Podstawowych Problemów Techniki PRACA DYPLOMOWA MAGISTERSKA Analiza numeryczna rozkładu i propagacji pola elektromagnetycznego w metamateriałach metodą FDTD Karol Lech Tarnowski Opiekun: dr hab.
Fizyka komputerowa(ii)
 Instytut Fizyki Fizyka komputerowa(ii) Studia magisterskie Prowadzący kurs: Dr hab. inż. Włodzimierz Salejda, prof. PWr Godziny konsultacji: Poniedziałki i wtorki w godzinach 13.00 15.00 pokój 223 lub
Instytut Fizyki Fizyka komputerowa(ii) Studia magisterskie Prowadzący kurs: Dr hab. inż. Włodzimierz Salejda, prof. PWr Godziny konsultacji: Poniedziałki i wtorki w godzinach 13.00 15.00 pokój 223 lub
Metody numeryczne rozwiązywania równań Maxwella w kwazijednowymiarowych strukturach fotonicznych
 Wydział Podstawowych Problemów Techniki Metody numeryczne rozwiązywania równań Maxwella w kwazijednowymiarowych strukturach fotonicznych Praca dyplomowa magisterska Szymon Kosydor Promotor: dr hab. inż.
Wydział Podstawowych Problemów Techniki Metody numeryczne rozwiązywania równań Maxwella w kwazijednowymiarowych strukturach fotonicznych Praca dyplomowa magisterska Szymon Kosydor Promotor: dr hab. inż.
Numeryczne rozwiązanie równania Schrodingera
 Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
Numeryczne rozwiązanie równania Schrodingera Równanie ruchu dla cząstki o masie m (elektron- cząstka elementarna o masie ~9.1 10-31 kg) Mechanika klasyczna - mechanika kwantowa 1. Druga zasada dynamiki
Fotonika. Plan: Wykład 14: podsumowanie, uzupełnienie
 Fotonika Wykład 14: podsumowanie, uzupełnienie Plan: Uzupełnienie: kryształy fotoniczne i metamateriały soczewka Pendrego, nadrozdzielczość Absorbery elektromagnetyczne elementy optyki fourierowskiej Optyka
Fotonika Wykład 14: podsumowanie, uzupełnienie Plan: Uzupełnienie: kryształy fotoniczne i metamateriały soczewka Pendrego, nadrozdzielczość Absorbery elektromagnetyczne elementy optyki fourierowskiej Optyka
KATEDRA TELEKOMUNIKACJI I FOTONIKI
 ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE WYDZIAŁ ELEKTRYCZNY KATEDRA TELEKOMUNIKACJI I FOTONIKI OPROGRAMOWANIE DO MODELOWANIA SIECI ŚWIATŁOWODOWYCH PROJEKTOWANIE FALOWODÓW PLANARNYCH (wydrukować
3. Umiejętność obsługi prostych przyrządów optycznych (UMIEJĘTNOŚĆ)
 Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical waveguides Kierunek studiów (jeśli dotyczy): Inżynieria Kwantowa Specjalność (jeśli
Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical waveguides Kierunek studiów (jeśli dotyczy): Inżynieria Kwantowa Specjalność (jeśli
III. Opis falowy. /~bezet
 Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Światłowody III. Opis falowy BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet Równanie falowe w próżni Teoria falowa Równanie Helmholtza Równanie bezdyspersyjne fali płaskiej, rozchodzącej
Fotonika. Plan: Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych
 Fotonika Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych S. Maier Plasmonics fundamentals and applications (Springer, 2007). Plan: Elementy plazmoniki i
Fotonika Wykład 15: Elementy plazmoniki: struktury cienkowarstwowe, elementy teorii ośrodków efektywnych S. Maier Plasmonics fundamentals and applications (Springer, 2007). Plan: Elementy plazmoniki i
Fotonika. Plan: Wykład 11: Kryształy fotoniczne
 Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Fotonika Wykład 11: Kryształy fotoniczne Plan: Kryształy fotoniczne Homogenizacja długofalowa Prawo załamania dla kryształów fotonicznych, superkolimacja Tw. Blocha, kryształy, kryształy fotoniczne, kryształy
Zał nr 4 do ZW. Dla grupy kursów zaznaczyć kurs końcowy. Liczba punktów ECTS charakterze praktycznym (P)
 Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
Fotonika. Plan: Wykład 3: Polaryzacja światła
 Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Fotonika Wykład 3: Polaryzacja światła Plan: Równania Maxwella w ośrodku optycznie liniowym Równania Maxwella dla fal monochromatycznych Polaryzacja światła Fala płaska spolaryzowana Polaryzacje liniowe,
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 6, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 6, 0.03.01 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 5 - przypomnienie ciągłość
Egzamin / zaliczenie na ocenę*
 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim: ŚWIATŁOWODY, ŚWIATŁOWODY Nazwa w języku angielskim: OPTICAL FIBERS Kierunek studiów (jeśli dotyczy):
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim: ŚWIATŁOWODY, ŚWIATŁOWODY Nazwa w języku angielskim: OPTICAL FIBERS Kierunek studiów (jeśli dotyczy):
Wykład 12: prowadzenie światła
 Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Fotonika Wykład 12: prowadzenie światła Plan: Mechanizmy prowadzenia światła Mechanizmy oparte na odbiciu całkowite wewnętrzne odbicie, odbicie od ośrodków przewodzących, fotoniczna przerwa wzbroniona
Egzamin / zaliczenie na ocenę*
 Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical fibers Kierunek studiów (jeśli dotyczy): Fizyka Techniczna Specjalność (jeśli dotyczy):
Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Światłowody Nazwa w języku angielskim Optical fibers Kierunek studiów (jeśli dotyczy): Fizyka Techniczna Specjalność (jeśli dotyczy):
Optyka Ośrodków Anizotropowych. Wykład wstępny
 Optyka Ośrodków Anizotropowych Wykład wstępny Cel kursu Zapoznanie z podstawami fizycznymi w optyce polaryzacyjnej. Jak zachowuje się fala elektromagnetyczna w ośrodku materialnym? Omówienie zastosowania
Optyka Ośrodków Anizotropowych Wykład wstępny Cel kursu Zapoznanie z podstawami fizycznymi w optyce polaryzacyjnej. Jak zachowuje się fala elektromagnetyczna w ośrodku materialnym? Omówienie zastosowania
Politechnika Wrocławska Wydział Podstawowych Problemów Techniki
 Politechnika Wrocławska Wydział Podstawowych Problemów Techniki specjalność FOTONIKA 3,5-letnie studia stacjonarne I stopnia (studia inżynierskie) FIZYKA TECHNICZNA Charakterystyka wykształcenia: - dobre
Politechnika Wrocławska Wydział Podstawowych Problemów Techniki specjalność FOTONIKA 3,5-letnie studia stacjonarne I stopnia (studia inżynierskie) FIZYKA TECHNICZNA Charakterystyka wykształcenia: - dobre
Egzamin / zaliczenie na ocenę*
 Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Podstawy optyki fizycznej i instrumentalnej Nazwa w języku angielskim Fundamentals of Physical and Instrumental Optics Kierunek
Zał. nr 4 do ZW 33/01 WYDZIAŁ PPT KARTA PRZEDMIOTU Nazwa w języku polskim: Podstawy optyki fizycznej i instrumentalnej Nazwa w języku angielskim Fundamentals of Physical and Instrumental Optics Kierunek
Wykład 17: Optyka falowa cz.2.
 Wykład 17: Optyka falowa cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Interferencja w cienkich warstwach Załamanie
Wykład 17: Optyka falowa cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Interferencja w cienkich warstwach Załamanie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 18, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 18, 23.04.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 17 - przypomnienie
Metody rozwiązania równania Schrödingera
 Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Metody rozwiązania równania Schrödingera Równanie Schrödingera jako algebraiczne zagadnienie własne Rozwiązanie analityczne dla skończonej i nieskończonej studni potencjału Problem rozwiązania równania
Podstawy Fizyki III Optyka z elementami fizyki współczesnej. wykład 18, Mateusz Winkowski, Łukasz Zinkiewicz
 Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Podstawy Fizyki III Optyka z elementami fizyki współczesnej wykład 18, 07.12.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Łukasz Zinkiewicz Radosław Łapkiewicz Wykład 17 - przypomnienie
Badanie uporządkowania magnetycznego w ultracienkich warstwach kobaltu w pobliżu reorientacji spinowej.
 Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Tel.: +48-85 7457229, Fax: +48-85 7457223 Zakład Fizyki Magnetyków Uniwersytet w Białymstoku Ul.Lipowa 41, 15-424 Białystok E-mail: vstef@uwb.edu.pl http://physics.uwb.edu.pl/zfm Praca magisterska Badanie
Zał. nr 4 do ZW. Wykład Ćwiczenia Laboratorium Projekt Seminarium
 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: OPTYKA NIELINIOWA Nazwa w języku angielskim: Nonlinear optics Kierunek studiów (jeśli dotyczy): Fizyka Techniczna Specjalność
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: OPTYKA NIELINIOWA Nazwa w języku angielskim: Nonlinear optics Kierunek studiów (jeśli dotyczy): Fizyka Techniczna Specjalność
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Metody Obliczeniowe Mikrooptyki i Fotoniki https://www.igf.fuw.edu.pl/pl/courses/lectures/metody-obliczen-95-021c/ Podstawy metody różnic skończonych (Basics of finite-difference methods) Podstawy metody
Zał nr 4 do ZW. Dla grupy kursów zaznaczyć kurs końcowy. Liczba punktów ECTS charakterze praktycznym (P)
 Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
Zał nr 4 do ZW WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim : Fizyka Nazwa w języku angielskim : Physics Kierunek studiów : Informatyka Specjalność (jeśli dotyczy) :
Katedra Elektrotechniki Teoretycznej i Informatyki
 Katedra Elektrotechniki Teoretycznej i Informatyki Przedmiot: Badania nieniszczące metodami elektromagnetycznymi Numer Temat: Badanie materiałów kompozytowych z ćwiczenia: wykorzystaniem fal elektromagnetycznych
Katedra Elektrotechniki Teoretycznej i Informatyki Przedmiot: Badania nieniszczące metodami elektromagnetycznymi Numer Temat: Badanie materiałów kompozytowych z ćwiczenia: wykorzystaniem fal elektromagnetycznych
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Widmo fal elektromagnetycznych
 Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Czym są fale elektromagnetyczne? Widmo fal elektromagnetycznych dr inż. Romuald Kędzierski Podstawowe pojęcia związane z falami - przypomnienie pole falowe część przestrzeni objęta w danej chwili falą
Metody Obliczeniowe Mikrooptyki i Fotoniki
 Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Metody Obliczeniowe Mikrooptyki i Fotoniki Kod USOS: 1103-4Fot4 Wykład (30h): R. Kotyński Wtorki 9:15-11:00, s.1.38 lub B4.17(ul. Pasteura 5) Ćwiczenia (45h): Wtorki, w godz. 14.15-16.30, s.1.7 lub B4.17
Różne reżimy dyfrakcji
 Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Def. MO Optyczne elementy o strukturze submm lub subμm, produkowane głównie metodami litograficznymi
 Mikro optyka MO Def. MO Optyczne elementy o strukturze submm lub subμm, produkowane głównie metodami litograficznymi Systemy bazujące na mikrooptyce Zalety systemów MO duże macierze wysoka dokładność pozycjonowania
Mikro optyka MO Def. MO Optyczne elementy o strukturze submm lub subμm, produkowane głównie metodami litograficznymi Systemy bazujące na mikrooptyce Zalety systemów MO duże macierze wysoka dokładność pozycjonowania
Agata Saternus piątek Dwójłomność kryształów, dwójłomność światłowodów, dwójłomność próżni (z ang. vacuum birefringence)
 Agata Saternus piątek 9.07.011 Dwójłomność kryształów, dwójłomność światłowodów, dwójłomność próżni (z ang. vacuum birefringence) Dwójłomność odkrył Rasmus Bartholin w 1669 roku, dwójłomność kryształu
Agata Saternus piątek 9.07.011 Dwójłomność kryształów, dwójłomność światłowodów, dwójłomność próżni (z ang. vacuum birefringence) Dwójłomność odkrył Rasmus Bartholin w 1669 roku, dwójłomność kryształu
Ośrodki dielektryczne optycznie nieliniowe
 Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Ośrodki dielektryczne optycznie nieliniowe Równania Maxwella roth rot D t B t = = przy czym tym razem wektor indukcji elektrycznej D ε + = ( ) Wektor polaryzacji jest nieliniową funkcją natężenia pola
Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość
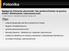 Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Fotonika Wykład 13: Elementy plazmoniki: fale powierzchniowe na granicy metali i dielektryków, nadrozdzielczość S. Maier Plasmonics fundamentals and applications (Springer, 007). Plan: związek dyspersyjny
Solitony i zjawiska nieliniowe we włóknach optycznych
 Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Solitony i zjawiska nieliniowe we włóknach optycznych Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone
Wprowadzenie do optyki nieliniowej
 Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Wprowadzenie do optyki nieliniowej Prezentacja zawiera kopie folii omawianych na wykładzie. Niniejsze opracowanie chronione jest prawem autorskim. Wykorzystanie niekomercyjne dozwolone pod warunkiem podania
Fotonika. Plan: Wykład 9: Interferencja w układach warstwowych
 Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Fotonika Wykład 9: Interferencja w układach warstwowych Plan: metody macierzowe - macierze przejścia i rozpraszania Proste układy warstwowe powłoki antyrefleksyjne interferometr Fabry-Pérot tunelowanie
Fotonika. Wykład (30h): R. Kotyński Wtorki 15:15-17:00, s. 1.40
 Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Wykład Ćwiczenia Laboratorium Projekt Seminarium Egzamin / zaliczenie na ocenę*
 Zał. nr do ZW 33/01 WYDZIAŁ Podstawowych problemów Techniki / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Projektowanie Materiałów i Sturktur Nazwa w języku angielskim Design of Materials and Structures
Zał. nr do ZW 33/01 WYDZIAŁ Podstawowych problemów Techniki / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Projektowanie Materiałów i Sturktur Nazwa w języku angielskim Design of Materials and Structures
Metody symulacji w nanotechnologii
 Metody symulacji w nanotechnologii Jan Iwaniszewski A. Formalizm operatorowy Załóżmy, że nasz układ kwantowy posiada dyskretny zbiór funkcji własnych ϕ k, k =,,.... Tworzą one bazę w całej przestrzeni
Metody symulacji w nanotechnologii Jan Iwaniszewski A. Formalizm operatorowy Załóżmy, że nasz układ kwantowy posiada dyskretny zbiór funkcji własnych ϕ k, k =,,.... Tworzą one bazę w całej przestrzeni
Fala EM w izotropowym ośrodku absorbującym
 Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
Fala EM w izotropowym ośrodku absorbującym Fala EM powoduje generację zmienne pole elektryczne E Zmienne co do kierunku i natężenia, Pole E Nie wywołuje w ośrodku prądu elektrycznego Powoduje ruch elektronów
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI 1. Wiedza z zakresu analizy I i algebry I
 WYDZIAŁ MECHANICZNY (w j. angielskim) Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim FIZYKA OGÓLNA Nazwa w języku angielskim GENERAL PHYSICS Kierunek studiów (jeśli dotyczy) MiBM Specjalność
WYDZIAŁ MECHANICZNY (w j. angielskim) Zał. nr 4 do ZW 33/01 KARTA PRZEDMIOTU Nazwa w języku polskim FIZYKA OGÓLNA Nazwa w języku angielskim GENERAL PHYSICS Kierunek studiów (jeśli dotyczy) MiBM Specjalność
Ciekłokrystaliczne światłowody fotoniczne
 Światło od zawsze fascynuje człowieka warunkuje ono jego istnienie. Nic więc dziwnego, że człowiek sięgnął po nie wykorzystują światło jako najszybszego posłańca promienie świetlne rozprzestrzeniają się
Światło od zawsze fascynuje człowieka warunkuje ono jego istnienie. Nic więc dziwnego, że człowiek sięgnął po nie wykorzystują światło jako najszybszego posłańca promienie świetlne rozprzestrzeniają się
Wykład Ćwiczenia Laboratorium Projekt Seminarium Liczba godzin zajęć zorganizowanych w Uczelni (ZZU)
 Wydział Podstawowych Problemów Techniki PWr KARTA PRZEDMIOTU Nazwa w języku polskim: Metody numeryczne w fizyce Nazwa w języku angielskim: Numerical methods in Physics Kierunek studiów: Fizyka techniczna
Wydział Podstawowych Problemów Techniki PWr KARTA PRZEDMIOTU Nazwa w języku polskim: Metody numeryczne w fizyce Nazwa w języku angielskim: Numerical methods in Physics Kierunek studiów: Fizyka techniczna
Wykład Ćwiczenia Laboratorium Projekt Seminarium Liczba godzin zajęć zorganizowanych w Uczelni (ZZU) Egzamin
 Zał. nr 3 do ZW Wydział Elektroniki PWr KARTA PRZEDMIOTU Nazwa w języku polskim: Fizyka 1.1A. Nazwa w języku angielskim: Physics 1.1A Kierunek studiów: Automatyka i Robotyka, Elektronika, Informatyka,
Zał. nr 3 do ZW Wydział Elektroniki PWr KARTA PRZEDMIOTU Nazwa w języku polskim: Fizyka 1.1A. Nazwa w języku angielskim: Physics 1.1A Kierunek studiów: Automatyka i Robotyka, Elektronika, Informatyka,
1 Płaska fala elektromagnetyczna
 1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
1 Płaska fala elektromagnetyczna 1.1 Fala w wolnej przestrzeni Rozwiązanie równań Maxwella dla zespolonych amplitud pól przemiennych sinusoidalnie, reprezentujące płaską falę elektromagnetyczną w wolnej
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką
 Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Problem Odwrotny rozchodzenia się fali Love'a w falowodach sprężystych obciążonych cieczą lepką Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Instytut Podstawowych Problemów Techniki PAN Zakład Teorii Ośrodków
Fale elektromagnetyczne w dielektrykach
 Fale elektromagnetyczne w dielektrykach Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia
Fale elektromagnetyczne w dielektrykach Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Krótka historia odkrycia
Fotonika. Wykład (30h): Rafał Kotyński, wtorki 15:15-17:00, s. 1.40
 Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Fotonika Fotonika to interdyscyplinarna dziedzina nauki i techniki, łącząca dokonania optyki, elektroniki i informatyki w celu opracowywania technik i urządzeń wykorzystujących promieniowanie elektromagnetyczne
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
UNIWERSYTET MARII CURIE-SKŁODOWSKIEJ W LUBLINIE
 UNIWERSYTET MARII CURIE-SKŁODOWSKIEJ W LUBLINIE Projekt Zintegrowany UMCS Centrum Kształcenia i Obsługi Studiów, Biuro ds. Kształcenia Ustawicznego telefon: +48 81 537 54 61 Podstawowe informacje o przedmiocie
UNIWERSYTET MARII CURIE-SKŁODOWSKIEJ W LUBLINIE Projekt Zintegrowany UMCS Centrum Kształcenia i Obsługi Studiów, Biuro ds. Kształcenia Ustawicznego telefon: +48 81 537 54 61 Podstawowe informacje o przedmiocie
Zastosowania metamateriałów o ujemnym współczynniku refrakcji w technice anten inteligentnych
 Zakład Zastosowań Technik Łączności Elektronicznej (Z-10) Zastosowania metamateriałów o ujemnym współczynniku refrakcji w technice anten inteligentnych Praca nr 10300016 Warszawa, grudzień 2006 1 Zastosowania
Zakład Zastosowań Technik Łączności Elektronicznej (Z-10) Zastosowania metamateriałów o ujemnym współczynniku refrakcji w technice anten inteligentnych Praca nr 10300016 Warszawa, grudzień 2006 1 Zastosowania
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyczny dualizm przestrzenno-czasowy: zastosowania w optyce kwantowej
 Sympozjum IFD, 28.11.2016 Optyczny dualizm przestrzenno-czasowy: zastosowania w optyce kwantowej Michał Karpiński Zakład Optyki IFD UW Optical Quantum Technologies Group, Clarendon Laboratory, University
Sympozjum IFD, 28.11.2016 Optyczny dualizm przestrzenno-czasowy: zastosowania w optyce kwantowej Michał Karpiński Zakład Optyki IFD UW Optical Quantum Technologies Group, Clarendon Laboratory, University
Laboratorium techniki laserowej. Ćwiczenie 5. Modulator PLZT
 Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Ćwiczenia z mikroskopii optycznej
 Ćwiczenia z mikroskopii optycznej Anna Gorczyca Rok akademicki 2013/2014 Literatura D. Halliday, R. Resnick, Fizyka t. 2, PWN 1999 r. J.R.Meyer-Arendt, Wstęp do optyki, PWN Warszawa 1979 M. Pluta, Mikroskopia
Ćwiczenia z mikroskopii optycznej Anna Gorczyca Rok akademicki 2013/2014 Literatura D. Halliday, R. Resnick, Fizyka t. 2, PWN 1999 r. J.R.Meyer-Arendt, Wstęp do optyki, PWN Warszawa 1979 M. Pluta, Mikroskopia
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Postulaty interpretacyjne mechaniki kwantowej Wykład 6
 Postulaty interpretacyjne mechaniki kwantowej Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl 19 września 2014 Karol Kołodziej Postulaty interpretacyjne mechaniki
Postulaty interpretacyjne mechaniki kwantowej Wykład 6 Karol Kołodziej Instytut Fizyki Uniwersytet Śląski, Katowice http://kk.us.edu.pl 19 września 2014 Karol Kołodziej Postulaty interpretacyjne mechaniki
Równania Maxwella. roth t
 , H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
, H wektory natężenia pola elektrycznego i magnetycznego D, B wektory indukcji elektrycznej i magnetycznej J gęstość prądu elektrycznego Równania Maxwella D roth t B rot+ t J Dla ośrodka izotropowego D
Pole elektromagnetyczne. Równania Maxwella
 Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
jest rozwiązaniem równania jednorodnego oraz dla pewnego to jest toŝsamościowo równe zeru.
 Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
Układy liniowe Układ liniowy pierwszego rzędu, niejednorodny. gdzie Jeśli to układ nazywamy jednorodnym Pamiętamy, Ŝe kaŝde równanie liniowe rzędu m moŝe zostać sprowadzone do układu n równań liniowych
ANALIZA WŁAŚCIWOŚCI ABSORPCJI POLA ELEKTROMAGNETYCZNEGO W WYBRANYCH METAMATERIAŁACH
 POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 018 DOI 10.1008/j.1897-0737.018.93.003 Mikołaj NOWAK * ANALIZA WŁAŚCIWOŚCI ABSORPCJI POLA ELEKTROMAGNETYCZNEGO W WYBRANYCH
POZNAN UNIVERSITY OF TECHNOLOGY ACADEMIC JOURNALS No 93 Electrical Engineering 018 DOI 10.1008/j.1897-0737.018.93.003 Mikołaj NOWAK * ANALIZA WŁAŚCIWOŚCI ABSORPCJI POLA ELEKTROMAGNETYCZNEGO W WYBRANYCH
Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie
 napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
napisał Michał Wierzbicki Prędkość fazowa i grupowa fali elektromagnetycznej w falowodzie Prędkość grupowa paczki falowej Paczka falowa jest superpozycją fal o różnej częstości biegnących wzdłuż osi z.
Symulacyjne metody wyceny opcji amerykańskich
 Metody wyceny Piotr Małecki promotor: dr hab. Rafał Weron Instytut Matematyki i Informatyki Politechniki Wrocławskiej Wrocław, 0 lipca 009 Metody wyceny Drzewko S 0 S t S t S 3 t S t St St 3 S t St St
Metody wyceny Piotr Małecki promotor: dr hab. Rafał Weron Instytut Matematyki i Informatyki Politechniki Wrocławskiej Wrocław, 0 lipca 009 Metody wyceny Drzewko S 0 S t S t S 3 t S t St St 3 S t St St
E wektor natęŝenia pola, a dr element obwodu, którego zwrot określa przyjęty kierunek obchodzenia danego oczka.
 Lista 9. do kursu Fizyka; rok. ak. 2012/13 sem. letni W. InŜ. Środ.; kierunek InŜ. Środowiska Tabele wzorów matematycznych (http://www.if.pwr.wroc.pl/~wsalejda/mat-wzory.pdf) i fizycznych (http://www.if.pwr.wroc.pl/~wsalejda/wzf1.pdf;
Lista 9. do kursu Fizyka; rok. ak. 2012/13 sem. letni W. InŜ. Środ.; kierunek InŜ. Środowiska Tabele wzorów matematycznych (http://www.if.pwr.wroc.pl/~wsalejda/mat-wzory.pdf) i fizycznych (http://www.if.pwr.wroc.pl/~wsalejda/wzf1.pdf;
Egzamin / zaliczenie na ocenę* CELE PRZEDMIOTU
 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: CIEKŁE KRYSZTAŁY I POLIMERY Nazwa w języku angielskim: Liquid crystals and polymers Kierunek studiów (jeśli dotyczy): Fizyka
WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim: CIEKŁE KRYSZTAŁY I POLIMERY Nazwa w języku angielskim: Liquid crystals and polymers Kierunek studiów (jeśli dotyczy): Fizyka
wartość oczekiwana choinki
 wartość oczekiwana choinki Plan seminarium cośo równaniu Schrödingera analityczne metody rozwiązywania algorytm & obliczenia Schrödinger w studni koniec choinka ortogonalna Coś o równaniu Schrödingera
wartość oczekiwana choinki Plan seminarium cośo równaniu Schrödingera analityczne metody rozwiązywania algorytm & obliczenia Schrödinger w studni koniec choinka ortogonalna Coś o równaniu Schrödingera
Piotr Targowski i Bernard Ziętek GENERACJA II HARMONICZNEJ ŚWIATŁA
 Instytut Fizyki Uniwersytet Mikołaja Kopernika Piotr Targowski i Bernard Ziętek Pracownia Optoelektroniki GENERACJA II HARMONICZNEJ ŚWIATŁA Zadanie VI Zakład Optoelektroniki Toruń 004 I. Cel zadania Celem
Instytut Fizyki Uniwersytet Mikołaja Kopernika Piotr Targowski i Bernard Ziętek Pracownia Optoelektroniki GENERACJA II HARMONICZNEJ ŚWIATŁA Zadanie VI Zakład Optoelektroniki Toruń 004 I. Cel zadania Celem
Wykład Ćwiczenia Laboratorium Projekt Seminarium 45
 Zał. nr 4 do ZW /202 WYDZIAŁ PPT / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Studenckie laboratorium obliczeniowe Nazwa w języku angielskim Student computational laboratory Kierunek studiów (jeśli
Zał. nr 4 do ZW /202 WYDZIAŁ PPT / STUDIUM KARTA PRZEDMIOTU Nazwa w języku polskim Studenckie laboratorium obliczeniowe Nazwa w języku angielskim Student computational laboratory Kierunek studiów (jeśli
WSPÓŁCZYNNIK GOTOWOŚCI SYSTEMU LOKOMOTYW SPALINOWYCH SERII SM48
 TECHNIKA TRANSPORTU SZYNOWEGO Andrzej MACIEJCZYK, Zbigniew ZDZIENNICKI WSPÓŁCZYNNIK GOTOWOŚCI SYSTEMU LOKOMOTYW SPALINOWYCH SERII SM48 Streszczenie W artykule wyznaczono współczynniki gotowości systemu
TECHNIKA TRANSPORTU SZYNOWEGO Andrzej MACIEJCZYK, Zbigniew ZDZIENNICKI WSPÓŁCZYNNIK GOTOWOŚCI SYSTEMU LOKOMOTYW SPALINOWYCH SERII SM48 Streszczenie W artykule wyznaczono współczynniki gotowości systemu
Przejścia optyczne w strukturach niskowymiarowych
 Współczynnik absorpcji w układzie dwuwymiarowym można opisać wyrażeniem: E E gdzie i oraz f są energiami stanu początkowego i końcowego elektronu, zapełnienie tych stanów opisane jest funkcją rozkładu
Współczynnik absorpcji w układzie dwuwymiarowym można opisać wyrażeniem: E E gdzie i oraz f są energiami stanu początkowego i końcowego elektronu, zapełnienie tych stanów opisane jest funkcją rozkładu
- Strumień mocy, który wpływa do obszaru ograniczonego powierzchnią A ( z minusem wpływa z plusem wypływa)
 37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
37. Straty na histerezę. Sens fizyczny. Energia dostarczona do cewki ferromagnetykiem jest znacznie większa od energii otrzymanej. Energia ta jest tworzona w ferromagnetyku opisanym pętlą histerezy, stąd
Prawdopodobieństwo i statystyka
 Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Statystyka i eksploracja danych
 Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
IV. Transmisja. /~bezet
 Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
ROZCHODZENIE SIĘ POWIERZCHNIOWYCH FAL LOVE A W FALOWODACH SPREśYSTYCH OBCIĄśONYCH NA POWIERZCHNI CIECZĄ LEPKĄ (NEWTONOWSKĄ)
 1 ROZCHODZENIE SIĘ POWIERZCHNIOWYCH FAL LOVE A W FALOWODACH SPREśYSTYCH OBCIĄśONYCH NA POWIERZCHNI CIECZĄ LEPKĄ (NEWTONOWSKĄ) Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Dr inŝ. Andrzej Balcerzak, Mgr
1 ROZCHODZENIE SIĘ POWIERZCHNIOWYCH FAL LOVE A W FALOWODACH SPREśYSTYCH OBCIĄśONYCH NA POWIERZCHNI CIECZĄ LEPKĄ (NEWTONOWSKĄ) Dr hab. Piotr Kiełczyński, prof. w IPPT PAN, Dr inŝ. Andrzej Balcerzak, Mgr
Fizyka - opis przedmiotu
 Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 06.1-WM-MiBM-P-09_15gen Wydział Kierunek Wydział Mechaniczny Mechanika i budowa maszyn / Automatyzacja i organizacja procesów
Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 06.1-WM-MiBM-P-09_15gen Wydział Kierunek Wydział Mechaniczny Mechanika i budowa maszyn / Automatyzacja i organizacja procesów
I. Wprowadzenie. Oddziaływanie światła z materią to wciąż nieustający przedmiot badań podstawowych
 dr hab. inż. Włodzimierz Salejda, prof. nadzw. Wrocław, 16.02.2014 Instytut Fizyki Politechnika Wrocławska Wybrzeże Wyspiańskiego 27 50-350 Wrocław tel. +48 71 320 20 20, fax: +48 71 328 36 96 e-mail:
dr hab. inż. Włodzimierz Salejda, prof. nadzw. Wrocław, 16.02.2014 Instytut Fizyki Politechnika Wrocławska Wybrzeże Wyspiańskiego 27 50-350 Wrocław tel. +48 71 320 20 20, fax: +48 71 328 36 96 e-mail:
Faculty of Applied Physics and Mathematics -> Department of Solid State Physics. dydaktycznych, objętych planem studiów
 Nazwa i kod przedmiotu Kierunek studiów Mechanika kwantowa, NAN1B0051 Nanotechnologia Poziom studiów I stopnia - inżynierskie Typ przedmiotu obowiąkowy Forma studiów stacjonarne Sposób realizacji na uczelni
Nazwa i kod przedmiotu Kierunek studiów Mechanika kwantowa, NAN1B0051 Nanotechnologia Poziom studiów I stopnia - inżynierskie Typ przedmiotu obowiąkowy Forma studiów stacjonarne Sposób realizacji na uczelni
EiT_S_I_F2. Elektronika I Telekomunikacja I stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu EiT_S_I_F2 Nazwa modułu FIZYKA 2 Nazwa modułu w języku angielskim Physics 2 Obowiązuje
KARTA MODUŁU / KARTA PRZEDMIOTU Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. Kod modułu EiT_S_I_F2 Nazwa modułu FIZYKA 2 Nazwa modułu w języku angielskim Physics 2 Obowiązuje
Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału
 Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Fizyka 2 Wykład 4 1 Jednowymiarowa mechanika kwantowa Rozpraszanie na potencjale Na początek rozważmy najprostszy przypadek: próg potencjału Niezależne od czasu równanie Schödingera ma postać: 2 d ( x)
Fala elektromagnetyczna o określonej częstotliwości ma inną długość fali w ośrodku niż w próżni. Jako przykłady policzmy:
 Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Rozważania rozpoczniemy od ośrodków jednorodnych. W takich ośrodkach zależność między indukcją pola elektrycznego a natężeniem pola oraz między indukcją pola magnetycznego a natężeniem pola opisana jest
Spis treœci. Wstêp... 9
 Spis treœci Wstêp... 9 1. Elementy analizy wektorowej i geometrii analitycznej... 11 1.1. Podstawowe pojêcia rachunku wektorowego... 11 1.2. Dodawanie i mno enie wektorów... 14 1.3. Uk³ady wspó³rzêdnych
Spis treœci Wstêp... 9 1. Elementy analizy wektorowej i geometrii analitycznej... 11 1.1. Podstawowe pojêcia rachunku wektorowego... 11 1.2. Dodawanie i mno enie wektorów... 14 1.3. Uk³ady wspó³rzêdnych
Wysokowydajne falowodowe źródło skorelowanych par fotonów
 Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Spis treści. Wykaz ważniejszych oznaczeń. Przedmowa 15. Wprowadzenie Ruch falowy w ośrodku płynnym Pola akustyczne źródeł rzeczywistych
 Spis treści Wykaz ważniejszych oznaczeń u Przedmowa 15 Wprowadzenie 17 1. Ruch falowy w ośrodku płynnym 23 1.1. Dźwięk jako drgania ośrodka sprężystego 1.2. Fale i liczba falowa 1.3. Przestrzeń liczb falowych
Spis treści Wykaz ważniejszych oznaczeń u Przedmowa 15 Wprowadzenie 17 1. Ruch falowy w ośrodku płynnym 23 1.1. Dźwięk jako drgania ośrodka sprężystego 1.2. Fale i liczba falowa 1.3. Przestrzeń liczb falowych
Instytut Fizyki Doświadczalnej Wydział Matematyki, Fizyki i Informatyki UNIWERSYTET GDAŃSKI
 Instytut Fizyki Doświadczalnej Wydział Matematyki, Fizyki i Informatyki UNIWERSYTET GDAŃSKI I. Zagadnienia do opracowania. 1. Podstawy teorii pasmowej. 2. Klasyfikacja ciał stałych w oparciu o teorię pasmową.
Instytut Fizyki Doświadczalnej Wydział Matematyki, Fizyki i Informatyki UNIWERSYTET GDAŃSKI I. Zagadnienia do opracowania. 1. Podstawy teorii pasmowej. 2. Klasyfikacja ciał stałych w oparciu o teorię pasmową.
Podstawy Automatyki. Wykład 5 - stabilność liniowych układów dynamicznych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Wykład 5 - stabilność liniowych układów dynamicznych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Stabilność O układzie możemy mówić, że jest stabilny gdy układ ten wytrącony ze stanu równowagi
Funkcje wymierne. Jerzy Rutkowski. Działania dodawania i mnożenia funkcji wymiernych określa się wzorami: g h + k l g h k.
 Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Funkcje wymierne Jerzy Rutkowski Teoria Przypomnijmy, że przez R[x] oznaczamy zbiór wszystkich wielomianów zmiennej x i o współczynnikach rzeczywistych Definicja Funkcją wymierną jednej zmiennej nazywamy
Optyczna spektroskopia oscylacyjna. w badaniach powierzchni
 Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
Optyczna spektroskopia oscylacyjna w badaniach powierzchni Zalety oscylacyjnej spektroskopii optycznej uŝycie fotonów jako cząsteczek wzbudzających i rejestrowanych nie wymaga uŝycia próŝni (moŝliwość
