Dwuetapowe algorytmy sterowania
|
|
|
- Natalia Kaczmarek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Dwuetapowe algorytmy sterowania Leszek Leszczyński Jerzy Pułaczewski Klasyczne algorytmy sterowania działają zazwyczaj w bliskim otoczeniu punktu pra cy, podczas gdy jakość sterowania znacząco pogarsza się w pozostałych przypad kach. W opozycji do klasycznych algorytmów na trzech przykładach zostają zapre zentowane algorytmy dwuetapowe. Proponowane podejście pozwala w prosty sposób uzupełniać niektóre braki klasycznych algorytmów. Przez układ wieloetapowy rozumiemy układ sterujący, składający się z dwóch lub więcej etapów sterowania, z których każdy ma miejsce w innym obszarze przestrzeni stanu obiektu sterowanego. Innymi słowy, dla układu wieloetapowego określa się dwa lub więcej algorytmów sterowania; poszczególne algorytmy są uruchamiane w zależności od stanu, w którym obiekt się znajduje. Uzasadnijmy przykładem celowość wprowadzenia tego typu układu. Załóżmy, że celem algorytmu sterowania jest przeprowadzenie robota przez skażony teren do punktu docelowego, przy czym istnieje wydzielona trasa (robot startuje z punktu spoza trasy). W przypadku klasycznym, algorytm sterowania będzie miał na celu znalezienie najkrótszej drogi, zazwyczaj ignorując istniejącą trasę. To zadanie może się okazać niewykonalne lub bardzo trudne do zrealizowania. W proponowanym przez autorów podejściu, celem algorytmu sterowania będzie sprowadzenie robota na drogę, którą łatwo już dotrzeć do punktu docelowego. W ten sposób, przy zachowaniu względnej prostoty, uzyskuje się układ działający we wszystkich przypadkach. Niestety, może się to wiązać z wydłużeniem czasu działania układu sterującego. Strukturę algorytmu wieloetapowego można w sposób schematyczny przedstawić jak na rys. 1 a. Układy sterowania S 1, S 2 S n działają niezależnie, natomiast układ nadzorcy O odpowiada za wybór odpowiedniego wyjścia u n. Oczywiście, nie jest tutaj wymagany wybór binarny, możliwa jest np. pewna suma ważona wyjść poszczególnych układów sterowania. Przedstawiona struktura ma zastosowanie w sytuacji, gdy dysponuje się już gotowymi układami sterującymi, których nie możemy modyfikować. Wadą tej struktury jest to, że niezależnie działające układy sterowania są stale uruchomione, co przekłada się na zajętość czasu procesora. Jeżeli istnieje możliwość wprowadzania modyfikacji do układów sterujących, lepiej jest zastosować strukturę jak na rys. 1 b. Do układów sterujących doprowadzony jest dodatkowy sygnał o n z zakresu [0, 1]. Jeżeli sygnał ten ma wartość 0, dany układ sterowania jest wyłączony (nie przeprowadza się żadnych obliczeń), w przeciwnym przypadku sygnał o n jest mnożony przez wyjście układu. Podstawowym problemem przy tworzeniu wieloetapowych algorytmów sterowania jest prawidłowe zaprojektowanie algorytmu nadzorcy. W tym problemie można upatrywać braku powszechności proponowanego rozwiązania w przypadku algorytmów analogowych. Aktualnie, dostępne są zarówno nowoczesne algorytmy, takie jak sieci neuronowe czy układy rozmyte (które, jak zostanie pokazane, dobrze nadają się do implementacji nadzorcy), jak i szybkie maszyny cyfrowe, dzięki którym możliwa jest implementacja tych algorytmów. Dalej zostaną przedstawione trzy przykłady ilustrujące możliwości zastosowań algorytmów dwuetapowych. Rys. 1. Struktury układu ze sterownikiem wieloetapowym Leszek Leszczyński, doc. dr inż. Jerzy Pułaczewski Instytut Automatyki i Informatyki Stosowanej, Wydział Elektroniki i Technik Informacyjnych, Politechnika Warszawska 12
2 Parkowanie ciężarówki tyłem Przykład ilustruje możliwość wykorzystania algorytmów dwuetapowych do kompensowania niepełnej wiedzy przy projektowaniu sterownika. Przez wiedzę rozumie się znajomość właściwego sposobu sterowania obiektem. Z sytuacją niepełnej wiedzy inżynier może mieć do czynienia w przypadku nieznajomości modelu i konieczności polegania na doświadczeniu eksperta. Pozyskanie tej wiedzy może być w szczególnych przypadkach kosztowne, zwłaszcza gdy ma ona postać niewerbalną. Rozpatrywany jest problem parkowania ciężarówki tyłem, który można sformułować w następujący sposób: Położenie ciężarówki jest określone przez trzy współrzędne f, x i y (rys. 2). Sterowaną wielkością jest kąt wychylenia kół q. Ciężarówka porusza się w jednym kierunku o stałą jednostkę odległości w każdym kroku. Kinematyka ciężarówki dana jest uproszczonymi wzorami: Rozwiązaniem problemu jest algorytm sterowania, który dla x [0, 20], f [ 90, 270 ] wygeneruje takie trajektorie θ 0 θ f dla θ [ 40, 40 ], że (x φ, φ φ ) = (10, 90 ). Jako wskaźnik jakości sterowania zastosowano sumę ważoną wartości położenia x ikąta f dla y = 30: e c = arttan(e x +0,0267e φ ) (2) Rys. 2. Strefa załadunkowa i symulowana ciężarówka (1) gdzie: e x i e φ oznaczają odpowiednio bezwzględny błąd położenia i kąta. Jako zadowalające przyjęto sterowanie z błędem mniejszym niż 0,4. Przyjęto, że odległość między ciężarówką a punktem załadunkowym (10,90 ) jest duża, więc wielkość y nie jest uznawana za wejście. To założenie w znakomity sposób upraszcza problem, natomiast oczywiście negatywnie wpływa na wyniki systemu w obszarze bliskim punktu załadunkowego. Jednym z podejść do problemu parkowania ciężarówki tyłem jest sterowanie rozmyte. Przykładowa metoda projektowania sterownika rozmytego została zaproponowana w [1]. Metodologia ta polega na odpowiednim doborze reguł rozmytych nałożonych na sterownik, przy arbitralnym doborze zbiorów rozmytych reprezentujących stan i sterowanie układu. Reguły te dobiera się na podstawie wiedzy eksperckiej, którą stanowią w tym przypadku przykładowe trajektorie sterowania. Takie trajektorie można uzyskać np. poprzez obserwację sterowania układem przez eksperta lub inny działający układ sterujący. Powtórzono eksperyment opisany w [1], w którym zasugerowano, że zastosowana metoda pozwala na prawidłowe wysterowanie ciężarówki dla wszystkich możliwych punktów początkowych z badanego przedziału. Autorom nie udało się powtórzyć tych wyników. Badany układ działał poprawnie jedynie w około 50 % przypadków, w pozostałych doprowadzał ciężarówkę zbyt daleko od celu. Jedną z możliwości poprawy działania sterownika jest rozszerzenie danych eksperckich. Należy mieć na uwadze, że pozyskanie wiedzy dotyczącej poprawnego sterowania może być kosztowne w przypadku ciężarówki taki koszt jest raczej znikomy, ale może być istotny w przypadku np. rakiety typu Cruise. Drugą możliwością jest oczywiście przeprojektowanie sterownika, tj. zmiana parametrów bądź całkowita zmiana algorytmu. Tego typu postępowania mają następujące wady: nie uwzględniają istnienia sterownika działającego w pewnych przypadkach; mogą być kosztowne; nie gwarantują poprawności działania. Zamiast tego, autorzy proponują wprowadzenie dodatkowego etapu sterowania, co oznacza zaprojektowanie sterownika dwuetapowego. Dodatkowy etap sterowania będzie miał na celu sprowadzenie stanu obiektu w obszar poprawnego działania, skąd sterownik drugiego etapu (czyli istniejący algorytm) efektywnie doprowadzi układ do pożądanego celu. Zaprojektowanie układu dwuetapowego wymaga w tym wypadku następujących kroków: 1 znalezienie obszarów niepoprawnego działania istniejącego sterownika; 2 zaprojektowanie sterownika dla tych obszarów; 3 zaprojektowanie układu nadzorcy. Pierwszy krok został wykonany poprzez wielokrotną symulację układu dla warunków początkowych zmieniających się ze stałym krokiem. Przypisując poszczególnym punktom wartości 0 lub 1 (w zależności od tego, czy układ zadziałał poprawnie), uzyskano mapę punktów startowych, dla których układ działa poprawnie. Posługując się tymi danymi, zaprojektowano układ nadzorcy wykorzystano do tego celu sieć neuronową, która miała odtwarzać kształt mapy. Na rys. 3 widoczna jest mapa uzyskana z symulacji oraz odtworzona przez sieć neuronową. Te obszary, w których działanie układu było nieprawidłowe, byłyby przejmowane przez sterownik pierwszego etapu. Gładkie przełączanie między dwoma sterownikami było zapewnione przez strukturę sieci zastosowano sigmoidalne funkcje aktywacji. 13
3 układu nadzorcy uzyskano satysfakcjonujące wyniki (rys. 4): układ działał poprawnie dla każdego punktu początkowego. Niewielkim nakładem pracy poprawiono zatem pierwotny algorytm, uzyskując w pełni sprawny układ sterowania. Poprawianie sterownika czasooptymalnego Rys. 3. Obszary prawidłowego działania sterownika Przy ocenie jakości sterowania danego algorytmu istotnym czynnikiem, oprócz stabilności i dokładności, jest szybkość sterowania w sensie czasu osiągania stanu ustalonego zgodnego z wartością zadaną. Jest to czynnik szczególnie istotny w przypadku instalacji działających non stop (np. zwiększenie prędkości działania robotów w fabryce samochodów o 1 % może oznaczać 1 samochód dziennie więcej) lub układów z natury wymagających dużej szybkości działania, np. systemów sterowniczych samolotów myśliwskich. Klasyczne algorytmy oparte na liniowej teorii układów sterowania (np. typu PID) oferują niewielką złożoność (a więc i cenę), prostotę doboru parametrów oraz dobrą dokładność sterowania, natomiast szybkość regulacji zazwyczaj nie jest duża. Regulatory tego typu są jednak bardzo popularne w przemyśle. Do przyspieszenia regulacji można stosować różnorodne algorytmy nieliniowe. Ich wadą jest jednak duża złożoność, trudny dobór struktury i parametrów oraz w ogólnym przypadku brak możliwości analizy. Pewnym pomysłem na szybką regulację jest algorytm czasooptymalny. Jest to algorytm z grubsza przybliżający ludzki sposób myślenia o szybkiej regulacji, tj. ustawianie maksymalnego możliwego sterowania, a następnie korektę (wyhamowanie, także stosując maksymalne sterowanie, ale z przeciwnym znakiem) aż do osiągnięcia wartości zadanej. Teoretycznie algorytm taki zapewnia optymalny (najmniejszy) czas regulacji. W praktyce jednak zastosowanie algorytmu czasooptymalnego wiąże się z dużymi problemami, wymagana jest co najmniej znajomość dokładnego modelu obiektu. Zastosowanie modelu przybliżonego (tak strukturalnie jak i co do parametrów), wraz z błędami pomiaru i skończoną częstością próbkowania prowadzi do niedopuszczalnego zachowania regulatora (zostanie to pokazane niżej). Błędów tych nie da się wyeliminować, co w zasadzie dyskwalifikuje ten algorytm. Rozpatrzmy serwomechanizm pozycyjny, opisany znormalizowanymi równaniami: (3) Rys. 4. Porównanie działania sterownika jedno- i dwuetapowego Układ sterujący pierwszego etapu zaprojektowano jako układ rozmyty, stosując arbitralnie dobrane reguły, w taki sposób, żeby układ ten sprowadzał obiekt w obszar poprawnego działania sterownika drugiego etapu. W wyniku połączenia obu sterowników i zastosowania omówionej sieci neuronowej jako Normalizacja oznacza tutaj, że na potrzeby regulacji skaluje się odpowiednie sygnały w taki sposób, aby uprościć stałe występujące w równaniach. W rozpatrywanym przypadku stała czasowa silnika została dobrana jako duża, co nie jest widoczne w znormalizowanych równaniach. Sterowanie czasooptymalne wymaga oddziaływania sygnałem u o maksymalnej dopuszczalnej amplitudzie (w przypadku układu liniowego). Trajektorie fazowe układu dla sterowania u [-1,1] opisuje się wzorami: Z rodziny trajektorii fazowych układu są wybierane takie, które przechodzą przez (x, y) = (0,0), przez co uzyskuje się równanie opisujące krzywą przełączeń: (4) (5) 14
4 Sterowanie w otoczeniu ograniczeń sterowania Rys. 5. Odpowiedź skokowa układu ze sterownikiem czasooptymalnym Rys. 6. Działanie układu dwustopniowego (linia ciągła) i liniowego (linia przerywana) Następnie, przyjmuje się następujące prawo sterowania: Działanie układu zostało przedstawione na rys. 5. Po osiągnięciu przez sterowany obiekt zadanej wartości kąta α występują niegasnące oscylacje o małej amplitudzie, spowodowane przełączaniem układu sterowania. Takie zachowanie układu jest w ogólnym przypadku niekorzystne i niepożądane, a jednocześnie niemożliwe do wyeliminowania w strukturze algorytmu czasooptymalnego. W celu eliminacji niepożądanych zachowań zostanie podjęta próba zastosowania algorytmu dwuetapowego. Zastosowano strukturę układu odpowiednio do rys. 1 b. Jako dodatkowy układ sterujący zastosowano regulator w układzie PDI, sygnał wyjściowy regulatora jest więc wypadkową sygnałów wyjściowych układów czasooptymalnego i PDI. O udziale każdego z tych układów w sterowaniu decyduje rozmyty układ nadzorcy. Sygnał wybierający z nadzorcy jest uzależniony od uchybu oraz prędkości kątowej obiektu, jeżeli uchyb i prędkość są małe, wtedy wybierany jest sygnał ze sterownika PDI, w przeciwnym przypadku wybierany jest układ czasooptymalny. Wartości progowe w układzie nadzorcy zostały dobrane eksperymentalnie, podobnie jak parametry sterownika PDI. Zastosowanie układu rozmytego zamiast prostego przełącznika zerojedynkowego jest podyktowane chęcią wyeliminowania gwałtownych zmian wartości sterowania. Przykładowe wyniki działania układu zostały przedstawione na rys. 6. Obserwuje się przyrost szybkości regulacji w stosunku do regulatora liniowego o około 20 %, przy niewielkim przeregulowaniu i braku uchybu. Poprzez połączenie regulacji liniowej i czasooptymalnej w układ dwuetapowy udało się uzyskać szybki, stabilny regulator. (6) Rozważmy układ sterowania z liniowym obiektem i ograniczeniami sterowania. Jako regulator zastosowany został typowy układ PID, z dobranymi eksperymentalnie nastawami. Układ pracuje w trybie pracy ciągłej i jest stale zakłócany sygnałem o dużej amplitudzie. Przykładowy przebieg został pokazany na rys. 7. Regulator poprawnie kompensuje zakłócenie, jednak w momencie osiągnięcia przez sygnał sterowania wartości górnego ograniczenia zakłócenie nie może być w pełni kompensowane, przez co powstaje znaczący uchyb. Po zmniejszeniu się wartości zakłócenia sterowanie pozostaje na ograniczeniu jeszcze przez pewien czas, co powoduje dodatkowy niepożądany uchyb wartości regulowanej. W przypadku nasycenia wartości sterowania następuje przerwanie pętli sprzężenia zwrotnego, ponieważ wartość sterowania może pozostać na ograniczeniu nawet w przypadku zmiany wartości wyjścia co oznacza, że suma w bloku całkującym regulatora może osiągnąć bardzo duże wartości. Po zmniejszeniu się błędu, wartość sumy może być na tyle duża, że zejście do normalnych wartości może zająć istotnie wiele czasu. Ten efekt nazywa się nakręcaniem (windup) i usuwa się go, wprowadzając dodatkową pętlę (tzw. anti-wind-up) do algorytmu regulacji. W przypadku algorytmu dyskretnego taką pętlę można alternatywnie wyrazić w postaci prostego warunku if.else. Na rys. 7 przedstawiono działanie pętli regulacji z dodatkowym warunkiem anti-wind-up. Błąd wynikający z narastania wartości sumy w integratorze został zniwelowany, pozostaje jednak znaczący uchyb w momencie osiągnięcia przez zakłócenie dużych wartości. Uchyb ten jest oczywiście niemożliwy do usunięcia. Możliwe jest jednak polepszenie pewnych wskaźników jakości sterowania, np. średniego błędu. Zmniejszenie średniego błędu może być istotne np. 15
5 w przypadku automatycznego pilota, jeżeli średnia odchyłka od planowanego kursu jest bliska zera, punkt docelowy zostanie osiągnięty niezależnie od bezwzględnych wartości uchybu. Polepszenie takie jest możliwe przez wyprzedzanie wystąpienia uchybu, poprzez wprowadzenie uchybu o przeciwnym znaku i podobnej amplitudzie. Wprowadźmy do układu dodatkowy blok regulacji nadrzędnej (pierwszy stopień sterowania). Załóżmy czas próbkowania bloku nadrzędnego jako dużo większy od czasu próbkowania bloku bezpośredniego. Wynika to z tego, że w pojedynczym kroku regulacji nadrzędnej w obiekcie powinny zaniknąć stany przejściowe i obiekt może zostać potraktowany jako statyczny o wzmocnieniu proporcjonalnym K p. Przyjęto następujące przybliżenie: (7) Taka wielkość sterowania jest wymagana do prawidłowej kompensacji zakłócenia w chwili k-tej. Z tej zależności, mając gotową predykcję wartości zakłócenia d p (k), obliczany jest ciąg predykowanych wartości sterowania. Z tych wartości otrzymuje się czasy t r i t s, odpowiadające najbliższej chwili, w której układ wejdzie na zakłócenia oraz chwili, w której te zakłócenia opuści. Dodatkowo zapamiętuje się wartość u, określającą maksymalną różnicę między sterowaniem a wartością zadaną, która przystaje do maksymalnej wartości uchybu, jaki wytworzy się w wyniku działania zakłócenia. Na podstawie tych wielkości na wyjście układu nadrzędnego wystawiana jest wartość poprawki: (8) Dla tak sformułowanego prostego algorytmu wykonano szereg eksperymentów symulacyjnych. Przyjęto czas próbkowania bloku nadrzędnego 10 razy dłuższy od czasu próbkowania regulatora bezpośredniego, który miał postać algorytmu PID z pętlą anti-wind-up. Jako zakłócenie przyjęto quasi-okresowe sygnały o różnych amplitudach i częstotliwościach. Do celów predykcji zastosowano model AR o raczej dużej złożoności. Przykładowy wynik symulacji znajduje się rys. 8. Dzięki zastosowaniu sterownika dwuetapowego udało się zredukować średnią wartość uchybu, co niestety pociągnęło za sobą zwiększenie błędu średniokwadratowego. Rys. 7. Układ liniowy z ograniczeniem sterowania, bez pętli anti-wind-up i z taką pętlą Rys. 8. Działanie algorytmu dwuetapowego dla różnych sygnałów zakłócenia 16
6 Podsumowanie Dwuetapowe algorytmy sterowania są wygodnym i prostym sposobem omijania problemów związanych z różnorodnymi ograniczeniami klasycznych algorytmów sterowania, takich jak nieliniowości, błędy modelowania i inne. Przykładowe zastosowania algorytmów dwuetapowych mogą dotyczyć sytuacji, w których: dysponuje się algorytmem klasycznym o odpowiednio dobranych parametrach; algorytm klasyczny działa poprawnie jedynie w pewnym zakresie zmienności zmiennych stanu; algorytm klasyczny ma cechy zmniejszające jakość sterowania w pewnym obszarze zakresu zmienności zmiennych stanu. Stosowanie algorytmów dwuetapowych w zasadzie wymaga stosowania sterowników cyfrowych. Ze względu na powszechną dostępność takich urządzeń oraz ich malejące ceny nie stanowi to przeszkody. Pewnym problemem może być jednak stosunkowo duży nakład obliczeń związany z układem nadzorcy, który może wymagać stosowania urządzeń o stosunkowo dużej wydajności. Bibliografia 1. Wang L., Mendel J.: Generating Fuzzy Rules by Learning from Examples. 2. Piegat A.: Modelowanie i sterowanie rozmyte, Oficyna Wydawnicza EXIT Osowski S.: Sieci neuronowe w ujęciu algorytmicznym, WNT Tatjewski P.: Sterowanie zaawansowane obiektów przemysłowych struktury i algorytmy, Oficyna Wydawnicza EXIT, REKLAMA REKLAMA
Obiekt. Obiekt sterowania obiekt, który realizuje proces (zaplanowany).
 SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
SWB - Systemy wbudowane w układach sterowania - wykład 13 asz 1 Obiekt sterowania Wejście Obiekt Wyjście Obiekt sterowania obiekt, który realizuje proces (zaplanowany). Fizyczny obiekt (proces, urządzenie)
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 206/207
Podstawy Automatyki. Wykład 9 - Dobór regulatorów. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Wykład 9 - Dobór regulatorów. Instytut Automatyki i Robotyki Warszawa, 2017 Dobór regulatorów Podstawową przesłanką przy wyborze rodzaju regulatora są właściwości dynamiczne obiektu regulacji. Rysunek:
Dobór parametrów regulatora - symulacja komputerowa. Najprostszy układ automatycznej regulacji można przedstawić za pomocą
 Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
Politechnika Świętokrzyska Wydział Mechatroniki i Budowy Maszyn Centrum Laserowych Technologii Metali PŚk i PAN Zakład Informatyki i Robotyki Przedmiot:Podstawy Automatyzacji - laboratorium, rok I, sem.
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Dla naszego obiektu ciągłego: przy czasie próbkowania T p =2.
 1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
1. Celem zadania drugiego jest przeprowadzenie badań symulacyjnych układu regulacji obiektu G(s), z którym zapoznaliśmy się w zadaniu pierwszym, i regulatorem cyfrowym PID, którego parametry zostaną wyznaczone
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Automatyka i pomiary wielkości fizykochemicznych. Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa.
 Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Automatyka i pomiary wielkości fizykochemicznych Instrukcja do ćwiczenia VI Dobór nastaw regulatora typu PID metodą Zieglera-Nicholsa. 1. Wprowadzenie Regulator PID (regulator proporcjonalno-całkująco-różniczkujący,
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Badanie i synteza kaskadowego adaptacyjnego układu regulacji do sterowania obiektu o
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 207/208
STEROWANIE MASZYN I URZĄDZEŃ I. Laboratorium. 8. Układy ciągłe. Regulator PID
 STEROWANIE MASZYN I URZĄDZEŃ I Laboratorium 8. Układy ciągłe. Regulator PID Opracował: dr hab. inż. Cezary Orlikowski Instytut Politechniczny 1 Blok funkcyjny regulatora PID przedstawiono na rys.1. Opis
STEROWANIE MASZYN I URZĄDZEŃ I Laboratorium 8. Układy ciągłe. Regulator PID Opracował: dr hab. inż. Cezary Orlikowski Instytut Politechniczny 1 Blok funkcyjny regulatora PID przedstawiono na rys.1. Opis
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II
 Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Automatyka i Regulacja Automatyczna Laboratorium Zagadnienia Seria II Zagadnienia na ocenę 3.0 1. Podaj transmitancję oraz naszkicuj teoretyczną odpowiedź skokową układu całkującego z inercją 1-go rzędu.
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku
 Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Układ regulacji ze sprzężeniem zwrotnym: - układ regulacji kaskadowej - układ regulacji stosunku Przemysłowe Układy Sterowania PID Opracowanie: dr inż. Tomasz Rutkowski Katedra Inżynierii Systemów Sterowania
Podstawy Automatyki. Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID. dr inż. Jakub Możaryn. Instytut Automatyki i Robotyki
 Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Wykład 7 - Jakość układu regulacji. Dobór nastaw regulatorów PID Instytut Automatyki i Robotyki Warszawa, 2015 Jakość układu regulacji Oprócz wymogu stabilności asymptotycznej, układom regulacji stawiane
Rys. 1 Otwarty układ regulacji
 Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
Automatyka zajmuje się sterowaniem, czyli celowym oddziaływaniem na obiekt, w taki sposób, aby uzyskać jego pożądane właściwości. Sterowanie często nazywa się regulacją. y zd wartość zadana u sygnał sterujący
WYDZIAŁ ELEKTRYCZNY KATEDRA AUTOMATYKI I ELEKTRONIKI. Badanie układu regulacji dwustawnej
 POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
POLITECHNIKA BIAŁOSTOCKA WYDZIAŁ ELEKTRYCZNY KATEDRA ATOMATYKI I ELEKTRONIKI ĆWICZENIE Nr 8 Badanie układu regulacji dwustawnej Dobór nastaw regulatora dwustawnego Laboratorium z przedmiotu: ATOMATYKA
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Optymalizacja ciągła
 Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
Optymalizacja ciągła 5. Metoda stochastycznego spadku wzdłuż gradientu Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 04.04.2019 1 / 20 Wprowadzenie Minimalizacja różniczkowalnej
AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 75 Electrical Engineering 2013 Łukasz NIEWIARA* Krzysztof ZAWIRSKI* AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ Zagadnienia
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 75 Electrical Engineering 2013 Łukasz NIEWIARA* Krzysztof ZAWIRSKI* AUTO-STROJENIE REGULATORA TYPU PID Z WYKORZYSTANIEM LOGIKI ROZMYTEJ Zagadnienia
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA
 Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Instrukcja do ćwiczenia 6 REGULACJA TRÓJPOŁOŻENIOWA Cel ćwiczenia: dobór nastaw regulatora, analiza układu regulacji trójpołożeniowej, określenie jakości regulacji trójpołożeniowej w układzie bez zakłóceń
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu
 Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Badanie kaskadowego układu regulacji na przykładzie serwomechanizmu 1. WSTĘP Serwomechanizmy są to przeważnie układy regulacji położenia. Są trzy główne typy zadań serwomechanizmów: - ruch point-to-point,
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 12. Regulacja dwu- i trójpołożeniowa (wg. Holejko, Kościelny: Automatyka procesów ciągłych)
Regulacja dwupołożeniowa (dwustawna)
 Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Regulacja dwupołożeniowa (dwustawna) I. Wprowadzenie Regulacja dwustawna (dwupołożeniowa) jest często stosowaną metodą regulacji temperatury w urządzeniach grzejnictwa elektrycznego. Polega ona na cyklicznym
Regulator PID w sterownikach programowalnych GE Fanuc
 Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
Regulator PID w sterownikach programowalnych GE Fanuc Wykład w ramach przedmiotu: Sterowniki programowalne Opracował na podstawie dokumentacji GE Fanuc dr inż. Jarosław Tarnawski Cel wykładu Przypomnienie
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH
 REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Reprezentacja
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Reprezentacja
Regulatory o działaniu ciągłym P, I, PI, PD, PID
 Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Regulatory o działaniu ciągłym P, I, PI, PD, PID Regulatory o działaniu ciągłym (analogowym) zmieniają wartość wielkości sterującej obiektem w sposób ciągły, tzn. wielkość ta może przyjmować wszystkie
Automatyka i sterowania
 Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Automatyka i sterowania Układy regulacji Regulacja i sterowanie Przykłady regulacji i sterowania Funkcje realizowane przez automatykę: regulacja sterowanie zabezpieczenie optymalizacja Automatyka i sterowanie
Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena LABORATORIUM 4. PODSTAW 5. AUTOMATYKI
 Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
Instytut Automatyki i Robotyki Prowadzący(a) Grupa Zespół data ćwiczenia Lp. Nazwisko i imię Ocena 1. 2. 3. LABORATORIUM 4. PODSTAW 5. AUTOMATYKI Ćwiczenie PA7b 1 Badanie jednoobwodowego układu regulacji
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH
 REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia I stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Pojęcie
REPREZENTACJA LICZBY, BŁĘDY, ALGORYTMY W OBLICZENIACH Transport, studia I stopnia rok akademicki 2012/2013 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Pojęcie
Podstawy Automatyki. Wykład 7 - obiekty regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
Wykład 7 - obiekty regulacji Instytut Automatyki i Robotyki Warszawa, 2018 Obiekty regulacji Obiekt regulacji Obiektem regulacji nazywamy proces technologiczny podlegający oddziaływaniu zakłóceń, zachodzący
PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa
 Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
Rok akademicki 2015/2016 Semestr letni PODSTAWY AUTOMATYKI I MIERNICTWA PRZEMYSŁOWEGO Laboratorium 3 Regulatory PID i ich strojenie, Regulacja dwupołożeniowa Wstęp teoretyczny: W układzie regulacji określa
4. Właściwości eksploatacyjne układów regulacji Wprowadzenie. Hs () Ys () Ws () Es () Go () s. Vs ()
 4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
4. Właściwości eksploatacyjne układów regulacji 4.1. Wprowadzenie Zu () s Zy ( s ) Ws () Es () Gr () s Us () Go () s Ys () Vs () Hs () Rys. 4.1. Schemat blokowy układu regulacji z funkcjami przejścia 1
LAB-EL LB-760A: regulacja PID i procedura samostrojenia
 Page 1 of 5 Copyright 2003-2010 LAB-EL Elektronika Laboratoryjna www.label.pl LAB-EL LB-760A: regulacja PID i procedura samostrojenia Nastawy regulatora PID W regulatorze LB-760A poczynając od wersji 7.1
Page 1 of 5 Copyright 2003-2010 LAB-EL Elektronika Laboratoryjna www.label.pl LAB-EL LB-760A: regulacja PID i procedura samostrojenia Nastawy regulatora PID W regulatorze LB-760A poczynając od wersji 7.1
Modelowanie jako sposób opisu rzeczywistości. Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka
 Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
Modelowanie jako sposób opisu rzeczywistości Katedra Mikroelektroniki i Technik Informatycznych Politechnika Łódzka 2015 Wprowadzenie: Modelowanie i symulacja PROBLEM: Podstawowy problem z opisem otaczającej
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
Nazwa przedmiotu: Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy Rodzaj zajęć: wykład, laboratorium Automatyka Automatics Forma studiów: studia stacjonarne Poziom kwalifikacji: I stopnia Liczba
1. Podstawowe pojęcia
 1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
1. Podstawowe pojęcia Sterowanie optymalne obiektu polega na znajdowaniu najkorzystniejszej decyzji dotyczącej zamierzonego wpływu na obiekt przy zadanych ograniczeniach. Niech dany jest obiekt opisany
Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy Anti-windup.
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Podstawy Automatyki Silnik prądu stałego (NI Elvis 2) Dobieranie nastaw regulatorów P, PI, PID. Filtr przeciwnasyceniowy
Temat: Projektowanie sterownika rozmytego. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Projektowanie sterownika rozmytego Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie System
Temat: Projektowanie sterownika rozmytego Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie System
1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI
 Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
Podstawy automatyki / Józef Lisowski. Gdynia, 2015 Spis treści PRZEDMOWA 9 WSTĘP 11 1. POJĘCIA PODSTAWOWE I RODZAJE UKŁADÓW AUTOMATYKI 17 1.1. Automatyka, sterowanie i regulacja 17 1.2. Obiekt regulacji
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
Nazwa przedmiotu: Kierunek: ENERGETYKA Rodzaj przedmiotu: kierunkowy ogólny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1. Zapoznanie studentów z własnościami
lim Np. lim jest wyrażeniem typu /, a
 Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Wykład 3 Pochodna funkcji złożonej, pochodne wyższych rzędów, reguła de l Hospitala, różniczka funkcji i jej zastosowanie, pochodna jako prędkość zmian 3. Pochodna funkcji złożonej. Jeżeli funkcja złożona
Sposoby modelowania układów dynamicznych. Pytania
 Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Sposoby modelowania układów dynamicznych Co to jest model dynamiczny? PAScz4 Modelowanie, analiza i synteza układów automatyki samochodowej równania różniczkowe, różnicowe, równania równowagi sił, momentów,
Temat: Projektowanie sterownika rozmytego. Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Projektowanie sterownika rozmytego Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
Temat: Projektowanie sterownika rozmytego Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe.
 Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe. zajecia.jakubw.pl/nai Literatura: S. Osowski, Sieci neuronowe w ujęciu algorytmicznym. WNT, Warszawa 997. PODSTAWOWE ZAGADNIENIA TECHNICZNE AI
Zagadnienia optymalizacji i aproksymacji. Sieci neuronowe. zajecia.jakubw.pl/nai Literatura: S. Osowski, Sieci neuronowe w ujęciu algorytmicznym. WNT, Warszawa 997. PODSTAWOWE ZAGADNIENIA TECHNICZNE AI
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
SIMATIC S Regulator PID w sterowaniu procesami. dr inż. Damian Cetnarowicz. Plan wykładu. I n t e l i g e n t n e s y s t e m y z e
 Plan wykładu I n t e l i g e n t n e s y s t e m y z e s p r zężeniem wizyjnym wykład 6 Sterownik PID o Wprowadzenie o Wiadomości podstawowe o Implementacja w S7-1200 SIMATIC S7-1200 Regulator PID w sterowaniu
Plan wykładu I n t e l i g e n t n e s y s t e m y z e s p r zężeniem wizyjnym wykład 6 Sterownik PID o Wprowadzenie o Wiadomości podstawowe o Implementacja w S7-1200 SIMATIC S7-1200 Regulator PID w sterowaniu
WYDZIAŁ PPT / KATEDRA INŻYNIERII BIOMEDYCZNEJ D-1 LABORATORIUM Z MIERNICTWA I AUTOMATYKI Ćwiczenie nr 7. Badanie jakości regulacji dwupołożeniowej.
 Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
REGULATOR PI W SIŁOWNIKU 2XI
 REGULATOR PI W SIŁOWNIKU 2XI Wydanie 1 lipiec 2012 r. 1 1. Regulator wbudowany PI Oprogramowanie sterownika Servocont-03 zawiera wbudowany algorytm regulacji PI (opcja). Włącza się go poprzez odpowiedni
REGULATOR PI W SIŁOWNIKU 2XI Wydanie 1 lipiec 2012 r. 1 1. Regulator wbudowany PI Oprogramowanie sterownika Servocont-03 zawiera wbudowany algorytm regulacji PI (opcja). Włącza się go poprzez odpowiedni
WZMACNIACZE OPERACYJNE Instrukcja do zajęć laboratoryjnych
 WZMACNIACZE OPERACYJNE Instrukcja do zajęć laboratoryjnych Tematem ćwiczenia są zastosowania wzmacniaczy operacyjnych w układach przetwarzania sygnałów analogowych. Ćwiczenie składa się z dwóch części:
WZMACNIACZE OPERACYJNE Instrukcja do zajęć laboratoryjnych Tematem ćwiczenia są zastosowania wzmacniaczy operacyjnych w układach przetwarzania sygnałów analogowych. Ćwiczenie składa się z dwóch części:
Laboratorium z podstaw automatyki
 Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
Wydział Inżynierii Mechanicznej i Mechatroniki Laboratorium z podstaw automatyki Dobór parametrów układu regulacji, Identyfikacja parametrów obiektów dynamicznych Kierunek studiów: Transport, Stacjonarne
REDUKCJA ZJAWISKA CHATTERINGU W ALGORYTMIE SMC W STEROWANIU SERWOMECHANIZMÓW ELEKTROHYDRAULICZNYCH
 REDUKCJA ZJAWISKA CHATTERINGU W ALGORYTMIE SMC W STEROWANIU SERWOMECHANIZMÓW ELEKTROHYDRAULICZNYCH Paweł Bachman, Uniwersytet Zielonogórski Instytut Edukacji Techniczno Informatycznej W artykule opisano
REDUKCJA ZJAWISKA CHATTERINGU W ALGORYTMIE SMC W STEROWANIU SERWOMECHANIZMÓW ELEKTROHYDRAULICZNYCH Paweł Bachman, Uniwersytet Zielonogórski Instytut Edukacji Techniczno Informatycznej W artykule opisano
Pomiar rezystancji metodą techniczną
 Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
Pomiar rezystancji metodą techniczną Cel ćwiczenia. Poznanie metod pomiarów rezystancji liniowych, optymalizowania warunków pomiaru oraz zasad obliczania błędów pomiarowych. Zagadnienia teoretyczne. Definicja
WYDZIAŁ PPT / KATEDRA INŻYNIERII BIOMEDYCZNEJ D-1 LABORATORIUM Z AUTOMATYKI I ROBOTYKI Ćwiczenie nr 4. Badanie jakości regulacji dwupołożeniowej.
 Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
Cel ćwiczenia: Zapoznanie się z zasadą działania regulatora dwupołożeniowego oraz ocena jakości regulacji dwupołożeniowej na przykładzie obiektu rzeczywistego (mikrotermostat) i badań symulacyjnych. Pytania
INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki
 Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
Opracowano na podstawie: INSTRUKCJA Regulacja PID, badanie stabilności układów automatyki 1. Kaczorek T.: Teoria sterowania, PWN, Warszawa 1977. 2. Węgrzyn S.: Podstawy automatyki, PWN, Warszawa 1980 3.
6. Zagadnienie parkowania ciężarówki.
 6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
6. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Metoda zaburz-obserwuj oraz metoda wspinania
 Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
Metoda zaburz-obserwuj oraz metoda wspinania Algorytm zaburz-obserwuj mierzy się moc (zwykle modułu) przed i po zmianie na tej podstawie podejmuje się decyzję o kierunku następnej zmiany Metoda wspinania
Regulator P (proporcjonalny)
 Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Regulator P (proporcjonalny) Regulator P (Proportional Controller) składa się z jednego członu typu P (proporcjonalnego), którego transmitancję określa wzmocnienie: W regulatorze tym sygnał wyjściowy jest
Tomasz Żabiński, tomz@prz-rzeszow.pl, 2006-03-14 90
 Poniżej przedstawiono zagadnienie automatycznej pracy suwnicy (Sawodny et al. 2002), będącej elementem np. zautomatyzowanej linii produkcyjnej. Opracowany system sterowania realizuje bezpieczny transport
Poniżej przedstawiono zagadnienie automatycznej pracy suwnicy (Sawodny et al. 2002), będącej elementem np. zautomatyzowanej linii produkcyjnej. Opracowany system sterowania realizuje bezpieczny transport
Dynamika procesu zmienna stała. programowalne zmiany parametrów r.
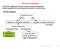 Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Sterowanie adaptacyjne Sterowanie adaptacyjne polega na dostosowywaniu (adaptacji) nastaw regulatora do zmian parametrów obiektu (w trakcie pracy) Techniki adaptacji Dynamika procesu zmienna stała regulator
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4
 Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Cyfrowe algorytmy sterowania AR S1 semestr 4 Projekt 4 MPC Sterowanie predykcyjne Cel: Poznanie podstaw regulacji predykcyjnej i narzędzi do badań symulacyjnych Wykonali: Konrad Słodowicz Patryk Frankowski
Politechnika Warszawska Instytut Automatyki i Robotyki. Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI
 Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
Politechnika Warszawska Instytut Automatyki i Robotyki Prof. dr hab. inż. Jan Maciej Kościelny PODSTAWY AUTOMATYKI 1. Dobór rodzaju i nastaw regulatorów PID Rodzaje regulatorów 2 Regulatory dwustawne (2P)
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MODELOWANIE I SYMULACJA UKŁADÓW STEROWANIA Kierunek: Mechatronika Rodzaj przedmiotu: Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1.
Nazwa przedmiotu: MODELOWANIE I SYMULACJA UKŁADÓW STEROWANIA Kierunek: Mechatronika Rodzaj przedmiotu: Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE C1.
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Automatyka i robotyka
 Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
Automatyka i robotyka Wykład 5 - Stabilność układów dynamicznych Wojciech Paszke Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski 1 z 43 Plan wykładu Wprowadzenie Stabilność modeli
INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE
 Temat: Podstawowe pojęcia z logiki rozmytej Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
Temat: Podstawowe pojęcia z logiki rozmytej Instrukcja do ćwiczeń przedmiotu INŻYNIERIA WIEDZY I SYSTEMY EKSPERTOWE Dr inż. Barbara Mrzygłód KISiM, WIMiIP, AGH mrzyglod@ agh.edu.pl 1 Wprowadzenie Sterowanie
Regulacja dwupołożeniowa.
 Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
Politechnika Krakowska Wydział Inżynierii Elektrycznej i Komputerowej Zakład eorii Sterowania Regulacja dwupołożeniowa. Kraków Zakład eorii Sterowania (E ) Regulacja dwupołożeniowa opis ćwiczenia.. Opis
ALGORYTM PROJEKTOWANIA ROZMYTYCH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO
 Szybkobieżne Pojazdy Gąsienicowe (2) Nr 2, 24 Mirosław ADAMSKI Norbert GRZESIK ALGORYTM PROJEKTOWANIA CH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO. WSTĘP
Szybkobieżne Pojazdy Gąsienicowe (2) Nr 2, 24 Mirosław ADAMSKI Norbert GRZESIK ALGORYTM PROJEKTOWANIA CH SYSTEMÓW EKSPERCKICH TYPU MAMDANI ZADEH OCENIAJĄCYCH EFEKTYWNOŚĆ WYKONANIA ZADANIA BOJOWEGO. WSTĘP
Sterowanie napędów maszyn i robotów
 Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
Wykład 7b - Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Instytut Automatyki i Robotyki Warszawa, 2014 Układy wieloobwodowe ze sprzężeniem od zmiennych stanu Zadanie przestawiania Postać modalna
1. Opis teoretyczny regulatora i obiektu z opóźnieniem.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie:. Opis teoretyczny regulatora i obiektu z opóźnieniem. W regulacji dwupołożeniowej sygnał sterujący przyjmuje dwie wartości: pełne załączenie i wyłączenie...
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie:. Opis teoretyczny regulatora i obiektu z opóźnieniem. W regulacji dwupołożeniowej sygnał sterujący przyjmuje dwie wartości: pełne załączenie i wyłączenie...
Podstawy Automatyki. Wykład 6 - Miejsce i rola regulatora w układzie regulacji. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Wykład 6 - Miejsce i rola regulatora w układzie regulacji Instytut Automatyki i Robotyki Warszawa, 2015 Regulacja zadajnik regulator sygnał sterujący (sterowanie) zespół wykonawczy przetwornik pomiarowy
Efekty kształcenia na kierunku AiR drugiego stopnia - Wiedza Wydziału Elektrotechniki, Automatyki i Informatyki Politechniki Opolskiej
 Efekty na kierunku AiR drugiego stopnia - Wiedza K_W01 K_W02 K_W03 K_W04 K_W05 K_W06 K_W07 K_W08 K_W09 K_W10 K_W11 K_W12 K_W13 K_W14 Ma rozszerzoną wiedzę dotyczącą dynamicznych modeli dyskretnych stosowanych
Efekty na kierunku AiR drugiego stopnia - Wiedza K_W01 K_W02 K_W03 K_W04 K_W05 K_W06 K_W07 K_W08 K_W09 K_W10 K_W11 K_W12 K_W13 K_W14 Ma rozszerzoną wiedzę dotyczącą dynamicznych modeli dyskretnych stosowanych
Inteligencja obliczeniowa
 Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
Ćwiczenie nr 3 Zbiory rozmyte logika rozmyta Sterowniki wielowejściowe i wielowyjściowe, relacje rozmyte, sposoby zapisu reguł, aproksymacja funkcji przy użyciu reguł rozmytych, charakterystyki przejściowe
Praktyka inżynierska korzystamy z tego co mamy. regulator. zespół wykonawczy. obiekt (model) Konfiguracja regulatora
 raktyka inżynierska korzystamy z tego co mamy Urządzenia realizujące: - blok funkcyjny D w sterowniku LC - moduł D w sterowniku LC - regulator wielofunkcyjny - prosty regulator cyfrowy zadajnik S e CV
raktyka inżynierska korzystamy z tego co mamy Urządzenia realizujące: - blok funkcyjny D w sterowniku LC - moduł D w sterowniku LC - regulator wielofunkcyjny - prosty regulator cyfrowy zadajnik S e CV
Szybkie prototypowanie w projektowaniu mechatronicznym
 Szybkie prototypowanie w projektowaniu mechatronicznym Systemy wbudowane (Embedded Systems) Systemy wbudowane (ang. Embedded Systems) są to dedykowane architektury komputerowe, które są integralną częścią
Szybkie prototypowanie w projektowaniu mechatronicznym Systemy wbudowane (Embedded Systems) Systemy wbudowane (ang. Embedded Systems) są to dedykowane architektury komputerowe, które są integralną częścią
Sterowanie z wykorzystaniem logiki rozmytej
 Sterowanie z wykorzystaniem logiki rozmytej konspekt seminarium Paweł Szołtysek 24 stycznia 2009 1 Wstęp 1.1 Podstawy logiki rozmytej Logika rozmyta jest rodzajem logiki wielowartościowej, stanowi uogólnienie
Sterowanie z wykorzystaniem logiki rozmytej konspekt seminarium Paweł Szołtysek 24 stycznia 2009 1 Wstęp 1.1 Podstawy logiki rozmytej Logika rozmyta jest rodzajem logiki wielowartościowej, stanowi uogólnienie
Problemy optymalizacji układów napędowych w automatyce i robotyce
 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Katedra Automatyki Autoreferat rozprawy doktorskiej Problemy optymalizacji układów napędowych
Politechnika Białostocka
 Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: ELEKTRONIKA EKS1A300024 Zastosowania wzmacniaczy operacyjnych w układach
Politechnika Białostocka Wydział Elektryczny Katedra Automatyki i Elektroniki Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: ELEKTRONIKA EKS1A300024 Zastosowania wzmacniaczy operacyjnych w układach
2. Wyznaczenie parametrów dynamicznych obiektu na podstawie odpowiedzi na skok jednostkowy, przy wykorzystaniu metody Küpfmüllera.
 1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
1. Celem projektu jest zaprojektowanie układu regulacji wykorzystującego regulator PI lub regulator PID, dla określonego obiektu składającego się z iloczynu dwóch transmitancji G 1 (s) i G 2 (s). Następnym
Podstawy automatyki. Energetyka Sem. V Wykład 1. Sem /17 Hossein Ghaemi
 Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Podstawy automatyki Energetyka Sem. V Wykład 1 Sem. 1-2016/17 Hossein Ghaemi Hossein Ghaemi Katedra Automatyki i Energetyki Wydział Oceanotechniki i Okrętownictwa Politechnika Gdańska pok. 222A WOiO Tel.:
Obliczenia polowe silnika przełączalnego reluktancyjnego (SRM) w celu jego optymalizacji
 Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
Akademia Górniczo Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Studenckie Koło Naukowe Maszyn Elektrycznych Magnesik Obliczenia polowe silnika
Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym
 Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym 1. Cel ćwiczenia Celem ćwiczenia jest analiza właściwości układu sterowania w torze otwartym, zamkniętym oraz zamkniętym z kompensacją zakłóceń.
Ćwiczenie nr 3 Układy sterowania w torze otwartym i zamkniętym 1. Cel ćwiczenia Celem ćwiczenia jest analiza właściwości układu sterowania w torze otwartym, zamkniętym oraz zamkniętym z kompensacją zakłóceń.
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki
 Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
Politechnika Warszawska Wydział Samochodów i Maszyn Roboczych Instytut Podstaw Budowy Maszyn Zakład Mechaniki http://www.ipbm.simr.pw.edu.pl/ Teoria maszyn i podstawy automatyki semestr zimowy 2017/2018
7. Zagadnienie parkowania ciężarówki.
 7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
7. Zagadnienie parkowania ciężarówki. Sterowniki rozmyte Aby móc sterować przebiegiem pewnych procesów lub też pracą urządzeń niezbędne jest stworzenie odpowiedniego modelu, na podstawie którego można
PRZETWORNIKI C / A PODSTAWOWE PARAMETRY
 PRZETWORIKI C / A PODSTAWOWE PARAMETRY Rozdzielczość przetwornika C/A - Określa ją liczba - bitów słowa wejściowego. - Definiuje się ją równieŝ przez wartość związaną z najmniej znaczącym bitem (LSB),
PRZETWORIKI C / A PODSTAWOWE PARAMETRY Rozdzielczość przetwornika C/A - Określa ją liczba - bitów słowa wejściowego. - Definiuje się ją równieŝ przez wartość związaną z najmniej znaczącym bitem (LSB),
Układy sterowania robotów przemysłowych. Warstwa programowania trajektorii ruchu. Warstwa wyznaczania trajektorii ruchu.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA RiSM Układy sterowania robotów przemysłowych. Warstwa programowania trajektorii ruchu. Warstwa wyznaczania trajektorii ruchu. Dr inż. Mariusz Dąbkowski Zadaniem
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA RiSM Układy sterowania robotów przemysłowych. Warstwa programowania trajektorii ruchu. Warstwa wyznaczania trajektorii ruchu. Dr inż. Mariusz Dąbkowski Zadaniem
Wysokowydajne falowniki wektorowe Micno KE300.
 Wysokowydajne falowniki wektorowe Micno KE300. Firma Shenzhen Micno Electric Co. jest przedsiębiorstwem zajmującym się zaawansowanymi technologiami. Specjalizuje się w pracach badawczorozwojowych, produkcji,
Wysokowydajne falowniki wektorowe Micno KE300. Firma Shenzhen Micno Electric Co. jest przedsiębiorstwem zajmującym się zaawansowanymi technologiami. Specjalizuje się w pracach badawczorozwojowych, produkcji,
4. UKŁADY II RZĘDU. STABILNOŚĆ. Podstawowe wzory. Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat. Transmitancja układu zamkniętego
 4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
4. UKŁADY II RZĘDU. STABILNOŚĆ Podstawowe wzory Układ II rzędu ze sprzężeniem zwrotnym Standardowy schemat (4.1) Transmitancja układu zamkniętego częstotliwość naturalna współczynnik tłumienia Odpowiedź
Podstawowe zastosowania wzmacniaczy operacyjnych
 ĆWICZENIE 0 Podstawowe zastosowania wzmacniaczy operacyjnych I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i właściwościami wzmacniaczy operacyjnych oraz podstawowych układów elektronicznych
ĆWICZENIE 0 Podstawowe zastosowania wzmacniaczy operacyjnych I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z budową i właściwościami wzmacniaczy operacyjnych oraz podstawowych układów elektronicznych
11. Dobór rodzaju, algorytmu i nastaw regulatora
 205 11. Dobór rodzaju, algorytmu i nastaw regulatora 11.1 Wybór rodzaju i algorytmu regulatora Poprawny wybór rodzaju regulatora i jego algorytmu uzależniony jest od znajomości (choćby przybliżonej) właściwości
205 11. Dobór rodzaju, algorytmu i nastaw regulatora 11.1 Wybór rodzaju i algorytmu regulatora Poprawny wybór rodzaju regulatora i jego algorytmu uzależniony jest od znajomości (choćby przybliżonej) właściwości
BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO
 Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
Ćwiczenie 11 BADANIE PRZERZUTNIKÓW ASTABILNEGO, MONOSTABILNEGO I BISTABILNEGO 11.1 Cel ćwiczenia Celem ćwiczenia jest poznanie rodzajów, budowy i właściwości przerzutników astabilnych, monostabilnych oraz
E2_PA Podstawy automatyki Bases of automatic. Elektrotechnika II stopień (I stopień / II stopień) Ogólnoakademicki (ogólno akademicki / praktyczny)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. P KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. P KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2012/2013
Sterowanie w programie ADAMS regulator PID. Przemysław Sperzyński
 Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Sterowanie w programie ADAMS regulator PID Przemysław Sperzyński Schemat regulatora K p e t e t = u zad t u akt (t) M = K p e t + K i e t + K d de(t) u zad uakt M K i e t K d de t Uchyb regulacji człony
Laboratorium elementów automatyki i pomiarów w technologii chemicznej
 POLITECHNIKA WROCŁAWSKA Wydziałowy Zakład Inżynierii Biomedycznej i Pomiarowej Laboratorium elementów automatyki i pomiarów w technologii chemicznej Instrukcja do ćwiczenia Regulacja dwupołożeniowa Wrocław
POLITECHNIKA WROCŁAWSKA Wydziałowy Zakład Inżynierii Biomedycznej i Pomiarowej Laboratorium elementów automatyki i pomiarów w technologii chemicznej Instrukcja do ćwiczenia Regulacja dwupołożeniowa Wrocław
Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych
 XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
XXXVIII MIĘDZYUCZELNIANIA KONFERENCJA METROLOGÓW MKM 06 Warszawa Białobrzegi, 4-6 września 2006 r. Symulacja sygnału czujnika z wyjściem częstotliwościowym w stanach dynamicznych Eligiusz PAWŁOWSKI Politechnika
ELEMENTY AUTOMATYKI PRACA W PROGRAMIE SIMULINK 2013
 SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
SIMULINK część pakietu numerycznego MATLAB (firmy MathWorks) służąca do przeprowadzania symulacji komputerowych. Atutem programu jest interfejs graficzny (budowanie układów na bazie logicznie połączonych
Lekcja : Tablice + pętle
 Lekcja : Tablice + pętle Wprowadzenie Oczywiście wiesz już jak dużo można osiągnąć za pomocą tablic oraz jak dużo można osiągnąć za pomocą pętli, jednak tak naprawdę prawdziwe możliwości daje połączenie
Lekcja : Tablice + pętle Wprowadzenie Oczywiście wiesz już jak dużo można osiągnąć za pomocą tablic oraz jak dużo można osiągnąć za pomocą pętli, jednak tak naprawdę prawdziwe możliwości daje połączenie
ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI
 1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
1 ĆWICZENIE 15 BADANIE WZMACNIACZY MOCY MAŁEJ CZĘSTOTLIWOŚCI 15.1. CEL ĆWICZENIA Celem ćwiczenia jest poznanie podstawowych właściwości wzmacniaczy mocy małej częstotliwości oraz przyswojenie umiejętności
Jeśli X jest przestrzenią o nieskończonej liczbie elementów:
 Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
