SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego. Kolorowane sieci Petriego 1
|
|
|
- Bogusław Tomczak
- 6 lat temu
- Przeglądów:
Transkrypt
1 SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1
2 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2
3 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu, bo nie pozwala rozróżnić stanów ani zdarzeń związanych z poszczególnymi wózkami Model z rysunku (b) pozwala na takie rozróżnienie, bo posiada 2 kolorowane (zindywidualizowane) znaczniki: < y > i < b >, a każda z tranzycji może się palić w dwóch kolorach: a i b. Kolorowane sieci Petriego 3
4 Tranzycja T 1 jest przygotowana ze względu na kolor y, jeżeli jest znacznik < y > w miescu P 1. Odpalenie T 1 w kolorze y powoduje usunięcie znacznika < y > z miejsca P 1 i dodanie znacznika < y > do miejsca P 2. Analogiczne, tranzycja T 1 jest przygotowana ze względu na kolor b, jeżeli jest znacznik < b > w miejscu P 1. Odpalenie T 1 w kolorze b powoduje usunięcie znacznka < b > z miejsca P 1 i dodanie znacznika < b > do miejsca P 2. Takie same reguły obowiązują dla tranzycji T 2 Kolorowane sieci Petriego 4
5 KONCEPCJA FUNKCJI W celu powiązania kolorów znaczników i kolorów palenia tranzycji przypisuje się wszystkim łukom w sieci określone funkcje. f (b) = b Tutaj jest to funkcja identyczności Id f (y) = y Kolorowane sieci Petriego 5
6 INNE FUNKCJE Wróćmy do pierwszego rysunku (model opisany zwykła siecią Petriego) i rozważmy jeden z wózków, np. żółty. Ruchy wózka w lewą i w prawą stronę są reprezentowane taką samą strukturą sieci. Możemy zatem zastąpić miejsca P y 1 (ruch w lewo) i Py 2 (ruch w prawo) jednym miejscem P y (ruch wózka), a tranzycje T y 1 (koniec ruchu w lewo) i T y 2 (koniec ruchu w prawo) jedną tranzycją T y (koniec ruchu w tym samym kierunku). Kolorowane sieci Petriego 6
7 Dla rozróznienia kierunków ruchu z miejscem P y wiążemy dwa możliwe kolory znaczników: < l > (ruch w lewo) i < r > (ruch w prawo). Tranzycja T y może się palić w dwóch kolorach: l (koniec ruchu w lewo) i p (koniec ruchu w prawo). Dla prawidłowego działania systemu znaczniki < l > i < r > muszą pojawiać się w miejscu P y 1 na przemian i podobnie tranzycja T y musi na przemian palić się w kolorze l i r. A zatem, tylko funkcja związana z łukiem (P y,t y ) jest identycznością, natomiast funkcja związana z łukiem (T y,p y ) powoduje zmianę znacznika f (P y,t y ) f (l) = l f (r) = r f (T y,p y ) f (l) = r f (r) = l Kolorowane sieci Petriego 7
8 KOLORY WEKTOROWE Za pomocą jednego miejsca i jednej tranzycji reprezentujemy ruch obu wózków. Miejsce P 1 zawiera znaczniki o kolorach dwuelementowych Tranzycja T 1 pali sie w czterech trybach identyfikowanych za pomocą kolorów dwuelementowych Funkcje f () przypisane łukom sieci przekształcają znaczniki dwuelementowe Kolorowane sieci Petriego 8
9 ZWIJANIE/ROZWIJANIE SIECI Kolorowane sieci Petriego 9
10 MULTIZBIORY Multizbiór określony na niepustym zbiorze S jest funkcją b : S N gdzie N jest zbiorem nieujemnych liczb całkowitych. Zbiór wszystkich skończonych multizbiorów określonych na zbiorze S oznacza się przez S MS Intuicyjnie, multizbiór jest zbiorem, który może zawierać wiele kopii elementów, łacznie z tym, że pewnych elementów może nie być (0 kopii). Wygodnie jest reprezentować multizbiory w postaci sumy b = b(s)s gdzie b(s) jest liczbą kopii elementu s w multizbiorze b. Kolorowane sieci Petriego 10
11 Na przykład: multizbiór {x,y,z,y} jest skończonym multizbiorem określonym na zbiorze {u,w,x,y,z}, który można zapisać jako Dla multizbiorów definiuje się: b 1 + b 2 = (b 1 (s) + b 2 (s)) n b = (nb(s))s b = x + 2y + z b 1 b 2 s S : b 1 (s) b 2 (s) b = b(s) b 2 b 1 = (b 2 (s) b 1 (s)) (określone dla b 1 b 2 ) Kolorowane sieci Petriego 11
12 CPN - DEFINICJA Kolorowana sieć Petriego jest szóstką CPN = (P,T,C,Pre,Post,M 0 ) P i T są zbiorami miejsc i tranzycji C jest zbiorem kolorów Pre() i Post() są funkcjami incydencji, określonymi dla trójek (p,t/c) P T C takich, że c C(t) jest możliwym kolorem palenia tranzycji t, przez: Pre(p,t/c) C MS Post(p,t/c) C MS Pre(p,t/c) 0 p t Post(p,t/c) 0 p t M 0 : P C MS jest markowaniem początkowym. Kolorowane sieci Petriego 12
13 PRZYKŁAD FUNKCJI INCYDENCJI Kolorowane sieci Petriego 13
14 EWOLUCJA MARKOWANIA Niech C(t) będzie zbiorem kolorów tranzycji t. Tranzycja t jest przygotowana ze względu na kolor c C(t) wtedy i tylko wtedy jeżeli p P, M(p) Pre(p,t/c) Przejście, ktore jest przygotowane ze względu na koloru c może w tym kolorze odpalić, w wyniku czego następuje zmiana markowania: p P, M (p) = M(p) Pre(p,t/c) + Post(p,t/c) Kolorowane sieci Petriego 14
15 PRZYKŁAD EWOLUCJI MARKOWANIA Startując z makowania M 1, dla ciągu paleń σ = t 1 /c 1,t 2 /c 2,...,t n /c k M k+1 (p) = M 1 (p) + k (Post(p,t j /c j ) Pre(p,t j /c j )), p P j=1 Kolorowane sieci Petriego 15
16 MODELOWANIE Każdą zwykła sieć Petriego z miejscami {p 1, p 2,..., p n } i tranzycjami {t 1,t 2,...,t m } można sprowadzić do sieci kolorowanej zawierającej tylko jedno miejsce P i jedną tranzycję T. Czy to ma jednak sens? C = C(P) +C(T ) C(P) = {p 1, p 2,..., p n }, C(T ) = {t 1,t 2,...,t m } Pre(P,T /t j ) = n i=1 X i j p i, Post(P,T /t j ) = n i=1 X i + j p i M0 c = n i=1 M 0(p i ) p i Kolorowane sieci Petriego 16
17 TRANSFORMACJA PN DO CPN - PRZYKŁAD Kolorowane sieci Petriego 17
18 MODELOWANIE - PRZYKŁAD W systemie występują współbieżnie dwa procesy produkcji: elementów umieszczonych na paletach typu l 1 i elementów umieszczonych na paletach typu l 2. Palety są wprowadzane na przemian jednego i drugiego typu. Palety wychodzące po odmontowaniu elementów przekazywane są z powrotem do systemu. Kolorowane sieci Petriego 18
19 MODEL 1 i {1,2} C i - paleta typu i-tego B i - palety w buforze we maszyny i-tej F i - maszyna i-ta jest wolna O i - maszyna i-ta jest zajęta T i - ładowanie maszyny i-tej T i - rozładowanie maszyny i-tej Kolorowane sieci Petriego 19
20 MODEL 1 c.d. Funkcja Succ(C i ) = C (i+1)mod 2 zapewnia wymaganą naprzemienność przepływu palet różnych typów Stan początkowy systemu jest zadany przez: w buforze maszyny m 1 jest n 1 palet pierwszego i n 2 palet drugiego typu M 0 (B 1 ) = n 1 C 1 + n 2 C 2 maszyny są dostępne i oprzyrządowane do realizacji elementów typu C 1 M 0 (F 1 ) = M 0 (F 2 ) = C 1 Kolorowane sieci Petriego 20
21 MODEL 2 Nie zawsze jest najlepiej używać prostych kolorów. Np. jeżeli liczba maszyn w linii wzrośnie, to model taki staje się bardziej złożony. Alternatywnie możemy związać palety z maszynami poprzez użycie kolorów dwuelementowych < c i,m j >. Obecność takiego znacznika w miejscu B oznacza, że w buforze maszyny j-tej jest paleta typu i-tego, a obecność < c i,m j > w miejscu F oznacza, że maszyna j-ta jest dostępna i przygotowana na przyjęcie części typu i-tego. Wówczas: Succ 1 (< c i,m j >) =< c (i+1)mod 2,m j > - funkcja wyznacza naprzemienny przepływ elementów c 1 i c 2 przez maszynę m j Succ 2 (< c i,m j >) =< c i,m ( j+1)mod 2 > - funkcja wyznacza przepływ palety c i naprzemian przez maszynę m 1 i m 2 Kolorowane sieci Petriego 21
22 MODEL 2 c.d. Kolorowane sieci Petriego 22
23 Stan początkowy systemu jest zadany przez: w buforze maszyny m 1 jest n 1 palet pierwszego i n 2 palet drugiego typu M 0 (B) = n 1 < c 1,m 1 > +n 2 < c 2,m 1 > maszyny m 1 i m 2 są dostępne i oprzyrządowane do realizacji elementów typu c 1 M 0 (F) =< c 1,m 1 > + < c 1,m 2 > Kolorowane sieci Petriego 23
24 ROZSZERZENIE MODELU 2 Jeżeli chcielibyśmy zamodelować linię produkcyjną złożoną z I typów palet (części) i J maszyn, to struktura modelu 2 (otrzymanego dla 2 typów palet i 2 maszyn) nie ulegnie zmianie. Jedyne modyfikacje to: 1. Funkcje Succ 1 i Succ 2 należy zdefiniować odpowiednio modulo I i modulo J. 2. markowanie początkowe M 0 (B) należy rozszerzyć do I znaczników, tj. M 0 (B) = I i=1 < c i,m 1 > 3. markowanie początkowe M 0 (F) należy rozszerzyć do J znaczników, tj. M 0 (F) = J j=1 < c 1,m j > Kolorowane sieci Petriego 24
25 TYPOWE FUNKCJE Kolorowane sieci Petriego 25
26 FUNKCJE NASTEPNIKA I DYSKOLORUJACA Kolorowane sieci Petriego 26
27 PRZENOŚNIK - KOLEJKA FIFO Transporter może jednocześnie przenosić co najwyżej 8 obiektów, które należą do q typów: o 1,...,o q. Model ma dostarczać bieżącej informacji o tym, które miejsca są wolne, a które zajęte i jakiego typu obiektem. Dwa typy znaczników: < o i,r j > - obiekt typu i-tego znajduje się w miejscu j-tym < r j > - miejsce j-te jest wolne Tranzycje T 1, T 2, T 3 reprezentują odpowiednio umieszczenie obiektu na przenośniku, zdjęcie obiektu z przenośnika i przesunięcie się transportera o jedno miejsce Kolorowane sieci Petriego 27
28 PRZENOŚNIK - MODEL Kolorowane sieci Petriego 28
29 LINIA MONTAŻOWA Produkowane są trzy różne typy wyrobów, każdy przez inną maszynę. Transporter dowozi odpowiednią paletę do odpowiedniej maszyny, gdzie paleta jest wprowadzana, jeżeli maszyna jest wolna. W przeciwnym przypadku transporter zatrzymuje się i czeka na jej zwolnienie; paleta zwalniająca maszynę umieszczana jest na transporterze i następnie przenoszona do wyjścia. Kolorowane sieci Petriego 29
30 Kolorowane sieci Petriego 30
31 MODYFIKACJE - NIESKIEROWANE CPN dwa modele skrzyżowania prosty system AGV Kolorowane sieci Petriego 31
32 SYSTEM TRANSPORTOWY Definicja 1 Dla sieci ścieżek U = (T,P,x) i n wózków, system transportowy jest siecią CPN N = N(U,n) = (P,T,C,Pre,Post,M 0 ) taką że: 1. P, T - zbiory miejsc i przejść 2. C - zbiór kolorów taki że: C(p) = {< h,t > h 1..n t x(p)} C(t) = {< h, p, p > h 1..n t x(p) x(p ) p p } 3. Pre, Post - funkcje incydencji zdefiniowane p P i t T ze względu na każdy kolor c C(t), c =< h,q,q >, przez: < h,t > jeżeli p = q Pre(p, t/c) = 0 w innym przypadku < h,t > jeżeli p = q Post(p, t/c) = 0 w innym przypadku gdzie: t x(q ) and x(q ) = 2 t t Kolorowane sieci Petriego 32
33 4. M 0 - markowanie początkowe takie że M 0 M i: p P, M(p) = 0 or M(p) C(p) h 1..n, p P takie że M(p) =< h,t > jeżeli M(p) =< h,t > i M(p ) =< h,t > to h h Kolorowane sieci Petriego 33
34 DYNAMIKA SYSTEMU M [ t 6 /(h 2, p 5, p 7 ) > M Definicja 2 Dla tranzycji t T i koloru c C(t), c =< h,q,q >: zdarzenie t/c jest przygotowane w.t.w. jeżeli M(q) =< h,t > and M(q ) = 0 0 if p = q M (p) = < h,t > jeżeli p = q t x(q ) gdzie: x(q ) = 2 t t M(p) w innym przypadku Kolorowane sieci Petriego 34
35 Jeżeli przy markowaniu M wystąpi zdarzenie t/c takie, że t T, c =< h,q,q > C(t) to nowe markowanie M jest określone przez: 0 jeżeli p = q M (p) = < h,t > jeżeli p = q M(p) w pozostalych przypadkach gdzie: t x(q ) i x(q ) = 2 t t. Kolorowane sieci Petriego 35
Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń)
 Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
miejsca przejścia, łuki i żetony
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego. Sieć Petriego
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Definicja sieci. Sieć Petriego jest czwórką C = ( P, T, I, O ), gdzie: P = { p 1, p 2,, p n } T = { t 1, t 2,, t m }
 Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
Kolorowanie płaszczyzny, prostych i okręgów
 Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
Kolorowanie płaszczyzny, prostych i okręgów Jadwiga Czyżewska Pisane pod kierunkiem W.Guzickiego W 2013 roku na II etapie VIII edycji Olimpiady Matematycznej Gimnazjalistów pojawiło się zadanie o następującej
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
TEORIA wiązań Magdalena Pawłowska Gr. 10B2
 TEORIA wiązań Magdalena Pawłowska Gr. 10B2 Techniki kombinatoryczne rozróżniania węzłów i splotów ØLiczba skrzyżowań, ØLiczba mostów, ØKolorowanie, ØIndeks zaczepienia, ØSzkic elementów arytmetyki węzłów.
TEORIA wiązań Magdalena Pawłowska Gr. 10B2 Techniki kombinatoryczne rozróżniania węzłów i splotów ØLiczba skrzyżowań, ØLiczba mostów, ØKolorowanie, ØIndeks zaczepienia, ØSzkic elementów arytmetyki węzłów.
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Automat ze stosem Automat ze stosem to szóstka
1. Sieci Petriego. Rys. 1-1 Przykład sieci Petriego
 1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
Przestrzenie wektorowe
 Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu.
 Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu. 1 Logika Klasyczna obejmuje dwie teorie:
Andrzej Wiśniewski Logika I Materiały do wykładu dla studentów kognitywistyki Wykład 11a. Składnia języka Klasycznego Rachunku Predykatów. Języki pierwszego rzędu. 1 Logika Klasyczna obejmuje dwie teorie:
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Internetowe Ko³o M a t e m a t yc z n e
 Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
Internetowe Ko³o M a t e m a t yc z n e Stowarzyszenie na rzecz Edukacji Matematycznej Zestaw 3 szkice rozwiązań zadań 1. Plansza do gry składa się z 15 ustawionych w rzędzie kwadratów. Pierwszy z graczy
Kolorowanie kalendarzy enova KADRY i PŁACE
 Kolorowanie kalendarzy enova KADRY i PŁACE (WERSJA 1.0) KATARZYNA DEPA Soneta Sp z o.o. ul. Wadowicka 8a, wejście B 31-415 Kraków tel./fax +48 (12) 261 36 41 http://www.enova.pl e-mail: place@enova.pl
Kolorowanie kalendarzy enova KADRY i PŁACE (WERSJA 1.0) KATARZYNA DEPA Soneta Sp z o.o. ul. Wadowicka 8a, wejście B 31-415 Kraków tel./fax +48 (12) 261 36 41 http://www.enova.pl e-mail: place@enova.pl
Okręgi na skończonej płaszczyźnie Mateusz Janus
 Okręgi na skończonej płaszczyźnie Mateusz Janus Skończona płaszczyzna, to płaszczyzna zawierająca skończoną liczbę punktów. Punkty utożsamiamy z parami liczb, które są resztami z dzielenia przez ustaloną
Okręgi na skończonej płaszczyźnie Mateusz Janus Skończona płaszczyzna, to płaszczyzna zawierająca skończoną liczbę punktów. Punkty utożsamiamy z parami liczb, które są resztami z dzielenia przez ustaloną
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
TEORIA GRAFÓW I SIECI Temat nr 1: Definicja grafu. Rodzaje i części grafów dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl tel.: 261-83-95-04, p.225/100
Wreferacie przedstawiono propozycję metody modelowania procesów transportowych
 Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 13/14 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Rysunek 1: Przykłady graficznej prezentacji klas.
 4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
4 DIAGRAMY KLAS. 4 Diagramy klas. 4.1 Wprowadzenie. Diagram klas - w ujednoliconym języku modelowania jest to statyczny diagram strukturalny, przedstawiający strukturę systemu w modelach obiektowych przez
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC
 Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów
Adaptacja sterownika PLC do obiektu sterowania. Synteza algorytmu procesu i sterowania metodą GRAFCET i SFC Proces technologiczny (etap procesu produkcyjnego/przemysłowego) podstawa współczesnych systemów
Wyrażenie nawiasowe. Wyrażenie puste jest poprawnym wyrażeniem nawiasowym.
 Wyrażenie nawiasowe Wyrażeniem nawiasowym nazywamy dowolny skończony ciąg nawiasów. Każdemu nawiasowi otwierającemu odpowiada dokładnie jeden nawias zamykający. Poprawne wyrażenie nawiasowe definiujemy
Wyrażenie nawiasowe Wyrażeniem nawiasowym nazywamy dowolny skończony ciąg nawiasów. Każdemu nawiasowi otwierającemu odpowiada dokładnie jeden nawias zamykający. Poprawne wyrażenie nawiasowe definiujemy
Maskowanie i selekcja
 Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
CZĘŚĆ PIERWSZA. Seminarium grupy RSPN. Piotr Lasek Uniwersytet Rzeszowski. Kontakt
 Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Wykład 4. Określimy teraz pewną ważną klasę pierścieni.
 Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
1. Synteza automatów Moore a i Mealy realizujących zadane przekształcenie 2. Transformacja automatu Moore a w automat Mealy i odwrotnie
 Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
Opracował: dr hab. inż. Jan Magott KATEDRA INFORMATYKI TECHNICZNEJ Ćwiczenia laboratoryjne z Logiki Układów Cyfrowych ćwiczenie 207 Temat: Automaty Moore'a i Mealy 1. Cel ćwiczenia Celem ćwiczenia jest
Drzewa BST i AVL. Drzewa poszukiwań binarnych (BST)
 Drzewa ST i VL Drzewa poszukiwań binarnych (ST) Drzewo ST to dynamiczna struktura danych (w formie drzewa binarnego), która ma tą właściwość, że dla każdego elementu wszystkie elementy w jego prawym poddrzewie
Drzewa ST i VL Drzewa poszukiwań binarnych (ST) Drzewo ST to dynamiczna struktura danych (w formie drzewa binarnego), która ma tą właściwość, że dla każdego elementu wszystkie elementy w jego prawym poddrzewie
Badania Operacyjne Ćwiczenia nr 4 (Materiały)
 Analiza wrażliwości Rozwiązanie programu liniowego jest dopiero początkiem analizy. Z punktu widzenia decydenta (menadżera) jest istotne, żeby wiedzieć jak na rozwiązanie optymalne wpływają zmiany parametrów
Analiza wrażliwości Rozwiązanie programu liniowego jest dopiero początkiem analizy. Z punktu widzenia decydenta (menadżera) jest istotne, żeby wiedzieć jak na rozwiązanie optymalne wpływają zmiany parametrów
Języki formalne i automaty Ćwiczenia 7
 Języki formalne i automaty Ćwiczenia 7 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Automaty... 2 Cechy automatów... 4 Łączenie automatów... 4 Konwersja automatu do wyrażenia
Języki formalne i automaty Ćwiczenia 7 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Automaty... 2 Cechy automatów... 4 Łączenie automatów... 4 Konwersja automatu do wyrażenia
Straszyński Kołodziejczyk, Paweł Straszyński. Wszelkie prawa zastrzeżone. FoamPro. Instrukcja obsługi
 FoamPro Instrukcja obsługi 1 Spis treści 1 Wstęp... 3 2 Opis Programu... 4 2.1 Interfejs programu... 4 2.2 Budowa projektu... 5 2.2.1 Elementy podstawowe... 5 2.2.2 Elementy grupowe... 5 2.2.3 Połączenia
FoamPro Instrukcja obsługi 1 Spis treści 1 Wstęp... 3 2 Opis Programu... 4 2.1 Interfejs programu... 4 2.2 Budowa projektu... 5 2.2.1 Elementy podstawowe... 5 2.2.2 Elementy grupowe... 5 2.2.3 Połączenia
Języki formalne i automaty Ćwiczenia 9
 Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Zadanie 4 Zadanie 5 Zadanie 6. Repetytorium z JFiZO. Jakub Michaliszyn 25 maja 2017
 Repetytorium z JFiZO Jakub Michaliszyn 25 maja 2017 dom(m) jest rekurencyjny wtw, gdy istnieje całkowita funkcja rekurencyjna t M (n) taka, że jeśli M(n) staje, to staje po dokładnie t M (n) krokach. dom(m)
Repetytorium z JFiZO Jakub Michaliszyn 25 maja 2017 dom(m) jest rekurencyjny wtw, gdy istnieje całkowita funkcja rekurencyjna t M (n) taka, że jeśli M(n) staje, to staje po dokładnie t M (n) krokach. dom(m)
Kolory elementów. Kolory elementów
 Wszystkie elementy na schematach i planach szaf są wyświetlane w kolorach. Kolory te są zawarte w samych elementach, ale w razie potrzeby można je zmienić za pomocą opcji opisanych poniżej, przy czym dotyczy
Wszystkie elementy na schematach i planach szaf są wyświetlane w kolorach. Kolory te są zawarte w samych elementach, ale w razie potrzeby można je zmienić za pomocą opcji opisanych poniżej, przy czym dotyczy
Zliczanie Podziałów Liczb
 Zliczanie Podziałów Liczb Przygotował: M. Dziemiańczuk 7 lutego 20 Streszczenie Wprowadzenie Przez podział λ nieujemnej liczby całkowitej n rozumiemy nierosnący ciąg (λ, λ 2,..., λ r ) dodatnich liczb
Zliczanie Podziałów Liczb Przygotował: M. Dziemiańczuk 7 lutego 20 Streszczenie Wprowadzenie Przez podział λ nieujemnej liczby całkowitej n rozumiemy nierosnący ciąg (λ, λ 2,..., λ r ) dodatnich liczb
1. Regulatory ciągłe liniowe.
 Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Laboratorium Podstaw Inżynierii Sterowania Ćwiczenie: Regulacja ciągła PID 1. Regulatory ciągłe liniowe. Zadaniem regulatora w układzie regulacji automatycznej jest wytworzenie sygnału sterującego u(t),
Dodatkowe możliwości RDF. Seminarium magisterskie Paweł Chrząszczewski
 Dodatkowe możliwości RDF Seminarium magisterskie Paweł Chrząszczewski Inne możliwości RDF RDF posiada szereg dodatkowych funkcji, takich jak wbudowane typy i właściwości reprezentujące grupy zasobów i
Dodatkowe możliwości RDF Seminarium magisterskie Paweł Chrząszczewski Inne możliwości RDF RDF posiada szereg dodatkowych funkcji, takich jak wbudowane typy i właściwości reprezentujące grupy zasobów i
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova
 Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Wstęp do sieci neuronowych, wykład 11 Łańcuchy Markova M. Czoków, J. Piersa 2010-12-21 1 Definicja Własności Losowanie z rozkładu dyskretnego 2 3 Łańcuch Markova Definicja Własności Losowanie z rozkładu
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii
 Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii Agnieszka Bojanowska Stefan Jackowski 24 listopada 2010 1 Podstawowe pojęcia Bedziemy uzywać następujących pojęć i przykładów dotyczących
Topologia Algebraiczna - Pomocnik studenta. 1. Język teorii kategorii Agnieszka Bojanowska Stefan Jackowski 24 listopada 2010 1 Podstawowe pojęcia Bedziemy uzywać następujących pojęć i przykładów dotyczących
Inżynieria Systemów Dynamicznych (4)
 Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Inżynieria Systemów Dynamicznych (4) liniowych (układów) Piotr Jacek Suchomski Katedra Systemów Automatyki WETI, Politechnika Gdańska 2 grudnia 2010 O czym będziemy mówili? 1 2 WE OKREŚLO 3 ASYMPTO 4 DYNAMICZ
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Ćwiczenie 1. Modelowanie prostego procesu
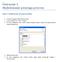 Ćwiczenie 1. Modelowanie prostego procesu Część 1. Definiowanie nowego projektu 1. Uruchom narzędzie TIBCO Business Studio. 2. Z menu wybierz File -> New -> Project... 3. W oknie dialogowym New Project
Ćwiczenie 1. Modelowanie prostego procesu Część 1. Definiowanie nowego projektu 1. Uruchom narzędzie TIBCO Business Studio. 2. Z menu wybierz File -> New -> Project... 3. W oknie dialogowym New Project
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
Przypadek praktyczny: United Caps Automatyczny magazyn wjezdny z systemem Pallet Shuttle dla producenta zakrętek
 Przypadek praktyczny: United Caps Automatyczny magazyn wjezdny z systemem Pallet Shuttle dla producenta zakrętek Lokalizacja: Luksemburg United Caps, spółka specjalizująca się w projektowaniu i produkcji
Przypadek praktyczny: United Caps Automatyczny magazyn wjezdny z systemem Pallet Shuttle dla producenta zakrętek Lokalizacja: Luksemburg United Caps, spółka specjalizująca się w projektowaniu i produkcji
Skrócona instrukcja korzystania z Platformy Zdalnej Edukacji w Gliwickiej Wyższej Szkole Przedsiębiorczości
 Skrócona instrukcja korzystania z Platformy Zdalnej Edukacji w Gliwickiej Wyższej Szkole Przedsiębiorczości Wstęp Platforma Zdalnej Edukacji Gliwickiej Wyższej Szkoły Przedsiębiorczości (dalej nazywana
Skrócona instrukcja korzystania z Platformy Zdalnej Edukacji w Gliwickiej Wyższej Szkole Przedsiębiorczości Wstęp Platforma Zdalnej Edukacji Gliwickiej Wyższej Szkoły Przedsiębiorczości (dalej nazywana
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki. Paweł Witas Nr albumu:178860
 Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Paweł Witas Nr albumu:178860 Symulator sieci Petriego ze znacznikami indywidualnymi Praca Magisterska na kierunku INFORMATYKA Praca wykonana
Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki Paweł Witas Nr albumu:178860 Symulator sieci Petriego ze znacznikami indywidualnymi Praca Magisterska na kierunku INFORMATYKA Praca wykonana
1. Operacje logiczne A B A OR B
 1. Operacje logiczne OR Operacje logiczne są operacjami działającymi na poszczególnych bitach, dzięki czemu można je całkowicie opisać przedstawiając jak oddziałują ze sobą dwa bity. Takie operacje logiczne
1. Operacje logiczne OR Operacje logiczne są operacjami działającymi na poszczególnych bitach, dzięki czemu można je całkowicie opisać przedstawiając jak oddziałują ze sobą dwa bity. Takie operacje logiczne
1. Opis okna podstawowego programu TPrezenter.
 OPIS PROGRAMU TPREZENTER. Program TPrezenter przeznaczony jest do pełnej graficznej prezentacji danych bieżących lub archiwalnych dla systemów serii AL154. Umożliwia wygodną i dokładną analizę na monitorze
OPIS PROGRAMU TPREZENTER. Program TPrezenter przeznaczony jest do pełnej graficznej prezentacji danych bieżących lub archiwalnych dla systemów serii AL154. Umożliwia wygodną i dokładną analizę na monitorze
Język UML w modelowaniu systemów informatycznych
 Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Reprezentacje grafów nieskierowanych Reprezentacje grafów skierowanych. Wykład 2. Reprezentacja komputerowa grafów
 Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
Wykład 2. Reprezentacja komputerowa grafów 1 / 69 Macierz incydencji Niech graf G będzie grafem nieskierowanym bez pętli o n wierzchołkach (x 1, x 2,..., x n) i m krawędziach (e 1, e 2,..., e m). 2 / 69
POMOC / INSTRUKCJA OBSŁUGI
 POMOC / INSTRUKCJA OBSŁUGI 1. Powiększanie mapy 2. Plakat 3. Schemat lekcji 4. Broszura informacyjna 5. Instrukcja obsługi Pasek narzędzi i menu wyboru Zmiana skali mapy Mini mapa - podgląd na położenie
POMOC / INSTRUKCJA OBSŁUGI 1. Powiększanie mapy 2. Plakat 3. Schemat lekcji 4. Broszura informacyjna 5. Instrukcja obsługi Pasek narzędzi i menu wyboru Zmiana skali mapy Mini mapa - podgląd na położenie
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Modelowanie całkowitoliczbowe
 1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
Lista zadań - Relacje
 MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
MATEMATYKA DYSKRETNA Lista zadań - Relacje Zadania obliczeniowe Zad. 1. Która z poniższych relacji jest funkcją? a) Relacja składająca się ze wszystkich par uporządkowanych, których poprzednikami są studenci,
Programowanie Równoległe i Rozproszone
 Programowanie Równoległe i Rozproszone Lucjan Stapp Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska (l.stapp@mini.pw.edu.pl) 1/30 PRiR MONITOR klasa z następującymi właściwościami: wszystkie
Programowanie Równoległe i Rozproszone Lucjan Stapp Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska (l.stapp@mini.pw.edu.pl) 1/30 PRiR MONITOR klasa z następującymi właściwościami: wszystkie
Elementy logiki. Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń
 Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Elementy logiki Wojciech Buszkowski Wydział Matematyki i Informatyki UAM Zakład Teorii Obliczeń 1 Klasyczny Rachunek Zdań 1.1 Spójniki logiczne Zdaniem w sensie logicznym nazywamy wyrażenie, które jest
Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych
 1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
Wielomiany podstawowe wiadomości
 Rozdział Wielomiany podstawowe wiadomości Funkcję postaci f s = a n s n + a n s n + + a s + a 0, gdzie n N, a i R i = 0,, n, a n 0 nazywamy wielomianem rzeczywistym stopnia n; jeżeli współczynniki a i
Rozdział Wielomiany podstawowe wiadomości Funkcję postaci f s = a n s n + a n s n + + a s + a 0, gdzie n N, a i R i = 0,, n, a n 0 nazywamy wielomianem rzeczywistym stopnia n; jeżeli współczynniki a i
ZESTAW OŚWIETLENIA SYGNALIZACYJNEGO SIEWNIKÓW MONOSEM
 Monosem, ref. 10640092 ZESTAW OŚWIETLENIA SYGNALIZACYJNEGO SIEWNIKÓW MONOSEM INSTRUKCJA OBSŁUGI, MONTAŻU I KONSERWACJI W JĘZYKU POLSKIM Wydanie: kwiecień 2013 INSTRUKCJA OBSŁUGI Niniejszą instrukcję obsługi
Monosem, ref. 10640092 ZESTAW OŚWIETLENIA SYGNALIZACYJNEGO SIEWNIKÓW MONOSEM INSTRUKCJA OBSŁUGI, MONTAŻU I KONSERWACJI W JĘZYKU POLSKIM Wydanie: kwiecień 2013 INSTRUKCJA OBSŁUGI Niniejszą instrukcję obsługi
x 2 = a RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych 2. Proste równania kwadratowe Równanie kwadratowe typu:
 RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
RÓWNANIA KWADRATOWE 1. Wprowadzenie do równań kwadratowych Przed rozpoczęciem nauki o równaniach kwadratowych, warto dobrze opanować rozwiązywanie zwykłych równań liniowych. W równaniach liniowych niewiadoma
Logika intuicjonistyczna
 Logika intuicjonistyczna Logika klasyczna oparta jest na pojęciu wartości logicznej zdania. Poprawnie zbudowane i jednoznaczne stwierdzenie jest w tej logice klasyfikowane jako prawdziwe lub fałszywe.
Logika intuicjonistyczna Logika klasyczna oparta jest na pojęciu wartości logicznej zdania. Poprawnie zbudowane i jednoznaczne stwierdzenie jest w tej logice klasyfikowane jako prawdziwe lub fałszywe.
Znajdowanie wyjścia z labiryntu
 Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
Znajdowanie wyjścia z labiryntu Zadanie to wraz z problemem pakowania najcenniejszego plecaka należy do problemów optymalizacji, które dotyczą znajdowania najlepszego rozwiązania wśród wielu możliwych
Matematyczne Podstawy Informatyki
 Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Matematyczne Podstawy Informatyki dr inż. Andrzej Grosser Instytut Informatyki Teoretycznej i Stosowanej Politechnika Częstochowska Rok akademicki 2013/2014 Informacje podstawowe 1. Konsultacje: pokój
Wykład 5: Specyfikacja na poziomie systemowym
 Systemy wbudowane Wykład 5: Specyfikacja na poziomie systemowym Ogólny model systemu informatycznego Sieć komunikujących się procesów P1 P3 P2 Kiedy procesy się aktywują? Czy jest synchronizacja między
Systemy wbudowane Wykład 5: Specyfikacja na poziomie systemowym Ogólny model systemu informatycznego Sieć komunikujących się procesów P1 P3 P2 Kiedy procesy się aktywują? Czy jest synchronizacja między
Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego
 Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
przy warunkach początkowych: 0 = 0, 0 = 0
 MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
MODELE MATEMATYCZNE UKŁADÓW DYNAMICZNYCH Podstawową formą opisu procesów zachodzących w członach lub układach automatyki jest równanie ruchu - równanie dynamiki. Opisuje ono zależność wielkości fizycznych,
Przykładowe zadanie z unikania blokad.
 Przykładowe zadanie z unikania blokad. Mamy system operacyjny, a w nim cztery procesy (,,,) i dwa zasoby (,), przy czym dysponujemy trzema egzemplarzami zasobu i trzema egzemplarzami zasobu. Oto zapotrzebowanie
Przykładowe zadanie z unikania blokad. Mamy system operacyjny, a w nim cztery procesy (,,,) i dwa zasoby (,), przy czym dysponujemy trzema egzemplarzami zasobu i trzema egzemplarzami zasobu. Oto zapotrzebowanie
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
SZTUCZNA INTELIGENCJA WYKŁAD 10. WNIOSKOWANIE W LOGICE ROZMYTEJ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska WNIOSKOWANIE W LOGICE DWUWARTOŚCIOWEJ W logice
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
1.1 Definicja. 1.2 Przykład. 1.3 Definicja. Niech G oznacza dowolny, niepusty zbiór.
 20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
Technologie i systemy oparte na logice rozmytej
 Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Zagadnienia I Technologie i systemy oparte na logice rozmytej Mają zastosowania w sytuacjach kiedy nie posiadamy wystarczającej wiedzy o modelu matematycznym rządzącym danym zjawiskiem oraz tam gdzie zbudowanie
Całki niewłaściwe. Całki w granicach nieskończonych
 Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
Całki niewłaściwe Całki w granicach nieskończonych Wiemy, co to jest w przypadku skończonego przedziału i funkcji ograniczonej. Okazuje się potrzebne uogólnienie tego pojęcia w różnych kierunkach (przedział
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy:
 Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
Zadanie 1. Oblicz prawdopodobieństwo, że rzucając dwiema kostkami do gry otrzymamy: a) sumę oczek równą 6, b) iloczyn oczek równy 6, c) sumę oczek mniejszą niż 11, d) iloczyn oczek będący liczbą parzystą,
HARMONOGRAMOWANIE OPERACYJNE Z OGRANICZENIAMI W IFS APPLICATIONS
 HARMONOGRAMOWANIE OPERACYJNE Z OGRANICZENIAMI W IFS APPLICATIONS Cele sterowania produkcją Dostosowanie asortymentu i tempa produkcji do spływających na bieżąco zamówień Dostarczanie produktu finalnego
HARMONOGRAMOWANIE OPERACYJNE Z OGRANICZENIAMI W IFS APPLICATIONS Cele sterowania produkcją Dostosowanie asortymentu i tempa produkcji do spływających na bieżąco zamówień Dostarczanie produktu finalnego
G. Wybrane elementy teorii grafów
 Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Dorota Miszczyńska, Marek Miszczyński KBO UŁ Wybrane elementy teorii grafów 1 G. Wybrane elementy teorii grafów Grafy są stosowane współcześnie w różnych działach nauki i techniki. Za pomocą grafów znakomicie
Ćwiczenia z przetwarzania tablic 2D
 Ćwiczenia z przetwarzania tablic 2D Wyświetlanie tablic 2D Jako wstęp do przetwarzania obrazów w pythonie przećwiczmy podstawowe operacje na dwuwymiarowych tablicach numpy w postaci których będziemy takie
Ćwiczenia z przetwarzania tablic 2D Wyświetlanie tablic 2D Jako wstęp do przetwarzania obrazów w pythonie przećwiczmy podstawowe operacje na dwuwymiarowych tablicach numpy w postaci których będziemy takie
Opis systemów dynamicznych w przestrzeni stanu. Wojciech Kurek , Gdańsk
 Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Opis systemów dynamicznych Mieczysław Brdyś 27.09.2010, Gdańsk Rozważmy układ RC przedstawiony na rysunku poniżej: wejscie u(t) R C wyjście y(t)=vc(t) Niech u(t) = 2 + sin(t) dla t t 0 gdzie t 0 to chwila
Indukcja. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
Indukcja Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Charakteryzacja zbioru liczb naturalnych Arytmetyka liczb naturalnych Jedną z najważniejszych teorii matematycznych jest arytmetyka
10. Kolorowanie wierzchołków grafu
 p. 10. Kolorowanie wierzchołków grafu 10.1 Definicje i twierdzenia Przez k-kolorowanie wierzchołków grafu G rozumiemy przyporzadkowanie każdemu wierzchołkowi grafu G jednego z k kolorów 1, 2,...,k. p.
p. 10. Kolorowanie wierzchołków grafu 10.1 Definicje i twierdzenia Przez k-kolorowanie wierzchołków grafu G rozumiemy przyporzadkowanie każdemu wierzchołkowi grafu G jednego z k kolorów 1, 2,...,k. p.
Ciała i wielomiany 1. przez 1, i nazywamy jedynką, zaś element odwrotny do a 0 względem działania oznaczamy przez a 1, i nazywamy odwrotnością a);
 Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
WASM AppInventor Lab 3. Rysowanie i animacja po kanwie PODSTAWY PRACY Z KANWAMI
 Rysowanie i animacja po kanwie PODSTAWY PRACY Z KANWAMI Kanwa, to komponent służący do rysowania. Można ją dodać w Designerze przeciągając komponent Canvas z sekcji Basic. W celu ustawienia obrazka jako
Rysowanie i animacja po kanwie PODSTAWY PRACY Z KANWAMI Kanwa, to komponent służący do rysowania. Można ją dodać w Designerze przeciągając komponent Canvas z sekcji Basic. W celu ustawienia obrazka jako
Polska Sieć Trakcyjna
 Dodatek do MS Train Simulator 1.x Polska Sieć Trakcyjna Instrukcja układania sieci na szlakach Po instalacji pakietu (pakietów) obiektów sieci, wpisów do plików *.ref i gantry.dat - zgodnie z instrukcją
Dodatek do MS Train Simulator 1.x Polska Sieć Trakcyjna Instrukcja układania sieci na szlakach Po instalacji pakietu (pakietów) obiektów sieci, wpisów do plików *.ref i gantry.dat - zgodnie z instrukcją
Zagadnienie transportowe
 Zagadnienie transportowe Firma X zawarła kontrakt na dostarczenie trawnika do wykończenia terenów wokół trzech zakładów U, V i W. Trawnik ma być dostarczony z trzech farm A, B i C. Zapotrzebowanie zakładów
Zagadnienie transportowe Firma X zawarła kontrakt na dostarczenie trawnika do wykończenia terenów wokół trzech zakładów U, V i W. Trawnik ma być dostarczony z trzech farm A, B i C. Zapotrzebowanie zakładów
Definicje wyższego poziomu
 Definicje wyższego poziomu Interpreter Scheme-a nie będzie narzekad w przypadku wystąpienia niezdefionowanej zmiennej w ciele wyrażenia lambda dopóki nie będzie zastosowana Przykład braku informacji o
Definicje wyższego poziomu Interpreter Scheme-a nie będzie narzekad w przypadku wystąpienia niezdefionowanej zmiennej w ciele wyrażenia lambda dopóki nie będzie zastosowana Przykład braku informacji o
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 14/15 Grafy podstawowe definicje Graf to para G=(V, E), gdzie V to niepusty i skończony zbiór, którego elementy nazywamy wierzchołkami
Języki programowania C i C++ Wykład: Typy zmiennych c.d. Operatory Funkcje. dr Artur Bartoszewski - Języki C i C++, sem.
 Języki programowania C i C++ Wykład: Typy zmiennych c.d. Operatory Funkcje 1 dr Artur Bartoszewski - Języki C i C++, sem. 1I- WYKŁAD programowania w C++ Typy c.d. 2 Typy zmiennych Instrukcja typedef -
Języki programowania C i C++ Wykład: Typy zmiennych c.d. Operatory Funkcje 1 dr Artur Bartoszewski - Języki C i C++, sem. 1I- WYKŁAD programowania w C++ Typy c.d. 2 Typy zmiennych Instrukcja typedef -
Kolorowanie wierzchołków Kolorowanie krawędzi Kolorowanie regionów i map. Wykład 8. Kolorowanie
 Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wykład 8. Kolorowanie 1 / 62 Kolorowanie wierzchołków - definicja Zbiory niezależne Niech G będzie grafem bez pętli. Definicja Mówimy, że G jest grafem k kolorowalnym, jeśli każdemu wierzchołkowi możemy
Wstęp Pierwsze kroki Pierwszy rysunek Podstawowe obiekty Współrzędne punktów Oglądanie rysunku...
 Wstęp... 5 Pierwsze kroki... 7 Pierwszy rysunek... 15 Podstawowe obiekty... 23 Współrzędne punktów... 49 Oglądanie rysunku... 69 Punkty charakterystyczne... 83 System pomocy... 95 Modyfikacje obiektów...
Wstęp... 5 Pierwsze kroki... 7 Pierwszy rysunek... 15 Podstawowe obiekty... 23 Współrzędne punktów... 49 Oglądanie rysunku... 69 Punkty charakterystyczne... 83 System pomocy... 95 Modyfikacje obiektów...
Program graficzny MS Paint.
 Program graficzny MS Paint. Program graficzny MS Paint (w starszych wersjach Windows Paintbrush lub mspaint) aplikacja firmy Microsoft w systemach Windows służąca do obróbki grafiki. SP 8 Lubin Zdjęcie:
Program graficzny MS Paint. Program graficzny MS Paint (w starszych wersjach Windows Paintbrush lub mspaint) aplikacja firmy Microsoft w systemach Windows służąca do obróbki grafiki. SP 8 Lubin Zdjęcie:
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Turing i jego maszyny
 Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
Wykład 11: Martyngały: definicja, twierdzenia o zbieżności
 RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
Języki formalne i automaty Ćwiczenia 4
 Języki formalne i automaty Ćwiczenia 4 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Sposób tworzenia deterministycznego automatu skończonego... 4 Intuicyjne rozumienie konstrukcji
Języki formalne i automaty Ćwiczenia 4 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Sposób tworzenia deterministycznego automatu skończonego... 4 Intuicyjne rozumienie konstrukcji
Indukowane Reguły Decyzyjne I. Wykład 3
 Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
Indukowane Reguły Decyzyjne I Wykład 3 IRD Wykład 3 Plan Powtórka Grafy Drzewa klasyfikacyjne Testy wstęp Klasyfikacja obiektów z wykorzystaniem drzewa Reguły decyzyjne generowane przez drzewo 2 Powtórzenie
