Rozszerzenia sieci Petriego
|
|
|
- Maksymilian Jastrzębski
- 6 lat temu
- Przeglądów:
Transkrypt
1 Rozszerzenia sieci Petriego
2 Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu dla konfliktowych przejść Dla złożonych procesów, tworzone modele ze względu na wielkość są trudne do specyfikacji i interpretacji Modele nie odzwierciedlają aspektów czasowych, np. czasu pozostawania żetonów w miejscach, uniemożliwiając wykonywanie analizy wydajnościowej Brak możliwości modelowania semantyki przepływu i przetwarzania danych
3 Rozszerzenia sieci Petriego Sieci Petriego są rozszerzane o następujące własności: Nowe typy łuków: zerujące i inhibitory Sieci priorytetowe Czasowe sieci Petriego Kolorowane sieci Petriego Czasowe i kolorowane sieci Petriego Hierarchiczna struktura sieci
4 Łuki zerujące Łuki zerujące są specjalnym rodzajem łuków służących do całkowitego zerowania zawartości przyłączonych do nich miejsc w wyniku odpalenia przejścia Dwie alternatywne notacje: P1 T1 T1 P1 Przejście konsumuje wszystkie żetony z miejsca wejściowego Odpalenie przejścia zeruje wszystkie żetony w miejscu wyjściowym
5 Inhibitory Łuki typu inhibitor, blokują odpalanie aktywnych przejść, kiedy miejsce połączone z przejściem za pomocą inhibitora zawiera żetony P1 P2 T1 P3 Aktywne przejście T1 nie może odpalić z powodu zablokowania przez miejsce P3.
6 Priorytetowe sieci Petriego Przez przypisanie przejściom sieci Petriego priorytetów można określić częściowy porządek w zbiorze przejść, który wyeliminuje lub ograniczy sytuacje niejednoznaczne brak determinizmu w działaniu sieci. Jeżeli aktywne są dwa przejścia, które rywalizują o ten sam zbiór żetonów, to odpalone zostanie przejście o wyższym priorytecie.
7 Priorytetowe sieci Petriego Formalnie, priorytetowa sieć Petriego jest uporządkowaną szóstką: (P, T, I, O, R, S), gdzie: P jest skończonym zbiorem miejsc, T jest skończonym zbiorem przejść, I : P x T > N jest funkcją wejść, N jest liczbą krawędzi między p i t, O : T x P > N jest funkcją wyjść, N jest liczbą krawędzi między t i p, R : T > N 0 jest funkcją priorytetów, przypisującą każdemu z przejść liczbę całkowitą nieujemną, S: P > N jest to funkcja odwzorowująca zbiór miejsc w zbiór liczb naturalnych reprezentujących liczbę żetonów w danym miejscu.
8 Przykład sieci priorytetowej W danym stanie sieci priorytetowej aktywne są przejścia, których miejsca wejściowe mają wystarczającą liczbę znaczników oraz ich priorytet jest nie mniejszy niż dowolnego innego przejścia, z którym jest w konflikcie. W danym stanie sieci aktywne są jedynie przejścia t 1 i t 3. Miejsce t 4 nie jest aktywne, bo ma priorytet mniejszy niż t 1 i t 3.
9 Przykład sieci priorytetowej Przejazd kolejowy przejazd pociągu ma większy priorytet od przejazdu samochodów (domyślny priorytet równy 0). t 1 t 4 samochód przed przejazdem opuść szlaban pociąg przed przejazdem samochód za przejazdem przejedź przez tory podniesiony szlaban pociąg za przejazdem przejedź przez przejazd
10 Sieci czasowe Sieci czasowe umożliwiają modelowanie czasu odpalenia przejść Proste pozwalają przypisać przejściom czas ich odpalenia liczony od momentu uaktywnienia przejścia Przedziałowe pozwalają przypisać przejściom przedział czasu [t min, t max ], w którym mogą być odpalone, liczony od momentu uaktywnienia danego przejścia.
11 Proste sieci czasowe Formalnie, czasowa sieć Petriego jest uporządkowaną szóstką: (P, T, I, O, σ, S), gdzie: σ : T -> Q, gdzie Q jest liczbą reprezentującą opóźnienie odpalenia przejścia t T. Aktywne przejście musi być odpalone po dokładnie σ jednostkach czasu, chyba że wcześniej zostanie dezaktywowane. Aktywne są przejścia: t1 i t3. Po dwóch jednostkach czasu odpali przejście t1. Jeżeli dwa aktywne przejścia mają takie same opóźnienie, odpalone zostanie niedeterministycznie wybrane jedno z nich.
12 Przedziałowe sieci czasowe Formalnie, przedziałowa czasowa sieć Petriego jest uporządkowaną szóstką: (P, T, I, O, σ, S), gdzie: σ : T -> Q Q, gdzie Q są liczbami reprezentującymi minimalny i maksymalny czas odpalenia przejścia t T Aktywne są przejścia: t1 i t3. W przedziale czasu [0-4] niedereministycznie może odpalić przejście t3, w przedziale czasu [2-4] przejście t1.
13 Przykład model protokołu komunikacyjnego W każdym ze stanów poniższej sieci Petriego, znajduje się dokładnie jeden znacznik reprezentujący jeden z 6 stanów, w którym może znajdować się protokół. t1 wygenerowanie wiadomości t2 wysłanie wiadomości przez nadawcę t3 odebranie wiadomości przez odbiorcę t4 wysłanie potwierdzenia przez odbiorcę t5 odebranie potwierdzenia przez nadawcę t6 zgubienie wiadomości t7 zgubienie potwierdzenia t8 żądanie ponowienia transmisji
14 Kolorowane sieci Petriego nowe własności Miejsca mają przypisane typy danych Znaczniki mają wartości Łuki mają przypisane wyrażenia logiczne (zastrzeżenia), które opisują warunki konsumowania żetonów z miejsc wejściowych Łuki mają przypisane wyrażenia typu przypisanego miejscom, określające sposób wyznaczania wartości konsumowanych i produkowanych żetonów
15 Typy i wartości danych Żetony mają kolor, czyli przypisane są im wartości Miejsca są typowane, mają przypisany zbiór kolorów
16 Wyznaczanie wartości żetonów W przejściach można zdefiniować wyrażenia wyznaczające wartości produkowanych żetonów in x add x+y y sum 0 1 Wartości produkowanych żetonów w miejscu sum jest sumą wartości konsumowanych żetonów.
17 Kolorowane sieci Petriego przykład zastrzeżenie: wyrażenie: zmienna: nazwa miejsca: typ miejsca: stała: zbiór znaczników: - dwa o wartości a - cztery o wartości b - trzy o wartości c
18 Rozszerzenie kolorowanych sieci Petriego o element czasu Każdy żeton ma przypisany znacznik czasowy Znacznik czasowy żetonu określa czas kiedy żeton może być najwcześniej skonsumowany 2 5
19 Rozszerzenie o element czasu Czas aktywowania przejścia odpowiada największemu znacznikowi czasowemu ze zbioru żetonów przeznaczonych do konsumpcji przez to przejście. Jeżeli w danym miejscu jest wiele żetonów, żeton o najmniejszym znaczniku czasowym jest konsumowany jako pierwszy. Przejście o najmniejszym czasie odpalenia będzie odpalone jako pierwsze. Przejścia są odpalane natychmiast, kiedy tylko mogą być odpalone. Produkowane żetony mogą mieć opóźnienie. Znaczniki czasowe produkowanych żetonów są równe czasowi odpalenia powiększonym o czas opóźnienia.
20 Ustalenie czasu aktywacji Czas aktywacji przejścia start w poniższym przykładzie wynosi: 2 = max{0,min{2,4,4}}. 0 4 wait done 2 start free stop 4 busy
21 Czas produkowania żetonów Żetony produkowane do miejsca busy mają opóźnienie równe = czas odpalenia przejścia start plus 3 jednostki opóźnienia 0 4 done 2 free 4 busy
22 Czas odpalenia przejścia Przejście start zostanie odpalone w jednostce czasu 2. Żeton wyprodukowany do miejsca busy będzie miał wartość =5 4 done free 4 5 busy
23 Hierarchiczne sieci Petriego Hierarchiczne sieci kolorowane umożliwiają tworzenie dużych modeli przez łączenie mniejszych fragmentów sieci zwanych pod stronami w wielopoziomową hierarchię stron. Całe fragmenty sieci mogą być zastępowane pojedynczymi przejściami podstawianymi. Strony sieci mogą być łączone za pomocą dwóch konstrukcji: Podstawiane przejścia, które służą do łączenia sieci podstron, z sieciami nad stron poprzez gniazda (miejsca w nadstronach) i miejsca portowe (miejsca w pod stronach) Fuzje miejsc, które są nierozróżnialnymi miejscami występującymi w różnych pod stronach sieci Umożliwia to modelowanie procesów na różnych poziomach abstrakcji
24 Strona główna sieci Strona główna sieci Sortowanie obejmuje trzy przejścia podstawiane Zliczanie HS (ang. hierarchy substitution): t2, t3 i t4 oraz odpowiadające im gniazda wejściowe i wyjściowe (p2,p5), (p3,p6) i (p4,p7). Hierarchia stron
25 Pod strony sieci Pod strona Zliczanie, zawiera dwa miejsca portowe: miejsce p8 typu IN odpowiadające gniazdom wejściowym, miejsce p9 typu OUT odpowiadające gniazdom wyjściowym, oraz fuzję miejsc: miejsce p10 które jest współdzielone przez wszystkie trzy wystąpienia strony licznik.
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Sieci Petriego. Sieć Petriego
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
miejsca przejścia, łuki i żetony
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń)
 Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego. Kolorowane sieci Petriego 1
 SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
Wykład 5: Specyfikacja na poziomie systemowym
 Systemy wbudowane Wykład 5: Specyfikacja na poziomie systemowym Ogólny model systemu informatycznego Sieć komunikujących się procesów P1 P3 P2 Kiedy procesy się aktywują? Czy jest synchronizacja między
Systemy wbudowane Wykład 5: Specyfikacja na poziomie systemowym Ogólny model systemu informatycznego Sieć komunikujących się procesów P1 P3 P2 Kiedy procesy się aktywują? Czy jest synchronizacja między
CZĘŚĆ PIERWSZA. Seminarium grupy RSPN. Piotr Lasek Uniwersytet Rzeszowski. Kontakt
 Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego
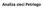 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Jeśli X jest przestrzenią o nieskończonej liczbie elementów:
 Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
Logika rozmyta 2 Zbiór rozmyty może być formalnie zapisany na dwa sposoby w zależności od tego z jakim typem przestrzeni elementów mamy do czynienia: Jeśli X jest przestrzenią o skończonej liczbie elementów
Modelowanie procesów współbieżnych
 Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Rozkład menu narzędzi
 Tylko administrator systemu ma dostęp do wszystkich opcji Narzędzi. Ustawienia urządzenia Ogólne Oszczędzanie energii Inteligentny Uruchamiany pracą Planowany Data i godzina Strefa czasowa (różnica dla
Tylko administrator systemu ma dostęp do wszystkich opcji Narzędzi. Ustawienia urządzenia Ogólne Oszczędzanie energii Inteligentny Uruchamiany pracą Planowany Data i godzina Strefa czasowa (różnica dla
Wstęp do informatyki. Maszyna RAM. Schemat logiczny komputera. Maszyna RAM. RAM: szczegóły. Realizacja algorytmu przez komputer
 Realizacja algorytmu przez komputer Wstęp do informatyki Wykład UniwersytetWrocławski 0 Tydzień temu: opis algorytmu w języku zrozumiałym dla człowieka: schemat blokowy, pseudokod. Dziś: schemat logiczny
Realizacja algorytmu przez komputer Wstęp do informatyki Wykład UniwersytetWrocławski 0 Tydzień temu: opis algorytmu w języku zrozumiałym dla człowieka: schemat blokowy, pseudokod. Dziś: schemat logiczny
Definicja sieci. Sieć Petriego jest czwórką C = ( P, T, I, O ), gdzie: P = { p 1, p 2,, p n } T = { t 1, t 2,, t m }
 Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
Sieci Petriego Źródła wykładu: 1. http://www.ia.pw.edu.pl/~sacha/petri.html 2.M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008 Definicja sieci Sieć Petriego jest czwórką
S Instrukcje programowania instrukcje obsługi Ethernetu
 S7-1200 Instrukcje programowania instrukcje obsługi Ethernetu Kontynuujemy opis instrukcji programowania sterowników S7-1200. W tym miesiącu skupiamy się na prezentacji i omówieniu instrukcji obsługujących
S7-1200 Instrukcje programowania instrukcje obsługi Ethernetu Kontynuujemy opis instrukcji programowania sterowników S7-1200. W tym miesiącu skupiamy się na prezentacji i omówieniu instrukcji obsługujących
TECHNOLOGIE OBIEKTOWE WYKŁAD 2. Anna Mroczek
 TECHNOLOGIE OBIEKTOWE WYKŁAD 2 Anna Mroczek 2 Diagram czynności Czym jest diagram czynności? 3 Diagram czynności (tak jak to definiuje język UML), stanowi graficzną reprezentację przepływu kontroli. 4
TECHNOLOGIE OBIEKTOWE WYKŁAD 2 Anna Mroczek 2 Diagram czynności Czym jest diagram czynności? 3 Diagram czynności (tak jak to definiuje język UML), stanowi graficzną reprezentację przepływu kontroli. 4
INFORMATYKA W SZKOLE. Podyplomowe Studia Pedagogiczne. Dr inż. Grażyna KRUPIŃSKA. D-10 pokój 227
 INFORMATYKA W SZKOLE Dr inż. Grażyna KRUPIŃSKA grazyna@fis.agh.edu.pl D-10 pokój 227 Podyplomowe Studia Pedagogiczne 2 Algorytmy Nazwa algorytm wywodzi się od nazwiska perskiego matematyka Muhamed ibn
INFORMATYKA W SZKOLE Dr inż. Grażyna KRUPIŃSKA grazyna@fis.agh.edu.pl D-10 pokój 227 Podyplomowe Studia Pedagogiczne 2 Algorytmy Nazwa algorytm wywodzi się od nazwiska perskiego matematyka Muhamed ibn
dwójkę liczącą Licznikiem Podział liczników:
 1. Dwójka licząca Przerzutnik typu D łatwo jest przekształcić w przerzutnik typu T i zrealizować dzielnik modulo 2 - tzw. dwójkę liczącą. W tym celu wystarczy połączyć wyjście zanegowane Q z wejściem D.
1. Dwójka licząca Przerzutnik typu D łatwo jest przekształcić w przerzutnik typu T i zrealizować dzielnik modulo 2 - tzw. dwójkę liczącą. W tym celu wystarczy połączyć wyjście zanegowane Q z wejściem D.
EGZAMIN MATURALNY Z INFORMATYKI. 10 maja 2017 POZIOM ROZSZERZONY. Godzina rozpoczęcia: 14:00 CZĘŚĆ I
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 2013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu. Układ graficzny CKE 2013 KOD UZUPEŁNIA ZDAJĄCY PESEL miejsce na naklejkę EGZAMIN MATURALNY Z INFORMATYKI POZIOM ROZSZERZONY
Problem detekcji zakończenia (I)
 Problem detekcji zakończenia (I) Plan wykładu Celem wykładu jest zapoznanie studenta z tematyką detekcji zakończenia. Wykład obejmie przedstawienie przykładów ilustrujących potrzebę problemy detekcji zakończenia
Problem detekcji zakończenia (I) Plan wykładu Celem wykładu jest zapoznanie studenta z tematyką detekcji zakończenia. Wykład obejmie przedstawienie przykładów ilustrujących potrzebę problemy detekcji zakończenia
Literatura. adów w cyfrowych. Projektowanie układ. Technika cyfrowa. Technika cyfrowa. Bramki logiczne i przerzutniki.
 Literatura 1. D. Gajski, Principles of Digital Design, Prentice- Hall, 1997 2. C. Zieliński, Podstawy projektowania układów cyfrowych, PWN, Warszawa 2003 3. G. de Micheli, Synteza i optymalizacja układów
Literatura 1. D. Gajski, Principles of Digital Design, Prentice- Hall, 1997 2. C. Zieliński, Podstawy projektowania układów cyfrowych, PWN, Warszawa 2003 3. G. de Micheli, Synteza i optymalizacja układów
1. Cel ćwiczenia. 2. Podłączenia urządzeń zewnętrznych w sterowniku VersaMax Micro
 1. Cel ćwiczenia Celem ćwiczenia jest zaprojektowanie sterowania układem pozycjonowania z wykorzystaniem sterownika VersaMax Micro oraz silnika krokowego. Do algorytmu pozycjonowania wykorzystać licznik
1. Cel ćwiczenia Celem ćwiczenia jest zaprojektowanie sterowania układem pozycjonowania z wykorzystaniem sterownika VersaMax Micro oraz silnika krokowego. Do algorytmu pozycjonowania wykorzystać licznik
Stan globalny. Krzysztof Banaś Systemy rozproszone 1
 Stan globalny Krzysztof Banaś Systemy rozproszone 1 Stan globalny Z problemem globalnego czasu jest związany także problem globalnego stanu: interesuje nas stan systemu rozproszonego w konkretnej pojedynczej
Stan globalny Krzysztof Banaś Systemy rozproszone 1 Stan globalny Z problemem globalnego czasu jest związany także problem globalnego stanu: interesuje nas stan systemu rozproszonego w konkretnej pojedynczej
LICZNIKI PODZIAŁ I PARAMETRY
 LICZNIKI PODZIAŁ I PARAMETRY Licznik jest układem służącym do zliczania impulsów zerojedynkowych oraz zapamiętywania ich liczby. Zależnie od liczby n przerzutników wchodzących w skład licznika pojemność
LICZNIKI PODZIAŁ I PARAMETRY Licznik jest układem służącym do zliczania impulsów zerojedynkowych oraz zapamiętywania ich liczby. Zależnie od liczby n przerzutników wchodzących w skład licznika pojemność
Kody Tunstalla. Kodowanie arytmetyczne
 Kody Tunstalla. Kodowanie arytmetyczne Kodowanie i kompresja informacji - Wykład 3 8 marca 2010 Kody Tunstalla Wszystkie słowa kodowe maja ta sama długość ale jeden kod może kodować różna liczbę liter
Kody Tunstalla. Kodowanie arytmetyczne Kodowanie i kompresja informacji - Wykład 3 8 marca 2010 Kody Tunstalla Wszystkie słowa kodowe maja ta sama długość ale jeden kod może kodować różna liczbę liter
Modelowanie i Analiza Systemów Informatycznych
 Paweł Skrobanek Modelowanie i Analiza Systemów Informatycznych Sieci Petriego (wersja poprawiona, 2013) Materiały są tłumaczeniem instrukcji laboratoryjnych p.t. Paweł Skrobanek Information Systems Analysis
Paweł Skrobanek Modelowanie i Analiza Systemów Informatycznych Sieci Petriego (wersja poprawiona, 2013) Materiały są tłumaczeniem instrukcji laboratoryjnych p.t. Paweł Skrobanek Information Systems Analysis
Przetwarzanie rozproszone
 Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
Sortowanie przez wstawianie Insertion Sort
 Sortowanie przez wstawianie Insertion Sort Algorytm sortowania przez wstawianie można porównać do sposobu układania kart pobieranych z talii. Najpierw bierzemy pierwszą kartę. Następnie pobieramy kolejne,
Sortowanie przez wstawianie Insertion Sort Algorytm sortowania przez wstawianie można porównać do sposobu układania kart pobieranych z talii. Najpierw bierzemy pierwszą kartę. Następnie pobieramy kolejne,
SFC zawiera zestaw kroków i tranzycji (przejść), które sprzęgają się wzajemnie przez połączenia
 Norma IEC-61131-3 definiuje typy języków: graficzne: schematów drabinkowych LD, schematów blokowych FBD, tekstowe: lista instrukcji IL, tekst strukturalny ST, grafów: graf funkcji sekwencyjnych SFC, graf
Norma IEC-61131-3 definiuje typy języków: graficzne: schematów drabinkowych LD, schematów blokowych FBD, tekstowe: lista instrukcji IL, tekst strukturalny ST, grafów: graf funkcji sekwencyjnych SFC, graf
Aby w pełni przetestować układ o trzech wejściach IN_0, IN_1 i IN_2 chcemy wygenerować wszystkie możliwe kombinacje sygnałów wejściowych.
 Generowanie sygnałów testowych VHDL Wariant współbieżny (bez procesu): sygnał
Generowanie sygnałów testowych VHDL Wariant współbieżny (bez procesu): sygnał
Odwzorowanie BPMN w sieć Petriego
 Odwzorowanie BPMN w sieć Petriego Proces odwzorowania Scenariusz procesu odwzorowania BPMN2PN BPMN Modeler plik XML BPMN Preprocesor plik XMI BPMN Narzędzie transformacji plik PNML Narzędzia analizy: ProM,
Odwzorowanie BPMN w sieć Petriego Proces odwzorowania Scenariusz procesu odwzorowania BPMN2PN BPMN Modeler plik XML BPMN Preprocesor plik XMI BPMN Narzędzie transformacji plik PNML Narzędzia analizy: ProM,
Analiza i projektowanie oprogramowania. Analiza i projektowanie oprogramowania 1/32
 Analiza i projektowanie oprogramowania Analiza i projektowanie oprogramowania 1/32 Analiza i projektowanie oprogramowania 2/32 Cel analizy Celem fazy określania wymagań jest udzielenie odpowiedzi na pytanie:
Analiza i projektowanie oprogramowania Analiza i projektowanie oprogramowania 1/32 Analiza i projektowanie oprogramowania 2/32 Cel analizy Celem fazy określania wymagań jest udzielenie odpowiedzi na pytanie:
Automatyka SPZ. 1. ZASADA DZIAŁANIA...2 2. SCHEMAT FUNKCJONALNY...6 3. PARAMETRY SPZ...7 4. WYKRESY CZASOWE DZIAŁANIA AUTOMATYKI SPZ...
 Automatyka SPZ. 1. ZASADA DZIAŁANIA...2 2. SCHEMAT FUNKCJONALNY...6 3. PARAMETRY SPZ...7 4. WYKRESY CZASOWE DZIAŁANIA AUTOMATYKI SPZ...9 Zabezpieczenia : ZCS 4E od: v 3.7 ZCR 4E od: v 5.1 ZZN 4E od: v
Automatyka SPZ. 1. ZASADA DZIAŁANIA...2 2. SCHEMAT FUNKCJONALNY...6 3. PARAMETRY SPZ...7 4. WYKRESY CZASOWE DZIAŁANIA AUTOMATYKI SPZ...9 Zabezpieczenia : ZCS 4E od: v 3.7 ZCR 4E od: v 5.1 ZZN 4E od: v
Urządzenia sieciowe. Tutorial 1 Topologie sieci. Definicja sieci i rodzaje topologii
 Tutorial 1 Topologie sieci Definicja sieci i rodzaje topologii Definicja 1 Sieć komputerowa jest zbiorem mechanizmów umożliwiających komunikowanie się komputerów bądź urządzeń komputerowych znajdujących
Tutorial 1 Topologie sieci Definicja sieci i rodzaje topologii Definicja 1 Sieć komputerowa jest zbiorem mechanizmów umożliwiających komunikowanie się komputerów bądź urządzeń komputerowych znajdujących
RS485 MODBUS Module 6RO
 Wersja 1.2 15.10.2012 wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
Wersja 1.2 15.10.2012 wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
Hardware mikrokontrolera X51
 Hardware mikrokontrolera X51 Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Hardware mikrokontrolera X51 (zegar)
Hardware mikrokontrolera X51 Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Hardware mikrokontrolera X51 (zegar)
Podstawy Projektowania Przyrządów Wirtualnych. Wykład 9. Wprowadzenie do standardu magistrali VMEbus. mgr inż. Paweł Kogut
 Podstawy Projektowania Przyrządów Wirtualnych Wykład 9 Wprowadzenie do standardu magistrali VMEbus mgr inż. Paweł Kogut VMEbus VMEbus (Versa Module Eurocard bus) jest to standard magistrali komputerowej
Podstawy Projektowania Przyrządów Wirtualnych Wykład 9 Wprowadzenie do standardu magistrali VMEbus mgr inż. Paweł Kogut VMEbus VMEbus (Versa Module Eurocard bus) jest to standard magistrali komputerowej
Modelowanie procesów współbieżnych
 Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Katedra Inżynierii Komputerowej Politechnika Częstochowska. Zastosowania protokołu ICMP Laboratorium podstaw sieci komputerowych
 Katedra Inżynierii Komputerowej Politechnika Częstochowska Zastosowania protokołu ICMP Laboratorium podstaw sieci komputerowych Cel ćwiczenia Zastosowania protokołu ICMP Celem dwiczenia jest zapoznanie
Katedra Inżynierii Komputerowej Politechnika Częstochowska Zastosowania protokołu ICMP Laboratorium podstaw sieci komputerowych Cel ćwiczenia Zastosowania protokołu ICMP Celem dwiczenia jest zapoznanie
ZASOBY ZMIENNYCH W STEROWNIKACH SAIA-BURGESS
 ZASOBY ZMIENNYCH W STEROWNIKACH SAIA-BURGESS Autorzy Wydanie Data : : : Zespół SABUR Sp. z o.o. 3.00 Sierpień 2013 2013 SABUR Sp. z o. o. Wszelkie prawa zastrzeżone Bez pisemnej zgody firmy SABUR Sp. z
ZASOBY ZMIENNYCH W STEROWNIKACH SAIA-BURGESS Autorzy Wydanie Data : : : Zespół SABUR Sp. z o.o. 3.00 Sierpień 2013 2013 SABUR Sp. z o. o. Wszelkie prawa zastrzeżone Bez pisemnej zgody firmy SABUR Sp. z
ĆWICZENIE 7. Wprowadzenie do funkcji specjalnych sterownika LOGO!
 ćwiczenie nr 7 str.1/1 ĆWICZENIE 7 Wprowadzenie do funkcji specjalnych sterownika LOGO! 1. CEL ĆWICZENIA: zapoznanie się z zaawansowanymi możliwościami mikroprocesorowych sterowników programowalnych na
ćwiczenie nr 7 str.1/1 ĆWICZENIE 7 Wprowadzenie do funkcji specjalnych sterownika LOGO! 1. CEL ĆWICZENIA: zapoznanie się z zaawansowanymi możliwościami mikroprocesorowych sterowników programowalnych na
GRUPA ĆWICZENIOWA (ZAKREŚL ODPOWIEDNIĄ): MG8 MG13 MB13 MD13 BT13
 Nazwisko i imię: Nr indeksu: 1 2 3 4 Σ MiNI/MatLic/AiPP/2014 2015/Kolokwium-IIA (30) GRUPA ĆWICZENIOWA (ZAKREŚL ODPOWIEDNIĄ): MG8 MG13 MB13 MD13 BT13 Uwaga: Za każde zadanie można uzyskać tę samą liczbę
Nazwisko i imię: Nr indeksu: 1 2 3 4 Σ MiNI/MatLic/AiPP/2014 2015/Kolokwium-IIA (30) GRUPA ĆWICZENIOWA (ZAKREŚL ODPOWIEDNIĄ): MG8 MG13 MB13 MD13 BT13 Uwaga: Za każde zadanie można uzyskać tę samą liczbę
Strefy dostępu i obwodowe
 R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 004 Wersja dokumentu: Rev. B Strefy dostępu i obwodowe Uwaga: Niniejszy dokument dotyczy RACS v5.2 (VISO 1.2.2 lub nowszy) Wprowadzenie
R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 004 Wersja dokumentu: Rev. B Strefy dostępu i obwodowe Uwaga: Niniejszy dokument dotyczy RACS v5.2 (VISO 1.2.2 lub nowszy) Wprowadzenie
Problem detekcji zakończenia
 Problem detekcji zakończenia Przykład sortowanie rozproszone Rozważmy problem sortowania rozproszonego zbioru X składającego się z v różnych liczb naturalnych, w środowisku rozproszonym o n węzłach (procesorach),
Problem detekcji zakończenia Przykład sortowanie rozproszone Rozważmy problem sortowania rozproszonego zbioru X składającego się z v różnych liczb naturalnych, w środowisku rozproszonym o n węzłach (procesorach),
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
WFiIS CEL ĆWICZENIA WSTĘP TEORETYCZNY
 WFiIS LABORATORIUM Z ELEKTRONIKI Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA CEL ĆWICZENIA Ćwiczenie
WFiIS LABORATORIUM Z ELEKTRONIKI Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA CEL ĆWICZENIA Ćwiczenie
Podstawy Informatyki Systemy sterowane przepływem argumentów
 Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Komputer i jego architektura Taksonomia Flynna 2 Komputer i jego architektura Taksonomia Flynna Komputer Komputer
Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Komputer i jego architektura Taksonomia Flynna 2 Komputer i jego architektura Taksonomia Flynna Komputer Komputer
W ielofunkcyjne linie wejściowe
 R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 010 Wersja dokumentu: Rev. B W ielofunkcyjne linie wejściowe Wprowadzenie W systemie RACS 5 istnieje możliwość przypisywania wielu
R o g e r A c c e s s C o n t r o l S y s t e m 5 Nota aplikacyjna nr 010 Wersja dokumentu: Rev. B W ielofunkcyjne linie wejściowe Wprowadzenie W systemie RACS 5 istnieje możliwość przypisywania wielu
Algorytm. a programowanie -
 Algorytm a programowanie - Program komputerowy: Program komputerowy można rozumieć jako: kod źródłowy - program komputerowy zapisany w pewnym języku programowania, zestaw poszczególnych instrukcji, plik
Algorytm a programowanie - Program komputerowy: Program komputerowy można rozumieć jako: kod źródłowy - program komputerowy zapisany w pewnym języku programowania, zestaw poszczególnych instrukcji, plik
Zasady analizy algorytmów
 Zasady analizy algorytmów A więc dziś w programie: - Kilka ważnych definicji i opisów formalnych - Złożoność: czasowa i pamięciowa - Kategorie problemów - Jakieś przykłady Problem: Zadanie możliwe do rozwiązania
Zasady analizy algorytmów A więc dziś w programie: - Kilka ważnych definicji i opisów formalnych - Złożoność: czasowa i pamięciowa - Kategorie problemów - Jakieś przykłady Problem: Zadanie możliwe do rozwiązania
Język skryptowy: Laboratorium 1. Wprowadzenie do języka Python
 Język skryptowy: Laboratorium 1. Wprowadzenie do języka Python Język PYTHON Podstawowe informacje Python to język skryptowy, interpretowany - co oznacza, że piszemy skrypt, a następnie wykonujemy go za
Język skryptowy: Laboratorium 1. Wprowadzenie do języka Python Język PYTHON Podstawowe informacje Python to język skryptowy, interpretowany - co oznacza, że piszemy skrypt, a następnie wykonujemy go za
Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony.
 GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
GRY (część 1) Zastosowanie: Modelowanie sytuacji konfliktowych, w których występują dwie antagonistyczne strony. Najbardziej znane modele: - wybór strategii marketingowych przez konkurujące ze sobą firmy
Information Systems Analysis
 THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
1. Sieci Petriego. Rys. 1-1 Przykład sieci Petriego
 1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
Wreferacie przedstawiono propozycję metody modelowania procesów transportowych
 Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Instrukcja wprowadzania graficznych harmonogramów pracy w SZOI Wg stanu na 21.06.2010 r.
 Instrukcja wprowadzania graficznych harmonogramów pracy w SZOI Wg stanu na 21.06.2010 r. W systemie SZOI została wprowadzona nowa funkcjonalność umożliwiająca tworzenie graficznych harmonogramów pracy.
Instrukcja wprowadzania graficznych harmonogramów pracy w SZOI Wg stanu na 21.06.2010 r. W systemie SZOI została wprowadzona nowa funkcjonalność umożliwiająca tworzenie graficznych harmonogramów pracy.
Język UML w modelowaniu systemów informatycznych
 Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 4 Diagramy aktywności I Diagram aktywności (czynności) (ang. activity
Paweł Kurzawa, Delfina Kongo
 Paweł Kurzawa, Delfina Kongo Pierwsze prace nad standaryzacją Obiektowych baz danych zaczęły się w roku 1991. Stworzona została grupa do prac nad standardem, została ona nazwana Object Database Management
Paweł Kurzawa, Delfina Kongo Pierwsze prace nad standaryzacją Obiektowych baz danych zaczęły się w roku 1991. Stworzona została grupa do prac nad standardem, została ona nazwana Object Database Management
MODELOWANIE STANDARDU PROFIBUS W ŚRODOWISKU LABVIEW
 Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 69 Politechniki Wrocławskiej Nr 69 Studia i Materiały Nr 33 2013 Krzysztof PODLEJSKI*, Jarosław SZAFRAN* Profibus, LabView, modelowanie
Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Nr 69 Politechniki Wrocławskiej Nr 69 Studia i Materiały Nr 33 2013 Krzysztof PODLEJSKI*, Jarosław SZAFRAN* Profibus, LabView, modelowanie
Definicje. Algorytm to:
 Algorytmy Definicje Algorytm to: skończony ciąg operacji na obiektach, ze ściśle ustalonym porządkiem wykonania, dający możliwość realizacji zadania określonej klasy pewien ciąg czynności, który prowadzi
Algorytmy Definicje Algorytm to: skończony ciąg operacji na obiektach, ze ściśle ustalonym porządkiem wykonania, dający możliwość realizacji zadania określonej klasy pewien ciąg czynności, który prowadzi
Wymiar poziomy: oś na której umieszczono instancje klasyfikatorów biorące udział w interakcji.
 Wymiar poziomy: oś na której umieszczono instancje klasyfikatorów biorące udział w interakcji. Wymiar pionowy: oś czasu przedstawiajaca ułożone chronologicznie komunikaty Podstawowe notacje graficzne Konceptualny
Wymiar poziomy: oś na której umieszczono instancje klasyfikatorów biorące udział w interakcji. Wymiar pionowy: oś czasu przedstawiajaca ułożone chronologicznie komunikaty Podstawowe notacje graficzne Konceptualny
Opis techniczny koncentratora wejść impulsowych KWI-1. APATOR SA,
 Opis techniczny koncentratora wejść impulsowych KWI-1 APATOR SA, www.apator.eu 1 SPIS TREŚCI STRONA 1. Funkcja KWI-1...3 2. Opis KWI-1...3 2.1. Wejścia impulsowe...3 2.2. Praca sieciowa M Bus...3 3. Stałe
Opis techniczny koncentratora wejść impulsowych KWI-1 APATOR SA, www.apator.eu 1 SPIS TREŚCI STRONA 1. Funkcja KWI-1...3 2. Opis KWI-1...3 2.1. Wejścia impulsowe...3 2.2. Praca sieciowa M Bus...3 3. Stałe
Technologie informacyjne - wykład 12 -
 Zakład Fizyki Budowli i Komputerowych Metod Projektowania Instytut Budownictwa Wydział Budownictwa Lądowego i Wodnego Politechnika Wrocławska Technologie informacyjne - wykład 12 - Prowadzący: Dmochowski
Zakład Fizyki Budowli i Komputerowych Metod Projektowania Instytut Budownictwa Wydział Budownictwa Lądowego i Wodnego Politechnika Wrocławska Technologie informacyjne - wykład 12 - Prowadzący: Dmochowski
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie
 Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie Wydział Elektrotechniki, Automatyki, Informatyki i Inżynierii Biomedycznej KATEDRA INFORMATYKI STOSOWANEJ ROZPRAWA DOKTORSKA MGR INŻ. WOJCIECH
Temat 1: Podstawowe pojęcia: program, kompilacja, kod
 Temat 1: Podstawowe pojęcia: program, kompilacja, kod wynikowy. Przykłady najprostszych programów. Definiowanie zmiennych. Typy proste. Operatory: arytmetyczne, przypisania, inkrementacji, dekrementacji,
Temat 1: Podstawowe pojęcia: program, kompilacja, kod wynikowy. Przykłady najprostszych programów. Definiowanie zmiennych. Typy proste. Operatory: arytmetyczne, przypisania, inkrementacji, dekrementacji,
Sterowniki Programowalne (SP)
 Sterowniki Programowalne (SP) Wybrane aspekty procesu tworzenia oprogramowania dla sterownika PLC Podstawy języka funkcjonalnych schematów blokowych (FBD) Politechnika Gdańska Wydział Elektrotechniki i
Sterowniki Programowalne (SP) Wybrane aspekty procesu tworzenia oprogramowania dla sterownika PLC Podstawy języka funkcjonalnych schematów blokowych (FBD) Politechnika Gdańska Wydział Elektrotechniki i
Część 3. Układy sekwencyjne. Układy sekwencyjne i układy iteracyjne - grafy stanów TCiM Wydział EAIiIB Katedra EiASPE 1
 Część 3 Układy sekwencyjne Układy sekwencyjne i układy iteracyjne - grafy stanów 18.11.2017 TCiM Wydział EAIiIB Katedra EiASPE 1 Układ cyfrowy - przypomnienie Podstawowe informacje x 1 x 2 Układ cyfrowy
Część 3 Układy sekwencyjne Układy sekwencyjne i układy iteracyjne - grafy stanów 18.11.2017 TCiM Wydział EAIiIB Katedra EiASPE 1 Układ cyfrowy - przypomnienie Podstawowe informacje x 1 x 2 Układ cyfrowy
Jednostka Sterująca - Menu
 Jednostka Sterująca - Menu Spis treści 1. Podział menu... 3 2. Tryb użytkownika... 4 2.1 Zdarzenia... 5 2.2 Urządzenia... 5 2.2.1 Błędy... 5 2.2.2 Porty... 5 2.2.3 Grupy... 5 2.2.4 Wszystkie... 5 2.3 Historia
Jednostka Sterująca - Menu Spis treści 1. Podział menu... 3 2. Tryb użytkownika... 4 2.1 Zdarzenia... 5 2.2 Urządzenia... 5 2.2.1 Błędy... 5 2.2.2 Porty... 5 2.2.3 Grupy... 5 2.2.4 Wszystkie... 5 2.3 Historia
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
LISTA 1 ZADANIE 1 a) 41 x =5 podnosimy obustronnie do kwadratu i otrzymujemy: 41 x =5 x 5 x przechodzimy na system dziesiętny: 4x 1 1=25 4x =24
 LISTA 1 ZADANIE 1 a) 41 x =5 podnosimy obustronnie do kwadratu i otrzymujemy: 41 x =5 x 5 x przechodzimy na system dziesiętny: 4x 1 1=25 4x =24 x=6 ODP: Podstawą (bazą), w której spełniona jest ta zależność
LISTA 1 ZADANIE 1 a) 41 x =5 podnosimy obustronnie do kwadratu i otrzymujemy: 41 x =5 x 5 x przechodzimy na system dziesiętny: 4x 1 1=25 4x =24 x=6 ODP: Podstawą (bazą), w której spełniona jest ta zależność
Systemy informatyczne. Modelowanie danych systemów informatycznych
 Modelowanie danych systemów informatycznych Diagramy związków encji Entity-Relationship Diagrams Modelowanie danych diagramy związków encji ERD (ang. Entity-Relationship Diagrams) diagramy związków encji
Modelowanie danych systemów informatycznych Diagramy związków encji Entity-Relationship Diagrams Modelowanie danych diagramy związków encji ERD (ang. Entity-Relationship Diagrams) diagramy związków encji
Podstawowe pojęcia. Własności próby. Cechy statystyczne dzielimy na
 Podstawowe pojęcia Zbiorowość statystyczna zbiór jednostek (obserwacji) nie identycznych, ale stanowiących logiczną całość Zbiorowość (populacja) generalna skończony lub nieskończony zbiór jednostek, które
Podstawowe pojęcia Zbiorowość statystyczna zbiór jednostek (obserwacji) nie identycznych, ale stanowiących logiczną całość Zbiorowość (populacja) generalna skończony lub nieskończony zbiór jednostek, które
W narzędziu typu Excel, Calc czy Gnumeric napisz formułę logiczną która wyznaczy wartośd przynależności dla podanej temperatury do zbioru gorąco.
 Zadanie 0 Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad wartośd funkcji przynależności
Zadanie 0 Wyobraźmy sobie, że chcemy oceniad czy dana temperatura świadczy o tym, że jest gorąco czy raczej zimno. A więc znając wartośd liczbową temperatury chcemy oceniad wartośd funkcji przynależności
Modelowanie danych, projektowanie systemu informatycznego
 Modelowanie danych, projektowanie systemu informatycznego Modelowanie odwzorowanie rzeczywistych obiektów świata rzeczywistego w systemie informatycznym Modele - konceptualne reprezentacja obiektów w uniwersalnym
Modelowanie danych, projektowanie systemu informatycznego Modelowanie odwzorowanie rzeczywistych obiektów świata rzeczywistego w systemie informatycznym Modele - konceptualne reprezentacja obiektów w uniwersalnym
MODELOWANIE PRZEPŁYWU DANYCH
 MODELOWANIE PRZEPŁYWU DANYCH 1. Diagram przepływu danych (DFD) 2. Weryfikacja modelu strukturalnego za pomocą DFD Modelowanie SI - GHJ 1 Definicja i struktura DFD Model części organizacji rozważany z punktu
MODELOWANIE PRZEPŁYWU DANYCH 1. Diagram przepływu danych (DFD) 2. Weryfikacja modelu strukturalnego za pomocą DFD Modelowanie SI - GHJ 1 Definicja i struktura DFD Model części organizacji rozważany z punktu
System plików. Warstwowy model systemu plików
 System plików System plików struktura danych organizująca i porządkująca zasoby pamięci masowych w SO. Struktura ta ma charakter hierarchiczny: urządzenia fizyczne strefy (partycje) woluminy (w UNIXie:
System plików System plików struktura danych organizująca i porządkująca zasoby pamięci masowych w SO. Struktura ta ma charakter hierarchiczny: urządzenia fizyczne strefy (partycje) woluminy (w UNIXie:
Na podstawie: Kirch O., Dawson T. 2000: LINUX podręcznik administratora sieci. Wydawnictwo RM, Warszawa. FILTROWANIE IP
 FILTROWANIE IP mechanizm decydujący, które typy datagramów IP mają być odebrane, które odrzucone. Odrzucenie oznacza usunięcie, zignorowanie datagramów, tak jakby nie zostały w ogóle odebrane. funkcja
FILTROWANIE IP mechanizm decydujący, które typy datagramów IP mają być odebrane, które odrzucone. Odrzucenie oznacza usunięcie, zignorowanie datagramów, tak jakby nie zostały w ogóle odebrane. funkcja
Mini Modbus 1AO. Moduł rozszerzający 1 wyjście analogowe, 2 wyjście cyfrowe. Wyprodukowano dla
 Wersja 1.0 14.08.2014 Wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
Wersja 1.0 14.08.2014 Wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
Automatyka SPZ. ZCR 4E; ZCS 4E; ZZN 4E; ZZN 5; ZRL 4E Automatyka SPZ
 Automatyka SPZ. 1. ZASADA DZIAŁANIA...2 2. SCHEMAT FUNKCJONALNY... 5 3. PARAMETRY SPZ...6 4. WYKRESY CZASOWE DZIAŁANIA AUTOMATYKI SPZ...8 Zabezpieczenia : ZCS 4E od: v 3.7 ZCR 4E od: v 5.1 ZZN 4E od: v
Automatyka SPZ. 1. ZASADA DZIAŁANIA...2 2. SCHEMAT FUNKCJONALNY... 5 3. PARAMETRY SPZ...6 4. WYKRESY CZASOWE DZIAŁANIA AUTOMATYKI SPZ...8 Zabezpieczenia : ZCS 4E od: v 3.7 ZCR 4E od: v 5.1 ZZN 4E od: v
Sterowniki Programowalne (SP) Wykład 11
 Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Bazy danych w sterowaniu
 Bazy danych w sterowaniu systemy transakcyjne sterowanie dostępem współbieżnym Stan spójny bazy danych zgodność z możliwym stanem reprezentowanego fragmentu świata rzeczywistego; spełnione są wszystkie
Bazy danych w sterowaniu systemy transakcyjne sterowanie dostępem współbieżnym Stan spójny bazy danych zgodność z możliwym stanem reprezentowanego fragmentu świata rzeczywistego; spełnione są wszystkie
E-book: Automatyzacja powiadomień SMS. CASE STUDY
 E-book: Automatyzacja powiadomień SMS. CASE STUDY CASE STUDY PRZEWODNIK JAK SKONFIGUROWAĆ FUNKCJĘ AUTOMATYZACJI na wybranym przykładzie Po zalogowaniu się do systemu (panel.serwersms.pl) pierwszym etapem
E-book: Automatyzacja powiadomień SMS. CASE STUDY CASE STUDY PRZEWODNIK JAK SKONFIGUROWAĆ FUNKCJĘ AUTOMATYZACJI na wybranym przykładzie Po zalogowaniu się do systemu (panel.serwersms.pl) pierwszym etapem
Przetwarzanie równoległesprzęt. Rafał Walkowiak Wybór
 Przetwarzanie równoległesprzęt 2 Rafał Walkowiak Wybór 17.01.2015 1 1 Sieci połączeń komputerów równoległych (1) Zadanie: przesyłanie danych pomiędzy węzłami przetwarzającymi, pomiędzy pamięcią a węzłami
Przetwarzanie równoległesprzęt 2 Rafał Walkowiak Wybór 17.01.2015 1 1 Sieci połączeń komputerów równoległych (1) Zadanie: przesyłanie danych pomiędzy węzłami przetwarzającymi, pomiędzy pamięcią a węzłami
Podstawy Informatyki Elementarne podzespoły komputera
 Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Reprezentacja informacji Podstawowe bramki logiczne 2 Przerzutniki Przerzutnik SR Rejestry Liczniki 3 Magistrala Sygnały
Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Reprezentacja informacji Podstawowe bramki logiczne 2 Przerzutniki Przerzutnik SR Rejestry Liczniki 3 Magistrala Sygnały
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04
 Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych kolekcji. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 04 Cel zajęć. Celem zajęć jest zapoznanie się ze sposobem działania popularnych kolekcji. Wprowadzenie teoretyczne. Rozważana w ramach niniejszych
Elżbieta Kula - wprowadzenie do Turbo Pascala i algorytmiki
 Elżbieta Kula - wprowadzenie do Turbo Pascala i algorytmiki Turbo Pascal jest językiem wysokiego poziomu, czyli nie jest rozumiany bezpośrednio dla komputera, ale jednocześnie jest wygodny dla programisty,
Elżbieta Kula - wprowadzenie do Turbo Pascala i algorytmiki Turbo Pascal jest językiem wysokiego poziomu, czyli nie jest rozumiany bezpośrednio dla komputera, ale jednocześnie jest wygodny dla programisty,
Wprowadzenie do algorytmiki
 Wprowadzenie do algorytmiki Pojecie algorytmu Powszechnie przyjmuje się, że algorytm jest opisem krok po kroku rozwiązania postawionego problemu lub sposób osiągnięcia jakiegoś celu. Wywodzi się z matematyki
Wprowadzenie do algorytmiki Pojecie algorytmu Powszechnie przyjmuje się, że algorytm jest opisem krok po kroku rozwiązania postawionego problemu lub sposób osiągnięcia jakiegoś celu. Wywodzi się z matematyki
W przypadku spostrzeżenia błędu proszę o przesłanie informacji na adres
 PROJEKTOWANIE LICZNIKÓW (skrót wiadomości) Autor: Rafał Walkowiak W przypadku spostrzeżenia błędu proszę o przesłanie informacji na adres rafal.walkowiak@cs.put.poznan.pl 1. Synchroniczne łączenie liczników
PROJEKTOWANIE LICZNIKÓW (skrót wiadomości) Autor: Rafał Walkowiak W przypadku spostrzeżenia błędu proszę o przesłanie informacji na adres rafal.walkowiak@cs.put.poznan.pl 1. Synchroniczne łączenie liczników
Plan wykładu. Statystyka opisowa. Statystyka matematyczna. Dane statystyczne miary położenia miary rozproszenia miary asymetrii
 Plan wykładu Statystyka opisowa Dane statystyczne miary położenia miary rozproszenia miary asymetrii Statystyka matematyczna Podstawy estymacji Testowanie hipotez statystycznych Żródła Korzystałam z ksiażek:
Plan wykładu Statystyka opisowa Dane statystyczne miary położenia miary rozproszenia miary asymetrii Statystyka matematyczna Podstawy estymacji Testowanie hipotez statystycznych Żródła Korzystałam z ksiażek:
RS485 MODBUS Module 8I8O
 Wersja 2.2 12.01.2014 wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
Wersja 2.2 12.01.2014 wyprodukowano dla Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w
RS485 MODBUS Module 6RO
 Wersja 2.0 19.12.2012 Dystrybutor Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w niniejszej
Wersja 2.0 19.12.2012 Dystrybutor Dziękujemy za wybór naszego produktu. Niniejsza instrukcja ułatwi Państwu prawidłową obsługę i poprawną eksploatację opisywanego urządzenia. Informacje zawarte w niniejszej
Podstawowe procedury przy tworzeniu programu do sterownika:
 Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
SYSTEM KONTROLI DOSTĘPU. XChronos
 SYSTEM KONTROLI DOSTĘPU XChronos Kontrola dostępu Najważniejsze cechy Kontrola dostępu do obiektów Szerokie możliwości raportowania Szeroki wybór technik identyfikacji Sterowanie ryglami i urządzeniami
SYSTEM KONTROLI DOSTĘPU XChronos Kontrola dostępu Najważniejsze cechy Kontrola dostępu do obiektów Szerokie możliwości raportowania Szeroki wybór technik identyfikacji Sterowanie ryglami i urządzeniami
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Diagramy czynności. Widok logiczny. Widok fizyczny
 Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
Obliczenia inspirowane Naturą Wykład 01 Modele obliczeń Jarosław Miszczak IITiS PAN Gliwice 05/10/2016 1 / 33 1 2 3 4 5 6 2 / 33 Co to znaczy obliczać? Co to znaczy obliczać? Deterministyczna maszyna Turinga
Adresacja IPv4 - podstawy
 Adresacja IPv4 - podstawy LAN LAN... MAN... LAN Internet Internet = sieć sieci Problem jak adresować urządzenia w takiej sieci? 1 Budowa adresu IP rozmiar adresu IP: 4 bajty (32 bity) Adres IP jest hierarchiczny
Adresacja IPv4 - podstawy LAN LAN... MAN... LAN Internet Internet = sieć sieci Problem jak adresować urządzenia w takiej sieci? 1 Budowa adresu IP rozmiar adresu IP: 4 bajty (32 bity) Adres IP jest hierarchiczny
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń.
 Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1. ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...5 3. FUNKCJE WYJŚCIOWE...6 4. FUNKCJE LOGICZNE...9 Zabezpieczenie : ZSN 5U od: v. 1.0
Funkcje: wejściowe, wyjściowe i logiczne. Konfigurowanie zabezpieczeń. 1. ZASADA DZIAŁANIA...2 2. FUNKCJE WEJŚCIOWE...5 3. FUNKCJE WYJŚCIOWE...6 4. FUNKCJE LOGICZNE...9 Zabezpieczenie : ZSN 5U od: v. 1.0
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 2 Temat: Schemat blokowy (algorytm) procesu selekcji wymiarowej
