Definicja sieci. Sieć Petriego jest czwórką C = ( P, T, I, O ), gdzie: P = { p 1, p 2,, p n } T = { t 1, t 2,, t m }
|
|
|
- Monika Jasińska
- 6 lat temu
- Przeglądów:
Transkrypt
1 Sieci Petriego Źródła wykładu: M. Szpyrka: Sieci Petriego w modelowaniu i analizie systemów współbieżnych, WNT 2008
2 Definicja sieci Sieć Petriego jest czwórką C = ( P, T, I, O ), gdzie: P = { p 1, p 2,, p n } T = { t 1, t 2,, t m } I : T P* O : T P* P T = {} zbiór miejsc zbiór tranzycji funkcja wejściowa funkcja wyjściowa I ( t j ) kolekcja miejsc wejściowych tranzycji t j # ( p i, I ( t j ) ) liczba wystąpień p i w I ( t j ) O ( t j ) kolekcja miejsc wyjściowych tranzycji t j # ( p i, O ( t j ) ) liczba wystąpień p i w O ( t j ) kolekcja = multi-zbiór 2
3 Reprezentacja graficzna p 1 t 1 t 2 p 2 p 3 P = { p 1, p 2, p 3, p 4 } T = { t 1, t 2, t 3 } I ( t 1 ) = { p 1 } I ( t 2 ) = { p 1 } I ( t 3 ) = { p 2, p 3 } p 4 t 3 O ( t 1 ) = { p 1, p 2 } O ( t 2 ) = { p 3, p 3 } O ( t 3 ) = { p 3, p 4 } # ( p i, I ( t j ) ) liczba łuków od miejsca p i do tranzycji t j # ( p i, O ( t j ) ) liczba łuków od tranzycji t j do miejsca p i 3
4 Znakowanie Znakowanie sieci jest funkcją µ : P N p 2 p 1 t 1 t 2 µ ( p 2 ) = 2 µ ( p 1 ) = 1 p 3 µ ( p 3 ) = 0 µ ( p 4 ) = 0 t 3 p 4 Definicja alternatywna Znakowanie sieci jest wektorem: µ = ( µ ( p 1 ), µ ( p 2 ),, µ ( p n ) ) Zbiór wszystkich możliwych znakowań: N n 4
5 Znakowana sieć Petriego jest parą Z = ( C,µ 0 ), gdzie: C sieć Petriego µ 0 : P N znakowanie początkowe Tranzycja jest wzbudzona w znakowaniu µ jeśli: p i P # ( p i, I ( t j ) ) µ( p i ) Wynikiem odpalenia wzbudzonej tranzycji t j w znakowaniu µ jest nowe znakowanie µ, takie że: p i P µ ( p i ) =µ( p i ) # ( p i, I ( t j ) ) + # ( p i, O ( t j ) ) 5
6 Sieć Petriego jako maszyna abstrakcyjna Znakowana sieć Petriego tworzy maszynę abstrakcyjną : przestrzeń stanów: N n funkcja przejścia: δ : N n T N n, gdzie: 1. Wartość δ ( µ, t j ) jest określona wtw. gdy: p i P # ( p i, I ( t j ) ) µ( p i ) Warunek wzbudzenia t j 2. Jeśli δ ( µ, t j ) jest określona, to δ ( µ, t j ) =µ, gdzie: p i P µ ( p i ) =µ( p i ) # ( p i, I ( t j ) ) + # ( p i, O ( t j ) ) Wynik odpalenia t j 6
7 Wykonanie sieci to odpalenie sekwencji wzbudzonych tranzycji zaczynając od znakowania początkowego t j0 t j1 t jk µ 0 µ 1 µ 2 µ k µ k+1 gdzie: t jk wzbudzona w znakowaniu µ k µ k+1 = δ ( µ k, t jk ) 7
8 Osiągalność znakowań Znakowanie µ k jest bezpośrednio osiągalne z µ l wtw., gdy: t j T µ k = δ ( µ l, t j ) Znakowanie µ k jest osiągalne z µ l wtw., gdy istnieje sekwencja znakowań µ l, µ l+1,..., µ l+n =µ k, taka że: i = l,..., l + n 1 µ i+1 jest bezpośrednio osiągalne z µ i Zbiór znakowań osiągalnych R ( C,µ 0 ) jest najmniejszym zbiorem, takim że: µ 0 R ( C, µ 0 ) jeśli µ l R ( C, µ 0 ) oraz istnieje tranzycja t j T taka,że µ k = δ ( µ l, t j ), to µ k R ( C, µ 0 ) 8
9 Zastosowania sieci Petriego Modelowanie przepływu sterowania w systemach współbieżnych Modelowanie zdarzeń złożonych Modelowanie konfliktów przy dostępie do zasobów 9
10 Bezpieczeństwo Właściwości sieci Miejsce p i P jest bezpieczne, jeśli: µ k R ( C, µ 0 ) µ k ( p i ) 1 Sieć ( C, µ 0 ) jest bezpieczna, jeśli wszystkie jej miejsca są bezpieczne Ograniczoność Miejsce p i P jest q-ograniczone, jeśli: µ k R ( C, µ 0 ) µ k ( p i ) q Sieć ( C, µ 0 ) jest ograniczona, jeśli wszystkie jej miejsca są q-ograniczone dla pewnego q 10
11 Zachowawczość Sieć ( C, µ 0 ) jest ściśle zachowawcza, jeśli: µ k R ( C, µ 0 ) i = 1.. n µ k ( p i ) = i = 1..n µ 0 ( p i ) Sieć ( C, µ 0 ) jest zachowawcza, jeśli istnieje taki dodatni wektor w = ( w 1, w 2,..., w n ), że: µ k R ( C, µ 0 ) i = 1.. n w i µ k ( p i ) = i = 1..n w i µ 0 ( p i ) 11
12 Żywotność Tranzycja t jest żywa, jeśli: µ k R ( C, µ 0 ) µ R ( C, µ k ) ( µ, t ) Dom ( δ ) Z dowolnego znakowania osiągalnego można dojść do takiego znakowania, w którym t będzie mogła odpalić Brak martwego kodu w każdym stanie wykonania programu Sieć ( C, µ 0 ) jest żywa, jeśli każda jej tranzycja jest żywa 12
13 Zakleszczenie Sieć ma zakleszczenie, jeśli: µ R ( C, µ 0 ) t T ( µ, t ) Dom ( δ ) Istnieje znakowanie, w którym żadna tranzycja nie jest wzbudzona Zawieszenie się wszystkich procesów programu Sieć jest wolna od zakleszczeń, jeśli: µ R ( C, µ 0 ) t T ( µ, t ) Dom ( δ ) 13
14 Osiągalność znakowania 1. Problem osiągalności: Czy dla danego µ k, µ k R ( C, µ 0 )? 2. Problem pokrycia: Porównanie wektorów Czy dla danego µ k istnieje µ l R ( C, µ 0 ) takie, że µ l µ k? 3. Osiągalność znakowania częściowego: Czy dla danego µ k określonego na zbiorze P x P istnieje µ l R ( C, µ 0 ) takie, że µ k ( p ) =µ l ( p ) dla p P x? 14
15 Drzewo osiągalności węzły znakowania łuki odpalenia tranzycji korzeń znakowanie początkowe liście znakowania końcowe lub powtórzone znakowanie graniczne znakowanie wewnętrzne znakowanie końcowe znakowanie powtórzone nowe, czekające na analizę znakowanie już poddane analizie bez wzbudzonych tranzycji już wcześniej analizowane Jeśli w gałęzi µ 0,..., µ k,..., µ l,... zachodzi: µ l jest większe od µ k p P µ l ( p ) µ k ( p ) oraz p i P µ l ( p i ) >µ k ( p i ), to przyjmuje się: µ l ( p i ) =ω 15
16 Algorytm konstrukcji drzewa osiągalności 1. Utwórz korzeń drzewa jako znakowanie graniczne µ 0 2. Dla każdego znakowania granicznego µ x : a. jeśli brak tranzycji wzbudzonych w µ x, to µ x jest znakowaniem końcowym (liść) b. jeśli w drzewie istnieje już znakowanie µ y, które nie jest znakowaniem granicznym i µ y =µ x, to µ x jest znakowaniem powtórzonym (liść) c. jeśli µ x nie jest ani końcowe ani powtórzone, to dla każdej wzbudzonej tranzycji t oblicz δ ( µ x, t ) i utwórz µ z : jeśli dla pewnego p Pµ x ( p ) =ω, to również µ z ( p ) =ω jeśli w drodze od korzenia do µ x istnieje znakowanie µ y takie, że δ ( µ x, t ) µ y oraz δ ( µ x, t )( p ) >µ y ( p ), to µ z ( p ) =ω w każdym innym przypadku µ z ( p ) = δ ( µ x, t )( p ) Znakowanie µ x staje się teraz wewnętrznym, a µ z granicznym 16
Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń)
 Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
Carl Adam Petri (1926-2010) Najkrótsza droga Maksymalny przepływ Najtańszy przepływ Analiza czynności (zdarzeń) Problemy statyczne Kommunikation mit Automaten praca doktorska (1962) opis procesów współbieżnych
1. Sieci Petriego. Rys. 1-1 Przykład sieci Petriego
 1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
1 1. Sieci Petriego Narzędzie wprowadzone przez Carla A. Petriego w 1962 roku do pierwotnie modelowania komunikacji z automatami. Obecnie narzędzie stosowane jest w modelowaniu systemów współbieżnych,
Analiza sieci Petriego
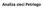 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Własności behawioralne sieci Petriego
Analiza sieci Petriego
 Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
Analiza sieci Petriego Przydatność formalnej analizy modelu procesów Szpital obsługa 272 pacjentów 29258 zdarzeń 264 różnych czynności Czy powyższy model jest poprawny? Tomasz Koszlajda Instytut Informatyki
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI
 WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
WOJSKOWA AKADEMIA TECHNICZNA WYDZIAŁ CYBERNETYKI Analiza i modelowanie Systemów Teleinformatycznych Sprawozdanie z ćwiczenia laboratoryjnego nr 6 Temat ćwiczenia: Modelowanie systemów równoległych z zastosowaniem
miejsca przejścia, łuki i żetony
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego. Sieć Petriego
 Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Sieci Petriego Sieć Petriego Formalny model procesów umożliwiający ich weryfikację Główne konstruktory: miejsca, przejścia, łuki i żetony Opis graficzny i matematyczny Formalna semantyka umożliwia pogłębioną
Zastosowanie kolorowej sieci Petriego do modelowania transakcji rozproszonej
 Marek IWANIAK, Włodzimierz KHADZHYNOV Wydział Elektroniki i Informatyki, Politechnika Koszalińska E mail: marek.iwaniak@tu.koszalin.pl, hadginov@ie.tu.koszalin.pl 1. Wstęp Zastosowanie kolorowej sieci
Marek IWANIAK, Włodzimierz KHADZHYNOV Wydział Elektroniki i Informatyki, Politechnika Koszalińska E mail: marek.iwaniak@tu.koszalin.pl, hadginov@ie.tu.koszalin.pl 1. Wstęp Zastosowanie kolorowej sieci
Spis treści. Przedmowa Wykaz oznaczeń Wstęp Układy kombinacyjne... 18
 Spis treści Przedmowa... 11 Wykaz oznaczeń... 13 1. Wstęp... 15 1.1. Układycyfrowe... 15 1.2. Krótki esej o projektowaniu.... 15 2. Układy kombinacyjne... 18 2.1. Podstawyprojektowaniaukładówkombinacyjnych...
Spis treści Przedmowa... 11 Wykaz oznaczeń... 13 1. Wstęp... 15 1.1. Układycyfrowe... 15 1.2. Krótki esej o projektowaniu.... 15 2. Układy kombinacyjne... 18 2.1. Podstawyprojektowaniaukładówkombinacyjnych...
Filogeneza: problem konstrukcji grafu (drzewa) zależności pomiędzy gatunkami.
 181 Filogeneza: problem konstrukcji grafu (drzewa) zależności pomiędzy gatunkami. 3. D T(D) poprzez algorytm łączenia sąsiadów 182 D D* : macierz łącząca sąsiadów n Niech TotDist i = k=1 D i,k Definiujemy
181 Filogeneza: problem konstrukcji grafu (drzewa) zależności pomiędzy gatunkami. 3. D T(D) poprzez algorytm łączenia sąsiadów 182 D D* : macierz łącząca sąsiadów n Niech TotDist i = k=1 D i,k Definiujemy
Wreferacie przedstawiono propozycję metody modelowania procesów transportowych
 Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Modelowanie procesów transportowych w magazynie elementów produkcyjnych Krzysztof Franczok 1 1 Fabryka Maszyn ROTOX Sp. z o.o. Pokój k/opola, kfranczok@op.pl Wreferacie przedstawiono propozycję metody
Modelowanie procesów współbieżnych
 Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Modelowanie procesów współbieżnych dr inż. Maciej Piotrowicz Katedra Mikroelektroniki i Technik Informatycznych PŁ piotrowi@dmcs.p.lodz.pl http://fiona.dmcs.pl/~piotrowi -> Modelowanie... Literatura M.
Zofia Kruczkiewicz, Algorytmu i struktury danych, Wykład 14, 1
 Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
Wykład Algorytmy grafowe metoda zachłanna. Właściwości algorytmu zachłannego:. W przeciwieństwie do metody programowania dynamicznego nie występuje etap dzielenia na mniejsze realizacje z wykorzystaniem
procesów Współbieżność i synchronizacja procesów Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak
 Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
Wykład prowadzą: Jerzy Brzeziński Dariusz Wawrzyniak Plan wykładu Abstrakcja programowania współbieżnego Instrukcje atomowe i ich przeplot Istota synchronizacji Kryteria poprawności programów współbieżnych
Sterowniki Programowalne (SP) Wykład 11
 Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Sterowniki Programowalne (SP) Wykład 11 Podstawy metody sekwencyjnych schematów funkcjonalnych (SFC) SP 2016 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI KATEDRA INŻYNIERII SYSTEMÓW STEROWANIA Kierunek: Automatyka
Logika Temporalna i Automaty Czasowe
 Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
Modelowanie i Analiza Systemów Informatycznych Logika Temporalna i Automaty Czasowe (4) Modelowa weryfikacja systemu Paweł Głuchowski, Politechnika Wrocławska wersja 2.1 Treść wykładu Własności współbieżnych
Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci
 KNWS 2010 239 Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci Agnieszka Lasota Streszczenie: W artykule zostały opisane wytyczne, wskazujące na celowość wspomagania
KNWS 2010 239 Modelowanie produkcji obudowy separatora olejowego za pomocą diagramów aktywności UML i -sieci Agnieszka Lasota Streszczenie: W artykule zostały opisane wytyczne, wskazujące na celowość wspomagania
Wstęp do Techniki Cyfrowej... Teoria automatów
 Wstęp do Techniki Cyfrowej... Teoria automatów Alfabety i litery Układ logiczny opisywany jest przez wektory, których wartości reprezentowane są przez ciągi kombinacji zerojedynkowych. Zwiększenie stopnia
Wstęp do Techniki Cyfrowej... Teoria automatów Alfabety i litery Układ logiczny opisywany jest przez wektory, których wartości reprezentowane są przez ciągi kombinacji zerojedynkowych. Zwiększenie stopnia
TEORIA GRAFÓW I SIECI
 TEORIA GRAFÓW I SIECI Temat nr 5: Sieci, drogi ekstremalne w sieciach, analiza złożonych przedsięwzięć (CPM i PERT) dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl
TEORIA GRAFÓW I SIECI Temat nr 5: Sieci, drogi ekstremalne w sieciach, analiza złożonych przedsięwzięć (CPM i PERT) dr hab. inż. Zbigniew TARAPATA, prof. WAT e-mail: zbigniew.tarapata@wat.edu.pl http://tarapata.edu.pl
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego. Kolorowane sieci Petriego 1
 SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
SIECI PETRIEGO WYŻSZEGO RZEDU Kolorowane sieci Petriego Kolorowane sieci Petriego 1 PRZYKŁAD - DWA POCIAGI Kolorowane sieci Petriego 2 KONCEPCJA KOLORÓW Model z rysunku (a) nie jest równoważny poprzedniemu,
ANALIZA POPRAWNOŚCI OPROGRAMOWANIA WSPÓŁBIEŻNEGO Z WYKORZYSTANIEM FUNKCJI OBSERWACJI
 AKADEMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWIE WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI, INFORMATYKI I ELEKTRONIKI Piotr Szwed ANALIZA POPRAWNOŚCI OPROGRAMOWANIA WSPÓŁBIEŻNEGO Z WYKORZYSTANIEM
AKADEMIA GÓRNICZO-HUTNICZA IM. STANISŁAWA STASZICA W KRAKOWIE WYDZIAŁ ELEKTROTECHNIKI, AUTOMATYKI, INFORMATYKI I ELEKTRONIKI Piotr Szwed ANALIZA POPRAWNOŚCI OPROGRAMOWANIA WSPÓŁBIEŻNEGO Z WYKORZYSTANIEM
CZĘŚĆ PIERWSZA. Seminarium grupy RSPN. Piotr Lasek Uniwersytet Rzeszowski. Kontakt
 Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
Sieci Petriego w CZĘŚĆ PIERWSZA Seminarium grupy RSPN Piotr Lasek Uniwersytet Rzeszowski Kontakt lasek@univ.rzeszow.pl Agenda Sieci Petriego w Snoopy 1. Wstęp a) podstawowe cechy i zalety sieci Petriego
ODWZOROWANIE DZIAŁANIA PROTOKOŁU DWUFAZOWEGO ZATWIERDZANIA Z WIELOMA UCZESTNIKAMI ZA POMOCĄ KOLOROWANEJ SIECI PETRIEGO
 STUDIA INFORMATICA 2013 Volume 34 Number 2A (111) Marek IWANIAK, Włodzimierz KHADZHYNOV Politechnika Koszalińska, Wydział Elektroniki i Informatyki ODWZOROWANIE DZIAŁANIA PROTOKOŁU DWUFAZOWEGO ZATWIERDZANIA
STUDIA INFORMATICA 2013 Volume 34 Number 2A (111) Marek IWANIAK, Włodzimierz KHADZHYNOV Politechnika Koszalińska, Wydział Elektroniki i Informatyki ODWZOROWANIE DZIAŁANIA PROTOKOŁU DWUFAZOWEGO ZATWIERDZANIA
Wstęp do programowania. Drzewa. Piotr Chrząstowski-Wachtel
 Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Wstęp do programowania Drzewa Piotr Chrząstowski-Wachtel Drzewa Drzewa definiują matematycy, jako spójne nieskierowane grafy bez cykli. Równoważne określenia: Spójne grafy o n wierzchołkach i n-1 krawędziach
Rozszerzenia sieci Petriego
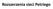 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego
 Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Rozszerzenia sieci Petriego Ograniczenia klasycznej sieci Petriego Trudność w modelowaniu specyficznych przepływów: testowania braku żetonów w danym miejscu, blokowania odpalania, itp. Brak determinizmu
Teoria grafów podstawy. Materiały pomocnicze do wykładu. wykładowca: dr Magdalena Kacprzak
 Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Teoria grafów podstawy Materiały pomocnicze do wykładu wykładowca: dr Magdalena Kacprzak Grafy zorientowane i niezorientowane Przykład 1 Dwa pociągi i jeden most problem wzajemnego wykluczania się Dwa
Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego
 Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
Politechnika Warszawska Wydział Elektroniki i Technik Informacyjnych Agnieszka Węgrzyn Symboliczna analiza układów sterowania binarnego z wykorzystaniem wybranych metod analizy sieci Petriego Rozprawa
WOJSKOWA AKADEMIA TECHNICZNA
 WOJSKOWA AKADEMIA TECHNICZNA PROJEKT MODELOWANIE SYSTEMÓW TELEINFORMATYCZNYCH Stopień, imię i nazwisko prowadzącego Stopień, imię i nazwisko słuchacza Grupa szkoleniowa dr inż. Zbigniew Zieliński inż.
WOJSKOWA AKADEMIA TECHNICZNA PROJEKT MODELOWANIE SYSTEMÓW TELEINFORMATYCZNYCH Stopień, imię i nazwisko prowadzącego Stopień, imię i nazwisko słuchacza Grupa szkoleniowa dr inż. Zbigniew Zieliński inż.
Grafy i sieci w informatyce - opis przedmiotu
 Grafy i sieci w informatyce - opis przedmiotu Informacje ogólne Nazwa przedmiotu Grafy i sieci w informatyce Kod przedmiotu 11.9-WI-INFD-GiSwI Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki
Grafy i sieci w informatyce - opis przedmiotu Informacje ogólne Nazwa przedmiotu Grafy i sieci w informatyce Kod przedmiotu 11.9-WI-INFD-GiSwI Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki
Algorytmy i Struktury Danych
 Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy i Struktury Danych Kopce Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 11 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych Wykład 11 1 / 69 Plan wykładu
Algorytmy metaheurystyczne Wykład 11. Piotr Syga
 Algorytmy metaheurystyczne Wykład 11 Piotr Syga 22.05.2017 Drzewa decyzyjne Idea Cel Na podstawie przesłanek (typowo zbiory rozmyte) oraz zbioru wartości w danych testowych, w oparciu o wybrane miary,
Algorytmy metaheurystyczne Wykład 11 Piotr Syga 22.05.2017 Drzewa decyzyjne Idea Cel Na podstawie przesłanek (typowo zbiory rozmyte) oraz zbioru wartości w danych testowych, w oparciu o wybrane miary,
Sieć (graf skierowany)
 Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
Sieci Sieć (graf skierowany) Siecia (grafem skierowanym) G = (V, A) nazywamy zbiór wierzchołków V oraz zbiór łuków A V V. V = {A, B, C, D, E, F}, A = {(A, B), (A, D), (A, C), (B, C),..., } Ścieżki i cykle
xx + x = 1, to y = Jeśli x = 0, to y = 0 Przykładowy układ Funkcja przykładowego układu Metody poszukiwania testów Porównanie tabel prawdy
 Testowanie układów kombinacyjnych Przykładowy układ Wykrywanie błędów: 1. Sklejenie z 0 2. Sklejenie z 1 Testem danego uszkodzenia nazywa się takie wzbudzenie funkcji (wektor wejściowy), które daje błędną
Testowanie układów kombinacyjnych Przykładowy układ Wykrywanie błędów: 1. Sklejenie z 0 2. Sklejenie z 1 Testem danego uszkodzenia nazywa się takie wzbudzenie funkcji (wektor wejściowy), które daje błędną
Podstawy Automatyki. Wykład 4 - algebra schematów blokowych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
koniec punkt zatrzymania przepływów sterowania na diagramie czynności
 Diagramy czynności opisują dynamikę systemu, graficzne przedstawienie uszeregowania działań obrazuje strumień wykonywanych czynności z ich pomocą modeluje się: - scenariusze przypadków użycia, - procesy
Diagramy czynności opisują dynamikę systemu, graficzne przedstawienie uszeregowania działań obrazuje strumień wykonywanych czynności z ich pomocą modeluje się: - scenariusze przypadków użycia, - procesy
Bioinformatyka Laboratorium, 30h. Michał Bereta
 Bioinformatyka Laboratorium, 30h Michał Bereta mbereta@pk.edu.pl www.michalbereta.pl 1 Filogenetyka molekularna wykorzystuje informację zawartą w sekwencjach aminokwasów lub nukleotydów do kontrukcji drzew
Bioinformatyka Laboratorium, 30h Michał Bereta mbereta@pk.edu.pl www.michalbereta.pl 1 Filogenetyka molekularna wykorzystuje informację zawartą w sekwencjach aminokwasów lub nukleotydów do kontrukcji drzew
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne
 E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
E: Rekonstrukcja ewolucji. Algorytmy filogenetyczne Przypominajka: 152 drzewo filogenetyczne to drzewo, którego liśćmi są istniejące gatunki, a węzły wewnętrzne mają stopień większy niż jeden i reprezentują
Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające
 Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Liczniki klasyfikacja Licznik asynchroniczny:
Technika Cyfrowa 1 wykład 11: liczniki sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Liczniki klasyfikacja Licznik asynchroniczny:
Łyżwy - omówienie zadania
 Komisja Regulaminowa XVI Olimpiady Informatycznej 1 UMK Toruń 12 luty 2009 1 Niniejsza prezentacja zawiera materiały dostarczone przez Komitet Główny Olimpiady Informatycznej. Treść zadania Wejście Wyjście
Komisja Regulaminowa XVI Olimpiady Informatycznej 1 UMK Toruń 12 luty 2009 1 Niniejsza prezentacja zawiera materiały dostarczone przez Komitet Główny Olimpiady Informatycznej. Treść zadania Wejście Wyjście
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II
 Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Algorytmy Równoległe i Rozproszone Część V - Model PRAM II Łukasz Kuszner pokój 209, WETI http://www.sphere.pl/ kuszner/ kuszner@sphere.pl Oficjalna strona wykładu http://www.sphere.pl/ kuszner/arir/ 2005/06
Information Systems Analysis
 THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
THE DEVELOPMENT OF THE POTENTIAL AND ACADEMIC PROGRAMMES OF WROCŁAW UNIVERSITY OF SCIENCE AND TECHNOLOGY Część 1 Sieci Petriego Materiały są tłumaczeniem i rozszerzeniem instrukcji laboratoryjnych p.t.
Wykład 1 Wprowadzenie do algorytmów. Zawartość wykładu 1. Wstęp do algorytmów i struktur danych 2. Algorytmy z rozgałęzieniami.
 Wykład 1 Wprowadzenie do algorytmów Zawartość wykładu 1. Wstęp do algorytmów i struktur danych 2. Algorytmy z rozgałęzieniami Wykaz literatury 1. N. Wirth - Algorytmy+Struktury Danych = Programy, WNT Warszawa
Wykład 1 Wprowadzenie do algorytmów Zawartość wykładu 1. Wstęp do algorytmów i struktur danych 2. Algorytmy z rozgałęzieniami Wykaz literatury 1. N. Wirth - Algorytmy+Struktury Danych = Programy, WNT Warszawa
Języki formalne i automaty Ćwiczenia 9
 Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Języki formalne i automaty Ćwiczenia 9 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Maszyna Mealy'ego... 2 Maszyna Moore'a... 2 Automat ze stosem... 3 Konwersja gramatyki bezkontekstowej
Wykład nr 3 Techniki Mikroprocesorowe. dr inż. Artur Cichowski
 Wykład nr 3 Techniki Mikroprocesorowe dr inż. Artur Cichowski Automat skończony jest przetwornikiem ciągu symboli wejściowych na ciąg symboli wyjściowych. Zbiory symboli wejściowych x X i wyjściowych y
Wykład nr 3 Techniki Mikroprocesorowe dr inż. Artur Cichowski Automat skończony jest przetwornikiem ciągu symboli wejściowych na ciąg symboli wyjściowych. Zbiory symboli wejściowych x X i wyjściowych y
Odwzorowanie BPMN w sieć Petriego
 Odwzorowanie BPMN w sieć Petriego Proces odwzorowania Scenariusz procesu odwzorowania BPMN2PN BPMN Modeler plik XML BPMN Preprocesor plik XMI BPMN Narzędzie transformacji plik PNML Narzędzia analizy: ProM,
Odwzorowanie BPMN w sieć Petriego Proces odwzorowania Scenariusz procesu odwzorowania BPMN2PN BPMN Modeler plik XML BPMN Preprocesor plik XMI BPMN Narzędzie transformacji plik PNML Narzędzia analizy: ProM,
Wykład 3. Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy
 Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
Wykład 3 Złożoność i realizowalność algorytmów Elementarne struktury danych: stosy, kolejki, listy Dynamiczne struktury danych Lista jest to liniowo uporządkowany zbiór elementów, z których dowolny element
Nierówność Krafta-McMillana, Kodowanie Huffmana
 Nierówność Krafta-McMillana, Kodowanie Huffmana Kodowanie i kompresja informacji - Wykład 2 1 marca 2010 Test na jednoznaczna dekodowalność Kod a jest prefiksem kodu b jeśli b jest postaci ax. x nazywamy
Nierówność Krafta-McMillana, Kodowanie Huffmana Kodowanie i kompresja informacji - Wykład 2 1 marca 2010 Test na jednoznaczna dekodowalność Kod a jest prefiksem kodu b jeśli b jest postaci ax. x nazywamy
Język UML w modelowaniu systemów informatycznych
 Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 7 Przeglądowe diagramy interakcji Przeglądowe diagramy interakcji wiążą
Język UML w modelowaniu systemów informatycznych dr hab. Bożena Woźna-Szcześniak Akademia im. Jan Długosza bwozna@gmail.com Wykład 7 Przeglądowe diagramy interakcji Przeglądowe diagramy interakcji wiążą
Twój wynik: 4 punktów na 6 możliwych do uzyskania (66,67 %).
 Powrót Twój wynik: 4 punktów na 6 możliwych do uzyskania (6667 %). Nr Opcja Punkty Poprawna Odpowiedź Rozważmy algorytm AVLSequence postaci: 1 Niech drzewo będzie rezultatem działania algorytmu AVLSequence
Powrót Twój wynik: 4 punktów na 6 możliwych do uzyskania (6667 %). Nr Opcja Punkty Poprawna Odpowiedź Rozważmy algorytm AVLSequence postaci: 1 Niech drzewo będzie rezultatem działania algorytmu AVLSequence
Poprawność semantyczna
 Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Poprawność składniowa Poprawność semantyczna Poprawność algorytmu Wypisywanie zdań z języka poprawnych składniowo Poprawne wartościowanie zdań języka, np. w języku programowania skutki wystąpienia wyróżnionych
Elementy kognitywistyki II: Sztuczna inteligencja. WYKŁAD III: Problemy agenta
 Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD III: Problemy agenta To już było: AI to dziedzina zajmująca się projektowaniem agentów Określenie agenta i agenta racjonalnego Charakterystyka PAGE
Elementy kognitywistyki II: Sztuczna inteligencja WYKŁAD III: Problemy agenta To już było: AI to dziedzina zajmująca się projektowaniem agentów Określenie agenta i agenta racjonalnego Charakterystyka PAGE
Metoda Tablic Semantycznych
 Procedura Plan Reguły Algorytm Logika obliczeniowa Instytut Informatyki Plan Procedura Reguły 1 Procedura decyzyjna Logiczna równoważność formuł Logiczna konsekwencja Procedura decyzyjna 2 Reguły α, β,
Procedura Plan Reguły Algorytm Logika obliczeniowa Instytut Informatyki Plan Procedura Reguły 1 Procedura decyzyjna Logiczna równoważność formuł Logiczna konsekwencja Procedura decyzyjna 2 Reguły α, β,
Laboratorium MATLA. Ćwiczenie 6 i 7. Mała aplikacja z GUI
 Laboratorium MATLA Ćwiczenie 6 i 7 Mała aplikacja z GUI Opracowali: - dr inż. Beata Leśniak-Plewińska dr inż. Jakub Żmigrodzki Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii Biomedycznej
Laboratorium MATLA Ćwiczenie 6 i 7 Mała aplikacja z GUI Opracowali: - dr inż. Beata Leśniak-Plewińska dr inż. Jakub Żmigrodzki Zakład Inżynierii Biomedycznej Instytut Metrologii i Inżynierii Biomedycznej
Algorytm - pojęcie algorytmu, sposób zapisu, poziom szczegółowości, czynności proste i strukturalne. Pojęcie procedury i funkcji.
 Algorytm - pojęcie algorytmu, sposób zapisu, poziom szczegółowości, czynności proste i strukturalne. Pojęcie procedury i funkcji. Maria Górska 9 stycznia 2010 1 Spis treści 1 Pojęcie algorytmu 3 2 Sposób
Algorytm - pojęcie algorytmu, sposób zapisu, poziom szczegółowości, czynności proste i strukturalne. Pojęcie procedury i funkcji. Maria Górska 9 stycznia 2010 1 Spis treści 1 Pojęcie algorytmu 3 2 Sposób
Typy danych. 2. Dane liczbowe 2.1. Liczby całkowite ze znakiem i bez znaku: 32768, -165, ; 2.2. Liczby rzeczywiste stało i zmienno pozycyjne:
 Strona 1 z 17 Typy danych 1. Dane tekstowe rozmaite słowa zapisane w różnych alfabetach: Rozwój metod badawczych pozwala na przesunięcie granicy poznawania otaczającego coraz dalej w głąb materii: 2. Dane
Strona 1 z 17 Typy danych 1. Dane tekstowe rozmaite słowa zapisane w różnych alfabetach: Rozwój metod badawczych pozwala na przesunięcie granicy poznawania otaczającego coraz dalej w głąb materii: 2. Dane
Diagramy czynności. Widok logiczny. Widok fizyczny
 Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Diagramy czynności System widoków 4+1 Kruchtena Widok logiczny Widok fizyczny Widok procesu Widok przypadków użycia Widok konstrukcji Diagramy czynności są jedynym diagramem w widoku procesu modelowanego
Modelowanie motywów łańcuchami Markowa wyższego rzędu
 Modelowanie motywów łańcuchami Markowa wyższego rzędu Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki 23 października 2008 roku Plan prezentacji 1 Źródła 2 Motywy i ich znaczenie Łańcuchy
Modelowanie motywów łańcuchami Markowa wyższego rzędu Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki 23 października 2008 roku Plan prezentacji 1 Źródła 2 Motywy i ich znaczenie Łańcuchy
WYKORZYSTANIE LOGIKI SEKWENTÓW GENTZENA DO SYMBOLICZNEJ ANALIZY SIECI PETRIEGO
 II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie WYKORZYSTANIE LOGIKI SEKWENTÓW GENTZENA DO SYMBOLICZNEJ ANALIZY SIECI PETRIEGO Jacek Tkacz Instytut
II Konferencja Naukowa KNWS'05 "Informatyka- sztuka czy rzemios o" 15-18 czerwca 2005, Z otniki Luba skie WYKORZYSTANIE LOGIKI SEKWENTÓW GENTZENA DO SYMBOLICZNEJ ANALIZY SIECI PETRIEGO Jacek Tkacz Instytut
Podstawy Automatyki. Wykład 4 - algebra schematów blokowych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2015 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
PROJEKT WSPÓŁFINANSOWANY ZE ŚRODKÓW UNII EUROPEJSKIEJ W RAMACH EUROPEJSKIEGO FUNDUSZU SPOŁECZNEGO OPIS PRZEDMIOTU
 OPIS PRZEDMIOTU Nazwa przedmiotu Systemy rozproszone Kod przedmiotu Wydział Wydział Matematyki, Fizyki i Techniki Instytut/Katedra Instytut Mechaniki i Informatyki Stosowanej Kierunek Informatyka Specjalizacja/specjalność
OPIS PRZEDMIOTU Nazwa przedmiotu Systemy rozproszone Kod przedmiotu Wydział Wydział Matematyki, Fizyki i Techniki Instytut/Katedra Instytut Mechaniki i Informatyki Stosowanej Kierunek Informatyka Specjalizacja/specjalność
MODELE SIECIOWE 1. Drzewo rozpinające 2. Najkrótsza droga 3. Zagadnienie maksymalnego przepływu źródłem ujściem
 MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
MODELE SIECIOWE 1. Drzewo rozpinające (spanning tree) w grafie liczącym n wierzchołków to zbiór n-1 jego krawędzi takich, że dowolne dwa wierzchołki grafu można połączyć za pomocą krawędzi należących do
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ. Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska
 SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
SYSTEMY UCZĄCE SIĘ WYKŁAD 4. DRZEWA REGRESYJNE, INDUKCJA REGUŁ Częstochowa 2014 Dr hab. inż. Grzegorz Dudek Wydział Elektryczny Politechnika Częstochowska DRZEWO REGRESYJNE Sposób konstrukcji i przycinania
Wyrażenie nawiasowe. Wyrażenie puste jest poprawnym wyrażeniem nawiasowym.
 Wyrażenie nawiasowe Wyrażeniem nawiasowym nazywamy dowolny skończony ciąg nawiasów. Każdemu nawiasowi otwierającemu odpowiada dokładnie jeden nawias zamykający. Poprawne wyrażenie nawiasowe definiujemy
Wyrażenie nawiasowe Wyrażeniem nawiasowym nazywamy dowolny skończony ciąg nawiasów. Każdemu nawiasowi otwierającemu odpowiada dokładnie jeden nawias zamykający. Poprawne wyrażenie nawiasowe definiujemy
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych
 Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Uniwersytet Zielonogórski Wydział Elektrotechniki, Informatyki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych ELEMENTY SZTUCZNEJ INTELIGENCJI Laboratorium nr 9 PRZESZUKIWANIE GRAFÓW Z
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych
 Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2013/14 Znajdowanie maksimum w zbiorze
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2013/14 Znajdowanie maksimum w zbiorze
Problem eliminacji nieprzystających elementów w zadaniu rozpoznania wzorca Marcin Luckner
 Problem eliminacji nieprzystających elementów w zadaniu rozpoznania wzorca Marcin Luckner Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska Elementy nieprzystające Definicja odrzucania Klasyfikacja
Problem eliminacji nieprzystających elementów w zadaniu rozpoznania wzorca Marcin Luckner Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska Elementy nieprzystające Definicja odrzucania Klasyfikacja
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Kompresja danych Streszczenie Studia Dzienne Wykład 10,
 1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
1 Kwantyzacja wektorowa Kompresja danych Streszczenie Studia Dzienne Wykład 10, 28.04.2006 Kwantyzacja wektorowa: dane dzielone na bloki (wektory), każdy blok kwantyzowany jako jeden element danych. Ogólny
Diagramy czynności. sekwencyjnych i współbieŝnych. pomiędzy uporządkowanymi ciągami czynności, akcji i obiektów
 Diagramy czynności Graficzne przedstawienie sekwencyjnych i współbieŝnych przepływów sterowania oraz danych pomiędzy uporządkowanymi ciągami czynności, akcji i obiektów Zastosowanie w modelowaniu scenariuszy
Diagramy czynności Graficzne przedstawienie sekwencyjnych i współbieŝnych przepływów sterowania oraz danych pomiędzy uporządkowanymi ciągami czynności, akcji i obiektów Zastosowanie w modelowaniu scenariuszy
Transformacja wiedzy w budowie i eksploatacji maszyn
 Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
Uniwersytet Technologiczno Przyrodniczy im. Jana i Jędrzeja Śniadeckich w Bydgoszczy Wydział Mechaniczny Transformacja wiedzy w budowie i eksploatacji maszyn Bogdan ŻÓŁTOWSKI W pracy przedstawiono proces
Dynamiczny przydział pamięci w języku C. Dynamiczne struktury danych. dr inż. Jarosław Forenc. Metoda 1 (wektor N M-elementowy)
 Rok akademicki 2012/2013, Wykład nr 2 2/25 Plan wykładu nr 2 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia niestacjonarne I stopnia Rok akademicki 2012/2013
Rok akademicki 2012/2013, Wykład nr 2 2/25 Plan wykładu nr 2 Informatyka 2 Politechnika Białostocka - Wydział Elektryczny Elektrotechnika, semestr III, studia niestacjonarne I stopnia Rok akademicki 2012/2013
Podstawowe procedury przy tworzeniu programu do sterownika:
 Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
Podstawowe procedury przy tworzeniu programu do sterownika: 1. Opracowanie algorytmu sterowania procesem, potwierdzonego przez technologa. 2. Oszacowanie wielkości obiektu, czyli liczby punktów (liczby
Sortowanie. Bartman Jacek Algorytmy i struktury
 Sortowanie Bartman Jacek jbartman@univ.rzeszow.pl Algorytmy i struktury danych Sortowanie przez proste wstawianie przykład 41 56 17 39 88 24 03 72 41 56 17 39 88 24 03 72 17 41 56 39 88 24 03 72 17 39
Sortowanie Bartman Jacek jbartman@univ.rzeszow.pl Algorytmy i struktury danych Sortowanie przez proste wstawianie przykład 41 56 17 39 88 24 03 72 41 56 17 39 88 24 03 72 17 41 56 39 88 24 03 72 17 39
Projektowanie Scalonych Systemów Wbudowanych VERILOG
 Projektowanie Scalonych Systemów Wbudowanych VERILOG OPIS BEHAWIORALNY proces Proces wątek sterowania lub przetwarzania danych, niezależny w sensie czasu wykonania, ale komunikujący się z innymi procesami.
Projektowanie Scalonych Systemów Wbudowanych VERILOG OPIS BEHAWIORALNY proces Proces wątek sterowania lub przetwarzania danych, niezależny w sensie czasu wykonania, ale komunikujący się z innymi procesami.
Sortowanie. Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania:
 Sortowanie Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania: podać strukturę danych dla elementów dynamicznego skończonego multi-zbioru S, względem którego są wykonywane następujące
Sortowanie Kolejki priorytetowe i algorytm Heapsort Dynamiczny problem sortowania: podać strukturę danych dla elementów dynamicznego skończonego multi-zbioru S, względem którego są wykonywane następujące
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych
 Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2014/15 Znajdowanie maksimum w zbiorze
Algorytmy równoległe: ocena efektywności prostych algorytmów dla systemów wielokomputerowych Rafał Walkowiak Politechnika Poznańska Studia inżynierskie Informatyka 2014/15 Znajdowanie maksimum w zbiorze
Modelowanie obiektowe - Ćw. 6.
 1 Modelowanie obiektowe - Ćw. 6. Treść zajęć: Dokumentacja przypadków użycia diagramy czynności. Poznane wcześniej diagramy przypadków użycia pokazują co system powinien robić. Natomiast diagramy czynności
1 Modelowanie obiektowe - Ćw. 6. Treść zajęć: Dokumentacja przypadków użycia diagramy czynności. Poznane wcześniej diagramy przypadków użycia pokazują co system powinien robić. Natomiast diagramy czynności
Modelowanie produkcji. Drzewo produktu
 Modelowanie produkcji Drzewo produktu Proces produkcji jednego produktu finalnego będziemy przedstawiać graficznie, odzwierciedlając kolejne etapy wytwarzania produktu. Proces produkcji jednego produktu
Modelowanie produkcji Drzewo produktu Proces produkcji jednego produktu finalnego będziemy przedstawiać graficznie, odzwierciedlając kolejne etapy wytwarzania produktu. Proces produkcji jednego produktu
Podstawy programowania III WYKŁAD 4
 Podstawy programowania III WYKŁAD 4 Jan Kazimirski 1 Podstawy UML-a 2 UML UML Unified Modeling Language formalny język modelowania systemu informatycznego. Aktualna wersja 2.3 Stosuje paradygmat obiektowy.
Podstawy programowania III WYKŁAD 4 Jan Kazimirski 1 Podstawy UML-a 2 UML UML Unified Modeling Language formalny język modelowania systemu informatycznego. Aktualna wersja 2.3 Stosuje paradygmat obiektowy.
TEORETYCZNE PODSTAWY INFORMATYKI
 1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
1 TEORETYCZNE PODSTAWY INFORMATYKI WFAiS UJ, Informatyka Stosowana I rok studiów, I stopień Wykład 14c 2 Definicje indukcyjne Twierdzenia dowodzone przez indukcje Definicje indukcyjne Definicja drzewa
Języki formalne i automaty Ćwiczenia 8
 Języki formalne i automaty Ćwiczenia 8 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Konwersja NFA do DFA... 2 Minimalizacja liczby stanów DFA... 4 Konwersja automatu DFA do
Języki formalne i automaty Ćwiczenia 8 Autor: Marcin Orchel Spis treści Spis treści... 1 Wstęp teoretyczny... 2 Konwersja NFA do DFA... 2 Minimalizacja liczby stanów DFA... 4 Konwersja automatu DFA do
Wstęp do programowania
 Wstęp do programowania Programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. X Jesień 2013 1 / 21 Dziel i zwyciężaj przypomnienie 1 Podział problemu na 2 lub
Wstęp do programowania Programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2013 P. Daniluk(Wydział Fizyki) WP w. X Jesień 2013 1 / 21 Dziel i zwyciężaj przypomnienie 1 Podział problemu na 2 lub
Wyznaczanie strategii w grach
 Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wyznaczanie strategii w grach Dariusz Banasiak Katedra Informatyki Technicznej W4/K9 Politechnika Wrocławska Definicja gry Teoria gier i konstruowane na jej podstawie programy stanowią jeden z głównych
Wstęp do programowania
 Wstęp do programowania Algorytmy zachłanne, programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk(Wydział Fizyki) WP w. IX Jesień 2014 1 / 26 Algorytmy zachłanne Strategia polegająca
Wstęp do programowania Algorytmy zachłanne, programowanie dynamiczne Paweł Daniluk Wydział Fizyki Jesień 2014 P. Daniluk(Wydział Fizyki) WP w. IX Jesień 2014 1 / 26 Algorytmy zachłanne Strategia polegająca
Asynchroniczne statyczne układy sekwencyjne
 Asynchroniczne statyczne układy sekwencyjne Układem sekwencyjnym nazywany jest układ przełączający, posiadający przynajmniej jeden taki stan wejścia, któremu odpowiadają, zależnie od sygnałów wejściowych
Asynchroniczne statyczne układy sekwencyjne Układem sekwencyjnym nazywany jest układ przełączający, posiadający przynajmniej jeden taki stan wejścia, któremu odpowiadają, zależnie od sygnałów wejściowych
Podstawy programowania 2. Temat: Drzewa binarne. Przygotował: mgr inż. Tomasz Michno
 Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
Instrukcja laboratoryjna 5 Podstawy programowania 2 Temat: Drzewa binarne Przygotował: mgr inż. Tomasz Michno 1 Wstęp teoretyczny Drzewa są jedną z częściej wykorzystywanych struktur danych. Reprezentują
12) Wadą modelu kaskadowego jest: Zagadnienia obowiązujące na egzaminie z inżynierii oprogramowania: 13) Wadą modelu opartego na prototypowaniu jest:
 Zagadnienia obowiązujące na egzaminie z inżynierii oprogramowania: 1) Oprogramowanie to: 2) Produkty oprogramowania w inżynierii oprogramowania można podzielić na: 3) W procesie wytwarzania oprogramowania
Zagadnienia obowiązujące na egzaminie z inżynierii oprogramowania: 1) Oprogramowanie to: 2) Produkty oprogramowania w inżynierii oprogramowania można podzielić na: 3) W procesie wytwarzania oprogramowania
Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań
 Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań Anna Manerowska, Michal Kozakiewicz 2.12.2009 1 Wstęp Jako projekt na przedmiot MEUM (Metody Ewolucyjne Uczenia Maszyn)
Algorytm indukcji klasyfikatora za pomocą EA z automatycznym przełączaniem ukierunkowań Anna Manerowska, Michal Kozakiewicz 2.12.2009 1 Wstęp Jako projekt na przedmiot MEUM (Metody Ewolucyjne Uczenia Maszyn)
Drzewa. Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew
 Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Drzewa Las - graf, który nie zawiera cykli Drzewo - las spójny Jeżeli graf G jest lasem, który ma n wierzchołków i k składowych, to G ma n k krawędzi. Własności drzew Niech T graf o n wierzchołkach będący
Podstawy Automatyki. Wykład 4 - algebra schematów blokowych. dr inż. Jakub Możaryn. Warszawa, Instytut Automatyki i Robotyki
 Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Wykład 4 - algebra schematów blokowych Instytut Automatyki i Robotyki Warszawa, 2017 Wstęp Schemat blokowy Schemat blokowy (strukturalny): przedstawia wzajemne powiązania pomiędzy poszczególnymi zespołami
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania MODELOWANIE I IDENTYFIKACJA Studia niestacjonarne Estymacja parametrów modeli, metoda najmniejszych kwadratów.
Turing i jego maszyny
 Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
Turing Magdalena Lewandowska Politechnika Śląska, wydział MS, semestr VI 20 kwietnia 2016 1 Kim był Alan Turing? Biografia 2 3 Mrówka Langtona Bomba Turinga 4 Biografia Kim był Alan Turing? Biografia Alan
Metody Kompilacji Wykład 1 Wstęp
 Metody Kompilacji Wykład 1 Wstęp Literatura: Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman: Compilers: Princiles, Techniques, and Tools. Addison-Wesley 1986, ISBN 0-201-10088-6 Literatura: Alfred V. Aho,
Metody Kompilacji Wykład 1 Wstęp Literatura: Alfred V. Aho, Ravi Sethi, Jeffrey D. Ullman: Compilers: Princiles, Techniques, and Tools. Addison-Wesley 1986, ISBN 0-201-10088-6 Literatura: Alfred V. Aho,
Technika Cyfrowa 1 wykład 12: sekwencyjne układy przełączające
 Technika Cyfrowa 1 wykład 12: sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Sekwencyjny układ przełączający układ przełączający
Technika Cyfrowa 1 wykład 12: sekwencyjne układy przełączające Dr inż. Jacek Mazurkiewicz Katedra Informatyki Technicznej e-mail: Jacek.Mazurkiewicz@pwr.edu.pl Sekwencyjny układ przełączający układ przełączający
Metody Kompilacji Wykład 3
 Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Metody Kompilacji Wykład 3 odbywa się poprzez dołączenie zasad(reguł) lub fragmentów kodu do produkcji w gramatyce. Włodzimierz Bielecki WI ZUT 2 Na przykład, dla produkcji expr -> expr 1 + term możemy
Wykład 2. Drzewa zbalansowane AVL i 2-3-4
 Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Wykład Drzewa zbalansowane AVL i -3-4 Drzewa AVL Wprowadzenie Drzewa AVL Definicja drzewa AVL Operacje wstawiania i usuwania Złożoność obliczeniowa Drzewa -3-4 Definicja drzewa -3-4 Operacje wstawiania
Przetwarzanie rozproszone
 Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
Wykład prowadzą: Jerzy Brzeziński Jacek Kobusiński Plan wykładu Proces sekwencyjny Komunikaty, kanały komunikacyjne Stan kanału Operacje komunikacyjne Model formalny procesu sekwencyjnego Zdarzenia Warunek
