BILANS ENERGETYCZNY POMIESZCZENIA ZE STRUKTURALNYM, FUNKCJONUJĄCYM W CYKLU DOBOWYM, MAGAZYNEM CIEPŁA Z MATERIAŁEM FAZOWO-ZMIENNYM
|
|
|
- Bogumił Makowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 RYSZARD WNUK BILANS ENERGETYCZNY POMIESZCZENIA ZE STRUKTURALNYM, FUNKCJONUJĄCYM W CYKLU DOBOWYM, MAGAZYNEM CIEPŁA Z MATERIAŁEM FAZOWO-ZMIENNYM ENERGY BALANCE OF THE ROOM EQUIPPED WITH PCM PLASTER BOARD AS A HEAT STORAGE UNIT OPERATING ON A DAILY BASIS S t r e z c z e n e A b t r a c t Przedmotem artykułu jet krótkotermnowy (dobowy) magazyn cepła z materałem ulegającym przemane fazowej (PCM). Jego podtawową funkcją jet zmagazynowane pozykanej w cągu dna energ promenowana łonecznego oddane jej powetrzu w pomezczenu w nocy. Sformułowano rozwązano zagadnene modelowana funkcjonowana powerzchnowego zaobnka cepła w warunkach wzajemnego wpółdzałana ceplnego z powetrzem wewnętrznym pomezczena, z jednoczenym uwzględnenem tacjonarnych w cągu doby oddzaływań środowka otoczena budynku. Podano równana chwlowych blanów energ ceplnej zaobnka powetrza wewnętrznego, na podtawe których wyprowadzono równana przebegów temperatury zaobnka powetrza wewnętrznego w przedzałach czaowych kolejnych etapów proceu przemany fazowej materału PCM w zaobnku. Słowa kluczowe: magazynowane cepła, ytem berny wykorzytujący energę promenowana łonecznego, materał ulegający przemane fazowej Integrated to nternal wall PCM (Phae Change Materal) baed torage unt aborb olar radaton durng daytme and releae the heat at nght. The feature of torage unt and t thermal charactertc are decrbed. The bac conervaton equaton of energy for the torage unt and nternal ar were provded and analytcally olved. Thermal performance obtaned from mathematcal calculaton for elected commercal PCM. Keyword: energy torage, pave olar ytem, Phae Change Materal Dr nŝ. Ryzard Wnuk, Zakład Problemów Eko-Budownctwa, Intytut Podtawowych Problemów Technk PAN.
2 7 Oznaczena A powerzchna [m ] C pojemność ceplna [J/K] c cepło właścwe [J/(kg K)] G gętość trumena energ promenowana łonecznego [W/m ] J gętość napromenowana [J/m ] m maa [kg] Q energa magazynowana w zaobnku cepła [J] t cza [] T temperatura [K] V objętość [m 3 ] ρ trumeń objętośc powetrza [m 3 /] νɺ gętość [kg/m 3 ] α wpółczynnk przejmowana cepła [W/(m K)] ϕ udzał objętoścowy materału fazowo-zmennego w kompozytowym zaobnku Indeky, 1,, 3 tan początkowy kolejne etapy funkcjonowana zaobnka a zaobnk (magazyn) cepła e, o, b odpowedno: otoczene budynku, okno, przegroda zewnętrzna I powetrze wewnątrz pomezczena PCM materał ulegający przemane fazowej (Phae Change Materal) S przemana fazowa 1. Wtęp Wykorzytane energ promenowana łonecznego, nezbędne w budownctwe energoozczędnym, wąŝe ę z konecznoścą magazynowana pozykwanej energ, której źródło charakteryzują okreowość zmenność parametrów. WyróŜnamy aktywne berne ytemy grzewcze wykorzytujące energę promenowana łonecznego. Podtawowym elementam kaŝdego ytemu ą kolektor zbornk akumulacyjny. W ytemach bernych, w których ne wytępuje mechanczne wymuzona cyrkulacja medum pośrednczącego w przekazywanu cepła, rolę kolektorów łonecznych mogą pełnać przezklena elementy budynku. Przez przezklena wnka do wnętrz promenowane łoneczne w forme fal wdzalnych oraz podczerwonych, a natępne jet pochłanane przez: ścany wewnętrzne, poadzk tropy lub przez pecjalne magazyny, które akumulują energę w cągu dna, a oddają ją w nocy. W nnejzym artykule jako magazyn cepła rozwa- Ŝana jet powerzchnowa wartwa tynku pomezczena, zawerająca materał ulegający przemane fazowej (Phae Change Materal PCM). Materał fazowo-zmenny moŝe być dodany, w forme zawerających go mkrokapuł, do tradycyjnych materałów budowlanych.
3 . Charakterytyka zaobnka jego oddzaływane z otoczenem 71 Zaobnk cepła o objętośc V a jet elementem przegrody budowlanej ma formę płyty o powerzchn A a. Zaobnk tanow kompozyt złoŝony z onowy (tynku, betonu), z rozmezczonym w nej równomerne materałem ulegającym przemane fazowej. Ry. 1. Zaobnk cepła jako kompozyt wartwy tynku ścan uftu oraz materału PCM Fg. 1. PCM baed torage unt a a layer of nternal wall Właścwośc fzyczne materału onowy ą natępujące: gętość ρ o, cepło właścwe c o. Materał PCM, którego udzał objętoścowy w kompozyce wyno φ, charakteryzują: gętość ρ PCM, cepło przemany fazowej C PCM oraz cepło właścwe c PCM (przyjęto równe w tanach tałym cekłym). Przemany fazowe przejść ze tanu tałego w cekły odwrotne zachodzą w tałej, określonej dla danego materału, temperaturze T. Przyjęto na- ρ = ϕρ + 1 ϕ ρ, po- tępujące podtawowe włanośc ceplne kompozytu: gętość ( ) jemność ceplna C = V [ ρ (1 ϕ ) c + ρ ϕ c ]. Powerzchna czołowa zaobnka wymena cepło z wnętrzem pomezczena w wynku konwekcj promenowana. Po- a a o o PCM PCM werzchna ta aborbuje energę promenowana łonecznego, której gętość wyno J a =A o J τ o /A, gdze J jet gętoścą całkowtego promenowana łonecznego padającego na ponowe przezklene przegrody zewnętrznej o powerzchn A o, a τ o jet wpółczynnkem przepuzczana promenowana przez zyby. Promenowane łoneczne docerające do wnętrza jet w całośc równomerne pochłanane przez powerzchne A wzytkch ścan, podłog uftu pomezczena. Gętość trumena promenowana aborbowanego przez wewnętrzne powerzchne pomezczena, w tym powerzchnę czołową zaobnka, wyno G = J / t, gdze t jet czaem trwana pory dzennej. D D a a W odneenu do płyty o grubośc d a tanowącej rozwaŝany zaobnk cepła, dla której wpółczynnk wymany cepła pomędzy ną a wnętrzem wyno α, moŝna przyjąć, Ŝe jeŝel jet pełnone kryterum małej lczby Bota ( B = α d / λ,15 ), to rozkład temperatury T a w obzarze zaobnka (płyty) jet prawe równomerny [1]. Take załoŝene a a przyjęto w modelowanu funkcjonowana zaobnka. a PCM o
4 7 3. Blane energ zaobnka cepła powetrza wewnątrz pomezczena Blan energ zaobnka, wynkający z jego napromenowana energą łoneczną oraz z oddzaływań z powetrzem wewnątrz pomezczena, przy załoŝenu adabatycznośc ścank tylnej zaobnka, ma potać de a ( ) = A G α A T T (1) a a a a Energę wewnętrzną kompozytowego zaobnka cepła zapano za pomocą funkcj Heavde a w potac E = C T + V ρ C ϕ{[ H ( t t ) H ( t t )] µ ( t) + H ( t t )} () a a a a PCM PCM 1 gdze t 1 oraz t określają czay odpowedno początku końca przemany fazowej, a wprowadzony parametr funkcyjny µ ( t) pełna natępujące warunk początkowe końcowe: t= t 1 t= t µ ( t) =, µ ( t) = 1, w przedzałach czau topnena krzepnęca materału ulegającego przemane fazowej. Podano formułowane blanów energ zaobnka ( powetrza wewnątrz) w zaleŝnośc od tanu materału PCM w zaobnku. I tak, rozróŝnono trzy etapy tanu ładowana: () przyrot temperatury zaobnka, a węc materału PCM pozotającego w tane tałym onowy (przy załoŝenu, Ŝe temperatury te ą równe), od temperatury początkowej T do a temperatury przemany fazowej T, () proce przemany fazowej, zachodzący w przedzale czau t = t t, () dalzy przyrot temperatury magazynu począwzy od temperatury T w etape tym PCM jet w tane cekłym. Warunk cągłośc temperatury magazy- 1 nu powetrza w pomezczenu na grancach określonych przedzałów czaowych funkcjonowana zaobnka ą natępujące T ( t) = T, T ( t) = T a1 t= t a3 1 t= t T ( t) = T ( t), T ( t) = T ( t) 1 t= t 3 1 t= t 1 t= t t= t W zaleŝnośc od warunków funkcjonowana zaobnka jego parametrów mogą wytępować wzytke trzy etapy lub moŝe wytępować mnej etapów podcza proceu magazynowana energ. W odwrotnej kolejnośc zachodzą etapy rozładowywana magazynu. Blan energ powetrza wewnątrz pomezczena zapano jak ponŝej (3) dt C = α A ( T T a a ) + A U b b ( T T + R G e b ) + G A + A U ( T T ) + e r r o o e + η ρ + ω ( 1 ) vɺ c ( T T ) w p e (4) gdze C = m c = ρ V c p p jet pojemnoścą ceplną powetrza w pomezczenu z powerzchnowym zaobnkem cepła, a pozczególne kolejne kładnk prawej trony opują: α A ( T T ) trumeń energ wymenanej pomędzy zaobnkem a powetrzem a a w pomezczenu,
5 73 A U ( T T + R ) b b e b e G oddzaływane otoczena zewnętrznego, gdze R jet oporem be wymany cepła pomędzy przegrodą zewnętrzną a otoczenem, G gętoścą trumena promenowana padającego na ponową D przegrodę zewnętrzną G = J / t, U b wpółczynnkem przenkana cepła przez neprzezroczytą przegrodę zewnętrzną o powerzchn A b, G A trumeń energ pochłonętej przez przegrody pomezczena nne r r nŝ magazyn cepła z PCM, których blane ne ą rozpatrywane, przy załoŝenu, Ŝe energa ta jet w całośc oddawana powetrzu wewnętrznemu, A U ( T T ) cepło wymenane przez okna pomezczena o powerzchn A o o e o z otoczenem zewnętrznym, przy wpółczynnku przenkana cepła okna U o, (1 η ) νρ ɺ c ( T T ) tratę cepła przez wentylację z odzykem cepła, przy prawnośc ω w p e rekuperatora η w, moc dodatkowego źródła cepła. Rozwązane blanów energ zaobnka powetrza przy braku przemany fazowej materału PCM w zaobnku Dla etapu, w którym ne natępuje przemana fazowa materału PCM, równane (1) ma potać dta C = A G α A a a a a ( T T a ) (5) d T dt dt a RóŜnczkując (4), otrzymamy C = α A A AU AU ( 1 ) v c, a a o o b b w p α η ɺ ρ do którego wtawene (5) daje równane róŝnczkowe II rzędu względem temperatury d T dt powetrza wewnątrz pomezczena w potac a + b + ct = d, przy warunkach początkowych dla etapu () t =, T = T, T = T, gdze a a CaC Ca a =, b = C + C + A U + A U + ( 1 η ) vρc A A ɺ α α a o o b b w p a a ( 1 ) ( 1 ) ɺ c = A U + A U + η vɺ ρc o o b b w p d = A G + A U + A U + η vρ c T + A U R G + G A + ω a b b o o w p e b b be r r Rozwązane ogólne ma natępującą potać T = C e + C e + d c (6) d r1 t rt / 1 b b + gdze = b 4 ac, r =, r =, a uwzględnając warunk początkowe, 1 a a określono tałe całkowana C 1 oraz C
6 74 r1 d, r d 1 C = T + r r c r r ( ) 1 1 ( ) ( ) ( ) ( 1 ) ɺ ( ) α A T T + A U T T + R G + G A + A U T T + η vρc T T + ω C r r a a b b e be r r o o e w p e ( ) 1 C = T d / c C 1 Temperaturę zaobnka, na podtawe równana (4), uwzględnając (6), zapano jako C r1 t rt 1 T = ( rc e + r C e 1 1 ) + α A + A U + A U + ( 1 η a a b b o o w ) vρ c T + p A A ɺ α α a a { A U A U ( 1 b b o o w ) vɺ c T A U R G G A p } e b b be r r η ρ ω α A a Blane energ zaobnka powetrza w etape przebegu przemany fazowej materału PCM Blan energ powetrza wewnątrz pomezczena wobec T = T wygląda natępująco a dt 1 + A A U A U ( 1 ) v c T a b b o o w p C α η ɺρ + (8) 1 { α A T + A U + A U + ( 1 η ) vρ c T + A U R G + G A + ω } = a b b o o w p e b b be r r C ɺ rozwązanem którego jet wyraŝene T = T C + C e 3 3 ( 1 ) α A + A U + A U + ( 1 η ) vɺ ρc C a b b o o w p t α A T + A U A U v c T A U R G G A a b b o o w p e b b be r r C T + + η ɺρ ω = 3 α A + A U + A U + η vɺ ρc ( 1 ) a b b o o w p gdze T jet temperaturą powetrza w czae t 1, czyl gdy magazyn cepła oąga temperaturę przemany fazowej T. Blan energ zaobnka na podtawe równań (1) () jet natępujący d ( ρ V C µ PCM PCM PCM ) = A G α A a a a ( T T ) (1) Po wtawenu (9) do (1) całkowanu blanu energ zaobnka w przedzale czau [ t, t ] otrzymano równane przetępne na cza przemany fazowej t jak natępuje 1 α A C C α A + A U + A U + η vɺ ρc a 3 ρ V C = + PCM PCM PCM a 3 α A + A U + A U + ( 1 η a b b o o w ) vɺ ρ cp ( 1 ) a b b o o w p ( 1 ) α A T + A U A U v c T A U R G G A a b b o o w p e b b be r r A G A T A + + η ɺρ ω + α + α t a a a a + α A + A U + A U + ( 1 η a b b o o w ) vɺ ρcp α A C C e ( ) α Aa + Ab Ub+ AoU o+ 1 ηw vɺ ρc p t C (7) (9) (11)
7 4. Przykład lczbowy 75 Analzowano funkcjonowane zaobnka w pomezczenu budynku energoozczędnego, pełnającego tandardy budynku paywnego []. Pomezczene ma powerzchnę 3 m, powerzchnę okna 7,5 m, wyokość,6 m. Strumeń powetrza wentylacyjnego wyno 1 m 3 /h/(m powerzchn), przy prawnośc rekuperacj,75. Zaobnk tanow wartwa tynku ścan wewnętrznych pomezczena o powerzchn A a = 71,6 m. Onową w zaobnku z materałem PCM jet tynk wapenny: c o = 84 J/(kg K), ρ o = 17 kg/m 3, λ o =,7 W/(m K). Udzał objętoścowy materału PCM (Mcronal@ DS. 58 X) w mezanne wyno φ =,5. Grubość płyty zaobnka d a =,5 m, objętość V a =,358. Mcronal@ DS. 58 X jet materałem handlowym o temperaturze topnena T = 3 C ceple topnena C PCM = 11 kj/kg. Włanośc te zweryfkowano w badanach kalorymetrem kanngowym. Na fotograf 1 przedtawono zdjęce mkrokopowe granulek PCM (średnce 5 µm) rozypanych na uwmarce. Wykonano wele model fzycznych (przykładowy pokazano na fot. 1) zaobnka, w tym jako mezanny tynku wapennego materału PCM o udzale objętoścowym PCM φ =,5. Oblczono temperatury magazynu powetrza, lośc magazynowanego cepła w zaobnku funkcjonującym w średnch dzennych warunkach napromenowana powerzchn ponowej temperaturach zewnętrznych pozczególnych meęcy roku. Wynk przedtawono w tab. 1. W oblczenach załoŝono, Ŝe ne funkcjonują dodatkowe źródła cepła ω =. W średnm pod względem warunków atmoferycznych dnu grudna tyczna temperatura zaobnka ne oąga welkośc temperatury przemany fazowej. Zyk łoneczne zapewnają jednak utrzymane temperatury powetrza na pozome ok. C. W pozotałych meącach okreu grzewczego w cągu dna zachodz przemana fazowa magazynowana jet energa do wykorzytana w nocy. W meącach letnch, ogranczając dotęp promenowana łonecznego (topeń przełonęca zyb ne jet jednak znaczący), magazyn tablzuje temperaturę powetrza wewnątrz pomezczena, utrzymując ją na pozome ok. 3 C (temperatura przemany fazowej), bez konecznośc chłodzena pomezczena. W oblczenach dla tego okreu załoŝono prawność rekuperacj η w =. Fot. 1. Mkrokopowe zdjęce materału PCM oraz wykonany model fzyczny zaobnka Photo 1. Mcrocope photo of PCM capule and PCM baed torage unt
8 76 Wynk oblczeń dla meęcy zmowych T a b e l a 1 Meąc X XI XII I II III Napromenowane powerzchn ponowej J [J/m /dzeń] Temperatura zewnętrzna T e [ C] 8,1 3,6 3,5,6 1, Temperatura powetrza na początku 3,,84,8,9 przemany fazowej T [ C] Magazyn ne Cza rozpoczęca przemany fazowej [h] 1,34 4,5 oąga,61 1,5 Cza etapu z przemaną fazową [h] 1,66 7,75 temperatury 9,39 1,5 Procent realzacj przemany fazowej 99 1 przemany Energa zmagazynowana w zaobnku 19,45 5,859 fazowej 9,7 17,17 w cągu dna [MJ] Temperatura powetrza w pomezczenu 3,11,87 19,6 19,6,86 3,1 na konec dna T [ C] D Temperatura magazynu na konec dna T [ C] D a ,8 19,8 3 3 Wynk oblczeń dla meęcy letnch T a b e l a Meąc IV V VI VII VIII IX Napromenowane J [J/m /dzeń] Temperatura zewnętrzna T e [ C] 7,8 13,8 17,3 19,1 18, 13,9 Załonęce okna w cągu dna [%] 13 16,5 8 4 Temperatura powetrza T [ C],88 3 3,7 3,1 Cza rozpoczęca przemany fazowej [h] 1,38 1,3 1,3 1,31 Cza etapu z przemaną fazową [h] 1,6 1,7 1,7 1,69 Procent realzacj przemany fazowej Temperatura powetrza po 1 h dna,96 3,9 3,16 3,19 5. Podumowane Zatoowane materału PCM podno efektywność magazynowana energ promenowana łonecznego. Zmnejzenu ulegają zapotrzebowane na energę do ogrzewana chłodzena, jak makymalne zapotrzebowane na moc ytemów grzewczych chłodzena. Zwękzene pojemnośc ceplnej truktur budynku przez wykorzytane materałów ulegających przemane fazowej podno komfort ceplny pomezczeń budynku przez zmnejzene wahań temperatury wewnętrznej. Przedtawony model analtyczny moŝe być narzędzem doboru oraz wtępnej oceny funkcjonowana przydatnośc zatoowana materału PCM. Dalzym etapem pracy jet ymulacja numeryczna funkcjonowana magazynu cepła z materałem PCM w okree całorocznym, określonym przez parametry Typowego Roku Meteorologcznego.
9 L t e r a t u r a 77 [1] T a l e r J., D u d a P., Rozwązywane protych odwrotnych zagadneń przewodzena cepła, WNT, Warzawa 3. [] W n u k R., Intalacje w domu paywnym energoozczędnym, Przewodnk Budowlany, Warzawa 7.
10 78
Opracowanie wskaźników energetycznych metoda miesięczna budynek mieszkalny bez inst. chłodu
 Konpekt do wykładu/ ćwczeń Konpekt do ćwczeń Opracowane wkaźnków energetycznych metoda meęczna budynek mezkalny bez nt. chłodu CARAKTERYSTYKA ENERGETYCZNA OBLICZENIA Zdefnowane grancy blanowej budynku
Konpekt do wykładu/ ćwczeń Konpekt do ćwczeń Opracowane wkaźnków energetycznych metoda meęczna budynek mezkalny bez nt. chłodu CARAKTERYSTYKA ENERGETYCZNA OBLICZENIA Zdefnowane grancy blanowej budynku
Wstęp do fizyki budowli
 Wstęp do fzyk budowl Xella Polska sp. z o.o. 0.06.200 Plan prezentacj Izolacyjność termczna Przenkane pary wodnej Podcągane kaplarne Wentylacja budynków Xella Polska sp. z o.o. 0.06.200 2 Współczynnk przewodzena
Wstęp do fzyk budowl Xella Polska sp. z o.o. 0.06.200 Plan prezentacj Izolacyjność termczna Przenkane pary wodnej Podcągane kaplarne Wentylacja budynków Xella Polska sp. z o.o. 0.06.200 2 Współczynnk przewodzena
METODA ELEMENTU SKOŃCZONEGO. Termokinetyka
 METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
METODA ELEMENTU SKOŃCZONEGO Termoknetyka Matematyczny ops ruchu cepła (1) Zasada zachowana energ W a Cepło akumulowane, [J] P we Moc wejścowa, [W] P wy Moc wyjścowa, [W] t przedzał czasu, [s] V q S(V)
Podstawy termodynamiki
 Podstawy termodynamk Temperatura cepło Praca jaką wykonuje gaz I zasada termodynamk Przemany gazowe zotermczna zobaryczna zochoryczna adabatyczna Co to jest temperatura? 40 39 38 Temperatura (K) 8 7 6
Podstawy termodynamk Temperatura cepło Praca jaką wykonuje gaz I zasada termodynamk Przemany gazowe zotermczna zobaryczna zochoryczna adabatyczna Co to jest temperatura? 40 39 38 Temperatura (K) 8 7 6
Współczynnik przenikania ciepła U v. 4.00
 Współczynnk przenkana cepła U v. 4.00 1 WYMAGANIA Maksymalne wartośc współczynnków przenkana cepła U dla ścan, stropów, stropodachów, oken drzw balkonowych podano w załącznku do Rozporządzena Mnstra Infrastruktury
Współczynnk przenkana cepła U v. 4.00 1 WYMAGANIA Maksymalne wartośc współczynnków przenkana cepła U dla ścan, stropów, stropodachów, oken drzw balkonowych podano w załącznku do Rozporządzena Mnstra Infrastruktury
3 BADANIE WYDAJNOŚCI SPRĘŻARKI TŁOKOWEJ. 1. Wprowadzenie
 3 BADANIE WYDAJNOŚCI SPRĘŻARKI TŁOKOWEJ. Wprowadzene Sprężarka jet podtawowym przykładem otwartego układu termodynamcznego. Jej zadanem jet medzy nnym podwyżzene cśnena gazu w celu: uzykane czynnka napędowego
3 BADANIE WYDAJNOŚCI SPRĘŻARKI TŁOKOWEJ. Wprowadzene Sprężarka jet podtawowym przykładem otwartego układu termodynamcznego. Jej zadanem jet medzy nnym podwyżzene cśnena gazu w celu: uzykane czynnka napędowego
f 4,3 m l 20 m 4 f l x x 2 y x l 2 4 4,3 20 x x ,86 x 0,043 x 2 y x 4 f l 2 x l 2 4 4, x dy dx tg y x ,86 0,086 x
 f l Ry. 3. Rozpatrywany łuk parabolczny 4 f l x x 2 y x l 2 f m l 2 m y x 4 2 x x 2 2 2,86 x,43 x 2 tg y x dy 4 f l 2 x l 2 4 2 2 x 2 2,86,86 x Mechanka Budowl Projekty Zgodne ze poobem rozwązywana układów
f l Ry. 3. Rozpatrywany łuk parabolczny 4 f l x x 2 y x l 2 f m l 2 m y x 4 2 x x 2 2 2,86 x,43 x 2 tg y x dy 4 f l 2 x l 2 4 2 2 x 2 2,86,86 x Mechanka Budowl Projekty Zgodne ze poobem rozwązywana układów
Zadanie 2. Dany jest szereg rozdzielczy przedziałowy, wyznaczyć następujące miary: 0 5 5 wariancja, odchylenie standardowe
 Zadane 1. Dany jet zereg przedzałowy, wyznaczyć natępujące mary: x n średna arytmetyczna 1 10 warancja, odchylene tandardowe 15 domnanta 3 0 medana 4 35 kurtoza 5 0 6 15 Zadane. Dany jet zereg rozdzelczy
Zadane 1. Dany jet zereg przedzałowy, wyznaczyć natępujące mary: x n średna arytmetyczna 1 10 warancja, odchylene tandardowe 15 domnanta 3 0 medana 4 35 kurtoza 5 0 6 15 Zadane. Dany jet zereg rozdzelczy
1. Komfort cieplny pomieszczeń
 1. Komfort ceplny pomeszczeń Przy określanu warunków panuących w pomeszczenu używa sę zwykle dwóch poęć: mkroklmat komfort ceplny. Przez poęce mkroklmatu wnętrz rozume sę zespół wszystkch parametrów fzycznych
1. Komfort ceplny pomeszczeń Przy określanu warunków panuących w pomeszczenu używa sę zwykle dwóch poęć: mkroklmat komfort ceplny. Przez poęce mkroklmatu wnętrz rozume sę zespół wszystkch parametrów fzycznych
-ignorowanie zmiennej wartości pieniądza w czasie, -niemoŝność porównywania projektów o róŝnych klasach ryzyka.
 Podstawy oceny ekonomcznej przedsęwzęć termo-modernzacyjnych modernzacyjnych -Proste (statyczne)-spb (prosty czas zwrotu nakładów nwestycyjnych) -ZłoŜone (dynamczne)-dpb, NPV, IRR,PI Cechy metod statycznych:
Podstawy oceny ekonomcznej przedsęwzęć termo-modernzacyjnych modernzacyjnych -Proste (statyczne)-spb (prosty czas zwrotu nakładów nwestycyjnych) -ZłoŜone (dynamczne)-dpb, NPV, IRR,PI Cechy metod statycznych:
1. SPRAWDZENIE WYSTEPOWANIA RYZYKA KONDENSACJI POWIERZCHNIOWEJ ORAZ KONDENSACJI MIĘDZYWARSTWOWEJ W ŚCIANIE ZEWNĘTRZNEJ
 Ćwczene nr 1 cz.3 Dyfuzja pary wodnej zachodz w kerunku od środowska o wyższej temperaturze do środowska chłodnejszego. Para wodna dyfundująca przez przegrody budowlane w okrese zmowym napotyka na coraz
Ćwczene nr 1 cz.3 Dyfuzja pary wodnej zachodz w kerunku od środowska o wyższej temperaturze do środowska chłodnejszego. Para wodna dyfundująca przez przegrody budowlane w okrese zmowym napotyka na coraz
PROGNOZOWANIE KSZTAŁTOWANIA SIĘ MIKROKLIMATU BUDYNKÓW INWENTARSKICH MOśLIWOŚCI I OGRANICZENIA
 InŜynera Rolncza 7/2005 Jan Radoń Katedra Budownctwa Weskego Akadema Rolncza w Krakowe PROGNOZOWANIE KSZTAŁTOWANIA SIĘ MIKROKLIMATU BUDYNKÓW INWENTARSKICH MOśLIWOŚCI I OGRANICZENIA Streszczene Opsano nawaŝnesze
InŜynera Rolncza 7/2005 Jan Radoń Katedra Budownctwa Weskego Akadema Rolncza w Krakowe PROGNOZOWANIE KSZTAŁTOWANIA SIĘ MIKROKLIMATU BUDYNKÓW INWENTARSKICH MOśLIWOŚCI I OGRANICZENIA Streszczene Opsano nawaŝnesze
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY. Zakład Budowy i Eksploatacji Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
Jakość cieplna obudowy budynków - doświadczenia z ekspertyz
 dr nż. Robert Geryło Jakość ceplna obudowy budynków - dośwadczena z ekspertyz Wdocznym efektem występowana znaczących mostków ceplnych w obudowe budynku, występującym na ogół przy nedostosowanu ntensywnośc
dr nż. Robert Geryło Jakość ceplna obudowy budynków - dośwadczena z ekspertyz Wdocznym efektem występowana znaczących mostków ceplnych w obudowe budynku, występującym na ogół przy nedostosowanu ntensywnośc
Wykład Turbina parowa kondensacyjna
 Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
α i = n i /n β i = V i /V α i = β i γ i = m i /m
 Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE
 Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
Inormatyka Podstawy Programowana 06/07 Projekt 6 6. ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH CAŁKOWANIE NUMERYCZNE 6. Równana algebraczne. Poszukujemy rozwązana, czyl chcemy określć perwastk rzeczywste równana:
POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ INŻYNIERII ŚRODOWISKA i ENERGETYKI INSTYTUT MASZYN i URZĄDZEŃ ENERGETYCZNYCH.
 POLITECHIKA ŚLĄSKA W GLIWICACH WYDZIAŁ IŻYIERII ŚRODOWISKA EERGETYKI ISTYTUT MASZY URZĄDZEŃ EERGETYCZYCH Turbna arowa II Laboratoru oarów azyn celnych (PM 8) Oracował: dr nż. Grzegorz Wcak Srawdzł: dr
POLITECHIKA ŚLĄSKA W GLIWICACH WYDZIAŁ IŻYIERII ŚRODOWISKA EERGETYKI ISTYTUT MASZY URZĄDZEŃ EERGETYCZYCH Turbna arowa II Laboratoru oarów azyn celnych (PM 8) Oracował: dr nż. Grzegorz Wcak Srawdzł: dr
ROZWIĄZYWANIE DWUWYMIAROWYCH USTALONYCH ZAGADNIEŃ PRZEWODZENIA CIEPŁA PRZY POMOCY ARKUSZA KALKULACYJNEGO
 OZWIĄZYWAIE DWUWYMIAOWYCH USALOYCH ZAGADIEŃ PZEWODZEIA CIEPŁA PZY POMOCY AKUSZA KALKULACYJEGO OPIS MEODY Do rozwązana ustalonego pola temperatury wyorzystana est metoda blansów elementarnych. W metodze
OZWIĄZYWAIE DWUWYMIAOWYCH USALOYCH ZAGADIEŃ PZEWODZEIA CIEPŁA PZY POMOCY AKUSZA KALKULACYJEGO OPIS MEODY Do rozwązana ustalonego pola temperatury wyorzystana est metoda blansów elementarnych. W metodze
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
4. Zjawisko przepływu ciepła
 . Zawso przepływu cepła P.Plucńs. Zawso przepływu cepła wymana cepła przez promenowane wymana cepła przez unoszene wymana cepła przez przewodzene + generowane cepła znane wartośc temperatury zolowany brzeg
. Zawso przepływu cepła P.Plucńs. Zawso przepływu cepła wymana cepła przez promenowane wymana cepła przez unoszene wymana cepła przez przewodzene + generowane cepła znane wartośc temperatury zolowany brzeg
Opracowanie wskaźników energetycznych metoda miesięczna budynek mieszkalny bez inst. chłodu
 Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Archtektury Studa dzenne, S2, rok IV Konspekt do ćwczeń Opracowane wskaźnków energetycznych metoda mesęczna budynek meszkalny bez nst.
Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Archtektury Studa dzenne, S2, rok IV Konspekt do ćwczeń Opracowane wskaźnków energetycznych metoda mesęczna budynek meszkalny bez nst.
V. TERMODYNAMIKA KLASYCZNA
 46. ERMODYNAMIKA KLASYCZNA. ERMODYNAMIKA KLASYCZNA ermodynamka jako nauka powstała w XIX w. Prawa termodynamk są wynkem obserwacj welu rzeczywstych procesów- są to prawa fenomenologczne modelu rzeczywstośc..
46. ERMODYNAMIKA KLASYCZNA. ERMODYNAMIKA KLASYCZNA ermodynamka jako nauka powstała w XIX w. Prawa termodynamk są wynkem obserwacj welu rzeczywstych procesów- są to prawa fenomenologczne modelu rzeczywstośc..
Opracowanie świadectwa energetycznego metoda miesięczna budynek mieszkalny bez inst. chłodu
 Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Archtektury Studa dzenne, specjalność BE, rok IV Konspekt do ćwczeń Opracowane śwadectwa energetycznego metoda mesęczna budynek meszkalny
Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Archtektury Studa dzenne, specjalność BE, rok IV Konspekt do ćwczeń Opracowane śwadectwa energetycznego metoda mesęczna budynek meszkalny
DIAGNOSTYKA WYMIENNIKÓW CIEPŁA Z UWIARYGODNIENIEM WYNIKÓW POMIARÓW EKPLOATACYJNYCH
 RYNEK CIEŁA 03 DIANOSYKA YMIENNIKÓ CIEŁA Z UIARYODNIENIEM YNIKÓ OMIARÓ EKLOAACYJNYCH Autorzy: rof. dr hab. nż. Henryk Rusnowsk Dr nż. Adam Mlejsk Mgr nż. Marcn ls Nałęczów, 6-8 paźdzernka 03 SĘ Elementam
RYNEK CIEŁA 03 DIANOSYKA YMIENNIKÓ CIEŁA Z UIARYODNIENIEM YNIKÓ OMIARÓ EKLOAACYJNYCH Autorzy: rof. dr hab. nż. Henryk Rusnowsk Dr nż. Adam Mlejsk Mgr nż. Marcn ls Nałęczów, 6-8 paźdzernka 03 SĘ Elementam
SYMULACJA KRZEPNIĘCIA OBJĘTOŚCIOWEGO METALI Z UWZGLĘDNIENIEM PRZECHŁODZENIA TEMPERATUROWEGO
 49/14 Archves of Foundry, Year 2004, Volume 4, 14 Archwum O dlewnctwa, Rok 2004, Rocznk 4, Nr 14 PAN Katowce PL ISSN 1642-5308 SYMULACJA KRZEPNIĘCIA OBJĘTOŚCIOWEGO METALI Z UWZGLĘDNIENIEM PRZECHŁODZENIA
49/14 Archves of Foundry, Year 2004, Volume 4, 14 Archwum O dlewnctwa, Rok 2004, Rocznk 4, Nr 14 PAN Katowce PL ISSN 1642-5308 SYMULACJA KRZEPNIĘCIA OBJĘTOŚCIOWEGO METALI Z UWZGLĘDNIENIEM PRZECHŁODZENIA
B u d y n e k b i u r o w y
 B u d y n e k b u r o w y Ochrona ceplna budynków Projektowa charakterytyka energetyczna Śwadectwo charakterytyk energetycznej 1. Ogólna charakterytyka projektowanego obektu Budynek burowy, wolnotojący,
B u d y n e k b u r o w y Ochrona ceplna budynków Projektowa charakterytyka energetyczna Śwadectwo charakterytyk energetycznej 1. Ogólna charakterytyka projektowanego obektu Budynek burowy, wolnotojący,
KONSPEKT WYKŁADU. nt. MECHANIKA OŚRODKÓW CIĄGŁYCH. Piotr Konderla
 Studa doktorancke Wydzał Budownctwa Lądowego Wodnego Poltechnk Wrocławskej KONSPEKT WYKŁADU nt. MECHANIKA OŚRODKÓW CIĄGŁYCH Potr Konderla paźdzernk 2014 2 SPIS TREŚCI Oznaczena stosowane w konspekce...
Studa doktorancke Wydzał Budownctwa Lądowego Wodnego Poltechnk Wrocławskej KONSPEKT WYKŁADU nt. MECHANIKA OŚRODKÓW CIĄGŁYCH Potr Konderla paźdzernk 2014 2 SPIS TREŚCI Oznaczena stosowane w konspekce...
2 PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ. 2.1 Wprowadzenie
 RAKTYCZNA REALIZACJA RZEMIANY ADIABATYCZNEJ. Wprowadzene rzeana jest adabatyczna, jeśl dla każdych dwóch stanów l, leżących na tej przeane Q - 0. Z tej defncj wynka, że aby zrealzować wyżej wyenony proces,
RAKTYCZNA REALIZACJA RZEMIANY ADIABATYCZNEJ. Wprowadzene rzeana jest adabatyczna, jeśl dla każdych dwóch stanów l, leżących na tej przeane Q - 0. Z tej defncj wynka, że aby zrealzować wyżej wyenony proces,
1. OKREŚLENIE PARAMETRÓW GEOTECHNICZNYCH
 Projekt z fundamentowana: MUR OPOROWY (tuda mgr) POSADOWIENIE NA PALACH WG PN-83/B-02482. OKREŚLENIE PARAMETRÓW GEOTECHNICZNYCH grunt G π P d T/Nm P / P r grunt zayp. Tabl.II.. Zetawene parametrów geotechncznych.
Projekt z fundamentowana: MUR OPOROWY (tuda mgr) POSADOWIENIE NA PALACH WG PN-83/B-02482. OKREŚLENIE PARAMETRÓW GEOTECHNICZNYCH grunt G π P d T/Nm P / P r grunt zayp. Tabl.II.. Zetawene parametrów geotechncznych.
Równoczesna wymiana ciepła przez konwekcję i promieniowanie
 Równoczesna wymana cepła przez konwekcję promenowane W warunkach rzeczywstych wymana cepła droga konwekcj promenowana najczęścej zachodz równocześne. Zakłada sę zatem z reguły, że gęstość strumena ceplnego
Równoczesna wymana cepła przez konwekcję promenowane W warunkach rzeczywstych wymana cepła droga konwekcj promenowana najczęścej zachodz równocześne. Zakłada sę zatem z reguły, że gęstość strumena ceplnego
OKREŚLANIE EFEKTYWNOŚCI ENERGETYCZNEJ KOLEKTORÓW SŁONECZNYCH
 Adran TRZĄSKI Aleksander PANEK Poltechnka Warszawska OKREŚLANIE EFEKTYWNOŚCI ENERGETYCZNEJ KOLEKTORÓW SŁONECZNYCH Powszechność stosowana kolektorów słonecznych wymaga dostarczena projektantom opsów metod
Adran TRZĄSKI Aleksander PANEK Poltechnka Warszawska OKREŚLANIE EFEKTYWNOŚCI ENERGETYCZNEJ KOLEKTORÓW SŁONECZNYCH Powszechność stosowana kolektorów słonecznych wymaga dostarczena projektantom opsów metod
Metody systemowe i decyzyjne w informatyce
 Metody ytemowe i decyzyjne w informatyce Ćwiczenia lita zadań nr 1 Prote zatoowania równań różniczkowych Zad. 1 Liczba potencjalnych użytkowników portalu połecznościowego wynoi 4 miliony oób. Tempo, w
Metody ytemowe i decyzyjne w informatyce Ćwiczenia lita zadań nr 1 Prote zatoowania równań różniczkowych Zad. 1 Liczba potencjalnych użytkowników portalu połecznościowego wynoi 4 miliony oób. Tempo, w
PROSTY MODEL SYMULACYJNY PRZEGRODY Z IZOLACJĄ TRANSPARENTNĄ THE SIMPLE SIMULATION MODEL OF THE WALL WITH TRANSPARENT INSULATION
 TOMASZ KISILEWICZ PROSTY MODEL SYMULACYJNY PRZEGRODY Z IZOLACJĄ TRANSPARENTNĄ THE SIMPLE SIMULATION MODEL OF THE WALL WITH TRANSPARENT INSULATION S t r e s z c z e n e A b s t r a c t W artykule przedstawono
TOMASZ KISILEWICZ PROSTY MODEL SYMULACYJNY PRZEGRODY Z IZOLACJĄ TRANSPARENTNĄ THE SIMPLE SIMULATION MODEL OF THE WALL WITH TRANSPARENT INSULATION S t r e s z c z e n e A b s t r a c t W artykule przedstawono
Model oceny systemu remontu techniki brygady zmechanizowanej w działaniach bojowych
 Bi u l e t y n WAT Vo l. LX, Nr 2, 20 Model oceny ytemu remontu techniki brygady zmechanizowanej w działaniach bojowych Marian Brzezińki Wojkowa Akademia Techniczna, Wydział Mechaniczny, Katedra Logityki,
Bi u l e t y n WAT Vo l. LX, Nr 2, 20 Model oceny ytemu remontu techniki brygady zmechanizowanej w działaniach bojowych Marian Brzezińki Wojkowa Akademia Techniczna, Wydział Mechaniczny, Katedra Logityki,
Sprawozdanie powinno zawierać:
 Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
Studia dzienne, S1, rok III Konspekt do ćwiczeń
 Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Arcektury Studa dzenne, S1, rok III Konspekt do ćwczeń Termomodernzacja budynków część 1 projektu: blans potrzeb ceplnych budynku Budynek
Zachodnopomorsk Unwersytet Technologczny w Szczecne Wydzał Budownctwa Arcektury Studa dzenne, S1, rok III Konspekt do ćwczeń Termomodernzacja budynków część 1 projektu: blans potrzeb ceplnych budynku Budynek
WADY W PROCEDURZE OBLICZANIA WSPÓŁCZYNNIKA PRZENIKANIA CIEPŁA DEFECT IN PROCEDURE OF CALCULATION OF COEFFICIENT OF PENETRATION OF WARMTH
 ANDRZEJ DYLLA, KRZYSZTOF PAWŁOWSKI WADY W PROCEDURZE OBLICZANIA WSPÓŁCZYNNIKA PRZENIKANIA CIEPŁA DEFECT IN PROCEDURE OF CALCULATION OF COEFFICIENT OF PENETRATION OF WARMTH Streszczene Głównym celem nnejszego
ANDRZEJ DYLLA, KRZYSZTOF PAWŁOWSKI WADY W PROCEDURZE OBLICZANIA WSPÓŁCZYNNIKA PRZENIKANIA CIEPŁA DEFECT IN PROCEDURE OF CALCULATION OF COEFFICIENT OF PENETRATION OF WARMTH Streszczene Głównym celem nnejszego
Zmiana entropii w przemianach odwracalnych
 Wykład 4 Zmana entrop w przemanach odwracalnych: przemany obegu Carnota, spręŝane gazu półdoskonałego ze schładzanem, zobaryczne wytwarzane przegrzewane pary techncznej rzemany zentropowe gazu doskonałego
Wykład 4 Zmana entrop w przemanach odwracalnych: przemany obegu Carnota, spręŝane gazu półdoskonałego ze schładzanem, zobaryczne wytwarzane przegrzewane pary techncznej rzemany zentropowe gazu doskonałego
MECHANIKA 2 MOMENT BEZWŁADNOŚCI. Wykład Nr 10. Prowadzący: dr Krzysztof Polko
 MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
Wykład 8. Silnik Stirlinga (R. Stirling, 1816)
 Wykład 8 Maszyny ceplne c.d. Rozkład Maxwella -wstęp Entalpa Entalpa reakcj chemcznych Entalpa przeman azowych Procesy odwracalne neodwracalne Entropa W. Domnk Wydzał Fzyk UW Termodynamka 018/019 1/6 Slnk
Wykład 8 Maszyny ceplne c.d. Rozkład Maxwella -wstęp Entalpa Entalpa reakcj chemcznych Entalpa przeman azowych Procesy odwracalne neodwracalne Entropa W. Domnk Wydzał Fzyk UW Termodynamka 018/019 1/6 Slnk
INSTYTUT ENERGOELEKTRYKI POLITECHNIKI WROCŁAWSKIEJ Raport serii SPRAWOZDANIA Nr LABORATORIUM TEORII I TEHCNIKI STEROWANIA INSTRUKCJA LABORATORYJNA
 Na prawach rękopiu do użytku łużbowego INSTYTUT ENEROELEKTRYKI POLITECHNIKI WROCŁAWSKIEJ Raport erii SPRAWOZDANIA Nr LABORATORIUM TEORII I TEHCNIKI STEROWANIA INSTRUKCJA LABORATORYJNA ĆWICZENIE Nr SPOSOBY
Na prawach rękopiu do użytku łużbowego INSTYTUT ENEROELEKTRYKI POLITECHNIKI WROCŁAWSKIEJ Raport erii SPRAWOZDANIA Nr LABORATORIUM TEORII I TEHCNIKI STEROWANIA INSTRUKCJA LABORATORYJNA ĆWICZENIE Nr SPOSOBY
MODELOWANIE PRZEPŁYWU POWIETRZA W KANAŁACH WENTYLACYJNYCH PIECZARKARNI
 Inżynera Rolncza 10(108)/2008 MODELOWANIE PRZEPŁYWU POWIETRZA W KANAŁACH WENTYLACYJNYCH PIECZARKARNI Leonard Vorontsov, Ewa Wachowcz Katedra Automatyk, Poltechnka Koszalńska Streszczene: W pracy przedstawono
Inżynera Rolncza 10(108)/2008 MODELOWANIE PRZEPŁYWU POWIETRZA W KANAŁACH WENTYLACYJNYCH PIECZARKARNI Leonard Vorontsov, Ewa Wachowcz Katedra Automatyk, Poltechnka Koszalńska Streszczene: W pracy przedstawono
Warszawa, 7 września 2012. dr inż. Ryszard Wnuk Krajowa Agencja Poszanowania Energii S.A. rwnuk@kape.gov.pl
 XLIV spotkanie Forum Energia Efekt Środowisko NFOŚiGW Warszawa, 7 września 2012 Domy słoneczne i magazynowanie ciepła dr inż. Ryszard Wnuk Krajowa Agencja Poszanowania Energii S.A. rwnuk@kape.gov.pl 1
XLIV spotkanie Forum Energia Efekt Środowisko NFOŚiGW Warszawa, 7 września 2012 Domy słoneczne i magazynowanie ciepła dr inż. Ryszard Wnuk Krajowa Agencja Poszanowania Energii S.A. rwnuk@kape.gov.pl 1
WYKŁAD V. IV.3. Modele konsolidacji ośrodka porowatego. ( ) 2 = ], J t G e Τ
![WYKŁAD V. IV.3. Modele konsolidacji ośrodka porowatego. ( ) 2 = ], J t G e Τ WYKŁAD V. IV.3. Modele konsolidacji ośrodka porowatego. ( ) 2 = ], J t G e Τ](/thumbs/73/68296983.jpg) WYKŁAD V IV.. Modee konodacj ośrodka porowatego. W poprzednm rozdzae przyjęśmy założene, że zkeet gruntowy jet całem neodkztałcanym, a jeże dopuzczamy jakeś odkztałcena fazy tałej, to ą to tyko zmany objętoścowe.
WYKŁAD V IV.. Modee konodacj ośrodka porowatego. W poprzednm rozdzae przyjęśmy założene, że zkeet gruntowy jet całem neodkztałcanym, a jeże dopuzczamy jakeś odkztałcena fazy tałej, to ą to tyko zmany objętoścowe.
 Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
ELEKTROCHEMIA. ( i = i ) Wykład II b. Nadnapięcie Równanie Buttlera-Volmera Równania Tafela. Wykład II. Równowaga dynamiczna i prąd wymiany
 Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
ZADANIE 9.5. p p T. Dla dwuatomowego gazu doskonałego wykładnik izentropy = 1,4 (patrz tablica 1). Temperaturę spiętrzenia obliczymy następująco
 ZADANIE 9.5. Do dyszy Bendemanna o rzekroju wylotowym A = mm doływa owetrze o cśnenu =,85 MPa temeraturze t = C, z rędkoścą w = 5 m/s. Cśnene owetrza w rzestrzen, do której wyływa owetrze z dyszy wynos
ZADANIE 9.5. Do dyszy Bendemanna o rzekroju wylotowym A = mm doływa owetrze o cśnenu =,85 MPa temeraturze t = C, z rędkoścą w = 5 m/s. Cśnene owetrza w rzestrzen, do której wyływa owetrze z dyszy wynos
Optymalizacja belki wspornikowej
 Leszek MIKULSKI Katedra Podstaw Mechank Ośrodków Cągłych, Instytut Mechank Budowl, Poltechnka Krakowska e mal: ps@pk.edu.pl Optymalzacja belk wspornkowej 1. Wprowadzene RozwaŜamy zadane optymalnego kształtowana
Leszek MIKULSKI Katedra Podstaw Mechank Ośrodków Cągłych, Instytut Mechank Budowl, Poltechnka Krakowska e mal: ps@pk.edu.pl Optymalzacja belk wspornkowej 1. Wprowadzene RozwaŜamy zadane optymalnego kształtowana
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania
 Poltechnka Poznańka Wydzał Budowy Mazyn Zarządzana Rozprawa doktorka Mgr nż. Jacek DIAKN Identyfkacja tanu utalonego model ymulacyjnych ytemów produkcyjnych Promotor: Prof. dr hab. nż Zenoba WEISS POZNAŃ
Poltechnka Poznańka Wydzał Budowy Mazyn Zarządzana Rozprawa doktorka Mgr nż. Jacek DIAKN Identyfkacja tanu utalonego model ymulacyjnych ytemów produkcyjnych Promotor: Prof. dr hab. nż Zenoba WEISS POZNAŃ
2012-10-11. Definicje ogólne
 0-0- Defncje ogólne Logstyka nauka o przepływe surowców produktów gotowych rodowód wojskowy Utrzyywane zapasów koszty zwązane.n. z zarożene kaptału Brak w dostawach koszty zwązane.n. z przestoje w produkcj
0-0- Defncje ogólne Logstyka nauka o przepływe surowców produktów gotowych rodowód wojskowy Utrzyywane zapasów koszty zwązane.n. z zarożene kaptału Brak w dostawach koszty zwązane.n. z przestoje w produkcj
Dobór zmiennych objaśniających
 Dobór zmennych objaśnających Metoda grafowa: Należy tak rozpąć graf na werzchołkach opsujących poszczególne zmenne, aby występowały w nm wyłączne łuk symbolzujące stotne korelacje pomędzy zmennym opsującym.
Dobór zmennych objaśnających Metoda grafowa: Należy tak rozpąć graf na werzchołkach opsujących poszczególne zmenne, aby występowały w nm wyłączne łuk symbolzujące stotne korelacje pomędzy zmennym opsującym.
Egzamin poprawkowy z Analizy II 11 września 2013
 Egzamn poprawkowy z nalzy II 11 wrześna 13 Uwag organzacyjne: każde zadane rozwązujemy na osobnej kartce Każde zadane należy podpsać menem nazwskem własnym oraz prowadzącego ćwczena Na wszelk wypadek prosmy
Egzamn poprawkowy z nalzy II 11 wrześna 13 Uwag organzacyjne: każde zadane rozwązujemy na osobnej kartce Każde zadane należy podpsać menem nazwskem własnym oraz prowadzącego ćwczena Na wszelk wypadek prosmy
Zaawansowane metody numeryczne
 Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
Wykład 9. jej modyfkacje. Oznaczena Będzemy rozpatrywać zagadnene rozwązana następującego układu n równań lnowych z n newadomym x 1... x n : a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 + a 22 x
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
BADANIA OPERACYJNE. Podejmowanie decyzji w warunkach niepewności. dr Adam Sojda
 BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
BADANIA OPERACYJNE Podejmowane decyzj w warunkach nepewnośc dr Adam Sojda Teora podejmowana decyzj gry z naturą Wynk dzałana zależy ne tylko od tego, jaką podejmujemy decyzję, ale równeż od tego, jak wystąp
Dla dzielnej X (dividend) i dzielnika D 0 (divisor) liczby Q oraz R takie, Ŝe
 zelene ekwencyjne zelene la dzelnej X (dvdend) dzelnka (dvor) lczby Q oraz R take, Ŝe X=Q R, R < nazywa ę lorazem Q (uotent) reztą R (remander) z dzelena X rzez. Równane dzelena moŝe meć rozwązana ełnające
zelene ekwencyjne zelene la dzelnej X (dvdend) dzelnka (dvor) lczby Q oraz R take, Ŝe X=Q R, R < nazywa ę lorazem Q (uotent) reztą R (remander) z dzelena X rzez. Równane dzelena moŝe meć rozwązana ełnające
Tensorowe. Wielkości fizyczne. Wielkości i Jednostki UŜywane w Elektryce Wielkość Fizyczna to właściwość fizyczna zjawisk lub obiektów,
 Welkośc Jednosk UŜywane w Elekryce Welkość Fzyczna o właścwość fzyczna zjawsk lub obeków, Przykłady: W. f.: kórą moŝna zmerzyć. czas, długość, naęŝene pola elekrycznego, przenkalność elekryczna kryszałów.
Welkośc Jednosk UŜywane w Elekryce Welkość Fzyczna o właścwość fzyczna zjawsk lub obeków, Przykłady: W. f.: kórą moŝna zmerzyć. czas, długość, naęŝene pola elekrycznego, przenkalność elekryczna kryszałów.
SPECYFIKACJA TECHNICZNA S-04.00. ROBOTY MUROWE
 TOM III - Specyfkacje Technczne SPECYFIKACJA TECHNICZNA S-04.00. ROBOTY MUROWE Remont rozbudowa budynku szatnowego przy boskach sportowych w Morynu. 42 są TOM III - Specyfkacje Technczne 1. WST P 1.1.
TOM III - Specyfkacje Technczne SPECYFIKACJA TECHNICZNA S-04.00. ROBOTY MUROWE Remont rozbudowa budynku szatnowego przy boskach sportowych w Morynu. 42 są TOM III - Specyfkacje Technczne 1. WST P 1.1.
Identyfikacja stopnia zanieczyszczenia powierzchni ogrzewalnych kotła parowego
 POLITECHNIKA KRAKOWSKA IM. TADEUSZA KOŚCIUSZKI WYDZIAŁ MECHANICZNY Identyfkacja stopna zaneczyszczena powerzchn ogrzewalnych kotła parowego Marcn Trojan Praca doktorska pod kerunkem prof. dr hab. nż. Jana
POLITECHNIKA KRAKOWSKA IM. TADEUSZA KOŚCIUSZKI WYDZIAŁ MECHANICZNY Identyfkacja stopna zaneczyszczena powerzchn ogrzewalnych kotła parowego Marcn Trojan Praca doktorska pod kerunkem prof. dr hab. nż. Jana
Pracownia Automatyki i Elektrotechniki Katedry Tworzyw Drzewnych Ćwiczenie 3. Analiza obwodów RLC przy wymuszeniach sinusoidalnych w stanie ustalonym
 ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
LABORATORIUM PRZYRZĄDÓW I UKŁADÓW MOCY. Ćwiczenie 3 B. Stany dynamiczne Przetwornica impulsowa
 90-924 Łódź, ul. Wólczańka 221/223, bud. B18 tel. (0)42 631 26 28 fak (0)42 636 03 27 e-mal ecretary@dmc.p.lodz.pl http://www.dmc.p.lodz.pl ABORATORIM PRZYRZĄDÓW I KŁADÓW MOCY Ćwczene 3 B Stany dynamczne
90-924 Łódź, ul. Wólczańka 221/223, bud. B18 tel. (0)42 631 26 28 fak (0)42 636 03 27 e-mal ecretary@dmc.p.lodz.pl http://www.dmc.p.lodz.pl ABORATORIM PRZYRZĄDÓW I KŁADÓW MOCY Ćwczene 3 B Stany dynamczne
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
Część teoretyczna IZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD
 Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
5. Rezonans napięć i prądów
 ezonans napęć prądów W-9 el ćwczena: 5 ezonans napęć prądów Dr hab nŝ Dorota Nowak-Woźny Wyznaczene krzywej rezonansowej dla szeregowego równoległego obwodu Zagadnena: Fzyczne podstawy zjawska rezonansu
ezonans napęć prądów W-9 el ćwczena: 5 ezonans napęć prądów Dr hab nŝ Dorota Nowak-Woźny Wyznaczene krzywej rezonansowej dla szeregowego równoległego obwodu Zagadnena: Fzyczne podstawy zjawska rezonansu
SYMULACJA KOMPUTEROWA NAPRĘŻEŃ DYNAMICZNYCH WE WRĘGACH MASOWCA NA FALI NIEREGULARNEJ
 Jan JANKOWSKI *), Maran BOGDANIUK *),**) SYMULACJA KOMPUTEROWA NAPRĘŻEŃ DYNAMICZNYCH WE WRĘGACH MASOWCA NA FALI NIEREGULARNEJ W referace przedstawono równana ruchu statku w warunkach falowana morza oraz
Jan JANKOWSKI *), Maran BOGDANIUK *),**) SYMULACJA KOMPUTEROWA NAPRĘŻEŃ DYNAMICZNYCH WE WRĘGACH MASOWCA NA FALI NIEREGULARNEJ W referace przedstawono równana ruchu statku w warunkach falowana morza oraz
Systemy Ochrony Powietrza Ćwiczenia Laboratoryjne
 ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
MODEL ODPOWIEDZI I SCHEMAT OCENIANIA ARKUSZA II. Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy maksymalną liczbę punktów.
 MODEL ODOWEDZ SCHEMAT OCENANA AKUSZA Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy makymalną liczbę punktów.. Amperomierz należy podłączyć zeregowo. Zadanie. Żaróweczki... Obliczenie
MODEL ODOWEDZ SCHEMAT OCENANA AKUSZA Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy makymalną liczbę punktów.. Amperomierz należy podłączyć zeregowo. Zadanie. Żaróweczki... Obliczenie
Podstawowe układy pracy tranzystora bipolarnego
 L A B O A T O I U M U K Ł A D Ó W L I N I O W Y C H Podtawowe układy pracy tranzytora bipolarnego Ćwiczenie opracował Jacek Jakuz 4. Wtęp Ćwiczenie umożliwia pomiar i porównanie parametrów podtawowych
L A B O A T O I U M U K Ł A D Ó W L I N I O W Y C H Podtawowe układy pracy tranzytora bipolarnego Ćwiczenie opracował Jacek Jakuz 4. Wtęp Ćwiczenie umożliwia pomiar i porównanie parametrów podtawowych
OBLICZENIA STRAT CIEPŁA BUDYNKU
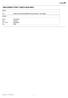 OBLICZENIA STRAT CIEPŁA BUDYNKU Projekt : Projekt termomodernizacji Biblioteki Gminnej w Mniowie - stan istniejący Inwestor : Gmina Mniów Ulica: Centralna 9 Kod i miasto: 26-080 Mniów Kraj: Polska - 1
OBLICZENIA STRAT CIEPŁA BUDYNKU Projekt : Projekt termomodernizacji Biblioteki Gminnej w Mniowie - stan istniejący Inwestor : Gmina Mniów Ulica: Centralna 9 Kod i miasto: 26-080 Mniów Kraj: Polska - 1
MODEL ODPOWIEDZI I SCHEMAT OCENIANIA ARKUSZA II. Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy maksymalną liczbę punktów.
 MODEL ODOWEDZ SCHEMAT OCENANA AKUSZA Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy makymalną liczbę punktów. Numer zadania Czynności unktacja Uwagi. Amperomierz należy podłączyć
MODEL ODOWEDZ SCHEMAT OCENANA AKUSZA Zdający może rozwiązać zadania każdą poprawną metodą. Otrzymuje wtedy makymalną liczbę punktów. Numer zadania Czynności unktacja Uwagi. Amperomierz należy podłączyć
Czynnik niezawodności w modelowaniu podróży i prognozowaniu ruchu
 Problemy Kolejnictwa Zezyt 165 (grudzień 2014) 53 Czynnik niezawodności w modelowaniu podróży i prognozowaniu ruchu Szymon KLEMBA 1 Strezczenie W artykule rozważano możliwości uwzględniania czynnika niezawodności
Problemy Kolejnictwa Zezyt 165 (grudzień 2014) 53 Czynnik niezawodności w modelowaniu podróży i prognozowaniu ruchu Szymon KLEMBA 1 Strezczenie W artykule rozważano możliwości uwzględniania czynnika niezawodności
Materiały ćwiczeniowe do małego kursu chemii teoretycznej Mechanika klasyczna
 Materały ćwczenowe do małego kuru chem teoretycznej Mechanka klayczna Opracowane: Potr Petelenz, Barbara Pac WSTĘP Podtawowe defncje równana Stan mechanczny układu n punktów materalnych (reprezentujących
Materały ćwczenowe do małego kuru chem teoretycznej Mechanka klayczna Opracowane: Potr Petelenz, Barbara Pac WSTĘP Podtawowe defncje równana Stan mechanczny układu n punktów materalnych (reprezentujących
OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI
 Oblczane rozkładów natęŝena ośwetlena. OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI T E R E N Y O T W A R T E Stosowana jest tzw. metoda punktowa, która polega na oblczanu w określonych
Oblczane rozkładów natęŝena ośwetlena. OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI T E R E N Y O T W A R T E Stosowana jest tzw. metoda punktowa, która polega na oblczanu w określonych
POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA
 Ćwczene O5 POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA 1. Cel zakres ćwczena Celem ćwczena jest poznane metod pomaru współczynnków odbca przepuszczana próbek płaskch 2. Ops stanowska laboratoryjnego
Ćwczene O5 POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA 1. Cel zakres ćwczena Celem ćwczena jest poznane metod pomaru współczynnków odbca przepuszczana próbek płaskch 2. Ops stanowska laboratoryjnego
1. Wstępna geometria skrzyżowania (wariant 1a)
 . Wtępna geometra rzyżowana (warant a) 2. Strutura erunowa ruchu 3. Warun geometryczne Srzyżowane et zloalzowane w śródmeścu o newelm ruchu pezych. Pochylene podłużne na wlotach nr 3 ne przeracza 0,5%,
. Wtępna geometra rzyżowana (warant a) 2. Strutura erunowa ruchu 3. Warun geometryczne Srzyżowane et zloalzowane w śródmeścu o newelm ruchu pezych. Pochylene podłużne na wlotach nr 3 ne przeracza 0,5%,
Weryfikacja hipotez dla wielu populacji
 Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Weryfkacja hpotez dla welu populacj Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Intelgencj Metod Matematycznych Wydzał Informatyk Poltechnk Szczecńskej 5. Parametryczne testy stotnośc w
Rozwiązywanie zadań optymalizacji w środowisku programu MATLAB
 Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
Rozwązywane zadań optymalzacj w środowsku programu MATLAB Zagadnene optymalzacj polega na znajdowanu najlepszego, względem ustalonego kryterum, rozwązana należącego do zboru rozwązań dopuszczalnych. Standardowe
ANALIZA JEDNOSTKOWYCH STRAT CIEPŁA W SYSTEMIE RUR PREIZOLOWANYCH
 ZESZYTY NAUKOWE POLITECHNIKI RZESZOWSKIEJ Nr 83 Budownctwo Inżynera Środowska z. 59 (4/1) 01 Bożena BABIARZ Barbara ZIĘBA Poltechnka Rzeszowska ANALIZA JEDNOSTKOWYCH STRAT CIEPŁA W SYSTEMIE RUR PREIZOLOWANYCH
ZESZYTY NAUKOWE POLITECHNIKI RZESZOWSKIEJ Nr 83 Budownctwo Inżynera Środowska z. 59 (4/1) 01 Bożena BABIARZ Barbara ZIĘBA Poltechnka Rzeszowska ANALIZA JEDNOSTKOWYCH STRAT CIEPŁA W SYSTEMIE RUR PREIZOLOWANYCH
Blok 7: Zasada zachowania energii mechanicznej. Zderzenia
 Blok 7 Zaada zachowana energ echancznej. Zderzena I. Sły zachowawcze nezachowawcze Słą zachowawczą nazyway łę która wzdłuż dowolnego zaknętego toru wykonuje pracę równą zeru. Słą zachowawczą nazyway łę
Blok 7 Zaada zachowana energ echancznej. Zderzena I. Sły zachowawcze nezachowawcze Słą zachowawczą nazyway łę która wzdłuż dowolnego zaknętego toru wykonuje pracę równą zeru. Słą zachowawczą nazyway łę
Dr inż. Andrzej Tatarek. Siłownie cieplne
 Dr nż. Andrzej Tatarek Słowne ceplne Wykład 2 Podstawowe przemany energetyczne Jednostkowe zużyce cepła energ chemcznej palwa w elektrown parowej 2 Podstawowe przemany Proces przetwarzana energ elektrycznej
Dr nż. Andrzej Tatarek Słowne ceplne Wykład 2 Podstawowe przemany energetyczne Jednostkowe zużyce cepła energ chemcznej palwa w elektrown parowej 2 Podstawowe przemany Proces przetwarzana energ elektrycznej
EDOMETRYCZNE MODUŁY ŚCISLIWOŚCI GRUNTU
 Dr inż. Grzegorz Straż Intrukcja do ćwiczeń laboratoryjnych pt: EDOMETRYCZNE MODUŁY ŚCISLIWOŚCI GRUNTU Wprowadzenie. Zalecenia dotyczące badań gruntów w edometrze: Zalecane topnie wywoływanego naprężenia:
Dr inż. Grzegorz Straż Intrukcja do ćwiczeń laboratoryjnych pt: EDOMETRYCZNE MODUŁY ŚCISLIWOŚCI GRUNTU Wprowadzenie. Zalecenia dotyczące badań gruntów w edometrze: Zalecane topnie wywoływanego naprężenia:
I. PRZEPŁYWY W BUDOWLACH
 9 I. PRZEPŁYWY W BUDOWLCH Zarys problematyk Fzyka budowl est edną z namłodszych dzedzn nżyner budowlane. Rozwnęła sę w latach 70-tych, główne w wynku kryzysu energetycznego, aczkolwek e podstawy są znaczne
9 I. PRZEPŁYWY W BUDOWLCH Zarys problematyk Fzyka budowl est edną z namłodszych dzedzn nżyner budowlane. Rozwnęła sę w latach 70-tych, główne w wynku kryzysu energetycznego, aczkolwek e podstawy są znaczne
BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH
 INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
Fizyka, technologia oraz modelowanie wzrostu kryształów
 Fizyka, technologia oraz modelowanie wzrotu kryztałów Staniław Krukowki i Michał Lezczyńki Intytut Wyokich Ciśnień PAN 01-14 Warzawa, ul Sokołowka 9/37 tel: 88 80 44 e-mail: tach@unipre.waw.pl, mike@unipre.waw.pl
Fizyka, technologia oraz modelowanie wzrotu kryztałów Staniław Krukowki i Michał Lezczyńki Intytut Wyokich Ciśnień PAN 01-14 Warzawa, ul Sokołowka 9/37 tel: 88 80 44 e-mail: tach@unipre.waw.pl, mike@unipre.waw.pl
KONSPEKT WYKŁADU. nt. METODA ELEMENTÓW SKOŃCZONYCH TEORIA I ZASTOSOWANIA. Piotr Konderla
 Studa doktorancke Wydzał Budownctwa Lądowego Wodnego Poltechnk Wrocławskej KONSPEKT WYKŁADU nt. METODA ELEMENTÓW SKOŃCZONYCH TEORIA I ZASTOSOWANIA Potr Konderla maj 2007 Kurs na Studach Doktoranckch Poltechnk
Studa doktorancke Wydzał Budownctwa Lądowego Wodnego Poltechnk Wrocławskej KONSPEKT WYKŁADU nt. METODA ELEMENTÓW SKOŃCZONYCH TEORIA I ZASTOSOWANIA Potr Konderla maj 2007 Kurs na Studach Doktoranckch Poltechnk
Komputerowe generatory liczb losowych
 . Perwszy generator Komputerowe generatory lczb losowych 2. Przykłady zastosowań 3. Jak generuje sę lczby losowe przy pomocy komputera. Perwszy generator lczb losowych L. H. C. Tppet - 927 Ksąż ążka -
. Perwszy generator Komputerowe generatory lczb losowych 2. Przykłady zastosowań 3. Jak generuje sę lczby losowe przy pomocy komputera. Perwszy generator lczb losowych L. H. C. Tppet - 927 Ksąż ążka -
Zastosowanie technik sztucznej inteligencji w analizie odwrotnej
 Zastosowane technk sztucznej ntelgencj w analze odwrotnej Ł. Sztangret, D. Szelga, J. Kusak, M. Petrzyk Katedra Informatyk Stosowanej Modelowana Akadema Górnczo-Hutncza, Kraków Motywacja Dokładność symulacj
Zastosowane technk sztucznej ntelgencj w analze odwrotnej Ł. Sztangret, D. Szelga, J. Kusak, M. Petrzyk Katedra Informatyk Stosowanej Modelowana Akadema Górnczo-Hutncza, Kraków Motywacja Dokładność symulacj
KONCEPCJA OCENY HYBRYDOWYCH SYSTEMÓW ENERGETYCZNYCH
 2-2010 PROBLEMY ESPLOATACJI 159 Robert DZIERŻAOWSI Poltechnka Warszawska OCCJA OCEY HYBRYDOWYCH SYSTEMÓW EERGETYCZYCH Słowa kluczowe Hybrydowy system energetyczny, skojarzony system energetyczny, generator
2-2010 PROBLEMY ESPLOATACJI 159 Robert DZIERŻAOWSI Poltechnka Warszawska OCCJA OCEY HYBRYDOWYCH SYSTEMÓW EERGETYCZYCH Słowa kluczowe Hybrydowy system energetyczny, skojarzony system energetyczny, generator
I..ROZWIĄZANIE DANEGO RUSZTU BELKOWEGO OD DANEGO OBCIĄŻENIA
 TO SIŁ układ przetrzenny przykład ruzt belkowy OZWIĄZNI USZTU LKOWO TOĄ SIŁ I OLIZNI PZISZZNI any jet ruzt belkowy jak na ryunku obok ozwązać go etodą ł porządzć wykrey ł przekrojowych dokonać kontrol
TO SIŁ układ przetrzenny przykład ruzt belkowy OZWIĄZNI USZTU LKOWO TOĄ SIŁ I OLIZNI PZISZZNI any jet ruzt belkowy jak na ryunku obok ozwązać go etodą ł porządzć wykrey ł przekrojowych dokonać kontrol
POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH. Badanie wentylatora
 POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Badanie wentylatora Laboratorium Pomiarów Mazyn Cieplnych (PM-3) Opracował: Sprawdził: Zatwierdził:
POLITECHNIKA ŚLĄSKA WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI INSTYTUT MASZYN I URZĄDZEŃ ENERGETYCZNYCH Badanie wentylatora Laboratorium Pomiarów Mazyn Cieplnych (PM-3) Opracował: Sprawdził: Zatwierdził:
MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5
 MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
OBLICZENIA STRAT CIEPŁA BUDYNKU
 OBLICZENIA STRAT CIEPŁA BUDYNKU Projekt : Projekt termomodernizacji Biblioteki Gminnej w Mniowie - stanpo wykonaniu termomodernizacji Inwestor : Gmina Mniów Ulica: Centralna 9 Kod i miasto: 26-080 Mniów
OBLICZENIA STRAT CIEPŁA BUDYNKU Projekt : Projekt termomodernizacji Biblioteki Gminnej w Mniowie - stanpo wykonaniu termomodernizacji Inwestor : Gmina Mniów Ulica: Centralna 9 Kod i miasto: 26-080 Mniów
Department of Civil Engineering and Geodesy WULS SGGW
 Gabrela RUTKOWSKA 1, Marcn PRZYBYTKOWSKI 1 Katedra Budownctwa Geodezj SGGW w Warszawe Department of Cvl Engneerng and Geodesy WULS SGGW Analza opłacalnośc oceplana wybranych budynków jednorodznnych. Część
Gabrela RUTKOWSKA 1, Marcn PRZYBYTKOWSKI 1 Katedra Budownctwa Geodezj SGGW w Warszawe Department of Cvl Engneerng and Geodesy WULS SGGW Analza opłacalnośc oceplana wybranych budynków jednorodznnych. Część
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
Wykład 4. Skręcanie nieskrępowane prętów o przekroju cienkościennym otwartym i zamkniętym. Pręt o przekroju cienkościennym otwartym
 Wykład 4. Skręane nekrępowane prętów o przekroju enkośennym otwartym zamknętym. Pręt o przekroju enkośennym otwartym la przekroju pręta pokazanego na ryunku przyjmjmy funkje naprężeń Prandtla, która tylko
Wykład 4. Skręane nekrępowane prętów o przekroju enkośennym otwartym zamknętym. Pręt o przekroju enkośennym otwartym la przekroju pręta pokazanego na ryunku przyjmjmy funkje naprężeń Prandtla, która tylko
Bryła fotometryczna i krzywa światłości.
 STUDIA NIESTACJONARNE ELEKTROTECHNIKA Laboratorum PODSTAW TECHNIKI ŚWIETLNEJ Temat: WYZNACZANIE BRYŁY FOTOMETRYCZNEJ ŚWIATŁOŚCI Opracowane wykonano na podstawe: 1. Laboratorum z technk śwetlnej (praca
STUDIA NIESTACJONARNE ELEKTROTECHNIKA Laboratorum PODSTAW TECHNIKI ŚWIETLNEJ Temat: WYZNACZANIE BRYŁY FOTOMETRYCZNEJ ŚWIATŁOŚCI Opracowane wykonano na podstawe: 1. Laboratorum z technk śwetlnej (praca
Płyny nienewtonowskie i zjawisko tiksotropii
 Płyny nenewtonowske zjawsko tksotrop ) Krzywa newtonowska, lnowa proporcjonalność pomędzy szybkoścą ścnana a naprężenem 2) Płyny zagęszczane ścnanem, naprężene wzrasta bardzej nż proporcjonalne do wzrostu
Płyny nenewtonowske zjawsko tksotrop ) Krzywa newtonowska, lnowa proporcjonalność pomędzy szybkoścą ścnana a naprężenem 2) Płyny zagęszczane ścnanem, naprężene wzrasta bardzej nż proporcjonalne do wzrostu
Michal Strzeszewski Piotr Wereszczynski. poradnik. Norma PN-EN 12831. Nowa metoda. obliczania projektowego. obciazenia cieplnego
 Mchal Strzeszewsk Potr Wereszczynsk Norma PN-EN 12831 Nowa metoda oblczana projektowego. obcazena ceplnego poradnk Mchał Strzeszewsk Potr Wereszczyńsk Norma PN EN 12831 Nowa metoda oblczana projektowego
Mchal Strzeszewsk Potr Wereszczynsk Norma PN-EN 12831 Nowa metoda oblczana projektowego. obcazena ceplnego poradnk Mchał Strzeszewsk Potr Wereszczyńsk Norma PN EN 12831 Nowa metoda oblczana projektowego
RZECZPOSPOLITA OPIS PATENTOWY
 RZECZPOSPOLITA OPIS PATENTOWY 4486 POLSKA Patent dodatkowy do patentunr Zgłoszono: 85 25 (P. 256445) Perwszeństwo Int. Cl.4 B65D 90/02 E04H 7/22 Int. Cl.5 B65D 88/52 B65D 90/02 E04H 7/22 URZĄD PATENTOWY
RZECZPOSPOLITA OPIS PATENTOWY 4486 POLSKA Patent dodatkowy do patentunr Zgłoszono: 85 25 (P. 256445) Perwszeństwo Int. Cl.4 B65D 90/02 E04H 7/22 Int. Cl.5 B65D 88/52 B65D 90/02 E04H 7/22 URZĄD PATENTOWY
