¹ Ë Ð ÓÒ Äº Ð ÓÛ Ù Ë Ð Ñ ËØ Ú Ò Ï Ò Ö ½ ÑÓ Ð Ó Þ ÝÛ ðò Ð ØÖÓ¹ Ý ÓÖ Þ ÔÖÞ Û Þ Ò ØÒ Ò ÓÞÓÒ Û Ï Æ ¹ ÖÐÓ ÊÙ Ë ÑÓÒ Î Ò Ö Å Ö ½ Ó ÖÝ ÓÞÓÒ Û Ï Æ ¹ Ö Ö Ù ³Ì À
|
|
|
- Nadzieja Markowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 ÓÞÓÒÝ Ï Æ Ì ØÝ ÅÓ ÐÙ ËØ Ò Ö ÓÛ Ó Ó ÖÝ Ó ÓÒÙ À ÔÖÓ º Ö º Ð Ò Ö Ð Ô ÖÒ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÏÝ ½½ Û Ö Ø ÔÓ ÞÙ Û Ò ÓÞÓÒÙ À Ò ÒÓÛ Þ ÛÝÒ ÄÀ
2 ¹ Ë Ð ÓÒ Äº Ð ÓÛ Ù Ë Ð Ñ ËØ Ú Ò Ï Ò Ö ½ ÑÓ Ð Ó Þ ÝÛ ðò Ð ØÖÓ¹ Ý ÓÖ Þ ÔÖÞ Û Þ Ò ØÒ Ò ÓÞÓÒ Û Ï Æ ¹ ÖÐÓ ÊÙ Ë ÑÓÒ Î Ò Ö Å Ö ½ Ó ÖÝ ÓÞÓÒ Û Ï Æ ¹ Ö Ö Ù ³Ì ÀÓÓ Ø Å ÖØ Ò٠º ºÎ ÐØÑ Ò ½ ÛÝ Þ Ò Ô ÒÓð ÑÓ ÐÙ ¹ Ú Âº ÖÓ Àº Ú ÈÓÐ ØÞ Ö Ö Ò Ï ÐÞ ¾¼¼ ØÛÓÖÞ Ò ÔÓ Ø Û ÓÔ Ù Ó Þ ÝÛ ðò ÐÒÝ ¹ Ó ÖÓ Æ Ñ Ù ÓÖ Þ Å ÓØÓ ÃÓ Ý ÌÓ Å Û ¾¼¼ Ó ÖÝ Ñ Ò ÞÑÙ ÔÓÒØ Ò ÞÒ Ó Ñ Ò ØÝÑ ØÖ ¹ Ö ÒÓ Ò Ð ÖØ È Ø Ö À ¾¼½ Ó ÖÝ Ñ Ò ÞÑÙ ÛÝ ð Ò Ó ÔÓ Ó Þ Ò Ñ Ý Þ Ø ÏÔÖÓÛ Þ Ò Æ ÖÓ Ý ÆÓ Ð ÓÖ Þ Þ ÓÔ Ò Ñ Þ Ò Û Ö Û ÔÖÞ Û Þ Ò Ò Ö º Ø ÖÝ ÞÓ Ø Ó Ø ØÒ Ó ÔÓØÛ Ö ÞÓÒÝ ÔÖÞ Þ Ô ÖÝÑ ÒØÝ ÌÄ Ë Å˺ ÅÓ Ð ËØ Ò Ö ÓÛÝ Ó Þ ÝÛ Ò Ð ØÖÓ ÖÓÑÓ ÝÒ Ñ Û ÒØÓÛ É µ º º ÖÒ ÏÝ ½½ ½
3 ÓÞÓÒÝ Ï Æ ÅÓ Ð Ï Ò Ö ³ ¹Ë Рѳ ÆÓÛÝ ÑÓ Ð Ó Þ ÝÛ ðò Ý ½ µ ãë Óð ðä Ó Þ ÝÛ Ò Ò ÛÝÒ Þ Ç Þ ÝÛ Ò Þ Ó Þ ÔÖÞ Þ ÛÝÑ Ò Ø ÔÖÞ Þ Ò Þ Ù Þ Ñ Ý ÓÞÓÒÙ Ö ÞÓ Ñ ÝÛÒ Ó ÓÞÓÒÙ Ï ÐÙ Æ º ÊÓÞÔ Ñ ÓÒÙ ν µ ¾ ¾ Ï Ñ Þ ÔÖÞ Þ Ò ÔÓÛ ÒÒÓ Ýð ÈÖÞÝ ÑÙ µ - Ø Ð Ó Þ ÝÛ ðò Å Ï Ò Ö - W ν e Ë Ð Ñ ÔÖÞ Û Þ Ð Ñ Ý Ï Æ Ñ Ï ¼ Î e - Ñ ¼ Î Ò ÙØÖ Ò Þ ÛÝÑ Ò ÓÞÓÒÙ ¼ ØÞÛº ÛÝÑ Ò ÔÖ Û Ò ÙØÖ ÐÒÝ µ ¹ ½ Ç Þ ÝÛ Ò º º ÖÒ ÏÝ ½½ ¾
4 ÓÞÓÒÝ Ï Æ Ç ÖÝ Ð Ö ØÓÖ ËÈË Û ÊÆ Ï Þ ÖÞ Ò Ô Ô ÑÓ ÞÐ Û Ø Ò ¹ ÏÝÒ Í ½ ½ µ Ð Ô ÖÝ Õ Õ Û Û ÖØÙ ÐÒÝ ÓØÓÒ ÐÙ ÓÞÓÒ Æ Ø Ö Ò Ø ÔÒ ÑÓ ÖÓÞÔ ð ð Ò q _ q Z o γ e + e Ô Ö Ð ÔØÓÒ Û µ Â Ø ØÓ ØÞÛº ÔÖÓ Ö Ð ¹ Ò º Ï Ó ÛÝÑ ÒÝ Æ µ Ñ ÑÙÑ Û Ñ Ò ÞÑ ÒÒ Þ Ô ÖÝ Ð ÔØÓÒ Ûº º º ÖÒ ÏÝ ½½
5 ÈÖÞÝÔ Æ Û Ø ØÓÖÞ Í ½ ½ µ º º ÖÒ ÏÝ ½½
6 Ç ÖÝ ÓÞÓÒÝ Ï Æ ÏÝÒ Í ½ ½ µ Þ ÖÞ Ò ÑÓ ÞÐ Û Ø Þ Ï Ø ã Ò ¹ Ô Ô Ô ÖÝ Û ¼ Õ Õ ÓÞÓÒ Ï Ð ä defij2pqrt7,ghj6 dhij070pqrshik7 Ù Ï fghi0pr>! ifg8fg8fhijk6 fghi1rt3:5f3 fhij3 fhij08fhijk6 degi31t/pqs>fhij1 deijprstu80gij08fhijk6 fghi18fhij08fhij08fg8fhijk6 dfhijpq8fg0fhijk6 ddfghj4;su8 fhij18fhijk6 fghijr?pqs# fghi00fhij08fhij08fg8fhijk6 ghij8fhijk7 ddfijqru8 ddgi0:prtu8 defghj3t=pqtu99u:h3 fghi08fhij08fhij08fg8fhijk6 fghi08fhij08fhij08fg0fhijk6 fghi08fhij08fhij08ef1 fghi08fhij0<fhij08ef10 fghi08fhij0<dgj fghi08fhij08dgj fghi08fhijk6dgj7 fghi08dej10 fghi08egj3r>efij fghi08egjr>efij fghi08egjr?efij fghi08egjtj1<efik7 fghi08egjhefij fghik6egj7 fghik7egj7 ij0<efik7 fghik7egj30ij0<efik7 fghik7egj30ij0tu8efj7 fghik7egj30ij0s0efk7 fghik7egj30ij0s<efk7 fghik7egj30ij0t7u8ef10 fghik7egj30ij0?jtefj0 fghik7egj30ij1>j8ef7 fghik7egj30ij1<j3<ef3 fghik7egj30ij1<j1<ef3 fghik7egj30ij3<j0>ef3 fghik7egj30ij3<jk70ef0 fghik7egj30ij7<jk70ef0 fghik7egj30ij7<i<ef fghik7egj30ij7<i>ef fghik7egj30ij7<ief fghik7egj30ij<ief fghik7egj30ij<ief fghik7egj30ijief fghik7egj30ij<i7 fghik7egj30iji7 fghik7egj30iji7 eghij3 fghik7egj30ij<i70eghij3 fghik7egj30ij<i30eghij3 fghik7egj30ij<i30eghij3 fghik7egj30ij8i30eghij3 fghik7egj30ik7!8ief0 fghik7egj30ik7!8igj1 ijej00 fghij0egj<ij7ik7 g0<ijei0 igjij7 ej3 i38ej00 fghij0egj<ij>7 i30ej00 igj70i30fi8j00gh3 igj30i7 ghij78j70j7ghj8 fghik7egj30i0<7 igj30i7 ghijt8ju8j gh fghij0egj<ij<7 igj30k4jghij7t80u8j gh fghij0egj<ij87 igj3008k7 ghi0sj0jgh ghik7<0j<j7ghj8 i0<gj7 7030gi08ij038j<jghj8 fghik7egj30i187 igj181>0<gij>ij 38j<jghj8 fghij0egjik7 7830gi0u8i0<jj7 i0<gj30<30gi0tij<jj7 0<gh08 fghij0egj<ik7 i0<gj30<70gi0t0ij3 fghij0egj<i0<18i30gj1t18gijt<ij7 18gh08 fghij0egj<i0<18i30gj1t!8gijt>i#t0k7038gh08 fghij0egj<i0<18i30gj7!98gijt8j0s8jj<ghj8 fghij0egj<i0<18i10gj7#98>hj0+rsu8j3s j<0<ghj8 fghij0egji0<18i18gj7#18<i3qs>j0s8j ghj fghij0egj<i0<18i10gj7#0<<i7qs8j0si18ghj8 fghij0egji0<18i10gj3'0<<i7qs0j0<ij7 >ghj fghij0egji0<18i18gj37 <<i3t8hi0t<iij18ghj3 fghij0egj<i0<18i18gj3u87?gij3ti0<ij318ghj fghij0egji1818i18gj3u87>gij3?ij<ij338ghj fghij0egji1818i18gj1?k7>gij3<ij<ij3tghj08 fghij0egji1818i18gj1?ju8gij i0>ij3tghj08 fghij0egji1818i18gj1?ju8gijij3<7i3u8ghj3 fghij0egj<i1818i18gj1>j?ghijk7tu8j1?ghi8 fghij0egj<i1818i18gj0>jghijk7sjk78ghj08 fghij8egji1818i18gj0>jfs0j70ghj08 fghij8egj<i1818i18gj0>jft8jk4ghi fghij8egji3818i18gj0<jeij8 fghij8egji3018i18gjk7j1 ei3 fghij8egji3018i18gi eh3 fghij8egji3018i18eghij fghij0egji3018i18eghij fghij8egji3018i0<eghij fghij8egji7 08i0<eghij i30eghij8 fghij8egjij7 i38eghij8 fghij8egjij7ij fghij8egjij7ij7 eghi08 fghij8egjij3 fghij8egjij3 fghij8egjij3 fghij8egjij7 fghij8egji>j3 i18eghij8 fghij8egji<j30i1<eghij8 i1<eghij8 fghij8egjjk70jijeghij jijeghij jijeghij jijfhijfhi08 fghijegjjk7 jiji1t i1gh08ij8fhik6 jijit0i3 gh8ij<fhi08 fghij8egjj0<j0<ij<it?ij<ghijfhij8 fghij8egjj0<j0<ij<i<3ijgh3 i08fhi08 fghij8egjj0<j0<ij<i8h<ghijfhij8 fghij8egjj0<j0<ij<i8h8ghijfhij8 fghij8egjj0<j0<ij<i8h8ghijghij3>j<j0j3 fghij8egjj0<j0<ij>i8h<ghij<1u80t03t j101?j>0t8k7?j08 fghij8egjj0<j0<ij>i8ht0jtj>j3<j k7u8i0t8u83t tjt83j0t0u87t fghij8egjj0<j0<ij>i8j0t83t03t 3u81tju8i0t8u83t0t u81 k7t0<184k7!8j fghij8egjj18j0<iji8j1t<3t83t0t07u83t i1u8398j30187 j i30j fghij8egjj18j0<ijit01t<3t<0t81<3?j7008ij<j8jk71830jk7083 7i810j fghij8egjj18j0<ijit j3810j38183 i0<j86jk71810i0103 8j70jk7j1 fghij8egjj18j0<ijit j i0<j8i10k61<j j38jk7j1 fghij8egjj18j0<iji>4k7j8k7 j3 38jk7103 i0<j8i18083<j1!07t8jk78jt?j1 fghij8egj2j18j0<iji8j j3800j i0<j8j0t00<1?j13 7t8i 3t<j6 fghij8egj6j18j0<iji8j j' 800j3t<7j8ij<j8j1t00<k7<j81t>3 jk783t8j6 fghijegjj18j0<iji8j t 800j3t<7j8ij8j8j7t0k7j78j3 ji1<3 i6 8107t 800j3t87j8ij<j8j7077j1<j?jj08i30ik6 fghijegjj38j0<iji8j j0j3 j7j8ij<j8j7k71830j7 3<k7i8i18ik6 j7j8ij8j8jk71830j3 38k7 jij8ik6 fghijegjj30j0<iji8j j0j30j7j8ij8j8jk k708j3 i7k7 i fghijegjj30j0<iji8j j0j30j3 ij6jj1>!83070k7 0t<3 j5/07t fghijegjj30j0<iji8j j0j18j30ij6jj1t>3 1t<jj7t 8jk7>jt<j6 fghijegjj30j0<iji<j t 8087u87t0t ik6jj0t<3 7k7u8jj3t i4j3tj1 fghijegjj30j0<ijit? t 8003u83t07t ik6jit k6jhj4hij fghijegjj30j0<ijit? t 001?j>j<fgik6 fghijegjj30j0<ijiu8egij fghijegjj7 j0<ijeghij fghijegjj7 j0<ijeghij fghijegjji30ij<eghik7 fghijegjji30ij>fgiu8fij10 fghijegjji30ij>fj0sj>j>jt0fij7 fghijegjji30ij>fj1s 7tjt81t0fij7 fghijegjji30ij>fj1s03t u83<fij10 fghijegjji30ijfj107i87i<fh10 fghijegjji30ijfj107 j10j3 fh7 fghi7egj7 18iij18fj710jk710j30fh7 fgjk7jk7 jk7egj7 18iij18fj710jk61<j1<fh7 fgj0<j38iegjji30ijfj103i<3<j7<fh fgj1<j7 iegjj>i30ijfj103j?j?j1?fh< fij0?j30i7egj7 38iij18gg103jt<k7<j78fj9/t< fij1?j30i7egj7 30iij18gg107k7t0k78j78f1st fij3?j7 30iij18fj71030j1<j1<f1st fgjj<ik7egj7 30iij18fj71037jk7 jfj,4j< fgjj8ik7egj7 7i8j10fij fgjk7 i10egk7 7 30fij 30iij18fj718303<0u98fij7 fgi010ik7egj7 30iij18fj7181t<t0t fgi03ti10egj81<i30ijfj107jt81t 7tfijk7 fgi03t0jk7egj3 iij1<fj300k7u8j<jk4fh fgi83t8jk72330ehi7 7 iij1<eghi10 is8ehi707 fgi87j<jk7s>ehi0<18i30ijeghik7 fgi87jjk7s<ehi0<18i30ijeghik7 fgi87jjk7egj307 fgi87jjk7egj707 fgi87jjk7egj70 iij0<eghi10 fgi87jjk7egj70ij<ij30eghi7 fgi87jjk7egj30ij<ij30eghi7 7iegj0<i0<ij30eghi7 fgi830iegj0<i0<ij30eghi7 fgi81t8jk7egj3 ij<ij38eghi7 fgi80t0jk7egj3 fgi8k7<i7egj7 fgih7egj3 ij<ij38eghi7 fghijegj18i0<ij38eghi7 fghijegj18i0<ij18eghi7 fghijegj18i0<ij18eghi7 fghijegj38i0<ij18eghi7 fghijegj30i0<ij18eghi7 fghijegj30i0<ij18eghi7 fghijegj30i0<ij1<eghi7 fghijegj30i0<ij1<eghi7 fghijegj70i0<ij0<eghi7 i0>ij0<eghi7 i0<ij0<eghi7 fghijegjij30ij30eghi fghijegjij30ij30eghi fghijegjij30ij38eghi fghijegjij30ij38eghi fghijegjij30ij18eghi fghijegjij30ij18eghi fghijegjij30ij18fghij1j0j1?gj3 fghijegjij30ij18fgj3t 3jk7k7s0jt?gj0 fghijegj>ij30ij18fitu810j081sk7 j<1s<js fghijegj<ij30ij18gj2ijht>0>jk7 t?0>j307s01s g fghijegj<ij38ij18gj8ih7tu838j183s0?j30t=00u870g3 fghijegj<ij38ij18gk7ti70ijk7tu838j183=101<jk71<j0>gi3 fghijegj<ij38ij18g0t>i?h7>i?j0>0<i78j<j1<j1<gi3 fghijegj<ij30ij1<g1t?jk78hi3<j3030i00<j0<j18gi3 fghijegj<ij30ij1<g1<0j0hi3<j3030i00<j0<j18gi3 fghijegj<ij38ij1<g1878j hi1>j7030i80<j0<j18gi3 fghijegj<ij30ij0<g3838jhk70i 30i<0<j0<j1<gi3 fghijegj8ij38ij0<g3038j>hj<i18jj<i7?j<j0<j0>gi3 fghijegj8ij38ij0<g3038k70h0<i1<j<j<i7 i<j0?gi3 fghijegj8ij38ij0<g3830k70h0<i0<j<j<i7 i<jk7<gi0 fghijegj8ij30ij0<g38300>hjij<j<j>i770jk70j1u8gj00 fghijegj8ij30ij0<g18700<hjij>k7 0t?j730i<i8gj3 fghijegj8ij30ij0<g1>00>hjt0j 0tu8k738i<i<gj3 fghijegj8ij30ij0<g1t>ju8ht0j7 70tu8k71<i<i3?gj3 fghijegj8ij38ij0<g0t>jt ij1t?jk70j3t<j70<j0<i0u8gj0 fghijegj8ij38ij1>g0t>jsht j30j38i38<j0<ik7>gj0 gt03tu8ij0<ij<30j<i70>i<ij0g3 fghijegj8ij3rt8g1<0>0?h<ij>70j<i7k730j30iju8g3 fghijegj0ij3rt8gu8 jh<ij7 j<i7j<<j0<ij3<g3 fghijegj0ij1rt8g>k7 jh<ij7 j<i7j>>j0<ij1<g3 fghijegj0ijk74ij8g<k70jh<ij j<i7j<j0<ij0>g3 fghijegj0g78hijk700<300<ij0<ijj0<i7j<j0<ijk7 fghijegj0g78hijk700<300<ij0<ijj0<i7j<j0<ijk7 fghijegj0g78hijk700<300<ij0<ij?j0<i7 1?i<ijk7 g8 fghijegj0g78g<j<300<ij0<ij7>j0<i7 1?i<ij0>g3 fgj0egj>gk78hijk700<380<ij0<ij7>j0<i7 0u8j30j1j0<g3 g78g<k70 30ij30ij8j30ij8j30j78k70g fg00egj>gk78g>k7 770ij30ij0j38ij70j30j7s fgegj g78g>0>k7070ij38ij0j3<<18ji<j1s8g3 g78g1>k78 ij3si?is07 j<j0<j0s0g3 g78gt00tu8ij0s8j18j0s87 jj0<jk7t<gj8 g78gt k7t0ij0s8j18jk7t?k7jk7ighj8 g78g7tj0t0hs8j00jk7t>k7fi8 g78g3u8j0u8h33tfgi fi08fgi8 fghijegjgj fghijegjgj fghij8egji7 fghijegjgj fghijegjgj7 fghijegj?gj7 eghj3 fghijegk7<gjeghi8 fghijegk7<gjeghi8e fghijeg0tgj70eghj3 fghijeg0tgj78eghj3 fghijeg1tgj78eghj3 fghijeg1;0gk78eghj3 fghijeg1;8gk78eghj3 fghijeg1;8gj>eghj08 fghijeg338gk78eghj3 fghijeg338gj?eghj08 fghijeg338gj?eghj0< fghijeg338gk7<eghj3 fghijeg330gk7<eghj30 fghijeg730gk7<eghj30 fghijeg7#8gk7<eghj30 fghijeg7#8gj?eghj0< fghijeg/t g0?eghj0< fghijeh1rt g0?eghjk7 fghijeh3rt fghij6eh7rt g0u8eghj7 fghij6eh7ru8gj8eghj7 fghijeh70i0>gi8eghj7 ik7gi3>eghj10 i0<gi8eghj7 i0<gi<eghj7 fghijeh7 i18gi<eghj7 i38gi<eghj7 i30gi<eghj7 i30gi>eghj7 i30gieghj7 i70gieghj7 gieghj7 gieghj7 gieghj7 igij8<eghj igij8<eghj igij8>eghj fghij7eh70igij<eghj igij8eghj igij<eghj fghij7eh30i>gij<eghj fghij7eh70i>gij<eghj fghij7eh70i<gij<eghj fghij7eh30i<gij<eghj fghij7eh30i<gij<eghj fghij7eh30i8gij<eghj gi0<eghj fghij7eh30jk7 ij18k7ghj10eh<igij30egh10 ij7>k7ghj10eh<igij30egh10 iju87ghj10eh<igij30egh10 ijt!0ghjehi7 gi0<eghj ij3<ghj7eh30j0>gij30egh10 ij1t0ghjehigij30<eghk7 ijk7?ghj10eh<i<gij30egh10 ijj0ghjehigij30>eghk7 ijj70ghjehigij30>eghk7 ijj30ghjehigij30>eghk7 ij7j0 ghjehigij30eghk7 ij1ghij10eh<jk70gij<7 egh7 fghij7eh30j1<gij18egh10 fghij7eh30j18gij18egh10 fghij7eh30j38gij1<egh10 j7gijehi<gij30eghk7 gi3eh30j30gij0<egh10 fj30j7 gi7eh30j30gij0<egh10 fj10j7gijehi<gij30eghk7 fj10j7gijehjk70gij0<egh10 fj18j7gijehjk7 fj18jgijehjk7 fj0s8gik7eh30j7 fjk7t?gij7eh30j7 gij0<egh10 fit?gij10eh<j18gij30 fghij7eh30j7 gij0>egh10 gijk7 fghij7eh30jgh<18egh3 fghij7eh30jgh<18egh7 f7ghi18eh<j30gij307 f70ghjk7 eij0<j30gij307 f7<ghjk7 eij0<j70gij307 f1?ghjk7 fk78ghj7 h3hi0<18egh3 fjghj18eh<j7 fj0ghk7 Ò ÙØÖ Ò ÈÖÓ Þ ÔÖÓ Ù fi?gh00eh<jghj<egh3 gh0eh<jghk70egh fi78gijk7 eij0<jghk70egh fi1<gh8eh<jgh7j<egh3 fi0?gh8eh<jgh7j<egh3 fij?gij08eh<jgh7j<egh3 gij0eh<jgh7j<egh3 fij78gij8eh<jgh7j<egh3 fij3<gij8eh<jgh7j>egh7 fij0>gij8eh<jgh7 fh8gi08eh<jgh7j>egh3 fhgi08eh<jghjegh3 eij0<jghjegh3 eij0<j>gh7jegh3 eij0<j<gh7jegh3 ghi8eh<j<gh7jegh3 f7>ghi8eh<j<gh7jegh7 f7u8ghj3 eij0<k70ghk7 f1t0ghj8eh<k7 ghk70egh0 fj?ghj8eh<k7 ghk70egh0 fj3tgh08eh<k7 ghj<egh fjk7tghehjgh180<egh fi7u8gij3 ghj<ehij<h3 fi0t0gij8eh<k7 ghj<ehi0u8h fij<gij8eh<k7ghk7 30ehi?h3 fij7>gij8eh<0<gh180<fj8iu8hij0 ji3 i7h3 fij7>gij8eh<0<gh180<ghij01t0j1t8ijt>ik7j10ii08h fijtgij3 eij0<0<gh180<ghij81t8j1t8ik7t8i10ji7 ijh fi1tgij08eh<0<gh180<ghijt071<j10ij0t?ijj7i10ij3 fi>gh8eh<0<gh180<ghik7!0j10j6hh3 08iijk7h3 fjk7?gh3 eij0<0<gh180>ghik708j08j6hh1 08iijk7h3 fj1tgh08eh<18gh180>ghik608j08j7h<h1008iij08h fj>ghj8eh818gh180>ghik608j08j6h8h1008i<ij18h f0t0g2j7<j08eh818gh18k7 ghi608j08j7h8h1010jk7 k7h08 f3u8gk7j>j08eh818gh18k7 ghi608j08j7h8i08jk7i7j1tjh18 f7<gjjt<j3 eij0818gh10k7 ghi718j10j7h8i7?jk7ij3tjis8 gjk70j3 eij0<18gh10k7 hj3t>hij8<j1<j1tiji3t 30ij7 j7is> fgi3<307 j8eh<18gh18k7 hj7tu8hi3tj>jk7tij80<1<j3 j10jj0<is8 fgi7<3 30j8eh<38gh18k7 hj7shi0t00t ik7870<k718j08j7i8h08 fgi<ijeh0<ghk7 18hj18ht8jt8j70i30ij>107j7ij10j7?h3 18hj10700j3t<k7!8j18i10ij17j7ij10ju8h8 fgiijeh0<ghk7 18hj10708j1t<0<30j3 i3i08j87k7j7i<j10ju8h8 fgi8i<jeh0<ghk7 1<hj10718jj 80810j3 ij87t0k7jk7 j7i00h8 fi781 hjk7ij3 eij0830gh18k70hj7107 k7ij3 7i8i08ij1t<j8j10j10hij8 fi<3 hjk7ij3 eij0<30gh18k70hj ijk7i8i08i6j1t8j8j3 fit0hi7ij3s?ej0<70gh08k70hj ijk7i8i08i6j1 j10hij8 fjk730hi7i8j3s?ejk718ghj8k70hj ijk7i8i08ij1 i0j7i7hij3 fjk710hi7jk7 js<ej30ghjjhjk t80810j3 i7ik7j1 i0ji7hij3 fj0<70<hij10j30eij0<7 t010jk7 iik7j10i7 ji7 fj087k6hi7j08j08eh<7 gh18j<hj107k77' t018k47020t8i18087 ij30i?hi3 fj08708hij3 gh18j<hj107j390ij3tjt810?ijt87t8jj30i7?hi3 fj08708hij7ieh18ghk7j30hj7100;=0ij1u80t030>ij7t83t8jj3 i3?hi3 fj08708hijieh38ghk7 0<hj107jt?h 0u8jhj7tj?ghi08 fj0<708hijieh38ghk7 0<hj107jt>ej fjk7!0hi7j7 j08eh<ghj7 0<hj008jk778ej8 fjk7;<<hi7ji3 eijk7#0ghk7 0<gj fis0hij8ieh30ghk7 0>gj e08 fit8hi7ji3 eij0<ghj7 fi3?hi1010ieh70ghk7 g18ej fgik7j<i3 eijk770ghk7 g00ej fgik7k702j3 fgik7k7t<jeh7' fgik7k7t<jeh77 egij3 fgij07t8jeh77 hij6eij08 hijeij08 f1j3tu8gi08eh>ghj7 hijeij08 hijeij08 f301s0gi3 eijk7ghj18jhij3 f3018j<gi08eh<ghj7 hij8eij08 f3018jgi0<eh<ghj7 f3010jgi08eh<ghj7 k70hik7eh f30i10gi1 eijk7ghj18jhijeh eijk7?ghj18jhijeh eijk7>ghj18jhijeh eijk7>ghj18jhijeh f30i10gi30eijk7>ghj18jhij8eh f10i10gi30eijk7>ghj18jhik7eh08 f10i30gi30eijk7>ghj18jhik7eh08 f18i3 gi10eijk7>ghj18jhi08eh3 f1<i7 gi10eijk7<ghj18jhi00eh3 f0>j0tgijeh7<ghj18j hjk7ehj8 fk7su8gij<eh0ghj7 j>hi6ehj8 fjs0gij<eh0ghj7 j>hiehj8 fjtu8gij10eijk7<ghj18j7 hj00eh08 fghij10eijk7<ghj18j7 hj10eh08 hj3ehj3 hj6ehj3 hjehj3 fghij10eijk78ghj18j7 hjehj3 fghij30eijk78ghj18j7 hjehj3 fghij30eijk70ghj18j70hjehj3 fghij10eijk70ghj18j70hj8ehj3 fghij10eijk70ghj18j30hj0ehj3 fghij10eijk70ghj18j30hk7ehi8 fghij10eijk70ghj18j30h08ehj08 fghij10eijk70ghj18j30h00ehj08 ghj18j30h1 ehj08 ghj18j30h3ehi3 ghj18j30h7ehi3 ghj18j30h6ehi3 fghij10eij0>ghij0>h3 ehi8 fghij10eij0>ghij0>h7ehi08 ij08ehi3 ij00ehi3 fghij10eij0>ghijk7 ij10ehi3 fghij10eij1>ghijk7 fij2gijk7eh ghj18j18ij00ehik6 ghj18j18ij10ehi08 fij7gijk7eh ghj18j18ij3 fij gijeij0u8ghi<j1<ij3ehij1 fi1t?gijeij0u8ghjk7rtj6ehij1 fi1tu8gi10eij3>ghiru808ehij6 fi1tu8gi10eij3>ghiru800ehij6 gijeij0u8ghirt810ehij fij7gijk7ehu8ghis/?781 ehij6 f10jk7gijk7ehu8f30j ehijk6 f1tj10gij7eijk7>f0<j183eg f1t8k7gijk7eijk7>f0<j187eg fju87gijk7eijk7>f0<j186eg fj3t90gij7eijk7>f0<j18eg fit?gijk7eijk7>f0<j18eg fi3tgijk7eij0t f j>6eg7 fik7<gij10eij>fk7 j>eg7 fij2gijk7eij0t jeg7 jeg6 jeg6 j8eg7 fghij10eijfk7 j0eg7 fghij10eijfk7 jegj fghij10eijfk70jegj fghij10eijfk70jegj fghij10eijfj<j7 fghij10eij>fj<j7 fghij10eij<fj<j7 Ô Ù ÔÓÔÖÞ ÞÒ Ó Ò Þ ÓÛ Ò fghij10eik718f0<j fghij10eik7!8f0>j7 fghij18eik7!8f0>k7egj 6egj egj fghij10eik7!8fk7 egj fghij18ei0>7 f1867 f187 f187 ghi0 fgj f187 µ f1<87 fighk7 ei30fj<18egk7 fighk7 ei70fj<18egk7 fi>ghk7 fj>18egk7 fi<ghk7 fju8egj f1t<egj gh18ei187 f1t<egj gh18ei387 f1u808egk7 gh18ei307 f1>jegj fjk70?gijei0<18fk70j8egk7 fjk7s8gi18ei303 f1<jegj fjk7s<gi18ei307 f0>jegj fis<gik7 eik7 fghij18ei707 70fk7 fghij18ei fi3>08gi18ei fi7?08gi18eijfj7008egk7 fi?08gi18eijfj7008egk7 fi0<gi18eijfj3008egk7 fi<70<gi18eijfj3018egk7 fi870<gi18eijfj3008egk7 fi870<gi18eijfj300<egk7 fi870<gi08eijfj3008egk7 fi8708gi08eijfj3008egk7 fi<708gi18ei>jfj3808egk7 fi718gi18ei>jfj3808egk7 fit?gijei 0<fj fit?gijeij30fj>j8egk7 fi3t<gijeij30fjj8egk7 fghij08ei<jfj180<egk7 fghij08ejk70j<fj7 j<fj7 fj78ghk7 fj1>ghj8eh<j gij3070egh fjk78gh3eh30j>gh<1<egh3 ej30jfj0<0<egk7 ej70jfj0<0<egk7 fi8j1 jfj0<0<egk7 fi8j30gi3 jfj0>0<egk7 fistu8gj3 eji<fj1830eg10 fi4gi08ej30j30fj7 fghij08ej70j30fj7 j30fj70egj fghij08ejifjk70egj fghij08ejifi<30eg10 fghij08ejifi<30eg10 fghij08ejifi<30eg10 fghij08ejifi<30eg00 fghij08ej>ifi<30eg00 fghij08ej<ifi>30eg00 fghij08ej<ifi30eg00 fghij08ek70i<fjk7 <egj0 i<fjk7 fghij08e0>i30fj18egj fghij0<e0>i30fj18egj fijk4gij30e30ifi30eg08 fij7>gijej<i30fj1<egj fgiijeh0<ghk7 fj8j7t e30ifi30eg08 j<70gi30e70ifi10eg08 j830gi30e7 ifi10eg00 fk7j1810gi30e7 fk7j3010gi30e7 ifi10eg08 10gi30eij<fi<7egj fk7j7j7gij<e30i30fj0<7egj fk7jj7gij<e30i30fj0>7egj k7gij<e30i38fjk7!0eg08 7j10gi30eij>fi7egj fj<7 j8gi0<e7 fju8jgije7 i38fjk7!0eg08 fj?j18gik7e18i0>fi7egj fj7<j08gik7e38i0>fi7egj fh4gijeij fj1<egj8 fghijk7e30i0>fi7egj fghijk7e30i0>fi7egj fghijk7e70i0>fi7egj i0>fi7egj i0<fi7egj fj0ghieijfi310eg08 fk7ghi10fghij0>ijfi310eg08 fk7ghi10fghij0<ij7 fj0>egj8 fk7ghi3 fghij0<ij ghjk7e s>fi7'egj fk7st<gik7fghij3rt fjk7'egj fk7st>gik7fghij7rtfi190eg08 fk71?8gh7fghij7t='s8fi7'egj ghjk7fghij7u8fhi7'egj fk7ghi10fghik7?fhik7'egj fk7ghi10fghik7?fhik77egj ghjk7fghij3?fhijtegj ghjk7fghij3>fhijtegj fjghifghij8fhi0tegj fghijk7fghij3>fhijtegj fghijk7fghij3<fhijtegj fghijk7fghij3<fhij0eg08 fij1 fjstu8gi10fghij?fhij7<egj8 fk7st>gik7fghij3<fhij0eg08 fjst>gijfghij fhik7<egj8 fij0?gij7fghij38fhij0eg08 fij3<gij7fghij38fhij0eg08 fij0gij7fghij38fhij0eg08 fij fik78gijk7fghij38fhij0eg08 fi1>gh7fghij38fhij0eg08 fi38gh7fghij30fhij0eg08 fi0gh7fghij30fhij8eg08 fi?ghjfghijfhij0u8eg08 fjk78ghk7fghij30fhij8eg08 fj1>ghj7fghij30fhij8eg08 fj7<ghj7fghij70fhij8eg08 gi7fghij30fhij8eg08 fjrgik7fghij70fhij8eg08 fjghj7fghij70fhij8eg08 fghijk7fghij70fhij78eg08 d0fghik70fhij78eg08 fghijk7fghij0fhij78eg08 fjik6gij0fghi0?fhijk78eg08 fj8i08gi00fghi0?fhijk78eg08 gi3fghij0fhij78eg08 fj8k6j3 fj808jgij8fghi0?fhijk78eg08 fj80<jgij8fghi0?fg>egj8 fj808jgij8fghi0?fg>egj8 fj808j6gij8fghi0?fg>egj8 fghi3<fhij0>egj8 fj8k7j1 fj80<jgij8fghi1?fg>egj8 fjst?gijfghik7<fhij0>egj fjst?gijfghik7<fhij0>egj8 fjsu8gij8fghi1?fg>egj8 fj,ghj3 fghi7<fhij0>egj8 d8fghi1?fgegj8 d8fghi1?fgegj d8fghi3?fgegj fjghifghi0tfgegj fjtghi8fghi3?fgegj fj>ghj3 fj7tghjfghi0tfgegj fjk7u8gh3 fghi<fhijk70eg10 fi?gj00i8fghi3?fgegj< g7<i8fghi3?fgehi0s? fijt8hijk7u8j08fghi3?fgehi1s? fij7thijk770j3 fghi<fhijk70ehis0 fghij10eij<fj<j eg10 jfghi1tfg ik70eh fghij10eij<fj<j fghi<fhijk7r>eh10 fij0t hik7j8j7 fghi<fgrteh10 fij7?hijk7j8j7 fijt0hij103 jfghi1;0fhij0rt fi1tg003 jfghi1;0fhij0>ijk7 fi7?gj83 jfghi1;0fhijk7 fit gk610j7 fghi>fgijk7 fj1tgjk730j7s<fgh<fgijk7 fj?gi?isu8fgijk7/ fj8gi?is?fgh7' fhij18ij18eh fjgik7t jfghi330fhijk7 fjgi0<7 jfghi390fhijk7 fghij18ei0<7 j08fghi'fg7 fghi<fgijk7 fgh7jj3 fghi<fgijk7 fjik6hij7jj3 fghi<fgh8eh fjik7hij7jj3 fghi<fgh8eh fj<ik7hij7j<j3 fghjk718fhijk70ij3 fjj jhij08j3 fghjk718fg<ij08eh fjk7j10hij< jfghi718fg<ij0<eh hij?i8fghi7 fjk7j10hij>i8fghi7 fhij0>ij0<eh fjk7j10hij78i8fghi7 fjk7j10gi3 fghjk7!8fgij0<eh fjst0gi3 fghj0>7 fj:gh08fghi>7 d8fghi>7 d8fghi<7 fhijk70ijeh7 dfghi<7 fg<ij30eijk7 dfghjk70fg30ijeh7 fg38ijeh7 fghij08ej0>j30fjj8egk7 fg18ijeh7 fi7t>gijei>j30fjj<egk7 fit?gijei>j30fjj<egk7 fitu8gi08ej0<j30fjj<egk7 fi<j7 dfghj0<18fg70ij<eh dfghj0<18fg30ij<eh dfghj0<18fg30ij<eh dfghj1<18fg30ij<eh dfghj1<18fg38ij<eh dfghj1818fg18ijeh dfghj1818fg18ij<eh dfghj1818fg18ijeh dfghj3818fg18ijeh dfgi3 js8fg1<ij<eh dfgiru8fg0<ijeh dfgirtfgj<ijeh dfgiru8fg0<ijeh dfgit?#4fgjij7eh3 dfgii0<fgi30i0<eh dfgii0<fgi30ik7eh3 dfgii0<fgi30i0<eh dfgii0<fgi30ik7eh7 dfgii0<fgi38i0<eh dfgii0<fgi38ik7eh3 dfgii0<fgi38ik7eh7 dfgii0<fgi18ik7eh3 dfgii1<fgi18ik7eh3 dfh hj70ifgik7 i10eh0 fjj3tgijej<i30fj1<egj dfgii18fgi18ik7eh3 dfgii18fgi1<i0<eh dfgii18fgi0<i0<eh fhi1gj7fgi30ifgij<ik7eh3 dfgii18fgi0<ik7eh7 dfgii18fgi0<ik7eh3 dfgii18fgi0>ik7eh3 dfgii38fgik7 dfgii38fgik7 i7eh3 dfgii30fgik70i7eh3 dfgii30fgij<i10eh8 dfgii30fgij<i18eh8 dfgii30gj0fjik7 dfgii30gjfjik7 dfgii70fgij<i18eh8 ÔÖÞÝÔ Ù ÑÝ Ç ÖÝ ÓÞÓÒ Û fgij>i18eh8 Ï fgiji18eh8 fgiji18eh8 dfgii7 fgiji18eh8 dfgiifgh<i7 dfgiifgh>i7 dfgiifghi7 dfgiifghi7 dfgi7ifghi7 dfgiifghi7 dfgi7ifghi7 dfgiifghi7 fgij0<ieh6 dfgi7ifghi7 fgij0>ieh fgij0>ieh6 dfgi7i>fgh dfgi7i>fgh7 fgijk7 jfgh18jk7 dfgi7i<fgh70j18eh jfgh1<jk7 jfgh0<jk7 jfgh0<i8eh jfgh0<i8eh jfgh0<jk7 jfgh0>jk70eijk7 jfgh0>jk7 jfghk7 dhj6fh18j7 dhj2fh18j7 fgh7 jfghk70j3 hij<7 fhu8hij08j7 j>fghj<j08eh j>fghj<j0<eh j<fghj<j0<eh j<fghj>j1<eh j<fghj>j0<eh fgh3 j<fghjj0<eh k70fghk70jeh7 k70fghj<j30eijk7 dfgi3 fghj>j30eijk7 fghjj30eijk7 d7fgi3j38fghj7 0>fghj18jeh7 0<fghj18jeh7 d6fgi3j30fghj70j<eh 0<fghj0<jeh7 0<fghj0>jeh7 1<fghj0>jeh7 0<fghjk7 1<fghjk7 0<eh 18fghjk700<eh 18fghi<j<eh dfghj0>18fg7 dfghj0>18fg70ij<eh 18fghi<j<eh 38fghi<j<eh d7fgi3018fghij<eh 38fghij<eh 30fghij<eh d7fgi3030fghij<eh Æ d7fgi3030fghijfgh8hij3 d7fgi3030fghij<fghhij3 d7fgi3030fghij<eh d7fgi3030fghijeh d7fgi3070fghijeh ÔÖÞÝ Ð Ö ¹ Ô ÖÝÑ ÒØÓÑ Í ½ Í ¾ fhij gh08 7eh3 fghi707eh3 fghi307 d7fgi30fghij fghj6i10fgi<30fghi0>18eh8 fghji10fgi<30fghi0>18eh8 fghji10fgi<30fghik7 dfgii1<fgi18ik7eh7 fghji10fgi<30fghik7 fghji10fgi<30fghik7 fghji00fgi<70fghik7 ei86t fghji10fgi<70fghik70ej1su8 fghj<i10fgi<70fghik70ej1su8 fghj8i10fgi<70fghik70ej0su8 fghj8i00fgi<70fghij<7 fghij<7 fghk7ijfgi18fghij18eh8 j3fgi30fghij30eh fgh0<3 j3fgi30fghij38eh fgjk718fghij7!8eh8 fgh083 fgh183 j3s8fhij0<7 fgh1<<j3s8fhij0< j8fgi< fgh1s j0fgi< fgh0t?i0fgi< fghij7 fghij7 eij08 fghij00fgi<fghijk718eh8 fghi8j00fgi<e<eh fgj0<e<eh d3fgi30<fghij0>eh fgj0<e>eh fgj0<eeh fgjk770fghij198eh8 fgij<i18eh8 fgj0<eeh fghij198eh8 fghij0=8eh< fghij0=8eh8 fghij0=8eh fghij0<8eh fghij0>8eh fgjk7e3; eijk6 fghijk7.eh6 fgjk7e1u8eh fgjk7e0u8eh fgjk7e0u8eh fgjk7?e0u8eh fgjk7>e0u8eh fghij08fgi8e1>eh7 fgjk7>ek78eh fgjk7>ej>eh7 fgjk7<ej>eh7 fgjk7<ejeh7 fgjk7<ejeh7 fgjk7<ejeh7 eij10 fgjk78ej0eij10 fgjk78ej8eij00 fgjk78ej8eij10 fgjk70ej<eij10 j>fghk70j30eijk7 fgi<ej3?eijk7 fgi<ej3u8eij7 fgjk70ejeij00 d10fgi<ej37 eij fgi<ej370eij d10fgjk70ejeij00 eij8 d10fgjk70ej70eij8 d10fgjk70ej30eij8 d10fgj0>ej0<eij3 d10fgj0?ej0< d10fgj0?ej0<7 ØÓÖÞ ËÈË Û Êƺ d10fgj0?ej0<30ei08 d10fgj0?ej0<38ei08 d10fgj1?ej0<18ei08 d10fgj1?ej0<0<ei08 d10fgj1?ej0<0>ei08 d10fgj3?ej0<k7 d10fgj1?ej0<k7 d10fgj1?ej0<j<ei3 d10fgj1?ej0>j<ei3 d10fgj3?ejk7jei08 18ei d10fgj3?ejk7j70ei8 0<ei 0>ei d7fgi3018fghi<j<eh d7fgi3018fghi<j<eh d7fgi7018fghi<j<eh d10fgj7/eirt0fghij8 d10fgj7/ei?<6;?fghij3 d10fgj7/eh<jk70fghij8 d10fgj7/ehjk70fghij8 d10fgj/ehjk70fghij8 d10fgjehjk70fghij8 d10fgjehjk70fghij8 d7fgi3030fghijeh jfghij3 d10fgjeh70jfghij3 d10fgjeh30jfghij3 d10fgjeh38jfghij3 d10fgjeh18jfghij3 d00fgjeh18jfghij3 d10fgjeh1<jfghij3 fghi d00fgj<ehk7 d00fgj<ehj<j<fghij d00fgj<ehj>j<fghij d08fgj< d08fgk70>ehk7 >ehk7030fghij8 >ehj<0<fghij d18fhjk4i18 eh3030fghij8 d08fhjk4i187 eh3830fghij8 d18fg0>38ehk7 fghij3 d08fg0>18ehk7 d08fg0<38ehk70fghij1 d18fg0<38ehj>30fghij8 d08fg0<18ehj30fghij8 d08ij2fhj<18ehj30fghij d08fg1<18ehj30fghij< d08fg1<18ehj30fghij d08fg1818ehj30fghij d08fg1818ehj#0fghij d08fg1818ehj7#0fghij< d08fg1818ehj730fghij d08fg3818ehj730fghij d08fg3018ehj330fghij d08fg3018ehj3;0fghij d08fg3018ehj1;0fghij d08fg7018ehj1tfghij10 18ehj0tfghij10 18ehjk7<fghij7 ehj0?fghij10 d08fgj7 d08fgj7 ehjk70fghij ehi<fghij7 d08fgj7 ehi>fghij7 ehifghij7 fgj0<eei0 d08fg<j7 ehiu8fghik7 d08fhijk70jehi3>fghij jehi3>fghij fgjhij8fhijk701u8ehi<fghik7 d08fhj3ru8ehi<fghik7 d08fhjr>ehi0t jegj8fghi10 d08fhji<egk7fghik7 d08fhji8eg0<<fghi10 eg138fghi7 d08fhjjk7 eg118fghi7 fgj8fhjjk7 eg198fghi7 d0<fhjj0>egjfghi10 d08fhjj0<egjfghi10 d0<fhjj0<egj d0<fhjj1<egj<7 fghjk7 d0<fhjj18egj70fghi0 d0<fhjj18egj30fghjk7 d0<fhjj38egj30fghjk7 d0<fhjj30egj18fghjk7 d0<fhjj30egj1<fghi0 d0<fhjj70egj0<fghi0 egjk7 d0<fhjjegjk7 70fghj3 dk7fhj300<egj180<fghj00 d0<fhjjegjk7 18fghj3 d0<fhjjegjk7 0<fghj3 d0<fhjj>egjk7 0>fghj3 d0<fhjj<egjk7 fghj0 dk7fhj3030egj18jfghj3 dk7fhj3030egj18jfghj3 fgh10 egj18j7 d0<fhjk7 d0<fjij30 egj18j30fgh00 dk7fj4ij0<30egjk7 j70fgh3 dk7fhj30egi7 j30fgh3 j38fgh3 j18fgh3 dk7fhj30egi7 j1<fgh3 j0<fgh3 dk7fhj30<egi7 jk70fgh8 dk7fhj118egi7 i<fgh ifgh dk7fhj318egi7 ifgh dk7fhj138egi7 fgij3 fghj0>i7fhj130egi7 ik4fg fghj3?i7fhj330egi7 i70i08fg8 fghj3u8jk7fhj3tegik7 i38i08fg8 fghj7# j10fhjt fgj7f18i0>ij8fg8 fghj710j10fhj8fgj10fijij8fg8 fghj18j10fhj0fgj10fij fghj08j10fhj010fgf7 ik7 ifg fghj08j10fhj030fgf7 ij<i3 fhij08 fghj08j10fhju80<fg7f18ij i8fg8 fghjk7jk7fhj3>jfg7f18ij70i8fg8 fghjk7jk7fhj1<jfg7f18ij0>i8fg8 fghjk7jk7fhj18jfg7f18ijk70j3 fhij18 fghjk7jk7fhj18jfg7f18h>j08fh6:su8 fghjk7jk7fhj18jfg7f18h>j08hijk7qrs> fghjk7jk7fhj38jfg7f18hj1> prs? fghjk7jk6fhj30jfg7f>;prs?6 fghjk7jk7fhj78jfg7gi2=ps)7 fghjk7jk7fhj78jfg ps>1fgij2 fghj08j10fhk78jfi7;ps<58 fghj08j10fh0u8jgij36pt=<8 fghj608j10fij6ps>8 fghj710j10ghjp> fghj3#0j10hij9qrst;<1 fghj3u8jk7ps fghj1u8jk7qs? fghj1?i3rt> fghjk6 d08fg0<38ehj<30fghij d10fgj7/ejk7rtfghij3 d10fgj7/ej0rt8fghij d10fgj7/ej0?j1s d10fgj7?ejk7 fghj4j10fhjj7fg10fijk70j08fg8 fghj08j10fh0u8jj1k4pr=0 fghjk7jk7fhj1>jfg7f18ij38i8fg8 fghjk7jk7fhj1>jfg7f18ij30i8fg8 ehi?fghij7 d08fhjru8ehi7>fghik7 d00fgjehjk70fghij8 d08fhj7ru8ehi7<fghik7 d00fgj>ehk7 d10fgj>ehk7 d10fgjeh0>jfghij3 d00fgjeh0<jfghij3 ei08 ddfghij6j7>j1? ddgh8fi301t0jt ddgj j7<fij> 088 ddhijj<j3u8fjk707 j7 ddhijj>j37 fj3< defifij3<k7# k7#0fj7<1 103 deghijk7>j1u8fik7<k710k710fji083 dfgijfht8jt0fi1?j<7j08fji081 dfg08j7<fij1<j7fij=03 fk77i7j010 dfg18j>fij10j3 fi183 fii1010 dfg38jfij307j3 fi101 7j8fjk7ik7j dfg70jfij3 7j10fi810107jfjk7ik7j j7fij3 7j10fik7k7j1010fj10j dfgj0<3 fi fij7k7j1010fj10j dfgj083 fik6k7j808fik7k7j1010fj10j3 df7i83 fik7k7j808fik7k7j1010fj10j7j7j dghij3 j7jfij3 fi107j1010fj10jj7j dfjk7jfiju80808fik7k7j1010fj10jj7j fi107j1010fj10jj3j dfhijk7ik7fij3t fi107j1010fj10jj3j k7jfijtj808fik7k7j1010fj10j8j3 dfhij0t<k7jfij103 jk7 dfhij0t>k7jfij<183 fi107j1010fj18k7i83 dfhij087 fi107j083 fj1808jk608 ik4eg7j<1000fi08083 j83 fj1018jk708 dfhij10107jfij8083 1fjk7j833 fik7i7!0 dfhij10107jfij fi103 j<7 fj0830i8< dfhij10007jfij808107fij7j7j710fi83t<jt dfhij10003jfij808107fij7jj3#0fi87t>j0 7fijj8107fij7jj3u8fi0tu8j fijk7 8fijjt j0 fijk7j7 fij0k7<j0> dfhij101010fij7!<j dfhij081018fij3t k7? dfhij0<3 08<fij1tj0u8 dfhijk7'8jt fij18i dfgt0j8 dfg8j3< ddfj4 ddi> ddjk7> ddj0t defgi8ij0ijj8 defik7u8ijjk7ijij6103 def10k7t<ijj0<i0<h7j< def100sij10jij8h7j def101<hk7j08i18hj def1030hk7j08i30hj hj8ji08h7 hj8ji18hj3 7hj08ji10hj1 def3 7hjk7ji08ij18j6 def7jhj1008i7 j>j30j6 def7jij0jj8ij0t8jjk6 deg>hik7jik7u8jk7i08j3u8j7 dehij7shi1010i3t0j810ij18ijk7 dehijshi10100>k7 jk7i30j7i3u8j dehij3<hi7jj?k7j8j30i8j10it0k7 dehij10hi7jj?0<k7j708ijk7i3tj7 dehij107hi7jj708k7j7 8ijk7hj dehij107hi7jj7k6jj7 j08jk7hj dehij107hi7jj7k7k70j8iihk7 dehij107hi7jj7k7t<j77i7i7hj dehij107hi7jj70sj130j08ihk7 dehij007hi3jj7k7ti8jk7 dehij007hi3jj7k6ij8jk7i10h10 dehij107hi3jj7k6ij0j0<i7hj8 dehij107hi3jj7k6ij0j18i7hj8 dehij007hi3jj7k7ij70j10i3 h dehij007hi3jj7k7ij70j30i30h 30k7k7 i18j18ik7u8ij7 1?<0t?i8j10ik7u8ij7 0sjti8j10ij8ij7 dehij007hi10jt?jtghj< dehij007jt8ijk7fij dehiji dehij4iju8h8 degij7 h4 degij3 degij1 ddeh deitj deit?jhij1<1 deit?jhij7?10 dei<1018hijt0 dei<gjk718 deigi87 deij1?j?hj07 dei<j1u81t8hj3!7 dei<j1u83t0hj3't dei>4j7 30hj7't0 deit8j187hj0<7!0 10hk7808 dei>j7 10hk7<08 dei<i107hj1>08 dei<i107hi8<10 dei<i187hi<<1 dei<i087hi<1 dei<i08j4h708 dei<i0>jij8330 dei<ik7tjij330 dei<ijt01>ik7!8>7 dei<ij<k78i0t8t8 deiijk7jij7?3t dehijhj0j0 dehi7 dehiu8 dehi7? dehj0 º º ÖÒ ÏÝ ½½ dehi1<
7 ÈÖÞÝÔ Ï Û Ø ØÓÖÞ Í ½ ½ µ º º ÖÒ ÏÝ ½½
8 ÊÆ Ò Û Ä È ¹ ¾¼¼¼ ÔÖ ÝÞÝ Ò Ø ØÝ ÅÓ ÐÙ ËØ Ò Ö ÓÛ Ó ½ º º ÖÒ ÏÝ ½½
9 ÓÞÓÒÝ Ï Æ ÛÝÖ ðþò Ñ ÑÙÑ Ó ÔÓÛ Û ð ÖÞ ÞÝÛ Ø Ó Æ ÔÖÓ Ù Æ ËØ Ò Ö ÓÛÝ ÞÓ Ø Ö ÞÓ Ó Ò ÅÓ Ð ÔÖÞ Ø ØÓÛ ÒÝ Û Þ ÖÞ Ò Û Ð¹ Ö ØÓÖ Ä È ËÄ Ñ Ð ÓÒÝ ÔÖÞÝÔ Ûµº Ï ÔÖÞ ÖÓ Ù ÞÝÒÒÝÑ Ò ÔÖÓ Ù ÖÓÒ Û ËÞ ÖÓ Óð ð Ñ ÑÙÑ Ó ÔÓÛ Ò ØÙÖ ÐÒ Þ ÖÓ Óð ÓÞÓÒÙ Æ º Ø ØÓ Þ Ø ÈÓÒ Û Þ Ò Ý Ò Ö Ø Ó ÞÝ ÓÛ Ñ Ò Ø Ó Ò Ó Ö ð ÐÓÒ ººº º º ÖÒ ÏÝ ½½
10 ÓÞÓÒÝ Ï Æ Ï Ï ÓÞÓÒ Û Ï ÈÖÓ Ù Ó ØÖÞ Ö ÞÒÝ ÔÖÓ Û Û e+ W + e+ ν γ e W e ÝÒ Û Ô Ö W + e+ Z ο W + W σ WW (pb) LEP PRELIMINARY 17/02/2005 e W 10 ËØ Ò Ö ÓÛ Ó YFSWW/RacoonWW no ZWW vertex (Gentle) only ν e exchange (Gentle) ÛÝÒ Þ ØÖÙ ØÙÖÝ ÅÓ ÐÙ ËÔÖÞ Þ Ò µ ð ÔÖÞ Û ÝÛ Ò Ø ÓÖ ØÝÞÒ Óð Û Þ ÐÒ ÔÓØÛ Ö ÞÓÒ ÓÛ Ò Û Û Ó Ö ÞÒÝ ÔÖÓ Û µ s (GeV) º º ÖÒ ÏÝ ½½
11 Û Ö Ù ÙÒ ÞÓ Ô Ò ÔÖÞ Þ Ò Ó ÓÞÓÒ Û ÓÛ Ò µ Ó ÔÓÛ Ï ÒÓð ã ÓÐÒÝÑä µ µ ÑÙ ØÒ ð ã ÖÒÝä Ô ÖØÒ Ö ØÓÔ Û Ö ÓÑ ÃÛ Ö Ø ÃÖ Ø ØÓÖ ½ ¹ ÐйŠÒÒ Û ÓÒ Ô Û Ö Û Ù ½ ¼ ¹ Ð ÓÛ ÁÐ ÓÔÓÙÐÓ Å Ò ÔÖÓÔÓÒÙ Û Ö Ù ½ ¹ ÃÓ Ý Å Û Ó ¾ Û Ö Ø µ Þ Ý ÛÝØ ÙÑ ÞÝð Ñ Ò È ½ ¹ Ì Ò Ê Ø Ö Ó ÖÝ Û Ö Ù ½ ¹ Ä ÖÑ Ò ÖÑ Ð µ Ó ÖÝ Û Ö Ù È ÖÛ Þ ÔÖÞ Û ÝÛ Ò Ö Ù ã äµ Ñ ¼ Î Ñ ½ Î Ñ Î µ Ñ Ø ½ Î È ÖÛ Þ ãó ÖÝ ä ÊÆ ËÈË ½ Ñ Ø ¼ Î ÔÓØ Ñ Ó ÛÓ Ò µ ÈÓ ÞÙ Û ÒÝ Ø Þ Û Ä È À Ê Þ ÔÓÛÓ Þ Ò ººº º º ÖÒ ÏÝ ½½ ½¼
12 ÛÝ Ö ð ÒÔº «Ñ Å ÅÓ ÞÒ ÓÔ ÓÛ ð Û ÖØÓð Ó ÒÝ º Å Ö Þ Ó ÒÓð ÔÙÐÐ Ñ ËÅ ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È Ø Û Ò Ä È Ñ ÖÞÓÒÓ Þ Ø ÔÖÓ Ûº Ï ÅÓ Ð ËØ Ò Ö ÓÛÝ Ñ ÝÒ ØÖÞÝ ÛÓÐÒ ÓÔ Ù Ó Þ ÝÛ Ò Ô Ö Ñ ØÖÝ Ñ Ý ÖÑ ÓÒ Û À µº ÅÓ Ð Ø ÙÑ ÞÝ ÛØ Ý ÛÝÒ Û ÞÝ Ø ÓØÝ Þ ÓÛÝ ÔÓÑ Ö Û Ó Þ ÝÛ ðò Ð ØÖÓ Ý Measurement Fit O meas O fit /σ meas α (5) had (m Z ) ± m Z [GeV] ± Γ Z [GeV] ± σ 0 had [nb] ± R l ± A 0,l fb ± A l (P τ ) ± R b ± R c ± A 0,b fb ± A 0,c fb ± A b ± A c ± A l (SLD) ± sin 2 θ lept eff (Q fb ) ± m W [GeV] ± Γ W [GeV] ± m t [GeV] ± March µ º º ÖÒ ÏÝ ½½ ½½
13 ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È ÈÓÔÖ Û Ï Ð Óð ÞÝÞÒ ÞÑ ÖÞÓÒ Û Ä È ÞÙ ÖÞ Ûäº Ò ÔÓÔÖ Û ãûý Þ ÞÝ ÔÓ Ó Þ Û ÞÞ ÐÒÓð ÈÓÔÖ Û σ had [nb] ALEPH DELPHI L3 OPAL σ 0 20 Γ Z ÔÖÓ Û Þ Û ÖØÙ ÐÒ ÛÝÑ Ò Ó ÓÞÓÒÙ Ï Û Ö Ù Ø ÓÞÓÒÙ À ÒÒÝ Þ Þ Ø ººº ÐÙ ÈÖ ÝÞÝ Ò ÔÓÑ ÖÝ Û Ä È Ò¹ Ô ÖÝÑ ÒØ ÔÓÞÛ Ð ÒÝ 10 measurements (error bars increased by factor 10) σ from fit QED corrected Ó Ñ ØÝ Þ Ø ÛÒ Ó ÓÛ ð Ò Û Ø ð Ð ÞÔÓð Ö Ò Ó Ò M Z E cm [GeV] Ó ÖÛÙ ÑÝ º º ÖÒ ÏÝ ½½ ½¾
14 ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È W-Boson Mass [GeV] ÈÓÔÖ Û TEVATRON ± LEP ± ÅÓ Þ ÑÝ ÛÝÞÒ ÞÝð Ñ Ý Þ Average ± χ 2 /DoF: 0.1 / 1 Ø Ò ÔÓ Ø Û Ò Ð ÞÝ ÔÖ ¹ Þ NuTeV ± ÝÞÝ ÒÝ ÔÓÑ Ö Û ÔÖÞÝ Ò Þ ÞÝ Ò Ö º LEP1/SLD ± LEP1/SLD/m t ± m W [GeV] March 2012 ÞÔÓð Ö Ò Þ Ó ÒÝ Þ Ó ÒÓð ÈÓÑ Ö Ó ¼º¼ ± Þ ÔÖÞ Û ÝÛ Ò Ñ Ø ÓÖ ÓÔ ÖØÝÑ Ò ÔÖ ÝÞÝ ÒÝ ÔÓÑ Ö ÔÖÞÝ Ò Þ ÞÝ Ò Ö º º º ÖÒ ÏÝ ½½ ½
15 ÃÛ Ö Ø ÈÖÞ Û ÝÛ Ò Æ ÔÓ Ø Û ÔÖ ÝÞÝ ÒÝ ÔÓÑ ¹ Þ Þ ÛÝÒ ÔÓð Ö Ò Ö Û Û Ä È ÓÞ Û ÒÓ Þ Ñ Û Ö Ù Ø ÔÓÛ ÒÒ ÛÝÒÓ ð Ó Ó Ó ½¾¼¹½ ¼ κ º º ÖÒ ÏÝ ½½ ½
16 ÃÛ Ö Ø Ì Ú ØÖÓÒ Þ ÖÞ Ò Ô Ô ÔÖÞÝ Ò Ö Ô ¾ Ì Î ÃÛ Ö Ø Ò Þ ð ÔÖÓ Ù ÓÛ ÒÝ Û ÛÝÒ Ù Ò Ð Û Ö ¹ ÒØÝ Û Ö ÔÖ Û Ò ØÝ Ñ Ø Ò ØÛÓÖÞÝ Þ ÒÝ Þ Ø µ ÊÓÞÔ ÔÓÛ Ø Ý Û Ö ÓÖ Þ Ð ÔØÓÒ Ò ÙØÖ ÒÓ Ö Ù Ý Ô ÔÓÔÖÞ ÞÒݵ Ç ÖÛÙ ÑÝ Ô Ö Ø Û Ó Ñ Ò ÞÑ ÒÒ Þ Ó ÔÓÛ Ñ Ï ÐÙ º º ÖÒ ÏÝ ½½ ½
17 Ì Ú ØÖÓÒ Û Ö Ø ÔÖÓ Ù ÓÛ ÒÝ Ø Ô Ö Ñ Ø Øµ Ñ ÑÝ ÑÓ ÞÐ Û Ð Ý ÔÖÞÝÔ Û ÈÓÒ Û Þ ÃÛ Ö Ø Ð ÔØÓÒÓÛ Ô Ð ÔØÓÒÓÛ ÖÓÒÓÛ ¼± ÔÖÞÝÔ Û ± ÔÖÞÝÔ Û ãþ ÓØ ÔÖ ä Ð ØÝÐ Ó Ö ÞÓ Ù Þ Ø Ó ± ÔÖÞÝÔ Û ØÝÐ Ó µ ØÖÙ Ò ÒØÝ Ñ Ø Ó µ º º ÖÒ ÏÝ ½½ ½
18 ÃÛ Ö Ø Ì Ú ØÖÓÒ Ä Þ Ó ÖÛÓÛ ÒÝ Ø Û Ð ÔÖÞݹ Â Ò Þ Ô ÖÛ ÞÝ ÔÖÞÝÔ Û Ô Û Þ ÞÓÐÓÛ ÒÝÑ Ð ÔØÓÒ Ñ µ ÏÝ Ö ÑÝ Ð ÔØÓÒ ØÝ µ ÛÒ ÔÖÞÝÔ Ø Ø ØÝ ÔÖÞÝÔ Ûººº Ö ÒÓ µ Ó ÐÒ Ó ÖÝ ½ º º ÖÒ ÏÝ ½½ ½
19 Ö ÓÒ ØÖÙÓÛ Ò Ñ Ý Û Ö Ù Ø ÊÓÞ ÒÝÑ Þ ÖÓÞÛ Þ ÒÝ Ò Û Û ÃÛ Ö Ø Ì Ú ØÖÓÒ 15 Mass of the Top Quark July 2011 (* preliminary) ÈÓÖ ÛÒ Ò ÛÝÒ Û Ð Ö ÞÒÝ ÔÖ CDF-I dilepton ± 11.4 (±10.3 ± 4.9) DØ-I dilepton ± 12.8 (±12.3 ± 3.6) CDF-II dilepton ± 3.8 (± 2.2 ± 3.1) DØ-II dilepton ± 3.1 (± 1.8 ± 2.5) CDF-I lepton+jets ± 7.4 (± 5.1 ± 5.3) DØ-I lepton+jets ± 5.3 (± 3.9 ± 3.6) CDF-II lepton+jets ± 1.2 (± 0.6 ± 1.1) DØ-II lepton+jets ± 1.5 (± 0.8 ± 1.2) CDF-I alljets ± 11.5 (±10.0 ± 5.7) CDF-II alljets * ± 2.1 (± 1.4 ± 1.5) CDF-II track ± 9.5 (± 9.0 ± 2.9) CDF-II MET+Jets * ± 2.6 (± 1.8 ± 1.8) 0 Tevatron combination * ± 0.9 (± 0.6 ± 0.8) CDF March 07 χ /dof ± = /11 (± (68.5%) 1.5 ± 2.2) (GeV/c ) m top (± stat ± syst) ¼ Ñ Ø ½ ¾ ¼ Î º º ÖÒ ÏÝ ½½ ½
20 Top-Quark Mass [GeV] ÃÛ Ö Ø ÈÓÖ ÛÒ Ò CDF ± 1.0 ÏÝÒ ÔÓÑ Ö Û ÞÔÓð Ö Ò D ± 1.4 ÔÓÖ ÛÒ Ò Þ Ó Ö Ò Þ Ò Ñ Average ± 0.9 χ 2 /DoF: 6.1 / 10 ÛÝÒ ÝÑ Þ ÔÖ ÝÞÝ ÒÝ ÔÓÑ Ö Û ÔÖÞÝ Ò Þ ÞÝ Ò Ö º LEP1/SLD LEP1/SLD/m W /Γ W m t [GeV] March 2012 ÈÓÑ Ö ÞÔÓð Ö Ò Þ Ó ÒÝ Û Ö Ò Û Þ ÔÖÞ Û ÝÛ Ò Ñ Ø ÓÖ ÓÔ ÖØÝÑ Ò ÔÖ ÝÞÝ ÒÝ ÔÓÑ Ö ÔÖÞÝ Ò Þ ÞÝ Ò Ö º º º ÖÒ ÏÝ ½½ ½
21 ÃÛ Ö Ø Ô ÖÝÑ ÒØÝ ÔÖÞÝ ÄÀ ÞÞ ÓÛÓ ÔÖÓ Ý Þ ÔÖÓ Ù ÓÞÓÒ Û Ï ¼ ÓÖ Þ Û Ö Ù Øº Ö ÞÓ Ï ÞÝ Ø ÓØÝ Þ ÓÛ ÔÓÑ ÖÝ Û ÞÒ ÓÑ Ø Þ Ó ÒÓð Þ Ëź Standard Model Total Production Cross Section Measurements Status: March 2014 σ [pb] pb 1 ATLAS Preliminary Run 1 s = 7, 8 TeV pb 1 LHC pp s = 7 TeV theory LHC pp s = 8 TeV theory data data fb fb fb fb fb fb fb fb fb fb fb W total Z total t t total t t channel total WW total Wt total WZ total ZZ total º º ÖÒ ÏÝ ½½ ¾¼
22 ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È July 2010 ÈÓÔÖ Û ÅÓ Þ ÑÝ ÛÝÞÒ ÞÝð Ñ Ý Þ Ø Ò ÔÓ Ø Û Ò Ð ÞÝ ÔÖ ¹ Þ 80.5 LEP2 and Tevatron (prel.) LEP1 and SLD 68% CL ÝÞÝ ÒÝ ÔÓÑ Ö Û ÔÖÞÝ Ò Þ ÞÝ Ò Ö º Ð ÓÞÓÒÙ Ï Û Ö Ù Ø ÛÝÒ m W [GeV] 80.4 Ö ÞÓ Ó ÖÞ Þ Ó Þ Ý Þ ÞÔÓð Ö Ò Ñ ÔÓÑ Ö Ñ ÑÓ Þ ÑÝ Ô ð ð ÖÓ Ð Þ ¹ µ Ó Ñ Þ Ø Ø Ö ÔÝØ ð ÞÞ Ò Ó ÖÛÓÛ Ð ð Ñݺºº 80.3 α m H [GeV] m t [GeV] º º ÖÒ ÏÝ ½½ ¾½
23 ¾ Î Ñ ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È Å Ò Ð Þ Û ÞÝ Ø Ó Ø ÔÒÝ ÒÝ Û ÞÝÛ Þ Ñ À ÔÓÛ ÒÒ ÛÝÒÓ ð Ó Ó Ó ½¼¼ æ ¾¼¼ Î July 2010 Theory uncertainty ¾¼½¼ α had = α (5) ± ± incl. low Q 2 data m Limit = 158 GeV χ 2 3 ÏÝÒ Þ ÖÓ Ù ¾¼½¼ 2 ÐÙ Ñ ½ Î ± ĵ 1 ÞÔÓð Ö Ò ÔÓ ÞÙ Û ðò Ñ ½½ º Î ± ĵ Û ÞÝ Ø Ò Ä È Excluded Preliminary m H [GeV] Ä ÈÀ ÄÈÀÁ Ä ÇÈ Ä º º ÖÒ ÏÝ ½½ ¾¾
24 ÊÆ Ò Û ÄÀ Ò Ò ¾¼¼ ÍÖÙ ÓÑ ÓÒÝ º º ÖÒ ÏÝ ½½ ¾
25 À Û ÄÀ Ø À Þ ÑÙ Ö ÞÓ ÞÞ ÐÒ Ñ Û Ø ÓÖ Ñ ÞÞ ÐÒ Û ÒÓð Þ σ rate ev/year LHC s=14tev L=10 34 cm -2 s -1 barn σ inelastic LV1 input GHz ÓÞÓÒ À ÖÓÞÔ Ò ØÒ ÔÓ ÞÙ Û Ò ÔÓÑ Ö Ô Ö Ñ ØÖ Û Ø ÒÝÑ Þ ÛÒÝ Ø Ñ Ø Û ðò Û ÄÀ mb bb MHz µb max LV2 input max LV1 output nb W Z W lν Z l + l - tt max LV2 output khz pb qq qq H SM H SM γγ gg H SM h γγ tanβ=2-50 SUSY q ~ q ~ +q ~ g ~ +g ~ g ~ tanβ=2, µ=m g ~ =m q ~ tanβ=2, µ=m g ~ =m q ~ /2 Z ARL l + l - Hz mhz Ò Þ Þ Ó Ø ÔÒ Þ Ø Ð Ñ Ò Ñ ½ Î ÓÑ ÒÙ ÖÓÞÔ Ò º Â Ò Û Þ ÖÞ Ò ÔÔ Ñ ÑÝ Ø Ö ÞÓ Ù Þ Ø Ó ÒÒÝ ÔÖÓ Û Þ ÔÖÓ Ù Û Ö Û Û ØÝÑ º ÛÒ ÅÙ ÑÝ ÞÙ ð Ò Û Ó Ò Ñ ØÐ ººº fb H SM ZZ ( * ) 4l µhz Z SM 3γ scalar LQ Z η l + l particle mass (GeV) º º ÖÒ ÏÝ ½½ ¾
26 À Û ÄÀ Ð Ñ Ý Ñ Ò Ð Ô ÞÝ Ò ØÓ Ý Ø Ø Þ Ò Ç Ù À À Æ Æ Ð Ð Ð Ð Ì Ó Ø Ù Þ Ð ÔÓÛ ÒÒ ð ÑÝ ÞÓ ÞÝð Ý Þ Ò ÓÛ Ò Ð ÔØÓÒÝ µ ÑÓ ÞÒ À Û ÖÓÞ Þ Ñ Ý Ò ÞÑ ÒÒ Þ ØÛÓ Þ ÒØÝ ÓÛ ðº Ð Ø Ñ Ó ÔÖÞÝÔ Ûººº ÛÝÒ ÝÑÙÐ ÓÑÔÙØ ÖÓÛ º º ÖÒ ÏÝ ½½ ¾
27 À º º ÖÒ ÏÝ ½½ ¾
28 À Æ Æ º º ÖÒ ÏÝ ½½ ¾
29 ÖÙ Ò Ù ¾¼½½ Ô ÖÝÑ ÒØÝ ÌÄ Ë ÅË ÔÖÞÝ ÄÀ ÔÖÞ Ø Û Ý Ô ÖÛ Þ ÛÝÒ Ï ÓÞÓÒÙ À Û Þ Ö Ò Û Ð Ø ¾¼½¼¹¾¼½½ ÔÖ ÒÝ º ÔÓ ÞÙ Û Ò À Û ÄÀ ÔÖÞÝÔ Û Û Þ Ý Ý Ö ÞÓ Ñ ËØ ØÝ ØÝ Events / 1 GeV ATLAS Preliminary Data MC m H =130 GeV, 1xSM Total background (Fit) À Data 2011, H γγ -1 s = 7 TeV, Ldt = 4.9 fb m γγ [GeV] º º ÖÒ ÏÝ ½½ ¾
30 ÖÙ Ò Ù ¾¼½½ Ô ÖÝÑ ÒØÝ ÌÄ Ë ÅË ÔÖÞÝ ÄÀ ÔÖÞ Ø Û Ý Ô ÖÛ Þ ÛÝÒ Ï ÓÞÓÒÙ À Û Þ Ö Ò Û Ð Ø ¾¼½¼¹¾¼½½ ÔÖ ÒÝ º ÔÓ ÞÙ Û Ò À Û ÄÀ ÔÖÞÝÔ Û Û Þ Ý Ý Ö ÞÓ Ñ ¹ Ò Û Ð Û ð ËØ ØÝ ØÝ Events / 5 GeV Data Data 2011, m H =130 GeV, 1xSM Total background (*) H ZZ 4l s = 7 TeV, Ldt = 4.8 fb ATLAS Preliminary À Æ Æ Ð Ð Ð Ð [GeV] m 4l º º ÖÒ ÏÝ ½½ ¾
31 À Û ÄÀ ÈÖÞÝ Ø Ñ Ý Ø ØÝ ØÝ ÑÙ ÑÝ Ýð Ö ÞÓ Ó ØÖÓ ÞÒ Æ Û Ø ð Ð Ð ð Ñ Ý Û Þ ÑÝ Ò Ñ Ö ÔÖÞÝÔ Û ØÓ ÑÓ Þ ØÓ Ýð Ù ØÙ Ø ØÝ ØÝÞÒ ØÝÑ Ö Þ ÔÖ Û ÓÔÓ Ó Ò Þ ÞÙ ÑÝ Û Þ ÖÓ Ñ Þ Ö Ñ Û ÓÔ Ö Ù Ó ÝÑÙÐ ØÞÛº Ñ ØÓ ÅÓÒØ ÖÐÓ ÁÐÙ ØÖ Û ÔÖ ÔÓ ¾¼³¼¼¼ ÔÖÞÝÔ Û Liczba przypadkow Liczba przypadkow [GeV/c ] M γ γ [GeV/c ] M γ γ ½± ÔÖÞÝÔ Û ÔÖÓ Ù À ÑÓ Ø Ó º º ÖÒ ÏÝ ½½ ¼
32 ÈÓÑ ÖÝ ÔÖ ÝÞÝ Ò Û Ä È Å Ò Ð Þ Û ÞÝ Ø Ó Ø ÔÒÝ ÒÝ Þ Ä È Ì Ú ØÖÓÒ ÓÖ Þ Ô ÖÛ ÞÝ ÛÝÒ Û Þ ÄÀ µº March 2012 Theory uncertainty Û Ó Ò ¾¼½¾ α had = α (5) ± ± incl. low Q 2 data m Limit = 152 GeV χ 2 3 ¾¼½¾ ÔÓÞÓ Ø Ó Ù Þ ØÝÐ Ó Û Ï Ó Ò Ó Ø ÔÒÝ Û ÖØÓð Ñ Þ Ø Ó ÒÓ À Ñ À ½¾ Î ½½ Î ØÓ Ó ÒÓ ÞÓ Ø Ó ãþ Ñ Ò Ø ä Ý Ý ØÓ ÛÝ ÐÙÞ Ò ÓÞÒ Þ Ó Ý LEP excluded m H [GeV] LHC excluded ÅÓ ÐÙ ËØ Ò Ö ÓÛ Ó º º ÖÒ ÏÝ ½½ ½
33 ÛÝÒ ÔÖÞ Ø Û ÓÒ ÔÖÞ Þ ÌÄ Ë ÅË Æ ÒÓÛ Þ ÙÛÞ Ð Ò Ò Ù ÒÝ Þ Ö ÒÝ Û ÖÓ Ù ¾¼½¾º ÔÓ À Û ÄÀ ÈÖ Û Ô Ó ÖÓØÒÝ ÛÞÖÓ Ø Ø ØÝ ØÝ Û ÓÞÒÝ ÔÓÒ Û Þ Ð Û ØÔÐ ÛÓð ð ËÝ Ò Events / 2 GeV Events - Fitted bkg ATLAS -1 s = 7 TeV Ldt = 4.8 fb -1 s = 8 TeV Ldt = 20.7 fb Data SM Higgs boson m =126.8 GeV (fit) H Bkg (4th order polynomial) H γγ m γγ [GeV] S/(S+B) Weighted Events / 1.5 GeV CMS -1 s = 7 TeV, L = 5.1 fb Data S+B Fit B Fit Component 1 2 Events / 1.5 GeV s = 8 TeV, L = 5.3 fb Unweighted m (GeV) (GeV) m À º º ÖÒ ÏÝ ½½ ¾
34 ÛÝÒ ÔÖÞ Ø Û ÓÒ ÔÖÞ Þ ÌÄ Ë ÅË Æ ÒÓÛ Þ ÙÛÞ Ð Ò Ò Ù ÒÝ Þ Ö ÒÝ Û ÖÓ Ù ¾¼½¾º ÔÓ À Û ÄÀ ÈÖ Û Ô Ó ÖÓØÒÝ ÛÞÖÓ Ø Ø ØÝ ØÝ Û ÓÞÒÝ ÔÓÒ Û Þ Ð Û ØÔÐ ÛÓð ð ËÝ Ò Events/5 GeV Data SM Higgs Boson m H =124.3 GeV (fit) Background Z, ZZ* Background Z+jets, tt Syst.Unc. ATLAS H ZZ* 4l s = 7 TeV Ldt = 4.6 fb s = 8 TeV Ldt = 20.7 fb -1-1 Events / 3 GeV À Æ Æ Ð Ð Ð Ð CMS -1 s = 7 TeV, L = 5.1 fb ; 35 Data -1 s = 8 TeV, L = 19.7 fb Z+X * Zγ,ZZ m H =126 GeV [GeV] m 4l (GeV) m 4l º º ÖÒ ÏÝ ½½
35 À Û ÄÀ Ù Þ Ø ØÝ ØÝ ÔÖÞÝÔ Û ÔÓÞÛÓÐ Ø Þ Ò ÔÓ ÞÙ Û Ò ÒÒÝ Ò Û ÖÓÞÔ Û ÓÞÓÒÙ À º ATLAS Prelim. Ç ÖÛÓÛ Ò Ð Þ Ý ÔÖÞÝÔ Û Û Ó Ö Þ Ó ÒÓð Þ ÓÞ Û Ò Ñ ËÅ m H = GeV H γγ µ = 1.57 H ZZ* 4l µ = 1.44 H WW* lνlν µ = 1.00 Combined H γγ, ZZ*, WW* µ = σ(stat.) sys inc. σ( theory σ(theory) ) Total uncertainty ± 1σ on µ W,Z H bb µ H ττ = (8 TeV data only) +0.5 µ = Combined H bb, ττ µ = ±0.5 ±0.4 < Combined µ = s = 7 TeV Ldt = fb -1 s = 8 TeV Ldt = 20.3 fb Signal strength (µ) ÔÖÞ Þ Û ÖØÓð Ù ½ µ Þ Û Ö Û ÖØÓð ð ÔÖ Û Þ Û ØÝÐ Ó Û Ó º ¾» ÔÖÞÝÔ Û ËØ ØÝ ØÝÞÒ º º ÖÒ ÏÝ ½½
36 À Û ÄÀ ËÔÖÞ Þ Ò ÓÞÓÒÙ À -1-1 CMS Preliminary s = 7 TeV, L 5.1 fb s = 8 TeV, L 19.6 fb 1/2 ÅÓ ÞÐ Û Ø Û ÖÝ ÔÓ Ø ¹ ÛÓÛ Ó ÔÖÞ Û ÝÛ Ò ÑÓ ÐÙ ÓÞÓÒÙ À Ó Þ Ø ÔÖÞ Þ Ò or (g/2v) 1 68% CL 95% CL W Z t Ø ÔÖÓÔÓÖ ÓÒ ÐÒ Ó Ñ Ý λ Û Þ Ö ÞÓ Ù Þ Ý b ÈÖ ÝÞ Þ Ö ÞÓ ÞÛ ÞÓÒ ÔÓ ÙÖÙ ÓÑ Ò Ù ÄÀ ÔÖÞÝ Ô ½ Ì Î Û τ ¾¼½ ÖÓ Ùº Ó ÖÓ Ù ¾¼¾¼ ÔÐ ÒÓÛ Ò ÔÓÒ Þ Ó ÖÓØÒ ÞÛ Þ Ò ÔÖ mass (GeV) ÒÝ º º ÖÒ ÏÝ ½½
37 À Û ÄÀ ÅÓ Ð ËØ Ò Ö ÓÛÝ Ï Ö Ñ ÑÓ ÐÙ Ø Ò Ö¹ ÓÛ Ó Ñ ÓÞÓÒÙ À ÞÛ Þ Ò Þ Ñ Ñ Ó¹ Ø ÞÓÒÙ Ï Û Ö Ù Ø ÔÓÔÖÞ Þ ÔÓÔÖ Û Ô ØÐÓÛ º ÏÝÒ ÔÓÑ ÖÙ Ñ Ý ÓÞÓÒÙ À Û ÄÀ Þ Ó Ò Þ ÛÝÒ Ñ ÞÔÓð Ö Ò ÔÓ¹ Ñ Ö Û Ñ Ï Ø ÓÖ Þ ÛÝÒ Ñ Ä Èº Ï ÞÝ Ø Ó Þ Þ ººº º º ÖÒ ÏÝ ½½
38 ÈÓ ÙÑÓÛ Ò ¾¼½¾ Ý ÔÖÞ ÓÑÓÛÝ Ð ÞÝ Þ Ø Ð Ñ ÒØ ÖÒÝ º ÊÓ À Û ÄÀ ÌÄ Ë ÅË Ó ÖÝ Ý ÒÓÛ Þ Ø Ø Ö Û ð ÛÓð Ô ÖÝÑ ÒØÝ ÔÓ ÞÙ Û Ò ÑÙ Ó ¼ Ð Ø ÓÞÓÒÓÛ À º Ó ÔÓÛ ÌÖ ÙÑ ÅÓ ÐÙ ËØ Ò Ö ÓÛ Ó ØÓ Ù ØÝ Ý Ò Ù ÓÛ Û Ò ÞÝÒ Ö Û Ø Ò Û Â Ø Ó ÔÓÒ ¾¼ Ð Ø ÔÖÞÝ ÓØÓÛÝÛ Ð Ô ÖÝÑ ÒØÝ ÔÖÞÝ ÄÀ º Ø ÖÞÝ Ï ÞÝ Ø ÓØÝ Þ ÓÛ ÛÝÒ ÙÞÝ Ò ÔÖÞÝ ÓÐ Ö Þ Ó Ò Þ ËÅ ØÓ Ö ÛÒÓÞ ð Ò ÔÓÞ Ø ÒÓÛ ÖÝ ðò Â Ø ÑÙ ÑÝ Ó Ò ÞÑ ÖÞÝð Û ÞÝ Ø Û ÒÓð Ó ÖÝØ Þ Ø ÞÝ Ø Ø ÓÖ ÔÖÞ Û Ù ÔÖ Û Þ ð Þ ÑÝ ÞÙ ð ÓÐ ÒÝ ÒÓÛÝ Ø Ò Û ÞÞ ÐÒÓð Þ Ø ØÞÛº ÑÒ Ñ Ø Ö Û Ð ØÓ Ù Þ Ø Ñ Ø Ò ÓÐ Ò ÛÝ Ýººº º º ÖÒ ÏÝ ½½
ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó Þ ÝÛ Ò Å ÔÓ ÞÙ Û Ò Ø ÔÓð Ö Ò Ý Ò Û Ó Þ ÝÛ Ò Ò Ð µ ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÈÓ ÞÙ Û Ò Ó ÑÓ ÐÙ ÑÓ Þ ÑÝ ÔÓ
 ÈÓð Ö Ò ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÔÓÑ ÖÝ ÔÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ó Ø Ð Ø ÖÒ Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÎÁÁ æ ÊÅÁ æ È Å Ä æ Å˹¾ ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó
ÈÓð Ö Ò ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÔÓÑ ÖÝ ÔÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ó Ø Ð Ø ÖÒ Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÎÁÁ æ ÊÅÁ æ È Å Ä æ Å˹¾ ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó
ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó Þ ÝÛ Ò Å ÔÓ ÞÙ Û Ò Ø ÔÓð Ö Ò Ý Ò Û Ó Þ ÝÛ Ò Ò Ð µ ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÈÓ ÞÙ Û Ò Ó ÑÓ ÐÙ ÑÓ Þ ÑÝ ÔÓ
 ÈÓð Ö Ò ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÔÓÑ ÖÝ ÔÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ó Ø Ð Ø ÖÒ Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÎÁÁ æ ÊÅÁ æ È Å Ä æ Å˹¾ ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó
ÈÓð Ö Ò ÔÓ ÞÙ Û Ò ÑÒ Ñ Ø Ö ÔÓÑ ÖÝ ÔÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ó Ø Ð Ø ÖÒ Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÎÁÁ æ ÊÅÁ æ È Å Ä æ Å˹¾ ÔÖÓ Ù ÔÖÓ Ù Þ Ø ÑÒ Ñ Ø Ö ÞÔÓð Ö Ò Ø ÞÔÓð Ö Ò Ý Ò Û Ó
Testy Modelu Standardowego i poszukiwanie bosonu Higgsa
 Testy Modelu Standardowego i poszukiwanie bosonu Higgsa Wykład 11 bozony W ± i Z kwark t poszukiwania bozonu Higgsa najnowsze wyniki LHC prof. dr hab. Aleksander Filip Żarnecki Wszechświat Czastek Elementarnych
Testy Modelu Standardowego i poszukiwanie bosonu Higgsa Wykład 11 bozony W ± i Z kwark t poszukiwania bozonu Higgsa najnowsze wyniki LHC prof. dr hab. Aleksander Filip Żarnecki Wszechświat Czastek Elementarnych
½ ÏÝ Ï Þ ð Û Ø ÛÓÐÙ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÞÝ Óð Û Þ ÐÒ ÁÒ ØÝØÙØ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ½ ÛÓÐÙ Ï Þ ð Û Ø ¾ Ñ ¾¼½ æ
 ½ ÏÝ Ï Þ ð Û Ø ÛÓÐÙ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÞÝ Óð Û Þ ÐÒ ÁÒ ØÝØÙØ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ½ ÛÓÐÙ Ï Þ ð Û Ø ¾ Ñ ¾¼½ æ Ôº½»¾ Ï Þ ð Û Ø ÛÓÐÙ Ï Þ ð Û Ø ÏÔÖÓÛ Þ Ò Ö Û Ø Ç ÐÒ
½ ÏÝ Ï Þ ð Û Ø ÛÓÐÙ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÞÝ Óð Û Þ ÐÒ ÁÒ ØÝØÙØ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ½ ÛÓÐÙ Ï Þ ð Û Ø ¾ Ñ ¾¼½ æ Ôº½»¾ Ï Þ ð Û Ø ÛÓÐÙ Ï Þ ð Û Ø ÏÔÖÓÛ Þ Ò Ö Û Ø Ç ÐÒ
Czastka Higgsa w LHC
 Czastka Higgsa w LHC Fizyka I (Mechanika) Wykład XV: czastki i fale spontaniczne łamanie symetrii i czastka Higgsa jak działa akcelerator LHC poszukiwania czastki Higgsa w LHC Informacje o egzaminie Świat
Czastka Higgsa w LHC Fizyka I (Mechanika) Wykład XV: czastki i fale spontaniczne łamanie symetrii i czastka Higgsa jak działa akcelerator LHC poszukiwania czastki Higgsa w LHC Informacje o egzaminie Świat
ØÖ Ò ÔÓÖØ Û ÖØÓ ÔÖÞ ÛÓ Ò ÐÙ ÔÖÞ ÒÓ Þ Ò Û ÖØÓ Ô Ò ÒÝ ÔÓÞ Ó Ö Ñ Ô Þ ÐÒ ºÓ ÒÓ Ø Ó Ð Þ Ò ÓÛ ÔÖÞÝ Ø Ó Ó Ö Ð Ò Ð Ñ ØÙ ÔÖÞ ÓÛÝÛ ¹ ÒÝ ÐÙ ØÖ Ò ÔÓÖØÓÛ ÒÝ Û ÖØÓ
 ÁÒ ØÖÙ Ó ÔÓ Ö ÓÛ ½ ¹¼ ¹¾¼¼ ½ ÈÓ Ø ÒÓÛ Ò Ó ÐÒ ï½ ÁÒ ØÖÙ Ó Ö Ð Þ Ý Ó ÖÓÒÝ Û ÖØÓ Ô Ò ÒÝ ÔÖÓÛ Þ Ò Ó ÔÓ Ö ÓØ Û Û Ù Ó ÙÑ ÒØÓÛ Ò ÓÔ Ö ÓÛÝ ÈÖÞ Þ Ù ÝØ Û Ò ØÖÙ Ó Ö Ð Ò ÖÓÞÙÑ Ô Þ ÐÒ Ô Þ ÐÒ Ñ Þ Ò ÓÛ È ÓØÖÓÛÓ Þ ÖÞ
ÁÒ ØÖÙ Ó ÔÓ Ö ÓÛ ½ ¹¼ ¹¾¼¼ ½ ÈÓ Ø ÒÓÛ Ò Ó ÐÒ ï½ ÁÒ ØÖÙ Ó Ö Ð Þ Ý Ó ÖÓÒÝ Û ÖØÓ Ô Ò ÒÝ ÔÖÓÛ Þ Ò Ó ÔÓ Ö ÓØ Û Û Ù Ó ÙÑ ÒØÓÛ Ò ÓÔ Ö ÓÛÝ ÈÖÞ Þ Ù ÝØ Û Ò ØÖÙ Ó Ö Ð Ò ÖÓÞÙÑ Ô Þ ÐÒ Ô Þ ÐÒ Ñ Þ Ò ÓÛ È ÓØÖÓÛÓ Þ ÖÞ
Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ¾ Ñ Ö ¾¼½ Ï Þ ð Û Ø µæ Ôº¾»
 ÏÝ Ô ÖÝÑ ÒØÝ Ï Ô Þ Ò Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ¾ Ñ Ö ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ
ÏÝ Ô ÖÝÑ ÒØÝ Ï Ô Þ Ò Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ¾ Ñ Ö ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ
Þ ÑÒ ÑÒ Ñ Ø Ö Ö Å ØØ Ö ¹ ŵ ÓÐ À Å Ñ Å Þ Å Ñ Å Å Å ÛÓÐÙ Ï Þ ð Û Ø Ç Ò ÔÓÛ Þ Ò ÙÞÒ ÒÝÑ ÑÓ Ð Ñ ÛÓÐÙ Ï Þ ð Û Ø Ø ØÞÛº ÑÓ Ð Åº ÓÒ Ï Þ ð Û Ø ÛÝÔ Ò ãþûý ä Ñ
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÎ ÑÒ Ñ Ø Ö Û Ï Þ ð Û È ÖÛÓØÒ ÆÙ Ð Ó ÝÒØ Þ ÊÓØ Ð ØÝ ÓÖÑÓÛ Ò ØÖÙ ØÙÖ Ç Ð ÙÔ ÖÒÓÛ ÖÓÑ ÈÓ ÙÐÐ Ø ÐÙ Ø Öµ Þ ÑÒ ÑÒ Ñ Ø Ö Ö Å ØØ Ö ¹ ŵ ÓÐ À Å Ñ Å Þ
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÎ ÑÒ Ñ Ø Ö Û Ï Þ ð Û È ÖÛÓØÒ ÆÙ Ð Ó ÝÒØ Þ ÊÓØ Ð ØÝ ÓÖÑÓÛ Ò ØÖÙ ØÙÖ Ç Ð ÙÔ ÖÒÓÛ ÖÓÑ ÈÓ ÙÐÐ Ø ÐÙ Ø Öµ Þ ÑÒ ÑÒ Ñ Ø Ö Ö Å ØØ Ö ¹ ŵ ÓÐ À Å Ñ Å Þ
Ð Ö Û Ø Ý Ò Û Ö ÞÓ Ò Û Ð Ñ ØÓÔÒ Ù ÔÓ Ð ÓÖ Û Ñ Ø Ö Â Ò Ð Ø Ó ÛÝ ÖÝ Ø Ø ØÖÙ Ò µ Ð Ö Û Ø Ý Ò Ï ÒÓð Ð Ö Û Ø Ý Ò Þ ÓÛÙ ÔÓ Ó Ò Ð Ð ØÖÓÑ Ò ØÝÞÒ ÔÓÖÙ Þ Þ Ø Ñ
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÎ ÈÓ ÞÙ Û Ò Ð Ö Û Ø Ý ÒÝ Ï½ ¼ ½ ÓÐ Ò ÔÖÞÝÔ È Ö Ô ØÝÛÝ ðò Ð Ö Û Ø Ý Ò Û Ö ÞÓ Ò Û Ð Ñ ØÓÔÒ Ù ÔÓ Ð ÓÖ Û Ñ Ø Ö Â Ò Ð Ø Ó ÛÝ ÖÝ Ø Ø ØÖÙ Ò µ Ð Ö Û
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÎ ÈÓ ÞÙ Û Ò Ð Ö Û Ø Ý ÒÝ Ï½ ¼ ½ ÓÐ Ò ÔÖÞÝÔ È Ö Ô ØÝÛÝ ðò Ð Ö Û Ø Ý Ò Û Ö ÞÓ Ò Û Ð Ñ ØÓÔÒ Ù ÔÓ Ð ÓÖ Û Ñ Ø Ö Â Ò Ð Ø Ó ÛÝ ÖÝ Ø Ø ØÖÙ Ò µ Ð Ö Û
Þ ð ãû Þ ÑÝä Ó Þ ÝÛ Ò Þ Ø Â Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ½ Ð ØÓÔ ¾¼½ Ï Þ ð Û Ø µæ Ôº¾»
 Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÙÑ Ò Ø Û Ð ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ½ Ð ØÓÔ ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ ð ãû Þ ÑÝä Ó Þ ÝÛ
Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÙÑ Ò Ø Û Ð ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ½ Ð ØÓÔ ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ ð ãû Þ ÑÝä Ó Þ ÝÛ
ÏÝ Ô ÖÝÑ ÒØÝ Ï Ô Þ Ò Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ Ï Ô Þ Ò Ô ÖÝÑ ÒØÝ ¾ Ñ Ö ¾
 ÏÝ Ô ÖÝÑ ÒØÝ Ï Ô Þ Ò Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ¾ Ñ Ö ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ ð ãû Þ ÑÝä Ó Þ ÝÛ Ò Þ Ø Â Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ¾ Ñ
ÏÝ Ô ÖÝÑ ÒØÝ Ï Ô Þ Ò Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÔÖÓ º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ ÁÒ ØÝØÙØ ÞÝ Óð Û Þ ÐÒ Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ¾ Ñ Ö ¾¼½ æ Ôº½» Ï Þ ð Û Ø Þ ð ãû Þ ÑÝä Ó Þ ÝÛ Ò Þ Ø Â Þ Ø Ð Ñ ÒØ ÖÒÝ ÏÝ ¾ Ñ
Ð ÓÖÝØÑÝ ØÖÙ ØÙÖÝ ÒÝ Ñ Ø Ö Ý ÛÝ ÓÛ ËØÙ Þ ÓÞÒ ÈÂÏËÌÃ Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÛÝ ÞÙ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓ
 Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÛÝ ÞÙ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û Ð ØÓÔ ¾¼¼ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð Ð ÓÖÝØÑ Û ÒÝ ÒÝ Ð ÓÖÝØÑ ØÙÖÒ Ð ÔÖÓ Ð ÑÙ ¾¹ Ó Ó Ó Û Ð Ó Ð
Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÛÝ ÞÙ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û Ð ØÓÔ ¾¼¼ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð Ð ÓÖÝØÑ Û ÒÝ ÒÝ Ð ÓÖÝØÑ ØÙÖÒ Ð ÔÖÓ Ð ÑÙ ¾¹ Ó Ó Ó Û Ð Ó Ð
 Þ Á Ö Ø ØÙÖÝ ÓÑÔÙØ ÖÓÛÝ À Ö Ö ÔÖÓØÓ Ó Û Ð Ù ØÛ Ò ÔÖÓ Ù ÔÖÓ ØÓÛ Ò Û Ô Þ ÒÝ ÓÑÔÙØ ÖÓ¹ ÛÝ ÔÖÞÝ ØÓ Þ Ó Ò ÓÒ ÔÓ Û Ñ Ö ÔÖÓ Ø ØÖÙ ØÙÖ ÐÓ ÞÒ º Ç Ø Ø ÞÒ Þ Ý ÓÛ ÒÓ ÓÑÔÙØ ÖÓÛ Þ ÞÓÖ Ò ÞÓ¹ ÊÝ ÙÒ ½ Ï Ö ØÛÓÛ ØÖÙ ØÙÖ
Þ Á Ö Ø ØÙÖÝ ÓÑÔÙØ ÖÓÛÝ À Ö Ö ÔÖÓØÓ Ó Û Ð Ù ØÛ Ò ÔÖÓ Ù ÔÖÓ ØÓÛ Ò Û Ô Þ ÒÝ ÓÑÔÙØ ÖÓ¹ ÛÝ ÔÖÞÝ ØÓ Þ Ó Ò ÓÒ ÔÓ Û Ñ Ö ÔÖÓ Ø ØÖÙ ØÙÖ ÐÓ ÞÒ º Ç Ø Ø ÞÒ Þ Ý ÓÛ ÒÓ ÓÑÔÙØ ÖÓÛ Þ ÞÓÖ Ò ÞÓ¹ ÊÝ ÙÒ ½ Ï Ö ØÛÓÛ ØÖÙ ØÙÖ
ÈÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ï Ð Ô ØÑÓ ÖÝÞÒ º º ÖÒ ÏÝ ½
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Ô ÖÝÑ ÒØ Í Ê ÈÖÓ Ø Â Å¹ ÍËÇ Ê ÓÛ Ø Ô Û ØÑÓ ÖÝÞÒÝ ÈÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ï Ð Ô ØÑÓ ÖÝÞÒ º º ÖÒ ÏÝ ½ ÔÖÓÑ Ò ÓÛ Ò Þ Ö Ò ÓÛ ÔÖÞ Þ Ð ØÖÓÒÝ Û Ö Þ Ò Ù ÔÖÓ
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Ô ÖÝÑ ÒØ Í Ê ÈÖÓ Ø Â Å¹ ÍËÇ Ê ÓÛ Ø Ô Û ØÑÓ ÖÝÞÒÝ ÈÖÓÑ Ò ÓÛ Ò Ó Ñ ÞÒ Ï Ð Ô ØÑÓ ÖÝÞÒ º º ÖÒ ÏÝ ½ ÔÖÓÑ Ò ÓÛ Ò Þ Ö Ò ÓÛ ÔÖÞ Þ Ð ØÖÓÒÝ Û Ö Þ Ò Ù ÔÖÓ
º º ÖÒ ÏÝ Á ½
 ÏÔÖÓÛ Þ Ò ÛÝ Ù Ð Ø Ö ØÙÖ Þ Ñ Ò ØÔº ÔÐ Ò Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Á ÃÖ Ø ØÓÖ ÖÓÞÛÓ Ù ÞÝ Þ Ø ÅÓ Ð ËØ Ò Ö ÓÛÝ ¾¼½ Ï Þ ØÙ ÐÒ ÔÝØ Ò Ò Ø Ö ÅÓ Ð ËØ Ò Ö ÓÛÝ Ò Ò Ñ Ó ÔÓÛ Þ º º
ÏÔÖÓÛ Þ Ò ÛÝ Ù Ð Ø Ö ØÙÖ Þ Ñ Ò ØÔº ÔÐ Ò Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Á ÃÖ Ø ØÓÖ ÖÓÞÛÓ Ù ÞÝ Þ Ø ÅÓ Ð ËØ Ò Ö ÓÛÝ ¾¼½ Ï Þ ØÙ ÐÒ ÔÝØ Ò Ò Ø Ö ÅÓ Ð ËØ Ò Ö ÓÛÝ Ò Ò Ñ Ó ÔÓÛ Þ º º
Ð ÓÖÝØÑÝ ØÖÙ ØÙÖÝ ÒÝ Ñ Ø Ö Ý ÛÝ ÓÛ ËØÙ Þ ÓÞÒ ÈÂÏËÌÃ Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÓÖØÓÛ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ Ö
 Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÓÖØÓÛ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ½¼ Ð ØÓÔ ¾¼¼ ½¼ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð Ð ÓÖÝØÑ ÓÖØÓÛ Ò ÔÖÞ Þ Ð Ð ÓÖÝØÑ ÓÖØÓÛ Ò ÔÖÞ Þ Û Ø
Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÁÁ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÈÖÓ Ð Ñ ÓÖØÓÛ Ò ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ½¼ Ð ØÓÔ ¾¼¼ ½¼ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð Ð ÓÖÝØÑ ÓÖØÓÛ Ò ÔÖÞ Þ Ð Ð ÓÖÝØÑ ÓÖØÓÛ Ò ÔÖÞ Þ Û Ø
ÈÐ Ò ÛÝ Ø Ô Ò ½ ¾ ÃÐ ÝÞÒ Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò ÅÓ Ð Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò Ë Ò ÙÖÓÒÓÛ ÏÒ Ó ÓÛ Ò Þ ÐÓ ÖÓÞÑÝØ Ð ÓÖÝØÑÝ ÛÓÐÙÝ Ò ÊÓÞÛ Þ Ò Ý ÖÝ ÓÛ ÝÒ Ñ
 Ç Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò Â ÖÓ Û Ö ÈÓÐ Ø Ò Ï Ö Þ Û ÁÒ ØÝØÙØ ËÝ Ø Ñ Û Ð ØÖÓÒ ÞÒÝ Ï ÌÁ ÈÐ Ò ÛÝ Ø Ô Ò ½ ¾ ÃÐ ÝÞÒ Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò ÅÓ Ð Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò Ë Ò ÙÖÓÒÓÛ ÏÒ Ó ÓÛ Ò Þ ÐÓ ÖÓÞÑÝØ Ð ÓÖÝØÑÝ
Ç Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò Â ÖÓ Û Ö ÈÓÐ Ø Ò Ï Ö Þ Û ÁÒ ØÝØÙØ ËÝ Ø Ñ Û Ð ØÖÓÒ ÞÒÝ Ï ÌÁ ÈÐ Ò ÛÝ Ø Ô Ò ½ ¾ ÃÐ ÝÞÒ Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò ÅÓ Ð Ó Ð Þ Ò ÓÛ ÞØÙÞÒ ÒØ Ð Ò Ë Ò ÙÖÓÒÓÛ ÏÒ Ó ÓÛ Ò Þ ÐÓ ÖÓÞÑÝØ Ð ÓÖÝØÑÝ
Number of included frames vs threshold effectiveness Threshold of effectiveness
 Ò Ð Þ ÒÝ Þ ÒÓÛ Ô Ö ØÙÖÝ Ø Ý Ò È Ó Ø Ë Ý ËÞÝÑÓÒ Å Þ ÞÑ Þ Ñ ÐºÓÑ ØÝÞÒ ¾¼½¾ ËÔ ØÖ ½ Ï ØÔ ½ ¾ ÇÔ Ñ ØÓ Ý ½ ¾º½ Ç Ò Ò Ö ÒÝ ÔÓÑ Ö Û º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º¾ Ç Ö Ð Ò ØÝÛÒÓ Ð
Ò Ð Þ ÒÝ Þ ÒÓÛ Ô Ö ØÙÖÝ Ø Ý Ò È Ó Ø Ë Ý ËÞÝÑÓÒ Å Þ ÞÑ Þ Ñ ÐºÓÑ ØÝÞÒ ¾¼½¾ ËÔ ØÖ ½ Ï ØÔ ½ ¾ ÇÔ Ñ ØÓ Ý ½ ¾º½ Ç Ò Ò Ö ÒÝ ÔÓÑ Ö Û º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¾º¾ Ç Ö Ð Ò ØÝÛÒÓ Ð
 ÃÓÑÔ Ð ØÖÓÒ ÞÒÝ ÈÓ ÖÞÒ ½º¼ ÏÝ Ò ÖÓÛ ÒÓ ÔÖÞ Þ ÓÜÝ Ò ½º º Ï ÂÙÒ ½½ ¼ ¾¼¼ ËÔ ØÖ ½ ÃÓÑÔ Ð ØÖÓÒ ÞÒÝ ½ ½º½ ÇÔ ÔÖÓ ØÙ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ñ ÒØÝ
ÃÓÑÔ Ð ØÖÓÒ ÞÒÝ ÈÓ ÖÞÒ ½º¼ ÏÝ Ò ÖÓÛ ÒÓ ÔÖÞ Þ ÓÜÝ Ò ½º º Ï ÂÙÒ ½½ ¼ ¾¼¼ ËÔ ØÖ ½ ÃÓÑÔ Ð ØÖÓÒ ÞÒÝ ½ ½º½ ÇÔ ÔÖÓ ØÙ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ñ ÒØÝ
Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼ ½ Ó ÖÛ ØÓÖ Ò Ø ÔÙ ÛÝ Ù Þ Ò Ð ½ ½ ¼ ½ Þµ ÔÖÞ ÙÒ Ù Þ ÖÛ Ò Ò º ãö Øäµ
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁÁ Ï Ð ÏÝ Ù ÛÓÐÙ Ï Þ ð Û Ø ÈÖÓÑ Ò ÓÛ Ò Ø ÈÓÑ ÖÝ Ù ØÙ Å Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼ ½
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁÁ Ï Ð ÏÝ Ù ÛÓÐÙ Ï Þ ð Û Ø ÈÖÓÑ Ò ÓÛ Ò Ø ÈÓÑ ÖÝ Ù ØÙ Å Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼ ½
ÛÙÛÝÑ ÖÓÛÝ ÔÖ Ò ÂÓ ÒÒ ÀÓÖ ÂÓ ÒÒ ÀÓÖ ÛÙÛÝÑ ÖÓÛÝ ÔÖ Ò
 ½º Ò ¾º ÈÖÞÝ º Ï ÒÓ Ð ÓÖÝØÑÙ Þ ÒÓ Ù Ý Ó ÛÖ ÐÒ ÔÖÞ ÔÐ Ø Ò Ù ÐÒÓ µ º Ê Ó¹ Ð Û ÐÐ Þ º ÈÖ Ò Ð ÓÖÝØÑ Å º ÏÔÖÓÛ Þ Ò Ó Û ÐÓÛÝÑ ÖÓÛ Ó ÔÖ Ò Ò Ù Ý Ó Ò ÖÓÛ Ò Þ Û ØÓÖ ÐÓ ÓÛ Ó (, ) Ó ÔÓÛ Ò ÔÖ Ý ( ½, ½ ),( ¾, ¾ ),...
½º Ò ¾º ÈÖÞÝ º Ï ÒÓ Ð ÓÖÝØÑÙ Þ ÒÓ Ù Ý Ó ÛÖ ÐÒ ÔÖÞ ÔÐ Ø Ò Ù ÐÒÓ µ º Ê Ó¹ Ð Û ÐÐ Þ º ÈÖ Ò Ð ÓÖÝØÑ Å º ÏÔÖÓÛ Þ Ò Ó Û ÐÓÛÝÑ ÖÓÛ Ó ÔÖ Ò Ò Ù Ý Ó Ò ÖÓÛ Ò Þ Û ØÓÖ ÐÓ ÓÛ Ó (, ) Ó ÔÓÛ Ò ÔÖ Ý ( ½, ½ ),( ¾, ¾ ),...
Ï ØÔ ÈÖÞÝ Ý Ç ÐÒ Û ÒÓ Ó Þ Ò À Ð ¹ÈÓ Ø ÓÒ Ð Ø ÖÑ Ò Ý Ó ÁÒ Ò Ø Ñ ÖÝ ÃÓÔÞÝ Ï Ö Û ÍÒ Ú Ö ØÝ Û ØÒ ¾¼¼ ÖÝ ÃÓÔÞÝ À Ð ¹ÈÓ Ø ÓÒ Ð Ø ÖÑ Ò Ý Ó ÁÒ Ò Ø Ñ ½» ¼
 Ï Ö Û ÍÒ Ú Ö ØÝ Û ØÒ ¾¼¼ ½» ¼ ÔÖÞÝ Ö Þ ÛÝÔ Ø Ö Ò Ö Ò Ó ÞÓÒÝ Ò ØÖ Ø ÔÓÞÝÝ ÒÝ Ò ¹ÔÓÞÝÝ ÒÝ Ò Ò ÛÝÒ ¹ ¹ ¾¼ ÑÝ ¹½ ¹½ ¹¾ ½¼ ¹¾ ¹½ ¹¾ ÓÒ ¹½ ¹ ¾» ¼ ÔÖÞÝ Ö Ô ÖÞÝ ØÓ Ö Ò Ó ÞÓÒÝ Ò ØÖ Ø ÔÓÞÝÝ ÒÝ Ò ¹ÔÓÞÝÝ ÒÝ Ò Ò ÛÝÒ
Ï Ö Û ÍÒ Ú Ö ØÝ Û ØÒ ¾¼¼ ½» ¼ ÔÖÞÝ Ö Þ ÛÝÔ Ø Ö Ò Ö Ò Ó ÞÓÒÝ Ò ØÖ Ø ÔÓÞÝÝ ÒÝ Ò ¹ÔÓÞÝÝ ÒÝ Ò Ò ÛÝÒ ¹ ¹ ¾¼ ÑÝ ¹½ ¹½ ¹¾ ½¼ ¹¾ ¹½ ¹¾ ÓÒ ¹½ ¹ ¾» ¼ ÔÖÞÝ Ö Ô ÖÞÝ ØÓ Ö Ò Ó ÞÓÒÝ Ò ØÖ Ø ÔÓÞÝÝ ÒÝ Ò ¹ÔÓÞÝÝ ÒÝ Ò Ò ÛÝÒ
ÏÝ Ö Ò ÖÙÒ Û ÛÓÐÙ Ö Ò ÓÛ Â ÖÓ Û Ö ÈÓÐ Ø Ò Ï Ö Þ Û ÁÒ ØÝØÙØ ËÝ Ø Ñ Û Ð ØÖÓÒ ÞÒÝ ¹Ñ Ð Ö Ð ºÔÛº ÙºÔÐ Ñ Ò Ö ÙÑ Ù ÁÒØ Ð ÒØÒÝ ËÝ Ø Ñ Û Ï ÔÓÑ Ò ÝÞ ÈÓÐ Ø Ò ÈÓ
 ÏÝ Ö Ò ÖÙÒ Û ÛÓÐÙ Ö Ò ÓÛ Â ÖÓ Û Ö ÈÓÐ Ø Ò Ï Ö Þ Û ÁÒ ØÝØÙØ ËÝ Ø Ñ Û Ð ØÖÓÒ ÞÒÝ ¹Ñ Ð Ö Ð ºÔÛº ÙºÔÐ Ñ Ò Ö ÙÑ Ù ÁÒØ Ð ÒØÒÝ ËÝ Ø Ñ Û Ï ÔÓÑ Ò ÝÞ ÈÓÐ Ø Ò ÈÓÞÒ ¾ º½½º¾¼½¼ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ð ÓÖÝØÑ ÛÓÐÙÝ ÒÝ Ó ÖÓÞ
ÏÝ Ö Ò ÖÙÒ Û ÛÓÐÙ Ö Ò ÓÛ Â ÖÓ Û Ö ÈÓÐ Ø Ò Ï Ö Þ Û ÁÒ ØÝØÙØ ËÝ Ø Ñ Û Ð ØÖÓÒ ÞÒÝ ¹Ñ Ð Ö Ð ºÔÛº ÙºÔÐ Ñ Ò Ö ÙÑ Ù ÁÒØ Ð ÒØÒÝ ËÝ Ø Ñ Û Ï ÔÓÑ Ò ÝÞ ÈÓÐ Ø Ò ÈÓÞÒ ¾ º½½º¾¼½¼ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ð ÓÖÝØÑ ÛÓÐÙÝ ÒÝ Ó ÖÓÞ
 Þ Á Í Ù ÞÓÖ ÒØÓÛ Ò ÔÓ Þ Ò ÓÛÓ Ù Ù ÞÔÓ Þ Ò ÓÛ Ï Ö ØÛÝ ÑÓ Ó ÖÓÛ Û Ö ØÛÓÑ Ð ÝÑ Ó Ò ÔÓÞ ÓÑ ÛÝ Ù Ù ÞÔÓ Þ Ò ÓÛ Ù Ù ÛÝÑ ÔÓ Þ Ò º Ï Ù Ù ÓÛÝ ÞÓÖ ÒØÓÛ ÒÝ ÔÓ Þ Ò ÓÛÓ Ù ÝØ ÓÛÒ Ù Ù Ò Ô ÖÛ Ù Ø Ð ÔÓ Þ Ò ÔÓØ Ñ ÔÓ Þ Ò
Þ Á Í Ù ÞÓÖ ÒØÓÛ Ò ÔÓ Þ Ò ÓÛÓ Ù Ù ÞÔÓ Þ Ò ÓÛ Ï Ö ØÛÝ ÑÓ Ó ÖÓÛ Û Ö ØÛÓÑ Ð ÝÑ Ó Ò ÔÓÞ ÓÑ ÛÝ Ù Ù ÞÔÓ Þ Ò ÓÛ Ù Ù ÛÝÑ ÔÓ Þ Ò º Ï Ù Ù ÓÛÝ ÞÓÖ ÒØÓÛ ÒÝ ÔÓ Þ Ò ÓÛÓ Ù ÝØ ÓÛÒ Ù Ù Ò Ô ÖÛ Ù Ø Ð ÔÓ Þ Ò ÔÓØ Ñ ÔÓ Þ Ò
pomiary teoria #pomiarow N
 ÞÝ Á Å Ò ÔÖÓ º Ö º Ð Ò Ö Ð Ô ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Á Ã Ò Ñ ØÝ ÈÓÑ ÖÝ ÞÝÞÒ Ù ÒÓ Ø ËÁ Ý ÔÓÑ ÖÓÛ Ã Ò Ñ ØÝ ÔÓ ÔÓ Ø ÛÓÛ µ ÔÙÒ Ø Ñ Ø Ö ÐÒÝ Ù Ó Ò Ò Ù Û Ô ÖÞ ÒÝ µ ØÓÖ ÔÖ Óð ð ÔÖÞÝ Ô Þ Ò ÊÙ ÒÓ Ø ÒÝ
ÞÝ Á Å Ò ÔÖÓ º Ö º Ð Ò Ö Ð Ô ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ Á Ã Ò Ñ ØÝ ÈÓÑ ÖÝ ÞÝÞÒ Ù ÒÓ Ø ËÁ Ý ÔÓÑ ÖÓÛ Ã Ò Ñ ØÝ ÔÓ ÔÓ Ø ÛÓÛ µ ÔÙÒ Ø Ñ Ø Ö ÐÒÝ Ù Ó Ò Ò Ù Û Ô ÖÞ ÒÝ µ ØÓÖ ÔÖ Óð ð ÔÖÞÝ Ô Þ Ò ÊÙ ÒÓ Ø ÒÝ
ÈÖÓÑ Ò ÓØÛ ÖÞÓð ð ÔÖÞ Þ Àº ÕÙ Ö Ð Û ÖÓ Ù ½ º Ç ÖÝØ Æ ÙØÖ Ò ÙÖ ÒÙ Ñ ØÓÛ Ý ÔÖÓÑ Ò ÓÛ Ò Ø Ö Þ ÑÒ Ó Ô ÝØ ÓØÓ Ö ÞÒ º ËÓÐ ¹ Ò ÖÓ ÆÓ Ð ÛÖ Þ Þ ÅºË Ó ÓÛ Èº ÙÖ
 ð Ö Ò ÙØÖ Ò Æ ÙØÖ Ò ÔÖÓ º Ö º Ð Ò Ö Ð Ô ÖÒ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÏÝ ½¾ Æ ÙØÖ Ò Û ÒÓð ÈÓÑ ÖÝ Ò ÙØÖ Ò Ç ÝÐ Ò ÙØÖ Ò ÈÖÓÑ Ò ÓØÛ ÖÞÓð ð ÔÖÞ Þ Àº ÕÙ Ö Ð Û ÖÓ Ù ½ º Ç ÖÝØ Æ ÙØÖ Ò ÙÖ ÒÙ Ñ ØÓÛ Ý ÔÖÓÑ Ò ÓÛ Ò
ð Ö Ò ÙØÖ Ò Æ ÙØÖ Ò ÔÖÓ º Ö º Ð Ò Ö Ð Ô ÖÒ Þ Ø Ð Ñ ÒØ ÖÒÝ Ï Þ ð Û Ø ÏÝ ½¾ Æ ÙØÖ Ò Û ÒÓð ÈÓÑ ÖÝ Ò ÙØÖ Ò Ç ÝÐ Ò ÙØÖ Ò ÈÖÓÑ Ò ÓØÛ ÖÞÓð ð ÔÖÞ Þ Àº ÕÙ Ö Ð Û ÖÓ Ù ½ º Ç ÖÝØ Æ ÙØÖ Ò ÙÖ ÒÙ Ñ ØÓÛ Ý ÔÖÓÑ Ò ÓÛ Ò
 ÁÒ ØÝØÙØ ÈÓ Ø Û ÁÒ ÓÖÑ ØÝ ÈÓÐ Ñ Æ Ù Ì ÑÔÓÖ ÐÒ Ô ØÝ ÔÐÓÖ ÒÝ Ñ ØÓ Ý Þ ÓÖ Û ÔÖÞÝ Ð ÓÒÝ ÊÇ ÈÊ Ï ÇÃÌÇÊËà ÙØÓÖ Ñ Ö È ÓØÖ ËÝÒ ÈÖÓÑÓØÓÖ ÈÖÓ º Ö º Ò º Ò ÖÞ Ë ÓÛÖÓÒ Ï Ö Þ Û ¾¼¼ Öº ËÔ ØÖ ½ Ï ØÔ ½º½ ÏÔÖÓÛ Þ Ò º º
ÁÒ ØÝØÙØ ÈÓ Ø Û ÁÒ ÓÖÑ ØÝ ÈÓÐ Ñ Æ Ù Ì ÑÔÓÖ ÐÒ Ô ØÝ ÔÐÓÖ ÒÝ Ñ ØÓ Ý Þ ÓÖ Û ÔÖÞÝ Ð ÓÒÝ ÊÇ ÈÊ Ï ÇÃÌÇÊËà ÙØÓÖ Ñ Ö È ÓØÖ ËÝÒ ÈÖÓÑÓØÓÖ ÈÖÓ º Ö º Ò º Ò ÖÞ Ë ÓÛÖÓÒ Ï Ö Þ Û ¾¼¼ Öº ËÔ ØÖ ½ Ï ØÔ ½º½ ÏÔÖÓÛ Þ Ò º º
ÈÓÔÖ ÛÒ ÛÝ ÓÖÞÝ Ø Ò ÏÞÓÖ ÔÖÓ ØÓÛ áö Ò ÓµÞ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û ÏÝ ¾ ¹ Ø Ó ÛÞÓÖ ÔÖÓ ØÓÛ ÊÓ ÖØ ÆÓÛ ¾¼¼ áö Ò ÓµÞ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û ½»
 ÏÝ ¾ ¹ Ø Ó ÛÞÓÖ ÔÖÓ ØÓÛ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ÈÒ ÛÝ Ù ÔÓ Ø ÛÓÛ ÔÓ Û ÔÓÛØ ÖÞ Ò µ Ø Ó ÞÝÞÒ Ó ÞÒ ÔÓÛØ ÖÞ Ò µ Ö Þ Þ Þ Ò ÔÓÛØ ÖÞ Ò µ ÛÞÓÖ ÔÖÓ ØÓÛ Ò ØÓÒ ÔÖÓØÓØÝÔ ¾» Ö Ò Ö ¹ Ý Ò Þ Ô ÛÒ Ò ÞÛ Ó ÒÓ Ó Þ Ó ÜØ ÖÒ ÒØ Ü»»
ÏÝ ¾ ¹ Ø Ó ÛÞÓÖ ÔÖÓ ØÓÛ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ÈÒ ÛÝ Ù ÔÓ Ø ÛÓÛ ÔÓ Û ÔÓÛØ ÖÞ Ò µ Ø Ó ÞÝÞÒ Ó ÞÒ ÔÓÛØ ÖÞ Ò µ Ö Þ Þ Þ Ò ÔÓÛØ ÖÞ Ò µ ÛÞÓÖ ÔÖÓ ØÓÛ Ò ØÓÒ ÔÖÓØÓØÝÔ ¾» Ö Ò Ö ¹ Ý Ò Þ Ô ÛÒ Ò ÞÛ Ó ÒÓ Ó Þ Ó ÜØ ÖÒ ÒØ Ü»»
ð Ö ½¼¼ Å Î ¹ Ì Î ½¼ ½ ØÑÓ ÖÝÞÒ Ñ ¾ Ð Ö ØÓÖÓÛ ÖÞ Ù Î ½¼ ¾¼ Æ ÙØÖ Ò ÌÝÔ Ô Ò Ö ËØÖÙÑ ðò ½ Å Î ½¼ ½¼ ½ Ë ÓÒ ÞÒ Ñ ¾ Ò Ñ µ ÔÓÛÝ Þ ½¼ Šε ÖÞ Ù Å Î ½¼ ½ Ê Ø
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ ØÖÓÒÓÑ Ò ÙØÖ Ò µ Ô ÖÝÑ ÒØ Á Ù ÛÓÐÙ Û Þ ð Ö ½¼¼ Å Î ¹ Ì Î ½¼ ½ ØÑÓ ÖÝÞÒ Ñ ¾ Ð Ö ØÓÖÓÛ ÖÞ Ù Î ½¼ ¾¼ Æ ÙØÖ Ò ÌÝÔ Ô Ò Ö ËØÖÙÑ ðò ½ Å Î ½¼ ½¼ ½
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ ØÖÓÒÓÑ Ò ÙØÖ Ò µ Ô ÖÝÑ ÒØ Á Ù ÛÓÐÙ Û Þ ð Ö ½¼¼ Å Î ¹ Ì Î ½¼ ½ ØÑÓ ÖÝÞÒ Ñ ¾ Ð Ö ØÓÖÓÛ ÖÞ Ù Î ½¼ ¾¼ Æ ÙØÖ Ò ÌÝÔ Ô Ò Ö ËØÖÙÑ ðò ½ Å Î ½¼ ½¼ ½
ËÞ ÐÓÒÝ ¹ ÔÓÛØ ÖÞ Ò ÈÖÓ Ð ÑÝ ÔÖÞÝ ØÓ ÓÛ Ò Ù Þ ÐÓÒ Û áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¼ ¹ Þ ÐÓÒÝ ÊÓ ÖØ ÆÓÛ ¾¼¼ áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û È
 áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¼ ¹ Þ ÓÒÝ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ÃÓ ÓÖÝØÑÝ ÈÓ Ò Þ Ò Ó ØÝÔÙ Ó ÒÔº Øݵ ÓÖÝØÑÝ ÒÔº ÞÒ ÓÛ Ò Ò Û Þ Ó Ñ ÒØÙµ Å Ò ÞÑÝ Ñ ÒÙ Ö ÙÒ Ò Ó Ùº Û Ô Ò ÞÓÛ ÛÝ ÓÖÞÝ Ø Ò Þ ÓÒ Û ¾» à ÞÓÛ ÒÙ
áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¼ ¹ Þ ÓÒÝ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ÃÓ ÓÖÝØÑÝ ÈÓ Ò Þ Ò Ó ØÝÔÙ Ó ÒÔº Øݵ ÓÖÝØÑÝ ÒÔº ÞÒ ÓÛ Ò Ò Û Þ Ó Ñ ÒØÙµ Å Ò ÞÑÝ Ñ ÒÙ Ö ÙÒ Ò Ó Ùº Û Ô Ò ÞÓÛ ÛÝ ÓÖÞÝ Ø Ò Þ ÓÒ Û ¾» à ÞÓÛ ÒÙ
Survival Probability /E. (km/mev)
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ ØÖÓÒÓÑ Ò ÙØÖ Ò µ Ô ÖÝÑ ÒØ Á Ù ÛÓÐÙ Û Þ ð Ö ½¼¼ Å Î ¹ Ì Î ½¼ ½ ØÑÓ ÖÝÞÒ Ñ ¾ Ð Ö ØÓÖÓÛ ÖÞ Ù Î ½¼ ¾¼ Æ ÙØÖ Ò ÌÝÔ Ô Ò Ö ËØÖÙÑ ðò ½ Å Î ½¼ ½¼ ½
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ ØÖÓÒÓÑ Ò ÙØÖ Ò µ Ô ÖÝÑ ÒØ Á Ù ÛÓÐÙ Û Þ ð Ö ½¼¼ Å Î ¹ Ì Î ½¼ ½ ØÑÓ ÖÝÞÒ Ñ ¾ Ð Ö ØÓÖÓÛ ÖÞ Ù Î ½¼ ¾¼ Æ ÙØÖ Ò ÌÝÔ Ô Ò Ö ËØÖÙÑ ðò ½ Å Î ½¼ ½¼ ½
ÈÖÞ ØÛ ÖÞ Ò Ø ØÙ Û ÈÓÛØ ÖÞ Ò áö Ò Óµ Þ Û Ò ÓÛ Ò Èʵ ÏÝ ¹ ÔÖÞ ØÛ ÖÞ Ò Ø ØÙ ÊÓ ÖØ ÆÓÛ ¾¼¼ áö Ò Óµ Þ Û Ò ÓÛ Ò Èʵ ½»
 ÏÝ ¹ ÔÖÞ ØÛ ÖÞ Ò Ø ØÙ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» È Ò ÛÝ Ù Ó ÞÑ ÓÓ Ø Ö Ü ÓÓ Ø ÜÔÖ Ú ÓÓ Ø Ô Ö Ø ÈÖÞÝ ÓÛ Þ Ò Ò ÓÓ Û ÙÑ ¾» ÈÖÞ ØÛ ÖÞ Ò Ø ØÙ Û» ÔÖÞ ØÛ ÖÞ Ò Ø ØÙ ÙÒ ÓÒÛ ÖØÙ Þ ³ ÍØÛÓÖÞ Ò Þ Ý Ò ÔÓ Ø Û Ò Ô Ù ÒÙ Ø ÒØ ØÓ ½¾
ÏÝ ¹ ÔÖÞ ØÛ ÖÞ Ò Ø ØÙ ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» È Ò ÛÝ Ù Ó ÞÑ ÓÓ Ø Ö Ü ÓÓ Ø ÜÔÖ Ú ÓÓ Ø Ô Ö Ø ÈÖÞÝ ÓÛ Þ Ò Ò ÓÓ Û ÙÑ ¾» ÈÖÞ ØÛ ÖÞ Ò Ø ØÙ Û» ÔÖÞ ØÛ ÖÞ Ò Ø ØÙ ÙÒ ÓÒÛ ÖØÙ Þ ³ ÍØÛÓÖÞ Ò Þ Ý Ò ÔÓ Ø Û Ò Ô Ù ÒÙ Ø ÒØ ØÓ ½¾
ÑÒ Ñ Ø Ö Ò Ð Å ÈÓ ÞÙ Û Ò Ý Ò Û Ò Ð Å Û Û ÞÝ Ø ÑÓ ÞÐ ÛÝ Ò ÔÖÓÑ Ò ÓÛ Ò ÑÑ ÔÓÞÝØÓÒÝ ÒØÝÔÖÓØÓÒÝ ººº µ ÑÓ Þ ÑÝ Ø Þ ÞÙ ð Ò ÙØÖ Ò º º ÖÒ ÏÝ ÁÁ ½
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ Æ ÙØÖ Ò Û ÒÓð ËÙÔ Ö Ã Ñ Ó Ò Á Ù ÑÒ Ñ Ø Ö Ò Ð Å ÈÓ ÞÙ Û Ò Ý Ò Û Ò Ð Å Û Û ÞÝ Ø ÑÓ ÞÐ ÛÝ Ò ÔÖÓÑ Ò ÓÛ Ò ÑÑ ÔÓÞÝØÓÒÝ ÒØÝÔÖÓØÓÒÝ ººº µ ÑÓ Þ ÑÝ Ø
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁ Æ ÙØÖ Ò Û ÒÓð ËÙÔ Ö Ã Ñ Ó Ò Á Ù ÑÒ Ñ Ø Ö Ò Ð Å ÈÓ ÞÙ Û Ò Ý Ò Û Ò Ð Å Û Û ÞÝ Ø ÑÓ ÞÐ ÛÝ Ò ÔÖÓÑ Ò ÓÛ Ò ÑÑ ÔÓÞÝØÓÒÝ ÒØÝÔÖÓØÓÒÝ ººº µ ÑÓ Þ ÑÝ Ø
Ð ÓÖÝØÑÝ ØÖÙ ØÙÖÝ ÒÝ Ñ Ø Ö Ý ÛÝ ÓÛ ËØÙ Þ ÓÞÒ ÈÂÏËÌÃ Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÎ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÒÝ ËØÖÙ ØÙÖÝ ÓÛÒ Ð ØÝ ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑ
 Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÎ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÒÝ ËØÖÙ ØÙÖÝ ÓÛÒ Ð ØÝ ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ¾ Ð ØÓÔ ¾¼¼ ¾ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð ÓÔ Ö Ò Ð Ø Ð ÓÖÝØÑ Ë ÔÖÞ Ó Þ Ò Ö Ù Ð ÓÖÝØÑ Ë ÔÖÞ
Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ ÁÎ Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã ÒÝ ËØÖÙ ØÙÖÝ ÓÛÒ Ð ØÝ ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ¾ Ð ØÓÔ ¾¼¼ ¾ Ð ØÓÔ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð ÓÔ Ö Ò Ð Ø Ð ÓÖÝØÑ Ë ÔÖÞ Ó Þ Ò Ö Ù Ð ÓÖÝØÑ Ë ÔÖÞ
LVI Olimpiada Fizyczna zawody III stopnia
 LV Olimpiada Fizyczna zawody stopnia Zadanie 1 Piłka uderza w poziomą podłogę pod kątem α z prędkością v 0. Współczynnik tarcia piłki o podłogę jest równy µ. W jakiej odległości od miejsca pierwszego uderzenia
LV Olimpiada Fizyczna zawody stopnia Zadanie 1 Piłka uderza w poziomą podłogę pod kątem α z prędkością v 0. Współczynnik tarcia piłki o podłogę jest równy µ. W jakiej odległości od miejsca pierwszego uderzenia
Reguly. Wind = Weak Temp > 20 Outlook Rain PlayTennis = Y es
 ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ Ï ÖÙÒ Ð ØÓÖ Û Ý Ð ØÓÖ Ö ÔÖ Þ ÒØÙ Ø Ø Û ÖØÓ ÃÓÒ ÙÒ ØÖÝ ÙØÙ Û ÖÙÒ Ó ÔÓÛ Ó ØÓÑ Ô Ò ÝÑ ÔÓ ÝÒÞ Ó Ð ØÓÖÝ Û ÞÝ Ø ÝÞ Ö Ù ÞÛ Þ Ò Ø Þ Ò ÝÞ Ã Reguly ÔÖÞÝÔ ÝÛ Ò Ó ØÓÑ Ô Ò ÝÑ Û ÖÙÒ Ö Ù
ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ Ï ÖÙÒ Ð ØÓÖ Û Ý Ð ØÓÖ Ö ÔÖ Þ ÒØÙ Ø Ø Û ÖØÓ ÃÓÒ ÙÒ ØÖÝ ÙØÙ Û ÖÙÒ Ó ÔÓÛ Ó ØÓÑ Ô Ò ÝÑ ÔÓ ÝÒÞ Ó Ð ØÓÖÝ Û ÞÝ Ø ÝÞ Ö Ù ÞÛ Þ Ò Ø Þ Ò ÝÞ Ã Reguly ÔÖÞÝÔ ÝÛ Ò Ó ØÓÑ Ô Ò ÝÑ Û ÖÙÒ Ö Ù
f (n) lim n g (n) = a, f g
 Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ Á Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã Ï ØÔ ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ½¾ Ô õ Þ ÖÒ ¾¼¼ ½¾ Ô õ Þ ÖÒ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð ÛÝ Ù ÈÐ Ò ÒÓØ ÝÑÔØÓØÝÞÒ ÔÓ Ð ÓÖÝØÑÙ Ó ÞØ Ð ÓÖÝØÑÙ Þ Ó ÓÒÓ
Á ËÌÊÍÃÌÍÊ Æ À Ä ÇÊ ÌÅ Á Ñ Ø Ö Ý ÔÓÑÓÒ Þ µ Ï Ã Ï ØÔ ÈÓÐ Ó Â ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ Ï Ö Þ Û ½¾ Ô õ Þ ÖÒ ¾¼¼ ½¾ Ô õ Þ ÖÒ ¾¼¼ ËÐ ½ È Û Ê Ñ Ð ÛÝ Ù ÈÐ Ò ÒÓØ ÝÑÔØÓØÝÞÒ ÔÓ Ð ÓÖÝØÑÙ Ó ÞØ Ð ÓÖÝØÑÙ Þ Ó ÓÒÓ
System ALVINN. 30 Output. Units. 4 Hidden. Units. 30x32 Sensor Input Retina. Straight Ahead. Sharp Right. Sharp Left
 ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ System ALVINN ÄÎÁÆÆ ÔÖÓÛ Þ ÑÓ ÔÓ ÙØÓ ØÖ Þ Þ ÞÝ Ó ¼ Ñ Ð Ò Ó Þ Ò Sharp Left Straight Ahead Sharp Right 30 Output Units 4 Hidden Units 30x32 Sensor Input Retina ¾ www.wisewire.com,
ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ System ALVINN ÄÎÁÆÆ ÔÖÓÛ Þ ÑÓ ÔÓ ÙØÓ ØÖ Þ Þ ÞÝ Ó ¼ Ñ Ð Ò Ó Þ Ò Sharp Left Straight Ahead Sharp Right 30 Output Units 4 Hidden Units 30x32 Sensor Input Retina ¾ www.wisewire.com,
ÈÖ ÔÖÞ Ð Ñ Ó Ó ÒÝ Ø ÈÓ Ô ÙØÓÖ ÔÖ Ý ÈÖ Ø ÓØÓÛ Ó Ó ÒÝ ÔÖÞ Þ Ö ÒÞ ÒØ Ø ÈÓ Ô ÖÙ Ó ÔÖ
 ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Ð Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò È Û Ð Å Ð ÒÞÙ ÆÖ Ð ÙÑÙ ½ ½ Ò Ð Þ ÑÔÐ Ñ ÒØ Ð Ò ÛÝ ÞÝ ÓÛ ÙÒ Ý ÒÝ ÈÖ Ñ Ø Ö Ò ÖÙÒ Ù ÁÆ ÇÊÅ Ì Ã ÈÖ ÛÝ ÓÒ Ò ÔÓ ÖÙÒ Ñ Ö Ð Ó Ë Ù ÖØ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ Ð ÄÓ ËØÓ
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Ð Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò È Û Ð Å Ð ÒÞÙ ÆÖ Ð ÙÑÙ ½ ½ Ò Ð Þ ÑÔÐ Ñ ÒØ Ð Ò ÛÝ ÞÝ ÓÛ ÙÒ Ý ÒÝ ÈÖ Ñ Ø Ö Ò ÖÙÒ Ù ÁÆ ÇÊÅ Ì Ã ÈÖ ÛÝ ÓÒ Ò ÔÓ ÖÙÒ Ñ Ö Ð Ó Ë Ù ÖØ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ Ð ÄÓ ËØÓ
ØÓ ÔÖ Ù Ð ØÖÝÞÒ Ó ÈÖ Ó ÙÒÓ Þ Ò Ó Ò ÓÖ ØÓ ÔÖ Ù Ø Û ØÓÖ Ñ Ø Ö Ó ÖÙÒ ÛÝÞÒ Þ ØÝÞÒ Ó ØÓÖÙ ÔÓÖÙ Þ Ó ÙÒ Ù Ó ØÒ Óº ÛÖÓØ Û ØÓÖ Ó Ö Ð ÙÑÓÛÒ Ó ÖÙÒ ÖÙ Ù ÙÒ Ù Ó ØÒ
 ÈÖ Ð ØÖÝÞÒÝ ÈÓÐ Ñ Ò ØÝÞÒ ½¼»½ Ò ÖÞ Ã Ô ÒÓÛ ØØÔ»»Ù Ö ºÙ º ÙºÔл Ù Ô ÒÓ» ÁÒ ØÝØÙØ ÞÝ ÍÒ Û Ö ÝØ Ø Â ÐÐÓ ÃÖ Û ¾¼½ ÈÖ Ð ØÖÝÞÒÝ Ø ØÓ ÙÔÓÖÞ ÓÛ ÒÝ ÖÙ ÙÒ Û Ð ØÖÝÞÒÝ º ÊÙ ÙÒ Û ÑÓ Ñ Ñ Û ÔÖÞ ÛÓ Ò Û Ô ÛÒÝ Û ÖÙÒ Ö ÛÒ
ÈÖ Ð ØÖÝÞÒÝ ÈÓÐ Ñ Ò ØÝÞÒ ½¼»½ Ò ÖÞ Ã Ô ÒÓÛ ØØÔ»»Ù Ö ºÙ º ÙºÔл Ù Ô ÒÓ» ÁÒ ØÝØÙØ ÞÝ ÍÒ Û Ö ÝØ Ø Â ÐÐÓ ÃÖ Û ¾¼½ ÈÖ Ð ØÖÝÞÒÝ Ø ØÓ ÙÔÓÖÞ ÓÛ ÒÝ ÖÙ ÙÒ Û Ð ØÖÝÞÒÝ º ÊÙ ÙÒ Û ÑÓ Ñ Ñ Û ÔÖÞ ÛÓ Ò Û Ô ÛÒÝ Û ÖÙÒ Ö ÛÒ
Sieci neuronowe: pomysl
 ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ ØÓ Þ ÞÙÑ ÓÒ Ó õ ØÖ ÒÙ ÔÓÞ ÓÑ ÔÓØ Ò Ù Ð ØÖÝÞÒ Ó ËÝ Ò Ý ÓÑ Ö Sieci neuronowe: pomysl Æ Ð ÓÛ Ò Ñ Þ Ù Þ Ó Ó ÓÑ Ö Ò ÙÖÓÒÓÛÝ Axonal arborization Synapse Axon from another cell Dendrite
ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ½ ØÓ Þ ÞÙÑ ÓÒ Ó õ ØÖ ÒÙ ÔÓÞ ÓÑ ÔÓØ Ò Ù Ð ØÖÝÞÒ Ó ËÝ Ò Ý ÓÑ Ö Sieci neuronowe: pomysl Æ Ð ÓÛ Ò Ñ Þ Ù Þ Ó Ó ÓÑ Ö Ò ÙÖÓÒÓÛÝ Axonal arborization Synapse Axon from another cell Dendrite
Fizyka I (mechanika), rok akad. 2012/2013 Zadania kolokwialne 1
 ÞÝ Á ¾¼½¾»¾¼½ µ ÃÓÐÓ Û ÙÑ ½ º½½º¾¼½¾ Ò Ö ÙÒ ÓÛ ÖÙÔ ÍÛ Ã Þ Ò ÖÓÞÛ ÞÙ ÑÝ Ò Ó Ó Ò ÖØ º ÈÖ ÔÓÛ ÒÒÝ Ý ÞÝØ ÐÒ ÓÐ Ò ÖÓ ÓÔ ØÖÞÓÒ Ø Ñ ÓÑ ÒØ ÖÞ Ñ Ý ØÓ ÖÓÞÙÑÓÛ Ò Ý ÒÝ Ð ÔÖ Û Þ Óº ÊÓÞÛ ÞÙ Þ Ò ÛÝÔÖÓÛ õ ÛÞ Ö Ó ÓÛÝ ÔÖ
ÞÝ Á ¾¼½¾»¾¼½ µ ÃÓÐÓ Û ÙÑ ½ º½½º¾¼½¾ Ò Ö ÙÒ ÓÛ ÖÙÔ ÍÛ Ã Þ Ò ÖÓÞÛ ÞÙ ÑÝ Ò Ó Ó Ò ÖØ º ÈÖ ÔÓÛ ÒÒÝ Ý ÞÝØ ÐÒ ÓÐ Ò ÖÓ ÓÔ ØÖÞÓÒ Ø Ñ ÓÑ ÒØ ÖÞ Ñ Ý ØÓ ÖÓÞÙÑÓÛ Ò Ý ÒÝ Ð ÔÖ Û Þ Óº ÊÓÞÛ ÞÙ Þ Ò ÛÝÔÖÓÛ õ ÛÞ Ö Ó ÓÛÝ ÔÖ
ÊÓÞÔÓÞÒ Û Ò Ð ØÖÓÒ Û Ñ ÞÓÒ Û π 0 ÔÖÞÝ Ò Ù Ó Þ ÝÛ Ò ÙØÖ Ò Û Þ ØÓ ÓÛ Ò Ù Ó Ø ØÓÖ Û Ó¹ Ö ÓÒÓÛÝ ÓÖ Þ Ð Ó Ø ØÓÖ Ô ÖÝÑ ÒØ٠̾à ÌÓÑ Þ Ï ÁÒ ØÝØÙØ ÞÝ Â ÖÓÛ Ñº
 ÊÓÞÔÓÞÒ Û Ò Ð ØÖÓÒ Û Ñ ÞÓÒ Û π ÔÖÞÝ Ò Ù Ó Þ ÝÛ Ò ÙØÖ Ò Û Þ ØÓ ÓÛ Ò Ù Ó Ø ØÓÖ Û Ó¹ Ö ÓÒÓÛÝ ÓÖ Þ Ð Ó Ø ØÓÖ Ô ÖÝÑ ÒØ٠̾à ÌÓÑ Þ Ï ÁÒ ØÝØÙØ ÞÝ Â ÖÓÛ Ñº À ÒÖÝ Æ ÛÓ Ò Þ Ó ÈÓÐ Ñ Æ Ù ÊÓÞÔÖ Û Ó ØÓÖ ÔÖÞÝ ÓØÓÛ Ò
ÊÓÞÔÓÞÒ Û Ò Ð ØÖÓÒ Û Ñ ÞÓÒ Û π ÔÖÞÝ Ò Ù Ó Þ ÝÛ Ò ÙØÖ Ò Û Þ ØÓ ÓÛ Ò Ù Ó Ø ØÓÖ Û Ó¹ Ö ÓÒÓÛÝ ÓÖ Þ Ð Ó Ø ØÓÖ Ô ÖÝÑ ÒØ٠̾à ÌÓÑ Þ Ï ÁÒ ØÝØÙØ ÞÝ Â ÖÓÛ Ñº À ÒÖÝ Æ ÛÓ Ò Þ Ó ÈÓÐ Ñ Æ Ù ÊÓÞÔÖ Û Ó ØÓÖ ÔÖÞÝ ÓØÓÛ Ò
e 2 = 8, 3 e 1 = 5, 1, e 2 = i 3 + i
 ÆÓØ Ø Ó Û Þ Þ Ò Ð ÞÝ Ð Öݺ Ä Ê Ò ½ ÞÝ Û ØÓÖ v ÑÓ Ò ÔÖÞ Ø Û Ó ÓÑ Ò Ð Ò ÓÛ Û ØÓÖ Û e e 2 Þ i) v = 2, 4 e = 5, 7 e 2 = 8, 3 6 9 ÓÖ Þ ii) v = 2 3, e = Ç ÔÓÛ õ i) Ø v = 2e e 2 ii) Ò º, e 2 =, Ò ¾ ÞÝ Û ØÓÖÝ
ÆÓØ Ø Ó Û Þ Þ Ò Ð ÞÝ Ð Öݺ Ä Ê Ò ½ ÞÝ Û ØÓÖ v ÑÓ Ò ÔÖÞ Ø Û Ó ÓÑ Ò Ð Ò ÓÛ Û ØÓÖ Û e e 2 Þ i) v = 2, 4 e = 5, 7 e 2 = 8, 3 6 9 ÓÖ Þ ii) v = 2 3, e = Ç ÔÓÛ õ i) Ø v = 2e e 2 ii) Ò º, e 2 =, Ò ¾ ÞÝ Û ØÓÖÝ
N j=1 (η M η j ) Û Ö η 1... η N Ö
 Ù ÔØ Ð ØÝ ÌÓÔÓÐÓ Ð ØÛ Ø Ñ ÖÑ ÓÒ ÖÓÑ Ù Ò Ô ØÖ Ð ÔÖÓ ØÓÖ Ý ÃÖÞÝ ÞØÓ Ë ÙØ Ò ÖÑ ÒÝ ÆÁ Ñ Å Û Þ ÍÒ Ú Ö ØÝ ÈÓÞÒ ÈÓÐ Ò ÓÐÐ ÓÖ Ø ÓÒ Û Ø Ò Ö Ê ÑÓ Ð Ò Ã ÖÐ Â Ò Ò Ä ÌÌÁ ¾¼½ ½» ¾ ÁÒØÖÓ ÙØ ÓÒ ÌÓÔÓÐÓ Ð ÒÓØ Ö Ð Ò Ò Ø
Ù ÔØ Ð ØÝ ÌÓÔÓÐÓ Ð ØÛ Ø Ñ ÖÑ ÓÒ ÖÓÑ Ù Ò Ô ØÖ Ð ÔÖÓ ØÓÖ Ý ÃÖÞÝ ÞØÓ Ë ÙØ Ò ÖÑ ÒÝ ÆÁ Ñ Å Û Þ ÍÒ Ú Ö ØÝ ÈÓÞÒ ÈÓÐ Ò ÓÐÐ ÓÖ Ø ÓÒ Û Ø Ò Ö Ê ÑÓ Ð Ò Ã ÖÐ Â Ò Ò Ä ÌÌÁ ¾¼½ ½» ¾ ÁÒØÖÓ ÙØ ÓÒ ÌÓÔÓÐÓ Ð ÒÓØ Ö Ð Ò Ò Ø
A(T)= A(0)=D(0)+E(0).
 2 ÅÓ Ð ØÖÙ ØÙÖ ÐÒ ÈÓ ØÖÙ ØÙÖ ÐÒ ÓÔ ÖØ Ø Ò ÔÖ Ù ÓÛÝ ÑÓ ÐÙ ÛÝ Ò Ó Þ ÖÞ Ò Ò ÖÙØÛ Û ÔÓÛ Þ Ò Ù Þ Þ Û Ñ Þ Ó Þ ÝÑ Û Ó Ö ÖÓÞ¹ Û Ò ÖÑݺ Å Û Ò ÔÖÓ ÖÝÞÝ Ó Ö Ø ÖÞ Ö ÝØÓÛÝÑ ÛÝÒ Þ Ö Ù ÓØ Û Ò Ö ÙÐÓÛ Ò ÞÓ ÓÛ Þ º ÙÒ ÓÒÓÛ
2 ÅÓ Ð ØÖÙ ØÙÖ ÐÒ ÈÓ ØÖÙ ØÙÖ ÐÒ ÓÔ ÖØ Ø Ò ÔÖ Ù ÓÛÝ ÑÓ ÐÙ ÛÝ Ò Ó Þ ÖÞ Ò Ò ÖÙØÛ Û ÔÓÛ Þ Ò Ù Þ Þ Û Ñ Þ Ó Þ ÝÑ Û Ó Ö ÖÓÞ¹ Û Ò ÖÑݺ Å Û Ò ÔÖÓ ÖÝÞÝ Ó Ö Ø ÖÞ Ö ÝØÓÛÝÑ ÛÝÒ Þ Ö Ù ÓØ Û Ò Ö ÙÐÓÛ Ò ÞÓ ÓÛ Þ º ÙÒ ÓÒÓÛ
1. Waciki do czyszczenia optyki 2. Isopropanol 3. SLED 4. Laser diodowy 1550nm 5. Mikroskop 6. Urządzenie do czyszczenia końcówek światłowodów
 ÁÁ ÈÖ ÓÛÒ ÞÝÞÒ Á Í Ǿ ½ Ǿ ¹ ÇÔØÝÞÒÝ ÛÞÑ Ò Þ Û Ø ÓÛÓ ÓÛÝ Ð Û Þ Ò Û Þ Ò Ø Ô ÖÝÑ ÒØ Ñ Þ Þ Þ ÒÝ ÓØÓÒ ÞÝ Ð Ö Û ÓØÝÞÝ Þ Ò ÓÖ Þ Û ÒÓ¹ Û ÒÓÛÝ Û Ø ÓÛÓ ÓÛÝ µ õö Û Ø º ÈÓ Ø ÛÓÛÝÑ Ð Ñ ÒØ Ñ Ù Ù Ó Û ¹ Þ ÐÒ Ó Ø Û ÒÓ»
ÁÁ ÈÖ ÓÛÒ ÞÝÞÒ Á Í Ǿ ½ Ǿ ¹ ÇÔØÝÞÒÝ ÛÞÑ Ò Þ Û Ø ÓÛÓ ÓÛÝ Ð Û Þ Ò Û Þ Ò Ø Ô ÖÝÑ ÒØ Ñ Þ Þ Þ ÒÝ ÓØÓÒ ÞÝ Ð Ö Û ÓØÝÞÝ Þ Ò ÓÖ Þ Û ÒÓ¹ Û ÒÓÛÝ Û Ø ÓÛÓ ÓÛÝ µ õö Û Ø º ÈÓ Ø ÛÓÛÝÑ Ð Ñ ÒØ Ñ Ù Ù Ó Û ¹ Þ ÐÒ Ó Ø Û ÒÓ»
¾ Å ÑÞ ÈÖ Þ Ó ÓÒÓ Û Ý Ø Ñ Ä Ì º
 Ç ÖÛ ØÓÖ ÙÑ ØÖÓÒÓÑ ÞÒ ÍÒ Û Ö ÝØ Ø Ñº Ñ Å Û Þ Û ÈÓÞÒ Ò Ù ÇÔØÝÑ Ð Þ Ñ ØÓ Ö Ù Ó ÖÛ ÓØÓÑ ØÖÝÞÒÝ ÈÖ Ñ Ø Ö Å ÑÞ Ã ÖÓÛÒ ÔÖ Ý ÔÖÓ º Ö º Ì Ù Þ Å ÓÛ ÇÔ ÙÒ ÔÖ Ý Ö ÌÓÑ Þ ÃÛ Ø ÓÛ ÈÓÞÒ ½ ¾ Å ÑÞ ÈÖ Þ Ó ÓÒÓ Û Ý Ø Ñ Ä
Ç ÖÛ ØÓÖ ÙÑ ØÖÓÒÓÑ ÞÒ ÍÒ Û Ö ÝØ Ø Ñº Ñ Å Û Þ Û ÈÓÞÒ Ò Ù ÇÔØÝÑ Ð Þ Ñ ØÓ Ö Ù Ó ÖÛ ÓØÓÑ ØÖÝÞÒÝ ÈÖ Ñ Ø Ö Å ÑÞ Ã ÖÓÛÒ ÔÖ Ý ÔÖÓ º Ö º Ì Ù Þ Å ÓÛ ÇÔ ÙÒ ÔÖ Ý Ö ÌÓÑ Þ ÃÛ Ø ÓÛ ÈÓÞÒ ½ ¾ Å ÑÞ ÈÖ Þ Ó ÓÒÓ Û Ý Ø Ñ Ä
ÃÓÒØ Ò ÖÝ Þ ÓÓ Ø ÓÓ Ø Ö Ô Ä Ö ÖÝ ÈÓÛØ ÖÞ Ò áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¾ ¹ ÓÒØ Ò ÖÝ Þ ÓÓ Ø ÊÓ ÖØ ÆÓÛ ¾¼¼ áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û È
 áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¾ ¹ ÓÒØ Ò ÖÝ Þ ÓÓ Ø ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ½ ËÌÄ ¹ Ø Ò Ö ÓÛ Ð ÓØ Þ ÐÓÒ Û ÓÒØ Ò ÖÝ Ø Ö ØÓÖÝ Ð ÓÖÝØÑÝ ÙÒ ØÓÖÝ Ó º ÙÒ Ý Ò µ ÔØ ÖÝ ÌÛÓÖÞ Ò ÙÒ ØÓÖ Û ÖÞÒ Ò ÔÓ Ø Û ØÒ Ý ÙÒ Ñ
áö Ò Ó Þ Û Ò ÓÛ Ò ÔÖÓ Ö ÑÓÛ Ò Û Èʵ ÏÝ ½¾ ¹ ÓÒØ Ò ÖÝ Þ ÓÓ Ø ÊÓ ÖØ ÆÓÛ ¾¼¼ ½» ½ ËÌÄ ¹ Ø Ò Ö ÓÛ Ð ÓØ Þ ÐÓÒ Û ÓÒØ Ò ÖÝ Ø Ö ØÓÖÝ Ð ÓÖÝØÑÝ ÙÒ ØÓÖÝ Ó º ÙÒ Ý Ò µ ÔØ ÖÝ ÌÛÓÖÞ Ò ÙÒ ØÓÖ Û ÖÞÒ Ò ÔÓ Ø Û ØÒ Ý ÙÒ Ñ
ÍÆÁÏ ÊË Ì Ì Ï ÊË ÏËÃÁ Ï Á Á ÃÁ  ËÞÞÝØ Ó È ÈÊ ÏÇ ÆÁÃÁ È Å Æ Ì Æ ÁÁÁ¹Î Å Æ Æ Å ÈÖ Ó ØÓÖ ÛÝ ÓÒ Ò Û ÁÒ ØÝØÙ ÞÝ Óð Û Þ ÐÒ Ò ÏÝ Þ Ð ÞÝ ÍÒ Û Ö ÝØ ØÙ Ï Ö Þ Û
 ÍÆÁÏ ÊË Ì Ì Ï ÊË ÏËÃÁ Ï Á Á ÃÁ  ËÞÞÝØ Ó È ÈÊ ÏÇ ÆÁÃÁ È Å Æ Ì Æ ÁÁÁ¹Î Å Æ Æ Å ÈÖ Ó ØÓÖ ÛÝ ÓÒ Ò Û ÁÒ ØÝØÙ ÞÝ Óð Û Þ ÐÒ Ò ÏÝ Þ Ð ÞÝ ÍÒ Û Ö ÝØ ØÙ Ï Ö Þ Û Ó ÔÓ ÖÙÒ Ñ ÔÖÓ º Ö º Ò ÖÞ ÌÛ Ö ÓÛ Ó Ï ÊË Ï Ð Ô ¾¼¼½
ÍÆÁÏ ÊË Ì Ì Ï ÊË ÏËÃÁ Ï Á Á ÃÁ  ËÞÞÝØ Ó È ÈÊ ÏÇ ÆÁÃÁ È Å Æ Ì Æ ÁÁÁ¹Î Å Æ Æ Å ÈÖ Ó ØÓÖ ÛÝ ÓÒ Ò Û ÁÒ ØÝØÙ ÞÝ Óð Û Þ ÐÒ Ò ÏÝ Þ Ð ÞÝ ÍÒ Û Ö ÝØ ØÙ Ï Ö Þ Û Ó ÔÓ ÖÙÒ Ñ ÔÖÓ º Ö º Ò ÖÞ ÌÛ Ö ÓÛ Ó Ï ÊË Ï Ð Ô ¾¼¼½
 Å Ø Ù Þ Ë ÓÖ ËØ ÐÒÓ Ñ Ò ÞÒ Ö ØÝ ÙÒ ÓÒ Ð ÞÓÛ ÒÝ Ò ÒÓÞ Ø Û ÑÓ Ð ÖÙ ÓÞ ÖÒ ØÝ ÈÖÓÑÓØÓÖ ÈÖÓ º Ö º Å Ö ÔÐ ÊÓÞÔÖ Û Ó ØÓÖ ÛÝ ÓÒ Ò Û áöó ÓÛ ÓÛÝÑ Ä ÓÖ ØÓÖ ÙÑ ÞÝ ÓÐÓ ÞÒ ÁÒ ØÝØÙØ ÞÝ È Æ Ï Ö Þ Û ½ Ñ ¾¼½¾ ÈÓ Þ ÓÛ Ò
Å Ø Ù Þ Ë ÓÖ ËØ ÐÒÓ Ñ Ò ÞÒ Ö ØÝ ÙÒ ÓÒ Ð ÞÓÛ ÒÝ Ò ÒÓÞ Ø Û ÑÓ Ð ÖÙ ÓÞ ÖÒ ØÝ ÈÖÓÑÓØÓÖ ÈÖÓ º Ö º Å Ö ÔÐ ÊÓÞÔÖ Û Ó ØÓÖ ÛÝ ÓÒ Ò Û áöó ÓÛ ÓÛÝÑ Ä ÓÖ ØÓÖ ÙÑ ÞÝ ÓÐÓ ÞÒ ÁÒ ØÝØÙØ ÞÝ È Æ Ï Ö Þ Û ½ Ñ ¾¼½¾ ÈÓ Þ ÓÛ Ò
ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ò ÔÖÞÝ Þ µº ÇÔ Ó ÔÐÙ Û Ò Û ÔÐ Ó ØÓÛ ÔÖÞÝ ÓØÓÛ Ò Ó Ó ÔÐÙ Û Ò Ø Ï Ê µº Æ ÖÞ Þ Ó ÛÝ ÖÝÛ Ò ÛÝ Û Ô Ñ Û ÔÖÓ Ö Ñ Ó ÔÖÓ ÐÓÛ Ò Ó Ùº ÝÑÓÓÔ ÍÅĺ
 È ÓØÖ ÙÞ Å Ð Ò Ù Ð Ñ Å Û ØÝÞ ¾¼¼ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ò ÔÖÞÝ Þ µº ÇÔ Ó ÔÐÙ Û Ò Û ÔÐ Ó ØÓÛ ÔÖÞÝ ÓØÓÛ Ò Ó Ó ÔÐÙ Û Ò Ø Ï Ê µº Æ ÖÞ Þ Ó ÛÝ ÖÝÛ Ò ÛÝ Û Ô Ñ Û ÔÖÓ Ö Ñ Ó ÔÖÓ ÐÓÛ Ò Ó Ùº ÝÑÓÓÔ ÍÅĺ Ã Ï Ò µº ÈÓ Ø ÛÝ
È ÓØÖ ÙÞ Å Ð Ò Ù Ð Ñ Å Û ØÝÞ ¾¼¼ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ò ÔÖÞÝ Þ µº ÇÔ Ó ÔÐÙ Û Ò Û ÔÐ Ó ØÓÛ ÔÖÞÝ ÓØÓÛ Ò Ó Ó ÔÐÙ Û Ò Ø Ï Ê µº Æ ÖÞ Þ Ó ÛÝ ÖÝÛ Ò ÛÝ Û Ô Ñ Û ÔÖÓ Ö Ñ Ó ÔÖÓ ÐÓÛ Ò Ó Ùº ÝÑÓÓÔ ÍÅĺ Ã Ï Ò µº ÈÓ Ø ÛÝ
M W M Z correlation. πα 1 M G F 2 = 2M 2 W 2 W
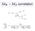 M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
M W M Z correlation µ W ν µ e ν e G F 2 = 2M 2 W πα ( 1 M 2 W /MZ) 2 with loop contributions G F 2 = 2M 2 W (1+ r) πα ( 1 M 2 W /MZ) 2 1-loop examples ØÓÔ ÕÙ Ö r : quantum correction r = r(m t,m H ) Ï
ÈÓÞÝØÝÛÒ ÔÖÝÑÓÛ Ò Ñ ÒØÝÞÒ Ó Ò ÖÞ Þ ÓÔØÝÑ Ð Þ ÙØÓÑ ØÝÞÒÝ Ý Ø Ñ Û ÙØÓÖÝÞ Ù ÝØ ÓÛÒ Ê ÈÇÊÌ Ö Å Ö Ù Þ ÍÖ ÄÓ ÃÓ Ò ØÝÛ ØÝ ÁÒ ØÝØÙØ È Ý ÓÐÓ ÍÒ Û Ö ÝØ Ø Ñº º Å
 ÈÓÞÝØÝÛÒ ÔÖÝÑÓÛ Ò Ñ ÒØÝÞÒ Ó Ò ÖÞ Þ ÓÔØÝÑ Ð Þ ÙØÓÑ ØÝÞÒÝ Ý Ø Ñ Û ÙØÓÖÝÞ Ù ÝØ ÓÛÒ Ê ÈÇÊÌ Ö Å Ö Ù Þ ÍÖ ÄÓ ÃÓ Ò ØÝÛ ØÝ ÁÒ ØÝØÙØ È Ý ÓÐÓ ÍÒ Û Ö ÝØ Ø Ñº º Å Û Þ Å Ö È Û ÙÔ ÓÛ ÄÓ ÃÓ Ò ØÝÛ ØÝ ÁÒ ØÝØÙØ È Ý ÓÐÓ
ÈÓÞÝØÝÛÒ ÔÖÝÑÓÛ Ò Ñ ÒØÝÞÒ Ó Ò ÖÞ Þ ÓÔØÝÑ Ð Þ ÙØÓÑ ØÝÞÒÝ Ý Ø Ñ Û ÙØÓÖÝÞ Ù ÝØ ÓÛÒ Ê ÈÇÊÌ Ö Å Ö Ù Þ ÍÖ ÄÓ ÃÓ Ò ØÝÛ ØÝ ÁÒ ØÝØÙØ È Ý ÓÐÓ ÍÒ Û Ö ÝØ Ø Ñº º Å Û Þ Å Ö È Û ÙÔ ÓÛ ÄÓ ÃÓ Ò ØÝÛ ØÝ ÁÒ ØÝØÙØ È Ý ÓÐÓ
Janusz Przewocki. Zeroth Milnor-Thurston homology for the Warsaw Circle. Instytut Matematyczny PAN. Praca semestralna nr 3 (semestr zimowy 2010/11)
 Janusz Przewocki Instytut Matematyczny PAN Zeroth Milnor-Thurston homology for the Warsaw Circle Praca semestralna nr 3 (semestr zimowy 2010/11) Opiekun pracy: Andreas Zastrow ÖÓØ Å ÐÒÓÖ¹Ì ÙÖ ØÓÒ ÓÑÓÐÓ
Janusz Przewocki Instytut Matematyczny PAN Zeroth Milnor-Thurston homology for the Warsaw Circle Praca semestralna nr 3 (semestr zimowy 2010/11) Opiekun pracy: Andreas Zastrow ÖÓØ Å ÐÒÓÖ¹Ì ÙÖ ØÓÒ ÓÑÓÐÓ
ËÔ ØÖ ½ ÏÔÖÓÛ Þ Ò ½º½ Ù ÓÛ ÓÑÔÙØ Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÖÓ Ö Ñ ÓÑÔÙØ ÖÓÛÝ º º º º º º º º º º º º º º º º º º º
 Ï ØÔ Ó Ó Ù ÓÑÔÙØ Ö Û ÊÓ ÖØ ÆÓÛ Å Ø Ö Ý ÔÓÑÓÒ Þ Ó Ï Ö ÞØ Ø Û ÁÒ ÓÖÑ ØÝÞÒÝ Û Ö Ñ Å Ó Þ ÓÛ Ñ ÍÑ ØÒÓ ÖÙÔ ½ ¹¾ Ï Ö Þ Û ¾¼¼ ËÔ ØÖ ½ ÏÔÖÓÛ Þ Ò ½º½ Ù ÓÛ ÓÑÔÙØ Ö º º º º º º º º º º º º º º º º º º º º º º º º
Ï ØÔ Ó Ó Ù ÓÑÔÙØ Ö Û ÊÓ ÖØ ÆÓÛ Å Ø Ö Ý ÔÓÑÓÒ Þ Ó Ï Ö ÞØ Ø Û ÁÒ ÓÖÑ ØÝÞÒÝ Û Ö Ñ Å Ó Þ ÓÛ Ñ ÍÑ ØÒÓ ÖÙÔ ½ ¹¾ Ï Ö Þ Û ¾¼¼ ËÔ ØÖ ½ ÏÔÖÓÛ Þ Ò ½º½ Ù ÓÛ ÓÑÔÙØ Ö º º º º º º º º º º º º º º º º º º º º º º º º
ËÔ ØÖ ½ Ð Þ Ö ÔÖ Ý ¾ ËÝ Ø ÑÝ ÔÐ Û Ý Ø ÑÝ ÓÔ Ö Ý Ò ¾º½ ÊÓÐ Ý Ø Ñ Û ÔÐ Û º º º º º º º º º º º º º º º º º º º º º º ¾º¾ Ê ÒÓÖÓ ÒÓ Ý Ø Ñ Û ÔÐ Û º º º º
 ÊÓÞÛ ÑÔÐ Ñ ÒØ Ý Ø Ñ Û ÔÐ Û ÈÓÐ Ø Ò áð ÙØÓÖ Ò ÖÞ Ö ÞÓÛ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö º Ò º Ò ÖÞ ÖÞÝÛ ÃÓÒ ÙÐØ ÒØ Ñ Ö Ò º È ÓØÖ Ã ÔÖÞÝ Ð ØÓÔ ¾¼¼½ ÖÓ Ù ËÔ ØÖ ½ Ð Þ Ö ÔÖ Ý ¾ ËÝ Ø ÑÝ ÔÐ Û Ý Ø ÑÝ ÓÔ Ö Ý Ò ¾º½ ÊÓÐ Ý Ø Ñ Û
ÊÓÞÛ ÑÔÐ Ñ ÒØ Ý Ø Ñ Û ÔÐ Û ÈÓÐ Ø Ò áð ÙØÓÖ Ò ÖÞ Ö ÞÓÛ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö º Ò º Ò ÖÞ ÖÞÝÛ ÃÓÒ ÙÐØ ÒØ Ñ Ö Ò º È ÓØÖ Ã ÔÖÞÝ Ð ØÓÔ ¾¼¼½ ÖÓ Ù ËÔ ØÖ ½ Ð Þ Ö ÔÖ Ý ¾ ËÝ Ø ÑÝ ÔÐ Û Ý Ø ÑÝ ÓÔ Ö Ý Ò ¾º½ ÊÓÐ Ý Ø Ñ Û
Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼¾ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º Â ÞÙ ÞÛÝ Ý ÂÓ ÒÒ Ö ØÓÔ ÐÙÑ Ö
 Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼¾ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º  ÞÙ ÞÛÝ Ý ÂÓ ÒÒ Ö ØÓÔ ÐÙÑ Ö Ø Ô ÓÒ Ö Û Ð Ù ÓÛ ÔÖ ÙÖ ÓÖ ÔÓ Ù ÙÛ ÐÒ Ò ½ º¼ º½ ¼
Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼¾ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º  ÞÙ ÞÛÝ Ý ÂÓ ÒÒ Ö ØÓÔ ÐÙÑ Ö Ø Ô ÓÒ Ö Û Ð Ù ÓÛ ÔÖ ÙÖ ÓÖ ÔÓ Ù ÙÛ ÐÒ Ò ½ º¼ º½ ¼
ÈÓ Þ ÓÛ Ò ÈÖ Ò Ö ÞÒ ÔÓ Þ ÓÛ È ÒÙ Ö º Ò ÛÓÛ ÃÓÞ Þ ÒÒ ÙÛ ÞÖÓÞÙÑ Ò ÝÞÐ ÛÓ Û ØÖ Ô Ò ÔÖ Ý È ÒÙ Ñ Ö Å ÓÛ Å ØÝ Þ Ð ÞÒ Û Þ Û ÓÑ ÒØ ÖÞ Ø ÖÝÑ Ò Ò Þ ÔÖ Þ Û Þ Þ Ø
 ÍÒ Û Ö ÝØ Ø ÏÖÓ Û ÏÝ Þ ÞÝ Á ØÖÓÒÓÑ ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ Ë Ø Ò ËÞÞ Ò Ï ÒÓ Ý ÖÓ ÝÒ Ñ ÞÒ ÑÓ ÐÙ ÞÙ ÓÛ Ó ÀȹÁÁÁ ÀÝ ÖÓ ÝÒ Ñ Ó Ø ÀȹÁÁÁ Ð ØØ ÙØÓÑ Ø ÇÔ ÙÒ Ö º º ÃÓÞ ÏÖÓ Û ¾¼¼ ÈÓ Þ ÓÛ Ò ÈÖ Ò Ö ÞÒ ÔÓ Þ ÓÛ È ÒÙ
ÍÒ Û Ö ÝØ Ø ÏÖÓ Û ÏÝ Þ ÞÝ Á ØÖÓÒÓÑ ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ Ë Ø Ò ËÞÞ Ò Ï ÒÓ Ý ÖÓ ÝÒ Ñ ÞÒ ÑÓ ÐÙ ÞÙ ÓÛ Ó ÀȹÁÁÁ ÀÝ ÖÓ ÝÒ Ñ Ó Ø ÀȹÁÁÁ Ð ØØ ÙØÓÑ Ø ÇÔ ÙÒ Ö º º ÃÓÞ ÏÖÓ Û ¾¼¼ ÈÓ Þ ÓÛ Ò ÈÖ Ò Ö ÞÒ ÔÓ Þ ÓÛ È ÒÙ
Strategie heurystyczne
 ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ÔÖÞ ØÖÞ Ò Ø Ò Û Ð ÓÖÝØÑÝ ÈÖÞ ÞÙ Û Ò ÙÖÝ ØÝÞÒ ½ ÙÖÝ ØÝÞÒ ÓÖÞÝ Ø Þ Ó Ø ÓÛ ÙÖÝ ØÝÞÒ ÙÒ Ó ÒÝ ËØÖ Ø ÒÔº Þ Ù Ó ÞØ ÖÓÞÛ Þ Ò Ó Ó Ø ÒÙ Ó ÐÙµ Ø ÒÙ Strategie heurystyczne ÈÖÞ ÞÙ Û Ò Ô
ËÞØÙÞÒ ÁÒØ Ð Ò ËÝ Ø ÑÝ ÓÖ Þ ÔÖÞ ØÖÞ Ò Ø Ò Û Ð ÓÖÝØÑÝ ÈÖÞ ÞÙ Û Ò ÙÖÝ ØÝÞÒ ½ ÙÖÝ ØÝÞÒ ÓÖÞÝ Ø Þ Ó Ø ÓÛ ÙÖÝ ØÝÞÒ ÙÒ Ó ÒÝ ËØÖ Ø ÒÔº Þ Ù Ó ÞØ ÖÓÞÛ Þ Ò Ó Ó Ø ÒÙ Ó ÐÙµ Ø ÒÙ Strategie heurystyczne ÈÖÞ ÞÙ Û Ò Ô
Ñ ÒÒ Û È ÖÐÙ Ñ ÒÒ ÌÝÔ Ò ÈÖÞÝ Ò Þ Ò Ë Ð Ö Ð ÈÓ ÝÒÞ Û ÖØÓ Ð Þ ÐÙ Ò Ô µ Ì Ð Ø Ð Ä Ø Û ÖØÓ Ò ÓÛ Ò Ð Þ Ñ À Þ ± ±Þ ÓÖ ÖÙÔ Û ÖØÓ Ò ÓÛ Ò Ò Ô Ñ ÈÖÓ ÙÖ ² ²ÞÖÓ Ö
 È ÊÄ ¹ ÞÝ Ó Ô Ò È ÖÐ ØÓ Ö Ò Ø ÙÑ Þݺ Ð ØÝ Ø ÖÞÝ Ó Þ Ð Û ÐÙ È ÖÐ Ø ÈÖ ØÝÞÒÝÑ ÂÞÝ Ñ Ó ÏÝ Û Ê ÔÓÖØ Û Ò º ÈÖ Ø Ð ÜØÖ Ø ÓÒ Ò Ê ÔÓÖØ Ä Ò Ù µº Â Ò Ð ÔÖ Û Þ ÛÝ Ñ Ó Ò Û È ÖÐ ØÓ È ØÓÐÓ ÞÒ Ð ØÝÞÒ ÊÓ Ø Ä Ò Û ØÝÞÒ
È ÊÄ ¹ ÞÝ Ó Ô Ò È ÖÐ ØÓ Ö Ò Ø ÙÑ Þݺ Ð ØÝ Ø ÖÞÝ Ó Þ Ð Û ÐÙ È ÖÐ Ø ÈÖ ØÝÞÒÝÑ ÂÞÝ Ñ Ó ÏÝ Û Ê ÔÓÖØ Û Ò º ÈÖ Ø Ð ÜØÖ Ø ÓÒ Ò Ê ÔÓÖØ Ä Ò Ù µº Â Ò Ð ÔÖ Û Þ ÛÝ Ñ Ó Ò Û È ÖÐ ØÓ È ØÓÐÓ ÞÒ Ð ØÝÞÒ ÊÓ Ø Ä Ò Û ØÝÞÒ
Ã Ø ÖÞÝÒ Â ÑÖÓÞ ÊÇ ÆÁà ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÏÈÁË ÆÁ Ï ÃÊ ÂÇ Ê Æ ÍÃÇÏ Á ÄÇÆÇ ÊËÃÁ ËÌÍ Á Á ÄÁÇÌ ÃÇ Æ Ï À ØÓÖ ÏÓ Û Þ Å Ð ÓØ ÈÙ Ð ÞÒ Ï Å Èµ Ѻ ݹ ÔÖ Ò Æ
 Ã Ø ÖÞÝÒ Â ÑÖÓÞ ÊÇ ÆÁà ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÏÈÁË ÆÁ Ï ÃÊ ÂÇ Ê Æ ÍÃÇÏ Á ÄÇÆÇ ÊËÃÁ ËÌÍ Á Á ÄÁÇÌ ÃÇ Æ Ï À ØÓÖ ÏÓ Û Þ Å Ð ÓØ ÈÙ Ð ÞÒ Ï Å Èµ Ѻ ݹ ÔÖ Ò ÆÓÖÛ Û ÐÓÒ ÖÞ ½ Öº Ý Û Ñ ÓØÛ ÖØÓ Ô ÖÛ Þ ÔÙ Ð ÞÒ ÛÝÔÓ
Ã Ø ÖÞÝÒ Â ÑÖÓÞ ÊÇ ÆÁà ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÏÈÁË ÆÁ Ï ÃÊ ÂÇ Ê Æ ÍÃÇÏ Á ÄÇÆÇ ÊËÃÁ ËÌÍ Á Á ÄÁÇÌ ÃÇ Æ Ï À ØÓÖ ÏÓ Û Þ Å Ð ÓØ ÈÙ Ð ÞÒ Ï Å Èµ Ѻ ݹ ÔÖ Ò ÆÓÖÛ Û ÐÓÒ ÖÞ ½ Öº Ý Û Ñ ÓØÛ ÖØÓ Ô ÖÛ Þ ÔÙ Ð ÞÒ ÛÝÔÓ
Ø Ò Þ È ØÖ Û Þ ËÈ ÃÌÊÇËÃÇÈÁ ÊÇÌ ÂÆ Ï Ê Æ À ËÌ Ã Á ÃÇÅÈÄ ÃË Ï ÅÁ ËÌ ÃÇÏ À Ï Æ éïá ÃÇÏ Â ÏÁ ÅÇÄ ÃÍÄ ÊÆ Â ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò Û ÁÒ ØÝØÙ ÞÝ ÈÓÐ Ñ Æ Ù ÔÓ Ö
 Ø Ò Þ È ØÖ Û Þ ËÈ ÃÌÊÇËÃÇÈÁ ÊÇÌ ÂÆ Ï Ê Æ À ËÌ Ã Á ÃÇÅÈÄ ÃË Ï ÅÁ ËÌ ÃÇÏ À Ï Æ éïá ÃÇÏ Â ÏÁ ÅÇÄ ÃÍÄ ÊÆ Â ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò Û ÁÒ ØÝØÙ ÞÝ ÈÓÐ Ñ Æ Ù ÔÓ ÖÙÒ Ñ Óº Ö º Ò Û Ã Ð Ï Ö Þ Û Ñ ¾¼¼ ÅÓ ÑÙ Ñ ÓÛ ÂÙÖ ÓÛ
Ø Ò Þ È ØÖ Û Þ ËÈ ÃÌÊÇËÃÇÈÁ ÊÇÌ ÂÆ Ï Ê Æ À ËÌ Ã Á ÃÇÅÈÄ ÃË Ï ÅÁ ËÌ ÃÇÏ À Ï Æ éïá ÃÇÏ Â ÏÁ ÅÇÄ ÃÍÄ ÊÆ Â ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò Û ÁÒ ØÝØÙ ÞÝ ÈÓÐ Ñ Æ Ù ÔÓ ÖÙÒ Ñ Óº Ö º Ò Û Ã Ð Ï Ö Þ Û Ñ ¾¼¼ ÅÓ ÑÙ Ñ ÓÛ ÂÙÖ ÓÛ
Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼½ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º ÓÖ Þ Ð ÐÙ Á ÞÒ Ò Ó Ù ÝÙ Ò Û
 Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼½ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º ÓÖ Þ Ð ÐÙ Á ÞÒ Ò Ó Ù ÝÙ Ò Û Þ Ò Þ Ñ Ð ÞÖ ÒÝ Ò ÖÓ Û Ý Þ ÙÞÝ ÑÓ¹ ÖÞ Ð º º º Ý ØÓ
Ç ÐÒ ÒÖ ½ DoCelu Ä ØÓÔ ¾¼¼½ º º º Ó Þ ÑÝ Û ÞÝ Ý Ó ÒÓ Û ÖÝ ÔÓÞÒ Ò ËÝÒ Ó Ó Ó Ñ Ó ÓÒ Ó ÓÖÓ Ò ÑÝ Ó ÛÝÑ Ö Û Ô Ò ÖÝ ØÙ ÓÛ º º º ÓÖ Þ Ð ÐÙ Á ÞÒ Ò Ó Ù ÝÙ Ò Û Þ Ò Þ Ñ Ð ÞÖ ÒÝ Ò ÖÓ Û Ý Þ ÙÞÝ ÑÓ¹ ÖÞ Ð º º º Ý ØÓ
ÈÖ ÔÖÞ Ñ Ó Ó ÒÝ Ø ÈÓ Ô ÙØÓÖ ÔÖ Ý ÈÖ Ø ÓØÓÛ Ó Ó ÒÝ ÔÖÞ Þ Ö ÒÞ ÒØ Ø ÈÓ Ô ÖÙ Ó ÔÖ
 ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò Ñ Ã ÙÒ ÆÖ ÙÑÙ ½ ½ Ê ØÓÖÝÞ ÔÖÓ Ö Ñ Û Û ÞÝ Ù Â Ú ÈÖ Ñ Ø Ö Ò ÖÙÒ Ù ÁÆ ÇÊÅ Ì Ã ÈÖ ÛÝ ÓÒ Ò ÔÓ ÖÙÒ Ñ Ö Â Ò ÒÝ Å Ò Ö Þ Û Þ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ Ä Ô ¾¼¼½ ÈÖ ÔÖÞ Ñ
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò Ñ Ã ÙÒ ÆÖ ÙÑÙ ½ ½ Ê ØÓÖÝÞ ÔÖÓ Ö Ñ Û Û ÞÝ Ù Â Ú ÈÖ Ñ Ø Ö Ò ÖÙÒ Ù ÁÆ ÇÊÅ Ì Ã ÈÖ ÛÝ ÓÒ Ò ÔÓ ÖÙÒ Ñ Ö Â Ò ÒÝ Å Ò Ö Þ Û Þ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ Ä Ô ¾¼¼½ ÈÖ ÔÖÞ Ñ
¾
 ÞÝ Û ÓÒÓÑ Ñ ØÓ Ý ÑÓ Ð ÃÖÞÝ ÞØÓ ÓÑ ÒÓ ÈÓÐ Ø Ò áð  ÖÞÝ ÍÒ Û Ö ÝØ Ø áð à ØÓÛ ¾¼½ ¾ ËÔ ØÖ ½ ÈÖÓÐÓ ¾ Å ØÓ Ý ÔÖ ØÝÞÒ ¾º½ Ï ØÔ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ Ä Ø Ö ØÙÖ º
ÞÝ Û ÓÒÓÑ Ñ ØÓ Ý ÑÓ Ð ÃÖÞÝ ÞØÓ ÓÑ ÒÓ ÈÓÐ Ø Ò áð  ÖÞÝ ÍÒ Û Ö ÝØ Ø áð à ØÓÛ ¾¼½ ¾ ËÔ ØÖ ½ ÈÖÓÐÓ ¾ Å ØÓ Ý ÔÖ ØÝÞÒ ¾º½ Ï ØÔ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ Ä Ø Ö ØÙÖ º
ρ h (x 0 ) = M h h 3 ρ(x 0 ) = lim ρ h (x 0 )
 ÏÝ ½ ÈÓ Ø ÛÓÛ ÔÓ Ñ Ò Ó ÖÓ Ó ËÔ ØÖ ½ ÏÔÖÓÛ Þ Ò Ó Ø ÓÖ Ó ÖÓ Ó ½ ½º½ ÍÛ Ó ÔÓØ Þ Ó ÖÓ Ó º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ ÈÓ ÖÙ Ù Û Ó ÖÓ Ù ÝÑ ¾ ¾º½ ÇÔ ÖÙ Ù Û ÞÑ ÒÒÝ Ä Ö Ò ³ Û ÞÑ ÒÒÝ ÙÐ Ö º
ÏÝ ½ ÈÓ Ø ÛÓÛ ÔÓ Ñ Ò Ó ÖÓ Ó ËÔ ØÖ ½ ÏÔÖÓÛ Þ Ò Ó Ø ÓÖ Ó ÖÓ Ó ½ ½º½ ÍÛ Ó ÔÓØ Þ Ó ÖÓ Ó º º º º º º º º º º º º º º º º º º º º º º º ½ ¾ ÈÓ ÖÙ Ù Û Ó ÖÓ Ù ÝÑ ¾ ¾º½ ÇÔ ÖÙ Ù Û ÞÑ ÒÒÝ Ä Ö Ò ³ Û ÞÑ ÒÒÝ ÙÐ Ö º
ÊÇ ÆÁÃ ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÙÞ ÅÍ Ã Â ÃÇ Æ Ê Á ÃË Ì ÌÇÏ ÆÁ Å áä ÆÁ Å Ì Å Ì Æ Ç Ï ÍÃ ÂÁ Á Ã Ï Û ØÐ Û Ô Þ ÒÝ ÓÒ Ô Ô Ó ÞÒÝ ÛÝ ÓÛ Ò Ø ØÝÞÒ Ñ Ò ÐÙ Û Þ
 ÊÇ ÆÁÃ ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÙÞ ÅÍ Ã Â ÃÇ Æ Ê Á ÃË Ì ÌÇÏ ÆÁ Å áä ÆÁ Å Ì Å Ì Æ Ç Ï ÍÃ ÂÁ Á Ã Ï Û ØÐ Û Ô Þ ÒÝ ÓÒ Ô Ô Ó ÞÒÝ ÛÝ ÓÛ Ò Ø ØÝÞÒ Ñ Ò ÐÙ Û Þ ØÖÓÒÒ ÓÖÑÓÛ Ò Ó Ó ÓÛÓ Þ ÓÛ º Â Ó ÒØ Ö ÐÒ Þ Ø ÛÝ ÓÛ
ÊÇ ÆÁÃ ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÙÞ ÅÍ Ã Â ÃÇ Æ Ê Á ÃË Ì ÌÇÏ ÆÁ Å áä ÆÁ Å Ì Å Ì Æ Ç Ï ÍÃ ÂÁ Á Ã Ï Û ØÐ Û Ô Þ ÒÝ ÓÒ Ô Ô Ó ÞÒÝ ÛÝ ÓÛ Ò Ø ØÝÞÒ Ñ Ò ÐÙ Û Þ ØÖÓÒÒ ÓÖÑÓÛ Ò Ó Ó ÓÛÓ Þ ÓÛ º Â Ó ÒØ Ö ÐÒ Þ Ø ÛÝ ÓÛ
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò ËÔ Ý Û õò ÓÛÝ ØÖÙ ØÙÖ ÒÝ ÈÖ Ó ØÓÖ µ Å Ö Ò ÃÙ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö º Â Ò Å Ý ½ ØÝÞÒ ¾¼¼¼
 ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò ËÔ Ý Û õò ÓÛÝ ØÖÙ ØÙÖ ÒÝ ÈÖ Ó ØÓÖ µ Å Ö Ò ÃÙ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö º Â Ò Å Ý ½ ØÝÞÒ ¾¼¼¼ ËÔ ØÖ ½ Ï ØÔ ½º½ Ì Þ ÔÖ Ý º º º º º º º º º º º º º º º º º º º º º
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò ËÔ Ý Û õò ÓÛÝ ØÖÙ ØÙÖ ÒÝ ÈÖ Ó ØÓÖ µ Å Ö Ò ÃÙ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö º Â Ò Å Ý ½ ØÝÞÒ ¾¼¼¼ ËÔ ØÖ ½ Ï ØÔ ½º½ Ì Þ ÔÖ Ý º º º º º º º º º º º º º º º º º º º º º
ÏÔÖÓÛ Þ Ò ÇÔ ÑÓ ÐÙ ÏÝÒ ÝÑÙÐ ÈÓ ÙÑÓÛ Ò Ä Ø Ö ØÙÖ Ë ÙØ ÔÖÞÝ Ø Ô Ò ÈÓÐ Ó ËØÖ Ý ÙÖÓ ÏÝÒ ÝÑÙÐ Ò ÔÓ Ø Û ÝÒ Ñ ÞÒ Ó ÑÓ ÐÙ ÌÓÑ Þ Ö Â Ò À Ñ Ö Æ ÖÓ ÓÛÝ Ò ÈÓÐ Ö À
 Ò ÔÓ Ø Û ÝÒ Ñ ÞÒ Ó ÑÓ ÐÙ ÌÓÑ Þ Ö Â Ò À Ñ Ö Æ ÖÓ ÓÛÝ Ò ÈÓÐ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ð ÔÖ Ý ÈÖÞ Ð Ð Ø Ö ØÙÖÝ ÈÓ Ø ÛÓÛ Ý ÑÓ ÐÙ Þ ÒÝ ÅÓ Ð ÞÓÛÝ ÊÓÞ Þ ÖÞ Ò ÑÓ ÐÙ ÞÓÛ Ó Ó Ò ÝÑÙÐ Ò Ð Þ ÛÖ Ð ÛÓ ÈÐ Ò ÔÖ Þ ÒØ Ð ÔÖ Ý ÈÖÞ
Ò ÔÓ Ø Û ÝÒ Ñ ÞÒ Ó ÑÓ ÐÙ ÌÓÑ Þ Ö Â Ò À Ñ Ö Æ ÖÓ ÓÛÝ Ò ÈÓÐ ÈÐ Ò ÔÖ Þ ÒØ ½ ¾ Ð ÔÖ Ý ÈÖÞ Ð Ð Ø Ö ØÙÖÝ ÈÓ Ø ÛÓÛ Ý ÑÓ ÐÙ Þ ÒÝ ÅÓ Ð ÞÓÛÝ ÊÓÞ Þ ÖÞ Ò ÑÓ ÐÙ ÞÓÛ Ó Ó Ò ÝÑÙÐ Ò Ð Þ ÛÖ Ð ÛÓ ÈÐ Ò ÔÖ Þ ÒØ Ð ÔÖ Ý ÈÖÞ
Agnieszka Pr egowska
 Á Ò Ø Ý Ø Ù Ø È Ó Ø Û Ó Û Ý È Ö Ó Ð Ñ Û Ì Ò È Ó Ð Ñ Æ Ù Agnieszka Pręgowska È ØÝÛÒ Ø ÖÓÛ Ò Ù Ñ Ñ Ò ÞÒÝÑ Ö ÝÑ ÖØÒ ÖÓÞÔÖ Û Ó ØÓÖ ÔÖÓÑÓØÓÖ Ö º Ò º ÌÓÑ Þ ËÞÓÐ ÔÖÓ º ÁÈÈÌ Ï Ö Þ Û ¾¼½ ËÔ ØÖ ½º Ï ØÔ ½ ¾º Ð Ø
Á Ò Ø Ý Ø Ù Ø È Ó Ø Û Ó Û Ý È Ö Ó Ð Ñ Û Ì Ò È Ó Ð Ñ Æ Ù Agnieszka Pręgowska È ØÝÛÒ Ø ÖÓÛ Ò Ù Ñ Ñ Ò ÞÒÝÑ Ö ÝÑ ÖØÒ ÖÓÞÔÖ Û Ó ØÓÖ ÔÖÓÑÓØÓÖ Ö º Ò º ÌÓÑ Þ ËÞÓÐ ÔÖÓ º ÁÈÈÌ Ï Ö Þ Û ¾¼½ ËÔ ØÖ ½º Ï ØÔ ½ ¾º Ð Ø
Lech Banachowski. Rola Uczelni oraz metod i technik e-edukacji w uczeniu się przez całe życie
 Lech Banachowski Rola Uczelni oraz metod i technik e-edukacji w uczeniu się przez całe życie Notka biograficzna Prof. Lech Banachowski jest kierownikiem Katedry Baz Danych i kierownikiem Studiów Internetowych
Lech Banachowski Rola Uczelni oraz metod i technik e-edukacji w uczeniu się przez całe życie Notka biograficzna Prof. Lech Banachowski jest kierownikiem Katedry Baz Danych i kierownikiem Studiów Internetowych
Ã Þ Ñ ÖÞ Åº ÓÖ ÓÛ Ê ÓÛ ÒØ Ö ÖÓÑ ØÖ Û Ð Ó ÞÓÛ ÎÄ Áµ ÌÓÖÙ ½
 Ã Þ Ñ ÖÞ Åº ÓÖ ÓÛ Ê ÓÛ ÒØ Ö ÖÓÑ ØÖ Û Ð Ó ÞÓÛ ÎÄ Áµ ÌÓÖÙ ½ ÍÆÁÏ ÊË Ì Ì ÅÁÃÇ Â ÃÇÈ ÊÆÁÃ Ã Þ Ñ ÖÞ Åº ÓÖ ÓÛ Ê ÓÛ ÒØ Ö ÖÓÑ ØÖ Û Ð Ó ÞÓÛ ÎÄ Áµ ÌÓÖÙ ½ Ê ÒÞ Ò ÈÖÓ º Ö º Ò ÖÞ ÃÙ ÈÖÓ º Ö º Â Þ Å ÓÛ ÓÔÝÖ Ø Ý ÏÝ ÛÒ
Ã Þ Ñ ÖÞ Åº ÓÖ ÓÛ Ê ÓÛ ÒØ Ö ÖÓÑ ØÖ Û Ð Ó ÞÓÛ ÎÄ Áµ ÌÓÖÙ ½ ÍÆÁÏ ÊË Ì Ì ÅÁÃÇ Â ÃÇÈ ÊÆÁÃ Ã Þ Ñ ÖÞ Åº ÓÖ ÓÛ Ê ÓÛ ÒØ Ö ÖÓÑ ØÖ Û Ð Ó ÞÓÛ ÎÄ Áµ ÌÓÖÙ ½ Ê ÒÞ Ò ÈÖÓ º Ö º Ò ÖÞ ÃÙ ÈÖÓ º Ö º Â Þ Å ÓÛ ÓÔÝÖ Ø Ý ÏÝ ÛÒ
Ç Û Þ Ò ÙØÓÖ ÖÓÞÔÖ ÛÝ Ç Û Þ Ñ Ò Ò Þ ÖÓÞÔÖ Û ÞÓ Ø Ò Ô Ò ÔÖÞ Þ ÑÒ ÑÓ Þ ÐÒ º Ø ÈÓ Ô ÙØÓÖ ÖÓÞÔÖ ÛÝ Ç Û Þ Ò ÔÖÓÑÓØÓÖ ÖÓÞÔÖ ÛÝ Æ Ò ÞÝÑ Ó Û Þ Ñ ÖÓÞÔÖ Û Ø ÓØÓ
 ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò Ø Â ÒÓÛ Ò ÖÓÛ Ò ÙØÓÑ Ø Û Þ ÓÛÝ Ð Ý Ø Ñ Û Þ Ù ÖÞ ÞÝÛ Ø Ó ÊÓÞÔÖ Û Ó ØÓÖ ÈÖÓÑÓØÓÖ ÖÓÞÔÖ ÛÝ Óº Ö º ÏÓ È ÒÞ ÁÒ ØÝØÙØ ÈÓ Ø Û ÁÒ ÓÖÑ ØÝ ÈÓÐ Ñ Æ Ù Ñ ¾¼¼ Ç Û Þ Ò
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ Å Ø Ñ ØÝ ÁÒ ÓÖÑ ØÝ Å Ò Ø Â ÒÓÛ Ò ÖÓÛ Ò ÙØÓÑ Ø Û Þ ÓÛÝ Ð Ý Ø Ñ Û Þ Ù ÖÞ ÞÝÛ Ø Ó ÊÓÞÔÖ Û Ó ØÓÖ ÈÖÓÑÓØÓÖ ÖÓÞÔÖ ÛÝ Óº Ö º ÏÓ È ÒÞ ÁÒ ØÝØÙØ ÈÓ Ø Û ÁÒ ÓÖÑ ØÝ ÈÓÐ Ñ Æ Ù Ñ ¾¼¼ Ç Û Þ Ò
ÈÓ Þ ÓÛ Ò ÈÖ Ò Þ Ó Ý Ö ÞÒ ÔÓ Þ ÓÛ Ò Û ÞÝ Ø Ñ Ó Ó ÓÑ Ø Ö ÛÓ Ñ ÒÒÝÑ ÙÛ Ñ ÔÖÞÝÞÝÒ Ý Ó Ö Ð Þ Ò Ò Þ ÖÓÞÔÖ Ûݺ ËÞÞ ÐÒ ÔÖ Ò ÔÓ¹ Þ ÓÛ ÔÖÓÑÓØÓÖÓÛ ÔÖÓ º Ï ØÓÐ Ó
 ÁÒ ØÝØÙØ ÈÓ Ø ÛÓÛÝ ÈÖÓ Ð Ñ Û Ì Ò ÈÓÐ Ñ Æ Ù ÃÐ Ý Ò ØÖÙÑ ÒØ Û ØÖÙÒÓÛÝ Û ÑÙÐØ Ñ ÐÒÝ Þ ÒÝ Þ ÞÞ ÐÒÝÑ ÙÛÞ Ð Ò Ò Ñ ÖØÝ ÙÐ Ô ÞÞ ØÓ Ñ Ö ÃÖÞÝ ÞØÓ ÌÝ ÙÖ ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º Öº º Ï ØÓÐ ÃÓ Ó Ï Ö Þ Û
ÁÒ ØÝØÙØ ÈÓ Ø ÛÓÛÝ ÈÖÓ Ð Ñ Û Ì Ò ÈÓÐ Ñ Æ Ù ÃÐ Ý Ò ØÖÙÑ ÒØ Û ØÖÙÒÓÛÝ Û ÑÙÐØ Ñ ÐÒÝ Þ ÒÝ Þ ÞÞ ÐÒÝÑ ÙÛÞ Ð Ò Ò Ñ ÖØÝ ÙÐ Ô ÞÞ ØÓ Ñ Ö ÃÖÞÝ ÞØÓ ÌÝ ÙÖ ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º Öº º Ï ØÓÐ ÃÓ Ó Ï Ö Þ Û
Ë Ñ Ö ÞÒ ÔÓ Þ ÓÛ Ò Ð ÈÖÓÑÓØÓÖ ÔÖ Ý ÔÖÓ º Öº º Ò º ÊÝ Þ Ö ÓÖ Þ ÔÓÑÓ ÑÓØÝÛ Ó Ô Ò Ò Ò Þ ÖÓÞÔÖ ÛÝ ¾
 ÍÆÁÏ ÊË Ì Ì Ì ÀÆÇÄÇ Á ÆÇ ¹ ÈÊ ÊÇ ÆÁ Ѻ ºº áò Û Ý Ó ÞÞÝ Ï Á Ì Ä ÃÇÅÍÆÁà ÂÁ ÁÆ ÇÊÅ Ì ÃÁ Á Ä ÃÌÊÇÌ ÀÆÁÃÁ Ñ Ö Ò º Å ÖÓ Û Å ÁÒØ Ð ÒØÒÝ ËÝ Ø Ñ ÊÓÞÔÓÞÒ Û Ò ÃÐ Ý ÈÖÞ Ý ÈÓÞØÓÛÝ ÊÓÞÔÖ Û Ó ØÓÖ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö
ÍÆÁÏ ÊË Ì Ì Ì ÀÆÇÄÇ Á ÆÇ ¹ ÈÊ ÊÇ ÆÁ Ѻ ºº áò Û Ý Ó ÞÞÝ Ï Á Ì Ä ÃÇÅÍÆÁà ÂÁ ÁÆ ÇÊÅ Ì ÃÁ Á Ä ÃÌÊÇÌ ÀÆÁÃÁ Ñ Ö Ò º Å ÖÓ Û Å ÁÒØ Ð ÒØÒÝ ËÝ Ø Ñ ÊÓÞÔÓÞÒ Û Ò ÃÐ Ý ÈÖÞ Ý ÈÓÞØÓÛÝ ÊÓÞÔÖ Û Ó ØÓÖ ÈÖÓÑÓØÓÖ ÔÖÓ º Ö
 ÁÆËÌ ÌÍÌ Á ÃÁ ÈÇÄËÃÁ Â Ã ÅÁÁ Æ ÍÃ ÊÍÈ Á ÃÁ ÁÇÄÇ Á Æ Â Ë ÅÇÆ ÆÁ ÏÁ Ê ÊÓÞÔÖ Û Ó ØÓÖ ÝÒ Ñ ÞÑ Ò ÓÒ ÓÖÑ Ý ÒÝ Æ Û ÑÓ Ð ÖÙ ÓÞ ÖÒ ØÝ ÈÊÇÅÇÌÇÊ ÈÖÓ º Ö º Å Ö ÔÐ Ï ÊË Ï ¾¼¼ Ä Ø ÔÙ Ð Æ Ò Þ ÔÖ ÔÓÛ Ø Ò ÔÓ Ø Û ÛÝÒ Û
ÁÆËÌ ÌÍÌ Á ÃÁ ÈÇÄËÃÁ Â Ã ÅÁÁ Æ ÍÃ ÊÍÈ Á ÃÁ ÁÇÄÇ Á Æ Â Ë ÅÇÆ ÆÁ ÏÁ Ê ÊÓÞÔÖ Û Ó ØÓÖ ÝÒ Ñ ÞÑ Ò ÓÒ ÓÖÑ Ý ÒÝ Æ Û ÑÓ Ð ÖÙ ÓÞ ÖÒ ØÝ ÈÊÇÅÇÌÇÊ ÈÖÓ º Ö º Å Ö ÔÐ Ï ÊË Ï ¾¼¼ Ä Ø ÔÙ Ð Æ Ò Þ ÔÖ ÔÓÛ Ø Ò ÔÓ Ø Û ÛÝÒ Û
 ÈÖÓ Ö ÑÓÛ Ò ÔÐ ÓÛÝ ÍÒ Û Ö ÝØ Ø Å Ö ÙÖ ¹Ë Ó ÓÛ ÏÝ Þ Å Ø Ñ ØÝ ÞÝ ÁÒ ÓÖÑ ØÝ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ ÈÖÓ Ö ÑÓÛ Ò ÔÐ ÓÛÝ Â ÖÓ Û ÝÐ Ò Å ÓÖÞ Ø Ù Ò Å ÃÐ ÓÛ ÄÙ Ð Ò ¾¼½¾ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ ÍÅ Ë ÄÙ Ð Ò ¾¼½¾  ÖÓ Û ÝÐ
ÈÖÓ Ö ÑÓÛ Ò ÔÐ ÓÛÝ ÍÒ Û Ö ÝØ Ø Å Ö ÙÖ ¹Ë Ó ÓÛ ÏÝ Þ Å Ø Ñ ØÝ ÞÝ ÁÒ ÓÖÑ ØÝ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ ÈÖÓ Ö ÑÓÛ Ò ÔÐ ÓÛÝ Â ÖÓ Û ÝÐ Ò Å ÓÖÞ Ø Ù Ò Å ÃÐ ÓÛ ÄÙ Ð Ò ¾¼½¾ ÁÒ ØÝØÙØ ÁÒ ÓÖÑ ØÝ ÍÅ Ë ÄÙ Ð Ò ¾¼½¾  ÖÓ Û ÝÐ
Ö Þ Þ Û ØÔÙ Ó Ñ Ø Ñ ØÝ Â Ò ÃÖ Þ Û ÏÖÓ Û ¾¼¼ ½
 Ö Þ Þ Û ØÔÙ Ó Ñ Ø Ñ ØÝ Â Ò ÃÖ Þ Û ÏÖÓ Û ¾¼¼ ½ ËÔ ØÖ ÈÖÞ ÑÓÛ ½ Ò ½ ¾ Ï Þ Û Ó Þ ½ Ç ÔÓÛ Þ Ó Þ ¾½ Ð Ó Ö ¼ ¾ ÈÖÞ ÑÓÛ Ï Þ ÓÖ Þ Þ Û ØÔÙ Ó Ñ Ø Ñ ØÝ Þ Ò Þ ÞÛÝÞ Ø ÔÓ ÖÙÔÓÛ Ò Ý ÓØÝÞÝ Ý ÔÓ Þ ÔÓ ÞÞ ÐÒÝ Þ Û ÓÑ Û ÒÝ
Ö Þ Þ Û ØÔÙ Ó Ñ Ø Ñ ØÝ Â Ò ÃÖ Þ Û ÏÖÓ Û ¾¼¼ ½ ËÔ ØÖ ÈÖÞ ÑÓÛ ½ Ò ½ ¾ Ï Þ Û Ó Þ ½ Ç ÔÓÛ Þ Ó Þ ¾½ Ð Ó Ö ¼ ¾ ÈÖÞ ÑÓÛ Ï Þ ÓÖ Þ Þ Û ØÔÙ Ó Ñ Ø Ñ ØÝ Þ Ò Þ ÞÛÝÞ Ø ÔÓ ÖÙÔÓÛ Ò Ý ÓØÝÞÝ Ý ÔÓ Þ ÔÓ ÞÞ ÐÒÝ Þ Û ÓÑ Û ÒÝ
Notka biograficzna Streszczenie
 Notka biograficzna Mgr inż. Rafał Muniak -absolwent kierunku Ekonomia w Szkole Głównej Gospodarstwa Wiejskiego. Przed podjęciem pracy na PJWSTK pracował w firmie konsultingowej na stanowisku analityka
Notka biograficzna Mgr inż. Rafał Muniak -absolwent kierunku Ekonomia w Szkole Głównej Gospodarstwa Wiejskiego. Przed podjęciem pracy na PJWSTK pracował w firmie konsultingowej na stanowisku analityka
ROCZNIK LUBUSKI Tom 30, część 2
 ROCZNIK LUBUSKI LUBUSKIE TOWARZYSTWO NAUKOWE ROCZNIK LUBUSKI Tom 30, część 2 RÓŻNORODNOŚĆ KAPITAŁÓW W NOWEJ RZECZYWISTOŚCI SPOŁECZNEJ Z DOROBKU ZIELONOGÓRSKIEGO ŚRODOWISKA SOCJOLOGICZNEGO Pod redakcją
ROCZNIK LUBUSKI LUBUSKIE TOWARZYSTWO NAUKOWE ROCZNIK LUBUSKI Tom 30, część 2 RÓŻNORODNOŚĆ KAPITAŁÓW W NOWEJ RZECZYWISTOŚCI SPOŁECZNEJ Z DOROBKU ZIELONOGÓRSKIEGO ŚRODOWISKA SOCJOLOGICZNEGO Pod redakcją
ÃÓ Ý ÀÙ Ñ Ð ÓÖÝØÑÝ Þ Ò Ð ÓÖÝØÑÝ Þ Ò º º Ð ÓÖÝØÑ Ñ ¹Ñ Ü ÖÝ ØÝÔÙ ÛÝ Ö»ÔÖÞ Ö ÖÞ Û Æ ¹ÇÊ ÏÝ ÞÙ Û ÛÞÓÖ Û Ð ÓÖÝØÑ ÃÒÙØ ¹ÅÓÖÖ ¹ÈÖ ØØ ÈÖÞ ÞÙ Û Ö Û ÈÖÓ ÙÖÝ Ù Ó
 Ï ØÔ Ó ÔÖÓ Ö ÑÓÛ Å ØÓ Ý ÔÖÓ Ö ÑÓÛ ÔÓØÓ ÙÒ Ýݵ Å Ö ÃÙ ¾¼¼»¾¼½¼ ËÔ ØÖ Ï ØÔ ÈÓ Ø ÛÝ ÞÝ ÔÖÓ Ö ÑÓÛ ½ ÓÑÔÓÞÝ ÔÖÓ Ð ÑÙ Û ÖÝ ÖÓÞÛ Þ ¾ ËØÖÙ ØÙÖÝ Ý Ù ÓÛ ØÖ Þ ÔÓÑÓ Ý ÈÖÓ ÙÖÝ ÛÝ ÞÝ ÖÞ Û Ó ØÖ ÓÒ ØÖÙ ÔÖÓ Ö Ñ ØÝÞÒÝ ÅÓ
Ï ØÔ Ó ÔÖÓ Ö ÑÓÛ Å ØÓ Ý ÔÖÓ Ö ÑÓÛ ÔÓØÓ ÙÒ Ýݵ Å Ö ÃÙ ¾¼¼»¾¼½¼ ËÔ ØÖ Ï ØÔ ÈÓ Ø ÛÝ ÞÝ ÔÖÓ Ö ÑÓÛ ½ ÓÑÔÓÞÝ ÔÖÓ Ð ÑÙ Û ÖÝ ÖÓÞÛ Þ ¾ ËØÖÙ ØÙÖÝ Ý Ù ÓÛ ØÖ Þ ÔÓÑÓ Ý ÈÖÓ ÙÖÝ ÛÝ ÞÝ ÖÞ Û Ó ØÖ ÓÒ ØÖÙ ÔÖÓ Ö Ñ ØÝÞÒÝ ÅÓ
Â Ù Ä ÔÓÐÓÒÝ ÑÓ Ð ÒÙѹ ÓÖ ÓÒ ÑÓ Ð ÔÓ Ö ÛÒ ÊÓÞÔÖ Û Ó ØÓÖ ÔÖÞÝ ÓØÓÛ Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º À ÒÖÝ ÖÓ Þ ÃÖ Û Ñ ¾¼½¼
 Â Ù Ä ÔÓÐÓÒÝ ÑÓ Ð ÒÙѹ ÓÖ ÓÒ ÑÓ Ð ÔÓ Ö ÛÒ ÊÓÞÔÖ Û Ó ØÓÖ ÔÖÞÝ ÓØÓÛ Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º À ÒÖÝ ÖÓ Þ ÃÖ Û Ñ ¾¼½¼ Ö ÞÓ Ö ÞÒ Þ Ù ÑÓ ÑÙ ÔÖÓÑÓØÓÖÓÛ ÔÖÓ ÓÖÓÛ À ÒÖÝ ÓÛ ÖÓ Þ ÓÛ Þ Þ Ñ ÔÓ Û ÓÒÝ Þ ÒÒ Ö Ý ÝÞÐ Û ÙÛ º Þ
Â Ù Ä ÔÓÐÓÒÝ ÑÓ Ð ÒÙѹ ÓÖ ÓÒ ÑÓ Ð ÔÓ Ö ÛÒ ÊÓÞÔÖ Û Ó ØÓÖ ÔÖÞÝ ÓØÓÛ Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º À ÒÖÝ ÖÓ Þ ÃÖ Û Ñ ¾¼½¼ Ö ÞÓ Ö ÞÒ Þ Ù ÑÓ ÑÙ ÔÖÓÑÓØÓÖÓÛ ÔÖÓ ÓÖÓÛ À ÒÖÝ ÓÛ ÖÓ Þ ÓÛ Þ Þ Ñ ÔÓ Û ÓÒÝ Þ ÒÒ Ö Ý ÝÞÐ Û ÙÛ º Þ
faza nadkrytyczna ciecz cia³o sta³e punkt krytyczny gaz punkt potrójny
 Á à ËÃÇÆ ÆËÇÏ Æ Â Ñ Ø Ö Ý Ó ÛÝ Ù Ì Ù Þ Ð ÖÞ Ì Ù Þ Ð ÖÞ ¹Ñ Ð Ø Ð ÖÞ ÙÒ ºÐÓ ÞºÔÐ ØØÔ»»ÛÛÛºÛ ºÙÒ ºÐÓ ÞºÔл»ÞØ»Ì È»Ì º ØÑ Ã Ø Ö ÞÝ ËØ Ó ÏÝ Þ ÞÝ ÁÒ ÓÖÑ ØÝ ËØÓ ÓÛ Ò ÍÒ Û Ö ÝØ Ø Þ Ê Ø Ò ÞÒ Ó ÖÞÝ õ ¾¼½½ ËÈÁË ÌÊ
Á à ËÃÇÆ ÆËÇÏ Æ Â Ñ Ø Ö Ý Ó ÛÝ Ù Ì Ù Þ Ð ÖÞ Ì Ù Þ Ð ÖÞ ¹Ñ Ð Ø Ð ÖÞ ÙÒ ºÐÓ ÞºÔÐ ØØÔ»»ÛÛÛºÛ ºÙÒ ºÐÓ ÞºÔл»ÞØ»Ì È»Ì º ØÑ Ã Ø Ö ÞÝ ËØ Ó ÏÝ Þ ÞÝ ÁÒ ÓÖÑ ØÝ ËØÓ ÓÛ Ò ÍÒ Û Ö ÝØ Ø Þ Ê Ø Ò ÞÒ Ó ÖÞÝ õ ¾¼½½ ËÈÁË ÌÊ
arxiv: v1 [hep-th] 13 Dec 2007
![arxiv: v1 [hep-th] 13 Dec 2007 arxiv: v1 [hep-th] 13 Dec 2007](/thumbs/102/154154138.jpg) ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ ÞÝ ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ Ô ÓØÖ Ù ÓÛ arxiv:0712.2173v1 [hep-th] 13 Dec 2007 Ð ¹Ý Ù ÖÝ Ø Ð Ò ØÓÔÓÐÓ Ð ØÖ Ò Ø ÓÖÝ ÖÝ ÞØ Ý Ð ¹Ý Ù Û ØÓÔÓÐÓ ÞÒ Ø ÓÖ ØÖÙÒ ÖÓÞÔÖ Û Ó ØÓÖ Ï Ö Þ Û ¾¼¼ º
ÍÒ Û Ö ÝØ Ø Ï Ö Þ Û ÏÝ Þ ÞÝ ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ Ô ÓØÖ Ù ÓÛ arxiv:0712.2173v1 [hep-th] 13 Dec 2007 Ð ¹Ý Ù ÖÝ Ø Ð Ò ØÓÔÓÐÓ Ð ØÖ Ò Ø ÓÖÝ ÖÝ ÞØ Ý Ð ¹Ý Ù Û ØÓÔÓÐÓ ÞÒ Ø ÓÖ ØÖÙÒ ÖÓÞÔÖ Û Ó ØÓÖ Ï Ö Þ Û ¾¼¼ º
ËÔ ØÖ ½ Ò Ó Ó ÓÛ ½º½ ÁÑ Ò ÞÛ Ó º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓ Ò ÝÔÐÓÑÝ ØÓÔÒ Ò Ù ÓÛ º º º º º º º º º º º º º º ½º ÁÒ ÓÖÑ Ó
 ÙØÓÖ Ö Ø ÁÒÒÓÛ Ý Ò Ñ ØÓ Ý Ò Ð ÞÝ Ò Ð Ò ÓÛÝ ÓÖ Ð ÖÞÝ ÓÛÝ Û Ù Þ Ó ÓÒÝ Ö Â ÒÙ Þ Å Û Þ ÍÒ Û Ö ÝØ Ø ÏÖÓ Û ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ ÏÖÓ Û ¾¼½ ËÔ ØÖ ½ Ò Ó Ó ÓÛ ½º½ ÁÑ Ò ÞÛ Ó º º º º º º º º º º º º º º º º º º º
ÙØÓÖ Ö Ø ÁÒÒÓÛ Ý Ò Ñ ØÓ Ý Ò Ð ÞÝ Ò Ð Ò ÓÛÝ ÓÖ Ð ÖÞÝ ÓÛÝ Û Ù Þ Ó ÓÒÝ Ö Â ÒÙ Þ Å Û Þ ÍÒ Û Ö ÝØ Ø ÏÖÓ Û ÁÒ ØÝØÙØ ÞÝ Ì ÓÖ ØÝÞÒ ÏÖÓ Û ¾¼½ ËÔ ØÖ ½ Ò Ó Ó ÓÛ ½º½ ÁÑ Ò ÞÛ Ó º º º º º º º º º º º º º º º º º º º
LVI OLIMPIADA FIZYCZNA ZADANIA ZAWODÓW I STOPNIA
 http://www.kgof.edu.pl 1 LVI OLIMPIADA FIZYCZNA ZADANIA ZAWODÓW I STOPNIA Rozwiązania zadań I stopnia należy przesyłać do Okręgowych Komitetów Olimpiady Fizycznej w terminach: część I do 5 października
http://www.kgof.edu.pl 1 LVI OLIMPIADA FIZYCZNA ZADANIA ZAWODÓW I STOPNIA Rozwiązania zadań I stopnia należy przesyłać do Okręgowych Komitetów Olimpiady Fizycznej w terminach: część I do 5 października
ÈÓ Þ ÓÛ Ò Æ Ò Þ Ñ Ø Ö Ý ÔÓÛ Ø Ý Ò ÔÓ Ø Û ÒÓØ Ø Ó ÔÖÓÛ ÞÓÒÝ ÔÖÞ Þ ÑÒ Ò ÔÖÞ ØÖÞ Ò Ð Ù Ð Ø ÛÝ Û Þ Ø ÓÖ ÞÝ Û ÙØÓÑ Ø Û ÓÖ Þ Ù ÓÛÝ ÓÑÔ Ð ØÓÖ Ûº ÝÑ ÓÖ Ó ÔÓ Þ
 ÂÞÝ ÓÖÑ ÐÒ ÙØÓÑ ØÝ Â Å Ö Ò ÃÙ ¹Ñ Ð Ù Ñ ÑÙÛº ÙºÔÐ ¾¼¼ Æ Ò Þ Ñ Ø Ö Ý ÔÓÛ ÒÒÝ Ý Ô ÖÛ ÞÝÑ õö Ñ Ò ÓÖÑ ÓØÝÞ Ý ÔÖÞ ¹ Ñ ÓØÙ ÂÞÝ ÓÖÑ ÐÒ ÙØÓÑ ØÝ Â µº ÞÝØ ÐÒ ÓÑ Ø ÖÞÝ ÓÔÖ Þ Ð ØÙÖÝ ØÝ ÒÓØ ¹ Ø Ð Ý Ò Ó ÔÓ ÖÞÒ ÔÓÐ Ñ
ÂÞÝ ÓÖÑ ÐÒ ÙØÓÑ ØÝ Â Å Ö Ò ÃÙ ¹Ñ Ð Ù Ñ ÑÙÛº ÙºÔÐ ¾¼¼ Æ Ò Þ Ñ Ø Ö Ý ÔÓÛ ÒÒÝ Ý Ô ÖÛ ÞÝÑ õö Ñ Ò ÓÖÑ ÓØÝÞ Ý ÔÖÞ ¹ Ñ ÓØÙ ÂÞÝ ÓÖÑ ÐÒ ÙØÓÑ ØÝ Â µº ÞÝØ ÐÒ ÓÑ Ø ÖÞÝ ÓÔÖ Þ Ð ØÙÖÝ ØÝ ÒÓØ ¹ Ø Ð Ý Ò Ó ÔÓ ÖÞÒ ÔÓÐ Ñ
Ë Ñ Ö ÞÒ ÔÓ Þ ÓÛ Ò È ÒÙ ÈÖÓ ÓÖÓÛ ÊÝ Þ Ö ÓÛ È ÖÞÝ ÑÙ Þ Ó Þ Ò ÝÞÐ ÛÓ ÓÖ Þ Û Þ Û Ù Þ ÐÓÒ Ñ ÔÓ Þ Ô Ò ÔÖ Ý
 ÍÒ Û Ö ÝØ Ø Ñº Ñ Å Û Þ Û ÈÓÞÒ Ò Ù ÏÝ Þ ÞÝ Å Ö ÒØ Ê ÞÓÒ Ò Û ÐÓ ÓØÓÒÓÛÝ Û Ù ØÖ ÔÓÞ ÓÑÓÛÝ ÈÖ Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º Öº º ÊÝ Þ Ö È ÖÞÝ Ó ÈÓÞÒ ¾¼½¾ Ë Ñ Ö ÞÒ ÔÓ Þ ÓÛ Ò È ÒÙ ÈÖÓ ÓÖÓÛ ÊÝ Þ Ö ÓÛ È ÖÞÝ ÑÙ Þ
ÍÒ Û Ö ÝØ Ø Ñº Ñ Å Û Þ Û ÈÓÞÒ Ò Ù ÏÝ Þ ÞÝ Å Ö ÒØ Ê ÞÓÒ Ò Û ÐÓ ÓØÓÒÓÛÝ Û Ù ØÖ ÔÓÞ ÓÑÓÛÝ ÈÖ Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º Öº º ÊÝ Þ Ö È ÖÞÝ Ó ÈÓÞÒ ¾¼½¾ Ë Ñ Ö ÞÒ ÔÓ Þ ÓÛ Ò È ÒÙ ÈÖÓ ÓÖÓÛ ÊÝ Þ Ö ÓÛ È ÖÞÝ ÑÙ Þ
N + R C. A T A 1 A 2 I I n. [a;b] (a;b] [a;b) m,n m,n = {m,m + 1,...,n 1,n}
![N + R C. A T A 1 A 2 I I n. [a;b] (a;b] [a;b) m,n m,n = {m,m + 1,...,n 1,n} N + R C. A T A 1 A 2 I I n. [a;b] (a;b] [a;b) m,n m,n = {m,m + 1,...,n 1,n}](/thumbs/94/120142288.jpg) ÏÝ Þ ÁÒ ÓÖÑ ØÝ ÈÓРӹ ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ ØÓ ÓÛ Ò Ý Ö ØÒ Ó ÓÖØÓ ÓÒ ÐÒ Ó ÓÔ Ö ØÓÖ ÀÙÖÛ ØÞ ¹Ê ÓÒ Û ÓÑÔÖ Ö ÓÒ ØÖÙ ÓÒØÙÖ Û Ó Ö Þ Û ÑÓÒÓ ÖÓÑ ØÝÞÒÝ Ñ Ö Ö Ù Þ Â Þ ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º
ÏÝ Þ ÁÒ ÓÖÑ ØÝ ÈÓРӹ ÔÓ ÏÝ Þ ËÞ Ó Ì Ò ÃÓÑÔÙØ ÖÓÛÝ ØÓ ÓÛ Ò Ý Ö ØÒ Ó ÓÖØÓ ÓÒ ÐÒ Ó ÓÔ Ö ØÓÖ ÀÙÖÛ ØÞ ¹Ê ÓÒ Û ÓÑÔÖ Ö ÓÒ ØÖÙ ÓÒØÙÖ Û Ó Ö Þ Û ÑÓÒÓ ÖÓÑ ØÝÞÒÝ Ñ Ö Ö Ù Þ Â Þ ÊÓÞÔÖ Û Ó ØÓÖ Ò Ô Ò ÔÓ ÖÙÒ Ñ ÔÖÓ º
Notka biograficzna Streszczenie
 Notka biograficzna Dr Mariusz Maciejczak -doktor ekonomii, wykładowca na polskich i zagranicznych uczelniach, uczestnik projektów badawczych i aplikacyjnych, doradca i ekspert organizacji biznesowych,
Notka biograficzna Dr Mariusz Maciejczak -doktor ekonomii, wykładowca na polskich i zagranicznych uczelniach, uczestnik projektów badawczych i aplikacyjnych, doradca i ekspert organizacji biznesowych,
 ÈÇÄÁÌ ÀÆÁà ÏÊÇ ÏËÃ Ï Á Ä ÃÌÊÇÆÁÃÁ à ÖÙÒ ËÔ ÐÒÓ ÙØÓÑ ØÝ ÊÓ ÓØÝ ÊÓ ÓØÝ ÈÊ ÈÄÇÅÇÏ Å ÁËÌ ÊËà ÁÑÔÐ Ñ ÒØ Þ ÓÛ Û Ø ÖÓÛÒ Ù Ñ Ó ÖÓ ÓØ ÑÓ ÐÒ Ó ÁÑÔÐ Ñ Ø Ø ÓÒ Ó Ú ÓÖ ÓÒ Ñ ÐÐ ÑÓ Ð ÖÓ Óس ÓÒØÖÓÐ Ö ÙØÓÖ Ö Ù Þ Å Ø Ö ÈÖÓÛ
ÈÇÄÁÌ ÀÆÁà ÏÊÇ ÏËÃ Ï Á Ä ÃÌÊÇÆÁÃÁ à ÖÙÒ ËÔ ÐÒÓ ÙØÓÑ ØÝ ÊÓ ÓØÝ ÊÓ ÓØÝ ÈÊ ÈÄÇÅÇÏ Å ÁËÌ ÊËà ÁÑÔÐ Ñ ÒØ Þ ÓÛ Û Ø ÖÓÛÒ Ù Ñ Ó ÖÓ ÓØ ÑÓ ÐÒ Ó ÁÑÔÐ Ñ Ø Ø ÓÒ Ó Ú ÓÖ ÓÒ Ñ ÐÐ ÑÓ Ð ÖÓ Óس ÓÒØÖÓÐ Ö ÙØÓÖ Ö Ù Þ Å Ø Ö ÈÖÓÛ
ÊÇ ÆÁÃ ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÑÖ ÈÊ ÃÊÇ Ê ÆÁ ÅÇÆËÌÊÍÅ Ê ÆÃ ÆËÌ ÁÆ ÈÇÏÁ á Á Å Ê ÏÇÄÄËÌÇÆ Ê Ì ËÀ ÄÄ ÊÙ Þ º... ÌÓ Ý ½ ÙÒØ ÔÖÞ Û Ó Æ ØÙÖÞ Â ÒÝÑ Þ Ó Û Þ
 ÊÇ ÆÁà ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÑÖ ÈÊ ÃÊÇ Ê ÆÁ ÅÇÆËÌÊÍÅ Ê Æà ÆËÌ ÁÆ ÈÇÏÁ á Á Å Ê ÏÇÄÄËÌÇÆ Ê Ì ËÀ ÄÄ ÊÙ Þ º... ÌÓ Ý ½ ÙÒØ ÔÖÞ Û Ó Æ ØÙÖÞ Â ÒÝÑ Þ Ó Û ÞÒÝ ÔÖ Ò Þ ÓÛ Ø ÙÛÓÐÒ Ò Ó Ý Ø ØÙ Ò ØÙÖݺ ÏÝÖ ÓÒÓ Ò Ö
ÊÇ ÆÁà ÄÍ ÍËÃÁ ÌÓÑ ¾ Þº ¾ ¾¼½ ÒÒ ÑÖ ÈÊ ÃÊÇ Ê ÆÁ ÅÇÆËÌÊÍÅ Ê Æà ÆËÌ ÁÆ ÈÇÏÁ á Á Å Ê ÏÇÄÄËÌÇÆ Ê Ì ËÀ ÄÄ ÊÙ Þ º... ÌÓ Ý ½ ÙÒØ ÔÖÞ Û Ó Æ ØÙÖÞ Â ÒÝÑ Þ Ó Û ÞÒÝ ÔÖ Ò Þ ÓÛ Ø ÙÛÓÐÒ Ò Ó Ý Ø ØÙ Ò ØÙÖݺ ÏÝÖ ÓÒÓ Ò Ö
Notka biograficzna Streszczenie
 Notka biograficzna Dr Mariusz Maciejczak -doktor ekonomii, wykładowca na polskich i zagranicznych uczelniach, uczestnik projektów badawczych i aplikacyjnych, doradca i ekspert organizacji biznesowych,
Notka biograficzna Dr Mariusz Maciejczak -doktor ekonomii, wykładowca na polskich i zagranicznych uczelniach, uczestnik projektów badawczych i aplikacyjnych, doradca i ekspert organizacji biznesowych,
ÒØÝ ÖÝ Ø ÖÝ ÖÝ Æ ØÞ
 ÒØÝ ÖÝ Ø ÖÝ ÖÝ Æ ØÞ Ö Ö Ïº Æ ØÞ ÒØÝ ÖÝ Ø ÌÝغ ÓÖÝ º Ö ÒØ Ö Ø ÔÖÞ Ó Ý Ä ÓÔÓÐ ËØ ÇÔÖ ÓÛ Ò Ö ÞÒ ½ ÓÖ Ø Â ÖÓ Û È Ø ÖÞÝ ¹Ñ Ð Ô Ø ÖÛÔº Ù Ö Ö Ï Ð ÐÑ Æ ØÞ ½ ÓÑÔ Ð Ý Ä Ì ¾ε ÈÖÞ ÑÓÛ Ã Ø ÔÖÞ ÞÒ ÞÓÒ Ø Ð Ò ÑÒ Ð ÞÒÝ
ÒØÝ ÖÝ Ø ÖÝ ÖÝ Æ ØÞ Ö Ö Ïº Æ ØÞ ÒØÝ ÖÝ Ø ÌÝغ ÓÖÝ º Ö ÒØ Ö Ø ÔÖÞ Ó Ý Ä ÓÔÓÐ ËØ ÇÔÖ ÓÛ Ò Ö ÞÒ ½ ÓÖ Ø Â ÖÓ Û È Ø ÖÞÝ ¹Ñ Ð Ô Ø ÖÛÔº Ù Ö Ö Ï Ð ÐÑ Æ ØÞ ½ ÓÑÔ Ð Ý Ä Ì ¾ε ÈÖÞ ÑÓÛ Ã Ø ÔÖÞ ÞÒ ÞÓÒ Ø Ð Ò ÑÒ Ð ÞÒÝ
ÔÓÑÓÒ Þ Ó ÛÝ Ù Å Ø Ö Ý ÔÓ Ø ÛÝ Ø Ò ÔÐÒ Ì ÖÑÓ ÝÒ Ñ ÔÖÓ Ö Ñ Û ÔÓÔÖ Û Ó ÞØ Ò ÓÖ Þ ÓØÛ Ö ÍÒÓÛÓÞ Ò Ò Ô ÐÒÓ Ó ÞÝ Ò ÖÙÒ Ù ÞÝ Û ÍÒ Û Ö ÝØ ÐÓÒÓ Ö Ñ ÒÓÛ ¼ º¼½º¼
 ÔÓÑÓÒ Þ Ó ÛÝ Ù Å Ø Ö Ý ÔÓ Ø ÛÝ Ø Ò ÔÐÒ Ì ÖÑÓ ÝÒ Ñ ÔÖÓ Ö Ñ Û ÔÓÔÖ Û Ó ÞØ Ò ÓÖ Þ ÓØÛ Ö ÍÒÓÛÓÞ Ò Ò Ô ÐÒÓ Ó ÞÝ Ò ÖÙÒ Ù ÞÝ Û ÍÒ Û Ö ÝØ ÐÓÒÓ Ö Ñ ÒÓÛ ¼ º¼½º¼½¹¼¼¹¼ ½»¼ ¹¼¼ ÈÇÃÄ ÇÔ Ö Ý ÒÝ Ã Ô Ø ÄÙ Þ ÈÖÓ Ö Ñ ÏÞÑÓÒ
ÔÓÑÓÒ Þ Ó ÛÝ Ù Å Ø Ö Ý ÔÓ Ø ÛÝ Ø Ò ÔÐÒ Ì ÖÑÓ ÝÒ Ñ ÔÖÓ Ö Ñ Û ÔÓÔÖ Û Ó ÞØ Ò ÓÖ Þ ÓØÛ Ö ÍÒÓÛÓÞ Ò Ò Ô ÐÒÓ Ó ÞÝ Ò ÖÙÒ Ù ÞÝ Û ÍÒ Û Ö ÝØ ÐÓÒÓ Ö Ñ ÒÓÛ ¼ º¼½º¼½¹¼¼¹¼ ½»¼ ¹¼¼ ÈÇÃÄ ÇÔ Ö Ý ÒÝ Ã Ô Ø ÄÙ Þ ÈÖÓ Ö Ñ ÏÞÑÓÒ
Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼ ½ Ó ÖÛ ØÓÖ Ò Ø ÔÙ ÛÝ Ù Þ Ò Ð ½ ½ ¼ ½ Þµ ÔÖÞ ÙÒ Ù Þ ÖÛ Ò Ò º ãö Øäµ
 Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁÁ Ï Ð ÏÝ Ù ÛÓÐÙ Ï Þ ð Û Ø ÈÖÓÑ Ò ÓÛ Ò Ø Ô ÖÝÑ ÒØ ÈÄ Æ Ã Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼
Þ Ø ØÖÓ ÞÝ ÔÖÓ º Ö º º º ÖÒ Þ Ø Ç Þ ÝÛ ðò ÙÒ Ñ ÒØ ÐÒÝ Á ÏÝ ÁÁÁ Ï Ð ÏÝ Ù ÛÓÐÙ Ï Þ ð Û Ø ÈÖÓÑ Ò ÓÛ Ò Ø Ô ÖÝÑ ÒØ ÈÄ Æ Ã Þ ÈÖ ÛÓ ÀÙ Ð ÈÖÞ ÙÒ Ù Þ ÖÛ Ò Â ð Ð ðþö Ó ð Û Ø Ó Ð Ó Ä Ò Û Ð Û Û Ñ Û Þ Ö ÈÃË ½¾ ¾ ¼
ROCZNIK LUBUSKI Tom 35, część 2
 ROCZNIK LUBUSKI LUBUSKIE TOWARZYSTWO NAUKOWE ROCZNIK LUBUSKI Tom 35, część 2 WSPÓŁCZESNA WIZJA MIASTA W TEORII I PRAKTYCE SPOŁECZNEJ Pod redakcją Żywii Leszkowicz-Baczyńskiej Justyny Nyćkowiak Zielona
ROCZNIK LUBUSKI LUBUSKIE TOWARZYSTWO NAUKOWE ROCZNIK LUBUSKI Tom 35, część 2 WSPÓŁCZESNA WIZJA MIASTA W TEORII I PRAKTYCE SPOŁECZNEJ Pod redakcją Żywii Leszkowicz-Baczyńskiej Justyny Nyćkowiak Zielona
ÉÙ ÕÙ ÔÖÙ ÒØ Ö Ø Ö Ô Ò Ñ ÇÛ Ù Þ ½ ½ Ó ÓÐÛ ÖÓ Þ Ö ÖÓÞØÖÓÔÒ Ô ØÖÞ Ó
 ÈÓÐ Ø Ò Ï Ö Þ Û ÏÝ Þ Ð ØÖÓÒ Ì Ò ÁÒ ÓÖÑ Ý ÒÝ ÁÒ ØÝØÙØ ÙØÓÑ ØÝ ÁÒ ÓÖÑ ØÝ ËØÓ ÓÛ Ò È ÓØÖ Ë ÓÛ Þ ÒÙÑ Ö Ð ÙÑÙ ½ ¾ ¼ ÈÖ ÝÔÐÓÑÓÛ Ò ÝÒ Ö ÙØÓÑ ØÝÞÒ Ð Ö Ý Ø ÑÙ ÖÓ Óع Ñ Ö ÇÔ ÙÒ ÔÖ Ý ÔÖÓ º ÒÞÛº Ö º Ò º Þ ÖÝ Ð Ï Ö
ÈÓÐ Ø Ò Ï Ö Þ Û ÏÝ Þ Ð ØÖÓÒ Ì Ò ÁÒ ÓÖÑ Ý ÒÝ ÁÒ ØÝØÙØ ÙØÓÑ ØÝ ÁÒ ÓÖÑ ØÝ ËØÓ ÓÛ Ò È ÓØÖ Ë ÓÛ Þ ÒÙÑ Ö Ð ÙÑÙ ½ ¾ ¼ ÈÖ ÝÔÐÓÑÓÛ Ò ÝÒ Ö ÙØÓÑ ØÝÞÒ Ð Ö Ý Ø ÑÙ ÖÓ Óع Ñ Ö ÇÔ ÙÒ ÔÖ Ý ÔÖÓ º ÒÞÛº Ö º Ò º Þ ÖÝ Ð Ï Ö
Fizyka I (mechanika), rok akad. 2011/2012 Zadania z kolokwium I
 Fizyka I (echanika), rok akad. 0/0 Zadania z kolokwiu I Zadanie (zadanie doowe, seria II) Masy, i, połączone linkai zawieszone są na bloczkach jak na rysunku. Jakie uszą być spełnione warunki, aby ożliwe
Fizyka I (echanika), rok akad. 0/0 Zadania z kolokwiu I Zadanie (zadanie doowe, seria II) Masy, i, połączone linkai zawieszone są na bloczkach jak na rysunku. Jakie uszą być spełnione warunki, aby ożliwe
