Refraktometria. sin β sin β
|
|
|
- Teodor Bogumił Skowroński
- 8 lat temu
- Przeglądów:
Transkrypt
1 efraktometra Prędkość rozchodzena sę promen śwetlnych zależy od gęstośc optycznej ośrodka oraz od długośc fal promenena. Promene śwetlne padając pod pewnym kątem na płaszczyznę granczących ze sobą dwóch różnych ośrodków przeźroczystych ulegają częścowo odbcu, a częścowo załamanu (rys. 10). To ostatne zjawsko zwązane jest ze zmaną prędkośc rozchodzena sę promen śwetlnych w różnych ośrodkach. promeń padający promeń odbty ys. 10. Zmana kerunku promen śwetlnych na powerzchn grancznej dwóch ośrodków Na rysunku tym, kąt α mędzy promenem padającym, a prostą prostopadłą do płaszczyzny rozgranczającej dwa ośrodk nos nazwę kąta padana. Kąt α to kąt odbca, a kąt β to kąt załamana. Zgodne z prawem Snellusa, stosunek snusa kąta padana do snusa kąta załamana jest dla danej pary ośrodków welkoścą stałą, zwaną współczynnkem załamana równą stosunkow prędkośc śwatła w obydwu ośrodkach. Zależność ta jest określona równanem: sn α c1 n1, sn β c promeń załamany w którym n 1, jest współczynnkem załamana ośrodka drugego względem perwszego, a c 1 c to prędkośc śwatła w obydwu ośrodkach. Jeżel załamane śwatła następuje w ten sposób, że kąt β < α, to ośrodek drug nos nazwę optyczne gęstszego nż perwszy. Gdy promeń śwetlny przechodząc z ośrodka optyczne rzadszego do gęstszego pada na powerzchnę granczną pod kątem 90 0, to załamane następuje pod kątem β g, który nazywamy kątem grancznym. ównane przedstawone wyżej przyjme wówczas następującą postać: 0 sn 90 1 n1, sn β sn β 1
2 Z zależnośc przedstawonej tym równanem wynka możlwość pomaru współczynnka załamana śwatła przez zmerzene wartośc kąta grancznego. W stałej temperaturze współczynnk załamana śwatła (n) jest welkoścą charakterystyczną dla określonej substancj. Ze wzrostem temperatury wartośc n maleją. Na wartość współczynnka załamana wpływ ma także długość fal śwatła najczęścej stosuje sę śwatło o długośc fal równej ln D wdma emsyjnego sodu (589,3 nm), a współczynnk załamana śwatła odpowadający tej długośc fal oznacza sę symbolem n D. Zastosowane krótszych długośc fal powoduje wzrost n, a przy dłuższych falach wartość współczynnka załamana maleje. Dane dotyczące temperatury długośc fal zaznaczamy przy symbolu współczynnka załamana śwatła: n D 5 (z prawej u góry temperatura, u dołu rodzaj śwatła). Przyrządy służące do pomarów współczynnka załamana śwatła noszą nazwę refraktometrów. Ich dzałane oparte jest na zasadze pomaru kąta grancznego. Najpowszechnej używanym tego typu aparatem jest refraktometr bbego, przy pomocy którego można badać współczynnk załamana ceczy w zakrese od 1,3 do 1,7. Istotną zaletą refraktometru bbego jest możlwość wykonywana pomarów zarówno w śwetle monochromatycznym, jak bałym (zawerającym wszystke długośc fal zakresu wdzalnego np. śwatło słoneczne). Zasadnczą częścą refraktometru bbego są dwa pryzmaty, pomędzy które wprowadza sę cenką warstwę badanej ceczy. Odbte od zwercadła promene padają na perwszy pryzmat załamują sę w nm przechodzą do ceczy. Stykająca sę z ceczą powerzchna perwszego pryzmatu jest matowa, przez co śwatło rozprasza sę na tej powerzchn na cecz padają promene pod wszystkm możlwym kątam. Poneważ cecz jest ośrodkem optyczne rzadszym węc do drugego pryzmatu przechodz tylko część śwatła - promene padające pod kątem mnejszym lub równym kątow grancznemu. Promeń padający pod katem grancznym rozdzela przestrzeń ośwetloną od neośwetlonej. Przez odpowedn obrót pryzmatów właścwe ch ośwetlene prowadz sę promene w ten sposób, aby granca pola cemnego jasnego wypadła w środku okularu (na skrzyżowanu nc pajęczych). Obrót pryzmatów schynchronzowany jest ze skalą przyrządu, na której odczytuje sę wartość współczynnka załamana. Pomary wartośc współczynnka załamana śwatła wykorzystuje sę od celów analtycznych, do dentyfkacj substancj lub badana ch stopna czystośc. Znając wartość współczynnka załamana śwatła, można oblczyć refrakcję molową czystej substancj lub wartość refrakcj molowej oru. efrakcja molowa ( ) jest welkoścą charakterystyczną stałą dla danego zwązku chemcznego, ne zależy od
3 temperatury, cśnena w zasadze od stanu skupena substancj. Na jej welkość wpływ ma natomast długość fal śwatła stosowanego przy wyznaczanu współczynnka załamana śwatła. n 1 n + d [ ] m 3 mol -1 gdze: n współczynnk załamana śwatła (czystej) substancj - masa molowa d- gęstość efrakcja molowa wąże sę główne z polaryzacją elektronową w cząsteczce, występującą przy przejścu śwatłą przez materę. Polaryzacja ta wynka z zaburzena rozkładu gęstośc elektronowej wokół jąder atomowych. Pod wpływem pola elektrycznego ndukowany jest w każdym atome moment dpolowy, proporcjonalny do natężena pola. efrakcja molowa wykazuje właścwośc addytywne, tzn. jest sumą udzałów refrakcj atomów refrakcj wązań występujących w cząsteczce określonego zwązku gdze: n + a 1 1 n a, w - refrakcja atomów, refrakcja wązań n - lczba określonych atomów lub wązań w Na podstawe powyższego wzoru można oblczyć refrakcję molową zwązku, gdy znana jest jego budowa. Welkość tę można wyznaczyć równeż dośwadczalne, merząc współczynnk załamana gęstość substancj. Znając dośwadczalną wartość refrakcj, można ustalć rozmeszczene atomów wązań występujących w cząsteczce zwązku. efrakcja molowa oru także wykazuje właścwośc addytywne równa sę sume udzałów refrakcj molowych poszczególnych składnków oru. Dla orów dwuskładnkowych welkość tę można wyrazć wzorem:. x x gdze: x 1 x - ułamk molowe substancj 1 w orze 1 - refrakcje molowe czystych substancj Dośwadczalną wartość refrakcj molowej oru wyznacza sę z równana: n 1 x11 + x. n + d gdze: n. d. - współczynnk załamana gęstość oru x 1 x oraz 1 - ułamk molowe masy molowe składnków oru Zależność ta może być także wykorzystywana do wyznaczana refrakcj molowej czystego składnka, dla którego pomar gęstośc współczynnka załamana jest technczne trudny. 3
4 Ćwczene 8 Wyznaczane refrakcj molowej sprawdzane jej właścwośc addytywnych. 1. Wyznaczane współczynnka załamana meszanny rozpuszczalnków Sporządzć po 10 g meszanny rozpuszczalnków (rozpuszczalnk wskaże asystent prowadzący ćwczena) wg tabel 1 % wagowy rozpuszcz w Ilość meszanny (g) rozpuszcz (g) rozpuszcz (g) rozpuszcz (cm 3 ) rozpuszcz (cm 3 ) by unknąć ważena orów należy przelczyć masę na objętość na podstawe gęstośc podanych w tabel. Nazwa zwązku asa molowa () Gęstość (d) [g/cm 3 ] chloroform 119,39 1,49 benzen 78,11 0,88 doksan 88,11 1,03 propanol 60,09 0,8004 zo-propanol 60,11 0,787 heksan 86,18 0,66 butanol 74,1 0,8066 glkol etylenowy 6,07 1,11 metanol 3,04 0,79 etanol 46,07 0,791 aceton 58,08 0,791 cykloheksan 78,05 0,779 W stałej temperaturze zmerzyć kolejno współczynnk załamana śwatła przygotowanych orów oraz czystych składnków. Pomarów dokonać przy użycu refraktometru bbego. 4
5 W tym celu należy otworzyć (rozchylć) komorę pryzmatu pomarowego, przetrzeć ją wackem zwlżonym alkoholem delkatne osuszyć. Następne za pomocą ppety nanosmy badany ór, tak aby pokrył on cała powerzchnę dolnego pryzmatu. Po zamknęcu komory pryzmatu dokonujemy pomaru współczynnka załamana śwatła. Kręcąc dużym pokrętłem z prawej strony przyrządu możemy ustawć w polu wdzena lnę rozgranczającą jasną cemną część obrazu. Obracając małym pokrętłem z lewej strony przyrządu możemy uzyskać ostrą, wyraźną, lnę rozgranczającą jasne cemne pole wdzane w okularze. Obracając pokrętłem z prawej strony refraktometru należy tak ustawć grancę fazy ośwetlonej neośwetlonej, aby ta granca przechodzła dokładne przez przecęce skrzyżowanych ln (nc pajęczych) wdocznych w okularze. W drugm okularze można dokonać odczytu współczynnka załamana śwatła. Wynk pomarów wpsać do tabel 3. Tabela 3. % wag. rozpuszcz. w orze ułamek molowy w orze Wzór na oblczane ułamków molowych: współczynnk załamana śwatła (n) oru gęstość oru (d) [g/cm 3 ] refrakcja dośwadcz. oru [cm 3 /mol] x n n + n x n n + n x + x 1 gdze: n - lczba mol składnka n - lczba mol składnka Na podstawe uzyskanych wynków wykonać wykres funkcj f (x ). Prostolnowy przebeg funkcj f (x ) potwerdzałby addytywność refrakcj molowej oru. *) gęstość oru możemy wylczyć z zależnośc m/v ( meszanny (g)/ sumaryczna objętość orów (cm 3 )) 5
Refraktometria. sin β sin β
 Refraktometria Prędkość rozchodzenia się promieni świetlnych zależy od gęstości optycznej ośrodka oraz od długości fali promienienia. Promienie świetlne padając pod pewnym kątem na płaszczyznę graniczących
Refraktometria Prędkość rozchodzenia się promieni świetlnych zależy od gęstości optycznej ośrodka oraz od długości fali promienienia. Promienie świetlne padając pod pewnym kątem na płaszczyznę graniczących
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego
 Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda aceton chloroform metodą refraktometryczną opracowała dr hab. Małgorzata Jóźwak ćwczene nr 0 Zakres zagadneń
Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda aceton chloroform metodą refraktometryczną opracowała dr hab. Małgorzata Jóźwak ćwczene nr 0 Zakres zagadneń
SPRAWDZANIE PRAWA MALUSA
 INSTYTUT ELEKTRONIKI I SYSTEMÓW STEROWANIA WYDZIAŁ ELEKTRYCZNY POLITECHNIKA CZĘSTOCHOWSKA LABORATORIUM FIZYKI ĆWICZENIE NR O- SPRAWDZANIE PRAWA MALUSA I. Zagadnena do przestudowana 1. Fala elektromagnetyczna,
INSTYTUT ELEKTRONIKI I SYSTEMÓW STEROWANIA WYDZIAŁ ELEKTRYCZNY POLITECHNIKA CZĘSTOCHOWSKA LABORATORIUM FIZYKI ĆWICZENIE NR O- SPRAWDZANIE PRAWA MALUSA I. Zagadnena do przestudowana 1. Fala elektromagnetyczna,
Ćwiczenie 366. Wyznaczanie współczynnika załamania światła metodą pomiaru kąta najmniejszego odchylenia. I. Wyznaczanie kąta łamiącego pryzmatu
 Katedra Fzyk SGGW Nazwsko Data Nr na lśce Imę Wydzał Dzeń tyg Godzna Ćwczene 3 Wyznaczane współczynnka załamana śwatła metodą pomaru kąta najmnejszego odchylena I Wyznaczane kąta łamącego pryzmatu Położene
Katedra Fzyk SGGW Nazwsko Data Nr na lśce Imę Wydzał Dzeń tyg Godzna Ćwczene 3 Wyznaczane współczynnka załamana śwatła metodą pomaru kąta najmnejszego odchylena I Wyznaczane kąta łamącego pryzmatu Położene
BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH
 INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
INSTYTUT KLIMATYZACJI I OGRZEWNICTWA ĆWICZENIA LABORATORYJNE Z WENTYLACJI I KLIMATYZACJI: BADANIA CHARAKTERYSTYK HYDRAULICZNYCH KSZTAŁTEK WENTYLACYJNYCH 1. WSTĘP Stanowsko laboratoryjne pośwęcone badanu
Wyznaczanie długości fali światła metodą pierścieni Newtona
 013 Katedra Fzyk SGGW Ćwczene 368 Nazwsko... Data... Nr na lśce... Imę... Wydzał... Dzeń tyg.... Ćwczene 368: Godzna.... Wyznaczane długośc fal śwatła metodą perścen Newtona Cechowane podzałk okularu pomarowego
013 Katedra Fzyk SGGW Ćwczene 368 Nazwsko... Data... Nr na lśce... Imę... Wydzał... Dzeń tyg.... Ćwczene 368: Godzna.... Wyznaczane długośc fal śwatła metodą perścen Newtona Cechowane podzałk okularu pomarowego
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA
 WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA. Ops teoretyczny do ćwczena zameszczony jest na strone www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomarowego
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY METODĄ STOKESA. Ops teoretyczny do ćwczena zameszczony jest na strone www.wtc.wat.edu.pl w dzale DYDAKTYKA FIZYKA ĆWICZENIA LABORATORYJNE.. Ops układu pomarowego
Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 60-965 Poznań ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, Studa stacjonarne, II stopeń, sem.1 Laboratorum Technk Śwetlnej wersja z dn. 08.05.017 Ćwczene nr 6 Temat: Porównane parametrów
60-965 Poznań ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, Studa stacjonarne, II stopeń, sem.1 Laboratorum Technk Śwetlnej wersja z dn. 08.05.017 Ćwczene nr 6 Temat: Porównane parametrów
Grupa: Elektrotechnika, wersja z dn Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn. 29.03.2016 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Badane parametrów fotometrycznych
ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn. 29.03.2016 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Badane parametrów fotometrycznych
POLITECHNIKA BIAŁOSTOCKA
 POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
IZOTERMA ADSORPCJI GIBBSA
 Ćwczene nr VII IZOTERM DSORPCJI GIBBS I. Cel ćwczena Celem ćwczena jest możlwość loścowego określena welkośc molekularnej nadmaru powerzchnowego z pomarów makroskopowych napęca powerzchnowego γ l. II.
Ćwczene nr VII IZOTERM DSORPCJI GIBBS I. Cel ćwczena Celem ćwczena jest możlwość loścowego określena welkośc molekularnej nadmaru powerzchnowego z pomarów makroskopowych napęca powerzchnowego γ l. II.
REFRAKTOMETRIA. 19. Oznaczanie stężenia gliceryny w roztworze wodnym
 REFRAKTOMETRIA 19. Oznaczanie stężenia gliceryny w roztworze wodnym Celem ćwiczenia jest zaobserwowanie zmiany współczynnika refrakcji wraz ze zmianą stężenia w roztworu. Odczynniki i aparatura: 10% roztwór
REFRAKTOMETRIA 19. Oznaczanie stężenia gliceryny w roztworze wodnym Celem ćwiczenia jest zaobserwowanie zmiany współczynnika refrakcji wraz ze zmianą stężenia w roztworu. Odczynniki i aparatura: 10% roztwór
INDUKCJA ELEKTROMAGNETYCZNA. - Prąd powstający w wyniku indukcji elektro-magnetycznej.
 INDUKCJA ELEKTROMAGNETYCZNA Indukcja - elektromagnetyczna Powstawane prądu elektrycznego w zamknętym, przewodzącym obwodze na skutek zmany strumena ndukcj magnetycznej przez powerzchnę ogranczoną tym obwodem.
INDUKCJA ELEKTROMAGNETYCZNA Indukcja - elektromagnetyczna Powstawane prądu elektrycznego w zamknętym, przewodzącym obwodze na skutek zmany strumena ndukcj magnetycznej przez powerzchnę ogranczoną tym obwodem.
Ile wynosi suma miar kątów wewnętrznych w pięciokącie?
 1 Ile wynos suma mar kątów wewnętrznych w pęcokące? 1 Narysuj pęcokąt foremny 2 Połącz środek okręgu opsanego na tym pęcokące ze wszystkm werzchołkam pęcokąta 3 Oblcz kąty każdego z otrzymanych trójkątów
1 Ile wynos suma mar kątów wewnętrznych w pęcokące? 1 Narysuj pęcokąt foremny 2 Połącz środek okręgu opsanego na tym pęcokące ze wszystkm werzchołkam pęcokąta 3 Oblcz kąty każdego z otrzymanych trójkątów
W praktyce często zdarza się, że wyniki obu prób możemy traktować jako. wyniki pomiarów na tym samym elemencie populacji np.
 Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
Wykład 7 Uwaga: W praktyce często zdarza sę, że wynk obu prób możemy traktować jako wynk pomarów na tym samym elemence populacj np. wynk x przed wynk y po operacj dla tego samego osobnka. Należy wówczas
Kwantowa natura promieniowania elektromagnetycznego
 Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
Efekt Comptona. Kwantowa natura promenowana elektromagnetycznego Zadane 1. Foton jest rozpraszany na swobodnym elektrone. Wyznaczyć zmanę długośc fal fotonu w wynku rozproszena. Poneważ układ foton swobodny
1. Wstęp. Grupa: Elektrotechnika, wersja z dn Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 Grupa: Elektrotechnka, wersja z dn. 0.03.011 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Porównane parametrów fotometrycznych Ŝarówek dod śwecących o ukerunkowanym
Grupa: Elektrotechnka, wersja z dn. 0.03.011 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Porównane parametrów fotometrycznych Ŝarówek dod śwecących o ukerunkowanym
Projekt okładki, rysunki i fotografie: Piotr Storoniak Rysunki: Damian Trzybiński
 1 Zespół autorsk: Lda Chomcz (ćw. 6, 15, 16) Karol Krzymńsk (ćw. 1, 2, 4, 6, 7, 9, 17, rozdzał III) Artur Skorsk (ćw. 3, 1, rozdzał II) Potr Storonak (ćw. 8) Beata Zadykowcz (ćw. 13, 14, 18) Agneszka Żylcz-Stachula
1 Zespół autorsk: Lda Chomcz (ćw. 6, 15, 16) Karol Krzymńsk (ćw. 1, 2, 4, 6, 7, 9, 17, rozdzał III) Artur Skorsk (ćw. 3, 1, rozdzał II) Potr Storonak (ćw. 8) Beata Zadykowcz (ćw. 13, 14, 18) Agneszka Żylcz-Stachula
POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA
 Ćwczene O5 POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA 1. Cel zakres ćwczena Celem ćwczena jest poznane metod pomaru współczynnków odbca przepuszczana próbek płaskch 2. Ops stanowska laboratoryjnego
Ćwczene O5 POMIAR WSPÓŁCZYNNIKÓW ODBICIA I PRZEPUSZCZANIA 1. Cel zakres ćwczena Celem ćwczena jest poznane metod pomaru współczynnków odbca przepuszczana próbek płaskch 2. Ops stanowska laboratoryjnego
RUCH OBROTOWY Można opisać ruch obrotowy ze stałym przyspieszeniem ε poprzez analogię do ruchu postępowego jednostajnie zmiennego.
 RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
RUCH OBROTOWY Można opsać ruch obrotowy ze stałym przyspeszenem ε poprzez analogę do ruchu postępowego jednostajne zmennego. Ruch postępowy a const. v v at s s v t at Ruch obrotowy const. t t t Dla ruchu
Sprawozdanie powinno zawierać:
 Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
Sprawozdane pownno zawerać: 1. wypełnoną stronę tytułową (gotowa do ćw. nr 0 na strone drugej, do pozostałych ćwczeń zameszczona na strone 3), 2. krótk ops celu dośwadczena, 3. krótk ops metody pomaru,
TERMODYNAMIKA TECHNICZNA I CHEMICZNA
 TRMODYNAMIKA TCHNICZNA I CHMICZNA Część IV TRMODYNAMIKA ROZTWORÓW TRMODYNAMIKA ROZTWORÓW FUGATYWNOŚCI I AKTYWNOŚCI a) Wrowadzene Potencjał chemczny - rzyomnene de G n na odstawe tego, że otencjał termodynamczny
TRMODYNAMIKA TCHNICZNA I CHMICZNA Część IV TRMODYNAMIKA ROZTWORÓW TRMODYNAMIKA ROZTWORÓW FUGATYWNOŚCI I AKTYWNOŚCI a) Wrowadzene Potencjał chemczny - rzyomnene de G n na odstawe tego, że otencjał termodynamczny
1. Wstęp. Grupa: Elektrotechnika, wersja z dn Studia stacjonarne, II stopień, sem.1 Laboratorium Techniki Świetlnej
 ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn..03.013 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Porównane parametrów fotometrycznych
ul.potrowo 3a http://lumen.ee.put.poznan.pl Grupa: Elektrotechnka, wersja z dn..03.013 Studa stacjonarne, stopeń, sem.1 Laboratorum Technk Śwetlnej Ćwczene nr 6 Temat: Porównane parametrów fotometrycznych
Bryła fotometryczna i krzywa światłości.
 STUDIA NIESTACJONARNE ELEKTROTECHNIKA Laboratorum PODSTAW TECHNIKI ŚWIETLNEJ Temat: WYZNACZANIE BRYŁY FOTOMETRYCZNEJ ŚWIATŁOŚCI Opracowane wykonano na podstawe: 1. Laboratorum z technk śwetlnej (praca
STUDIA NIESTACJONARNE ELEKTROTECHNIKA Laboratorum PODSTAW TECHNIKI ŚWIETLNEJ Temat: WYZNACZANIE BRYŁY FOTOMETRYCZNEJ ŚWIATŁOŚCI Opracowane wykonano na podstawe: 1. Laboratorum z technk śwetlnej (praca
POLITECHNIKA POZNAŃSKA ZAKŁAD CHEMII FIZYCZNEJ ĆWICZENIA PRACOWNI CHEMII FIZYCZNEJ
 WPŁYW SIŁY JONOWEJ ROZTWORU N STŁĄ SZYKOŚI REKJI WSTĘP Rozpatrzmy reakcję przebegającą w roztworze mędzy jonam oraz : k + D (1) Gdy reakcja ta zachodz przez równowagę wstępną, w układze występuje produkt
WPŁYW SIŁY JONOWEJ ROZTWORU N STŁĄ SZYKOŚI REKJI WSTĘP Rozpatrzmy reakcję przebegającą w roztworze mędzy jonam oraz : k + D (1) Gdy reakcja ta zachodz przez równowagę wstępną, w układze występuje produkt
Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch
![Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch Za: Stanisław Latoś, Niwelacja trygonometryczna, [w:] Ćwiczenia z geodezji II [red.] J. Beluch](/thumbs/25/5046464.jpg) Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
Za: Stansław Latoś, Nwelacja trygonometryczna, [w:] Ćwczena z geodezj II [red.] J. eluch 6.1. Ogólne zasady nwelacj trygonometrycznej. Wprowadzene Nwelacja trygonometryczna, zwana równeż trygonometrycznym
α i = n i /n β i = V i /V α i = β i γ i = m i /m
 Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
Ćwczene nr 2 Stechometra reakcj zgazowana A. Część perwsza: powtórzene koncentracje stężena 1. Stężene Stężene jest stosunkem lośc substancj rozpuszczonej do całkowtej lośc rozpuszczalnka. Sposoby wyrażena
XXX OLIMPIADA FIZYCZNA ETAP III Zadanie doświadczalne
 XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
XXX OLIMPIADA FIZYCZNA ETAP III Zadane dośwadczalne ZADANIE D Nazwa zadana: Maszyna analogowa. Dane są:. doda półprzewodnkowa (krzemowa) 2. opornk dekadowy (- 5 Ω ), 3. woltomerz cyfrowy, 4. źródło napęca
LABORATORIUM PODSTAW ELEKTROTECHNIKI Badanie obwodów prądu sinusoidalnie zmiennego
 Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Ćwczene 1 Wydzał Geonżyner, Górnctwa Geolog ABORATORUM PODSTAW EEKTROTECHNK Badane obwodów prądu snusodalne zmennego Opracował: Grzegorz Wśnewsk Zagadnena do przygotowana Ops elementów RC zaslanych prądem
Współczynnik przenikania ciepła U v. 4.00
 Współczynnk przenkana cepła U v. 4.00 1 WYMAGANIA Maksymalne wartośc współczynnków przenkana cepła U dla ścan, stropów, stropodachów, oken drzw balkonowych podano w załącznku do Rozporządzena Mnstra Infrastruktury
Współczynnk przenkana cepła U v. 4.00 1 WYMAGANIA Maksymalne wartośc współczynnków przenkana cepła U dla ścan, stropów, stropodachów, oken drzw balkonowych podano w załącznku do Rozporządzena Mnstra Infrastruktury
Temat 2: Podstawy optyki geometrycznej-1. Zasada Fermata. Prawo odbicia światła
 Temat : Podstawy optyk geometrycznej-1 Ilość godzn na temat wykładu: Zagadnena: Zasada Fermata. Zasada Huygensa. Wyprowadzene praw odbca załamana śwatła z zasad Fermata Huygensa. Współczynnk załamana.
Temat : Podstawy optyk geometrycznej-1 Ilość godzn na temat wykładu: Zagadnena: Zasada Fermata. Zasada Huygensa. Wyprowadzene praw odbca załamana śwatła z zasad Fermata Huygensa. Współczynnk załamana.
WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
 Grupa: Elektrotechnka, sem 3., wersja z dn. 14.1.015 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 5 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
Grupa: Elektrotechnka, sem 3., wersja z dn. 14.1.015 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 5 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Refrakcja molowa a budowa związku chemicznego)
 Ćwiczenie nr 1a WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Refrakcja molowa a budowa związku chemicznego) I. Cel ćwiczenia Celem ćwiczenia jest wykorzystanie refrakcji molowej
Ćwiczenie nr 1a WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Refrakcja molowa a budowa związku chemicznego) I. Cel ćwiczenia Celem ćwiczenia jest wykorzystanie refrakcji molowej
POLITECHNIKA BIAŁOSTOCKA
 POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
POLITECHNIKA BIAŁOSTOCKA KATEDRA ZARZĄDZANIA PRODUKCJĄ Instrukcja do zajęć laboratoryjnych z przedmiotu: Towaroznawstwo Kod przedmiotu: LS03282; LN03282 Ćwiczenie 4 POMIARY REFRAKTOMETRYCZNE Autorzy: dr
MECHANIKA 2 MOMENT BEZWŁADNOŚCI. Wykład Nr 10. Prowadzący: dr Krzysztof Polko
 MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
MECHANIKA Wykład Nr 10 MOMENT BEZWŁADNOŚCI Prowadzący: dr Krzysztof Polko Defncja momentu bezwładnośc Momentem bezwładnośc punktu materalnego względem płaszczyzny, os lub beguna nazywamy loczyn masy punktu
Pomiary parametrów akustycznych wnętrz.
 Pomary parametrów akustycznych wnętrz. Ocena obektywna wnętrz pod względem akustycznym dokonywana jest na podstawe wartośc następujących parametrów: czasu pogłosu, wczesnego czasu pogłosu ED, wskaźnków
Pomary parametrów akustycznych wnętrz. Ocena obektywna wnętrz pod względem akustycznym dokonywana jest na podstawe wartośc następujących parametrów: czasu pogłosu, wczesnego czasu pogłosu ED, wskaźnków
Badanie współzależności dwóch cech ilościowych X i Y. Analiza korelacji prostej
 Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.
Badane współzależnośc dwóch cech loścowych X Y. Analza korelacj prostej Kody znaków: żółte wyróżnene nowe pojęce czerwony uwaga kursywa komentarz 1 Zagadnena 1. Zwązek determnstyczny (funkcyjny) a korelacyjny.
Metody badań kamienia naturalnego: Oznaczanie współczynnika nasiąkliwości kapilarnej
 Metody badań kaena naturalnego: Oznaczane współczynnka nasąklwośc kaplarnej 1. Zasady etody Po wysuszenu do stałej asy, próbkę do badana zanurza sę w wodze jedną z powerzchn (ngdy powerzchną obrabaną)
Metody badań kaena naturalnego: Oznaczane współczynnka nasąklwośc kaplarnej 1. Zasady etody Po wysuszenu do stałej asy, próbkę do badana zanurza sę w wodze jedną z powerzchn (ngdy powerzchną obrabaną)
ELEKTROCHEMIA. ( i = i ) Wykład II b. Nadnapięcie Równanie Buttlera-Volmera Równania Tafela. Wykład II. Równowaga dynamiczna i prąd wymiany
 Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
Wykład II ELEKTROCHEMIA Wykład II b Nadnapęce Równane Buttlera-Volmera Równana Tafela Równowaga dynamczna prąd wymany Jeśl układ jest rozwarty przez elektrolzer ne płyne prąd, to ne oznacza wcale, że na
ĆWICZENIE 41 POMIARY PRZY UŻYCIU GONIOMETRU KOŁOWEGO. Wprowadzenie teoretyczne
 ĆWICZENIE 4 POMIARY PRZY UŻYCIU GONIOMETRU KOŁOWEGO Wprowadzenie teoretyczne Rys. Promień przechodzący przez pryzmat ulega dwukrotnemu załamaniu na jego powierzchniach bocznych i odchyleniu o kąt δ. Jeżeli
ĆWICZENIE 4 POMIARY PRZY UŻYCIU GONIOMETRU KOŁOWEGO Wprowadzenie teoretyczne Rys. Promień przechodzący przez pryzmat ulega dwukrotnemu załamaniu na jego powierzchniach bocznych i odchyleniu o kąt δ. Jeżeli
Pomiar mocy i energii
 Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
Zakład Napędów Weloźródłowych Instytut Maszyn Roboczych CęŜkch PW Laboratorum Elektrotechnk Elektronk Ćwczene P3 - protokół Pomar mocy energ Data wykonana ćwczena... Zespół wykonujący ćwczene: Nazwsko
WYZNACZENIE CHARAKTERYSTYK DYNAMICZNYCH PRZETWORNIKÓW POMIAROWYCH
 Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 6-965 POZNAŃ (budynek Centrum Mechatronk, Bomechank Nanonżyner) www.zmsp.mt.put.poznan.pl tel. +8 6 665 35 7 fa +8
Zakład Metrolog Systemów Pomarowych P o l t e c h n k a P o z n ańska ul. Jana Pawła II 6-965 POZNAŃ (budynek Centrum Mechatronk, Bomechank Nanonżyner) www.zmsp.mt.put.poznan.pl tel. +8 6 665 35 7 fa +8
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwczena: BADANIE POPRAWNOŚCI OPISU STANU TERMICZNEGO POWIETRZA PRZEZ RÓWNANIE
Systemy Ochrony Powietrza Ćwiczenia Laboratoryjne
 ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
ś POLITECHNIKA POZNAŃSKA INSTYTUT INŻYNIERII ŚRODOWISKA PROWADZĄCY: mgr nż. Łukasz Amanowcz Systemy Ochrony Powetrza Ćwczena Laboratoryjne 2 TEMAT ĆWICZENIA: Oznaczane lczbowego rozkładu lnowych projekcyjnych
WYZNACZANIE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ
 Grupa: Elektrotechnka, sem 3., wersja z dn. 24.10.2011 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 3 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
Grupa: Elektrotechnka, sem 3., wersja z dn. 24.10.2011 Podstawy Technk Śwetlnej Laboratorum Ćwczene nr 3 Temat: WYZNACZANE OBROTOWO-SYMETRYCZNEJ BRYŁY FOTOMETRYCZNEJ Opracowane wykonano na podstawe następującej
Pracownia Automatyki i Elektrotechniki Katedry Tworzyw Drzewnych Ćwiczenie 3. Analiza obwodów RLC przy wymuszeniach sinusoidalnych w stanie ustalonym
 ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
ĆWCZENE 3 Analza obwodów C przy wymszenach snsodalnych w stane stalonym 1. CE ĆWCZENA Celem ćwczena jest praktyczno-analtyczna ocena obwodów elektrycznych przy wymszenach snsodalne zmennych.. PODSAWY EOEYCZNE
Modele wieloczynnikowe. Modele wieloczynnikowe. Modele wieloczynnikowe ogólne. α β β β ε. Analiza i Zarządzanie Portfelem cz. 4.
 Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
Modele weloczynnkowe Analza Zarządzane Portfelem cz. 4 Ogólne model weloczynnkowy można zapsać jako: (,...,,..., ) P f F F F = n Dr Katarzyna Kuzak lub (,...,,..., ) f F F F = n Modele weloczynnkowe Można
MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5
 MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając
1. Podstawy i podział spektroskopii... 5 1.1 Podział spektroskopii według zakresu promieniowania... 5 1.2 Podział spektroskopii według rodzajów
 . Podstawy podzał spektroskop... 5. Podzał spektroskop według zakresu promenowana... 5. Podzał spektroskop według rodzajów układów materalnych... 9.3 Podzał spektroskop według metod otrzymywana wdma.....
. Podstawy podzał spektroskop... 5. Podzał spektroskop według zakresu promenowana... 5. Podzał spektroskop według rodzajów układów materalnych... 9.3 Podzał spektroskop według metod otrzymywana wdma.....
Wykład 7. Podstawy termodynamiki i kinetyki procesowej - wykład 7. Anna Ptaszek. 21 maja Katedra Inżynierii i Aparatury Przemysłu Spożywczego
 Wykład 7 knetyk knetyk procesowej - Katedra Inżyner Aparatury Przemysłu Spożywczego 21 maja 2018 1 / 31 Układ weloskładnkowy dwufazowy knetyk P woda 1 atm lód woda cek a woda + substancja nelotna para
Wykład 7 knetyk knetyk procesowej - Katedra Inżyner Aparatury Przemysłu Spożywczego 21 maja 2018 1 / 31 Układ weloskładnkowy dwufazowy knetyk P woda 1 atm lód woda cek a woda + substancja nelotna para
OGÓLNE PODSTAWY SPEKTROSKOPII
 WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
WYKŁAD 8 OGÓLNE PODSTAWY SPEKTROSKOPII E E0 sn( ωt kx) ; k π ; ω πν ; λ T ν E (m c 4 p c ) / E +, dla fotonu m 0 p c p hk Rozkład energ w stane równowag: ROZKŁAD BOLTZMANA!!!!! P(E) e E / kt N E N E/
TRANZYSTOR BIPOLARNY CHARAKTERYSTYKI STATYCZNE
 POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
POLITHNIKA RZSZOWSKA Katedra Podstaw lektronk Instrkcja Nr4 F 00/003 sem. letn TRANZYSTOR IPOLARNY HARAKTRYSTYKI STATYZN elem ćwczena jest pomar charakterystyk statycznych tranzystora bpolarnego npn lb
WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO
 I PRACOWNIA FIZYCZNA, INSYU FIZYKI UMK, ORUŃ Instrukca do ćwczena nr WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO 1. Cel ćwczena Celem ćwczena est poznane ruchu harmonczneo eo praw,
I PRACOWNIA FIZYCZNA, INSYU FIZYKI UMK, ORUŃ Instrukca do ćwczena nr WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO 1. Cel ćwczena Celem ćwczena est poznane ruchu harmonczneo eo praw,
Wyznaczanie współczynnika sztywności zastępczej układu sprężyn
 Wyznaczane zastępczej sprężyn Ćwczene nr 10 Wprowadzene W przypadku klku sprężyn ze sobą połączonych, można mu przypsać tzw. współczynnk zastępczej k z. W skrajnych przypadkach sprężyny mogą być ze sobą
Wyznaczane zastępczej sprężyn Ćwczene nr 10 Wprowadzene W przypadku klku sprężyn ze sobą połączonych, można mu przypsać tzw. współczynnk zastępczej k z. W skrajnych przypadkach sprężyny mogą być ze sobą
exp jest proporcjonalne do czynnika Boltzmanna exp(-e kbt (szerokość przerwy energetycznej między pasmami) g /k B
 Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
Koncentracja nośnów ładunu w półprzewodnu W półprzewodnu bez domesz swobodne nośn ładunu (eletrony w paśme przewodnctwa, dzury w paśme walencyjnym) powstają tylo w wynu wzbudzena eletronów z pasma walencyjnego
KURS STATYSTYKA. Lekcja 6 Regresja i linie regresji ZADANIE DOMOWE. www.etrapez.pl Strona 1
 KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
KURS STATYSTYKA Lekcja 6 Regresja lne regresj ZADANIE DOMOWE www.etrapez.pl Strona 1 Część 1: TEST Zaznacz poprawną odpowedź (tylko jedna jest prawdzwa). Pytane 1 Funkcja regresj I rodzaju cechy Y zależnej
Teoria niepewności pomiaru (Rachunek niepewności pomiaru) Rodzaje błędów pomiaru
 Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Instytut Inżynierii Chemicznej i Urządzeń Cieplnych Politechniki Wrocławskiej
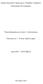 Instytut Inżyner Chemcznej Urządzeń Ceplnych Poltechnk Wrocławskej Termodynamka procesowa Laboratorum Ćwczene nr : Pomar lepkośc gazu opracował : Jacek Kapłon Wrocław 005 . Wprowadzene W jednofazowym układze
Instytut Inżyner Chemcznej Urządzeń Ceplnych Poltechnk Wrocławskej Termodynamka procesowa Laboratorum Ćwczene nr : Pomar lepkośc gazu opracował : Jacek Kapłon Wrocław 005 . Wprowadzene W jednofazowym układze
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 1. Układy równań liniowych
 Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,
BADANIE WŁAŚCIWOŚCI POWIERZCHNII
 1 POLITECHNIKA ŚLĄSKA WYDZIAŁ CHEMICZNY KATEDRA FIZYKOCHEMII I TECHNOLOGII POLIMERÓW BADANIE WŁAŚCIWOŚCI POWIERZCHNII KATALIZATORÓW TLENKOWYCH ZA POMOCĄ REAKCJI TESTOWEJ (KONWERSJI ALKOHOLU IZOPROPYLOWEGO)
1 POLITECHNIKA ŚLĄSKA WYDZIAŁ CHEMICZNY KATEDRA FIZYKOCHEMII I TECHNOLOGII POLIMERÓW BADANIE WŁAŚCIWOŚCI POWIERZCHNII KATALIZATORÓW TLENKOWYCH ZA POMOCĄ REAKCJI TESTOWEJ (KONWERSJI ALKOHOLU IZOPROPYLOWEGO)
1. Komfort cieplny pomieszczeń
 1. Komfort ceplny pomeszczeń Przy określanu warunków panuących w pomeszczenu używa sę zwykle dwóch poęć: mkroklmat komfort ceplny. Przez poęce mkroklmatu wnętrz rozume sę zespół wszystkch parametrów fzycznych
1. Komfort ceplny pomeszczeń Przy określanu warunków panuących w pomeszczenu używa sę zwykle dwóch poęć: mkroklmat komfort ceplny. Przez poęce mkroklmatu wnętrz rozume sę zespół wszystkch parametrów fzycznych
20. Oznaczanie stężenia acetonu w czterochloroetanie
 REFRAKTOMETRIA 20. Oznaczanie stężenia acetonu w czterochloroetanie Odczynniki i aparatura: Aceton Czterochloroetan Refraktometr Pulfricha PR-2 Wykonanie ćwiczenia: 1. 15 minut przed pomiarami włączyć
REFRAKTOMETRIA 20. Oznaczanie stężenia acetonu w czterochloroetanie Odczynniki i aparatura: Aceton Czterochloroetan Refraktometr Pulfricha PR-2 Wykonanie ćwiczenia: 1. 15 minut przed pomiarami włączyć
WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Pomiar refrakcji molowej i sprawdzenie jej addytywności)
 Ćwiczenie nr 1b WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Pomiar refrakcji molowej i sprawdzenie jej addytywności) I. Cel ćwiczenia Celem ćwiczenia jest teoretyczne i doświadczalne
Ćwiczenie nr 1b WYKORZYSTANIE POMIARU REFRAKCJI MOLOWEJ DO BADAŃ FIZYKOCHEMICZNYCH (Pomiar refrakcji molowej i sprawdzenie jej addytywności) I. Cel ćwiczenia Celem ćwiczenia jest teoretyczne i doświadczalne
7.8. RUCH ZMIENNY USTALONY W KORYTACH PRYZMATYCZNYCH
 WYKŁAD 7 7.8. RUCH ZMIENNY USTALONY W KORYTACH PRYZMATYCZNYCH 7.8.. Ogólne równane rucu Rucem zmennym w korytac otwartyc nazywamy tak przepływ, w którym parametry rucu take jak prędkość średna w przekroju
WYKŁAD 7 7.8. RUCH ZMIENNY USTALONY W KORYTACH PRYZMATYCZNYCH 7.8.. Ogólne równane rucu Rucem zmennym w korytac otwartyc nazywamy tak przepływ, w którym parametry rucu take jak prędkość średna w przekroju
Zestaw zadań 4: Przestrzenie wektorowe i podprzestrzenie. Liniowa niezależność. Sumy i sumy proste podprzestrzeni.
 Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
Zestaw zadań : Przestrzene wektorowe podprzestrzene. Lnowa nezależność. Sumy sumy proste podprzestrzen. () Wykazać, że V = C ze zwykłym dodawanem jako dodawanem wektorów operacją mnożena przez skalar :
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE
 LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwzee r 4 Temat: Wyzazee współzyka załamaa ezy refraktometrem Abbego.. Wprowadzee Śwatło, przy przejśu przez graę dwóh ośrodków, zmea swój
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwzee r 4 Temat: Wyzazee współzyka załamaa ezy refraktometrem Abbego.. Wprowadzee Śwatło, przy przejśu przez graę dwóh ośrodków, zmea swój
Pomiary dawek promieniowania wytwarzanego w liniowych przyspieszaczach na użytek radioterapii
 Pomary dawek promenowana wytwarzanego w lnowych przyspeszaczach na użytek radoterap Włodzmerz Łobodzec Zakład Radoterap Szptala m. S. Leszczyńskego w Katowcach Cel radoterap napromenene obszaru PTV zaplanowaną,
Pomary dawek promenowana wytwarzanego w lnowych przyspeszaczach na użytek radoterap Włodzmerz Łobodzec Zakład Radoterap Szptala m. S. Leszczyńskego w Katowcach Cel radoterap napromenene obszaru PTV zaplanowaną,
Falowa natura światła
 Falowa natura światła Christiaan Huygens Thomas Young James Clerk Maxwell Światło jest falą elektromagnetyczną Barwa światło zależy od jej długości (częstości). Optyka geometryczna Optyka geometryczna
Falowa natura światła Christiaan Huygens Thomas Young James Clerk Maxwell Światło jest falą elektromagnetyczną Barwa światło zależy od jej długości (częstości). Optyka geometryczna Optyka geometryczna
I. Elementy analizy matematycznej
 WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
WSTAWKA MATEMATYCZNA I. Elementy analzy matematycznej Pochodna funkcj f(x) Pochodna funkcj podaje nam prędkość zman funkcj: df f (x + x) f (x) f '(x) = = lm x 0 (1) dx x Pochodna funkcj podaje nam zarazem
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego
 Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda-kwas octowychloroform metodą potencjometryczną ćwczene nr 9 Opracowała dr hab. Małgorzata Jóźwak Zakres
Katedra Chem Fzycznej Unwersytetu Łódzkego Wyznaczane współczynnka podzału Nernsta w układze: woda-kwas octowychloroform metodą potencjometryczną ćwczene nr 9 Opracowała dr hab. Małgorzata Jóźwak Zakres
Część teoretyczna IZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD
 Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
Część teoretyczna ZOLACYJNOŚĆ AKUSTYCZNA PRZEGRÓD Energa dźwęku padającego na przegrodę będze częścowo odbta, częścowo pochłonęta, a ch stosunek będze zależał od stosunku mpedancj akustycznej materału
Wykład Turbina parowa kondensacyjna
 Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Wykład 9 Maszyny ceplne turbna parowa Entropa Równane Claususa-Clapeyrona granca równowag az Dośwadczena W. Domnk Wydzał Fzyk UW ermodynamka 08/09 /5 urbna parowa kondensacyjna W. Domnk Wydzał Fzyk UW
Laboratorium ochrony danych
 Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Laboratorum ochrony danych Ćwczene nr Temat ćwczena: Cała skończone rozszerzone Cel dydaktyczny: Opanowane programowej metody konstruowana cał skończonych rozszerzonych GF(pm), poznane ch własnośc oraz
Badanie właściwości optycznych roztworów.
 ĆWICZENIE 4 (2018), STRONA 1/6 Badanie właściwości optycznych roztworów. Cel ćwiczenia - wyznaczenie skręcalności właściwej sacharozy w roztworach wodnych oraz badanie współczynnika załamania światła Teoria
ĆWICZENIE 4 (2018), STRONA 1/6 Badanie właściwości optycznych roztworów. Cel ćwiczenia - wyznaczenie skręcalności właściwej sacharozy w roztworach wodnych oraz badanie współczynnika załamania światła Teoria
Płyny nienewtonowskie i zjawisko tiksotropii
 Płyny nenewtonowske zjawsko tksotrop ) Krzywa newtonowska, lnowa proporcjonalność pomędzy szybkoścą ścnana a naprężenem 2) Płyny zagęszczane ścnanem, naprężene wzrasta bardzej nż proporcjonalne do wzrostu
Płyny nenewtonowske zjawsko tksotrop ) Krzywa newtonowska, lnowa proporcjonalność pomędzy szybkoścą ścnana a naprężenem 2) Płyny zagęszczane ścnanem, naprężene wzrasta bardzej nż proporcjonalne do wzrostu
Portfele zawierające walor pozbawiony ryzyka. Elementy teorii rynku kapitałowego
 Portel nwestycyjny ćwczena Na podst. Wtold Jurek: Konstrukcja analza rozdzał 5 dr chał Konopczyńsk Portele zawerające walor pozbawony ryzyka. lementy teor rynku kaptałowego 1. Pożyczane penędzy amy dwa
Portel nwestycyjny ćwczena Na podst. Wtold Jurek: Konstrukcja analza rozdzał 5 dr chał Konopczyńsk Portele zawerające walor pozbawony ryzyka. lementy teor rynku kaptałowego 1. Pożyczane penędzy amy dwa
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY. Zakład Budowy i Eksploatacji Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA
 PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA W PILE INSTYTUT POLITECHNICZNY Zakład Budowy Eksploatacj Maszyn PRACOWNIA TERMODYNAMIKI TECHNICZNEJ INSTRUKCJA Temat ćwczena: PRAKTYCZNA REALIZACJA PRZEMIANY ADIABATYCZNEJ.
Pole magnetyczne. Za wytworzenie pola magnetycznego odpowiedzialny jest ładunek elektryczny w ruchu
 Pole magnetyczne Za wytworzene pola magnetycznego odpowedzalny jest ładunek elektryczny w ruchu Źródła pola magnetycznego Źródła pola magnetycznego I Sła Lorentza - wektor ndukcj magnetycznej Sła elektryczna
Pole magnetyczne Za wytworzene pola magnetycznego odpowedzalny jest ładunek elektryczny w ruchu Źródła pola magnetycznego Źródła pola magnetycznego I Sła Lorentza - wektor ndukcj magnetycznej Sła elektryczna
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORYJNE Z FIZYKI. SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr 0. Badanie rozkładu rzutu śnieżkami do celu
 WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząca(y)... grupa... podgrupa... zespół... semestr roku akademckego... student(ka)... SPRAWOZDANIE
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząca(y)... grupa... podgrupa... zespół... semestr roku akademckego... student(ka)... SPRAWOZDANIE
 Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Zadane 1: Wyznacz średne ruchome 3-okresowe z następujących danych obrazujących zużyce energ elektrycznej [kwh] w pewnym zakładze w mesącach styczeń - lpec 1998 r.: 400; 410; 430; 40; 400; 380; 370. Zadane
Ćwiczenie 2. Parametry statyczne tranzystorów bipolarnych
 Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
Ćwczene arametry statyczne tranzystorów bpolarnych el ćwczena odstawowym celem ćwczena jest poznane statycznych charakterystyk tranzystorów bpolarnych oraz metod dentyfkacj parametrów odpowadających m
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORYJNE Z FIZYKI. SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr 0. Badanie rozkładu rzutu śnieżkami do celu
 WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząc(a/y)... grupa... podgrupa... zespół... semestr... roku akademckego... student(ka)... SPRAWOZDANIE
WOJSKOWA AKADEMIA TECHNICZNA ĆWICZENIA LABORATORJNE Z FIZKI trzec termn wpsu zalczena do USOSu upływa...prowadząc(a/y)... grupa... podgrupa... zespół... semestr... roku akademckego... student(ka)... SPRAWOZDANIE
Ćwiczenie Nr 8 Współczynnik załamania refraktometr Abbego
 Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 8 Współczynnik załamania refraktometr Abbego Zagadnienia: załamanie światła na anicy dwóch ośrodków, prawo Snelliusa, zjawisko całkowitego
Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 8 Współczynnik załamania refraktometr Abbego Zagadnienia: załamanie światła na anicy dwóch ośrodków, prawo Snelliusa, zjawisko całkowitego
Laboratorium Akustyki Architektonicznej Ćw. 4
 Laboratorum Akustyk Archtektoncznej Ćw. 4 POMARY ZOLACYJNOŚC AKUSTYCZNEJ PRZEGRODY BUDOWLANEJ. Cel ćwczena Celem ćwczena jest zapoznane sę z metodą pomaru zolacyjnośc akustycznej przegród budowlanych.
Laboratorum Akustyk Archtektoncznej Ćw. 4 POMARY ZOLACYJNOŚC AKUSTYCZNEJ PRZEGRODY BUDOWLANEJ. Cel ćwczena Celem ćwczena jest zapoznane sę z metodą pomaru zolacyjnośc akustycznej przegród budowlanych.
STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ],
![STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ], STATECZNOŚĆ SKARP. α - kąt nachylenia skarpy [ o ], φ - kąt tarcia wewnętrznego gruntu [ o ],](/thumbs/27/11347185.jpg) STATECZNOŚĆ SKARP W przypadku obektu wykonanego z gruntów nespostych zaprojektowane bezpecznego nachylena skarp sprowadza sę do przekształcena wzoru na współczynnk statecznośc do postac: tgφ tgα = n gdze:
STATECZNOŚĆ SKARP W przypadku obektu wykonanego z gruntów nespostych zaprojektowane bezpecznego nachylena skarp sprowadza sę do przekształcena wzoru na współczynnk statecznośc do postac: tgφ tgα = n gdze:
BADANIE KONCENTRACJI NAPRĘŻEŃ DOŚWIADCZALNE WYZNACZANIE WSPÓŁCZYNNIKA KSZTAŁTU METODĄ ELASTOOPTYCZNĄ. Oprac.: dr inż. Ludomir J.
 BADANIE KONCENTRACJI NAPRĘŻEŃ DOŚWIADCZALNE WYZNACZANIE WSPÓŁCZYNNIKA KSZTAŁTU METODĄ ELASTOOPTYCZNĄ 1. WPROWADZENIE Oprac.: dr nż. Ludomr J. Jankowsk Elastooptyka ([1], [], [3],[5]), mmo rozwoju nnych
BADANIE KONCENTRACJI NAPRĘŻEŃ DOŚWIADCZALNE WYZNACZANIE WSPÓŁCZYNNIKA KSZTAŁTU METODĄ ELASTOOPTYCZNĄ 1. WPROWADZENIE Oprac.: dr nż. Ludomr J. Jankowsk Elastooptyka ([1], [], [3],[5]), mmo rozwoju nnych
Egzamin poprawkowy z Analizy II 11 września 2013
 Egzamn poprawkowy z nalzy II 11 wrześna 13 Uwag organzacyjne: każde zadane rozwązujemy na osobnej kartce Każde zadane należy podpsać menem nazwskem własnym oraz prowadzącego ćwczena Na wszelk wypadek prosmy
Egzamn poprawkowy z nalzy II 11 wrześna 13 Uwag organzacyjne: każde zadane rozwązujemy na osobnej kartce Każde zadane należy podpsać menem nazwskem własnym oraz prowadzącego ćwczena Na wszelk wypadek prosmy
Ćwiczenie Nr 6 Skręcenie płaszczyzny polaryzacji
 Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 6 Skręcenie płaszczyzny polaryzacji Zagadnienia: polaryzacja światła, metody otrzymywania światła spolaryzowanego, budowa polarymetru, zjawisko
Instytut Fizyki, Uniwersytet Śląski Chorzów 2018 r. Ćwiczenie Nr 6 Skręcenie płaszczyzny polaryzacji Zagadnienia: polaryzacja światła, metody otrzymywania światła spolaryzowanego, budowa polarymetru, zjawisko
1. SPRAWDZENIE WYSTEPOWANIA RYZYKA KONDENSACJI POWIERZCHNIOWEJ ORAZ KONDENSACJI MIĘDZYWARSTWOWEJ W ŚCIANIE ZEWNĘTRZNEJ
 Ćwczene nr 1 cz.3 Dyfuzja pary wodnej zachodz w kerunku od środowska o wyższej temperaturze do środowska chłodnejszego. Para wodna dyfundująca przez przegrody budowlane w okrese zmowym napotyka na coraz
Ćwczene nr 1 cz.3 Dyfuzja pary wodnej zachodz w kerunku od środowska o wyższej temperaturze do środowska chłodnejszego. Para wodna dyfundująca przez przegrody budowlane w okrese zmowym napotyka na coraz
Kształtowanie się firm informatycznych jako nowych elementów struktury przestrzennej przemysłu
 PRACE KOMISJI GEOGRAFII PRZEMY SŁU Nr 7 WARSZAWA KRAKÓW 2004 Akadema Pedagogczna, Kraków Kształtowane sę frm nformatycznych jako nowych elementów struktury przestrzennej przemysłu Postępujący proces rozwoju
PRACE KOMISJI GEOGRAFII PRZEMY SŁU Nr 7 WARSZAWA KRAKÓW 2004 Akadema Pedagogczna, Kraków Kształtowane sę frm nformatycznych jako nowych elementów struktury przestrzennej przemysłu Postępujący proces rozwoju
KOMPUTEROWE SYMULACJE CIECZY
 KOMPUTEROWE SYMULACJE CIECZY Najwcześnejsze eksperymenty (ruchy Browna) Współczesne metody (rozpraszane neutronów) Teoretyczne modele ceczy Struktura ceczy dynamka cząsteczek Symulacje komputerowe 1 Ponad
KOMPUTEROWE SYMULACJE CIECZY Najwcześnejsze eksperymenty (ruchy Browna) Współczesne metody (rozpraszane neutronów) Teoretyczne modele ceczy Struktura ceczy dynamka cząsteczek Symulacje komputerowe 1 Ponad
Wyznaczenie promienia hydrodynamicznego cząsteczki metodą wiskozymetryczną. Część 2. Symulacje komputerowe
 Rafał Górnak Wyznaczene promena hydrodynamcznego cząsteczk metodą wskozymetryczną. Część. Symulacje komputerowe Pojęca podstawowe Symulacje komputerowe, zasady dynamk Newtona, dynamka molekularna, potencjał
Rafał Górnak Wyznaczene promena hydrodynamcznego cząsteczk metodą wskozymetryczną. Część. Symulacje komputerowe Pojęca podstawowe Symulacje komputerowe, zasady dynamk Newtona, dynamka molekularna, potencjał
Twierdzenie Bezouta i liczby zespolone Javier de Lucas. Rozwi azanie 2. Z twierdzenia dzielenia wielomianów, mamy, że
 Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam
3. ŁUK ELEKTRYCZNY PRĄDU STAŁEGO I PRZEMIENNEGO
 3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
3. ŁUK ELEKTRYCZNY PRĄDU STŁEGO I PRZEMIENNEGO 3.1. Cel zakres ćwczena Celem ćwczena jest zapoznane sę z podstawowym właścwoścam łuku elektrycznego palącego sę swobodne, w powetrzu o cśnentmosferycznym.
Wyznaczenie współczynnika podziału kwasu octowego pomiędzy fazą organiczną a wodną
 Ćwzene 13 Wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną a wodną Cel ćwzena Celem ćwzena jest wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną (butanolem) a wodną w oparu
Ćwzene 13 Wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną a wodną Cel ćwzena Celem ćwzena jest wyznazene współzynnka podzału kwasu otowego pomędzy fazą anzną (butanolem) a wodną w oparu
OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI
 Oblczane rozkładów natęŝena ośwetlena. OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI T E R E N Y O T W A R T E Stosowana jest tzw. metoda punktowa, która polega na oblczanu w określonych
Oblczane rozkładów natęŝena ośwetlena. OBLICZANIE ROZKŁADÓW NATĘśENIA OŚWIETLENIA I ROZKŁADÓW LUMINANCJI T E R E N Y O T W A R T E Stosowana jest tzw. metoda punktowa, która polega na oblczanu w określonych
WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH
 Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Metrologa Wspomagana Komputerowo - Zegrze, 9-22 05.997 WSPOMAGANE KOMPUTEROWO POMIARY CZĘSTOTLIWOŚCI CHWILOWEJ SYGNAŁÓW IMPULSOWYCH dr nż. Jan Ryszard Jask, dr nż. Elgusz Pawłowsk POLITECHNIKA lubelska
Instrukcja do ćwiczeń laboratoryjnych
 UNIWERSYTET GDAŃSKI WYDZIAŁ CHEMII Pracowna studencka Katedry Analzy Środowska Instrukcja do ćwczeń laboratoryjnych Ćwczene nr 2 WYZNACZANIE WSPÓŁCZYNNIKA PDZIAŁU WYBRANYCH ZANIECZYSZCZEŃ RGANICZNYCH ŚRDWISKA
UNIWERSYTET GDAŃSKI WYDZIAŁ CHEMII Pracowna studencka Katedry Analzy Środowska Instrukcja do ćwczeń laboratoryjnych Ćwczene nr 2 WYZNACZANIE WSPÓŁCZYNNIKA PDZIAŁU WYBRANYCH ZANIECZYSZCZEŃ RGANICZNYCH ŚRDWISKA
Teoria niepewności pomiaru (Rachunek niepewności pomiaru) Rodzaje błędów pomiaru
 Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Pomary fzyczne - dokonywane tylko ze skończoną dokładnoścą. Powodem - nedoskonałość przyrządów pomarowych neprecyzyjność naszych zmysłów borących udzał w obserwacjach. Podawane samego tylko wynku pomaru
Proces narodzin i śmierci
 Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
Proces narodzn śmerc Jeżel w ewnej oulacj nowe osobnk ojawają sę w sosób losowy, rzy czym gęstość zdarzeń na jednostkę czasu jest stała w czase wynos λ, oraz lczba osobnków n, które ojawły sę od chwl do
