Zeszyty naukowe nr 9
|
|
|
- Amelia Kowal
- 8 lat temu
- Przeglądów:
Transkrypt
1 Zeszyty naukowe nr 9 Wyższej Szkoły Ekonomicznej w Bochni 2011 Piotr Fijałkowski O pewnym modelu zależności wahań notowań giełdowych akcji na GPW od kapitalizacji spółki Streszczenie Niniejsza praca opisuje próbę budowy modelu ekonometrycznego zależności wahań notowań akcji na Giełdzie Papierów Wartościowych w Warszawie od kapitalizacji spółek. Danymi do modelu są notowania akcji z 50 kolejnych sesji Giełdy Papierów Wartościowych Abstract The present article describes the attempt to construction of an econometric model of dependence between the fluctuations of stock quotations on Warsaw Stock Exchange and the capitalizations of companies. The data to the model are the stock quotations from 50 following sessions of Warsaw Stock Exchange. 1. Wstęp Prawidłowością obserwowaną na rynkach akcji jest fakt, że większa kapitalizacja spółki często wiąże się ze stosunkowo mniejszymi wahaniami cen akcji. Jest to zasada, której mechanizm jest dość łatwy do zrozumienia podobne zainteresowanie inwestorów małą spółką podnosi cenę jej akcji w większym stopniu, niż spółki dużej, ze względu na różnicę wartości podaży. Mechanizm ten jest wykorzystywany przez kapitał spekulacyjny, co oczywiście może jeszcze bardziej wzmocnić ten efekt. Spektakularnym przykładem z Giełdy Papierów Wartościowych w Warszawie (GPW) może tu być bardzo skuteczna spekulacja akcjami spółek o bardzo niewielkiej kapitalizacji Domplast S.A., Chemiskór S.A. i EchoPress S.A., którą zajmowała się w latach grupa inwestorów zwana poznańską WIRR-ówką.
2 160 Celem niniejszej pracy jest próba budowy modelu ekonometrycznego opisującego zależności wahań notowań akcji spółek na GPW (zmienna wyjaśniana od ich kapitalizacji (zmienna wyjaśniająca x). Model taki, choćby niedoskonały, mógłby być ciekawym statystycznym potwierdzeniem rzeczywistego istnienia takiej prawidłowości. Aby precyzyjnie opisać model, uściślimy zagadnienie. Przez kapitalizację będziemy rozumieć iloczyn liczby akcji danej spółki i średniego kursu akcji. Miarą wahania cen akcji jest w niniejszej pracy współczynnik ich zmienności, czyli iloraz odchylenia standardowego przez wartość średnią ceny akcji w pewnym okresie. Ze względu na nieporównywalność walorów, jakimi są akcje różnych spółek, odchylenie standardowe nie byłoby odpowiednią miarą wahania cen. Będziemy rozważać cztery modele - liniowy, potęgowy, wykładniczy i logarytmiczny, które mogłyby opisać wspomnianą zależność. 2. Dane Dane do niniejszego opracowania pochodzą ze strony internetowej [4]. Wybór źródła jest podyktowany jego wiarygodnością i możliwością pobierania danych w postaci plików xls, a więc w formie gotowej do dalszego przetwarzania. Poniżej przedstawione jest tabelaryczne zestawienie liczby akcji, średnich kursów akcji i współczynników zmienności z 50 kolejnych notowań w dniach od do włącznie dla wszystkich spółek notowanych na GPW, które brały udział we wszystkich tych notowaniach. Średnie kursy zostały policzone jako średnie arytmetyczne kursów zamknięcia sesji. Kapitalizacja x jest rozumiana tu jako iloczyn liczby akcji przez średni kurs akcji w milionach złotych. Tabela1. Liczba akcji, średni kurs, kapitalizacja x i współczynniki zmienności y dla spółek, które brały udział we wszystkich sesjach GPW w dniach na podstawie [4] L.p. Skrót nazwy Liczba akcji spółki Średni kurs (PLN) Kapital. x (mln PLN) Wsp. zmien. y L.p. Skrót nazwy spółki Liczba akcji Średni kurs (PLN) Kapital.x (mln PLN) Wsp. zmien. y 1. 06N , ,6466 0, KOM , ,9865 0, N , ,4441 0, KOV , ,7206 0, ABC , ,7830 0, KPX , ,5970 0, ABM , ,3892 0, KRB , ,7000 0, ABS , ,2035 0, KRI , ,4605 0, ACE , ,4201 0, KSW , ,8860 0, ACP , ,1610 0, KTY , ,1980 0,0227
3 ACS , ,4264 0, KZS , ,8319 0, ACT , ,6388 0, LBW , ,5261 0, ADD , ,5237 0, LCC , ,4079 0, ADS , ,6572 0, LEN , ,3965 0, ADV , ,4932 0, LPP , ,0020 0, AGM , ,6722 0, LST , ,7517 0, AGO , ,6440 0, LTS , ,9200 0, ALC , ,3660 0, LWB , ,2020 0, ALM , ,1909 0, MAK , ,4951 0, ALT , ,9398 0, MAR ,4164 2,2600 0, AMB , ,4986 0, MCI , ,4171 0, AMC , ,7626 0, MCR , ,6301 0, APL , ,5080 0, MDS , ,7458 0, APT , ,8039 0, MEW , ,4072 0, ARM , ,8560 0, MIC ,7832 7,0932 0, ARR , ,0306 0, MIL , ,8610 0, ART ,0586 0,2505 0, MIP , ,3142 0, AST , ,9250 0, MIT , ,3744 0, ATC , ,3520 0, MLK , ,0630 0, ATE , ,0249 0, MMP , ,3230 0, ATG , ,7552 0, MNI , ,5307 0, ATM , ,6250 0, MOL , ,9400 0, ATO , ,9210 0, MON , ,3535 0, ATP , ,8025 0, MRB , ,1850 0, ATR , ,3993 0, MSA , ,9182 0, ATS , ,1276 0, MSC , ,5500 0, ATT , ,5220 0, MSO , ,5764 0, AUX , ,5804 0, MSP , ,6448 0, AZC , ,6659 0, MSW , ,6680 0, BBC , ,9685 0, MSX , ,2440 0, BBD , ,2498 0, MSZ , ,6658 0, BBZ , ,5713 0, MVP , ,5482 0, BCM , ,0632 0, MWT , ,6276 0, BDX , ,2530 0, MZA , ,7200 0, BDZ , ,1335 0, NEM , ,6460 0, BHW , ,5000 0, NET , ,2370 0, BIO , ,2464 0, NGS , ,6195 0, BLI , ,5856 0, NOV , ,0458 0,1290
4 BMC , ,0168 0, NTT , ,1368 0, BMI , ,4654 0, NVS , ,2240 0, BMP , ,7175 0, NWR , ,1500 0, BPC , ,0479 0, O2O , ,5332 0, BPH , ,4950 0, OBL , ,1447 0, BPM , ,1568 0, ODL , ,6945 0, BPN , ,6010 0, OIL , ,6556 0, BRE , ,6600 0, OPG , ,1099 0, BRK , ,2316 0, OPN , ,5781 0, BRS , ,3480 0, OPT , ,4232 0, BSK , ,5900 0, ORB , ,1600 0, BTG ,0398 3,9800 0, ORL , ,9044 0, BTM , ,7930 0, ORN , ,1045 0, BVD , ,1690 0, OTM , ,0952 0, BZW , ,5900 0, PAT , ,0725 0, CCC , ,5870 0, PBG , ,9270 0, CCI , ,9880 0, PCE , ,5100 0, CDC , ,9950 0, PCG , ,9948 0, CER , ,6892 0, PCI , ,8247 0, CEZ , ,7400 0, PEK , ,9972 0, CFL , ,8030 0, PEO , ,5900 0, CHS , ,7071 0, PEP , ,3861 0, CIA , ,3813 0, PFR ,4624 8,2626 0, CIE , ,9570 0, PGD , ,4368 0, CMP , ,9841 0, PGE , ,0700 0, CMR , ,5865 0, PGF , ,3903 0, CNG , ,3729 0, PGM , ,3885 0, COG , ,6436 0, PGN , ,8800 0, CPA , ,9997 0, PHO , ,0640 0, CPE , ,3915 0, PJP , ,4567 0, CPS , ,2800 0, PKN , ,9200 0, CRM , ,9699 0, PKO , ,7500 0, CST , ,9320 0, PLJ , ,8158 0, CTC , ,6796 0, PLT , ,8133 0, CZP , ,9402 0, PLX , ,8912 0, DAM , ,6202 0, PLZ , ,9480 0, DBC , ,1880 0, PMA , ,6701 0, DFP ,6004 7,0229 0, PMD , ,5952 0,0254
5 DGA , ,4054 0, PMP , ,9704 0, DOM , ,6190 0, PND , ,6367 0, DPL , ,7427 0, POL ,4472 2,7950 0, DRE , ,3565 0, POZ , ,4583 0, DSS , ,9144 0, PPS , ,7938 0, DUD , ,8285 0, PQA , ,0553 0, EAT , ,5780 0, PRC , ,2017 0, ECD , ,9559 0, PRM , ,5781 0, ECH , ,1140 0, PRO , ,6942 0, EEF , ,5518 0, PRT , ,1443 0, EEX , ,8256 0, PSW , ,3929 0, EFH , ,5046 0, PTI , ,6840 0, EKO , ,4674 0, PUE , ,0750 0, EKP , ,6336 0, PXM , ,7450 0, ELS , ,3943 0, PZU , ,1200 0, EMC , ,3676 0, RBC , ,4090 0, EMF , ,2230 0, RBW , ,4572 0, EMP , ,8510 0, RCU , ,0726 0, ENA , ,5220 0, RDG , ,8801 0, EPD , ,2372 0, RDL , ,4176 0, EPI , ,8370 0, RDN , ,4479 0, EPL , ,6530 0, RFK , ,0210 0, ERG , ,7460 0, RHD , ,7904 0, ETL , ,2965 0, RLP , ,6481 0, EUC , ,1936 0, RMK , ,5556 0, EUI , ,3348 0, RNK , ,3602 0, EUR , ,4190 0, ROB , ,5349 0, FAM , , , RON , ,2219 0, FCL , ,4830 0, RPC , ,5465 0, FER , ,3639 0, RUN , ,5999 0, FMF , ,9930 0, SFG , ,7784 0, FON , ,4800 0, SFS , ,2522 0, FSG , , , SGN , ,5648 0, FTE , ,8275 0, SGR , ,0873 0, GCN , ,2604 0, SKL , ,5580 0, GNB , ,6830 0, SKO , ,7164 0, GNT , ,0980 0, SKT , ,9568 0, GOA , ,1163 0, SME , ,8095 0,0391
6 GPF ,0622 9,1353 0, SNK , ,8795 0, GPH , ,2380 0, SNS , ,6100 0, GPW , ,2560 0, SNW , ,6728 0, GRI , ,6844 0, SOB , ,3720 0, GRJ , ,4762 0, SRT , ,4271 0, GRL , ,0299 0, SSI , ,7519 0, GTC , ,1730 0, STF , ,4260 0, GTN , ,1400 0, STP , ,9560 0, GWR , ,4920 0, STX , ,9571 0, GZU , ,4504 0, SWD , ,8374 0, HBP , ,892 0, SZR , ,2160 0, HDR , ,4841 0, TEL , ,2981 0, HDX , ,0394 0, TFO , ,4170 0, HEF ,4920 8,0981 0, TIN , ,2924 0, HEL , ,8970 0, TLX , ,5944 0, HGN , ,6538 0, TPE , ,3800 0, HMS ,1538 3,0522 0, TPS , ,9200 0, HOT , ,4164 0, TRI , ,7038 0, HRT ,5182 5,4231 0, TRK , ,0422 0, HTM , ,4610 0, TSG , ,4063 0, HWE , ,7384 0, TUP , ,3986 0, IDM , ,7204 0, TVL , ,4417 0, IGR , ,4206 0, TVN , ,1550 0, IMX , ,2646 0, ULM , ,1133 0, INB ,0902 5,5002 0, VED , ,8557 0, INC , ,4517 0, VEN ,0210 6,5763 0, IND , ,0887 0, VIC ,0978 4,1967 0, INK , ,4446 0, VIN , ,4032 0, INL , ,2675 0, VIV , ,7500 0, IPL , ,1772 0, VST , ,9718 0, IPO , ,0120 0, VTR , ,2691 0, IPX , ,6800 0, WAS , ,9289 0, ITG , ,5677 0, WBY ,2814 5,6061 0, ITX , ,1764 0, WDM , ,4945 0, IZN , ,9195 0, WDX , ,4598 0, IZO , ,5934 0, WFM , ,1521 0, JAG , ,1460 0, WIK , ,0532 0, JPR , ,1392 0, WLB , ,4537 0,0820
7 JTZ , ,3562 0, WXF , ,6932 0, JWC , ,5146 0, XPL , ,9392 0, K2I , ,3147 0, ZAK , ,8958 0, KCH , ,6540 0, ZAP , ,666 0, KER , ,2610 0, ZKA , ,1296 0, KFL , ,9451 0, ZLR , ,0626 0, KGH , ,2000 0, ZRE , ,3518 0, KGN , ,3730 0, ZST , ,9344 0, KLR , ,9516 0, ZWC , ,5760 0, KMP , ,9511 0, Modele zależności Hipotetyczna zależność między kapitalizacją spółki x i współczynnikiem zmienności y nie musi być silna i, jeśli w ogóle występuje, niekoniecznie musi mieć charakter liniowy. Poniżej rozważamy, prócz liniowego, trzy modele nieliniowe, które mogłyby opisywać tę zależność - potęgowy, wykładniczy i logarytmiczny. Są to modele sprowadzalne do modelu liniowego przez zamianę zmiennych, często występujące w zastosowaniach ekonometrii Model liniowy Konstrukcję modelu liniowego zaczynamy od wyznaczenia współczynnika korelacji liniowej między zmiennymi x i y ze wzoru (zobacz na przykład [1], s.481): r n i n ( ( x x)( y = 1 i i ( x, =. 2 n 2 x = i i x) ( y i= i 1 1 W przypadku wartości współczynnika korelacji istotnie różnej od zera ma sens konstrukcja modelu liniowego postaci (zobacz na przykład [1], s ) y = α x + β + ε, gdzie ε jest składnikiem losowym. Parametry α i β estymujemy za pomocą metody najmniejszych kwadratów, która polega na minimalizacji wartości wyrażenia n 2 = ( y ˆi ), i 1 i y
8 166 gdzie (y i )są wartościami obserwowanymi (rzeczywistymi) zmiennej y, a ( ŷ i ) teoretycznymi, to znaczy obliczonymi według wzoru: yˆ = ax b. i i + Z powyższego kryterium otrzymujemy następujące wzory pozwalające obliczyć oceny a i b parametrów strukturalnych α i β modelu: a n ( i= 1 = n xi x)( yi, 2 ( x x) i= 1 b = y ax. Miarą dopasowania wartości rzeczywistych i teoretycznych może być współczynnik determinacji r 2 ( x,, którego wartości bliskie 1 wskazują na dobre dopasowanie oszacowanego modelu do danych (zobacz [3], s.41) Model potęgowy Przez model potęgowy rozumiemy hipotetyczną zależność postaci α ε y = βx e. Logarytmując obie strony powyższej równości, sprowadzamy model potęgowy do modelu liniowego: ln y = α ln x + ln β + ε. Przyjmując β '= ln β, x'= ln x, y'= ln y, uzyskujemy równość y ' = α x' + β ' + ε. Jest to tak zwana postać liniowa modelu potęgowego. Po wyznaczeniu wartości zmiennych x i y możemy wyznaczyć dla nich współczynnik korelacji liniowej, na podstawie którego ocenimy celowość konstrukcji modelu potęgowego. Jeżeli współczynnik ten okaże się istotny, to tak jak w modelu liniowym znajdujemy oceny a i b współczynników α i β odpowiednio. b' Po wyznaczeniu b = e, znajdujemy oszacowaną postać modelu potęgowego. i
9 Model wykładniczy Przez model wykładniczy rozumiemy hipotetyczną zależność postaci x ε y = βα e Logarytmując obie strony powyższej równości, sprowadzimy model potęgowy do modelu liniowego: ln y = xlnα + ln β + ε. Przyjmując β '= ln β, α'= lnα, y'= ln y, uzyskujemy postać liniową modelu wykładniczego: y ' = α ' x + β ' + ε. Dalej postępujemy analogicznie jak w przypadku modelu potęgowego. Model logarytmiczny Przez model logarytmiczny rozumiemy tu hipotetyczną zależność postaci y = α ln x + β + ε. Przyjmując x'= ln x, uzyskujemy postać liniową modelu logarytmicznego: y = α x'+ β + ε. Dalej postępujemy analogicznie jak w poprzednich przypadkach. 4. Wybór modelu i konstrukcja Z przedstawionego w rozdziale 3 opisu wynika, że wyboru najbardziej odpowiedniego modelu można dokonać na podstawie współczynnika korelacji odpowiednich zmiennych w modelu zlinearyzowanym. Obliczamy zatem współczynniki korelacji r ( x,, r ( x', y' ), r( x, y' ) i r ( x', : r ( x, = 0,099, r ( x', y') = 0,351, r ( x, y') = 0,126, r ( x', = 0,283.
10 168 Zagadnienie statystycznego przetestowania istotności tych współczynników dla całej populacji notowań jest trudne ze względu na charakter zmiennych x i y są one estymacjami odpowiednio średniej kapitalizacji i współczynnika zmienności dla wszystkich notowań danej spółki uzyskane z próby 50 notowań z określonego okresu. Tymczasem standardowe testy istotności współczynnika korelacji dotyczą jego estymacji na próbie rzeczywistych wartości danych. Problem, jak zbudować test w naszym przypadku, jest interesujący i chyba niełatwy zrezygnujemy tu z prób jego rozwiązania. Powyższe zestawienie pokazuje, że największą wartość bezwzględną współczynnika korelacji mają zmienne x i y, co oznacza wybór modelu potęgowego. Wyznaczamy oceny parametrów strukturalnych: a = 0,125, b ' = 2,388. Oszacowanie zlinearyzowanego modelu ma zatem postać: y ' = 0,125x' 2, ε. Współczynnik determinacji dla tego modelu wynosi r 2 ( x', y') = 0, 123, co oczywiście oznacza, że dopasowanie modelu do danych rzeczywistych jest bardzo słabe. b' 2,388 Po wyznaczeniu b = e = e = 0, 092 uzyskujemy oszacowany model potęgowy dla zmiennych x i y: lub y = 0,092x y 0,092 0,125 e ε = e. 8 x ε 5. Wnioski Ujemne współczynniki korelacji zdają się potwierdzać prawidłowość polegającą na mniejszych wahaniach kursów akcji spółek o większej kapitalizacji. Fakt, że otrzymany model jest słabo zgodny z danymi rzeczywistymi nie jest specjalnie zaskakujący istnieją inne czynniki wpływających na wahania kursów. Czynnikiem zwiększającym wahania kursów akcji niezwiązanym z małą kapitalizacją spółki może być przewidywanie wysokich zysków spółek inwestujących w nowe technologie. Przykładem mogą być spółki z branży
11 169 informatycznej, których notowania szybko rosły pod koniec lat dziewięćdziesiątych ubiegłego stulecia. Korekta nadmiernych oczekiwań wobec zysków z nowych technologii spowodowała odwrócenie trendu wzrostowego i w latach notowania tych spółek szybko spadły, nawet o 80% w przypadku Amazon, czy Yahoo! (zobacz [2], s. 410). Mechanizm taki jest wzmacniany przez efekt samospełniającej się prognozy, gdy prognozowany wzrost cen akcji stymuluje zwiększony popyt spowodowany nadzieją na zyski z inwestycji w akcje, co powoduje dalszy wzrost notowań. W sytuacji, gdy dalszy wzrost nie ma uzasadnienia fundamentalnego i rynek przez dłuższy czas dostatecznie nie koryguje cen, dochodzi do powstania bąbla spekulacyjnego (zobacz [2], s.422 i 449). Pękniecie bąbla, czyli gwałtowna korekta, wyzwala mechanizm samospełniającej się przepowiedni w odwrotnym kierunku prognozowany spadek notowań zwiększa liczbę chętnych do pozbycia się zniżkujących walorów, przez co spadek pogłębia się. W rezultacie rynki, które nadmiernie zwyżkują, mają tendencje do nadmiernych spadków po odwróceniu się trendu ([2], s.449). Przyczyna dużego wahnięcia kursu akcji może oczywiście mieć charakter całkiem fundamentalny informacja o dobrych wynikach finansowych z reguły powoduje wzrost, a informacja przeciwna spadek kursu akcji.
12 170 Bibliografia 1. Aczel A.D., Statystyka w zarządzaniu, PWN, Warszawa 2000, ISBN Begg D., Fisher S., Dornbush R., Mikroekonomia, PWE, Warszawa 2007, IBSN Welfe A., Ekonometria, PWE, Warszawa 2008, ISBN
Struktura portfela akcyjnego funduszy inwestycyjnych
 www.analizy.pl 29-11-2004 Struktura portfela akcyjnego funduszy inwestycyjnych Kategorie lokat Wartość papierów udziałowych (akcje polskie i zagraniczne, akcje NFI, prawa do akcji, prawa poboru, udziały
www.analizy.pl 29-11-2004 Struktura portfela akcyjnego funduszy inwestycyjnych Kategorie lokat Wartość papierów udziałowych (akcje polskie i zagraniczne, akcje NFI, prawa do akcji, prawa poboru, udziały
PRZEGLĄD STATYSTYCZNY R. LIX ZESZYT 3 2012 ANETA ZGLIŃSKA-PIETRZAK ZASTOSOWANIE METODY BOOTSTRAPOWEJ W ANALIZIE PORTFELOWEJ 1.
 PRZEGLĄD STATYSTYCZNY R. LIX ZESZYT 3 2012 ANETA ZGLIŃSKA-PIETRZAK ZASTOSOWANIE METODY BOOTSTRAPOWEJ W ANALIZIE PORTFELOWEJ 1. WSTĘP Metody bootstrapowe, zwane też sznurowadłowymi (zob. np. Domański, Pruska,
PRZEGLĄD STATYSTYCZNY R. LIX ZESZYT 3 2012 ANETA ZGLIŃSKA-PIETRZAK ZASTOSOWANIE METODY BOOTSTRAPOWEJ W ANALIZIE PORTFELOWEJ 1. WSTĘP Metody bootstrapowe, zwane też sznurowadłowymi (zob. np. Domański, Pruska,
GPW: Uchwała Nr 1168/2015 Zarządu Giełdy Papierów Wartościowych
 2015-11-18 12:55 GPW: Uchwała Nr 1168/2015 Zarządu Giełdy Papierów Wartościowych Uchwała Nr 1168/2015 Zarządu Giełdy Papierów Wartościowych w Warszawie S.A. z dnia 18 listopada 2015 r. Na podstawie 20
2015-11-18 12:55 GPW: Uchwała Nr 1168/2015 Zarządu Giełdy Papierów Wartościowych Uchwała Nr 1168/2015 Zarządu Giełdy Papierów Wartościowych w Warszawie S.A. z dnia 18 listopada 2015 r. Na podstawie 20
Ponad Rynek. Tygodniowa Analiza Portfelowa Akcji 7/2009, 17 lutego 2009
 Tygodniowa Analiza Portfelowa Akcji 7/009, 7 lutego 009 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
Tygodniowa Analiza Portfelowa Akcji 7/009, 7 lutego 009 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
KurS przy zmianie Strony. SzerSmug przy zmianie. Ile trwa Sygnał. Stopa Zwr
 KurS KurS Maximum Minimum Szer Smug od dziś od dziś SYGNAŁ Data Mav odl kursudodlkursudo Security Name Ticker Symbol KurS Pow, SMUG Pon,Smug Smug Smug w % Ob Strona Ob Strona ZMIANY STRONY Zmiany w dniach
KurS KurS Maximum Minimum Szer Smug od dziś od dziś SYGNAŁ Data Mav odl kursudodlkursudo Security Name Ticker Symbol KurS Pow, SMUG Pon,Smug Smug Smug w % Ob Strona Ob Strona ZMIANY STRONY Zmiany w dniach
Ponad Rynek. Tygodniowa Analiza Portfelowa Akcji 6/2009, 10 lutego 2009
 Tygodniowa Analiza Portfelowa Akcji 6/009, 0 lutego 009 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
Tygodniowa Analiza Portfelowa Akcji 6/009, 0 lutego 009 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
Ponad Rynek. Tygodniowa Analiza Portfelowa Akcji 26/2008, 18 listopada 2008
 Tygodniowa Analiza Portfelowa Akcji 6/008, 8 listopada 008 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
Tygodniowa Analiza Portfelowa Akcji 6/008, 8 listopada 008 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuŝszy niŝ 4 sesje, na których średni
Ile trwa Sygnał. SzerSmug przy zmianie
 KurS KurS Maximum Minimum Szer Smug od dziś od dziś SYGNAŁ Data Mav odl kursudo odlkursudo Security Name Ticker Symbol KurS Pow, SMUG Pon,Smug Smug Smug w % Ob Strona Ob Strona ZMIANY STRONY Zmiany w dniach
KurS KurS Maximum Minimum Szer Smug od dziś od dziś SYGNAŁ Data Mav odl kursudo odlkursudo Security Name Ticker Symbol KurS Pow, SMUG Pon,Smug Smug Smug w % Ob Strona Ob Strona ZMIANY STRONY Zmiany w dniach
Dywidendy za 2017 r. wypłacane w II półroczu'18. Dzień wypłaty
 Spółka Data WZA Ostatnie notowanie z prawem do dywidendy Dzień wypłaty Dywidenda na akcję Stopa dywidendy APN (APLISENS) 05-cze-18 03-lip-18 19-lip-18 0.32 PLN 2.6% uchwalona BFC (BIOFACTOR) 25-cze-18
Spółka Data WZA Ostatnie notowanie z prawem do dywidendy Dzień wypłaty Dywidenda na akcję Stopa dywidendy APN (APLISENS) 05-cze-18 03-lip-18 19-lip-18 0.32 PLN 2.6% uchwalona BFC (BIOFACTOR) 25-cze-18
-> Spółka musi być niedoceniona przez innych inwestorów. (Wykorzystujemy wskaźniki niedowartościowania).
 187 Poniższy portfel jest kontynuacją eksperymentu inwestycyjnego, który przeprowadzałem na moim blogu. Analiza wyników po 12 tygodniach pokazała, że strategia inwestycyjna oparta niemal wyłącznie na analizie
187 Poniższy portfel jest kontynuacją eksperymentu inwestycyjnego, który przeprowadzałem na moim blogu. Analiza wyników po 12 tygodniach pokazała, że strategia inwestycyjna oparta niemal wyłącznie na analizie
Specjalistyczny Fundusz Inwestycyjny Otwarty Telekomunikacji Polskiej Bilans na dzień (tysiące złotych)
 Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Bilans na dzień 30.06.2004 30.06.2004 31.12.2003 30.06.2003 258 573 203 337 149 749 Lokaty pieniężne krótkoterminowe 455 269 15 Należności
Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Bilans na dzień 30.06.2004 30.06.2004 31.12.2003 30.06.2003 258 573 203 337 149 749 Lokaty pieniężne krótkoterminowe 455 269 15 Należności
3. Modele tendencji czasowej w prognozowaniu
 II Modele tendencji czasowej w prognozowaniu 1 Składniki szeregu czasowego W teorii szeregów czasowych wyróżnia się zwykle następujące składowe szeregu czasowego: a) składowa systematyczna; b) składowa
II Modele tendencji czasowej w prognozowaniu 1 Składniki szeregu czasowego W teorii szeregów czasowych wyróżnia się zwykle następujące składowe szeregu czasowego: a) składowa systematyczna; b) składowa
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2009 Fundusz " UFK ZrównowaŜony"
 Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2009 Fundusz " UFK ZrównowaŜony" I. AKTYWA NETTO FUNDUSZU I. Aktywa 42 716 313,50 59 705 578,27 1. Lokaty 42 716 313,50
Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2009 Fundusz " UFK ZrównowaŜony" I. AKTYWA NETTO FUNDUSZU I. Aktywa 42 716 313,50 59 705 578,27 1. Lokaty 42 716 313,50
Eurofundusz Indeksowy Otwarty Fundusz Inwestycyjny Bilans na dzień 31.12.2001 (tysiące złotych)
 Aktywa Lokaty Środki pieniężne Eurofundusz Indeksowy Otwarty Fundusz Inwestycyjny Bilans na dzień 31.12.2001 Inwestycje w krajowe papiery wartościowe 31.12.2001 31.12.2000 7 878 13 408,1 Lokaty pieniężne
Aktywa Lokaty Środki pieniężne Eurofundusz Indeksowy Otwarty Fundusz Inwestycyjny Bilans na dzień 31.12.2001 Inwestycje w krajowe papiery wartościowe 31.12.2001 31.12.2000 7 878 13 408,1 Lokaty pieniężne
Narzędzia statystyczne i ekonometryczne. Wykład 1. dr Paweł Baranowski
 Narzędzia statystyczne i ekonometryczne Wykład 1 dr Paweł Baranowski Informacje organizacyjne Wydział Ek-Soc, pok. B-109 pawel@baranowski.edu.pl Strona: baranowski.edu.pl (w tym materiały) Konsultacje:
Narzędzia statystyczne i ekonometryczne Wykład 1 dr Paweł Baranowski Informacje organizacyjne Wydział Ek-Soc, pok. B-109 pawel@baranowski.edu.pl Strona: baranowski.edu.pl (w tym materiały) Konsultacje:
Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych
 Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych 3.1. Estymacja parametrów i ocena dopasowania modeli z jedną zmienną 23. Właściciel komisu w celu zbadania
Estymacja parametrów modeli liniowych oraz ocena jakości dopasowania modeli do danych empirycznych 3.1. Estymacja parametrów i ocena dopasowania modeli z jedną zmienną 23. Właściciel komisu w celu zbadania
Ponad Rynek. Tygodniowa Analiza Portfelowa Akcji 10/2009, 10 marca 2009
 Ponad ynek ygodniowa Analiza Portfelowa Akcji /9, marca 9 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuższy niż 4 sesje, na których średni
Ponad ynek ygodniowa Analiza Portfelowa Akcji /9, marca 9 Opracowanie zawiera analizę portfelową spółek wchodzących w skład indeksu WIG, notowanych na GPW przez okres dłuższy niż 4 sesje, na których średni
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2010 Fundusz " UFK Zrównoważony"
 Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2010 Fundusz " UFK Zrównoważony" I. AKTYWA NETTO FUNDUSZU I. Aktywa 59 705 578,27 51 084 957,16 1. Lokaty 59 705 578,27
Roczne sprawozdanie ubezpieczeniowego funduszu kapitałowego sporządzone na dzień 31/12/2010 Fundusz " UFK Zrównoważony" I. AKTYWA NETTO FUNDUSZU I. Aktywa 59 705 578,27 51 084 957,16 1. Lokaty 59 705 578,27
Analiza ekonomiczna decyzji biznesowych LABORATORIUM
 Analiza ekonomiczna decyzji biznesowych LABORATORIUM Prof. dr hab. inż. Edward Radosiński kierownik Katedry Badań Operacyjnych, Finansów i Zastosowań Informatyki K4/W8, Wydział Informatyki i Zarządzania
Analiza ekonomiczna decyzji biznesowych LABORATORIUM Prof. dr hab. inż. Edward Radosiński kierownik Katedry Badań Operacyjnych, Finansów i Zastosowań Informatyki K4/W8, Wydział Informatyki i Zarządzania
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Ekonomiczna wartość dodana EVA
 Ekonomiczna wartość dodana EVA Ranking Spółek Giełdowych 2011 Wrocław, 2012 r. [Wpisz tekst] Opracowanie: Rafał Krawczyk Konsultant biznesowy VBA rafal.krawczyk@vba.pl Współpraca: Dariusz Ciborski Łukasz
Ekonomiczna wartość dodana EVA Ranking Spółek Giełdowych 2011 Wrocław, 2012 r. [Wpisz tekst] Opracowanie: Rafał Krawczyk Konsultant biznesowy VBA rafal.krawczyk@vba.pl Współpraca: Dariusz Ciborski Łukasz
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Pioneer Akcji Fundusz Inwestycyjny Otwarty Bilans na dzień (tysiące złotych) Aktywa (razem)
 Bilans na dzień 30.06.2004 ` Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne 30.06.2004 31.12.2003 30.06.2003 377 706 184 826 35 127 Środki na bieżących rachunkach bankowych 3 733 1 036
Bilans na dzień 30.06.2004 ` Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne 30.06.2004 31.12.2003 30.06.2003 377 706 184 826 35 127 Środki na bieżących rachunkach bankowych 3 733 1 036
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka - adres mailowy: nnehrebecka@wne.uw.edu.pl - strona internetowa: www.wne.uw.edu.pl/nnehrebecka - dyżur: wtorek 18.30-19.30 sala 302 lub 303 - 80% oceny: egzaminy -
Stanisław Cichocki Natalia Nehrebecka - adres mailowy: nnehrebecka@wne.uw.edu.pl - strona internetowa: www.wne.uw.edu.pl/nnehrebecka - dyżur: wtorek 18.30-19.30 sala 302 lub 303 - 80% oceny: egzaminy -
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Stanisław Cichocki. Natalia Nehrebecka
 Stanisław Cichocki Natalia Nehrebecka - adres mailowy: scichocki@o2.pl - strona internetowa: www.wne.uw.edu.pl/scichocki - dyżur: po zajęciach lub po umówieniu mailowo - 80% oceny: egzaminy - 20% oceny:
Stanisław Cichocki Natalia Nehrebecka - adres mailowy: scichocki@o2.pl - strona internetowa: www.wne.uw.edu.pl/scichocki - dyżur: po zajęciach lub po umówieniu mailowo - 80% oceny: egzaminy - 20% oceny:
Statystyka opisowa. Wykład V. Regresja liniowa wieloraka
 Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Statystyka opisowa. Wykład V. e-mail:e.kozlovski@pollub.pl Spis treści 1 Prosta regresji cechy Y względem cech X 1,..., X k. 2 3 Wyznaczamy zależność cechy Y od cech X 1, X 2,..., X k postaci Y = α 0 +
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Ekonometria. Modele dynamiczne. Paweł Cibis 27 kwietnia 2006
 Modele dynamiczne Paweł Cibis pcibis@o2.pl 27 kwietnia 2006 1 Wyodrębnianie tendencji rozwojowej 2 Etap I Wyodrębnienie tendencji rozwojowej Etap II Uwolnienie wyrazów szeregu empirycznego od trendu Etap
Modele dynamiczne Paweł Cibis pcibis@o2.pl 27 kwietnia 2006 1 Wyodrębnianie tendencji rozwojowej 2 Etap I Wyodrębnienie tendencji rozwojowej Etap II Uwolnienie wyrazów szeregu empirycznego od trendu Etap
parametrów strukturalnych modelu = Y zmienna objaśniana, X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających,
 诲 瞴瞶 瞶 ƭ0 ƭ 瞰 parametrów strukturalnych modelu Y zmienna objaśniana, = + + + + + X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających, α 0, α 1, α 2,,α k parametry strukturalne modelu, k+1 parametrów
诲 瞴瞶 瞶 ƭ0 ƭ 瞰 parametrów strukturalnych modelu Y zmienna objaśniana, = + + + + + X 1,X 2,,X k zmienne objaśniające, k zmiennych objaśniających, α 0, α 1, α 2,,α k parametry strukturalne modelu, k+1 parametrów
Ekonomiczna wartość dodana EVA
 Ekonomiczna wartość dodana EVA Ranking Spółek Giełdowych I półrocze 2012 Wrocław, 2012 r. [Wpisz tekst] Opracowanie: Rafał Krawczyk Konsultant biznesowy VBA rafal.krawczyk@vba.pl Współpraca: Dariusz Ciborski
Ekonomiczna wartość dodana EVA Ranking Spółek Giełdowych I półrocze 2012 Wrocław, 2012 r. [Wpisz tekst] Opracowanie: Rafał Krawczyk Konsultant biznesowy VBA rafal.krawczyk@vba.pl Współpraca: Dariusz Ciborski
Ocena zróżnicowania wartości wskaźników wykorzystywanych w podejściu porównawczym w wybranych sektorach na Giełdzie Papierów Wartościowych w Warszawie
 ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO nr 804 Finanse, Rynki Finansowe, Ubezpieczenia nr 67 (2014) s. 449 459 Ocena zróżnicowania wartości wskaźników wykorzystywanych w podejściu porównawczym w wybranych
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO nr 804 Finanse, Rynki Finansowe, Ubezpieczenia nr 67 (2014) s. 449 459 Ocena zróżnicowania wartości wskaźników wykorzystywanych w podejściu porównawczym w wybranych
O LICZBIE ABONENTÓW TELEFONII KOMÓRKOWEJ W POLSCE ZDANIEM TRZECH STATYSTYKÓW
 Rafał Czyżycki, Marcin Hundert, Rafał Klóska Wydział Zarządzania i Ekonomiki Usług Uniwersytet Szczeciński O LICZBIE ABONENTÓW TELEFONII KOMÓRKOWEJ W POLSCE ZDANIEM TRZECH STATYSTYKÓW Wprowadzenie Poruszana
Rafał Czyżycki, Marcin Hundert, Rafał Klóska Wydział Zarządzania i Ekonomiki Usług Uniwersytet Szczeciński O LICZBIE ABONENTÓW TELEFONII KOMÓRKOWEJ W POLSCE ZDANIEM TRZECH STATYSTYKÓW Wprowadzenie Poruszana
FORECASTING THE DISTRIBUTION OF AMOUNT OF UNEMPLOYED BY THE REGIONS
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Folia Univ. Agric. Stetin. 007, Oeconomica 54 (47), 73 80 Mateusz GOC PROGNOZOWANIE ROZKŁADÓW LICZBY BEZROBOTNYCH WEDŁUG MIAST I POWIATÓW FORECASTING THE DISTRIBUTION
Zeszyty naukowe nr 9
 Zeszyty aukowe r 9 Wyższej Szkoły Ekoomiczej w Bochi 2011 Piotr Fijałkowski Model zależości otowań giełdowych a przykładzie otowań ołowiu i spółki Orzeł Biały S.A. Streszczeie Niiejsza praca opisuje próbę
Zeszyty aukowe r 9 Wyższej Szkoły Ekoomiczej w Bochi 2011 Piotr Fijałkowski Model zależości otowań giełdowych a przykładzie otowań ołowiu i spółki Orzeł Biały S.A. Streszczeie Niiejsza praca opisuje próbę
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
Teoretyczne podstawy analizy indeksowej klasyfikacja indeksów, konstrukcja, zastosowanie
 Teoretyczne podstawy analizy indeksowej klasyfikacja indeksów, konstrukcja, zastosowanie Szkolenie dla pracowników Urzędu Statystycznego nt. Wybrane metody statystyczne w analizach makroekonomicznych dr
Teoretyczne podstawy analizy indeksowej klasyfikacja indeksów, konstrukcja, zastosowanie Szkolenie dla pracowników Urzędu Statystycznego nt. Wybrane metody statystyczne w analizach makroekonomicznych dr
Stanisław Cichocki. Natalia Nehrebecka Katarzyna Rosiak-Lada
 Stanisław Cichocki Natalia Nehrebecka Katarzyna Rosiak-Lada 1. Sprawy organizacyjne Zasady zaliczenia 2. Czym zajmuje się ekonometria? 3. Formy danych statystycznych 4. Model ekonometryczny 2 1. Sprawy
Stanisław Cichocki Natalia Nehrebecka Katarzyna Rosiak-Lada 1. Sprawy organizacyjne Zasady zaliczenia 2. Czym zajmuje się ekonometria? 3. Formy danych statystycznych 4. Model ekonometryczny 2 1. Sprawy
Specjalistyczny Fundusz Inwestycyjny Otwarty Telekomunikacji Polskie Bilans na dzień (tysiące złotych)
 Specjalistyczny Fundusz Inwestycyjny Otwarty Telekomunikacji Polskie Bilans na dzień 31.12.2004 Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne 31.12.2004 31.12.2003 322 144 203 337 Lokaty
Specjalistyczny Fundusz Inwestycyjny Otwarty Telekomunikacji Polskie Bilans na dzień 31.12.2004 Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne 31.12.2004 31.12.2003 322 144 203 337 Lokaty
Ekonometryczna analiza popytu na wodę
 Jacek Batóg Uniwersytet Szczeciński Ekonometryczna analiza popytu na wodę Jednym z czynników niezbędnych dla funkcjonowania gospodarstw domowych oraz realizacji wielu procesów technologicznych jest woda.
Jacek Batóg Uniwersytet Szczeciński Ekonometryczna analiza popytu na wodę Jednym z czynników niezbędnych dla funkcjonowania gospodarstw domowych oraz realizacji wielu procesów technologicznych jest woda.
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
Analiza współzależności zjawisk
 Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Wiadomości ogólne o ekonometrii
 Wiadomości ogólne o ekonometrii Materiały zostały przygotowane w oparciu o podręcznik Ekonometria Wybrane Zagadnienia, którego autorami są: Bolesław Borkowski, Hanna Dudek oraz Wiesław Szczęsny. Ekonometria
Wiadomości ogólne o ekonometrii Materiały zostały przygotowane w oparciu o podręcznik Ekonometria Wybrane Zagadnienia, którego autorami są: Bolesław Borkowski, Hanna Dudek oraz Wiesław Szczęsny. Ekonometria
OTWARTE FUNDUSZE EMERYTALNE W POLSCE Struktura funduszy emerytalnych pod względem liczby członków oraz wielkości aktywów
 OTWARTE FUNDUSZE EMERYTALNE W POLSCE Struktura funduszy emerytalnych pod względem liczby członków oraz wielkości aktywów Tomasz Gruszczyk Informatyka i Ekonometria I rok, nr indeksu: 156012 Sopot, styczeń
OTWARTE FUNDUSZE EMERYTALNE W POLSCE Struktura funduszy emerytalnych pod względem liczby członków oraz wielkości aktywów Tomasz Gruszczyk Informatyka i Ekonometria I rok, nr indeksu: 156012 Sopot, styczeń
e) Oszacuj parametry modelu za pomocą MNK. Zapisz postać modelu po oszacowaniu wraz z błędami szacunku.
 Zajęcia 4. Estymacja i weryfikacja modelu model potęgowy Wersja rozszerzona W pliku Funkcja produkcji.xls zostały przygotowane przykładowe dane o produkcji, kapitale i zatrudnieniu dla 27 przedsiębiorstw
Zajęcia 4. Estymacja i weryfikacja modelu model potęgowy Wersja rozszerzona W pliku Funkcja produkcji.xls zostały przygotowane przykładowe dane o produkcji, kapitale i zatrudnieniu dla 27 przedsiębiorstw
Informacja o wysokości parametrów dla derywatów na 3 lutego 2016 r.
 Informacja o wysokości parametrów dla derywatów na 3 lutego 2016 r. Dom Maklerski informuje, że inwestycje w derywaty obarczone są dużym ryzykiem. Wykorzystanie dźwigni finansowej daje możliwość osiągnięcia
Informacja o wysokości parametrów dla derywatów na 3 lutego 2016 r. Dom Maklerski informuje, że inwestycje w derywaty obarczone są dużym ryzykiem. Wykorzystanie dźwigni finansowej daje możliwość osiągnięcia
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI REGRESJA LINIOWA Powtórka Powtórki Kowiariancja cov xy lub c xy - kierunek zależności Współczynnik korelacji liniowej Pearsona r siła liniowej zależności Istotność
Statystyka. Wykład 8. Magdalena Alama-Bućko. 10 kwietnia Magdalena Alama-Bućko Statystyka 10 kwietnia / 31
 Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 8 Magdalena Alama-Bućko 10 kwietnia 2017 Magdalena Alama-Bućko Statystyka 10 kwietnia 2017 1 / 31 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
P: Czy studiujący i niestudiujący preferują inne sklepy internetowe?
 2 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia czy pomiędzy zmiennymi istnieje związek/zależność. Stosujemy go w sytuacji, kiedy zmienna zależna mierzona jest na skali
2 Test niezależności chi-kwadrat stosuje się (między innymi) w celu sprawdzenia czy pomiędzy zmiennymi istnieje związek/zależność. Stosujemy go w sytuacji, kiedy zmienna zależna mierzona jest na skali
Pioneer Otwarty Fundusz Inwestycyjny Agresywnego Inwestowania Bilans na dzień (tysiące złotych) Zbyte jednostki uczestnictwa
 Aktywa Lokaty Środki pieniężne Należności Pioneer Otwarty Fundusz Inwestycyjny Agresywnego Inwestowania Bilans na dzień 31.12.2001 Inwestycje w papiery wartościowe Środki na bieżących rachunkach bankowych
Aktywa Lokaty Środki pieniężne Należności Pioneer Otwarty Fundusz Inwestycyjny Agresywnego Inwestowania Bilans na dzień 31.12.2001 Inwestycje w papiery wartościowe Środki na bieżących rachunkach bankowych
INSTRUMENTY ZARZĄDZANIA RYZYKIEM NOTOWANE NA WARSZAWSKIEJ GIEŁDZIE PAPIERÓW WARTOŚCIOWYCH. Streszczenie
 Karol Klimczak Studenckie Koło Naukowe Stosunków Międzynarodowych TIAL przy Katedrze Stosunków Międzynarodowych Wydziału Ekonomiczno-Socjologicznego Uniwersytetu Łódzkiego INSTRUMENTY ZARZĄDZANIA RYZYKIEM
Karol Klimczak Studenckie Koło Naukowe Stosunków Międzynarodowych TIAL przy Katedrze Stosunków Międzynarodowych Wydziału Ekonomiczno-Socjologicznego Uniwersytetu Łódzkiego INSTRUMENTY ZARZĄDZANIA RYZYKIEM
Etapy modelowania ekonometrycznego
 Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
Etapy modelowania ekonometrycznego jest podstawowym narzędziem badawczym, jakim posługuje się ekonometria. Stanowi on matematyczno-statystyczną formę zapisu prawidłowości statystycznej w zakresie rozkładu,
Specjalistyczny Fundusz Inwestycyjny Otwarty Telekomunikacji Polskiej Bilans na dzień (tysiące złotych)
 Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Bilans na dzień 30.06.2003 30.06.2003 31.12.2002 30.06.2002 149 749 92 821 42 756 Lokaty pieniężne krótkoterminowe 15 5 141 2 888 Należności
Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Bilans na dzień 30.06.2003 30.06.2003 31.12.2002 30.06.2002 149 749 92 821 42 756 Lokaty pieniężne krótkoterminowe 15 5 141 2 888 Należności
Analiza zdarzeń Event studies
 Analiza zdarzeń Event studies Dobromił Serwa akson.sgh.waw.pl/~dserwa/ef.htm Leratura Campbell J., Lo A., MacKinlay A.C.(997) he Econometrics of Financial Markets. Princeton Universy Press, Rozdział 4.
Analiza zdarzeń Event studies Dobromił Serwa akson.sgh.waw.pl/~dserwa/ef.htm Leratura Campbell J., Lo A., MacKinlay A.C.(997) he Econometrics of Financial Markets. Princeton Universy Press, Rozdział 4.
A.Światkowski. Wroclaw University of Economics. Working paper
 A.Światkowski Wroclaw University of Economics Working paper 1 Planowanie sprzedaży na przykładzie przedsiębiorstwa z branży deweloperskiej Cel pracy: Zaplanowanie sprzedaży spółki na rok 2012 Słowa kluczowe:
A.Światkowski Wroclaw University of Economics Working paper 1 Planowanie sprzedaży na przykładzie przedsiębiorstwa z branży deweloperskiej Cel pracy: Zaplanowanie sprzedaży spółki na rok 2012 Słowa kluczowe:
JEDNORÓWNANIOWY LINIOWY MODEL EKONOMETRYCZNY
 JEDNORÓWNANIOWY LINIOWY MODEL EKONOMETRYCZNY Będziemy zapisywać wektory w postaci (,, ) albo traktując go jak macierz jednokolumnową (dzięki temu nie będzie kontrowersji przy transponowaniu wektora ) Model
JEDNORÓWNANIOWY LINIOWY MODEL EKONOMETRYCZNY Będziemy zapisywać wektory w postaci (,, ) albo traktując go jak macierz jednokolumnową (dzięki temu nie będzie kontrowersji przy transponowaniu wektora ) Model
Pioneer Pierwszy Polski Otwarty Fundusz Inwestycyjny Bilans na dzień (tysiące złotych)
 Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Pioneer Pierwszy Polski Otwarty Fundusz Inwestycyjny Bilans na dzień 31.12.2001 31.12.2001 31.12.2000 580 766 721 622 Środki na bieżących
Aktywa Lokaty Inwestycje w papiery wartościowe Środki pieniężne Pioneer Pierwszy Polski Otwarty Fundusz Inwestycyjny Bilans na dzień 31.12.2001 31.12.2001 31.12.2000 580 766 721 622 Środki na bieżących
t y x y'y x'x y'x x-x śr (x-x śr)^2
 Na podstawie:w.samuelson, S.Marks Ekonomia menedżerska Zadanie 1 W przedsiębiorstwie toczy się dyskusja na temat wpływu reklamy na wielkość. Dział marketingu uważa, że reklama daje wysoce pozytywne efekty,
Na podstawie:w.samuelson, S.Marks Ekonomia menedżerska Zadanie 1 W przedsiębiorstwie toczy się dyskusja na temat wpływu reklamy na wielkość. Dział marketingu uważa, że reklama daje wysoce pozytywne efekty,
ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO
 ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO Wprowadzenie Zmienność koniunktury gospodarczej jest kształtowana przez wiele różnych czynników ekonomicznych i pozaekonomicznych. Znajomość zmienności poszczególnych
ANALIZA DYNAMIKI DOCHODU KRAJOWEGO BRUTTO Wprowadzenie Zmienność koniunktury gospodarczej jest kształtowana przez wiele różnych czynników ekonomicznych i pozaekonomicznych. Znajomość zmienności poszczególnych
BIULETYN PORANNY. GPW 28 kwietnia 2009. ŚWIAT Nasdaq
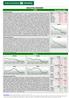 BIULETYN PORANNY GPW 28 kwietnia 2009 Komentarz poranny Wczorajsza sesja zakończyła się spadkiem indeksów, ale skala ruchu nie była znacząca. Po słabszym otwarciu WIG- 20 odnotował spadek do dziennego
BIULETYN PORANNY GPW 28 kwietnia 2009 Komentarz poranny Wczorajsza sesja zakończyła się spadkiem indeksów, ale skala ruchu nie była znacząca. Po słabszym otwarciu WIG- 20 odnotował spadek do dziennego
EKONOMETRIA. Prof. dr hab. Eugeniusz Gatnar.
 EKONOMETRIA Prof. dr hab. Eugeniusz Gatnar egatnar@mail.wz.uw.edu.pl Sprawy organizacyjne Wykłady - prezentacja zagadnień dotyczących: budowy i weryfikacji modelu ekonometrycznego, doboru zmiennych, estymacji
EKONOMETRIA Prof. dr hab. Eugeniusz Gatnar egatnar@mail.wz.uw.edu.pl Sprawy organizacyjne Wykłady - prezentacja zagadnień dotyczących: budowy i weryfikacji modelu ekonometrycznego, doboru zmiennych, estymacji
INSTRUMENTY FINANSOWE PRZYJĘTE DO KDPW / FINANCIAL INSTRUMENTS REGISTERED AT KDPW
 AKCJE EMITENTÓW KRAJOWYCH / SHARES OF DOMESTIC ISSUERS Sponsor emisji sponsor Emitent / r: Zakłady Tłuszczowe "Kruszwica" SA PLKRUSZ00016 KSW 16 946 549 7,48 922 seria E / series E 648 000 7,48 2009-03-09
AKCJE EMITENTÓW KRAJOWYCH / SHARES OF DOMESTIC ISSUERS Sponsor emisji sponsor Emitent / r: Zakłady Tłuszczowe "Kruszwica" SA PLKRUSZ00016 KSW 16 946 549 7,48 922 seria E / series E 648 000 7,48 2009-03-09
-> Spółka musi być niedoceniona przez innych inwestorów. (Wykorzystujemy wskaźniki niedowartościowania).
 48 Poniższy portfel jest kontynuacją eksperymentu inwestycyjnego, który przeprowadzałem na moim blogu. Analiza wyników po 12 tygodniach pokazała, że strategia inwestycyjna oparta niemal wyłącznie na analizie
48 Poniższy portfel jest kontynuacją eksperymentu inwestycyjnego, który przeprowadzałem na moim blogu. Analiza wyników po 12 tygodniach pokazała, że strategia inwestycyjna oparta niemal wyłącznie na analizie
STATYSTYKA. Rafał Kucharski. Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND, Finanse i Rachunkowość, rok 2
 STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND Finanse i Rachunkowość rok 2 Analiza dynamiki Szereg czasowy: y 1 y 2... y n 1 y n. y t poziom (wartość) badanego zjawiska w
STATYSTYKA Rafał Kucharski Uniwersytet Ekonomiczny w Katowicach 2015/16 ROND Finanse i Rachunkowość rok 2 Analiza dynamiki Szereg czasowy: y 1 y 2... y n 1 y n. y t poziom (wartość) badanego zjawiska w
Statystyka. Wykład 13. Magdalena Alama-Bućko. 12 czerwca Magdalena Alama-Bućko Statystyka 12 czerwca / 30
 Statystyka Wykład 13 Magdalena Alama-Bućko 12 czerwca 2017 Magdalena Alama-Bućko Statystyka 12 czerwca 2017 1 / 30 Co wpływa na zmiany wartości danej cechy w czasie? W najbardziej ogólnym przypadku, na
Statystyka Wykład 13 Magdalena Alama-Bućko 12 czerwca 2017 Magdalena Alama-Bućko Statystyka 12 czerwca 2017 1 / 30 Co wpływa na zmiany wartości danej cechy w czasie? W najbardziej ogólnym przypadku, na
Regresja linearyzowalna
 1 z 5 2007-05-09 23:22 Medycyna Praktyczna - portal dla lekarzy Regresja linearyzowalna mgr Andrzej Stanisz z Zakładu Biostatystyki i Informatyki Medycznej Collegium Medicum UJ w Krakowie Data utworzenia:
1 z 5 2007-05-09 23:22 Medycyna Praktyczna - portal dla lekarzy Regresja linearyzowalna mgr Andrzej Stanisz z Zakładu Biostatystyki i Informatyki Medycznej Collegium Medicum UJ w Krakowie Data utworzenia:
Statystyka. Wykład 9. Magdalena Alama-Bućko. 24 kwietnia Magdalena Alama-Bućko Statystyka 24 kwietnia / 34
 Statystyka Wykład 9 Magdalena Alama-Bućko 24 kwietnia 2017 Magdalena Alama-Bućko Statystyka 24 kwietnia 2017 1 / 34 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
Statystyka Wykład 9 Magdalena Alama-Bućko 24 kwietnia 2017 Magdalena Alama-Bućko Statystyka 24 kwietnia 2017 1 / 34 Tematyka zajęć: Wprowadzenie do statystyki. Analiza struktury zbiorowości miary położenia
KLASYFIKACJA SPÓŁEK PUBLICZNYCH NA PODSTAWIE ICH POZYCJI KONKURENCYJNEJ W SEKTORZE BUDOWLANYM
 Anna Turczak Zachodniopomorska Szkoła Biznesu ul. Żołnierska 53, 71-210 Szczecin aturczak@zpsb.szczecin.pl KLASYFIKACJA SPÓŁEK PUBLICZNYCH NA PODSTAWIE ICH POZYCJI KONKURENCYJNEJ W SEKTORZE BUDOWLANYM
Anna Turczak Zachodniopomorska Szkoła Biznesu ul. Żołnierska 53, 71-210 Szczecin aturczak@zpsb.szczecin.pl KLASYFIKACJA SPÓŁEK PUBLICZNYCH NA PODSTAWIE ICH POZYCJI KONKURENCYJNEJ W SEKTORZE BUDOWLANYM
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego
 Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
Korelacja oznacza współwystępowanie, nie oznacza związku przyczynowo-skutkowego Współczynnik korelacji opisuje siłę i kierunek związku. Jest miarą symetryczną. Im wyższa korelacja tym lepiej potrafimy
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
przedmiotu Nazwa Pierwsza studia drugiego stopnia
 Nazwa przedmiotu K A R T A P R Z E D M I O T U ( S Y L L A B U S ) O p i s p r z e d m i o t u Kod przedmiotu EKONOMETRIA UTH/I/O/MT/zmi/ /C 1/ST/2(m)/1Z/C1.1.5 Język wykładowy ECONOMETRICS JĘZYK POLSKI
Nazwa przedmiotu K A R T A P R Z E D M I O T U ( S Y L L A B U S ) O p i s p r z e d m i o t u Kod przedmiotu EKONOMETRIA UTH/I/O/MT/zmi/ /C 1/ST/2(m)/1Z/C1.1.5 Język wykładowy ECONOMETRICS JĘZYK POLSKI
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Analiza autokorelacji
 Analiza autokorelacji Oblicza się wartości współczynników korelacji między y t oraz y t-i (dla i=1,2,...,k), czyli współczynniki autokorelacji różnych rzędów. Bada się statystyczną istotność tych współczynników.
Analiza autokorelacji Oblicza się wartości współczynników korelacji między y t oraz y t-i (dla i=1,2,...,k), czyli współczynniki autokorelacji różnych rzędów. Bada się statystyczną istotność tych współczynników.
ANALIZA REGRESJI SPSS
 NLIZ REGRESJI SPSS Metody badań geografii społeczno-ekonomicznej KORELCJ REGRESJ O ile celem korelacji jest zmierzenie siły związku liniowego między (najczęściej dwoma) zmiennymi, o tyle w regresji związek
NLIZ REGRESJI SPSS Metody badań geografii społeczno-ekonomicznej KORELCJ REGRESJ O ile celem korelacji jest zmierzenie siły związku liniowego między (najczęściej dwoma) zmiennymi, o tyle w regresji związek
Analiza zależności liniowych
 Narzędzie do ustalenia, które zmienne są ważne dla Inwestora Analiza zależności liniowych Identyfikuje siłę i kierunek powiązania pomiędzy zmiennymi Umożliwia wybór zmiennych wpływających na giełdę Ustala
Narzędzie do ustalenia, które zmienne są ważne dla Inwestora Analiza zależności liniowych Identyfikuje siłę i kierunek powiązania pomiędzy zmiennymi Umożliwia wybór zmiennych wpływających na giełdę Ustala
KARTA PRZEDMIOTU. 12. PRZEDMIOTOWE EFEKTY KSZTAŁCENIA Odniesienie do kierunkowych efektów kształcenia (symbol)
 KARTA PRZEDMIOTU 1. NAZWA PRZEDMIOTU: Ekonometria 2. KIERUNEK: MATEMATYKA 3. POZIOM STUDIÓW: I stopnia 4. ROK/ SEMESTR STUDIÓW: III/6 5. LICZBA PUNKTÓW ECTS: 5 6. LICZBA GODZIN: 30 / 30 7. TYP PRZEDMIOTU
KARTA PRZEDMIOTU 1. NAZWA PRZEDMIOTU: Ekonometria 2. KIERUNEK: MATEMATYKA 3. POZIOM STUDIÓW: I stopnia 4. ROK/ SEMESTR STUDIÓW: III/6 5. LICZBA PUNKTÓW ECTS: 5 6. LICZBA GODZIN: 30 / 30 7. TYP PRZEDMIOTU
Podstawy ekonometrii. Opracował: dr hab. Eugeniusz Gatnar prof. WSBiF
 Podstawy ekonometrii Opracował: dr hab. Eugeniusz Gatnar prof. WSBiF Cele przedmiotu: I. Ogólne informacje o przedmiocie. - Opanowanie podstaw teoretycznych, poznanie przykładów zastosowań metod modelowania
Podstawy ekonometrii Opracował: dr hab. Eugeniusz Gatnar prof. WSBiF Cele przedmiotu: I. Ogólne informacje o przedmiocie. - Opanowanie podstaw teoretycznych, poznanie przykładów zastosowań metod modelowania
REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ. Analiza regresji i korelacji
 Statystyka i opracowanie danych Ćwiczenia 5 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ MODEL REGRESJI LINIOWEJ Analiza regresji
Statystyka i opracowanie danych Ćwiczenia 5 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA I KORELACJA MODEL REGRESJI LINIOWEJ MODEL REGRESJI WIELORAKIEJ MODEL REGRESJI LINIOWEJ Analiza regresji
Regresja i Korelacja
 Regresja i Korelacja Regresja i Korelacja W przyrodzie często obserwujemy związek między kilkoma cechami, np.: drzewa grubsze są z reguły wyższe, drewno iglaste o węższych słojach ma większą gęstość, impregnowane
Regresja i Korelacja Regresja i Korelacja W przyrodzie często obserwujemy związek między kilkoma cechami, np.: drzewa grubsze są z reguły wyższe, drewno iglaste o węższych słojach ma większą gęstość, impregnowane
Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do:
 Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
Ekonometria. Zajęcia
 Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
Ekonometria Zajęcia 16.05.2018 Wstęp hipoteza itp. Model gęstości zaludnienia ( model gradientu gęstości ) zakłada, że gęstość zaludnienia zależy od odległości od okręgu centralnego: y t = Ae βx t (1)
Statystyka opisowa Opracował: dr hab. Eugeniusz Gatnar, prof. WSBiF
 Statystyka opisowa Opracował: dr hab. Eugeniusz Gatnar, prof. WSBiF 120 I. Ogólne informacje o przedmiocie Cel przedmiotu: Opanowanie podstaw teoretycznych, poznanie przykładów zastosowań metod statystycznych.
Statystyka opisowa Opracował: dr hab. Eugeniusz Gatnar, prof. WSBiF 120 I. Ogólne informacje o przedmiocie Cel przedmiotu: Opanowanie podstaw teoretycznych, poznanie przykładów zastosowań metod statystycznych.
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Metodologia badań psychologicznych. Wykład 12. Korelacje
 Metodologia badań psychologicznych Lucyna Golińska SPOŁECZNA AKADEMIA NAUK Wykład 12. Korelacje Korelacja Korelacja występuje wtedy gdy dwie różne miary dotyczące tych samych osób, zdarzeń lub obiektów
Metodologia badań psychologicznych Lucyna Golińska SPOŁECZNA AKADEMIA NAUK Wykład 12. Korelacje Korelacja Korelacja występuje wtedy gdy dwie różne miary dotyczące tych samych osób, zdarzeń lub obiektów
Które z wymienionych miar obrazują zmiany zjawiska w czasie? Uczniowie winni wskazać: przyrost absolutny, przyrost względny, tempo wzrostu, indeks.
 Praca zaliczeniowa Ewa Nowak Scenariusz lekcji ze statystyki Giełda jest dynamiczna 245 min. I) Cele a) wiedza: po lekcji uczeń - zna miary dynamiki i sposób ich wyliczania, - potrafi wymienić pojęcia
Praca zaliczeniowa Ewa Nowak Scenariusz lekcji ze statystyki Giełda jest dynamiczna 245 min. I) Cele a) wiedza: po lekcji uczeń - zna miary dynamiki i sposób ich wyliczania, - potrafi wymienić pojęcia
Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych (X1, X2, X3,...) na zmienną zależną (Y).
 Statystyka i opracowanie danych Ćwiczenia 12 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA WIELORAKA Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych
Statystyka i opracowanie danych Ćwiczenia 12 Izabela Olejarczyk - Wożeńska AGH, WIMiIP, KISIM REGRESJA WIELORAKA Regresja wielokrotna jest metodą statystyczną, w której oceniamy wpływ wielu zmiennych niezależnych
Notowania. Pragma Faktoring Umowa faktoringowa z maksymalnym limitem w kwocie 130 tys. PLN
 19 kwietnia 2013 2013-04-19 TRIGON COVERAGE CCC W I kwartale strata netto powyżej 30 mln PLN W wypowiedzi dla prasy wiceprezes przyznaje, że w I kwartale strata grupy jest wysoka i przekracza 30 mln PLN.
19 kwietnia 2013 2013-04-19 TRIGON COVERAGE CCC W I kwartale strata netto powyżej 30 mln PLN W wypowiedzi dla prasy wiceprezes przyznaje, że w I kwartale strata grupy jest wysoka i przekracza 30 mln PLN.
Analiza Współzależności
 Statystyka Opisowa z Demografią oraz Biostatystyka Analiza Współzależności Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka
Statystyka Opisowa z Demografią oraz Biostatystyka Analiza Współzależności Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka
Inwestycje funduszy emerytalnych na rynku akcji grudzień 2004
 Czy jesteś już naszym subskrybentem? To najprostszy i najszybszy sposób otrzymywania naszych raportów. Za darmo. http://www.analizy.pl/subskrypcja.shtml www.analizy.pl 28-01-2005 Inwestycje funduszy emerytalnych
Czy jesteś już naszym subskrybentem? To najprostszy i najszybszy sposób otrzymywania naszych raportów. Za darmo. http://www.analizy.pl/subskrypcja.shtml www.analizy.pl 28-01-2005 Inwestycje funduszy emerytalnych
Prace magisterskie 1. Założenia pracy 2. Budowa portfela
 1. Założenia pracy 1 Założeniem niniejszej pracy jest stworzenie portfela inwestycyjnego przy pomocy modelu W.Sharpe a spełniającego następujące warunki: - wybór akcji 8 spółek + 2 papiery dłużne, - inwestycja
1. Założenia pracy 1 Założeniem niniejszej pracy jest stworzenie portfela inwestycyjnego przy pomocy modelu W.Sharpe a spełniającego następujące warunki: - wybór akcji 8 spółek + 2 papiery dłużne, - inwestycja
Korelacja krzywoliniowa i współzależność cech niemierzalnych
 Korelacja krzywoliniowa i współzależność cech niemierzalnych Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki Szczecińskiej
Korelacja krzywoliniowa i współzależność cech niemierzalnych Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki Szczecińskiej
Ciągi liczbowe. Zbigniew Koza. Wydział Fizyki i Astronomii
 Ciągi liczbowe Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2015 Co to są ciągi? Ciąg skończony o wartościach w zbiorze A to dowolna funkcja f: 1,2,, n A Ciąg nieskończony o wartościach w zbiorze
Ciągi liczbowe Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2015 Co to są ciągi? Ciąg skończony o wartościach w zbiorze A to dowolna funkcja f: 1,2,, n A Ciąg nieskończony o wartościach w zbiorze
K wartość kapitału zaangażowanego w proces produkcji, w tys. jp.
 Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
Sprawdzian 2. Zadanie 1. Za pomocą KMNK oszacowano następującą funkcję produkcji: Gdzie: P wartość produkcji, w tys. jp (jednostek pieniężnych) K wartość kapitału zaangażowanego w proces produkcji, w tys.
Wykład Centralne twierdzenie graniczne. Statystyka matematyczna: Estymacja parametrów rozkładu
 Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Wykład 11-12 Centralne twierdzenie graniczne Statystyka matematyczna: Estymacja parametrów rozkładu Centralne twierdzenie graniczne (CTG) (Central Limit Theorem - CLT) Centralne twierdzenie graniczne (Lindenberga-Levy'ego)
Prognozowanie na podstawie modelu ekonometrycznego
 Prognozowanie na podstawie modelu ekonometrycznego Przykład. Firma usługowa świadcząca usługi doradcze w ostatnich kwartałach (t) odnotowała wynik finansowy (yt - tys. zł), obsługując liczbę klientów (x1t)
Prognozowanie na podstawie modelu ekonometrycznego Przykład. Firma usługowa świadcząca usługi doradcze w ostatnich kwartałach (t) odnotowała wynik finansowy (yt - tys. zł), obsługując liczbę klientów (x1t)
Istota funkcjonowania przedsiębiorstwa produkcyjnego. dr inż. Andrzej KIJ
 Istota funkcjonowania przedsiębiorstwa produkcyjnego dr inż. Andrzej KIJ 1 Popyt rynkowy agregacja krzywych popytu P p2 p1 D1 q1 D2 q2 Q 2 Popyt rynkowy agregacja krzywych popytu P p2 p1 D1 +D2 D1 D2 q1
Istota funkcjonowania przedsiębiorstwa produkcyjnego dr inż. Andrzej KIJ 1 Popyt rynkowy agregacja krzywych popytu P p2 p1 D1 q1 D2 q2 Q 2 Popyt rynkowy agregacja krzywych popytu P p2 p1 D1 +D2 D1 D2 q1
Budowa portfela inwestycyjnego za pomocą siły relatywnej i elementy pairs trading
 Budowa portfela inwestycyjnego za pomocą siły relatywnej i elementy pairs trading Krzysztof Borowski KBC Securities Krzysztof Borowski - Analiza techniczna 1 AT / AF Metody analizy na giełdzie: Analiza
Budowa portfela inwestycyjnego za pomocą siły relatywnej i elementy pairs trading Krzysztof Borowski KBC Securities Krzysztof Borowski - Analiza techniczna 1 AT / AF Metody analizy na giełdzie: Analiza
