Unimodalne odwzorowania kwadratowe
|
|
|
- Paweł Karpiński
- 6 lat temu
- Przeglądów:
Transkrypt
1 Dynamika Ukadów Nieliniowych 2009 Wykład 3 1 Unimodalne odwzorowania kwadratowe Najbardziej znane s dwa odwzorowania: - kwadratowe x n+1 = 1 - a x n 2 lub równowanie x n+1 = C - x n 2 - logistyczne x n+1 = r x n (1 - x n ) (x n ) Oba odwzorowania s ze sob blisko spokrewnione i nale do szerokiej klasy topologicznie równowanych jednowymiarowych odwzorowań unimodalnych, które s okrelone na skoczonym odcinku posiadaj pojedycze, gadkie maksimum. Odwzorowania te s nieodwracalne: nie mona napisa jednoznacznie: x n = -1 (x n+1 ) gdzie (x) - dane odwzorowanie unimodalne np. logistyczne.
2 Dynamika Ukadów Nieliniowych 2009 Wykład 3 2 Pochodzenie odwzorowania logistycznego: Odwzorowanie logistyczne pojawia si bezporednio w demografii. W modelu zmian populacji gdy pokolenia nie zachodz na siebie (jak to si dzieje np. u owadów): - najprostsze prawo zakada sta szybko reprodukcji z pokolenia na pokolenie: x n+1 = r x n Bardziej wyrafinowanie: zaoy, e zdolno reprodukcji maleje gdy populacja ronie: opisuje to odwzorowanie logistyczne x n+1 = r x n (1 - x n ) Podstawowe wasnoci odwzorowania logistycznego I. Dla 0 < r 1 wszystkie warunki początkowe prowadzą do 0. II. Dla r > 1 wszystkie x 0 < 0 d do - podobnie wszystkie x 0 > 1 d do - III. Dla r = 4 istnieje przeksztacenie wspórzdnych x= 2 sin y 2 które wie kolejne iteracje odwzorowania logistycznego (x) z iteracjami odwzorowania trójktnego (y) dla a = 1.0.
3 (x) Dynamika Ukadów Nieliniowych 2009 Wykład 3 3 Konsekwencje własności III: Skoro odwzorowanie trójktne dla parametru a= 1.0 jest chaotyczne tak samo bdzie si zachowywa odwzorowanie logistyczne dla r = 4.0 Odwzorowanie logistyczne dla r = 4 bdzie miao tyle samo (niestabilnych) punktów staych co odwzorowanie trójktne tzn. w granicy n nieskoczenie wiele Orbity periodyczne s gste w [0,1] dla odwzorowania trójktnego dla a= 1.0, wic s te gste dla odwzorowania logistycznego z r = 4 Naturalna miara niezmiennicza dla odwzorowania trójktnego ρ(y) = 1 Skoro istnieje przeksztacenie wspórzdnych x = x(y) to czsto odwiedzania odcinka x, x+dx dla odwzorowania logistycznego musi by taka sama jak często odwiedzania odcinka y, y+dy dla odwzorowania trójktnego tj. ρ 1 (x)dx = ρ(y) dy 12 inaczej 1 Jeli wstawi posta y(x) to (x) = dy(x) ( dx y (x) ) ( x )= x ( 1- x ) x Naturalna miara niezmiennicza odwzorowania logistyczneg dla r = 4 ma osobliwoci w x = 0 i x =
4 Dynamika Ukadów Nieliniowych 2009 Wykład 3 4 IV. Dla 1 r 3 odwzorowanie logistyczne ma dwa punkty stae: x * = 0 - niestabilny dla wszystkich r > 1 x * = 1-1/r - stabilny dla 1 < r < 3 sprawdzenie: df ( x= 1-1 / r dx ) = 2 - r < 1 V. Mona pokaza, e dla 1 < r < 3 wszystkie warunki pocztkowe x 0 є (0,1) d do x * = 1-1/r [0,1] jest basenem atrakcji x * Przykład: Program logistic Parametry: parametr kontrolny zmieniać od r < 1 do 3.1 i obserwować zachowanie układu warunek początkowy dowolny z basenu atrakcji (0,1) rząd złożenia 1 VI. Dla r = 4 niestabilne punkty stae s gste w (0,1) Co si dzieje dla 3 < r < 4? Rozpatrzmy dwukrotnie zoone odwzorowanie logistyczne tj. 2 (x). Dla r < 3 mamy jeden punkt stay. Dla r = 3 2 (x) jest styczne do przektnej wykresu odwzorowania. Dla r > 3 pojawiaj si dwa nowe punkty stae 2 (x). Nie s one punktami staymi (x) wic tworz one orbit o okresie 2.
5 Dynamika Ukadów Nieliniowych 2009 Wykład 3 5 Jednoczenie widzimy, e punkt stay stabilny dla r < 3 przesta by stabilny (prosz sprawdzi (!) warunek stabilnoci tego punktu staego dla r >3): Przykład: Program logistic Parametry: rząd złożenia 2 warunek początkowy dowolny z basenu atrakcji (0,1) parametr kontrolny najpierw r = trajektoria zbiega do pojedynczego punktu stałego x * = Następnie zmienić parametr kontrolny na r = 3.1; Punkt stały x * = traci stabilność. Trajektoria zbiega do 2 różnych stabilnych punktów stałych w x * = oraz x * = Następnie zmienić rząd złożenia na 1 (skorzystać z klawisza zmień rząd złożenia a nie poprzez klawisz parametry ). Trajektoria jest orbitą o okresie 2 składającą się z ww. punktów stałych.
6 Dynamika Ukadów Nieliniowych 2009 Wykład 3 6 Bifurkacja podwajania okresu linia przerywana - niestabilny punkt stay; linia ciga - stabilny punkt stay Inaczej patrzc na ten sam problem: - dla 1 < r < 3 widzielimy, e wszystkie warunki pocztkowe x 0 є (0,1) s przycigane do x * = 1-1/r - wspóczynnik stabilnoci punktu staego x * λ = 2 -r Otrzymuje wartość λ 1 = 1 dla r = 1 i maleje do λ 1 = -1 gdy r = 3 (punkt bifurkacji)
7 Dynamika Ukadów Nieliniowych 2009 Wykład Wspóczynnik stabilnoci orbit o okresie 2 λ 2 = '(e)'(f) gdzie e,f punkty orbity; λ 2 = 1 dla r = 3 i maleje osigajc warto -1 dla pewnego r = r 1 > 3. Dla r > r 1 orbita o okresie 2 przestaa by stabilna bo λ 2 > 1. - Dla parametru kontrolnego r = r 1 oba punkty orbity o okresie 2 podlegaj bifurkacji. Obraz jest podobny jak przy podwojeniu okresu dla r = 3 tyle e rol peni teraz 2 a rol 2 - odwzorowanie czterokrotnie złoone 4. Przykład: Program logistic Parametry: rząd złożenia 4 warunek początkowy dowolny z basenu atrakcji (0,1) parametr kontrolny najpierw r = 3.41 trajektoria zbiega do 2 punktów stałych. Następnie zmienić parametr kontrolny na r = 3.5; Punkty stałe tracą stabilność. Trajektoria zbiega do 4 innych stabilnych punktów stałych. Następnie zmienić rząd złożenia na 1 (skorzystać z klawisza zmień rząd złożenia a nie poprzez klawisz parametry ). Trajektoria jest orbitą o okresie 4 składającą się z ww. punktów stałych.
8 Dynamika Ukadów Nieliniowych 2009 Wykład dalsze powikszanie parametru kontronego r prowadzi do ponownej bifurkacji podwajania okresu przy r = r 2. - przy dalszym wzrocie parametru powstaje nieskoczona kaskada bifurkacji podwajania: w kadym obszarze parametru kontrolnego r m-1 < r r m stabilne s orbity o okresie 2 m. Ćwiczenie: Spróbuj znaleźć wartości parametru kontrolnego odpowiadające następnym punktom podwojenia okresu. Podpowiedź: dobre wartości parametru kontrolnego to: r = 3.54, 3.56, 3.565, Zidentyfikuj orbity jakim te punkty odpowiadają odpowiadają. - Feigenbaum pokaza (1978), e obszar stabilnoci orbity o okresie 2 m maleje w przyblieniu w stosunku geometrycznym: r r m m+1 - r - r m-1 m m ˆ - istnieje więc punkt akumulacji r = , w którym liczba bifurkacji podwajania okresu osiga nieskoczono stała Feigenbauma
9 Dynamika Ukadów Nieliniowych 2009 Wykład 3 9 Orbity superstabilne S to orbity o okresie 2 m, których wspóczynnik stabilnoci znika. Dzieje si tak dla pewnego r = r ms. Wspólczynnik stabilnoci orbity okresowej okrelony jest przez iloczyn pochodnych odwzorowania w punktach należących do tej orbity. Dla orbity o okresie 2 m : = 0 1 ˆm ( xˆ ) ( xˆ )... ( x ) gdzie ^ oznacza punkt na orbicie. Widzimy, e punkt krytyczny odwzorowania tj. punkt w maksimum odwzorowania ley na orbicie superstabilnej. W tym punkcie pochodna znika znika też współczynnik stabilności całej orbity. Niech d m bdzie odlegoci punktu krytycznego od najbliszego sporód pozostaych 2 m -1 punktów orbity periodycznej.
10 Dynamika Ukadów Nieliniowych 2009 Wykład 3 10 Ten najbliszy punkt jest przesunity o 1/2 okresu od punktu krytycznego: d m = 2 m-1 ( 1 2 )- 1 2 d d m m+1 Okazuje si, e m ˆ Druga stała Fiegenbauma Przykład: orbity superstabilne Program logistic Parametry: rząd złożenia 1 parametr kontrolny najpierw r = warunek początkowy dowolny z basenu atrakcji (0,1) Trajektoria zbiega do orbity o okresie 2: x = oraz x = Jest to więc z dobrym przybliżeniem orbita superstabilna. Natomiast dla np. r = 3.15 orbita nie przechodzi przez x = 0.5 więc nie jest superstabilna.
11 Dynamika Ukadów Nieliniowych 2009 Wykład 3 11 A co si dzieje za punktem akumulacji dla r > r? - powikszanie r powyej r powoduje "zderzanie si" brzegów pasm widocznych na wykresie bifurkacyjnym a dla r = 4 iteracje wypeniaj cay odcinek [0,1]. - ciemne linie na wykresie bifurkacyjnym s obrazami punktu krytycznego (punktów krytycznych) odwzorowania. Tworz tzw."szkielet" wykresu bifurkacyjnego. Analiza ewolucji punktów krytycznych odwzorowania pozwala przewidzie wiele jego wasnoci np. punkty zderzania si pasm chaotycznych. - bifurkacje tangencjalne (styczne, siodło-węzeł) powoduj powstawanie okien periodycznych. Okna te s gste w caym obszarze [r,4]. Tzn. Jeeli dane jest r, dla którego odwzorowanie jest chaotyczne to w maym otoczeniu [r-ε,r+ε] mona znale okna periodyczne niezalenie od wielkoci ε. Okno najlepiej widoczne - o okresie 3 powstaje na skutek bifurkacji tangencjalnej 3-krotnie złożonego odwzorowania logistycznego 3 Przykład: Program logistic Parametry: rząd złożenia 3 parametr kontrolny najpierw r = 3.825
12 Dynamika Ukadów Nieliniowych 2009 Wykład 3 12 warunek początkowy 0.5 Trajektoria przechodzi przez kanał intermitencyjny a potem błądzi chaotycznie dopóki nie wejdzie do następnego kanału. Układ znajduje się w stanie chaotycznym zwanym intermitencją I rodzaju. Zmień parametr kontrolny na r = 3.84 posługując się klawiszem Dodaj wykres po bifurkacji. Następnie użyj Zmień rząd złożenia na 1. W ten sposób zmieniamy tylko rząd złożenia a nie parametr kontrolny! Obserwuj trajektorię o okresie 3. Trajektoria ta przechodzi przez wszystkie stabilne punkty stałe odwzorowania 3-krotnie złożonego. W ten sposób powstaje jednoczenie przycigajca orbita o okresie 3 (atraktor) oraz niestabilna (odpychajca) orbita - repeler o okresie 3. Kryzys: zderzenie chaotycznego rozwizania stabilnego z niestabiln orbit periodyczn. Kryzysy powstają bo w trakcie bifurkacji powstają też repelery. Przy zmianie parametru kontrolnego zmieniają swoje położenie i dlatego może dojść do zderzenia z atraktorem. Przykład: Dla r = 4 równania logistycznego dochodzi do kryzysu brzegowego w wyniku, którego trajektoria zbiega do -. Do tego tematu wrócimy przy omawianiu przepywów cigych i układów o wikszej liczby wymiarów.
13 Dynamika Ukadów Nieliniowych 2009 Wykład 3 13 Twierdzenie Szarkowskiego (porządek Szarkowskiego): Dany jest cig: 3,5,7,..., 2 x 3, 2 x 5, 2 x 7,..., 2 2 x 3, 2 2 x 5, 2 2 x 7,..., 2 m,..., 2 5, 2 4, 2 3, 2 2, 2, 1 Niech odwzorowanie cige okrelone na caej osi rzeczywistej ma orbit o okresie p. Jeeli p wystpuje w powyszym cigu przed inn liczb cakowit l to dane odwzorowanie ma równie orbit periodyczn o okresie l. (Nic nie wiadomo o jej stabilnoci!). Wyej napisany cig nosi nazw cigu uniwersalnego bo wykazano, e wystpuje on dla innych odwzorowa ni logistyczne. Pojcie to ma sens najprawdopodobniej tylko dla jednowymiarowych odwzorowa unimodlanych. Dla wicej ni jednowymiarowych odwzorowa nie tylko nie stwierdzono uporzdkowania trajektorii periodycznych ale te zdarzaj si wspóistniejce atraktory periodyczne o rónych basenach atrakcji. Li i Yorke ("Period three implies chaos", Am. Math. Monthly 82, 985, 1975) wykazali, e gdy si pojawia trajektoria periodyczna o okresie 3 to z tego wynika, e istnieje równie nieprzeliczalna liczba trajektorii, które pozostaj nieperiodyczne na zawsze. Wprowadzili termin "chaos" dla okrelenia takiej sytuacji.
14 Dynamika Ukadów Nieliniowych 2009 Wykład 3 14 Jak zobaczymy w swoim czasie bifurkacja podwajania okresu bifurkacja tangencjalna (styczna) opisane powyej maj swoje odpowiedniki dla odwzorowa wicej ni jednowymiarowych i dla przepywów (równania róniczkowe). Wykadnik Lapunowa dla odwzorowania logistycznego: Dla r = 4 znalelimy naturaln gsto niezmiennicz 1 ( x )= -1 1 x ( 1- x ) N-1 1 Wykadnik Lapunowa dany jest przez: = lim ln ( xn ) N N co mona obliczy posugujc si naturaln miar niezmiennicz jako: = 1 ( x ) ( x ) = ln 2 i jest taki sam dla odwzorowania namiotowego Δ(x) z parametrem a = 1. Wniosek: Wykadnik Lapunowa nie zaley jak wida od wyboru wspórzdnych. N=0 1 0
15 Dynamika Ukadów Nieliniowych 2009 Wykład 3 15 Wpyw szumu na podwajanie okresu Szum w deterministycznych układach jest zawsze obecny: albo jest on numeryczny albo te pochodzi z pomiaru. Rodzaje szumu w układach dynamicznych: a) szum addytywny x (1 ) f ( x, p) n 1 n n gdzie f jest odwzorowaniem p jest parametrem kontrolnym, ξ n jest dodatnio określoną zmienną losową o zadanym rozkładzie (najczęściej równomiernym lub normalnym, ale może być też np. szumem dychotomicznym) ε parametr określający moc szumu Czynnik 1- ε dodaje się po to aby utrzymać wartości x n+1 wewnątrz basenu atrakcji odwzorowania tj. aby x є (0,1). b) szum parametryczny x f x, p p ) ( n 1 n 0 n gdzie ξ n jest zmienną losową tym razem zawartą w przedziale [-1,1] Δp określa zakres zmian parametru kontrolnego p c) szum pomiarowy ( zabrudzenie sygnału szumem ): szum nie zmienia dynamiki układu ale występuje w sygnale i zniekształca go.
16 Dynamika Ukadów Nieliniowych 2009 Wykład 3 16 ad a) Syntetycznie biorc: szum powoduje skrócenie kaskady podwajania okresu - staje si ona skoczona i chaos pojawia si nieco przed r. Aby zobaczy nastpne "pitro" kaskady trzeba zmniejszy szum. Szum wpywa te na wykadnik Lapunowa. Chocia Schuster i inni autorzy podrczników twierdz, e szum nie niszczy przejcia do chaosu w r = r dla odwzorowa unimodalnych to trzeba pamita, e w niektórych pracach dowodzi si, e szum numeryczny (zaokrglenia) moe sztucznie stabilizowa periodyczne rozwizania równa róniczkowych zwyczajnych.
ϕ(t k ; p) dla pewnego cigu t k }.
 VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
VI. Trajektorie okresowe i zbiory graniczne. 1. Zbiory graniczne. Rozważamy równanie (1.1) x = f(x) z funkcją f : R n R n określoną na całej przestrzeni R n. Będziemy zakładać, że funkcja f spełnia założenia,
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań.
 III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
III. Układy liniowe równań różniczkowych. 1. Pojęcie stabilności rozwiązań. Analiza stabilności rozwiązań stanowi ważną część jakościowej teorii równań różniczkowych. Jej istotą jest poszukiwanie odpowiedzi
czyli o szukaniu miejsc zerowych, których nie ma
 zerowych, których nie ma Instytut Fizyki im. Mariana Smoluchowskiego Centrum Badania Systemów Złożonych im. Marka Kaca Uniwersytet Jagielloński Metoda Metoda dla Warszawa, 9 stycznia 2006 Metoda -Raphsona
zerowych, których nie ma Instytut Fizyki im. Mariana Smoluchowskiego Centrum Badania Systemów Złożonych im. Marka Kaca Uniwersytet Jagielloński Metoda Metoda dla Warszawa, 9 stycznia 2006 Metoda -Raphsona
Proste modele o zªo»onej dynamice
 Proste modele o zªo»onej dynamice czyli krótki wst p do teorii chaosu Tomasz Rodak Festiwal Nauki, Techniki i Sztuki 2018 April 17, 2018 Dyskretny model pojedynczej populacji Rozwa»my pojedyncz populacj
Proste modele o zªo»onej dynamice czyli krótki wst p do teorii chaosu Tomasz Rodak Festiwal Nauki, Techniki i Sztuki 2018 April 17, 2018 Dyskretny model pojedynczej populacji Rozwa»my pojedyncz populacj
Wykład z modelowania matematycznego.
 Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Załóżmy, że równanie różniczkowe x (t) = f (t, x) (1) ma rozwiązanie ogólne x(t) = ϕ(t, c). (2) Rodzina funkcji
Intermitencja. Często wiry i przepływ laminarny się przeplatają wtedy mówimy o. intermitencji przestrzennej:
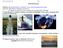 Dynamika układów nieliniowych 2009 Wykład 5 1 Intermitencja Odrónia si intermitencj w dziedzinie czasu i intermitencj przestrzenn Znaczenie sownikowe terminu intermitency: to intermit: to stop for a time,
Dynamika układów nieliniowych 2009 Wykład 5 1 Intermitencja Odrónia si intermitencj w dziedzinie czasu i intermitencj przestrzenn Znaczenie sownikowe terminu intermitency: to intermit: to stop for a time,
II. Równania autonomiczne. 1. Podstawowe pojęcia.
 II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
II. Równania autonomiczne. 1. Podstawowe pojęcia. Definicja 1.1. Niech Q R n, n 1, będzie danym zbiorem i niech f : Q R n będzie daną funkcją określoną na Q. Równanie różniczkowe postaci (1.1) x = f(x),
Uniwersalność wykresu bifurkacyjnego w uogólnionym odwzorowaniu logistycznym
 Uniwersalność wykresu bifurkacyjnego w uogólnionym odwzorowaniu logistycznym Oskar Amadeusz Prośniak pod opieką prof. dr hab. Karola Życzkowskiego 29 września 2015 Instytut Fizyki UJ 1 Wstęp Celem tej
Uniwersalność wykresu bifurkacyjnego w uogólnionym odwzorowaniu logistycznym Oskar Amadeusz Prośniak pod opieką prof. dr hab. Karola Życzkowskiego 29 września 2015 Instytut Fizyki UJ 1 Wstęp Celem tej
KLUCZ PUNKTOWANIA ODPOWIEDZI
 Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartoci funkcji dla danych argumentów i jej miejsca zerowego. Zdajcy
Egzamin maturalny maj 009 MATEMATYKA POZIOM PODSTAWOWY KLUCZ PUNKTOWANIA ODPOWIEDZI Zadanie 1. Matematyka poziom podstawowy Wyznaczanie wartoci funkcji dla danych argumentów i jej miejsca zerowego. Zdajcy
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Rodzinę odwzorowań {f i : X X} k i=1 nazywamy iterowanym układem funkcyjnym (ang. IFS iterated function system).
 Iterowane układy funkcyjne Fraktale i chaos K. Leśniak X przestrzeń metryczna (w szczególności X R lub X C R 2 ). Rodzinę odwzorowań {f i : X X} k i= nazywamy iterowanym układem funkcyjnym (ang. IFS iterated
Iterowane układy funkcyjne Fraktale i chaos K. Leśniak X przestrzeń metryczna (w szczególności X R lub X C R 2 ). Rodzinę odwzorowań {f i : X X} k i= nazywamy iterowanym układem funkcyjnym (ang. IFS iterated
Iteracyjne rozwiązywanie równań
 Elementy metod numerycznych Plan wykładu 1 Wprowadzenie Plan wykładu 1 Wprowadzenie 2 Plan wykładu 1 Wprowadzenie 2 3 Wprowadzenie Metoda bisekcji Metoda siecznych Metoda stycznych Plan wykładu 1 Wprowadzenie
Elementy metod numerycznych Plan wykładu 1 Wprowadzenie Plan wykładu 1 Wprowadzenie 2 Plan wykładu 1 Wprowadzenie 2 3 Wprowadzenie Metoda bisekcji Metoda siecznych Metoda stycznych Plan wykładu 1 Wprowadzenie
TEORIA CHAOSU. Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska
 TEORIA CHAOSU Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska Wydział MiNI Politechnika Warszawska Rok akademicki 2015/2016 Semestr letni Krótki kurs historii matematyki DEFINICJA
TEORIA CHAOSU Autorzy: Szymon Sapkowski, Karolina Seweryn, Olaf Skrabacz, Kinga Szarkowska Wydział MiNI Politechnika Warszawska Rok akademicki 2015/2016 Semestr letni Krótki kurs historii matematyki DEFINICJA
Zastosowanie wykładników Lapunowa do badania stabilności sieci elektroenergetycznej
 Zastosowanie wykładników Lapunowa do badania stabilności sieci elektroenergetycznej dr inż. Olgierd Małyszko Katedra Elektroenergetyki i Napędów Elektrycznych, Wydział Elektryczny Zachodniopomorski Uniwersytet
Zastosowanie wykładników Lapunowa do badania stabilności sieci elektroenergetycznej dr inż. Olgierd Małyszko Katedra Elektroenergetyki i Napędów Elektrycznych, Wydział Elektryczny Zachodniopomorski Uniwersytet
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
Twierdzenie 2: Własności pola wskazujące na istnienie orbit
 Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
Cykle graniczne Dotychczas zajmowaliśmy się głównie znajdowaniem i badaniem stabilności punktów stacjonarnych. Wiele ciekawych procesów ma naturę cykliczną. Umiemy już sobie poradzić z cyklicznością występującą
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Stała w przedsionku chaosu
 36 Stała w przedsionku chaosu Mateusz Denys Student V roku fizyki na Uniwersytecie Warszawskim Liczba π, pierwiastek z dwóch, podstawa logarytmów naturalnych to stałe matematyczne znane od wieków. Każda
36 Stała w przedsionku chaosu Mateusz Denys Student V roku fizyki na Uniwersytecie Warszawskim Liczba π, pierwiastek z dwóch, podstawa logarytmów naturalnych to stałe matematyczne znane od wieków. Każda
Metody numeryczne I Równania nieliniowe
 Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Metody numeryczne I Równania nieliniowe Janusz Szwabiński szwabin@ift.uni.wroc.pl Metody numeryczne I (C) 2004 Janusz Szwabiński p.1/66 Równania nieliniowe 1. Równania nieliniowe z pojedynczym pierwiastkiem
Równania ró»niczkowe I rz du (RRIR) Twierdzenie Picarda. Anna D browska. WFTiMS. 23 marca 2010
 WFTiMS 23 marca 2010 Spis tre±ci 1 Denicja 1 (równanie ró»niczkowe pierwszego rz du) Równanie y = f (t, y) (1) nazywamy równaniem ró»niczkowym zwyczajnym pierwszego rz du w postaci normalnej. Uwaga 1 Ogólna
WFTiMS 23 marca 2010 Spis tre±ci 1 Denicja 1 (równanie ró»niczkowe pierwszego rz du) Równanie y = f (t, y) (1) nazywamy równaniem ró»niczkowym zwyczajnym pierwszego rz du w postaci normalnej. Uwaga 1 Ogólna
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
W. Guzicki Zadanie IV z Informatora Maturalnego poziom rozszerzony 1
 W. Guzicki Zadanie IV z Informatora Maturalnego poziom rozszerzony 1 Zadanie IV. Dany jest prostokątny arkusz kartony o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe
W. Guzicki Zadanie IV z Informatora Maturalnego poziom rozszerzony 1 Zadanie IV. Dany jest prostokątny arkusz kartony o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Zadania z analizy matematycznej - sem. II Rachunek ró»niczkowy funkcji wielu zmiennych
 Zadania z analizy matematycznej - sem II Rachunek ró»niczkowy funkcji wielu zmiennych Denicja (Pochodne cz stkowe dla funkcji trzech zmiennych) Niech D R 3 b dzie obszarem oraz f : D R f = f y z) P 0 =
Zadania z analizy matematycznej - sem II Rachunek ró»niczkowy funkcji wielu zmiennych Denicja (Pochodne cz stkowe dla funkcji trzech zmiennych) Niech D R 3 b dzie obszarem oraz f : D R f = f y z) P 0 =
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
2) R stosuje w obliczeniach wzór na logarytm potęgi oraz wzór na zamianę podstawy logarytmu.
 ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
ZAKRES ROZSZERZONY 1. Liczby rzeczywiste. Uczeń: 1) przedstawia liczby rzeczywiste w różnych postaciach (np. ułamka zwykłego, ułamka dziesiętnego okresowego, z użyciem symboli pierwiastków, potęg); 2)
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
MODELOWANIE RZECZYWISTOŚCI
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN Szkoła Wyższa Psychologii Społecznej d.wojcik@nencki.gov.pl dwojcik@swps.edu.pl tel. 022 5892 424 http://www.neuroinf.pl/members/danek/swps/
Pochodna funkcji c.d.-wykład 5 ( ) Funkcja logistyczna
 Pochodna funkcji c.d.-wykład 5 (5.11.07) Funkcja logistyczna Rozważmy funkcję logistyczną y = f 0 (t) = 40 1+5e 0,5t Funkcja f może być wykorzystana np. do modelowania wzrostu masy ziaren kukurydzy (zmienna
Pochodna funkcji c.d.-wykład 5 (5.11.07) Funkcja logistyczna Rozważmy funkcję logistyczną y = f 0 (t) = 40 1+5e 0,5t Funkcja f może być wykorzystana np. do modelowania wzrostu masy ziaren kukurydzy (zmienna
Dynamika Uk adów Nieliniowych 2009 Wykład 11 1 Synchronizacja uk adów chaotycznych O synchronizacji mówiliśmy przy okazji języków Arnolda.
 Dynamika Ukadów Nieliniowych 2009 Wykład 11 1 Synchronizacja ukadów chaotycznych O synchronizacji mówiliśmy przy okazji języków Arnolda. Wtedy była to synchronizacja stanów periodycznych. Wiecej na ten
Dynamika Ukadów Nieliniowych 2009 Wykład 11 1 Synchronizacja ukadów chaotycznych O synchronizacji mówiliśmy przy okazji języków Arnolda. Wtedy była to synchronizacja stanów periodycznych. Wiecej na ten
Matematyka licea ogólnokształcące, technika
 Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Egzamin test GRUPA A (c) maleje na przedziale (1, 6). 0, ,5 1
 Matematyka dla Biologów Warszawa, stycznia 04. Imię i nazwisko:... Egzamin test GRUPA A nr indeksu:... Przy każdym z podpunktów wpisz, czy jest on prawdziwy (TAK) czy fałszywy (NIE). Za każde pytanie można
Matematyka dla Biologów Warszawa, stycznia 04. Imię i nazwisko:... Egzamin test GRUPA A nr indeksu:... Przy każdym z podpunktów wpisz, czy jest on prawdziwy (TAK) czy fałszywy (NIE). Za każde pytanie można
OCENIANIE ARKUSZA POZIOM ROZSZERZONY
 Numer zadania... Etapy rozwizania zadania Przeksztacenie wzoru funkcji do danej postaci f ( x) lub f ( x) x x. I sposób rozwizania podpunktu b). Zapisanie wzoru funkcji w postaci sumy OCENIANIE ARKUSZA
Numer zadania... Etapy rozwizania zadania Przeksztacenie wzoru funkcji do danej postaci f ( x) lub f ( x) x x. I sposób rozwizania podpunktu b). Zapisanie wzoru funkcji w postaci sumy OCENIANIE ARKUSZA
Efekt motyla i dziwne atraktory
 O układzie Lorenza Wydział Matematyki i Informatyki Uniwersytet Mikołaja kopernika Toruń, 3 grudnia 2009 Spis treści 1 Wprowadzenie Wyjaśnienie pojęć 2 O dziwnych atraktorach 3 Wyjaśnienie pojęć Dowolny
O układzie Lorenza Wydział Matematyki i Informatyki Uniwersytet Mikołaja kopernika Toruń, 3 grudnia 2009 Spis treści 1 Wprowadzenie Wyjaśnienie pojęć 2 O dziwnych atraktorach 3 Wyjaśnienie pojęć Dowolny
Dynamika nieliniowa i chaos deterministyczny. Fizyka układów złożonych
 Dynamika nieliniowa i chaos deterministyczny Fizyka układów złożonych Wahadło matematyczne F θ = mgsinθ Druga zasada dynamiki: ma = mgsinθ a = d2 x dt 2 = gsinθ Długość łuku: x = Lθ Równanie ruchu: θ ሷ
Dynamika nieliniowa i chaos deterministyczny Fizyka układów złożonych Wahadło matematyczne F θ = mgsinθ Druga zasada dynamiki: ma = mgsinθ a = d2 x dt 2 = gsinθ Długość łuku: x = Lθ Równanie ruchu: θ ሷ
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE. Marta Zelmańska
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
ANALIZA NUMERYCZNA. Grzegorz Szkibiel. Wiosna 2014/15
 ANALIZA NUMERYCZNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Metoda Eulera 3 1.1 zagadnienia brzegowe....................... 3 1.2 Zastosowanie ró»niczki...................... 4 1.3 Output do pliku
ANALIZA NUMERYCZNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Metoda Eulera 3 1.1 zagadnienia brzegowe....................... 3 1.2 Zastosowanie ró»niczki...................... 4 1.3 Output do pliku
Bifurkacje. Ewa Gudowska-Nowak Nowak. Plus ratio quam vis
 Bifurkacje Nowak Plus ratio quam vis M. Kac Complex Systems Research Center, M. Smoluchowski Institute of Physics, Jagellonian University, Kraków, Poland 2008 Gªówna idea.. Pozornie "dynamika" ukªadów
Bifurkacje Nowak Plus ratio quam vis M. Kac Complex Systems Research Center, M. Smoluchowski Institute of Physics, Jagellonian University, Kraków, Poland 2008 Gªówna idea.. Pozornie "dynamika" ukªadów
W. Guzicki Próbna matura, grudzień 2014 r. poziom rozszerzony 1
 W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
W. Guzicki Próbna matura, grudzień 01 r. poziom rozszerzony 1 Próbna matura rozszerzona (jesień 01 r.) Zadanie 18 kilka innych rozwiązań Wojciech Guzicki Zadanie 18. Okno na poddaszu ma mieć kształt trapezu
Mechanika kwantowa Schrödingera
 Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Dynamika Uk»adów Nieliniowych 2009 Wykład 2 1. Uk»ady dynamiczne
 Dynamika Uk»adów ieliniowych 29 Wykład 2 Uk»ady dynamiczne Uk»adem dynamicznym b dziemy nazywali deterministyczn recept na dokonanie ewolucji w czasie stanu danego uk»adu. Czas moóe byƒ albo dyskretny
Dynamika Uk»adów ieliniowych 29 Wykład 2 Uk»ady dynamiczne Uk»adem dynamicznym b dziemy nazywali deterministyczn recept na dokonanie ewolucji w czasie stanu danego uk»adu. Czas moóe byƒ albo dyskretny
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Granice funkcji wielu zmiennych.
 AM WNE 008/009. Odpowiedzi do zada«przygotowawczych do czwartego kolokwium. Granice funkcji wielu zmiennych. Zadanie. Zadanie. Pochodne. (a) 0, Granica nie istnieje, (c) Granica nie istnieje, (d) Granica
AM WNE 008/009. Odpowiedzi do zada«przygotowawczych do czwartego kolokwium. Granice funkcji wielu zmiennych. Zadanie. Zadanie. Pochodne. (a) 0, Granica nie istnieje, (c) Granica nie istnieje, (d) Granica
Podręcznik. Przykład 1: Wyborcy
 MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 5892 424 http://www.neuroinf.pl/members/danek/swps/ Iwo Białynicki-Birula Iwona Białynicka-Birula
MODELOWANIE RZECZYWISTOŚCI Daniel Wójcik Instytut Biologii Doświadczalnej PAN d.wojcik@nencki.gov.pl tel. 5892 424 http://www.neuroinf.pl/members/danek/swps/ Iwo Białynicki-Birula Iwona Białynicka-Birula
1 Relacje i odwzorowania
 Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Relacje i odwzorowania Relacje Jacek Kłopotowski Zadania z analizy matematycznej I Wykazać, że jeśli relacja ρ X X jest przeciwzwrotna i przechodnia, to jest przeciwsymetryczna Zbadać czy relacja ρ X X
Matematyka 1. Šukasz Dawidowski. Instytut Matematyki, Uniwersytet l ski
 Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Pochodna funkcji Niech a, b R, a < b. Niech f : (a, b) R b dzie funkcj oraz x, x 0 (a, b) b d ró»nymi punktami przedziaªu (a, b). Wyra»enie
Matematyka 1 Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Pochodna funkcji Niech a, b R, a < b. Niech f : (a, b) R b dzie funkcj oraz x, x 0 (a, b) b d ró»nymi punktami przedziaªu (a, b). Wyra»enie
Twierdzenie Li-Yorke a Twierdzenie Szarkowskiego
 Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Twierdzenie Li-Yorke a Twierdzenie Szarkowskiego Autor: Kamil Jaworski 11 marca 2012 Spis treści 1 Wstęp 2 1.1 Podstawowe pojęcia........................
Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Twierdzenie Li-Yorke a Twierdzenie Szarkowskiego Autor: Kamil Jaworski 11 marca 2012 Spis treści 1 Wstęp 2 1.1 Podstawowe pojęcia........................
Chaotyczne generatory liczb pseudolosowych
 Chaotyczne generatory liczb pseudolosowych Michał Krzemiński michalkrzeminski@wp.pl Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Chaotyczne generatory liczb pseudolosowych -
Chaotyczne generatory liczb pseudolosowych Michał Krzemiński michalkrzeminski@wp.pl Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Chaotyczne generatory liczb pseudolosowych -
Wykład 15. Matematyka 3, semestr zimowy 2011/ listopada 2011
 Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
Wykład 5 Matematyka 3, semestr zimowy / 9 listopada W trakcie tego i następnych kilku wykładów zajmować się będziemy analizą zespoloną, czyli różniczkowaniem i całkowaniem funkcji argumentu zespolonego
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych
 Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
Zadania do wykładu Jakościowa Teoria Równań Różniczkowych Zwyczajnych [ ] e Zadanie 1 Pokazać, że X(t) = 2t cos t sin t e 2t jest specjalną macierzą fundamentalną w sin t cos t [ 2 cos chwili τ = 0 układu
SPIS TREŚCI WSTĘP... 8 1. LICZBY RZECZYWISTE 2. WYRAŻENIA ALGEBRAICZNE 3. RÓWNANIA I NIERÓWNOŚCI
 SPIS TREŚCI WSTĘP.................................................................. 8 1. LICZBY RZECZYWISTE Teoria............................................................ 11 Rozgrzewka 1.....................................................
SPIS TREŚCI WSTĘP.................................................................. 8 1. LICZBY RZECZYWISTE Teoria............................................................ 11 Rozgrzewka 1.....................................................
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum. w roku szkolnym 2012/2013
 Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Próbny egzamin z matematyki dla uczniów klas II LO i III Technikum w roku szkolnym 2012/2013 I. Zakres materiału do próbnego egzaminu maturalnego z matematyki: 1) liczby rzeczywiste 2) wyrażenia algebraiczne
Siły wewnętrzne - związki różniczkowe
 Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Siły wewnętrzne - związki różniczkowe Weźmy dowolny fragment belki obciążony wzdłuż osi obciążeniem n(x) oraz poprzecznie obciążeniem q(x). Na powyższym rysunku zwroty obciążeń są zgodne z dodatnimi zwrotami
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/
 Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Matematyka z el. statystyki, # 4 /Geodezja i kartografia I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Akademicka 15, p.211a, bud. Agro
Równanie przewodnictwa cieplnego (II)
 Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
Wykład 5 Równanie przewodnictwa cieplnego (II) 5.1 Metoda Fouriera dla pręta ograniczonego 5.1.1 Pierwsze zagadnienie brzegowe dla pręta ograniczonego Poszukujemy rozwiązania równania przewodnictwa spełniającego
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
ROZKŁAD MATERIAŁU DO II KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. LICZBA TEMAT GODZIN LEKCYJNYCH Potęgi, pierwiastki i logarytmy (8 h) Potęgi 3 Pierwiastki 3 Potęgi o wykładnikach
Ekstremalnie fajne równania
 Ekstremalnie fajne równania ELEMENTY RACHUNKU WARIACYJNEGO Zaczniemy od ogólnych uwag nt. rachunku wariacyjnego, który jest bardzo przydatnym narz dziem mog cym posªu»y do rozwi zywania wielu problemów
Ekstremalnie fajne równania ELEMENTY RACHUNKU WARIACYJNEGO Zaczniemy od ogólnych uwag nt. rachunku wariacyjnego, który jest bardzo przydatnym narz dziem mog cym posªu»y do rozwi zywania wielu problemów
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Zaawansowane metody numeryczne
 Wykład 1 Zadanie Definicja 1.1. (zadanie) Zadaniem nazywamy zagadnienie znalezienia rozwiązania x spełniającego równanie F (x, d) = 0, gdzie d jest zbiorem danych (od których zależy rozwiązanie x), a F
Wykład 1 Zadanie Definicja 1.1. (zadanie) Zadaniem nazywamy zagadnienie znalezienia rozwiązania x spełniającego równanie F (x, d) = 0, gdzie d jest zbiorem danych (od których zależy rozwiązanie x), a F
Chaos w układach dynamicznych: miary i kryteria chaosu
 : miary i kryteria chaosu Uniwersytet Śląski w Katowicach, Wydział Matematyki, Fizyki i Chemii 27.08.14 : miary i kryteria chaosu Temat tego referatu jest związany z teorią układów dynamicznych która ma
: miary i kryteria chaosu Uniwersytet Śląski w Katowicach, Wydział Matematyki, Fizyki i Chemii 27.08.14 : miary i kryteria chaosu Temat tego referatu jest związany z teorią układów dynamicznych która ma
Wykład Analiza jakościowa równań różniczkowych
 Na podstawie książki J. Rusinka, Równania różniczkowe i różnicowe w zarządzaniu, Oficna Wdawnicza WSM, Warszawa 2005. 21 maja 2012 Definicja Stabilność Niech = F (x, ) będzie równaniem różniczkowm. Rozwiązanie
Na podstawie książki J. Rusinka, Równania różniczkowe i różnicowe w zarządzaniu, Oficna Wdawnicza WSM, Warszawa 2005. 21 maja 2012 Definicja Stabilność Niech = F (x, ) będzie równaniem różniczkowm. Rozwiązanie
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Pochodne funkcji wraz z zastosowaniami - teoria
 Pochodne funkcji wraz z zastosowaniami - teoria Pochodne Definicja 2.38. Niech f : O(x 0 ) R. Jeżeli istnieje skończona granica f(x 0 + h) f(x 0 ) h 0 h to granicę tę nazywamy pochodną funkcji w punkcie
Pochodne funkcji wraz z zastosowaniami - teoria Pochodne Definicja 2.38. Niech f : O(x 0 ) R. Jeżeli istnieje skończona granica f(x 0 + h) f(x 0 ) h 0 h to granicę tę nazywamy pochodną funkcji w punkcie
ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY
 ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY Numer lekcji 1 2 Nazwa działu Lekcja organizacyjna. Zapoznanie z programem nauczania i kryteriami wymagań Zbiór liczb rzeczywistych i jego 3 Zbiór
ROZKŁAD MATERIAŁU NAUCZANIA KLASA 1, ZAKRES PODSTAWOWY Numer lekcji 1 2 Nazwa działu Lekcja organizacyjna. Zapoznanie z programem nauczania i kryteriami wymagań Zbiór liczb rzeczywistych i jego 3 Zbiór
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
 Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej
 Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej Denicja 1. Niech X = R n b dzie przestrzeni unormowan oraz d(x, y) = x y.
Zadania z analizy matematycznej - sem. II Ekstrema funkcji wielu zmiennych, twierdzenia o funkcji odwrotnej i funkcji uwikªanej Denicja 1. Niech X = R n b dzie przestrzeni unormowan oraz d(x, y) = x y.
ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES PODSTAWOWY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES PODSTAWOWY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. TEMAT Równania i nierówności (30h) LICZBA GODZIN LEKCYJNYCH Liczby wymierne 3 Liczby niewymierne 1 Zapisywanie
ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES PODSTAWOWY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. TEMAT Równania i nierówności (30h) LICZBA GODZIN LEKCYJNYCH Liczby wymierne 3 Liczby niewymierne 1 Zapisywanie
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Matematyka I. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12
 Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
Matematyka I Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr zimowy 2018/2019 Wykład 12 Egzamin Termin: 28.01, godz. 10.15-11.45, sala 309 3 pytania teoretyczne 2 zadania wybór pytań i wybór zadań
Wykład 6, pochodne funkcji. Siedlce
 Wykład 6, pochodne funkcji Siedlce 20.12.2015 Definicja pochodnej funkcji w punkcie Niech f : (a; b) R i niech x 0 ; x 1 (a; b), x0 x1. Wyrażenie nazywamy ilorazem różnicowym funkcji f między punktami
Wykład 6, pochodne funkcji Siedlce 20.12.2015 Definicja pochodnej funkcji w punkcie Niech f : (a; b) R i niech x 0 ; x 1 (a; b), x0 x1. Wyrażenie nazywamy ilorazem różnicowym funkcji f między punktami
PORÓWNANIE TREŚCI ZAWARTYCH W OBOWIĄZUJĄCYCH STANDARDACH EGZAMINACYJNYCH Z TREŚCIAMI NOWEJ PODSTAWY PROGRAMOWEJ
 PORÓWNANIE TREŚCI ZAWARTYCH W OBOWIĄZUJĄCYCH STANDARDACH EGZAMINACYJNYCH Z TREŚCIAMI NOWEJ PODSTAWY PROGRAMOWEJ L.p. 1. Liczby rzeczywiste 2. Wyrażenia algebraiczne bada, czy wynik obliczeń jest liczbą
PORÓWNANIE TREŚCI ZAWARTYCH W OBOWIĄZUJĄCYCH STANDARDACH EGZAMINACYJNYCH Z TREŚCIAMI NOWEJ PODSTAWY PROGRAMOWEJ L.p. 1. Liczby rzeczywiste 2. Wyrażenia algebraiczne bada, czy wynik obliczeń jest liczbą
I Rok LOGISTYKI: wykªad 2 Pochodna funkcji. iloraz ró»nicowy x y x
 I Rok LOGISTYKI: wykªad 2 Pochodna funkcji Niech f jest okre±lona w Q(x 0, δ) i x Q(x 0, δ). Oznaczenia: x = x x 0 y = y y 0 = f(x 0 + x) f(x 0 ) y x = f(x 0 + x) f(x 0 ) iloraz ró»nicowy x y x = tgβ,
I Rok LOGISTYKI: wykªad 2 Pochodna funkcji Niech f jest okre±lona w Q(x 0, δ) i x Q(x 0, δ). Oznaczenia: x = x x 0 y = y y 0 = f(x 0 + x) f(x 0 ) y x = f(x 0 + x) f(x 0 ) iloraz ró»nicowy x y x = tgβ,
Fale biegnące w równaniach reakcji-dyfuzji
 Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Fale biegnące w równaniach reakcji-dyfuzji Piotr Bartłomiejczyk Politechnika Gdańska Między teorią a zastosowaniami: Matematyka w działaniu Będlewo, 25 30 maja 2015 P. Bartłomiejczyk Fale biegnące 1 /
Specjalistyczna Pracownia Komputerowa Obliczanie widma Lapunowa
 Arkadiusz Neubauer IV rok, Fizyka z Informatyką. Specjalistyczna Pracownia Komputerowa Obliczanie widma Lapunowa 1 Problem fizyczny W poniższej pracy przedstawiono numeryczną metodę obliczania widma Lapunowa
Arkadiusz Neubauer IV rok, Fizyka z Informatyką. Specjalistyczna Pracownia Komputerowa Obliczanie widma Lapunowa 1 Problem fizyczny W poniższej pracy przedstawiono numeryczną metodę obliczania widma Lapunowa
Niestabilne orbity okresowe a (niektóre) własności układów chaotycznych
 Niestabilne orbity okresowe a (niektóre) własności układów chaotycznych Justyna Signerska,Jan Pyrzowski Politechnika Gdańska, Akademia Medyczna w Gdańsku Hel 2008 p.1/3 Outline Podstawowe definicje Hel
Niestabilne orbity okresowe a (niektóre) własności układów chaotycznych Justyna Signerska,Jan Pyrzowski Politechnika Gdańska, Akademia Medyczna w Gdańsku Hel 2008 p.1/3 Outline Podstawowe definicje Hel
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
Pochodne. Zbigniew Koza. Wydział Fizyki i Astronomii
 Pochodne Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2015 MOTYWACJA Rozpatrzmy gładką funkcję np. y x = x 2 w okolicach punktu (1,1) x 0 = 1, y 0 = f x 0 = 1 powiększmy wykres wokół (x 0, f(x 0
Pochodne Zbigniew Koza Wydział Fizyki i Astronomii Wrocław, 2015 MOTYWACJA Rozpatrzmy gładką funkcję np. y x = x 2 w okolicach punktu (1,1) x 0 = 1, y 0 = f x 0 = 1 powiększmy wykres wokół (x 0, f(x 0
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
 27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Chaos, fraktale i statystyka
 Bogumiła Koprowska Elżbieta Kukla 1 Przykłady Odwzorowanie logistyczne Odwzorowanie trójkątne 2 Historia 3 Fraktale Zbiór Mandelbrota i zbiór Julii Przykłady fraktali 4 Podstawowe pojęcia Układy dynamiczne
Bogumiła Koprowska Elżbieta Kukla 1 Przykłady Odwzorowanie logistyczne Odwzorowanie trójkątne 2 Historia 3 Fraktale Zbiór Mandelbrota i zbiór Julii Przykłady fraktali 4 Podstawowe pojęcia Układy dynamiczne
Ruch jednostajnie zmienny prostoliniowy
 Ruch jednostajnie zmienny prostoliniowy Przyspieszenie w ruchu jednostajnie zmiennym prostoliniowym Jest to taki ruch, w którym wektor przyspieszenia jest stały, co do wartości (niezerowej), kierunku i
Ruch jednostajnie zmienny prostoliniowy Przyspieszenie w ruchu jednostajnie zmiennym prostoliniowym Jest to taki ruch, w którym wektor przyspieszenia jest stały, co do wartości (niezerowej), kierunku i
Zadania z analizy matematycznej - sem. I Pochodne funkcji, przebieg zmienności funkcji
 Zadania z analizy matematycznej - sem. I Pochodne funkcji przebieg zmienności funkcji Definicja 1. Niech f : (a b) R gdzie a < b oraz 0 (a b). Dla dowolnego (a b) wyrażenie f() f( 0 ) = f( 0 + ) f( 0 )
Zadania z analizy matematycznej - sem. I Pochodne funkcji przebieg zmienności funkcji Definicja 1. Niech f : (a b) R gdzie a < b oraz 0 (a b). Dla dowolnego (a b) wyrażenie f() f( 0 ) = f( 0 + ) f( 0 )
ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ.
 ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. TEMAT Równania i nierówności (36 h) LICZBA GODZIN LEKCYJNYCH Liczby wymierne 3 Liczby niewymierne 1 Zapisywanie
ROZKŁAD MATERIAŁU DO 1 KLASY LICEUM (ZAKRES ROZSZERZONY) A WYMAGANIA PODSTAWY PROGRAMOWEJ. TEMAT Równania i nierówności (36 h) LICZBA GODZIN LEKCYJNYCH Liczby wymierne 3 Liczby niewymierne 1 Zapisywanie
JAK PROSTO I SKUTECZNIE WYKORZYSTAĆ ARKUSZ KALKULACYJNY DO OBLICZENIA PARAMETRÓW PROSTEJ METODĄ NAJMNIEJSZYCH KWADRATÓW
 JAK PROSTO I SKUTECZNIE WYKORZYSTAĆ ARKUSZ KALKULACYJNY DO OBLICZENIA PARAMETRÓW PROSTEJ METODĄ NAJMNIEJSZYCH KWADRATÓW Z tego dokumentu dowiesz się jak wykorzystać wbudowane funkcje arkusza kalkulacyjnego
JAK PROSTO I SKUTECZNIE WYKORZYSTAĆ ARKUSZ KALKULACYJNY DO OBLICZENIA PARAMETRÓW PROSTEJ METODĄ NAJMNIEJSZYCH KWADRATÓW Z tego dokumentu dowiesz się jak wykorzystać wbudowane funkcje arkusza kalkulacyjnego
Metody numeryczne. Sformułowanie zagadnienia interpolacji
 Ćwiczenia nr 4. Sformułowanie zagadnienia interpolacji Niech będą dane punkty x 0,..., x n i wartości y 0,..., y n, takie że i=0,...,n y i = f (x i )). Szukamy funkcji F (funkcji interpolującej), takiej
Ćwiczenia nr 4. Sformułowanie zagadnienia interpolacji Niech będą dane punkty x 0,..., x n i wartości y 0,..., y n, takie że i=0,...,n y i = f (x i )). Szukamy funkcji F (funkcji interpolującej), takiej
Matematyka i Statystyka w Finansach. Rachunek Różniczkowy
 Rachunek Różniczkowy Ciąg liczbowy Link Ciągiem liczbowym nieskończonym nazywamy każdą funkcję a która odwzorowuje zbiór liczb naturalnych N w zbiór liczb rzeczywistych R a : N R. Tradycyjnie wartość a(n)
Rachunek Różniczkowy Ciąg liczbowy Link Ciągiem liczbowym nieskończonym nazywamy każdą funkcję a która odwzorowuje zbiór liczb naturalnych N w zbiór liczb rzeczywistych R a : N R. Tradycyjnie wartość a(n)
jest ciągiem elementów z przestrzeni B(R, R)
 Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
Wykład 2 1 Ciągi Definicja 1.1 (ciąg) Ciągiem w zbiorze X nazywamy odwzorowanie x: N X. Dla uproszczenia piszemy x n zamiast x(n). Przykład 1. x n = n jest ciągiem elementów z przestrzeni R 2. f n (x)
( ) Pochodne. Załómy, e funkcja f jest okrelona w pewnym otoczeniu punktu x 0. Liczb
 Pocodne Załómy, e unkcja jest okrelona w pewnym otoczeniu punktu. Liczb ( + ) ( ) nazywamy ilorazem rónicowym unkcji w punkcie dla przyrostu. Pocodn ( ) unkcji w punkcie nazywamy granic ilorazu rónicowego,
Pocodne Załómy, e unkcja jest okrelona w pewnym otoczeniu punktu. Liczb ( + ) ( ) nazywamy ilorazem rónicowym unkcji w punkcie dla przyrostu. Pocodn ( ) unkcji w punkcie nazywamy granic ilorazu rónicowego,
Rachunek ró»niczkowy funkcji jednej zmiennej
 Lista Nr 5 Rachunek ró»niczkowy funkcji jednej zmiennej 5.0. Obliczanie pochodnej funkcji Pochodne funkcji podstawowych. f() = α f () = α α. f() = log a f () = ln a '. f() = ln f () = 3. f() = a f () =
Lista Nr 5 Rachunek ró»niczkowy funkcji jednej zmiennej 5.0. Obliczanie pochodnej funkcji Pochodne funkcji podstawowych. f() = α f () = α α. f() = log a f () = ln a '. f() = ln f () = 3. f() = a f () =
Dystrybucje. Marcin Orchel. 1 Wstęp Dystrybucje Pochodna dystrybucyjna Przestrzenie... 5
 Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
N ma rozkład Poissona z wartością oczekiwaną równą 100 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach:
 Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
KADD Minimalizacja funkcji
 Minimalizacja funkcji n-wymiarowych Forma kwadratowa w n wymiarach Procedury minimalizacji Minimalizacja wzdłuż prostej w n-wymiarowej przestrzeni Metody minimalizacji wzdłuż osi współrzędnych wzdłuż kierunków
Minimalizacja funkcji n-wymiarowych Forma kwadratowa w n wymiarach Procedury minimalizacji Minimalizacja wzdłuż prostej w n-wymiarowej przestrzeni Metody minimalizacji wzdłuż osi współrzędnych wzdłuż kierunków
Rachunek różniczkowy funkcji dwóch zmiennych
 Rachunek różniczkowy funkcji dwóch zmiennych Definicja Spis treści: Wykres Ciągłość, granica iterowana i podwójna Pochodne cząstkowe Różniczka zupełna Gradient Pochodna kierunkowa Twierdzenie Schwarza
Rachunek różniczkowy funkcji dwóch zmiennych Definicja Spis treści: Wykres Ciągłość, granica iterowana i podwójna Pochodne cząstkowe Różniczka zupełna Gradient Pochodna kierunkowa Twierdzenie Schwarza
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Matematyka dyskretna. Andrzej Łachwa, UJ, /15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
Matematyka dyskretna Andrzej Łachwa, UJ, 2013 andrzej.lachwa@uj.edu.pl 7/15 Rachunek różnicowy Dobrym narzędziem do obliczania skończonych sum jest rachunek różnicowy. W rachunku tym odpowiednikiem operatora
