4. Zależności między współrzędnymi tłowymi i terenowymi
|
|
|
- Edyta Brzozowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 4. Zależności między wsółrzędnymi tłowymi i terenowymi Oracowanie zdjęć fotogrametrycznych, srowadzające się do określenia terenowych wsółrzędnych omierzonych unktów, może yć rzerowadzone - jak już wiadomo - metodą ciągłą (autogrametryczną) lu unktową. Punktowe rozwiązanie jest oarte o omiar wsółrzędnych tłowych (za omocą stereokomaratora lu monokomaratora); do omiaru wsółrzędnych tłowych można wykorzystać również cyfrową stację fotogrametryczną. Stoień złożoności oliczeń zależy od rodzaju zdjęć. Poszczególne warianty, oczynając od najrostszego do najardziej ogólnego, zostaną rozatrzone w odrozdziałach Naziemne wcięcia kątowe Przyrównaliśmy orzednio fotogrametryczne wyznaczanie ołożenia unktu do rzestrzennego wcięcia w rzód. Różnica rzede wszystkim srowadza się do ominięcia kątów, ale w szczególnych wyadkach i ta droga oliczeń ywa stosowana. Dlatego rzedstawimy zależności omiędzy wsółrzędnymi tłowymi (zdjęcia oziomego) i kątami : oziomym - α i ionowym β Z rysunku 4.1 wynikają zależności: tg α = x c k z cosα tgβ = /4.1/ c k c k Rys Odwzorowanie unktu na zdjęciu oziomym, jego wsółrzędne tłowe i kąty. Znając orientację osi kamery - na rzykład jej azymut - można oliczyć wsółrzędne, stosując rzestrzenne wcięcie w rzód. Nie tym jednak sosoem rzerowadza się oliczenia fotogrametryczne; można je wykonać ardziej rosto, o czym mówią nastęne rozdziały Zdjęcia normalne W rzyadku zdjęć oziomych, normalnych, wcięcie w rzód rozwiązujemy w oarciu o zależności wynikające z rys Przyjmujemy ortogonalny układ wsółrzędnych o oczątku w unkcie O 1 (środek rzutów na stanowisku lewym), oś Y skierowaną zgodnie z osią kamery, oś X rosnącą w rawo, oś Z - ionowo w górę. 43
2 Rys Odwzorowanie unktu P na zdjęciu normalnym - rzut oziomy. Znając wsółrzędne tłowe x, z (zdjęcie lewe), i x (zdjęcie rawe) możemy zaisać dla unktu P: Y : c k = :, gdzie = x - x, X : x = Y :c k Z : z = Y : c k z czego wynikają zależności: Y = c k X = x' Z = z' /4.2/ W rzyadku analogicznych zdjęć lotniczych (gdyy udało się wykonać zdjęcia ściśle ionowe, oydwa z tej samej wysokości), wzory 4.2 rzyjmą ostać: Z = c k X = x' Y = y' /4.3/ 4.3. Zdjęcia oziome, zwrócone Rys Odwzorowanie unktu P na zdjęciach oziomych, zwróconych w lewo. W rzyadku zdjęć oziomych, gdy osie kamer - wzajemnie równoległe - nie są rostoadłe do azy, można dla unktu P zaisać zależność: Y : c k = (O L K + KL) : 44
3 gdzie: O L K = cosψ, KL = x.. sinψ : c k skąd: x" sinψ Y = cos ψ + lu: Y Y Y = ( cosψ + x" sinψ ) X = x' Z = z' /4.4/ W rzyadku zdjęć zwróconych w rawo, w nawiasie wzoru na Y należy zmienić znak (+) na (- ). Dla analogicznych zdjęć lotniczych: Z Z Z = ( cosψ + x" sinψ ) X = x' Y = y' /4.5/ Z ionowymi zdjęciami lotniczymi, równoległymi, nierostoadłymi do azy mieliyśmy do czynienia wtedy, gdyy zostały wykonane z różnej wysokości Przestrzenne wsółrzędne tłowe W rzyadku zdjęć o dowolnej orientacji, rzestrzenne wcięcie w rzód staje się ardziej złożone, ale stosunkowo rosto można je rozwiązać sosoami fotogrametrii analitycznej. W tym celu wrowadzimy ojęcie rzestrzennych wsółrzędnych tłowych (rys.4.4, 4.5). Rys Odwzorowanie unktu P na zdjęciu oziomym, r - wektor wodzący unktu P i jego składowe (x, y, z) - rzestrzenne wsółrzędne tłowe unktu P. Znając wsółrzędne tłowe (x, z ) unktu P (rys. 4.4) możemy określić składowe wektora r : x = x, y = c k, z = z, co można zaisać macierzowo: x' r = z' /4.6/ Macierz ta zawiera rzestrzenne wsółrzędne tłowe unktu na zdjęciu oziomym. Analogicznie można zaisać rzestrzenne wsółrzędne tłowe zdjęcia ionowego (wg. rys. 4.5): x' r = y' c k /4.7/ 45
4 Rys Odwzorowanie unktu P na zdjęciu ionowym, wektor wodzący unktu P i jego składowe (x, y, z) - rzestrzenne wsółędne tłowe unktu P 4.5. Macierz transformacji W rzyadku zdjęć lotniczych o dowolnej orientacji (w raktyce - dla zdjęć rawie ionowych ), określenie składowych wektora r w rzestrzennym układzie tłowym (x, y, z) wymaga uwzględnienia kątów: ω, ϕ, κ (rys. 4.7). Składowe te można oliczyć wg. zależności macierzowej: x x' = y M y' /4.8/ z c k gdzie M oznacza macierz orotu (3x3), zwaną także macierzą transformacji; zawiera ona funkcje sinus i cosinus kątów ω, ϕ, κ. Rys.4.6. Przestrzenny układ wsółrzędnych tłowych zdjęcia nieionowego. 46
5 Z z κ y y x x κ z z ϕ y y ω ϕ κ ϕ ω x x y x z ω Rys.4.7. Elementy transformacji rzestrzennych wsółrzędnych tłowych. x κ x ϕ z ω Postać macierzy transformacji M można wyrowadzić, dokonując kolejno trzech transformacji łaskich, zgodnie z rys Orót o kąt κ (wokół osi z, w łaszczyżnie x, y) : x κ = x cosκ + y y κ = y cosκ - x z κ = z analogicznie o kolejnym orocie o kąt ϕ (wokół osi y, w łaszczyżnie xz): x κϕ = x κ cos ϕ + y κ y κϕ = y κ z κϕ = z κ cosϕ - x κ i wreszcie - o kolejnym orocie - o kąt ω (orót wokół osi x w łaszczyżnie yz), otrzymamy wartości : x κϕω, y κϕω, z κϕω, które ędą szukanymi składowymi wektora r (x, y, z), co można zaisać: x cosκ cosϕ = y sinω cosκ + cosω z cosω cosκ + sinω cosϕ sinω + cosω cosκ cosω + sinω cosκ x' sinω cosϕ y' cosω cosϕ c k /4.9/ Zaisana owyżej macierz orotu M, jest macierzą ortogonalną, co oznacza że suma kwadratów elementów każdej kolumny jest równa 1, zaś suma iloczynów odowiadających soie elementów w każdych dwu kolumnach jest równa Warunki: kolinearności i komlanarności Jeśli umiemy określić składowe wektora r (wg. wzoru 4.7), to możemy rozwiązać wcięcie w rzód, zaisując wielkości znane (x, y, c k ), oraz szukane wsółrzedne terenowe unktu P (X, Y, Z) w zależności zwanej równaniem kolinearności lu warunkiem kolinearności (czyli wsółliniowości - wektorów r i R wg. rys. 4.8): R = λ. M. r (4.10) gdzie: λ- skalar stanowiący wsółczynnik skalowy (łatwy do eliminacji w trakcie oliczeń), zaś macierzowy zais wsółrzędnych wektora R zawiera wsółrzędne terenowe unktu P: X R = Y Z /4.11/ 47
6 Jest oczywiste, że wcięcie w rzód wymaga zaisania równań kolinearności dla oydwu zdjęć rzedstawionych na rys Na ogół do rozwiązania wcięcia w rzód stosuje się równanie komlanarności (czyli wsółłaszczyznowości wektorów: azy B, R 1 i R 2 ). Jak wiadomo, warunkiem wsółłaszczyznowości wektorów jest zerowa wartość ich iloczynu mieszanego, czyli r r r B R R 0 (4.12) 1 2 = Rys.4.8. Wektory równań kolinearności i komlanarności. Zais warunku kolinearności najczęściej jest wykorzystywany do fotogrametrycznego wcięcia wstecz - określenia elementów orientacji zewnętrznej (a więc nie tylko wsółrzędnych środka rzutów X o, Y o, Z o, ale także kątów κ, ϕ, ω ). Danymi do wcięcia wstecz są wsółrzędne fotounktów - zidentyfikowanych na zdjęciach unktów o znanych wsółrzędnych terenowych (X, Y, Z). W tym rzyadku równanie 1.11 rozisujemy ardziej szczegółowo: X X Y Yo Z Z o o r = λ M /4.13/ Powyższe informacje o stosowanych w fotogrametrii metodach analitycznych, należy uzuełnić kilkoma uwagami końcowymi. Oisane metody analityczne zakładają ostęowanie oliczeniowe w którym określa się elementy orientacji oszczególnych zdjęć, ay nastęnie wyliczyć wsółrzędne terenowe unktów. Odmienne ostęowanie jest raktykowane w rzyadku samokaliracyjnego rozwiązywania sieci wiązek: już na etaie ustalania elementów orientacji wiązki są łączone w jedną, wsólną, rzestrzenną sieć geometryczną, rzy uwzględnieniu warunków rzecinania się wszystkich jednoimiennych romieni do unktów oiektu omiaru. W jednym etaie wylicza się zarówno elementy orientacji zdjęć (wraz z łędami orazowania), jak i szukane wsółrzędne 48
7 unktów. Dla wielu zdjęć tworzy się rzestrzenną sieć rzecinających się kierunków - do unktów znanych jak i wyznaczanych. Takie ostęowanie rzynosi znaczne korzyści: orzez silne związanie geometryczne sieci rzestrzennej można ograniczyć liczę unktów kontrolnych; także z unktu widzenia zasad wyrównania oserwacji, takie ostęowanie jest ardziej orawne. Niewiadome (w tym łędy orazowania) są wyznaczane nie tylko na odstawie unktów kontrolnych, ale z wszystkich unktów mierzonych na wielu zdjęciach. Ten sosó rozwiązania sieci wiązek nosi nazwę samokaliracji Charakteryzuje go złożoność algorytmów i orogramowania. Wymagana jest znaczna licza nadliczowych zdjęć. Na otrzey oracowania zdjęć niemetrycznych (lu metrycznych o nieewnych elementach orientacji) stworzono metodę kaliracji w trakcie rozwiązywania zadania omiarowego ( ng. on the jo calliration). Jej zasady oisano w literaturze [ ]. Podstawę ostęowania oliczeniowego stanowią jak wiadomo unkty kontrolne. Licza i rozmieszczenie unktów kontrolnych zależą od zastosowanej metody. Bez unktów kontrolnych oywają się oczywiście najmniej racochłonne - metody oarte na danych nominalnych; oliczenie wsółrzędnych rzerowadza się o wrowadzeniu danych olowych do odowiednich wzorów. Wśród metod zakładających korekcję, najoularniejsze są korekcje kątowych elementów orientacji kamery wystarczają do tego 3 unkty kontrolne (dla każdego zdjęcia); w rzyadku korekcji łędów orazu niezędna jest znajomość 5 8 unktów (dla każdego zdjęcia). Najmniejsze wymagania wziąwszy od uwagę liczę stosowanych zdjęć mają rozwiązania sieci wiązek rozwiązywane na drodze samokaliracji 3 unkty XYZ. Jak wynika z wcześniejszych rozważań, w klasycznych rozwiązaniach oierających się na geometrii odoieństw ewien rolem stwarza znalezienie wartości kątowych elementów orientacji wiązki, uwikłanych w funkcje wyrazów ortogonalnej macierzy orotu. Z tego owodu, większość oeracji oliczeniowych wymagała ostęowania iteracyjnego. Niedogodność ta nie wystęuje w rozwiązaniach analitycznych wywodzących się z geometrii rzutowej, którym oświęcono nastęny rozdział Przekształcenia oarte o geometrię rzutową Geometria rzutowa zajmuje się rzekształceniami utworów geometrycznych w rzestrzeni rzutowej. Za rzestrzeń rzutową uważa się rzestrzeń euklidesową wzogaconą o elementy niewłaściwe: unkt niewłaściwy (rostej), rostą niewłaściwą (łaszczyzny), łaszczyznę niewłaściwą (rzestrzeni). Przekształcenia rzutowe są rezultatem: rzutowania (z unktu dla nas najważniejsze, alo z rostej), lu rzecinania (łaszczyzną dla nas najważniejsze, lu rostą). Utwory to ziory elementów zasadniczych (unktów, rostych, łaszczyzn); dla nas najważniejszymi utworami są: łaszczyzna unktów (ziór unktów należących do tej samej łaszczyzny), wiązka rostych (ziór rostych rzestrzeni mających jeden wsólny unkt), rzestrzeń unktów (ziór unktów rzestrzeni). Pojęcie elementów niewłaściwych należy rozumieć nastęująco: roste równoległe mają wsólny unkt niewłaściwy (w ± ), łaszczyzny równoległe rzecinają się we wsólnej rostej niewłaściwej (w ), rzestrzeń unktów osiada łaszczyznę niewłaściwą (w ). Utworami wzajemnie rzutowymi nazywamy takie utwory, które owstały w wyniku skończonej liczy rzekształceń rzutowych (rzutowań, lu rzecinań); dadzą się one zawsze srowadzić do ołożenia ersektywicznego tzn. do ołożenia w którym jeden jest rzutem lu rzecięciem drugiego; rzykład takich rzekształceń ilustuje rys
8 Fotomaa Zdjęcie lotnicze Maa Teren Rys Łańcuch rzekształceń rzutowych omiędzy terenem a fotomaą Wzajemną rzutowość dwóch łaszczyzn unktów (n. łaszczyzny fotogramu i łaskiej owierzchni elewacji udynku, czy łaskiego terenu) określają cztery elementy homologiczne w naszym rzyadku cztery ary odowiadających soie unktów, od warunkiem, że żadne trzy nie leżą na tej samej rostej. Zaisem matematycznym który określa wzajemną rzutowość tych utworów są równania: x = ax + Y + c dx + ey +1 fx + gy + h y = /4.14/ dx + ey +1 Licza wystęujących wsółczynników (a... h) otwierdza wcześniejsze twierdzenie - cztery ary unktów, dla których możemy zaisać (łącznie) 8 równań, ozwalają oliczyć wartości 8 wsółczynników. Zależności te oatruje się zastrzeżeniem matematycznym wykluczającym rzynależność trzech unktów do jednej rostej. We wzorach tych, XY i xy to ortokartezjańskie układy wsółrzędnych (n. wsółrzędne tłowe i terenowe). Inną arę utworów, których wzajemna rzutowość może mieć raktyczne znaczenie stanowią: łaszczyzna unktów (fotogramu) i rzestrzeń unktów (mierzonego oiektu). Zais matematyczny tej zależności jest znany od nazwą DLT (ang. Direct Linear Transformation ezośrednia transformacja liniowa): x = ax + Y + cz + d ex + fy + gz +1 hx + jy + kz + l y = /4.15/ ex + fy + gz +1 Ze względu na liczę wsółczynników (11) zależność ta nazywana jest także jedenastoarametrową. 50
Orientacja zewnętrzna pojedynczego zdjęcia
 Orientacja zewnętrzna pojedynczego zdjęcia Proces opracowania fotogrametrycznego zdjęcia obejmuje: 1. Rekonstrukcję kształtu wiązki promieni rzutujących (orientacja wewnętrzna ck, x, y punktu głównego)
Orientacja zewnętrzna pojedynczego zdjęcia Proces opracowania fotogrametrycznego zdjęcia obejmuje: 1. Rekonstrukcję kształtu wiązki promieni rzutujących (orientacja wewnętrzna ck, x, y punktu głównego)
4. Analityczne metody stosowane w fotogrametrii inżynieryjnej
 4. Analityczne metody stosowane w fotogrametrii inżynieryjnej Większość pomiarów zaliczanych do geodezji inżynieryjnej, czy fotogrametrii inżynieryjnej ma na celu wyznaczenie współrzędnych punktów kontrolowanych,
4. Analityczne metody stosowane w fotogrametrii inżynieryjnej Większość pomiarów zaliczanych do geodezji inżynieryjnej, czy fotogrametrii inżynieryjnej ma na celu wyznaczenie współrzędnych punktów kontrolowanych,
Temat ćwiczenia: Wyznaczenie elementów orientacji zewnętrznej pojedynczego zdjęcia lotniczego
 Uniwersytet Rolniczy w Krakowie Wydział InŜynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Wyznaczenie elementów orientacji zewnętrznej pojedynczego zdjęcia lotniczego
Uniwersytet Rolniczy w Krakowie Wydział InŜynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Wyznaczenie elementów orientacji zewnętrznej pojedynczego zdjęcia lotniczego
Podstawy fotogrametrii i teledetekcji
 Podstawy fotogrametrii i teledetekcji Józef Woźniak Zakład Geodezji i Geoinformatyki Wrocław, 2013 Fotogrametria analityczna Metody pozyskiwania danych przestrzennych Plan prezentacji bezpośrednie pomiary
Podstawy fotogrametrii i teledetekcji Józef Woźniak Zakład Geodezji i Geoinformatyki Wrocław, 2013 Fotogrametria analityczna Metody pozyskiwania danych przestrzennych Plan prezentacji bezpośrednie pomiary
Aerotriangulacja. 1. Aerotriangulacja z niezależnych wiązek. 2. Aerotriangulacja z niezależnych modeli
 Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Przykładowe zadania z matematyki na poziomie podstawowym wraz z rozwiązaniami
 8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
8 Liczba 9 jest równa A. B. C. D. 9 5 C Przykładowe zadania z matematyki na oziomie odstawowym wraz z rozwiązaniami Zadanie. (0-) Liczba log jest równa A. log + log 0 B. log 6 + log C. log 6 log D. log
Aerotriangulacja metodą niezależnych wiązek w programie AEROSYS. blok Bochnia
 Aerotriangulacja metodą niezależnych wiązek w programie AEROSYS blok Bochnia - 2014 Zdjęcia lotnicze okolic Bochni wykonane kamerą cyfrową DMCII-230 w dn.21.10.2012r Parametry zdjęć: Ck = 92.0071mm, skala
Aerotriangulacja metodą niezależnych wiązek w programie AEROSYS blok Bochnia - 2014 Zdjęcia lotnicze okolic Bochni wykonane kamerą cyfrową DMCII-230 w dn.21.10.2012r Parametry zdjęć: Ck = 92.0071mm, skala
FOTOMAPA I ORTOFOTOMAPA NUMERYCZNY MODEL TERENU
 FTMAPA I RTFTMAPA Zdjęcie lotnicze a mapa Zniekształcenia zdjęć lotniczych wpływ nachylenia zdjęcia wpływ rzeźby terenu Modele rzutu środkowego Przetwarzanie rzutowe rtorektyfikacja Terminologia Aspekty
FTMAPA I RTFTMAPA Zdjęcie lotnicze a mapa Zniekształcenia zdjęć lotniczych wpływ nachylenia zdjęcia wpływ rzeźby terenu Modele rzutu środkowego Przetwarzanie rzutowe rtorektyfikacja Terminologia Aspekty
AUTORKA: ELŻBIETA SZUMIŃSKA NAUCZYCIELKA ZESPOŁU SZKÓŁ OGÓLNOKSZTAŁCĄCYCH SCHOLASTICUS W ŁODZI ZNANE RÓWNANIA PROSTEJ NA PŁASZCZYŹNIE I W PRZESTRZENI
 UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
UTORK: ELŻBIET SZUMIŃSK NUCZYCIELK ZESPOŁU SZKÓŁ OGÓLNOKSZTŁCĄCYCH SCHOLSTICUS W ŁODZI ZNNE RÓWNNI PROSTEJ N PŁSZCZYŹNIE I W PRZESTRZENI SPIS TREŚCI: PROST N PŁSZCZYŻNIE Str 1. Równanie kierunkowe prostej
Obóz Naukowy Olimpiady Matematycznej Gimnazjalistów
 Obóz Naukowy Olimiady Matematycznej Gimnazjalistów Liga zadaniowa 01/01 Seria VII styczeń 01 rozwiązania zadań 1. Udowodnij, że dla dowolnej dodatniej liczby całkowitej n liczba n! jest odzielna rzez n!
Obóz Naukowy Olimiady Matematycznej Gimnazjalistów Liga zadaniowa 01/01 Seria VII styczeń 01 rozwiązania zadań 1. Udowodnij, że dla dowolnej dodatniej liczby całkowitej n liczba n! jest odzielna rzez n!
TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD 10
 TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD 10 Fotogrametria to technika pomiarowa oparta na obrazach fotograficznych. Wykorzystywana jest ona do opracowywani map oraz do różnego rodzaju zadań pomiarowych.
TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD 10 Fotogrametria to technika pomiarowa oparta na obrazach fotograficznych. Wykorzystywana jest ona do opracowywani map oraz do różnego rodzaju zadań pomiarowych.
Rozdział 2. Krzywe stożkowe. 2.1 Elipsa. Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie
 Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Rozdział Krzywe stożkowe Krzywe stożkowe są zadane ogólnym równaniem kwadratowym na płaszczyźnie x + By + Cxy + Dx + Ey + F = 0. (.) W zależności od relacji pomiędzy współczynnikami otrzymujemy elipsę,
Funkcje liniowe i wieloliniowe w praktyce szkolnej. Opracowanie : mgr inż. Renata Rzepińska
 Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Funkcje liniowe i wieloliniowe w praktyce szkolnej Opracowanie : mgr inż. Renata Rzepińska . Wprowadzenie pojęcia funkcji liniowej w nauczaniu matematyki w gimnazjum. W programie nauczania matematyki w
Instrukcja do laboratorium z fizyki budowli. Ćwiczenie: Pomiar i ocena hałasu w pomieszczeniu
 nstrukcja do laboratorium z fizyki budowli Ćwiczenie: Pomiar i ocena hałasu w omieszczeniu 1 1.Wrowadzenie. 1.1. Energia fali akustycznej. Podstawowym ojęciem jest moc akustyczna źródła, która jest miarą
nstrukcja do laboratorium z fizyki budowli Ćwiczenie: Pomiar i ocena hałasu w omieszczeniu 1 1.Wrowadzenie. 1.1. Energia fali akustycznej. Podstawowym ojęciem jest moc akustyczna źródła, która jest miarą
ANALIZA ZALEśNOŚCI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA CELU I STANOWISKA OGNIOWEGO
 ZESZYTY NAUKOWE WSOWL Nr (148) 8 ISSN 1731-8157 Sławomir KRZYśANOWSKI ANALIZA ZALEśNOŚI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA ELU I STANOWISKA OGNIOWEGO Jednym z ierwszych etaów nauczania rzedmiotu
ZESZYTY NAUKOWE WSOWL Nr (148) 8 ISSN 1731-8157 Sławomir KRZYśANOWSKI ANALIZA ZALEśNOŚI KĄTA PODNIESIENIA LUFY OD WZAJEMNEGO POŁOśENIA ELU I STANOWISKA OGNIOWEGO Jednym z ierwszych etaów nauczania rzedmiotu
3. Kinematyka podstawowe pojęcia i wielkości
 3. Kinematya odstawowe ojęcia i wielości Kinematya zajmuje się oisem ruchu ciał. Ruch ciała oisujemy w ten sosób, że odajemy ołożenie tego ciała w ażdej chwili względem wybranego uładu wsółrzędnych. Porawny
3. Kinematya odstawowe ojęcia i wielości Kinematya zajmuje się oisem ruchu ciał. Ruch ciała oisujemy w ten sosób, że odajemy ołożenie tego ciała w ażdej chwili względem wybranego uładu wsółrzędnych. Porawny
3. FUNKCJA LINIOWA. gdzie ; ół,.
 1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
1 WYKŁAD 3 3. FUNKCJA LINIOWA FUNKCJĄ LINIOWĄ nazywamy funkcję typu : dla, gdzie ; ół,. Załóżmy na początek, że wyraz wolny. Wtedy mamy do czynienia z funkcją typu :.. Wykresem tej funkcji jest prosta
GEOMETRIA WYKREŚLNA I RYSUNEK TECHNICZNY
 Instytut Geologii, Uniwersytet im. A. Mickiewicza w oznaniu GEOMETRIA WYKREŚLNA I RYSUNEK TECHNICZNY prof. UAM, dr hab. Jędrze Wierzbicki racownia Geologii Inżynierskie i Geotechniki p. 251, e-mail: wi@amu.edu.pl
Instytut Geologii, Uniwersytet im. A. Mickiewicza w oznaniu GEOMETRIA WYKREŚLNA I RYSUNEK TECHNICZNY prof. UAM, dr hab. Jędrze Wierzbicki racownia Geologii Inżynierskie i Geotechniki p. 251, e-mail: wi@amu.edu.pl
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Temat ćwiczenia: Opracowanie stereogramu zdjęć naziemnych na VSD.
 Uniwersytet Rolniczy w Krakowie Wydział Inżynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Opracowanie stereogramu zdjęć naziemnych na VSD. Instrukcja do ćwiczeń dla
Uniwersytet Rolniczy w Krakowie Wydział Inżynierii Środowiska i Geodezji Katedra Fotogrametrii i Teledetekcji Temat ćwiczenia: Opracowanie stereogramu zdjęć naziemnych na VSD. Instrukcja do ćwiczeń dla
Elementy geometrii analitycznej w R 3
 Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
Rozdział 12 Elementy geometrii analitycznej w R 3 Elementy trójwymiarowej przestrzeni rzeczywistej R 3 = {(x,y,z) : x,y,z R} możemy interpretować co najmniej na trzy sposoby, tzn. jako: zbiór punktów (x,
M10. Własności funkcji liniowej
 M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
M10. Własności funkcji liniowej dr Artur Gola e-mail: a.gola@ajd.czest.pl pokój 3010 Definicja Funkcję określoną wzorem y = ax + b, dla x R, gdzie a i b są stałymi nazywamy funkcją liniową. Wykresem funkcji
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II
 ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
ZAGADNIENIA PROGRAMOWE I WYMAGANIA EDUKACYJNE DO TESTU PRZYROSTU KOMPETENCJI Z MATEMATYKI DLA UCZNIA KLASY II POZIOM ROZSZERZONY Równania i nierówności z wartością bezwzględną. rozwiązuje równania i nierówności
Rachunek wektorowy - wprowadzenie. dr inż. Romuald Kędzierski
 Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Rachunek wektorowy - wprowadzenie dr inż. Romuald Kędzierski Graficzne przedstawianie wielkości wektorowych Długość wektora jest miarą jego wartości Linia prosta wyznaczająca kierunek działania wektora
Układy współrzędnych
 Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
Układy współrzędnych Układ współrzędnych matematycznie - funkcja przypisująca każdemu punktowi danej przestrzeni skończony ciąg (krotkę) liczb rzeczywistych zwanych współrzędnymi punktu. Układ współrzędnych
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
INTERPRETACJA WYNIKÓW BADANIA WSPÓŁCZYNNIKA PARCIA BOCZNEGO W GRUNTACH METODĄ OPARTĄ NA POMIARZE MOMENTÓW OD SIŁ TARCIA
 Górnictwo i Geoinżynieria Rok 3 Zeszyt 008 Janusz aczmarek* INTERPRETACJA WYNIÓW BADANIA WSPÓŁCZYNNIA PARCIA BOCZNEGO W GRUNTACH METODĄ OPARTĄ NA POMIARZE MOMENTÓW OD SIŁ TARCIA 1. Wstę oncecję laboratoryjnego
Górnictwo i Geoinżynieria Rok 3 Zeszyt 008 Janusz aczmarek* INTERPRETACJA WYNIÓW BADANIA WSPÓŁCZYNNIA PARCIA BOCZNEGO W GRUNTACH METODĄ OPARTĄ NA POMIARZE MOMENTÓW OD SIŁ TARCIA 1. Wstę oncecję laboratoryjnego
Matematyka licea ogólnokształcące, technika
 Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Matematyka licea ogólnokształcące, technika Opracowano m.in. na podstawie podręcznika MATEMATYKA w otaczającym nas świecie zakres podstawowy i rozszerzony Funkcja liniowa Funkcję f: R R określoną wzorem
Drgania układu o wielu stopniach swobody
 Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ. 1. Ciała
 ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 1. Ciała Definicja 1. Układ { ; 0, 1; +, } złożony ze zbioru, dwóch wyróżnionych elementów 0, 1 oraz dwóch działań +:, : nazywamy ciałem
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 1. Ciała Definicja 1. Układ { ; 0, 1; +, } złożony ze zbioru, dwóch wyróżnionych elementów 0, 1 oraz dwóch działań +:, : nazywamy ciałem
TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD IX
 TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD IX to technika pomiarowa oparta na obrazach fotograficznych. Taki obraz uzyskiwany jest dzięki wykorzystaniu kamery lub aparatu. Obraz powstaje na specjalnym
TELEDETEKCJA Z ELEMENTAMI FOTOGRAMETRII WYKŁAD IX to technika pomiarowa oparta na obrazach fotograficznych. Taki obraz uzyskiwany jest dzięki wykorzystaniu kamery lub aparatu. Obraz powstaje na specjalnym
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa. P. F. Góra
 Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Wstęp do metod numerycznych Uwarunkowanie Eliminacja Gaussa P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Uwarunkowanie zadania numerycznego Niech ϕ : R n R m będzie pewna funkcja odpowiednio wiele
Geometria analityczna
 Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Geometria analityczna Wektory Zad Dane są wektory #» a, #» b, #» c Znaleźć długość wektora #» x (a #» a = [, 0, ], #» b = [0,, 3], #» c = [,, ], #» x = #» #» a b + 3 #» c ; (b #» a = [,, ], #» b = [,,
Przekształcenia geometryczne w grafice komputerowej. Marek Badura
 Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
Przekształcenia geometryczne w grafice komputerowej Marek Badura PRZEKSZTAŁCENIA GEOMETRYCZNE W GRAFICE KOMPUTEROWEJ Przedstawimy podstawowe przekształcenia geometryczne na płaszczyźnie R 2 (przestrzeń
( n) Łańcuchy Markowa X 0, X 1,...
 Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład II
 Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Równania różniczkowe liniowe rzędu pierwszego
 Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
Katedra Matematyki i Ekonomii Matematycznej SGH 21 kwietnia 2016 Wstęp Definicja Równanie różniczkowe + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to
5 Równania różniczkowe zwyczajne rzędu drugiego
 5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
GEOMETRIA ANALITYCZNA W PRZESTRZENI Położenie punktu w przestrzeni określamy za pomocą trzech liczb (x, y, z). Liczby te odpowiadają rzutom na osie układu współrzędnych: każdy rzut wzdłuż płaszczyzny równoległej
Geometria w R 3. Iloczyn skalarny wektorów
 Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: KONWEKCJA SWOBODNA W POWIETRZU OD RURY Konwekcja swobodna od rury
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: KONWEKCJA SWOBODNA W POWIETRZU OD RURY Konwekcja swobodna od rury
Matematyka z kluczem
 Matematyka z kluczem Ois założonych osiągnięć ucznia Ogólny ois osiągnięć Ois ogólnych lanowanych osiągnięć ucznia odajemy z odziałem na oszczególne oziomy. Ułatwi to nauczycielom określenie szczegółowych
Matematyka z kluczem Ois założonych osiągnięć ucznia Ogólny ois osiągnięć Ois ogólnych lanowanych osiągnięć ucznia odajemy z odziałem na oszczególne oziomy. Ułatwi to nauczycielom określenie szczegółowych
6 6.1 Projektowanie profili
 6 Niwelacja rofilów 6.1 Projektowanie rofili Niwelacja rofilów Niwelacja rofilów olega na określeniu wysokości ikiet niwelacją geometryczną, trygonometryczną lub tachimetryczną usytuowanych wzdłuŝ osi
6 Niwelacja rofilów 6.1 Projektowanie rofili Niwelacja rofilów Niwelacja rofilów olega na określeniu wysokości ikiet niwelacją geometryczną, trygonometryczną lub tachimetryczną usytuowanych wzdłuŝ osi
MECHANIK NR 3/2015 59
 MECHANIK NR 3/2015 59 Bogusław PYTLAK 1 toczenie, owierzchnia mimośrodowa, tablica krzywych, srzężenie osi turning, eccentric surface, curve table, axis couling TOCZENIE POWIERZCHNI MIMOŚRODOWYCH W racy
MECHANIK NR 3/2015 59 Bogusław PYTLAK 1 toczenie, owierzchnia mimośrodowa, tablica krzywych, srzężenie osi turning, eccentric surface, curve table, axis couling TOCZENIE POWIERZCHNI MIMOŚRODOWYCH W racy
Lista nr 1 - Liczby zespolone
 Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Lista nr - Liczby zespolone Zadanie. Obliczyć: a) ( 3 i) 3 ( 6 i ) 8 c) (+ 3i) 8 (i ) 6 + 3 i + e) f*) g) ( 3 i ) 77 ( ( 3 i + ) 3i 3i h) ( + 3i) 5 ( i) 0 i) i ( 3 i ) 4 ) +... + ( 3 i ) 0 Zadanie. Przedstawić
Przestrzeń unitarna. Jacek Kłopotowski. 23 października Katedra Matematyki i Ekonomii Matematycznej SGH
 Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Rachunek całkowy funkcji wielu zmiennych
 Rachunek całkowy funkcji wielu zmiennych Całki potrójne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki olitechnika Białostocka 1
Rachunek całkowy funkcji wielu zmiennych Całki potrójne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki olitechnika Białostocka 1
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych. Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych
 RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych wyliczamy według wzoru (x, x 2,..., x n ) f(x, x 2,..., x n )
RÓŻNICZKOWANIE FUNKCJI WIELU ZMIENNYCH: rachunek pochodnych dla funkcji wektorowych Pochodne cząstkowe funkcji rzeczywistej wielu zmiennych wyliczamy według wzoru (x, x 2,..., x n ) f(x, x 2,..., x n )
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju
 Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
 TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
FUNKCJA LINIOWA. Zadanie 1. (1 pkt) Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y = ax + b.
 FUNKCJA LINIOWA Zadanie 1. (1 pkt) Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y = ax + b. Jakie znaki mają współczynniki a i b? R: Przedstawiona prosta, jest wykresem funkcji
FUNKCJA LINIOWA Zadanie 1. (1 pkt) Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej y = ax + b. Jakie znaki mają współczynniki a i b? R: Przedstawiona prosta, jest wykresem funkcji
Równania różniczkowe liniowe wyższych rzędów o stałych współcz
 Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
Równania różniczkowe liniowe wyższych rzędów o stałych współczynnikach Katedra Matematyki i Ekonomii Matematycznej SGH 12 maja 2016 Równanie liniowe n-tego rzędu Definicja Równaniem różniczkowym liniowym
ciężkości. Długości celowych d są wtedy jednakowe. Do wstępnych i przybliżonych analiz dokładności można wykorzystywać wzór: m P [cm] = ± 0,14 m α
![ciężkości. Długości celowych d są wtedy jednakowe. Do wstępnych i przybliżonych analiz dokładności można wykorzystywać wzór: m P [cm] = ± 0,14 m α ciężkości. Długości celowych d są wtedy jednakowe. Do wstępnych i przybliżonych analiz dokładności można wykorzystywać wzór: m P [cm] = ± 0,14 m α](/thumbs/66/55588895.jpg) ciężkości. Długości celowych d są wtedy jednakowe. Do wstępnych i przybliżonych analiz dokładności można wykorzystywać wzór: m [cm] = ±,4 m α [cc] d [km] * (9.5) β d 9.7. Zadanie Hansena β d Rys. 9.7.
ciężkości. Długości celowych d są wtedy jednakowe. Do wstępnych i przybliżonych analiz dokładności można wykorzystywać wzór: m [cm] = ±,4 m α [cc] d [km] * (9.5) β d 9.7. Zadanie Hansena β d Rys. 9.7.
= i Ponieważ pierwiastkami stopnia 3 z 1 są (jak łatwo wyliczyć) liczby 1, 1+i 3
 ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
ZESTAW I 1. Rozwiązać równanie. Pierwiastki zaznaczyć w płaszczyźnie zespolonej. z 3 8(1 + i) 3 0, Sposób 1. Korzystamy ze wzoru a 3 b 3 (a b)(a 2 + ab + b 2 ), co daje: (z 2 2i)(z 2 + 2(1 + i)z + (1 +
ALGEBRA z GEOMETRIA, ANALITYCZNA,
 ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
ALGEBRA z GEOMETRIA, ANALITYCZNA, MAT00405 PRZEKSZTAL CANIE WYRAZ EN ALGEBRAICZNYCH, WZO R DWUMIANOWY NEWTONA Uprościć podane wyrażenia 7; (b) ( 6)( + ); (c) a 5 6 8a ; (d) ( 5 )( 5 + ); (e) ( 45x 4 y
Geometria Lista 0 Zadanie 1
 Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
Geometria Lista 0 Zadanie 1. Wyznaczyć wzór na pole równoległoboku rozpiętego na wektorach u, v: (a) nie odwołując się do współrzędnych tych wektorów; (b) odwołując się do współrzędnych względem odpowiednio
Instytut Fizyki Politechniki Wrocławskiej. Laboratorium Fizyki Cienkich Warstw. Ćwiczenie nr 9
 Instytut Fizyki Politechniki Wrocławskiej Laboratorium Fizyki Cienkich Warstw Ćwiczenie nr 9 Wyznaczanie stałych otycznych cienkich warstw metali metodą elisometryczną Oracowanie: dr Krystyna Żukowska
Instytut Fizyki Politechniki Wrocławskiej Laboratorium Fizyki Cienkich Warstw Ćwiczenie nr 9 Wyznaczanie stałych otycznych cienkich warstw metali metodą elisometryczną Oracowanie: dr Krystyna Żukowska
Elastyczność popytu. Rodzaje elastyczności popytu. e p = - Pamiętajmy, że rozpatrujemy wielkości względne!!! Wzory na elastyczność cenową popytu D
 lastyczność oytu Rodzaje elastyczności oytu > lastyczność cenowa oytu - lastyczność mieszana oytu - e m = < lastyczność dochodowa oytu - e i lastyczność cenowa oytu - lastyczność cenowa oytu jest to stosunek
lastyczność oytu Rodzaje elastyczności oytu > lastyczność cenowa oytu - lastyczność mieszana oytu - e m = < lastyczność dochodowa oytu - e i lastyczność cenowa oytu - lastyczność cenowa oytu jest to stosunek
WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23
 WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23 RÓWNOWAGA SIŁ Siła owierzchniowa FS nds Siła objętościowa FV f dv Warunek konieczny równowagi łynu F F 0 S Całkowa ostać warunku równowagi łynu V nds f dv 0
WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23 RÓWNOWAGA SIŁ Siła owierzchniowa FS nds Siła objętościowa FV f dv Warunek konieczny równowagi łynu F F 0 S Całkowa ostać warunku równowagi łynu V nds f dv 0
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne. 1. Badanie przelewu o ostrej krawędzi
 Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. Badanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. Badanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA
 Dr inż. Andrzej Polka Katedra Dynamiki Maszyn Politechnika Łódzka RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA Streszczenie: W pracy opisano wzajemne położenie płaszczyzny parasola
Dr inż. Andrzej Polka Katedra Dynamiki Maszyn Politechnika Łódzka RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA Streszczenie: W pracy opisano wzajemne położenie płaszczyzny parasola
Przykład 4.1. Ściag stalowy. L200x100x cm 10 cm I120. Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym
 Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
Przykład 4.1. Ściag stalowy Obliczyć dopuszczalną siłę P rozciagającą ściąg stalowy o przekroju pokazanym na poniższym rysunku jeśli naprężenie dopuszczalne wynosi 15 MPa. Szukana siła P przyłożona jest
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A
 PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
PYTANIA KONTROLNE STAN NAPRĘŻENIA, ODKSZTAŁCENIA PRAWO HOOKE A TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej
3. PŁASKI STAN NAPRĘŻENIA I ODKSZTAŁCENIA
 3. PŁASKI STAN NAPRĘŻNIA I ODKSZTAŁCNIA 1 3. 3. PŁASKI STAN NAPRĘŻNIA I ODKSZTAŁCNIA Analizując płaski stan naprężenia posługujemy się składowymi tensora naprężenia w postaci wektora {,,y } (3.1) Za dodatnie
3. PŁASKI STAN NAPRĘŻNIA I ODKSZTAŁCNIA 1 3. 3. PŁASKI STAN NAPRĘŻNIA I ODKSZTAŁCNIA Analizując płaski stan naprężenia posługujemy się składowymi tensora naprężenia w postaci wektora {,,y } (3.1) Za dodatnie
Etap 1. Rysunek: Układy odniesienia
 Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Geometria analityczna - przykłady
 Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
Geometria analityczna - przykłady 1. Znaleźć równanie ogólne i równania parametryczne prostej w R 2, któr przechodzi przez punkt ( 4, ) oraz (a) jest równoległa do prostej x + 5y 2 = 0. (b) jest prostopadła
2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I
![2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I 2 1 3 c c1. e 1, e 2,..., e n A= e 1 e 2...e n [ ] M. Przybycień Matematyczne Metody Fizyki I](/thumbs/88/115575416.jpg) Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
Liniowa niezależno ność wektorów Przykład: Sprawdzić czy następujące wektory z przestrzeni 3 tworzą bazę: e e e3 3 Sprawdzamy czy te wektory są liniowo niezależne: 3 c + c + c3 0 c 0 c iei 0 c + c + 3c3
GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA
 MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s.8-86, Gliwice 007 GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA EUGENIUSZ
MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s.8-86, Gliwice 007 GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA EUGENIUSZ
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1 Równania różniczkowe zwyczajne
 Równania różniczkowe zwyczajne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki Politechnika Białostocka Równania różniczkowe Równaniem
Równania różniczkowe zwyczajne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki Politechnika Białostocka Równania różniczkowe Równaniem
Algebra linowa w pigułce
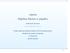 Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
Algebra Algebra linowa w pigułce Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych Wydział Informatyki w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Algebra
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
FUNKCJA KWADRATOWA. 1. Definicje i przydatne wzory. lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax 2 + bx + c
 FUNKCJA KWADRATOWA 1. Definicje i przydatne wzory DEFINICJA 1. Funkcja kwadratowa lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax + bx + c taką, że a, b, c R oraz a 0. Powyższe wyrażenie
FUNKCJA KWADRATOWA 1. Definicje i przydatne wzory DEFINICJA 1. Funkcja kwadratowa lub trójmianem kwadratowym nazywamy funkcję postaci: f(x) = ax + bx + c taką, że a, b, c R oraz a 0. Powyższe wyrażenie
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne. 1. Badanie przelewu o ostrej krawędzi
 Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. adanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. adanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
W-23 (Jaroszewicz) 20 slajdów Na podstawie prezentacji prof. J. Rutkowskiego
 Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
O MACIERZACH I UKŁADACH RÓWNAŃ
 O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
Układ współrzędnych dwu trój Wykład 2 "Układ współrzędnych, system i układ odniesienia"
 Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
Układ współrzędnych Układ współrzędnych ustanawia uporządkowaną zależność (relację) między fizycznymi punktami w przestrzeni a liczbami rzeczywistymi, czyli współrzędnymi, Układy współrzędnych stosowane
Układy równań liniowych, macierze, Google
 Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
Układ równań linowych { x+2y = 6, 3x y = 4 (0) Spotkania z Matematyka Układy równań liniowych, macierze, Google Aleksander Denisiuk denisjuk@matman.uwm.edu.pl Uniwersytet Warmińsko-Mazurski w Olsztynie
i = [ 0] j = [ 1] k = [ 0]
![i = [ 0] j = [ 1] k = [ 0] i = [ 0] j = [ 1] k = [ 0]](/thumbs/70/62901734.jpg) Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Ćwiczenia nr TEMATYKA: Układy współrzędnych: kartezjański, walcowy (cylindryczny), sferyczny (geograficzny), Przekształcenia: izometryczne, nieizometryczne. DEFINICJE: Wektor wodzący: wektorem r, ρ wodzącym
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, , tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Rozwiązanie:
 Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Zadanie 3 Oblicz jeżeli wiadomo, że liczby 8 2,, 1, 6 11 6 11, tworzą ciąg arytmetyczny. Wyznacz różnicę ciągu. Uprośćmy najpierw liczby dane w treści zadania: 8 2, 2 2 2 2 2 2 6 11 6 11 6 11 26 11 6 11
Zaawansowane metody numeryczne
 Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
TENSOMETRIA ZARYS TEORETYCZNY
 TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
TENSOMETRIA ZARYS TEORETYCZNY Stan naprężenia jest niemożliwy do pomiaru, natomiast łatwo zmierzyć stan odkształcenia na powierzchni zewnętrznej badanej konstrukcji. Aby wyznaczyć stan naprężenia trzeba
Lokalna odwracalność odwzorowań, odwzorowania uwikłane
 Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cieplnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cieplnych
 Laboratorium Termodynamiki i Pomiarów Maszyn Cielnych Przeływomierze zwężkowe POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cielnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cielnych LABORATORIUM
Laboratorium Termodynamiki i Pomiarów Maszyn Cielnych Przeływomierze zwężkowe POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cielnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cielnych LABORATORIUM
Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne
 46 III. Przekształcenia w przestrzeni trójwymiarowej Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne Złożone obiekty trójwymiarowe można uważać,
46 III. Przekształcenia w przestrzeni trójwymiarowej Z ostatniego wzoru i zależności (3.20) można obliczyć n6. Otrzymujemy (3.23) 3.5. Transformacje geometryczne Złożone obiekty trójwymiarowe można uważać,
Jakobiany. Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu
 Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wstęp do Robotyki c W. Szynkiewicz, 29 1 Jakobiany Kinematykę we współrzędnych możemy potraktować jako operator przekształcający funkcje czasu ( t )z(t)=k(x(t)) Ponieważ funkcje w powyższym równaniu są
Wielomiany podstawowe wiadomości
 Rozdział Wielomiany podstawowe wiadomości Funkcję postaci f s = a n s n + a n s n + + a s + a 0, gdzie n N, a i R i = 0,, n, a n 0 nazywamy wielomianem rzeczywistym stopnia n; jeżeli współczynniki a i
Rozdział Wielomiany podstawowe wiadomości Funkcję postaci f s = a n s n + a n s n + + a s + a 0, gdzie n N, a i R i = 0,, n, a n 0 nazywamy wielomianem rzeczywistym stopnia n; jeżeli współczynniki a i
GEOMETRIA ANALITYCZNA W PRZESTRZENI
 Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
Wykład z Podstaw matematyki dla studentów Inżynierii Środowiska Wykład 13. Egzaminy I termin wtorek 31.01 14:00 Aula A Wydział Budownictwa II termin poprawkowy czwartek 9.02 14:00 Aula A Wydział Budownictwa
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE
 27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
27. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE 27.1. Wiadomości wstępne Równaniem różniczkowym cząstkowym nazywamy związek w którym występuje funkcja niewiadoma u dwóch lub większej liczby zmiennych niezależnych i
Fotogrametryczny pomiar lin odciągowych z wykorzystaniem przekształceń rzutowych
 rchiwum Fotogrametrii, Kartografii i Teledetekcji Vol., Kraków 00 ISBN 3-73-0-7 Fotogrametryczny pomiar lin odciągowych z wykorzystaniem przekształceń rzutowych Regina Tokarczyk, Władysław Mierzwa kademia
rchiwum Fotogrametrii, Kartografii i Teledetekcji Vol., Kraków 00 ISBN 3-73-0-7 Fotogrametryczny pomiar lin odciągowych z wykorzystaniem przekształceń rzutowych Regina Tokarczyk, Władysław Mierzwa kademia
Wykład 3 Równania rózniczkowe cd
 7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
7 grudnia 2010 Definicja Równanie różniczkowe dy dx + p (x) y = q (x) (1) nazywamy równaniem różniczkowym liniowym pierwszego rzędu. Jeśli q (x) 0, to równanie (1) czyli równanie dy dx + p (x) y = 0 nazywamy
W wielu obliczeniach w matematyce bądź fizyce wykonanie niektórych kroków zależy od spełnienia warunku.
 W wielu obliczeniach w matematyce bądź fizyce wykonanie niektórych kroków zależy od spełnienia warunku. Nie wolno dzielić przez zero i należy sprawdzić, czy dzielna nie jest równa zeru. W dziedzinie liczb
W wielu obliczeniach w matematyce bądź fizyce wykonanie niektórych kroków zależy od spełnienia warunku. Nie wolno dzielić przez zero i należy sprawdzić, czy dzielna nie jest równa zeru. W dziedzinie liczb
Układy równań i równania wyższych rzędów
 Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Rozdział Układy równań i równania wyższych rzędów Układy równań różniczkowych zwyczajnych Wprowadzenie W poprzednich paragrafach zajmowaliśmy się równaniami różniczkowymi y = f(x, y), których rozwiązaniem
Podstawy robotyki. Wykład II. Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska
 Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Podstawy robotyki Wykład II Ruch ciała sztywnego w przestrzeni euklidesowej Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Preliminaria matematyczne
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
Geometria analityczna
 Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
Geometria analityczna Paweł Mleczko Teoria Informacja (o prostej). postać ogólna prostej: Ax + By + C = 0, A + B 0, postać kanoniczna (kierunkowa) prostej: y = ax + b. Współczynnik a nazywamy współczynnikiem
