Konstruowanie Baz Danych Relacyjny Model Danych I
|
|
|
- Kamil Ostrowski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Studia podyplomowe In»ynieria oprogramowania wspóªnansowane przez Uni Europejsk w ramach Europejskiego Funduszu Spoªecznego Projekt Studia podyplomowe z zakresu wytwarzania oprogramowania oraz zarz dzania projektami w rmach informatycznych realizowany w ramach Programu Operacyjnego Kapitaª Ludzki Konstruowanie Baz Danych Relacyjny Model Danych I Antoni Lig za ligeza@agh.edu.pl
2 Konstruowanie baz danych: Relacyjny model danych I 2 Poj cie atrybutu Dane reprezentowane w jakiejkolwiek formie, np. w pewnym pliku, arkuszu kalkulacyjnym, bazie danych, bazie wiedzy, itp. odnosz si zawsze do pewnego obiektu lub zbioru obiektów i charakteryzuj wybrane ich wªasno±ci b d ce przedmiotem zainteresowania. Dla danego zagadnienia, zazwyczaj na etapie projektu systemu informatycznego, dokonuje si wyboru tych wªasno±ci oraz stopnia szczegóªowo±ci ich reprezentacji. Do opisu wªasno±ci obiektów reprezentowanych w bazie danych wykorzystuje si wybrany zestaw atrybutów, a dla wyra»enia ich warto±ci z zadan dokªadno±ci okre±la si dziedziny atrybutów. W praktyce cz sto dziedzin atrybutu deniuje si poprzez podanie typu danych, rozmiaru pola, wi zów spójno±ci (lokalnych, np. reguªy poprawno±ci). Przez atrybut obiektu rozumie si pewn jego wªasno±, cech lub charakterystyk, pozwalaj c cz ±ciowo opisa ten obiekt. Przykªadami atrybutów mog by kolor, ksztaªt, waga, cena, wiek, marka, typ, numer seryjny, itp. Atrybuty przyjmuj warto±ci z okre±lonego zbioru (dziedziny), przy czym normalnie (cho milcz co) zakªada si,»e w danym momencie dla danego obiektu wybrany atrybut przyjmuje pojedyncz warto± ; co wi cej, przyjmuje si najcz ±ciej,»e jest to warto± atomiczna, tzn. taka, która traktowana jest jako pojedynczy symbol i nie jest dalej analizowana po k tem jej struktury wewn trznej, zawarto±ci, elementów skªadowych, itd. Wymaganie co do atomicznego charakteru warto±ci atrybutów stanowi jeden z podstawowych kanonów relacyjnych baz danych; w bardziej zaawansowanych modelach mo»e ono by jednak osªabione, poprzez dopuszczenie warto±ci zªo»onych, takich jak zbiory, przedziaªy, czy nawet struktury. Wymaganie atomicznego charakter warto±ci atrybutów uwarunkowane jest d»eniem do maksymalnej przejrzysto±ci modelu relacyjnych baz danych i jego zgodno±ci z teori, a przede wszystkim d»eniem do uzyskania du»ej efektywno i operacji algebraicznych.
3 Konstruowanie baz danych: Relacyjny model danych I 3 Poj cie atrybutu zagadnienia formalne Z matematycznego punktu widzenia atrybut jest funkcj a wi c pewnego rodzaju odwzorowniem, które ka»demu obiektowi przypisuje pewn warto± cechy któr ten atrybut deniuje. Denicja 1 Niech bedzie dany pewnien zbiór D i zwany dziedzin. Attrybutem A i o dziedzinie D i okre±lonym na zbiorze obiektów E nazywamy dowoln funkcj postaci: A i : E D i. Uwaga: z denicji poj cia funcji wynika,»e je»eli A i (e j ) = d 1 ji oraz A i (e j ) = d 2 ji to d1 ji = d 2 j2 ; dla danego obiektu atrybut mo»e przyjmowa tylko jedn warto±! Warto±c ta mo»e powtarza si dla wielu ró»nych obiektów (s one wtedy nierozró»nialne z punktu widzenia warto±ci tego atrybutu). Niech: E = {e 1, e 2,..., e m } oznacza zbiór m rozwa»anych obiektów (encji), A = {A 1, A 2,..., A n } oznacza zbiór n atrybutów reprezentuj cych wybrane wªasno±ci obiektów ze zbioru E, D 1, D 2,..., D n oznacza dziedziny powy»szych atrybutów. Zapis warto±ci atrybutu dla wybranego obiektu przybiera form : Uwaga: zapis postaci: A i (e j ) = d ji, (1) A i = d j nie mówi dla jakiego obiektu okre±lono warto± atrybutu A j ; jest on stosowany jako selektor (warunek logiczny), który deniuje (wybiera) pewien podzbiór E ij zbioru obiektów E, dla których ten warunek jest speªniony; matematycznie: E ij = {e E: A i (e) = d j }.
4 Konstruowanie baz danych: Relacyjny model danych I 4 Warto±ci i dziedziny atrybutów Ka»dy atrybut przyjmuje warto±ci z okre±lonego zbioru, zadanego jawnie lub domy±lnie, stanowi cego jego dziedzin. Przyjmijmy nast puj ce standardowe oznaczenia: A = {A 1, A 2,..., A n } ustalony zbiór atrybutów, D 1, D 2,..., D n ustalony zbiór dziedzin tych atrybutów. Z ka»dym atrybutem A i A zwi zana jest dziedzina D i, i = 1, 2,..., n. Dziedzina atrybutu mo»e by zadana jawnie, np. poprzez wyliczenie elementów w postaci sko«czonego zbioru (ekstensjonalnie), lub mo»e by zadana niejawnie w przypadku trudno±ci wyliczenia wszystkich potencjalnych elementów tej dziedziny. Przykªadem pierwszej dziedziny mo»e by zbiór warto±ci atrybutu dzie«_tygodnia w postaci {poniedziaªek, wtorek, ±roda, czwartek, pi tek, sobota, niedziela}. Przykªadem drugiej dziedziny mo»e by zbiór warto±ci atrybutu nazwisko trudno tutaj wyliczy wszystkie mo»liwe napisy, które mogªyby by uznane za nazwiska; z drugiej strony, przyj cie za dziedzin tego atrybutu zbioru napisów o ograniczonej dªugo±ci maksymalnej dopuszcza napisy typu Aaaaa czy xyz, które trudno uzna za realne nazwiska. W takiej sytuacji dziedzin zadaje si zazwyczaj cz ±ciowo, poprzez okre±lenie typu i rozmiaru pola, oraz ewentualnie reguª poprawno±ci. Dany atrybut dla danego obiektu mo»e przyjmowa w danej chwili czasu pojedyncz warto± mówimy tutaj o funkcyjnym charakterze zale»no±ci warto±ci atrybutu od wybranych parametrów (obiektu, chwili czasu, ewentualnie dodatkowych czynników). Dobrymi przykªadami warto±ci atrybutów s np. warto±ci zmiennych opisuj cych stan i zachowanie si ukªadów zycznych, precyzyjne dane pomiarowe, warto±ci wielko±ci zycznych, takich jak temperatura, pr dko±, napi cie, nat»enie, itp. Natomiast cz sto nie maj tego charakteru gromadzone ª cznie dane pochodz ce z pewnych obserwacji, np. warto±ci charakteryzuj ce objawy wyst puj ce ª cznie u chorego jak {gor czka, duszno±ci, bóle, wysypka}, czy te» nieformalne opisy tekstowe.
5 Konstruowanie baz danych: Relacyjny model danych I 5 Rodzaje dziedzin Dziedziny nominalne i cz ±ciowo uporz dkowane Dziedzina atrybutu mo»e tworzy pewn struktur ; typowe z nich to: dziedziny binarne dziedzina taka zawiera dokªadnie dwa elementy, np. 0 i 1 lub okre±lenia tak oraz nie; dodatkowo, mo»e by narzucona relacja porz dkuj ca te elementy, np. 0 1, dziedziny trójwarto±ciowe dziedzina taka zawiera dokªadnie trzy elementy, np. {tak, nie, brak_danych}, {TRUE, FALSE, NULL} lub {, 0, +}; mo»e by okre±lona relacja porz dku, np. 0 +, dziedziny nominalne (nieuporz dkowane) s to sko«czone (lub rzadziej niesko«czone) zbiory nazw, które nie s powi zane ze sob»adn relacj porz dkuj c ; typowymi przykªadami mog by np. zbiory dopuszczalnych kolorów, ksztaªtów, itp.; zbiory takie mo»na jednak porz dkowa leksykogracznie, dziedziny cz ±ciowo uporz dkowane podobnie jak wy»ej, zbiory sko«czone lub niesko«czone z relacj cz ±ciowego porz dku takie dziedziny wyst puj stosunkowo rzadko; przykªadem mo»e by zbiór warto±ci mieszanych typu {list_zwykªy, list_ekspresowy, list_polecony, paczka_zwykªa, paczka_warto±ciowa, przesyªka_kurierska} stanowi - cych warto±ci atrybutu rodzaj_przesyªki z cz ±ciowym porz dkiem (wzgl dem czasu dostarczenia) ustalonym przez relacj list_zwykªy list_ekspresowy, list_ekspresowy przesyªka_kurierska, list_polecony list_ekspresowy, list_ekspresowy przesyªka_kurierska, dziedziny tworz ce struktur kraty dziedziny takie wraz z wprowadzon relacj cz ±ciowego porz dku tworz struktur kraty; typowym przykªadem mog by specykacje typów,
6 Konstruowanie baz danych: Relacyjny model danych I 6 Rodzaje dziedzin Dziedziny uporz dkowane dziedziny uporz dkowane sko«czone lub niesko«czone zbiory warto±ci uporz dkowanych (liniowo), np. {nb,nm,ns,z,ps,pm,pb}, gdzie nb du»y ujemny, nm ±redni ujemny, ns maªy ujemny, z okoªo zera, ps maªy dodatni, pm ±redni dodatni, pb du»y dodatni, z uporz dkowaniem np nm ns z ps pm pb; mo»e to by te» pewien zbiór napisów (imion, nazwisk, nazw wªasnych) z relacj porz dku alfabetycznego; analogiczny charakter ma zbiór ocen! dziedziny liczbowe ze wzgl du na liczne zastosowania i specyczny charakter wyró»niono je jako osobny rodzaj, cho w istocie nale» do klasy zbiorów uporz dkowanych wyró»nia je jednak okre±lona arytmetyka pozwalaj ca realizowa operacje obliczeniowe, w tym wszelkiego rodzaju przeliczenia, obliczanie warto±ci funkcji, obliczanie funkcji sumarycznych (takich jak: suma, ±rednia, wariancja, odchylenie standardowe, itp.); przykªady obejmuj dowolne podzbiory zbioru liczb naturalnych, caªkowitych, czy rzeczywistych, a tak»e daty i czas, liczby zapisane w innym ni» dziesi tny ukªadzie pozycyjnym, walut, procenty, itp. Cz sto spotykane typy danych to: bajt, liczba caªkowita (krótka, dªuga), liczba rzeczywista (pojedynczej, podwójnej precyzji), data, waluta, procenty Dla dziedzin tego typu istnieje zwykle mo»liwo± konwersji typu.
7 Konstruowanie baz danych: Relacyjny model danych I 7 Inne typy danych Dane specjalizowane nie maj charakteru atomicznego, a ich zapis i interpretacja odbywa si przy pomocy specjalnych narz dzi. Ich przetwarzanie wymaga znajomo±ci strutury oraz specjalizowanego oprogramowania, np.: dane typu tekstowego mog zawiera dowolne pliki tekstowe; w bazach danych okre±la si je jako tzw. pola typu memo, przy czym nie wykonuje si na nich»adnych operacji, poza obróbk za pomoc edytora tekstu, dane typu d¹wi k zapisywane s w postaci specjalnych plików, w bazach danych jedyne ich zastosowanie polega na odtwarzaniu nagranej sekwencji; specjalistyczna obróbka mo»liwa jest przy zastosowaniu odpowiednich narz dzi, przy czym mo»e ona mie na celu np. rozpoznanie mowy i przetªumaczenie do postaci zapisu w pewnym j zyku symbolicznym, albo np. rozpoznanie osoby na podstawie jej wypowiedzi, dane typu obraz zapisywane s w postaci specjalnych plików w okre±lonym formacie, ich zastosowanie polega na odtwarzaniu (prezentacji) obrazu; specjalistyczna obróbka mo»liwa jest przy zastosowaniu odpowiednich narz dzi, przy czym mo»e ona mie na celu analiz i rozpoznawanie obrazu, porównywanie obrazów, itp. (Istniej specjalizowane bazy danych, w których mo»liwe jest wyszukiwanie na podstawie wzorca), dane typu sekwencja wideo podobie jak obrazy, dane typu hyperª cze umo»liwiaj uruchomienie usªugi sieciowej, wiedza jako dane wiedza, o ile stanowi przedmiot dalszej analizy czy przetwarzania (na wy»szym poziomie), mo»e równie» stanowi dane wyj±ciowe dla tego procesu; przykªadem mog by zbiory reguª lub programy logiczne, których wªasno±ci, s przedmiotem dalszej analizy. Baza danych zawieraj ca zbiory procedur mo»e te» by wykorzystywana do wspomagania lub automatycznej syntezy programów w oparciu o dobór istniej cych komponentów o podanych specykacjach.
8 Konstruowanie baz danych: Relacyjny model danych I 8
9 Konstruowanie baz danych: Relacyjny model danych I 9 Przykªadowe wªasno±ci pól: ACCESS W systemie ACCESS mo»na zdeniowa nast puj ce wªasno±ci pól tabeli: Rozmiar pola okre±la maksymalny rozmiar danych przechowywanych w polu (tekst i liczba), Nowe warto±ci tylko dla autonumer; mo»na wybra generowanie przyrostowe lub losowe, Format deniuje szablon wy±wietlania zawarto±ci danego pola, Miejsca dziesi tne deniuje ilo± miejsc po przecinku (liczby), Maska wprowadzania deniuje szablon dla wprowadzania danych, Tytuª pozwala poda etykiet kolumny tabeli, Warto± domy±lna pozwala zdeniowa standardow warto± wprowadzan automatycznie, Reguªa poprawno±ci deniuje warunek, jaki musz speªnia wszystkie warto±ci w danym polu, Komunikat o bª dzie pozwala zdeniowa tekst wy±wietlany przy naruszeniu reguªy poprawno±ci, Wymagane okre±la czy dane pole musi zosta wypeªnione, czy te» mo»e pozosta puste, Zerowa dªugo± dozwolona pozwala zapisa w polu ªa«cuch zerowej dªugo±ci (zamienia puste pola tekstowe na ªa«cuchy zerowej dªugo±ci), Indeksowane pozwala wyspecykowa» danie indeksowania pola (mo»liwe jest indeksowanie z powtórzeniami lub bez), Odno±nik pozwala wybra typ formantu (dla typów tekst, liczba, logiczne) jako list, pole wyboru, lub list rozwijaln (pole kombi) (osi galne przez zakªadk ; mo»e by tworzone przy pomocy kreatora).
10 Konstruowanie baz danych: Relacyjny model danych I 10 Dla pól tekstowych: Format pola: ACCESS <Szablon>;<String zerowej dªugo±ci>;<null> <Szablon> sekcja deniuj ca sposób wyprowadzania tekstu, <String zerowej dªugo±ci> - sekcja deniuj ca co zostanie wyprowadzone w przypadku, gdy pole zawiera string zerowej dªugo±ci (""), <Null> sekcja deniuj ca co zostanie wyprowadzone w przypadku, gdy pole zawiera warto± Null. Na telefonu"[czerwony];"telefon nieznany"[niebieski] spowoduje wypisanie numeru telefonu zawartego w polu i odpowiednich komunikatów w przypadku jego braku lub nieznajomo±ci. Dla liczb obowi zuje format: <Szablon dodatnich>;<szablon ujemnych>;<szablon zera>;<null> <Szablon dodatnich> deniuje sposób wyprowadzania liczb dodatnich, <Szablon ujemnych> deniuje sposób wyprowadzania liczb ujemnych, <Szablon zera> deniuje, co b dzie wypisane gdy w polu jest warto± zero, <Null> deniuje, co b dzie wypisane gdy pole jest puste. Na przykªad: 0,00;"Ujemna cena!"[czerwony];"zero"[zielony];"brak"[niebieski] wy±wietli cen z dokªadno±ci do dwóch miejsc po przecinku, oraz wskazane komunikaty w sytuacjach wyj tkowych.
11 Konstruowanie baz danych: Relacyjny model danych I 11 Format danych: ACCESS Znaczenie symboli "TEKST" wy±wietla podany w cudzysªowach tekst, (spacja) wy±wietla spacj,! wymusza lewostronne wyrównanie danych w polu, wypeªnia wole pole podanym znakiem, \ powoduje wy±wietlenie nast puj cego po nim znaku, [kolor] powoduje wy±wietlanie zawarto±ci pola w zadanym kolorze (Black, Blue, Green, Cyan, Red, Magenta, Yellow, White),, separator cz ±ci dziesi tnej, 0 cyfra lub zero; wyst pienie obowi zkowe, # cyfra lub spacja, % wy±wietla liczb w postaci procentu, E-, e-, E+, e+ notacja eksponencjalna (dla caªy tekst, pojedynczy znak lub spacja, & pojedynczy znak lub nic, > powoduje wypisanie tekstu du»ymi literami, < powoduje wypisanie tekstu maªymi literami, Dla typu data istnieje szereg symboli specjalnych (vide: Help).
12 Konstruowanie baz danych: Relacyjny model danych I 12 Maska wprowadzania: ACCESS Schemat i przykªady masek Maska wprowadzania stanowi szablon i ltr u»ytczny przy wprowadzaniu danych do pola; realizuje równie» proste transformacje. Maska zapewnia elementarna kontrol poprawno±ci wprowadzanych danych. Schemat maski wprowadzania jest nast puj cy: <Szablon maski>;<przechowanie znaku>;<znak maski> <Szablon maski> deniuje posta maski, <Przechowanie znaku> 0 oznacza,»e znaki maski maj by przechowywane w tabeli; 1 oznacza,»e znaki maski nie b d przechowywane w tabeli (standardowo 1), <Znak maski> znak reprezentuj cy w masce pojedynczy symbol (standardowo _. Na przykªad, dla przechowywania numerów ISBN mo» posªu»y si mask : ISBN 00\-00000\-00\-0;1;\_ a dla numerów telefonów mo»na posªu»y si mask : (9\-99) 000\-00\-00!;0;\_ Maska wprowadzania mo»e peªni rol (i) szablonu, (ii) ltru poprawno±ci oraz (iii) by zastosowana do przeksztaªcania (formatowania) wprowadzanych symboli. Typowe maski wprowadzania dogodnie jest tworzy przy wykorzystaniu Kreatora masek.
13 Konstruowanie baz danych: Relacyjny model danych I 13 Maska wprowadzania: ACCESS Znaczenie symboli u»ywanych w maskach wprowadzania: 0 cyfra, pozycja wymagana, 9 cyfra lub spacja, pozycja nie wymagana, # cyfra lub spacja, pozycja nie wymagana (puste miejsca konwertowane na spacje, dozwolone + i -), L litera, pozycja wymagana,? litera, pozycja opcjonalna, A litera lub cyfra, pozycja wymagana, a litera lub cyfra, pozycja opcjonalna, & dowolny znak lub spacja, pozycja wymagana, C dowolny znak lub spacja, pozycja opcjonalna,! wy±wietlanie znaków od prawej do lewej, Password Hasªo powoduje utajnienie wprowadzanych znakó (s zast pione ), > powoduje,»e wprowadzane za tym symbolem znaki b d konwertowane na du»e, < powoduje,»e wprowadzane za tym symbolem znaki b d konwertowane na maªe,.,:;-/ znak dziesi tny, separatory tysi cy, daty i czasu; zale»ne od ustawie«w Panelu sterowania, \ literalne cytowanie nast pnego znaku.
i, lub, nie Cegieªki buduj ce wspóªczesne procesory. Piotr Fulma«ski 5 kwietnia 2017
 i, lub, nie Cegieªki buduj ce wspóªczesne procesory. Piotr Fulma«ski Uniwersytet Šódzki, Wydziaª Matematyki i Informatyki UŠ piotr@fulmanski.pl http://fulmanski.pl/zajecia/prezentacje/festiwalnauki2017/festiwal_wmii_2017_
i, lub, nie Cegieªki buduj ce wspóªczesne procesory. Piotr Fulma«ski Uniwersytet Šódzki, Wydziaª Matematyki i Informatyki UŠ piotr@fulmanski.pl http://fulmanski.pl/zajecia/prezentacje/festiwalnauki2017/festiwal_wmii_2017_
Autor: dr inż. Katarzyna Rudnik
 Bazy danych Wykład 2 MS Access Obiekty programu, Reprezentacja danych w tabeli, Indeksy, Relacje i ich sprzężenia Autor: dr inż. Katarzyna Rudnik Obiekty programu MS ACCESS Obiekty typu Tabela są podstawowe
Bazy danych Wykład 2 MS Access Obiekty programu, Reprezentacja danych w tabeli, Indeksy, Relacje i ich sprzężenia Autor: dr inż. Katarzyna Rudnik Obiekty programu MS ACCESS Obiekty typu Tabela są podstawowe
Konstruowanie Baz Danych Wprowadzenie do projektowania. Normalizacja
 Studia podyplomowe In»ynieria oprogramowania wspóªnansowane przez Uni Europejsk w ramach Europejskiego Funduszu Spoªecznego Projekt Studia podyplomowe z zakresu wytwarzania oprogramowania oraz zarz dzania
Studia podyplomowe In»ynieria oprogramowania wspóªnansowane przez Uni Europejsk w ramach Europejskiego Funduszu Spoªecznego Projekt Studia podyplomowe z zakresu wytwarzania oprogramowania oraz zarz dzania
JAO - J zyki, Automaty i Obliczenia - Wykªad 1. JAO - J zyki, Automaty i Obliczenia - Wykªad 1
 J zyki formalne i operacje na j zykach J zyki formalne s abstrakcyjnie zbiorami sªów nad alfabetem sko«czonym Σ. J zyk formalny L to opis pewnego problemu decyzyjnego: sªowa to kody instancji (wej±cia)
J zyki formalne i operacje na j zykach J zyki formalne s abstrakcyjnie zbiorami sªów nad alfabetem sko«czonym Σ. J zyk formalny L to opis pewnego problemu decyzyjnego: sªowa to kody instancji (wej±cia)
Metody numeryczne i statystyka dla in»ynierów
 Kierunek: Automatyka i Robotyka, II rok Wprowadzenie PWSZ Gªogów, 2009 Plan wykªadów Wprowadzenie, podanie zagadnie«, poj cie metody numerycznej i algorytmu numerycznego, obszar zainteresowa«i stosowalno±ci
Kierunek: Automatyka i Robotyka, II rok Wprowadzenie PWSZ Gªogów, 2009 Plan wykªadów Wprowadzenie, podanie zagadnie«, poj cie metody numerycznej i algorytmu numerycznego, obszar zainteresowa«i stosowalno±ci
Baza danych - Access. 2 Budowa bazy danych
 Baza danych - Access 1 Baza danych Jest to zbiór danych zapisanych zgodnie z okre±lonymi reguªami. W w»szym znaczeniu obejmuje dane cyfrowe gromadzone zgodnie z zasadami przyj tymi dla danego programu
Baza danych - Access 1 Baza danych Jest to zbiór danych zapisanych zgodnie z okre±lonymi reguªami. W w»szym znaczeniu obejmuje dane cyfrowe gromadzone zgodnie z zasadami przyj tymi dla danego programu
Relacj binarn okre±lon w zbiorze X nazywamy podzbiór ϱ X X.
 Relacje 1 Relacj n-argumentow nazywamy podzbiór ϱ X 1 X 2... X n. Je±li ϱ X Y jest relacj dwuargumentow (binarn ), to zamiast (x, y) ϱ piszemy xϱy. Relacj binarn okre±lon w zbiorze X nazywamy podzbiór
Relacje 1 Relacj n-argumentow nazywamy podzbiór ϱ X 1 X 2... X n. Je±li ϱ X Y jest relacj dwuargumentow (binarn ), to zamiast (x, y) ϱ piszemy xϱy. Relacj binarn okre±lon w zbiorze X nazywamy podzbiór
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
2 Liczby rzeczywiste - cz. 2
 2 Liczby rzeczywiste - cz. 2 W tej lekcji omówimy pozostaªe tematy zwi zane z liczbami rzeczywistymi. 2. Przedziaªy liczbowe Wyró»niamy nast puj ce rodzaje przedziaªów liczbowych: (a) przedziaªy ograniczone:
2 Liczby rzeczywiste - cz. 2 W tej lekcji omówimy pozostaªe tematy zwi zane z liczbami rzeczywistymi. 2. Przedziaªy liczbowe Wyró»niamy nast puj ce rodzaje przedziaªów liczbowych: (a) przedziaªy ograniczone:
Listy i operacje pytania
 Listy i operacje pytania Iwona Polak iwona.polak@us.edu.pl Uniwersytet l ski Instytut Informatyki pa¹dziernika 07 Który atrybut NIE wyst puje jako atrybut elementów listy? klucz elementu (key) wska¹nik
Listy i operacje pytania Iwona Polak iwona.polak@us.edu.pl Uniwersytet l ski Instytut Informatyki pa¹dziernika 07 Który atrybut NIE wyst puje jako atrybut elementów listy? klucz elementu (key) wska¹nik
x y x y x y x + y x y
 Algebra logiki 1 W zbiorze {0, 1} okre±lamy dziaªania dwuargumentowe,, +, oraz dziaªanie jednoargumentowe ( ). Dziaªanie x + y nazywamy dodawaniem modulo 2, a dziaªanie x y nazywamy kresk Sheera. x x 0
Algebra logiki 1 W zbiorze {0, 1} okre±lamy dziaªania dwuargumentowe,, +, oraz dziaªanie jednoargumentowe ( ). Dziaªanie x + y nazywamy dodawaniem modulo 2, a dziaªanie x y nazywamy kresk Sheera. x x 0
Matematyka wykªad 1. Macierze (1) Andrzej Torój. 17 wrze±nia 2011. Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej
 Matematyka wykªad 1 Macierze (1) Andrzej Torój Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej 17 wrze±nia 2011 Plan wykªadu 1 2 3 4 5 Plan prezentacji 1 2 3 4 5 Kontakt moja strona internetowa:
Matematyka wykªad 1 Macierze (1) Andrzej Torój Wy»sza Szkoªa Zarz dzania i Prawa im. H. Chodkowskiej 17 wrze±nia 2011 Plan wykªadu 1 2 3 4 5 Plan prezentacji 1 2 3 4 5 Kontakt moja strona internetowa:
1. Wprowadzenie do C/C++
 Podstawy Programowania :: Roman Grundkiewicz :: 014 Zaj cia 1 1 rodowisko Dev-C++ 1. Wprowadzenie do C/C++ Uruchomienie ±rodowiska: Start Programs Developments Dev-C++. Nowy projekt: File New Project lub
Podstawy Programowania :: Roman Grundkiewicz :: 014 Zaj cia 1 1 rodowisko Dev-C++ 1. Wprowadzenie do C/C++ Uruchomienie ±rodowiska: Start Programs Developments Dev-C++. Nowy projekt: File New Project lub
Technologie Informacyjne
 Technologie Informacyjne Wykªad 5 Paweª Witkowski MIM UW Wiosna 2012 P. Witkowski (MIM UW) Technologie Informacyjne Wiosna 2012 1 / 1 WYSZUKAJ.PIONOWO WYSZUKAJ.PIONOWO(kryterium wyszukiwania; macierz;
Technologie Informacyjne Wykªad 5 Paweª Witkowski MIM UW Wiosna 2012 P. Witkowski (MIM UW) Technologie Informacyjne Wiosna 2012 1 / 1 WYSZUKAJ.PIONOWO WYSZUKAJ.PIONOWO(kryterium wyszukiwania; macierz;
Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY
 Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY PB 2 PB 1 Projekt z wyznaczania reduktów zbioru Liczba osób realizuj cych projekt: 1-2 osoby 1. Wczytanie danych w formatach arf,
Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY PB 2 PB 1 Projekt z wyznaczania reduktów zbioru Liczba osób realizuj cych projekt: 1-2 osoby 1. Wczytanie danych w formatach arf,
1 Metody iteracyjne rozwi zywania równania f(x)=0
 1 Metody iteracyjne rozwi zywania równania f()=0 1.1 Metoda bisekcji Zaªó»my,»e funkcja f jest ci gªa w [a 0, b 0 ]. Pierwiastek jest w przedziale [a 0, b 0 ] gdy f(a 0 )f(b 0 ) < 0. (1) Ustalmy f(a 0
1 Metody iteracyjne rozwi zywania równania f()=0 1.1 Metoda bisekcji Zaªó»my,»e funkcja f jest ci gªa w [a 0, b 0 ]. Pierwiastek jest w przedziale [a 0, b 0 ] gdy f(a 0 )f(b 0 ) < 0. (1) Ustalmy f(a 0
ANALIZA NUMERYCZNA. Grzegorz Szkibiel. Wiosna 2014/15
 ANALIZA NUMERYCZNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Metoda Eulera 3 1.1 zagadnienia brzegowe....................... 3 1.2 Zastosowanie ró»niczki...................... 4 1.3 Output do pliku
ANALIZA NUMERYCZNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Metoda Eulera 3 1.1 zagadnienia brzegowe....................... 3 1.2 Zastosowanie ró»niczki...................... 4 1.3 Output do pliku
Zbiory i odwzorowania
 Zbiory i odwzorowania 1 Sposoby okre±lania zbiorów 1) Zbiór wszystkich elementów postaci f(t), gdzie t przebiega zbiór T : {f(t); t T }. 2) Zbiór wszystkich elementów x zbioru X speªniaj cych warunek ϕ(x):
Zbiory i odwzorowania 1 Sposoby okre±lania zbiorów 1) Zbiór wszystkich elementów postaci f(t), gdzie t przebiega zbiór T : {f(t); t T }. 2) Zbiór wszystkich elementów x zbioru X speªniaj cych warunek ϕ(x):
Metodydowodzenia twierdzeń
 1 Metodydowodzenia twierdzeń Przez zdanie rozumiemy dowolne stwierdzenie, które jest albo prawdziwe, albo faªszywe (nie mo»e by ono jednocze±nie prawdziwe i faªszywe). Tradycyjnie b dziemy u»ywali maªych
1 Metodydowodzenia twierdzeń Przez zdanie rozumiemy dowolne stwierdzenie, które jest albo prawdziwe, albo faªszywe (nie mo»e by ono jednocze±nie prawdziwe i faªszywe). Tradycyjnie b dziemy u»ywali maªych
A = n. 2. Ka»dy podzbiór zbioru sko«czonego jest zbiorem sko«czonym. Dowody tych twierdze«(elementarne, lecz nieco nu» ce) pominiemy.
 Logika i teoria mnogo±ci, konspekt wykªad 12 Teoria mocy, cz ± II Def. 12.1 Ka»demu zbiorowi X przyporz dkowujemy oznaczany symbolem X obiekt zwany liczb kardynaln (lub moc zbioru X) w taki sposób,»e ta
Logika i teoria mnogo±ci, konspekt wykªad 12 Teoria mocy, cz ± II Def. 12.1 Ka»demu zbiorowi X przyporz dkowujemy oznaczany symbolem X obiekt zwany liczb kardynaln (lub moc zbioru X) w taki sposób,»e ta
Wst p do informatyki. Systemy liczbowe. Piotr Fulma«ski. 21 pa¹dziernika 2010. Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska
 Wst p do informatyki Systemy liczbowe Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 21 pa¹dziernika 2010 Spis tre±ci 1 Liczby i ich systemy 2 Rodzaje systemów liczbowych
Wst p do informatyki Systemy liczbowe Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 21 pa¹dziernika 2010 Spis tre±ci 1 Liczby i ich systemy 2 Rodzaje systemów liczbowych
Wyra»enia logicznie równowa»ne
 Wyra»enia logicznie równowa»ne Denicja. Wyra»enia rachunku zda«nazywamy logicznie równowa»nymi, gdy maj równe warto±ci logiczne dla dowolnych warto±ci logicznych zmiennych zdaniowych. 1 Przykªady: Wyra»enia
Wyra»enia logicznie równowa»ne Denicja. Wyra»enia rachunku zda«nazywamy logicznie równowa»nymi, gdy maj równe warto±ci logiczne dla dowolnych warto±ci logicznych zmiennych zdaniowych. 1 Przykªady: Wyra»enia
1 Bª dy i arytmetyka zmiennopozycyjna
 1 Bª dy i arytmetyka zmiennopozycyjna Liczby w pami ci komputera przedstawiamy w ukªadzie dwójkowym w postaci zmiennopozycyjnej Oznacza to,»e s one postaci ±m c, 01 m < 1, c min c c max, (1) gdzie m nazywamy
1 Bª dy i arytmetyka zmiennopozycyjna Liczby w pami ci komputera przedstawiamy w ukªadzie dwójkowym w postaci zmiennopozycyjnej Oznacza to,»e s one postaci ±m c, 01 m < 1, c min c c max, (1) gdzie m nazywamy
Statystyka. Šukasz Dawidowski. Instytut Matematyki, Uniwersytet l ski
 Statystyka Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Statystyka Statystyka: nauka zajmuj ca si liczbowym opisem zjawisk masowych oraz ich analizowaniem, zbiory informacji liczbowych. (Sªownik
Statystyka Šukasz Dawidowski Instytut Matematyki, Uniwersytet l ski Statystyka Statystyka: nauka zajmuj ca si liczbowym opisem zjawisk masowych oraz ich analizowaniem, zbiory informacji liczbowych. (Sªownik
Ÿ1 Oznaczenia, poj cia wst pne
 Ÿ1 Oznaczenia, poj cia wst pne Symbol sumy, j, k Z, j k: k x i = x j + x j+1 + + x k. i=j Przykªad 1.1. Oblicz 5 i=1 2i. Odpowied¹ 1.1. 5 i=1 2i = 2 1 + 2 2 + 2 3 + 2 4 + 2 5 = 2 + 4 + 8 + 16 + 32 = 62.
Ÿ1 Oznaczenia, poj cia wst pne Symbol sumy, j, k Z, j k: k x i = x j + x j+1 + + x k. i=j Przykªad 1.1. Oblicz 5 i=1 2i. Odpowied¹ 1.1. 5 i=1 2i = 2 1 + 2 2 + 2 3 + 2 4 + 2 5 = 2 + 4 + 8 + 16 + 32 = 62.
Obliczenia arytmetyczne. Konkatenacja pól. Aliasy kolumn. Aliasy tabel. Co dalej? Rozdział 4. Korzystanie z funkcji. Zastosowanie funkcji
 O autorze Wprowadzenie Rozdział 1. Relacyjne bazy danych i SQL Język i logika Definicja SQL Microsoft SQL Server, Oracle i MySQL Inne bazy danych Relacyjne bazy danych Klucze główne i obce Typy danych
O autorze Wprowadzenie Rozdział 1. Relacyjne bazy danych i SQL Język i logika Definicja SQL Microsoft SQL Server, Oracle i MySQL Inne bazy danych Relacyjne bazy danych Klucze główne i obce Typy danych
KLASYCZNE ZDANIA KATEGORYCZNE. ogólne - orzekaj co± o wszystkich desygnatach podmiotu szczegóªowe - orzekaj co± o niektórych desygnatach podmiotu
 ➏ Filozoa z elementami logiki Na podstawie wykªadów dra Mariusza Urba«skiego Sylogistyka Przypomnij sobie: stosunki mi dzy zakresami nazw KLASYCZNE ZDANIA KATEGORYCZNE Trzy znaczenia sªowa jest trzy rodzaje
➏ Filozoa z elementami logiki Na podstawie wykªadów dra Mariusza Urba«skiego Sylogistyka Przypomnij sobie: stosunki mi dzy zakresami nazw KLASYCZNE ZDANIA KATEGORYCZNE Trzy znaczenia sªowa jest trzy rodzaje
Twierdzenie Wainera. Marek Czarnecki. Warszawa, 3 lipca Wydziaª Filozoi i Socjologii Uniwersytet Warszawski
 Twierdzenie Wainera Marek Czarnecki Wydziaª Filozoi i Socjologii Uniwersytet Warszawski Wydziaª Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 3 lipca 2009 Motywacje Dla dowolnej
Twierdzenie Wainera Marek Czarnecki Wydziaª Filozoi i Socjologii Uniwersytet Warszawski Wydziaª Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 3 lipca 2009 Motywacje Dla dowolnej
wiczenie nr 3 z przedmiotu Metody prognozowania kwiecie«2015 r. Metodyka bada«do±wiadczalnych dr hab. in». Sebastian Skoczypiec Cel wiczenia Zaªo»enia
 wiczenie nr 3 z przedmiotu Metody prognozowania kwiecie«2015 r. wiczenia 1 2 do wiczenia 3 4 Badanie do±wiadczalne 5 pomiarów 6 7 Cel Celem wiczenia jest zapoznanie studentów z etapami przygotowania i
wiczenie nr 3 z przedmiotu Metody prognozowania kwiecie«2015 r. wiczenia 1 2 do wiczenia 3 4 Badanie do±wiadczalne 5 pomiarów 6 7 Cel Celem wiczenia jest zapoznanie studentów z etapami przygotowania i
System zarządzania bazą danych (SZBD) Proces przechodzenia od świata rzeczywistego do jego informacyjnej reprezentacji w komputerze nazywać będziemy
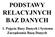 System zarządzania bazą danych (SZBD) Proces przechodzenia od świata rzeczywistego do jego informacyjnej reprezentacji w komputerze nazywać będziemy modelowaniem, a pewien dobrze zdefiniowany sposób jego
System zarządzania bazą danych (SZBD) Proces przechodzenia od świata rzeczywistego do jego informacyjnej reprezentacji w komputerze nazywać będziemy modelowaniem, a pewien dobrze zdefiniowany sposób jego
Wykªad 4. Funkcje wielu zmiennych.
 Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 4. Funkcje wielu zmiennych. Zbiory na pªaszczy¹nie i w przestrzeni.
Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 4. Funkcje wielu zmiennych. Zbiory na pªaszczy¹nie i w przestrzeni.
Logika dla matematyków i informatyków Wykªad 1
 Logika dla matematyków i informatyków Wykªad 1 Stanisªaw Goldstein Wydziaª Matematyki i Informatyki UŠ 16 lutego 2016 Wszech±wiat matematyczny skªada si wyª cznie ze zbiorów. Liczby naturalne s zdeniowane
Logika dla matematyków i informatyków Wykªad 1 Stanisªaw Goldstein Wydziaª Matematyki i Informatyki UŠ 16 lutego 2016 Wszech±wiat matematyczny skªada si wyª cznie ze zbiorów. Liczby naturalne s zdeniowane
1. Wprowadzenie do C/C++
 Podstawy Programowania - Roman Grundkiewicz - 013Z Zaj cia 1 1 rodowisko Dev-C++ 1. Wprowadzenie do C/C++ Uruchomienie ±rodowiska: Start Programs Developments Dev-C++. Nowy projekt: File New Project lub
Podstawy Programowania - Roman Grundkiewicz - 013Z Zaj cia 1 1 rodowisko Dev-C++ 1. Wprowadzenie do C/C++ Uruchomienie ±rodowiska: Start Programs Developments Dev-C++. Nowy projekt: File New Project lub
Indeksowane rodziny zbiorów
 Logika i teoria mnogo±ci, konspekt wykªad 7 Indeksowane rodziny zbiorów Niech X b dzie przestrzeni zbiorem, którego podzbiorami b d wszystkie rozpatrywane zbiory, R rodzin wszystkich podzbiorów X za± T
Logika i teoria mnogo±ci, konspekt wykªad 7 Indeksowane rodziny zbiorów Niech X b dzie przestrzeni zbiorem, którego podzbiorami b d wszystkie rozpatrywane zbiory, R rodzin wszystkich podzbiorów X za± T
Maszyny Turinga i problemy nierozstrzygalne. Maszyny Turinga i problemy nierozstrzygalne
 Maszyny Turinga Maszyna Turinga jest automatem ta±mowym, skª da si z ta±my (tablicy symboli) potencjalnie niesko«czonej w prawo, zakªadamy,»e w prawie wszystkich (tzn. wszystkich poza sko«czon liczb )
Maszyny Turinga Maszyna Turinga jest automatem ta±mowym, skª da si z ta±my (tablicy symboli) potencjalnie niesko«czonej w prawo, zakªadamy,»e w prawie wszystkich (tzn. wszystkich poza sko«czon liczb )
Podstawy modelowania w j zyku UML
 Podstawy modelowania w j zyku UML dr hab. Bo»ena Wo¹na-Szcze±niak Akademia im. Jan Dªugosza bwozna@gmail.com Wykªad 2 Zwi zki mi dzy klasami Asocjacja (ang. Associations) Uogólnienie, dziedziczenie (ang.
Podstawy modelowania w j zyku UML dr hab. Bo»ena Wo¹na-Szcze±niak Akademia im. Jan Dªugosza bwozna@gmail.com Wykªad 2 Zwi zki mi dzy klasami Asocjacja (ang. Associations) Uogólnienie, dziedziczenie (ang.
Aplikacje bazodanowe. Laboratorium 1. Dawid Poªap Aplikacje bazodanowe - laboratorium 1 Luty, 22, / 37
 Aplikacje bazodanowe Laboratorium 1 Dawid Poªap Aplikacje bazodanowe - laboratorium 1 Luty, 22, 2017 1 / 37 Plan 1 Informacje wst pne 2 Przygotowanie ±rodowiska do pracy 3 Poj cie bazy danych 4 Relacyjne
Aplikacje bazodanowe Laboratorium 1 Dawid Poªap Aplikacje bazodanowe - laboratorium 1 Luty, 22, 2017 1 / 37 Plan 1 Informacje wst pne 2 Przygotowanie ±rodowiska do pracy 3 Poj cie bazy danych 4 Relacyjne
Zadania z kolokwiów ze Wst pu do Informatyki. Semestr II.
 Zadania z kolokwiów ze Wst pu do Informatyki. Semestr II. Poni»sze zadania s wyborem zada«z kolokwiów ze Wst pu do Informatyki jakie przeprowadziªem w ci gu ostatnich lat. Marek Zawadowski Zadanie 1 Napisz
Zadania z kolokwiów ze Wst pu do Informatyki. Semestr II. Poni»sze zadania s wyborem zada«z kolokwiów ze Wst pu do Informatyki jakie przeprowadziªem w ci gu ostatnich lat. Marek Zawadowski Zadanie 1 Napisz
Aproksymacja funkcji metod najmniejszych kwadratów
 Aproksymacja funkcji metod najmniejszych kwadratów Teoria Interpolacja polega na znajdowaniu krzywej przechodz cej przez wszystkie w zªy. Zdarzaj si jednak sytuacje, w których dane te mog by obarczone
Aproksymacja funkcji metod najmniejszych kwadratów Teoria Interpolacja polega na znajdowaniu krzywej przechodz cej przez wszystkie w zªy. Zdarzaj si jednak sytuacje, w których dane te mog by obarczone
XVII Warmi«sko-Mazurskie Zawody Matematyczne
 1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
1 XVII Warmi«sko-Mazurskie Zawody Matematyczne Kategoria: klasa VIII szkoªy podstawowej i III gimnazjum Olsztyn, 16 maja 2019r. Zad. 1. Udowodnij,»e dla dowolnych liczb rzeczywistych x, y, z speªniaj cych
WST P DO TEORII INFORMACJI I KODOWANIA. Grzegorz Szkibiel. Wiosna 2013/14
 WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 2013/14 Spis tre±ci 1 Kodowanie i dekodowanie 4 1.1 Kodowanie a szyfrowanie..................... 4 1.2 Podstawowe poj cia........................
WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 2013/14 Spis tre±ci 1 Kodowanie i dekodowanie 4 1.1 Kodowanie a szyfrowanie..................... 4 1.2 Podstawowe poj cia........................
Macierze i Wyznaczniki
 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja 1. Tablic nast puj cej postaci a 11 a 12... a 1n a 21 a 22... a 2n A =... a m1 a m2... a mn nazywamy macierz o m wierszach i n kolumnach,
Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja 1. Tablic nast puj cej postaci a 11 a 12... a 1n a 21 a 22... a 2n A =... a m1 a m2... a mn nazywamy macierz o m wierszach i n kolumnach,
Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych.
 Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych. Denicja Mówimy,»e funkcja
Wykªad jest prowadzony w oparciu o podr cznik Analiza matematyczna 2. Denicje, twierdzenia, wzory M. Gewerta i Z. Skoczylasa. Wykªad 7. Ekstrema lokalne funkcji dwóch zmiennych. Denicja Mówimy,»e funkcja
Statystyka matematyczna
 Statystyka matematyczna Aleksandra Ki±lak-Malinowska akis@uwm.edu.pl http://wmii.uwm.edu.pl/ akis/ Czym zajmuje si statystyka? Statystyka zajmuje si opisywaniem i analiz zjawisk masowych otaczaj cej czªowieka
Statystyka matematyczna Aleksandra Ki±lak-Malinowska akis@uwm.edu.pl http://wmii.uwm.edu.pl/ akis/ Czym zajmuje si statystyka? Statystyka zajmuje si opisywaniem i analiz zjawisk masowych otaczaj cej czªowieka
Elementy geometrii w przestrzeni R 3
 Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
Elementy geometrii w przestrzeni R 3 Z.Šagodowski Politechnika Lubelska 29 maja 2016 Podstawowe denicje Wektorem nazywamy uporz dkowan par punktów (A,B) z których pierwszy nazywa si pocz tkiem a drugi
MiASI. Modelowanie analityczne. Piotr Fulma«ski. 18 stycznia Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska
 MiASI Modelowanie analityczne Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 18 stycznia 2010 Spis tre±ci 1 Czym jest modelowanie analityczne? 2 Podstawowe kategorie poj ciowe
MiASI Modelowanie analityczne Piotr Fulma«ski Wydziaª Matematyki i Informatyki, Uniwersytet Šódzki, Polska 18 stycznia 2010 Spis tre±ci 1 Czym jest modelowanie analityczne? 2 Podstawowe kategorie poj ciowe
CAŠKOWANIE METODAMI MONTE CARLO Janusz Adamowski
 III. CAŠKOWAIE METODAMI MOTE CARLO Janusz Adamowski 1 1 azwa metody Podstawowym zastosowaniem w zyce metody Monte Carlo (MC) jest opis zªo-»onych ukªadów zycznych o du»ej liczbie stopni swobody. Opis zªo»onych
III. CAŠKOWAIE METODAMI MOTE CARLO Janusz Adamowski 1 1 azwa metody Podstawowym zastosowaniem w zyce metody Monte Carlo (MC) jest opis zªo-»onych ukªadów zycznych o du»ej liczbie stopni swobody. Opis zªo»onych
Podstawy modelowania w j zyku UML
 Podstawy modelowania w j zyku UML dr hab. Bo»ena Wo¹na-Szcze±niak Akademia im. Jan Dªugosza bwozna@gmail.com Wykªad 8 Diagram pakietów I Diagram pakietów (ang. package diagram) jest diagramem strukturalnym,
Podstawy modelowania w j zyku UML dr hab. Bo»ena Wo¹na-Szcze±niak Akademia im. Jan Dªugosza bwozna@gmail.com Wykªad 8 Diagram pakietów I Diagram pakietów (ang. package diagram) jest diagramem strukturalnym,
Koªo Naukowe Robotyków KoNaR. Plan prezentacji. Wst p Rezystory Potencjomerty Kondensatory Podsumowanie
 Plan prezentacji Wst p Rezystory Potencjomerty Kondensatory Podsumowanie Wst p Motto W teorii nie ma ró»nicy mi dzy praktyk a teori. W praktyce jest. Rezystory Najwa»niejsze parametry rezystorów Rezystancja
Plan prezentacji Wst p Rezystory Potencjomerty Kondensatory Podsumowanie Wst p Motto W teorii nie ma ró»nicy mi dzy praktyk a teori. W praktyce jest. Rezystory Najwa»niejsze parametry rezystorów Rezystancja
Zdzisªaw Dzedzej, Katedra Analizy Nieliniowej pok. 611 Kontakt:
 Zdzisªaw Dzedzej, Katedra Analizy Nieliniowej pok. 611 Kontakt: zdzedzej@mif.pg.gda.pl www.mif.pg.gda.pl/homepages/zdzedzej () 5 pa¹dziernika 2016 1 / 1 Literatura podstawowa R. Rudnicki, Wykªady z analizy
Zdzisªaw Dzedzej, Katedra Analizy Nieliniowej pok. 611 Kontakt: zdzedzej@mif.pg.gda.pl www.mif.pg.gda.pl/homepages/zdzedzej () 5 pa¹dziernika 2016 1 / 1 Literatura podstawowa R. Rudnicki, Wykªady z analizy
Metody numeryczne. Wst p do metod numerycznych. Dawid Rasaªa. January 9, 2012. Dawid Rasaªa Metody numeryczne 1 / 9
 Metody numeryczne Wst p do metod numerycznych Dawid Rasaªa January 9, 2012 Dawid Rasaªa Metody numeryczne 1 / 9 Metody numeryczne Czym s metody numeryczne? Istota metod numerycznych Metody numeryczne s
Metody numeryczne Wst p do metod numerycznych Dawid Rasaªa January 9, 2012 Dawid Rasaªa Metody numeryczne 1 / 9 Metody numeryczne Czym s metody numeryczne? Istota metod numerycznych Metody numeryczne s
Dział 1. Działania na ułamkach zwykłych i dziesi tnych Ucze :
 Klasa VI Rozdział konieczne podstawowe rozszerzaj ce dopełniaj ce wykraczaj ce Dostrzeganie prawidłowo ci wykonuje działania na ułamkach dziesi tnych z pomoc kalkulatora (5.8); wykonuje działania na ułamkach
Klasa VI Rozdział konieczne podstawowe rozszerzaj ce dopełniaj ce wykraczaj ce Dostrzeganie prawidłowo ci wykonuje działania na ułamkach dziesi tnych z pomoc kalkulatora (5.8); wykonuje działania na ułamkach
Przeksztaªcenia liniowe
 Przeksztaªcenia liniowe Przykªady Pokaza,»e przeksztaªcenie T : R 2 R 2, postaci T (x, y) = (x + y, x 6y) jest przeksztaªceniem liniowym Sprawdzimy najpierw addytywno± przeksztaªcenia T Niech v = (x, y
Przeksztaªcenia liniowe Przykªady Pokaza,»e przeksztaªcenie T : R 2 R 2, postaci T (x, y) = (x + y, x 6y) jest przeksztaªceniem liniowym Sprawdzimy najpierw addytywno± przeksztaªcenia T Niech v = (x, y
Wektory w przestrzeni
 Wektory w przestrzeni Informacje pomocnicze Denicja 1. Wektorem nazywamy uporz dkowan par punktów. Pierwszy z tych punktów nazywamy pocz tkiem wektora albo punktem zaczepienia wektora, a drugi - ko«cem
Wektory w przestrzeni Informacje pomocnicze Denicja 1. Wektorem nazywamy uporz dkowan par punktów. Pierwszy z tych punktów nazywamy pocz tkiem wektora albo punktem zaczepienia wektora, a drugi - ko«cem
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Macierze. 1 Podstawowe denicje. 2 Rodzaje macierzy. Denicja
 Macierze 1 Podstawowe denicje Macierz wymiaru m n, gdzie m, n N nazywamy tablic liczb rzeczywistych (lub zespolonych) postaci a 11 a 1j a 1n A = A m n = [a ij ] m n = a i1 a ij a in a m1 a mj a mn W macierzy
Macierze 1 Podstawowe denicje Macierz wymiaru m n, gdzie m, n N nazywamy tablic liczb rzeczywistych (lub zespolonych) postaci a 11 a 1j a 1n A = A m n = [a ij ] m n = a i1 a ij a in a m1 a mj a mn W macierzy
WST P DO TEORII INFORMACJI I KODOWANIA. Grzegorz Szkibiel. Wiosna 2013/14
 WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 203/4 Spis tre±ci Kodowanie i dekodowanie 4. Kodowanie a szyfrowanie..................... 4.2 Podstawowe poj cia........................
WST P DO TEORII INFORMACJI I KODOWANIA Grzegorz Szkibiel Wiosna 203/4 Spis tre±ci Kodowanie i dekodowanie 4. Kodowanie a szyfrowanie..................... 4.2 Podstawowe poj cia........................
Wzorce projektowe kreacyjne
 Wzorce projektowe kreacyjne Krzysztof Ciebiera 14 pa¹dziernika 2005 1 1 Wst p 1.1 Podstawy Opis Ogólny Podstawowe informacje Wzorce kreacyjne sªu» do uabstrakcyjniania procesu tworzenia obiektów. Znaczenie
Wzorce projektowe kreacyjne Krzysztof Ciebiera 14 pa¹dziernika 2005 1 1 Wst p 1.1 Podstawy Opis Ogólny Podstawowe informacje Wzorce kreacyjne sªu» do uabstrakcyjniania procesu tworzenia obiektów. Znaczenie
Instrukcja obsługi Norton Commander (NC) wersja 4.0. Autor: mgr inż. Tomasz Staniszewski
 Instrukcja obsługi Norton Commander (NC) wersja 4.0 Autor: mgr inż. Tomasz Staniszewski ITM Zakład Technologii Maszyn, 15.10.2001 2 1.Uruchomienie programu Aby uruchomić program Norton Commander standardowo
Instrukcja obsługi Norton Commander (NC) wersja 4.0 Autor: mgr inż. Tomasz Staniszewski ITM Zakład Technologii Maszyn, 15.10.2001 2 1.Uruchomienie programu Aby uruchomić program Norton Commander standardowo
Programowanie funkcyjne. Wykªad 13
 Programowanie funkcyjne. Wykªad 13 Siªa wyrazu rachunku lambda Zdzisªaw Spªawski Zdzisªaw Spªawski: Programowanie funkcyjne. Wykªad 13, Siªa wyrazu rachunku lambda 1 Wst p Warto±ci logiczne Liczby naturalne
Programowanie funkcyjne. Wykªad 13 Siªa wyrazu rachunku lambda Zdzisªaw Spªawski Zdzisªaw Spªawski: Programowanie funkcyjne. Wykªad 13, Siªa wyrazu rachunku lambda 1 Wst p Warto±ci logiczne Liczby naturalne
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
Wnioskowanie Boolowskie i teoria zbiorów przybli»onych
 Wnioskowanie Boolowskie i teoria zbiorów przybli»onych 4 Zbiory przybli»one Wprowadzenie do teorii zbiorów przybli»onych Zªo»ono± problemu szukania reduktów 5 Wnioskowanie Boolowskie w obliczaniu reduktów
Wnioskowanie Boolowskie i teoria zbiorów przybli»onych 4 Zbiory przybli»one Wprowadzenie do teorii zbiorów przybli»onych Zªo»ono± problemu szukania reduktów 5 Wnioskowanie Boolowskie w obliczaniu reduktów
Materiaªy do Repetytorium z matematyki
 Materiaªy do Repetytorium z matematyki 0/0 Dziaªania na liczbach wymiernych i niewymiernych wiczenie Obliczy + 4 + 4 5. ( + ) ( 4 + 4 5). ( : ) ( : 4) 4 5 6. 7. { [ 7 4 ( 0 7) ] ( } : 5) : 0 75 ( 8) (
Materiaªy do Repetytorium z matematyki 0/0 Dziaªania na liczbach wymiernych i niewymiernych wiczenie Obliczy + 4 + 4 5. ( + ) ( 4 + 4 5). ( : ) ( : 4) 4 5 6. 7. { [ 7 4 ( 0 7) ] ( } : 5) : 0 75 ( 8) (
Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY
 Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY PB 2 PB 1 Projekt z grupowania danych - Rough k-medoids Liczba osób realizuj cych projekt: 1 osoba 1. Wczytanie danych w formatach
Granular Computing 9999 pages 15 METODY SZTUCZNEJ INTELIGENCJI - PROJEKTY PB 2 PB 1 Projekt z grupowania danych - Rough k-medoids Liczba osób realizuj cych projekt: 1 osoba 1. Wczytanie danych w formatach
PRAWA ZACHOWANIA. Podstawowe terminy. Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc
 PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
PRAWA ZACHOWANIA Podstawowe terminy Cia a tworz ce uk ad mechaniczny oddzia ywuj mi dzy sob i z cia ami nie nale cymi do uk adu za pomoc a) si wewn trznych - si dzia aj cych na dane cia o ze strony innych
1 Klasy. 1.1 Denicja klasy. 1.2 Skªadniki klasy.
 1 Klasy. Klasa to inaczej mówi c typ który podobnie jak struktura skªada si z ró»nych typów danych. Tworz c klas programista tworzy nowy typ danych, który mo»e by modelem rzeczywistego obiektu. 1.1 Denicja
1 Klasy. Klasa to inaczej mówi c typ który podobnie jak struktura skªada si z ró»nych typów danych. Tworz c klas programista tworzy nowy typ danych, który mo»e by modelem rzeczywistego obiektu. 1.1 Denicja
przewidywania zapotrzebowania na moc elektryczn
 do Wykorzystanie do na moc elektryczn Instytut Techniki Cieplnej Politechnika Warszawska Slide 1 of 20 do Coraz bardziej popularne staj si zagadnienia zwi zane z prac ¹ródªa energii elektrycznej (i cieplnej)
do Wykorzystanie do na moc elektryczn Instytut Techniki Cieplnej Politechnika Warszawska Slide 1 of 20 do Coraz bardziej popularne staj si zagadnienia zwi zane z prac ¹ródªa energii elektrycznej (i cieplnej)
Funkcje, wielomiany. Informacje pomocnicze
 Funkcje, wielomiany Informacje pomocnicze Przydatne wzory: (a + b) 2 = a 2 + 2ab + b 2 (a b) 2 = a 2 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (a b) 3 = a 3 3a 2 b + 3ab 2 b 3 a 2 b 2 = (a + b)(a
Funkcje, wielomiany Informacje pomocnicze Przydatne wzory: (a + b) 2 = a 2 + 2ab + b 2 (a b) 2 = a 2 2ab + b 2 (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 (a b) 3 = a 3 3a 2 b + 3ab 2 b 3 a 2 b 2 = (a + b)(a
Rachunek zda«. Relacje. 2018/2019
 Rachunek zda«. Relacje. 2018/2019 Zdanie logiczne. Zdaniem logicznym nazywamy ka»de wyra»enie, któremu mo»na przyporz dkowa jedn z dwóch warto±ci logicznych: 0 czyli faªsz b d¹ 1 czyli prawda. Zdanie logiczne.
Rachunek zda«. Relacje. 2018/2019 Zdanie logiczne. Zdaniem logicznym nazywamy ka»de wyra»enie, któremu mo»na przyporz dkowa jedn z dwóch warto±ci logicznych: 0 czyli faªsz b d¹ 1 czyli prawda. Zdanie logiczne.
Matematyka dyskretna dla informatyków
 Matematyka dyskretna dla informatyków Cz ± I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szyma«ski Uniwersytet im. Adama Mickiewicza Pozna«2007 2 Podstawowe zasady i prawa przeliczania
Matematyka dyskretna dla informatyków Cz ± I: Elementy kombinatoryki Jerzy Jaworski Zbigniew Palka Jerzy Szyma«ski Uniwersytet im. Adama Mickiewicza Pozna«2007 2 Podstawowe zasady i prawa przeliczania
Programowanie i struktury danych 1 / 44
 Programowanie i struktury danych 1 / 44 Lista dwukierunkowa Lista dwukierunkowa to liniowa struktura danych skªadaj ca si z ci gu elementów, z których ka»dy pami ta swojego nast pnika i poprzednika. Operacje
Programowanie i struktury danych 1 / 44 Lista dwukierunkowa Lista dwukierunkowa to liniowa struktura danych skªadaj ca si z ci gu elementów, z których ka»dy pami ta swojego nast pnika i poprzednika. Operacje
PRZYPOMNIENIE Ka»d przestrze«wektorow V, o wymiarze dim V = n < nad ciaªem F mo»na jednoznacznie odwzorowa na przestrze«f n n-ek uporz dkowanych:
 Plan Spis tre±ci 1 Homomorzm 1 1.1 Macierz homomorzmu....................... 2 1.2 Dziaªania............................... 3 2 Ukªady równa«6 3 Zadania 8 1 Homomorzm PRZYPOMNIENIE Ka»d przestrze«wektorow
Plan Spis tre±ci 1 Homomorzm 1 1.1 Macierz homomorzmu....................... 2 1.2 Dziaªania............................... 3 2 Ukªady równa«6 3 Zadania 8 1 Homomorzm PRZYPOMNIENIE Ka»d przestrze«wektorow
Ukªady równa«liniowych
 dr Krzysztof yjewski Mechatronika; S-I 0 in» 7 listopada 206 Ukªady równa«liniowych Informacje pomocnicze Denicja Ogólna posta ukªadu m równa«liniowych z n niewiadomymi x, x, x n, gdzie m, n N jest nast
dr Krzysztof yjewski Mechatronika; S-I 0 in» 7 listopada 206 Ukªady równa«liniowych Informacje pomocnicze Denicja Ogólna posta ukªadu m równa«liniowych z n niewiadomymi x, x, x n, gdzie m, n N jest nast
Zastosowania matematyki
 Zastosowania matematyki Monika Bartkiewicz 1 / 126 ...czy«cie dobrze i po»yczajcie niczego si nie spodziewaj c(šk. 6,34-35) Zagadnienie pobierania procentu jest tak stare jak gospodarka pieni»na. Procent
Zastosowania matematyki Monika Bartkiewicz 1 / 126 ...czy«cie dobrze i po»yczajcie niczego si nie spodziewaj c(šk. 6,34-35) Zagadnienie pobierania procentu jest tak stare jak gospodarka pieni»na. Procent
Oba zbiory s uporz dkowane liniowo. Badamy funkcj w pobli»u kresów dziedziny. Pewne punkty szczególne (np. zmiana denicji funkcji).
 Plan Spis tre±ci 1 Granica 1 1.1 Po co?................................. 1 1.2 Denicje i twierdzenia........................ 4 1.3 Asymptotyka, granice niewªa±ciwe................. 7 2 Asymptoty 8 2.1
Plan Spis tre±ci 1 Granica 1 1.1 Po co?................................. 1 1.2 Denicje i twierdzenia........................ 4 1.3 Asymptotyka, granice niewªa±ciwe................. 7 2 Asymptoty 8 2.1
Przetwarzanie sygnaªów
 Przetwarzanie sygnaªów Laboratorium 1 - wst p do C# Dawid Poªap Przetwarzanie sygnaªów Pa¹dziernik, 2018 1 / 17 Czego mo»na oczekiwa wzgl dem programowania w C# na tych laboratoriach? Dawid Poªap Przetwarzanie
Przetwarzanie sygnaªów Laboratorium 1 - wst p do C# Dawid Poªap Przetwarzanie sygnaªów Pa¹dziernik, 2018 1 / 17 Czego mo»na oczekiwa wzgl dem programowania w C# na tych laboratoriach? Dawid Poªap Przetwarzanie
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej
 Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Opis programu do wizualizacji algorytmów z zakresu arytmetyki komputerowej 3.1 Informacje ogólne Program WAAK 1.0 służy do wizualizacji algorytmów arytmetyki komputerowej. Oczywiście istnieje wiele narzędzi
Funkcje wielu zmiennych
 dr Krzysztof yjewski Informatyka I rok I 0 in» 12 stycznia 2016 Funkcje wielu zmiennych Informacje pomocnicze Denicja 1 Niech funkcja f(x y) b dzie okre±lona przynajmniej na otoczeniu punktu (x 0 y 0 )
dr Krzysztof yjewski Informatyka I rok I 0 in» 12 stycznia 2016 Funkcje wielu zmiennych Informacje pomocnicze Denicja 1 Niech funkcja f(x y) b dzie okre±lona przynajmniej na otoczeniu punktu (x 0 y 0 )
Ekonometria - wykªad 8
 Ekonometria - wykªad 8 3.1 Specykacja i werykacja modelu liniowego dobór zmiennych obja±niaj cych - cz ± 1 Barbara Jasiulis-Goªdyn 11.04.2014, 25.04.2014 2013/2014 Wprowadzenie Ideologia Y zmienna obja±niana
Ekonometria - wykªad 8 3.1 Specykacja i werykacja modelu liniowego dobór zmiennych obja±niaj cych - cz ± 1 Barbara Jasiulis-Goªdyn 11.04.2014, 25.04.2014 2013/2014 Wprowadzenie Ideologia Y zmienna obja±niana
Systemy baz danych. mgr inż. Sylwia Glińska
 Systemy baz danych Wykład 1 mgr inż. Sylwia Glińska Baza danych Baza danych to uporządkowany zbiór danych z określonej dziedziny tematycznej, zorganizowany w sposób ułatwiający do nich dostęp. System zarządzania
Systemy baz danych Wykład 1 mgr inż. Sylwia Glińska Baza danych Baza danych to uporządkowany zbiór danych z określonej dziedziny tematycznej, zorganizowany w sposób ułatwiający do nich dostęp. System zarządzania
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA. W obu podpunktach zakªadamy,»e kolejno± ta«ców jest wa»na.
 Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zadanko 1 (12p.) Na imprezie w Noc Kupaªy s 44 dziewczyny. Nosz one 11 ró»nych imion, a dla ka»dego imienia s dokªadnie 4 dziewczyny o tym imieniu przy czym ka»da
Zad. 1 Zad. 2 Zad. 3 Zad. 4 Zad. 5 SUMA Zadanko 1 (12p.) Na imprezie w Noc Kupaªy s 44 dziewczyny. Nosz one 11 ró»nych imion, a dla ka»dego imienia s dokªadnie 4 dziewczyny o tym imieniu przy czym ka»da
System Informatyczny CELAB. Przygotowanie programu do pracy - Ewidencja Czasu Pracy
 Instrukcja obsługi programu 2.11. Przygotowanie programu do pracy - ECP Architektura inter/intranetowa System Informatyczny CELAB Przygotowanie programu do pracy - Ewidencja Czasu Pracy Spis treści 1.
Instrukcja obsługi programu 2.11. Przygotowanie programu do pracy - ECP Architektura inter/intranetowa System Informatyczny CELAB Przygotowanie programu do pracy - Ewidencja Czasu Pracy Spis treści 1.
Matematyka dyskretna dla informatyków
 UNIWERSYTET IM. ADAMA MICKIEWICZA W POZNANIU Jerzy Jaworski, Zbigniew Palka, Jerzy Szyma«ski Matematyka dyskretna dla informatyków uzupeænienia Pozna«007 A Notacja asymptotyczna Badaj c du»e obiekty kombinatoryczne
UNIWERSYTET IM. ADAMA MICKIEWICZA W POZNANIU Jerzy Jaworski, Zbigniew Palka, Jerzy Szyma«ski Matematyka dyskretna dla informatyków uzupeænienia Pozna«007 A Notacja asymptotyczna Badaj c du»e obiekty kombinatoryczne
Macierze i Wyznaczniki
 dr Krzysztof yjewski Mechatronika; S-I.in». 5 pa¹dziernika 6 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja. Tablic nast puj cej postaci a a... a n a a... a n A =... a m a m...
dr Krzysztof yjewski Mechatronika; S-I.in». 5 pa¹dziernika 6 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja. Tablic nast puj cej postaci a a... a n a a... a n A =... a m a m...
Zestaw 1 ZESTAWY A. a 1 a 2 + a 3 ± a n, gdzie skªadnik a n jest odejmowany, gdy n jest liczb parzyst oraz dodawany w przeciwnym.
 ZESTAWY A Zestaw 1 Organizacja plików: Wszystkie pliki oddawane do sprawdzenia nale»y zapisa we wspólnym folderze o nazwie b d cej numerem indeksu, umieszczonym na pulpicie. Oddajemy tylko ¹ródªa programów
ZESTAWY A Zestaw 1 Organizacja plików: Wszystkie pliki oddawane do sprawdzenia nale»y zapisa we wspólnym folderze o nazwie b d cej numerem indeksu, umieszczonym na pulpicie. Oddajemy tylko ¹ródªa programów
det A := a 11, ( 1) 1+j a 1j det A 1j, a 11 a 12 a 21 a 22 Wn. 1 (Wyznacznik macierzy stopnia 2:). = a 11a 22 a 33 +a 12 a 23 a 31 +a 13 a 21 a 32
 Wyznacznik Def Wyznacznikiem macierzy kwadratowej nazywamy funkcj, która ka»dej macierzy A = (a ij ) przyporz dkowuje liczb det A zgodnie z nast puj cym schematem indukcyjnym: Dla macierzy A = (a ) stopnia
Wyznacznik Def Wyznacznikiem macierzy kwadratowej nazywamy funkcj, która ka»dej macierzy A = (a ij ) przyporz dkowuje liczb det A zgodnie z nast puj cym schematem indukcyjnym: Dla macierzy A = (a ) stopnia
Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH"
 Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH" Autorzy: Adrian Stanula Grzegorz Stopa Mariusz Sasko Data: 14 XI 2008 rok Spis tre±ci 1 Sformuªowanie zadania projektowego.
Projekt konceptualny z Baz Danych "Centralny system zarz dzania salami na AGH" Autorzy: Adrian Stanula Grzegorz Stopa Mariusz Sasko Data: 14 XI 2008 rok Spis tre±ci 1 Sformuªowanie zadania projektowego.
Wykªad 6: Model logitowy
 Wykªad 6: Model logitowy Ekonometria Stosowana SGH Model logitowy 1 / 18 Plan wicze«1 Modele zmiennej jako±ciowej idea 2 Model logitowy Specykacja i interpretacja parametrów Dopasowanie i restrykcje 3
Wykªad 6: Model logitowy Ekonometria Stosowana SGH Model logitowy 1 / 18 Plan wicze«1 Modele zmiennej jako±ciowej idea 2 Model logitowy Specykacja i interpretacja parametrów Dopasowanie i restrykcje 3
Instalacja programu. Omówienie programu. Jesteś tu: Bossa.pl
 Jesteś tu: Bossa.pl Program Quotes Update to niewielkie narzędzie ułatwiające pracę inwestora. Jego celem jest szybka i łatwa aktualizacja plików lokalnych z historycznymi notowaniami spółek giełdowych
Jesteś tu: Bossa.pl Program Quotes Update to niewielkie narzędzie ułatwiające pracę inwestora. Jego celem jest szybka i łatwa aktualizacja plików lokalnych z historycznymi notowaniami spółek giełdowych
Wojewódzki Konkurs Matematyczny
 sumaryczna liczba punktów (wypeªnia sprawdzaj cy) Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów 13 luty 2014 Czas 90 minut 1. Otrzymujesz do rozwi zania 10 zada«zamkni tych oraz 5 zada«otwartych.
sumaryczna liczba punktów (wypeªnia sprawdzaj cy) Wojewódzki Konkurs Matematyczny dla uczniów gimnazjów 13 luty 2014 Czas 90 minut 1. Otrzymujesz do rozwi zania 10 zada«zamkni tych oraz 5 zada«otwartych.
Lekcja 12 - POMOCNICY
 Lekcja 12 - POMOCNICY 1 Pomocnicy Pomocnicy, jak sama nazwa wskazuje, pomagaj Baltiemu w programach wykonuj c cz ± czynno±ci. S oni szczególnie pomocni, gdy chcemy ci g polece«wykona kilka razy w programie.
Lekcja 12 - POMOCNICY 1 Pomocnicy Pomocnicy, jak sama nazwa wskazuje, pomagaj Baltiemu w programach wykonuj c cz ± czynno±ci. S oni szczególnie pomocni, gdy chcemy ci g polece«wykona kilka razy w programie.
Ekonometria Bayesowska
 Ekonometria Bayesowska Wykªad 9: Metody numeryczne: MCMC Andrzej Torój 1 / 17 Plan wykªadu Wprowadzenie 1 Wprowadzenie 3 / 17 Plan prezentacji Wprowadzenie 1 Wprowadzenie 3 3 / 17 Zastosowanie metod numerycznych
Ekonometria Bayesowska Wykªad 9: Metody numeryczne: MCMC Andrzej Torój 1 / 17 Plan wykªadu Wprowadzenie 1 Wprowadzenie 3 / 17 Plan prezentacji Wprowadzenie 1 Wprowadzenie 3 3 / 17 Zastosowanie metod numerycznych
Teoretyczne Podstawy Informatyki
 Instytut Informatyki Stosowanej Teoretyczne Podstawy Informatyki Wykªad 2. J zyki i gramatyki formalne Zdzisªaw Spªawski Zdzisªaw Spªawski: Teoretyczne Podstawy Informatyki, Wykªad 2. J zyki i gramatyki
Instytut Informatyki Stosowanej Teoretyczne Podstawy Informatyki Wykªad 2. J zyki i gramatyki formalne Zdzisªaw Spªawski Zdzisªaw Spªawski: Teoretyczne Podstawy Informatyki, Wykªad 2. J zyki i gramatyki
Listy Inne przykªady Rozwi zywanie problemów. Listy w Mathematice. Marcin Karcz. Wydziaª Matematyki, Fizyki i Informatyki.
 Wydziaª Matematyki, Fizyki i Informatyki 10 marca 2008 Spis tre±ci Listy 1 Listy 2 3 Co to jest lista? Listy List w Mathematice jest wyra»enie oddzielone przecinkami i zamkni te w { klamrach }. Elementy
Wydziaª Matematyki, Fizyki i Informatyki 10 marca 2008 Spis tre±ci Listy 1 Listy 2 3 Co to jest lista? Listy List w Mathematice jest wyra»enie oddzielone przecinkami i zamkni te w { klamrach }. Elementy
Lekcja 9 - LICZBY LOSOWE, ZMIENNE
 Lekcja 9 - LICZBY LOSOWE, ZMIENNE I STAŠE 1 Liczby losowe Czasami spotkamy si z tak sytuacj,»e b dziemy potrzebowa by program za nas wylosowaª jak ± liczb. U»yjemy do tego polecenia: - liczba losowa Sprawd¹my
Lekcja 9 - LICZBY LOSOWE, ZMIENNE I STAŠE 1 Liczby losowe Czasami spotkamy si z tak sytuacj,»e b dziemy potrzebowa by program za nas wylosowaª jak ± liczb. U»yjemy do tego polecenia: - liczba losowa Sprawd¹my
Analizy populacyjne, ªadunki atomowe
 Dodatek do w. # 3 i # 4 Šadunki atomowe, analizy populacyjne Q A = Z A N A Q A efektywny ªadunek atomu A, Z A N A liczba porz dkowa dla atomu A (czyli ªadunek j dra) efektywna liczba elektronów przypisana
Dodatek do w. # 3 i # 4 Šadunki atomowe, analizy populacyjne Q A = Z A N A Q A efektywny ªadunek atomu A, Z A N A liczba porz dkowa dla atomu A (czyli ªadunek j dra) efektywna liczba elektronów przypisana
Projektowanie bazy danych
 Projektowanie bazy danych Pierwszą fazą tworzenia projektu bazy danych jest postawienie definicji celu, założeo wstępnych i określenie podstawowych funkcji aplikacji. Każda baza danych jest projektowana
Projektowanie bazy danych Pierwszą fazą tworzenia projektu bazy danych jest postawienie definicji celu, założeo wstępnych i określenie podstawowych funkcji aplikacji. Każda baza danych jest projektowana
Strategia czy intuicja?
 Strategia czy intuicja czyli o grach niesko«czonych Instytut Matematyki Uniwersytetu Warszawskiego Grzegorzewice, 29 sierpnia 2009 Denicja gry Najprostszy przypadek: A - zbiór (na ogóª co najwy»ej przeliczalny),
Strategia czy intuicja czyli o grach niesko«czonych Instytut Matematyki Uniwersytetu Warszawskiego Grzegorzewice, 29 sierpnia 2009 Denicja gry Najprostszy przypadek: A - zbiór (na ogóª co najwy»ej przeliczalny),
Bazy danych Podstawy teoretyczne
 Pojcia podstawowe Baza Danych jest to zbiór danych o okrelonej strukturze zapisany w nieulotnej pamici, mogcy zaspokoi potrzeby wielu u!ytkowników korzystajcych z niego w sposóbs selektywny w dogodnym
Pojcia podstawowe Baza Danych jest to zbiór danych o okrelonej strukturze zapisany w nieulotnej pamici, mogcy zaspokoi potrzeby wielu u!ytkowników korzystajcych z niego w sposóbs selektywny w dogodnym
ARYTMETYKA MODULARNA. Grzegorz Szkibiel. Wiosna 2014/15
 ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
ARYTMETYKA MODULARNA Grzegorz Szkibiel Wiosna 2014/15 Spis tre±ci 1 Denicja kongruencji i jej podstawowe wªasno±ci 3 2 Systemy pozycyjne 8 3 Elementy odwrotne 12 4 Pewne zastosowania elementów odwrotnych
