Zajęcia 8 - Równoważność warunków oprocentowania
|
|
|
- Roman Karpiński
- 9 lat temu
- Przeglądów:
Transkrypt
1 Zajęcia 8 - Równoważność warunków oprocentowania Zadanie 1 Mając roczną stopę oprocentowania prostego 18% wyznaczyć równoważną stopę: 1. miesięczną. 2. tygodniową letnią. Uzasadnić wyniki. Czy czas oprocentowania miał wpływ na wynik? Zadanie 2 Bank A stosuje oprocentowanie półroczne składane przy stopie nominalnej 12%, zaś bank B oprocentowanie kwartalne składane przy stopie nominalnej 12%. Bez użycia kalkulatora zbadać, czy warunki oprocentowania proponowane przez te banki są równoważne. Zadanie 3 W banku A obowiązuje półroczna kapitalizacja odsetek przy stopie nominalnej 18%, w banku B obowiązuje kwartalna kapitalizacji odsetek przy stopie nominalnej r. Ile musi wynosić stopa r, aby warunki oprocentowania w banku A i B były równoważne? Zadanie 4 Mając roczną stopę oprocentowania składanego rocznego 11% wyznaczyć równoważną stopę: 1. miesięczną. 2. tygodniową letnią. Wyznaczyć stopy nominalne w każdym z trzech podpunktów i omówić zależność. Zadanie 5 Mając półroczną stopę 6% wyznaczyć równoważną stopę kwartalną w modelu oprocentowania składanego. Zadanie 6 Przy użyciu rocznego czynnika akumulacji wykazać nierównoważność stóp oprocentowania składanego i 4 = 3, 3% oraz i 12 = 1, 3%, a następnie obliczyć: 1. stopę i 12 równoważną stopie i 4 = 3, 3%. 2. stopę i 4 równoważną stopie i 12 = 1, 3% Zadanie 7 Model oprocentowania półrocznego składanego ze stopą nominalną 23% zamienić na model oprocentowania 1. kwartalnego składanego 2. rocznego składanego 1
2 zachowując równoważność warunków oprocentowania. Zadanie 8 Mając nominalną stopę 19% w modelu oprocentowania składanego z dzienną kapitalizacją odsetek wyznaczyć nominalną stopę oprocentowania składanego rocznego z zachowaniem równoważności warunków oprocentowania. Zadanie 9 Obliczyć 1. tygodniową 2. miesięczną 3. roczną stopę równoważną stopie kwartalnej 3% w modelu oprocentowania składanego. Zadanie 10 Sprawdzić, czy równoważne są następujący stopy oprocentowania składanego: kwartalna stopa 3% oraz półroczna stopa 6%. Zadanie 11 Zbadać bez użycia kalkulatora równoważność warunków oprocentowania przy stopach rocznych 12% w kapitalizacji rocznej i 12% w kapitalizacji ciągłej. Zadanie 12 Zbadać bez użycia kalkulatora równoważność warunków oprocentowania przy stopach rocznych 12% i 12, 5% w kapitalizacji ciągłej. Zadanie 13 Dla stopy rocznej 24% oprocentowania rocznego obliczyć równoważną stopę podokresową oprocentowania 1. półrocznego, 2. kwartalnego, 3. miesięcznego, 4. ciągłego, a następnie przy użyciu stopy podokresowej obliczyć dwuletnie odsetki od kapitału 1000 zł. Zadanie 14 Jeśli roczna stopa procentowa w modelu kaptalizacji ciągłej wynosi 10%, to jakie powinny być równoważne stopy nominalne oraz roczne dla kapitalizacji 1. miesięcznej? 2. półrocznej? 2
3 Stopa efektywna Zadanie 15 For the $10000 investment given in Example 1 find the effective rate of interest for each of the fours years. Zadanie 16 Assume that F n = n. Find r ef,5, r ef,10. Zadanie 17 If F 4 = 1000 and r ef,n =.01n, where n is a positive integer, find F 7. Zadanie 18 W modelu oprocentowania prostego wyznaczyć efektywną stopę procentową w każdym roku trzyletniej inwestycji, jeśli roczna stopa (nominalna) wynosi 10% Zadanie 19 Wyznaczyć stopę efektywną w modelu oprocentowania składanego przy kwartalnej kapitalizacji odsetek i stopie nominalnej 9% oraz podać roczny czynnik akumulacji. Zadanie 20 Zamierzamy wpłacić na rachunek bankowy kwotę , 00 zł. Bank A oferuje nominalną stopę r A = 3% przy półrocznej kapitalizacji odsetek, bank B oferuje nominalną stopę r B = 2, 8% przy dziennej kapitalizacji odsetek, zaś bank C oferuje nominalną stopę r C = 2, 4% przy miesięcznej kapitalizacji odsetek. Wyznaczając stopę efektywną sprawdzić, który bank oferuje najkorzystniejsze warunki oprocentowania? Zadanie 21 Pewien kapitał ulokowano na procent składany. Kapitalizacja odsetek następuje pod koniec każdego kwartału, a efektywna stopa procentowa jest równa 13%. Ile wynosi równoważna kwartalna stopa procentowa a ile nominalna? Zadanie 22 Efektywna stopa procentowa wynosi 14%. Obliczyć równoważną okresową i nominalną stopę oprocentowania składanego przy kapitalizacji a) co kwartał. b) co 1,5 miesiąca. c) ciągłej. Zadanie 23 Dla każdej stopy oprocentowania składanego: i 4 = 5%, i 1 = 20%, i 2 = 10, 5%, r ef = 19%, r c = 19% obliczyć stopę efektywną. Zadanie 24 Pewien kapitał złożono na procent składany. Kapitalizacja odsetek następuje co kwartał, a efektywna stopa procentowa jest równa 13%. Ile wynosi zgodna stopa procentowa odpowiadająca tej efektywnej a ile nominalna? Zadanie 25 Wyznaczyć stopę efektywną dla rocznej stopy 11, 9% przy ciągłej kapitalizacji odsetek. Zadanie 26 Dane są stopy oprocentowania składanego r 4, i 1, r c, i 2, przy czym r 4 = ln(1 + i 1 ) = r c = i 2 = 12%. 3
4 a) Co oznacza każda z tych stóp? b) Dla każdej stopy podać (obliczyć) stopę nominalną, roczny czynnik akumulacji, stopę efektywną oraz równoważną stopę oprocentowania ciągłego. Zadanie 27 Firma zamierza sprzedać nieruchomość drogą przetargu. Otrzymała oferty od trzech nabywców. Pierwszy z nich chciałby ją kupić natychmiast regulując należność gotówką w wysokości zł, drugi proponuje sume zł przy uregulowaniu należności za rok, trzeci zaś gotów jest zapłacić zł, ale po upływie 3 lat. Którą ofertę powinna wybrać firma, jeśli istnieje możliwość ulokowania gotówki w banku na procent składany 12% w skali roku? Zadanie 28 Bank A oferuje rachunek oszczędnościowy oprocentowany 4, 15% w skali roku przy miesięcznej kapitalizacji odsetek. Bank B oferuje lokatę terminową 6-miesięczną oprocentowaną 4, 20% w skali roku. Która z ofert bankowych jest korzystniejsza, jeśli w ciągu 6 miesięcy nie planujemy żadnej wypłaty? Zadanie 29 Assume that F n = 100(1, 1) n. Find r ef,5, r ef,10. Zadanie 30 Jaka jest efektywna i nominalna stopa procentowa w modelu kapitalizacji ciągłej, jeśli roczny czynnk akumulacji wynosi 1, 2? Zadanie 31 Jaka jest efektywna i nominalna stopa procentowa w modelu kapitalizacji miesięcznej, jeśli roczny czynnik akumulacji wynosi 1, 11? Zadanie 32 Wyznaczyć stopę efektywną dla nominalnej stopy procentowej 17% przy prostej kapitalizacji odsetek? Zadanie 33 Pewien kapitał złożono na procent składany. Kapitalizacja odsetek następuje co miesiąc, a efektywna stopa procentowa wynosi 10, 5%. Ile wynosi równoważna stopa miesięczna a ile nominalna? Zadanie 34 Find the accumulated value of $500 invested for five years at 8% per annum convertible quarterly. Find r ef,1, r ef,5 Zadanie 35 Wyznaczyć stopę efektywną dla każdego z czterech lat inwestycji przy rocznej stopie procentowej 12% i odsetkach prostych? Zadanie 36 Kwotę zł ulokowano na rachunku na okres 2 lat. Nominalna stopa procentowa wynosiła 9%. Jaki będzie stan konta po tym okresie, jeśli kapitalizacja odsetek miała miejsce pod koniec każdego kwartału. Wyznacz efektywną stopę dla każdego roku. Zadanie 37 Złożono w banku kapitał w wysokości , 00 zł. Po upływie 10 lat kwota kapitału wzrosła do , 00 jp. Jaka będzie kwota kapitału po upływie dalszych 4 lat? Zadanie 38 Ulokowano w banku depozyt w wysokości zł na 14% w skali roku przy kwartalnej kapitalizacji odsetek. Czy warunki oprocentowania się pogorszą, jeśli stopa procentowa będzie obniżona o 1, 4 pkt procentowego i kapitalizacja kwartalna zostanie zastąpiona kapitalizacją miesięczną? Oblicz zysk bądź stratę właściciela depozytu. 4
5 Zadanie 39 Bank A oferuje rachunek oszczędnościowy oprocentowany 5, 25% w skali roku przy dziennej kapitalizacji odsetek. Bank B oferuje lokatę terminową 3- miesięczną oprocentowaną 6% w skali roku. Która z ofert bankowych jest korzystniejsza, jeśli w ciągu roku nie planujemy żadnej wypłaty? 5
Zadania do wykładu Matematyka bankowa 1
 Zadania do wykładu Matematyka bankowa 1 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Matematyka bankowa 1 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Matematyka bankowa 1
 Zadania do wykładu Matematyka bankowa 1 Dorota Klim Instytut Matematyki i Informatyki, Państwowej Wyższej Szkoły Zawodowej w Płocku E-mail address: klimdr@math.uni.ldz.pl http://math.uni.lodz.pl/ klimdr/
Zadania do wykładu Matematyka bankowa 1 Dorota Klim Instytut Matematyki i Informatyki, Państwowej Wyższej Szkoły Zawodowej w Płocku E-mail address: klimdr@math.uni.ldz.pl http://math.uni.lodz.pl/ klimdr/
Zadania do wykładu Matematyka bankowa 1
 Zadania do wykładu Matematyka bankowa 1 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Matematyka bankowa 1 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zajęcia 1. Pojęcia: - Kapitalizacja powiększenie kapitału o odsetki, które zostały przez ten kapitał wygenerowane
 Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
Zajęcia 1 Pojęcia: - Procent setna część całości; w matematyce finansowej korzyści płynące z użytkowania kapitału (pojęcie używane zamiennie z terminem: odsetki) - Kapitalizacja powiększenie kapitału o
Licz i zarabiaj matematyka na usługach rynku finansowego
 Licz i zarabiaj matematyka na usługach rynku finansowego Przedstawiony zestaw zadań jest przeznaczony dla uczniów szkół ponadgimnazjalnych i ma na celu ukazanie praktycznej strony matematyki, jej zastosowania
Licz i zarabiaj matematyka na usługach rynku finansowego Przedstawiony zestaw zadań jest przeznaczony dla uczniów szkół ponadgimnazjalnych i ma na celu ukazanie praktycznej strony matematyki, jej zastosowania
2. Funkcja akumulacji i wartość przyszła
 2. Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600,
2. Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600,
Zadania do wykładu Matematyka bankowa 1 i 2
 Zadania do wykładu Matematyka bankowa 1 i 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address:
Zadania do wykładu Matematyka bankowa 1 i 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address:
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady
 Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
Wydział Matematyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady Łódź 2006 Rozdział 1 Oprocentowanie lokaty
Funkcja akumulacji i wartość przyszła
 Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
Funkcja akumulacji i wartość przyszła
 Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
System finansowy gospodarki. Zajęcia nr 5 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
System finansowy gospodarki Zajęcia nr 5 Matematyka finansowa Wartość pieniądza w czasie 1 złoty posiadany dzisiaj jest wart więcej niż 1 złoty posiadany w przyszłości, np. za rok. Powody: Suma posiadana
Zadania do wykładu Matematyka bankowa 2
 Zadania do wykładu Matematyka bankowa 2 Dorota Klim Instytut Matematyki i Informatyki, PWSZ w Płocku E-mail address: klimdr@math.uni.ldz.pl http://math.uni.lodz.pl/ klimdr/ Bibliografia [1] M. Podgórska,
Zadania do wykładu Matematyka bankowa 2 Dorota Klim Instytut Matematyki i Informatyki, PWSZ w Płocku E-mail address: klimdr@math.uni.ldz.pl http://math.uni.lodz.pl/ klimdr/ Bibliografia [1] M. Podgórska,
[1 ] M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN
![[1 ] M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN [1 ] M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN](/thumbs/63/48894660.jpg) LITERATURA: [1 ] M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN [2 ] E. Smaga, Arytmetyka finansowa, PWN [3 ] M. Sobczyk, Matematyka finansowa, Placet [4 ] M. Szałański, Podstawy matematyki finansowej,
LITERATURA: [1 ] M. Podgórska, J. Klimkowska, Matematyka finansowa, PWN [2 ] E. Smaga, Arytmetyka finansowa, PWN [3 ] M. Sobczyk, Matematyka finansowa, Placet [4 ] M. Szałański, Podstawy matematyki finansowej,
mgr Katarzyna Niewińska; Wydział Zarządzania UW Ćwiczenia 2
 Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Ćwiczenia 2 Wartość pieniądza w czasie Zmienna wartość pieniądza w czasie jest pojęciem, które pozwala porównać wartość różnych sum pieniężnych otrzymanych w różnych okresach czasu. Czy 1000 PLN otrzymane
Matematyka I dla DSM zbiór zadań
 I Sumowanie skończone W zadaniach -4 obliczyć podaną sumę. Matematyka I dla DSM zbiór zadań do użytku wewnętrznego dr Leszek Rudak Uniwersytet Warszawski Wydział Zarządzania. 5 i. i= 4 i 3. i= 5 ( ) i
I Sumowanie skończone W zadaniach -4 obliczyć podaną sumę. Matematyka I dla DSM zbiór zadań do użytku wewnętrznego dr Leszek Rudak Uniwersytet Warszawski Wydział Zarządzania. 5 i. i= 4 i 3. i= 5 ( ) i
Funkcja akumulacji i wartość przyszła
 Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
Funkcja akumulacji i wartość przyszła Zadanie 1 An investment of $10000 is made into a fund at time t=0. The fund develops the following balances over the next 4 years: F (0) = 10000, F (1) = 10600, F
System finansowy gospodarki. Zajęcia nr 6 Matematyka finansowa
 System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
System finansowy gospodarki Zajęcia nr 6 Matematyka finansowa Rachunek rentowy (annuitetowy) Mianem rachunku rentowego określa się regularne płatności w stałych odstępach czasu przy założeniu stałej stopy
Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona.
 Temat: Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona. Zadanie Przez 2 lata na koniec każdego miesiąca wpłacamy 200
Temat: Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona. Zadanie Przez 2 lata na koniec każdego miesiąca wpłacamy 200
Rachunek rent. Pojęcie renty. Wartość początkowa i końcowa renty. Renty o stałych ratach. Renta o zmiennych ratach. Renta uogólniona.
 Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
Temat: Rachunek rent Pojęcie renty Wartość początkowa i końcowa renty Renty o stałych ratach Renta o zmiennych ratach Renta uogólniona Zadanie 1 Przez 2 lata na koniec każdego miesiąca wpłacamy 1 000 PLN
ZADANIE 1. NAJWIEKSZY INTERNETOWY ZBIÓR ZADAŃ Z MATEMATYKI
 ZADANIE 1 Na budowę domu możesz zaciagn ać pożyczkę w wysokości 63450 e. Do wyboru sa dwa warianty spłaty: I w każdym miesiacu spłacasz równe raty, każda w wysokości 2% pożyczonej kwoty. II pierwsza rata
ZADANIE 1 Na budowę domu możesz zaciagn ać pożyczkę w wysokości 63450 e. Do wyboru sa dwa warianty spłaty: I w każdym miesiacu spłacasz równe raty, każda w wysokości 2% pożyczonej kwoty. II pierwsza rata
Zastosowanie matematyki w finansach i bankowości
 Zastosowanie matematyki w finansach i bankowości Maciej Wolny I. Kalkulacja wartości pieniądza w czasie... 1 II. Nominalna, efektywna i realna stopa procentowa... 4 III. Spłata kredytów w równych i różnych
Zastosowanie matematyki w finansach i bankowości Maciej Wolny I. Kalkulacja wartości pieniądza w czasie... 1 II. Nominalna, efektywna i realna stopa procentowa... 4 III. Spłata kredytów w równych i różnych
Zadania do wykładu Matematyka bankowa 2
 Zadania do wykładu Matematyka bankowa 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Matematyka bankowa 2 Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min.
 zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
zaliczenie na ocenę z elementarnej matematyki finansowej I rok MF, 21 czerwca 2012 godz. 8:15 czas trwania 120 min. Imię nazwisko:... numer indeksu:... nr zadania zad.1 zad.2 zad.3 zad.4 zad.5 zad.6 zad.7
Sprawdzian 4- lokaty i kredyty
 Sprawdzian 4- lokaty i kredyty Przykładowetypowe) zadania ZADANIE. Pan X wpłacił 000 zł do banku na czteroletni a lokatę oprocentowana w wysokości 8% rocznie. Odsetki dopisywane były do kapitału w końcu
Sprawdzian 4- lokaty i kredyty Przykładowetypowe) zadania ZADANIE. Pan X wpłacił 000 zł do banku na czteroletni a lokatę oprocentowana w wysokości 8% rocznie. Odsetki dopisywane były do kapitału w końcu
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Matematyka Finansowa dla liderów dr Aneta Kaczyńska Uniwersytet Ekonomiczny w Poznaniu 30 listopada 2017 r. Dr Tomaszie Projektami EKONOMICZNY UNIWERSYTET DZIECIĘCY Copywrite
Akademia Młodego Ekonomisty Matematyka Finansowa dla liderów dr Aneta Kaczyńska Uniwersytet Ekonomiczny w Poznaniu 30 listopada 2017 r. Dr Tomaszie Projektami EKONOMICZNY UNIWERSYTET DZIECIĘCY Copywrite
WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu)
 WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu) PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we wzorach oznaczamy
WARTOŚĆ PIENIĄDZA W CZASIE c.d. (WACC + Spłata kredytu) PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we wzorach oznaczamy
OPŁACALNOŚĆ INWESTYCJI
 3/27/2011 Ewa Kusideł ekusidel@uni.lodz.pl 1 OPŁACALNOŚĆ INWESTYCJI www.kep.uni.lodz.pl\ewakusidel 3/27/2011 Inwestycje i ryzyko na rynku nieruchomości 2 Inwestycja Inwestycja Nakład na zwiększenie lub
3/27/2011 Ewa Kusideł ekusidel@uni.lodz.pl 1 OPŁACALNOŚĆ INWESTYCJI www.kep.uni.lodz.pl\ewakusidel 3/27/2011 Inwestycje i ryzyko na rynku nieruchomości 2 Inwestycja Inwestycja Nakład na zwiększenie lub
Procent prosty Def.: Procent prosty Zad. 1. Zad. 2. Zad. 3
 Procent prosty Zakładając konto w banku, decydujesz się na określone oprocentowanie tego rachunku. Zależy ono między innymi od czasu, w jakim zobowiązujesz się nie naruszać stanu konta, czyli tzw. lokaty
Procent prosty Zakładając konto w banku, decydujesz się na określone oprocentowanie tego rachunku. Zależy ono między innymi od czasu, w jakim zobowiązujesz się nie naruszać stanu konta, czyli tzw. lokaty
Informacja dla lokat terminowych założonych do dnia Obowiązująca od LOKATY TERMINOWE ZWYKŁE
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla lokat terminowych założonych do dnia 13.04.2014 Obowiązująca od 01.05.2014 LOKATY TERMINOWE ZWYKŁE Lokaty terminowe obowiązuje dla lokat
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla lokat terminowych założonych do dnia 13.04.2014 Obowiązująca od 01.05.2014 LOKATY TERMINOWE ZWYKŁE Lokaty terminowe obowiązuje dla lokat
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
1940, 17 = K 4 = K 2 (1, 05)(1 + x 200 )3. Stąd, po wstawieniu K 2 dostaję:
 Poniższe rozwiązania są jedynie przykładowe. Każde z tych zadań da się rozwiązać na wiele sposobów, ale te na pewno są dobre (i prawdopodobnie najprostsze). Komentarze (poza odpowiedziami) są zbędne -
Poniższe rozwiązania są jedynie przykładowe. Każde z tych zadań da się rozwiązać na wiele sposobów, ale te na pewno są dobre (i prawdopodobnie najprostsze). Komentarze (poza odpowiedziami) są zbędne -
6SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 6SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
6SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3
 Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3 Uwaga! Każde ćwiczenie rozpoczynamy od stworzenia w katalogu Moje dokumenty swojego własnego katalogu roboczego, w którym będziecie Państwo zapisywać swoje pliki.
Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3 Uwaga! Każde ćwiczenie rozpoczynamy od stworzenia w katalogu Moje dokumenty swojego własnego katalogu roboczego, w którym będziecie Państwo zapisywać swoje pliki.
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Informacja obowiązująca od 01.07.2015
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3. Zadanie 1 Amortyzacja środków trwałych
 Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3 Uwaga! Każde ćwiczenie rozpoczynamy od stworzenia w katalogu Moje dokumenty swojego własnego katalogu roboczego, w którym będziecie Państwo zapisywać swoje pliki.
Arkusz kalkulacyjny MS EXCEL ĆWICZENIA 3 Uwaga! Każde ćwiczenie rozpoczynamy od stworzenia w katalogu Moje dokumenty swojego własnego katalogu roboczego, w którym będziecie Państwo zapisywać swoje pliki.
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Matematyka finansowa 17.05.2003
 1. Na początku roku (w chwili t = 0 ) portfel pewnego funduszu inwestycyjnego składa się z 40% obligacji typu I oraz 60% obligacji typu II. O obligacjach typu I oraz typu II wiadomo, że: (i) obligacja
1. Na początku roku (w chwili t = 0 ) portfel pewnego funduszu inwestycyjnego składa się z 40% obligacji typu I oraz 60% obligacji typu II. O obligacjach typu I oraz typu II wiadomo, że: (i) obligacja
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
INDEKS FINANSISTY. Monika Skrzydłowska. PWSZ w Chełmie. wrzesień Projekt dofinansowała Fundacja mbanku
 INDEKS FINANSISTY Monika Skrzydłowska PWSZ w Chełmie wrzesień 2017 Projekt dofinansowała Fundacja mbanku Monika Skrzydłowska (PWSZ w Chełmie) INDEKS FINANSISTY wrzesień 2017 1 / 40 Spis treści 1 Wprowadzenie
INDEKS FINANSISTY Monika Skrzydłowska PWSZ w Chełmie wrzesień 2017 Projekt dofinansowała Fundacja mbanku Monika Skrzydłowska (PWSZ w Chełmie) INDEKS FINANSISTY wrzesień 2017 1 / 40 Spis treści 1 Wprowadzenie
1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku
 1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku miesiąca a każda następna miesięczna wpłata jest (a) Większa
1. Jaką kwotę zgromadzimy po 3 latach na lokacie bankowej jeśli roczna NSP wynosi 4%, pierwsza wpłata wynosi 300 zl i jest dokonana na poczatku miesiąca a każda następna miesięczna wpłata jest (a) Większa
Akademia Młodego Ekonomisty
 Akademia Młodego Ekonomisty Matematyka finansowa wokół nas Michał Trzęsiok Uniwersytet Ekonomiczny w Katowicach 20 października 2014 r. Czym jest pieniądz? Pieniądz - dobro, które jest powszechnie akceptowane
Akademia Młodego Ekonomisty Matematyka finansowa wokół nas Michał Trzęsiok Uniwersytet Ekonomiczny w Katowicach 20 października 2014 r. Czym jest pieniądz? Pieniądz - dobro, które jest powszechnie akceptowane
KOMUNIKAT z dnia 17.08.2015 r. dotyczący oprocentowania rachunków bankowych Meritum Banku
 KOMUNIKAT z dnia 17.08.2015 r. dotyczący oprocentowania rachunków bankowych I. Rachunki oszczędnościowo-rozliczeniowe i oszczędnościowe dla Klientów Indywidualnych Nazwa Konto z Gwarancją Konto Oszczędnościowe
KOMUNIKAT z dnia 17.08.2015 r. dotyczący oprocentowania rachunków bankowych I. Rachunki oszczędnościowo-rozliczeniowe i oszczędnościowe dla Klientów Indywidualnych Nazwa Konto z Gwarancją Konto Oszczędnościowe
4. Strumienie płatności: okresowe wkłady oszczędnościowe
 4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
4. Strumienie płatności: okresowe wkłady oszczędnościowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 4. Strumienie w Krakowie)
METODY OCENY PROJEKTÓW INWESTYCYJNYCH WPROWADZENIE WARTOŚĆ PIENIĄDZA W CZASIE. Ćwiczenia nr 1 i 2
 METODY OCENY PROJEKTÓW INWESTYCYJNYCH WPROWADZENIE WARTOŚĆ PIENIĄDZA W CZASIE Ćwiczenia nr 1 i 2 - Cel ćwiczeń - Komunikacja email: i.ratuszniak@efficon.pl, w temacie - mopi - Konsultacje: pokój: 428,
METODY OCENY PROJEKTÓW INWESTYCYJNYCH WPROWADZENIE WARTOŚĆ PIENIĄDZA W CZASIE Ćwiczenia nr 1 i 2 - Cel ćwiczeń - Komunikacja email: i.ratuszniak@efficon.pl, w temacie - mopi - Konsultacje: pokój: 428,
Zastosowania matematyki
 Zastosowania matematyki Monika Bartkiewicz 1 / 143 Dyskonto-przypomnienie Obliczanie kapitaªu pocz tkowego P v na podstawie znanej warto±ci kapitaªu ko«cowego F v nazywa si dyskontowaniem kapitaªu F v.
Zastosowania matematyki Monika Bartkiewicz 1 / 143 Dyskonto-przypomnienie Obliczanie kapitaªu pocz tkowego P v na podstawie znanej warto±ci kapitaªu ko«cowego F v nazywa si dyskontowaniem kapitaªu F v.
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH. Dla klientów indywidualnych. obowiązująca od dnia
 Załącznik nr 1 do Uchwały Nr 13./Z/2013 Zarządu BS w Podegrodziu z dnia 11.04.2013 r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Załącznik nr 1 do Uchwały Nr 13./Z/2013 Zarządu BS w Podegrodziu z dnia 11.04.2013 r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH. Dla klientów indywidualnych. w Banku Spółdzielczym w Podegrodziu
 Załącznik nr 1 do Uchwały Nr 27/Z/2013 Zarządu BS w Podegrodziu z dnia 24.07.2013 Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Załącznik nr 1 do Uchwały Nr 27/Z/2013 Zarządu BS w Podegrodziu z dnia 24.07.2013 Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Dariusz Wardowski Katedra Analizy Nieliniowej. Bankowość i metody statystyczne w biznesie - zadania i przykłady część II
 Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Wydział Matematyki i Informatyki Uniwersytetu Łódzkiego w Łodzi Dariusz Wardowski Katedra Analizy Nieliniowej Bankowość i metody statystyczne w biznesie - zadania i przykłady część II Łódź 2008 Rozdział
Wartość przyszła pieniądza
 O koszcie kredytu nie można mówić jedynie na podstawie wysokości płaconych odsetek. Dla pożyczającego pieniądze najważniejszą kwestią jest kwota, jaką będzie musiał zapłacić za korzystanie z cudzych środków
O koszcie kredytu nie można mówić jedynie na podstawie wysokości płaconych odsetek. Dla pożyczającego pieniądze najważniejszą kwestią jest kwota, jaką będzie musiał zapłacić za korzystanie z cudzych środków
INFLACJA
 INFLACJA Zadanie 1 i. Nakłady na pewne działania z pewnym roku wzrosły o 10%, a inflacja roczna (w tym roku) wyniosła 5%. O ile, realnie wzrosły nakłady? A jeżeli nakłady wzrosły o 30%, a inflacja roczny
INFLACJA Zadanie 1 i. Nakłady na pewne działania z pewnym roku wzrosły o 10%, a inflacja roczna (w tym roku) wyniosła 5%. O ile, realnie wzrosły nakłady? A jeżeli nakłady wzrosły o 30%, a inflacja roczny
WACC Montaż finansowy Koszt kredytu
 WACC Montaż finansowy Koszt kredytu Na następne zajęcia proszę przygotować listę zakupów niezbędną do realizacji projektu. PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Zdefiniuj stopę procentową
WACC Montaż finansowy Koszt kredytu Na następne zajęcia proszę przygotować listę zakupów niezbędną do realizacji projektu. PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Zdefiniuj stopę procentową
Funkcje w MS Excel. Arkadiusz Banasik arkadiusz.banasik@polsl.pl
 Funkcje w MS Excel Arkadiusz Banasik arkadiusz.banasik@polsl.pl Plan prezentacji Wprowadzenie Funkcje matematyczne Funkcje logiczne Funkcje finansowe Podsumowanie 2/27 Wprowadzenie Funkcje: Są elementami
Funkcje w MS Excel Arkadiusz Banasik arkadiusz.banasik@polsl.pl Plan prezentacji Wprowadzenie Funkcje matematyczne Funkcje logiczne Funkcje finansowe Podsumowanie 2/27 Wprowadzenie Funkcje: Są elementami
Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE
 Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE Zmianą wartości pieniądza w czasie zajmują się FINANSE. Finanse to nie to samo co rachunkowość. Rachunkowość to opowiadanie JAK BYŁO i JAK JEST Finanse zajmują
Paulina Drozda WARTOŚĆ PIENIĄDZA W CZASIE Zmianą wartości pieniądza w czasie zajmują się FINANSE. Finanse to nie to samo co rachunkowość. Rachunkowość to opowiadanie JAK BYŁO i JAK JEST Finanse zajmują
Matematyka bankowa 1 1 wykład
 Matematyka bankowa 1 1 wykład Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Matematyka bankowa 1 1 wykład Dorota Klim Department of Nonlinear Analysis, Faculty of Mathematics and Computer Science, University of Łódź, Banacha 22, 90-238 Łódź, Poland E-mail address: klimdr@math.uni.ldz.pl
Akademia Młodego Ekonomisty Matematyka finansowa dla liderów Albert Tomaszewski Grupy 1-2 Zadanie 1.
 Grupy 1-2 Zadanie 1. Sprawdźcie ofertę dowolnych 5 banków i wybierzcie najlepszą ofertę oszczędnościową (lokatę lub konto oszczędnościowe). Obliczcie, jaki zwrot przyniesie założenie jednej takiej lokaty
Grupy 1-2 Zadanie 1. Sprawdźcie ofertę dowolnych 5 banków i wybierzcie najlepszą ofertę oszczędnościową (lokatę lub konto oszczędnościowe). Obliczcie, jaki zwrot przyniesie założenie jednej takiej lokaty
ZASADY I TERMINY KAPITALIZACJI ODSETEK
 OPROCENTOWANIE ŚRODKÓW PIENIĘŻNYCH W WALUTACH WYMIENIALNYCH GROMADZONYCH NA RACHUNKACH BANKOWYCH I KREDYTÓW W WALUTACH WYMIENIALNYCH UDZIELANYCH PRZEZ PKO BANK POLSKI S.A. KLIENTOM RYNKU DETALICZNEGO:
OPROCENTOWANIE ŚRODKÓW PIENIĘŻNYCH W WALUTACH WYMIENIALNYCH GROMADZONYCH NA RACHUNKACH BANKOWYCH I KREDYTÓW W WALUTACH WYMIENIALNYCH UDZIELANYCH PRZEZ PKO BANK POLSKI S.A. KLIENTOM RYNKU DETALICZNEGO:
WACC Montaż finansowy Koszt kredytu
 WACC Montaż finansowy Koszt kredytu PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Zdefiniuj stopę procentową i dyskontową Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we
WACC Montaż finansowy Koszt kredytu PYTANIA KONTROLNE Co oznacza pojęcie kapitalizacja odsetek? Zdefiniuj stopę procentową i dyskontową Co oznacza pojęcie wartość przyszła i bieżąca? Jakimi symbolami we
Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH. Dla klientów indywidualnych. w Banku Spółdzielczym w Podegrodziu
 Załącznik nr 3 do Uchwały Nr 8/Z/2014 Zarządu BS w Podegrodziu z dnia 14.01.2014r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Załącznik nr 3 do Uchwały Nr 8/Z/2014 Zarządu BS w Podegrodziu z dnia 14.01.2014r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych w Banku Spółdzielczym
Tabela oprocentowania produktów bankowych w ABS Banku Spółdzielczym
 Tabela oprocentowania produktów bankowych w ABS Banku Spółdzielczym Spis treści: WSTĘP... 3 KLIENCI INDYWIDUALNI... 4 KONTA OSOBISTE... 4 Tabela 1 RACHUNKI OSZCZĘDNOŚCIOWO-ROZLICZENIOWE...4 Tabela 2 RACHUNEK
Tabela oprocentowania produktów bankowych w ABS Banku Spółdzielczym Spis treści: WSTĘP... 3 KLIENCI INDYWIDUALNI... 4 KONTA OSOBISTE... 4 Tabela 1 RACHUNKI OSZCZĘDNOŚCIOWO-ROZLICZENIOWE...4 Tabela 2 RACHUNEK
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171)
 Przedmiot: MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171) Prowadzący wykład: dr Krzysztof Samotij, e-mail: krzysztof.samotij@pwr.edu.pl Czas i miejsce wykładu: poniedziałki (wg definicji J.M. Rektora) g. 9:15-11:00,
Przedmiot: MODELOWANIE RYNKÓW FINANSOWYCH (MAP1171) Prowadzący wykład: dr Krzysztof Samotij, e-mail: krzysztof.samotij@pwr.edu.pl Czas i miejsce wykładu: poniedziałki (wg definicji J.M. Rektora) g. 9:15-11:00,
2a. Przeciętna stopa zwrotu
 2a. Przeciętna stopa zwrotu Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2a. Przeciętna stopa zwrotu Matematyka
2a. Przeciętna stopa zwrotu Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2a. Przeciętna stopa zwrotu Matematyka
Matematyka podstawowa V. Ciągi
 Matematyka podstawowa V Ciągi Teoria ciąg arytmetyczny - pierwszy wyraz ciągu - różnica Kolejny wyraz ciągu arytmetycznego powstaje przez dodanie do poprzedniego różnicy. = + Np. =2,=3 :2,5,8,11 = 4,=2
Matematyka podstawowa V Ciągi Teoria ciąg arytmetyczny - pierwszy wyraz ciągu - różnica Kolejny wyraz ciągu arytmetycznego powstaje przez dodanie do poprzedniego różnicy. = + Np. =2,=3 :2,5,8,11 = 4,=2
I = F P. P = F t a(t) 1
 6. Modele wartości pieniądza w czasie. Współczynnik akumulacji kapitału. Kapitalizacja okresowa, kapitalizacja ciągła. Wartość bieżąca, wartość przyszła. Pojęcia kredytu, renty, renty wieczystej, zadłużenia
6. Modele wartości pieniądza w czasie. Współczynnik akumulacji kapitału. Kapitalizacja okresowa, kapitalizacja ciągła. Wartość bieżąca, wartość przyszła. Pojęcia kredytu, renty, renty wieczystej, zadłużenia
Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino
 Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Ćwiczenia 5 Pojęcie benchmarku, tracking error Wskaźniki efektywności Sharpe a, Treynora, Jensena, Information Ratio, Sortino Renata Karkowska, Wydział Zarządzania UW 1 Współczynnik Sharpe a Renata Karkowska,
Matematyka finansowa. Ćwiczenia ZPI. Ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
Matematyka finansowa Ćwiczenia ZPI 1 Zadanie 1. Procent składany W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku
Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH. Dla klientów indywidualnych. w Banku Spółdzielczym w Podegrodziu
 Załącznik nr 1 do Uchwały Nr 27/Z/2014 Zarządu Banku Spółdzielczego w Podegrodziu z dnia 09-10-2014 r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych
Załącznik nr 1 do Uchwały Nr 27/Z/2014 Zarządu Banku Spółdzielczego w Podegrodziu z dnia 09-10-2014 r Bank Spółdzielczy w Podegrodziu TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH Dla klientów indywidualnych
BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA. OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku Spółdzielczym w Nowym Sączu
 Załącznik do Uchwały Nr 13 z dnia 05.03.2015 r. Zarządu Banku Spółdzielczego w Nowym Sączu BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku
Załącznik do Uchwały Nr 13 z dnia 05.03.2015 r. Zarządu Banku Spółdzielczego w Nowym Sączu BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku
KARTA PRACY Z PROCENTÓW - nowa
 KARTA PRACY Z PROCENTÓW - nowa ZADANIE 1. Zamień procenty na ułamki ( : 100 ) 25%= 50%= % % 62%= 16 % 138%= 11 % 2%= 33 % 2340%= 3 % 0,4%= 66 % 0,35%= % 1,05%= 1%= 2,3%= 4%= 27,4%= 16%= 0,004%= 28%= %
KARTA PRACY Z PROCENTÓW - nowa ZADANIE 1. Zamień procenty na ułamki ( : 100 ) 25%= 50%= % % 62%= 16 % 138%= 11 % 2%= 33 % 2340%= 3 % 0,4%= 66 % 0,35%= % 1,05%= 1%= 2,3%= 4%= 27,4%= 16%= 0,004%= 28%= %
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE
 WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
WARTOŚĆ PIENIĄDZA W CZASIE WPROWADZENIE PYTANIA KONTROLNE Różnica pomiędzy: inwestycją, projektem inwestycyjnym, przedsięwzięciem inwestycyjnym Rodzaje inwestycji ze względu na cel Wartość pieniądza w
Elementy matematyki finansowej w programie Maxima
 Maxima-03_windows.wxm 1 / 8 Elementy matematyki finansowej w programie Maxima 1 Wartość pieniądza w czasie Umiejętność przenoszenia kwot pieniędzy w czasie, a więc obliczanie ich wartości na dany moment,
Maxima-03_windows.wxm 1 / 8 Elementy matematyki finansowej w programie Maxima 1 Wartość pieniądza w czasie Umiejętność przenoszenia kwot pieniędzy w czasie, a więc obliczanie ich wartości na dany moment,
Oprocentowanie rachunku oszczędnościowego KSO (Książeczka) Oprocentowanie Lokaty odnawialnej 2,7 na 7 dni. Oprocentowanie Lokaty 3 na 4
 OPROCENTOWANIE RACHUNKÓW: Oprocentowanie rachunków oszczędnościowo rozliczeniowych i rachunku bieżącego IKS Zero IKS Senior / IKS Deponent IKS Classic / IKS Med / IKS VIP / IKS Udziałowiec Tandem IKS Zwykłe
OPROCENTOWANIE RACHUNKÓW: Oprocentowanie rachunków oszczędnościowo rozliczeniowych i rachunku bieżącego IKS Zero IKS Senior / IKS Deponent IKS Classic / IKS Med / IKS VIP / IKS Udziałowiec Tandem IKS Zwykłe
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO
 SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
SPÓŁDZIELCZA KASA OSZCZĘDNOŚCIOWO-KREDYTOWA JAWORZNO Informacja dla rachunków lokat terminowych i rachunków oszczędnościowo-rozliczeniowych wycofanych z bieżącej oferty SKOK "Jaworzno". (Produkty obsługiwane
Temat 1: Wartość pieniądza w czasie
 Temat 1: Wartość pieniądza w czasie Inwestycja jest w istocie bieżącym wyrzeczeniem się dla przyszłych korzyści. Ale teraźniejszość jest względnie dobrze znana, natomiast przyszłość to zawsze tajemnica.
Temat 1: Wartość pieniądza w czasie Inwestycja jest w istocie bieżącym wyrzeczeniem się dla przyszłych korzyści. Ale teraźniejszość jest względnie dobrze znana, natomiast przyszłość to zawsze tajemnica.
Nauka o finansach. Prowadzący: Dr Jarosław Hermaszewski
 Nauka o finansach Prowadzący: Dr Jarosław Hermaszewski WARTOŚĆ PIENIĄDZA W CZASIE Wykład 4 Prawda ekonomiczna Pieniądz, który mamy realnie w ręku, dziś jest wart więcej niż oczekiwana wartość tej samej
Nauka o finansach Prowadzący: Dr Jarosław Hermaszewski WARTOŚĆ PIENIĄDZA W CZASIE Wykład 4 Prawda ekonomiczna Pieniądz, który mamy realnie w ręku, dziś jest wart więcej niż oczekiwana wartość tej samej
STOPA PROCENTOWA I STOPA ZWROTU
 Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Piotr Cegielski, MAI, MRICS, CCIM STOPA PROCENTOWA I STOPA ZWROTU (Wybrane fragmenty artykułu opublikowanego w C.H. Beck Nieruchomości, numer 9 z 2011 r. Całość dostępna pod adresem internetowym: www.nieruchomosci.beck.pl)
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 16 maja 2005 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Komisja Egzaminacyjna dla Aktuariuszy XXXV Egzamin dla Aktuariuszy z 6 maja 005 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU A Czas egzaminu: 00 minut . Inwestorzy
Bank Spółdzielczy w Głogówku
 Bank Spółdzielczy w Głogówku Grupa BPS Załącznik do Uchwały nr 34/2018/Z Zarządu Banku Spółdzielczego w Głogówku z dnia 16.02.2018r. obowiązuje od 22.02.2018r. Tabela oprocentowania rachunków bankowych
Bank Spółdzielczy w Głogówku Grupa BPS Załącznik do Uchwały nr 34/2018/Z Zarządu Banku Spółdzielczego w Głogówku z dnia 16.02.2018r. obowiązuje od 22.02.2018r. Tabela oprocentowania rachunków bankowych
Charakterystyka i wycena kontraktów terminowych forward
 Charakterystyka i wycena kontraktów terminowych forward Profil wypłaty forward Profil wypłaty dla pozycji długiej w kontrakcie terminowym Long position Zysk/strata Cena spot Profil wypłaty dla pozycji
Charakterystyka i wycena kontraktów terminowych forward Profil wypłaty forward Profil wypłaty dla pozycji długiej w kontrakcie terminowym Long position Zysk/strata Cena spot Profil wypłaty dla pozycji
Zadania do wykładu Rachunek efektywności projektów inwestycyjnych
 Zadania do wykładu Rachunek efektywności projektów inwestycyjnych Dorota Klim Instytut Nauk Ekonomicznych i Informatyki, Państwowa Wyższa Szkoła Zawodowa w Płocku E-mail address: klimdr@math.uni.ldz.pl
Zadania do wykładu Rachunek efektywności projektów inwestycyjnych Dorota Klim Instytut Nauk Ekonomicznych i Informatyki, Państwowa Wyższa Szkoła Zawodowa w Płocku E-mail address: klimdr@math.uni.ldz.pl
Czym jest ciąg? a 1, a 2, lub. (a n ), n = 1,2,
 Ciągi liczbowe Czym jest ciąg? Ciąg liczbowy, to funkcja o argumentach naturalnych, której wartościami są liczby rzeczywiste. Wartość ciągu dla liczby naturalnej n oznaczamy symbolem a n i nazywamy n-tym
Ciągi liczbowe Czym jest ciąg? Ciąg liczbowy, to funkcja o argumentach naturalnych, której wartościami są liczby rzeczywiste. Wartość ciągu dla liczby naturalnej n oznaczamy symbolem a n i nazywamy n-tym
LOKATY RENTIERSKIE min. kwota 500 zł oprocentowanie zmienne
 oszczędzania TABELE OPROCENTOWAŃ LOKAT LOKATY TERMINOWE kwota min. 500 zł oprocentowanie zmienne oprocentowanie stałe Lokata PRIMA 7 dni - 0,50 % 1 m-c 1,00 % 1,00 % 2 m-ce 1,00 % - 3 m-ce 1,25 % 1,25
oszczędzania TABELE OPROCENTOWAŃ LOKAT LOKATY TERMINOWE kwota min. 500 zł oprocentowanie zmienne oprocentowanie stałe Lokata PRIMA 7 dni - 0,50 % 1 m-c 1,00 % 1,00 % 2 m-ce 1,00 % - 3 m-ce 1,25 % 1,25
Matematyka finansowa 04.04.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LVI Egzamin dla Aktuariuszy z 4 kwietnia 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
Ćwiczenia ZPI 1 W banku A oprocentowanie lokat 4% przy kapitalizacji kwartalnej. W banku B oprocentowanie lokat 4,5% przy kapitalizacji miesięcznej. W banku A ulokowano kwotę 1000 zł. Jaki kapitał należy
BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA. OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku Spółdzielczym w Nowym Sączu
 Załącznik do Uchwały Nr 5/2019 z dnia 30.01.2019 r. Zarządu Banku Spółdzielczego w Nowym Sączu BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku
Załącznik do Uchwały Nr 5/2019 z dnia 30.01.2019 r. Zarządu Banku Spółdzielczego w Nowym Sączu BANK SPÓŁDZIELCZY W NOWYM SĄCZU TABELA OPROCENTOWANIA PRODUKTÓW BANKOWYCH dla klientów indywidualnych w Banku
TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia 2015 r.)
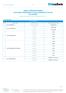 Duma Przedsiębiorcy 1/8 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia ) 1. Oprocentowanie LOKATY TERMINOWE L.p. Nazwa Lokaty umowny Oprocentowanie
Duma Przedsiębiorcy 1/8 TABELA OPROCENTOWANIA AKTUALNIE OFEROWANYCH LOKAT BANKOWYCH W PLN DLA SPÓŁEK (Zaktualizowana w dniu 18 sierpnia ) 1. Oprocentowanie LOKATY TERMINOWE L.p. Nazwa Lokaty umowny Oprocentowanie
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r.
 TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
TABELA OPROCENTOWANIA DLA RACHUNKÓW W RAMACH KONT BGŻOptima (roczna stopa oprocentowania) Obowiązuje od dnia 28 maja 2015 r. Część 1. Rachunki Oszczędnościowe w złotych prowadzone w ramach Kont BGŻOptima:
Powtórzenie. Ćwiczenia ZPI. Katarzyna Niewińska, ćwiczenia do wykładu Zarządzanie portfelem inwestycyjnym 1
 Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Powtórzenie Ćwiczenia ZPI 1 Zadanie 1. Średnia wartość stopy zwrotu dla wszystkich spółek finansowych wynosi 12%, a odchylenie standardowe 5,1%. Rozkład tego zjawiska zbliżony jest do rozkładu normalnego.
Egzamin dla Aktuariuszy z 26 października 1996 r.
 Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 26 października 1996 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:.... Czas egzaminu: l OO minut Ośrodek Doskonalenia
Komisja Egzaminacyjna dla Aktuariuszy Egzamin dla Aktuariuszy z 26 października 1996 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:.... Czas egzaminu: l OO minut Ośrodek Doskonalenia
Forward Rate Agreement
 Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Forward Rate Agreement Nowoczesne rynki finansowe oferują wiele instrumentów pochodnych. Należą do nich: opcje i warranty, kontrakty futures i forward, kontrakty FRA (Forward Rate Agreement) oraz swapy.
Bank Spółdzielczy w Głogówku
 Bank Spółdzielczy w Głogówku Grupa BPS Załącznik do Uchwały nr 125/2016/Z Zarządu Banku Spółdzielczego w Głogówku z dnia 24.10.2016r. Tabela oprocentowania rachunków bankowych i lokat terminowych w Banku
Bank Spółdzielczy w Głogówku Grupa BPS Załącznik do Uchwały nr 125/2016/Z Zarządu Banku Spółdzielczego w Głogówku z dnia 24.10.2016r. Tabela oprocentowania rachunków bankowych i lokat terminowych w Banku
Tabela oprocentowania dla konsumentów
 KONTA Konto Osobiste Oprocentowanie konta 0,10% Brak kwoty minimalnej. zmienne obowiązuje od 18.05.2015 r. Miesięczna kapitalizacja odsetek. Odsetki za niedozwolone saldo debetowe oraz odsetki za przekroczenie
KONTA Konto Osobiste Oprocentowanie konta 0,10% Brak kwoty minimalnej. zmienne obowiązuje od 18.05.2015 r. Miesięczna kapitalizacja odsetek. Odsetki za niedozwolone saldo debetowe oraz odsetki za przekroczenie
Akademia Młodego Ekonomisty
 Temat spotkania: Matematyka finansowa dla liderów Temat wykładu: Matematyka finansowa wokół nas Prowadzący: Szkoła Główna Handlowa w Warszawie 14 października 2014 r. Matematyka finansowa dla liderów Po
Temat spotkania: Matematyka finansowa dla liderów Temat wykładu: Matematyka finansowa wokół nas Prowadzący: Szkoła Główna Handlowa w Warszawie 14 października 2014 r. Matematyka finansowa dla liderów Po
Tabela oprocentowania dla konsumentów
 konta Konto osobiste konta 0,50% Brak kwoty minimalnej. zmienne obowiązuje od 12.08.2013 r. Miesięczna kapitalizacja odsetek. Odsetki za niedozwolone saldo debetowe - 4-krotność stopy kredytu lombardowego
konta Konto osobiste konta 0,50% Brak kwoty minimalnej. zmienne obowiązuje od 12.08.2013 r. Miesięczna kapitalizacja odsetek. Odsetki za niedozwolone saldo debetowe - 4-krotność stopy kredytu lombardowego
Procenty zadania maturalne z rozwiązaniami
 Każde zadanie 1 punkt. 1. Cena towaru bez podatku VAT jest równa 60 zł. Towar ten wraz z podatkiem VAT w wysokości 22% kosztuje 0,22 60 = 13,20 kwota VAT 60 + 13,20 = 73,20 Odp. A 2. Wskaż liczbę, której
Każde zadanie 1 punkt. 1. Cena towaru bez podatku VAT jest równa 60 zł. Towar ten wraz z podatkiem VAT w wysokości 22% kosztuje 0,22 60 = 13,20 kwota VAT 60 + 13,20 = 73,20 Odp. A 2. Wskaż liczbę, której
KOMUNIKAT Z DNIA 4 MAJA 2015 r. zasady prowadzenia wybranych rachunków terminowych lokat oszczędnościowych
 KOMUNIKAT Z DNIA 4 MAJA 2015 r. zasady prowadzenia wybranych rachunków terminowych lokat oszczędnościowych Lokata Dynamiczna Adm. (wycofana z oferty z dniem 20.04.2015) 2.. 3. Wypłata przed terminem powoduje
KOMUNIKAT Z DNIA 4 MAJA 2015 r. zasady prowadzenia wybranych rachunków terminowych lokat oszczędnościowych Lokata Dynamiczna Adm. (wycofana z oferty z dniem 20.04.2015) 2.. 3. Wypłata przed terminem powoduje
