PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA ZA POMOCĄ ROZKŁADÓW PRAWDOPODOBIEŃSTWA EWAPOTRANSPIRACJI WSKAŹNIKOWEJ
|
|
|
- Marcin Sobolewski
- 6 lat temu
- Przeglądów:
Transkrypt
1 Act Agrophysic, 9, 13(), PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA ZA POMOCĄ ROZKŁADÓW PRAWDOPODOBIEŃSTWA EWAPOTRANSPIRACJI WSKAŹNIKOWEJ Edwrd Gąsiorek, Jonn Kmińsk, ElŜbiet Musił Ktedr Mtemtyki, Uniwersytet Przyrodniczy we Wrocłwiu ul. Grunwldzk 53, Wrocłw e-mil: elzbiet.musil@up.wroc.pl S t r e s z c z e n i e. Do końc lt 9-tych XX wieku metod był powszechnie stosowną metodą obliczni ewpotrnspircji wskźnikowej. Obecnie njczęściej stosowną metodą wyznczni ewpotrnspircji wskźnikowej jest metod -Monteith w modyfikcji Allen i współutorów. Now modyfikcj metody -Monteith weryfikown przez wielu bdczy w róŝnych regionch Polski i n świecie umoŝliwi dokłdniejszą ocenę zdolności ewporcyjnej tmosfery, dltego jest metodą preferowną. W prcy przeprowdzono bdni n dnych pochodzących z trzech stcji doświdczlnych Bydgoszcz (1945-3), Łódź ( ) orz Wrocłw (1964-). Do wyznczonych sum ewpotrnspircji wskźnikowej w okresie wegetcyjnym z pomocą metody i - Monteith dopsowno funkcje rozkłdu prwdopodobieństw. Weryfikcję hipotezy o zgodności rozkłdów empirycznych z rozkłdem gmm przeprowdzono z pomocą testu chi-kwdrt. Nstępnie uŝywjąc rozkłdów gmm przeprowdzono podził okresów wegetcyjnych n: mokre, średnio-mokre, suche i brdzo suche w bdnych regionch i wielolecich. W wymienionych okresch wegetcyjnych porównno wyniki uzyskne z pomocą obu metod: i -Monteith. Przeprowdzone porównni wskzują n to, Ŝe metod dje zwyŝone wrtości ewpotrnspircji wskźnikowej w wybrnych regionch. S ł o w kluczowe: ewpotrnspircj wskźnikow, rozkłd gmm WSTĘP Ewpotrnspircj, jko jedn ze skłdowych bilnsu wodnego jest brdzo wŝnym czynnikiem przy projektowniu i eksplotcji systemów meliorcyjnych. Stnowi on wŝny element bdń hydrologicznych. Dokłdność oszcowni ewpotrnspircji m wpływ n ocenę zpsów wody glebowej, niedoborów wodnych roślin, tkŝe zpotrzebowni n wodę do nwodnień. Powszechnie
2 34 E. GĄSIOREK i in. stosowną metodą obliczni ewpotrnspircji jest sposób pośredni polegjący n ocenie ewpotrnspircji wskźnikowej ze stndrdowej pokrywy roślinnej, jką jest trw o stłej jednkowej wysokości dobrze zoptrzonej w wodę. Równnie opublikowne w 1948 roku ( 1948) było przełomem w modelowniu procesu ewpotrnspircji wskźnikowej. W literturze moŝn spotkć wiele innych propozycji dotyczących wyznczni wrtości ewpotrnspircji wskźnikowej. MoŜn wyznczć tę wielkość n podstwie formuł empirycznych (np. wzór Bc, Turc, Mtul, i innych), tkŝe jko wielkość mierzoną (prownie z wolnej powierzchni wodnej, lub ewpotrnspircj stndrdowej pokrywy roślinnej). Do końc lt 9-tych XX wieku zlecną i powszechnie stosowną metodą obliczni ewpotrnspircji wskźnikowej był wzór, z grnicą stosowny w modyfikcji FAO (Doorenbos i Pruitt 1977), ntomist w Polsce w modyfikcji frncuskiej (Srnck i in. 1983) z wielkością promieniowni słonecznego oblicznego według Podogrockiego (Podogrocki 1977). Obecnie powszechnie stosowną metodą wyznczni ewpotrnspircji wskźnikowej jest metod -Monteith. Metod -Monteith (Allen i in. 1994, 1994b), (Feddes i Lenselink 1994), umoŝliwi dokłdniejszą ocenę zdolności ewporcyjnej tmosfery, dltego jest metodą preferowną przez wielu bdczy. Celem prcy jest porównnie metody i metody -Monteith w okresch wegetcyjnych mokrych, średnio-mokrych, suchych i brdzo suchych, wyznczonych z pomocą rozkłdów prwdopodobieństw ewpotrnspircji wskźnikowej w nstępujących regionch Polski: w Bydgoszczy (1945-3), Łodzi ( ) orz Wrocłwiu (1964-). MATERIAŁ I METODY Pierwszy etp bdń, to wyznczenie ewpotrnspircji wskźnikowej z pomocą metody. Wg wzoru wrtość ewpotrnspircji wskźnikowej wyrŝ się nstępującym wzorem: ( R n + G ) + E γ γ n (1) ET = ( R n + G ) + E = + γ γ 8, γ gdzie: R n promieniownie netto (W m - ); G ciepło odprowdzone do gleby (W m - ); E zdolność ewporcyjn powietrz (W m - ); nchylenie krzywej opisującej ciśnienie nsyconej pry wodnej jko funkcję tempertury, hp K -1 ; γ stł psychrometryczn równ,655 hp K -1 ; n liczb dni w okresie, dl którego wykonywno obliczeni (dekd, miesiąc). W równniu nleŝy uwzględnić nstępujący fkt: Wszystkie strumienie energii płynące od powierzch-
3 PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA 343 ni czynnej mją umownie znk ujemny (są rozchodowymi skłdnikmi bilnsu cieplnego) i są generowne przez powierzchnię czynną, ntomist wszystkie strumienie energii płynące do powierzchni czynnej mją znk dodtni. Drugi etp bdń, to wyznczenie wrtości ewpotrnspircji wskźnikowej metodą -Monteith w modyfikcji Allen i współutorów (Allen i in. 1994, 1994b), (Feddes i Lenselink 1994). Monteith (Monteith 1973) wprowdził do wzoru (1) opór, jki stwi szt roślinn prze wodnej wędrującej z gleby do tmosfery. Opór ten łączy nstępujące opory: opór gleby (opór przy przepływie wody z gleby do otoczeni korzeni), opór korzeniowy (opór przy wnikniu wody do korzeni), opór nczyniowy (opór przepływu wody w wiązce nczyniowej), opór liściowy (opór przepływu wody w tknkch liści), opór szprkowy (opór przejści pry wodnej z wnętrz liści do tmosfery) i nzwł ten opór oporem sklepieni szty roślinnej (r c ). Wrtości ewpotrnspircji wskźnikowej wg wzoru -Monteith są nstępujące: ET o = ( Rn + G) + ρ c p d / γ r γ n () rc r γ 8,34 W prezentownej w prcy metodzie -Monteith przyjęto z (Allen i in. 1994, 1994b), Ŝe ewpotrnspircj wskźnikow jest to ewpotrnspircj hipotetycznej rośliny, jką jest trw o stłej jednkowej wysokości równej 1cm, w pełni zkrywjąc glebę w wrunkch ktywnego rozwoju i nieogrniczonego dostępu wody, stłym lbedo wynoszącym,3, i stłej oporności stomtycznej równej 7 s m -1. Opór erodynmiczny r zwny inczej oporem dyfuzji turbulencyjnej definiuje się jko opór w obszrze ogrniczonym poziomem z = d + z orz poziomem w tmosferze n wysokości pomirowej x. Opór erodynmiczny wyzncz się nstępująco: x dz r = (3) K d + z o k v( z d ) K M = (4) x d ln zh gdzie: x wysokość pomirow (m), z wysokość zmienn (m), r opór erodynmiczny (s m 1 ), k stł von Krmn =,41 ( ), v prędkość witru n wysokości z (m s 1 ), z o prmetr szorstkości przy trnsporcie ciepł i pry wodnej m
4 344 E. GĄSIOREK i in. (m), z h prmetr szorstkości przy wyminie pędu (m), d wrstw przesunięci płszczyzny zerowej (m). r x d = ln z h x d + z dz k vz k vd = x d 1 = ln zh k v x d + zo k v k vz k x d x d ln ln zh zo dz = vd k v (5) Przy obliczenich oporu erodynmicznego dl hipotetycznej rośliny, jką jest trw o stłej wysokości h równej 1 cm uwzględniono nstępujące wrunki: d = / 3h; zo =,13h ; zh =,1z o. Uwzględnienie wymienionych zleŝności pozwl wyznczyć wrtość oporu erodynmicznego 8 r =, który jest funkcją zmiennej prędkości witru ν mierzonej n wysokości m. v W proponownej metodzie wyznczni ewpotrnspircji wskźnikowej pomij się strumień ciepł glebowego, gdyŝ w wrunkch zdefiniownych jko stndrdowe m on niewielki udził w bilnsie cieplnym runi trwistej (Łbędzki 1999, Kspersk-Wołowicz i Łbędzki 4, Roguski i in., Musił 1). WYNIKI I DYSKUSJA Do bdń wykorzystno dne pochodzące z trzech stcji doświdczlnych: Bydgoszcz (1945-3), Łódź ( ) orz Wrocłw-Swojec (1964-). Porównnie ewpotrnspircji wskźnikowej wyznczonej metodą i -Monteith dl stcji Bydgoszcz przedstwi rysunek 1. Anliz wykresu pozwl wyciągnąć nstępujący wniosek: zdecydownie mniejsze wrtości ewpotrnspircji wskźnikowej otrzymno stosując metodę -Monteith w modyfikcji Allen i współutorów (Allen i in. 1994, 1994b, Fedder i Lenselink 1994), zlecną przez FAO i ICID i powszechnie stosowną n świecie od 199 roku (Allen i in. 1994b, 1998), (Fedder i Lensellink 1994, Smith 199).
5 PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA , -Monteith 5, 45, ET (mm) 4, 35, 3, 5,, Lt-Yers Rys. 1. Ewpotrnspircj wskźnikow w okresie wegetcyjnym (IV-IX) w wieloleciu n stcji Bydgoszcz Fig.1. Reference evpotrnspirtion in the growing seson (IV-IX) in the yers t the Bydgoszcz observtory Nstępnie do sum ewpotrnspircji wskźnikowej w okresie wegetcyjnym wg, i -Monteith dopsowno funkcję rozkłdu prwdopodobieństw. Przy dopsowywniu funkcji rozkłdu prwdopodobieństw wykorzystno rozkłd gmm. Zmienn losow X podleg rozkłdowi gmm o prmetrch p, λ>, jeŝeli jej gęstość prwdopodobieństw jest określon wzorem: 1 p 1 x x exp( ) dl x > f ( x) = p λ Γ( p) λ (6) dl x Weryfikcję hipotezy o zgodności rozkłdów empirycznych z rozkłdem gmm przeprowdzono z pomocą testu zgodności χ Person. Nstępnie wyznczono prmetry skli i ksztłtu rozkłdu gmm orz wyznczono kwntyle rzędu,;,5 i,8 oznczone odpowiednio przez x,, x,5 i x,8 tego rozkłdu, przyjmując nstępującą klsyfikcję: okres wegetcyjny w dnym roku uwŝ się z mokry, jeŝeli sum ewpotrnspircji wskźnikowej
6 346 E. GĄSIOREK i in. w tym okresie nie przekrcz x,, z średni jeŝeli sum ewpotrnspircji w okresie wegetcyjnym jest większ niŝ x, lecz nie przekrcz x,5, z suchy jeŝeli sum ewpotrnspircji w okresie wegetcyjnym jest większ niŝ x,5 lecz nie przekrcz x,8 i z brdzo suchy jeŝeli sum ewpotrnspircji w okresie wegetcyjnym jest większ niŝ x,8. W tbelch 1-4 zostły zmieszczone wrtości ewpotrnspircji wskźnikowej klsyfikujące okresy wegetcyjne jko mokre, średnio-mokre, suche orz brdzo suche dl trzech stcji bdwczych. Tbel 1. Weryfikcj hipotezy o zgodności rozkłdu gmm z rozkłdem empirycznym dl sumy ewpotrnspircji wskźnikowej w okresie wegetcyjnym wyznczonej metodą: i -Monteith Tble 1. Verifiction of the hypothesis on consistency of gmm distribution to empiricl distribution in cse of reference evpotrnspirtion using in the growing seson obtined by nd -Monteith methods Stcj Observtory Wielolecie Period χ obl p-wrtość p-vlue -Monteith χ obl p-wrtość p-vlue Wrocłw-Swojec 1964-,88,645 3,5,17 Bydgoszcz ,4,57 6,37,17 Łódź ,3,15 1,67,64 χ obl jest wrtością sttystyki χ, ntomist p jest njniŝszym poziomem istotności α, przy którym hipotez zerow mogłby być odrzucon przy otrzymnej wrtości sttystyki χ. Tbel. Prmetry skli i ksztłtu rozkłdu gmm dl stcji Wrocłw-Swojec (1964-) Tble. Prmeters of scle nd shpe for gmm distribution t the Wrocłw-Swojec observtory (1964-) Ewpotrnspircj wskźnikow Reference evpotrnspirtion Rozkłd Γ Γ distribution Prmetr Prmeter Skli-β Scle-β Ksztłtu- α Shpe-α Rząd kwntyl Quntile rnk,,5,8 3,39 156, Monteith,97 1,
7 PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA 347 Tbel 3. Prmetry skli i ksztłtu rozkłdu gmm dl stcji Bydgoszcz (1945-3) Tble 3. Prmeters of scle nd shpe for gmm distribution t the Bydgoszcz observtory (1945-3) Ewpotrnspircj wskźnikow Reference evpotrnspirtion Rozkłd Γ Γ distribution Prmetr Prmeter Skli-β Scle-β Ksztłtu-α Shpe-α Rząd kwntyl Quntile rnk,,5,8 3,4 114, Monteith 1,73 147, Tbel 4. Prmetry skli i ksztłtu rozkłdu gmm dl stcji Łódź ( ) Tble 4. Prmeters of scle nd shpe for gmm distribution t the Łódź observtory ( ) Ewpotrnspircj wskźnikow Reference evpotrnspirtion Rozkłd Γ Γ distribution Prmetr Prmeter skli-β scle-β ksztłtu-α Shpe-α Rząd kwntyl Quntile rnk,,5,8 6,59 68, Monteith,96 86, Szczegółow nliz okresów wegetcyjnych mokrych, średnio-mokrych, suchych i brdzo suchych n wszystkich stcjch przedstwion jest n rysunkch i 3. N rysunku przedstwione są wrtości ewpotrnspircji wskźnikowej wyznczone metodą i -Monteith kolejno dl stcji: ) Bydgoszcz, b) Wrocłw orz c) Łódź. Rysunki te umoŝliwiją porównnie wrtości ewpotrnspircji wskźnikowej wyznczonej dwiem metodmi w okresch wegetcyjnych mokrych, średnio-mokrych, suchych i brdzo suchych. N rysunku 3 grficznie przedstwiono zminy klimtycznego bilnsu wodnego wyznczonego metodą i - Monteith w okresch wegetcyjnych mokrych, średnio-mokrych, suchych i brdzo suchych n wszystkich bdnych stcjch. Anliz rysunku skłni do nstępujących wniosków: Metodą otrzymuje się zdecydownie większe wrtości ewpotrnspircji wskźnikowej niŝ metodą -Monteith. W rejonie Wrocłwi wrtości ET wyznczone metodmi i -Monteith w okresch wegetcyjnych mokrych, średnio-mokrych, suchych i brdzo suchych rozkłdją się mniej więcej tk smo. Tką smą prwidłowość moŝemy obserwowć w przypdku Bydgoszczy i Łodzi. RóŜnice polegją n tym, Ŝe w bdnych okresch wegetcyjnych moŝliwości wchłnini pry wodnej przez wrstwę tmosfery leŝącą nd powierzchnią prującą są njwiększe we Wrocłwiu njmniejsze w Bydgoszczy i Łodzi.
8 348 E. GĄSIOREK i in. Bydgoszcz ET (mm) lt średnie lt mokre -Monteith Miesiące-Months b lt średnie lt mokre Wrocłw ET (mm) Monteith Miesiące-Months c Łódź ET (mm) lt średnie lt mokre -Monteith Miesiące - Months Rys.. Ewpotrnspircj wskźnikow w okresie wegetcyjnym (IV-IX) wyznczon metodą i -Monteith dl: ) Bydgoszczy (1945-3), b) Wrocłwi (1964-), c) Łodzi ( ) Fig.. Reference evpotrnspirtion in the growing seson (IV-IX) obtined using nd -Monteith methods for: ) Bydgoszcz (1945-3), b) Wrocłw (1964-), c) Łódź ( )
9 PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA 349 KBW (mm) Monteith Bydgoszcz Miesiące-Months lt średnie lt mokre b KBW (mm) Monteith Wrocłw lt średnie lt mokre -6-8 Miesice - Months c KBW (mm) Monteith Łódź Miesiące -Months lt średnie lt mokre Rys. 3. Średnie miesięczne sumy klimtycznego bilnsu wodnego (KBW) w okresie wegetcyjnym (IV-IX) dl: ) Bydgoszczy (1945-3), b) Wrocłwi (1964-), i c) Łodzi ( ) Fig. 3. Men monthly sums of climtic wter blnce (CWB) in the growing seson (IV-IX) for: ) Bydgoszcz (1945-3), b) Wrocłw (1964-), c) Łódź ( )
10 35 E. GĄSIOREK i in. Anlizując rysunek 3 moŝn stwierdzić, Ŝe klimtyczny bilns wodny wyznczony n podstwie metody jest dl Wrocłwi w zsdzie ujemny, (dodtni jest tylko od lipc w okresie wegetcyjnym średnio-mokrym). W Bydgoszczy i Łodzi jest dodtni tylko w okresie wegetcyjnym mokrym. Tk sytucj związn jest z przewgą ewpotrnspircji wskźnikowej wyznczonej metodą nd opdmi. Klimtyczny bilns wodny wyznczony n podstwie ewpotrnspircji wskźnikowej wg -Monteith w Łodzi jest dodtni we wszystkich okresch wegetcyjnych. W Bydgoszczy i we Wrocłwiu jest dodtni w okresch wegetcyjnych mokrych, średnio-mokrych i suchych, ntomist w okresch brdzo suchych jest ujemny. WNIOSKI 1. Rozkłd sum ewpotrnspircji wskźnikowej wyznczonej metodą orz -Monteith w okresie wegetcyjnym (IV-IX) moŝn przybli- Ŝyć rozkłdem gmm. Z pomocą rozkłdu gmm wyznczono grniczne wrtości ewpotrnspircji wskźnikowej określjące okresy wegetcyjne jko mokre, średnio-mokre, suche orz brdzo suche we wszystkich bdnych rejonch.. Przeestymowne wrtości ewpotrnspircji wskźnikowej wyznczone metodą określją klimtyczny bilns wodny w zsdzie jko ujemny, co ozncz w przypdku tej metody wyznczni ewpotrnspircji wskźnikowej przewgę prowni nd opdem. 3. Metod -Monteith okzł się metodą lepiej chrkteryzującą okresy wegetcyjne brdzo suche i częściowo suche jko te, dl których klimtyczny bilns wodny jest ujemny, co ozncz deficyty wody jedynie w tych okresch. PIŚMIENNICTWO Allen R.G., Pereir L.S., Res D., Smith M., Crop evpotrnspirtion. Guidelines for computing crop wter requirements. Irrig. Drin. Pper no. 56, Rome: FAO. Allen R.G., Smith M., Pereir L.S., Perrier A., An updte for the clcultion of reference evpotrnspirtion. ICID Bulletin, 43(), Allen R.G., Smith M., Perrier A., Pereir L.S., 1994b. An updte for the definition of reference evpotrnspirtion. ICID Bulletin, 43(), Feddes R.A., Lenselink K.J., Evpotrnspirtion. ILRI Publiction 16. Dringe Principles nd Applictions. Wgeningen, Doorenbos J.,Pruitt W..,1977. Guidelines for predicting crop wter requirements. Irrig. Drin. Pper, no. 4 Rome: FAO. Kspersk-Wołowicz W., Łbędzki L., 4. Porównnie ewpotrnspircji wskźnikowej według i -Monteith w róŝnych regionch Polski. Wod-Środowisko-Obszry Wiejskie, t. 4, z. (11),
11 PORÓWNANIE METODY PENMANA I PENMANA-MONTEITHA 351 Łbędzki L., Przydtność wzoru -Monteith do obliczni ewpotrnspircji wskźnikowej i rzeczywistej uŝytków zielonych. Widomości Instytutu Meliorcji i UŜytków Zielonych, T. XX, z., Monteith J., Principles of environmentl physics. Americn Elsevier Publ. Co., N.Y. 41. Musił E., 1. Modelownie procesu ewpotrnspircji rzeczywistej i prognozownie jego tendencji. ZNAR we Wrocłwiu, nr 41, Rozprwy CLXXXII Podogrocki J, Zmienność czsow promieniowni cłkowitego w Polsce. Zesz. Nuk. ART. W Olsztynie. Rolnictwo, Roguski W., Łbędzki L., Kspersk W.,. Anliz wybrnych wzorów do obliczni prowni wskźnikowego n potrzeby nwdnini uŝytków zielonych. IMUZ, Flęty, t., z. 1 (4), H.L.,1948. Nturl evportion from open wter, bre soi lnd Grss. Proc. Roy. Soc. London A, 193, Srnck S., Brzesk J., Świerczyńsk H., Wybrne metody wyznczni ewpotrnspircji potencjlnej. Mteriły Bdwcze, Wrszw: IMGW. Smith M., 199. Report on the expert consulttion on revision of FAO methodologies for crop wter requirements. Lnd nd Wter Development Division, Rome: FAO. COMPARISON OF THE PENMAN AND PENMAN-MONTEITH METHODS BY MEANS OF PROBABILITY DISTRIBUTIONS OF REFERENCE EVAPOTRANSPIRATION Edwrd Gąsiorek, Jonn Kmińsk, ElŜbiet Musił Deprtment of Mthemtics, Wrocłw University of Environmentl nd Life Sciences ul. Grunwldzk 53, Wrocłw e-mil: elzbiet.musil@up.wroc.pl Ab s t r c t. Till the lte 9-ties of the th century the method hd been used widely to evlute the reference evpotrnspirtion. Nowdys, the most frequently used method is tht of -Monteith, modified by Allen nd co-uthors. A new modifiction of the -Monteith method, verified by mny reserchers worldwide nd in different regions of Polnd, enbles more ccurte evlution of the tmospheric evportion bility, therefore it is preferred. In this study, dt from sttions in Bydgoszcz (1945-3), Łódź ( ) nd Wrocłw (1964-) were nlysed. The sums of reference evpotrnspirtion in the growing seson, clculted by mens of the nd -Monteith methods, were fitted to the function of probbility distribution. The verifiction of hypothesis on consistency of empiricl distribution to gmm distribution ws performed using the Chi squre test. Then, by mens of gmm distribution, the growing sesons in the exmined regions nd multi-yer periods were clssified s: wet, medium wet, dry nd very dry. In the bove mentioned sesons, the results obtined by the use of nd -Monteith methods were compred. Those comprisons reveled tht the vlues of reference evpotrnspirtion, clculted by the method, re overestimted in the selected regions. K e y wo r d s : reference evpotrnspirtion, gmm distribution
MODELOWANIE EWAPOTRANSPIRACJI WSKAŹNIKOWEJ W RÓŻNYCH REGIONACH POLSKI MODELLING OF REFERENCE EVAPOTRANSPIRATION IN VARIOUS REGIONS OF POLAND
 Modelowanie ewapotranspiracji wskaźnikowej INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr 7/008, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 69 80 Komisja Technicznej
Modelowanie ewapotranspiracji wskaźnikowej INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr 7/008, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 69 80 Komisja Technicznej
PORÓWNANIE EWAPOTRANSPIRACJI WSKAŹNIKOWEJ WEDŁUG PENMANA I PENMANA-MONTEITHA W RÓŻNYCH REGIONACH POLSKI
 WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2004: t. 4 z. 2a () WATER-ENVIRONMENT-RURAL AREAS s. 23 36 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2004 PORÓWNANIE EWAPOTRANSPIRACJI WSKAŹNIKOWEJ
WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2004: t. 4 z. 2a () WATER-ENVIRONMENT-RURAL AREAS s. 23 36 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2004 PORÓWNANIE EWAPOTRANSPIRACJI WSKAŹNIKOWEJ
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Wykład 2. Pojęcie całki niewłaściwej do rachunku prawdopodobieństwa
 Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Wykłd 2. Pojęcie cłki niewłściwej do rchunku prwdopodobieństw dr Mriusz Grządziel 4 mrc 24 Pole trpezu krzywoliniowego Przypomnienie: figurę ogrniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Modelowanie i obliczenia techniczne. Metody numeryczne w modelowaniu: Różniczkowanie i całkowanie numeryczne
 Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
Modelownie i obliczeni techniczne Metody numeryczne w modelowniu: Różniczkownie i cłkownie numeryczne Pochodn unkcji Pochodn unkcji w punkcie jest deiniown jko grnic ilorzu różnicowego (jeżeli istnieje):
ZASTOSOWANIE RÓWNANIA NASGRO DO OPISU KRZYWYCH PROPAGACYJI PĘKNIĘĆ ZMĘCZENIOWYCH
 Sylwester KŁYSZ *, **, nn BIEŃ **, Pweł SZBRCKI ** ** Instytut Techniczny ojsk Lotniczych, rszw * Uniwersytet rmińsko-mzurski, Olsztyn ZSTOSONIE RÓNNI NSGRO DO OPISU KRZYYCH PROPGCYJI PĘKNIĘĆ ZMĘCZENIOYCH
Sylwester KŁYSZ *, **, nn BIEŃ **, Pweł SZBRCKI ** ** Instytut Techniczny ojsk Lotniczych, rszw * Uniwersytet rmińsko-mzurski, Olsztyn ZSTOSONIE RÓNNI NSGRO DO OPISU KRZYYCH PROPGCYJI PĘKNIĘĆ ZMĘCZENIOYCH
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO
 MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
ZESZYTY NAUKOWE UNIWERSYTETU SZCZECIŃSKIEGO NR 424 PRACE INSTYTUTU KULTURY FIZYCZNEJ NR 22 2005
 ZEZYTY NAUKOWE UNIWERYTETU ZCZECIŃKIEGO NR 424 PRACE INTYTUTU KULTURY FIZYCZNEJ NR 22 2005 MARIA MAKRI PRAWNOŚĆ FIZYCZNA I AKTYWNOŚĆ RUCHOWA KOBIET W WIEKU 20 60 LAT 1. Wstęp Dobr sprwność fizyczn jest
ZEZYTY NAUKOWE UNIWERYTETU ZCZECIŃKIEGO NR 424 PRACE INTYTUTU KULTURY FIZYCZNEJ NR 22 2005 MARIA MAKRI PRAWNOŚĆ FIZYCZNA I AKTYWNOŚĆ RUCHOWA KOBIET W WIEKU 20 60 LAT 1. Wstęp Dobr sprwność fizyczn jest
N(0, 1) ) = φ( 0, 3) = 1 φ(0, 3) = 1 0, 6179 = 0, 3821 < t α 1 e t dt α > 0. f g = fg. f = e t f = e t. U nas: g = t α 1 g = (α 1)t α 2
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
< f g = fg. f = e t f = e t. U nas: e t (α 1)t α 2 dt = 0 + (α 1)Γ(α 1)
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Metody określania macierzy przemieszczeń w modelowaniu przewozów pasażerskich. mgr inż. Szymon Klemba Warszawa, r.
 Metody określni mcierzy przemieszczeń w modelowniu przewozów psżerskich mgr inż. Szymon Klemb Wrszw, 2.07.2013r. SPIS TREŚCI 1 Podstwy teoretyczne 2 Rol mcierzy przemieszczeń 3 Metody wyznczni mcierzy
Metody określni mcierzy przemieszczeń w modelowniu przewozów psżerskich mgr inż. Szymon Klemb Wrszw, 2.07.2013r. SPIS TREŚCI 1 Podstwy teoretyczne 2 Rol mcierzy przemieszczeń 3 Metody wyznczni mcierzy
Matematyka finansowa 10.03.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część I
 Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
usuwa niewymierność z mianownika wyrażenia typu
 Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
Wymgni edukcyjne n poszczególne oceny z mtemtyki Kls pierwsz zkres podstwowy. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
2. Tensometria mechaniczna
 . Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
. Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
2. Na ich rozwiązanie masz 90 minut. Piętnaście minut przed upływem tego czasu zostaniesz o tym poinformowany przez członka Komisji Konkursowej.
 Kod uczni... MAŁOPOLSKI KONKURS MATEMATYCZNY dl uczniów gimnzjów Rok szkolny 03/0 ETAP SZKOLNY - 5 pździernik 03 roku. Przed Tobą zestw zdń konkursowych.. N ich rozwiąznie msz 90 minut. Piętnście minut
Kod uczni... MAŁOPOLSKI KONKURS MATEMATYCZNY dl uczniów gimnzjów Rok szkolny 03/0 ETAP SZKOLNY - 5 pździernik 03 roku. Przed Tobą zestw zdń konkursowych.. N ich rozwiąznie msz 90 minut. Piętnście minut
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych M O D E L O W A N I E I S Y M U L A C J A
 POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
Wspomaganie obliczeń za pomocą programu MathCad
 Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
Wprowdzenie do Mthcd' Oprcowł:M. Detk P. Stąpór Wspomgnie oliczeń z pomocą progrmu MthCd Definicj zmiennych e f g h 8 Przykłd dowolnego wyrŝeni Ay zdefinowc znienną e wyierz z klwitury kolejno: e: e f
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych
 POLITECHNIKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych S Y S T E M Y E L E K T R O M E C H A N I C Z N E PROJEKT/LABORATORIUM ĆWICZENIE (SPS) SILNIK PRĄDU
POLITECHNIKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych S Y S T E M Y E L E K T R O M E C H A N I C Z N E PROJEKT/LABORATORIUM ĆWICZENIE (SPS) SILNIK PRĄDU
Układ elektrohydrauliczny do badania siłowników teleskopowych i tłokowych
 TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
Warunki pogodowe w lipcu, sierpniu i wrześniu 1988 roku w Calypsobyen (Zachodni Spitsbergen)
 Andrzej F. Gluz Instytut Nuk o Ziemi Uniwersytet Mrii Curie-Skłodowskiej w Lulinie Wyprwy Geogrficzne U M C S w Lulinie n Spitsergen 1986 1988 Sesj Polrn 1989 Wrunki pogodowe w lipcu, sierpniu i wrześniu
Andrzej F. Gluz Instytut Nuk o Ziemi Uniwersytet Mrii Curie-Skłodowskiej w Lulinie Wyprwy Geogrficzne U M C S w Lulinie n Spitsergen 1986 1988 Sesj Polrn 1989 Wrunki pogodowe w lipcu, sierpniu i wrześniu
ZMIENNOŚĆ CZASOWA KLIMATYCZNEGO BILANSU WODNEGO MAŁYCH PIENIN W LATACH
 WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2004: t. 4 z. 2b (12) WATER-ENVIRONMENT-RURAL AREAS s. 135 146 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2004 ZMIENNOŚĆ CZASOWA KLIMATYCZNEGO
WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2004: t. 4 z. 2b (12) WATER-ENVIRONMENT-RURAL AREAS s. 135 146 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2004 ZMIENNOŚĆ CZASOWA KLIMATYCZNEGO
ROLE OF CUSTOMER IN BALANCED DEVELOPMENT OF COMPANY
 FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Foli Univ. Agric. Stetin. 2007, Oeconomic 254 (47), 117 122 Jolnt KONDRATOWICZ-POZORSKA ROLA KLIENTA W ZRÓWNOWAŻONYM ROZWOJU FIRMY ROLE OF CUSTOMER IN BALANCED
FOLIA UNIVERSITATIS AGRICULTURAE STETINENSIS Foli Univ. Agric. Stetin. 2007, Oeconomic 254 (47), 117 122 Jolnt KONDRATOWICZ-POZORSKA ROLA KLIENTA W ZRÓWNOWAŻONYM ROZWOJU FIRMY ROLE OF CUSTOMER IN BALANCED
Zastosowanie analizy widmowej sygnału ultradwikowego do okrelenia gruboci cienkich warstw
 AMME 1 1th JUBILEE INTERNATIONAL SC IENTIFIC CONFERENCE Zstosownie nlizy widmowej sygnłu ultrdwikowego do okreleni gruboci cienkich wrstw A. Kruk Wydził Metlurgii i Inynierii Mteriłowej, Akdemi Górniczo-Hutnicz
AMME 1 1th JUBILEE INTERNATIONAL SC IENTIFIC CONFERENCE Zstosownie nlizy widmowej sygnłu ultrdwikowego do okreleni gruboci cienkich wrstw A. Kruk Wydził Metlurgii i Inynierii Mteriłowej, Akdemi Górniczo-Hutnicz
Modelowanie 3 D na podstawie fotografii amatorskich
 Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri Środowisk w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri Środowisk w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Komisja Egzaminacyjna dla Aktuariuszy LII Egzamin dla Aktuariuszy z 15 marca 2010 r. Część I Matematyka finansowa
 Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
( ) Lista 2 / Granica i ciągłość funkcji ( z przykładowymi rozwiązaniami)
 List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
List / Grnic i ciągłość funkcji ( z przykłdowymi rozwiąznimi) Korzystjąc z definicji grnicy (ciągowej) funkcji uzsdnić podne równości: sin ) ( + ) ; b) ; c) + 5 Obliczyć grnice funkcji przy orz : + ) f
OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW
 Ktedr Technicznego Zbezpieczeni Okrętów Lbortorium Bdń Cech PoŜrowych Mteriłów OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW Metody bdń 1 pren 45545-2:
Ktedr Technicznego Zbezpieczeni Okrętów Lbortorium Bdń Cech PoŜrowych Mteriłów OCHRONA PRZECIWPOśAROWA TABORU KOLEJOWEGO WYMAGANIA PRZECIWPOśAROWE DLA MATERIAŁÓW I KOMPONENTÓW Metody bdń 1 pren 45545-2:
Katedra Chemii Fizycznej Uniwersytetu Łódzkiego. Energia aktywacji jodowania acetonu. opracowała dr B. Nowicka, aktualizacja D.
 Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
Ktedr Chemii Fizycznej Uniwersytetu Łódzkiego Energi ktywcji jodowni cetonu oprcowł dr B. Nowick, ktulizcj D. Wliszewski ćwiczenie nr 8 Zkres zgdnień obowiązujących do ćwiczeni 1. Cząsteczkowość i rzędowość
Katedra Matematyki, Uniwersytet Przyrodniczy we Wrocławiu
 Inżynieria Ekologiczna Vol. 39, 2014, 155 165 DOI: 10.12912/2081139X.59 PORÓWNANIE WSKAŹNIKÓW: STANDARYZOWANEGO OPADU (SPI), STANDARYZOWANEJ EWAPOTRANSPIRACJI WSKAŹNIKOWEJ (SEI) ORAZ STANDARYZOWANEGO KLIMATYCZNEGO
Inżynieria Ekologiczna Vol. 39, 2014, 155 165 DOI: 10.12912/2081139X.59 PORÓWNANIE WSKAŹNIKÓW: STANDARYZOWANEGO OPADU (SPI), STANDARYZOWANEJ EWAPOTRANSPIRACJI WSKAŹNIKOWEJ (SEI) ORAZ STANDARYZOWANEGO KLIMATYCZNEGO
http://www.clausius-tower-society.koszalin.pl/index.html
 yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
yłd rc zminy objętości czynni roboczego rc techniczn w ułdzie otwrtym n przyłdzie turbiny RównowŜność prcy i ciepł w obiegu zmniętym I zsd termodynmii dl zminy stnu msy ontrolnej Szczególne przypdi I zsdy
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część I Matematyka finansowa
 Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
smoleńska jako nierozwiązywalny konflikt?
 D y s k u s j smoleńsk jko nierozwiązywlny konflikt? Wiktor Sorl Michł Bilewicz Mikołj Winiewski Wrszw, 2014 1 Kto nprwdę stł z zmchmi n WTC lub z zbójstwem kżnej Diny? Dlczego epidemi AIDS rozpowszechnił
D y s k u s j smoleńsk jko nierozwiązywlny konflikt? Wiktor Sorl Michł Bilewicz Mikołj Winiewski Wrszw, 2014 1 Kto nprwdę stł z zmchmi n WTC lub z zbójstwem kżnej Diny? Dlczego epidemi AIDS rozpowszechnił
Zadanie 5. Kratownica statycznie wyznaczalna.
 dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
dnie 5. Krtownic sttycznie wyznczln. Wyznczyć wrtości sił w prętch krtownicy sttycznie wyznczlnej przedstwionej n Rys.1: ). metodą nlitycznego równowżeni węzłów, ). metodą gricznego równowżeni węzłów;
Materiały pomocnicze do ćwiczeń z przedmiotu: Ogrzewnictwo, wentylacja i klimatyzacja II. Klimatyzacja
 Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Mteriły pomocnicze do ćwiczeń z przedmiotu: Orzewnictwo, wentylcj i klimtyzcj II. Klimtyzcj Rozdził 1 Podstwowe włsności powietrz jko nośnik ciepł mr inż. Anieszk Sdłowsk-Słę Mteriły pomocnicze do klimtyzcji.
Pomiary ciśnień i sprawdzanie manometrów
 Poiry ciśnień i srwdznie noetrów Instrukcj do ćwiczeni nr 2 Miernictwo energetyczne - lbortoriu Orcowł: dr inŝ. ElŜbiet Wróblewsk Zkłd Miernictw i Ochrony Atosfery Wrocłw, grudzień 2008 r. I. WSTĘP Ciśnienie
Poiry ciśnień i srwdznie noetrów Instrukcj do ćwiczeni nr 2 Miernictwo energetyczne - lbortoriu Orcowł: dr inŝ. ElŜbiet Wróblewsk Zkłd Miernictw i Ochrony Atosfery Wrocłw, grudzień 2008 r. I. WSTĘP Ciśnienie
Ćwiczenie 6 Wpływ dawki kwasu acetylosalicylowego na jego farmakokinetykę
 Ćwiczenie 6 Wpływ dwki kws cetyloslicylowego n jego frmkokinetykę Celem ćwiczeni jest zbdnie wpływ dwki kws cetyloslicylowego n jego frmkokinetykę. Wprowdzenie: Ćwiczenie poleg n oznczeni ilości slicylnów
Ćwiczenie 6 Wpływ dwki kws cetyloslicylowego n jego frmkokinetykę Celem ćwiczeni jest zbdnie wpływ dwki kws cetyloslicylowego n jego frmkokinetykę. Wprowdzenie: Ćwiczenie poleg n oznczeni ilości slicylnów
WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH
 Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
Ochron przeciwwybuchow Michł Świerżewski WENTYLACJA PRZESTRZENI POTENCJALNIE ZAGROŻONYCH WYBUCHEM MIESZANIN GAZOWYCH 1. Widomości ogólne Zgodnie z postnowienimi rozporządzeni Ministr Sprw Wewnętrznych
Próba określenia czynników determinujących wyniki ocen wprowadzenia euro przez mieszkańców Unii Europejskiej
 Mieczysłw Kowerski Wyższ Szkoł Zrządzni I Administrcji w Zmościu Ewelin Włodrczyk Wyższ Szkoł Zrządzni I Administrcji w Zmościu Prób określeni czynników determinujących wyniki ocen wprowdzeni euro przez
Mieczysłw Kowerski Wyższ Szkoł Zrządzni I Administrcji w Zmościu Ewelin Włodrczyk Wyższ Szkoł Zrządzni I Administrcji w Zmościu Prób określeni czynników determinujących wyniki ocen wprowdzeni euro przez
MODELOWANIE CHARAKTERYSTYK RDZENI FERROMAGNETYCZNYCH
 Krzysztof Górecki Akdemi orsk w Gdyni Klin Detk Pomorsk Wyższ Szkoł Nuk Stosownych w Gdyni ODELOWANIE CHARAKTERYSTYK RDZENI FERROAGNETYCZNYCH Artykuł dotyczy modelowni chrkterystyk rdzeni ferromgnetycznych.
Krzysztof Górecki Akdemi orsk w Gdyni Klin Detk Pomorsk Wyższ Szkoł Nuk Stosownych w Gdyni ODELOWANIE CHARAKTERYSTYK RDZENI FERROAGNETYCZNYCH Artykuł dotyczy modelowni chrkterystyk rdzeni ferromgnetycznych.
Prace Koła Matematyków Uniwersytetu Pedagogicznego w Krakowie (2014)
 Prce Koł Mt. Uniw. Ped. w Krk. 1 014), 1-5 edgogicznego w Krkowie PKoło Mtemtyków Uniwersytetu Prce Koł Mtemtyków Uniwersytetu Pedgogicznego w Krkowie 014) Bet Gwron 1 Kwdrtury Newton Cotes Streszczenie.
Prce Koł Mt. Uniw. Ped. w Krk. 1 014), 1-5 edgogicznego w Krkowie PKoło Mtemtyków Uniwersytetu Prce Koł Mtemtyków Uniwersytetu Pedgogicznego w Krkowie 014) Bet Gwron 1 Kwdrtury Newton Cotes Streszczenie.
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Biotechnologi w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt n przyszłość
Zadania. I. Podzielność liczb całkowitych
 Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Uszczelnienie przepływowe w maszyn przepływowych oraz sposób diagnozowania uszczelnienia przepływowego zwłaszcza w maszyn przepływowych
 Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
Uszczelnienie przepływowe w mszyn przepływowych orz sposób dignozowni uszczelnieni przepływowego zwłszcz w mszyn przepływowych Przedmiotem wynlzku jest uszczelnienie przepływowe mszyn przepływowych orz
WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ KONSTRUKCJI DREWNIANYCH
 95 ROCZNII INŻYNIERII BUDOWLANEJ ZESZYT 3/03 omisj Inżynierii Budowlnej Oddził Polskiej Akdemii Nuk w towicch WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ ONSTRUCJI DREWNIANYCH mil PAWLI, Zbigniew
95 ROCZNII INŻYNIERII BUDOWLANEJ ZESZYT 3/03 omisj Inżynierii Budowlnej Oddził Polskiej Akdemii Nuk w towicch WPŁYW WILGOTNOŚCI NA SZTYWNOŚCIOWE TŁUMIENIE DRGAŃ ONSTRUCJI DREWNIANYCH mil PAWLI, Zbigniew
Propozycja przedmiotowego systemu oceniania wraz z określeniem wymagań edukacyjnych (zakres podstawowy)
 Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Propozycj przedmiotowego systemu ocenini wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Proponujemy, by omwijąc dne zgdnienie progrmowe lub rozwiązując zdnie, nuczyciel określł do jkiego zkresu
Przykład 2.5. Figura z dwiema osiami symetrii
 Przkłd 5 Figur z dwiem osimi smetrii Polecenie: Wznczć główne centrlne moment bezwłdności orz kierunki główne dl poniższej figur korzstjąc z metod nlitcznej i grficznej (konstrukcj koł Mohr) 5 5 5 5 Dl
Przkłd 5 Figur z dwiem osimi smetrii Polecenie: Wznczć główne centrlne moment bezwłdności orz kierunki główne dl poniższej figur korzstjąc z metod nlitcznej i grficznej (konstrukcj koł Mohr) 5 5 5 5 Dl
CAŁKA OZNACZONA JAKO SUMA SZEREGU
 CAŁKA OZNACZONA JAKO SUMA SZEREGU Rozwżmy funkcję ciągłą x f(x) o wrtościch nieujemnych określoną n przedzile [, b]. Ustlmy [będzie to problem sttystyczny polegjący n dokłdnym sprecyzowniu informcji o
CAŁKA OZNACZONA JAKO SUMA SZEREGU Rozwżmy funkcję ciągłą x f(x) o wrtościch nieujemnych określoną n przedzile [, b]. Ustlmy [będzie to problem sttystyczny polegjący n dokłdnym sprecyzowniu informcji o
Weryfikacja modelowa jest analizą statyczną logiki modalnej
 Weryfikcj modelow jest nlizą sttyczną logiki modlnej Mrcin Sulikowski MIMUW 15 grudni 010 1 Wstęp Weryfikcj systemów etykietownych 3 Flow Logic 4 Weryfikcj modelow nliz sttyczn Co jest czym czego? Weryfikcj
Weryfikcj modelow jest nlizą sttyczną logiki modlnej Mrcin Sulikowski MIMUW 15 grudni 010 1 Wstęp Weryfikcj systemów etykietownych 3 Flow Logic 4 Weryfikcj modelow nliz sttyczn Co jest czym czego? Weryfikcj
CHARAKTERYSTYKA TEKSTURY WYBRANYCH MIKSÓW TŁUSZCZOWYCH. Ewa Jakubczyk, Ewa Gondek, Karolina Samborska
 Zeszyty Problemowe Postępów Nuk Rolniczych nr 579, 214, 17 26 CHRKTERYSTYK TEKSTURY WYBRNYCH MIKSÓW TŁUSZCZOWYCH Ew Jkubczyk, Ew Gondek, Krolin Smborsk Szkoł Główn Gospodrstw Wiejskiego w Wrszwie Streszczenie.
Zeszyty Problemowe Postępów Nuk Rolniczych nr 579, 214, 17 26 CHRKTERYSTYK TEKSTURY WYBRNYCH MIKSÓW TŁUSZCZOWYCH Ew Jkubczyk, Ew Gondek, Krolin Smborsk Szkoł Główn Gospodrstw Wiejskiego w Wrszwie Streszczenie.
LISTA02: Projektowanie układów drugiego rzędu Przygotowanie: 1. Jakie własności ma równanie 2-ego rzędu & x &+ bx&
 LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
temperatura
 tempertur 2.3 3.3 Rys. 9. Przestrzenny rozkłd dnych: powierzchni geosttystyczn (rozkłd tempertury powierzchni morz zrejestrowny przez stelitę jest rezulttem dziłni prw fizyki; powierzchni sttystyczn (zwierjąc
tempertur 2.3 3.3 Rys. 9. Przestrzenny rozkłd dnych: powierzchni geosttystyczn (rozkłd tempertury powierzchni morz zrejestrowny przez stelitę jest rezulttem dziłni prw fizyki; powierzchni sttystyczn (zwierjąc
Wyrównanie sieci niwelacyjnej
 1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
1. Wstęp Co to jest sieć niwelcyjn Po co ją się wyrównje Co chcemy osiągnąć 2. Metod pośrednicząc Wyrównnie sieci niwelcyjnej Metod pośrednicząc i metod grpow Mmy sieć skłdjącą się z szereg pnktów. Niektóre
Wymagania na poszczególne oceny z matematyki w Zespole Szkół im. St. Staszica w Pile. Kl. I poziom podstawowy
 Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
Wymgni n poszczególne oceny z mtemtyki w Zespole Szkół im. St. Stszic w Pile. LICZBY RZECZYWISTE Kl. I poziom podstwowy podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych
ZMIANY W STRUKTURZE BILANSU CIEPLNEGO I KLIMATYCZNEGO BILANSU WODNEGO DLA LASU IGLASTEGO
 WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2007: t. 7 z. 2b (21) WATER-ENVIRONMENT-RURAL AREAS s. 111 119 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2007 ZMIANY W STRUKTURZE BILANSU CIEPLNEGO
WODA-ŚRODOWISKO-OBSZARY WIEJSKIE 2007: t. 7 z. 2b (21) WATER-ENVIRONMENT-RURAL AREAS s. 111 119 www.imuz.edu.pl Instytut Melioracji i Użytków Zielonych w Falentach, 2007 ZMIANY W STRUKTURZE BILANSU CIEPLNEGO
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY
 WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE IIc ZAKRES PODSTAWOWY I ROZSZERZONY. JĘZYK MATEMATYKI oblicz wrtość bezwzględną liczby rzeczywistej stosuje interpretcję geometryczną wrtości bezwzględnej liczby
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
WEKTORY skalary wektory W ogólnym przypadku, aby określić wektor, należy znać:
 WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
WEKTORY Wśród wielkości fizycznych występujących w fizyce możn wyróżnić sklry i wektory. Aby określić wielkość sklrną, wystrczy podć tylko jedną liczbę. Wielkościmi tkimi są ms, czs, tempertur, objętość
PORÓWNANIE WSKAŹNIKA STANDARYZOWANEGO OPADU (SPI) WYZNACZONEGO ZA POMOCĄ ROZKŁADU GAMMA I ROZKŁADU NORMALNEGO DLA MIESIĘCZNYCH SUM OPADÓW
 INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr /III/2012, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 197 208 Komisja Technicznej Infrastruktury Wsi Porównanie
INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr /III/2012, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 197 208 Komisja Technicznej Infrastruktury Wsi Porównanie
3. F jest lewostronnie ciągła
 Def. Zmienną losową nzywmy funkcję X: tką, że x R : { : X( ) < x }. Ozn.: zmist pisd A = { : X( ) < x } piszemy A = { X < x } zdrzenie poleg n tym, że X( )
Def. Zmienną losową nzywmy funkcję X: tką, że x R : { : X( ) < x }. Ozn.: zmist pisd A = { : X( ) < x } piszemy A = { X < x } zdrzenie poleg n tym, że X( )
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Oznaczenia: K wymagania konieczne; P wymagania podstawowe; R wymagania rozszerzające; D wymagania dopełniające; W wymagania wykraczające
 Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
Wymgni edukcyjne z mtemtyki ls 2 b lo Zkres podstwowy Oznczeni: wymgni konieczne; wymgni podstwowe; R wymgni rozszerzjące; D wymgni dopełnijące; W wymgni wykrczjące Temt lekcji Zkres treści Osiągnięci
I POCHODNA - INTERPRETACJA GEOMETRYCZNA
 I ROK GOSPODARKA PRZESTRZENNA semestr I POCHODNA - INTERPRETACJA GEOMETRYCZNA Przpomnijm definicję ilorzu róŝnicowego : Definicj (ilorzu róŝnicowego) : Ilorzem róŝnicowm funkcji f : (,b) R odpowidjącm
I ROK GOSPODARKA PRZESTRZENNA semestr I POCHODNA - INTERPRETACJA GEOMETRYCZNA Przpomnijm definicję ilorzu róŝnicowego : Definicj (ilorzu róŝnicowego) : Ilorzem róŝnicowm funkcji f : (,b) R odpowidjącm
PODSTAWY ALGEBRY MACIERZY. Operacje na macierzach
 PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
PODSTWY LGEBRY MCIERZY WIERSZ i, KOLUMN (j) Mcierz m,n, gdzie m to ilość wierszy, n ilość kolumn i,j element mcierzy z itego wiersz, jtej kolumny Opercje n mcierzch Równość mcierzy m,n = B m,n. def i,j
OCENA BARWY ORAZ ZAWARTOŚCI BARWNIKÓW KAROTENOIDOWYCH W OWOCACH POMIDORA NOWYCH LINII HODOWLANYCH
 BROMAT. CHEM. TOKSYKOL. XLII, 2009, 3, str. 926 931 Ew Jbłońsk-Ryś, Mrt Zlewsk-Koron OCENA BARWY ORAZ ZAWARTOŚCI BARWNIKÓW KAROTENOIDOWYCH W OWOCACH POMIDORA NOWYCH LINII HODOWLANYCH Ktedr Technologii
BROMAT. CHEM. TOKSYKOL. XLII, 2009, 3, str. 926 931 Ew Jbłońsk-Ryś, Mrt Zlewsk-Koron OCENA BARWY ORAZ ZAWARTOŚCI BARWNIKÓW KAROTENOIDOWYCH W OWOCACH POMIDORA NOWYCH LINII HODOWLANYCH Ktedr Technologii
POWŁOKI ELEKTROISKROWE WC-CO MODYFIKOWANE WIĄZKĄ LASEROWĄ. 88 Powłoki elektroiskrowe WC-Co modyfikowane wiązką laserową. Wstęp
 Rdek N.,* Szlpko J.** *Ktedr Inżynierii Eksplotcji Politechnik Świętokrzysk, Kielce, Polsk **Khmelnitckij Uniwersytet Nrodowy, Khmelnitckij, Ukrin Wstęp 88 POWŁOKI ELEKTROISKROWE WC-CO MODYFIKOWANE WIĄZKĄ
Rdek N.,* Szlpko J.** *Ktedr Inżynierii Eksplotcji Politechnik Świętokrzysk, Kielce, Polsk **Khmelnitckij Uniwersytet Nrodowy, Khmelnitckij, Ukrin Wstęp 88 POWŁOKI ELEKTROISKROWE WC-CO MODYFIKOWANE WIĄZKĄ
REWOLUCJA MOBILNEGO INTERNETU RAPORT EMPIRYCZNE BADANIE MOBILNYCH. Audytel W POLSCE USŁUG DOSTĘPU DO INTERNETU. Warszawa,21.01.2009 r.
 REWOLUCJA MOBILNEGO INTERNETU W POLSCE RAPORT EMPIRYCZNE BADANIE MOBILNYCH USŁUG DOSTĘPU DO INTERNETU Wrszw,21.01.2009 r. Audytel Dził Bdń i Anliz Audytel S.A. Rport Extel S.A. do uŝytku wewnętrznego Streszczenie
REWOLUCJA MOBILNEGO INTERNETU W POLSCE RAPORT EMPIRYCZNE BADANIE MOBILNYCH USŁUG DOSTĘPU DO INTERNETU Wrszw,21.01.2009 r. Audytel Dził Bdń i Anliz Audytel S.A. Rport Extel S.A. do uŝytku wewnętrznego Streszczenie
Ewapotranspiracja i jej wpływ na plonowanie roślin
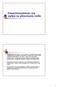 Ewapotranspiracja i jej wpływ na plonowanie roślin Ewaporacja, parowanie są to procesy, w wyniku których woda znajdująca się na powierzchni terenu w ciekłym lub stałym stanie skupienia przechodzi w stan
Ewapotranspiracja i jej wpływ na plonowanie roślin Ewaporacja, parowanie są to procesy, w wyniku których woda znajdująca się na powierzchni terenu w ciekłym lub stałym stanie skupienia przechodzi w stan
ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etapy rozwiązania zadania , 3 5, 7
 Próbn egzmin mturln z mtemtki Numer zdni ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etp rozwiązni zdni Liczb punktów Podnie wrtości b: b = Sporządzenie wkresu funkcji g Uwgi dl egzmintorów 4 Krzw
Próbn egzmin mturln z mtemtki Numer zdni ODPOWIEDZI I SCHEMAT PUNKTOWANIA POZIOM ROZSZERZONY Etp rozwiązni zdni Liczb punktów Podnie wrtości b: b = Sporządzenie wkresu funkcji g Uwgi dl egzmintorów 4 Krzw
Równania i nierówności kwadratowe z jedną niewiadomą
 50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
50 REPETYTORIUM 31 Równni i nierówności kwdrtowe z jedną niewidomą Równnie wielominowe to równość dwóch wyrżeń lgebricznych Kżd liczb, któr po podstwieniu w miejscu niewidomej w równniu o jednej niewidomej
Fizyka. Kurs przygotowawczy. na studia inżynierskie. mgr Kamila Haule
 Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
Fizyk Kurs przygotowwczy n studi inżynierskie mgr Kmil Hule Dzień 3 Lbortorium Pomir dlczego mierzymy? Pomir jest nieodłączną częścią nuki. Stopień znjomości rzeczy często wiąże się ze sposobem ich pomiru.
TRANSCOMP XIV INTERNATIONAL CONFERENCE COMPUTER SYSTEMS AIDED SCIENCE, INDUSTRY AND TRANSPORT
 TRANSCOMP XIV INTRNATIONAL CONFRNC COMPUTR SYSTMS AIDD SCINC, INDUSTRY AND TRANSPORT Dignostyk, hmulce, pomiry drogowe trnsport, Andrzej GAJK Wojciech SZCZYPIŃSKI-SALA Piotr STRZĘPK 1 OCNA MTOD POMIARÓW
TRANSCOMP XIV INTRNATIONAL CONFRNC COMPUTR SYSTMS AIDD SCINC, INDUSTRY AND TRANSPORT Dignostyk, hmulce, pomiry drogowe trnsport, Andrzej GAJK Wojciech SZCZYPIŃSKI-SALA Piotr STRZĘPK 1 OCNA MTOD POMIARÓW
Podstawy Konstrukcji Maszyn
 Podstwy Konstrukcji Mszyn Wykłd 3 ObciąŜeni zienne Dr inŝ. Jcek Czrnigowski ienność obciąŝeń Klsyfikcj obciąŝeń: ObciąŜeni stłe Wrtość, kierunek i zwrot nie ulegją zinie w czsie O zienności ustlonej ObciąŜeni
Podstwy Konstrukcji Mszyn Wykłd 3 ObciąŜeni zienne Dr inŝ. Jcek Czrnigowski ienność obciąŝeń Klsyfikcj obciąŝeń: ObciąŜeni stłe Wrtość, kierunek i zwrot nie ulegją zinie w czsie O zienności ustlonej ObciąŜeni
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 9. ZBIORY ROZMYTE Częstochow 204 Dr hb. inż. Grzegorz Dudek Wydził Elektryczny Politechnik Częstochowsk ZBIORY ROZMYTE Klsyczne pojęcie zbioru związne jest z logiką dwuwrtościową
SZTUCZNA INTELIGENCJA WYKŁAD 9. ZBIORY ROZMYTE Częstochow 204 Dr hb. inż. Grzegorz Dudek Wydził Elektryczny Politechnik Częstochowsk ZBIORY ROZMYTE Klsyczne pojęcie zbioru związne jest z logiką dwuwrtościową
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Mteriły dydktyczne n zjęci wyrównwcze z mtemtyki dl studentów pierwszego roku kierunku zmwinego Inżynieri i Gospodrk Wodn w rmch projektu Er inżynier pewn lokt n przyszłość Projekt Er inżynier pewn lokt
Spis treści. Wstęp... 4
 pis treści Wstęp... 4 Zdni mturlne......................................................... 5 1. Funkcj kwdrtow... 5. Wielominy... 7. Trygonometri... 9 4. Wrtość bezwzględn... 11 5. Plnimetri... 15 6.
pis treści Wstęp... 4 Zdni mturlne......................................................... 5 1. Funkcj kwdrtow... 5. Wielominy... 7. Trygonometri... 9 4. Wrtość bezwzględn... 11 5. Plnimetri... 15 6.
Zaokrąglanie i zapisywanie wyników obliczeń przybliżonych
 Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
Edwrd Musił Oddził Gdński SEP Zokrąglnie i zpisywnie wyników obliczeń przybliżonych Inżynier wykonuje nieml wyłącznie obliczeni przybliżone i powinien mieć nieustnnie n względzie dokłdność, jką chce uzyskć
INSTRUKCJA. - Jak rozwiązywać zadania wysoko punktowane?
 INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
Instytut Mechatroniki i Systemów Informatycznych. Podstawy pomiaru i analizy sygnałów wibroakustycznych wykorzystywanych w diagnostyce
 ĆWICZEIE 1 Podstwy pomiru i nlizy sygnłów wibrokustycznych wykorzystywnych w dignostyce Cel ćwiczeni Poznnie podstwowych, mierzlnych wrtości procesów wibrokustycznych wykorzystywnych w dignostyce, metod
ĆWICZEIE 1 Podstwy pomiru i nlizy sygnłów wibrokustycznych wykorzystywnych w dignostyce Cel ćwiczeni Poznnie podstwowych, mierzlnych wrtości procesów wibrokustycznych wykorzystywnych w dignostyce, metod
WYMAGANIA EDUKACYJNE Z MATEMATYKI W KLASIE Ib ZAKRES PODSTAWOWY
 . LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje liczbę do odpowiedniego zbioru liczb stosuje cechy podzielności
. LICZBY RZECZYWISTE podje przykłdy liczb: nturlnych, cłkowitych, wymiernych, niewymiernych, pierwszych i złożonych orz przyporządkowuje liczbę do odpowiedniego zbioru liczb stosuje cechy podzielności
4. RACHUNEK WEKTOROWY
 4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
Wysokocyklowa analiza zmęczeniowa cylindrów hydraulicznych z uwzględnieniem wpływu napręŝenia średniego
 Mteriły XIII Konferencji Informtyk w Technologii Metli KomPlsTech2006 Szczwnic 15-18 styczni 2006 Wysokocyklow nliz zmęczeniow cylindrów hydrulicznych z uwzględnieniem wpływu npręŝeni średniego Tomsz Bednrek
Mteriły XIII Konferencji Informtyk w Technologii Metli KomPlsTech2006 Szczwnic 15-18 styczni 2006 Wysokocyklow nliz zmęczeniow cylindrów hydrulicznych z uwzględnieniem wpływu npręŝeni średniego Tomsz Bednrek
SUSZE METEOROLOGICZNE WE WROCŁAWIU-SWOJCU W PÓŁROCZU CIEPŁYM (IV IX) W WIELOLECIU
 INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr 8/2/2010, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 89 102 Komisja Technicznej Infrastruktury Wsi Susze meteorologiczne...
INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr 8/2/2010, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 89 102 Komisja Technicznej Infrastruktury Wsi Susze meteorologiczne...
POMIAR, JEGO OPRACOWANIE I INTERPRETACJA
 POMIAR, JEGO OPRACOWANIE I INTERPRETACJA N wynik kżdego pomiru wpływ duż ilość czynników. Większość z nich jest nieidentyfikowln, sił ich oddziływni zmieni się w sposób przypdkowy. Z tego względu, chociż
POMIAR, JEGO OPRACOWANIE I INTERPRETACJA N wynik kżdego pomiru wpływ duż ilość czynników. Większość z nich jest nieidentyfikowln, sił ich oddziływni zmieni się w sposób przypdkowy. Z tego względu, chociż
Prosta metoda sprawdzania fundamentów ze względu na przebicie
 Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
Konstrkcje Elementy Mteriły Prost metod sprwdzni fndmentów ze względ n przebicie Prof dr b inż Micł Knff, Szkoł Główn Gospodrstw Wiejskiego w Wrszwie, dr inż Piotr Knyzik, Politecnik Wrszwsk 1 Wprowdzenie
1 Definicja całki oznaczonej
 Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
Definicj cłki oznczonej Niech dn będzie funkcj y = g(x) ciągł w przedzile [, b]. Przedził [, b] podzielimy n n podprzedziłów punktmi = x < x < x
2. FUNKCJE WYMIERNE Poziom (K) lub (P)
 Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Kls drug poziom podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych redukuje wyrzy
Algorytmy graficzne. Filtry wektorowe. Filtracja obrazów kolorowych
 Algorytmy grficzne Filtry wektorowe. Filtrcj orzów kolorowych Filtrcj orzów kolorowych Metody filtrcji orzów kolorowych możn podzielić n dwie podstwowe klsy: Metody komponentowe (component-wise). Cechą
Algorytmy grficzne Filtry wektorowe. Filtrcj orzów kolorowych Filtrcj orzów kolorowych Metody filtrcji orzów kolorowych możn podzielić n dwie podstwowe klsy: Metody komponentowe (component-wise). Cechą
f(x)dx (1.7) b f(x)dx = F (x) = F (b) F (a) (1.2)
 Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Temat lekcji Zakres treści Osiągnięcia ucznia
 ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
ln wynikowy kls 2c i 2e - Jolnt jąk Mtemtyk 2. dl liceum ogólnoksztłcącego, liceum profilownego i technikum. sztłcenie ogólne w zkresie podstwowym rok szkolny 2015/2016 Wymgni edukcyjne określjące oceny:
Integralność konstrukcji
 1 Integrlność konstrukcji Wykłd Nr 5 PROJEKTOWANIE W CELU UNIKNIĘCIA ZMĘCZENIOWEGO Wydził Inżynierii Mechnicznej i Robotyki Ktedr Wytrzymłości, Zmęczeni Mteriłów i Konstrukcji http://zwmik.imir.gh.edu.pl/dydktyk/imir/index.htm
1 Integrlność konstrukcji Wykłd Nr 5 PROJEKTOWANIE W CELU UNIKNIĘCIA ZMĘCZENIOWEGO Wydził Inżynierii Mechnicznej i Robotyki Ktedr Wytrzymłości, Zmęczeni Mteriłów i Konstrukcji http://zwmik.imir.gh.edu.pl/dydktyk/imir/index.htm
( ) Elementy rachunku prawdopodobieństwa. f( x) 1 F (x) f(x) - gęstość rozkładu prawdopodobieństwa X f( x) - dystrybuanta rozkładu.
 Elementy rchunku prwdopodoeństw f 0 f() - gęstość rozkłdu prwdopodoeństw X f d P< < = f( d ) F = f( tdt ) - dystryunt rozkłdu E( X) = tf( t) dt - wrtość średn D ( X) = E( X ) E( X) - wrncj = f () F ()
Elementy rchunku prwdopodoeństw f 0 f() - gęstość rozkłdu prwdopodoeństw X f d P< < = f( d ) F = f( tdt ) - dystryunt rozkłdu E( X) = tf( t) dt - wrtość średn D ( X) = E( X ) E( X) - wrncj = f () F ()
Przekształcenia automatów skończonych
 Przeksztłceni utomtów skończonych Teori utomtów i języków formlnych Dr inŝ. Jnusz Mjewski Ktedr Informtyki Konstrukcj utomtu skończonego n podstwie wyrŝeni regulrnego (lgorytm Thompson) Wejście: wyrŝenie
Przeksztłceni utomtów skończonych Teori utomtów i języków formlnych Dr inŝ. Jnusz Mjewski Ktedr Informtyki Konstrukcj utomtu skończonego n podstwie wyrŝeni regulrnego (lgorytm Thompson) Wejście: wyrŝenie
Kodowanie liczb. Kodowanie stałopozycyjne liczb całkowitych. Niech liczba całkowita a ma w systemie dwójkowym postać: Kod prosty
 Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
Kodownie licz Kodownie stłopozycyjne licz cłkowitych Niech licz cłkowit m w systemie dwójkowym postć: nn 0 Wtedy może yć on przedstwion w postci ( n+)-itowej przy pomocy trzech niżej zdefiniownych kodów
ROZPORZĄDZENIE MINISTRA INFRASTRUKTURY 1) z dnia 16 grudnia 2004 r.
 Typ/orgn wydjący Rozporządzenie/Minister Infrstruktury Tytuł w sprwie szczegółowych wrunków i trybu wydwni zezwoleń n przejzdy pojzdów nienormtywnych Skrócony opis pojzdy nienormtywne Dt wydni 16 grudni
Typ/orgn wydjący Rozporządzenie/Minister Infrstruktury Tytuł w sprwie szczegółowych wrunków i trybu wydwni zezwoleń n przejzdy pojzdów nienormtywnych Skrócony opis pojzdy nienormtywne Dt wydni 16 grudni
