W siła działająca na bryłę zredukowana do środka masy ( = 0
|
|
|
- Józef Łukasik
- 7 lat temu
- Przeglądów:
Transkrypt
1 Popęd i popęd bryły Bryła w ruchu posępowym. Zasada pędu i popędu ma posać: p p S gdie: p m v pęd bryły w ruchu posępowym S c W d popęd siły diałającej na bryłę w ruchu posępowym aś: v c prędkość środka masy bryły (równa prędkości kaŝdego punku) W siła diałająca na bryłę redukowana do środka masy ( 0 M ) c Prof. Edmund Wibrod
2 Pokrę i krę bryły w ruchu posępowym obroowym i płaskim Zasada kręu kręu i pokręu ora asada achowania kręu. Dla ruchu posępowego obroowego i płaskiego bryły słusne są asady kręu kręu i pokręu ora asada achowania kręu kóre moŝemy sformułować w posaci nasępujących wierdeń. Twierdenie Pochodna wględem casu kręu ciała wględem punku jes równa momenowi sił ewnęrnych diałających na o ciało wględem ego samego punku K & M. (4.68) Równanie (4.68) moŝemy eŝ predsawić w posaci Twierdenie K K M d. (4.69) Pokrę sił ewnęrnych wględem punku diałających na ciało jes równy pryrosowi kręu ego ciała Twierdenie 3 JeŜeli momen sił ewnęrnych diałających na ciało wględem punku jes równy ero o krę ego ciała wględem punku nie moŝe ulec mianie K cons. (4.70) Prof. Edmund Wibrod
3 Pokrę i krę bryły w ruchu posępowym wględem nieruchomego punku oblicamy: Π M d r W d r S pokrę K r mv krę bryły w ruchu posępowym c gdie: r wekor promień o pocąku w punkcie i końcu w środku masy ciała v prędkość środka masy bryły (jednakowa dla wsyskich punków) m masa bryły. mv K r Krę bryły w ruchu posępowym Prof. Edmund Wibrod
4 Pokrę i krę bryły w ruchu obroowym oblicamy nasępująco. Równanie (4.77) preksałcamy do posaci d ( J ω ) M d a po scałkowaniu J ω d( J ω ) M d J ω orymujemy J ω J ω M d (4.83) gdie: J ω M d krę bryły w ruchu obroowym pokrę (impuls momenu). Prof. Edmund Wibrod
5 Pokrę i krę bryły w ruchu płaskim wględem dowolnego nieruchomego punku oblicamy: Π ( M + r W ) d pokrę siły i momenu diałającego na bryłę K K + r mv krę bryły wględem punku gdie: K krę ciała wględem środka masy r wekor a pocąku w punkcie i końcu w środku masy bryły v prędkość środka masy bryły m masa bryły. v r K Krę bryły w ruchu płaskim Prof. Edmund Wibrod
6 Praca i energia bryły w ruchu posępowym obroowym i płaskim Zasada energii i pracy ma w ym prypadku posać podobną jak dla punku maerialnego. Pryros energii kineycnej pry premiescaniu ciała jednego połoŝenia w drugie jes równy pracy wsyskich sił ewnęrnych diałających na o ciało E E E L (4.7) gdie: E energia kineycna bryły w połoŝeniu pocąkowym E energia kineycna bryły w połoŝeniu końcowym L praca sił i ewnęrnych wykonana na drode od połoŝenia pocąkowego do końcowego bryły. RóŜnickową posać asady energii orymamy pre róŝnickowanie (4.7) wględem casu E& N (4.73) gdie: E energia kineycna bryły dl N d moc. Prof. Edmund Wibrod
7 Pracę i energię bryły w ruchu posępowym moŝemy oblicyć określając najpierw energię kineycną masy elemenarnej a) dm v b) or W dr Bryła w ruchu posępowym: a) określanie energii kineycnej b) określanie pracy sił pryłoŝonych do bryły de dmv co po scałkowaniu daje energię kineycną bryły w ruchu posępowym w posaci mv E gdie: m masa bryły v prędkość punku bryły (jednakowa dla wsyskich punków). Pracę sił pryłoŝonych do ciała porusającego się ruchem posępowym (rys. 4.5b) moŝemy oblicyć określając najpierw pracę elemenarną dl W dr skąd L r r dl r r W dr. (4.7) Prof. Edmund Wibrod
8 Pracę i energię bryły w ruchu obroowym oblicamy preksałcając kolei równanie (4.77) nasępująco J ω M dϕ d d co moŝemy dalej apisać pryjmuje posać dϕ J d ω J ω d ω M d ϕ d po scałkowaniu ω ϕ J ωdω M dϕ ω ϕ E E L (4.84) gdie: E J ω energia kineycna bryły w ruchu obroowym L ϕ M dϕ praca par sił (momenów) diałających na bryłę na drode od ϕ ϕ do ϕ. Prof. Edmund Wibrod
9 Praca i energia bryły w ruchu płaskim jes odpowiednio sumą pracy ora energii ruchu posępowego środka masy i ruchu obroowego bryły wględem osi prechodącej pre środek masy. Energię kineycną oblicamy więc v E m + J ω. (4.9) Z kolei praca wykonana pre siły i momeny pryłoŝone do ciała redukowane do jego środka masy jes sumą s ϕ ϕ (4.93) s ϕ L W ds + M d gdie: s s droga prebya pre środek masy bryły ϕ ϕ ką obrou bryły. Prof. Edmund Wibrod
10 blicanie reakcji dynamicnych łoŝysk Do oblicania reakcji dynamicnych łoŝysk w ruchu obroowym bryły sosujemy asadę d Alembera: l B x x da ρ da n B y A x ω ε y x dm A y y kreślanie reakcji dynamicnych łoŝysk bryły ruchu obroowym W prypadku oblicania reakcji dynamicnych łoŝysk (rys. 4.7) warunki równowagi bryły są nasępujące: A x + B x + da n sin + da cos 0 B y l + da n cos da sin 0 A y + B y + da n cos da sin 0 B x l + da n sin + da cos 0 gdie: dan dmρω da dm ερ a ponado: ρ sin x ρ cos y. (4.79) Prof. Edmund Wibrod
11 Po podsawieniu (4.79) do (4.78) orymujemy: ω Ax + Bx + xdm + ydm 0 Ay + By + ω ydm ε xdm 0 ε + ω ε 0 Byl ydm xdm (4.80) ω Bxl + xdm + ydm 0 ε a po skorysaniu aleŝności: xdm x m ( ) m ydm y m ( m) xdm D x (4.8) ( m) ydm D y ( m) Prof. Edmund Wibrod
12 orymujemy: x x ω ε y y ω ε A + B x m y m A + B y m + x m y ω y ε x B l D + D. (4.8) x ω x ε y B l D D Z powyŝsych równań wynika Ŝe reakcje dynamicne w łoŝyskach będą równe ero gdy spełnione będą dwa warunki: ) środek masy leŝy na osi obrou bryły (x y 0) ) oś obrou jes jedną głównych osi bewładności obracającej się bryły (D x D y 0). Wirnik w kórym spełnione są e warunki naywamy wyrównowaŝonym. Prof. Edmund Wibrod
Zasada pędu i popędu, krętu i pokrętu, energii i pracy oraz d Alemberta bryły w ruchu postępowym, obrotowym i płaskim
 Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
Zasada pędu i popędu, kręu i pokręu, energii i pracy oraz d Alembera bryły w ruchu posępowym, obroowym i płaskim Ruch posępowy bryły Pęd ciała w ruchu posępowym obliczamy, jak dla punku maerialnego, skupiając
>> ω z, (4.122) Przybliżona teoria żyroskopu
 Prybliżona teoria żyroskopu Żyroskopem naywamy ciało materialne o postaci bryły obrotowej (wirnika), osadone na osi pokrywającej się osią geometrycną tego ciała wanej osią żyroskopową. ζ K θ ω η ω ζ y
Prybliżona teoria żyroskopu Żyroskopem naywamy ciało materialne o postaci bryły obrotowej (wirnika), osadone na osi pokrywającej się osią geometrycną tego ciała wanej osią żyroskopową. ζ K θ ω η ω ζ y
Opis ruchu we współrzędnych prostokątnych (kartezjańskich)
 Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
Opis ruchu we współrędch prosokąch (karejańskich) Opis ruchu we współrędch prosokąch jes podob do opisu a pomocą wekora wodącego, kórego pocąek leż w pocąku układu odiesieia. Położeie. Położeie puku A
Ruch płaski. Bryła w ruchu płaskim. (płaszczyzna kierująca) Punkty bryły o jednakowych prędkościach i przyspieszeniach. Prof.
 Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Ruch płaski Ruchem płaskim nazywamy ruch, podczas kórego wszyskie punky ciała poruszają się w płaszczyznach równoległych do pewnej nieruchomej płaszczyzny, zwanej płaszczyzną kierującą. Punky bryły o jednakowych
Wyznaczyć prędkości punktów A i B
 Wyzaczaie prędkości i przyspieszeia puku ciała w ruchu płaskim (a) Wyzaczyć prędkości puków i Dae: rad/s; ε 0; 5 cm; 5 cm 48 mechaika echicza kiemayka 3 Wyzaczaie prędkości i przyspieszeia puku ciała w
Wyzaczaie prędkości i przyspieszeia puku ciała w ruchu płaskim (a) Wyzaczyć prędkości puków i Dae: rad/s; ε 0; 5 cm; 5 cm 48 mechaika echicza kiemayka 3 Wyzaczaie prędkości i przyspieszeia puku ciała w
Dynamika punktu materialnego
 Naa -Japonia W-3 (Jaosewic 1 slajdów Dynamika punku maeialnego Dynamika Układ inecjalny Zasady dynamiki: piewsa asada dynamiki duga asada dynamiki; pęd ciała popęd siły ecia asada dynamiki (pawo akcji
Naa -Japonia W-3 (Jaosewic 1 slajdów Dynamika punku maeialnego Dynamika Układ inecjalny Zasady dynamiki: piewsa asada dynamiki duga asada dynamiki; pęd ciała popęd siły ecia asada dynamiki (pawo akcji
Wyznaczanie reakcji dynamicznych oraz wyważanie ciała w ruchu obrotowym wokół stałej osi 8
 Wnacanie reakcji dnaicnch ora wważanie ciała w ruchu oroow wokół sałej osi 8 Wprowadenie Jeśli dowolne ciało swne o asie jes w ruchu oroow wokół osi, o na podporach powsają reakcje A i B. Składowe ch reakcji
Wnacanie reakcji dnaicnch ora wważanie ciała w ruchu oroow wokół sałej osi 8 Wprowadenie Jeśli dowolne ciało swne o asie jes w ruchu oroow wokół osi, o na podporach powsają reakcje A i B. Składowe ch reakcji
Zasady dynamiki Isaak Newton (1686 r.)
 Zasady dynamiki Isaak Newton (1686 r.) I (zasada bezwładności) Istnieje taki układ odniesienia, w którym ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, jeśli nie działają
Zasady dynamiki Isaak Newton (1686 r.) I (zasada bezwładności) Istnieje taki układ odniesienia, w którym ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, jeśli nie działają
2.1 Zagadnienie Cauchy ego dla równania jednorodnego. = f(x, t) dla x R, t > 0, (2.1)
 Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Wykład 2 Sruna nieograniczona 2.1 Zagadnienie Cauchy ego dla równania jednorodnego Równanie gań sruny jednowymiarowej zapisać można w posaci 1 2 u c 2 2 u = f(x, ) dla x R, >, (2.1) 2 x2 gdzie u(x, ) oznacza
Ruch obrotowy bryły sztywnej. Bryła sztywna - ciało, w którym odległości między poszczególnymi punktami ciała są stałe
 Ruch obrotowy bryły sztywnej Bryła sztywna - ciało, w którym odległości między poszczególnymi punktami ciała są stałe Ruch obrotowy ruch po okręgu P, t 1 P 1, t 1 θ 1 θ Ruch obrotowy ruch po okręgu P,
Ruch obrotowy bryły sztywnej Bryła sztywna - ciało, w którym odległości między poszczególnymi punktami ciała są stałe Ruch obrotowy ruch po okręgu P, t 1 P 1, t 1 θ 1 θ Ruch obrotowy ruch po okręgu P,
Podstawy fizyki sezon 1 V. Ruch obrotowy 1 (!)
 Podstawy fizyki sezon 1 V. Ruch obrotowy 1 (!) Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Kinematyka ruchu
Podstawy fizyki sezon 1 V. Ruch obrotowy 1 (!) Agnieszka Obłąkowska-Mucha WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Kinematyka ruchu
Wykład FIZYKA I. 2. Kinematyka punktu materialnego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wykład FIZYKA I. Kinemayka punku maerialnego Kaedra Opyki i Fooniki Wydział Podsawowych Problemów Techniki Poliechnika Wrocławska hp://www.if.pwr.wroc.pl/~wozniak/fizyka1.hml Miejsce konsulacji: pokój
Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego
 POLTECHNKA ŚLĄSKA WYDZAŁ CHEMCZNY KATEDRA FZYKOCHEM TECHNOLOG POLMERÓW LABORATORUM Z FZYK Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego WYZNACZANE MOMENTÓW BEZWŁADNOŚC
POLTECHNKA ŚLĄSKA WYDZAŁ CHEMCZNY KATEDRA FZYKOCHEM TECHNOLOG POLMERÓW LABORATORUM Z FZYK Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego WYZNACZANE MOMENTÓW BEZWŁADNOŚC
będzie momentem Twierdzenie Steinera
 Wykład z fizyki, Piotr Posmykiewicz. Niech 90 oznacza moment bezwładności względem osi przechodzącej przez środek masy ciała o masie i niech będzie momentem bezwładności tego ciała względem osi równoległej
Wykład z fizyki, Piotr Posmykiewicz. Niech 90 oznacza moment bezwładności względem osi przechodzącej przez środek masy ciała o masie i niech będzie momentem bezwładności tego ciała względem osi równoległej
ver b drgania harmoniczne
 ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
ver-28.10.11 b drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne N = n=1 A n cos nω n Fig (...) analiza Fouriera małe drgania E p E E k jeden sopień swobody: E p -A E p A 0
Opis ruchu obrotowego
 Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
Opis ruchu obrotowego Oprócz ruchu translacyjnego ciała obserwujemy w przyrodzie inną jego odmianę: ruch obrotowy Ruch obrotowy jest zawsze względem osi obrotu W ruchu obrotowym wszystkie punkty zakreślają
MECHANIKA 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO. Wykład Nr 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
PRAWA ZACHOWANIA Prawa zachowania najbardziej fundamentalne prawa:
 PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
PRW ZCHOWNI Pawa achowania nabadie fundamentalne pawa: o ewnętne : pawo achowania pędu, pawo achowania momentu pędu, pawo achowania enegii; o wewnętne : pawa achowania np. całkowite licb nukleonów w eakci
Powierzchnie stopnia drugiego
 Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
Algebra WYKŁAD 3 Powierchnie sopnia drugiego Deinicja Powierchnią sopnia drugiego kwadrką nawam biór punków presreni rójwmiarowej, spełniającch równanie A B C D E F G H I K gdie A, B,, K są sałmi i prnajmniej
ψ przedstawia zależność
 Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
Ruch falowy 4-4 Ruch falowy Ruch falowy polega na rozchodzeniu się zaburzenia (odkszałcenia) w ośrodku sprężysym Wielkość zaburzenia jes, podobnie jak w przypadku drgań, funkcją czasu () Zaburzenie rozchodzi
II.2 Położenie i prędkość cd. Wektory styczny i normalny do toru. II.3 Przyspieszenie
 II. Położenie i prędkość cd. Wekory syczny i normalny do oru. II.3 Przyspieszenie Wersory cylindrycznego i sferycznego układu współrzędnych krzywoliniowych Wyrażenia na prędkość w układach cylindrycznym
II. Położenie i prędkość cd. Wekory syczny i normalny do oru. II.3 Przyspieszenie Wersory cylindrycznego i sferycznego układu współrzędnych krzywoliniowych Wyrażenia na prędkość w układach cylindrycznym
Pochodna kierunkowa i gradient Równania parametryczne prostej przechodzącej przez punkt i skierowanej wzdłuż jednostkowego wektora mają postać:
 ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
ochodna kierunkowa i gradient Równania parametrcne prostej prechodącej pre punkt i skierowanej wdłuż jednostkowego wektora mają postać: Oblicam pochodną kierunkową u ( u, u ) 1 + su + su 1 (, ) d d d ˆ
Guanajuato, Mexico, August 2015
 Guanajuao Meico Augus 15 W-3 Jaosewic 1 slajdów Dnamika punku maeialnego Dnamika Układ inecjaln Zasad dnamiki: piewsa asada dnamiki duga asada dnamiki pęd ciała popęd sił ecia asada dnamiki pawo akcji
Guanajuao Meico Augus 15 W-3 Jaosewic 1 slajdów Dnamika punku maeialnego Dnamika Układ inecjaln Zasad dnamiki: piewsa asada dnamiki duga asada dnamiki pęd ciała popęd sił ecia asada dnamiki pawo akcji
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Równania różniczkowe. Lista nr 2. Literatura: N.M. Matwiejew, Metody całkowania równań różniczkowych zwyczajnych.
 Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
Równania różniczkowe. Lisa nr 2. Lieraura: N.M. Mawiejew, Meody całkowania równań różniczkowych zwyczajnych. W. Krysicki, L. Włodarski, Analiza Maemayczna w Zadaniach, część II 1. Znaleźć ogólną posać
cz.2 Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321
 Wkład 8: Brła stwna c. Dr inż. Zbigniew Sklarski Katedra Elektroniki, paw. C-, pok.3 skla@agh.edu.pl http://laer.uci.agh.edu.pl/z.sklarski/ 05.04.08 Wdiał nformatki, Elektroniki i Telekomunikacji - Teleinformatka
Wkład 8: Brła stwna c. Dr inż. Zbigniew Sklarski Katedra Elektroniki, paw. C-, pok.3 skla@agh.edu.pl http://laer.uci.agh.edu.pl/z.sklarski/ 05.04.08 Wdiał nformatki, Elektroniki i Telekomunikacji - Teleinformatka
MECHANIKA OGÓLNA (II)
 MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
MECHNIK GÓLN (II) Semestr: II (Mechanika I), III (Mechanika II), rok akad. 2013/2014 Liczba godzin: sem. II *) - wykład 30 godz., ćwiczenia 30 godz. sem. III *) - wykład 30 godz., ćwiczenia 30 godz., ale
Fizyka 1 (mechanika) AF14. Wykład 9
 Fizyka 1 (mechanika) 1100-1AF14 Wykład 9 Jerzy Łusakowski 05.12.2016 Plan wykładu Żyroskopy, bąki, etc. Toczenie się koła Ruch w polu sił centralnych Żyroskopy, bąki, etc. Niezrównoważony żyroskop L m
Fizyka 1 (mechanika) 1100-1AF14 Wykład 9 Jerzy Łusakowski 05.12.2016 Plan wykładu Żyroskopy, bąki, etc. Toczenie się koła Ruch w polu sił centralnych Żyroskopy, bąki, etc. Niezrównoważony żyroskop L m
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
Fizyka 1 Wróbel Wojciech. w poprzednim odcinku
 w popzednim odcinku 1 Zasady zachowania: enegia mechaniczna E E const. k p E p ()+E k (v) = 0 W układzie zachowawczym odosobnionym całkowita enegia mechaniczna, czyli suma enegii potencjalnej, E p, zaówno
w popzednim odcinku 1 Zasady zachowania: enegia mechaniczna E E const. k p E p ()+E k (v) = 0 W układzie zachowawczym odosobnionym całkowita enegia mechaniczna, czyli suma enegii potencjalnej, E p, zaówno
Ćwiczenie 13. Wyznaczanie ruchliwości i koncentracji nośników prądu w półprzewodnikach metodą efektu Halla. Cel ćwiczenia
 Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
Fizyka 11. Janusz Andrzejewski
 Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
Fizyka 11 Ruch okresowy Każdy ruch powtarzający się w regularnych odstępach czasu nazywa się ruchem okresowym lub drganiami. Drgania tłumione ruch stopniowo zanika, a na skutek tarcia energia mechaniczna
DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Rys Model układu
 Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
Ćwiczenie 7 DRGANIA SWOBODNE UKŁADU O DWÓCH STOPNIACH SWOBODY. Cel ćwiczenia Doświadczalne wyznaczenie częstości drgań własnych układu o dwóch stopniach swobody, pokazanie postaci drgań odpowiadających
drgania h armoniczne harmoniczne
 ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
ver-8..7 drgania harmoniczne drgania Fourier: częsość podsawowa + składowe harmoniczne () An cos( nω + ϕ n ) N n Fig (...) analiza Fouriera małe drgania E p E E k E p ( ) jeden sopień swobody: -A A E p
VII.1 Pojęcia podstawowe.
 II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
Bryła sztywna. Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka
 Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Bryła sztywna Fizyka I (B+C) Wykład XXIII: Przypomnienie: statyka Moment bezwładności Prawa ruchu Energia ruchu obrotowego Porównanie ruchu obrotowego z ruchem postępowym Przypomnienie Równowaga bryły
Zginanie Proste Równomierne Belki
 Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
DYNAMIKA KONSTRUKCJI
 10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
10. DYNAMIKA KONSTRUKCJI 1 10. 10. DYNAMIKA KONSTRUKCJI 10.1. Wprowadzenie Ogólne równanie dynamiki zapisujemy w posaci: M d C d Kd =P (10.1) Zapis powyższy oznacza, że równanie musi być spełnione w każdej
Podstawy fizyki wykład 4
 Podstawy fizyki wykład 4 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Podstawy fizyki wykład 4 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
pionowe od kół suwnic, zgodnie z warunków równowagi statecznej (rys. 6.4) dla
 6.7. Prkład oblicania słupa pełnościennego esakad podsuwnicowej Pełnościenne słup esakad podsuwnicowej podpierają or podsuwnicowe na kórch pracują suwnice pomosowe naorowe o udźwigach i paramerach echnicnch
6.7. Prkład oblicania słupa pełnościennego esakad podsuwnicowej Pełnościenne słup esakad podsuwnicowej podpierają or podsuwnicowe na kórch pracują suwnice pomosowe naorowe o udźwigach i paramerach echnicnch
Praca domowa nr 1. Metodologia Fizyki. Grupa 1. Szacowanie wartości wielkości fizycznych Zad Stoisz na brzegu oceanu, pogoda jest idealna,
 Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
Praca domowa nr. Meodologia Fizyki. Grupa. Szacowanie warości wielkości fizycznych Zad... Soisz na brzegu oceanu, pogoda jes idealna, powierze przeźroczyse; proszę oszacować jak daleko od Ciebie znajduje
ZADANIA Z FUNKCJI ANALITYCZNYCH LICZBY ZESPOLONE
 . Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
. Oblicyć: ZADANIA Z FUNKCJI ANALITYCZNYCH a) ( 7i) ( 9i); b) (5 i)( + i); c) 4+3i ; LICZBY ZESPOLONE d) 3i 3i ; e) pierwiastki kwadratowe 8 + i.. Narysować biór tych licb espolonych, które spełniają warunek:
R o z d z i a ł 4 MECHANIKA CIAŁA SZTYWNEGO
 R o z d z i a ł 4 MECHANIKA CIAŁA SZTYWNEGO 4.1. Bryła sztywna W dotychczasowych rozważaniach traktowaliśmy wszystkie otaczające nas ciała jako punkty materialne lub zbiory punktów materialnych. Jest to
R o z d z i a ł 4 MECHANIKA CIAŁA SZTYWNEGO 4.1. Bryła sztywna W dotychczasowych rozważaniach traktowaliśmy wszystkie otaczające nas ciała jako punkty materialne lub zbiory punktów materialnych. Jest to
Podstawy fizyki wykład 4
 Podstawy fizyki wykład 4 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Podstawy fizyki wykład 4 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Zestaw zadań 12: Przekształcenia liniowe. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t. x y + 2t 2x 3y + 5z t x z t
 Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
Zesaw adań : Preksałcenia liniowe () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + +, b) n = m = 3, ϕ( +, 3 + + + +, d) n = m = 3, ϕ( +, c) n = m = 3, ϕ( e) n
3. WSPÓŁCZYNNIK ŚCINANIA (KOREKCYJNY)
 Cęść 1. WSPÓŁCZYNNIK ŚCINANIA (KOEKCYJNY) 1.. WSPÓŁCZYNNIK ŚCINANIA (KOEKCYJNY).1. Wstęp Współcynnik κ naywany współcynnikiem ścinania jest wielkością ewymiarową, ależną od kstałtu prekroju. Występuje
Cęść 1. WSPÓŁCZYNNIK ŚCINANIA (KOEKCYJNY) 1.. WSPÓŁCZYNNIK ŚCINANIA (KOEKCYJNY).1. Wstęp Współcynnik κ naywany współcynnikiem ścinania jest wielkością ewymiarową, ależną od kstałtu prekroju. Występuje
y 1 y 2 = f 2 (t, y 1, y 2,..., y n )... y n = f n (t, y 1, y 2,..., y n ) f 1 (t, y 1, y 2,..., y n ) y = f(t, y),, f(t, y) =
 Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
Uk lady równań różniczkowych Pojȩcia wsȩpne Uk ladem równań różniczkowych nazywamy uk lad posaci y = f (, y, y 2,, y n ) y 2 = f 2 (, y, y 2,, y n ) y n = f n (, y, y 2,, y n ) () funkcje f j, j =, 2,,
W takim modelu prawdopodobieństwo konfiguracji OR wynosi. 0, 21 lub , 79. 6
 achunek prawdopodobieństwa MP6 Wydiał Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab.. Jurlewic Prykłady do listy : Prestreń probabilistycna. Prawdopodobieństwo klasycne. Prawdopodobieństwo
achunek prawdopodobieństwa MP6 Wydiał Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab.. Jurlewic Prykłady do listy : Prestreń probabilistycna. Prawdopodobieństwo klasycne. Prawdopodobieństwo
I. DYNAMIKA PUNKTU MATERIALNEGO
 I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
I. DYNAMIKA PUNKTU MATERIALNEGO A. RÓŻNICZKOWE RÓWNANIA RUCHU A1. Bryła o masie m przesuwa się po chropowatej równi z prędkością v M. Podać dynamiczne równania ruchu bryły i rozwiązać je tak, aby wyznaczyć
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej
 MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
MECHANIKA II. Dynamika ruchu obrotowego bryły sztywnej Daniel Lewandowski Politechnika Wrocławska, Wydział Mechaniczny, Katedra Mechaniki i Inżynierii Materiałowej http://kmim.wm.pwr.edu.pl/lewandowski/
Siły oporu prędkość graniczna w spadku swobodnym
 FIZYKA I Wykład III Mechanika: Pojęcia podstawowe dynamika i punktu historiamaterialnego (VI) Siły oporu prędkość graniczna w spadku swobodnym s = v 0 t + at v 0 = 0; a = g; s = h h = gt F o = k v F g
FIZYKA I Wykład III Mechanika: Pojęcia podstawowe dynamika i punktu historiamaterialnego (VI) Siły oporu prędkość graniczna w spadku swobodnym s = v 0 t + at v 0 = 0; a = g; s = h h = gt F o = k v F g
MECHANIKA 2. Praca, moc, energia. Wykład Nr 11. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 11 Praca, moc, energia Prowadzący: dr Krzysztof Polko PRACA MECHANICZNA SIŁY STAŁEJ Pracą siły stałej na prostoliniowym przemieszczeniu w kierunku działania siły nazywamy iloczyn
MECHANIKA 2 Wykład Nr 11 Praca, moc, energia Prowadzący: dr Krzysztof Polko PRACA MECHANICZNA SIŁY STAŁEJ Pracą siły stałej na prostoliniowym przemieszczeniu w kierunku działania siły nazywamy iloczyn
MiBM sem. III Zakres materiału wykładu z fizyki
 MiBM sem. III Zakres materiału wykładu z fizyki 1. Dynamika układów punktów materialnych 2. Elementy mechaniki relatywistycznej 3. Podstawowe prawa elektrodynamiki i magnetyzmu 4. Zasady optyki geometrycznej
MiBM sem. III Zakres materiału wykładu z fizyki 1. Dynamika układów punktów materialnych 2. Elementy mechaniki relatywistycznej 3. Podstawowe prawa elektrodynamiki i magnetyzmu 4. Zasady optyki geometrycznej
Drgania. W Y K Ł A D X Ruch harmoniczny prosty. k m
 Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
Wykład z fizyki Piotr Posmykiewicz 119 W Y K Ł A D X Drgania. Drgania pojawiają się wtedy, gdy układ zostanie wytrącony ze stanu równowagi stabilnej. MoŜna przytoczyć szereg znanych przykładów: kołysząca
12 RUCH OBROTOWY BRYŁY SZTYWNEJ I. a=εr. 2 t. Włodzimierz Wolczyński. Przyspieszenie kątowe. ε przyspieszenie kątowe [ ω prędkość kątowa
 Włodzimierz Wolczyński Przyspieszenie kątowe 1 RUCH OROTOWY RYŁY SZTYWNEJ I = = ε przyspieszenie kątowe [ ] ω prędkość kątowa = = T okres, = - częstotliwość s=αr v=ωr a=εr droga = kąt x promień prędkość
Włodzimierz Wolczyński Przyspieszenie kątowe 1 RUCH OROTOWY RYŁY SZTYWNEJ I = = ε przyspieszenie kątowe [ ] ω prędkość kątowa = = T okres, = - częstotliwość s=αr v=ωr a=εr droga = kąt x promień prędkość
Pojęcia podstawowe 1
 Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Tomasz Lubera Pojęcia podsawowe aa + bb + dd + pp + rr + ss + Kineyka chemiczna dział chemii fizycznej zajmujący się przebiegiem reakcji chemicznych w czasie, ich mechanizmami oraz wpływem różnych czynników
Równa Równ n a i n e i ru r ch u u ch u po tor t ze (równanie drogi) Prędkoś ędkoś w ru r ch u u ch pros pr t os ol t i ol n i io i wym
 Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
Mechanika ogólna Wykład nr 14 Elementy kinematyki i dynamiki 1 Kinematyka Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez
 Ż ć Ó Ś Ó ć Ę Ó Ś ź Ż Ż Ó Ż ź Ó ÓŚ Ć Ó ź Ó ź Ó Ź ć Ę Ó Ś Ż Ó Ó Ń Ą ź ź Ź Ś Ą Ą Ś Ą Ś ć ć ź ź Ó Ó Ę Ź Ą Ź Ę ĘŚ ć ź Ę Ę ź Ę ć Ś Ś Ę Ż Ż ć Ść ć ć Ń Ż Ś ć Ż Ż Ż Ż Ż Ó Ą Ę Ę Ę Ą Ż Ż Ż Ź Ż ć Ś Ż Ż Ż Ż Ż ć Ś
Ż ć Ó Ś Ó ć Ę Ó Ś ź Ż Ż Ó Ż ź Ó ÓŚ Ć Ó ź Ó ź Ó Ź ć Ę Ó Ś Ż Ó Ó Ń Ą ź ź Ź Ś Ą Ą Ś Ą Ś ć ć ź ź Ó Ó Ę Ź Ą Ź Ę ĘŚ ć ź Ę Ę ź Ę ć Ś Ś Ę Ż Ż ć Ść ć ć Ń Ż Ś ć Ż Ż Ż Ż Ż Ó Ą Ę Ę Ę Ą Ż Ż Ż Ź Ż ć Ś Ż Ż Ż Ż Ż ć Ś
Zestaw zadań 12: Przekształcenia liniowe. Macierze przekształceń liniowych. z z + 2 2x + y. x y z. x y + 2t 2x + 3y + 5z t x + z t
 Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
Zesaw adań : Preksałcenia liniowe. Maciere preksałceń liniowch () Kóre podanch niżej preksałceń ϕ : K n K m są preksałceniami liniowmi: a) n = m = 3, ϕ( + ) = +, b) n = m = 3, ϕ( ) = +, 3 + + + +, d) n
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM
 ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
ZADANIA Z GEOMETRII RÓŻNICZKOWEJ NA PIERWSZE KOLOKWIUM. Koło o promieniu n płszczyźnie Oxy oczy się bez poślizgu wzdłuż osi Ox. Miejsce geomeryczne opisne przez punk M leżący n obwodzie ego koł jes cykloidą.
Dynamika Newtonowska trzy zasady dynamiki
 Dynamika Newtonowska trzy zasady dynamiki I. Zasada bezwładności Gdy działające siły równoważą się ciało fizyczne pozostaje w spoczynku lubporusza się ruchem prostoliniowym ze stałą prędkością. II. Zasada
Dynamika Newtonowska trzy zasady dynamiki I. Zasada bezwładności Gdy działające siły równoważą się ciało fizyczne pozostaje w spoczynku lubporusza się ruchem prostoliniowym ze stałą prędkością. II. Zasada
Podstawy robotyki wykład VI. Dynamika manipulatora
 Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
Podstawy robotyki Wykład VI Robert Muszyński Janusz Jakubiak Instytut Informatyki, Automatyki i Robotyki Politechnika Wrocławska Dynamika opisuje sposób zachowania się manipulatora poddanego wymuszeniu
2. Pręt skręcany o przekroju kołowym
 2. Pręt skręcany o przekroju kołowym Przebieg wykładu : 1. Sformułowanie zagadnienia 2. Warunki równowagi kąt skręcenia 3. Warunek geometryczny kąt odkształcenia postaciowego 4. Związek fizyczny Prawo
2. Pręt skręcany o przekroju kołowym Przebieg wykładu : 1. Sformułowanie zagadnienia 2. Warunki równowagi kąt skręcenia 3. Warunek geometryczny kąt odkształcenia postaciowego 4. Związek fizyczny Prawo
PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE. WALCOWE (równoległe) STOŻKOWE (kątowe) ŚLIMAKOWE HIPERBOIDALNE. o zebach prostych. walcowe. o zębach.
 CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
i j k Oprac. W. Salejda, L. Bujkiewicz, G.Harań, K. Kluczyk, M. Mulak, J. Szatkowski. Wrocław, 1 października 2015
 WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
WM-E; kier. MBM, lisa za. nr. p. (z kary przemiou): Rozwiązywanie zaań z zakresu: ransformacji ukłaów współrzęnych, rachunku wekorowego i różniczkowo-całkowego o kursu Fizyka.6, r. ak. 05/6; po koniec
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej
 mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
mechanika analityczna 1 nierelatywistyczna L.D.Landau, E.M.Lifszyc Krótki kurs fizyki teoretycznej ver-28.06.07 współrzędne uogólnione punkt materialny... wektor wodzący: prędkość: przyspieszenie: liczba
Lista nr Znaleźć rozwiązania ogólne następujących równań różniczkowych: a) y = y t,
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE B Lisa nr 1 1. Napisać równanie różniczkowe, jakie spełnia napięcie u = u() na okładkach kondensaora w obwodzie zawierającym połączone szeregowo oporność R i pojemność C,
C d u. Po podstawieniu prądu z pierwszego równania do równania drugiego i uporządkowaniu składników lewej strony uzyskuje się:
 Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Zadanie. Obliczyć przebieg napięcia na pojemności C w sanie przejściowym przebiegającym przy nasępującej sekwencji działania łączników: ) łączniki Si S są oware dla < 0, ) łącznik S zamyka się w chwili
Mechanika ogólna. Kinematyka. Równania ruchu punktu materialnego. Podstawowe pojęcia. Równanie ruchu po torze (równanie drogi)
 Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Kinematyka Mechanika ogólna Wykład nr 7 Elementy kinematyki Dział mechaniki zajmujący się matematycznym opisem układów mechanicznych oraz badaniem geometrycznych właściwości ich ruchu, bez wnikania w związek
Fale biegnące. y t=0 vt. y = f(x), t = 0 y = f(x - vt), t ogólne równanie fali biegnącej w prawo
 ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
ale (mechaniczne) ala - rozchodzenie się się zaburzenia (w maerii) nie dzięki ruchowi posępowemu samej maerii ale dzięki oddziałwaniu (sprężsemu) Rodzaje i cech fal Rodzaj zaburzenia mechaniczne elekromagneczne
Ruch kulisty bryły. Kąty Eulera. Precesja regularna
 Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
4.2. Obliczanie przewodów grzejnych metodą dopuszczalnego obciążenia powierzchniowego
 4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
4.. Obliczanie przewodów grzejnych meodą dopuszczalnego obciążenia powierzchniowego Meodą częściej sosowaną w prakyce projekowej niż poprzednia, jes meoda dopuszczalnego obciążenia powierzchniowego. W
Drgania układu o wielu stopniach swobody
 Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Drgania układu o wielu stopniach swobody Rozpatrzmy układ składający się z n ciał o masach m i (i =,,..., n, połączonych między sobą i z nieruchomym podłożem za pomocą elementów sprężystych o współczynnikach
Analiza Matematyczna Praca domowa
 Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Analiza Matematyczna Praca domowa J. de Lucas Zadanie 1. Pokazać, że dla wszystkich n naturalnych ( n ) exp kx k dx 1 dx n = 1 n (e k 1). (0,1) n k=1 n! k=1 Zadanie. Obliczyć dla dowolnego n. (0,1) n (x
Ruch falowy, ośrodek sprężysty
 W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
W-9 (Jaroszewicz) 5 slajdów Ruch falow, ośrodek sprężs ę Pojęcie ruchu falowego rodzaje fal Równanie fali płaskiej paraer fali Równanie falowe prędkość propagacji, energia i pęd przenoszone przez falę
MECHANIKA 2 Wykład Nr 9 Dynamika układu punktów materialnych
 MECHANIKA 2 Wykład Nr 9 Dynamika układu punktów materialnych Prowadzący: dr Krzysztof Polko Dynamiczne równania ruchu układu punktów materialnych Układem punktów materialnych nazwiemy zbiór punktów w sensie
MECHANIKA 2 Wykład Nr 9 Dynamika układu punktów materialnych Prowadzący: dr Krzysztof Polko Dynamiczne równania ruchu układu punktów materialnych Układem punktów materialnych nazwiemy zbiór punktów w sensie
Ruch pod wpływem sił zachowawczych
 Ruch pod wpływem sił zachowawczych Fizyka I (B+C) Wykład XV: Energia potencjalna Siły centralne Ruch w polu grawitacyjnym Pole odpychajace Energia potencjalna Równania ruchu Znajomość energii potencjalnej
Ruch pod wpływem sił zachowawczych Fizyka I (B+C) Wykład XV: Energia potencjalna Siły centralne Ruch w polu grawitacyjnym Pole odpychajace Energia potencjalna Równania ruchu Znajomość energii potencjalnej
Materiały pomocnicze 5 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej
 Materiały pomocnicze 5 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Wielkości dynamiczne w ruchu postępowym. a. Masa ciała jest: - wielkością skalarną, której wielkość jest niezmienna
Materiały pomocnicze 5 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Wielkości dynamiczne w ruchu postępowym. a. Masa ciała jest: - wielkością skalarną, której wielkość jest niezmienna
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
WYZNACZANIE ZREDUKOWANEGO MOMENTU BEZWŁADNOŚCI UKŁADU MECHANICZNEGO I MASOWYCH MOMENTÓW BEZWŁADNOŚCI TARCZ KOŁOWYCH
 Ćwicenie WYZNACZANI ZRDUKOWANGO MOMNTU BZWŁADNOŚCI UKŁADU MCHANICZNGO I MASOWYCH MOMNTÓW BZWŁADNOŚCI TARCZ KOŁOWYCH Cel ćwicenia Celem ćwicenia jes doświadcalne wynacenie ukowanego momenu ewładności ruchomych
Ćwicenie WYZNACZANI ZRDUKOWANGO MOMNTU BZWŁADNOŚCI UKŁADU MCHANICZNGO I MASOWYCH MOMNTÓW BZWŁADNOŚCI TARCZ KOŁOWYCH Cel ćwicenia Celem ćwicenia jes doświadcalne wynacenie ukowanego momenu ewładności ruchomych
V.4 Ruch w polach sił zachowawczych
 r. akad. 5/ 6 V.4 Ruch w polach sił zachowawczych. Ruch cząstki w potencjale jednowyiarowy. Ruch w polu siły centralnej. Wzór Bineta 3. Przykład: całkowanie wzoru Bineta dla siły /r Dodatek: całkowanie
r. akad. 5/ 6 V.4 Ruch w polach sił zachowawczych. Ruch cząstki w potencjale jednowyiarowy. Ruch w polu siły centralnej. Wzór Bineta 3. Przykład: całkowanie wzoru Bineta dla siły /r Dodatek: całkowanie
cx siła z jaką element tłumiący działa na to ciało.
 Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
Drgania układu o jedny sopniu swobody Rozparzy układ składający się z ciała o asie połączonego z nierucoy podłoże za poocą eleenu sprężysego o współczynniku szywności k oraz eleenu łuiącego o współczynniku
Drgania prętów (kamerton, cymbałki )
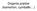 Draia pręów kamero, cymbałki Roważaliśmy iaie belek y M F ϕ d MdM FdF E - moduł Youa J - eomerycy mome bewładości w prekroju d diała mome MdM h M M Mome skręcający ależy od położeia, w prekroju diała mome
Draia pręów kamero, cymbałki Roważaliśmy iaie belek y M F ϕ d MdM FdF E - moduł Youa J - eomerycy mome bewładości w prekroju d diała mome MdM h M M Mome skręcający ależy od położeia, w prekroju diała mome
Zasady dynamiki Newtona. Pęd i popęd. Siły bezwładności
 Zasady dynamiki Newtona Pęd i popęd Siły bezwładności Copyright by pleciuga@o2.pl Inercjalne układy odniesienia Układy inercjalne to takie układy odniesienia, względem których wszystkie ciała nie oddziałujące
Zasady dynamiki Newtona Pęd i popęd Siły bezwładności Copyright by pleciuga@o2.pl Inercjalne układy odniesienia Układy inercjalne to takie układy odniesienia, względem których wszystkie ciała nie oddziałujące
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Rozruch silnika prądu stałego
 Rozruch silnika prądu sałego 1. Model silnika prądu sałego (SPS) 1.1 Układ równań modelu SPS Układ równań modelu silnika prądu sałego d ua = Ra ia + La ia + ea d równanie obwodu wornika d uf = Rf if +
Rozruch silnika prądu sałego 1. Model silnika prądu sałego (SPS) 1.1 Układ równań modelu SPS Układ równań modelu silnika prądu sałego d ua = Ra ia + La ia + ea d równanie obwodu wornika d uf = Rf if +
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
RÓWNANIA RÓŻNICZKOWE WYKŁAD 13 Geomeria różniczkowa Geomeria różniczkowa o dział maemayki, w kórym do badania obieków geomerycznych wykorzysuje się meody opare na rachunku różniczkowym. Obieky geomeryczne
, to: Energia całkowita w ruchu harmonicznym prostym jest proporcjonalna do kwadratu amplitudy.
 Wykład z fizyki Piotr Posmykiewicz 4 Podstawiając to do wzoru na energię kinetyczną: K = ma sin t + ( δ ) Podstawiając = k / m K = ka sin t ( + δ ) -5 Energia kinetyczna w ruchu harmonicznym prostym Energia
Wykład z fizyki Piotr Posmykiewicz 4 Podstawiając to do wzoru na energię kinetyczną: K = ma sin t + ( δ ) Podstawiając = k / m K = ka sin t ( + δ ) -5 Energia kinetyczna w ruchu harmonicznym prostym Energia
Część I. MECHANIKA. Wykład KINEMATYKA PUNKTU MATERIALNEGO. Ruch jednowymiarowy Ruch na płaszczyźnie i w przestrzeni.
 Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Część I. MECHANIKA Wykład.. KINEMATYKA PUNKTU MATERIALNEGO Ruch jednowymiarowy Ruch na płaszczyźnie i w przesrzeni 1 KINEMATYKA PUNKTU MATERIALNEGO KINEMATYKA zajmuje się opisem ruchu ciał bez rozparywania
Rozwiązanie. Metoda I Stosujemy twierdzenie, mówiące że rzuty prędkości dwóch punktów ciała sztywnego na prostą łączącą te punkty są sobie równe.
 Wyzczie prędkości i przyspieszeń cił w ruchu posępowym, obroowym i płskim orz chwilowych środków obrou w ruchu płskim. Ruch korbowodu część II Zdie.. Prę o długości L ślizg się jedym końcem (puk po podłodze,
Wyzczie prędkości i przyspieszeń cił w ruchu posępowym, obroowym i płskim orz chwilowych środków obrou w ruchu płskim. Ruch korbowodu część II Zdie.. Prę o długości L ślizg się jedym końcem (puk po podłodze,
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
Dodawanie i mnożenie liczb zespolonych są działaniami wewnętrznymi tzn., że ich wynikiem jest liczba zespolona.
 Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
Wykład - LICZBY ZESPOLONE Algebra licb espolonych, repreentacja algebraicna i geometrycna, geometria licb espolonych. Moduł, argument, postać trygonometrycna, wór de Moivre a.' Zbiór Licb Zespolonych Niech
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
Prawa ruchu: dynamika
 Prawa ruchu: dynamika Fizyka I (B+C) Wykład X: Dynamika ruchu po okręgu siła dośrodkowa Prawa ruchu w układzie nieinercjalnym siły bezwładności Prawa ruchu w układzie obracajacym się siła odśrodkowa siła
Prawa ruchu: dynamika Fizyka I (B+C) Wykład X: Dynamika ruchu po okręgu siła dośrodkowa Prawa ruchu w układzie nieinercjalnym siły bezwładności Prawa ruchu w układzie obracajacym się siła odśrodkowa siła
Zasady oceniania karta pracy
 Zadanie 1.1. 5) stosuje zasadę zachowania energii oraz zasadę zachowania pędu do opisu zderzeń sprężystych i niesprężystych. Zderzenie, podczas którego wózki łączą się ze sobą, jest zderzeniem niesprężystym.
Zadanie 1.1. 5) stosuje zasadę zachowania energii oraz zasadę zachowania pędu do opisu zderzeń sprężystych i niesprężystych. Zderzenie, podczas którego wózki łączą się ze sobą, jest zderzeniem niesprężystym.
Mechanika ogólna II Kinematyka i dynamika
 Mechanika ogólna II Kineatyka i dynaika kierunek Budownictwo, se. III ateriały poocnicze do ćwiczeń opracowanie: dr inŝ. Piotr Dębski, dr inŝ. Irena Wagner TREŚĆ WYKŁADU Kineatyka: Zakres przediotu. Przestrzeń,
Mechanika ogólna II Kineatyka i dynaika kierunek Budownictwo, se. III ateriały poocnicze do ćwiczeń opracowanie: dr inŝ. Piotr Dębski, dr inŝ. Irena Wagner TREŚĆ WYKŁADU Kineatyka: Zakres przediotu. Przestrzeń,
Kinematyka W Y K Ł A D I. Ruch jednowymiarowy. 2-1 Przemieszczenie, prędkość. x = x 2 - x x t
 Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Wykład z fizyki. Pior Posmykiewicz W Y K Ł A D I Ruch jednowymiarowy Kinemayka Zaczniemy wykład z fizyki od badania przedmioów będących w ruchu. Dział fizyki, kóry zajmuje się badaniem ruchu ciał bez wnikania
Funkcje pola we współrzędnych krzywoliniowych cd.
 Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
Metody Lagrange a i Hamiltona w Mechanice
 Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
Meody Lagrange a i Hamilona w Mechanice Mariusz Przybycień Wydział Fizyki i Informayki Sosowanej Akademia Górniczo-Hunicza Wykład 7 M. Przybycień (WFiIS AGH) Meody Lagrange a i Hamilona... Wykład 7 1 /
