Elementy programowania liniowego
|
|
|
- Kajetan Krupa
- 8 lat temu
- Przeglądów:
Transkrypt
1 Instytut Sterowania i Systemów Informatycznych Politechnika Zielonogórska Metody i techniki optymalizacji Elementy programowania liniowego Poniższe zadania należy rozwiązać z zastosowaniem programów Excel oraz Lindo i Lingo. 1. Firma produkuje dwa produkty A i B, których rynek zbytu jest nieograniczony. Każdy z produktów wymaga obróbki na każdej z maszyn I, II, III. Czasy obróbki (w godzinach) dla każdego z produktów są następujące: I II III A B Tygodniowy czas pracy maszyn I, II, III wynosi odpowiednio 40, 36 i 36 godzin. Zysk ze sprzedaży jednej sztuki A i B stanowi odpowiednio 5 i 3$. Określić tygodniowe normy produkcji wyrobów A i B maksymalizujące zysk. 2. Firma potrzebuje węgiel z zawartosćią fosforu nie większą niż 0.03% i zawartością cynku nie większą niż 3.25%. Dostępne są trzy gatunki węgla A, B i C po następujących cenach za tonę: Gatunek węgla Zaw. P [%] Zaw. Zn [%] Cena [$] A B C Jak należy je zmieszać, aby otrzymać najniższą cenę i jednocześnie spełnić ograniczenia na zawartość zanieczyszczeń? Zadanie rozwiązać metodą graficzną. 3. Środki do czyszczenia podłóg ocenia się na podstawie trzech wskaźników: a) własności czyszczących, b) własności dezynfekujących, c) drażniącego działania na skórę. Każdy z tych wskaźników ocenia się w skali liniowej od 0 do 100 jednostek. Produkt wypuszczany na rynek powinien mieć w skrajnym przypadku 60 jednostek własności czyszczących i 60 jednostek własności dezynfekujących w odpowiednich skalach. Jednocześnie działanie podrażniające skórę powinno być minimalne. Końcowy produkt powinien być mieszanką trzech podstawowych środków czyszczących o własnościach przedstawionych w tabeli: Środek Dział. czyszczące Dział. dezynfekujące Dział. podrażniające A B C
2 Sformułować zadanie znajdowania optymalnej mieszanki jako zadanie programowania liniowego. 4. Firma produkuje dwa produkty A i B, sprzedawane odpowiednio po 8 i 15 centów za opakowanie. Rynek zbytu dla każdego z nich jest praktycznie nieograniczony. Produkt A wytwarza się na maszynie 1, a produkt B na maszynie 2. Następnie oba produkty pakuje się w fabryce. 1 kg surowca kosztuje 6 centów. Maszyna 1 przetwarza 5000 kg w godzinę ze stratami 10%. Maszyna 2 obrabia 4000 kg/h ze stratami 20%. Maszyna 1 jest dostępna przez 6 godzin dziennie, a jej praca kosztuje 288 $/h. Maszyna 2 jest dostępna przez 5 godzin dziennie, a jej wykorzystanie kosztuje 336 $/h. Opakowanie produktu A waży 1/4 kg, a opakowanie produktu B 1/3 kg. Dział dokonujący pakowania może pracować przez 10 h dziennie z kosztami 360 $/h. W ciągu 1 h można zapakować szt. A i 8000 szt. B. Firma chce określić takie wartości x 1 i x 2 zapotrzebowania na surowce do produkcji A i B (w tonach), dla których dzienny zysk będzie maksymalny. Sformułować przedstawiony problem jako ZPL, a następnie rozwiązać go graficznie. 5. W dwóch punktach A i B pewnej miejscowości istnieje zapotrzebowanie na dodatkowy transport. W punkcie A potrzeba 5 dodatkowych autobusów, a w punkcie B 7. Wiadomo, że 3, 4 i 5 autobusów można otrzymać odpowiednio z garaży G 1, G 2 i G 3. Jak należy rozdzielić te autobusy między punkty A i B, aby zminimalizować ich całkowity przebieg? Odległości z garaży do punktów A i B przedstawia poniższa tabela: Garaż Odległość od punktów A B G G G Fabryka produkuje dwa modele samochodów: droższy A i tańszy B. Zatrudnionych jest w niej 1000 robotników niewykwalifikowanych i 800 wykwalifikowanych, z których każdy pracuje 40 godzin w tygodniu. Do wyprodukowania jednego egzemplarza modelu A potrzeba 30 roboczogodzin pracy niewykwalifikowanej i 50 roboczogodzin pracy wykwalifikowanej; do wyprodukowania jednego egzemplarza modelu B potrzeba odpowiednio 40 i 20 roboczogodzin. Każdy egzemplarz B wymaga wydatków na surowiec i wyposażenie na poziomie 500 $, podczas gdy każdy egzemplarz A wymaga kosztów rzędu 1500 $. Całkowite koszty nie powinny przekraczać $ tygodniowo. Pracownicy odprowadzający samochody z fabryki pracują pięć dni w tygodniu i mogą zabrać nie więcej niż 210 maszyn dziennie. Każdy sprzedany model A przynosi firmie 1000 $ zysku, a każdy model B 500 $ zysku. Jaką wielkość produkcji każdego z modeli jest optymalna? Co można zarekomendować w celu podwyższenia zysku firmy? 7. Firma produkuje trzy produkty A, B i C, przy czym do wytworzenia każdego z nich wymagana jest obróbka na wszystkich czterech stanowiskach I, II, III, IV. 2
3 Produkt Czas obróbki, h Zysk, $ I II III IV A B C Czas pracy każdego ze stanowisk wynosi odpowiednio 84, 42, 21 i 42 h. Określić które z produktów i w jakich ilościach należy produkować. 8. Producent napojów bezalkoholowych dysponuje dwoma maszynami do rozlewania A i B. Maszyna A jest zaprojektowana dla butelek półlitrowych, a maszyna B dla litrowych, jednak każda z nich może być wykorzystana do napełniania obu typów butelek, chociaż wiąże się to z pewną utratą efektywności, co przedstawia poniższa tabela: Maszyna Liczba butelek produkowanych w ciągu 1 min. Butelki półlitrowe Butelki litrowe A B Każda z maszyn pracuje po 6 h dziennie przez 5 roboczych dni tygodnia. Zysk ze sprzedaży jednej butelki półlitrowej stanowi 4 centy, a od litrowej 10 centów. Tygodniowa produkcja nie może przekroczyć l. Rynek nie przyjmuje więcej niż butelek półlitrowych i litrowych. Producent chce zmaksymalizować swój zysk przy dostępnych środkach. Sformułować odpowiednie ZPL i znaleźć optymalne rozwiązanie. 9. Firma reklamuje swoją produkcję za pomocą czterech środków masowego przekazu: telewizji, radia, gazet i plakatów. Na podstawie rozmaitych doświadczeń z przeszłości wiadomo, że te środki prowadzą do zwiększenia zysku odpowiednio o 10, 3, 7 i 4 $ w przeliczeniu na 1 $ przeznaczony na reklamę. Rozdział budżetu na poszczególne środki ograniczono następująco: (a) pełny budżet nie powinien przekraczać $; (b) należy przeznaczyć nie więcej niż 40 % budżetu na telewizję i nie więcej niż 20 % na plakaty; (c) wskutek atrakcyjności radia dla młodzieży należy nań przeznaczyć w skrajnym przypadku połowę tego, co na telewizję. Sformułować zadanie rozdzialu pieniędzy na poszczególne środki jako ZPL i rozwiązać wykorzystując metodę sympleks. 10. Firma zajmuje się zestawianiem diety, zawierającej w skrajnym przypadku 20 jednostek białek, 30 j. węglowodanów, 10 j. tłuszczów i 40 j. witamin. Jak osiągnąć ten cel w najtańszy sposób przy zestawionych w tabeli cenach za 1 kg (lub 1l) pięciu dostępnych produktów? 3
4 Chleb Soja Ryba Owoce Mleko Białka Węglowodany Tłuszcze Witaminy Cena Kompania naftowa kupuje ropę naftową ze źródeł W, X, Y i Z, a następnie zajmuje się jej przetworzeniem, produkując trzy rodzaje smarów A, B i C. Istnieje ograniczenie na chłonność rynku dla każdego rodzaju smaru: Smar Skład, % Możliwa ilość do sprzedania [galony] A nie mniej niż 10 (W) nie więcej niż 25 (Z) B nie mniej niż 15 (W) C nie mniej niż 20 (X) nie więcej niż 50 (Y) Ceny (w jednostkach umownych) za jeden galon surowca i gotowego produktu przedstawiono poniżej Surowiec Smar X Y Z W A B C Zakładając, że ropa jest dostępna w nieograniczonych ilościach, sformułować zadanie maksymalizacji zysku jako ZPL i znaleźć rozwiązanie optymalne. 12. Fabryka włókiennicza powinna pracować 24 godziny na dobę zgodnie z poniższą tabelą: Godzina [h] Minimalna koniecz na liczba tkaczy Każdy z tkaczy powinien pracować 8 godzin bez przerwy. Znaleźć minimalną liczbę tkaczy spełniającą podane warunki. 13. Dziecko w pewnym wieku potrzebuje dziennie co najmniej 120 jednostek witaminy A, 60 jednostek witaminy D, 36 jednostek witaminy C oraz 180 jednostek witaminy E. Witaminy te zawarte są w dwóch produktach P 1 i P 2. Ze względu na uboczne szkodliwe działanie witaminy A należy dostarczyć jej co najwyżej 240 jednostek. Zawartość poszczególnych witamin w jednostce produktu oraz ceny jednostkowe produktów podaje poniższa tablica. P 1 P 2 A 6 3 D 1 3 C 9 1 E 6 6 Cena
5 Ile należy zakupić produktu P 1 i P 2, aby dostarczyć dziecku witamin w wymaganych ilościach przy minimalnym koszcie zakupu produktów P 1 i P 2? 14. Kompania kontroluje trzy fabryki F 1, F 2 i F 3 produkujące 50, 25 i 25 tys. szt. pewnego produktu tygodniowo. Zawarto umowy z czterema odbiorcami C 1, C 2, C 3 i C 4, którzy potrzebują tygodniowo odpowiednio 15, 20, 20 i 30 tys. szt. Koszty produkcji i transportu 1 tys. szt. produktu do odbiorców przedstawiono poniżej: Fabryka Odbiorca C 1 C 2 C 3 C 4 F F F Określić minimalny koszt ogólny i wielkości produkcji. 15. Firma zaproponawała właścicielom trzech linii lotniczych przewóz brygad specjalistów do różnych części świata. Koszt przewozu w funtach szterlingach przedstawiono w tabelce: Linia lotnicza Sydney Kalkuta Bejrut Dallas San Paulo I II III Administracja firmy postanowiła, że kontrakty na przewozy będą zawierane z właścicielami linii I, II, III w stosunku 2:3:2 i powiadomiła o tym kierującego przewozami, a także zakomunikowała, że z 70 wyznaczonych na bieżący rok przewozów 10 jest do Sydney, 15 do Kalkuty, 20 do Bejrutu, 10 do Dallas i 15 do San Paulo. Jak należy zawrzeć kontrakty, aby zminimalizować koszt przewozów przy ograniczeniach narzuconych przez administrację? 16. Pewien produkt wytwarza się w dwóch zakładach i wysyła do dwóch odbiorców. Ich potrzeby na najbliższe dwa miesiące przedstawiono w tabeli: Odbiorca Zapotrzebowanie Sierpień Wrzesień Jednostkowy koszt transportu produktu z zakładów do odbiorców określa tabela: Zakład Odbiorca Jednostkowy koszt produkcji (w jednostkach umownych) i wielkość produkcji wg planu na dwa miesiące przedstawiono poniżej: 5
6 Zakład Koszt produkcji, j.u. Wielkość Sierpień Wrzesień Sierpień Wrzesień Produkt można przechowywać przez okres miesiąca i dopiero wtedy wysłać go do odbiorcy. Koszt magazynowania wynosi 0.5 w pierwszym zakładzie i 0.6 w drugim. Określić optymalne plany produkcji i plany dostaw traktując zagadnienie jako transportowe. 17. Firma przewozowa powinna w ciągu tego samego dnia pobrać pięć towarów w punktach A, B, C, D, E i dostarczyć je odpowiednio do punktów a, b, c, d, e. Odległości (w km) między punktami załadunku i punktami przeznaczenia są następujące: A a B b C c D d E e Firma dysponuje pięcioma ciężarówkami dwóch typów X i Y w punktach S, T, U, V, W (typy ciężarówek: X w S, Y w T, X w U, X w V i Y w W). Ciężarówki typu X są nowsze o ekonomiczniejsze od ciężarówek typu Y. Koszty przejazdu jednego kilometra (w centach) dla ciężarówek obu typów (włączając paliwo, ubezpieczenie, konserwację, itd.) są następujące: Pusta Załadowana X Y Odległości od garaży do punktów przeznaczenia przedstawia tabela: A B C D E S T U V W Przydzielić zadania kierowcom ciężarówek tak, aby zminimalizować koszty. Założyć, że wszystkie ładunki mają w przybliżeniu jednakowy rozmiar i wymagają jednakowej pracy przy pakowaniu, ułożeniu, itd. 18. W systemie radarowym przeznaczonym do automatycznego śledzenia obiektów powietrznych przeprowadza się obliczenia określające względną wiarygodność tego, ze dany sygnał odbity odpowiada któremuś z obserwowanych obiektów. Rezultaty przedstawia tabela: Sygnał odbity Obiekt
7 Zakładając, że celem jest skojarzenie sygnałów odbitych z obiektami w taki sposób, aby zmaksymalizować iloczyn wiarygodności, sprowadzić zadanie do pewnego problemu przydziału, a następnie rozwiązać go dla przedstawionych danych. 19. Linia lotnicza obsługuje trzy miasta A, B, C. Przeloty odbywają się w ciągu dnia przez siedem dni tygodnia. Koszt postoju samolotu we wszystkich trzech portach lotniczych wynosi kt 2, gdzie T oznacza czas postoju. Jak należy przydzielić samoloty poszczególnym liniom aby zminimalizować koszty? Należy uwzględnić, że samolot nie może wystartować wcześniej niż jedną godzinę po wylądowaniu, gdyż w tym czasie dokonuje się kontroli technicznej i przeprowadza przygotowania do startu. Wylot Przybycie Miasto Godzina Miasto Godzina A 8:00 B 12:00 A 9:00 C 12:00 A 10:00 B 14:00 A 14:00 B 18:00 A 18:00 B 22:00 A 20:00 C 23:00 B 7:00 A 11:00 B 9:00 A 13:00 B 13:00 A 17:00 B 18:00 A 22:00 C 9:00 A 12:00 C 15:00 A 18: Kłody o długości 5,6 m są cięte w tartaku na kawałki 1,2 m, 1.6 i 1,9 m. Tartak ma wykonać dzienny plan produkcji, który zakłada oddanie 200 kłód o długości 1,2 m, 300 kłód o długości 1,6 m oraz 100 kłód o długości 1,9 m. W jaki sposób należy pociąć kłody, aby z jednej strony wykonać plan, z drugiej zaś uzyskać jak najmniej odpadu? Za odpad przyjmuje się kawałki drewna krótsze niż 1,2 m. Zbudować model matematyczny tego zagadnienia. 21. Trzech importerów hurtowników H 1, H 2, H 3 zaopatruje co 3 dni w banany cztery sklepy S 1, S 2, S 3, S 4. W czasie transportu część bananów ulega zapsuciu. Procentowy poziom ubytku bananów, zależny od czasu trwania transportu, ofertę (podaż) dostawców A i oraz zgłaszane zapotrzebowanie sklepów B j w kg zawiera poniższa tabela: Dostawcy Odbiorcy A i S 1 S 2 S 3 S 4 H 1 2,0 3,0 4,0 1, H 2 5,0 7,0 3,0 2, H 3 1,0 4,0 8,0 3, B j Jak sformułować zadanie doboru takiego planu dostaw, który zapewni minimalizację ilości zepsutych bananów? 7
8 22. Na początku dnia roboczego z parku autobusów wyjeżdża na linię x 1 maszyn, po godzinie dochodzi do nich następne x 2 autobusów, a po następnej godzinie dodatkowo x 3 autobusów. Każdy autobus kursuje po trasie bez przerwy przez 8 godzin. Minimalna konieczna liczba maszyn na linii w i-tej godzinie dnia pracy (i = 1, 2,..., 10) wynosi b i. Przekroczenie tej liczby prowadzi do dodatkowych kosztów w ciągu i-tej godziny w wielkości c i zł na każdy dodatkowy autobus. Sformułować matematycznie zadanie określenia liczby maszyn x 1, x 2 oraz x 3 wyjeżdżających na linię w pierwszych godzinach dnia roboczego, tak aby dodatkowe koszty w ciągu całego dnia były minimalne. 23. W wydziale pewnego zakładu znajduje się 100 obrabiarek typu T 1 oraz 200 obrabiarek typu T 2, a na każdej z nich można wytwarzać detale A 1 i A 2. Wydajność obrabiarek w ciągu doby, zysk z jednego detalu i minimalny dobowy plan produkcji przedstawia poniższa tabela. Rodzaj Wydajność szt./dobę Zysk z 1 szt. Minimalny plan detalu T 1 T 2 zł dobowy szt. A A Sformułować zadanie określenia liczby x ij obrabiarek typu T i, i = 1, 2, które należy przeznaczyć do produkcji detali A j, j = 1, 2 w taki sposób, aby zysk był maksymalny. 24. Zakład wytwarza dwa produkty A 1 i A 2 wykorzystując surowiec, którego zapas wynosi b ton. Zgodnie z planem, produkcja A 1 powinna stanowić co najmniej 60 % całej produkcji zakładu. Zużycie surowca na wytworzenie 1 tony produktu A 1 i A 2 wynosi odpowiednio a 1 i a 2. Cena 1 tony gotowego produktu A 1 i A 2 wynosi odpowiednio c 1 i c 2 zł. (a) Sformułować ZPL maksymalizujące zysk zakładu. (b) Zapisać je w postaci standardowej. (c) Zapisać otrzymaną postać standardową stosując zapis macierzowy. 8
Zagadnienie transportowe i zagadnienie przydziału
 Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Temat: Zagadnienie transportowe i zagadnienie przydziału Zadanie 1 Trzy piekarnie zlokalizowane na terenie miasta są zaopatrywane w mąkę z trzech magazynów znajdujących się na peryferiach. Zasoby mąki
Lista 1 PL metoda geometryczna
 Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Lista 1 PL metoda geometryczna 1.1. Znajdź maksimum funkcji celuf(x 1,x 2 )=5x 1 +7x 2 przy ograniczeniach: 2x 1 +2x 2 600, 2x 1 +4x 2 1000, x i 0 dlai=1,2 1.2. Znajdź maksimum funkcji celuf(x 1,x 2 )=2x
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych"
 Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Zadanie laboratoryjne "Wybrane zagadnienia badań operacyjnych" 1. Zbudować model optymalizacyjny problemu opisanego w zadaniu z tabeli poniżej. 2. Rozwiązać zadanie jak w tabeli poniżej z wykorzystaniem
Badania operacyjne. Lista zadań projektowych nr 2
 Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
Badania operacyjne Lista zadań projektowych nr 2 1. Trzy PGR-y mają odstawić do czterech punktów skupu pszenicę w następujących ilościach: PGR I - 100 ton, PGR II - 250 ton, PGR III - 100 ton. Punkty skupu
ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 3 ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA 3.3. ZADANIA Wykorzystując
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 3 ZADANIE TRANSPORTOWE I PROBLEM KOMIWOJAŻERA 3.3. ZADANIA Wykorzystując
Ćwiczenia laboratoryjne - 7. Problem (diety) mieszanek w hutnictwie programowanie liniowe. Logistyka w Hutnictwie Ćw. L. 7
 Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
Ćwiczenia laboratoryjne - 7 Problem (diety) mieszanek w hutnictwie programowanie liniowe Ćw. L. 7 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym zapisem
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Przedmiot: Nr ćwiczenia: 3 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie dynamiczne Cel ćwiczenia: Formułowanie i rozwiązywanie problemów optymalizacyjnych
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700
 Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
Zagadnienie diety Marta prowadzi hodowlę zwierząt. Minimalne dzienne zapotrzebowanie hodowli na mikroelementy M1, M2 i M3 wynosi 300, 800 i 700 jednostek, przy czym dla mikroelementu M1 maksymalna dzienna
METODY OBLICZENIOWE OPTYMALIZACJI zadania
 METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
METODY OBLICZENIOWE OPTYMALIZACJI zadania Przedstawione dalej zadania rozwiąż wykorzystując Excel/Solver. Zadania 8 są zadaniami optymalizacji liniowej, zadania 9, dotyczą optymalizacji nieliniowej. Przed
Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ).
 PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
PROGRAMOWANIE LINIOWE Zbudować model matematyczny do poniższych zagadnień (ułożyć program matematyczny ). Problem. Przedsiębiorstwo przewozowe STAR zajmuje się dostarczaniem lodów do sklepów. Dane dotyczące
Przykładowe zadania rozwiązywane na ćwiczeniach
 Przykładowe zadania rozwiązywane na ćwiczeniach Zad.. Określić ilość kursów poszczególnych środków transportu, przy których koszty przewozu gotowych wyrobów z przedsiębiorstwa do hurtowni będą najniższe.
Przykładowe zadania rozwiązywane na ćwiczeniach Zad.. Określić ilość kursów poszczególnych środków transportu, przy których koszty przewozu gotowych wyrobów z przedsiębiorstwa do hurtowni będą najniższe.
Modelowanie całkowitoliczbowe
 1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
1 Modelowanie całkowitoliczbowe Zmienne binarne P 1 Firma CMC rozważa budowę nowej fabryki w miejscowości A lub B lub w obu tych miejscowościach. Bierze również pod uwagę budowę co najwyżej jednej hurtowni
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Przedmiot: Nr ćwiczenia: 1 Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Temat: Programowanie liniowe Cel ćwiczenia: Opanowanie umiejętności modelowania i rozwiązywania problemów
Badania Operacyjne Ćwiczenia nr 5 (Materiały)
 ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
ZADANIE 1 Zakład produkuje trzy rodzaje papieru: standardowy do kserokopiarek i drukarek laserowych (S), fotograficzny (F) oraz nabłyszczany do drukarek atramentowych (N). Każdy z rodzajów papieru wymaga
ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI
 Wstęp ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI Problem podejmowania decyzji jest jednym z zagadnień sterowania nadrzędnego. Proces podejmowania decyzji
Wstęp ZASTOSOWANIE PROGRAMOWANIA LINIOWEGO W ZAGADNIENIACH WSPOMAGANIA PROCESU PODEJMOWANIA DECYZJI Problem podejmowania decyzji jest jednym z zagadnień sterowania nadrzędnego. Proces podejmowania decyzji
Wykład z modelowania matematycznego. Zagadnienie transportowe.
 Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Wykład z modelowania matematycznego. Zagadnienie transportowe. 1 Zagadnienie transportowe zostało sformułowane w 1941 przez F.L.Hitchcocka. Metoda rozwiązania tego zagadnienia zwana algorytmem transportowymópracowana
Ekonometria Programowanie Liniowe. Robert Pietrzykowski
 Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
Ekonometria Programowanie Liniowe Robert Pietrzykowski ZADANIE: Przedsiębiorstwo produkuje dwa wyroby: W1 i W2. Ograniczeniem w procesie produkcji jest czas pracy trzech maszyn: M1, M2 i M3. W tablicy
Ćwiczenia laboratoryjne - 7. Zagadnienie transportowoprodukcyjne. programowanie liniowe
 Ćwiczenia laboratoryjne - 7 Zagadnienie transportowoprodukcyjne ZT-P programowanie liniowe Ćw. L. 8 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym
Ćwiczenia laboratoryjne - 7 Zagadnienie transportowoprodukcyjne ZT-P programowanie liniowe Ćw. L. 8 Konstrukcja modelu matematycznego Model matematyczny składa się z: Funkcji celu będącej matematycznym
c j x x
 ZESTAW 1 Numer indeksu Test jest wielokrotnego wyboru We wszystkich mają być nieujemne 1 Pewien towar jest zmagazynowany w miejscowości A 1 w ilości 700 ton, w miejscowości 900 ton Ma być on przewieziony
ZESTAW 1 Numer indeksu Test jest wielokrotnego wyboru We wszystkich mają być nieujemne 1 Pewien towar jest zmagazynowany w miejscowości A 1 w ilości 700 ton, w miejscowości 900 ton Ma być on przewieziony
=B8*E8 ( F9:F11 F12 =SUMA(F8:F11)
 Microsoft EXCEL - SOLVER 2. Elementy optymalizacji z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Microsoft EXCEL - SOLVER 2. Elementy optymalizacji z wykorzystaniem dodatku Microsoft Excel Solver Cele Po ukończeniu tego laboratorium słuchacze potrafią korzystając z dodatku Solver: formułować funkcję
Ćwiczenia laboratoryjne - Dobór optymalnego asortymentu produkcji programowanie liniowe. Logistyka w Hutnictwie Ćw. L.
 Ćwiczenia laboratoryjne - Dobór optymalnego asortymentu produkcji programowanie liniowe Ćw. L. Typy optymalizacji Istnieją trzy podstawowe typy zadań optymalizacyjnych: Optymalizacja statyczna- dotyczy
Ćwiczenia laboratoryjne - Dobór optymalnego asortymentu produkcji programowanie liniowe Ćw. L. Typy optymalizacji Istnieją trzy podstawowe typy zadań optymalizacyjnych: Optymalizacja statyczna- dotyczy
1-2. Formułowanie zadań decyzyjnych. Metoda geometryczna
 -. Formułowanie zadań decyzyjnych. Metoda geometryczna Zagadnienie wyznaczania optymalnego asortymentu produkcji Firma zamierza uruchomić produkcję dwóch wyrobów A i B. Cenę zbytu oszacowano na zł/kg dla
-. Formułowanie zadań decyzyjnych. Metoda geometryczna Zagadnienie wyznaczania optymalnego asortymentu produkcji Firma zamierza uruchomić produkcję dwóch wyrobów A i B. Cenę zbytu oszacowano na zł/kg dla
ZAGADNIENIE TRANSPORTOWE
 ZAGADNENE TRANSPORTOWE Definicja: Program liniowy to model, w którym warunki ograniczające oraz funkcja celu są funkcjami liniowymi. W skład każdego programu liniowego wchodzą: zmienne decyzyjne, ograniczenia
ZAGADNENE TRANSPORTOWE Definicja: Program liniowy to model, w którym warunki ograniczające oraz funkcja celu są funkcjami liniowymi. W skład każdego programu liniowego wchodzą: zmienne decyzyjne, ograniczenia
Algebra liniowa. Macierze i układy równań liniowych
 Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Programowanie liniowe
 Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Badania operacyjne Ćwiczenia 4 Programowanie liniowe Dualizm w programowaniu liniowym Plan zajęć Dualizm w programowaniu liniowym Projektowanie programu dualnego Postać programu dualnego Przykład 1 Rozwiązania
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne. Temat ćwiczenia:
 Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Instrukcja do ćwiczeń laboratoryjnych z przedmiotu: Badania operacyjne Temat ćwiczenia: Programowanie liniowe, metoda geometryczna, dobór struktury asortymentowej produkcji Zachodniopomorski Uniwersytet
Definicja problemu programowania matematycznego
 Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Definicja problemu programowania matematycznego minimalizacja lub maksymalizacja funkcji min (max) f(x) gdzie: x 1 x R n x 2, czyli: x = [ ] x n przy ograniczeniach (w skrócie: p.o.) p.o. g i (x) = b i
Badania operacyjne. Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie:
 Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
Badania operacyjne Dr hab. inż. Adam Kasperski, prof. PWr. Pokój 509, budynek B4 adam.kasperski@pwr.edu.pl Materiały do zajęć dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia
Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego
 Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego Wstęp Spośród różnych analitycznych metod stosowanych do rozwiązywania problemów optymalizacji procesów technologicznych
Optymalizacja procesów technologicznych przy zastosowaniu programowania liniowego Wstęp Spośród różnych analitycznych metod stosowanych do rozwiązywania problemów optymalizacji procesów technologicznych
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO
 ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
ZAGADNIENIA PROGRAMOWANIA LINIOWEGO Maciej Patan Uniwersytet Zielonogórski WSTĘP często spotykane w życiu codziennym wybór asortymentu produkcji jakie wyroby i w jakich ilościach powinno produkować przedsiębiorstwo
Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE 2.3. ZADANIA W zadaniach 2.1 2.20
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 2 PROGRAMOWANIE LINIOWE CAŁKOWITOLICZBOWE 2.3. ZADANIA W zadaniach 2.1 2.20
TECHNIK LOGISTYK Zadanie egzaminacyjne etap praktyczny
 TECHNIK LOGISTYK Zadanie egzaminacyjne etap praktyczny Opracuj projekt realizacji czynności logistycznych zakładu przetwórstwa owocowo - warzywnego związanych z wyborem dostawców i przewoźnika. zużywa
TECHNIK LOGISTYK Zadanie egzaminacyjne etap praktyczny Opracuj projekt realizacji czynności logistycznych zakładu przetwórstwa owocowo - warzywnego związanych z wyborem dostawców i przewoźnika. zużywa
Pyt.1. Podać warunki jakie musi spełniać model matematyczny dla możliwości rozwiązywania metodami programowania liniowego.
 Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Firma produkująca płatki śniadaniowe rozważa wypuszczenie na rynek nowego produktu. Ma to być mieszanka pszenicy, ryżu i kukurydzy. Normy zawartości przedstawia tabela: Dane Pszenica Ryż Kukurydza Zawartość
Politechnika Wrocławska, Wydział Informatyki i Zarządzania. Optymalizacja
 Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Politechnika Wrocławska, Wydział Informatyki i Zarządzania Optymalizacja Dla podanych niżej problemów decyzyjnych (zad.1 zad.5) należy sformułować zadania optymalizacji, tj.: określić postać zmiennych
Wskaźniki pomiaru i oceny podsystemu - zaopatrzenia
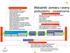 1 S T W Zaopatrzenie zakupy Mierniki strukturalne i ramowe liczba zakupionych części wolumen zakupionych materiałów pozycje zamówień na miesiąc liczba dostawców kwota umów ramowych struktura zamówień liczba
1 S T W Zaopatrzenie zakupy Mierniki strukturalne i ramowe liczba zakupionych części wolumen zakupionych materiałów pozycje zamówień na miesiąc liczba dostawców kwota umów ramowych struktura zamówień liczba
Zad.1. Microsoft Excel - Raport wyników Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto pocz tkowa Warto cowa Komórka Nazwa Warto
 Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Zad.1. Przedsiębiorstwo może wytwarzać trzy typy maszyn: tokarki, piły, frezarki zużywając dwa ograniczone zasoby: energię elektryczną i siłę roboczą w następujących proporcjach: energia (KWH / jedn.)
Zadanie transportowe i problem komiwojażera. Tadeusz Trzaskalik
 Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
Zadanie transportowe i problem komiwojażera Tadeusz Trzaskalik 3.. Wprowadzenie Słowa kluczowe Zbilansowane zadanie transportowe Rozwiązanie początkowe Metoda minimalnego elementu macierzy kosztów Metoda
4. PROGRAMOWANIE LINIOWE
 4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
4. PROGRAMOWANIE LINIOWE Programowanie liniowe jest jednym z działów badań operacyjnych. Celem badań operacyjnych jest pomoc w podejmowaniu optymalnych z pewnego punktu widzenia decyzji. Etapy rozwiązywania
OPTYMALIZACJA DYSKRETNA
 Temat nr a: odelowanie problemów decyzyjnych, c.d. OPTYALIZACJA DYSKRETA Zagadnienia decyzyjne, w których chociaż jedna zmienna decyzyjna przyjmuje wartości dyskretne (całkowitoliczbowe), nazywamy dyskretnymi
Temat nr a: odelowanie problemów decyzyjnych, c.d. OPTYALIZACJA DYSKRETA Zagadnienia decyzyjne, w których chociaż jedna zmienna decyzyjna przyjmuje wartości dyskretne (całkowitoliczbowe), nazywamy dyskretnymi
Wykład 7. Informatyka Stosowana. Magdalena Alama-Bućko. 16 kwietnia Magdalena Alama-Bućko Wykład 7 16 kwietnia / 23
 Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Wykład 7 Informatyka Stosowana Magdalena Alama-Bućko 16 kwietnia 2018 Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 1 / 23 Programowanie liniowe Magdalena Alama-Bućko Wykład 7 16 kwietnia 2018 2 / 23
Rozwiązanie Ad 1. Model zadania jest następujący:
 Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
Przykład. Hodowca drobiu musi uzupełnić zawartość dwóch składników odżywczych (A i B) w produktach, które kupuje. Rozważa cztery mieszanki: M : M, M i M. Zawartość składników odżywczych w poszczególnych
ZAGADNIENIE TRANSPORTOWE
 ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
ZAGADNIENIE TRANSPORTOWE ZT jest specyficznym problemem z zakresu zastosowań programowania liniowego. ZT wykorzystuje się najczęściej do: optymalnego planowania transportu towarów, przy minimalizacji kosztów,
Wydział Matematyki Programowanie liniowe Ćwiczenia. Zestaw 1. Modelowanie zadań programowania liniowego.
 Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Wydział Matematyki Programowanie liniowe Ćwiczenia Zestaw. Modelowanie zadań programowania liniowego. Zadania dotyczące zagadnienia planowania produkcji Zadanie.. Zapisać następujące zadanie w postaci
Zadanie egzaminacyjne
 Przykłady wybranych fragmentów prac egzaminacyjnych z komentarzami Technik logistyk 342[04] Zadanie egzaminacyjne Opracuj projekt realizacji czynności logistycznych zakładu przetwórstwa owocowowarzywnego
Przykłady wybranych fragmentów prac egzaminacyjnych z komentarzami Technik logistyk 342[04] Zadanie egzaminacyjne Opracuj projekt realizacji czynności logistycznych zakładu przetwórstwa owocowowarzywnego
Programowanie nieliniowe
 Rozdział 5 Programowanie nieliniowe Programowanie liniowe ma zastosowanie w wielu sytuacjach decyzyjnych, jednak często zdarza się, że zależności zachodzących między zmiennymi nie można wyrazić za pomocą
Rozdział 5 Programowanie nieliniowe Programowanie liniowe ma zastosowanie w wielu sytuacjach decyzyjnych, jednak często zdarza się, że zależności zachodzących między zmiennymi nie można wyrazić za pomocą
Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02
 Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Optymalizacja całkowitoliczbowa Przykład. Wspomaganie Zarządzania Przedsiębiorstwem Laboratorium 02 Firma stolarska produkuje dwa rodzaje stołów Modern i Classic, cieszących się na rynku dużym zainteresowaniem,
Halabarda A Halabarda B Zapas [t] Stal Drewno
![Halabarda A Halabarda B Zapas [t] Stal Drewno Halabarda A Halabarda B Zapas [t] Stal Drewno](/thumbs/53/31217238.jpg) Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Statystyka. Zadanie 1.
 Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
Statystyka Zadanie 1. W przedsiębiorstwie Statexport pracuje 100 pracowników fizycznych i 25 umysłowych. Typowy wiek pracownika fizycznego kształtuje się w przedziale od 30 do 40 lat. Średnia wieku pracowników
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych. Badania operacyjne. Dr inż.
 Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
Instytut Konstrukcji i Eksploatacji Maszyn Katedra Logistyki i Systemów Transportowych Badania operacyjne Dr inż. Artur KIERZKOWSKI Wprowadzenie Badania operacyjne związana jest ściśle z teorią podejmowania
OPTYMALIZACJA W LOGISTYCE
 OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
OPTYMALIZACJA W LOGISTYCE Zagadnienie przydziału dr Zbigniew Karwacki Katedra Badań Operacyjnych UŁ Zagadnienie przydziału 1 Można wyodrębnić kilka grup problemów, których zadaniem jest alokacja szeroko
SCENARIUSZ LEKCJI. Streszczenie. Czas realizacji. Podstawa programowa Etap edukacyjny: IV, przedmiot: informatyka (poziom podstawowy )
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
EKONOMIKA TRANSPORTU ANALIZA WSKAŹNIKOWA ANALIZA WSKAŹNIKOWA MARCIN FOLTYŃSKI
 EKONOMIKA RANSPORU Główną ideą tworzenia wskaźników w transporcie jest przeprowadzenie diagnozy stanu bieżącego systemu transportowego, którego podstawowym elementem są środki transportu 2 e V V gdzie:
EKONOMIKA RANSPORU Główną ideą tworzenia wskaźników w transporcie jest przeprowadzenie diagnozy stanu bieżącego systemu transportowego, którego podstawowym elementem są środki transportu 2 e V V gdzie:
Programowanie liniowe
 Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
Badania operacyjne Problem Model matematyczny Metoda rozwiązania Znaleźć optymalny program produkcji. Zmaksymalizować 1 +3 2 2 3 (1) Przy ograniczeniach 3 1 2 +2 3 7 (2) 2 1 +4 2 12 (3) 4 1 +3 2 +8 3 10
Iwona Konarzewska Programowanie celowe - wprowadzenie. Katedra Badań Operacyjnych UŁ
 1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
1 Iwona Konarzewska Programowanie celowe - wprowadzenie Katedra Badań Operacyjnych UŁ 2 Programowanie celowe W praktycznych sytuacjach podejmowania decyzji często występuje kilka celów. Problem pojawia
Wieloetapowe zagadnienia transportowe
 Przykład 1 Wieloetapowe zagadnienia transportowe Dwóch dostawców o podaży 40 i 45 dostarcza towar do trzech odbiorców o popycie 18, 17 i 26 za pośrednictwem dwóch punktów pośrednich o pojemnościach równych
Przykład 1 Wieloetapowe zagadnienia transportowe Dwóch dostawców o podaży 40 i 45 dostarcza towar do trzech odbiorców o popycie 18, 17 i 26 za pośrednictwem dwóch punktów pośrednich o pojemnościach równych
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Metody Ilościowe w Socjologii wykład 4 BADANIA OPERACYJNE dr inż. Maciej Wolny AGENDA I. Badania operacyjne podstawowe definicje II. Metodologia badań operacyjnych III. Wybrane zagadnienia badań operacyjnych
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa
 Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
Ćwiczenia pierwsze Badania operacyjne (budowanie modelu matematycznego) kierunek: matematyka, studia I specjalność: matematyka finansowa dr Jarosław Kotowicz 02 października 2015r. Zadanie 1 ([1, Przykład
Programowanie liniowe. Tadeusz Trzaskalik
 Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
Programowanie liniowe Tadeusz Trzaskalik .. Wprowadzenie Słowa kluczowe Model matematyczny Cel, środki, ograniczenia Funkcja celu funkcja kryterium Zmienne decyzyjne Model optymalizacyjny Układ warunków
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli?
 Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
Dodatek Solver Teoria Dodatek Solver jest częścią zestawu poleceń czasami zwaną narzędziami analizy typu co-jśli (analiza typu co, jeśli? : Proces zmieniania wartości w komórkach w celu sprawdzenia, jak
1. Który z warunków nie jest właściwy dla powyższego zadania programowania liniowego? 2. Na podstawie poniższej tablicy można odczytać, że
 Stwierdzeń będzie. Przy każdym będzie należało ocenić, czy jest to stwierdzenie prawdziwe, czy fałszywe i zaznaczyć x w tabelce odpowiednio przy prawdzie, jeśli jest ono prawdziwe lub przy fałszu, jeśli
Stwierdzeń będzie. Przy każdym będzie należało ocenić, czy jest to stwierdzenie prawdziwe, czy fałszywe i zaznaczyć x w tabelce odpowiednio przy prawdzie, jeśli jest ono prawdziwe lub przy fałszu, jeśli
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zadanie projektowe 2 Czas realizacji: 6 godzin Maksymalna liczba
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Struktury i Algorytmy Wspomagania Decyzji Zadanie projektowe 2 Czas realizacji: 6 godzin Maksymalna liczba
METODY WIELOKRYTERIALNE
 Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 4 METODY WIELOKRYTERIALNE 4.3. ZADANIA Zadanie 4.1 Wykorzystując tryb konwersacyjny
Standardowe zadanie programowania liniowego. Gliwice 1
 Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Standardowe zadanie programowania liniowego 1 Standardowe zadanie programowania liniowego Rozważamy proces, w którym zmiennymi są x 1, x 2,, x n. Proces poddany jest m ograniczeniom, zapisanymi w postaci
Środki produkcji Jedn. nakłady środka W1 Jedn. nakłady środka W2 I 6 6 II 10 5
 PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
PROGRAMOWANIE LINIOWE ZADANIA TEKSTOWE 5. Zakład produkuje dwa typy wózków: S i H. Zysk ze sprzedaży jednego wózka typu S wynosi 2850 zł a wózka typu H 6270 zł. Koszt produkcji jednego wózka typu S wynosi
Rachunkowość zarządcza
 Rachunkowość zarządcza Dorota Kuchta www.ioz.pwr.wroc.pl/pracownicy/kuchta/dydaktyka.htm 1 Podstawowa literatura Gabrusewicz W., Kamela-Sowińska A., Poetschke H., Rachunkowość zarządcza, PWE, Warszawa
Rachunkowość zarządcza Dorota Kuchta www.ioz.pwr.wroc.pl/pracownicy/kuchta/dydaktyka.htm 1 Podstawowa literatura Gabrusewicz W., Kamela-Sowińska A., Poetschke H., Rachunkowość zarządcza, PWE, Warszawa
Wykład z modelowania matematycznego. Algorytm sympleks.
 Wykład z modelowania matematycznego. Algorytm sympleks. 1 Programowanie matematyczne jest to zbiór metod poszukiwania punktu optymalizującego (minimalizującego lub maksymalizującego) wartość funkcji rzeczywistej
Wykład z modelowania matematycznego. Algorytm sympleks. 1 Programowanie matematyczne jest to zbiór metod poszukiwania punktu optymalizującego (minimalizującego lub maksymalizującego) wartość funkcji rzeczywistej
WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIEŃ TRANSPORTOWYCH Z KRYTERIUM KOSZTÓW
 WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIEŃ TRANSPORTOWYCH Z KRYTERIUM KOSZTÓW Zadania transportowe Zadania transportowe są najczęściej rozwiązywanymi problemami w praktyce z zakresu optymalizacji
WYKORZYSTANIE NARZĘDZIA Solver DO ROZWIĄZYWANIA ZAGADNIEŃ TRANSPORTOWYCH Z KRYTERIUM KOSZTÓW Zadania transportowe Zadania transportowe są najczęściej rozwiązywanymi problemami w praktyce z zakresu optymalizacji
Ekonometria - ćwiczenia 10
 Ekonometria - ćwiczenia 10 Mateusz Myśliwski Zakład Ekonometrii Stosowanej Instytut Ekonometrii Kolegium Analiz Ekonomicznych Szkoła Główna Handlowa 14 grudnia 2012 Wprowadzenie Optymalizacja liniowa Na
Ekonometria - ćwiczenia 10 Mateusz Myśliwski Zakład Ekonometrii Stosowanej Instytut Ekonometrii Kolegium Analiz Ekonomicznych Szkoła Główna Handlowa 14 grudnia 2012 Wprowadzenie Optymalizacja liniowa Na
Zarządzanie produkcją dr Mariusz Maciejczak. PROGRAMy. Istota sterowania
 Zarządzanie produkcją dr Mariusz Maciejczak PROGRAMy www.maciejczak.pl Istota sterowania W celu umożliwienia sobie realizacji złożonych celów, każda organizacja tworzy hierarchię planów. Plany różnią się
Zarządzanie produkcją dr Mariusz Maciejczak PROGRAMy www.maciejczak.pl Istota sterowania W celu umożliwienia sobie realizacji złożonych celów, każda organizacja tworzy hierarchię planów. Plany różnią się
Badania operacyjne. te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze.
 BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
BADANIA OPERACYJNE Badania operacyjne Badania operacyjne są sztuką dawania złych odpowiedzi na te praktyczne pytania, na które inne metody dają odpowiedzi jeszcze gorsze. T. Sayty 2 Standardowe zadanie
Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18
![Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18 Halabarda A Halabarda B Zapas [t] Stal 1 2 20 Drewno 2 1 18](/thumbs/27/9894738.jpg) Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Zadanie 1 Zamkowa zbrojownia produkuje dwa rodzaje halabard: A i B, które stały się jej przebojem eksportowym. Jednostkowy zysk osiągany na halabardzie A równa się 1 dukatowi, a na halabardzie B 3 dukatom.
Plan wykładu. Przykład. Przykład 3/19/2011. Przykład zagadnienia transportowego. Optymalizacja w procesach biznesowych Wykład 2 DECYZJA?
 /9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
/9/ Zagadnienie transportowe Optymalizacja w procesach biznesowych Wykład --9 Plan wykładu Przykład zagadnienia transportowego Sformułowanie problemu Własności zagadnienia transportowego Metoda potencjałów
Programowanie liniowe
 Programowanie liniowe Schemat postępowania w badaniach operacyjnych decydent sytuacja decyzyjna decyzje decyzje dopuszczalne niedopuszczalne kryterium wyboru zadanie decyzyjne zmienne decyzyjne warunki
Programowanie liniowe Schemat postępowania w badaniach operacyjnych decydent sytuacja decyzyjna decyzje decyzje dopuszczalne niedopuszczalne kryterium wyboru zadanie decyzyjne zmienne decyzyjne warunki
Estymacja przedziałowa
 Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski Metody analizy danych ćwiczenia Estymacja przedziałowa Program ćwiczeń obejmuje następująca zadania: 1. Dom handlowy prowadzący
Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski Metody analizy danych ćwiczenia Estymacja przedziałowa Program ćwiczeń obejmuje następująca zadania: 1. Dom handlowy prowadzący
Przykład wykorzystania dodatku SOLVER 1 w arkuszu Excel do rozwiązywania zadań programowania matematycznego
 Przykład wykorzystania dodatku SOLVER 1 w arkuszu Ecel do rozwiązywania zadań programowania matematycznego Firma produkująca samochody zaciągnęła kredyt inwestycyjny w wysokości mln zł na zainstalowanie
Przykład wykorzystania dodatku SOLVER 1 w arkuszu Ecel do rozwiązywania zadań programowania matematycznego Firma produkująca samochody zaciągnęła kredyt inwestycyjny w wysokości mln zł na zainstalowanie
Logistyka zaopatrzenia i produkcji
 Wydział Nauk Ekonomicznych Szkoła Główna Gospodarstwa Wiejskiego w Warszawie Logistyka zaopatrzenia i produkcji Wybrane instrukcje do gry piwnej (bez arkuszy analitycznych) Przyg. L. Wicki 2009-2015 4
Wydział Nauk Ekonomicznych Szkoła Główna Gospodarstwa Wiejskiego w Warszawie Logistyka zaopatrzenia i produkcji Wybrane instrukcje do gry piwnej (bez arkuszy analitycznych) Przyg. L. Wicki 2009-2015 4
Excel - użycie dodatku Solver
 PWSZ w Głogowie Excel - użycie dodatku Solver Dodatek Solver jest narzędziem używanym do numerycznej optymalizacji nieliniowej (szukanie minimum funkcji) oraz rozwiązywania równań nieliniowych. Przed pierwszym
PWSZ w Głogowie Excel - użycie dodatku Solver Dodatek Solver jest narzędziem używanym do numerycznej optymalizacji nieliniowej (szukanie minimum funkcji) oraz rozwiązywania równań nieliniowych. Przed pierwszym
Algorytmy i Struktury Danych.
 Algorytmy i Struktury Danych. Programowanie Dynamiczne dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 14 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Algorytmy i Struktury Danych. Programowanie Dynamiczne dr hab. Bożena Woźna-Szcześniak bwozna@gmail.com Jan Długosz University, Poland Wykład 14 Bożena Woźna-Szcześniak (AJD) Algorytmy i Struktury Danych.
Barbadoska 16 mb 24 mb Afrykańska 16 mb 10 mb
 I. Ćwiczenia 2 Firma McCain jest światowym potentatem w branży frytek. W swojej fabryce, która znajduje się w Buriey (stan Idaho), produkuje frytki Golden Longs oraz frytki My Fries Classic. Fabryka zaopatruje
I. Ćwiczenia 2 Firma McCain jest światowym potentatem w branży frytek. W swojej fabryce, która znajduje się w Buriey (stan Idaho), produkuje frytki Golden Longs oraz frytki My Fries Classic. Fabryka zaopatruje
EGZAMIN POTWIERDZAJĄCY KWALIFIKACJE W ZAWODZIE Rok 2017 CZĘŚĆ PRAKTYCZNA
 Arkusz zawiera informacje prawnie Układ graficzny CKE 2016 chronione do momentu rozpoczęcia egzaminu Nazwa kwalifikacji: Obsługa klientów i kontrahentów Oznaczenie kwalifikacji: A.29 Numer zadania: 01
Arkusz zawiera informacje prawnie Układ graficzny CKE 2016 chronione do momentu rozpoczęcia egzaminu Nazwa kwalifikacji: Obsługa klientów i kontrahentów Oznaczenie kwalifikacji: A.29 Numer zadania: 01
Zadanie TRAMAG 1 Przedstawienie problemu
 Zadanie TRAMAG 1 Przedstawienie problemu Firma TRAMAG jest firmą świadczącą kompleksowe usługi przewozu, przeładunku i magazynowania produktów chemii gospodarczej. Głównym długookresowym celem firmy jest
Zadanie TRAMAG 1 Przedstawienie problemu Firma TRAMAG jest firmą świadczącą kompleksowe usługi przewozu, przeładunku i magazynowania produktów chemii gospodarczej. Głównym długookresowym celem firmy jest
Analiza korelacji i regresji dwóch zmiennych losowych
 Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
Analiza korelacji i regresji dwóch zmiennych losowych 1. Badano zależność między ilością godzin przebywania samolotu w powietrzu ( nalot lotniczy) a ilością wypadków. Na podstawie zebranych danych z pewnego
ANKIETA. Proszę o podanie następujących danych: 1. Typ zakładu/rodzaj wytwarzanych produktów..
 ANKIETA METRYCZKA Proszę o podanie następujących danych: 1. Typ zakładu/rodzaj wytwarzanych produktów.. 2. Okres funkcjonowania zakładu: mniej niż rok od 1 2 lat od 3 5 lat 6-9 lat powyżej 9 lat 3. Liczba
ANKIETA METRYCZKA Proszę o podanie następujących danych: 1. Typ zakładu/rodzaj wytwarzanych produktów.. 2. Okres funkcjonowania zakładu: mniej niż rok od 1 2 lat od 3 5 lat 6-9 lat powyżej 9 lat 3. Liczba
ZAGADNIENIA TRANSPORTOWE
 ZAGADNIENIA TRANSPORTOWE Maciej Patan Uniwersytet Zielonogórski WPROWADZENIE opracowano w 1941 r. (F.L. Hitchcock) Jest to problem opracowania planu przewozu pewnego jednorodnego produktu z kilku różnych
ZAGADNIENIA TRANSPORTOWE Maciej Patan Uniwersytet Zielonogórski WPROWADZENIE opracowano w 1941 r. (F.L. Hitchcock) Jest to problem opracowania planu przewozu pewnego jednorodnego produktu z kilku różnych
Rozdział 1 PROGRAMOWANIE LINIOWE
 1.3. ZADANIA Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 1 PROGRAMOWANIE LINIOWE W zadaniach 1.1 1.40 zakłada się, że
1.3. ZADANIA Wprowadzenie do badań operacyjnych z komputerem Opisy programów, ćwiczenia komputerowe i zadania. T. Trzaskalik (red.) Rozdział 1 PROGRAMOWANIE LINIOWE W zadaniach 1.1 1.40 zakłada się, że
Studia stacjonarne I stopnia
 Studia stacjonarne I stopnia Kierunek Logistyka sem. 1 Logistyka Ćwiczenia 5 Mierniki i wskaźniki logistyczne Transport Logistyka przedsiębiorstwa Logistyka marketingowa Logistyka materiałowa Logistyka
Studia stacjonarne I stopnia Kierunek Logistyka sem. 1 Logistyka Ćwiczenia 5 Mierniki i wskaźniki logistyczne Transport Logistyka przedsiębiorstwa Logistyka marketingowa Logistyka materiałowa Logistyka
EGZAMIN POTWIERDZAJĄCY KWALIFIKACJE W ZAWODZIE Rok 2018 CZĘŚĆ PRAKTYCZNA
 Arkusz zawiera informacje prawnie Układ graficzny CKE 2017 chronione do momentu rozpoczęcia egzaminu Nazwa kwalifikacji: Organizacja i nadzorowanie transportu Oznaczenie kwalifikacji: A.28 Numer zadania:
Arkusz zawiera informacje prawnie Układ graficzny CKE 2017 chronione do momentu rozpoczęcia egzaminu Nazwa kwalifikacji: Organizacja i nadzorowanie transportu Oznaczenie kwalifikacji: A.28 Numer zadania:
RACHUNEK KOSZTÓW I CONTROLLING LOGISTYKI Controlling operacyjny w łańcuchu dostaw
 1 RHUNEK KSZTÓW I NTRLLING LGISTKI ontrolling operacyjny w łańcuchu dostaw RHUNEK KSZTÓW I NTRLLING LGISTKI UTR: M KLIŃSKI UTR: M KLIŃSKI 2 Identyfikacja podsystemów logistyki w stanach statycznych i dynamicznych
1 RHUNEK KSZTÓW I NTRLLING LGISTKI ontrolling operacyjny w łańcuchu dostaw RHUNEK KSZTÓW I NTRLLING LGISTKI UTR: M KLIŃSKI UTR: M KLIŃSKI 2 Identyfikacja podsystemów logistyki w stanach statycznych i dynamicznych
Analiza danych przy uz yciu Solvera
 Analiza danych przy uz yciu Solvera Spis treści Aktywacja polecenia Solver... 1 Do jakich zadań wykorzystujemy Solvera?... 1 Zadanie 1 prosty przykład Solvera... 2 Zadanie 2 - Optymalizacja programu produkcji
Analiza danych przy uz yciu Solvera Spis treści Aktywacja polecenia Solver... 1 Do jakich zadań wykorzystujemy Solvera?... 1 Zadanie 1 prosty przykład Solvera... 2 Zadanie 2 - Optymalizacja programu produkcji
Programowanie liniowe całkowitoliczbowe
 Programowanie liniowe całkowitoliczbowe Jeżeli w zadaniu programowania liniowego pewne (lub wszystkie) zmienne musza przyjmować wartości całkowite, to takie zadanie nazywamy zadaniem programowania liniowego
Programowanie liniowe całkowitoliczbowe Jeżeli w zadaniu programowania liniowego pewne (lub wszystkie) zmienne musza przyjmować wartości całkowite, to takie zadanie nazywamy zadaniem programowania liniowego
Rachunek kosztów działań sterowany czasem TD ABC
 Projektowanie procesów dr Mariusz Maciejczak www.maciejczak.pl Rachunek kosztów działań sterowany czasem TD ABC ABC Rachunek kosztów działań Nośniki kosztów Mierniki częstotliwości i intensywności z jaką
Projektowanie procesów dr Mariusz Maciejczak www.maciejczak.pl Rachunek kosztów działań sterowany czasem TD ABC ABC Rachunek kosztów działań Nośniki kosztów Mierniki częstotliwości i intensywności z jaką
RACHUNEK KOSZTÓW _ ZADANIA
 RACHUNEK KOSZTÓW _ ZADANIA Zadania_Kalkulacja podziałowa prosta, współczynnikowa i odjemna Przykład_1 wyprodukowano 80 sztuk wyrobów gotowych i 50 sztuk wyrobów zaawansowanych w 40% z punktu widzenia poniesionych
RACHUNEK KOSZTÓW _ ZADANIA Zadania_Kalkulacja podziałowa prosta, współczynnikowa i odjemna Przykład_1 wyprodukowano 80 sztuk wyrobów gotowych i 50 sztuk wyrobów zaawansowanych w 40% z punktu widzenia poniesionych
Nazwa kwalifikacji: Organizacja i nadzorowanie transportu Oznaczenie kwalifikacji: A.28 Numer zadania: 01
 Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2017 Nazwa kwalifikacji: Organizacja i nadzorowanie transportu Oznaczenie kwalifikacji: A.28 Numer zadania:
Arkusz zawiera informacje prawnie chronione do momentu rozpoczęcia egzaminu Układ graficzny CKE 2017 Nazwa kwalifikacji: Organizacja i nadzorowanie transportu Oznaczenie kwalifikacji: A.28 Numer zadania:
Modele i narzędzia optymalizacji w systemach informatycznych zarządzania
 Politechnika Poznańska Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Joanna Józefowska POZNAŃ 2010/11 Spis treści Rozdział 1. Metoda programowania dynamicznego........... 5
Politechnika Poznańska Modele i narzędzia optymalizacji w systemach informatycznych zarządzania Joanna Józefowska POZNAŃ 2010/11 Spis treści Rozdział 1. Metoda programowania dynamicznego........... 5
Zadanie A. Pestycydy. Wejście. Wyjście. Przykłady. Techniki optymalizacyjne Sosnowiec, semestr zimowy 2016/2017
 Zadanie A. Pestycydy Aby uprawiać pewną roślinę musimy ją nawozić mieszanką zawierającą wszystkie potrzebne składniki odżywcze w ilości (podawanej w gramach) nie mniejszej niż przewiduje norma. Taką mieszankę
Zadanie A. Pestycydy Aby uprawiać pewną roślinę musimy ją nawozić mieszanką zawierającą wszystkie potrzebne składniki odżywcze w ilości (podawanej w gramach) nie mniejszej niż przewiduje norma. Taką mieszankę
Problem zarządzania produkcją i zapasami
 Problem zarządzania produkcją i zapasami Wykorzystamy zasadę optymalności Bellmana do poradzenia sobie z zarządzaniem zapasami i produkcją w określonym czasie z punktu widzenia istniejącego i mogącego
Problem zarządzania produkcją i zapasami Wykorzystamy zasadę optymalności Bellmana do poradzenia sobie z zarządzaniem zapasami i produkcją w określonym czasie z punktu widzenia istniejącego i mogącego
METODA SYMPLEKS. Maciej Patan. Instytut Sterowania i Systemów Informatycznych Uniwersytet Zielonogórski
 METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
METODA SYMPLEKS Maciej Patan Uniwersytet Zielonogórski WSTĘP Algorytm Sympleks najpotężniejsza metoda rozwiązywania programów liniowych Metoda generuje ciąg dopuszczalnych rozwiązań x k w taki sposób,
Łańcuch dostaw Łańcuch logistyczny
 Zarządzanie logistyką Dr Mariusz Maciejczak Łańcuch dostaw Łańcuch logistyczny www.maciejczak.pl Łańcuch logistyczny a łańcuch dostaw Łańcuch dostaw w odróżnieniu od łańcucha logistycznego dotyczy integracji
Zarządzanie logistyką Dr Mariusz Maciejczak Łańcuch dostaw Łańcuch logistyczny www.maciejczak.pl Łańcuch logistyczny a łańcuch dostaw Łańcuch dostaw w odróżnieniu od łańcucha logistycznego dotyczy integracji
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE
 PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
PROBLEMY DECYZYJNE KRÓTKOOKRESOWE OPTYMALNA STRUKTURA PRODUKCJI Na podstawie: J. Wermut, Rachunkowość zarządcza, ODDK, Gdańsk 2013 1 DECYZJE KRÓTKOOKRESOWE Decyzje krótkookresowe to takie, które dotyczą
Badania operacyjne. Dr Michał Kulej. Pokój 509, budynek B4 Forma zaliczenia wykładu: egzamin pisemny.
 Badania operacyjne Dr Michał Kulej. Pokój 509, budynek B4 michal.kulej@pwr.wroc.pl Materiały do zajęć będa dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia wykładu: egzamin
Badania operacyjne Dr Michał Kulej. Pokój 509, budynek B4 michal.kulej@pwr.wroc.pl Materiały do zajęć będa dostępne na stronie: www.ioz.pwr.wroc.pl/pracownicy/kasperski Forma zaliczenia wykładu: egzamin
