Topologiczny diagram fazowy półprzewodników IV-VI
|
|
|
- Barbara Dagmara Bukowska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Topologiczny diagram fazowy półprzewodników IV-VI Tomasz Story (IF PAN) Półprzewodniki IV-VI jako materiały topologiczne Koncepcje teoretyczne stanów topologicznch w materiałach IV-VI i ich weryfikacja doświadczalna Topologiczny diagram fazowy - powierzchniowe (3D) i krawędziowe (2D) stany elektronowe Podsumowanie
2 Izolatory topologiczne: podstawowa właściwości fizyczne Silne oddziaływanie spin-orbita E so E G Odwrócona symetria pasm Nieparzysta liczba stożków Diraca Metaliczne, helikalne spinowo stany powierzchniowe Ochrona topologiczna
3 Inwersja pasm w półprzewodnikach P. Barone et al., Phys. Rev. B (2013)
4 Izolatory topologiczne 3D Bi, Sb półmetale z silnym oddziaływaniem spin-orbita Bi 1-x Sb x półprzewodnikowy stop materiał termoelektryczny L. Fu & C. Kane przewidywania teoretyczne dla Bi 1-x Sb x (PRB 2007) Weryfikacja doświadczalna: Hsieh et al., Nature 2008
5 Topologiczne stany elektronowe krawędziowe w heterostrukturach 2D powierzchniowe w kryształach 3D S. Murakami, J. Phys. Conf. Ser. 302, (2011)
6 Topologiczne stany elektronowe Metody doświadczalne: Fotoemisyjna spektroskopia elektronowa z rozdzielczością kątową ( ARPES) i spinową (SRPES) Skaningowa mikroskopia i spektroskopia tunelowa (STM) Transport elektronowy; magneto-przewodnictwo Magneto-optyka Mikro-magnetometria (np. mikro-squid) Magnetyzm, nadprzewodnictwo ( )
7 DOS Core level Fotoemisyjna spektroskopia elektronowa Vacuum level Intensity hn Valence band Energy Energy analyzer hn e - Sample Electron detector Secondary electrons Kinetic energy Binding energy E F
8 Fotoemisja metoda badania powierzchni kryształów photons electrons nm nm W. Mönch Semiconductor surfaces and interfaces 1993
9 Półprzewodniki rodziny IV-VI Binarne związki chemiczne: PbTe, PbSe, PbS, SnTe, GeTe Podstawieniowe roztwory stałe: Pb 1-x Sn x Te, Pb 1-x Sn x Se Półprzewodniki półmagnetyczne: Sn 1-x Mn x Te
10 Półprzewodniki rodziny IV-VI Struktura NaCl Wąska (0-0.3 ev), prosta przerwa energetyczna w punkcie L - 4 doliny Oddziaływanie relatywistyczne 1-go rzędu Małe masy efektywne, duże ruchliwości elektronów i dziur Materiały termoelektryczne i optoelektroniczne (lasery podczerwone).
11 Struktura elektronowa półprzewodników IV-VI Oddziaływania relatywistyczne w PbTe i PbSnTe
12 300 K Pb 1-x Sn x Te podstawieniowy roztwór stały 0,4 0,3 R. Dornhaus, G. Nimtz, and B. Schlicht, Springer Tracts in Modern Physics vol. 98, Narrow-Gap Semiconductors (Springer, Berlin, 1983) Pb 1-x Sn x Te L 6 0,2 0,1 L K E g (ev) 0,0-0,1-0,2 L K -0,3 L 6 TCI -0,4 0,0 0,2 0,4 0,6 0,8 1,0 Sn content, x
13 Podstawieniowy roztwór stały Pb 1-x Sn x Se 0,3 300 K Pb 1-x Sn x Se L 6 0,2 195 K L + 6 E g (ev) 0,1 0,0 77 K 4 K ü exp. data ý ţ A.J. Strauss x=0.23 x=0.27 x=0.30 L + 6-0,1 L 6 TCI -0,2 0 0,1 0,2 0,3 0,4 Sn content, x
14 Topologiczne izolatory krystaliczne: SnTe - wskazania teorii SnTe - teoretyczna analiza topologiczna wskazuje na stany elektronowe TCI z 4 stożkami Diraca w pobliżu punktów X strefy Brillouina (powierzchniowej) Przejście Lifshitza - zmiana kształtu powierzchni Fermiego T.H. Hsieh,L. Fu, Nature Commun. 3, 982 (2012).
15 Topologiczne izolatory krystaliczne: SnTe vs PbTe analiza teoretyczna PbTe trywialny izolator pasmowy E G >0 SnTe topologiczny izolator krystaliczny (TCI) E G <0 T.H. Hsieh, H. Lin, J. Liu, W. Duan, A. Bansil, L. Fu, Nature Commun. 3, 982 (2012).
16 Struktura elektronowa Pb 1-x Sn x Te - obliczenia metodą ciasnego wiązania PbSnTe w obszarze inwersji pasm: A) izolator pasmowy B) zerowa przerwa C) odwrócona przerwa - TCI D) SnTe - TCI S. Safaei, P. Kacman, R. Buczko, Phys. Rev. B 88, (2013)
17 Izolatory topologiczne a topologiczne izolatory krystaliczne Metaliczne stany powierzchniowe (krawędziowe) o liniowej dyspersji (Diraca). Symetria pasma przewodnictwa i pasma walencyjnego odwrócona w wyniku oddziaływań relatywistycznych (spinowo-orbitalnych). Ochrona topologiczna i brak rozpraszania do tyłu. Polaryzacja spinowa (helikalność). Mechanizm ochrona topologicznej: symetria odwrócenia czasu - zwierciadlana symetria krystaliczna Rozmieszczenie i liczba stożków Diraca nieparzysta (TRI) / parzysta Niezmiennik topologiczny: liczba Cherna (Z 2 ) zwierciadlana liczba Cherna
18 Wzrost monokryształów PbSnSe metodą SSVG A. Szczerbakow, monokryształ Pb 0.76 Sn 0.24 Se w ampule kwarcowej
19 Pomiary struktury elektronowej (ARPES) Pb 0.77 Sn 0.23 Se T=199 K E T=284 K E G vs. T T=144 K T=126 K T=111 K k
20 Strefa Brillouina dla powierzchni (001)
21 Struktura elektronowa - ARPES Relacje dyspersji w obszarze stożka Diraca dla różnych temperatur P. Dziawa, B.J. Kowalski, K. Dybko et al., Nat. Mat. 11, 1023 (2012)
22 Struktura elektronowa ARPES Relacje dyspersji E(k) dla kierunków X- i X-M
23 Struktura elektronowa - ARPES Przekroje powierzchni Fermiego E(k x, k y ) dla różnych energii wiązania
24 B.E. (ev) Dirac point Dirac point Pb 0.67 Sn 0.33 Se, T=87 K, hn=18.5 ev B.E. (ev) X 0.4 M X M X X Theory- R. Buczko, P. Kacman, S. Safaei X
25 Izolator trywialny (pasmowy) PbSe a topologiczny izolator krystaliczny Pb 1-x Sn x Se x=0, 0.15, 0.19, 0.23, 0.30, 0.37 T=300 K 0,3 300 K Pb 1-x Sn x Se L 6 0,2 195 K L + 6 T= 200 K E g (ev) 0,1 0,0 77 K 4 K ü exp. data ý ţ A.J. Strauss x=0.23 x=0.27 x=0.30 L + 6 T=100 K -0,1 L 6 TCI -0,2 0 0,1 0,2 0,3 0,4 Sn content, x T=9 K B.M. Wojek, P. Dziawa, B.J. Kowalski et al., Phys. Rev. B (R) (2014)
26 Cienkie warstwy Pb 1-x Sn x Se/BaF 2 (111) C.P. Polley, P. Dziawa et al., Phys. Rev. B 89, (2014)
27 Polaryzacja spinowa stanów TCI: obliczenia modelowe Pb 0.76 Sn 0.24 Se B.M. Wojek, R. Buczko et al., Phys. Rev. B 87, (2013)
28 Polaryzacja spinowa stanów topologicznych w SnTe S. Safaei, P. Kacman, R. Buczko, Phys. Rev. B 88, (2013) Obiczenia metodą ciasnego wiązania
29 Polaryzacja spinowa stanów TCI: eksperyment SRPES Pb 0.76 Sn 0.24 Se B.M. Wojek, R. Buczko et al., Phys. Rev. B 87, (2013)
30 Polaryzacja spinowa stanów TCI: SRPES Pb 0.6 Sn 0.4 Te S.-Y. Xu et al., Nat. Commun. 3, 1192 (2012).
31 Spektroskopia tunelowa STM I. Zeljkovic et al., Nat. Mat. 14, 318 (2015)
32 STM interferencje kwazi-cząstek quasi-particle interference (QPI) A. Gyenis et al., Phys. Rev. B 88, (2013) Princeton group
33 Spektroskopia tunelowa STM - Pb 1-x Sn x Se Y. Okada et al., Science 341, 1496 (2013)
34 Dystorsja sieci krystalicznej a stany topologiczne
35 Dystorsja sieci krystalicznej a stany topologicznego izolatora krystalicznego B.M. Wojek et al., Nat. Commun. 6, 8463 (2015)
36 Kontrola właściwości elektrycznych objętości kryształów TCI Domieszki o właściwościach głębokich centrów: grupa III: In lub metale przejściowe (V, Mo) R. Zhong et al., Phys. Rev. B 91, (2015)
37 Transport elektronowy Pomiary magnetooporowe: Efekt słabej antylokalizacji (WAL) efekty interferencyjne i s-o Efekt Subnikowa de Haasa (kwantowe oscylacje magnetooporu) Efekt Nernsta-Ettingshausena - K. Dybko et al., arxiv: Punkt inwersji pasm (x,t)
38 Tranzystor topologiczny 2D TCI
39 Dwuwymiarowy izolator topologiczny (2D TI) w ultra cienkich warstwach SnTe i SnSe (111) S. Safaei, M. Galicka, P. Kacman, R. Buczko, New J. Phys. 17, (2015)
40 Podsumowanie Topologiczne izolatory krystaliczne (TCI) nowa klasa materiałów półprzewodnikowych, dla których na powierzchniach wysokiej symetrii obserwuje się metaliczne stany elektronowe chronione topologicznie. Pb 1-x Sn x Se i Pb 1-x Sn x Te półprzewodniki rodziny IV-VI modelowe materiały TCI, w których obserwuje się indukowane temperaturą przejście od stanu izolatora pasmowego (trywialnego) do stanu topologicznego izolatora krystalicznego (3D). Weryfikacja doświadczalna koncepcji teoretycznych pomiary fotoemisyjne (ARPES, SRPES) i STM. Analiza teoretyczna struktury elektronowej w obszarze inwersji symetrii pasm. Topologiczny diagram fazowy (x, T, dystorsja sieci): 3D TCI potwierdzone doświadczalnie 2D TCI, 2D TI - przewidywania teoretyczne
41 Materiały topologiczne - nowość w fizyce ciała stałego czy materiały nowej elektroniki? Długa lista pomysłów teoretycznych wykorzystujących polaryzację spinową stanów topologicznych, możliwość otwierania i zamykani przerwy energetycznej i reżim transportu elektronowego bez rozpraszania nośników. Spintronika: źródła prądu spinowo spolaryzowanego (spinowego). Termoelektryczność: nowa realizacja idei kryształu elektronowego/szkła fononowego. Optoelektronika : materiały magnetooptyczne o kontrolowanej przerwie energetycznej. Elektronika: nowe tranzystory polowe; nanopołączenia elektryczne. Ważna zaleta izolatorów topologicznych: skalę temperatur ogranicza energia przerwy energetycznej (0.1 ev to ok K) temperatura pokojowa. Poważny (ale usuwalny) kłopot technologiczny: to raczej półprzewodniki niż izolatory przewodzenie objętości kryształu zwykle dominuje
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Podstawy Fizyki Półprzewodników
 Podstawy Fizyki Półprzewodników Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski konsultacje: poniedziałek godz. 15:00-17:00, pok. 310 A-1 WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
Podstawy Fizyki Półprzewodników Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski konsultacje: poniedziałek godz. 15:00-17:00, pok. 310 A-1 WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Leonard Sosnowski
 Admiralty Research Laboratory w Teddington, Anglia (1945-1947). Leonard Sosnowski J. Starkiewicz, L. Sosnowski, O. Simpson, Nature 158, 28 (1946). L. Sosnowski, J. Starkiewicz, O. Simpson, Nature 159,
Admiralty Research Laboratory w Teddington, Anglia (1945-1947). Leonard Sosnowski J. Starkiewicz, L. Sosnowski, O. Simpson, Nature 158, 28 (1946). L. Sosnowski, J. Starkiewicz, O. Simpson, Nature 159,
Badania powierzchni kryształów i struktur epitaksjalnych. Bogdan J. Kowalski IF PAN
 Badania powierzchni kryształów i struktur epitaksjalnych Bogdan J. Kowalski IF PAN Co to jest powierzchnia? o GaN (0001) A Co to jest powierzchnia? 8 4 0 0 0.4 0.8 mm GaAs (110) Jak opisać powierzchnie:
Badania powierzchni kryształów i struktur epitaksjalnych Bogdan J. Kowalski IF PAN Co to jest powierzchnia? o GaN (0001) A Co to jest powierzchnia? 8 4 0 0 0.4 0.8 mm GaAs (110) Jak opisać powierzchnie:
Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu.
 Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu. Agnieszka Wołoś Instytut Fizyki Polskiej Akademii Nauk Uniwersytet Warszawski Instytut Technologii Materiałów Elektronicznych A. Hruban, G. Strzelecka,
Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu. Agnieszka Wołoś Instytut Fizyki Polskiej Akademii Nauk Uniwersytet Warszawski Instytut Technologii Materiałów Elektronicznych A. Hruban, G. Strzelecka,
Spintronika fotonika: analogie
 : analogie Paweł Wójcik, Maciej Wołoszyn, Bartłomiej Spisak W oparciu o wykład wygłoszony podczas konferencji 2nd World Congress of Smart Materials, Singapur, March 2-6, 2016 Wprowadzenie dla niespecjalistów
: analogie Paweł Wójcik, Maciej Wołoszyn, Bartłomiej Spisak W oparciu o wykład wygłoszony podczas konferencji 2nd World Congress of Smart Materials, Singapur, March 2-6, 2016 Wprowadzenie dla niespecjalistów
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Dr inż. Zbigniew Szklarski
 Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH
 Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Rok akademicki: 2016/2017 Kod: NIM s Punkty ECTS: 5. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Fizyka ciała stałego Rok akademicki: 2016/2017 Kod: NIM-1-306-s Punkty ECTS: 5 Wydział: Metali Nieżelaznych Kierunek: Inżynieria Materiałowa Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Fizyka ciała stałego Rok akademicki: 2016/2017 Kod: NIM-1-306-s Punkty ECTS: 5 Wydział: Metali Nieżelaznych Kierunek: Inżynieria Materiałowa Specjalność: Poziom studiów: Studia I stopnia
Struktura pasmowa ciał stałych
 Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Materiały używane w elektronice
 Materiały używane w elektronice Typ Rezystywność [Wm] Izolatory (dielektryki) Over 10 5 półprzewodniki 10-5 10 5 przewodniki poniżej 10-5 nadprzewodniki (poniżej 20K) poniżej 10-15 Model pasm energetycznych
Materiały używane w elektronice Typ Rezystywność [Wm] Izolatory (dielektryki) Over 10 5 półprzewodniki 10-5 10 5 przewodniki poniżej 10-5 nadprzewodniki (poniżej 20K) poniżej 10-15 Model pasm energetycznych
Podstawy fizyki wykład 4
 D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Projekt FPP "O" Kosma Jędrzejewski 13-12-2013
 Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
Projekt FPP "O" Kosma Jędrzejewski --0 Projekt polega na wyznaczeniu charakterystyk gęstości stanów nośników ładunku elektrycznego w obszarze aktywnym lasera półprzewodnikowego GaAs. Wyprowadzenie wzoru
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Modele kp Studnia kwantowa
 Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Przewodnictwo elektryczne ciał stałych. Fizyka II, lato
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
3.4 Badanie charakterystyk tranzystora(e17)
 152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
Przewodnictwo elektryczne ciał stałych
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2011 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Ciała stałe. Literatura: Halliday, Resnick, Walker, t. 5, rozdz. 42 Orear, t. 2, rozdz. 28 Young, Friedman, rozdz
 Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Lasery półprzewodnikowe. przewodnikowe. Bernard Ziętek
 Lasery półprzewodnikowe przewodnikowe Bernard Ziętek Plan 1. Rodzaje półprzewodników 2. Parametry półprzewodników 3. Złącze p-n 4. Rekombinacja dziura-elektron 5. Wzmocnienie 6. Rezonatory 7. Lasery niskowymiarowe
Lasery półprzewodnikowe przewodnikowe Bernard Ziętek Plan 1. Rodzaje półprzewodników 2. Parametry półprzewodników 3. Złącze p-n 4. Rekombinacja dziura-elektron 5. Wzmocnienie 6. Rezonatory 7. Lasery niskowymiarowe
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Poznań, 11 sierpnia 2014 r.
 Kierownik Zakładu: prof. dr hab. Ryszard Czajka e-mail: ryszard.czajka@put.poznan.pl tel.: 61-665 3234, 61-665 3162 Wydział Fizyki Technicznej Instytut Fizyki, ul. Nieszawska 13 A, 60-965 POZNAŃ Zakład
Kierownik Zakładu: prof. dr hab. Ryszard Czajka e-mail: ryszard.czajka@put.poznan.pl tel.: 61-665 3234, 61-665 3162 Wydział Fizyki Technicznej Instytut Fizyki, ul. Nieszawska 13 A, 60-965 POZNAŃ Zakład
Wykład IV. Dioda elektroluminescencyjna Laser półprzewodnikowy
 Wykład IV Dioda elektroluminescencyjna Laser półprzewodnikowy Półprzewodniki - diagram pasmowy Kryształ Si, Ge, GaAs Struktura krystaliczna prowadzi do relacji dyspersji E(k). Krzywizna pasm decyduje o
Wykład IV Dioda elektroluminescencyjna Laser półprzewodnikowy Półprzewodniki - diagram pasmowy Kryształ Si, Ge, GaAs Struktura krystaliczna prowadzi do relacji dyspersji E(k). Krzywizna pasm decyduje o
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Czym jest prąd elektryczny
 Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Przyrządy półprzewodnikowe
 Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 5 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 5 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
!!!DEL są źródłami światła niespójnego.
 Dioda elektroluminescencyjna DEL Element czynny DEL to złącze p-n. Gdy zostanie ono spolaryzowane w kierunku przewodzenia, to w obszarze typu p, w warstwie o grubości rzędu 1µm, wytwarza się stan inwersji
Dioda elektroluminescencyjna DEL Element czynny DEL to złącze p-n. Gdy zostanie ono spolaryzowane w kierunku przewodzenia, to w obszarze typu p, w warstwie o grubości rzędu 1µm, wytwarza się stan inwersji
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Wprowadzenie do ekscytonów
 Proces absorpcji można traktować jako tworzenie się, pod wpływem zewnętrznego pola elektrycznego, pary elektron-dziura, które mogą być opisane w przybliżeniu jednoelektronowym. Dokładniejszym podejściem
Proces absorpcji można traktować jako tworzenie się, pod wpływem zewnętrznego pola elektrycznego, pary elektron-dziura, które mogą być opisane w przybliżeniu jednoelektronowym. Dokładniejszym podejściem
Jak TO działa? Co to są półprzewodniki? TRENDY: Prawo Moore a. Google: Jacek Szczytko Login: student Hasło: *******
 Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Cel ćwiczenia: Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporności elektrycznej monokryształu germanu od temperatury.
 WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne
 Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 8 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 8 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Złącze p-n: dioda. Przewodnictwo półprzewodników. Dioda: element nieliniowy
 Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Złącze p-n: dioda Półprzewodniki Przewodnictwo półprzewodników Dioda Dioda: element nieliniowy Przewodnictwo kryształów Atomy dyskretne poziomy energetyczne (stany energetyczne); określone energie elektronów
Struktura energetyczna ciał stałych. Fizyka II, lato
 Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
30/01/2018. Wykład XI: Właściwości elektryczne. Treść wykładu: Wprowadzenie
 Wykład XI: Właściwości elektryczne JERZY LIS Wydział Inżynierii Materiałowej i Ceramiki Katedra Ceramiki i Materiałów Ogniotrwałych Treść wykładu: 1. Wprowadzenie 2. a) wiadomości podstawowe b) przewodniki
Wykład XI: Właściwości elektryczne JERZY LIS Wydział Inżynierii Materiałowej i Ceramiki Katedra Ceramiki i Materiałów Ogniotrwałych Treść wykładu: 1. Wprowadzenie 2. a) wiadomości podstawowe b) przewodniki
Laboratorium inżynierii materiałowej LIM
 Laboratorium inżynierii materiałowej LIM wybrane zagadnienia fizyki ciała stałego czyli skrót skróconego skrótu dr hab. inż.. Ryszard Pawlak, P prof. PŁP Fizyka Ciała Stałego I. Wstęp Związki Fizyki Ciała
Laboratorium inżynierii materiałowej LIM wybrane zagadnienia fizyki ciała stałego czyli skrót skróconego skrótu dr hab. inż.. Ryszard Pawlak, P prof. PŁP Fizyka Ciała Stałego I. Wstęp Związki Fizyki Ciała
II. WYBRANE LASERY. BERNARD ZIĘTEK IF UMK www.fizyka.umk.pl/~ /~bezet
 II. WYBRANE LASERY BERNARD ZIĘTEK IF UMK www.fizyka.umk.pl/~ /~bezet Laser gazowy Laser He-Ne, Mechanizm wzbudzenia Bernard Ziętek IF UMK Toruń 2 Model Bernard Ziętek IF UMK Toruń 3 Rozwiązania stacjonarne
II. WYBRANE LASERY BERNARD ZIĘTEK IF UMK www.fizyka.umk.pl/~ /~bezet Laser gazowy Laser He-Ne, Mechanizm wzbudzenia Bernard Ziętek IF UMK Toruń 2 Model Bernard Ziętek IF UMK Toruń 3 Rozwiązania stacjonarne
W1. Właściwości elektryczne ciał stałych
 W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
Spektroskopia modulacyjna
 Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Podstawy krystalografii
 Podstawy krystalografii Kryształy Pojęcie kryształu znane było już w starożytności. Nazywano tak ciała o regularnych kształtach i gładkich ścianach. Już wtedy podejrzewano, że te cechy związane są ze szczególną
Podstawy krystalografii Kryształy Pojęcie kryształu znane było już w starożytności. Nazywano tak ciała o regularnych kształtach i gładkich ścianach. Już wtedy podejrzewano, że te cechy związane są ze szczególną
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Zaburzenia periodyczności sieci krystalicznej
 Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru
 Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane. Piotr Perlin Instytut Wysokich Ciśnień PAN
 Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Badania powierzchni kryształów i struktur epitaksjalnych. Bogdan J. Kowalski IF PAN
 Badania powierzchni kryształów i struktur epitaksjalnych Bogdan J. Kowalski IF PAN Co to jest powierzchnia? A o Co to jest powierzchnia? GaN(0001) 8 4 0 0 0.4 0.8 mm GaAs (110) Przykład: powierzchnia GaAs
Badania powierzchni kryształów i struktur epitaksjalnych Bogdan J. Kowalski IF PAN Co to jest powierzchnia? A o Co to jest powierzchnia? GaN(0001) 8 4 0 0 0.4 0.8 mm GaAs (110) Przykład: powierzchnia GaAs
Przyrządy i układy półprzewodnikowe
 Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
Recenzja rozprawy doktorskiej mgr Małgorzaty Bukały
 Warszawa, 25. kwietnia 2012 r. Prof. dr hab. Grzegorz Karczewski Instytut Fizyki Polska Akademia Nauk Al. Lotników 32/46 02-668 Warszawa Recenzja rozprawy doktorskiej mgr Małgorzaty Bukały zatytułowanej:
Warszawa, 25. kwietnia 2012 r. Prof. dr hab. Grzegorz Karczewski Instytut Fizyki Polska Akademia Nauk Al. Lotników 32/46 02-668 Warszawa Recenzja rozprawy doktorskiej mgr Małgorzaty Bukały zatytułowanej:
Proste struktury krystaliczne
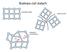 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Repeta z wykładu nr 6. Detekcja światła. Plan na dzisiaj. Metal-półprzewodnik
 Repeta z wykładu nr 6 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 - kontakt omowy
Repeta z wykładu nr 6 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 - kontakt omowy
Przejścia promieniste
 Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
Przejście promieniste proces rekombinacji elektronu i dziury (przejście ze stanu o większej energii do stanu o energii mniejszej), w wyniku którego następuje emisja promieniowania. E Długość wyemitowanej
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
elektryczne ciał stałych
 Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.2017 1 2 Własności elektryczne
Wykład 23: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.2017 1 2 Własności elektryczne
Recenzja osiągnięć naukowych dr. Łukasza Plucińskiego w związku z postępowaniem habilitacyjnym.
 Prof. dr hab. Józef Korecki Katedra Fizyki Ciała Stałego Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza w Krakowie oraz Instytut Katalizy i Fizykochemii Powierzchni im. Jerzego Habera
Prof. dr hab. Józef Korecki Katedra Fizyki Ciała Stałego Wydział Fizyki i Informatyki Stosowanej Akademia Górniczo-Hutnicza w Krakowie oraz Instytut Katalizy i Fizykochemii Powierzchni im. Jerzego Habera
WYZNACZANIE STAŁEJ PLANCKA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH. Irena Jankowska-Sumara, Magdalena Krupska
 1 II PRACOWNIA FIZYCZNA: FIZYKA ATOMOWA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH Irena Jankowska-Sumara, Magdalena Krupska Cel ćwiczenia Celem ćwiczenia jest wyznaczenie
1 II PRACOWNIA FIZYCZNA: FIZYKA ATOMOWA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH Irena Jankowska-Sumara, Magdalena Krupska Cel ćwiczenia Celem ćwiczenia jest wyznaczenie
Fizyka 3.3. prof.dr hab. Ewa Popko p.231a
 Fizyka 3.3 prof.dr hab. Ewa Popko www.if.pwr.wroc.pl/~popko ewa.popko@pwr.edu.pl p.231a Fizyka 3.3 Literatura 1.J.Hennel Podstawy elektroniki półprzewodnikowej WNT Warszawa 1995. 2. B. Ziętek, Optoelektronika,
Fizyka 3.3 prof.dr hab. Ewa Popko www.if.pwr.wroc.pl/~popko ewa.popko@pwr.edu.pl p.231a Fizyka 3.3 Literatura 1.J.Hennel Podstawy elektroniki półprzewodnikowej WNT Warszawa 1995. 2. B. Ziętek, Optoelektronika,
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Fizyka i inżynieria materiałów Prowadzący: Ryszard Pawlak, Ewa Korzeniewska, Jacek Rymaszewski, Marcin Lebioda, Mariusz Tomczyk, Maria Walczak
 Fizyka i inżynieria materiałów Prowadzący: Ryszard Pawlak, Ewa Korzeniewska, Jacek Rymaszewski, Marcin Lebioda, Mariusz Tomczyk, Maria Walczak Instytut Systemów Inżynierii Elektrycznej Politechnika Łódzka
Fizyka i inżynieria materiałów Prowadzący: Ryszard Pawlak, Ewa Korzeniewska, Jacek Rymaszewski, Marcin Lebioda, Mariusz Tomczyk, Maria Walczak Instytut Systemów Inżynierii Elektrycznej Politechnika Łódzka
Zagadnienie do ćwiczeń na 2 Pracowni Fizycznej Dr Urszula Majewska
 Ćwiczenie nr 1-4pkt Wyznaczanie współczynników załamania ośrodków ciekłych i gazowych za pomocą interferometru 1. Interferencja światła Drgania harmoniczne Faza drgań Faza fali Kiedy stosujemy prawa fizyki
Ćwiczenie nr 1-4pkt Wyznaczanie współczynników załamania ośrodków ciekłych i gazowych za pomocą interferometru 1. Interferencja światła Drgania harmoniczne Faza drgań Faza fali Kiedy stosujemy prawa fizyki
Wprowadzenie do struktur niskowymiarowych
 Wprowadzenie do struktur niskowymiarowych W litym krysztale ruch elektronów i dziur nie jest ograniczony przestrzennie. Struktury niskowymiarowe pozwalają na ograniczenie (częściowe lub całkowite) ruchu
Wprowadzenie do struktur niskowymiarowych W litym krysztale ruch elektronów i dziur nie jest ograniczony przestrzennie. Struktury niskowymiarowe pozwalają na ograniczenie (częściowe lub całkowite) ruchu
elektryczne ciał stałych
 Wykład 22: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
Wykład 22: Przewodnictwo elektryczne ciał stałych Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Własności elektryczne ciał
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 13 Janusz Andrzejewski Scaledlugości Janusz Andrzejewski 2 Scaledługości Simple molecules
Fizyka 2 wykład 13 Janusz Andrzejewski Scaledlugości Janusz Andrzejewski 2 Scaledługości Simple molecules
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
W drugiej części przedstawiono podstawowe wiadomości z fizyki atomowej, fizyki ciała stałego oraz fizyki jądrowej.
 W drugiej części przedstawiono podstawowe wiadomości z fizyki atomowej, fizyki ciała stałego oraz fizyki jądrowej. Na całość pracy składają się dwie części (cz. I Fizyka klasyczna J. Massalski, M. Massalska).
W drugiej części przedstawiono podstawowe wiadomości z fizyki atomowej, fizyki ciała stałego oraz fizyki jądrowej. Na całość pracy składają się dwie części (cz. I Fizyka klasyczna J. Massalski, M. Massalska).
Wykład FIZYKA II. 14. Fizyka ciała stałego. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II 14. Fizyka ciała stałego Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ MATERIA SKONDENSOWANA Każdy pierwiastek bądź
Wykład FIZYKA II 14. Fizyka ciała stałego Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ MATERIA SKONDENSOWANA Każdy pierwiastek bądź
W5. Rozkład Boltzmanna
 W5. Rozkład Boltzmanna Podstawowym rozkładem w klasycznej fizyce statystycznej jest rozkład Boltzmanna E /( kt ) f B ( E) Ae gdzie: A jest stałą normalizacyjną, k stałą Boltzmanna 5 k 8.61710 ev / K Został
W5. Rozkład Boltzmanna Podstawowym rozkładem w klasycznej fizyce statystycznej jest rozkład Boltzmanna E /( kt ) f B ( E) Ae gdzie: A jest stałą normalizacyjną, k stałą Boltzmanna 5 k 8.61710 ev / K Został
Struktura energetyczna ciał stałych
 011-05-0 Struktura energetyczna ciał stałych Fizyka II dla Elektroniki, lato 011 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona
011-05-0 Struktura energetyczna ciał stałych Fizyka II dla Elektroniki, lato 011 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona
Aleksandra Banaś Dagmara Zemła WPPT/OPTOMETRIA
 Aleksandra Banaś Dagmara Zemła WPPT/OPTOMETRIA B V B C ZEWNĘTRZNE POLE ELEKTRYCZNE B C B V B D = 0 METAL IZOLATOR PRZENOSZENIE ŁADUNKÓW ELEKTRYCZNYCH B C B D B V B D PÓŁPRZEWODNIK PODSTAWOWE MECHANIZMY
Aleksandra Banaś Dagmara Zemła WPPT/OPTOMETRIA B V B C ZEWNĘTRZNE POLE ELEKTRYCZNE B C B V B D = 0 METAL IZOLATOR PRZENOSZENIE ŁADUNKÓW ELEKTRYCZNYCH B C B D B V B D PÓŁPRZEWODNIK PODSTAWOWE MECHANIZMY
KĄTOWO-ROZDZIELCZA SPEKTROSKOPIA FOTOEMISYJNA, CZYLI STRUKTURA PASMOWA OD A, PRZEZ Γ, DO K
 KĄTOWO-ROZDZIELCZA SPEKTROSKOPIA FOTOEMISYJNA, CZYLI STRUKTURA PASMOWA OD A, PRZEZ Γ, DO K Bogdan J. Kowalski Instytut Fizyki Polskiej Akademii Nauk, Aleja Lotników 32/46, PL-02 668 Warszawa Streszczenie:
KĄTOWO-ROZDZIELCZA SPEKTROSKOPIA FOTOEMISYJNA, CZYLI STRUKTURA PASMOWA OD A, PRZEZ Γ, DO K Bogdan J. Kowalski Instytut Fizyki Polskiej Akademii Nauk, Aleja Lotników 32/46, PL-02 668 Warszawa Streszczenie:
Badanie pól elektrycznych w azotkach metodami optycznymi
 Badanie pól elektrycznych w azotkach metodami optycznymi Krzysztof Zieleniewski Pod opieką dr. Anety Drabińskiej Proseminarium Fizyki Ciała Stałego, 8 kwietnia 2010 O czym będzie? Dlaczego azotki? Dlaczego
Badanie pól elektrycznych w azotkach metodami optycznymi Krzysztof Zieleniewski Pod opieką dr. Anety Drabińskiej Proseminarium Fizyki Ciała Stałego, 8 kwietnia 2010 O czym będzie? Dlaczego azotki? Dlaczego
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 6 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 6 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 2003
 Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
Podstawowe właściwości fizyczne półprzewodników WYKŁAD 1 SMK J. Hennel: Podstawy elektroniki półprzewodnikowej, WNT, W-wa 003 1. Wiązania atomów w krysztale Siły wiążące atomy w kryształ mają charakter
FIZYKA WSPÓŁCZESNA. Janusz Adamowski
 FIZYKA WSPÓŁCZESNA Janusz Adamowski 1 Wykłady dla studentów 2. stopnia studiów inżynierskich AGH Motto wykładów: FIZYKA (WSPÓŁCZESNA) stanowi podstawę działania przyrządów obecnej i przyszłej techniki
FIZYKA WSPÓŁCZESNA Janusz Adamowski 1 Wykłady dla studentów 2. stopnia studiów inżynierskich AGH Motto wykładów: FIZYKA (WSPÓŁCZESNA) stanowi podstawę działania przyrządów obecnej i przyszłej techniki
Dyslokacje w kryształach. ach. Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska
 Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
METALE. Cu 8.50 1.35 1.56 7.0 8.2 Ag 5.76 1.19 1.38 5.5 6.4 Au 5.90 1.2 1.39 5.5 6.4
 MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
MAL Zestawienie właściwości gazu elektronowego dla niektórych metali: n cm -3 k cm -1 v cm/s ε e ε /k Li 4.6 10 1.1 10 8 1.3 10 8 4.7 5.5 10 4 a.5 0.9 1.1 3.1 3.7 K 1.34 0.73 0.85.1.4 Rb 1.08 0.68 0.79
