Laboratorium grafiki komputerowej i animacji. Ćwiczenie III - Biblioteka OpenGL - wprowadzenie, obiekty trójwymiarowe: punkty, linie, wielokąty
|
|
|
- Szczepan Góra
- 8 lat temu
- Przeglądów:
Transkrypt
1 Laboratorium grafiki komputerowej i animacji Ćwicenie III - Biblioteka OpenGL - wprowadenie, obiekty trójwymiarowe: punkty, linie, wielokąty Prygotowanie do ćwicenia: 1. Zaponać się ogólną charakterystyką biblioteki OpenGL. 2. Zaponać się e sposobem konstruowania prymitywów graficnych OpenGL. 3. Zaponać się asadami tworenia aplikacji OpenGL na platformie Windows - estaw funkcji "wgl", biblioteka GLAUX. 4. Zaponać się prykładowymi programami dostarconymi wprowadeniem do ćwicenia. Prebieg ćwicenia: 1. Założenia: a. Celem prac na kilku następnych ajęciach jest skonstruowanie modelu graficnego manipulatora Puma (Siatka całego manipulatora pokaan jest na rysunku 1.1.). b. Predmiotem obecnych ajęć jest prygotowanie siatek elementów składowych manipulatora: walca i dwu ramion. c. Wynikiem prac na disiejsych ajęciach ma być program bliżony w diałaniu do programu puma_elementy.ee dostarconego do materiałów laboratoryjnych. d. Realiacja ćwicenia polega na modyfikacji kodu programu gl_template dołąconego do materiałów laboratoryjnych. e. W realiacji prac worować się należy na rowiąaniach pryjętych w programie triangle również dołąconym do materiałów laboratoryjnych. Rysunek 1.1 Graficny model manipulatora Puma (siatka) 2. Uwagi do sposobu realiacji celu ajęć laboratoryjnych: a. W programie gl_template wbudowano możliwość obracania tworonych modeli pry pomocy klawisy strałek.
2 b. Obiekty graficne należy tworyć w funkcji RenderScene() programu gl_template. c. Pry tworeniu amkniętych brył klucową rolę odgrywa takie aprojektowanie wielokątów, aby były wrócone na ewnątr ewnętrnymi powierchniami. Umożliwia to później pryspiesenie obliceń sceny pre odrucenie wewnętrnych powierchni w obliceniach. Uprasca się wówcas również procedura oświetlania obiektów. W wiąku tym podcas realiacji ćwicenia należy wrócić scególną uwagę na odpowiednie dobieranie kolejności podawania wierchołków wielokątów. Pomocne okaać się może wywołanie funkcji: glpolygonmode(gl_back,gl_line); umiescone w funkcji RenderScene(). Wewnętrne ściany wielokątów będą wtedy rysowane w postaci siatki, natomiast ewnętrne ostaną w całości amalowane. Wywołanie funkcji glpolygonmode(gl_front_and_back,gl_line) umożliwi postreganie aprojektowanej bryły w postaci siatki. d. Każdy tworonych na scenie obiektów ma powiąany e sobą układ współrędnych. Modele brył tworyć należy w taki sposób, aby dawać sobie sprawę, gdie najduje się układ współrędnych powiąany bryłą (Pocątkowy baowy układ współrędnych sceny najduje się na środku okna i tym układem współrędnych należy wiąać kolejno projektowane siatki brył). e. Brył amkniętych nie należy tworyć prymitywów do odworowywania linii. f. Wsystkie tworone w ramach ćwiceń modele stanowić mają bryły amknięte, w wiąku tym należy precyyjnie uwględnić każdą e ścian bryły (walec powinien awierać obie podstawy, wielościany powinny posiadać definiowane wsystkie ściany najlepiej w postaci osobnych wielokątów GL_QUADS, GL_TRANGLES, GL_POLYGON). g. Każdy elementów manipulatora najwygodniej amknąć w jednej funkcji. W parametrach wywołania funkcji nie należy uwględniać położenia elementu na scenie (Sposób romiescania elementów na scenie określony ostanie na kolejnych ajęciach). h. Sposób uupełnienia menu na potreby programu można worować na programie triangle. i. Model walca na potreby programu najwygodniej definiować w taki sposób, aby można było adawać jego promień i wysokość, np.: void walec(double h, double r). j. Fragment programu awierający definicję cęści walca może mieć następującą postać: void walec(double h, double r) double angle,,y; glbegin(gl_triangle_fan); glverte3d(0.0f, 0.0f, 0.0f); for(angle = 0.0f; angle <= (2.0f*GL_PI); angle += (GL_PI/8.0f)) = r*sin(angle); y = r*cos(angle); glverte3d(, y, 0.0);
3 glbegin(gl_quad_strip); for(angle = 0.0f; angle >= -(2.0f*GL_PI); angle -= (GL_PI/8.0f)) = r*sin(angle); y = r*cos(angle); glverte3d(, y, h); glverte3d(, y, 0); 3. Prebieg ćwicenia: a. Załadować do VS projekt GL_Template (Jest to kompletny projekt wiążący interfejs Windows interfejsem OpenGL. Jego struktura jest taka, jak omówiona we wprowadeniu do ćwicenia. Podstawowa funkcja do pisania kodu w OpenGL to RenderScene.). b. Dokońcyć realiację seścianu astosowaniem skryptu OpenGL. Współrędne wierchołków seścianu pokaano na rysunku 3.1. Funkcja seścian powinna być wywołana w funkcji RenderScene. (-20,20,-20) y (-20,20,20) (-20,-20,-20) (-20,-20,20) (20,20,-20) (20,20,20) (20,-20,-20) (20,-20,20) Rys. 3.1 Współrędne wierchołków seścianu Fragment kodu funkcji seścian amiescono poniżej: void sescian(void) glbegin(gl_quads); glcolor3d(1,0.5,0); glverte3d( 20, 20, 20); glverte3d(-20, 20, 20); glverte3d(-20,-20, 20); glverte3d( 20,-20, 20); glcolor3d(0,0.5,1); glverte3d( 20, 20, 20); glverte3d( 20,-20, 20);
4 glverte3d( 20,-20,-20); glverte3d( 20, 20,-20); Uwagi: W rysowaniu seścianu astosowano pojedynce cworokąty. Można pryjąć asadę, że, jeśli amieramy tworyć siatkę ostrymi krawędiami, to stosujemy do jej tworenia pojedynce wielokąty. Należy pamiętać, aby wsystkie ściany seścianu były wrócone prawą stroną na ewnątr. c. Opracować funkcję rysującą walec godnie aleceniami i i j. W realiacji funkcji rysującej walec astosować wachlar trójkątów (GL_TRIANGLE_FAN) do wyrysowania podstawy ora łańcuch cworokątów (GL_QUAD_STRIP) do wyrysowania tworącej walca. Uwagi: W rysowaniu walca astosowano parametrycne równanie okręgu do wynacenia wierchołków trójkątów tworących prybliżenie koła: [ ] Należy samodielnie rowiąać problem wyrysowania drugiej podstawy skierowanej prawą stroną na ewnątr walca. Orientację walca i parametry go opisujące w lokalnym układie współrędnych opisuje rysunek 3.2 y r h Rys. 3.2 Orientacja modelu walca i interpretacja jego parametrów. d. Opracować funkcję rysującą ramię robota. Ramię robota, pokaane na rysunku 3.3, można skonstruować dwu połówek walca i 4 cworokątów. Funkcja ramie może mieć prototyp: void ramie(double r1, double r2, double h, double d);
5 y h r1 d r2 Rys. 3.3 Orientacja modelu ramienia i jego parametry.
Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
 Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Laboratorium grafiki komputerowej i animacji. Ćwiczenie IV - Biblioteka OpenGL - transformacje przestrzenne obiektów
 Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
Laboratorium grafiki komputerowej i animacji Ćwicenie IV - Biblioteka OpenGL - transformacje prestrenne obiektów Prgotowanie do ćwicenia: 1. Zaponać się transformacjami prestrennmi (obrót, presunięcie,
Elementarne obiekty geometryczne, bufory. Dorota Smorawa
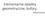 Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
ORGANIZACJA I ZARZĄDZANIE
 P O L I T E C H N I K A W A R S Z A W S K A WYDZIAŁ BUDOWNICTWA, MECHANIKI I PETROCHEMII INSTYTUT INŻYNIERII MECHANICZNEJ ORGANIZACJA I ZARZĄDZANIE Optymaliacja transportu wewnętrnego w akładie mechanicnym
P O L I T E C H N I K A W A R S Z A W S K A WYDZIAŁ BUDOWNICTWA, MECHANIKI I PETROCHEMII INSTYTUT INŻYNIERII MECHANICZNEJ ORGANIZACJA I ZARZĄDZANIE Optymaliacja transportu wewnętrnego w akładie mechanicnym
3 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
OZNACZENIE NIERUCHOMOŚCI KTÓREJ DOTYCZY UWAGA (numery działek lub inne określenie terenu objętego uwagą) USTALENIA PROJEKTU PLANU DZIAŁKA OBRĘB 10/2,
 Załącnik Nr 2 do Uchwały Nr... Rady Krakowa dnia... O SPOSOBIE ROZPATRZE UWAG DO MIEJSCOWEGO ZAGOSPODAROWA PRZESTRZENNEGO OBSZARU PARK RZECZNY DRWINKA - PODEDWORZE W KRAKOWIE, W TYM UWAG ZGŁOSZONYCH W
Załącnik Nr 2 do Uchwały Nr... Rady Krakowa dnia... O SPOSOBIE ROZPATRZE UWAG DO MIEJSCOWEGO ZAGOSPODAROWA PRZESTRZENNEGO OBSZARU PARK RZECZNY DRWINKA - PODEDWORZE W KRAKOWIE, W TYM UWAG ZGŁOSZONYCH W
OpenGL - charakterystyka
 OpenGL - charakterystyka OpenGL jest interfejsem programowym aplikacji zestawem funkcji umożliwiających tworzenie interaktywnej grafiki 3D. Program oparty na OpenGL musi być pisany z zastosowaniem języka
OpenGL - charakterystyka OpenGL jest interfejsem programowym aplikacji zestawem funkcji umożliwiających tworzenie interaktywnej grafiki 3D. Program oparty na OpenGL musi być pisany z zastosowaniem języka
Zatem standardowe rysowanie prymitywów wygląda następująco:
 Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Języki interpretowane Interpreted languages PRZEWODNIK PO PRZEDMIOCIE
 Jęyki interpretowane Interpreted languages Informatyka Stacjonarne IO2_02 Obowiąkowy w ramach specjalności: Inżynieria oprogramowania II stopień Rok: I Semestr: II wykład, laboratorium 1W, 2L 3 ECTS I
Jęyki interpretowane Interpreted languages Informatyka Stacjonarne IO2_02 Obowiąkowy w ramach specjalności: Inżynieria oprogramowania II stopień Rok: I Semestr: II wykład, laboratorium 1W, 2L 3 ECTS I
MES W ANALIZIE SPRĘŻYSTEJ UKŁADÓW PRĘTOWYCH
 MES W ANALIZIE SPRĘŻYS UKŁADÓW PRĘOWYCH Prykłady obliceń Belki Lidia FEDOROWICZ Jan FEDOROWICZ Magdalena MROZEK Dawid MROZEK Gliwice 7r. 6-4 Lidia Fedorowic, Jan Fedorowic, Magdalena Mroek, Dawid Mroek
MES W ANALIZIE SPRĘŻYS UKŁADÓW PRĘOWYCH Prykłady obliceń Belki Lidia FEDOROWICZ Jan FEDOROWICZ Magdalena MROZEK Dawid MROZEK Gliwice 7r. 6-4 Lidia Fedorowic, Jan Fedorowic, Magdalena Mroek, Dawid Mroek
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM. Rok szkolny 2015/16
 WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM Rok skolny 2015/16 POZIOMY WYMAGAŃ EDUKACYJNYCH: (2) - ocena dopscająca (2); (3) - ocena dostatecna (3); (4) - ocena dobra (4);
WYMAGANIA NA POSZCZEGÓLNE OCENY Z MATEMATYKI W KLASACH I - III GIMNAZJUM Rok skolny 2015/16 POZIOMY WYMAGAŃ EDUKACYJNYCH: (2) - ocena dopscająca (2); (3) - ocena dostatecna (3); (4) - ocena dobra (4);
ĆWICZENIE 5 BADANIE ZASILACZY UPS
 ĆWICZENIE 5 BADANIE ZASILACZY UPS Cel ćwicenia: aponanie budową i asadą diałania podstawowych typów asilacy UPS ora pomiar wybranych ich parametrów i charakterystyk. 5.1. Podstawy teoretycne 5.1.1. Wstęp
ĆWICZENIE 5 BADANIE ZASILACZY UPS Cel ćwicenia: aponanie budową i asadą diałania podstawowych typów asilacy UPS ora pomiar wybranych ich parametrów i charakterystyk. 5.1. Podstawy teoretycne 5.1.1. Wstęp
Jakie nowe możliwości daje właścicielom i zarządcom budynków znowelizowana Ustawa termomodrnizacyjna
 dr inż. Wiesław Sarosiek mgr inż. Beata Sadowska mgr inż. Adam Święcicki Katedra Podstaw Budownictwa i Fiyki Budowli Politechniki Białostockiej Narodowa Agencja Posanowania Energii S.A. Filia w Białymstoku
dr inż. Wiesław Sarosiek mgr inż. Beata Sadowska mgr inż. Adam Święcicki Katedra Podstaw Budownictwa i Fiyki Budowli Politechniki Białostockiej Narodowa Agencja Posanowania Energii S.A. Filia w Białymstoku
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 INSTRUKCJA DO ĆWICZENIA NR 3. Optymalizacja wielowarstwowych płyt laminowanych
 Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
Document: Exercise-03-manual --- 2014/12/10 --- 8:54--- page 1 of 8 PRZEDMIOT TEMAT KATEDRA MECHANIKI STOSOWANEJ Wydiał Mechanicny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 3 1. CEL ĆWICZENIA Wybrane
OpenGL model oświetlenia
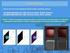 Składowe światła OpenGL Światło otaczające (ambient) OpenGL model oświetlenia Nie pochodzi z żadnego określonego kierunku. Powoduje równomierne oświetlenie obiektów na wszystkich powierzchniach i wszystkich
Składowe światła OpenGL Światło otaczające (ambient) OpenGL model oświetlenia Nie pochodzi z żadnego określonego kierunku. Powoduje równomierne oświetlenie obiektów na wszystkich powierzchniach i wszystkich
UKŁADY TENSOMETRII REZYSTANCYJNEJ
 Ćwicenie 8 UKŁADY TESOMETII EZYSTACYJEJ Cel ćwicenia Celem ćwicenia jest ponanie: podstawowych właściwości metrologicnych tensometrów, asad konstrukcji pretworników siły, ora budowy stałoprądowych i miennoprądowych
Ćwicenie 8 UKŁADY TESOMETII EZYSTACYJEJ Cel ćwicenia Celem ćwicenia jest ponanie: podstawowych właściwości metrologicnych tensometrów, asad konstrukcji pretworników siły, ora budowy stałoprądowych i miennoprądowych
1. Prymitywy graficzne
 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy
Wymiana ciepła przez żebra
 Katedra Silników Spalinowych i Pojadów TH ZKŁD TERMODYNMIKI Wymiana ciepła pre era - - Cel ćwicenia Celem ćwicenia jet adanie wpływu atoowania eer na intenywność wymiany ciepła. Badanie preprowada ię na
Katedra Silników Spalinowych i Pojadów TH ZKŁD TERMODYNMIKI Wymiana ciepła pre era - - Cel ćwicenia Celem ćwicenia jet adanie wpływu atoowania eer na intenywność wymiany ciepła. Badanie preprowada ię na
INFORMATYKA TECHNICZNA Badanie możliwości wykorzystania języka AutoLISP i środowiska VisualLISP w systemie CAx
 INFORMATYKA TECHNICZNA Badanie możliwości wykorzystania języka AutoLISP i środowiska VisualLISP w systemie CAx 1. WPROWADZENIE Program AutoCAD ma wielu użytkowników i zajmuje znaczące miejsce w graficznym
INFORMATYKA TECHNICZNA Badanie możliwości wykorzystania języka AutoLISP i środowiska VisualLISP w systemie CAx 1. WPROWADZENIE Program AutoCAD ma wielu użytkowników i zajmuje znaczące miejsce w graficznym
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
3. Zapas stabilności układów regulacji 3.1. Wprowadzenie
 3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
Temat: Transformacje 3D
 Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Analiza transformatora
 ĆWICZENIE 4 Analia transformatora. CEL ĆWICZENIA Celem ćwicenia jest ponanie bodowy, schematu astępcego ora ocena pracy transformatora.. PODSTAWY TEORETYCZNE. Budowa Podstawowym adaniem transformatora
ĆWICZENIE 4 Analia transformatora. CEL ĆWICZENIA Celem ćwicenia jest ponanie bodowy, schematu astępcego ora ocena pracy transformatora.. PODSTAWY TEORETYCZNE. Budowa Podstawowym adaniem transformatora
URZĄD MIEJSKI W SŁUPSKU Wydział Zdrowia i Spraw Społecznych. SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*)1) z wykonania zadania publicznego...
 SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*)1) wykonania adania publicnego... (nawa adania) w okresie od... do..., określonego w umowie nr..., awartej w dniu..., pomiędy... a... (nawa organu lecającego) (nawa organiacji
SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*)1) wykonania adania publicnego... (nawa adania) w okresie od... do..., określonego w umowie nr..., awartej w dniu..., pomiędy... a... (nawa organu lecającego) (nawa organiacji
W takim modelu prawdopodobieństwo konfiguracji OR wynosi. 0, 21 lub , 79. 6
 achunek prawdopodobieństwa MP6 Wydiał Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab.. Jurlewic Prykłady do listy : Prestreń probabilistycna. Prawdopodobieństwo klasycne. Prawdopodobieństwo
achunek prawdopodobieństwa MP6 Wydiał Elektroniki, rok akad. 8/9, sem. letni Wykładowca: dr hab.. Jurlewic Prykłady do listy : Prestreń probabilistycna. Prawdopodobieństwo klasycne. Prawdopodobieństwo
Optymalizacja (w matematyce) termin optymalizacja odnosi się do problemu znalezienia ekstremum (minimum lub maksimum) zadanej funkcji celu.
 TEMATYKA: Optymaliacja nakładania wyników pomiarów Ćwicenia nr 6 DEFINICJE: Optymaliacja: metoda wynacania najlepsego (sukamy wartości ekstremalnej) rowiąania punktu widenia określonego kryterium (musimy
TEMATYKA: Optymaliacja nakładania wyników pomiarów Ćwicenia nr 6 DEFINICJE: Optymaliacja: metoda wynacania najlepsego (sukamy wartości ekstremalnej) rowiąania punktu widenia określonego kryterium (musimy
ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI ENERGII
 Zesyty Problemowe Masyny Elektrycne Nr 9/211 15 Marcin Fice, Rafał Setlak Politechnika Śląska, Gliwice ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI
Zesyty Problemowe Masyny Elektrycne Nr 9/211 15 Marcin Fice, Rafał Setlak Politechnika Śląska, Gliwice ANALIZA ROZDZIAŁU SIŁ HAMOWANIA POJAZDU HYBRYDOWEGO Z NAPĘDEM NA KOŁA TYLNE W ASPEKCIE REKUPERACJI
SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*) 1) w okresie od... do..., określonego w umowie nr..., zawartej w dniu..., pomiędzy... a...
 SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*) 1) wykonania adania publicnego... (nawa adania) w okresie od... do..., określonego w umowie nr..., awartej w dniu..., pomiędy... a.. (nawa organu lecającego) (nawa organiacji
SPRAWOZDANIE (CZĘŚCIOWE*/KOŃCOWE*) 1) wykonania adania publicnego... (nawa adania) w okresie od... do..., określonego w umowie nr..., awartej w dniu..., pomiędy... a.. (nawa organu lecającego) (nawa organiacji
Podstawowe zasady. modelowania śrub i spoin
 Podstawowe zasady modelowania śrub i spoin oraz innych skomplikowanych obiektów Podstawowe zasady modelowania śrub i spoin oraz innych skomplikowanych obiektów 1 Zasady przygotowania modelu śruby 1. Poszczególne
Podstawowe zasady modelowania śrub i spoin oraz innych skomplikowanych obiektów Podstawowe zasady modelowania śrub i spoin oraz innych skomplikowanych obiektów 1 Zasady przygotowania modelu śruby 1. Poszczególne
Zginanie Proste Równomierne Belki
 Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
Zginanie Proste Równomierne Belki Prebieg wykładu : 1. Rokład naprężeń w prekroju belki. Warunki równowagi. Warunki geometrycne 4. Zwiąek fiycny 5. Wskaźnik wytrymałości prekroju na ginanie 6. Podsumowanie
Zaproszenie do współpracy przy organizacji wydarzeń społecznych (CSR) w zakresie warsztatów edukacyjnych na PGE Narodowym
 Zaprosenie do współpracy pry organiacji wydareń społecnych (CSR) w akresie warstatów edukacyjnych na m WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre PL.202+
Zaprosenie do współpracy pry organiacji wydareń społecnych (CSR) w akresie warstatów edukacyjnych na m WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre PL.202+
TEMAT: Próba statyczna rozciągania metali. Obowiązująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1
 ĆWICZENIE NR 1 TEMAT: Próba statycna rociągania metali. Obowiąująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1 Podać nacenie następujących symboli: d o -.....................................................................
ĆWICZENIE NR 1 TEMAT: Próba statycna rociągania metali. Obowiąująca norma: PN-EN 10002-1:2002(U) Zalecana norma: PN-91/H-04310 lub PN-EN10002-1+AC1 Podać nacenie następujących symboli: d o -.....................................................................
3. Zapas stabilności układów regulacji 3.1. Wprowadzenie
 3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
3. Zapas stabilności układów regulacji 3.. Wprowadenie Dla scharakteryowania apasu stabilności roważymy stabilny układ regulacji o nanym schemacie blokowym: Ws () Gs () Ys () Hs () Rys. 3.. Schemat blokowy
Materiał szkoleniowy Gdańsk, 1 lutego 2005 r. Opracowanie: Joanna Folejewska Szkoła Podstawowa nr 55 ul. Wolności 6A, 80-538 Gdańsk Lider Programu
 Materiał skoleniowy 1 lutego 2005 r. Opracowanie: Folejewska Skoła Podstawowa nr 55 ul. Wolności 6A, 80-538 Gdańsk Lider Programu ORTOGRAFFITI: Aleksandra Bućko Skolny dieciom rowojową Program Edukacyjno-Terapeutycny
Materiał skoleniowy 1 lutego 2005 r. Opracowanie: Folejewska Skoła Podstawowa nr 55 ul. Wolności 6A, 80-538 Gdańsk Lider Programu ORTOGRAFFITI: Aleksandra Bućko Skolny dieciom rowojową Program Edukacyjno-Terapeutycny
Wymagania edukacyjne z matematyki w klasie V Matematyka z plusem
 Wymagania edukacyjne matematyki w klasie V Matematyka plusem Poiomy wymagań edukacyjnych K koniecny ocena dopuscająca P podstawowy ocena dostatecna R roserający ocena dobra D dopełniający ocena bardo dobra
Wymagania edukacyjne matematyki w klasie V Matematyka plusem Poiomy wymagań edukacyjnych K koniecny ocena dopuscająca P podstawowy ocena dostatecna R roserający ocena dobra D dopełniający ocena bardo dobra
Katedra Geotechniki i Budownictwa Drogowego. WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Mazurski
 Katedra Geotechniki i Budownictwa Drogowego WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Maurski Mechanika Gruntów dr inż. Ireneus Dyka http://pracownicy.uwm.edu.pl/i.dyka e-mail: i.dyka@uwm.edu.pl
Katedra Geotechniki i Budownictwa Drogowego WYDZIAŁ NAUK TECHNICZNYCH Uniwersytet Warmińsko-Maurski Mechanika Gruntów dr inż. Ireneus Dyka http://pracownicy.uwm.edu.pl/i.dyka e-mail: i.dyka@uwm.edu.pl
PLAN REALIZACJI MATERIAŁU NAUCZANIA Z MATEMATYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH
 Matematyka plusem dla gimnajum PLAN REALIZACJI MATERIAŁU NAUCZANIA Z MATEMATYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH OPRACOWANO NA PODSTAWIE PROGRAMU MATEMATYKA Z PLUSEM
Matematyka plusem dla gimnajum PLAN REALIZACJI MATERIAŁU NAUCZANIA Z MATEMATYKI W KLASIE PIERWSZEJ GIMNAZJUM WRAZ Z OKREŚLENIEM WYMAGAŃ EDUKACYJNYCH OPRACOWANO NA PODSTAWIE PROGRAMU MATEMATYKA Z PLUSEM
Laboratorium 1. Część I. Podstawy biblioteki graficznej OpenGL.
 Laboratorium 1 Część I Podstawy biblioteki graficznej OpenGL. I. Konfiguracja środowiska 1. Ściągamy bibliotekę freeglut i rozpakujemy do głównego folderu dysku systemowego np. C:\freeglut 2. Uruchamiamy
Laboratorium 1 Część I Podstawy biblioteki graficznej OpenGL. I. Konfiguracja środowiska 1. Ściągamy bibliotekę freeglut i rozpakujemy do głównego folderu dysku systemowego np. C:\freeglut 2. Uruchamiamy
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie
 GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
Rurka Pitota Model FLC-APT-E, wersja wyjmowana Model FLC-APT-F, wersja stała
 Pomiar prepływu Rurka Pitota Model FLC-APT-E, wersja wyjmowana Model FLC-APT-F, wersja stała Karta katalogowa WIKA FL 10.05 FloTec Zastosowanie Produkcja i rafinacja oleju Udatnianie i dystrybucja wody
Pomiar prepływu Rurka Pitota Model FLC-APT-E, wersja wyjmowana Model FLC-APT-F, wersja stała Karta katalogowa WIKA FL 10.05 FloTec Zastosowanie Produkcja i rafinacja oleju Udatnianie i dystrybucja wody
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
Ruch kulisty bryły. Kąty Eulera. Precesja regularna
 Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Ruch kulist brł. Kąt Eulera. Precesja regularna Ruchem kulistm nawam ruch, w casie którego jeden punktów brł jest stale nieruchom. Ruch kulist jest obrotem dookoła chwilowej osi obrotu (oś ta mienia swoje
Funkcje pola we współrzędnych krzywoliniowych cd.
 Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
Funkcje pola we współrędnych krywoliniowych cd. Marius Adamski 1. spółrędne walcowe. Definicja. Jeżeli M jest rutem punktu P na płascynę xy, a r i ϕ są współrędnymi biegunowymi M, to mienne u = r, v =
ANALIZA KONSTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY
 Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
Cw3_biornik.doc ANALIZA KONTRUKCJI POWŁOKOWEJ. CIENKOŚCIENNY ZBIORNIK CIŚNIENIOWY 1. W P R O W A D Z E N I E Ciało utworone pre dwie akrwione powierchnie nawane jest powłoką, jeśli preciętna odlełość pomięd
Niniejsze zapytanie nie stanowi zapytania ofertowego w rozumieniu przepisów Prawa o Zamówieniach Publicznych.
 Zapytanie o informację na ofertę monitoringu mediów Narodowego WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre sp. siedibą w Warsawie (dalej również jako lub
Zapytanie o informację na ofertę monitoringu mediów Narodowego WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre sp. siedibą w Warsawie (dalej również jako lub
Systemy wirtualnej rzeczywistości. Komponenty i serwisy
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD
 Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Zapytanie o informację na ofertę przygotowania wideorelacji z wybranych wydarzeń odbywających się na PGE Narodowym
 Zapytanie o informację na ofertę prygotowania wideorelacji wybranych wydareń odbywających się na m WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre PL.202+ sp.
Zapytanie o informację na ofertę prygotowania wideorelacji wybranych wydareń odbywających się na m WSTĘP Na podstawie Umowy dierżawy i powierenia arądania Stadionem m w Warsawie awartej pre PL.202+ sp.
KOSZTORYS ŚLEPY NA WYPOSAŻENIOWE - MEBLE
 KOSZTORYS ŚLEPY NA WYPOSAŻENIOWE - MEBLE Klasyfikacja robót wg. Wspólnego Słownika Zamówień 45212330-8 Roboty budowlane w akresie bibliotek 45451000-3 SST - 4 - Dostarcenie i montaż wyposażenia biblioteki
KOSZTORYS ŚLEPY NA WYPOSAŻENIOWE - MEBLE Klasyfikacja robót wg. Wspólnego Słownika Zamówień 45212330-8 Roboty budowlane w akresie bibliotek 45451000-3 SST - 4 - Dostarcenie i montaż wyposażenia biblioteki
Informacje uzupełniające: Wyboczenie z płaszczyzny układu w ramach portalowych. Spis treści
 S032a-PL-EU Informacje uupełniające: Wybocenie płascyny układu w ramach portalowych Ten dokument wyjaśnia ogólną metodę (predstawioną w 6.3.4 E1993-1-1 sprawdania nośności na wybocenie płascyny układu
S032a-PL-EU Informacje uupełniające: Wybocenie płascyny układu w ramach portalowych Ten dokument wyjaśnia ogólną metodę (predstawioną w 6.3.4 E1993-1-1 sprawdania nośności na wybocenie płascyny układu
Badanie wymiennika ciepła typu płaszczowo-rurowy
 Badanie wymiennika ciepła typu płascowo-rurowy opracował Damian Joachimiak . Rodaje wymienników ciepła. Wymiennik ciepła (prenośnik ciepła) jest to urądenie, w którym ciepło prekaywane jest od jednego
Badanie wymiennika ciepła typu płascowo-rurowy opracował Damian Joachimiak . Rodaje wymienników ciepła. Wymiennik ciepła (prenośnik ciepła) jest to urądenie, w którym ciepło prekaywane jest od jednego
5. Badanie transformatora jednofazowego
 5. Badanie transformatora jednofaowego Celem ćwicenia jest ponanie budowy i asady diałania transformatora jednofaowego, jego metod badania i podstawowych charakterystyk. 5.. Wiadomości ogólne 5... Budowa
5. Badanie transformatora jednofaowego Celem ćwicenia jest ponanie budowy i asady diałania transformatora jednofaowego, jego metod badania i podstawowych charakterystyk. 5.. Wiadomości ogólne 5... Budowa
2. ELEMENTY TEORII PRĘTÓW SILNIE ZAKRZYWIONYCH (Opracowano na podstawie [9, 11, 13, 34, 51])
![2. ELEMENTY TEORII PRĘTÓW SILNIE ZAKRZYWIONYCH (Opracowano na podstawie [9, 11, 13, 34, 51]) 2. ELEMENTY TEORII PRĘTÓW SILNIE ZAKRZYWIONYCH (Opracowano na podstawie [9, 11, 13, 34, 51])](/thumbs/88/115066441.jpg) P Litewka Efektywny eement skońcony o dżej krywiźnie ELEENTY TEOII PĘTÓW SILNIE ZKZYWIONYCH (Opracowano na podstawie [9,, 3, 34, 5]) Premiescenia i odkstałcenia osiowe Pre pręty sinie akrywione romie się
P Litewka Efektywny eement skońcony o dżej krywiźnie ELEENTY TEOII PĘTÓW SILNIE ZKZYWIONYCH (Opracowano na podstawie [9,, 3, 34, 5]) Premiescenia i odkstałcenia osiowe Pre pręty sinie akrywione romie się
AKADEMIA GÓRNICZO-HUTNICZA im. Stanisława Staszica w Krakowie. Wydział Inżynierii Mechanicznej i Robotyki Katedra Automatyzacji Procesów
 AKADEMIA GÓRNICZO-HUTNICZA im. Stanisława Stasica w Krakowie Wydiał Inżynierii Mechanicnej i Robotyki Katedra Automatyacji Procesów ROZPRAWA DOKTORSKA Układy redukcji drgań tłumikami magnetoreologicnymi
AKADEMIA GÓRNICZO-HUTNICZA im. Stanisława Stasica w Krakowie Wydiał Inżynierii Mechanicnej i Robotyki Katedra Automatyacji Procesów ROZPRAWA DOKTORSKA Układy redukcji drgań tłumikami magnetoreologicnymi
GEOMETRIA PRZESTRZENNA (STEREOMETRIA)
 GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
GEOMETRIA PRZESTRZENNA (STEREOMETRIA) WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. Na początek omówimy
Grafika inżynierska geometria wykreślna. 5a. Obroty i kłady. Rozwinięcie wielościanu.
 Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Grafika inżynierska geometria wykreślna 5a. Obroty i kłady. Rozwinięcie wielościanu. dr inż. arch. Anna Wancław Politechnika Gdańska, Wydział Architektury Studia inżynierskie, kierunek Gospodarka przestrzenna,
Generowanie ruchu robota dwunożnego z wykorzystaniem danych opisujących chód człowieka
 Pomiary Automatyka obotyka 3/29 Generowanie ruchu robota dwunożnego wykorystaniem danych opisujących chód cłowieka Maciej T. Trojnacki W artykule predstawiono metodę generowania ruchu robota dwunożnego
Pomiary Automatyka obotyka 3/29 Generowanie ruchu robota dwunożnego wykorystaniem danych opisujących chód cłowieka Maciej T. Trojnacki W artykule predstawiono metodę generowania ruchu robota dwunożnego
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
str 1 WYMAGANIA EDUKACYJNE ( ) - matematyka - poziom podstawowy Dariusz Drabczyk
 str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
str 1 WYMAGANIA EDUKACYJNE (2017-2018) - matematyka - poziom podstawowy Dariusz Drabczyk Klasa 3e: wpisy oznaczone jako: (T) TRYGONOMETRIA, (PII) PLANIMETRIA II, (RP) RACHUNEK PRAWDOPODOBIEŃSTWA, (ST)
UZĘBIENIA CZOŁOWE O ŁUKOWO KOŁOWEJ LINII ZĘBÓW KSZTAŁTOWANE NARZĘDZIEM JEDNOOSTRZOWYM
 MODELOWANIE INŻYNIESKIE ISSN 896-77X 40, s. 7-78, Gliwice 00 UZĘBIENIA CZOŁOWE O ŁUKOWO KOŁOWEJ LINII ZĘBÓW KSZTAŁTOWANE NAZĘDZIEM JEDNOOSTZOWYM PIOT FĄCKOWIAK Instytut Technologii Mechanicnej, Politechnika
MODELOWANIE INŻYNIESKIE ISSN 896-77X 40, s. 7-78, Gliwice 00 UZĘBIENIA CZOŁOWE O ŁUKOWO KOŁOWEJ LINII ZĘBÓW KSZTAŁTOWANE NAZĘDZIEM JEDNOOSTZOWYM PIOT FĄCKOWIAK Instytut Technologii Mechanicnej, Politechnika
Strukturalne elementy symetrii. Krystalograficzne grupy przestrzenne.
 Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
Uniwerstet Śląski Insttut Chemii Zakład Krstalografii Laboratorium Krstalografii Strukturalne element smetrii. Krstalograficne grup prestrenne. god. Cel ćwicenia: aponanie się diałaniem elementów smetrii
PRZEDMIOTOWY SYSTEM OCENIANIA
 PRZEDMIOTOWY SYSTEM OCENIANIA Predmiot: informatyka akres podstawowy Klasy: pierwse LO i TE Program naucania: Informatyka nie tylko dla ucniów. Podręcnik. Zakres podstawowy Realiowany w Zespole Skół Ekonomicnych
PRZEDMIOTOWY SYSTEM OCENIANIA Predmiot: informatyka akres podstawowy Klasy: pierwse LO i TE Program naucania: Informatyka nie tylko dla ucniów. Podręcnik. Zakres podstawowy Realiowany w Zespole Skół Ekonomicnych
SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ KATEDRA TECHNIKI POŻARNICZEJ
 SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ KATEDRA TECHNIKI POŻARNICZEJ ZAKŁAD ELEKTROENERGETYKI Ćwicenie: URZĄDZENIA PRZECIWWYBUCHOWE BADANIE TRANSFORMATORA JEDNOFAZOWEGO Opracował: kpt.dr inż. R.Chybowski Warsawa
SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ KATEDRA TECHNIKI POŻARNICZEJ ZAKŁAD ELEKTROENERGETYKI Ćwicenie: URZĄDZENIA PRZECIWWYBUCHOWE BADANIE TRANSFORMATORA JEDNOFAZOWEGO Opracował: kpt.dr inż. R.Chybowski Warsawa
Ćwiczenie 13. Wyznaczanie ruchliwości i koncentracji nośników prądu w półprzewodnikach metodą efektu Halla. Cel ćwiczenia
 Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
Ćwicenie 13 Wynacanie ruchliwości i koncentracji nośników prądu w półprewodnikach metodą efektu alla Cel ćwicenia Celem ćwicenia jest aponanie się e jawiskiem alla, stałoprądowa metoda badania efektu alla,
Pochylenia, Lustro. Modelowanie ramienia. Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części)
 Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
Pochylenia, Lustro Zagadnienia. Wyciągnięcie/dodania/bazy, Pochylenia ścian, Lustro (ewent. wstawianie części, łączenie części) Wykonajmy model korbowodu jak na rys. 1 (zobacz też rys. 29, str. 11). Rysunek
STEROWANIE ADAPTACYJNE RUCHEM ROBOTA PODWODNEGO W PŁ ASZCZYŹ NIE PIONOWEJ
 ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLVII NR 4 (167) 2006 Jery Garus Akademia Marynarki Wojennej STEROWANIE ADAPTACYJNE RUCHEM ROBOTA PODWODNEGO W PŁ ASZCZYŹ NIE PIONOWEJ STRESZCZENIE W artykule
ZESZYTY NAUKOWE AKADEMII MARYNARKI WOJENNEJ ROK XLVII NR 4 (167) 2006 Jery Garus Akademia Marynarki Wojennej STEROWANIE ADAPTACYJNE RUCHEM ROBOTA PODWODNEGO W PŁ ASZCZYŹ NIE PIONOWEJ STRESZCZENIE W artykule
ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE
 KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 6 nr Archiwum Technologii Masn i Automatacji 6 ROMAN STANIEK * ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE W artkule predstawiono ależności matematcne
KOMISJA BUDOWY MASZYN PAN ODDZIAŁ W POZNANIU Vol. 6 nr Archiwum Technologii Masn i Automatacji 6 ROMAN STANIEK * ZŁOŻONE RUCHY OSI OBROTOWYCH STEROWANYCH NUMERYCZNIE W artkule predstawiono ależności matematcne
Karta (sylabus) modułu/przedmiotu
 Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Materiały budowlane I Construction materials Rok: I Semestr: 2 MK_20 Rodaje ajęć i licba godin: Studia stacjonarne
Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Materiały budowlane I Construction materials Rok: I Semestr: 2 MK_20 Rodaje ajęć i licba godin: Studia stacjonarne
HAMOWANIE REKUPERACYJNE W MIEJSKIM POJEŹDZIE HYBRYDOWYM Z NAPĘDEM NA KOŁA TYLNE
 ELEKTRYKA 213 Zesyt 1 (225) Rok LIX Marcin FICE Politechnika Śląska w Gliwicach HAMOWANIE REKUPERACYJNE W MIEJSKIM POJEŹDZIE HYBRYDOWYM Z NAPĘDEM NA KOŁA TYLNE Strescenie. W artykule predstawiono wyniki
ELEKTRYKA 213 Zesyt 1 (225) Rok LIX Marcin FICE Politechnika Śląska w Gliwicach HAMOWANIE REKUPERACYJNE W MIEJSKIM POJEŹDZIE HYBRYDOWYM Z NAPĘDEM NA KOŁA TYLNE Strescenie. W artykule predstawiono wyniki
Plan wynikowy, klasa 3 ZSZ
 Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Grafika Komputerowa Materiały Laboratoryjne
 Grafika Komputerowa Materiały Laboratoryjne Laboratorium 6 Processing c.d. Wstęp Laboratorium 6 poszerza zagadnienie generowania i przetwarzania obrazów z wykorzystaniem języka Processing 2, dedykowanego
Grafika Komputerowa Materiały Laboratoryjne Laboratorium 6 Processing c.d. Wstęp Laboratorium 6 poszerza zagadnienie generowania i przetwarzania obrazów z wykorzystaniem języka Processing 2, dedykowanego
Układy równań - Przykłady
 Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
Układy równań - Prykłady Dany układ równań rowiąać trea sposobai: (a) korystając e worów Craera, (b) etodą aciery odwrotnej, (c) etodą eliinacji Gaussa, + y + = y = y = (a) Oblicy wynacnik deta aciery
PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE. WALCOWE (równoległe) STOŻKOWE (kątowe) ŚLIMAKOWE HIPERBOIDALNE. o zebach prostych. walcowe. o zębach.
 CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
CZOŁOWE OWE PRZEKŁADNIE STOŻKOWE PRZEKŁADNIE ZĘBATE CZOŁOWE ŚRUBOWE WALCOWE (równoległe) STOŻKOWE (kątowe) HIPERBOIDALNE ŚLIMAKOWE o ebach prostych o ębach prostych walcowe walcowe o ębach śrubowych o
Okręgi i proste na płaszczyźnie
 Okręgi i proste na płaszczyźnie 1 Kąt środkowy i pole wycinka koła rozpoznawać kąty środkowe, obliczać kąt środkowy oparty na zadanym łuku, obliczać długość okręgu i łuku okręgu, obliczać pole koła, pierścienia,
Okręgi i proste na płaszczyźnie 1 Kąt środkowy i pole wycinka koła rozpoznawać kąty środkowe, obliczać kąt środkowy oparty na zadanym łuku, obliczać długość okręgu i łuku okręgu, obliczać pole koła, pierścienia,
Województwa Dolnośląskiego
 Kontrole 2010 r. Data ropocęcia Organ kontrolujący Predmiot 20.01.2010 r. Urąd Marsałkowski Planowa kontrola systemowa 17.02.2010 r. Wojewoda Dolnośląski - Opracowywanie, aktualiowanie i upowsechnianie
Kontrole 2010 r. Data ropocęcia Organ kontrolujący Predmiot 20.01.2010 r. Urąd Marsałkowski Planowa kontrola systemowa 17.02.2010 r. Wojewoda Dolnośląski - Opracowywanie, aktualiowanie i upowsechnianie
Badanie transformatora jednofazowego
 BADANIE TRANSFORMATORA JEDNOFAZOWEGO Cel ćwicenia Ponanie budowy i asady diałania ora metod badania i podstawowych charakterystyk transformatora jednofaowego. I. WIADOMOŚCI TEORETYCZNE Budowa i asada diałania
BADANIE TRANSFORMATORA JEDNOFAZOWEGO Cel ćwicenia Ponanie budowy i asady diałania ora metod badania i podstawowych charakterystyk transformatora jednofaowego. I. WIADOMOŚCI TEORETYCZNE Budowa i asada diałania
Badanie transformatora jednofazowego. (Instrukcja do ćwiczenia)
 1 Badanie transformatora jednofaowego (Instrukcja do ćwicenia) Badanie transformatora jednofaowego. CEL ĆICZENI: Ponanie asady diałania, budowy i właściwości.transformatora jednofaowego. 1 IDOMOŚCI TEORETYCZNE
1 Badanie transformatora jednofaowego (Instrukcja do ćwicenia) Badanie transformatora jednofaowego. CEL ĆICZENI: Ponanie asady diałania, budowy i właściwości.transformatora jednofaowego. 1 IDOMOŚCI TEORETYCZNE
Fizyka 3.3 III. DIODA ZENERA. 1. Zasada pomiaru.
 Fiyka 3.3 III. DIODA ZENERA Cel ćwicenia: Zaponanie się asadą diałania diody Zenera, wynacenie jej charakterystyki statycnej, napięcia wbudowanego ora napięcia Zenera. 1) Metoda punkt po punkcie 1. Zasada
Fiyka 3.3 III. DIODA ZENERA Cel ćwicenia: Zaponanie się asadą diałania diody Zenera, wynacenie jej charakterystyki statycnej, napięcia wbudowanego ora napięcia Zenera. 1) Metoda punkt po punkcie 1. Zasada
Przykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krzywej temperatura-czas
 Dokument Ref: SX043a-PL-EU Strona 1 5 Prykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krywej temperatura-cas Wykonał Z. Sokol Data styceń 006 Sprawdił F. Wald Data styceń
Dokument Ref: SX043a-PL-EU Strona 1 5 Prykład: Projektowanie poŝarowe nieosłoniętego słupa stalowego według standardowej krywej temperatura-cas Wykonał Z. Sokol Data styceń 006 Sprawdił F. Wald Data styceń
Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA.
 Zadanie PUMA Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA. Cały projekt składa się z następujących elementów: 1. Animacja ramion
Zadanie PUMA Zadanie polega na zbudowaniu i wyświetleniu przykładowej animowanej sceny przedstawiającej robota spawalniczego typu PUMA. Cały projekt składa się z następujących elementów: 1. Animacja ramion
Scenariusz lekcji. scharakteryzować budowę procedury w języku Logo; rozróżnić etapy tworzenia i wykonania procedury;
 1 TEMAT LEKCJI Definiowanie i wywoływanie własnych procedur 2 CELE LEKCJI 2.1 Wiadomości Uczeń potrafi: scharakteryzować budowę procedury w języku Logo; rozróżnić etapy tworzenia i wykonania procedury;
1 TEMAT LEKCJI Definiowanie i wywoływanie własnych procedur 2 CELE LEKCJI 2.1 Wiadomości Uczeń potrafi: scharakteryzować budowę procedury w języku Logo; rozróżnić etapy tworzenia i wykonania procedury;
PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3
 PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3 I. FUNKCJE grupuje elementy w zbiory ze względu na wspólne cechy wymienia elementy zbioru rozpoznaje funkcje wśród przyporządkowań
PRZEDMIOTOWE ZASADY OCENIANIA I WYMAGANIA EDUKACYJNE Z MATEMATYKI Klasa 3 I. FUNKCJE grupuje elementy w zbiory ze względu na wspólne cechy wymienia elementy zbioru rozpoznaje funkcje wśród przyporządkowań
Zadania domowe. Ćwiczenie 2. Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL
 Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Grafika 3D OpenGL część II
 #include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
#include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
Animacje z zastosowaniem suwaka i przycisku
 Animacje z zastosowaniem suwaka i przycisku Animacja Pole równoległoboku Naukę tworzenia animacji uruchamianych na przycisk zaczynamy od przygotowania stosunkowo prostej animacji, za pomocą, której można
Animacje z zastosowaniem suwaka i przycisku Animacja Pole równoległoboku Naukę tworzenia animacji uruchamianych na przycisk zaczynamy od przygotowania stosunkowo prostej animacji, za pomocą, której można
Przeciąganie po profilach, Dodanie/baza przez wyciągnięcie po ścieŝce
 Przeciąganie po profilach, Dodanie/baza przez wyciągnięcie po ścieŝce Zagadnienia. Tworzenie brył przez Przeciąganie po profilach i Dodanie/baza przez wyciągnięcie po ścieŝce. Geometria odniesienia, Płaszczyzna.
Przeciąganie po profilach, Dodanie/baza przez wyciągnięcie po ścieŝce Zagadnienia. Tworzenie brył przez Przeciąganie po profilach i Dodanie/baza przez wyciągnięcie po ścieŝce. Geometria odniesienia, Płaszczyzna.
Grafika inżynierska i podstawy projektowania Kod przedmiotu
 Grafika inżynierska i podstawy projektowania - opis przedmiotu Informacje ogólne Nazwa przedmiotu Grafika inżynierska i podstawy projektowania Kod przedmiotu 06.9-WM-BHP-P-18_14L_pNadGenAF7UG Wydział Kierunek
Grafika inżynierska i podstawy projektowania - opis przedmiotu Informacje ogólne Nazwa przedmiotu Grafika inżynierska i podstawy projektowania Kod przedmiotu 06.9-WM-BHP-P-18_14L_pNadGenAF7UG Wydział Kierunek
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE. Rozwiązania. Wartość bezwzględna jest odległością na osi liczbowej.
 Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
Arkusz maturalny nr 2 poziom podstawowy ZADANIA ZAMKNIĘTE Rozwiązania Zadanie 1 Wartość bezwzględna jest odległością na osi liczbowej. Stop Istnieje wzajemnie jednoznaczne przyporządkowanie między punktami
SolidWorks 2017 : projektowanie maszyn i konstrukcji : praktyczne przykłady / Jerzy Domański. Gliwice, cop Spis treści
 SolidWorks 2017 : projektowanie maszyn i konstrukcji : praktyczne przykłady / Jerzy Domański. Gliwice, cop. 2017 Spis treści Wprowadzenie 9 Część I. Praca z programem 11 Rozdział 1. Wprowadzenie do programu
SolidWorks 2017 : projektowanie maszyn i konstrukcji : praktyczne przykłady / Jerzy Domański. Gliwice, cop. 2017 Spis treści Wprowadzenie 9 Część I. Praca z programem 11 Rozdział 1. Wprowadzenie do programu
Karta (sylabus) modułu/przedmiotu
 Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Regulacja rek River regulation Rok: IV Semestr: 7 MK_65 Rodaje ajęć i licba godin: Studia stacjonarne Studia
Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Regulacja rek River regulation Rok: IV Semestr: 7 MK_65 Rodaje ajęć i licba godin: Studia stacjonarne Studia
Zasady rekrutacji uczniów do I Liceum Ogólnokształcącego im. Tadeusza Kościuszki na rok szkolny 2015/2016
 Zasady rekrutacji ucniów do I Liceum Ogólnokstałcącego im. Tadeusa Kościuski na rok skolny 201/2016 Podstawa prawna: Roporądenie Ministra Edukacji Narodowej i Sportu dnia 20 lutego 2004 roku w sprawie
Zasady rekrutacji ucniów do I Liceum Ogólnokstałcącego im. Tadeusa Kościuski na rok skolny 201/2016 Podstawa prawna: Roporądenie Ministra Edukacji Narodowej i Sportu dnia 20 lutego 2004 roku w sprawie
PROGNOZA OSIADANIA BUDYNKU W ZWIĄZKU ZE ZMIANĄ SPOSOBU POSADOWIENIA THE PROGNOSIS OF BUILDING SETTLEMENT DUE TO CHANGES OF FOUNDATION
 XXVI Konferencja awarie budowlane 213 Naukowo-Technicna ZYGMUNT MEYER, meyer@ut.edu.pl Zachodniopomorski Uniwersytet Technologicny w cecinie, Katedra Geotechniki MARIUZ KOWALÓW, m.kowalow@gco-consult.com
XXVI Konferencja awarie budowlane 213 Naukowo-Technicna ZYGMUNT MEYER, meyer@ut.edu.pl Zachodniopomorski Uniwersytet Technologicny w cecinie, Katedra Geotechniki MARIUZ KOWALÓW, m.kowalow@gco-consult.com
Karta (sylabus) modułu/przedmiotu
 Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Ogrewnictwo Heating Engineering Rok: III Semestr: 6 MK_60 Rodaje ajęć i licba godin: Studia stacjonarne Studia
Karta (sylabus) modułu/predmiotu Budownictwo (Nawa kierunku studiów) Studia I Stopnia Predmiot: Ogrewnictwo Heating Engineering Rok: III Semestr: 6 MK_60 Rodaje ajęć i licba godin: Studia stacjonarne Studia
DWUCZĘŚCIOWE ŁOŻYSKO POROWATE
 PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 1 14 maja 1999 r. Karol Kremiński Politechnika Warsawska DWUCZĘŚCIOWE ŁOŻYSKO POROWATE SŁOWA KLUCZOWE: łożysko śligowe, tuleja porowata, prepuscalność
PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 1 14 maja 1999 r. Karol Kremiński Politechnika Warsawska DWUCZĘŚCIOWE ŁOŻYSKO POROWATE SŁOWA KLUCZOWE: łożysko śligowe, tuleja porowata, prepuscalność
PRZEKROJE POWIERZCHNI ORAZ PRZENIKANIA SIĘ POWIERZCHNI I WIELOŚCIANÓW REALIZOWANE ZA POMOCĄ PROGRAMU AUTOCAD W PRZESTRZENI E3
 Andrzej KOCH, Krzysztof PAŁAC, Tomasz SULIMA SAMUJŁŁO Wydział Matematyki Stosowanej, Pracownia Geometrii Wykreślnej Akademia Górniczo Hutnicza PRZEKROJE POWIERZCHNI ORAZ PRZENIKANIA SIĘ POWIERZCHNI I WIELOŚCIANÓW
Andrzej KOCH, Krzysztof PAŁAC, Tomasz SULIMA SAMUJŁŁO Wydział Matematyki Stosowanej, Pracownia Geometrii Wykreślnej Akademia Górniczo Hutnicza PRZEKROJE POWIERZCHNI ORAZ PRZENIKANIA SIĘ POWIERZCHNI I WIELOŚCIANÓW
Ćwiczenie nr 3 Edycja modeli bryłowych
 Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
Ćwiczenie nr 3 Edycja modeli bryłowych 1. Fazowanie oraz zaokrąglanie. Wykonaj element pokazany na rys. 1a. Wymiary elementu: średnice 100 i 40. Długość wałków 30 i 100 odpowiednio. Następnie wykonaj fazowanie
ZRÓŻNICOWANA EFEKTYWNOŚĆ EKSPLOATACYJNYCH DODATKÓW PRZECIWCIERNYCH DO OLEJÓW SMARNYCH
 PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 15-16 maja 1997 r. Zbigniew Zalis Politechnika Opolska w Opolu ZRÓŻNICOWANA EFEKTYWNOŚĆ EKSPLOATACYJNYCH DODATKÓW PRZECIWCIERNYCH DO OLEJÓW SMARNYCH
PROBLEMY NIEKONWENCJONALNYCH UKŁADÓW ŁOŻYSKOWYCH Łódź, 15-16 maja 1997 r. Zbigniew Zalis Politechnika Opolska w Opolu ZRÓŻNICOWANA EFEKTYWNOŚĆ EKSPLOATACYJNYCH DODATKÓW PRZECIWCIERNYCH DO OLEJÓW SMARNYCH
MODEL MUNDELLA-FLEMINGA
 Danuta Miłasewic Uniwersytet Sceciński MODEL MUNDELLA-FLEMINGA 1. OPIS MODELU MUNDELLA-FLEMINGA Model ten, stworony na pocątku lat seśćdiesiątych XX wieku pre Roberta A. Mundella i Markusa Fleminga, opisuje
Danuta Miłasewic Uniwersytet Sceciński MODEL MUNDELLA-FLEMINGA 1. OPIS MODELU MUNDELLA-FLEMINGA Model ten, stworony na pocątku lat seśćdiesiątych XX wieku pre Roberta A. Mundella i Markusa Fleminga, opisuje
Transformator Φ M. uzwojenia; siła elektromotoryczna indukowana w i-tym zwoju: dφ. = z1, z2 liczba zwojów uzwojenia pierwotnego i wtórnego.
 Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
Transformator Φ r Φ M Φ r i i u u Φ i strumień magnetycny prenikający pre i-ty wój pierwsego uwojenia; siła elektromotorycna indukowana w i-tym woju: dφ ei, licba wojów uwojenia pierwotnego i wtórnego.
Programowanie obiektowe
 Laboratorium z przedmiotu Programowanie obiektowe - zestaw 07 Cel zajęć. Celem zajęć jest zapoznanie z praktycznymi aspektami tworzenia aplikacji okienkowych w C#. Wprowadzenie teoretyczne. Rozważana w
Laboratorium z przedmiotu Programowanie obiektowe - zestaw 07 Cel zajęć. Celem zajęć jest zapoznanie z praktycznymi aspektami tworzenia aplikacji okienkowych w C#. Wprowadzenie teoretyczne. Rozważana w
