1. Prymitywy graficzne
|
|
|
- Artur Marszałek
- 8 lat temu
- Przeglądów:
Transkrypt
1 1. Prymitywy graficzne Prymitywy graficzne są elementarnymi obiektami jakie potrafi bezpośrednio rysować, określony system graficzny (DirectX, OpenGL itp.) są to: punkty, listy linii, serie linii, listy trójkątów i serie trójkątów. 1.1 Lista punktów (point list) System graficzny wyświetlający listę punktów rysuje na ekranie punkty w takiej kolejności w jakiej zapisano je w odpowiedniej tablicy, czy też buforze wierzchołków. Typowym zastosowaniem tego typu prymitywów graficznych jest rysowanie gwiazd. P2(-5,10,1) P4(5,10,1) P1(-10,1,1) P3(0,1,1) P5(10,1,1) Rys 1 przedstawiający w jaki sposób rysowana jest lista punków. TVector3 Points[] = TVector3(-10.0, 1.0, 1.0), TVector3( -5.0, 10.0, 1.0), TVector3( 0.0, 1.0, 1.0), TVector3( 5.0, 10.0, 1.0), TVector3( 10.0, 1.0, 1.0), 1.2 Lista linii (line list) System graficzny wyświetlając listę linii pobiera z bufora (tablicy) wierzchołków parę sąsiadujących elementów i rysuje na ekranie linie łączącą te dwa wierzchołki. Także oczywiste jest, że dla narysowania N linii bufor powinien zawierać 2N wierzchołków. Dodatkowo należy pamiętać o odpowiedniej organizacji (ułożeniu) wierzchołków, aby narysować obiekt o żądanych kształtach. P2(10,15,0) P4(20,15,0) P1(5,5,0) P3(15,5,0) Rys. 2 przedstawiający w jaki sposób łączone są wierzchołki rysowanymi liniami Linie mogą być wykorzystywane do reprezentacji krawędzi brył, tzw. druciaków, przy rysowaniu efektu deszczu lub do imitowania wszelkiego typu strzałów lasera. W niektórych - 1 -
2 systemach graficznych (np. DirectX) znacznie poważniejszym zastosowaniem linii jest antialiasing krawędziowy, który polega na dwukrotnym rysowaniu sceny z tym, że drugim razem używamy tylko linii, które są w odpowiedni sposób wygładzane. TVector3 Vertices[] = TVector3(-5.0, 5.0, 0.0), TVector3(-10.0, 15.0, 0.0), TVector3(-15.0, 5.0, 0.0), TVector3(-20.0, 15.0, 0.0), 1.3 Seria linii (line strip) W tym trybie linie rysowane są na zasadzie łączenia kolejnych wierzchołków, także wierzchołki muszą być odpowiednio ułożone w buforze, aby w efekcie dać sensowny rysunek. Ten typ prymitywów znakomicie nadaje się do rysowania np. płaszczyzn generowanych w programowo. P2(10,15,0) P4(20,15,0) P1(5,5,0) P3(15,5,0) Rys. 3 przedstawiający w jaki sposób łączone są kolejne wierzchołki rysowanymi liniami, dając w efekcie łamaną Należy pamiętać, iż rysowanych linii będzie o jedną mniej niż wierzchołków. TVector3 Vertices[] = TVector3(-5.0, 5.0, 0.0), TVector3(-10.0, 15.0, 0.0), TVector3(-15.0, 5.0, 0.0), TVector3(-20.0, 15.0, 0.0), - 2 -
3 1.4 Lista trójkątów (triangle list) Trójkąty są podstawą wszelkiego typu wypełnianych brył. Prymitywy będące listą trójkątów tworzone są z kolejnych trzech wierzchołków, których liczba musi być podzielna przez trzy. P2(0,15,0) P4(10,15,0) P6(20,15,0) P1(-5,5,0) P3(5,5,0) P5(15,5,0) Rys. 4 przedstawiający sposób rysowania trójkątów, w oparciu o listę trójkątów Podczas operacji rysowania wnętrze trójkąta może być wypełnione pojedynczym kolorem, teksturą lub kolory będą interpolowane między wierzchołkami TVector3 Vertices[] = TVector3(-5.0, -5.0, 0.0), TVector3( 0.0, 5.0, 0.0), TVector3( 5.0, -5.0, 0.0), TVector3(10.0, 5.0, 0.0), TVector3(15.0, -5.0, 0.0), TVector3(20.0, 5.0, 0.0) 1.5 Seria trójkątów (Triangle Strip) Przy użyciu tego typu prymitywów rysowana jest seria (taśma ang. strip) trójkątów. Kolejne trójkąty wyznaczane są przez trzy wierzchołki począwszy od wierzchołka będącego numerem trójkąta w taśmie. I tak dla pierwszego trójkąta pobierane są wierzchołki 1,2,3, dla drugiego 2,3,4 itd. Także od razu widać, iż można narysować N-2 trójkątów, gdzie N- liczba wierzchołków. Tak jak Line Strip, ten typ prymitywów znakomicie służy do rysowania powierzchni generowanych programowo oraz do rysowania dowolnych wielokątów na podstawie podanych wierzchołków. P2(0,15,0) P4(10,15,0) P1(-5,5,0) P3(5,5,0) P5(15,5,0) Rys. 5 przedstawia sposób łączenia kolejnych wierzchołków w trójkąty
4 TVector3 Vertices[] = TVector3(-5.0, -5.0, 0.0), TVector3( 0.0, 5.0, 0.0), TVector3( 5.0, -5.0, 0.0), TVector3(10.0, 5.0, 0.0), TVector3(15.0, -5.0, 0.0), TVector3(20.0, 5.0, 0.0) 1.6 Triangle Fan W tym typie prymitywów wszystkie rysowane trójkąty mają wspólny wierzchołek i jest nim pierwszy punkt w buforze. Przy rysowaniu pierwszego trójkąta pobierane są wierzchołki 1,2,3, przy rysowaniu drugiego 1,3,4 itd. P2(0,15,0) P3(1,10,0) P1(-5,5,0) P4(3,5,0) P5(2,0,0) P6(1,-5,0) Rys. 6 przedstawia sposób współdzielenia pierwszego wierzchołka przez wszystkie trójkąty TVector3Vertices[] = TVector3(-5.0, 5.0, 0.0), TVector3( 0.0,15.0, 0.0), TVector3( 1.0,10.0, 0.0), TVector3( 3.0, 5.0, 0.0), TVector3( 2.0, 0.0, 0.0), TVector3( 1.0,-5.0, 0.0), 1.7 Indeksowane listy linii i trójkątów. Indeksowane listy linii i trójkątów są bardzo podobne do zwykłych list linii i trójkątów, jedyną różnicą jest to, że system graficzny (lub nasz program) pobiera pary lub trójki wierzchołków z tablicy na podstawie informacji zawartej w tablicy (buforze) indeksów. Przykład organizacji brył z zastosowaniem tego typu prymitywów znajduje się w podrozdziale 2.2 i
5 2. Reprezentacja obiektów 2.1 Reprezentacja punktowa Tego typu metoda oczywiście jest najprostsza i wymaga mniejszej ilości danych niż pozostałe (krawędziowa, wypełniana). W reprezentacji punktowej potrzebne są jedynie współrzędne (x,y,z) kolejnych punktów tworzących daną bryłę Przykładowa konstrukcja sześcianu może wyglądać następująco: TVector3v[8]; v[0] = TVector3 (-4.5, 4.5,-4.5 ); v[1] = TVector3 ( 4.5, 4.5,-4.5 ); v[2] = TVector3 ( 4.5,-4.5,-4.5 ); v[3] = TVector3 (-4.5,-4.5,-4.5 ); v[4] = TVector3 (-4.5, 4.5, 4.5 ); v[5] = TVector3 ( 4.5, 4.5, 4.5 ); v[6] = TVector3 ( 4.5,-4.5, 4.5 ); v[7] = TVector3 (-4.5,-4.5, 4.5 ); Tak zdefiniowana kostka zbudowana jest z 8 punktów leżących symetrycznie względem punktu (0,0,0) układu współrzędnych oraz w odległości równej 9 jednostek od siebie. W zasadzie bryła zdefiniowana w ten sposób może zostać bezpośrednio narysowana na ekranie. Przypomnę, że każdy z wierzchołków sześcianu powinien zostać poddany właściwym transformacjom, czyli przemnożony kolejno przez: macierz transformacji świata, macierz widoku, macierz projekcji i macierz skalowania pola widoku. Dodatkowo należy pamiętać o podzieleniu przez współrzędną w każdego z otrzymanych, w wyniku transformacji, wektorów. W przypadku reprezentacji punktowej nie musimy zajmować się problemem usuwania niewidocznych powierzchni, czy punktów. Rys. 7 Przykład reprezentacji punktowej obiektu - 5 -
6 2.2 Reprezentacja krawędziowa Wizualizacja szkieletowa polega na rysowaniu krawędzi sianek danego obiektu. W metodzie tej poza współrzędnymi wierzchołków potrzebujemy informacji, które z wierzchołków mamy łączyć liniami. Tego typu tablica często nazywana jest indeksem wierzchołków tworzących linie. Przyglądając się rysunkowi sześcianu, mieszczącemu się na sąsiedniej stronie, spróbujemy teraz stworzyć tablicę połączeń dla linii. Może ona wyglądać tak: WORD Line_Index[]= 0,1,1,2,2,3,3,0, // linie tworzące ściankę przednią 4,5,5,6,6,7,7,4, // linie tworzące ściankę tylną 0,4,1,5,3,7,2,6, // pozostałe linie Rys 8 Przykład reprezentacji krawędziowej (szkieletowej) obiektu Chcąc narysować bryłę zdefiniowaną w ten sposób należy tak jak poprzednio każdy z wierzchołków sześcianu przemnożyć kolejno przez: macierz transformacji świata, macierz widoku, macierz projekcji i macierz skalowania pola widoku oraz podzielić przez współrzędną w. Następnie mając wyznaczone współrzędne punktów w przestrzenie ekranu można przejść do właściwej procedury rysującej linie między odpowiednimi wierzchołkami. W pseudokodzie może wyglądać to następująco:... TVector3 tab2d[8];/*tablica współrzędnych punktów w przestrzeni ekranu*/ - 6 -
7 ... for(int a=0;a<ilość_krawędzi;a++) int x1,y1,x2,y2; x1=tab2d[line_index[a*2]].x; y1=tab2d[line_index[a*2]].y; x2=tab2d[line_index[a*2+1]].x; y2=tab2d[line_index[a*2+1]].y; Line(x1,y1,x2,y2);} V4 V5 V0 V1 V7 V6 V3 V2 Rys 9.Sześcian z zaznaczonymi krawędziami oraz trójkątami, tworzącymi jego ścianki W przypadku definiowania połączeń między wierzchołkami tworzącymi linie nie ma specjalnych wymogów dotyczących kolejności wierzchołków. Jedynym kryterium jest kształt uzyskany w wyniku połączeń. Następstwem tych faktów jest niemożliwość eliminacji linii, które należałoby uznać za niewidoczne, także obiekty rysowane za pomocą linii w pełni oddają druciane modele brył. 2.3 Reprezentacja wypełniana Reprezentacja wypełniana polega na rysowaniu pojedynczych ścianek bryły z zastosowaniem określonego modelu cieniowania (płaskie, Gouraud a, Phong a). Metoda ta bazuje na siatkach wielokątów - które są zbiorem punktów, krawędzi oraz wielokątów tak połączonych, że każda z krawędzi jest wspólna przynajmniej dla dwóch wielokątów. Krawędź zawsze łączy dwa wierzchołki, a wielokąt jest zamkniętą sekwencją krawędzi. Dla naszych potrzeb stosowane wielokąty ograniczymy jedynie do trójkątów, gdyż dowolny wielokąt może być reprezentowany odpowiednią liczbą trójkątów. Jak widać na rys. 9 sześcian może być reprezentowany za pomocą 6 czworokątnych ścian lub 12 trójkątnych. Chcąc zdefiniować pełny opis sześcianu poza tablicą współrzędnych wierzchołków musimy stworzyć odpowiednią tablicę definiującą numery wierzchołków przynależnych do danej ścianki, dodatkowo musimy zadbać, aby ich kolejność była zgodna z ruchem wskazówek zegara
8 Przykładowo, przednia ścianka sześcianu z rys. 3 tworzona jest z dwóch trójkątów, które powinny składać się z wierzchołków wymienionych w następującej kolejności trójkąt 1: v0, v1, v2; trójkąt 2: v2,v3, v0. Podążając tym tokiem rozumowania możemy stworzyć tablicę indeksów wierzchołków, dla wszystkich 12 trójkątów tworzących sześcian. Ma ona następującą postać WORD Triangle_Index[]= 0,1,2,2,3,0, // przednia ścianka 6,5,4,4,7,6, // tylna ścianka 4,5,1,1,0,4, // górna ścianka 1,5,6,6,2,1, // prawa ścianka 7,4,0,0,3,7, // lewa ścianka 2,6,7,7,3,2 // dolna ścianka Rys 10 Przykład reprezentacji wypełnianej obiektu z zastosowaniem cieniowania Gouraud a. Procedura rysowania bryły wypełnianej jest podobna do poprzedniej także: każdy z wierzchołków sześcianu przemnożyć kolejno przez: macierz transformacji świata, macierz widoku, macierz projekcji i macierz skalowania pola widoku oraz podzielić przez współrzędną w. Następnie mając wyznaczone współrzędne punktów w przestrzenie ekranu można przejść do właściwej procedury rysującej wypełniane trójkąty, składające się z odpowiednich wierzchołków. W pseudokodzie może wyglądać to następująco: - 8 -
9 ... TVector3 tab2d[8];/*tablica współrzędnych punktów w przestrzeni ekranu*/... for(int a=0;a<ilość_scian;a++) int x1,y1,x2,y2,x3,y3; x1=tab2d[triangle _Index[a*3]].x; y1=tab2d[triangle _Index[a*3]].y; x2=tab2d[triangle _Index[a*3+1]].x; y2=tab2d[triangle _Index[a*3+1]].y; x3=tab2d[triangle _Index[a*3+2]].x; y3=tab2d[triangle _Index[a*3+2]].y; Triangle(x1,y1,x2,y2,x3,y3); } Zadania do wykonania w trakcie ćwiczeń Napisać procedurę reprezentującą bryłę w postaci punktowej Napisać procedurę rysującą linie od punktu (x1,y1) do punktu (x2,y2) Napisać procedurę reprezentującą bryłę w postaci szkieletowej Napisać procedurę reprezentującą bryłę w postaci wypełnianej (zastosować cieniowanie płaskie lub Gouraud a). Procedura powinna sprawdzać widoczność ścian. Rozszerzyć program z poprzedniego punktu o algorytm z-bufora. Algorytm z-bufor należy zaimplementować w funkcji cieniującej wielokąty
Grafika komputerowa Tekstury
 . Tekstury Tekstury są dwuwymiarowymi obrazkami nakładanymi na obiekty lub ich części, w celu poprawienia realizmu rysowanych brył oraz dodatkowego określenia cech ich powierzchni np. przez nałożenie obrazka
. Tekstury Tekstury są dwuwymiarowymi obrazkami nakładanymi na obiekty lub ich części, w celu poprawienia realizmu rysowanych brył oraz dodatkowego określenia cech ich powierzchni np. przez nałożenie obrazka
Zatem standardowe rysowanie prymitywów wygląda następująco:
 Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Instrukcja laboratoryjna 10 Grafika komputerowa 3D Temat: Prymitywy Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Prymitywy proste figury geometryczne,
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Laboratorium grafiki komputerowej i animacji. Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny
 Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
Laboratorium grafiki komputerowej i animacji Ćwiczenie V - Biblioteka OpenGL - oświetlenie sceny Przygotowanie do ćwiczenia: 1. Zapoznać się ze zdefiniowanymi w OpenGL modelami światła i właściwości materiałów.
3 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Laboratorium nr 3 1/5 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Rysowanie prymitywów 3 Przygotował: mgr inż. Maciej Lasota 1) Rysowanie prymitywów Podstawową rodziną funkcji wykorzystywanych
Systemy wirtualnej rzeczywistości. Podstawy grafiki 3D
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Podstawy grafiki 3D Wstęp: W drugiej części przedstawione zostaną podstawowe mechanizmy
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Podstawy grafiki 3D Wstęp: W drugiej części przedstawione zostaną podstawowe mechanizmy
Grafika Komputerowa Wykład 5. Potok Renderowania Oświetlenie. mgr inż. Michał Chwesiuk 1/38
 Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Wykład 5 Potok Renderowania Oświetlenie mgr inż. 1/38 Podejście śledzenia promieni (ang. ray tracing) stosuje się w grafice realistycznej. Śledzone są promienie przechodzące przez piksele obrazu wynikowego
Zadania domowe. Ćwiczenie 2. Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL
 Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Zadania domowe Ćwiczenie 2 Rysowanie obiektów 2-D przy pomocy tworów pierwotnych biblioteki graficznej OpenGL Zadanie 2.1 Fraktal plazmowy (Plasma fractal) Kwadrat należy pokryć prostokątną siatką 2 n
Nadają się do automatycznego rysowania powierzchni, ponieważ może ich być dowolna ilość.
 CAD 3W zajęcia nr 2 Rysowanie prostych powierzchni trójwymiarowych. 1. 3wpow (3dface) powierzchnia trójwymiarowa Rysujemy ją tak, jak pisze się literę S (w przeciwieństwie do powierzchni 2W (solid), którą
CAD 3W zajęcia nr 2 Rysowanie prostych powierzchni trójwymiarowych. 1. 3wpow (3dface) powierzchnia trójwymiarowa Rysujemy ją tak, jak pisze się literę S (w przeciwieństwie do powierzchni 2W (solid), którą
RENDERING W CZASIE RZECZYWISTYM. Michał Radziszewski
 RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
RENDERING W CZASIE RZECZYWISTYM Michał Radziszewski Plan wykładu Programy geometrii wprowadzenie Miejsce w potoku graficznym Wejścia i wyjścia programów geometrii Wierzchołki, prymitywy, ich nowe rodzaje
KGGiBM GRAFIKA INŻYNIERSKA Rok III, sem. VI, sem IV SN WILiŚ Rok akademicki 2011/2012
 Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Rysowanie precyzyjne 7 W ćwiczeniu tym pokazane zostaną wybrane techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2012, między innymi wykorzystanie punktów charakterystycznych. Narysować
Elementarne obiekty geometryczne, bufory. Dorota Smorawa
 Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
Elementarne obiekty geometryczne, bufory Dorota Smorawa Elementarne obiekty Tworząc scenę 3D, od najprostszej, po najbardziej skomplikowaną, używamy obiektów złożonych, przede wszystkim podstawowych, elementarnych
Graniastosłupy mają dwie podstawy, a ich ściany boczne mają kształt prostokątów.
 GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
GRANIASTOSŁUPY I OSTROSŁUPY Bryły czyli figury przestrzenne dzielimy na: graniastosłupy ostrosłupy bryły obrotowe Graniastosłupy i ostrosłupy nazywamy wielościanami Graniastosłupy mają dwie podstawy, a
AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne.
 AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne. RYSOWANIE 2D Polecenie LINIA Polecenie LINIA tworzy linię, której punkty
AUTOCAD teoria i zadania z podstaw rysowania Rysowanie linii, prostej, półprostej, punktu, trasy, polilinii. Zadania geodezyjne. RYSOWANIE 2D Polecenie LINIA Polecenie LINIA tworzy linię, której punkty
Rysowanie precyzyjne. Polecenie:
 7 Rysowanie precyzyjne W ćwiczeniu tym pokazane zostaną różne techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2010, między innymi wykorzystanie punktów charakterystycznych. Z uwagi na
7 Rysowanie precyzyjne W ćwiczeniu tym pokazane zostaną różne techniki bardzo dokładnego rysowania obiektów w programie AutoCAD 2010, między innymi wykorzystanie punktów charakterystycznych. Z uwagi na
Temat: Transformacje 3D
 Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Instrukcja laboratoryjna 11 Grafika komputerowa 3D Temat: Transformacje 3D Przygotował: dr inż. Grzegorz Łukawski, mgr inż. Maciej Lasota, mgr inż. Tomasz Michno 1 Wstęp teoretyczny Bardzo często programując
Algorytmy grafiki rastrowej. Mirosław Głowacki Wykład z Grafiki Komputerowej
 Algorytmy grafiki rastrowej Mirosław Głowacki Wykład z Grafiki Komputerowej Wypełnianie prymitywów Mirosław Głowacki Wykład z Grafiki Komputerowej Wypełnianie prymitywów Zadanie wypełniania prymitywów
Algorytmy grafiki rastrowej Mirosław Głowacki Wykład z Grafiki Komputerowej Wypełnianie prymitywów Mirosław Głowacki Wykład z Grafiki Komputerowej Wypełnianie prymitywów Zadanie wypełniania prymitywów
2 Przygotował: mgr inż. Maciej Lasota
 Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Laboratorium nr 2 1/6 Grafika Komputerowa 3D Instrukcja laboratoryjna Temat: Manipulowanie przestrzenią 2 Przygotował: mgr inż. Maciej Lasota 1) Manipulowanie przestrzenią Istnieją dwa typy układów współrzędnych:
Elementy okna MatLab-a
 MatLab część IV 1 Elementy okna MatLab-a 2 Elementy okna MatLab-a 3 Wykresy i przydatne polecenia Wywołanie funkcji graficznej powoduje automatyczne otwarcie okna graficznego Kolejne instrukcje graficzne
MatLab część IV 1 Elementy okna MatLab-a 2 Elementy okna MatLab-a 3 Wykresy i przydatne polecenia Wywołanie funkcji graficznej powoduje automatyczne otwarcie okna graficznego Kolejne instrukcje graficzne
GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych
 GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy
GRAFIKA CZASU RZECZYWISTEGO Podstawy syntezy grafiki 3D i transformacji geometrycznych Grafika komputerowa i wizualizacja, Bioinformatyka S1, II Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy
w jednym kwadrat ziemia powietrze równoboczny pięciobok
 Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Wielościany Definicja 1: Wielościanem nazywamy zbiór skończonej ilości wielokątów płaskich spełniających następujące warunki: 1. każde dwa wielokąty mają bok lub wierzchołek wspólny albo nie mają żadnego
Grafika Komputerowa Wykład 4. Synteza grafiki 3D. mgr inż. Michał Chwesiuk 1/30
 Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Wykład 4 mgr inż. 1/30 Synteza grafiki polega na stworzeniu obrazu w oparciu o jego opis. Synteza obrazu w grafice komputerowej polega na wykorzystaniu algorytmów komputerowych do uzyskania obrazu cyfrowego
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Powierzchnia obiektu 3D jest renderowana jako czarna jeżeli nie jest oświetlana żadnym światłem (wyjątkiem są obiekty samoświecące) Oświetlenie
Animowana grafika 3D. Opracowanie: J. Kęsik.
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Rzutowanie Równoległe Perspektywiczne Rzutowanie równoległe Rzutowanie równoległe jest powszechnie używane w rysunku technicznym - umożliwienie
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie
 GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
GRAFIKA KOMPUTEROWA 7: Kolory i cieniowanie http://galaxy.agh.edu.pl/~mhojny Prowadzący: dr inż. Hojny Marcin Akademia Górniczo-Hutnicza Mickiewicza 30 30-059 Krakow pawilon B5/p.406 tel. (+48)12 617 46
4. Rysowanie krzywych
 1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
1. Operator plot y x \begin{tikzpicture} \draw[->] (-0.2,0) -- (4.2,0) node[right] {$x$}; \draw[->] (0,-1.2) -- (0,4.2) node[above] {$y$}; \draw (3,4) -- (3,3) plot coordinates{(2,3) (3,0) (4,3)}; \end{tikzpicture}
Obiekt 2: Świątynia Zeusa
 Obiekt 2: Świątynia Zeusa Rys 2-1. Wyobrażenie greckiej świątyni ku czci Zeusa Prezentowane w tym dokumencie zadanie polega na narysowaniu bryły, będącej wyobrażeniem greckiej świątyni ku czci Zeusa. Poniżej
Obiekt 2: Świątynia Zeusa Rys 2-1. Wyobrażenie greckiej świątyni ku czci Zeusa Prezentowane w tym dokumencie zadanie polega na narysowaniu bryły, będącej wyobrażeniem greckiej świątyni ku czci Zeusa. Poniżej
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5
 Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
Ćwiczenie 9. Rzutowanie i wymiarowanie Strona 1 z 5 Problem I. Model UD Dana jest bryła, której rzut izometryczny przedstawiono na rysunku 1. (W celu zwiększenia poglądowości na rysunku 2. przedstawiono
DesignCAD 3D Max 24.0 PL
 DesignCAD 3D Max 24.0 PL Październik 2014 DesignCAD 3D Max 24.0 PL zawiera następujące ulepszenia i poprawki: Nowe funkcje: Tryb RedSDK jest teraz dostępny w widoku 3D i jest w pełni obsługiwany przez
DesignCAD 3D Max 24.0 PL Październik 2014 DesignCAD 3D Max 24.0 PL zawiera następujące ulepszenia i poprawki: Nowe funkcje: Tryb RedSDK jest teraz dostępny w widoku 3D i jest w pełni obsługiwany przez
XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY
 pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
pitagoras.d2.pl XII. GEOMETRIA PRZESTRZENNA GRANIASTOSŁUPY Graniastosłup to wielościan posiadający dwie identyczne i równoległe podstawy oraz ściany boczne będące równoległobokami. Jeśli podstawy graniastosłupa
WYKŁAD 3 WYPEŁNIANIE OBSZARÓW. Plan wykładu: 1. Wypełnianie wieloboku
 WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
WYKŁ 3 WYPŁNINI OSZRÓW. Wypełnianie wieloboku Zasada parzystości: Prosta, która nie przechodzi przez wierzchołek przecina wielobok parzystą ilość razy. Plan wykładu: Wypełnianie wieloboku Wypełnianie konturu
Zad. 6: Sterowanie robotem mobilnym
 Zad. 6: Sterowanie robotem mobilnym 1 Cel ćwiczenia Utrwalenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie dziedziczenia
Zad. 6: Sterowanie robotem mobilnym 1 Cel ćwiczenia Utrwalenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie dziedziczenia
Transformacje. dr Radosław Matusik. radmat
 www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja m.in. przestrzeni modelu, świata, kamery oraz projekcji, a także omówienie sposobów oświetlania i cieniowania obiektów. Pierwsze
www.math.uni.lodz.pl/ radmat Cel wykładu Celem wykładu jest prezentacja m.in. przestrzeni modelu, świata, kamery oraz projekcji, a także omówienie sposobów oświetlania i cieniowania obiektów. Pierwsze
Materiały pomocnicze do programu AutoCAD 2014
 Łukasz Przeszłowski Politechnika Rzeszowska im. I. Łukasiewicza Wydział Budowy Maszyn i Lotnictwa Katedra Konstrukcji Maszyn Materiały pomocnicze do programu AutoCAD 2014 UWAGA: Są to materiały pomocnicze
Łukasz Przeszłowski Politechnika Rzeszowska im. I. Łukasiewicza Wydział Budowy Maszyn i Lotnictwa Katedra Konstrukcji Maszyn Materiały pomocnicze do programu AutoCAD 2014 UWAGA: Są to materiały pomocnicze
Rys 3-1. Rysunek wałka
 Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Obiekt 3: Wałek Rys 3-1. Rysunek wałka W tym dokumencie zostanie zaprezentowany schemat działania w celu przygotowania trójwymiarowego rysunku wałka. Poniżej prezentowane są sugestie dotyczące narysowania
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania.
 Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Oświetlenie. Modelowanie oświetlenia sceny 3D. Algorytmy cieniowania. Chcąc osiągnąć realizm renderowanego obrazu, należy rozwiązać problem świetlenia. Barwy, faktury i inne właściwości przedmiotów postrzegamy
Systemy wirtualnej rzeczywistości. Komponenty i serwisy
 Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Uniwersytet Zielonogórski Instytut Sterowania i Systemów Informatycznych Systemy wirtualnej rzeczywistości Laboratorium Komponenty i serwisy Wstęp: W trzeciej części przedstawione zostaną podstawowe techniki
Trójwymiarowa grafika komputerowa rzutowanie
 Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Trójwymiarowa grafika komputerowa rzutowanie Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej Rzutowanie w przestrzeni 3D etapy procesu rzutowania określenie rodzaju rzutu określenie
Podstawy Processingu. Diana Domańska. Uniwersytet Śląski
 Podstawy Processingu Diana Domańska Uniwersytet Śląski Processing jest językiem programowania opartym na języku Java. Jest on nastawiony na aplikacje związane z grafiką, animacją. Projekt został zainicjowany
Podstawy Processingu Diana Domańska Uniwersytet Śląski Processing jest językiem programowania opartym na języku Java. Jest on nastawiony na aplikacje związane z grafiką, animacją. Projekt został zainicjowany
Synteza i obróbka obrazu. Modelowanie obiektów 3D
 Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
Synteza i obróbka obrazu Modelowanie obiektów 3D Grafika 2D a 3D W obu przypadkach efekt jest taki sam: rastrowy obraz 2D. W grafice 2D od początku operujemy tylko w dwóch wymiarach, przekształcając obraz
Grafika Komputerowa Wykład 6. Teksturowanie. mgr inż. Michał Chwesiuk 1/23
 Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Wykład 6 mgr inż. 1/23 jest to technika w grafice komputerowej, której celem jest zwiększenie szczegółowości renderowanych powierzchni za pomocą tekstur. jest to pewna funkcja (najczęściej w formie bitmapy)
Bartosz Bazyluk SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok
 SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
SYNTEZA GRAFIKI 3D Grafika realistyczna i czasu rzeczywistego. Pojęcie sceny i kamery. Grafika Komputerowa, Informatyka, I Rok Synteza grafiki 3D Pod pojęciem syntezy grafiki rozumiemy stworzenie grafiki
WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje.
 WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje. Tworzenie z formatu A4 formatów podstawowych. Rodzaje linii Najważniejsze zastosowania linii: - ciągła gruba do rysowania widocznych krawędzi
WYKŁAD 2 Znormalizowane elementy rysunku technicznego. Przekroje. Tworzenie z formatu A4 formatów podstawowych. Rodzaje linii Najważniejsze zastosowania linii: - ciągła gruba do rysowania widocznych krawędzi
Rys. 1. Rozpoczynamy rysunek pojedynczej części
 Inventor cw1 Otwieramy nowy rysunek typu Inventor Part (ipt) pojedyncza część. Wykonujemy to następującym algorytmem, rys. 1: 1. Na wstędze Rozpocznij klikamy nowy 2. W oknie dialogowym Nowy plik klikamy
Inventor cw1 Otwieramy nowy rysunek typu Inventor Part (ipt) pojedyncza część. Wykonujemy to następującym algorytmem, rys. 1: 1. Na wstędze Rozpocznij klikamy nowy 2. W oknie dialogowym Nowy plik klikamy
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH
 STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
STEREOMETRIA CZYLI GEOMETRIA W 3 WYMIARACH Stereometria jest działem geometrii, którego przedmiotem badań są bryły przestrzenne oraz ich właściwości. WZAJEMNE POŁOŻENIE PROSTYCH W PRZESTRZENI 2 proste
10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu.
 Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
Waldemar Izdebski - Wykłady z przedmiotu SIT 91 10.3. Typowe zadania NMT W niniejszym rozdziale przedstawimy podstawowe zadania do jakich może być wykorzystany numerycznego modelu terenu. 10.3.1. Wyznaczanie
Rysowanie punktów na powierzchni graficznej
 Rysowanie punktów na powierzchni graficznej Tworzenie biblioteki rozpoczniemy od podstawowej funkcji graficznej gfxplot() - rysowania pojedynczego punktu na zadanych współrzędnych i o zadanym kolorze RGB.
Rysowanie punktów na powierzchni graficznej Tworzenie biblioteki rozpoczniemy od podstawowej funkcji graficznej gfxplot() - rysowania pojedynczego punktu na zadanych współrzędnych i o zadanym kolorze RGB.
Plan wykładu. Akcelerator 3D Potok graficzny
 Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Plan wykładu Akcelerator 3D Potok graficzny Akcelerator 3D W 1996 r. opracowana została specjalna karta rozszerzeń o nazwie marketingowej Voodoo, którą z racji wspomagania procesu generowania grafiki 3D
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki
 Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 2 Temat: Modelowanie powierzchni swobodnych 3D przy użyciu programu Autodesk Inventor Spis treści 1.
Politechnika Warszawska Wydział Mechatroniki Instytut Automatyki i Robotyki Ćwiczenie laboratoryjne 2 Temat: Modelowanie powierzchni swobodnych 3D przy użyciu programu Autodesk Inventor Spis treści 1.
Ćwiczenie R-3. Modelowanie w Rhino - zaawansowane modelowanie powierzchni
 Grafika komputerowa Ćwiczenie R-3 Modelowanie w Rhino - zaawansowane modelowanie powierzchni Instrukcja laboratoryjna opracował: Marcin Skotnicki Człowiek - najlepsza inwestycja Projekt współfinansowany
Grafika komputerowa Ćwiczenie R-3 Modelowanie w Rhino - zaawansowane modelowanie powierzchni Instrukcja laboratoryjna opracował: Marcin Skotnicki Człowiek - najlepsza inwestycja Projekt współfinansowany
Ćwiczenia nr 4. TEMATYKA: Rzutowanie
 TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
TEMATYKA: Rzutowanie Ćwiczenia nr 4 DEFINICJE: Rzut na prostą: rzutem na prostą l (zwaną rzutnią) w kierunku rzutowania k (k l) nazywamy przekształcenie płaszczyzny przyporządkowujące: a) Punktom prostej
Zadanie I. 2. Gdzie w przestrzeni usytuowane są punkty (w której ćwiartce leży dany punkt): F x E' E''
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2012/2013 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Maskowanie i selekcja
 Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
Maskowanie i selekcja Maska prostokątna Grafika bitmapowa - Corel PHOTO-PAINT Pozwala definiować prostokątne obszary edytowalne. Kiedy chcemy wykonać operacje nie na całym obrazku, lecz na jego części,
GRK 4. dr Wojciech Palubicki
 GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
GRK 4 dr Wojciech Palubicki Uproszczony Potok Graficzny (Rendering) Model Matrix View Matrix Projection Matrix Viewport Transform Object Space World Space View Space Clip Space Screen Space Projection
RZUT CECHOWANY DACHY, NASYPY, WYKOPY
 WYZNACZANIE DACHÓW: RZUT CECHOWANY DACHY, NASYPY, WYKOPY Ograniczymy się do dachów złożonych z płaskich wielokątów nazywanych połaciami, z linią okapu (linią utworzoną przez swobodne brzegi połaci) w postaci
WYZNACZANIE DACHÓW: RZUT CECHOWANY DACHY, NASYPY, WYKOPY Ograniczymy się do dachów złożonych z płaskich wielokątów nazywanych połaciami, z linią okapu (linią utworzoną przez swobodne brzegi połaci) w postaci
Oświetlenie obiektów 3D
 Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Synteza i obróbka obrazu Oświetlenie obiektów 3D Opracowanie: dr inż. Grzegorz Szwoch Politechnika Gdańska Katedra Systemów Multimedialnych Rasteryzacja Spłaszczony po rzutowaniu obraz siatek wielokątowych
Modelowanie i wstęp do druku 3D Wykład 1. Robert Banasiak
 Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Modelowanie i wstęp do druku 3D Wykład 1 Robert Banasiak Od modelu 3D do wydruku 3D Typowa droga...czasem wyboista... Pomysł!! Modeler 3D Przygotowanie modelu do druku Konfiguracja Programu do drukowania
Scenariusz lekcji matematyki w kl. IV
 Scenariusz lekcji matematyki w kl. IV TEMAT LEKCJI: Okrąg i koło. Treści nauczania z podstawy programowej : Wielokąty, koła, okręgi. Uczeń wskazuje na rysunku, a także rysuje cięciwę, średnicę, promień
Scenariusz lekcji matematyki w kl. IV TEMAT LEKCJI: Okrąg i koło. Treści nauczania z podstawy programowej : Wielokąty, koła, okręgi. Uczeń wskazuje na rysunku, a także rysuje cięciwę, średnicę, promień
Czy pamiętasz? Zadanie 1. Rozpoznaj wśród poniższych brył ostrosłupy i graniastosłupy.
 1. Bryły Tradycyjna futbolówka jest zszyta z 3232 kawałków. Gdybyśmy ją rozcięli, ujrzelibyśmy siatkę dwudziestościanu ściętego. Kulisty kształt piłka otrzymuje dzięki wypełnieniu sprężonym powietrzem.
1. Bryły Tradycyjna futbolówka jest zszyta z 3232 kawałków. Gdybyśmy ją rozcięli, ujrzelibyśmy siatkę dwudziestościanu ściętego. Kulisty kształt piłka otrzymuje dzięki wypełnieniu sprężonym powietrzem.
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do
 0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
0. OpenGL ma układ współrzędnych taki, że oś y jest skierowana (względem monitora) a) w dół b) w górę c) w lewo d) w prawo e) w kierunku do obserwatora f) w kierunku od obserwatora 1. Obrót dookoła osi
(1,10) (1,7) (5,5) (5,4) (2,1) (0,0) Grafika 3D program POV-Ray - 73 -
 Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Temat 10: Tworzenie brył obrotowych poprzez obrót krzywych (lathe). W poprzednim temacie wymodelowaliśmy kieliszek obracając krzywą Beziera wokół osi Y. Zastosowaliśmy w tym celu polecenie lathe. Krzywa
Zad. 5: Sterowanie robotem mobilnym
 Zad. 5: Sterowanie robotem mobilnym 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie
Zad. 5: Sterowanie robotem mobilnym 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas, czynności oraz przypadków użycia. Wykorzystanie
Laboratorium 1. Część I. Podstawy biblioteki graficznej OpenGL.
 Laboratorium 1 Część I Podstawy biblioteki graficznej OpenGL. I. Konfiguracja środowiska 1. Ściągamy bibliotekę freeglut i rozpakujemy do głównego folderu dysku systemowego np. C:\freeglut 2. Uruchamiamy
Laboratorium 1 Część I Podstawy biblioteki graficznej OpenGL. I. Konfiguracja środowiska 1. Ściągamy bibliotekę freeglut i rozpakujemy do głównego folderu dysku systemowego np. C:\freeglut 2. Uruchamiamy
Ćwiczenie R-2. Modelowanie w Rhino - metody tworzenia powierzchni z krzywych
 Grafika komputerowa Ćwiczenie R-2 Modelowanie w Rhino - metody tworzenia powierzchni z krzywych Instrukcja laboratoryjna opracował: Marcin Skotnicki Człowiek - najlepsza inwestycja Projekt współfinansowany
Grafika komputerowa Ćwiczenie R-2 Modelowanie w Rhino - metody tworzenia powierzchni z krzywych Instrukcja laboratoryjna opracował: Marcin Skotnicki Człowiek - najlepsza inwestycja Projekt współfinansowany
Rok akademicki 2005/2006
 GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
GEOMETRIA WYKREŚLNA ĆWICZENIA ZESTAW I Rok akademicki 2005/2006 Zadanie I. 1. Według podanych współrzędnych punktów wykreślić je w przestrzeni (na jednym rysunku aksonometrycznym) i określić, gdzie w przestrzeni
Baltie 3. Podręcznik do nauki programowania dla klas I III gimnazjum. Tadeusz Sołtys, Bohumír Soukup
 Baltie 3 Podręcznik do nauki programowania dla klas I III gimnazjum Tadeusz Sołtys, Bohumír Soukup Czytanie klawisza lub przycisku myszy Czytaj klawisz lub przycisk myszy - czekaj na naciśnięcie Polecenie
Baltie 3 Podręcznik do nauki programowania dla klas I III gimnazjum Tadeusz Sołtys, Bohumír Soukup Czytanie klawisza lub przycisku myszy Czytaj klawisz lub przycisk myszy - czekaj na naciśnięcie Polecenie
Animowana grafika 3D. Opracowanie: J. Kęsik. kesik@cs.pollub.pl
 Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Podstawowe pojęcia Modelowanie i wyświetlenie struktury trójwymiarowej wymaga zajęcia się wieloma aspektami oprócz samego dodania trzeciej
Animowana grafika 3D Opracowanie: J. Kęsik kesik@cs.pollub.pl Podstawowe pojęcia Modelowanie i wyświetlenie struktury trójwymiarowej wymaga zajęcia się wieloma aspektami oprócz samego dodania trzeciej
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie
 Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Rozwiązywanie równań różniczkowych cząstkowych metodą elementów skończonych - wprowadzenie Wprowadzenie Metoda Elementów Skończonych (MES) należy do numerycznych metod otrzymywania przybliżonych rozwiązań
Podstawowe komendy. Ćwiczenie 1
 Podstawowe komendy Program (język) komputerowy LOGO powstał w latach sześćdziesiątych w USA. Stworzył go Seymour Papert. Uczniowie bawiący się z LOGO wydają polecenia komendy, które wykonuje żółw pojawiający
Podstawowe komendy Program (język) komputerowy LOGO powstał w latach sześćdziesiątych w USA. Stworzył go Seymour Papert. Uczniowie bawiący się z LOGO wydają polecenia komendy, które wykonuje żółw pojawiający
Wizualizacja 3D obiektów i systemów biomedycznych
 Wizualizacja 3D obiektów i systemów biomedycznych Krzysztof Gdawiec Instytut Informatyki Uniwersytet Śląski Wejście: przykładowe zbiory danych Wyjście: obraz Dziedzina: przestrzeń 2D (pozycje pikseli)
Wizualizacja 3D obiektów i systemów biomedycznych Krzysztof Gdawiec Instytut Informatyki Uniwersytet Śląski Wejście: przykładowe zbiory danych Wyjście: obraz Dziedzina: przestrzeń 2D (pozycje pikseli)
Druga aplikacja Prymitywy, alpha blending, obracanie bitmap oraz mały zestaw przydatnych funkcji wyświetlających własnej roboty.
 Przyszedł czas na rysowanie własnych figur, czyli prymitywy, obracanie bitmap, oraz alpha blending-czyli półprzezroczystość. Będę opisywał tylko rzeczy nowe-nie ma potrzeby abym się powtarzał. Zaczynajmny
Przyszedł czas na rysowanie własnych figur, czyli prymitywy, obracanie bitmap, oraz alpha blending-czyli półprzezroczystość. Będę opisywał tylko rzeczy nowe-nie ma potrzeby abym się powtarzał. Zaczynajmny
WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ
 Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
Zapis i Podstawy Konstrukcji Widoki i przekroje przedmiotów 1 WIDOKI I PRZEKROJE PRZEDMIOTÓW LINIE PRZENIKANIA BRYŁ Rzutami przedmiotów mogą być zarówno widoki przestawiające zewnętrzne kształty przedmiotów
narzędzie Linia. 2. W polu koloru kliknij kolor, którego chcesz użyć. 3. Aby coś narysować, przeciągnij wskaźnikiem w obszarze rysowania.
 Elementy programu Paint Aby otworzyć program Paint, należy kliknąć przycisk Start i Paint., Wszystkie programy, Akcesoria Po uruchomieniu programu Paint jest wyświetlane okno, które jest w większej części
Elementy programu Paint Aby otworzyć program Paint, należy kliknąć przycisk Start i Paint., Wszystkie programy, Akcesoria Po uruchomieniu programu Paint jest wyświetlane okno, które jest w większej części
Grafika trójwymiarowa
 Strona 1 Grafika 3D w systemie Android Wprowadzenie do OpenGL ES Podstawy rysowania Rzutowanie i kamera Klasa GLSurfaceView Algorytm rysowania Tekstury Strona 2 Grafika 3D w systemie Android W komputerach,
Strona 1 Grafika 3D w systemie Android Wprowadzenie do OpenGL ES Podstawy rysowania Rzutowanie i kamera Klasa GLSurfaceView Algorytm rysowania Tekstury Strona 2 Grafika 3D w systemie Android W komputerach,
Grafika 2D. Animacja Zmiany Kształtu. opracowanie: Jacek Kęsik
 Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
Grafika 2D Animacja Zmiany Kształtu opracowanie: Jacek Kęsik Wykład przedstawia podstawy animacji zmiany kształtu - morfingu Animacja zmiany kształtu Podstawowe pojęcia Zlewanie (Dissolving / cross-dissolving)
PODSTAWOWE KONSTRUKCJE GEOMETRYCZNE
 PODSTAWOWE KONSTRUKCJE GEOMETRYCZNE Dane będę rysował na czarno. Różne etapy konstrukcji kolorami: (w kolejności) niebieskim, zielonym, czerwonym i ewentualnie pomarańczowym i jasnozielonym. 1. Prosta
PODSTAWOWE KONSTRUKCJE GEOMETRYCZNE Dane będę rysował na czarno. Różne etapy konstrukcji kolorami: (w kolejności) niebieskim, zielonym, czerwonym i ewentualnie pomarańczowym i jasnozielonym. 1. Prosta
TWORZENIE SZEŚCIANU. Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian
 TWORZENIE SZEŚCIANU Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian ZADANIE Twoim zadaniem jest zaprojektowanie a następnie wydrukowanie (za pomocą drukarki 3D)
TWORZENIE SZEŚCIANU Sześcian to trójwymiarowa bryła, w której każdy z sześciu boków jest kwadratem. Sześcian ZADANIE Twoim zadaniem jest zaprojektowanie a następnie wydrukowanie (za pomocą drukarki 3D)
dodatkowe operacje dla kopca binarnego: typu min oraz typu max:
 ASD - ćwiczenia IX Kopce binarne własność porządku kopca gdzie dla każdej trójki wierzchołków kopca (X, Y, Z) porządek etykiet elem jest następujący X.elem Y.elem oraz Z.elem Y.elem w przypadku kopca typu
ASD - ćwiczenia IX Kopce binarne własność porządku kopca gdzie dla każdej trójki wierzchołków kopca (X, Y, Z) porządek etykiet elem jest następujący X.elem Y.elem oraz Z.elem Y.elem w przypadku kopca typu
Tworzenie nowego rysunku Bezpośrednio po uruchomieniu programu zostanie otwarte okno kreatora Nowego Rysunku.
 1 Spis treści Ćwiczenie 1...3 Tworzenie nowego rysunku...3 Ustawienia Siatki i Skoku...4 Tworzenie rysunku płaskiego...5 Tworzenie modeli 3D...6 Zmiana Układu Współrzędnych...7 Tworzenie rysunku płaskiego...8
1 Spis treści Ćwiczenie 1...3 Tworzenie nowego rysunku...3 Ustawienia Siatki i Skoku...4 Tworzenie rysunku płaskiego...5 Tworzenie modeli 3D...6 Zmiana Układu Współrzędnych...7 Tworzenie rysunku płaskiego...8
Zad. 3: Rotacje 2D. Demonstracja przykładu problemu skończonej reprezentacji binarnej liczb
 Zad. 3: Rotacje 2D 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich struktur
Zad. 3: Rotacje 2D 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich struktur
Zad. 5: Rotacje 3D. 1 Cel ćwiczenia. 2 Program zajęć. 3 Opis zadania programowego
 Zad. 5: Rotacje 3D 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas. Praktyczne zweryfikowanie wcześniejszej konstrukcji programu. Jeśli
Zad. 5: Rotacje 3D 1 Cel ćwiczenia Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Tworzenie diagramu klas. Praktyczne zweryfikowanie wcześniejszej konstrukcji programu. Jeśli
EGZAMIN MATURALNY OD ROKU SZKOLNEGO
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 204/205 MATEMATYKA POZIOM PODSTAWOWY PRZYKŁADOWY ZESTAW ZADAŃ (A) W czasie trwania egzaminu zdający może korzystać z zestawu wzorów matematycznych, linijki i cyrkla
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 204/205 MATEMATYKA POZIOM PODSTAWOWY PRZYKŁADOWY ZESTAW ZADAŃ (A) W czasie trwania egzaminu zdający może korzystać z zestawu wzorów matematycznych, linijki i cyrkla
Plan wynikowy, klasa 3 ZSZ
 Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Plan wynikowy, klasa 3 ZSZ Nazwa działu Temat Liczba godzin 1. Trójkąty prostokątne powtórzenie 1. Trygonometria (10 h) 2. Funkcje trygonometryczne kąta ostrego 3. 4. Trygonometria zastosowania 5. 6. Związki
Uniwersytet Zielonogórski. Kurs: Autodesk 3D Studio MAX Komputerowa grafika 3D. 3dsmax Teksturowanie obiektów 3D
 Uniwersytet Zielonogórski Kurs: Autodesk 3D Studio MAX Komputerowa grafika 3D 3dsmax Teksturowanie obiektów 3D opracował: dr inż Andrzej Czajkowski, aczajkowski@issiuzzgorapl 1 Cel ćwiczenia Celem ćwiczenia
Uniwersytet Zielonogórski Kurs: Autodesk 3D Studio MAX Komputerowa grafika 3D 3dsmax Teksturowanie obiektów 3D opracował: dr inż Andrzej Czajkowski, aczajkowski@issiuzzgorapl 1 Cel ćwiczenia Celem ćwiczenia
WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ. Instrukcja obsługi aplikacji
 /30 WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ Instrukcja obsługi aplikacji Aby rozpocząć pracę z aplikacją, należy zarejestrować się w celu założenia konta. Wystarczy wpisać imię, nazwisko, adres
/30 WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ Instrukcja obsługi aplikacji Aby rozpocząć pracę z aplikacją, należy zarejestrować się w celu założenia konta. Wystarczy wpisać imię, nazwisko, adres
Grafika 3D OpenGL część II
 #include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
#include #include #include float kat=0.0f; void renderujscene(void) { glclearcolor(1.0f,1.0f,1.0f,1.0f); glclear(gl_color_buffer_bit); glpushmatrix(); glrotatef(kat,0,0,1);
1 Automaty niedeterministyczne
 Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
Szymon Toruńczyk 1 Automaty niedeterministyczne Automat niedeterministyczny A jest wyznaczony przez następujące składniki: Alfabet skończony A Zbiór stanów Q Zbiór stanów początkowych Q I Zbiór stanów
EGZAMIN MATURALNY Z MATEMATYKI
 Miejsce na naklejkę z kodem szkoły dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-R1A1P-052 POZIOM ROZSZERZONY Czas pracy 150 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 15
Miejsce na naklejkę z kodem szkoły dysleksja EGZAMIN MATURALNY Z MATEMATYKI MMA-R1A1P-052 POZIOM ROZSZERZONY Czas pracy 150 minut Instrukcja dla zdającego 1. Sprawdź, czy arkusz egzaminacyjny zawiera 15
Kurs ZDAJ MATURĘ Z MATEMATYKI - MODUŁ 13 Teoria stereometria
 1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
1 GRANIASTOSŁUPY i OSTROSŁUPY wiadomości ogólne Aby tworzyć wzory na OBJĘTOŚĆ i POLE CAŁKOWITE graniastosłupów musimy znać pola figur płaskich a następnie na ich bazie stosować się do zasady: Objętość
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył
 Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Ćwiczenie nr 5 i 6 Przygotowanie dokumentacji technicznej dla brył Zadanie A Celem będzie wykonanie rysunku pokazanego NA KOŃCU zadania. Rysując proszę się posłużyć podanymi tam wymiarami. Pamiętajmy o
Przyrządy do kreślenia, plansza połażenie prostych i odcinków, kąty, domino, krzyżówka, kartki z gotowymi figurami.
 Powtórzenie wiadomości o figurach geometrycznych. 1. Cele lekcji a) Wiadomości Uczeń: - zna podstawowe figury geometryczne, - zna własności figur, - zna pojęcie kąta oraz wierzchołka i ramion kąta. b)
Powtórzenie wiadomości o figurach geometrycznych. 1. Cele lekcji a) Wiadomości Uczeń: - zna podstawowe figury geometryczne, - zna własności figur, - zna pojęcie kąta oraz wierzchołka i ramion kąta. b)
PL B1. POLITECHNIKA LUBELSKA, Lublin, PL BUP 15/15. JANUSZ W. SIKORA, Dys, PL MACIEJ NOWICKI, Lublin, PL KAMIL ŻELAZEK, Lublin, PL
 PL 223387 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 223387 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 410338 (22) Data zgłoszenia: 03.12.2014 (51) Int.Cl.
PL 223387 B1 RZECZPOSPOLITA POLSKA (12) OPIS PATENTOWY (19) PL (11) 223387 (13) B1 Urząd Patentowy Rzeczypospolitej Polskiej (21) Numer zgłoszenia: 410338 (22) Data zgłoszenia: 03.12.2014 (51) Int.Cl.
Pytania do spr / Własności figur (płaskich i przestrzennych) (waga: 0,5 lub 0,3)
 Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Pytania zamknięte / TEST : Wybierz 1 odp prawidłową. 1. Punkt: A) jest aksjomatem in. pewnikiem; B) nie jest aksjomatem, bo można go zdefiniować. 2. Prosta: A) to zbiór punktów; B) to zbiór punktów współliniowych.
Wymagania edukacyjne z matematyki dla klasy III gimnazjum
 Wymagania edukacyjne z matematyki dla klasy III gimnazjum Poziomy wymagań edukacyjnych: K konieczny dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je zatem opanować każdy
Wymagania edukacyjne z matematyki dla klasy III gimnazjum Poziomy wymagań edukacyjnych: K konieczny dotyczą zagadnień elementarnych, stanowiących swego rodzaju podstawę, powinien je zatem opanować każdy
Obiekty trójwymiarowe AutoCAD 2013 PL
 Spis treści Rozdział I Wprowadzenie... 11 Zakres materiału... 13 Przyjęta konwencja oznaczeń... 13 Instalowanie plików rysunków... 16 Rozdział II Narzędzia nawigacji 3D... 19 Interfejs programu... 19 Współrzędne
Spis treści Rozdział I Wprowadzenie... 11 Zakres materiału... 13 Przyjęta konwencja oznaczeń... 13 Instalowanie plików rysunków... 16 Rozdział II Narzędzia nawigacji 3D... 19 Interfejs programu... 19 Współrzędne
WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ. Instrukcja obsługi aplikacji
 /30 WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ Instrukcja obsługi aplikacji Aby rozpocząć pracę z aplikacją, należy zarejestrować się w celu założenia konta. Wystarczy wpisać imię, nazwisko, adres
/30 WIZUALIZER 3D APLIKACJA DOBORU KOSTKI BRUKOWEJ Instrukcja obsługi aplikacji Aby rozpocząć pracę z aplikacją, należy zarejestrować się w celu założenia konta. Wystarczy wpisać imię, nazwisko, adres
a) 7 b) 19 c) 21 d) 34
 Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
Zadanie 1. Pytania testowe dotyczące podstawowych własności grafów. Zadanie 2. Przy każdym z zadań może się pojawić polecenie krótkiej charakterystyki algorytmu. Zadanie 3. W zadanym grafie sprawdzenie
KONSPEKT do przeprowadzenia lekcji matematyki
 Zespół Szkół im A. Mickiewicza we Wręczycy Wielkiej Szkoła Podstawowa Przedmiot: Matematyka, klasa VI b. Podręcznik: Matematyka wokół nas Prowadzący: mgr Ewa Mika KONSPEKT do przeprowadzenia lekcji matematyki
Zespół Szkół im A. Mickiewicza we Wręczycy Wielkiej Szkoła Podstawowa Przedmiot: Matematyka, klasa VI b. Podręcznik: Matematyka wokół nas Prowadzący: mgr Ewa Mika KONSPEKT do przeprowadzenia lekcji matematyki
GRK 2. dr Wojciech Palubicki
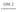 GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
GRK dr Wojciech Palubicki Macierz wektor produkt jako Transformacja T: R n R m T Ԧx = A Ԧx Przemieszczanie wierzchołków - Transformacje Skalowanie Rotacja Translacja -y -y Macierz rotacji M wobec punktu
Agnieszka Kamińska, Dorota Ponczek. Matematyka na czasie Gimnazjum, klasa 3 Rozkład materiału i plan wynikowy
 Agnieszka Kamińska, Dorota Ponczek Matematyka na czasie Gimnazjum, klasa Rozkład materiału i plan wynikowy I. FUNKCJE 1 1. Pojęcie funkcji zbiór i jego elementy pojęcie przyporządkowania pojęcie funkcji
Agnieszka Kamińska, Dorota Ponczek Matematyka na czasie Gimnazjum, klasa Rozkład materiału i plan wynikowy I. FUNKCJE 1 1. Pojęcie funkcji zbiór i jego elementy pojęcie przyporządkowania pojęcie funkcji
