Lublin, 27 XI 2015 r. Nadprzewodnictwo. możliwość realizowania ujemnego oporu. Tadeusz Domański Instytut Fizyki UMCS
|
|
|
- Edward Rybak
- 6 lat temu
- Przeglądów:
Transkrypt
1 Lublin, 27 XI 2015 r. Nadprzewodnictwo możliwość realizowania ujemnego oporu Tadeusz Domański Instytut Fizyki UMCS
2 Lublin, 27 XI 2015 r. Nadprzewodnictwo możliwość realizowania ujemnego oporu Tadeusz Domański Instytut Fizyki UMCS
3 Nadprzewodnictwo dlaczego taki temat?
4 Nadprzewodnictwo dlaczego taki temat? Aspekty poznawcze: za badania przyznano już 5 Nagród Nobla z fizyki (w sumie dla 10 osób)
5 Nadprzewodnictwo dlaczego taki temat? Aspekty poznawcze: za badania przyznano już 5 Nagród Nobla z fizyki (w sumie dla 10 osób) Aspekty technologiczne: nowe technologie m.in. w transporcie, medycynie itp.
6 Nadprzewodnictwo dlaczego taki temat? Aspekty poznawcze: za badania przyznano już 5 Nagród Nobla z fizyki (w sumie dla 10 osób) Aspekty technologiczne: nowe technologie m.in. w transporcie, medycynie itp. Aspekty ekonomiczne: olbrzymie oszcze dności w wydatkach na energetyke
7 Aspekty ekonomiczne fakty Na energii elektrycznej sie : rynkowa cene składaja koszty produkcji, koszty przesyłania. Straty w przesyłaniu energii około 7 procent. wynosza Dzie ki zastosowaniu nadprzewodników można byłoby zredukować straty do 0!
8 Opór elektryczny istota zjawiska
9 Opór elektryczny istota zjawiska Pod wpływem zewne trznych pól (elektrycznego, magnetycznego, gradientu temperatur) elektrony walencyjne sa zmuszone do przemieszczania.
10 Opór elektryczny istota zjawiska Ruch elektronów odbywa sie w sieci jonów ulegaja c procesom rozpraszania, co przejawia sie makroskopowo jako opór.
11 Opór elektryczny istota zjawiska Opór całkowity wynosi R = ρ l A,
12 Opór elektryczny istota zjawiska Opór całkowity wynosi R = ρ l A, gdzie opór właściwy ρ
13 Opór elektryczny istota zjawiska Opór całkowity wynosi R = ρ l A, gdzie opór właściwy ρ zależy od: rodzaju materiału,
14 Opór elektryczny istota zjawiska Opór całkowity wynosi R = ρ l A, gdzie opór właściwy ρ zależy od: rodzaju materiału, temperatury.
15 Opór elektryczny przykłady w temperaturze 20 o C
16 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m aluminium żelazo 2, Ω m 1, Ω m
17 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m aluminium żelazo 2, Ω m 1, Ω m grafit german krzem 2, Ω m 4, Ω m 6, Ω m
18 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m aluminium żelazo 2, Ω m 1, Ω m grafit german krzem diament guma teflon 2, Ω m 4, Ω m 6, Ω m Ω m Ω m Ω m
19 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m aluminium żelazo 2, Ω m 1, Ω m grafit german krzem diament guma teflon 2, Ω m 4, Ω m 6, Ω m Ω m Ω m Ω m Wartości oporu różnia sie o ponad 30 rze dów wielkości!
20 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m. przewodniki aluminium 2, Ω m żelazo grafit german krzem diament guma teflon 1, Ω m 2, Ω m 4, Ω m 6, Ω m Ω m Ω m Ω m Wartości oporu różnia sie o ponad 30 rze dów wielkości!
21 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m. przewodniki aluminium 2, Ω m żelazo 1, Ω m grafit 2, Ω m 4, Ω m german. półprzewodniki krzem diament guma teflon 6, Ω m Ω m Ω m Ω m Wartości oporu różnia sie o ponad 30 rze dów wielkości!
22 Opór elektryczny przykłady w temperaturze 20 o C miedź 1, Ω m. przewodniki aluminium 2, Ω m żelazo 1, Ω m grafit 2, Ω m 4, Ω m german. półprzewodniki krzem 6, Ω m diament Ω m Ω m guma. izolatory teflon Ω m Wartości oporu różnia sie o ponad 30 rze dów wielkości!
23 Nadprzewodniki science fiction? Czy sa takie materiały, w których opór elektryczny całkowicie znika?
24 Nadprzewodniki science fiction? Czy sa takie materiały, w których opór elektryczny całkowicie znika? Futurystyczne perspektywy: Można byłoby przesyłać nimi energie od solarów rozmieszczonych na Saharze.
25 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika.
26 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
27 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
28 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
29 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
30 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
31 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
32 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
33 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
34 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
35 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
36 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
37 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
38 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
39 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
40 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika. opor, temperatura [K]
41 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika.
42 Odkrycie nadprzewodnictwa 8 kwietnia 1911 r. Stan nadprzewodza cy odkryto (przypadkowo) podczas badania oporu rte ci. Poniżej temperatury T c = 4,2 K (czyli -269 o C) opór całkowicie zanika.. (Lejda, Holandia) Heike Kamerlingh Onnes
43 Nadprzewodniki efekt Meissnera
44 Nadprzewodniki efekt Meissnera Nadprzewodniki charakteryzuja sie jednocześnie idealnym diamagnetyzmem. Zjawisko to polega na całkowitym ekranowaniu pola magnetycznego. W. Meissner, R. Ochsenfeld ( 1933 r. )
45 Nadprzewodniki efekt Meissnera Zjawisko Meissnera wykorzystuje sie np. do profilowania linii sił pola magnetycznego.
46 Nadprzewodniki efekt Meissnera W ten sposób można skompensować siłe grawitacji, uzyskuja c efekt lewitacji.
47 Nadprzewodniki efekt Meissnera W ten sposób można skompensować siłe grawitacji, uzyskuja c efekt lewitacji.
48 Nadprzewodniki efekt Meissnera W ten sposób można skompensować siłe grawitacji, uzyskuja c efekt lewitacji.
49 Nadprzewodniki efekt Meissnera Perspektywa: Skarpety lewituja ce wraz z właścicielem?
50 Nadprzewodniki kolejne odkrycia
51 Nadprzewodniki kolejne odkrycia Stan nadprzewodza cy został później odkryty w kilku innych pierwiastkach oraz stopach. Oto wybrane przykłady:
52 Nadprzewodniki kolejne odkrycia Stan nadprzewodza cy został później odkryty w kilku innych pierwiastkach oraz stopach. Oto wybrane przykłady: 80 ciekly N 2 60 T c (K) ciekly H 2 Nb 3 Ge Nb 3 Sn Nb Pb NbN V Si Nb Al Ge 3 Hg rok
53 Nadprzewodniki kolejne odkrycia Stan nadprzewodza cy został później odkryty w kilku innych pierwiastkach oraz stopach. Oto wybrane przykłady: 80 ciekly N 2 skroplony azot 60 T c (K) ciekly H 2 Nb 3 Ge Nb 3 Sn Nb Pb NbN V Si Nb Al Ge 3 Hg rok skroplony neon skroplony wodór skroplony hel
54 Zagadka nadprzewodnictwa problemy z wyjaśnieniem
55 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak:
56 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak: R. Feynman
57 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak:. R. Feynman W. Heisenberg
58 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak:.. R. Feynman W. Heisenberg N. Bohr
59 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak:.. R. Feynman W. Heisenberg N. Bohr A. Einstein
60 Zagadka nadprzewodnictwa problemy z wyjaśnieniem Przez niemal 50 lat nie potrafiono wyjaśnić mechanizmu odpowiedzialnego za stan nadprzewodza cy. Problemem tym zajmowali sie tacy wybitni naukowcy, jak:.. R. Feynman W. Heisenberg N. Bohr A. Einstein No one is smart enough to explain it R. Feynman
61 Istota nadprzewodnictwa pomocne fakty Kluczowe znaczenie dla zrozumienia mechanizmu (konwencjonalnego) nadprzewodnictwa miało:
62 Istota nadprzewodnictwa pomocne fakty Kluczowe znaczenie dla zrozumienia mechanizmu (konwencjonalnego) nadprzewodnictwa miało: odkrycie efektu izotopowego (1950 r.) T c 1 M M - masa jonów
63 Teoria nadprzewodnictwa 1957 r. Za opracowanie mikroskopowej teorii nadprzewodnictwa (tzw. teorie BCS) przyznano Nagrode Nobla w 1972 roku.
64 Nadprzewodnictwo zjawisko emergentne
65 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego:
66 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera)
67 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: w pary (Coopera) ła cza sie i kolektywnie na zewne trzne zaburzenia reaguja
68 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera) i kolektywnie reaguja na zewne trzne zaburzenia (jak gigantyczny superatom identycznych obiektów!)
69 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera) i kolektywnie reaguja na zewne trzne zaburzenia (jak gigantyczny superatom identycznych obiektów!) Kondensat par Coopera jest odpowiedzialny za:
70 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera) i kolektywnie reaguja na zewne trzne zaburzenia (jak gigantyczny superatom identycznych obiektów!) Kondensat par Coopera jest odpowiedzialny za: idealne przewodnictwo (ruch bez rozpraszania)
71 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera) i kolektywnie reaguja na zewne trzne zaburzenia (jak gigantyczny superatom identycznych obiektów!) Kondensat par Coopera jest odpowiedzialny za: idealne przewodnictwo idealny diamagnetyzm (ruch bez rozpraszania) (efekt Meissnera)
72 Nadprzewodnictwo zjawisko emergentne Elektrony w powierzchni Fermiego: ła cza sie w pary (Coopera) i kolektywnie reaguja na zewne trzne zaburzenia (jak gigantyczny superatom identycznych obiektów!) Kondensat par Coopera jest odpowiedzialny za: idealne przewodnictwo idealny diamagnetyzm (ruch bez rozpraszania) (efekt Meissnera) nowe zjawiska (efekt Josephsona, wiry kwantowe itp.)
73 Efekt Josephsona pra d par Coopera
74 Efekt Josephsona pra d par Coopera nadprzew. 1 izolator nadprzew. 2 I > 0 U=0 Zła cze utworzone z dwóch nadprzewodników i cienkiej warstwy izolatora.
75 Efekt Josephsona pra d par Coopera SQUID Superconducting QUantum Interferometer Device. Takie urza dzenia sa w stanie wykryć bardzo małe pola magnetyczne T.
76 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć
77 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć Alex Müller, Georg Bednorz / IBM Rüschlikon, Szwajcaria / W 1986 r. odkryto, że materiał ceramiczny La 2 x Sr x CuO 4 (który dla x=0 jest izolatorem typu Motta) w zakresie domieszkowania 0,05 < x < 0,25 staje nadprzewodnikiem. sie Maksymalna temperatura krytyczna La 2 x Sr x CuO 4 wynosi T c =36 K.
78 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć Alex Müller, Georg Bednorz. Nagroda Nobla, 1987 r. / IBM Rüschlikon, Szwajcaria / W 1986 r. odkryto, że materiał ceramiczny La 2 x Sr x CuO 4 (który dla x=0 jest izolatorem typu Motta) w zakresie domieszkowania 0,05 < x < 0,25 staje sie nadprzewodnikiem. Maksymalna temperatura krytyczna La 2 x Sr x CuO 4 wynosi T c =36 K.
79 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć Odkrycie to zapocza tkowało burzliwy okres historii rozwoju nadprzewodnictwa.
80 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć Odkrycie to zapocza tkowało burzliwy okres historii rozwoju nadprzewodnictwa. 180 * HgBa 2 Ca 2 Cu 3 O 8+δ HgBa 2 Ca 2 Cu 3 O 8+δ 120 Tl 2 Ba 2 Ca 2 Cu 3 O 10 T c (K) ciekly N 2 Bi 2 Ba 2 Ca 2 Cu 3 O 10 YBa 2 Cu 3 O 7 δ La 2 δ Sr δ CuO 4 20 ciekly H Nb 2 Nb 3 Sn 3 Ge Hg Pb Nb NbN V Si Nb Al Ge rok
81 Nadprzewodniki wysokotemperaturowe nowa epoka odkryć Odkrycie to zapocza tkowało burzliwy okres historii rozwoju nadprzewodnictwa. 180 * HgBa 2 Ca 2 Cu 3 O 8+δ HgBa 2 Ca 2 Cu 3 O 8+δ T c (K) ciekly N 2 Tl 2 Ba 2 Ca 2 Cu 3 O 10 Bi 2 Ba 2 Ca 2 Cu 3 O 10 YBa 2 Cu 3 O 7 δ temp. pow. Ksie życa skroplony azot La 2 δ Sr δ CuO 4 20 ciekly H Nb 2 Nb 3 Sn 3 Ge Hg Pb Nb NbN V Si Nb Al Ge rok temp. pow. Plutonu skroplony wodór skroplony hel
82 Nadprzewodnictwo w nanoukładach
83 Nadprzewodnictwo w nanoukładach jak można uzyskać nano nadprzewodniki? / efekt bliskości /
84 Nadprzewodnictwo w nanoukładach jak można uzyskać nano nadprzewodniki? / efekt bliskości / jak można zaobserwować nano nadprzewodnictwo? / spektroskopia tunelowania /
85 Nadprzewodnictwo w nanoukładach jak można uzyskać nano nadprzewodniki? / efekt bliskości / jak można zaobserwować nano nadprzewodnictwo? / spektroskopia tunelowania / gdzie można zastosować nano nadprzewodniki? / aspekty praktyczne /
86 Efekt bliskości zaindukowane parowanie elektronów
87 Efekt bliskości zaindukowane parowanie elektronów Każdy materiał umieszczony w kontakcie z nadprzewodnikiem
88 Efekt bliskości zaindukowane parowanie elektronów Każdy materiał umieszczony w kontakcie z nadprzewodnikiem absorbuje pary elektronowe do odległości ξ n.
89 Efekt bliskości zaindukowane parowanie elektronów Każdy materiał umieszczony w kontakcie z nadprzewodnikiem absorbuje pary elektronowe do odległości ξ n. Rozmiary przestrzenne obiektów nanoskopowych sa L ξ n!
90 2. Nano nadprzewodnictwo: w czym sie przejawia?
91 Nadprzewodnictwo w nanoukładach charakterystyczne cechy
92 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 1. Kwantowy Efekt Rozmiarowy dyskretne widmo stan normalny nadprzewodnik
93 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 1. Kwantowy Efekt Rozmiarowy dyskretne widmo stan normalny nadprzewodnik Kryterium Andersona: nadprzewodnictwo, gdy > ε i+1 ε i
94 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 2. Blokada kulombowska (konfrontacja parowania z odpychaniem) Nieparzysta / parzysta liczba electronów ma kluczowe znaczenie!
95 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 2. Blokada kulombowska (konfrontacja parowania z odpychaniem) Nieparzysta / parzysta liczba electronów ma kluczowe znaczenie! Potencjał kulombowski U jest zazwyczaj dużo mniejszy od, dlatego jego wpływ może być w praktyce obserwowany jedynie poprzez: u 0 v ( kwantowe przejście fazowe )
96 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 2. Blokada kulombowska (konfrontacja parowania z odpychaniem) Nieparzysta / parzysta liczba electronów ma kluczowe znaczenie! Potencjał kulombowski U jest zazwyczaj dużo mniejszy od, dlatego jego wpływ może być w praktyce obserwowany jedynie poprzez: u 0 v ( kwantowe przejście fazowe ) Konsekwencje fizyczne: odwrócenie pra du Josephson a (w zła czach S-QD-S) aktywacja/zablokowanie efektu Kondo (w zła czach N-QD-S)
97 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 3. Efekt Kondo w obecności parowania ( to screen or not to screen ) R. Maurand, Ch. Schönenberger, Physics 6, 75 (2013).
98 Nadprzewodnictwo w nanoukładach charakterystyczne cechy 3. Efekt Kondo w obecności parowania ( to screen or not to screen ) R. Maurand, Ch. Schönenberger, Physics 6, 75 (2013). stany w pobliżu energii Fermiego sa zabronione konfrontacja zjawiska Kondo z parowaniem (nietrywialna relacja)
99 Domieszka (kropka) kwantowa w ośrodku nadprzewodza cym
100 Przypadek bez korelacji U d = 0 ε d = 0 ρ d (ω) / Γ S ω / Γ S 2 Rezonanse pod-przerwowe, tzw. stany Andreeva (Shiby). J. Barański and T. Domański, J. Phys.: Condens. Matter 25, (2013).
101 Stany podprzerwowe doświadczalne wyniki Magnetic field [Tesla] Przewodnictwo różniczkowe nanorurek sprze żonych z wanadem (S) i złotem (N) / zewne trzne pole magnetyczne B wpływa na wartość (B) / Eduardo J.H. Lee,..., S. De Franceschi, Nature Nanotechnology 9, 79 (2014).
102 Przyapdek wielopoziomowych domieszek a) b) STM tip d I/ d V subgap structure V a) Schemat STM oraz b) przewodnictwo różniczkowe wielopoziomowej domieszki kwantowej na powierzchni nadprzewodnika. R. Žitko, O. Bodensiek, and T. Pruschke, Phys. Rev. B 83, (2011).
103 Przypadek łańcuchów kwantowych wyniki dośw.
104 Przypadek łańcuchów kwantowych wyniki dośw. Łańcuch atomów na powierzchni (nadprzewodza cego) ołowiu Pomiary STM wskazały na obecność: stanów zwia zanych typu Majorany! S. Nadj-Perge,..., and A. Yazdani, Science 346, 602 (2014). / Princeton University, Princeton (NJ), USA /
105 Przypadek łańcuchów kwantowych wyniki dośw. Nanodrut InSb mie dzy metalem (złoto) i nadprzewodnikiem (Nb-Ti-N) di/dv zmierzone w 70 mk dla różnych pól B wykazało: wzmocnienie przewodnictwa zaindukowane stanem Majorany V. Mourik,..., and L.P. Kouwenhoven, Science 336, 1003 (2012). / Kavli Institute of Nanoscience, Delft Univ., Netherlands /
106 3. Nano nadprzewodnictwo: aspekty praktyczne
107 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev.
108 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S V
109 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S elektron
110 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S elektron
111 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S elektron
112 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S dziura para Cooper a
113 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S dziura para Cooper a
114 Odbicia Andreev a zasadnicza idea Rozpatrzmy proces tunelowania elektronów z elektrody normalnej N (np. metalu) do elektrody nadprzewodza cej S dla małych napie ć ev. N S dziura para Cooper a Konwersja elektronu w pare z wytworzeniem dziury jest tzw. odbiciem Andreev a.
115 Odbicia Andreev a w układach trój-terminalnych
116 Odbicia Andreev a w układach trój-terminalnych P. Cadden-Zimansky, Northwestern University (2008).
117 Odbicia Andreev a w układach trój-terminalnych elektron P. Cadden-Zimansky, Northwestern University (2008).
118 Odbicia Andreev a w układach trój-terminalnych elektron zwykłe tunelowanie P. Cadden-Zimansky, Northwestern University (2008).
119 Odbicia Andreev a w układach trój-terminalnych elektron zwykłe tunelowanie odbicie Andreev a P. Cadden-Zimansky, Northwestern University (2008).
120 Odbicia Andreev a w nanoukładach N QD S Rozpatrzmy kropke kwantowa (QD) na zła czu mie dzy metalem (N) i elektroda nadprzewodza ca (S)
121 Odbicia Andreev a w nanoukładach N QD S Rozpatrzmy kropke kwantowa (QD) na zła czu mie dzy metalem (N) i elektroda nadprzewodza ca (S) V = µ N - µ S N Γ N QD Γ S V G S metal QD nadprzewodnik
122 Odbicia Andreev a w nanoukładach N QD S Rozpatrzmy kropke kwantowa (QD) na zła czu mie dzy metalem (N) i elektroda nadprzewodza ca (S) V = µ N - µ S N Γ N QD Γ S V G S metal QD nadprzewodnik Układ ten jest szczególnym wariantem tranzystora jednoelektronowego (SET).
123 Spektroskopia Andreev a doświadczalna realizacja # 1 Tokyo (Japonia) T c 1K 152µeV QD : InAs rozmiar 100 nm bramka : GaAs domieszkowany krzemem R.S. Deacon et al, Phys. Rev. Lett. 104, (2010).
124 Spektroskopia Andreev a doświadczalna realizacja # 2 Paryż (Francja) QD : nanorurka we glowa S : aluminium U 2 mev 0, 15meV J.-D. Pillet, R. Žitko, and M.F. Goffman, Phys. Rev. B 88, (2013).
125 Spektroskopia Andreev a dos wiadczalna realizacja # 3 Grenoble/Madryt (Francja/Hiszpania) QD : półprzewodnikowy nanodrut InAs/InP S : wanad 0.55meV U 3 10 N : złoto E.J.H. Lee et al, Phys. Rev. Lett. 109, (2012).
126 Zła cza 3-elektrodowe krzyżowe odbicia Andreev a
127 Zła cza 3-elektrodowe krzyżowe odbicia Andreev a Kropka kwantowa (QD) w konfiguracji 3-elektrodowej L, R electrody normalne, S nadprzewodnik, QD kropka kwantowa G. Michałek, T. Domański, B.R. Bułka & K.I. Wysokiński, Scientific Reports 5, (2015).
128 Zła cza 3-elektrodowe krzyżowe odbicia Andreev a Opór pra du tunelowego 2R RS,LS /D R [e 2 /h] max: 2e 2 /h e 0 =0 G R =G L G S =G L +G R G S =(G L +G R ) 3 min: -1/4e 2 /h k B T/G L R RS,LS V RS /I LS G S /G L Ujemny opór w przypadku dużego sprze żenia Γ S!
129 Zła cza 3-elektrodowe krzyżowe odbicia Andreev a Napie cie wygenerowane na elektrodzie R. ev R / L k B T/G L G S /G L =2 G S /G L =4 G S /G L =6 e 0 =0 G R =G L ev L / L Odwrotny znak napie cia (tzn. ujemny opór) dla silnych sprze żeń Γ S.
130 Odbicia Andreev a dalsze perspektywy
131 Odbicia Andreev a dalsze perspektywy Odbicia Andreev a umożliwiaja separacje pra du ładunkowego od cieplnego F. Mazza, S. Valentini, R. Bosisio, G. Benenti, V. Giovannetti, R. Fazio & F. Tadddei, Phys. Rev. B 91, (2015).
132 Odbicia Andreev a dalsze perspektywy Nanoskopowy termometr, działaja cy w zakresie do 7 mk. A.V. Feshchenko, L. Casparis,..., J.P. Pekola & D.M. Zumbühl, Phys. Rev. Appl. 4, (2015). T. Faivre, D.S. Golubev and J.P. Pekola, Appl. Phys. Lett. 106, (2015). Zalety urza dzenia: nie powoduje samo-ogrzewania działa w kriogenicznych temperaturach może termicznie monitorować kwantowe bit-y
133 Podsumowanie
134 Podsumowanie Nano-nadprzewodniki:
135 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości
136 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y)
137 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y) W obszarze miliwoltowych napie ć obserwujemy:
138 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y) W obszarze miliwoltowych napie ć obserwujemy: egzotyczne charakterystyki transportowe (np. ujemny opór)
139 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y) W obszarze miliwoltowych napie ć obserwujemy: egzotyczne charakterystyki transportowe (np. ujemny opór) separacje pra du ładunkowego od cieplnego
140 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y) W obszarze miliwoltowych napie ć obserwujemy: egzotyczne charakterystyki transportowe (np. ujemny opór) pra du ładunkowego od cieplnego separacje realizacje enigmatycznych kwazicza stek typu Majorany
141 Podsumowanie Nano-nadprzewodniki: można uzsykać poprzez efekt bliskości charakteryzuja sie kwazicza stkami Andreev a (Shib y) W obszarze miliwoltowych napie ć obserwujemy: egzotyczne charakterystyki transportowe (np. ujemny opór) pra du ładunkowego od cieplnego separacje realizacje enigmatycznych kwazicza stek typu Majorany
142 Stany spla tane elektronów rozbijanie par
143 Stany spla tane elektronów rozbijanie par Elektrony uwolniene z par Coopera zachowuja spla tanie kwantowe. L. Hofstetter, S. Csonka, J. Nygård, C. Schönenberger, Nature 461, 960 (2009).
144 Stany spla tane elektronów rozbijanie par Możliwe kanały de parowania. L.G. Herrmann et al, Phys. Rev. Lett. 104, (2010).
Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych
 LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach konwencjonalnych i topologicznych Tadeusz Domański Uniwersytet M. Curie-Skłodowskiej LTN - Lublin 29 XI 2018 r. Nadprzewodnictwo w materiałach
Lublin, 23 X 2012 r. Nadprzewodnictwo. - od badań podstawowych do zastosowań. Tadeusz Domański Instytut Fizyki UMCS
 Lublin, 23 X 2012 r. Nadprzewodnictwo - od badań podstawowych do zastosowań Tadeusz Domański Instytut Fizyki UMCS Lublin, 23 X 2012 r. Nadprzewodnictwo - od badań podstawowych do zastosowań Tadeusz Domański
Lublin, 23 X 2012 r. Nadprzewodnictwo - od badań podstawowych do zastosowań Tadeusz Domański Instytut Fizyki UMCS Lublin, 23 X 2012 r. Nadprzewodnictwo - od badań podstawowych do zastosowań Tadeusz Domański
Nadprzewodniki: właściwości i zastosowania
 Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania Tadeusz Domański Instytut Fizyki Uniwersytet M. Curie-Skłodowskiej Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania
Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania Tadeusz Domański Instytut Fizyki Uniwersytet M. Curie-Skłodowskiej Lublin, 21 września 2012 r. Nadprzewodniki: właściwości i zastosowania
Zamiast przewodnika z miedzi o bardzo dużych rozmiarach możemy zastosowad niewielki nadprzewodnik niobowo-tytanowy
 Nadprzewodniki Nadprzewodnictwo Nadprzewodnictwo stan materiału polegający na zerowej rezystancji, jest osiągany w niektórych materiałach w niskiej temperaturze. Nadprzewodnictwo zostało wykryte w 1911
Nadprzewodniki Nadprzewodnictwo Nadprzewodnictwo stan materiału polegający na zerowej rezystancji, jest osiągany w niektórych materiałach w niskiej temperaturze. Nadprzewodnictwo zostało wykryte w 1911
NADPRZEWODNIKI WYSOKOTEMPERATUROWE (NWT) W roku 1986 Alex Muller i Georg Bednorz odkryli. miedziowo-lantanowym, w którym niektóre atomy lantanu były
 FIZYKA I TECHNIKA NISKICH TEMPERATUR NADPRZEWODNICTWO NADPRZEWODNIKI WYSOKOTEMPERATUROWE (NWT) W roku 1986 Alex Muller i Georg Bednorz odkryli nadprzewodnictwo w złożonym tlenku La 2 CuO 4 (tlenku miedziowo-lantanowym,
FIZYKA I TECHNIKA NISKICH TEMPERATUR NADPRZEWODNICTWO NADPRZEWODNIKI WYSOKOTEMPERATUROWE (NWT) W roku 1986 Alex Muller i Georg Bednorz odkryli nadprzewodnictwo w złożonym tlenku La 2 CuO 4 (tlenku miedziowo-lantanowym,
Nadprzewodniki. W takich materiałach kiedy nastąpi przepływ prądu może on płynąć nawet bez przyłożonego napięcia przez długi czas! )Ba 2. Tl 0.2.
 Nadprzewodniki Pewna klasa materiałów wykazuje prawie zerową oporność (R=0) poniżej pewnej temperatury zwanej temperaturą krytyczną T c Większość przewodników wykazuje nadprzewodnictwo dopiero w temperaturze
Nadprzewodniki Pewna klasa materiałów wykazuje prawie zerową oporność (R=0) poniżej pewnej temperatury zwanej temperaturą krytyczną T c Większość przewodników wykazuje nadprzewodnictwo dopiero w temperaturze
Nadprzewodniki nowe fakty i teorie
 Warszawa, 13 września 2005 r. Nadprzewodniki nowe fakty i teorie T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Schemat referatu: Schemat referatu: Wste
Warszawa, 13 września 2005 r. Nadprzewodniki nowe fakty i teorie T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Schemat referatu: Schemat referatu: Wste
Nadprzewodnictwo i nadciekłość w układach oddziałuja. cych mieszanin bozonowo-fermionowych. Tadeusz Domański
 Toruń, 22 września 2006 r. Nadprzewodnictwo i nadciekłość w układach oddziałuja cych mieszanin bozonowo-fermionowych Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures
Toruń, 22 września 2006 r. Nadprzewodnictwo i nadciekłość w układach oddziałuja cych mieszanin bozonowo-fermionowych Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH
 Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Ciała stałe. Literatura: Halliday, Resnick, Walker, t. 5, rozdz. 42 Orear, t. 2, rozdz. 28 Young, Friedman, rozdz
 Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
S. Baran - Podstawy fizyki materii skondensowanej Nadprzewodnictwo. Nadprzewodnictwo
 Nadprzewodnictwo Definicja, odkrycie nadprzewodnictwo spadek oporu elektrycznego do zera poniżej charakterystycznej temperatury zwanej temperaturą krytyczną. Po raz pierwszy zaobserwował nadprzewodnictwo
Nadprzewodnictwo Definicja, odkrycie nadprzewodnictwo spadek oporu elektrycznego do zera poniżej charakterystycznej temperatury zwanej temperaturą krytyczną. Po raz pierwszy zaobserwował nadprzewodnictwo
Struktura elektronowa
 Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Nadpłynność i nadprzewodnictwo
 Nadpłynność i nadprzewodnictwo Krzysztof Byczuk Instytut Fizyki Teoretycznej, Wydział Fizyki, Uniwersytet Warszawski 13 marzec 2019 www.fuw.edu.pl/ byczuk Tarcie, opór, dysypacja... pomaga... przeszkadza...
Nadpłynność i nadprzewodnictwo Krzysztof Byczuk Instytut Fizyki Teoretycznej, Wydział Fizyki, Uniwersytet Warszawski 13 marzec 2019 www.fuw.edu.pl/ byczuk Tarcie, opór, dysypacja... pomaga... przeszkadza...
Kondensat Bosego-Einsteina okiem teoretyka
 Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
Kondensat Bosego-Einsteina okiem teoretyka Krzysztof Sacha Instytut Fizyki im. M. Smoluchowskiego, Uniwersytet Jagielloński Plan: Kondensacja Bosego-Einsteina. Teoretyczny opis kondensatu. Przyk lady.
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
LEWITACJA MAGNETYCZNA Z WYKORZYSTANIEM ZJAWISKA NADPRZEWODNICTWA
 LEWITACJA MAGNETYCZNA Z WYKORZYSTANIEM ZJAWISKA NADPRZEWODNICTWA Prof. nz. dr hab. inż. Antoni Cieśla, AKADEMIA GÓRNICZO - HUTNICZA Wydział EAIiIB Katedra Elektrotechniki i Elektroenergetyki Agenda wykładu:
LEWITACJA MAGNETYCZNA Z WYKORZYSTANIEM ZJAWISKA NADPRZEWODNICTWA Prof. nz. dr hab. inż. Antoni Cieśla, AKADEMIA GÓRNICZO - HUTNICZA Wydział EAIiIB Katedra Elektrotechniki i Elektroenergetyki Agenda wykładu:
Wybrane zastosowania nadprzewodników wysokotemperaturowych
 Wybrane zastosowania nadprzewodników wysokotemperaturowych Ryszard Pałka Department of Electrical Engineering West Pomeranian University of Technology Szczecin KETiI Zakres prezentacji 1. Wprowadzenie
Wybrane zastosowania nadprzewodników wysokotemperaturowych Ryszard Pałka Department of Electrical Engineering West Pomeranian University of Technology Szczecin KETiI Zakres prezentacji 1. Wprowadzenie
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie. Anna Rutkowska IMM sem. 2 mgr
 Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie Anna Rutkowska IMM sem. 2 mgr Gdańsk, 2012 Spis treści: 1. Nadprzewodnictwo...3 2. Efekt Meissnera...5 2.1 Lewitacja...5 3. Zastosowanie...6 3.1
Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie Anna Rutkowska IMM sem. 2 mgr Gdańsk, 2012 Spis treści: 1. Nadprzewodnictwo...3 2. Efekt Meissnera...5 2.1 Lewitacja...5 3. Zastosowanie...6 3.1
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
POLITECHNIKA GDAŃSKA NADPRZEWODNICTWO I EFEKT MEISSNERA
 POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY KATEDRA ENERGETYKI I APARATURY PRZEMYSŁOWEJ NADPRZEWODNICTWO I EFEKT MEISSNERA Katarzyna Mazur Inżynieria Mechaniczno-Medyczna Sem. 9 1. Przypomnienie istotnych
POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY KATEDRA ENERGETYKI I APARATURY PRZEMYSŁOWEJ NADPRZEWODNICTWO I EFEKT MEISSNERA Katarzyna Mazur Inżynieria Mechaniczno-Medyczna Sem. 9 1. Przypomnienie istotnych
Przyrządy i układy półprzewodnikowe
 Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
) (*#)$+$$ poniedziałki 13:30-15:00 wtorki 12:00-14:00 pitek 8:30-10:00
 poniedziałki 13:30-15:00 wtorki 12:00-14:00 pitek 8:30-10:00 8 wykładów, 3 wiczenia: w, w, w, w, c, w, w, c, w, w, c(kolo) kolokwium na ostatnich cw. historia zerowy opór efekt Meissnera temperatura, pole
poniedziałki 13:30-15:00 wtorki 12:00-14:00 pitek 8:30-10:00 8 wykładów, 3 wiczenia: w, w, w, w, c, w, w, c, w, w, c(kolo) kolokwium na ostatnich cw. historia zerowy opór efekt Meissnera temperatura, pole
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Najzimniejsze atomy. Tadeusz Domański. Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie.
 Odolanów, 10 lipca 2008 r. Najzimniejsze atomy Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman Referat be dzie dotyczyć : kondensacji i nadciekłości
Odolanów, 10 lipca 2008 r. Najzimniejsze atomy Tadeusz Domański Instytut Fizyki, Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman Referat be dzie dotyczyć : kondensacji i nadciekłości
Czym jest prąd elektryczny
 Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Nadprzewodnikowe zasobniki energii (SMES)
 Nadprzewodnikowe zasobniki energii (SMES) Superconducting Magnetic Energy Storage dr hab. inŝ. Antoni Cieśla, prof. n. Wydział EAIiE Katedra Elektrotechniki i Elektroenergetyki Agenda wystąpienia: 1. Gromadzenie
Nadprzewodnikowe zasobniki energii (SMES) Superconducting Magnetic Energy Storage dr hab. inŝ. Antoni Cieśla, prof. n. Wydział EAIiE Katedra Elektrotechniki i Elektroenergetyki Agenda wystąpienia: 1. Gromadzenie
Cel ćwiczenia: Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporności elektrycznej monokryształu germanu od temperatury.
 WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
WFiIS PRACOWNIA FIZYCZNA I i II Imię i nazwisko: 1. 2. TEMAT: ROK GRUPA ZESPÓŁ NR ĆWICZENIA Data wykonania: Data oddania: Zwrot do poprawy: Data oddania: Data zliczenia: OCENA Cel ćwiczenia: Wyznaczenie
Konwersatorium 1. Zagadnienia na konwersatorium
 Konwersatorium 1 Zagadnienia na konwersatorium 1. Omów reguły zapełniania powłok elektronowych. 2. Podaj konfiguracje elektronowe dla atomów Cu, Ag, Au, Pd, Pt, Cr, Mo, W. 3. Wyjaśnij dlaczego występują
Konwersatorium 1 Zagadnienia na konwersatorium 1. Omów reguły zapełniania powłok elektronowych. 2. Podaj konfiguracje elektronowe dla atomów Cu, Ag, Au, Pd, Pt, Cr, Mo, W. 3. Wyjaśnij dlaczego występują
Wykład 21: Studnie i bariery cz.2.
 Wykład 21: Studnie i bariery cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Przykłady tunelowania: rozpad alfa, synteza
Wykład 21: Studnie i bariery cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Przykłady tunelowania: rozpad alfa, synteza
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Przyrządy półprzewodnikowe
 Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
Przyrządy półprzewodnikowe Prof. Zbigniew Lisik Katedra Przyrządów Półprzewodnikowych i Optoelektronicznych pokój: 116 e-mail: zbigniew.lisik@p.lodz.pl wykład 30 godz. laboratorium 30 godz WEEIiA E&T Metal
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Fizyka Laserów wykład 10. Czesław Radzewicz
 Fizyka Laserów wykład 10 Czesław Radzewicz Struktura energetyczna półprzewodników Regularna budowa kryształu okresowy potencjał Funkcja falowa elektronu. konsekwencje: E ψ r pasmo przewodnictwa = u r e
Fizyka Laserów wykład 10 Czesław Radzewicz Struktura energetyczna półprzewodników Regularna budowa kryształu okresowy potencjał Funkcja falowa elektronu. konsekwencje: E ψ r pasmo przewodnictwa = u r e
Kwazicza stki Bogoliubova w nadprzewodnikach
 Lublin, 20 stycznia 2009 r. Kwazicza stki Bogoliubova w nadprzewodnikach TADEUSZ DOMAŃSKI http://kft.umcs.lublin.pl/doman/lectures Plan referatu: Plan referatu: Wprowadzenie / istota stanu nadprzewodza
Lublin, 20 stycznia 2009 r. Kwazicza stki Bogoliubova w nadprzewodnikach TADEUSZ DOMAŃSKI http://kft.umcs.lublin.pl/doman/lectures Plan referatu: Plan referatu: Wprowadzenie / istota stanu nadprzewodza
WŁAŚCIWOŚCI ELEKTRYCZNE. Oddziaływanie pola elektrycznego na materiał. Przewodnictwo elektryczne. Podstawy Nauki o Materiałach
 Podstawy Nauki o Materiałach WŁAŚCIWOŚCI ELEKTRYCZNE Oddziaływanie pola elektrycznego na materiał Pole elektromagnetyczne MATERIAŁ Przepływ prądu Polaryzacja Odkształcenie Namagnesowanie... Przepływ prądu
Podstawy Nauki o Materiałach WŁAŚCIWOŚCI ELEKTRYCZNE Oddziaływanie pola elektrycznego na materiał Pole elektromagnetyczne MATERIAŁ Przepływ prądu Polaryzacja Odkształcenie Namagnesowanie... Przepływ prądu
Pierwiastki nadprzewodzące
 Pierwiastki nadprzewodzące http://www.magnet.fsu.edu/education/tutorials/magnetacademy/superconductivity101/fullarticle.html Materiały nadprzewodzące Rodzaj Materiał c (K) Uwagi Związki międzymetaliczne
Pierwiastki nadprzewodzące http://www.magnet.fsu.edu/education/tutorials/magnetacademy/superconductivity101/fullarticle.html Materiały nadprzewodzące Rodzaj Materiał c (K) Uwagi Związki międzymetaliczne
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY
 POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY Techniki niskotemperaturowe w Inżynierii Mechaniczno Medycznej Zmiana własności ciał w temperaturach kriogenicznych Prowadzący: dr inż. Waldemar Targański Emilia
POLITECHNIKA GDAŃSKA WYDZIAŁ MECHANICZNY Techniki niskotemperaturowe w Inżynierii Mechaniczno Medycznej Zmiana własności ciał w temperaturach kriogenicznych Prowadzący: dr inż. Waldemar Targański Emilia
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Podstawy fizyki wykład 4
 D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
Wykład 12 V = 4 km/s E 0 =.08 e V e = = 1 Å
 Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Nadprzewodniki wysokotemperaturowe. Zastosowania nadprzewodników starych i nowych. Koniec odkryć?
 Nadprzewodniki wysokotemperaturowe. Zastosowania nadprzewodników starych i nowych. Koniec odkryć? 1 Główne nadprzewodniki Compound wysokotemperaturowe:t c T b liquid nitrogen Hg-1223 Tl-2223 Tl-1223 Bi-2223
Nadprzewodniki wysokotemperaturowe. Zastosowania nadprzewodników starych i nowych. Koniec odkryć? 1 Główne nadprzewodniki Compound wysokotemperaturowe:t c T b liquid nitrogen Hg-1223 Tl-2223 Tl-1223 Bi-2223
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru
 Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Duży, mały i zerowy opór. Od czego zależy, czy materiał przewodzi prąd?
 Duży, mały i zerowy opór Od czego zależy, czy materiał przewodzi prąd? 2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning is a trademark used herein under license. Page 1 Przewodnictwo
Duży, mały i zerowy opór Od czego zależy, czy materiał przewodzi prąd? 2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning is a trademark used herein under license. Page 1 Przewodnictwo
Badanie charakterystyki diody
 Badanie charakterystyki diody Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk prądowo napięciowych różnych diod półprzewodnikowych. Wstęp Dioda jest jednym z podstawowych elementów elektronicznych,
Badanie charakterystyki diody Cel ćwiczenia Celem ćwiczenia jest poznanie charakterystyk prądowo napięciowych różnych diod półprzewodnikowych. Wstęp Dioda jest jednym z podstawowych elementów elektronicznych,
Nagrody Nobla z dziedziny fizyki ciała. Natalia Marczak Fizyka Stosowana, semestr VII
 Nagrody Nobla z dziedziny fizyki ciała stałego Natalia Marczak Fizyka Stosowana, semestr VII Zaczęł ęło o się od Alfred Bernhard Nobel (1833 1896) Nadprzewodnictwo Kamerlingh-Onnes Heike (1853-1926) 1926)
Nagrody Nobla z dziedziny fizyki ciała stałego Natalia Marczak Fizyka Stosowana, semestr VII Zaczęł ęło o się od Alfred Bernhard Nobel (1833 1896) Nadprzewodnictwo Kamerlingh-Onnes Heike (1853-1926) 1926)
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
Repeta z wykładu nr 5. Detekcja światła. Plan na dzisiaj. Złącze p-n. złącze p-n
 Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 5 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Cia!a sta!e. W!asno"ci elektryczne cia! sta!ych. Inne w!asno"ci
 Cia!a sta!e Podstawowe w!asno"ci cia! sta!ych Struktura cia! sta!ych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencja! kontaktowy
Cia!a sta!e Podstawowe w!asno"ci cia! sta!ych Struktura cia! sta!ych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencja! kontaktowy
Proste struktury krystaliczne
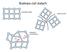 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Nadprzewodniki wysokotemperatu rowe. I nie tylko.
 Nadprzewodniki wysokotemperatu rowe. I nie tylko. Odkrycie nadprzewodnictwa: H. Kamerlingh Onnes (1911) Table from Burns Pierwiastki Li: pierwiastek o najwyższej T c K. Shimizu et al., Nature 419, 597
Nadprzewodniki wysokotemperatu rowe. I nie tylko. Odkrycie nadprzewodnictwa: H. Kamerlingh Onnes (1911) Table from Burns Pierwiastki Li: pierwiastek o najwyższej T c K. Shimizu et al., Nature 419, 597
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych komputera kwantowego
 Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
W1. Właściwości elektryczne ciał stałych
 W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
W1. Właściwości elektryczne ciał stałych Względna zmiana oporu właściwego przy wzroście temperatury o 1 0 C Materiał Opór właściwy [m] miedź 1.68*10-8 0.0061 żelazo 9.61*10-8 0.0065 węgiel (grafit) 3-60*10-3
dr inż. Beata Brożek-Pluska SERS La boratorium La serowej
 dr inż. Beata Brożek-Pluska La boratorium La serowej Spektroskopii Molekularnej PŁ Powierzchniowo wzmocniona sp ektroskopia Ramana (Surface Enhanced Raman Spectroscopy) Cząsteczki zaadsorbowane na chropowatych
dr inż. Beata Brożek-Pluska La boratorium La serowej Spektroskopii Molekularnej PŁ Powierzchniowo wzmocniona sp ektroskopia Ramana (Surface Enhanced Raman Spectroscopy) Cząsteczki zaadsorbowane na chropowatych
Nanofizyka co wiemy, a czego jeszcze szukamy?
 Nanofizyka co wiemy, a czego jeszcze szukamy? Maciej Maśka Zakład Fizyki Teoretycznej UŚ Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ...czyli dlaczego NANO
Nanofizyka co wiemy, a czego jeszcze szukamy? Maciej Maśka Zakład Fizyki Teoretycznej UŚ Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ...czyli dlaczego NANO
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Wzrost pseudomorficzny. Optyka nanostruktur. Mody wzrostu. Ekscyton. Sebastian Maćkowski
 Wzrost pseudomorficzny Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 naprężenie
Wzrost pseudomorficzny Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 naprężenie
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
Nadprzewodniki wysokotemperaturowe. Joanna Mieczkowska
 Nadprzewodniki wysokotemperaturowe Joanna Mieczkowska Zastosowanie nadprzewodnictwa na szeroką skalę, szczególnie do przesyłania energii na duże odległości, było dotychczas ograniczone z powodu konieczności
Nadprzewodniki wysokotemperaturowe Joanna Mieczkowska Zastosowanie nadprzewodnictwa na szeroką skalę, szczególnie do przesyłania energii na duże odległości, było dotychczas ograniczone z powodu konieczności
Domieszki w półprzewodnikach
 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Układ SI. Nazwa Symbol Uwagi. Odległość jaką pokonujeświatło w próżni w czasie 1/ s
 Układ SI Wielkość Nazwa Symbol Uwagi Długość metr m Masa kilogram kg Czas sekunda s Odległość jaką pokonujeświatło w próżni w czasie 1/299 792 458 s Masa walca wykonanego ze stopu platyny z irydem przechowywanym
Układ SI Wielkość Nazwa Symbol Uwagi Długość metr m Masa kilogram kg Czas sekunda s Odległość jaką pokonujeświatło w próżni w czasie 1/299 792 458 s Masa walca wykonanego ze stopu platyny z irydem przechowywanym
Spektroskopia modulacyjna
 Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Spektroskopia modulacyjna pozwala na otrzymanie energii przejść optycznych w strukturze z bardzo dużą dokładnością. Charakteryzuje się również wysoką czułością, co pozwala na obserwację słabych przejść,
Lublin, 7 VI ultrazimnych atomów. T. Domański. Instytut Fizyki UMCS.
 Lublin, 7 VI 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Tematem tego Sympozjum sa różne zjawiska fizyczne, które maja miejsce
Lublin, 7 VI 2006 Nadciekłość w układach ultrazimnych atomów T. Domański Instytut Fizyki UMCS http://kft.umcs.lublin.pl/doman/lectures Tematem tego Sympozjum sa różne zjawiska fizyczne, które maja miejsce
Teoria pasmowa. Anna Pietnoczka
 Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Teoria pasmowa Anna Pietnoczka Opis struktury pasmowej we współrzędnych r, E Zmiana stanu elektronów przy zbliżeniu się atomów: (a) schemat energetyczny dla atomów sodu znajdujących się w odległościach
Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie.
 Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie. Aleksandra Galikowska IMM, sem.2, st.ii Spis treści 1. Wstęp, historia... 3 2. Nadprzewodnictwo... 4 3. Własności nadprzewodników... 5 3. Teoria
Nadprzewodnictwo i efekt Meissnera oraz ich wykorzystanie. Aleksandra Galikowska IMM, sem.2, st.ii Spis treści 1. Wstęp, historia... 3 2. Nadprzewodnictwo... 4 3. Własności nadprzewodników... 5 3. Teoria
Struktura pasmowa ciał stałych
 Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Struktura pasmowa ciał stałych dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Spis treści 1. Pasmowa teoria ciała stałego 2 1.1. Wstęp do teorii..............................................
Zastosowanie sieci tensorowych w obliczeniach procedurą numerycznej grupy renormalizacji
 Zastosowanie sieci tensorowych w obliczeniach procedurą numerycznej grupy renormalizacji Kacper Wrześniewski, Ireneusz Weymann 23 maja 2017 Wydział Fizyki, Uniwersytet im. Adama Mickiewicza w Poznaniu
Zastosowanie sieci tensorowych w obliczeniach procedurą numerycznej grupy renormalizacji Kacper Wrześniewski, Ireneusz Weymann 23 maja 2017 Wydział Fizyki, Uniwersytet im. Adama Mickiewicza w Poznaniu
3.4 Badanie charakterystyk tranzystora(e17)
 152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
152 Elektryczność 3.4 Badanie charakterystyk tranzystora(e17) Celem ćwiczenia jest wyznaczenie charakterystyk tranzystora npn w układzie ze wspólnym emiterem W E. Zagadnienia do przygotowania: półprzewodniki,
Elektryczne właściwości materii. Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej.
 Elektryczne właściwości materii Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki I
Elektryczne właściwości materii Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki I
Podstawy fizyki ciała stałego półprzewodniki domieszkowane
 Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman ( ) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd.
 Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
XII. NANOSTRUKTURY PÓŁPRZEWODNIKOWE Janusz Adamowski
 XII. NANOSTRUKTURY PÓŁPRZEWODNIKOWE Janusz Adamowski 1 1 Wstęp Na wykładzie tym zostaną omówione dwa typy nanostruktur półprzewodnikowych: (1) kropki kwantowe, (2) druty kwantowe (nanodruty). 2 Wprowadzenie
XII. NANOSTRUKTURY PÓŁPRZEWODNIKOWE Janusz Adamowski 1 1 Wstęp Na wykładzie tym zostaną omówione dwa typy nanostruktur półprzewodnikowych: (1) kropki kwantowe, (2) druty kwantowe (nanodruty). 2 Wprowadzenie
Inne koncepcje wiązań chemicznych. 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań?
 Inne koncepcje wiązań chemicznych 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań? Model VSEPR wiązanie pary elektronowe dzielone między atomy tworzące wiązanie.
Inne koncepcje wiązań chemicznych 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań? Model VSEPR wiązanie pary elektronowe dzielone między atomy tworzące wiązanie.
Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC
 Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC J. Łażewski, M. Sternik, P.T. Jochym, P. Piekarz politypy węglika krzemu SiC >250 politypów, najbardziej stabilne: 3C, 2H, 4H i 6H
Wpływ defektów punktowych i liniowych na własności węglika krzemu SiC J. Łażewski, M. Sternik, P.T. Jochym, P. Piekarz politypy węglika krzemu SiC >250 politypów, najbardziej stabilne: 3C, 2H, 4H i 6H
Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
 Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
Półprzewodniki i elementy z półprzewodników homogenicznych Ryszard J. Barczyński, 2012 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Publikacja
N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji
 Katowice, 12 listopada 2008 r. N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Plan referatu:
Katowice, 12 listopada 2008 r. N a d p r z e w o d n i c t w o - przegla d faktów i koncepcji T. DOMAŃSKI Uniwersytet M. Curie-Skłodowskiej w Lublinie http://kft.umcs.lublin.pl/doman/lectures Plan referatu:
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 13 Janusz Andrzejewski Scaledlugości Janusz Andrzejewski 2 Scaledługości Simple molecules
Fizyka 2 wykład 13 Janusz Andrzejewski Scaledlugości Janusz Andrzejewski 2 Scaledługości Simple molecules
Stara i nowa teoria kwantowa
 Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Stara i nowa teoria kwantowa Braki teorii Bohra: - podane jedynie położenia linii, brak natężeń -nie tłumaczy ilości elektronów na poszczególnych orbitach - model działa gorzej dla atomów z więcej niż
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie. Co to jest ekscyton? Co to jest ekscyton? e πε. E = n. Sebastian Maćkowski
 Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Co to jest ekscyton? Co to jest ekscyton? h 2 2 2 e πε m* 4 0ε s Φ
Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Co to jest ekscyton? Co to jest ekscyton? h 2 2 2 e πε m* 4 0ε s Φ
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Laboratorium z Konwersji Energii. Ogniwo fotowoltaiczne
 Laboratorium z Konwersji Energii Ogniwo fotowoltaiczne 1.0 WSTĘP Energia słoneczna jest energią reakcji termojądrowych zachodzących w olbrzymiej odległości od Ziemi. Zachodzące na Słońcu przemiany helu
Laboratorium z Konwersji Energii Ogniwo fotowoltaiczne 1.0 WSTĘP Energia słoneczna jest energią reakcji termojądrowych zachodzących w olbrzymiej odległości od Ziemi. Zachodzące na Słońcu przemiany helu
Studnia kwantowa. Optyka nanostruktur. Studnia kwantowa. Gęstość stanów. Sebastian Maćkowski
 Studnia kwantowa Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Studnia kwantowa
Studnia kwantowa Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Studnia kwantowa
Repeta z wykładu nr 8. Detekcja światła. Przypomnienie. Efekt fotoelektryczny
 Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne
 Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
Zjawiska zachodzące w półprzewodnikach Przewodniki samoistne i niesamoistne Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego. Zadania elektroniki: Urządzenia elektroniczne
