Martyngały a rynki finansowe
|
|
|
- Rafał Klimek
- 8 lat temu
- Przeglądów:
Transkrypt
1 Jest to zapis odczytu wygłoszonego na XXXIII Szkole Matematyki Poglądowej Metody klasyczne i współczesne, sierpień Martyngały a rynki finansowe Jacek JAKUBOWSKI, Warszawa 1. Okazuje się, że teoria martyngałów część teorii procesów stochastycznych jest podstawowym narzędziem we współczesnej matematyce finansowej. Celem tego artykułu jest przedstawienie podstawowych idei prowadzących do tego związku. Aby uniknąć trudności technicznych ograniczę się do najprostszego przypadku tj. przypadku dyskretnej i skończonej przestrzeni probabilistycznej (Ω, M, P). Zacznę od opisu klasycznego zadania hazardu (gra w orła i reszkę ), przypomnę co to jest warunkowa wartość oczekiwana, wprowadzę pojęcie martyngału, a skończę na zagadnieniach wyceny pewnych aktywów (instrumentów pochodnych) na rynkach finansowych (dla niektórych gra na giełdzie to nieklasyczny hazard). 2. Rozważmy najprostszą sytuację gry w orła i reszkę. Gracze A i B grają rzucając symetryczną monetą. W pojedynczej kolejce gracz wygrywa 1 zł z prawdopodobieństwem 1/2 i przegrywa 1 zł z prawdopodobieństwem 1/2. Zasadniczo gra kończy się, gdy jeden z graczy zostanie zrujnowany. Gracze mogą jednak umówić się inaczej (np. wycofywać się z gry w dogodnym dla siebie momencie). Wyniki poszczególnych kolejek są niezależne, zatem wygrane pierwszego gracza w kolejnych partiach są niezależnymi zmiennymi losowymi ξ 1,..., ξ n,..., przy czym P(ξ i = 1) = 1/2 = P(ξ i = 1). Korzystając z metod rachunku prawdopodobieństwa można zbadać tę grę (znaleźć szansę wygrania ustalonej kwoty, szansę przegrania całego kapitału czyli ruiny, szansę wygrania k zł nim przegramy n zł itp.). Wygrana gracza A po n grach jest równa sumie wygranych w pojedynczych kolejkach: S n = ξ ξ n. Przy badaniu zachowania ciągu zmiennych losowych (S n ) n wykorzystuje się związek S n+1 = S n + ξ n+1, zatem do S n dodajemy niezależną od S n zmienną losową ξ n+1 o średniej zero, czyli intuicyjnie: jeśli znamy S n (np. jest równe 7), to S n+1 daje średnio to samo (formalnie E(S n+1 S n = 7) = 7). Ta własność jest bardzo przydatna przy badaniu ciągu (S n ) n. Warto wykorzystać to spostrzeżenie i uogólnić rozumowanie, aby móc stosować teorię do szerszej klasy zagadnień np. zagadnienia ruiny przy osłabionych założeniach o grze. Chcemy pozbyć się założenia o niezależności zmiennych losowych ξ i zachowując własność uśrednienia tzn. własność E(S n+1 S n = k) = k. W następnym punkcie zajmiemy się formalnym opisem takiego uogólnienia. 3. Jeśli dysponujemy jakąś cząstkową wiedzą o zjawisku, np. wiemy, że zaszło zdarzenie A (P(A) > 0), to mamy do czynienia z prawdopodobieństwem warunkowym P( A) (dla przypomnienia P(B A) = P(A B)/P(A)). Przy ustalonym A, funkcja B P(B A) jest rozkładem prawdopodobieństwa na M, który będziemy oznaczać P A. Dla zmiennej losowej X możemy mówić o rozkładzie warunkowym X, gdy wiemy, że zaszło zdarzenie A, tzn. o P A (X = x i ) = P(X = x i A) dla wszystkich wartości x i, i = 1,...,k przyjmowanych przez zmienną losową X. Rozpatrujemy także wartość oczekiwaną zmiennej losowej X, gdy wiemy, że zaszło A tzn. E(X A) = k x i P(X = x i A) i=1 Jest to klasyczna definicja wartości oczekiwanej zmiennej losowej X względem rozkładu prawdopodobieństwa P A. Stąd oznaczenie E(X A) i interpretacja jako 13
2 wartości średniej X, gdy wiemy, że zaszło zdarzenie A. Wielkość tę możemy wyrazić za pomocą wyjściowego rozkładu prawdopodobieństwa P, a mianowicie E(X A) = 1 X(ω) P(ω). P(A) ω A Zawsze zachodzi jedno ze zdarzeń A lub A = Ω \ A. Stąd dla rozbicia F = {A, A } przestrzeni Ω możemy zdefiniować nową zmienną losową: E(X F)(ω) przyjmującą wartość E(X A), gdy ω A oraz równą E(X A ), gdy ω A. Przykład 1. Niech X będzie liczbą orłów otrzymaną przy trzykrotnym rzucie symetryczną monetą, natomiast A zdarzeniem polegającym na wypadnięciu reszki w pierwszym rzucie. Wtedy dla rozbicia F = {A, A } { 1, ω A, E(X F) = 2, ω A. Ta idea w naturalny sposób przenosi się na rozbicie skończone. Niech Ω = l i=1 A i, gdzie zdarzenia A i są parami rozłączne i mają dodatnie prawdopodobieństwa. Wtedy F = {A 1,...,A l } jest rozbiciem przestrzeni Ω. Definicja 1. Warunkową wartością oczekiwaną X pod warunkiem rozbicia F = {A 1,...,A l } będziemy nazywać zmienną losową E(X F)(ω) = l E(X A j )1 Aj (ω) j=1 tzn. E(X F)(ω) jest równe E(X A j ), gdy ω A j. Tak zdefiniowana warunkowa wartość oczekiwana jest uśrednieniem X na elementach rozbicia tzn. jest stała na elementach rozbicia i na każdym z nich ta stała jest równa średniej wartości X na nim. Wymienimy teraz kilka podstawowych własności warunkowej wartości oczekiwanej względem rozbicia F: i) Jeśli X jest stała na zbiorach A i, to E(X F) = X. ii) Jeśli X 0, to E(X F) 0. iii) E(αX 1 + βx 2 F) = αe(x 1 F) + βe(x 2 F) dla α, β R. iv) EX = E(E(X F)). v) Jeśli F i X są niezależne (tzn. P(X = x i A j ) = P(X = x i )P(A j ) dla każdych i, j), to E(X F) = EX. W dalszym ciągu σ(x) będzie oznaczać rozbicie Ω generowane przez zmienną losową X tzn. σ(x) = {{X = x 1 },...,{X = x k }} i analogicznie σ(x 1,...,X n ) = {{X 1 = x 1 }... {X n = x n } : x i X i (Ω), i = 1,...,n}. Przykład 2. Gdy X 1,...,X 10 są niezależnymi zmiennymi losowymi o średniej zero, to korzystając z własności warunkowej wartości oczekiwanej otrzymujemy E(X X 10 σ(x 1,...,X 4 )) = X X 4 + E(X X 10 ) = X X 4. Definicja 2. Mówimy, że ciąg zmiennych losowych X n jest martyngałem, jeśli E(X n+1 F n ) = X n dla wszystkich n, gdzie F n = σ(x 1,...,X n ). Warto zauważyć, że dla martyngału zachodzi EX n = EX 1, czyli wartość średnia zmiennych losowych tworzących martyngał jest stała. Przykład 3. Niech X n = ξ ξ n, gdzie ξ i są niezależnymi zmiennymi losowymi takimi, że Eξ i = 0, i = 1, Wtedy E(X n+1 F n ) = X n + E(ξ n+1 F n ) = X n + E(ξ n+1 ) = X n, zatem(x n ) n=1 jest martyngałem. 14
3 Stąd sumy X n niezależnych zmiennych losowych o średniej zero są szczególnym przypadkiem martyngału. Czyli własność prawdziwa dla martyngałów jest prawdziwa i dla takich sum. W szczególności błądzenia przypadkowe, grę w orła i reszkę opisaną w punkcie 2 itp. można badać korzystając z tego, że tworzą one martyngał. Jednocześnie pojęcie martyngału jest pojęciem ogólniejszym od pojęcia sumy niezależnych zmiennych losowych o średniej zero. Przykład 4. (Model Pólyi) Urna zawiera b 0 białych i c 0 czarnych kul (b 0, c 0 1). Losujemy kulę z urny, zwracamy ją i dokładamy m kul tego samego koloru. Niech b n, c n oznaczają liczbę kul białych i czarnych po n-tym losowaniu. Definiujemy X n = c n /(b n + c n ) jest to ułamek kul czarnych w urnie po n-tym losowaniu, n = 0, 1, 2,.... Okazuje się, że (X n ) n=0 jest martyngałem (patrz np. [4]). 4. Rozważmy najprostszy model rynku finansowego rynek jednookresowy dwustanowy. Na tym rynku zilustrujemy najważniejsze pojęcia matematyki finansowej. Na rynku jednookresowym dwustanowym transakcje odbywają się w dwu chwilach czasu: chwili 0 i chwili T. Przyjmujemy także założenie, że rynek jest rynkiem idealnym tzn. oprocentowanie kredytów i depozytów bankowych jest jednakowe, inwestorzy nie ponoszą żadnych kosztów, tzn. kosztów transakcji, kosztów prowizji, nie płacą podatków itp., nie ma ograniczeń w dostępie do kredytów oraz rynek jest płynny, tzn. możemy kupić lub sprzedać dowolną liczbę aktywów. Założymy także, że są możliwe dwa scenariusze wypadków, zatem przestrzeń zdarzeń elementarnych to Ω = {ω 1, ω 2 }, przy czym ω 1 oznacza sytuację interpretowaną jako korzystna, zaś ω 2 jako niekorzystna, a prawdopodobieństwo P jest takie, że P({ω 1 }) = p > 0, P({ω 2 }) = 1 p > 0. Przyjmujemy, że na tym rynku istnieją dwa papiery wartościowe: jeden ryzykowny (np. akcje) i drugi pozbawiony ryzyka inwestycja polegająca na włożeniu pieniędzy na rachunek bankowy. Są to instrumenty bazowe na tym rynku. Niech: S t oznacza cenę papieru ryzykownego (za jedną jednostkę) w chwili t, B t oznacza cenę papieru bez ryzyka (za jedną jednostkę) w chwili t, gdzie t {0, T }. Zakładamy, że stopa procentowa jest stała i wynosi r w okresie czasu od 0 do T. Zatem w naszym przypadku mamy Natomiast (1) S 0 = s, S T (ω) = B 0 = 1, B T = 1 + r. { S u, gdy ω = ω 1, S d, gdy ω = ω 2, bo zmienna losowa S T przyjmuje dwie wartości, gdyż mamy do czynienia z dwoma scenariuszami. Możemy bez starty ogólności przyjąć, że S u > S d (dlatego ω 1 nazwaliśmy scenariuszem korzystnym). Cenę S T możemy też zapisać w innej postaci: (2) S T = S 0 Z = sz, gdzie zmienna losowa Z(ω) = { u, gdy ω = ω 1, d, gdy ω = ω 2, wskazuje, o ile procent zmieniła się cena początkowa. Na rynku istnieje wiele instrumentów pochodnych, tzn. takich, których cena zależy od cen aktywów podstawowych. Przykładem takiego instrumentu jest europejska opcja kupna. Posiadacz takiej opcji ma prawo (i nie jest to obowiązek) do kupienia określonego w umowie aktywa w ustalonej chwili T za ustaloną z góry cenę K. Zatem, gdy mu się to opłaca, realizuje swoje prawo 15
4 i zyskuje S T K, a gdy mu się nie opłaca, nie robi nic. W rezultacie otrzymuje wypłatę (S T K) +. Nie tylko europejską opcję kupna, ale każde aktywo pochodne można utożsamiać z wypłatą X generowaną przez to aktywo. Wypłata X zależy od scenariusza, więc jest zmienną losową określoną na Ω. Wiemy, ile można uzyskać posiadając europejską opcję kupna. Powstaje pytanie, ile za opcje powinniśmy zapłacić (jest to problem wyceny opcji). Pierwsza próba wyceny kontraktu związana jest z zastosowaniem metod wykorzystywanych m.in. w matematyce ubezpieczeniowej. Przykład 5. Aktywo ryzykowne kosztuje S 0 = 1 w chwili t = 0. Zakładamy, że możliwe (i równo prawdopodobne) są dwa scenariusze wydarzeń do chwili T i cena aktywa ryzykownego w chwili T = 1 wynosi S 1 (ω 1 ) = 7 lub S 1 (ω 2 ) = 1. Wiemy także, że cena aktywa bez ryzyka wynosi B 0 = 1 na początku okresu i B 1 = 2 na końcu. Interesuje nas, jak wycenić opcję kupna dającą wypłatę końcową C 1 = (S 1 K) +, gdy K = 3. Korzystając z metod z matematyki ubezpieczeniowej przypuszczamy, że cena ta jest wartością obecną opcji, a tę liczymy jako zdyskontowaną wartość oczekiwaną wypłaty. Wobec tego cena opcji C 0 jest równa C 0 = B 0 E(C 1 ) = 1 [0, , 5 0] = 1, B 1 2 ponieważ C 1 (ω 1 ) = 4, C 1 (ω 2 ) = 0. Tak liczona cena opcji jest równa 1, ale nikt rozsądny nie będzie kupował opcji za cenę równą 1, gdyż lepiej kupić za tę cenę akcję. Wynika to z faktu, że gdy cena akcji wzrośnie to akcja jest warta 7, a opcja daje wypłatę 4, a gdy cena akcji się nie zmieni to akcja jest warta 1, a opcja jest bezwartościowa. Akcja daje zawsze większy zysk niż opcja. Tu oczywiście widać, że tak wyznaczona cena zależy od wyboru prawdopodobieństwa P, zatem od oszacowania rynku przez inwestora. Gdy dla innego inwestora oszacowanie szans zmian na rynku P jest inne, to i wartość zdyskontowana wypłaty będzie inna. Zatem mamy drugi argument przemawiający za tym, że wielkości obliczonej według powyższego sposobu nie można przyjąć za cenę opcji. Taki model nie spełniałby podstawowego wymogu jedyności ceny aktywa pochodnego. Okazuje się, że można dobrze wycenić wypłatę korzystając z idei portfela replikującego. Portfel ϕ = (α 0, β 0 ) jest to para liczb, gdzie α 0 jest liczbą posiadanych akcji w chwili zero, zaś β 0 jest wysokością wkładu bankowego (ewentualnie wielkością kredytu, gdy β 0 < 0) w chwili zero. Dla przykładu, portfel (7, 3) oznacza, że w portfelu jest siedem akcji, tzn. inwestor kupił 7 akcji i pożyczył 3 jednostki z banku. Każda para (α, β) R 2 tworzy portfel, co odzwierciedla fakt, że można handlować dowolną liczbą aktywów, dopuszczenie wartości ujemnych β oznacza, że możemy dowolnie dużo pożyczać, a dopuszczenie wartości ujemnych α oznacza, że rynek ten dopuszcza także krótką sprzedaż akcji. Krótka sprzedaż polega na pożyczeniu i sprzedaży akcji w chwili 0 oraz odkupieniu tej samej liczby akcji i ich zwrocie w chwili T. Zbiór wszystkich możliwych portfeli oznaczać będziemy przez Φ. W modelu, który przyjęliśmy, Φ = R 2. Niech ϕ = (α 0, β 0 ) będzie portfelem inwestora, który sprzedał wypłatę X. Wartość portfela V t (ϕ) w chwili t wynosi dla t = 0 i t = T, odpowiednio: V 0 (ϕ) = α 0 S 0 + β 0, V T (ϕ) = α 0 S T + β 0 (1 + r). Tak jest, gdyż portfel ustaliliśmy w chwili t = 0 i nie ulega on zmianie do chwili T. Inwestor sprzedający wypłatę X musi umieć ją zabezpieczyć tzn. wartość portfela ϕ, który zbudował sprzedający wypłatę za otrzymane ze sprzedaży pieniądze, musi w chwili T być równa X, czyli portfel ϕ musi replikować wypłatę X: V T (ϕ)(ω i ) = X(ω i ) dla i = 1, 2. Portfel ϕ jest doskonałym zabezpieczeniem wypłaty X, gdyż eliminuje całkowicie ryzyko. Na pytanie dla jakich wypłat istnieje portfel replikujący odpowiada 16
5 Twierdzenie 1. Dla każdej wypłaty istnieje dokładnie jeden portfel replikujący. Dla wypłaty X ma on postać (3) α 0 = Xu X d S u S d, β 0 = Xd S u X u S d (1 + r)(s u S d ), gdzie X u = X(ω 1 ), X d = X(ω 2 ). Dowód. Portfel replikujący ϕ = (α 0, β 0 ) dla wypłaty X jest zadany przez układ równości α 0 S u + (1 + r)β 0 = X u, α 0 S d + (1 + r)β 0 = X d i ma dokładnie jedno rozwiązanie dane wzorem (3) dla dowolnych X u, X d, zatem dla dowolnej wypłaty portfel jest wyznaczony jednoznacznie. Naturalne jest zdefiniowanie racjonalnej ceny wypłaty X jako początkowej inwestycji potrzebnej do konstrukcji portfela replikującego, tzn. (4) Π 0 (X) def = V 0 (ϕ), gdzie ϕ jest portfelem replikującym. Z tej definicji wynika, że racjonalna cena wypłaty nie zależy od subiektywnych prawdopodobieństw zmian cen akcji, tzn. nie zależy od prawdopodobieństwa P. Korzystając z tw. 1 otrzymujemy, że cena racjonalna wypłaty X jest równa (5) Π 0 (X) = α 0 S 0 + β 0 = Xu X d S u S d S 0 + Xd S u X u S d (1 + r)(s u S d ). Przykład 6. Wycenimy opcję z przykładu 5. Portfel ϕ = (α, β) jest portfelem replikującym, gdy 7α + 2β = 4, α + 2β = 0. Ten układ równań ma dokładnie jedno rozwiązanie: α = 2/3, β = 1/3. Stąd C 0 = V 0 (ϕ) = 2/3 1/3 = 1/3. Znając skład portfela replikującego wystawca opcji wie, jak wygenerować wielkość (S T K) + w chwili T, dysponując zapłatą za opcję. Zatem potrafi rozwiązać problem zabezpieczenia wypłaty (drugi podstawowy problem matematyki finansowej dalej tym problemem w tym artykule nie będziemy się zajmować). Powyższy model rynku trzeba jeszcze poprawić, gdyż dopuszcza on sytuację, że dla dodatniej wypłaty X > 0 może okazać się, że jej cena jest ujemna, czyli Π 0 (X) < 0. W takim przypadku można by osiągnąć zysk bez ryzyka przy pomocy odpowiedniej strategii. Przykład 7. Gdy S 0 = 10, S d = 12, S u = 13, X d = 5, X u = 15, r = 0, 1, to z (5) otrzymujemy Π 0 (X) = 50/11. Ale na tym rynku możemy osiągnąć zysk bez ryzyka pożyczając 10 jednostek z banku i kupując za tę kwotę akcję. Wtedy w chwili T sprzedając akcję otrzymujemy co najmniej 12, a do banku musimy zwrócić 11. Chcemy takie sytuacje wykluczyć, zatem chcemy z rynku wykluczyć portfel ϕ (nazywany arbitrażem lub portfelem arbitrażowym) dla którego V 0 (ϕ) = 0, V T (ϕ) 0, ω Ω V T (ϕ)(ω) > 0. Mówimy, że model rynku M = (S, B, Φ) jest wolny od arbitrażu, gdy nie ma możliwości arbitrażu w klasie portfeli Φ. Interpretacja portfela arbitrażowego jest klarowna: nie mając nic na początku, stosując strategię ϕ, na końcu operacji nic nie stracimy, a dla pewnych scenariuszy mamy zysk dodatni. Istnienie możliwości arbitrażu świadczy o serii poważnych błędów w wycenie instrumentów na rynku. Takie błędy są bardzo szybko wychwytywane i wykorzystywane przez arbitrażystów, skutkiem czego rynek szybko wraca do równowagi. Zatem model rynku powinien być modelem bez możliwości arbitrażu. Zbadamy wobec tego, jakie warunki trzeba narzucić na model rynku, by na rynku nie było możliwości arbitrażu. 17
6 Twierdzenie 2. Rynek jest wolny od arbitrażu wtedy i tylko wtedy, gdy (6) S d < (1 + r)s 0 < S u. Dowód. (nie wprost) Niech jedna z powyższych nierówności nie zachodzi. Załóżmy, że S 0 (1 + r) S u. Wtedy portfel ϕ = ( 1, S 0 ) jest arbitrażem. Gdy S d (1 + r), to ϕ = (1, S 0 ) jest arbitrażem. Sprzeczność. Chcemy wykazać, że nie istnieje arbitraż. Weźmy portfel ϕ = (α, β), taki że V 0 (ϕ) = 0, tzn. αs 0 + β = 0. Gdy α = 0, to β = 0, zatem ϕ = (0, 0), V T (ϕ) 0 i portfel nie jest portfelem arbitrażowym. Gdy α 0, to β = αs 0 i ten portfel w chwili T ma wartość: { α(s u S 0 (1 + r)) dla ω = ω 1, V T (ϕ) = αs T + β(1 + r) = α(s d S 0 (1 + r)) dla ω = ω 2. Korzystając z (6) otrzymujemy, że portfel ϕ z kapitałem początkowym równym zero i α 0, w chwili końcowej T przyjmuje wartości różnych znaków, a mianowicie: gdy α > 0, to V T (ϕ)(ω 1 ) > 0 i V T (ϕ)(ω 2 ) < 0, a gdy α < 0 to zachodzą nierówności przeciwne. Zatem portfel ϕ o wartości początkowej zero nie może być arbitrażem. Z tego twierdzenia wynika, że rynek z przykładu 5. jest wolny od arbitrażu, a na rynku z przykładu 7. istnieje arbitraż, który zresztą w tym przykładzie wskazaliśmy. Od tego momentu będziemy zakładali, że na rynku M zawsze zachodzi warunek (6). Wykluczenie równości w (6) ma sens ekonomiczny, gdyż wtedy wykluczamy sytację, w której na rynku są dwa aktywa, ale jednym z nich nikt nie handluje. Istotnie, gdy S d = (1 + r)s 0, to zawsze należy inwestować w akcje, bo w najgorszym przypadku dadzą tyle, co depozyt w banku, a gdy S u = (1 + r)s 0, to zawsze należy wkładać pieniądze do banku, bo depozyt da nie mniejszy zysk niż akcje i to bez żadnego ryzyka. W obu tych przypadkach rynek nie jest płynny i z rynku znika jeden z rodzajów aktywów. Definicja 3. Na rynku M bez możliwości arbitrażu cenę racjonalną instrumentu pochodnego X nazywamy ceną arbitrażową X w chwili t = 0 na rynku M. Okazuje się, że istnieje alternatywne podejście do wyceny instrumentów pochodnych na rynku bez możliwości arbitrażu, opierające się na liczeniu wartości oczekiwanej względem pewnej wyróżnionej miary probabilistycznej. Przykład 8. Przyjmijmy, że S 0 = 3, S d = 1, S u = 7, K = 3, X = (S T K) + i niech r = 0. Wtedy X d = 0, X u = 4. Łatwo obliczyć, że portfel replikujący ma postać: α = 2/3 i β = 2/3, a stąd C 0 = 4/3. Zatem C 0 [0, 4], a więc dla q = 1/3 C 0 = qx(ω 1 ) + (1 q)x(ω 2 ) tzn. C 0 = E Q X, gdzie Q({ω 1 }) = q = 1/3, Q({ω 2 }) = 1 q. Dla tej miary probabilistycznej Q zachodzi także S 0 = 3 = 7/3 + 2/3 = E Q S T. Czy jest to przypadek wynikający ze szczególnego doboru danych? Czy cena jest wartością oczekiwaną wypłaty względem pewnego rozkładu? W tym przykładzie q nie zależy od prawdopodobieństwa subiektywnego P, zależy zaś od wypłaty X = f(s T ), a jednocześnie dla cen akcji zachodzi S 0 = E Q S T. Chciałoby się, aby w sytuacji ogólnej q zależało tylko od cen S T, a nie zależało od postaci funkcji f. Okazuje się, że tak jest w istocie. Pokazanie tego będzie naszym celem. Dla rynku bez możliwości arbitrażu z założenia (6) wynika, że S 0 (1 + r) jest kombinacją wypukłą końców odcinka tzn. istnieje γ (0, 1), takie że (7) S 0 (1 + r) = γs u + (1 γ)s d. Liczby γ i (1 γ) zadają nowe prawdopodobieństwo Q, takie że 18 Q(Z = u) = γ, Q(Z = d) = 1 γ.
7 Wtedy (8) S 0 = r E QS T, czyli otrzymaliśmy wzór przedstawiający cenę dzisiejszą jako zdyskontowaną wartość oczekiwaną ceny jutrzejszej względem prawdopodobieństwa Q. Zwykle ważne są nie wielkości cen, a proporcje pomiędzy nimi. W tym celu wyrażamy wszystko w terminach wartości jakiegoś ustalonego aktywa. Wygodne jest znormalizowanie cen tak, by jednostka na rachunku bankowym miała stałą wartość. Czyli B zdyskontowany proces wartości jednostki na rachunku bankowym spełnia B0 = BT = 1 i wtedy zamiast procesu cen rozważamy zdyskontowany proces cen S : S 0 = S 0, S T = S T 1 + r. Z (8) dla miary Q zachodzi S 0 = E Q S T. Dla rynku jednookresowego dwustanowego jest to równoważne faktowi, że S jest Q-martyngałem. Stąd Definicja 4. Miarę probabilistyczną P nazywamy miarą martyngałową dla zdyskontowanego procesu cen S, gdy 1 > P (ω 1 ) > 0 oraz S jest martyngałem względem P (tzn. S jest martyngałem na przestrzeni probabilistycznej (Ω, M, P ).) Lemat 1. Na rynku M istnieje miara martyngałowa P dla zdyskontowanego procesu cen S wtedy i tylko wtedy, gdy jedyne rozwiązanie równania (9) S 0 (1 + r) = γs u + (1 γ)s d, względem γ, należy do przedziału (0, 1). Dowód. Gdy P jest miarą martyngałową, to zachodzi S 0 = E P S T, a stąd przyjmując γ = P ({ω 1 }) otrzymujemy (9) i oczywiście γ = P ({ω 1 }) (0, 1). Gdy (9) ma rozwiązanie γ (0, 1), to definiując miarę probabilistyczną P wzorem P ({ω 1 }) = γ i P ({ω 2 }) = 1 γ otrzymujemy miarę P spełniającą S 0 = E P S T. Stąd P jest miarą martyngałową. Warto zauważyć, że jedyne rozwiązanie równania (9) jest postaci (10) γ = (1 + r)s 0 S d S u S d, więc miara martyngałowa P jest zadana przez wielkości wyznaczające cenę i przez wielkość stopy procentowej. Twierdzenie 3. Rynek M = (S, B, Φ) jest wolny od arbitrażu wtedy i tylko wtedy, gdy istnieje miara martyngałowa dla zdyskontowanego procesu cen S. Wtedy cena arbitrażowa w chwili 0 dowolnej wypłaty X w chwili T jest dana wzorem ( ) X (11) Π 0 (X) = E P, 1 + r gdzie P jest miarą martyngałową. Dowód. Pierwsza część twierdzenia wynika z lematu 1, tw. 2, wzoru (10) oraz z tego, że 19 γ = (1 + r)s 0 S d S u S d (0, 1) S d < (1 + r)s 0 < S u.
8 Został do udowodnienia wzór (11) podający cenę arbitrażową. Niech ϕ = (α 0, β 0 ) będzie jedynym portfelem replikującym X (istnieje na mocy twierdzenia 1). Wówczas: E P ( ) X = E P 1 + r ( ) ( VT (ϕ) α0 S T = E P 1 + r 1 + r + (1 + r)β ) 0 = 1 + r = α 0 E P (S T) + β 0 = α 0 S 0 + β 0 = V 0 (ϕ) = Π 0 (X), przy czym trzecia od końca równość wynika z faktu, iż P jest miarą martyngałową, ostatnia zaś z definicji Π 0. Przykład 9. Obliczmy cenę opcji z przykładu 5 korzystając ze wzorów (10) i (11). Otrzymujemy γ = 1/6 i Π 0 (X) = 1/6 4/2 = 1/3. Oczywiście otrzymaliśmy ten sam wynik co w przykładzie 6. Gdy Ω zawiera n scenariuszy i na rynku można handlować w chwilach 0, 1,...,T, to dla dużych n, T metoda badania, czy rynek jest wolny od arbitrażu, wykorzystująca portfele samofinansujące się, jest zwykle mało przydatna ze względu na ogromną liczbę dopuszczalnych strategii. To samo dotyczy problemów wyceny. Natomiast zbadanie, czy na danym rynku istnieje miara probabilistyczną P, taka że zdyskontowany proces cen S t = S t /B t, t = 0, 1,...,T, jest martyngałem względem P jest znacznie prostsze. Z analogonów podanych tu twierdzeń wynika, że wtedy znamy własności rynku. Również liczenie cen za pomocą uogólnienia wzoru (11), które to dla wypłat replikowalnych ma dokładnie taką samą postać, jest łatwe. Ta metoda przenosi się także na przypadek dowolnej Ω i czasu ciągłego. 5. Elementarny wykład rachunku prawdopodobieństwa można znaleźć w [2] lub [5]. Więcej informacji o martyngałach czytelnik znajdzie w książkach [1], [4], [7], a o działaniu rynków finansowych w [3], [8] lub w pierwszym rozdziale [6]. Literatura [1] T. Bojdecki, 1977, Martyngały z czasem dyskretnym, zarys teorii i przykłady zastosowań, Wyd. UW, Wyd. I, Warszawa. [2] W. Feller, 1966, Wstęp do rachunku prawdopodobieństwa, t. I, PWN, Warszawa. [3] J.C. Hull, 1997, Options, Futures, and Other Derivatives, Prentice-Hall, Englewood Cliffs. [4] J. Jakubowski, R. Sztencel, 2001, Wstęp do teorii prawdopodobieństwa, Wyd. II. Script, Warszawa. [5] J. Jakubowski, R. Sztencel, 2002, Rachunek prawdopodobieństwa dla (prawie) każdego, Wydawnictwo Script, Warszawa. [6] J. Jakubowski, A. Palczewski, M. Rutkowski, Ł. Stettner, 2003, Matematyka finansowa. Instrumenty pochodne, Wyd. I. WNT Warszawa. [7] A. N. Shiryaev, 1980, Wierojatnost, Nauka, Moskwa. [8] A. Weron, R. Weron, 1998, Inżynieria finansowa, WNT, Warszawa. 20
Matematyka finansowa w pakiecie Matlab
 Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Matematyka finansowa w pakiecie Matlab Wykład 5. Wycena opcji modele dyskretne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK Kurs letni dla studentów studiów zamawianych na kierunku Matematyka
Teoria opcji 2018/19. Instytut Matematyki Uniwersytet Gdański. (IM UG) Teoria opcji 1 / 49
 Teoria opcji Instytut Matematyki Uniwersytet Gdański 2018/19 (IM UG) Teoria opcji 1 / 49 Sprawy organizacyjne Kontakt i strona E-mail: mwrzosek@mat.ug.edu.pl Konsultacje: środa, 12 14, p.323 Materiały:
Teoria opcji Instytut Matematyki Uniwersytet Gdański 2018/19 (IM UG) Teoria opcji 1 / 49 Sprawy organizacyjne Kontakt i strona E-mail: mwrzosek@mat.ug.edu.pl Konsultacje: środa, 12 14, p.323 Materiały:
Modele matematyczne rynków instrumentów pochodnych I
 Matematyka stosowana Modele matematyczne rynków instrumentów pochodnych I Jacek Jakubowski jakub@mimuw.edu.pl Uniwersytet Warszawski, 2011 Streszczenie. Wykład jest wprowadzeniem do modelowania rynków
Matematyka stosowana Modele matematyczne rynków instrumentów pochodnych I Jacek Jakubowski jakub@mimuw.edu.pl Uniwersytet Warszawski, 2011 Streszczenie. Wykład jest wprowadzeniem do modelowania rynków
Wykład 11: Martyngały: definicja, twierdzenia o zbieżności
 RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
RAP 412 14.01.2009 Wykład 11: Martyngały: definicja, twierdzenia o zbieżności Wykładowca: Andrzej Ruciński Pisarz:Mirosława Jańczak 1 Wstęp Do tej pory zajmowaliśmy się ciągami zmiennych losowych (X n
Zatem, jest wartością portfela (wealth) w chwili,. j=1
 Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Model Rynku z czasem dyskretnym n = 0,1,2, S 1 (n), S 2,, S m (n) - czas - ceny m aktywów obciążanych ryzykiem (akcji) w momencie : dodatnie zmienne losowe. - cena aktywa wolnego od ryzyka (obligacji)
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa
 Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
Ćwiczenia z metodyki nauczania rachunku prawdopodobieństwa 25 marca 209 Zadanie. W urnie jest b kul białych i c kul czarnych. Losujemy n kul bez zwracania. Jakie jest prawdopodobieństwo, że pierwsza kula
WYKŁAD 3. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Uniwersytet Warszawski. 1 Instytut Matematyki
 WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
Podstawy nauk przyrodniczych Matematyka
 Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy XLIX Egzamin dla Aktuariuszy z 6 kwietnia 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym
 Edward Stachowski Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym W podstawie programowej obowiązującej na egzaminie maturalnym od 05r pojawiły się nowe treści programowe Wśród
Edward Stachowski Prawdopodobieństwo warunkowe Twierdzenie o prawdopodobieństwie całkowitym W podstawie programowej obowiązującej na egzaminie maturalnym od 05r pojawiły się nowe treści programowe Wśród
i=7 X i. Zachodzi EX i = P(X i = 1) = 1 2, i {1, 2,..., 11} oraz EX ix j = P(X i = 1, X j = 1) = 1 7 VarS 2 2 = 14 3 ( 5 2 =
 Kombinatoryka W tej serii zadań można znaleźć pojawiające się na egzaminach zadania dotyczące problemu wyznaczania prostych parametrów rozkładu w przypadku zgadnień kombinatorycznych. Zadania te wymagają
Kombinatoryka W tej serii zadań można znaleźć pojawiające się na egzaminach zadania dotyczące problemu wyznaczania prostych parametrów rozkładu w przypadku zgadnień kombinatorycznych. Zadania te wymagają
Prawdopodobieństwo. Prawdopodobieństwo. Jacek Kłopotowski. Katedra Matematyki i Ekonomii Matematycznej SGH. 16 października 2018
 Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Katedra Matematyki i Ekonomii Matematycznej SGH 16 października 2018 Definicja σ-algebry Definicja Niech Ω oznacza zbiór niepusty. Rodzinę M podzbiorów zbioru Ω nazywamy σ-algebrą (lub σ-ciałem) wtedy
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy
 Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Instrumenty pochodne 2014 Wycena equity derivatives notowanych na GPW w obliczu wysokiego ryzyka dywidendy Jerzy Dzieża, WMS, AGH Kraków 28 maja 2014 (Instrumenty pochodne 2014 ) Wycena equity derivatives
Ćwiczenia: Ukryte procesy Markowa lista 1 kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II
 Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
Ćwiczenia: Ukryte procesy Markowa lista kierunek: matematyka, specjalność: analiza danych i modelowanie, studia II dr Jarosław Kotowicz Zadanie. Dany jest łańcuch Markowa, który może przyjmować wartości,,...,
zdarzenie losowe - zdarzenie którego przebiegu czy wyniku nie da się przewidzieć na pewno.
 Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3
 Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Zmienna losowa i jej
Rachunek prawdopodobieństwa (Elektronika, studia niestacjonarne) Wykład 3 Przygotowując wykład korzystam głównie z książki Jakubowski, Sztencel Wstęp do teorii prawdopodobieństwa. Zmienna losowa i jej
Matematyka finansowa 30.09.2013 r. Komisja Egzaminacyjna dla Aktuariuszy. LXV Egzamin dla Aktuariuszy z 30 września 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXV Egzamin dla Aktuariuszy z 30 września 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
Metody probabilistyczne
 Metody probabilistyczne 6. Momenty zmiennych losowych Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 8.11.2018 1 / 47 Funkcje zmiennych losowych Mierzalna funkcja Y
Metody probabilistyczne 6. Momenty zmiennych losowych Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 8.11.2018 1 / 47 Funkcje zmiennych losowych Mierzalna funkcja Y
Matematyka finansowa 15.12.2008 r. Komisja Egzaminacyjna dla Aktuariuszy. XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy XLVIII Egzamin dla Aktuariuszy z 15 grudnia 2008 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Matematyka finansowa 03.10.2011 r. Komisja Egzaminacyjna dla Aktuariuszy. LVIII Egzamin dla Aktuariuszy z 3 października 2011 r.
 Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LVIII Egzamin dla Aktuariuszy z 3 października 2011 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Komisja Egzaminacyjna dla Aktuariuszy LXX Egzamin dla Aktuariuszy z 23 marca 2015 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Rozważmy
Matematyka finansowa 13.12.2010 r. Komisja Egzaminacyjna dla Aktuariuszy. LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Komisja Egzaminacyjna dla Aktuariuszy LV Egzamin dla Aktuariuszy z 13 grudnia 2010 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pan
Wykład z równań różnicowych
 Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Wykład z równań różnicowych 1 Wiadomości wstępne Umówmy się, że na czas tego wykładu zrezygnujemy z oznaczania n-tego wyrazu ciągu symbolem typu x n, y n itp. Zamiast tego pisać będziemy x (n), y (n) itp.
Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne
 Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne 5.3 Rozkłady warunkowe i warunkowa wartość oczekiwana Katarzyna Rybarczyk-Krzywdzińska semestr zimowy 2015/2016 Prawdopodobieństwo wyraża postawę
Rachunek prawdopodobieństwa Rozdział 5. Rozkłady łączne 5.3 Rozkłady warunkowe i warunkowa wartość oczekiwana Katarzyna Rybarczyk-Krzywdzińska semestr zimowy 2015/2016 Prawdopodobieństwo wyraża postawę
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Zmienna losowa. Rozkład skokowy
 Temat: Zmienna losowa. Rozkład skokowy Kody kolorów: żółty nowe pojęcie pomarańczowy uwaga * - materiał nadobowiązkowy Anna Rajfura, Matematyka i statystyka matematyczna na kierunku Rolnictwo SGGW 1 Zagadnienia
Temat: Zmienna losowa. Rozkład skokowy Kody kolorów: żółty nowe pojęcie pomarańczowy uwaga * - materiał nadobowiązkowy Anna Rajfura, Matematyka i statystyka matematyczna na kierunku Rolnictwo SGGW 1 Zagadnienia
Komisja Egzaminacyjna dla Aktuariuszy. XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I. Matematyka finansowa
 Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
Komisja Egzaminacyjna dla Aktuariuszy XXXII Egzamin dla Aktuariuszy z 7 czerwca 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Trzy osoby biorą
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
Matematyka finansowa 15.06.2015 r. Komisja Egzaminacyjna dla Aktuariuszy. LXXI Egzamin dla Aktuariuszy z 15 czerwca 2015 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
Komisja Egzaminacyjna dla Aktuariuszy LXXI Egzamin dla Aktuariuszy z 1 czerwca 201 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Pracownik
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH
 O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
O PEWNEJ ANOMALII W WYCENIE INSTRUMENTÓW DŁUŻNYCH A. KARPIO KATEDRA EKONOMETRII I STATYSTYKI SGGW W WARSZAWIE Krzywa dochodowości Obligacja jest papierem wartościowym, którego wycena opiera się na oczekiwanych
Wykład 4. Określimy teraz pewną ważną klasę pierścieni.
 Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Wykład 2 Zmienne losowe i ich rozkłady
 Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
Wykład 2 Zmienne losowe i ich rozkłady Magdalena Frąszczak Wrocław, 11.10.2017r Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe Doświadczenie
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures
 10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
10. Instrumenty pochodne: kontrakty terminowe typu forward/futures Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie Matematyka finansowa rzegorz Kosiorowski (Uniwersytet Ekonomiczny 10. winstrumenty
Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe
 Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe 4.0. Rozkłady zmiennych losowych, dystrybuanta. Katarzyna Rybarczyk-Krzywdzińska Wprowadzenie Rozważmy eksperymenty 1 gra Bolka w ruletkę w kasynie;
Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe 4.0. Rozkłady zmiennych losowych, dystrybuanta. Katarzyna Rybarczyk-Krzywdzińska Wprowadzenie Rozważmy eksperymenty 1 gra Bolka w ruletkę w kasynie;
Przykład 1 W przypadku jednokrotnego rzutu kostką przestrzeń zdarzeń elementarnych
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Dwa równania kwadratowe z częścią całkowitą
 Dwa równania kwadratowe z częścią całkowitą Andrzej Nowicki Wydział Matematyki i Informatyki Uniwersytet M. Kopernika w Toruniu anow @ mat.uni.torun.pl 4 sierpnia 00 Jeśli r jest liczbą rzeczywistą, to
Dwa równania kwadratowe z częścią całkowitą Andrzej Nowicki Wydział Matematyki i Informatyki Uniwersytet M. Kopernika w Toruniu anow @ mat.uni.torun.pl 4 sierpnia 00 Jeśli r jest liczbą rzeczywistą, to
Statystyka i eksploracja danych
 Wykład I: Formalizm statystyki matematycznej 17 lutego 2014 Forma zaliczenia przedmiotu Forma zaliczenia Literatura Zagadnienia omawiane na wykładach Forma zaliczenia przedmiotu Forma zaliczenia Literatura
Wykład I: Formalizm statystyki matematycznej 17 lutego 2014 Forma zaliczenia przedmiotu Forma zaliczenia Literatura Zagadnienia omawiane na wykładach Forma zaliczenia przedmiotu Forma zaliczenia Literatura
Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995.
 Bibliografia Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995. Elton E.J., Gruber M.J., Nowoczesna teoria portfelowa i analiza papierów wartościowych,
Bibliografia Dobija M., Smaga E.; Podstawy matematyki finansowej i ubezpieczeniowej, PWN Warszawa- -Kraków 1995. Elton E.J., Gruber M.J., Nowoczesna teoria portfelowa i analiza papierów wartościowych,
Wycena papierów wartościowych - instrumenty pochodne
 Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Matematyka finansowa - 8 Wycena papierów wartościowych - instrumenty pochodne W ujęciu probabilistycznym cena akcji w momencie t jest zmienną losową P t o pewnym (zwykle nieznanym) rozkładzie prawdopodobieństwa,
Inwestycje finansowe. Wycena obligacji. Stopa zwrotu z akcji. Ryzyko.
 Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
Inwestycje finansowe Wycena obligacji. Stopa zwrotu z akcji. yzyko. Inwestycje finansowe Instrumenty rynku pieniężnego (np. bony skarbowe). Instrumenty rynku walutowego. Obligacje. Akcje. Instrumenty pochodne.
III. ZMIENNE LOSOWE JEDNOWYMIAROWE
 III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
III. ZMIENNE LOSOWE JEDNOWYMIAROWE.. Zmienna losowa i pojęcie rozkładu prawdopodobieństwa W dotychczas rozpatrywanych przykładach każdemu zdarzeniu była przyporządkowana odpowiednia wartość liczbowa. Ta
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 20 lutego 2017 Magdalena Alama-Bućko Statystyka matematyczna 20 lutego 2017 1 / 21 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 20 lutego 2017 Magdalena Alama-Bućko Statystyka matematyczna 20 lutego 2017 1 / 21 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
Komisja Egzaminacyjna dla Aktuariuszy LXIV Egzamin dla Aktuariuszy z 17 czerwca 2013 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1. Rozważamy
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej
 5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
Metody probabilistyczne
 Metody probabilistyczne 2. Aksjomatyczna definicja prawdopodobieństwa Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 10.10.2017 1 / 33 Klasyczna definicja prawdopodobieństwa
Metody probabilistyczne 2. Aksjomatyczna definicja prawdopodobieństwa Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 10.10.2017 1 / 33 Klasyczna definicja prawdopodobieństwa
Statystyka podstawowe wzory i definicje
 1 Statystyka podstawowe wzory i definicje Średnia arytmetyczna to suma wszystkich liczb (a 1, a 2,, a n) podzielona przez ich ilość (n) Przykład 1 Dany jest zbiór liczb {6, 8, 11, 2, 5, 3}. Oblicz średnią
1 Statystyka podstawowe wzory i definicje Średnia arytmetyczna to suma wszystkich liczb (a 1, a 2,, a n) podzielona przez ich ilość (n) Przykład 1 Dany jest zbiór liczb {6, 8, 11, 2, 5, 3}. Oblicz średnią
Układy równań i nierówności liniowych
 Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Układy równań i nierówności liniowych Wiesław Krakowiak 1 grudnia 2010 1 Układy równań liniowych DEFINICJA 11 Układem równań m liniowych o n niewiadomych X 1,, X n, nazywamy układ postaci: a 11 X 1 + +
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 26 lutego 2018 Magdalena Alama-Bućko Statystyka matematyczna 26 lutego 2018 1 / 16 Wykład : 10h (przez 10 tygodni po 45 minut) zaliczenie wykładu
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 26 lutego 2018 Magdalena Alama-Bućko Statystyka matematyczna 26 lutego 2018 1 / 16 Wykład : 10h (przez 10 tygodni po 45 minut) zaliczenie wykładu
Rozdział 1. Zmienne losowe, ich rozkłady i charakterystyki. 1.1 Definicja zmiennej losowej
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Zbiór możliwych wyników eksperymentu będziemy nazywać przestrzenią zdarzeń elementarnych i oznaczać Ω, natomiast
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Zbiór możliwych wyników eksperymentu będziemy nazywać przestrzenią zdarzeń elementarnych i oznaczać Ω, natomiast
P (A B) P (B) = 1/4 1/2 = 1 2. Zakładamy, że wszystkie układy dwójki dzieci: cc, cd, dc, dd są jednakowo prawdopodobne.
 Wykład Prawdopodobieństwo warunkowe Dwukrotny rzut symetryczną monetą Ω {OO, OR, RO, RR}. Zdarzenia: Awypadną dwa orły, Bw pierwszym rzucie orzeł. P (A) 1 4, 1. Jeżeli już wykonaliśmy pierwszy rzut i wiemy,
Wykład Prawdopodobieństwo warunkowe Dwukrotny rzut symetryczną monetą Ω {OO, OR, RO, RR}. Zdarzenia: Awypadną dwa orły, Bw pierwszym rzucie orzeł. P (A) 1 4, 1. Jeżeli już wykonaliśmy pierwszy rzut i wiemy,
Metody probabilistyczne
 Metody probabilistyczne. Twierdzenia graniczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 20.2.208 / 26 Motywacja Rzucamy wielokrotnie uczciwą monetą i zliczamy
Metody probabilistyczne. Twierdzenia graniczne Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 20.2.208 / 26 Motywacja Rzucamy wielokrotnie uczciwą monetą i zliczamy
Ważne rozkłady i twierdzenia
 Ważne rozkłady i twierdzenia Rozkład dwumianowy i wielomianowy Częstość. Prawo wielkich liczb Rozkład hipergeometryczny Rozkład Poissona Rozkład normalny i rozkład Gaussa Centralne twierdzenie graniczne
Ważne rozkłady i twierdzenia Rozkład dwumianowy i wielomianowy Częstość. Prawo wielkich liczb Rozkład hipergeometryczny Rozkład Poissona Rozkład normalny i rozkład Gaussa Centralne twierdzenie graniczne
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych:
 W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych: Zmienne losowe skokowe (dyskretne) przyjmujące co najwyżej przeliczalnie wiele wartości Zmienne losowe ciągłe
W rachunku prawdopodobieństwa wyróżniamy dwie zasadnicze grupy rozkładów zmiennych losowych: Zmienne losowe skokowe (dyskretne) przyjmujące co najwyżej przeliczalnie wiele wartości Zmienne losowe ciągłe
TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1
 TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1 Podstawowym pojęciem dotyczącym transakcji arbitrażowych jest wartość teoretyczna kontraktu FV. Na powyższym diagramie przedstawiono wykres oraz wzór,
TRANSAKCJE ARBITRAŻOWE PODSTAWY TEORETYCZNE cz. 1 Podstawowym pojęciem dotyczącym transakcji arbitrażowych jest wartość teoretyczna kontraktu FV. Na powyższym diagramie przedstawiono wykres oraz wzór,
Parametr Λ w populacji ubezpieczonych ma rozkład dany na półosi dodatniej gęstością: 3 f
 Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE
 INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE OPCJE / DEFINICJA Opcja jest prawem do zakupu lub sprzedaży określonej ilości wyspecyfikowanego przedmiotu (tzw. instrumentu bazowego)
INSTRUMENTY POCHODNE OPCJE EUROPEJSKIE OPCJE AMERYKAŃSKIE OPCJE EGZOTYCZNE OPCJE / DEFINICJA Opcja jest prawem do zakupu lub sprzedaży określonej ilości wyspecyfikowanego przedmiotu (tzw. instrumentu bazowego)
F t+ := s>t. F s = F t.
 M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
M. Beśka, Całka Stochastyczna, wykład 1 1 1 Wiadomości wstępne 1.1 Przestrzeń probabilistyczna z filtracją Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną i niech F = {F t } t 0 będzie rodziną
Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe
 Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe Nierówność Czebyszewa Niech X będzie zmienną losową o skończonej wariancji V ar(x). Wtedy wartość oczekiwana E(X) też jest skończona i
Wykład 6 Centralne Twierdzenie Graniczne. Rozkłady wielowymiarowe Nierówność Czebyszewa Niech X będzie zmienną losową o skończonej wariancji V ar(x). Wtedy wartość oczekiwana E(X) też jest skończona i
Ciała i wielomiany 1. przez 1, i nazywamy jedynką, zaś element odwrotny do a 0 względem działania oznaczamy przez a 1, i nazywamy odwrotnością a);
 Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
Elementy matematyki finansowej
 ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
ROZDZIAŁ 2 Elementy matematyki finansowej 1. Procent składany i ciągły Stopa procentowa i jest związana z podstawową jednostką czasu, jaką jest zwykle jeden rok. Jeśli pożyczamy komuś 100 zł na jeden rok,
Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga
 RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
RAP 412 21.01.2009 Wykład 11: Martyngały: Twierdzenie o zbieżności i Hoeffdinga Wykładowca: Andrzej Ruciński Pisarz: Łukasz Waszak 1 Wstęp Na ostatnim wykładzie przedstawiliśmy twierdzenie o zbieżności
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
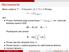 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
1 Funkcja użyteczności
 1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
Inżynieria Finansowa: 6. Wycena martyngałowa, dynamiczna replikacja i model dwumianowy
 Inżynieria Finansowa: 6. Wycena martyngałowa, dynamiczna replikacja i model dwumianowy Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Kwiecień 2017 r. Warszawa, Szkoła Główna Handlowa Wycena pochodnych:
Inżynieria Finansowa: 6. Wycena martyngałowa, dynamiczna replikacja i model dwumianowy Piotr Bańbuła Katedra Ekonomii Ilościowej, KAE Kwiecień 2017 r. Warszawa, Szkoła Główna Handlowa Wycena pochodnych:
Prawdopodobieństwo
 Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
9 Funkcje Użyteczności
 9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
OGÓLNE RENTY ŻYCIOWE
 OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
OGÓLNE RENTY ŻYCIOWE M. BIENIEK Rentą życiową nazywamy kontrakt między ubezpieczycielem a ubezpieczonym, w którym ubezpieczony w zamian za określoną opłatę, zwaną składką, otrzymuje ciąg z góry określonych
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
Matematyka finansowa 26.05.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I
 Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Komisja Egzaminacyjna dla Aktuariuszy LXVII Egzamin dla Aktuariuszy z 26 maja 2014 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1. Przyjmijmy
Matematyka finansowa 11.10.2004 r. Komisja Egzaminacyjna dla Aktuariuszy. XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r.
 Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Komisja Egzaminacyjna dla Aktuariuszy XXXIII Egzamin dla Aktuariuszy - 11 października 2004 r. Część I Matematyka finansowa Imię i nazwisko osoby egzaminowanej:... WERSJA TESTU Czas egzaminu: 100 minut
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. LXI Egzamin dla Aktuariuszy z 1 października 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Komisja Egzaminacyjna dla Aktuariuszy LXI Egzamin dla Aktuariuszy z 1 października 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014
 Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Matematyka ubezpieczeń majątkowych 1.10.2012 r.
 Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zdarzenia losowe i prawdopodobieństwo
 Rozdział 1 Zdarzenia losowe i prawdopodobieństwo 1.1 Klasyfikacja zdarzeń Zdarzenie elementarne pojęcie aprioryczne, które nie może być zdefiniowane. Odpowiednik pojęcia punkt w geometrii. Zdarzenie elementarne
Rozdział 1 Zdarzenia losowe i prawdopodobieństwo 1.1 Klasyfikacja zdarzeń Zdarzenie elementarne pojęcie aprioryczne, które nie może być zdefiniowane. Odpowiednik pojęcia punkt w geometrii. Zdarzenie elementarne
Matematyka finansowa 10.12.2012 r. Komisja Egzaminacyjna dla Aktuariuszy. LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy LXII Egzamin dla Aktuariuszy z 10 grudnia 2012 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut 1 1.
Prawdopodobieństwo i statystyka
 Wykład I: Formalizm teorii prawdopodonieństwa 6 października 2014 Forma zaliczenia przedmiotu Forma zaliczenia Literatura Dostępność treści wykładów 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin dwuczęściowy:
Wykład I: Formalizm teorii prawdopodonieństwa 6 października 2014 Forma zaliczenia przedmiotu Forma zaliczenia Literatura Dostępność treści wykładów 1 Zaliczenie ćwiczeń rachunkowych. 2 Egzamin dwuczęściowy:
Zmienne losowe. dr Mariusz Grządziel Wykład 12; 20 maja 2014
 Zmienne losowe dr Mariusz Grządziel Wykład 2; 20 maja 204 Definicja. Zmienna losowa nazywamy dyskretna (skokowa), jeśli zbiór jej wartości x, x 2,..., można ustawić w ciag. Zmienna losowa X, która przyjmuje
Zmienne losowe dr Mariusz Grządziel Wykład 2; 20 maja 204 Definicja. Zmienna losowa nazywamy dyskretna (skokowa), jeśli zbiór jej wartości x, x 2,..., można ustawić w ciag. Zmienna losowa X, która przyjmuje
Drugie kolokwium z Rachunku Prawdopodobieństwa, zestaw A
 Drugie kolokwium z Rachunku Prawdopodobieństwa, zestaw A Zad. 1. Korzystając z podanych poniżej mini-tablic, oblicz pierwszy, drugi i trzeci kwartyl rozkładu N(10, 2 ). Rozwiązanie. Najpierw ogólny komentarz
Drugie kolokwium z Rachunku Prawdopodobieństwa, zestaw A Zad. 1. Korzystając z podanych poniżej mini-tablic, oblicz pierwszy, drugi i trzeci kwartyl rozkładu N(10, 2 ). Rozwiązanie. Najpierw ogólny komentarz
Modele rynku, kontrakty terminowe, spekulacje
 Modele rynku, kontrakty terminowe, spekulacje Marcin Abram WFAIS UJ w Krakowie 9 marca 2009 Założenia modelu Cena rozpatrywanego obiektu zmienia się skokowo co czas δt. Bezwzględna wartość zmiany ceny
Modele rynku, kontrakty terminowe, spekulacje Marcin Abram WFAIS UJ w Krakowie 9 marca 2009 Założenia modelu Cena rozpatrywanego obiektu zmienia się skokowo co czas δt. Bezwzględna wartość zmiany ceny
Prawa wielkich liczb, centralne twierdzenia graniczne
 , centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
, centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008
 Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
3. Podstawowe pojęcia statystyki matematycznej i rachunku prawdopodobieństwa wykład z Populacja i próba
 3. Podstawowe pojęcia statystyki matematycznej i rachunku prawdopodobieństwa wykład z 12.03.2007 Populacja i próba Populacja- zbiorowość skończona lub nieskończona, w stosunku do której mają być formułowane
3. Podstawowe pojęcia statystyki matematycznej i rachunku prawdopodobieństwa wykład z 12.03.2007 Populacja i próba Populacja- zbiorowość skończona lub nieskończona, w stosunku do której mają być formułowane
Forward kontrakt terminowy o charakterze rzeczywistym (z dostawą instrumentu bazowego).
 Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Kontrakt terminowy (z ang. futures contract) to umowa pomiędzy dwiema stronami, z których jedna zobowiązuje się do kupna, a druga do sprzedaży, w określonym terminie w przyszłości (w tzw. dniu wygaśnięcia)
Statystyka matematyczna
 Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 25 lutego 2019 Magdalena Alama-Bućko Statystyka matematyczna 25 lutego 2019 1 / 18 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Statystyka matematyczna Wykład 1 Magdalena Alama-Bućko 25 lutego 2019 Magdalena Alama-Bućko Statystyka matematyczna 25 lutego 2019 1 / 18 Wykład : 10h (przez 10 tygodni po 45 minut) Ćwiczenia : 15h (45
Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe
 Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe 4.1. Zmienne losowe dyskretne. Katarzyna Rybarczyk-Krzywdzińska Definicja/Rozkład Zmienne losowe dyskretne Definicja Zmienną losową, która skupiona
Rachunek prawdopodobieństwa Rozdział 4. Zmienne losowe 4.1. Zmienne losowe dyskretne. Katarzyna Rybarczyk-Krzywdzińska Definicja/Rozkład Zmienne losowe dyskretne Definicja Zmienną losową, która skupiona
4,5. Dyskretne zmienne losowe (17.03; 31.03)
 4,5. Dyskretne zmienne losowe (17.03; 31.03) Definicja 1 Zmienna losowa nazywamy dyskretna (skokowa), jeśli zbiór jej wartości x 1, x 2,..., można ustawić w ciag. Zmienna losowa X, która przyjmuje wszystkie
4,5. Dyskretne zmienne losowe (17.03; 31.03) Definicja 1 Zmienna losowa nazywamy dyskretna (skokowa), jeśli zbiór jej wartości x 1, x 2,..., można ustawić w ciag. Zmienna losowa X, która przyjmuje wszystkie
Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do:
 Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
Jesteś tu: Bossa.pl Opcje na WIG20 - wprowadzenie Opcja jest to prawo przysługujące nabywcy opcji wobec jej wystawcy do: żądania w ustalonym terminie dostawy instrumentu bazowego po określonej cenie wykonania
domykanie relacji, relacja równoważności, rozkłady zbiorów
 1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
1 of 8 2012-03-28 17:45 Logika i teoria mnogości/wykład 5: Para uporządkowana iloczyn kartezjański relacje domykanie relacji relacja równoważności rozkłady zbiorów From Studia Informatyczne < Logika i
Pochodna funkcji odwrotnej
 Pochodna funkcji odwrotnej Niech będzie dana w przedziale funkcja różniczkowalna i różnowartościowa. Wiadomo, że istnieje wówczas funkcja odwrotna (którą oznaczymy tu : ), ciągła w przedziale (lub zależnie
Pochodna funkcji odwrotnej Niech będzie dana w przedziale funkcja różniczkowalna i różnowartościowa. Wiadomo, że istnieje wówczas funkcja odwrotna (którą oznaczymy tu : ), ciągła w przedziale (lub zależnie
Opcje podstawowe własności.
 Opcje podstawowe własności. Opcja jest to rodzaj umowy między dwoma podmiotami i jednocześnie instrument finansowy. Opcje kupna (call) dają posiadaczowi prawo do kupienia określonego w umowie aktywa (bazowego)
Opcje podstawowe własności. Opcja jest to rodzaj umowy między dwoma podmiotami i jednocześnie instrument finansowy. Opcje kupna (call) dają posiadaczowi prawo do kupienia określonego w umowie aktywa (bazowego)
= A. A - liczba elementów zbioru A. Lucjan Kowalski
 Lucjan Kowalski ZADANIA, PROBLEMY I PARADOKSY W PROBABILISTYCE Przypomnienie. Ω - zbiór zdarzeń elementarnych. A zdarzenie (podzbiór Ω). A - liczba elementów zbioru A Jeśli zdarzeń elementarnych jest skończenie
Lucjan Kowalski ZADANIA, PROBLEMY I PARADOKSY W PROBABILISTYCE Przypomnienie. Ω - zbiór zdarzeń elementarnych. A zdarzenie (podzbiór Ω). A - liczba elementów zbioru A Jeśli zdarzeń elementarnych jest skończenie
