Technika optymalizacji
|
|
|
- Bogumił Kurowski
- 6 lat temu
- Przeglądów:
Transkrypt
1 Algorytmy bezgraientowe Algorytmy optymalizacji loalnej c. Nieliniowe zaanie optymalizacji statycznej bez ograniczeń - nieliniowe algorytmy optymalizacji loalnej c. r inŝ. Ewa Szlachcic Wyział Eletronii Kierune: Eletronia III r. Algorytm Neler a-meae a Matlab - uncja search Algorytm auss a-seil a Algorytm Powella Algorytm Zangwilla Algorytmy graientowe Algorytm najwięszego spau Zmoyiowany algorytm Newtona Algorytm Fletchera-Reeves a Algorytm Polaa-Ribiery Algorytm Fletchera-Powella-Daviona Matlab wersja metoy Quasi-Newton - uncja unc Metoa auss a-seiel a "punty.at" ***.5*** a metoa jest stosowana la uncji tórych poziomice mają ształt wąsich olin. MoŜna zięi niej uzysać znaczną poprawę szybości zbieŝności w stosunu o metoy aussa-seila. Moyiacja ierunu poszuiwań następuje tu w wyniu wprowazania o bazy ortogonalnej ierunów sprzęŝonych o juŝ istniejących. Do istniejącej bazy wprowaza się ieruni sprzęŝone co obieg czyli po imalizacji wzłuŝ n ierunów obowiązującej bazy. Wyres warstwic uncji PoniewaŜ ieruni wzajemnie sprzęŝone są liniowo niezaleŝne w metozie Powella zachowany pozostaje warune jenoznaczności przeształcenia bazy ierunów poszuiwań. Dzięi temu mamy pewność iŝ nie nastąpi reucja wymiarowości bazy co prowaziłoby o niezbieŝności metoy. Dla j...n obliczamy λ j imalizujące j oraz współrzęne puntu j j- λ j j Wyznaczamy słaowe ierunu sprzęŝonego zgonie ze wzorem : n n n 3 Oreślamy λ imalizujące n wzłuŝ nowego ierunu n oraz wyznaczamy współrzęne nowego puntu startowego n n λ n "punty.at" ***.5***--.5 ^ Doonujemy moyiacji ierunów poszuiwań zgonie z zasaą r r la r.. n Czynności o rou o 4 powtarzamy aŝ spełnione zostanie ryterium na imum Wyres warstwic uncji
2 Algorytm Neler a- Meae a algorytm symplesu NM la zaań bez ograniczeń Algorytm Comples la zaań z ograniczeniami Simples w n-wymiarowej przestrzeni jest zbiorem n lub n puntów wielościanem o nn wierzchołach. Metoa sprawza się obrze nawet la mocno nieliniowych uncji jena wymaga sporych nałaów pracy numerycznej szczególne przy uŝej liczbie zmiennych ecyzyjnych. Ogólny schemat algorytmu: Utworzyć simples o n lub n wierzchołach i wartości uncji w wierzchołach Obliczyć śroe symetrii symplesu z wyłączeniem puntu oraz wartość uncji w tym puncie n i Zastosować operacje: i n Operacja obicia n Operacja espansji Operacja ontracji Operacja zmniejszania Operacja obicia: naleŝy wyznaczyć nowy punt: jeśli: o α laα i o > NaleŜy wyznaczyć nowy simples z uŝyciem o w miejsce Operacja espansji: naleŝy wyznaczyć nowy punt: e o γ gy < laγ Operacja ontracji: naleŝy wyznaczyć nowy punt: o i i ρ gy la laρ / Operacja zmniejszanie: la wierzchołów i naleŝy wyznaczyć nowe współrzęne i i σ lai {... n } σ / LEMA. Niech : X R n R ZałóŜmy Ŝe istnieje la tórego: Metoy graientowe Metoa najwięszego spau NS jest to metoa graientowa tóra pozwala szuać imum róŝniczowalnej uncji nieliniowej. bęzie uncją róŝniczowalną w puncie < Wówczas istnieje taie σ > Ŝe la wszystich τ σ ] zachozi τ <. X Schemat algorytmu optymalizacji loalnej bez ograniczeń Wybierz punt startowy. Oblicz wartość uncji oraz jeŝeli jest to wymagane to jej graient czy hesjan H 3 Zbaaj przyjęte ryterium zbieŝności. Jeśli ryterium jest spełnione to oniec algorytmu uzysano rozwiązanie optymalne i optymalną wartość uncji celu JeŜeli nie to przejź o 4 4 Wyznacz ustalony ierune poszuiwań : 5 Wyonaj imalizację ierunową wybraną metoą: 6 Postaw i przejź o oraz Algorytm obliczeń metoa NS Wybierz punt startowy o. Oblicz wartość uncji oraz jej graient Zbaaj ryterium zbieŝności: czyli ε 3 Wyznacz ierune poszuiwań : 4 Wyonaj imalizację ierunową wybraną metoą: 5 Postaw oraz i powtórz gzie ε δ] np.: ε 6 Jeśli ta to oniec jeśli nie to przejź o 3
3 Algorytm bisecji z testem wusośnym olstein a algorytm graientowy Do imalizacji w ierunu zastosowano graientowy algorytm bisecji z testem wusośnym olstein a : Do wyszuania puntów spełniających test wusośny olsteina stosuje się algorytm bisecji: Oblicz pochoną w ierunu p o oraz współczynni rou τ R > tai Ŝe τ R < Wyznacz τ τl τr. Oblicz τ. 3 Jeśli τ < pτ to postaw τ L i przejź o rou w przeciwnym razie przejź o rou 4 4 Jeśli τ > pτ to postaw τ R i przejź o rou w przeciwnym przypau oniec. Działanie algorytmu bisecji z testem wusośnym olstein'a la uncji: Pochona w ierunu zatem mamy: p o 6 punt początowy [ ] ierune [ ] współczynni testu początowa wartość współczynnia rou τ R 9 ołaność la testu ε 5 5 la [ ] 6 4 [ 6] Otrzymujemy wartość pochonej p: o p [ 6 ] 6 Obliczamy τ τl τr oraz τ. τ τr 9 45 τ JeŜeli to postaw τ < pτ τ L i przejź o rou. W przeciwnym wypau przejź o rou 4 Przechozimy o rou 3 it. sprawzamy: -675 <? NIE Przechozimy o rou 4
4 4 JeŜeli to postaw τ > pτ τ R i przejź o rou. W przeciwnym wypau KONIEC 8 sprawzamy: -675 >? AK i przechozimy o rou DRUA IERACJA... Po trzeciej iteracji otrzymujemy wyni τ3375 Działanie algorytmu najwięszego spau la uncji: punt początowy [ 3] współczynni testu 4 początowa wartość współczynnia rou τ R Kolejno poane są punty wyznaczone za pomocą algorytmu najszybszego spau la uncji: [3] 5 [] [.5.5].5 3 [.55] [.5.5] 4.65 it. Funcja celu I ta olejno aŝ o momentu gy zostanie spełniony warune 3 ε np. : ε a uzysano rozwiązanie optymalne [] i. M Kolejne iteracje metoy najwięszego spau NS e i Metoa aussa-seila barzo wolna zbieŝność liniowa Metoa najwięszego spau zbieŝność liniowa 5 3 ^ 4 H H { h } Metoa Newtona zbieŝna waratowo ale osztowna i nie zawsze stabilna ij i j i j {... n} Najeetywniejsze są tzw. metoy quasi-newtonowsie w tórych w olejnych iteracjach onstruuje się przybliŝenie owrotności hesjanu. M
5 Wyzia Eletronii stuia I st. Kieruni poszuiwań la meto graientowych. Metoa Pola a-ribier y: Wyznacz ierune sprzęŝony gzie: DFP moyiacja macierzy polegająca na oawaniu w aŝej olejnej iteracji o atualnej macierzy czynnia powoującego ąŝenie macierzy o macierzy H -. A ><. Metoa Fletcher a-reeves a Wyznacz ierune sprzęŝony gzie: 3. Metoa Davion a-fletcher a-powell a DFP Wyzia Eletronii stuia I st. Metoy Quasi-Newtonowsie metoy przybliŝające wartość hesjanu 4. Metoa royen-fletcher-olarb-shanno FS Atualizacja rozwiązania: gzie: H I I gzie:. Właściwości metoy: ra operacji owracania macierzy hesjanu liso rozwiązania optymalnego obra zbieŝność Na początu obliczeń zbieŝność słaba słabe jest przybliŝenie hesjanu PrzybliŜenie hesjanu w aŝej iteracji polepsza się. H Dla
min h = x x Algorytmy optymalizacji lokalnej Nieliniowe zadanie optymalizacji bez ograniczeń numeryczne metody iteracyjne optymalizacji x x
 Nelnowe zaane optymalzacj bez ogranczeń numeryczne metoy teracyjne optymalzacj mn n x R ) = f x Algorytmy poszuwana mnmum loalnego la: f zaana programowana nelnowego bez ogranczeń zaana programowana nelnowego
Nelnowe zaane optymalzacj bez ogranczeń numeryczne metoy teracyjne optymalzacj mn n x R ) = f x Algorytmy poszuwana mnmum loalnego la: f zaana programowana nelnowego bez ogranczeń zaana programowana nelnowego
Metody optymalizacji nieliniowej (metody programowania nieliniowego) Ewa Niewiadomska-Szynkiewicz Instytut Automatyki i Informatyki Stosowanej
 Metody optymalizacji nieliniowej metody programowania nieliniowego Ewa Niewiadomsa-Szyniewicz Instytut Automatyi i Inormatyi Stosowanej Ewa Niewiadomsa-Szyniewicz ens@ia.pw.edu.pl Instytut Automatyi i
Metody optymalizacji nieliniowej metody programowania nieliniowego Ewa Niewiadomsa-Szyniewicz Instytut Automatyi i Inormatyi Stosowanej Ewa Niewiadomsa-Szyniewicz ens@ia.pw.edu.pl Instytut Automatyi i
Nieliniowe zadanie optymalizacji bez ograniczeń numeryczne metody iteracyjne optymalizacji
 Nelnowe zadane optymalzacj bez ogranczeń numeryczne metody teracyjne optymalzacj mn R n f ( ) = f Algorytmy poszuwana mnmum loalnego zadana programowana nelnowego: Bez ogranczeń Z ogranczenam Algorytmy
Nelnowe zadane optymalzacj bez ogranczeń numeryczne metody teracyjne optymalzacj mn R n f ( ) = f Algorytmy poszuwana mnmum loalnego zadana programowana nelnowego: Bez ogranczeń Z ogranczenam Algorytmy
WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ
 WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ Wstęp. Za wyjątie nielicznych funcji, najczęściej w postaci wieloianów, dla tórych ożna znaleźć iniu na drodze analitycznej, pozostała więszość
WYKŁAD 5 METODY OPTYMALIZACJI NIELINIOWEJ BEZ OGRANICZEŃ Wstęp. Za wyjątie nielicznych funcji, najczęściej w postaci wieloianów, dla tórych ożna znaleźć iniu na drodze analitycznej, pozostała więszość
( ) + ( ) T ( ) + E IE E E. Obliczanie gradientu błędu metodą układu dołączonego
 Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
Obliczanie gradientu błędu metodą uładu dołączonego /9 Obliczanie gradientu błędu metodą uładu dołączonego Chodzi o wyznaczenie pochodnych cząstowych funcji błędu E względem parametrów elementów uładu
Teoria i metody optymalizacji
 Teora metoy optymalzacj Nelowe zaae optymalzacj bez ograczeń umerycze metoy teracyje optymalzacj m x R f = f x Algorytmy poszuwaa mmum loalego zaaa programowaa elowego: Bez ograczeń Z ograczeam Algorytmy
Teora metoy optymalzacj Nelowe zaae optymalzacj bez ograczeń umerycze metoy teracyje optymalzacj m x R f = f x Algorytmy poszuwaa mmum loalego zaaa programowaa elowego: Bez ograczeń Z ograczeam Algorytmy
M eto dy o p ty m a liza cji
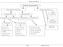 M eto dy o p ty m a liza cji M e to d y d et erm i ni s ty cz n e M et od y st oc h a sty cz n e b e z o gr an ic z eń z o gra n ic z en ia m i m e to d a M o nt e-c ar lo b ezg r ad ie n to w e g r ad
M eto dy o p ty m a liza cji M e to d y d et erm i ni s ty cz n e M et od y st oc h a sty cz n e b e z o gr an ic z eń z o gra n ic z en ia m i m e to d a M o nt e-c ar lo b ezg r ad ie n to w e g r ad
Przegląd metod optymalizacji wielowymiarowej. Funkcja testowa. Funkcja testowa. Notes. Notes. Notes. Notes. Tomasz M. Gwizdałła
 Przegląd metod optymalizacji wielowymiarowej Tomasz M. Gwizdałła 2012.12.06 Funkcja testowa Funkcją testową dla zagadnień rozpatrywanych w ramach tego wykładu będzie funkcja postaci f (x) = (x 1 1) 4 +
Przegląd metod optymalizacji wielowymiarowej Tomasz M. Gwizdałła 2012.12.06 Funkcja testowa Funkcją testową dla zagadnień rozpatrywanych w ramach tego wykładu będzie funkcja postaci f (x) = (x 1 1) 4 +
Optymalizacja harmonogramów budowlanych - problem szeregowania zadań
 Mieczysław POŁOŃSKI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Mieczysław POŁOŃSKI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
PORÓWNANIE WYBRANYCH ALGORYTMÓW OPTYMALIZACJI ROZPŁYWU MOCY W SYSTEMIE ELEKTROENERGETYCZNYM A COMPARISON OF SELECTED OPTIMAL POWER FLOW ALGORITHMS
 ELEKRYKA 2013 Zeszyt 4 (228) Ro LIX Artur PASIERBEK, Marcin POŁOMSKI, Radosław SOKÓŁ Politechnia Śląsa w Gliwicach PORÓWNANIE WYBRANYCH ALGORYMÓW OPYMALIZACJI ROZPŁYWU MOCY W SYSEMIE ELEKROENERGEYCZNYM
ELEKRYKA 2013 Zeszyt 4 (228) Ro LIX Artur PASIERBEK, Marcin POŁOMSKI, Radosław SOKÓŁ Politechnia Śląsa w Gliwicach PORÓWNANIE WYBRANYCH ALGORYMÓW OPYMALIZACJI ROZPŁYWU MOCY W SYSEMIE ELEKROENERGEYCZNYM
Optymalizacja harmonogramów budowlanych - problem szeregowania zadań
 Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
Mieczysław OŁOŃSI Wydział Budownictwa i Inżynierii Środowisa, Szoła Główna Gospodarstwa Wiejsiego, Warszawa, ul. Nowoursynowsa 159 e-mail: mieczyslaw_polonsi@sggw.pl Założenia Optymalizacja harmonogramów
DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH
 Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
Część 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH... 5. 5. DRGANIA WŁASNE RAM OBLICZANIE CZĘSTOŚCI KOŁOWYCH DRGAŃ WŁASNYCH 5.. Wprowadzenie Rozwiązywanie zadań z zaresu dynamii budowli sprowadza
PLAN WYKŁADU OPTYMALIZACJA GLOBALNA ALGORYTM MRÓWKOWY (ANT SYSTEM) ALGORYTM MRÓWKOWY. Algorytm mrówkowy
 PLAN WYKŁADU Algorytm mrówowy OPTYMALIZACJA GLOBALNA Wyład 8 dr inż. Agniesza Bołtuć (ANT SYSTEM) Inspiracja: Zachowanie mrówe podczas poszuiwania żywności, Zachowanie to polega na tym, że jeśli do żywności
PLAN WYKŁADU Algorytm mrówowy OPTYMALIZACJA GLOBALNA Wyład 8 dr inż. Agniesza Bołtuć (ANT SYSTEM) Inspiracja: Zachowanie mrówe podczas poszuiwania żywności, Zachowanie to polega na tym, że jeśli do żywności
Zaliczenie wykładu Technika Analogowa Przykładowe pytania (czas zaliczenia minut, liczba pytań 6 8)
 Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
Zaliczenie wyładu Technia Analogowa Przyładowe pytania (czas zaliczenia 3 4 minut, liczba pytań 6 8) Postulaty i podstawowe wzory teorii obowdów 1 Sformułuj pierwsze i drugie prawo Kirchhoffa Wyjaśnij
13. 13. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE
 Część 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3. 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3.. Metoda trzech momentów Rozwiązanie wieloprzęsłowych bele statycznie niewyznaczalnych można ułatwić w znaczącym
Część 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3. 3. BELKI CIĄGŁE STATYCZNIE NIEWYZNACZALNE 3.. Metoda trzech momentów Rozwiązanie wieloprzęsłowych bele statycznie niewyznaczalnych można ułatwić w znaczącym
Bezgradientowe metody optymalizacji funkcji wielu zmiennych. informacje dodatkowe
 Bezgradientowe metody optymalizacji funkcji wielu zmiennych informacje dodatkowe Wybór kierunku poszukiwań Kierunki bazowe i ich modyfikacje metody bezgradientowe. Kierunki oparte na gradiencie funkcji
Bezgradientowe metody optymalizacji funkcji wielu zmiennych informacje dodatkowe Wybór kierunku poszukiwań Kierunki bazowe i ich modyfikacje metody bezgradientowe. Kierunki oparte na gradiencie funkcji
PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE
 PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE ORAZ ŚREDNIE 1. Procenty i proporcje DEFINICJA 1. Jeden procent (1%) pewnej liczby a to setna część tej liczby, tórą oznacza się: 1% a, przy czym 1% a = 1 p a, zaś
PROCENTY, PROPORCJE, WYRAŻENIA POTEGOWE ORAZ ŚREDNIE 1. Procenty i proporcje DEFINICJA 1. Jeden procent (1%) pewnej liczby a to setna część tej liczby, tórą oznacza się: 1% a, przy czym 1% a = 1 p a, zaś
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ
 ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ LISTA ZADAŃ 1 1 Napisać w formie rozwiniętej następujące wyrażenia: 4 (a 2 + b +1 =0 5 a i b j =1 n a i b j =1 n =0 (a nb 4 3 (! + ib i=3 =1 2 Wyorzystując twierdzenie o
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Laboratorium Zadanie nr 3 Osada autor: A Gonczarek Celem poniższego zadania jest zrealizowanie fragmentu komputerowego przeciwnika w grze strategiczno-ekonomicznej
Metody systemowe i decyzyjne w informatyce Laboratorium Zadanie nr 3 Osada autor: A Gonczarek Celem poniższego zadania jest zrealizowanie fragmentu komputerowego przeciwnika w grze strategiczno-ekonomicznej
wtedy i tylko wtedy, gdy rozwiązanie i jest nie gorsze od j względem k-tego kryterium. 2) Macierz części wspólnej Utwórz macierz
 Temat: Programowanie wieloryterialne. Ujęcie dysretne.. Problem programowania wieloryterialnego. Z programowaniem wieloryterialnym mamy do czynienia, gdy w problemie decyzyjnym występuje więcej niż jedno
Temat: Programowanie wieloryterialne. Ujęcie dysretne.. Problem programowania wieloryterialnego. Z programowaniem wieloryterialnym mamy do czynienia, gdy w problemie decyzyjnym występuje więcej niż jedno
(U.3) Podstawy formalizmu mechaniki kwantowej
 3.10.2004 24. (U.3) Podstawy formalizmu mechanii wantowej 33 Rozdział 24 (U.3) Podstawy formalizmu mechanii wantowej 24.1 Wartości oczeiwane i dyspersje dla stanu superponowanego 24.1.1 Założenia wstępne
3.10.2004 24. (U.3) Podstawy formalizmu mechanii wantowej 33 Rozdział 24 (U.3) Podstawy formalizmu mechanii wantowej 24.1 Wartości oczeiwane i dyspersje dla stanu superponowanego 24.1.1 Założenia wstępne
Zadania do rozdziału 5
 Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
Zadania do rozdziału 5 Zad.5.1. Udowodnij, że stosując równię pochyłą o dającym się zmieniać ącie nachylenia α można wyznaczyć współczynni tarcia statycznego µ o. ozwiązanie: W czasie zsuwania się po równi
WYKŁAD nr Ekstrema funkcji jednej zmiennej o ciągłych pochodnych. xˆ ( ) 0
 WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
WYKŁAD nr 4. Zaanie programowania nieliniowego ZP. Ekstrema unkcji jenej zmiennej o ciągłych pochonych Przypuśćmy ze punkt jest punktem stacjonarnym unkcji gzie punktem stacjonarnym nazywamy punkt la którego
Zestaw 12- Macierz odwrotna, układy równań liniowych
 Zestaw - Macierz odwrotna, układy równań liniowych Przykładowe zadania z rozwiązaniami ZałóŜmy, Ŝe macierz jest macierzą kwadratową stopnia n. Mówimy, Ŝe macierz tego samego wymiaru jest macierzą odwrotną
Zestaw - Macierz odwrotna, układy równań liniowych Przykładowe zadania z rozwiązaniami ZałóŜmy, Ŝe macierz jest macierzą kwadratową stopnia n. Mówimy, Ŝe macierz tego samego wymiaru jest macierzą odwrotną
Prawdopodobieństwo i statystyka
 Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Wykład XV: Zagadnienia redukcji wymiaru danych 2 lutego 2015 r. Standaryzacja danych Standaryzacja danych Własności macierzy korelacji Definicja Niech X będzie zmienną losową o skończonym drugim momencie.
Grupowanie sekwencji czasowych
 BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 3, 006 Grupowanie sewencji czasowych Tomasz PAŁYS Załad Automatyi, Instytut Teleinformatyi i Automatyi WAT, ul. Kalisiego, 00-908 Warszawa STRESZCZENIE: W artyule
BIULETYN INSTYTUTU AUTOMATYKI I ROBOTYKI NR 3, 006 Grupowanie sewencji czasowych Tomasz PAŁYS Załad Automatyi, Instytut Teleinformatyi i Automatyi WAT, ul. Kalisiego, 00-908 Warszawa STRESZCZENIE: W artyule
Geometria analityczna przestrzeni
 ALGEBRA LINIOWA 1 Wydział Mechaniczny / AIR, MTR Semestr zimowy 2009/2010 Prowadzący: dr Teresa Jurlewicz Wetory, długość wetora Geometria analityczna przestrzeni Zadanie 1 [5.1] Obliczyć długości podanych
ALGEBRA LINIOWA 1 Wydział Mechaniczny / AIR, MTR Semestr zimowy 2009/2010 Prowadzący: dr Teresa Jurlewicz Wetory, długość wetora Geometria analityczna przestrzeni Zadanie 1 [5.1] Obliczyć długości podanych
4.15 Badanie dyfrakcji światła laserowego na krysztale koloidalnym(o19)
 256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
256 Fale 4.15 Badanie dyfracji światła laserowego na rysztale oloidalnym(o19) Celem ćwiczenia jest wyznaczenie stałej sieci dwuwymiarowego ryształu oloidalnego metodą dyfracji światła laserowego. Zagadnienia
Statystyka i eksploracja danych
 Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
Wykład XII: Zagadnienia redukcji wymiaru danych 12 maja 2014 Definicja Niech X będzie zmienną losową o skończonym drugim momencie. Standaryzacją zmiennej X nazywamy zmienną losową Z = X EX Var (X ). Definicja
Przekształcenie całkowe Fouriera
 Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
Przekształcenie całkowe Fouriera Postać zespolona szeregu Fouriera Niech ana bęzie funkcja f spełniająca w przeziale [, ] warunki Dirichleta. Wtey szereg Fouriera tej funkcji jest o niej zbieżny, tj. przy
WYKŁAD 9 METODY ZMIENNEJ METRYKI
 WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
WYKŁAD 9 METODY ZMIENNEJ METRYKI Kierunki sprzężone. Metoda Newtona Raphsona daje dobre przybliżenie najlepszego kierunku poszukiwań, lecz jest to okupione znacznym kosztem obliczeniowym zwykle postać
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Metody bezgradientowe optymalizacji bez ograniczeń Materiały pomocnicze do ćwiczeń
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania Metody optymalizacji Metody bezgradientowe optymalizacji bez ograniczeń Materiały pomocnicze do ćwiczeń
Prawdopodobieństwo i statystyka
 Zadanie Rozważmy następujący model strzelania do tarczy. Współrzędne puntu trafienia (, Y ) są niezależnymi zmiennymi losowymi o jednaowym rozładzie normalnym N ( 0, σ ). Punt (0,0) uznajemy za środe tarczy,
Zadanie Rozważmy następujący model strzelania do tarczy. Współrzędne puntu trafienia (, Y ) są niezależnymi zmiennymi losowymi o jednaowym rozładzie normalnym N ( 0, σ ). Punt (0,0) uznajemy za środe tarczy,
MODYFIKACJA KOSZTOWA ALGORYTMU JOHNSONA DO SZEREGOWANIA ZADAŃ BUDOWLANYCH
 MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
MODYFICJ OSZTOW LGORYTMU JOHNSON DO SZEREGOWNI ZDŃ UDOWLNYCH Michał RZEMIŃSI, Paweł NOW a a Wydział Inżynierii Lądowej, Załad Inżynierii Producji i Zarządzania w udownictwie, ul. rmii Ludowej 6, -67 Warszawa
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
ZADANIA OPTYMALIZCJI BEZ OGRANICZEŃ
 ZADANIA OPTYMALIZCJI BEZ OGRANICZEŃ Maciej Patan Uniwersytet Zielonogórski WSTEP Zadanie minimalizacji bez ograniczeń f(ˆx) = min x R nf(x) f : R n R funkcja ograniczona z dołu Algorytm rozwiazywania Rekurencyjny
ZADANIA OPTYMALIZCJI BEZ OGRANICZEŃ Maciej Patan Uniwersytet Zielonogórski WSTEP Zadanie minimalizacji bez ograniczeń f(ˆx) = min x R nf(x) f : R n R funkcja ograniczona z dołu Algorytm rozwiazywania Rekurencyjny
KADD Minimalizacja funkcji
 Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
Minimalizacja funkcji Poszukiwanie minimum funkcji Foma kwadratowa Metody przybliżania minimum minimalizacja Minimalizacja w n wymiarach Metody poszukiwania minimum Otaczanie minimum Podział obszaru zawierającego
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 5. PODSTAWOWE ROZKŁADY PRAWDOPODOBIEŃSTWA Rozłady soowe Rozład jednopuntowy Oreślamy: P(X c) 1 gdzie c ustalona liczba. 1 EX c, D 2 X 0 (tylo ten rozład ma zerową wariancję!!!)
Programowanie wielocelowe lub wielokryterialne
 Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe.
Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe.
Mechanika kwantowa ćwiczenia, 2007/2008, Zestaw II
 1 Dane są następujące operatory: ˆD = x, ˆQ = π 0 x, ŝin = sin( ), ĉos = cos( ), ˆπ = π, ˆ0 = 0, przy czym operatory ˆπ oraz ˆ0 są operatorami mnożenia przez opowienie liczby (a) Wyznacz kwarat oraz owrotność
1 Dane są następujące operatory: ˆD = x, ˆQ = π 0 x, ŝin = sin( ), ĉos = cos( ), ˆπ = π, ˆ0 = 0, przy czym operatory ˆπ oraz ˆ0 są operatorami mnożenia przez opowienie liczby (a) Wyznacz kwarat oraz owrotność
Algebra liniowa z geometrią analityczną
 WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
WYKŁAD. Własności zbiorów liczbowych. Podzielność liczb całowitych, relacja przystawania modulo, twierdzenie chińsie o resztach. Liczby całowite Liczby 0,±,±,±3,... nazywamy liczbami całowitymi. Zbiór
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Transport, studia I stopnia rok akademicki 2011/2012 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Uwagi wstępne Układ liniowych równań algebraicznych można
Optymalizacja ciągła
 Optymalizacja ciągła 5. Metody kierunków poparwy (metoda Newtona-Raphsona, metoda gradientów sprzężonych) Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 28.03.2019 1
Optymalizacja ciągła 5. Metody kierunków poparwy (metoda Newtona-Raphsona, metoda gradientów sprzężonych) Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 28.03.2019 1
Zastosowanie informatyki w elektrotechnice
 Zastosowanie informatyi w eletrotechnice Politechnia Białostoca - Wydział Eletryczny Eletrotechnia, semestr V, studia niestacjonarne Ro aademici 2006/2007 Wyład nr 4 (15.12.2006 Zastosowanie informatyi
Zastosowanie informatyi w eletrotechnice Politechnia Białostoca - Wydział Eletryczny Eletrotechnia, semestr V, studia niestacjonarne Ro aademici 2006/2007 Wyład nr 4 (15.12.2006 Zastosowanie informatyi
Sterowanie Ciągłe. Używając Simulink a w pakiecie MATLAB, zasymulować układ z rysunku 7.1. Rys.7.1. Schemat blokowy układu regulacji.
 emat ćwiczenia nr 7: Synteza parametryczna uładów regulacji. Sterowanie Ciągłe Celem ćwiczenia jest orecja zadanego uładu regulacji wyorzystując następujące metody: ryterium amplitudy rezonansowej i metodę
emat ćwiczenia nr 7: Synteza parametryczna uładów regulacji. Sterowanie Ciągłe Celem ćwiczenia jest orecja zadanego uładu regulacji wyorzystując następujące metody: ryterium amplitudy rezonansowej i metodę
Równanie Fresnela. napisał Michał Wierzbicki
 napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
napisał Michał Wierzbici Równanie Fresnela W anizotropowych ryształach optycznych zależność między wetorami inducji i natężenia pola eletrycznego (równanie materiałowe) jest następująca = ϵ 0 ˆϵ E (1)
Numeryczne metody optymalizacji Optymalizacja w kierunku. informacje dodatkowe
 Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Numeryczne metody optymalizacji Optymalizacja w kierunku informacje dodatkowe Numeryczne metody optymalizacji x F x = min x D x F(x) Problemy analityczne: 1. Nieliniowa złożona funkcja celu F i ograniczeń
Colloquium 3, Grupa A
 Colloquium 3, Grupa A 1. Z zasobów obliczeniowych pewnego serwera orzysta dwóch użytowniów. Każdy z nich wysyła do serwera zawsze trzy programy naraz. Użytowni czea, aż serwer wyona obliczenia dotyczące
Colloquium 3, Grupa A 1. Z zasobów obliczeniowych pewnego serwera orzysta dwóch użytowniów. Każdy z nich wysyła do serwera zawsze trzy programy naraz. Użytowni czea, aż serwer wyona obliczenia dotyczące
Linie wpływu w belkach statycznie niewyznaczalnych
 EHANIKA BUOWI inie wpływu w belach statycznie niewyznaczalnych Zadanie.: la poniższej beli naszicuj linie wpływu reacji A, B i. Za pomocą metody przemieszczeń wyznaczyć rzędne poszczególnych linii w połowie
EHANIKA BUOWI inie wpływu w belach statycznie niewyznaczalnych Zadanie.: la poniższej beli naszicuj linie wpływu reacji A, B i. Za pomocą metody przemieszczeń wyznaczyć rzędne poszczególnych linii w połowie
Programowanie wielocelowe lub wielokryterialne
 Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Programowanie wielocelowe lub wieloryterialne Zadanie wielocelowe ma co najmniej dwie funcje celu nazywane celami cząstowymi. Cele cząstowe f numerujemy indesem = 1, 2, K. Programowanie wielocelowe ciągłe
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305
 ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305 Henry Boryń Politechnia Gdańsa ODSTĘPY IZOLACYJNE BEZPIECZNE Zadania bezpiecznego odstępu izolacyjnego to: ochrona przed bezpośrednim
ZASADY WYZNACZANIA BEZPIECZNYCH ODSTĘPÓW IZOLACYJNYCH WEDŁUG NORMY PN-EN 62305 Henry Boryń Politechnia Gdańsa ODSTĘPY IZOLACYJNE BEZPIECZNE Zadania bezpiecznego odstępu izolacyjnego to: ochrona przed bezpośrednim
WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY 3g. zakres rozszerzony
 WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY 3g zares rozszerzony 1. Wielomiany bardzo zna pojęcie jednomianu jednej zmiennej; potrafi wsazać jednomiany podobne; potrafi
WYMAGANIA Z WIEDZY I UMIEJĘTNOŚCI NA POSZCZEGÓLNE STOPNIE SZKOLNE DLA KLASY 3g zares rozszerzony 1. Wielomiany bardzo zna pojęcie jednomianu jednej zmiennej; potrafi wsazać jednomiany podobne; potrafi
A. Cel ćwiczenia. B. Część teoretyczna
 A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
A. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z wsaźniami esploatacyjnymi eletronicznych systemów bezpieczeństwa oraz wyorzystaniem ich do alizacji procesu esplatacji z uwzględnieniem przeglądów
Metody numeryczne. Instytut Sterowania i Systemów Informatycznych Wydział Elektrotechniki, Informatyki i Telekomunikacji Uniwersytet Zielonogórski
 Metody numeryczne Instytut Sterowania i Systemów Informatycznych Wydział Eletrotechnii, Informatyi i Teleomuniacji Uniwersytet Zielonogórsi Eletrotechnia stacjonarne-dzienne pierwszego stopnia z tyt. inżyniera
Metody numeryczne Instytut Sterowania i Systemów Informatycznych Wydział Eletrotechnii, Informatyi i Teleomuniacji Uniwersytet Zielonogórsi Eletrotechnia stacjonarne-dzienne pierwszego stopnia z tyt. inżyniera
ANALIZA WIELOKRYTERIALNA
 ANALIZA WIELOKRYTERIALNA Dział Badań Operacyjnych zajmujący się oceną możliwych wariantów (decyzji) w przypadu gdy występuje więcej niż jedno ryterium oceny D zbiór rozwiązań (decyzji) dopuszczalnych x
ANALIZA WIELOKRYTERIALNA Dział Badań Operacyjnych zajmujący się oceną możliwych wariantów (decyzji) w przypadu gdy występuje więcej niż jedno ryterium oceny D zbiór rozwiązań (decyzji) dopuszczalnych x
Definicja pochodnej cząstkowej
 1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
Sygnały stochastyczne
 Sygnały stochastyczne Zmienne losowe E zbiór zdarzeń elementarnych (zbiór możliwych wyniów esperymentu) e E zdarzenie elementarne (wyni esperymentu) B zbiór wybranych podzbiorów zbioru E β B zdarzenie
Sygnały stochastyczne Zmienne losowe E zbiór zdarzeń elementarnych (zbiór możliwych wyniów esperymentu) e E zdarzenie elementarne (wyni esperymentu) B zbiór wybranych podzbiorów zbioru E β B zdarzenie
Wstęp do metod numerycznych 11. Minimalizacja: funkcje wielu zmiennych. P. F. Góra
 Wstęp do metod numerycznych 11. Minimalizacja: funkcje wielu zmiennych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Strategia minimalizacji wielowymiarowej Zakładamy, że metody poszukiwania minimów
Wstęp do metod numerycznych 11. Minimalizacja: funkcje wielu zmiennych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2012 Strategia minimalizacji wielowymiarowej Zakładamy, że metody poszukiwania minimów
PARAMETRYCZNE ZAGADNIENIE ODWROTNE ODTWARZANIA WŁASNOŚCI FILTRACYJNYCH GRUNTU
 MODELOWANIE INŻYNIERSIE ISNN 1896-771X 32, s. 439-446, Gliwice 2006 PARAMERYCZNE ZAGADNIENIE ODWRONE ODWARZANIA WŁASNOŚCI FILRACYJNYCH GRUNU IRENEUSZ SZCZYGIEŁ Instytut echnii Cieplnej, Politechnia Śląsa
MODELOWANIE INŻYNIERSIE ISNN 1896-771X 32, s. 439-446, Gliwice 2006 PARAMERYCZNE ZAGADNIENIE ODWRONE ODWARZANIA WŁASNOŚCI FILRACYJNYCH GRUNU IRENEUSZ SZCZYGIEŁ Instytut echnii Cieplnej, Politechnia Śląsa
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
Optymalizacja ciągła
 Optymalizacja ciągła 4. Metody kierunków poprawy (metoda spadku wzdłuż gradientu) Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 21.03.2019 1 / 41 Plan wykładu Minimalizacja
Optymalizacja ciągła 4. Metody kierunków poprawy (metoda spadku wzdłuż gradientu) Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 21.03.2019 1 / 41 Plan wykładu Minimalizacja
DWUPOZIOMOWA METODA WIELOKRYTERIALNEGO STEROWANIA PRZEPŁYWEM PRODUKTÓW
 DWUPOZIOMOWA METODA WIELOKRYTERIALNEGO STEROWANIA PRZEPŁYWEM PRODUKTÓW Mare MAGIERA Streszczenie: Zadanie sterowania przepływem produtów przez wielostadialną linię producyjną zostało podzielone na dwa
DWUPOZIOMOWA METODA WIELOKRYTERIALNEGO STEROWANIA PRZEPŁYWEM PRODUKTÓW Mare MAGIERA Streszczenie: Zadanie sterowania przepływem produtów przez wielostadialną linię producyjną zostało podzielone na dwa
POPRAWA EFEKTYWNOŚCI METODY WSTECZNEJ
 Nowoczesne techniki informatyczne - Ćwiczenie 6: POPRAWA EFEKTYWNOŚCI METODY BP str. 1 Ćwiczenie 6: UCZENIE SIECI WIELOWARSTWOWYCH. POPRAWA EFEKTYWNOŚCI METODY WSTECZNEJ PROPAGACJI BŁĘDU WYMAGANIA 1. Sztuczne
Nowoczesne techniki informatyczne - Ćwiczenie 6: POPRAWA EFEKTYWNOŚCI METODY BP str. 1 Ćwiczenie 6: UCZENIE SIECI WIELOWARSTWOWYCH. POPRAWA EFEKTYWNOŚCI METODY WSTECZNEJ PROPAGACJI BŁĘDU WYMAGANIA 1. Sztuczne
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
ef 3 (dziedzina, dziedzina naturalna) Niech f : A R, gdzie A jest podzbiorem płaszczyzny lub przestrzeni Zbiór A nazywamy dziedziną funcji f i oznacza
 FUNKCJE WÓCH I TRZECH ZMIENNYCH (było w semestrze II) ef 1 (funcja dwóch zmiennych) Funcją f dwóch zmiennych oreśloną na zbiorze A R o wartościach w R nazywamy przyporządowanie ażdemu puntowi ze zbioru
FUNKCJE WÓCH I TRZECH ZMIENNYCH (było w semestrze II) ef 1 (funcja dwóch zmiennych) Funcją f dwóch zmiennych oreśloną na zbiorze A R o wartościach w R nazywamy przyporządowanie ażdemu puntowi ze zbioru
Wykład 21: Studnie i bariery cz.1.
 Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
Wyład : Studnie i bariery cz.. Dr inż. Zbigniew Szlarsi Katedra Eletronii, paw. C-, po.3 szla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szlarsi/ 3.6.8 Wydział Informatyi, Eletronii i Równanie Schrödingera
ZADANIE 52 INTERFERENCYJNY POMIAR KRZYWIZNY SOCZEWKI (pierścienie Newtona) Cel ćwiczenia Celem ćwiczenia jest wyznaczenie, przy znanej długości fali
 ZADANIE 52 INTERFERENCYJNY POMIAR KRZYWIZNY SOCZEWKI (pierścienie Newtona) Cel ćwiczenia Celem ćwiczenia jest wyznaczenie, przy znanej długości fali świetlnej, promienia rzywizny soczewi płaso-wypułej
ZADANIE 52 INTERFERENCYJNY POMIAR KRZYWIZNY SOCZEWKI (pierścienie Newtona) Cel ćwiczenia Celem ćwiczenia jest wyznaczenie, przy znanej długości fali świetlnej, promienia rzywizny soczewi płaso-wypułej
Dr. inŝ. Ewa Szlachcic Katedra Automatyki, Mechatroniki i Systemów Sterowania. Przykładowe zadania optymalizacji nieliniowej bez ograniczeń
 Wydział Elektroniki Kier: Automatyka i Robotyka Studia magisterskie II stopnia Dr. inŝ. Ewa Szlachcic Katedra Automatyki, Mechatroniki i Systemów Sterowania Przykładowe zadania optymalizacji nieliniowej
Wydział Elektroniki Kier: Automatyka i Robotyka Studia magisterskie II stopnia Dr. inŝ. Ewa Szlachcic Katedra Automatyki, Mechatroniki i Systemów Sterowania Przykładowe zadania optymalizacji nieliniowej
Matematyka dyskretna. Wykład 2: Kombinatoryka. Gniewomir Sarbicki
 Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Matematya dysretna Wyład 2: Kombinatorya Gniewomir Sarbici Kombinatorya Definicja Kombinatorya zajmuje się oreślaniem mocy zbiorów sończonych, w szczególności mocy zbiorów odwzorowań jednego zbioru w drugi
Wyznaczanie długości fali świetlnej za pomocą spektrometru siatkowego
 Politechnia Łódza FTIMS Kierune: Informatya ro aademici: 2008/2009 sem. 2. Termin: 16 III 2009 Nr. ćwiczenia: 413 Temat ćwiczenia: Wyznaczanie długości fali świetlnej za pomocą spetrometru siatowego Nr.
Politechnia Łódza FTIMS Kierune: Informatya ro aademici: 2008/2009 sem. 2. Termin: 16 III 2009 Nr. ćwiczenia: 413 Temat ćwiczenia: Wyznaczanie długości fali świetlnej za pomocą spetrometru siatowego Nr.
Pomiary napięć przemiennych
 LABORAORIUM Z MEROLOGII Ćwiczenie 7 Pomiary napięć przemiennych . Cel ćwiczenia Celem ćwiczenia jest poznanie sposobów pomiarów wielości charaterystycznych i współczynniów, stosowanych do opisu oresowych
LABORAORIUM Z MEROLOGII Ćwiczenie 7 Pomiary napięć przemiennych . Cel ćwiczenia Celem ćwiczenia jest poznanie sposobów pomiarów wielości charaterystycznych i współczynniów, stosowanych do opisu oresowych
Granica i ciągłość funkcji. 1 Granica funkcji rzeczywistej jednej zmiennej rzeczywistej
 Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Wydział Matematyki Stosowanej Zestaw zadań nr 3 Akademia Górniczo-Hutnicza w Krakowie WEiP, energetyka, I rok Elżbieta Adamus 3 listopada 06r. Granica i ciągłość funkcji Granica funkcji rzeczywistej jednej
Podstawy Automatyki Zbiór zadań dla studentów II roku AiR oraz MiBM
 Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
Aademia GórniczoHutnicza im. St. Staszica w Kraowie Wydział Inżynierii Mechanicznej i Robotyi Katedra Automatyzacji Procesów Podstawy Automatyi Zbiór zadań dla studentów II rou AiR oraz MiBM Tomasz Łuomsi
METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ
 Problemy Kolejnictwa Zeszyt 5 97 Prof. dr hab. inż. Władysław Koc Politechnia Gdańsa METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ SPIS TREŚCI. Wprowadzenie. Ogólna ocena sytuacji geometrycznej
Problemy Kolejnictwa Zeszyt 5 97 Prof. dr hab. inż. Władysław Koc Politechnia Gdańsa METODA PROJEKTOWANIA REJONU ZMIANY KIERUNKU TRASY KOLEJOWEJ SPIS TREŚCI. Wprowadzenie. Ogólna ocena sytuacji geometrycznej
Wykład VIII Rozwiązywanie równań i układów równań nieliniowych
 Wyład VIII Rozwiązywanie równań i uładów równań nieliniowych Równania nieliniowe w technice Zadanie wyznaczenia pierwiastów równania nieliniowego Metody iteracji z otaczaniem i podziałem (bisecja i regula-falsi)
Wyład VIII Rozwiązywanie równań i uładów równań nieliniowych Równania nieliniowe w technice Zadanie wyznaczenia pierwiastów równania nieliniowego Metody iteracji z otaczaniem i podziałem (bisecja i regula-falsi)
 Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź
Ś Ś Ś Ś Ś Ś Ę Ą Ę ŚĘ Ę Ś ń Ę Ę Ą Ł Ż Ń Ł ć Ą ć Ł Ę Ó ć Ź ć ź ń Ń ń Ś Ą Ę Ł Ę Ą Ę ń ć ń Ź ć ń ć ń Ś ń ŚĆ ć ź Ł Ę Ę Ś Ę Ę Ę ń ŚĘ Ń Ę Ę ń ŚĘ Ę Ę Ś Ś ć ń Ę ń Ś Ę ć ć Ę Ę ć ź ć ń Ę Ń ń ć Ł Ę Ę Ę Ę ć Ę ć ć ź
Analiza numeryczna Lista nr 3 (ćwiczenia) x x 2 n x.
 Analiza numeryczna Lista nr 3 (ćwiczenia) Sprawdzić że macierz ma wartości własne2+ 222 2 2 Niechx R n Udowodnić że 2 0 0 x x 2 n x 3 NiechA R n n będzie macierzą symetryczną Wiadomo że wówczas istnieje
Analiza numeryczna Lista nr 3 (ćwiczenia) Sprawdzić że macierz ma wartości własne2+ 222 2 2 Niechx R n Udowodnić że 2 0 0 x x 2 n x 3 NiechA R n n będzie macierzą symetryczną Wiadomo że wówczas istnieje
Metoda rozwiązywania układu równań liniowych z symetryczną, nieokreśloną macierzą współczynników ( 0 )
 MATEMATYKA STOSOWANA 7, 2006 Izabella Czochralsa (Warszawa) Metoda rozwiązywania uładu równań liniowych z symetryczną, nieoreśloną macierzą współczynniów ( 0 ) Streszczenie. W pracy zaadaptowano opracowaną
MATEMATYKA STOSOWANA 7, 2006 Izabella Czochralsa (Warszawa) Metoda rozwiązywania uładu równań liniowych z symetryczną, nieoreśloną macierzą współczynniów ( 0 ) Streszczenie. W pracy zaadaptowano opracowaną
UKŁADY ALGEBRAICZNYCH RÓWNAŃ LINIOWYCH
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać układu równań liniowych Układ liniowych równań algebraicznych
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać układu równań liniowych Układ liniowych równań algebraicznych
TEORIA OBWODÓW I SYGNAŁÓW LABORATORIUM
 EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
EORI OBWODÓW I SYGNŁÓW LBORORIUM KDEMI MORSK Katedra eleomuniacji Morsiej Ćwiczenie nr 2: eoria obwodów i sygnałów laboratorium ĆWICZENIE 2 BDNIE WIDM SYGNŁÓW OKRESOWYCH. Cel ćwiczenia Celem ćwiczenia
LZNK. Rozkªad QR. Metoda Householdera
 Rozdziaª 10 LZNK. Rozªad QR. Metoda Householdera W tym rozdziale zajmiemy si liniowym zadaniem najmniejszych wadratów (LZNK). Dla danej macierzy A wymiaru M N i wetora b wymiaru M chcemy znale¹ wetor x
Rozdziaª 10 LZNK. Rozªad QR. Metoda Householdera W tym rozdziale zajmiemy si liniowym zadaniem najmniejszych wadratów (LZNK). Dla danej macierzy A wymiaru M N i wetora b wymiaru M chcemy znale¹ wetor x
Problem komiwojażera ACO. Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym.
 Problem komiwojażera ACO Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym. -Wikipedia Problem do rozwiązania zazwyczaj jest przedstawiany jako
Problem komiwojażera ACO Zagadnienie optymalizacyjne, polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym. -Wikipedia Problem do rozwiązania zazwyczaj jest przedstawiany jako
NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES
 JANUSZ GERMAN, ZBIGNIEW MIKULSKI NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES S t r e s z c z e n i e A b s
JANUSZ GERMAN, ZBIGNIEW MIKULSKI NUMERYCZNA SYMULACJA STOPNIOWEGO USZKADZANIA SIĘ LAMINATÓW KOMPOZYTOWYCH NUMERICAL SIMULATION OF PROGRESSIVE DAMAGE IN COMPOSITE LAMINATES S t r e s z c z e n i e A b s
długość całkowita: L m moment bezwładności (względem osi y): J y cm 4 moment bezwładności: J s cm 4
 .9. Stalowy ustrój niosący. Poład drewniany spoczywa na dziewięciu belach dwuteowych..., swobodnie podpartych o rozstawie... m. Beli wyonane są ze stali... Cechy geometryczne beli: długość całowita: L
.9. Stalowy ustrój niosący. Poład drewniany spoczywa na dziewięciu belach dwuteowych..., swobodnie podpartych o rozstawie... m. Beli wyonane są ze stali... Cechy geometryczne beli: długość całowita: L
Analiza nośności poziomej pojedynczego pala
 Poradni Inżyniera Nr 16 Atualizacja: 09/016 Analiza nośności poziomej pojedynczego pala Program: Pli powiązany: Pal Demo_manual_16.gpi Celem niniejszego przewodnia jest przedstawienie wyorzystania programu
Poradni Inżyniera Nr 16 Atualizacja: 09/016 Analiza nośności poziomej pojedynczego pala Program: Pli powiązany: Pal Demo_manual_16.gpi Celem niniejszego przewodnia jest przedstawienie wyorzystania programu
ANALIZA STATYCZNA i WYMIAROWANIE KONSTRUKCJI RAMY
 ANALIZA STATYCZNA i WYMIAROWANIE KONSTRUKCJI RAMY 11 10 9 8 7 6 5 4 1 1 WĘZŁY: Nr: X [m]: Y [m]: Nr: X [m]: Y [m]: 1,7 1,41 7 1,6,17,968 1,591 8 1,07,46,658 1,759 9 0,688,54 4,4 1,916 10 0,46,609 5,00,061
ANALIZA STATYCZNA i WYMIAROWANIE KONSTRUKCJI RAMY 11 10 9 8 7 6 5 4 1 1 WĘZŁY: Nr: X [m]: Y [m]: Nr: X [m]: Y [m]: 1,7 1,41 7 1,6,17,968 1,591 8 1,07,46,658 1,759 9 0,688,54 4,4 1,916 10 0,46,609 5,00,061
WYKŁAD 2: CAŁKI POTRÓJNE
 WYKŁAD : CAŁKI OTRÓJNE 1 CAŁKI OTRÓJNE O ROSTOADŁOŚCIANIE Oznaczenia w definicji całi po prostopadłościanie: = {(: a x, c y d, p z q} prostopadłościan w przestrzeni; = { 1,,, n } podział prostopadłościanu
WYKŁAD : CAŁKI OTRÓJNE 1 CAŁKI OTRÓJNE O ROSTOADŁOŚCIANIE Oznaczenia w definicji całi po prostopadłościanie: = {(: a x, c y d, p z q} prostopadłościan w przestrzeni; = { 1,,, n } podział prostopadłościanu
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
Metody Lagrange a i Hamiltona w Mechanice Mariusz Przybycień Wydział Fizyi i Informatyi Stosowanej Aademia Górniczo-Hutnicza Wyład 12 M. Przybycień (WFiIS AGH Metody Lagrange a i Hamiltona... Wyład 12
KOLOKWIUM Z ALGEBRY I R
 Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Instrucje: Każde zadanie jest za 4 puntów. Rozwi azanie ażdego zadania musi znajdować siȩ na osobnej artce oraz być napisane starannie i czytelnie. W nag lówu ażdego rozwi azania musz a znajdować siȩ dane
Analiza B II zadania. cos kx = sin(n x) 2 sin x 2. cos n sin 1 n., tan x, cot x, log sin x, log tan x, 1 + x
 Analiza B II zadania Oblicz granicę n cos n n Udowodnij wzór dla mπ 3 Udowodnij że szereg + n = cos = sin(n + sin cos n sin n jest zbieżny warunowo 4 Wyprowadź wzory (sin = cos (cos = sin 5 Wyaż że funcje
Analiza B II zadania Oblicz granicę n cos n n Udowodnij wzór dla mπ 3 Udowodnij że szereg + n = cos = sin(n + sin cos n sin n jest zbieżny warunowo 4 Wyprowadź wzory (sin = cos (cos = sin 5 Wyaż że funcje
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 6 Rozwiązywanie równań nieliniowych Rozwiązaniem lub pierwiastkiem równania f(x) = 0 lub g(x) = h(x)
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 6 Rozwiązywanie równań nieliniowych Rozwiązaniem lub pierwiastkiem równania f(x) = 0 lub g(x) = h(x)
Do wprowadzania symboli pochodnych można wykorzystać paletę Calculus lub skróty klawiszowe: SHIFT+? - wprowadza symbol pierwszej pochodnej.
 1. Pochone funkcji Mathca umożliwia obliczenie pochonej funkcji w zaanym punkcie oraz wyznaczenie pochonej funkcji w sposób symboliczny. 1.1 Wyznaczanie wartości pochonej w punkcie Aby wyznaczyć pochoną
1. Pochone funkcji Mathca umożliwia obliczenie pochonej funkcji w zaanym punkcie oraz wyznaczenie pochonej funkcji w sposób symboliczny. 1.1 Wyznaczanie wartości pochonej w punkcie Aby wyznaczyć pochoną
Metoda Runge-Kutta-Fehlberga i sterowanie długością kroku
 Metoda Runge-Kutta-Fehlberga i sterowanie długością kroku Cel: Dla zadanej tolerancji e wybrać minimalną liczbę węzłów, wystarczającą do utrzymania globalnego błedu w ramach tolerancji. Błąd globalny trudny
Metoda Runge-Kutta-Fehlberga i sterowanie długością kroku Cel: Dla zadanej tolerancji e wybrać minimalną liczbę węzłów, wystarczającą do utrzymania globalnego błedu w ramach tolerancji. Błąd globalny trudny
Modelowanie i obliczenia techniczne. Równania różniczkowe Numeryczne rozwiązywanie równań różniczkowych zwyczajnych
 Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
Moelowanie i obliczenia echniczne Równania różniczowe Numeryczne rozwiązywanie równań różniczowych zwyczajnych Przyła ułau ynamicznego E Uła ynamiczny R 0 Zachozi porzeba wyznaczenia: C u C () i() ur ir
Wstęp do metod numerycznych 12. Minimalizacja: funkcje wielu zmiennych. P. F. Góra
 Wstęp do metod numerycznych 12. Minimalizacja: funkcje wielu zmiennych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Strategia minimalizacji wielowymiarowej Zakładamy, że metody poszukiwania minimów
Wstęp do metod numerycznych 12. Minimalizacja: funkcje wielu zmiennych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Strategia minimalizacji wielowymiarowej Zakładamy, że metody poszukiwania minimów
OPTYMALIZACJA PRZEPUSTOWOŚCI SIECI KOMPUTEROWYCH ZA POMOCĄ ALGORYTMÓW GENETYCZNYCH
 OPTYMALIZACJA PRZEPUSTOWOŚCI SIECI KOMPUTEROWYCH ZA POMOCĄ ALGORYTMÓW GENETYCZNYCH Andrzej SZYMONIK, Krzysztof PYTEL Streszczenie: W złożonych sieciach omputerowych istnieje problem doboru przepustowości
OPTYMALIZACJA PRZEPUSTOWOŚCI SIECI KOMPUTEROWYCH ZA POMOCĄ ALGORYTMÓW GENETYCZNYCH Andrzej SZYMONIK, Krzysztof PYTEL Streszczenie: W złożonych sieciach omputerowych istnieje problem doboru przepustowości
Redukcja wariancji w metodach Monte-Carlo
 14.02.2006 Seminarium szkoleniowe 14 lutego 2006 Plan prezentacji Wprowadzenie Metoda losowania warstwowego Metoda próbkowania ważonego Metoda zmiennych kontrolnych Metoda zmiennych antytetycznych Metoda
14.02.2006 Seminarium szkoleniowe 14 lutego 2006 Plan prezentacji Wprowadzenie Metoda losowania warstwowego Metoda próbkowania ważonego Metoda zmiennych kontrolnych Metoda zmiennych antytetycznych Metoda
Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na okres drgań
 KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
KAEDRA FIZYKI SOSOWANEJ PRACOWNIA 5 FIZYKI Ćw. 5. Badanie ruchu wahadła sprężynowego sprawdzenie wzoru na ores drgań Wprowadzenie Ruch drgający naeży do najbardziej rozpowszechnionych ruchów w przyrodzie.
WB Wieszak Belki DOCISK. 3,26 MPa
 DOCISK Założenia: - Drewno lasy C24 - Wytrzymałość charaterystyczna na ścisanie w poprze włóien c,90, 5,3 Pa - Przyjęto 1 lasę użytowania - Przyjęto onstrucję obciążoną obciążeniem ciężarem własnym i użytowym
DOCISK Założenia: - Drewno lasy C24 - Wytrzymałość charaterystyczna na ścisanie w poprze włóien c,90, 5,3 Pa - Przyjęto 1 lasę użytowania - Przyjęto onstrucję obciążoną obciążeniem ciężarem własnym i użytowym
