prof. dr hab. Zbigniew Klusek Cz. 1
|
|
|
- Angelika Michalik
- 6 lat temu
- Przeglądów:
Transkrypt
1 prof. dr hab. Zbigniew Klusek Cz. 1
2 Nowe wyzwania Koszty budowy fabryki: kilkanaście miliardów $ Co 18 miesięcy podwaja się liczba tranzystorów Tranzystory z bramką nm w masowej produkcji Na razie proces skalowania się udaje POJAWIA SIĘ MOTYWACJA DO WPROWADZANIA TECHNOLOGII OPARTYCH NA NOWYCH ZJAWISKACH I MATERIAŁACH
3 Nowe wyzwania Poszukujemy nowych wewnętrznych kwantowych stopni swobody elektronu J.J. Thomson m e- e- m O. Stern, W. Gerlach
4 Nowe możliwości s=+1 m e- e- s=+1 m m e- e- s=-1 m s=-1
5 Nowe możliwości s=+1 m e- e- s=+1 m e- e- m s=-1 m s=-1 h + s=+1 m s=+1 m h + h + h + m s=-1 m s=-1
6 Wymiarowość układów węglowych 3-D 0-D fulereny grafit nanorurki węglowe 1-D
7 Grafen 2-D Kryterium Lindemanna 2 2 R R R = a L.D. Landau R.E. Peierls R.E. Peierls, Helv. Phys. Acta 7 (1934) 61. R.E. Peierls, Ann. I.H. Poincare 5 ( 1935) 177. L.D. Landau, Phys. Z. Sowjetunion 11 ( 1937) 26.
8 Grafen 2-D R.E. Peierls L.D. Landau R.E. Peierls, Helv. Phys. Acta 7 (1934) 61. R.E. Peierls, Ann. I.H. Poincare 5 ( 1935) 177. L.D. Landau, Phys. Z. Sowjetunion 11 ( 1937) 26. W przybliżeniu harmonicznym, fluktuacje termiczne niszczą długozasięgowe uporządkowanie co prowadzi do procesu topnienia sieci 2-D w dowolnej temperaturze. Kryterium Lindemanna 2 2 R R R = a N.D. Mermin, H. Wagner N.D. Mermin Długozasięgowe uporządkowanie magnetyczne nie istnieje w 1-D i 2-D. Później wynik ten został rozszerzony na długozasięgowe uporządkowanie sieci krystalicznej (Mermin) N.D. Mermin, H. Wagner, Phys. Rev. Lett. 17 (1966) N.D. Mermin Phys. Rev. 176 (1968) 250.
9 Grafen 2-D
10 2-D (grafen?) w 3-D Poza przybliżenie harmoniczne Struktury 2-D w przestrzeni 3-D D.R. Nelson, L. Peliti, J. Phys. 48 (1987) L. Radzihovsky, P. Le Doussal, Phys. Rev. Lett. 69 (1992) D.R. Nelson, T. Piran, S. Weinberg, Statiscical Mechanics of Membrans and Surfaces (World Scientific 2004)
11 2-D (grafen?) w 3-D Morgenstern, RWTH Aachen Germany Klusek, UL Lodz Poland
12 Grafen można wytworzyć!!!!!!!! Andre Geim Kostya Novoselov
13 Grafen można wytworzyć!!!!!!!! grafit/grafeny grafit/grafeny A. Geim i K. Novoselov zaprezentowali prostą metodę otrzymywania grafenu
14 Grafen można wytworzyć!!!!!!!! A. Geim i K. Novoselov zaprezentowali prostą metodę identyfikacji grafenu grafit/grafeny SiO 2 /Si
15 Grafen można zidentyfikować Teoria Fresnela grafen/sio 2 /Si Współczynnik załamania grafen SiO 2 Si(100) n0 n2 n 1 3 n P. Blake, et al. Appl. Phys. Lett. 91, (2007). I. Wlasny, P. Dabrowski,, arxiv: v1 (2011).
16 Grafen można zidentyfikować Więcej niż 10 warstw Jedna warstwa Dwie warstwy Trzy warstwy Grafen w Zakładzie Fizyki i Technologii Struktur Nanometrowych Uniwersytetu Łódzkiego
17 Intensity [arb. units] Intensity [arb. units] Grafen można zidentyfikować 2D pik podwójny rezonans Graphene/SiO 2 /Si Bilayer/SiO 2 /Si Monolayer graphene Lorentz fit Bilayer graphene Lorentz fit Raman Shift [cm -1 ] Raman Shift [cm -1 ] SiO 2
18 Grafen można zidentyfikować Powszechna procedura identyfikacji 1 - warstwa - 1 komponent 2 - warstwy - 4 komponenty 3 - warstwy - 15 komponentów ->6 Więcej niż 5 warstw 2 komponenty jak w graficie
19 Grafen można zidentyfikować Teoria/Eksperyment A.C. Ferrari
20 Grafen można zidentyfikować 2D pik podwójny rezonans q, q K K 0 f
21 Grafen można zidentyfikować System STM/AFM/XPS/UPS ARPES/AES/LEED/KPM do badania własności grafenu
22 Zaczął się bum grafenowy Wszystkich zafascynowały własności elektryczne grafenu grafen ścieżka
23 Zaczął się bum grafenowy Physical Review Online Archive
24 Zaczął się bum grafenowy
25 Zaczął się bum grafenowy for groundbreaking experiments regarding the two-dimensional material graphene" Ig Nobel 2000 Nazwa pochodzi z języka angielskiego "ignoble" znaczy niegodziwy Novoselov Geim The 2000 Ig Nobel Prize in Physics shared by Andrey Geim and Michael Berry The Physics of Flying Frogs
26 Zaczął się bum grafenowy AntyNobel z Fizyki Ig Nobel in Physics 2000
27 Zaczął się bum grafenowy A. Geim K. Novoselov
28 Zaczął się bum grafenowy Richard Smalley / 1996 Harold Kroto / 1996 Robert Curl / 1996 Kostya Novoselov/2010 Andre Geim/2010 Sumio Iijima
29 Zaczął się bum grafenowy
30 Historia
31 Kontrowersje.. Walt de Heer Georgia Institute of Technology, Atlanta de Herr napisał list do Komitetu Noblowskiego
32 Kontrowersje.. October K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva, and A. A. Firsov Electric Field Effect in Atomically Thin Carbon Films December J. Phys. Chem. B2004, vol. 108, Claire Berger, Zhimin Song, Tianbo Li, Xuebin Li, Asmerom Y. Ogbazghi, Rui Feng, Zhenting Dai, Alexei N. Marchenkov, Edward H. Conrad, Phillip N. First, and Walt A. de Heer Ultrathin Epitaxial Graphite: 2D Electron Gas Properties and a Route toward Graphene-based Nanoelectronics
33 Kontrowersje.. Walt de Heer Georgia Institute of Technology, Atlanta
34 Kontrowersje.. Eksfoljacja mechaniczna Manchester, Science 04 Grube warstwy? Kurtz PRB1990 Ebbesen Adv Mat 1995 Ohashi Tanso 1997 Ruoff APL1999 Gan Surf Sci2003 Metoda CVD McConville 1986 (on Ni) Land 1992 (on Pt) Metoda transferu: Geim & Novoselov Nature Mat. (2007) Realizacja : MIT (2008) Yu(2008) Hong (2009) Ruoff (2009) Epitaksjalny wzrost na SiC Bommel 1975 Nagashima 1993 Forbeaux 1998 de Heer 2004 HRL 2009 IBM 2009 Eeksfoljacja chemiczna Benjamin Brodie Phil Trans.1859 Ruess & Vogt 1948 Boehm & Hofmann 1962 Ruoff 2007 Coleman 2008 Manchester 2008
35 Kontrowersje.. NSF Proposal, 2001 Patterned Graphite Nanoelectronics 3 cytowania naszej pracy w NSF Proposal, 2001 w różnych aspektach grantu, Z. Waqar, E. Denisov, T. Kompaniets, I. Makarenko, A. Titkov, and A. Bhatti Appl. Surf. Sci., vol. 161, p. 508, 2000.
36 Kontrowersje.. armchair zig-zag K. Kobayashi Phys. Rev. B 48 (1993) R. Tamura, M. Tsukada Phys. Rev. B 49 (1994) M. Fujita, K. Wakabayashi, K. Nakada, K. Kusakabe J. Phys. Soc. Jpn. 65 (1996) K. Nakada, M. Fujita, G. Dresselhaus, M. Dresselhaus Phys. Rev. B 54 (1996) K. Wakabayashi, M. Fujita, H. Ajiki, M. Sigrist Phys. Rev. B 59 (1999) R. Tamura, K. Akagi, M. Tsukada, S. Itoh, S. Ihara Phys. Rev. B 56 (1999) Y. Miyamoto, K. Nakada, M. Fujita Phys. Rev. B 59 (1999) 9858.
37 Kontrowersje.., Z. Waqar, E. Denisov, T. Kompaniets, I. Makarenko, A. Titkov, A. Bhatti, Appl. Surf. Sci. 161, pp , (2000)., Z. Waqar, W. Kozlowski, P. Kowlaczyk, E. Denisov, et al. Appl. Surf. Sci. 187, pp , (2002)., P.K. Datta, W. Kozlowski, Corr. Sci. 45, pp , (2003)., W. Kozlowski, P. Kowalczyk, A. Busiakiewicz, W. Olejniczak, et al. Acta Phys. Super. 6, pp , (2004). STM/STS 0.35 nm 0.35 nm d a Profil LDOS na krawędzi 5 d tunneling current [na] Profil I/V bias [V] Początek badań na Uniwersytecie Łódzkim 1999 rok di/dv [na/v] E F bias [V] c b a tunneling current [na] Profil I/V bias [V]
38 Kontrowersje.., Appl. Surf. Sci. 108, pp , (1997)., Appl. Surf. Sci. 125, pp , (1998)., Appl. Surf. Sci. 151, pp , (1999)., et al. Appl. Surf. Sci. 161, pp , (2000)., Vacuum 63, (2001) 139., et al. Appl. Surf. Sci. 187, pp , (2002)., et al. Corr. Sci. 45, pp , (2003)., Acta Phys. Super. 6, pp , (2004)., et al. Appl. Surf. Sci. 252, pp , (2005). NSF Proposal, 2001 Patterned Graphite Nanoelectronics 5 4 d c di/dv [na/v] bias [V] b a Krawędzie zig-zag armchair STM/STS
39 Kontrowersje.. NSF Proposal, 2001 Patterned Graphite Nanoelectronics Referee responses: not interesting ; not possible ; premature W latach udowodnili, że to możliwe Grant z Intela w 2003 oraz grant z NSF w 2004 Patent w 2003
40 Kontrowersje.. Confinement Controlled Sublimation
41 Kontrowersje.. Science 22 October 2004: Vol. 306 no pp
42 Kontrowersje..
43 Kontrowersje.. A może Phil Kim powinien być również laureatem Nagrody Nobla z Fizyki za 2010? Kostia Novoselov Andre Geim Phil Kim
44 Grafen na Uniwersytecie Łódzkim 20 lat minęło Bazylea D 3-D
45 Grafen na Uniwersytecie Łódzkim H H H H H T=1500 K Ir(111) H [111] Grafen/Ir(111) Początek badań w Łodzi 1999 rok Ir (111) A. F. Ioffe Physical-Technical Institute Russian Academy of Sciences St. Petersburg, Russia Solid State Electronics Department, Research Institute of Physics St. Petersburg University St. Petersburg, Russia
46 Grafen na Uniwersytecie Łódzkim 10 nm x 10 nm Pierwsza próba opublikowania rezultatów w roku 2000 nie powiodła się
47 Grafen grafit dwuwarstwa grafenowa grafen
48 Grafen sieć rzeczywista A B Komórka elementarna 2 atomy Dwie podsieci trójkątne Bravaisgo Symetria inwersji
49 Grafen Potrzebne do koncepcji pseudospinu Mamy dwie orientacje wiązań tzn. mamy dwa rodzaje atomów węgla. Z chemicznego punktu widzenia nie ma to znaczenia.
50 Grafen sieć odwrotna Kmórka elementarna sieci odwrotnej Konstrukcja Wignera-Seitza a 1 b 1 a 2 b 2 b a = 2 b a = b a = 0 b a =
51 Grafen struktura elektronowa pz pz A B B p z s A p z
52 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie?, = f k, k E k k x y x y A B A B L.D. Landau R.E. Peierls t t' Philip Russel Wallace, 1947 t=2.8-3 ev przeskok pomiędzy dwoma różnymi podsieciami t =0.1eV przeskok w ramach tej samej sieci Hˆ t a b h. c. t a a b b h. c. ' s, i s, j s, i s, j s, i s, j = i, j, s i, j, s
53 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie? P.R. Wallace, Phys. Rev. 71 (1947) 622. Single hexagonal layer Graphene -1986
54 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie? ˆ ' s, i s, j +.. c t a, i, j, i, j hc.. H -t a b h - s as bs bs i, j, s i, j, s = + +, 3 ' x y = = t + k - f k E k k E k f t 3ak y 3 f k = 2cos 3ak y + 4cos cos kxx 2 2
55 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie?
56 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie? k y Rozwijamy funkcję f(k) w otoczeniu punktów K i K K K G k x k 4 =,0 + 3a p K 4 4 =,0 ; K' = -,0 3a 3a ka = + 2 cos 2 ik y a / 3 ik y a / 2 3 f k e e - x 4 KK, ' =,0 ; = 1 3a 3 a = - / 2 x - y + f k p ip O pa 2
57 Grafen teoria ciasnego wiązania Jakie jest widmo energii kwazicząstek w grafenie? 0 -tf k 0 px -ipy = -tf 0 k 0 H v * p x + ip y S 1 sf k 1 0 = sf k * 0 px -ipy H = v = vs x px + s y py = vs p px + ipy 0 s x i =, s y = 1 0 i 0 W. Pauli E =v k
58 Grafen teoria ciasnego wiązania t ' 0 Jakie jest widmo energii kwazicząstek w grafenie? Pasmo przewodnictwa Punkt Diraca E =vf k Pasmo walencyjne
59 Grafen - struktura pasmowa Relatywistyczna zależność pomiędzy energią, pędem i masą spoczynkową E = m c + p c A. Einstein Przypadek cząstek z zerową masą spoczynkową m0 = 0 E = cp = c k Wydział Fizyki i Informatyki Stosowanej UŁ
60 Grafen - struktura pasmowa fermiony z masą Vˆ = E 2m 2 * e - + Vˆ = E 2m * h P. A. M. Dirac E. Schrodinger bezmasowe fermiony H. Weyl
61 Grafen - struktura pasmowa H 3 3 K = - at s xkx + s yky = - ats k 2 2 H. Weyl H = v s k + s k = v s k K F x x y y F vf c s x i =, s y = 1 0 i 0 W. Pauli i 1 0 s =, s, s x = 1 0 y = i 0 z 0-1 Wydział Fizyki i Informatyki Stosowanej UŁ
62 Masa efektywna d E( k) m = dk dk * 2 i, j i j i,j odpowiadają kierunkom x,y,z E( k) 1 E( k) 1 E( k) kx kxk y kxk z E( k) 1 E( k) 1 E( k) * = m k ykx k y k yk z E( k) 1 E( k) 1 E( k) kz kx kz k y k z
63 Masa efektywna m = * E 2 k m = k E k * 2 1 Masa efektywna dla liniowej zależności dyspersyjnej Masa efektywna dla dowolnej zależności dyspersyjnej m 1 = 2 E 2 k * 2 k m = k = E vf k * 2 1
64 Grafen - struktura pasmowa Trochę eksperymentu
65 Grafen - struktura pasmowa i H K = - at kx + ky i 0 H K at kx -iky 2 = 3 - at kx + iky 0 2 det H - EI = 0 K równanie wiekowe równanie sekularne at kx -iky det H K - EI = det - E = at kx + iky 0 2
66 Grafen - struktura pasmowa 3 2 det H K - EI = E - at kx + ky = E = at k + k 4 2 x y E 3 E = at k + k 2 E =vf k 2 2 x y k x k y Bezmasowe Fermiony Diraca
67 ARPES kątowo rozdzielcza fotoemisja elektronów k T ex z, = f k, k E k k x y x y a k ex k y ex k x ex f k II ex y x
68 ARPES kątowo rozdzielcza fotoemisja elektronów
69 ARPES kątowo rozdzielcza fotoemisja elektronów
70 ARPES kątowo rozdzielcza fotoemisja elektronów E D E D
71 Grafen - struktura pasmowa E(k)->D(E) Zależność dyspersyjna Funkcja gęstości stanów E D(E) k y k x E F E Bezmasowe Fermiony Diraca Funkcja gęstości stanów s enm
72 Grafen - struktura pasmowa Ruchliwość nośników Przewodnictwo elektryczne m = v E U V E = d cm d cm v = t s s enm cm V s cm V s cm V s Grafen na SiO 2 Grafen na SiO 2 bez zanieczyszczeń Grafen zawieszony T=300 K Bez domieszkowania Si cm V s Ge cm V s GaAs cm V s InSb cm V s
73 grafen/4h-sic(0001) H interkalacja grafen/sic J.M. Baranowski, M. Możdżonek, P. Dąbrowski, K. Grodecki, P. Osewski, W. Kozłowski, M. Kopciuszyński, M. Jałochowski, W. Strupiński Graphene, 2, (2013) domieszkowanie typu n E domieszkowanie typu p E E F E D n-type ARPES E F E D D(E) E D D(E) E F E D E F
74 Oddziaływanie grafenu z metalami i izolatorami
75 Oddziaływanie grafenu z metalami STM, P. Dabrowski, P. Kowalczyk, W. Kozlowski, W. Olejniczak, P. Blake, M. Szybowicz, T. Runka, Applied Physics Letters 95, (2009). J. Sławińska, I. Własny, P. Dąbrowski,, I. Zasada Physical Review B, 85, (2012) STM [111] Au(111) [111] [110] [112] [110] [112] Cu(111)
76 DFT: Oddziaływanie grafen-metal Własności elektronowe grafenu ulegają zmianie na skutek oddziaływania z metalami Oddziaływanie grafen-metal silne/słabe chemisorpcja fizysorpcja Co(111) Ni(111) Pd(111) Al(111) Ag(111) Cu(111) Au(111) Pt(111)
77 grafen/ge(001)/si Przed wygrzaniem Po wygrzaniu ML BL P. Dabrowski, M. Rogala, I. Pasternak, J. M. Baranowski, W. Strupinski, M. Kopciuszynski, R. Zdyb, M. Jalochowski, I. Lutsyk, Nano Res. doi: /s First Online:06 May 2017
78 grafen/4h-sic(0001) N doped STM DFT P. Dąbrowski, M. Rogala, I. Własny,, M. Kopciuszyński, M. Jałochowski, W. Strupiński, J.M. Baranowski Carbon 94, (2015)
79 grafen/4h-sic(0001) N doped undoped doped 0.3% N n-type n-type STS+DFT STS+DFT E F E D P. Dąbrowski, M. Rogala, I. Własny,, M. Kopciuszyński, M. Jałochowski, W. Strupiński, J.M. Baranowski Carbon 94, (2015)
80 Grafen w zewnętrznym potencjale E H 3 3 K = - at s xkx + s yky = - ats k 2 2 Złamanie przestrzennej symetrii inwersji H K = - at s xkx + s yky + s z = - ats k + s z
81 Grafen - struktura pasmowa 3 1 H K = - ats k + sz 2 2 H K at kx - iky 2 2 = at kx + iky E = at kx + ky Wydział Fizyki i Informatyki Stosowanej UŁ
82 Grafen - struktura pasmowa E E półmetal izolator k y k y k x k x Bezmasowe Fermiony Diraca 3 E = at k + k 2 E =v k F 2 2 x y Fermiony Diraca z masą E = at kx + ky + 4 2
83 Grafen/usunięcie degeneracji E E izolator izolator k y k y k x k x Fermiony Diraca z masą E = at kx + ky Fermiony Diraca z masą E = at kx + ky Struktura pasmowa jest symetryczna wokół punktu k=0 Pasma są podwójnie zdegenerowane
84 ARPES kątowo rozdzielcza fotoemisja elektronów
85 ARPES kątowo rozdzielcza fotoemisja elektronów
86 grafen/4h-sic(0001) H interkalacja grafen/sic J.M. Baranowski, M. Możdżonek, P. Dąbrowski, K. Grodecki, P. Osewski, W. Kozłowski, M. Kopciuszyński, M. Jałochowski, W. Strupiński Graphene, 2, (2013) grafen/sic+h E F E D n-type ARPES E D E F p-type ARPES E F E D E D E F
87 Grafen - struktura pasmowa fermiony z masą Vˆ = E 2m 2 * e - + Vˆ = E 2m * h P. A. M. Dirac E. Schrodinger bezmasowe fermiony H. Weyl
88 Równanie Diraca H = ca P + m c K s I 0 a = = s 0 0 I i 1 0 s = s s x = 1 0 y = i 0 z r, t 1 r, t r, t r, t - + = i ca mc i 3 r, t t 3 r, t r, t r, t 4 4
89 Grafen (Dirac -> Weyl) 2 HK = ca P + m0c ca P v F 0 kx -ikya( r) A( r) E kx iky 0 = + B( r) B( r) v ( ) ( ) ( ) F s k r = E r
90 Co to jest pseudospin Dwie podsieci A i B dwa stopnie swobody elektron scharakteryzowany jest przez amplitudę prawdopodobieństwa, że znajduje się w danej podsieci Baza dwóch podsieci przypomina układ ze spinem B A A B t A + i B e i cos + sin e 2 2
91 Co to jest pseudospin A B A() r B () r i A + e B
92 Co to jest pseudospin pseudospin K pseudospin przeskok z B do A przeskok z A do B v F 0 kx -ikya( r) A( r) E kx iky 0 = + B( r) B( r)
93 Symetrie symetria translacji symetria inwersji przestrzennej ˆ f ( r ) = f ( r + R ) R ˆr = -r Hˆ, ˆ R = 0 E k = E -k Energia cząstki poruszającej się w prawo jest równa energii cząstki poruszającej się w lewo. Zasada słuszna dla cząstek ze spinem w górę i w dół.
94 Symetria inwersji przestrzennej grafen h-bn C C B N Symetria inwersji przestrzennej złamana C C B N
95 Symetrie symetria translacji symetria inwersji przestrzennej symetria inwersji czasu ˆ f ( r ) = f ( r + R ) R ˆr = -r t -t Hˆ, ˆ R = 0 E k = E -k, = -, E k E k Energia cząstki poruszającej się w prawo jest równa energii cząstki poruszającej się w lewo. Zasada słuszna dla cząstek ze spinem w górę i w dół. Energia cząstki poruszającej się w prawo ze spinem do góry jest równa energii cząstki poruszającej się w lewo ze spinem w dół
96 Symetria inwersji czasu k y k y K M K K K G k x G k x t -t, = -, E k E k
97 Symetria inwersji czasu H = v s k K F H = v s ' k =, x y s ' = -s, s s s s K' F x y H K 0 kx -iky = vf kx + iky 0 H K' 0 -kx -iky = vf - kx + iky 0
98 Pełny Hamiltonian v F 0 kx - iky 0 0 AK ( r) AK ( r) kx iky BK ( r) BK ( r) = E k -ik ( r) ( r) x y AK ' AK ' kx + iky 0 BK '( r) B K '( r)
99 Struktura elektronowa grafenu pseudospin k y pseudospin K K G K k x K v F 0 -k -ik ( r) ( r) x y AK ' AK ' = E - kx + iky 0 BK '( r) BK '( r) v F 0 kx -ikyak ( r) AK ( r) E kx iky 0 = + BK ( r) BK ( r)
100 Struktura elektronowa grafenu K E K K k y G k x K K K
101 Grafen skrętność H = v s k = v ksn K F F σ σ s k = = + 1 k s k = = -1 k k k Skrętność prawoskrętne lewoskrętne Elektrony i dziury z tym samym wektorem falowym mają przeciwne prędkości grupowe s k K + - s k = +1 = -1 k s s k
102 Grafen skrętność K - + K + - k y G E k x - + K + - K K + - K - +
103 Grafen rozpraszanie s K s s K s k k k k - + s + - s s s k k k k
104 Grafen - struktura pasmowa Ruchliwość nośników Przewodnictwo elektryczne m = v E U V E = d cm d cm v = t s s enm cm V s cm V s cm V s Grafen na SiO 2 Grafen na SiO 2 bez zanieczyszczeń Grafen zawieszony T=300 K Bez domieszkowania Si cm V s Ge cm V s GaAs cm V s InSb cm V s
105 Valleytronika K Symetria inwersji czasu K K' K Potrzebujemy wielkości fizycznej która odróżni K od K Spin jako przykład Spin do góry i spin do dołu przechodzą w siebie na skutek inwersji czasu. Kierunek spinu rozróżniamy za pomocą przeciwnych momentów magnetycznych. Moment magnetyczny jest pseudowektorem, który jest nieparzysty na skutek symetrii inwersji czasu. Medium do detekcji pole magnetyczne. Pseudospin Wielkości fizyczne które są nieparzyste na skutek symetrii inwersji czasu nadają się do detekcji pseudospinu. W krzywizna Berry ego P. Berry
106 Krzywizna Berry ego P Koneksja afinczna wyraża ideę prześnienia równoległego wektorów stycznych wzdłuż krzywych. Miarą krzywizny jest stopień rozbieżności przy przemieszczaniu wektorów wzdłuż krzywych. R Q
107 Faza Berry ego E k () k k t t k () t Ewolucja stanu na skutek adiabatycznej rotacji wektora falowego. Rotację modelujemy za pomocą k(t) k Przyjmujemy, że w dowolnej chwili czasu t stan pozostaje stanem własnym hmiltonianu () t ĥ k t który zależy od czasu tylko poprzez k(t).
108 Faza Berry ego () t i = E () t k() t t Rozwiązanie musi być proporcjonalne do () k () t t - () ( ) i t t e ( t) k() t ( t ) ( t ) = 1 = k ( t) k ( t) () t jest nieznaną fazą
109 Faza Berry ego k() t i + () t = E t 1 () t = E -i k ( t) k ( t) k ( t) t k ( t) k ( t) k ( t) t 1 ( t) = E dt ' -i dt ' t ' t k ( t ') k ( t ') k ( t ') 0 0 Faza na skutek ewolucji adiabatycznej
110 Koneksja Berry ego t cykl = - i dt ' = -i dk k ( t ') k ( t ') k ( t ') k k ( t ') t ' 0 Definiujemy potencjał wektorowy Koneksja Berry ego A -i k k ( t ') k k ( t ')
111 Krzywizna Berry ego Fazę Berry ego można przedstawić w formie analogicznej jak w przypadku strumienia magnetycznego x y A dk A dk dk = = k k k z Krzywizna Berry ego k k z A Pełni rolę pola magnetycznego prostopadłego do powierzchni zamkniętej przez krzywą całkowania W = A k k
112 Valleytronika 1 En ( k) vn ( k) = k 1 En ( k) e vn( k ) = - E Wn( k ) k Prędkość związana energią pasma Pełny opis prędkości Kiedy krzywizna Berry ego nie może być pominięta?
113 Valleytronika 2D sieć heksagonalna symetria odwrócenia czasu W ( k) = -W (-k) przestrzenna inwersja symetrii W ( k) = W (-k) n n n n W krysztale z jednoczesną symetrią odwrócenia czasu i symetrią inwersji przestrzennej krzywizna Berryego znika 1 En ( k) vn ( k) = k W krysztale w którym symetria odwrócenia czasu lub symetrią inwersji przestrzennej jest złamana krzywizna Berryego pozostaje 1 En ( k) e vn( k ) = - E Wn( k ) k Łamiemy symetrię inwersji przestrzennej grafenu (dwuwarstwa grafenowa, pole elektryczne)
114 Dolinotronika (Valleytronika) Dolinowy Efekt Halla E e EW ( ) n k e EW ( ) n k K e- e- K
115 KONIEC Cz. 1
Oddziaływanie grafenu z metalami
 Oddziaływanie grafenu z metalami Oddziaływanie grafenu z metalami prof. dr hab. Zbigniew Klusek Grafen dla czego intryguje? v E U V E d cm d cm v t s en Transport dyfuzyjny Transport kwantowy balistyczny
Oddziaływanie grafenu z metalami Oddziaływanie grafenu z metalami prof. dr hab. Zbigniew Klusek Grafen dla czego intryguje? v E U V E d cm d cm v t s en Transport dyfuzyjny Transport kwantowy balistyczny
Grafen. Poprzednio. Poprzednio
 Elektronika plastikowa i organiczna Grafen Poprzednio Poprzednio Metody syntezy związków organicznych pozwalają na tworzenie półprzewodników organicznych o zadanych własnościach mechanicznych i elektrooptycznych
Elektronika plastikowa i organiczna Grafen Poprzednio Poprzednio Metody syntezy związków organicznych pozwalają na tworzenie półprzewodników organicznych o zadanych własnościach mechanicznych i elektrooptycznych
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową. Metody wytwarzania
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Wykład 12 V = 4 km/s E 0 =.08 e V e = = 1 Å
 Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Grafen i jego własności
 Grafen i jego własności Jacek Baranowski Instytut Technologii Materiałów Elektronicznych Wydział Fizyki, Uniwersytet Warszawski W Polsce są duże pokłady węgla, niestety nie można ich przerobić na grafen,
Grafen i jego własności Jacek Baranowski Instytut Technologii Materiałów Elektronicznych Wydział Fizyki, Uniwersytet Warszawski W Polsce są duże pokłady węgla, niestety nie można ich przerobić na grafen,
na dnie (lub w szczycie) pasma pasmo jest paraboliczne, ale masa wyznaczona z krzywizny niekoniecznie = m 0
 Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
Koncepcja masy efektywnej swobodne elektrony k 1 1 E( k) E( k) =, = m m k krzywizna E(k) określa masę cząstek elektrony prawie swobodne - na dnie pasma masa jest dodatnia, ale niekoniecznie = masie swobodnego
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Modele kp wprowadzenie
 Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Modele kp wprowadzenie Komórka elementarna i komórka sieci odwrotnej Funkcje falowe elektronu w krysztale Struktura pasmowa Przybliżenie masy efektywnej Naprężenia: potencjał deformacyjny, prawo Hooka
Absorpcja związana z defektami kryształu
 W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
W rzeczywistych materiałach sieć krystaliczna nie jest idealna występują różnego rodzaju defekty. Podział najważniejszych defektów ze względu na właściwości optyczne: - inny atom w węźle sieci: C A atom
Ciała stałe. Literatura: Halliday, Resnick, Walker, t. 5, rozdz. 42 Orear, t. 2, rozdz. 28 Young, Friedman, rozdz
 Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Ciała stałe Podstawowe własności ciał stałych Struktura ciał stałych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencjał kontaktowy
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafen perspektywy zastosowań
 Grafen perspektywy zastosowań Paweł Szroeder 3 czerwca 2014 Spis treści 1 Wprowadzenie 1 2 Właściwości grafenu 2 3 Perspektywy zastosowań 2 3.1 Procesory... 2 3.2 Analogoweelementy... 3 3.3 Czujniki...
Grafen perspektywy zastosowań Paweł Szroeder 3 czerwca 2014 Spis treści 1 Wprowadzenie 1 2 Właściwości grafenu 2 3 Perspektywy zastosowań 2 3.1 Procesory... 2 3.2 Analogoweelementy... 3 3.3 Czujniki...
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach
 Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Funkcja rozkładu Fermiego-Diraca w różnych temperaturach 1 f FD ( E) = E E F exp + 1 kbt Styczna do krzywej w punkcie f FD (E F )=0,5 przecina oś energii i prostą f FD (E)=1 w punktach odległych o k B
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO.
 GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
GAZ ELEKTRONÓW SWOBODNYCH POWYŻEJ ZERA BEZWZGLĘDNEGO. Funkcja rozkładu Fermiego-Diraca T=0K T>0K 1 f ( E ) = 0 dla dla E E F E > EF f ( E, T ) 1 = E E F kt e + 1 1 T>0K Funkcja rozkładu Fermiego-Diraca
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Domieszki w półprzewodnikach
 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU
 X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
X. RÓWNANIE SCHRÖDINGERA NIEZALEŻNE OD CZASU Równanie Schrődingera niezależne od czasu to równanie postaci: ħ 2 2m d 2 x dx 2 V xx = E x (X.1) Warunki regularności na x i a) skończone b) ciągłe c) jednoznaczne
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków).
 Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
Właściwości chemiczne i fizyczne pierwiastków powtarzają się w pewnym cyklu (zebrane w grupy 2, 8, 8, 18, 18, 32 pierwiastków). 1925r. postulat Pauliego: Na jednej orbicie może znajdować się nie więcej
The role of band structure in electron transfer kinetics at low dimensional carbons
 The role of band structure in electron transfer kinetics at low dimensional carbons Paweł Szroeder Instytut Fizyki, Uniwersytet Mikołaja Kopernika, ul. Grudziądzka 5/7, 87-100 Toruń, Poland Reakcja przeniesienia
The role of band structure in electron transfer kinetics at low dimensional carbons Paweł Szroeder Instytut Fizyki, Uniwersytet Mikołaja Kopernika, ul. Grudziądzka 5/7, 87-100 Toruń, Poland Reakcja przeniesienia
Wstęp do Optyki i Fizyki Materii Skondensowanej. Mateusz Goryca
 Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Elektron fala stojąca wokół jądra Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkowy
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH
 Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Nadprzewodnictwo w nanostrukturach metalicznych Paweł Wójcik Wydział Fizyki i Informatyki Stosowanej, AGH Współpraca: Akademickie Centrum Materiałów i Nanotechnologii dr Michał Zegrodnik, prof. Józef Spałek
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru
 Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Fizyka silnie skorelowanych elektronów na przykładzie międzymetalicznych związków ceru Rafał Kurleto 4.3.216 ZFCS IF UJ Rafał Kurleto Sympozjum doktoranckie 4.3.216 1 / 15 Współpraca dr hab. P. Starowicz
Rozszczepienie poziomów atomowych
 Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Rozszczepienie poziomów atomowych Poziomy energetyczne w pojedynczym atomie Gdy zbliżamy atomy chmury elektronowe nachodzą na siebie (inaczej: funkcje falowe elektronów zaczynają się przekrywać) Na skutek
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 2006 Instytut Fizyki Uniwersytetu Szczecińskiego Rezonansowe oddziaływanie układu atomowego z promieniowaniem "! "!! # $%&'()*+,-./-(01+'2'34'*5%.25%&+)*-(6
Podstawy Fizyki Półprzewodników
 Podstawy Fizyki Półprzewodników Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski konsultacje: poniedziałek godz. 15:00-17:00, pok. 310 A-1 WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
Podstawy Fizyki Półprzewodników Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski konsultacje: poniedziałek godz. 15:00-17:00, pok. 310 A-1 WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
S. Baran - Podstawy fizyki materii skondensowanej Pasma energetyczne. Pasma energetyczne
 Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Pasma energetyczne Niedostatki modelu gazu Fermiego elektronów swobodnych Pomimo wielu sukcesów model nie jest w stanie wyjaśnić następujących zagadnień: 1. różnica między metalami, półmetalami, półprzewodnikami
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Modele kp Studnia kwantowa
 Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Modele kp Studnia kwantowa Przegląd modeli pozwalających obliczyć strukturę pasmową materiałów półprzewodnikowych. Metoda Fal płaskich Transformata Fouriera Przykładowe wyniki Model Kaine Hamiltonian z
Domieszki w półprzewodnikach
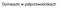 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Czym jest prąd elektryczny
 Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
Prąd elektryczny Ruch elektronów w przewodniku Wektor gęstości prądu Przewodność elektryczna Prawo Ohma Klasyczny model przewodnictwa w metalach Zależność przewodności/oporności od temperatury dla metali,
C h można przedstawić w bazie wektorów bazowych grafenu (*) (**) Nanorurki węglowe (jednościenne)
 Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
Nanorurki węglowe (jednościenne) zwinięte paski arkusza grafenu (wstęgi grafenowej) (węzły sieciowe Bravais i węzły podsieci) wstęgi: chiralna fotelowa zykzak komórka elementarna jednoznacznie definiuje
Przyrządy i układy półprzewodnikowe
 Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
Przyrządy i układy półprzewodnikowe Prof. dr hab. Ewa Popko ewa.popko@pwr.edu.pl www.if.pwr.wroc.pl/~popko p.231a A-1 Zawartość wykładu Wy1, Wy2 Wy3 Wy4 Wy5 Wy6 Wy7 Wy8 Wy9 Wy10 Wy11 Wy12 Wy13 Wy14 Wy15
STRUKTURA KRYSTALICZNA
 PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
P R A C O W N I A
 P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
P R A C O W N I A www.tremolo.pl M E T O D Y B A D A Ń M A T E R I A Ł Ó W (WŁAŚCIWOŚCI ELEKTRYCZNE, MAGNETYCZNE I AKUSTYCZNE) Ewelina Broda Robert Gabor ĆWICZENIE NR 3 WYZNACZANIE ENERGII AKTYWACJI I
IX. MECHANIKA (FIZYKA) KWANTOWA
 IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
IX. MECHANIKA (FIZYKA) KWANTOWA IX.1. OPERACJE OBSERWACJI. a) klasycznie nie ważna kolejność, w jakiej wykonujemy pomiary. AB = BA A pomiar wielkości A B pomiar wielkości B b) kwantowo wartość obserwacji
Półprzewodniki samoistne. Struktura krystaliczna
 Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Półprzewodniki samoistne Struktura krystaliczna Si a5.43 A GaAs a5.63 A ajczęściej: struktura diamentu i blendy cynkowej (ZnS) 1 Wiązania chemiczne Wiązania kowalencyjne i kowalencyjno-jonowe 0K wszystkie
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk
 Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Atom wodoru w mechanice kwantowej. Równanie Schrödingera
 Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Fizyka atomowa Atom wodoru w mechanice kwantowej Moment pędu Funkcje falowe atomu wodoru Spin Liczby kwantowe Poprawki do równania Schrödingera: struktura subtelna i nadsubtelna; przesunięcie Lamba Zakaz
Przerwa energetyczna w germanie
 Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Ćwiczenie 1 Przerwa energetyczna w germanie Cel ćwiczenia Wyznaczenie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu od temperatury. Wprowadzenie Eksperymentalne badania
Elementy teorii powierzchni metali
 Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Krawędź absorpcji podstawowej
 Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
Obecność przerwy energetycznej między pasmami przewodnictwa i walencyjnym powoduje obserwację w eksperymencie absorpcyjnym krawędzi podstawowej. Dla padającego promieniowania oznacza to przejście z ośrodka
S. Baran - Podstawy fizyki materii skondensowanej Półprzewodniki. Półprzewodniki
 Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Półprzewodniki Definicja i własności Półprzewodnik materiał, którego przewodnictwo rośnie z temperaturą (opór maleje) i w temperaturze pokojowej wykazuje wartości pośrednie między przewodnictwem metali,
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
1 Struktura pasmowa grafenu
 1 Struktura pasmowa grafenu Ze względu na swoją prostotę kryształ grafenu oraz grafitu stanowi jedną z najlepiej zbadanych teoretycznie struktur w fizyce ciała stałego. Strukturę pasmową daje się stosunkowo
1 Struktura pasmowa grafenu Ze względu na swoją prostotę kryształ grafenu oraz grafitu stanowi jedną z najlepiej zbadanych teoretycznie struktur w fizyce ciała stałego. Strukturę pasmową daje się stosunkowo
Spis treści. Przedmowa redaktora do wydania czwartego 11
 Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Mechanika kwantowa : teoria nierelatywistyczna / Lew D. Landau, Jewgienij M. Lifszyc ; z jęz. ros. tł. Ludwik Dobrzyński, Andrzej Pindor. - Wyd. 3. Warszawa, 2012 Spis treści Przedmowa redaktora do wydania
Dr inż. Zbigniew Szklarski
 Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład 1: Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
S. Baran - Podstawy fizyki materii skondensowanej Gaz Fermiego elektronów swobodnych. Gaz Fermiego elektronów swobodnych
 Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Gaz Fermiego elektronów swobodnych charakter idea Teoria metali Paula Drudego Teoria metali Arnolda (1900 r.) Sommerfelda (1927 r.) klasyczna kwantowa elektrony przewodnictwa elektrony przewodnictwa w
Jak TO działa? Co to są półprzewodniki? TRENDY: Prawo Moore a. Google: Jacek Szczytko Login: student Hasło: *******
 Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Chiralność w fizyce jądrowej. na przykładzie Cs
 Chiralność w fizyce jądrowej 124 na przykładzie Cs Tomasz Marchlewski Uniwersytet Warszawski Seminarium Fizyki Jądra Atomowego 6 kwietnia 2017 1 Słowo chiralność Chiralne obiekty: Obiekty będące swoimi
Chiralność w fizyce jądrowej 124 na przykładzie Cs Tomasz Marchlewski Uniwersytet Warszawski Seminarium Fizyki Jądra Atomowego 6 kwietnia 2017 1 Słowo chiralność Chiralne obiekty: Obiekty będące swoimi
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
Leonard Sosnowski
 Admiralty Research Laboratory w Teddington, Anglia (1945-1947). Leonard Sosnowski J. Starkiewicz, L. Sosnowski, O. Simpson, Nature 158, 28 (1946). L. Sosnowski, J. Starkiewicz, O. Simpson, Nature 159,
Admiralty Research Laboratory w Teddington, Anglia (1945-1947). Leonard Sosnowski J. Starkiewicz, L. Sosnowski, O. Simpson, Nature 158, 28 (1946). L. Sosnowski, J. Starkiewicz, O. Simpson, Nature 159,
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych
 III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu.
 Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu. Agnieszka Wołoś Instytut Fizyki Polskiej Akademii Nauk Uniwersytet Warszawski Instytut Technologii Materiałów Elektronicznych A. Hruban, G. Strzelecka,
Trójwymiarowe izolatory topologiczne - chalkogenki bizmutu. Agnieszka Wołoś Instytut Fizyki Polskiej Akademii Nauk Uniwersytet Warszawski Instytut Technologii Materiałów Elektronicznych A. Hruban, G. Strzelecka,
STRUKTURA CIAŁA STAŁEGO
 STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
Mechanika kwantowa Schrödingera
 Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Fizyka 2 Wykład 2 1 Mechanika kwantowa Schrödingera Hipoteza de Broglie a wydawała się nie zgadzać z dynamiką Newtona. Mechanika kwantowa Schrödingera zawiera mechanikę kwantową jako przypadek graniczny
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych komputera kwantowego
 Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Cia!a sta!e. W!asno"ci elektryczne cia! sta!ych. Inne w!asno"ci
 Cia!a sta!e Podstawowe w!asno"ci cia! sta!ych Struktura cia! sta!ych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencja! kontaktowy
Cia!a sta!e Podstawowe w!asno"ci cia! sta!ych Struktura cia! sta!ych Przewodnictwo elektryczne teoria Drudego Poziomy energetyczne w krysztale: struktura pasmowa Metale: poziom Fermiego, potencja! kontaktowy
Proste struktury krystaliczne
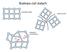 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Symetrie. D. Kiełczewska, wykład 5 1
 Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
Symetrie Symetrie a prawa zachowania Spin Parzystość Spin izotopowy Multiplety hadronowe Niezachowanie parzystości w oddz. słabych Sprzężenie ładunkowe C Symetria CP Zależność spinowa oddziaływań słabych
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab.
 WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych
 Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Studnia skończona. Heterostruktury półprzewodnikowe studnie kwantowe (cd) Heterostruktury mogą mieć różne masy efektywne w różnych obszarach:
 Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia skończona Heterostruktury mogą mieć różne masy efektywne w różnych obszarach: V z Okazuje się, że zamiana nie jest dobrym rozwiązaniem problemu
Heterostruktury półprzewodnikowe studnie kwantowe (cd) Studnia skończona Heterostruktury mogą mieć różne masy efektywne w różnych obszarach: V z Okazuje się, że zamiana nie jest dobrym rozwiązaniem problemu
Metody pomiarowe spinowego efektu Halla w nanourządzeniach elektroniki spinowej
 Metody pomiarowe spinowego efektu Halla w nanourządzeniach elektroniki spinowej Monika Cecot, Witold Skowroński, Sławomir Ziętek, Tomasz Stobiecki Wisła, 13.09.2016 Plan prezentacji Spinowy efekt Halla
Metody pomiarowe spinowego efektu Halla w nanourządzeniach elektroniki spinowej Monika Cecot, Witold Skowroński, Sławomir Ziętek, Tomasz Stobiecki Wisła, 13.09.2016 Plan prezentacji Spinowy efekt Halla
ZASADY ZALICZENIA PRZEDMIOTU MBS
 ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
ZASADY ZALICZENIA PRZEDMIOTU MBS LABORATORIUM - MBS 1. ROZWIĄZYWANIE WIDM kolokwium NMR 25 kwietnia 2016 IR 30 maja 2016 złożone 13 czerwca 2016 wtorek 6.04 13.04 20.04 11.05 18.05 1.06 8.06 coll coll
Układ okresowy. Przewidywania teorii kwantowej
 Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Elektryczne własności ciał stałych Izolatory (w temperaturze pokojowej) w praktyce - nie przewodzą prądu elektrycznego. Ich oporność jest b. duża. Np. diament ma oporność większą od miedzi 1024 razy Metale
Mechanika kwantowa. Jak opisać atom wodoru? Jak opisać inne cząsteczki?
 Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Mechanika kwantowa Jak opisać atom wodoru? Jak opisać inne cząsteczki? Mechanika kwantowa Równanie Schrödingera Ĥ E ψ H ˆψ = Eψ operator różniczkow Hamiltona energia funkcja falowa h d d d + + m d d dz
Przewodnictwo elektryczne ciał stałych. Fizyka II, lato
 Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Przewodnictwo elektryczne ciał stałych Fizyka II, lato 2016 1 Własności elektryczne ciał stałych Komputery, kalkulatory, telefony komórkowe są elektronicznymi urządzeniami półprzewodnikowymi wykorzystującymi
Repeta z wykładu nr 4. Detekcja światła. Dygresja. Plan na dzisiaj
 Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
IV. Transmisja. /~bezet
 Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Światłowody IV. Transmisja BERNARD ZIĘTEK http://www.fizyka.umk.pl www.fizyka.umk.pl/~ /~bezet 1. Tłumienność 10 7 10 6 Tłumienność [db/km] 10 5 10 4 10 3 10 2 10 SiO 2 Tłumienność szkła w latach (za A.
Ruch ładunków w polu magnetycznym
 Ruch ładunków w polu magnetycznym Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Ruch ładunków w polu magnetycznym
Ruch ładunków w polu magnetycznym Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Ruch ładunków w polu magnetycznym
Dr inż. Zbigniew Szklarski
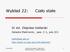 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Zaburzenia periodyczności sieci krystalicznej
 Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Zaburzenia periodyczności sieci krystalicznej Defekty liniowe dyslokacja krawędziowa dyslokacja śrubowa dyslokacja mieszana Defekty punktowe obcy atom w węźle luka w sieci (defekt Schottky ego) obcy atom
Model uogólniony jądra atomowego
 Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Model uogólniony jądra atomowego Jądro traktowane jako chmura nukleonów krążąca w średnim potencjale Średni potencjał może być sferyczny ale także trwale zdeformowany lub może zależeć od czasu (wibracje)
Ekscyton w morzu dziur
 Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Światło fala, czy strumień cząstek?
 1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
1 Światło fala, czy strumień cząstek? Teoria falowa wyjaśnia: Odbicie Załamanie Interferencję Dyfrakcję Polaryzację Efekt fotoelektryczny Efekt Comptona Teoria korpuskularna wyjaśnia: Odbicie Załamanie
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics)
 Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
