Problemy dywidendowe dla procesu ryzyka typu Lévy ego
|
|
|
- Eleonora Matysiak
- 8 lat temu
- Przeglądów:
Transkrypt
1 Problemy dywidendowe dla procesu ryzyka typu Lévy ego Zbigniew Palmowski Wspólne prace z F. Avramem, S. Baranem, P. Azcue, N. Muler R. Loeffenem, A. Kyprianou, M. Pistoriusem I. Czarna, E. Marciniak Zagadnienia aktuarialne - teoria i praktyka, 2014
2 Ekonomiczny punkt widzenia 2 Słowo dywidenda pochodzi od łacińskiego słowa dividendum, które oznacza rzecz, która ma być podzielona i zwykle oznacza część akcji rozprowadzanych pomiędzy akcjonariuszy;
3 Ekonomiczny punkt widzenia 2 Słowo dywidenda pochodzi od łacińskiego słowa dividendum, które oznacza rzecz, która ma być podzielona i zwykle oznacza część akcji rozprowadzanych pomiędzy akcjonariuszy; Dywidendy sa wypłacane z opodatkowanych dochodów oraz też podlegaja opodatkowaniu; Wycena firm metoda DCF;
4 Ekonomiczny punkt widzenia 2 Słowo dywidenda pochodzi od łacińskiego słowa dividendum, które oznacza rzecz, która ma być podzielona i zwykle oznacza część akcji rozprowadzanych pomiędzy akcjonariuszy; Dywidendy sa wypłacane z opodatkowanych dochodów oraz też podlegaja opodatkowaniu; Wycena firm metoda DCF; Sa dwie strony polityki wypłaty dywidend: z jednej strony menadżerowie staraja sie zminimalizować wypłatę dywidend aby na przykład zwiększyć inwestycje, z drugie strony akcjonariusze pragna zmaksymalizować jej wypłatę, m.in także dlatego aby zwiększyć efektywnośc firmy;
5 Ekonomiczny punkt widzenia 2 Słowo dywidenda pochodzi od łacińskiego słowa dividendum, które oznacza rzecz, która ma być podzielona i zwykle oznacza część akcji rozprowadzanych pomiędzy akcjonariuszy; Dywidendy sa wypłacane z opodatkowanych dochodów oraz też podlegaja opodatkowaniu; Wycena firm metoda DCF; Sa dwie strony polityki wypłaty dywidend: z jednej strony menadżerowie staraja sie zminimalizować wypłatę dywidend aby na przykład zwiększyć inwestycje, z drugie strony akcjonariusze pragna zmaksymalizować jej wypłatę, m.in także dlatego aby zwiększyć efektywnośc firmy; Wypłata dywidend może być jeszcze jedna miara ryzyka (firma w słabej kondycji finansowej wypłaca mała dywidendę);
6 Ekonomiczny punkt widzenia 2 Słowo dywidenda pochodzi od łacińskiego słowa dividendum, które oznacza rzecz, która ma być podzielona i zwykle oznacza część akcji rozprowadzanych pomiędzy akcjonariuszy; Dywidendy sa wypłacane z opodatkowanych dochodów oraz też podlegaja opodatkowaniu; Wycena firm metoda DCF; Sa dwie strony polityki wypłaty dywidend: z jednej strony menadżerowie staraja sie zminimalizować wypłatę dywidend aby na przykład zwiększyć inwestycje, z drugie strony akcjonariusze pragna zmaksymalizować jej wypłatę, m.in także dlatego aby zwiększyć efektywnośc firmy; Wypłata dywidend może być jeszcze jedna miara ryzyka (firma w słabej kondycji finansowej wypłaca mała dywidendę); W trakcie tej prezentacji będziemy koncentrować się tylko na zysku akcjonariuszy.
7 Model Craméra-Lundberga 3 Zwykle rezerwy firmy ubezpieczeniowej sa modelowane przez proces Craméra-Lundberga: gdzie X t = x + pt N t C k - ciag niezależnych zmiennych losowych o jednakowym rozkładzie F (tzw. roszczenia) k=1 C k N t - niezależny proces Poissona z intensywnościa λ p - intensywność wpłaty składki
8 Proces Lévy ego 4 X t - spektralnie ujemny proces Lévy ego, który nie jest subordynatorem, będzie modelować rezerwy firmy ubezpieczeniowej przed wypłata dywidend X t - proces ze niezależnymi i stacjonarnymi przyrostami, który nie ma dodatnich skoków
9 Proces Lévy ego 5 X t - spektralnie ujemny proces Lévy ego, który nie jest subordynatorem, będzie modelować rezerwy firmy ubezpieczeniowej przed wypłata dywidend X t - proces ze niezależnymi i stacjonarnymi przyrostami, który nie ma dodatnich skoków Formuła Lévy ego-chinczyna: Ee iθx t = e Ψ(θ)t gdzie Ψ(θ) = ipθ + σ2 ( 2 θ2 + ) 1 e iθx Π X (dx) (, 1) ( + 1 e iθx + iθx ) Π X (dx) ( 1,0) oraz zakładamy, że ( 1,0) (1 x2 ) Π X (dx) <
10 Motywacja 6 Motywacja rozważań dowolnych spektralnie ujemnych procesów Lévy ego: obok skoków modelujemy małe perturbacje Brownowskie i martyngałowe;
11 Motywacja 6 Motywacja rozważań dowolnych spektralnie ujemnych procesów Lévy ego: obok skoków modelujemy małe perturbacje Brownowskie i martyngałowe; wszystkie wzory dane w jednolitym języku tzw. funkcji skalujacych (brak potrzeby rozważania kolejnych przypadków różnych rozkładów roszczeń);
12 Motywacja 6 Motywacja rozważań dowolnych spektralnie ujemnych procesów Lévy ego: obok skoków modelujemy małe perturbacje Brownowskie i martyngałowe; wszystkie wzory dane w jednolitym języku tzw. funkcji skalujacych (brak potrzeby rozważania kolejnych przypadków różnych rozkładów roszczeń); krótsze dowody niż dla klasycznego procesu ryzyka (kosztem bardziej zaawansowanej wiedzy poczatkowej);
13 Motywacja 6 Motywacja rozważań dowolnych spektralnie ujemnych procesów Lévy ego: obok skoków modelujemy małe perturbacje Brownowskie i martyngałowe; wszystkie wzory dane w jednolitym języku tzw. funkcji skalujacych (brak potrzeby rozważania kolejnych przypadków różnych rozkładów roszczeń); krótsze dowody niż dla klasycznego procesu ryzyka (kosztem bardziej zaawansowanej wiedzy poczatkowej); te same metody pojawiaja się przy wycenie opcji i innych problemach matematyki finansowej;
14 Problem De Finettiego Zakładamy, że X t p.w. 7
15 Problem De Finettiego Zakładamy, że X t p.w. Proces regulowany: U π t = X t D π t 8 gdzie Dt π jest łaczn a ilości a wypłaconych dywidend do czasu t
16 Problem De Finettiego Zakładamy, że X t p.w. Proces regulowany: U π t = X t D π t 9 gdzie Dt π jest łaczn a ilości a wypłaconych dywidend do czasu t τ π - moment likwidacji firmy w postaci jednorazowej wypłaty (wtedy U π τ π = 0)
17 Problem De Finettiego Zakładamy, że X t p.w. Proces regulowany: U π t = X t D π t 10 gdzie Dt π jest łaczn a ilości a wypłaconych dywidend do czasu t τ π - moment likwidacji firmy w postaci jednorazowej wypłaty (wtedy U π τ π = 0) π = (τ π, D π t ) - strategia wypłaty dywidend polega na wyborze niemalejacego, lewostronnie ciagłego F-adaptowalnego procesu Dt π π oraz momentu τ
18 Problem De Finettiego Zakładamy, że X t p.w. Proces regulowany: U π t = X t D π t 11 gdzie Dt π jest łaczn a ilości a wypłaconych dywidend do czasu t τ π - moment likwidacji firmy w postaci jednorazowej wypłaty (wtedy U π τ π = 0) π = (τ π, D π t ) - strategia wypłaty dywidend polega na wyborze niemalejacego, lewostronnie ciagłego F-adaptowalnego procesu Dt π π oraz momentu τ Obserwujemy proces U π do czasu τ π σ π, gdzie σ π = inf{t 0 : U π t < 0}
19 Impulsowa kontrola 12 Zakładamy, że dla t < σ π D π t := D π t + D π t < U π t Do każdej wypłaty moga być dodane koszty transakcyjne w wysokości K 0 (przypadek K = 0 oznacza ich brak). Wtedy dodatkowo zakładamy, że D π t K W tym przypadku π jest dyktowane przez ciag czasów zatrzymania 0 T 1 T 2 T 3 < T 4 <... reprezentujacy momenty wypłat oraz przez ciag J i K F Ti -mierzalnych, dodatnich zmiennych losowych opisujacych wielkość wypłat. Dodatkowo: gdzie N π t = #{k : T k t} D π t = N π t k=1 J k
20 Funkcja wypłaty 13 Średnie zdyskontowane łaczne dywidendy: gdzie [ σ π τ ] π D π (x) = E x e qt (dd π t K) + 0 t 0 (dd π s K) + = { D π t jeśli K = 0, s t 1 { D π t >K}( Dt π K) jeśli K > 0 oraz E x oznacza średnia kiedy X 0 = x.
21 Funkcja wypłaty 14 Średnie zdyskontowane łaczne dywidendy: gdzie [ σ π τ ] π D π (x) = E x e qt (dd π t K) + 0 t 0 (dd π s K) + = { D π t jeśli K = 0, s t 1 { D π t >K}( Dt π K) jeśli K > 0 oraz E x oznacza średnia kiedy X 0 = x. Funkcja kary Gerbera-Shiu: ] Ww(x) π = E x [e q(σπ τ π) w (U π σ π τ ) π gdzie w jest funkcja kary (dla uproszczenia zakładamy, że w(0) = 0)
22 Funkcja wypłaty 15 Średnie zdyskontowane łaczne dywidendy: gdzie [ σ π τ ] π D π (x) = E x e qt (dd π t K) + 0 t 0 (dd π s K) + = { D π t jeśli K = 0, s t 1 { D π t >K}( Dt π K) jeśli K > 0 oraz E x oznacza średnia kiedy X 0 = x. Funkcja kary Gerbera-Shiu: ] Ww(x) π = E x [e q(σπ τ π) w (U π σ π τ ) π gdzie w jest funkcja kary (dla uproszczenia zakładamy, że w(0) = 0) Funkcja wypłaty: v π (x) = D π (x) + W π w(x)
23 Cel 16 Celem jest znalezienie (optymalnej) strategii która maksymalizuje v π (x) = E x [ σ π τ π 0 π = (τ, D ) e qt (dd π t K) + ] ] + E x [e q(σπ τ π) w (U π σ π τ ) π Wtedy v (x) = sup π v π (x) = v π (x)
24 Strategia barierowa π a dla K = 0 17
25 Strategia barierowa π a dla K = 0 18 Jeśli bariera jest zbyt wysoko to nie zdołamy spędzić na niej zbyt wiele czasu (zebrać dużo dywidend) a jeśli jest zbyt nisko to zbyt szybko uzyskamy ruinę. Możemy więc spodziewać się optymalnej wysokości bariery.
26 Czas lokalny w maksimum 19 Dla strategii barierowej w a z K = 0: D π a t = a X t a, gdzie X t = sup s t X s oraz {U π a t, t σ π a ; U π a 0 = x} = D {a Y t, t σ a ; Y 0 = a x} gdzie Y t = (a X t ) X t jest procesem odbitym w supremum i σ a = inf{t > 0 : Y t > a} jest pierwszym momentem wyjścia tego procesu z przedziału [0, a]
27 Proces regulowany raz jeszcze 20
28 Zdyskontowany czas lokalny 21
29 Dwuwymiarowy subordynator 22 D π a (x) = σa 0 e qt dd π a t = = 0 0 e qdπa, 1 t 1 (sups t ɛ s a)dt e qξ t 1 (sups t η s a)dt gdzie η t = η t η t oraz (ξ, η) = {(ξ t, η t ) : t 0} jest dwuwymiarowym subordynatorem
30 Dwuwymiarowy subordynator 23 D π a (x) = σa 0 e qt dd π a t = = 0 0 e qdπa, 1 t 1 (sups t ɛ s a)dt e qξ t 1 (sups t η s a)dt gdzie η t = η t η t oraz (ξ, η) = {(ξ t, η t ) : t 0} jest dwuwymiarowym subordynatorem Twierdzenie 1. (Kyprianou i Palmowski (2007)) Dla n = 1, 2, 3,... mamy: [( E 0 ) n ] e qξ t 1 (sups t η s a)dt = n! n k=1 1 Λ(qk) + ν Λ(qk) (a, ) gdzie Λ(q) jest wykładnikiem Laplace a ξ oraz ν Λ(q) jest miara Lévy ego procesu η rozpatrywanego względem nowej miary dp Λ(q) t dp t = e Λ(q)t qξ t
31 Strategia barierowa π a dla K = 0 24 W π a w (x) = E x [ e qσ πa w(u π a σ πa ) ]
32 Strategia barierowa π a dla K = 0 25 W π a w (x) = E x [ e qσ πa w(u π a σ πa ) ] ] = E x [ t 0 e qt w(u π a t + X t )1 {t<σ πa, X t <U πa t } = a 0 y w(y z)π X (dz)r (q) (x, dy) = a 0 K w (y)r (q) (x, dy) gdzie R (q) (x, dy) jest rezolwenta procesu odbitego w maximum Y zabitego przy wyjściu z przedziału [0, a]: R (q) (x, dy) = = e qt P x (Y t dy, t < σ a )dt [ 0 W (q) (x) W (q) (a) W (q) (a y) W (q) (x y) + W (q) (x) W (q) (a) W (q) (0)δ a (dy) ] dy
33 Funkcje skalujace Wykładnik Laplace a: ψ(θ): 26 E[e θx t ] = e tψ(θ) Φ(q) - największy pierwiastek równania ψ(θ) = q Pierwsza funkcja skalujaca: W (q) : [0, ) [0, ): 0 e θx W (q) (y)dy = (ψ(θ) q) 1, θ > Φ(q) W (q) jest różniczkowalna (niekoniecznie w sposób ciagły) oraz Druga funkcja skalujaca: W (x) = W (0) (x) Z (q) (y) = 1 + q y 0 W (q) (z) dz
34 Strategia barierowa π a dla K > 0 27
35 Strat. likw.-barierowa π b,a, K > 0 28 π b,a dla a = (a, a + ) oraz b > 0
36 Strat. likw.-barierowa π b,a, K = 0 29 π b,a dla a > b oraz b > 0 ("graniczny przypadek"dla a + = a = a) Dla uproszczenia będziemy dla obu przypadków używać tego samego oznaczenia π b,a
37 Funkcja wypłaty dla π b,a Definiujemy: 30 w(x) = w(x b), K w (y) = y w(y + z)π X (dz) < F w (x) = x 0 W (q) (x y)k w (y)dy
38 Funkcja wypłaty dla π b,a Definiujemy: 31 w(x) = w(x b), K w (y) = y w(y + z)π X (dz) < F w (x) = x 0 W (q) (x y)k w (y)dy Twierdzenie 2. (Avram, Palmowski i Pistorius (2014)) w(x) x < b v πb,a := v b,a (x) = W (q) (x b)g b (a) + F w (x b) x [b, a + ] gdzie G b (a) := [ a K F w (a b) W (q) (a b) 1 F w (a b) W (q) (a b) jeśli K > 0 jeśli K = 0 oraz a = a + a, g(a b) = g(a + b) g(a b).
39 Optymalność π b,a Wybieramy optymalne bariery a = (a, a +) i b (dla K = 0: a = a = a + ). Niech: I w := sup I w (x), I w (x) = Γw(x) qw(x) x>0 gdzie 32 Af(x) = σ2 2 f (x)+pf (x)+ 0 [ f(x + y) f(x) f (x)y1 { y <1} ] ΠX (dy)
40 Optymalność π b,a Wybieramy optymalne bariery a = (a, a +) i b (dla K = 0: a = a = a + ). Niech: I w := sup I w (x), I w (x) = Γw(x) qw(x) x>0 gdzie 33 Γf(x) = σ2 2 f (x)+pf (x)+ 0 [ f(x + y) f(x) f (x)y1 { y <1} ] ΠX (dy) Twierdzenie 3. (i) Jeśi Iw 0, to dla każdego x > 0 optymalna strategia jest likwidacja, tzn. τ = 0. Załóżmy, że I w > 0. Wtedy (ii) π b,a jest optymaln a strategi a w zbiorze wszystkich strategii ograniczonych przez a + ; (iii) jeśli (Av b,a qv b,a )(x) 0 dla x > a +, to π b,a jest optymaln a strategia oraz v = v b,a. W szczególności, jeśli miara skoków Π X ma wypukła gęstość to strategia barierowo-likwidacyjna jest zawsze optymalna.
41 Azcue i Muler 2005 Cramér-Lundberg proces z roszczeniami o rozkładzie Gamma: 34 F (dx) = xe x dx, z intensywnościa dyskonta q = 0.1, intensywnościa zgłoszeń Poissonowskich λ = 10, intensywnościa składek: p = 2( )λ. Wtedy: v (x) = x x [0, 1.803) e x 9.431e x e x x [1.803, 10.22) x x 10.22
42 Strategia bandowa π b,a 35
43 π b,a, K = 0 36 Twierdzenie 4. Niech K = 0. Dla i 1 oraz v πb,a := v b,a (x): W (q) (x b i 1 )G wi 1 (a i, b i 1 ) + F wi 1 (x b i 1 ) x [b i 1, a i ) v b,a (x) = v b,a (a i ) + x a i x [a i, b i ) gdzie F wi 1 (x b i 1 ) = w i 1(b i 1 )F 1 (x) + w i 1 (b i 1 )F 0 (x) + F wi 1,0 (x) oraz w i 1,0 (x) = v b,a (x b i 1 ) v b,a (b i 1 ) (x b i 1 )v b,a (b i 1 )
44 Optymalność π b,a 37 Optymalne bandy: a i jest dane poprzez smooth fit condition of singular control : 0 = lim v x a a,b (x) = lim v i x a a,b (x), i b i > 0 jest zdeterminowane poprzez smooth fit condition : 1 = lim v x b a,b (x) = lim v i x b a,b (x) i jeśli X jest o nieograniczonym wahaniu lub przez continuous fit condition : jeśli X ma ograniczone wahanie. lim v x b a,b (x) = lim v i x b a,b (x) i Twierdzenie 5. Strategia π b,a dopuszczalnych strategii. jest optymaln a strategi a spośród wszystkich
45 Wykładnicze roszczenia Exp(µ) Niech gdzie C k = Exp(µ). X t = x + pt N t k=1 C k 38
46 Wykładnicze roszczenia Exp(µ) Niech gdzie C k = Exp(µ). Wtedy X t = x + pt N t k=1 C k 39 ( ) W (q) (x) = p 1 A + e q+ (q)x A e q (q)x, Z (q) (x) = p 1 q (q ) + (q) 1 A + e q+ (q)x q (q) 1 A e q (q)x gdzie A ± = µ+q± (q) q + (q) q (q) ψ(θ) = q: oraz q+ (q) = Φ(q) i q (q) rozwiazuj a równanie q ± (q) = q + λ µp ± (q + λ µp) 2 + 4pqµ 2p
47 Wykładnicze roszczenia Exp(µ) Niech gdzie C k = Exp(µ). Wtedy X t = x + pt N t k=1 C k 40 ( ) W (q) (x) = p 1 A + e q+ (q)x A e q (q)x, Z (q) (x) = p 1 q (q ) + (q) 1 A + e q+ (q)x q (q) 1 A e q (q)x gdzie A ± = µ+q± (q) q + (q) q (q) ψ(θ) = q: oraz q+ (q) = Φ(q) i q (q) rozwiazuj a równanie q ± (q) = q + λ µp ± (q + λ µp) 2 + 4pqµ 2p Rozważmy kawałkami liniowa funkcję Gerbera-Shiu: w(x) = cx1 {x<0} + (x K)1 {x>0}
48 Wykładnicze roszczenia Exp(µ) 41 Strategia likwidacyjna jest optymalna jeśli: gdzie I w 0 c max {c 1, c 2 } c 1 = (pµ/λ+k(µ+ qµ λ )), c 2 = 1+Kµ+ q λ exp { ( pµ λ q + Kµ 1) + } Jeśli c [c 1, c 2 ), to optymalna strategia jest strategia barierowa-likwidacyjna π b,a z b > 0. Jeśli c < min{c 1, c 2 }, to optymalna strategia jest strategia barierowa π a (czyli b = 0).
49 Erlang (2, µ), K = 0 42 W (q) (x) = 3 D j e ρ jx gdzie ρ 1 > 0 > ρ 2 > µ > ρ 3 sa pierwiastkami równania ψ(θ) = q oraz D j = (ρ j+µ) 2 p k j (ρ j ρ k. Rozważmy liniowa funkcję kary: ) j=1 w(x) = cx, dla x < 0 Jeśli I w 0 c µp/(2λ) > 1, to strategia likwidacyjna jest optymalna dla wszystkich x > 0 (τ = 0).
50 Erlang (2, µ), K = 0 43 W (q) (x) = 3 D j e ρ jx gdzie ρ 1 > 0 > ρ 2 > µ > ρ 3 sa pierwiastkami równania ψ(θ) = q oraz D j = (ρ j+µ) 2 p k j (ρ j ρ k. Rozważmy liniowa funkcję kary: ) j=1 w(x) = cx, dla x < 0 Jeśli Iw 0 c µp/(2λ) > 1, to strategia likwidacyjna jest optymalna dla wszystkich x > 0 (τ = 0). Numeryczny przykład Biorac c = 0.2, λ = 10, µ = 1, p = 21.4, q = 0.1 Optymalna strategia jest 2-bandowa strategia: v (x) = 0.2x for x < 0 x for 0 x e x e x e x for < x x for x >
51 Paryskie dywidendy Proces regulowany: U π t = X t D π t 43 gdzie Dt π jest łaczn a ilości a wypłaconych dywidend do czasu t Od teraz załóżmy brak funkcji kary, tzn. w(x) = 0 dla x < 0. Wtedy zawsze b = 0 oraz rozważamy tylko strategię barierowa π a. Obserwujemy proces U π do czasu ruiny σ, gdzie σ = σ π,ζ = inf{t > 0 : t sup{s t : U π s 0} ζ, U π t < 0}
52 Paryska strategia barierowa π a 44 X t a z,z t
53 Paryskie funkcje skalujace 45 gdzie V (q) (x) = e Φ(q)x P Φ(q) x (τ ζ = ), τ ζ = inf{t > 0 : t sup{s t : X s 0} ζ, X t > 0} Twierdzenie 6. (Czarna i Palmowski (2011), Loeffen, Czarna, Palmowski (2013)) Dla x 0: P x (τ ζ 0 W (0) (x + z)zp(x ζ dz) < ) = 1 EX 1 0 zp(x ζ dz)
54 Wykładnicze roszczenia Exp(µ) 46 Niech gdzie C k = Exp(µ). Wtedy: gdzie X t = x + pt P x (τ ζ < ) =e ( λ p µ)x (1 N t k=1 C k ) pµ λ e λζ pµ + e λζ µ D ζ 2 D 2 = pζ 0 (pζ t)e µt µλζ I 1 (2 tµλζ)dt t
55 Funkcja wypłaty dla π a 47 Przypomnijmy, że funkcja wartości liczona do klasycznej ruiny jest równa: W (q) (x), x a, W (q) (a) v πa (x) = x a + W (q) (a) x > a W (q) (a), Twierdzenie 7. (Czarna i Palmowski (2014)) Funkcja wartości liczona do paryskiej ruiny wynosi: v ζ π a (x) = V (q) (x), x a, V (q) (a) x a + V (q) (a) V (q) (a), x > a
56 Optymalność π a 48 Twierdzenie 8. Przypuśćmy, że miara skoków ma gęstość monotonicznie malejac a, to wtedy strategia barierowa jest optymalna dla obu problemów optymalizacyjnych z klasyczna i paryska ruina. W szczególności, optymalna bariera dla problemu z klasyczna ruina wynosi: a = inf{a > 0 : W (q) (a) W (q) (y) dla każdego y 0}, zaś dla problemu z paryskim opóźnieniem w momencie ruiny: a,ζ = inf{a > 0 : V (q) (a) V (q) (y) dla każdego y 0}. Dodatkowo jeśli W (q) C 2 (R), to optymalne bariery rozwiazuj a następujace równania: W (q) (a ) = 0, V (q) (a,ζ ) = 0.
57 Model Craméra-Lundberga X t = x + pt N t i=1 C i Exp(ξ) C i 49 dla oraz dla a = 1 q + (q) q (q) log q (q) 2 (ξ + q (q)) q + (q) 2 (ξ + q + (q)) q ± (q) = q + λ ξp ± (q + λ ξp) 2 + 4pqξ 2 a,ζ = 2p [( ) ( λ q D log 1 pξ q λ q ξ q λ q pξ q λ q (1 D) pφ(q) D = 1 ζ z λ q = λξ/ξ q i ξ q = ξ + q + (q) 0 pξq e (λ q+pξ q )t t 1 I 1 (2t pλ q ξ)dt λ q )]
58 C-L - an. numeryczna 50 Bierzemy następujace parametry procesu ryzyka: ξ = 2, λ = 2, q = 0.1, p = 2.5. Wtedy a = ζ a,ζ Tabela 1: Optymalna wyskość bariery dla różnych paryskich opóźnień. x v(x) v a,ζ(x) Tabela 2: Łaczna ilość zdyskontowanych dywidend dla klasycznej i paryskiej ruiny dla różnych kapitałów poczatkowych
59 Model z wpłatami 51 Niech π = {D π t, R π t, t 0} będa niemalejacymi F-adaptowalnymi procesami opisujacymi łaczn a ilość wypłaconych dywidend oraz łaczn a ilość wpłat utrzymujacych proces powyżej zera Regulowany proces: Funkcja wartości: v (x) = sup π U π t = X t D π t + R π t [ E x e qt dd π t ϕ 0 0 e qt dr π t ] gdzie ϕ > 1 jest kosztem operacyjnym zwiazanym z wpłata jednostkowego kapitału
60 Optymalna startegia 52 v a (x) = ϕ(z (q) (x) + ψ (0 + )/q) + Z (q) (x) x a + v a (a) [ ] 1 ϕz (q) (a) qw (q) (a) 0 x a, x > a gdzie Z (q) (y) = y 0 Z (q) (z)dz = y + q y z 0 0 W (q) (w)dwdz Twierdzenie 9. (Avram, Palmowski i Pistorius (2007)) Optymalna strategia jest strategia barierowa z bariera: a = inf{a > 0 : G(a) 0} gdzie G(a) := [ϕz (q) (a) 1]W (q) (a) ϕqw (q) (a) 2.
61 Wycena typu DCF 53 DCF - Discounted Cash Flow (wycena firm metoda przepływów pieniężnych) Funkcja wartości: [ σ σ ] v (x) = sup E x e qt dl π t ϕ e qt dr π t π,σ 0 Twierdzenie 10. (Gajek i Kuciński (2011), Palmowski i Loeffen (2014)) Jeśli miara skoków ma gęstość monotonicznie malejac a, to optymalna strategia jest strategia π b,a polegajaca na odbiciu od a i wpłatach sprawiajacych, że regulowany proces jest nieujemny do czasu pierwszego zejścia poniżej poziomu b. Wycena PZU ta metoda dała kwotę 8,03 bn EUR zaś wycena rynkowa dawała w 2010 kwotę: 7,97 bn EUR. 0
62 Optymalna strategia dla DCF 54 a U p -b,a t -b
63 Składki zależne od rezerw 55 Proces rezerw (nieregulowany) jest opisany przez równanie: X t = x + t 0 p(x s )ds N t k=1 C k, gdzie p jest deterministyczna dodatnia, niemalejac a i Lipschitzowska funkcja a N t procesem Poissona z intensywnościa λ.
64 Problem optymalizacji dywidend 56 Proces regulowany U π t spełnia równanie: U π t = x + t 0 p(u π s )ds N t k=1 C k D π t, oznacza skumulowan a war- gdzie π jest dopuszczalna strategia dla której Dt π tość wypłaconych dywidend do chwili t włacznie. Uwaga! W modelu z p const NIE zachodzi równość U π t = X t D π t jak to jest m.in. w modelu Craméra-Lundberga lub w modelach z procesem Lévy ego X.
65 Cel 57 Celem jest znalezienie (optymalnej) strategii która maksymalizuje π = (τ, D ) v π (x) = E x [ σ π 0 ] [ e qt dd π t + E x e qσ π w (U π σ ) ] π Wtedy v (x) = sup π v π (x) = v π (x)
66 Strategia barierowa 58 a
67 Strategia barierowa 59 Zdefiniujmy funkcje: W q (x) = lim E x [e qτ y +, τ + y y < τ 0 ]/E 0 [e qτ y +, τ + y < τ 0 ] ] G q,w (x) = E x [e qτ 0 w(xτ 0 )I {τ 0 < }, gdzie τ a + = inf{t 0 : X t > a}, τ0 = inf{t 0 : X t < 0}. Załóżmy, że rozkład F ma ciagł a gestość. Wtedy funkcje W q, G q,w sa różniczkowalne dla każdego u > 0. Twierdzenie 11. (Marciniak i Palmowski (2014)) Dla strategii barierowej π a mamy: ( ) W q (x) 1 G W q(a) q,w(a) + G q,w (x), x a, v a (x) = v π a(x) = x a + v a (a), x > a.
68 Optymalność 60 Niech H q(y) := W q(y) 1 G q,w(y). Kandydat na barierę optymalna: { } a = sup a 0 : H q(a) H q(u) dla u 0, gdzie H q(0) = lim u 0 H q(u). Twierdzenie 12. Załóżmy, że H q(a) H q(b) dla wszystkich a a b. Wówczas strategia barierowa z barier a a jest optymalna tj. v (x) = v a (x).
69 Uwaga 61 Przypomnijmy, że dla x a mamy: v a (x) = W ( ) q(x) 1 G W q,w(a) + G q(a) q,w (x) Zauważmy też, że: lim u W q (x) = + and lim u G q,w (x) = 0. Oznacza to, że funkcja wartości (przy dodatkowych założeniach) jest kombinacja liniowa dwóch funkcji Gerbera-Shiu: niestabilnej, która znika na ujemnej półosi (odpowiada ona wypłatom dywidendowym, w naszym przypadku jest to funkcja W q ) oraz stabilnej (odpowiada ona wypłacie kary za ruinę, w naszym przypadku jest to funkcja G q,w ).
70 Przykład 62 Załóżmy, że szkody maja rozkład wykładniczy z parametrem µ. Niech p(x) = c + ɛx dla ɛ < q. Funkcje W q i G q,w sa rozwiazaniami równań: AW q (x) = qw q (x) dla x 0, W q (x) = 0 dla x < 0 AG q,w = qg q,w (x) + ω(x) dla x 0, G q,w (x) = w(x) dla x < 0 gdzie oraz A = ( d dx + µ)( p(x) d dx ω(x) = u + q) λµ w(x z)df (z)
71 Przykład 63 Niech: oraz s 1 (x) = U ( q ɛ λ+q + 1, + 1, µx + µc ) λ+q ɛ ɛ (ɛx + c) ɛ exp( µx) Gg(x) = ( U(x) Γ(q/ɛ+1) Γ((q+λ)/(1+ɛ)) x 0 ( 1 µ ) (λ+q)/ɛ (ɛx + c) (λ+q)/ɛ exp( µx µc ) ɛ ɛ ɛ ) M(v) M(x) U(v) + M(0) U(x) U(v) g(v) dv, U(0) x gdzie U(x) i M(x) sa funkcjami Kummera, g(x) = λ ( +µ) ω(x). Wtedy: p(x) x G q,w (x) = (s 1 (x) + Gg(x)), 0 Dodatkowo: W q (x) = M ( q ɛ λ+q + 1, + 1, µx + µc ) λ+q ɛ ɛ (ɛx + c) ɛ exp( µx)
72 Przykład 64 Przypomnijmy, że: G q,w (u) = (s 1 (u) + Gg(u)) W q (x) = M ( q ɛ λ+q + 1, + 1, µx + µc ) λ+q ɛ ɛ (ɛx + c) ɛ exp( µx) Zatem: H q(x) = W q(x) 1 G q,w(x) i możemy znaleźć optymalna barierę a rozwiazuj ac równanie H q(a ) = 0.
73 Funkcja użyteczności 65 U π t = X t t 0 c s ds Funkcja wartości: ( v (x) = v(x) = sup E dla funkcji użyteczności m, na przykład dla m(x) = xα, α (0, 1) α 0 ) e qt m(c t )dt Optymalna strategia jest funkcja c od obecnych rezerw, gdzie: c (x) = (m ) 1 (v x ).
74 C-L z wykładniczymi roszczeniami 66 Dla m(x) = xα przy dodatkowych założeniach funkcja wartości rozwi azuje α następujace równanie: µv xx + (ξµ β λ)v x ξβv + ξ 1 α α v(0) = µ β + λ v x(0) + v α 1 α x 1 α α(β + λ) v x(0) α 1 α v 1 1 α x v xx = 0 Twierdzenie 13. (Baran i Palmowski (2014)) Dla dużych wartości poczatko- wego kapitału x mamy: v(x) v x (x) c (x) ( ) 1 1 α α αβ x 1 α ( ) ( α 1 α 2α 1 αβ ( ) 1 α 1 α α αβ (1 α) x α ) 1 α α 2α 1 x α
75 Dwuwymiarowy p. ryzyka 67 Rozważamy teraz dwuwymiarowy proces ryzyka, kiedy dwie firmy (lub dwie gałęzie jednej firmy) połaczone sa poprzez proporcjonalna reasekurację. To znaczy będziemy zakładać, że firmy dziela sie roszczeniami (dla uproszczenia zakładamy, że dziela się nimi po równo) oraz intensywnościami wpłat w proporcji p 1 do p 2. Czyli: X t = (X 1 (t), X 2 (t)) = ( x 1 + p 1 t N t i=1 C i, x 2 + p 2 t N t i=1 C i ). dla p 1 > p 2.
76 Dwuwymiarowy p. ryzyka 68 Two possible surplus trajectories: X 2 3 Initial surpluses Slope p 2 p 1 2 Ruin 1 Initial surpluses Slope X 1 Ruin
77 Dwuwymiarowy p. ryzyka 69 Proces regulowany: gdzie U t = (U 1 (t), U 2 (t)) = X t D π t D π t = (D π 1(t), D π 2(t)) opisuje wypłatę dywidend przez każda z firm. Niech: v (x 1, x 2 ) = v (x) = sup π gdzie σ = inf{t 0 : U 1 (t)u 2 (t) < 0}. E x (1, 1) σ 0 e qt dd π t Funkcja wartości v (x 1, x 2 ) opisuje średnia zdyskontowana sumę łacznych dywidend płaconych przez obie firmy do czasu ruiny jednej z nich.
78 Równanie 70 Twierdzenie 14. (Czarna i Palmowski (2014)) Av(x) := p v x (x) (λ + q)v(x) + λ min(x1,x2) 0 v(x (1, 1)u) df (u) = 0 Znaleziono też rozwiazanie powyższego równania przy określonej strategii wypłaty dywidend polegajacej na odbiciu od prostej w dwóch wymiarach. Strategia ta determinuje warunki berzegowe dla tego równania. Ta strategia nie jest jednak optymalna w zbiorze wszystkich strategii dopuszczalnych.
79 Ham. - Jac. - Bell. 71 Twierdzenie 15. (Azcue, Muler i Palmowski (2014)) Funkcja wartości jest rozwiazaniem lepkościowym następujacego systemu HJB: max{av(x), 1 x 1 v(x), x 2 v(x)} = 0. Przykład Roszczenia wykładnicze: p 1 = 2, p 2 = 1, q = 0, 05 C k Exp ( ) 6 5
80 Azcue, Muler i Palmowski (2014) 72
81 DZIEKUJ E BARDZO ZA UWAGE!!!!! 73
82 Literatura 74 I. Czarna, Z. Palmowski, De Finetti s dividend problem and impulse control for a two-dimensional insurance risk process. Stochastic Models 27 (2011), I. Czarna, Z. Palmowski, Ruin probability with Parisian delay for a spectrally negative Lévy risk process. Journal of Applied Probability 48(4) (2011), I. Czarna, Z. Palmowski, Dividend problem with Parisian delay for a spectrally negative Lévy risk process. Journal of Optimization Theory and Applications (2013). F. Avram, Z. Palmowski, M. Pistorius, On Gerber-Shiu functions and optimal dividend distribution for a Lévy risk-process in the presence of a penalty function. Złożony do publikacji, (2014). H. Albrecher, C. Constantinescu, Z. Palmowski, G. Regensburger, M. Rosenkranz, On Gerber-Shiu functions for models with premiums dependent on reserves. SIAM Journal on Applied Mathematics 73(1) (2013), S. Baran, Z. Palmowski, Optimizing expected utility of dividend payments for a Erlang risk process. Złożony do publikacji, (2014).
83 Literatura 75 R. Loeffen, I. Czarna, Z. Palmowski, Parisian ruin probability for spectrally negative Lévy processes. Bernoulli 19(2) (2013), F. Avram, Z. Palmowski, M. Pistorius, On the optimal dividend problem for a spectrally negative Lévy process. Annals of Applied Probability 17(1) (2007), A. Kyprianou, Z. Palmowski, Distributional study of De Finetti s dividend problem for a general Lévy insurance risk process. Journal of Applied Probability 44(2) (2007), E. Marciniak, Z. Palmowski On optimal dividend problem for an insurance risk models with surplus-dependent premiums. W przygotowaniu, (2014). P. Azcue, N. Muler, Z. Palmowski Optimal dividend payments for a twodimensional risk process. W przygotowaniu, (2014).
Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego
 Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego Zbigniew Palmowski Wspólna praca z I. Czarna Zagadnienia aktuarialne: teoria i praktyka, Wrocław Ekonomiczny
Problem wyboru optymalnej dywidendy z paryskim opóźnieniem dla spektralnie ujemnych procesów Lévy ego Zbigniew Palmowski Wspólna praca z I. Czarna Zagadnienia aktuarialne: teoria i praktyka, Wrocław Ekonomiczny
Parametr Λ w populacji ubezpieczonych ma rozkład dany na półosi dodatniej gęstością: 3 f
 Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008
 Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Przemysław Klusik Instytut Matematyczny, Uniwersytet Wrocławski Ogólnopolska Konferencja Naukowa Zagadnienia Aktuarialne - Teoria i praktyka Warszawa, 9 11 czerwca 2008 (UWr) Zagadnienia Aktuarialne -
Problem optymalizacji oczekiwanej użyteczności wypłat dywidend w modelu Craméra-Lundberga 1
 Roczniki Kolegium Analiz Ekonomicznych Zeszyt 31/213 Sebastian Baran Zbigniew Palmowski Problem optymalizacji oczekiwanej użyteczności wypłat dywidend w modelu Craméra-Lundberga 1 Streszczenie W niniejszej
Roczniki Kolegium Analiz Ekonomicznych Zeszyt 31/213 Sebastian Baran Zbigniew Palmowski Problem optymalizacji oczekiwanej użyteczności wypłat dywidend w modelu Craméra-Lundberga 1 Streszczenie W niniejszej
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami:
 Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:
Zadanie 1. Zmienne losowe X 1, X 2 są niezależne i mają taki sam rozkład z atomami: Pr(X 1 = 0) = 6/10, Pr(X 1 = 1) = 1/10, i gęstością: f(x) = 3/10 na przedziale (0, 1). Wobec tego Pr(X 1 + X 2 5/3) wynosi:
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Zadanie 1. są niezależne i mają rozkład z atomami: ( ),
 Zadanie. Zmienne losowe są niezależne i mają rozkład z atomami: ( ) ( ) i gęstością: ( ) na przedziale ( ). Wobec tego ( ) wynosi: (A) 0.2295 (B) 0.2403 (C) 0.2457 (D) 0.25 (E) 0.269 Zadanie 2. Niech:
Zadanie. Zmienne losowe są niezależne i mają rozkład z atomami: ( ) ( ) i gęstością: ( ) na przedziale ( ). Wobec tego ( ) wynosi: (A) 0.2295 (B) 0.2403 (C) 0.2457 (D) 0.25 (E) 0.269 Zadanie 2. Niech:
Egzamin z matematyki ubezpieczeniowej (MUMIO), semestr zimowy 2013/14
 ZESTAW A IMIȨ I NAZWISKO: Egzamin z matematyki ubezpieczeniowej (MUMIO), semestr zimowy 2/4 Data: 224 Egzaminar: Ryszard Szekli INSTRUKCJE: Rozwiązując test zakreślamy literką X POPRAWNE ODPOWIEDZI W TABELCE
ZESTAW A IMIȨ I NAZWISKO: Egzamin z matematyki ubezpieczeniowej (MUMIO), semestr zimowy 2/4 Data: 224 Egzaminar: Ryszard Szekli INSTRUKCJE: Rozwiązując test zakreślamy literką X POPRAWNE ODPOWIEDZI W TABELCE
Własność iteracyjności składek ubezpieczeniowych wyznaczonych w oparciu o teorię skumulowanej perspektywy Kahnemana-Tversky
 Własność iteracyjności składek ubezpieczeniowych wyznaczonych w oparciu o teorię skumulowanej perspektywy Kahnemana-Tversky ego Marek Kałuszka Michał Krzeszowiec Ogólnopolska Konferencja Naukowa Zagadnienia
Własność iteracyjności składek ubezpieczeniowych wyznaczonych w oparciu o teorię skumulowanej perspektywy Kahnemana-Tversky ego Marek Kałuszka Michał Krzeszowiec Ogólnopolska Konferencja Naukowa Zagadnienia
Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1
 Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Równania różniczkowe pierwszego rzędu Równaniem różniczkowym zwyczajnym pierwszego rzędu nazywamy równanie postaci (R) y = f(x, y). Najogólniejszą
Biotechnologia, Chemia, Chemia Budowlana - Wydział Chemiczny - 1 Równania różniczkowe pierwszego rzędu Równaniem różniczkowym zwyczajnym pierwszego rzędu nazywamy równanie postaci (R) y = f(x, y). Najogólniejszą
Matematyka ubezpieczeń majątkowych r.
 Zadanie 1. W pewnej populacji podmiotów każdy podmiot narażony jest na ryzyko straty X o rozkładzie normalnym z wartością oczekiwaną równą μ i wariancją równą. Wszystkie podmioty z tej populacji kierują
Zadanie 1. W pewnej populacji podmiotów każdy podmiot narażony jest na ryzyko straty X o rozkładzie normalnym z wartością oczekiwaną równą μ i wariancją równą. Wszystkie podmioty z tej populacji kierują
Zadanie 1. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k =
 Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 1.10.2012 r.
 Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Matematyka ubezpieczeń majątkowych 4.04.0 r. Zadanie. Przy danej wartości λ parametru ryzyka Λ liczby szkód generowane przez ubezpieczającego się w kolejnych latach to niezależne zmienne losowe o rozkładzie
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
1 Funkcja użyteczności
 1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
1 Funkcja użyteczności Funkcja użyteczności to funkcja, której wartościami są wartości użyteczności (satysfakcji, komfortu psychicznego). Można mówić o użyteczności różnych zjawisk. Użyteczność pieniądza
Zadania z Rachunku Prawdopodobieństwa III - 1
 Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Zadania z Rachunku Prawdopodobieństwa III - 1 Funkcją tworzącą momenty (transformatą Laplace a) zmiennej losowej X nazywamy funkcję M X (t) := Ee tx, t R. 1. Oblicz funkcję tworzącą momenty zmiennych o
Wykład 7: Warunkowa wartość oczekiwana. Rozkłady warunkowe.
 Rachunek prawdopodobieństwa MAP3040 WPPT FT, rok akad. 2010/11, sem. zimowy Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 7: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Warunkowa wartość oczekiwana.
Rachunek prawdopodobieństwa MAP3040 WPPT FT, rok akad. 2010/11, sem. zimowy Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 7: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Warunkowa wartość oczekiwana.
Quantile hedging. czyli jak tanio i dobrze zabezpieczyć opcję. Michał Krawiec, Piotr Piestrzyński
 czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
czyli jak tanio i dobrze zabezpieczyć opcję Michał Krawiec Piotr Piestrzyński Koło Naukowe Probabilistyki i Statystyki Matematycznej Uniwersytet Wrocławski Niedziela, 19 kwietnia 2015 Przykład (opis problemu)
N ma rozkład Poissona z wartością oczekiwaną równą 100 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach:
 Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
Zadanie. O niezależnych zmiennych losowych N, M M, M 2, 3 wiemy, że: N ma rozkład Poissona z wartością oczekiwaną równą 00 M, M M mają ten sam rozkład dwupunktowy o prawdopodobieństwach: 2, 3 Pr( M = )
01. dla x 0; 1 2 wynosi:
 Matematyka ubezpieczeń majątkowych 0.0.04 r. Zadanie. Ryzyko X ma rozkład z atomami: Pr X 0 08. Pr X 0. i gęstością: f X x 0. dla x 0; Ryzyko Y ma rozkład z atomami: Pr Y 0 07. Pr Y 0. i gęstością: fy
Matematyka ubezpieczeń majątkowych 0.0.04 r. Zadanie. Ryzyko X ma rozkład z atomami: Pr X 0 08. Pr X 0. i gęstością: f X x 0. dla x 0; Ryzyko Y ma rozkład z atomami: Pr Y 0 07. Pr Y 0. i gęstością: fy
Prawdopodobieństwo i statystyka
 Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
Wykład VII: Rozkład i jego charakterystyki 22 listopada 2016 Uprzednio wprowadzone pojęcia i ich własności Definicja zmiennej losowej Zmienna losowa na przestrzeni probabilistycznej (Ω, F, P) to funkcja
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadanie 1. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną:
 Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
2. Wykaż, że moment pierwszego skoku w procesie Poissona. S 1 := inf{t : N t > 0} jest zmienną losową o rozkładzie wykładniczym z parametrem λ.
 Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Zadania z Procesów Stochastycznych 1 1. Udowodnij, że z prawdopodobieństwem 1 trajektorie procesu Poissona są niemalejące, przyjmują wartości z Z +, mają wszystkie skoki równe 1 oraz dążą do nieskończoności.
Procesy stochastyczne 2.
 Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Procesy stochastyczne 2. Listy zadań 1-3. Autor: dr hab.a. Jurlewicz WPPT Matematyka, studia drugiego stopnia, I rok, rok akad. 211/12 1 Lista 1: Własność braku pamięci. Procesy o przyrostach niezależnych,
Wykład 3 Jednowymiarowe zmienne losowe
 Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Wykład 3 Jednowymiarowe zmienne losowe Niech (Ω, F, P ) będzie ustaloną przestrzenią probabilistyczną Definicja 1 Jednowymiarowa zmienna losowa (o wartościach rzeczywistych), określoną na przestrzeni probabilistycznej
Matematyka ubezpieczeń majątkowych r.
 Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Zadanie. W pewnej populacji kierowców każdego jej członka charakteryzują trzy zmienne: K liczba przejeżdżanych kilometrów (w tysiącach rocznie) NP liczba szkód w ciągu roku, w których kierowca jest stroną
Geometryczna zbieżność algorytmu Gibbsa
 Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
z przedziału 0,1 liczb dodatnich. Rozważmy dwie zmienne losowe:... ma złożony rozkład dwumianowy o parametrach 1,q i, gdzie X, wszystkie składniki X
 Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20:
 Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20: E X 20 8 oraz znamy następujące charakterystyki dotyczące przedziału 10, 20 : 3 Pr
Zadanie 1. O rozkładzie pewnego ryzyka X posiadamy następujące informacje: znamy oczekiwaną wartość nadwyżki ponad 20: E X 20 8 oraz znamy następujące charakterystyki dotyczące przedziału 10, 20 : 3 Pr
zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych
 zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych 1. [E.A 5.10.1996/zad.4] Funkcja gęstości dana jest wzorem { 3 x + 2xy + 1 y dla (x y) (0 1) (0 1) 4 4 P (X > 1 2 Y > 1 2 ) wynosi:
zadania z rachunku prawdopodobieństwa zapożyczone z egzaminów aktuarialnych 1. [E.A 5.10.1996/zad.4] Funkcja gęstości dana jest wzorem { 3 x + 2xy + 1 y dla (x y) (0 1) (0 1) 4 4 P (X > 1 2 Y > 1 2 ) wynosi:
Dokumentacja. Portal Mathfinance Wycena opcji paryskich metoda. Wiktor Madejski
 Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
Dokumentacja Portal Mathfinance Wycena opcji paryskich metoda PDE Wiktor Madejski Spis treści 1 Wstęp 2 2 Opcje paryskie 2 2.1 Układ PDE dla opcji paryskich..................... 2 2.2 Schemat numeryczny..........................
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
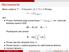 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Przykład 1 W przypadku jednokrotnego rzutu kostką przestrzeń zdarzeń elementarnych
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
22 Pochodna funkcji definicja
 22 Pochodna funkcji definicja Rozważmy funkcję f : (a, b) R, punkt x 0 b = +. (a, b), dopuszczamy również a = lub Definicja 33 Mówimy, że funkcja f jest różniczkowalna w punkcie x 0, gdy istnieje granica
22 Pochodna funkcji definicja Rozważmy funkcję f : (a, b) R, punkt x 0 b = +. (a, b), dopuszczamy również a = lub Definicja 33 Mówimy, że funkcja f jest różniczkowalna w punkcie x 0, gdy istnieje granica
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu.
 Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Ćwiczenia 7 - Zmienna losowa i jej rozkład. Parametry rozkładu. A Teoria Definicja A.1. Niech (Ω, F, P) będzie przestrzenią probabilistyczną. Zmienną losową określoną na przestrzeni Ω nazywamy dowolną
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Proces rezerwy w czasie dyskretnym z losową stopą procentową i losową składką
 z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
z losową stopą procentową i losową składką Instytut Matematyki i Informatyki Politechniki Wrocławskiej 10 czerwca 2008 Oznaczenia Wprowadzenie ξ n liczba wypłat w (n 1, n], Oznaczenia Wprowadzenie ξ n
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA
 PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA 1. Trójkę (Ω, F, P ), gdzie Ω, F jest σ-ciałem podzbiorów Ω, a P jest prawdopodobieństwem określonym na F, nazywamy przestrzenią probabilistyczną. 2. Rodzinę F
PEWNE FAKTY Z RACHUNKU PRAWDOPODOBIEŃSTWA 1. Trójkę (Ω, F, P ), gdzie Ω, F jest σ-ciałem podzbiorów Ω, a P jest prawdopodobieństwem określonym na F, nazywamy przestrzenią probabilistyczną. 2. Rodzinę F
Rozdział 1. Wektory losowe. 1.1 Wektor losowy i jego rozkład
 Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
Rozdział 1 Wektory losowe 1.1 Wektor losowy i jego rozkład Definicja 1 Wektor X = (X 1,..., X n ), którego każda współrzędna jest zmienną losową, nazywamy n-wymiarowym wektorem losowym (krótko wektorem
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Programowanie nieliniowe. Badania operacyjne Wykład 3 Metoda Lagrange a
 Programowanie nieliniowe Badania operacyjne Wykład 3 Metoda Lagrange a Plan wykładu Przykład problemu z nieliniową funkcją celu Sformułowanie problemu programowania matematycznego Podstawowe definicje
Programowanie nieliniowe Badania operacyjne Wykład 3 Metoda Lagrange a Plan wykładu Przykład problemu z nieliniową funkcją celu Sformułowanie problemu programowania matematycznego Podstawowe definicje
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
Matematyka ubezpieczeń majątkowych..00 r. Zadanie. Proces szkód w pewnym ubezpieczeniu jest złożonym procesem Poissona z oczekiwaną liczbą szkód w ciągu roku równą λ i rozkładem wartości szkody o dystrybuancie
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ
 ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
ANALIZA MATEMATYCZNA Z ELEMENTAMI STATYSTYKI MATEMATYCZNEJ FUNKCJE DWÓCH ZMIENNYCH RZECZYWISTYCH Definicja 1. Niech A będzie dowolnym niepustym zbiorem. Metryką w zbiorze A nazywamy funkcję rzeczywistą
5 Równania różniczkowe zwyczajne rzędu drugiego
 5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
5 Równania różniczkowe zwyczajne rzędu drugiego Definicja 5.1. Równaniem różniczkowym zwyczajnym rzędu drugiego nazywamy równanie postaci F ( x, y, y, y ) = 0, (12) w którym niewiadomą jest funkcja y =
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych)
 Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
Jak trudne jest numeryczne całkowanie (O złożoności zadań ciągłych) Uniwersytet Warszawski Wydział Matematyki, Informatyki i Mechaniki leszekp@mimuw.edu.pl Horyzonty 2014 17-03-2014 Będlewo Zadania numeryczne
2. ZASTOSOWANIA POCHODNYCH. (a) f(x) = ln 3 x ln x, (b) f(x) = e2x x 2 2.
 2. ZASTOSOWANIA POCHODNYCH. Koniecznie trzeba znać: twierdzenia o ekstremach (z wykorzystaniem pierwszej i drugiej pochodnej), Twierdzenie Lagrange a, Twierdzenie Taylora (z resztą w postaci Peano, Lagrange
2. ZASTOSOWANIA POCHODNYCH. Koniecznie trzeba znać: twierdzenia o ekstremach (z wykorzystaniem pierwszej i drugiej pochodnej), Twierdzenie Lagrange a, Twierdzenie Taylora (z resztą w postaci Peano, Lagrange
Fizyka statystyczna, elementy termodynamiki nierównowagowej Cele, zakres zagadnień
 Fizyka statystyczna, elementy termodynamiki nierównowagowej Cele, zakres zagadnień Narzędzia przypomnienie podstawowych definicji i twierdzeń z rachunku prawdopodobienstwa; podstawowe rozkłady statystyczne
Fizyka statystyczna, elementy termodynamiki nierównowagowej Cele, zakres zagadnień Narzędzia przypomnienie podstawowych definicji i twierdzeń z rachunku prawdopodobienstwa; podstawowe rozkłady statystyczne
Modelowanie zależności. Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski
 Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Modelowanie zależności pomiędzy zmiennymi losowymi Matematyczne podstawy teorii ryzyka i ich zastosowanie R. Łochowski P Zmienne losowe niezależne - przypomnienie Dwie rzeczywiste zmienne losowe X i Y
Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów.
 Rachunek prawdopodobieństwa MAP1181 Wydział PPT, MS, rok akad. 213/14, sem. zimowy Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów.
Rachunek prawdopodobieństwa MAP1181 Wydział PPT, MS, rok akad. 213/14, sem. zimowy Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów.
poprzez reasekurację proporcjonalną w modelu Jan Matuszewski Uniwersytet Warszawski
 Minimalizacja prawdopodobieństwa ruiny poprzez reasekurację proporcjonalną w modelu Sparre Andersena Jan Matuszewski Uniwersytet Warszawski Prezentacja powstała w oparciu o wyniki uzyskane w pracy magisterskiej
Minimalizacja prawdopodobieństwa ruiny poprzez reasekurację proporcjonalną w modelu Sparre Andersena Jan Matuszewski Uniwersytet Warszawski Prezentacja powstała w oparciu o wyniki uzyskane w pracy magisterskiej
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sp. ze stałymi kosztami za transakcje
 Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Analiza portfelowa w czasie ciagłym dla ogólnych cen zakupu i sprzedaży ze stałymi kosztami za transakcje Instytut Matematyczny PAN Problem bez stałych kosztów za transakcje (Ω, F, (F t ), P) przestrzeń
Całki krzywoliniowe skierowane
 Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
Całki krzywoliniowe skierowane Zamiana całki krzywoliniowej skierowanej na całkę pojedyńcza. Twierdzenie Greena. Zastosowania całki krzywoliniowej skierowanej. Małgorzata Wyrwas Katedra Matematyki Wydział
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej
 5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
5.1 Stopa Inflacji - Dyskonto odpowiadające sile nabywczej Stopa inflacji, i, mierzy jak szybko ceny się zmieniają jako zmianę procentową w skali rocznej. Oblicza się ją za pomocą średniej ważonej cząstkowych
4 Kilka klas procesów
 Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Marek Beśka, Całka Stochastyczna, wykład 4 48 4 Kilka klas procesów 4.1 Procesy rosnące i przestrzenie V,, loc Jak poprzednio niech (Ω, F, F, P ) będzie zupełną bazą stochastyczną. Definicja 4.1 Proces
Matematyka ubezpieczeń majątkowych 6.04.2009 r.
 Matematyka ubezpieczeń majątkowych 6.04.009 r. Zadanie. Niech N oznacza liczbę szkód zaszłych w ciągu roku z pewnego ubezpieczenia z czego: M to liczba szkód zgłoszonych przed końcem tego roku K to liczba
Matematyka ubezpieczeń majątkowych 6.04.009 r. Zadanie. Niech N oznacza liczbę szkód zaszłych w ciągu roku z pewnego ubezpieczenia z czego: M to liczba szkód zgłoszonych przed końcem tego roku K to liczba
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
1 Warunkowe wartości oczekiwane
 Warunkowe wartości oczekiwane W tej serii zadań rozwiążemy różne zadania związane z problemem warunkowania.. (Eg 48/) Załóżmy, że X, X, X 3, X 4 są niezależnymi zmiennymi losowymi o jednakowym rozkładzie
Warunkowe wartości oczekiwane W tej serii zadań rozwiążemy różne zadania związane z problemem warunkowania.. (Eg 48/) Załóżmy, że X, X, X 3, X 4 są niezależnymi zmiennymi losowymi o jednakowym rozkładzie
1 Pochodne wyższych rzędów
 Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
Pochodne wyższych rzędów Pochodną rzędu drugiego lub drugą pochodną funkcji y = f(x) nazywamy pochodną pierwszej pochodnej tej funkcji. Analogicznie definiujemy pochodne wyższych rzędów, jako pochodne
Matematyka finansowa r. Komisja Egzaminacyjna dla Aktuariuszy. L Egzamin dla Aktuariuszy z 5 października 2009 r.
 Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Komisja Egzaminacyjna dla Aktuariuszy L Egzamin dla Aktuariuszy z 5 października 2009 r. Część I Matematyka finansowa WERSJA TESTU A Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 0 minut 1 1.
Podstawy Informatyki Elementy teorii masowej obsługi
 Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Wprowadzenie Źródło, kolejka, stanowisko obsługi Notacja Kendalla 2 Analiza systemu M/M/1 Wyznaczenie P n (t) Wybrane
Podstawy Informatyki alina.momot@polsl.pl http://zti.polsl.pl/amomot/pi Plan wykładu 1 Wprowadzenie Źródło, kolejka, stanowisko obsługi Notacja Kendalla 2 Analiza systemu M/M/1 Wyznaczenie P n (t) Wybrane
2. Kombinacja liniowa rozwiązań zeruje się w pewnym punkcie wtedy i tylko wtedy, gdy zeruje się w każdym punkcie.
 Wniosek 1 Rozpatrzmy układ równań postaci: y 1 = a 11 (x)y 1 + + a 1n (x)y n y 2 = a 21 (x)y 1 + + a 2n (x)y n y n = a n1 (x)y 1 + + a nn (x)y n (1) o współczynnikach ciągłych w przedziale J 1 Rozwiązanie
Wniosek 1 Rozpatrzmy układ równań postaci: y 1 = a 11 (x)y 1 + + a 1n (x)y n y 2 = a 21 (x)y 1 + + a 2n (x)y n y n = a n1 (x)y 1 + + a nn (x)y n (1) o współczynnikach ciągłych w przedziale J 1 Rozwiązanie
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty
 WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
WYKŁADY Z RACHUNKU PRAWDOPODOBIEŃSTWA I wykład 4 Przekształcenia zmiennej losowej, momenty Agata Boratyńska Agata Boratyńska Rachunek prawdopodobieństwa, wykład 4 / 9 Przekształcenia zmiennej losowej X
Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów.
 Rachunek prawdopodobieństwa MAT1332 Wydział Matematyki, Matematyka Stosowana Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów. Warunkowa
Rachunek prawdopodobieństwa MAT1332 Wydział Matematyki, Matematyka Stosowana Wykładowca: dr hab. Agnieszka Jurlewicz Wykład 12: Warunkowa wartość oczekiwana. Rozkłady warunkowe. Mieszanina rozkładów. Warunkowa
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 5.0.00 r. Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej µ wariancji oraz momencie centralnym µ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X
Matematyka ubezpieczeń majątkowych 5.0.00 r. Zadanie. Dla dowolnej zmiennej losowej X o wartości oczekiwanej µ wariancji oraz momencie centralnym µ k rzędu k zachodzą nierówności (typu Czebyszewa): ( X
Funkcje rzeczywiste jednej. Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski
 Funkcje rzeczywiste jednej zmiennej rzeczywistej Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski Definicje Funkcją (odwzorowaniem) f, odwzorowującą zbiór D w zbiór P nazywamy
Funkcje rzeczywiste jednej zmiennej rzeczywistej Matematyka Studium doktoranckie KAE SGH Semestr letni 2008/2009 R. Łochowski Definicje Funkcją (odwzorowaniem) f, odwzorowującą zbiór D w zbiór P nazywamy
Zadania z Analizy Funkcjonalnej I Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?
 Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
Zadania z Analizy Funkcjonalnej I - 1 1. Które z poniższych przestrzeni metrycznych są przestrzeniami unormowanymi?. a) X = R, x = arctg x ; b) X = R n, d(x, y) = x 1 y 1 + x 2 y 2 + max i 3 x i y i ;
XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r.
 Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Komisja Egzaminacyjna dla Aktuariuszy XLIV Egzamin dla Aktuariuszy z 3 grudnia 2007 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa,
Matematyka II. Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 2018/2019 wykład 13 (27 maja)
 Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
Matematyka II Bezpieczeństwo jądrowe i ochrona radiologiczna Semestr letni 208/209 wykład 3 (27 maja) Całki niewłaściwe przedział nieograniczony Rozpatrujemy funkcje ciągłe określone na zbiorach < a, ),
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3.
 RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
RACHUNEK PRAWDOPODOBIEŃSTWA WYKŁAD 3. ZMIENNA LOSOWA JEDNOWYMIAROWA. Zmienną losową X nazywamy funkcję (praktycznie każdą) przyporządkowującą zdarzeniom elementarnym liczby rzeczywiste. X : Ω R (dokładniej:
Krzysztof Kępczyński Zagadnienie paryskiej ruiny w gaussowskim modelu ryzyka
 Uniwersytet Wrocław Wydział Matematyki i Informatyki Instytut matematyczny specjalność: zastosowania rachunku prawdopodobieństwa i statystyki Krzysztof Kępczyński Zagadnienie paryskiej ruiny w gaussowskim
Uniwersytet Wrocław Wydział Matematyki i Informatyki Instytut matematyczny specjalność: zastosowania rachunku prawdopodobieństwa i statystyki Krzysztof Kępczyński Zagadnienie paryskiej ruiny w gaussowskim
Funkcja tworząca Funkcja charakterystyczna. Definicja i własności Funkcja tworząca momenty
 momenty Oprócz omówionych już do tej pory charakterystyk rozkładów bardzo wygodnym i skutecznym narzędziem badanie zmiennej losowej są tzw. transformaty jej rozkładu: funkcje tworzące i funkcje charakterystyczne.
momenty Oprócz omówionych już do tej pory charakterystyk rozkładów bardzo wygodnym i skutecznym narzędziem badanie zmiennej losowej są tzw. transformaty jej rozkładu: funkcje tworzące i funkcje charakterystyczne.
LX Egzamin dla Aktuariuszy z 28 maja 2012 r.
 Komisja Egzaminacyjna dla Aktuariuszy LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa, 28
Komisja Egzaminacyjna dla Aktuariuszy LX Egzamin dla Aktuariuszy z 28 maja 2012 r. Część II Matematyka ubezpieczeń życiowych Imię i nazwisko osoby egzaminowanej:... Czas egzaminu: 100 minut Warszawa, 28
Jak wyznaczyć premię za ryzyko? kilka słów o modelu Arrowa - Pratta
 Jak wyznaczyć premię za ryzyko? kilka słów o modelu Arrowa - Pratta Instytut Matematyki Politechniki Łódzkiej Poznań, 13.05.2017 r. Pojęcia wstępne u - funkcja użyteczności u : R R, u - ciągła, ściśle
Jak wyznaczyć premię za ryzyko? kilka słów o modelu Arrowa - Pratta Instytut Matematyki Politechniki Łódzkiej Poznań, 13.05.2017 r. Pojęcia wstępne u - funkcja użyteczności u : R R, u - ciągła, ściśle
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE. Marta Zelmańska
 RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE Marta Zelmańska Toruń 009 1 Rozdział 1 Wstęp Definicja 1. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie: F (t, x, x, x,..., x (n) ) = 0 (1.1) Rozwiązaniem równania
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Centralne twierdzenie graniczne
 Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 4 Ważne uzupełnienie Dwuwymiarowy rozkład normalny N (µ X, µ Y, σ X, σ Y, ρ): f XY (x, y) = 1 2πσ X σ Y 1 ρ 2 { [ (x ) 1
Instytut Sterowania i Systemów Informatycznych Universytet Zielonogórski Wykład 4 Ważne uzupełnienie Dwuwymiarowy rozkład normalny N (µ X, µ Y, σ X, σ Y, ρ): f XY (x, y) = 1 2πσ X σ Y 1 ρ 2 { [ (x ) 1
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Notatki z Analizy Matematycznej 3. Jacek M. Jędrzejewski
 Notatki z Analizy Matematycznej 3 Jacek M. Jędrzejewski ROZDZIAŁ 6 Różniczkowanie funkcji rzeczywistej 1. Pocodna funkcji W tym rozdziale rozważać będziemy funkcje rzeczywiste określone w pewnym przedziale
Notatki z Analizy Matematycznej 3 Jacek M. Jędrzejewski ROZDZIAŁ 6 Różniczkowanie funkcji rzeczywistej 1. Pocodna funkcji W tym rozdziale rozważać będziemy funkcje rzeczywiste określone w pewnym przedziale
ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA
 ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA DYNAMICZNYCH LOKAT KAPITAŁOWYCH Krzysztof Gąsior Uniwersytet Rzeszowski Streszczenie Celem referatu jest zaprezentowanie praktycznego zastosowania
ZASTOSOWANIE ZASADY MAKSIMUM PONTRIAGINA DO ZAGADNIENIA DYNAMICZNYCH LOKAT KAPITAŁOWYCH Krzysztof Gąsior Uniwersytet Rzeszowski Streszczenie Celem referatu jest zaprezentowanie praktycznego zastosowania
W2 Podstawy rachunku prawdopodobieństwa (przypomnienie)
 W2 Podstawy rachunku prawdopodobieństwa (przypomnienie) Henryk Maciejewski Jacek Jarnicki Marek Woda www.zsk.iiar.pwr.edu.pl Rachunek prawdopodobieństwa - przypomnienie 1. Zdarzenia 2. Prawdopodobieństwo
W2 Podstawy rachunku prawdopodobieństwa (przypomnienie) Henryk Maciejewski Jacek Jarnicki Marek Woda www.zsk.iiar.pwr.edu.pl Rachunek prawdopodobieństwa - przypomnienie 1. Zdarzenia 2. Prawdopodobieństwo
Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa
 Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
O pewnych klasach funkcji prawie okresowych (niekoniecznie ograniczonych)
 (niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
(niekoniecznie ograniczonych) Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza, Poznań Będlewo, 25-30 maja 2015 Funkcje prawie okresowe w sensie Bohra Definicja Zbiór E R nazywamy względnie
Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE. Joanna Sawicka
 Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE Joanna Sawicka Plan prezentacji Model Poissona-Gamma ze składnikiem regresyjnym Konstrukcja optymalnego systemu Bonus- Malus Estymacja
Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE Joanna Sawicka Plan prezentacji Model Poissona-Gamma ze składnikiem regresyjnym Konstrukcja optymalnego systemu Bonus- Malus Estymacja
Pochodna funkcji. Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji.
 Pochodna funkcji Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji. Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika
Pochodna funkcji Pochodna funkcji w punkcie. Różniczka funkcji i obliczenia przybliżone. Zastosowania pochodnych. Badanie funkcji. Małgorzata Wyrwas Katedra Matematyki Wydział Informatyki Politechnika
1 Równania różniczkowe zwyczajne
 Równania różniczkowe zwyczajne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki Politechnika Białostocka Równania różniczkowe Równaniem
Równania różniczkowe zwyczajne wykład z MATEMATYKI Budownictwo studia niestacjonarne sem. II, rok ak. 2008/2009 Katedra Matematyki Wydział Informatyki Politechnika Białostocka Równania różniczkowe Równaniem
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza
 1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza x µ x = 06e. dożyje wieku największej śmiertelności (tzn. takiego wieku, w którym
1. Oblicz prawdopodobieństwo zdarzenia, że noworodek wybrany z populacji, w której śmiertelnością rządzi prawo Gompertza x µ x = 06e. dożyje wieku największej śmiertelności (tzn. takiego wieku, w którym
Równanie przewodnictwa cieplnego (I)
 Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Wykład 4 Równanie przewodnictwa cieplnego (I) 4.1 Zagadnienie Cauchy ego dla pręta nieograniczonego Rozkład temperatury w jednowymiarowym nieograniczonym pręcie opisuje funkcja u = u(x, t), spełniająca
Zagadnienia stacjonarne
 Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
Zagadnienia stacjonarne Karol Hajduk 19 grudnia 2012 Nierówność wariacyjna (u (t), v u(t)) + a(u, v u) + Ψ(v) Ψ(u) (f, v u), v V. Zagadnienie stacjonarne ma postać (u (t) = 0): a(u, v u) + Ψ(v) Ψ(u) (f,
Przestrzeń probabilistyczna
 Przestrzeń probabilistyczna (Ω, Σ, P) Ω pewien niepusty zbiór Σ rodzina podzbiorów tego zbioru P funkcja określona na Σ, zwana prawdopodobieństwem. Przestrzeń probabilistyczna (Ω, Σ, P) Ω pewien niepusty
Przestrzeń probabilistyczna (Ω, Σ, P) Ω pewien niepusty zbiór Σ rodzina podzbiorów tego zbioru P funkcja określona na Σ, zwana prawdopodobieństwem. Przestrzeń probabilistyczna (Ω, Σ, P) Ω pewien niepusty
9 Funkcje Użyteczności
 9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
9 Funkcje Użyteczności Niech u(x) oznacza użyteczność wynikającą z posiadania x jednostek pewnego dobra. Z założenia, 0 jest punktem referencyjnym, czyli u(0) = 0. Należy to zinterpretować jako użyteczność
ELEKTROTECHNIKA Semestr 2 Rok akad / ZADANIA Z MATEMATYKI Zestaw Oblicz pochodne cząstkowe rzędu drugiego funkcji:
 ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
ZADANIA Z MATEMATYKI Zestaw. Oblicz pochodne cząstkowe funkcji: a) f(x, y) = x sin y x b) f(x, y) = e y +x 2 c) f(x, y, z) = z cos x+y z 2. Oblicz pochodne cząstkowe rzędu drugiego funkcji: 3. Wyznacz
21 maja, Mocna własność Markowa procesu Wienera. Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126
 Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
Mocna własność Markowa procesu Wienera Procesy Stochastyczne, wykład 13, T. Byczkowski, Procesy Stochastyczne, PPT, Matematyka MAP1126 21 maja, 2012 Mocna własność Markowa W = (W 1,..., W d ) oznaczać
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
