Department of Hydraulic Engineering and Environmental Recultivation WAU. Department of Hydraulics and Hydrology Technical University of Gdańsk
|
|
|
- Nina Wolska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Janusz KUBRAK 1, Michał SZYDŁOWSKI 2 1 Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department o Hydraulic Engineering and Environmental Recultivation WAU 2 Katedra Hydrauliki i Hydrologii Politechniki Gdańskiej Department o Hydraulics and Hydrology Technical University o Gdańsk Zastosowanie modelu Singha i Quiroga do prognozowania hydrogramu wypływu wody przez prostokątną wyrwę w zaporze ziemnej Singh and Quiroga model application or prediction o hydrograph or earth dam rectangular reach outlow Wprowadzenie Przelanie się wody nad koroną zapory ziemnej jest częstą przyczyną katastro zapór. Dlatego też w prognozach awarii zapór ziemnych rozważa się skutki przejścia ali powodziowej w dolinie powstałej w następstwie wypływu wody przez wyrwę w zaporze. Przelewanie się wody nad koroną zapoczątkowuje proces tworzenia się wyrwy w zaporze, który trwa do momentu całkowitego opróżnienia ziornika lu do chwili sztucznego lu samoczynnego powstrzymania rozmywania wyrwy. Proces tworzenia się wyrwy w zaporze jest ardzo złożony i do dziś nie doczekał się pełnego wyjaśnienia. Charakterystykę modeli tworzenia się wyrwy w zaporze ziemnej znaleźć można w pracach Singha i Scarlatosa (1988, Singha i Quirogi (1988. Cechą wspólną tych modeli jest opis przepływu w ziorniku pełnymi równaniami hydrodynamicznymi (Lou 1981, Ponce i Tsivoglou 1981 lu ich uproszczoną ormą (Benoist 1983, Brown i Rogers 1981, Cristoano 1973, Fread 1977, 1984, Singh i Scarlatos 1988 i stosowanie warunku ruchu krytycznego lu równania przepływu przez przelew o szerokiej koronie jako prawego warunku rzegowego zadawanego w przekroju wyrwy. Początkowy kształt wyrwy przyjmowany ył zwykle jako prostokątny, trójkątny, trapezowy (Cristoano 1973, Fread 1977, Fread 1984, Singh i Scarlatos 1988 lu paraoliczny (Brown i Rogers Niektórzy autorzy w swoich modelach uwzględniali położenie wody dolnej (Fread 1977, Lou 1981, Ponce i Tsivoglou 1981, Singh i Scarlatos 1988 oraz stailność ścian wyrwy w warunkach raku (Fread 1984, 1985 lu występowania wody w gruncie zapory (Singh i Scarlatos Zastosowanie większości modeli wymaga określenia wymiarów ziornika i zapory, jak również izycznych cech gruntu w korpusie
2 zapory, np. średniej średnicy ziaren gruntu, kąta tarcia wewnętrznego i kohezji. Jednym z najtrudniejszych zadań jest zdeiniowanie początkowej wielkości i kształtu wyrwy. Nie iorąc nawet pod uwagę stopnia uproszczenia modelu, istnieje znaczna rozieżność uzyskiwanych z nich wyników wskutek szerokiej zmienności wartości wprowadzonych parametrów. Natężenie ruchu rumowiska w przekroju wyrwy w trakcie jej rozmywania olicza się za pomocą empirycznych zależności (Cristoano 1965, Lou 1981, jak i ogólnie znanych wzorów na natężenie ruchu rumowiska, takich jak Schoklitscha (Brown i Rogers 1977, 1981, Meyera Petera i Muellera (Fread 1984, Ponce i Tsivoglou 1981, Smarta (Fread 1985 lu Einsteina i Browna (Scarlatos i Singh 1986, Singh i Scarlatos Doświadczenia na modelach izycznych z rozmywalną wyrwą w zaporze (Singh i Scarlatos 1985, Quiroga i Singh 1987 wykazały, że stosowanie ormuł na intensywność ruchu rumowiska wleczonego, takich jak Browna, Einsteina i Bagnolda jest rozszerzeniem ich ważności poza warunki przyjmowane przy ich wyprowadzeniu. Ekstrapolacja taka powinna yć potwierdzona doświadczalnie, lecz z raku odpowiednich danych zwykle się jej nie przeprowadza, dlatego wiarygodność inormacji uzyskiwana z wszystkich tak udowanych modeli udzi uzasadnione wątpliwości. Celowym yło zdeiniowanie prędkości rozmywania zapory w unkcji ogólnych parametrów (wysokości zapory, pojemności i głęokości ziornika, charakterystyk materiału, co pozwoliłoy uprościć matematyczny opis procesu rozmywania zapory i podać jego analityczne rozwiązania. Singh i Quiroga (1988 podali ezwymiarowe rozwiązanie do oliczania czasu tworzenia się wyrw prostokątnych i trójkątnych oraz wznoszącej się części hydrogramu wypływu przez wyrwę. W artykule wyprowadzono zależności do oliczania czasu rozmywania prostokątnej wyrwy w zaporze dla dwu różnych wartości parametru n, charakteryzującego szykość tworzenia się wyrwy. Oliczony czas tworzenia się wyrwy i zmian jej krawędzi w czasie, wykorzystano do przykładowych oliczeń hydrogramu wypływu przez wyrwę w zaporze. Rozwiązanie Singha i Quiroga (1988 Model rozmywania wyrwy w zaporze ziemnej oparto na założeniu, że wyrwa jest prostokątna i dopływ wody do ziornika jest równy odpływowi z niego przez urządzenia upustowe (rys.1. W oszarze ziornika oowiązuje równanie ciągłości: A dh = (1 dt s va w
3 korona zapory krawędź wyrwy w czasie t = Z H H - H h-z krawędź wyrwy po czasie t z krawędź wyrwy po czasie T H RYSUNEK 1. Schemat do oliczania czasu tworzenia się prostokątnej wyrwy w zaporze ziemnej FIGURE 1. Idealized reach section or calculation o reach ormulation time o earth dam A s - powierzchnia ziornika [m 2 ], h rzędna zwierciadła wody w ziorniku [m], A w powierzchnia przekroju strumienia w wyrwie [m 2 ], v średnia prędkość przepływu wody wyrwie [m/s], t czas [s]. Średnią prędkość przepływu wody w wyrwie wyrażono jak prędkość wypływu wody przez niezatopiony otwór: v = C (2 a v (h z C v współczynnik prędkości zależny od kształtu wyrwy, którego wartość Singh i Quiroga przyjmują zmienną w granicach 1,2 1,7 [m 1/2 s], a wykładnik równy,5, z rzędna krawędzi wyrwy [m]. Prędkość oniżania się krawędzi wyrwy w czasie zdeiniowano jako proporcjonalną do średniej prędkości wypływu wody z wyrwy w potędze "n" oraz stałego dla danego gruntu współczynnika proporcjonalności E, nazwanego dalej współczynnikiem erozyjności i uzależnionego od parametrów gruntu, z którego zudowana jest zapora: dz dt n = E v (3 E współczynnik erozyjności, n ezwymiarowy wykładnik, od którego zależą jednostki E.
4 Założenie to jest stosunkowo proste, aczkolwiek poprawne, ponieważ erozja wyrwy jest zależna od naprężeń stycznych i w konsekwencji do średniej prędkości przepływu w wyrwie. Z wyprowadzonych w ten sposó zależności określić można położenie dolnej krawędzi wyrwy w trakcie opróżniania ziornika i całkowity czas tworzenia się wyrwy. W celu określenia jednoznacznego rozwiązania prolemu określono warunki początkowe: h( = H, z( = Z (4 H rzędna zwierciadła wody w ziorniku w chwili awarii [m], Z początkowa rzędna spodu wyrwy [m]. Wprowadzono zależności normalizacyjne określone równaniami (5, (6, (7: h' h H H H = (5 h' ezwymiarowa rzędna zwierciadła wody w ziorniku, H rzędna posadowienia zapory [m]. Dla h = H, wartość ezwymiarowej rzędnej jest równa odpowiednio równa h' = ; z' z H Z H h' = 1, zaś dla h = H jest = (6 z' - ezwymiarowa rzędna spodu wyrwy. Dla z = Z ta ezwymiarowa rzędna przyjmuje wartość z'= 1, a dla z = H wartość z' = ; t t ' = (7 T t' ezwymiarowa wielkość reprezentująca czas, T całkowity czas tworzenia się wyrwy liczony od chwili zaistnienia wypływu przez wyrwę do osiągnięcia rzędnej podłoża zapory przez krawędź wyrwy [s]. Dla t =, wartość t' =, zaś dla t = T, ezwymiarowa wartość t' = 1. Wartości rzędnych H, Z i H stanowią znane dane wysokościowe zapory. Jak pokazano poniżej możliwe jest wyprowadzenie zależności dla T na podstawie zdeiniowanych ilorazów ezwymiarowych. Najpierw podano ogólną metodę otrzymania ezwymiarowego analitycznego rozwiązania procesu erozji wyrwy w zaporze ziemnej. Następnie podano szczegółowe rozwiązania. W czasie analiz przyjęto, że A s w równaniu (1 pozostaje stałe i wykładnik a =,5. Założenie to oznacza niezmienność pola przekroju ziornika wraz z głęokością i oliczanie średniej prędkości przepływu w wyrwie jak dla wypływu przez mały niezatopiony otwór. Pole przekroju strumienia w prostokątnej wyrwie olicza się z zależności:
5 A w = (h z (8 gdzie szerokość wyrwy [m]. Wprowadzając równania (8 i (2 do równania (1 otrzymano: dh dt C A v 1,5 = (h z (9 s Podstawiając v z równania (2 do równania (3 otrzymano: dz dt = E (1 n,5n Cv (h z W celu uogólnienia rozwiązania, wyprowadzono wyrażenie, które wiąże h od z, a następnie wyrażenie uzależniające h od z i t. Dzieląc równanie (9 przez (1 otrzymuje się: dh dt dz dt skąd dh dz = E Cv As n Cv (h z 1,5 (h z,5n (3 n / 2 = (h z (11 n 1 AsE Cv Wyznaczając h z równania (5 oraz z z równania (6 otrzymano: h = h' (H-H +H z = z' (Z-H +H i podstawiając oie zależności do równania (11, tzn. dh = (H -H d h ' dz = (Z -H d z ' uzyskano: dh dz (H H dh' (3 n / 2 = (h z [(H H h' (Z H z ] (12 (Z (3 n / 2 = = ' n 1 n 1 H dz' AsE Cv AsE Cv Podstawiając dalej: H Z 2 3 n ( (H H (13 n 1 A E C = s v 2 3 n ( (Z H (14 n 1 A E C = s v równanie (12 przekształcono do postaci: dh' dz' Z H (3 n / 2 = (Hh' Zz' (15 Najpierw zróżniczkowano wyrażenie w nawiasie (H h '-Zz, ' tzn.
6 d dh' (Hh' Zz' = H Z dz' dz' i z wyrażenia tego wyznaczono dh ', tzn. dz' dh' 1 d(hh' Zz' = + Z dz' H Z (16 po czym porównano wyznaczoną w ten sposó wartość poprzedniego równania, tzn. Z 2 H 1 d(hh' Zz' H dz' ( ( 3 n / Hh' Zz' = + Z Po przekształceniach otrzymano: d( Hh' Zz' ( ( n Hh' Zz' / 2 = Z dz' 3 1 skąd po scałkowaniu uzyskano: d( Hh' Zz' ( ( n Hh' Zz' / 2 dh' dz' z wartością wyznaczoną z = Zz' + K ( Bezwymiarowe równanie (17 wiąże rzędną zwierciadła wody z rzędną krawędzi prostokątnej wyrwy. Równanie (17 jest zależne od dwóch parametrów: H i Z. Oa parametry są ezwymiarowe i oliczane na podstawie znanych wielkości początkowych. Podstawiając h wyznaczone z równania (5 oraz t z równania (7 do (9 otrzymano: dh' T = dt' H 1,5 ( Hh' Zz' 2 n 3 n n T E n 1 CvT AsE C = (19 v gdzie T jest ezwymiarowym parametrem. Dzieląc równanie (18 przez (15 otrzymano: dz' T,5n = ( Hh' Zz' (2 dt' Z Odejmując równanie (2 od (18 otrzymano: d( Hh' Zz',5 ( Hh' Zz' ( Hh' Zz' = Tt' + K (21 1,5n (18 Równanie (21 wiąże położenie zwierciadła wody z ziorniku H z rzędną krawędzi prostokątnej wyrwy Z. Ponieważ wartość T określana z równania (19 jest uzależnione od T, więc olicza się T z równania (21.
7 Badania własne Wykorzystując ogólne zależności podane przez Singha i Quiroga (1988 wyprowadzono wzory do oliczania czasu tworzenia się wyrwy T dla dwu wartości wykładnika, tzn. n=2 i n=4 (taela 1. Natężenie wypływu przez prostokątna wyrwę olicza się ze wzoru: Q = C v [ h '' (H-H ] 1.5 (36 Singh i Quiroga (1988 do oliczeń hydrogramu wypływu przez wyrwę w zaporze wykorzystali przykładowe dane dla zapory Teton w stanie Idaho (USA, która uległa katastroie 5 czerwca 1976 roku. W oliczeniach przyjęto: H = m, Z = m, H =1538 m, A s = m 2, C v =1.5 m.5 /s, szerokość wyrwy =65 m. Oliczenia wykonano dla wartości wykładnika n=2, E =.45 oraz n=4 oraz E =.45. Wartości parametru erozyjności E dorano tak, ay uzyskać zgodność oliczonych maksymalnych natężeń wypływu przez wyrwę z oserwowanymi. Oliczone czasy rozmywania prostokątnej wyrwy i maksymalne natężenia przepływu yły równe:
8 Taela 1. Zestawienie równań do oliczania czasu tworzenia się wyrwy w zaporze ziemnej Tale 1. Equations or calculation o reach ormulation time o the earth dam Dla n=2 równanie (17 ma postać: d ( Hh' Zz' = Zz' ( + K (22,5 Hh' Zz' 1 Skąd po scałkowaniu trzymano: 2 Hh' Zz' + ln Hh' Zz' 1 = Zz ' + (23 [ ( ] K Dla n=4 równanie (17 ma postać: d ( Hh' Zz' = ( + Zz' K (29,5 Hh' Zz' 1 Skąd po scałkowaniu otrzymano: Hh ' Zz' 2 Hh Zz' 2ln 1 Hh ' Zz' = Zz' + (3 ( ( K Z warunków początkowych dla z ' = 1, h ' = 1 wyznaczono stałą K: 2 H Z + ln H Z 1 Z = [ ( ] K a następnie przekształcono równanie (22 do postaci: 2 Hh' Zz' 1 z' = 1 + Hh' Zz' H Z + ln (24 Z H Z 1 Ponieważ h' jest zdeiniowane w unkcji z', więc należy uzależnić h ' - z ' od t '. W tym celu korzysta się z równania (21: d ( Hh ' Zz' = Tt' ( ( + 1, 5 K (25 Hh' Zz' Hh' Zz' Po oliczeniu całki otrzymano: Hh ' Zz' 2 ln = Tt' + K (26 Hh' Zz' 1 Czas T olicza się z równania (26 przy t ' = 1 i z ' = i przyjęciu h ' = h ", gdzie h " wyznacza się z równania (24: T 1 1/ H Z = 2ln (27 '' 1 1/ Hh Z warunków początkowych dla z ' = 1, h ' = 1 wyznaczono stałą K: K = H + Z 2 H Z 2ln 1 H Z ( Z a następnie przekształcono równanie (29 do postaci: H Hh' + 2 Hh' z Hh' Zz' + 2ln 1 H Z 2 ( ( ln ( 1 Hh' Zz' = Ponieważ h ' jest zdeiniowane w unkcji z', więc należy uzależnić h-z ' ' od t '. W tym celu korzysta się z równania (21: d ( Hh' Zz ' 1,5 ( Hh' Zz' ( Hh' Zz' = Tt' + 2 K (31 (32 Po oliczeniu całki otrzymano: 2 1 2ln 1 = Tt' + K (33 Hh' Zz' Hh' Zz' Czas T olicza się z równania (33 przy t ' = 1 i z ' = i przyjęciu h ' = h ", gdzie h " wyznacza się z równania (31: T = + 2ln 1 2ln 1 Hh" Hh" H Z H Z (34
9 n=2 n=4 T =4766 s T =581 s Q=59858 m 3 /s Q=65893 m 3 /s. Na podstawie oserwacji katastroy oszacowano maksymalne natężenie wypływu przez wyrwę równe Q=65 m 3 /s (Fread Z porównania widać, że oliczone wartości maksymalnego natężenia wypływu przez wyrwę są ardzo zliżone do oszacowanej na podstawie oserwacji. RYSUNEK 2. Prognozowany i oszacowany hydrogram wypływu przez wyrwę w zaporze Teton FIGURE 2. Predicted and oserved reach outlow hydrographs or the Teton Dam
10 Q [m 3 /s] t [s] rozw iązanie rów nań nieustalonego przepływ u w ziorniku rozwiązanie Singa i Quiroga dla n=2 Na rys.2 pokazano prognozowane części hydrogramu wypływu przez wyrwę w zaporze Teton oliczone podanymi w taeli 1 wzorami oraz dodatkowo z modelu opracowanego przez Freada (1985. Jak widać, wartość wykładnika n w omówionym rozwiązaniu wpływa na przeieg zmian położenia spodu wyrwy w czasie (rys.3 Rozwiązanie Singha i Quiroga pozwala wyznaczyć jedynie wznoszącą się gałąź hydrogramu podczas opróżniania ziornika przez wyrwę w zaporze w założeniu stałości powierzchni ziornika A s. Określenie całego hydrogramu wypływu przez wyrwę możliwe jest przy wykorzystaniu oliczonej zmienności rzędnej krawędzi wyrwy w czasie z zależności (24, (31 i rozwiązaniu równań nieustalonego przepływu w ziorniku (rys.3. Lewy warunek rzegowy rozwiązania równań ruchu stanowi hydrogram dopływu do ziornika, zaś prawy warunek - równanie przepływu przez przelew o szerokiej koronie. Nie wykonano takich oliczeń dla zapory Teton, gdyż nie dysponowano przekrojami poprzecznymi tego ziornika. W związku z tym wykonano je dla ziornika, dla którego posiadano niezędne dane. Ziornik opisano 8 przekrojami poprzecznymi. W oszarze ziornika rozwiązywano jednowymiarowe równania nieustalonego przepływu Kurak (1988. Otrzymany hydrogram wypływu ze ziornika dla wyrwy o szerokość =75.5 m pokazano na rys. 4. W oliczeniach przyjęto: H =16.5 m, Z =158.5 m, H =152.5 m, A s =5 m 2, C v =1.5 m.5 /s. Oliczenia wykonano dla wartości wykładnika n=2 i E =.45.
11 Q [m 3 /s] t [s] rozw iązanie rów nań nieustalonego przepływ u w ziorniku rozwiązanie Singa i Quiroga dla n=2 RYSUNEK 4. Hydrogram wypływu przez wyrwę w zaporze oliczony na podstawie rozwiązania nieustalonego przepływu w ziorniku oraz oniżania się krawędzi wyrwy z rozwiązania Singha i Quiroga FIGURE 4. The predicted hydrograph or dam reach outlow otained rom the usteady low solution in reservoir and reach ottom elevation calculated ater Singh and Quiroga method Podsumowanie Stosunkowo proste rozwiązanie procesu rozmywania wyrwy w zaporze ziemnej powstałej wskutek przelania się wody nad koroną podane przez Singha i Quiroga pozwala oliczać czas rozmywania prostokątnej wyrwy, zmianę położenia krawędzi wyrwy w czasie i natężenie wypływu przez wyrwę. Porównanie wyników oliczeń natężenia wypływu z wartościami szacowanymi na podstawie oserwacji i uzyskanymi ze złożonego modelu zudowanego przez Freada (1987 potwierdza wysoką zieżność oliczanych wartości. Wykorzystano uzyskane z oliczeń wyprowadzonymi wzorami inormacje o zmienności położenia wyrwy w czasie do oliczania wypływ przez wyrwę w założeniu nieustalonego przepływu wody w ziorniku. Uzyskany z oliczeń hydrogram opróżniania ziornika wskutek powstania wyrwy może yć z powodzeniem stosowany do analiz hydraulicznych warunków przejścia ali powodziowej w dolinie poniżej zapory.
12 Adnotacje Artykuł powstał w ramach projektu adawczego 6P6S inansowanego przez KBN. Literatura BENOIST G. 1983: Calcul de l'erosion d'une digue par surverse. Departement laoratoire national d'hydraulique, Chatou. BROWN R.J., ROGERS D.C. 1977: A simulation o the hydraulics events during and ollowing the Teton Dam ailure. Proc. Dam-Break Flood Routing Model Workshop, Md., BROWN R J., ROGERS D.C. 1981: User manual or program Brdam. Engineering and Research Center, Bureau o Reclamation, Denver. CRISTOFANO E.A. 1973: Method o computing erosion rate or ailure o dams. Unpulished preliminary report to United States Bureau o Reclamation, Denver, Kolorado. FRAED D.L. 1984: DAMBRK, The NWS dam-reak lood orecasting model. National Weather Service, Maryland. FREAD D.L. 1985: BREACH, An erosion model or earthen dam ailures. NWS Report, Oceanic and Atmospheric Administration, Silver Spring. FREAD D.L. 1977: The development and testing o a dam-reak lood orecasting model. Proc. o Dam-Break Flood Routing Model Workshop, US Department o Commerce, National Technical Inormation Service. KUBRAK J. 1989: Modele numeryczne rozprzestrzeniania się ali wypływającej przez wyrwę w zaporze. Rozprawy Naukowe i Monograie SGGW, Warszawa. LOU W.C. 1981: Mathematical modeling o earth dam reaches. Thesis presented to Colorado State Univ., at Fort Collins, in partial ulillment o the requirements or the degree o Doctor o Philosophy. PONCE V.M., TSIVOGLOU A.J. 1981: Modeling gradual dam reaches. J.Hydraulic Division, Vol.17. no.7. SINGH V.P., QUIROGA A.C. 1988: Dimensional analytical solutions or dam-reak erosion. J.Hydraulic Research, Vol.26, no.2. SINGH V.P., SCARLATOS P.D. 1988: Analysis o gradual earth-dam ailure. J.Hydraulic Engineering, Vol.114, no.1. Summary The earth dams reach erosion is analyzed using dimensionless analytical solutions or rectangular reach given y Singh and Quiroga (1988. Data or the historical ailure o Teton Dam are used to test these solutions. The calculated changes o reach ottom elevation with time are used or prediction reach outlow hydrograph. The one-dimensional unsteady low model in reservoir was applied or prediction reach outlow hydrograph. Author's address: Janusz Kurak Katedra Inżynierii Wodnej i Rekultywacji Środowiska Wydział Inżynierii i Kształtowania Środowiska SGGW
13 2-787 Warszawa, Nowoursynowska 166 Michał Szydłowski Katedra Hydrauliki i Hydrologii Wydział Budownictwa Wodnego i Inżynierii Środowiska Politechniki Gdańskiej 8-95 Gdańsk, ul. Narutowicza 11/12
Department of Hydraulic Engineering and Environmental Recultivation WAU. Department of Hydraulics and Hydrology Technical University of Gdańsk
 Janusz KUBRAK 1, Michał SZYDŁOWSKI 2 1 Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WAU 2 Katedra Hydrauliki i Hydrologii
Janusz KUBRAK 1, Michał SZYDŁOWSKI 2 1 Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WAU 2 Katedra Hydrauliki i Hydrologii
Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS
 Zbigniew POPEK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS Weryfikacja wybranych wzorów empirycznych do określania
Zbigniew POPEK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS Weryfikacja wybranych wzorów empirycznych do określania
Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości
 LABORATORIUM MECHANIKI PŁYNÓW Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA, WYDZ. BMiP, PŁOCK
LABORATORIUM MECHANIKI PŁYNÓW Nieustalony wypływ cieczy ze zbiornika przewodami o różnej średnicy i długości dr inż. Jerzy Wiejacha ZAKŁAD APARATURY PRZEMYSŁOWEJ POLITECHNIKA WARSZAWSKA, WYDZ. BMiP, PŁOCK
Wyznaczenie stref zagrożenia powodziowego na terenach otaczających zbiornik Kolbudy II. ENERGA Elektrownie Straszyn sp. z o.o.
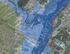 Wyznaczenie stref zagrożenia powodziowego na terenach otaczających zbiornik Kolbudy II ENERGA Elektrownie Straszyn sp. z o.o. Awarie zapór i wałów Górowo Iławeckie Gdańsk, Kanał Raduni 2000 Lipiec 2001
Wyznaczenie stref zagrożenia powodziowego na terenach otaczających zbiornik Kolbudy II ENERGA Elektrownie Straszyn sp. z o.o. Awarie zapór i wałów Górowo Iławeckie Gdańsk, Kanał Raduni 2000 Lipiec 2001
MECHANIKA PŁYNÓW LABORATORIUM
 MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 6 Wyznaczanie współczynnika wydatku przelewu Celem ćwiczenia jest wyznaczenie wartości współczynnika wydatku dla różnyc rodzajów przelewów oraz sporządzenie ic
MECHANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 6 Wyznaczanie współczynnika wydatku przelewu Celem ćwiczenia jest wyznaczenie wartości współczynnika wydatku dla różnyc rodzajów przelewów oraz sporządzenie ic
Proces kształtowania koryt rzecznych
 Proces kształtowania koryt rzecznych Proces kształtowania i przeorażania koryt rzecznych zależy od wzajemnych relacji między: reżimem przepływu wody i transportem rumowiska Proces ten opisał Lane za pomocą
Proces kształtowania koryt rzecznych Proces kształtowania i przeorażania koryt rzecznych zależy od wzajemnych relacji między: reżimem przepływu wody i transportem rumowiska Proces ten opisał Lane za pomocą
Przepływy laminarne - zadania
 Zadanie 1 Warstwa cieczy o wysokości = 3mm i lepkości v = 1,5 10 m /s płynie równomiernie pod działaniem siły ciężkości po płaszczyźnie nachylonej do poziomu pod kątem α = 15. Wyznaczyć: a) Rozkład prędkości.
Zadanie 1 Warstwa cieczy o wysokości = 3mm i lepkości v = 1,5 10 m /s płynie równomiernie pod działaniem siły ciężkości po płaszczyźnie nachylonej do poziomu pod kątem α = 15. Wyznaczyć: a) Rozkład prędkości.
MODELOWANIE BIFURKACJI PRZEPŁYWU W KANALE OTWARTYM Z PRZELEWEM BOCZNYM MODELING OF FLOW BIFURCATION IN THE OPEN CHANNEL WITH SIDE WEIR
 TOMASZ SIUTA MODELOWANIE BIFURKACJI PRZEPŁYWU W KANALE OTWARTYM Z PRZELEWEM BOCZNYM MODELING OF FLOW BIFURCATION IN THE OPEN CHANNEL WITH SIDE WEIR S t r e s z c z e n i e A b s t r a c t W artykule przedstawiono
TOMASZ SIUTA MODELOWANIE BIFURKACJI PRZEPŁYWU W KANALE OTWARTYM Z PRZELEWEM BOCZNYM MODELING OF FLOW BIFURCATION IN THE OPEN CHANNEL WITH SIDE WEIR S t r e s z c z e n i e A b s t r a c t W artykule przedstawiono
Filtracja - zadania. Notatki w Internecie Podstawy mechaniki płynów materiały do ćwiczeń
 Zadanie 1 W urządzeniu do wyznaczania wartości współczynnika filtracji o powierzchni przekroju A = 0,4 m 2 umieszczono próbkę gruntu. Różnica poziomów h wody w piezometrach odległych o L = 1 m wynosi 0,1
Zadanie 1 W urządzeniu do wyznaczania wartości współczynnika filtracji o powierzchni przekroju A = 0,4 m 2 umieszczono próbkę gruntu. Różnica poziomów h wody w piezometrach odległych o L = 1 m wynosi 0,1
Dr inż. Witold Sterpejkowicz-Wersocki Katedra Hydrotechniki PG
 OBLICZENIA FILTRACJI PRZEZ KORPUS I PODŁOŻE ZAPORY ZIEMNEJ Dr inż. Witold Sterpejkowicz-Wersocki Katedra Hydrotechniki PG OBLICZENIA FILTRACYJNE składają się z: 1) jednostkowego wydatku filtracyjnego (q)
OBLICZENIA FILTRACJI PRZEZ KORPUS I PODŁOŻE ZAPORY ZIEMNEJ Dr inż. Witold Sterpejkowicz-Wersocki Katedra Hydrotechniki PG OBLICZENIA FILTRACYJNE składają się z: 1) jednostkowego wydatku filtracyjnego (q)
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Grzegorz Siwek. Studenckie Koło Naukowe Geografów UMCS im. A. Malickiego w Lublinie. Naukowa Sieć Studentów Geoinformatyki
 Grzegorz Siwek Studenckie Koło Naukowe Geografów UMCS im. A. Malickiego w Lublinie Naukowa Sieć Studentów Geoinformatyki Produkt Obrony Cywilnej USA HEC = Hydrologic Engineering Center RAS = River Analysis
Grzegorz Siwek Studenckie Koło Naukowe Geografów UMCS im. A. Malickiego w Lublinie Naukowa Sieć Studentów Geoinformatyki Produkt Obrony Cywilnej USA HEC = Hydrologic Engineering Center RAS = River Analysis
Opracowanie koncepcji ochrony przed powodzią opis ćwiczenia projektowego
 Opracowanie koncepcji ochrony przed powodzią opis ćwiczenia projektowego 1. Położenie analizowanej rzeki Analizowaną rzekę i miejscowość, w pobliżu której należy zlokalizować suchy zbiornik, należy odszukać
Opracowanie koncepcji ochrony przed powodzią opis ćwiczenia projektowego 1. Położenie analizowanej rzeki Analizowaną rzekę i miejscowość, w pobliżu której należy zlokalizować suchy zbiornik, należy odszukać
PRACE NAUKOWO-PRZEGLĄDOWE
 PRACE NAUKOWO-PRZEGLĄDOWE Przegląd Naukowy Inżynieria i Kształtowanie Środowiska nr (47), 00: 43 5 (Prz. Nauk. Inż. Kszt. Środ. (47), 00) Scientific Review Engineering and Environmental Sciences No (47),
PRACE NAUKOWO-PRZEGLĄDOWE Przegląd Naukowy Inżynieria i Kształtowanie Środowiska nr (47), 00: 43 5 (Prz. Nauk. Inż. Kszt. Środ. (47), 00) Scientific Review Engineering and Environmental Sciences No (47),
BADANIE PRZELEWU MIERNICZEGO
 BADANIE PRZELEWU MIERNICZEGO Pytania zaliczające: 1. Pomiar przepływu za pomocą jednego z przelewów mierniczych. 2. Charakterystyka przelewu mierniczego. METODA PRZELEWOWA bezpośrednia metoda pomiaru przepływu;
BADANIE PRZELEWU MIERNICZEGO Pytania zaliczające: 1. Pomiar przepływu za pomocą jednego z przelewów mierniczych. 2. Charakterystyka przelewu mierniczego. METODA PRZELEWOWA bezpośrednia metoda pomiaru przepływu;
Charakterystyka hydrauliczna jazu Jaktorów na rzece Pisia Tuczna Hydraulic characteristics of Jaktorów weir on Pisia Tuczna River
 Sławomir BAJKOWSKI, Piotr SIWICKI, Janusz URBAŃSKI Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Charakterystyka
Sławomir BAJKOWSKI, Piotr SIWICKI, Janusz URBAŃSKI Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Charakterystyka
Przepływ w korytach otwartych. kanał otwarty przepływ ze swobodną powierzchnią
 Przepływ w korytach otwartych kanał otwarty przepływ ze swobodną powierzchnią Przepływ w korytach otwartych Przewody otwarte dzielimy na: Naturalne rzeki strumienie potoki Sztuczne kanały komunikacyjne
Przepływ w korytach otwartych kanał otwarty przepływ ze swobodną powierzchnią Przepływ w korytach otwartych Przewody otwarte dzielimy na: Naturalne rzeki strumienie potoki Sztuczne kanały komunikacyjne
Ćwiczenie laboratoryjne Parcie wody na stopę fundamentu
 Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
Ćwiczenie laboratoryjne Parcie na stopę fundamentu. Cel ćwiczenia i wprowadzenie Celem ćwiczenia jest wyznaczenie parcia na stopę fundamentu. Natężenie przepływu w ośrodku porowatym zależy od współczynnika
ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI
 Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
Budownictwo 18 Mariusz Poński ZASTOSOWANIE RACHUNKU OPERATORÓW MIKUS- IŃSKIEGO W PEWNYCH ZAGADNIENIACH DYNAMIKI KONSTRUKCJI 1. Metody transformacji całkowych Najczęściej spotykaną metodą rozwiązywania
9. Mimośrodowe działanie siły
 9. MIMOŚRODOWE DZIŁIE SIŁY 1 9. 9. Mimośrodowe działanie siły 9.1 Podstawowe wiadomości Mimośrodowe działanie siły polega na jednoczesnym działaniu w przekroju pręta siły normalnej oraz dwóc momentów zginającyc.
9. MIMOŚRODOWE DZIŁIE SIŁY 1 9. 9. Mimośrodowe działanie siły 9.1 Podstawowe wiadomości Mimośrodowe działanie siły polega na jednoczesnym działaniu w przekroju pręta siły normalnej oraz dwóc momentów zginającyc.
1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8
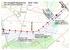 H h = 0,8H Przykładowe obliczenia odwodnienia autor: mgr inż. Marek Motylewicz strona 1 z 5 1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8 1:m1 1:m2 c Przyjęte parametry: rów o przekroju trapezowym
H h = 0,8H Przykładowe obliczenia odwodnienia autor: mgr inż. Marek Motylewicz strona 1 z 5 1. Obliczenia rowu przydrożnego prawostronnego odcinki 6-8 1:m1 1:m2 c Przyjęte parametry: rów o przekroju trapezowym
MODELOWANIE WYPŁYWU WODY PRZEZ HIPOTETYCZNĄ WYRWĘ W ZAPORZE ZBIORNIKA RZYMÓWKA
 INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr IV/1/2015, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 993 1005 Komisja Technicznej Infrastruktury Wsi DOI: http://dx.medra.org/10.14597/infraeco.2015.4.1.079
INFRASTRUKTURA I EKOLOGIA TERENÓW WIEJSKICH INFRASTRUCTURE AND ECOLOGY OF RURAL AREAS Nr IV/1/2015, POLSKA AKADEMIA NAUK, Oddział w Krakowie, s. 993 1005 Komisja Technicznej Infrastruktury Wsi DOI: http://dx.medra.org/10.14597/infraeco.2015.4.1.079
ANALIZA ROZKŁADU CIŚNIEŃ I PRĘDKOŚCI W PRZEWODZIE O ZMIENNYM PRZEKROJU
 Dr inż. Paweł PIETKIEWICZ Dr inż. Wojciech MIĄSKOWSKI Dr inż. Krzysztof NALEPA Piotr LESZCZYŃSKI Uniwersytet Warmińsko-Mazurski w Olsztynie DOI: 10.17814/mechanik.2015.7.283 ANALIZA ROZKŁADU CIŚNIEŃ I
Dr inż. Paweł PIETKIEWICZ Dr inż. Wojciech MIĄSKOWSKI Dr inż. Krzysztof NALEPA Piotr LESZCZYŃSKI Uniwersytet Warmińsko-Mazurski w Olsztynie DOI: 10.17814/mechanik.2015.7.283 ANALIZA ROZKŁADU CIŚNIEŃ I
Zapora ziemna analiza przepływu nieustalonego
 Przewodnik Inżyniera Nr 33 Aktualizacja: 01/2017 Zapora ziemna analiza przepływu nieustalonego Program: MES - przepływ wody Plik powiązany: Demo_manual_33.gmk Wprowadzenie Niniejszy Przewodnik przedstawia
Przewodnik Inżyniera Nr 33 Aktualizacja: 01/2017 Zapora ziemna analiza przepływu nieustalonego Program: MES - przepływ wody Plik powiązany: Demo_manual_33.gmk Wprowadzenie Niniejszy Przewodnik przedstawia
Opracowanie koncepcji budowy suchego zbiornika
 Opracowanie koncepcji budowy suchego zbiornika Temat + opis ćwiczenia i materiały pomocnicze są dostępne na stronie: http://ziw.sggw.pl/dydaktyka/zbigniew Popek 7. Określić współrzędne hydrogramu fali
Opracowanie koncepcji budowy suchego zbiornika Temat + opis ćwiczenia i materiały pomocnicze są dostępne na stronie: http://ziw.sggw.pl/dydaktyka/zbigniew Popek 7. Określić współrzędne hydrogramu fali
prof. dr hab. inż. Tomaszek Henryk Instytut Techniczny Wojsk Lotniczych, ul. Księcia Bolesława 6, Warszawa, tel.
 prof. dr hab. inż. Tomaszek Henryk Instytut Techniczny Wojsk Lotniczych, ul. Księcia Bolesława 6, 01-494 Warszawa, tel. +48 22 685 19 56 dr inż. Jasztal Michał Wojskowa Akademia Techniczna, ul. Kaliskiego
prof. dr hab. inż. Tomaszek Henryk Instytut Techniczny Wojsk Lotniczych, ul. Księcia Bolesława 6, 01-494 Warszawa, tel. +48 22 685 19 56 dr inż. Jasztal Michał Wojskowa Akademia Techniczna, ul. Kaliskiego
PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
Zadania do ćwiczeń z tematyki podstawowej opory cieplne, strumienie, obliczanie oporów wielowarstwowych ścian, etc
 Zadania do ćwiczeń z tematyki podstawowej opory cieplne, strumienie, oliczanie oporów wielowarstwowyc ścian, etc zad (rysunek nie oddaje skali układu cieplnego) papier laca ciepło Oliczyć równoważną przewodność
Zadania do ćwiczeń z tematyki podstawowej opory cieplne, strumienie, oliczanie oporów wielowarstwowyc ścian, etc zad (rysunek nie oddaje skali układu cieplnego) papier laca ciepło Oliczyć równoważną przewodność
Projekt nr 2 Charakterystyki aerodynamiczne płata
 Projekt nr Charakterystyki aerodynamiczne płata W projekcie tym należy wyznaczyć dwie podstawowe symetryczne charakterystyki aerodynamiczne płata nośnego samolotu istotne do oliczeń osiągów samolotu: Cx()
Projekt nr Charakterystyki aerodynamiczne płata W projekcie tym należy wyznaczyć dwie podstawowe symetryczne charakterystyki aerodynamiczne płata nośnego samolotu istotne do oliczeń osiągów samolotu: Cx()
Laboratorium. Hydrostatyczne Układy Napędowe
 Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Pomiary hydrometryczne w zlewni rzek
 Pomiary hydrometryczne w zlewni rzek Zagożdżonka onka i Zwoleńka Hydrometric measurements in Zwoleńka & Zagożdżonka onka catchments Anna Sikorska, Kazimierz Banasik, Anna Nestorowicz, Jacek Gładecki Szkoła
Pomiary hydrometryczne w zlewni rzek Zagożdżonka onka i Zwoleńka Hydrometric measurements in Zwoleńka & Zagożdżonka onka catchments Anna Sikorska, Kazimierz Banasik, Anna Nestorowicz, Jacek Gładecki Szkoła
TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA
 Doświadczenie nr 1 TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA 1. Cel ćwiczenia Instrukcja dla studenta (opracowana przez dr Danutę Piwowarską ) Celem
Doświadczenie nr 1 TEMAT : WYZNACZANIE WYKŁADNIKA POTĘGOWEGO CZASU WYPŁYWU WODY W ZALEŻNOŚCI OD GŁĘBOKOŚCI ZBIORNIKA 1. Cel ćwiczenia Instrukcja dla studenta (opracowana przez dr Danutę Piwowarską ) Celem
Pochodna i różniczka funkcji oraz jej zastosowanie do rachunku błędów pomiarowych
 Pochodna i różniczka unkcji oraz jej zastosowanie do rachunku błędów pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją symbolami:
Pochodna i różniczka unkcji oraz jej zastosowanie do rachunku błędów pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją symbolami:
Ćw. 1. BADANIE PRZEBIEGÓW NAGRZEWANIA SIĘ I STYGNIĘCIA PRZEWODÓW PRZY OBCIĄŻENIU PRZERYWANYM
 Ćw. 1. BADANIE PRZEBIEGÓW NAGRZEWANIA SIĘ I SYGNIĘCIA PRZEWODÓW PRZY OBCIĄŻENIU PRZERYWANYM 1. Wprowadzenie 1.1. Wiadomości podstawowe W eksploatacji urządzeń elektroenergetycznych i ich elementów, a do
Ćw. 1. BADANIE PRZEBIEGÓW NAGRZEWANIA SIĘ I SYGNIĘCIA PRZEWODÓW PRZY OBCIĄŻENIU PRZERYWANYM 1. Wprowadzenie 1.1. Wiadomości podstawowe W eksploatacji urządzeń elektroenergetycznych i ich elementów, a do
WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH
 WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH Pomiar strumienia masy i strumienia objętości metoda objętościowa, (1) q v V metoda masowa. (2) Obiekt badań Pomiar
WYKŁAD 10 METODY POMIARU PRĘDKOŚCI, STRUMIENIA OBJĘTOŚCI I STRUMIENIA MASY W PŁYNACH Pomiar strumienia masy i strumienia objętości metoda objętościowa, (1) q v V metoda masowa. (2) Obiekt badań Pomiar
NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 85 Electrical Engineering 016 Krzysztof KRÓL* NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU W artykule zaprezentowano
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 85 Electrical Engineering 016 Krzysztof KRÓL* NATĘŻENIE POLA ELEKTRYCZNEGO PRZEWODU LINII NAPOWIETRZNEJ Z UWZGLĘDNIENIEM ZWISU W artykule zaprezentowano
Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW
 Zbigniew POPEK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Zmienność natężenia ruchu rumowiska wleczonego w czasie
Zbigniew POPEK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Zmienność natężenia ruchu rumowiska wleczonego w czasie
Pochodna i różniczka funkcji oraz jej zastosowanie do obliczania niepewności pomiarowych
 Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Ć W I C Z E N I E N R M-2
 INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
INSYU FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I ECHNOLOGII MAERIAŁÓW POLIECHNIKA CZĘSOCHOWSKA PRACOWNIA MECHANIKI Ć W I C Z E N I E N R M- ZALEŻNOŚĆ OKRESU DRGAŃ WAHADŁA OD AMPLIUDY Ćwiczenie M-: Zależność
Termodynamika. Część 12. Procesy transportu. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
Termodynamika Część 12 Procesy transportu Janusz Brzychczyk, Instytut Fizyki UJ Zjawiska transportu Zjawiska transportu są typowymi procesami nieodwracalnymi zachodzącymi w przyrodzie. Zjawiska te polegają
MECHANIKA PŁYNÓW LABORATORIUM
 MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
MECANIKA PŁYNÓW LABORATORIUM Ćwiczenie nr 4 Współpraca pompy z układem przewodów. Celem ćwiczenia jest sporządzenie charakterystyki pojedynczej pompy wirowej współpracującej z układem przewodów, przy różnych
OCENA SKUTKÓW AWARII ZAPORY ZIEMNEJ ZBIORNIKA RETENCYJNEGO W PRZECZYCACH
 Acta Sci. Pol., Formatio Circumiectus 9 (3) 2010, 35 44 OCENA SKUTKÓW AWARII ZAPORY ZIEMNEJ ZBIORNIKA RETENCYJNEGO W PRZECZYCACH Jerzy Machajski * Politechnika Wrocławska Streszczenie. W pracy przedstawiono
Acta Sci. Pol., Formatio Circumiectus 9 (3) 2010, 35 44 OCENA SKUTKÓW AWARII ZAPORY ZIEMNEJ ZBIORNIKA RETENCYJNEGO W PRZECZYCACH Jerzy Machajski * Politechnika Wrocławska Streszczenie. W pracy przedstawiono
LABORATORIUM ELEKTROAKUSTYKI. ĆWICZENIE NR 1 Drgania układów mechanicznych
 LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
LABORATORIUM ELEKTROAKUSTYKI ĆWICZENIE NR Drgania układów mechanicznych Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z właściwościami układów drgających oraz metodami pomiaru i analizy drgań. W ramach
DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA
 71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA CIEPŁA
 39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
39/19 ARCHIWUM ODLEWNICTWA Rok 006, Rocznik 6, Nr 19 Archives of Foundry Year 006, Volume 6, Book 19 PAN - Katowice PL ISSN 164-5308 WYKORZYSTANIE SYSTEMU Mathematica DO ROZWIĄZYWANIA ZAGADNIEŃ PRZEWODZENIA
Badanie transformatora
 Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Skrypt 23. Geometria analityczna. Opracowanie L7
 Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 2 Geometria analityczna 1.
Projekt Innowacyjny program nauczania matematyki dla liceów ogólnokształcących współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Skrypt 2 Geometria analityczna 1.
Wyniki badań transportu rumowiska rzecznego w korycie rzeki Zagożdżonki Results of sediment transport in the Zagożdżonka riverbed
 Zbigniew POPEK, Kazimierz BANASIK, Leszek HEJDUK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Wyniki
Zbigniew POPEK, Kazimierz BANASIK, Leszek HEJDUK Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Recultivation WULS SGGW Wyniki
Opracowanie koncepcji budowy suchego zbiornika
 Opracowanie koncepcji budowy suchego zbiornika Temat + opis ćwiczenia i materiały pomocnicze są dostępne na stronie: http://ziw.sggw.pl/dydaktyka/zbigniew Popek 10. Hydrogram miarodajnej fali wezbraniowej
Opracowanie koncepcji budowy suchego zbiornika Temat + opis ćwiczenia i materiały pomocnicze są dostępne na stronie: http://ziw.sggw.pl/dydaktyka/zbigniew Popek 10. Hydrogram miarodajnej fali wezbraniowej
OPORY RUCHU w ruchu turbulentnym
 Katedra Inżynierii Wodnej i Geotechniki Wydział Inżynierii Środowiska i Geodezji Uniwersytet Rolniczy im. Hugona Kołłątaja w Krakowie dr hab. inż. Leszek Książ ążek OPORY RUCHU w ruchu turbulentnym Hydraulika
Katedra Inżynierii Wodnej i Geotechniki Wydział Inżynierii Środowiska i Geodezji Uniwersytet Rolniczy im. Hugona Kołłątaja w Krakowie dr hab. inż. Leszek Książ ążek OPORY RUCHU w ruchu turbulentnym Hydraulika
mgr inż. Małgorzata Leja BM 4329 Katedra Inżynierii Wodnej i Geotechniki Uniwersytet Rolniczy Hugona Kołłątaja w Krakowie Kraków,
 mgr inż. Małgorzata Leja BM 4329 Katedra Inżynierii Wodnej i Geotechniki Uniwersytet Rolniczy Hugona Kołłątaja w Krakowie Kraków, 11.02.2013 Wstęp Cel projektu Procesy morfologiczne Materiały i metody
mgr inż. Małgorzata Leja BM 4329 Katedra Inżynierii Wodnej i Geotechniki Uniwersytet Rolniczy Hugona Kołłątaja w Krakowie Kraków, 11.02.2013 Wstęp Cel projektu Procesy morfologiczne Materiały i metody
Hydraulika i hydrologia
 Zad. Sprawdzić możliwość wyparcia filtracyjnego gruntu w dnie wykopu i oszacować wielkość dopływu wody do wykopu o wymiarach w planie 0 x 0 m. 8,00 6,00 4,00 -,00 Piaski średnioziarniste k = 0,0004 m/s
Zad. Sprawdzić możliwość wyparcia filtracyjnego gruntu w dnie wykopu i oszacować wielkość dopływu wody do wykopu o wymiarach w planie 0 x 0 m. 8,00 6,00 4,00 -,00 Piaski średnioziarniste k = 0,0004 m/s
OCENA ZAGROśENIA I SYSTEM OCHRONY PRZED POWODZIĄ. Wykład 7 kwietnia 2008 roku - część 2. Wykład 14 kwietnia 2008 roku
 OCENA ZAGROśENIA I SYSTEM OCHRONY PRZED POWODZIĄ Wykład 7 kwietnia 008 roku - część. Wykład 4 kwietnia 008 roku Ocena zagroŝenia i system ochrony przed powodzią Zakres: Ocena zagroŝenia powodziowego. Podstawy
OCENA ZAGROśENIA I SYSTEM OCHRONY PRZED POWODZIĄ Wykład 7 kwietnia 008 roku - część. Wykład 4 kwietnia 008 roku Ocena zagroŝenia i system ochrony przed powodzią Zakres: Ocena zagroŝenia powodziowego. Podstawy
MECHANIKA PŁYNÓW - LABORATORIUM
 MECHANIKA PŁYNÓW - LABORATORIUM Ćwiczenie nr 1 Wypływ cieczy przez przystawki Celem ćwiczenia jest eksperymentalne wyznaczenie współczynnika wydatku przystawki przy wypływie ustalonym, nieustalonym oraz
MECHANIKA PŁYNÓW - LABORATORIUM Ćwiczenie nr 1 Wypływ cieczy przez przystawki Celem ćwiczenia jest eksperymentalne wyznaczenie współczynnika wydatku przystawki przy wypływie ustalonym, nieustalonym oraz
Q t lub precyzyjniej w postaci różniczkowej. dq dt Jednostką natężenia prądu jest amper oznaczany przez A.
 Prąd elektryczny Dotychczas zajmowaliśmy się zjawiskami związanymi z ładunkami spoczywającymi. Obecnie zajmiemy się zjawiskami zachodzącymi podczas uporządkowanego ruchu ładunków, który często nazywamy
Prąd elektryczny Dotychczas zajmowaliśmy się zjawiskami związanymi z ładunkami spoczywającymi. Obecnie zajmiemy się zjawiskami zachodzącymi podczas uporządkowanego ruchu ładunków, który często nazywamy
Obszar Oddziaływania Kanał Zaborowski
 1 Obszar Oddziaływania Kanał Zaborowski Dokumentacja końcowa z symulacyjnych obliczeń hydraulicznych LIFE12 NAT/PL/000084 Wetlands conservation and restoration in Puszcza Kampinoska Natura 2000 site 2
1 Obszar Oddziaływania Kanał Zaborowski Dokumentacja końcowa z symulacyjnych obliczeń hydraulicznych LIFE12 NAT/PL/000084 Wetlands conservation and restoration in Puszcza Kampinoska Natura 2000 site 2
Badanie transformatora
 Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Ćwiczenie 14 Badanie transformatora 14.1. Zasada ćwiczenia Transformator składa się z dwóch uzwojeń, umieszczonych na wspólnym metalowym rdzeniu. Do jednego uzwojenia (pierwotnego) przykłada się zmienne
Tok postępowania przy projektowaniu fundamentu bezpośredniego obciążonego mimośrodowo wg wytycznych PN-EN 1997-1 Eurokod 7
 Tok postępowania przy projektowaniu fundamentu bezpośredniego obciążonego mimośrodowo wg wytycznych PN-EN 1997-1 Eurokod 7 I. Dane do projektowania - Obciążenia stałe charakterystyczne: V k = (pionowe)
Tok postępowania przy projektowaniu fundamentu bezpośredniego obciążonego mimośrodowo wg wytycznych PN-EN 1997-1 Eurokod 7 I. Dane do projektowania - Obciążenia stałe charakterystyczne: V k = (pionowe)
on behavior of flood embankments
 Michał Grodecki * Wpływ hydrogramu fali powodziowej na zachowanie się wałów przeciwpowodziowych Influence of a flood wave hydrograph on behavior of flood embankments Streszczenie Abstract W artykule przedstawiono
Michał Grodecki * Wpływ hydrogramu fali powodziowej na zachowanie się wałów przeciwpowodziowych Influence of a flood wave hydrograph on behavior of flood embankments Streszczenie Abstract W artykule przedstawiono
ZESZYTY NAUKOWE NR 10(82) AKADEMII MORSKIEJ W SZCZECINIE. Analiza strat ciśnieniowych w kanałach pompy MP-05
 ISSN 1733-8670 ZESZYTY NAUKOWE NR 10(82) AKADEMII MORSKIEJ W SZCZECINIE IV MIĘDZYNARODOWA KONFERENCJA NAUKOWO-TECHNICZNA E X P L O - S H I P 2 0 0 6 Adam Komorowski Analiza strat ciśnieniowych w kanałach
ISSN 1733-8670 ZESZYTY NAUKOWE NR 10(82) AKADEMII MORSKIEJ W SZCZECINIE IV MIĘDZYNARODOWA KONFERENCJA NAUKOWO-TECHNICZNA E X P L O - S H I P 2 0 0 6 Adam Komorowski Analiza strat ciśnieniowych w kanałach
Ruch rumowiska rzecznego
 Ruch rumowiska rzecznego Woda płynąca w korytach rzecznych transportuje materiał stały tzw. rumowisko rzeczne, które ze względu na mechanizm transportu dzielimy na rumowisko unoszone i wleczone. Rumowisko
Ruch rumowiska rzecznego Woda płynąca w korytach rzecznych transportuje materiał stały tzw. rumowisko rzeczne, które ze względu na mechanizm transportu dzielimy na rumowisko unoszone i wleczone. Rumowisko
Rozkłady prędkości przepływu wody w korytach z roślinnością wodną Distributions of water velocities in open-channels with aquatic vegetation
 Adam WÓJTOWICZ, Elżbieta KUBRAK, Marcin KRUKOWSKI Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Restoration WULS SGGW Rozkłady
Adam WÓJTOWICZ, Elżbieta KUBRAK, Marcin KRUKOWSKI Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW w Warszawie Department of Hydraulic Engineering and Environmental Restoration WULS SGGW Rozkłady
Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2)
![Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2) Wzór Żurawskiego. Belka o przekroju kołowym. Składowe naprężenia stycznego można wyrazić następująco (np. [1,2]): T r 2 y ν ) (1) (2)](/thumbs/101/149183432.jpg) Przykłady rozkładu naprężenia stycznego w przekrojach belki zginanej nierównomiernie (materiał uzupełniający do wykładu z wytrzymałości materiałów I, opr. Z. Więckowski, 11.2018) Wzór Żurawskiego τ xy
Przykłady rozkładu naprężenia stycznego w przekrojach belki zginanej nierównomiernie (materiał uzupełniający do wykładu z wytrzymałości materiałów I, opr. Z. Więckowski, 11.2018) Wzór Żurawskiego τ xy
dr hab. inż. Andrzej Tiukało, prof. IMGW-PIB Ogrodzieniec, marca 2017 r.
 Wykorzystanie mapy zagrożenia i ryzyka powodziowego do wyznaczenia negatywnych konsekwencji zalania lub podtopienia potencjalnych źródeł zanieczyszczenia środowiska. dr hab. inż. Andrzej Tiukało, prof.
Wykorzystanie mapy zagrożenia i ryzyka powodziowego do wyznaczenia negatywnych konsekwencji zalania lub podtopienia potencjalnych źródeł zanieczyszczenia środowiska. dr hab. inż. Andrzej Tiukało, prof.
Liczba godzin Liczba tygodni w tygodniu w semestrze
 15. Przedmiot: WYTRZYMAŁOŚĆ MATERIAŁÓW Kierunek: Mechatronika Specjalność: mechatronika systemów energetycznych Rozkład zajęć w czasie studiów Liczba godzin Liczba godzin Liczba tygodni w tygodniu w semestrze
15. Przedmiot: WYTRZYMAŁOŚĆ MATERIAŁÓW Kierunek: Mechatronika Specjalność: mechatronika systemów energetycznych Rozkład zajęć w czasie studiów Liczba godzin Liczba godzin Liczba tygodni w tygodniu w semestrze
Analiza wymiarowa jest działem matematyki stosowanej, którego zadaniem jest wyznaczenie, poprawnej pod względem wymiarowym, postaci wzorów fizycznych.
 Analiza wymiarowa Prof. dr hab. Małgorzata Jaros, prof. SGGW Analiza wymiarowa jest działem matematyki stosowanej, którego zadaniem jest wyznaczenie, poprawnej pod względem wymiarowym, postaci wzorów fizycznych.
Analiza wymiarowa Prof. dr hab. Małgorzata Jaros, prof. SGGW Analiza wymiarowa jest działem matematyki stosowanej, którego zadaniem jest wyznaczenie, poprawnej pod względem wymiarowym, postaci wzorów fizycznych.
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
i elementy z półprzewodników homogenicznych część II
 Półprzewodniki i elementy z półprzewodników homogenicznych część II Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
Półprzewodniki i elementy z półprzewodników homogenicznych część II Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego
Wprowadzenie. Małgorzata KLENIEWSKA. nawet już przy stosunkowo niewielkim stężeniu tego gazu w powietrzu atmosferycznym.
 Małgorzata KLENIEWSKA Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Zakład Meteorologii i Klimatologii Department of Hydraulic Engineering and Environmental Restoration WAU Division of Meteorology
Małgorzata KLENIEWSKA Katedra Inżynierii Wodnej i Rekultywacji Środowiska SGGW Zakład Meteorologii i Klimatologii Department of Hydraulic Engineering and Environmental Restoration WAU Division of Meteorology
Wymagania edukacyjne z matematyki dla klasy II gimnazjum wg programu Matematyka z plusem
 Wymagania edukacyjne z matematyki dla klasy II gimnazjum wg programu Matematyka z plusem Ocenę dopuszczającą otrzymuje uczeń, który umie: 1.zapisywać potęgi w postaci iloczynów 2. zapisywać iloczyny jednakowych
Wymagania edukacyjne z matematyki dla klasy II gimnazjum wg programu Matematyka z plusem Ocenę dopuszczającą otrzymuje uczeń, który umie: 1.zapisywać potęgi w postaci iloczynów 2. zapisywać iloczyny jednakowych
Laboratorium komputerowe z wybranych zagadnień mechaniki płynów
 FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
1.1 Przegląd wybranych równań i modeli fizycznych. , u x1 x 2
 Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
Temat 1 Pojęcia podstawowe 1.1 Przegląd wybranych równań i modeli fizycznych Równaniem różniczkowym cząstkowym rzędu drugiego o n zmiennych niezależnych nazywamy równanie postaci gdzie u = u (x 1, x,...,
WYMAGANIA PROGRAMOWE Z MATEMATYKI KLASA II
 WYMAGANIA PROGRAMOWE Z MATEMATYKI KLASA II POTĘGI zna pojęcie potęgi o wykładniku naturalnym rozumie pojęcie potęgi o wykładniku naturalnym umie zapisać potęgę w postaci iloczynu umie zapisać iloczyn jednakowych
WYMAGANIA PROGRAMOWE Z MATEMATYKI KLASA II POTĘGI zna pojęcie potęgi o wykładniku naturalnym rozumie pojęcie potęgi o wykładniku naturalnym umie zapisać potęgę w postaci iloczynu umie zapisać iloczyn jednakowych
Renaturyzacja rzek i ich dolin. Wykład 1, 2. - Cechy hydromorfologiczne rzek naturalnych i przekształconych.
 Renaturyzacja rzek i ich dolin Wykład 1, 2 - Cechy hydromorfologiczne rzek naturalnych i przekształconych. - Wpływ antropopresji na cechy dolin rzecznych. - Określenie stanu ekologicznego rzek i stopnia
Renaturyzacja rzek i ich dolin Wykład 1, 2 - Cechy hydromorfologiczne rzek naturalnych i przekształconych. - Wpływ antropopresji na cechy dolin rzecznych. - Określenie stanu ekologicznego rzek i stopnia
Zagrożenia powodziowe w dorzeczu górnej Wisły na przykładzie modelowania potencjalnych skutków katastrof budowli piętrzących Michał Piórecki
 Zagrożenia powodziowe w dorzeczu górnej Wisły na przykładzie modelowania potencjalnych skutków katastrof budowli piętrzących Michał Piórecki Ośrodek Koordynacyjno Informacyjny Ochrony Przeciwpowodziowej
Zagrożenia powodziowe w dorzeczu górnej Wisły na przykładzie modelowania potencjalnych skutków katastrof budowli piętrzących Michał Piórecki Ośrodek Koordynacyjno Informacyjny Ochrony Przeciwpowodziowej
RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA
 Dr inż. Andrzej Polka Katedra Dynamiki Maszyn Politechnika Łódzka RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA Streszczenie: W pracy opisano wzajemne położenie płaszczyzny parasola
Dr inż. Andrzej Polka Katedra Dynamiki Maszyn Politechnika Łódzka RÓWNANIE DYNAMICZNE RUCHU KULISTEGO CIAŁA SZTYWNEGO W UKŁADZIE PARASOLA Streszczenie: W pracy opisano wzajemne położenie płaszczyzny parasola
MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ
 Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Jarosław MAŃKOWSKI * Andrzej ŻABICKI * Piotr ŻACH * MODELOWANIE POŁĄCZEŃ TYPU SWORZEŃ OTWÓR ZA POMOCĄ MES BEZ UŻYCIA ANALIZY KONTAKTOWEJ 1. WSTĘP W analizach MES dużych konstrukcji wykonywanych na skalę
Suche zbiorniki przeciwpowodziowe. Michał Szydłowski, prof.pg Kierownik Katedry Hydrotechniki Wydział Inżynierii Lądowej i Środowiska PG
 Michał Szydłowski, prof.pg Kierownik Katedry Hydrotechniki Wydział Inżynierii Lądowej i Środowiska PG Trzy integralne strategie ograniczania skutków powodzi Trzymać wodę z daleka od ludzi Trzymać ludzi
Michał Szydłowski, prof.pg Kierownik Katedry Hydrotechniki Wydział Inżynierii Lądowej i Środowiska PG Trzy integralne strategie ograniczania skutków powodzi Trzymać wodę z daleka od ludzi Trzymać ludzi
PROGNOZA HYDROGRAMU WYPŁYWU POWSTAŁEGO W WYNIKU SYMULACJI AWARII ZAPORY BESKO
 115 DOROTA MIROSŁAW-ŚWIĄTEK, MARIA MERKEL, KAMIL MAŃK, ANNA KOSIK* PROGNOZA HYDROGRAMU WYPŁYWU POWSTAŁEGO W WYNIKU SYMULACJI AWARII ZAPORY BESKO PREDICTION OF THE OUTFLOW HYDROGRAPH FOLLOWING THE BESKO
115 DOROTA MIROSŁAW-ŚWIĄTEK, MARIA MERKEL, KAMIL MAŃK, ANNA KOSIK* PROGNOZA HYDROGRAMU WYPŁYWU POWSTAŁEGO W WYNIKU SYMULACJI AWARII ZAPORY BESKO PREDICTION OF THE OUTFLOW HYDROGRAPH FOLLOWING THE BESKO
Załącznik D (EC 7) Przykład analitycznej metody obliczania oporu podłoża
 Załącznik D (EC 7) Przykład analitycznej metody obliczania oporu podłoża D.1 e używane w załączniku D (1) Następujące symbole występują w Załączniku D: A' = B' L efektywne obliczeniowe pole powierzchni
Załącznik D (EC 7) Przykład analitycznej metody obliczania oporu podłoża D.1 e używane w załączniku D (1) Następujące symbole występują w Załączniku D: A' = B' L efektywne obliczeniowe pole powierzchni
MODYFIKACJA RÓWNANIA DO OPISU KRZYWYCH WÖHLERA
 Sylwester KŁYSZ Janusz LISIECKI Instytut Techniczny Wojsk Lotniczych Tomasz BĄKOWSKI Jet Air Sp. z o.o. PRACE NAUKOWE ITWL Zeszyt 27, s. 93 97, 2010 r. DOI 10.2478/v10041-010-0003-0 MODYFIKACJA RÓWNANIA
Sylwester KŁYSZ Janusz LISIECKI Instytut Techniczny Wojsk Lotniczych Tomasz BĄKOWSKI Jet Air Sp. z o.o. PRACE NAUKOWE ITWL Zeszyt 27, s. 93 97, 2010 r. DOI 10.2478/v10041-010-0003-0 MODYFIKACJA RÓWNANIA
WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM
 Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
Na ocenę dopuszczającą uczeń umie : WYMAGANIA EDUKACYJN KRYTERIA OCENY Z MATEMATYKI W KLASIE II GIMNAZJUM stosować cztery podstawowe działania na liczbach wymiernych, zna kolejność wykonywania działań
ZESPÓŁ SZKÓŁ W OBRZYCKU
 Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
Matematyka na czasie Program nauczania matematyki w gimnazjum ZGODNY Z PODSTAWĄ PROGRAMOWĄ I z dn. 23 grudnia 2008 r. Autorzy: Agnieszka Kamińska, Dorota Ponczek ZESPÓŁ SZKÓŁ W OBRZYCKU Wymagania edukacyjne
Indukcja elektromagnetyczna Faradaya
 Indukcja elektromagnetyczna Faradaya Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Po odkryciu Oersteda zjawiska
Indukcja elektromagnetyczna Faradaya Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Po odkryciu Oersteda zjawiska
Wyboczenie ściskanego pręta
 Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
Wszelkie prawa zastrzeżone Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: 1. Wstęp Wyboczenie ściskanego pręta oprac. dr inż. Ludomir J. Jankowski Zagadnienie wyboczenia
ĆWICZENIE Z PRZEDMIOTU OCHRONA ŚRODOWISKA W BUDOWNICTWIE WODNYM
 ĆWICZENIE Z PRZEDMIOTU OCHRONA ŚRODOWISKA W BUDOWNICTWIE WODNYM Tema: Określenie czas i przebieg zamulenia małego zbiornika wodnego Projekowana objęość zbiornika V =.. [ys m 3 ] Powierzchnia zlewni do
ĆWICZENIE Z PRZEDMIOTU OCHRONA ŚRODOWISKA W BUDOWNICTWIE WODNYM Tema: Określenie czas i przebieg zamulenia małego zbiornika wodnego Projekowana objęość zbiornika V =.. [ys m 3 ] Powierzchnia zlewni do
SZCZEGÓŁOWY OPIS OSIĄGNIĘĆ NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA DRUGA
 SZCZEGÓŁOWY OPIS OSIĄGNIĘĆ NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA DRUGA DZIAŁ I: POTĘGI I PIERWIASTKI zna i rozumie pojęcie potęgi o wykładniku naturalnym (2) umie zapisać potęgę w postaci iloczynu (2)
SZCZEGÓŁOWY OPIS OSIĄGNIĘĆ NA POSZCZEGÓLNE OCENY MATEMATYKA KLASA DRUGA DZIAŁ I: POTĘGI I PIERWIASTKI zna i rozumie pojęcie potęgi o wykładniku naturalnym (2) umie zapisać potęgę w postaci iloczynu (2)
J. Szantyr Wykład nr 27 Przepływy w kanałach otwartych I
 J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
J. Szantyr Wykład nr 7 Przepływy w kanałach otwartych Przepływy w kanałach otwartych najczęściej wymuszane są działaniem siły grawitacji. Jako wstępny uproszczony przypadek przeanalizujemy spływ warstwy
WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA KOŁA NA ZMIANĘ SZTYWNOŚCI ZAZĘBIENIA
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum
 Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
Przedmiotowe zasady oceniania i wymagania edukacyjne z matematyki dla klasy drugiej gimnazjum I. POTĘGI I PIERWIASTKI oblicza wartości potęg o wykładnikach całkowitych liczb różnych od zera zapisuje liczbę
Stosowane metody wykrywania nieszczelności w sieciach gazowych
 Stosowane metody wykrywania nieszczelności w sieciach gazowych Andrzej Osiadacz, Łukasz Kotyński Zakład Systemów Ciepłowniczych i Gazowniczych Wydział Inżynierii Środowiska Politechniki Warszawskiej Międzyzdroje,
Stosowane metody wykrywania nieszczelności w sieciach gazowych Andrzej Osiadacz, Łukasz Kotyński Zakład Systemów Ciepłowniczych i Gazowniczych Wydział Inżynierii Środowiska Politechniki Warszawskiej Międzyzdroje,
RÓWNANIE MOMENTÓW PĘDU STRUMIENIA
 RÓWNANIE MOMENTÓW PĘDU STRUMIENIA Przepływ osiowo-symetryczny ustalony to przepływ, w którym parametry nie zmieniają się wzdłuż okręgów o promieniu r, czyli zależą od promienia r i długości z, a nie od
RÓWNANIE MOMENTÓW PĘDU STRUMIENIA Przepływ osiowo-symetryczny ustalony to przepływ, w którym parametry nie zmieniają się wzdłuż okręgów o promieniu r, czyli zależą od promienia r i długości z, a nie od
Analiza wpływu sterowania retencją korytową małego cieku na redukcję fal wezbraniowych przy wykorzystaniu modeli Hec Ras i Hec ResSim
 Analiza wpływu sterowania retencją korytową małego cieku na redukcję fal wezbraniowych przy wykorzystaniu modeli Hec Ras i Hec ResSim mgr inż. Bartosz Kierasiński Zakład Zasobów Wodnych Instytut Technologiczno-Przyrodniczy
Analiza wpływu sterowania retencją korytową małego cieku na redukcję fal wezbraniowych przy wykorzystaniu modeli Hec Ras i Hec ResSim mgr inż. Bartosz Kierasiński Zakład Zasobów Wodnych Instytut Technologiczno-Przyrodniczy
Przedmiotowy system oceniania dla uczniów z obowiązkiem dostosowania wymagań edukacyjnych z matematyki w kl.ii
 Matematyka klasa II kryteria oceniania dla uczniów z obowiązkiem dostosowania wymagań edukacyjnych opracowano na podstawie programu MATEMATYKA Z PLUSEM DZIAŁ 1. POTĘGI zna i rozumie pojęcie potęgi o wykładniku
Matematyka klasa II kryteria oceniania dla uczniów z obowiązkiem dostosowania wymagań edukacyjnych opracowano na podstawie programu MATEMATYKA Z PLUSEM DZIAŁ 1. POTĘGI zna i rozumie pojęcie potęgi o wykładniku
Przedmiotowy system oceniania z matematyki kl.ii
 DZIAŁ 1. POTĘGI Matematyka klasa II - wymagania programowe zna i rozumie pojęcie potęgi o wykładniku naturalnym (K) umie zapisać potęgę w postaci iloczynu (K) umie zapisać iloczyn jednakowych czynników
DZIAŁ 1. POTĘGI Matematyka klasa II - wymagania programowe zna i rozumie pojęcie potęgi o wykładniku naturalnym (K) umie zapisać potęgę w postaci iloczynu (K) umie zapisać iloczyn jednakowych czynników
Przewód wydatkujący po drodze
 Przewód wydatkujący po drodze Współczesne wodociągi, występujące w postaci mniej lub bardziej złożonych systemów obiektów służą do udostępniania wody o pożądanej jakości i w oczekiwanej ilości. Poszczególne
Przewód wydatkujący po drodze Współczesne wodociągi, występujące w postaci mniej lub bardziej złożonych systemów obiektów służą do udostępniania wody o pożądanej jakości i w oczekiwanej ilości. Poszczególne
Mechanika i Budowa Maszyn
 Mechanika i Budowa Maszyn Materiały pomocnicze do ćwiczeń Wyznaczanie sił wewnętrznych w belkach statycznie wyznaczalnych Andrzej J. Zmysłowski Andrzej J. Zmysłowski Wyznaczanie sił wewnętrznych w belkach
Mechanika i Budowa Maszyn Materiały pomocnicze do ćwiczeń Wyznaczanie sił wewnętrznych w belkach statycznie wyznaczalnych Andrzej J. Zmysłowski Andrzej J. Zmysłowski Wyznaczanie sił wewnętrznych w belkach
Kinetyka. energia swobodna, G. postęp reakcji. stan 1 stan 2. kinetyka
 Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
Kinetyka postęp reakcji energia swobodna, G termodynamika kinetyka termodynamika stan 1 stan 2 Kinetyka Stawia dwa pytania: 1) Jak szybko biegną reakcje? 2) W jaki sposób przebiegają reakcje? 1) Jak szybko
Analiza mobilizacji oporu pobocznicy i podstawy pala na podstawie interpretacji badań modelowych
 Analiza mobilizacji oporu pobocznicy i podstawy pala na podstawie interpretacji badań modelowych Prof. dr hab. inż. Zygmunt Meyer, mgr inż. Krzysztof Żarkiewicz Zachodniopomorski Uniwersytet Technologiczny
Analiza mobilizacji oporu pobocznicy i podstawy pala na podstawie interpretacji badań modelowych Prof. dr hab. inż. Zygmunt Meyer, mgr inż. Krzysztof Żarkiewicz Zachodniopomorski Uniwersytet Technologiczny
