4. Obliczanie rozpywów mocy w duych systemach elektroenergetycznych

Wykad 3 Spadki i straty napicia. Straty przesyowe mocy. Analiza promieniowych ukadów przesyowych.

1 Wykad 3 Spadki i straty napicia. Straty przesyowe mocy. Analiza promieniowych kadów przesyowych. 3.1. Spadki i straty napicia. Straty przesyowe. a rys. 3.1. pokazano wykres wektorowy napi# odnosz$cy

ANALIZA OBWODÓW DLA PRZEBIEGÓW SINUSOIDALNYCH METODĄ LICZB ZESPOLONYCH

ANAZA OBWODÓW DA PZBGÓW SNUSODANYH MTODĄ ZB ZSPOONYH. Wprowadzn. Wprowadź fnkcję zspoloną znnj rzczwstj (czas) o następjącj postac: F( t) F F j t j jt t+ Fnkcj tj przporządkj na płaszczźn zspolonj wktor

8. PRDY I NAPICIA PRZY ZWARCIACH NIESYMETRYCZNYCH

8. PRDY APCA PRY WARCACH YMTRYCYCH 8.. Wprowadzenie Przez impedancj obwodu zwarciowego rozumie si impedancj widzian z miejsca zwarcia, przy zao$eniu, $e wszystkie siy elektromotoryczne s równe zeru. Twierdzenie

1 SEE wykad 2 Schematy zastpcze linii i transformatorów. Wykady dostpne na stronie: http://zss.ie.pwr.wroc.pl/studenci

1 EE wykad chematy zastpcze linii i transformatorów. Wykady dostpne na stronie: http://zss.ie.pwr.wroc.pl/stdenci Wykad chematy zastpcze linii i transformatorów. waga! Wykad zosta przeniesiony z s.305

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 03 3 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U d o s t p n i e n i e t e l e b i m ó w i n a g ł o n i e n i

Schematy zastępcze tranzystorów

haty zastępz tanzystoów kst tn pztawa kótko zasady spoządzana odl zastępzyh dla tanzystoów bpolanyh oaz unpolanyh Nalży paętać, ż są to odl ałosynałow, a wę słuszn tylko wyłązn pzy założnu, ż dany lnt

Całkowanie numeryczne funkcji. Kwadratury Gaussa.

Cłkon nuryczn unkc. Kdrtury Guss. Rozżyy:. -D -punkto kdrtur Guss tod prostokątó. -D tod trpzó. -D -punkto kdrtur Guss 4. Zn grnc cłkon unoron d t dt 5. -D n-punkto kdrtur Guss 6. -D -punkto kdrtur Guss

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa

W Z Ó R U M O W Y z a w a r t a w G d y n i w d n i u 2 0 1 4 r po m i d z y G d y s k i m O r o d k i e m S p o r t u i R e k r e a c j i j e d n o s t k a b u d e t o w a ( 8 1-5 3 8 G d y n i a ), l

1 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu B L A C H A R Z Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów

BADANIE ODBIORNIKÓW R, L, C W OBWODZIE PRDU SINUSOIDALNEGO

Cel wiczenia BADANIE ODBIORNIKÓW R, L, C W OBWODZIE PRDU SINUSOIDALNEGO Cele wiczenia jest poznanie etod technicznych wyznaczania podstawowych paraetrów pojedynczych odbiorników o charakterze R, L, C i

Mariusz RADWAŃSKI 1. które w przybliżeniu można zapisać w postaci [2, 5, 6]:

Marusz RADWAŃSKI 1 Poltchnka Warszawska, Instytut Elktronrgtyk (1) do:10.15199/48.2015.05.30 Współzalżność nastawń przkładn poprzcznych przsuwnków fazowych wpływaąca na stany pracy systmu lktronrgtyczngo

Opis i zakres czynności sprzątania obiektów Gdyńskiego Centrum Sportu

O p i s i z a k r e s c z y n n o c is p r z» t a n i a o b i e k t ó w G d y s k i e g o C e n t r u m S p o r t u I S t a d i o n p i ł k a r s k i w G d y n i I A S p r z» t a n i e p r z e d m e c

I n f o r m a c j e n a t e m a t p o d m i o t u k t ó r e m u z a m a w i a j» c y p o w i e r z y łk p o w i e r z y l i p r o w a d z e p o s t p

A d r e s s t r o n y i n t e r n e t o w e j, n a k t ó r e j z a m i e s z c z o n a b d z i e s p e c y f i k a c j a i s t o t n y c h w a r u n k ó w z a m ó w i e n i a ( j e e ld io t y c z y )

1.7 Zagadnienia szczegółowe związane z równaniem ruchu Moment bezwładności i moment zamachowy

.7 Zagadnna zczgółow zwązan z równan ruchu.7. ont bzwładnośc ont zaachowy Równan równowag ł dzałających na lnt ay d poazany na ry..8 będz ało potać: df a tąd lntarny ont dynaczny: d d ϑ d r * d d ϑ r d

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S i R D Z P I 2 7 1 0 3 62 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A Z a p e w n i e n i e z a s i l a n i ea n e r g e t y c z ne g o

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 70 1 3 7 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U d o s t p n i e n i e w r a z z r o z s t a w i e n i e m o g

Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 1. Układy równań liniowych

Zaawansowane metody numeryczne Komputerowa analza zagadneń różnczkowych 1. Układy równań lnowych P. F. Góra http://th-www.f.uj.edu.pl/zfs/gora/ semestr letn 2006/07 Podstawowe fakty Równane Ax = b, x,

1 0 2 / m S t a n d a r d w y m a g a ñ - e g z a m i n m i s t r z o w s k i dla zawodu R A D I E S T E T A Kod z klasyfikacji zawodów i sp e cjaln o ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

Teoria Sygnałów. II rok Geofizyki III rok Informatyki Stosowanej. Wykład 5 ( ) ( ) ( ) ( ) ( ) ( ) ( ) Transformacja Hilberta. sgn( + = + = + lim.

Tora Synałów II rok Gozyk III rok Inormatyk Stosowanj Wykład 5 ) sn( d d d F Najprw nzbędny rzltat. Transormacja Forra (w sns rancznym) nkcj sn() F lm π sn Z twrdzna o dalnośc wynka, ż π sn Transormacja

Jak zwiększyć efektywność i radość z wykonywanej pracy? Motywacja do pracy - badanie, szkolenie

Jak zwększyć fktywność radość z wykonywanj pracy? Motywacja do pracy - badan, szkoln czym sę zajmujmy? szkolna, symulacj Komunkacja, współpraca Cągł doskonaln Zarządzan zspołm Rozwój talntów motywacja

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 0 4 52 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A W y k o n a n i e p o m i a r ó w i n s t a l a c j i e l e k t r y c

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 07 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f U s ł u g i s p r z» t a n i a o b i e k t Gó w d y s k i e g o C e n

4. Podzielnica uniwersalna 4.1. Budowa podzielnicy

4. Podelnca unwersalna 4.. Budowa podelncy Podelnca jest pryrądem podałowym, który stanow specjalne wyposażene frearek unwersalnych. Podstawowym astosowanem podelncy jest dokonywane podału kątowego. Jest

Zawód: z d u n I. Etap teoretyczny (część pisemna i ustna) egzaminu obejmuje: Z a k r e s w i a d o m o ś c i i u m i e j ę t n o ś c i w ł a ś c i w

9 4 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu Z D U N Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów szkoln

SPECYFIKACJA ISTOTNYCH WARUNKÓW ZAMÓWIENIA

Z a m a w i a j» c y G D Y S K I O R O D E K S P O R T U I R E K R E A C J I J E D N O S T K A B U D E T O W A 8 1 5 3 8 G d y n i a, u l O l i m p i j s k a 5k 9 Z n a k s p r a w y G O S I R D Z P I

n ó g, S t r o n a 2 z 1 9

Z n a k s p r a w y G O S I R D Z P I2 7 1 0 6 3 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A D o s t a w a w r a z z m o n t a e m u r z» d z e s i ł o w n i z

(EN 10270:1-SH oraz DIN 17223, C; nr mat ) (EN 10270:3-NS oraz DIN 17224, nr mat )

(EN 10270:1-SH orz DIN 17223, C; nr mt. 1.1200) (EN 10270:3-NS orz DIN 17224, nr mt. 1.4310) d Fn K Dm k Dz L1 Ln L0 Legend d - Dm - Dz - L0 - n - czynn zwoi Ln - Fn - c - K - k - Fn stl nierdzewn = 1kg

Twierdzenia o przyrostach

Twirdznia o przyrosach Jżli w sici liniow zwrzy dwa węzły, iędzy kóryi panu napięci, o przyrosy (dodani lub un prądów w gałęziach sici oży obliczyć włączaąc iędzy węzły idaln źródło napięciow o sil lkroooryczn

Markowa. ZałoŜenia schematu Gaussa-

ZałoŜena scheatu Gaussa- Markowa I. Model jest nezennczy ze względu na obserwacje: f f f3... fl f, czyl y f (x, ε) II. Model jest lnowy względe paraetrów. y βo + β x +ε Funkcja a być lnowa względe paraetrów

MATEMATYKA POZIOM ROZSZERZONY Kryteria oceniania odpowiedzi. Arkusz A II. Strona 1 z 5

MATEMATYKA POZIOM ROZSZERZONY Krytera ocenana odpowedz Arkusz A II Strona 1 z 5 Odpowedz Pytane 1 2 3 4 5 6 7 8 9 Odpowedź D C C A B 153 135 232 333 Zad. 10. (0-3) Dana jest funkcja postac. Korzystając

y f x 0 f x 0 x x 0 x 0 lim 0 h f x 0 lim x x0 - o ile ta granica właściwa istnieje. f x x2 Definicja pochodnych jednostronnych 1.5 0.

Matematyka ZLic - 3 Pochodne i różniczki funkcji jednej zmiennej Definicja Pochodną funkcji f w punkcie x, nazwiemy liczbę oznaczaną symbolem f x lub df x dx, równą granicy właściwej f x lim h - o ile

Twierdzenie Bezouta i liczby zespolone Javier de Lucas. Rozwi azanie 2. Z twierdzenia dzielenia wielomianów, mamy, że

Twerdzene Bezouta lczby zespolone Javer de Lucas Ćwczene 1 Ustal dla których a, b R można podzelć f 1 X) = X 4 3X 2 + ax b przez f 2 X) = X 2 3X+2 Oblcz a b Z 5 jeżel zak ladamy, że f 1 f 2 s a welomanam

14.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe.

Matematyka 4/ 4.Rozwiązywanie zadań tekstowych wykorzystujących równania i nierówności kwadratowe. I. Przypomnij sobie:. Wiadomości z poprzedniej lekcji... Że przy rozwiązywaniu zadań tekstowych wykorzystujących

P 0max. P max. = P max = 0; 9 20 = 18 W. U 2 0max. U 0max = q P 0max = p 18 2 = 6 V. D = T = U 0 = D E ; = 6

XL OLIMPIADA WIEDZY TECHNICZNEJ Zawody II stopnia Rozwi zania zada dla grupy elektryczno-elektronicznej Rozwi zanie zadania 1 Sprawno przekszta tnika jest r wna P 0ma a Maksymaln moc odbiornika mo na zatem

WYNIKI EGZAMINU MATURALNEGO 2010 r.

OKE Łomż 00 stron z 5 powt M. Olsztyn WYNIKI EGZAMINU MATURALNEGO 00 r. Powt M. Olsztyn CZĘŚĆ I Dn zmszczon w częśc I sprwozdn dotyczą mturlngo po rz prwszy. bsolwntów, którzy przystąpl do gzmnu. Ops populcj

2.1. Ruch, gradient pr dko ci, tensor pr dko ci odkszta cenia, Ruchem cia a B nazywamy dostatecznie g adko zale ne od czasu t jego odkszta cenie

Rozdzia 2 Ruch i kinematyka 2.. Ruch, gradient pr dko ci, tensor pr dko ci odkszta cenia, wirowo Ruchem cia a B nazywamy dostatecznie g adko zale ne od czasu t jego odkszta cenie t, tzn. B X! t (X) =x

Rozdział 1. Nazwa i adres Zamawiającego Gdyńskie Centrum Sportu jednostka budżetowa w Gdyni Rozdział 2. Informacja o trybie i stosowaniu przepisów

Z n a k s p r a w y G C S D Z P I 2 7 1 0 2 8 2 0 1 5 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e ro b ó t b u d o w l a n y c h w b u d y n k u H

2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l

Podstawowe obiekty AutoCAD-a

LINIA Podstawowe obiekty AutoCAD-a Zad1: Narysowa lini o pocztku w punkcie o współrzdnych (100, 50) i kocu w punkcie (200, 150) 1. Wybierz polecenie rysowania linii, np. poprzez kilknicie ikony. W wierszu

Zawód: stolarz meblowy I. Etap teoretyczny (część pisemna i ustna) egzaminu obejmuje: Z ak res wi ad omoś c i i u mi ej ę tn oś c i wł aś c i wyc h d

4 6 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu S T O L A R Z M E B L O W Y Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

Równania ró»niczkowe I rz du (RRIR) Twierdzenie Picarda. Anna D browska. WFTiMS. 23 marca 2010

WFTiMS 23 marca 2010 Spis tre±ci 1 Denicja 1 (równanie ró»niczkowe pierwszego rz du) Równanie y = f (t, y) (1) nazywamy równaniem ró»niczkowym zwyczajnym pierwszego rz du w postaci normalnej. Uwaga 1 Ogólna

9 7 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu F O T O G R A F Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów

Ł Ł Ś Ś ź Ć ź ź ź Ń Ł Ż Ś ź Ę Ż Ń Ę ź ź ź Ę ź Ł Ę ź Ę Ę Ę ź ź Ś ź ź Ł Ł Ź Ę Ł Ś ź Ę Ę Ę ń ź Ą ó Ę ĘĘ ź Ę ź Ą Ł Ę Ł Ą ź Ę ó Ź Ś ź Ń Ę Ę ĘĘ Ą Ś Ę Ł Ę Ć Ź ź Ź Ę Ę Ź ź Ź Ź Ź Ł Ż Ł Ę ź Ż Ź ź Ź Ź Ź Ź Ą Ż ŚĆ

Ź Ę Ę Ś Ś Ś ć Ę ć Ś ć Ź Ż Ś ć Ż Ź Ż Ą Ż Ę Ś Ź Ę Ź Ż Ó Ś ć ć Ś Ż Ć ź Ś Ń Ź ć Ó ź Ś Ń ź Ń Ź Ź ź Ż Ź Ź Ź Ź Ż Ź ć Ż Ę ź Ę ź ć Ń ć ć ć ć Ź Ę Ą ć Ę ć Ń ć ć Ź Ż ć Ó Ó Ó Ż ć Ó Ż Ę Ą Ź Ó Ń Ł ź ź Ń ć ć Ż ć Ś Ą

Ł Ł ń ń Ą ń ń Ś ń Ź ń ń ń Ż ń Ł ń Ś ń ń ń Ą Ą Ł Ż ń ń Ś ń Ź ń ń ć Ź ń ć Ś ć ć ń Ź ń Ą Ł Ł Ę ĘĘ Ż Ź ć Ł ń Ś Ą Ł Ł Ł Ą Ę Ę ń Ń ń Ź ń ć Ż ń Ż Ś ń Ń ń Ń Ź Ą ć Ł ń ć ć Ź Ą Ą Ą Ź Ą Ł Ą Ś ń ń Ś Ś Ą Ć ŚĆ Ł ć Ż

Ą Ń Ś Ę ź Ś Ś ź ź Ś Ś ź Ł Ś Ś Ś Ł ĘĘ Ś Ś Ś ć Ś Ś Ś Ś Ł Ó Ś Ł ć Ś Ść Ś Ś Ś Ń ć Ś Ł Ś Ź Ą ć ć Ł ź Ś Ą Ś Ł Ą Ś Ś Ą Ś Ś ź Ś ć Ł ć ć Ł Ł ć Ź ć ć Ś ć ź Ź ć Ś ć ć ć Ś Ą Ś Ś Ś ć Ś Ść Ś ć Ł ć Ś ć Ś Ś Ń ć ć Ł Ś

啇c go b kt ᆗ匷 y l y s l g y l. P ysł ᆗ匷 ᆗ匷 s ob kt b o l go ᆗ匷 l. P ysł ᆗ匷ᆗ匷.. ᆗ匷ᆗ匷ᆗ匷 ᆗ匷ᆗ匷ᆗ匷ᆗ匷 啇c go Pᆗ匷ᆗ匷 ᆗ匷 ᆗ匷 s 啇c go l. ᆗ匷. 呷b s ᆗ匷ᆗ匷 ᆗ匷2-500 ᆗ匷 s o ot o co 啇c go ᆗ匷 P ó O g Z I s y TECHPLAN ᆗ匷 ᆗ匷

Spis świadectw wydanych przez COCH w 2006 r.

Numer świadectwa Spis świadectw wydanych przez COCH w 2006 r. Numer rejestracyjny (punkt 3 świadectwa) Uznaje się jako (punkt 6 świadectwa) Nr protokołu badań (punkt 7.2.3 świadectwa) Data waŝności świadectwa

1 Metody iteracyjne rozwi zywania równania f(x)=0

1 Metody iteracyjne rozwi zywania równania f()=0 1.1 Metoda bisekcji Zaªó»my,»e funkcja f jest ci gªa w [a 0, b 0 ]. Pierwiastek jest w przedziale [a 0, b 0 ] gdy f(a 0 )f(b 0 ) < 0. (1) Ustalmy f(a 0

1 8 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu M E C H A N I K - O P E R A T O R P O J A Z D Ó W I M A S Z Y N R O L N I C Z Y C H K o d z k l a s y f i k a c j i

Gdyńskim Ośrodkiem Sportu i Rekreacji jednostka budżetowa

Z a ł» c z n i k n r 5 d o S p e c y f i k a c j i I s t o t n y c h W a r u n k Zó aw m ó w i e n i a Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 1 2 0 14 W Z Ó R U M O W Y z a w a r t a w Gd y n

Rozwi zanie równania ró»niczkowego metod operatorow (zastosowanie transformaty Laplace'a).

Rozwi zania zada«z egzaminu podstawowego z Analizy matematycznej 2.3A (24/5). Rozwi zanie równania ró»niczkowego metod operatorow (zastosowanie transformaty Laplace'a). Zadanie P/4. Metod operatorow rozwi

Gramatyki regularne i automaty skoczone

Gramatyki regularne i automaty skoczone Alfabet, jzyk, gramatyka - podstawowe pojcia Co to jest gramatyka regularna, co to jest automat skoczony? Gramatyka regularna Gramatyka bezkontekstowa Translacja

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 2 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f O b s ł u g a o p e r a t o r s k a u r a w i s a m o j e z d n

Zagadnienia. Prąd elektryczny. Siła elektromotoryczna. Siła elektromotoryczna SEM. W = q. b) i. Źródło wykonuje pracę nad ładunkami kosztem

Zagada Prąd lryczy. Sła lrmrycza SEM. Zasada dzałaa ga. dal rzczys źródł apęca. Opór ęrzy źródła 4. Sa jały sa zarca a) Wszys puy przda mają a sam pcjał. Elry sbd pruszają sę ąrz przda przypadych ruach.

1 0 2 / c S t a n d a r d w y m a g a ń e g z a m i n c z e l a d n i c z y dla zawodu R A D I E S T E T A Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji

WYNIKI KOLOKWIUM Z FUNDAMENTOWANIA SM/sem.1

Na kolokwium konieczny jest do okazania dowód osobisty lub legitymacja studencka 1 WYNIKI KOLOKWIUM Z FUNDAMENTOWANIA SM/sem.1 GHB003321W W.Brząkała I termin (na przedostatnim wykładzie) = PONIEDZIAŁEK

Rozdział 1. Nazwa i adres Zamawiającego Gdyński Ośrodek Sportu i Rekreacji jednostka budżetowa Rozdział 2.

Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 5 32 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f W y k o n a n i e p r z e g l» d ó w k o n s e r w a c y j n o -

EGZAMIN MATURALNY Z MATEMATYKI

ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZCIA EGZAMINU! Miejsce na naklejk MMA-R_P-08 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 008 Czas pracy 80 minut Instrukcja dla

Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych

Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych Piotr Modliński Wydział Geodezji i Kartografii PW 13 stycznia 2012 P. Modliński, GiK PW Rozw.

WYNIKI MISTRZOSTW KATOWIC W PŁYWANIU SZKÓŁ PONADPODSTAWOWYCH ( R.)

WYNIKI MISTRZOSTW KATOWIC W PŁYWANIU SZKÓŁ PONADPODSTAWOWYCH (12.10.2018 R.) 100 metrów stylem zmiennym dziewcząt 1 WB X LO 1:25,52 17 2 KK I LO 1:25,77 15 3 MZ II LO 1:28,70 14 4 AP III LO 1:30,81 13

Czyli L = P a wi c wzór (1) dla n=1 jest prawdziwy. Czyli L = P a wi c wzór (1) dla n=2 jest prawdziwy.

1.59 1 + +... + n = n(n+1) (1) Sprawd¹my wzór dla n=1: L = 1 P = 1(1+1) = = 1 Czyli L = P a wi c wzór (1) dla n=1 jest prawdziwy. Sprawd¹my wzór dla n=: L = 1 + = 3 P = (+1) = 6 = 3 Czyli L = P a wi c

Kurs wyrównawczy dla kandydatów i studentów UTP

Kurs wyrównawczy dla kandydatów i studentów UTP Część III Funkcja wymierna, potęgowa, logarytmiczna i wykładnicza Magdalena Alama-Bućko Ewa Fabińska Alfred Witkowski Grażyna Zachwieja Uniwersytet Technologiczno

( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 2. r s. ( i. REGRESJA (jedna zmienna) e s = + Y b b X. x x x n x. cov( (kowariancja) = (współczynnik korelacji) = +

REGRESJA jda zma + prota rgrj zmj wzgldm. przlo wartoc paramtrów trukturalch cov r waga: a c cov kowaracja d r cov wpółczk korlacj Waracja rztowa. Nch gdz + wtd czl ozacza rd tadardow odchl od protj rgrj.

ZAGĘSZCZARKI REWERSYJNE

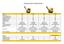Typ LG 160 LG 160 LG 200 LG 200 Masa [kg] 161 175 217 231 Siła wymuszająca [kn] 28 28 36 36 Prędkość liniowa [m/min] 22 22 25 25 Szerokość płyty [mm] 450 450 500 500 Długość płyty [mm] 655 650 700 700

Rachunek ró»niczkowy funkcji jednej zmiennej

Lista Nr 5 Rachunek ró»niczkowy funkcji jednej zmiennej 5.0. Obliczanie pochodnej funkcji Pochodne funkcji podstawowych. f() = α f () = α α. f() = log a f () = ln a '. f() = ln f () = 3. f() = a f () =

2 3 / m S t a n d a r d w y m a g a ń e g z a m i n m i s t r z o w s k i dla zawodu L A K I E R N I K S A M O C H O D O W Y Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy

Służą opisowi oraz przewidywaniu przyszłego kształtowania się zależności gospodarczych.

MODEL EOOMERYCZY MODEL EOOMERYCZY DEFIICJA Modl konomtrczn jst równanm matmatcznm (lub układm równao), któr przdstawa zasadncz powązana loścow pomędz rozpatrwanm zjawskam konomcznm., uwzględnającm tlko

Portfele zawierające walor pozbawiony ryzyka. Elementy teorii rynku kapitałowego

Portel nwestycyjny ćwczena Na podst. Wtold Jurek: Konstrukcja analza rozdzał 5 dr chał Konopczyńsk Portele zawerające walor pozbawony ryzyka. lementy teor rynku kaptałowego 1. Pożyczane penędzy amy dwa

lim lim 4) lim lim lim lim lim x 3 e e lim lim x lim lim 2 lim lim lim Zadanie 1 Wyznacz dziedziny następujących funkcji: log x x 6x

Tmat : Funkcj jdnj zminnj Zadani Wyznacz dzidziny następujących funkcji: ) f ) f 5) log 6 ) f ) f 7 Zadani Oblicz granic funkcji: log f 5 6) f 7 8 ) ) ) 8 7 ) 5) 6) 7) 8) 9) 5 5 7 7 7 6 0) 6 ) ) 9) 0)

ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM ROZSZERZONY. S x 3x y. 1.5 Podanie odpowiedzi: Poszukiwane liczby to : 2, 6, 5.

Nr zadania Nr czynno ci... ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM ROZSZERZONY Etapy rozwi zania zadania Wprowadzenie oznacze : x, x, y poszukiwane liczby i zapisanie równania: x y lub: zapisanie

f(x, y) = arctg x y. f(u) = arctg(u), u(x, y) = x y. x = 1 1 y = y y = 1 1 +

Różnczkowalność pocodne Ćwczene. Znaleźć pocodne cz astkowe funkcj f(x, y) = arctg x y. Rozw azane: Wdać, że funkcj f można napsać jako f(u(x, y)) gdze f(u) = arctg(u), u(x, y) = x y. Korzystaj ac z reg

EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA

EFEKTYWNA STOPA PROCENTOWA O RÓWNOWAŻNA STPOPA PROCENTOWA Nekedy zachodz koneczność zany okesu kapt. z ównoczesny zachowane efektów opocentowane. Dzeje sę tak w nektóych zagadnenach ateatyk fnansowej np.

I 3 + d l a : B E, C H, C Y, C Z, ES, F R, G B, G R, I E, I T, L T, L U V, P T, S K, S I

M G 6 6 5 v 1. 2 0 1 5 G R I L L G A Z O W Y T R Ó J P A L N I K O W Y M G 6 6 5 I N S T R U K C J A U 7 Y T K O W A N I A I B E Z P I E C Z E Ń S T W A S z a n o w n i P a s t w o, D z i ę k u j e m y

0 ( 1 ) Q = Q T W + Q W + Q P C + Q P R + Q K T + Q G K + Q D M =

M O D E L O W A N I E I N Y N I E R S K I E n r 4 7, I S S N 1 8 9 6-7 7 1 X O P T Y M A L I Z A C J A K O N S T R U K C J I F O R M Y W T R Y S K O W E J P O D K Ą T E M E F E K T Y W N O C I C H O D

Zawód: monter instalacji i urządzeń sanitarnych I. Etap teoretyczny (część pisemna i ustna) egzaminu obejmuje: Z ak res w iadomoś ci i umieję tnoś ci

8 8 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu M O N T E R I N S T A L A C J I I U R Z Ą D Z E Ń S A N I T A R N Y C H Kod z klasyfikacji zawodów i sp e cjaln oś

Funkcje charakterystyczne zmiennych losowych, linie regresji 1-go i 2-go rodzaju

Funkcje charakterystyczne zmiennych losowych, linie regresji -go i 2-go rodzaju Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki

Teoria Sygnałów. II rok Geofizyki III rok Informatyki Stosowanej. Wykład 4. iωα. Własności przekształcenia Fouriera. α α

ora Sygałów rok Gozyk rok ormatyk Stosowaj Wykład 4 Własośc przkształca ourra własość. Przkształc ourra jst low [ β g ] βg dowód: rywaly całkowa jst opracją lową. własość. wrdz o podobństw [ ] dowód :

Ś ź ć ź ć Ź ć ź ć Ą ć ć ć Ą ć ź ć ź ć Ś ć ć ć ć Ą Ą ć ć ć ć ć ć Ś ć Ź ć ć Ą ć ó ń ć ć ó ć ó ń ć ć ć ó ó ń ć ó Śń ó ó ć ó ó ó ó ć ó ń ó ó ó ó Ą ć ź ó ó ó ń ó ó ń ó ó ó ź ó ó ó ó Ść ć Ą ź ć ć ć ć Ś Ą ć ć

5ilAtlzarcielc 6wipro jekt6rtrealizowanycn-z

mn mn mn 52 811 MAC pwzn z k PzAku Ku 2 / fy ylln n 0 \zn Ku Rnln lzb bhunkw w Wzwl wwzw 1 wu /zwzku 1 " nmn,/:zwzku lk MAC Wyzzlnn A. CH A1+A2 A2. hy mjkw B. WAT B+82 127 84,7 82. Wyl mjkw. HmwZxulT AB

25. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU. y +y tgx=sinx

5. RÓWNANIA RÓŻNICZKOWE PIERWSZEGO RZĘDU 5.1. Pojęcia wstępne. Klasfikacja równań i rozwiązań Rozróżniam dwa zasadnicze tp równań różniczkowch: równania różniczkowe zwczajne i równania różniczkowe cząstkowe.

Katalog sygnałów pomiarowych. Obowiązuje od 10 marca 2015 roku

Załącznik nr 3 do Standardu technicznego nr 2/DTS/2015 - sygnały przesyłane z obiektów elektroenergetycznych do systemu SCADA w TAURON Dystrybucja S.A. Katalog sygnałów pomiarowych Obowiązuje od 10 marca

WYDZIAŁ INFORMATYKI I ZARZĄDZANIA, studia niestacjonarne ANALIZA MATEMATYCZNA1, lista zadań 1

WYDZIAŁ INFORMATYKI I ZARZĄDZANIA, studia niestacjonarne ANALIZA MATEMATYCZNA, lista zadań. Dla podanych ciągów napisać wzory określające wskazane wyrazy tych ciągów: a) a n = n 3n +, a n+, b) b n = 3

Wrocław, dnia 31 marca 2017 r. Poz UCHWAŁA NR XXXVII/843/17 RADY MIEJSKIEJ WROCŁAWIA. z dnia 23 marca 2017 r.

ZENN URZĘY EÓZTA LNŚLĄE, 31 2017.. 1547 UHAŁA NR XXXV/843/17 RAY EE RŁAA 23 2017. p ó p gó N p. 18. 2 p 15 8 1990. ą g (. U. 2016. p. 814, 1579 1948). 210. 1. 4 14 g 2016. p pą ę - ś (. U. 2017. p. 60),

1 Ró»niczka drugiego rz du i ekstrema

Plan Spis tre±ci 1 Pochodna cz stkowa 1 1.1 Denicja................................ 1 1.2 Przykªady............................... 2 1.3 Wªasno±ci............................... 2 1.4 Pochodne wy»szych

WPROWADZENIE DO TEORII DECYZJI STATYSTYCZNYCH

Ćwczene nr 1 Statystyczne metody wspomagana decyzj Teora decyzj statystycznych WPROWADZENIE DO TEORII DECYZJI STATYSTYCZNYCH Problem decyzyjny decyzja pocągająca za sobą korzyść lub stratę. Proces decyzyjny

6 0 / m S t a n d a r d w y m a g a ń - e g z a m i n m i s t r z o w s k i dla zawodu K R A W I E C Kod z klasyfikacji zawodów i sp e cjaln oś ci dla p ot r ze b r yn ku p r acy Kod z klasyfikacji zawodów

Róniczka. f x. V Vx. Zadanie 4. Znale maksymalny błd bezwzgldny i wzgldny powstały przy obliczaniu objtoci stoka, jeli promie podstawy wynosi

Róniczka Wraenie d nazwa si róniczk pierwszego rzdu czci liniow przrostu wartoci unkcji Zastosowanie róniczki do oblicze przblionch: Zadanie Za pomoc róniczki oblicz przblion warto liczb Wkorzstam wzór

Rozdział 1. Nazwa i adres Zamawiającego Rozdział 2. Informacja o trybie i stosowaniu przepisów Rozdział 3. Przedmiot zamówienia

Z n a k s p r a w y G O S I R D Z P I 2 7 1 0 1 0 2 0 1 4 S P E C Y F I K A C J A I S T O T N Y C H W A R U N K Ó W Z A M Ó W I E N I A f S p r z» t a n i e i u t r z y m a n i e c z y s t o c i g d y

CAŠKA NIEOZNACZONA. Politechnika Lubelska. Z.Šagodowski. 18 lutego 2016

WYKŠAD CAŠKA NIEOZNACZONA Z.Šagodowski Politechnika Lubelska 8 lutego 06 Denicja CAŠKA NIEOZNACZONA Funkcja F jest funkcja pierwotn funkcji f na przedziale A, je»eli Zauwa»my,ze F (x) = f (x), dla ka»dego

O F E R T A H o t e l Z A M E K R Y N * * * * T a m, g d z i e b łł k i t j e z i o r p r z e p l a t a s ił z s o c z y s t z i e l e n i t r a w, a r a d o s n e t r e l e p t a z m i a r o w y m s z

Temat: Pochodna funkcji. Zastosowania

Tmat: Pochodna funkcji. Zastosowania A n n a R a j f u r a, M a t m a t y k a s m s t r, W S Z i M w S o c h a c z w i Kody kolorów: Ŝółty now pojęci pomarańczowy uwaga A n n a R a j f u r a, M a t m a

( t) UKŁADY TRÓJFAZOWE

KŁDY TRÓJFW kładm wilofazowym nazywamy zbiór obwodów lktrycznych (fazowych) w których działają napięcia żródłow sinusoidaln o jdnakowj częstotliwości przsunięt względm sibi w fazi i wytwarzan przważni

Ś Ń ź Ś ź Ś Ś Ś Ś Ś Ś Ś Ą Ś Ż ż ż Ż ć ć ź ź ÓĆ ć Ż Ą ć Ż ż ć Ą Ł Ś Ń ć Ś Ą Ą ż Ż Ą ź Ą ź Ą ż Ś Ń Ł Ś Ś Ó Ą ż ż Ś Ń Ł Ś ż ź ź Ą ć ż ż ć ć ż ć ż Ą ż Ł ż ć ż ż Ż ż ż ż ć Ąć ż ż ż Ż Ż ż ż ć ż ć ż ż ż Ż ż ż

Politechnika Wrocławska Instytut Maszyn, Napędów i Pomiarów Elektrycznych. Materiał ilustracyjny do przedmiotu. (Cz. 2)

Poltchnka Wrocławska nstytut Maszyn, Napędów Pomarów Elktrycznych Matrał lustracyjny do przdmotu EEKTOTEHNKA (z. ) Prowadzący: Dr nż. Potr Zlńsk (-9, A0 p.408, tl. 30-3 9) Wrocław 004/5 PĄD ZMENNY Klasyfkacja

Metoda Elementów Skończonych w Modelowaniu Układów Mechatronicznych. Układy prętowe (Scilab)

Mtoda Elmntów Skończonych w Modlowaniu Układów Mchatronicznych Układy prętow (Scilab) str.1 I. MES 1D układy prętow. Podstawow informacj Istotą mtody lmntów skończonych jst sposób aproksymacji cząstkowych