WYZNACZANIE MAP ZAGROŻENIA POWODZIOWEGO: TEORIA I PRAKTYKA

Transkrypt

1 337 WYZNACZANIE MAP ZAGROŻENIA POWODZIOWEGO: TEORIA I PRAKTYKA Renata J. Romanowicz 1, Adam Kiczko 2, Marzena Osuch 3 Streszczenie: W niniejszej pracy przedstawiony jest wpływ niepewności na wyznaczanie stref zagrożenia powodziowego. W tym celu dokonano porównania dwóch podejść do modelowania przepływów wezbraniowych. Pierwsze bazuje na powszechnie stosownym modelowaniu deterministycznym, nieuwzględniającym elementu losowości, w drugim uwzględniona została niepewność obserwacji i struktury modelu, poprzez przyjęcie stochastycznego charakteru parametrów i wymuszeń modelu. Do wyznaczenia rozkładów prawdopodobieństwa symulowanych rzędnych lustra wody oraz wyznaczonych zasięgów zalewów zastosowano bayesowską teorię stochastyczną. Modele przepływu zostały zaimplementowane dla zlewni Górnej Narwi. Wyniki badań wskazują na duże znaczenie niepewności na uzyskiwane wyniki. Słowa kluczowe: mapy prawdopodobieństwa zalewisk powodziowych, bayesowska analiza niepewności, model przepływu HEC-RAS, przepływy maksymalne roczne. WPROWADZENIE W modelowaniu systemów przyrodniczych stosowane są dwa zasadnicze podejścia: deterministyczne i stochastyczne. W pierwszym z nich, błędy obserwacji wejść i wyjść systemu, takie jak przepływy, stany wód, opady deszczu, temperatura powietrza, są pomijane. W drugim podejściu uwzględniany jest wspływ błędów na uzyskiwane wyniki. W obu podejściach procesy fizyczne mogą być opisane za pomocą modeli wyprowadzonych na podstawie zasad zachowania masy, energii czy pędu. Modele takie opisane są za pomocą równań różniczkowych cząstkowych, które ze względu na swój nieliniowy charakter oraz złożone warunki brzegowe i początkowe, nie mają rozwiązań analitycznych, lecz są rozwiązywane za pomocą metod numerycznych, przy założeniu szeregu uproszczeń dotyczących struktury modelu. Przykładem tego typu modelu jest np. model transformacji przepływu opisany równaniami Saint Venanta. Model ten stanowi podstawę popularnych pakietów numerycznych takich jak MIKE11 ( czy HEC-RAS UNET (Barkau, 1993), stosowanych w praktyce do wyznaczania zasięgu powodzi. Należy podkreślić, że dwu- oraz trzy-wymiarowe modele hydrodynamiczne są bardziej odpowiednie do modelowania skomplikowanych procesów przepływu w ciekach naturalnych, jednak ich zastosowanie jest znacznie mniej powszechne z uwagi na ograniczoną ilość danych niezbędnych do prawidłowej identyfikacji oraz weryfikacji tego typu modeli. Modele przepływu (zarówno jedno- jak i dwu- i trzy-wymiarowe) wymagają określenia parametrów szorstkości, geometrii koryta i obszarów zalewowych, które zwykle są określane na podstawie pomiarów. Ze względu na błędy pomiarowe, wynikające z konieczności wprowadzania przybliżeń i aproksymacji oraz ze względu na przybliżony charakter rozwiązań numerycznych, obliczane wartości stanów wody w rzece obarczone są dużą niepewnością (Grayson i inni 1992; Horritt, 2000; Hankin i inni, 2001). 1 Renata J. Romanowicz Instytut Geofizyki Polskiej Akademii Nauk, romanowicz@igf.edu.pl 2 Adam Kiczko Instytut Geofizyki Polskiej Akademii Nauk, akiczko@igf.edu.pl 3 Marzena Osuch Instytut Geofizyki Polskiej Akademii Nauk, marz@igf.edu.pl

2 338 W zalecanej obecnie w Polsce metodyce wyznaczania zasięgu stref zalewowych o określonym prawdopodobieństwie proponuje się deterministyczne symulacje jednowymiarowego modelu przepływu dla fal o podanym prawdopodobieństwie przewyższenia (Radczuk i inni, 2001; Kitkowski i Nieznański, 2009). W podejściu tym nie są brane pod uwagę niepewności wynikające z błędów obserwacji używanych przy estymacji parametrów modelu, uproszczeń strukturalnych oraz braku dokładnej znajomości warunków początkowych i brzegowych (w tym również niepewności fali o zadanym prawdopodobieństwie przewyższenia). Tak określone mapy zasięgu wezbrania są następnie używane do określania map ryzyka powodzi. Są one uzyskiwane poprzez przemnożenie prawdopodobieństwa wystąpienia powodzi przez potencjalne straty uzyskane na podstawie informacji o zaludnieniu, infrastrukturze zlewni oraz metodach jej użytkowania. Przy wyznaczaniu tych map zakłada się, że niepewność wynikająca z braku oszacowania prawdopodobieństwa wystąpienia zalewisk jest mała w porównaniu z niepewnością związaną z potencjalnymi kosztami szkód. Należy podkreślić, że czysto deterministyczne podejście do modelowania zasięgu zalewisk nie jest już stosowane w praktyce hydrologicznej krajów Unii Europejskiej od ponad dziesięciu lat (Anselmo i inni, 1996). W związku z tym już najwyższy czas, aby metody uwzględniające niepewności procesów środowiska stały się powszechnie stosowanym w Polsce podejściem w modelowaniu hydrologicznym nie tylko na etapie badań rozwojowych, ale również w zastosowaniach praktycznych. Celem pracy jest oszacowanie wpływu niepewności na wyznaczanie stref zagrożenia powodziowego. W celu oszacowania niepewności symulowanych prognoz stanów wody w rzece oraz przepływów zastosujemy, opartą na teorii Bayesa, Uogólnioną Metodę Estymacji Niepewności przy pomocy Funkcji Wiarygodności, popularnie określaną za angielskim akronimem GLUE (ang. Generalised Likelihood Uncertainty Estimation) (Beven i Binley, 1992). W podejściu tym zakłada się, że w przypadku skomplikowanych modeli środowiska z nadmierną liczbą parametrów w porównaniu z ilością dostępnych obserwacji systemu, problem odwrotny nie posiada rozwiązania. W związku z powyższym nie istnieje jednoznacznie określony zbiór parametrów, który optymalizuje wybrany wskaźnik jakości działania modelu. W pracy Romanowicz i inni (1994), wykazano, że przy określonych założeniach podejście to jest analogiczne do analizy bayesowskiej. W celu uniknięcia trudności związanych z dużą wymiarowością problemu, w metodzie GLUE do próbkowania przestrzeni parametrów, stosuje się technikę Monte Carlo. Polega ona na estymacji wag związanych z różnymi zbiorami parametrów, w oparciu o arbitralnie wybrane kryterium oceny działania modelu. Wagi te są następnie używane do wyznaczenia prawdopodobieństwa predykcji zmiennych wyjściowych modelu. Wybór kryterium oceny działania modelu może być równoważny wyborowi rozkładu losowego błędów (różnicy pomiędzy symulowanymi i obserwowanymi zmiennymi) (Romanowicz i inni, 1996). Ponieważ podejście to wymaga wielokrotnych symulacji, jego użycie ograniczone jest do stosunkowo prostych modeli. Pomimo to, zostało ono z sukcesem zastosowane zarówno do problemów o parametrach skupionych, jak i rozłożonych. Oprócz niepewności związanej ze strukturą i parametrami modelu, na estymowany zasięg stref zagrożenia powodziowego, wpływ ma również niepewność oszacowania fali o określonym prawdopodobieństwie przewyższenia (tzw. woda 10-, 100- czy też 1000-letnia). W następnych rozdziałach przedstawiono w skrócie elementy składające się na określenie stref zagrożenia powodziowego, wyznaczenie fali o określonym prawdopodobieństwie przewyższenia, prognoz przepływów na podstawie jednowymiarowego modelu przepływu oraz przedyskutujemy różnice wynikające z uwzględnienia niepewności wejść i parametrów modelu przepływu w porównaniu z stosowanym w praktyce podejściem deterministycznym. Rozważania te będą zilustrowane na przykładzie 7- kilometrowego odcinka rzeki Górnej Narwi pomiędzy Bondarami i ujściem Narewki.

3 339 WYZNACZANIE ROZKŁADÓW PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH Metody wyznaczania przepływów maksymalnych o określonym prawdopodobieństwie przekroczenia opierają się na dopasowaniu znanych analitycznych rozkładów do ciągów przepływów maksymalnych. Ze względu na krótkie ciągi pomiarowe, metody te obarczone są dużymi błędami (Strupczewski i inni, 2002). W niniejszej pracy wykorzystano 30-letni ciąg przepływów maksymalnych rocznych, pomierzonych na wodowskazie w Bondarach. Do empirycznego rozkładu prawdopodobieństwa, wyznaczonego zgodnie z formułą Weibulla, dopasowywano 9 rozkładów prawdopodobieństwa najczęściej stosowanych do opisu przepływów maksymalnych rocznych (ekspotencjalny, GEV, Gumbel, Weibull, logarytmiczno-normalny, logarytmiczno-normalny o trzech parametrach, Gamma, Pearson typ III, log- Pearson typ III). Parametry tych rozkładów były estymowane za pomocą czterech metod: największej wiarygodności (MLM), momentów (MOM), momentów ważonych prawdopodobieństwem (PWM), a dla rozkładu log-pearsona typu III za pomocą metody rekomendowanej przez Water Resources Council (WRC). Statystyczne testy zgodności nie doprowadziły do odrzucenia żadnego rozkładu i na ich podstawie trudno było określić jeden najlepszy rozkład. Dlatego zastosowano cztery dodatkowe kryteria określające dopasowanie rozkładów: kryteria informacyjne Akaike i bayesowskie, średni bezwzględny wskaźnik odchylenia (MADI) i średni kwadratowy wskaźnik odchylenia (MSDI). Na podstawie tych czterech dodatkowych kryteriów oraz testu zgodności χ 2 jako najlepszy przyjęto rozkład logarytmiczno-normalny o dwóch parametrach (LN2), estymowany za pomocą metody największej wiarygodności (MLM). Dla najlepszego rozkładu prawdopodobieństwa LN2 MLM wygenerowano syntetyczne fale wezbraniowe i przeprowadzono symulacje ich transformacji. Rys. 1 ilustruje porównanie rozkładu empirycznego z analizowanymi rozkładami teoretycznymi, natomiast na rys. 2 przedstawiony został estymowany rozkład logarytmicznonormalny z 95% przedziałami ufności (linie kreskowane) oraz rozkład empiryczny oznaczony czarnymi kółkami. Rys. 1. Porównanie rozkładu empirycznego z analizowanymi rozkładami teoretycznymi

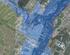
4 340 Rys. 2. Porównanie rozkładu empirycznego (czarne kółka) i rozkładem logarytmiczno-normalnym estymowanym metodą maksymalnej wiarygodności. Linie kreskowane przedstawiają 95% przedziały ufności dla rozkładu teoretycznego STOSOWANA W PRAKTYCE METODYKA OKREŚLANIA ZAGROŻENIA POWODZIOWEGO Zgodnie z zaleceniami przedstawionymi, między innymi, w Radczuk i inni (2001) i Kitkowski i Nieznański (2009), stosowana w praktyce deterministyczna metodyka określania zagrożenia powodziowego składa się z następujących etapów pośrednich: Budowa jednowymiarowego modelu przepływu (tu HEC RAS) w oparciu o dostępną informację o geometrii rzeki oraz terenów zalewowych z uwzględnieniem istniejących konstrukcji inżynieryjnych (mosty, itp.). Deterministyczna kalibracja i weryfikacja jednowymiarowego modelu przepływu w oparciu o dostępne pomiary stanów wody. Wyznaczenie fal powodziowych o zadanych prawdopodobieństwach przewyższenia (p=10%, p=1% oraz p=0.1%). Wyznaczenie zasięgu wezbrania na podstawie symulacji modelu przepływu dla fal o określonym prawdopodobieństwie wystąpienia. Tak określone mapy są następnie używane do oszacowania potencjalnych strat na podstawie informacji o zaludnieniu, infrastrukturze zlewni oraz metod jej użytkowania. Rys. 3 przedstawia mapę zasięgu wezbrania dla Górnej Narwi miedzy Bondarami i Narewką uzyskaną na podstawie deterministycznej prognozy maksymalnych stanów wody dla fali 1000-letniej.

5 341 OKREŚLANIE MAP PRAWDOPODOBIEŃSTWA ZAGROŻENIA POWODZIOWEGO METODĄ STOCHASTYCZNĄ Stochastyczne podejście do wyznaczania zagrożenia powodziowego uwzględniające niepewności obserwacji (zarówno warunków początkowych i brzegowych jak też struktury modelu i obserwacji używanych do estymacji parametrów modelu) składa się z następujących etapów: 1. Budowa, kalibracja i weryfikacja deterministyczna jednowymiarowego modelu przepływu bazując na obserwacjach historycznych. Rys. 3. Zasięg wody 1000-letniej, podejście deterministyczne. 2. Generacja rozkładów a priori dla parametrów modelu (współczynników szorstkości) oraz warunków brzegowych (dopływy boczne) przy użyciu metody próbkowania Latin Hypercube. 3. Stochastyczna kalibracja modelu w oparciu o historyczne pomiary stanów wody: kalibracja modelu uwzględniająca wielokrotne symulacje jednowymiarowego modelu przepływu dla losowo wybranych parametrów modelu (współczynników szorstkości), warunków początkowych (przepływów historycznych) oraz losowych warunków brzegowych (dopływów bocznych). 4. Bayesowskie warunkowanie predykcji modelu na dostępnych obserwacjach (wersja metody GLUE) w celu wyznaczenia rozkładów a posteriori parametrów modelu. 5. Stochastyczna weryfikacja modelu: weryfikacja modelu w oparciu o wielokrotne symulacje dla przepływów historycznych innych niż stosowane podczas kalibracji; rozkład a posteriori parametrów uzyskany w czasie kalibracji służy do wyznaczenia rozkładów a posteriori predykcji modelu (maksymalnych stanów wody w przekrojach poprzecznych analizowanego odcinka rzeki). 6. Generacja wiązek fal wezbraniowych o zadanym prawdopodobieństwie wystąpienia. 7. Wielokrotna symulacja jednowymiarowego modelu przepływu dla losowo wybranych

6 342 parametrów (współczynników szorstkości), warunków początkowych (wiązka fal o zadanym prawdopodobieństwie) oraz losowych warunków brzegowych (dopływów bocznych). 8. Wyznaczanie predykcji a posteriori wyjść modelu w postaci rozkładu stanów wody w przekrojach poprzecznych analizowanego odcinka rzeki dla fal powodziowych o określonym prawdopodobieństwie przewyższenia oraz wyznaczenie map prawdopodobieństwa maksymalnego zasięgu wezbrania. Etapy 1-5 służą do wyznaczenia rozkładów a posteriori parametrów modelu przepływu i stanowią stochastyczne rozwinięcie dwóch pierwszych etapów podejścia deterministycznego przedstawionego w rozdziale 3. Etap 6 pokrywa się z etapem 3 podejścia deterministycznego, natomiast etapy 7-8 są rozwinięciem stochastycznym etapu 4-tego z podejścia deterministycznego. Szersze omówienie poszczególnych etapów wyznaczania map prawdopodobieństwa zasięgu wezbrania znajduje się w pracach Romanowicz i inni (1996), Romanowicz i Beven (1998, 2003), Romanowicz i inni (2005) oraz Kiczko i inni (2007). Rys. 4. Zasięg wody 1000-letniej, wyznaczony z zastosowaniem metody GLUE Proponowane tu podejście różni się od poprzednio opisanych poprzez uwzględnienie niepewności fal wezbraniowych. W tym celu oszacowano niepewność kwantyli dla fal o określonym prawdopodobieństwie przewyższenia, odpowiadającym fali 100-letniej oraz 1000-letniej. Na tej podstawie wygenerowano wiązki o 10- elementach przy założeniu rozkładu normalnego dla kwantyli. Bardziej poprawnym statystycznie byłoby założenie niepewności parametrów rozkładu log-normalnego, z którego generowane są kwantyle. Jednak ze względu na poglądowy charakter tej pracy, zastosowano prostszą metodę, która nie zmienia zasadniczo wyników rozważań. Ponadto, w celu uwzględnienia prawdopodobieństwa prób z kwantyli (elementów wiązki) w oszacowaniu całkowitego prawdopodobieństwa predykcji modelu, założono niezależność modelu statystycznego wejść od modelu statystycznego parametrów opisujących przejście fali i przemnożono oba prawdopodobieństwa (Romanowicz i inni, 2006).

7 343 Na rys. 4 przedstawiona jest mapa prawdopodobieństwa zagrożenia powodziowego. Pole o najbardziej jasnym odcieniu szarego odpowiada prawdopodobieństwu zalania 0,05 (5%), ciemniejszy odcień odpowiada prawdopodobieństwu zalania 0,5 (50%), a najciemniejszy odcień odpowiada prawdopodobieństwu zalania 0,95 (95%). PORÓWNANIE WYNIKÓW I DYSKUSJA Metoda wyznaczania map zagrożenia powodziowego dla fali o zadanym prawdopodobieństwie przewyższenia, zgodna z praktykowanym podejściem (Kitkowski i Nieznański, 2009) jest niewątpliwie znacznie prostsza od podejścia uwzględniającego niepewność zarówno fali wejściowej jak i parametrów modelu transformacji fali. Przy porównaniu obu podejść, należy pamiętać, że uzyskane mapy przedstawiają diametralnie różne wielkości. Podczas gdy mapa deterministyczna (rys. 3) przedstawia tereny zalane dla wygenerowanej fali powodziowej uzyskane na postawie maksymalnych wysokości stanów wody dla pojedynczej symulacji modelu transformacji fali wezbraniowej (w tym wypadku HEC-RAS), mapa z rys. 4 przedstawia zmieniające się przestrzennie prawdopodobieństwa zasięgu wezbrania. Mapy prawdopodobieństwa zasięgu wezbrania są wymagane przy wyznaczaniu ryzyka związanego z powodzią (Radczuk i inni, 2001). W wypadku deterministycznych map zagrożenia powodziowego zachodzi pytanie, jakie prawdopodobieństwo należy im przypisać aby móc je użyć do wyznaczenia ryzyka powodziowego, jak również porównać z mapami prawdopodobieństwa zagrożenia powodziowego. Dla lepszego wyjaśnienia problemu, rys. 5 przedstawia dystrybuantę stanów wody na przekroju 5 w pobliżu wsi Słobódka z zaznaczonym stanem wody odpowiadającym fali wezbraniowej z podejścia deterministycznego dla wody 100-letniej. 1 Woda 100-letnia przek. nr: 5 Dystrybuanta (cdf) H [m] Rys. 5. Dystrybuanta (cdf) stanów w rzece w przekroju poprzecznym 5 w pobliżu wsi Słobódka dla wody 100-letniej z uwzględnieniem niepewności kwantyli fali powodziowej oraz niepewności parametrycznej modelu przepływu. Linią przerywaną zaznaczono stan wody odpowiadający fali wezbraniowej w podejściu deterministycznym, gwiazdki oznaczają kwantyle o prawdopodobieństwie przekroczenia 0,05, 0,5 i 0,95 Z rys. 5 wynika, że wygenerowana fala wezbraniowa w podejściu deterministycznym odpowiada prawdopodobieństwu przewyższenia 0,3 co oznacza, że prawdopodobieństwo,

8 344 że stan wody będzie niższy niż stan wody wyznaczony w podejściu deterministycznym (na danym przekroju rzeki) wynosi 0,7. Tak więc granice zalewisk dla rozważanego przekroju wyznaczone za pomocą metody deterministycznej nie odpowiadają ani maksymalnemu prawdopodobnemu zalaniu ani zalaniu z prawdopodobieństwem 0,5. Ponadto, każdy z przekrojów poprzecznych na analizowanym odcinku rzeki będzie się charakteryzował inną dystrybuantą stanów wody oraz inną relacją ze stanem wody wyznaczonym w podejściu deterministycznym. Ze względu na brak możliwości bezpośredniego porównania deterministycznej mapy zasięgu wezbrania z stochastyczną mapą prawdopodobieństwa zasięgu wezbrania, założono, że mapa deterministyczna reprezentuje prawdopodobieństwo wystąpienia 0,5. Rys. 6 przedstawia porównanie map zasięgu wezbrania o prawdopodobieństwie 0,5, uzyskanych metodą stochastyczną i deterministyczną. Na rys. 6 zasięg wezbrania wyznaczony metodą deterministyczną pokazany jest kolorem jaśniejszym natomiast zasięg wezbrania uzyskany metodą stochastyczną jest zaznaczony kolorem ciemniejszym. Tak wiec zakładając, że deterministyczna mapa zasięgu wezbrania odpowiada 0,5 prawdopodobieństwu zalania, zaniża ona obszar zalewisk. Rys. 6. Zasięg wody 100-letniej, porównanie wyników podejścia stochastycznego (zasięg o prawdopodobieństwie 0,5) i deterministycznego Podsumowując, w pracy pokazano, że stosowana obecnie podejście deterministyczne w wyznaczania zagrożenia powodziowego (pojedyncza realizacja modelu transformacji fali wezbraniowej) nie daje odpowiedzi na pytanie, jakie są prawdopodobieństwa zagrożenia powodziowego, i tym samym nie spełnia wymogów Dyrektywy Wodnej UE (2007/60/EC). Przedstawione tu rozważania wskazują również na niejednoznaczność związaną z reprezentacją deterministycznej mapy zasięgu wezbrania, gdyż prawdopodobieństwo wystąpienia zalewisk uzyskanych z pojedynczej realizacji ze zbioru możliwych realizacji jest nieokreślone. W zależności od tego, jakie prawdopodobieństwo przypiszemy tej mapie, uzyskamy inną wartość ryzyka powodzi (dla przypomnienia, ryzyko jest zdefiniowane jako prawdopodobień-

9 345 stwo wystąpienia powodzi pomnożone przez potencjalne straty). Tak więc nie można twierdzić, że niepewność wynikająca z braku oszacowania prawdopodobieństwa wystąpienia zalewisk jest mała w porównaniu z niepewnością związaną z potencjalnymi kosztami szkód bez określenia tej niepewności. LITERATURA Anzelmo V., Galatei G., Palmieri S., Rossi U., Todini E., 1996: Flood risk assessment using an integrated hydrological and hydraulic modeling approach: a case study. J. Hydrol., 175, s Barkau R.L., 1993: UNET, one-dimensional flow through a full network of open channels, user s manual version 2.1., Publication CPD-66, U.S. Army Corps of Engineers, Davis, CA, Hydrologic Engineering Center. Beven K.J, Binley A., 1992: The future of distributed models: model calibration and uncertainty prediction. Hydrological Processes, 6, s Grayson R.B., Moore I.D., McMahon T.A., 1992: Physically-based hydrologic modeling, 2, Is the concept realistic? Water Resour. Res., 28, s Hankin B.G., Hardy R., Kettle H., Beven K.J., 2001: Using CFD in a GLUE framework to model the flow and dispersion characteristics of a natural fluvial dead zone. Earth Surface Processes and Landforms, 26 (6), s Horritt M.S., 2000: Calibration of a two-dimensional finite element flood flow model using satellite radar imagery. Water Resources Research, 36 (11), s Kiczko, A., Romanowicz R.J., Pappenberger F., 2007: Flood Risk Analysis Of The Warsaw Reach Of The Vistula River, 11th Conference of the ERB, Luksemburg. Kitkowski K., Nieznański P., 2009: Mapy terenów zalewowych w dolinie Odry na obszarze województwa dolnośląskiego. Gospodarka Wodna, nr 3. Radczuk L., Szymkiewicz R., Jełowicki J., Żyszkowska W., Brun J.-F., 2001: Wyznaczanie stref zagrożenia powodziowego. Drukarnia Oficyny Wydawniczej READ-ME w Łodzi. Romanowicz R., Beven K.J., Tawn J., 1994: Evaluation of Predictive Uncertainty in Nonlinear Hydrological Models Using a Bayesian Approach, in: Statistics for the Environment 2, Water Related Issues, Eds. Barnett V., Turkman K.F., s , Romanowicz R., Beven K.J., Tawn J., 1996: Bayesian calibration of flood inundation models. In: Anderson M.G., Walling D.E., Bates P.D. (red.), Floodplain Processes, John Wiley and Sons, Chichester, UK, s Romanowicz R.J., Beven K.J., 1998: Dynamic real time predictions of flood inundation probabilities. Hydrological Sciences Journal, 43, Romanowicz R.J., Beven K.J., 2003: Estimation of flood inundation probabilities as conditioned on event inundation maps. Water Resources Research, VOL. 39, nr 3, /2001WR Romanowicz R.J., Beven K.J., Young P., 2005: Assessing the risk of flood inundation in real time, Proceedings of ACTIF 2nd Workshop, Delft, th November 2004, Romanowicz R.J, Beven K.J., Young P.C., 2006: Uncertainty propagation in a sequential model for flood forecasting, in: Predictions in Ungauged Basins: Promise and Progress (Proceedings of symposium S7 held during the 7th IAHS Scientific Assembly at Foz do Iguacu, Brazil, April 2005), IAHS Publ. 303, s Strupczewski, W.G., Węglarczyk S., Singh V.P., 2002: Model error in flood frequency estimation. Acta Geophysica Pol., 50(2), s

10 346 DERIVATION OF FLOOD RISK MAPS: THEORY AND PRACTICE Summary: This paper discusses methods of deriving flood inundation maps for the purpose of flood risk assessment. The deterministic approach, commonly used in practice, is compared with the stochastic approach that takes into account the uncertainty related to model parameters and initial and boundary conditions. The discussion is illustrated by the example of the Upper Narew river reach. The 1-D HEC-RAS model is used for flow routing. It is calibrated and validated using historical data from the site. The deterministic approach consists of simulating the propagation of a flood wave with an assumed probability of exceedence. The maps of inundation outlines are derived from maximum water levels simulated by a distributed flow routing model (here the HEC-RAS). The stochastic approach applies multiple sampling from the a priori distribution of parameters and random initial and boundary conditions. The same HEC-RAS model is used for the flow routing and the resulting posterior distributions of parameters are used to build the maps of flood inundation probabilities. We apply Bayesian conditioning of the posterior distribution of parameters based on available historical observations. A comparison of the results of both approaches is possible only when the deterministic inundation outlines are given a specific probability value. The paper demonstrates the ambiguity of the deterministic procedure in the derivation of flood inundation probabilities. Key words: maximum annual flow, flow routing model HEC-RAS, Bayesian uncertainty estimation, maps of flood inundation probabilities.