PORÓWNANIE PRZEPŁYWÓW MAKSYMALNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA W MAŁEJ RZECE WYŻYNNEJ

Transkrypt

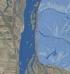
1 MONOGRAFIE KOMITETU GOSPODARKI WODNEJ PAN z. XX 2014 Andrzej BYCZKOWSKI 1, Janusz OSTROWSKI 2, Kazimierz BANASIK 1 1 Szkoła Główna Gospodarstwa Wiejskiego w Warszawie Wydział Budownictwa i Inżynierii Środowiska 2 Instytut Meteorologii i Gospodarki Wodnej PIB PORÓWNANIE PRZEPŁYWÓW MAKSYMALNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA W MAŁEJ RZECE WYŻYNNEJ 1. WPROWADZENIE Przepływy maksymalne roczne o określonym prawdopodobieństwie przewyższenia dla zlewni, w których istnieją wieloletnie ciągi obserwacyjne, określa się przy zastosowaniu ogólnie przyjętych metod, opartych na analizie rozkładów prawdopodobieństwa przepływów maksymalnych. Dyskusyjnymi problemami mogą tu być jedynie dobór właściwego typu rozkładu prawdopodobieństwa oraz metody szacowania parametrów tego rozkładu. W przypadku zlewni, w których nie są prowadzone wieloletnie obserwacje stanów wody oraz pomiary przepływu, stosuje się metody pośrednie, charakteryzujące się większym stopniem niepewności. Zalicza się do nich metody analogii hydrologicznej oraz empiryczne. W pracy podano wyniki obliczeń przepływów maksymalnych rocznych (WQ p ) metodą statystyczną oraz metodami pośrednimi dla rzeki Świśliny w jej górnym biegu, położonej na Wyżynie Kielecko-Sandomierskiej (rys. 1). Powierzchnia zlewni do rozpatrywanego profilu Rzepin wynosi 118 km 2. Długość cieku głównego od źródeł do wodowskazu wynosi 28,2 km, a średni spadek 3,8. Zlewnia użytkowana jest rolniczo; grunty orne stanowią ok. 83% jej powierzchni, użytki zielone ok. 4%, a lasy niespełna 13%. Zbiór danych pomiarowych do obliczeń z okresu (w tym z lat , tj. realizacji programu małych zlewni IMGW (Ostrowski 1994) uzyskano z Centralnej Bazy Danych Historycznych (CBDH) IMGW-PIB. Monografia KGW-PAN, z. XX, tom 1.indb :46:21

2 34 A. Byczkowski, J. Ostrowski, K. Banasik Rys. 1. Lokalizacja i sieć rzeczna zlewni Świśliny po profil Rzepin 2. OSZACOWANIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH METODĄ BEZPOŚREDNIĄ (STATYSTYCZNĄ) Problematyka oszacowania przepływów maksymalnych WQ p na podstawie danych pomiarowych (metodą statystyczną) została szeroko omówiona w literaturze hydrologicznej (Kaczmarek 1970; Ozga-Zielińska, Brzeziński 1994; Byczkowski 1999). W niniejszym artykule badania zrealizowano przy wykorzystaniu ciągu przepływów maksymalnych z okresu 35 lat ( ). Obliczenia przeprowadzono przy zastosowaniu metody tradycyjnej, wykorzystując maksymalne przepływy, jakie wystąpiły w danym roku hydrologicznym AM (Banasik, Byczkowski 2007, 2010), przy użyciu programu komputerowego Q maxp opracowanego w IMGW (Ozga- -Zielińska i in. 1999). Obliczenia przepływów WQ poprzedzone były analizą jednorodności ciągu obserwacyjnego przy pomocy metod statystycznych. Przeprowadzono tu weryfikację: Elementów odstających wg testu Grubbsa-Becka, Niezależności elementów próby wg testu run, Stacjonarności serii przy zastosowaniu trzech testów: Kruskala-Wallisa, Spearmana na trend wartości średniej, Spearmana na trend wariancji. Badania jednorodności serii przepływów maksymalnych wskazują, że 35-letnia seria spełnia wszystkie warunki jednorodności na poziomie istotności µ = 0,05. Chronologiczny ciąg przepływów maksymalnych rocznych przedstawiono na rys. 2. Miary statystyczne ciągu wynoszą: współczynnik zmienności c v = 0,926, współczynnik asymetrii c s = 1,521. Dobór najbardziej wiarygodnej funkcji rozkładu prawdopodobieństwa spośród rozkładów: gamma, Weibulla, log-normalnego i log-gamma, o dolnym ograniczeniu Monografia KGW-PAN, z. XX, tom 1.indb :46:21

3 Porównanie przepływów maksymalnych o określonym prawdopodobieństwie Rys. 2. Przepływy maksymalne roczne w układzie chronologicznym Świśliny w profilu Rzepin Rys. 3. Przepływy maksymalne prawdopodobne Świśliny w profilu Rzepin Tablica 1 Wyniki obliczeń przepływów maksymalnych rocznych WQ o określonym prawdopodobieństwie przewyższenia; rzeka: Świślina, profil: Rzepin, A = 118 km 2, okres Prawdopodobieństwo przewyższenia p [%] Przepływ maksymalny WQ p Odpływy jednostkowe Wq p [m 3 s -1 km 2 ] 0,1 86,30 0,734 1,0 56,5 0,479 2,0 47,6 0,403 5,0 36,0 0,305 10,0 27,3 0,231 50,0 8,32 0,070 Monografia KGW-PAN, z. XX, tom 1.indb :46:22

4 36 A. Byczkowski, J. Ostrowski, K. Banasik x = e 0, został dokonany przy zastosowaniu informacyjnego kryterium Akaike (Mutua 1994). Analiza wykazała, że rozkład gamma (Pearsona T3) najlepiej wyrównuje ciąg przepływów maksymalnych rocznych. Parametry rozkładu prawdopodobieństwa przepływów maksymalnych rocznych (AM) oraz przepływy maksymalne WQ p obliczono metodą największej wiarygodności. Wyniki podano w tablicy 1. oraz przedstawiono na rys OSZACOWANIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH METODAMI POŚREDNIMI 3.1. Oszacowanie przepływów maksymalnych rocznych na podstawie map izorei Do oszacowania wartości przepływów maksymalnych rocznych wykorzystano mapy obszarowego rozkładu maksymalnych odpływów jednostkowych podane w Atlasie hydrologicznym Polski (Stachý 1987). Podane są tu izoreje maksymalnych odpływów jednostkowych Wq p dla p = 1% oraz p = 50%. Wartości przepływów maksymalnych oblicza się ze wzoru: WQ p = Wq p A (1) gdzie: WQ przepływ maksymalny o prawdopodobieństwie przewyższenia p% p [m3 s -1 ] Wq p maksymalny odpływ jednostkowy o prawdopodobieństwie przewyższenia p% odczytywany z Atlasu Hydrologicznego Polski [m 3 s -1 km -2 ] W tablicy 2 zestawiono wartości WQ p obliczone metodą statystyczną oraz metodą izorei. Zauważa się znaczne różnice pomiędzy wartościami odpływów jednostkowych, określonych metodą statystyczną, oraz odczytanych z mapy izorei. Zlewnia górnej Świśliny na mapie izorei (dla p = 1%) położona jest w obszarze, dla którego można przyjąć Wq 1% ok. 1,5 m 3 s -1 km -2. Charakterystyce tej odpowiada przepływ w profilu Rzepin WQ 1% = 177 m 3 s -1. W porównaniu z wartością uzyskaną przy zastosowaniu metody statystycznej różnica względna wynosi 213%. Dla p = 50%, p [%] Tablica 2 Porównanie odpływów jednostkowych obliczonych metodą statystyczną (Wq p) oraz odpływów uzyskanych z mapy izorei (Wq p,) dla Świśliny w przekroju Rzepin WQ p Metoda bezpośrednia (statystyczna) Wq p [m 3 s -1 km -2 ] WQ p Metoda pośrednia (wg mapy izorei) Wq p, [m 3 s -1 km -2 ] WQ p, Różnica = Wq p, Wq p [m 3 s -1 km -2 ] Różnica względna δ = 100% Wq p 1 0,479 56,5 1, , ,070 8,32 0,20 23,6 0, [%] Monografia KGW-PAN, z. XX, tom 1.indb :46:22

5 Porównanie przepływów maksymalnych o określonym prawdopodobieństwie badana zlewnia leży w obszarze, dla którego wartość Wq 50% wynosi 0,2 m 3 s -1 km -2. W tym przypadku różnica względna to 186%. Biorąc pod uwagę, że maksymalne odpływy jednostkowe obliczone metodą statystyczną wynoszą odpowiednio Wq 1% = 0,48 m 3 s -1 km -2, a Wq 50% = 0,07 m 3 s -1 km -2 (tablica 1), to wniosek jest taki, że wartości określone z mapy izorei są zbyt duże Oszacowanie przepływów maksymalnych rocznych metodą regionalnych krzywych prawdopodobieństwa Metoda ta opiera się na kwantylach bezwymiarowej krzywej prawdopodobieństwa obliczanych ze wzoru: μ p = WQ p WQ 50% (2) gdzie: μ p kwantyl bezwymiarowej krzywej prawdopodobieństwa przepływów maksymalnych, WQ p przepływ maksymalny o prawdopodobieństwie przewyższenia p %, WQ 50% przepływ maksymalny o prawdopodobieństwie przewyższenia p 50% [m3 s -1 ]. Wartości kwantyli (µ p ) zostały określone przez Stachỳ i Fal (1986) dla wszystkich profili wodowskazowych w Polsce, dla których istniały długie serie obserwacyjne. Obszar kraju podzielono na 12 regionów, dla których obliczono średnie wartości (µ p ), biorąc pod uwagę wybrane zlewnie w danym regionie. W ten sposób otrzymano rzędne regionalnych bezwymiarowych krzywych prawdopodobieństwa (µ p ) dla każdego regionu. Wartości przepływów maksymalnych o prawdopodobieństwie przewyższenia p% oblicza się z zależności: WQ p = μ p WQ 50% (3) Oznaczenia jak we wzorze 2. Metoda ta, wg zaleceń jej autorów, umożliwia obliczanie przepływów maksymalnych o określonym (niskim) prawdopodobieństwie przewyższenia na podstawie krótkich ciągów obserwacyjnych (8 < N 15 lat), stanowiących podstawę wyznaczenia WQ 50%. Stosując zależność opisaną równaniem (3), wyznaczono przepływ WQ 1% i porównano go z odpowiednim przepływem wyznaczonym metodą bezpośrednią. Wartości kwantyla µ 1% dla regionu 3b, w którym znajduje się zlewnia rzeki Świśliny, po profil Rzepin wynosi 4,28 (Stachỳ i Fal 1986; Byczkowski 1999). Kwantyl ten, ustalony wg przepływów prawdopodobnych uzyskanych za pomocą metody bezpośredniej, zestawionych w tablicy 1, przyjmuje wartość 6,79. Przyjmując do wzoru 3 przepływ maksymalny o prawdopodobieństwie przewyższenia 50% z tablicy 1, tj. obliczony metodą bezpośrednią WQ 50% = 8,32 m 3 s -1, natomiast przepływ maksymalny o prawdopodobieństwie przewyższenia 1%, wg Monografia KGW-PAN, z. XX, tom 1.indb :46:22

6 38 A. Byczkowski, J. Ostrowski, K. Banasik metody regionalnych krzywych prawdopodobieństwa, wyniesie WQ 1% = 35,6 m 3 s -1 (tablica 3). Porównanie zastosowania metody regionalnych krzywych prawdopodobieństwa z wynikami metody bezpośredniej dla WQ 1% przedstawiono w tablicy 3. Oszacowany metodą krzywych regionalnych przepływ WQ 1% jest o 37% niższy od odpowiedniego przepływu obliczonego metodą bezpośrednią. Warto tu zwrócić uwagę, że przepływ WQ 50%, kluczowy w metodzie krzywych regionalnych, a ustalony na podstawie krótkich ciągów obserwacyjnych, szczególnie w przypadku małych zlewni, może znacznie się różnić od odpowiedniej wartości dla długich ciągów, co w konsekwencji będzie dodatkową przyczyną niedokładnych szacunków WQ p (Banasik i in. 2003). Tablica 3 Porównanie wartości przepływów maksymalnych rocznych WQ 1% obliczonych metodą statystyczną oraz metodą regionalnych krzywych prawdopodobieństwa Metoda bezpośrednia (statystyczna) WQ 1 Metoda pośrednia (regionalne krzywe podobieństwa) μ 1% (region 3b) WQ 1,, Różnica = WQ 1,, WQ 1 Różnica względna δ = 100% WQ 1 56,5 4,28 35,6-20,9-37 [%] 4. WNIOSKI 1. Metody pośrednie zastosowane w opracowaniu opierają się na uogólnionych wartościach przepływów, określonych dla dużej liczby stacji wodowskazowych, czynnych w konkretnym, wydzielonym regionie i dotyczą przeciętnych warunków dla danego regionu. Jeżeli warunki formowania się odpływów maksymalnych w rozpatrywanej zlewni odbiegają od przeciętnych dla regionu, wówczas wartości otrzymane metodą statystyczną oraz przy zastosowaniu metod pośrednich mogą być w dużym stopniu zróżnicowane. 2. Wartości WQ p uzyskane na podstawie map izorei wykazują, że w przypadku małych zlewni wartości WQ p mogą być przypadkowe. Należy wziąć pod uwagę, że stopień uogólnienia wartości Wq p na mapie jest na tyle znaczny, że lokalne obszarowe zróżnicowania rozkładu wartości Wq p mogą nie być uchwycone w skali mapy. Metoda ta może dawać zadowalające wyniki dla większych zlewni, które w skali mapy mogą być zlokalizowane z większą dokładnością, a miejscowa zmienność wartości Wq p nie ma istotnego wpływu na wartości Wq p oszacowane na podstawie mapy. 3. Wartości kwantyli regionalnych krzywych prawdopodobieństwa (µ p ) określone zostały przez Stachý i Fal (1986) dla zlewni o różnej powierzchni. W małych zlewniach warunki tworzenia się odpływu mogą znacznie różnić się od przeciętnych warunków panujących w regionie. Wartości kwantyla µ 1% dla regionu 3b, w którym leży zlewnia górnej Świśliny wynosi µ 1% = 4,28, natomiast Monografia KGW-PAN, z. XX, tom 1.indb :46:22

7 Porównanie przepływów maksymalnych o określonym prawdopodobieństwie wartość określona na podstawie danych pomiarowych metodą statystyczną dla profilu Rzepin µ 1% = 6,79. Rozbieżność powyższa wydaje się potwierdzać tezę, że w małych zlewniach występuje większe względne zróżnicowanie przepływów wezbraniowych niż w zlewniach dużych. Po porównaniu wartości współczynnika asymetrii, obliczonych na podstawie ciągu pomiarowego, oraz wartości dla regionu, reguła ta potwierdza się. Współczynnik asymetrii dla Świśliny w profilu Rzepin wynosi c s = 1,52, a odpowiednia wartość dla regionu 3b równa jest jedynie c = 0,80. s 4. W tej sytuacji opieranie się na wartościach kwantyli µ p przeciętnych dla regionu może prowadzić do znacznych błędów. Wydaje się, że w tabeli podającej wartości kwantyli µ p, wypośrodkowane dla poszczególnych regionów, powinny być również podane granice, w jakich zawierają się wartości kwantyli µ p, określone dla poszczególnych rozpatrywanych zlewni. 5. Metody pośrednie, zwłaszcza w przypadku małych zlewni, należy w praktyce inżynierskiej stosować z dużą ostrożnością. Niemniej jednak metody te, w porównaniu ze wzorami empirycznymi stosowanymi dawniej, powinny zapewniać wyniki obarczone znacznie mniejszymi błędami, wobec czego wymagają dalszych weryfikacji. ESTIMATION OF PROBABLE FLOOD FLOWS IN SMALL UPLAND RIVER WITH THE USE OF DIRECT AND INDIRECT METHODS Abstract Direct (statistical) and indirect methods have been applied for estimating T-year flood flows at the gauging station of a small (A = 118 km 2 ) upland river of Swislina, located in Kielce-Sandomierz Uplands ca. 150 km south of Warsaw. River flow data of the period , used for statistical analysis were collected by state hydrological service (the Institute of Meteorology and Water Management in Warsaw). Comparison of the study results showed significant differences of T-year flood flows estimated with various methods. This confirms the need to continue the improvement of indirect methods for small ungauged basins. Key words: hydrological characteristics, small watershed, T-year flood flows BIBLIOGRAFIA Banasik K., Byczkowski A., 2007, Probable annual floods in small lowland river estimated with the use of various sets of data, Annals of Warsaw University of Life Sciences SGGW, Land Reclamation, 38, 3-10, pdf Banasik K., Byczkowski A., 2010, Porównanie przepływów maksymalnych rocznych w małej zlewni rolniczej wyznaczonych różnymi sposobami, [w:] Hydrologia w Inżynierii i Gospodarce Wodnej, B. Więzik (red.), monografia Komitetu Inżynierii Środowiska PAN, 68 (1), Banasik K., Byczkowski A., Gładecki J., 2003, Prediction of T-year flood discharge from small river basin using direct and indirect methods, Annals of Warsaw University of Life Sciences SGGW, Land Reclamation, 34, 3-8 Monografia KGW-PAN, z. XX, tom 1.indb :46:22

8 40 A. Byczkowski, J. Ostrowski, K. Banasik Byczkowski A., 1999, Hydrologia, T. I, Wydawnictwo SGGW, Warszawa Kaczmarek Z., 1970, Metody statystyczne w hydrologii i meteorologii, PIHM, Instrukcje i podręczniki, 78, WKŁ, Warszawa Mutua F.M., 1994, The use of the Akaike information criterion in the identyfication of on optimum flood frequency model, Hydrological Science Journal, 39 (3), Ostrowski J., 1994, Model regionalny małej zlewni MOREMAZ-1, Materiały Badawcze IMGW, seria: Hydrologia i Oceanologia, 17, Warszawa Ozga-Zielińska M., Brzeziński J., 1994, Hydrologia stosowana, PWN, Warszawa Ozga-Zielińska M., Brzeziński J., Ozga-Zieliński B., 1999, Zasady obliczania największych przepływów rocznych o określonym prawdopodobieństwie przewyższenia przy projektowaniu obiektów budownictwa hydrotechnicznego, Materiały Badawcze IMGW, seria: Hydrologia i Oceanologia, 27, Warszawa Stachý J. (red.), 1987, Atlas hydrologiczny Polski, IMGW, Wyd. Komunikacji i Łączności, Warszawa Stachỳ J., Fal B., 1986, Zasady obliczania maksymalnych przepływów prawdopodobnych, Prace Instytutu Badawczego Dróg i Mostów, 3-4 Adres do korespondencji Corresponding author: prof. dr hab. Andrzej Byczkowski, Szkoła Główna Gospodarstwa Wiejskiego w Warszawie, Wydział Budownictwa i Inżynierii Środowiska, Katedra Inżynierii Wodnej, Warszawa, ul. Nowoursynowska 166, kazimierz_banasik@ sggw.pl Monografia KGW-PAN, z. XX, tom 1.indb :46:22