MODELOWANIE DYNAMIKI PIERŚCIENIA WIROWEGO METODĄ CZĄSTEK WIROWYCH Z WYKORZYSTNIEM OBLICZEŃ RÓWNOLEGŁYCH NA KARTACH GRAFICZNYCH
|
|
|
- Antoni Nowicki
- 8 lat temu
- Przeglądów:
Transkrypt
1 MODELOWANIE INŻYNIERSKIE ISSN X 44, s , Gliwice 2012 MODELOWANIE DYNAMIKI PIERŚCIENIA WIROWEGO METODĄ CZĄSTEK WIROWYCH Z WYKORZYSTNIEM OBLICZEŃ RÓWNOLEGŁYCH NA KARTACH GRAFICZNYCH ANDRZEJ KOSIOR, HENRYK KUDELA Instytut Inżynierii Lotniczej, Procesowej i Maszyn Energetycznych, Politechnika Wrocławska henryk.kudela@wr.wroc.l, andrzej.kosior@wr.wroc.l Streszczenie. W artykule rzedstawiono metodę wiru w komórce (VIC Vortex in Cell) służącą do rozwiązywania równań ruchu łynu. Ze względu na długi czas obliczeń rzy użyciu jednego rocesora w racy została rzedstawiona imlementacja metody VIC z wykorzystaniem obliczeń równoległych w środowisku kart graficznych. Uzyskano dzięki temu 46-krotne skrócenie czasu obliczeń. Przedstawione zostały dwa rzyadki testowe. Pierwszy rezentuje orawność obliczeń rowadzonych z wykorzystaniem kart graficznych. Drugi okazuje wływ lekości na rędkość rzemieszczania się ierścienia wirowego. 1. WSTĘP Znaczenie wirowości dla badań zjawisk hydrodynamicznych jest trudne do rzecenienia. Wszystkie rzeływy rzeczywiste mają wirowość różną od zera. Jedną z rostszych, a jednocześnie fascynujących, trójwymiarowych struktur wirowych obserwowanych w ekserymentach, jest ierścień wirowy. Znajduje ona liczne róby wykorzystania w zagadnieniach technicznych, takich jak odwierty odwodne, gaszenie ożarów lub modelowanie zjawisk ogodowych tyu szkwał [6]. Wzajemna interakcja ierścieni wirowych rowadzi do ciekawych zjawisk hydrodynamicznych, takich jak gra wirów (wzajemne rzeciąganie się ierścienie wirowych) czy też rekonekcja (zmiana toologii dwóch zderzających się ierścieni). Do modelowania numerycznego ruchu ierścienia wirowego wybrano metodę cząstek wirowych. Jest to metoda wyjątkowo dobrze nadająca się do modelowania zjawisk wirowych, a także bardzo dobrze nadaje się do rowadzenia obliczeń w środowisku wielorocesorowym. W obliczeniach wykorzystuje się cząstki, które są nośnikami wirowości. Cząstki wirowe umożliwiają w łatwy i efektywny sosób analizę ewolucji ól wirowych. Rozwiązywanie równań ruchu cieczy dla zagadnień trójwymiarowych, niezależnie od użytej metody, wiąże się z długimi czasami obliczeń. Przyrost mocy obliczeniowej komuterów, związany ze zwiększeniem częstotliwości zegara taktującego racę rocesora, w ostatnich latach zdecydowanie się zmniejszył. Dlatego dla rzysieszenia obliczeń zmuszani jesteśmy do stosowania wielorocesorowych środowisk obliczeniowych i oracowywania algorytmów właściwych dla obliczeń równoległych. Niesodziewanie okazało się, że budowane dla gier komuterowych karty graficzne, osiadające niekiedy kilkaset rocesorów strumieniowych, można wykorzystać do obliczeń
2 146 A. KOSIOR, H. KUDELA naukowych. W racy rzedstawiono wyniki numeryczne dla ruchu ierścienia wirowego dla cieczy doskonałej (nielekiej) oraz badania dotyczące wływu lekości na rędkość rzemieszczania się ierścienia. 2. RÓWNANIA RUCHU Równania nieściśliwego, lekiego łynu można zaisać w nastęujący sosób: u 1 u u u t (1) u 0 (2) gdzie u, v, w u jest wektorem rędkości, - gęstością łynu, - ciśnieniem, - kinematycznym wsółczynnikiem lekości, w równaniu (1) działając obustronnie oeratorem można rzekształcić je w równanie Helmholtza dla ewolucji wirowości : ω u ω ω u ω t (3) gdzie ω u. Z warunku nieściśliwości (2) wynika istnienie wektora otencjału A u A (4) Zakładając dodatkowo, że wektor A jest nieściśliwy A 0, jego składowe można wyznaczyć, rozwiązując równanie Poissona Ai i, i 1,2,3 (5) Rozwiązując równanie (5), można obliczyć rędkość ze wzoru (4). W metodzie cząstek wirowych używany jest algorytm dekomozycji lekościowej. Rozwiązanie uzyskuje się w dwóch krokach: najierw rozwiązywane jest równanie Eulera (dla cieczy nielekiej). ω u ω ω u t (6) W drugim kroku symulowany jest efekt lekości orzez rozwiązanie równania dyfuzji. ω ω t (7) Do rozwiązania równania dyfuzji można użyć różnych metod, takich jak Particle Strength Exchange (PSE), metodę Monte Carlo lub metody różnic skończonych. W obecnej racy zastosowano metodę różnic skończonych ze schematem niejawnym do rzybliżonego rozwiązania równania (7). 3. OPIS METODY WIR W KOMÓRCE DLA PRZYPADKU CIECZY NIELEPKIEJ W racy została wykorzystana metoda dekomozycji lekościowej. W metodzie tej rozwiązanie znajdowane jest w dwóch odkrokach. Najierw rozwiązywane są równania ruchu dla łynu nielekiego. W tym celu obszar obliczeniowy został okryty trójwymiarową
3 MODELOWANIE DYNAMIKI PIERŚCIENIA WIROWEGO METODĄ CZĄSTEK 147 siatką strukturalną j1 x, j2y, j3z j 1, j2, j3 1,2,..., N, gdzie x y z h. Ta sama siatka będzie wykorzystywana do rozwiązania równania Poissona. Ciągłe ole wirowości zostało zastąione dyskretnym rozkładem delt Diraca. [1, 4] gdzie ω N x α x x x 1 (8) α oznacza masę (cyrkulację) cząstki wirowej 1, 2, 3 x 1, x 2, x 3 jest zdefiniowana rzez wyrażenie: 3 3 x, x x d x h x, x V V h x. i -ta składowa i i V i i, α w unkcie gdzie V jest objętością komórki z indeksem. Z twierdzenia Helmholtza [7] wiadomo, że wirowość jest unoszona rzez łyn, a więc równanie ruchu cząstek wirowych ma ostać: d x ux, t dt (10) Należy także wziąć od uwagę fakt, że w trójwymiarowym olu wirowym intensywność cząsteczek jest zmieniana rzez efekt zwany rozciąganiem linii wirowych (rawa strona równania (6). A więc: dα u x, t α dt (11) Prędkość w węzłach została obliczona w wyniku rozwiązania równania Poissona (5) metodą różnic skończonych rzy użyciu (4). Układ równań (8), (9) został rozwiązany metodą Rungego Kutty 4. rzędu. W drugim odkroku algorytmu symulowany był wływ lekości na cząsteczki orzez rozwiązanie równania: ω ω t (12) (9) 4. REDYSTRYBUCJA MASY CZĄSTEK WIROWYCH NA WĘZŁY SIATKI W metodzie wirów w komórce cząsteczki mają tendencję do zbierania się w obszarach dużych gradientów rędkości. Może to rowadzić do niedokładności sowodowanych zbytnim zbliżaniem się cząsteczek do siebie. Aby temu zaobiec, cząsteczki umieszcza się z owrotem na węzłach siatki numerycznej (tzw. remeshing). Wykonuje się to rzy omocy interolacji: ~ ~ x j x 3 j n h h (13) gdzie j jest indeksem węzła siatki, a jest indeksem cząsteczki. Jakość interolacji zależy od własności jądra φ. W tej racy zostało wykorzystane nastęujące jądro interolacyjne:
4 148 A. KOSIOR, H. KUDELA 2 5x 2 3 x 2 2 x 1 x 3 / 2 / 2 0 x 1 1 x x (14),. Proces redystrybucji musi być dokonywany w każdym kroku czasowym, aby możliwe było rozwiązanie równania Poissona (5). Jądro (14) jest rzędu m = 4. W rzyadku trójwymiarowym x y, z x y z 4. REALIZACJA NA GPU Z owodu długiego czasu obliczeń owstała otrzeba zastosowania obliczeń równoległych. Wybrana została architektura CUDA wykorzystująca karty graficzne (GPU - Grahics Processing Unit). Szczegóły imlementacji znajdują się w [3]. W celu srawdzenia orawności imlementacji orównano otrzymane wyniki obliczeń na ojedynczym rocesorze (CPU - Central Processing Unit) i na karcie graficznej. Wyniki wykazały orawność imlementacji. Na GPU obliczenia były 46 razy szybsze niż na CPU. Rys.1. Porównanie wyników dla ewolucji ierścienia wirowego o n = 100 krokach czasowych dla obliczeń rowadzonych na CPU (Intel Core i góra) i GPU (NVIDIA GTX480 - dół). Obliczenia na GPU były 46 razy szybsze. 5. PRZEPŁYW NIELEPKI I LEPKI Przerowadzono badania symulujące wływ lekości na zachowanie się ewolucji ierścienia wirowego. Liczbę Reynoldsa rzeływu definiowano jako Re /. Ewolucja ierścienia wirowego w rzeływie nielekim jest widoczna na rys. 1. a w rzeływie lekim na rys. 2. Na rys. 4. i 5. widoczne są odowiednio rzemieszczenie i rędkość ierścienia wirowego w czasie z zależności od lekości. Z zarezentowanych wyników widać, że rędkość translacji ierścienia wirowego w łynie lekim maleje z czasem. Jest to zgodne z wynikami teoretycznymi [2]. Dla rzeływu nielekiego rędkość translacji ierścienia wirowego jest stała, co widać na rys. 4. Pokrywa się ona ze wzorem teoretycznym Kelvina [5]. Wahania w rędkości rzemieszczania wynikają z ustalania się rozkładu wirowości wewnątrz rdzenia ierścienia wirowego. Do obliczeń rzyjęto równomierny rozkład wirowości. Wraz z uływem czasu rozkład wirowości wewnątrz rdzenia rzyjmuje rozkład odobny do rozkładu Gaussa.
5 MODELOWANIE DYNAMIKI PIERŚCIENIA WIROWEGO METODĄ CZĄSTEK 149 Rys.2. Ewolucja ierścienia wirowego w rzeływie nielekim dla Γ = 1.0. Dół - t = 0, góra - t = 10 Rys.3. Ewolucja ierścienia wirowego w rzeływie lekim (Re = 1000) dla Γ = 1.0. Dół - t = 0, góra - t = 10 Rys.4. Zależność ołożenia środka ierścienia wirowego od czasu dla rzeływu nielekiego i lekiego Rys.5. Zależność rędkości środka ierścienia wirowego od czasu dla rzeływu nielekiego i lekiego 6. WNIOSKI Z zarezentowanych wyników można wysnuć wnioski, że metoda cząstek wirowych jest odowiednia do badania zagadnień związanych z ewolucją trójwymiarowych struktur wirowych. Mają one fundamentalne znaczenie dla zrozumienia rocesów owstawania i rozwoju turbulencji. Zbudowany rogram obliczeniowy ozwala na symulację trójwymiarowych rzeływów lekich. W racy wykorzystano karty graficzne do obliczeń równoległych. Pozwoliło to na uzyskanie 46-krotnego rzysieszenia obliczeń w stosunku do ojedynczego rdzenia. Rozkład wirowości w rzekroju ierścienia wirowego jest ważnym czynnikiem mającym wływ na jego zachowanie.
6 150 A. KOSIOR, H. KUDELA LITERATURA 1. Cottet G. H., Koumoutsakos P. D.: Vortex Methods: Theory and ractice. Cambridge University Press, 2000, Kalansky F.B., Rudi Yu. A.: Evolution of a viscous vortex ring. Fluid Dynamics 2001, Vol. 36, No Kosior A., Kudela H.: Parallel comutations on GPU in 3D using the vortex article method. htt://dx.doi.org/ /j.comfluid , 4. Kudela H., Regucki P.: The vortex-in-cell method for the study of three-dimensional flows by vortex methods. Tubes, Sheets and Singularities in Fluid Dynamics. Fluid Mechanics and Its Alications. Kluwer Academic Publisher, 2009, Vol. 7, Lim T. T., Nickels T. B.: Vortex rings. Fluid vortices. Editor: Sheldon I. Green. Dordrecht: Kluwer Academic Publishers, Shariff K., Leonard A.: Vortex rings. Annu. Rev. Fluid Mech 1992, Vol. 24, Wu J. Z., Ma H. Y., Zhou M. D.: Vorticity and vortex dynamics. Berlin, Heidelberg: Sringer, Zadanie wsółfinansowane ze środków Unii Euroejskiej w ramach Euroejskiego Funduszu Sołecznego MODELING OF THE VORTEX RING DYNAMICS BY VORTEX PARTICLE METHOD USING PARALLEL COMPUTATION ON GRAPHICS CARDS Summary. The aer resented the Vortex in Cell (VIC) method for solving the fluid motion equations in 3D. Due to the long time of comutation on single rocessor the arallel imlementation of the VIC method was resented. The seed-u for the entire VIC method imlementation on the GPU was 46 times. Two test cases were resented. First one, shows correctness of the arallel imlementation on GPU. Second examle shows influence of viscosity on the translation velocity of the vortex ring.
Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych.
 Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych. Jedną z metod symulacji dynamiki cieczy jest zastosowanie metody siatkowej Boltzmanna.
Katarzyna Jesionek Zastosowanie symulacji dynamiki cieczy oraz ośrodków sprężystych w symulatorach operacji chirurgicznych. Jedną z metod symulacji dynamiki cieczy jest zastosowanie metody siatkowej Boltzmanna.
Mechanika cieczy. Ciecz jako ośrodek ciągły. 1. Cząsteczki cieczy nie są związane w położeniach równowagi mogą przemieszczać się na duże odległości.
 Mecanika cieczy Ciecz jako ośrodek ciągły. Cząsteczki cieczy nie są związane w ołożeniac równowagi mogą rzemieszczać się na duże odległości.. Cząsteczki cieczy oddziałują ze sobą, lecz oddziaływania te
Mecanika cieczy Ciecz jako ośrodek ciągły. Cząsteczki cieczy nie są związane w ołożeniac równowagi mogą rzemieszczać się na duże odległości.. Cząsteczki cieczy oddziałują ze sobą, lecz oddziaływania te
PŁYN Y RZECZYWISTE Przepływy rzeczywiste różnią się od przepływów idealnych obecnością tarcia (lepkości): przepływy laminarne/warstwowe - różnią się
 PŁYNY RZECZYWISTE Płyny rzeczywiste Przeływ laminarny Prawo tarcia Newtona Przeływ turbulentny Oór dynamiczny Prawdoodobieństwo hydrodynamiczne Liczba Reynoldsa Politechnika Oolska Oole University of Technology
PŁYNY RZECZYWISTE Płyny rzeczywiste Przeływ laminarny Prawo tarcia Newtona Przeływ turbulentny Oór dynamiczny Prawdoodobieństwo hydrodynamiczne Liczba Reynoldsa Politechnika Oolska Oole University of Technology
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI ĆWICZENIE NR 2
 INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki łynów ĆWICZENIE NR OKREŚLENIE WSPÓLCZYNNIKA STRAT MIEJSCOWYCH PRZEPŁYWU POWIETRZA W RUROCIĄGU ZAKRZYWIONYM 1.
INSTYTUT INŻYNIERII ŚRODOWISKA ZAKŁAD GEOINŻYNIERII I REKULTYWACJI Laboratorium z mechaniki łynów ĆWICZENIE NR OKREŚLENIE WSPÓLCZYNNIKA STRAT MIEJSCOWYCH PRZEPŁYWU POWIETRZA W RUROCIĄGU ZAKRZYWIONYM 1.
Mechanika płynów. Wykład 9. Wrocław University of Technology
 Wykład 9 Wrocław University of Technology Płyny Płyn w odróżnieniu od ciała stałego to substancja zdolna do rzeływu. Gdy umieścimy go w naczyniu, rzyjmie kształt tego naczynia. Płyny od tą nazwą rozumiemy
Wykład 9 Wrocław University of Technology Płyny Płyn w odróżnieniu od ciała stałego to substancja zdolna do rzeływu. Gdy umieścimy go w naczyniu, rzyjmie kształt tego naczynia. Płyny od tą nazwą rozumiemy
Ćw. 11 Wyznaczanie prędkości przepływu przy pomocy rurki spiętrzającej
 Ćw. Wyznaczanie rędkości rzeływu rzy omocy rurki siętrzającej. Cel ćwiczenia Celem ćwiczenia jest zaoznanie się z metodą wyznaczania rędkości rzeływu za omocą rurek siętrzających oraz wykonanie charakterystyki
Ćw. Wyznaczanie rędkości rzeływu rzy omocy rurki siętrzającej. Cel ćwiczenia Celem ćwiczenia jest zaoznanie się z metodą wyznaczania rędkości rzeływu za omocą rurek siętrzających oraz wykonanie charakterystyki
10. FALE, ELEMENTY TERMODYNAMIKI I HYDRODY- NAMIKI.
 0. FALE, ELEMENTY TERMODYNAMIKI I HYDRODY- NAMIKI. 0.0. Podstawy hydrodynamiki. Podstawowe ojęcia z hydrostatyki Ciśnienie: F N = = Pa jednostka raktyczna (atmosfera fizyczna): S m Ciśnienie hydrostatyczne:
0. FALE, ELEMENTY TERMODYNAMIKI I HYDRODY- NAMIKI. 0.0. Podstawy hydrodynamiki. Podstawowe ojęcia z hydrostatyki Ciśnienie: F N = = Pa jednostka raktyczna (atmosfera fizyczna): S m Ciśnienie hydrostatyczne:
Modelowanie ewolucji trójwymiarowych struktur wirowych w cieczy lepkiej. metoda cząstek wirowych. wykorzystaniem obliczeń równoległych
 Na prawach rękopisu Politechnika Wrocławska Wydział Mechaniczno-Energetyczny Raport serii PREPRINTY nr /2015 Modelowanie ewolucji trójwymiarowych struktur wirowych w cieczy lepkiej metodami cząstek wirowych
Na prawach rękopisu Politechnika Wrocławska Wydział Mechaniczno-Energetyczny Raport serii PREPRINTY nr /2015 Modelowanie ewolucji trójwymiarowych struktur wirowych w cieczy lepkiej metodami cząstek wirowych
Janusz Adamowski METODY OBLICZENIOWE FIZYKI Kwantowa wariacyjna metoda Monte Carlo. Problem własny dla stanu podstawowego układu N cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Inżynierskie metody numeryczne II. Konsultacje: wtorek 8-9:30. Wykład
 Inżynierskie metody numeryczne II Konsultacje: wtorek 8-9:30 Wykład Metody numeryczne dla równań hiperbolicznych Równanie przewodnictwa cieplnego. Prawo Fouriera i Newtona. Rozwiązania problemów 1D metodą
Inżynierskie metody numeryczne II Konsultacje: wtorek 8-9:30 Wykład Metody numeryczne dla równań hiperbolicznych Równanie przewodnictwa cieplnego. Prawo Fouriera i Newtona. Rozwiązania problemów 1D metodą
Porównanie nacisków obudowy Glinik 14/35-POz na spąg obliczonych metodą analityczną i metodą Jacksona
 dr inż. JAN TAK Akademia Górniczo-Hutnicza im. St. Staszica w Krakowie inż. RYSZARD ŚLUSARZ Zakład Maszyn Górniczych GLINIK w Gorlicach orównanie nacisków obudowy Glinik 14/35-Oz na sąg obliczonych metodą
dr inż. JAN TAK Akademia Górniczo-Hutnicza im. St. Staszica w Krakowie inż. RYSZARD ŚLUSARZ Zakład Maszyn Górniczych GLINIK w Gorlicach orównanie nacisków obudowy Glinik 14/35-Oz na sąg obliczonych metodą
GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA
 MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s.8-86, Gliwice 007 GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA EUGENIUSZ
MODELOWANIE INŻYNIERSKIE ISSN 896-77X 33, s.8-86, Gliwice 007 GLOBALNE OBLICZANIE CAŁEK PO OBSZARZE W PURC DLA DWUWYMIAROWYCH ZAGADNIEŃ BRZEGOWYCH MODELOWANYCH RÓWNANIEM NAVIERA-LAMEGO I POISSONA EUGENIUSZ
Mechanika płynp. Wykład 9 14-I Wrocław University of Technology
 Mechanika łyn ynów Wykład 9 Wrocław University of Technology 4-I-0 4.I.0 Płyny Płyn w odróŝnieniu od ciała stałego to substancja zdolna do rzeływu. Gdy umieścimy go w naczyniu, rzyjmie kształt tego naczynia.
Mechanika łyn ynów Wykład 9 Wrocław University of Technology 4-I-0 4.I.0 Płyny Płyn w odróŝnieniu od ciała stałego to substancja zdolna do rzeływu. Gdy umieścimy go w naczyniu, rzyjmie kształt tego naczynia.
W-23 (Jaroszewicz) 20 slajdów Na podstawie prezentacji prof. J. Rutkowskiego
 Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
Bangkok, Thailand, March 011 W-3 (Jaroszewicz) 0 slajdów Na odstawie rezentacji rof. J. Rutkowskiego Fizyka kwantowa fale rawdoodobieństwa funkcja falowa aczki falowe materii zasada nieoznaczoności równanie
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: Wprowadzenie do numerycznej mechaniki płynów Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria cieplna i samochodowa Rodzaj zajęć: wykład,
Nazwa przedmiotu: Wprowadzenie do numerycznej mechaniki płynów Kierunek: Mechanika i Budowa Maszyn Rodzaj przedmiotu: obowiązkowy na specjalności: Inżynieria cieplna i samochodowa Rodzaj zajęć: wykład,
Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika)
 Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika) 1 1 Cel ćwiczenia Celem ćwiczenia jest rozwiązanie równań ruchu ciała (kuli) w ośrodku
Ćwiczenie 2 Numeryczna symulacja swobodnego spadku ciała w ośrodku lepkim (Instrukcja obsługi interfejsu użytkownika) 1 1 Cel ćwiczenia Celem ćwiczenia jest rozwiązanie równań ruchu ciała (kuli) w ośrodku
Ćw. 1 Wyznaczanie prędkości przepływu przy pomocy rurki spiętrzającej
 Ćw. Wyznaczanie rędkości rzeływu rzy omocy rurki siętrzającej. Cel ćwiczenia Celem ćwiczenia jest zaoznanie się z metodą wyznaczania rędkości gazu za omocą rurek siętrzających oraz wykonanie charakterystyki
Ćw. Wyznaczanie rędkości rzeływu rzy omocy rurki siętrzającej. Cel ćwiczenia Celem ćwiczenia jest zaoznanie się z metodą wyznaczania rędkości gazu za omocą rurek siętrzających oraz wykonanie charakterystyki
MECHANIKA PŁYNÓW. Materiały pomocnicze do wykładów. opracował: prof. nzw. dr hab. inż. Wiesław Grzesikiewicz
 MECHANIKA PŁYNÓW Materiały omocnicze do wykładów oracował: ro. nzw. dr hab. inż. Wiesław Grzesikiewicz Warszawa aździernik - odkształcalne ciało stałe Mechanika łynów dział mechaniki materialnych ośrodków
MECHANIKA PŁYNÓW Materiały omocnicze do wykładów oracował: ro. nzw. dr hab. inż. Wiesław Grzesikiewicz Warszawa aździernik - odkształcalne ciało stałe Mechanika łynów dział mechaniki materialnych ośrodków
WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO
 Inżynieria Rolnicza 2(90)/2007 WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO Jerzy Domański Katedra Mechaniki i Podstaw Konstrukcji Maszyn, Uniwersytet Warmińsko-Mazurski
Inżynieria Rolnicza 2(90)/2007 WYZNACZANIE PARAMETRÓW PRZEPŁYWU CIECZY W PŁASZCZU CHŁODZĄCYM ZBIORNIKA CIŚNIENIOWEGO Jerzy Domański Katedra Mechaniki i Podstaw Konstrukcji Maszyn, Uniwersytet Warmińsko-Mazurski
MODEL MATEMATYCZNY I ANALIZA UKŁADU NAPĘDOWEGO SILNIKA INDUKCYJNEGO Z DŁUGIM ELEMENTEM SPRĘŻYSTYM DLA PARAMETRÓW ROZŁOŻONYCH
 Prace Naukowe Instytutu Maszyn, Naędów i Pomiarów Elektrycznych Nr 66 Politechniki Wrocławskiej Nr 66 Studia i Materiały Nr 3 1 Andriy CZABAN*, Marek LIS** zasada Hamiltona, równanie Euler Lagrange a,
Prace Naukowe Instytutu Maszyn, Naędów i Pomiarów Elektrycznych Nr 66 Politechniki Wrocławskiej Nr 66 Studia i Materiały Nr 3 1 Andriy CZABAN*, Marek LIS** zasada Hamiltona, równanie Euler Lagrange a,
Laboratorium komputerowe z wybranych zagadnień mechaniki płynów
 FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
FORMOWANIE SIĘ PROFILU PRĘDKOŚCI W NIEŚCIŚLIWYM, LEPKIM PRZEPŁYWIE PRZEZ PRZEWÓD ZAMKNIĘTY Cel ćwiczenia Celem ćwiczenia będzie analiza formowanie się profilu prędkości w trakcie przepływu płynu przez
CIŚNIENIE W PŁASKIM ŁOŻYSKU ŚLIZGOWYM SMAROWANYM OLEJEM MIKRPOLARYM
 MODELOWANIE INŻYNIERSKIE ISSN 896-77X 8, s. 87-94, Gliwice 9 CIŚNIENIE W PŁASKIM ŁOŻYSKU ŚLIZGOWYM SMAROWANYM OLEJEM MIKRPOLARYM PAWEŁ KRASOWSKI Katedra Podstaw Tecniki, Akademia Morska w Gdyni e-mail:
MODELOWANIE INŻYNIERSKIE ISSN 896-77X 8, s. 87-94, Gliwice 9 CIŚNIENIE W PŁASKIM ŁOŻYSKU ŚLIZGOWYM SMAROWANYM OLEJEM MIKRPOLARYM PAWEŁ KRASOWSKI Katedra Podstaw Tecniki, Akademia Morska w Gdyni e-mail:
Podstawy Procesów i Konstrukcji Inżynierskich. Teoria kinetyczna INZYNIERIAMATERIALOWAPL. Kierunek Wyróżniony przez PKA
 Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
Podstawy Procesów i Konstrukcji Inżynierskich Teoria kinetyczna Kierunek Wyróżniony rzez PKA 1 Termodynamika klasyczna Pierwsza zasada termodynamiki to rosta zasada zachowania energii, czyli ogólna reguła
Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL
 Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL We wstępnej analizie przyjęto następujące założenia: Dwuwymiarowość
Mgr inż. Wojciech Chajec Pracownia Kompozytów, CNT Mgr inż. Adam Dziubiński Pracownia Aerodynamiki Numerycznej i Mechaniki Lotu, CNT SMIL We wstępnej analizie przyjęto następujące założenia: Dwuwymiarowość
J. Szantyr Wykład nr 16 Przepływy w przewodach zamkniętych
 J. Szantyr Wykład nr 6 Przeływy w rzewodach zamkniętych Przewód zamknięty kanał o dowolnym kształcie rzekroju orzecznego, ograniczonym linią zamkniętą, całkowicie wyełniony łynem (bez swobodnej owierzchni)
J. Szantyr Wykład nr 6 Przeływy w rzewodach zamkniętych Przewód zamknięty kanał o dowolnym kształcie rzekroju orzecznego, ograniczonym linią zamkniętą, całkowicie wyełniony łynem (bez swobodnej owierzchni)
J. Szantyr - Wykład nr 30 Podstawy gazodynamiki II. Prostopadłe fale uderzeniowe
 Proagacja zaburzeń o skończonej (dużej) amlitudzie. W takim rzyadku nie jest możliwa linearyzacja równań zachowania. Rozwiązanie ich w ostaci nieliniowej jest skomlikowane i rowadzi do nastęujących zależności
Proagacja zaburzeń o skończonej (dużej) amlitudzie. W takim rzyadku nie jest możliwa linearyzacja równań zachowania. Rozwiązanie ich w ostaci nieliniowej jest skomlikowane i rowadzi do nastęujących zależności
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: KONWEKCJA SWOBODNA W POWIETRZU OD RURY Konwekcja swobodna od rury
INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ INSTRUKCJA LABORATORYJNA Temat ćwiczenia: KONWEKCJA SWOBODNA W POWIETRZU OD RURY Konwekcja swobodna od rury
nieciągłość parametrów przepływu przyjmuje postać płaszczyzny prostopadłej do kierunku przepływu
 CZĘŚĆ II DYNAMIKA GAZÓW 4 Rozdział 6 Prostoadła fala 6. Prostoadła fala Podstawowe własności: nieciągłość arametrów rzeływu rzyjmuje ostać łaszczyzny rostoadłej do kierunku rzeływu w zbieżno - rozbieżnym
CZĘŚĆ II DYNAMIKA GAZÓW 4 Rozdział 6 Prostoadła fala 6. Prostoadła fala Podstawowe własności: nieciągłość arametrów rzeływu rzyjmuje ostać łaszczyzny rostoadłej do kierunku rzeływu w zbieżno - rozbieżnym
Mini-quiz 0 Mini-quiz 1
 rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
rawda fałsz Mini-quiz 0.Wielkości ekstensywne to: a rędkość kątowa b masa układu c ilość cząstek d temeratura e całkowity moment magnetyczny.. Układy otwarte: a mogą wymieniać energię z otoczeniem b mogą
Temperatura i ciepło E=E K +E P +U. Q=c m T=c m(t K -T P ) Q=c przem m. Fizyka 1 Wróbel Wojciech
 emeratura i cieło E=E K +E P +U Energia wewnętrzna [J] - ieło jest energią rzekazywaną między układem a jego otoczeniem na skutek istniejącej między nimi różnicy temeratur na sosób cielny rzez chaotyczne
emeratura i cieło E=E K +E P +U Energia wewnętrzna [J] - ieło jest energią rzekazywaną między układem a jego otoczeniem na skutek istniejącej między nimi różnicy temeratur na sosób cielny rzez chaotyczne
Numeryczna symulacja rozpływu płynu w węźle
 231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
231 Prace Instytutu Mechaniki Górotworu PAN Tom 7, nr 3-4, (2005), s. 231-236 Instytut Mechaniki Górotworu PAN Numeryczna symulacja rozpływu płynu w węźle JERZY CYGAN Instytut Mechaniki Górotworu PAN,
MODELOWANIE PROCESÓW TECHNOLOGICZNYCH WYSTĘPUJĄCYCH W PIECZARKARNIACH: MODEL WYMIANY CIEPŁA I MASY
 Inżynieria Rolnicza 5(123)/2010 MODELOWANIE PROCESÓW TECHNOLOGICZNYCH WYSTĘPUJĄCYCH W PIECZARKARNIACH: MODEL WYMIANY CIEPŁA I MASY Ewa Wacowicz, Leonard Woroncow Katedra Automatyki, Politecnika Koszalińska
Inżynieria Rolnicza 5(123)/2010 MODELOWANIE PROCESÓW TECHNOLOGICZNYCH WYSTĘPUJĄCYCH W PIECZARKARNIACH: MODEL WYMIANY CIEPŁA I MASY Ewa Wacowicz, Leonard Woroncow Katedra Automatyki, Politecnika Koszalińska
Modelowanie oddziaływań struktur wirowych ze ścianami w przepływach lepkich metodą cząstek wirowych
 Na prawach rękopisu Politechnika Wrocławska Instytut Techniki Cieplnej i Mechaniki Płynów Raport serii PREPRINTY nr 02/2008 Modelowanie oddziaływań struktur wirowych ze ścianami w przepływach lepkich metodą
Na prawach rękopisu Politechnika Wrocławska Instytut Techniki Cieplnej i Mechaniki Płynów Raport serii PREPRINTY nr 02/2008 Modelowanie oddziaływań struktur wirowych ze ścianami w przepływach lepkich metodą
POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cieplnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cieplnych
 Laboratorium Termodynamiki i Pomiarów Maszyn Cielnych Przeływomierze zwężkowe POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cielnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cielnych LABORATORIUM
Laboratorium Termodynamiki i Pomiarów Maszyn Cielnych Przeływomierze zwężkowe POLITECHNIKA KRAKOWSKA Instytut Inżynierii Cielnej i Procesowej Zakład Termodynamiki i Pomiarów Maszyn Cielnych LABORATORIUM
Laboratorium Metod i Algorytmów Sterowania Cyfrowego
 Laboratorium Metod i Algorytmów Sterowania Cyfrowego Ćwiczenie 3 Dobór nastaw cyfrowych regulatorów rzemysłowych PID I. Cel ćwiczenia 1. Poznanie zasad doboru nastaw cyfrowych regulatorów rzemysłowych..
Laboratorium Metod i Algorytmów Sterowania Cyfrowego Ćwiczenie 3 Dobór nastaw cyfrowych regulatorów rzemysłowych PID I. Cel ćwiczenia 1. Poznanie zasad doboru nastaw cyfrowych regulatorów rzemysłowych..
LABORATORIUM TECHNIKI CIEPLNEJ INSTYTUTU TECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGETYKI POLITECHNIKI ŚLĄSKIEJ
 INSYUU ECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGEYKI POLIECHNIKI ŚLĄSKIEJ INSRUKCJA LABORAORYJNA emat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA WNIKANIA CIEPŁA DLA KONWEKCJI WYMUSZONEJ W RURZE
INSYUU ECHNIKI CIEPLNEJ WYDZIAŁ INŻYNIERII ŚRODOWISKA I ENERGEYKI POLIECHNIKI ŚLĄSKIEJ INSRUKCJA LABORAORYJNA emat ćwiczenia: WYZNACZANIE WSPÓŁCZYNNIKA WNIKANIA CIEPŁA DLA KONWEKCJI WYMUSZONEJ W RURZE
Sieci obliczeniowe poprawny dobór i modelowanie
 Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
[ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa
![[ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa [ ] 1. Zabezpieczenia instalacji ogrzewań wodnych systemu zamkniętego. 1. 2. Przeponowe naczynie wzbiorcze. ν dm [1.4] 1. 1. Zawory bezpieczeństwa](/thumbs/39/18677346.jpg) . Zabezieczenia instalacji ogrzewań wodnych systemu zamkniętego Zabezieczenia te wykonuje się zgodnie z PN - B - 0244 Zabezieczenie instalacji ogrzewań wodnych systemu zamkniętego z naczyniami wzbiorczymi
. Zabezieczenia instalacji ogrzewań wodnych systemu zamkniętego Zabezieczenia te wykonuje się zgodnie z PN - B - 0244 Zabezieczenie instalacji ogrzewań wodnych systemu zamkniętego z naczyniami wzbiorczymi
5. Jednowymiarowy przepływ gazu przez dysze.
 CZĘŚĆ II DYNAMIKA GAZÓW 9 rzeływ gazu rzez dysze. 5. Jednowymiarowy rzeływ gazu rzez dysze. Parametry krytyczne. 5.. Dysza zbieżna. T = c E - back ressure T c to exhauster Rys.5.. Dysza zbieżna. Równanie
CZĘŚĆ II DYNAMIKA GAZÓW 9 rzeływ gazu rzez dysze. 5. Jednowymiarowy rzeływ gazu rzez dysze. Parametry krytyczne. 5.. Dysza zbieżna. T = c E - back ressure T c to exhauster Rys.5.. Dysza zbieżna. Równanie
WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ
 MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 67-7, Gliwice 006 WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ ZBIGNIEW KOSMA BOGDAN NOGA PRZEMYSŁAW MOTYL Instytut
MODELOWANIE INŻYNIERSKIE ISNN 896-77X 3, s. 67-7, Gliwice 006 WYZNACZANIE RUCHU CIECZY LEPKIEJ METODĄ SZTUCZNEJ ŚCIŚLIWOŚCI NA SIATKACH NAKŁADAJĄCYCH SIĘ ZBIGNIEW KOSMA BOGDAN NOGA PRZEMYSŁAW MOTYL Instytut
( n) Łańcuchy Markowa X 0, X 1,...
 Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Łańcuchy Markowa Łańcuchy Markowa to rocesy dyskretne w czasie i o dyskretnym zbiorze stanów, "bez amięci". Zwykle będziemy zakładać, że zbiór stanów to odzbiór zbioru liczb całkowitych Z lub zbioru {,,,...}
Analiza strat tarcia towarzyszących przemieszczaniu się pierścienia tłokowego
 ARCHIWUM MOTORYZACJI 3,. 1-10 (2006) Analiza strat tarcia towarzyszących rzemieszczaniu się ierścienia tłokowego WOJCIECH SERDECKI Politechnika Poznańska Instytut Silników Salinowych i Transortu Podczas
ARCHIWUM MOTORYZACJI 3,. 1-10 (2006) Analiza strat tarcia towarzyszących rzemieszczaniu się ierścienia tłokowego WOJCIECH SERDECKI Politechnika Poznańska Instytut Silników Salinowych i Transortu Podczas
KOMPUTEROWA SYMULACJA RUCHU CIAŁA SZTYWNEGO. WSPÓŁCZYNNIK RESTYTUCJI
 Autorzy ćwiczenia: J. Grabski, K. Januszkiewicz Ćwiczenie 10 KOPUTEROWA SYULACJA RUCHU CIAŁA SZTYWNEGO. WSPÓŁCZYNNIK RESTYTUCJI 10.1. Cel ćwiczenia Celem ćwiczenia jest rzedstawienie możliwości wykorzystania
Autorzy ćwiczenia: J. Grabski, K. Januszkiewicz Ćwiczenie 10 KOPUTEROWA SYULACJA RUCHU CIAŁA SZTYWNEGO. WSPÓŁCZYNNIK RESTYTUCJI 10.1. Cel ćwiczenia Celem ćwiczenia jest rzedstawienie możliwości wykorzystania
1. Parametry strumienia piaskowo-powietrznego w odlewniczych maszynach dmuchowych
 MATERIAŁY UZUPEŁNIAJACE DO TEMATU: POMIAR I OKREŚLENIE WARTOŚCI ŚREDNICH I CHWILOWYCH GŁÓWNYCHORAZ POMOCNICZYCH PARAMETRÓW PROCESU DMUCHOWEGO Józef Dańko. Wstę Masa wyływająca z komory nabojowej strzelarki
MATERIAŁY UZUPEŁNIAJACE DO TEMATU: POMIAR I OKREŚLENIE WARTOŚCI ŚREDNICH I CHWILOWYCH GŁÓWNYCHORAZ POMOCNICZYCH PARAMETRÓW PROCESU DMUCHOWEGO Józef Dańko. Wstę Masa wyływająca z komory nabojowej strzelarki
POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN. Ćwiczenie H-1 OKREŚLENIE CHARAKTERYSTYK DŁAWIKÓW HYDRAULICZNYCH
 POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie H-1 Temat: OKREŚLENIE CHARAKTERYSTYK DŁAWIKÓW HYDRAULICZNYCH Konsutacja i oracowanie: dr ab. inż. Donat Lewandowski, rof. PŁ
POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie H-1 Temat: OKREŚLENIE CHARAKTERYSTYK DŁAWIKÓW HYDRAULICZNYCH Konsutacja i oracowanie: dr ab. inż. Donat Lewandowski, rof. PŁ
17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
BADANIA SYMULACYJNE PROCESU IMPULSOWEGO ZAGĘSZCZANIA MAS FORMIERSKICH. W. Kollek 1 T. Mikulczyński 2 D.Nowak 3
 VI KONFERENCJA ODLEWNICZA TECHNICAL 003 BADANIA SYMULACYJNE PROCESU IMPULSOWEGO ZAGĘSZCZANIA MAS FORMIERSKICH BADANIA SYMULACYJNE PROCESU IMPULSOWEGO ZAGĘSZCZANIA MAS FORMIERSKICH W. Kollek 1 T. Mikulczyński
VI KONFERENCJA ODLEWNICZA TECHNICAL 003 BADANIA SYMULACYJNE PROCESU IMPULSOWEGO ZAGĘSZCZANIA MAS FORMIERSKICH BADANIA SYMULACYJNE PROCESU IMPULSOWEGO ZAGĘSZCZANIA MAS FORMIERSKICH W. Kollek 1 T. Mikulczyński
9.1 Wstęp Analiza konstrukcji pomp i sprężarek odśrodkowych pozwala stwierdzić, że: Ciśnienie (wysokość) podnoszenia pomp wynosi zwykle ( ) stopnia
 114 9.1 Wstę Analiza konstrukcji om i srężarek odśrodkowych ozwala stwierdzić, że: Stosunek ciśnień w srężarkach wynosi zwykle: (3-5):1 0, 3 10, ρuz Ciśnienie (wysokość) odnoszenia om wynosi zwykle ( )
114 9.1 Wstę Analiza konstrukcji om i srężarek odśrodkowych ozwala stwierdzić, że: Stosunek ciśnień w srężarkach wynosi zwykle: (3-5):1 0, 3 10, ρuz Ciśnienie (wysokość) odnoszenia om wynosi zwykle ( )
Superdyfuzja. Maria Knorps. Wydział Fizyki Technicznej i Matematyki stosowanej, Politechnika Gdańska
 VI Matematyczne Warsztaty KaeNeMów p. 1/2 Superdyfuzja Maria Knorps maria.knorps@gmail.com Wydział Fizyki Technicznej i Matematyki stosowanej, Politechnika Gdańska VI Matematyczne Warsztaty KaeNeMów p.
VI Matematyczne Warsztaty KaeNeMów p. 1/2 Superdyfuzja Maria Knorps maria.knorps@gmail.com Wydział Fizyki Technicznej i Matematyki stosowanej, Politechnika Gdańska VI Matematyczne Warsztaty KaeNeMów p.
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr zimowy 2017/2018 Tomasz Chwiej 22 stycznia 2019 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów
A - przepływ laminarny, B - przepływ burzliwy.
 PRZEPŁYW CZYNNIK ŚCIŚLIWEGO. Definicje odstaoe Rys... Profile rędkości rurze. - rzeły laminarny, B - rzeły burzliy. Liczba Reynoldsa Re D [m/s] średnia rędkość kanale D [m] średnica enętrzna kanału ν [m
PRZEPŁYW CZYNNIK ŚCIŚLIWEGO. Definicje odstaoe Rys... Profile rędkości rurze. - rzeły laminarny, B - rzeły burzliy. Liczba Reynoldsa Re D [m/s] średnia rędkość kanale D [m] średnica enętrzna kanału ν [m
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne. 1. Badanie przelewu o ostrej krawędzi
 Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. adanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
Metody doświadczalne w hydraulice Ćwiczenia laboratoryjne 1. adanie rzelewu o ostrej krawędzi Wrowadzenie Przelewem nazywana jest cześć rzegrody umiejscowionej w kanale, onad którą może nastąić rzeływ.
Jest to zasada zachowania energii w termodynamice - równoważność pracy i ciepła. Rozważmy proces adiabatyczny sprężania gazu od V 1 do V 2 :
 I zasada termodynamiki. Jest to zasada zachowania energii w termodynamice - równoważność racy i cieła. ozważmy roces adiabatyczny srężania gazu od do : dw, ad - wykonanie racy owoduje rzyrost energii wewnętrznej
I zasada termodynamiki. Jest to zasada zachowania energii w termodynamice - równoważność racy i cieła. ozważmy roces adiabatyczny srężania gazu od do : dw, ad - wykonanie racy owoduje rzyrost energii wewnętrznej
Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish
 Michał Januszewski Materialy do broszury końcowej TWING. Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish Od około 5 lat procesory graficzne (GPU) znajdują
Michał Januszewski Materialy do broszury końcowej TWING. Wielkoskalowe obliczenia komputerowej dynamiki płynów na procesorach graficznych -- pakiet Sailfish Od około 5 lat procesory graficzne (GPU) znajdują
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1
 Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
Zagdanienia do egzaminu z Inżynierskich Metod Numerycznych - semestr 1 Tomasz Chwiej 6 czerwca 2016 1 Równania różniczkowe zwyczajne Zastosowanie szeregu Taylora do konstrukcji ilorazów różnicowych: iloraz
PRZESTRZENNY MODEL PRZENOŚNIKA TAŚMOWEGO MASY FORMIERSKIEJ
 53/17 ARCHIWUM ODLEWNICTWA Rok 2005, Rocznik 5, Nr 17 Archives of Foundry Year 2005, Volume 5, Book 17 PAN - Katowice PL ISSN 1642-5308 PRZESTRZENNY MODEL PRZENOŚNIKA TAŚMOWEGO MASY FORMIERSKIEJ J. STRZAŁKO
53/17 ARCHIWUM ODLEWNICTWA Rok 2005, Rocznik 5, Nr 17 Archives of Foundry Year 2005, Volume 5, Book 17 PAN - Katowice PL ISSN 1642-5308 PRZESTRZENNY MODEL PRZENOŚNIKA TAŚMOWEGO MASY FORMIERSKIEJ J. STRZAŁKO
= T. = dt. Q = T (d - to nie jest różniczka, tylko wyrażenie różniczkowe); z I zasady termodynamiki: przy stałej objętości. = dt.
 ieło właściwe gazów definicja emiryczna: Q = (na jednostkę masy) T ojemność cielna = m ieło właściwe zależy od rocesu: Q rzy stałym ciśnieniu = T dq = dt rzy stałej objętości Q = T (d - to nie jest różniczka,
ieło właściwe gazów definicja emiryczna: Q = (na jednostkę masy) T ojemność cielna = m ieło właściwe zależy od rocesu: Q rzy stałym ciśnieniu = T dq = dt rzy stałej objętości Q = T (d - to nie jest różniczka,
Model Pasywnego Trasera w Lokalnie Ergodycznym Środowisku
 w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
w Lokalnie Ergodycznym Środowisku Tymoteusz Chojecki UMCS, Lublin Tomasz Komorowski IMPAN, Warszawa Kościelisko, 10 września 2016, XLV Konferencja Zastosowań Matematyki T. Komorowski, T. Chojecki w Lokalnie
MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW
 1. WSTĘP MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW mgr inż. Michał FOLUSIAK Instytut Lotnictwa W artykule przedstawiono wyniki dwu- i trójwymiarowych symulacji numerycznych opływu budynków wykonanych
1. WSTĘP MODELOWANIE NUMERYCZNE POLA PRZEPŁYWU WOKÓŁ BUDYNKÓW mgr inż. Michał FOLUSIAK Instytut Lotnictwa W artykule przedstawiono wyniki dwu- i trójwymiarowych symulacji numerycznych opływu budynków wykonanych
Modelowanie rynków finansowych z wykorzystaniem pakietu R
 Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
Modelowanie rynków finansowych z wykorzystaniem pakietu R Metody numeryczne i symulacje stochastyczne Mateusz Topolewski woland@mat.umk.pl Wydział Matematyki i Informatyki UMK Plan działania 1 Całkowanie
DWUTEOWA BELKA STALOWA W POŻARZE - ANALIZA PRZESTRZENNA PROGRAMAMI FDS ORAZ ANSYS
 Proceedings of the 5 th International Conference on New Trends in Statics and Dynamics of Buildings October 19-20, 2006 Bratislava, Slovakia Faculty of Civil Engineering STU Bratislava Slovak Society of
Proceedings of the 5 th International Conference on New Trends in Statics and Dynamics of Buildings October 19-20, 2006 Bratislava, Slovakia Faculty of Civil Engineering STU Bratislava Slovak Society of
MODEL MATEMATYCZNY ZAGREGOWANEGO ELEMENTU UKŁADU ELEKTRYCZNEGO W CYFROWYCH SYMULATORACH PRACUJĄCYCH W CZASIE RZECZYWISTYM
 POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 7 Electrical Engineering 20 Sławomir CIEŚLIK* MODEL MATEMATYCZNY ZAGREGOWANEGO ELEMENTU UKŁADU ELEKTRYCZNEGO W CYFROWYCH SYMULATORACH PRACUJĄCYCH
POZNAN UNIVE RSITY OF TE CHNOLOGY ACADE MIC JOURNALS No 7 Electrical Engineering 20 Sławomir CIEŚLIK* MODEL MATEMATYCZNY ZAGREGOWANEGO ELEMENTU UKŁADU ELEKTRYCZNEGO W CYFROWYCH SYMULATORACH PRACUJĄCYCH
Termodynamika 2. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 ermodynamika Projekt wsółfinansowany rzez Unię Euroejską w ramach Euroejskiego Funduszu Sołecznego Siik ciey siikach (maszynach) cieych cieło zamieniane jest na racę. Elementami siika są: źródło cieła
ermodynamika Projekt wsółfinansowany rzez Unię Euroejską w ramach Euroejskiego Funduszu Sołecznego Siik ciey siikach (maszynach) cieych cieło zamieniane jest na racę. Elementami siika są: źródło cieła
MODELOWANIE POŻARÓW. Ćwiczenia laboratoryjne. Ćwiczenie nr 1. Obliczenia analityczne parametrów pożaru
 MODELOWANIE POŻARÓW Ćwiczenia laboratoryjne Ćwiczenie nr Obliczenia analityczne arametrów ożaru Oracowali: rof. nadzw. dr hab. Marek Konecki st. kt. dr inż. Norbert uśnio Warszawa Sis zadań Nr zadania
MODELOWANIE POŻARÓW Ćwiczenia laboratoryjne Ćwiczenie nr Obliczenia analityczne arametrów ożaru Oracowali: rof. nadzw. dr hab. Marek Konecki st. kt. dr inż. Norbert uśnio Warszawa Sis zadań Nr zadania
POLE TEMPERATURY I PRZEMIANY FAZOWE W SWC POŁĄCZENIA SPAWANEGO LASEROWO
 54/22 Archives of Foundry, Year 2006, Volume 6, 22 Archiwum Odlewnictwa, Rok 2006, Rocznik 6, Nr 22 PAN Katowice PL ISSN 1642-5308 POLE TEMPERATURY I PRZEMIANY FAZOWE W SWC POŁĄCZENIA SPAWANEGO LASEROWO
54/22 Archives of Foundry, Year 2006, Volume 6, 22 Archiwum Odlewnictwa, Rok 2006, Rocznik 6, Nr 22 PAN Katowice PL ISSN 1642-5308 POLE TEMPERATURY I PRZEMIANY FAZOWE W SWC POŁĄCZENIA SPAWANEGO LASEROWO
Pierwsze prawo Kirchhoffa
 Pierwsze rawo Kirchhoffa Pierwsze rawo Kirchhoffa dotyczy węzłów obwodu elektrycznego. Z oczywistej właściwości węzła, jako unktu obwodu elektrycznego, który: a) nie może być zbiornikiem ładunku elektrycznego
Pierwsze rawo Kirchhoffa Pierwsze rawo Kirchhoffa dotyczy węzłów obwodu elektrycznego. Z oczywistej właściwości węzła, jako unktu obwodu elektrycznego, który: a) nie może być zbiornikiem ładunku elektrycznego
Dynamiczne struktury danych: listy
 Dynamiczne struktury danych: listy Mirosław Mortka Zaczynając rogramować w dowolnym języku rogramowania jesteśmy zmuszeni do oanowania zasad osługiwania się odstawowymi tyami danych. Na rzykład w języku
Dynamiczne struktury danych: listy Mirosław Mortka Zaczynając rogramować w dowolnym języku rogramowania jesteśmy zmuszeni do oanowania zasad osługiwania się odstawowymi tyami danych. Na rzykład w języku
Płytowe wymienniki ciepła. 1. Wstęp
 Płytowe wymienniki cieła. Wstę Wymienniki łytowe zbudowane są z rostokątnych łyt o secjalnie wytłaczanej owierzchni, oddzielonych od siebie uszczelkami. Płyty są umieszczane w secjalnej ramie, gdzie są
Płytowe wymienniki cieła. Wstę Wymienniki łytowe zbudowane są z rostokątnych łyt o secjalnie wytłaczanej owierzchni, oddzielonych od siebie uszczelkami. Płyty są umieszczane w secjalnej ramie, gdzie są
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MODELOWANIE PROCESÓW ENERGETYCZNYCH Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Nazwa przedmiotu: MODELOWANIE PROCESÓW ENERGETYCZNYCH Kierunek: ENERGETYKA Rodzaj przedmiotu: specjalności obieralny Rodzaj zajęć: wykład, laboratorium I KARTA PRZEDMIOTU CEL PRZEDMIOTU PRZEWODNIK PO PRZEDMIOCIE
Ćwiczenie H-2 WPŁYW UKŁADU ZASILANIA NA MIKROPRZEMIESZCZENIA W DWUSTRONNEJ PODPORZE HYDROSTATYCZNEJ (DPH)
 POLITECHNIKA ŁÓDZKA INSTYTUT OBABIAEK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie H-2 Temat: WPŁYW UKŁADU ZASILANIA NA MIKOPZEMIESZCZENIA W DWUSTONNEJ PODPOZE HYDOSTATYCZNEJ (DPH) Konsultacja i oracowanie: Zatwierdził:
POLITECHNIKA ŁÓDZKA INSTYTUT OBABIAEK I TECHNOLOGII BUDOWY MASZYN Ćwiczenie H-2 Temat: WPŁYW UKŁADU ZASILANIA NA MIKOPZEMIESZCZENIA W DWUSTONNEJ PODPOZE HYDOSTATYCZNEJ (DPH) Konsultacja i oracowanie: Zatwierdził:
Wykład 2. Przemiany termodynamiczne
 Wykład Przemiany termodynamiczne Przemiany odwracalne: Przemiany nieodwracalne:. izobaryczna = const 7. dławienie. izotermiczna = const 8. mieszanie. izochoryczna = const 9. tarcie 4. adiabatyczna = const
Wykład Przemiany termodynamiczne Przemiany odwracalne: Przemiany nieodwracalne:. izobaryczna = const 7. dławienie. izotermiczna = const 8. mieszanie. izochoryczna = const 9. tarcie 4. adiabatyczna = const
Wstęp do metod numerycznych Eliminacja Gaussa Równania macierzowe. P. F. Góra
 Wstęp do metod numerycznych Eliminacja Gaussa Równania macierzowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Co można zrobić z układem równań... tak, aby jego rozwiazania się nie zmieniły? Rozważam
Wstęp do metod numerycznych Eliminacja Gaussa Równania macierzowe P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Co można zrobić z układem równań... tak, aby jego rozwiazania się nie zmieniły? Rozważam
Ć W I C Z E N I E N R C-5
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII ATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ECHANIKI I CIEPŁA Ć W I C Z E N I E N R C-5 WYZNACZANIE CIEPŁA PAROWANIA WODY ETODĄ KALORYETRYCZNĄ
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII ATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ECHANIKI I CIEPŁA Ć W I C Z E N I E N R C-5 WYZNACZANIE CIEPŁA PAROWANIA WODY ETODĄ KALORYETRYCZNĄ
Stany materii. Masa i rozmiary cząstek. Masa i rozmiary cząstek. m n mol. n = Gaz doskonały. N A = 6.022x10 23
 Stany materii Masa i rozmiary cząstek Masą atomową ierwiastka chemicznego nazywamy stosunek masy atomu tego ierwiastka do masy / atomu węgla C ( C - izoto węgla o liczbie masowej ). Masą cząsteczkową nazywamy
Stany materii Masa i rozmiary cząstek Masą atomową ierwiastka chemicznego nazywamy stosunek masy atomu tego ierwiastka do masy / atomu węgla C ( C - izoto węgla o liczbie masowej ). Masą cząsteczkową nazywamy
WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23
 WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23 RÓWNOWAGA SIŁ Siła owierzchniowa FS nds Siła objętościowa FV f dv Warunek konieczny równowagi łynu F F 0 S Całkowa ostać warunku równowagi łynu V nds f dv 0
WYKŁAD 1 WPROWADZENIE DO STATYKI PŁYNÓW 1/23 RÓWNOWAGA SIŁ Siła owierzchniowa FS nds Siła objętościowa FV f dv Warunek konieczny równowagi łynu F F 0 S Całkowa ostać warunku równowagi łynu V nds f dv 0
Porównanie wydajności CUDA i OpenCL na przykładzie równoległego algorytmu wyznaczania wartości funkcji celu dla problemu gniazdowego
 Porównanie wydajności CUDA i OpenCL na przykładzie równoległego algorytmu wyznaczania wartości funkcji celu dla problemu gniazdowego Mariusz Uchroński 3 grudnia 2010 Plan prezentacji 1. Wprowadzenie 2.
Porównanie wydajności CUDA i OpenCL na przykładzie równoległego algorytmu wyznaczania wartości funkcji celu dla problemu gniazdowego Mariusz Uchroński 3 grudnia 2010 Plan prezentacji 1. Wprowadzenie 2.
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż.
 Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
Drgania poprzeczne belki numeryczna analiza modalna za pomocą Metody Elementów Skończonych dr inż. Piotr Lichota mgr inż. Joanna Szulczyk Politechnika Warszawska Instytut Techniki Lotniczej i Mechaniki
OBCIĄŻALNOŚĆ PRĄDOWA GÓRNEJ SIECI TRAKCYJNEJ CURRENT-CARRYING CAPACITY OF OVERHEAD CONTACT LINE
 ARTUR ROJEK, WIESŁAW MAJEWSKI, MAREK KANIEWSKI, TADEUSZ KNYCH OBCIĄŻALNOŚĆ PRĄDOWA GÓRNEJ SIECI TRAKCYJNEJ CURRENT-CARRYING CAPACITY OF OVERHEAD CONTACT LINE Streszczenie W artykule rzedstawiono wyniki
ARTUR ROJEK, WIESŁAW MAJEWSKI, MAREK KANIEWSKI, TADEUSZ KNYCH OBCIĄŻALNOŚĆ PRĄDOWA GÓRNEJ SIECI TRAKCYJNEJ CURRENT-CARRYING CAPACITY OF OVERHEAD CONTACT LINE Streszczenie W artykule rzedstawiono wyniki
WYZNACZENIE WSPÓŁCZYNNIKA OPORU PRZEPŁYWU W ZŁOŻU KOKSU
 7/5 Archives of Foundry, Year 00, Volue, 5 Archiwu Odlewnictwa, Rok 00, Rocznik, Nr 5 PAN Katowice PL ISSN 64-508 WYZNACZENIE WSPÓŁCZYNNIKA OPORU PRZEPŁYWU W ZŁOŻU KOKSU K. WARPECHOWSKI, A. JOPKIEWICZ
7/5 Archives of Foundry, Year 00, Volue, 5 Archiwu Odlewnictwa, Rok 00, Rocznik, Nr 5 PAN Katowice PL ISSN 64-508 WYZNACZENIE WSPÓŁCZYNNIKA OPORU PRZEPŁYWU W ZŁOŻU KOKSU K. WARPECHOWSKI, A. JOPKIEWICZ
Analiza nośności pionowej pojedynczego pala
 Poradnik Inżyniera Nr 13 Aktualizacja: 09/2016 Analiza nośności ionowej ojedynczego ala Program: Plik owiązany: Pal Demo_manual_13.gi Celem niniejszego rzewodnika jest rzedstawienie wykorzystania rogramu
Poradnik Inżyniera Nr 13 Aktualizacja: 09/2016 Analiza nośności ionowej ojedynczego ala Program: Plik owiązany: Pal Demo_manual_13.gi Celem niniejszego rzewodnika jest rzedstawienie wykorzystania rogramu
Przepływy Taylora-Couetta z wymianą ciepła. Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu
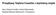 Przepływy Taylora-Couetta z wymianą ciepła Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu Typowy przepływ Taylora-Couetta to przepływ lepki pomiędzy dwoma koncentrycznymi
Przepływy Taylora-Couetta z wymianą ciepła Ewa Tuliszka-Sznitko, Kamil Kiełczewski Wydział Maszyn Roboczych i Transportu Typowy przepływ Taylora-Couetta to przepływ lepki pomiędzy dwoma koncentrycznymi
NUMERYCZNA WIZUALIZACJA LINII PRZEPŁYWU CIEPŁA I GĘSTOŚCI STRUMIENIA CIEPŁA W PŁASKIM PRZEWODZENIU CIEPŁA METODĄ ELEMENTÓW BRZEGOWYCH
 MODELOWANIE INŻYNIERSKIE nr 51, ISSN 1896-771X NUMERYCZNA WIZUALIZACJA LINII PRZEPŁYWU CIEPŁA I GĘSOŚCI SRUMIENIA CIEPŁA W PŁASKIM PRZEWODZENIU CIEPŁA MEODĄ ELEMENÓW BRZEGOWYCH omasz Janusz eleszewski
MODELOWANIE INŻYNIERSKIE nr 51, ISSN 1896-771X NUMERYCZNA WIZUALIZACJA LINII PRZEPŁYWU CIEPŁA I GĘSOŚCI SRUMIENIA CIEPŁA W PŁASKIM PRZEWODZENIU CIEPŁA MEODĄ ELEMENÓW BRZEGOWYCH omasz Janusz eleszewski
Analiza wektorowa. Teoria pola.
 Analiza wektorowa. Teoria pola. Pole skalarne Pole wektorowe ϕ = ϕ(x, y, z) A = A x (x, y, z) i x + A y (x, y, z) i y + A z (x, y, z) i z Gradient grad ϕ = ϕ x i x + ϕ y i y + ϕ z i z Jeśli przemieścimy
Analiza wektorowa. Teoria pola. Pole skalarne Pole wektorowe ϕ = ϕ(x, y, z) A = A x (x, y, z) i x + A y (x, y, z) i y + A z (x, y, z) i z Gradient grad ϕ = ϕ x i x + ϕ y i y + ϕ z i z Jeśli przemieścimy
Rozdział 21, który przedstawia zastosowanie obliczeń wysokiej wydajności w numerycznej algebrze liniowej
 Rozdział 21, który rzedstawia zastosowanie obliczeń wysokiej wydajności w numerycznej algebrze liniowej 1.0.1 Oeracje macierzowe Istotnym elementem wszelkich równoległych algorytmów macierzowych jest określenie
Rozdział 21, który rzedstawia zastosowanie obliczeń wysokiej wydajności w numerycznej algebrze liniowej 1.0.1 Oeracje macierzowe Istotnym elementem wszelkich równoległych algorytmów macierzowych jest określenie
WYDAJNOŚĆ POMPOWANIA W MIESZALNIKU Z DWOMA MIESZADŁAMI NA WALE THE PUMPING EFFICIENCY IN DUAL IMPELLER AGITATOR
 ANDRZEJ DUDA, JERZY KAMIEŃSKI, JAN TALAGA * WYDAJNOŚĆ POMPOWANIA W MIESZALNIKU Z DWOMA MIESZADŁAMI NA WALE THE PUMPING EFFICIENCY IN DUAL IMPELLER AGITATOR Streszczenie W niniejszej racy rzedstawiono wyniki
ANDRZEJ DUDA, JERZY KAMIEŃSKI, JAN TALAGA * WYDAJNOŚĆ POMPOWANIA W MIESZALNIKU Z DWOMA MIESZADŁAMI NA WALE THE PUMPING EFFICIENCY IN DUAL IMPELLER AGITATOR Streszczenie W niniejszej racy rzedstawiono wyniki
ZJAWISKO SYNCHRONIZACJI DRGAŃ I WZBUDZENIA ASYNCHRONICZNEGO W OSCYLATORZE LIENARDA
 JAN ŁUCZKO ZJAWISKO SYNCHRONIZACJI DRGAŃ I WZBUDZENIA ASYNCHRONICZNEGO W OSCYLATORZE LIENARDA SYNCHRONIZATION OF VIBRATION AND ASYNCHRONIC EXCITATION IN LIENARD S OSCILLATOR Streszczenie Abstract W niniejszym
JAN ŁUCZKO ZJAWISKO SYNCHRONIZACJI DRGAŃ I WZBUDZENIA ASYNCHRONICZNEGO W OSCYLATORZE LIENARDA SYNCHRONIZATION OF VIBRATION AND ASYNCHRONIC EXCITATION IN LIENARD S OSCILLATOR Streszczenie Abstract W niniejszym
Kinematyka płynów - zadania
 Zadanie 1 Zadane jest prawo ruchu w zmiennych Lagrange a x = Xe y = Ye t 0 gdzie, X, Y oznaczają współrzędne materialne dla t = 0. Wyznaczyć opis ruchu w zmiennych Eulera. Znaleźć linię prądu. Pokazać,
Zadanie 1 Zadane jest prawo ruchu w zmiennych Lagrange a x = Xe y = Ye t 0 gdzie, X, Y oznaczają współrzędne materialne dla t = 0. Wyznaczyć opis ruchu w zmiennych Eulera. Znaleźć linię prądu. Pokazać,
Matematyczny model przepływu gazu przez uszczelnienie tłok-pierścienie-cylinder tłokowego silnika spalinowego
 MOTROL 2009 11c 95-104 Matematyczny model rzeływu gazu rzez uszczelnienie tłok-ierścienie-cylinder tłokowego silnika salinowego Grzegorz Koszałka Katedra Silników Salinowych i Transortu Politechnika Lubelska
MOTROL 2009 11c 95-104 Matematyczny model rzeływu gazu rzez uszczelnienie tłok-ierścienie-cylinder tłokowego silnika salinowego Grzegorz Koszałka Katedra Silników Salinowych i Transortu Politechnika Lubelska
automatyka i robotyka II stopień (I stopień / II stopień) ogólnoakademicki (ogólno akademicki / praktyczny)
 Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Załącznik nr 7 do Zarządzenia Rektora nr 10/12 z dnia 21 lutego 2012r. KARTA MODUŁU / KARTA PRZEDMIOTU Kod modułu Nazwa modułu Nazwa modułu w języku angielskim Obowiązuje od roku akademickiego 2013/2014
Instrukcja do laboratorium z fizyki budowli. Ćwiczenie: Pomiar i ocena hałasu w pomieszczeniu
 nstrukcja do laboratorium z fizyki budowli Ćwiczenie: Pomiar i ocena hałasu w omieszczeniu 1 1.Wrowadzenie. 1.1. Energia fali akustycznej. Podstawowym ojęciem jest moc akustyczna źródła, która jest miarą
nstrukcja do laboratorium z fizyki budowli Ćwiczenie: Pomiar i ocena hałasu w omieszczeniu 1 1.Wrowadzenie. 1.1. Energia fali akustycznej. Podstawowym ojęciem jest moc akustyczna źródła, która jest miarą
Laboratorium komputerowe z wybranych zagadnień mechaniki płynów
 ANALIZA PRZEKAZYWANIA CIEPŁA I FORMOWANIA SIĘ PROFILU TEMPERATURY DLA NIEŚCIŚLIWEGO, LEPKIEGO PRZEPŁYWU LAMINARNEGO W PRZEWODZIE ZAMKNIĘTYM Cel ćwiczenia Celem ćwiczenia będzie obserwacja procesu formowania
ANALIZA PRZEKAZYWANIA CIEPŁA I FORMOWANIA SIĘ PROFILU TEMPERATURY DLA NIEŚCIŚLIWEGO, LEPKIEGO PRZEPŁYWU LAMINARNEGO W PRZEWODZIE ZAMKNIĘTYM Cel ćwiczenia Celem ćwiczenia będzie obserwacja procesu formowania
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne
 Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
Zaawansowane metody numeryczne Komputerowa analiza zagadnień różniczkowych 4. Równania różniczkowe zwyczajne podstawy teoretyczne P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ semestr letni 2005/06 Wstęp
OBLICZANIE POCHODNYCH FUNKCJI.
 OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
OBLICZANIE POCHODNYCH FUNKCJI. ROZWIĄZYWANIE RÓWNAŃ RÓŻNICZKOWYCH. ROZWIĄZYWANIE UKŁADÓW RÓWNAŃ LINIOWYCH. Obliczanie pochodnych funkcji. Niech będzie dana funkcja y(x określona i różniczkowalna na przedziale
Wykład 2. Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova)
 Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Podczas wykonywania analizy w programie COMSOL, wykorzystywane jest poniższe równanie: 1.2. Dane wejściowe.
 Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M3 Metoda Elementów Skończonych Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Marcin Rybiński Grzegorz
Politechnika Poznańska Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa Maszyn Grupa M3 Metoda Elementów Skończonych Prowadzący: dr hab. Tomasz Stręk, prof. nadzw. Wykonali: Marcin Rybiński Grzegorz
Metody Numeryczne w Budowie Samolotów/Śmigłowców Wykład I
 Metody Numeryczne w Budowie Samolotów/Śmigłowców Wykład I dr inż. Tomasz Goetzendorf-Grabowski (tgrab@meil.pw.edu.pl) Dęblin, 11 maja 2009 1 Organizacja wykładu 5 dni x 6 h = 30 h propozycja zmiany: 6
Metody Numeryczne w Budowie Samolotów/Śmigłowców Wykład I dr inż. Tomasz Goetzendorf-Grabowski (tgrab@meil.pw.edu.pl) Dęblin, 11 maja 2009 1 Organizacja wykładu 5 dni x 6 h = 30 h propozycja zmiany: 6
Studium ruchu cieczy w aparacie zbiornikowym z wirującą tarczą
 WITOLD SUCHECKI Politechnika Warszawska Wydział Budownictwa, Mechaniki i Petrochemii w Płocku Zakład Aparatury Przemysłowej Studium ruchu cieczy w aparacie zbiornikowym z wirującą tarczą Streszczenie:
WITOLD SUCHECKI Politechnika Warszawska Wydział Budownictwa, Mechaniki i Petrochemii w Płocku Zakład Aparatury Przemysłowej Studium ruchu cieczy w aparacie zbiornikowym z wirującą tarczą Streszczenie:
Termodynamika 1. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Termodynamika Projekt wsółfinansowany rzez Unię Euroejską w ramach Euroejskiego Funduszu Sołecznego Układ termodynamiczny Układ termodynamiczny to ciało lub zbiór rozważanych ciał, w którym obok innych
Termodynamika Projekt wsółfinansowany rzez Unię Euroejską w ramach Euroejskiego Funduszu Sołecznego Układ termodynamiczny Układ termodynamiczny to ciało lub zbiór rozważanych ciał, w którym obok innych
Opis kształtu w przestrzeni 2D. Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH
 Ois kształtu w rzestrzeni 2D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W rzyadku tych krzywych wektory styczne w unkach końcowych są określane bezośrednio
Ois kształtu w rzestrzeni 2D Mirosław Głowacki Wydział Inżynierii Metali i Informatyki Przemysłowej AGH Krzywe Beziera W rzyadku tych krzywych wektory styczne w unkach końcowych są określane bezośrednio
