Informatyka kwantowa
|
|
|
- Zofia Góra
- 6 lat temu
- Przeglądów:
Transkrypt
1 VI Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Informatyka kwantowa Ryszard Tanaś 16 października 2003
2 Spis treści 1 Rozwój komputerów Początki Obwody scalone miniaturyzacja Prawo Moore a Zasada Landauera Bit Orzeł czy reszka? Definicja Entropia Shannona Zapisywanie (kodowanie) informacji Operacje na bitach bramki logiczne. 16
3 3 Kubit (qubit) Definicja Sfera Blocha Reguła Feynmana Kwantowe, czyli nielogiczne bramki logiczne Rejestry kwantowe Stany splątane Algorytmy kwantowe Kwantowa faktoryzacja Komputer kwantowy liczy już do 15! Kilka uwag na koniec 128
4 1 Rozwój komputerów 1.1 Początki ENIAC, luty 1946 (Electronic Numerical Integrator and Computer) lamp elektronowych 5000 dodawań/s 357 mnożeń/s 175 kw energii
5 1.2 Obwody scalone miniaturyzacja Komputery stają się coraz mniejsze szybsze tańsze
6 1.3 Prawo Moore a Tranzystorów/chip Itanium 2 Pentium 4 Pentium III Pentium II Pentium Lata Rozwój układów scalonych (Intel)
7 10 3 Rozmiary bramki [nm] Lata Rozmiary elementów obwodu scalonego (SIA Roadmap 2000/2001)
8 Jak długo prawo Moore a będzie jeszcze obowiązywać?
9 Jak długo prawo Moore a będzie jeszcze obowiązywać? Obecna technologia to 0.13 µm = 130 nm Przygotowana jest już technologia 90 nm Już obecnie na jedną bramkę logiczną potrzeba mniej niż 1000 elektronów.
10 Jak długo prawo Moore a będzie jeszcze obowiązywać? Obecna technologia to 0.13 µm = 130 nm Przygotowana jest już technologia 90 nm Już obecnie na jedną bramkę logiczną potrzeba mniej niż 1000 elektronów. Czy istnieją fizyczne granice miniaturyzacji?
11 Jak długo prawo Moore a będzie jeszcze obowiązywać? Obecna technologia to 0.13 µm = 130 nm Przygotowana jest już technologia 90 nm Już obecnie na jedną bramkę logiczną potrzeba mniej niż 1000 elektronów. Czy istnieją fizyczne granice miniaturyzacji? Przewiduje się, że około roku 2020 technologia zejdzie do rozmiarów, przy których niezbędne jest uwzględnienie praw fizyki obowiązujących w mikroświecie, czyli mechaniki kwantowej.
12 Earth Simulator marzec 2002, Yokohama 5120 procesorów, 0.15µm 500 MHz NEC 640 węzłów po 8 CPU 40 TFLOPS, tera = wysokość szafy 2m miniaturyzacja?
13 1.4 Zasada Landauera Rolf Landauer ( ) Wymazanie jednego bitu informacji wymaga straty energii (wydzielenia ciepła) o wartości co najmniej kt ln 2 Informacja jest wielkością fizyczną!
14 2 Bit 2.1 Orzeł czy reszka?
15 2 Bit 2.1 Orzeł czy reszka?
16 2 Bit 2.1 Orzeł czy reszka?
17 2 Bit 2.1 Orzeł czy reszka?
18 2 Bit 2.1 Orzeł czy reszka?
19 2 Bit 2.1 Orzeł czy reszka?
20 2 Bit 2.1 Orzeł czy reszka?
21 2 Bit 2.1 Orzeł czy reszka?
22 2 Bit 2.1 Orzeł czy reszka?
23 2 Bit 2.1 Orzeł czy reszka? Rzut monetą pozwala wybrać losowo jedną z dwóch wykluczających się możliwości:
24 2 Bit 2.1 Orzeł czy reszka? Rzut monetą pozwala wybrać losowo jedną z dwóch wykluczających się możliwości: orzeł
25 2 Bit 2.1 Orzeł czy reszka? Rzut monetą pozwala wybrać losowo jedną z dwóch wykluczających się możliwości: orzeł albo reszka.
26 2 Bit 2.1 Orzeł czy reszka? Rzut monetą pozwala wybrać losowo jedną z dwóch wykluczających się możliwości: orzeł albo reszka. Kiedy poznajemy wynik rzutu monetą uzyskujemy jeden bit informacji.
27 2.2 Definicja Niech A będzie zdarzeniem losowym, które występuje z prawdopodobieństwem P (A) (w przypadku rzutu monetą P (A) = 1/2). Jeśli dowiadujemy się, że takie zdarzenie nastąpiło, to uzyskujemy bitów informacji. I(A) = log 2 1 P (A) = log = log 2 2 = 1
28 2.2 Definicja Niech A będzie zdarzeniem losowym, które występuje z prawdopodobieństwem P (A) (w przypadku rzutu monetą P (A) = 1/2). Jeśli dowiadujemy się, że takie zdarzenie nastąpiło, to uzyskujemy bitów informacji. I(A) = log 2 1 P (A) = log = log 2 2 = 1 Jeden bit to ilość informacji jaką uzyskujemy kiedy zachodzi jedna z dwóch alternatywnych, jednakowo prawdopodobnych możliwości.
29 2.3 Entropia Shannona Claude E. Shannon ( ) Twórca matematycznych podstaw informatyki H = i P (A i ) log 2 1 P (A i ) = i P (A i ) log 2 P (A i ) określa średnią informację (entropię) źródła informacji
30 2.4 Zapisywanie (kodowanie) informacji
31 2.4 Zapisywanie (kodowanie) informacji
32 2.4 Zapisywanie (kodowanie) informacji
33 2.4 Zapisywanie (kodowanie) informacji
34 2.4 Zapisywanie (kodowanie) informacji
35 2.4 Zapisywanie (kodowanie) informacji
36 2.4 Zapisywanie (kodowanie) informacji
37 2.4 Zapisywanie (kodowanie) informacji
38 2.4 Zapisywanie (kodowanie) informacji
39 2.4 Zapisywanie (kodowanie) informacji
40 2.4 Zapisywanie (kodowanie) informacji
41 2.4 Zapisywanie (kodowanie) informacji
42 2.4 Zapisywanie (kodowanie) informacji
43 2.4 Zapisywanie (kodowanie) informacji
44 2.4 Zapisywanie (kodowanie) informacji
45 2.4 Zapisywanie (kodowanie) informacji
46 2.4 Zapisywanie (kodowanie) informacji
47 2.4 Zapisywanie (kodowanie) informacji 0
48 2.4 Zapisywanie (kodowanie) informacji 0 1
49 2.4 Zapisywanie (kodowanie) informacji 0 1 1
50 2.4 Zapisywanie (kodowanie) informacji
51 2.4 Zapisywanie (kodowanie) informacji
52 2.4 Zapisywanie (kodowanie) informacji
53 2.4 Zapisywanie (kodowanie) informacji
54 2.4 Zapisywanie (kodowanie) informacji
55 2.4 Zapisywanie (kodowanie) informacji
56 2.4 Zapisywanie (kodowanie) informacji
57 2.4 Zapisywanie (kodowanie) informacji
58 2.4 Zapisywanie (kodowanie) informacji
59 2.4 Zapisywanie (kodowanie) informacji
60 2.4 Zapisywanie (kodowanie) informacji
61 2.4 Zapisywanie (kodowanie) informacji
62 2.4 Zapisywanie (kodowanie) informacji
63 2.4 Zapisywanie (kodowanie) informacji
64 2.4 Zapisywanie (kodowanie) informacji l
65 2.4 Zapisywanie (kodowanie) informacji l Układając monety możemy (teoretycznie) zapisać dowolną informację.
66 Słowo bit zapisane w ten sposób
67 Słowo bit zapisane w ten sposób
68 Słowo bit zapisane w ten sposób
69 Słowo bit zapisane w ten sposób Bardzo kosztowny i bardzo wolny zapis informacji! Jedna litera = 1 bajt = 8 bitów = 8 Pamięć mojego komputera: 256 MB = mld
70 2.5 Operacje na bitach bramki logiczne
71 2.5 Operacje na bitach bramki logiczne Bramki jednobitowe??? Bramki jednobitowe są odwracalne
72 0 NOT 1
73 1 NOT 0
74 2.5.2 Bramki dwubitowe???? Nieodwracalne
75 ????? Odwracalne
76 0 0 AND 0
77 0 1 AND 0
78 1 0 AND 0
79 1 1 AND 1
80 0 0 OR 0
81 0 1 OR 1
82 1 0 OR 1
83 1 1 OR 1
84 0 0 XOR 0
85 0 1 XOR 1
86 1 0 XOR 1
87 1 1 XOR 0
88 0 0 CNOT 0 0 Sterowane zaprzeczenie
89 0 1 CNOT 0 1
90 1 0 CNOT 1 1
91 1 1 CNOT 1 0
92 3 Kubit (qubit) 3.1 Definicja Klasyczny bit może przyjmować tylko dwie wartości {0, 1} ({orzeł,reszka}, {TAK,NIE}). Układ znajduje się albo w stanie 0 (orzeł,tak) albo w stanie 1 (reszka,nie).
93 3 Kubit (qubit) 3.1 Definicja Klasyczny bit może przyjmować tylko dwie wartości {0, 1} ({orzeł,reszka}, {TAK,NIE}). Układ znajduje się albo w stanie 0 (orzeł,tak) albo w stanie 1 (reszka,nie). Kwantowym odpowiednikiem klasycznego bitu jest dowolny układ dwustanowy: dwa poziomy atomu, spin połówkowy, foton o dwóch wzajemnie ortogonalnych stanach polaryzacji, itp.
94 3 Kubit (qubit) 3.1 Definicja Klasyczny bit może przyjmować tylko dwie wartości {0, 1} ({orzeł,reszka}, {TAK,NIE}). Układ znajduje się albo w stanie 0 (orzeł,tak) albo w stanie 1 (reszka,nie). Kwantowym odpowiednikiem klasycznego bitu jest dowolny układ dwustanowy: dwa poziomy atomu, spin połówkowy, foton o dwóch wzajemnie ortogonalnych stanach polaryzacji, itp. Taki układ to qubit (quantum bit); po polsku kubit.
95 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów
96 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A 1 1
97 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A A A 1 = Ψ
98 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A A A 1 = Ψ Ψ Ψ = A A 1 2 = 1
99 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A A A 1 = Ψ Ψ Ψ = A A 1 2 = = 1 1 = = 1 0 = 0
100 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A A A 1 = Ψ Ψ Ψ = A A 1 2 = = 1 1 = = 1 0 = 0 Kubit reprezentuje obydwa stany: stan 0 z amplitudą A 0 stan 1 z amplitudą A 1
101 Weźmy układ kwantowy o stanach 0 i 1. Kubit (qubit) to dowolna superpozycja tychże stanów Ψ = A A A A 1 = Ψ Ψ Ψ = A A 1 2 = = 1 1 = = 1 0 = 0 Kubit reprezentuje obydwa stany: stan 0 z amplitudą A 0 stan 1 z amplitudą A 1 Pomiar w bazie { 0, 1 } daje: stan 0 z prawdopodobieństwem A 0 2 stan 1 z prawdopodobieństwem A 1 2
102 3.2 Sfera Blocha Kubitem jest np. spin połówkowy, który w stałym polu magnetycznym może ustawić się zgodnie z kierunkiem pola lub przeciwnie do tego kierunku. Mamy więc dwa stany i, które możemy też nazwać 0 i 1. Ewolucja takiego spinu to ruch jego końca po sferze o jednostkowym promieniu, zwanej sferą Blocha.
103 3.2 Sfera Blocha Kubitem jest np. spin połówkowy, który w stałym polu magnetycznym może ustawić się zgodnie z kierunkiem pola lub przeciwnie do tego kierunku. Mamy więc dwa stany i, które możemy też nazwać 0 i 1. Ewolucja takiego spinu to ruch jego końca po sferze o jednostkowym promieniu, zwanej sferą Blocha. Ale nie tylko spin połówkowy, ale dowolny kubit może graficznie być reprezentowany jako punkt na takiej sferze. Ewolucja kubitu to ruch punktu po sferze Blocha.
104 3.2 Sfera Blocha Kubitem jest np. spin połówkowy, który w stałym polu magnetycznym może ustawić się zgodnie z kierunkiem pola lub przeciwnie do tego kierunku. Mamy więc dwa stany i, które możemy też nazwać 0 i 1. Ewolucja takiego spinu to ruch jego końca po sferze o jednostkowym promieniu, zwanej sferą Blocha. Ale nie tylko spin połówkowy, ale dowolny kubit może graficznie być reprezentowany jako punkt na takiej sferze. Ewolucja kubitu to ruch punktu po sferze Blocha. A wygląda to tak...
105 0 z x y
106 z x y 1
107 z x y Ψ = 1 2 ( )
108 Ψ = 1 2 ( 0 1 ) z x y
109 z x y Ψ = 1 2 ( 0 + i 1 )
110 Ψ = 1 2 ( 0 i 1 ) z x y
111 Ψ = cos θ eiϕ sin θ 2 1 z x y
112 z x y Ψ = sin θ 2 0 eiϕ cos θ 2 1
113 Przyjęliśmy tutaj następującą konwencję dotyczącą kolorowania kubitów:
114 Przyjęliśmy tutaj następującą konwencję dotyczącą kolorowania kubitów: Każdy kubit (punkt na sferze) ma własny kolor
115 Przyjęliśmy tutaj następującą konwencję dotyczącą kolorowania kubitów: Każdy kubit (punkt na sferze) ma własny kolor Dwa ortogonalne kubity (punkty na antypodach) mają kolory dopełniające (ich zmieszanie daje kolor biały lub odcień szarości)
116 Kubit jest kwantową monetą, której stan ewoluując w czasie reprezentuje jednocześnie orła i reszkę, 0 i 1.
117 Kubit jest kwantową monetą, której stan ewoluując w czasie reprezentuje jednocześnie orła i reszkę, 0 i 1. Podobnie jak koziołkująca w powietrzu moneta, dopóki nie spadnie na ziemię, reprezentuje zarówno orła jak i reszkę.
118 Kubit jest kwantową monetą, której stan ewoluując w czasie reprezentuje jednocześnie orła i reszkę, 0 i 1. Podobnie jak koziołkująca w powietrzu moneta, dopóki nie spadnie na ziemię, reprezentuje zarówno orła jak i reszkę. Dopiero pomiar w określonej bazie zmusza ją do wyboru jednej z dwóch możliwości.
119 Kubit jest kwantową monetą, której stan ewoluując w czasie reprezentuje jednocześnie orła i reszkę, 0 i 1. Podobnie jak koziołkująca w powietrzu moneta, dopóki nie spadnie na ziemię, reprezentuje zarówno orła jak i reszkę. Dopiero pomiar w określonej bazie zmusza ją do wyboru jednej z dwóch możliwości. Wybór bazy określa jaki stan będziemy mierzyli, ale w każdej bazie mamy tylko dwie alternatywne możliwości.
120 Kubit jest kwantową monetą, której stan ewoluując w czasie reprezentuje jednocześnie orła i reszkę, 0 i 1. Podobnie jak koziołkująca w powietrzu moneta, dopóki nie spadnie na ziemię, reprezentuje zarówno orła jak i reszkę. Dopiero pomiar w określonej bazie zmusza ją do wyboru jednej z dwóch możliwości. Wybór bazy określa jaki stan będziemy mierzyli, ale w każdej bazie mamy tylko dwie alternatywne możliwości. Kwantowe monety różnią się jednak od monet klasycznych!
121 1 50 % % 1 Płytka światłodzieląca
122 1 50 % % 1 Foton padający drogą 0...
123 1 50 % % 1 z prawdopodobieństwem 50% zostanie zarejestrowany przez detektor 0...
124 1 50 % % 1 lub przez detektor 1
125 1 50 % % 1 Podobnie z fotonem padającym drogą 1
126 1 50 % % 1
127 1 50 % % 1 Wyniki są losowe, jak w przypadku rzutu monetą.
128 Interferometr Macha-Zehndera
129 Policzmy klasycznie prawdopodobieństwo zarejestrowania fotonu przez detektor 0 Foton padający drogą 0
130 przechodzi przez płytkę z prawdopodobieństwem 1 2
131 przechodzi przez drugą płytkę i dociera do detektora z prawdopodobieństwem
132 Ale jest też druga droga. Foton odbija się od pierwszej płytki
133 i od drugiej płytki. Całkowite prawdopodobieństwo wynosi więc: = 1 2
134 Podobnie dla detektora 1, mamy:
135
136
137
138 = 1 2 Wynik jest losowy, jak w przypadku rzutu monetą.
139 A w rzeczywistości, czyli kwantowo, może być tak:...
140 foton padający drogą 0 trafia z prawdopodobieństwem 100% do detektora 1...
141 a foton padający drogą 1...
142 trafia na pewno do detektora 0 Wynik jest drastycznie różny od klasycznego!
143 Co się dzieje? Złożenie dwóch płytek światłodzielących, z których każda daje wynik losowy (jak rzut monetą) dało w rezultacie wynik absolutnie pewny!
144 Co się dzieje? Złożenie dwóch płytek światłodzielących, z których każda daje wynik losowy (jak rzut monetą) dało w rezultacie wynik absolutnie pewny! Foton jest kubitem, a płytka światłodzieląca jest bramką kwantową!
145 Co się dzieje? Złożenie dwóch płytek światłodzielących, z których każda daje wynik losowy (jak rzut monetą) dało w rezultacie wynik absolutnie pewny! Foton jest kubitem, a płytka światłodzieląca jest bramką kwantową! Kwantowe monety różnią się od klasycznych!
146 Co się dzieje? Złożenie dwóch płytek światłodzielących, z których każda daje wynik losowy (jak rzut monetą) dało w rezultacie wynik absolutnie pewny! Foton jest kubitem, a płytka światłodzieląca jest bramką kwantową! Kwantowe monety różnią się od klasycznych! Jak więc działa płytka światłodzieląca?
147
148
149
150
151
152 0 1
153 i 2 ( 0 i 1 ) 0 1
154 i 2 ( 0 i 1 ) ( 0 + i 1 ) 1 Płytka tworzy superpozycje stanów!
155 3.3 Reguła Feynmana W mechanice kwantowej dodają się amplitudy a nie prawdopodobieństwa. Richard P. Feynman ( ) Tam na dole jest jeszcze dużo miejsca! W 1982 r. Feynman pokazał, że nie da się symulować efektywnie procesów kwantowych na komputerach klasycznych.
156 Foton padający drogą 0 jest kubitem w stanie 0 Dodajemy amplitudy!
157 Przejście przez pierwszą płytkę: 1 2
158 Zmiana fazy: e iθ 2
159 Przejście przez drugą płytkę: e iθ 2 1 2
160 Dodajemy druga drogę. Odbicie na pierwszej płytce: 1 2 eiθ 2 + i 2
161 I znowu odbicie: 1 2 eiθ 2 + i i 2 2 = 1 2 (eiθ 1)
162 Amplituda stanu 0 w detektorze 0 jest równa A 0 = 1 2 (eiθ 1)
163 Amplituda stanu 0 w detektorze 0 jest równa A 0 = 1 2 (eiθ 1) Prawdopodobieństwo zarejestrowania w detektorze 0 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 0 = (eiθ 1) = 1 (1 cos θ) 2
164 Amplituda stanu 0 w detektorze 0 jest równa A 0 = 1 2 (eiθ 1) Prawdopodobieństwo zarejestrowania w detektorze 0 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 0 = (eiθ 1) = 1 (1 cos θ) 2 Dla θ = 0 prawdopodobieństwo to jest równe zero.
165 Amplituda stanu 0 w detektorze 0 jest równa A 0 = 1 2 (eiθ 1) Prawdopodobieństwo zarejestrowania w detektorze 0 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 0 = (eiθ 1) = 1 (1 cos θ) 2 Dla θ = 0 prawdopodobieństwo to jest równe zero. Foton nigdy nie trafi do detektora 0!
166 Amplituda stanu 0 w detektorze 0 jest równa A 0 = 1 2 (eiθ 1) Prawdopodobieństwo zarejestrowania w detektorze 0 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 0 = (eiθ 1) = 1 (1 cos θ) 2 Dla θ = 0 prawdopodobieństwo to jest równe zero. Foton nigdy nie trafi do detektora 0! Zmieniając fazę θ możemy dowolnie zmieniać prawdopodobieństwo.
167 Teraz detektor 1. Znowu, foton padający drogą 0
168 Przejście przez pierwszą płytkę: 1 2
169 Zmiana fazy: e iθ 2
170 Odbicie: e iθ 2 i 2
171 I druga droga. Odbicie: e iθ 2 i 2 + i 2
172 0 1 0 Przejście: e iθ 2 1 i 2 + i = i 2 (eiθ + 1)
173 Amplituda stanu 0 w detektorze 1 jest równa A 1 = i 2 (eiθ + 1)
174 Amplituda stanu 0 w detektorze 1 jest równa A 1 = i 2 (eiθ + 1) Prawdopodobieństwo zarejestrowania w detektorze 1 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 1 = i 2 2 (eiθ + 1) = 1 (1 + cos θ) 2
175 Amplituda stanu 0 w detektorze 1 jest równa A 1 = i 2 (eiθ + 1) Prawdopodobieństwo zarejestrowania w detektorze 1 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 1 = i 2 2 (eiθ + 1) = 1 (1 + cos θ) 2 Dla θ = 0 prawdopodobieństwo to jest równe jeden. Foton zawsze trafi do detektora 1!
176 Amplituda stanu 0 w detektorze 1 jest równa A 1 = i 2 (eiθ + 1) Prawdopodobieństwo zarejestrowania w detektorze 1 fotonu, który wpadł drogą 0 do interferometru wynosi więc: P 1 = i 2 2 (eiθ + 1) = 1 (1 + cos θ) 2 Dla θ = 0 prawdopodobieństwo to jest równe jeden. Foton zawsze trafi do detektora 1! Interferometr Macha-Zehndera dziala jak bramka logiczna NOT.
177 Skoro cały interferometr to bramka logiczna NOT, to jedna płytka światłodzieląca to NOT! NOT NOT = NOT NOT NOT
178 Interferencja kwantowa pozwala uzyskać operacje logiczne niedostępne w informatyce klasycznej
179 Interferencja kwantowa pozwala uzyskać operacje logiczne niedostępne w informatyce klasycznej Czy takie nielogiczne bramki logiczne mogą się do czegoś przydać?
180 Interferencja kwantowa pozwala uzyskać operacje logiczne niedostępne w informatyce klasycznej Czy takie nielogiczne bramki logiczne mogą się do czegoś przydać? Okazuje się, że tak!
181 3.4 Kwantowe, czyli nielogiczne bramki logiczne 0 NOT 1
182 1 NOT 0
183 a 0 + b 1 NOT a 1 + b 0
184 a 0 + b 1 θ a 0 + be iθ 1 Bramka fazowa
185 0 H 1 2 ( ) Bramka Hadamarda
186 1 H 1 2 ( 0 1 )
187 0 NOT 1+i i 2 1
188 1 NOT 1 i i 2 1
189 Ψ U Ψ Ogólnie
190 3.5 Rejestry kwantowe Rzucając dwie monety możemy uzyskać cztery różne rezultaty:
191 3.5 Rejestry kwantowe Rzucając dwie monety możemy uzyskać cztery różne rezultaty:
192 3.5 Rejestry kwantowe Rzucając dwie monety możemy uzyskać cztery różne rezultaty:
193 3.5 Rejestry kwantowe Rzucając dwie monety możemy uzyskać cztery różne rezultaty:
194 3.5 Rejestry kwantowe Rzucając dwie monety możemy uzyskać cztery różne rezultaty:
195 Co możemy zapisać: 00 = 0 01 = 1 10 = 2 11 = 3
196 Co możemy zapisać: 00 = 0 01 = 1 10 = 2 11 = 3 Dla kubitów wygląda to tak: 00 = 0 01 = 1 10 = 2 11 = 3
197 Ale kubity mogą być w stanie superpozycji, i nasz dwukubitowy rejestr może wyglądać tak
198 Ale kubity mogą być w stanie superpozycji, i nasz dwukubitowy rejestr może wyglądać tak albo tak
199 Ale kubity mogą być w stanie superpozycji, i nasz dwukubitowy rejestr może wyglądać tak albo tak albo tak
200 W pierwszym przypadku mamy stan kwantowy Ψ = 1 2 ( ) 1 2 ( )
201 W pierwszym przypadku mamy stan kwantowy Ψ = 1 2 ( ) 1 2 ( ) = 1 2 ( )
202 W pierwszym przypadku mamy stan kwantowy Ψ = 1 2 ( ) 1 2 ( ) = 1 2 ( ) = 1 ( ) 2
203 W pierwszym przypadku mamy stan kwantowy Ψ = 1 2 ( ) 1 2 ( ) = 1 2 ( ) = 1 ( ) 2 Mamy zatem dwukubitowy rejestr, który przechowuje z jednakowymi amplitudami jednocześnie cztery liczby, {0, 1, 2, 3}.
204 Klasycznie na przechowanie czterech liczb potrzebujemy czterech rejestrów dwubitowych każda liczba w innym rejestrze.
205 Klasycznie na przechowanie czterech liczb potrzebujemy czterech rejestrów dwubitowych każda liczba w innym rejestrze. Gdybyśmy dysponowali rejestrem kwantowym złożonym z N kubitów, to moglibyśmy przechować w takim rejestrze 2 N liczb!
206 Klasycznie na przechowanie czterech liczb potrzebujemy czterech rejestrów dwubitowych każda liczba w innym rejestrze. Gdybyśmy dysponowali rejestrem kwantowym złożonym z N kubitów, to moglibyśmy przechować w takim rejestrze 2 N liczb! Przy N = 300 liczba ta przekraczałaby liczbę atomów we wszechświecie!
207 Klasycznie na przechowanie czterech liczb potrzebujemy czterech rejestrów dwubitowych każda liczba w innym rejestrze. Gdybyśmy dysponowali rejestrem kwantowym złożonym z N kubitów, to moglibyśmy przechować w takim rejestrze 2 N liczb! Przy N = 300 liczba ta przekraczałaby liczbę atomów we wszechświecie! Komputer kwantowy wykonuje operacje na całym rejestrze, czyli na wszyskich 2 N liczbach jednocześnie. Nazywa się to kwantowym parallelizmem.
208 Klasycznie na przechowanie czterech liczb potrzebujemy czterech rejestrów dwubitowych każda liczba w innym rejestrze. Gdybyśmy dysponowali rejestrem kwantowym złożonym z N kubitów, to moglibyśmy przechować w takim rejestrze 2 N liczb! Przy N = 300 liczba ta przekraczałaby liczbę atomów we wszechświecie! Komputer kwantowy wykonuje operacje na całym rejestrze, czyli na wszyskich 2 N liczbach jednocześnie. Nazywa się to kwantowym parallelizmem. Kwantowe monety różnią się od klasycznych!
209 3.6 Stany splątane Przypuśćmy, że udało nam się przygotować rejestr dwukubitowy w stanie Ψ = 1 2 ( )
210 3.6 Stany splątane Przypuśćmy, że udało nam się przygotować rejestr dwukubitowy w stanie Ψ = 1 2 ( ) Taki stan nie daje się zapisać w postaci iloczynu dwóch kubitów!
211 3.6 Stany splątane Przypuśćmy, że udało nam się przygotować rejestr dwukubitowy w stanie Ψ = 1 2 ( ) Taki stan nie daje się zapisać w postaci iloczynu dwóch kubitów! Kubity tworzące taki rejestr nie mają indywidualnych kolorów są białe w naszej konwencji (kolor biały można otrzymać na wiele sposobów mieszając ze sobą kolory dopełniające).
212 Wyobraźmy sobie, że mamy dwie kwantowe monety w stanie splątanym.
213 Wyobraźmy sobie, że mamy dwie kwantowe monety w stanie splątanym. Jedną ma Ala a drugą Bolek.
214 Wyobraźmy sobie, że mamy dwie kwantowe monety w stanie splątanym. Jedną ma Ala a drugą Bolek. Ala rzuca monetę i wypadł jej orzeł.
215 Wyobraźmy sobie, że mamy dwie kwantowe monety w stanie splątanym. Jedną ma Ala a drugą Bolek. Ala rzuca monetę i wypadł jej orzeł.
216 Wyobraźmy sobie, że mamy dwie kwantowe monety w stanie splątanym. Jedną ma Ala a drugą Bolek. Ala rzuca monetę i wypadł jej orzeł. Wtedy Bolek rzucając swoją monetę musi uzyskać reszkę, jakkolwiek daleko nie byłby oddalony od Ali.
217 I na odwrót:
218 I na odwrót:
219 I na odwrót:
220 I na odwrót: Mechanika kwantowa jest nielokalna!
221 I na odwrót: Mechanika kwantowa jest nielokalna! Kwantowe monety naprawdę różnią się od klasycznych!
222 I na odwrót: Mechanika kwantowa jest nielokalna! Kwantowe monety naprawdę różnią się od klasycznych! Jak uzyskać stan splątany?
223 0 0 CNOT 0 0 Sterowane zaprzeczenie
224 0 1 CNOT 0 1
225 1 0 CNOT 1 1
226 1 1 CNOT 1 0
227 1 2 ( 0 1 ) 1 CNOT??
228 1 2 ( 0 1 ) 1 CNOT } Ψ
229 Otrzymujemy taki właśnie stan splątany Ψ = 1 2 ( )
230 Otrzymujemy taki właśnie stan splątany Ψ = 1 2 ( ) Po co nam stany splątane?
231 Otrzymujemy taki właśnie stan splątany Ψ = 1 2 ( ) Po co nam stany splątane? Stany splątane pozwalają np. na kwantową teleportację czy gęste kodowanie.
232 Otrzymujemy taki właśnie stan splątany Ψ = 1 2 ( ) Po co nam stany splątane? Stany splątane pozwalają np. na kwantową teleportację czy gęste kodowanie. Potrafimy już wytwarzać stany splątane!
233 4 Algorytmy kwantowe Co potrafi komputer kwantowy?
234 4 Algorytmy kwantowe Co potrafi komputer kwantowy? Komputer kwantowy potrafi np.
235 4 Algorytmy kwantowe Co potrafi komputer kwantowy? Komputer kwantowy potrafi np. szybko faktoryzować liczby algorytm Shora,
236 4 Algorytmy kwantowe Co potrafi komputer kwantowy? Komputer kwantowy potrafi np. szybko faktoryzować liczby algorytm Shora, czy też przeszukiwać bazę danych algorytm Grovera.
237 4.1 Kwantowa faktoryzacja Peter Shor Twórca kwantowego algorytmu faktoryzacji liczb.
238 Systemy kryptograficzne (RSA) z kluczem publicznym wykorzystują fakt, że rozkład dużej liczby na czynniki jest trudny (czasochłonny)
239 Systemy kryptograficzne (RSA) z kluczem publicznym wykorzystują fakt, że rozkład dużej liczby na czynniki jest trudny (czasochłonny) Najszybszy obecnie algorytm wymaga czasu exp[( 64 9 )1/3 (ln ln N) 2/3 ] faktoryzacja liczby 400 cyfrowej wymagałaby lat
240 Systemy kryptograficzne (RSA) z kluczem publicznym wykorzystują fakt, że rozkład dużej liczby na czynniki jest trudny (czasochłonny) Najszybszy obecnie algorytm wymaga czasu exp[( 64 9 )1/3 (ln ln N) 2/3 ] faktoryzacja liczby 400 cyfrowej wymagałaby lat W 1994 r. RSA 129 został złamany na 1600 stacjach roboczych w ciągu 8 miesięcy
241 Systemy kryptograficzne (RSA) z kluczem publicznym wykorzystują fakt, że rozkład dużej liczby na czynniki jest trudny (czasochłonny) Najszybszy obecnie algorytm wymaga czasu exp[( 64 9 )1/3 (ln ln N) 2/3 ] faktoryzacja liczby 400 cyfrowej wymagałaby lat W 1994 r. RSA 129 został złamany na 1600 stacjach roboczych w ciągu 8 miesięcy Algorytm kwantowy Petera Shora wymaga czasu (ln N) 2+ɛ komputer kwantowy, który faktoryzowałby liczbę 130 cyfrową w ciągu miesiąca, sfaktoryzowałby liczbę 400 cyfrową w czasie krótszym niż 3 lata
242 Chcemy sfaktoryzować liczbę N, N = 15. Wybieramy liczbę losową 1 < X < N 1 względnie pierwszą z N, tzn. taką, że NW D(N, X) = 1, powiedzmy X = 2.
243 Chcemy sfaktoryzować liczbę N, N = 15. Wybieramy liczbę losową 1 < X < N 1 względnie pierwszą z N, tzn. taką, że NW D(N, X) = 1, powiedzmy X = 2. Przygotowujemy rejestr kwantowy w stanie superpozycji wszystkich liczb od 0 do 15 A = 1 ( ) 4
244 Chcemy sfaktoryzować liczbę N, N = 15. Wybieramy liczbę losową 1 < X < N 1 względnie pierwszą z N, tzn. taką, że NW D(N, X) = 1, powiedzmy X = 2. Przygotowujemy rejestr kwantowy w stanie superpozycji wszystkich liczb od 0 do 15 A = 1 ( ) 4 Co zapisujemy dla skrótu tak: A
245 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B.
246 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku!
247 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A
248 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B
249 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4
250 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4 B
251 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4 B
252 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4 B
253 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4 B
254 Wykonujemy operację X A mod N, wykorzystując kwantowy parallelizm i wyniki umieszczamy w rejestrze B. Komputer kwantowy wykonuje taką operację w jednym kroku! A B Zauważamy, że wyniki w rejestrze B są okresowe z okresem r = 4 B Komputer kwantowy potrafi szybko znajdować okres funkcji!
255 Jeśli r jest nieparzyste, to wybieramy inne X i zaczynamy procedurę od nowa.
256 Jeśli r jest nieparzyste, to wybieramy inne X i zaczynamy procedurę od nowa. Jeśli r jest parzyste, obliczamy P = X r/2 1 lub P = X r/2 + 1 i sprawdzamy czy P jest dzielnikiem N. W naszym przykładzie r = 4 i P = 2 4/2 1 = 3 lub P = 2 4/2 + 1 = 5.
257 Jeśli r jest nieparzyste, to wybieramy inne X i zaczynamy procedurę od nowa. Jeśli r jest parzyste, obliczamy P = X r/2 1 lub P = X r/2 + 1 i sprawdzamy czy P jest dzielnikiem N. W naszym przykładzie r = 4 i P = 2 4/2 1 = 3 lub P = 2 4/2 + 1 = 5. Hurra!!! 15/3 = 5 15/5 = 3
258 Jeśli r jest nieparzyste, to wybieramy inne X i zaczynamy procedurę od nowa. Jeśli r jest parzyste, obliczamy P = X r/2 1 lub P = X r/2 + 1 i sprawdzamy czy P jest dzielnikiem N. W naszym przykładzie r = 4 i P = 2 4/2 1 = 3 lub P = 2 4/2 + 1 = 5. Hurra!!! 15/3 = 5 15/5 = 3 Ten wynik udało się już uzyskać eksperymentalnie!
259 4.2 Komputer kwantowy liczy już do 15! Wiedza i Życie, maj 2002
260 Isaac L. Chuang i jego procesor kwantowy
261 5 Kilka uwag na koniec Kubit to nowa jednostka informacji informacji kwantowej
262 5 Kilka uwag na koniec Kubit to nowa jednostka informacji informacji kwantowej Informatyka kwantowa zajmuje się metodami przetwarzania informacji kwantowej
263 5 Kilka uwag na koniec Kubit to nowa jednostka informacji informacji kwantowej Informatyka kwantowa zajmuje się metodami przetwarzania informacji kwantowej Superpozycja i splątanie kubitów to podwaliny informatyki kwantowej
264 5 Kilka uwag na koniec Kubit to nowa jednostka informacji informacji kwantowej Informatyka kwantowa zajmuje się metodami przetwarzania informacji kwantowej Superpozycja i splątanie kubitów to podwaliny informatyki kwantowej Kwantowe monety różnią się od klasycznych!
265 Za lat 20 wielu z Was z pewnością będzie specjalistami w dziedzinie informatyki kwantowej Powodzenia!
Fizyka dla wszystkich
 Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
Informatyka kwantowa. Zaproszenie do fizyki. Zakład Optyki Nieliniowej. wykład z cyklu. Ryszard Tanaś. mailto:tanas@kielich.amu.edu.
 Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
XIII Poznański Festiwal Nauki i Sztuki. Wydziale Fizyki UAM
 XIII Poznański Festiwal Nauki i Sztuki na Wydziale Fizyki UAM XIII Poznański Festival Nauki i Sztuki na Wydziale Fizyki UAM Od informatyki klasycznej do kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas
XIII Poznański Festiwal Nauki i Sztuki na Wydziale Fizyki UAM XIII Poznański Festival Nauki i Sztuki na Wydziale Fizyki UAM Od informatyki klasycznej do kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 13
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 13 Spis treści 19 Algorytmy kwantowe 3 19.1 Bit kwantowy kubit (qubit)........... 3 19. Twierdzenie
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 13 Spis treści 19 Algorytmy kwantowe 3 19.1 Bit kwantowy kubit (qubit)........... 3 19. Twierdzenie
VII Festiwal Nauki i Sztuki. Wydziale Fizyki UAM
 VII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Teleportacja stanów atomowych Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 14 października 2004
VII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Teleportacja stanów atomowych Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 14 października 2004
Informatyka kwantowa. Karol Bartkiewicz
 Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
Quantum Computer I (QC) Zapis skrócony. Zapis skrócony
 Quantum Computer I (QC) Jacek Szczytko, Wydział Fizyki UW. Komputery kwantowe a. Logika bramek b. Kwantowe algorytmy c. Jak zbudować taki komputer? "Where a calculator on the Eniac is equipped with vacuum
Quantum Computer I (QC) Jacek Szczytko, Wydział Fizyki UW. Komputery kwantowe a. Logika bramek b. Kwantowe algorytmy c. Jak zbudować taki komputer? "Where a calculator on the Eniac is equipped with vacuum
W5. Komputer kwantowy
 W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski
 VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
Wstęp do komputerów kwantowych
 Obwody kwantowe Uniwersytet Łódzki, Wydział Fizyki i Informatyki Stosowanej 2008/2009 Obwody kwantowe Bramki kwantowe 1 Algorytmy kwantowe 2 3 4 Algorytmy kwantowe W chwili obecnej znamy dwie obszerne
Obwody kwantowe Uniwersytet Łódzki, Wydział Fizyki i Informatyki Stosowanej 2008/2009 Obwody kwantowe Bramki kwantowe 1 Algorytmy kwantowe 2 3 4 Algorytmy kwantowe W chwili obecnej znamy dwie obszerne
Historia. Zasada Działania
 Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Komputery Kwantowe. Sprawy organizacyjne Literatura Plan. Komputery Kwantowe. Ravindra W. Chhajlany. 27 listopada 2006
 Sprawy organizacyjne Literatura Plan Ravindra W. Chhajlany 27 listopada 2006 Ogólne Sprawy organizacyjne Literatura Plan Współrzędne: Pokój 207, Zakład Elektroniki Kwantowej. Telefon: (0-61)-8295005 Email:
Sprawy organizacyjne Literatura Plan Ravindra W. Chhajlany 27 listopada 2006 Ogólne Sprawy organizacyjne Literatura Plan Współrzędne: Pokój 207, Zakład Elektroniki Kwantowej. Telefon: (0-61)-8295005 Email:
Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku
 Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku Wstęp czyli (próba) odpowiedzi na pewne pytania (Silna) Teza Church
Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku Wstęp czyli (próba) odpowiedzi na pewne pytania (Silna) Teza Church
dr inż. Andrzej Skorupski Wydział Elektroniki i Technik Informacyjnych Politechnika Warszawska
 dr inż. Andrzej Skorupski Wydział Elektroniki i Technik Informacyjnych Politechnika Warszawska Zasilacz pierwszego polskiego komputera UMC1 produkowanego seryjnie w ELWRO opracowanego w katedrze kierowanej
dr inż. Andrzej Skorupski Wydział Elektroniki i Technik Informacyjnych Politechnika Warszawska Zasilacz pierwszego polskiego komputera UMC1 produkowanego seryjnie w ELWRO opracowanego w katedrze kierowanej
Algorytm Grovera. Kwantowe przeszukiwanie zbiorów. Robert Nowotniak
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 13 listopada 2007 Plan wystapienia 1 Informatyka Kwantowa podstawy 2 Opis problemu (przeszukiwanie zbioru) 3 Intuicyjna
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 13 listopada 2007 Plan wystapienia 1 Informatyka Kwantowa podstawy 2 Opis problemu (przeszukiwanie zbioru) 3 Intuicyjna
O informatyce kwantowej
 O informatyce kwantowej Piotr Gawron Instytut Informatyki Teoretycznej i Stosowanej PAN Posiedzenie PTM Gliwice Piotr Gawron (IITiS PAN) O informatyce kwantowej 6 października 009 1 / 33 Plan wystąpienia
O informatyce kwantowej Piotr Gawron Instytut Informatyki Teoretycznej i Stosowanej PAN Posiedzenie PTM Gliwice Piotr Gawron (IITiS PAN) O informatyce kwantowej 6 października 009 1 / 33 Plan wystąpienia
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń.
 Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń. 3.2. Niezależność zdarzeń Katarzyna Rybarczyk-Krzywdzińska Niezależność dwóch zdarzeń Intuicja Zdarzenia losowe
Rachunek prawdopodobieństwa Rozdział 3. Prawdopodobieństwo warunkowe i niezależność zdarzeń. 3.2. Niezależność zdarzeń Katarzyna Rybarczyk-Krzywdzińska Niezależność dwóch zdarzeń Intuicja Zdarzenia losowe
Wstęp do algorytmiki kwantowej
 Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Komputer kwantowy - co to właściwie jest? Komputer kwantowy Komputer, którego zasada działania nie może zostać wyjaśniona bez użycia formalizmu mechaniki
Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Komputer kwantowy - co to właściwie jest? Komputer kwantowy Komputer, którego zasada działania nie może zostać wyjaśniona bez użycia formalizmu mechaniki
Algorytm faktoryzacji Petera Shora dla komputera kwantowego
 Algorytm faktoryzacji Petera Shora dla komputera kwantowego Peter Shor (ur. 14 sierpnia 1959 roku w USA Matematyk oraz informatyk teoretyk Autor kwantowego Algorytmu Shora Pracuje w AT&T Bell Laboratories
Algorytm faktoryzacji Petera Shora dla komputera kwantowego Peter Shor (ur. 14 sierpnia 1959 roku w USA Matematyk oraz informatyk teoretyk Autor kwantowego Algorytmu Shora Pracuje w AT&T Bell Laboratories
Informatyka Kwantowa Sekcja Informatyki Kwantowej prezentacja
 Informatyka Kwantowa Sekcja Informatyki Kwantowej prezentacja Robert Nowotniak Wydział FTIMS, Politechnika Łódzka XV konferencja SIS, 26 października 2007 Streszczenie Informatyka kwantowa jest dziedziną
Informatyka Kwantowa Sekcja Informatyki Kwantowej prezentacja Robert Nowotniak Wydział FTIMS, Politechnika Łódzka XV konferencja SIS, 26 października 2007 Streszczenie Informatyka kwantowa jest dziedziną
Arytmetyka liczb binarnych
 Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Wartość dwójkowej liczby stałoprzecinkowej Wartość dziesiętna stałoprzecinkowej liczby binarnej Arytmetyka liczb binarnych b n-1...b 1 b 0,b -1 b -2...b -m = b n-1 2 n-1 +... + b 1 2 1 + b 0 2 0 + b -1
Podstawy systemów kryptograficznych z kluczem jawnym RSA
 Podstawy systemów kryptograficznych z kluczem jawnym RSA RSA nazwa pochodząca od nazwisk twórców systemu (Rivest, Shamir, Adleman) Systemów z kluczem jawnym można używać do szyfrowania operacji przesyłanych
Podstawy systemów kryptograficznych z kluczem jawnym RSA RSA nazwa pochodząca od nazwisk twórców systemu (Rivest, Shamir, Adleman) Systemów z kluczem jawnym można używać do szyfrowania operacji przesyłanych
Wprowadzenie do teorii komputerów kwantowych
 Wprowadzenie do teorii komputerów kwantowych mgr inż. Olga Siedlecka olga@icis.pcz.pl Instytut Informatyki Teoretycznej i Stosowanej Wprowadzenie do teorii komputerów kwantowych p.1/35 Plan seminarium
Wprowadzenie do teorii komputerów kwantowych mgr inż. Olga Siedlecka olga@icis.pcz.pl Instytut Informatyki Teoretycznej i Stosowanej Wprowadzenie do teorii komputerów kwantowych p.1/35 Plan seminarium
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 24, Radosław Chrapkiewicz, Filip Ozimek
 odstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 4, 5.05.0 wykład: pokazy: ćwiczenia: Michał Karpiński Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 3 - przypomnienie argumenty
odstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 4, 5.05.0 wykład: pokazy: ćwiczenia: Michał Karpiński Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 3 - przypomnienie argumenty
V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski
 V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski 1 1 Wprowadzenie Wykład ten poświęcony jest dokładniejszemu omówieniu własności kwantowych bramek logicznych (kwantowych operacji logicznych). Podstawowymi
V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski 1 1 Wprowadzenie Wykład ten poświęcony jest dokładniejszemu omówieniu własności kwantowych bramek logicznych (kwantowych operacji logicznych). Podstawowymi
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA
 RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
RACHUNEK PRAWDOPODOBIEŃSTWA I KOMBINATORYKA Doświadczenia losowe Rachunek prawdopodobieństwa zajmuje się zdarzeniami jakie zachodzą, gdy przeprowadzamy doświadczenia losowe. Mówimy, że doświadczenie jest
Protokół teleportacji kwantowej
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 7
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 7 Spis treści 11 Algorytm ElGamala 3 11.1 Wybór klucza.................... 3 11.2 Szyfrowanie.....................
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 7 Spis treści 11 Algorytm ElGamala 3 11.1 Wybór klucza.................... 3 11.2 Szyfrowanie.....................
Komputery kwantowe. Szymon Pustelny Student SMP, Instytut Fizyki UJ
 6 FOTON 8, Lato 2003 Komputery kwantowe Szymon Pustelny Student SMP, Instytut Fizyki UJ Wstęp Współcześnie coraz głośniej mówi się o ograniczeniach stojących przed rozwojem klasycznych komputerów. Zakrojone
6 FOTON 8, Lato 2003 Komputery kwantowe Szymon Pustelny Student SMP, Instytut Fizyki UJ Wstęp Współcześnie coraz głośniej mówi się o ograniczeniach stojących przed rozwojem klasycznych komputerów. Zakrojone
Technika cyfrowa Inżynieria dyskretna cz. 2
 Sławomir Kulesza Technika cyfrowa Inżynieria dyskretna cz. 2 Wykład dla studentów III roku Informatyki Wersja 5.0, 10/10/2015 Generacje układów scalonych Stopień scalenia Liczba elementów aktywnych Zastosowania
Sławomir Kulesza Technika cyfrowa Inżynieria dyskretna cz. 2 Wykład dla studentów III roku Informatyki Wersja 5.0, 10/10/2015 Generacje układów scalonych Stopień scalenia Liczba elementów aktywnych Zastosowania
Gry kwantowe na łańcuchach spinowych
 Gry kwantowe na łańcuchach spinowych Jarosław Miszczak we współpracy z Piotrem Gawronem i Zbigniewem Puchałą Instytut Informatyki Teoretycznej i Stosowanej PAN w Gliwicach J.A.M., Z. Puchała, P. Gawron
Gry kwantowe na łańcuchach spinowych Jarosław Miszczak we współpracy z Piotrem Gawronem i Zbigniewem Puchałą Instytut Informatyki Teoretycznej i Stosowanej PAN w Gliwicach J.A.M., Z. Puchała, P. Gawron
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, Kryptografia: algorytmy asymetryczne (RSA)
 Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, 7.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 14, 7.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt.
 P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
P r a w d o p o d o b i eństwo Lekcja 1 Temat: Lekcja organizacyjna. Program. Kontrakt. Lekcja 2 Temat: Podstawowe pojęcia związane z prawdopodobieństwem. Str. 10-21 1. Doświadczenie losowe jest to doświadczenie,
- nowe wyzwanie. Feliks Kurp
 INFORMATYKA KWANTOWA - nowe wyzwanie Feliks Kurp 2006 2 Plan wystąpienia: 1. Dlaczego informatyka kwantowa? 2. Grupy i ludzie zajmujący się informatyką kwantową 3. Fenomeny mechaniki kwantowej 4. Podstawy
INFORMATYKA KWANTOWA - nowe wyzwanie Feliks Kurp 2006 2 Plan wystąpienia: 1. Dlaczego informatyka kwantowa? 2. Grupy i ludzie zajmujący się informatyką kwantową 3. Fenomeny mechaniki kwantowej 4. Podstawy
Kryptografia kwantowa. Marta Michalska
 Kryptografia kwantowa Marta Michalska Główne postacie Ewa podsłuchiwacz Alicja nadawca informacji Bob odbiorca informacji Alicja przesyła do Boba informacje kanałem, który jest narażony na podsłuch. Ewa
Kryptografia kwantowa Marta Michalska Główne postacie Ewa podsłuchiwacz Alicja nadawca informacji Bob odbiorca informacji Alicja przesyła do Boba informacje kanałem, który jest narażony na podsłuch. Ewa
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, Kryptografia: algorytmy asymetryczne (RSA)
 Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, 19.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 15, 19.06.2005 1 Kryptografia: algorytmy asymetryczne (RSA) Niech E K (x) oznacza szyfrowanie wiadomości x kluczem K (E od encrypt, D K (x)
Podstawy informatyki kwantowej
 Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Prawdopodobieństwo geometryczne
 Prawdopodobieństwo geometryczne Krzysztof Jasiński Wydział Matematyki i Informatyki UMK, Toruń V Lieceum Ogólnokształące im. Jana Pawała II w Toruniu 13.03.2014 Krzysztof Jasiński (WMiI UMK) Prawdopodobieństwo
Prawdopodobieństwo geometryczne Krzysztof Jasiński Wydział Matematyki i Informatyki UMK, Toruń V Lieceum Ogólnokształące im. Jana Pawała II w Toruniu 13.03.2014 Krzysztof Jasiński (WMiI UMK) Prawdopodobieństwo
Kwantowe przelewy bankowe foton na usługach biznesu
 Kwantowe przelewy bankowe foton na usługach biznesu Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Zakupy w Internecie Secure Socket Layer Bazuje na w wymianie klucza metodą RSA Jak mogę przesłać
Kwantowe przelewy bankowe foton na usługach biznesu Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Zakupy w Internecie Secure Socket Layer Bazuje na w wymianie klucza metodą RSA Jak mogę przesłać
Podejścia do realizacji modelu obliczeń kwantowych
 Podejścia do realizacji modelu obliczeń kwantowych Instytut Informatyki Uniwersytetu Wrocławskiego 18 maja 2007 Jak reprezentować qubit? Główne zasady Warunki dla obliczeń kwantowych Spin Oscylator harmoniczny
Podejścia do realizacji modelu obliczeń kwantowych Instytut Informatyki Uniwersytetu Wrocławskiego 18 maja 2007 Jak reprezentować qubit? Główne zasady Warunki dla obliczeń kwantowych Spin Oscylator harmoniczny
Kryptografia kwantowa
 Kryptografia kwantowa Krzysztof Maćkowiak DGA SECURE 2006 Plan referatu Wprowadzenie, podstawowe pojęcia Algorytm Grovera Algorytm Shora Algorytm Bennetta-Brassarda Algorytm Bennetta Praktyczne zastosowanie
Kryptografia kwantowa Krzysztof Maćkowiak DGA SECURE 2006 Plan referatu Wprowadzenie, podstawowe pojęcia Algorytm Grovera Algorytm Shora Algorytm Bennetta-Brassarda Algorytm Bennetta Praktyczne zastosowanie
Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych
 1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
1 Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych 1. Podstawowe operacje logiczne dla cyfr binarnych Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne fałsz i prawda, to działanie
Miary splątania kwantowego
 kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
Zadanie 1. Potęgi (14 pkt)
 2 Egzamin maturalny z informatyki Zadanie 1. otęgi (14 pkt) W poniższej tabelce podane są wartości kolejnych potęg liczby 2: k 0 1 2 3 4 5 6 7 8 9 10 2 k 1 2 4 8 16 32 64 128 256 512 1024 Ciąg a=(a 0,
2 Egzamin maturalny z informatyki Zadanie 1. otęgi (14 pkt) W poniższej tabelce podane są wartości kolejnych potęg liczby 2: k 0 1 2 3 4 5 6 7 8 9 10 2 k 1 2 4 8 16 32 64 128 256 512 1024 Ciąg a=(a 0,
Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe
 Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Modelowanie Preferencji a Ryzyko. Dlaczego w dylemat więźnia warto grać kwantowo?
 Modelowanie Preferencji a Ryzyko Dlaczego w dylemat więźnia warto grać kwantowo? Marek Szopa U n iwe r s y t e t Ś l ą s k i INSTYTUT FIZYKI im. Augusta Chełkowskiego Zakład Fizyki Teoretycznej Klasyczny
Modelowanie Preferencji a Ryzyko Dlaczego w dylemat więźnia warto grać kwantowo? Marek Szopa U n iwe r s y t e t Ś l ą s k i INSTYTUT FIZYKI im. Augusta Chełkowskiego Zakład Fizyki Teoretycznej Klasyczny
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI. Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub
 RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
RACHUNEK PRAWDOPODOBIEŃSTWA ZADANIA Z ROZWIĄZANIAMI Uwaga! Dla określenia liczebności zbioru (mocy zbioru) użyto zamiennie symboli: Ω lub 1. W grupie jest 15 kobiet i 18 mężczyzn. Losujemy jedną osobę
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 8
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 8 Spis treści 13 Szyfrowanie strumieniowe i generatory ciągów pseudolosowych 3 13.1 Synchroniczne
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 8 Spis treści 13 Szyfrowanie strumieniowe i generatory ciągów pseudolosowych 3 13.1 Synchroniczne
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 07 - Podstawy obliczeń kwantowych Jarosław Miszczak IITiS PAN Gliwice 27/10/2016 1 / 29 1 Wprowadzenie Obliczanie Motywacja fizyczna Motywacja kryptograficzna 2 2 /
Obliczenia inspirowane Naturą Wykład 07 - Podstawy obliczeń kwantowych Jarosław Miszczak IITiS PAN Gliwice 27/10/2016 1 / 29 1 Wprowadzenie Obliczanie Motywacja fizyczna Motywacja kryptograficzna 2 2 /
Wykład 2. Informatyka Stosowana. 8 października 2018, M. A-B. Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41
 Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
Wykład 2 Informatyka Stosowana 8 października 2018, M. A-B Informatyka Stosowana Wykład 2 8 października 2018, M. A-B 1 / 41 Elementy logiki matematycznej Informatyka Stosowana Wykład 2 8 października
Strategie kwantowe w teorii gier
 Uniwersytet Jagielloński adam.wyrzykowski@uj.edu.pl 18 stycznia 2015 Plan prezentacji 1 Gra w odwracanie monety (PQ penny flip) 2 Wojna płci Definicje i pojęcia Równowagi Nasha w Wojnie płci 3 Kwantowanie
Uniwersytet Jagielloński adam.wyrzykowski@uj.edu.pl 18 stycznia 2015 Plan prezentacji 1 Gra w odwracanie monety (PQ penny flip) 2 Wojna płci Definicje i pojęcia Równowagi Nasha w Wojnie płci 3 Kwantowanie
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Wprowadzenie do kombinatoryki
 Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Wprowadzenie do kombinatoryki http://www.matemaks.pl/kombinatoryka.html Kombinatoryka jest działem matematyki, który pomaga odpowiedzieć na pytania typu: "ile jest możliwych wyników w rzucie monetą?",
Komputery kwantowe - mit czy rzeczywistość?
 Działanie realizowane w ramach projektu Absolwent informatyki lub matematyki specjalistą na rynku pracy Komputery kwantowe - mit czy rzeczywistość? Wykład 7 Aneta Polewko-Klim Projekt współfinansowany
Działanie realizowane w ramach projektu Absolwent informatyki lub matematyki specjalistą na rynku pracy Komputery kwantowe - mit czy rzeczywistość? Wykład 7 Aneta Polewko-Klim Projekt współfinansowany
Teleportacja stanów atomowych z wykorzystaniem kwantowej interferencji pól wychodzących z dwóch rezonatorów
 Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Grzegorz Chimczak Teleportacja stanów atomowych z wykorzystaniem kwantowej interferencji pól wychodzących z dwóch rezonatorów Praca doktorska
Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Grzegorz Chimczak Teleportacja stanów atomowych z wykorzystaniem kwantowej interferencji pól wychodzących z dwóch rezonatorów Praca doktorska
Splątanie a przesyłanie informacji
 Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
VIII Festiwal Nauki i Sztuki. Wydziale Fizyki UAM
 VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Kryptografia kwantowa raz jeszcze Ryszard Tanaś http://zon8physdamuedupl/~tanas 13 października 2005
VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Kryptografia kwantowa raz jeszcze Ryszard Tanaś http://zon8physdamuedupl/~tanas 13 października 2005
Kwantowa kooperacja. Robert Nowotniak. Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Zadanie 1. Suma silni (11 pkt)
 2 Egzamin maturalny z informatyki Zadanie 1. Suma silni (11 pkt) Pojęcie silni dla liczb naturalnych większych od zera definiuje się następująco: 1 dla n = 1 n! = ( n 1! ) n dla n> 1 Rozpatrzmy funkcję
2 Egzamin maturalny z informatyki Zadanie 1. Suma silni (11 pkt) Pojęcie silni dla liczb naturalnych większych od zera definiuje się następująco: 1 dla n = 1 n! = ( n 1! ) n dla n> 1 Rozpatrzmy funkcję
Podstawy nauk przyrodniczych Matematyka
 Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
Podstawy nauk przyrodniczych Matematyka Elementy rachunku prawdopodobieństwa dr inż. Małgorzata Szeląg Zakład Genetyki Molekularnej Człowieka tel. 61 829 59 04 malgorzata.szelag@amu.edu.pl Pokój 1.118
1. Operacje logiczne A B A OR B
 1. Operacje logiczne OR Operacje logiczne są operacjami działającymi na poszczególnych bitach, dzięki czemu można je całkowicie opisać przedstawiając jak oddziałują ze sobą dwa bity. Takie operacje logiczne
1. Operacje logiczne OR Operacje logiczne są operacjami działającymi na poszczególnych bitach, dzięki czemu można je całkowicie opisać przedstawiając jak oddziałują ze sobą dwa bity. Takie operacje logiczne
Wykorzystanie metod ewolucyjnych w projektowaniu algorytmów kwantowych
 Wykorzystanie metod ewolucyjnych w projektowaniu algorytmów kwantowych mgr inż. Robert Nowotniak Politechnika Łódzka 1 października 2008 Robert Nowotniak 1 października 2008 1 / 18 Plan referatu 1 Informatyka
Wykorzystanie metod ewolucyjnych w projektowaniu algorytmów kwantowych mgr inż. Robert Nowotniak Politechnika Łódzka 1 października 2008 Robert Nowotniak 1 października 2008 1 / 18 Plan referatu 1 Informatyka
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 1
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8physdamuedupl/~tanas Wykład 1 Spis treści 1 Kryptografia klasyczna wstęp 4 11 Literatura 4 12 Terminologia 6 13 Główne postacie
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8physdamuedupl/~tanas Wykład 1 Spis treści 1 Kryptografia klasyczna wstęp 4 11 Literatura 4 12 Terminologia 6 13 Główne postacie
Algorytmy i struktury danych. Wykład 4
 Wykład 4 Różne algorytmy - obliczenia 1. Obliczanie wartości wielomianu 2. Szybkie potęgowanie 3. Algorytm Euklidesa, liczby pierwsze, faktoryzacja liczby naturalnej 2017-11-24 Algorytmy i struktury danych
Wykład 4 Różne algorytmy - obliczenia 1. Obliczanie wartości wielomianu 2. Szybkie potęgowanie 3. Algorytm Euklidesa, liczby pierwsze, faktoryzacja liczby naturalnej 2017-11-24 Algorytmy i struktury danych
Doświadczenie i zdarzenie losowe
 Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Doświadczenie i zdarzenie losowe Doświadczenie losowe jest to takie doświadczenie, które jest powtarzalne w takich samych warunkach lub zbliżonych, a którego wyniku nie można przewidzieć jednoznacznie.
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego
 Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego Piotr Rybak Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Piotr Rybak (Migacz UWr) Odkrywanie algorytmów kwantowych 1 / 17 Spis
Odkrywanie algorytmów kwantowych za pomocą programowania genetycznego Piotr Rybak Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Piotr Rybak (Migacz UWr) Odkrywanie algorytmów kwantowych 1 / 17 Spis
Kwantowe stany splątane. Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017
 B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
zdarzenie losowe - zdarzenie którego przebiegu czy wyniku nie da się przewidzieć na pewno.
 Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Rachunek prawdopodobieństwa Podstawowym celem rachunku prawdopodobieństwa jest określanie szans zajścia pewnych zdarzeń. Pojęcie podstawowe rachunku prawdopodobieństwa to: zdarzenie losowe - zdarzenie
Komputery Kwantowe. Ravindra W. Chhajlany. 16 stycznia Komputery Kwantowe
 Ravindra W. Chhajlany 16 stycznia 2007 Plan Przeszukiwanie nieuporządkowanej bazy danych: I Przykłady 1. Z ksiązki adresowej, podaj nazwę użytkownika do którego przypisany jest jakiś numer telefonu, np.
Ravindra W. Chhajlany 16 stycznia 2007 Plan Przeszukiwanie nieuporządkowanej bazy danych: I Przykłady 1. Z ksiązki adresowej, podaj nazwę użytkownika do którego przypisany jest jakiś numer telefonu, np.
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 6a
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 6a Spis treści 10 Trochę matematyki (c.d.) 3 10.19 Reszty kwadratowe w Z p.............. 3 10.20
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 6a Spis treści 10 Trochę matematyki (c.d.) 3 10.19 Reszty kwadratowe w Z p.............. 3 10.20
Prawdopodobieństwo
 Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
Prawdopodobieństwo http://www.matemaks.pl/ Wstęp do rachunku prawdopodobieństwa http://www.matemaks.pl/wstep-do-rachunku-prawdopodobienstwa.html Rachunek prawdopodobieństwa pomaga obliczyć szansę zaistnienia
1. Matematyka Fizyki Kwantowej: Cześć Druga
 . Matematyka Fizyki Kwantowej: Cześć Druga Piotr Szańkowski I. PRZESTRZEŃ WEKTOROWA Kolejnym punktem naszej jest ogólna struktura matematyczna mechaniki kwantowej, która jest strukturą przestrzeni wektorowej
. Matematyka Fizyki Kwantowej: Cześć Druga Piotr Szańkowski I. PRZESTRZEŃ WEKTOROWA Kolejnym punktem naszej jest ogólna struktura matematyczna mechaniki kwantowej, która jest strukturą przestrzeni wektorowej
Nanostruktury, spintronika, komputer kwantowy
 Nanostruktury, spintronika, komputer kwantowy Wykªad dla uczniów Gimnazjum Nr 2 w Krakowie I. Nanostruktury Skala mikrometrowa 1µm (mikrometr) = 1 milionowa cz ± metra = 10 6 m obiekty mikrometrowe, np.
Nanostruktury, spintronika, komputer kwantowy Wykªad dla uczniów Gimnazjum Nr 2 w Krakowie I. Nanostruktury Skala mikrometrowa 1µm (mikrometr) = 1 milionowa cz ± metra = 10 6 m obiekty mikrometrowe, np.
Kwantowa implementacja paradoksu Parrondo
 Kwantowa implementacja paradoksu Parrondo Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN, Gliwice oraz Zakład Fizyki Teoretycznej, Uniwersytet Śląski, Katowice 7 Czerwca 2005 Plan
Kwantowa implementacja paradoksu Parrondo Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN, Gliwice oraz Zakład Fizyki Teoretycznej, Uniwersytet Śląski, Katowice 7 Czerwca 2005 Plan
L.O. św. Marii Magdaleny w Poznaniu, O POŻYTKACH PŁYN ACYCH Z RZUCANIA MONETA. Tomasz Łuczak
 L.O. św. Marii Magdaleny w Poznaniu, 27.11.2015 O POŻYTKACH PŁYN ACYCH Z RZUCANIA MONETA Tomasz Łuczak NA POCZATEK DOBRA WIADOMOŚĆ! Dzięki naszym o hojnym sponsorom: Poznańskiej Fundacji Matematycznej
L.O. św. Marii Magdaleny w Poznaniu, 27.11.2015 O POŻYTKACH PŁYN ACYCH Z RZUCANIA MONETA Tomasz Łuczak NA POCZATEK DOBRA WIADOMOŚĆ! Dzięki naszym o hojnym sponsorom: Poznańskiej Fundacji Matematycznej
Rachunek prawdopodobieństwa- wykład 2
 Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
Rachunek prawdopodobieństwa- wykład 2 Pojęcie dyskretnej przestrzeni probabilistycznej i określenie prawdopodobieństwa w tej przestrzeni dr Marcin Ziółkowski Instytut Matematyki i Informatyki Uniwersytet
kondensat Bosego-Einsteina
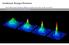 kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
Internet kwantowy. (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak. Instytut Informatyki Teoretycznej i Stosowanej PAN
 Internet kwantowy (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN 16. stycznia 2012 Plan wystąpienia 1 Skąd się biorą stany kwantowe? Jak
Internet kwantowy (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN 16. stycznia 2012 Plan wystąpienia 1 Skąd się biorą stany kwantowe? Jak
Systemy liczbowe. 1. Przedstawić w postaci sumy wag poszczególnych cyfr liczbę rzeczywistą R = (10).
 Wprowadzenie do inżynierii przetwarzania informacji. Ćwiczenie 1. Systemy liczbowe Cel dydaktyczny: Poznanie zasad reprezentacji liczb w systemach pozycyjnych o różnych podstawach. Kodowanie liczb dziesiętnych
Wprowadzenie do inżynierii przetwarzania informacji. Ćwiczenie 1. Systemy liczbowe Cel dydaktyczny: Poznanie zasad reprezentacji liczb w systemach pozycyjnych o różnych podstawach. Kodowanie liczb dziesiętnych
Wykład 8. Informatyka Stosowana. 26 listopada 2018 Magdalena Alama-Bućko. Informatyka Stosowana Wykład , M.A-B 1 / 31
 Wykład 8 Informatyka Stosowana 26 listopada 208 Magdalena Alama-Bućko Informatyka Stosowana Wykład 8 26..208, M.A-B / 3 Definicja Ciagiem liczbowym {a n }, n N nazywamy funkcję odwzorowujac a zbiór liczb
Wykład 8 Informatyka Stosowana 26 listopada 208 Magdalena Alama-Bućko Informatyka Stosowana Wykład 8 26..208, M.A-B / 3 Definicja Ciagiem liczbowym {a n }, n N nazywamy funkcję odwzorowujac a zbiór liczb
Temat: Kryptografia kwantowa. Autor: Tomasz Stachlewski. Data: październik Krótkie wprowadzenie
 Temat: Kryptografia kwantowa Autor: Tomasz Stachlewski Data: październik 2007 1. Krótkie wprowadzenie Na sam początek zadajmy sobie pytanie Jaka była przyczyna stworzenia pierwszych komputerów? Nie da
Temat: Kryptografia kwantowa Autor: Tomasz Stachlewski Data: październik 2007 1. Krótkie wprowadzenie Na sam początek zadajmy sobie pytanie Jaka była przyczyna stworzenia pierwszych komputerów? Nie da
Teoretyczne podstawy informatyki
 Teoretyczne podstawy informatyki Wykład 12a: Prawdopodobieństwo i algorytmy probabilistyczne http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Teoria prawdopodobieństwa
Teoretyczne podstawy informatyki Wykład 12a: Prawdopodobieństwo i algorytmy probabilistyczne http://hibiscus.if.uj.edu.pl/~erichter/dydaktyka2010/tpi-2010 Prof. dr hab. Elżbieta Richter-Wąs 1 Teoria prawdopodobieństwa
Wykorzystanie metod ewolucyjnych sztucznej inteligencji w projektowaniu algorytmów kwantowych
 Wykorzystanie metod ewolucyjnych sztucznej inteligencji w projektowaniu algorytmów kwantowych Robert Nowotniak Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 3 czerwca
Wykorzystanie metod ewolucyjnych sztucznej inteligencji w projektowaniu algorytmów kwantowych Robert Nowotniak Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka 3 czerwca
Prawdopodobieństwo geometryczne
 Prawdopodobieństwo geometryczne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Uniwersyteckie Koło Matematyczne 23 kwietnia 2009 r. Bartosz Ziemkiewicz (WMiI UMK) Prawdopodobieństwo geometryczne
Prawdopodobieństwo geometryczne Bartosz Ziemkiewicz Wydział Matematyki i Informatyki UMK, Toruń Uniwersyteckie Koło Matematyczne 23 kwietnia 2009 r. Bartosz Ziemkiewicz (WMiI UMK) Prawdopodobieństwo geometryczne
Kryptografia kwantowa
 Kryptografia kwantowa Wykład popularno-naukowy dla młodzieży szkół średnich Ryszard Tanaś http://zon8physdamuedupl/~tanas 20 marca 2002 Enigma niemiecka maszyna szyfrująca Marian Rejewski Jerzy Różycki
Kryptografia kwantowa Wykład popularno-naukowy dla młodzieży szkół średnich Ryszard Tanaś http://zon8physdamuedupl/~tanas 20 marca 2002 Enigma niemiecka maszyna szyfrująca Marian Rejewski Jerzy Różycki
Układy kombinacyjne 1
 Układy kombinacyjne 1 Układy kombinacyjne są to układy cyfrowe, których stany wyjść są zawsze jednoznacznie określone przez stany wejść. Oznacza to, że doprowadzając na wejścia tych układów określoną kombinację
Układy kombinacyjne 1 Układy kombinacyjne są to układy cyfrowe, których stany wyjść są zawsze jednoznacznie określone przez stany wejść. Oznacza to, że doprowadzając na wejścia tych układów określoną kombinację
Luty 2001 Algorytmy (7) 2000/2001 s-rg@siwy.il.pw.edu.pl
 System dziesiętny 7 * 10 4 + 3 * 10 3 + 0 * 10 2 + 5 *10 1 + 1 * 10 0 = 73051 Liczba 10 w tym zapisie nazywa się podstawą systemu liczenia. Jeśli liczba 73051 byłaby zapisana w systemie ósemkowym, co powinniśmy
System dziesiętny 7 * 10 4 + 3 * 10 3 + 0 * 10 2 + 5 *10 1 + 1 * 10 0 = 73051 Liczba 10 w tym zapisie nazywa się podstawą systemu liczenia. Jeśli liczba 73051 byłaby zapisana w systemie ósemkowym, co powinniśmy
Materiały dla finalistów
 Materiały dla finalistów Malachoviacus Informaticus 2016 11 kwietnia 2016 Wprowadzenie Poniższy dokument zawiera opisy zagadnień, które będą niezbędne do rozwiązania zadań w drugim etapie konkursu. Polecamy
Materiały dla finalistów Malachoviacus Informaticus 2016 11 kwietnia 2016 Wprowadzenie Poniższy dokument zawiera opisy zagadnień, które będą niezbędne do rozwiązania zadań w drugim etapie konkursu. Polecamy
Wstęp do Modelu Standardowego
 Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
Wstęp do Modelu Standardowego Plan (Uzupełnienie matematyczne II) Abstrakcyjna przestrzeń stanów Podstawowe własności Iloczyn skalarny amplitudy prawdopodobieństwa Operatory i ich hermitowskość Wektory
Dr inż. Robert Wójcik, p. 313, C-3, tel Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska
 Dr inż. Robert Wójcik, p. 313, C-3, tel. 320-27-40 Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska E-mail: Strona internetowa: robert.wojcik@pwr.edu.pl google: Wójcik
Dr inż. Robert Wójcik, p. 313, C-3, tel. 320-27-40 Katedra Informatyki Technicznej (K-9) Wydział Elektroniki (W-4) Politechnika Wrocławska E-mail: Strona internetowa: robert.wojcik@pwr.edu.pl google: Wójcik
Seminarium: Efekty kwantowe w informatyce
 Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 5
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 5 Spis treści 9 Algorytmy asymetryczne RSA 3 9.1 Algorytm RSA................... 4 9.2 Szyfrowanie.....................
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 5 Spis treści 9 Algorytmy asymetryczne RSA 3 9.1 Algorytm RSA................... 4 9.2 Szyfrowanie.....................
Zastosowanie Excela w matematyce
 Zastosowanie Excela w matematyce Komputer w dzisiejszych czasach zajmuje bardzo znamienne miejsce. Trudno sobie wyobrazić jakąkolwiek firmę czy instytucję działającą bez tego urządzenia. W szkołach pierwsze
Zastosowanie Excela w matematyce Komputer w dzisiejszych czasach zajmuje bardzo znamienne miejsce. Trudno sobie wyobrazić jakąkolwiek firmę czy instytucję działającą bez tego urządzenia. W szkołach pierwsze
P (A B) P (B) = 1/4 1/2 = 1 2. Zakładamy, że wszystkie układy dwójki dzieci: cc, cd, dc, dd są jednakowo prawdopodobne.
 Wykład Prawdopodobieństwo warunkowe Dwukrotny rzut symetryczną monetą Ω {OO, OR, RO, RR}. Zdarzenia: Awypadną dwa orły, Bw pierwszym rzucie orzeł. P (A) 1 4, 1. Jeżeli już wykonaliśmy pierwszy rzut i wiemy,
Wykład Prawdopodobieństwo warunkowe Dwukrotny rzut symetryczną monetą Ω {OO, OR, RO, RR}. Zdarzenia: Awypadną dwa orły, Bw pierwszym rzucie orzeł. P (A) 1 4, 1. Jeżeli już wykonaliśmy pierwszy rzut i wiemy,
Informacja w perspektywie obliczeniowej. Informacje, liczby i obliczenia
 Informacja w perspektywie obliczeniowej Informacje, liczby i obliczenia Cztery punkty odniesienia (dla pojęcia informacji) ŚWIAT ontologia fizyka UMYSŁ psychologia epistemologia JĘZYK lingwistyka nauki
Informacja w perspektywie obliczeniowej Informacje, liczby i obliczenia Cztery punkty odniesienia (dla pojęcia informacji) ŚWIAT ontologia fizyka UMYSŁ psychologia epistemologia JĘZYK lingwistyka nauki
Symulacja obliczeń kwantowych
 Model kwantowych bramek logicznych w NumPy Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 10 października 2007 Plan prezentacji 1 Python
Model kwantowych bramek logicznych w NumPy Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 10 października 2007 Plan prezentacji 1 Python
