Fizyka, technologia oraz modelowanie wzrostu kryształów
|
|
|
- Marek Małek
- 8 lat temu
- Przeglądów:
Transkrypt
1 Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-42 Warszawa, ul Sokołowska 29/37 tel: stach@unipress.waw.pl, mike@unipress.waw.pl Zbigniew Żytkiewicz Instytut Fizyki PAN Warszawa, Al. Lotników 32/46 zytkie@ifpan.edu.pl Wykład 2 godz./tydzień piątek Interdyscyplinarne Centrum Modelowania UW Budynek Wydziału Geologii UW sala
2 Wykład 4. Równowagowe własności powierzchni krystalicznych Fazy skondensowane (stała, ciekła) ujemna entalpia układu Energia oddziaływania np. potencjał Lennarda-Jonesa (gazy szlachetne) E ( r) = ε r σ 2 r σ 6 V/ε r/σ Do entalpii układu (jego energii wiązania) daje wkład wiele warstw atomowych.
3 Własności energetyczne warstw powierzchniowych Gęstość oraz energia oddziaływania zmienia się w sposób ciągły Energia Gęstość Grubość warstwy powierzchniowej może być bardzo różna, jednak w wielu przypadkach, np. kryształy półprzewodników lub kryształy jonowe, może to być wiele warstw atomowych. Stosuje się wiele różnych przybliżeń do opisu własności powierzchni, jednak najprostszym jest opis Gibbsa
4 Model powierzchni Gibbsa Model Gibbsa jednorodne własności faz objętościowych i dodatkowa gęstość (masy, energii, itp.) przypisywana powierzchni gdy zachodzi taka potrzeba Energia Można wybrać położenie powierzchni tak, aby znikała powierzchniowa gęstość masy lub powierzchniowa gęstość energii. Gęstość W przypadku układy zawierającego kilka składników można wybrać położenie tak aby znikała powierzchniowa gęstość jednego ze składników.
5 Opis standardowy znika powierzchniowa gęstość masy Energia swobodna kryształu F jest sumą wkładu objętościowego i powierzchniowego: F = V s f s r (T, p, r) dv + V l f l r (T, p, r) dv + S γ( θ, ϕ,t,p) ds µ l,s - potencjał chemiczny (s,l) f l,s - gęstość energii swobodnej na jednostkę objętości faz (s,l) γ - gęstość energii powierzchniowej Energia swobodna w modelu Gibbsa jest więc równa: F = f s (T, p)v s + f l (T, p)v l + γ( θ, ϕ,t, p)a
6 Napięcie powierzchniowe - i powierzchniowa gęstość energii Powierzchniowa gęstość energii γ ( θ,t,p) ds = γ( θ,t, p)a Praca potrzebna na zwiększenie obwodu = zmiana energii powierzchni F = Napięcie powierzchniowe siła działające na jednostkę długości obwodu powierzchni σ r A W = r r dlσ* δx r σδa = r σ F pow = γδa σ r = γ
7 Zwilżanie powierzchni Rozważmy 3 układy: faza stała(), faza gazowa(3) oraz inna faza (ciekła lub stała - 2) Własności energetyczne powierzchni są określone przez ich energie powierzchniowe (napięcia powierzchniowe):γ 2, γ 3, γ 23. (A) (B) Całkowite zwilżanie powierzchni (A) zachodzi gdy γ 3 > γ2 + γ 23
8 Częściowe zwilżanie powierzchni kąt zwilżania Częściowe zwilżanie powierzchni (A) zachodzi gdy γ γ 3 < γ2 + γ 23 3 > γ2 γ 23 Kąt zwilżania powierzchni definiujemy jako γ 3 = γ 2 + γ 23 cos ( θ) γ 2 θ γ 3 γ 23
9 Brak zwilżania Kąt zwilżania powierzchni γ 3 = γ 2 + γ 23 cos ( θ) γ 2 θ γ 3 γ 23 Brak zwilżania powierzchni (A) zachodzi gdy γ 2 > γ3 + γ 23
10 Warunki stabilności (V,T) Układy zamknięty warunek na stabilności - fluktuacje izotermicznoizochoryczne δf 0 δf = p δv p2δv + γδa + µ δn + µ 2δN 2 0 N = N + N2 = V = V + V2 = const const Równania równowagi δn δv = δ N 2 = V 2 T = const δt = 0 p δa = p2 + γ µ ( p,t) = µ 2( p,t) δv Stan równowagi zależy od kształtu powierzchni
11 Powierzchnia płaska U,V,N U 2,V 2,N 2 p,t,ρ p 2,T 2,ρ 2 Równania równowagi p δa = p2 + γ µ ( p,t) = µ 2( p,t) δv Dla powierzchni płaskiej wielkość powierzchni nie zależy od objętości faz: δa δv Warunki równowagi nie zależą od ich rozmiaru są to wartości umieszczane na diagramach fazowych = 0 p = p 2 T = = T2 Tp
12 Powierzchnia zakrzywiona przypadek izotropowy Równania równowagi p δa = p2 + γ δv µ ( p,t ) ( p,t ) = µ 2 U,V,N p,t,ρ U 2,V 2,N 2 Fazy izotropowe - kula: p 2,T 2,ρ 2 V = 4πR 3 3 A = 4πR 2 δa δv = 2 R = κ + κ 2 κ, κ 2 - krzywizny powierzchni Warunki równowagi zależą od rozmiaru faz p p2 2γ + R = T = T2 T p
13 Powierzchnia zakrzywiona efekt Gibbsa-Thompsona Równania równowagi p = p2 + 2γ R U,V,N p,t,ρ Przesunięcie ciśnienia zmiana warunku równowagi chemicznej U 2,V 2,N 2 p 2,T 2,ρ 2 µ ( + dp,t + dt) = µ ( p,t dt) p 2 + Efekt Gibbsa - Thompsona zmiana temperatury równowagi powierzchni zakrzywionej
14 Powierzchnia płaska Efekt Gibbsa-Thompsona Powierzchnia zakrzywiona µ (,T) = ( p,t) p µ 2 µ ( + dp,t + dt) = µ ( p,t dt) p 2 + Po rozwinięciu otrzymujemy: vdp s dt = s2dt dt = vdp s s 2 = (V / T dp ( S S )/ N S S L N)dp 2 = Vdp 2 = p Efekt Gibbsa - Thompsona zmiana temperatury równowagi powierzchni zakrzywionej T = T p - 2 d R o d o = T p γ = ( S - S ) L l s γ - długość kapilarna L ciepło przemiany na jednostkę objętości
15 Powierzchnia zakrzywiona przypadek anizotropowy Równania równowagi p = p 2 + γ Dla powierzchni są zdefiniowane dwa promienie krzywizny R oraz R 2 które dają rozmiar obszaru fazy 2. Zmiana ta powoduje zmianę potencjału chemicznego µ ( θ, ϕ) + R R ( + dp,t + dt) = µ ( p,t dt) p R 2 R Efekt Gibbsa - Thompsona zmiana temperatury równowagi powierzchni zakrzywionej: T = Tm - do( θ, ϕ) + do( θ, ϕ) R R 2 γ = T m ( θ, ϕ) ( S - S ) l s = γ ( θ, ϕ) L
16 Przypadek anizotropowy - równowagowy kształt powierzchni kryształów W przypadku kryształów energią powierzchniowa zależy od orientacji, tzn. zachodzi γ = γ(θ,ϕ) Wykres tej zależności jest to tzw. γ - plot - wyznaczenie na jego podstawie równowagowego kształtu kryształu nosi nazwę konstrukcji (twierdzenia) Wulfa. Równowagowy kształt kryształu jest wyznaczony przez minimalną obwiednię utworzoną przez płaszczyzny prostopadłe do linii wychodzących ze środka wykresu i przechodzące przez punkty przecięcia linii i tego wykresu Stąd wyznaczenie równowagowego kształtu sprowadza się do wyznaczenia zależności γ(θ,ϕ).
17 dθ Konstrukcja Wulfa E θ E 2 Dana jest zależność energii powierzchniowej od kątów γ(θ,ϕ) Obliczamy wielkość energii powierzchniowej dla kąta dθ Dla przypadku Dla przypadku E2 = E2dl E dl cosθ E dl cosθ E = Edl = = W przypadku gdy E 2 > (E /cosθ) to realizowany będzie przypadek, w przypadku odwrotnym przypadek 2. Jest to konstrukcja Wulfa
18 Kryształ Kossela najprostszy model kryształu Siec kwadratowa (2d) lub regularna( 3d) Oddziaływanie najbliższych sąsiadów Energia oddziaływania nie zależy od kierunku (φ - energia wiązania dwu atomów) Z liczba sąsiadów (d=2 Z=4, d=3 Z=6) φ φ Modyfikacje Oddziaływanie anizotropowe Oddziaływanie drugich sąsiadów φ X φ nn φ Y φ nnn
19 Powierzchnie w krysztale Kossela Powierzchnia układ atomów które nie maja wysycanych wiązań (mają złamane wiązania - broken bonds ) φ Energia kryształu (bez uwzględnienia powierzchni): E S ZNsφ = = Nbond Sφ 2 Energia kryształu (z powierzchnią): Energia powierzchni: E E = N S+ A S bond A φ E NsZφ = + Nbond 2 S+ A A Jest to uproszczony lecz zupełny opis powierzchni dla fazy stałej i fazy gazowej φ
20 Powierzchnie kryształ-ciecz w modelu Kossela Energia wiązania atomów w krysztale - φ ss Energia wiązania atomów w cieczy - φ ll E S E l N Zφ 2 s ss = = Nbond SS N Zφ 2 l ll = = Nbond ll φ φ ll ss Energia wiązania atomu w cieczy i w krysztale - φ sl φ ll φ sl Energia układu z powierzchnią: E S+ A+ L N = bond ls φ ls + N bond ss φ ss N bond ll φ ll φ ss Każde wiązanie łączy dwa atomy, stąd energia powierzchni jest równa: E A = Nbond A φ sl φ ll + φ 2 Jest to zupełny opis powierzchni dla fazy ciekłej i fazy stałej ss
21 Przykład (2d) - powierzchnie (0) oraz powierzchnie nachylone (vicinal surfaces) Powierzchnia (0) Powierzchnia nachylona (vicinal) α ( α) tg = n γ n = tg ( α) ( α) = φ( + n) cos( α) = cos( α) + sin( α) n szerokość stopnia (w stałych sieciowych) [ ] φ φ γ - plot wykres ma wcięcie (cusp) dla płaszczyzn o niskich wskaźnikach Millera (T = 0)
22 2-d kryształ Kossela Równowagowy kształt kryształu można policzyć dokładnie C. Rotmann and M Wortis (Phys. Rev B 24 (98) 6274) { } - - (, T ) = k T cos sinh ( cos ) + sin sinh ( sin ) γ θ θ α θ θ α θ RW B α = b b + sin 2 + b cos ( θ θ) 2 b = ϕ 2 sinh 2 ϕ cosh 2 2 Nie ma osobliwości przejścia fazowego
23 2-d kryształ Kossela - zależność kształtu od temperatury kt/ϕ = 0 kt/ϕ = 0.3 kt/ϕ = 0. kt/ϕ = 0.6
24 Weryfikacja wyniku Rotmana i Wortisa Monte Carlo wykonane przez Saito i Ueta (989r) Gaz sieciowy w równowadze z kryształem Kossela. Czas uśredniania Konfiguracja chwilowa Konfiguracje uśrednione. ϕ kt = 20 3 = 6.666(6) ϕ kt = 0 3 = 3.333(3) ϕ kt = 20 3 = 6.666(6)
25 Powierzchnie 2-d oraz 3-d Stopień jest obiektem -d
26 Struktura powierzchni 3-d F S K Powierzchnie o niskich wskaźnikach Millera nazywamy powierzchniami płaskimi (F flat) Warstwy atomowe zakończone są brzegiem. Brzeg warstwy nazywamy stopniami (S step lub L ledge) Koniec rzędu atomów w stopniu nazywamy kinkiem (K kink) Model nosi nazwę modelu TLK terrace ledge - kink
27 Rodzaje powierzchni 3-d Powierzchnia S(stepped) Powierzchnia F(flat) Powierzchnia K(kinked)
28 3-d Kossel klasyfikacja Rotmana i Wortisa Diagram fazowy Ciemne kropki - punkty osobliwe przejścia od powierzchni gładkiej do powierzchni zakrzywionej
29 Oddziaływanie drugich sąsiadów (przyciąganie nnn) klasyfikacja Rotmana i Wortisa Diagram fazowy
30 Oddziaływanie drugich sąsiadów (odpychanie nnn) klasyfikacja Rotmana i Wortisa Diagram fazowy
31 Mikroskopowa struktura powierzchni powierzchnie gładkie i szorstkie Szorstkość powierzchni definiujemy jako: R N - N N o o N - ilość złamanych wiązań N o - minimalna ilość złamanych wiązań gladka szorstka Parametr szorstkości zdefiniowany w ten sposób nie jest tożsamy z szorstkością mierzona np. przy pomocy mikroskopu sił atomowych (AFM)
32 Przejście fazowe powierzchnia gładka powierzchnia szorstka: wyniki analityczne Model pojedynczej warstwy: Teoria pola średniego (przybliżenie Bragga Williamsa) Energia swobodna układu jest równa: [ ( - x) ln ( - x) + Z φ x ( - x) ] F = kt x ln x Zφ/kT=3 x N N at o Zφ/kT=2 F/kT Zφ/kT= Przejście fazowe dla Zφ=2kT x
33 Przejście fazowe powierzchnia gładka powierzchnia szorstka: wyniki symulacji komputerowych Model ze stopniami Pseudoperiodyczne warunki brzegowe Przybliżenie SOS Leamy & Gilmer α kt φ = kt ε
34 Przejście fazowe powierzchnia gładka powierzchnia szorstka: wyniki symulacji komputerowych Różnica energii układu ze stopniami oraz bez stopni: α kt φ = kt ε Przejście fazowe dla kt = 0.6φ
35 Równowagowa struktura stopni Stopień obiekt -d Nie występuje przejście fazowe dla struktury stopnia Stopień - obiekt szorstki obecność dużej gęstości kinków Stopień obiekt na którym odbywa się wymiana atomów
36 Powierzchnie kryształów rzeczywistych bez atomów obcych Na powierzchni kryształów rzeczywistych może zajść efekt Jahna-Tellera: spontaniczne złamanie symetrii dla obniżenia energii układu Wyróżniamy dwa rodzaje efektów: relaksację i rekonstrukcje powierzchni Relaksacja powierzchni: zmiana położeń atomów zachowująca symetrię translacyjną sieci (równoległą do powierzchni) Rekonstrukcja powierzchni: zmiana położeń atomów w sieci naruszająca symetrie sieci Bravais
37 Relaksacja powierzchni Występuje w przypadku metali wiązania prawie izotropowe Zachowanie elektrostatycznej struktury powierzchni Powierzchnia prosta Powierzchnia zrelaksowana
38 Powierzchnie ulegające rekonstrukcji przykłady 2x rekonstrukcja brakującego rzędu 2x rekonstrukcja parowania Symetria sieci notacja Wooda
39 Powierzchnia o wskaźnikach krystalograficznych (hkl) Notacja (symbol) Wooda a, a 2 - wektory translacji prymitywnych powierzchni Symbol chemiczny, np. C S(hkl) κ a r r b, a r r b Rϕ o Obrót o kąt ϕº (Dla ϕ=0 symbol jest pomijany) c centrowana p prosta (domyślna w przypadku braku symbolu) b, b 2 - wektory translacji prymitywnych sieci objętościowej Notacja Wooda jest niekiedy niejednoznaczna (dla sieci regularnej)
40 Symbol Wooda - przykłady ( x) ( 2 x) ( 2x2) ( 2x2) ( 2x 2)
41 Powierzchnie półprzewodników rekonstrukcja Silne, kierunkowe wiązania Tendencja do wysycenia przez tworzenie wiązań równoległych do powierzchni: łańcuchów, dimerów itp. Struktura powierzchni może ulec zmianie na skutek przyłączenia obcych atomów wysycających złamane wiązania Rekonstrukcja może sięgać kilku warstw atomowych Ładunki związane ze stanami powierzchniowymi tworzą pola które mogą sięgać głęboko do wnętrza półprzewodnika
42 Skanningowy mikroskop tunelowy (Scanning Tunneling Microscope STM) Nobel Laureates: Heinrich Rohrer and Gerd Binnig
43 Działanie skanningowego mikroskopu tunelowego Oddziaływanie końcówki mikroskopu z powierzchnią Zależność prądu tunelowania od odległości d. K oraz k są stałymi STM osiąga rozdzielczość atomową!
44 Mikroskop sił atomowych (AFM Atomic Force Microscope) Atomic Force Microscope - NovaScan ESPM II OSPM II
45 Działanie mikroskopu sił atomowych Oddziaływanie końcówki mikroskopu z powierzchnią Detekcja ruchu końcówki mikroskopu odbity promień lasera Rozdzielczość atomowa powierzchni miki w roztworze wodnym. Odległość pomiędzy sąsiadującymi wypukłościami wynosi 5.4 Å.
46 Powierzchnie półprzewodników łańcuchy zig-zak kation-anion Powierzchnia (0) x - schemat Powierzchnia InP (0) x - STM Aniony kółka pełne Kationy kółka puste Zapełnione złamane wiązanie Puste złamane wiązanie
47 Powierzchnie półprzewodników łańcuchy związane wiązaniami π Schemat powierzchni () półprzewodników grupy IV Łańcuchy Pandey a z ugięciem (a) - dodatnie ugięcie (a) - powierzchnia idealna (b) - ujemne ugięcie (b) - powierzchnia zrelaksowana
48 Powierzchnie półprzewodników łańcuchy związane wiązaniami π (ładunek elektryczny) Rozkład ładunku na powierzchni C() 2x Widok z boku Widok z góry Stan antywiążący Stan wiążący
49 Powierzchnie półprzewodników łańcuchy Seiwatza Powierzchnia () półprzewodników grupy IV potrójne złamane wiązanie (TDB triple dangling bonds) Idealna powierzchnia TDB IV() Łańcuch Seiwatza widok z boku Łańcuch Seiwatza widok z góry
50 Powierzchnie półprzewodników - dimery Dimery symetryczne - schemat powstawania Dimery asymetryczne schemat powstawania
51 Powierzchnie półprzewodników dimery rozkład ładunku Powierzchnia GaAs (00) 2x4 As kółka pełne Ga kółka puste
52 Powierzchnie półprzewodników- dimery: układy mostkowe Powierzchnia C terminated SiC (00) c (2x2) Skręcony dimer Skręcona grupa mostkowa C kółka pełne; Si kółka puste
53 Powierzchnie półprzewodników adatomy Adatomy (atomy zaadsorbowane) na powierzchni () kryształów o strukturze diamentu lub blendy cynkowej Adatomy kółka szare
54 Powierzchnie półprzewodników adatomy Si () 7x7 DAS (dimer adatom stacking fault) Adatomy na powierzchni Si () - model STM obraz Adatomy kółka szare
55 Si() rekonstrukcja (7x7) - obrazy STM 3-d model Model - R.M. Tromp (IBM) Obraz STM
56 Adsorpcja Fizysorpcja przyłączanie atomów do powierzchni kryształu/cieczy bez tworzenia wiązań chemicznych. Siły wiążące siły Lennarda Jonesa. Na ogół nie prowadzi do lokalizacji atomu na powierzchni Chemisorpcja przyłączenie atomu do powierzchni kryształu/cieczy powodujące powstanie wiązania chemicznego. Na ogół prowadzi do lokalizacji atomów w węzłach sieci krystalograficznej. Często prowadzi do zmian wiązania w przyłączanych cząsteczkach chemicznych.
57 Fizysorpcja izoterma Langmuira Zakładamy ze istnieje pewna liczba węzłów na których mogą być zaadsorbowane cząstki Pokryciem Γ nazywamy stosunek liczby obsadzonych wezłów do liczby wszystkich węzłów Pokrycie zależy min. od energii wiązania na powierzchni Dla danego układu (tzn. dla określonej energii wiązania) pokrycie jest funkcja ciśnienia gazu nad powierzchnia i temperatury: Γ = Γ o P + P P 2 ( T) Γ E kt o = Γ( P ) 5 2 b P ( T) = P Γ = = CT exp 2 2 E b energia wiązania do powierzchni
58 Przykład - adsorpcja CO/Pd()
59 Chemisorpcja Adsorpcja molekularna Adsorpcja dysocjatywna E dis Energy 0 E dis Energy 0 5 E bar 5 E bar distance distance
60 Oddziaływanie N 2 z Ga(l) N 2 Energia bariery na rozpad Excess energy [ev] ev 4.8 ev 3.2 ev N2 molecule horizontally and cluster of 9 atoms In Ga Al Ga Energia dysocjacji swobodnej cząsteczki N ev/cząsteczkę Distance from surface(a) S. Krukowski and Z. Romanowski Obliczenia kwantowe, Dmol, QM DFT
61 Dysocjacja N 2 na powierzchni Ga 3,5 3,0.0A N - N spacing [A] 2,5 2,0,5.6A 2.6A,0 0,8,2,6 2,0 2,4 2,8 3,2 3,6 4,0 d [A] S. Krukowski and Z. Romanowski Dmol, QM DFT
62 Rozpuszczanie innych gazów O 2 i H 2 O 2 na powierzchni metali H 2 na powierzchni metali Excess energy [ev] ev -.8 ev -3.8 ev One layer Me surface clusters: Al Ga In 2.9 ev Excess energy [ev] ev.4 ev.8 ev H 3.2 ev 2 molecule and 27 atom cluste in one layer: Al: 3.2eV Al - back: 2.3eV Ga:3.0eV Ga - back: 2.0eV In: 2.9eV 2.3 ev In - back:.8ev 2.0 ev Distance from surface [A] Distance from surfacei [A] Brak bariery energetycznej E bar = 2.0 ev (Ga) S. Krukowski & Z. Romanowski, QM DFT
63 Rozpuszczanie CO CO na powierzchni metali OC na powierzchni metali Excess energy [ev] ev 3.6 ev 2.4 ev 4.0 ev CO molecule and 27 atom cluster in one layer 2.9 ev O closer to the surface Al: 4.0eV Al - back: 2.8eV Ga: 2.9eV In: 4.0eV In - back: 3.6eV 2.8 ev Excess energy [ev] ev 0.3 ev 2.2 ev.9 ev CO molecule and 27 atom cluster in one layer: Al: 2.2eV Al - back:.9ev Ga: 2.0eV Ga - back: 2.0eV In: 2.4eV In - back: 2.4eV 0.7 ev 2.0 ev 0.3 ev Distance from surface [A] Distance from surface [A] E bar = 2.0 ev (Ga) S. Krukowski & Z. Romanowski, QM DFT
Fizyka, technologia oraz modelowanie wzrostu kryształów
 Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-42 Warszawa, ul Sokołowska 29/37 tel: 88 80 244 e-mail: stach@unipress.waw.pl,
Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-42 Warszawa, ul Sokołowska 29/37 tel: 88 80 244 e-mail: stach@unipress.waw.pl,
Fizyka, technologia oraz modelowanie wzrostu kryształów
 Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
Fizyka, technologia oraz modelowanie wzrostu kryształów Stanisław Krukowski i Michał Leszczyński Instytut Wysokich Ciśnień PAN 0-4 Warszawa, ul Sokołowska 9/37 tel: 88 80 44 e-mail: stach@unipress.waw.pl,
Krystalizacja. Zarodkowanie
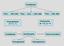 Krystalizacja Ciecz ciało stałe Para ciecz ciało stałe Para ciało stałe Przechłodzenie T = T L - T c Przesycenie p = p g - p z > 0 Krystalizacja Zarodkowanie Rozrost zarodków Homogeniczne Heterogeniczne
Krystalizacja Ciecz ciało stałe Para ciecz ciało stałe Para ciało stałe Przechłodzenie T = T L - T c Przesycenie p = p g - p z > 0 Krystalizacja Zarodkowanie Rozrost zarodków Homogeniczne Heterogeniczne
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
Zadania treningowe na kolokwium
 Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Zadania treningowe na kolokwium 3.12.2010 1. Stan układu binarnego zawierającego n 1 moli substancji typu 1 i n 2 moli substancji typu 2 parametryzujemy za pomocą stężenia substancji 1: x n 1. Stabilność
Wiązania chemiczne. Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych. 5 typów wiązań
 Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
Elementy teorii powierzchni metali
 Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Fizyka statystyczna Fenomenologia przejść fazowych. P. F. Góra
 Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
Fizyka statystyczna Fenomenologia przejść fazowych P. F. Góra http://th-www.if.uj.edu.pl/zfs/gora/ 2015 Przejście fazowe transformacja układu termodynamicznego z jednej fazy (stanu materii) do innej, dokonywane
Powierzchnie cienkie warstwy nanostruktury. Józef Korecki, C1, II p., pok. 207
 Powierzchnie cienkie warstwy nanostruktury Józef Korecki, C1, II p., pok. 207 korecki@uci.agh.edu.pl http://korek.uci.agh.edu.pl/priv/jk.htm Obiekty niskowymiarowe Powierzchnia Cienkie warstwy Wielowarstwy
Powierzchnie cienkie warstwy nanostruktury Józef Korecki, C1, II p., pok. 207 korecki@uci.agh.edu.pl http://korek.uci.agh.edu.pl/priv/jk.htm Obiekty niskowymiarowe Powierzchnia Cienkie warstwy Wielowarstwy
BUDOWA KRYSTALICZNA CIAŁ STAŁYCH. Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale
 BUDOWA KRYSTALICZNA CIAŁ STAŁYCH Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale na: kryształy ciała o okresowym regularnym uporządkowaniu atomów, cząsteczek w całej swojej
BUDOWA KRYSTALICZNA CIAŁ STAŁYCH Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale na: kryształy ciała o okresowym regularnym uporządkowaniu atomów, cząsteczek w całej swojej
Statyka Cieczy i Gazów. Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał
 Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
Statyka Cieczy i Gazów Temat : Podstawy teorii kinetyczno-molekularnej budowy ciał 1. Podstawowe założenia teorii kinetyczno-molekularnej budowy ciał: Ciała zbudowane są z cząsteczek. Pomiędzy cząsteczkami
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY
 WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
WŁASNOŚCI CIAŁ STAŁYCH I CIECZY Polimery Sieć krystaliczna Napięcie powierzchniowe Dyfuzja 2 BUDOWA CIAŁ STAŁYCH Ciała krystaliczne (kryształy): monokryształy, polikryształy Ciała amorficzne (bezpostaciowe)
Wykład 5. Komórka elementarna. Sieci Bravais go
 Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
STRUKTURA CIAŁA STAŁEGO
 STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
Zjawiska powierzchniowe
 Zjawiska powierzchniowe Adsorpcja Model Langmuira Model BET 1 Zjawiska powierzchniowe Adsorpcja Proces gromadzenia się substancji z wnętrza fazy na granicy międzyfazowej; Wynika z tego, że w obszarze powierzchniowym
Zjawiska powierzchniowe Adsorpcja Model Langmuira Model BET 1 Zjawiska powierzchniowe Adsorpcja Proces gromadzenia się substancji z wnętrza fazy na granicy międzyfazowej; Wynika z tego, że w obszarze powierzchniowym
Fizyka Ciała Stałego
 Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Sieć przestrzenna. c r. b r. a r. komórka elementarna. r r
 Sieć przestrzenna c r b r r r u a r vb uvw = + + w c v a r komórka elementarna V = r r a ( b c) v Układy krystalograficzne (7) i Sieci Bravais (14) Triclinic (P) a b c, α β γ 90 ο Monoclinic (P) a b c,
Sieć przestrzenna c r b r r r u a r vb uvw = + + w c v a r komórka elementarna V = r r a ( b c) v Układy krystalograficzne (7) i Sieci Bravais (14) Triclinic (P) a b c, α β γ 90 ο Monoclinic (P) a b c,
Nauka o Materiałach Wykład II Monokryształy Jerzy Lis
 Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
STRUKTURA KRYSTALICZNA
 PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
Termodynamika fazy powierzchniowej Zjawisko sorpcji Adsorpcja fizyczna: izoterma Langmuira oraz BET Zjawiska przylegania
 ermodynamika zjawisk powierzchniowych 3.6.1. ermodynamika fazy powierzchniowej 3.6.2. Zjawisko sorpcji 3.6.3. Adsorpcja fizyczna: izoterma Langmuira oraz BE 3.6.4. Zjawiska przylegania ZJAWISKA PWIERZCHNIWE
ermodynamika zjawisk powierzchniowych 3.6.1. ermodynamika fazy powierzchniowej 3.6.2. Zjawisko sorpcji 3.6.3. Adsorpcja fizyczna: izoterma Langmuira oraz BE 3.6.4. Zjawiska przylegania ZJAWISKA PWIERZCHNIWE
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Elektrostatyka ŁADUNEK. Ładunek elektryczny. Dr PPotera wyklady fizyka dosw st podypl. n p. Cząstka α
 Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ
 CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ Ciepło i temperatura Pojemność cieplna i ciepło właściwe Ciepło przemiany Przejścia między stanami Rozszerzalność cieplna Sprężystość ciał Prawo Hooke a Mechaniczne
CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ Ciepło i temperatura Pojemność cieplna i ciepło właściwe Ciepło przemiany Przejścia między stanami Rozszerzalność cieplna Sprężystość ciał Prawo Hooke a Mechaniczne
Wykład 1. Anna Ptaszek. 5 października Katedra Inżynierii i Aparatury Przemysłu Spożywczego. Chemia fizyczna - wykład 1. Anna Ptaszek 1 / 36
 Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Wykład 1 Katedra Inżynierii i Aparatury Przemysłu Spożywczego 5 października 2015 1 / 36 Podstawowe pojęcia Układ termodynamiczny To zbiór niezależnych elementów, które oddziałują ze sobą tworząc integralną
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wstęp. Krystalografia geometryczna
 Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 1 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 1 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Wykład 14 Przejścia fazowe
 Wykład 14 Przejścia fazowe Z izoterm gazu Van der Waalsa (rys.14.1) wynika, że dla T < T k izotermy zawierają obszary w których gaz Van der Waalsa zachowuje się niefizycznie. W tych niefizycznych obszarach
Wykład 14 Przejścia fazowe Z izoterm gazu Van der Waalsa (rys.14.1) wynika, że dla T < T k izotermy zawierają obszary w których gaz Van der Waalsa zachowuje się niefizycznie. W tych niefizycznych obszarach
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 4 v.16 Wiązanie metaliczne Wiązanie metaliczne Zajmujemy się tylko metalami dlatego w zasadzie interesuje nas tylko wiązanie metaliczne.
Wykład 3. Entropia i potencjały termodynamiczne
 Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Wykład 3 Entropia i potencjały termodynamiczne dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 1 stycznia 2017 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
FIZYKA POWIERZCHNI I NANOSTRUKTURY. Wykład odbędzie się w II semstrze 2005/2006
 FIZYKA POWIERZCHNI I NANOSTRUKTURY dr hab. Zbigniew Postawa Zakład Fizyki Doświadczalnej pok. 016 Tel. 5626 e-mail: zp@castor.if.uj.edu.pl H H C H H C H H Wykład odbędzie się w II semstrze 2005/2006 Bez
FIZYKA POWIERZCHNI I NANOSTRUKTURY dr hab. Zbigniew Postawa Zakład Fizyki Doświadczalnej pok. 016 Tel. 5626 e-mail: zp@castor.if.uj.edu.pl H H C H H C H H Wykład odbędzie się w II semstrze 2005/2006 Bez
Wykład 4. Przypomnienie z poprzedniego wykładu
 Wykład 4 Przejścia fazowe materii Diagram fazowy Ciepło Procesy termodynamiczne Proces kwazistatyczny Procesy odwracalne i nieodwracalne Pokazy doświadczalne W. Dominik Wydział Fizyki UW Termodynamika
Wykład 4 Przejścia fazowe materii Diagram fazowy Ciepło Procesy termodynamiczne Proces kwazistatyczny Procesy odwracalne i nieodwracalne Pokazy doświadczalne W. Dominik Wydział Fizyki UW Termodynamika
S. Baran - Podstawy fizyki materii skondensowanej Wiązania chemiczne w ciałach stałych. Wiązania chemiczne w ciałach stałych
 Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wstęp do Optyki i Fizyki Materii Skondensowanej. Mateusz Goryca
 Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Termodynamiczny opis przejść fazowych pierwszego rodzaju
 Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Wykład II Przejścia fazowe 1 Termodynamiczny opis przejść fazowych pierwszego rodzaju Woda występuje w trzech stanach skupienia jako ciecz, jako gaz, czyli para wodna, oraz jako ciało stałe, a więc lód.
Pasmowa teoria przewodnictwa. Anna Pietnoczka
 Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Pasmowa teoria przewodnictwa elektrycznego Anna Pietnoczka Wpływ rodzaju wiązań na przewodność próbki: Wiązanie jonowe - izolatory Wiązanie metaliczne - przewodniki Wiązanie kowalencyjne - półprzewodniki
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Wykład VI. Teoria pasmowa ciał stałych
 Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład VI Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Podstawy termodynamiki
 Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Podstawy termodynamiki Organizm żywy z punktu widzenia termodynamiki Parametry stanu Funkcje stanu: U, H, F, G, S I zasada termodynamiki i prawo Hessa II zasada termodynamiki Kierunek przemian w warunkach
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Wykład III. Teoria pasmowa ciał stałych
 Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Wykład III Teoria pasmowa ciał stałych Energia elektronu (ev) Powstawanie pasm w krysztale sodu pasmo walencyjne (zapełnione częściowo) Konfiguracja w izolowanym atomie Na: 1s 2 2s 2 2p 6 3s 1 Ne Położenie
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5. Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego
 Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Szkła specjalne Przejście szkliste i jego termodynamika Wykład 5 Ryszard J. Barczyński, 2017 Materiały edukacyjne do użytku wewnętrznego Czy przejście szkliste jest termodynamicznym przejściem fazowym?
Równowagi fazowe. Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny
 Równowagi fazowe Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny Równowaga termodynamiczna Przemianom fazowym towarzyszą procesy, podczas których nie zmienia się skład chemiczny układu, polegają
Równowagi fazowe Zakład Chemii Medycznej Pomorski Uniwersytet Medyczny Równowaga termodynamiczna Przemianom fazowym towarzyszą procesy, podczas których nie zmienia się skład chemiczny układu, polegają
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii
 Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Seria 2, ćwiczenia do wykładu Od eksperymentu do poznania materii 8.1.21 Zad. 1. Obliczyć ciśnienie potrzebne do przemiany grafitu w diament w temperaturze 25 o C. Objętość właściwa (odwrotność gęstości)
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/\~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne......................
Ciała stałe. Ciała krystaliczne. Ciała amorficzne. Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami.
 Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
Elektrodynamika Część 1 Elektrostatyka Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 1 Literatura 3 2 Elektrostatyka 4 2.1 Pole elektryczne....................
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
Podstawy fizyki wykład 2
 D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
Warunki izochoryczno-izotermiczne
 WYKŁAD 5 Pojęcie potencjału chemicznego. Układy jednoskładnikowe W zależności od warunków termodynamicznych potencjał chemiczny substancji czystej definiujemy następująco: Warunki izobaryczno-izotermiczne
WYKŁAD 5 Pojęcie potencjału chemicznego. Układy jednoskładnikowe W zależności od warunków termodynamicznych potencjał chemiczny substancji czystej definiujemy następująco: Warunki izobaryczno-izotermiczne
MATERIA. = m i liczby całkowite. ciała stałe. - kryształy - ciała bezpostaciowe (amorficzne) - ciecze KRYSZTAŁY. Periodyczność
 MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 8 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 8 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne
 Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Transport jonów: kryształy jonowe
 Transport jonów: kryształy jonowe JONIKA I FOTONIKA MICHAŁ MARZANTOWICZ Jodek srebra AgI W 42 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie
Transport jonów: kryształy jonowe JONIKA I FOTONIKA MICHAŁ MARZANTOWICZ Jodek srebra AgI W 42 K strukturalne przejście fazowe I rodzaju do fazy α stopiona podsieć kationowa. Fluorek ołowiu PbF 2 zdefektowanie
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
prof. dr hab. Małgorzata Jóźwiak
 Czy równowaga w przyrodzie i w chemii jest korzystna? prof. dr hab. Małgorzata Jóźwiak 1 Pojęcie równowagi łańcuch pokarmowy równowagi fazowe równowaga ciało stałe - ciecz równowaga ciecz - gaz równowaga
Czy równowaga w przyrodzie i w chemii jest korzystna? prof. dr hab. Małgorzata Jóźwiak 1 Pojęcie równowagi łańcuch pokarmowy równowagi fazowe równowaga ciało stałe - ciecz równowaga ciecz - gaz równowaga
Temat 27. Termodynamiczne modele blokowe wzrostu kryształów
 Temat 27. Termodynamiczne modele blokowe wzrostu kryształów W modelach blokowych wzrostu kryształów wszystkie zjawiska zachodzące na powierzchni kryształu zostały sprowadzone do przyłączania i odłączania
Temat 27. Termodynamiczne modele blokowe wzrostu kryształów W modelach blokowych wzrostu kryształów wszystkie zjawiska zachodzące na powierzchni kryształu zostały sprowadzone do przyłączania i odłączania
PODSTAWY CHEMII INŻYNIERIA BIOMEDYCZNA. Wykład 2
 PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
PODSTAWY CEMII INŻYNIERIA BIOMEDYCZNA Wykład Plan wykładu II,III Woda jako rozpuszczalnik Zjawisko dysocjacji Równowaga w roztworach elektrolitów i co z tego wynika Bufory ydroliza soli Roztwory (wodne)-
WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ MATERIAŁ. Właściwości materiałów. Właściwości materiałów
 WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ Właściwości materiałów O możliwości zastosowania danego materiału decydują jego właściwości użytkowe; Zachowanie się danego materiału w środowisku pracy to zaplanowana
WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ Właściwości materiałów O możliwości zastosowania danego materiału decydują jego właściwości użytkowe; Zachowanie się danego materiału w środowisku pracy to zaplanowana
STRUKTURA PASM ENERGETYCZNYCH
 PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
PODSTAWY TEORII PASMOWEJ Struktura pasm energetycznych Teoria wa Struktura wa stałych Półprzewodniki i ich rodzaje Półprzewodniki domieszkowane Rozkład Fermiego - Diraca Złącze p-n (dioda) Politechnika
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }
![Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] } Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }](/thumbs/64/51033976.jpg) Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
S ścianki naczynia w jednostce czasu przekazywany
 FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
FIZYKA STATYSTYCZNA W ramach fizyki statystycznej przyjmuje się, że każde ciało składa się z dużej liczby bardzo małych cząstek, nazywanych cząsteczkami. Cząsteczki te znajdują się w ciągłym chaotycznym
Ogólny schemat postępowania
 Ogólny schemat postępowania 1. Należy zdecydować, który rozkład prawdopodobieństwa chcemy badać. Rozkład oznaczamy przez P; zależy od zespołu statystycznego. 2. Narzucamy warunek równowagi szczegółowej,
Ogólny schemat postępowania 1. Należy zdecydować, który rozkład prawdopodobieństwa chcemy badać. Rozkład oznaczamy przez P; zależy od zespołu statystycznego. 2. Narzucamy warunek równowagi szczegółowej,
Nanostruktury i nanotechnologie
 Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Nanostruktury i nanotechnologie Heterozłącza Efekty kwantowe Nanotechnologie Z. Postawa, "Fizyka powierzchni i nanostruktury" 1 Termin oddania referatów do 19 I 004 Zaliczenie: 1 I 004 Z. Postawa, "Fizyka
Czym się różni ciecz od ciała stałego?
 Szkła Czym się różni ciecz od ciała stałego? gęstość Czy szkło to ciecz czy ciało stałe? Szkło powstaje w procesie chłodzenia cieczy. Czy szkło to ciecz przechłodzona? kryształ szkło ciecz przechłodzona
Szkła Czym się różni ciecz od ciała stałego? gęstość Czy szkło to ciecz czy ciało stałe? Szkło powstaje w procesie chłodzenia cieczy. Czy szkło to ciecz przechłodzona? kryształ szkło ciecz przechłodzona
Przejścia kwantowe w półprzewodnikach (kryształach)
 Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Przejścia kwantowe w półprzewodnikach (kryształach) Rozpraszanie na nieruchomej sieci krystalicznej (elektronów, neutronów, fotonów) zwykłe odbicie Bragga (płaszczyzny krystaliczne odgrywają rolę rys siatki
Wykład 21: Studnie i bariery cz.2.
 Wykład 21: Studnie i bariery cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Przykłady tunelowania: rozpad alfa, synteza
Wykład 21: Studnie i bariery cz.2. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.321 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 1 Przykłady tunelowania: rozpad alfa, synteza
Elektryczne własności ciał stałych
 Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności elektryczne trzeba zdefiniować kilka wielkości Oporność właściwa (albo przewodność) ładunek [C] = 1/
XXXI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne
 XXXI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne Rozwiąż dowolnie przez siebie wybrane dwa zadania spośród poniższych trzech: Nazwa zadania: ZADANIE T A. Oblicz moment bezwładności jednorodnego
XXXI OLIMPIADA FIZYCZNA ETAP WSTĘPNY Zadanie teoretyczne Rozwiąż dowolnie przez siebie wybrane dwa zadania spośród poniższych trzech: Nazwa zadania: ZADANIE T A. Oblicz moment bezwładności jednorodnego
Efekty strukturalne przemian fazowych
 Efekty strukturalne przemian fazowych Literatura 1. Zbigniew Kędzierski PRZEMIANY FAZOWE W UKŁADACH SKONDESOWANYCH, AGH Uczelniane Wydawnictwa Naukowo Dydaktyczne, 003. Marek Blicharski INŻYNIERIA MATERIAŁOWA
Efekty strukturalne przemian fazowych Literatura 1. Zbigniew Kędzierski PRZEMIANY FAZOWE W UKŁADACH SKONDESOWANYCH, AGH Uczelniane Wydawnictwa Naukowo Dydaktyczne, 003. Marek Blicharski INŻYNIERIA MATERIAŁOWA
STRUKTURA MATERIAŁÓW
 STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
Linie sił pola elektrycznego
 Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Nauka o Materiałach. Wykład VIII. Odkształcenie materiałów właściwości sprężyste. Jerzy Lis
 Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Symulacja Monte Carlo izotermy adsorpcji w układzie. ciało stałe-gaz
 Ćwiczenie nr 2 Symulacja Monte Carlo izotermy adsorpcji w układzie ciało stałe-gaz I. Cel ćwiczenia Celem ćwiczenia jest określenie wpływu parametrów takich jak temperatura, energia oddziaływania cząsteczka-powierzchnia
Ćwiczenie nr 2 Symulacja Monte Carlo izotermy adsorpcji w układzie ciało stałe-gaz I. Cel ćwiczenia Celem ćwiczenia jest określenie wpływu parametrów takich jak temperatura, energia oddziaływania cząsteczka-powierzchnia
Wykład 18 Dielektryk w polu elektrycznym
 Wykład 8 Dielektryk w polu elektrycznym Polaryzacja dielektryka Dielektryk (izolator), w odróżnieniu od przewodnika, nie posiada ładunków swobodnych zdolnych do przemieszczenia się na duże odległości.
Wykład 8 Dielektryk w polu elektrycznym Polaryzacja dielektryka Dielektryk (izolator), w odróżnieniu od przewodnika, nie posiada ładunków swobodnych zdolnych do przemieszczenia się na duże odległości.
Przewodność elektryczna ciał stałych. Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki
 Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
Przewodność elektryczna ciał stałych Elektryczne własności ciał stałych Izolatory, metale i półprzewodniki Elektryczne własności ciał stałych Do sklasyfikowania różnych materiałów ze względu na ich własności
STRUKTURA IDEALNYCH KRYSZTAŁÓW
 BUDOWA WEWNĘTRZNA MATERIAŁÓW METALICZNYCH Zakres tematyczny y 1 STRUKTURA IDEALNYCH KRYSZTAŁÓW 2 1 Sieć przestrzenna kryształu TRANSLACJA WĘZŁA TRANSLACJA PROSTEJ SIECIOWEJ TRANSLACJA PŁASZCZYZNY SIECIOWEJ
BUDOWA WEWNĘTRZNA MATERIAŁÓW METALICZNYCH Zakres tematyczny y 1 STRUKTURA IDEALNYCH KRYSZTAŁÓW 2 1 Sieć przestrzenna kryształu TRANSLACJA WĘZŁA TRANSLACJA PROSTEJ SIECIOWEJ TRANSLACJA PŁASZCZYZNY SIECIOWEJ
Diagramy fazowe graficzna reprezentacja warunków równowagi
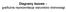 Diagramy fazowe graficzna reprezentacja warunków równowagi Faza jednorodna część układu, oddzielona od innych części granicami faz, na których zachodzi skokowa zmiana pewnych własności fizycznych. B 0
Diagramy fazowe graficzna reprezentacja warunków równowagi Faza jednorodna część układu, oddzielona od innych części granicami faz, na których zachodzi skokowa zmiana pewnych własności fizycznych. B 0
Właściwości defektów punktowych w stopach Fe-Cr-Ni z pierwszych zasad
 Właściwości defektów punktowych w stopach Fe-Cr-Ni z pierwszych zasad Jan S. Wróbel Wydział Inżynierii Materiałowej Politechnika Warszawska we współpracy z: D. Nguyen-Manh, S.L. Dudarev, K.J. Kurzydłowski
Właściwości defektów punktowych w stopach Fe-Cr-Ni z pierwszych zasad Jan S. Wróbel Wydział Inżynierii Materiałowej Politechnika Warszawska we współpracy z: D. Nguyen-Manh, S.L. Dudarev, K.J. Kurzydłowski
1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych.
 Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Tematy opisowe 1. Kryształy jonowe omówić oddziaływania w kryształach jonowych oraz typy struktur jonowych. 2. Dlaczego do kadłubów statków, doków, falochronów i filarów mostów przymocowuje się płyty z
Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania
 Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania I. Elektroujemność pierwiastków i elektronowa teoria wiązań Lewisa-Kossela
Cz. I Materiał powtórzeniowy do sprawdzianu dla klas II LO - Wiązania chemiczne + przykładowe zadania i proponowane rozwiązania I. Elektroujemność pierwiastków i elektronowa teoria wiązań Lewisa-Kossela
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych
 III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
III.4 Gaz Fermiego. Struktura pasmowa ciał stałych Jan Królikowski Fizyka IVBC 1 Gaz Fermiego Gaz Fermiego to gaz swobodnych, nie oddziałujących, identycznych fermionów w objętości V=a 3. Poszukujemy N(E)dE
Rozwiązanie: Zadanie 2
 Podstawowe pojęcia. Definicja kryształu. Sieć przestrzenna i sieć krystaliczna. Osie krystalograficzne i jednostki osiowe. Ściana jednostkowa i stosunek osiowy. Położenie węzłów, prostych i płaszczyzn
Podstawowe pojęcia. Definicja kryształu. Sieć przestrzenna i sieć krystaliczna. Osie krystalograficzne i jednostki osiowe. Ściana jednostkowa i stosunek osiowy. Położenie węzłów, prostych i płaszczyzn
Stany skupienia materii
 Stany skupienia materii Ciała stałe Ciecze Płyny Gazy Plazma 1 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -
Stany skupienia materii Ciała stałe Ciecze Płyny Gazy Plazma 1 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny
 Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Termodynamika Część 6 Związki i tożsamości termodynamiczne Potencjały termodynamiczne Warunki równowagi termodynamicznej Potencjał chemiczny Janusz Brzychczyk, Instytut Fizyki UJ Związek pomiędzy równaniem
Elektrodynamika Część 2 Specjalne metody elektrostatyki Ryszard Tanaś Zakład Optyki Nieliniowej, UAM
 Elektrodynamika Część 2 Specjalne metody elektrostatyki Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 3 Specjalne metody elektrostatyki 3 3.1 Równanie Laplace
Elektrodynamika Część 2 Specjalne metody elektrostatyki Ryszard Tanaś Zakład Optyki Nieliniowej, UAM http://zon8.physd.amu.edu.pl/~tanas Spis treści 3 Specjalne metody elektrostatyki 3 3.1 Równanie Laplace
Wykład 17 Izolatory i przewodniki
 Wykład 7 Izolatory i przewodniki Wszystkie ciała możemy podzielić na przewodniki i izolatory albo dielektryki. Przewodnikami są wszystkie metale, roztwory kwasów i zasad, roztopione soli, nagrzane gazy
Wykład 7 Izolatory i przewodniki Wszystkie ciała możemy podzielić na przewodniki i izolatory albo dielektryki. Przewodnikami są wszystkie metale, roztwory kwasów i zasad, roztopione soli, nagrzane gazy
Model elektronów swobodnych w metalu
 Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Model elektronów swobodnych w metalu Stany elektronu w nieskończonej trójwymiarowej studni potencjału - dozwolone wartości wektora falowego k Fale stojące - warunki brzegowe znikanie funkcji falowej na
Laboratorium techniki laserowej. Ćwiczenie 5. Modulator PLZT
 Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Laboratorium techniki laserowej Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdaoska Gdańsk 006 1.Wstęp Rozwój techniki optoelektronicznej spowodował poszukiwania nowych materiałów
Laboratorium z Krystalografii. 2 godz.
 Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
3. Przejścia fazowe pomiędzy trzema stanami skupienia materii:
 Temat: Zmiany stanu skupienia. 1. Energia sieci krystalicznej- wielkość dzięki której można oszacować siły przyciągania w krysztale 2. Energia wiązania sieci krystalicznej- ilość energii potrzebnej do
Temat: Zmiany stanu skupienia. 1. Energia sieci krystalicznej- wielkość dzięki której można oszacować siły przyciągania w krysztale 2. Energia wiązania sieci krystalicznej- ilość energii potrzebnej do
17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 17 KLASYCZNA DYNAMIKA MOLEKULARNA 17.1 Podstawy metod symulacji komputerowych dla klasycznych układów wielu cząstek Rozważamy układ N punktowych cząstek
