Modelowanie ryzyka kredytowego: Model Mertona - estymacja
|
|
|
- Ryszard Czarnecki
- 4 lat temu
- Przeglądów:
Transkrypt
1 Modelowanie ryzyka kredytowego: Model Mertona - estymacja Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2010 Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
2 Estymacja wartości aktywów i ich zmienności 1 Problem w zastosowaniu Modelu Mertona: Rzadko kiedy możemy obserwować wartość aktywów firmy V, o ich zmienności σ V już nie wspominając. 2 Pozostaje nam estymowanie obydwu wartosci z obserwowanych cen akcji firmy przy założeniu że znamy wartość nominalną długu. Zasadniczo wygląda to bardzo prosto: Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
3 W modelu Mertona mamy Stosując wzór Ito otrzymujemy S t = C(V t, L, σ v, r, T t) ds t = (...)dt + v C(V t, L, σ V, r, T t)σ V V t dw t Jaka jest zmienność cen akcji σ S (t)? otrzymujemy więc ds t = (...)dt + σ S (t)s t dw t = (...)dt + v C(V t, L, σ V, r, T t)σ V V t S t S t dw t σ S (t) = v C(V t, L, σ V, r, T t)σ V V t S t Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
4 Jeżeli obserwujemy S t i σ S (t) to mamy dwa równania z dwiema niewiadomymi V t i σ V S t = C(V t, L, σ v, r, T t) σ S (t) = v C(V t, L, σ V, r, T t)σ V V t S t Otrzymane nieliniowe równani można rozwiązać numerycznie i otrzymać V t i σ V, ale mamy PROBLEM σ S nie jest parametrem ale procesem stochastycznym!! 1 Jeżeli dźwignia L t := Vt S t jest mała to C (V t ) jest bardzo bliskie 1. 2 Wtedy σ S (t) σ V V t S t = σ V L t. 3 Jeżeli ponadto L t nie zmienia się bardzo przez obserwowany okres to S wygląda jak geometryczny ruch Brown a i można sprobować estymować jego parametry tak jak w modelu Black a Scholes a. Vassalou i Xing(2004) zaproponowali pewien schemat iteracyjny który działa dobrze nawet gdy zmiany L t w obserwowanym okresie są znaczące. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
5 Vassalou i Xing Załóżmy, że zaobserwowaliśmy szereg czasowy cen akcji S t0, S t1,..., S tn. W n-tym kroku otrzymujemy z estymacji zmienności σv n poprawioną estymację σv n+1. 1 Obliczyć V t0 (σv n ),..., V t N (σv n ) z S t 0,..., S tn odwracając funkcję C jako funkcję V. 2 Estymować σv n+1 tak jakby V t0 (σv n ),..., V t N (σv n ) było geometrycznym ruchem Browna tzn. gdzie σ n+1 V = ξ = 1 N t 1 N t N ln i=1 ( N ln i=1 ( Vti V ti 1 ) ( Vti V ti 1 ) ξ) 2, = 1 ( ) N t ln VtN. V t0 3 Korzystając z poprawionej estymacji σv n+1 wykonujemy podaną procedure ponownie wstawiając σv n+1 w miejsce σv n+1. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
6 Opisana procedura wymaga pewnej wartości początkowej σ 0 V i warunku zatrzymania. Jako warunek początkowy można wziąść np. trakując S jak w modelu Blacka Scholes a i stosując poprawkę z L t tzn. 1 Estymować zmienność akcji jak w modelu Blacka-Scholes a wtedy otrzymujemy pewne σ S. 2 Stosując wzór σ S (t) = L t σ V wyznaczyć σ V. Uwaga W praktyce okazuje się że ta procedura jest szybko zbieżna i wybór punktu startu nie jest bardzo ważny. Uwaga Zaletą tej metody jest to że można ją bardzo szybko zaimplementować!! Wynik numeryczne pokazują, że estymator jest nie identyczny ale bardzo bliski estymatorowi największej wiarogodności (MLE) którym się teraz zajmiemy. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
7 Estymacja MLE w modelu Mertona Przypomnimy elementarny wyniki z rachunku prawdopodobieństwa/statystyki. Niech X będzie zmienną losową o gęstości na R n danej funkcją f (x 1,..., x n ; θ), gdzie θ jest parametrem o wartościach w pewnym otwartym podzbiorze Θ R k. Niech T R n R n które zależy od θ, piszemy skrótowo y = T (x; θ) dla y = (T 1 (x; θ),..., T n (x; θ)). Załóżmy że T jest 1 na 1 i różniczkowalna w sposób ciągły dla każdego θ. Niech T 1 oznacza odwzorowanie do T odwrotne względem x przy ustalonym theta tzn. x = T 1 (y; θ) y = T (x; θ). Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
8 Niech J T oznacza Jakobian T który jest dany wzorem. x 1 T 1 (x; θ) x n T 1 (x; θ) J T (x) = det.. x 1 T n (x; θ) x n T n (x; θ) gęstość zmiennej losowej Y = T (X ; θ) jest dana wzorem g(y; θ) = f (T 1 (y; θ))j T 1(y; θ) = f (T 1 1 (y; θ)) J T (T 1 (y; θ)). Weźmy szczególne przekształcenie T takie że y 1 = T 1 (x 1 ; θ),..., y n = T 1 (x n ; θ), wtedy pochodne xi T j = 0 dla i j i otrzymujemy 1 n J T (T 1 (y; θ)) = i=1 1 xi T i (Ti 1 (y i ; θ); θ) Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
9 Przyjmując dla uproszczenia zapisu mamy x i (θ) = T 1 (y i ; θ) 1 n J T (T 1 (y; θ)) = i=1 1 xi T i (Ti 1 (y i ; θ); θ) W modelu Mertona proces aktywów firmy V jest rozwiązaniem SDE dv t = µv t dt + σv t dw t parametrami są więc µ i σ. Z postaci rozwiązani mamy że gęstość warunkowa V ti pod warunkiem V ti jest postaci φ(v i v i 1 ; µ, θ) [ 1 = σ 2π(t i t i 1 ) exp ln(v i /v i 1 ) (µ 1 2 σ2 )(t i t i 1 ) 2σ 2 (t i t i 1 ) ] 2 1 v i. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
10 Z własności markowa gęstość łączna V t1,..., V tn pod warunkiem V 0 = v 0 natomiast jest postaci n φ(v 1,..., v n v 0, µ, σ) = φ(v i v i 1 ; µ, θ) Gdybyśmy obserwowali V to moglibyśmy teraz przejść do wyprowadzenia estymatora MLE. Jednakże obserwujemy S -cenę akcji. Wiemy natomiast jaki jest związek między ceną akcji a wartością aktywów w modelu Mertona i=1 S ti = C(V ti ; σ, T t i ) korzystając z tego związku możemy napisać postać gęstości obserwowanych wielkości S t1,..., S tn i otrzymujemy n 1 L(s 1,..., s n s 0, σ, µ) = φ(v i (σ) v i 1 (σ); µ, θ) C i (v i(σ); σ) gdzie i=1 v i (σ) = C 1 (s i ; σ, T t i ), C i := v C(v i(σ), σ, T t i ), Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
11 Stąd zlogarytmowana funkcja wiarogodności jest log L(s 1,..., s n s 0, µ, σ) = 1 2 n log 2π n log σ σ 2 n i=1 n 1 n v i=1 i (σ) i=1 n log(t i t i 1 ) i=1 [ ln(v i (σ)/v i 1 (σ)) (µ 1 2 σ2 )(t i t i 1 ) log N(d 1 (σ)). t i t i 1 Dla ustalonego σ obserwowane S 0 daje nam ustaloną wartość V 0. Jednak ponieważ maksymalizujemy po σ to znajdujemy V 0 w procedurze estymacji. Kiedy ta wartość jest znana to otrzymujemy cały ciąg V t1 ( σ),..., V tn ( σ) które zgadzają się z prawdziwymi wartościami aktywów jeżeli σ jest równa prawdziwej wartości. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18 ] 2
12 Eksperyment Przedstawiona metoda działa całkiem dobrze jeżeli spełnione są założenia modelu. Zilustruje to następujący przykład. Wykonaliśmy symulację symulację startując z V 0 = 100 na 50 tygodni do przodu obserwacji aktywów firmy o zmienności σ = 0.2 i µ = 0.1. Na koniec roku otrzymaliśmy V 1 = Dla otrzymanych wyników symulacji zastosowaliśmy procedurę MLE i otrzymaliśmy dla długu o terminie wykupu 3 lata wyniki Uwaga Nominał V 1 σ SD σ µ SD µ Błąd estymacji dryfu jest bardzo duży!! Stosowanie tej metody do wyznaczenia rzeczywistych prawdopodobieństw bankructwa jest obarczone dużym ryzykiem. Błąd nie dotyka V 1 ponieważ V 1 nie zależy od µ. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
13 Opisaną procedure można zastosować w innych modelach (np. Black-Cox), tutaj mogliśmy napisać bezpośrednią postać funkcji wiarogodności. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
14 KMV - model Mertona w praktyce W 1990 powstała firma KMV - (założyciele Kealhofer, McQuown i Vasicek) która wprowadziła bardzo popularna implementacje modelu Mertona (od 2002 Moody s KMV). Spójrzmy na model Mertona przy prawdopodobieństwie rzeczywistym. Mamy wtedy V T = V 0 e (µ σ2 /2)T +σ V W T Wtedy prawdopodobieństwo skończenia poniżej L ( ln V 0 L P(V T L) = 1 N + (µ ) σ2 /2)T =: EDF Merton σ V T nazywamy Oczekiwaną Częstością Defaultów (Expected-Default-Frequency), DD Merton := ln V 0 L + (µ σ2 /2)T σ V T = E P(ln V T ) ln L σ V T mierzy Odległość od Defaultu (Distance-to-Default) w modelu Mertona. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
15 Zauważmy, że 1 Jeżeli w T mamy V T = L to mamy DD Merton = 0. 2 W modelu Mertona DD Merton może być ujemna. Można wykorzystać wielkości do DD Merton do sprawdzenia czy model jest dobry do szacowania prawdopodobieństw bankructwa. Jak?? Można np sprawadzić jak dobrze DD Merton w historii przewidywało bankructwo. 1 Ustalić horyzont T = 1. 2 Podzielić DD na przedziały wystarczająco duże aby w każdym przedziale było wystarczająco dużo firm, i wystarczająco małe aby prawdopodobieństwo defualtów w przedziale było można uznać za stałe na tym przedziale. 3 Wyznaczyć empiryczne częstości bankructw dla danych przedziałów. 4 Wtedy częstość rzeczywistych bankructw w każdym przedziale można uznać za dobre przybliżenie prawdopodobieństwa bankructwa dla danego przedziału. Porównać empiryczne częstości z modelowymi. 5 W praktyce okazuje się, że empiryczne częstości defaultów znacznie różnią się od tych przewidywanych przez model Mertona Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
16 1 Pomimo tego DD może być dobrym sposobem mierzenia ryzyka kredytowego firm, dzielenia ich na różne klasy ryzyka. 2 Można liczyć DD i stosować empiryczne/historyczne dane do szacowania prawdopodobieństw defaultów. 3 Moody s KMV stosuje właśnie taką idee, biorąc nieco inną odległość od defaultu w horyzoncie T=1 rok DD KMV := 1 σ V V 0 L V 0, gdzie punkt defaultu L stosowany przez KMV jest zadany wzorem L := short-term debt + 0, 5 long-term debt. Taki wybór ma odzwierciedlać fakt, że dla długów krótkoterminowych nominał będzie wymagany do spłacenie szybciej, a w przypadku długu długoterminowego w horyzoncie 1 roku wymagane będą do spłacenia tylko kupony. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
17 1 Korzystając z bazy danych historycznych defaultów firma KMV dla ustalonego horyzontu T estymuje proporcje firm które zbankrutowały w danym horyzoncie czasu o DD KMV leżącym w ustalonym małym przedziale. 2 Ta proporcja jest empiryczną estymacją EDF. Jest to oczywiście malejąca funkcja DD KMV. 3 Gdzie tu jest ukryty model Mertona? 4 W estymacji wartości aktywów firmy V 0 i ich zmienności σ V. 5 Implicite KMV zakłada że firmy o tym samym DD KMV mają takie samo prawdopodobieństwo defaultu. 6 W DD KMV nie uwzględniamy dryfu który ma istotny wpływ na prawdopodobieństwo defaultu. 7 Jeżeli horyzont jest krotki np 1 rok to ma to jego wpływ jest mały. Co innego dla średnich i długich horyzontów. Jak widzieliśmy estymacja dryfu metodą największej wiarogodności jest obarczona dużym błędem więc można argumentować, że uwzględnianie jego w DD nie dodaje żadnej informacji. Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
18 Literatura Crosbie, P. i Bohn, J. Modeling default risk, Moodys KMV web page, 2003 Bohn, J. R. A survey of contingent-claims approaches to risky debt valuation, Journal of Risk Finance 1:1 18, Duan, J. Maximum likelihood estimation using price data of the derivatives contract, Mathematical Finance 4: , 1994 (Correction: 2000 Mathematical Finance 10(4): ) Ericsson, J. i J. Reneby. The valuation of corporate liabilities: theory and tests. Working paper, McGill University, Montreal Ericsson, J. i J. Reneby. Estimating structural bond pricing models. Working paper, McGill University, Montreal Hull J., Nelken I. i White A. Merton s Model, Credit Risk, and Volatility Skews Journal of Credit Risk Vol 1, No 1 (2004) 1-27 Niewęgłowski (MiNI PW) Model Mertona Warszawa / 18
r u du. Proces wartości aktywów firmy V. Proces bariery v wykorzystywany do zdefiniowania defaultu. moment defaultu τ.
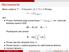 Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Wprowadzenie Mamy ustalone T > 0 horyzont, (Ω, F, P) z F filtracja, F = {F t } t [0,T ] oraz Proces chwilowej stopy procentowej r = (r t ) t [0,T ], tzn. rachunek bankowy spełnia ODE: db t = B t r t dt,
Mirosław Wójciak Akademia Ekonomiczna w Katowicach Aleksandra Wójcicka Akademia Ekonomiczna w Poznaniu
 DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Katedra Ekonometrii i Statystyki, Uniwersytet Mikołaja Kopernika w Toruniu Mirosław Wójciak Akademia Ekonomiczna
DYNAMICZNE MODELE EKONOMETRYCZNE X Ogólnopolskie Seminarium Naukowe, 4 6 września 2007 w Toruniu Katedra Ekonometrii i Statystyki, Uniwersytet Mikołaja Kopernika w Toruniu Mirosław Wójciak Akademia Ekonomiczna
Modelowanie ryzyka kredytowego Zadania 1.
 1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
1 Ex-dividend prices Modelowanie ryzyka kredytowego Zadania 1. Mariusz Niewęgłowski 19 października 2014 Definicja 1. Dla każdego t [0, T ] cena ex-dividend wypłaty (X, A, X, Z, τ) ( ) S t := B t E Q Bu
Rozdział 2: Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów
 Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Rozdział : Metoda największej wiarygodności i nieliniowa metoda najmniejszych kwadratów W tym rozdziale omówione zostaną dwie najpopularniejsze metody estymacji parametrów w ekonometrycznych modelach nieliniowych,
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Laboratorium JAVA Zadanie nr 2 Rozpoznawanie liter autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z problemem klasyfikacji
Metody systemowe i decyzyjne w informatyce Laboratorium JAVA Zadanie nr 2 Rozpoznawanie liter autorzy: A. Gonczarek, J.M. Tomczak Cel zadania Celem zadania jest zapoznanie się z problemem klasyfikacji
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji.
 I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
I. Pochodna i różniczka funkcji jednej zmiennej. 1. Definicja pochodnej funkcji i jej interpretacja fizyczna. Istnienie pochodnej funkcji. Niech x 0 R i niech f będzie funkcją określoną przynajmniej na
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. - funkcja dwóch zmiennych,
 IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
IX. Rachunek różniczkowy funkcji wielu zmiennych. 1. Funkcja dwóch i trzech zmiennych - pojęcia podstawowe. Definicja 1.1. Niech D będzie podzbiorem przestrzeni R n, n 2. Odwzorowanie f : D R nazywamy
Modele zapisane w przestrzeni stanów
 Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
Modele zapisane w przestrzeni stanów Modele Przestrzeni Stanów (State Space Models) sa to modele, w których część parametrów jest nieobserwowalna i losowa. Zachowanie wielowymiarowej zmiennej y t zależy
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization
 Wrocław University of Technology SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization Jakub M. Tomczak Studenckie Koło Naukowe Estymator jakub.tomczak@pwr.wroc.pl 4.1.213 Klasteryzacja Zmienne
Wrocław University of Technology SPOTKANIE 6: Klasteryzacja: K-Means, Expectation Maximization Jakub M. Tomczak Studenckie Koło Naukowe Estymator jakub.tomczak@pwr.wroc.pl 4.1.213 Klasteryzacja Zmienne
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A
 Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Modelowanie ryzyka kredytowego: MODEL BLACK-COX A Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014 Niewęgłowski MiNI PW Modele wartości firmy Warszawa
Zadanie 1. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną:
 Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
Zadanie. Ilość szkód N ma rozkład o prawdopodobieństwach spełniających zależność rekurencyjną: Pr Pr ( = k) ( N = k ) N = + k, k =,,,... Jeśli wiemy, że szkód wynosi: k= Pr( N = k) =, to prawdopodobieństwo,
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 7 i 8 1 / 9 EFEKTYWNOŚĆ ESTYMATORÓW, próba
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 7 i 8 - Efektywność estymatorów, przedziały ufności Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 7 i 8 1 / 9 EFEKTYWNOŚĆ ESTYMATORÓW, próba
Niech X i Y będą niezależnymi zmiennymi losowymi o rozkładach wykładniczych, przy czym Y EX = 4 i EY = 6. Rozważamy zmienną losową Z =.
 Prawdopodobieństwo i statystyka 3..00 r. Zadanie Niech X i Y będą niezależnymi zmiennymi losowymi o rozkładach wykładniczych, przy czym Y EX 4 i EY 6. Rozważamy zmienną losową Z. X + Y Wtedy (A) EZ 0,
Prawdopodobieństwo i statystyka 3..00 r. Zadanie Niech X i Y będą niezależnymi zmiennymi losowymi o rozkładach wykładniczych, przy czym Y EX 4 i EY 6. Rozważamy zmienną losową Z. X + Y Wtedy (A) EZ 0,
Pochodna i różniczka funkcji oraz jej zastosowanie do rachunku błędów pomiarowych
 Pochodna i różniczka unkcji oraz jej zastosowanie do rachunku błędów pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją symbolami:
Pochodna i różniczka unkcji oraz jej zastosowanie do rachunku błędów pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją symbolami:
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 13 i 14 - Statystyka bayesowska
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 13 i 14 - Statystyka bayesowska Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 13 i 14 1 / 15 MODEL BAYESOWSKI, przykład wstępny Statystyka
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 13 i 14 - Statystyka bayesowska Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 13 i 14 1 / 15 MODEL BAYESOWSKI, przykład wstępny Statystyka
Stochastyczne równania różniczkowe, model Blacka-Scholesa
 Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Stochastyczne równania różniczkowe, model Blacka-Scholesa Marcin Orchel Spis treści 1 Wstęp 1 1.1 Błądzenie losowe................................ 1 1. Proces Wienera................................. 1.3
Rozwiązywanie równań nieliniowych
 Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Rozwiązywanie równań nieliniowych Marcin Orchel 1 Wstęp Przykłady wyznaczania miejsc zerowych funkcji f : f(ξ) = 0. Wyszukiwanie miejsc zerowych wielomianu n-tego stopnia. Wymiar tej przestrzeni wektorowej
Modele DSGE. Jerzy Mycielski. Maj Jerzy Mycielski () Modele DSGE Maj / 11
 Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Modele DSGE Jerzy Mycielski Maj 2008 Jerzy Mycielski () Modele DSGE Maj 2008 1 / 11 Modele DSGE DSGE - Dynamiczne, stochastyczne modele równowagi ogólnej (Dynamic Stochastic General Equilibrium Model)
Idea. θ = θ 0, Hipoteza statystyczna Obszary krytyczne Błąd pierwszego i drugiego rodzaju p-wartość
 Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
Idea Niech θ oznacza parametr modelu statystycznego. Dotychczasowe rozważania dotyczyły metod estymacji tego parametru. Teraz zamiast szacować nieznaną wartość parametru będziemy weryfikowali hipotezę
Metoda największej wiarogodności
 Wprowadzenie Założenia Logarytm funkcji wiarogodności Metoda Największej Wiarogodności (MNW) jest bardziej uniwersalną niż MNK metodą szacowania wartości nieznanych parametrów Wprowadzenie Założenia Logarytm
Wprowadzenie Założenia Logarytm funkcji wiarogodności Metoda Największej Wiarogodności (MNW) jest bardziej uniwersalną niż MNK metodą szacowania wartości nieznanych parametrów Wprowadzenie Założenia Logarytm
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
Matematyka ubezpieczeń majątkowych 0.0.005 r. Zadanie. Likwidacja szkody zaistniałej w roku t następuje: w tym samym roku z prawdopodobieństwem 0 3, w następnym roku z prawdopodobieństwem 0 3, 8 w roku
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω)
 PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
PROCESY STOCHASTYCZNE. PEWNE KLASY PROCESÓW STOCHASTYCZNYCH Definicja. Procesem stochastycznym nazywamy rodzinę zmiennych losowych X(t) = X(t, ω) określonych na tej samej przestrzeni probabilistycznej
Laboratorium 5 Przybliżone metody rozwiązywania równań nieliniowych
 Uniwersytet Zielonogórski Wydział Informatyki, Elektrotechniki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych Elektrotechnika niestacjonarne-zaoczne pierwszego stopnia z tyt. inżyniera
Uniwersytet Zielonogórski Wydział Informatyki, Elektrotechniki i Telekomunikacji Instytut Sterowania i Systemów Informatycznych Elektrotechnika niestacjonarne-zaoczne pierwszego stopnia z tyt. inżyniera
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/
 Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA HAZARDU cz. II: CDS y - swapy kredytowe
 Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Modelowanie ryzyka kredytowego MODELOWANIE ZA POMOCA FUNKCJI HAZARDU cz. II: CDS y - swapy kredytowe Mariusz Niewęgłowski Wydział Matematyki i Nauk Informacyjnych, Politechniki Warszawskiej Warszawa 2014
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Prawdopodobieństwo i statystyka r.
 Zadanie. Niech (X, Y) ) będzie dwuwymiarową zmienną losową, o wartości oczekiwanej (μ, μ, wariancji każdej ze współrzędnych równej σ oraz kowariancji równej X Y ρσ. Staramy się obserwować niezależne realizacje
Zadanie. Niech (X, Y) ) będzie dwuwymiarową zmienną losową, o wartości oczekiwanej (μ, μ, wariancji każdej ze współrzędnych równej σ oraz kowariancji równej X Y ρσ. Staramy się obserwować niezależne realizacje
Szeregi czasowe, analiza zależności krótkoi długozasięgowych
 Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
Szeregi czasowe, analiza zależności krótkoi długozasięgowych Rafał Weron rweron@im.pwr.wroc.pl Definicje Mając dany proces {X t } autokowariancję definiujemy jako : γ(t, t ) = cov(x t, X t ) = = E[(X t
Parametr Λ w populacji ubezpieczonych ma rozkład dany na półosi dodatniej gęstością: 3 f
 Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Zadanie. W kolejnych latach t =,,,... ubezpieczony charakteryzujący się parametrem ryzyka Λ generuje N t szkód. Dla danego Λ = λ zmienne N, N, N,... są warunkowo niezależne i mają (brzegowe) rozkłady Poissona:
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 2 autorzy: A. Gonczarek, J.M. Tomczak Metody estymacji Zad. 1 Pojawianie się spamu opisane jest zmienną losową x o rozkładzie dwupunktowym
Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 2 autorzy: A. Gonczarek, J.M. Tomczak Metody estymacji Zad. 1 Pojawianie się spamu opisane jest zmienną losową x o rozkładzie dwupunktowym
MODELOWANIE ZMIENNOŚCI CEN AKCJI MODEL ADDYTYWNY MODEL MULTIPLIKATYWNY
 MODELOWANIE ZMIENNOŚCI CEN AKCJI MODEL ADDYTYWNY MODEL MULTIPLIKATYWNY Modele zmienności aktywów z czasem dyskretnym / Model addytywny Przyjmijmy następujące oznaczenia: S(0) - cena początkowa akcji S(k)
MODELOWANIE ZMIENNOŚCI CEN AKCJI MODEL ADDYTYWNY MODEL MULTIPLIKATYWNY Modele zmienności aktywów z czasem dyskretnym / Model addytywny Przyjmijmy następujące oznaczenia: S(0) - cena początkowa akcji S(k)
Agata Boratyńska Statystyka aktuarialna... 1
 Agata Boratyńska Statystyka aktuarialna... 1 ZADANIA NA ĆWICZENIA Z TEORII WIAROGODNOŚCI Zad. 1. Niech X 1, X 2,..., X n będą niezależnymi zmiennymi losowymi z rozkładu wykładniczego o wartości oczekiwanej
Agata Boratyńska Statystyka aktuarialna... 1 ZADANIA NA ĆWICZENIA Z TEORII WIAROGODNOŚCI Zad. 1. Niech X 1, X 2,..., X n będą niezależnymi zmiennymi losowymi z rozkładu wykładniczego o wartości oczekiwanej
Lokalna odwracalność odwzorowań, odwzorowania uwikłane
 Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Lokalna odwracalność odwzorowań, odwzorowania uwikłane Katedra Matematyki i Ekonomii Matematycznej Szkoła Główna Handlowa 17 maja 2012 Definicja Mówimy, że odwzorowanie F : X R n, gdzie X R n, jest lokalnie
Estymacja gęstości prawdopodobieństwa metodą selekcji modelu
 Estymacja gęstości prawdopodobieństwa metodą selekcji modelu M. Wojtyś Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska Wisła, 7 grudnia 2009 Wstęp Próba losowa z rozkładu prawdopodobieństwa
Estymacja gęstości prawdopodobieństwa metodą selekcji modelu M. Wojtyś Wydział Matematyki i Nauk Informacyjnych Politechnika Warszawska Wisła, 7 grudnia 2009 Wstęp Próba losowa z rozkładu prawdopodobieństwa
Stanisław Cichocki Natalia Nehrebecka. Wykład 7
 Stanisław Cichocki Natalia Nehrebecka Wykład 7 1 1. Metoda Największej Wiarygodności MNW 2. Założenia MNW 3. Własności estymatorów MNW 4. Testowanie hipotez w MNW 2 1. Metoda Największej Wiarygodności
Stanisław Cichocki Natalia Nehrebecka Wykład 7 1 1. Metoda Największej Wiarygodności MNW 2. Założenia MNW 3. Własności estymatorów MNW 4. Testowanie hipotez w MNW 2 1. Metoda Największej Wiarygodności
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 2 autorzy: A. Gonczarek, J.M. Tomczak Metody estymacji ML Zad. 1 Pojawianie się spamu opisane jest zmienną losową x o rozkładzie dwupunktowym
Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 2 autorzy: A. Gonczarek, J.M. Tomczak Metody estymacji ML Zad. 1 Pojawianie się spamu opisane jest zmienną losową x o rozkładzie dwupunktowym
Modelowanie wybranych pojęć matematycznych. semestr letni, 2016/2017 Wykład 10 Własności funkcji cd.
 Modelowanie wybranych pojęć matematycznych semestr letni, 206/207 Wykład 0 Własności funkcji cd. Ciągłość funkcji zastosowania Przybliżone rozwiązywanie równań Znajdziemy przybliżone rozwiązanie równania
Modelowanie wybranych pojęć matematycznych semestr letni, 206/207 Wykład 0 Własności funkcji cd. Ciągłość funkcji zastosowania Przybliżone rozwiązywanie równań Znajdziemy przybliżone rozwiązanie równania
Metoda największej wiarygodności
 Metoda największej wiarygodności Próbki w obecności tła Funkcja wiarygodności Iloraz wiarygodności Pomiary o różnej dokładności Obciążenie Informacja z próby i nierówność informacyjna Wariancja minimalna
Metoda największej wiarygodności Próbki w obecności tła Funkcja wiarygodności Iloraz wiarygodności Pomiary o różnej dokładności Obciążenie Informacja z próby i nierówność informacyjna Wariancja minimalna
Mikroekonometria 3. Mikołaj Czajkowski Wiktor Budziński
 Mikroekonometria 3 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Mikroekonometria 3 Mikołaj Czajkowski Wiktor Budziński Zadanie 1. Wykorzystując dane me.hedonic.dta przygotuj model oszacowujący wartość kosztów zewnętrznych rolnictwa 1. Przeprowadź regresję objaśniającą
Oznacza to, że chcemy znaleźć minimum, a właściwie wartość najmniejszą funkcji
 Wykład 11. Metoda najmniejszych kwadratów Szukamy zależności Dane są wyniki pomiarów dwóch wielkości x i y: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Przypuśćmy, że nanieśliśmy je na wykres w układzie
Wykład 11. Metoda najmniejszych kwadratów Szukamy zależności Dane są wyniki pomiarów dwóch wielkości x i y: (x 1, y 1 ), (x 2, y 2 ),..., (x n, y n ). Przypuśćmy, że nanieśliśmy je na wykres w układzie
Wstęp. Regresja logistyczna. Spis treści. Hipoteza. powrót
 powrót Spis treści 1 Wstęp 2 Regresja logistyczna 2.1 Hipoteza 2.2 Estymacja parametrów 2.2.1 Funkcja wiarygodności 3 Uogólnione modele liniowe 3.1 Rodzina wykładnicza 3.1.1 Rozkład Bernouliego 3.1.2 Rozkład
powrót Spis treści 1 Wstęp 2 Regresja logistyczna 2.1 Hipoteza 2.2 Estymacja parametrów 2.2.1 Funkcja wiarygodności 3 Uogólnione modele liniowe 3.1 Rodzina wykładnicza 3.1.1 Rozkład Bernouliego 3.1.2 Rozkład
STATYSTYKA
 Wykład 1 20.02.2008r. 1. ROZKŁADY PRAWDOPODOBIEŃSTWA 1.1 Rozkład dwumianowy Rozkład dwumianowy, 0 1 Uwaga: 1, rozkład zero jedynkowy. 1 ; 1,2,, Fakt: Niech,, będą niezależnymi zmiennymi losowymi o jednakowym
Wykład 1 20.02.2008r. 1. ROZKŁADY PRAWDOPODOBIEŃSTWA 1.1 Rozkład dwumianowy Rozkład dwumianowy, 0 1 Uwaga: 1, rozkład zero jedynkowy. 1 ; 1,2,, Fakt: Niech,, będą niezależnymi zmiennymi losowymi o jednakowym
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 4 1 / 23 ZAGADNIENIE ESTYMACJI Zagadnienie
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 4 - zagadnienie estymacji, metody wyznaczania estymatorów Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 4 1 / 23 ZAGADNIENIE ESTYMACJI Zagadnienie
METODY ESTYMACJI PUNKTOWEJ. nieznanym parametrem (lub wektorem parametrów). Przez X będziemy też oznaczać zmienną losową o rozkładzie
 METODY ESTYMACJI PUNKTOWEJ X 1,..., X n - próbka z rozkładu P θ, θ Θ, θ jest nieznanym parametrem (lub wektorem parametrów). Przez X będziemy też oznaczać zmienną losową o rozkładzie P θ. Definicja. Estymatorem
METODY ESTYMACJI PUNKTOWEJ X 1,..., X n - próbka z rozkładu P θ, θ Θ, θ jest nieznanym parametrem (lub wektorem parametrów). Przez X będziemy też oznaczać zmienną losową o rozkładzie P θ. Definicja. Estymatorem
Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE. Joanna Sawicka
 Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE Joanna Sawicka Plan prezentacji Model Poissona-Gamma ze składnikiem regresyjnym Konstrukcja optymalnego systemu Bonus- Malus Estymacja
Szacowanie optymalnego systemu Bonus-Malus przy pomocy Pseudo-MLE Joanna Sawicka Plan prezentacji Model Poissona-Gamma ze składnikiem regresyjnym Konstrukcja optymalnego systemu Bonus- Malus Estymacja
Całkowanie numeryczne
 Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
Całkowanie numeryczne Poniżej omówione zostanie kilka metod przybliżania operacji całkowania i różniczkowania w szczególności uzależnieniu pochodnej od jej różnic skończonych gdy równanie różniczkowe mamy
6.4 Podstawowe metody statystyczne
 156 Wstęp do statystyki matematycznej 6.4 Podstawowe metody statystyczne Spóbujemy teraz w dopuszczalnym uproszczeniu przedstawić istotę analizy statystycznej. W szczególności udzielimy odpowiedzi na postawione
156 Wstęp do statystyki matematycznej 6.4 Podstawowe metody statystyczne Spóbujemy teraz w dopuszczalnym uproszczeniu przedstawić istotę analizy statystycznej. W szczególności udzielimy odpowiedzi na postawione
Prawdopodobieństwo i statystyka
 Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Wykład XIII: Prognoza. 26 stycznia 2015 Wykład XIII: Prognoza. Prognoza (predykcja) Przypuśćmy, że mamy dany ciąg liczb x 1, x 2,..., x n, stanowiących wyniki pomiaru pewnej zmiennej w czasie wielkości
Wykład 1 Próba i populacja. Estymacja parametrów z wykorzystaniem metody bootstrap
 Wykład 1 Próba i populacja. Estymacja parametrów z wykorzystaniem metody bootstrap Magdalena Frąszczak Wrocław, 21.02.2018r Tematyka Wykładów: Próba i populacja. Estymacja parametrów z wykorzystaniem metody
Wykład 1 Próba i populacja. Estymacja parametrów z wykorzystaniem metody bootstrap Magdalena Frąszczak Wrocław, 21.02.2018r Tematyka Wykładów: Próba i populacja. Estymacja parametrów z wykorzystaniem metody
Wstęp do Metod Systemowych i Decyzyjnych Opracowanie: Jakub Tomczak
 Wstęp do Metod Systemowych i Decyzyjnych Opracowanie: Jakub Tomczak 1 Wprowadzenie. Zmienne losowe Podczas kursu interesować nas będzie wnioskowanie o rozpatrywanym zjawisku. Poprzez wnioskowanie rozumiemy
Wstęp do Metod Systemowych i Decyzyjnych Opracowanie: Jakub Tomczak 1 Wprowadzenie. Zmienne losowe Podczas kursu interesować nas będzie wnioskowanie o rozpatrywanym zjawisku. Poprzez wnioskowanie rozumiemy
Wnioskowanie statystyczne. Statystyka w 5
 Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Wnioskowanie statystyczne tatystyka w 5 Rozkłady statystyk z próby Próba losowa pobrana z populacji stanowi realizacje zmiennej losowej jak ciąg zmiennych losowych (X, X,... X ) niezależnych i mających
Rozkład normalny, niepewność standardowa typu A
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
Matematyka ubezpieczeń majątkowych 1.10.2012 r.
 Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Zadanie. W pewnej populacji każde ryzyko charakteryzuje się trzema parametrami q, b oraz v, o następującym znaczeniu: parametr q to prawdopodobieństwo, że do szkody dojdzie (może zajść co najwyżej jedna
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Wstęp do analitycznych i numerycznych metod wyceny opcji
 Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
Wstęp do analitycznych i numerycznych metod wyceny opcji Jan Palczewski Wydział Matematyki, Informatyki i Mechaniki Uniwersytet Warszawski Warszawa, 16 maja 2008 Jan Palczewski Wycena opcji Warszawa, 2008
EGZAMIN MAGISTERSKI, 18 września 2013 Biomatematyka
 Biomatematyka Liczebność populacji pewnego gatunku jest modelowana przez równanie różnicowe w którym N k stałymi. rn 2 n N n+1 =, A+Nn 2 oznacza liczebność populacji w k tej generacji, a r i A są dodatnimi
Biomatematyka Liczebność populacji pewnego gatunku jest modelowana przez równanie różnicowe w którym N k stałymi. rn 2 n N n+1 =, A+Nn 2 oznacza liczebność populacji w k tej generacji, a r i A są dodatnimi
System prognozowania rynków energii
 System prognozowania rynków energii STERMEDIA Sp. z o. o. Software Development Grupa IT Kontrakt ul. Ostrowskiego13 Wrocław Poland tel.: 0 71 723 43 22 fax: 0 71 733 64 66 http://www.stermedia.eu Piotr
System prognozowania rynków energii STERMEDIA Sp. z o. o. Software Development Grupa IT Kontrakt ul. Ostrowskiego13 Wrocław Poland tel.: 0 71 723 43 22 fax: 0 71 733 64 66 http://www.stermedia.eu Piotr
Stopę zbieżności ciagu zmiennych losowych a n, takiego, że E (a n ) < oznaczamy jako a n = o p (1) prawdopodobieństwa szybciej niż n α.
 Stopy zbieżności Stopę zbieżności ciagu zmiennych losowych a n, takiego, że a n oznaczamy jako a n = o p (1 p 0 a Jeśli n p n α 0, to a n = o p (n α i mówimy a n zbiega według prawdopodobieństwa szybciej
Stopy zbieżności Stopę zbieżności ciagu zmiennych losowych a n, takiego, że a n oznaczamy jako a n = o p (1 p 0 a Jeśli n p n α 0, to a n = o p (n α i mówimy a n zbiega według prawdopodobieństwa szybciej
STATYSTYKA MATEMATYCZNA WYKŁAD stycznia 2010
 STATYSTYKA MATEMATYCZNA WYKŁAD 14 18 stycznia 2010 Model statystyczny ROZKŁAD DWUMIANOWY ( ) {0, 1,, n}, {P θ, θ (0, 1)}, n ustalone P θ {K = k} = ( ) n θ k (1 θ) n k, k k = 0, 1,, n Geneza: Rozkład Bernoulliego
STATYSTYKA MATEMATYCZNA WYKŁAD 14 18 stycznia 2010 Model statystyczny ROZKŁAD DWUMIANOWY ( ) {0, 1,, n}, {P θ, θ (0, 1)}, n ustalone P θ {K = k} = ( ) n θ k (1 θ) n k, k k = 0, 1,, n Geneza: Rozkład Bernoulliego
Podstawowe modele probabilistyczne
 Wrocław University of Technology Podstawowe modele probabilistyczne Maciej Zięba maciej.zieba@pwr.edu.pl Rozpoznawanie Obrazów, Lato 2018/2019 Pojęcie prawdopodobieństwa Prawdopodobieństwo reprezentuje
Wrocław University of Technology Podstawowe modele probabilistyczne Maciej Zięba maciej.zieba@pwr.edu.pl Rozpoznawanie Obrazów, Lato 2018/2019 Pojęcie prawdopodobieństwa Prawdopodobieństwo reprezentuje
Zad. 4 Należy określić rodzaj testu (jedno czy dwustronny) oraz wartości krytyczne z lub t dla określonych hipotez i ich poziomów istotności:
 Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
Zadania ze statystyki cz. 7. Zad.1 Z populacji wyłoniono próbę wielkości 64 jednostek. Średnia arytmetyczna wartość cechy wyniosła 110, zaś odchylenie standardowe 16. Należy wyznaczyć przedział ufności
5. Rozwiązywanie układów równań liniowych
 5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
5. Rozwiązywanie układów równań liniowych Wprowadzenie (5.1) Układ n równań z n niewiadomymi: a 11 +a 12 x 2 +...+a 1n x n =a 10, a 21 +a 22 x 2 +...+a 2n x n =a 20,..., a n1 +a n2 x 2 +...+a nn x n =a
Rozpoznawanie obrazów
 Rozpoznawanie obrazów Ćwiczenia lista zadań nr 7 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Rozpoznawanie obrazów Ćwiczenia lista zadań nr 7 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Wprowadzenie do teorii ekonometrii. Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe
 Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Wprowadzenie do teorii ekonometrii Wykład 1 Warunkowa wartość oczekiwana i odwzorowanie liniowe Zajęcia Wykład Laboratorium komputerowe 2 Zaliczenie EGZAMIN (50%) Na egzaminie obowiązują wszystkie informacje
Prawa wielkich liczb, centralne twierdzenia graniczne
 , centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
, centralne twierdzenia graniczne Katedra matematyki i ekonomii matematycznej 17 maja 2012, centralne twierdzenia graniczne Rodzaje zbieżności ciągów zmiennych losowych, centralne twierdzenia graniczne
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu
 1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
1 Metody rozwiązywania równań nieliniowych. Postawienie problemu Dla danej funkcji ciągłej f znaleźć wartości x, dla których f(x) = 0. (1) 2 Przedział izolacji pierwiastka Będziemy zakładać, że równanie
Znaleźć wzór ogólny i zbadać istnienie granicy ciągu określonego rekurencyjnie:
 Ciągi rekurencyjne Zadanie 1 Znaleźć wzór ogólny i zbadać istnienie granicy ciągu określonego rekurencyjnie: w dwóch przypadkach: dla i, oraz dla i. Wskazówka Należy poszukiwać rozwiązania w postaci, gdzie
Ciągi rekurencyjne Zadanie 1 Znaleźć wzór ogólny i zbadać istnienie granicy ciągu określonego rekurencyjnie: w dwóch przypadkach: dla i, oraz dla i. Wskazówka Należy poszukiwać rozwiązania w postaci, gdzie
8 Całka stochastyczna względem semimartyngałów
 M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
M. Beśka, Całka Stochastyczna, wykład 8 148 8 Całka stochastyczna względem semimartyngałów 8.1 Całka stochastyczna w M 2 Oznaczmy przez Ξ zbiór procesów postaci X t (ω) = ξ (ω)i {} (t) + n ξ i (ω)i (ti,
Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }
![Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] } Zespół kanoniczny N,V, T. acc o n =min {1, exp [ U n U o ] }](/thumbs/64/51033976.jpg) Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Zespół kanoniczny Zespół kanoniczny N,V, T acc o n =min {1, exp [ U n U o ] } Zespół izobaryczno-izotermiczny Zespół izobaryczno-izotermiczny N P T acc o n =min {1, exp [ U n U o ] } acc o n =min {1, exp[
Metody systemowe i decyzyjne w informatyce
 Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 3 Metody estymacji. Estymator największej wiarygodności Zad. 1 Pojawianie się spamu opisane jest zmienną losową y o rozkładzie zero-jedynkowym
Metody systemowe i decyzyjne w informatyce Ćwiczenia lista zadań nr 3 Metody estymacji. Estymator największej wiarygodności Zad. 1 Pojawianie się spamu opisane jest zmienną losową y o rozkładzie zero-jedynkowym
Pochodna i różniczka funkcji oraz jej zastosowanie do obliczania niepewności pomiarowych
 Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Pochodna i różniczka unkcji oraz jej zastosowanie do obliczania niepewności pomiarowych Krzyszto Rębilas DEFINICJA POCHODNEJ Pochodna unkcji () w punkcie określona jest jako granica: lim 0 Oznaczamy ją
Algorytmy w teorii liczb
 Łukasz Kowalik, ASD 2004: Algorytmy w teorii liczb 1 Algorytmy w teorii liczb Teoria liczb jest działem matemtyki dotyczącym własności liczb naturalnych. Rozważa się zagadnienia związane z liczbami pierwszymi,
Łukasz Kowalik, ASD 2004: Algorytmy w teorii liczb 1 Algorytmy w teorii liczb Teoria liczb jest działem matemtyki dotyczącym własności liczb naturalnych. Rozważa się zagadnienia związane z liczbami pierwszymi,
Matematyka. rok akademicki 2008/2009, semestr zimowy. Konwersatorium 1. Własności funkcji
 . Własności funkcji () Wyznaczyć dziedzinę funkcji danej wzorem: y = 2 2 + 5 y = +4 y = 2 + (2) Podać zbiór wartości funkcji: y = 2 3, [2, 5) y = 2 +, [, 4] y =, [3, 6] (3) Stwierdzić, czy dana funkcja
. Własności funkcji () Wyznaczyć dziedzinę funkcji danej wzorem: y = 2 2 + 5 y = +4 y = 2 + (2) Podać zbiór wartości funkcji: y = 2 3, [2, 5) y = 2 +, [, 4] y =, [3, 6] (3) Stwierdzić, czy dana funkcja
1. Przyszła długość życia x-latka
 Przyszła długość życia x-latka Rozważmy osobę mającą x lat; oznaczenie: (x) Jej przyszłą długość życia oznaczymy T (x), lub krótko T Zatem x+t oznacza całkowitą długość życia T jest zmienną losową, której
Przyszła długość życia x-latka Rozważmy osobę mającą x lat; oznaczenie: (x) Jej przyszłą długość życia oznaczymy T (x), lub krótko T Zatem x+t oznacza całkowitą długość życia T jest zmienną losową, której
Elementy modelowania matematycznego
 Elementy modelowania matematycznego Modelowanie algorytmów klasyfikujących. Podejście probabilistyczne. Naiwny klasyfikator bayesowski. Modelowanie danych metodą najbliższych sąsiadów. Jakub Wróblewski
Elementy modelowania matematycznego Modelowanie algorytmów klasyfikujących. Podejście probabilistyczne. Naiwny klasyfikator bayesowski. Modelowanie danych metodą najbliższych sąsiadów. Jakub Wróblewski
1. Pochodna funkcji. 1.1 Pierwsza pochodna - definicja i własności Definicja pochodnej
 . Pierwsza pochodna - definicja i własności.. Definicja pochodnej Definicja Niech f : a, b) R oraz niech 0 a, b). Mówimy, że funkcja f ma pochodna w punkcie 0, którą oznaczamy f 0 ), jeśli istnieje granica
. Pierwsza pochodna - definicja i własności.. Definicja pochodnej Definicja Niech f : a, b) R oraz niech 0 a, b). Mówimy, że funkcja f ma pochodna w punkcie 0, którą oznaczamy f 0 ), jeśli istnieje granica
Rozwiązania prac domowych - Kurs Pochodnej. x 2 4. (x 2 4) 2. + kπ, gdzie k Z
 1 Wideo 5 1.1 Zadanie 1 1.1.1 a) f(x) = x + x f (x) = x + f (x) = 0 x + = 0 x = 1 [SZKIC] zatem w x = 1 występuje minimum 1.1. b) f(x) = x x 4 f (x) = x(x 4) x (x) (x 4) f (x) = 0 x(x 4) x (x) (x 4) =
1 Wideo 5 1.1 Zadanie 1 1.1.1 a) f(x) = x + x f (x) = x + f (x) = 0 x + = 0 x = 1 [SZKIC] zatem w x = 1 występuje minimum 1.1. b) f(x) = x x 4 f (x) = x(x 4) x (x) (x 4) f (x) = 0 x(x 4) x (x) (x 4) =
Spis treści Wstęp Estymacja Testowanie. Efekty losowe. Bogumiła Koprowska, Elżbieta Kukla
 Bogumiła Koprowska Elżbieta Kukla 1 Wstęp Czym są efekty losowe? Przykłady Model mieszany 2 Estymacja Jednokierunkowa klasyfikacja (ANOVA) Metoda największej wiarogodności (ML) Metoda największej wiarogodności
Bogumiła Koprowska Elżbieta Kukla 1 Wstęp Czym są efekty losowe? Przykłady Model mieszany 2 Estymacja Jednokierunkowa klasyfikacja (ANOVA) Metoda największej wiarogodności (ML) Metoda największej wiarogodności
Rynek, opcje i równania SDE
 Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Rynek, opcje i równania SDE Adam Majewski Uniwersytet Gdański kwiecień 2009 Adam Majewski (Uniwersytet Gdański) Rynek, opcje i równania SDE kwiecień 2009 1 / 16 1 Rynek, portfel inwestycyjny, arbitraż
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
z przedziału 0,1 liczb dodatnich. Rozważmy dwie zmienne losowe:... ma złożony rozkład dwumianowy o parametrach 1,q i, gdzie X, wszystkie składniki X
 Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Zadanie. Mamy dany ciąg liczb q, q,..., q n z przedziału 0,, oraz ciąg m, m,..., m n liczb dodatnich. Rozważmy dwie zmienne losowe: o X X X... X n, gdzie X i ma złożony rozkład dwumianowy o parametrach,q
Metody probabilistyczne
 Metody probabilistyczne 13. Elementy statystki matematycznej I Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 17.01.2019 1 / 30 Zagadnienia statystki Przeprowadzamy
Metody probabilistyczne 13. Elementy statystki matematycznej I Wojciech Kotłowski Instytut Informatyki PP http://www.cs.put.poznan.pl/wkotlowski/ 17.01.2019 1 / 30 Zagadnienia statystki Przeprowadzamy
XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych
 Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O górnym ograniczeniu zysku ze strategii handlowej opartej na kointegracji XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych Zależność kointegracyjna
Rafał M. Łochowski Szkoła Główna Handlowa w Warszawie O górnym ograniczeniu zysku ze strategii handlowej opartej na kointegracji XI Konferencja Metody Ilościowe w Badaniach Ekonomicznych Zależność kointegracyjna
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa.
 VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
VII. Elementy teorii stabilności. Funkcja Lapunowa. 1. Stabilność w sensie Lapunowa. W rozdziale tym zajmiemy się dokładniej badaniem stabilności rozwiązań równania różniczkowego. Pojęcie stabilności w
SMOP - wykład. Rozkład normalny zasady przenoszenia błędów. Ewa Pawelec
 SMOP - wykład Rozkład normalny zasady przenoszenia błędów Ewa Pawelec 1 iepewność dla rozkładu norm. Zamiast dodawania całych zakresów uwzględniamy prawdopodobieństwo trafienia dwóch wartości: P x 1, x
SMOP - wykład Rozkład normalny zasady przenoszenia błędów Ewa Pawelec 1 iepewność dla rozkładu norm. Zamiast dodawania całych zakresów uwzględniamy prawdopodobieństwo trafienia dwóch wartości: P x 1, x
Finanse i Rachunkowość studia niestacjonarne Wprowadzenie do teorii ciągów liczbowych (treść wykładu z 21 grudnia 2014)
 dr inż. Ryszard Rębowski DEFINICJA CIĄGU LICZBOWEGO Finanse i Rachunkowość studia niestacjonarne Wprowadzenie do teorii ciągów liczbowych (treść wykładu z grudnia 04) Definicja ciągu liczbowego Spośród
dr inż. Ryszard Rębowski DEFINICJA CIĄGU LICZBOWEGO Finanse i Rachunkowość studia niestacjonarne Wprowadzenie do teorii ciągów liczbowych (treść wykładu z grudnia 04) Definicja ciągu liczbowego Spośród
Ekonometria Finansowa II EARF. Michał Rubaszek
 Ekonometria Finansowa II EARF Michał Rubaszek 1 Cele - Zapoznanie z charakterystykami szeregów finansowych - Omówienie jednowymiarowych metod liczenia VaR - Omówienie wielowymiarowych metod liczenia VaR
Ekonometria Finansowa II EARF Michał Rubaszek 1 Cele - Zapoznanie z charakterystykami szeregów finansowych - Omówienie jednowymiarowych metod liczenia VaR - Omówienie wielowymiarowych metod liczenia VaR
Zawansowane modele wyborów dyskretnych
 Zawansowane modele wyborów dyskretnych Jerzy Mycielski Uniwersytet Warszawski grudzien 2013 Jerzy Mycielski (Uniwersytet Warszawski) Zawansowane modele wyborów dyskretnych grudzien 2013 1 / 16 Model efektów
Zawansowane modele wyborów dyskretnych Jerzy Mycielski Uniwersytet Warszawski grudzien 2013 Jerzy Mycielski (Uniwersytet Warszawski) Zawansowane modele wyborów dyskretnych grudzien 2013 1 / 16 Model efektów
WYKŁAD 3. Witold Bednorz, Paweł Wolff. Rachunek Prawdopodobieństwa, WNE, Uniwersytet Warszawski. 1 Instytut Matematyki
 WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
WYKŁAD 3 Witold Bednorz, Paweł Wolff 1 Instytut Matematyki Uniwersytet Warszawski Rachunek Prawdopodobieństwa, WNE, 2010-2011 Schemmat Bernouliego Rzucamy 10 razy moneta, próba Bernouliego jest pojedynczy
ROZWIĄZYWANIE RÓWNAŃ NIELINIOWYCH
 Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
Transport, studia I stopnia Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Adam Wosatko Postać ogólna równania nieliniowego Często występującym, ważnym problemem obliczeniowym
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 3 - model statystyczny, podstawowe zadania statystyki matematycznej
 WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 3 - model statystyczny, podstawowe zadania statystyki matematycznej Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 3 1 / 8 ZADANIE z rachunku
WYKŁADY ZE STATYSTYKI MATEMATYCZNEJ wykład 3 - model statystyczny, podstawowe zadania statystyki matematycznej Agata Boratyńska Agata Boratyńska Statystyka matematyczna, wykład 3 1 / 8 ZADANIE z rachunku
Rozpoznawanie obrazów
 Rozpoznawanie obrazów Ćwiczenia lista zadań nr 5 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
Rozpoznawanie obrazów Ćwiczenia lista zadań nr 5 autorzy: A. Gonczarek, J.M. Tomczak Przykładowe problemy Klasyfikacja binarna Dla obrazu x zaproponowano dwie cechy φ(x) = (φ 1 (x) φ 2 (x)) T. Na obrazie
166 Wstęp do statystyki matematycznej
 166 Wstęp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwiązać nasz zasadniczy problem związany z identyfikacją cechy populacji generalnej
166 Wstęp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwiązać nasz zasadniczy problem związany z identyfikacją cechy populacji generalnej
Definicja 1 Statystyką nazywamy (mierzalną) funkcję obserwowalnego wektora losowego
 Rozdział 1 Statystyki Definicja 1 Statystyką nazywamy (mierzalną) funkcję obserwowalnego wektora losowego X = (X 1,..., X n ). Uwaga 1 Statystyka jako funkcja wektora zmiennych losowych jest zmienną losową
Rozdział 1 Statystyki Definicja 1 Statystyką nazywamy (mierzalną) funkcję obserwowalnego wektora losowego X = (X 1,..., X n ). Uwaga 1 Statystyka jako funkcja wektora zmiennych losowych jest zmienną losową
Tydzień nr 9-10 (16 maja - 29 maja), Równania różniczkowe, wartości własne, funkcja wykładnicza od operatora - Matematyka II 2010/2011L
 Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Tydzień nr 9-10 (16 maja - 29 maja) Równania różniczkowe wartości własne funkcja wykładnicza od operatora - Matematyka II 2010/2011L Wszelkie pytania oraz uwagi o błędach proszę kierować na przemek.majewski@gmail.com
Geometryczna zbieżność algorytmu Gibbsa
 Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
Geometryczna zbieżność algorytmu Gibbsa Iwona Żerda Wydział Matematyki i Informatyki, Uniwersytet Jagielloński 6 grudnia 2013 6 grudnia 2013 1 / 19 Plan prezentacji 1 Algorytm Gibbsa 2 Tempo zbieżności
Zaawansowane metody numeryczne
 Wykład 1 Zadanie Definicja 1.1. (zadanie) Zadaniem nazywamy zagadnienie znalezienia rozwiązania x spełniającego równanie F (x, d) = 0, gdzie d jest zbiorem danych (od których zależy rozwiązanie x), a F
Wykład 1 Zadanie Definicja 1.1. (zadanie) Zadaniem nazywamy zagadnienie znalezienia rozwiązania x spełniającego równanie F (x, d) = 0, gdzie d jest zbiorem danych (od których zależy rozwiązanie x), a F
