Macierze - obliczanie wyznacznika macierzy z użyciem permutacji
|
|
|
- Jarosław Jaworski
- 9 lat temu
- Przeglądów:
Transkrypt
1 Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl r. Typeset by FoilTEX
2 Streszczenie Celem wykładu jest wprowadzenie pojęcia macierzy oraz podstawowych operacji na macierzach i zapoznanie słuchaczy z własnościami tychże operacji. Macierze są obiektami matematycznymi o bardzo szerokich zastosowaniach w matematyce, zarówno szkolnej, jak i wyższej. Stosuje się je między innymi do rozwiązywania układów równań liniowych postaci { ax + by = c1 cx + dy = c 2. Jednak w wykładzie tym, interesującymi dla nas będą fakty dotyczące macierzy i operacji na nich, a nie zastosowania. 1
3 Definicja macierzy Definicja 1. Niech m, n N. Macierzą o wymiarach m n o współczynnikach rzeczywistych nazywamy każdą funkcję A: {1,..., m} {1,..., n} R. Macierz jest zatem funkcją, która przyporządkowuje parze i, j liczb naturalnych, gdzie i {1,..., m}, j {1,..., n} liczbę rzeczywistą Ai, j, często oznaczaną symbolem a ij. 2
4 Jak rozumieć definicję macierzy? Macierz o wymiarach m n możemy traktować jako tablicę o m wierszach i n kolumnach. We wierszu o numerze i a w kolumnie o numerze j takiej tablicy umieszczamy wartość funkcji A w punkcie o współrzędnych i, j, czyli Ai, j, uzyskując np. dla m = 2, n = 3: A = A1, 1 A1, 2 A1, 3 A2, 1 A2, 2 A2, 3, czyli A = a11 a 12 a 13. a 21 a 22 a 23 3
5 Przykładowe macierze A = a 11 = A1, 1 = 3, a 12 = A1, 2 = 2, a 23 = A2, 3 = 8 2, a 32 = A3, 2 = 2, a 43 = A4, 3 = 7. Poniżej macierz kwadratowa, czyli macierz o jednakowej liczbie kolumn i wierszy m = n = B =
6 Dodawanie macierzy Definicja 2. Niech A, B będą macierzami o wymiarach m n, m, n N i współczynnikach rzeczywistych. Sumą macierzy A i B nazywamy macierz C = A + B o wymiarach m n taką, że c ij = a ij + b ij, dla dowolnej pary liczb i {1,..., m}, j {1,..., n}. A = B = C = A + B =
7 Mnożenie macierzy przez liczbę Oznaczmy przez M m n R zbiór wszystkich macierzy o współczynnikach rzeczywistych. Niech A M m n R, t R. Wynikiem mnożenia macierzy A przez liczbę t jest macierz B = ta taka, że dla dowolnej pary liczb i {1,..., m}, j {1,..., n} mamy równość b ij = ta ij. Na przykład dla mamy B = ta = 1 2 t = 1 2, A = = 2 3,
8 Mnożenie macierzy przez macierz Niech A M m n R, B M n k R, m, n, k N. Definicja 3. Iloczynem macierzy A i B nazywamy macierz C = AB M m k R taką, że dla dowolnej pary liczb i {1,..., m}, j {1,..., n} zachodzi równość gdzie n c ij = a ir b rj, r=1 n z r = z 1 + z 2 + z z n 1 + z n. r=1 7
9 Przykład. [Mnożenie macierzy przez macierz] A = B = AB = C = AB =
10 Istotne uwagi Dodawać do siebie można tylko macierze o jednakowych wymiarach, ale niekoniecznie kwadratowe Macierze A i B możemy pomnożyć tylko wtedy, gdy liczba kolumn macierzy A odpowiada liczbie wierszy macierzy B, Mnożenie macierzy na ogół nie jest przemienne AB BA, a często nawet niewykonalne jest mnożenie BA, pomimo, że możemy wykonać mnożenie AB, 9
11 Ćwiczenia Ćwiczenie 1. Mając dane macierze A i B znajdź ich sumę C. Pomnóż każdą spośród macierzy A, B i C przez liczby 2 i 3. A = B = Ćwiczenie 2. Wykonaj mnożenie macierzy A = B =
12 Permutacje Zmierzamy do określenia wyznacznika macierzy kwadratowej. Definicja 4. Bijekcją nazywamy każdą funkcję f : X Y taką, że i jeżeli x 1 x 2, to fx 1 fx 2, f różnowartościowa ii dla dowolnego y Y istnieje element x X taki, że fx = y. f na Definicja 5. Niech n N. Permutacją zbioru {1, 2,..., n}, nazywamy każdą bijekcję f : {1, 2,..., n} {1, 2,..., n}. Permutacje oznaczamy często literkami greckimi σ, τ,... zamiast f, g,..., a zapisujemy w następującej postaci 11
13 n f1 f2... fn. 12
14 Przykłady permutacji, składanie permutacji Permutacje składamy w następujący sposób. Składając f = z g = , uzyskujemy g f = = ; g f1 = gf1 = g4 = 1, g f2 = gf2 = g2 = 3, g f3 = gf3 = g1 = 2, g f4 = gf4 = g3 = 4. Zbiór wszystkich permutacji zbioru {1, 2,..., n} oznaczamy symbolem S n. 13
15 Cykle, transpozycje Definicja 6. Mówimy, że permutacja f S n zachowuje liczbę i {1, 2,..., n}, o ile fi = i. Definicja 7. Niech i 1, i 2,..., i k różne liczby ze zbioru {1, 2,..., n}, k n. Jeżeli permutacja f S n zachowuje pozostałe n k liczb ze zbioru {1, 2,..., n} oraz fi 1 = i 2, fi 2 = i 3,..., fi k 1 = i k, fi k = i 1, to mówimy, że f jest cyklem długości k i oznaczamy i 1 i 2... i k. Cykl długości 1 zachowuje każdy element zbioru, a cykl i j długości 2 nazywamy transpozycją = , = 1 4 3, =
16 Rozkład permutacji na cykle i transpozycje Definicja 8. Niech k, l n Mówimy, że cykle f = i 1 i 2... i k, g = j 1 j 2... j l są rozłączne, o ile zbiory {i 1, i 2,..., i k }, {j 1, j 2,..., j l } są rozłączne. Zauważmy, że jeżeli cykle f, g są rozłączne, to g f = f g. Twierdzenie 9. Każda permutacja f S n jest złożeniem pewnej liczby cykli rozłącznych. Przedstawienie permutacji f w postaci złożenia cykli rozłącznych jest jednoznaczne z dokładnością do porządku czynników kolejności składania Przykład: = Każda permutacja z S n jest złożeniem pewnej liczby transpozy- Wniosek 10. cji. 15
17 Dowód. Zauważmy, że i 1 i 2... i k = i 1 i k i 1 i 3 i 1 i 2. Teza wniosku wynika z Twierdzenia 6. Ćwiczenie 3. Sprawdzić, że =
18 Rozkład permutacji na cykle i transpozycje Uwaga 11. Rozkład permutacji na iloczyn złożenie transpozycji nie jest jednoznaczny. Na przykład, w S 4 zachodzą równości = = = = = = Uwaga 12. Przypomnijmy, że rozkład permutacji na cykle rozłączne jest jednoznaczny z dokładnością do kolejności ich składania. 17
19 Parzystość, nieparzystość i znak permutacji Twierdzenie 13. Jeżeli f = g 1 g 2... g r, r N jest jednym z rozkładów permutacji f S n na iloczyn transpozycji, to liczba sgnf = 1 r, nazywana znakiem permutacji f, zależy jedynie od f, a nie zależy od rozkładu. Zatem parzystość liczby r jest taka sama w każdym rozkładzie permutacji f na iloczyn transpozycji. Jeżeli również g S n, to sgng f = sgng sgnf. Definicja 14. Permutację f S n nazywamy parzystą, jeśli sgnf = 1. Jeśli sgnf = 1, to mówimy, że f jest permutacją nieparzystą. Uwaga 15. Liczba elementów zbioru S n, tj. permutacji zbioru {1, 2,..., n}, wynosi n! = n. 18
20 Wyznacznik macierzy Definicja 16. nazywamy liczbę Niech n N, A M n n R. Wyznacznikiem macierzy A deta = f S n sgnf a f11 a f22... a fnn. Przykład 17. Niech n = 1, A = a 11, wówczas S 1 = {id {1} } = { 1 1 } oraz deta = sgnid {1} a 11 = a 11. Przykład 18. Niech n = 2, A = a 11 a 12 a 21 a , wówczas S 2 = { , } = {1 22 1, 1 2} =: {f, g} oraz deta = sgnf a f11 a f22 +sgng a g11 a g22 = a 11 a 22 a 21 a
21 Przykład 19. Niech n = 3, A = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 M 3 3 R, wtedy S 3 = oraz { , , , , = {1 22 1, 2 3, 1 2, , , 1 3} =: {f 1, f 2, f 3, f 4, f 5, f 6 }, } deta = sgnf 1 a f1 11 a f1 22 a f sgnf 2 a f2 11 a f2 22 a f sgnf 3 a f3 11 a f3 22 a f sgnf 4 a f4 11 a f4 22 a f sgnf 5 a f5 11 a f5 22 a f sgnf 6 a f6 11 a f6 22 a f
22 deta = a 11 a 22 a 33 a 11 a 32 a 23 a 21 a 12 a 33 + a 21 a 32 a 13 + a 31 a 12 a 23 a 31 a 22 a
23 Istotne uwagi Wyznacznik macierzy definiuje się tylko dla macierzy kwadratowych o jednakowej liczbie wierszy i kolumn. Składanie permutacji na ogół nie jest przemienne, ale składanie rozłącznych cykli jest przemienne. Każdą permutację można w sposób jednoznaczny z dokładnością do kolejności składania przedstawić w postaci złożenia pewnej ilości rozłącznych cykli. Każdą permutację można przedstawić w postaci złożenia pewnej ilości transpozycji. Przedstawienie to nie jest jednoznaczne, ale parzystość liczby czynników rozkładu jest taka sama dla każdego z przedstawień. Identyczność jest permutacją parzystą, a każda transpozycja jest permutacją nieparzystą. 22
24 Ćwiczenia Podaj przykład permutacji f, g S n takich, że g f f g. Przedstaw poniższe permutacje w postaci złożenia rozłącznych cykli f = , g = Przedstaw powyższe permutacje w postaci złożenia transpozycji. Wypisz wszystkie permutacje zbioru {1, 2, 3, 4}. Ile elementów ma zbiór S 7? 23
25 Ćwiczenia Zastanów się kiedy dla jakich wymiarów dwie macierze możemy zarówno dodać do siebie, jak i pomnożyć przez siebie. Oblicz wyznacznik macierzy A =
26 Zadania Napisać programy np. w języku Pascal realizujące algorytmy: dodawania macierzy o podanych przez użytkownika wymiarach, mnożenia macierzy przez liczbę, mnożenia macierzy o podanych przez użytkownika wymiarach, obliczania wyznacznika macierzy dowolnego wymiaru. 25
27 Bibliografia G. Banaszak, W. Gajda, Elementy algebry liniowej cz. Naukowo-Techniczne, Warszawa 2002 I, Wydawnictwa 26
1 Macierze i wyznaczniki
 1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
Macierz o wymiarach m n. a 21. a 22. A =
 Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
Treści programowe. Matematyka. Efekty kształcenia. Literatura. Terminy wykładów i ćwiczeń. Warunki zaliczenia. tnij.org/ktrabka
 Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Grupy. Permutacje 1. (G2) istnieje element jednostkowy (lub neutralny), tzn. taki element e G, że dla dowolnego a G zachodzi.
 Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element
15. Macierze. Definicja Macierzy. Definicja Delty Kroneckera. Definicja Macierzy Kwadratowej. Definicja Macierzy Jednostkowej
 15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
Ekoenergetyka Matematyka 1. Wykład 3.
 Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
5 Wyznaczniki. 5.1 Definicja i podstawowe własności. MIMUW 5. Wyznaczniki 25
 MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
1 Zbiory i działania na zbiorach.
 Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Lista. Algebra z Geometrią Analityczną. Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami:
 Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
ALGEBRA LINIOWA. Wykład 2. Analityka gospodarcza, sem. 1. Wydział Zarządzania i Ekonomii Politechnika Gdańska
 ALGEBRA LINIOWA Wykład 2 Analityka gospodarcza, sem 1 Wydział Zarządzania i Ekonomii Politechnika Gdańska dr inż Natalia Jarzębkowska, CNMiKnO semzimowy 2018/2019 2/17 Macierze Niech M = {1, 2,, m} i N
ALGEBRA LINIOWA Wykład 2 Analityka gospodarcza, sem 1 Wydział Zarządzania i Ekonomii Politechnika Gdańska dr inż Natalia Jarzębkowska, CNMiKnO semzimowy 2018/2019 2/17 Macierze Niech M = {1, 2,, m} i N
DB Algebra liniowa semestr zimowy 2018
 DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
Wyk lad 4 Dzia lania na macierzach. Określenie wyznacznika
 Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
φ(x 1,..., x n ) = a i x 2 i +
 Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze
 Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze Polsko-Japońska Wyższa Szkoła Technik Komputerowych Katedra Informatyki Stosowanej Spis treści Spis treści 1 Wektory
Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze Polsko-Japońska Wyższa Szkoła Technik Komputerowych Katedra Informatyki Stosowanej Spis treści Spis treści 1 Wektory
Macierze i Wyznaczniki
 dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
Wyznaczniki. Mirosław Sobolewski. Wydział Matematyki, Informatyki i Mechaniki UW. 6. Wykład z algebry liniowej Warszawa, listopad 2013
 Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Algebra. Jakub Maksymiuk. lato 2018/19
 Algebra Jakub Maksymiuk lato 2018/19 Algebra W1/0 Zbiory z działaniami Podstawowe własności Potęgi Tabelka działania Przykłady Grupa symetryczna Algebra W1/1 Podstawowe własności Definicja: Działaniem
Algebra Jakub Maksymiuk lato 2018/19 Algebra W1/0 Zbiory z działaniami Podstawowe własności Potęgi Tabelka działania Przykłady Grupa symetryczna Algebra W1/1 Podstawowe własności Definicja: Działaniem
MATEMATYKA I SEMESTR ALK (PwZ) 1. Sumy i sumy podwójne : Σ i ΣΣ
 MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 4. Informatyka Stosowana. Magdalena Alama-Bućko. 25 marca Magdalena Alama-Bućko Wykład 4 25 marca / 25
 Wykład 4 Informatyka Stosowana Magdalena Alama-Bućko 25 marca 2019 Magdalena Alama-Bućko Wykład 4 25 marca 2019 1 / 25 Macierze Magdalena Alama-Bućko Wykład 4 25 marca 2019 2 / 25 Macierza wymiaru m n
Wykład 4 Informatyka Stosowana Magdalena Alama-Bućko 25 marca 2019 Magdalena Alama-Bućko Wykład 4 25 marca 2019 1 / 25 Macierze Magdalena Alama-Bućko Wykład 4 25 marca 2019 2 / 25 Macierza wymiaru m n
Algebra WYKŁAD 3 ALGEBRA 1
 Algebra WYKŁAD 3 ALGEBRA 1 Liczby zespolone Postać wykładnicza liczby zespolonej Niech e oznacza stałą Eulera Definicja Równość e i cos isin nazywamy wzorem Eulera. ALGEBRA 2 Liczby zespolone Każdą liczbę
Algebra WYKŁAD 3 ALGEBRA 1 Liczby zespolone Postać wykładnicza liczby zespolonej Niech e oznacza stałą Eulera Definicja Równość e i cos isin nazywamy wzorem Eulera. ALGEBRA 2 Liczby zespolone Każdą liczbę
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn x 1 x 2... x m ...
 Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
3. Wykład Układy równań liniowych.
 31 Układy równań liniowych 3 Wykład 3 Definicja 31 Niech F będzie ciałem Układem m równań liniowych o niewiadomych x 1,, x n, m, n N, o współczynnikach z ciała F nazywamy układ równań postaci: x 1 + +
31 Układy równań liniowych 3 Wykład 3 Definicja 31 Niech F będzie ciałem Układem m równań liniowych o niewiadomych x 1,, x n, m, n N, o współczynnikach z ciała F nazywamy układ równań postaci: x 1 + +
Wyznaczniki. Algebra. Aleksander Denisiuk
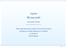 Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
O MACIERZACH I UKŁADACH RÓWNAŃ
 O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
Definicja macierzy Typy i właściwości macierzy Działania na macierzach Wyznacznik macierzy Macierz odwrotna Normy macierzy RACHUNEK MACIERZOWY
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy funkcję
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy funkcję
Met Me ody numer yczne Wykład ykład Dr inż. Mic hał ha Łanc Łan zon Instyt Ins ut Elektr Elektr echn iki echn i Elektrot Elektr echn olo echn
 Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
Zastosowania wyznaczników
 Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
RACHUNEK MACIERZOWY. METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6. Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska
 RACHUNEK MACIERZOWY METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy
RACHUNEK MACIERZOWY METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy
Działania na przekształceniach liniowych i macierzach
 Działania na przekształceniach liniowych i macierzach Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 5 wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa,
Działania na przekształceniach liniowych i macierzach Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 5 wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa,
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści 0 Wyrażenia algebraiczne, indukcja matematyczna 2 2 2 1 Geometria analityczna w R 2 3 3 3 2 Liczby zespolone 4 4 4 3
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści 0 Wyrażenia algebraiczne, indukcja matematyczna 2 2 2 1 Geometria analityczna w R 2 3 3 3 2 Liczby zespolone 4 4 4 3
Zestaw 12- Macierz odwrotna, układy równań liniowych
 Zestaw - Macierz odwrotna, układy równań liniowych Przykładowe zadania z rozwiązaniami Załóżmy, że macierz jest macierzą kwadratową stopnia n. Mówimy, że macierz tego samego wymiaru jest macierzą odwrotną
Zestaw - Macierz odwrotna, układy równań liniowych Przykładowe zadania z rozwiązaniami Załóżmy, że macierz jest macierzą kwadratową stopnia n. Mówimy, że macierz tego samego wymiaru jest macierzą odwrotną
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 2 marca 2017 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod m)),
MACIERZE I WYZNACZNIKI
 Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Zadania z algebry liniowej - sem. I Przestrzenie liniowe, bazy, rząd macierzy
 Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
Wykład 7 Macierze i wyznaczniki
 Wykład 7 Macierze i wyznaczniki Andrzej Sładek sladek@ux2mathusedupl Instytut Matematyki, Uniwersytet Śląski w Katowicach Andrzej Sładek (Instytut Matematyki, Uniwersytet Śląski Wykład w Katowicach) 7
Wykład 7 Macierze i wyznaczniki Andrzej Sładek sladek@ux2mathusedupl Instytut Matematyki, Uniwersytet Śląski w Katowicach Andrzej Sładek (Instytut Matematyki, Uniwersytet Śląski Wykład w Katowicach) 7
Metody i analiza danych
 2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
Matematyka dyskretna
 Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
Matematyka dyskretna Wykład 6: Ciała skończone i kongruencje Gniewomir Sarbicki 24 lutego 2015 Relacja przystawania Definicja: Mówimy, że liczby a, b Z przystają modulo m (co oznaczamy jako a = b (mod
Kody blokowe Wykład 2, 10 III 2011
 Kody blokowe Wykład 2, 10 III 2011 Literatura 1. R.M. Roth, Introduction to Coding Theory, 2006 2. W.C. Huffman, V. Pless, Fundamentals of Error-Correcting Codes, 2003 3. D.R. Hankerson et al., Coding
Kody blokowe Wykład 2, 10 III 2011 Literatura 1. R.M. Roth, Introduction to Coding Theory, 2006 2. W.C. Huffman, V. Pless, Fundamentals of Error-Correcting Codes, 2003 3. D.R. Hankerson et al., Coding
, A T = A + B = [a ij + b ij ].
![, A T = A + B = [a ij + b ij ]. , A T = A + B = [a ij + b ij ].](/thumbs/98/137554993.jpg) 1 Macierze Jeżeli każdej uporządkowanej parze liczb naturalnych (i, j), 1 i m, 1 j n jest przyporządkowana dokładnie jedna liczba a ij, to mówimy, że jest określona macierz prostokątna A = a ij typu m
1 Macierze Jeżeli każdej uporządkowanej parze liczb naturalnych (i, j), 1 i m, 1 j n jest przyporządkowana dokładnie jedna liczba a ij, to mówimy, że jest określona macierz prostokątna A = a ij typu m
MATEMATYKA I SEMESTR ALK (PwZ) 1. Sumy i sumy podwójne : Σ i ΣΣ
 MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
Algebra z Geometrią Analityczną. { x + 2y = 5 x y = 9. 4x + 5y 3z = 9, 2x + 4y 3z = 1. { 2x + 3y + z = 5 4x + 5y 3z = 9 7 1,
 Lista Algebra z Geometrią Analityczną Układy równań. Zadanie 1 Wyjaśnij na czym polega metoda elininacji Gaussa rozwiązując układ równań: { x + 2y = 5 x y = 9 Zadanie 2 Rozwiąż układ równań metodą eliminacji
Lista Algebra z Geometrią Analityczną Układy równań. Zadanie 1 Wyjaśnij na czym polega metoda elininacji Gaussa rozwiązując układ równań: { x + 2y = 5 x y = 9 Zadanie 2 Rozwiąż układ równań metodą eliminacji
1. Liczby zespolone i
 Zadania podstawowe Liczby zespolone Zadanie Podać część rzeczywistą i urojoną następujących liczb zespolonych: z = ( + 7i)( + i) + ( 5 i)( + 7i), z = + i, z = + i i, z 4 = i + i + i i Zadanie Dla jakich
Zadania podstawowe Liczby zespolone Zadanie Podać część rzeczywistą i urojoną następujących liczb zespolonych: z = ( + 7i)( + i) + ( 5 i)( + 7i), z = + i, z = + i i, z 4 = i + i + i i Zadanie Dla jakich
2 Rachunek macierzowy, metoda eliminacji Gaussa-Jordana Wprowadzenie teoretyczne Zadania... 9
 Spis treści 1 Podstawowe struktury algebraiczne 2 11 Grupa, pierścień, ciało 2 12 Grupy permutacji 4 13 Pierścień wielomianów, algorytm Euklidesa, największy wspólny dzielnik 6 14 Zadania 7 2 Rachunek
Spis treści 1 Podstawowe struktury algebraiczne 2 11 Grupa, pierścień, ciało 2 12 Grupy permutacji 4 13 Pierścień wielomianów, algorytm Euklidesa, największy wspólny dzielnik 6 14 Zadania 7 2 Rachunek
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Uniwersytet Kazimierza Wielkiego w Bydgoszczy Zespół Szkół nr 5 Mistrzostwa Sportowego XV Liceum Ogólnokształcące w Bydgoszczy
 Uniwersytet Kazimierza Wielkiego w Bydgoszczy Zespół Szkół nr 5 Mistrzostwa Sportowego XV Liceum Ogólnokształcące w Bydgoszczy Matematyka, królowa nauk Edycja X - etap 2 Bydgoszcz, 16 kwietnia 2011 Fordoński
Uniwersytet Kazimierza Wielkiego w Bydgoszczy Zespół Szkół nr 5 Mistrzostwa Sportowego XV Liceum Ogólnokształcące w Bydgoszczy Matematyka, królowa nauk Edycja X - etap 2 Bydgoszcz, 16 kwietnia 2011 Fordoński
Układy równań. Kinga Kolczyńska - Przybycień 22 marca Układ dwóch równań liniowych z dwiema niewiadomymi
 Układy równań Kinga Kolczyńska - Przybycień 22 marca 2014 1 Układ dwóch równań liniowych z dwiema niewiadomymi 1.1 Pojęcie układu i rozwiązania układu Układem dwóch równań liniowych z dwiema niewiadomymi
Układy równań Kinga Kolczyńska - Przybycień 22 marca 2014 1 Układ dwóch równań liniowych z dwiema niewiadomymi 1.1 Pojęcie układu i rozwiązania układu Układem dwóch równań liniowych z dwiema niewiadomymi
1 Macierz odwrotna metoda operacji elementarnych
 W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Analiza numeryczna Kurs INP002009W. Wykłady 6 i 7 Rozwiązywanie układów równań liniowych. Karol Tarnowski A-1 p.
 Analiza numeryczna Kurs INP002009W Wykłady 6 i 7 Rozwiązywanie układów równań liniowych Karol Tarnowski karol.tarnowski@pwr.wroc.pl A-1 p.223 Plan wykładu Podstawowe pojęcia Własności macierzy Działania
Analiza numeryczna Kurs INP002009W Wykłady 6 i 7 Rozwiązywanie układów równań liniowych Karol Tarnowski karol.tarnowski@pwr.wroc.pl A-1 p.223 Plan wykładu Podstawowe pojęcia Własności macierzy Działania
Przestrzenie wektorowe, liniowa niezależność wektorów, bazy przestrzeni wektorowych
 Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
Wyk lad 3 Wyznaczniki
 1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
1 Określenie wyznacznika Wyk lad 3 Wyznaczniki Niech A bedzie macierza kwadratowa stopnia n > 1 i niech i, j bed a liczbami naturalnymi n Symbolem A ij oznaczać bedziemy macierz kwadratowa stopnia n 1
; B = Wykonaj poniższe obliczenia: Mnożenia, transpozycje etc wykonuję programem i przepisuję wyniki. Mam nadzieję, że umiesz mnożyć macierze...
 Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Macierze Lekcja I: Wprowadzenie
 Macierze Lekcja I: Wprowadzenie Wydział Matematyki Politechniki Wrocławskiej Definicja Niech dane będą dwie liczby naturalne dodatnie m i n. Układ m n liczb ułożonych w prostokątną tablicę złożoną z m
Macierze Lekcja I: Wprowadzenie Wydział Matematyki Politechniki Wrocławskiej Definicja Niech dane będą dwie liczby naturalne dodatnie m i n. Układ m n liczb ułożonych w prostokątną tablicę złożoną z m
OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY
 OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY Dodawanie i odejmowanie macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach! Wynikiem tych operacji jest macierz o takich samych
OPERACJE NA MACIERZACH DODAWANIE I ODEJMOWANIE MACIERZY Dodawanie i odejmowanie macierzy jest możliwe tylko dla dwóch macierzy o takich samych wymiarach! Wynikiem tych operacji jest macierz o takich samych
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera
 Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Wyk lad 4 Macierz odwrotna i twierdzenie Cramera 1 Odwracanie macierzy I n jest elementem neutralnym mnożenia macierzy w zbiorze M n (R) tzn A I n I n A A dla dowolnej macierzy A M n (R) Ponadto z twierdzenia
Algorytm Euklidesa. ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90),
 Algorytm Euklidesa ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90), (d) NWD(120, 168, 280), (e) NWD(30, 42, 70, 105), (f) NWW[120, 195], (g)
Algorytm Euklidesa ZADANIE 1. Oblicz korzystając z algorytmu Euklidesa: (a) NWD(120, 195), (b) NWD(80, 208), (c) NWD(36, 60, 90), (d) NWD(120, 168, 280), (e) NWD(30, 42, 70, 105), (f) NWW[120, 195], (g)
det[a 1,..., A i,..., A j,..., A n ] + det[a 1,..., ka j,..., A j,..., A n ] Dowód Udowodniliśmy, że: det[a 1,..., A i + ka j,..., A j,...
![det[a 1,..., A i,..., A j,..., A n ] + det[a 1,..., ka j,..., A j,..., A n ] Dowód Udowodniliśmy, że: det[a 1,..., A i + ka j,..., A j,... det[a 1,..., A i,..., A j,..., A n ] + det[a 1,..., ka j,..., A j,..., A n ] Dowód Udowodniliśmy, że: det[a 1,..., A i + ka j,..., A j,...](/thumbs/93/111637753.jpg) Wykład 14 Wyznacznik macierzy cd Twierdzenie 1 Niech A będzie macierzą kwadratową i niech A i, A j będą dwiema różnymi jej kolumnami, wtedy dla dowolnego k K: det[a 1,, A i,, A j,, A n ] det[a 1,, A i
Wykład 14 Wyznacznik macierzy cd Twierdzenie 1 Niech A będzie macierzą kwadratową i niech A i, A j będą dwiema różnymi jej kolumnami, wtedy dla dowolnego k K: det[a 1,, A i,, A j,, A n ] det[a 1,, A i
1 Elementy logiki i teorii mnogości
 1 Elementy logiki i teorii mnogości 11 Elementy logiki Notatki do wykładu Definicja Zdaniem logicznym nazywamy zdanie oznajmujące, któremu przysługuje jedna z dwu logicznych ocen prawda (1) albo fałsz
1 Elementy logiki i teorii mnogości 11 Elementy logiki Notatki do wykładu Definicja Zdaniem logicznym nazywamy zdanie oznajmujące, któremu przysługuje jedna z dwu logicznych ocen prawda (1) albo fałsz
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u
 Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
Wykład 4 Udowodnimy teraz, że jeśli U, W są podprzetrzeniami skończenie wymiarowej przestrzeni V to zachodzi wzór: dim(u + W ) = dim U + dim W dim(u W ) Rzeczywiście U W jest podprzetrzenią przestrzeni
Układy równań liniowych i metody ich rozwiązywania
 Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
Układy równań liniowych i metody ich rozwiązywania Łukasz Wojciechowski marca 00 Dany jest układ m równań o n niewiadomych postaci: a x + a x + + a n x n = b a x + a x + + a n x n = b. a m x + a m x +
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki Spis treści strona główna 1 Wyrażenia algebraiczne, indukcja matematyczna 2 2 Geometria analityczna w R 2 Liczby zespolone 4 4 Wielomiany
Pytania i polecenia podstawowe
 Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
Pytania i polecenia podstawowe Liczby zespolone a) 2 i 1 + 2i 1 + 2i 3 + 4i, c) 1 i 2 + i a) 4 + 3i (2 i) 2, c) 1 3i a) i 111 (1 + i) 100, c) ( 3 i) 100 Czy dla dowolnych liczb z 1, z 2 C zachodzi równość:
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Algebra z geometrią analityczną zadania z odpowiedziami
 Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
Algebra z geometrią analityczną zadania z odpowiedziami Maciej Burnecki opracowanie Spis treści I Wyrażenia algebraiczne, indukcja matematyczna 2 II Geometria analityczna w R 2 4 III Liczby zespolone 5
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn a 1j a 2j R i = , C j =
 11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
Matematyka liczby zespolone. Wykład 1
 Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Matematyka liczby zespolone Wykład 1 Siedlce 5.10.015 Liczby rzeczywiste Zbiór N ={0,1,,3,4,5, } nazywamy zbiorem Liczb naturalnych, a zbiór N + ={1,,3,4, } nazywamy zbiorem liczb naturalnych dodatnich.
Treści programowe. Matematyka 1. Efekty kształcenia. Literatura. Warunki zaliczenia. Ogólne własności funkcji. Definicja 1. Funkcje elementarne.
 Treści programowe Matematyka 1 Katarzyna Trąbka-Więcław Funkcje elementarne. Granica funkcji, własności granic, wyrażenia nieoznaczone, ciągłość funkcji. Pochodna funkcji w punkcie i w przedziale, pochodne
Treści programowe Matematyka 1 Katarzyna Trąbka-Więcław Funkcje elementarne. Granica funkcji, własności granic, wyrażenia nieoznaczone, ciągłość funkcji. Pochodna funkcji w punkcie i w przedziale, pochodne
Lista. Algebra z Geometrią Analityczną. Zadanie 1 Zapisz za pomocą spójników logicznych i kwantyfikatorów: x jest większe niż 6 lub mniejsze niż 4
 Lista Algebra z Geometrią Analityczną Zadanie 1 Zapisz za pomocą spójników logicznych i kwantyfikatorów: x jest większe niż 6 lub mniejsze niż 4 jeżeli x jest podzielne przez 4 to jest podzielne przez
Lista Algebra z Geometrią Analityczną Zadanie 1 Zapisz za pomocą spójników logicznych i kwantyfikatorów: x jest większe niż 6 lub mniejsze niż 4 jeżeli x jest podzielne przez 4 to jest podzielne przez
MACIERZE. Sobiesiak Łukasz Wilczyńska Małgorzata
 MACIERZE Sobiesiak Łukasz Wilczyńska Małgorzata Podstawowe pojęcia dotyczące macierzy Nie bez przyczyny zaczynamy od pojęcia macierzy, które jest niezwykle przydatne we wszystkich zastosowaniach, obliczeniach
MACIERZE Sobiesiak Łukasz Wilczyńska Małgorzata Podstawowe pojęcia dotyczące macierzy Nie bez przyczyny zaczynamy od pojęcia macierzy, które jest niezwykle przydatne we wszystkich zastosowaniach, obliczeniach
Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań.
 Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań. Wydział Matematyki Politechniki Wrocławskiej Układy Cramerowskie Układem Cramera nazywamy układ równań liniowych: AX = B, w którym A jest macierzą
Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań. Wydział Matematyki Politechniki Wrocławskiej Układy Cramerowskie Układem Cramera nazywamy układ równań liniowych: AX = B, w którym A jest macierzą
Podstawowe działania w rachunku macierzowym
 Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Baza w jądrze i baza obrazu ( )
 Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
Przykład Baza w jądrze i baza obrazu (839) Znajdź bazy jądra i obrazu odwzorowania α : R 4 R 3, gdzie α(x, y, z, t) = (x + 2z + t, 2x + y 3z 5t, x y + z + 4t) () zór ten oznacza, że α jest odwzorowaniem
 http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
Wykład Ćwiczenia Laboratorium Projekt Seminarium Liczba godzin zajęć zorganizowanych w Uczelni ,5 1
 Zał. nr 4 do ZW WYDZIAŁ ***** KARTA PRZEDMIOTU Nazwa w języku polskim ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ B Nazwa w języku angielskim Algebra and Analytic Geometry B Kierunek studiów (jeśli dotyczy): Specjalność
Zał. nr 4 do ZW WYDZIAŁ ***** KARTA PRZEDMIOTU Nazwa w języku polskim ALGEBRA Z GEOMETRIĄ ANALITYCZNĄ B Nazwa w języku angielskim Algebra and Analytic Geometry B Kierunek studiów (jeśli dotyczy): Specjalność
Zaawansowane metody numeryczne
 Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ
 ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów.
 5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
Projekt Informatyka przepustką do kariery współfinansowany ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 Zajęcia 1 Pewne funkcje - funkcja liniowa dla gdzie -funkcja kwadratowa dla gdzie postać kanoniczna postać iloczynowa gdzie równanie kwadratowe pierwiastki równania kwadratowego: dla dla wzory Viete a
Zajęcia 1 Pewne funkcje - funkcja liniowa dla gdzie -funkcja kwadratowa dla gdzie postać kanoniczna postać iloczynowa gdzie równanie kwadratowe pierwiastki równania kwadratowego: dla dla wzory Viete a
2. Układy równań liniowych
 2. Układy równań liniowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2. Układy równań liniowych zima 2017/2018 1 /
2. Układy równań liniowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2. Układy równań liniowych zima 2017/2018 1 /
cx cx 1,cx 2,cx 3,...,cx n. Przykład 4, 5
 Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Postać Jordana macierzy
 Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Rozdział 8 Postać Jordana macierzy Niech F = R lub F = C Macierz J r λ) F r r postaci λ 1 0 0 0 λ 1 J r λ) = 0 λ 1 0 0 λ gdzie λ F nazywamy klatką Jordana stopnia r Oczywiście J 1 λ) = [λ Definicja 81
Algebra liniowa II. Lista 1. 1 u w 0 1 v 0 0 1
 Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z].
![Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z]. Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z].](/thumbs/66/54501363.jpg) 1. Wykład 1: Grupy i izomorfizmy grup. Definicja 1.1. Niech A będzie niepustym zbiorem. Działaniem wewnętrznym(lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym
1. Wykład 1: Grupy i izomorfizmy grup. Definicja 1.1. Niech A będzie niepustym zbiorem. Działaniem wewnętrznym(lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy
 Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
