Grupy. Permutacje 1. (G2) istnieje element jednostkowy (lub neutralny), tzn. taki element e G, że dla dowolnego a G zachodzi.
|
|
|
- Daniel Jasiński
- 8 lat temu
- Przeglądów:
Transkrypt
1 Grupy. Permutacje 1 1 Definicja grupy Niech G będzie zbiorem. Działaniem na zbiorze G nazywamy odwzorowanie (oznaczane, jak mnożenie, przez ) przyporządkowujące każdej parze uporządkowanej (a, b) G G element a b zbioru G. Definicja. Zbiór G wraz z działaniem nazywamy grupą, jeśli są spełnione następujące własności: (G1) działanie jest łączne, tzn. dla dowolnych elementów a, b, c G zachodzi (a b) c = a (b c); (G2) istnieje element jednostkowy (lub neutralny), tzn. taki element e G, że dla dowolnego a G zachodzi a e = e a = a; (G3) dla każdego elementu a G istnieje element odwrotny, tzn. taki element a 1 G, że zachodzi a a 1 = a 1 a = e. Grupę zwykle zapisujemy w postaci (G, ). Niekiedy zamiast a b piszemy po prostu ab, itp. Fakt 1. Niech (G, ) będzie grupą. Dla dowolnych a, b G zachodzi Dla k N i a G oznaczmy i Ponadto, a 0 := e. (a b) 1 = b 1 a 1. a k := } a.{{.. a}, k czynników a k := a} 1.{{.. a 1 }. k czynników Warto zauważyć, że w definicji grupy nie żąda się, by działanie było przemienne, tzn. by a b = b a dla dowolnych a, b G. Gdy dla pewnych elementów a, b grupy (G, ) zachodzi a b = b a, to mówimy, że elementy te komutują.
2 2 Skompilował Janusz Mierczyński Fakt 2. Jeśli a i b komutują, to (a b) k = a k b k = b k a k dla dowolnego k Z. Definicja. Grupę (G, ) nazywamy grupą przemienną (lub abelową), gdy dla dowolnych a, b G zachodzi a b = b a. Inaczej mówiąc, grupa abelowa to taka grupa, że dowolne dwa jej elementy komutują. Definicja. Rzędem grupy (G, ) nazywamy liczbę elementów zbioru G. Rząd grupy oznaczamy przez G. Przykład 1. (R, +), gdzie R jest zbiorem liczb rzeczywistych, a + jest działaniem dodawania, jest grupą: elementem neutralnym jest zero, elementem odwrotnym do a R jest a. Jest to grupa abelowa. Przykład 2. (R \ {0}, ), gdzie jest działaniem mnożenia, jest grupą: elementem neutralnym jest 1, elementem odwrotnym do a R jest 1/a. Jest to grupa abelowa. Przykład 3. (R, ), gdzie jest działaniem mnożenia, nie jest grupą: nie ma elementu odwrotnego do zera. Przykład 4. Niech n będzie liczbą naturalną. Oznaczmy przez GL(n, R) zbiór wszystkich kwadratowych macierzy nieosobliwych stopnia n o elementach rzeczywistych. (GL(n, R), ), gdzie jest działaniem mnożenia macierzy, jest grupą: elementem neutralnym jest macierz jednostkowa, elementem odwrotnym do macierzy A jest macierz odwrotna A 1. Dla n 2 jest to grupa nieabelowa. 2 Grupy permutacji 2.1 Podstawowe własności Będziemy rozpatrywali X, zbiór n-elementowy, utożsamiany ze zbiorem liczb naturalnych od 1 do n, czyli X = {1,..., n}. Definicja. Permutacją zbioru n-elementowego {1,..., n} nazywamy odwzorowanie π : {1,..., n} {1,..., n} takie, że dla dowolnych dwóch liczb i, j {1,..., n}, i j, zachodzi π(i) π(j). Inaczej mówiąc, permutacja to różnowartościowe odwzorowanie zbioru {1,..., n} w siebie.
3 Grupy. Permutacje 3 Permutację π : {1,..., n} {1,..., n} zapisujemy jako n. π(1) π(2)... π(n) Definicja. Permutację n n zbioru n-elementowego nazywamy permutacją identycznościową (lub tożsamościową), i oznaczamy przez I. Definicja. Złożeniem lub iloczynem dwóch permutacji π, ϱ zbioru n-elementowego nazywamy permutację π ϱ zdefiniowaną jako (π ϱ)(i) := π(ϱ(i)) dla wszystkich i {1,..., n}. W przypadku składania permutacji ważna jest kolejność czynników. Na przykład, niech π =, ϱ = Wówczas π ϱ = 1 2 3, ale ϱ π = Ponieważ X jest zbiorem skończonym, każda permutacja π zbioru X, będąc odwzorowaniem różnowartościowym, jest też odwzorowaniem na zbiór X. Wobec tego, poniższa definicja ma sens: Definicja. Permutacją odwrotną do permutacji π zbioru n-elementowego nazywamy permutację π 1 zdefiniowaną jako ( π 1 (i) = j ) ( π(j) = i ). Fakt 3. Dla permutacji π, ϱ, σ zbioru n-elementowego zachodzą następujące równości: (i) (ii) (ii) (π ϱ) σ = π (ϱ σ), π I = I π = π, π π 1 = π 1 π = I.
4 4 Skompilował Janusz Mierczyński Z powyższego faktu wynika, że zbiór wszystkich permutacji zbioru n-elementowego wraz z działaniem składania permutacji tworzy grupę. Grupę tę nazywamy grupą symetryczną (lub grupą permutacji) stopnia n, i oznaczamy przez (S n, ) (lub przez S n ). Przypominam, że dla π S n i k N oznaczamy oraz Ponadto, π 0 = I. π k = π π π k = π 1 π 1 (k czynników), (k czynników). Przypominam też, że dla dowolnych π, ρ S n zachodzi (π ϱ) 1 = ϱ 1 π 1. Fakt 4. Rząd grupy (S n, ) wynosi n!. Zauważmy, że S 1 = {I}, S 2 = {I, (1 2)}. Są to grupy abelowe. Natomiast wszystkie grupy S n dla n 3 są nieabelowe. 2.2 Cykle Definicja. Niech i 1, i 2,..., i r będą parami różnymi elementami zbioru {1,..., n}. Oznaczmy przez (i 1 i 2... i r ) permutację π S n taką, że π(i 1 ) = i 2, π(i 2 ) = i 3,..., π(i r 1 ) = i r, π(i r ) = i 1, oraz π(i) = i dla i {1,..., n} \ {i 1,..., i r }. Permutację (i 1 i 2... i r ) nazywamy cyklem długości r. Przykład. Permutacja jest cyklem. Zauważmy, że można go zapisać na cztery sposoby: ( ), lub ( ), lub ( ), lub ( ). Definicja. Cykle (i 1 i 2... i r ), (j 1 j 2... j s ) S n są rozłączne, jeśli nie mają wspólnego elementu. Łatwo zauważyć, że dla rozłącznych cykli (i 1 i 2... i r ), (j 1 j 2... j s ) S n zachodzi (i 1 i 2... i r ) (j 1 j 2... j s ) = (j 1 j 2... j s ) (i 1 i 2... i r ) (inaczej mówiąc, cykle rozłączne komutują).
5 Grupy. Permutacje 5 Twierdzenie 1 (Rozkład permutacji na cykle rozłączne). Każdą permutację można przedstawić w postaci złożenia parami rozłącznych cykli. Przykład. Pokażemy teraz, w jaki sposób możemy otrzymać rozkład permutacji na cykle rozłączne jak w powyższym twierdzeniu. Niech S Wybieramy jakiś element ze zbioru X, powiedzmy 1, i rozpatrujemy π(1), π 2 (1), π 3 (1), itd. W naszym przykładzie, π(1) = 3, π 2 (1) = π(3) = 8, π 3 (1) = π(8) = 4, π 4 (1) = π(4) = 1. Zatem jednym z cykli będzie ( ). Bierzemy teraz pewien element ze zbioru {1,..., 8}\{1, 3, 4, 8}, powiedzmy 2. Ponieważ π(2) = 2, drugim cyklem będzie (2). Dalej, bierzemy jakiś element ze zbioru {1,..., 8} \ {1, 2, 3, 4, 8}, powiedzmy 5. Ponieważ π(5) = 5, trzecim cyklem będzie (5). Weźmy teraz π(6) = 7 i π 2 (6) = π(7) = 6. Czwartym cyklem będzie (6 7). Ponieważ wyczerpaliśmy już wszystkie elementy zbioru {1,..., 8}, rozkład permutacji na cykle ma postać = ( ) (2) (5) (6 7) Często cykli długości jeden nie zapisuje się; na przykład, powyższą równość zapisuje się jako = ( ) (6 7) Permutację tożsamościową niekiedy zapisujemy jako (1). Rozkład permutacji na cykle rozłączne, o którym jest mowa w Twierdzeniu 1, jest jednoznaczny w tym sensie, że czynniki (czyli parami rozłączne cykle) są zawsze takie same, tylko ich kolejność może się zmieniać. 2.3 Transpozycje. Permutacje parzyste i nieparzyste Definicja. Transpozycją nazywamy cykl długości 2. Twierdzenie 2 (Rozkład cyklu na transpozycje). Każdy cykl długości r jest złożeniem r 1 transpozycji (niekoniecznie rozłącznych). Na przykład, (i 1 i 2... i r ) = (i 1 i 2 ) (i 2 i 3 ) (i r 1 i r ).
6 6 Skompilował Janusz Mierczyński W odróżnieniu od rozkładu permutacji na cykle rozłączne, rozkład cyklu na transpozycje nie jest jednoznaczny. Na przykład, (1 2 3) = (1 2) (2 3) = (2 3) (1 3). Ponadto, cykle nierozłączne nie muszą komutować. Wnioskiem z Twierdzenia 1 i Twierdzenia 2 jest następujący fakt. Fakt 5. Każda permutacja jest złożeniem transpozycji. Rozkład permutacji na transpozycje, o którym mowa w powyższym fakcie, nie jest jednoznaczny. Jednak dla ustalonej permutacji liczba transpozycji w rozkładzie jest albo parzysta, albo nieparzysta. Definicja. Permutację π S n nazywamy parzystą, gdy jest permutacją identycznościową lub gdy można ją przedstawić jako złożenie parzystej liczby transpozycji. Definicja. Permutację π S n nazywamy nieparzystą, gdy można ją przedstawić jako złożenie nieparzystej liczby transpozycji. (i) Złożenie dwóch permutacji parzystych jest permutacją parzy- Fakt 6. stą. (ii) Złożenie dwóch permutacji nieparzystych jest permutacją parzystą. (i) Złożenie permutacji parzystej i nieparzystej jest permutacją nieparzystą. Permutacja tożsamościowa jest permutacją parzystą. Z powyższego faktu łatwo można wywnioskować, że permutacja odwrotna do permutacji parzystej [nieparzystej] jest permutacją parzystą [nieparzystą]. Zatem zbiór wszystkich permutacji parzystych zbioru n-elementowego wraz z działaniem składania permutacji tworzy grupę, zwaną grupą alternującą stopnia n, i oznaczaną przez (A n, ) (lub przez A n ). Jej rząd wynosi 1 n! (dla 2 n 2). 2.4 Inwersje Definicja. Dla permutacji π S n, parę (π(i), π(j)) nazywamy inwersją, gdy i < j oraz π(i) > π(j). Twierdzenie 3. Permutacja π S n parzystą [nieparzystą] liczbę inwersji. jest parzysta [nieparzysta], gdy ma Przykład. Rozpatrzmy znów permutację S
7 Grupy. Permutacje 7 Wypisujemy jej inwersje: (π(1), π(2)), (π(1), π(4)), (π(2), π(4)), (π(3), π(4)), (π(3), π(5)), (π(3), π(6)), (π(3), π(7)), (π(3), π(8)), (π(5), π(8)), (π(6), π(7)), (π(6), π(8)), (π(7), π(8)). Jest ich 12, zatem π jest permutacją parzystą. Powyższe zgadza się z wnioskiem otrzymanym poprzez rozkład permutacji na transpozycje: (1 3) (3 8) (8 4) (6 7). 3 Literatura Powyższe przedstawienie zostało oparte na następujących pozycjach: W. J. Gilbert, W. K. Nicholson, Algebra współczesna z zastosowaniami, przełożył W. Bartol, WNT, Warszawa, 2008, str J. Klukowski, I. Nabiałek, Algebra dla studentów, wydanie czwarte uzupełnione, WNT, Warszawa, 2004, str
Ciała i wielomiany 1. przez 1, i nazywamy jedynką, zaś element odwrotny do a 0 względem działania oznaczamy przez a 1, i nazywamy odwrotnością a);
 Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
Ciała i wielomiany 1 Ciała i wielomiany 1 Definicja ciała Niech F będzie zbiorem, i niech + ( dodawanie ) oraz ( mnożenie ) będą działaniami na zbiorze F. Definicja. Zbiór F wraz z działaniami + i nazywamy
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów.
 5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
5. Algebra działania, grupy, grupy permutacji, pierścienie, ciała, pierścień wielomianów. Algebra jest jednym z najstarszych działów matematyki dotyczącym początkowo tworzenia metod rozwiązywania równań
Chcąc wyróżnić jedno z działań, piszemy np. (, ) i mówimy, że działanie wprowadza w STRUKTURĘ ALGEBRAICZNĄ lub, że (, ) jest SYSTEMEM ALGEBRAICZNYM.
 DEF. DZIAŁANIE DWUARGUMENTOWE Działaniem dwuargumentowym w niepsutym zbiorze nazywamy każde odwzorowanie iloczynu kartezjańskiego :. Inaczej mówiąc, w zbiorze jest określone działanie dwuargumentowe, jeśli:
DEF. DZIAŁANIE DWUARGUMENTOWE Działaniem dwuargumentowym w niepsutym zbiorze nazywamy każde odwzorowanie iloczynu kartezjańskiego :. Inaczej mówiąc, w zbiorze jest określone działanie dwuargumentowe, jeśli:
2. FUNKCJE. jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy FUNKCJĄ, lub
 WYKŁAD 2 1 2. FUNKCJE. 2.1.PODSTAWOWE DEFINICJE. Niech będą dane zbiory i. Jeżeli każdemu elementowi x ze zbioru,, przyporządkujemy jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy
WYKŁAD 2 1 2. FUNKCJE. 2.1.PODSTAWOWE DEFINICJE. Niech będą dane zbiory i. Jeżeli każdemu elementowi x ze zbioru,, przyporządkujemy jeden i tylko jeden element y ze zbioru, to takie przyporządkowanie nazwiemy
Podstawowe struktury algebraiczne
 Maciej Grzesiak Podstawowe struktury algebraiczne 1. Wprowadzenie Przedmiotem algebry było niegdyś przede wszystkim rozwiązywanie równań. Obecnie algebra staje się coraz bardziej nauką o systemach matematycznych.
Maciej Grzesiak Podstawowe struktury algebraiczne 1. Wprowadzenie Przedmiotem algebry było niegdyś przede wszystkim rozwiązywanie równań. Obecnie algebra staje się coraz bardziej nauką o systemach matematycznych.
Zestaw 2. Definicje i oznaczenia. inne grupy V 4 grupa czwórkowa Kleina D n grupa dihedralna S n grupa symetryczna A n grupa alternująca.
 Zestaw 2 Definicja grupy Definicje i oznaczenia grupa zbiór z działaniem łącznym, posiadającym element neutralny, w którym każdy element posiada element odwrotny grupa abelowa (przemienna) grupa, w której
Zestaw 2 Definicja grupy Definicje i oznaczenia grupa zbiór z działaniem łącznym, posiadającym element neutralny, w którym każdy element posiada element odwrotny grupa abelowa (przemienna) grupa, w której
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji
 Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Podstawowe struktury algebraiczne
 Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
Rozdział 1 Podstawowe struktury algebraiczne 1.1. Działania wewnętrzne Niech X będzie zbiorem niepustym. Dowolną funkcję h : X X X nazywamy działaniem wewnętrznym w zbiorze X. Działanie wewnętrzne, jak
1. R jest grupą abelową względem działania + (tzn. działanie jest łączne, przemienne, istnieje element neutralny oraz element odwrotny)
 Rozdział 1 Pierścienie i ideały Definicja 1.1 Pierścieniem nazywamy trójkę (R, +, ), w której R jest zbiorem niepustym, działania + : R R R i : R R R są dwuargumentowe i spełniają następujące warunki dla
Rozdział 1 Pierścienie i ideały Definicja 1.1 Pierścieniem nazywamy trójkę (R, +, ), w której R jest zbiorem niepustym, działania + : R R R i : R R R są dwuargumentowe i spełniają następujące warunki dla
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Macierz o wymiarach m n. a 21. a 22. A =
 Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
Działania Definicja: Działaniem wewnętrznym w niepustym zbiorze G nazywamy funkcję działającą ze zbioru GxG w zbiór G.
 Działania Definicja: Działaniem wewnętrznym w niepustym zbiorze G nazywamy funkcję działającą ze zbioru GxG w zbiór G. Przykłady działań wewnętrznych 1. Dodawanie i mnożenie są działaniami wewnętrznymi
Działania Definicja: Działaniem wewnętrznym w niepustym zbiorze G nazywamy funkcję działającą ze zbioru GxG w zbiór G. Przykłady działań wewnętrznych 1. Dodawanie i mnożenie są działaniami wewnętrznymi
Wykład 4. Określimy teraz pewną ważną klasę pierścieni.
 Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Wykład 4 Określimy teraz pewną ważną klasę pierścieni. Twierdzenie 1 Niech m, n Z. Jeśli n > 0 to istnieje dokładnie jedna para licz q, r, że: m = qn + r, 0 r < n. Liczbę r nazywamy resztą z dzielenia
Algebra. Jakub Maksymiuk. lato 2018/19
 Algebra Jakub Maksymiuk lato 2018/19 Algebra W1/0 Zbiory z działaniami Podstawowe własności Potęgi Tabelka działania Przykłady Grupa symetryczna Algebra W1/1 Podstawowe własności Definicja: Działaniem
Algebra Jakub Maksymiuk lato 2018/19 Algebra W1/0 Zbiory z działaniami Podstawowe własności Potęgi Tabelka działania Przykłady Grupa symetryczna Algebra W1/1 Podstawowe własności Definicja: Działaniem
1 Działania na zbiorach
 M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
M. Beśka, Wstęp do teorii miary, rozdz. 1 1 1 Działania na zbiorach W rozdziale tym przypomnimy podstawowe działania na zbiorach koncentrując się na własnościach tych działań, które będą przydatne w dalszej
Teoria ciała stałego Cz. I
 Teoria ciała stałego Cz. I 1. Elementy teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3
Teoria ciała stałego Cz. I 1. Elementy teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3
FUNKCJE. (odwzorowania) Funkcje 1
 FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
FUNKCJE (odwzorowania) Funkcje 1 W matematyce funkcja ze zbioru X w zbiór Y nazywa się odwzorowanie (przyporządkowanie), które każdemu elementowi zbioru X przypisuje jeden, i tylko jeden element zbioru
Zadania z algebry liniowej - sem. I Struktury algebraiczne
 Zadania z algebry liniowej - sem. I Struktury algebraiczne Definicja 1. Działaniem dwuargumentowym w niepustym zbiorze A nazywamy każdą funkcję : A A A, tzn. taką funkcję, że zachodzi a,b A (a, b) ((a,
Zadania z algebry liniowej - sem. I Struktury algebraiczne Definicja 1. Działaniem dwuargumentowym w niepustym zbiorze A nazywamy każdą funkcję : A A A, tzn. taką funkcję, że zachodzi a,b A (a, b) ((a,
Algebra abstrakcyjna
 Algebra abstrakcyjna Przykłady 1. Sama liczba 0 tworzy grupę (rzędu 1) ze względu na zwykłe dodawanie, również liczba 1 tworzy grupę (rzędu 1) ze względu na zwykłe mnożenie.. Liczby 1 i 1 stanowią grupą
Algebra abstrakcyjna Przykłady 1. Sama liczba 0 tworzy grupę (rzędu 1) ze względu na zwykłe dodawanie, również liczba 1 tworzy grupę (rzędu 1) ze względu na zwykłe mnożenie.. Liczby 1 i 1 stanowią grupą
Liczby zespolone. x + 2 = 0.
 Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Liczby zespolone 1 Wiadomości wstępne Rozważmy równanie wielomianowe postaci x + 2 = 0. Współczynniki wielomianu stojącego po lewej stronie są liczbami całkowitymi i jedyny pierwiastek x = 2 jest liczbą
Przykładowe zadania z teorii liczb
 Przykładowe zadania z teorii liczb I. Podzielność liczb całkowitych. Liczba a = 346 przy dzieleniu przez pewną liczbę dodatnią całkowitą b daje iloraz k = 85 i resztę r. Znaleźć dzielnik b oraz resztę
Przykładowe zadania z teorii liczb I. Podzielność liczb całkowitych. Liczba a = 346 przy dzieleniu przez pewną liczbę dodatnią całkowitą b daje iloraz k = 85 i resztę r. Znaleźć dzielnik b oraz resztę
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 12B/14 Permutacje bez punktów stałych Nieporządek na zbiorze X to permutacja taka, że dla dowolnego, czyli permutacja "bez punktów
1. Elementy (abstrakcyjnej) teorii grup
 1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
1 Określenie pierścienia
 1 Określenie pierścienia Definicja 1. Niech P będzie zbiorem, w którym określone są działania +, (dodawanie i mnożenie). Mówimy, że struktura (P, +, ) jest pierścieniem, jeżeli spełnione są następujące
1 Określenie pierścienia Definicja 1. Niech P będzie zbiorem, w którym określone są działania +, (dodawanie i mnożenie). Mówimy, że struktura (P, +, ) jest pierścieniem, jeżeli spełnione są następujące
DB Algebra liniowa semestr zimowy 2018
 DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
Matematyka dyskretna. Andrzej Łachwa, UJ, /10
 Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
Matematyka dyskretna Andrzej Łachwa, UJ, 2018 andrzej.lachwa@uj.edu.pl 10/10 Podziały i liczby Stirlinga Liczba Stirlinga dla cykli (często nazywana liczbą Stirlinga pierwszego rodzaju) to liczba permutacji
1. Liczby zespolone. Jacek Jędrzejewski 2011/2012
 1. Liczby zespolone Jacek Jędrzejewski 2011/2012 Spis treści 1 Liczby zespolone 2 1.1 Definicja liczby zespolonej.................... 2 1.2 Postać kanoniczna liczby zespolonej............... 1. Postać
1. Liczby zespolone Jacek Jędrzejewski 2011/2012 Spis treści 1 Liczby zespolone 2 1.1 Definicja liczby zespolonej.................... 2 1.2 Postać kanoniczna liczby zespolonej............... 1. Postać
Przestrzenie liniowe
 Rozdział 4 Przestrzenie liniowe 4.1. Działania zewnętrzne Niech X oraz F będą dwoma zbiorami niepustymi. Dowolną funkcję D : F X X nazywamy działaniem zewnętrznym w zbiorze X nad zbiorem F. Przykład 4.1.
Rozdział 4 Przestrzenie liniowe 4.1. Działania zewnętrzne Niech X oraz F będą dwoma zbiorami niepustymi. Dowolną funkcję D : F X X nazywamy działaniem zewnętrznym w zbiorze X nad zbiorem F. Przykład 4.1.
Matematyka dyskretna. Andrzej Łachwa, UJ, A/15
 Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2015 andrzej.lachwa@uj.edu.pl 10A/15 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Algebra liniowa. 1. Macierze.
 Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
1 Równania różniczkowe zwyczajne liniowe pierwszego rzędu
 Równania różniczkowe zwyczajne liniowe I-go rzędu 1 1 1 Równania różniczkowe zwyczajne liniowe pierwszego rzędu Równaniem różniczkowym zwyczajnym liniowym pierwszego rzędu nazywamy równanie postaci (RL1)
Równania różniczkowe zwyczajne liniowe I-go rzędu 1 1 1 Równania różniczkowe zwyczajne liniowe pierwszego rzędu Równaniem różniczkowym zwyczajnym liniowym pierwszego rzędu nazywamy równanie postaci (RL1)
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
0 + 0 = 0, = 1, = 1, = 0.
 5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
5 Kody liniowe Jak już wiemy, w celu przesłania zakodowanego tekstu dzielimy go na bloki i do każdego z bloków dodajemy tak zwane bity sprawdzające. Bity te są w ścisłej zależności z bitami informacyjnymi,
15. Macierze. Definicja Macierzy. Definicja Delty Kroneckera. Definicja Macierzy Kwadratowej. Definicja Macierzy Jednostkowej
 15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy
 Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Grupy, pierścienie i ciała
 Grupy, pierścienie i ciała Definicja: Niech A będzie niepustym zbiorem. Działaniem wewnętrznym (lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym zbiorem.
Grupy, pierścienie i ciała Definicja: Niech A będzie niepustym zbiorem. Działaniem wewnętrznym (lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym zbiorem.
Matematyka dyskretna. 1. Relacje
 Matematyka dyskretna 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produktu kartezjańskiego X Y, którego elementami są pary uporządkowane (x, y), takie, że x X i y Y. Uwaga 1.1 Jeśli
Matematyka dyskretna 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produktu kartezjańskiego X Y, którego elementami są pary uporządkowane (x, y), takie, że x X i y Y. Uwaga 1.1 Jeśli
2 Kongruencje 5. 4 Grupy 9. 5 Grupy permutacji Homomorfizmy grup Pierścienie 16
 DB Algebra dla informatyków 1 semestr letni 2018 1 Spis treści 1 Podzielność w Z, algorytm Euklidesa 2 2 Kongruencje 5 3 Twierdzenia: Fermata, Eulera i Wilsona 7 4 Grupy 9 5 Grupy permutacji 12 6 Homomorfizmy
DB Algebra dla informatyków 1 semestr letni 2018 1 Spis treści 1 Podzielność w Z, algorytm Euklidesa 2 2 Kongruencje 5 3 Twierdzenia: Fermata, Eulera i Wilsona 7 4 Grupy 9 5 Grupy permutacji 12 6 Homomorfizmy
1.1 Definicja. 1.2 Przykład. 1.3 Definicja. Niech G oznacza dowolny, niepusty zbiór.
 20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
20. Definicje i przykłady podstawowych struktur algebraicznych (grupy, pierścienie, ciała, przestrzenie liniowe). Pojęcia dotyczące przestrzeni liniowych (liniowa zależność i niezależność układu wektorów,
Relacje binarne. Def. Relację ϱ w zbiorze X nazywamy. antysymetryczną, gdy x, y X (xϱy yϱx x = y) spójną, gdy x, y X (xϱy yϱx x = y)
 Relacje binarne Niech X będzie niepustym zbiorem. Jeśli ϱ X X to mówimy, że ϱ jest relacją w zbiorze X. Zamiast pisać (x, y) ϱ będziemy stosować zapis xϱy. Def. Relację ϱ w zbiorze X nazywamy zwrotną,
Relacje binarne Niech X będzie niepustym zbiorem. Jeśli ϱ X X to mówimy, że ϱ jest relacją w zbiorze X. Zamiast pisać (x, y) ϱ będziemy stosować zapis xϱy. Def. Relację ϱ w zbiorze X nazywamy zwrotną,
1 Macierze i wyznaczniki
 1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
Przestrzenie wektorowe
 Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
1 Grupy. 1.1 Grupy. 1.2 Podgrupy. 1.3 Dzielniki normalne. 1.4 Homomorfizmy
 1 Grupy 1.1 Grupy 1.1.1. Niech G będzie taką grupa, że (ab) 2 = a 2 b 2 dla dowolnych a, b G. Udowodnić, że grupa G jest abelowa. 1.1.2. Niech G będzie taką grupa, że (ab) 1 = a 1 b 1 dla dowolnych a,
1 Grupy 1.1 Grupy 1.1.1. Niech G będzie taką grupa, że (ab) 2 = a 2 b 2 dla dowolnych a, b G. Udowodnić, że grupa G jest abelowa. 1.1.2. Niech G będzie taką grupa, że (ab) 1 = a 1 b 1 dla dowolnych a,
2 Rachunek macierzowy, metoda eliminacji Gaussa-Jordana Wprowadzenie teoretyczne Zadania... 9
 Spis treści 1 Podstawowe struktury algebraiczne 2 11 Grupa, pierścień, ciało 2 12 Grupy permutacji 4 13 Pierścień wielomianów, algorytm Euklidesa, największy wspólny dzielnik 6 14 Zadania 7 2 Rachunek
Spis treści 1 Podstawowe struktury algebraiczne 2 11 Grupa, pierścień, ciało 2 12 Grupy permutacji 4 13 Pierścień wielomianów, algorytm Euklidesa, największy wspólny dzielnik 6 14 Zadania 7 2 Rachunek
1 Zbiory i działania na zbiorach.
 Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Wyznaczniki. Algebra. Aleksander Denisiuk
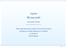 Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Zbiory, relacje i funkcje
 Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Zbiory, relacje i funkcje Zbiory będziemy zazwyczaj oznaczać dużymi literami A, B, C, X, Y, Z, natomiast elementy zbiorów zazwyczaj małymi. Podstawą zależność między elementem zbioru a zbiorem, czyli relację
Definicja odwzorowania ciągłego i niektóre przykłady
 Odwzorowania Pojęcie odwzorowania pomiędzy dwoma zbiorami było już definiowane, ale dawno, więc nie od rzeczy będzie przypomnieć, że odwzorowaniem nazywamy sposób przyporządkowania (niekoniecznie każdemu)
Odwzorowania Pojęcie odwzorowania pomiędzy dwoma zbiorami było już definiowane, ale dawno, więc nie od rzeczy będzie przypomnieć, że odwzorowaniem nazywamy sposób przyporządkowania (niekoniecznie każdemu)
1 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych
 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
φ(x 1,..., x n ) = a i x 2 i +
 Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
Teoria na egzamin z algebry liniowej Wszystkie podane pojęcia należy umieć określić i podać pprzykłady, ewentualnie kontrprzykłady. Ponadto należy znać dowody tam gdzie to jest zaznaczone. Liczby zespolone.
III. Funkcje rzeczywiste
 . Pojęcia podstawowe Załóżmy, że dane są dwa niepuste zbiory X i Y. Definicja. Jeżeli każdemu elementowi x X przyporządkujemy dokładnie jeden element y Y, to mówimy, że na zbiorze X została określona funkcja
. Pojęcia podstawowe Załóżmy, że dane są dwa niepuste zbiory X i Y. Definicja. Jeżeli każdemu elementowi x X przyporządkujemy dokładnie jeden element y Y, to mówimy, że na zbiorze X została określona funkcja
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Uwaga 1.2. Niech (G, ) będzie grupą, H 1, H 2 < G. Następujące warunki są równoważne:
 1. Wykład 1: Produkty grup. Produkty i koprodukty grup abelowych. Przypomnijmy konstrukcje słabych iloczynów (sum) prostych i iloczynów (sum) prostych grup znane z kursowego wykładu algebry. Ze względu
1. Wykład 1: Produkty grup. Produkty i koprodukty grup abelowych. Przypomnijmy konstrukcje słabych iloczynów (sum) prostych i iloczynów (sum) prostych grup znane z kursowego wykładu algebry. Ze względu
Algebra liniowa. Macierze i układy równań liniowych
 Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Algebra liniowa Macierze i układy równań liniowych Własności wyznaczników det I = 1, det(ab) = det A det B, det(a T ) = det A. Macierz nieosobliwa Niech A będzie macierzą kwadratową wymiaru n n. Mówimy,
Matematyka dyskretna. Andrzej Łachwa, UJ, A/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna Andrzej Łachwa, UJ, 2016 andrzej.lachwa@uj.edu.pl 9A/14 Permutacje Permutacja zbioru skończonego X to bijekcja z X w X. Zbiór permutacji zbioru oznaczamy przez, a permutacje małymi
Matematyka dyskretna. Andrzej Łachwa, UJ, /14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 11/14 Współczynniki multimianowe (wielomianowe) Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu. Odpowiadały one
Matematyka dyskretna Andrzej Łachwa, UJ, 2012 andrzej.lachwa@uj.edu.pl 11/14 Współczynniki multimianowe (wielomianowe) Współczynniki dwumianowe pojawiały się przy rozwinięciu dwumianu. Odpowiadały one
Zbiory, funkcje i ich własności. XX LO (wrzesień 2016) Matematyka elementarna Temat #1 1 / 16
 Zbiory, funkcje i ich własności XX LO (wrzesień 2016) Matematyka elementarna Temat #1 1 / 16 Zbiory Zbiory ograniczone, kresy Zbiory ograniczone, min, max, sup, inf Zbiory ograniczone 1 Zbiór X R jest
Zbiory, funkcje i ich własności XX LO (wrzesień 2016) Matematyka elementarna Temat #1 1 / 16 Zbiory Zbiory ograniczone, kresy Zbiory ograniczone, min, max, sup, inf Zbiory ograniczone 1 Zbiór X R jest
5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych.
 5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych. Przeprowadzimy obecnie skróconą klasyfikację skończonych grup prostych. 5.1.
5. Wykład 5: Grupy proste. Definicja 5.1. Grupę (G, ) nazywamy grupą prostą, gdy G nie zawiera właściwych podgrup normalnych. Przeprowadzimy obecnie skróconą klasyfikację skończonych grup prostych. 5.1.
Funkcja jest różnowartościowa w zbiorze A wtedy i tylko wtedy, gdy różnym argumentom funkcja ta przyporządkowuje różne wartości.
 Gdy mamy daną funkcję, poza określeniem jej dziedziny i miejsca zerowego możemy badad szczególne własności, takie jak: monotonicznośd, różnowartościowośd, parzystośd, nieparzystośd. Na temat monotoniczności
Gdy mamy daną funkcję, poza określeniem jej dziedziny i miejsca zerowego możemy badad szczególne własności, takie jak: monotonicznośd, różnowartościowośd, parzystośd, nieparzystośd. Na temat monotoniczności
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1
 W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Relacje. opracował Maciej Grzesiak. 17 października 2011
 Relacje opracował Maciej Grzesiak 17 października 2011 1 Podstawowe definicje Niech dany będzie zbiór X. X n oznacza n-tą potęgę kartezjańską zbioru X, tzn zbiór X X X = {(x 1, x 2,..., x n ) : x k X dla
Relacje opracował Maciej Grzesiak 17 października 2011 1 Podstawowe definicje Niech dany będzie zbiór X. X n oznacza n-tą potęgę kartezjańską zbioru X, tzn zbiór X X X = {(x 1, x 2,..., x n ) : x k X dla
Przestrzeń unitarna. Jacek Kłopotowski. 23 października Katedra Matematyki i Ekonomii Matematycznej SGH
 Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
Katedra Matematyki i Ekonomii Matematycznej SGH 23 października 2018 Definicja iloczynu skalarnego Definicja Iloczynem skalarnym w przestrzeni liniowej R n nazywamy odwzorowanie ( ) : R n R n R spełniające
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn a 1j a 2j R i = , C j =
 11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
Indukcja matematyczna. Zasada minimum. Zastosowania.
 Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
Indukcja matematyczna. Zasada minimum. Zastosowania. Arkadiusz Męcel Uwagi początkowe W trakcie zajęć przyjęte zostaną następujące oznaczenia: 1. Zbiory liczb: R - zbiór liczb rzeczywistych; Q - zbiór
 http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
Zasada indukcji matematycznej
 Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
Ćwiczenia 1 - Pojęcie grupy i rzędu elementu
 Algebra 1 Ćwiczenia 1 - Pojęcie grupy i rzędu elementu Definicje i podstawowe własności Definicja 1. Niech X będzie niepustym zbiorem. Działaniem w zbiorze X nazywamy dowolne odwzorowanie (funkcję) działające
Algebra 1 Ćwiczenia 1 - Pojęcie grupy i rzędu elementu Definicje i podstawowe własności Definicja 1. Niech X będzie niepustym zbiorem. Działaniem w zbiorze X nazywamy dowolne odwzorowanie (funkcję) działające
; B = Wykonaj poniższe obliczenia: Mnożenia, transpozycje etc wykonuję programem i przepisuję wyniki. Mam nadzieję, że umiesz mnożyć macierze...
 Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Tekst na niebiesko jest komentarzem lub treścią zadania. Zadanie. Dane są macierze: A D 0 ; E 0 0 0 ; B 0 5 ; C Wykonaj poniższe obliczenia: 0 4 5 Mnożenia, transpozycje etc wykonuję programem i przepisuję
Dystrybucje. Marcin Orchel. 1 Wstęp Dystrybucje Pochodna dystrybucyjna Przestrzenie... 5
 Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Dystrybucje Marcin Orchel Spis treści 1 Wstęp 1 1.1 Dystrybucje................................... 1 1.2 Pochodna dystrybucyjna............................ 3 1.3 Przestrzenie...................................
Dlaczego nie wystarczają liczby wymierne
 Dlaczego nie wystarczają liczby wymierne Analiza zajmuje się problemami, w których pojawia się przejście graniczne. Przykładami takich problemów w matematyce bądź fizyce mogą być: 1. Pojęcie prędkości
Dlaczego nie wystarczają liczby wymierne Analiza zajmuje się problemami, w których pojawia się przejście graniczne. Przykładami takich problemów w matematyce bądź fizyce mogą być: 1. Pojęcie prędkości
Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi.
 Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Logika Jest to zasadniczo powtórka ze szkoły średniej, być może z niektórymi rzeczami nowymi. Często słowu "logika" nadaje się szersze znaczenie niż temu o czym będzie poniżej: np. mówi się "logiczne myślenie"
Funkcja kwadratowa. f(x) = ax 2 + bx + c = a
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax, a R \ {0}.
Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze
 Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze Polsko-Japońska Wyższa Szkoła Technik Komputerowych Katedra Informatyki Stosowanej Spis treści Spis treści 1 Wektory
Wprowadzenie do metod numerycznych Wykład 3 Metody algebry liniowej I Wektory i macierze Polsko-Japońska Wyższa Szkoła Technik Komputerowych Katedra Informatyki Stosowanej Spis treści Spis treści 1 Wektory
Rodzinę spełniającą trzeci warunek tylko dla sumy skończonej nazywamy ciałem (algebrą) w zbiorze X.
 1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
1 σ-ciała Definicja 1.1 (σ - ciało) σ - ciałem (σ - algebrą) w danym zbiorze X (zwanym przestrzenią) nazywamy rodzinę M pewnych podzbiorów zbioru X, spełniającą trzy warunki: 1 o M; 2 o jeśli A M, to X
Zapisujemy:. Dla jednoczesnego podania funkcji (sposobu przyporządkowania) oraz zbiorów i piszemy:.
 Funkcja Funkcją (stosuje się też nazwę odwzorowanie) określoną na zbiorze o wartościach w zbiorze nazywamy przyporządkowanie każdemu elementowi dokładnie jednego elementu. nazywamy argumentem, zaś wartością
Funkcja Funkcją (stosuje się też nazwę odwzorowanie) określoną na zbiorze o wartościach w zbiorze nazywamy przyporządkowanie każdemu elementowi dokładnie jednego elementu. nazywamy argumentem, zaś wartością
Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań
 Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań Przekształcenia liniowe, diagonalizacja macierzy 1. Podano współrzędne wektora v w bazie B. Znaleźć współrzędne tego wektora w bazie B, gdy: a) v = (1,
Algebra Liniowa 2 (INF, TIN), MAP1152 Lista zadań Przekształcenia liniowe, diagonalizacja macierzy 1. Podano współrzędne wektora v w bazie B. Znaleźć współrzędne tego wektora w bazie B, gdy: a) v = (1,
1 Elementy logiki i teorii mnogości
 1 Elementy logiki i teorii mnogości 11 Elementy logiki Notatki do wykładu Definicja Zdaniem logicznym nazywamy zdanie oznajmujące, któremu przysługuje jedna z dwu logicznych ocen prawda (1) albo fałsz
1 Elementy logiki i teorii mnogości 11 Elementy logiki Notatki do wykładu Definicja Zdaniem logicznym nazywamy zdanie oznajmujące, któremu przysługuje jedna z dwu logicznych ocen prawda (1) albo fałsz
Funkcja kwadratowa. f(x) = ax 2 + bx + c,
 Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Funkcja kwadratowa. Funkcją kwadratową nazywamy funkcję f : R R określoną wzorem gdzie a, b, c R, a 0. f(x) = ax 2 + bx + c, Szczególnym przypadkiem funkcji kwadratowej jest funkcja f(x) = ax 2, a R \
Zadania z algebry liniowej - sem. I Przestrzenie liniowe, bazy, rząd macierzy
 Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
Zajęcia nr. 3 notatki
 Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Zajęcia nr. 3 notatki 22 kwietnia 2005 1 Funkcje liczbowe wprowadzenie Istnieje nieskończenie wiele funkcji w matematyce. W dodaktu nie wszystkie są liczbowe. Rozpatruje się funkcje które pobierają argumenty
Funkcje elementarne. Matematyka 1
 Funkcje elementarne Matematyka 1 Katarzyna Trąbka-Więcław Funkcjami elementarnymi nazywamy: funkcje wymierne (w tym: wielomiany), wykładnicze, trygonometryczne, odwrotne do wymienionych (w tym: funkcje
Funkcje elementarne Matematyka 1 Katarzyna Trąbka-Więcław Funkcjami elementarnymi nazywamy: funkcje wymierne (w tym: wielomiany), wykładnicze, trygonometryczne, odwrotne do wymienionych (w tym: funkcje
LOGIKA I TEORIA ZBIORÓW
 LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
LOGIKA I TEORIA ZBIORÓW Logika Logika jest nauką zajmującą się zdaniami Z punktu widzenia logiki istotne jest, czy dane zdanie jest prawdziwe, czy nie Nie jest natomiast istotne o czym to zdanie mówi Definicja
Notatki do wykładu Geometria Różniczkowa I
 Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 1 listopada 013 1 Odwzorowanie styczne i cofnięcie formy cd: 1.1 Transport pola wektorowego i cofnięcie formy W poprzednim paragrafie
Notatki do wykładu Geometria Różniczkowa I Katarzyna Grabowska, KMMF 1 listopada 013 1 Odwzorowanie styczne i cofnięcie formy cd: 1.1 Transport pola wektorowego i cofnięcie formy W poprzednim paragrafie
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z].
![Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z]. Definicja1.2.Niech Abędzieniepustymzbiorem,a i działaniamiwa. (1)Mówimy,że jestłączne,jeżeli. x,y,z A[x (y z) = (x y) z].](/thumbs/66/54501363.jpg) 1. Wykład 1: Grupy i izomorfizmy grup. Definicja 1.1. Niech A będzie niepustym zbiorem. Działaniem wewnętrznym(lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym
1. Wykład 1: Grupy i izomorfizmy grup. Definicja 1.1. Niech A będzie niepustym zbiorem. Działaniem wewnętrznym(lub, krótko, działaniem) w zbiorze A nazywamy funkcję : A A A. Niech ponadto B będzie niepustym
Treści programowe. Matematyka. Efekty kształcenia. Literatura. Terminy wykładów i ćwiczeń. Warunki zaliczenia. tnij.org/ktrabka
 Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
5 Wyznaczniki. 5.1 Definicja i podstawowe własności. MIMUW 5. Wyznaczniki 25
 MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
Rachunek prawdopodobieństwa
 Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rachunek prawdopodobieństwa Sebastian Rymarczyk srymarczyk@afm.edu.pl Tematyka zajęć 1. Elementy kombinatoryki. 2. Definicje prawdopodobieństwa. 3. Własności prawdopodobieństwa. 4. Zmienne losowe, parametry
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria Środowiska w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Inżynieria Środowiska w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era
O funkcjach : mówimy również, że są określone na zbiorze o wartościach w zbiorze.
 1. Definicja funkcji f:x->y. Definicja dziedziny, przeciwdziedziny, zbioru wartości. Przykłady. I definicja: Funkcją nazywamy relację, jeśli spełnia następujące warunki: 1) 2) 1,2 [(1 2)=> 1=2] Inaczej
1. Definicja funkcji f:x->y. Definicja dziedziny, przeciwdziedziny, zbioru wartości. Przykłady. I definicja: Funkcją nazywamy relację, jeśli spełnia następujące warunki: 1) 2) 1,2 [(1 2)=> 1=2] Inaczej
MACIERZE I WYZNACZNIKI
 Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Wyk lad 2 Podgrupa grupy
 Wyk lad 2 Podgrupa grupy Definicja 2.1. Pod grupy (G,, e) nazywamy taki podzbiór H G, że e H, h 1 H dla każdego h H oraz h 1 h 2 H dla dowolnych h 1, h 2 H. Jeśli H jest grupy G, to bedziemy pisali H G.
Wyk lad 2 Podgrupa grupy Definicja 2.1. Pod grupy (G,, e) nazywamy taki podzbiór H G, że e H, h 1 H dla każdego h H oraz h 1 h 2 H dla dowolnych h 1, h 2 H. Jeśli H jest grupy G, to bedziemy pisali H G.
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne.
 Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
Logarytmy. Funkcje logarytmiczna i wykładnicza. Równania i nierówności wykładnicze i logarytmiczne. Definicja. Niech a i b będą dodatnimi liczbami rzeczywistymi i niech a. Logarytmem liczby b przy podstawie
1 Podstawowe oznaczenia
 Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Poniżej mogą Państwo znaleźć skondensowane wiadomości z wykładu. Należy je traktować jako przegląd pojęć, które pojawiły się na wykładzie. Materiały te nie są w pełni tożsame z tym co pojawia się na wykładzie.
Przykład 1 W przypadku jednokrotnego rzutu kostką przestrzeń zdarzeń elementarnych
 Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
Rozdział 1 Zmienne losowe, ich rozkłady i charakterystyki 1.1 Definicja zmiennej losowej Niech Ω będzie przestrzenią zdarzeń elementarnych. Definicja 1 Rodzinę S zdarzeń losowych (zbiór S podzbiorów zbioru
