Macierze Lekcja I: Wprowadzenie
|
|
|
- Dorota Kwiecień
- 7 lat temu
- Przeglądów:
Transkrypt
1 Macierze Lekcja I: Wprowadzenie Wydział Matematyki Politechniki Wrocławskiej
2 Definicja Niech dane będą dwie liczby naturalne dodatnie m i n. Układ m n liczb ułożonych w prostokątną tablicę złożoną z m wierszy i n kolumn nazywamy macierzą. a 1,1 a 1,2... a 1,n a 2,1 a 2,2... a 2,n A = a m,1 a m,2... a m,n Zbiór macierzy mxn oznaczamy symbolem M m,n. Jeśli chcemy napiać, że macierz A ma m wierszy i n kolumn to piszemy A M m,n
3 Definicja Podczas tych zajęć będziemy czasem posługiwali się angielskimi odpowiednikami nazw poszczególnych pojęć. Dlaczego?
4 Definicja Podczas tych zajęć będziemy czasem posługiwali się angielskimi odpowiednikami nazw poszczególnych pojęć. Dlaczego? Angielskie nazwy występują w technice i oprogramowaniu komputerowym. Część funkcji programów bierze swoje nazwy z j. angielskiego.
5 Definicja Podczas tych zajęć będziemy czasem posługiwali się angielskimi odpowiednikami nazw poszczególnych pojęć. Dlaczego? Angielskie nazwy występują w technice i oprogramowaniu komputerowym. Część funkcji programów bierze swoje nazwy z j. angielskiego. I tak angielska nazwa dla macierzy to:
6 Zastosowanie macierzy Współcześnie dostępnych jest wiele programów komputerowych, których zasada działania opiera się na zasadach obliczeniowych macierzy (czyli na tych, które poznamy.
7 Zastosowanie macierzy Współcześnie dostępnych jest wiele programów komputerowych, których zasada działania opiera się na zasadach obliczeniowych macierzy (czyli na tych, które poznamy. Jednym z takich programów jest Matlab. Niestety jest to program komercyjny i potrzeba na niego zakupić licencję :(
8 Zastosowanie macierzy Współcześnie dostępnych jest wiele programów komputerowych, których zasada działania opiera się na zasadach obliczeniowych macierzy (czyli na tych, które poznamy. Jednym z takich programów jest Matlab. Niestety jest to program komercyjny i potrzeba na niego zakupić licencję :( Są jednak inne darmowe programy oparte na licencji GNU GPL. Przykładami są GNU Octave oraz Scilab.
9 Scilab Część przykładów będzie pokazywana w programie Scilab. Jest to oprogramowanie darmowe i można je pobrać ze strony producenta ( Obecnie najnowszą wersją jest Scilab i jest ona dostępna na różne systemy operacyjne.
10 Scilab Część przykładów będzie pokazywana w programie Scilab. Jest to oprogramowanie darmowe i można je pobrać ze strony producenta ( Obecnie najnowszą wersją jest Scilab i jest ona dostępna na różne systemy operacyjne. Do programu można dodatkowo pobrać moduł Xcos, który służy do przeprowadzania różnego rodzaju symulacji. I tak na przykład można wykonać symulację obwodów elektrycznych i sprawdzić jak zmienia się napięcie w obwodzie RLC w różnych warunkach. Zatem warto zapoznać się z tym programem!
11 Scilab
12 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0.
13 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0. Macierz kwadratowa (square matrix) to macierz, w której m = n
14 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0. Macierz kwadratowa (square matrix) to macierz, w której m = n Główna przekątna (main diagonal) to elementy a i,i, i = 1,..., n. Występuje w macierzach kwadratowych!
15 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0. Macierz kwadratowa (square matrix) to macierz, w której m = n Główna przekątna (main diagonal) to elementy a i,i, i = 1,..., n. Występuje w macierzach kwadratowych! Macierz trójkątna (triangular matrix) charakteryzuje się tym, że elementy powyżej lub poniżej głównej przekątnej są równe 0. Jeśli są to elementy powyżej to mówimy o macierzy trójkątnej dolnej (lower triangular matrix). W przeciwnym wypadku jest to macierz trójkątna górna (upper triangular matrix).
16 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0. Macierz kwadratowa (square matrix) to macierz, w której m = n Główna przekątna (main diagonal) to elementy a i,i, i = 1,..., n. Występuje w macierzach kwadratowych! Macierz trójkątna (triangular matrix) charakteryzuje się tym, że elementy powyżej lub poniżej głównej przekątnej są równe 0. Jeśli są to elementy powyżej to mówimy o macierzy trójkątnej dolnej (lower triangular matrix). W przeciwnym wypadku jest to macierz trójkątna górna (upper triangular matrix). Macierz diagonalna (diagonal matrix) posiada tylko niezerową główną przekątną. Jest szczególnie ważna przy potęgowaniu macierzy. Niestety to działanie wykracza poza ramy tego kursu :(
17 Podstawowe definicje Macierzą zerową nazywamy macierz, w której każdy element jest równy 0. Macierz kwadratowa (square matrix) to macierz, w której m = n Główna przekątna (main diagonal) to elementy a i,i, i = 1,..., n. Występuje w macierzach kwadratowych! Macierz trójkątna (triangular matrix) charakteryzuje się tym, że elementy powyżej lub poniżej głównej przekątnej są równe 0. Jeśli są to elementy powyżej to mówimy o macierzy trójkątnej dolnej (lower triangular matrix). W przeciwnym wypadku jest to macierz trójkątna górna (upper triangular matrix). Macierz diagonalna (diagonal matrix) posiada tylko niezerową główną przekątną. Jest szczególnie ważna przy potęgowaniu macierzy. Niestety to działanie wykracza poza ramy tego kursu :( Szczególną macierzą diagonalną jest macierz jednostkowa (identity matrix). Oznaczana przez literę I. Wtedy a i,i = 1, i = 1,..., n.
18 Macierz a wektor Często stosowanym pojęciem jest wektor. Można go traktować jako macierz, w której jeden z wymiarów jest równy 1.
19 Macierz a wektor Często stosowanym pojęciem jest wektor. Można go traktować jako macierz, w której jeden z wymiarów jest równy 1. W algebrze macierze wykorzystywane są przy rozwiązywaniu układów równań liniowych. W zaawansowanej matematyce występują o wiele częściej. A czy w życiu codziennym?
20 Działania na macierzach: dodawanie Pierwszym działaniem, które poznamy jest dodawanie macierzy.
21 Działania na macierzach: dodawanie Pierwszym działaniem, które poznamy jest dodawanie macierzy. Przypuśćmy, że dane mamy dwie macierze A = [a i,j ] oraz B = [b i,j ]. Co istotne: A, B M m,n!
22 Działania na macierzach: dodawanie Pierwszym działaniem, które poznamy jest dodawanie macierzy. Przypuśćmy, że dane mamy dwie macierze A = [a i,j ] oraz B = [b i,j ]. Co istotne: A, B M m,n! W wyniku dodawania macierzy dostajemy nową macierz C M m,n : C = A + B c i,j = a i,j + b i,j, gdzie c i,j są elementami nowej macierzy C.
23 Działania na macierzach: dodawanie Pierwszym działaniem, które poznamy jest dodawanie macierzy. Przypuśćmy, że dane mamy dwie macierze A = [a i,j ] oraz B = [b i,j ]. Co istotne: A, B M m,n! W wyniku dodawania macierzy dostajemy nową macierz C M m,n : C = A + B c i,j = a i,j + b i,j, gdzie c i,j są elementami nowej macierzy C.Mówiąc najprościej: dodajemy do siebie elementy na tych samych pozycjach w każdej z macierzy. Co istotne: jest to działanie przemienne: A + B = B + A.
24 Działania na macierzach: mnożenie przez liczbę (skalar) Dana niech będzie macierz A = [a i,j ], A M m,n oraz liczba α R.
25 Działania na macierzach: mnożenie przez liczbę (skalar) Dana niech będzie macierz A = [a i,j ], A M m,n oraz liczba α R. Wtedy: B = α A b i,j = α a i,j, gdzie b i,j są elementami nowej macierzy B.
26 Działania na macierzach: mnożenie przez liczbę (skalar) Dana niech będzie macierz A = [a i,j ], A M m,n oraz liczba α R. Wtedy: B = α A b i,j = α a i,j, gdzie b i,j są elementami nowej macierzy B.Mówiąc najprościej: mnożymy przez liczbę α każdy wyraz macierzy A. Co istotne: jest to działanie przemienne: α A = A α.
27 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność)
28 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność)
29 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność) 3 A + 0 = A
30 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność) 3 A + 0 = A 4 A + ( A) = A + A = 0
31 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność) 3 A + 0 = A 4 A + ( A) = A + A = 0 5 α(a + B) = αa + αb 6 (α + β)a = αa + βa
32 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność) 3 A + 0 = A 4 A + ( A) = A + A = 0 5 α(a + B) = αa + αb 6 (α + β)a = αa + βa 7 1 A = A
33 Kilka własności Niech A, B M m,n oraz α, β R. Wtedy: 1 A + B = B + A (przemienność) 2 A + (B + C) = (A + B) + C (łączność) 3 A + 0 = A 4 A + ( A) = A + A = 0 5 α(a + B) = αa + αb 6 (α + β)a = αa + βa 7 1 A = A 8 (αβ)a = α(βa)
34 Działania na macierzach: transponowanie macierzy Dana niech będzie macierz A = [a i,j ], A M m,n. Transpozycją macierzy A nazywamy macierz B = A T b i,j = a j,i.
35 Działania na macierzach: transponowanie macierzy Dana niech będzie macierz A = [a i,j ], A M m,n. Transpozycją macierzy A nazywamy macierz Zauważmy, że A T M n,m. B = A T b i,j = a j,i.
36 Działania na macierzach: transponowanie macierzy Dana niech będzie macierz A = [a i,j ], A M m,n. Transpozycją macierzy A nazywamy macierz B = A T b i,j = a j,i. Zauważmy, że A T M n,m. Mówimy, że macierz A jest symetryczna jeżeli A = A T. Mówimy, że macierz jest antysymetryczna jeżeli A = A T.
37 Działania na macierzach: mnożenie macierzy Chyba najbardziej skomplikowane. Niech A = [a i,j ], A M m,n oraz B = [b i,j ], B M n,k. Zwróćmy uwagę na wymiary poszczególnych macierzy!
38 Działania na macierzach: mnożenie macierzy Chyba najbardziej skomplikowane. Niech A = [a i,j ], A M m,n oraz B = [b i,j ], B M n,k. Zwróćmy uwagę na wymiary poszczególnych macierzy! W wyniku mnożenia macierzy dostajemy macierz C = [c i,j ], C M m,k o elementach c i,j = a i,1 b 1,j + a i,2 b 2,j +...a i,n b n,j.
39 Działania na macierzach: mnożenie macierzy Chyba najbardziej skomplikowane. Niech A = [a i,j ], A M m,n oraz B = [b i,j ], B M n,k. Zwróćmy uwagę na wymiary poszczególnych macierzy! W wyniku mnożenia macierzy dostajemy macierz C = [c i,j ], C M m,k o elementach c i,j = a i,1 b 1,j + a i,2 b 2,j +...a i,n b n,j. UWAGA! Mnożenie macierzy NIE jest przemienne!
40 Kilka własności Choć mnożenie macierzy nie jest przemienne, to jednak zachowane są inne własności: 1 A(B + C) = AB + AC
41 Kilka własności Choć mnożenie macierzy nie jest przemienne, to jednak zachowane są inne własności: 1 A(B + C) = AB + AC 2 (B + C)A = BA + CA
42 Kilka własności Choć mnożenie macierzy nie jest przemienne, to jednak zachowane są inne własności: 1 A(B + C) = AB + AC 2 (B + C)A = BA + CA 3 A(αB) = (αa)b = α(ab)
43 Kilka własności Choć mnożenie macierzy nie jest przemienne, to jednak zachowane są inne własności: 1 A(B + C) = AB + AC 2 (B + C)A = BA + CA 3 A(αB) = (αa)b = α(ab) 4 (AB)C = A(BC)
44 Kilka własności Choć mnożenie macierzy nie jest przemienne, to jednak zachowane są inne własności: 1 A(B + C) = AB + AC 2 (B + C)A = BA + CA 3 A(αB) = (αa)b = α(ab) 4 (AB)C = A(BC) 5 AI = IA = A dla macierzy kwadratowych.
45 Przykłady w Scilab
46 Podziękowania Dziękuję za uwagę
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
ALGEBRA LINIOWA. Wykład 2. Analityka gospodarcza, sem. 1. Wydział Zarządzania i Ekonomii Politechnika Gdańska
 ALGEBRA LINIOWA Wykład 2 Analityka gospodarcza, sem 1 Wydział Zarządzania i Ekonomii Politechnika Gdańska dr inż Natalia Jarzębkowska, CNMiKnO semzimowy 2018/2019 2/17 Macierze Niech M = {1, 2,, m} i N
ALGEBRA LINIOWA Wykład 2 Analityka gospodarcza, sem 1 Wydział Zarządzania i Ekonomii Politechnika Gdańska dr inż Natalia Jarzębkowska, CNMiKnO semzimowy 2018/2019 2/17 Macierze Niech M = {1, 2,, m} i N
Treści programowe. Matematyka. Efekty kształcenia. Literatura. Terminy wykładów i ćwiczeń. Warunki zaliczenia. tnij.org/ktrabka
 Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
Treści programowe Matematyka Katarzyna Trąbka-Więcław Elementy algebry liniowej. Macierze i wyznaczniki. Ciągi liczbowe, granica ciągu i granica funkcji, rachunek granic, wyrażenia nieoznaczone, ciągłość
1 Macierze i wyznaczniki
 1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
1 Macierze i wyznaczniki 11 Definicje, twierdzenia, wzory 1 Macierzą rzeczywistą (zespoloną) wymiaru m n, gdzie m N oraz n N, nazywamy prostokątną tablicę złożoną z mn liczb rzeczywistych (zespolonych)
Macierz o wymiarach m n. a 21. a 22. A =
 Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
Macierze 1 Macierz o wymiarach m n A = a 11 a 12 a 1n a 21 a 22 a 2n a m1 a m2 a mn Mat m n (R) zbiór macierzy m n o współczynnikach rzeczywistych Analogicznie określamy Mat m n (Z), Mat m n (Q) itp 2
Met Me ody numer yczne Wykład ykład Dr inż. Mic hał ha Łanc Łan zon Instyt Ins ut Elektr Elektr echn iki echn i Elektrot Elektr echn olo echn
 Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
Metody numeryczne Wykład 3 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Pojęcia podstawowe Algebra
RACHUNEK MACIERZOWY. METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6. Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska
 RACHUNEK MACIERZOWY METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy
RACHUNEK MACIERZOWY METODY OBLICZENIOWE Budownictwo, studia I stopnia, semestr 6 Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy
macierze jednostkowe (identyczności) macierze diagonalne, które na przekątnej mają same
 1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
1 Macierz definicja i zapis Macierzą wymiaru m na n nazywamy tabelę a 11 a 1n A = a m1 a mn złożoną z liczb (rzeczywistych lub zespolonych) o m wierszach i n kolumnach (zamiennie będziemy też czasem mówili,
15. Macierze. Definicja Macierzy. Definicja Delty Kroneckera. Definicja Macierzy Kwadratowej. Definicja Macierzy Jednostkowej
 15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
15. Macierze Definicja Macierzy. Dla danego ciała F i dla danych m, n IN funkcję A : {1,...,m} {1,...,n} F nazywamy macierzą m n ( macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
Macierze. Rozdział Działania na macierzach
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i, j) (i 1,..., n; j 1,..., m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F R lub F C, nazywamy macierzą (rzeczywistą, gdy
Definicja macierzy Typy i właściwości macierzy Działania na macierzach Wyznacznik macierzy Macierz odwrotna Normy macierzy RACHUNEK MACIERZOWY
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy funkcję
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Czym jest macierz? Definicja Macierzą A nazywamy funkcję
O MACIERZACH I UKŁADACH RÓWNAŃ
 O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
O MACIERZACH I UKŁADACH RÓWNAŃ Problem Jak rozwiązać podany układ równań? 2x + 5y 8z = 8 4x + 3y z = 2x + 3y 5z = 7 x + 8y 7z = Definicja Równanie postaci a x + a 2 x 2 + + a n x n = b gdzie a, a 2, a
Ekoenergetyka Matematyka 1. Wykład 3.
 Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
Ekoenergetyka Matematyka Wykład 3 MACIERZE Macierzą wymiaru n m, gdzie nm, nazywamy prostokątną tablicę złożoną z n wierszy i m kolumn: a a2 a j am a2 a22 a2 j a2m [ a ] nm A ai ai 2 a aim - i-ty wiersz
Rozdział 5. Macierze. a 11 a a 1m a 21 a a 2m... a n1 a n2... a nm
 Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Rozdział 5 Macierze Funkcję, która każdej parze liczb naturalnych (i,j) (i = 1,,n;j = 1,,m) przyporządkowuje dokładnie jedną liczbę a ij F, gdzie F = R lub F = C, nazywamy macierzą (rzeczywistą, gdy F
Modelowanie danych hodowlanych
 Modelowanie danych hodowlanych 1. Wykład wstępny 2. Algebra macierzowa 3. Wykorzystanie różnych źródeł informacji w predykcji wartości hodowlanej 4. Kowariancja genetyczna pomiędzy spokrewnionymi osobnikami
Modelowanie danych hodowlanych 1. Wykład wstępny 2. Algebra macierzowa 3. Wykorzystanie różnych źródeł informacji w predykcji wartości hodowlanej 4. Kowariancja genetyczna pomiędzy spokrewnionymi osobnikami
1 Zbiory i działania na zbiorach.
 Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
Matematyka notatki do wykładu 1 Zbiory i działania na zbiorach Pojęcie zbioru jest to pojęcie pierwotne (nie definiuje się tego pojęcia) Pojęciami pierwotnymi są: element zbioru i przynależność elementu
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn a 1j a 2j R i = , C j =
 11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
11 Algebra macierzy Definicja 11.1 Dla danego ciała F i dla danych m, n N funkcję A : {1,..., m} {1,..., n} F nazywamy macierzą m n (macierzą o m wierszach i n kolumnach) o wyrazach z F. Wartość A(i, j)
a 11 a a 1n a 21 a a 2n... a m1 a m2... a mn x 1 x 2... x m ...
 Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
Wykład 15 Układy równań liniowych Niech K będzie ciałem i niech α 1, α 2,, α n, β K. Równanie: α 1 x 1 + α 2 x 2 + + α n x n = β z niewiadomymi x 1, x 2,, x n nazywamy równaniem liniowym. Układ: a 21 x
MACIERZE. Sobiesiak Łukasz Wilczyńska Małgorzata
 MACIERZE Sobiesiak Łukasz Wilczyńska Małgorzata Podstawowe pojęcia dotyczące macierzy Nie bez przyczyny zaczynamy od pojęcia macierzy, które jest niezwykle przydatne we wszystkich zastosowaniach, obliczeniach
MACIERZE Sobiesiak Łukasz Wilczyńska Małgorzata Podstawowe pojęcia dotyczące macierzy Nie bez przyczyny zaczynamy od pojęcia macierzy, które jest niezwykle przydatne we wszystkich zastosowaniach, obliczeniach
MATEMATYKA I SEMESTR ALK (PwZ) 1. Sumy i sumy podwójne : Σ i ΣΣ
 MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
DB Algebra liniowa semestr zimowy 2018
 DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
DB Algebra liniowa semestr zimowy 2018 SPIS TREŚCI Teoria oraz większość zadań w niniejszym skrypcie zostały opracowane na podstawie książek: 1 G Banaszak, W Gajda, Elementy algebry liniowej cz I, Wydawnictwo
PODSTAWY AUTOMATYKI. MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
 WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI Katedra Inżynierii Systemów Sterowania PODSTAWY AUTOMATYKI MATLAB - komputerowe środowisko obliczeń naukowoinżynierskich - podstawowe operacje na liczbach i macierzach.
D1. Algebra macierzy. D1.1. Definicje
 D1. Algebra macierzy W niniejszym dodatku podamy podstawowe operacje macierzowe oraz niektóre techniki algebry macierzowej nie dbając szczególnie o formalizm matematyczny. Zakres jest wystarczający dla
D1. Algebra macierzy W niniejszym dodatku podamy podstawowe operacje macierzowe oraz niektóre techniki algebry macierzowej nie dbając szczególnie o formalizm matematyczny. Zakres jest wystarczający dla
Wykład 4. Informatyka Stosowana. Magdalena Alama-Bućko. 25 marca Magdalena Alama-Bućko Wykład 4 25 marca / 25
 Wykład 4 Informatyka Stosowana Magdalena Alama-Bućko 25 marca 2019 Magdalena Alama-Bućko Wykład 4 25 marca 2019 1 / 25 Macierze Magdalena Alama-Bućko Wykład 4 25 marca 2019 2 / 25 Macierza wymiaru m n
Wykład 4 Informatyka Stosowana Magdalena Alama-Bućko 25 marca 2019 Magdalena Alama-Bućko Wykład 4 25 marca 2019 1 / 25 Macierze Magdalena Alama-Bućko Wykład 4 25 marca 2019 2 / 25 Macierza wymiaru m n
Algebra liniowa z geometria
 Algebra liniowa z geometria Materiały do ćwiczeń Zespół matematyków przy WEEiA Spis treści 1 Macierze i wyznaczniki 5 11 Macierze i ich rodzaje 5 12 Operacje na macierzach 6 13 Wyznacznik macierzy 8 14
Algebra liniowa z geometria Materiały do ćwiczeń Zespół matematyków przy WEEiA Spis treści 1 Macierze i wyznaczniki 5 11 Macierze i ich rodzaje 5 12 Operacje na macierzach 6 13 Wyznacznik macierzy 8 14
Analiza numeryczna Kurs INP002009W. Wykłady 6 i 7 Rozwiązywanie układów równań liniowych. Karol Tarnowski A-1 p.
 Analiza numeryczna Kurs INP002009W Wykłady 6 i 7 Rozwiązywanie układów równań liniowych Karol Tarnowski karol.tarnowski@pwr.wroc.pl A-1 p.223 Plan wykładu Podstawowe pojęcia Własności macierzy Działania
Analiza numeryczna Kurs INP002009W Wykłady 6 i 7 Rozwiązywanie układów równań liniowych Karol Tarnowski karol.tarnowski@pwr.wroc.pl A-1 p.223 Plan wykładu Podstawowe pojęcia Własności macierzy Działania
A A A A A A A A A n n
 DODTEK NR GEBR MCIERZY W dodatku tym podamy najważniejsze definicje rachunku macierzowego i omówimy niektóre funkcje i transformacje macierzy najbardziej przydatne w zastosowaniach numerycznych a w szczególności
DODTEK NR GEBR MCIERZY W dodatku tym podamy najważniejsze definicje rachunku macierzowego i omówimy niektóre funkcje i transformacje macierzy najbardziej przydatne w zastosowaniach numerycznych a w szczególności
Pokazać, że wyżej zdefiniowana struktura algebraiczna jest przestrzenią wektorową nad ciałem
 Zestaw zadań 9: Przestrzenie wektorowe. Podprzestrzenie () Wykazać, że V = C ze zwykłym dodawaniem jako dodawaniem wektorów i operacją mnożenia przez skalar : C C C, (z, v) z v := z v jest przestrzenią
Zestaw zadań 9: Przestrzenie wektorowe. Podprzestrzenie () Wykazać, że V = C ze zwykłym dodawaniem jako dodawaniem wektorów i operacją mnożenia przez skalar : C C C, (z, v) z v := z v jest przestrzenią
Algebra macierzy
 Algebra macierzy Definicja macierzy Macierze Macierze Macierze Działania na macierzach Działania na macierzach A + B = B + A (prawo przemienności dodawania) (A + B) + C = A + (B + C) (prawo łączności dodawania)
Algebra macierzy Definicja macierzy Macierze Macierze Macierze Działania na macierzach Działania na macierzach A + B = B + A (prawo przemienności dodawania) (A + B) + C = A + (B + C) (prawo łączności dodawania)
MACIERZE. ZWIĄZEK Z ODWZOROWANIAMI LINIOWYMI.
 MAIERZE. ZWIĄZEK Z ODWZOROWANIAMI LINIOWYMI. k { 1,,..., k} Definicja 1. Macierzą nazyway każde odwzorowanie określone na iloczynie kartezjański.wartość tego odwzorowania na parze (i,j) k j oznaczay aij
MAIERZE. ZWIĄZEK Z ODWZOROWANIAMI LINIOWYMI. k { 1,,..., k} Definicja 1. Macierzą nazyway każde odwzorowanie określone na iloczynie kartezjański.wartość tego odwzorowania na parze (i,j) k j oznaczay aij
Algebra WYKŁAD 3 ALGEBRA 1
 Algebra WYKŁAD 3 ALGEBRA 1 Liczby zespolone Postać wykładnicza liczby zespolonej Niech e oznacza stałą Eulera Definicja Równość e i cos isin nazywamy wzorem Eulera. ALGEBRA 2 Liczby zespolone Każdą liczbę
Algebra WYKŁAD 3 ALGEBRA 1 Liczby zespolone Postać wykładnicza liczby zespolonej Niech e oznacza stałą Eulera Definicja Równość e i cos isin nazywamy wzorem Eulera. ALGEBRA 2 Liczby zespolone Każdą liczbę
Przekształcenia liniowe
 Algebra Przekształcenia liniowe Aleksandr Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra
Algebra Przekształcenia liniowe Aleksandr Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra
dr Mariusz Grządziel 15,29 kwietnia 2014 Przestrzeń R k R k = R R... R k razy Elementy R k wektory;
 Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Wykłady 8 i 9 Pojęcia przestrzeni wektorowej i macierzy Układy równań liniowych Elementy algebry macierzy dodawanie, odejmowanie, mnożenie macierzy; macierz odwrotna dr Mariusz Grządziel 15,29 kwietnia
Algebra liniowa. 1. Macierze.
 Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
Algebra liniowa 1 Macierze Niech m oraz n będą liczbami naturalnymi Przestrzeń M(m n F) = F n F n będącą iloczynem kartezjańskim m egzemplarzy przestrzeni F n z naturalnie określonymi działaniami nazywamy
, A T = A + B = [a ij + b ij ].
![, A T = A + B = [a ij + b ij ]. , A T = A + B = [a ij + b ij ].](/thumbs/98/137554993.jpg) 1 Macierze Jeżeli każdej uporządkowanej parze liczb naturalnych (i, j), 1 i m, 1 j n jest przyporządkowana dokładnie jedna liczba a ij, to mówimy, że jest określona macierz prostokątna A = a ij typu m
1 Macierze Jeżeli każdej uporządkowanej parze liczb naturalnych (i, j), 1 i m, 1 j n jest przyporządkowana dokładnie jedna liczba a ij, to mówimy, że jest określona macierz prostokątna A = a ij typu m
3. Wykład Układy równań liniowych.
 31 Układy równań liniowych 3 Wykład 3 Definicja 31 Niech F będzie ciałem Układem m równań liniowych o niewiadomych x 1,, x n, m, n N, o współczynnikach z ciała F nazywamy układ równań postaci: x 1 + +
31 Układy równań liniowych 3 Wykład 3 Definicja 31 Niech F będzie ciałem Układem m równań liniowych o niewiadomych x 1,, x n, m, n N, o współczynnikach z ciała F nazywamy układ równań postaci: x 1 + +
Analiza matematyczna i algebra liniowa Macierze
 Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
Analiza matematyczna i algebra liniowa Macierze Wojciech Kotłowski Instytut Informatyki Politechniki Poznańskiej email: imię.nazwisko@cs.put.poznan.pl pok. 2 (CW) tel. (61)665-2936 konsultacje: poniedziałek
1 Macierz odwrotna metoda operacji elementarnych
 W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
W tej części skupimy się na macierzach kwadratowych. Zakładać będziemy, że A M(n, n) dla pewnego n N. Definicja 1. Niech A M(n, n). Wtedy macierzą odwrotną macierzy A (ozn. A 1 ) nazywamy taką macierz
Wyk lad 4 Dzia lania na macierzach. Określenie wyznacznika
 Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Wyk lad 4 Dzia lania na macierzach Określenie wyznacznika 1 Określenie macierzy Niech K bedzie dowolnym cia lem oraz niech n i m bed a dowolnymi liczbami naturalnymi Prostokatn a tablice a 11 a 12 a 1n
Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań.
 Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań. Wydział Matematyki Politechniki Wrocławskiej Układy Cramerowskie Układem Cramera nazywamy układ równań liniowych: AX = B, w którym A jest macierzą
Macierze Lekcja V: Wzory Cramera. Macierzowe układy równań. Wydział Matematyki Politechniki Wrocławskiej Układy Cramerowskie Układem Cramera nazywamy układ równań liniowych: AX = B, w którym A jest macierzą
Zadania egzaminacyjne
 Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Rozdział 13 Zadania egzaminacyjne Egzamin z algebry liniowej AiR termin I 03022011 Zadanie 1 Wyznacz sumę rozwiązań równania: (8z + 1 i 2 2 7 iz 4 = 0 Zadanie 2 Niech u 0 = (1, 2, 1 Rozważmy odwzorowanie
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji
 Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
Macierze - obliczanie wyznacznika macierzy z użyciem permutacji I LO im. F. Ceynowy w Świeciu Radosław Rudnicki joix@mat.uni.torun.pl 17.03.2009 r. Typeset by FoilTEX Streszczenie Celem wykładu jest wprowadzenie
Własności wyznacznika
 Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Własności wyznacznika Rozwinięcie Laplace a względem i-tego wiersza: n det(a) = ( 1) i+j a ij M ij (A), j=1 gdzie M ij (A) to minor (i, j)-ty macierzy A, czyli wyznacznik macierzy uzyskanej z macierzy
Macierze. 1 Podstawowe denicje. 2 Rodzaje macierzy. Denicja
 Macierze 1 Podstawowe denicje Macierz wymiaru m n, gdzie m, n N nazywamy tablic liczb rzeczywistych (lub zespolonych) postaci a 11 a 1j a 1n A = A m n = [a ij ] m n = a i1 a ij a in a m1 a mj a mn W macierzy
Macierze 1 Podstawowe denicje Macierz wymiaru m n, gdzie m, n N nazywamy tablic liczb rzeczywistych (lub zespolonych) postaci a 11 a 1j a 1n A = A m n = [a ij ] m n = a i1 a ij a in a m1 a mj a mn W macierzy
Wykład 14. Elementy algebry macierzy
 Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 14 Elementy algebry macierzy dr Mariusz Grządziel 26 stycznia 2009 Układ równań z dwoma niewiadomymi Rozważmy układ równań z dwoma niewiadomymi: a 11 x + a 12 y = h 1 a 21 x + a 22 y = h 2 a 11,
Wykład 7 Macierze i wyznaczniki
 Wykład 7 Macierze i wyznaczniki Andrzej Sładek sladek@ux2mathusedupl Instytut Matematyki, Uniwersytet Śląski w Katowicach Andrzej Sładek (Instytut Matematyki, Uniwersytet Śląski Wykład w Katowicach) 7
Wykład 7 Macierze i wyznaczniki Andrzej Sładek sladek@ux2mathusedupl Instytut Matematyki, Uniwersytet Śląski w Katowicach Andrzej Sładek (Instytut Matematyki, Uniwersytet Śląski Wykład w Katowicach) 7
Macierze i Wyznaczniki
 dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
dr Krzysztof Żyjewski MiBM; S-I 0.inż. 0 października 04 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Definicja. Iloczynem macierzy A = [a ij m n, i macierzy B = [b ij n p nazywamy macierz
Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych
 Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych Piotr Modliński Wydział Geodezji i Kartografii PW 13 stycznia 2012 P. Modliński, GiK PW Rozw.
Rozwiązywanie układów równań liniowych metody dokładne Materiały pomocnicze do ćwiczeń z metod numerycznych Piotr Modliński Wydział Geodezji i Kartografii PW 13 stycznia 2012 P. Modliński, GiK PW Rozw.
Algebra. macierzy brzegowych z zastosowaniami. Micha Kolupa Zbigniew Âleszyƒski
 Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski Algebra macierzy brzegowych z zastosowaniami Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski
Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski Algebra macierzy brzegowych z zastosowaniami Algebra macierzy brzegowych z zastosowaniami Micha Kolupa Zbigniew Âleszyƒski
Zadania z algebry liniowej - sem. I Przestrzenie liniowe, bazy, rząd macierzy
 Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
Zadania z algebry liniowej - sem I Przestrzenie liniowe bazy rząd macierzy Definicja 1 Niech (K + ) będzie ciałem (zwanym ciałem skalarów a jego elementy nazywać będziemy skalarami) Przestrzenią liniową
4 Przekształcenia liniowe
 MIMUW 4. Przekształcenia liniowe 16 4 Przekształcenia liniowe Obok przestrzeni liniowych, podstawowym obiektem algebry liniowej są przekształcenia liniowe. Rozpatrując przekształcenia liniowe między przestrzeniami
MIMUW 4. Przekształcenia liniowe 16 4 Przekształcenia liniowe Obok przestrzeni liniowych, podstawowym obiektem algebry liniowej są przekształcenia liniowe. Rozpatrując przekształcenia liniowe między przestrzeniami
Podstawowe działania w rachunku macierzowym
 Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Podstawowe działania w rachunku macierzowym Marcin Detka Katedra Informatyki Stosowanej Kielce, Wrzesień 2004 1 MACIERZE 1 1 Macierze Macierz prostokątną A o wymiarach m n (m wierszy w n kolumnach) definiujemy:
Lista. Algebra z Geometrią Analityczną. Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami:
 Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Lista Algebra z Geometrią Analityczną Zadanie 1 Przypomnij definicję grupy, które z podanych struktur są grupami: (N, ), (Z, +) (Z, ), (R, ), (Q \ {}, ) czym jest element neutralny i przeciwny w grupie?,
Krótkie wprowadzenie do macierzy i wyznaczników
 Radosław Marczuk Krótkie wprowadzenie do macierzy i wyznaczników 12 listopada 2005 1. Macierze Macierzą nazywamy układ liczb(rzeczywistych, bądź zespolonych), funkcji, innych macierzy w postaci: A a 11
Radosław Marczuk Krótkie wprowadzenie do macierzy i wyznaczników 12 listopada 2005 1. Macierze Macierzą nazywamy układ liczb(rzeczywistych, bądź zespolonych), funkcji, innych macierzy w postaci: A a 11
"Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub
 "Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub Def. Macierzą odwrotną do macierzy A M(n) i deta nazywamy macierz A - M(n) taką, że A A - A - A Tw.
"Bieda przeczy matematyce; gdy się ją podzieli na więcej ludzi, nie staje się mniejsza." Gabriel Laub Def. Macierzą odwrotną do macierzy A M(n) i deta nazywamy macierz A - M(n) taką, że A A - A - A Tw.
Matematyka dyskretna. Andrzej Łachwa, UJ, B/14
 Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Matematyka dyskretna Andrzej Łachwa, UJ, 2019 andrzej.lachwa@uj.edu.pl 2B/14 Relacje Pojęcia: relacja czyli relacja dwuargumentowa relacja w zbiorze A relacja n-argumentowa Relacja E = {(x, x): x S} jest
Zastosowania wyznaczników
 Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
Zastosowania wyznaczników Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 7.wykład z algebry liniowej Warszawa, listopad 2012 Mirosław Sobolewski (UW) Warszawa, listopad 2012 1 / 17
Wyznaczniki. Mirosław Sobolewski. Wydział Matematyki, Informatyki i Mechaniki UW. 6. Wykład z algebry liniowej Warszawa, listopad 2013
 Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Wyznaczniki Mirosław Sobolewski Wydział Matematyki, Informatyki i Mechaniki UW 6. Wykład z algebry liniowej Warszawa, listopad 2013 Mirosław Sobolewski (UW) Warszawa, listopad 2013 1 / 13 Terminologia
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy
 Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
Wektor, prosta, płaszczyzna; liniowa niezależność, rząd macierzy Justyna Winnicka Na podstawie podręcznika Matematyka. e-book M. Dędys, S. Dorosiewicza, M. Ekes, J. Kłopotowskiego. rok akademicki 217/218
2. Układy równań liniowych
 2. Układy równań liniowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2. Układy równań liniowych zima 2017/2018 1 /
2. Układy równań liniowych Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie zima 2017/2018 rzegorz Kosiorowski (Uniwersytet Ekonomiczny w Krakowie) 2. Układy równań liniowych zima 2017/2018 1 /
04 Układy równań i rozkłady macierzy - Ćwiczenia. Przykład 1 A =
 04 Układy równań i rozkłady macierzy - Ćwiczenia 1. Wstęp Środowisko Matlab można z powodzeniem wykorzystać do rozwiązywania układów równań z wykorzystaniem rozkładów macierzy m.in. Rozkładu Choleskiego,
04 Układy równań i rozkłady macierzy - Ćwiczenia 1. Wstęp Środowisko Matlab można z powodzeniem wykorzystać do rozwiązywania układów równań z wykorzystaniem rozkładów macierzy m.in. Rozkładu Choleskiego,
Zaawansowane metody numeryczne
 Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Wykład 10 Rozkład LU i rozwiązywanie układów równań liniowych Niech będzie dany układ równań liniowych postaci Ax = b Załóżmy, że istnieją macierze L (trójkątna dolna) i U (trójkątna górna), takie że macierz
Jak łatwo zauważyć, zbiór form symetrycznych (podobnie antysymetrycznych) stanowi podprzestrzeń przestrzeni L(V, V, K). Oznaczamy ją Sym(V ).
 Odwzorowania n-liniowe; formy n-liniowe Definicja 1 Niech V 1,..., V n, U będą przestrzeniami liniowymi nad ciałem K. Odwzorowanie G: V 1 V n U nazywamy n-liniowym, jeśli dla każdego k [n] i wszelkich
Odwzorowania n-liniowe; formy n-liniowe Definicja 1 Niech V 1,..., V n, U będą przestrzeniami liniowymi nad ciałem K. Odwzorowanie G: V 1 V n U nazywamy n-liniowym, jeśli dla każdego k [n] i wszelkich
Układy równań liniowych
 Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
Układy równań liniowych Niech K będzie ciałem. Niech n, m N. Równanie liniowe nad ciałem K z niewiadomymi (lub zmiennymi) x 1, x 2,..., x n K definiujemy jako formę zdaniową zmiennej (x 1,..., x n ) K
MACIERZE I WYZNACZNIKI
 Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Wykłady z matematyki inżynierskiej IMiF UTP 07 MACIERZ DEFINICJA. Macierza o m wierszach i n kolumnach nazywamy przyporza dkowanie każdej uporza dkowanej parze liczb naturalnych (i, j), gdzie 1 i m, 1
Rozwiązywanie układów równań liniowych
 Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
Rozwiązywanie układów równań liniowych Marcin Orchel 1 Wstęp Jeśli znamy macierz odwrotną A 1, to możęmy znaleźć rozwiązanie układu Ax = b w wyniku mnożenia x = A 1 b (1) 1.1 Metoda eliminacji Gaussa Pierwszy
ALGEBRA Z GEOMETRIĄ MACIERZE ODWZOROWAŃ LINIOWYCH
 ALGEBRA Z GEOMETRIĄ 1/10 MACIERZE ODWZOROWAŃ LINIOWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 12, 08.01.2014 Typeset by Jakub Szczepanik. Motywacje 2/10 W celu wykonania obliczeń numerycznych w zagadnieniach
ALGEBRA Z GEOMETRIĄ 1/10 MACIERZE ODWZOROWAŃ LINIOWYCH Piotr M. Hajac Uniwersytet Warszawski Wykład 12, 08.01.2014 Typeset by Jakub Szczepanik. Motywacje 2/10 W celu wykonania obliczeń numerycznych w zagadnieniach
PODSTAWY RACHUNKU WEKTOROWEGO
 Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Transport, studia niestacjonarne I stopnia, semestr I Instytut L-5, Wydział Inżynierii Lądowej, Politechnika Krakowska Adam Wosatko Ewa Pabisek Skalar Definicja Skalar wielkość fizyczna (lub geometryczna)
Algebra liniowa z geometrią
 Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Algebra liniowa z geometrią Maciej Czarnecki 15 stycznia 2013 Spis treści 1 Geometria płaszczyzny 2 1.1 Wektory i skalary........................... 2 1.2 Macierze, wyznaczniki, układy równań liniowych.........
Obliczenia w programie MATLAB
 Obliczenia w programie MATLAB Na zajęciach korzystamy z programu MATLAB, w którym wykonywać będziemy większość obliczeń. Po uruchomieniu programu w zależności od wersji i konfiguracji może pojawić się
Obliczenia w programie MATLAB Na zajęciach korzystamy z programu MATLAB, w którym wykonywać będziemy większość obliczeń. Po uruchomieniu programu w zależności od wersji i konfiguracji może pojawić się
Metody i analiza danych
 2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
2015/2016 Metody i analiza danych Macierze Laboratorium komputerowe 2 Anna Kiełbus Zakres tematyczny 1. Funkcje wspomagające konstruowanie macierzy 2. Dostęp do elementów macierzy. 3. Działania na macierzach
Podstawowe struktury algebraiczne
 Maciej Grzesiak Podstawowe struktury algebraiczne 1. Wprowadzenie Przedmiotem algebry było niegdyś przede wszystkim rozwiązywanie równań. Obecnie algebra staje się coraz bardziej nauką o systemach matematycznych.
Maciej Grzesiak Podstawowe struktury algebraiczne 1. Wprowadzenie Przedmiotem algebry było niegdyś przede wszystkim rozwiązywanie równań. Obecnie algebra staje się coraz bardziej nauką o systemach matematycznych.
Niezb. ednik matematyczny. Niezb. ednik matematyczny
 Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Niezb ednik matematyczny Niezb ednik matematyczny Liczby zespolone I Rozważmy zbiór R R (zbiór par liczb rzeczywistych) i wprowadźmy w nim nastepuj ace dzia lania: z 1 + z 2 = (x 1, y 1 ) + (x 2, y 2 )
Przestrzenie wektorowe, liniowa niezależność wektorów, bazy przestrzeni wektorowych
 Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Grupa, cia lo Zadanie 1. Jakie w lasności w zbiorze liczb naturalnych, ca lkowitych, wymiernych, rzeczywistych maj dzia lania a b = a b, a b = a 2 + b 2, a b = a+b, a b = b. 2 Zadanie 2. Pokazać, że (R
Algebra liniowa II. Lista 1. 1 u w 0 1 v 0 0 1
 Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
Algebra liniowa II Lista Zadanie Udowodnić, że jeśli B b ij jest macierzą górnotrójkątną o rozmiarze m m, to jej wyznacznik jest równy iloczynowi elementów leżących na głównej przekątnej: det B b b b mm
III TUTORIAL Z METOD OBLICZENIOWYCH
 III TUTORIAL Z METOD OBLICZENIOWYCH ALGORYTMY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH Opracowanie: Agata Smokowska Marcin Zmuda Trzebiatowski Koło Naukowe Mechaniki Budowli KOMBO Spis treści: 1. Wstęp do
III TUTORIAL Z METOD OBLICZENIOWYCH ALGORYTMY ROZWIĄZYWANIA UKŁADÓW RÓWNAŃ LINIOWYCH Opracowanie: Agata Smokowska Marcin Zmuda Trzebiatowski Koło Naukowe Mechaniki Budowli KOMBO Spis treści: 1. Wstęp do
5 Wyznaczniki. 5.1 Definicja i podstawowe własności. MIMUW 5. Wyznaczniki 25
 MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
MIMUW 5 Wyznaczniki 25 5 Wyznaczniki Wyznacznik macierzy kwadratowych jest funkcją det : K m n K, (m = 1, 2, ) przypisującą każdej macierzy kwadratowej skalar, liniowo ze względu na każdy wiersz osobno
cx cx 1,cx 2,cx 3,...,cx n. Przykład 4, 5
 Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Laboratorium Techniki Obliczeniowej i Symulacyjnej
 Ćwiczenie 10. Metody numeryczne rozwiązywania układów równań liniowych. Opracował: dr inż. Sebastian Dudzik 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z algorytmami numerycznymi przetwarzania
Ćwiczenie 10. Metody numeryczne rozwiązywania układów równań liniowych. Opracował: dr inż. Sebastian Dudzik 1. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z algorytmami numerycznymi przetwarzania
WYBRANE DZIAŁY ANALIZY MATEMATYCZNEJ. Wykład II
 Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Wykład II I. Algebra wektorów 2.1 Iloczyn wektorowy pary wektorów. 2.1.1 Orientacja przestrzeni Załóżmy, że trójka wektorów a, b i c jest niekomplanarna. Wynika z tego, że żaden z tych wektorów nie jest
Spis treści Wstęp Liczby zespolone Funkcje elementarne zmiennej zespolonej Wielomiany Macierze i wyznaczniki
 Spis treści Wstęp ii 1 Liczby zespolone 1 1.1 Definicja i działania, liczby sprzężone......................... 1 1.2 Moduł, argument, postać trygonometryczna..................... 2 1.3 Działania na liczbach
Spis treści Wstęp ii 1 Liczby zespolone 1 1.1 Definicja i działania, liczby sprzężone......................... 1 1.2 Moduł, argument, postać trygonometryczna..................... 2 1.3 Działania na liczbach
Metody numeryczne Wykład 4
 Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
Metody numeryczne Wykład 4 Dr inż. Michał Łanczont Instytut Elektrotechniki i Elektrotechnologii E419, tel. 4293, m.lanczont@pollub.pl, http://m.lanczont.pollub.pl Zakres wykładu Metody skończone rozwiązywania
MATEMATYKA I SEMESTR ALK (PwZ) 1. Sumy i sumy podwójne : Σ i ΣΣ
 MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
MATEMATYKA I SEMESTR ALK (PwZ). Sumy i sumy podwójne : Σ i ΣΣ.. OKREŚLENIE Ciąg liczbowy = Dowolna funkcja przypisująca liczby rzeczywiste pierwszym n (ciąg skończony), albo wszystkim (ciąg nieskończony)
Przestrzenie wektorowe
 Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Rozdział 4 Przestrzenie wektorowe Rozważania dotyczące przestrzeni wektorowych rozpoczniemy od kilku prostych przykładów. Przykład 4.1. W przestrzeni R 3 = {(x, y, z) : x, y, z R} wprowadzamy dwa działania:
Wyk lad 5 W lasności wyznaczników. Macierz odwrotna
 Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Wyk lad 5 W lasności wyznaczników Macierz odwrotna 1 Operacje elementarne na macierzach Bardzo ważne znaczenie w algebrze liniowej odgrywaja tzw operacje elementarne na wierszach lub kolumnach macierzy
Analiza funkcjonalna 1.
 Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
Analiza funkcjonalna 1. Wioletta Karpińska Semestr letni 2015/2016 0 Bibliografia [1] Banaszczyk W., Analiza matematyczna 3. Wykłady. (http://math.uni.lodz.pl/ wbanasz/am3/) [2] Birkholc A., Analiza matematyczna.
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ
 ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
ALGEBRA LINIOWA Z ELEMENTAMI GEOMETRII ANALITYCZNEJ WSHE, O/K-CE 10. Homomorfizmy Definicja 1. Niech V, W będą dwiema przestrzeniami liniowymi nad ustalonym ciałem, odwzorowanie ϕ : V W nazywamy homomorfizmem
Matematyka dyskretna. 1. Relacje
 Matematyka dyskretna 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produktu kartezjańskiego X Y, którego elementami są pary uporządkowane (x, y), takie, że x X i y Y. Uwaga 1.1 Jeśli
Matematyka dyskretna 1. Relacje Definicja 1.1 Relacją dwuargumentową nazywamy podzbiór produktu kartezjańskiego X Y, którego elementami są pary uporządkowane (x, y), takie, że x X i y Y. Uwaga 1.1 Jeśli
R n = {(x 1, x 2,..., x n ): x i R, i {1,2,...,n} },
 nazywa- Definicja 1. Przestrzenią liniową R n my zbiór wektorów R n = {(x 1, x 2,..., x n ): x i R, i {1,2,...,n} }, z określonymi działaniami dodawania wektorów i mnożenia wektorów przez liczby rzeczywiste.
nazywa- Definicja 1. Przestrzenią liniową R n my zbiór wektorów R n = {(x 1, x 2,..., x n ): x i R, i {1,2,...,n} }, z określonymi działaniami dodawania wektorów i mnożenia wektorów przez liczby rzeczywiste.
Metody numeryczne II. Układy równań liniowych
 Metody numeryczne II. Układy równań liniowych Oleksandr Sokolov Wydział Fizyki, Astronomii i Informatyki Stosowanej UMK (2016/17) http://fizyka.umk.pl/~osokolov/mnii/ Układ równań liniowych Układem równań
Metody numeryczne II. Układy równań liniowych Oleksandr Sokolov Wydział Fizyki, Astronomii i Informatyki Stosowanej UMK (2016/17) http://fizyka.umk.pl/~osokolov/mnii/ Układ równań liniowych Układem równań
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI. Wprowadzenie do środowiska Matlab
 LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
LABORATORIUM 3 ALGORYTMY OBLICZENIOWE W ELEKTRONICE I TELEKOMUNIKACJI Wprowadzenie do środowiska Matlab 1. Podstawowe informacje Przedstawione poniżej informacje maja wprowadzić i zapoznać ze środowiskiem
Macierze i Wyznaczniki
 Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja 1. Tablic nast puj cej postaci a 11 a 12... a 1n a 21 a 22... a 2n A =... a m1 a m2... a mn nazywamy macierz o m wierszach i n kolumnach,
Macierze i Wyznaczniki Kilka wzorów i informacji pomocniczych: Denicja 1. Tablic nast puj cej postaci a 11 a 12... a 1n a 21 a 22... a 2n A =... a m1 a m2... a mn nazywamy macierz o m wierszach i n kolumnach,
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wyznaczniki. Algebra. Aleksander Denisiuk
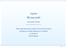 Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Algebra Wyznaczniki Aleksander Denisiuk denisjuk@pjwstk.edu.pl Polsko-Japońska Wyższa Szkoła Technik Komputerowych zamiejscowy ośrodek dydaktyczny w Gdańsku ul. Brzegi 55 80-045 Gdańsk Algebra p. 1 Wyznaczniki
Wyznaczniki 3.1 Wyznaczniki stopni 2 i 3
 3 Wyznaczniki 31 Wyznaczniki stopni 2 i 3 Wyznacznik macierzy 2 2 Dana jest macierz [ ] a b A Mat c d 2 2 (R) Wyznacznikiem macierzy A nazywamy liczbę mamy a A c b ad bc d Wyznacznik macierzy A oznaczamy
3 Wyznaczniki 31 Wyznaczniki stopni 2 i 3 Wyznacznik macierzy 2 2 Dana jest macierz [ ] a b A Mat c d 2 2 (R) Wyznacznikiem macierzy A nazywamy liczbę mamy a A c b ad bc d Wyznacznik macierzy A oznaczamy
1. Zbadać liniową niezależność funkcji x, 1, x, x 2 w przestrzeni liniowej funkcji ciągłych na przedziale [ 1, ).
 B 2 Suma Zbadać, czy liniowo niezależne wektory u, v, w stanowią bazę przestrzeni liniowej lin { u + 2 v + w, u v + 2 w, 3 u + 5 w } 2 Współrzędne wektora (, 4, 5, 4 ) w pewnej bazie podprzestrzeni U R
B 2 Suma Zbadać, czy liniowo niezależne wektory u, v, w stanowią bazę przestrzeni liniowej lin { u + 2 v + w, u v + 2 w, 3 u + 5 w } 2 Współrzędne wektora (, 4, 5, 4 ) w pewnej bazie podprzestrzeni U R
WEKTORY I MACIERZE. Strona 1 z 11. Lekcja 7.
 Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
Strona z WEKTORY I MACIERZE Wektory i macierze ogólnie nazywamy tablicami. Wprowadzamy je:. W sposób jawny: - z menu Insert Matrix, - skrót klawiszowy: {ctrl}+m, - odpowiedni przycisk z menu paska narzędziowego
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
, to liczby γ +δi oraz γ δi opisują pierwiastki z a+bi.
 Zestaw 1 Liczby zespolone 1 Zadania do przeliczenia Nie będziemy robić na ćwiczeniach S 1 Policz wartość 1 + i + (2 + i)(i 3) 1 i Zadania domowe x y(1 + i) 1 Znajdź liczby rzeczywiste x, y takie, że +
Zestaw 1 Liczby zespolone 1 Zadania do przeliczenia Nie będziemy robić na ćwiczeniach S 1 Policz wartość 1 + i + (2 + i)(i 3) 1 i Zadania domowe x y(1 + i) 1 Znajdź liczby rzeczywiste x, y takie, że +
