TEX/L A TEX przykładowy dokument
|
|
|
- Jadwiga Michalak
- 8 lat temu
- Przeglądów:
Transkrypt
1 TEX/L A TEX przykładowy dokument Paweł Syty stycznia 5 Wstęp To jest przykładowy, dość rozbudowany dokument w L A TEX-u. Wprowadzono w nim podział na rozdziały, na końcu dołączono spisy treści, rysunków, tabel oraz literatury. Dodatkowo, drukowany jest tytuł i autor dokumentu oraz data jego utworzenia. Rozdział omawia polonizację L A TEX-a. W rozdziale mamy małą próbkę tego, w czym TEX jest bezkonkurencyjny składaniu wzorów matematycznych. Rozdział 4 demonstruje tworzenie tabel i wypunktowań oraz wstawianie rysunków postscriptowych do dokumentów. W rozdziale 5 omówione zostały najczęściej używane kroje czcionek oraz ich rozmiary. Ostatni rozdział omawia tworzenie plików PDF. Na końcu dokumentu załączono spis tabel i rysunków zamieszczonych w dokumencie, spis wykorzystanej literatury oraz rzecz jasna spis treści. Polonizacja L A TEX-a Dzięki dołączeniu pakietu polski, możemy w dokumencie używać polskich znaków diakrytycznych. Pakiet ten dodatkowo spolszcza nazwy części składowych dokumentu (np. mamy Spis treści zamiast Contents, Literaturę zamiast Bibliography, polskie nazwy dni i miesięcy itp.). Ponadto, wprowadza on inne drobne usprawnienia, np. nazwy funkcji trygonometrycznych będą zapisywane zgodnie z polską tradycją (np. tg a nie tan na zapis tangensa). Przy tworzeniu większych dokumentów polskojęzycznych, dobrym rozwiązaniem jest stosowanie zamiast jednej ze standardowych klas (które siłą rzeczy stosują anglo-amerykańskie wzorce), klas, które stosują do dokumentu polskie zasady i zwyczaje typograficzne. Takimi polskimi klasami są np. klasy mwart, mwrep oraz mwbk odpowiedniki klas article, report oraz book. Pełna nazwa pakietu polonizacyjnego to PLaTeX.
2 Trochę matematyki Twierdzenie (Twierdzenie Pitagorasa, źródło: []) Jeżeli a i b są długościami przyprostokątnych trójkąta prostokątnego, zaś c długością jego przeciwprostokątnej, to zachodzi związek: a + b = c. Iloczyn wektorowy wektorów a i b wyraża się następującym wyznacznikiem ponadto, zachodzi ( a b )i = j= k= ˆ i ˆ j ˆ k a b = a a a ; b b b ɛ ijk a j b k, ɛ ijk = ɛ jik = ɛ jki =... }{{} Tensor Levi-Civity Z kolei, iloczyn skalarny wektorów wyliczamy ze wzoru a b = a i b i. i= Wzór na długość krzywej y = y(x) na odcinku [x, x ] ma postać (patrz []) I[y(x)] = x x + y (x) dx. () Wyrażenie po prawej stronie wzoru () jest tzw. funkcjonałem, ponieważ jego argumentami są funkcje. Równania Eulera dla bryły sztywnej (w układzie odniesienia związanym z bryłą) mają postać: I ω = (I I )ω ω + D I ω = (I I )ω ω + D () I ω = (I I )ω ω + D W powyższym układzie równań, I i oznacza moment bezwładności bryły względem i-tej osi, ω i to i-ta składowa prędkości kątowej bryły, zaś D i jest momentem siły obracającym bryłę wokół i-tej osi. Funkcję Delta Kroneckera definiujemy następująco: dla m = n δ mn = dla m n.
3 4 Tabele, wypunktowania, rysunki 4. Tabele Poniżej dwie przykładowe tabele. Program cena netto cena brutto jakość obsługa Microsoft Word 7 zł 854 zł taka sobie łatwa Adobe Pagemaker zł 66 zł może być dość trudna TEX/L A TEX zupełnie za darmo... to chyba widać? trudna łatwa Tabela : Zestawienie popularnych programów do składu tekstów Funkcja Argument (ϕ) sin(ϕ) cos(ϕ) tg(ϕ) ctg(ϕ) - π 6 = π 4 = 45 π = 6 π = 9 - Tabela : Wartości funkcji trygonometrycznych dla wybranych kątów 4. Wypunktowania Języki programowania dzielimy na: imperatywne program składa się ze zmiennych oraz modyfikujących je operacji, z jawnie określonym przepływem sterowania przykłady: C, Pascal obiektowe funkcyjne logiczne inne
4 4. Rysunki Rysunek : Wykres funkcji y(x) = x(x )(x )(x 6) oraz prostej stycznej do niej w dwóch różnych punktach Rysunek : Trójwymiarowy wykres funkcji z(x, y) = sin xy Rysunki oraz zostały wykonane przy użyciu programu Mathematica i zapisane w formacie Encapsulated Postscript (EPS). 5 Czcionki i stopień pisma Co prawda nie należy przesadzać z używaniem zbyt wielu krojów oraz stopni pisma w jednym dokumencie, niemniej jednak możliwość ich zmiany jest czasami przydatna. Wskazane jest jednak nie zmieniać ich bezpośrednio. Warto w zamian zdefiniować dodatkowe polecenie odnoszące się do całej grupy elementów, które chcemy wyróżnić i w dokumencie użyć tego nowego polecenia. Dzięki takiemu podejściu zachowujemy oddzielenie formy od treści dokumentu, co jest podstawową ideą L A TEX-a. 4
5 Poniżej przedstawione są podstawowe kroje i odmiany czcionek: krój/odmiana polecenie krój szeryfowy \textrm{... } krój bezszeryfowy \textsf{... } grotesk \texttt{... } pismo jasne \textmd{... } pismo grube \textbf{... } odmiana prosta \textup{... } odmiana pochyła \textsl{... } kursywa \textit{... } kapitaliki \textsc{... } głowna czcionka dokumentu \textnormal{... } Stopnie pisma (efekt końcowy oczywiście zależny jest od wyboru podstawowego stopnia pisma w preambule): rozmiar polecenie największy {\Huge... } ogromny {\huge... } bardzo duży {\LARGE... } większy {\Large... } duży {\large... } normalny {\normalsize... } mały {\small... } mniejszy {\footnotesize... } bardzo mały {\scriptsize... } mikroskopijny {\tiny... } 6 Tworzenie plików PDF Do tworzenia popularnych plików PDF (Adobe Portable Document Format) służy program pdflatex. Uruchamia się go analogicznie jak L A TEX-a, ale w wyniku, zamiast pliku DVI, otrzymujemy PDF. Niestety, metoda ta nie pozwala na dołączanie rysunków postscriptowych (PS, EPS) do dokumentu. Najprostszą metodą otrzymania pliku PDF z rysunkami jest wykorzystanie darmowego narzędzia dvipdfm, konwertującego pliki DVI na PDF. Alternatywnie, można programem dvips przekonwertować plik DVI na Postscript (PS) i z niego utworzyć PDF-a za 5
6 pomocą np. Adobe Acrobata/Distillera. Można też użyć programu emulującego drukarkę PDFową i wydrukować na niej plik DVI lub PS, otrzymując plik PDF. Taką wirtualną PDF-ową drukarką jest np. darmowy QPrinter. Spis tabel Zestawienie popularnych programów do składu tekstów Wartości funkcji trygonometrycznych dla wybranych kątów Spis rysunków Dwuwymiarowy wykres funkcji Trójwymiarowy wykres funkcji Literatura [] Pitagoras Dzieła, Ateny, 4 PNE [] W. Krysicki, W. Włodarski Analiza matematyczna w zadaniach, Warszawa, PWN, 99 Spis treści Wstęp Polonizacja L A TEX-a Trochę matematyki 4 Tabele, wypunktowania, rysunki 4. Tabele Wypunktowania Rysunki Czcionki i stopień pisma 4 6 Tworzenie plików PDF 5 6
Podstawowe komendy i możliwości system składu drukarskiego L A TEX
 Podstawowe komendy i możliwości system składu drukarskiego L A TEX Paweł Woźny Rafał Nowak Wrocław, 7 października 2007 Spis treści Rozdział 2. Podrozdział..................................... 2.. Podpodrozdział...............................
Podstawowe komendy i możliwości system składu drukarskiego L A TEX Paweł Woźny Rafał Nowak Wrocław, 7 października 2007 Spis treści Rozdział 2. Podrozdział..................................... 2.. Podpodrozdział...............................
Spis treści -1. Copyright c 2001 by Marcin Woliński
 Spis treści -1 Fonty w T E Xu NFSS Stopnie pisma Polecenia odziedziczone z L A T E Xa 2.09 Nowe polecenia L A T E Xa 2ε Opis fontu w NFSS Standardowe układy fontów L A T E Xa 2ε Układy znaków L A T E Xa
Spis treści -1 Fonty w T E Xu NFSS Stopnie pisma Polecenia odziedziczone z L A T E Xa 2.09 Nowe polecenia L A T E Xa 2ε Opis fontu w NFSS Standardowe układy fontów L A T E Xa 2ε Układy znaków L A T E Xa
Hipotetyczna praca dyplomowa
 Hipotetyczna praca dyplomowa Twoje imię i nazwisko Spis treści 1 Matematyka 4 1.1 Wzory............................... 4 1.2 Twierdzenie i lemat........................ 4 1.3 Tabela...............................
Hipotetyczna praca dyplomowa Twoje imię i nazwisko Spis treści 1 Matematyka 4 1.1 Wzory............................... 4 1.2 Twierdzenie i lemat........................ 4 1.3 Tabela...............................
IIIa. Fonty w LATEX-u
 w LaTeX-u IIIa. w L A TEX-u 10 marca 2014 IIIa. w LATEX-u w LaTeX-u Pojęcie fontu Fontem nazywa się pełny zbiór charakterystycznych znaków danego pisma (wraz ze znakami przestankowymi etc.) utrwalony w
w LaTeX-u IIIa. w L A TEX-u 10 marca 2014 IIIa. w LATEX-u w LaTeX-u Pojęcie fontu Fontem nazywa się pełny zbiór charakterystycznych znaków danego pisma (wraz ze znakami przestankowymi etc.) utrwalony w
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ
 METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
METODY MATEMATYCZNE I STATYSTYCZNE W INŻYNIERII CHEMICZNEJ Wykład 3 Elementy analizy pól skalarnych, wektorowych i tensorowych Prof. Antoni Kozioł, Wydział Chemiczny Politechniki Wrocławskiej 1 Analiza
Funkcje trygonometryczne w trójkącie prostokątnym
 Funkcje trygonometryczne w trójkącie prostokątnym Oznaczenia boków i kątów trójkąta prostokątnego użyte w definicjach Sinus Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
Funkcje trygonometryczne w trójkącie prostokątnym Oznaczenia boków i kątów trójkąta prostokątnego użyte w definicjach Sinus Sinusem kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych
 Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
Krzywe stożkowe Lekcja II: Okrąg i jego opis w różnych układach współrzędnych Wydział Matematyki Politechniki Wrocławskiej Okrąg Okrąg jest szczególną krzywą stożkową. Wyznacza nam koło, które jest podstawą
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas
 3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
3. KINEMATYKA Kinematyka jest częścią mechaniki, która zajmuje się opisem ruchu ciał bez wnikania w jego przyczyny. Oznacza to, że nie interesuje nas oddziaływanie między ciałami, ani też rola, jaką to
1 Zacznijmy od początku... 2 Tryb tekstowy. 2.1 Wyliczenia
 1 Zacznijmy od początku... L A TEX 1 jest systemem składu umożliwiającym między innymi tworzenie dokumentów naukowych i technicznych o wysokiej jakości typograficznej. Oczywiście oprócz tego L A TEXumożliwia
1 Zacznijmy od początku... L A TEX 1 jest systemem składu umożliwiającym między innymi tworzenie dokumentów naukowych i technicznych o wysokiej jakości typograficznej. Oczywiście oprócz tego L A TEXumożliwia
VII.1 Pojęcia podstawowe.
 II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
II.1 Pojęcia podstawowe. Jan Królikowski Fizyka IBC 1 Model matematyczny ciała sztywnego Zbiór punktów materialnych takich, że r r = const; i, j= 1,... N i j Ciało sztywne nie ulega odkształceniom w wyniku
L A T E X- wprowadzenie
 L A T E X- wprowadzenie Katarzyna Grzelak październik 2009 K.Grzelak (IFD UW) 1 / 36 Najprostszy tekst w L A T E X u Zawartość przykładowego pliku zerowy.tex : \documentclass{article} \begin{document}
L A T E X- wprowadzenie Katarzyna Grzelak październik 2009 K.Grzelak (IFD UW) 1 / 36 Najprostszy tekst w L A T E X u Zawartość przykładowego pliku zerowy.tex : \documentclass{article} \begin{document}
Sylabus Moduł 2: Przetwarzanie tekstów
 Sylabus Moduł 2: Przetwarzanie tekstów Niniejsze opracowanie przeznaczone jest dla osób zamierzających zdać egzamin ECDL (European Computer Driving Licence) na poziomie podstawowym. Publikacja zawiera
Sylabus Moduł 2: Przetwarzanie tekstów Niniejsze opracowanie przeznaczone jest dla osób zamierzających zdać egzamin ECDL (European Computer Driving Licence) na poziomie podstawowym. Publikacja zawiera
ABC systemu L A TEX. Marcin SZPYRKA. 11 grudnia 2006
 ABC systemu L A TEX Marcin SZPYRKA 11 grudnia 006 1 Wprowadzenie L A TEX (wymawiamy latech ) jest systemem składu drukarskiego, nadającym się do tworzenia różnego rodzaju dokumentów. L A TEX jest zbiorem
ABC systemu L A TEX Marcin SZPYRKA 11 grudnia 006 1 Wprowadzenie L A TEX (wymawiamy latech ) jest systemem składu drukarskiego, nadającym się do tworzenia różnego rodzaju dokumentów. L A TEX jest zbiorem
Matematyka stosowana i metody numeryczne
 Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
Ewa Pabisek Adam Wosatko Piotr Pluciński Matematyka stosowana i metody numeryczne Konspekt z wykładu 14 Rachunekwektorowy W celu zdefiniowania wektora a należy podać: kierunek(prostą na której leży wektor)
1 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych
 Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
Rozwiązywanie układów równań. Wyznaczniki. 2 Wektory kilka faktów użytkowych 2. Wektory. 2.. Wektor jako n ka liczb W fizyce mamy do czynienia z pojęciami lub obiektami o różnym charakterze. Są np. wielkości,
GRAFIKA KOMPUTEROWA podstawy matematyczne. dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel.
 GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
GRAFIKA KOMPUTEROWA podstawy matematyczne dr inż. Hojny Marcin pokój 406, pawilon B5 E-mail: mhojny@metal.agh.edu.pl Tel. (12) 617 46 37 Plan wykładu 1/4 ZACZNIEMY OD PRZYKŁADOWYCH PROCEDUR i PRZYKŁADÓW
Fonty w dokumenach L A TEXowych
 Fonty w dokumenach L A TEXowych Marcin Woliński BachoTEX, 1 maja 2008 Dla ustalenia uwagi Zakładamy (na chwilę) następującą preambułę dokumenu: \documentclass{mwart} \usepackage{polski} \usepackage[utf8]{inputenc}
Fonty w dokumenach L A TEXowych Marcin Woliński BachoTEX, 1 maja 2008 Dla ustalenia uwagi Zakładamy (na chwilę) następującą preambułę dokumenu: \documentclass{mwart} \usepackage{polski} \usepackage[utf8]{inputenc}
Podstawy systemu L A TEX część 2
 Imię Nazwisko Podstawy systemu L A TEX część 2 05.03.2007 Część I Podstawy 1. Podział tekstu 1.1. Podział linii \\ lub \newline łamanie linii bez justowania linebreak łamanie linii z justowaniem \nolinebreak
Imię Nazwisko Podstawy systemu L A TEX część 2 05.03.2007 Część I Podstawy 1. Podział tekstu 1.1. Podział linii \\ lub \newline łamanie linii bez justowania linebreak łamanie linii z justowaniem \nolinebreak
Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem.
 1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
1 Wektory Co to jest wektor? Jest to obiekt posiadający: moduł (długość), kierunek wraz ze zwrotem. 1.1 Dodawanie wektorów graficzne i algebraiczne. Graficzne - metoda równoległoboku. Sprowadzamy wektory
S88 Badanie rzutu kostką sześcienną
 S88 Badanie rzutu kostką sześcienną Andrzej Kapanowski 29 lutego 2012 Streszczenie Celem ćwiczenia jest zbadanie rzutu kostką sześcienną. Dokument ma być pomocą przy przygotowywaniu opracowania z ćwiczenia
S88 Badanie rzutu kostką sześcienną Andrzej Kapanowski 29 lutego 2012 Streszczenie Celem ćwiczenia jest zbadanie rzutu kostką sześcienną. Dokument ma być pomocą przy przygotowywaniu opracowania z ćwiczenia
Funkcje dwóch zmiennych
 Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
Funkcje dwóch zmiennych Andrzej Musielak Str Funkcje dwóch zmiennych Wstęp Funkcja rzeczywista dwóch zmiennych to funkcja, której argumentem jest para liczb rzeczywistych, a wartością liczba rzeczywista.
TRYGONOMETRIA. 1. Definicje i własności funkcji trygonometrycznych
 TRYGONOMETRIA. Definicje i własności funkcji trygonometrycznych Funkcje trygonometryczne kąta ostrego można zdefiniować przy użyciu trójkąta prostokątnego: c a α b DEFINICJA. Sinusem kąta ostrego α w trójkącie
TRYGONOMETRIA. Definicje i własności funkcji trygonometrycznych Funkcje trygonometryczne kąta ostrego można zdefiniować przy użyciu trójkąta prostokątnego: c a α b DEFINICJA. Sinusem kąta ostrego α w trójkącie
Równania dla potencjałów zależnych od czasu
 Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
Równania dla potencjałów zależnych od czasu Potencjały wektorowy A( r, t i skalarny ϕ( r, t dla zależnych od czasu pola elektrycznego E( r, t i magnetycznego B( r, t definiujemy poprzez następujące zależności
INFORMATYKA I L A TEX
 Wykład INFORMATYKA I L A TEX Marta Tyran-Kamińska semestr letni 2004/2005 Twierdzenia 28 W preambule \newtheorem{nazwa}[wnazwa]{nagłówek}[podział] W treści dokumentu \begin{nazwa}[dodatkowy opis] Treść
Wykład INFORMATYKA I L A TEX Marta Tyran-Kamińska semestr letni 2004/2005 Twierdzenia 28 W preambule \newtheorem{nazwa}[wnazwa]{nagłówek}[podział] W treści dokumentu \begin{nazwa}[dodatkowy opis] Treść
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO. dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury
 KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
KINEMATYKA I DYNAMIKA CIAŁA STAŁEGO dr inż. Janusz Zachwieja wykład opracowany na podstawie literatury Funkcje wektorowe Jeśli wektor a jest określony dla parametru t (t należy do przedziału t (, t k )
ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR 2 POZIOM PODSTAWOWY. Etapy rozwiązania zadania
 Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
Przykładowy zestaw zadań nr z matematyki ODPOWIEDZI I SCHEMAT PUNKTOWANIA ZESTAW NR POZIOM PODSTAWOWY Nr zadania Nr czynności Etapy rozwiązania zadania Liczba punktów Uwagi. Podanie dziedziny funkcji f:
MECHANIKA 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO. Wykład Nr 2. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
MECHANIKA 2 Wykład Nr 2 RUCH POSTĘPOWY I OBROTOWY CIAŁA SZTYWNEGO Prowadzący: dr Krzysztof Polko WSTĘP z r C C(x C,y C,z C ) r C -r B B(x B,y B,z B ) r C -r A r B r B -r A A(x A,y A,z A ) Ciało sztywne
1 Funkcje dwóch zmiennych podstawowe pojęcia
 1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
1 Funkcje dwóch zmiennych podstawowe pojęcia Definicja 1 Funkcją dwóch zmiennych określoną na zbiorze A R 2 o wartościach w zbiorze R nazywamy przyporządkowanie każdemu punktowi ze zbioru A dokładnie jednej
MECHANIKA 2 KINEMATYKA. Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
MECHANIKA 2 KINEMATYKA Wykład Nr 5 RUCH KULISTY I RUCH OGÓLNY BRYŁY Prowadzący: dr Krzysztof Polko Określenie położenia ciała sztywnego Pierwszy sposób: Określamy położenia trzech punktów ciała nie leżących
13. Równania różniczkowe - portrety fazowe
 13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
13. Równania różniczkowe - portrety fazowe Grzegorz Kosiorowski Uniwersytet Ekonomiczny w Krakowie rzegorz Kosiorowski (Uniwersytet Ekonomiczny 13. wrównania Krakowie) różniczkowe - portrety fazowe 1 /
Instytut Mechaniki i Inżynierii Obliczeniowej Wydział Mechaniczny Technologiczny Politechnika Śląska
 Instytut Mechaniki i Inżynierii Obliczeniowej www.imio.polsl.pl fb.com/imiopolsl @imiopolsl Wydział Mechaniczny Technologiczny Politechnika Śląska Języki programowania z programowaniem obiektowym Laboratorium
Instytut Mechaniki i Inżynierii Obliczeniowej www.imio.polsl.pl fb.com/imiopolsl @imiopolsl Wydział Mechaniczny Technologiczny Politechnika Śląska Języki programowania z programowaniem obiektowym Laboratorium
Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz
 Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz Dr inż. Janusz Dębiński 1 2.1. Przestrzeń i płaszczyzna Podstawowe definicje Punkt - najmniejszy bezwymiarowy
Dr inż. Janusz Dębiński Mechanika ogólna Wykład 2 Podstawowe wiadomości z matematyki Kalisz Dr inż. Janusz Dębiński 1 2.1. Przestrzeń i płaszczyzna Podstawowe definicje Punkt - najmniejszy bezwymiarowy
8. TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO.
 WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
WYKŁAD 6 1 8. TRYGONOMETRIA. 8.1. FUNKCJE TRYGONOMETRYCZNE KĄTA OSTREGO. SINUSEM kąta nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta do przeciwprostokątnej w trójkącie prostokątnym : =. COSINUSEM
Zasada indukcji matematycznej
 Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
Zasada indukcji matematycznej Twierdzenie 1 (Zasada indukcji matematycznej). Niech ϕ(n) będzie formą zdaniową zmiennej n N 0. Załóżmy, że istnieje n 0 N 0 takie, że 1. ϕ(n 0 ) jest zdaniem prawdziwym,.
SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD
 Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Dr inż. Jacek WARCHULSKI Dr inż. Marcin WARCHULSKI Mgr inż. Witold BUŻANTOWICZ Wojskowa Akademia Techniczna SPOSOBY POMIARU KĄTÓW W PROGRAMIE AutoCAD Streszczenie: W referacie przedstawiono możliwości
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
CAŁOŚĆ OPRACOWANIA POWINNA ZAWIERAĆ MAKSYMALNIE 10 STRON.
 CAŁOŚĆ OPRACOWANIA POWINNA ZAWIERAĆ MAKSYMALNIE 10 STRON. REDAKCJA NIE INGERUJE W ZAWARTOŚĆ MERYTORYCZNĄ NADESŁANYCH ARTYKUŁÓW I NIE DOKONUJE KOREKTY PISOWNI. REDAKCJA PRZYJMUJE PLIKI WYŁĄCZNIE W FORMACIE
CAŁOŚĆ OPRACOWANIA POWINNA ZAWIERAĆ MAKSYMALNIE 10 STRON. REDAKCJA NIE INGERUJE W ZAWARTOŚĆ MERYTORYCZNĄ NADESŁANYCH ARTYKUŁÓW I NIE DOKONUJE KOREKTY PISOWNI. REDAKCJA PRZYJMUJE PLIKI WYŁĄCZNIE W FORMACIE
Funkcją sinus kąta α nazywamy stosunek przyprostokątnej leżącej naprzeciw kąta α do przeciwprostokątnej w trójkącie prostokątnym, i opisujemy jako:
 1. Trygonometria 1.1Wprowadzenie Jednym z podstawowych działów matematyki który wykorzystywany jest w rozwiązywaniu problemów technicznych jest trygonometria. W szkole średniej wprowadzone zostały podstawowe
1. Trygonometria 1.1Wprowadzenie Jednym z podstawowych działów matematyki który wykorzystywany jest w rozwiązywaniu problemów technicznych jest trygonometria. W szkole średniej wprowadzone zostały podstawowe
Analiza stanu naprężenia - pojęcia podstawowe
 10. ANALIZA STANU NAPRĘŻENIA - POJĘCIA PODSTAWOWE 1 10. 10. Analiza stanu naprężenia - pojęcia podstawowe 10.1 Podstawowy zapisu wskaźnikowego Elementy konstrukcji znajdują się w przestrzeni fizycznej.
10. ANALIZA STANU NAPRĘŻENIA - POJĘCIA PODSTAWOWE 1 10. 10. Analiza stanu naprężenia - pojęcia podstawowe 10.1 Podstawowy zapisu wskaźnikowego Elementy konstrukcji znajdują się w przestrzeni fizycznej.
SIMR 2016/2017, Analiza 2, wykład 1, Przestrzeń wektorowa
 SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
SIMR 06/07, Analiza, wykład, 07-0- Przestrzeń wektorowa Przestrzeń wektorowa (liniowa) - przestrzeń (zbiór) w której określone są działania (funkcje) dodawania elementów i mnożenia elementów przez liczbę
Ćwiczenie M-2 Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego Cel ćwiczenia: II. Przyrządy: III. Literatura: IV. Wstęp. l Rys.
 Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
Ćwiczenie M- Pomiar przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego. Cel ćwiczenia: pomiar przyśpieszenia ziemskiego przy pomocy wahadła fizycznego.. Przyrządy: wahadło rewersyjne, elektroniczny
LaTeX wprowadzenie. Piotr Kustra. Faculty of Metals Engineering and Industrial Computer Science. Department of Applied Computer Science and Modelling
 LaTeX wprowadzenie Piotr Kustra Faculty of Metals Engineering and Industrial Computer Science Department of Applied Computer Science and Modelling LaTeX co to jest? LaTeX jest to system składu umoŝliwiający
LaTeX wprowadzenie Piotr Kustra Faculty of Metals Engineering and Industrial Computer Science Department of Applied Computer Science and Modelling LaTeX co to jest? LaTeX jest to system składu umoŝliwiający
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 6 2016/2017, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora.
 1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
1. Podstawy matematyki 1.1. Geometria analityczna W naukach technicznych większość rozpatrywanych wielkości możemy zapisać w jednej z trzech postaci: skalara, wektora oraz tensora. Skalarem w fizyce nazywamy
Liczby zespolone. Magdalena Nowak. 23 marca Uniwersytet Śląski
 Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Uniwersytet Śląski 23 marca 2012 Ciało liczb zespolonych Rozważmy zbiór C = R R, czyli C = {(x, y) : x, y R}. W zbiorze C definiujemy następujące działania: dodawanie: mnożenie: (a, b) + (c, d) = (a +
Nazwisko i imię: Zespół: Data: Ćwiczenie nr 1: Wahadło fizyczne. opis ruchu drgającego a w szczególności drgań wahadła fizycznego
 Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
Nazwisko i imię: Zespół: Data: Cel ćwiczenia: Ćwiczenie nr 1: Wahadło fizyczne opis ruchu drgającego a w szczególności drgań wahadła fizycznego wyznaczenie momentów bezwładności brył sztywnych Literatura
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ
 RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
RUCH OBROTOWY- MECHANIKA BRYŁY SZTYWNEJ Wykład 7 2012/2013, zima 1 MOMENT PĘDU I ENERGIA KINETYCZNA W RUCHU PUNKTU MATERIALNEGO PO OKRĘGU Definicja momentu pędu L=mrv=mr 2 ω L=Iω I= mr 2 p L r ω Moment
SCENARIUSZ LEKCJI. Streszczenie. Czas realizacji. Podstawa programowa
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
Mechanika. Wykład 2. Paweł Staszel
 Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
Mechanika Wykład 2 Paweł Staszel 1 Przejście graniczne 0 2 Podstawowe twierdzenia o pochodnych: pochodna funkcji mnożonej przez skalar pochodna sumy funkcji pochodna funkcji złożonej pochodna iloczynu
BIBLIOGRAFIA W WORD 2007
 BIBLIOGRAFIA W WORD 2007 Ćwiczenie 1 Tworzenie spisu literatury (bibliografii) Word pozwala utworzyć jedną listę główną ze źródłami (cytowanymi książkami czy artykułami), która będzie nam służyć w różnych
BIBLIOGRAFIA W WORD 2007 Ćwiczenie 1 Tworzenie spisu literatury (bibliografii) Word pozwala utworzyć jedną listę główną ze źródłami (cytowanymi książkami czy artykułami), która będzie nam służyć w różnych
Pole magnetyczne magnesu w kształcie kuli
 napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
napisał Michał Wierzbicki Pole magnetyczne magnesu w kształcie kuli Rozważmy kulę o promieniu R, wykonaną z materiału ferromagnetycznego o stałej magnetyzacji M = const, skierowanej wzdłuż osi z. Gęstość
Dodatkowe pakiety i polecenia L A TEXowe
 Dodatkowe pakiety i polecenia L A TEXowe 3 grudnia 2007 1 Ustawienia strony Do zmian ustawień strony warto użyć pakietu geometry, tj. w preambule wpisujemy: \usepackage[]{geometry} Dostępne opcje pakietu
Dodatkowe pakiety i polecenia L A TEXowe 3 grudnia 2007 1 Ustawienia strony Do zmian ustawień strony warto użyć pakietu geometry, tj. w preambule wpisujemy: \usepackage[]{geometry} Dostępne opcje pakietu
INSTRUKCJA PRZYGOTOWANIA MATERIAŁU AUTORSKIEGO POD WZGLĘDEM TECHNICZNYM INFORMACJE OGÓLNE
 [Załącznik nr 1] INSTRUKCJA PRZYGOTOWANIA MATERIAŁU AUTORSKIEGO POD WZGLĘDEM TECHNICZNYM INFORMACJE OGÓLNE Tekst powinien być zapisany w programie Microsoft Office Word (doc, docx, rtf ) i przekazany za
[Załącznik nr 1] INSTRUKCJA PRZYGOTOWANIA MATERIAŁU AUTORSKIEGO POD WZGLĘDEM TECHNICZNYM INFORMACJE OGÓLNE Tekst powinien być zapisany w programie Microsoft Office Word (doc, docx, rtf ) i przekazany za
KATEGORIA OBSZAR WIEDZY
 Moduł 3 - Przetwarzanie tekstów - od kandydata wymaga się zaprezentowania umiejętności wykorzystywania programu do edycji tekstu. Kandydat powinien wykonać zadania o charakterze podstawowym związane z
Moduł 3 - Przetwarzanie tekstów - od kandydata wymaga się zaprezentowania umiejętności wykorzystywania programu do edycji tekstu. Kandydat powinien wykonać zadania o charakterze podstawowym związane z
ECDL/ICDL Przetwarzanie tekstów Moduł B3 Sylabus - wersja 5.0
 ECDL/ICDL Przetwarzanie tekstów Moduł B3 Sylabus - wersja 5.0 Przeznaczenie sylabusa Dokument ten zawiera szczegółowy sylabus dla modułu ECDL/ICDL Przetwarzanie tekstów. Sylabus opisuje zakres wiedzy i
ECDL/ICDL Przetwarzanie tekstów Moduł B3 Sylabus - wersja 5.0 Przeznaczenie sylabusa Dokument ten zawiera szczegółowy sylabus dla modułu ECDL/ICDL Przetwarzanie tekstów. Sylabus opisuje zakres wiedzy i
MECHANIKA 2. Wykład Nr 3 KINEMATYKA. Temat RUCH PŁASKI BRYŁY MATERIALNEJ. Prowadzący: dr Krzysztof Polko
 MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
MECHANIKA 2 Wykład Nr 3 KINEMATYKA Temat RUCH PŁASKI BRYŁY MATERIALNEJ Prowadzący: dr Krzysztof Polko Pojęcie Ruchu Płaskiego Rys.1 Ruchem płaskim ciała sztywnego nazywamy taki ruch, w którym wszystkie
Zajmijmy się najpierw pierwszym równaniem. Zapiszmy je w postaci trygonometrycznej, podstawiając z = r(cos ϕ + i sin ϕ).
 Zad (0p) Zaznacz na płaszczyźnie zespolonej wszystkie z C, które spełniają równanie ( iz 3 z z ) Re [(z + 3) ( z 3) = 0 Szukane z C spełniają: iz 3 = z z Re [(z + 3) ( z 3) = 0 Zajmijmy się najpierw pierwszym
Zad (0p) Zaznacz na płaszczyźnie zespolonej wszystkie z C, które spełniają równanie ( iz 3 z z ) Re [(z + 3) ( z 3) = 0 Szukane z C spełniają: iz 3 = z z Re [(z + 3) ( z 3) = 0 Zajmijmy się najpierw pierwszym
Etap 1. Rysunek: Układy odniesienia
 Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Wprowadzenie. Jaś i Małgosia kręcą się na karuzeli symetrycznej dwuramiennej. Siedzą na karuzeli zwróceni do siebie twarzami, symetrycznie względem osi obrotu karuzeli. Jaś ma dropsa, którego chce dać
Troszkę Geometrii. Kinga Kolczyńska - Przybycień
 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Kilka słów o mierzeniu Otóż jak sama nazwa Geometria (z gr geo-ziemia, metria-miara) ma ona coś wspólnego
Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Spis tresci O Geometrii 1 O Geometrii 2 3 4 5 6 7 Kilka słów o mierzeniu Otóż jak sama nazwa Geometria (z gr geo-ziemia, metria-miara) ma ona coś wspólnego
Nie tylko Power Point
 Nie tylko Power Point Prezentacje w L A TEX-u Maciej Matyka maq@panoramix.ift.uni.wroc.pl Nie Tylko Power Point p. 1/19 Dlaczego Power Point? Dlaczego Power Point jest najczęściej używanym programem do
Nie tylko Power Point Prezentacje w L A TEX-u Maciej Matyka maq@panoramix.ift.uni.wroc.pl Nie Tylko Power Point p. 1/19 Dlaczego Power Point? Dlaczego Power Point jest najczęściej używanym programem do
Podstawy fizyki wykład 4
 Podstawy fizyki wykład 4 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Podstawy fizyki wykład 4 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
L A TEX - bardzo krótkie wprowadzenie
 1 Wstęp L A TEX - bardzo krótkie wprowadzenie (wersja 0.2) Marzena M. Tefelska L A TEXjest systemem umożliwiającym zaawansowane składanie tekstu. Daje możliwość przygotowywania zarówno prostych tekstów,
1 Wstęp L A TEX - bardzo krótkie wprowadzenie (wersja 0.2) Marzena M. Tefelska L A TEXjest systemem umożliwiającym zaawansowane składanie tekstu. Daje możliwość przygotowywania zarówno prostych tekstów,
FUNKCJE LICZBOWE. Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y.
 FUNKCJE LICZBOWE Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y. Innymi słowy f X Y = {(x, y) : x X oraz y Y }, o ile (x, y) f oraz (x, z) f pociąga
FUNKCJE LICZBOWE Na zbiorze X określona jest funkcja f : X Y gdy dowolnemu punktowi x X przyporządkowany jest punkt f(x) Y. Innymi słowy f X Y = {(x, y) : x X oraz y Y }, o ile (x, y) f oraz (x, z) f pociąga
EGZAMIN MATURALNY Z MATEMATYKI
 ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZĘCIA EGZAMINU! Miejsce na naklejkę MMA-R_P-08 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 008 Czas pracy 80 minut Instrukcja
ARKUSZ ZAWIERA INFORMACJE PRAWNIE CHRONIONE DO MOMENTU ROZPOCZĘCIA EGZAMINU! Miejsce na naklejkę MMA-R_P-08 EGZAMIN MATURALNY Z MATEMATYKI POZIOM ROZSZERZONY MAJ ROK 008 Czas pracy 80 minut Instrukcja
Numeryczne rozwiązywanie równań różniczkowych ( )
 Numeryczne rozwiązywanie równań różniczkowych Równanie różniczkowe jest to równanie, w którym występuje pochodna (czyli różniczka). Przykładem najprostszego równania różniczkowego może być: y ' = 2x które
Numeryczne rozwiązywanie równań różniczkowych Równanie różniczkowe jest to równanie, w którym występuje pochodna (czyli różniczka). Przykładem najprostszego równania różniczkowego może być: y ' = 2x które
Technologie informacyjne. semestr I, studia niestacjonarne I stopnia Elektrotechnika rok akademicki 2013/2014 Pracownia nr 2 dr inż.
 Technologie informacyjne semestr I, studia niestacjonarne I stopnia Elektrotechnika rok akademicki 2013/2014 Pracownia nr 2 dr inż. Adam Idźkowski Podstawy Informatyki Pracownia nr 3 2 MS WORD 2007 Podstawy
Technologie informacyjne semestr I, studia niestacjonarne I stopnia Elektrotechnika rok akademicki 2013/2014 Pracownia nr 2 dr inż. Adam Idźkowski Podstawy Informatyki Pracownia nr 3 2 MS WORD 2007 Podstawy
Wprowadzenie do rysowania w 3D. Praca w środowisku 3D
 Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
Wprowadzenie do rysowania w 3D 13 Praca w środowisku 3D Pierwszym krokiem niezbędnym do rozpoczęcia pracy w środowisku 3D programu AutoCad 2010 jest wybór odpowiedniego obszaru roboczego. Można tego dokonać
SPIS ILUSTRACJI, BIBLIOGRAFIA
 SPIS ILUSTRACJI, BIBLIOGRAFIA Ćwiczenie 1 Automatyczne tworzenie spisu ilustracji 1. Wstaw do tekstu roboczego kilka rysunków (WSTAWIANIE OBRAZ z pliku). 2. Ustaw kursor w wersie pod zdjęciem i kliknij
SPIS ILUSTRACJI, BIBLIOGRAFIA Ćwiczenie 1 Automatyczne tworzenie spisu ilustracji 1. Wstaw do tekstu roboczego kilka rysunków (WSTAWIANIE OBRAZ z pliku). 2. Ustaw kursor w wersie pod zdjęciem i kliknij
Ćwiczenia nr 4. Arkusz kalkulacyjny i programy do obliczeń statystycznych
 Ćwiczenia nr 4 Arkusz kalkulacyjny i programy do obliczeń statystycznych Arkusz kalkulacyjny składa się z komórek powstałych z przecięcia wierszy, oznaczających zwykle przypadki, z kolumnami, oznaczającymi
Ćwiczenia nr 4 Arkusz kalkulacyjny i programy do obliczeń statystycznych Arkusz kalkulacyjny składa się z komórek powstałych z przecięcia wierszy, oznaczających zwykle przypadki, z kolumnami, oznaczającymi
TRYGONOMETRIA FUNKCJE TRYGONOMETRYCZNE KĄTA SKIEROWANEGO
 TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
TRYGONOMETRIA Trygonometria to dział matematyki, którego przedmiotem badań są związki między bokami i kątami trójkątów oraz tzw. funkcje trygonometryczne. Trygonometria powstała i rozwinęła się głównie
Podstawy fizyki wykład 4
 Podstawy fizyki wykład 4 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Podstawy fizyki wykład 4 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, W11, PWr Dynamika Obroty wielkości liniowe a kątowe energia kinetyczna w ruchu obrotowym moment bezwładności moment siły II zasada
Temat 1. Więcej o opracowywaniu tekstu
 Temat 1. Więcej o opracowywaniu tekstu Cele edukacyjne Celem tematu 1. jest uporządkowanie i rozszerzenie wiedzy uczniów na temat opracowywania dokumentów tekstowych (m.in. stosowania tabulatorów, spacji
Temat 1. Więcej o opracowywaniu tekstu Cele edukacyjne Celem tematu 1. jest uporządkowanie i rozszerzenie wiedzy uczniów na temat opracowywania dokumentów tekstowych (m.in. stosowania tabulatorów, spacji
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..)
 Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
Wykład 2 - zagadnienie dwóch ciał (od praw Keplera do prawa powszechnego ciążenia i z powrotem..) 24.02.2014 Prawa Keplera Na podstawie obserwacji zgromadzonych przez Tycho Brahe (głównie obserwacji Marsa)
RÓWNANIA RÓŻNICZKOWE WYKŁAD 1
 RÓWNANIA RÓŻNICZKOWE WYKŁAD 1 Przedmiot realizowany w układzie wykład 2 godz. tygodniowo ćwiczenia 2 godz. tygodniowo Regulamin zaliczeń www.mini.pw.edu.pl/~figurny 2 Program zajęć Równania różniczkowe
RÓWNANIA RÓŻNICZKOWE WYKŁAD 1 Przedmiot realizowany w układzie wykład 2 godz. tygodniowo ćwiczenia 2 godz. tygodniowo Regulamin zaliczeń www.mini.pw.edu.pl/~figurny 2 Program zajęć Równania różniczkowe
O 2 O 1. Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego
 msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
msg M 7-1 - Temat: Wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego Zagadnienia: prawa dynamiki Newtona, moment sił, moment bezwładności, dynamiczne równania ruchu wahadła fizycznego,
Podstawy systemu L A TEX
 systemu L A TEX wersja 0.5 27 kwietnia 2006 1 2 3 4 5 1 Zalogować się do systemu. 2 Otworzyć okienko terminala. 3 Korzystać z podstawowych komend systemowych Linuksa: tworzenie katalogów i plików, kopiowanie
systemu L A TEX wersja 0.5 27 kwietnia 2006 1 2 3 4 5 1 Zalogować się do systemu. 2 Otworzyć okienko terminala. 3 Korzystać z podstawowych komend systemowych Linuksa: tworzenie katalogów i plików, kopiowanie
cx cx 1,cx 2,cx 3,...,cx n. Przykład 4, 5
 Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
Matematyka ZLic - 07 Wektory i macierze Wektorem rzeczywistym n-wymiarowym x x 1, x 2,,x n nazwiemy ciąg n liczb rzeczywistych (tzn odwzorowanie 1, 2,,n R) Zbiór wszystkich rzeczywistych n-wymiarowych
BADANIE ELEKTRYCZNEGO OBWODU REZONANSOWEGO RLC
 Ćwiczenie 45 BADANE EEKTYZNEGO OBWOD EZONANSOWEGO 45.. Wiadomości ogólne Szeregowy obwód rezonansowy składa się z oporu, indukcyjności i pojemności połączonych szeregowo i dołączonych do źródła napięcia
Ćwiczenie 45 BADANE EEKTYZNEGO OBWOD EZONANSOWEGO 45.. Wiadomości ogólne Szeregowy obwód rezonansowy składa się z oporu, indukcyjności i pojemności połączonych szeregowo i dołączonych do źródła napięcia
Wykład 5. Zagadnienia omawiane na wykładzie w dniu r
 Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
Wykład 5. Zagadnienia omawiane na wykładzie w dniu 14.11.2018r Definicja (iloraz różnicowy) Niech x 0 R oraz niech funkcja f będzie określona przynajmnniej na otoczeniu O(x 0 ). Ilorazem różnicowym funkcji
Podstawy Informatyki i Technologii Informacyjnej
 Automatyka i Robotyka, Rok I Komputerowe przetwarzanie tekstu PWSZ Gªogów, 2009 Nomenklatura Edytor tekstu (ang. word processor) - program komputerowy sªu» cy tworzeniu, edycji i odpowiedniemu formatowaniu
Automatyka i Robotyka, Rok I Komputerowe przetwarzanie tekstu PWSZ Gªogów, 2009 Nomenklatura Edytor tekstu (ang. word processor) - program komputerowy sªu» cy tworzeniu, edycji i odpowiedniemu formatowaniu
Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego
 POLTECHNKA ŚLĄSKA WYDZAŁ CHEMCZNY KATEDRA FZYKOCHEM TECHNOLOG POLMERÓW LABORATORUM Z FZYK Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego WYZNACZANE MOMENTÓW BEZWŁADNOŚC
POLTECHNKA ŚLĄSKA WYDZAŁ CHEMCZNY KATEDRA FZYKOCHEM TECHNOLOG POLMERÓW LABORATORUM Z FZYK Wyznaczanie momentów bezwładności brył sztywnych metodą zawieszenia trójnitkowego WYZNACZANE MOMENTÓW BEZWŁADNOŚC
Wykład 16. P 2 (x 2, y 2 ) P 1 (x 1, y 1 ) OX. Odległość tych punktów wyraża się wzorem: P 1 P 2 = (x 1 x 2 ) 2 + (y 1 y 2 ) 2
 Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Wykład 16 Geometria analityczna Przegląd wiadomości z geometrii analitycznej na płaszczyźnie rtokartezjański układ współrzędnych powstaje przez ustalenie punktu początkowego zwanego początkiem układu współrzędnych
Paradygmaty programowania
 Paradygmaty programowania Jacek Michałowski, Piotr Latanowicz 15 kwietnia 2014 Jacek Michałowski, Piotr Latanowicz () Paradygmaty programowania 15 kwietnia 2014 1 / 12 Zadanie 1 Zadanie 1 Rachunek predykatów
Paradygmaty programowania Jacek Michałowski, Piotr Latanowicz 15 kwietnia 2014 Jacek Michałowski, Piotr Latanowicz () Paradygmaty programowania 15 kwietnia 2014 1 / 12 Zadanie 1 Zadanie 1 Rachunek predykatów
O pisaniu prac matematycznych po polsku
 O pisaniu prac matematycznych po polsku Adam Maria Syzyf Instytut Matematyki Stosownej 15 listopada 2010 Streszczenie Tekst niniejszy należy traktować jako wstępną wersję. Nie mam czasu, aby go dopracować.
O pisaniu prac matematycznych po polsku Adam Maria Syzyf Instytut Matematyki Stosownej 15 listopada 2010 Streszczenie Tekst niniejszy należy traktować jako wstępną wersję. Nie mam czasu, aby go dopracować.
Projekt Era inżyniera pewna lokata na przyszłość jest współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Biotechnologia w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era inżyniera
Materiały dydaktyczne na zajęcia wyrównawcze z matematyki dla studentów pierwszego roku kierunku zamawianego Biotechnologia w ramach projektu Era inżyniera pewna lokata na przyszłość Projekt Era inżyniera
 http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
http://www-users.mat.umk.pl/~pjedrzej/matwyz.html 1 Opis przedmiotu Celem przedmiotu jest wykształcenie u studentów podstaw języka matematycznego i opanowanie przez nich podstawowych pojęć dotyczących
Bezbolesny wstęp do LATEX
 Bezbolesny wstęp do L A TEX 27 kwietnia 2004 Historia Ciekawe informacje o TEX-ie Czym jest L A TEX? jest doskonałym, darmowym (również wolnym) systemem składu tekstu, służącym między innymi do przygotowywania
Bezbolesny wstęp do L A TEX 27 kwietnia 2004 Historia Ciekawe informacje o TEX-ie Czym jest L A TEX? jest doskonałym, darmowym (również wolnym) systemem składu tekstu, służącym między innymi do przygotowywania
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu
 Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Technikum Nr 2 im. gen. Mieczysława Smorawińskiego w Zespole Szkół Ekonomicznych w Kaliszu Wymagania edukacyjne niezbędne do uzyskania poszczególnych śródrocznych i rocznych ocen klasyfikacyjnych z obowiązkowych
Podstawy obsługi pakietu GNU octave.
 Podstawy obsługi pakietu GNU octave. (wspomaganie obliczeń inżynierskich) Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z obsługą pakietu GNU octave. W ćwiczeniu wprowadzono opis podstawowych komend
Podstawy obsługi pakietu GNU octave. (wspomaganie obliczeń inżynierskich) Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z obsługą pakietu GNU octave. W ćwiczeniu wprowadzono opis podstawowych komend
Zad. 3: Układ równań liniowych
 1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
1 Cel ćwiczenia Zad. 3: Układ równań liniowych Wykształcenie umiejętności modelowania kluczowych dla danego problemu pojęć. Definiowanie właściwego interfejsu klasy. Zwrócenie uwagi na dobór odpowiednich
MATEMATYKA 8. Funkcje trygonometryczne kąta ostrego (α < 90 ). Stosunki długości boków trójkąta prostokątnego nazywamy funkcjami trygonometrycznymi.
 INSTYTUT MEDICUS Kurs przygotowawczy do matury i rekrutacji na studia medyczne Rok 017/018 www.medicus.edu.pl tel. 501 38 39 55 MATEMATYKA 8 FUNKCJE TRYGONOMETRYCZNE. Funkcje trygonometryczne kąta ostrego
INSTYTUT MEDICUS Kurs przygotowawczy do matury i rekrutacji na studia medyczne Rok 017/018 www.medicus.edu.pl tel. 501 38 39 55 MATEMATYKA 8 FUNKCJE TRYGONOMETRYCZNE. Funkcje trygonometryczne kąta ostrego
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ
 KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
KRYTERIA OCENIANIA Z MATEMATYKI W OPARCIU O PODSTAWĘ PROGRAMOWĄ I PROGRAM NAUCZANIA MATEMATYKA 2001 DLA KLASY DRUGIEJ TREŚCI KSZTAŁCENIA WYMAGANIA PODSTAWOWE WYMAGANIA PONADPODSTAWOWE Liczby wymierne i
Dr Kazimierz Sierański www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach
 Dr Kazimierz Sierański kazimierz.sieranski@pwr.edu.pl www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach Forma zaliczenia kursu: egzamin końcowy Grupa kursów -warunkiem
Dr Kazimierz Sierański kazimierz.sieranski@pwr.edu.pl www. If.pwr.wroc.pl/~sieranski Konsultacje pok. 320 A-1: codziennie po ćwiczeniach Forma zaliczenia kursu: egzamin końcowy Grupa kursów -warunkiem
Fale elektromagnetyczne
 Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
Fale elektromagnetyczne dr inż. Ireneusz Owczarek CMF PŁ ireneusz.owczarek@p.lodz.pl http://cmf.p.lodz.pl/iowczarek 2012/13 Plan wykładu Spis treści 1. Analiza pola 2 1.1. Rozkład pola...............................................
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie Teoria sprężystości jest działem mechaniki, zajmującym się bryłami sztywnymi i ciałami plastycznymi. Sprężystość zajmuje się odkształceniami
Przygotowywanie dokumentu do pracy
 Przygotowywanie dokumentu do pracy 1. Wczytywanie tekstu źródłowego (dostępne w menu Plik/Otwórz) Wczytując tekst, nie będący zapisany w rodzimym formacie programu (w tym przypadku MS Word) trzeba pamiętać,
Przygotowywanie dokumentu do pracy 1. Wczytywanie tekstu źródłowego (dostępne w menu Plik/Otwórz) Wczytując tekst, nie będący zapisany w rodzimym formacie programu (w tym przypadku MS Word) trzeba pamiętać,
Mechanika. Wykład 7. Paweł Staszel
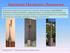 Mechanika Wykład 7 Paweł Staszel 1 Dynamika bryły sztywnej Bryłą (ciałem) sztywnym nazywamy zbiór cząstek zachowujących stałe odległości między sobą. Pomijamy więc zjawiska związane z powstawaniem odkształceń
Mechanika Wykład 7 Paweł Staszel 1 Dynamika bryły sztywnej Bryłą (ciałem) sztywnym nazywamy zbiór cząstek zachowujących stałe odległości między sobą. Pomijamy więc zjawiska związane z powstawaniem odkształceń
Geometria w R 3. Iloczyn skalarny wektorów
 Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Geometria w R 3 Andrzej Musielak Str 1 Geometria w R 3 Działania na wektorach Wektory w R 3 możemy w naturalny sposób dodawać i odejmować, np.: [2, 3, 1] + [ 1, 2, 1] = [1, 5, 2] [2, 3, 1] [ 1, 2, 1] =
Mechanika Kwantowa. Maciej J. Mrowiński. 24 grudnia Funkcja falowa opisująca stan pewnej cząstki ma następującą postać: 2 x 2 )
 Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Mechanika Kwantowa Maciej J. Mrowiński 4 grudnia 11 Zadanie MK1 Funkcja falowa opisująca stan pewnej cząstki w chwili t = ma następującą postać: A(a Ψ(x,) = x ) gdy x [ a,a] gdy x / [ a,a] gdzie a +. Wyznacz
Wymagania edukacyjne z informatyki dla klasy szóstej szkoły podstawowej.
 Wymagania edukacyjne z informatyki dla klasy szóstej szkoły podstawowej. Dział Zagadnienia Wymagania podstawowe Wymagania ponadpodstawowe Arkusz kalkulacyjny (Microsoft Excel i OpenOffice) Uruchomienie
Wymagania edukacyjne z informatyki dla klasy szóstej szkoły podstawowej. Dział Zagadnienia Wymagania podstawowe Wymagania ponadpodstawowe Arkusz kalkulacyjny (Microsoft Excel i OpenOffice) Uruchomienie
