ASTRONOMIA JANUSZA WILANDA
|
|
|
- Jakub Wilczyński
- 7 lat temu
- Przeglądów:
Transkrypt
1 ASTRONOMIA JANUSZA WILANDA Część 1 Podstawy astronomii Warszawa, Piotrków Tryb r. 1
2 Spis treści : 1. Wstęp 3 2. Moje początki z astronomią 3 3. Kierunki świata i rodzaje współrzędnych 4 4. Współrzędne horyzontalne 6 5. Współrzędne równikowe 8 6. Ruch Słońca po niebie KsięŜyc, jego widoczność, zakrycia, zaćmienia Widoczność gwiazd Widoczność planet Skala jasności ciał niebieskich Gwiazdy Zakończenie 32 2
3 PODSTAWY ASTRONOMII 1. Wstęp Program AstroJaWil zacząłem pisać na początku 2002 roku. Od tej pory stale go rozbudowuję. JuŜ kilka razy próbowałem napisać pełną instrukcję do programu, ale nigdy nie udało mi się dogonić jego aktualnej wersji. Częste zmiany w programie (na lepsze, mam nadzieję) szybko dezaktualizowały instrukcję. Pod koniec 2009 roku rozpocząłem kolejną próbę wykonania obszerniejszej instrukcji, ale tym razem mam wizję innego podejścia do tematu. ZauwaŜyłem, Ŝe część uŝytkowników AstroJaWila rozpoczyna dopiero poznawanie nieba, astronomii i praktycznie od razu napotykają na problemy w zrozumieniu niektórych typowo astronomicznych pojęć. I właśnie tutaj zamierzam napisać wystarczająco obszerne wyjaśnienia podstaw astronomii, aby było łatwiej zrozumieć, jak to się dzieje na niebie. Mam tylko małą nadzieję, Ŝe nie zanudzę i da się przez ten materiał łatwo przebrnąć. Nie jest to kompendium wiedzy astronomicznej, a jedynie wierzchołek góry lodowej. Pozostałą wiedzę o kosmosie doradzam juŝ zgłębiać z ksiąŝek, które obszerniej tłumaczą te zagadnienia. Moim celem jest, aby czytelnik zapoznał się z podstawami astronomii, co ułatwi mu poznawanie kosmosu, szczególnie przy posługiwaniu się moim programem AstroJaWil. Polecam zainstalować sobie program oraz przestudiować część drugą Astronomii Janusza Wilanda, czyli instrukcję do programu AstroJaWil. 2. Moje początki z astronomią Dawno, dawno temu, kiedy miałem kilka lat, jechaliśmy z bratem i rodzicami taksówką gdzieś do centrum Warszawy, do miejsca, gdzie obecnie stoją Wars, Sawa i Junior (wtedy pamiętam były tam jakieś Ŝółte budynki). Podczas tej jazdy mój starszy brat pochwalił się, Ŝe wie, w którym kierunku jest północ. Rodzice zdziwili się taką wiedzą brata, a we mnie utkwiło na długie lata pytanie, skąd on wiedział, Ŝe akurat tam jest północ? Czy to moŝna faktycznie wiedzieć? PrzecieŜ ani na niebie, ani w ruchomej taksówce nie było to zaznaczone. Gryzło mnie to pytanie długo i po paru latach stała się moją obsesją wiedza, jak są ustawione kierunki świata, gdziekolwiek się znalazłem. Zostało mi to do dziś. 3
4 Astronomia Janusza Wilanda Podstawy astronomii 3. Kierunki świata i rodzaje współrzędnych Rys. nr 1 kierunki świata. Z oznaczeniem kierunków świata i współrzędnymi ludzie mają duŝe problemy. Aby opisać komuś co się widziało na niebie nie wystarczy powiedzieć, Ŝe wczoraj wieczorem widziałem jakąś jasną gwiazdę nad kominem. Na podstawie tych danych nie określimy, co to była za gwiazda. Aby móc jednoznacznie określić, co i gdzie się widziało, naleŝy zrozumieć istotę róŝnych pomocnych nam współrzędnych. Do naszej praktycznej, amatorskiej astronomii wystarczy opanować w podstawowym zakresie współrzędne: geograficzne, horyzontalne i równikowe. Ale po kolei. Rys. nr 2 Długość geograficzna Ziemia widziana znad bieguna północnego. 4
5 Astronomia Janusza Wilanda Podstawy astronomii Rys. nr 3 Szerokość geograficzna Ziemia z boku i widoczność Słońca. Współrzędne geograficzne. śyjemy na Ziemi i nie zanosi się, aby się to w najbliŝszych latach zmieniło. Dla dokładnego określenia, w którym miejscu na Ziemi się znajdujemy, do dalszych matematycznych obliczeń potrzebne są dane liczbowe. Nie wystarczy powiedzieć, Ŝe w Polsce. Wszystkie współrzędne muszą być podane w wielkościach liczbowych. Powierzchnia Ziemi ma kształt podobny do powierzchni kuli (nazywamy go geoidą) i aby dokładnie wskazać punkt na tej powierzchni trzeba podać dwie wartości współrzędnych. Pierwsza to szerokość geograficzna (oznaczana literą ϕ), których miejsca na Ziemi na północ od równika mają szerokość geograficzną północną, a na południe od równika szerokość geograficzną południową. Szerokość geograficzna przyjmuje wartości z przedziału -90 do +90. Jest to kąt pomiędzy płaszczyzną równika ziemskiego, a naszym miejscem. Wierzchołek tego kąta jest w środku Ziemi. Ziemianie zamieszkujący naszą planetę na północ od równika mają dodatnie wartości szerokości geograficznej, a ci, co są na południu, np. mieszkańcy Australii, muszą podawać swoją szerokość geograficzną jako ujemną. Natomiast, aby określić długość geograficzną trzeba było sztucznie zaznaczyć na Ziemi początek układu współrzędnych. W przypadku szerokości geograficznej równik ziemski jest określony jednoznacznie, lecz dla długości geograficznej trudno wskazać gdzie jest początek równika, czy równoleŝnika. Tak się jednak historycznie w dziejach ludzkości ułoŝyło, iŝ mieszkańcy tej trzeciej planety od Słońca uznali, Ŝe punkt Greenwich (dzielnica Londynu) jest w tym względzie najwaŝniejszy i od niego mamy obliczać długość geograficzną. Dlaczego ten, a nie inny punkt, to odsyłam do innych ksiąŝek. My przyjmujemy do wiadomości, Ŝe południk przechodzący przez Greenwich jest początkiem współrzędnej określanej długością geograficzną i jej wartość w tym miejscu wynosi 0 (zero). 5
6 Długość geograficzna (oznaczana symbolem λ), jest to kąt pomiędzy południkami przechodzącymi przez Greenwich i przez nasze miejsce. Mamy więc punkt zaczepienia dla naliczania długości geograficznej. Na zachód od Greenwich jest długość zachodnia (np. oznaczenie 5 W), a na wschód długość geograficzna wschodnia (np. 21 E). W naszych obliczeniach, literek W czy E nie da się pomnoŝyć i trzeba umówić się co do znaku. Aby było łatwiej zapamiętać przyjmujemy, iŝ skoro Greenwich jest w Europie i na wschód od tego punktu jest zdecydowanie więcej mieszkańców naszego kontynentu, to uznajemy, Ŝe właśnie na wschód są wartości dodatnie. Zresztą bohaterowie kultowego filmu Seksmisja teŝ nie mieli wątpliwości, w którym kierunku naleŝy szukać cywilizacji. Dla przykładu współrzędne Warszawy to 52 N i 021 E, czyli szerokość geogr. φ = +52 i długość geogr. λ = +21. Czasem moŝna się spotkać z długością geograficzną wyraŝoną w mierze czasowej, gdyŝ ta miara jest łatwiejsza do prowadzenia róŝnych obliczeń astronomicznych. I tak, dla Warszawy, długość λ = 021 E = +1godz. 24 min. Przelicznik miary czasowej i kątowej jest prosty: jeden pełny obrót, czyli 360 trwa 24 godziny, zatem 15 odpowiada 1 godzinie czasowej (360/15 = 24). Przypominam takŝe, Ŝe południk danej miejscowości jest to łuk od bieguna północnego poprzez dane miejsce na Ziemi aŝ do bieguna południowego. Wszystkie południki mają tę samą długość w kilometrach. RównoleŜniki mają róŝną długość. NajdłuŜszy równoleŝnik to równik jego długość wynosi km, a koło południkowe przechodzące przez dwa bieguny ma km. Ta róŝnica wskazuje na wielkość spłaszczenia biegunowego Ziemi. Pytanie nr 1. Znajdujecie się dokładnie na biegunie północnym. W którym kierunku moŝecie wykonać pierwszy krok? 4. Współrzędne horyzontalne Chcąc określić jednoznacznie jaki obiekt widzimy na niebie naleŝy podać swoje współrzędne geograficzne, datę, dokładny czas oraz współrzędne horyzontalne obiektu, czyli azymut i wysokość. Dopiero mając te wszystkie dane będziemy mogli wyliczyć, jaki to jest obiekt. Azymut i wysokość są to współrzędne horyzontalne, właściwe dla danego miejsca obserwacji. Ten sam obiekt dla dwóch obserwatorów w róŝnych miejscach będzie miał inny azymut i inną wysokość. Ale wróćmy do współrzędnych horyzontalnych. Wysokość jest to wielkość kąta wzniesienia obiektu nad płaszczyzną horyzontu. Jeśli gwiazda wschodzi lub zachodzi, to jej wysokość wynosi 0 (zero). Jeśli znajduje się wysoko nad nami, w najwyŝszym punkcie, czyli mamy wysokość = 90, wtedy mówimy, iŝ gwiazda znajduje się w zenicie. Punkt przeciwny do zenitu, czyli dokładnie pod nami, ma wysokość równą -90. Punkt ten nazywa się nadir. Czyli nad horyzontem wszystkie wysokości są dodatnie, a pod nim przyjmują wartości ujemne. 6
7 Astronomia Janusza Wilanda Podstawy astronomii Rys. nr 4 azymut astronomiczny i geograficzny Z azymutem jest juŝ troszkę bardziej złoŝona sprawa. Azymut jest to kąt liczony poziomo wzdłuŝ linii horyzontu. Tak, jak w przypadku długości geograficznej, mamy jeden wyznaczony charakterystyczny punkt na Ziemi (Greenwich), to we współrzędnych horyzontalnych, dla azymutu mamy dwa takie punkty na horyzoncie. W typowym miejscu obserwacji na Ziemi mamy tak zwany południk lokalny. Jest to koło wielkie przechodzące przez zenit, nadir i przez bieguny. To koło wielkie przecina się z horyzontem w dwóch punktach. Te punkty wyznaczają dokładnie: kierunek S (południowy) i N (północny). Zatem mamy dwa charakterystyczne punkty na horyzoncie, od których moŝna określać azymut. I tak się równieŝ stało, Ŝe są dwa systemy określania azymutów. Pierwszy, nazywamy go geograficzny, przyjmuje za początek azymutów kierunek N. Azymuty te liczone są zgodnie z biegiem wskazówek zegara właśnie od północy geograficznej. Czyli mamy w tym przypadku dla punktu N (północ) Az = 0, E (wschód) Az = 90, S (południe) Az = 180, W (zachód) Az = 270. KaŜdy z nas obserwując niebo zauwaŝył, iŝ patrząc w kierunku południowym widzimy duŝo więcej gwiazd w ciągu roku, niŝ w kierunku północnym, gdzie widoczne są tylko te same okołobiegunowe konstelacje. Na południu, co miesiąc mamy widoczne inne gwiazdy. Podczas swojej wędrówki po nieboskłonie w ciągu doby kaŝda gwiazda osiąga swoje najwyŝsze połoŝenie na niebie zwane kulminacją górną, mówimy wtedy gwiazda góruje, a takŝe gwiazda ta osiąga swoje najniŝsze połoŝenie zwane kulminacją dolną, mówimy wtedy gwiazda dołuje. Obydwie te kulminacje mają miejsce wtedy, kiedy gwiazda przecina południk lokalny danego miejsca obserwacji. W astronomii obserwacyjnej uŝywany jest takŝe system określania azymutów, nazwijmy go astronomiczny, w którym azymut liczony jest od kierunku południowego. W przeciwieństwie do geograficznego, gdzie azymuty (liczone od kierunku N) były w przedziale 0-360, to w astronomicznym azymuty przyjmują wartości od 0 do +180 licząc na zachód od południa lokalnego i od 0 do -180 licząc na wschód od kierunku S. Jak widać wschodnia część horyzontu ma azymuty ujemne, a zachodnia dodatnie, czyli odwrotnie jak znaki w przypadku wyznaczania długości geograficznej. W programie AstroJaWil uŝywam prawie wszędzie astronomicznego systemu azymutów, ale na prośbę niektórych uŝytkowników, bardzo przyzwyczajonych do tego geograficznego, wprowadziłem moŝliwość wyboru systemu w funkcji HORYZONT, jednej z najczęściej uŝywanej funkcji programu. 7
8 Jakoś udało nam się przebrnąć przez gąszcz pojęć przy okazji współrzędnych horyzontalnych, zatem czas przejść do krótkiego omówienia następnych współrzędnych, jakie są nieodzowne do stosowania w astronomii. Pytanie nr 2. Jaką wartość liczbową przyjmuje wysokość bieguna północnego widocznego z miejscowości o szerokości geograficznej ϕ = +52 stopnie? 5. Współrzędne równikowe Jeśli dostalibyśmy od kogoś informację o tym, Ŝe widział na wysokości 30 i azymucie +45, danego dnia, o konkretnej godzinie, będąc w określonym miejscu na Ziemi, jakiś ciekawy obiekt, to moglibyśmy wyliczyć sobie gdzie na niebie ten dany obiekt byłby wtedy u nas widoczny. Aby jednak ułatwić dokładne określanie połoŝenia wśród gwiazd obiektów na niebie zostały wprowadzone współrzędne zwane równikowymi. Generalnie układ współrzędnych równikowych jest rzutem siatki współrzędnych geograficznych Ziemi na niebo. Odpowiednikiem szerokości geograficznej we współrzędnych równikowych jest deklinacja oznaczana grecką literą δ (delta) oraz współrzędna liczona wzdłuŝ równika niebieskiego, czyli rektascensja oznaczana literą α (alfa). Deklinacje północne przyjmują wartości od 0 (równik niebieski) do +90 (biegun północny), a deklinacje południowe od 0 do -90 (biegun południowy). Rektascensja liczona jest od tzw. Punktu Barana w kierunku wschodnim w mierze czasowej od 0 do 24 godzin. Punkt Barana jest to miejsce, w którym Słońce w swojej wędrówce rocznej przecina równik niebieski przechodząc z półkuli południowej na północną. Dzieje się to w okolicy 20 marca. Najprostsza definicja Punktu Barana: jest to miejsce przecięcia się równika niebieskiego z ekliptyką na początku wiosny. Wprowadziłem nowe pojęcie, ekliptyka, które teŝ muszę objaśnić. Najprościej rzecz ujmując ekliptyka jest to linia na niebie, po której Słońce porusza się w ciągu roku na tle gwiazd. Ekliptyka jest kołem wielkim nachylonym do równika niebieskiego pod kątem ok. 23,5. Pamiętamy, iŝ oś wirowania Ziemi (obrót dobowy) jest nachylona do płaszczyzny, w której obiega Słońce w ciągu roku, pod kątem ok. 66,5. Dzięki temu mamy pory roku. 8
9 Rys. nr 5 droga Słońca wśród gwiazd w układzie współrzędnych równikowych Ruch Słońca po niebie jest dość złoŝony, co opiszę w następnym rozdziale. Podając dwie współrzędne obiektu rektascensję i deklinację jednoznacznie określamy na niebie miejsce, gdzie znajduje się wskazany obiekt. Wtedy nie ma znaczenia, gdzie się na Ziemi znajdujemy. Kiedy podamy alfę i deltę, to wiadomo gdzie tego obiektu szukać. Przy okazji wspomnę, iŝ Ziemia kręcąc się podczas obiegu rocznego Słońca, jest bardzo podobna w swoim ruchu do bączka, którego chyba kaŝdy, jako dziecko rozkręcał na podłodze. Pamiętacie jak ten bączek podczas szybkiego wirowania kiwał się na boki? Niestety Ziemia takŝe tak samo kiwa się na boki i takie jedno boczne kółko trwa ok lat (tzw. Rok Platona). Promień tego kółka wynosi ok. 23,5. W tym czasie biegun północny zatacza spore kółko na niebie. Ten ruch nazywamy precesją osi ziemskiej. Obecnie biegun ten przebywa w okolicy Gwiazdy Polarnej. Za lat, po przebyciu prawie połowy swojego kółka, biegun północny znajdzie się w okolicach Wegi w Lutni. PołoŜenie bieguna zmienia się w czasie i równieŝ Punkt Barana wędruje po niebie. Dwadzieścia wieków temu Hipparch wskazał na niebie punkt, w którym ekliptyka przecinała równik i tam gdzie Słońce na wiosnę znajdowało się na równiku było ono w gwiazdozbiorze Barana, stąd nazwa Punkt Barana. Analogicznie po przeciwnej stronie nazwany został Punkt Wagi, kiedy Słońce będąc w Wadze przecinało na początku jesieni równik niebieski, idąc w kierunku deklinacji południowych. Tak było dawno temu. Teraz nie znajdziemy Punktu Barana w konstelacji Barana. Precesja od tamtego czasu zrobiła juŝ swoje i obecnie Punkt Barana znajduje się w gwiazdozbiorze Ryb, a Punkt Wagi teraz jest w Pannie. Jak z tego wynika, tzw. Punkt Barana zmienia swoje miejsce na niebie, a to pociąga za sobą fakt, Ŝe początek układu współrzędnych równikowych równieŝ nie jest stały i niestety teŝ zmienia swoje połoŝenie. Tak więc współrzędne gwiazd zmieniają się w czasie. Aby astronomowie nie oszaleli od tych zmian, zostały wprowadzone tak zwane epoki. Umówiono się, Ŝe główne epoki do przeliczania współrzędnych gwiazd występują co 50 lat. Współrzędne gwiazd w katalogach podawane są na epoki np czy , a niedługo pewnie juŝ będzie uŝywana epoka
10 Astronomia Janusza Wilanda Podstawy astronomii Póki co, podając współrzędne równikowe gwiazdy naleŝy podawać jaka jest epoka tych współrzędnych. Aby obserwacje planet, komet czy innych ciał moŝna było ze sobą porównać, naleŝy podawać epokę współrzędnych. To jest tylko skutek precesji. Ale są takŝe i inne drobniejsze ruchy wpływające na zmianę współrzędnych równikowych takie jak nutacja i aberracja, których nie będę tu omawiał. Do naszych bardzo amatorskich obserwacji wystarczy wiedzieć, Ŝe coś takiego istnieje. Do super dokładnych obliczeń współrzędnych gwiazd naleŝy jeszcze uwzględnić ruchy własne gwiazd. Prócz samych ruchów Ziemi gwiazdy poruszają się takŝe same z siebie po niebie, co przy dłuŝszych okresach czasu to znacząco wpływa na zmianę ich współrzędnych. Najszybszą gwiazdą na naszym niebie (zaraz po Słońcu) jest Gwiazda Barnarda, która obecnie znajduje się w WęŜowniku. Jej ruch własny jest największy i wynosi 10.3 na rok. Jasność tej gwiazdy jest niestety dość słaba tylko 9,57 mag, ale jest wystarczająco jasna, aby co roku wykonywać jej zdjęcie i po kilku latach będziemy mogli pochwalić się sekwencją z widoczną zmianą połoŝenia Gwiazdy Barnarda wśród pobliskich jej gwiazd. Rys. nr 6 Przekrój sfery niebieskiej przez południk lokalny. Patrząc z danego miejsca obserwacji charakterystyczne jest to, Ŝe równik niebieski styka się z teoretycznym horyzontem w dwóch punktach: punkt wschodu (E) i zachodu (W). Poza tym równik, jako okrąg na niebie, jest stale zawsze w tym samym miejscu. Jest on nachylony do płaszczyzny horyzontu pod kątem równym 90 - ϕ. Na przykład, w Warszawie, równik niebieski przecina lokalny południk na wysokości h = = Ruch Słońca po niebie Co jest ciekawego w tym, co widzimy kaŝdego dnia? Słońce wschodzi, mamy dzień, Słońce góruje i zachodzi. Po zachodzie Słońca mamy zmierzch cywilny. Gdy Słońce osiągnie wysokość 6 pod horyzontem zaczyna się zmierzch nawigacyjny. Niebo dalej się ściemnia umoŝliwiając Ŝeglarzom nawigację okrętową. Kiedy Słońce osiąga wysokość 12 pod horyzontem, wtedy zaczyna się zmierzch astronomiczny. Jak Słońce zanurzy się 18 stopni pod horyzont, 10
11 Astronomia Janusza Wilanda Podstawy astronomii to mamy początek czarnej nocy astronomicznej. Nad ranem mamy odwrotną kolejność i tak przy Słońcu na wysokości -18 mamy początek świtu astronomicznego. Potem jak wysokość Słońca osiągnie wartość -12 zaczyna się świt nawigacyjny, a przy -6 mamy juŝ świt cywilny. Wkrótce znowu wschodzi Słońce i mamy znowu dzień i tak w kółko. Rozpoczynamy budowę naszego Układu Słonecznego od ustawienia po środku naszej wyobraźni Ŝółtej, jasnej i gorącej kulki to oczywiście jest Słońce. Dookoła Słońca prawie po okręgu poziomo obiega Słońce mała kuleczka, to jest nasza Ziemia. Patrząc na tę płaszczyznę elipsy (prawie kołowa) lekko z góry widzimy, Ŝe Ziemia obiega Słońce w lewo w kierunku przeciwnym do ruchu wskazówek zegara. Płaszczyznę, po której porusza się Ziemia dookoła Słońca nazywamy płaszczyzną ekliptyki. Oczywiście taki jeden obieg trwa jeden rok. W tym czasie nasza kuleczka Ziemia obraca się wokół swojej osi tak szybko, Ŝe podczas jednego obiegu wykona nieco ponad 365 obrotów wokół swojej osi. Teraz wyobraźmy sobie, Ŝe oś obrotu tej kuleczki jest nachylona do płaszczyzny ekliptyki pod kątem ok. 66,5. ZałóŜmy teŝ, Ŝe oś wirowania Ziemi zachowuje równoległość przez cały obiegu dookoła Słońca. Jeśli to, co napisałem będziemy w stanie w wyobraźni sobie obracać i powiększać, to szybko zrozumiemy zjawiska widoczne na niebie. Mała powtórka: Płaszczyzna obiegu Ziemi dookoła Słońca to płaszczyzna ekliptyki. Ziemia obiega dookoła Słońca po elipsie zbliŝonej do okręgu, ale jednak to jest elipsa. Oś wirowania Ziemi nachylona jest do tej płaszczyzny pod kątem 66,5 i przyjmujemy, Ŝe zachowuje cały czas równoległość do siebie. Na razie do opanowania ruchów Słońca precesję zostawiamy w spokoju. Analizując powyŝsze załoŝenia moŝemy dojść do wyjaśnienia ruchów Słońca obserwowanych z Ziemi. Rys. nr 7 roczny ruch Ziemi wokół Słońca śeby nie było za prosto, to do naszych rozwaŝań dołoŝymy jeszcze czas i kalendarz. Doba została podzielona na 24 równe godziny. To wiemy i wydaje się 11
12 nam to bardzo oczywiste. Ale pytanie: jaka jest definicja tej doby? - to juŝ nie jest takie oczywiste. Narzucającą się jest odpowiedź, Ŝe doba jest to czas, podczas którego Ziemia wykonuje jeden obrót wokół swojej osi. Lecz ta wydawałoby się prawidłowa odpowiedź, nie jest odpowiedzią jednoznaczną. Jeśli przyjmiemy, Ŝe jeden obrót Ziemi, to jest czas pomiędzy dwoma górowaniami jakiejś dalekiej gwiazdy, np. Aldebarana, to mierząc ten czas naszymi zegarkami stwierdzimy, Ŝe upłynęło 23 godz. 56 min i 4 sek. Czas jaki upłynął pomiędzy górowaniami tej samej gwiazdy jest definicją doby gwiazdowej. Jednak nasze Ŝycie jest dostosowane do ruchu naszego Słońca i za dobę, która ma 24 godziny, przyjęto dawniej 1/365,2422 roku zwrotnikowego (czas pomiędzy dwoma kolejnymi przejściami Słońca przez Punkt Barana). Ta doba nazywa się średnią dobą słoneczną. Czyli godzina jest to 1/24 średniej doby słonecznej. Teraz króciutko o kalendarzu. Kalendarz juliański wprowadzony przez Juliusza Cezara obowiązywał od 1 stycznia 45 r. p.n.e. (do tej pory jest stosowany w astronomii) liczył sobie 365 dni i ćwierć dnia. Ta ćwiartka powodowała, Ŝe po czterech kolejnych latach trzeba było dodać jeden dzień, aby ruch Słońca na niebie dopasować do naszego kalendarza. Stąd lata przestępne z lutym mającym 29 dni zamiast normalnie 28. Jednak średni rok zwrotnikowy trwa nie 365,25 dni, lecz jest bliŝej wartości 365,2422 dni, więc z biegiem lat występowała coraz większa róŝnica pomiędzy kalendarzem, a wynikającym z niego połoŝeniem Słońca. Kalendarz juliański opóźniał się o jedną dobę na kaŝde 128 lat. Aby dopasować kalendarz do roku astronomicznego, na zlecenie papieŝa Grzegorza XIII został opracowany nowy kalendarz, który modyfikuje kalendarz juliański o poprawkę, iŝ jeśli ilość lat podzielna jest przez 100, a nie jest podzielna przez 400, to luty w tym roku ma 28 dni. Ponadto w 1582 roku po 5 października nastąpił dzień 14 października, aby nadrobić opóźnienie. I tak lata 1700, 1800 i 1900 miały luty z 28 dniami, a rok 1600 i 2000 były to zwykłe przestępne lata z lutym 29-cio dniowym. Kalendarz gregoriański dopiero za 3323 lat będzie wykazywał błąd 1 doby. 12
13 Rys. nr 8 - Widoczność Słońca w Warszawie (azymuty geograficzne). Wracając do ruchów naszego Słońca, przypominam, iŝ Ziemia obiega Słońce po elipsie. Ten fakt wywołuje następujące skutki: Ziemia na swojej orbicie ok. 3 lipca jest w aphelium, czyli w punkcie najdalej odległym od Słońca (ok. 152 mln km) oraz ok. 3 stycznia znajduje się w peryhelium, czyli najbliŝej Słońca (ok. 147 mln km). Ponadto, zgodnie z prawami Keplera, jeśli Ziemia porusza się po elipsie, to jej orbitalna prędkość liniowa jest większa w peryhelium niŝ w aphelium. Zakładamy, Ŝe ruch obrotowy Ziemi jest stały, (bardzo duŝa masa Ziemi i brak tarcia w próŝni), a przed chwilą stwierdziliśmy, Ŝe Ziemia obiega Słońce czasem szybciej, czasem wolniej. I właśnie te dwa fakty skutkują tym, Ŝe dla obserwatora z Ziemi prędkość kątowa Słońca na niebie nie jest stała, lecz zmienia się. Znaczy to, Ŝe czas pomiędzy dwoma kolejnymi górowaniami Słońca w danym miejscu takŝe się zmienia. Aby odmierzane godziny czasu były jednakowe, to nie moŝna było się wzorować na Słońcu, tylko wprowadzono pojęcie Słońce średnie i czas średni słoneczny, który to płynął jednostajnie, a Słońce prawdziwe wykonuje wokół Słońca średniego cykliczne wahania. Jeśli do tego ruchu prawdziwego Słońca dodamy skutek nachylenia osi wirowania Ziemi do płaszczyzny ekliptyki (czyli zmiana połoŝenia względem równika o +/-23,5, to otrzymamy wykres ruchu rocznego Słońca na niebie zwanego analemmą. RóŜnicę czasu pomiędzy średnim czasem słonecznym, a czasem Słońca prawdziwego nazywamy równaniem czasu. Największą róŝnicę (-16 min) pomiędzy średnim czasem słonecznym i prawdziwym słonecznym 13
14 mamy na początku listopada, a na początku lutego wartość ta wynosi ok. +14 min. Równanie czasu cztery razy w roku przyjmuje wartość zero i wtedy czas średni słoneczny pokrywa się ze Słońcem prawdziwym. Występuje to 15 kwietnia, 13 czerwca, 1 września i 25 grudnia. Gdybyśmy na stałe ustawili aparat fotograficzny z obiektywem szerokokątnym i na jednej i tej samej klatce naświetlali przez cały rok co kilka dni, z bardzo krótkim czasem naświetlania zdjęcie Słońca dokładnie o tej samej godzinie danej strefy czasowej, np. 12:00 UT, to na zdjęciu otrzymamy wykres analemmy. Rys. nr 9 diagram analemmy Powróćmy teraz do widoczności Słońca z miejsca obserwacji. Zapewne wszyscy zauwaŝyli, Ŝe zimą Słońce świeci nisko nad horyzontem, a latem wysoko. Jest to skutek nachylenia osi wirowania Ziemi do płaszczyzny obiegu dookoła Słońca (ekliptyka). W poprzednim rozdziale napisałem, iŝ z danego miejsca na Ziemi równik niebieski zawsze jest widoczny w tym samym miejscu, natomiast ekliptyka jest nachylona do równika. Latem Słońce znajduje się 23,5 nad równikiem i w Warszawie (ϕ = 52 ) osiąga maksymalną wysokość h = ,5 = 61,5, a zimą, kiedy Słońce osiąga połoŝenie południowe jego wysokość maksymalna (podczas górowania) wynosi h = 38-23,5 = 14,5. Przypominam, iŝ 38 jest to stała wysokość równika niebieskiego w Warszawie (90 - ϕ). 14
15 7. KsięŜyc, jego widoczność, zakrycia i zaćmienia Drugim ciałem Układu Słonecznego, którego nie sposób nie zauwaŝyć na niebie, to jest KsięŜyc. Fascynuje on widocznymi gołym okiem na jego powierzchni ciemnymi plamami, które przy pewnej wyobraźni tworzą na niebie okrągłą twarz. Co ciekawe widoczna jest zawsze tylko ta sama twarz. Wielu z nas dochodzi wówczas do błędnego wniosku, iŝ KsięŜyc nie obraca się, a pytanie o czas obrotu KsięŜyca wokół jego własnej osi sprawia takŝe problem. Ale odpowiedź nie jest trudna, jak tylko wyobrazicie sobie patrząc z góry obiegający KsięŜyc Ziemię w średniej odległości 384 tys. km i cały czas pokazujący nam tę samą stronę. Odpowiedź wtedy jest prosta: KsięŜyc wykonuje jeden obrót wokół swojej osi dokładnie w tym samym czasie, w jakim wykona jeden obieg dookoła Ziemi. Jeden średni obieg KsięŜyca dookoła Ziemi zwany miesiącem gwiazdowym (syderycznym) trwa 27 dni 7 godz. 43 min i 11,5 sek. W tym uśrednionym czasie KsięŜyc znajdzie się, ogólnie mówiąc, w tym samym miejscu na tle gwiazd. Ciągle piszę ogólnie, ok., średnio, gdyŝ zarówno Ziemia jak i KsięŜyc krąŝą po swych orbitach po elipsach, a nie okręgach i nic tu nie ma stałego, wszystko musimy uśredniać, aby poznać rząd wielkości. Kiedy ten nasz KsięŜyc znajdzie się po tym miesiącu syderycznym w tym samym miejscu na niebie, czyli po ponad 27 dniach, to Ziemia w tym czasie wykonała ok. 1/12 obiegu dookoła Słońca. Zatem jeśliby zacząć liczyć czas obiegu KsięŜyca poczynając od nowiu, to stwierdzimy, iŝ po tych ponad 27 dniach KsięŜyc jeszcze nie dogonił Słońca. Brakuje mu ok. 30 na niebie. Na to, aby obserwowany z Ziemi KsięŜyc wykonał jeden obieg na niebie, względem Słońca (powiedzmy od nowiu do nowiu) potrzeba średnio: 29 dni 12 godz. 44 min i 2,9 sek. Jest to tak zwany miesiąc synodyczny. Rys. nr 10 fazy KsięŜyca - widok z Ziemi. 15
16 Rys. nr 11 fazy KsięŜyca - widok znad bieguna północnego Ziemi Strzałka pokazuje kierunek ruchu KsięŜyca Omawiając KsięŜyc nie sposób nie wspomnieć o fazach KsięŜyca, których kolejność kaŝdy powinien znać. Począwszy od nowiu, kiedy KsięŜyc jest przy Słońcu (nie widzimy go). Potem mamy okres, kiedy KsięŜyc ma kształt literki D ( dopełnia, mój kolega mówi duŝeje ). Po ok. tygodniu od nowiu widzimy tylko prawą połowę oświetloną, a właśnie tu muszę napisać uzupełnienie. Jak KsięŜyc jest w małej fazie to wyraźnie widać prócz jasnego rogalika oświetlonej części tarczy KsięŜyca przez Słońce, takŝe dopełnienie tarczy do pełnego kółka. Widoczne jest to w postaci takiej szarej poświaty. Nazywamy to światłem popielatym. Jest to światło słoneczne odbite od chmur na Ziemi, które oświetla tę nocną część KsięŜyca i dlatego jest widoczna z Ziemi. Światło popielate najlepiej widoczne jest wiosną tuŝ po nowiu, wkrótce po zachodzie Słońca. O tej porze roku wieczorem ekliptyka schodzi do horyzontu pod duŝym kątem i KsięŜyc jest widoczny dość wysoko. Analogicznie, na jesieni, rano przed wschodem Słońca takŝe dobrze widać światło popielate na starym KsięŜycu tuŝ przed złączeniem KsięŜyca ze Słońcem. Fazę tę nazywamy nowiem. Podczas nowiu KsięŜyca nie jesteśmy w stanie zobaczyć, gdyŝ jest blisko Słońca. Tylko podczas zaćmień Słońca moŝna zobaczyć KsięŜyc podczas nowiu. 16
17 Światło popielate (z lewej strony) z prawej prześwietlony rogal światła słonecznego padającego bezpośrednio na KsięŜyc. fot. Janusz Wiland Po ok. siedmiu dniach od nowiu widzimy oświetloną przez Słońce prawą połówkę KsięŜyca i mamy wtedy pierwszą kwadrę. (Pamiętajcie, iŝ dla obserwatora na Ziemi na półkuli południowej KsięŜyc podczas pierwszej kwadry ma oświetloną lewą połówkę tarczy, a widoczna twarz jest odwrócona do góry nogami ). Po ok dniach od nowiu widzimy jasno oświetloną całą tarczę KsięŜyca. Ta faza KsięŜyca nazywa się pełnią. Jest to najmniej poŝądany moment na obserwacje astronomiczne dla miłośnika astronomii. Na KsięŜycu prawie wcale nie widać kraterów, a jego blask zdecydowanie przytłumia widoczne gwiazdy, a szczególnie utrudnia obserwację wszelkich mgławic. Po następnym tygodniu nad ranem obserwujemy ostatnią kwadrę i w tym czasie znowu na KsięŜycu w pobliŝu terminatora, czyli linii stanowiącej granicę pomiędzy nocna i dzienną stroną KsięŜyca (Słońce dla obserwatora na KsięŜycu znajduje się na horyzoncie) widać wspaniale kratery i inne szczegóły na jego powierzchni (tak jak podczas I kwadry) góry, wały, doliny i uskoki rzucają długie cienie, co jest wspaniale widoczne przez nasze teleskopy. Po następnym tygodniu KsięŜyc znowu osiąga nów i tak skończył się miesiąc synodyczny. 17
18 Warto tutaj napisać, iŝ KsięŜyc w pierwszej kwadrze najlepiej obserwować wieczorem na wiosnę, w pełni zimą, a w ostatniej kwadrze nad ranem jesienią. W tym czasie KsięŜyc widoczny jest wysoko na niebie. KsięŜyc obiega Ziemię w płaszczyźnie, która jest nachylona do płaszczyzny ekliptyki (płaszczyzna obiegu Ziemi dookoła Słońca) pod kątem ok. 5,1. Powinienem dodać niestety, bowiem, gdyby te płaszczyzny dokładnie się pokrywały, mielibyśmy co miesiąc zaćmienie Słońca i KsięŜyca. W związku z tym te najefektowniejsze zjawiska na niebie zachodzą bardzo rzadko. Rys. nr 12 płaszczyzna orbity KsięŜyca nachylona do ekliptyki pod kątem 5,1 Kiedy KsięŜyc w swojej wędrówce po niebie przecina płaszczyznę ekliptyki ze strony południowej na północną mówimy, iŝ KsięŜyc jest w węźle wstępującym. Oczywiście po przeciwnej stronie, kiedy KsięŜyc przechodzi przez ekliptykę z północnej strony na południową, mówimy, iŝ KsięŜyc jest w węźle zstępującym. Aby doszło do zaćmienia Słońca lub KsięŜyca warunkiem koniecznym jest, aby podczas nowiu (dla zaćmień Słońca) i pełni (dla zaćmień KsięŜyca) KsięŜyc znajdował się blisko któregoś z węzłów, czyli musi znajdować się bliziutko ekliptyki. Bo tylko wówczas moŝe dojść do zaćmienia, kiedy te trzy ciała znajdą się w jednej linii, tzw. linii węzłów. Zatem, aby doszło do zaćmienia musi być spełniony warunek, Ŝe linia węzłów KsięŜyca przecina Słońce i w tym samym momencie KsięŜyc znajduje się w którymś z węzłów. Rys. nr 13 schemat zaćmienia Słońca i KsięŜyca. 18
19 Częściowe zaćmienie Słońca r. fot. Janusz Wiland Całkowite zaćmienie Słońca r. fot. Tomasz Zwoliński 19
20 Zaćmienia Słońca zdarzają się wyłącznie podczas nowiu. Wtedy KsięŜyc zasłania swoją tarczą tarczę Słońca. Napisano juŝ wiele na temat najefektowniejszego zjawiska na niebie, jakim jest niewątpliwie całkowite zaćmienie Słońca. Gorąco polecam przeŝyć samemu, na własne oczy i ciało (wyraźnie odczuwalna zmiana temperatury powietrza) to fantastyczne zjawisko. UwaŜam, Ŝe warto poświęcić większość swoich oszczędności, aby wybrać się na wyprawę tam, gdzie będzie widoczna całkowita faza zaćmienia. Niestety w Polsce najbliŝsze takie całkowite zaćmienie nastąpi 7 X 2135, a co gorsza nawet w Europie nie nastąpi to prędko. Ostatnie widoczne w Polsce całkowite zaćmienie Słońca było 30 czerwca 1954 r., które znam tylko z opowieści mojej mamy. Za moich juŝ czasów wybrałem się razem z grupą łódzko-warszawską PTMA nad Balaton, aby tam zobaczyć całkowite zaćmienie Słońca w dniu 11 sierpnia 1999 r. Mieliśmy wiele szczęścia, gdyŝ przy pięknej pogodzie podziwialiśmy to cudowne zjawisko w pełnej krasie. Do opisu naszej relacji i innych grup odsyłam do specjalnego numeru URANII POSTĘPY ASTRONOMII z roku 1999 zatytułowanego Dane nam było Słońca zaćmienie. Dla obserwatora na Ziemi widoczna średnica tarczy Słońca i KsięŜyca jest niemal tej samej wielkości - ok. pół stopnia. To jest wyjątkowy zbieg okoliczności, Ŝe Słońce jest tyle samo razy większe niŝ KsięŜyc, co odległość Ziemia-Słońce w stosunku do odległości Ziemia-KsięŜyc. PoniewaŜ Ziemia i KsięŜyc nie posiadają orbit kołowych, lecz eliptyczne, ten stoŝek cienia KsięŜyca czasami wchodzi w głąb powierzchni Ziemi i wtedy dochodzi do całkowitych zaćmień. Ale zdarza się teŝ, Ŝe KsięŜyc jest w okolicach perygeum (punkt najbliŝszy Ziemi) i jednocześnie Ziemia przechodzi w pobliŝu peryhelium (punkt Ziemi najbliŝej Słońca). Wówczas stoŝek cienia KsięŜyca nie dochodzi do powierzchni Ziemi i mamy tzw. obrączkowe zaćmienie Słońca. KsięŜyc mający wtedy mniejszą niŝ Słońce widomą na niebie średnicę tarczy nie zakryje całej tarczy naszej dziennej gwiazdy, tylko będzie widoczna dookoła KsięŜyca jasna obwódka, tzw. obrączka. Podczas centralnego zaćmienia obrączkowego nie zrobi się tak ciemno jak podczas całkowitej fazy. Podczas zaćmienia całkowitego maksymalnie średnica stoŝka cienia KsięŜyca przecinająca powierzchnię Ziemi wynosi ok. 270 km. Zatem jest to zjawisko bardzo rzadkie. Warto tu dodać, iŝ kaŝdego roku KsięŜyc oddala się od Ziemi o ok. 4 cm i wkrótce przyjdą takie czasy, Ŝe nie będziemy mieli na Ziemi juŝ w ogóle całkowitych zaćmień Słońca. Będą wyłącznie same obrączkowe. Ale spokojnie, to jeszcze nie nastąpi za naszego Ŝycia. NajbliŜsze częściowe zaćmienie Słońca zobaczymy w Polsce 4 stycznia 2011 r. 20
21 O wiele częściej jesteśmy w stanie zobaczyć całkowite zaćmienie KsięŜyca, które jest widoczne z całej półkuli Ziemi, z której widoczny jest KsięŜyc podczas zaćmienia. W czasie fazy całkowitej KsięŜyc przybiera ceglasto czerwony kolor z uwagi na promienie słoneczne, które załamywane są w naszej atmosferze. Podczas przejścia światła przez naszą grubą atmosferę (zostają rozproszone na pyłach w atmosferze najkrótsze niebieskie fale), przez którą przechodzą tylko czerwone promienie widma światła słonecznego i padają na ciemny KsięŜyc znajdujący się całkowicie w stoŝku cienia. Gdybyśmy podczas całkowitego zaćmienia KsięŜyca znajdowali się wtedy na KsięŜycu i spojrzeli na Ziemię, to widzielibyśmy czarne kółko tarczy Ziemi i dookoła jasny, ceglasto-czerwony krąg. Czasem po wielkich wybuchach wulkanów do atmosfery dostaje się tak wiele pyłu, Ŝe nasza atmosfera zatrzymuje prawie całe światło od Słońca i wtedy podczas całkowitych zaćmień KsięŜyc znika nam z pola widzenia. Gdzie się on wtedy znajduje, widzimy tylko po braku gwiazd w tym miejscu. Składanka zdjęć wykonanych podczas zaćmienia KsięŜyca 5 II 1990 fot. Janusz Wiland NajbliŜsze widoczne z Polski całkowite zaćmienie KsięŜyca będzie 15 czerwca 2011 roku. Jeśli utworzymy sobie wykres prostokątny dla współrzędnych ekliptycznych, gdzie ekliptyka jest poziomą kreską na środku mapy, to na tym wykresie droga KsięŜyca będzie widoczna jako sinusoida, przecinająca się z linią ekliptyki w dwóch miejscach (węzłach). Węzły te wykonują pełen obieg wokół ekliptyki w ciągu ok. 18 lat, zatem co ten okres czasu KsięŜyc przechodzi przez te same obszary na niebie. W ciągu tych 18 lat KsięŜyc zakryje wszystkie gwiazdy 21
22 zaznaczone na tej mapie odległe na 5,1 stopnia poniŝej i powyŝej ekliptyki. Jak widać w obszarze tym, którym KsięŜyc zakrywa gwiazdy, moŝna znaleźć kilka bardzo jasnych gwiazd takich jak: Aldebaran, Spica, Antares, Regulus i dwie bardzo jasne gromady otwarte gwiazd M44 śłóbek w Raku i M45 Plejady w Byku. Kiedy dochodzi do zakryć tych gwiazd i gromad gwiazd obserwatorzy zjawisk zakryciowych mają wtedy święto. Osobiście obserwuję zjawiska zakryciowe od 1979 roku i uwaŝam je za bardzo atrakcyjne, gdyŝ na własne oczy moŝna zobaczyć jak szybko KsięŜyc porusza się wśród gwiazd. Kiedy KsięŜyc (w fazie pomiędzy nowiem a pełnią) zbliŝa się do gwiazdy, mam wtedy zawsze emocje. Gwiazda sobie wyraźnie świeci, KsięŜyc zbliŝa się do niej i w pewnym momencie gwiazda raptownie znika. Zdarza się, Ŝe zobaczymy jak na ułamek sekundy przed całkowitym zniknięciem gwiazda tylko lekko przygaśnie. Do takiej sytuacji dochodzi, kiedy zakrywana gwiazda jest gwiazdą podwójną i KsięŜyc zakryje najpierw jeden składnik i przez ułamek sekundy świeci jeszcze drugi składnik. Całe szczęście, Ŝe na KsięŜycu nie ma atmosfery i te zakrycia są tak znakomicie widoczne. Przy jasnym brzegu KsięŜyca moŝemy zaobserwować zakrycia tylko tych kilku najjaśniejszych gwiazd. KsięŜyc po niebie porusza się w ruchu dobowym, tak jak Słońce, ze wschodu na zachód. Lecz wśród gwiazd jego ruch odbywa się w przeciwnym kierunku do ruchu dobowego, czyli z zachodu na wschód. Zatem, jak juŝ pisałem, po nowiu KsięŜyc zakrywa gwiazdy swą wschodnią, (lewą) ciemną stroną, a odkrywa prawą, oświetloną przez Słońce jasną stroną tarczy. Po pełni KsięŜyca jest odwrotnie. KsięŜyc zakrywa gwiazdy jasnym brzegiem, a odkrywa ciemnym. Tak więc po pełni obserwujemy odkrycia gwiazd zza ciemnej strony KsięŜyca. Są to trudniejsze zjawiska do obserwacji, gdyŝ gwiazdę widzimy dopiero w momencie odkrycia trzeba dokładnie wiedzieć, w którym miejscu zza KsięŜyca wyjdzie gwiazda. Bardzo rzadko, ale zdarza się, Ŝe KsięŜyc w swym ruchu po niebie zakrywa swą tarczą jasną gwiazdę nie centralnie, ale na skraju tarczy, swym brzegiem. Wtedy moŝe dojść to tzw. zakrycia brzegowego. Jest to jedno z najefektowniejszych zjawisk zakryciowych, gdyŝ gwiazda moŝe zniknąć i pojawić się za pojedynczymi górami kilkanaście razy w ciągu jednej minuty. Kiedy do takich zakryć jasnych gwiazd przez KsięŜyc dochodzi przy jego ciemnej stronie, wtedy obserwatorzy zjawisk zakryciowych zbierają się i urządzają wspólną wyprawę do obliczonego miejsca, gdzie będzie granica przebiegu tego zjawiska. Obserwatorzy rozstawiają się co kilkaset metrów i rejestrują dokładnie swoją pozycję geograficzną i wszystkie momenty zakryć i odkryć danej gwiazdy. KaŜdy obserwator uzyska inne wyniki, które po złoŝeniu w całość dają wykres profilu KsięŜyca widocznego w tym miejscu. Traktujemy to prawie jak wyprawę na KsięŜyc. MoŜemy po zbiorowej obserwacji zobaczyć na wykresie góry, które zaobserwowaliśmy na KsięŜycu. Zainteresowanych obserwacjami tych zjawisk odsyłam do Sekcji Obserwacji Pozycji i Zakryć PTMA. 22
23 Zakrycie Wenus przez KsięŜyc 1 XII 2008 fot. Wojciech Piskorz Do prześlicznych widoków na niebie zaliczam zakrycia jasnych planet przez KsięŜyc. Wszystkie planety poruszają się po orbitach bardzo zbliŝonych do ekliptyki, w związku z tym znajdują się one czasem na drodze KsięŜyca. Do najefektowniejszych tego typu zjawisk moŝna zaliczyć zakrycie/odkrycie w nocy ciemną stroną najjaśniejszej widocznej z Ziemi planety Wenus. Zjawisko takie było widoczne 7 X 1988, lecz z powodu chmur było ono widoczne tylko w północno-wschodniej Polsce. 1 XII 2008 doszło do niesamowitej potrójnej koniunkcji Jowisza, Wenus i KsięŜyca. Wieczorem tego dnia doszło do zakrycia Wenus przez KsięŜyc. Niestety pogoda okazała się łaskawa tylko w niektórych południowych regionach Polski. Następne takie nocne zakrycie Wenus będziemy mogli zobaczyć dopiero w piątek 1 kwietnia 2044 r. 8. Widoczność gwiazd Opisu samych konstelacji i co w nich ciekawego moŝna zobaczyć nie będę tutaj umieszczał. Zostało to zrobione w innych ksiąŝkach (np. Przemysław Rudź Niebo na weekend ) oraz w moim programie AstroJaWil, do którego instrukcję opisałem w osobnej ksiąŝeczce. Ograniczę się tutaj tylko do podziału gwiazdozbiorów na pewne grupy, przy okazji omawiana ruchów sfery niebieskiej. 23
24 Astronomia Janusza Wilanda Podstawy astronomii Gwiazdy nas otaczające moŝna podzielić na trzy grupy pod względem widoczności: gwiazdy nie zachodzące (zawsze znajdujące się nad horyzontem), wschodzące i zachodzące oraz nigdy nie wschodzące (zawsze będące pod horyzontem). Rys. nr 14 Widoczność gwiazd w Warszawie. Gwiazdy nie zachodzące, to te, które widoczne są kaŝdej nocy. Czy w dzień, czy w nocy, gwiazdy te są zawsze nad horyzontem. MoŜemy zapisać wzorem, iŝ gwiazdy nie zachodzą w danej miejscowości o szerokości geograficznej ϕ, jeśli ich deklinacja jest większa niŝ (90 - ϕ). Gwiazdy z pasa o przedziale deklinacji (90 - ϕ) do +(90 - ϕ) wschodzą i zachodzą i są widoczne dla nas tylko wtedy, kiedy znajdują się nad horyzontem. Skrajny przypadek występuje dla gwiazd o deklinacji równej +(90 - ϕ), kiedy gwiazda w kulminacji dolnej styka się z horyzontem, a gwiazda o deklinacji (90 - ϕ) w swojej kulminacji górnej tylko osiągnie na moment wysokość równą 0 w punkcie S przecięcia się linii horyzontu z południkiem lokalnym. Pozostałe gwiazdy o deklinacjach leŝących dalej na południe niŝ (90 - ϕ) są dla nas niewidoczne. Dodam, iŝ na biegunie północnym widać tylko połowę nieba z gwiazdami o deklinacji północnej (równik pokrywa się tam z horyzontem). Analogicznie jest na biegunie południowym, gdzie widać tylko gwiazdy o deklinacji południowej (wartości ujemne). Na równiku obserwator moŝe w ciągu roku zobaczyć wszystkie moŝliwe gwiazdy. Obydwa bieguny widoczne są tam na horyzoncie po przeciwnych stronach, a równik niebieski przechodzi jak wszędzie przez punkt wschodu i zachodu oraz, tym razem, przez zenit. Słońce i gwiazdy widoczne z równika wschodzą i zachodzą prostopadle do horyzontu. Po zachodzie Słońca bardzo szybko robi się ciemno, bowiem czas, kiedy Słońce osiągnie wysokość 18 pod horyzontem (noc astronomiczna), jest najkrótszy na całej kuli ziemskiej. 24
25 9. Widoczność planet Planety obiegają Słońce po orbitach połoŝonych w niewielkich nachyleniach do ekliptyki. Tak więc planety Układu Słonecznego widzimy z Ziemi zawsze w pobliŝu ekliptyki. Dane tabelaryczne o kaŝdej z nich znajdziecie w programie AstroJaWil. Teraz wskaŝę tylko najwaŝniejsze elementy ich widoczności z Ziemi. W Układzie Słonecznym są dwie planety, Merkury i Wenus, których orbity leŝą wewnątrz orbity Ziemi. Rys. nr 15 orbita Ziemi i planety wewnętrznej na przykładzie Wenus Merkury porusza się po orbicie o dość duŝym mimośrodzie (0,2056), co powoduje, Ŝe w peryhelium zbliŝa się on na 46 mln km do Słońca, a w aphelium oddala od niego na 69,8 mln km. Przez ten mimośród jego maksymalne elongacje osiągają wartości od 17 do 27,8 w zaleŝności od ustawienia widocznej orbity z Ziemi. Złączenie dolne występuje wtedy, kiedy Merkury znajdzie się pomiędzy Ziemią a Słońcem. W przypadku, kiedy Merkury znajdzie się w swoim węźle (analogicznie jak dla KsięŜyca) dojdzie wówczas do tranzytu Merkurego przed tarczą Słońca. Następne takie tranzyt zobaczymy 9 maja 2016 i 11 listopada Złączenie górne występuje wtedy, kiedy Merkury przechodzi za Słońcem. Merkury nie ma naturalnych satelitów. 25
26 Wenus jest to najjaśniejszy obiekt na niebie po Słońcu i KsięŜycu. Druga planeta wewnętrzna ma orbitę wewnątrz orbity Ziemi. Tak samo jak Merkury, Wenus oddala się od Słońca teŝ tylko na pewną odległość kątową. Maksymalna elongacja od Słońca, to ok. 46. Mimośród orbity jest mały (0,0067), czyli ma ona kształt bliski okręgu. Średnia odległość Wenus od Słońca to ok. 108 mln km. Wenus w złączeniu dolnym takŝe potrafi przejść przed tarczą Słońca. Ostatnio obserwowaliśmy takie zjawisko 8 czerwca 2004 roku, a następne będziemy mogli obserwować 6 czerwca Będzie to dla nas ostatnie przejście Wenus przed tarczą Słońca widoczne z terenów Polski. Następne przejście Wenus przed tarczą Słońca nasi potomkowie zobaczą 11 czerwca 2247 roku. Wenus nie ma naturalnych satelitów. Pozostałe planety, które nazywamy zewnętrznymi, posiadają orbity większe niŝ Ziemia, toteŝ kaŝda z nich ma połoŝenie względem Ziemi zwane opozycją, dwie kwadratury i złączenie ze Słońcem. Rys. nr 16 orbita Ziemi i planety zewnętrznej na przykładzie Marsa Data opozycji Odległość mln km Średnica tarczy sek. kątowe ,2 14, ,7 13, ,8 15, ,2 18, ,5 24,2 Tabela 1 - NajbliŜsze opozycje Marsa 26
27 Mars, będący najbliŝszą planetą, obiega Słońce po orbicie zewnętrznej o mimośrodzie 0,09338, co jest juŝ dość wyraźną elipsą. Planeta ta, co ok. 780 dni jest w opozycji, czyli znajduje się po przeciwnej stronie niŝ Słońce. Obserwujemy ją wtedy przez całą noc. Góruje około północy i jest to analogiczna sytuacja, jaka występuje podczas pełni KsięŜyca. Eliptyczność orbity Marsa sprawia, Ŝe podczas kolejnych opozycji odległość Ziemia Mars przyjmuje zdecydowanie róŝne wartości. Co ok. 15 lat występuje tak zwana Wielka Opozycja Marsa, kiedy moment opozycji przypada w pobliŝu peryhelium Marsa. Jeśli na to nałoŝy się zbieŝność, Ŝe Ziemia w tym czasie będzie w aphelium, wtedy podczas takiej opozycji odległość z Ziemi do Marsa będzie wynosiła tylko 55,8 mln km, a tarcza Marsa będzie miała wielkość aŝ 25. Tak było w ostatnich dniach sierpnia 2003 roku. Podczas opozycji Marsa 29 I 2010 planeta będzie miała tarczę o widomej wielkości tylko 14 i będzie w odległości ok. 100 mln km od Ziemi. Te dwie opozycje, i , będą opozycjami w środku 15-to letniego cyklu, zatem Mars będzie miał najmniejszą widoczną tarczkę, bo będzie najdalej od Ziemi. Lecz nie zraŝa to miłośników obserwacji planet, którzy i w takich warunkach obserwują szczegóły na tarczy Czerwonej Planety. Mars ma dwa księŝyce (Fobos i Dejmos), które nie są widoczne przez nasze teleskopy. Pomiędzy orbitami Marsa i Jowisza rozpościera się pas planetoid. Olbrzymia grawitacja Jowisza nie pozwoliła, aby setki tysięcy tych okruchów skalnych połączyło się w jedną planetę. Przez to do dziś oglądamy je w miejscu, gdzie powinna była powstać planeta. Dla nabrania pewności, Ŝe tam powinna znaleźć się planeta moŝna przeanalizować empiryczną regułę Titiusa-Bodego. Z tabelki widać, Ŝe brakuje tam planety, a pozostałe rzeczywiste planety ułoŝyły swoje orbity całkiem zgodnie z regułą, której postać jest następująca: a = 0,4 + 0,3 * k Gdzie: a - średnia odległość planety od Słońca wyraŝona w jednostkach astronomicznych (j.a. jest to średnia odległość Ziemia-Słońce, ok. 150 mln km), k = 0, 1, 2, 4, 8,..., (ciąg kolejnych potęg dwójki wraz z zerem). Planeta k średnia odległość od Słońca w j.a. wg reguły rzeczywista Merkury 0 0,4 0,39 Wenus 1 0,7 0,72 Ziemia 2 1,0 1,00 Mars 4 1,6 1,52 pas planetoid 8 2,8 2,17-3,64 Jowisz 16 5,2 5,20 Saturn 32 10,0 9,54 Uran 64 19,6 19,2 Neptun ,8 30,1 Tabela 2 - Reguła Titiusa-Bodego w liczbach 27
28 Jowisz obiega Słońce w ciągu około 12 lat. PoniewaŜ ekliptyka przecina na niebie 12 gwiazdozbiorów zodiakalnych, Jowisz mniej więcej co roku widziany jest w innym gwiazdozbiorze. Ale tutaj mała dygresja. Na skutek precesji obecnie ekliptyka przechodzi przez 13 gwiazdozbiorów! Pomiędzy Skorpionem, a Strzelcem Słońce pod koniec roku kilkanaście dni znajduje się w gwiazdozbiorze WęŜownika. Obecnie, na przełomie 2009/2010 Jowisz znajduje się w KozioroŜcu i z kaŝdym rokiem jego warunki obserwacyjne poprawiają się, gdyŝ deklinacja Jowisza systematycznie zmienia się w kierunku północnym. W Byku i Bliźniętach, a więc wysoko na niebie, Jowisza będziemy oglądali w latach Jowisz znajduje się juŝ w odległości 778 mln km od Słońca, a więc 5 razy dalej niŝ Ziemia. Opozycje Jowisza przypadają co 399 dni. Wokół Jowisza krąŝą cztery jasne księŝyce: Io, Europa, Ganimedes i Calisto, które bez problemu juŝ widać przez lornetkę. Z pomocą programu AstroJaWil moŝna zaplanować sobie obserwację licznych zjawisk zachodzących pomiędzy tymi księŝycami takimi jak wzajemne zakrycia, zaćmienia przez tarczę Jowisza, przejście przed tarczą. Przy duŝych powiększeniach (teleskop, luneta) widać nawet cienie tych księŝyców na tarczy planety, ale do tego potrzebny jest dobry sprzęt i bardzo stabilna atmosfera. Jowisz ma obecnie odkrytych ponad 60 księŝyców, ale są one tak małe, Ŝe nie zobaczymy ich przez nasze teleskopy. Saturn krąŝy jeszcze dalej od Słońca niŝ Jowisz, bo średnio w odległości 1427 mln km. Przez małe lunetki, a nawet przez duŝe lornety dojrzymy juŝ charakterystyczne dla tej planety pierścienie i najjaśniejszy księŝyc Saturna (Tytan). Dysponując teleskopem o średnicy cm dostrzeŝemy takŝe jeszcze kilka słabszych naturalnych satelitów Saturna (Rhea, Dione, Mimas, Japetus). Saturn obiega Słońce w 29,5 roku, co sprawia, Ŝe bardzo nieznacznie przemieszcza się wśród gwiazd. Pod koniec 2009 roku Saturn przebywa w pobliŝu równika niebieskiego w Pannie i jego warunki obserwacyjne niestety z kaŝdym rokiem pogarszają się, gdyŝ w tym miejscu ekliptyka idzie coraz niŝej w kierunku deklinacji południowych. Saturn będzie widoczny coraz niŝej nad horyzontem przez wiele lat. Ponownie znajdzie się w okolicach równika niebieskiego dopiero około 2026 roku i wtedy jego widoczność będzie dobra, a gdy osiągnie maksymalne północne połoŝenie na ekliptyce (rok 2033), to wtedy będą jego najlepsze warunki obserwacyjne. Saturn ma obecnie odkrytych ponad 60 księŝyców, ale są one tak małe, Ŝe nie zobaczymy ich przez nasze teleskopy. Uran jest widoczny jak gwiazdka ok. 6 mag i trzeba wiedzieć dokładnie gdzie on się znajduje wśród gwiazd, aby go odnaleźć. Przy stabilnej atmosferze i duŝym powiększeniu moŝemy zobaczyć jego niebieskawą tarczkę. Obieg dookoła Słońca zajmuje mu juŝ 84 lata, tak więc jego połoŝenie nieznacznie się zmienia wśród gwiazd. Na początku 2010 roku Urana obserwujemy na granicy gwiazdozbiorów Ryb i KozioroŜca w pobliŝu równika niebieskiego. Z kaŝdym rokiem jego warunki obserwacyjne będą się poprawiały. Uran ma prawie 30 zarejestrowanych księŝyców, z czego najjaśniejsze Miranda, Ariel, Umbriel, Tytania i Oberon są na granicy widoczności przez nasze duŝe teleskopy. Najjaśniejsze z nich osiągają jasność zaledwie ok. 13,0 i 13,2 mag. Neptun jest juŝ słabiutkim punkcikiem na niebie (jasność ok. 8 mag). Aby go rozpoznać, nieodzowna jest dokładna mapka. Neptun obiega Słońce raz na prawie 165 lat. Obecnie przebywa w KozioroŜcu, w pobliŝu równika. W tamtych 28
29 okolicach będziemy go jeszcze długo obserwować. Wśród 13-tu naturalnych księŝyców Neptuna najjaśniejszym jest Tryton o jasności 13,0 mag. 10. Skala jasności gwiazd Jasności gwiazd i obiektów na niebie określamy w tzw. wielkościach gwiazdowych magnitudo. Nie jest to skala liniowa, lecz logarytmiczna. Jednakowe przyrosty jednostek skali jasności nie odpowiadają takim samym przyrostom jasności. Za zero tej skali przyjęto jasność najjaśniejszych gwiazd widocznych bardzo dobrze gołym okiem, jak np. Wega i Capella. Ich jasność wynosi 0 mag. Gwiazdy najsłabsze, ledwo widoczne w warunkach czarnej nocy, mają jasność +6 mag. Choć są tacy, obdarzeni znakomitym wzrokiem, którzy widzą w idealnych warunkach gwiazdy o jasności nawet +7mag. Zasięg wizualny słynnego teleskopu o średnicy zwierciadła 508 cm na Mt Palomar wynosi +21 mag, a teleskop Hubble a, mimo iŝ ma dwukrotnie mniejszą średnicę zwierciadła, moŝe zarejestrować obiekty o jasności +28 mag. Idąc od gwiazd zerowych w stronę jaśniejszych obiektów przechodzimy do ujemnych wartości jasności. I tak Syriusz, najjaśniejsza gwiazda nieba nocnego, ma jasność -1,54 mag, Jowisz ok. -2,5 mag, Wenus (najjaśniejsza planeta) w maksimum osiąga jasność ok. -4,6 mag. KsięŜyc w pełni ma jasność -12 mag, a Słońce ma -26 mag. RóŜnica jasności świecenia dwóch gwiazd wynosząca jednej magnitudo, jest to współczynnik ok. 2,5 razy w natęŝeniu oświetlenia. RóŜnica dwóch magnitudo określa przyrost natęŝenia światła równy 2,5*2,5 = 6,25 razy. Dla 3 magnitudo mamy przyrost jasności 2,5*2,5*2,5 = 15,6 razy. Stąd przy róŝnicy jasności 5 mag (2,5*2,5*2,5*2,5*2,5=97,7) moŝna powiedzieć, Ŝe ta słabsza gwiazda świeci ok.100 razy słabiej niŝ ta jaśniejsza. lp jasność konstelacja nazwa własna odl. lata św. 1 1,54 α CMa Syriusz 8,61 2 0,62 α Car Kanopus 312,73 3 0,27 α 1 Cen Alfa Centauri 4,36 4 0,05 α Boo Arktur 36, ,03 α Lyr Wega 25, ,21 α 1 Aur Capella 42, ,18 β Ori Rigel 772, ,4 α CMi Procjon 11, ,45 α Eri Achernar 143, ,45 α Ori Betelgeuza 427, ,61 β Cen Hadar 525, ,76 α Aql Altair 16, ,87 α Tau Aldebaran 65, ,98 α Vir Spika 262, ,06 α Sco Antares 604,02 Tabela nr 3 Wykaz najjaśniejszych gwiazd i ich jasności 29
Ruch obiegowy Ziemi. Ruch obiegowy Ziemi. Cechy ruchu obiegowego. Cechy ruchu obiegowego
 Ruch obiegowy Ziemi Ruch obiegowy Ziemi Ziemia obiega Słońce po drodze zwanej orbitą ma ona kształt lekko wydłużonej elipsy Czas pełnego obiegu wynosi 365 dni 5 godzin 48 minut i 46 sekund okres ten nazywamy
Ruch obiegowy Ziemi Ruch obiegowy Ziemi Ziemia obiega Słońce po drodze zwanej orbitą ma ona kształt lekko wydłużonej elipsy Czas pełnego obiegu wynosi 365 dni 5 godzin 48 minut i 46 sekund okres ten nazywamy
( W.Ogłoza, Uniwersytet Pedagogiczny w Krakowie, Pracownia Astronomiczna)
 TEMAT: Analiza zdjęć ciał niebieskich POJĘCIA: budowa i rozmiary składników Układu Słonecznego POMOCE: fotografie róŝnych ciał niebieskich, przybory kreślarskie, kalkulator ZADANIE: Wykorzystując załączone
TEMAT: Analiza zdjęć ciał niebieskich POJĘCIA: budowa i rozmiary składników Układu Słonecznego POMOCE: fotografie róŝnych ciał niebieskich, przybory kreślarskie, kalkulator ZADANIE: Wykorzystując załączone
Wędrówki między układami współrzędnych
 Wykład udostępniam na licencji Creative Commons: Wędrówki między układami współrzędnych Piotr A. Dybczyński Układ równikowy godzinny i układ horyzontalny zenit północny biegun świata Z punkt wschodu szerokość
Wykład udostępniam na licencji Creative Commons: Wędrówki między układami współrzędnych Piotr A. Dybczyński Układ równikowy godzinny i układ horyzontalny zenit północny biegun świata Z punkt wschodu szerokość
Elementy astronomii w geografii
 Elementy astronomii w geografii Prowadzący: Marcin Kiraga kiraga@astrouw.edu.pl Podstawowe podręczniki: Jan Mietelski, Astronomia w geografii Eugeniusz Rybka, Astronomia ogólna Podręczniki uzupełniające:
Elementy astronomii w geografii Prowadzący: Marcin Kiraga kiraga@astrouw.edu.pl Podstawowe podręczniki: Jan Mietelski, Astronomia w geografii Eugeniusz Rybka, Astronomia ogólna Podręczniki uzupełniające:
Pozorne orbity planet Z notatek prof. Antoniego Opolskiego. Tomasz Mrozek Instytut Astronomiczny UWr Zakład Fizyki Słońca CBK PAN
 Pozorne orbity planet Z notatek prof. Antoniego Opolskiego Tomasz Mrozek Instytut Astronomiczny UWr Zakład Fizyki Słońca CBK PAN Początek Młody miłośnik astronomii patrzy w niebo Młody miłośnik astronomii
Pozorne orbity planet Z notatek prof. Antoniego Opolskiego Tomasz Mrozek Instytut Astronomiczny UWr Zakład Fizyki Słońca CBK PAN Początek Młody miłośnik astronomii patrzy w niebo Młody miłośnik astronomii
Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
 Geografia listopad Liceum klasa I, poziom rozszerzony XI Ziemia we wszechświecie Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
Geografia listopad Liceum klasa I, poziom rozszerzony XI Ziemia we wszechświecie Zapisy podstawy programowej Uczeń: 2. 1) wyjaśnia cechy budowy i określa położenie różnych ciał niebieskich we Wszechświecie;
Jowisz i jego księŝyce
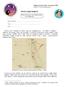 Jowisz i jego księŝyce Obserwacje przez niewielką lunetkę np: Galileoskop Międzynarodowy Rok Astronomii 2009 Projekt Jesteś Galileuszem Imię i Nazwisko 1 :... Adres:... Wiek:... Jowisza łatwo odnaleźć
Jowisz i jego księŝyce Obserwacje przez niewielką lunetkę np: Galileoskop Międzynarodowy Rok Astronomii 2009 Projekt Jesteś Galileuszem Imię i Nazwisko 1 :... Adres:... Wiek:... Jowisza łatwo odnaleźć
Ruchy planet. Wykład 29 listopada 2005 roku
 Ruchy planet planety wewnętrzne: Merkury, Wenus planety zewnętrzne: Mars, Jowisz, Saturn, Uran, Neptun, Pluton Ruch planet wewnętrznych zachodzi w cyklu: koniunkcja dolna, elongacja wschodnia, koniunkcja
Ruchy planet planety wewnętrzne: Merkury, Wenus planety zewnętrzne: Mars, Jowisz, Saturn, Uran, Neptun, Pluton Ruch planet wewnętrznych zachodzi w cyklu: koniunkcja dolna, elongacja wschodnia, koniunkcja
Dyfrakcja to zdolność fali do uginania się na krawędziach przeszkód. Dyfrakcja światła stanowi dowód na to, że światło ma charakter falowy.
 ZAŁĄCZNIK V. SŁOWNICZEK. Czas uniwersalny Czas uniwersalny (skróty: UT lub UTC) jest taki sam, jak Greenwich Mean Time (skrót: GMT), tzn. średni czas słoneczny na południku zerowym w Greenwich, Anglia
ZAŁĄCZNIK V. SŁOWNICZEK. Czas uniwersalny Czas uniwersalny (skróty: UT lub UTC) jest taki sam, jak Greenwich Mean Time (skrót: GMT), tzn. średni czas słoneczny na południku zerowym w Greenwich, Anglia
Układy współrzędnych równikowych
 Wykład udostępniam na licencji Creative Commons: Układy współrzędnych równikowych Piotr A. Dybczyński 15 października 2013 Układ współrzędnych sferycznych Taki układ wydaje się prosty. Sytuacja komplikuje
Wykład udostępniam na licencji Creative Commons: Układy współrzędnych równikowych Piotr A. Dybczyński 15 października 2013 Układ współrzędnych sferycznych Taki układ wydaje się prosty. Sytuacja komplikuje
Tomasz Ściężor. Almanach Astronomiczny na rok 2012
 Tomasz Ściężor Almanach Astronomiczny na rok 2012 Klub Astronomiczny Regulus Kraków 2011 1 Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna część tej
Tomasz Ściężor Almanach Astronomiczny na rok 2012 Klub Astronomiczny Regulus Kraków 2011 1 Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna część tej
CZY TE SCENY TO TYLKO FIKCJA LITERACKA CZY. CZY STAROśYTNI EGIPCJANIE FAKTYCZNIE UMIELI TAK DOBRZE PRZEWIDYWAĆ ZAĆMIENIA?
 MOTYW ZAĆMIENIA SŁOŃCA S W POWIEŚCI I FILMIE FARAON M CZY TE SCENY TO TYLKO FIKCJA LITERACKA CZY TEś CHOĆBY SZANSA MOśLIWO LIWOŚCI? CZY STAROśYTNI EGIPCJANIE FAKTYCZNIE UMIELI TAK DOBRZE PRZEWIDYWAĆ ZAĆMIENIA?
MOTYW ZAĆMIENIA SŁOŃCA S W POWIEŚCI I FILMIE FARAON M CZY TE SCENY TO TYLKO FIKCJA LITERACKA CZY TEś CHOĆBY SZANSA MOśLIWO LIWOŚCI? CZY STAROśYTNI EGIPCJANIE FAKTYCZNIE UMIELI TAK DOBRZE PRZEWIDYWAĆ ZAĆMIENIA?
Cykl Metona. Liceum Klasy I III Doświadczenie konkursowe nr 1
 Liceum Klasy I III Doświadczenie konkursowe nr 1 Rok 2017 1. Wstęp teoretyczny Od czasów prehistorycznych życie człowieka regulują trzy regularnie powtarzające się cykle astronomiczne. Pierwszy z nich
Liceum Klasy I III Doświadczenie konkursowe nr 1 Rok 2017 1. Wstęp teoretyczny Od czasów prehistorycznych życie człowieka regulują trzy regularnie powtarzające się cykle astronomiczne. Pierwszy z nich
1. Obserwacje nieba 2. Gwiazdozbiór na północnej strefie niebieskiej 3. Gwiazdozbiór na południowej strefie niebieskiej 4. Ruch gwiazd 5.
 Budowa i ewolucja Wszechświata Autor: Weronika Gawrych Spis treści: 1. Obserwacje nieba 2. Gwiazdozbiór na północnej strefie niebieskiej 3. Gwiazdozbiór na południowej strefie niebieskiej 4. Ruch gwiazd
Budowa i ewolucja Wszechświata Autor: Weronika Gawrych Spis treści: 1. Obserwacje nieba 2. Gwiazdozbiór na północnej strefie niebieskiej 3. Gwiazdozbiór na południowej strefie niebieskiej 4. Ruch gwiazd
Opozycja... astronomiczna...
 Opozycja... astronomiczna... Pojęcie opozycja bez dodatków ją bliżej określających jest intuicyjnie zrozumiałe. Wyraz ma swoją etymologię łacińską - oppositio i oznacza przeciwstawienie. Przenosząc to
Opozycja... astronomiczna... Pojęcie opozycja bez dodatków ją bliżej określających jest intuicyjnie zrozumiałe. Wyraz ma swoją etymologię łacińską - oppositio i oznacza przeciwstawienie. Przenosząc to
NACHYLENIE OSI ZIEMSKIEJ DO PŁASZCZYZNY ORBITY. Orbita tor ciała niebieskiego lub sztucznego satelity krążącego wokół innego ciała niebieskiego.
 RUCH OBIEGOWY ZIEMI NACHYLENIE OSI ZIEMSKIEJ DO PŁASZCZYZNY ORBITY Orbita tor ciała niebieskiego lub sztucznego satelity krążącego wokół innego ciała niebieskiego. OBIEG ZIEMI WOKÓŁ SŁOŃCA W czasie równonocy
RUCH OBIEGOWY ZIEMI NACHYLENIE OSI ZIEMSKIEJ DO PŁASZCZYZNY ORBITY Orbita tor ciała niebieskiego lub sztucznego satelity krążącego wokół innego ciała niebieskiego. OBIEG ZIEMI WOKÓŁ SŁOŃCA W czasie równonocy
Zadania do testu Wszechświat i Ziemia
 INSTRUKCJA DLA UCZNIA Przeczytaj uważnie czas trwania tekstu 40 min. ). W tekście, który otrzymałeś są zadania. - z luką - rozszerzonej wypowiedzi - zadania na dobieranie ). Nawet na najłatwiejsze pytania
INSTRUKCJA DLA UCZNIA Przeczytaj uważnie czas trwania tekstu 40 min. ). W tekście, który otrzymałeś są zadania. - z luką - rozszerzonej wypowiedzi - zadania na dobieranie ). Nawet na najłatwiejsze pytania
Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych.
 Wykład udostępniam na licencji Creative Commons: Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych. Piotr A. Dybczyński Związek czasu słonecznego z gwiazdowym. Zadanie:
Wykład udostępniam na licencji Creative Commons: Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych. Piotr A. Dybczyński Związek czasu słonecznego z gwiazdowym. Zadanie:
XXXIX OLIMPIADA GEOGRAFICZNA Zawody III stopnia pisemne podejście 2
 -2/1- Zadanie 8. W każdym z poniższych zdań wpisz lub podkreśl poprawną odpowiedź. XXXIX OLIMPIADA GEOGRAFICZNA Zawody III stopnia pisemne podejście 2 A. Słońce nie znajduje się dokładnie w centrum orbity
-2/1- Zadanie 8. W każdym z poniższych zdań wpisz lub podkreśl poprawną odpowiedź. XXXIX OLIMPIADA GEOGRAFICZNA Zawody III stopnia pisemne podejście 2 A. Słońce nie znajduje się dokładnie w centrum orbity
Tomasz Ściężor. Almanach Astronomiczny na rok 2013
 Tomasz Ściężor Almanach Astronomiczny na rok 2013 Klub Astronomiczny Regulus Kraków 2012 1 Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna część tej
Tomasz Ściężor Almanach Astronomiczny na rok 2013 Klub Astronomiczny Regulus Kraków 2012 1 Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna część tej
Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych.
 Wykład udostępniam na licencji Creative Commons: Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych. Piotr A. Dybczyński Związek czasu słonecznego z gwiazdowym. Zadanie:
Wykład udostępniam na licencji Creative Commons: Wyznaczanie długości i szerokości geograficznej z obserwacji astronomicznych. Piotr A. Dybczyński Związek czasu słonecznego z gwiazdowym. Zadanie:
Gdzie się znajdujemy na Ziemi i w Kosmosie
 Gdzie się znajdujemy na Ziemi i w Kosmosie Realizując ten temat wspólnie z uczniami zajęliśmy się określeniem położenia Ziemi w Kosmosie. Cele: Rozwijanie umiejętności określania kierunków geograficznych
Gdzie się znajdujemy na Ziemi i w Kosmosie Realizując ten temat wspólnie z uczniami zajęliśmy się określeniem położenia Ziemi w Kosmosie. Cele: Rozwijanie umiejętności określania kierunków geograficznych
PROSZĘ UWAŻNIE SŁUCHAĆ NA KOŃCU PREZENTACJI BĘDZIE TEST SPRAWDZAJĄCY
 PROSZĘ UWAŻNIE SŁUCHAĆ NA KOŃCU PREZENTACJI BĘDZIE TEST SPRAWDZAJĄCY RUCH OBROTOWY ZIEMI Ruch obrotowy to ruch Ziemi wokół własnej osi. Oś Ziemi jest teoretyczną linią prostą, która przechodzi przez Biegun
PROSZĘ UWAŻNIE SŁUCHAĆ NA KOŃCU PREZENTACJI BĘDZIE TEST SPRAWDZAJĄCY RUCH OBROTOWY ZIEMI Ruch obrotowy to ruch Ziemi wokół własnej osi. Oś Ziemi jest teoretyczną linią prostą, która przechodzi przez Biegun
Odległość kątowa. Liceum Klasy I III Doświadczenie konkursowe 1
 Liceum Klasy I III Doświadczenie konkursowe 1 Rok 2015 1. Wstęp teoretyczny Patrząc na niebo po zachodzie Słońca mamy wrażenie, że znajdujemy się pod rozgwieżdżoną kopułą. Kopuła ta stanowi połowę tzw.
Liceum Klasy I III Doświadczenie konkursowe 1 Rok 2015 1. Wstęp teoretyczny Patrząc na niebo po zachodzie Słońca mamy wrażenie, że znajdujemy się pod rozgwieżdżoną kopułą. Kopuła ta stanowi połowę tzw.
Październikowe tajemnice skrywane w blasku Słońca
 Październikowe tajemnice skrywane w blasku Słońca Do tej pory zajmowaliśmy się po części opisem nieba nocnego. I to nie powinno dziwić: wszak ta pora nadaje się na obserwacje rozgwieżdżonego nieba. Tymczasem
Październikowe tajemnice skrywane w blasku Słońca Do tej pory zajmowaliśmy się po części opisem nieba nocnego. I to nie powinno dziwić: wszak ta pora nadaje się na obserwacje rozgwieżdżonego nieba. Tymczasem
Piotr Brych Wzajemne zakrycia planet Układu Słonecznego
 Piotr Brych Wzajemne zakrycia planet Układu Słonecznego 27 sierpnia 2006 roku nastąpiło zbliżenie Wenus do Saturna na odległość 0,07 czyli 4'. Odległość ta była kilkanaście razy większa niż średnica tarcz
Piotr Brych Wzajemne zakrycia planet Układu Słonecznego 27 sierpnia 2006 roku nastąpiło zbliżenie Wenus do Saturna na odległość 0,07 czyli 4'. Odległość ta była kilkanaście razy większa niż średnica tarcz
Tomasz Ściężor. Almanach Astronomiczny na rok 2014
 Tomasz Ściężor Almanach Astronomiczny na rok 2014 Klub Astronomiczny Regulus Kraków 2013 1 Recenzent prof. dr hab. Jerzy M. Kreiner Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie
Tomasz Ściężor Almanach Astronomiczny na rok 2014 Klub Astronomiczny Regulus Kraków 2013 1 Recenzent prof. dr hab. Jerzy M. Kreiner Skład komputerowy almanachu wykonał autor publikacji Tomasz Ściężor Wszelkie
Inne Nieba. Gimnazjum Klasy I III Doświadczenie konkursowe nr 4
 Gimnazjum Klasy I III Doświadczenie konkursowe nr 4 Rok 2017 1. Wstęp teoretyczny Układ Słoneczny jest niezwykle skomplikowanym mechanizmem. Mnogość parametrów przekłada się na mnogość zjawisk, jakie można
Gimnazjum Klasy I III Doświadczenie konkursowe nr 4 Rok 2017 1. Wstęp teoretyczny Układ Słoneczny jest niezwykle skomplikowanym mechanizmem. Mnogość parametrów przekłada się na mnogość zjawisk, jakie można
Księżyc to ciało niebieskie pochodzenia naturalnego.
 2b. Nasz Księżyc Księżyc to ciało niebieskie pochodzenia naturalnego. Obiega on największe ciała układów planetarnych, tj. planeta, planeta karłowata czy planetoida. W niektórych przypadkach kiedy jest
2b. Nasz Księżyc Księżyc to ciało niebieskie pochodzenia naturalnego. Obiega on największe ciała układów planetarnych, tj. planeta, planeta karłowata czy planetoida. W niektórych przypadkach kiedy jest
Tellurium szkolne [ BAP_1134000.doc ]
![Tellurium szkolne [ BAP_1134000.doc ] Tellurium szkolne [ BAP_1134000.doc ]](/thumbs/23/2075108.jpg) Tellurium szkolne [ ] Prezentacja produktu Przeznaczenie dydaktyczne. Kosmograf CONATEX ma stanowić pomoc dydaktyczną w wyjaśnianiu i demonstracji układu «ZIEMIA - KSIĘŻYC - SŁOŃCE», zjawiska nocy i dni,
Tellurium szkolne [ ] Prezentacja produktu Przeznaczenie dydaktyczne. Kosmograf CONATEX ma stanowić pomoc dydaktyczną w wyjaśnianiu i demonstracji układu «ZIEMIA - KSIĘŻYC - SŁOŃCE», zjawiska nocy i dni,
Przykładowe zagadnienia.
 Wykład udostępniam na licencji Creative Commons: Przykładowe zagadnienia. Piotr A. Dybczyński Z BN E N h W Nd A S BN Z t δ N S α BS zenit północny biegun świata BN miejscowy południk astronomiczny Z punkt
Wykład udostępniam na licencji Creative Commons: Przykładowe zagadnienia. Piotr A. Dybczyński Z BN E N h W Nd A S BN Z t δ N S α BS zenit północny biegun świata BN miejscowy południk astronomiczny Z punkt
Niebo nad nami Styczeń 2018
 Niebo nad nami Styczeń 2018 Comiesięczny kalendarz astronomiczny STOWARZYSZENIE NA RZECZ WIEDZY I ROZWOJU WiR KOPERNIK WWW.WIRKOPERNIK.PL CZARNA 857, 37-125 CZARNA TEL: 603 155 527 E-MAIL: kontakt@wirkopernik.pl
Niebo nad nami Styczeń 2018 Comiesięczny kalendarz astronomiczny STOWARZYSZENIE NA RZECZ WIEDZY I ROZWOJU WiR KOPERNIK WWW.WIRKOPERNIK.PL CZARNA 857, 37-125 CZARNA TEL: 603 155 527 E-MAIL: kontakt@wirkopernik.pl
ZAŁĄCZNIK IV. Obliczanie rotacji / translacji obrazów.
 ZAŁĄCZNIK IV. Obliczanie rotacji / translacji obrazów. Jak to zostało przedstawione w części 5.2.1, jeżeli zrobimy Słońcu zdjęcie z jakiegoś miejsca na powierzchni ziemi w danym momencie t i dokładnie
ZAŁĄCZNIK IV. Obliczanie rotacji / translacji obrazów. Jak to zostało przedstawione w części 5.2.1, jeżeli zrobimy Słońcu zdjęcie z jakiegoś miejsca na powierzchni ziemi w danym momencie t i dokładnie
RUCH OBROTOWY I OBIEGOWY ZIEMI
 1. Wpisz w odpowiednich miejscach następujące nazwy: Równik, Zwrotnika Raka, Zwrotnik Koziorożca iegun Południowy, iegun Północny Koło Podbiegunowe Południowe Koło Podbiegunowe Południowe RUCH OROTOWY
1. Wpisz w odpowiednich miejscach następujące nazwy: Równik, Zwrotnika Raka, Zwrotnik Koziorożca iegun Południowy, iegun Północny Koło Podbiegunowe Południowe Koło Podbiegunowe Południowe RUCH OROTOWY
Niebo na wakacje. Bartłomiej Zakrzewski
 Strona 1 Niebo na wakacje Bartłomiej Zakrzewski Niniejszy artykuł jest w zamyśle propozycją wykorzystania wolnego czasu podczas właśnie rozpoczętych wakacji. Zaprezentowane informacje zachęcają do samodzielnego
Strona 1 Niebo na wakacje Bartłomiej Zakrzewski Niniejszy artykuł jest w zamyśle propozycją wykorzystania wolnego czasu podczas właśnie rozpoczętych wakacji. Zaprezentowane informacje zachęcają do samodzielnego
Niebo nad nami Wrzesień 2017
 Niebo nad nami Wrzesień 2017 Comiesięczny kalendarz astronomiczny STOWARZYSZENIE NA RZECZ WIEDZY I ROZWOJU WiR KOPERNIK WWW.WIRKOPERNIK.PL CZARNA 857, 37-125 CZARNA TEL: 603 155 527 E-MAIL: kontakt@wirkopernik.pl
Niebo nad nami Wrzesień 2017 Comiesięczny kalendarz astronomiczny STOWARZYSZENIE NA RZECZ WIEDZY I ROZWOJU WiR KOPERNIK WWW.WIRKOPERNIK.PL CZARNA 857, 37-125 CZARNA TEL: 603 155 527 E-MAIL: kontakt@wirkopernik.pl
LX Olimpiada Astronomiczna 2016/2017 Zadania z zawodów III stopnia. S= L 4π r L
 LX Olimpiada Astronomiczna 2016/2017 Zadania z zawodów III stopnia 1. Przyjmij, że prędkość rotacji różnicowej Słońca, wyrażoną w stopniach na dobę, można opisać wzorem: gdzie φ jest szerokością heliograficzną.
LX Olimpiada Astronomiczna 2016/2017 Zadania z zawodów III stopnia 1. Przyjmij, że prędkość rotacji różnicowej Słońca, wyrażoną w stopniach na dobę, można opisać wzorem: gdzie φ jest szerokością heliograficzną.
Przykład testu z astronomicznych podsatw geografii Uzupełnić puste pola : Wybarć własciwe odpowiedzi a,b,c,d,e... (moŝe byc kilka poprawnych!!
 Przykład testu z astronomicznych podsatw geografii Uzupełnić puste pola : Wybarć własciwe odpowiedzi a,b,c,d,e.... (moŝe byc kilka poprawnych!!) 1. Astronomia zajmuje się badaniem 2. Z powodu zjawiska
Przykład testu z astronomicznych podsatw geografii Uzupełnić puste pola : Wybarć własciwe odpowiedzi a,b,c,d,e.... (moŝe byc kilka poprawnych!!) 1. Astronomia zajmuje się badaniem 2. Z powodu zjawiska
Przykładowe zagadnienia.
 Wykład udostępniam na licencji Creative Commons: Przykładowe zagadnienia. Piotr A. Dybczyński Z BN E N h W Nd A S BN Z δ N t S α BS zenit północny biegun świata BN miejscowy południk astronomiczny Z punkt
Wykład udostępniam na licencji Creative Commons: Przykładowe zagadnienia. Piotr A. Dybczyński Z BN E N h W Nd A S BN Z δ N t S α BS zenit północny biegun świata BN miejscowy południk astronomiczny Z punkt
Ściąga eksperta. Ruch obiegowy i obrotowy Ziemi. - filmy edukacyjne on-line. Ruch obrotowy i obiegowy Ziemi.
 Ruch obiegowy i obrotowy Ziemi Ruch obrotowy i obiegowy Ziemi Ruch obiegowy W starożytności uważano, że wszystkie ciała niebieskie wraz ze Słońcem poruszają się wokół Ziemi. Jest to tzw. teoria geocentryczna.
Ruch obiegowy i obrotowy Ziemi Ruch obrotowy i obiegowy Ziemi Ruch obiegowy W starożytności uważano, że wszystkie ciała niebieskie wraz ze Słońcem poruszają się wokół Ziemi. Jest to tzw. teoria geocentryczna.
24 godziny 23 godziny 56 minut 4 sekundy
 Ruch obrotowy Ziemi Podstawowe pojęcia Ruch obrotowy, inaczej wirowy to ruch Ziemi wokół własnej osi. Oś Ziemi jest teoretyczną linią prostą, która przechodzi przez Biegun Północny i Biegun Południowy.
Ruch obrotowy Ziemi Podstawowe pojęcia Ruch obrotowy, inaczej wirowy to ruch Ziemi wokół własnej osi. Oś Ziemi jest teoretyczną linią prostą, która przechodzi przez Biegun Północny i Biegun Południowy.
Astronomia. Wykład IV. Waldemar Ogłoza. >> dla studentów. Wykład dla studentów fizyki
 Astronomia Wykład IV Wykład dla studentów fizyki Waldemar Ogłoza www.as.up.krakow.pl >> dla studentów Ruch obrotowy Ziemi Efekty ruchu wirowego Ziemi Zjawisko dnia i nocy Spłaszczenie Ziemi przez siłę
Astronomia Wykład IV Wykład dla studentów fizyki Waldemar Ogłoza www.as.up.krakow.pl >> dla studentów Ruch obrotowy Ziemi Efekty ruchu wirowego Ziemi Zjawisko dnia i nocy Spłaszczenie Ziemi przez siłę
Sprawozdanie z działalności koła w ramach konkursu A jednak się kręci.
 Sprawozdanie z działalności koła w ramach konkursu A jednak się kręci. I Zespół Szkół nr 1 w Wadowicach Ul. Słowackiego 4 II Kółko geograficzne, prowadzący ElŜbieta Włoch III Liczba członków 6 osób z klas
Sprawozdanie z działalności koła w ramach konkursu A jednak się kręci. I Zespół Szkół nr 1 w Wadowicach Ul. Słowackiego 4 II Kółko geograficzne, prowadzący ElŜbieta Włoch III Liczba członków 6 osób z klas
Skala jasności w astronomii. Krzysztof Kamiński
 Skala jasności w astronomii Krzysztof Kamiński Obserwowana wielkość gwiazdowa (magnitudo) Skala wymyślona prawdopodobnie przez Hipparcha, który podzielił gwiazdy pod względem jasności na 6 grup (najjaśniejsze:
Skala jasności w astronomii Krzysztof Kamiński Obserwowana wielkość gwiazdowa (magnitudo) Skala wymyślona prawdopodobnie przez Hipparcha, który podzielił gwiazdy pod względem jasności na 6 grup (najjaśniejsze:
Poza przedstawionymi tutaj obserwacjami planet (Jowisza, Saturna) oraz Księżyca, zachęcamy również do obserwowania plam na Słońcu.
 Zachęcamy do eksperymentowania z amatorską fotografią nieba. W przygotowaniu się do obserwacji ciekawych zjawisk może pomóc darmowy program Stellarium oraz strony internetowe na przykład spaceweather.com
Zachęcamy do eksperymentowania z amatorską fotografią nieba. W przygotowaniu się do obserwacji ciekawych zjawisk może pomóc darmowy program Stellarium oraz strony internetowe na przykład spaceweather.com
wersja
 www.as.up.krakow.pl wersja 2013-01-12 STAŁE: π = 3.14159268... e = 2.718281828... Jednostka astronomiczna 1 AU = 149.6 mln km = 8 m 19 s świetlnych Rok świetlny [l.y.] = c t = 9460730472580800 m = 9.46
www.as.up.krakow.pl wersja 2013-01-12 STAŁE: π = 3.14159268... e = 2.718281828... Jednostka astronomiczna 1 AU = 149.6 mln km = 8 m 19 s świetlnych Rok świetlny [l.y.] = c t = 9460730472580800 m = 9.46
Ziemia we Wszechświecie lekcja powtórzeniowa
 Scenariusz lekcji Scenariusz lekcji powtórzeniowej do podręczników PULS ZIEMI 1 i PLANETA NOWA 1 45 min Ziemia we Wszechświecie lekcja powtórzeniowa t Hasło programowe: Ziemia we Wszechświecie/Ruchy Ziemi.
Scenariusz lekcji Scenariusz lekcji powtórzeniowej do podręczników PULS ZIEMI 1 i PLANETA NOWA 1 45 min Ziemia we Wszechświecie lekcja powtórzeniowa t Hasło programowe: Ziemia we Wszechświecie/Ruchy Ziemi.
Konkurs Astronomiczny Astrolabium IV Edycja 26 kwietnia 2017 roku Klasy I III Gimnazjum Test Konkursowy
 Instrukcja Zaznacz prawidłową odpowiedź. Tylko jedna odpowiedź jest poprawna. Czas na rozwiązanie testu wynosi 60 minut. 1. 11 kwietnia 2017 roku była pełnia Księżyca. Pełnia w dniu 11 kwietnia będzie
Instrukcja Zaznacz prawidłową odpowiedź. Tylko jedna odpowiedź jest poprawna. Czas na rozwiązanie testu wynosi 60 minut. 1. 11 kwietnia 2017 roku była pełnia Księżyca. Pełnia w dniu 11 kwietnia będzie
1. * Wyjaśnij, dlaczego w kalendarzu gregoriańskim wprowadzono lata przestępne na zasadach opisanych powyŝej...
 Zadania oznaczone * - zakres rozszerzony Zadania 1i 2 wykonaj po przeczytaniu poniŝszego tekstu. Od 1582 r. powszechnie w świecie jest uŝywany kalendarz gregoriański. Przyjęto w nim załoŝenie, tak jak
Zadania oznaczone * - zakres rozszerzony Zadania 1i 2 wykonaj po przeczytaniu poniŝszego tekstu. Od 1582 r. powszechnie w świecie jest uŝywany kalendarz gregoriański. Przyjęto w nim załoŝenie, tak jak
Grawitacja - powtórka
 Grawitacja - powtórka 1. Oceń prawdziwość każdego zdania. Zaznacz, jeśli zdanie jest prawdziwe, lub, jeśli jest A. Jednorodne pole grawitacyjne istniejące w obszarze sali lekcyjnej jest wycinkiem centralnego
Grawitacja - powtórka 1. Oceń prawdziwość każdego zdania. Zaznacz, jeśli zdanie jest prawdziwe, lub, jeśli jest A. Jednorodne pole grawitacyjne istniejące w obszarze sali lekcyjnej jest wycinkiem centralnego
Sztuczny satelita Ziemi. Ruch w polu grawitacyjnym
 Sztuczny satelita Ziemi Ruch w polu grawitacyjnym Sztuczny satelita Ziemi Jest to obiekt, któremu na pewnej wysokości nad powierzchnią Ziemi nadano prędkość wystarczającą do uzyskania przez niego ruchu
Sztuczny satelita Ziemi Ruch w polu grawitacyjnym Sztuczny satelita Ziemi Jest to obiekt, któremu na pewnej wysokości nad powierzchnią Ziemi nadano prędkość wystarczającą do uzyskania przez niego ruchu
Sprawdzian 2. Fizyka Świat fizyki. Astronomia. Sprawdziany podsumowujące. sin = 0,0166 cos = 0,9999 tg = 0,01659 ctg = 60,3058
 Imię i nazwisko Data Klasa Wersja A Sprawdzian.. Jedna jednostka astronomiczna to odległość jaką przebywa światło (biegnące z szybkością 300 000 km/h) w ciągu jednego roku. jaką przebywa światło (biegnące
Imię i nazwisko Data Klasa Wersja A Sprawdzian.. Jedna jednostka astronomiczna to odległość jaką przebywa światło (biegnące z szybkością 300 000 km/h) w ciągu jednego roku. jaką przebywa światło (biegnące
Człowiek najlepsza inwestycja. Fot.NASA FENIKS PRACOWNIA DYDAKTYKI ASTRONOMII
 Fot.NASA FENIKS PRACOWNIA DYDAKTYKI ASTRONOMII PROPOZYCJA ĆWICZEŃ DZIENNYCH Z ASTRONOMII DLA UCZESTNIKÓW PROGRAMU FENIKS dr hab. Piotr Gronkowski, prof. UR gronk@univ.rzeszow.pl Uniwersytet Rzeszowski
Fot.NASA FENIKS PRACOWNIA DYDAKTYKI ASTRONOMII PROPOZYCJA ĆWICZEŃ DZIENNYCH Z ASTRONOMII DLA UCZESTNIKÓW PROGRAMU FENIKS dr hab. Piotr Gronkowski, prof. UR gronk@univ.rzeszow.pl Uniwersytet Rzeszowski
Egzamin maturalny z fizyki i astronomii 5 Poziom podstawowy
 Egzamin maturalny z fizyki i astronomii 5 Poziom podstawowy 14. Kule (3 pkt) Dwie małe jednorodne kule A i B o jednakowych masach umieszczono w odległości 10 cm od siebie. Kule te oddziaływały wówczas
Egzamin maturalny z fizyki i astronomii 5 Poziom podstawowy 14. Kule (3 pkt) Dwie małe jednorodne kule A i B o jednakowych masach umieszczono w odległości 10 cm od siebie. Kule te oddziaływały wówczas
LIV Olimpiada Astronomiczna 2010 / 2011 Zawody III stopnia
 LIV Olimpiada Astronomiczna 2010 / 2011 Zawody III stopnia 1. Wskutek efektów relatywistycznych mierzony całkowity strumień promieniowania od gwiazdy, która porusza się w kierunku obserwatora z prędkością
LIV Olimpiada Astronomiczna 2010 / 2011 Zawody III stopnia 1. Wskutek efektów relatywistycznych mierzony całkowity strumień promieniowania od gwiazdy, która porusza się w kierunku obserwatora z prędkością
Projekt instalacji astronomicznych w miejscach publicznych Krakowa
 Polska: www.astronomia2009.pl Małopolska: www.as.up.krakow.pl/2009 Projekt instalacji astronomicznych w miejscach publicznych Krakowa W grudniu 2007 podczas 62 zgromadzenia Ogólnego ONZ postanowiono, Ŝe
Polska: www.astronomia2009.pl Małopolska: www.as.up.krakow.pl/2009 Projekt instalacji astronomicznych w miejscach publicznych Krakowa W grudniu 2007 podczas 62 zgromadzenia Ogólnego ONZ postanowiono, Ŝe
1 Co to jest gwiazda? 2 Gwiazdozbiór. 3 Przedstawienie
 Maria Myśkow Spis treści 1 Co to jest gwiazda?...3 2 Gwiazdozbiór...3 3 Przedstawienie...3 4 Znak zodiaku...4 4.1 Zodiak astronomiczny...4 4.2 Zodiak astrologiczny...5 5 Ekliptyka...6 6 Bibliografia:...6
Maria Myśkow Spis treści 1 Co to jest gwiazda?...3 2 Gwiazdozbiór...3 3 Przedstawienie...3 4 Znak zodiaku...4 4.1 Zodiak astronomiczny...4 4.2 Zodiak astrologiczny...5 5 Ekliptyka...6 6 Bibliografia:...6
Aplikacje informatyczne w Astronomii. Internet źródło informacji i planowanie obserwacji astronomicznych
 Aplikacje informatyczne w Astronomii Internet źródło informacji i planowanie obserwacji astronomicznych Skrót kursu: Tydzień I wstęp i planowanie pokazów popularnonaukowych a) współrzędne niebieskie układy
Aplikacje informatyczne w Astronomii Internet źródło informacji i planowanie obserwacji astronomicznych Skrót kursu: Tydzień I wstęp i planowanie pokazów popularnonaukowych a) współrzędne niebieskie układy
Fizyka i Chemia Ziemi
 Fizyka i Chemia Ziemi Temat 4: Ruch geocentryczny i heliocentryczny planet T.J. Jopek jopek@amu.edu.pl IOA UAM Układ Planetarny - klasyfikacja. Planety grupy ziemskiej: Merkury Wenus Ziemia Mars 2. Planety
Fizyka i Chemia Ziemi Temat 4: Ruch geocentryczny i heliocentryczny planet T.J. Jopek jopek@amu.edu.pl IOA UAM Układ Planetarny - klasyfikacja. Planety grupy ziemskiej: Merkury Wenus Ziemia Mars 2. Planety
3a. Ruch obiegowy Ziemi
 3a. Ruch obiegowy Ziemi Ziemia obiega gwiazdę znajdującą się w środku naszego układu planetarnego, czyli Słońce. Ta konstatacja, dzisiaj absolutnie niekwestionowana, z trudem dochodziła do powszechnej
3a. Ruch obiegowy Ziemi Ziemia obiega gwiazdę znajdującą się w środku naszego układu planetarnego, czyli Słońce. Ta konstatacja, dzisiaj absolutnie niekwestionowana, z trudem dochodziła do powszechnej
Czas w astronomii. Krzysztof Kamiński
 Czas w astronomii Krzysztof Kamiński Czas gwiazdowy - kąt godzinny punktu Barana; lokalny na danym południku Ziemi; związany z układem równikowym równonocnym; odzwierciedla niejednorodności rotacji Ziemi
Czas w astronomii Krzysztof Kamiński Czas gwiazdowy - kąt godzinny punktu Barana; lokalny na danym południku Ziemi; związany z układem równikowym równonocnym; odzwierciedla niejednorodności rotacji Ziemi
PODRĘCZNA INSTRUKCJA ASTRO-EXCELA
 2015 rok Janusz Bańkowski, Bełchatów Patronat programu SOS PTMA PODRĘCZNA INSTRUKCJA ASTRO-EXCELA Wstęp Arkusz kalkulacyjny MS Excel to doskonałe narzędzie obliczeniowe wszechstronnego użytku. Za pomocą
2015 rok Janusz Bańkowski, Bełchatów Patronat programu SOS PTMA PODRĘCZNA INSTRUKCJA ASTRO-EXCELA Wstęp Arkusz kalkulacyjny MS Excel to doskonałe narzędzie obliczeniowe wszechstronnego użytku. Za pomocą
Cykl saros. Szkoła Podstawowa Klasy VII-VIII Gimnazjum Klasa III Doświadczenie konkursowe 4
 Szkoła Podstawowa Klasy VII-VIII Gimnazjum Klasa III Doświadczenie konkursowe 4 Rok 2019 1. Wstęp teoretyczny Zaćmienia Słońca należą do najbardziej spektakularnych widowisk na niebie. Zachodzą one wtedy,
Szkoła Podstawowa Klasy VII-VIII Gimnazjum Klasa III Doświadczenie konkursowe 4 Rok 2019 1. Wstęp teoretyczny Zaćmienia Słońca należą do najbardziej spektakularnych widowisk na niebie. Zachodzą one wtedy,
Krzywe stożkowe Lekcja V: Elipsa
 Krzywe stożkowe Lekcja V: Elipsa Wydział Matematyki Politechniki Wrocławskiej Czym jest elipsa? Elipsa jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem α < β < π 2 (gdzie α jest
Krzywe stożkowe Lekcja V: Elipsa Wydział Matematyki Politechniki Wrocławskiej Czym jest elipsa? Elipsa jest krzywą stożkową powstałą przez przecięcie stożka płaszczyzną pod kątem α < β < π 2 (gdzie α jest
Rozwiązania przykładowych zadań
 Rozwiązania przykładowych zadań Oblicz czas średni i czas prawdziwy słoneczny na południku λ=45 E o godzinie 15 00 UT dnia 1 VII. Rozwiązanie: RóŜnica czasu średniego słonecznego T s w danym miejscu i
Rozwiązania przykładowych zadań Oblicz czas średni i czas prawdziwy słoneczny na południku λ=45 E o godzinie 15 00 UT dnia 1 VII. Rozwiązanie: RóŜnica czasu średniego słonecznego T s w danym miejscu i
STYCZEŃ Mgławica Koński Łeb Barnard 33 wewnątrz IC 434 w Orionie Źródło: NASA
 Johannes Kepler Teleskop Keplera Mgławica Koński Łeb Barnard wewnątrz IC w Orionie Źródło: NASA STYCZEŃ 0 stycznia hm Ziemia znajduje się najbliżej Słońca w peryhelium. stycznia częściowe zaćmienie Słońca.
Johannes Kepler Teleskop Keplera Mgławica Koński Łeb Barnard wewnątrz IC w Orionie Źródło: NASA STYCZEŃ 0 stycznia hm Ziemia znajduje się najbliżej Słońca w peryhelium. stycznia częściowe zaćmienie Słońca.
4. Ruch obrotowy Ziemi
 4. Ruch obrotowy Ziemi Jednym z pierwszych dowodów na ruch obrotowy Ziemi było doświadczenie, wykazujące ODCHYLENIE CIAŁ SWOBODNIE SPADAJĄCYCH Z WIEŻY: gdy ciało zostanie zrzucone z wysokiej wieży, to
4. Ruch obrotowy Ziemi Jednym z pierwszych dowodów na ruch obrotowy Ziemi było doświadczenie, wykazujące ODCHYLENIE CIAŁ SWOBODNIE SPADAJĄCYCH Z WIEŻY: gdy ciało zostanie zrzucone z wysokiej wieży, to
Konkurs Astronomiczny Astrolabium III Edycja 25 marca 2015 roku Klasy I III Liceum Ogólnokształcącego Test Konkursowy
 Instrukcja Zaznacz prawidłową odpowiedź. Tylko jedna odpowiedź jest poprawna. Czas na rozwiązanie testu wynosi 75 minut. 1. Przyszłość. Ludzie mieszkają w stacjach kosmicznych w kształcie okręgu o promieniu
Instrukcja Zaznacz prawidłową odpowiedź. Tylko jedna odpowiedź jest poprawna. Czas na rozwiązanie testu wynosi 75 minut. 1. Przyszłość. Ludzie mieszkają w stacjach kosmicznych w kształcie okręgu o promieniu
Ziemia jako zegar Piotr A. Dybczyński
 Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
Układy współrzędnych równikowych
 Wykład udostępniam na licencji Creative Commons: Układy współrzędnych równikowych Piotr A. Dybczyński Taki układ wydaje się prosty. Sytuacja komplikuje się gdy musimy narysować i używać dwóch lub trzech
Wykład udostępniam na licencji Creative Commons: Układy współrzędnych równikowych Piotr A. Dybczyński Taki układ wydaje się prosty. Sytuacja komplikuje się gdy musimy narysować i używać dwóch lub trzech
Współrzędne geograficzne
 Współrzędne geograficzne Siatka kartograficzna jest to układ południków i równoleżników wykreślony na płaszczyźnie (mapie); jest to odwzorowanie siatki geograficznej na płaszczyźnie. Siatka geograficzna
Współrzędne geograficzne Siatka kartograficzna jest to układ południków i równoleżników wykreślony na płaszczyźnie (mapie); jest to odwzorowanie siatki geograficznej na płaszczyźnie. Siatka geograficzna
Układ Słoneczny. Pokaz
 Układ Słoneczny Pokaz Rozmiary planet i Słońca Orbity planet Planety typu ziemskiego Merkury Najmniejsza planeta U.S. Brak atmosfery Powierzchnia podobna do powierzchni Księżyca zryta kraterami część oświetlona
Układ Słoneczny Pokaz Rozmiary planet i Słońca Orbity planet Planety typu ziemskiego Merkury Najmniejsza planeta U.S. Brak atmosfery Powierzchnia podobna do powierzchni Księżyca zryta kraterami część oświetlona
Fizyka i Chemia Ziemi
 Fizyka i Chemia Ziemi Temat 5: Zjawiska w układzie Ziemia - Księżyc T.J. Jopek jopek@amu.edu.pl IOA UAM 2012-01-26 T.J.Jopek, Fizyka i chemia Ziemi 1 Ruch orbitalny Księżyca Obserwowane tarcze Księżyca
Fizyka i Chemia Ziemi Temat 5: Zjawiska w układzie Ziemia - Księżyc T.J. Jopek jopek@amu.edu.pl IOA UAM 2012-01-26 T.J.Jopek, Fizyka i chemia Ziemi 1 Ruch orbitalny Księżyca Obserwowane tarcze Księżyca
Ruch Gwiazd. Szkoła Podstawowa Klasy IV VI Doświadczenie konkursowe nr 3
 Szkoła Podstawowa Klasy IV VI Doświadczenie konkursowe nr 3 Rok 2017 1. Wstęp teoretyczny Ludzka wyobraźnia łączy rozproszone po niebie gwiazdy w pewne charakterystyczne wzory, ułatwiające nawigację po
Szkoła Podstawowa Klasy IV VI Doświadczenie konkursowe nr 3 Rok 2017 1. Wstęp teoretyczny Ludzka wyobraźnia łączy rozproszone po niebie gwiazdy w pewne charakterystyczne wzory, ułatwiające nawigację po
b. Ziemia w Układzie Słonecznym sprawdzian wiadomości
 a. b. Ziemia w Układzie Słonecznym sprawdzian wiadomości 1. Cele lekcji Cel ogólny: podsumowanie wiadomości o Układzie Słonecznym i miejscu w nim Ziemi. Uczeń: i. a) Wiadomości zna planety Układu Słonecznego,
a. b. Ziemia w Układzie Słonecznym sprawdzian wiadomości 1. Cele lekcji Cel ogólny: podsumowanie wiadomości o Układzie Słonecznym i miejscu w nim Ziemi. Uczeń: i. a) Wiadomości zna planety Układu Słonecznego,
Analiza danych. 7 th International Olympiad on Astronomy & Astrophysics 27 July 5 August 2013, Volos Greece. Zadanie 1.
 Analiza danych Zadanie 1. Zdjęcie 1 przedstawiające część gwiazdozbioru Wielkiej Niedźwiedzicy, zostało zarejestrowane kamerą CCD o rozmiarze chipu 17mm 22mm. Wyznacz ogniskową f systemu optycznego oraz
Analiza danych Zadanie 1. Zdjęcie 1 przedstawiające część gwiazdozbioru Wielkiej Niedźwiedzicy, zostało zarejestrowane kamerą CCD o rozmiarze chipu 17mm 22mm. Wyznacz ogniskową f systemu optycznego oraz
KONKURS ASTRONOMICZNY
 SZKOLNY KLUB PRZYRODNICZY ALTAIR KONKURS ASTRONOMICZNY ETAP PIERWSZY 1. Jakie znasz ciała niebieskie? Gwiazdy, planety, planety karłowate, księŝyce, planetoidy, komety, kwazary, czarne dziury, ciemna materia....
SZKOLNY KLUB PRZYRODNICZY ALTAIR KONKURS ASTRONOMICZNY ETAP PIERWSZY 1. Jakie znasz ciała niebieskie? Gwiazdy, planety, planety karłowate, księŝyce, planetoidy, komety, kwazary, czarne dziury, ciemna materia....
Układ Słoneczny Pytania:
 Układ Słoneczny Pytania: Co to jest Układ Słoneczny? Czy znasz nazwy planet? Co jeszcze znajduje się w Układzie Słonecznym poza planetami? Co to jest Układ Słoneczny Układ Słoneczny to układ ciał niebieskich,
Układ Słoneczny Pytania: Co to jest Układ Słoneczny? Czy znasz nazwy planet? Co jeszcze znajduje się w Układzie Słonecznym poza planetami? Co to jest Układ Słoneczny Układ Słoneczny to układ ciał niebieskich,
Tomasz Ściężor. Almanach Astronomiczny na rok 2015
 Tomasz Ściężor Almanach Astronomiczny na rok 2015 Polskie Towarzystwo Astronomiczne Warszawa 2014 RECENZENT Jerzy M. Kreiner OPRACOWANIE TECHNICZNE I SKŁAD Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna
Tomasz Ściężor Almanach Astronomiczny na rok 2015 Polskie Towarzystwo Astronomiczne Warszawa 2014 RECENZENT Jerzy M. Kreiner OPRACOWANIE TECHNICZNE I SKŁAD Tomasz Ściężor Wszelkie prawa zastrzeżone. Żadna
Rotacja. W układzie związanym z planetą: siła odśrodkowa i siła Coroilisa. Potencjał efektywny w najprostszym przypadku (przybliżenie Roche a):
 Rotacja W układzie związanym z planetą: siła odśrodkowa i siła Coroilisa. Potencjał efektywny w najprostszym przypadku (przybliżenie Roche a): Φ = ω2 r 2 sin 2 (θ) 2 GM r Z porównania wartości potencjału
Rotacja W układzie związanym z planetą: siła odśrodkowa i siła Coroilisa. Potencjał efektywny w najprostszym przypadku (przybliżenie Roche a): Φ = ω2 r 2 sin 2 (θ) 2 GM r Z porównania wartości potencjału
Cairns (Australia): Szerokość: 16º 55' " Długość: 145º 46' " Sapporo (Japonia): Szerokość: 43º 3' " Długość: 141º 21' 15.
 5 - Obliczenia przejścia Wenus z 5-6 czerwca 2012 r. 5.1. Wybieranie miejsca obserwacji. W tej części zajmiemy się nadchodzącym tranzytem Wenus, próbując wyobrazić sobie sytuację jak najbardziej zbliżoną
5 - Obliczenia przejścia Wenus z 5-6 czerwca 2012 r. 5.1. Wybieranie miejsca obserwacji. W tej części zajmiemy się nadchodzącym tranzytem Wenus, próbując wyobrazić sobie sytuację jak najbardziej zbliżoną
ETAP II. Astronomia to nauka. pochodzeniem i ewolucją. planet i gwiazd. na wydarzenia na Ziemi.
 ETAP II Konkurencja I Ach te definicje! (każda poprawnie ułożona definicja warta jest aż dwa punkty) Astronomia to nauka o ciałach niebieskich zajmująca się badaniem ich położenia, ruchów, odległości i
ETAP II Konkurencja I Ach te definicje! (każda poprawnie ułożona definicja warta jest aż dwa punkty) Astronomia to nauka o ciałach niebieskich zajmująca się badaniem ich położenia, ruchów, odległości i
Ziemia jako zegar Piotr A. Dybczyński
 Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
Rozmiar Księżyca. Szkoła Podstawowa Klasy I III Doświadczenie konkursowe nr 2
 Szkoła Podstawowa Klasy I III Doświadczenie konkursowe nr 2 Rok 2017 1. Wstęp teoretyczny Księżyc jest znacznie mniejszy od Ziemi. Ma on kształt w przybliżeniu kulisty o promieniu około 1740 km. Dla porównania
Szkoła Podstawowa Klasy I III Doświadczenie konkursowe nr 2 Rok 2017 1. Wstęp teoretyczny Księżyc jest znacznie mniejszy od Ziemi. Ma on kształt w przybliżeniu kulisty o promieniu około 1740 km. Dla porównania
BADANIE WYNIKÓW KLASA 1
 BADANIE WYNIKÓW KLASA 1 Zad. 1 (0-1p) Wielki Mur Chiński ma obecnie długość około 2500km. Jego długość na mapie w skali 1:200 000 000 wynosi A. 125 cm B. 12,5 cm C. 1,25 cm D. 0,125 cm Zad. 2 (0-1p) Rzeka
BADANIE WYNIKÓW KLASA 1 Zad. 1 (0-1p) Wielki Mur Chiński ma obecnie długość około 2500km. Jego długość na mapie w skali 1:200 000 000 wynosi A. 125 cm B. 12,5 cm C. 1,25 cm D. 0,125 cm Zad. 2 (0-1p) Rzeka
S T Y C Z E Ń. Mgławica Kooski Łeb Barnard 33 wewnątrz IC 434 w Orionie Źródło: NASA
 Johannes Kepler Teleskop Keplera Mgławica Kooski Łeb Barnard wewnątrz IC w Orionie Źródło: NASA S T Y C Z E Ń 0 stycznia hm Ziemia znajduje się najbliżej Słońca w peryhelium. stycznia częściowe zaćmienie
Johannes Kepler Teleskop Keplera Mgławica Kooski Łeb Barnard wewnątrz IC w Orionie Źródło: NASA S T Y C Z E Ń 0 stycznia hm Ziemia znajduje się najbliżej Słońca w peryhelium. stycznia częściowe zaćmienie
Aplikacje informatyczne w Astronomii. Internet źródło informacji i planowanie obserwacji astronomicznych
 Aplikacje informatyczne w Astronomii Internet źródło informacji i planowanie obserwacji astronomicznych Planowanie obserwacji ciał Układu Słonecznego Plan zajęć: planety wewnętrzne planety zewnętrzne systemy
Aplikacje informatyczne w Astronomii Internet źródło informacji i planowanie obserwacji astronomicznych Planowanie obserwacji ciał Układu Słonecznego Plan zajęć: planety wewnętrzne planety zewnętrzne systemy
Prezentacja. Układ Słoneczny
 Prezentacja Układ Słoneczny Układ Słoneczny Układ Słoneczny układ planetarny składający się ze Słońca i powiązanych z nim grawitacyjnie ciał niebieskich. Ciała te to osiem planet, 166 znanych księżyców
Prezentacja Układ Słoneczny Układ Słoneczny Układ Słoneczny układ planetarny składający się ze Słońca i powiązanych z nim grawitacyjnie ciał niebieskich. Ciała te to osiem planet, 166 znanych księżyców
LVII Olimpiada Astronomiczna 2013/2014 Zadania zawodów III stopnia
 Zadanie 1. LVII Olimpiada Astronomiczna 2013/2014 Zadania zawodów III stopnia Z północnego bieguna księżycowego wystrzelono pocisk, nadając mu prędkość początkową równą lokalnej pierwszej prędkości kosmicznej.
Zadanie 1. LVII Olimpiada Astronomiczna 2013/2014 Zadania zawodów III stopnia Z północnego bieguna księżycowego wystrzelono pocisk, nadając mu prędkość początkową równą lokalnej pierwszej prędkości kosmicznej.
Odległość kątowa. Szkoła średnia Klasy I IV Doświadczenie konkursowe 5
 Szkoła średnia Klasy I IV Doświadczenie konkursowe 5 Rok 2019 1. Wstęp teoretyczny Patrząc na niebo po zachodzie Słońca, mamy wrażenie, że znajdujemy się pod rozgwieżdżoną kopułą. Kopuła ta stanowi połowę
Szkoła średnia Klasy I IV Doświadczenie konkursowe 5 Rok 2019 1. Wstęp teoretyczny Patrząc na niebo po zachodzie Słońca, mamy wrażenie, że znajdujemy się pod rozgwieżdżoną kopułą. Kopuła ta stanowi połowę
Materiały edukacyjne Tranzyt Wenus Zestaw 3. Paralaksa. Zadanie 1. Paralaksa czyli zmiana
 Materiały edukacyjne Tranzyt Wenus 2012 Zestaw 3. Paralaksa Zadanie 1. Paralaksa czyli zmiana Paralaksa to zjawisko pozornej zmiany położenia obiektu oglądanego z dwóch kierunków. W praktyce najłatwiej
Materiały edukacyjne Tranzyt Wenus 2012 Zestaw 3. Paralaksa Zadanie 1. Paralaksa czyli zmiana Paralaksa to zjawisko pozornej zmiany położenia obiektu oglądanego z dwóch kierunków. W praktyce najłatwiej
14 POLE GRAWITACYJNE. Włodzimierz Wolczyński. Wzór Newtona. G- stała grawitacji 6, Natężenie pola grawitacyjnego.
 Włodzimierz Wolczyński 14 POLE GRAWITACYJNE Wzór Newtona M r m G- stała grawitacji Natężenie pola grawitacyjnego 6,67 10 jednostka [ N/kg] Przyspieszenie grawitacyjne jednostka [m/s 2 ] Praca w polu grawitacyjnym
Włodzimierz Wolczyński 14 POLE GRAWITACYJNE Wzór Newtona M r m G- stała grawitacji Natężenie pola grawitacyjnego 6,67 10 jednostka [ N/kg] Przyspieszenie grawitacyjne jednostka [m/s 2 ] Praca w polu grawitacyjnym
nawigację zliczeniową, która polega na określaniu pozycji na podstawie pomiaru przebytej drogi i jej kierunku.
 14 Nawigacja dla żeglarzy nawigację zliczeniową, która polega na określaniu pozycji na podstawie pomiaru przebytej drogi i jej kierunku. Rozwiązania drugiego problemu nawigacji, tj. wyznaczenia bezpiecznej
14 Nawigacja dla żeglarzy nawigację zliczeniową, która polega na określaniu pozycji na podstawie pomiaru przebytej drogi i jej kierunku. Rozwiązania drugiego problemu nawigacji, tj. wyznaczenia bezpiecznej
Jaki jest Wszechświat?
 1 Jaki jest Wszechświat? Od najmłodszych lat posługujemy się terminem KOSMOS. Lubimy gry komputerowe czy filmy, których akcja rozgrywa się w Kosmosie, na przykład Gwiezdne Wojny. Znamy takie słowa, jak
1 Jaki jest Wszechświat? Od najmłodszych lat posługujemy się terminem KOSMOS. Lubimy gry komputerowe czy filmy, których akcja rozgrywa się w Kosmosie, na przykład Gwiezdne Wojny. Znamy takie słowa, jak
Biuletyn Astronomiczny nr 2
 Biuletyn Astronomiczny nr 2 W kwietniu skupimy się przede wszystkim na opisie rozgwieżdżonego nieba ponieważ takie interesujące zjawiska jak koniunkcje Księżyca z planetami czy zakrycia gwiazd przez Księżyc,
Biuletyn Astronomiczny nr 2 W kwietniu skupimy się przede wszystkim na opisie rozgwieżdżonego nieba ponieważ takie interesujące zjawiska jak koniunkcje Księżyca z planetami czy zakrycia gwiazd przez Księżyc,
Badanie faz Księżyca oraz ich wpływu na poziom wody mórz i oceanów na Ziemi
 Badanie faz Księżyca oraz ich wpływu na poziom wody mórz i oceanów na Ziemi Projekt badawczy wykonała: Nina Bąkowska kl. IIA Publiczne Gimnazjum w Pokoju 2014 rok Spis treści: I. Opis faz Księżyca II.
Badanie faz Księżyca oraz ich wpływu na poziom wody mórz i oceanów na Ziemi Projekt badawczy wykonała: Nina Bąkowska kl. IIA Publiczne Gimnazjum w Pokoju 2014 rok Spis treści: I. Opis faz Księżyca II.
Wenus na tle Słońca. Sylwester Kołomański Tomasz Mrozek. Instytut Astronomiczny Uniwersytetu Wrocławskiego
 Wenus na tle Słońca Sylwester Kołomański Tomasz Mrozek Instytut Astronomiczny Uniwersytetu Wrocławskiego Instytut Astronomiczny UWr Czym się zajmujemy? uczymy studentów, prowadzimy badania naukowe (astrofizyka
Wenus na tle Słońca Sylwester Kołomański Tomasz Mrozek Instytut Astronomiczny Uniwersytetu Wrocławskiego Instytut Astronomiczny UWr Czym się zajmujemy? uczymy studentów, prowadzimy badania naukowe (astrofizyka
Astronomia. Znając przyspieszenie grawitacyjne planety (ciała), obliczyć możemy ciężar ciała drugiego.
 Astronomia M = masa ciała G = stała grawitacji (6,67 10-11 [N m 2 /kg 2 ]) R, r = odległość dwóch ciał/promień Fg = ciężar ciała g = przyspieszenie grawitacyjne ( 9,8 m/s²) V I = pierwsza prędkość kosmiczna
Astronomia M = masa ciała G = stała grawitacji (6,67 10-11 [N m 2 /kg 2 ]) R, r = odległość dwóch ciał/promień Fg = ciężar ciała g = przyspieszenie grawitacyjne ( 9,8 m/s²) V I = pierwsza prędkość kosmiczna
Ziemia jako zegar Piotr A. Dybczyński
 Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
Wykład udostępniam na licencji Creative Commons: Ziemia jako zegar Piotr A. Dybczyński Czas gwiazdowy N N N N N N N N N N N s = 0h N s = 0h Czemu taka dziwna tarcza? N s = 0h Czemu taka dziwna tarcza?
