Wstępna redukcja obrazów z kamer CCD
|
|
|
- Karol Jakubowski
- 9 lat temu
- Przeglądów:
Transkrypt
1 Wstępna redukcja obrazów z kamer CCD Wstępna obróbka obrazów pochodzących z urządzeń takich jak kamery CCD, czy CMOS polega na usunięciu lub zminimalizowaniu niepoŝądanych efektów dawanych przez te urządzenia (i optykę teleskopu) podczas eksponowania obrazu obiektu. Przebiega ona w trzech etapach (klasyczna trójka redukcyjna ): 1. redukcja na BIAS, 2. redukcja na DARK, 3. redukcja na FLAT, By wykonać powyŝsze etapy obróbki naleŝy, prócz oczywiście właściwego obrazu obiektu (OBJECT), wykonać szereg pomocniczych ekspozycji pamiętając, Ŝe zwiększenie stosunku S/N w obrazach słuŝących redukcji osiąga się zwiększając liczbę obrazów pomocniczych. W ogólności mamy: S ~ N frame gdzie: N frame - liczba zdjęć N Musimy otrzymać szereg (rzędu dziesiątek) 1. obrazów BIAS (odcięty dopływ światła i t exp = 0.0): 2. obrazów DARK (odcięty dopływ światła i t exp (DARK) t exp (OBJECT)) 3. obrazów FLAT (FLATFIELD) (równomiernie i izotropowo emitująca światło powierzchnia: tło nieba o zmierzchu/świcie, ekran oświetlony światłem nieba lub sztucznym źródłem światła - UWAGA na efekt koloru oświetlenia) 209
2 Mamy więc: B ( x, y), i = 1, N, t 0. 0 D ( x, y), j = 1, N, t F ( x, y), k = 1, N, t O( x, y),, texp PoniŜej symbol: <... > oznacza średnią (medianę lub średnią z procedurą odcięcia Kσ) po obrazach dla konkretnego (x,y); wynikiem jest obraz, oznacza średnią z sygnałów pixli dla danego obrazu; wynikiem jest liczba, Zacieramy ręce i przystępujemy do redukcji: i k j B D F B exp D exp F exp O 1. BIAS B ( x, y) = B ( x, y) B ( x, y) = B ( x, y) B ( x, y) dla kontroli i i D ( x, y) = D ( x, y) B ( x, y) j j F ( x, y) = F ( x, y) B ( x, y) k k O ( x, y) = O ( x, y) B ( x, y) i 210
3 2. DARK Tu szczególnie waŝne jest zastosowanie procedur składania obrazów innych niŝ zwykła średnia (np. mediana, odcięcie Kσ), by nie mnoŝyć, a raczej usuwać efekty promieniowania jonizującego, głównie kosmicznego CRH (Cosmic Ray Hit) których ilość narasta proporcjonalnie do czasu ekspozycji i ilości obrazów DARK. D ( x, y) = D ( x, y) j D ( x, y) = D ( x, y) D ( x, y) dla kontroli j j texp Fk ( x, y) = Fk ( x, y) D x y D (, ) t texp O ( x, y) = O ( x, y) D x y D (, ) t F exp O exp 3. FLAT F ( x, y) = F ( x, y), f = F ( x, y) F ( x, y) = f k O ( x, y) = f k Fk ( x, y) F ( x, y) O ( x, y) F ( x, y) dla kontroli 211
4 Przykładowe obrazy średnie BIAS, DARK, FLAT... BIAS Wzrost jasności do brzegu jest efektem generowania sygnału ciemnego podczas odczytu obrazu BIAS trwającego pojedyncze sekundy. Jasne fragmenty kolumn to efekt hot pixel na początku kaŝdego fragmentu. FLAT dla kamery wraz z teleskopem. Spadek jasności od centrum do brzegów jest efektem winietowania. Małe ciemne pierścienie to dyfrakcja światła na pyłkach leŝących na szybce zamykającej próŝnię, większe, na pyłkach leŝących na filtrach. BIAS FLAT DARK FLAT kontrolny DARK Jasne pasma to e- fekt zmiennej przewodności cieplnej pomiędzy matrycą CCD a zimną płytą termoelektrycznego urządzenia chłodzącego. Jasne pixle i klastery to hot pixels i efekty promieniowania jonizującego. FLAT kontrolny powstaje przez redukcję indywidualnej ekspozycji FLAT przy pomocyśredniego FLAT (tzw. Master Flat) 212
5 ...i wynik redukcji obrazu obiektu przed po 213
6 Pakiety oprogramowania słuŝące do wstępnej (i nie tylko) obróbki zdjęć z kamer CCD Pakiety te powinny umoŝliwiać między innymi: - działania arytmetyczne na obrazach, liczenie funkcji z obrazów, porównywanie obrazów itp., - analizę statystyczną obrazów (momenty rozkładu i parametry statystyczne), - liczenie róŝnych transformat (FFT, itp.), - transformacje geometryczne (afiniczne itp.), - wykrywanie i rozpoznawanie typów obiektów i czyszczenie zdjęć (z CRH itp.), - filtrowanie i dekonwolucję (filtr splotowy, Winera itp., dekonwolucja MEM itp.), - pisanie własnych skryptów wykorzystujących elementy pakietu, - rozbudowę pakietów dzięki zdobycznemu oprogramowaniu. MIDAS (Munich Image Data Analysis System) ESO, IRAF (Image Reduction and Analysis Facility) NOAO Tuscon, USA, AIPS (Astronomical Image Processing System) NRAO, USA, IDL (The Data Visualization & Analysis Platform) ITT Corporation, USA, Podstawowy format zapisu danych uŝywany w astrofizyce obserwacyjnej (i nie tylko) to FITS (Flexible Image Transport System), przykładowe referencje: D.C. Wells et al. 1981, Astron. Astrophys. Supp. Ser. 44, 363 R.J. Hanish et al. 2001, Astron. Astrophys. 376, 359. Zbiór z danymi zawiera nagłówek opisujący formę zapisu danych, warunki otrzymania danych, informacje o metodach i historii redukcji oraz o uŝytym oprogramowaniu. Dalsza część zbioru zawiera dane liczbowe uszeregowane względem dowolnej liczby osi. W ten sposób równie łatwy jest zapis typu 1-D (np. widmo), 2-D (obraz), 3-D (dane ze spektroskopu obrazującego), 4-D (dane ze spektropolarymetru obrazującego)
7 słowo kluczowe (keyword) Przykład nagłówka zbioru FITS. SIMPLE = T / FITS STANDARD BITPIX = 16 / FITS BITS/PIXEL NAXIS = 2 / NUMBER OF AXES NAXIS1 =1024 / LENGTH OF AXIS1 NAXIS2 =1024 / LENGTH OF AXIS2 AXIS10 = 1 / ZERO OF AXIS1 AXIS20 = 1 / ZERO OF AXIS2 BSCALE = E+0 / REAL = ADU*BSCALE + BZERO sposób odtworzenia rzeczywistej wartości BZERO = / sygnału dla pixla OBJECT = 'p17 ' / BIAS,DARK,FLAT,COMMON NAME OF THE OBJECT RA = '03:48:14' / EPOCH 2000 DEC = '50:26:48' / EPOCH 2000 OBSERVER= 'waniak ' WEATHER = 'clear fog' CCD-TEMP = -21 AIR-TEMP = 25 EXPTIME = '20.00 ' FILTER = 'R ' / BESSELL FILTER GAIN = 1 / GAIN NUMBER BINNING = 3 komentarz fragment absolutnie niezbędny / OBSERVER / WEATHER INFO / CCD TEMPERATURE / AIR TEMPERATURE / EXPOSURE DURATION [SEC] informacja, Ŝe jest to FITS ilość bitów na pixel (1,2,4-zapis danych REAL) ilość osi ilość pixli wzdłuŝ osi 1 ilość pixli wzdłuŝ osi 2 FILENAME = 'p17r0001.fit' / ORIGINAL FILE NAME DATE-OBS = '29/10/2007' / DD/MM/YYYY TIME-OBS = '23:56:58.90' / HH:MM:SS.SS UT OF THE EXPOSURE START MID-TIME = / Middle of exp [h] JD = / Julian Day (mid exp) HEL_CORR= HJD = / Heliocentric Julian Day (mid exp) END 215
8 Fotometria obiektów na zdjęciach z kamer CCD W zaleŝności od rozmiaru obrazu obiektu w porównaniu z PSF pełnego systemu obrazującego mamy do czynienia z fotometrią: obiektów zwartych, punktowych, gwiazdopodobnych (kierunkowy profil jasności powierzchniowej ma mniejsze rozmiary niŝ PSF, informacja o kierunkowym rozkładzie jasności powierzchniowej jest praktycznie utracona), zmierzyć moŝna jedynie pełną jasność obiektu, scałkowaną po profilu kierunkowym, obiektów rozciągłych (kierunkowy profil jasności powierzchniowej przewyŝsza rozmiarami PSF), ( ) B k r zmierzyć moŝna jasność powierzchniową, informacja kierunkowa choć zniekształcona przez PSF moŝe być wykorzystana w badaniach obiektów, np. odtworzona odpowiednim modelem obiektu, czy zjawiska. obiektów rozciągłych małych w porównaniu z PSF (kierunkowy profil jasności powierzchniowej ma rozmiary porównywalne z PSF), przy odpowiednim próbkowaniu i wysokim S/N moŝliwe jest odtworzenie estymaty oryginalnego profilu kierunkowego B k r dzięki ~ metodom rekonstrukcji i dekonwolucji obrazu. Tak czy siak, chcąc otrzymać pełną jasność lub jasność powierzchniową obiektu naleŝy jego fotometrię skalibrować poprzez obserwacje standardów fotometrycznych, a te z reguły są gwiazdami o znanych magnitudach systemowych lub/i widmach. Czyli fotometrii obiektów zwartych raczej nie unikniemy. ( ) B k r ( ) 216
9 Metody fotometrii gwiazdowej z wykorzystaniem zdjęć z kamer CCD Dwa najbardziej podstawowe podejścia do tego zagadnienia to: fotometria aperturowa (wyznaczenie pełnego sygnału w obrazie obiektu zwartego poprzez zliczanie sygnałów dla elementów obrazu zawartych w umownej aperturze obejmującej obiekt z jednoczesnym odjęciem sygnału pochodzącego od tła), fotometria profilowa (wyznaczenie jasności poprzez wyznaczenie normalizacji funkcji PSF optymalnie dopasowanej do profilu obiektu z jednoczesnym wyznaczeniem poziomu sygnału pochodzącego od tła). Sposoby programowej realizacji fotometrii gwiazdowej to: metoda interaktywna (operator wskazuje obiekty, których jasność naleŝy wyznaczyć; w przypadku fotometrowania wielu zdjęć tego samego pola ułatwieniem jest wzorzec (templet) zawierający pozycje obiektów, uŝywany przez program dla analizy kolejnych zdjęć), metoda automatyczna (program samodzielnie wykrywa istotne obiekty na zdjęciu, odrzuca obiekty nie gwiazdowe np. CRH, galaktyki a dla wyselekcjonowanych obrazów gwiazd mierzy jasności), metoda kombinowana (stosowana w przypadku iteracyjnej procedury automatycznej mającej podwyŝszyć jakość fotometrii; ingerencja operatora pomaga w selekcji gwiazd przeznaczonych do sfotometrowania lub do wyznaczenia PSF). 217
10 Fotometria aperturowa. Rozpoczyna się od właściwego, obiektywnego scentrowania apertury na obrazie gwiazdy. Operator najczęściej dokonuje jedynie wskazania obiektu. Stosuje się np.: wyznaczenie środka powierzchniowego rozkładu jasności profilu obiektu, brzegowe rozkłady jasności profilu obiektu względem osi X,Y (np. dopasowanie funkcji Gaussa). Apertura (najczęściej kołowa, choć niekoniecznie) o promieniu r 1 obejmuje obiekt a dodatkowy pierścień o promieniu wewnętrznym r 2 i zewnętrznym r 3 słuŝy wyznaczeniu poziomu tła nieba. Przez tło nieba rozumie się wszelkie oświetlenie detektora nie pochodzące od fotometrowanego obiektu (świecenie nieba, słabe gwiazdy, obiekty rozciągłe, słabe CRH, światło rozproszone w optyce itp.). Poziom jego sygnału otrzymuje się jako: średnią z wartości sygnałów w pierścieniu (dobre statystycznie, ale tło musi być czyste ), dopasowanie poziomu tła zmieniającego się liniowo, kwadratowo,..., lub zagiętego (uwaga na zaleŝności o zbyt wysokich potęgach), medianę rozkładu wartości sygnałów w pierścieniu (odporne na małe zwarte zakłócenia ), modę rozkładu wartości sygnałów w pierścieniu (najbezpieczniejsze, modę przybliŝa się wartością 3 Median-2 Mean. Fotometrię aperturową stosuje się chętnie w przypadku: braku izoplanatyzmu i silnej zaleŝności PSF od pozycji na zdjęciu, fotometrii prowadzonej pomiędzy zdjęciami o wyraźnie róŝnych PSF (np. nawiązania fotometryczne, wyznaczanie ekstykcji). Fotometrii aperturowej nie stosuje się w przypadku: gęstych pól gwiazdowych (nakładanie się profili sąsiednich gwiazd), obrazów prześwietlonych i z wyraźnymi defektami (np. CRH). 218
11 Problem doboru promienia diafragmy w fotometrii aperturowej. ZaleŜność pełnego sygnału od promienia diaframy opisuje krzywa wzrostu (rys. prawy, czerwona). Jak widać gwiazda nie zanika nigdy. Z drugiej strony formalny błąd fotometrii aperturowej zaleŝy od promienia diafragmy (rys. prawy, niebieskie) osiągając minimum dla promienia diafragmy mniejszego w przypadku gwiazd słabszych i większego w przypadku gwiazd jaśniejszych. Wynika to z formalnego wyraŝenia na pełny błąd fotometrii aperturowej: tot star sky RON DARK FLAT σ = σ + σ + σ + σ + σ Mimo, Ŝe jest to błąd formalny w przypadku dobrze prowadzonej analizy jest on dobrze skorelowany z błędem faktycznym otrzymanym z wielokrotnych pomiarów gwiazd (rys. lewy). Measured photometric error [mag] Arbitrary magnitude error 2 mag error Photometric error 1 [mag] Theoretical photometric error [mag] Aperture radius [pix]
12 W związku z tym fotometrię aperturową gwiazd prowadzi się w dwu reŝimach: błąd fotometrii zdominowany przez pełny sygnał gwiazdy (jasna gwiazda, niskie tło, rozmiar diafragmy nie stanowi problemu), błąd fotometrii zdominowany przez sygnał tła (słaba gwiazda, jasne tło, im większa diafragma tym gorzej), W celu utrzymania prawie niezmiennego magnitudowego błędu fotometrii (mag error) od jasności obiektu, stosujemy diafragmę o promieniu zaleŝnym od jasności gwiazdy. W związku z zaleŝnością sygnału fotometrycznego od promienia diafragmy naleŝy skorygować otrzymane magnitudy na aktualny promień diafragmy przeliczając je przy wykorzystaniu krzywej wzrostu na jeden, zadany promień diafragmy. Jest to tzw. korekcja aperturowa (aperture correction). A jak się ma promień apertury do problemu izoplanatyzmu zdjęć obiektów? Oj ma się, ma! Dla fotometrii róŝnicowej wykonywanej na jednym obrazie: w przypadku izoplanatyzmu - wynik nie zaleŝy od promienia apertury (stałość krzywej wzrostu po polu zdjęcia) (moŝna stosować aperturę minimalizującą mag error), w przypadku braku izoplanatyzmu - wynik zaleŝy od promienia apertury (najlepiej stosować moŝliwie jak największą aperturę). I jeszcze dwa zagadnienia związane z fotometrią aperturową: problem właściwej interpolacji sygnału dla pixli częściowo zawartych w aperturze, problem właściwego doboru pierścienia słuŝącego określeniu poziomu tła - w sytuacji izoplanatyzmu obrazu nie ma problemu. Wynik fotometrii nie jest czuły na rozmiar pierścienia. W sytuacji przeciwnej, wskazany wybór moŝliwie jak najdalszego pierścienia. Wzrost szerokości pierścienia powoduje spadek składowej błędu fotometrii pochodzącej od tła. 220
13 Fotometria profilowa. Startuje się od znalezienia PSF charakteryzującego dane zdjęcie. PSF opisywane moŝe być za pomocą: funkcji analitycznej, której parametry określone zostają poprzez jej dopasowanie LSQ do pewnej liczby wyselekcjonowanych gwiazd (odpowiednio jasne i samotne ). Najczęściej stosuje się następujące funkcje: Gauss (uwzględniona eliptyczność i dowolny kąt pozycyjny elipsy): G( x, y) = g exp[ ( α X + β Y + γ XY) ] a = 2 β = 2 2σ Lorentz: L( x, y) = l 1 x 2σ y 2 2 δ 1+ ( α X + β Y + γ XY ) X = x x Y = y y Moffat (1969, uzyskana z profili gwiazd na kliszach, najlepszy wykładnik δ to 4, Racine 1996): Penny (suma funkcji Gaussa i Lorentza): 2 2 (, ) = [ 1+ α + β + γ ] M x y m X Y XY (, ) = (, ) + (, ) P x y G x y L x y mapy z wartościami PSF wyznaczonymi z grupy wyselekcjonowanych gwiazd. Zmieniające się ułoŝenie profili gwiazd względem siatki pixli umoŝliwia zwiększenie gęstości próbkowania PSF w porównaniu z próbkowaniem pojedynczego profilu. W zaleŝności od stopnia izoplanatyzmu PSF moŝliwe są dwa podejścia: izoplanatyzm - parametry analitycznego przybliŝenia PSF lub wyznaczona mapa PSF niezmienne po polu obrazu, brak izoplanatyzmu - parametry analitycznego przybliŝenia PSF lub wyznaczona mapa PSF zmieniające się w sposób np. liniowy lub kwadratowy ze współrzędnymi na obrazie (moŝliwość uwzględnienia aberracji optycznych pozaosiowych) 221 δ 0 0
14 Uwaga: W przypadku izoplanatycznej PSF niedoskonałość dopasowania funkcji analitycznej nie ma większego znaczenia dla wyniku profilowej fotometrii róŝnicowej prowadzonej w ramach danego zdjęcia (np. wydłuŝone profile gwiazd moŝna fitować profilami kołowo-symetrycznymi). Relative signal X [pix] Porównanie profili Gaussa, Lorentza i Moffata z obserwowanym profilem gwiazdy (kwadraty). Jak widać ani Gauss, ani Lorentz, ale Moffat z wykładnikiem 4 najlepiej oddaje rzeczywisty kształt profilu PSF. Większość szanujących się programów przeznaczonych do fotometrowania obiektów zwartych ma zarówno opcję fotometrii aperturowej jak i profilowej. Przykłady takich programów to: DAOPHOT (Dominion Astrophysical Observatory PHOTometry, aut. Stetson), dophot (do PHOTometry, aut. Schechter), ROMAPHOT (ROMA PHOTometry), Inne programy słuŝące rozpoznawaniu, klasyfikowaniu i fotometrowaniu róŝnych obiektów to np.: INVENTORY (aut. Kruszewski), SEXTRACTOR Większość programów realizujących fotometrię obiektów zwartych rozpoczyna działanie od zidentyfikowania tych obiektów w wejściowym obrazie. Stosowane kryteria wyboru obejmują m.in. : minimalny dopuszczalny poziom sygnału w obiekcie, kryteria kształtu (np. stopień okrągłości pozwalający odrzucić fragmenty kolumn o wyŝszym sygnale), kryteria profilu (np. stopień ostrości pozwalający odrzucić CRH i obiekty rozciągłe). 222
15 Idea działania programu DAOPHOT. 1.Wstępna analiza zdjęcia, np. filtrowanie (filtr wygładzająco-kontrastorowy na bazie Gaussa) (cel: zwiększenie wykrywalności gwiazd, obniŝenie wykrywalności CRH i obiektów rozciągłych), 2.Wybór kandydatów na obiekty gwiazdowe przy zastosowaniu 3 powyŝszych (i innych) kryteriów, 3.Fotometria aperturowa gwiazd dla wielu apertur (X,Y, mag, mag error), 4.Wybór gwiazd słuŝących określeniu PSF, 5.Określenie PSF (analityczne, mapa ze skokiem 0.5 pix.) (stałe lub zmienne po polu obrazu), 6.Fotometria profilowa gwiazd w oparciu o PSF (moŝliwość jednoczesnego dopasowania PSF do 60 gwiazd w wyselekcjonowanych przez program grupach), 7.Odjęcie od zdjęcia wejściowego syntetycznego obrazu powstałego przez umieszczenie PSF w wyznaczonych dla gwiazd pozycjach (obraz O-C), 8.Analiza obrazu O-C w celu wykrycia nie znalezionych poprzednio obiektów gwiazdowych, 9.Przeprowadzenie fotometrii wykrytych gwiazd. itd., itp. COORstar: dmap.nxy : Coordinates of all stars in an observed file a fiducial star positions. PSFNlist: dlst.psf : Star numbers to be used for making a PSF. PIXSizea: : pixelsize in arcseconds (used only by `dpar` program dao_re: 7.55 : RE ad noise dao_ga: 1.41 : GA in ADU dao_lo: 1.0 : LO west counts dao_ls: 0.2 : LS Low Sharpness cutoff dao_hs: 1.0 : HS High Sharpness cutoff dao_lr: -1.0 : LR Low Roundness cutoff dao_hr: 1.0 : HR High Roundness cutoff dao_hi: : HI ghest counts alowed by ADC converter dao_fw: 5.0 : FW (initial FWHM of PSF, seeing) dao_th: 3.0 : TH reshold w sigma tla. dao_wa: -1 : WA tch,1 display,-1 do not display info. on a screen dao_fi: 10.0 : FI tting radius dao_ps: 12.0 : PS f radius of substruction of PSF from a star image dao_va: 0 : VA -1,0,1,2, - model: only analytic fit,flat linear,square dao_ex: 9 : EX tra Passes dao_an: 1 : AN - Analytic model PSF (1-Gauss, 2-Moffat (Beta=1.5) 3-Mofat (Beta=2.5), 4-Lorentz, 5-Penny (Gausian + Lorentz, four parameters free), 6-Penny: 5 parameters free. dao_is: 15.0 : IS Inner Sky radius (different than all_is, pg. 58 pt. 5.) dao_os: 20.0 : OS Outer Sky radius ALLSTAR PARAMETERS (Manual pg. 57,58,59) Fragment zbioru DAOPHOT.OPT zawierającego m. in. wartości parametrów analizy obrazu i fotometrii profilowej. all_fi: 5.0 : FI Fitting radius all_ce: 6.0 : CE Clipping Exponent all_is: 2.0 : IS Inner Sky radius (should be sma ll: see pg. 58 pt. 5.) all_os: 20.0 : OS Outer Sky radius 223
16 Idea działania programu DoPHOT. 1.UŜycie jedynie analitycznej reprezentacji PSF w postaci fragmentu potęgowego rozwinięcia funkcji Gaussa (dla profili niedopróbkowanych na ogół pracuje lepiej niŝ reprezentacja PSF jako mapy): D x, y d z z z δ δ + B, z = αx + βy + γ XY, α = =, X = x x Y = y y 2 6 2σ β 2σ ( ) = ( ) ( ) x y 2.Poziom lokalnego tła jako jeden z dopasowywanych parametrów (B), 3.Zastąpienie jednoczesnego dopasowywania profilu PSF do wielu obiektów (znane z programu DAOPHOT) dopasowywaniem do potencjalnych obiektów gwiazdowych spełniających zmieniające się od iteracji do iteracji kryteria (np. malejący poziom sygnału), 4.Klasyfikowanie obiektów (gwiazda, CRH, obiekt rozciągły), 5.Dodawanie kolejnych obiektów gwiazdowych do listy obiektów i jednoczesne odejmowanie ich profili od obrazu wejściowego (działanie przypominające algorytm CLEAN Högbom 1974), 6.MoŜliwość wykonania fotometrii aperturowej. Schemat ideowy działania programu DoPHOT. 224
17 Fotometria obiektów gwiazdowych o zmiennej jasności w gęstych polach - ISM (Image Subtraction Method). Stosuje się ją do wykrywania zmienności i fotometrowania zmiennych obiektów gwiazdopodobnych znajdujących się w gęstych polach gwiazdowych utrudniających lub uniemoŝliwiających przeprowadzenie fotometrii profilowej (przy odległości centrów obiektów mniejszej niŝ 0.37 FWHM PSF DAOPHOT traktuje je jako jeden obiekt), a tym bardziej fotometrii aperturowej. Bazuje ona na odejmowaniu od siebie obrazów tego samego pola gwiazdowego uzyskanych w pewnym odstępie czasu. Istotą ISM jest: właściwe zgranie astrometryczne zdjęć uzyskane dzięki zastosowaniu: przeskalowań, obrotów, przesunięć transformacji wyŝszego stopnia, właściwe zgranie fotometryczne zdjęć odjęcie tła nieba, przeskalowanie sygnałów w oparciu o średnią jasność grupy odpowiednio dobranych obiektów, właściwe zgranie PSF - splot zdjęcia charakteryzującego się węŝszym PSF (f 1 (x,y)) z funkcją rozmywającą F(x,y) dającą efektywny PSF bliski temu, jaki ma zdjęcie uzyskane z szerszym PSF (f 2 (x,y)). ~ I x, y = F x, y I x, y f x, y = F x, y f x, y ( ) ( ) ( ) ( ) ( ) ( ) I = ~, 2 ( x, y) I 1 ( x y ) ( ) ( ) ~ I2 x, y I1 x, y 225
Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky"
 Uniwersytet Warszawski Wydział Fizyki Bartłomiej Włodarczyk Nr albumu: 306849 Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky" Praca przygotowana w ramach Pracowni Fizycznej II-go stopnia pod
Uniwersytet Warszawski Wydział Fizyki Bartłomiej Włodarczyk Nr albumu: 306849 Analiza danych z nowej aparatury detekcyjnej "Pi of the Sky" Praca przygotowana w ramach Pracowni Fizycznej II-go stopnia pod
Pomiary jasności nieba z użyciem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN
 Pomiary jasności nieba z użyciem aparatu cyfrowego Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum Wrocławia Pomiary
Pomiary jasności nieba z użyciem aparatu cyfrowego Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum Wrocławia Pomiary
Przegląd funkcji i możliwości programu
 Akademia Pedagogiczna, 10.01.2006 JastroCam Przegląd funkcji i możliwości programu Marek Budyn rayn@infostrade.com.pl Podstawowe cechy programu Dostosowanie do podstawowych czynności wykonywanych w trakcji
Akademia Pedagogiczna, 10.01.2006 JastroCam Przegląd funkcji i możliwości programu Marek Budyn rayn@infostrade.com.pl Podstawowe cechy programu Dostosowanie do podstawowych czynności wykonywanych w trakcji
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek cięŝkości ułoŝenie przestrzenne momenty wyŝszych rzędów promienie max-min centryczność
Fotometria CCD 5. Metoda odejmowania obrazów
 Fotometria CCD 5. Metoda odejmowania obrazów Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Gęste pole: M92 Gęste pole: M92 Gęste pole: okolice centrum Galaktyki
Fotometria CCD 5. Metoda odejmowania obrazów Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Gęste pole: M92 Gęste pole: M92 Gęste pole: okolice centrum Galaktyki
Laboratorium optycznego przetwarzania informacji i holografii. Ćwiczenie 6. Badanie właściwości hologramów
 Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 6. Badanie właściwości hologramów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska Gdańsk 2006 1. Cel
Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 6. Badanie właściwości hologramów Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska Gdańsk 2006 1. Cel
Gwiazdy zmienne. na przykładzie V729 Cygni. Janusz Nicewicz
 Gwiazdy zmienne na przykładzie V729 Cygni Plan prezentacji Czym są gwiazdy zmienne? Rodzaje gwiazd zmiennych Układy podwójne gwiazd Gwiazdy zmienne zaćmieniowe Model Roche'a V729 Cygni Obserwacje Analiza
Gwiazdy zmienne na przykładzie V729 Cygni Plan prezentacji Czym są gwiazdy zmienne? Rodzaje gwiazd zmiennych Układy podwójne gwiazd Gwiazdy zmienne zaćmieniowe Model Roche'a V729 Cygni Obserwacje Analiza
ASTROFOTOGRAFIA Z IRIS
 ASTROFOTOGRAFIA Z IRIS DOMINIK GRONKIEWICZ Klub Astronomiczny Almukantarat Tę pracę można rozpowszechniać wyłącznie w całości w celach edukacyjnych i dydaktycznych. TROCHĘ TEORII 2 Naświetlenie zdjęć to
ASTROFOTOGRAFIA Z IRIS DOMINIK GRONKIEWICZ Klub Astronomiczny Almukantarat Tę pracę można rozpowszechniać wyłącznie w całości w celach edukacyjnych i dydaktycznych. TROCHĘ TEORII 2 Naświetlenie zdjęć to
Laboratorium optycznego przetwarzania informacji i holografii. Ćwiczenie 4. Badanie optycznej transformaty Fouriera
 Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 4. Badanie optycznej transformaty Fouriera Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska Gdańsk
Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 4. Badanie optycznej transformaty Fouriera Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska Gdańsk
Mikroskop teoria Abbego
 Zastosujmy teorię dyfrakcji do opisu sposobu powstawania obrazu w mikroskopie: Oświetlacz typu Köhlera tworzy równoległą wiązkę światła, padającą na obserwowany obiekt (płaszczyzna 0 ); Pole widzenia ograniczone
Zastosujmy teorię dyfrakcji do opisu sposobu powstawania obrazu w mikroskopie: Oświetlacz typu Köhlera tworzy równoległą wiązkę światła, padającą na obserwowany obiekt (płaszczyzna 0 ); Pole widzenia ograniczone
Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN
 Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum
Pomiary jasności tła nocnego nieba z wykorzystaniem aparatu cyfrowego. Tomek Mrozek 1. Instytut Astronomiczny UWr 2. Zakład Fizyki Słońca CBK PAN Jasność nieba Jasność nieba Jelcz-Laskowice 20 km od centrum
Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky
 Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky Maciej Zielenkiewicz 5 marca 2010 1 Wstęp 1.1 Projekt Pi of the Sky Celem projektu jest poszukiwanie
Ocena błędów systematycznych związanych ze strukturą CCD danych astrometrycznych prototypu Pi of the Sky Maciej Zielenkiewicz 5 marca 2010 1 Wstęp 1.1 Projekt Pi of the Sky Celem projektu jest poszukiwanie
Wykład 10 - Charakterystyka podstawowych systemów gwiazdowych: otoczenie Słońca, Galaktyka, gromady gwiazd, galaktyki, grupy i gromady galaktyk
 Wykład 10 - Charakterystyka podstawowych systemów gwiazdowych: otoczenie Słońca, Galaktyka, gromady gwiazd, galaktyki, grupy i gromady galaktyk 28.04.2014 Dane o kinematyce gwiazd Ruchy własne gwiazd (Halley
Wykład 10 - Charakterystyka podstawowych systemów gwiazdowych: otoczenie Słońca, Galaktyka, gromady gwiazd, galaktyki, grupy i gromady galaktyk 28.04.2014 Dane o kinematyce gwiazd Ruchy własne gwiazd (Halley
Fotometria i modelowanie planetoid
 Fotometria i modelowanie planetoid Pakiet Starlink. Metoda inwersji krzywych zmian blasku Anna Marciniak Obserwatorium Astronomiczne UAM, Poznań 21 marca 2015 Planetoidy - skamieniałe planetezymale (NASA/JPL-Caltech/JAXA/ESA)
Fotometria i modelowanie planetoid Pakiet Starlink. Metoda inwersji krzywych zmian blasku Anna Marciniak Obserwatorium Astronomiczne UAM, Poznań 21 marca 2015 Planetoidy - skamieniałe planetezymale (NASA/JPL-Caltech/JAXA/ESA)
Poszukiwanie gwiazd zmiennych w eksperymencie Pi of the Sky
 Poszukiwanie gwiazd zmiennych w eksperymencie Pi of the Sky Łukasz Obara Wydział Fizyki, Uniwersytet Warszawski Plan prezentacji Eksperyment Pi of the Sky Projekt GLORIA Środowisko LUIZA i zaimplementowana
Poszukiwanie gwiazd zmiennych w eksperymencie Pi of the Sky Łukasz Obara Wydział Fizyki, Uniwersytet Warszawski Plan prezentacji Eksperyment Pi of the Sky Projekt GLORIA Środowisko LUIZA i zaimplementowana
Aerotriangulacja. 1. Aerotriangulacja z niezależnych wiązek. 2. Aerotriangulacja z niezależnych modeli
 Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Aerotriangulacja 1. Aerotriangulacja z niezależnych wiązek 2. Aerotriangulacja z niezależnych modeli Definicja: Cel: Kameralne zagęszczenie osnowy fotogrametrycznej + wyznaczenie elementów orientacji zewnętrznej
Skala jasności w astronomii. Krzysztof Kamiński
 Skala jasności w astronomii Krzysztof Kamiński Obserwowana wielkość gwiazdowa (magnitudo) Skala wymyślona prawdopodobnie przez Hipparcha, który podzielił gwiazdy pod względem jasności na 6 grup (najjaśniejsze:
Skala jasności w astronomii Krzysztof Kamiński Obserwowana wielkość gwiazdowa (magnitudo) Skala wymyślona prawdopodobnie przez Hipparcha, który podzielił gwiazdy pod względem jasności na 6 grup (najjaśniejsze:
Aproksymacja funkcji a regresja symboliczna
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(x), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(x), zwaną funkcją aproksymującą
Laboratorium Informatyki Optycznej ĆWICZENIE 2. Koherentne korelatory optyczne i hologram Fouriera
 ĆWICZENIE 2 Koherentne korelatory optyczne i hologram Fouriera 1. Wprowadzenie Historycznie jednym z ważniejszych zastosowań korelatorów optycznych było rozpoznawanie obrazów, pozwalały np. na analizę
ĆWICZENIE 2 Koherentne korelatory optyczne i hologram Fouriera 1. Wprowadzenie Historycznie jednym z ważniejszych zastosowań korelatorów optycznych było rozpoznawanie obrazów, pozwalały np. na analizę
Rys. 1 Schemat układu obrazującego 2f-2f
 Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Ćwiczenie 15 Obrazowanie. Celem ćwiczenia jest zbudowanie układów obrazujących w świetle monochromatycznym oraz zaobserwowanie różnic w przypadku obrazowania za pomocą różnych elementów optycznych, zwracając
Definicja pochodnej cząstkowej
 1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
1 z 8 gdzie punkt wewnętrzny Definicja pochodnej cząstkowej JeŜeli iloraz ma granicę dla to granicę tę nazywamy pochodną cząstkową funkcji względem w punkcie. Oznaczenia: Pochodną cząstkową funkcji względem
Laboratorium Optyki Falowej
 Marzec 2019 Laboratorium Optyki Falowej Instrukcja do ćwiczenia pt: Filtracja optyczna Opracował: dr hab. Jan Masajada Tematyka (Zagadnienia, które należy znać przed wykonaniem ćwiczenia): 1. Obraz fourierowski
Marzec 2019 Laboratorium Optyki Falowej Instrukcja do ćwiczenia pt: Filtracja optyczna Opracował: dr hab. Jan Masajada Tematyka (Zagadnienia, które należy znać przed wykonaniem ćwiczenia): 1. Obraz fourierowski
Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD
 Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 CCD CCD = Charge Coupled Device (urządzenie o sprzężeniu ładunkowym)
Fotometria CCD 3. Kamera CCD. Kalibracja obrazów CCD Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 CCD CCD = Charge Coupled Device (urządzenie o sprzężeniu ładunkowym)
Analiza obrazów - sprawozdanie nr 2
 Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Analiza obrazów - sprawozdanie nr 2 Filtracja obrazów Filtracja obrazu polega na obliczeniu wartości każdego z punktów obrazu na podstawie punktów z jego otoczenia. Każdy sąsiedni piksel ma wagę, która
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy
 Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
Rozpoznawanie obrazów na przykładzie rozpoznawania twarzy Wykorzystane materiały: Zadanie W dalszej części prezentacji będzie omawiane zagadnienie rozpoznawania twarzy Problem ten można jednak uogólnić
7. Wyznaczanie poziomu ekspozycji
 7. Wyznaczanie poziomu ekspozycji Wyznaczanie poziomu ekspozycji w przypadku promieniowania nielaserowego jest bardziej złożone niż w przypadku promieniowania laserowego. Wynika to z faktu, że pracownik
7. Wyznaczanie poziomu ekspozycji Wyznaczanie poziomu ekspozycji w przypadku promieniowania nielaserowego jest bardziej złożone niż w przypadku promieniowania laserowego. Wynika to z faktu, że pracownik
Diagnostyka obrazowa
 Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Diagnostyka obrazowa Ćwiczenie drugie Podstawowe przekształcenia obrazu 1 Cel ćwiczenia Ćwiczenie ma na celu zapoznanie uczestników kursu Diagnostyka obrazowa z podstawowymi przekształceniami obrazu wykonywanymi
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 5 Tomasz Kwiatkowski 3 listopad 2010 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 5 1/41 Plan wykładu Podstawy optyki geometrycznej Załamanie światła, soczewki Odbicie
Wstęp do astrofizyki I Wykład 5 Tomasz Kwiatkowski 3 listopad 2010 r. Tomasz Kwiatkowski, Wstęp do astrofizyki I, Wykład 5 1/41 Plan wykładu Podstawy optyki geometrycznej Załamanie światła, soczewki Odbicie
Zygmunt Wróbel i Robert Koprowski. Praktyka przetwarzania obrazów w programie Matlab
 Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Zygmunt Wróbel i Robert Koprowski Praktyka przetwarzania obrazów w programie Matlab EXIT 2004 Wstęp 7 CZĘŚĆ I 9 OBRAZ ORAZ JEGO DYSKRETNA STRUKTURA 9 1. Obraz w programie Matlab 11 1.1. Reprezentacja obrazu
Przetwarzanie obrazu
 Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
Przetwarzanie obrazu Przekształcenia kontekstowe Liniowe Nieliniowe - filtry Przekształcenia kontekstowe dokonują transformacji poziomów jasności pikseli analizując za każdym razem nie tylko jasność danego
oraz kilka uwag o cyfrowej rejestracji obrazów
 oraz kilka uwag o cyfrowej rejestracji obrazów Matryca CCD i filtry Bayera Matryca CCD i filtry Bayera Demozaikowanie Metody demozaikowania Tradycyjne metody interpolacyjne (nienajlepsze efekty) Variable
oraz kilka uwag o cyfrowej rejestracji obrazów Matryca CCD i filtry Bayera Matryca CCD i filtry Bayera Demozaikowanie Metody demozaikowania Tradycyjne metody interpolacyjne (nienajlepsze efekty) Variable
Filtracja obrazów. w dziedzinie częstotliwości. w dziedzinie przestrzennej
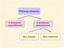 Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Filtracja obrazów w dziedzinie częstotliwości w dziedzinie przestrzennej filtry liniowe filtry nieliniowe Filtracja w dziedzinie częstotliwości Obraz oryginalny FFT2 IFFT2 Obraz po filtracji f(x,y) H(u,v)
Cykle życia gwiazd. Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ. Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak
 [ Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ [Wpis]z Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak Fotometria gromad gwiazdowych z programem SalsaJ Wstęp Fotometria to
[ Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ [Wpis]z Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak Fotometria gromad gwiazdowych z programem SalsaJ Wstęp Fotometria to
Cykle życia gwiazd. Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ. Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak
 [ Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ [Wpis]z Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak Fotometria gromad gwiazdowych z programem SalsaJ Wstęp Fotometria to
[ Fotometria gromad gwiazdowych z wykorzystaniem programu SalsaJ [Wpis]z Autorzy: Daniel Duggan & Sarah Roberts Redakcja: Dawid Basak Fotometria gromad gwiazdowych z programem SalsaJ Wstęp Fotometria to
OPTYKA GEOMETRYCZNA I INSTRUMENTALNA
 1100-1BO15, rok akademicki 2018/19 OPTYKA GEOMETRYCZNA I INSTRUMENTALNA dr hab. Rafał Kasztelanic Wykład 6 Optyka promieni 2 www.zemax.com Diafragmy Pęk promieni świetlnych, przechodzący przez układ optyczny
1100-1BO15, rok akademicki 2018/19 OPTYKA GEOMETRYCZNA I INSTRUMENTALNA dr hab. Rafał Kasztelanic Wykład 6 Optyka promieni 2 www.zemax.com Diafragmy Pęk promieni świetlnych, przechodzący przez układ optyczny
w analizie wyników badań eksperymentalnych, w problemach modelowania zjawisk fizycznych, w analizie obserwacji statystycznych.
 Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Aproksymacja funkcji a regresja symboliczna Problem aproksymacji funkcji polega na tym, że funkcję F(), znaną lub określoną tablicą wartości, należy zastąpić inną funkcją, f(), zwaną funkcją aproksymującą
Astrofotografia dla początkujących. Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski
 Astrofotografia dla początkujących Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski Podstawowe pytania Chcę fotografowad niebo: Mam budżet: Miejsce obserwacji: Poświęcony czas (na jedną noc):
Astrofotografia dla początkujących Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski Podstawowe pytania Chcę fotografowad niebo: Mam budżet: Miejsce obserwacji: Poświęcony czas (na jedną noc):
Rekonstrukcja obrazu (Image restoration)
 Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Rekonstrukcja obrazu (Image restoration) Celem rekonstrukcji obrazu cyfrowego jest odtworzenie obrazu oryginalnego na podstawie obrazu zdegradowanego. Obejmuje ona identyfikację procesu degradacji i próbę
Podstawy OpenCL część 2
 Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Podstawy OpenCL część 2 1. Napisz program dokonujący mnożenia dwóch macierzy w wersji sekwencyjnej oraz OpenCL. Porównaj czasy działania obu wersji dla różnych wielkości macierzy, np. 16 16, 128 128, 1024
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 5 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, shortinst Wstęp do astrofizyki I,
Wstęp do astrofizyki I Wykład 5 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, shortinst Wstęp do astrofizyki I,
ĘŚCIOWO KOHERENTNYM. τ), gdzie Γ(r 1. oznacza centralną częstotliwość promieniowania quasi-monochromatycznego.
 OBRAZOWANIE W OŚWIETLENIU CZĘŚ ĘŚCIOWO KOHERENTNYM 1. Propagacja światła a częś ęściowo koherentnego prof. dr hab. inŝ. Krzysztof Patorski Krzysztof PoniŜej zajmiemy się propagacją promieniowania quasi-monochromatycznego,
OBRAZOWANIE W OŚWIETLENIU CZĘŚ ĘŚCIOWO KOHERENTNYM 1. Propagacja światła a częś ęściowo koherentnego prof. dr hab. inŝ. Krzysztof Patorski Krzysztof PoniŜej zajmiemy się propagacją promieniowania quasi-monochromatycznego,
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE
 LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwiczenie nr 6 Temat: Wyznaczenie stałej siatki dyfrakcyjnej i dyfrakcja światła na otworach kwadratowych i okrągłych. 1. Wprowadzenie Fale
LABORATORIUM FIZYKI PAŃSTWOWEJ WYŻSZEJ SZKOŁY ZAWODOWEJ W NYSIE Ćwiczenie nr 6 Temat: Wyznaczenie stałej siatki dyfrakcyjnej i dyfrakcja światła na otworach kwadratowych i okrągłych. 1. Wprowadzenie Fale
PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ
 LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
LABORATORIUM MECHANIKI PŁYNÓW Ćwiczenie N 7 PROFIL PRĘDKOŚCI W RURZE PROSTOLINIOWEJ . Cel ćwiczenia Doświadczalne i teoretyczne wyznaczenie profilu prędkości w rurze prostoosiowej 2. Podstawy teoretyczne:
Wielkości gwiazdowe. Systematyka N.R. Pogsona, który wprowadza zasadę, że różniaca 5 wielkości gwiazdowych to stosunek natężeń równy 100
 Wielkości gwiazdowe Ptolemeusz w Almageście 6 wielkości gwiazdowych od 1 do 6 mag. 1830 r, John Herschel wiąże skalę wielkości gwiazdowych z natężeniem globlanym światła gwiazd, mówiąc, że różnicom w wielkościach
Wielkości gwiazdowe Ptolemeusz w Almageście 6 wielkości gwiazdowych od 1 do 6 mag. 1830 r, John Herschel wiąże skalę wielkości gwiazdowych z natężeniem globlanym światła gwiazd, mówiąc, że różnicom w wielkościach
Atmosfera ziemska w obserwacjach promieni kosmicznych najwyższych energii. Jan Pękala Instytut Fizyki Jądrowej PAN
 Atmosfera ziemska w obserwacjach promieni kosmicznych najwyższych energii Jan Pękala Instytut Fizyki Jądrowej PAN Promienie kosmiczne najwyższych energii Widmo promieniowania kosmicznego rozciąga się na
Atmosfera ziemska w obserwacjach promieni kosmicznych najwyższych energii Jan Pękala Instytut Fizyki Jądrowej PAN Promienie kosmiczne najwyższych energii Widmo promieniowania kosmicznego rozciąga się na
Politechnika Świętokrzyska. Laboratorium. Cyfrowe przetwarzanie sygnałów. Ćwiczenie 8. Filtracja uśredniająca i statystyczna.
 Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Politechnika Świętokrzyska Laboratorium Cyfrowe przetwarzanie sygnałów Ćwiczenie 8 Filtracja uśredniająca i statystyczna. Cel ćwiczenia Celem ćwiczenia jest zdobycie umiejętności tworzenia i wykorzystywania
Laboratorium optycznego przetwarzania informacji i holografii. Ćwiczenie 3. Częstotliwości przestrzenne struktur okresowych
 Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 3. Częstotliwości przestrzenne struktur okresowych Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska
Laboratorium optycznego przetwarzania informacji i holografii Ćwiczenie 3. Częstotliwości przestrzenne struktur okresowych Katedra Optoelektroniki i Systemów Elektronicznych, WETI, Politechnika Gdańska
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX Lokalne transformacje obrazów Joanna Ratajczak, Wrocław, 28 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami lokalnych
Proste metody przetwarzania obrazu
 Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Operacje na pikselach obrazu (operacje punktowe, bezkontekstowe) Operacje arytmetyczne Dodanie (odjęcie) do obrazu stałej 1 Mnożenie (dzielenie) obrazu przez stałą Operacje dodawania i mnożenia są operacjami
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 8 AiR III
 1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
1 Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania wyłącznie do własnych, prywatnych potrzeb i może
Β2 - DETEKTOR SCYNTYLACYJNY POZYCYJNIE CZUŁY
 Β2 - DETEKTOR SCYNTYLACYJNY POZYCYJNIE CZUŁY I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z zasadą działania detektorów pozycyjnie czułych poprzez pomiar prędkości światła w materiale scyntylatora
Β2 - DETEKTOR SCYNTYLACYJNY POZYCYJNIE CZUŁY I. Cel ćwiczenia Celem ćwiczenia jest zapoznanie się z zasadą działania detektorów pozycyjnie czułych poprzez pomiar prędkości światła w materiale scyntylatora
Oszacowywanie możliwości wykrywania śmieci kosmicznych za pomocą teleskopów Pi of the Sky
 Mirosław Należyty Agnieszka Majczyna Roman Wawrzaszek Marcin Sokołowski Wilga, 27.05.2010. Obserwatorium Astronomiczne Uniwersytetu Warszawskiego i Instytut Problemów Jądrowych w Warszawie Oszacowywanie
Mirosław Należyty Agnieszka Majczyna Roman Wawrzaszek Marcin Sokołowski Wilga, 27.05.2010. Obserwatorium Astronomiczne Uniwersytetu Warszawskiego i Instytut Problemów Jądrowych w Warszawie Oszacowywanie
Ekspansja Wszechświata
 Ekspansja Wszechświata Odkrycie Hubble a w 1929 r. Galaktyki oddalają się od nas z prędkościami wprost proporcjonalnymi do odległości. Prędkości mierzymy za pomocą przesunięcia ku czerwieni efekt Dopplera
Ekspansja Wszechświata Odkrycie Hubble a w 1929 r. Galaktyki oddalają się od nas z prędkościami wprost proporcjonalnymi do odległości. Prędkości mierzymy za pomocą przesunięcia ku czerwieni efekt Dopplera
Wszechświat: spis inwentarza. Typy obiektów Rozmieszczenie w przestrzeni Symetrie
 Wszechświat: spis inwentarza Typy obiektów Rozmieszczenie w przestrzeni Symetrie Curtis i Shapley 1920 Heber D. Curtis 1872-1942 Mgławice spiralne są układami gwiazd równoważnymi Drodze Mlecznej Mgławice
Wszechświat: spis inwentarza Typy obiektów Rozmieszczenie w przestrzeni Symetrie Curtis i Shapley 1920 Heber D. Curtis 1872-1942 Mgławice spiralne są układami gwiazd równoważnymi Drodze Mlecznej Mgławice
Wstęp do astrofizyki I
 Wstęp do astrofizyki I Wykład 15 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
Wstęp do astrofizyki I Wykład 15 Tomasz Kwiatkowski Uniwersytet im. Adama Mickiewicza w Poznaniu Wydział Fizyki Instytut Obserwatorium Astronomiczne Tomasz Kwiatkowski, OA UAM Wstęp do astrofizyki I, Wykład
Reprezentacja i analiza obszarów
 Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Cechy kształtu Topologiczne Geometryczne spójność liczba otworów liczba Eulera szkielet obwód pole powierzchni środek ciężkości ułożenie przestrzenne momenty wyższych rzędów promienie max-min centryczność
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Filtracja obrazu operacje kontekstowe Podział metod filtracji obrazu Metody przestrzenne i częstotliwościowe Metody liniowe i nieliniowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu
Kodowanie transformacyjne. Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG
 Kodowanie transformacyjne Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG Zasada Zasada podstawowa: na danych wykonujemy transformacje która: Likwiduje korelacje Skupia energię w kilku komponentach
Kodowanie transformacyjne Plan 1. Zasada 2. Rodzaje transformacji 3. Standard JPEG Zasada Zasada podstawowa: na danych wykonujemy transformacje która: Likwiduje korelacje Skupia energię w kilku komponentach
GWIEZDNE INTERFEROMETRY MICHELSONA I ANDERSONA
 GWIEZNE INTERFEROMETRY MICHELSONA I ANERSONA Cel ćwiczenia Celem ćwiczenia jest zestawienie i demonstracja modelu gwiezdnego interferometru Andersona oraz laboratoryjny pomiar wymiaru sztucznej gwiazdy.
GWIEZNE INTERFEROMETRY MICHELSONA I ANERSONA Cel ćwiczenia Celem ćwiczenia jest zestawienie i demonstracja modelu gwiezdnego interferometru Andersona oraz laboratoryjny pomiar wymiaru sztucznej gwiazdy.
Automatyzacja teleskopu Celestron CGE Pro w OA UJ
 Automatyzacja teleskopu Celestron CGE Pro w OA UJ tomasz.szymanski@oa.uj.edu.pl Tomasz Szymański Obserwatorium Astronomiczne Uniwersytetu Jagiellońskiego 3-04-2012 Plan 1 Schemat modelu 2 Sprzęt 3 Oprogramowanie
Automatyzacja teleskopu Celestron CGE Pro w OA UJ tomasz.szymanski@oa.uj.edu.pl Tomasz Szymański Obserwatorium Astronomiczne Uniwersytetu Jagiellońskiego 3-04-2012 Plan 1 Schemat modelu 2 Sprzęt 3 Oprogramowanie
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI
 FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
FILTRACJE W DZIEDZINIE CZĘSTOTLIWOŚCI ( frequency domain filters) Każdy człon F(u,v) zawiera wszystkie wartości f(x,y) modyfikowane przez wartości członów wykładniczych Za wyjątkiem trywialnych przypadków
Zamiana reprezentacji wektorowej na rastrową - rasteryzacja
 MODEL RASTROWY Siatka kwadratów lub prostokątów stanowi elementy rastra. Piksel - pojedynczy element jest najmniejszą rozróŝnialną jednostką powierzchniową, której własności są opisane atrybutami. Model
MODEL RASTROWY Siatka kwadratów lub prostokątów stanowi elementy rastra. Piksel - pojedynczy element jest najmniejszą rozróŝnialną jednostką powierzchniową, której własności są opisane atrybutami. Model
Operacje morfologiczne w przetwarzaniu obrazu
 Przekształcenia morfologiczne obrazu wywodzą się z morfologii matematycznej działu matematyki opartego na teorii zbiorów Wykorzystuje się do filtracji morfologicznej, wyszukiwania informacji i analizy
Przekształcenia morfologiczne obrazu wywodzą się z morfologii matematycznej działu matematyki opartego na teorii zbiorów Wykorzystuje się do filtracji morfologicznej, wyszukiwania informacji i analizy
( W.Ogłoza, Uniwersytet Pedagogiczny w Krakowie, Pracownia Astronomiczna)
 TEMAT: Analiza zdjęć ciał niebieskich POJĘCIA: budowa i rozmiary składników Układu Słonecznego POMOCE: fotografie róŝnych ciał niebieskich, przybory kreślarskie, kalkulator ZADANIE: Wykorzystując załączone
TEMAT: Analiza zdjęć ciał niebieskich POJĘCIA: budowa i rozmiary składników Układu Słonecznego POMOCE: fotografie róŝnych ciał niebieskich, przybory kreślarskie, kalkulator ZADANIE: Wykorzystując załączone
Ciężkie wspaniałego początki
 Ciężkie wspaniałego początki opowieść prawdziwa Filip Kucharski Pod kierunkiem Dominka Gronkiewicza http://pomagacze.blogspot.com Spis treści 1. Trudności w astrofotografii. 2. Uzyskane zdjęcie. 3. Widoczne
Ciężkie wspaniałego początki opowieść prawdziwa Filip Kucharski Pod kierunkiem Dominka Gronkiewicza http://pomagacze.blogspot.com Spis treści 1. Trudności w astrofotografii. 2. Uzyskane zdjęcie. 3. Widoczne
Anna Barnacka. Obserwacje gwiazd zmiennych zaćmieniowych
 Anna Barnacka Akademia Pedagogiczna im. Komisji Edukacji Narodowej w Krakowie Instytut Fizyki Katedra Astronomii Obserwacje gwiazd zmiennych zaćmieniowych Szybko rozwijająca się technika umożliwia sięganie
Anna Barnacka Akademia Pedagogiczna im. Komisji Edukacji Narodowej w Krakowie Instytut Fizyki Katedra Astronomii Obserwacje gwiazd zmiennych zaćmieniowych Szybko rozwijająca się technika umożliwia sięganie
KP, Tele i foto, wykład 3 1
 Krystian Pyka Teledetekcja i fotogrametria sem. 4 2007/08 Wykład 3 Promieniowanie elektromagnetyczne padające na obiekt jest w części: odbijane refleksja R rozpraszane S przepuszczane transmisja T pochłaniane
Krystian Pyka Teledetekcja i fotogrametria sem. 4 2007/08 Wykład 3 Promieniowanie elektromagnetyczne padające na obiekt jest w części: odbijane refleksja R rozpraszane S przepuszczane transmisja T pochłaniane
Polecenie ŚWIATPUNKT - ŚWIATŁO PUNKTOWE
 Polecenie ŚWIATPUNKT - ŚWIATŁO PUNKTOWE Tworzy światło punktowe emitujące światło we wszystkich kierunkach. Lista monitów Wyświetlane są następujące monity. Określ położenie źródłowe : Podaj wartości
Polecenie ŚWIATPUNKT - ŚWIATŁO PUNKTOWE Tworzy światło punktowe emitujące światło we wszystkich kierunkach. Lista monitów Wyświetlane są następujące monity. Określ położenie źródłowe : Podaj wartości
Wartość netto (zł) (kolumna 3x5)
 Postępowanie WB.2420.9.2012.NG ZAŁĄCZNIK NR 6 Zadanie nr 2 L.p. Nazwa asortymentu parametry techniczne Ilość Nazwa wyrobu, nazwa producenta, określenie marki, modelu, znaku towarowego Cena jednostkowa
Postępowanie WB.2420.9.2012.NG ZAŁĄCZNIK NR 6 Zadanie nr 2 L.p. Nazwa asortymentu parametry techniczne Ilość Nazwa wyrobu, nazwa producenta, określenie marki, modelu, znaku towarowego Cena jednostkowa
Optyka instrumentalna
 Optyka instrumentalna wykład 7 20 kwietnia 2017 Wykład 6 Optyka geometryczna cd. Przybliżenie przyosiowe Soczewka, zwierciadło Ogniskowanie, obrazowanie Macierze ABCD Punkty kardynalne układu optycznego
Optyka instrumentalna wykład 7 20 kwietnia 2017 Wykład 6 Optyka geometryczna cd. Przybliżenie przyosiowe Soczewka, zwierciadło Ogniskowanie, obrazowanie Macierze ABCD Punkty kardynalne układu optycznego
Kamera internetowa: prosty instrument astronomiczny. Dr Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski
 Kamera internetowa: prosty instrument astronomiczny Dr Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski Detektory promieniowania widzialnego Detektory promieniowania widzialnego oko błona fotograficzna
Kamera internetowa: prosty instrument astronomiczny Dr Tomasz Mrozek Instytut Astronomiczny Uniwersytet Wrocławski Detektory promieniowania widzialnego Detektory promieniowania widzialnego oko błona fotograficzna
MODULATOR CIEKŁOKRYSTALICZNY
 ĆWICZENIE 106 MODULATOR CIEKŁOKRYSTALICZNY 1. Układ pomiarowy 1.1. Zidentyfikuj wszystkie elementy potrzebne do ćwiczenia: modulator SLM, dwa polaryzatory w oprawie (P, A), soczewka S, szary filtr F, kamera
ĆWICZENIE 106 MODULATOR CIEKŁOKRYSTALICZNY 1. Układ pomiarowy 1.1. Zidentyfikuj wszystkie elementy potrzebne do ćwiczenia: modulator SLM, dwa polaryzatory w oprawie (P, A), soczewka S, szary filtr F, kamera
Cyfrowe przetwarzanie obrazów i sygnałów Wykład 9 AiR III
 1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
1 Na podstawie materiałów autorstwa dra inż. Marka Wnuka. Niniejszy dokument zawiera materiały do wykładu z przedmiotu Cyfrowe Przetwarzanie Obrazów i Sygnałów. Jest on udostępniony pod warunkiem wykorzystania
Navigare necesse est. Roman Werpachowski CFT PAN 22 września 2007
 Navigare necesse est Roman Werpachowski CFT PAN 22 września 2007 O czym będzie? 1) Po co nam nawigacja? 2) Nawigacja na sferze 3) Znajdowanie drogi na lądzie: grafy Zaczniemy od nawigacji, ale poŝeglujemy
Navigare necesse est Roman Werpachowski CFT PAN 22 września 2007 O czym będzie? 1) Po co nam nawigacja? 2) Nawigacja na sferze 3) Znajdowanie drogi na lądzie: grafy Zaczniemy od nawigacji, ale poŝeglujemy
Różne reżimy dyfrakcji
 Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Różne reżimy
Teoria błędów pomiarów geodezyjnych
 PodstawyGeodezji Teoria błędów pomiarów geodezyjnych mgr inŝ. Geodeta Tomasz Miszczak e-mail: tomasz@miszczak.waw.pl Wyniki pomiarów geodezyjnych będące obserwacjami (L1, L2,, Ln) nigdy nie są bezbłędne.
PodstawyGeodezji Teoria błędów pomiarów geodezyjnych mgr inŝ. Geodeta Tomasz Miszczak e-mail: tomasz@miszczak.waw.pl Wyniki pomiarów geodezyjnych będące obserwacjami (L1, L2,, Ln) nigdy nie są bezbłędne.
Zbigniew Sołtys - Komputerowa Analiza Obrazu Mikroskopowego 2016 część 7
 7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
7. NORMALIZACJA I BINARYZACJA ADAPTATYWNA 7.1. Normalizacja lokalna Zwykłe konwolucje działają w jednakowy sposób na całym obrazie. Plugin Local Normalization przeprowadza filtrowanie Gaussa w zależności
Obserwacje fotometryczne planetoid
 Obserwacje fotometryczne planetoid Anna Borucka 2002-01-14 Streszczenie Sprawozdanie dotyczy obserwacji planetoidy 54 Alexandra wykonanej w Borowcu 8-go października 2001. Dalej przedstawiono redukcję
Obserwacje fotometryczne planetoid Anna Borucka 2002-01-14 Streszczenie Sprawozdanie dotyczy obserwacji planetoidy 54 Alexandra wykonanej w Borowcu 8-go października 2001. Dalej przedstawiono redukcję
Dopasowywanie modelu do danych
 Tematyka wykładu dopasowanie modelu trendu do danych; wybrane rodzaje modeli trendu i ich właściwości; dopasowanie modeli do danych za pomocą narzędzi wykresów liniowych (wykresów rozrzutu) programu STATISTICA;
Tematyka wykładu dopasowanie modelu trendu do danych; wybrane rodzaje modeli trendu i ich właściwości; dopasowanie modeli do danych za pomocą narzędzi wykresów liniowych (wykresów rozrzutu) programu STATISTICA;
Wpływ pól magnetycznych na rotację materii w galaktykach spiralnych. Joanna Jałocha-Bratek, IFJ PAN
 Wpływ pól magnetycznych na rotację materii w galaktykach spiralnych. Joanna Jałocha-Bratek, IFJ PAN c Czy pola magnetyczne mogą wpływać na kształt krzywych rotacji? W galaktykach spiralnych występuje wielkoskalowe,
Wpływ pól magnetycznych na rotację materii w galaktykach spiralnych. Joanna Jałocha-Bratek, IFJ PAN c Czy pola magnetyczne mogą wpływać na kształt krzywych rotacji? W galaktykach spiralnych występuje wielkoskalowe,
Aby pobrać program FotoSender naleŝy na stronę www.fotokoda.pl lub www.kodakwgalerii.astral.pl i kliknąć na link Program do wysyłki zdjęć Internetem.
 FotoSender 1. Pobranie i instalacja programu Aby pobrać program FotoSender naleŝy na stronę www.fotokoda.pl lub www.kodakwgalerii.astral.pl i kliknąć na link Program do wysyłki zdjęć Internetem. Rozpocznie
FotoSender 1. Pobranie i instalacja programu Aby pobrać program FotoSender naleŝy na stronę www.fotokoda.pl lub www.kodakwgalerii.astral.pl i kliknąć na link Program do wysyłki zdjęć Internetem. Rozpocznie
Simp-Q. Porady i wskazówki
 Simp-Q Porady i wskazówki ROZWÓJ ZESTAWÓW BEZCIENIOWYCH Pierwsza generacja Najnowsza generacja Profesjonalne studio idealne dla zawodowych fotografów. Zestawy bezcieniowe Simp-Q to rewolucyjne i kompletne
Simp-Q Porady i wskazówki ROZWÓJ ZESTAWÓW BEZCIENIOWYCH Pierwsza generacja Najnowsza generacja Profesjonalne studio idealne dla zawodowych fotografów. Zestawy bezcieniowe Simp-Q to rewolucyjne i kompletne
PRZYSŁONY. Przysłona aperturowa APERTURE STOP (ogranicza ilość promieni pochodzących od obiektu)
 ELEMENTY PRZYSŁONY Przysłona aperturowa APERTURE STOP (ogranicza ilość promieni pochodzących od obiektu) Przysłona polowa FIELD STOP (całkowicie zasłania promienie) Źrenica wejściowa Źrenica wejściowa
ELEMENTY PRZYSŁONY Przysłona aperturowa APERTURE STOP (ogranicza ilość promieni pochodzących od obiektu) Przysłona polowa FIELD STOP (całkowicie zasłania promienie) Źrenica wejściowa Źrenica wejściowa
Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji
 Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Fotonika Wykład 6: Reprezentacja informacji w układzie optycznym; układy liniowe w optyce; podstawy teorii dyfrakcji Plan: pojęcie sygnału w optyce układy liniowe filtry liniowe, transformata Fouriera,
Odległość mierzy się zerami
 Odległość mierzy się zerami Jednostki odległości w astronomii jednostka astronomiczna AU, j.a. rok świetlny l.y., r.św. parsek pc średnia odległość Ziemi od Słońca odległość przebyta przez światło w próżni
Odległość mierzy się zerami Jednostki odległości w astronomii jednostka astronomiczna AU, j.a. rok świetlny l.y., r.św. parsek pc średnia odległość Ziemi od Słońca odległość przebyta przez światło w próżni
Cyfrowe Przetwarzanie Obrazów i Sygnałów
 Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Cyfrowe Przetwarzanie Obrazów i Sygnałów Laboratorium EX3 Globalne transformacje obrazów Joanna Ratajczak, Wrocław, 2018 1 Cel i zakres ćwiczenia Celem ćwiczenia jest zapoznanie się z własnościami globalnych
Filtracja obrazu operacje kontekstowe
 Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
Filtracja obrazu operacje kontekstowe Główne zadania filtracji Usunięcie niepożądanego szumu z obrazu Poprawa ostrości Usunięcie określonych wad obrazu Poprawa obrazu o złej jakości technicznej Rekonstrukcja
PLAN WYNIKOWY DLA KLASY DRUGIEJ POZIOM PODSTAWOWY I ROZSZERZONY. I. Proste na płaszczyźnie (15 godz.)
 PLAN WYNIKOWY DLA KLASY DRUGIEJ POZIOM PODSTAWOWY I ROZSZERZONY I. Proste na płaszczyźnie (15 godz.) Równanie prostej w postaci ogólnej Wzajemne połoŝenie dwóch prostych Nierówność liniowa z dwiema niewiadomymi
PLAN WYNIKOWY DLA KLASY DRUGIEJ POZIOM PODSTAWOWY I ROZSZERZONY I. Proste na płaszczyźnie (15 godz.) Równanie prostej w postaci ogólnej Wzajemne połoŝenie dwóch prostych Nierówność liniowa z dwiema niewiadomymi
BADANIE INTERFEROMETRU YOUNGA
 Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Celem ćwiczenia jest: BADANIE INTERFEROMETRU YOUNGA 1. poznanie podstawowych właściwości interferometru z podziałem czoła fali w oświetleniu monochromatycznym i świetle białym, 2. demonstracja możliwości
Ćw.6. Badanie własności soczewek elektronowych
 Pracownia Molekularne Ciało Stałe Ćw.6. Badanie własności soczewek elektronowych Brygida Mielewska, Tomasz Neumann Zagadnienia do przygotowania: 1. Budowa mikroskopu elektronowego 2. Wytwarzanie wiązki
Pracownia Molekularne Ciało Stałe Ćw.6. Badanie własności soczewek elektronowych Brygida Mielewska, Tomasz Neumann Zagadnienia do przygotowania: 1. Budowa mikroskopu elektronowego 2. Wytwarzanie wiązki
Fotometria 1. Systemy fotometryczne.
 Fotometria 1. Systemy fotometryczne. Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Fotometria Fotometria to jedna z podstawowych technik obserwacyjnych. Pozwala
Fotometria 1. Systemy fotometryczne. Andrzej Pigulski Instytut Astronomiczny Uniwersytetu Wrocławskiego Produkty HELAS-a, 2010 Fotometria Fotometria to jedna z podstawowych technik obserwacyjnych. Pozwala
FOTOMETRIA OBIEKTÓW PUNKTOWYCH Z UŻYCIEM PROGRAMU SalsaJ
 FOTOMETRIA OBIEKTÓW PUNKTOWYCH Z UŻYCIEM PROGRAMU SalsaJ Opracowanie: Paulina Sowicka, Grzegorz Sęk Młodzieżowe Obserwatorium Astronomiczne w Niepołomicach Program SalsaJ został napisany przez zespół EU-HOU
FOTOMETRIA OBIEKTÓW PUNKTOWYCH Z UŻYCIEM PROGRAMU SalsaJ Opracowanie: Paulina Sowicka, Grzegorz Sęk Młodzieżowe Obserwatorium Astronomiczne w Niepołomicach Program SalsaJ został napisany przez zespół EU-HOU
DETEKCJA W MIKRO- I NANOOBJĘTOŚCIACH. Ćwiczenie nr 3 Detektor optyczny do pomiarów fluorescencyjnych
 DETEKCJA W MIKRO- I NANOOBJĘTOŚCIACH Ćwiczenie nr 3 Detektor optyczny do pomiarów fluorescencyjnych Cel ćwiczenia: Celem ćwiczenia jest zaznajomienie się z zasadą działania i zastosowaniami detektora optycznego
DETEKCJA W MIKRO- I NANOOBJĘTOŚCIACH Ćwiczenie nr 3 Detektor optyczny do pomiarów fluorescencyjnych Cel ćwiczenia: Celem ćwiczenia jest zaznajomienie się z zasadą działania i zastosowaniami detektora optycznego
Propagacja w przestrzeni swobodnej (dyfrakcja)
 Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Propagacja
Fotonika Wykład 7 - Sposoby wyznaczania obrazu dyfrakcyjnego - Przykłady obrazów dyfrakcyjnych w polu dalekim obliczonych przy użyciu dyskretnej transformaty Fouriera - Elementy dyfrakcyjne Propagacja
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych
 Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
Parametryzacja obrazu na potrzeby algorytmów decyzyjnych Piotr Dalka Wprowadzenie Z reguły nie stosuje się podawania na wejście algorytmów decyzyjnych bezpośrednio wartości pikseli obrazu Obraz jest przekształcany
BIBLIOTEKA PROGRAMU R - BIOPS. Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat
 BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
BIBLIOTEKA PROGRAMU R - BIOPS Narzędzia Informatyczne w Badaniach Naukowych Katarzyna Bernat Biblioteka biops zawiera funkcje do analizy i przetwarzania obrazów. Operacje geometryczne (obrót, przesunięcie,
Tworzenie buforów w ArcView
 W celu utworzenia buforów naleŝy najpierw zdefiniować jednostki odległości. W tym celu naleŝy wybrać polecenie: View/Properties... W polach Map Units: oraz Distance units: naleŝy wskazać jednostki odległości
W celu utworzenia buforów naleŝy najpierw zdefiniować jednostki odległości. W tym celu naleŝy wybrać polecenie: View/Properties... W polach Map Units: oraz Distance units: naleŝy wskazać jednostki odległości
Ćw.1. Monitorowanie temperatury
 Ćw.1. Monitorowanie temperatury Wstęp Ćwiczenie przedstawia metodę monitorowania temperatury w obecności pola elektromagnetycznego przy użyciu czujników światłowodowych. Specjalna technologia kryształów
Ćw.1. Monitorowanie temperatury Wstęp Ćwiczenie przedstawia metodę monitorowania temperatury w obecności pola elektromagnetycznego przy użyciu czujników światłowodowych. Specjalna technologia kryształów
Wstęp do fotografii. piątek, 15 października 2010. ggoralski.com
 Wstęp do fotografii ggoralski.com element światłoczuły soczewki migawka przesłona oś optyczna f (ogniskowa) oś optyczna 1/2 f Ogniskowa - odległość od środka układu optycznego do ogniska (miejsca w którym
Wstęp do fotografii ggoralski.com element światłoczuły soczewki migawka przesłona oś optyczna f (ogniskowa) oś optyczna 1/2 f Ogniskowa - odległość od środka układu optycznego do ogniska (miejsca w którym
