Mirosław Dąbrowski. Gry matematyczne. dla uczniów klas 1 3 i starszych. Część 2
|
|
|
- Emilia Cieślik
- 9 lat temu
- Przeglądów:
Transkrypt
1 Mirosław Dąbrowski Gry matematyczne dla uczniów klas 1 3 i starszych Część 2 Opole 2016
2 Spis treści Wstęp 5 Rozdział 1 Gry wykorzystujące dziesięciościenne kostki z liczbami Dwa warunki 1 11 Cztery warunki 1 14 Parzyste i nieparzyste 1 17 Dwa warunki 2 20 Cztery warunki 2 22 Parzyste i nieparzyste 2 25 Same podzielne 1 28 Same podzielne 2 30 Podzielna, niepodzielna 32 Trzy w linii 34 Zwierzak 37 Rozdział 2 Gry na planszy stu liczb 41 Ślizgawka 44 Ruchome schody 47 Winda 1 50 Winda 2 53 Krótkie, dłuższe i najdłuższe 1 54 Krótkie, dłuższe i najdłuższe 2 57 Na skos 1 58 Na skos 2 60 Pełne dziesiątki 61 Dziesiątki i jedności 64 W dół 66 Parzyste i nieparzyste 70 Trzy w linii 1 75 W linii 77 Trzy w linii 2 80 Zjazd 82 Cztery w linii 85 Po kolei 88 Bingo 90 Trzy w linii 3 93 Dzieli, nie dzieli? 95 3
3 Rozdział 3 Gry strategiczne 100 Dwie wieże Dwie wieże Trzy wieże 108 Do środka Do środka 1 (Plansza 2) 113 Do środka Do środka 2 (Plansza 2) 117 Do środka 2 (Plansza 3) 118 Trzy w linii (Kółko i krzyżyk) 119 Trzy w linii (Plansza 2) 121 Trzy w linii (Plansza 3) 122 Trzy w linii (Plansza 4) 123 Trzy w linii (Plansza 5) 124 Trzy w linii (Plansza 6) wygrywa! wygrywa! 129 Pierwszy do 100! 131 Mur 134 Pasek 137 Rozdział 4 Gry różne 139 Wyścig na centymetrze 141 Drabina 144 Jak najbliżej celu! 148 Bingo 150 Prostokąty Prostokąty Wielokąty 158 Kropki Kropki
4 Wstęp Do czego służą gry? Gdyby zadać takie pytanie nauczycielom klas 1 3 lub nauczycielom matematyki w klasach 4 6, prawdopodobnie (prawdopodobnie, bo nie przeprowadzałem nigdy takiej ankiety wśród większej grupy) najczęściej pojawiłaby się odpowiedź: do ćwiczenia rachunków. Czasem ankietowani dodaliby pewnie: ale na słupkach robi się to lepiej i jest mniej hałasu. Obie te wypowiedzi są, w mej ocenie, naturalną konsekwencją naszego rozumienia szkolnej matematyki (i to nie tylko na poziomie szkoły podstawowej), jako nauki przede wszystkich o rachowaniu, a także tradycji jej podającego nauczania. Od lat powtarzam przy okazji różnych konferencji i spotkań z nauczycielami: matematyka to nauka nie o rachowaniu, lecz o strukturach i prawidłowościach. Matematyk przede wszystkim bada własności różnorodnych struktur i istniejące w nich prawidłowości. Bada, bo uprawianie matematyki to proces, w którym analizujemy różne sytuacje i przypadki, dokonujemy uogólnień, formułujemy hipotezy, podejmujemy próby ich weryfikacji, dostrzegamy i formułujemy prawidłowości, przewidujemy, szukamy argumentów potrzebnych do przekonania oponentów Uczeń też może i powinien to robić! Na zadane wyżej pytanie dotyczące celu stosowania gier proponuję więc zupełnie inną odpowiedź: gry dydaktyczne są doskonałą okazją do wspólnego uprawiania matematyki. I temu właśnie, czyli wspólnemu uprawianiu matematyki, przy okazji i dzięki grom dydaktycznym, poświęcone są obie części tej książki. Jeśli chcemy korzystać w swojej pracy z gier i możliwie efektywnie je wykorzystywać, warto poświęcić trochę czasu na refleksję o tym, jak grać z dziećmi. Na początek kilka praktycznych wskazówek (więcej i dokładniej na ten temat w rozdziale 1. części pierwszej): 1. Zawsze warto zacząć od wcześniejszego zagrania samemu w grę, którą chce się wykorzystać podczas zajęć. Grę powinniśmy dobrze znać i to od środka, tzn. powinniśmy mieć w niej swoje własne doświadczenia. Ułatwi nam to m.in. zrozumienie sytuacji powstających podczas gry w klasie. 2. Koniecznie musimy zadbać o stworzenie właściwych warunków organizacyjnych dla przeprowadzenia wybranej gry: przygotować większą niż to konieczne liczbę potrzebnych pomocy: plansz, pionków itp.; odpowiednio zagospodarować przestrzeń klasy. 3. Warto stworzyć właściwy, poważny klimat wokół tego, co będziemy na lekcji robić. Zamiast zwyczajowego: Teraz trochę się pobawimy proponuję np.: Teraz będziemy ćwiczyć wykonywanie obliczeń, w tym celu zagramy w grę. Z gry korzystamy nie po to, aby uczniowie się pobawili, lecz po to, aby wykreować bogatą edukacyjnie sytuację, która pozwoli im poszerzyć własną wiedzę matematyczną. 4. Zanim zacznie się rozgrywka, upewnijmy się, że uczniowie zrozumieli reguły gry, oszczędzi nam to czasu i sporo nerwów. Dobrym pomysłem jest rozegranie pokazowej partii, np. w układzie nauczyciel kontra uczeń albo uczniowie. 5. Jeśli już zdecydowaliśmy się na grę, pamiętajmy, że najlepiej, by dzieci zagrały w nią kilka razy z rzędu. Podczas rozgrywek młodzi gracze zbierają doświadczenie, zaczynają szukać prawidłowości i budować indywidualne strategie zwiększające szanse na sukces. Powinniśmy dać im 5
5 Gry matematyczne dla uczniów klas 1 3 i starszych szansę wykorzystania swoich spostrzeżeń w kolejnych rundach gry. Może to dać szybką nagrodę i zmotywować dziecko do kolejnych samodzielnych poszukiwań. 6. Nie zmieniajmy reguł w trakcie gry i nie zastępujmy jednej gry inną. Jeżeli gra przestanie być atrakcyjna dla uczniów, przerwijmy ją i przejdźmy do innej aktywności. Zaoszczędzimy sobie dzięki temu bolesnej sytuacji, gdy nagle okazuje się, że znaczna część uczniów nie wie, w co ma teraz grać i robi coś zupełnie innego niż byśmy chcieli. 7. My też podczas gry musimy być aktywni, choć nieco inaczej niż dzieci. Być może, najlepszym rozwiązaniem jest spokojne przemieszczanie się od grupy do grupy, gdy uczniowie grają w parach lub większych grupach, i obserwowanie, jak w poszczególnych zespołach rozwija się rozgrywka. Nie ingerujmy w rozgrywkę, nie decydujmy się pochopnie na interwencje, pozwalajmy dzieciom na samodzielność w inny sposób nie nauczą się jej. 8. Jedną z pierwszych rzeczy, którą musimy sobie uświadomić, gdy wprowadzamy gry na zajęcia, to to, że to nie my mamy grać. To uczniowie mają podejmować decyzje, robić błędy, wyciągać z nich naukę Musimy powstrzymać chęć podpowiadania, jaki ruch byłby najlepszy, czy co w tej sytuacji trzeba zrobić. 9. Jeśli dzieci polubiły jakąś grę, nie rezygnujmy z niej zbyt szybko. Wracajmy do niej, gdy zaistnieje ku temu okazja na pewno nie będzie to czas stracony. Możemy także sięgnąć po jakąś jej modyfikację. Warto zachęcać dzieci do zmieniania i wymyślania gier, zwłaszcza takich, które realizują pewne konkretne cele, np. pomogą kolegom szybciej się nauczyć dzielić czy porównywać liczby. 10. Zawsze powinniśmy zachęcać uczniów do rozmowy o tym, co się podczas rozgrywki wydarzyło ciekawego, dziwnego, zabawnego, co było trudne, co było łatwe i dlaczego, co zauważyli, jakie metody postępowania sobie wypracowali. Jest to nie tylko okazja do podzielenia się własnymi spostrzeżeniami czy odkryciami oraz do poznania cudzych, ale przede wszystkim okazja do wspólnego uczenia się matematyki. 11. Po rozegraniu kilku partii dzieci mają już bogate, różnorodne doświadczenia związane z grą. Warto to wykorzystać, formułując zagadki, problemy, zadania tekstowe dotyczące tego, co podczas gry się działo czy mogło dziać. Zdobyte doświadczenie sprawia, że uczniowie dobrze rozumieją zadawane pytania czy formułowane zadania i chętniej angażują się w ich rozwiązywanie. 12. Gry są doskonałym narzędziem do indywidualizacji, zwłaszcza gdy dzieci grają w parach lub większych grupach. Wystarczy np. zaproponować poszczególnym zespołom różne modyfikacje tej samej gry, dobierając ich poziom trudności do aktualnych potrzeb konkretnych uczniów. 13. Po zakończeniu rozgrywek zawsze warto podsumować to, co się w ich trakcie działo z matematycznego punktu widzenia, np.: Dziś ćwiczyliśmy mnożenie liczb czy Dziś badaliśmy własności liczb wielocyfrowych. Zbierzmy jeszcze raz najważniejsze wnioski z gry. To nadaje głębszy sens temu, co uczniowie robili i zachęca do właściwego podejścia do gier w przyszłości gra to okazja, najczęściej przyjemna i wciągająca, do nauczenia się czegoś ważnego. 14. W gry należy grać często i systematycznie. Gry wprowadzane na zajęcia sporadycznie nie przyniosą dobrego skutku efekty edukacyjne będą znikome czy wręcz zerowe, a sytuacja zostanie przez uczniów wykorzystana przede wszystkim do odreagowania szkolnej (najczęściej nudnej) codzienności. Co więcej, dzieci muszą się nauczyć grać tak, aby dawało im to wymierne merytoryczne korzyści. Im wcześniej tę naukę zaczną, tym lepiej dla nich i dla nas. A co możemy otrzymać w zamian? Podczas tak stosowanych gier dzieci będą (por. rozdział 1, część pierwsza): ćwiczyć i rozwijać konkretne matematyczne umiejętności, w tym także, oczywiście, obliczeniowe; poznawać konkretne matematyczne pojęcia i pogłębiać ich rozumienie; dostrzegać wzajemne związki między pojęciami i faktami; dostrzegać nowe prawidłowości i je wykorzystywać; w różnorodny sposób posługiwać się notacją matematyczną; 6
6 Wstęp słuchać i czytać ze zrozumieniem; uczyć się przestrzegania przyjętych reguł; uczyć się akceptować przegraną i rozsądnie cieszyć się z wygranej; komunikować się i dyskutować (zarówno w układzie uczeń uczeń, jak i uczeń nauczyciel); współdziałać i współpracować (w większych i mniejszych grupach); przewidywać, planować i podejmować decyzje; analizować i badać konsekwencje; budować, testować i ulepszać strategie, czyli będą uczyć się matematyki skutecznie skutecznie, bo dzięki własnej aktywności, dzięki sukcesywnie rosnącej wierze w swoje siły i możliwości oraz dzięki rosnącej motywacji do uczenia się w ogóle. Niektóre z przytoczonych w tej części gier znalazłem w różnych materiałach czy książkach, często tak dawno, że już nie pamiętam źródła. O kilku mi opowiedziano. Resztę wymyśliłem sam lub razem ze współpracownikami. Część z tych gier była, znowu przed laty, wykorzystana w pakiecie edukacyjnym dla klas 1 3 Przygoda z klasą. Dziękuję Wydawnictwom Szkolnym i Pedagogicznym za wyrażenie zgody na ich umieszczenie w niniejszej książce. W obu częściach publikacji łącznie opisałem ponad sto gier, do każdej dołączając jeszcze niektóre z możliwych modyfikacji oraz przykładowe zadania czy problemy do rozwiązania. To ogromnie bogaty materiał edukacyjny. Zachęcam jednak także do wymyślania gier samemu i razem z uczniami, gdyż jest to nie tylko kształcące, ale również zwyczajnie przyjemne. Powtórzę raz jeszcze: gra to nie tylko okazja do ćwiczenia obliczeń, przede wszystkim to doskonała okazja do wspólnego nauczenia się czegoś matematycznie ważnego. Warto spróbować! 7
7 Gry różne Wyścig na centymetrze Gra dla 2-4 osób Pomoce: centymetr krawiecki, po jednym kolorowym spinaczu (klamerce itp.) dla każdego gracza, kostka dziesięciościenna z liczbami od 1 do 10. Gracze ustalają, w jakiej kolejności będą wykonywać ruchy. Gracz rozpoczynający grę rzuca kostką i umieszcza swój spinacz na polu centymetra z wyrzuconą liczbą. To samo, kolejno, robią pozostali gracze. Pierwszy gracz znowu rzuca kostką i przesuwa swój spinacz na centymetrze o tyle pól, jaki wynik rzutu uzyskał. Teraz rzuca kostką i przesuwa swój spinacz drugi gracz, potem trzeci. I tak kolejno na zmianę. Wygrywa ten gracz, który jako pierwszy dojdzie do ostatniego pola centymetra albo go przejdzie i zejdzie z centymetra. Początek przykładowej rozgrywki (dla 4 osób) Gracz 1 (spinacz czerwony): Gracz 2 (spinacz niebieski): Gracz 3 (spinacz zielony): Gracz 3 (spinacz żółty): Gracz 1 (spinacz czerwony): Gracz 2 (spinacz niebieski): Gracz 3 (spinacz zielony): Gracz 3 (spinacz żółty): 141
8 Gry matematyczne dla uczniów klas 1 3 i starszych Gracz 1 (spinacz czerwony): Gracz 2 (spinacz niebieski): Gracz 3 (spinacz zielony): Gracz 3 (spinacz żółty): Modyfikacje: 1. Gracz rzuca kostką sześcienną. Reszta reguł bez zmian. 2. Gracz rzuca dwiema dziesięciościennymi kostkami z liczbami od 1 do 10, po czym uzyskane wyniki dodaje albo odejmuje według uznania. Jeśli spinacz gracza trafi na pole z dziesiątkami: 10, 20, 30, 130, 140 gracz ma dodatkowy rzut. 3. Gracz rzuca trzema dziesięciościennymi kostkami z liczbami od 1 do 10. Wybiera dwie z wylosowanych liczb i je dodaje albo odejmuje według uznania. Jeśli spinacz gracza trafi na pole z dziesiątkami: 10, 20, 30, 130, 140 gracz ma dodatkowy rzut. Komentarz: Centymetr krawiecki jest bardzo ciekawą pomocą arytmetyczną, która może m.in. oswajać z uporządkowaniem liczb naturalnych oraz z samymi liczbami i ich zapisem, i to nie tylko podczas dokonywania nim pomiarów. Ta gra to właśnie ilustruje. Żeby wziąć w niej świadomy udział, dzieci wcale nie muszą operować liczbami w zakresie 150 wystarczy, jeśli robią to w zakresie 10, bo tylko to jest potrzebne do samodzielnego wykonywania kolejnych ruchów. Udział w grze pozwoli im rozwinąć intuicje dotyczące większych liczb, oswoić się z ich zapisem, a nawet nauczyć się je porównywać i dodawać (np. przez doliczanie). W czasie gry w naturalny sposób dzieci sprawdzają, jaka jest kolejność graczy, kto jest najdalej, a kto najbliżej, o ile pól jest jeden zawodnik przed czy za drugim. Przed rzutem np. analizują, ile muszą wyrzucić, żeby wyprzedzić znajdującego się przed nimi gracza itp. Okazji do budowania wiedzy arytmetycznej powstaje mnóstwo. I, jak zawsze, powstaje mnóstwo okazji do wspólnego układania i rozwiązywania różnorodnych zadań tekstowych, np.: Marek stał na polu 33. Wyrzucił 5. Na jakim polu stanie? Janek z pola 22 przeszedł na pole 29. Co wyrzucił? Po wyrzuceniu liczby 4 spinacz Ani znalazł się na polu 48. Na jakim polu znajdował się przed tym ruchem? A na jakim polu stał przed swoim ruchem Zbyszek, jeśli po przesunięciu się o 5 pól znalazł się na polu 41? W kolejnym swoim ruchu Marek przesunął swój spinacz z pola 38 na pole 46. Co wyrzucił? Ania, żeby wyprzedzić Janka, musiała wyrzucić 7 albo więcej. Ania stała na polu 33. A gdzie stał Janek? Po trzecim ruchu pionek Zbyszka stanął na polu 20. Jakie liczby Zbyszek mógł wyrzucić w tych trzech rzutach? 142
9 5 Gry różne Warto mieć świadomość, że żeby rozwiązać np. pierwsze zadanie o Zbyszku, dzieci wcale nie muszą umieć dodawać z przekraczaniem progu mają centymetr, który sprawia, że żadnych progów nie ma, mogą np. przeliczyć pola na centymetrze, odliczyć na palcach itp. Gra pozwala dzieciom na budowanie różnorodnych strategii obliczeniowych, ale żeby faktycznie zaczęły je budować, musimy pozwolić im na samodzielność. Modyfikacja 1 ogranicza długość wykonywanych ruchów, co wydłuża czas trwania gry. Warto w takiej sytuacji skrócić trasę wyścigu. Modyfikacja 2 znacząco przyspiesza grę i, dodatkowo, wzmacnia proces dopełniania do pełnych dziesiątek. Jednak udział w niej wymaga już umiejętności dodawania liczb w zakresie 20. W modyfikacji 3 dzieci mają jeszcze więcej okazji do wykonywania obliczeń, planowania, przewidywania. Propozycje zagadnień do wspólnego zbadania i przedyskutowania: Przyjrzyjcie się uważnie, jak wygląda centymetr krawiecki. W jaki sposób ułożone są na nim i zapisane liczby? W jaki sposób można na tym centymetrze dodawać i odejmować? Jakie najtrudniejsze obliczenie potraficie z jego pomocą wykonać?
33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I
 150 Mirosław Dąbrowski 33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
150 Mirosław Dąbrowski 33. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I
 124 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Mirosław Dąbrowski 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie
124 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Mirosław Dąbrowski 25. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie
34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II
 157 Mirosław Dąbrowski 34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
157 Mirosław Dąbrowski 34. NIE TYLKO WORECZKI CZYLI O ROZUMIENIU SYSTEMU DZIESIĘTNEGO, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
Mirosław Dąbrowski. Gry matematyczne. (nie tylko) dla klas 1 3
 Mirosław Dąbrowski Gry matematyczne (nie tylko) dla klas 1 3 Opole 2015 Spis treści Wstęp 5 Rozdział 1 Jak i dlaczego warto grać 7 Rozdział 2 Dwuosobowe proste gry planszowe 12 Trzy w linii 1 14 Od 1 do
Mirosław Dąbrowski Gry matematyczne (nie tylko) dla klas 1 3 Opole 2015 Spis treści Wstęp 5 Rozdział 1 Jak i dlaczego warto grać 7 Rozdział 2 Dwuosobowe proste gry planszowe 12 Trzy w linii 1 14 Od 1 do
Pora na gry planszowe
 Mirosław Dąbrowski Pora na gry planszowe Dzieci lubią gry i zabawy, dorośli na ogół zresztą też. To wspólne upodobanie może być bardzo dobrym punktem wyjścia do miłego i pożytecznego spędzenia czasu. Proponujemy
Mirosław Dąbrowski Pora na gry planszowe Dzieci lubią gry i zabawy, dorośli na ogół zresztą też. To wspólne upodobanie może być bardzo dobrym punktem wyjścia do miłego i pożytecznego spędzenia czasu. Proponujemy
Działania uczniów klasy 3a wg Scenariusza zajęć edukacyjnych z matematyki Wykorzystanie w edukacji matematycznej własnej gry planszowej
 Działania uczniów klasy 3a wg Scenariusza zajęć edukacyjnych z matematyki Wykorzystanie w edukacji matematycznej własnej gry planszowej rok szkolny 2016/2017 OPRACOWANO W RAMACH PROJEKTU "PODNOSZENIA KOMPETENCJI
Działania uczniów klasy 3a wg Scenariusza zajęć edukacyjnych z matematyki Wykorzystanie w edukacji matematycznej własnej gry planszowej rok szkolny 2016/2017 OPRACOWANO W RAMACH PROJEKTU "PODNOSZENIA KOMPETENCJI
9. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. III
 46 Mirosław Dąbrowski 9. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. III Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości podczas
46 Mirosław Dąbrowski 9. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. III Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości podczas
Runda 5: zmiana planszy: < < i 6 rzutów.
 1. Gry dotyczące systemu dziesiętnego Pomoce: kostka dziesięciościenna i/albo karty z cyframi. KaŜdy rywalizuje z kaŝdym. KaŜdy gracz rysuje planszę: Prowadzący rzuca dziesięciościenną kostką albo losuje
1. Gry dotyczące systemu dziesiętnego Pomoce: kostka dziesięciościenna i/albo karty z cyframi. KaŜdy rywalizuje z kaŝdym. KaŜdy gracz rysuje planszę: Prowadzący rzuca dziesięciościenną kostką albo losuje
16. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. II
 80 Mirosław Dąbrowski 16. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
80 Mirosław Dąbrowski 16. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. II Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
XXI Krajowa Konferencja SNM
 1 XXI Krajowa Konferencja SNM AKTYWNOŚCI MATEMATYCZNE Ewa Szelecka (Częstochowa) ewaszel@poczta.onet.pl Małgorzata Pyziak (Rzeszów) mmpskarp@interia.pl Projekty, gry dydaktyczne i podręcznik interaktywny
1 XXI Krajowa Konferencja SNM AKTYWNOŚCI MATEMATYCZNE Ewa Szelecka (Częstochowa) ewaszel@poczta.onet.pl Małgorzata Pyziak (Rzeszów) mmpskarp@interia.pl Projekty, gry dydaktyczne i podręcznik interaktywny
Rachunki trudne i nudne? Nie muszą, mogą być ciekawe!
 Rachunki trudne i nudne? Nie muszą, mogą być ciekawe! Jolanta Biernat konsultant RODN WOM Bielsko-Biała jolanta.biernat@gmail.com Katarzyna Parcia konsultant RODN WOM Bielsko-Biała kparcia@wombb.edu.pl
Rachunki trudne i nudne? Nie muszą, mogą być ciekawe! Jolanta Biernat konsultant RODN WOM Bielsko-Biała jolanta.biernat@gmail.com Katarzyna Parcia konsultant RODN WOM Bielsko-Biała kparcia@wombb.edu.pl
Metryczka Justyna Płonka Szkoła Podstawowa nr 1 z Oddziałami Integracyjnymi im. Jana III Sobieskiego w Kozach
 Metryczka Justyna Płonka Szkoła Podstawowa nr 1 z Oddziałami Integracyjnymi im. Jana III Sobieskiego w Kozach Temat: Dzielenie z resztą Dział: Liczby i działania Klasa: IV szkoły podstawowej Czas realizacji:
Metryczka Justyna Płonka Szkoła Podstawowa nr 1 z Oddziałami Integracyjnymi im. Jana III Sobieskiego w Kozach Temat: Dzielenie z resztą Dział: Liczby i działania Klasa: IV szkoły podstawowej Czas realizacji:
BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA DLA KLASY VI. CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących zdrowie.
 BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA SCENARIUSZ DOTYCZĄCY UZALEŻNIEŃ TEMAT: Bieg po zdrowie. CZAS TRWANIA: 2 godz. lekcyjne. DLA KLASY VI CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących
BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA SCENARIUSZ DOTYCZĄCY UZALEŻNIEŃ TEMAT: Bieg po zdrowie. CZAS TRWANIA: 2 godz. lekcyjne. DLA KLASY VI CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących
Opinie nauczycieli klas 1-3 o edukacji językowej i edukacji matematycznej
 Opinie nauczycieli klas 1-3 o edukacji językowej i edukacji matematycznej Edukacja językowa Treść pozycji skali Dzieci z rodzin o niskim poziomie wykształcenia rodziców powinny uczyć się razem w jednej
Opinie nauczycieli klas 1-3 o edukacji językowej i edukacji matematycznej Edukacja językowa Treść pozycji skali Dzieci z rodzin o niskim poziomie wykształcenia rodziców powinny uczyć się razem w jednej
Moneta 1 Moneta 2 Kostka O, R O,R 1,2,3,4,5, Moneta 1 Moneta 2 Kostka O O ( )
 Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Nowa matura kombinatoryka i rachunek prawdopodobieństwa Zadania zamknięte (0 1 pkt) 1. Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo
Tytuł. Autor. Dział. Innowacyjne cele edukacyjne. Czas. Przebieg. Etap 1 - wprowadzenie. Etap 2 - algorytm 3. Sztuka szybkiego liczenia Cz.
 Tytuł Sztuka szybkiego liczenia Cz. II Autor Dariusz Kulma Dział Liczby wymierne Innowacyjne cele edukacyjne Zapoznanie uczniów z technikami szybkiego liczenia w pamięci niestosowanymi na lekcjach matematyki:
Tytuł Sztuka szybkiego liczenia Cz. II Autor Dariusz Kulma Dział Liczby wymierne Innowacyjne cele edukacyjne Zapoznanie uczniów z technikami szybkiego liczenia w pamięci niestosowanymi na lekcjach matematyki:
BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA DLA KLASY III. CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących zdrowie
 BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA SCENARIUSZ DOTYCZĄCY UZALEŻNIEŃ TEMAT: Bieg po zdrowie. CZAS TRWANIA: 2 godz. lekcyjne. DLA KLASY III CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących
BEZPIECZNE DZIECKO- PRZYJACIEL SZNUPKA SCENARIUSZ DOTYCZĄCY UZALEŻNIEŃ TEMAT: Bieg po zdrowie. CZAS TRWANIA: 2 godz. lekcyjne. DLA KLASY III CEL GŁÓWNY: Nabywanie umiejętności wyboru zachowań promujących
PROGRAM ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA UCZNIÓW KLASY IV. Realizowanych w ramach projektu: SZKOŁA DLA KAŻDEGO
 PROGRAM ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA UCZNIÓW KLASY IV Realizowanych w ramach projektu: SZKOŁA DLA KAŻDEGO Opracowała: Marzanna Leśniewska I. WSTĘP Matematyka potrzebna jest każdemu. Spotykamy się
PROGRAM ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA UCZNIÓW KLASY IV Realizowanych w ramach projektu: SZKOŁA DLA KAŻDEGO Opracowała: Marzanna Leśniewska I. WSTĘP Matematyka potrzebna jest każdemu. Spotykamy się
Scenariusz lekcji matematyki w klasie VI
 Scenariusz lekcji matematyki w klasie VI Dział programowy: LICZBY WYMIERNE Temat lekcji: Powtórzenie działań na liczbach wymiernych. Cele główne: o powtórzenie i utrwalenie wiadomości i umiejętności z
Scenariusz lekcji matematyki w klasie VI Dział programowy: LICZBY WYMIERNE Temat lekcji: Powtórzenie działań na liczbach wymiernych. Cele główne: o powtórzenie i utrwalenie wiadomości i umiejętności z
Roboty grają w karty
 Roboty grają w karty Wstęp: Roboty grają w karty - to propozycja lekcji łączącej edukację matematyczną z programowaniem i elementami robotyki. Uczniowie będą tworzyć skrypty w aplikacji Blockly, jednocześnie
Roboty grają w karty Wstęp: Roboty grają w karty - to propozycja lekcji łączącej edukację matematyczną z programowaniem i elementami robotyki. Uczniowie będą tworzyć skrypty w aplikacji Blockly, jednocześnie
SCENARIUSZE ZAJĘĆ KLASA 1 DIDASKO Ewa Kapczyńska, Krystyna Tomecka
 TEMAT: Spotkanie z liczbą 12 Miesiąc: luty Tydzień nauki: 21 Kształtowanie umiejętności: edukacja matematyczna ( 7.2; 7.3; 7.4. ;7.5; 7.8), edukacja społeczna (5.4) Materiały i środki dydaktyczne: kartoniki
TEMAT: Spotkanie z liczbą 12 Miesiąc: luty Tydzień nauki: 21 Kształtowanie umiejętności: edukacja matematyczna ( 7.2; 7.3; 7.4. ;7.5; 7.8), edukacja społeczna (5.4) Materiały i środki dydaktyczne: kartoniki
SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA
 SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA Temat lekcji Co lepsze strategia czy przypadek? Gra dydaktyczna. Na podstawie pracy
SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA Temat lekcji Co lepsze strategia czy przypadek? Gra dydaktyczna. Na podstawie pracy
gra Chińczyk dla 6 osób
 CHIŃCZYK Chińczyk to popularna gra planszowa dla dwóch, trzech lub czterech osób, w której celem graczy jest przejście dookoła planszy czterema pionkami z pozycji początkowych na końcowe. Pierwszy gracz,
CHIŃCZYK Chińczyk to popularna gra planszowa dla dwóch, trzech lub czterech osób, w której celem graczy jest przejście dookoła planszy czterema pionkami z pozycji początkowych na końcowe. Pierwszy gracz,
Załącznik do Uchwały Nr 1/2014/2015 Rady Pedagogicznej Szkoły Podstawowej w Czernikowie z dnia 15.09.2014 r.
 Celem doskonalenia sprawności rachunkowej należy: stosować różnorodne ćwiczenia doskonalące sprawność rachunkową, dostosowane do indywidualnych możliwości uczniów; wykorzystywać codzienne okazje do utrwalania
Celem doskonalenia sprawności rachunkowej należy: stosować różnorodne ćwiczenia doskonalące sprawność rachunkową, dostosowane do indywidualnych możliwości uczniów; wykorzystywać codzienne okazje do utrwalania
6. TWORZYMY OPOWIEŚĆ DO RZUTÓW KOSTKĄ CZYLI O UKŁADANIU OPOWIADAŃ
 6. TWORZYMY OPOWIEŚĆ DO RZUTÓW KOSTKĄ CZYLI O UKŁADANIU OPOWIADAŃ 27 Małgorzata Sieńczewska 6. TWORZYMY OPOWIEŚĆ DO RZUTÓW KOSTKĄ CZYLI O UKŁADANIU OPOWIADAŃ Cele ogólne w szkole podstawowej: zdobycie
6. TWORZYMY OPOWIEŚĆ DO RZUTÓW KOSTKĄ CZYLI O UKŁADANIU OPOWIADAŃ 27 Małgorzata Sieńczewska 6. TWORZYMY OPOWIEŚĆ DO RZUTÓW KOSTKĄ CZYLI O UKŁADANIU OPOWIADAŃ Cele ogólne w szkole podstawowej: zdobycie
Kto jeszcze gra w domino?
 Mirosław Dąbrowski Kto jeszcze gra w domino? Domino, choć wciąż jeszcze można jego zestawy kupić w sklepach z zabawkami, nie należy już chyba do bardzo popularnych dziecięcych rozrywek. Szkoda, bo gra
Mirosław Dąbrowski Kto jeszcze gra w domino? Domino, choć wciąż jeszcze można jego zestawy kupić w sklepach z zabawkami, nie należy już chyba do bardzo popularnych dziecięcych rozrywek. Szkoda, bo gra
Scenariusz lekcji. Opracował: Paweł Słaby
 Scenariusz lekcji 1. Informacje wstępne: Klasa: uczniowie szkoły ponadgimnazjalnej, realizujący poziom podstawowy bądź rozszerzony; Czas trwania zajęć: 45 minut; Nauczany przedmiot: matematyka.. Temat
Scenariusz lekcji 1. Informacje wstępne: Klasa: uczniowie szkoły ponadgimnazjalnej, realizujący poziom podstawowy bądź rozszerzony; Czas trwania zajęć: 45 minut; Nauczany przedmiot: matematyka.. Temat
12. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I
 56 Mirosław Dąbrowski 12. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości podczas
56 Mirosław Dąbrowski 12. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości podczas
Z CZEGO SKŁADA SIĘ PAKIET EDUKACYJNY GRAMY W PIKTOGRAMY
 25 Rozdział 7. Z CZEGO SKŁADA SIĘ PAKIET EDUKACYJNY GRAMY W PIKTOGRAMY Przewodnik Przewodnik złożony jest z dwóch części. Pierwsza teoretyczna przypomina nauczycielom prawidłowości uczenia się, wskazania
25 Rozdział 7. Z CZEGO SKŁADA SIĘ PAKIET EDUKACYJNY GRAMY W PIKTOGRAMY Przewodnik Przewodnik złożony jest z dwóch części. Pierwsza teoretyczna przypomina nauczycielom prawidłowości uczenia się, wskazania
Rola rodziców w kształtowaniu motywacji do nauki. Zespół Szkół w Rycerce Górnej
 Rola rodziców w kształtowaniu motywacji do nauki Zespół Szkół w Rycerce Górnej CO TO JEST MOTYWACJA? Na słowo MOTYWACJA składają się dwa słówka: Motyw i Akcja. Czyli aby podjąć jakieś określone działanie
Rola rodziców w kształtowaniu motywacji do nauki Zespół Szkół w Rycerce Górnej CO TO JEST MOTYWACJA? Na słowo MOTYWACJA składają się dwa słówka: Motyw i Akcja. Czyli aby podjąć jakieś określone działanie
Program edukacyjny wspierający nauczanie matematyki w klasach III - VII
 Program edukacyjny wspierający nauczanie matematyki w klasach III - VII Teresa Świrska Aleksandra Jakubowska Małgorzata Niedziela Wrocław 2019 I. W S T Ę P Intencją autorów programu Z kalkulatorem, kartami
Program edukacyjny wspierający nauczanie matematyki w klasach III - VII Teresa Świrska Aleksandra Jakubowska Małgorzata Niedziela Wrocław 2019 I. W S T Ę P Intencją autorów programu Z kalkulatorem, kartami
SCENARIUSZ LEKCJI. - pracować w sposób wytrwały i samodzielny, - pracować zgodnie z pozytywnymi postawami etycznymi, - dobrze organizować pracę,
 SCENARIUSZ LEKCJI 1. Informacje wstępne Klasa VI PSP 20 w Opolu Czas trwania zajęć 45 minut Nauczany przedmiot matematyka Nauczyciel przedmiotu Małgorzata Jackowska 2. Program nauczania Matematyka z plusem
SCENARIUSZ LEKCJI 1. Informacje wstępne Klasa VI PSP 20 w Opolu Czas trwania zajęć 45 minut Nauczany przedmiot matematyka Nauczyciel przedmiotu Małgorzata Jackowska 2. Program nauczania Matematyka z plusem
SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA
 SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA Temat lekcji: Krzyżówka liczbowa Dobrze poukładany człowiek Na podstawie pracy Justyny
SCENARIUSZ ZAJĘĆ SZKOLNEGO KOŁA NAUKOWEGO Z PRZEDMIOTU MATEMATYKA PROWADZONEGO W RAMACH PROJEKTU AKADEMIA UCZNIOWSKA Temat lekcji: Krzyżówka liczbowa Dobrze poukładany człowiek Na podstawie pracy Justyny
7. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I
 7. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I 37 Mirosław Dąbrowski 7. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez
7. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I 37 Mirosław Dąbrowski 7. ILE TO KOSZTUJE CZYLI OD ZAGADKI DO ZADANIA TEKSTOWEGO, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez
SCENARIUSZ LEKCJI MATEMATYKI W KLASIE 1 GIMNAZJUM
 SCENARIUSZ LEKCJI MATEMATYKI W KLASIE GIMNAZJUM Temat: Ćwiczenia w dodawaniu i odejmowaniu liczb wymiernych Cele ogólne: - utrwalenie reguł dodawania i odejmowania liczb wymiernych, - wyrabianie sprawności
SCENARIUSZ LEKCJI MATEMATYKI W KLASIE GIMNAZJUM Temat: Ćwiczenia w dodawaniu i odejmowaniu liczb wymiernych Cele ogólne: - utrwalenie reguł dodawania i odejmowania liczb wymiernych, - wyrabianie sprawności
Scenariusz lekcji matematyki Równania pierwszego stopnia z jedną niewiadomą w zadaniach.
 Scenariusz lekcji matematyki Równania pierwszego stopnia z jedną niewiadomą w zadaniach. Opracowała: mgr inż. Monika Grzegorczyk 1. Temat lekcji: Równania pierwszego stopnia z jedną niewiadomą w zadaniach.
Scenariusz lekcji matematyki Równania pierwszego stopnia z jedną niewiadomą w zadaniach. Opracowała: mgr inż. Monika Grzegorczyk 1. Temat lekcji: Równania pierwszego stopnia z jedną niewiadomą w zadaniach.
DZIAŁANIA NA LICZBACH WYMIERNYCH - ZADANIA TEKSTOWE
 Danuta Węgrowska Pracownia Edukacji Matematycznej, Fizycznej i Chemicznej ŁCDNiKP DZIAŁANIA NA LICZBACH WYMIERNYCH - ZADANIA TEKSTOWE III etap edukacji (klasa I) Cele kształcenia Cele ogólne: doskonalenie
Danuta Węgrowska Pracownia Edukacji Matematycznej, Fizycznej i Chemicznej ŁCDNiKP DZIAŁANIA NA LICZBACH WYMIERNYCH - ZADANIA TEKSTOWE III etap edukacji (klasa I) Cele kształcenia Cele ogólne: doskonalenie
KLASA O PROFILU MATEMATYCZNO-INFORMATYCZNYM
 KLASA O PROFILU MATEMATYCZNO-INFORMATYCZNYM COS SIN I. Część matematyczna Uczniowie, którzy będą uczyć się w tej klasie będą mieli możliwość rozwijać swoje talenty matematyczne, a pozyskaną wiedzę weryfikować
KLASA O PROFILU MATEMATYCZNO-INFORMATYCZNYM COS SIN I. Część matematyczna Uczniowie, którzy będą uczyć się w tej klasie będą mieli możliwość rozwijać swoje talenty matematyczne, a pozyskaną wiedzę weryfikować
KWIECIEŃ klasa 2 MATEMATYKA
 26. tydzień nauki Jak dzielimy? Jak mnożymy? Temat: Jak dzielimy? Jak mnożymy? Mnożenie i dzielenie liczb w zakresie 50. 7.6 Zagadki matematyczne zapisywanie działań. 7.8 Rozwiązywanie zadań tekstowych
26. tydzień nauki Jak dzielimy? Jak mnożymy? Temat: Jak dzielimy? Jak mnożymy? Mnożenie i dzielenie liczb w zakresie 50. 7.6 Zagadki matematyczne zapisywanie działań. 7.8 Rozwiązywanie zadań tekstowych
Autor: Małgorzata Urbańska. Temat lekcji: Pieszy i znaki
 Autor: Małgorzata Urbańska Klasa I Edukacja: techniczna, społeczna, matematyczna, plastyczna, Cel zajęć: - zapoznanie z zasadami bezpiecznego poruszania się po drodze, - kształtowanie umiejętności dbania
Autor: Małgorzata Urbańska Klasa I Edukacja: techniczna, społeczna, matematyczna, plastyczna, Cel zajęć: - zapoznanie z zasadami bezpiecznego poruszania się po drodze, - kształtowanie umiejętności dbania
Szkole Podstawowej nr 6. im. Henryka Sienkiewicza. w Pruszkowie
 Raport z Ogólnopolskiego Sprawdzianu Kompetencji Trzecioklasisty Operon w roku szkolnym 2012/2013 w Szkole Podstawowej nr 6 im. Henryka Sienkiewicza w Pruszkowie Opracowanie: mgr Anna Frączek mgr Magdalena
Raport z Ogólnopolskiego Sprawdzianu Kompetencji Trzecioklasisty Operon w roku szkolnym 2012/2013 w Szkole Podstawowej nr 6 im. Henryka Sienkiewicza w Pruszkowie Opracowanie: mgr Anna Frączek mgr Magdalena
PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe
 PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe DOMI mnożenie w zakresie 50 28 klocków, 56 zadań Prosta, powszechnienie znana, a jednocześnie atrakcyjna forma uczenia się poprzez
PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe DOMI mnożenie w zakresie 50 28 klocków, 56 zadań Prosta, powszechnienie znana, a jednocześnie atrakcyjna forma uczenia się poprzez
Scenariusz lekcji matematyki w klasie I gimnazjum z wykorzystaniem metod aktywizujących prowadząca: mgr Daniela Moch
 Scenariusz lekcji matematyki w klasie I gimnazjum z wykorzystaniem metod aktywizujących prowadząca: mgr Daniela Moch Temat: Działania na liczbach wymiernych zadania tekstowe. Cele ogólne - edukacyjne lekcji:
Scenariusz lekcji matematyki w klasie I gimnazjum z wykorzystaniem metod aktywizujących prowadząca: mgr Daniela Moch Temat: Działania na liczbach wymiernych zadania tekstowe. Cele ogólne - edukacyjne lekcji:
UMIEJĘTNOŚCI JĘZYKOWE
 Raport z Ogólnopolskiego Sprawdzianu Kompetencji Trzecioklasisty OPERON 2016 w Szkole Podstawowej nr 6 im. Henryka Sienkiewicza w Pruszkowie Ogólnopolski Sprawdzian Kompetencji Trzecioklasisty odbył się
Raport z Ogólnopolskiego Sprawdzianu Kompetencji Trzecioklasisty OPERON 2016 w Szkole Podstawowej nr 6 im. Henryka Sienkiewicza w Pruszkowie Ogólnopolski Sprawdzian Kompetencji Trzecioklasisty odbył się
W przyszłość bez barier
 Program zajęć dla dzieci z trudnościami w zdobywaniu umiejętności matematycznych w klasach I III w Szkole Podstawowej w Łysowie realizowany w ramach projektu W przyszłość bez barier PO KL.09.01.02-14-071/13
Program zajęć dla dzieci z trudnościami w zdobywaniu umiejętności matematycznych w klasach I III w Szkole Podstawowej w Łysowie realizowany w ramach projektu W przyszłość bez barier PO KL.09.01.02-14-071/13
Scenariusz zajęć do programu kształcenia Myślę- działam- idę w świat
 Scenariusz zajęć do programu kształcenia Myślę- działam- idę w świat Aur: Danuta Szymczak Klasa II Edukacja: polonistyczna, muzyczna, społeczna, matematyczna. Cel/cele zajęć: -doskonalenie umiejętności
Scenariusz zajęć do programu kształcenia Myślę- działam- idę w świat Aur: Danuta Szymczak Klasa II Edukacja: polonistyczna, muzyczna, społeczna, matematyczna. Cel/cele zajęć: -doskonalenie umiejętności
OCENIANIE KSZTAŁTUJĄCE
 OCENIANIE KSZTAŁTUJĄCE Co to jest ocenianie kształtujące? Ocenianie jest integralną częścią procesu edukacyjnego. Najczęściej mamy do czynienia z ocenianiem podsumowującym, które dzięki testom i egzaminom,
OCENIANIE KSZTAŁTUJĄCE Co to jest ocenianie kształtujące? Ocenianie jest integralną częścią procesu edukacyjnego. Najczęściej mamy do czynienia z ocenianiem podsumowującym, które dzięki testom i egzaminom,
I etap edukacyjny, uczeń kończący klasę III, edukacja matematyczna
 Scenariusz zajęć I etap edukacyjny, uczeń kończący klasę III, edukacja matematyczna Temat: Telefony Treści kształcenia: 8) uczeń wykonuje łatwe obliczenia pieniężne (cena, ilość, wartość) i radzi sobie
Scenariusz zajęć I etap edukacyjny, uczeń kończący klasę III, edukacja matematyczna Temat: Telefony Treści kształcenia: 8) uczeń wykonuje łatwe obliczenia pieniężne (cena, ilość, wartość) i radzi sobie
DZIELENIE SIĘ WIEDZĄ I POMYSŁAMI SPOTKANIE ZESPOŁU SAMOKSZTAŁCENIOWEGO
 DZIELENIE SIĘ WIEDZĄ I POMYSŁAMI SPOTKANIE ZESPOŁU SAMOKSZTAŁCENIOWEGO Mariusz Pielucha nauczyciel nauczania początkowego Szkoła Podstawowa w Kaźmierzu. CEL: Wykorzystanie szablonów kratkowych do wprowadzenia
DZIELENIE SIĘ WIEDZĄ I POMYSŁAMI SPOTKANIE ZESPOŁU SAMOKSZTAŁCENIOWEGO Mariusz Pielucha nauczyciel nauczania początkowego Szkoła Podstawowa w Kaźmierzu. CEL: Wykorzystanie szablonów kratkowych do wprowadzenia
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1
 W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
W. Guzicki Zadanie 41 z Informatora Maturalnego poziom podstawowy 1 W tym tekście zobaczymy rozwiązanie zadania 41 z Informatora o egzaminie maturalnym z matematyki od roku szkolnego 014/015 oraz rozwiązania
Pak Pa iet e eduk acyjn eduk acyjn Gram Gram w piktogram pikt ogram Pomaga skutecznie i ciekawie ucz ć y ema ki!
 Pakiet edukacyjny Gramyw piktogramy Pomaga skutecznie i ciekawie i uczyć ć matematyki! t Pakiet edukacyjny Gramy w piktogramy przygotowany jest w 3 wariantach: dla klas I III szkoły podstawowej dla klas
Pakiet edukacyjny Gramyw piktogramy Pomaga skutecznie i ciekawie i uczyć ć matematyki! t Pakiet edukacyjny Gramy w piktogramy przygotowany jest w 3 wariantach: dla klas I III szkoły podstawowej dla klas
Scenariusz nr 9. Blok tematyczny: Bezpiecznie na wakacje
 Autor scenariusza: Maria Piotrowska Blok tematyczny: Bezpiecznie na wakacje Scenariusz nr 9 I. Tytuł scenariusza zajęć : " Wielka gra planszowa " Utrwalenie wiadomości. II. Czas realizacji: 2 jednostki
Autor scenariusza: Maria Piotrowska Blok tematyczny: Bezpiecznie na wakacje Scenariusz nr 9 I. Tytuł scenariusza zajęć : " Wielka gra planszowa " Utrwalenie wiadomości. II. Czas realizacji: 2 jednostki
20. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. I
 98 Mirosław Dąbrowski 20. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
98 Mirosław Dąbrowski 20. CO TU PASUJE CZYLI O DOSTRZEGANIU ZWIĄZKÓW, PODOBIEŃSTW I RÓŻNIC, CZ. I Cele ogólne w szkole podstawowej: zdobycie przez uczniów umiejętności wykorzystywania posiadanych wiadomości
PRZYKŁADOWE SCENARIUSZE ZAJĘĆ
 PRZYKŁADOWE SCENARIUSZE ZAJĘĆ SCENARIUSZ NR 1 Temat zajęć: Obliczanie pól i obwodów prostokątów. Cele zajęć: Uczeń: Zna jednostki pola; Umie obliczyć pole i obwód prostokąta i kwadratu; Wykorzystuje swoje
PRZYKŁADOWE SCENARIUSZE ZAJĘĆ SCENARIUSZ NR 1 Temat zajęć: Obliczanie pól i obwodów prostokątów. Cele zajęć: Uczeń: Zna jednostki pola; Umie obliczyć pole i obwód prostokąta i kwadratu; Wykorzystuje swoje
SPRAWOZDANIE Z ZAJĘĆ WYRÓWNAWCZYCH Z MATEMATYKI DLA KLAS IV-VII
 Tytuł projektu: Lokata w dziecięce umysły Zadanie nr 3 : Zajęcia wyrównawcze z matematyki dla klas IV-VII Imię i nazwisko osoby prowadzącej zajęcia: Dorota Siejkowska SPRAWOZDANIE Z ZAJĘĆ WYRÓWNAWCZYCH
Tytuł projektu: Lokata w dziecięce umysły Zadanie nr 3 : Zajęcia wyrównawcze z matematyki dla klas IV-VII Imię i nazwisko osoby prowadzącej zajęcia: Dorota Siejkowska SPRAWOZDANIE Z ZAJĘĆ WYRÓWNAWCZYCH
AKADEMIA DLA MŁODYCH PRZEWODNIK TRENERA. PRACA ŻYCIE UMIEJĘTNOŚCI
 PRACA ŻYCIE UMIEJĘTNOŚCI www.akademiadlamlodych.pl PODRĘCZNIK WPROWADZENIE Akademia dla Młodych to nowa inicjatywa mająca na celu wspieranie ludzi młodych w rozwijaniu umiejętności niezbędnych w ich miejscu
PRACA ŻYCIE UMIEJĘTNOŚCI www.akademiadlamlodych.pl PODRĘCZNIK WPROWADZENIE Akademia dla Młodych to nowa inicjatywa mająca na celu wspieranie ludzi młodych w rozwijaniu umiejętności niezbędnych w ich miejscu
SCENARIUSZ LEKCJI. kategoria B zrozumienie. Uczeń :
 SCENARIUSZ LEKCJI 1. Informacje wstępne: Data : 01.10.2012 Klasa : I A Czas trwania zajęć : 45 minut Nauczany przedmiot: matematyka 2. Program nauczania: Matematyka z plusem. Program nauczania matematyki
SCENARIUSZ LEKCJI 1. Informacje wstępne: Data : 01.10.2012 Klasa : I A Czas trwania zajęć : 45 minut Nauczany przedmiot: matematyka 2. Program nauczania: Matematyka z plusem. Program nauczania matematyki
GRA EDUKACYJNA INNA NIŻ WSZYSTKIE
 GRA EDUKACYJNA INNA NIŻ WSZYSTKIE Przewodnik 5 9 Daje LAT dorosłym możliwość wspólnej zabawy z dziećmi Mnóstwo zabawy, mnóstwo nauki! Od 1967 Zawartość 4 5... Wstęp 6 7... Zasady gry 8... Grając w iknow
GRA EDUKACYJNA INNA NIŻ WSZYSTKIE Przewodnik 5 9 Daje LAT dorosłym możliwość wspólnej zabawy z dziećmi Mnóstwo zabawy, mnóstwo nauki! Od 1967 Zawartość 4 5... Wstęp 6 7... Zasady gry 8... Grając w iknow
Scenariusz zajęć nr 8
 Autor scenariusza: Małgorzata Marzycka Blok tematyczny: Świat wokół nas Scenariusz zajęć nr 8 Temat dnia: Zabawy matematyką. I. Czas realizacji: 2 jednostki lekcyjne. II. Czynności przed lekcyjne: przygotowanie
Autor scenariusza: Małgorzata Marzycka Blok tematyczny: Świat wokół nas Scenariusz zajęć nr 8 Temat dnia: Zabawy matematyką. I. Czas realizacji: 2 jednostki lekcyjne. II. Czynności przed lekcyjne: przygotowanie
DODAWANIE I ODEJMOWANIE SUM ALGEBRAICZNYCH
 DODAWANIE I ODEJMOWANIE SUM ALGEBRAICZNYCH Cele operacyjne Uczeń umie: budować wyrażenia algebraiczne, opuszczać nawiasy, redukować wyrazy podobne, dodawać i odejmować sumy algebraiczne. Metody nauczania
DODAWANIE I ODEJMOWANIE SUM ALGEBRAICZNYCH Cele operacyjne Uczeń umie: budować wyrażenia algebraiczne, opuszczać nawiasy, redukować wyrazy podobne, dodawać i odejmować sumy algebraiczne. Metody nauczania
Elementy Skarbnicy odkrywców dla klas 1-3
 Elementy Skarbnicy odkrywców dla klas 1-3 Pomoce Gra matematyczna Mistrz mnożenia i dzielenia Do czego mogą być przydatne? Doskonalenie mnożenia i dzielenia w zakresie 30 Gra matematyczna Poszukiwacze
Elementy Skarbnicy odkrywców dla klas 1-3 Pomoce Gra matematyczna Mistrz mnożenia i dzielenia Do czego mogą być przydatne? Doskonalenie mnożenia i dzielenia w zakresie 30 Gra matematyczna Poszukiwacze
Nr art. 25516 XXL Papillon
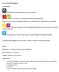 Nr art. 25516 XXL Papillon Gra wspomaga: Naukę rozpoznawania kolorów: podstawowych i pochodnych Ruch w czasie gry / poznawanie liczb i kształtów, pojmowanie ilości: połączenie ruchu i rozwijanie umiejętności
Nr art. 25516 XXL Papillon Gra wspomaga: Naukę rozpoznawania kolorów: podstawowych i pochodnych Ruch w czasie gry / poznawanie liczb i kształtów, pojmowanie ilości: połączenie ruchu i rozwijanie umiejętności
Program Coachingu dla młodych osób
 Program Coachingu dla młodych osób "Dziecku nie wlewaj wiedzy, ale zainspiruj je do działania " Przed rozpoczęciem modułu I wysyłamy do uczestników zajęć kwestionariusz 360 Moduł 1: Samoznanie jako część
Program Coachingu dla młodych osób "Dziecku nie wlewaj wiedzy, ale zainspiruj je do działania " Przed rozpoczęciem modułu I wysyłamy do uczestników zajęć kwestionariusz 360 Moduł 1: Samoznanie jako część
Gra w kolory program nauczania edukacji wczesnoszkolnej
 Scenariusz zajęć z edukacji wczesnoszkolnej 1. Informacje wstępne: Data 12 II 2013 Klasa II c 2. Realizowany program nauczania Gra w kolory program nauczania edukacji wczesnoszkolnej Autorka Ewa Stolarczyk
Scenariusz zajęć z edukacji wczesnoszkolnej 1. Informacje wstępne: Data 12 II 2013 Klasa II c 2. Realizowany program nauczania Gra w kolory program nauczania edukacji wczesnoszkolnej Autorka Ewa Stolarczyk
Opracował: Rafał Górniak Gra symulacyjna Budujemy wiatraki
 Gra symulacyjna Budujemy wiatraki Cele gry - poznanie interesów różnych grup społecznych, których dotyczy budowa farmy wiatrowej - poznanie/ lepsze zrozumienie zalet i wad elektrowni wiatrowych - rozwój
Gra symulacyjna Budujemy wiatraki Cele gry - poznanie interesów różnych grup społecznych, których dotyczy budowa farmy wiatrowej - poznanie/ lepsze zrozumienie zalet i wad elektrowni wiatrowych - rozwój
EGZAMIN W KLASIE TRZECIEJ GIMNAZJUM W ROKU SZKOLNYM 2017/2018 CZĘŚĆ 2. MATEMATYKA ZASADY OCENIANIA ROZWIĄZAŃ ZADAŃ
 EGZAMIN W KLASIE TRZECIEJ GIMNAZJUM W ROKU SZKOLNYM 2017/2018 CZĘŚĆ 2. MATEMATYKA ZASADY OCENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ GM-M8 KWIECIEŃ 2018 Zadanie 1. (0 1) I. Wykorzystanie i tworzenie informacji. Umiejętność
EGZAMIN W KLASIE TRZECIEJ GIMNAZJUM W ROKU SZKOLNYM 2017/2018 CZĘŚĆ 2. MATEMATYKA ZASADY OCENIANIA ROZWIĄZAŃ ZADAŃ ARKUSZ GM-M8 KWIECIEŃ 2018 Zadanie 1. (0 1) I. Wykorzystanie i tworzenie informacji. Umiejętność
Cele nauczania: a)poznawcze: Cele ogólne kształcenia: -uczeń umie odejmować ułamki dziesiętne. Aktywności matematyczne:
 Konspekt lekcji matematyki: Klasa: czwarta Prowadzący: Elżbieta Kruczek, nauczyciel Samorządowej Szkoły Podstawowej w Brześciu (z wykorzystaniem podręcznika Matematyka z plusem) Temat: Odejmowanie ułamków
Konspekt lekcji matematyki: Klasa: czwarta Prowadzący: Elżbieta Kruczek, nauczyciel Samorządowej Szkoły Podstawowej w Brześciu (z wykorzystaniem podręcznika Matematyka z plusem) Temat: Odejmowanie ułamków
Realizacja podstawy programowej w klasach IV VI szkoły podstawowej poprzez różne formy aktywności
 Realizacja podstawy programowej w klasach IV VI szkoły podstawowej poprzez różne formy aktywności Małgorzata Tubielewicz tubielewicz@womczest.edu.pl Co to są metody aktywizujące? Metody aktywizujące to
Realizacja podstawy programowej w klasach IV VI szkoły podstawowej poprzez różne formy aktywności Małgorzata Tubielewicz tubielewicz@womczest.edu.pl Co to są metody aktywizujące? Metody aktywizujące to
Po drabinie do celu. Spotkanie 2. fundacja. Realizator projektu:
 T Spotkanie 2 Po drabinie do celu Projekt finansowany ze środków Ministerstwa Edukacji Narodowej w ramach Narodowego Programu Zdrowia Realizator projektu: fundacja e d u k a c j i p o z y t y w n e j Grupa
T Spotkanie 2 Po drabinie do celu Projekt finansowany ze środków Ministerstwa Edukacji Narodowej w ramach Narodowego Programu Zdrowia Realizator projektu: fundacja e d u k a c j i p o z y t y w n e j Grupa
Wyniki sprawdzianu zewnętrznego klas szóstych uczniów SP10 w latach 2008-2012 na tle miasta, województwa, kraju:
 Efekty różnorodnych działań przygotowujących uczniów do sprawdzianu zewnętrznego analiza oferty zajęć wspierających oraz materiałów przygotowywanych przez nauczycieli Dzięki zaangażowaniu nauczycieli,
Efekty różnorodnych działań przygotowujących uczniów do sprawdzianu zewnętrznego analiza oferty zajęć wspierających oraz materiałów przygotowywanych przez nauczycieli Dzięki zaangażowaniu nauczycieli,
Projekt Otwarte Przedszkola został zrealizowany w Zespole Placówek Oświatowych w Zatorach. Byliśmy jedną z nielicznych placówek w powiecie pułtuskim
 Projekt Otwarte Przedszkola został zrealizowany w Zespole Placówek Oświatowych w Zatorach. Byliśmy jedną z nielicznych placówek w powiecie pułtuskim uczestniczących w projekcie. Wzięło w nim udział 48
Projekt Otwarte Przedszkola został zrealizowany w Zespole Placówek Oświatowych w Zatorach. Byliśmy jedną z nielicznych placówek w powiecie pułtuskim uczestniczących w projekcie. Wzięło w nim udział 48
Scenariusz zajęć z edukacji wczesnoszkolnej
 Scenariusz zajęć z edukacji wczesnoszkolnej 1. Informacje wstępne: Data 5 III 2013 Klasa II c 2. Realizowany program nauczania Gra w kolory program nauczania edukacji wczesnoszkolnej Autorka Ewa Stolarczyk
Scenariusz zajęć z edukacji wczesnoszkolnej 1. Informacje wstępne: Data 5 III 2013 Klasa II c 2. Realizowany program nauczania Gra w kolory program nauczania edukacji wczesnoszkolnej Autorka Ewa Stolarczyk
ZGŁOSZENIE DOBREJ PRAKTYKI
 ZGŁOSZENIE DOBREJ PRAKTYKI Sulechów, 18.11.2013 r. NAZWA SZKOŁY DANE SZKOŁY ( adres, telefon, e-mail) IMIĘ I NAZWISKO AUTORA/AUTORÓW DOBREJ PRAKTYKI TYTUŁ PRZEDSIĘWZIĘCIA RODZAJ PRZEDSIĘWZIĘCIA ( np. innowacja,
ZGŁOSZENIE DOBREJ PRAKTYKI Sulechów, 18.11.2013 r. NAZWA SZKOŁY DANE SZKOŁY ( adres, telefon, e-mail) IMIĘ I NAZWISKO AUTORA/AUTORÓW DOBREJ PRAKTYKI TYTUŁ PRZEDSIĘWZIĘCIA RODZAJ PRZEDSIĘWZIĘCIA ( np. innowacja,
Matematyka na przełomie
 Matematyka na przełomie Na przełomie klasy 3/4 ROZPORZĄDZENIE MINISTRA EDUKACJI NARODOWEJ z dnia 27 sierpnia 2012 r. w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w
Matematyka na przełomie Na przełomie klasy 3/4 ROZPORZĄDZENIE MINISTRA EDUKACJI NARODOWEJ z dnia 27 sierpnia 2012 r. w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w
PUBLIKACJA PODSUMOWUJACA ZAJĘCIA DODATKOWE Z MATEMATYKI. realizowane w ramach projektu Stąd do przyszłości. nr. POKL.09.01.
 Mołodiatycze, 22.06.2012 PUBLIKACJA PODSUMOWUJACA ZAJĘCIA DODATKOWE Z MATEMATYKI realizowane w ramach projektu Stąd do przyszłości nr. POKL.09.01.02-06-090/11 Opracował: Zygmunt Krawiec 1 W ramach projektu
Mołodiatycze, 22.06.2012 PUBLIKACJA PODSUMOWUJACA ZAJĘCIA DODATKOWE Z MATEMATYKI realizowane w ramach projektu Stąd do przyszłości nr. POKL.09.01.02-06-090/11 Opracował: Zygmunt Krawiec 1 W ramach projektu
Wewnątrzszkolne Doskonalenie Nauczycieli Nowatorskie metody nauczania
 Wewnątrzszkolne Doskonalenie Nauczycieli Nowatorskie metody nauczania Zapraszam na szkolenie on line prezentujące dwie nowoczesne metody pracy: coaching i mentoring. Idea i definicja coachingu Coaching,
Wewnątrzszkolne Doskonalenie Nauczycieli Nowatorskie metody nauczania Zapraszam na szkolenie on line prezentujące dwie nowoczesne metody pracy: coaching i mentoring. Idea i definicja coachingu Coaching,
Obliczanie procentu danej liczby i liczby na podstawie jej. procentu jako umiejętności kluczowe w pracy doradcy. inwestycyjnego.
 1 Obliczanie procentu danej liczby i liczby na podstawie jej procentu jako umiejętności kluczowe w pracy doradcy inwestycyjnego. Czas trwania zajęć: ok. 40 minut Kontekst w jakim wprowadzono doświadczenie:
1 Obliczanie procentu danej liczby i liczby na podstawie jej procentu jako umiejętności kluczowe w pracy doradcy inwestycyjnego. Czas trwania zajęć: ok. 40 minut Kontekst w jakim wprowadzono doświadczenie:
OGÓLNA CHARAKTERYSTYKA GRY PLANSZA
 OGÓLNA CHARAKTERYSTYKA GRY Na bezdrożach Afryki to gra planszowa przeznaczona dla 2 4 osób. W niniejszej książce zamieszczono 4 komplety gry, tak aby w rozgrywce mogło naraz uczestniczyć 16 uczniów (jeśli
OGÓLNA CHARAKTERYSTYKA GRY Na bezdrożach Afryki to gra planszowa przeznaczona dla 2 4 osób. W niniejszej książce zamieszczono 4 komplety gry, tak aby w rozgrywce mogło naraz uczestniczyć 16 uczniów (jeśli
JAK MOTYWOWAĆ DZIECKO DO NAUKI
 JAK MOTYWOWAĆ DZIECKO DO NAUKI Motywacja to: CO TO JEST MOTYWACJA? stan gotowości człowieka do podjęcia określonego działania, w tym przypadku chęć dziecka do uczenia się, dążenie do rozwoju, do zaspokajania
JAK MOTYWOWAĆ DZIECKO DO NAUKI Motywacja to: CO TO JEST MOTYWACJA? stan gotowości człowieka do podjęcia określonego działania, w tym przypadku chęć dziecka do uczenia się, dążenie do rozwoju, do zaspokajania
SPRAWOZDANIE Z ZAJĘĆ KOŁO MATEMATYCZNE DLA KLAS IV-VII
 Tytuł projektu: Lokata w dziecięce umysły Zadanie nr 3 : Koło matematyczne dla klas IV-VII Imię i nazwisko osoby prowadzącej zajęcia: Dorota Siejkowska SPRAWOZDANIE Z ZAJĘĆ KOŁO MATEMATYCZNE DLA KLAS IV-VII
Tytuł projektu: Lokata w dziecięce umysły Zadanie nr 3 : Koło matematyczne dla klas IV-VII Imię i nazwisko osoby prowadzącej zajęcia: Dorota Siejkowska SPRAWOZDANIE Z ZAJĘĆ KOŁO MATEMATYCZNE DLA KLAS IV-VII
Koło matematyczne 2abc
 Koło matematyczne 2abc Autor: W. Kamińska 17.09.2015. Zmieniony 08.12.2015. "TO CO MUSIAŁEŚ ODKRYĆ SAMODZIELNIE, ZOSTANIE W TWYM UMYŚLE ŚCIEŻKĄ, KTÓRĄ W RAZIE POTRZEBY MOŻESZ PÓJŚĆ RAZ JESZCZE" G. CH.
Koło matematyczne 2abc Autor: W. Kamińska 17.09.2015. Zmieniony 08.12.2015. "TO CO MUSIAŁEŚ ODKRYĆ SAMODZIELNIE, ZOSTANIE W TWYM UMYŚLE ŚCIEŻKĄ, KTÓRĄ W RAZIE POTRZEBY MOŻESZ PÓJŚĆ RAZ JESZCZE" G. CH.
PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa III szkoła podstawowa marzec 2015
 PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa III szkoła podstawowa marzec 205 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad.
PŁOCKA MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA MATEMATYKA klasa III szkoła podstawowa marzec 205 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad.
Temat lekcji: Dzielniki, wielokrotności, podzielność liczb naturalnych.
 Klasa: IV, V Przedmiot: matematyka Temat lekcji: Dzielniki, wielokrotności, podzielność liczb naturalnych. Cele: Podczas lekcji uczeń: określa dzielniki ćwiczy sprawność rachunkową dzielenia oblicza wielokrotności
Klasa: IV, V Przedmiot: matematyka Temat lekcji: Dzielniki, wielokrotności, podzielność liczb naturalnych. Cele: Podczas lekcji uczeń: określa dzielniki ćwiczy sprawność rachunkową dzielenia oblicza wielokrotności
SCENARIUSZ LEKCJI W KLASIE I GIMNAZJUM
 Opracowała Elżbieta Tomczak SCENARIUSZ LEKCJI W KLASIE I GIMNAZJUM Motto lekcji: To, co musiałeś odkryć samodzielnie, zostawia w twym umyśle ścieżkę, którą w razie potrzeby możesz pójść jeszcze raz. Georg
Opracowała Elżbieta Tomczak SCENARIUSZ LEKCJI W KLASIE I GIMNAZJUM Motto lekcji: To, co musiałeś odkryć samodzielnie, zostawia w twym umyśle ścieżkę, którą w razie potrzeby możesz pójść jeszcze raz. Georg
Odwrócona lekcja odwrócona klasa lub odwrócone nauczanie
 Odwrócona lekcja odwrócona klasa lub odwrócone nauczanie Odwrócona lekcja odwrócona klasa lub odwrócone nauczanie Odwrócona lekcja to propozycja na potwierdzone naukowo teorie dotyczące nauczania wyprzedzającego
Odwrócona lekcja odwrócona klasa lub odwrócone nauczanie Odwrócona lekcja odwrócona klasa lub odwrócone nauczanie Odwrócona lekcja to propozycja na potwierdzone naukowo teorie dotyczące nauczania wyprzedzającego
SPOSOBY NA DOBRY POCZĄTEK ROKU SZKOLNEGO
 SPOSOBY NA DOBRY POCZĄTEK ROKU SZKOLNEGO 1. Zadbanie, aby dziecko miało stałe miejsce do uczenia się, w którym znajdują się wszystkie potrzebne przedmioty. 2. Podczas odrabiania lekcji ważne jest stworzenie
SPOSOBY NA DOBRY POCZĄTEK ROKU SZKOLNEGO 1. Zadbanie, aby dziecko miało stałe miejsce do uczenia się, w którym znajdują się wszystkie potrzebne przedmioty. 2. Podczas odrabiania lekcji ważne jest stworzenie
Program zajęć wyrównawczych z matematyki dla grupy 6.1. zajęcia pozalekcyjne realizowane w ramach projektu
 Program zajęć wyrównawczych z matematyki dla grupy 6.1 zajęcia pozalekcyjne realizowane w ramach projektu " One Two Three - eksperymentujemy z matematyką i językiem angielskim - program rozwijania kompetencji
Program zajęć wyrównawczych z matematyki dla grupy 6.1 zajęcia pozalekcyjne realizowane w ramach projektu " One Two Three - eksperymentujemy z matematyką i językiem angielskim - program rozwijania kompetencji
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 2014
 MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
MIĘDZYSZKOLNA LIGA PRZEDMIOTOWA EDUKACJA MATEMATYCZNA klasa III PŁOCK 204 KARTA PUNKTACJI ZADAŃ (wypełnia komisja konkursowa): Numer zadania Zad. Zad. 2 Zad. 3 Zad. 4 Zad. 5 Zad. 6 Zad. 7 Zad. 8 SUMA PUNKTÓW
WYKORZYSTANIE KOMPUTERA NA LEKCJI MATEMATYKI W I KLASIE GIMNAZJUM.
 WYKORZYSTANIE KOMPUTERA NA LEKCJI MATEMATYKI W I KLASIE GIMNAZJUM. Rozwój techniki komputerowej oraz oprogramowania stwarza nowe możliwości dydaktyczne dla każdego przedmiotu nauczanego w szkole. Nowoczesne
WYKORZYSTANIE KOMPUTERA NA LEKCJI MATEMATYKI W I KLASIE GIMNAZJUM. Rozwój techniki komputerowej oraz oprogramowania stwarza nowe możliwości dydaktyczne dla każdego przedmiotu nauczanego w szkole. Nowoczesne
KONSPEKT MATEMATYKA. Temat lekcji: Rozwiązujemy zadania tekstowe wykorzystując dodawanie i odejmowanie ułamków dziesiętnych.
 KONSPEKT MATEMATYKA Przedmiot: matematyka Klasa: 5 Temat lekcji: Rozwiązujemy zadania tekstowe wykorzystując dodawanie i odejmowanie ułamków dziesiętnych. Cel lekcji wynikający z podstawy programowej:
KONSPEKT MATEMATYKA Przedmiot: matematyka Klasa: 5 Temat lekcji: Rozwiązujemy zadania tekstowe wykorzystując dodawanie i odejmowanie ułamków dziesiętnych. Cel lekcji wynikający z podstawy programowej:
Danuta Sterna: Strategie dobrego nauczania
 : Strategie dobrego nauczania Strategie dobrego nauczania Strategie oceniania kształtującego I. Określanie i wyjaśnianie uczniom celów uczenia się i kryteriów sukcesu. II. Organizowanie w klasie dyskusji,
: Strategie dobrego nauczania Strategie dobrego nauczania Strategie oceniania kształtującego I. Określanie i wyjaśnianie uczniom celów uczenia się i kryteriów sukcesu. II. Organizowanie w klasie dyskusji,
DOMINO MATEMATYCZNE PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe 1. DOMI dopełnianie do klocków, 56 zadań
 DOMINO MATEMATYCZNE PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe 1. DOMI dopełnianie do 30 28 klocków, 56 zadań Prosta, powszechnienie znana, a jednocześnie atrakcyjna forma
DOMINO MATEMATYCZNE PRZEZNACZENIE dla dzieci na zajęcia pozalekcyjne indywidualne i grupowe 1. DOMI dopełnianie do 30 28 klocków, 56 zadań Prosta, powszechnienie znana, a jednocześnie atrakcyjna forma
Temat: Moja miejscowość, mój dom. - scenariusz zajęć z elementami kodowania
 Temat: Moja miejscowość, mój dom - scenariusz zajęć z elementami kodowania Wiek: edukacja przedszkolna, edukacja wczesnoszkolna Autor: Anna Świć Czas trwania: 30-60 min (uzależniony od wieku, możliwości
Temat: Moja miejscowość, mój dom - scenariusz zajęć z elementami kodowania Wiek: edukacja przedszkolna, edukacja wczesnoszkolna Autor: Anna Świć Czas trwania: 30-60 min (uzależniony od wieku, możliwości
Renata Krzemińska. nauczyciel matematyki i informatyki
 Program zajęć wyrównawczych w Gimnazjum Matematyka J1 w ramach projektu pn. Czym skorupka za młodu nasiąknie - rozwój kompetencji kluczowych uczniów Zespołu Szkół w Nowej Wsi Lęborskiej Renata Krzemińska
Program zajęć wyrównawczych w Gimnazjum Matematyka J1 w ramach projektu pn. Czym skorupka za młodu nasiąknie - rozwój kompetencji kluczowych uczniów Zespołu Szkół w Nowej Wsi Lęborskiej Renata Krzemińska
Metody: pogadanka, pokaz, symulacja, ćwiczenie interaktywne, ćwiczenia praktyczne.
 Scenariusz zajęć nr 13 Temat: Jak mądrze robić zakupy? Cele operacyjne: Uczeń: rozróżnia będące w obiegu monety i banknot 10 zł, odczytuje wartość pieniędzy, wymienia banknoty na bilon, ustala listę zakupów,
Scenariusz zajęć nr 13 Temat: Jak mądrze robić zakupy? Cele operacyjne: Uczeń: rozróżnia będące w obiegu monety i banknot 10 zł, odczytuje wartość pieniędzy, wymienia banknoty na bilon, ustala listę zakupów,
Karta pracy do doświadczeń
 1 Karta pracy do doświadczeń UWAGA: Pola z poleceniami zapisanymi niebieską czcionką i ramkami z przerywaną linią wypełniają uczniowie uczestniczący w zajęciach. A. Temat w formie pytania badawczego lub
1 Karta pracy do doświadczeń UWAGA: Pola z poleceniami zapisanymi niebieską czcionką i ramkami z przerywaną linią wypełniają uczniowie uczestniczący w zajęciach. A. Temat w formie pytania badawczego lub
ARKUSZ OBSERWACYJNY LEKCJI. Uwagi nauczyciela hospitującego lekcję koleżeńską na temat zajęć:
 Temat zajęć: Proporcjonalność odwrotna. Lekcja dla uczniów klasy: II c Data zajęć: 17 marzec 2005r. 1. Przebieg lekcji. Nauczycielka zgodnie z przyjętymi celami wprowadziła pojęcie proporcjonalności odwrotnej,
Temat zajęć: Proporcjonalność odwrotna. Lekcja dla uczniów klasy: II c Data zajęć: 17 marzec 2005r. 1. Przebieg lekcji. Nauczycielka zgodnie z przyjętymi celami wprowadziła pojęcie proporcjonalności odwrotnej,
MATEMATYCZNY TURNIEJ KLAS Szkoła a Podstawowa nr 26 im.andrzeja Struga W Krakowie
 MATEMATYCZNY TURNIEJ KLAS Szkoła a Podstawowa nr 26 im.andrzeja Struga W Krakowie Jest to konkurs matematyczny, który w Naszej Szkole ma już dość długą tradycję. Pomysł powstał na spotkaniu zespołu nauczycieli
MATEMATYCZNY TURNIEJ KLAS Szkoła a Podstawowa nr 26 im.andrzeja Struga W Krakowie Jest to konkurs matematyczny, który w Naszej Szkole ma już dość długą tradycję. Pomysł powstał na spotkaniu zespołu nauczycieli
Gra- Oblicz i zaznacz właściwy wynik- puzzle. matematyczno - przyrodnicze
 TYTUŁ AUTOR EDUKACJA Gra- Oblicz i zaznacz właściwy wynik- puzzle Aneta Kryszczak Uczeń wykonuje dzielenie, doskonali umiejętność posługiwanie się pojęciami matematycznymi; I WSKAZÓWKI AUTO dzielenie Uczeń
TYTUŁ AUTOR EDUKACJA Gra- Oblicz i zaznacz właściwy wynik- puzzle Aneta Kryszczak Uczeń wykonuje dzielenie, doskonali umiejętność posługiwanie się pojęciami matematycznymi; I WSKAZÓWKI AUTO dzielenie Uczeń
