Ryszard Horodecki, członek korespondent PAN W LABIRYNCIE KWANTOWYCH KORELACJI
|
|
|
- Irena Mazurek
- 6 lat temu
- Przeglądów:
Transkrypt
1 Ryszard Horodecki, członek korespondent PAN W LABIRYNCIE KWANTOWYCH KORELACJI Fenomen kwantowych korelacji zogniskował wysiłek wielu ośrodków naukowych zarówno po stronie teorii, jak i eksperymentu. Historia jego sięga korzeniami odkrycia kwantowego obrazu Natury, które wstrząsnęło podstawami nauk przyrodniczych. Na początku ubiegłego wieku harmonia sfer deterministycznego opisu świata rozbiła się o zjawisko promieniowania ciała doskonale czarnego, z którym stykali się nasi przodkowie przy wypieku chleba, kiedy po kolorze ścianek pieca, bez termometru szacowali temperaturę. Aby być w zgodzie z eksperymentem, Max Planck (9) musiał założyć, że atomy mogą wysyłać i pochłaniać promieniowanie tylko w ściśle określonych porcjach energetycznych kwantach energii, które Albert Einstein potem utożsamił z fotonami kwantami światła. Dopiero pod koniec XX wieku dzięki niebywałemu rozwojowi kwantowych technologii udało się wytworzyć źródła pojedynczych fotonów, a także rejestrujące je detektory. Te osobliwe nośniki informacji nie tylko poruszają się z prędkością światła, ale także wykonują drgania w dowolnych kierunkach w płaszczyźnie prostopadłej do kierunku ruchu. Dzięki polaryzatorom możemy filtrować określony kierunek drgań. Gdy foton spolaryzowany w płaszczyźnie poziomej skierujemy na kryształ kalcytu, to z pewnością (prawdopodobieństwem ) trafi on do górnego detektora (rys.. Podobnie foton pionowy zawsze trafi do dolnego (rys.. Co się jednak stanie gdy na kryształ skierujemy foton spolaryzowany ukośnie (rys.c)? Otóż wtedy nie można przewidzieć, którą z dróg wybierze. Ta wewnętrzna probabilistyczna natura fotonu, jak wiele innych zjawisk kwantowych, wyłamuje się z deterministycznej harmonii sfer. Szukając języka dla kwantowej fenomenologii Heisenberg (95) i Schrödinger (96) odkryli dwie twarze mikroświata, jako alternatywne reprezentacje tej samej matematycznej struktury, nazwane mechaniką kwantową. Nowy język wzbogacony i sformalizowany jawił się jak inskrypcja na kamieniu z Rossetty. Miejsce klasycznej czasoprzestrzeni jako areny fizycznych zdarzeń zajęła abstrakcyjna przestrzeń Hilberta. W tej przestrzeni z każdym układem fizycznym jest stowarzyszona funkcja falowa (stan czysty układu), maksymalna probabilistyczna informacja o układzie. Inskrypcja stanowi instrukcję zbiór przepisów określających sposób probabilistycznego przewidywania wyników przyszłych pomiarów w laboratoriach. To kolosalne odkrycie drastycznie zmieniło nasze wyobrażenia o naturze mikroobiektów. c) wiat Nauki, Grudzie 99 Rys. Foton spolaryzowany skierowany na kryszta kalcytu: polaryzacja pozioma polaryzacja pionowa c) polaryzacja uko na foton w stanie superpozycji pod wp ywem pomiaru decyduje si z prawdopodobie stwem prawd ( ) = prawd ( ) = / na przej cie do stanu lub. 5
2 W powyższym przykładzie inskrypcja żąda, aby foton spolaryzowany ukośnie padający na kryształ kalcytu zachowywał się tak, jakby był w stanie będącym superpozycją stanów polaryzacji poziomej i pionowej. Dopiero pod wpływem pomiaru, foton decyduje się z prawdopodobieństwem równym kwadratowi czynnika liczbowego występującego w superpozycji p= ( = na przejście do stanu lub odpowiadających polaryzacji poziomej (górny detektor) i pionowej (dolny detektor) (rys. c). Bardzo trudno było wyabstrahować zdawałoby się oczywisty fakt, że foton niesie jednostkę kwantowej informacji kwantowy bit (kubit). Pojęcie to ( zrewolucjonizowało nasze myślenie o naturze informacji. Można się tylko dziwić, że kwantowa inskrypcja przez pół wieku kryła banalną tajemnicę kubitu nie można wiernie skopiować. Ta właśnie cecha odróżnia kwantową informację od klasycznej i legła u podstaw kwantowej kryptografii. Zdumiewającą przepowiednią kwantowej inskrypcji jest istnienie w Naturze osobliwych korelacji między własnościami odległych cząstek nazwanych splątaniem. Szczęśliwie, fizycy znaleźli wiele metod wytwarzania w laboratorium splątanej pary fotonów. Na przykład, skierowując wiązkę lasera na kryształ beta boranu baru można wytworzyć pary fotonów o skorelowanych polaryzacjach. wi zka laserowa polaryzacja pozioma A kryszta BBO polaryzacja pionowa B Lab. Alicji Lab. Bogdana prawd.½ pomiar prawd.½ Rys. Generacja par fotonów skorelowanych w polaryzacjach; fotony spl tane w polaryzacji pod wp ywem pomiaru decyduj si z prawdopodobie stwem p=/ na przej cie do stanu A B lub A B 53
3 Na rys. a są to fotony wylatujące wzdłuż linii przecięcia się stożków górnego z polaryzacją poziomą i dolnego z pionową. Ponieważ nie potrafimy odróżnić, z którego stożka pochodzi foton, kwantowa inskrypcja zmusza nas do zapisu tej sytuacji jako superpozycji maksymalnie splątanych fotonów, tj. = ( + ). Jeśli teraz bliźniacze A B A B fotony poślemy do odległych laboratoriów Alicji (A) i Bogdana (B), którzy mierzą polaryzacje używając identycznie ustawionych polaryzatorów, to pod wpływem pomiaru fotony decydują się z prawdopodobieństwem p = ( = na przejście do stanu A B lub A B (rys.. Fizycznie oznacza to, że gdy Alicja na swoim fotonie zaobserwuje polaryzację poziomą, ma pewność, że foton Bogdana był spolaryzowany pionowo i vice versa. Rezultaty ich własnych pomiarów pojawiają się z prawdopodobieństwem p =, czyli są zupełnie przypadkowe. Kiedy jednak porównają swoje wyniki (np. przez telefon), to odkryją, że mają idealnie skorelowane losowe ciągi bitów (rys.. Korelacje te są niezwykłe. Jak pokazał Bell, są one silniejsze niż wynikałoby to z naturalnych założeń, że fotony mają określone wartości polaryzacji przed pomiarem i nie ma oddziaływań szybszych od światła między laboratoriami. Są z natury monogamiczne, tzn. para maksymalnie splątanych fotonów jest kompletnie odkorelowana od reszty świata, co oznacza, że wyników tych nikt wcześniej nie mógł znać. Artur Ekert jako pierwszy spostrzegł, że własność monogamii splątania pozwala generować bezpieczny klucz kryptograficzny. Rzeczywiście, jakakolwiek próba doplątania się do maksymalnie skorelowanej pary degraduje jej korelacje, co zostanie wykryte przez Alicję i Bogdana. Wkrótce splątanie stało się zasobem nie tylko dla kwantowej kryptografii, ale także dla kwantowej teleportacji i gęstego kodowania. Pamiętam, jak silne wrażenie zrobił na mnie fakt, że te kanoniczne efekty były zakodowane w kwantowej inskrypcji. Moja pasja udzieliła się wtedy synom, którzy otrzymali wykształcenie na rodzimym Uniwersytecie Gdańskim. Już jako studenci włączyli się w pracę badawczą. W naturalny sposób powstał więc zespół, który miał potem wejść do współpracy ze ( światowymi liderami z kwantowej informatyki. Na początku lat dziewięćdziesiątych tylko kilka zespołów na świecie zajmowało się rozszyfrowywaniem niezwykle złożonej struktury kwantowego splątania. Pisząc w 993 roku swoją pracę Układy informacyjnie spójne miałem odczucie, że szczelina między kwantowym splątaniem a klasycznymi korelacjami jest wejściem do labiryntu pełnego niespodzianek. Moja przygoda z nim zaczęła się od paradoksu Schrödingera, który najlepiej widać na rys. b. Polaryzacje fotonów zmierzone niezależnie przez każdego z partnerów są kompletnie chaotyczne, podczas gdy na odległość są idealnie skorelowane. W następnym roku, wraz z synem Pawłem dowiedliśmy, że to właśnie splątanie jest odpowiedzialne za kwantowy porządek niewystępujący w świecie klasycznym. Nie byłem wtedy świadom, że dotknęliśmy rdzenia informacji kwantowej i że nasz rezultat odegra rolę w odkryciu ujemnej kwantowej informacji przez Michała Horodeckiego, Jonathana Oppenheima i Andreasa Wintera, którzy przebywali wówczas w Instytucie Newtona w Cambridge. Praktyczna detekcja kwantowego splątania. Doświadczalnicy najlepiej wiedzą, jak delikatnym zasobem jest splątanie. Niezwykle czułe na zaburzenia środowiska, podlega szybko degradacji.w naszym przykładzie oznacza to, że ciągi losowe Alicji i Bogdana nie są stuprocentowo skorelowane, pojawiają się błędy. Mówimy wtedy, że splątane fotony przechodzą ze stanu czystego do stanu mieszanego z zaszumionym splątaniem (rys.3. Niestabilność splątania zmobilizowała fizyków do pracy nad fundamentalnym zagadnieniem: jak weryfikować, destylować i opisywać ilościowo splątanie wytworzone w laboratorium? W 996 roku, pracując nad pierwszym problemem dowiedliśmy, że stan przygotowany w laboratorium jest splątany wtedy i tylko wtedy, gdy istnieje taka wielkość obserwowalna (tzw. świadek splątani, której wartość średnia w tym stanie jest ujemna, podczas gdy jest ona zawsze nieujemna dla wszystkich niesplątanych stanów zwanych separowalnymi. Był to kamień węgielny detekcji splątania w laboratorium. Popularność detekcji splątania metodą świadków wynika z jej prostoty i ekonomii. 54
4 Rys. 3 Dzia anie szumu; destylacja spl tania. Często wystarczy pomierzyć tylko jedną lub dwie obserwable (np. wartości spinu lub polaryzacji), aby stwierdzić obecność splątania. Metoda świadków jest szeroko stosowana m.in. w kwantowej kryptografii, kwantowej optyce, nanofizyce, spinowych układach, wielokrotnych kwantowych eksperymentach NMR, detekcji wieloukładowego splątania oraz ilościowaniu splątania. Związane splątanie tajemnicza inwencja Natury. Równolegle z nami pracował zespół C. H. Bennetta nad problemem, jak odwrócić degradację czystego splątania. Owocem ich pracy był protokół destylacji zaszumionego splątania. Czyżby autorzy odkryli uniwersalną, maszynę do destylacji splątania? Natychmiast postanowiliśmy wypróbować protokół. Sprawdził się on dla wszystkich zaszumionych stanów splątanych układów złożonych z dwóch kubitów. Gdy jednak przeszliśmy do bardziej skomplikowanych układów, okazało się, że nie tylko ten protokół nie zadziała, ale żaden inny nie wydestyluje z nich splątania. Mglisty busz kwantowego formalizmu maskował fundamentalne ograniczenie: środowisko może w sposób nieodwracalny uwięzić splątanie w szumie! Było to dla nas fascynujące. Oznaczało, że istnieje osobliwy rodzaj związanego splątania, które nie daje się wydestylować do czystej postaci. Zatem w przyrodzie występują przynajmniej dwa rodzaje zaszumionego splątania: swobodne (destylowalne) i związane (niedestylowalne) (rys. 3. Odkrycie związanego splątania (998) poruszyło fizyków (Bound entanglement tells us that life is not so simple ) i wywołało szereg fundamentalnych pytań dotyczących jego natury. Z początku wydawało się, że jest ono pasywne, gdyż jest niezdatne do wykonania nieklasycznych zadań, takich, jak teleportacja kubitu. Jednak w następnym roku, bazując na termodynamicznych analogiach, udało nam się znaleźć protokół, który pozwala aktywować związane splątanie. Otworzyło to nowe kierunki badań. W szczególności P. Shor i inni odkryli silniejszy efekt tzw. superaktywację splątania, który gra ważną rolę w kwantowej komunikacji, a którego G. Smith i J. Yard podali ostatnio komunikacyjny wariant legitymujący się dziwną algebrą: dwa kanały kwantowe o zerowej pojemności połączone mają pojemność niezerową. Pod koniec ubiegłego wieku nie było żadnych podstaw, aby podejrzewać, że związane splątanie może być przydatne do kwantowej kryptografii. Dlatego fizycy byli zaskoczeni, kiedy mój zespół udowodnił, że choć związane splątanie jest niedestylowalne, można z niego otrzymać klucz kryptograficzny. Prowadziło to do nowego typu protokołu kryptograficznego w reżimie szumu, dla którego ani słynny protokół C. B. Bennetta i G. Brassarda, ani jego destylacyjne wersje nie są w stanie pracować. Zespół koordynowany przez K. Banaszka i P. Horodeckiego współpracujący w ramach Narodowego Laboratorium Technologii Kwantowych pokazał po raz pierwszy doświadczalnie, że mimo trudności z destylacją splątania można wydajnie przesyłać klucz kryptograficzny. Splątanie związane w laboratorium. Eksperymentalna realizacja stanów ze związanym splątaniem okazała się niemałym wyzwaniem. Dopiero w 9 roku zespół M. Bourennane ze Sztokholmu wytworzył je na świetle, lecz eksperyment nie był w pełni przekonywujący. Wkrótce zespół Rainera Kaltenbaeka z Waterloo, w którego skład wchodził Marco 55
5 Piani, wytworzył prawdziwe (stabilne) związane splątanie na świetle. W tym samym roku niezależnie związane splątanie zostało zrealizowane w Dortmundzie na NMR, w Innsbrucku na jonach i w Hanowerze na świetle w ciągłym reżimie. W roku zespół F. Kanedyz Japonii wykonał po raz pierwszy w laboratorium przewidzianą przez nas w 999 roku aktywację związanego splątania. Kwantowe korelacje bez splątania. Nie jest tu miejsce na pełną prezentację rezultatów zespołu, trudno jednak pominąć odkrycie innego rodzaju kwantowych korelacji, które mogą istnieć nawet bez kwantowego splątania. Mój zespół był jednym z pierwszych, który badał naturę tych korelacji. W roku wraz z Jonathanem Oppenheimem, który przygodę z kwantową informacją rozpoczął w moim zespole, odkryliśmy związek między korelacjami kwantowymi a termodynamiką. W szczególności pokazaliśmy, że korelacje te stanowią cenny zasób dla mikrosilników. Kilka lat później w pracy z Marco Pianim, przebywającym wówczas na stażu podoktorskim w Gdańsku, dowiedliśmy fundamentalnego twierdzenia: kwantowych korelacji bez splątania nie można rozgłaszać lokalnie. Była to pierwsza operacyjna charakteryzacja tych korelacji. Obecnie wielkim wyzwaniem jest opis ilościowy wielocząstkowych kwantowych korelacji. Pierwszy krok w kierunku zbudowania jednolitych podstaw takiego opisu polegał na wprowadzeniu postulatów (z C. H. Bennettem i A. Grudką), które musi spełniać każda dobra miara takich korelacji. Ponadto uzyskaliśmy wiele innych wyników dotyczących np. nierówności Bella, aksjomatyzacji miar splątania, kwantowej teleportacji oraz kanałów kwantowych. Wyniki te są obecnie szeroko cytowane. Moi uczniowie, a także ich uczniowie rozwijają zastosowania kwantowego splątania w kryptografii, komunikacji kwantowej, kwantowym obliczaniu ze szczególnym uwzględnieniem teorii korekcji błędu oraz związki kwantowego splątania z termodynamiką. Obecnie w zespole prowadzone są m.in. badania z zakresu teorii korelacji kwantowych, zasad nieoznaczoności, ogólnej charakteryzacji zasobów kwantowych, włączając tzw. kwantową kontekstualność. O żywotności kwantowej informatyki świadczy przyznanie w roku grantu Europejskiej Komisji ds. Badań Naukowych w konkursie Ideas Advanced Grant, a także fakt, że nasza publikacja w Reviews of Modern Physics znalazła się na trzeciej pozycji na liście najczęściej cytowanych prac (tzw. hot papers) z fizyki opublikowanych w ostatnich dwóch latach. Piśmiennictwo. R. Horodecki, P. Horodecki, M. Horodecki, K. Horodecki (9). Quantum entanglement, Rev. Mod. Phys. 8,865.. B. Terhal, M. Wolf, A. Doherty (3). Quantum Entanglement: A Modern Perspective. Physics Today 56, R. Horodecki (). Bound entanglement mysterious invention of Nature, Europhysics News 4, G. Alber, T. Beth, M.Horodecki, P. Horodecki, R. Horodecki, M. Rottler, H. Weinfurter, R. F. Werner, A. Zeilinger, Quantum information: an introduction to basic theoretical concept and experiments, (). Quantum Information Book Series: Springer Tract in Modern, 73,5. 5. M. Horodecki, J. Oppenheim, A. Winter (5). Partial quantum information, Nature 436, K. Modi, A. Brodutch, H. Cable, T. Paterek, V. Vedral (). Quantum discord and other measures of quantum correlations, przesłane do Rev. Mod. Phys. (arxiv:.638). 56
Kryptografia kwantowa. Marta Michalska
 Kryptografia kwantowa Marta Michalska Główne postacie Ewa podsłuchiwacz Alicja nadawca informacji Bob odbiorca informacji Alicja przesyła do Boba informacje kanałem, który jest narażony na podsłuch. Ewa
Kryptografia kwantowa Marta Michalska Główne postacie Ewa podsłuchiwacz Alicja nadawca informacji Bob odbiorca informacji Alicja przesyła do Boba informacje kanałem, który jest narażony na podsłuch. Ewa
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman ( ) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd.
 Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski
 VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
VIII. TELEPORTACJA KWANTOWA Janusz Adamowski 1 1 Wprowadzenie Teleportacja kwantowa polega na przesyłaniu stanów cząstek kwantowych na odległość od nadawcy do odbiorcy. Przesyłane stany nie są znane nadawcy
Splątanie a przesyłanie informacji
 Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
Splątanie a przesyłanie informacji Jarosław A. Miszczak 21 marca 2003 roku Plan referatu Stany splątane Co to jest splątanie? Gęste kodowanie Teleportacja Przeprowadzone eksperymenty Możliwości wykorzystania
Wielcy rewolucjoniści nauki
 Isaak Newton Wilhelm Roentgen Albert Einstein Max Planck Wielcy rewolucjoniści nauki Erwin Schrödinger Werner Heisenberg Niels Bohr dr inż. Romuald Kędzierski W swoim słynnym dziele Matematyczne podstawy
Isaak Newton Wilhelm Roentgen Albert Einstein Max Planck Wielcy rewolucjoniści nauki Erwin Schrödinger Werner Heisenberg Niels Bohr dr inż. Romuald Kędzierski W swoim słynnym dziele Matematyczne podstawy
Kwantowe stany splątane. Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017
 B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
Miary splątania kwantowego
 kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
kwantowego Michał Kotowski michal.kotowski1@gmail.com K MISMaP, Uniwersystet Warszawski Studenckie Koło Fizyki UW (SKFiz UW) 24 kwietnia 2010 kwantowego Spis treści 1 2 Stany czyste i mieszane Matematyczny
Różne oblicza splątania kwantowego
 Różne oblicza splątania kwantowego Ryszard Horodecki Krajowe Centrum Informatyki Kwantowej, Zakład Optyki i Informacji Kwantowej Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański Various
Różne oblicza splątania kwantowego Ryszard Horodecki Krajowe Centrum Informatyki Kwantowej, Zakład Optyki i Informacji Kwantowej Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański Various
W5. Komputer kwantowy
 W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
Kwantowe stany splątane w układach wielocząstkowych. Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017
 Kwantowe stany splątane w układach wielocząstkowych Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017 Otton Nikodym oraz Stefan Banach rozmawiają na ławce na krakowskich plantach
Kwantowe stany splątane w układach wielocząstkowych Karol Życzkowski (UJ / CFT PAN) 44 Zjazd PTF Wrocław, 12 września 2017 Otton Nikodym oraz Stefan Banach rozmawiają na ławce na krakowskich plantach
VIII Festiwal Nauki i Sztuki. Wydziale Fizyki UAM
 VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Kryptografia kwantowa raz jeszcze Ryszard Tanaś http://zon8physdamuedupl/~tanas 13 października 2005
VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM VIII Festiwal Nauki i Sztuki na Wydziale Fizyki UAM Kryptografia kwantowa raz jeszcze Ryszard Tanaś http://zon8physdamuedupl/~tanas 13 października 2005
interpretacje mechaniki kwantowej fotony i splątanie
 mechaniki kwantowej fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Twierdzenie o nieklonowaniu Jak sklonować stan kwantowy? klonowanie
mechaniki kwantowej fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Twierdzenie o nieklonowaniu Jak sklonować stan kwantowy? klonowanie
Wprowadzenie do optycznej kryptografii kwantowej
 Wprowadzenie do optycznej kryptografii kwantowej o tym jak kryptografia kwantowa jest być może najważniejszym zastosowaniem współczesnej optyki kwantowej prehistoria kryptografii kwantowej 983 (97!) Stephen
Wprowadzenie do optycznej kryptografii kwantowej o tym jak kryptografia kwantowa jest być może najważniejszym zastosowaniem współczesnej optyki kwantowej prehistoria kryptografii kwantowej 983 (97!) Stephen
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit jest jednostką informacji tzn. jest "najmniejszą możliwą
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW
 fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, Sprawozdanie z pracy naukowej w roku 2005
 Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2006-01-10 Sprawozdanie z pracy naukowej w roku 2005 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2006-01-10 Sprawozdanie z pracy naukowej w roku 2005 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
bity kwantowe zastosowania stanów splątanych
 bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
bity kwantowe zastosowania stanów splątanych Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Bit kwantowy zawiera więcej informacji niż bit klasyczny
WYKŁAD 15. Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego
 WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
WYKŁAD 15 Gęstość stanów Zastosowanie: oscylatory kwantowe (ª bosony bezmasowe) Formalizm dla nieoddziaływujących cząstek Bosego lub Fermiego 1 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bosony
Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury.
 1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
1 Ciało doskonale czarne absorbuje całkowicie padające promieniowanie. Parametry promieniowania ciała doskonale czarnego zależą tylko jego temperatury. natężenie natężenie teoria klasyczna wynik eksperymentu
O symetrycznej rozszerzalności stanów kwantowych i jej zastosowaniach
 Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Katedra Fizyki Teoretycznej i Informatyki Kwantowej Streszczenie rozprawy doktorskiej O symetrycznej rozszerzalności stanów kwantowych
Politechnika Gdańska Wydział Fizyki Technicznej i Matematyki Stosowanej Katedra Fizyki Teoretycznej i Informatyki Kwantowej Streszczenie rozprawy doktorskiej O symetrycznej rozszerzalności stanów kwantowych
Kwantowe przelewy bankowe foton na usługach biznesu
 Kwantowe przelewy bankowe foton na usługach biznesu Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Zakupy w Internecie Secure Socket Layer Bazuje na w wymianie klucza metodą RSA Jak mogę przesłać
Kwantowe przelewy bankowe foton na usługach biznesu Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Zakupy w Internecie Secure Socket Layer Bazuje na w wymianie klucza metodą RSA Jak mogę przesłać
Historia. Zasada Działania
 Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Protokół teleportacji kwantowej
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 9 stycznia 008 Teleportacja kwantowa 1993 Propozycja teoretyczna protokołu teleportacji
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 24, Radosław Chrapkiewicz, Filip Ozimek
 odstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 4, 5.05.0 wykład: pokazy: ćwiczenia: Michał Karpiński Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 3 - przypomnienie argumenty
odstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 4, 5.05.0 wykład: pokazy: ćwiczenia: Michał Karpiński Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Wykład 3 - przypomnienie argumenty
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
Kryptografia kwantowa
 Kryptografia kwantowa Wykład popularno-naukowy dla młodzieży szkół średnich Ryszard Tanaś http://zon8physdamuedupl/~tanas 20 marca 2002 Enigma niemiecka maszyna szyfrująca Marian Rejewski Jerzy Różycki
Kryptografia kwantowa Wykład popularno-naukowy dla młodzieży szkół średnich Ryszard Tanaś http://zon8physdamuedupl/~tanas 20 marca 2002 Enigma niemiecka maszyna szyfrująca Marian Rejewski Jerzy Różycki
Informatyka kwantowa. Karol Bartkiewicz
 Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
Informatyka kwantowa Karol Bartkiewicz Informacja = Wielkość fizyczna Jednostka informacji: Zasada Landauera: I A =log 2 k B T ln 2 1 P A R. Landauer, Fundamental Physical Limitations of the Computational
Wysokowydajne falowodowe źródło skorelowanych par fotonów
 Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
Obliczenia inspirowane Naturą Wykład 12 - Algorytmy i protokoły kwantowe Jarosław Miszczak IITiS PAN Gliwice 19/05/2016 1 / 39 1 Motywacja rozwoju informatyki kwantowej. 2 Stany kwantowe. 3 Notacja Diraca.
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne.
 Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
Kwantowe własności promieniowania, ciało doskonale czarne, zjawisko fotoelektryczne zewnętrzne. DUALIZM ŚWIATŁA fala interferencja, dyfrakcja, polaryzacja,... kwant, foton promieniowanie ciała doskonale
Internet kwantowy. (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak. Instytut Informatyki Teoretycznej i Stosowanej PAN
 Internet kwantowy (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN 16. stycznia 2012 Plan wystąpienia 1 Skąd się biorą stany kwantowe? Jak
Internet kwantowy (z krótkim wstępem do informatyki kwantowej) Jarosław Miszczak Instytut Informatyki Teoretycznej i Stosowanej PAN 16. stycznia 2012 Plan wystąpienia 1 Skąd się biorą stany kwantowe? Jak
Kryptografia kwantowa
 Kryptografia kwantowa Krzysztof Maćkowiak DGA SECURE 2006 Plan referatu Wprowadzenie, podstawowe pojęcia Algorytm Grovera Algorytm Shora Algorytm Bennetta-Brassarda Algorytm Bennetta Praktyczne zastosowanie
Kryptografia kwantowa Krzysztof Maćkowiak DGA SECURE 2006 Plan referatu Wprowadzenie, podstawowe pojęcia Algorytm Grovera Algorytm Shora Algorytm Bennetta-Brassarda Algorytm Bennetta Praktyczne zastosowanie
Fizyka klasyczna. - Mechanika klasyczna prawa Newtona - Elektrodynamika prawa Maxwella - Fizyka statystyczna -Hydrtodynamika -Astronomia
 Fizyka klasyczna - Mechanika klasyczna prawa Newtona - Elektrodynamika prawa Maxwella - Fizyka statystyczna -Hydrtodynamika -Astronomia Zaczniemy historię od optyki W połowie XiX wieku Maxwell wprowadził
Fizyka klasyczna - Mechanika klasyczna prawa Newtona - Elektrodynamika prawa Maxwella - Fizyka statystyczna -Hydrtodynamika -Astronomia Zaczniemy historię od optyki W połowie XiX wieku Maxwell wprowadził
Fizyka dla wszystkich
 Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
Fizyka dla wszystkich Wykład popularny dla młodzieży szkół średnich Splątane kubity czyli rzecz o informatyce kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas 21 kwietnia 2004 Spis treści 1
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A / B 2 1 hν exp( ) 1 kt (24)
 n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
n n 1 2 = exp( ε ε ) 1 / kt = exp( hν / kt) (23) 2 to wzór (22) przejdzie w następującą równość: ρ (ν) = B B A 1 2 / B hν exp( ) 1 kt (24) Powyższe równanie określające gęstość widmową energii promieniowania
Kwantowa kooperacja. Robert Nowotniak. Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka
 Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Wydział Fizyki Technicznej, Informatyki i Matematyki Stosowanej Politechnika Łódzka Sekcja Informatyki Kwantowej, 17 maja 2007 Materiały źródłowe Prezentacja oparta jest na publikacjach: Johann Summhammer,
Niezwykłe cechy informacji kwantowej
 Niezwykłe cechy informacji kwantowej Michał Horodecki Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański 1. Wstęp Koncepcja informacji kwantowej zrodziła się na pograniczu dwóch dziedzin:
Niezwykłe cechy informacji kwantowej Michał Horodecki Instytut Fizyki Teoretycznej i Astrofizyki, Uniwersytet Gdański 1. Wstęp Koncepcja informacji kwantowej zrodziła się na pograniczu dwóch dziedzin:
O spl ataniu kwantowym s lów kilka
 O spl ataniu kwantowym s lów kilka Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski http://www.physik.uni-augsburg.de/theo3/kbyczuk/index.html 30 styczeń 2006 Rozważania Einsteina,
O spl ataniu kwantowym s lów kilka Krzysztof Byczuk Instytut Fizyki Teoretycznej, Uniwersytet Warszawski http://www.physik.uni-augsburg.de/theo3/kbyczuk/index.html 30 styczeń 2006 Rozważania Einsteina,
XIII Poznański Festiwal Nauki i Sztuki. Wydziale Fizyki UAM
 XIII Poznański Festiwal Nauki i Sztuki na Wydziale Fizyki UAM XIII Poznański Festival Nauki i Sztuki na Wydziale Fizyki UAM Od informatyki klasycznej do kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas
XIII Poznański Festiwal Nauki i Sztuki na Wydziale Fizyki UAM XIII Poznański Festival Nauki i Sztuki na Wydziale Fizyki UAM Od informatyki klasycznej do kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas
Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe
 Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Informatyka kwantowa. Zaproszenie do fizyki. Zakład Optyki Nieliniowej. wykład z cyklu. Ryszard Tanaś. mailto:tanas@kielich.amu.edu.
 Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
Zakład Optyki Nieliniowej http://zon8.physd.amu.edu.pl 1/35 Informatyka kwantowa wykład z cyklu Zaproszenie do fizyki Ryszard Tanaś Umultowska 85, 61-614 Poznań mailto:tanas@kielich.amu.edu.pl Spis treści
Podstawy informatyki kwantowej
 Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład FIZYKA II. 11. Optyka kwantowa. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Wykład FIZYKA II 11. Optyka kwantowa Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ FIZYKA KLASYCZNA A FIZYKA WSPÓŁCZESNA Fizyka klasyczna
Jak wygrywać w brydża znając mechanikę kwantową?
 Jak wygrywać w brydża znając mechanikę kwantową? Tomasz Kisielewski 15 grudnia 2014 Podstawowe zasady brydża Brydż jest grą karcianą dla czterech osób grających w drużynach po dwie osoby. Gra składa się
Jak wygrywać w brydża znając mechanikę kwantową? Tomasz Kisielewski 15 grudnia 2014 Podstawowe zasady brydża Brydż jest grą karcianą dla czterech osób grających w drużynach po dwie osoby. Gra składa się
IX. KRYPTOGRAFIA KWANTOWA Janusz Adamowski
 IX. KRYPTOGRAFIA KWANTOWA Janusz Adamowski 1 1 Wstęp Wykład ten stanowi wprowadzenie do kryptografii kwantowej. Kryptografia kwantowa jest bardzo obszerną i szybko rozwijającą się dziedziną obliczeń kwantowych,
IX. KRYPTOGRAFIA KWANTOWA Janusz Adamowski 1 1 Wstęp Wykład ten stanowi wprowadzenie do kryptografii kwantowej. Kryptografia kwantowa jest bardzo obszerną i szybko rozwijającą się dziedziną obliczeń kwantowych,
o pomiarze i o dekoherencji
 o pomiarze i o dekoherencji Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW pomiar dekoherencja pomiar kolaps nieoznaczoność paradoksy dekoherencja Przykładowy
o pomiarze i o dekoherencji Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW pomiar dekoherencja pomiar kolaps nieoznaczoność paradoksy dekoherencja Przykładowy
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach
 Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Efekt Comptona. Efektem Comptona nazywamy zmianę długości fali elektromagnetycznej w wyniku rozpraszania jej na swobodnych elektronach Efekt Comptona. p f Θ foton elektron p f p e 0 p e Zderzenia fotonów
Paradoksy mechaniki kwantowej
 Wykład XX Paradoksy mechaniki kwantowej Chociaż przewidywania mechaniki kwantowej są w doskonałej zgodności z eksperymentem, interpretacyjna strona teorii budzi poważne spory. Przebieg zjawisk w świecie
Wykład XX Paradoksy mechaniki kwantowej Chociaż przewidywania mechaniki kwantowej są w doskonałej zgodności z eksperymentem, interpretacyjna strona teorii budzi poważne spory. Przebieg zjawisk w świecie
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, Sprawozdanie z pracy naukowej w roku 2004
 Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2005-01-10 Sprawozdanie z pracy naukowej w roku 2004 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2005-01-10 Sprawozdanie z pracy naukowej w roku 2004 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Wykład 13 Mechanika Kwantowa
 Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
Wykład 13 Mechanika Kwantowa Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 25 maja 2016 Maciej J. Mrowiński (IF PW) Wykład 13 25 maja 2016 1 / 21 Wprowadzenie Sprawy organizacyjne
kondensat Bosego-Einsteina
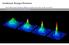 kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
kondensat Bosego-Einsteina Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW Podziękowania dla Dr. M. Zawady (Krajowe Laboratorium Fizyki Atomowej, Molekularnej
Optyka kwantowa wprowadzenie. Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej
 Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
Optyka kwantowa wprowadzenie Początki modelu fotonowego Detekcja pojedynczych fotonów Podstawowe zagadnienia optyki kwantowej Krótka (pre-)historia fotonu (1900-1923) Własności światła i jego oddziaływania
Zwiększanie losowości
 Zwiększanie losowości Maciej Stankiewicz Wydział Matematyki, Fizyki i Informatyki UG Krajowe Centrum Informatyki Kwantowej XIII Matematyczne Warsztaty KaeNeMów Hel, 20-22 maja 2016 Maciej Stankiewicz Zwiększanie
Zwiększanie losowości Maciej Stankiewicz Wydział Matematyki, Fizyki i Informatyki UG Krajowe Centrum Informatyki Kwantowej XIII Matematyczne Warsztaty KaeNeMów Hel, 20-22 maja 2016 Maciej Stankiewicz Zwiększanie
Wykład Ćwiczenia Laboratorium Projekt Seminarium 30 30
 Zał. nr do ZW 33/01 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim Podstawy fizyki kwantowej Nazwa w języku angielskim Fundamental of Quantum Physics Kierunek studiów (jeśli
Zał. nr do ZW 33/01 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI KARTA PRZEDMIOTU Nazwa w języku polskim Podstawy fizyki kwantowej Nazwa w języku angielskim Fundamental of Quantum Physics Kierunek studiów (jeśli
Kryptografia. z elementami kryptografii kwantowej. Ryszard Tanaś Wykład 13
 Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 13 Spis treści 19 Algorytmy kwantowe 3 19.1 Bit kwantowy kubit (qubit)........... 3 19. Twierdzenie
Kryptografia z elementami kryptografii kwantowej Ryszard Tanaś http://zon8.physd.amu.edu.pl/~tanas Wykład 13 Spis treści 19 Algorytmy kwantowe 3 19.1 Bit kwantowy kubit (qubit)........... 3 19. Twierdzenie
Plan Zajęć. Ćwiczenia rachunkowe
 Plan Zajęć 1. Termodynamika, 2. Grawitacja, Kolokwium I 3. Elektrostatyka + prąd 4. Pole Elektro-Magnetyczne Kolokwium II 5. Zjawiska falowe 6. Fizyka Jądrowa + niepewność pomiaru Kolokwium III Egzamin
Plan Zajęć 1. Termodynamika, 2. Grawitacja, Kolokwium I 3. Elektrostatyka + prąd 4. Pole Elektro-Magnetyczne Kolokwium II 5. Zjawiska falowe 6. Fizyka Jądrowa + niepewność pomiaru Kolokwium III Egzamin
OPTYKA. Leszek Błaszkieiwcz
 OPTYKA Leszek Błaszkieiwcz Ojcem optyki jest Witelon (1230-1314) Zjawisko odbicia fal promień odbity normalna promień padający Leszek Błaszkieiwcz Rys. Zjawisko załamania fal normalna promień padający
OPTYKA Leszek Błaszkieiwcz Ojcem optyki jest Witelon (1230-1314) Zjawisko odbicia fal promień odbity normalna promień padający Leszek Błaszkieiwcz Rys. Zjawisko załamania fal normalna promień padający
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, Sprawozdanie z pracy naukowej w roku 2006
 Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2007-01-18 Sprawozdanie z pracy naukowej w roku 2006 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2007-01-18 Sprawozdanie z pracy naukowej w roku 2006 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
LABORATORIUM Z FIZYKI
 LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
LABORATORIUM Z FIZYKI LABORATORIUM Z FIZYKI I PRACOWNIA FIZYCZNA C w Gliwicach Gliwice, ul. Konarskiego 22, pokoje 52-54 Regulamin pracowni i organizacja zajęć Sprawozdanie (strona tytułowa, karta pomiarowa)
Optyka. Wykład V Krzysztof Golec-Biernat. Fale elektromagnetyczne. Uniwersytet Rzeszowski, 8 listopada 2017
 Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Optyka Wykład V Krzysztof Golec-Biernat Fale elektromagnetyczne Uniwersytet Rzeszowski, 8 listopada 2017 Wykład V Krzysztof Golec-Biernat Optyka 1 / 17 Plan Swobodne równania Maxwella Fale elektromagnetyczne
Instytut Fizyki Teoretycznej i Astrofizyki Gdańsk, Uniwersytet Gdański. Informacja o współpracy z zagranicą w roku 2004
 Instytut Fizyki Teoretycznej i Astrofizyki Gdańsk, 2005-02-14 Uniwersytet Gdański Informacja o współpracy z zagranicą w roku 2004 Współpraca Instytutu Fizyki Teoretycznej i Astrofizyki z partnerami zagranicznymi
Instytut Fizyki Teoretycznej i Astrofizyki Gdańsk, 2005-02-14 Uniwersytet Gdański Informacja o współpracy z zagranicą w roku 2004 Współpraca Instytutu Fizyki Teoretycznej i Astrofizyki z partnerami zagranicznymi
Ćwiczenie 363. Polaryzacja światła sprawdzanie prawa Malusa. Początkowa wartość kąta 0..
 Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Godzina... Polaryzacja światła sprawdzanie prawa Malusa Początkowa wartość kąta 0.. 1 25 49 2 26 50 3 27 51 4 28 52 5 29 53 6 30 54
Nazwisko... Data... Nr na liście... Imię... Wydział... Dzień tyg.... Godzina... Polaryzacja światła sprawdzanie prawa Malusa Początkowa wartość kąta 0.. 1 25 49 2 26 50 3 27 51 4 28 52 5 29 53 6 30 54
TEORIE KWANTOWE JAKO PODSTAWA NOWOCZESNEJ KRYPTOGRAFII QUANTUM TEORIIES AS MODERN CRYPTOGRAPHY BASIS
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ Seria: ORGANIZACJA I ZARZĄDZANIE z. XX XXXX Nr kol. XXXX Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania Instytut Ekonometrii i Informatyki TEORIE
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ Seria: ORGANIZACJA I ZARZĄDZANIE z. XX XXXX Nr kol. XXXX Marcin SOBOTA Politechnika Śląska Wydział Organizacji i Zarządzania Instytut Ekonometrii i Informatyki TEORIE
Statystyka nieoddziaływujących gazów Bosego i Fermiego
 Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Statystyka nieoddziaływujących gazów Bosego i Fermiego Bozony: fotony (kwanty pola elektromagnetycznego, których liczba nie jest zachowana mogą być pojedynczo pochłaniane lub tworzone. W konsekwencji,
Sprawozdanie z pracy naukowej w roku SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ
 Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2008-01-28 Sprawozdanie z pracy naukowej w roku 2007 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Instytut Fizyki Teoretycznej i Astrofizyki Uniwersytet Gdański Gdańsk, 2008-01-28 Sprawozdanie z pracy naukowej w roku 2007 1. SYNTETYCZNE PODSUMOWANIE DZIAŁALNOŚCI NAUKOWO-BADAWCZEJ Źródła finansowania
Podstawy fizyki kwantowej
 Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Wykład I Prolog Przy końcu XIX wieku fizyka, którą dzisiaj określamy jako klasyczną, zdawała się być nauką ostateczną w tym sensie, że wszystkie jej podstawowe prawa były już ustanowione, a efektem dalszego
Falowa natura materii
 r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
r. akad. 2012/2013 wykład I - II Podstawy Procesów i Konstrukcji Inżynierskich Falowa natura materii 1 r. akad. 2012/2013 Podstawy Procesów i Konstrukcji Inżynierskich Warunki zaliczenia: Aby uzyskać dopuszczenie
Seminarium: Efekty kwantowe w informatyce
 Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
Seminarium: Efekty kwantowe w informatyce Aleksander Mądry Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Sprawy organizacyjne Spotykamy się w piątki o 12:15 w sali 105. Każdy kto będzie
Kwantowa natura promieniowania
 Kwantowa natura promieniowania Promieniowanie ciała doskonale czarnego Ciało doskonale czarne ciało, które absorbuje całe padające na nie promieniowanie bez względu na częstotliwość. Promieniowanie ciała
Kwantowa natura promieniowania Promieniowanie ciała doskonale czarnego Ciało doskonale czarne ciało, które absorbuje całe padające na nie promieniowanie bez względu na częstotliwość. Promieniowanie ciała
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny
 POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
POSTULATY MECHANIKI KWANTOWEJ cd i formalizm matematyczny Funkcja Falowa Postulat 1 Dla każdego układu istnieje funkcja falowa (funkcja współrzędnych i czasu), która jest ciągła, całkowalna w kwadracie,
Promieniowanie X. Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X
 Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
Promieniowanie X Jak powstaje promieniowanie rentgenowskie Budowa lampy rentgenowskiej Widmo ciągłe i charakterystyczne promieniowania X Lampa rentgenowska Lampa rentgenowska Promieniowanie rentgenowskie
PODSTAWY MECHANIKI KWANTOWEJ
 PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
PODSTAWY MECHANIKI KWANTOWEJ De Broglie, na podstawie analogii optycznych, w roku 194 wysunął hipotezę, że cząstki materialne także charakteryzują się dualizmem korpuskularno-falowym. Hipoteza de Broglie
Teleportacja czy mamy juŝ technologię XII wieku?
 Teleportacja czy mamy juŝ technologię XII wieku? Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Energize! Teleportacja w Startreku Czas teleportacji: 2-5s, Zasięg: 40000km Wchodzimy do transportera
Teleportacja czy mamy juŝ technologię XII wieku? Rafał Demkowicz-Dobrzański Centrum Fizyki Teoretycznej PAN Energize! Teleportacja w Startreku Czas teleportacji: 2-5s, Zasięg: 40000km Wchodzimy do transportera
Fizyka - opis przedmiotu
 Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 13.2-WI-INFP-F Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki Informatyka / Sieciowe systemy informatyczne
Fizyka - opis przedmiotu Informacje ogólne Nazwa przedmiotu Fizyka Kod przedmiotu 13.2-WI-INFP-F Wydział Kierunek Wydział Informatyki, Elektrotechniki i Automatyki Informatyka / Sieciowe systemy informatyczne
Bozon Higgsa prawda czy kolejny fakt prasowy?
 Bozon Higgsa prawda czy kolejny fakt prasowy? Sławomir Stachniewicz, IF PK 1. Standardowy model cząstek elementarnych Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami
Bozon Higgsa prawda czy kolejny fakt prasowy? Sławomir Stachniewicz, IF PK 1. Standardowy model cząstek elementarnych Model Standardowy to obecnie obowiązująca teoria cząstek elementarnych, które są składnikami
Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku
 Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku Wstęp czyli (próba) odpowiedzi na pewne pytania (Silna) Teza Church
Peter W. Shor - Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. 19 listopada 2004 roku Wstęp czyli (próba) odpowiedzi na pewne pytania (Silna) Teza Church
h 2 h p Mechanika falowa podstawy pˆ 2
 Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Mechanika falowa podstawy Hipoteza de Broglie a Zarówno promieniowanie jak i cząstki materialne posiadają naturę dwoistą korpuskularno-falową. Z każdą mikrocząstką można związać pewien proces falowy pierwotnie
Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały
 WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
WYKŁAD 1 Teorie wiązania chemicznego i podstawowe zasady mechaniki kwantowej Zjawiska, które zapowiadały nadejście nowej ery w fizyce i przybliżały sformułowanie praw fizyki kwantowej: promieniowanie katodowe
KWANTOWA DYSTRYBUCJA KLUCZA: STAN WIEDZY
 Zeszyty Naukowe WSEI seria: TRANSPORT I INFORMATYKA, 7(1/2017), s. 17 26 inż. Michał MAJ Wyższa Szkoła Ekonomii i Innowacji w Lublinie KWANTOWA DYSTRYBUCJA KLUCZA: STAN WIEDZY QUANTUM KEY DISTRIBUTION.
Zeszyty Naukowe WSEI seria: TRANSPORT I INFORMATYKA, 7(1/2017), s. 17 26 inż. Michał MAJ Wyższa Szkoła Ekonomii i Innowacji w Lublinie KWANTOWA DYSTRYBUCJA KLUCZA: STAN WIEDZY QUANTUM KEY DISTRIBUTION.
Podstawy fizyki kwantowej
 Podstawy fizyki kwantowej Fizyka kwantowa - co to jest? Światło to fala czy cząstka? promieniowanie termiczne efekt fotoelektryczny efekt Comptona fale materii de Broglie a równanie Schrodingera podstawa
Podstawy fizyki kwantowej Fizyka kwantowa - co to jest? Światło to fala czy cząstka? promieniowanie termiczne efekt fotoelektryczny efekt Comptona fale materii de Broglie a równanie Schrodingera podstawa
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym
 II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
Jądra o wysokich energiach wzbudzenia
 Jądra o wysokich energiach wzbudzenia 1. Utworzenie i rozpad jądra złożonego a) model statystyczny 2. Gigantyczny rezonans dipolowy (GDR) a) w jądrach w stanie podstawowym b) w jądrach w stanie wzbudzonym
Jądra o wysokich energiach wzbudzenia 1. Utworzenie i rozpad jądra złożonego a) model statystyczny 2. Gigantyczny rezonans dipolowy (GDR) a) w jądrach w stanie podstawowym b) w jądrach w stanie wzbudzonym
Fizyka współczesna. 4 października 2017
 Fizyka współczesna 4 października 2017 Fizyka współczesna Fizyka (za Encyclopeadia Britannica): Nauka badajaca strukturę materii oraz oddziaływania między podstawowymi elementami obserwowalnego Wszechświata.
Fizyka współczesna 4 października 2017 Fizyka współczesna Fizyka (za Encyclopeadia Britannica): Nauka badajaca strukturę materii oraz oddziaływania między podstawowymi elementami obserwowalnego Wszechświata.
Fizyka 3.3 WYKŁAD II
 Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Fizyka 3.3 WYKŁAD II Promieniowanie elektromagnetyczne Dualizm korpuskularno-falowy światła Fala elektromagnetyczna Strumień fotonów o energii E F : E F = hc λ c = 3 10 8 m/s h = 6. 63 10 34 J s Światło
Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu rubidowego
 Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Prof. dr hab. Jan Mostowski Instytut Fizyki PAN Warszawa Warszawa, 15 listopada 2010 r. Recenzja pracy doktorskiej mgr Tomasza Świsłockiego pt. Wpływ oddziaływań dipolowych na własności spinorowego kondensatu
Pole elektromagnetyczne. Równania Maxwella
 Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
Pole elektromagnetyczne (na podstawie Wikipedii) Pole elektromagnetyczne - pole fizyczne, za pośrednictwem którego następuje wzajemne oddziaływanie obiektów fizycznych o właściwościach elektrycznych i
Ćwiczenia z mikroskopii optycznej
 Ćwiczenia z mikroskopii optycznej Anna Gorczyca Rok akademicki 2013/2014 Literatura D. Halliday, R. Resnick, Fizyka t. 2, PWN 1999 r. J.R.Meyer-Arendt, Wstęp do optyki, PWN Warszawa 1979 M. Pluta, Mikroskopia
Ćwiczenia z mikroskopii optycznej Anna Gorczyca Rok akademicki 2013/2014 Literatura D. Halliday, R. Resnick, Fizyka t. 2, PWN 1999 r. J.R.Meyer-Arendt, Wstęp do optyki, PWN Warszawa 1979 M. Pluta, Mikroskopia
WYMAGANIA WSTĘPNE W ZAKRESIE WIEDZY, UMIEJĘTNOŚCI I INNYCH KOMPETENCJI
 Zał. nr 4 do ZW 33/01 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI, Instytut Fizyki (wykład w j. angielskim) KARTA PRZEDMIOTU Nazwa w języku polskim Klasyczna i kwantowa kryptografia Nazwa w języku angielskim
Zał. nr 4 do ZW 33/01 WYDZIAŁ PODSTAWOWYCH PROBLEMÓW TECHNIKI, Instytut Fizyki (wykład w j. angielskim) KARTA PRZEDMIOTU Nazwa w języku polskim Klasyczna i kwantowa kryptografia Nazwa w języku angielskim
Wstęp do algorytmiki kwantowej
 Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Komputer kwantowy - co to właściwie jest? Komputer kwantowy Komputer, którego zasada działania nie może zostać wyjaśniona bez użycia formalizmu mechaniki
Koło naukowe fizyków Migacz, Uniwersytet Wrocławski Komputer kwantowy - co to właściwie jest? Komputer kwantowy Komputer, którego zasada działania nie może zostać wyjaśniona bez użycia formalizmu mechaniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Szczegółowe wymagania edukacyjne na poszczególne oceny śródroczne i roczne z przedmiotu: FIZYKA. Nauczyciel przedmiotu: Marzena Kozłowska
 Szczegółowe wymagania edukacyjne na poszczególne oceny śródroczne i roczne z przedmiotu: FIZYKA Nauczyciel przedmiotu: Marzena Kozłowska Szczegółowe wymagania edukacyjne zostały sporządzone z wykorzystaniem
Szczegółowe wymagania edukacyjne na poszczególne oceny śródroczne i roczne z przedmiotu: FIZYKA Nauczyciel przedmiotu: Marzena Kozłowska Szczegółowe wymagania edukacyjne zostały sporządzone z wykorzystaniem
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics)
 Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
Szczegółowy program właściwy dla standardowej ścieżki kształcenia na kierunku astronomia. Semestr I. 60 120 14 Egzamin. 45 75 9 Egzamin 75 2.
 B3. Program studiów liczba punktów konieczna dla uzyskania kwalifikacji (tytułu zawodowego) określonej dla rozpatrywanego programu kształcenia - 180 łączna liczba punktów, którą student musi uzyskać na
B3. Program studiów liczba punktów konieczna dla uzyskania kwalifikacji (tytułu zawodowego) określonej dla rozpatrywanego programu kształcenia - 180 łączna liczba punktów, którą student musi uzyskać na
Fizyka. Program Wykładu. Program Wykładu c.d. Kontakt z prowadzącym zajęcia. Rok akademicki 2013/2014. Wydział Zarządzania i Ekonomii
 Fizyka Wydział Zarządzania i Ekonomii Kontakt z prowadzącym zajęcia dr Paweł Możejko 1e GG Konsultacje poniedziałek 9:00-10:00 paw@mif.pg.gda.pl Rok akademicki 2013/2014 Program Wykładu Mechanika Kinematyka
Fizyka Wydział Zarządzania i Ekonomii Kontakt z prowadzącym zajęcia dr Paweł Możejko 1e GG Konsultacje poniedziałek 9:00-10:00 paw@mif.pg.gda.pl Rok akademicki 2013/2014 Program Wykładu Mechanika Kinematyka
Termodynamika. Część 11. Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna. Janusz Brzychczyk, Instytut Fizyki UJ
 Termodynamika Część 11 Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna Janusz Brzychczyk, Instytut Fizyki UJ Układ otwarty rozkład wielki kanoniczny Rozważamy układ w równowadze termicznej
Termodynamika Część 11 Układ wielki kanoniczny Statystyki kwantowe Gaz fotonowy Ruchy Browna Janusz Brzychczyk, Instytut Fizyki UJ Układ otwarty rozkład wielki kanoniczny Rozważamy układ w równowadze termicznej
Wykład 14. Termodynamika gazu fotnonowego
 Wykład 14 Termodynamika gazu fotnonowego dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 16 stycznia 217 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
Wykład 14 Termodynamika gazu fotnonowego dr hab. Agata Fronczak, prof. PW Wydział Fizyki, Politechnika Warszawska 16 stycznia 217 dr hab. A. Fronczak (Wydział Fizyki PW) Wykład: Elementy fizyki statystycznej
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale.
 VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
VII. CZĄSTKI I FALE VII.1. POSTULAT DE BROGLIE'A (1924) De Broglie wysunął postulat fal materii tzn. małym cząstkom przypisał fale. Światło wykazuje zjawisko dyfrakcyjne. Rys.VII.1.Światło padające na
Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów
 Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) VII OSKNF 8 XI 2008 Plan Po co nam optyka kwantowa? Czerwony + Czerwony = Niebieski?
Optyczny wzmacniacz parametryczny jako źródło splątanych par fotonów Radosław Chrapkiewicz, Piotr Migdał (SKFiz UW) VII OSKNF 8 XI 2008 Plan Po co nam optyka kwantowa? Czerwony + Czerwony = Niebieski?
Teoria grawitacji. Grzegorz Hoppe (PhD)
 Teoria grawitacji Grzegorz Hoppe (PhD) Oddziaływanie grawitacyjne nie zostało dotychczas poprawnie opisane i pozostaje jednym z nie odkrytych oddziaływań. Autor uważa, że oddziaływanie to jest w rzeczywistości
Teoria grawitacji Grzegorz Hoppe (PhD) Oddziaływanie grawitacyjne nie zostało dotychczas poprawnie opisane i pozostaje jednym z nie odkrytych oddziaływań. Autor uważa, że oddziaływanie to jest w rzeczywistości
