REDUNDANCJA W SYSTEMACH DOSTAW
|
|
|
- Krzysztof Biernacki
- 6 lat temu
- Przeglądów:
Transkrypt
1 REDUNDANCJA W SYSTEMACH DOSTAW Wacław GIERULSKI, Sławomir LUŚCIŃSKI, Ryszard SERAFIN Streszczenie: W praktyce wyboru dostawców stosowane są systemy redundantne, w których ten sam asortyment dostarczany jest przez dwóch dostawców. Podział ilościowy bywa nierównomierny i zakłada dostawcę dominującego, który w większym stopniu spełnia wymagania. W prezentowanej pracy pokazano uzasadnienie dla stosowania takiego systemu oparte na analizach statystycznych, w którym jako kryterium podziału przyjęto minimalizację skutków zaburzeń w dostawach. Słowa kluczowe: niezgodności dostaw, system dwóch dostawców, miary statystyczne, rozwiązanie optymalne, eksperymenty symulacyjne. 1. Wstęp Wybór i ocena dostawców jest ważnym zagadnieniem, szczególnie w przypadku dążenia do redukcji zapasów w systemach produkcji masowej. Wymagana jest wtedy pełna zgodność dostaw z zamówieniami, a wszelkie zaburzenia mogą niekorzystnie wpływać na realizacje procesu produkcyjnego. W procedurze wyboru dostawców przeprowadzana jest ocena przed rozpoczęciem dostaw, uzupełniana poprzez późniejsze okresowe weryfikacje [8]. W przypadku powtarzalnych dostaw może być stosowana ocena, która wykorzystuje miary statystyczne. Jest to zgodne z koncepcją zarządzania ryzykiem dostaw [7], która uzależnia współpracę z dostawcami od wyników analizy danych uzyskanych z poprzednio realizowanych dostaw. Istnieją systemy, w których zaopatrzenie w ten sam asortyment produktów zapewnia równolegle dwóch dostawców. Jest to jeden ze sposobów zmniejszania niepewności dostaw poprzez wprowadzenie pewnego rodzaju redundancji w systemie zaopatrzenia. Podział zamówienia pomiędzy dostawców może być równomierny, ale często w takich systemach przyjmuje się podział przy którym jeden z nich pełni dominującą rolę i dostarcza zdecydowanie większą ilość a drugi zdecydowanie mniejsza ilość produktów. Ocena dostawców przeprowadzana okresowo może zmienić tą proporcje podziału. Argumentem dla takiego podziału jest wprowadzenie konkurencji pomiędzy dostawcami, brak natomiast uzasadnienia, że taki podział jest optymalny. Można podjąć próbę określenia optymalnego podziału zamówień pomiędzy dostawców zgodnie z pewnym jednoznacznie określonym kryterium. W proponowanej tutaj metodzie kryterium dotyczy minimalizacji zmienności wynikającej z niezgodności dostaw. Oczywiście tego rodzaju podejście może być stosowane tylko w przypadku produkcji masowej, gdy dostawy tego samego asortymentu realizowane są wielokrotnie przez długie okresy czasu. 2. Podział zamówień pomiędzy dostawców Wykorzystywanie dwóch źródeł dostaw dla tego samego produktu zwiększa bezpieczeństwo w procesie zaopatrzenia. Łatwiej w takim systemie unikać problemów z zaopatrzeniem w przypadku niewywiązywania się jednego z dostawców ze swoich 936
2 zobowiązań dotyczących ilości i jakości dostarczanych produktów. Jest wtedy do dyspozycji drugi dostawca, który może łagodzić powstałe problemy. Jednak nawet w przypadku realizacji zamówień zgodnie z ustaleniami, dostawy obarczone są pewnymi niezgodnościami o charakterze losowym. Niezgodności w dostawach powodują, że ilości przyjmowanych do magazynu produktów są mniejsze od zamawianych. Wynika to z mniejszej niż zamawiana ilości, oraz nieakceptowanej jakości części dostarczanych produktów. W racjonalnej gospodarce magazynowej ze względu na koszty, stan zapasów łącznie z zapasem bezpieczeństwa powinien być utrzymywany na niskim poziomie przy zagwarantowaniu ciągłości produkcji. Ważnym czynnikiem zmniejszającym poziom zapasów jest zmniejszenie w dostawach zmienności o charakterze losowym co można osiągnąć przez odpowiedni dobór współczynnika podziału zamówień pomiędzy dwóch dostawców. Zmienności dotyczące dostaw w wymiarze statystycznym są cechą dostawców. Opisuje to probabilistyczny model oceny dostawców [1], który określa miary zmienności w formie rozkładów prawdopodobieństwa. Model ten zakłada, że zmienność w dostawach, której miarą jest wariancja (lub odchylenie standardowe) jest stałą cechą dostawcy. W przedstawionej metodzie wyznaczania współczynnika podziału pomiędzy dwóch dostawców analizy teoretyczne prowadzone są dla strategii zaopatrzeniowej o stałej wielkości zamówień [3]. W praktyce strategia taka zakłada także stały okres pomiędzy dostawami i nie uwzględnia bieżących stanów zapasów oraz prognozowanego zapotrzebowania [8]. Jest to prosty system zaopatrzenia stosowany głównie w przypadku stabilnych sytuacji dotyczących wielkości produkcji i niezgodności występujących w realizowanych dostawach. Zamawiane produkty przyjmowane są do magazynu po upływie czasu określonego jako czas realizacji. Ilości produktów przyjmowane do magazynu mimo stałych wielkości zamówień nie są stałe, są mniejsze od ilości zamawianych na skutek występujących niezgodności o losowym charakterze (rys. 1). Stan zapasów Zamówienia Dostawy Pobieranie do produkcji Okres między dostawami Zapas bezpieczeństwa Okres między zamówieniami Czas realizacji Składanie zamówień Jednostka terminowania Rys. 1. Model dostaw ze stała wielkością zamówień W metodzie wyznaczania optymalnego współczynnika podziału zamówień pomiędzy dwóch dostawców analizowana jest zmienność, która wynika z niedoborów spowodowanych 937
3 niekompletnością oraz nieodpowiednią jakością dostaw. Przyjęto założenie, że znane są parametry statystyczne charakteryzuje zmienność niedoborów każdego dostawcy [4, 9]. Dla przeprowadzenia teoretycznych rozważań przyjęto następujące oznaczenia: X ilość zamawianego produkty γ współczynnik podziału zamówienia pomiędzy dwóch dostawców, X1 ilość produktu dobrej jakości przyjmowany od dostawcy 1, X2 ilość produktu dobrej jakości przyjmowany od dostawcy 2, Y1 niezgodności dotyczące ilości produktu od dostawcy 1, Y2 niezgodności dotyczące ilości produktu od dostawcy 2. Niedobory wynikające z niezgodności, oznaczane jako Y1, Y2 są to zmiennymi losowymi i odnoszą się do całkowitej wielkości zamówienia oznaczanego jako X. Tak więc ilości produktów przyjmowanych do magazynu z uwzględnieniem występujących niezgodności (także zmienne losowe) w przypadku zakupów realizowanych w całości przez jednego dostawcę są następujące: X1 = X Y1 jeżeli X2 = 0 (1) X2 = X Y2 jeżeli X1 = 0 (2) Natomiast w przypadku realizacji zamówienia przez dwóch dostawców, po uwzględnieniu współczynnika podziału γ ilości przyjmowane od każdego z nich wynoszą odpowiednio: X1 = γ (X Y1) (3) X2 = (1 γ) (X Y2) (4) Dla wyznaczenia wariancji będącej miarą zmienności łącznej dostawy wyznaczana jest wariancja sumy dostaw X1, X2. σ (X1 + X2) = σ [γ (X Y1) + (1 γ) (X Y2)] (5) Dla modelu realizacji zaopatrzenia o stałej wielkości zamawianej partii (rys. 1), która obejmuje łączną wielkość zamówienia, obowiązuje warunek: X = const (6) Po uwzględnieniu podstawowych własności dotyczących wariancji [10] wykonując proste przekształcenia otrzymano: σ (X1 + X2) = σ [γ Y1 + (1 γ) Y2] (7) Następnie wykorzystując wzór dla wariancji sumy zmiennych losowych, po przekształceniach otrzymano następujące wyrażenie, w którym cov oznacza kowariancję zmiennych losowych. σ (X1 + X2) = σ (γ Y1) + σ ((1 γ) Y2) + cov(γ Y1, (1 γ) Y2) (8) 938
4 Oznaczając symbolem E wartość oczekiwaną zmiennej losowej (wartość średnia), wyrażenie określające kowariancje może być obliczone jako: cov(γ Y1, (1 γ) Y2) = E(γ Y1 (1 γ) Y2) E(γ Y1) E((1 γ) Y2) (9) Skąd ostatecznie, po odpowiednich przekształceniach otrzymano zależność określającą poszukiwaną wariancję sumy dostaw z uwzględnieniem współczynnika podziału: σ (X1 + X2) = γ σ (Y1) + (1 γ) σ (Y2) + +γ (1 γ) E(Y1 Y2) γ (1 γ) E(Y1) E(Y2) (10) Obliczona w ten sposób wariancja sumy zmiennych losowych X1, X2, może być traktowana jako funkcja współczynnika podziału γ: σ (X1 + X2) = f(γ) (11) f(γ) = γ A + γ B + C (12) Gdzie wprowadzonym dla uproszczenia zapisu parametrom A, B, C przypisano następujące wyrażenia: A = σ (Y1) + σ (Y2) [E(Y1 Y2) E(Y1) E(Y2)] (13) B = 2 σ (Y2) + [E(Y1 Y2) E(Y1) E(Y2)] (14) C = σ (Y2) (15) Funkcja f(γ) może posiadać ekstremum (minimum albo maksimum), dla wartości argumentu γ, przy którym pochodna pierwszego rzędu przyjmuje wartość zerową, czyli: ( ) = 2 γ A + B = 0 (16) Natomiast warunkiem koniecznym, żeby było to minimum funkcji jest dodatnia wartość pochodnej drugiego rzędu: ( ) = 2 A > 0 czyli A > 0 (17) Po spełnieniu tego warunku dotyczącego parametru A, można obliczyć optymalną wartość współczynnika podziału γ, czyli taką przy której występuje minimalna zmienność niezgodności dostaw: γ = (18) Ponieważ miarą zmienności w przeprowadzanej analizie jest wariancja, jest to wartość γ dla której wariancja 2 oraz związane z nią odchylenie standardowe sumy zmiennych X1, X2 przyjmuje minimalną wartość. 939
5 3. Przykład numeryczny Praktyczne działania dla wyznaczanie optymalnego współczynnika podziału można pokazać na prostym przykładzie bazującym na eksperymencie numerycznym [3]. W tym celu wygenerowano dwa sygnały losowe Y1 oraz Y2 o rozkładzie normalnym (rys. 2), które obrazują niezgodności występujące w dostawach. Sygnały losowe otrzymano wykorzystując pakiet Vensim [5], który posiada wbudowany generator liczb losowych o rozkładzie normalnym. Rys. 2. Sygnały Y1, Y2 w eksperymencie numerycznym Dla wygenerowanych przykładowych danych (rys. 2) obliczono odpowiednie parametry statystyczne, wyznaczono współczynniki A, B, C oraz optymalną wartość współczynnika podziału γ. Obliczenia przeprowadzono z wykorzystaniem arkusza kalkulacyjnego Excel, a uzyskane wyniki zamieszczono w tabeli 1. Tabela 1. Obliczanie współczynnika podziału Parametry statystyczne Wyniki Wielkość Wartość Współczynnik Wartość 2 (Y1) 13,974 A 17,461 2 (Y2) 3,355 B -28,078 E(Y1) 10,113 C 13,974 E(Y2) 5,671 E(Y1*Y2) 57,216 γ - optymalne 0,8041 Spełnienie warunku (A > 0) wskazuje, że współczynnik γ przyjmuje wartość optymalną, dla której podział zamówień zapewnia minimalną wartość wariancji, czyli najmniejszą zmienność. Uwzględniając otrzymane wyniki, wariancja wyrażona w funkcji współczynnika γ ma następującą postać: σ (X1 + X2) = f(γ) = 17,461 γ 28,078 γ + 13,974 (19) 940
6 Na rys. 3 pokazano wykres funkcji f(γ), czyli wariancję sumy dostaw (X1+X2) w funkcji współczynnika podziału γ. Wariancja dla optymalnej wartości współczynnika podziału wynosi 2,6864 a odchylenie standardowe 1,6390. Rys. 3. Wariancja w funkcji współczynnika podziału (przykład numeryczny) Wyniki analizy wskazują, że optymalna wartość wskaźnika podziału γ wynosi 0,8041 (w przybliżeniu 0,8), czyli dostawca 1 powinien dostarczać 80% produktów a dostawca 2 pozostałe 20%. Na rys. 4 pokazano wielkości niezgodności dla warunków optymalnego podziału. Rys. 4. Sygnały dla optymalnej wartości współczynnika podziału 4. Zmienne wielkości dostaw Wyznaczenie optymalnej wartości współczynnika γ w sposób analityczny jest możliwe tylko dla modelu zaopatrzenia o stałej ilości zamawianego produktu (warunek 6). W przypadku innych modeli zaopatrzenia poszukiwanie rozwiązania możliwe jest na drodze eksperymentalnej poprzez wybór wartości współczynnika, który zapewni najmniejszą zmienność niezgodności. Mogą to być symulacyjne eksperymenty komputerowe wykonywane z uwzględnieniem wybranej strategii zaopatrzeniowej oraz parametrów 941
7 statystycznych charakteryzujących zmienność niedoborów każdego dostawcy Jedną z często stosowanych strategii realizuje system dostaw o stałym okresie pomiędzy zamówieniami i zmiennej ilości zależnej od stanów magazynowych [8]. Ilość zamawianego produktu ma dopełnić stan magazynowy do poziomu zapasu nominalnego. Ilość ta jest określana w momencie składania zamówienia (rys. 5). Stan zapasów Zamówienia Dostawy Pobieranie do produkcji Zapas nominalny Okres między dostawami Zapas bezpieczeństwa Okres między zamówieniami Czas realizacji Składanie zamówień Jednostka terminowania Rys. 5. Model dostaw ze zmienną wielkością zamówień W chwili dostawy stan zapasów w magazynie jest niższy o produkty pobrane do produkcji w czasie pomiędzy momentem składania zamówienia i momentem realizacji dostawy. Ponadto dostawy mogą być pomniejszone o ilość spowodowaną niezgodnościami. Na rys. 6 przedstawiono model symulacyjny zbudowany w programie Vensim realizujący taki system dostaw [2, 5]. Rys. 6. Model symulacyjny w programie Vensim W tabeli 2 zamieszczono zestawienie zmiennych występujących w modelu symulacyjnym łącznie z wiążącym je zależnościami. Pominięto natomiast przypisane tym zmiennym jednostki miar. 942
8 Tabela 2. Zmienne modelu symulacyjnego Lp. Zmienne Opis 1. Bloki całkujące (sumujące) 1.1 magazyn = przyjęto wydano Stan zapasów w magazynie wartość początkowa = pobrano z zapasu = pobieranie z zapasu wartość początkowa = 0 2. Zależności funkcyjne 2.1 wydano = IF THEN ELSE(magazyn>=plan produkcji, plan produkcji, magazyn) 2.2 niedobory = IF THEN ELSE (magazyn<plan produkcji, plan produkcji magazyn, 0) 943 Łączna ilość pobrana z zapasu bezpieczeństwa Ilość produktów pobieranych z magazynu Ilość brakujących w magazynie produktów potrzebnych dla realizacji planu produkcji 2.3 zamówienie = IF THEN ELSE( licznik=1, ilość, 0) Określenie terminu składania zamówienia 2.4 licznik = PULSE TRAIN(0, 1, okres, 50) Licznik dla określania terminów składania zamówienia 2.5 ilość = IF THEN ELSE(magazyn<zapas nominalny, zapas nominalny-magazyn, 0) Wielkość zamówienia dla jednej partii dostaw 2.6 wahania = INTEGER( RANDOM UNIFORM(-5, 5, 0)) Część losowo zmienna planu produkcyjnego 2.7 plan produkcji = optymalny + wahania Plan produkcji jako suma części stałej i losowo zmiennej 2.8 zakupy 1 = DELAY FIXED(IF THEN ELSE(zamówienie>0, INTEGER( współczynnik podziału*(zamówienie-niezgodności 1)), 0), czas realizacji, 0) Produkty spełniające wymagania jakościowe dostarczone przez dostawcę zakupy 2 = DELAY FIXED(IF THEN ELSE(zamówienie>0, INTEGER((1-współczynnik podziału)*(zamówienie-niezgodności 2)), 0), czas realizacji, 0) Produkty spełniające wymagania jakościowe dostarczone przez dostawcę niezgodności 1 = INTEGER(RANDOM NORMAL(2, 25, 11, 2, 0)) Niezgodności dostawcy 1 zmienna losowa 2.11 niezgodności 2 = INTEGER(RANDOM NORMAL(0, 20, 12, 4, 0)) Niezgodności dostawcy 2 zmienna losowa 2.12 przyjęto = zakupy 1+zakupy 2 Produkty przyjęte do magazynu 2.13 pobieranie z zapasu = IF THEN ELSE(magazyn<zapas bezpieczeństwa, zapas bezpieczeństwa-magazyn, 0) Ilość produktu pobierana z zapasu bezpieczeństwa 3. Wartości stałe 3.1 współczynnik podziału = 0, 0.1, 0.2,..0.8, 0.9, 1 Podział pomiędzy dostawców 3.2 optymalny = 12 Część stała planu produkcji 3.3 okres = 3 Czas pomiędzy zamówieniami 3.4 czas realizacji = 2 Czas realizacji zamówienia 3.5 zapas nominalny = zapas bezpieczeństwa = 15 Centralnym elementem modelu jest blok sumujący magazyn do którego dostarczane są produkty przyjęto i z którego pobierane są produkty produkcja. Pobieranie produktów jest zgodne z planem produkcji o ile nie występują niedobory w magazynie. W modelu
9 generowany jest losowo zmienny plan produkcji, w którym występują pewne ograniczone wahania wokół wartości optymalnej. Zamówienia produktów wystawiane są cyklicznie w ustalonych okresach czasu. Zakupy realizowane są z pewnym opóźnieniem względem zamówień wynikającym z koniecznego czasu realizacji. Zakupione produkty dostarczane są przez dwóch dostawców w ilościach obliczanych w blokach zakupy 1 oraz zakupy 2. Podział pomiędzy dostawców określa parametr określany w bloku współczynnik podziału. W blokach niezgodności 1 oraz niezgodności 2 określane są w formie funkcji losowych udziały niedoborów w dostawach. Pozawala to na obliczenie rzeczywiście dostarczanych do magazynu produktów. Dla magazynu określany jest zapas bezpieczeństwa jako poziom, który powinien być naruszany tylko w wyjątkowych sytuacjach. W modelu zmienna pobieranie z zapasu pokazuje kolejne wielkości naruszenia zapasu bezpieczeństwa a w bloku pobrano a zapasu obliczana jest całkowita ilość produktów pobieranych z zapasu bezpieczeństwa w analizowanym okresie. Tą całkowita ilość produktów pobieranych z zapasu bezpieczeństwa przyjęto jako miarę przy doborze współczynnika podziału. Tak więc współczynnik podziału powinien być dobierany tak, żeby łączna ilość produktów pobieranych z zapasu bezpieczeństwa była najmniejsza. W symulacjach komputerowych korzystając z modelu przedstawionego na rys. 6 badano proces zaopatrzenia magazynu do którego dostarczane są zamawiane produkty i z którego pobierane są produkty potrzebne do produkcji. Spośród szeregu przeprowadzonych symulacji pokazano tutaj dwa przypadki, nazywane Symulacja 1 oraz Symulacja 2. Symulacje przeprowadzano dla wartości współczynnika podziału γ z zakresu <0,1> zmienianej z krokiem 0,1. W wyniku wyznaczono zależność pomiędzy ilością pobieranych produktów a współczynnikiem podziału. Zależność tą przedstawiono w postaci tabelarycznej (tabela 3) oraz w postaci wykresów (rys. 7). Tabela 3. Wyniki badań symulacyjnych Pobrano Współczynnik podziału γ z zapasu 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 Symulacja Symulacja Rys. 7. Wykorzystywanie zapasu bezpieczeństwa 944
10 Na rysunkach zamieszczono dodatkowo linie trendu. Skorzystano tutaj z narzędzia Excela wybierając trend wielomianowy. Równania linii trendu dla symulacji 1 (Z 1) oraz symulacji 2 (Z 2) przyjmują następującą postać: Z = 38,576 γ 50,124 γ + 0,6496 (20) Z = 34,848 γ 20,03 γ + 78,727 (21) Z równań tych można obliczyć optymalne wartości współczynnika γ dla którego zmienna Z 1 oraz Z 2 przyjmuje wartość minimalną. Wyniki zamieszczono w tabeli 4 gdzie dodatkowo drogą symulacji wyznaczono wielkości wykorzystywanego zapasu bezpieczeństwa. Tabela 4. Parametry optymalne dla przykładów symulacyjnych Parametry Symulacja 1 Symulacja 2 γ - optymalne 0,649 0,287 Z linia trendu 92,919 75,85 Z - symulacje Dla wyznaczonych na podstawie linii trendu wartości współczynnika podziału przeprowadzono symulacje weryfikujące wynik analizy. Wyniki w postaci graficznej przedstawiono na rys. 8 (symulacja 1) oraz rys. 9 (symulacja 2). Wyniki liczbowe zamieszczono w tabeli 4 (ostatni wiersz). Ich wartości, zbliżone do wartości teoretycznych określonych przez linie trendu wskazują na pozytywny wynik weryfikacji. Rys. 8. Wyniki symulacji 1 945
11 Rys. 9. Wyniki symulacji 2 Przyjęcie ilości produktów pobieranych z zapasu bezpieczeństwa jako miarę doboru współczynnika podziału nie jest sprzeczne z poprzednim przykładem, gdzie współczynnik ten uzależniany był od wariancji. W obydwóch przypadkach efektem analizy jest możliwość zmniejszenia poziomu zapasu bezpieczeństwa co jednocześnie wiąże się z obniżeniem kosztów. 5. Podsumowanie Przedstawiona praca wpisuje się w nabierający coraz większego znaczenia obszar nazywany inżynierią danych [6]. Rozwój technik informatycznych ułatwia obecnie gromadzenie dużych ilości danych i wykonywanie różnego rodzaju analiz wspomagających procesy decyzyjne. Zagadnienie wspomagania procesów decyzyjnych wpisane w istotę inżynierii danych jednoznacznie wiąże się z systemami zarządzania jakością. Jedna z ośmiu zasad zarządzania przedstawiona w aktualnej normie ISO 9000 wskazuje na konieczność podejmowania decyzji na podstawie faktów (zasada 7). A właśnie rzeczywiste dane w postaci ilościowej, związane z realizowanymi procesami są odzwierciedleniem faktów. Podobnie koncepcja Six Sigma przypisuje kluczowe znaczenie pomiarom będących źródłem danych co pokazuje następujące stwierdzenie: Nie możemy poprawić czegoś, o czym nie wiemy. Nie dowiemy się, póki nie zmierzymy. Zaproponowana w pracy metoda określania współczynnika podziału zamówień w systemach redundantnych jest kolejną propozycją usprawniania gospodarki zaopatrzeniowej. Metoda dla przypadku stałych ilości zamawianych produktów przedstawiona w pracy [3] została tutaj rozszerzona na przypadki dowolnej strategii realizacji dostaw. Pozwala ona na obniżenie poziomu zapasów co jest zgodne z wszechobecną koncepcją odchudzania (Lean) w zastosowaniu do procesów produkcyjnych. Jest to także pewien przyczynek do prac nad zagadnieniami adaptacyjnego zarządzania ryzykiem dostaw w procesach produkcyjnych [7]. W pracy zamieszczono jedynie rozważania teoretyczne oraz symulacje komputerowe, natomiast następnym etapem powinna być weryfikacja przedstawionej metody w warunkach rzeczywistych dostaw. 946
12 Literatura 1. Gierulski W., Luściński S., Serafim R.: Probabilistyczne miary oceny dostawców w łańcuchu logistycznym produkcji masowej Logistyka 4/2015, str Gierulski W., Luściński S., Serafim R.: Symulacja komputerowa procesów logistycznych z wykorzystaniem programu vensim. [w:] Innowacje w zarządzaniu i inżynierii produkcji, pod red. R.Knosali, Oficyna Wydawnicza Polskiego Towarzystwa Zarządzania Produkcją, Opole Gierulski W.: Modelowanie w inżynierii systemów. Monografia, Politechnika Świętokrzyska (w druku). 4. Jóźwiak J. Podgórski J.: Statystyka od podstaw, PWE, Warszawa Krupa K.: Modelowanie symulacje i prognozowanie systemy ciągłe. Wydawnictwo naukowo-techniczne. Warszawa Luściński S.: Perspectives on data engineering: emerging role in organisation development. [w:] Innowacje w zarządzaniu i inżynierii produkcji, pod red. R.Knosali, Oficyna Wydawnicza Polskiego Towarzystwa Zarządzania Produkcją, Opole Serafin R.: Koncepcja systemu adaptacyjnego zarządzania ryzykiem dostaw w procesach produkcyjnych. Zarządzanie przedsiębiorstwem. Nr Skowronek C., Sarjusz-Wolski Z.: Logistyka w przedsiębiorstwie. Warszawa: Państwowe Wydawnictwo Ekonomiczne, Sobczyk M.: Statystyka, PWN, Warszawa, Internet: Dr hab. inż. Wacław GIERULSKI, prof. nadzw. PŚk. Dr inż. Sławomir LUŚCIŃSKI Katedra Inżynierii Produkcji Wydział Zarządzania i Modelowania Komputerowego Politechnika Świętokrzyska Kielce, Aleja Tysiąclecia PP 7 waclaw.gierulski@tu.kielce.pl luscinski@tu.kielce.pl Mgr inż. Ryszard SERAFIN Katedra Zarządzania i Inżynierii Produkcji Wydział Inżynierii Produkcji i Logistyki Politechnika Opolska Opole, ul. Ozimska 75 r.serafin@po.opole.pl 947
SYMULACJA KOMPUTEROWA PROCESÓW LOGISTYCZNYCH Z WYKORZYSTANIEM PROGRAMU VENSIM
 SYMULACJA KOMPUTEROWA PROCESÓW LOGISTYCZNYCH Z WYKORZYSTANIEM PROGRAMU VENSIM Wacław GIERULSKI, Sławomir LUŚCIŃSKI, Ryszard SERAFIN Streszczenie: W artykule pokazano możliwości zastosowania metody symulacji
SYMULACJA KOMPUTEROWA PROCESÓW LOGISTYCZNYCH Z WYKORZYSTANIEM PROGRAMU VENSIM Wacław GIERULSKI, Sławomir LUŚCIŃSKI, Ryszard SERAFIN Streszczenie: W artykule pokazano możliwości zastosowania metody symulacji
Sterowanie wielkością zamówienia w Excelu - cz. 3
 Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych
 dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
SCENARIUSZ LEKCJI. TEMAT LEKCJI: Zastosowanie średnich w statystyce i matematyce. Podstawowe pojęcia statystyczne. Streszczenie.
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI
 WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
WYZNACZANIE NIEPEWNOŚCI POMIARU METODAMI SYMULACYJNYMI Stefan WÓJTOWICZ, Katarzyna BIERNAT ZAKŁAD METROLOGII I BADAŃ NIENISZCZĄCYCH INSTYTUT ELEKTROTECHNIKI ul. Pożaryskiego 8, 04-703 Warszawa tel. (0)
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz.
 14.12.2005 r. Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz. 2 3.2. Implementacja w Excelu (VBA for
14.12.2005 r. Wykorzystanie nowoczesnych technik prognozowania popytu i zarządzania zapasami do optymalizacji łańcucha dostaw na przykładzie dystrybucji paliw cz. 2 3.2. Implementacja w Excelu (VBA for
Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa
 Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Spis treści Elementy Modelowania Matematycznego Wykład 4 Regresja i dyskryminacja liniowa Romuald Kotowski Katedra Informatyki Stosowanej PJWSTK 2009 Spis treści Spis treści 1 Wstęp Bardzo często interesujący
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa. Diagnostyka i niezawodność robotów
 Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
Instytut Politechniczny Państwowa Wyższa Szkoła Zawodowa Diagnostyka i niezawodność robotów Laboratorium nr 6 Model matematyczny elementu naprawialnego Prowadzący: mgr inż. Marcel Luzar Cele ćwiczenia:
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Spacery losowe generowanie realizacji procesu losowego
 Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Spacery losowe generowanie realizacji procesu losowego Michał Krzemiński Streszczenie Omówimy metodę generowania trajektorii spacerów losowych (błądzenia losowego), tj. szczególnych procesów Markowa z
Estymacja parametrów w modelu normalnym
 Estymacja parametrów w modelu normalnym dr Mariusz Grządziel 6 kwietnia 2009 Model normalny Przez model normalny będziemy rozumieć rodzine rozkładów normalnych N(µ, σ), µ R, σ > 0. Z Centralnego Twierdzenia
Estymacja parametrów w modelu normalnym dr Mariusz Grządziel 6 kwietnia 2009 Model normalny Przez model normalny będziemy rozumieć rodzine rozkładów normalnych N(µ, σ), µ R, σ > 0. Z Centralnego Twierdzenia
Pobieranie prób i rozkład z próby
 Pobieranie prób i rozkład z próby Marcin Zajenkowski Marcin Zajenkowski () Pobieranie prób i rozkład z próby 1 / 15 Populacja i próba Populacja dowolnie określony zespół przedmiotów, obserwacji, osób itp.
Pobieranie prób i rozkład z próby Marcin Zajenkowski Marcin Zajenkowski () Pobieranie prób i rozkład z próby 1 / 15 Populacja i próba Populacja dowolnie określony zespół przedmiotów, obserwacji, osób itp.
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Weryfikacja hipotez statystycznych. KG (CC) Statystyka 26 V / 1
 Weryfikacja hipotez statystycznych KG (CC) Statystyka 26 V 2009 1 / 1 Sformułowanie problemu Weryfikacja hipotez statystycznych jest drugą (po estymacji) metodą uogólniania wyników uzyskanych w próbie
Weryfikacja hipotez statystycznych KG (CC) Statystyka 26 V 2009 1 / 1 Sformułowanie problemu Weryfikacja hipotez statystycznych jest drugą (po estymacji) metodą uogólniania wyników uzyskanych w próbie
PROGNOZOWANIE I SYMULACJE EXCEL 1 AUTOR: MARTYNA MALAK PROGNOZOWANIE I SYMULACJE EXCEL 1 AUTOR: MARTYNA MALAK
 1 PROGNOZOWANIE I SYMULACJE 2 http://www.outcome-seo.pl/excel1.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodatek Solver jest dostępny w menu Narzędzia. Jeżeli Solver nie jest
1 PROGNOZOWANIE I SYMULACJE 2 http://www.outcome-seo.pl/excel1.xls DODATEK SOLVER WERSJE EXCELA 5.0, 95, 97, 2000, 2002/XP i 2003. 3 Dodatek Solver jest dostępny w menu Narzędzia. Jeżeli Solver nie jest
7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej
 7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej Definicja 1 n-elementowa losowa próba prosta nazywamy ciag n niezależnych zmiennych losowych o jednakowych rozkładach
7. Estymacja parametrów w modelu normalnym(14.04.2008) Pojęcie losowej próby prostej Definicja 1 n-elementowa losowa próba prosta nazywamy ciag n niezależnych zmiennych losowych o jednakowych rozkładach
LOGISTYKA. Zapas: definicja. Zapasy: podział
 LOGISTYKA Zapasy Zapas: definicja Zapas to określona ilość dóbr znajdująca się w rozpatrywanym systemie logistycznym, bieżąco nie wykorzystywana, a przeznaczona do późniejszego przetworzenia lub sprzedaży.
LOGISTYKA Zapasy Zapas: definicja Zapas to określona ilość dóbr znajdująca się w rozpatrywanym systemie logistycznym, bieżąco nie wykorzystywana, a przeznaczona do późniejszego przetworzenia lub sprzedaży.
STATYSTYKA MATEMATYCZNA WYKŁAD 4. WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X.
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki
 Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Akademia Górniczo-Hutnicza Wydział Elektrotechniki, Automatyki, Informatyki i Elektroniki Przetwarzanie Sygnałów Studia Podyplomowe, Automatyka i Robotyka. Wstęp teoretyczny Zmienne losowe Zmienne losowe
Zadania przykładowe na egzamin. przygotował: Rafał Walkowiak
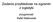 Zadania przykładowe na egzamin z logistyki przygotował: Rafał Walkowiak Punkt zamawiania Proszę określić punkt dokonywania zamawiania jeżeli: zapas bezpieczeństwa wynosi 10 sztuk, czas realizacji zamówienia
Zadania przykładowe na egzamin z logistyki przygotował: Rafał Walkowiak Punkt zamawiania Proszę określić punkt dokonywania zamawiania jeżeli: zapas bezpieczeństwa wynosi 10 sztuk, czas realizacji zamówienia
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Jerzy Berdychowski. Informatyka. w turystyce i rekreacji. Materiały do zajęć z wykorzystaniem programu. Microsoft Excel
 Jerzy Berdychowski Informatyka w turystyce i rekreacji Materiały do zajęć z wykorzystaniem programu Microsoft Excel Warszawa 2006 Recenzenci prof. dr hab. inż. Tomasz Ambroziak prof. dr hab. inż. Leszek
Jerzy Berdychowski Informatyka w turystyce i rekreacji Materiały do zajęć z wykorzystaniem programu Microsoft Excel Warszawa 2006 Recenzenci prof. dr hab. inż. Tomasz Ambroziak prof. dr hab. inż. Leszek
Metody Ilościowe w Socjologii
 Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
Metody Ilościowe w Socjologii wykład 2 i 3 EKONOMETRIA dr inż. Maciej Wolny AGENDA I. Ekonometria podstawowe definicje II. Etapy budowy modelu ekonometrycznego III. Wybrane metody doboru zmiennych do modelu
Rozdział 8. Regresja. Definiowanie modelu
 Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Rozdział 8 Regresja Definiowanie modelu Analizę korelacji można traktować jako wstęp do analizy regresji. Jeżeli wykresy rozrzutu oraz wartości współczynników korelacji wskazują na istniejąca współzmienność
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Rozkład normalny, niepewność standardowa typu A
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
Podstawy Metrologii i Technik Eksperymentu Laboratorium Rozkład normalny, niepewność standardowa typu A Instrukcja do ćwiczenia nr 1 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy
3. Modele tendencji czasowej w prognozowaniu
 II Modele tendencji czasowej w prognozowaniu 1 Składniki szeregu czasowego W teorii szeregów czasowych wyróżnia się zwykle następujące składowe szeregu czasowego: a) składowa systematyczna; b) składowa
II Modele tendencji czasowej w prognozowaniu 1 Składniki szeregu czasowego W teorii szeregów czasowych wyróżnia się zwykle następujące składowe szeregu czasowego: a) składowa systematyczna; b) składowa
W1. Wprowadzenie. Statystyka opisowa
 W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
W1. Wprowadzenie. Statystyka opisowa dr hab. Jerzy Nakielski Zakład Biofizyki i Morfogenezy Roślin Plan wykładu: 1. O co chodzi w statystyce 2. Etapy badania statystycznego 3. Zmienna losowa, rozkład
Rok akademicki: 2012/2013 Kod: JFM s Punkty ECTS: 3. Poziom studiów: Studia I stopnia Forma i tryb studiów: Stacjonarne
 Nazwa modułu: Statystyka inżynierska Rok akademicki: 2012/2013 Kod: JFM-1-210-s Punkty ECTS: 3 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
Nazwa modułu: Statystyka inżynierska Rok akademicki: 2012/2013 Kod: JFM-1-210-s Punkty ECTS: 3 Wydział: Fizyki i Informatyki Stosowanej Kierunek: Fizyka Medyczna Specjalność: Poziom studiów: Studia I stopnia
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr Temat: Karty kontrolne przy alternatywnej ocenie właściwości.
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr Temat: Karty kontrolne przy alternatywnej ocenie właściwości.
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI
 DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
DWUKROTNA SYMULACJA MONTE CARLO JAKO METODA ANALIZY RYZYKA NA PRZYKŁADZIE WYCENY OPCJI PRZEŁĄCZANIA FUNKCJI UŻYTKOWEJ NIERUCHOMOŚCI mgr Marcin Pawlak Katedra Inwestycji i Wyceny Przedsiębiorstw Plan wystąpienia
ECONOMIC ORDER QUANTITY (EOQ)
 Systemy Logistyczne Wojsk nr 41/2014 MODEL EKONOMICZNEJ WIELKOŚCI ZAMÓWIENIA (EOQ) ECONOMIC ORDER QUANTITY (EOQ) Małgorzata GRZELAK Jarosław ZIÓŁKOWSKI Wojskowa Akademia Techniczna Wydział Logistyki Instytut
Systemy Logistyczne Wojsk nr 41/2014 MODEL EKONOMICZNEJ WIELKOŚCI ZAMÓWIENIA (EOQ) ECONOMIC ORDER QUANTITY (EOQ) Małgorzata GRZELAK Jarosław ZIÓŁKOWSKI Wojskowa Akademia Techniczna Wydział Logistyki Instytut
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Analiza współzależności zjawisk
 Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Wykład z Technologii Informacyjnych. Piotr Mika
 Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Wykład z Technologii Informacyjnych Piotr Mika Uniwersalna forma graficznego zapisu algorytmów Schemat blokowy zbiór bloków, powiązanych ze sobą liniami zorientowanymi. Jest to rodzaj grafu, którego węzły
Korzystanie z podstawowych rozkładów prawdopodobieństwa (tablice i arkusze kalkulacyjne)
 Korzystanie z podstawowych rozkładów prawdopodobieństwa (tablice i arkusze kalkulacyjne) Przygotował: Dr inż. Wojciech Artichowicz Katedra Hydrotechniki PG Zima 2014/15 1 TABLICE ROZKŁADÓW... 3 ROZKŁAD
Korzystanie z podstawowych rozkładów prawdopodobieństwa (tablice i arkusze kalkulacyjne) Przygotował: Dr inż. Wojciech Artichowicz Katedra Hydrotechniki PG Zima 2014/15 1 TABLICE ROZKŁADÓW... 3 ROZKŁAD
Spis treści. Przedmowa
 Spis treści Przedmowa 1.1. Magazyn i magazynowanie 1.1.1. Magazyn i magazynowanie - podstawowe wiadomości 1.1.2. Funkcje i zadania magazynów 1.1.3. Rodzaje magazynów 1.1.4. Rodzaje zapasów 1.1.5. Warunki
Spis treści Przedmowa 1.1. Magazyn i magazynowanie 1.1.1. Magazyn i magazynowanie - podstawowe wiadomości 1.1.2. Funkcje i zadania magazynów 1.1.3. Rodzaje magazynów 1.1.4. Rodzaje zapasów 1.1.5. Warunki
Wstęp do teorii niepewności pomiaru. Danuta J. Michczyńska Adam Michczyński
 Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
Wstęp do teorii niepewności pomiaru Danuta J. Michczyńska Adam Michczyński Podstawowe informacje: Strona Politechniki Śląskiej: www.polsl.pl Instytut Fizyki / strona własna Instytutu / Dydaktyka / I Pracownia
6. Zmienne losowe typu ciagłego ( ) Pole trapezu krzywoliniowego
 6. Zmienne losowe typu ciagłego (2.04.2007) Pole trapezu krzywoliniowego Przypomnienie: figurę ograniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją ciągłą; proste x = a, x = b, a < b, oś OX
6. Zmienne losowe typu ciagłego (2.04.2007) Pole trapezu krzywoliniowego Przypomnienie: figurę ograniczoną przez: wykres funkcji y = f(x), gdzie f jest funkcją ciągłą; proste x = a, x = b, a < b, oś OX
PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem
 1 PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem DANE I INFORMACJE 2 Planowanie przepływów jest ciągłym procesem podejmowania decyzji, które decydują o efektywnym
1 PROCESY I TECHNOLOGIE INFORMACYJNE Dane i informacje w zarządzaniu przedsiębiorstwem DANE I INFORMACJE 2 Planowanie przepływów jest ciągłym procesem podejmowania decyzji, które decydują o efektywnym
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH
 WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
WSKAZÓWKI DO WYKONANIA SPRAWOZDANIA Z WYRÓWNAWCZYCH ZAJĘĆ LABORATORYJNYCH Dobrze przygotowane sprawozdanie powinno zawierać następujące elementy: 1. Krótki wstęp - maksymalnie pół strony. W krótki i zwięzły
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych. Wykład tutora na bazie wykładu prof. Marka Stankiewicza
 Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych Wykład tutora na bazie wykładu prof. Marka Stankiewicza Po co zajęcia w I Pracowni Fizycznej? 1. Obserwacja zjawisk i
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych Wykład tutora na bazie wykładu prof. Marka Stankiewicza Po co zajęcia w I Pracowni Fizycznej? 1. Obserwacja zjawisk i
PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI MARCIN FOLTYŃSKI
 PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI WŁAŚCIWIE PO CO ZAPASY?! Zasadniczą przyczyną utrzymywania zapasów jest występowanie nieciągłości w przepływach materiałów i towarów. MIEJSCA UTRZYMYWANIA ZAPASÓW
PODSTAWY LOGISTYKI ZARZĄDZANIE ZAPASAMI WŁAŚCIWIE PO CO ZAPASY?! Zasadniczą przyczyną utrzymywania zapasów jest występowanie nieciągłości w przepływach materiałów i towarów. MIEJSCA UTRZYMYWANIA ZAPASÓW
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych)
 Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Szukanie rozwiązań funkcji uwikłanych (równań nieliniowych) Funkcja uwikłana (równanie nieliniowe) jest to funkcja, która nie jest przedstawiona jawnym przepisem, wzorem wyrażającym zależność wartości
Ważne rozkłady i twierdzenia c.d.
 Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Ważne rozkłady i twierdzenia c.d. Funkcja charakterystyczna rozkładu Wielowymiarowy rozkład normalny Elipsa kowariacji Sploty rozkładów Rozkłady jednostajne Sploty z rozkładem normalnym Pobieranie próby
Rok akademicki: 2013/2014 Kod: ZIE n Punkty ECTS: 6. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Statystyka opisowa i ekonomiczna Rok akademicki: 2013/2014 Kod: ZIE-1-205-n Punkty ECTS: 6 Wydział: Zarządzania Kierunek: Informatyka i Ekonometria Specjalność: - Poziom studiów: Studia I
Nazwa modułu: Statystyka opisowa i ekonomiczna Rok akademicki: 2013/2014 Kod: ZIE-1-205-n Punkty ECTS: 6 Wydział: Zarządzania Kierunek: Informatyka i Ekonometria Specjalność: - Poziom studiów: Studia I
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych. Wykład tutora na bazie wykładu prof. Marka Stankiewicza
 Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych Wykład tutora na bazie wykładu prof. Marka tankiewicza Po co zajęcia w I Pracowni Fizycznej? 1. Obserwacja zjawisk i efektów
Podstawy opracowania wyników pomiarów z elementami analizy niepewności pomiarowych Wykład tutora na bazie wykładu prof. Marka tankiewicza Po co zajęcia w I Pracowni Fizycznej? 1. Obserwacja zjawisk i efektów
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Pakiet edukacyjny do nauki przedmiotów ścisłych i kształtowania postaw przedsiębiorczych
 ZESPÓŁ SZKÓŁ HANDLOWO-EKONOMICZNYCH IM. MIKOŁAJA KOPERNIKA W BIAŁYMSTOKU Pakiet edukacyjny do nauki przedmiotów ścisłych i kształtowania postaw przedsiębiorczych Mój przedmiot matematyka spis scenariuszy
ZESPÓŁ SZKÓŁ HANDLOWO-EKONOMICZNYCH IM. MIKOŁAJA KOPERNIKA W BIAŁYMSTOKU Pakiet edukacyjny do nauki przedmiotów ścisłych i kształtowania postaw przedsiębiorczych Mój przedmiot matematyka spis scenariuszy
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 9 Temat: Karty kontrolne przy alternatywnej ocenie właściwości.
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 9 Temat: Karty kontrolne przy alternatywnej ocenie właściwości.
MODELE LINIOWE. Dr Wioleta Drobik
 MODELE LINIOWE Dr Wioleta Drobik MODELE LINIOWE Jedna z najstarszych i najpopularniejszych metod modelowania Zależność między zbiorem zmiennych objaśniających, a zmienną ilościową nazywaną zmienną objaśnianą
MODELE LINIOWE Dr Wioleta Drobik MODELE LINIOWE Jedna z najstarszych i najpopularniejszych metod modelowania Zależność między zbiorem zmiennych objaśniających, a zmienną ilościową nazywaną zmienną objaśnianą
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania wybranych technik regresyjnych do modelowania współzależności zjawisk Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki
KARTA KURSU. (do zastosowania w roku ak. 2015/16) Kod Punktacja ECTS* 4
 KARTA KURSU (do zastosowania w roku ak. 2015/16) Nazwa Statystyka 1 Nazwa w j. ang. Statistics 1 Kod Punktacja ECTS* 4 Koordynator Dr hab. Tadeusz Sozański (koordynator, wykłady) Dr Paweł Walawender (ćwiczenia)
KARTA KURSU (do zastosowania w roku ak. 2015/16) Nazwa Statystyka 1 Nazwa w j. ang. Statistics 1 Kod Punktacja ECTS* 4 Koordynator Dr hab. Tadeusz Sozański (koordynator, wykłady) Dr Paweł Walawender (ćwiczenia)
Generowanie ciągów pseudolosowych o zadanych rozkładach przykładowy raport
 Generowanie ciągów pseudolosowych o zadanych rozkładach przykładowy raport Michał Krzemiński Streszczenie Projekt dotyczy metod generowania oraz badania własności statystycznych ciągów liczb pseudolosowych.
Generowanie ciągów pseudolosowych o zadanych rozkładach przykładowy raport Michał Krzemiński Streszczenie Projekt dotyczy metod generowania oraz badania własności statystycznych ciągów liczb pseudolosowych.
Biostatystyka, # 3 /Weterynaria I/
 Biostatystyka, # 3 /Weterynaria I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, p. 221 bud. CIW, e-mail: zdzislaw.otachel@up.lublin.pl
Biostatystyka, # 3 /Weterynaria I/ dr n. mat. Zdzisław Otachel Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, p. 221 bud. CIW, e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka - Statystyka matematyczna Mathematical statistics 2, 2, 0, 0, 0
 Nazwa przedmiotu: Kierunek: Matematyka - Statystyka matematyczna Mathematical statistics Inżynieria materiałowa Materials Engineering Rodzaj przedmiotu: Poziom studiów: forma studiów: obowiązkowy studia
Nazwa przedmiotu: Kierunek: Matematyka - Statystyka matematyczna Mathematical statistics Inżynieria materiałowa Materials Engineering Rodzaj przedmiotu: Poziom studiów: forma studiów: obowiązkowy studia
Analiza Statystyczna
 Lekcja 5. Strona 1 z 12 Analiza Statystyczna Do analizy statystycznej wykorzystać można wbudowany w MS Excel pakiet Analysis Toolpak. Jest on instalowany w programie Excel jako pakiet dodatkowy. Oznacza
Lekcja 5. Strona 1 z 12 Analiza Statystyczna Do analizy statystycznej wykorzystać można wbudowany w MS Excel pakiet Analysis Toolpak. Jest on instalowany w programie Excel jako pakiet dodatkowy. Oznacza
Testowanie hipotez statystycznych.
 Bioinformatyka Wykład 6 Wrocław, 7 listopada 2011 Temat. Weryfikacja hipotez statystycznych dotyczących proporcji. Test dla proporcji. Niech X 1,..., X n będzie próbą statystyczną z 0-1. Oznaczmy odpowiednio
Bioinformatyka Wykład 6 Wrocław, 7 listopada 2011 Temat. Weryfikacja hipotez statystycznych dotyczących proporcji. Test dla proporcji. Niech X 1,..., X n będzie próbą statystyczną z 0-1. Oznaczmy odpowiednio
ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII
 STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII Streszczenie W artykule przedstawiono
STUDIA I PRACE WYDZIAŁU NAUK EKONOMICZNYCH I ZARZĄDZANIA NR 31 Ewa Dziawgo Uniwersytet Mikołaja Kopernika w Toruniu ANALIZA WRAŻLIWOŚCI CENY OPCJI O UWARUNKOWANEJ PREMII Streszczenie W artykule przedstawiono
Statystyki: miary opisujące rozkład! np. : średnia, frakcja (procent), odchylenie standardowe, wariancja, mediana itd.
 Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Wnioskowanie statystyczne obejmujące metody pozwalające na uogólnianie wyników z próby na nieznane wartości parametrów oraz szacowanie błędów tego uogólnienia. Przewidujemy nieznaną wartości parametru
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Regresja i Korelacja
 Regresja i Korelacja Regresja i Korelacja W przyrodzie często obserwujemy związek między kilkoma cechami, np.: drzewa grubsze są z reguły wyższe, drewno iglaste o węższych słojach ma większą gęstość, impregnowane
Regresja i Korelacja Regresja i Korelacja W przyrodzie często obserwujemy związek między kilkoma cechami, np.: drzewa grubsze są z reguły wyższe, drewno iglaste o węższych słojach ma większą gęstość, impregnowane
Wykład 5: Statystyki opisowe (część 2)
 Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Wykład 5: Statystyki opisowe (część 2) Wprowadzenie Na poprzednim wykładzie wprowadzone zostały statystyki opisowe nazywane miarami położenia (średnia, mediana, kwartyle, minimum i maksimum, modalna oraz
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania
 Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA I WSPOMAGANIA DECYZJI Rozproszone programowanie produkcji z wykorzystaniem
Politechnika Gdańska Wydział Elektrotechniki i Automatyki Katedra Inżynierii Systemów Sterowania KOMPUTEROWE SYSTEMY STEROWANIA I WSPOMAGANIA DECYZJI Rozproszone programowanie produkcji z wykorzystaniem
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014
 Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienne losowe i ich rozkłady. Momenty zmiennych losowych. Wrocław, 10 października 2014 Zmienne losowe i ich rozkłady Doświadczenie losowe: Rzut monetą Rzut kostką Wybór losowy n kart z talii 52 Gry losowe
Zmienna losowa i jej rozkład Dystrybuanta zmiennej losowej Wartość oczekiwana zmiennej losowej
 Zmienna losowa i jej rozkład Dystrybuanta zmiennej losowej Wartość oczekiwana zmiennej losowej c Copyright by Ireneusz Krech ikrech@ap.krakow.pl Instytut Matematyki Uniwersytet Pedagogiczny im. KEN w Krakowie
Zmienna losowa i jej rozkład Dystrybuanta zmiennej losowej Wartość oczekiwana zmiennej losowej c Copyright by Ireneusz Krech ikrech@ap.krakow.pl Instytut Matematyki Uniwersytet Pedagogiczny im. KEN w Krakowie
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/
 Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Matematyka z el. statystyki, # 6 /Geodezja i kartografia II/ Uniwersytet Przyrodniczy w Lublinie Katedra Zastosowań Matematyki i Informatyki ul. Głęboka 28, bud. CIW, p. 221 e-mail: zdzislaw.otachel@up.lublin.pl
Zadanie 1. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k =
 Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Matematyka ubezpieczeń majątkowych 0.0.006 r. Zadanie. Liczba szkód N w ciągu roku z pewnego ryzyka ma rozkład geometryczny: k 5 Pr( N = k) =, k = 0,,,... 6 6 Wartości kolejnych szkód Y, Y,, są i.i.d.,
Spis treści 3 SPIS TREŚCI
 Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Spis treści 3 SPIS TREŚCI PRZEDMOWA... 1. WNIOSKOWANIE STATYSTYCZNE JAKO DYSCYPLINA MATEMATYCZNA... Metody statystyczne w analizie i prognozowaniu zjawisk ekonomicznych... Badania statystyczne podstawowe
Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11,
 1 Kwantyzacja skalarna Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11, 10.05.005 Kwantyzacja polega na reprezentowaniu dużego zbioru wartości (być może nieskończonego) za pomocą wartości
1 Kwantyzacja skalarna Kodowanie i kompresja Streszczenie Studia Licencjackie Wykład 11, 10.05.005 Kwantyzacja polega na reprezentowaniu dużego zbioru wartości (być może nieskończonego) za pomocą wartości
MODELOWANIE KOSZTÓW USŁUG ZDROWOTNYCH PRZY
 MODELOWANIE KOSZTÓW USŁUG ZDROWOTNYCH PRZY WYKORZYSTANIU METOD STATYSTYCZNYCH mgr Małgorzata Pelczar 6 Wprowadzenie Reforma służby zdrowia uwypukliła problem optymalnego ustalania kosztów usług zdrowotnych.
MODELOWANIE KOSZTÓW USŁUG ZDROWOTNYCH PRZY WYKORZYSTANIU METOD STATYSTYCZNYCH mgr Małgorzata Pelczar 6 Wprowadzenie Reforma służby zdrowia uwypukliła problem optymalnego ustalania kosztów usług zdrowotnych.
Statystyka matematyczna i ekonometria
 Statystyka matematyczna i ekonometria prof. dr hab. inż. Jacek Mercik B4 pok. 55 jacek.mercik@pwr.wroc.pl (tylko z konta studenckiego z serwera PWr) Konsultacje, kontakt itp. Strona WWW Elementy wykładu.
Statystyka matematyczna i ekonometria prof. dr hab. inż. Jacek Mercik B4 pok. 55 jacek.mercik@pwr.wroc.pl (tylko z konta studenckiego z serwera PWr) Konsultacje, kontakt itp. Strona WWW Elementy wykładu.
Matematyka ubezpieczeń majątkowych r.
 Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Matematyka ubezpieczeń majątkowych 3..007 r. Zadanie. Każde z ryzyk pochodzących z pewnej populacji charakteryzuje się tym że przy danej wartości λ parametru ryzyka Λ rozkład wartości szkód z tego ryzyka
Regresja logistyczna (LOGISTIC)
 Zmienna zależna: Wybór opcji zachodniej w polityce zagranicznej (kodowana jako tak, 0 nie) Zmienne niezależne: wiedza o Unii Europejskiej (WIEDZA), zamieszkiwanie w regionie zachodnim (ZACH) lub wschodnim
Zmienna zależna: Wybór opcji zachodniej w polityce zagranicznej (kodowana jako tak, 0 nie) Zmienne niezależne: wiedza o Unii Europejskiej (WIEDZA), zamieszkiwanie w regionie zachodnim (ZACH) lub wschodnim
Teoria portfelowa H. Markowitza
 Aleksandra Szymura szymura.aleksandra@yahoo.com Teoria portfelowa H. Markowitza Za datę powstania teorii portfelowej uznaje się rok 95. Wtedy to H. Markowitz opublikował artykuł zawierający szczegółowe
Aleksandra Szymura szymura.aleksandra@yahoo.com Teoria portfelowa H. Markowitza Za datę powstania teorii portfelowej uznaje się rok 95. Wtedy to H. Markowitz opublikował artykuł zawierający szczegółowe
Streszczenie: Zasady projektowania konstrukcji budowlanych z uwzględnieniem aspektów ich niezawodności wg Eurokodu PN-EN 1990
 Streszczenie: W artykule omówiono praktyczne podstawy projektowania konstrukcji budowlanych wedłu Eurokodu PN-EN 1990. Podano metody i procedury probabilistyczne analizy niezawodności konstrukcji. Podano
Streszczenie: W artykule omówiono praktyczne podstawy projektowania konstrukcji budowlanych wedłu Eurokodu PN-EN 1990. Podano metody i procedury probabilistyczne analizy niezawodności konstrukcji. Podano
Estymacja wektora stanu w prostym układzie elektroenergetycznym
 Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Zakład Sieci i Systemów Elektroenergetycznych LABORATORIUM INFORMATYCZNE SYSTEMY WSPOMAGANIA DYSPOZYTORÓW Estymacja wektora stanu w prostym układzie elektroenergetycznym Autorzy: dr inż. Zbigniew Zdun
Rok akademicki: 2030/2031 Kod: ZZIP n Punkty ECTS: 3. Poziom studiów: Studia I stopnia Forma i tryb studiów: -
 Nazwa modułu: Logistyka Rok akademicki: 2030/2031 Kod: ZZIP-1-604-n Punkty ECTS: 3 Wydział: Zarządzania Kierunek: Zarządzanie i Inżynieria Produkcji Specjalność: - Poziom studiów: Studia I stopnia Forma
Nazwa modułu: Logistyka Rok akademicki: 2030/2031 Kod: ZZIP-1-604-n Punkty ECTS: 3 Wydział: Zarządzania Kierunek: Zarządzanie i Inżynieria Produkcji Specjalność: - Poziom studiów: Studia I stopnia Forma
Szczegółowy rozkład materiału dla klasy 3b poziom rozszerzny cz. 1 - liceum
 Szczegółowy rozkład materiału dla klasy b poziom rozszerzny cz. - liceum WYDAWNICTWO PAZDRO GODZINY Lp. Tematyka zajęć Liczba godzin I. Funkcja wykładnicza i funkcja logarytmiczna. Potęga o wykładniku
Szczegółowy rozkład materiału dla klasy b poziom rozszerzny cz. - liceum WYDAWNICTWO PAZDRO GODZINY Lp. Tematyka zajęć Liczba godzin I. Funkcja wykładnicza i funkcja logarytmiczna. Potęga o wykładniku
Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów. Dawid Doliński
 Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów Dawid Doliński Dlaczego MonZa? Korzyści z wdrożenia» zmniejszenie wartości zapasów o 40 %*» podniesienie poziomu obsługi
Zarządzanie Zapasami System informatyczny do monitorowania i planowania zapasów Dawid Doliński Dlaczego MonZa? Korzyści z wdrożenia» zmniejszenie wartości zapasów o 40 %*» podniesienie poziomu obsługi
OPISU MODUŁU KSZTAŁCENIA (SYLABUS) dla przedmiotu Logistyka na kierunku Zarządzanie
 dr Andrzej Podleśny Poznań, dnia 1 października 2017 roku OPISU MODUŁU KSZTAŁCENIA (SYLABUS) dla przedmiotu Logistyka na kierunku Zarządzanie I. Informacje ogólne 1. Nazwa modułu kształcenia: Logistyka
dr Andrzej Podleśny Poznań, dnia 1 października 2017 roku OPISU MODUŁU KSZTAŁCENIA (SYLABUS) dla przedmiotu Logistyka na kierunku Zarządzanie I. Informacje ogólne 1. Nazwa modułu kształcenia: Logistyka
Statystyka matematyczna. dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt
 Statystyka matematyczna dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt Zasady zaliczenia przedmiotu: część wykładowa Maksymalna liczba punktów do zdobycia 40. Egzamin będzie
Statystyka matematyczna dr Katarzyna Góral-Radziszewska Katedra Genetyki i Ogólnej Hodowli Zwierząt Zasady zaliczenia przedmiotu: część wykładowa Maksymalna liczba punktów do zdobycia 40. Egzamin będzie
1 Podstawy rachunku prawdopodobieństwa
 1 Podstawy rachunku prawdopodobieństwa Dystrybuantą zmiennej losowej X nazywamy prawdopodobieństwo przyjęcia przez zmienną losową X wartości mniejszej od x, tzn. F (x) = P [X < x]. 1. dla zmiennej losowej
1 Podstawy rachunku prawdopodobieństwa Dystrybuantą zmiennej losowej X nazywamy prawdopodobieństwo przyjęcia przez zmienną losową X wartości mniejszej od x, tzn. F (x) = P [X < x]. 1. dla zmiennej losowej
Komputerowa Analiza Danych Doświadczalnych
 Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
Komputerowa Analiza Danych Doświadczalnych Prowadząca: dr inż. Hanna Zbroszczyk e-mail: gos@if.pw.edu.pl tel: +48 22 234 58 51 konsultacje: poniedziałek, 10-11, środa: 11-12 www: http://www.if.pw.edu.pl/~gos/students/kadd
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 4 Temat: Analiza korelacji i regresji dwóch zmiennych
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 4 Temat: Analiza korelacji i regresji dwóch zmiennych
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, Spis treści
 Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
Z Wikipedii, wolnej encyklopedii.
 Rozkład normalny Rozkład normalny jest niezwykle ważnym rozkładem prawdopodobieństwa w wielu dziedzinach. Nazywa się go także rozkładem Gaussa, w szczególności w fizyce i inżynierii. W zasadzie jest to
Rozkład normalny Rozkład normalny jest niezwykle ważnym rozkładem prawdopodobieństwa w wielu dziedzinach. Nazywa się go także rozkładem Gaussa, w szczególności w fizyce i inżynierii. W zasadzie jest to
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
Symulacja obrotów magazynowych
 Symulacja obrotów magazynowych Wykorzystanie symulacji komputerowej w zarządzaniu przedsiębiorstwem stanowi obecnie jeden z dynamiczniej rozwijających się kierunków badań. Możliwość sięgnięcia w przyszłość
Symulacja obrotów magazynowych Wykorzystanie symulacji komputerowej w zarządzaniu przedsiębiorstwem stanowi obecnie jeden z dynamiczniej rozwijających się kierunków badań. Możliwość sięgnięcia w przyszłość
BŁĘDY W POMIARACH BEZPOŚREDNICH
 Podstawy Metrologii i Technik Eksperymentu Laboratorium BŁĘDY W POMIARACH BEZPOŚREDNICH Instrukcja do ćwiczenia nr 2 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy Metrologii
Podstawy Metrologii i Technik Eksperymentu Laboratorium BŁĘDY W POMIARACH BEZPOŚREDNICH Instrukcja do ćwiczenia nr 2 Zakład Miernictwa i Ochrony Atmosfery Wrocław, listopad 2010 r. Podstawy Metrologii
Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich
 Podstawy Metrologii i Technik Eksperymentu Laboratorium Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich Instrukcja do ćwiczenia nr 4 Zakład Miernictwa
Podstawy Metrologii i Technik Eksperymentu Laboratorium Sprawdzenie narzędzi pomiarowych i wyznaczenie niepewności rozszerzonej typu A w pomiarach pośrednich Instrukcja do ćwiczenia nr 4 Zakład Miernictwa
Rachunek prawdopodobieństwa WZ-ST1-AG--16/17Z-RACH. Liczba godzin stacjonarne: Wykłady: 15 Ćwiczenia: 30. niestacjonarne: Wykłady: 9 Ćwiczenia: 18
 Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Analityka gospodarcza I. Informacje podstawowe Nazwa przedmiotu Rachunek prawdopodobieństwa Nazwa przedmiotu w j. ang. Język prowadzenia przedmiotu
Karta przedmiotu Wydział: Wydział Zarządzania Kierunek: Analityka gospodarcza I. Informacje podstawowe Nazwa przedmiotu Rachunek prawdopodobieństwa Nazwa przedmiotu w j. ang. Język prowadzenia przedmiotu
Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony. Klasa I (90 h)
 Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony (według podręczników z serii MATeMAtyka) Klasa I (90 h) Temat Liczba godzin 1. Liczby rzeczywiste 15
Propozycja szczegółowego rozkładu materiału dla 4-letniego technikum, zakres podstawowy i rozszerzony (według podręczników z serii MATeMAtyka) Klasa I (90 h) Temat Liczba godzin 1. Liczby rzeczywiste 15
KOMPUTEROWA SYMULACJA PROCESÓW ZWIĄZANYCH Z RYZYKIEM PRZY WYKORZYSTANIU ŚRODOWISKA ADONIS
 KOMPUTEROWA SYMULACJA PROCESÓW ZWIĄZANYCH Z RYZYKIEM PRZY WYKORZYSTANIU ŚRODOWISKA ADONIS Bogdan RUSZCZAK Streszczenie: Artykuł przedstawia metodę komputerowej symulacji czynników ryzyka dla projektu inwestycyjnego
KOMPUTEROWA SYMULACJA PROCESÓW ZWIĄZANYCH Z RYZYKIEM PRZY WYKORZYSTANIU ŚRODOWISKA ADONIS Bogdan RUSZCZAK Streszczenie: Artykuł przedstawia metodę komputerowej symulacji czynników ryzyka dla projektu inwestycyjnego
Rozkład normalny Parametry rozkładu zmiennej losowej Zmienne losowe wielowymiarowe
 Statystyka i opracowanie danych W4 Rozkład normalny Parametry rozkładu zmiennej losowej Zmienne losowe wielowymiarowe Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Rozkład normalny wykres funkcji gęstości
Statystyka i opracowanie danych W4 Rozkład normalny Parametry rozkładu zmiennej losowej Zmienne losowe wielowymiarowe Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Rozkład normalny wykres funkcji gęstości
