ISSN PL INSTYTUT CHEMII I TECHNIKI JĄDROWEJ INSTITUTE OF NUCLEAR CHEMISTRY AND TECHNOLOGY WARSZAWA 7BM 1
|
|
|
- Eugeniusz Sebastian Kwiecień
- 8 lat temu
- Przeglądów:
Transkrypt
1 ISSN PL INSTYTUT CHEMII I TECHNIKI JĄDROWEJ INSTITUTE OF NUCLEAR CHEMISTRY AND TECHNOLOGY WARSZAWA 7BM 1
2 RAPORTY IChTJ. SERIA B nr 2/96 TEST KOMETKOWY. 2. ANALIZA STATYSTYCZNA WYNIKÓW Marcin Kruszewski Warszawa 1996
3 ZESPÓŁ REDAKCYJNY dr Wiktor Smułek, Ewa Godlewska, Sylwester Wojtas WYDAWCA Instytut Chemii i Techniki Jądrowej ul. Dorodna 16, Warszawa tel.: (0-22) ; telex: ichtj pl: fax: (0-22) ; sekdyrn@orange. ichtj.waw.pl Raport zosta! wydany w postaci otrzymanej od Autora Symbol UKD: Symbol INIS: Cl 1.00 Słowa kluczowe: ANALIZA STATYSTYCZNA, TEST KOMETKOWY
4 Test kometkowy. 2. Anal za statystyczna wyników W pracy opisano niektóre metody statystyczne używane do oceny wyników otrzymanych testem kometkowym. Metody statystyczne opisano na przykładzie pakietu Statistica w oparciu o podręcznik Biostatistical analysis, J.H. Zar, Prentice-Hall International, Inc., Comet assay. 2. Statistical analysis of results Statistical methods commonly used for analysis of results of the comet assay was described, based on the Statistica analytical software. NEXT PAQE(S) left BLANK
5 SPIS TREŚCI 1. Analiza pojedynczej próbki 1.1. Analiza rozkładu próbki 1.2. Ocena skośności ^ 1.3. Ocena kurtozy 2. Określenie homogenności połączonych doświadczeń 8 3. Porównanie średnich dwóch próbek ( 3.1. Rozkład normalny Wariancje są równe Próby niezależne Próby zależne Wariancje nie są równe 3.2. Rozkład nie jest normalny Próby niezależne Próby zależne g 4. Porównanie wielu prób 4.1. Rozkłady normalne i wariancje jednakowe * i* * ' * i 1 _. ~~ _* *** A 4.2. Rozkłady nienormalne i/lub niejednakowe wariancje 4.3. Porównania wielokrotne post hoc / (7 /O 5. Badanie zależności między zmiennymi 5.1. Korelacja Zmienne o rozkładzie normalnym Zmienne o rozkładzie nienormalnym Porównanie dwóch współczynników korelacji Porównanie więcej niż dwóch współczynników korelacji Regresja "! Obliczanie kąta nachylenia prostej regresji (b) Błąd standardowy wartości b Punkt przecięcia z osią OYi jego błąd standardowy I Obliczanie X dla znanego Y Sprawdzenie istotności obliczonego współczynnika nachylenia prostej regresji Porównanie dwóch współczynników nachylenia prostych regresji /-/ Porównanie dwóch elewacji _ Porównywanie punktów na prostych regresji -^ Porównanie więcej niż dwóch współczynników nachylenia prostych regresji Porównanie post hoc więcej niż dwóch prostych regresji ^ Porównanie więcej niż dwóch elewacji Porównanie post hoc więcej niż dwóch elewacji prostych regresji / 5.3. Diagram porównania prostych regresji z: I I 8 6. Literatura NEXT PAGE(S) left BLANK
6 1. ANALIZA POJEDYNCZEJ PRÓBKI 1.1. ANALIZA ROZKŁADU PRÓBKI Analiza ma na celu określenie czy rozkład próbki jest normalny, oraz określenie parametrów rozkładu (kurtozy i symetrii (skośności)). Ponieważ parametry badanego rozkładu określa się na podstawie próbki badanej, hipotezę należy sprawdzić testem Shapiro-Wilka lub testem Kołmogonorowa-Smirnowa, z poprawką Lilleforce'a. Ho: rozkład próbki jest normalny HA: rozkład próbki nie jest normalny Jeżeli p<0,05 należy odrzucić Ho (rozkład próbki nie jest normalny) OCENA SKOŚNOŚCI Skośność (yi) jest trzecim momentem średniej ([1], str.81). Statystyczną ocenę skośności prowadzi się w zasadzie dopiero dla dużych próbek n>150 (odpowiednia statystyka została opisana w [1], str. 118). Jeżeli: Yi=0 to rozkład jest symetryczny; Yi<0 próbka pochodzi z populacji w której średnia jest mniejsza niż mediana; yi>0 próbka pochodzi z populacji w której średnia jest większa niż mediana. Dla małych próbek można sprawdzić symetrię rozkładu korzystając z tabeli B.20 w [1]. Wartość (yi) obliczoną dla rozkładu porównuje się z wartością w tabeli B.20 dla danego poziomu istotności: oc<2) = 0,05 dla testu dwustronnego i a<i) = 0,025 dla testu jednostronnego OCENA KURTOZY Kurtoza (y 2 ) jest czwarty momentem średniej ([1], str.81). Jej statystyczną ocenę prowadzi się dla próbek n>1000 (odpowiednia statystyka została opisana w [1], str. 119). Na podstawie obliczonej wartości (y 2 ) można dokonać ogólnej oceny kurtozy. Populacje mające: (y 2 ) = 0 są normalne (mezokurtyczne); (y 2 ) < 0 (platykurtyczne) mogą pochodzić z dwóch populacji o takiej samej wariancji ale różnych średnich; (y 2 ) > 0 (mezokurtyczne) mogą pochodzić z dwóch populacji o takiej samej średniej ale różnych wariancjach. We wszystkich przykładach uważa się, że poziom istotności p=0.05 jest wystarczający
7 2. OKREŚLENIE HOMOGENNOŚCI POŁĄCZONYCH DOŚWIADCZEŃ Połączenie wyników dwóch doświadczeń i ich wspólna analiza zwiększa moc testu (większe n). Możliwość połączenia wyników dwóch próbek określa się za pomocą testu heterogenności x", opierając się na założeniu, że yj połączonych wyników równe jest sumie x" poszczególnych prób. Ho: próbki są homogenne HA: próbki nie są homogenne Należy przeprowadzić analizę rozkładu prób testem % 2 dopasowując je do rozkładu normalnego i zsumować poszczególne wartości, następnie testem % 2 przeprowadzić analizę rozkładu połączonych prób, dopasowując je do tego samego rozkładu. Od sumy yj dla poszczególnych prób odjąć wartość y? dla prób połączonych. Na podstawie otrzymanej wartości sprawdzić istotność Ho dla ilości stopni swobody DF = (ilość prób) - 1. Jeżeli p<0,05 należy odrzucić Ho (próbki są heterogenne) i nie można ich połączyć. 3. PORÓWNANIE ŚREDNICH DWÓCH PRÓBEK 3.1. ROZKŁAD NORMALNY W przypadku potwierdzenia normalności rozkładu należy sprawdzić czy wariancje obu porównywanych prób są równe. Do porównania wariancji używa się testu F Fischera lub testu Lavene'a. Ho: wariancje są równe HA: wariancje nie są równe Jeżeli p<0,05 należy odrzucić Ho (wariancje nie są równe). Uwaga: Test F Fischera często jest zawarty w module analizy testem t-studenta (np. w pakiecie Statistica) i nie ma potrzeby oddzielnego obliczania tego testu Wariancje są równe Próby niezależne W przypadku stwierdzenia równości wariancji do porównania dwóch średnich należy użyć testu t-studenta dla prób niezależnych. Ho: Średnie są równe : Średnie nie są równe Jeżeli p<0,05 należy odrzucić Ho (średnie nie są równe). Uwaga: Testem t-studenta można także sprawdzać hipotezy jednostronne np. Ho: średnia 1> średnia2 : średnia I<średnia Próby zależne W przypadku stwierdzenia równości wariancji do porównania dwóch średnich należy użyć testu t-studenta dla prób zależnych.
8 H o : Średnie są równe : Średnie nie są równe Jeżeli p<0,05 należy odrzucić H o (średnie nie są równe). Uwaga: Test t jest mocny jeżeli ilość obserwacji w próbach jest jednakowa i jednakowe są wariancje prób. Testem t-studenta można także sprawdzać hipotezy jednostronne np. Ho: średnia 1> średnia2 : średnia I<średnia Wariancje nie są równe Jeżeli n>30 a różnica wariancji nie jest duża i/lub próby nie są równe, to można użyć testu t-studenta z poprawką na osobną ocenę wariancji lub innych testów np. Cochran-Coxa. Jeżeli różnica wariancji jest duża to lepiej użyć któregoś z testów nieparametrycznych (patrz 3.2.) ROZKŁAD NIE JEST NORMALNY W przypadku stwierdzenia, że rozkład nie jest normalny do porównania dwóch średnich należy użyć testów nieparametrycznych Próby niezależne Do porównania dwóch średnich prób niezależnych należy użyć testu U Mann-Whitney'a (korzystny) lub testu Kołmogonorowa-Smirnowa dla dwóch prób. Korzystnie jest przeprowadzić oba testy, chociaż test Mann-Whitney'a jest silniejszy niż test Kołmogonorowa-Smirnowa dla dwóch prób, to ten ostatni jest bardziej czuły na różnice w kształcie rozkładów. Ho: Średnie są równe : Średnie nie są równe Jeżeli p<0,05 należy odrzucić Ho (średnie nie są równe) Próby zależne Do porównania dwóch średnich prób zależnych należy użyć testu znakowego różnic (sign test) lub testu Wilcoxona dla par powiązanych. Ho: Średnie są równe : Średnie nie są równe Jeżeli p<0,05 należy odrzucić Ho (średnie nie są równe). 4. PORÓWNANIE WIELU PRÓB Najczęściej stosowany sposób porównania wielu prób poprzez wielokrotne porównanie parami testem t-studenta, nie jest odpowiedni i może prowadzić do mylnej oceny istotności różnicy średnich. Prawdopodobieństwo popełnienia błędu I rodzaju (odrzucenie hipotezy zerowej jeżeli w istocie jest ona prawdziwa) przy porównaniu parami testem t-studenta 10 średnich wynosi 0,63 przy poziomie ufności a=0,05. Porównanie takie powinno się prowadzić metodą jednoczynnikowej analizy wariancji (one-way ANOVA), dwuczynnikowej analizy
9 wariancji (two-way ANOVA) lub wieloczynnikowej analizy wariancji (MANOVA) (dla prób o rozkładzie normalnym) lub ich nieparametrycznymi odpowiednikami, np. ANOVA Kruskal- Wallisa (dla prób o rozkładzie nienormalnym) ROZKŁADY NORMALNE I WARIANCJE JEDNAKOWE Do porównania średnich kilku prób mających normalne rozkłady i jednakowe wariancje używa się jednoczynnikowej analizy wariancji (one-way ANOVA). Jednoczynnikowej analizy wariancji można także użyć, jeżeli różnica między wariancjami nie jest zbyt duża i (1) n>10 oraz (2) średnie grup nie są skorelowane z odchyleniem standardowym. H o : Średnie są równe : Średnie nie są równe Jeżeli p<0,05 należy odrzucić H o (średnie nie są równe). Uwaga 1: Istnieją przynajmniej trzy typy analizy ANOVA. Model I i II i III. Analiza typu I powinna być prowadzona jeżeli zakłada się stały wpływ efektu na zmienne, np. wzrastająca dawka czynnika, analiza typu II - kiedy efekt jest rzeczywiście losowy, np. porównanie średnich kontroli. Model III występuje w przypadku gdy działanie czynnika jest mieszane, czyli zachodzi stały i losowy wpływ efektu na zmienne. I Uwaga 2: Przy przeprowadzaniu analizy metodą dwuczynnikowej analizy wariancji korzystnie jest mieć jednakową ilość powtórzeń w każdym punkcie, jednakże możliwe jest też przeprowadzenie takiej analizy przy niejednakowej ilości powtórzeń ROZKłADY NIENORMALNE I/LUB NIEJEDNAKOWE WARIANCJE Do porównania średnich kilku prób mających nienormalne rozkłady i/lub niejednakowe wariancje używa się testu Kruskal-Wallisa, zwanego też analizą wariancji według rang. Test ten można też stosować wszędzie tam gdzie stosuje się jednoczynnikowy test ANOVA, wtedy test Kruskal-Wallisa, ma moc 95% testu ANOVA. Testu Kruskal-Wallisa można też użyć do nieparametrycznej analizy dwuczynnikowej 4.3. PORÓWNANIA WIELOKROTNE POST HOC Często po odrzuceniu hipotezy o równości wariancji, zachodzi potrzeba wzajemnego porównania poszczególnych prób (wariancji), w celu określenia, które próby różnią się, a które nie. Chociaż często stosowane jest porównanie parami testem t-studenta, nie jest to najlepszy sposób takiej analizy. Po odrzuceniu Ho można przeprowadzić analizę post hoc, w celu znalezienia średnich odbiegających. Pakiet Statistika zawiera następujące testy umożliwiające analizę post hoc. test LSD (odpowiednik testu t-studenta), test Scheffe'a, test Neuman-Keulsa, test Duncana, test Tukey'a. Korzystnie jest porównać wyniki kilku testów. Najczęściej używane (i zalecane) są testy Tukey'a (Tukey Honest Significant Difference test) i test Neuman-Keulsa. Testy te powinny być stosowane przede wszystkim w przypadku analizy ANOVA typu I. Jeżeli próbki nie są równej wielkości można użyć testu Tukey'a dla nierównych wielkości próbek (Tukey HSD test for unequal sample size), zwanego też testem Spjotvoll-Stoline. 10
10 Do porównań wielokrotnych prób nieparametrycznych stosuje się odmianę testu Tukey'a, w którym rangi nadaje się sumom, a nie średnim ([1], str. 199). Pakiet Statistica oferuje też inne rodzaje analizy wariancji, takie jak dwuczynnikowa analiza wariancji, wieloczynnikowa analiza wariancji, czy hierarchiczna analiza wariancji (nested ANOVA), jednakże dokładny opis tych metod wykracza poza ramy tego opracowania. Dokładny opis wymienionych metod zamieszczony jest w [1], str BADANIE ZALEŻNOŚCI MIĘDZY ZMIENNYMI Na podstawie wyników doświadczalnych można sprawdzić czy zmierzone wielkości zależą od siebie, czy też ich wzajemne powiązanie jest przypadkowe. Różnica między regresją a korelacją polega na tym, że w przypadku regresji zakładamy a priori, że Y zależy od X, natomiast badając korelację określamy czy Y zależy od A'i czy Xzależy od Y. Po stwierdzeniu, że badane wielkości zależą od siebie (korelacja) można obliczyć krzywą regresji, a więc sposób w jaki Y zmienia się w zależności od X KORELACJA Zmienne o rozkładzie normalnym Stopień zależności od siebie dwóch badanych wielkości oznacza się jako współczynnik korelacji r (1), a jego błąd standardowy s r określony jest wzorem (2), w którym n oznacza liczbę punktów na podstawie których przeprowadzono korelację. (o Za pomocą testu t-studenta należy sprawdzić istotność statystyczną obliczonego współczynnika korelacji według wzoru (3): * = -, (3) w którym r oznacza obliczony współczynnik korelacji, s r obliczony według wzoru (2) błąd standardowy. Ilość stopni swobody oblicza się v = n - 2, gdzie n to liczba punktów, na podstawie których przeprowadzono korelację. Ho:r = O :r*0 Hipotezę zerową Ho: r = 0 odrzuca się na korzyść : r#0, jeżeli / > t a(2 ) lv. Za pomocą testu t-studenta można także testować hipotezy jednostronne. 11
11 Zmienne o rozkładzie nienormalnym Jeżeli bada się korelację zmiennych o rozkładzie nienormalnym należy zastosować test korelacji rang Spearmana lub analogiczny test Kendala. Odpowiednia statystyka została opisana w [1], str Porównanie dwóch współczynników korelacji Program Statistica oferuje także możliwość porównania dwóch współczynników korelacji i określenia istotności różnicy między nimi. Odpowiednia statystyka została opisana w [1], str Porównanie więcej niż dwóch współczynników korelacji Do porównania więcej niż dwóch współczynników korelacji wykorzystuje się wzór (4): (4) I=I w którym /; oznacza ilość punktów na podstawie których obliczono korelację, a Ho', n = r 2 = ric i*.\'. T\ ^ r 2 ^ Tic Obliczoną wartość porównuje się z wartością / a dla v = k - 1 stopni swobody (k liczba porównywanych współczynników korelacji). Hipotezę Ho: n = r 2 = rt (elewacje nie są równe) odrzuca się, jeżeli wartość obliczona jest większa niż niż wartość prawdopodobieństwa %~ av. Po odrzuceniu hipotezy o równości współczynników korelacji możliwe jest porównanie post hoc poszczególnych współczynników, w celu znalezienia współczynników korelacji różniących się od innych. Odpowiednia statystyka jest opisana w [1], str (5) 5.2. REGRESJA Po stwierdzeniu zależności pomiędzy zmiennymi, można zbadać w jaki sposób zmienna zależna zależy od zmiennej niezależnej. Do określania zależności między zmiennymi używa się najczęściej metody najmniejszych kwadratów. W tym opracowaniu zostanie omówiona jedynie regresja prostoliniowa, ponieważ jej statystyczne podstawy są najlepiej poznane i jest ona najczęściej używana, jednakże pakiet Statistica oferuje także możliwości stosowania regresji nieliniowej. Jeżeli zależność pomiędzy zmiennymi jest prostoliniowa, to wyrażają wzór (6): y = bx + a, (6) w którym b oznacza współczynnik regresji, odpowiadający kątowi nachylenia prostej regresji (slope), natomiast a odpowiada punktowi przecięcia prostej regresji z osią OY (Y intercept/ 12
12 Obliczar ie kąta nachylenia prostej regresji (b) Najlepsze przybliżenie wartości b określa wzór (7)- w którym y x 2 ' n (8) n (9) Błąd standardowy wartości b Błąd standardowy wartości b określony jest wzorem (10): (10) w którym s r, x oznacza błąd standardowy regresji określony wzorem (11): tss-rss w którym (12) (13) n Wartość s r, x jest bezpośrednio związana z współczynnikiem regresji i błędem standardowym y (s y ) i można ją także obliczyć ze wzoru (14) s r.x (14) Punkt przecięcia z osią OY i jego błąd standardowy Najlepszym przybliżeniem wartości a jest a = y-bx, (15) w którym y i x są wartościami średnimi. Błąd standardowy wartości a określony jest wzorem (16): s, = n w którym x jest wartością średnią, a Sy, x oznacza błąd standardowy regresji określony wzorem (11) lub (14). (16)
13 Obliczanie A'dla znanego Y Znając równanie prostej regresji oraz wartość y :, można na podstawie wzoru (17) obliczyć wartość X (inverse prediction) B, - ^, (.7) (1-a) przedziały ufności obliczonego x] nie są symetryczne względem wyznaczonego xi i oblicza sieje ze wzoru (18) w +*?.-y) t L L K K n \r V >#A ' y x~ v n w którym / = t a{2)an.2h K = tf-fisl \, s b określone jest wzorem (10)., (18) Sprawdzenie istotności obliczonego współczynnika nachylenia prostej regresji Za pomocą testu t-studenta można sprawdzić istotność statystyczną obliczonego współczynnika nachylenia prostej regresji. H o : bi = 0 : b, * 0 Odpowiednia statystyka opisana jest wzorem (19): / = ^-, (19) w którym s b jest błędem standardowym obliczonym z wzoru (10). Obliczoną wartość porównuje się z wartością testu t dla n-2 stopni swobody Porównanie dwóch współczynników nachylenia prostych regresji Dwa kąty nachylenia można porównać testem t-studenta. Statystyka jest opisana wzorem: / = ^ Ł, (20) w którym (rss) <+ (rss) : Indeksy dolne / / 2 odnoszą się do analizowanych prostych regresji. Otrzymaną wartość porównuje się z krytyczną wartością / dla v = /// + ni - 4 stopni swobody. Jeżeli współczynniki nachylenia prostej nie są równe, można obliczyć punkt przecięcia krzywych X,Yr. X. = a -~ a ', (23) J bb
14 r, =a,+a 2 * / =a *,- (24) Natomiast jeżeli Ho: bi=b2 to można obliczyć wartość wspólnego współczynnika nachylenia prostej regresji b c wyrażoną wzorem (25): = Porównanie dwóch elewacji Po odrzuceniu Ho: bi=b2 można przyjąć, że badane populacje są różne. Jednakże, jeżeli kąty nachylenia prostych są takie same, to proste te mogą mieć różny punkt przecięcia z osią OY (elewacja). Do określenia, czy elewacja obu prostych regresji jest taka sama używa się testu t-studenta : / = 1 1 I \MS C I (y - y \ 2 MS C = ^ c c * A c DF C (27) (28) (30) Otrzymaną wartość t porównuje się z wartością / w tablicach dla v = DFc stopni swobody. Jeżeli dwie elewacje prostych regresji nie różnią się znamiennie to można obliczyć wspólną dla obu prostych elewację: (3D Jeżeli stwierdzono, że obie proste regresji mają takie same kąty nachylenia i elewacje to wspólna prosta regresji dla obu populacji wyników będzie miała wzór: Y,=a c +b c X, (33) Porównywanie punktów na prostych regresji Jeżeli stwierdzono, że dwie proste regresji mają takie same współczynniki nachylenia i takie same elewacje, to proste te są takie same i ich punkty nie różnią się ze statystycznego punktu widzenia. Jeżeli dwie proste regresji mają takie same współczynniki nachylenia, ale różne elewacje, to proste te są równoległe, a punkty na ich leżące różnią się od siebie. Jeżeli dwie proste regresji mają różne współczynniki nachylenia, to proste te przecinają się i można sprawdzić, które z punktów tych prostych różnią się. Porównania dokonuje się testem t- Studenta: 15
15 (34) "»> (I* 2 ), Otrzymaną wartość / porównuje się z wartością / w tablicach dla v = //, f /ij - 4 stopni swobody. Testu należy jednak używać z ostrożnością ponieważ zakłada, że każda z przewidywanych wartości Y związana jest z taką samą wariancją. Test jest najsilniejszy, jeżeli obie proste mają takie same X i // Porównanie więcej niż dwóch współczynników nachylenia prostych regresji Do porównania więcej niż dwóch współczynników prostych prostych regresji używa się procedury znanej jako analiza kowariancji. H o : p, = p 2 = Pk i _} w którym F = fcss-pss} { k-l ) pss DF 1=1 I.*. Z 4 1=1 DF = Y(n, -2) =Yn-lk. 1=1 1=1 (35) (36) (37) (38) Jeżeli stwierdzono, że kąty nachylenia prostych regresji nie różnią się, to można obliczyć wspólny kąt nachylenia prostych regresji: T HI Porównanie post hoc więcej niż dwóch prostych regresji Jeżeli porównanie kilku kątów nachylenia prostych regresji wykazało, że nie są one równe, to do porównania poszczególnych par kątów nachylenia prostych regresji należy użyć testu Tukey'a lub jeżeli porównuje się z kontrolą testu Dunnett'a lub Scheffe'a. Odpowiednia statystyka opisana jest w [1], str.302.
16 Porównanie więcej niż dwóch elewacji Do porównania więcej niż dwóch elewacji używa się procedury znanej jako analiza kowariancji. ftss-css\ w którym DF C % (41) 4 1 = 1 V A (42) -k-\. (43) We wzorze tss oznacza całkowitą sumę kwadratów (total Sum of Squares), a zmienne A,, B t i C,, oznaczają odpowiednio 2x, Jjcy, Zy 2 obliczone dla wszystkich punktów regresji traktowanych jakby należały do jednej prostej Porównanie post hoc więcej niż dwóch elewacji prostych regresji Jeżeli porównanie kilku elewacji prostych regresji wykazało, że nie są one równe, to do znalezienia najbardziej odbiegających elewacji prostych regresji można użyć testu Tukey'a lub jeżeli porównuje się z kontrolą testu Dunnett'a lub Scheffe'a. Odpowiednia statystyka opisana jest w [1], str.3o3.
17 5.3. DIAGRAM PORÓWNANIA PROSTYCH REGRESJI Rysunek przedstawia schemat blokowy ilustrujący sposób porównania prostych regresji. Ile linii? k>2 Sprawdzić H o : bi=b 2 (Rozdz.5.2.6) Sprawdzić H o : b]=b:=...=b k (Rozdz.5.2.9) Ho prawdziwa Ho fałszywa Ho prawdziwa H o fałszywa 1. Obliczyć wspólny kąt STOP 1. Obliczyć wspólny kąt 1. Porównania nachylenia (b) (Rozdz.5.2.6) nachylenia (b) (Rozdz.5.2.9) wielokrotne kątów 2. Sprawdzić H o : Obie elewacje 2. Sprawdzić Ho: Wszystkie nachylenia (b) równe (Rozdz.5.2.7) elewacje równe (Rozdz ) (Rozdz ) 2. STOP Ho prawdziwa Ho fałszywa H o prawdziwa Ho fałszywa 1. Obliczyć wspólną STOP 1. Obliczyć wspólną 1. Porównania wielokrotne elewację (Rozdz.5.2.7) elewację (Rozdz ) elewacji (Rozdz ) 2. STOP 2. STOP 2. STOP Rys. Schemat blokowy ilustrujący sposób porównania prostych regresji. 6. LITERATURA [1]. Zar J.H.: Biostatistical analysis. Prentice-Hall International, Inc., 1984.
Statystyczna analiza danych w programie STATISTICA (wykład 2) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Statystyczna analiza danych w programie STATISTICA (wykład ) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Weryfikacja (testowanie) hipotez statystycznych
Przykład 1. (A. Łomnicki)
 Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
Plan wykładu: 1. Wariancje wewnątrz grup i między grupami do czego prowadzi ich ocena 2. Rozkład F 3. Analiza wariancji jako metoda badań założenia, etapy postępowania 4. Dwie klasyfikacje a dwa modele
Testy nieparametryczne
 Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
Testy nieparametryczne Testy nieparametryczne możemy stosować, gdy nie są spełnione założenia wymagane dla testów parametrycznych. Stosujemy je również, gdy dane można uporządkować według określonych kryteriów
PDF created with FinePrint pdffactory Pro trial version http://www.fineprint.com
 Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
Analiza korelacji i regresji KORELACJA zależność liniowa Obserwujemy parę cech ilościowych (X,Y). Doświadczenie jest tak pomyślane, aby obserwowane pary cech X i Y (tzn i ta para x i i y i dla różnych
STATYSTYKA I DOŚWIADCZALNICTWO. Wykład 2
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
STATYSTYKA I DOŚWIADCZALNICTWO Wykład Parametry przedziałowe rozkładów ciągłych określane na podstawie próby (przedziały ufności) Przedział ufności dla średniej s X t( α;n 1),X + t( α;n 1) n s n t (α;
Przedmowa Wykaz symboli Litery alfabetu greckiego wykorzystywane w podręczniku Symbole wykorzystywane w zagadnieniach teorii
 SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
SPIS TREŚCI Przedmowa... 11 Wykaz symboli... 15 Litery alfabetu greckiego wykorzystywane w podręczniku... 15 Symbole wykorzystywane w zagadnieniach teorii mnogości (rachunku zbiorów)... 16 Symbole stosowane
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice
 Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Księgarnia PWN: George A. Ferguson, Yoshio Takane - Analiza statystyczna w psychologii i pedagogice Przedmowa do wydania polskiego Przedmowa CZĘŚĆ I. PODSTAWY STATYSTYKI Rozdział 1 Podstawowe pojęcia statystyki
Testowanie hipotez statystycznych. Wnioskowanie statystyczne
 Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Testowanie hipotez statystycznych Wnioskowanie statystyczne Hipoteza statystyczna to dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Hipotezy
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
Analiza wariancji - ANOVA Analizę wariancji, często określaną skrótem ANOVA (Analysis of Variance), zawdzięczamy angielskiemu biologowi Ronaldowi A. Fisherowi, który opracował ją w 1925 roku dla rozwiązywania
TESTY NIEPARAMETRYCZNE. 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa.
 TESTY NIEPARAMETRYCZNE 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa. Standardowe testy równości średnich wymagają aby badane zmienne losowe
TESTY NIEPARAMETRYCZNE 1. Testy równości średnich bez założenia normalności rozkładu zmiennych: Manna-Whitney a i Kruskala-Wallisa. Standardowe testy równości średnich wymagają aby badane zmienne losowe
Testy post-hoc. Wrocław, 6 czerwca 2016
 Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
Testy post-hoc Wrocław, 6 czerwca 2016 Testy post-hoc 1 metoda LSD 2 metoda Duncana 3 metoda Dunneta 4 metoda kontrastów 5 matoda Newman-Keuls 6 metoda Tukeya Metoda LSD Metoda Least Significant Difference
1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe
 Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Zjazd 7. SGGW, dn. 28.11.10 r. Matematyka i statystyka matematyczna Tematy 1. Jednoczynnikowa analiza wariancji 2. Porównania szczegółowe nna Rajfura 1 Zagadnienia Przykład porównania wielu obiektów w
Importowanie danych do SPSS Eksportowanie rezultatów do formatu MS Word... 22
 Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
Spis treści Przedmowa do wydania pierwszego.... 11 Przedmowa do wydania drugiego.... 15 Wykaz symboli.... 17 Litery alfabetu greckiego wykorzystywane w podręczniku.... 17 Symbole wykorzystywane w zagadnieniach
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki
 Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Tablica Wzorów Rachunek Prawdopodobieństwa i Statystyki Spis treści I. Wzory ogólne... 2 1. Średnia arytmetyczna:... 2 2. Rozstęp:... 2 3. Kwantyle:... 2 4. Wariancja:... 2 5. Odchylenie standardowe:...
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski
 Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Projekt zaliczeniowy z przedmiotu Statystyka i eksploracja danych (nr 3) Kamil Krzysztof Derkowski Zadanie 1 Eksploracja (EXAMINE) Informacja o analizowanych danych Obserwacje Uwzględnione Wykluczone Ogółem
Jak sprawdzić normalność rozkładu w teście dla prób zależnych?
 Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Jak sprawdzić normalność rozkładu w teście dla prób zależnych? W pliku zalezne_10.sta znajdują się dwie zmienne: czasu biegu przed rozpoczęciem cyklu treningowego (zmienna 1) oraz czasu biegu po zakończeniu
Analiza wariancji i kowariancji
 Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Analiza wariancji i kowariancji Historia Analiza wariancji jest metodą zaproponowaną przez Ronalda A. Fishera. Po zakończeniu pierwszej wojny światowej był on pracownikiem laboratorium statystycznego w
Analiza wariancji. dr Janusz Górczyński
 Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
Analiza wariancji dr Janusz Górczyński Wprowadzenie Powiedzmy, że badamy pewną populację π, w której cecha Y ma rozkład N o średniej m i odchyleniu standardowym σ. Powiedzmy dalej, że istnieje pewien czynnik
KORELACJE I REGRESJA LINIOWA
 KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
KORELACJE I REGRESJA LINIOWA Korelacje i regresja liniowa Analiza korelacji: Badanie, czy pomiędzy dwoma zmiennymi istnieje zależność Obie analizy się wzajemnie przeplatają Analiza regresji: Opisanie modelem
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4
 Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Modele i wnioskowanie statystyczne (MWS), sprawozdanie z laboratorium 4 Konrad Miziński, nr albumu 233703 31 maja 2015 Zadanie 1 Wartości oczekiwane µ 1 i µ 2 oszacowano wg wzorów: { µ1 = 0.43925 µ = X
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Elementy statystyki STA - Wykład 5
 STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
STA - Wykład 5 Wydział Matematyki i Informatyki Uniwersytet im. Adama Mickiewicza 1 ANOVA 2 Model jednoczynnikowej analizy wariancji Na model jednoczynnikowej analizy wariancji możemy traktować jako uogólnienie
ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH
 1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
1 ALGORYTMICZNA I STATYSTYCZNA ANALIZA DANYCH WFAiS UJ, Informatyka Stosowana II stopień studiów 2 Wnioskowanie statystyczne dla zmiennych numerycznych Porównywanie dwóch średnich Boot-strapping Analiza
Założenia do analizy wariancji. dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW
 Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
Założenia do analizy wariancji dr Anna Rajfura Kat. Doświadczalnictwa i Bioinformatyki SGGW anna_rajfura@sggw.pl Zagadnienia 1. Normalność rozkładu cechy Testy: chi-kwadrat zgodności, Shapiro-Wilka, Kołmogorowa-Smirnowa
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 6 Metody sprawdzania założeń w analizie wariancji: -Sprawdzanie równości (jednorodności) wariancji testy: - Cochrana - Hartleya - Bartletta -Sprawdzanie zgodności
Statystyka. Rozkład prawdopodobieństwa Testowanie hipotez. Wykład III ( )
 Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Statystyka Rozkład prawdopodobieństwa Testowanie hipotez Wykład III (04.01.2016) Rozkład t-studenta Rozkład T jest rozkładem pomocniczym we wnioskowaniu statystycznym; stosuje się go wyznaczenia przedziału
Spis treści. Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów. Wstęp Wprowadzenie...
 Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Księgarnia PWN: Bruce M. King, Edward W. Minium - Statystyka dla psychologów i pedagogów Wstęp... 13 1. Wprowadzenie... 19 1.1. Statystyka opisowa.................................. 21 1.2. Wnioskowanie
Analiza wariancji - ANOVA
 Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Analiza wariancji - ANOVA Analiza wariancji jest metodą pozwalającą na podział zmienności zaobserwowanej wśród wyników eksperymentalnych na oddzielne części. Każdą z tych części możemy przypisać oddzielnemu
Matematyka i statystyka matematyczna dla rolników w SGGW WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE
 WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE Było: Przykład. W doświadczeniu polowym załoŝonym w układzie całkowicie losowym w czterech powtórzeniach porównano
WYKŁAD 11 DOŚWIADCZENIE JEDNOCZYNNIKOWE W UKŁADZIE CAŁKOWICIE LOSOWYM PORÓWNANIA SZCZEGÓŁOWE Było: Przykład. W doświadczeniu polowym załoŝonym w układzie całkowicie losowym w czterech powtórzeniach porównano
Analizy wariancji ANOVA (analysis of variance)
 ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
ANOVA Analizy wariancji ANOVA (analysis of variance) jest to metoda równoczesnego badania istotności różnic między wieloma średnimi z prób pochodzących z wielu populacji (grup). Model jednoczynnikowy analiza
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski
 Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
Statystyka od podstaw Janina Jóźwiak, Jarosław Podgórski Książka jest nowoczesnym podręcznikiem przeznaczonym dla studentów uczelni i wydziałów ekonomicznych. Wykład podzielono na cztery części. W pierwszej
JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA
 JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A a liczba poziomów (j=1..a), n i liczba powtórzeń w i tej populacji
JEDNOCZYNNIKOWA ANALIZA WARIANCJI, ANOVA 1 Obserwowana (badana) cecha Y Czynnik wpływający na Y (badany) A A i i ty poziom czynnika A a liczba poziomów (j=1..a), n i liczba powtórzeń w i tej populacji
weryfikacja hipotez dotyczących parametrów populacji (średnia, wariancja)
 PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
PODSTAWY STATYSTYKI. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5. Testy parametryczne (na
LABORATORIUM 3. Jeśli p α, to hipotezę zerową odrzucamy Jeśli p > α, to nie mamy podstaw do odrzucenia hipotezy zerowej
 LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
LABORATORIUM 3 Przygotowanie pliku (nazwy zmiennych, export plików.xlsx, selekcja przypadków); Graficzna prezentacja danych: Histogramy (skategoryzowane) i 3-wymiarowe; Wykresy ramka wąsy; Wykresy powierzchniowe;
Wydział Matematyki. Testy zgodności. Wykład 03
 Wydział Matematyki Testy zgodności Wykład 03 Testy zgodności W testach zgodności badamy postać rozkładu teoretycznego zmiennej losowej skokowej lub ciągłej. Weryfikują one stawiane przez badaczy hipotezy
Wydział Matematyki Testy zgodności Wykład 03 Testy zgodności W testach zgodności badamy postać rozkładu teoretycznego zmiennej losowej skokowej lub ciągłej. Weryfikują one stawiane przez badaczy hipotezy
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak
 Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
Podstawy statystyki dla psychologów. Podręcznik akademicki. Wydanie drugie poprawione. Wiesław Szymczak Autor prezentuje spójny obraz najczęściej stosowanych metod statystycznych, dodatkowo omawiając takie
Wykład 9 Testy rangowe w problemie dwóch prób
 Wykład 9 Testy rangowe w problemie dwóch prób Wrocław, 18 kwietnia 2018 Test rangowy Testem rangowym nazywamy test, w którym statystyka testowa jest konstruowana w oparciu o rangi współrzędnych wektora
Wykład 9 Testy rangowe w problemie dwóch prób Wrocław, 18 kwietnia 2018 Test rangowy Testem rangowym nazywamy test, w którym statystyka testowa jest konstruowana w oparciu o rangi współrzędnych wektora
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Jednoczynnikowa analiza wariancji i porównania wielokrotne (układ losowanych bloków randomized block design RBD) Układ losowanych bloków Stosujemy, gdy podejrzewamy,
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Jednoczynnikowa analiza wariancji i porównania wielokrotne (układ losowanych bloków randomized block design RBD) Układ losowanych bloków Stosujemy, gdy podejrzewamy,
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Testowanie hipotez. Marcin Zajenkowski. Marcin Zajenkowski () Testowanie hipotez 1 / 25
 Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
Testowanie hipotez Marcin Zajenkowski Marcin Zajenkowski () Testowanie hipotez 1 / 25 Testowanie hipotez Aby porównać ze sobą dwie statystyki z próby stosuje się testy istotności. Mówią one o tym czy uzyskane
STATYSTYKA MATEMATYCZNA WYKŁAD 4. Testowanie hipotez Estymacja parametrów
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
STATYSTYKA MATEMATYCZNA WYKŁAD 4 Testowanie hipotez Estymacja parametrów WSTĘP 1. Testowanie hipotez Błędy związane z testowaniem hipotez Etapy testowana hipotez Testowanie wielokrotne 2. Estymacja parametrów
Weryfikacja hipotez statystycznych
 Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Weryfikacja hipotez statystycznych Hipoteza Test statystyczny Poziom istotności Testy jednostronne i dwustronne Testowanie równości wariancji test F-Fishera Testowanie równości wartości średnich test t-studenta
Wprowadzenie do analizy korelacji i regresji
 Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
Statystyka dla jakości produktów i usług Six sigma i inne strategie Wprowadzenie do analizy korelacji i regresji StatSoft Polska Wybrane zagadnienia analizy korelacji Przy analizie zjawisk i procesów stanowiących
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA
 ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
ANALIZA WARIANCJI - KLASYFIKACJA JEDNOCZYNNIKOWA Na poprzednich zajęciach omawialiśmy testy dla weryfikacji hipotez, że dwie populacje o rozkładach normalnych mają jednakowe wartości średnie. Co jednak
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI
 ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
ĆWICZENIE 11 ANALIZA KORELACJI I REGRESJI Korelacja 1. Współczynnik korelacji 2. Współczynnik korelacji liniowej definicja 3. Estymacja współczynnika korelacji 4. Testy istotności współczynnika korelacji
Zadania ze statystyki cz. 8 I rok socjologii. Zadanie 1.
 Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Zadania ze statystyki cz. 8 I rok socjologii Zadanie 1. W potocznej opinii pokutuje przekonanie, że lepsi z matematyki są chłopcy niż dziewczęta. Chcąc zweryfikować tę opinię, przeprowadzono badanie w
Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona;
 LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
LABORATORIUM 4 Testowanie hipotez dla dwóch zmiennych zależnych. Moc testu. Minimalna liczność próby; Regresja prosta; Korelacja Pearsona; dwie zmienne zależne mierzalne małe próby duże próby rozkład normalny
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 7 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 2. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez 5.
Testowanie hipotez. Hipoteza prosta zawiera jeden element, np. H 0 : θ = 2, hipoteza złożona zawiera więcej niż jeden element, np. H 0 : θ > 4.
 Testowanie hipotez Niech X = (X 1... X n ) będzie próbą losową na przestrzeni X zaś P = {P θ θ Θ} rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby X. Definicja 1. Hipotezą zerową Θ
Testowanie hipotez Niech X = (X 1... X n ) będzie próbą losową na przestrzeni X zaś P = {P θ θ Θ} rodziną rozkładów prawdopodobieństwa określonych na przestrzeni próby X. Definicja 1. Hipotezą zerową Θ
SIGMA KWADRAT. Weryfikacja hipotez statystycznych. Statystyka i demografia CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY
 SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Weryfikacja hipotez statystycznych Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
SIGMA KWADRAT CZWARTY LUBELSKI KONKURS STATYSTYCZNO-DEMOGRAFICZNY Weryfikacja hipotez statystycznych Statystyka i demografia PROJEKT DOFINANSOWANY ZE ŚRODKÓW NARODOWEGO BANKU POLSKIEGO URZĄD STATYSTYCZNY
Statystyka matematyczna dla leśników
 Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyka matematyczna dla leśników Wydział Leśny Kierunek leśnictwo Studia Stacjonarne I Stopnia Rok akademicki 03/04 Wykład 5 Testy statystyczne Ogólne zasady testowania hipotez statystycznych, rodzaje
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski
 Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
Statystyczna analiza danych w programie STATISTICA 7.1 PL (wykład 3) Dariusz Gozdowski Katedra Doświadczalnictwa i Bioinformatyki Wydział Rolnictwa i Biologii SGGW Dwuczynnikowa analiza wariancji (2-way
JEDNOCZYNNIKOWA ANOVA
 Analizę ANOVA wykorzystujemy do wykrycia różnic pomiędzy średnimi w więcej niż dwóch grupach/więcej niż w dwóch pomiarach JEDNOCZYNNIKOWA ANOVA porównania jednej zmiennej pomiędzy więcej niż dwoma grupami
Analizę ANOVA wykorzystujemy do wykrycia różnic pomiędzy średnimi w więcej niż dwóch grupach/więcej niż w dwóch pomiarach JEDNOCZYNNIKOWA ANOVA porównania jednej zmiennej pomiędzy więcej niż dwoma grupami
OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA. z wykorzystaniem programu obliczeniowego Q maxp
 tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
tel.: +48 662 635 712 Liczba stron: 15 Data: 20.07.2010r OBLICZENIE PRZEPŁYWÓW MAKSYMALNYCH ROCZNYCH O OKREŚLONYM PRAWDOPODOBIEŃSTWIE PRZEWYŻSZENIA z wykorzystaniem programu obliczeniowego Q maxp DŁUGIE
Jednoczynnikowa analiza wariancji
 Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
Jednoczynnikowa analiza wariancji Zmienna zależna ilościowa, numeryczna Zmienna niezależna grupująca (dzieli próbę na więcej niż dwie grupy), nominalna zmienną wyrażoną tekstem należy w SPSS przerekodować
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI. Test zgodności i analiza wariancji Analiza wariancji
 WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
WIELKA SGH-OWA POWTÓRKA ZE STATYSTYKI Test zgodności i analiza wariancji Analiza wariancji Test zgodności Chi-kwadrat Sprawdza się za jego pomocą ZGODNOŚĆ ROZKŁADU EMPIRYCZNEGO Z PRÓBY Z ROZKŁADEM HIPOTETYCZNYM
Prawdopodobieństwo i rozkład normalny cd.
 # # Prawdopodobieństwo i rozkład normalny cd. Michał Daszykowski, Ivana Stanimirova Instytut Chemii Uniwersytet Śląski w Katowicach Ul. Szkolna 9 40-006 Katowice E-mail: www: mdaszyk@us.edu.pl istanimi@us.edu.pl
# # Prawdopodobieństwo i rozkład normalny cd. Michał Daszykowski, Ivana Stanimirova Instytut Chemii Uniwersytet Śląski w Katowicach Ul. Szkolna 9 40-006 Katowice E-mail: www: mdaszyk@us.edu.pl istanimi@us.edu.pl
dr hab. Dariusz Piwczyński, prof. nadzw. UTP
 dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
dr hab. Dariusz Piwczyński, prof. nadzw. UTP Porównanie większej niż 2 liczby grup (k>2) Zmienna zależna skala przedziałowa Zmienna niezależna skala nominalna lub porządkowa 2 Istota teorii analizy wariancji
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH
 RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
RÓWNOWAŻNOŚĆ METOD BADAWCZYCH Piotr Konieczka Katedra Chemii Analitycznej Wydział Chemiczny Politechnika Gdańska Równoważność metod??? 2 Zgodność wyników analitycznych otrzymanych z wykorzystaniem porównywanych
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć)
 Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
Szczegółowy program kursu Statystyka z programem Excel (30 godzin lekcyjnych zajęć) 1. Populacja generalna a losowa próba, parametr rozkładu cechy a jego ocena z losowej próby, miary opisu statystycznego
( x) Równanie regresji liniowej ma postać. By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : Gdzie:
 ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
ma postać y = ax + b Równanie regresji liniowej By obliczyć współczynniki a i b należy posłużyć się następującymi wzorami 1 : xy b = a = b lub x Gdzie: xy = też a = x = ( b ) i to dane empiryczne, a ilość
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, Spis treści
 Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
Statystyka w zarzadzaniu / Amir D. Aczel, Jayavel Sounderpandian. Wydanie 2. Warszawa, 2018 Spis treści Przedmowa 13 O Autorach 15 Przedmowa od Tłumacza 17 1. Wprowadzenie i statystyka opisowa 19 1.1.
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych.
 Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Statystyka i opracowanie danych- W 8 Wnioskowanie statystyczne. Testy statystyczne. Weryfikacja hipotez statystycznych. Dr Anna ADRIAN Paw B5, pok407 adan@agh.edu.pl Hipotezy i Testy statystyczne Każde
Badanie zgodności dwóch rozkładów - test serii, test mediany, test Wilcoxona, test Kruskala-Wallisa
 Badanie zgodności dwóch rozkładów - test serii, test mediany, test Wilcoxona, test Kruskala-Wallisa Test serii (test Walda-Wolfowitza) Założenie. Rozpatrywane rozkłady są ciągłe. Mamy dwa uporządkowane
Badanie zgodności dwóch rozkładów - test serii, test mediany, test Wilcoxona, test Kruskala-Wallisa Test serii (test Walda-Wolfowitza) Założenie. Rozpatrywane rozkłady są ciągłe. Mamy dwa uporządkowane
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 4 Inne układy doświadczalne 1) Układ losowanych bloków Stosujemy, gdy podejrzewamy, że może występować systematyczna zmienność między powtórzeniami np. - zmienność
Matematyka i statystyka matematyczna dla rolników w SGGW
 Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Było: Testowanie hipotez (ogólnie): stawiamy hipotezę, wybieramy funkcję testową f (test statystyczny), przyjmujemy poziom istotności α; tym samym wyznaczamy obszar krytyczny testu (wartość krytyczną funkcji
Statystyka matematyczna Testowanie hipotez i estymacja parametrów. Wrocław, r
 Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
Statystyka matematyczna Testowanie hipotez i estymacja parametrów Wrocław, 18.03.2016r Plan wykładu: 1. Testowanie hipotez 2. Etapy testowania hipotez 3. Błędy 4. Testowanie wielokrotne 5. Estymacja parametrów
, a ilość poziomów czynnika A., b ilość poziomów czynnika B. gdzie
 Test Scheffego, gdzie (1) n to ilość powtórzeń (pomiarów) w jednej grupie (zabiegu) Test NIR Istnieje wiele testów dla porównań wielokrotnych opartych o najmniejszą istotna różnicę między średnimi (NIR).
Test Scheffego, gdzie (1) n to ilość powtórzeń (pomiarów) w jednej grupie (zabiegu) Test NIR Istnieje wiele testów dla porównań wielokrotnych opartych o najmniejszą istotna różnicę między średnimi (NIR).
Statystyka Opisowa z Demografią oraz Biostatystyka. Aleksander Denisiuk. denisjuk@euh-e.edu.pl
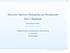 Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
Statystyka Opisowa z Demografią oraz Biostatystyka TesttStudenta Aleksander Denisiuk denisjuk@euh-e.edu.pl Elblaska Uczelnia Humanistyczno-Ekonomiczna ul. Lotnicza 2 82-300 Elblag oraz Biostatystyka p.
POLITECHNIKA OPOLSKA
 POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 4 Temat: Analiza korelacji i regresji dwóch zmiennych
POLITECHNIKA OPOLSKA WYDZIAŁ MECHANICZNY Katedra Technologii Maszyn i Automatyzacji Produkcji Laboratorium Podstaw Inżynierii Jakości Ćwiczenie nr 4 Temat: Analiza korelacji i regresji dwóch zmiennych
Wykład 3 Hipotezy statystyczne
 Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
Wykład 3 Hipotezy statystyczne Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu obserwowanej zmiennej losowej (cechy populacji generalnej) Hipoteza zerowa (H 0 ) jest hipoteza
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI
 LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
Zadania ze statystyki cz.8. Zadanie 1.
 Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
Zadania ze statystyki cz.8. Zadanie 1. Wykonano pewien eksperyment skuteczności działania pewnej reklamy na zmianę postawy. Wylosowano 10 osobową próbę studentów, których poproszono o ocenę pewnego produktu,
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI
 LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
LABORATORIUM 8 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI WERYFIKACJA HIPOTEZ Hipoteza statystyczna jakiekolwiek przypuszczenie dotyczące populacji generalnej- jej poszczególnych
Testowanie hipotez statystycznych.
 Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
VI WYKŁAD STATYSTYKA. 9/04/2014 B8 sala 0.10B Godz. 15:15
 VI WYKŁAD STATYSTYKA 9/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 6 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności, zasady
VI WYKŁAD STATYSTYKA 9/04/2014 B8 sala 0.10B Godz. 15:15 WYKŁAD 6 WERYFIKACJA HIPOTEZ STATYSTYCZNYCH PARAMETRYCZNE TESTY ISTOTNOŚCI Weryfikacja hipotez ( błędy I i II rodzaju, poziom istotności, zasady
Testowanie hipotez statystycznych.
 Bioinformatyka Wykład 4 Wrocław, 17 października 2011 Temat. Weryfikacja hipotez statystycznych dotyczących wartości oczekiwanej w dwóch populacjach o rozkładach normalnych. Model 3. Porównanie średnich
Bioinformatyka Wykład 4 Wrocław, 17 października 2011 Temat. Weryfikacja hipotez statystycznych dotyczących wartości oczekiwanej w dwóch populacjach o rozkładach normalnych. Model 3. Porównanie średnich
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki 3. Zmienne losowe 4. Populacje i próby danych 5. Testowanie hipotez i estymacja parametrów 6. Test t 7. Test
Stanisław Cichocki. Natalia Nehrebecka. Wykład 9
 Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Stanisław Cichocki Natalia Nehrebecka Wykład 9 1 1. Dodatkowe założenie KMRL 2. Testowanie hipotez prostych Rozkład estymatora b Testowanie hipotez prostych przy użyciu statystyki t 3. Przedziały ufności
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności. dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl
 Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Statystyka w pracy badawczej nauczyciela Wykład 4: Analiza współzależności dr inż. Walery Susłow walery.suslow@ie.tu.koszalin.pl Statystyczna teoria korelacji i regresji (1) Jest to dział statystyki zajmujący
Uwaga. Decyzje brzmią różnie! Testy parametryczne dotyczące nieznanej wartości
 TESTOWANIE HIPOTEZ Przez hipotezę statystyczną rozumiemy, najogólniej mówiąc, pewną wypowiedź na temat rozkładu, z którego pochodzi próbka. Hipotezy dzielimy na parametryczne i nieparametryczne. Parametrycznymi
TESTOWANIE HIPOTEZ Przez hipotezę statystyczną rozumiemy, najogólniej mówiąc, pewną wypowiedź na temat rozkładu, z którego pochodzi próbka. Hipotezy dzielimy na parametryczne i nieparametryczne. Parametrycznymi
Statystyczna analiza danych (molekularnych) analiza wariancji ANOVA
 Statystyczna analiza danych (molekularnych) analiza wariancji ANOVA Anna Gambin 19 maja 2013 Spis treści 1 Przykład: Model liniowy dla ekspresji genów 1 2 Jednoczynnikowa analiza wariancji 3 2.1 Testy
Statystyczna analiza danych (molekularnych) analiza wariancji ANOVA Anna Gambin 19 maja 2013 Spis treści 1 Przykład: Model liniowy dla ekspresji genów 1 2 Jednoczynnikowa analiza wariancji 3 2.1 Testy
Statystyka matematyczna i ekonometria
 Statystyka matematyczna i ekonometria Wykład 5 dr inż. Anna Skowrońska-Szmer zima 2017/2018 Hipotezy 2 Hipoteza zerowa (H 0 )- hipoteza o wartości jednego (lub wielu) parametru populacji. Traktujemy ją
Statystyka matematyczna i ekonometria Wykład 5 dr inż. Anna Skowrońska-Szmer zima 2017/2018 Hipotezy 2 Hipoteza zerowa (H 0 )- hipoteza o wartości jednego (lub wielu) parametru populacji. Traktujemy ją
Oszacowanie i rozkład t
 Oszacowanie i rozkład t Marcin Zajenkowski Marcin Zajenkowski () Oszacowanie i rozkład t 1 / 31 Oszacowanie 1 Na podstawie danych z próby szacuje się wiele wartości w populacji, np.: jakie jest poparcie
Oszacowanie i rozkład t Marcin Zajenkowski Marcin Zajenkowski () Oszacowanie i rozkład t 1 / 31 Oszacowanie 1 Na podstawie danych z próby szacuje się wiele wartości w populacji, np.: jakie jest poparcie
TESTOWANIE HIPOTEZ STATYSTYCZNYCH
 TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
TETOWANIE HIPOTEZ TATYTYCZNYCH HIPOTEZA TATYTYCZNA przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcyjnej lub wartości parametrów). Prawdziwość tego przypuszczenia jest oceniana na
X Y 4,0 3,3 8,0 6,8 12,0 11,0 16,0 15,2 20,0 18,9
 Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
Zadanie W celu sprawdzenia, czy pipeta jest obarczona błędem systematycznym stałym lub zmiennym wykonano szereg pomiarów przy różnych ustawieniach pipety. Wyznacz równanie regresji liniowej, które pozwoli
Statystyka i Analiza Danych
 Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Warsztaty Statystyka i Analiza Danych Gdańsk, 20-22 lutego 2014 Zastosowania analizy wariancji w opracowywaniu wyników badań empirycznych Janusz Wątroba StatSoft Polska Centrum Zastosowań Matematyki -
Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą w oddzielnej kolumnie.
 STATISTICA INSTRUKCJA - 1 I. Wprowadzanie danych Podstawowe / Nowy / Arkusz Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą
STATISTICA INSTRUKCJA - 1 I. Wprowadzanie danych Podstawowe / Nowy / Arkusz Dane dotyczące wartości zmiennej (cechy) wprowadzamy w jednej kolumnie. W przypadku większej liczby zmiennych wprowadzamy każdą
STATYSTYKA MATEMATYCZNA
 STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
STATYSTYKA MATEMATYCZNA 1. Wykład wstępny. Teoria prawdopodobieństwa i elementy kombinatoryki. Zmienne losowe i ich rozkłady 3. Populacje i próby danych, estymacja parametrów 4. Testowanie hipotez statystycznych
RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA MATEMATYCZNA
 RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA MATEMATYCZNA LISTA 10 1.Dokonano 8 pomiarów pewnej odległości (w m) i otrzymano: 201, 195, 207, 203, 191, 208, 198, 210. Wiedząc,że błąd pomiaru ma rozkład normalny
RACHUNEK PRAWDOPODOBIEŃSTWA I STATYSTYKA MATEMATYCZNA LISTA 10 1.Dokonano 8 pomiarów pewnej odległości (w m) i otrzymano: 201, 195, 207, 203, 191, 208, 198, 210. Wiedząc,że błąd pomiaru ma rozkład normalny
), którą będziemy uważać za prawdziwą jeżeli okaże się, że hipoteza H 0
 Testowanie hipotez Każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy nazywamy hipotezą statystyczną. Hipoteza określająca jedynie wartości nieznanych parametrów liczbowych badanej cechy
Testowanie hipotez Każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy nazywamy hipotezą statystyczną. Hipoteza określająca jedynie wartości nieznanych parametrów liczbowych badanej cechy
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE
 STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
STATYSTYKA - PRZYKŁADOWE ZADANIA EGZAMINACYJNE 1 W trakcie badania obliczono wartości średniej (15,4), mediany (13,6) oraz dominanty (10,0). Określ typ asymetrii rozkładu. 2 Wymień 3 cechy rozkładu Gauss
Statystyka. #5 Testowanie hipotez statystycznych. Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik. rok akademicki 2016/ / 28
 Statystyka #5 Testowanie hipotez statystycznych Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2016/2017 1 / 28 Testowanie hipotez statystycznych 2 / 28 Testowanie hipotez statystycznych
Statystyka #5 Testowanie hipotez statystycznych Aneta Dzik-Walczak Małgorzata Kalbarczyk-Stęclik rok akademicki 2016/2017 1 / 28 Testowanie hipotez statystycznych 2 / 28 Testowanie hipotez statystycznych
Eksploracja Danych. Testowanie Hipotez. (c) Marcin Sydow
 Testowanie Hipotez Wprowadzenie Testy statystyczne: pocz. XVII wieku (prace J.Arbuthnotta, liczba urodzeń noworodków obu płci w Londynie) Testowanie hipotez: Karl Pearson (pocz. XX w., testowanie zgodności,
Testowanie Hipotez Wprowadzenie Testy statystyczne: pocz. XVII wieku (prace J.Arbuthnotta, liczba urodzeń noworodków obu płci w Londynie) Testowanie hipotez: Karl Pearson (pocz. XX w., testowanie zgodności,
Zadanie 1. Analiza Analiza rozkładu
 Zadanie 1 data lab.zad 1; input czas; datalines; 85 3060 631 819 805 835 955 595 690 73 815 914 ; run; Analiza Analiza rozkładu Ponieważ jesteśmy zainteresowani wyznaczeniem przedziału ufności oraz weryfikacja
Zadanie 1 data lab.zad 1; input czas; datalines; 85 3060 631 819 805 835 955 595 690 73 815 914 ; run; Analiza Analiza rozkładu Ponieważ jesteśmy zainteresowani wyznaczeniem przedziału ufności oraz weryfikacja
Zawartość. Zawartość
 Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Opr. dr inż. Grzegorz Biesok. Wer. 2.05 2011 Zawartość Zawartość 1. Rozkład normalny... 3 2. Rozkład normalny standardowy... 5 3. Obliczanie prawdopodobieństw dla zmiennych o rozkładzie norm. z parametrami
Błędy przy testowaniu hipotez statystycznych. Decyzja H 0 jest prawdziwa H 0 jest faszywa
 Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Weryfikacja hipotez statystycznych Hipotezą statystyczną nazywamy każde przypuszczenie dotyczące nieznanego rozkładu badanej cechy populacji, o prawdziwości lub fałszywości którego wnioskuje się na podstawie
Rozkłady statystyk z próby
 Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
Rozkłady statystyk z próby Rozkłady statystyk z próby Przypuśćmy, że wykonujemy serię doświadczeń polegających na 4 krotnym rzucie symetryczną kostką do gry, obserwując liczbę wyrzuconych oczek Nr kolejny
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5
 STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
STATYSTYKA I DOŚWIADCZALNICTWO Wykład 5 Analiza korelacji - współczynnik korelacji Pearsona Cel: ocena współzależności między dwiema zmiennymi ilościowymi Ocenia jedynie zależność liniową. r = cov(x,y
