Elektrostatyka. mgr inż. Grzegorz Strzeszewski. 20 kwietnia 2013 r. ZespółSzkółnr2wWyszkowie. mgr inż. Grzegorz Strzeszewski Elektrostatyka
|
|
|
- Szczepan Wasilewski
- 8 lat temu
- Przeglądów:
Transkrypt
1 Elektrostatyka mgr inż. Grzegorz Strzeszewski ZespółSzkółnr2wWyszkowie 20 kwietnia 2013 r.
2 Nauka jest dla tych, którzy chcą być mądrzejsi, którzy chcą wykorzystywać swój umysł do poznawania otaczającego nas świata. Jeżeliktośchcewżyciupozostaćciemnyigłupi,tonatakiego nie ma siły. Musimy mu pozwolić takim zostać.
3 Pole elektryczne Pole elektryczne jest to stan przestrzeni, gdzie na umieszczone w niej ładunki elektryczne działają siły elektrostatyczne. Ładunek elektryczny w przyrodzie występują dwa rodzaje ładunków, które umownie oznaczamy jako dodatnie i ujemne. Jednostką ładunku elektrycznego jest 1 Culomb, 1 C. Ładunek elektronu: e = 1, C. Prawo zachowania ładunku: W układzie odosobnionym, suma algebraiczna zgromadzonych tam ładunków nie zmienia się.
4 Prawo zachowania ładunku Prawo zachowania ładunku(postać matematyczna) dla n ładunków będących w odosobnieniu: i=n Q = Q 1 +Q 2 +Q 3 + +Q n = Q i = const. Z prawa zachowania ładunku wynika, że ładunku elektrycznego nie można stworzyć ani zniszczyć. Można jedynie spowodować przejście pewnej liczby ładunków z jednego ciała do drugiego. Podczas elektryzacji przy powstawaniu ładunku jednego znaku musi powstać ta sama ilość ładunku przeciwnego znaku. Elektryzacja jest procesem przekazywania ładunków elektrycznych z jednego ciała do drugiego. i=1
5 Sposoby elektryzacji przez pocieranie, drogą indukcji(influencji), przez zetknięcie ciała z ciałem mającycm nadmiar ładunków danego rodzaju. Równowaga ładunków elektrycznych w otaczającym nas świecie jest podstawowym prawem natury. Ładunek elektronu i równy mu co do wartości ładunek protonu są najmniejszymi porcjami ładunku występującymi ( w przyrodzie. ) Wprawdzie kwarki mają ładunki ułamkowe 1 3 e, 2 3 e alesąone uwięzione w nukleonach jąder atomów.
6 Gęstość ładunków W elektrostatyce ładunki elektryczne traktujemy jako nieskończenie podzielne i nieruchome. Rozróżniamy trzy rodzaje gęstości ładunku: objętościowa ρ, gdy ładunki rozmieszczone są w obszarze o objętości V, powierzchniowa σ, gdy ładunki rozłożone są na powierzchni S, liniowaτ,gdyładunkirozłożonesąnaprzewodzieodługości l. Odpowiednie gęstości definiujemy jako: ρ = Q V [ C m 3 ], σ = Q S [ C m 2 ], τ = Q l [ C m].
7 Pole elektrostatyczne Dookoła ciała naelektryzowanego powstaje pole elektryczne, które działa na inne umieszczone w pobliżu ładunki. W celu wyobrażenia sobie pola elektrycznego wygodnie jest posłużyć się obrazem graficznym tego pola. + Rysunek: Obraz pola elektrostatycznego, utworzony przez odosobniony dodatni ładunek punktowy.
8 Pole elektrostatyczne c. d. _ Rysunek: Obraz pola elektrostatycznego, utworzony przez odosobniony ujemny ładunek punktowy.
9 Obrazy graficzne pola Q _ 1 + Q 2 Rysunek: Linie pola elektrostatycznego dwóch ładunków różnoimiennych. Układdwóchładunkówróżnoimiennych,takichże Q 1 = Q 2 nazywamy dipolem elektrycznym.
10 Obrazy graficzne pola c. d. + Q 1 =Q 2 + Rysunek: Linie sił pola elektrostatycznego dwóch ładunków jednoimiennych(dodatnich).
11 Pole równomierne +Q -Q Rysunek: Pole równomierne powstałe między dwoma równoległymi płytkami metalowymi.
12 Natężenie pola elektrycznego Natężeniepolaelektrycznego Ewdowolnympunkcie,wktórym istnieje, określamy jako stosunek siły działającej na umieszczony w tym punkcie ładunek próbny do wartości tego ładunku. E = F q. Natężenie pola elektrycznego jest wielkością wektorową. Zwrot wektora Ejestzgodnyzezwrotemwektorasiły F. Ładunekpróbny q,toładunekdodatninatylemały,żejegopole własne jest do pominięcia.
13 Natężenie pola elektrycznego Jednostką natężenia pola elektrycznego jest: V m. Kierunek natężenia pola elektrycznego jest zgodny z kierunkiem siły działającej na dodatni ładunek q. Natężenie pola elektrycznego, pochodzące od kilku ładunków jest sumą wektorową natężeń od poszczególnych ładunków: E = E 1 + E E n = i=n i=1 E i.
14 Prawo Coulomba Jeżeli w polu elektrostatycznym wytworzonym przez ładunek punktowy Q 1,umieścimydrugiładunekpunktowy Q 2,tobędziena niego działać siła określona wzorem: F = Q 1Q 2 4πεr 2. Kierunek działania siły leży na prostej łączącej te ładunki, a jej zwrot zależy od znaków ładunków: jednoimienne odpychają się a różnoimienne przyciągają. r odległość między ładunkami, mierzona w metrach. +Q F -F _ + -Q r
15 Przenikalność elektryczna ε ε =ε 0 ε r ε przenikalnośćelektrycznabezwzględna,mierzonajestw F m, ε 0 przenikalnośćelektrycznapróżni, ε 0 =8, F m, ε r przenikalnośćelektrycznaśrodowiska,wktórymznajdująsię ładunki(przenikalność względna). Przenikalnośćelektrycznawzględnaε r jestwielkością bezwymiarową. Określa ona ile razy przenikalność danego środowiska jest większa od przenikalności elektrycznej próżni.
16 ε r niektórychdielektryków Materiał ε r Materiał ε r próżnia 1 parafina 2,0 2,5 powietrze 1, 0006 bakelit 3, 5 6, 0 papierizolac. 1,8 5,8 porcelana 4,5 6,0 olejizolac. 2,2 2,5 szkło 3,0 8,0 guma 2,5 2,8 mika 4,0 6,0 ebonit 2,0 3,5 marmur 6,0 8,0 wodadestyl. 80 rutylon TiO 2 100
17 Potencjał i napięcie elektryczne Napięciem elektrycznym między dwoma punktami A i B nazywamy stosunek pracy W, którą wykonują siły pola elektrycznego podczas przemieszczania ładunku próbnego q z punktu A do B. U AB = W q = E l. Potencjałemelektrycznym V A wpunkcie Apolaelektrycznego nazywamy stosunek pracy wykonanej podczas przemieszczania ładunku próbnego z punktu A do nieskończoności, do ładunku próbnego q. V A = W AB, B. q
18 Powierzchnie ekwipotencjalne Powierzchnie ekwipotencjalne są to miejsca geometryczne punktów równego potencjału. powierzchnie ekwipotencjalne _ V 1 =const V 2 =const V 3 =const
19 Indukcja elektryczna Wektor indukcji elektrycznej określamy następująco: D =ε 0 E + P, gdzie: P wektor polaryzacji elektrycznej, określony jako: P =κ E. κ =ε 0 κ r, κ podatność elektryczna(bezwzględna). ε r =1+κ r, D =ε E.
20 Strumień indukcji elektrycznej Strumień indukcji elektrycznej Ψ zdefiniowany jest jako iloczyn indukcjielektrycznej Dipowierzchni S,prostopadłejdowektora D. Powierzchnia S powinna być tak dobrana, aby można było przyjąć, że wartość indukcji jest stała na całej powierzchni S. Ψ = DS. Jednostkąindukcjielektrycznej D (D)jestkulombnametr kwadratowy C m 2. Jednostką strumienia indukcji elektrycznej Ψ(krócej: strumienia elektrycznego) jest kulomb C.
21 Twierdzenie Gaussa Strumień indukcji elektrycznej Ψ, przenikający powierzchnię zamkniętą S 0,równyjestsumieładunkówznajdującychsięw obszarze ograniczonym tą powierzhnią: i=n Ψ = Q i, i=1 n ilośćładunkówwewnątrzpowierzchni S 0. 1 Q Q2 S 0 Q n
22 Pole elektryczne kuli Kula odosobniona, naładowana ładunkiem Q. Q R r Natężenie pola elektrycznego w odległości r od środka kuli ma wartość: E = Q 4πεr 2. Wektornatężeniapola Ejestrównoległydopromienia rajego zwrot zależy od znaku ładunku Q.
23 Pole wokół przewodu Pole elektryczne wokół odosobnionego przewodu prostoliniowego o gęstości liniowej ładunku τ. r Wartość natężenia pola elektrycznego jest stała wzdłuż dowolnego okręgu wokół przewodu i równa: E = τ 2πεr. Natężenie pola elektrycznego jest odwrotnie proporcjonalne do odległości od przewodu.
24 Pojemność elektryczna Kondensator elektryczny jest układem dwóch przewodników (okładzin) rozdzielonych środowiskiem izolacyjnym(dielektrykiem). Pojemność elektryczna kondensatora jest wielkością charakteryzującą jego zdolność do gromadzenia ładunku elektrycznego. Doświadczalnie stwierdzono, że ładunek zgromadzony na okładkach kondensatora jest wprost proporcjonalny do napięcia przyłożonego do kondensatora U i jego pojemności C: Q = CU. Pojemność kondensatora mierzona jest w faradach(f). Farad jest pojemnością dużą. W praktyce posługujemy się jednostkami mniejszymi:µf, nf, pf.
25 Praktyczne jednostki pojemności elektrycznej Pojemność elektryczna kondensatorów mierzona jest w faradach(f). 1 F = 1 C 1 V. Farad jest pojemnością dużą a więc niepraktyczną w technicznych zastosowaniach. W praktyce, do pomiaru pojemności kondensatorów posługujemy się jednostkami mniejszymi. Jednostką milion razy mniejszą do farada jest mikrofarad(1 µf) 1µF =10 6 F =0, F. Nanofarad(1 nf) jest jednostką tysiąc razy mniejszą od mikrofarada 1 nf =10 3 µf =10 9 F =0, F. Pikofarad(1 pf) jest jednostką tysiąc razy mniejszą od nanofarada 1 pf =10 3 nf =10 6 µf =10 12 F =0, F.
26 Kondensator płaski ε d U Pojemność kondensatora płaskiego: C = εs d. Pojemność kondensatora jest tym większa im większa jest powierzchnia okładzin i im mniejsza odległość między nimi. Pojemność kondensatora zależy także od własności dielektryka umieszczonego między jego okładzinami.
27 Rodzaje kondensatorów papierowe okładziny wykonuje się z dwóch pasków folii aluminiowej, przedzielonych papierem nasyconym parafiną lub olejem, mikowe buduje się je jako płaskie, niezwjalne, ceramiczne dielektrykiem jest zazwyczaj dwutlenek tytanu lub jego związki, elektrolityczne stosowane tylko w obwodach prądu stałego, polistyrenowe i poliestrowe wykonywane są z metalizowanej folii poliestrowej, powietrzne, zazwyczaj o regulowanej pojemności.
28 _ Szeregowe łączenie kondensatorów C1 C 2 C3 -Q +Q -Q +Q -Q +Q + U 1 U 2 U 3 U Pojemność zastępcza: C z = C 1 C 2 C 3 C 1 C 2 +C 2 C 3 +C 1 C 3, lub 1 C z = 1 C C C 3.
29 Łączenie szeregowe pojemności Pojemność zastępcza n kondensatorów połączonych szeregowo: 1 = i=n 1 =. C z C 1 C 2 C n C i=1 i Inna postać wzoru na pojemność zastępczą n kondensatorów połączonych szeregowo: C z = C 1 C 2 C n C 2 C 3 C n +C 1 C 3 C n + +C 1 C 2 C n 1. Stosując skróconą notację matematyczną dla sumy i iloczynu wielu składników(n liczba kondensatorów połączonych szeregowo), ostatni wzór można przepisać w postaci bardziej zwięzłej. Otrzymamy wtedy tak zwany wzór Strzeszewskiego.
30 Wzór Strzeszewskiego Wzór na pojemność zastępczą n kondensatorów połączonych szeregowo zapisany w zwięzłej postaci jako wzór Strzeszewskiego: C z = gdzie: i=n C i = C 1 C 2 C n, i=1 j=n C j = C 2 C 3 C n +C }{{} 1 C 3 C n + +C }{{} 1 C 2 C n 1. }{{} j=1 j k brak C 1 brak C 2 brak C n
31 Szeregowe łączenie kondensatorów c. d. Podstawiając we wzorze Strzeszewskiego kolejne liczby naturalne w miejsce n, otrzymujemy: n =2 C z = C 1 C 2 C 1 +C 2, n =3 n =4 itd. C z = C z = C 1 C 2 C 3 C 1 C 2 +C 2 C 3 +C 1 C 3, C 1 C 2 C 3 C 4 C 1 C 2 C 3 +C 1 C 2 C 4 +C 1 C 3 C 4 +C 2 C 3 C 4,
32 Przykład Obliczyć pojemność zastępczą układu pięciu kondensatorów połączonych szeregowo: C1 C2 C3 C4 C5 Dane: C 1 = 2 F; C 2 = 4 F; C 3 = 3 F; C 4 = 5 F; C 5 = 6 F. Rozwiązanie: Do wyznaczenia pojemności zastępczej wykorzystamy wzór Strzeszewskiego(n = 5): C z = = = = (µF) 5 ( )(µF) 4 = = µf = µf 0,69µF.
33 Równoległe łączenie kondensatorów + _ U +Q 1 +Q 2 +Q 3 C1 C 2 C3 -Q1 -Q2 -Q3 Pojemność zastępcza: C z = C 1 +C 2 +C 3. Pojemność zastępcza n kondensatorów połączonych równolegle: i=n C z = C 1 +C 2 + +C n = C i. i=1
34 Energia pola elektrycznego Ładowanie kondensatora związane jest z doprowadzeniem do niego energii. Energia zgromadzona jest w polu elektrycznym kondensatora. Ilość zgromadzonej w polu elektrycznym energii obliczamy według wzoru: W e = CU2 2. Jednostką energii jest dżul(1 J). Ponieważ Q = CU, mamy wzory równoważne na energię zgromadzoną w polu elektrycznym: W e = QU 2, W e = Q2 2C.
35 Przykłady Przykład Obliczyć pracę wykonaną przy przesuwaniu w powietrzu ładunku Q 1 = C =5 pcznajdującegosięwpoluelektrycznym wytworzonymprzezładunek Q = C =200µC.Ładunek Q 1 przesuniętoodpunktu r A =0,5 modładunku Qdopunktu r B =1,5 modładunku Qwzdłużprostejłączącejobaładunki. VA VB +Q + Q 1 r A r B Wskazówki:ε r =1dlapowietrza, W = Q 1 (V A V B ),potencjał wytworzonyprzezładunek Qrównyjest V = Q 4πεr. (Odpowiedź: W 12µJ).
36 Przykłady Przykład Obliczyć siłę działającą między dwoma ładunkami punktowymi: Q 1 =1 mc,iq 2 = 1 mcumieszczonymiwodległości r =0,4 modsiebie. Rozwiązanie: Stosujemy prawo Coulomba +Q+ F -F -Q r F = Q 1Q 2 4πεr 2 = ( 1) ,14 8, (0,4) 2 56 kn. Ładunki są różnoimienne, dlatego obliczona siła ma znak minus(ładunki przyciągają się). _
37 Przykłady Przykład Obliczyć pojemność zwijki kondensatorowej o następujących danych: długośćfoliialuminiowej l =10,4 m,szerokość b =12 cm,grubość izolacji d =0,1 mm,przenikalnośćelektrycznawzględnaε r =4,5. Rozwiązanie: W kondensatorze zwijkowym okładziny pracują obustronnie. Pole powierzchni okładziny obliczamy wówczas z wzoru: Pojemność kondensatora S =2bl =2 10,4 m 0,0001 m 2,5 m 2. C =ε 0 ε r S d =8, ,5 2, µF.
38 Przykłady Przykład Kondensatorogrubościizolacji d =0,1 mmipojemności C =12µFpodłączonodo źródła napięcia stałego U = 1200 V. Obliczyć ładunek zgromadzony na okładzinach oraz natężenie pola w kondensatorze. Obliczyć energię zgromadzoną w polu elektrycznym kondensatora. Rozwiązanie: Ładunek zgromadzony na okładzinach: Natężenie pola elektrycznego: Energia pola elektrycznego: Q = CU = F 1200 V =14,4 mc. E = U d =1200 V 10 4 m =12 MV m, W e = CU2 2 = =86,4 J.
39 Przykłady Przykład Obliczyć pojemność zastępczą: dane: C 1 =10µF, C 2 =20µF, C 3 =30µF. b) a) C1 C2 C1 C2 d) c) C1 C2 C3 C1 C2 C3 Odpowiedź:a)6,67µF,b)30µF,c)50µF,d)60µF.
40 Przykłady Przykład Obliczyć pojemność zastępczą oraz ładunek i napięcie na poszczególnych kondensatorach przy zasilaniu układu kondensatorów napięciem U. Dane: C 1 =10µF, C 2 =20µF, C 3 =30µF, C 4 =50µF, C 5 = 40µF, C 6 =70µF, U =1000 V. a) b) C4 C1 C2 C1 C2 C5 C3 C3 C6 Odpowiedź:a) C z =15µF,b) C z 18,67µF.
41 Dziękuję za uwagę.
POLE ELEKTRYCZNE PRAWO COULOMBA
 POLE ELEKTRYCZNE PRAWO COULOMBA gdzie: Q, q ładunki elektryczne wyrażone w kulombach [C] r - odległość między ładunkami Q i q wyrażona w [m] ε - przenikalność elektryczna bezwzględna środowiska, w jakim
POLE ELEKTRYCZNE PRAWO COULOMBA gdzie: Q, q ładunki elektryczne wyrażone w kulombach [C] r - odległość między ładunkami Q i q wyrażona w [m] ε - przenikalność elektryczna bezwzględna środowiska, w jakim
Lekcja 40. Obraz graficzny pola elektrycznego.
 Lekcja 40. Obraz graficzny pola elektrycznego. Polem elektrycznym nazywamy obszar, w którym na wprowadzony doń ładunek próbny q działa siła. Pole elektryczne występuje wokół ładunków elektrycznych i ciał
Lekcja 40. Obraz graficzny pola elektrycznego. Polem elektrycznym nazywamy obszar, w którym na wprowadzony doń ładunek próbny q działa siła. Pole elektryczne występuje wokół ładunków elektrycznych i ciał
Podstawy fizyki wykład 8
 Podstawy fizyki wykład 8 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Ładunek elektryczny Grecy ok. 600 r p.n.e. odkryli, że bursztyn potarty o wełnę przyciąga inne (drobne) przedmioty. słowo
Podstawy fizyki wykład 8 Dr Piotr Sitarek Instytut Fizyki, Politechnika Wrocławska Ładunek elektryczny Grecy ok. 600 r p.n.e. odkryli, że bursztyn potarty o wełnę przyciąga inne (drobne) przedmioty. słowo
Podstawowe własności elektrostatyczne przewodników: Pole E na zewnątrz przewodnika jest prostopadłe do jego powierzchni
 KONDENSATORY Podstawowe własności elektrostatyczne przewodników: Natężenie pola wewnątrz przewodnika E = 0 Pole E na zewnątrz przewodnika jest prostopadłe do jego powierzchni Potencjał elektryczny wewnątrz
KONDENSATORY Podstawowe własności elektrostatyczne przewodników: Natężenie pola wewnątrz przewodnika E = 0 Pole E na zewnątrz przewodnika jest prostopadłe do jego powierzchni Potencjał elektryczny wewnątrz
Elektrostatyka ŁADUNEK. Ładunek elektryczny. Dr PPotera wyklady fizyka dosw st podypl. n p. Cząstka α
 Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
Elektrostatyka ŁADUNEK elektron: -e = -1.610-19 C proton: e = 1.610-19 C neutron: 0 C n p p n Cząstka α Ładunek elektryczny Ładunek jest skwantowany: Jednostką ładunku elektrycznego w układzie SI jest
Fizyka 2 Wróbel Wojciech. w poprzednim odcinku
 Fizyka w poprzednim odcinku Obliczanie natężenia pola Fizyka Wyróżniamy ładunek punktowy d Wektor natężenia pola d w punkcie P pochodzący od ładunku d Suma składowych x-owych wektorów d x IĄGŁY ROZKŁAD
Fizyka w poprzednim odcinku Obliczanie natężenia pola Fizyka Wyróżniamy ładunek punktowy d Wektor natężenia pola d w punkcie P pochodzący od ładunku d Suma składowych x-owych wektorów d x IĄGŁY ROZKŁAD
Ładunki elektryczne. q = ne. Zasada zachowania ładunku. Ładunek jest cechąciała i nie można go wydzielićz materii. Ładunki jednoimienne odpychają się
 Ładunki elektryczne Ładunki jednoimienne odpychają się Ładunki różnoimienne przyciągają się q = ne n - liczba naturalna e = 1,60 10-19 C ładunek elementarny Ładunek jest cechąciała i nie można go wydzielićz
Ładunki elektryczne Ładunki jednoimienne odpychają się Ładunki różnoimienne przyciągają się q = ne n - liczba naturalna e = 1,60 10-19 C ładunek elementarny Ładunek jest cechąciała i nie można go wydzielićz
Strumień Prawo Gaussa Rozkład ładunku Płaszczyzna Płaszczyzny Prawo Gaussa i jego zastosowanie
 Problemy elektrodynamiki. Prawo Gaussa i jego zastosowanie przy obliczaniu pól ładunku rozłożonego w sposób ciągły. I LO im. Stefana Żeromskiego w Lęborku 19 marca 2012 Nowe spojrzenie na prawo Coulomba
Problemy elektrodynamiki. Prawo Gaussa i jego zastosowanie przy obliczaniu pól ładunku rozłożonego w sposób ciągły. I LO im. Stefana Żeromskiego w Lęborku 19 marca 2012 Nowe spojrzenie na prawo Coulomba
Dielektryki. właściwości makroskopowe. Ryszard J. Barczyński, 2016 Materiały dydaktyczne do użytku wewnętrznego
 Dielektryki właściwości makroskopowe Ryszard J. Barczyński, 2016 Materiały dydaktyczne do użytku wewnętrznego Przewodniki i izolatory Przewodniki i izolatory Pojemność i kondensatory Podatność dielektryczna
Dielektryki właściwości makroskopowe Ryszard J. Barczyński, 2016 Materiały dydaktyczne do użytku wewnętrznego Przewodniki i izolatory Przewodniki i izolatory Pojemność i kondensatory Podatność dielektryczna
Ładunki elektryczne i siły ich wzajemnego oddziaływania. Pole elektryczne. Copyright by pleciuga@ o2.pl
 Ładunki elektryczne i siły ich wzajemnego oddziaływania Pole elektryczne Copyright by pleciuga@ o2.pl Ładunek punktowy Ładunek punktowy (q) jest to wyidealizowany model, który zastępuje rzeczywiste naelektryzowane
Ładunki elektryczne i siły ich wzajemnego oddziaływania Pole elektryczne Copyright by pleciuga@ o2.pl Ładunek punktowy Ładunek punktowy (q) jest to wyidealizowany model, który zastępuje rzeczywiste naelektryzowane
Podstawy fizyki sezon 2 2. Elektrostatyka 2
 Podstawy fizyki sezon 2 2. Elektrostatyka 2 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Strumień wektora
Podstawy fizyki sezon 2 2. Elektrostatyka 2 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Strumień wektora
21 ELEKTROSTATYKA. KONDENSATORY
 Włodzimierz Wolczyński Pojemność elektryczna 21 ELEKTROSTATYKA. KONDENSATORY - dla przewodników - dla kondensatorów C pojemność elektryczna Q ładunek V potencjał, U napięcie jednostka farad 1 r Pojemność
Włodzimierz Wolczyński Pojemność elektryczna 21 ELEKTROSTATYKA. KONDENSATORY - dla przewodników - dla kondensatorów C pojemność elektryczna Q ładunek V potencjał, U napięcie jednostka farad 1 r Pojemność
UKŁADY KONDENSATOROWE
 UKŁADY KONDENSATOROWE 3.1. Wyprowadzić wzory na: a) pojemność kondensatora sferycznego z izolacją jednorodną (ε), b) pojemność kondensatora sferycznego z izolacją warstwową (ε 1, ε 2 ) c) pojemność odosobnionej
UKŁADY KONDENSATOROWE 3.1. Wyprowadzić wzory na: a) pojemność kondensatora sferycznego z izolacją jednorodną (ε), b) pojemność kondensatora sferycznego z izolacją warstwową (ε 1, ε 2 ) c) pojemność odosobnionej
Lekcja 43. Pojemność elektryczna
 Lekcja 43. Pojemność elektryczna Pojemność elektryczna przewodnika zależy od: Rozmiarów przewodnika, Obecności innych przewodników, Ośrodka w którym się dany przewodnik znajduje. Lekcja 44. Kondensator
Lekcja 43. Pojemność elektryczna Pojemność elektryczna przewodnika zależy od: Rozmiarów przewodnika, Obecności innych przewodników, Ośrodka w którym się dany przewodnik znajduje. Lekcja 44. Kondensator
WŁAŚCIWOŚCI IDEALNEGO PRZEWODNIKA
 WŁAŚCIWOŚCI IDEALNEGO PRZEWODNIKA Idealny przewodnik to materiał zawierająca nieskończony zapas zupełnie swobodnych ładunków. Z tej definicji wynikają podstawowe własności elektrostatyczne idealnych przewodników:
WŁAŚCIWOŚCI IDEALNEGO PRZEWODNIKA Idealny przewodnik to materiał zawierająca nieskończony zapas zupełnie swobodnych ładunków. Z tej definicji wynikają podstawowe własności elektrostatyczne idealnych przewodników:
Pojemność elektryczna. Pojemność elektryczna, Kondensatory Energia elektryczna
 Pojemność elektryczna Pojemność elektryczna, Kondensatory Energia elektryczna Pojemność elektryczna - kondensatory Kondensator : dwa przewodniki oddzielone izolatorem zwykle naładowane ładunkami o przeciwnych
Pojemność elektryczna Pojemność elektryczna, Kondensatory Energia elektryczna Pojemność elektryczna - kondensatory Kondensator : dwa przewodniki oddzielone izolatorem zwykle naładowane ładunkami o przeciwnych
Wymiana ciepła. Ładunek jest skwantowany. q=n. e gdzie n = ±1, ±2, ±3 [1C = 6, e] e=1, C
![Wymiana ciepła. Ładunek jest skwantowany. q=n. e gdzie n = ±1, ±2, ±3 [1C = 6, e] e=1, C Wymiana ciepła. Ładunek jest skwantowany. q=n. e gdzie n = ±1, ±2, ±3 [1C = 6, e] e=1, C](/thumbs/63/50333873.jpg) Wymiana ciepła Ładunek jest skwantowany ładunek elementarny ładunek pojedynczego elektronu (e). Każdy ładunek q (dodatni lub ujemny) jest całkowitą wielokrotnością jego bezwzględnej wartości. q=n. e gdzie
Wymiana ciepła Ładunek jest skwantowany ładunek elementarny ładunek pojedynczego elektronu (e). Każdy ładunek q (dodatni lub ujemny) jest całkowitą wielokrotnością jego bezwzględnej wartości. q=n. e gdzie
ŁADUNEK I MATERIA Ładunki elektryczne są ściśle związane z atomową budową materii. Materia składa się z trzech rodzajów cząstek elementarnych:
 POLE ELEKTRYCZNE Ładunek i materia Ładunek elementarny. Zasada zachowania ładunku Prawo Coulomba Elektryzowanie ciał Pole elektryczne i pole zachowawcze Natężenie i strumień pola elektrycznego Prawo Gaussa
POLE ELEKTRYCZNE Ładunek i materia Ładunek elementarny. Zasada zachowania ładunku Prawo Coulomba Elektryzowanie ciał Pole elektryczne i pole zachowawcze Natężenie i strumień pola elektrycznego Prawo Gaussa
Wykład 8 ELEKTROMAGNETYZM
 Wykład 8 ELEKTROMAGNETYZM Równania Maxwella dive = ρ εε 0 prawo Gaussa dla pola elektrycznego divb = 0 rote = db dt prawo Gaussa dla pola magnetycznego prawo indukcji Faradaya rotb = μμ 0 j + εε 0 μμ 0
Wykład 8 ELEKTROMAGNETYZM Równania Maxwella dive = ρ εε 0 prawo Gaussa dla pola elektrycznego divb = 0 rote = db dt prawo Gaussa dla pola magnetycznego prawo indukcji Faradaya rotb = μμ 0 j + εε 0 μμ 0
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics)
 Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
Fizyka współczesna Co zazwyczaj obejmuje fizyka współczesna (modern physics) Koniec XIX / początek XX wieku Lata 90-te XIX w.: odkrycie elektronu (J. J. Thomson, promienie katodowe), promieniowania Roentgena
ELEKTRONIKA ELM001551W
 ELEKTRONIKA ELM001551W Podstawy elektrotechniki i elektroniki Definicje prądu elektrycznego i wielkości go opisujących: natężenia, gęstości, napięcia. Zakres: Oznaczenia wielkości fizycznych i ich jednostek,
ELEKTRONIKA ELM001551W Podstawy elektrotechniki i elektroniki Definicje prądu elektrycznego i wielkości go opisujących: natężenia, gęstości, napięcia. Zakres: Oznaczenia wielkości fizycznych i ich jednostek,
ELEKTROSTATYKA. cos tg60 3
 Włodzimierz Wolczyński 45 POWTÓRKA 7 ELEKTROSTATYKA Zadanie 1 Na nitkach nieprzewodzących o długościach 1 m wiszą dwie jednakowe metalowe kuleczki. Po naładowaniu obu ładunkiem jednoimiennym 1μC nitki
Włodzimierz Wolczyński 45 POWTÓRKA 7 ELEKTROSTATYKA Zadanie 1 Na nitkach nieprzewodzących o długościach 1 m wiszą dwie jednakowe metalowe kuleczki. Po naładowaniu obu ładunkiem jednoimiennym 1μC nitki
Ładunek elektryczny. Ładunek elektryczny jedna z własności cząstek elementarnych
 Ładunek elektryczny Ładunek elektryczny jedna z własności cząstek elementarnych http://pl.wikipedia.org/wiki/%c5%81a dunek_elektryczny ładunki elektryczne o takich samych znakach się odpychają a o przeciwnych
Ładunek elektryczny Ładunek elektryczny jedna z własności cząstek elementarnych http://pl.wikipedia.org/wiki/%c5%81a dunek_elektryczny ładunki elektryczne o takich samych znakach się odpychają a o przeciwnych
Elektrostatyka. A. tyle samo B. będzie 2 razy mniejsza C. będzie 4 razy większa D. nie da się obliczyć bez znajomości odległości miedzy ładunkami
 Elektrostatyka Zadanie 1. Dwa jednoimienne ładunki po 10C każdy odpychają się z siłą 36 10 8 N. Po dwukrotnym zwiększeniu odległości między tymi ładunkami i dwukrotnym zwiększeniu jednego z tych ładunków,
Elektrostatyka Zadanie 1. Dwa jednoimienne ładunki po 10C każdy odpychają się z siłą 36 10 8 N. Po dwukrotnym zwiększeniu odległości między tymi ładunkami i dwukrotnym zwiększeniu jednego z tych ładunków,
Dielektryki polaryzację dielektryka Dipole trwałe Dipole indukowane Polaryzacja kryształów jonowych
 Dielektryki Dielektryk- ciało gazowe, ciekłe lub stałe niebędące przewodnikiem prądu elektrycznego (ładunki elektryczne wchodzące w skład każdego ciała są w dielektryku związane ze sobą) Jeżeli do dielektryka
Dielektryki Dielektryk- ciało gazowe, ciekłe lub stałe niebędące przewodnikiem prądu elektrycznego (ładunki elektryczne wchodzące w skład każdego ciała są w dielektryku związane ze sobą) Jeżeli do dielektryka
Elektryczne właściwości materii. Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej.
 Elektryczne właściwości materii Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki I
Elektryczne właściwości materii Materiały dydaktyczne dla kierunku Technik Optyk (W10) Szkoły Policealnej Zawodowej. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki I
Ładunek elektryczny. Zastosowanie równania Laplace a w elektro- i magnetostatyce. Joanna Wojtal. Wprowadzenie. Podstawowe cechy pól siłowych
 6 czerwca 2013 Ładunek elektryczny Ciała fizyczne mogą być obdarzone (i w znacznej większości faktycznie są) ładunkiem elektrycznym. Ładunek ten może być dodatni lub ujemny. Kiedy na jednym ciele zgromadzonych
6 czerwca 2013 Ładunek elektryczny Ciała fizyczne mogą być obdarzone (i w znacznej większości faktycznie są) ładunkiem elektrycznym. Ładunek ten może być dodatni lub ujemny. Kiedy na jednym ciele zgromadzonych
Elektrostatyka. Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego
 Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Elektrostatyka Prawo Coulomba Natężenie pola elektrycznego Energia potencjalna pola elektrycznego 1 Prawo Coulomba odpychanie naelektryzowane szkło nie-naelektryzowana miedź F 1 4 0 q 1 q 2 r 2 0 8.85
Elektryczne właściwości materiałów. Materiały dydaktyczne dla kierunku Technik Optyk (W12) Kwalifikacyjnego kursu zawodowego.
 Elektryczne właściwości materiałów Materiały dydaktyczne dla kierunku Technik Optyk (W) Kwalifikacyjnego kursu zawodowego. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki
Elektryczne właściwości materiałów Materiały dydaktyczne dla kierunku Technik Optyk (W) Kwalifikacyjnego kursu zawodowego. Podział materii ze względu na jej właściwości Przewodniki elektryczne: Przewodniki
Linie sił pola elektrycznego
 Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Wykład 5 5.6. Linie sił pola elektrycznego Pamiętamy, że we wzorze (5.) określiliśmy natężenie pola elektrycznego przy pomocy ładunku próbnego q 0, którego wielkość dążyła do zera. Robiliśmy to po to,
Elektrostatyka. Potencjał pola elektrycznego Prawo Gaussa
 Elektrostatyka Potencjał pola elektrycznego Prawo Gaussa 1 Potencjał pola elektrycznego Energia potencjalna zależy od (ładunek próbny) i Q (ładunek który wytwarza pole), ale wielkość definiowana jako:
Elektrostatyka Potencjał pola elektrycznego Prawo Gaussa 1 Potencjał pola elektrycznego Energia potencjalna zależy od (ładunek próbny) i Q (ładunek który wytwarza pole), ale wielkość definiowana jako:
Wykład 17 Izolatory i przewodniki
 Wykład 7 Izolatory i przewodniki Wszystkie ciała możemy podzielić na przewodniki i izolatory albo dielektryki. Przewodnikami są wszystkie metale, roztwory kwasów i zasad, roztopione soli, nagrzane gazy
Wykład 7 Izolatory i przewodniki Wszystkie ciała możemy podzielić na przewodniki i izolatory albo dielektryki. Przewodnikami są wszystkie metale, roztwory kwasów i zasad, roztopione soli, nagrzane gazy
4.1.1 Elektryzowanie ciał. Zasada zachowania ładunku
 Rozdział 4 Pole elektryczne 4.1 Ładunki elektryczne 4.1.1 Elektryzowanie ciał. Zasada zachowania ładunku W niniejszym rozdziale zostaną przedstawione wybrane zagadnienia elektrostatyki. Elektrostatyka
Rozdział 4 Pole elektryczne 4.1 Ładunki elektryczne 4.1.1 Elektryzowanie ciał. Zasada zachowania ładunku W niniejszym rozdziale zostaną przedstawione wybrane zagadnienia elektrostatyki. Elektrostatyka
Badanie rozkładu pola elektrycznego
 Ćwiczenie 8 Badanie rozkładu pola elektrycznego 8.1. Zasada ćwiczenia W wannie elektrolitycznej umieszcza się dwie metalowe elektrody, połączone ze źródłem zmiennego napięcia. Kształt przekrojów powierzchni
Ćwiczenie 8 Badanie rozkładu pola elektrycznego 8.1. Zasada ćwiczenia W wannie elektrolitycznej umieszcza się dwie metalowe elektrody, połączone ze źródłem zmiennego napięcia. Kształt przekrojów powierzchni
kondensatory Jednostkę pojemności [Q/V] przyjęto nazywać faradem i oznaczać literą F.
![kondensatory Jednostkę pojemności [Q/V] przyjęto nazywać faradem i oznaczać literą F. kondensatory Jednostkę pojemności [Q/V] przyjęto nazywać faradem i oznaczać literą F.](/thumbs/65/54307331.jpg) Pojemność elektryczna i kondensatory Umieśćmy na przewodniku ładunek. Przyjmijmy zero potencjału w nieskończoności. Potencjał przewodnika jest proporcjonalny do ładunku (dlaczego?). Współczynnik proporcjonalności
Pojemność elektryczna i kondensatory Umieśćmy na przewodniku ładunek. Przyjmijmy zero potencjału w nieskończoności. Potencjał przewodnika jest proporcjonalny do ładunku (dlaczego?). Współczynnik proporcjonalności
Pojemność elektryczna, Kondensatory Energia elektryczna
 Pojemność elektryczna Pojemność elektryczna, Kondensatory Energia elektryczna 1 Pojemność elektryczna - kondensatory Kondensator : dwa przewodniki oddzielone izolatorem zwykle naładowane ładunkami o przeciwnych
Pojemność elektryczna Pojemność elektryczna, Kondensatory Energia elektryczna 1 Pojemność elektryczna - kondensatory Kondensator : dwa przewodniki oddzielone izolatorem zwykle naładowane ładunkami o przeciwnych
Wykład 4 i 5 Prawo Gaussa i pole elektryczne w materii. Pojemność.
 Wykład 4 i 5 Prawo Gaussa i pole elektryczne w materii. Pojemność. Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 21 marca 2016 Maciej J. Mrowiński (IF PW) Wykład 4 i 5 21
Wykład 4 i 5 Prawo Gaussa i pole elektryczne w materii. Pojemność. Maciej J. Mrowiński mrow@if.pw.edu.pl Wydział Fizyki Politechnika Warszawska 21 marca 2016 Maciej J. Mrowiński (IF PW) Wykład 4 i 5 21
Wykład 2. POLE ELEKTROMEGNETYCZNE:
 Wykład 2. POLE ELEKTROMEGNETYCZNE: Ładunek elektryczny Ładunki elektryczne: -dodatnie i ujemne - skwantowane, czyli że mają pewną najmniejszą wartość, której nie można już dalej podzielić. Nie można ładunków
Wykład 2. POLE ELEKTROMEGNETYCZNE: Ładunek elektryczny Ładunki elektryczne: -dodatnie i ujemne - skwantowane, czyli że mają pewną najmniejszą wartość, której nie można już dalej podzielić. Nie można ładunków
2 K A T E D R A F I ZYKI S T O S O W AN E J
 2 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 2. Łączenie i pomiar pojemności i indukcyjności Wprowadzenie Pojemność
2 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 2. Łączenie i pomiar pojemności i indukcyjności Wprowadzenie Pojemność
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 3 Janusz Andrzejewski Prąd elektryczny Prąd elektryczny to uporządkowany ruch swobodnych ładunków. Ruchowi chaotycznemu nie towarzyszy przepływ prądu. Strzałki szare - to nieuporządkowany(chaotyczny)
FIZYKA 2 wykład 3 Janusz Andrzejewski Prąd elektryczny Prąd elektryczny to uporządkowany ruch swobodnych ładunków. Ruchowi chaotycznemu nie towarzyszy przepływ prądu. Strzałki szare - to nieuporządkowany(chaotyczny)
Wykład 2. POLE ELEKTROMEGNETYCZNE:
 Wykład 2. POLE ELEKTROMEGNETYCZNE: Ładunek elektryczny Ładunki elektryczne: -dodatnie i ujemne - skwantowane, czyli że mają pewną najmniejszą wartość, której nie można już dalej podzielić. Nie można ładunków
Wykład 2. POLE ELEKTROMEGNETYCZNE: Ładunek elektryczny Ładunki elektryczne: -dodatnie i ujemne - skwantowane, czyli że mają pewną najmniejszą wartość, której nie można już dalej podzielić. Nie można ładunków
autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 22 ELEKTROSTATYKA CZĘŚĆ 2. KONDENSATORY
 autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 22 ELEKTROSTATYKA CZĘŚĆ 2. KONDENSATORY Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania Zadanie 1 1 punkt TEST JEDNOKROTNEGO
autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 22 ELEKTROSTATYKA CZĘŚĆ 2. KONDENSATORY Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania Zadanie 1 1 punkt TEST JEDNOKROTNEGO
cz.3 dr inż. Zbigniew Szklarski
 Wykład : lektrostatyka cz.3 dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Przykłady Jaka musiałaby być powierzchnia okładki kondensatora płaskiego, aby, przy odległości
Wykład : lektrostatyka cz.3 dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Przykłady Jaka musiałaby być powierzchnia okładki kondensatora płaskiego, aby, przy odległości
Badanie rozkładu pola elektrycznego
 Ćwiczenie 8 Badanie rozkładu pola elektrycznego 8.1. Zasada ćwiczenia W wannie elektrolitycznej umieszcza się dwie metalowe elektrody, połączone ze źródłem zmiennego napięcia. Kształt przekrojów powierzchni
Ćwiczenie 8 Badanie rozkładu pola elektrycznego 8.1. Zasada ćwiczenia W wannie elektrolitycznej umieszcza się dwie metalowe elektrody, połączone ze źródłem zmiennego napięcia. Kształt przekrojów powierzchni
Elektrostatyka, część pierwsza
 Elektrostatyka, część pierwsza ZADANIA DO PRZEROBIENIA NA LEKJI 1. Dwie kulki naładowano ładunkiem q 1 = 1 i q 2 = 3 i umieszczono w odległości r = 1m od siebie. Oblicz siłę ich wzajemnego oddziaływania.
Elektrostatyka, część pierwsza ZADANIA DO PRZEROBIENIA NA LEKJI 1. Dwie kulki naładowano ładunkiem q 1 = 1 i q 2 = 3 i umieszczono w odległości r = 1m od siebie. Oblicz siłę ich wzajemnego oddziaływania.
Materiały pomocnicze 10 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej
 Materiały pomocnicze 10 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Siła Coulomba. F q q = k r 1 = 1 4πεε 0 q q r 1. Pole elektrostatyczne. To przestrzeń, w której na ładunek
Materiały pomocnicze 10 do zajęć wyrównawczych z Fizyki dla Inżynierii i Gospodarki Wodnej 1. Siła Coulomba. F q q = k r 1 = 1 4πεε 0 q q r 1. Pole elektrostatyczne. To przestrzeń, w której na ładunek
Prąd elektryczny 1/37
 Prąd elektryczny 1/37 Prąd elektryczny Prądem elektrycznym w przewodniku metalowym nazywamy uporządkowany ruch elektronów swobodnych pod wpływem sił pola elektrycznego. Prąd elektryczny może również płynąć
Prąd elektryczny 1/37 Prąd elektryczny Prądem elektrycznym w przewodniku metalowym nazywamy uporządkowany ruch elektronów swobodnych pod wpływem sił pola elektrycznego. Prąd elektryczny może również płynąć
FIZYKA 2. Janusz Andrzejewski
 FIZYKA 2 wykład 3 Janusz Andrzejewski Prawo Coulomba a prawo Newtona Janusz Andrzejewski 2 Natężenie i potencjał pola elektrycznego A q A B q A D q A C q A q 0 D B C A E E E E r r r r 0 0 + + + + + + D
FIZYKA 2 wykład 3 Janusz Andrzejewski Prawo Coulomba a prawo Newtona Janusz Andrzejewski 2 Natężenie i potencjał pola elektrycznego A q A B q A D q A C q A q 0 D B C A E E E E r r r r 0 0 + + + + + + D
Podstawy fizyki sezon 2 2. Elektrostatyka 2
 Podstawy fizyki sezon 2 2. Elektrostatyka 2 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Zebranie faktów
Podstawy fizyki sezon 2 2. Elektrostatyka 2 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Zebranie faktów
Pojemność elektryczna
 Pojemność elektryczna Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Pojemność elektryczna Umieśćmy na pewnym
Pojemność elektryczna Ryszard J. Barczyński, 2016 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Pojemność elektryczna Umieśćmy na pewnym
Podstawy Elektroniki i Elektrotechniki
 Podstawy Elektroniki i Elektrotechniki Sławomir Mamica mamica@amu.edu.pl Obwody prądu elektrycznego http://main5.amu.edu.pl/~zfp/sm/home.html Plan. Krótko o elektryczności Ładunek elektryczny Pole elektryczne
Podstawy Elektroniki i Elektrotechniki Sławomir Mamica mamica@amu.edu.pl Obwody prądu elektrycznego http://main5.amu.edu.pl/~zfp/sm/home.html Plan. Krótko o elektryczności Ładunek elektryczny Pole elektryczne
Elektrostatyka. Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
 Elektrostatyka Projekt współfinansowany przez Unię Europejską w ramach Europejskiego unduszu Społecznego Ładunek elektryczny Materia zbudowana jest z atomów. Atom składa się z dodatnie naładowanego jądra
Elektrostatyka Projekt współfinansowany przez Unię Europejską w ramach Europejskiego unduszu Społecznego Ładunek elektryczny Materia zbudowana jest z atomów. Atom składa się z dodatnie naładowanego jądra
Elektrostatyczna energia potencjalna U
 Elektrostatyczna energia potencjalna U Żeby zbliżyć do siebie dwa ładunki jednoimienne trzeba wykonać pracę przeciwko siłom pola nadając ładunkowi energię potencjalną. Podobnie trzeba wykonać pracę przeciwko
Elektrostatyczna energia potencjalna U Żeby zbliżyć do siebie dwa ładunki jednoimienne trzeba wykonać pracę przeciwko siłom pola nadając ładunkowi energię potencjalną. Podobnie trzeba wykonać pracę przeciwko
Wykład 8: Elektrostatyka Katarzyna Weron
 Wykład 8: Elektrostatyka Katarzyna Weron Matematyka Stosowana Przewodniki i izolatory Przewodniki - niektóre ładunki ujemne mogą się dość swobodnie poruszać: metalach, wodzie, ciele ludzkim, Izolatory
Wykład 8: Elektrostatyka Katarzyna Weron Matematyka Stosowana Przewodniki i izolatory Przewodniki - niektóre ładunki ujemne mogą się dość swobodnie poruszać: metalach, wodzie, ciele ludzkim, Izolatory
znak minus wynika z faktu, że wektor F jest zwrócony
 Wykład 6 : Pole grawitacyjne. Pole elektrostatyczne. Prąd elektryczny Pole grawitacyjne Każde dwa ciała o masach m 1 i m 2 przyciągają się wzajemnie siłą grawitacji wprost proporcjonalną do iloczynu mas,
Wykład 6 : Pole grawitacyjne. Pole elektrostatyczne. Prąd elektryczny Pole grawitacyjne Każde dwa ciała o masach m 1 i m 2 przyciągają się wzajemnie siłą grawitacji wprost proporcjonalną do iloczynu mas,
Pole magnetyczne. Magnes wytwarza wektorowe pole magnetyczne we wszystkich punktach otaczającego go przestrzeni.
 Pole magnetyczne Magnes wytwarza wektorowe pole magnetyczne we wszystkich punktach otaczającego go przestrzeni. naładowane elektrycznie cząstki, poruszające się w przewodniku w postaci prądu elektrycznego,
Pole magnetyczne Magnes wytwarza wektorowe pole magnetyczne we wszystkich punktach otaczającego go przestrzeni. naładowane elektrycznie cząstki, poruszające się w przewodniku w postaci prądu elektrycznego,
Obwodem elektrycznym nazywamy zespół połączonych ze sobą elementów, umożliwiający zamknięty obieg prądu.
 Opracował: mgr inż. Marcin Wieczorek www.marwie.net.pl Obwód elektryczny i jego schemat. Obwodem elektrycznym nazywamy zespół połączonych ze sobą elementów, umożliwiający zamknięty obieg prądu. Schemat
Opracował: mgr inż. Marcin Wieczorek www.marwie.net.pl Obwód elektryczny i jego schemat. Obwodem elektrycznym nazywamy zespół połączonych ze sobą elementów, umożliwiający zamknięty obieg prądu. Schemat
POWTÓRKA PRZED KONKURSEM CZĘŚĆ 14 ZADANIA ZAMKNIĘTE
 DO ZDOBYCIA PUNKTÓW 50 POWTÓRKA PRZED KONKURSEM CZĘŚĆ 14 Jest to powtórka przed etapem rejonowym (głównie elektrostatyka). ZADANIA ZAMKNIĘTE łącznie pkt. zamknięte otwarte SUMA zadanie 1 1 pkt Po włączeniu
DO ZDOBYCIA PUNKTÓW 50 POWTÓRKA PRZED KONKURSEM CZĘŚĆ 14 Jest to powtórka przed etapem rejonowym (głównie elektrostatyka). ZADANIA ZAMKNIĘTE łącznie pkt. zamknięte otwarte SUMA zadanie 1 1 pkt Po włączeniu
Pojęcie ładunku elektrycznego
 Elektrostatyka Trochę historii Zjawisko elektryzowania się niektórych ciał było znane już w starożytności. O zjawisku przyciągania drobnych, lekkich ciał przez potarty suknem bursztyn wspomina Tales z
Elektrostatyka Trochę historii Zjawisko elektryzowania się niektórych ciał było znane już w starożytności. O zjawisku przyciągania drobnych, lekkich ciał przez potarty suknem bursztyn wspomina Tales z
Podstawy fizyki sezon 2 3. Prąd elektryczny
 Podstawy fizyki sezon 2 3. Prąd elektryczny Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Prąd elektryczny
Podstawy fizyki sezon 2 3. Prąd elektryczny Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Prąd elektryczny
Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI.
 Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI. 1. Ładunki q 1 =3,2 10 17 i q 2 =1,6 10 18 znajdują się w próżni
Przykładowe zadania/problemy egzaminacyjne. Wszystkie bezwymiarowe wartości liczbowe występujące w treści zadań podane są w jednostkach SI. 1. Ładunki q 1 =3,2 10 17 i q 2 =1,6 10 18 znajdują się w próżni
Wykład 18 Dielektryk w polu elektrycznym
 Wykład 8 Dielektryk w polu elektrycznym Polaryzacja dielektryka Dielektryk (izolator), w odróżnieniu od przewodnika, nie posiada ładunków swobodnych zdolnych do przemieszczenia się na duże odległości.
Wykład 8 Dielektryk w polu elektrycznym Polaryzacja dielektryka Dielektryk (izolator), w odróżnieniu od przewodnika, nie posiada ładunków swobodnych zdolnych do przemieszczenia się na duże odległości.
Kondensator. Kondensator jest to układ dwóch przewodników przedzielonych
 Kondensatory Kondensator Kondensator jest to układ dwóch przewodników przedzielonych dielektrykiem, na których zgromadzone są ładunki elektryczne jednakowej wartości ale o przeciwnych znakach. Budowa Najprostsze
Kondensatory Kondensator Kondensator jest to układ dwóch przewodników przedzielonych dielektrykiem, na których zgromadzone są ładunki elektryczne jednakowej wartości ale o przeciwnych znakach. Budowa Najprostsze
Plan Zajęć. Ćwiczenia rachunkowe
 Plan Zajęć 1. Termodynamika, 2. Grawitacja, Kolokwium I 3. Elektrostatyka + prąd 4. Pole Elektro-Magnetyczne Kolokwium II 5. Zjawiska falowe 6. Fizyka Jądrowa + niepewność pomiaru Kolokwium III Egzamin
Plan Zajęć 1. Termodynamika, 2. Grawitacja, Kolokwium I 3. Elektrostatyka + prąd 4. Pole Elektro-Magnetyczne Kolokwium II 5. Zjawiska falowe 6. Fizyka Jądrowa + niepewność pomiaru Kolokwium III Egzamin
1 K A T E D R A F I ZYKI S T O S O W AN E J
 1 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 1. Łączenie i pomiar oporu Wprowadzenie Prąd elektryczny Jeżeli w przewodniku
1 K A T E D R A F I ZYKI S T O S O W AN E J P R A C O W N I A P O D S T A W E L E K T R O T E C H N I K I I E L E K T R O N I K I Ćw. 1. Łączenie i pomiar oporu Wprowadzenie Prąd elektryczny Jeżeli w przewodniku
KONKURS FIZYCZNY CZĘŚĆ 3. Opracowanie Agnieszka Janusz-Szczytyńska
 KONKURS FIZYCZNY CZĘŚĆ 3 Opracowanie Agnieszka Janusz-Szczytyńska ZAGADNIENIA DO KONKURSU ETAP II Kolorem czerwonym zaznaczone są zagadnienia wykraczające poza program nauczania, na zielono zagadnienia,
KONKURS FIZYCZNY CZĘŚĆ 3 Opracowanie Agnieszka Janusz-Szczytyńska ZAGADNIENIA DO KONKURSU ETAP II Kolorem czerwonym zaznaczone są zagadnienia wykraczające poza program nauczania, na zielono zagadnienia,
Elektryczność i Magnetyzm
 Elektryczność i Magnetyzm Wykład: Piotr Kossacki Pokazy: Kacper Oreszczuk, Magda Grzeszczyk, Paweł Trautman Wykład szósty 14 marca 019 Z ostatniego wykładu Doświadczenie Millikana Potencjał i pole od dipola
Elektryczność i Magnetyzm Wykład: Piotr Kossacki Pokazy: Kacper Oreszczuk, Magda Grzeszczyk, Paweł Trautman Wykład szósty 14 marca 019 Z ostatniego wykładu Doświadczenie Millikana Potencjał i pole od dipola
RÓWNANIA MAXWELLA. Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego?
 RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
RÓWNANIA MAXWELLA Czy pole magnetyczne może stać się źródłem pola elektrycznego? Czy pole elektryczne może stać się źródłem pola magnetycznego? Wykład 3 lato 2012 1 Doświadczenia Wykład 3 lato 2012 2 1
Elektrostatyka. Już starożytni Grecy wiedzieli, że potarty o tkaninę bursztyn przyciąga drobne lekkie przedmioty.
 Elektrostatyka Już starożytni Grecy wiedzieli, że potarty o tkaninę bursztyn przyciąga drobne lekkie przedmioty. Pozostawało to odosobnioną ciekawostką aż do XVIw., kiedy Wlliam Gilbert wykazał, że podobną
Elektrostatyka Już starożytni Grecy wiedzieli, że potarty o tkaninę bursztyn przyciąga drobne lekkie przedmioty. Pozostawało to odosobnioną ciekawostką aż do XVIw., kiedy Wlliam Gilbert wykazał, że podobną
Wykład 14: Indukcja cz.2.
 Wykład 14: Indukcja cz.. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 10.05.017 Wydział Informatyki, Elektroniki i 1 Przykład
Wykład 14: Indukcja cz.. Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 10.05.017 Wydział Informatyki, Elektroniki i 1 Przykład
autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 21 ELEKTROSTATYKA CZĘŚĆ 1. POLE CENTRALNE I JEDNORODNE
 autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 21 ELEKTROSTATYKA CZĘŚĆ 1. POLE CENTRALNE I JEDNORODNE Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania TEST JEDNOKROTNEGO
autor: Włodzimierz Wolczyński rozwiązywał (a)... ARKUSIK 21 ELEKTROSTATYKA CZĘŚĆ 1. POLE CENTRALNE I JEDNORODNE Rozwiązanie zadań należy zapisać w wyznaczonych miejscach pod treścią zadania TEST JEDNOKROTNEGO
Guma Guma. Szkło Guma
 1 Ładunek elektyczny jest cechą mateii. Istnieją dwa odzaje ładunków, nazywane dodatnimi i ujemnymi. Ładunki jednoimienne się odpychają, podczas gdy ładunki óżnoimeinne się pzyciągają Guma Guma Szkło Guma
1 Ładunek elektyczny jest cechą mateii. Istnieją dwa odzaje ładunków, nazywane dodatnimi i ujemnymi. Ładunki jednoimienne się odpychają, podczas gdy ładunki óżnoimeinne się pzyciągają Guma Guma Szkło Guma
Podstawy fizyki sezon 2 1. Elektrostatyka 1
 Biblioteka AGH Podstawy fizyki sezon 2 1. Elektrostatyka 1 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha
Biblioteka AGH Podstawy fizyki sezon 2 1. Elektrostatyka 1 Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha
Fizyka 2 Wróbel Wojciech. w poprzednim odcinku
 w poprzednim odcinku 1 Model przewodnictwa metali Elektrony przewodnictwa dla metalu tworzą tzw. gaz elektronowy Elektrony poruszają się chaotycznie (ruchy termiczne), ulegają zderzeniom z atomami sieci
w poprzednim odcinku 1 Model przewodnictwa metali Elektrony przewodnictwa dla metalu tworzą tzw. gaz elektronowy Elektrony poruszają się chaotycznie (ruchy termiczne), ulegają zderzeniom z atomami sieci
ELEKTROSTATYKA. Zakład Elektrotechniki Teoretycznej Politechniki Wrocławskiej, I-7, W-5
 ELEKTROSTATYKA 2.1 Obliczyć siłę, z jaką działają na siebie dwa ładunki punktowe Q 1 = Q 2 = 1C umieszczone w odległości l km od siebie, a z jaką siłą - w tej samej odległości - dwie jednogramowe kulki
ELEKTROSTATYKA 2.1 Obliczyć siłę, z jaką działają na siebie dwa ładunki punktowe Q 1 = Q 2 = 1C umieszczone w odległości l km od siebie, a z jaką siłą - w tej samej odległości - dwie jednogramowe kulki
PROGRAM INDYWIDUALNEGO TOKU NAUCZANIA DLA UCZNIÓW KLASY II
 POGAM INDYWIDUALNEGO TOKU NAUCZANIA DLA UCZNIÓW KLASY II Opracowała: mgr Joanna Kondys Cele do osiągnięcia: etapowe udział w olimpiadzie fizycznej udział w konkursie fizycznym dla szkół średnich docelowe
POGAM INDYWIDUALNEGO TOKU NAUCZANIA DLA UCZNIÓW KLASY II Opracowała: mgr Joanna Kondys Cele do osiągnięcia: etapowe udział w olimpiadzie fizycznej udział w konkursie fizycznym dla szkół średnich docelowe
R o z d z i a ł 7 POLE ELEKTRYCZNE
 R o z d z i a ł 7 POLE ELEKTRYCZNE Zjawiska elektryczne towarzyszyły człowiekowi od samego początku jego pojawienia się. Wyładowania atmosferyczne napawały grozą, zaś zjawiska bioelektryczne i elektryzacja
R o z d z i a ł 7 POLE ELEKTRYCZNE Zjawiska elektryczne towarzyszyły człowiekowi od samego początku jego pojawienia się. Wyładowania atmosferyczne napawały grozą, zaś zjawiska bioelektryczne i elektryzacja
Fizyka 2 Podstawy fizyki
 Fizyka Podstawy fizyki dr hab. inż. Wydział Fizyki e-mail: wrobel.studia@gmail.com konsultacje: Gmach Mechatroniki, pok. 34; środa 13-14 i po umówieniu mailowym http://www.if.pw.edu.pl/~wrobel/simr_f_17.html
Fizyka Podstawy fizyki dr hab. inż. Wydział Fizyki e-mail: wrobel.studia@gmail.com konsultacje: Gmach Mechatroniki, pok. 34; środa 13-14 i po umówieniu mailowym http://www.if.pw.edu.pl/~wrobel/simr_f_17.html
cz. 2. dr inż. Zbigniew Szklarski
 Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
Wykład 14: Pole magnetyczne cz.. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Prąd elektryczny jako źródło pola magnetycznego - doświadczenie Oersteda Kiedy przez
Indukcja magnetyczna pola wokół przewodnika z prądem. dr inż. Romuald Kędzierski
 Indukcja magnetyczna pola wokół przewodnika z prądem dr inż. Romuald Kędzierski Pole magnetyczne wokół pojedynczego przewodnika prostoliniowego Założenia wyjściowe: przez nieskończenie długi prostoliniowy
Indukcja magnetyczna pola wokół przewodnika z prądem dr inż. Romuald Kędzierski Pole magnetyczne wokół pojedynczego przewodnika prostoliniowego Założenia wyjściowe: przez nieskończenie długi prostoliniowy
Pole elektromagnetyczne
 Pole elektromagnetyczne Pole magnetyczne Strumień pola magnetycznego Jednostką strumienia magnetycznego w układzie SI jest 1 weber (1 Wb) = 1 N m A -1. Zatem, pole magnetyczne B jest czasem nazywane gęstością
Pole elektromagnetyczne Pole magnetyczne Strumień pola magnetycznego Jednostką strumienia magnetycznego w układzie SI jest 1 weber (1 Wb) = 1 N m A -1. Zatem, pole magnetyczne B jest czasem nazywane gęstością
Wykład 15: Indukcja. Dr inż. Zbigniew Szklarski. Katedra Elektroniki, paw. C-1, pok
 Wykład 15: Indukcja Dr inż. Zbigniew zklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ 1 Pole magnetyczne a prąd elektryczny Do tej pory omawiano skutki
Wykład 15: Indukcja Dr inż. Zbigniew zklarski Katedra Elektroniki, paw. -1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ 1 Pole magnetyczne a prąd elektryczny Do tej pory omawiano skutki
Fizyka 2 Wróbel Wojciech. w poprzednim odcinku
 w poprzednim odcinku 1 Potencjał pola elektrycznego U ab ΔV W q b a F dx q b a F q dx b a (x)dx U gradv ab ΔV b a dv dv dv x,y,z i j k (x)dx dx dy dz Natężenie pola wskazuje kierunek w którym potencjał
w poprzednim odcinku 1 Potencjał pola elektrycznego U ab ΔV W q b a F dx q b a F q dx b a (x)dx U gradv ab ΔV b a dv dv dv x,y,z i j k (x)dx dx dy dz Natężenie pola wskazuje kierunek w którym potencjał
Wykład FIZYKA II. 1. Elektrostatyka. Dr hab. inż. Władysław Artur Woźniak
 Wykład FIZYKA II. Elektrostatyka Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ ELEKTROMAGNETYZM Już starożytni Grecy Potarty kawałek
Wykład FIZYKA II. Elektrostatyka Dr hab. inż. Władysław Artur Woźniak Instytut Fizyki Politechniki Wrocławskiej http://www.if.pwr.wroc.pl/~wozniak/ ELEKTROMAGNETYZM Już starożytni Grecy Potarty kawałek
Rozdział 1. Pole elektryczne i elektrostatyka
 Rozdział 1. Pole elektryczne i elektrostatyka 2018 Spis treści Ładunek elektryczny Prawo Coulomba Pole elektryczne Prawo Gaussa Zastosowanie prawa Gaussa: Izolowany przewodnik Zastosowanie prawa Gaussa:
Rozdział 1. Pole elektryczne i elektrostatyka 2018 Spis treści Ładunek elektryczny Prawo Coulomba Pole elektryczne Prawo Gaussa Zastosowanie prawa Gaussa: Izolowany przewodnik Zastosowanie prawa Gaussa:
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej
 Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
Linia dwuprzewodowa Obliczanie pojemności linii dwuprzewodowej 1. Wstęp Pojemność kondensatora można obliczyć w prosty sposób znając wartości zgromadzonego na nim ładunku i napięcia między okładkami: Q
Zwój nad przewodzącą płytą METODA ROZDZIELENIA ZMIENNYCH
 METODA ROZDZIELENIA ZMIENNYCH (2) (3) (10) (11) Modelowanie i symulacje obiektów w polu elektromagnetycznym 1 Rozwiązania równań (10-11) mają ogólną postać: (12) (13) Modelowanie i symulacje obiektów w
METODA ROZDZIELENIA ZMIENNYCH (2) (3) (10) (11) Modelowanie i symulacje obiektów w polu elektromagnetycznym 1 Rozwiązania równań (10-11) mają ogólną postać: (12) (13) Modelowanie i symulacje obiektów w
Elektrostatyka Elektryczność nas otacza i tworzy...
 Elektrostatyka Elektryczność nas otacza i tworzy... Ryszard J. Barczyński, 2010 2015 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Elektryczność
Elektrostatyka Elektryczność nas otacza i tworzy... Ryszard J. Barczyński, 2010 2015 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Elektryczność
Elektrostatyka, cz. 1
 Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Podstawy elektromagnetyzmu Wykład 3 Elektrostatyka, cz. 1 Prawo Coulomba F=k q 1 q 2 r 2 1 q1 q 2 Notka historyczna: 1767: John Priestley - sugestia 1771: Henry Cavendish - eksperyment 1785: Charles Augustin
Przewodniki w polu elektrycznym
 Przewodniki w polu elektrycznym Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Przewodniki to ciała takie, po
Przewodniki w polu elektrycznym Ryszard J. Barczyński, 2017 Politechnika Gdańska, Wydział FTiMS, Katedra Fizyki Ciała Stałego Materiały dydaktyczne do użytku wewnętrznego Przewodniki to ciała takie, po
Elektrostatyka, cz. 2
 Podstawy elektromagnetyzmu Wykład 4 Elektrostatyka, cz. Praca, energia, pojemność i kondensatory, ekrany elektrostatyczne Energia Praca w polu elektrostatycznym dw =F dl=q E dl W = L F d L=q L E d L=q
Podstawy elektromagnetyzmu Wykład 4 Elektrostatyka, cz. Praca, energia, pojemność i kondensatory, ekrany elektrostatyczne Energia Praca w polu elektrostatycznym dw =F dl=q E dl W = L F d L=q L E d L=q
Elektrostatyczna energia potencjalna. Potencjał elektryczny
 Elektrostatyczna energia potencjalna Potencjał elektryczny Elektrostatyczna energia potencjalna U Żeby zbliżyć do siebie dwa ładunki jednoimienne trzeba wykonać pracę przeciwko siłą pola nadając ładunkowi
Elektrostatyczna energia potencjalna Potencjał elektryczny Elektrostatyczna energia potencjalna U Żeby zbliżyć do siebie dwa ładunki jednoimienne trzeba wykonać pracę przeciwko siłą pola nadając ładunkowi
25P3 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - III POZIOM PODSTAWOWY
 25P3 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - III Hydrostatyka Gazy Termodynamika Elektrostatyka Prąd elektryczny stały POZIOM PODSTAWOWY Rozwiązanie zadań należy zapisać w wyznaczonych
25P3 POWTÓRKA FIKCYJNY EGZAMIN MATURALNYZ FIZYKI I ASTRONOMII - III Hydrostatyka Gazy Termodynamika Elektrostatyka Prąd elektryczny stały POZIOM PODSTAWOWY Rozwiązanie zadań należy zapisać w wyznaczonych
Imię i nazwisko ucznia Data... Klasa...
 Przygotowano za pomocą programu Ciekawa fizyka. Bank zadań Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2011 strona 1 Imię i nazwisko ucznia Data...... Klasa... Zadanie 1. Między
Przygotowano za pomocą programu Ciekawa fizyka. Bank zadań Copyright by Wydawnictwa Szkolne i Pedagogiczne sp. z o.o., Warszawa 2011 strona 1 Imię i nazwisko ucznia Data...... Klasa... Zadanie 1. Między
ELEKTROSTATYKA. Ze względu na właściwości elektryczne ciała dzielimy na przewodniki, izolatory i półprzewodniki.
 ELEKTROSTATYKA Ładunkiem elektrycznym nazywamy porcję elektryczności. Ładunkiem elementarnym e nazywamy najmniejszą wartość ładunku zaobserwowaną w przyrodzie. Jego wartość jest równa wartości ładunku
ELEKTROSTATYKA Ładunkiem elektrycznym nazywamy porcję elektryczności. Ładunkiem elementarnym e nazywamy najmniejszą wartość ładunku zaobserwowaną w przyrodzie. Jego wartość jest równa wartości ładunku
Podstawy fizyki sezon 2 3. Prąd elektryczny
 Podstawy fizyki sezon 2 3. Prąd elektryczny Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Prąd elektryczny
Podstawy fizyki sezon 2 3. Prąd elektryczny Agnieszka Obłąkowska-Mucha AGH, WFIiS, Katedra Oddziaływań i Detekcji Cząstek, D11, pok. 111 amucha@agh.edu.pl http://home.agh.edu.pl/~amucha Prąd elektryczny
Magnetyzm. Magnetyzm zdolność do przyciągania małych kawałków metalu. Bar Magnet. Magnes. Kompas N N. Iron filings. Biegun południowy.
 Magnetyzm Magnetyzm zdolność do przyciągania małych kawałków metalu Magnes Bar Magnet S S N N Iron filings N Kompas S Biegun południowy Biegun północny wp.lps.org/kcovil/files/2014/01/magneticfields.ppt
Magnetyzm Magnetyzm zdolność do przyciągania małych kawałków metalu Magnes Bar Magnet S S N N Iron filings N Kompas S Biegun południowy Biegun północny wp.lps.org/kcovil/files/2014/01/magneticfields.ppt
Pole magnetyczne Ziemi. Pole magnetyczne przewodnika z prądem
 Pole magnetyczne Własność przestrzeni polegającą na tym, że na umieszczoną w niej igiełkę magnetyczną działają siły, nazywamy polem magnetycznym. Pole takie wytwarza ruda magnetytu, magnes stały (czyli
Pole magnetyczne Własność przestrzeni polegającą na tym, że na umieszczoną w niej igiełkę magnetyczną działają siły, nazywamy polem magnetycznym. Pole takie wytwarza ruda magnetytu, magnes stały (czyli
cz. 2. dr inż. Zbigniew Szklarski
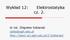 Wykład 2: lektrostatyka cz. 2. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Dygresja matematyczna - operatory Operator przyporządkowuje np. polu skalarnemu odpowiednie
Wykład 2: lektrostatyka cz. 2. dr inż. Zbigniew zklarski szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.zklarski/ Dygresja matematyczna - operatory Operator przyporządkowuje np. polu skalarnemu odpowiednie
Badanie własności hallotronu, wyznaczenie stałej Halla (E2)
 Badanie własności hallotronu, wyznaczenie stałej Halla (E2) 1. Wymagane zagadnienia - ruch ładunku w polu magnetycznym, siła Lorentza, pole elektryczne - omówić zjawisko Halla, wyprowadzić wzór na napięcie
Badanie własności hallotronu, wyznaczenie stałej Halla (E2) 1. Wymagane zagadnienia - ruch ładunku w polu magnetycznym, siła Lorentza, pole elektryczne - omówić zjawisko Halla, wyprowadzić wzór na napięcie
