Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Informatyki Stosowanej i Modelowania
|
|
|
- Adrian Kozieł
- 8 lat temu
- Przeglądów:
Transkrypt
1 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Informatyki Stosowanej i Modelowania Rozprawa doktorska Modelowanie wieloskalowe metodą automatów komórkowych własności materiałów odkształcanych plastycznie mgr inż. Jerzy Gawąd Promotor: Prof. dr hab. inż. Maciej Pietrzyk Kraków 2007
2 Podziękowania Składam podziękowania wszystkim osobom, które przez swoje działania lub ich zaniechanie przyczyniły się do powstania tej pracy. W szczególności chciałbym podziękować: Panu Profesorowi dr hab. inż. Maciejowi Pietrzykowi za opiekę nad pracą oraz cenne i wnoszące wiele inspirujących wątpliwości dyskusje. Panu Profesorowi dr hab. Romanowi Kuziakowi za umożliwienie przeprowadzenia badań doświadczalnych. Agacie za cierpliwość oraz wsparcie i otuchę. Praca naukowa finansowana ze środków budżetowych na naukę w latach jako projekt badawczy 3 T08A i
3 Spis treści Spis rysunków Spis tabel iv vii Wykaz najważniejszych oznaczeń viii Skróty viii Lista symboli ix 1 Wstęp 1 2 Wybrane problemy modelowania mikrostruktury Rekrystalizacja Klasyczne modele zmian mikrostruktury podczas rekrystalizacji Symulacja komputerowa procesów rekrystalizacji Metoda Monte-Carlo MES i teoria plastyczności kryształów MES i metoda zmiennej wewnętrznej Automaty komórkowe w modelowaniu rekrystalizacji Automaty komórkowe zarys metody Automaty komórkowe w symulacji rozwoju mikrostruktury Modele CA rekrystalizacji Podstawowe problemy modelowania CA procesów rekrystalizacji Wieloskalowa metoda symulacji CAFE Zastosowania CAFE w modelowaniu krystalizacji Metoda CAFE w modelowaniu rekrystalizacji statycznej Zastosowania CAFE w modelowaniu odkształceń plastycznych Podsumowanie Teza i cele pracy 43 4 Model CAFE Model skali makro Model mechaniczny Model cieplny Model CA dynamicznej rekrystalizacji Stan komórek Siatka komórek ii
4 SPIS TREŚCI Definicje sąsiedztwa w modelu Rozwój gęstości dyslokacji w modelu CA Reguły zmiany stanu komórek Tworzenie mikrostruktur początkowych Połączenie automatów komórkowych z MES Wyniki Wpływ definicji sąsiedztwa na rozrost ziarna w ośrodku izotropowym Tworzenie początkowych obrazów mikrostruktury Algorytm swobodnego wzrostu ziaren Przetwarzanie doświadczalnych obrazów mikrostruktury Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Stabilność obliczeń CA Obliczenia krytycznej gęstości dyslokacji Rozrost zarodka w złączu potrójnym Zarodkowanie i rozrost zrekrystalizowanych ziaren Analiza jakościowa modelu CAFE Wielopikowa krzywa naprężenia uplastyczniającego Jednopikowa krzywa naprężenia uplastyczniającego Podsumowanie Weryfikacja modelu Zastosowanie analizy odwrotnej do weryfikacji modelu CAFE Weryfikacja danymi literaturowymi Weryfikacja doświadczalna Dyskusja Model CA dynamicznej rekrystalizacji Własności odkształcanego metalu i połączenie CA-MES Identyfikacja parametrów modelu Podsumowanie i wnioski 150 A Implementacja modelu CAFE DRX 156 A.1 Biblioteka caengine A.2 Biblioteka cadrx A.3 Program cadrx A.4 Biblioteka userhard integracja modelu CA z MES Bibliografia 162 iii
5 Spis rysunków 2.1 Standardowe definicje sąsiedztwa w przestrzeniach 2D: von Neumanna, (b) Moore a, (c) heksagonalne Schematyczna ilustracja periodycznego warunku brzegowego dla dwuwymiarowej siatki komórek CA Krzywe naprężenia dla dρ/dt = 10 i czterech różnych rozmiarów ziarna początkowego i przy ustalonym rozmiarze ziarna końcowego, uzyskane w symulacji CA DRX oraz obrazy mikrostruktury w t = t Schemat rozwoju mikrostruktury naszyjnikowej w trakcie DRX Wpływ zmiany prędkości odkształcenia na krzywą naprężenia dla trzech różnych średnich rozmiarów ziarna początkowego oraz porównanie krzywych naprężenia i prędkości zarodkowania pod wpływem zmiany prędkości odkształcenia, uzyskane w symulacji CA DRX Porównanie krzywych płynięcia miedzi OFHC, pochodzących z symulacji CA i z doświadczenia Symulacja CA zmian mikrostruktury na poszczególnych etapach odkształcenia dla stali HY Symulacja CA rozwoju mikrostruktury w trakcie DRX i MDRX Sąsiedztwo heksagonalne, powstające przez modyfikację sąsiedztwa Moore a Obrazy mikrostruktur uzyskane z wykorzystaniem różnych definicji sąsiedztwa Sąsiedztwo o promieniu r w siatce nieregularnej Schemat dynamicznego przyporządkowania komórek i elementów skończonych w modelu 3D CAFE Proces osiowosymetrycznego ściskania próbek walcowych Wycinek siatki komórek CA z zaznaczonym przypisaniem do ziaren Przykład interpretacji układu stanu komórek w obrębie sąsiedztwa Przykład wprowadzenia zależności geometrycznych do sąsiedztwa Moore a, definiowanego jako graf z wagami w 1,..., w Alternatywne konfiguracje sąsiedztwa heksagonalnego losowo komutowanego Schemat dynamicznej rekrystalizacji, przybliżany regułami przejścia modelu CA Granica ziarna pomiędzy dwoma kryształami o kącie wzajemnej dezorientacji θ Zależność energii i ruchliwości granicy ziarna od kąta dezorientacji.. 71 iv
6 SPIS RYSUNKÓW 4.9 Schemat połączenia symulacji CA i elementu skończonego w punktach całkowania Gaussa Ilustracja połączenia z elementami w siatce MES zróżnicowanych pod względem wielkości ziarna symulacji CA Wpływ definicji sąsiedztwa na kształt wzrastającego ziarna Przebieg symulacji swobodnego wzrostu ziaren w wybranych krokach czasowych Obrazy mikrostruktury, uzyskane dla różnych schematów podziału siatki obliczeniowej w symulacji swobodnego wzrostu ziaren Rozkład względnej wielkości ziarna dla różnych schematów podziału siatki CA i gęstości zarodkowania w siatce Ułamek powierzchni przypisanej do ziaren, uzyskany z wykorzystaniem różnych schematów podziału siatki obliczeniowej i gęstości zarodkowania Kolejne etapy generowania reprezentacji mikrostruktury na podstawie danych z mikroskopii świetlnej Rozkład klas orientacji i względnej wielkości ziarna w reprezentacji mikrostruktury, wygenerowanej na podstawie danych z mikroskopii świetlnej Porównanie wartości naprężenia uplastyczniającego, uzyskanych na podstawie analitycznego rozwiązania równania rozwoju gęstości dyslokacji i obliczonego w modelu CA Wpływ definicji sąsiedztwa na średnie krytyczne gęstości dyslokacji w siatce CA Układ kątów dezorientacji granic ziaren w domenie obliczeniowej z zarodkiem w złączu potrójnym Rozrost zarodka w złączu potrójnym dla różnych kątów dezorientacji, podanych w tabeli 5.2, wiersz Rozrost zarodka w złączu potrójnym dla różnych kątów dezorientacji, podanych w tabeli 5.2, wiersz Rozrost zarodka w złączu potrójnym dla różnych kątów dezorientacji, podanych w tabeli 5.2, wiersz Rozkład gęstości dyslokacji w siatce obliczeniowej dla wzrostu zarodka w złączu potrójnym Schematyczna ilustracja gęstości dyslokacji na froncie dynamicznej rekrystalizacji Zarodkowanie i wzrost ziaren w trakcie DRX dla wybranych ułamków rekrystalizacji Uzyskany w obliczeniach CA obraz mikrostruktury dla wielopikowej krzywej σ f Ułamki rekrystalizacji przynależne do kolejnych cykli rekrystalizacji i odpowiadający im wielopikowy wykres naprężenia uplastyczniającego Naprężenie uplastyczniające oraz zastępczy ułamek rekrystalizacji: (a) uzyskany z modelu CAFE, (b) na podstawie pracy [71] (przypadek wielopikowej krzywej σ f ) v
7 SPIS RYSUNKÓW 5.20 Mapy rozkładu w siatce CA przynależności do cyklu rekrystalizacji i gęstości dyslokacji Średnia wielkość ziarna dla wielopikowej krzywej naprężenia uplastyczniającego. Linią przerywaną zaznaczono D 0 / Rozkłady wielkości ziarna dla wielopikowej krzywej naprężenia uplastyczniającego w wybranych odkształceniach Uzyskana w symulacji CA liczba zarodków i komórek przyłączonych do wzrastających ziaren w kolejnych krokach czasowych (przypadek wielopikowej krzywej σ f ) Wyniki makroskopowe rozwiązania CAFE dla wielopikowej krzywej naprężenia uplastyczniającego Ułamki rekrystalizacji przynależne do kolejnych cykli rekrystalizacji Naprężenie uplastyczniające oraz zastępczy ułamek rekrystalizacji: (a) uzyskany z modelu CAFE, (b) na podstawie pracy [71] (przypadek jednopikowej krzywej σ f ) Zmiana wielkości ziarna w trakcie odkształcenia dla jednopikowej krzywej naprężenia uplastyczniającego Uzyskana w symulacji CA liczba zarodków i komórek przyłączonych do wzrastających ziaren w kolejnych krokach czasowych (przypadek jednopikowej krzywej σ f ) Wyniki makroskopowe rozwiązania CAFE dla jednopikowej krzywej naprężenia uplastyczniającego Schemat rozszerzonego algorytmu obliczeń odwrotnych Naprężenia otrzymane w doświadczeniu spęczania miedzianych próbek walcowych Porównanie naprężenia uplastyczniającego, obliczonego przez model CA na podstawie zidentyfikowanych parametrów z naprężeniami wyznaczonymi doświadczalnie Porównanie średniej wielkości ziarna zmierzonej po zakończeniu doświadczenia i uzyskanej z modelu CA Siły nacisku obliczone przez model CAFE na podstawie zidentyfikowanych parametrów modelu CA Uzyskany w badaniach metalograficznych rozkład wielkości ziarna dla stali 16NiCrMo13: (a) próbka wyżarzona, (b) próbka odkształcona do ε = Naprężenie uplastyczniające σ f wyznaczone metodą odwrotną dla badanej stali oraz porównanie sił zmierzonych i obliczonych Rozkład wielkości ziarna w początkowej reprezentacji mikrostruktury w modelu CA, wygenerowanej algorytmem swobodnego wzrostu ziarna Wyniki obliczeń odwrotnych prowadzonych dla modelu CA DRX w stali Wyniki uzyskane z modelu CAFE na podstawie parametrów modelu CA, wyznaczonych w drodze obliczeń odwrotnych A.1 Diagram współpracy dla klasy DRXSimulationNode vi
8 Spis tabel 5.1 Schematy podziału siatki obliczeniowej na podobszary oraz gęstości zarodkowania, wykorzystane w testowaniu generatora mikrostruktur Układy kątów dezorientacji zarodka w złączu potrójnym względem osnowy Skład chemiczny badanej technicznie czystej miedzi 99.94% Cu Wybrane do analizy warunki procesu spęczania próbek z Cu oraz średnica ziarna po zakończeniu procesu Wartości parametrów modelu CA dynamicznej rekrystalizacji, zidentyfikowane dla miedzi w drodze obliczeń odwrotnych Skład chemiczny badanej stali 16NiCrMo13 wyrażony w procentach wagowych Wartości parametrów modelu CAFE, zidentyfikowane w drodze obliczeń odwrotnych dla stali 16NiCrMo vii
9 Wykaz najważniejszych oznaczeń Skróty CA automaty komórkowe (ang. Cellular Automata) CP-FEM MES oparta na teorii plastyczności kryształów (ang. Crystal Plasticity FEM ), DRX rekrystalizacja dynamiczna (ang. dynamic recrystallization) DRV dynamiczne zdrowienie (ang. dynamic recovery) EBSD dyfrakcja elektronów wstecznie rozproszonych 1 (ang. Electron Back Scattered Diffraction) FEM metoda elementów skończonych (ang. Finite Element Method), MES GB granica ziarna (ang. grain boundary) IVM model ze zmienną wewnętrzną (ang. Internal Variable Model) JMAK Johnson-Mehl-Avrami-Kolmogorow MC Monte-Carlo MCA ruchome automaty komórkowe (ang. Movable Cellular Automata) MDRX rekrystalizacja metadynamiczna (ang. metadynamic recrystallization) MES metoda elementów skończonych PSN zarodkowanie stymulowane cząsteczkami (ang. Particle Stimulated Nucleation) RX rekrystalizacja SRX rekrystalizacja statyczna (ang. static recrystallization) 1 Tłumaczenie skrótu EBSD wg [9] viii
10 Lista symboli b C wektor Burgersa komórka CA c p (T ) ciepło właściwe d D D c D e D gr ε ε ε i ε V ε F c F e φ gr f j Γ γ przemieszczenie narzędzia względem położenia na początku spęczania średnia średnica zastępcza ziarna średnia średnica ziarna uzyskana w symulacji CAFE doświadczenia średnia średnica ziarna uzyskana w doświadczeniu średnica zastępcza ziarna odkształcenie prędkość odkształcenia intensywność prędkości odkształcenia objętościowa prędkość odkształcenia tensor prędkości odkształcenia siła obliczona przez model CAFE siła zmierzona orientacja ziarna częstość względna występowania ziarna w j-tej klasie wielkości reguła zmiany stanu komórki CA energia granicy ziarna ix
11 LISTA SYMBOLI γ m energia wysokokątowej granicy ziarna G(ρ, t) funkcja dystrybucji gęstości dyslokacji I gr k k(t ) λ l M 0 M identyfikator ziarna stała Boltzmanna przewodność cieplna mnożnik Lagrange a średnia droga swobodna dyslokacji atermiczny współczynnik ruchliwości granicy ziarna ruchliwość (mobilność) granicy ziarna µ moduł sprężystości poprzecznej m M m N współczynnik tarcia ruchliwość wysokokątowej granicy ziarna liczba komórek w sąsiedztwie N (C) sąsiedztwo komórki C N D N gr n gr n P P Q Q gb Q s Q dalekie sąsiedztwo liczba ziaren reprezentowanych w siatce CA liczba komórek przynależnych do ziarna wektor jednostkowy normalny do powierzchni liczba podobszarów w siatce CA wektor warunków procesu energia aktywacji ruchliwości granicy ziarna energia (lub entalpia) aktywacji ruchliwości granicy ziarna energia aktywacji samodyfuzji prędkość generowania ciepła w wyniku odkształcenia x
12 LISTA SYMBOLI ρ 0 R ρ CA ρ c ρ gr σ 0 σ f S gr σ i gęstość dyslokacji w materiale wyżarzonym uniwersalna stała gazowa średnia gęstość dyslokacji w siatce CA krytyczna gęstość dyslokacji średnia gęstość dyslokacji w ziarnie naprężenie początkowe naprężenie uplastyczniające powierzchnia ziarna intensywność naprężenia S τ [N D (C)] stan dalekiego sąsiedztwa S u σ t 0.5 θ τ T t θ k θ m τ X X Z powierzchnia jednostkowa komórki CA tensor naprężeń Cauchy ego czas połówkowy rekrystalizacji kąt dezorientacji granicy ziarna średnia energia na jednostkę długości linii dyslokacji temperatura czas kąt dezorientacji pomiędzy komórką i k-tym sąsiadem kąt dezorientacji wysokokątowej granicy ziarna numer kroku czasowego (czas dyskretny) ułamek rekrystalizacji wektor parametrów modelu, symulującego proces F parametr Zenera-Hollomona xi
13 Rozdział 1 Wstęp Przedmioty wykonane z metalu towarzyszą ludzkości od zamierzchłych czasów, od wtedy także datuje się rozwój wiedzy dotyczącej otrzymywania wyrobów metalowych o pożądanych właściwościach. Wiedza ta obecnie obejmuje ogromny zasób informacji o zjawiskach zachodzących w metalach w różnych stanach skupienia i pozwala na technologiczną kontrolę procesu wytwarzania wyrobów. Proces ten składa się z wielu etapów, z których każdy pośrednio wpływa na końcowe właściwości wyrobu. Umiejętne prowadzenie tego procesu, mające podstawy w zrozumieniu zjawisk zachodzących w materiale, umożliwia sterowanie szeregiem właściwości materiału, które decydują o późniejszym zastosowaniu otrzymanego wyrobu. Przeróbka plastyczna na gorąco jest podstawową metodą otrzymywania wyrobów z metali i ich stopów. Niemal każdy przedmiot wykonany z metalu na jakimś etapie przetwarzania poddany był tego typu obróbce. Dlatego przewidywanie i kontrola przebiegu odkształcenia plastycznego na gorąco odgrywa szczególną rolę. Metody matematyczne i numeryczne są najnowszym narzędziem wspomagającym przewidywanie zachowania materiału w trakcie przeróbki. Symulacje prowadzone z wykorzystaniem tych metod obejmują zjawiska zachodzące w bardzo różnych skalach wymiarów geometrycznych i czasu. Zazwyczaj jednak opis matematyczny procesu koncentruje się na pojedynczej skali, przy czym w większości zagadnień inżynierskich jest to skala makro. W tej dziedzinie wieloletni rozwój metod komputerowego wspomagania projektowania procesów pozwala na zadowalająco dokładne rozwiązywanie problemów przeróbki plastycznej na gorąco. Obecnie dominującą metodą, przydatną w numerycznej analizie zagadnień związanych z mechaniką ośrodków ciągłych i równaniami transportu ciepła, jest metoda elementów skończonych (MES). W ostatnich latach obserwowany jest silny trend poszukiwania metod obliczeniowych, pozwalających na powiązanie makroskopowego opisu procesu z jednoczesnym przewidywaniem stanu mikrostruktury i jej zmian w trakcie i po odkształceniu. 1
14 1. Wstęp Oddaje to zapotrzebowanie technologiczne, obejmujące kontrolę zarówno kształtu wyrobu, stanu naprężeń w materiale jak i jego mikrostruktury. Z punktu widzenia technologicznego istotne jest więc stworzenie narzędzia, umożliwiającego prognozowanie właściwości wyrobu w zależności od zastosowanych warunków termomechanicznych procesu. Ponieważ własności materiału w dużej mierze zależą od mikrostruktury, kluczowe dla konstrukcji takiego narzędzia jest poprawne odtworzenie jej stanu oraz zmian jakim podlega w trakcie przetwarzania. Szczególną rolę odgrywa przewidywanie przebiegu rekrystalizacji, będącej jednym z najważniejszych zjawisk, likwidujących efekt umocnienia i wpływających na mikrostrukturę materiału. Z tego względu celowe jest skoncentrowanie uwagi na wybranych własnościach materiału, najmocniej wpływających na przebieg procesu odkształcenia plastycznego, do których zaliczyć należy przede wszystkim naprężenie uplastyczniające oraz powiązany z nim stan mikrostruktury, obejmujący między innymi wielkość ziarna. Określenie charakterystyki plastyczności materiału i powiązanie jej z opisem zmian, zachodzących w mikrostrukturze podczas odkształcenia, jest kluczowe dla poprawnego przeprowadzenia symulacji numerycznej, a tym samym dla możliwości jej zastosowania jako wiarygodnego narzędzia, wspomagającego projektowanie procesów wytwórczych. Niniejsza praca przedstawia próbę stworzenia nowego narzędzia obliczeniowego, łączącego rozbudowany opis zmian zachodzących w mikrostrukturze podczas dynamicznej rekrystalizacji z makroskopowym modelem MES procesu przeróbki plastycznej na gorąco. Połączenie to koncentruje się na wzajemnym powiązaniu charakterystyki naprężenia uplastyczniającego i wpływu mikrostrukturalnych procesów dynamicznych. Nadrzędnym celem, jaki postawił sobie autor, było zbudowanie wieloskalowego modelu, opisującego zmiany własności metali odkształcanych plastycznie w wysokich temperaturach, wykorzystując konwencjonalne metody opisujące umocnienie metalu połączone z opracowanym modelem rozwoju mikrostruktury. Spośród wielu metod, umożliwiających symulację zjawisk w skali mikro, wybrano metodę automatów komórkowych. W świetle dostępnych danych literaturowych, metoda ta pozwala na dostatecznie precyzyjne odtworzenie szeregu zjawisk, wpływających na rozwój mikrostruktury. Zaletą metody jest zastosowany w niej paradygmat, zakładający opis złożonego układu poprzez modelowanie lokalnych interakcji pomiędzy jego podstawowymi częściami składowymi. Metoda umożliwia także elastyczne dostosowanie reprezentacji wiedzy do rozwiązywanego problemu. W opisanym rozwiązaniu wprowadzone zostało dwukierunkowe powiązanie pomiędzy modelami zjawisk, zachodzących jednocześnie w różnych skalach geometrycznych, oraz wymagających sprzężenia w skali czasu. 2
15 Rozdział 2 Wybrane problemy modelowania mikrostruktury W rozdziale tym przedstawiono wybrane zagadnienia związane z modelowaniem rozwoju mikrostruktury. Tematyka ta jest bardzo rozległa, co znajduje odzwierciedlenie w dotyczącej jej obszernej bibliografii. Szczególną uwagę poświęcono tworzeniu modeli matematycznych procesu rekrystalizacji dynamicznej. W niniejszym rozdziale omówiono tylko stosunkowo niewielki podzbiór publikacji, poświęconych zagadnieniom blisko powiązanych z tematyką rozprawy. 2.1 Rekrystalizacja Proces rekrystalizacji (RX) odkształconych plastycznie metali i ich stopów odgrywa szczególną rolę w ich przetwarzaniu. Pozwala na odzyskanie plastyczności po odkształceniu w niskich temperaturach. W przypadku metali, które nie przechodzą przemiany fazowej w trakcie chłodzenia, rekrystalizacja pozwala na wytworzenie całkowicie nowej struktury ziarnowej, co przy umiejętnym prowadzeniu procesu umożliwia kontrolę mikrostruktury wyrobu końcowego. Rekrystalizacja jest procesem tworzenia nowej struktury ziarnowej w odkształconym materiale poprzez powstawanie i migrację granic wysokokątowych, wynikających ze zmagazynowanej energii odkształcenia. Granice wysokokątowe charakteryzują się kątem dezorientacji powyżej [25]. Na proces rekrystalizacji składają się dwa podstawowe podprocesy: zarodkowania nowych ziaren oraz ich dalszy rozrost. Zarodkowanie można podzielić na dwie klasy, zarodkowanie homogeniczne i zarodkowanie heterogeniczne. Zarodkowanie homogeniczne następuje w dowolnym miejscu mikrostruktury. Warunkiem zajścia zarodkowania homogenicznego jest, aby po- 3
16 2.1. Rekrystalizacja wstające klastry nowej fazy były w kontakcie wyłącznie z poprzednią fazą, wolną od jakichkolwiek wtrąceń. Z kolei zarodkowanie heterogeniczne następuje w przypadku, gdy nowa faza wydziela się na innej fazie lub wtrąceniach, które ograniczają ją przestrzennie [54]. Zarodkowanie rekrystalizacji zachodzi heterogenicznie, a preferowanymi miejscami tworzenia się zarodków są granice ziaren, złącza potrójne, wtrącenia oraz pasma odkształcenia wewnątrz ziaren [82]. Rozrost ziarna warunkowany jest przede wszystkim prędkością migracji frontów rekrystalizacji, dla której siłą pędną jest różnica energii swobodnej przed i za frontem [4]. Rekrystalizacja statyczna (SRX) jest procesem tworzenia nowej struktury ziarnowej odkształconego materiału w podwyższonej temperaturze. Struktura ta tworzy się w drodze powstawania wolnych od dyslokacji obszarów, nazywanych zarodkami, których wzrost następuje w odkształconej osnowie [52]. Proces nazywany jest także rekrystalizacją pierwotną (ang. primary recrystallization) i zachodzi powyżej tzw. temperatury rekrystalizacji, wyższej niż temperatura zdrowienia [94]. Rekrystalizacja wtórna polega na wzroście niektórych ziaren kosztem innych. Proces ten nazywany jest także anormalnym wzrostem ziaren (ang. abnormal grain growth) [94, 116]. Rekrystalizacja dynamiczna (DRX) następuje jednocześnie z odkształceniem, a jej siła pędna jest w przybliżeniu stała [94]. Przebieg rekrystalizacji dynamicznej zależy od wielu czynników, w tym zewnętrznych, takich jak temperatura, odkształcenie i prędkość odkształcenia, oraz czynników wewnętrznych powiązanych z właściwościami struktury materiału, w szczególności z energią błędu ułożenia. Rekrystalizacja dynamiczna cechuje się mniejszą wrażliwością na temperaturę niż SRX oraz znacznie większą wrażliwością na prędkość odkształcenia [25]. Powszechnie uznawane jest, że do wystąpienia DRX niezbędne jest przekroczenie odkształcenia krytycznego ε c [6, 64] lub krytycznej gęstości dyslokacji ρ c. Wprowadzane są także kryteria bazujące na bilansie energii zmagazynowanej w materiale [41, 92]. Metale i ich stopy o niskiej i średniej energii błędu ułożenia np. miedź, nikiel, aluminium, stale austenityczne łatwiej podlegają DRX. Szeroki opis rozwoju wiedzy dotyczącej dynamicznej rekrystalizacji przedstawił McQueen w pracy [76]. W literaturze polskiej dostępna jest monografia [4] autorstwa L. Błaża, poświęcona dynamicznym procesom w metalach, w szczególności dynamicznej rekrystalizacji. Obszerną dyskusję czynników, wpływających na kinetykę rekrystalizacji statycznej, przedstawiono w pracy Blicharskiego i Gorczycy [8]. 4
17 2.2. Klasyczne modele zmian mikrostruktury podczas rekrystalizacji 2.2 Klasyczne modele zmian mikrostruktury podczas rekrystalizacji Istnieje szereg modeli opisujących procesy rekrystalizacji, spośród których najszerzej przyjętym jest model JMAK (Johnson-Mehl-Avrami-Kolmogorow). Innym klasycznym podejściem jest teoria idealnego wzrostu ziaren von Neumanna [144]. Modelowanie procesów rekrystalizacji doczekało się obszernego zbioru publikacji. Ich przegląd wychodzi poza ramy niniejszej rozprawy. Autor uważa jednak, że należy wspomnieć o najważniejszych spośród modeli matematycznych, służących opisowi rekrystalizacji. Modele te stosowane są powszechnie jako część opisu materiału w metodzie elementów skończonych. Rekrystalizacja statyczna Rekrystalizacja statyczna jest dominującym procesem odbudowy mikrostruktury w materiałach odkształcanych na gorąco. SRX zachodzi, jeśli odkształcenie materiału jest większe od odkształcenia krytycznego dla zajścia SRX i jednocześnie mniejsze od odkształcenia krytycznego dla zajścia DRX. Kinetyka rekrystalizacji statycznej jest opisywana poprzez równanie JMAK o ogólnej postaci: X(t) = 1 exp ( Kt n ) (2.1) gdzie: t czas, X ułamek rekrystalizacji po czasie t, K, n parametry. W równaniu (2.1) wprowadza się czas połówkowy t 0.5, zależny od szeregu czynników, w tym odkształcenia, prędkości odkształcenia, temperatury, początkowego rozmiaru ziarna, parametru Zenera-Hollomona i innych. Równanie (2.1) przyjmuje wówczas postać: [ ( ) t n ] X(t) = 1 exp ln 2 t 0.5 Wykładnik potęgowy n przyjmuje wartości z zakresu 1 < n < 2. (2.2) Rekrystalizacja dynamiczna Opis dynamicznej rekrystalizacji jest bardziej złożony od opisu SRX, gdyż w jej trakcie następuje odkształcenie materiału. W literaturze istnieje wiele prac, opisujących charakterystyki materiału, podlegającego DRX. Jedną z najważniejszych charakterystyk jest naprężenie uplastyczniające σ f. Przebieg DRX w dużym stopniu zależy od warunków odkształcenia: temperatury T oraz prędkości odkształcenia ε. Zmiana tych parametrów wpływa na przebieg charakterystyki odkształcenia materiału. Dlatego warunki odkształcenia często zastępuje się jednym parametrem, nazywanym temperaturowo zredukowaną prędko- 5
18 2.3. Symulacja komputerowa procesów rekrystalizacji ścią odkształcenia lub parametrem Zenera-Hollomona [4]: ( ) Q Z = ε exp RT (2.3) gdzie: Z parametr Zenera-Hollomona, Q energia aktywacji wysokotemperaturowego odkształcenia, R uniwersalna stała gazowa, T temperatura w skali bezwzględnej. Wiele spośród konwencjonalnych modeli DRX uzależnia od parametru Z naprężenie uplastyczniające oraz parametry mikrostruktury, takie jak wielkość ziarna i podziarna po procesie. 2.3 Symulacja komputerowa procesów rekrystalizacji Podrozdział ten jest poświęcony przeglądowi metod symulacyjnych, wykorzystywanych do przewidywania zmian mikrostruktury oraz stanu materiału w wyniku odkształcenia. Szczególną uwagę poświęcono procesom rekrystalizacji, które zachodzą w materiale w trakcie odkształcenia. Ze względu na ważną rolę, jaką odgrywają procesy rekrystalizacji w formowaniu materiałów polikrystalicznych, duża liczba prac została poświęcona analizie fizycznej, matematycznej i numerycznej tych zjawisk. W dalszej części podrozdziału pokrótce przedstawiono wybrane próby zastosowania różnych metod obliczeniowych. Szczególna uwaga poświęcona zostanie metodom, pozwalającym na bezpośrednie ujęcie topologii modelowanego układu, zatem dającym możliwość odtworzenia przestrzennego układu ziaren (lub ich płaskiego przekroju) w materiale. Z oczywistych względów przegląd ten ograniczony jest do prac blisko związanych z przedmiotem rozprawy. Natomiast podsumowanie wybranych prac dotyczących zastosowania metody automatów komórkowych, wykorzystywanej w niniejszej pracy, przedstawiono w podrozdziale 2.4. Ponieważ praca ta nie ma na celu przeprowadzenia wyczerpującego przeglądu stosowanych metod, pominięto szereg obecnych w literaturze prac związanych z analitycznym, statystycznym i empirycznym opisem procesów rekrystalizacji, opisem metalograficznym, a także wiele publikacji podejmujących tematykę numerycznej symulacji rekrystalizacji, np. z wykorzystaniem metody pola fazowego (ang. Phase field method) [141] lub metody wierzchołków (ang. Vertex method). W literaturze dotyczącej rozważanego zagadnienia istnieją prace [49, 80, 114] podsumowujące rozwój modelowania zjawisk rekrystalizacji i dostarczające obszernego przeglądu stosowanych metod obliczeniowych. Pominięto także liczne przykłady zastosowania 6
19 2.3. Symulacja komputerowa procesów rekrystalizacji klasycznych modeli rekrystalizacji, omówionych w podrozdziale Metoda Monte-Carlo Symulacje Monte-Carlo wykorzystywane są powszechnie w modelowaniu zjawisk związanych z rekrystalizacją (np. prace [11 13, 31, 49, 50, 69, 79, 83, , 109, 117, 132, ]). Obszerny przegląd zastosowań MC w symulacji rozwoju mikrostruktury przedstawiono w pracach [80, 114]. Szczególnie intensywnie rozwijane były zagadnienia związane ze wzrostem ziaren, w tym anormalnym rozrostem ziaren [27, 50, 80, 116, 134]. Jedne z najwcześniejszych symulacji MC wzrostu ziaren przedstawiono w pracy [133], opisującej model 2D rozrostu ziaren, oraz w pracy [3], w której zaprezentowano model trójwymiarowy. W metodzie MC wprowadza się dyskretyzację domeny obliczeniowej za pomocą siatki obliczeniowej. Symulacje 2D wykorzystują zwykle siatki regularne, w tym trójkątne, prostokątne i sześciokątne. W węzłach siatki obliczane jest prawdopodobieństwo zmiany stanu, bazujące na lokalnej zmianie energii układu. Z tego względu metoda Monte-Carlo jest stosowana z powodzeniem w symulacji układów dążących do minimum energetycznego, np. poprzez minimalizację energii granic międzyziarnowych. Najczęściej spotykane są w literaturze podejścia wykorzystujące tzw. wielospinowy model Pottsa. W większości z wymienionych prac rozważa się obszary zawierające co najwyżej kilka tysięcy ziaren. Duży postęp odnotowano w symulacji MC powstawania i rozwoju tekstury, np. [50, 79]. W zdecydowanej większości prac czas symulacji wyrażany jest w jednostkach MCS (Monte-Carlo Step), co znacznie ogranicza możliwość bezpośredniego porównywania wyników obliczeń i doświadczeń. Arbitralne jednostki występują często także w kluczowym dla metody problemie doboru wartości energii zmiany spinu. Stosunkowo niewielka jest liczba publikacji, poświęconych symulacji dynamicznej rekrystalizacji za pomocą MC, np. prace [85 88, 115]. Prace te koncentrują się raczej na jakościowym opisie DRX, nie wprowadzając powiązania z rzeczywistymi parametrami materiałowymi i warunkami odkształcenia. Warte zauważenia są stosunkowo liczne próby połączenia MC z innymi technikami obliczeniowymi, takimi jak MES [109, 110, 128] lub CA [117]. Symulacje MC wzrostu ziaren zastosowano np. do generowania początkowych mikrostruktur w obliczeniach plastyczności kryształów, bazujących na MES [127]. Elementy podejścia MC wykorzystywane są także w pracach dotyczących zastosowań niedeterministycznych automatów komórkowych, głównie w konstrukcji reguł przejścia, np. w pracach [106, 108]. 7
20 2.3. Symulacja komputerowa procesów rekrystalizacji MES i teoria plastyczności kryształów Kolejna grupa metod bazuje na wykorzystaniu w MES teorii plastyczności kryształów (ang. Crystal Plasticity FEM, CP-FEM ) i zależności krystalograficznych do budowy modelu konstytutywnego materiału. W podejściu tym bazuje się na założeniu, że głównym mechanizmem odkształceń plastycznych w większości metali jest poślizg po różnych płaszczyznach krystalograficznych. Metoda CP-FEM łączy to założenie z metodą elementów skończonych, przyjmując, że wynikowe odkształcenie pochodzi od wkładu wszystkich systemów poślizgu [118]. Zastosowania różnorodnych wariantów tej metody posiadają obszerną bibliografię [72], a przegląd najważniejszych dokonań w zakresie rozwoju metody można znaleźć np. w [20]. W wielu publikacjach [77] korzysta się z dyskretyzacji MES struktury ziaren w próbce. Najczęściej pojedyncze ziarno jest dyskretyzowane za pomocą jednego lub więcej elementu skończonego [126]. Wykorzystywane są siatki 2D [128] oraz 3D (elementy sześciościenne i czworościenne) [20, 126, 128, 129] MES i metoda zmiennej wewnętrznej Omawiane w niniejszym podrozdziale podejście do symulacji rekrystalizacji nie należy do grupy metod, opisujących w bezpośredni sposób topologię mikrostruktury. Koncepcje leżące u podstaw metody zmiennej wewnętrznej (IVM) są jednak w dużym stopniu wykorzystywane w niniejszej rozprawie, stąd konieczność omówienia wybranych publikacji związanych z zastosowaniem IVM. Większość kodów MES z zakresu symulacji procesów przeróbki plastycznej wykorzystuje jako model konstytutywny materiału równania opisujące naprężenie uplastyczniające σ f. Oparte są one zwykle na empirycznych zależnościach, wiążących σ f ze zmiennymi zewnętrznymi, takimi jak temperatura i prędkość odkształcenia oraz makroskopowymi parametrami, opisującymi stan materiału. Przykładem takiego powiązania są wykorzystywane powszechnie równania, w których σ f jest funkcją potęgową odkształcenia i prędkości odkształcenia. Równania te wykorzystują makroskopowe wartości jako parametry stanu, np. odkształcenie lub skład chemiczny materiału. Podejście to posiada fundamentalną wadę, gdyż właściwości mechaniczne zależą bardziej od stanu mikrostruktury niż od składu chemicznego [119]. Słabością wykorzystania modeli konstytutywnych tego typu jest również brak możliwości śledzenia historii procesu odkształcenia i towarzyszących mu zjawisk, zachodzących w materiale. Model zmiennej wewnętrznej w dużej mierze pozwala na wyeliminowanie tych ograniczeń. Opracowany przez Sandströma i Lagneborga model DRX [124], wykorzystujący 8
21 2.3. Symulacja komputerowa procesów rekrystalizacji koncepcję IVM, był jednym z pierwszych, które opisywały i wyjaśniały obserwowalne doświadczalnie zachowanie materiału podlegającego DRX. Podstawowa idea budowy modelu zakładała, że w materiale wyróżnić można obszary umocnione, takie jak granice ziaren i podziaren, oraz obszary umocnione w mniejszym stopniu, takie jak wnętrza ziaren. Każdy z tych obszarów wnosi odmienny wkład w naprężenie uplastyczniające. Dla każdego z obszarów opracowano równania rozwoju ilości dyslokacji, opisanych za pomocą gęstości dyslokacji. Założono, że siłą pędną rekrystalizacji jest różnica gęstości dyslokacji w obszarach rozdzielonych granicą ziaren. Metoda zmiennej wewnętrznej opisana w pracy [120] bazuje na założeniach przedstawionych w pracach [124, 125]. Przyjęto, że wykorzystywany w MES model konstytutywny materiału zależy nie tylko od warunków związanych z deformacją materiału, takich jak odkształcenie, prędkość odkształcenia i temperatura, ale także od zmiennej zależnej od czasu i reprezentującej lokalną gęstość dyslokacji. Wprowadzono równanie opisujące rozwój gęstości dyslokacji w czasie o postaci: dg(ρ, t) = φ( ε) g(ε) R (2.4) dt R = vγ τρg(ρ, t) (2.5) D gdzie: G(ρ, t) funkcja dystrybucji gęstości dyslokacji, φ( ε) reprezentuje atermiczny wzrost ilości dyslokacji, g(ε) opisuje aktywowane cieplnie zdrowienie, R człon odpowiadający za zmiany wynikające z zajścia rekrystalizacji, γ ułamek ruchliwych granic ziaren, ρ gęstość dyslokacji, ε odkształcenie, τ średnia energia na jednostkę długości linii dyslokacji, D średnia wielkość ziarna. Równanie (2.4) jest rozwiązywane w przedziałach, dyskretyzujących gęstość dyslokacji, wraz z równaniami opisującymi zmianę średniej wielkości ziarna. Zależności te przyjmują postać następujących równań różniczkowych: dd dx = D dt dt dd dt = σ sm 0 D ln N (2.6) ( ) exp Qm (2.7) RT dx dt = vγ D mτg iρ i (2.8) gdzie: N liczba nowych ziaren powstających z ziarna pierwotnego, m 0 współczynnik ruchliwości granic międzyziarnowych, Q m energia aktywacji ruchu granic, X ułamek objętości zrekrystalizowanego materiału. Równanie (2.6) opisuje rozdrobnienie ziarna w wyniku rekrystalizacji i rozwiązywane jest jedynie przy ρ > ρ c, gdzie ρ c jest krytyczną gęstością dyslokacji, niezbędną do rozpoczęcia rekrystalizacji. 9
22 2.3. Symulacja komputerowa procesów rekrystalizacji Z kolei zależność (2.7) wyraża zmianę średniej wielkości ziarna D w wyniku rozrostu ziaren. Do obliczenia naprężenia uplastyczniającego w punktach całkowania MES wykorzystano równanie: σ = αµb ρ (2.9) gdzie: α współczynnik rzędu jedności, µ moduł sprężystości poprzecznej, b wektor Burgersa. Inne podejście bazujące na połączeniu równań rozwoju populacji dyslokacji z MES przedstawiono w pracy [1]. Wykorzystano tam trzy zmienne wewnętrzne, reprezentujące odpowiednio gęstość dyslokacji wewnątrz podziaren, średnią wielkość podziarna oraz średnią dezorientację granic pomiędzy podziarnami. Kolejny model MES wykorzystujący równania rozwoju gęstości dyslokacji opisano w pracy [131]. W modelu rozwoju mikrostruktury wprowadzono równania statystyczne pozwalające na obliczenie liczby zarodków w objętości materiału. Równania te uwzględniały także liczbę anihilowanych potencjalnych zarodków. Założono, że zajście kolejnych cykli rekrystalizacji możliwe jest wyłącznie w obszarze zrekrystalizowanym w poprzednim cyklu. Model nie uwzględniał natomiast orientacji zarodków, przyjmując stałą ruchliwość granic ziaren. W kontekście niniejszej rozprawy warto także wspomnieć o dwóch pracach, poświęconych aplikacji IVM, pomimo, że nie są bezpośrednio związane z rekrystalizacją. W pierwszej z nich [119] wprowadzono trzy zmienne wewnętrzne, jednak reprezentowały one populacje dyslokacji, należących do odrębnych klas. Podział na klasy przeprowadzono ze względu na ruchliwość (mobilność) dyslokacji oraz ich ułożenie w materiale. Wyodrębnione zostały następujące klasy populacji dyslokacji: dyslokacje mobilne, przemieszczające się przez strukturę komórkową, dyslokacje nieruchome wewnątrz komórek, nieruchome dyslokacje, znajdujące się w ścianach komórek. Dla każdej klasy wprowadzono równanie rozwoju dyslokacji w postaci ρ = ρ + ρ, gdzie ρ + i ρ reprezentują odpowiednio prędkość wzrostu i spadku gęstości dyslokacji. Równania opisujące prędkości przyrostu dyslokacji ρ + uzależniono od makroskopowej prędkości odkształcenia ε. Zaproponowany model pozwalał na uwzględnienie pojawiania się wydzieleń oraz ich wpływu na umocnienie materiału poprzez blokowanie poślizgu dyslokacji. W pracy [70] dokonano rozwinięcia modelu opisanego w [119]. Podobnie jak w [119] zmienne wewnętrzne powiązano z klasami dyslokacji. Rozważano zagadnienie adaptacji siatki MES (ang. remeshing) w kontekście zmiennej wewnętrznej. Do 10
23 2.3. Symulacja komputerowa procesów rekrystalizacji przeniesienia wartości zmiennych wewnętrznych w trakcie generowania nowej siatki wykorzystano algorytm wyboru najbliższego sąsiada w starej siatce obliczeniowej [70]. Stwierdzono, że przeniesienie obliczonych wartości zmiennych wewnętrznych do nowo utworzonych elementów skończonych nie prowadzi do dużej utraty dokładności symulacji [70]. Warto zauważyć, że nie brano pod uwagę zmiennej liczby elementów w siatce i problemów związanych ze wzrostem i zmniejszeniem liczby punktów całkowania. Interesującym jest, że w pracy [70] zasugerowano możliwość włączenia symulacji, opartej o metodę automatów komórkowych, do modelu konstytutywnego materiału w kodzie MES. Zagadnienie to pozostawiono jednak jako otwarte i wymagające dalszych prac. Podsumowując można stwierdzić, że cechą wspólną konstrukcji omawianych wcześniej modeli jest ukierunkowanie na ilościowy opis odpowiedzi modelowanego materiału, ze stosunkowo niewielkim uwzględnieniem mechanizmów procesów, których działanie manifestowane jest odpowiedzią materiału. Nie oznacza to bynajmniej, że opis procesów składowych był pomijany, przeciwnie, autorzy modeli IVM dołożyli wielu starań dla wprowadzenia możliwie pełnego fizykalnego opisu procesów składowych. Tym niemniej zastosowanie np. równań opisujących ewolucję wielkości ziarna pomija między innymi geometryczne zależności w mikrostrukturze, kształt ziaren, długość i charakter granic ziaren obecnych w materiale, zróżnicowanie umocnienia w pojedynczych ziarnach i inne czynniki. Pominięcie niejednorodności w mikrostrukturze materiału jest koniecznym uproszczeniem, gdyż opis materiału sprowadzany jest do kilku wartości skalarnych, trudnych do bezpośredniego powiązania np. ze złożonym mechanizmem ruchu granic ziaren. Stąd można określać tą grupę metod jako modele fenomenologiczne, mające dobre uzasadnienie fizyczne. Warto także zauważyć, że podejścia wykorzystujące IVM w metodzie elementów skończonych należą do grupy metod wieloskalowych, pomimo, że w większości prac ich autorzy nie wprowadzają takiej klasyfikacji. Jednak zmienne wewnętrzne zazwyczaj opisują zjawiska o wiele rzędów wielkości mniejsze od wymiarów obiektów, dla których MES dostarcza opisu makroskopowego. Dlatego zaszeregowanie połączonych modeli IVM-MES do kategorii modeli wieloskalowych wydaje się uzasadnione. Skala mikro i poniżej występuje w przypadku gdy prowadzone są obliczenia gęstości dyslokacji, z kolei obliczenia wielkości ziaren dotyczą skali mezo. Opis zachowania materiału w IVM bazuje na podejściu statystycznym, operując średnimi wartościami interesujących cech materiału. Podejście takie siłą rzeczy ogranicza szczegółowość dostarczanego opisu materiału. Pojawia się zatem pytanie czy można wprowadzić rozwiązanie, dające opis zarówno statystyczny, mówiący o cechach materiału w ujęciu średnim, oraz bardziej szczegółowy wgląd w mechanizmy wybranych procesów i 11
24 2.4. Automaty komórkowe w modelowaniu rekrystalizacji zjawisk, zachodzących w materiale. 2.4 Automaty komórkowe w modelowaniu rekrystalizacji Zawarta w tym podrozdziale część pracy ma na celu przeprowadzenie przeglądu istniejących modeli dotyczących rekrystalizacji i zjawisk z nią związanych, zbudowanych w oparciu o metodę automatów komórkowych (ang. Cellular Automata), CA 1. Omawiane zagadnienie obejmuje stosunkowo szeroką grupę zjawisk, w tym rekrystalizację statyczną, dynamiczną i metadynamiczną. Podrozdział jest poświęcony najistotniejszym problemom, związanym z symulacją SRX i DRX za pomocą automatów komórkowych Automaty komórkowe zarys metody Rozwój koncepcji automatów komórkowych łączy się z pracami wybitnego matematyka Johna von Neumanna. W swoich zainteresowaniach von Neumann nie ograniczał się do zagadnień teoretycznych, zajmował się między innymi zjawiskiem samoreplikacji organizmów żywych [145]. Stanisław Ulam zasugerował mu wykorzystanie automatów komórkowych jako platformy badawczej procesów istotnych dla tego zjawiska. Von Neumann położył fundamenty teorii obliczeń za pomocą sieci automatów skończonych, pomocnej w wyjaśnieniu działania złożonych systemów obecnych w świecie przyrody oraz w projektowaniu skomplikowanych sztucznych systemów [81]. Według klasycznej definicji automaty komórkowe są matematycznym modelem systemu fizycznego, w którym czas i przestrzeń są dyskretne, a własności fizyczne przyjmują wartości należące do skończonego zbioru [148]. Automat komórkowy składa się z regularnej siatki z dyskretną zmienną w każdej komórce. Stan automatu komórkowego jest całkowicie określony przez wartości zmiennych stanu w siatce. Ewolucja CA przebiega w dyskretnych krokach czasowych poprzez wpływ na zmienne w siatce ze strony zmiennych sąsiednich. Sąsiedztwo dobierane jest zazwyczaj w taki sposób, aby obejmowało komórkę i wszystkie komórki bezpośrednio do niej przyległe. W przestrzeniach 2D najczęściej wykorzystywane są sąsiedztwa von Neumanna i Moore a, niekiedy stosuje się także inne, np. heksagonalne (rysunek 2.1). Wszystkie wartości w siatce są aktualizowane symultanicznie na podstawie wartości w sąsiedztwie w poprzednim kroku czasowym, poprzez zastosowanie lokalnych reguł 1 W dalszej części pracy konsekwentnie wykorzystywany jest skrót anglojęzycznej nazwy metody, preferowany przez autora rozprawy. 12
25 2.4. Automaty komórkowe w modelowaniu rekrystalizacji i 1 j i 1 j 1 i 1 j i 1 j+1 i 1 j 1 i 1 j i i j 1 C i,j j+1 i i j 1 C i,j j+1 i i j 1 C i,j j+1 i+1 j i+1 j 1 i+1 j i+1 j+1 i+1 j 1 i+1 j (a) (b) (c) Rysunek 2.1: Standardowe definicje sąsiedztwa komórki C w przestrzeniach 2D: (a) von Neumanna, (b) Moore a, (c) heksagonalne. Indeksy i, j oznaczają położenie w siatce obliczeniowej przejścia stanu. Reguła przejścia stanu nazywana jest lokalną jeżeli wykorzystuje jedynie wartości zmiennych stanu w obrębie sąsiedztwa oraz nie wymaga informacji o stanie całego automatu komórkowego lub stanu jego arbitralnie wybranej komórki. Jeżeli reguła zmiany stanu komórki bazuje na liczbie komórek sąsiednich, przyjmujących określony stan, wówczas jest ona nazywana totalistyczną. W praktycznych zastosowaniach zmienne opisujące stan komórek w siatce mogą przyjmować także wartości ciągłe. Sposób konstruowania reguł przejścia stanu oraz definicja sąsiedztwa są zwykle dobierane w sposób ukierunkowany na odtworzenie podstawowych interakcji, zachodzących w symulowanym systemie. Niekiedy wykorzystuje się także reguły przejścia, uzależnione od realizacji zmiennej losowej, podobnie jak ma to miejsce w metodzie MC. Automaty komórkowe, bazujące na takim podejściu, nazywane są probabilistycznymi Automaty komórkowe w symulacji rozwoju mikrostruktury Raabe w książkach [99, 105] poświęcił po jednym rozdziale zastosowaniom automatów komórkowych w inżynierii materiałowej, ze szczególnym uwzględnieniem wykorzystania CA w symulacji rozwoju mikrostruktury. Zawarty w pracy [99] sformalizowany opis metody oraz przykłady wykorzystania deterministycznych i probabilistycznych automatów komórkowych mogą służyć jako dobry przewodnik po zastosowaniach CA w inżynierii materiałów. Wśród przykładów wymienia się modelowanie rekrystalizacji i zjawiska wzrostu krystalitów, krzepnięcia dendrytycznego, rozwoju wzorców struktur dyslokacyjnych, przemian fazowych oraz zachowania materiałów dwufazowych. Praca [99] zawiera także listę publikacji do roku 1998 oraz krótki 13
26 2.4. Automaty komórkowe w modelowaniu rekrystalizacji przegląd literatury przedmiotu. W ostatnich latach w literaturze napotkać można obszerną grupę publikacji, podejmujących tematykę symulacji przemian fazowych z wykorzystaniem automatów komórkowych, np. [65, 66]. W literaturze polskojęzycznej Burbelko opublikował monografię [10], poświęconą symulacji krystalizacji dendrytycznej z wykorzystaniem CA. Praca ta zawiera bogaty przegląd bibliograficzny, poświęcony modelowaniu zjawisk krystalizacji, zarówno z wykorzystaniem modeli konwencjonalnych jak i przy użyciu CA Modele CA rekrystalizacji W literaturze dotyczącej zagadnień rozważanych w niniejszej rozprawie, istnieją prace podsumowujące rozwój modelowania zjawisk rekrystalizacji oraz dostarczające przeglądu stosowanych metod obliczeniowych (np. [49, 80, 114]). Publikacje te poświęcają jednak automatom komórkowym stosunkowo niewielką uwagę, koncentrując się głównie na metodzie Monte-Carlo (MC) Pottsa. Stosunkowo obszerną grupę modeli SRX oraz DRX, zarówno klasycznych, jak i opartych o symulację CA rozwoju mikrostruktury, omówił w swojej rozprawie doktorskiej Kroc [57]. Zasadniczym celem budowy modelu rekrystalizacji, opartego o metodę automatów komórkowych, jest powiązanie gęstości dyslokacji oraz parametrów opisujących rozwój mikrostruktury z obrazem tej mikrostruktury. Przez obraz mikrostruktury należy rozumieć informację o przestrzennym ułożeniu ziaren oraz ich wielkości i orientacji. W metodzie CA reprezentacja ta przekłada się na rozmieszczenie na siatce CA informacji o stanie komórek, w tym ich przynależności do poszczególnych ziaren, oraz innych danych, potrzebnych w obliczeniach, np. lokalnej gęstości dyslokacji, orientacji itp. Automaty komórkowe stosowane w modelowaniu zjawisk rekrystalizacji najczęściej wykorzystują podział modelowanego obszaru z wykorzystaniem regularnej siatki komórek. W literaturze można napotkać w większości modele dwuwymiarowe (2D), zdecydowanie rzadsze są przykłady modeli trójwymiarowych (3D), m.in. [18, 19, 39, 75, 84, 100]. W przypadku modeli 2D siatka automatów komórkowych traktowana jest jako obraz zgładu mikrostruktury, natomiast dla modeli 3D jako przestrzennie ułożone, sąsiadujące ziarna. Do przeprowadzenia symulacji DRX lub SRX z wykorzystaniem CA wymagane jest utworzenie obrazu mikrostruktury początkowej. Wszystkie znane autorowi dotychczasowe prace, dotyczące tego zagadnienia, wykorzystują odrębny algorytm tworzenia mikrostruktury początkowej, zwykle opierający się na założeniu swobodnego rozrostu ziarna [21] lub np. w wyniku wcześniejszej SRX [57, 58]. W przypadku symulacji SRX wykorzystywano także obrazy badanej próbki, uzyskane za pomocą 14
27 2.4. Automaty komórkowe w modelowaniu rekrystalizacji C n,m C n,0 C n,j C n,m C n,0 C 0,m C 0,0 C 0,j C 0,m C 0, C i,m C i,0 C i,j C i,m C i, C n,m C n,0 C n,j C n,m C n,0 C 0,m C 0,0 C 0,j C 0,m C 0,0 Rysunek 2.2: Schematyczna ilustracja periodycznego warunku brzegowego dla dwuwymiarowej siatki komórek CA. Indeksy i, j reprezentują położenie komórek w siatce, linie wskazują miejsca nałożenia periodycznego warunku brzegowego metody EBSD [107]. W większości przypadków na brzegach siatki automatów komórkowych zakłada się periodyczne warunki brzegowe. Służy to częściowemu ograniczeniu wpływu rozmiaru siatki obliczeniowej na uzyskiwane wyniki oraz wyeliminowaniu anomalii przy tworzeniu sąsiedztwa dla komórek na brzegach siatki. Sposób nakładania periodycznego warunku brzegowego przedstawiono schematycznie na rysunku 2.2. Napotkać można także nieliczne prace, w których obliczenia CA są prowadzone bez wprowadzania periodycznych warunków brzegowych, np. [136]. Jak można się spodziewać, w literaturze brak powszechnego konsensusu dotyczącego przyjmowanego typu sąsiedztwa. Wykorzystywane są standardowe sąsiedztwa Moore a i von Neumanna (lub ich odpowiedniki w 3D), ale często także wprowadzane są inne definicje sąsiedztwa. Rekrystalizacja statyczna i rozrost ziarna Duża część prac, poświęconych modelowaniu za pomocą CA procesów rekrystalizacji, koncentruje się na rekrystalizacji statycznej. Jedną z najwcześniej opublikowanych prac z tego zakresu jest publikacja Hesselbartha i Göbela [48]. W podejściu przedstawionym w tej pracy zakłada się, że komórki CA mogą znajdować się w jednym z dwóch dyskretnych stanów: zrekrystalizowanym i niezrekrystalizowanym. Autorzy oparli się na fundamentalnym założeniu, że proces rekrystalizacji składa się z dwóch niezależnych podprocesów - zarodkowania i wzrostu ziarna. Niewiele późniejsza praca [7] prezentuje zastosowanie CA do symulacji rozrostu ziaren. Pomimo stosunkowo prostej konstrukcji modelu uzyskane wyniki wskazują 15
28 2.4. Automaty komórkowe w modelowaniu rekrystalizacji na poprawne odwzorowanie co najmniej rozkładu wielkości ziaren w mikrostrukturze wynikowej. W pracy tej zamiast wprowadzania równań określających kinetykę wzrostu ziaren proponuje się zastosowanie bariery energetycznej (podobnie jak w modelach MC), której przekroczenie warunkuje rozrost ziarna. Autorzy wprowadzają też pojęcie orientacji ziarna, choć wykorzystywana jest ona wyłącznie do określenia zderzenia ziaren, a nie do wyznaczenia prędkości ruchu granicy. Natomiast wydaje się, że w pracy tej mylnie interpretowane zostały reguły przejścia stanu komórek, prowadzące do migracji granicy ziarna w wyniku jej krzywizny. Nie umniejsza to zalet przedstawionej w pracy metody, która może być wykorzystywana jako wydajny sposób generowania początkowych reprezentacji mikrostruktury dla dalszych obliczeń, np. w symulacji SRX i DRX. W pracy [18] Davies opublikował dwa modele 3D dla wzrostu ziarna, różniące się równaniem prędkości ruchu granicy ziarna. W pracy tej zastosowano probabilistyczne reguły wzrostu ziarna. Zarodkowanie zostało uwzględnione za pomocą arbitralnie dobranego równania. Ułamki rekrystalizacji uzyskane z obu modeli zostały porównane z wynikiem doświadczalnym oraz rozwiązaniem analitycznym. Porównanie to wskazuje na dobrą zdolność obu modeli do odtworzenia zachowania się materiału. Kinetyka zarodkowania homogenicznego i heterogenicznego w materiale jednofazowym była przedmiotem pracy [40]. Opracowany został model zarówno 2D jak i 3D. Rozważano zarodkowanie w schemacie z wysyceniem miejsc zarodkowania oraz ze stałą prędkością zarodkowania. Na podstawie przeprowadzonych testów obliczeniowych autorzy stwierdzili, że dla zarodkowania o stałej prędkości uzyskiwane są mikrostruktury blaszkowe. Ponadto stwierdzono, że dla niskich prędkości zarodkowania uzyskiwane są struktury z ziarnami grupującymi się w klastry. Natomiast dla wysokich prędkości zarodkowania uzyskano strukturę naszyjnikową (ang. necklace structure), podobną do mikrostruktur uzyskiwanych w wyniku DRX. Kolejny model 3D zaproponowano w pracy [75]. Praca ta wnosi interesujące uwagi zarówno do konstrukcji obliczeniowej modelu jak i do uwzględnienia w nim zarodkowania oraz wzrostu ziaren. W pracy tej proponuje się m. in. nowe rodzaje sąsiedztwa wraz z kryteriami ich stosowalności. Ponadto przedstawiono przykład implementacji, w której zastosowano połączenie szybkiej pamięci operacyjnej, wykorzystywanej do śledzenia frontu ruchu granic ziaren, oraz wolniejszej pamięci dyskowej, służącej do przechowywania informacji o wnętrzu ziaren. Rozwiązanie to pozwala na prowadzenie obliczeń dla siatek o dużej gęstości. Model umożliwia symulację zachowania mikrostruktury w trakcie rekrystalizacji i obejmuje rozwój tekstury oraz anizotropię wzrostu ziaren poprzez zróżnicowanie prędkości wzrostu ziaren w zależności od orientacji. 16
29 2.4. Automaty komórkowe w modelowaniu rekrystalizacji W pracy [19] zaprezentowano model CA pozwalający na symulację rekrystalizacji z uwzględnieniem składowych tekstury. Uzyskane wyniki zostały porównane z rezultatami doświadczenia. Otrzymano dobrą zgodność oszacowanej kinetyki zjawiska, natomiast rozkład rozmiaru ziarna cechował się stosunkowo dużymi rozbieżnościami względem danych doświadczalnych. Kroc poświęcił swoją rozprawę doktorską [57] budowie modelu dynamicznej rekrystalizacji, opartego o CA. Ponieważ jednak potraktował on DRX jako uogólnienie SRX, w pracy tej znaleźć można także propozycję nowego modelu dla tego drugiego zjawiska. Nowością w modelu jest włączenie parametrów probabilistycznych do reguł przejścia, opisujących zarówno zarodkowanie jak i rozrost ziaren. Takie sformułowanie problemu pozwoliło m.in. na uzyskanie globularnego kształtu rosnących ziaren z wykorzystaniem standardowego sąsiedztwa Moore a. W pracy tej wprowadzono także dodatkową dyskretną zmienną stanu, określaną jako czas oczekiwania (ang. wait time), wspomagającą kontrolowanie kinetyki procesu. Rollett i Raabe [117] opracowali hybrydowy model rekrystalizacji, łączący model MC Pottsa i automaty komórkowe. Motywacją tej pracy była perspektywa wyeliminowania wad poszczególnych modeli obliczeniowych w zakresie uwzględnienia sił pędnych rozrostu ziaren. Autorzy pracy [117] stwierdzają, że ograniczeniem CA jest brak możliwości uwzględnienia krzywizny granicy ziarna jako siły pędnej rozrostu ziarna, z kolei MC nie daje zadowalających rezultatów w zakresie uwzględnienia energii zmagazynowanej w postaci defektów struktury [117]. Oprócz opisu modelu hybrydowego praca zawiera interesujący rozdział dotyczący skalowania parametrów modelu dla uzyskania wartości fizycznych. Rekrystalizacja dynamiczna Przedstawiony w poprzednim podrozdziale przegląd prac dotyczących rekrystalizacji statycznej świadczy o stosunkowo długim zainteresowaniu badaczy rozwojem modeli CA w tym zakresie. Zdecydowanie mniejszym zainteresowaniem cieszyła się DRX. Świadczy o tym fakt, że (zgodnie z rozeznaniem autora) do roku 2000 ukazała się zaledwie jedna szerokodostępna publikacja [39], poruszająca tą tematykę. W pracy tej zaproponowano pierwszy model DRX oparty o automaty komórkowe. Podejście to oparto na wcześniejszej pracy [48], dotyczącej rekrystalizacji statycznej. Podstawą modelu było śledzenie gęstości dyslokacji w komórkach, która warunkowała zarodkowanie i rozrost ziaren [39]. W pracy zademonstrowano m.in. zmianę charakteru krzywej naprężenia w zależności od stosunku rozmiaru ziarna początkowego i końcowego. Uzyskane wyniki są zgodne z tezami pracy Sakai [123], w której przedstawiono kryterium strukturalne przejścia charakterystyki krzywej płynięcia materiału z jed- 17
30 2.4. Automaty komórkowe w modelowaniu rekrystalizacji nopikowej do wielopikowej. Kryterium to zakłada, że dla co najmniej dwukrotnego rozdrobnienia ziarna na krzywej naprężenia uzyskuje się pojedynczy pik, natomiast dla mniejszego rozdrobnienia krzywa ta zawiera oscylacje. Przykładowe krzywe naprężenia uplastyczniającego, uzyskane w pracy [39], przedstawiono na rysunku 2.3a. (a) (b) (c) Rysunek 2.3: (a) krzywe naprężenia dla dρ/dt = 10 i czterech różnych rozmiarów ziarna początkowego i przy ustalonym rozmiarze ziarna końcowego, uzyskane w symulacji CA DRX; obraz mikrostruktury w t = t 0.5 : (b) dρ/dt = 10, (c) dρ/dt = 1000 (wg [39]) Spełnienie kryterium Sakai stanowiło duży postęp w porównaniu do wcześniejszych prac, wykorzystujących metodę MC, (np. [85]), których kryterium wypełnione było jedynie z dużym przybliżeniem. Praca [39] przynosi także propozycję nowego typu siedmioelementowego sąsiedztwa, prowadzącego do globularnego kształtu rozrastających się ziaren. Ponadto zaprezentowano tworzenie się struktur naszyjnikowych dla dużych wartości dρ/dt (rysunki 2.3b i 2.3c). Struktura naszyjnikowa powstaje w wyniku zarodkowania na granicach rozrastających się niewielkich ziaren wtórnych. W ten sposób na granicach ziaren pierwotnych obserwuje się dużą liczbę niewielkich ziaren, układających się warstwami w charakterystyczne pierścienie. Kolejne warstwy ziaren wrastają w obszar ziaren pierwotnych. Mechanizm powstawania takiej mikrostruktury w trakcie DRX omówiono w pracy [93], a zaczerpniętą z niej schematyczną ilustrację rozwoju struktury naszyjnikowej przedstawiono na rysunku 2.4. Uzyskane w pracy [39] wyniki wskazują na możliwość odtworzenia takiego rodzaju mikrostruktury w drodze obliczeń CA. Kroc w swojej rozprawie doktorskiej [57] jako pierwszy wprowadził do symulacji DRX metodą CA rozwiązanie równania różniczkowego, opisującego rozwój dyslokacji z uwzględnieniem umocnienia i zdrowienia. Oprócz równania opracowanego oryginalnie przez Kocksa i Meckinga [78] przetestował on szereg jego wariantów. W jednej z konkluzji zawartych w pracy [57] stwierdzono jednak, że dobór postaci 18
31 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Rysunek 2.4: Schematyczna ilustracja kolejnych etapów rozwoju mikrostruktury naszyjnikowej w trakcie DRX (wg [93]) równania różniczkowego nie wpływa znacząco na charakter krzywej opisującej gęstość dyslokacji w trakcie DRX. Wykorzystanie modelu Kocksa-Meckinga rozważane było wcześniej w pracy [39], jednak nie został on tam ostatecznie zastosowany. W pracy [57] podjęto także zagadnienie wpływu zmiany prędkości odkształcenia na przebieg DRX. Przeprowadzone obliczenia obejmowały analizę zależności krzywych umocnienia od prędkości odkształcenia oraz wpływu zmiany prędkości odkształcenia na przebieg procesu. Stwierdzono, że dla skokowej zmiany prędkości odkształcenia możliwe jest uzyskanie z modelu CA charakterystyki naprężenia uplastyczniającego, która jest jakościowo zgodna z obserwowanymi doświadczalnie. Przykłady wyników uzyskanych w pracy [57] przedstawiono na rysunku 2.5. Podsumowanie najistotniejszych zagadnień poruszanych w [57] można odnaleźć w późniejszych pracach [58, 62] tego samego autora. Wadą pracy [57] jest brak przedstawienia wyników dla rzeczywistych materiałów. Otrzymane wyniki mają więc charakter jakościowy - autor pozostaje na etapie obliczeń dla arbitralnych jednostek czasu, odkształcenia, naprężenia itp. Utrudnia to zarówno praktyczne zastosowanie rezultatów pracy, jak i weryfikację poprzez porównanie z opublikowanymi danymi doświadczalnymi. Ding i Guo ze współpracownikami opublikowali cykl artykułów [21, 22, 24, 96], prezentujących zaawansowany model DRX. W pracy [21], niezależnie od [57], pojawia się koncepcja wykorzystania równania Kocksa-Meckinga. Przedstawiony model uwzględniał również orientację ziaren i wpływ dezorientacji granic na kinetykę wzrostu ziaren. Uzyskane wyniki symulacji porównano z rezultatami prób spęczania na gorąco, przeprowadzonych na miedzi OFHC o wysokiej czystości (ang. Oxygen Free High Conductivity), otrzymując zadowalającą zgodność (rysunek 2.6). Model ten pozwalał także na śledzenie rozwoju mikrostruktury dla różnych odkształceń na przykładzie stali HY-100 [96] (rysunek 2.7). 19
32 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Rysunek 2.5: Wpływ zmiany prędkości odkształcenia (schemat ε 1, ε 2 > ε 1, ε 3 = ε 1 ) w modelu CA DRX na: a) krzywą naprężenia dla trzech różnych średnich rozmiarów ziarna początkowego (MSG), b) prędkość zarodkowania (wg [57]) Rysunek 2.6: Porównanie krzywych płynięcia miedzi OFHC dla zestawu temperatur ( K) i prędkości odkształcenia s 1. a) wyniki symulacji, b) wyniki doświadczalne (wg [21]) 20
33 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Rysunek 2.7: Symulacja CA zmian mikrostruktury na poszczególnych etapach odkształcenia dla stali HY-100 (T = 1100 C, ε = 0.01 s 1 ) (wg [96]) Kugler i Turk [63] opracowali model, podsumowujący poprzednio przedstawione rozwiązania dotyczące DRX. W pracy wprowadzono generalizację wcześniejszych modeli [21, 39, 58], pozwalającą także na uwzględnienie mięknięcia materiału w trakcie rekrystalizacji metadynamicznej (MDRX). Prezentowany w [63] model pozwala na wprowadzenie przerwy w odkształceniu i towarzyszącego jej wytrzymania w podwyższonej temperaturze. Rysunek 2.8, zaczerpnięty z pracy [63], przedstawia rozwój mikrostruktury w trakcie procesu. Przerwa w odkształceniu i towarzyszące jej wytrzymanie w podwyższonej temperaturze skutkuje rozrostem ziarna, co zostało poprawnie odtworzone przez model (rysunek 2.8c). W pracy [63] przedstawiono także kolejne potwierdzenie dla kryterium Sakai zmiany charakteru krzywej płynięcia, podanego w [123]. W pracy [74], powstałej z udziałem autora rozprawy, przedstawiono powiązanie modelu zmiennej wewnętrznej IVM z CA. W pracy tej wykorzystano uprzednio zidentyfikowane parametry modelu IVM jako zmienne wejściowe dla symulacji CA. Uzyskane z obu modeli krzywe naprężenia nie zostały jednak porównane, gdyż rezultat obliczeń CA przedstawiono w jednostkach umownych. W dalszych pracach tego samego zespołu autorów [34, 35] przedstawiono kolejną propozycję modelu DRX. W pracach tych ponownie wykorzystano współczynniki otrzymane z modelu IVM jako zmienne wejściowe symulacji CA. Uzyskane wyniki porównano z danymi doświadczalnymi, uzyskując dość dobrą zgodność dla małych prędkości odkształcenia (0.1 s 1 ) oraz znaczące rozbieżności dla większych prędkości (1 s 1 ). Praca [34] zawiera także kolejne modelowe potwierdzenie dla kryterium strukturalnego, podanego w [123]. Ponadto zaprezentowano przykłady wpływu są- 21
34 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Rysunek 2.8: Symulacja CA rozwoju mikrostruktury: a) przy odkształceniu 0.17 i b) 0.4, c) po wytrzymaniu w temperaturze 750 K przez 100 s, d) przy dalszym odkształceniu 0.9 (wg [63]) siedztwa zarówno na otrzymywane mikrostruktury jak i uzyskiwane wykresy naprężenia. Svyetlichnyy i Milenin w pracy [136] badali wpływ prędkości zarodkowania i prędkości rozrostu ziaren na charakter krzywej naprężenia. W pracy wskazano m.in., że krytyczna gęstość dyslokacji nie wyznacza jednoznacznie ani odkształcenia pikowego, ani naprężenia pikowego. Uzyskane w pracy [136] wartości naprężenia uplastyczniającego wskazują dobrą jakościową zgodność z danymi dostępnymi w literaturze Podstawowe problemy modelowania CA procesów rekrystalizacji Dobór siatki obliczeniowej W większości dotychczasowych prac wykorzystywano siatki regularne o komórkach kwadratowych (2D) lub sześciennych (3D). Porównanie wpływu siatki o komórkach kwadratowych i heksagonalnych zostało przedyskutowane w pracach [59, 60], w których rozważano przykład kurczenia się doskonale okrągłych ziaren (przez doskonale okrągłe należy rozumieć w tym wypadku: doskonale okrągłe w granicach rozdzielczości siatki obliczeniowej). Stwierdzono, że całkowity obszar zajmowany przez ziarna jest liniową funkcją czasu dla obydwu rodzajów siatki. Podobne wyniki uzyskali autorzy pracy [7], wykorzystując siatkę regularną kwadratową i sąsiedztwo von Neumanna. Nowością w pracy [60] jest wskazanie, że współczynnik kierunkowy (nachylenie) tej funkcji liniowej silnie zależy od przyjętego sąsiedztwa. 22
35 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Zastosowanie siatek regularnych w symulacji rozrostu ziarna powoduje pojawienie się sztucznej anizotropii, wynikającej z ograniczonej liczby możliwych kierunków wzrostu. Wyeliminowanie tego ograniczenia było motywacją m. in. dla pracy [53]. Zastosowano tam siatkę nieregularną 3D, o losowym położeniu komórek. W wyniku uzyskano niemal idealnie okrągłe ziarna przed zderzeniem. Dobór sąsiedztwa Dobór sąsiedztwa wpływa w dużym stopniu na zachowanie modelu CA. Wpływ ten obserwować można zarówno w kinetyce procesu, jak i w uzyskanym kształcie symulowanych ziaren, a co za tym idzie w końcowej mikrostrukturze. Szczególnie istotne jest uzyskanie ziaren o kształcie możliwie zbliżonym do globularnego (np. sześciokątne lub ośmiokątne w przypadku symulacji 2D) na etapach symulacji poprzedzających zderzenie rozrastających się ziaren. Autorzy poszczególnych prac proponują rozmaite strategie, prowadzące do odtworzenia globularnego kształtu ziaren w trakcie wzrostu. Dobór sąsiedztwa jest arbitralnie obieralną częścią konstrukcji modelu, choć uzależniony jest od rodzaju siatki i liczby wymiarów. Różni autorzy przyjmują wybrane typy sąsiedztwa, jak sąsiedztwo von Neumanna [21, 24] lub Moore a [57, 136]. Goetz i Seetharaman [39] zastosowali sąsiedztwo zbudowane z 7 komórek, dzięki czemu uzyskano kształt ziaren przed zderzeniem zbliżony do ośmiokątnego. W pracy [48] przetestowano kilka rodzajów sąsiedztwa, zarówno klasyczne von Neumanna i Moore a jak i rozszerzone sąsiedztwo Moore a o szerokości ściany r = 2, oraz sąsiedztwo heksagonalne. Ten ostatni typ sąsiedztwa wykorzystywano także w jednej z wcześniejszych prac autora niniejszej rozprawy [35]. Odmienne podejście do odtworzenia globularnego kształtu ziaren zaproponowano w [57]. Wykorzystuje się tam sąsiedztwo Moore a, natomiast w regułach przejścia uwzględniono probabilistyczne zachowanie ruchu granic ziaren. Podejście to zastosowano zarówno w modelach SRX i DRX, przedstawionych w pracy [57]. W obu przypadkach zachowano globularny kształt ziaren w trakcie rozrostu. Metodę podaną w [57] z powodzeniem zastosowano później w pracy [63], z tym, że jako bazowe wykorzystano sąsiedztwo von Neumanna. W pracy [89] zastosowano sąsiedztwo heksagonalne, powstające przez modyfikację sąsiedztwa Moore a. Modyfikacja polegała na wykorzystywaniu jedynie sześciu komórek sąsiednich, wyznaczonych poprzez odrzucenie jednej spośród diagonalnych par komórek. W kolejnych krokach czasowych diagonalne pary komórek wykorzystywano naprzemiennie. Układ sąsiedztwa przedstawia rysunek 2.9. Ten rodzaj sąsiedztwa prowadzi do równoosiowego, ośmiokątnego kształtu ziaren przed zderze- 23
36 2.4. Automaty komórkowe w modelowaniu rekrystalizacji Rysunek 2.9: Sąsiedztwo heksagonalne, powstające przez modyfikację sąsiedztwa Moore a. Sąsiadami komórki 5 w nieparzystych krokach czasowych są: (1, 2, 4, 6, 8, 9); w parzystych (2, 3, 4, 6, 7, 8) (wg [89]) niem [89]. Davies w pracy [17] rozważał wpływ rodzaju sąsiedztwa na kinetykę modelu rekrystalizacji. Przedmiotem jego badań były standardowe sąsiedztwo von Neumanna oraz zmodyfikowane sąsiedztwo Moore a, opisane w pracy [89]. Konkluzją z pracy [17] jest brak wpływu rodzaju sąsiedztwa na kinetykę zjawiska. Autor [17] zastosował statystyczny test t-test, w wyniku którego stwierdził, że z 95% pewnością rodzaj sąsiedztwa nie wpływa na wartość parametru eksponenty czasowej (eksponenty Avramiego) w modelu Johnson-Mehl-Avrami-Kolmogorov (JMAK). Wpływ doboru sąsiedztwa na symulowany rozwój mikrostruktury oraz na przebiegi krzywych naprężenia badano w pracy [34], opublikowanej przez autora niniejszej rozprawy. W pracy tej potwierdzono znany wcześniej wpływ sąsiedztwa na kształt ziaren. Ponadto wskazano, że wykresy naprężenia uplastyczniającego, uzyskiwane w symulacjach różniących się wyłącznie typem sąsiedztwa, odbiegają od siebie znacznie. Wynik ten tłumaczono wpływem łącznej długości granic ziarna, która jest efektywnie różna dla sąsiedztwa von Neumanna i heksagonalnego. Problem doboru sąsiedztwa, pozwalającego na odtworzenie realistycznych kształtów ziaren w trakcie wzrostu, poruszany był we wcześniejszych pracach autora niniejszej rozprawy. W kolejnej pracy tego samego zespołu [36] porównano wpływ rodzaju sąsiedztwa na przebieg DRX, w tym na kształt ziaren uzyskiwanych w trakcie symulacji procesu. Przykłady kształtu wzrastających w trakcie DRX ziaren, uzyskane dla trzech różnych definicji sąsiedztwa, przedstawiono na rysunku Porównanie obrazów mikrostruktur wskazuje, że ziarna najbardziej zbliżone do owalnych uzyskano z wykorzystaniem sąsiedztwa pseudo-heksagonalnego, podobnego w budowie do zaproponowanego w pracy [89] (rysunek 2.10c). 24
37 2.4. Automaty komórkowe w modelowaniu rekrystalizacji (a) (b) (c) Rysunek 2.10: Obrazy mikrostruktur uzyskane z wykorzystaniem różnych definicji sąsiedztwa: (a) Moore a, (b) von Neumanna, (c) pseudo-heksagonalnego (wg [36]) Rysunek 2.11: Sąsiedztwo o promieniu r w siatce nieregularnej (wg [53]) W przypadku modeli 3D interesującą koncepcję przedstawiono w pracy [75]. Zastosowano tam specjalny parametr x, określający maksymalny możliwy przyrost wielkości ziarna w trakcie pojedynczego kroku CA. Dla poszczególnych rodzajów sąsiedztwa obliczono odpowiadające im zakresy wartości x, a następnie dobierano takie rozszerzenie sąsiedztwa, aby przyrosty ziarna nie przekraczały dopuszczalnych wartości. Praca [75] zawiera też analizę wpływu rozmiaru sąsiedztwa na kształt ziaren przed zderzeniem. Sugeruje się, że zadowalające wyniki (tj. sferyczny kształt ziaren) uzyskiwane są dla sąsiedztwa o promieniu około 7 komórek. W pracy [53] wykorzystano siatkę nieregularną 3D. Sąsiedztwo w tej siatce, przedstawione schematycznie na rysunku 2.11, zdefiniowano jako zbiór komórek, oddalonych od komórki centralnej mniej niż promień sąsiedztwa r. Na rysunku 2.11 szarymi kwadratami oznaczono komórki w siatce, leżące poza sąsiedztwem komórki centralnej, natomiast czarnymi zaznaczono komórki przynależne do sąsiedztwa o promieniu r. Uzyskane w pracy [53] wyniki wskazują, że rezultatem zastosowania tego rodzaju sąsiedztwa jest uzyskanie niemal doskonale globularnego kształtu ziaren przed ich zderzeniem. Nakład obliczeniowy, konieczny do wyznaczania sąsiedztwa 25
38 2.4. Automaty komórkowe w modelowaniu rekrystalizacji każdej komórki, jest jednak poważnym ograniczeniem tej metody. Zarodkowanie nowych ziaren Poprawne uwzględnienie procesu powstawania nowych ziaren jest kluczowe dla opisu zjawiska rekrystalizacji. Paradoksalnie, właśnie ten element sprawia największe trudności w budowie modeli opartych o CA. Jak zostanie pokazane w dalszej części podrozdziału, w szeregu prac składowa ta jest przenoszona do oddzielnego modelu, który jedynie współdziała z CA. Jedną z przyczyn takiego postępowania jest trudność w poprawnym uwzględnieniu w modelu zjawisk prowadzących do pojawienia się zarodka, zachodzą one bowiem w skali o rzędy wielkości mniejszej niż skala używana w symulacji. Wyodrębnienie osobnego modelu zarodkowania, stowarzyszonego z symulacją CA, znaleźć można również w pracach dotyczących krystalizacji, np. dla polimerów [102] lub struktur globularnych, wykorzystywanych w formowaniu tiksotropowym [34]. Zarodkowanie SRX Algorytm zarodkowania przedstawiony w [75] zakłada, że zarodki nowych ziaren tworzone są na w każdym kroku symulacji, a ich liczba zależna jest od czasu i temperatury. Jako zarodek w pracy [75] rozumiana jest sfera o określonym rozmiarze (co oznacza, że zarodek składa się z wielu komórek CA), orientacji krystalograficznej i położeniu w przestrzeni. Utworzone zarodki są rozmieszczane losowo w siatce CA. Ponieważ model zakłada, że jest możliwe utworzenie zarodka wyłącznie wewnątrz osnowy, rzeczywista liczba powstałych zarodków sukcesywnie spada w trakcie symulacji. Jak zatem widać, w pracy [75] model kinetyki zarodkowania został przeniesiony na zewnątrz CA i nie jest bezpośrednio zależny od stanu komórek CA. W pracy [107] przyjęto, że miejsca zarodkowania wyznaczane są jedynie na początku symulacji. Odpowiada to schematowi wysycenia miejsc zarodkowania (ang. site saturated nucleation). W pracy tej przyjęto, że do zajścia zarodkowania wymagane jest spełnienie kryteriów termodynamicznej i kinetycznej niestabilności, jednak określenie lokalizacji w siatce miejsc zarodkowania zostało zrealizowane przez dodatkowy algorytm, pracujący poza zestawem reguł zmiany stanu CA. Zarodkowanie homogeniczne i heterogeniczne było przedmiotem badań w pracy [40]. W homogenicznym schemacie zarodkowania przyjęto, że zarodki pojawiają się w losowych miejscach na początku symulacji. Natomiast symulację zarodkowania heterogenicznego przeprowadzono dwuetapowo. W pierwszym etapie za pomocą zarodkowania homogenicznego wygenerowano strukturę początkową dla etapu drugiego. W drugim etapie wprowadzono zasadę, że nowe zarodki mogą pojawiać się 26
39 2.4. Automaty komórkowe w modelowaniu rekrystalizacji wyłącznie na granicach wcześniejszych ziaren. W tym etapie przeprowadzono obliczenia dla schematu z wysyceniem miejsc zarodkowania oraz ze stałą prędkością zarodkowania. Problem uwzględnienia w modelu CA powstawania tekstury i jej wpływu na przebieg procesu rekrystalizacji poruszono w pracy [104], w której przyjęto, że proces zarodkowania nie wprowadza nowych orientacji. W momencie powstania zarodka ziarna gęstość dyslokacji zostaje lokalnie obniżona do zera, jednak oryginalna orientacja komórki zostaje zachowana. Wykorzystanie takiego modelu zarodkowania opiera się na założeniu, że nowe ziarna pojawiają się w obszarach o dużej dezorientacji pomiędzy sąsiednimi podziarnami. Takie założenia można przyjąć np. dla aluminium o wysokiej czystości [52, 104]. W pracy [104] nie wprowadza się jawnie założenia o istnieniu granic ziaren a jedynie o kącie dezorientacji pomiędzy komórkami w siatce CA. Pozwala to na zastosowanie fenomenologicznego podejścia, w którym kryterium zarodkowania bazuje na termodynamicznej niestabilności obszaru o o dużej dezorientacji [104]. Zarodkowanie DRX Proces zarodkowania DRX wydaje się bardziej złożony niż w przypadku symulacji rekrystalizacji statycznej. Zwykle nie jest możliwe wykorzystanie założenia o wysyceniu miejsc zarodkowania, a tworzenie zarodków odbywa się heterogenicznie i ze zmienną w czasie kinetyką, zależną od przebiegu procesu odkształcenia. W praktycznie wszystkich pracach powstanie zarodka nowego ziarna uzależnione jest od jednoczesnego spełnienia szeregu warunków. Jako pierwszy warunek przyjmuje się, że zarodkowanie następuje wyłącznie na granicach ziaren, zarówno pierwotnych jak i wtórnych. Założenie to odpowiada zarodkowaniu w wyniku wybrzuszenia granic ziaren [21]. Mechanizm ten znajduje dobre potwierdzenie doświadczalne [21], jednak wiadomo też, że uprzywilejowanymi miejscami zarodkowania są również wtrącenia obcych faz, granice podziaren i struktur bliźniaczych i inne nieciągłości występujące w mikrostrukturze. Jak dotąd autorowi znany jest zaledwie jeden model DRX oparty o CA i opisany w pracy [38], wykorzystujący inne miejsca zarodkowania niż granice ziaren. W pracy tej wprowadzono do modelu zarodkowanie na wydzieleniach (PSN) (ang. Particle Stimulated Nucleation). Kolejny warunek związany jest z krytyczną gęstością dyslokacji. Sprawdzany jest warunek, czy gęstość dyslokacji przekracza wartość krytyczną dla zarodkowania ρ c. Wartość ta jest przyjmowana jako stała dla ustalonej prędkości odkształcenia i temperatury [63, 136] lub obliczana na podstawie równania Robertsa i Ahlblo- 27
40 2.4. Automaty komórkowe w modelowaniu rekrystalizacji ma [21, 23, 24, 96, 113]: ( ) 20γ ε 1/3 ρ c = (2.10) 3blMτ 2 gdzie: ρ c krytyczna gęstość dyslokacji, γ energia granicy ziarna, ε prędkość odkształcenia, b wektor Burgersa, l średnia droga swobodna dyslokacji, M ruchliwość (mobilność) granicy ziarna, τ średnia energia na jednostkę długości linii dyslokacji. W odróżnieniu od pozostałych prac dotyczących DRX, w pracy [57] przyjęto warunek przekroczenia krytycznej różnicy gęstości dyslokacji. Różnica ta obliczana jest pomiędzy komórką a tym spośród jej sąsiadów, który posiada największą gęstość dyslokacji. Zatem zamiast gęstości dyslokacji w pracy [57] do wyznaczenia miejsc zarodkowania wykorzystano lokalną niejednorodność (gradient) gęstości dyslokacji. Stosunkowo dużą trudnością wydaje się określenie liczby zarodków pojawiających się w kolejnych krokach symulacji oraz ich rozmieszczenia w siatce obliczeniowej. Szczególnie istotne jest to w przypadku przyjęcia założenia, że gęstość dyslokacji jest identyczna w całych ziarnach bądź np. w komórkach, które dołączają do ziaren w tych samych krokach czasowych. W literaturze można wyróżnić cztery rozwiązania tego problemu. Pierwsze z nich wykorzystano np. w pracach [21, 22, 96, 136]. Podstawą rozwiązania jest wprowadzenie równania, pozwalającego na obliczenie liczby zarodków lub prędkości zarodkowania w każdym kroku czasowym. Wartości te uzależniane są od parametrów symulowanego procesu, takich jak temperatura i prędkość odkształcenia. Następnie obliczona liczba zarodków jest rozmieszczana losowo w przestrzeni automatów komórkowych poprzez zmienienie stanów wybranych w ten sposób komórek. Zatem wybrane komórki są wyznaczane do zostania zarodkiem nowego ziarna. Można więc stwierdzić, że tworzenie zarodków jest rolą modelu zewnętrznego względem CA. Co więcej, przeczy ono założeniu lokalności oddziaływań w modelach CA, gdyż zakłada ingerencję zewnętrznego modelu, dysponującego globalną wiedzą o całym układzie. Wiedza ta obejmować musi efektywną prędkość zarodkowania. Podejście takie pomimo podanego wcześniej zastrzeżenia posiada także ważną zaletę, jaką jest dość dokładna kontrola nad procesem zarodkowania. Drugie rozwiązanie zostało zaproponowane w pracy [40]. Wykorzystuje się w nim jednocześnie dwa mechanizmy: pierwszym jest zapewnienie niejednorodności ρ poprzez wyznaczenie N losowych komórek, w których gęstość dyslokacji zostaje obniżona (zwykle o połowę) w wyniku dynamicznego zdrowienia. Postępowanie takie pośrednio wynika z faktu, że w pracy tej celowo nie wykorzystano do obliczania gęstości dyslokacji żadnego wariantu modelu Kocksa-Meckinga, stąd konieczne było uwzględnienie procesów umocnienia i zdrowienia w inny sposób. Drugi mechanizm 28
41 2.4. Automaty komórkowe w modelowaniu rekrystalizacji polega na wyznaczeniu P komórek jako potencjalnych miejsc zarodkowania. Rozwiązanie to cechuje się podobnymi słabościami co podejście pierwsze, wynikającymi z ingerencji w przestrzeń CA na podstawie wiedzy dostępnej wyłącznie globalnie. Krytyka tego mechanizmu podana została też w [57]. Trzecie rozwiązanie jest zdecydowanie lepiej wkomponowane w paradygmat CA. Zakłada się w nim, że utworzenie zarodka wymaga przekroczenia pewnej dodatkowej bariery, realizowanej za pomocą liczby losowej skorygowanej o zadany współczynnik. Podejście to pozwala na wbudowanie zarodkowania w reguły przejścia CA, stosowane lokalnie w obrębie sąsiedztwa. Rozwiązanie to zostało wykorzystane w pracach [57, 63]. Odmienne od przedstawionych wyżej jest rozwiązanie ostatnie, wykorzystywane we wcześniejszych pracach [34, 35] autora niniejszej rozprawy. Główną koncepcją tego rozwiązania jest ominięcie utrudnień, wynikających z lokalnej (w obrębie całego ziarna lub jego granicy) jednorodności zmiennej stanu, determinującej zajście zarodkowania w wyniku przekroczenia wartości krytycznej. Metoda ta polega na zapewnieniu niejednorodności tej zmiennej w całej siatce CA lub w jej obszarach powiązanych z pojedynczymi ziarnami. Dzięki temu proces zarodkowania można sprowadzić do deterministycznych reguł przejścia stanu CA. W odróżnieniu od rozwiązania drugiego, nie jest konieczne losowe wyznaczanie zarodków. Wadą metody jest konieczność zmiany sposobu obliczania gęstości dyslokacji na taką, która zapewni jednoczesną zgodność ilościową z równaniami rozwoju gęstości dyslokacji i niejednorodną dystrybucję ρ w siatce komórek CA. Możliwe jest przeprowadzenie różnych rozwiązań dla tego problemu, niektóre z nich przedyskutowano w podrozdziale Podrozdział ten zawiera szczegółowy opis metody wykorzystywanej w niniejszej rozprawie i spełniającej wskazane wcześniej założenia. Rozrost ziarna Rozrost ziaren jest drugim najistotniejszym procesem zachodzącym w trakcie rekrystalizacji i związany jest ściśle z migracją granic ziaren [44]. Stosowane w większości omawianych prac modele kinetyki wzrostu ziaren zakładają, że prędkość wzrostu ziarna jest proporcjonalna do iloczynu ruchliwości granicy ziarna M oraz siły pędnej F. Zależność taka jest powszechnie uznawana [8]. Ruchliwość (mobilność) M granicy ziarna jest ilościową miarą kinetycznych właściwości granicy ziarna i głównym parametrem, opisującym proces ruchu granicy [43]. Oprócz konwencjonalnych parametrów termodynamicznych, takich jak temperatura i ciśnienie, ruchliwość zależna jest od orientacji sąsiednich ziaren i dezorientacji granicy międzyziarnowej [43]. Ruchliwość granicy ziarna M w pracach [21, 29
42 2.4. Automaty komórkowe w modelowaniu rekrystalizacji 24, 57, 63, 96, 136], dotyczących symulacji DRX za pomocą CA, traktuje się jako aktywowaną cieplnie i niezależną jawnie od dezorientacji granicy ziarna. W pracach [21, 24, 63, 96, 136] ruchliwość granicy ziarna wyrażono równaniem: M = D sb kt (2.11) gdzie: D s współczynnik samodyfuzji granicy, b wektor Burgersa, k stała Boltzmanna, T temperatura w skali bezwzględnej. Zależność (2.11) opisuje ruchliwość granic niskokątowych [52]. Dla granic wysokokątowych zależność opisująca ruchliwość granicy przyjmuje postać równania typu Arrheniusa [52]. Ruchliwość jest silnie zależna od temperatury i opisywana jest jednym z równań: ( M = M 0 exp Q ) RT (2.12) lub M = M 0 exp ( ) Qgb kt (2.13) gdzie: Q gb energia (lub entalpia) aktywacji ruchliwości granicy ziarna, Q energia aktywacji ruchliwości granicy ziarna, M 0 współczynnik ruchliwości granicy ziarna. W pracach [106, 108, 146] równanie (2.13), wyrażające ruchliwość granicy ziarna, wyprowadzone zostało z podstawowych zależności termodynamicznych. Model CA rozwoju mikrostruktury w trakcie rekrystalizacji w stalach IF był przedmiotem powiązanych tematycznie prac [106, 107]. W pracy [106] wykorzystywano równanie (2.13) do określenia prawdopodobieństwa zmiany stanu przez komórki CA. W pracy tej M 0 oraz Q gb wyrażono jako funkcje różnicy orientacji pomiędzy komórkami CA. Z kolei w pracy [107], poruszającej podobne zagadnienia, wykorzystywana jest empiryczna zależność ruchliwości granicy ziarna od kąta dezorientacji θ, z pominięciem wpływu temperatury: 1 M(θ) = exp ( 2(θ 15) ) + 1 (2.14) Do wyznaczenia ruchliwości granicy ziarna wykorzystuje się także równanie Shivindlermana [11, 51, 52], opisujące sigmoidalną zależność M od kąta dezorientacji granicy: ( M(θ) = M m [1 exp B θ ) n ] θ m (2.15) gdzie: θ kąt dezorientacji granicy ziarna, θ m kąt dezorientacji wysokokątowej 30
43 2.4. Automaty komórkowe w modelowaniu rekrystalizacji granicy ziarna, M m ruchliwość wysokokątowej granicy ziarna, B, n parametry. Kąt dezorientacji dla granicy wysokokątowej przyjmuje się jako θ m 15. W równaniu (2.15) nie wprowadza się zależności od temperatury, jednak w przypadku, gdy energia aktywacji granic wysoko i niskokątowych jest różna, zależność taką należy uwzględnić. Dla niektórych materiałów jak np. Al równanie (2.15) może być stosowane w całym zakresie temperatury [51]. Równanie to zostało także zastosowanie w pracy [13] do opisu ruchliwości granicy ziarna w symulacji MC rekrystalizacji statycznej zachodzącej w Ti oraz dla stali IF w pracy [12]. W wielu opisywanych wcześniej pracach energię granicy ziarna traktuje się jako składową siły napędowej rozrostu ziarna. Znajduje to potwierdzenie w rozważaniach teoretycznych i doświadczalnych [146]. W pracach [21, 22, 24, 63, 96, 107] wykorzystuje się równanie Reada-Shockleya (2.16), opisujące zależność energii granicy ziarna od kąta jej dezorientacji: ( θ γ = γ m 1 ln θ ) θ m θ m gdzie: γ m energia wysokokątowej granicy ziarna, (2.16) Równanie (2.16) jest z powodzeniem wykorzystywane także w pracach stosujących metodę MC, np. w [150]. W pracy [107] wykorzystano aproksymację równania (2.16) dla kątów θ m < 15. W niektórych pracach poświęconych symulacji MC procesów rekrystalizacji wykorzystywana jest zmodyfikowana wersja równania (2.16) [11 13, 50, 109] w postaci: ( ) θ γ m θ γ = m 1 ln θ θ m : θ θm (2.17) γ m : θ > θ m W pracach [21, 22], dotyczących symulacji CA DRX, wyprowadzono na bazie teorii zarodkowania równanie, wyrażające siłę pędną wzrostu. Rozważany jest bilans energii swobodnej układu, składającego się z i-tego ziarna o promieniu r i i średniej gęstości dyslokacji ρ i, wzrastającego o przyrost dr i w odkształconej osnowie o gęstości dyslokacji ρ m. Energia granicy pomiędzy ziarnem i osnową wyrażona jest przez γ i. Zmiana energii w podanym układzie dana jest równaniem: dw i = dw sur i + dw vol i (2.18) dw sur i = d ( 4πr 2 i γ i ) = 8πri γ i dr i (2.19) dw vol i = 4πr 2 i τ (ρ m ρ i ) dr i (2.20) Człon dwi vol wyraża zmianę energii wewnętrznej układu przy zmianie gęstości dyslokacji na froncie rekrystalizacji. Składowa dwi vol jest proporcjonalna do energii 31
44 2.4. Automaty komórkowe w modelowaniu rekrystalizacji odkształcenia, zmagazynowanej w postaci dyslokacji w obszarze pomiędzy r i i r i + dr i, z kolei dwi sur jest zmianą energii granicy na powierzchni ziarna, związaną ze zmianą powierzchni. Siła pędna wzrostu ziarna wynika z różnicy energii swobodnej przed i za frontem rekrystalizacji i wyrażona jest jako: F i = dw i dr i = 4πr 2 i τ (ρ m ρ i ) 8πr i γ i (2.21) Kugler i Turk [63] zastosowali równanie siły pędnej, uwzględniające różnicę gęstości dyslokacji [8, 52] i krzywiznę granicy ziarna [52]: F = µb 2 (ρ 1 ρ 0 ) 2 γ r (2.22) gdzie: p szerokość komórki CA, ρ 1, ρ 0 gęstość dyslokacji przed i za frontem rekrystalizacji, r promień ziarna. Kolejnym problemem, związanym uwzględnieniem w symulacjach CA rozrostu ziarna i ruchu granicy międzyziarnowej, jest dostosowanie kinetyki wzrostu do rozdzielczości siatki obliczeniowej i promienia sąsiedztwa. W większości takich symulacji reguły zmiany stanu uruchamiane są synchronicznie, a prędkość migracji granicy zależy bezpośrednio od liczby wykonanych kroków czasowych. Davies w pracy [18] uzależnia wzrost ziarna od parametru probabilistycznego, związanego z równaniem prędkości wzrostu. W pracy tej wskazano możliwość włączenia arbitralnego modelu prędkości wzrostu ziarna do modelu opartego o CA. W pracy [21] wprowadzono do reguł zmiany stanu parametr probabilistyczny, pozwalający na określenie dozwolonego obszaru wzrostu w obrębie sąsiedztwa i promienia wzrostu ziarna w następnym kroku czasowym. Prace te nie prezentują jednak metody uwzględnienia dużych prędkości wzrostu, przekraczającej ograniczenia kinetyki wynikające z topologii siatki i sąsiedztwa. Inny sposób adaptacji kinetyki ruchu granicy ziarna do możliwości siatki obliczeniowej podany został w pracy [63], w której zaproponowano metodę dostosowania długości kroku czasowego w zależności od maksymalnej prędkości ruchu granicy w poprzednim kroku czasowym. Z kolei Kroc w pracy [57] zaproponował wprowadzenie dyskretnej zmiennej stanu, będącej licznikiem ustawianym na zadaną wartość przy każdej zmianie stanu komórki i dekrementowanym do zera w kolejnych krokach czasowych. W podejściu tym zmiana stanu dozwolona jest wyłącznie w przypadku, gdy zmienna ta przyjmuje wartość zero. Metoda pozwala na zmniejszenie prędkości ruchu granicy ziarna i zarodkowania, jednak nie daje możliwości uwzględnienia procesów zachodzących z dużą prędkością oraz czasowych zmian kinetyki tych procesów. Uwzględnienie częściowego zajścia rekrystalizacji w objętości materiału, repre- 32
45 2.4. Automaty komórkowe w modelowaniu rekrystalizacji zentowanej przez komórkę CA, pozwala na dokładniejszą kontrolę kinetyki ruchu granicy. W pracy [63] wprowadzono dodatkową zmienną, nazywaną długością komórki, pozwalającą na oszacowanie przyrostu rekrystalizacji wewnątrz komórki CA w trakcie kroku czasowego. Próbę uniezależnienia od topologii siatki podjęto w pracy [75], w której rozważano problem wzrostu kierunkowego ziaren. Zaproponowano tam rozszerzenie sąsiedztwa w taki sposób, aby wyeliminować problemy z oszacowaniem prędkości wzrostu występujące dla standardowych typów sąsiedztwa. Wykorzystane tam dostosowanie topologii sąsiedztwa do kinetyki wzrostu ziaren nie pozwalało jednak na adaptatywne uwzględnianie jej zmian. Przedstawiony w pracy [62] uproszczony model ruchu granic ziaren zademonstrowano na przykładzie układu, złożonego z czterech ziaren o różnej orientacji. W opisywanym tam modelu założono, że jedyną siłę napędową ruchu granicy jest minimalizacja długości linii granicy ziarna w obrębie sąsiedztwa. Pomimo daleko idących uproszczeń modelu udało się uzyskać efekt formowania złączy pomiędzy trzema ziarnami (ang. triple junctions). Więcej uzyskanych w drodze obliczeń typów układów granic pomiędzy ziarnami przedstawiono w pracy [61]. Rozwój tekstury W pracy [19] zaproponowano model 3D statycznej rekrystalizacji, zawierający elementy prognozowania rozwoju tekstury. Wprowadzone zostały trzy klasy tekstury, kubiczna, losowa oraz tekstura walcowania, które powiązano z różnymi prędkościami migracji granic ziaren. Wyniki symulacji dla trzech tekstur osobno oraz rozważanych łącznie zostały porównane z danymi doświadczalnymi w postaci rozkładów wielkości ziarna. Rozbieżności pomiędzy wynikami doświadczalnymi i obliczeniami tłumaczono pominięciem w modelu termodynamicznie niestabilnych ziaren, które w rzeczywistym doświadczeniu pochłaniane są przez inne ziarna. W pracy [75] przedstawiono wyniki modelowania 3D rekrystalizacji. Mikrostrukturę początkową wygenerowano na podstawie informacji uzyskanych doświadczalnie, z założeniem losowego rozkładu orientacji oraz zarodkowania z wysyconymi miejscami zarodkowania. Do opisu orientacji wykorzystano trzy kąty Eulera. Przyjęto, że granice niskokątowe są nieruchome. Założono także, że najwyższą ruchliwość posiadają granice o dezorientacji ±5.78 wokół , natomiast pozostałe granice posiadają ruchliwość pięciokrotnie niższą. Otrzymane w wyniku obliczeń diagramy ODF pozostają w dobrej zgodności z wynikami doświadczalnymi, otrzymanymi dla materiału o losowym rozkładzie orientacji ziaren, w którym zarodkowanie rekrystalizacji następuje na wtrąceniach faz obcych. Warto jednak zaznaczyć, że w modelu 33
46 2.5. Wieloskalowa metoda symulacji CAFE opisanym w [75] nie uwzględniano zarodkowania na wtrąceniach, zatem porównanie wyników nie wydaje się do końca wiarygodne. Niedawno Raabe i Hantcherli [107] zademonstrowali wykorzystanie CA do symulacji rozwoju tekstury w trakcie SRX w stalach IF. Do wygenerowania mikrostruktury początkowej wykorzystano dane, pochodzące z badań rzeczywistej próbki, prowadzonych metodą EBSD, w tym informacje o składowych tekstury w próbce. Na podstawie tych danych przeprowadzono powiązanie orientacji z poszczególnymi ziarnami, co zostało następnie uwzględnione podczas symulacji rozwoju mikrostruktury w trakcie SRX. W pracach dotyczących modelowania DRX za pomocą CA używa się co prawda pojęć orientacji ziaren oraz rozrostu zależnego od kąta dezorientacji granic ziaren, jednak według rozeznania autora w żadnej z nich nie przedstawiono wyczerpującej analizy uzyskanej tekstury. 2.5 Wieloskalowa metoda symulacji CAFE W tym podrozdziale przedstawiony zostanie przegląd sposobów konstruowania modeli symulacyjnych, bazujących na połączeniu automatów komórkowych z metodą elementów skończonych. Akronim będący nazwą metody pochodzi od Cellular Automata Finite Element i wedle wiedzy autora został po raz pierwszy wprowadzony w pracy [111]. Jest to stosunkowo nowa problematyka, rozwijana na przestrzeni ostatniej dekady. Ogólna koncepcja tego podejścia opiera się na wykorzystaniu CA do symulacji procesu zmian mikrostruktury materiału w skali mikro i wykorzystaniu wyników obliczeń w modelu materiału w symulacji MES. Kolejnym krokiem jest wykorzystanie w modelu CA wyniku, uzyskanego z metody elementów skończonych i wyrażającego wybrane parametry makroskopowe. Konkretne realizacje tej koncepcji, opisane w dalszej części rozdziału, różnią się znacznie między sobą. Podejmowane są próby jednoczesnego skonstruowania modelu całej domeny obliczeniowej z wykorzystaniem CA i MES, z kolei w innych podejściach symulacje CA wykorzystywane są do modelowania odpowiedzi materiału w skali mikro i oszacowania wybranych makroskopowych parametrów procesu, wówczas połączenie MES i CA następuje w punktach całkowania. Napotkać można także sekwencyjne połączenia rozwiązania MES i CA, wówczas jedna z metod dostarcza danych wejściowych dla drugiej Zastosowania CAFE w modelowaniu krystalizacji Pierwsze prace dotyczące metody CAFE opublikowano dla zagadnień krzepnięcia. W pracach [30, 111] przedstawiono połączenie symulacji MES i CA, prowadzonych 34
47 2.5. Wieloskalowa metoda symulacji CAFE dla rozwoju struktur dendrytycznych podczas krzepnięcia wlewka. W podejściu tym równanie różniczkowe opisujące pole temperatury rozwiązywane jest za pomocą MES. Natomiast CA wykorzystano do opisu rozwoju mikrostruktury i uwalniania w wyniku krzepnięcia ciepła przemiany fazowej. Modelowany obszar został w całości zdyskretyzowany oddzielnymi siatkami MES i CA. Wykorzystywana była regularna, czworokątna siatka CA, wielokrotnie gęstsza od siatki MES, która zbudowana była z elementów trójkątnych. Dla tak zdefiniowanej dyskretyzacji obszaru określone zostały funkcje interpolujące pomiędzy węzłami siatki MES i komórkami CA. Rozwinięciem koncepcji przedstawionej wcześniej w publikacji [30] jest praca [29]. Wykorzystano w niej symulacje 3D MES i CA oraz zaproponowano zaawansowaną technikę podziału domeny obliczeniowej na obszary ze względu na charakter zachodzących zjawisk. Służy temu wprowadzenie dodatkowych poziomów grupowania komórek CA. Autorzy [29] wprowadzili nową koncepcję łączenia CA i MES, bazującą na zgrupowaniu komórek. Wyodrębniono bloki, będące zbiorami komórek, oraz okna, powstałe przez zgrupowanie bloków. Ponadto wprowadzone zostały zmienne w czasie i uzależnione od przebiegu procesu powiązania pomiędzy elementami skończonymi i blokami komórek. Schemat łączenia elementów i bloków przestawiono na rysunku Obliczenia pola temperatury używano do określenia lokalnego przechłodzenia w skali mikrostruktury, wprowadzając siłę napędową do wzrostu dendrytów. Opisywany model uwzględnia też powstawanie i rozwój tekstury. W pracy [28], będącej kontynuacją omawianych wcześniej badań tych samych Autorów, przedstawiono porównanie wyników symulacji oraz pomiarów metodą EBSD próbek wykonanych z różnych materiałów i poddanych różnego rodzaju obróbce. Zarówno obrazy mikrostruktury jak i otrzymane figury biegunowe wskazują na bardzo dobrą zgodność obliczeń i prób doświadczalnych. Podane w pracy dokładne informacje o rozmiarze obliczanego problemu (liczby komórek CA i elementów MES) oraz czasie obliczeń na komputerze o przeciętnej wydajności, pozwalają na bardzo pozytywną ocenę zastosowanych usprawnień modelu, wprowadzonych w [29]. Założenia przyjęte w [29] zostały zweryfikowane w pracy [47]. Obliczenia wykonane modelem CAFE porównano z wynikami obliczeń metodą śledzenia frontu FT (ang. front tracking). Jako główne słabości przyjętej metody łączenia obliczeń CA i MES uznano przeszacowanie ciepła uwalnianego w trakcie krzepnięcia. Jako remedium zaproponowano wprowadzenie korekty, uwzględniającej stopniowe oddawanie ciepła krzepnięcia i biorącej pod uwagę lokalną entalpię objętościową i ułamek objętości komórek w regionie krzepnięcia. Kolejne zastosowanie CAFE w modelowaniu krzepnięcia przedstawiono w [143]. Cały obszar został zdyskretyzowany za pomocą oddzielnych siatek CA i MES, na- 35
48 2.5. Wieloskalowa metoda symulacji CAFE Rysunek 2.12: Schemat dynamicznego przyporządkowania komórek i elementów skończonych w modelu 3D CAFE. Na rysunku zaznaczono bloki, okna i komórki CA a także stan węzłów i elementów MES oraz bloków (wg [29]) kładających się na wzajem. Obliczone w MES pole temperatury interpolowano na środki komórek CA, a sprzężenie zwrotne bazowało na uwolnieniu ciepła przemiany fazowej w trakcie krystalizacji Metoda CAFE w modelowaniu rekrystalizacji statycznej Połączenie metody elementów skończonych z automatami komórkowymi zasugerował Gottstein w pracy [45], wprowadzającej koncepcję modelowania zintegrowanego (ang. Integrated modeling) procesów rekrystalizacji. W pracy tej przedyskutowano dwa podejścia do wieloskalowego, zintegrowanego rozwiązania zadań, wymagających łączenia modeli zjawisk zachodzących w różnych skalach czasu i przestrzeni. Pierwsze z nich bazuje na jednoczesnym (synchronicznym, bezpośrednim) połączeniu różnych metod symulacyjnych dla problemów różnej skali. Drugie zakłada sekwencyjne połączenie, wymagające cyklicznego przekazywania parametrów pomiędzy obliczeniami, rozwiązującymi problemy w różnych skalach [45]. Przykład modelowania zintegrowanego przedstawiono w pracy [42]. Wykorzystano tam połączenie modelu CA 3D rekrystalizacji statycznej, opisanego w pracy [75], oraz symulacji MES 3D procesu walcowania na gorąco, wykorzystującej model zmiennej wewnętrznej, opisany w pracy [119]. W rozwiązaniu tym model MES dostarcza obliczonych w elementach skończonych gęstości dyslokacji po zakończeniu procesu jako danych początkowych dla symulacji CA rekrystalizacji. Symulację CA przeprowa- 36
49 2.5. Wieloskalowa metoda symulacji CAFE dzano dla danych wejściowych pochodzących z każdego elementu skończonego w siatce MES, jednakże w pracy [42] nie podano szczegółów połączenia pomiędzy CA i MES. Opisane w [42] rozwiązanie nie wprowadza wyraźnego wzajemnego sprzężenia pomiędzy modelami w skali mikro i makro oraz nie uwzględniany jest wpływ zajścia rekrystalizacji w trakcie odkształcenia. Można zatem stwierdzić, że kaskadowe przeprowadzenie obliczeń dla skali makro i mikro nie pozwala na uwzględnienie jednoczesnego zajścia wielu zjawisk, istotnych w trakcie walcowania na gorąco. Z drugiej strony, w tym procesie przeróbki plastycznej decydującą rolę odgrywają procesy strukturalne o charakterze statycznym, zachodzące w przerwach pomiędzy przepustami [4], zatem w procesie omawianym w pracy [45] pełne sprzężenie zwrotne pomiędzy modelami CA i MES nie jest niezbędne. Połączenie metody automatów komórkowych z symulacją MES, bazującą na teorii plastyczności kryształów (CP-FEM), opisano w pracy [103]. Zarówno symulacja CA jak i MES prowadzona była w przestrzeni 2D. Probabilistyczny model CA wykorzystano do wspomagania symulacji CP-FEM w wyznaczaniu miejsc zarodkowania nowych ziaren. Połączenie CA-MES przeprowadzono poprzez zastępujące operacje: translację zmiennych stanu CP-FEM na zmienne stanu, używane przez CA; mapowanie punktów całkowania w elementach skończonych na kwadratowej siatce CA na komórki; obliczenie w wyznaczonej w poprzedniej operacji komórce CA siły pędnej do wzrostu oraz ruchliwości, a także prawdopodobieństwa zmiany stanu, w tym powstania zarodka. Rozwiązanie wykorzystane w pracy [103] zakłada zbudowanie modelu CA dla tej samej domeny obliczeniowej, która wykorzystywana jest przez MES. Podejście takie jest uzasadnione, gdyż CP-FEM i CA opisują zjawiska zachodzące w podobnych skalach. Metoda CP-FEM należy do grupy modeli skali mikro, a ze względu na złożoność obliczeniową nie jest stosowana do symulacji dużych obiektów. Zatem sposób łączenia, bazujący na dyskretyzacji wspólnej domeny obliczeniowej, w niewielkim stopniu nadaje się do łączenia CA i klasycznego MES, stosowanego w inżynierskich symulacjach procesów przeróbki plastycznej Zastosowania CAFE w modelowaniu odkształceń plastycznych Das w rozprawie doktorskiej [14] rozważał zastosowanie połączenia CA z MES w symulacji rozwoju mikrostruktury w wyniku pękania warstw tlenkowych w procesie walcowania. Głównym przedmiotem zainteresowania rozprawy były inicjacja i rozwój pęknięć w warstwie tlenkowej podczas tego procesu. W podejściu tym wprowadzono połączenie pomiędzy komórkami CA i obszarami w pobliżu punktów całkowania wewnątrz elementów skończonych. Celem tego zabiegu było dostarczenie 37
50 2.5. Wieloskalowa metoda symulacji CAFE danych mikrostrukturalnych, zawartych w przestrzeniach CA, do punktów całkowania Gaussa, w których na tej podstawie obliczana była następnie wartość naprężenia. Opisana w pracy[14] metodyka konstruowania modelu CAFE składa się z sześciu następujących po sobie etapów: 1. zdefiniowanie opisu procesu metalurgicznego z wykorzystaniem CA, 2. połączenie obszaru ciągłego z mikrostrukturą oraz dostosowanie wejść symulacji MES, 3. połączenie CA z MES, 4. aproksymacja odkształceń wewnątrz CA, 5. uśrednienie wartości zwracanych przez CA do MES, 6. uaktualnienie CA poprzez zastosowanie macierzy transformacji. Połączenie pomiędzy komórkami CA i elementami skończonymi sprowadza się do geometrycznego odwzorowania, wskazującego która komórka CA leży w którym elemencie skończonym. Wykorzystywany w [14] kod MES Abaqus Standard udostępnia informacje o budowie siatki, tzn. położeniu węzłów i macierzy połączeń. Wprowadzono dodatkową procedurę, bazującą na danych o strukturze siatki i łączącą konkretne elementy z konkretnymi przestrzeniami CA. Odwzorowanie przeprowadzono z zastosowaniem pomocniczej procedury triangulacji. W modelu [14] założono, że odkształcenie siatki MES prowadzi do odkształcenia komórek CA. W tym celu wprowadzono macierz transformacji, pozwalającą na geometryczne przekształcenie siatek CA z uwzględnieniem ścinania i obrotu. Wieloskalowy model 3D CAFE pękania kruchego i plastycznego opracowano w pracy [130]. W podejściu tym oddzielono zachowanie makroskopowe materiału od jego strukturalnej odpowiedzi na odkształcenie. W części strukturalnej wprowadzone zostały zagnieżdżone przestrzenie CA, odpowiadające założeniu, że pękanie plastyczne zachodzi w skali większej niż inicjujące je pękanie kruche. Z kolei zachowanie makroskopowe uwzględniono za pomocą MES, w której do punktów całkowania w elementach skończonych przypisano zagnieżdżone przestrzenie CA. Rolą tych przestrzeni było obliczenie naprężenia. Rozmiary komórek w każdej przestrzeni CA nie zostały powiązane ani ze sobą, ani z rozmiarem elementu skończonego, do którego zostały przypisane. Jedynym kryterium doboru rozmiaru komórek CA były skale wielkości w których zachodzą modelowane zjawiska pękania [130]. W pracy [130] wprowadzono także interesującą generalizację klasycznego modelu CA, która bazuje 38
51 2.5. Wieloskalowa metoda symulacji CAFE na koncepcji zmiennych stanu komórek oraz właściwości komórek, stałych w trakcie symulacji. Wykorzystywany w pracy [130] model struktur ziarnowych zakłada opis każdego ziarna przez pojedynczy kąt orientacji. Odstępstwo od opisu krystalograficznego za pomocą dwóch kątów, podanego w [55], lub za pomocą trzech kątów Eulera, uzasadniano złożonością obliczeniową, niezbędną do oszacowania kąta dezorientacji pomiędzy ziarnami. Dzięki założeniu, że orientację ziarna można opisać za pomocą pojedynczego kąta α, możliwy jest uproszczony sposób obliczania dezorientacji pomiędzy ziarnami m i l o orientacji odpowiednio α m i α l jako θ = α m α l [130]. Zastosowanie metody CAFE do symulacji rozwoju mikrostruktury w trakcie rekrystalizacji było przedmiotem prac [15, 16], które opublikował Das ze współpracownikami. W przedstawianym w [15, 16] modelu wykorzystano schemat budowy CAFE, opisany we wcześniejszej pracy doktorskiej [14]. Wykorzystano symulację 2D CA, bazującą na początkowej reprezentacji zgładu mikrostruktury. W pracy [16] zastosowano równania, służące obliczaniu gęstości dyslokacji: dρ i CA = dρ i+ CA dρ i CA (2.23) dρ i+ CA = M bl dεi CA (2.24) ( ) Q dρ i CA = A 1 ρ i CA exp dε i CA (2.25) RT i CA gdzie: dρ i CA całkowity przyrost gęstości dyslokacji w komórce CA, dρ i+ CA przyrost gęstości dyslokacji w komórce CA wynikający z przyrostu odkształcenia, dρ i CA spadek gęstości dyslokacji w komórce CA w wyniku zdrowienia, M współczynnik Taylora (ang. Taylor factor), l = C/Z q średnia droga swobodna dyslokacji, Z parametr Zenera-Hollomona, Q pozorna energia aktywacji, TCA i temperatura, A 1, C, q współczynniki. Opisany w pracach [15, 16] model rekrystalizacji zakładał, że zarodkowanie może następować na granicach ziaren pierwotnych pod warunkiem osiągnięcia krytycznej gęstości dyslokacji. Powstałe ziarna zrekrystalizowane rozrastały się oparciu o proste reguły zmiany stanu, stosowane z wykorzystaniem sąsiedztwa Moore a. Rozrost ziaren następował do momentu zderzenia z innymi zrekrystalizowanymi ziarnami. W trakcie odkształcenia w komórkach zrekrystalizowanych następowało zwiększanie gęstości dyslokacji. Model rekrystalizacji podany w pracach [15, 16] wprowadza szereg uproszczeń. Przyjęty tam model wzrostu ziaren nie umożliwia wprowadzenia siły pędnej. Nie uwzględnia także wpływu temperatury oraz orientacji na prędkość wzrostu zrekry- 39
52 2.5. Wieloskalowa metoda symulacji CAFE stalizowanych ziaren. Z kolei założenie o powstawaniu zarodków wyłącznie na granicach ziaren pierwotnych oraz rozroście ziaren do momentu zderzenia może być utrzymane wyłącznie dla rekrystalizacji statycznej. Ponadto krytyczna gęstość dyslokacji, potrzebna na granicy międzyziarnowej do zapoczątkowania rekrystalizacji, przyjmowana jest jako stała, ok m 2. Kolejnym uproszczeniem jest obliczanie średniej drogi swobodnej dyslokacji l jako funkcji parametru Zenera-Hollomona, a więc w sposób niezależny od odkształcenia i czasu. Zależność opisująca l wykorzystywana w [15, 16] zakłada niejawnie, że á priori znana jest końcowa wielkość podziarna. Połączenie CA z modelem 2D MES, wykorzystującym teorię plastyczności kryształów (CP-FEM), na przykładzie przemiany fazowej austenit-ferryt zaproponowano w pracy [66]. W przeciwieństwie do omawianych wcześniej przykładów zastosowania CAFE, nie wprowadzono sprzężenia zwrotnego pomiędzy CA i MES. Symulacja MES odkształcenia plastycznego dostarczała jedynie początkowych wartości zmiennych stanu dla CA. Dane uzyskane z siatki MES zostały za pomocą procedury interpolacyjnej przepisane na regularną siatkę CA. Następnie prowadzono symulację CA przemiany fazowej Fe γ w Fe α. W podejściu tym każde ziarno w próbce jest dyskretyzowane za pomocą wielu elementów skończonych, a rozmiary prostokątnej próbki przed odkształceniem są bardzo niewielkie i wynoszą 200 µm na każdym boku. Niedawno w pracy [98] przedstawiono połączenie rozwiązania opartego o metodę elementów skończonych z automatami komórkowymi dla zjawiska dynamicznej rekrystalizacji w materiale dwufazowym. Przykładowy materiał składał się z faz α i β, z udziałem 25% fazy α. W podejściu tym na całej domenie obliczeniowej wprowadzono oddzielną dyskretyzację MES i CA. Wprowadzano znacznie gęstszą siatkę CA, pokrywającą ten sam obszar co siatka MES. W niewiele wcześniejszej pracy [97] tych samych autorów wykorzystano tą samą siatkę dla symulacji CA i MES. Omawiana realizacja modelu CAFE wykorzystywała metodę elementów skończonych do wyznaczenia rozkładu naprężeń i odkształceń w domenie obliczeniowej. W pracy oparto się na założeniu, że całkowita prędkość odkształcenia ε może być wyrażona jako suma: ε = ε e + ε p + ε c (2.26) gdzie ε e, ε p i ε c wyrażają odpowiednio części sprężystą, plastyczną oraz wynikającą z zajścia DRX, uzyskiwaną w oparciu o wyniki pochodzące z części CA modelu. Tensor ε c ij wyrażono jako funkcję zależną od czasu t oraz tensora odkształceń sprężystych 40
53 2.6. Podsumowanie ε e ij w chwili t 0 : ε c ij = εe ij(t 0 ) t ( ) t sech 2 t0 t (2.27) gdzie: t długość kroku czasowego, t 0 czas rozpoczęcia zarodkowania w modelu CA. W modelu opisanym w [98] pomiędzy CA i MES wymieniane są tensory odkształceń i naprężeń oraz zmienna reprezentująca czas. Obliczenia podzielono na małe kroki odkształcenia. Po każdym kroku odkształcenia tensory odkształceń i naprężeń pochodzące z MES rzutowano na siatkę CA. Następnie, przy założeniu izotermiczności i stanu ustalonego odkształceń i naprężeń, przeprowadzano obliczenia CA, oparte na modelu omawianym w pracach [22, 96]. Powiązanie pomiędzy CA i MES oparte jest na zależności (2.27) i uwzględnia głównie wpływ zarodkowania. Jako kryterium zarodkowania wykorzystano przekroczenie krytycznej gęstości dyslokacji, zadanej równaniem (2.10), na granicy pomiędzy fazami α β lub granicy β β. 2.6 Podsumowanie Przedstawiona w rozdziale analiza literatury nie wyczerpuje wszystkich zagadnień, związanych z modelowaniem procesów rekrystalizacji. Pozwala jednak na syntetyczne ujęcie stanu badań, dotyczących modelowania dynamicznej rekrystalizacji za pomocą CA i metod wieloskalowych. Zgodnie z wiedzą Autora można sformułować następujące podsumowanie: Jak dotąd w literaturze nie przedstawiono modelu, łączącego metodę CA i MES w opisie dynamicznej rekrystalizacji i pozwalającego na symulację dużych próbek, a więc o rozmiarach porównywalnych z wykorzystywanymi w próbach plastometrycznych. Istnieją jedynie prace wprowadzające dyskretyzację MES na tej samej siatce obliczeniowej co CA. Powstały także nieliczne prace, opisujące próby łączenia CA i MES dla rekrystalizacji statycznej. Istnieją prace, rozważające wpływ zmiennych warunków odkształcenia (np. zmiany prędkości odkształcenia) na proces DRX, symulowany za pomocą CA. Jednakże zmiana warunków zadawana była skokowo i nie wynikała z makroskopowego przebiegu procesu. Odwzorowanie globularnego kształtu ziaren na prostokątnej siatce CA wciąż pozostaje zagadnieniem otwartym. Kontrola kinetyki wzrostu ziaren opiera się na wyznaczeniu siły pędnej wzrostu i ruchliwości granicy. Przebieg wzrostu 41
54 2.6. Podsumowanie ziaren oraz sposób jego reprezentacji w modelu CA jest stosunkowo słabo opisany w literaturze. Dotychczas nie przedstawiono metody wyznaczania długości kroku czasowego metody CA w symulacji dynamicznej rekrystalizacji. Nie opracowano też metody automatycznego doboru kroku czasowego i adaptowania go do kinetyki procesu. Modele zarodkowania nowych ziaren, wykorzystywane w symulacjach CA dynamicznej rekrystalizacji, bazują zazwyczaj na globalnej wiedzy o stanie układu, co sprzeczne jest z podstawowym założeniem metody CA o lokalności oddziaływań. Metoda zmiennej wewnętrznej pozwala na analizę rozwoju gęstości dyslokacji oraz wielkości ziarna. Jednakże opis zachodzących zmian pomija wpływ zależności topologicznych i morfologicznych, obecnych w mikrostrukturze. Nie uwzględniane są bezpośrednio interakcje lokalne, w szczególności zachodzące na granicach ziaren. IVM dostarcza statystycznego opisu zmian w mikrostrukturze. Ilościowy opis zjawisk, zachodzących w trakcie odkształcenia na gorąco, uzyskiwany z IVM, znajduje dobre potwierdzenie doświadczalne. Metody symulacji skali mikro dla SRX oferują szerszy opis procesów mikrostrukturalnych w porównaniu opracowanymi dotychczas metodami symulacji DRX. Opracowane dotychczas modele CA rekrystalizacji statycznej obejmują zarówno zmiany wielkości ziarna oraz zmiany tekstury. Możliwe jest również przeprowadzenie analizy rozkładów tych cech materiału za pomocą automatów komórkowych. 42
55 Rozdział 3 Teza i cele pracy Przedstawiona wcześniej analiza literatury oraz rozważania dotyczące pożądanych kierunków rozwoju symulacji DRX pozwalają na sformułowanie następującej tezy: Możliwe jest opracowanie wieloskalowego modelu własności materiału odkształcanego na gorąco, wykorzystującego połączenie metody elementów skończonych i automatów komórkowych i uwzględniającego zajście dynamicznej rekrystalizacji. W porównaniu z dotychczasowymi metodami model ten pozwoli na lepsze odwzorowanie podstaw fizycznych DRX w skali mikro. Ponadto umożliwi na przeniesienie cech materiału, obliczanych w skali mikro, do opisu własności materiału w metodzie elementów skończonych, oraz przeniesienie wpływu zachowania materiału w skali makro do modelu symulacyjnego skali mikro. W porównaniu z metodą zmiennej wewnętrznej opracowany model uwzględni w większym stopniu zależności topologiczne, istniejące w mikrostrukturze. Model ten pozwoli na prowadzenie obliczeń, wykorzystując lokalne interakcje pomiędzy elementarnymi objętościami materiału, zamiast opisywać zachowanie materiału w sposób uśredniony. Model wieloskalowy udostępni niektóre składowe opisu ilościowego, trudne do uzyskania z zastosowaniem dotychczasowych metod, m. in. rozkład wielkości ziarna w różnych obszarach odkształcanego materiału, oraz opis zmiany ułamka rekrystalizacji dla każdego cyklu rekrystalizacji z osobna. Celem pracy, mającym wykazać postawioną tezę, jest opracowanie modelu łączącego metodę elementów skończonych z metodą automatów komórkowych. Model ten pozwala na prowadzenie symulacji zachowania się materiału odkształcanego na gorąco. W modelu tym makroskopowe zachowanie materiału jest opisywane przez MES, a zachowanie w skali mikro, obejmujące proces DRX, jest uwzględnione za pomocą automatów komórkowych. Osiągnięcie celu pracy wymaga opracowania modeli dla każdej z wymienionych skal z osobna oraz następnie ich połączenia. Bazując na analizie literatury, przedsta- 43
56 3. Teza i cele pracy wionej w poprzednim rozdziale, można sformułować następujące główne cele cząstkowe: Zaadaptowanie kodu MES, rozwiązującego problem termomechaniczny i pełniącego rolę modelu skali makro, do potrzeb modelu CAFE. Opracowanie i zaimplementowanie modelu CA, uwzględniającego podstawowe procesy zachodzące w trakcie DRX. Opracowany model powinien wykorzystywać bieżący stan wiedzy, dotyczący modelowania DRX za pomocą CA. Ponadto powinien rozwiązać niektóre problemy, pojawiające się podczas budowania modeli z tej grupy, znane z literatury związanej z zagadnieniem. Opracowanie i zaimplementowanie metody łączenia symulacji CA i MES. Przeprowadzenie obliczeń weryfikujących działanie modelu CA oraz CAFE oraz porównanie z wynikiem doświadczenia. Realizacja celu pracy wymaga rozwiązania szeregu problemów cząstkowych. Należy do nich zaliczyć także wprowadzenie usprawnień w porównaniu z dotychczasowymi rozwiązaniami. W części pracy poświęconej modelowaniu rozwoju mikrostruktury cele te obejmują: 1. Opracowanie metody pozwalającej na uzyskanie globularnego kształtu wzrastających ziaren w osnowie o właściwościach zbliżonych do izotropowych. 2. Wprowadzenie reprezentacji i uwzględnienia w obliczeniach elementów mikrostruktury, takich jak ziarna, w sposób nie naruszający założeń metody automatów komórkowych. 3. Opracowanie metody tworzenia początkowej reprezentacji mikrostruktury, wykorzystywanej w symulacji DRX. 4. Uzależnienie prędkości wzrostu ziaren w trakcie rekrystalizacji od lokalnych parametrów, takich jak gęstość dyslokacji oraz kąt dezorientacji granicy międzyziarnowej. 5. Usprawnienie modelu zarodkowania poprzez wyeliminowanie sztucznych mechanizmów, takich jak konieczność globalnego wyznaczania komórek, które staną się zarodkami rekrystalizacji, oraz wprowadzanie prędkości zarodkowania. 6. Opracowanie metody adaptacji kroku czasowego CA w zależności od warunków odkształcenia i parametrów opisujących materiał. 44
57 3. Teza i cele pracy 7. Wprowadzenie opisu rozwoju gęstości dyslokacji na poziomie ziaren, z uwzględnieniem niejednorodnego rozkładu gęstości dyslokacji w ziarnach. 8. Wyeliminowanie założenia o stałych makroskopowych parametrach procesu w trakcie symulacji CA i powiązanie ich z rozwiązaniem problemu termomechanicznego. 9. Ocena czy model poprawnie odzwierciedla kryterium strukturalne, wiążące charakter krzywej naprężenia uplastyczniającego z wielkością ziarna. Sprawdzenie czy w przypadku rozrostu ziarna w wyniku DRX, model symulacyjny wskazuje pojawienie się dużych ziaren. 10. Wprowadzenie możliwości analizy współistniejących frontów rekrystalizacji oraz obliczania ułamków rekrystalizacji dla każdego frontu. Cele cząstkowe związane z makroskopową i wieloskalową analizą procesu odkształcenia obejmują: 1. Rozszerzenie opisu bazującego na IVM o relacje geometryczne, pochodzące z reprezentacji mikrostruktury. 2. Wzbogacenie opisu materiału, wykorzystywanego przez MES, o informacje o rozkładzie wielkości ziarna, zamiast tylko średniej wielkości ziarna. 3. Zastosowanie w MES modelu materiału, wykorzystującego reprezentację wiedzy w postaci regułowej. Wykazanie, że reprezentacja ta jest potencjalnie szersza od opisu bazującego na równaniach ewolucji. Wykazanie możliwości zastosowania wiedzy regułowej, uzupełnianej wzajemnie przez równania ewolucji. 4. Opracowanie, na bazie algorytmu obliczeń odwrotnych, metody uwzględnienia danych doświadczalnych, niosących informację o stanie mikrostruktury po odkształceniu. 45
58 Rozdział 4 Model CAFE Opracowany w niniejszej rozprawie model własności materiału odkształcanego plastycznie na gorąco bazuje na podobnych założeniach co modele MES ze zmienną wewnętrzną (IVM). W każdym elemencie siatki MES przechowywana jest zmienna stanu, zależna od czasu oraz parametrów termomechanicznych. Główną różnicą pomiędzy modelami IVM i prezentowanym rozwiązaniem jest budowa zmiennej wewnętrznej. Opisywane w rozdziale modele IV wykorzystują zmienne, będące pojedynczymi skalarami lub zestawem powiązanych ze sobą wartości skalarnych. Zmienne te reprezentują istotne z punktu widzenia przebiegu modelowanego procesu wielkości średnie, takie jak gęstość dyslokacji, orientacja ziaren, wielkość ziarna, ułamek rekrystalizacji i inne. Ewolucja zmiennych stanu w tych modelach opisywana jest zazwyczaj równaniami różniczkowymi zwyczajnymi, w których zmienną niezależną jest odkształcenie ε lub czas t. Przebieg symulacji procesu jest całkowicie deterministyczny. W przypadku przedstawianego modelu CAFE zmienna wewnętrzna, reprezentująca stan materiału, posiada budowę złożoną. Najistotniejszą jej częścią jest przestrzeń komórek CA, odzwierciedlająca z zadaną dokładnością obraz mikrostruktury, charakteryzowany w każdej komórce przez szereg zmiennych stanu. Zmienne te reprezentują gęstość dyslokacji, orientację, ułamek rekrystalizacji i inne parametry, istotne dla przebiegu procesu. Każda komórka reprezentuje pewną objętość materiału. Oprócz przestrzeni CA wprowadzane są także struktury danych, pozwalające na reprezentację pojedynczych ziaren. Ewolucja stanu zmiennej wewnętrznej opisywana jest za pomocą stosowanych dla każdej komórki CA, w obrębie zdefiniowanego sąsiedztwa, reguł przejścia stanu. Przekształcenie stanu przestrzeni komórek dokonywane jest w kolejnych krokach czasowych, poprzez synchroniczne uruchomienie dla każdej komórki reguł przejścia. Możliwe jest uzupełnienie reguł przejścia stanu o rozwiązanie równań rozwoju zmiennej stanu. Pojęcie zmiennej niezależnej, wyra- 46
59 4. Model CAFE żającej czas, wprowadzane jest pomocniczo, gdyż zmiany stanu CA zależą od liczby dokonanych przekształceń w przestrzeni CA, a nie bezpośrednio od czasu. Metoda automatów komórkowych pozwala na wprowadzenie czynnika probabilistycznego, przez co przebieg symulacji procesu nie jest deterministyczny. W przeciwieństwie do omawianych wcześniej modeli IVM, podejście CAFE umożliwia włączenie do MES bardziej szczegółowego opisu mechanizmów procesów, zachodzących w odkształcanym materiale. W szczególności, CAFE umożliwia wprowadzenie do symulacji zależności topologicznych w domenie obliczeniowej reprezentującej mikrostrukturę, w tym: podział na ziarna i wyróżnienie granic międzyziarnowych, orientację poszczególnych ziaren, gęstość dyslokacji charakteryzującą ziarna oraz jej niejednorodny rozkład wewnątrz ziarna. Potencjalnie możliwe, aczkolwiek wykraczające poza zakres niniejszej rozprawy, jest rozszerzenie opisu mikrostruktury, uwzględniające na przykład: obecność struktur podziarnowych, ograniczanych granicami niskokątowymi, oraz rozkład orientacji wewnątrz ziarna, wynikający z niewielkich rotacji sieci krystalicznej w obrębie ziarna, istnienie wydzieleń innych faz w postaci dyspersyjnej lub w postaci ziaren innej fazy, a także ich wpływ na procesy zachodzące w materiale, zmianę własności wybranych obszarów materiału w czasie lub w wyniku przemiany fazowej, skład chemiczny wybranych obszarów mikrostruktury i segregację chemiczną np. na granicach ziaren. W niniejszej pracy jako przykład procesu przeróbki plastycznej na gorąco wykorzystano proces spęczania osiowosymetrycznych próbek walcowych. Do makroskopowego opisu procesu zastosowano model termomechaniczny, oparty o metodę elementów skończonych, opisany w rozdziale 4.1. Rozdział 4.2 opisuje opracowany model rozwoju mikrostruktury i gęstości dyslokacji, zbudowany z wykorzystaniem automatów komórkowych i przystosowany do połączenia z metodą elementów skończonych. 47
60 4.1. Model skali makro 4.1 Model skali makro W niniejszej rozprawie do opisu zachowania się materiału w ujęciu makroskopowym wykorzystano rozwiązanie problemu termomechanicznego, oparte o metodę elementów skończonych. Jako przykład procesu przeróbki plastycznej wykorzystano osiowosymetryczne ściskanie próbek walcowych (rysunek 4.1). Zastosowano model 2D, w którym, dzięki symetrii procesu, symulowana jest 1 / 4 próbki. Omawiany kod MES o nazwie comp axi, został opracowany w Katedrze Informatyki Stosowanej i Modelowania. Na przestrzeni ostatnich lat był on sukcesywnie rozwijany i uzupełniany, również przy udziale autora niniejszej rozprawy. Szczegóły zastosowanego rozwiązania MES wykraczają poza ramy pracy, a wyczerpujący opis tego modelu podano w pracach [68, 90]. Dla utrzymania spójności wywodu przytoczono jedynie najważniejsze założenia wykorzystywanego modelu MES. (a) (b) Rysunek 4.1: Ilustracja procesu osiowosymetrycznego ściskania próbek walcowych: (a) zmiana wymiarów próbki w trakcie odkształcenia, (b) siatka 2D elementów skończonych z zaznaczonymi węzłami, nałożona na 1 / 4 odkształconej próbki Przyjęto, że rozważany jest ośrodek ciągły o objętości V, którego powierzchnię podzielić można na dwie części: powierzchnię swobodną S 0, powierzchnię styku z narzędziem S T. W przyjętym modelu zastosowano rozwiązanie quasistacjonarne, polegające na podzieleniu całego procesu odkształcenia na małe kroki czasowe t i przeprowadzeniu rozwiązania stacjonarnego dla każdego z nich. Po określeniu rzeczywistego pola prędkości w danym kroku, metodą Eulera obliczane są przemieszczenia węzłów siatki po czasie t. Problem mechaniczny i problem niestacjonarnego przepływu ciepła rozwiązywane są naprzemiennie, z wykorzystaniem tej samej siatki elementów skończonych. 48
61 4.1. Model skali makro Model mechaniczny Opisywane rozwiązanie bazuje na sformułowaniu wariacyjnym. Rozwiązywane jest różniczkowe równanie równowagi naprężeń, przy pominięciu wpływu grawitacji i sił masowych: σ = 0 (4.1) gdzie: σ tensor naprężeń Cauchy ego, W rozwiązaniu przyjmuje się następujące warunki brzegowe: δv i = 0 na S v (4.2) n T σ = f na S n (4.3) gdzie: v i prędkość w węzłach siatki, δv i dowolna wariacja v i, n wektor normalny do powierzchni, f siła tarcia. Słaba forma równania równowagi (4.1) przyjmuje postać: ( σ ij ) δv i dv = 0 (4.4) V Po scałkowaniu przez części równania (4.4) otrzymuje się następującą zależność: σ δvdv (σδv) dv = 0 (4.5) V V Zastosowanie teorii o dywergencji, z uwzględnieniem, że tensor stanu naprężenia jest symetryczny, prowadzi do równania: σ ij ε ij dω δv T fds F = 0 (4.6) V S F Wykorzystane sformułowanie oparte jest na fundamentalnej pracy [67] oraz późniejszych pracach, wykorzystujących podobne założenia. Przyjęto, że modelowany ośrodek jest materiałem sztywno-plastycznym, spełniającym warunek plastycznego płynięcia Hubera-Misesa. Sformułowanie sztywno-plastyczne oparte jest na zasadzie ekstremum, stwierdzającej, że dla ciała o objętości V odkształcanego plastycznie, z zadanymi kinetycznymi warunkami brzegowymi w postaci siły f działającej na powierzchni brzegu S T i prędkości v zadanej na pozostałej powierzchni, oraz z zachowanym warunkiem nieściśliwości ε V = 0, rozwiązanie rzeczywiste jest osiągane dla minimum funkcjonału mocy, otrzymanego z zależności (4.6) po nałożeniu wa- 49
62 4.1. Model skali makro runku nieściśliwości: J = V (σ i ε i + λ ε V ) dv S T f T vds T (4.7) gdzie: ε V objętościowa prędkość odkształcenia, λ mnożnik Lagrange a, σ i intensywność naprężenia, ε i intensywność prędkości odkształcenia. Dla problemu osiowosymetrycznego ściskania siły działające na brzegu są siłami tarcia. W opisywanym rozwiązaniu MES wykorzystywany jest model tarcia Coulomba. W objętości V pomijany jest wpływ sił ciężkości i sił bezwładności. Intensywność naprężenia σ i wyrażona jest równaniem: σ i = 2 3 σt Eσ (4.8) gdzie: E macierz tożsamościowa. Tensor prędkości odkształcenia ε przyjmuje postać: ε = 1 2 ( v + T v ) (4.9) gdzie: v wektor prędkości. Równanie określające intensywność prędkości odkształcenia ε i przyjmuje postać: ε i = 2 3 εt E ε (4.10) Powiązanie między składowymi dewiatora tensora naprężenia oraz wektorem prędkości odkształcenia jest przyjmowane zgodnie z prawem plastycznego płynięcia Levy-Misesa: gdzie: σ f naprężenie uplastyczniające. σ = 2 σ f E ε (4.11) 3 ε i Dyskretyzacja równania (4.7) jest przeprowadzana w typowy dla MES sposób. Wykorzystywane są elementy czworokątne czterowęzłowe. Otrzymany układ równań nieliniowych rozwiązywany jest za pomocą metody Newtona-Raphsona. Rozwiązaniem równania (4.7) jest rzeczywiste pole prędkości w węzłach siatki [56]. W opisywanym sformułowaniu naprężenie uplastyczniające σ f jest jedyną własnością, charakteryzującą materiał. Wartość naprężenia uplastyczniającego w warunkach odkształcenia na gorąco jest uzależniona od szeregu parametrów, w tym temperatury T, odkształcenia ε, prędkości odkształcenia ε, czasu t i innych: σ f = σ f (t, ε, ε, T,...) (4.12) 50
63 4.1. Model skali makro W literaturze istnieje szereg prac, wprowadzających różnorodne zależności określające σ f jako funkcję (4.12). Szeroki przegląd modeli naprężenia uplastyczniającego, ukierunkowany na zastosowanie w MES, przedstawiono np. w pracy [46]. Omawiany model MES umożliwia wykorzystanie dużej grupy funkcji o ogólnej postaci równania (4.12). Ponadto kod ten umożliwia wykorzystanie modelu zmiennej wewnętrznej IVM, opisanego w rozdziale W niniejszej pracy sformułowano zależność naprężenia uplastyczniającego jako funkcję wymienionych wcześniej parametrów oraz zmiennej ρ, interpretowanej jako gęstość dyslokacji, zależnej od czasu t i uwzględniającej historię procesu: σ f = σ f ( t, ε, ε, T, ρ(t, ε, T, ρ) ) (4.13) Naprężenie uplastyczniające jest obliczane w trakcie rozwiązania problemu mechanicznego wielokrotnie. Wartość ta jest potrzebna do obliczeń w każdym kroku czasowym metody Newtona-Raphsona, dla każdego punktu całkowania Gaussa w elementach skończonych. Istotne jest, że w opisywanym rozwiązaniu MES wartość naprężenia uplastyczniającego nie zmienia się w kolejnych krokach metody Newtona- Raphsona. Oznacza to, że wartość σ f może być obliczana jako funkcja jednej zmiennej niezależnej, jaką jest czas t. Założenie to ułatwia w dużym stopniu konstrukcję zależności, opisującej zmienną wewnętrzną ρ Model cieplny W opisywanym modelu MES rozwiązanie problemu mechanicznego połączone jest z problemem transportu ciepła. W przypadku symulacji procesu przeróbki plastycznej na gorąco rozwiązanie zagadnienia cieplnego wymaga uwzględnienia generowania ciepła w wyniku pracy odkształcenia i pracy siły tarcia, oraz wymiany ciepła z otoczeniem. Problem przewodnictwa cieplnego opisywany jest równaniem Fouriera: [k(t ) T ] + Q(T ) = c p (T )ρ(t ) T t (4.14) gdzie: k(t ) przewodność cieplna, Q prędkość generowania ciepła w wyniku odkształcenia, c p (T ) ciepło właściwe, ρ(t ) gęstość, T temperatura w skali bezwzględnej, t czas. W rozwiązaniu równania (4.14) zastosowano warunek brzegowy, uwzględniający strumień ciepła pochodzący od tarcia q oraz wymianę ciepła z otoczeniem: k T n = q + α (T a T ) (4.15) 51
64 4.2. Model CA dynamicznej rekrystalizacji gdzie: α współczynnik wymiany ciepła, T a temperatura otoczenia lub narzędzia, n wektor jednostkowy normalny do powierzchni. Rozważany proces ma charakter niestacjonarny, dlatego w rozwiązaniu numerycznym równania (4.14) zastosowano schemat całkowania Galerkina. Szczegóły zastosowania metody ważonych reziduów Galerkina podano w pracy [68]. 4.2 Model CA dynamicznej rekrystalizacji Jak wynika z przeglądu literatury, przedstawionego w rozdziale 2.4, tworzenie modelu CA dla procesów rekrystalizacji składa się z następujących etapów: określenie zmiennych stanu, charakterystycznych dla rozwiązywanego problemu, wybór siatki obliczeniowej, zdefiniowanie rodzaju sąsiedztwa, opracowanie reguł zmiany stanu komórek CA. Dodatkowo do przeprowadzenia symulacji CA procesów rekrystalizacji wymagane jest utworzenie początkowej reprezentacji mikrostruktury w siatce CA. Podane wyżej etapy budowy modelu omówiono w kolejnych podrozdziałach Stan komórek Każda komórka w siatce CA posiada stan, oznaczany jako S(C). W przypadku klasycznej definicji automatów komórkowych, stan ten jest dyskretny, o przeliczalnej liczbie poziomów. Stan komórek CA może się składać z wielu zmiennych, nazywanych zmiennymi stanu. W opisywanym modelu wprowadzono także zmienne stanu o charakterze ciągłym. Podejście takie wykorzystywane było w szeregu wcześniejszych prac dotyczących rekrystalizacji, przytoczonych w rozdziale 2.4 (m. in. [21, 33, 57, 63, 136]), gdyż pozwala na lepsze dostosowanie opisu matematycznego do rzeczywistego zjawiska. Stan każdej komórki w siatce opisywany jest za pomocą szeregu zmiennych. Najważniejszą spośród nich jest lokalna gęstość dyslokacji ρ. Sposób wyznaczania gęstości dyslokacji w komórkach CA przedyskutowano szczegółowo w rozdziale Ponieważ w modelu wprowadza się reprezentację ziaren, każda komórka w siatce posiada zmienną stanu I, identyfikującą ziarno, do którego przynależy. Dokładny opis reprezentacji ziaren w modelu zawarto w podrozdziale
65 4.2. Model CA dynamicznej rekrystalizacji Kolejna zmienna stanu reprezentuje udział powierzchni zrekrystalizowanej w komórce i oznaczana jest jako X. Zmienna ta przyjmuje wartości z zakresu [0, 1]. Odgrywa ona istotną rolę w kontroli wzrostu zrekrystalizowanych ziaren. Pomocniczą funkcję w uruchamianiu reguł zmiany stanu pełni zmienna dyskretna L, oznaczająca tzw. poziom rekrystalizacji. Przyjmuje ona wartość 0 dla komórek przynależnych do ziaren pierwotnych, obecnych w mikrostrukturze, i wartości dodatnie dla komórek przynależnych do ziaren zrekrystalizowanych. Dodatkowo, dla potrzeb analizy zachowania modelu, wprowadzono także szereg pomocniczych zmiennych, pełniących rolę markerów i nie mających wpływu na działanie modelu. Szerszy opis tych zmiennych wraz z przykładami ich użycia przedstawiono w rozdziale 5.4 w dalszej części pracy Siatka komórek Metoda automatów komórkowych bazuje na podziale domeny obliczeniowej na podobszary, nazywane komórkami. Komórki te w dalszej części pracy nazywane są komórkami CA. Podobszary te zazwyczaj są rozłączne i tworzą siatkę, nazywaną przestrzenią komórek. W niniejszej pracy zastosowano dwuwymiarową siatkę komórek. Na brzegach obszaru wprowadzono periodyczne warunki brzegowe. Siatka obliczeniowa przyjmuje wówczas logicznie postać dwuwymiarowego torusa. Zabieg ten pozwala na uniknięcie anomalii na brzegach oraz częściowo uniezależnia rozwiązanie od rozmiaru siatki obliczeniowej. Uproszczoną ilustrację wykorzystanego periodycznego warunku brzegowego przedstawiono na rysunku 2.2 na stronie 15. W zastosowanym podejściu obraz zgładu mikrostruktury dyskretyzowany jest za pomocą prostokątnej siatki komórek CA. Każda komórka reprezentuje skończoną objętość (lub powierzchnię) materiału. Wybór gęstości siatki obliczeniowej wynika z kompromisu pomiędzy rozdzielczością reprezentacji mikrostruktury i złożonością obliczeniową. Zależności geometryczne w siatce CA Metoda automatów komórkowych nie wprowadza zależności geometrycznych do siatki komórek, zarówno w przypadkach jednowymiarowych jak i wielowymiarowych. Metoda nie wprowadza bowiem jawnych założeń, dotyczących odległości pomiędzy komórkami. Ponadto założenia takie nie muszą być formułowane w trakcie tworzenia reguł zmiany stanu. W szczególności, w totalistycznych automatach komórkowych nie jest istotna żadna zależność geometryczna oprócz liczby sąsiadów posiadających 53
66 4.2. Model CA dynamicznej rekrystalizacji określony stan. Wprowadza to odróżnienie od większości zastosowań metody różnic skończonych, gdzie dyskretyzacja przestrzeni ma zazwyczaj jednoznaczne powiązanie geometryczne. Powiązanie to wynika bezpośrednio z rozwiązywanego równania różniczkowego cząstkowego, w którym występują człony zależne od wymiarów geometrycznych. Specyficzne zastosowania CA mogą nakładać wymóg wprowadzenia relacji geometrycznych. Konieczność ta pojawia się w przypadkach, gdy z pewnych względów wygodnie jest interpretować stan siatki jako analog rzeczywistego obiektu. W obliczeniach CA, związanych z ewolucją mikrostruktury, przyjmuje się, że stan siatki komórek odzwierciedla obraz wybranych cech mikrostruktury. W przypadku 2D jest on interpretowany jako zgład przekroju przez określoną objętość materiału polikrystalicznego, natomiast dla 3D reprezentuje przestrzenny układ krystalitów w zadanej objętości. Wprowadzana jest co najmniej jedna zmienna stanu komórek CA, reprezentująca cechę wyróżniającą poszczególne krystality, przy czym może ona posiadać podstawy w wiedzy o materiałach. Dobór cechy jest ograniczony i nie powinien mieć charakteru arbitralnego. Przykładowo, wybór zmiennej stanu reprezentującej fazę, skład chemiczny lub gęstość dyslokacji może nie pozwalać na jednoznaczne rozróżnienie pomiędzy przylegającymi do siebie krystalitami, lub rozróżnienie to jest utrudnione. Wymagania łatwej rozróżnialności spełniają orientacja krystalograficzna lub klasa orientacji krystalograficznej, które pozwalają na wyraźne wyznaczenie granic pomiędzy krystalitami. W opisywanym modelu jako wyróżnik przypisania komórki CA do ziarna wybrano najwygodniejszą w użyciu, jednak całkowicie sztuczną cechę, jaką jest numer porządkowy ziarna. Dzięki temu komórki, które dzielą ze sobą wartość tej zmiennej stanu, łączone są logicznie w struktury reprezentujące ziarna. Na rysunku 4.2 przedstawiono wycinek siatki, zawierający komórki CA charakteryzowane przez różne wartości przypisania do ziarna. Komórki oznaczone liczbami 1,..., 6 przypisane są do ziaren o odpowiadającym im numerze. Interpretacja siatki automatów komórkowych jako obrazu mikrostruktury nie jest możliwa bez wprowadzenia pewnych relacji geometrycznych. W dalszej części podrozdziału omówione zostaną pokrótce wybrane schematy powiązania komórek CA z wielkościami geometrycznymi w przypadkach dwuwymiarowych (2D). Zależności geometryczne na poziomie siatki W przypadku prostokątnych siatek 2D najprostszą metodą jest powiązanie jednostkowych przyrostów dla indeksów siatki i, j z wielkościami x, y. W konsekwencji takiego rozwiązania należy dla niektórych standardowych typów sąsiedztwa wprowadzić zróżnicowanie odległości od komórki centralnej. Np. w przypadku sąsiedztwa Moore a komórki leżące na 54
67 4.2. Model CA dynamicznej rekrystalizacji Rysunek 4.2: Wycinek siatki komórek CA z zaznaczonym przypisaniem do ziaren diagonalach będą posiadały odległość x 2 + y 2, natomiast komórki przyległe w pionie i poziomie odpowiednio y i x. Zastosowanie totalistycznych reguł w obrębie sąsiedztwa jest wówczas nadal możliwe, jednak wiąże się to z wprowadzeniem założeń co do: rodzaju wykorzystywanego sąsiedztwa oraz jego topologicznej niezmienności, odpowiednich wag, reprezentujących odległość, przypisanych do poszczególnych sąsiadów. Założenie o topologicznej niezmienności utrudnia konstruowanie reguł przejścia, gdyż wymusza ich powiązanie z wybranym rodzajem sąsiedztwa. Zmiana definicji sąsiedztwa oznacza, że niezbędne będzie także zmodyfikowanie reguł przejścia. Z drugiej strony, założenie to umożliwia interpretowanie pewnych układów stanów komórek w sąsiedztwie, tak jak uczyniono to np. w pracy [10]. Przykład interpretacji układów stanu komórek przedstawiono na rysunku 4.3. Zależności geometryczne na poziomie sąsiedztwa Założenie o wykorzystaniu konkretnego typu sąsiedztwa w regułach przejścia stanu komórek CA jest dużym ograniczeniem w budowie modelu. Jego wpływ można ograniczyć lub całkowicie wyeliminować, wprowadzając zależności geometryczne na poziomie definicji sąsiedztwa. Najprostszą realizacją tej koncepcji jest uwzględnienie w definicji sąsiedztwa wag, wyrażających odległości. Sąsiedztwo jest wówczas grafem z wagami, który w ogólnym przypadku może posiadać dowolną topologię. Na rysunku 4.4 przedstawiono ilustrację tej koncepcji na przykładzie sąsiedztwa Moore a. Podejście takie pozwala na stosowanie reguł przejścia stanu o dużym stopniu ogólności. 55
68 4.2. Model CA dynamicznej rekrystalizacji Rysunek 4.3: Przykład interpretacji układu stanu komórek w obrębie sąsiedztwa (wg [10]). a) - granica płaska, b) narożnik c) kąt. Litery w obrębie komórek oznaczają stan: L ciecz, S ciało stałe, liczby oznaczają typ komórki Rysunek 4.4: Przykład wprowadzenia zależności geometrycznych do sąsiedztwa Moore a, definiowanego jako graf z wagami w 1,..., w 8 56
69 4.2. Model CA dynamicznej rekrystalizacji Zależności geometryczne na poziomie komórki W podejściu tym siatki automatów komórkowych nie posiadają jawnie zadanych wymiarów geometrycznych. Komórki w siatce nie posiadają zdefiniowanego kształtu, lecz jedynie powierzchnię, którą zajmują. Wielkość domeny obliczeniowej, reprezentowanej za pomocą siatki, charakteryzowana jest przez liczbę komórek w siatce, oraz powierzchnię pojedynczej komórki. Oczywiście, bardzo łatwe jest wyliczenie szerokości i długości siatki (przy założeniu, że jest ona prostokątna), jednak wielkościami tymi nie operuje się w obliczeniach. Zamiast tego, używane są pojęcia powierzchni jednostkowej komórki S u oraz ułamka powierzchni, nie powiązane bezpośrednio z kształtem komórek. Podejście takie wykazuje pewne podobieństwo do metody MCA (ang. Movable Cellular Automata), opisanej m. in. w pracy [95], jednak w przeciwieństwie do niej zakłada, że wszystkie komórki w siatce posiadają jednakową powierzchnię, stałą w czasie, oraz nie dopuszcza nakładania się komórek. Możliwe jest natomiast wprowadzenie zmiennej stanu, określającej ułamek powierzchni. Metoda automatów komórkowych w swoich podstawach skupia się na zmianach stanu komórek. Omawiane wcześniej sposoby wprowadzania zależności geometrycznych wiążą się z ograniczeniami konstrukcji sąsiedztwa, co sprawia, że oprócz stanu sąsiadów na zmianę stanu komórki wpływa również budowa sąsiedztwa. Omawiana metoda, bazująca na parametrze geometrycznym zadanym powierzchnią komórki, w dużym stopniu wolna jest od tego ograniczenia. Łatwe jest budowanie reguł w totalistycznych automatach komórkowych, reguły te są niezależne od rodzaju sąsiedztwa, a jedynie od liczby sąsiadów. W omawianym modelu CA wykorzystano zależności geometryczne na poziomie komórki. Wszelkie wielkości geometryczne, wykorzystywane w obliczeniach (np. średnica ziarna), muszą zostać przeliczone na podstawie informacji o powierzchni pojedynczej komórki S u Definicje sąsiedztwa w modelu W opisywanych w literaturze zastosowaniach metody automatów komórkowych w przestrzeniach dwuwymiarowych najczęściej wykorzystuje się sąsiedztwo Moore a lub von Neumanna. Niekiedy stosowane są również bardziej złożone definicje sąsiedztwa. Przegląd rodzajów sąsiedztwa wykorzystywanych w symulacji zjawiska rekrystalizacji oraz najważniejsze problemy związane z doborem sąsiedztwa przedstawiono w rozdziale
70 4.2. Model CA dynamicznej rekrystalizacji i 1 j 1 i 1 j i 1 j i 1 j+1 i i j 1 C i,j j+1 i i j 1 C i,j j+1 i+1 j i+1 j+1 i+1 j 1 i+1 j (a) (b) Rysunek 4.5: Alternatywne konfiguracje sąsiedztwa heksagonalnego losowo komutowanego komórki C i,j. Indeksy i, j oznaczają położenie komórek w siatce obliczeniowej Sąsiedztwo pseudo-heksagonalne Prowadzenie obliczeń z wykorzystaniem standardowych rodzajów sąsiedztwa w siatkach reprezentujących topologiczne zależności, jak ma to miejsce w przypadku symulacji rozwoju mikrostruktury, pociąga za sobą szereg niedogodności. Jedną z najistotniejszych jest sztuczna anizotropia wzrostu ziaren. Problem ten pojawiał się we wcześniejszych pracach, m. in. [10, 18, 36, 57, 59, 60]. W opisywanym modelu wykorzystano podejście bazujące na niedeterministycznej definicji sąsiedztwa. Każda komórka C o położeniu w siatce wyznaczonej przez indeksy i, j posiada sześciu sąsiadów. Wyznaczani są oni poprzez operację losowego usunięcia z sąsiedztwa Moore a dwóch spośród sąsiadów leżących na diagonali. Sąsiedztwo to nazywane jest w dalszej części pracy heksagonalnym losowo komutowanym lub pseudo-heksagonalnym. Możliwe układy sąsiedztwa przedstawiono na rysunku 4.5. Wyznaczenie sąsiedztwa przeprowadzane jest dla każdej komórki C przed uruchomieniem reguł przejścia stanu, zatem układ sąsiedztwa dla każdej komórki C jest niedeterministyczny. Podobne podejście zastosowano w pracach [17, 89], jednak usuwanie sąsiadów miało charakter deterministyczny. W parzystych krokach czasowych metody wykorzystywano sąsiedztwo przedstawione na rysunku 4.5a, w krokach nieparzystych 4.5b. Wykorzystywane sąsiedztwo N komórki C definiowane jest jako zbiór sześciu komórek: N (C) = {C 1,..., C N } (4.16) gdzie: C komórka CA, N (C) sąsiedztwo komórki C, N liczba komórek w sąsiedztwie. Losowy wybór diagonalnych komórek do usunięcia z sąsiedztwa Moore a powoduje, że komórka o indeksach i, j może posiadać dwa zbiory sąsiadów. Indeksy i, j, 58
71 4.2. Model CA dynamicznej rekrystalizacji określające położenie komórek-sąsiadów w siatce, wyznaczane są w następujący sposób: N (C i,j ) = {C i 1,j 1, C i 1,j, C i,j 1, C i,j+1, C i+1,j, C i+1,j+1 } (4.17) N (C i,j ) = {C i 1,j, C i 1,j+1, C i,j 1, C i,j+1, C i+1,j 1, C i+1,j } (4.18) Stan każdej komórki w sąsiedztwie N (C) może być testowany (odczytywany) przez komórkę C, jednak nie może być zmieniany. Zbiór zawierający stany sąsiadów komórki C oznaczany jest jako: S (N (C)) = {S(C 1 ),..., S(C N )} (4.19) Zarówno dla sąsiedztwa oraz dla zbioru stanów komórek sąsiedztwa wprowadzana jest suriekcja f, odwzorowującą liczbę naturalną k [1, N] na element zbioru Y : y Y k [1, N] f(k) = y (4.20) Funkcja f wykorzystywana jest do numerowania komórek oraz ich stanów, przynależnych do sąsiedztwa komórki C i,j : C N (C i,j ) k [1, N] f(k) = C (4.21) S (C) S (N (C i,j )) k [1, N] f(k) = S (N (C i,j )) (4.22) Funkcja f, numerująca elementy zbiorów, zapisywana jest równoważnie poprzez operator wyłuskania, oznaczany jako [ ] : N (C)[k] = C k (4.23) S (N (C)) [k] = S(C k ) (4.24) Ważną zaletą sąsiedztwa heksagonalnego losowo komutowanego jest wprowadzenie czynnika losowego do definicji sąsiedztwa. Dzięki temu reguły przejścia stanu komórek CA mogą być ściśle deterministyczne, co upraszcza ich konstrukcję. Z punktu widzenia symulacji DRX istotne jest, że ten rodzaj sąsiedztwa umożliwia uzyskiwanie ziaren, które w trakcie wzrostu, a przed zderzeniem z innymi rozrastającymi się ziarnami, mają kształt w przybliżeniu globularny. W trakcie analizy działania modelu należy uwzględniać niedeterministyczny charakter omawianego sąsiedztwa. Jego wpływ przejawia się między innymi we wszelkich obliczeniach prowadzonych w obrębie sąsiedztwa. Szczególnie widoczne jest to w przypadku komórek leżących na granicach ziaren. Obliczane tam parametry, ta- 59
72 4.2. Model CA dynamicznej rekrystalizacji kie jak energia i ruchliwość granicy ziarna lub krytyczna gęstość dyslokacji, mogą przyjmować w tej samej komórce różne wartości, w zależności od tego, które komórki przynależą do sąsiedztwa. Dalekie sąsiedztwo W rzeczywistych materiałach polikrystalicznych istnieją obszary materiału, nazywane ziarnami, wewnątrz których pewne zjawiska, takie jak ruch dyslokacji, zachodzą w uprzywilejowany, łatwy sposób. Co więcej, obszary te są wewnętrznie w dużym stopniu koherentne i oddzielone od siebie wyraźnie zaznaczoną granicą. Ziarna są pojedynczymi kryształami o określonej orientacji, mogącymi zawierać niedoskonałości oraz strukturę podziarnową. Kluczowe dla przedstawianej argumentacji jest to, że wewnątrz ziaren zachodzą oddziaływania dalszego zasięgu niż bezpośrednie otoczenie o promieniu porównywalnym do wyznaczanego przez standardowe sąsiedztwa Moore a lub von Neumanna oraz sąsiedztwo pseudo-heksagonalne. Istnienie w rzeczywistych materiałach ziaren oraz ich udowodniony wpływ na zachowanie materiału są powodem wprowadzenia do modelu specjalnego rodzaju sąsiedztwa, pozwalającego na reprezentację ziaren. Sąsiedztwo to nazywane jest dalekim i oznaczane jest w dalszej części pracy jako N D. Każde ziarno reprezentowane jest przez pojedynczą instancję (egzemplarz) dalekiego sąsiedztwa. Lista ziaren obecnych w siatce CA jest jedną ze składowych opisywanego modelu symulacyjnego. Dalekie sąsiedztwo - cechy Dalekie sąsiedztwo (N D ) posiada szereg cech, odróżniających je od powszechnie spotykanych typów sąsiedztwa. Najważniejszym wyróżnikiem jest posiadanie przez dalekie sąsiedztwo wewnętrznego stanu. Stan ten pochodzi od stanu komórek przynależnych do N D i uzyskiwany jest poprzez operacje sumowania, uśredniania lub podobne. Każda komórka w siatce CA przynależy do dokładnie jednego dalekiego sąsiedztwa, co oznacza, że odwzorowanie N D (C) jest jednoznaczne. Stan dalekiego sąsiedztwa S τ [N D (C)] opisywany jest przez następujące parametry: ρ gr średnia gęstość dyslokacji w ziarnie, φ gr orientacja ziarna, n gr liczba komórek przynależnych do ziarna, I gr identyfikator ziarna. 60
73 4.2. Model CA dynamicznej rekrystalizacji Dalekie sąsiedztwo nie posiada ustalonej topologii. Zamiast tego, opisywane jest przez liczbę komórek przynależnych do niego, a topologia wynika z konfiguracji przynależnych komórek w siatce CA. Zarówno stan N D jak i jego topologia mogą zmieniać się w czasie. Zmiana topologii następuje poprzez przyłączanie i odłączanie komórek CA. W szczególności, N D o liczbie przynależnych komórek równej 0 zanika i jest usuwane z listy ziaren obecnych w siatce. Pomocniczo w każdym ziarnie przechowywana jest lista komórek przynależnych do danego N D. Dozwolone jest uzyskiwanie informacji o stanie dalekiego sąsiedztwa przez komórki CA do niego przynależne. Ponieważ stan ten wynika z uogólnienia stanu pewnego (zazwyczaj niewielkiego) podzbioru komórek CA, nie zachodzi naruszenie fundamentalnego założenia przyjmowanego w metodzie automatów komórkowych, że stan żadnej z komórek nie jest zmieniany na podstawie wiedzy o globalnym stanie układu (całej siatki komórek). Założenie to mogłoby zostać naruszone w przypadku, gdyby w skład dalekiego sąsiedztwa weszły wszystkie komórki w siatce. Jednakże w omawianym zastosowaniu sytuacja taka zazwyczaj nie zachodzi. Dalekie sąsiedztwo służy do reprezentacji ziaren, a w wypadku materiałów polikrystalicznych można dobrać takie rozmiary siatki, aby obecne w niej było od kilkunastu do kilku tysięcy ziaren. Opis geometryczny dalekiego sąsiedztwa Powierzchnia ziarna, reprezentowanego w siatce komórek za pomocą N D, jest obliczana jako iloczyn liczby komórek przynależnych do ziarna n gr i powierzchni pojedynczej komórki S u : S gr = n gr S u (4.25) gdzie: S gr powierzchnia ziarna, S u powierzchnia jednostkowa komórki CA. Bezwymiarowa średnica pozorna ziarna, zależna wyłącznie od liczby komórek przynależnych do ziarna, obliczana jest jako: ngr D p = 2 π (4.26) Średnica zastępcza ziarna D gr zależna jest od powierzchni pojedynczej komórki CA i wyrażana jest przez średnicę pozorną ziarna: D gr = D p S u (4.27) 61
74 4.2. Model CA dynamicznej rekrystalizacji Średnia średnica zastępcza ziarna w siatce CA obliczana jest ze wzoru: D = 1 N gr D gr (4.28) N gr gdzie: N gr liczba ziaren reprezentowanych w siatce CA. Dysponując doświadczalnie wyznaczoną średnią średnicą D ziarna w próbce, można łatwo zastosować równanie (4.27) do wyliczenia S u w wygenerowanym obrazie mikrostruktury. Ponieważ średnia średnica pozorna jest charakterystyczna dla obrazu wygenerowanego, przyjmuje się wówczas doświadczalnie wyznaczoną średnią średnicę ziarna jako średnicę zastępczą D gr. i= Rozwój gęstości dyslokacji w modelu CA Dla każdego ziarna, reprezentowanego w modelu przez egzemplarz dalekiego sąsiedztwa, przeprowadzane są obliczenia średniej gęstości dyslokacji. Rozwój gęstości dyslokacji ρ, przy założeniu, że jedynymi mechanizmami wpływającymi na zmianę ρ jest umocnienie i dynamiczne zdrowienie, jest opisany równaniem różniczkowym zwyczajnym: dρ dt =A Bρ (4.29) A = k 1 ε (4.30) bl ( ) B =k 2 ε m Qs exp (4.31) RT gdzie: b wektor Burgersa, l średnia droga swobodna dyslokacji, Q s energia aktywacji samodyfuzji, k 1, k 2, m współczynniki. Przy założeniu, że ρ t=0 = ρ 0 = 0, rozwiązanie analityczne równania (4.29) przyjmuje postać: ρ = A ( B + 1 A ) exp ( Bt) (4.32) B Typowa gęstość dyslokacji w materiale wyżarzonym ρ 0 wynosi m 2. W materiale poddanym bardzo dużym odkształceniom gęstość dyslokacji wzrasta do m 2 [94, 121]. Obliczanie przyrostu gęstości dyslokacji w komórkach CA Równanie (4.29) określa średnią gęstość dyslokacji w materiale w chwili t. W opisywanym modelu gęstość ta charakteryzuje ziarno, rozumiane jako pojedynczy krystalit i reprezentowane przez dalekie sąsiedztwo. Jednakże we wnętrzu ziarna lokalne 62
75 4.2. Model CA dynamicznej rekrystalizacji gęstości dyslokacji mogą odbiegać znacznie od wartości średniej [8]. Możliwe jest także występowanie obszarów o dużej kumulacji dyslokacji, przylegających do obszarów o relatywnie niewielkiej gęstości dyslokacji [8]. W rzeczywistości zdrowienie dynamiczne prowadzi do utworzenia silnie wyzdrowionych obszarów, a więc także rozkład gęstości dyslokacji musi być silnie zróżnicowany, zarówno w osnowie jak też w ziarnach utworzonych w wyniku DRX [4]. Z tego powodu nie jest realistyczne założenie, że we wszystkich komórkach CA przynależnych do ziarna gęstość dyslokacji jest identyczna. Z opisanych wyżej powodów niezbędne staje się opracowanie metody, pozwalającej na uzyskanie niejednorodnej gęstości dyslokacji w komórkach przynależnych do ziarna, jednocześnie utrzymując założenie, że średnia gęstości dyslokacji spełnia równanie (4.29). Ponadto założenie o niejednorodności gęstości dyslokacji jest istotne m. in. dla działania algorytmu zarodkowania, omówionego w podrozdziale w dalszej części pracy. W opracowanym modelu osiągnięto ten cel poprzez wprowadzenie niedeterministycznego algorytmu obliczania przyrostów gęstości dyslokacji w komórkach CA. Wartość przyrostu ρ gr wewnątrz ziarna pomiędzy krokiem τ 1 i τ, obliczona z równania (4.29), wyrażana jest równaniem: ρ gr = ρ gr (τ ) ρ gr (τ 1) (4.33) W rozwiązaniu równania (4.29) przyjmuje się jako warunek początkowy gęstość dyslokacji z kroku poprzedniego. Rozwiązanie przeprowadzane jest numerycznie. W niniejszej pracy wprowadzono model dystrybucji przyrostu dyslokacji pomiędzy komórki przynależne do dalekiego sąsiedztwa. Przy jego konstrukcji przyjęto następujące założenia: Przyrost gęstości dyslokacji obejmuje wszystkie spośród n gr komórek przynależnych do ziarna. Gęstość dyslokacji we wszystkich komórkach w ziarnie zwiększana jest o x ρ gr, gdzie x [0, 1] jest parametrem modelu dystrybucji. Pozostały przyrost (1 x) ρ gr kierowany jest do p komórek, wybranych w sposób pseudolosowy. Zatem te komórki otrzymują większe przyrosty ρ. Procedura wyznaczania komórek, w których przyrost ρ będzie większy, realizowana jest poprzez losowanie ze zwracaniem. Zgodnie z powyższymi założeniami w modelu dystrybucji wprowadza się dwa parametry, przyjmujące wartościach z zakresu [0, 1] i odpowiadające za udział poszczególnych przyrostów w przyroście średnim, wyrażonym równaniem (4.33): 63
76 4.2. Model CA dynamicznej rekrystalizacji x ułamek przyrostu ρ gr, kierowany do wszystkich komórek, q ułamek przyrostu, kierowany do p komórek. Wymagane jest określenie takiej liczby komórek p, dla której rozdział (1 x) ρ gr będzie gwarantował spełnienie równania (4.33): n gr ρ gr = n gr x ρ gr + p(q x) ρ gr (4.34) n gr = n gr x + p(q x) (4.35) Po przekształceniu równania (4.35) otrzymana zostaje liczba komórek p, pomiędzy które zostaje rozlosowana część (1 x) przyrostu ρ gr : p = n gr 1 x q x (4.36) Tożsamościowy względem (4.36) jest związek, określający ułamek przyrostu, kierowany do p komórek: q = x + n gr 1 x p (4.37) Każda komórka CA jest jednoznacznie przyporządkowana do ziarna poprzez relację N D (C). Dlatego możliwe jest wyznaczenie przyrostu gęstości dyslokacji w kroku czasowym osobno dla każdej komórki zawartej w ziarnie: ρ τ = ρ τ 1 + ρ(n D (C), C) (4.38) gdzie: ρ(n D (C), C) przyrost gęstości dyslokacji w komórce C, przynależnej do ziarna N D (C). Inne metody obliczania przyrostu gęstości dyslokacji Przedstawiony wyżej sposób wprowadzenia przyrostów gęstości dyslokacji do siatki CA oferuje szereg zalet, m. in. zapewnia ilościową zgodność z rozwiązaniem analitycznym dla odkształceń mniejszych od wymaganych do zajścia DRX, a więc do przekroczenia ρ c w komórkach CA i zapoczątkowania zarodkowania. Rozwiązanie to posiada jednak pewne wady. Między innymi, aby obliczyć średnią gęstość dyslokacji w ziarnie ρ gr, wymagane jest przeglądanie wszystkich komórek do niego przynależnych. Ponieważ procedura ta stosowana jest dla wszystkich ziaren, oznacza to konieczność przeglądania wszystkich komórek w siatce CA w każdym kroku czasowym. Co więcej, operacja ta jest prowadzona bez względu na to, czy nastąpiły zjawiska, powodujące spadek ρ gr, a wynikające z zajścia DRX. 64
77 4.2. Model CA dynamicznej rekrystalizacji W dalszej części podrozdziału krótko zarysowano inne możliwości rozwiązania problemu obliczania przyrostu ρ w komórkach CA. Wszystkie z tych metod były wykorzystywane na pewnych etapach rozwoju opisywanego modelu, stąd kolejność ich omawiania wynika z porządku chronologicznego. Ze względu na występujące w nich niedogodności zostały one jednak zastąpione przez opisany wcześniej model, zapewniający niejednorodny rozkład gęstości dyslokacji w obrębie ziaren. Metoda z działem dyslokacji. Najwcześniejsza z wykorzystywanych metod obliczania przyrostu gęstości dyslokacji w siatce CA wprowadzała koncepcję działa dyslokacji. Sformułowanie to zakłada, że znana jest arbitralnie średnia gęstość dyslokacji w całej siatce CA ρ τ odpowiadająca krokowi czasowemu τ. Wartość ta obliczana jest zgodnie z równaniem (4.32). Na podstawie wartości ρ τ 1 w poprzednim kroku czasowym obliczany jest przyrost ρ. Następnie za pomocą funkcji losowej z zadanym rozkładem prawdopodobieństwa wyznacza się wartości paczki dyslokacji ρ p i, i (1, N), kierowane do poszczególnych komórek CA w siatce. Zachowany jest warunek: ρ = N ρ p i (4.39) i=1 Zmienna N zazwyczaj przyjmuje wartość większą od liczby komórek w siatce, tj. N nm, gdzie n, m są odpowiednio liczbami komórek na poziomym i pionowym boku siatki prostokątnej. Uwzględnienie spadku wartości ρ wynikającego z zajścia DRX wymaga wprowadzenia globalnej zmiennej ρ ann, aktualizowanej przez komórki CA w trakcie stosowania reguł przejścia stanu i przechowującej informację o zanihilowanych dyslokacjach. Następnie wartość ρ t korygowana jest o spadek gęstości dyslokacji ρ ann, spowodowany DRX i odnotowany w całej siatce CA: ρ t = ρ t ρ ann (4.40) Metoda z działem dyslokacji nie wymaga wprowadzania koncepcji dalekiego sąsiedztwa. Wykazuje ona jednak szereg niedoskonałości, o różnych źródłach pochodzenia, dlatego obecnie nie jest stosowana. Zasadnicze zastrzeżenie do metody opiera się na niezgodności z podstawowym założeniem przyjmowanym dla automatów komórkowych, o braku zewnętrznego arbitra, dysponującego wiedzą o stanie całego systemu. Metoda z powiadamianiem. W metodzie tej wprowadzane są struktury danych reprezentujące ziarna (dalekie sąsiedztwo). Ziarna te są powiadamiane o spadku 65
78 4.2. Model CA dynamicznej rekrystalizacji gęstości dyslokacji w komórkach CA w wyniku DRX oraz o zmianie przypisania komórek od ziarna. W podejściu tym równanie rozwoju gęstości dyslokacji (4.29) rozwiązywane jest numerycznie. Ponieważ liczba komórek CA w ziarnie jest zmienna, powiązanej z nią gęstości dyslokacji nie można traktować jako niezależną od objętości. Powoduje to szereg utrudnień w interpretacji stanu dalekiego sąsiedztwa. W metodzie z powiadamianiem obliczenie ρ gr nie wymaga przeglądania wszystkich komórek przynależnych do ziarna. Jest to najważniejsza zaleta tej metody. Metoda zmiennej czasowej. Metoda ta opiera się na założeniu, że każdemu ziarnu przypisana jest zmienna stanu, reprezentująca jego wiek, a więc czas jaki upłynął od chwili jego powstania. W przypadku ziaren pierwotnych czas ten równy jest bieżącemu czasowi symulacji. Rozwój gęstości dyslokacji w każdym ziarnie opisywane jest przez równanie analityczne (4.32). W ziarnie wprowadzana jest także zmienna ρ d, reprezentująca spadek ρ, spowodowany odłączeniem komórek CA od ziarna w wyniku DRX. W każdym kroku czasowym obliczana jest gęstość dyslokacji, skorygowana o efekt zajścia DRX na obrzeżach ziarna: ρ t = ρ t ρ d (4.41) Do zalet metody ze zmienną czasową należy możliwość przeprowadzenia dokładnego, analitycznego rozwiązania równania (4.29) dla każdego ziarna z osobna. Metoda posiada jednak szereg niedoskonałości, utrudniających jej zastosowanie. Do najważniejszych należy zaliczyć utrudnione wprowadzenie korekty ρ d, gdyż liczba komórek przynależnych do ziarna jest zmienna, a więc ρ d nie może być traktowane jako wartość niezależna od objętości. Drugim poważnym ograniczeniem jest, że wartość ρ t+1 nie zależy od ρ t Reguły zmiany stanu komórek Reguły zmiany stanu komórek, nazywane także regułami przejścia, stanowią podstawę opisu modelowanego zjawiska przy wykorzystaniu metody automatów komórkowych. Reguły przejścia Γ definiują w jaki sposób stan S komórki C zmieni się w następnym kroku czasowym τ +1. Reguły te są stosowane (uruchamiane) dla każdej komórki w siatce w sposób synchroniczny. Nowy stan komórki wynika z jej stanu w poprzednim kroku czasowym oraz ze stanu komórek sąsiednich: ( ( ) ) S τ +1 = Γ S τ, S τ N (C) (4.42) 66
79 4.2. Model CA dynamicznej rekrystalizacji Rysunek 4.6: Schemat dynamicznej rekrystalizacji, przybliżany regułami przejścia modelu CA (wg [123, 149]) W prezentowanym modelu reguły przejścia wykorzystują także informację o stanie dalekiego sąsiedztwa komórki, omawianego w rozdziale Zatem równanie (4.42) uzupełnione o stan dalekiego sąsiedztwa S τ [N D (C)] przyjmuje postać: ( ( ) ( S τ +1 = Γ S τ, S τ N (C), Sτ ND (C) )) (4.43) Z równania (4.43) wynika, że wszelkie obliczenia, niezbędne do wyznaczenia nowego stanu komórki, dokonywane są na podstawie lokalnych (w obrębie sąsiedztwa) wartości zmiennych stanu. Zatem do jednoznacznego wyznaczenia wartości zmiennej stanu komórki przynależnej do sąsiedztwa wystarczający jest operator wyłuskania, zadany równaniem (4.23) i przyjmujący jako argument liczbę naturalną k. W dalszej części rozdziału wykorzystywana jest zatem notacja skrócona. Przykładowo, zapis ρ k lub ρ[k] oznacza zmienną stanu ρ w komórce N (C)[k]. Taka sama notacja stosowana jest do oznaczania parametrów, obliczanych na podstawie stanu komórki C i k-tej komórki sąsiedniej 1. Przedstawiany model opisuje zmiany topologiczne, zachodzące w mikrostrukturze podczas DRX i towarzyszący im efekt w postaci zmiany gęstości dyslokacji. Reguły przejścia stanu przybliżają schemat dynamicznej rekrystalizacji, opisany między innymi w pracach [123, 149] i przedstawiony na rysunku 4.6. Wedle tego schematu, do zapoczątkowania rekrystalizacji i utworzenia zarodka zrekrystalizowanego ziarna niezbędne jest przekroczenie krytycznej gęstości dyslokacji ρ c na granicy pomiędzy ziarnami. Utworzenie zarodka powoduje lokalne obniżenie gęstości dyslokacji do wartości ρ 0, odpowiadającej gęstości dyslokacji w materiale nieodkształconym. Utworzony zarodek rozrasta się, jednocześnie w wyniku odkształcenia wzrasta w nim gęstość dyslokacji. Front wzrostu przyjmuje wartość ρ 0. Zderzenie z innymi rozrastającymi się ziarnami prowadzi do zahamowania wzrostu i utworzenia nowej 1 Zapis z wykorzystaniem operatora [ ] stosowany jest w przypadku parametrów, zawierających w oznaczeniu indeks dolny 67
80 4.2. Model CA dynamicznej rekrystalizacji granicy międzyziarnowej. Wraz z dalszym wzrostem gęstości dyslokacji, wywołanym odkształceniem, na nowo utworzonych granicach międzyziarnowych ponownie mogą pojawić się zarodki. Granice ziaren Szczególnymi obszarami w siatce CA są komórki, które znajdują się na granicach ziaren. W modelu nie wprowadza się specjalnego stanu komórek, oznaczającego istnienie granicy międzyziarnowej. Wystarczające jest, aby w komórce C spełniony był warunek: k = 1,..., N : N D (C) N D (C k ). Pomocniczo wprowadza się podzbiór sąsiedztwa, zawierający komórki sąsiednie przynależne do innego ziarna: O = {C i N (C) : N D (C) N D (C i ), i = 1,..., N} (4.44) Orientacja każdej komórki może być jednoznacznie wyznaczona na podstawie stanu jej dalekiego sąsiedztwa. Kąt dezorientacji obliczany jest na podstawie wartości bezwzględnej różnicy orientacji φ pomiędzy komórką a jej k-tym sąsiadem φ k : θ k = φ φ k (4.45) gdzie: θ k kąt dezorientacji pomiędzy komórką i k-tym sąsiadem. Podobny sposób obliczania kąta dezorientacji, bazujący na wartości bezwzględnej, zastosowano m. in. w pracach [130, 150]. Na rysunku 4.7 przedstawiono schematycznie metodę obliczania dezorientacji, przy założeniu tej samej płaszczyzny krystalograficznej. Ponieważ w obecnym modelu orientacja komórki jest jednoznaczna z orientacją ziarna, θ k przyjmuje wartości niezerowe wyłącznie na granicach ziaren. Dla komórek leżących na granicach ziaren obliczane są ruchliwość granicy M, energia granicy γ oraz krytyczna gęstość dyslokacji ρ c, niezbędna do utworzenia zarodka zrekrystalizowanego ziarna. Wartości te w modelu uzależniono bezpośrednio lub pośrednio od kąta dezorientacji granicy. Zatem w przypadku komórek sąsiadujących z więcej niż jednym ziarnem możliwe jest uzyskanie różnych wartości wymienionych parametrów dla różnych sąsiadów. Ze względu na niedeterministyczny charakter sąsiedztwa N, możliwe jest także uzyskanie różnych wartości tych parametrów w kolejnych krokach czasowych lub w kolejnych uruchomieniach symulacji. Ruchliwość granicy ziarna wyrażono jako iloczyn aktywowanej cieplnie ruchliwości granicy wysokokątowej, obliczanej z zależności (2.13) i ruchliwości powiązanej z 68
81 4.2. Model CA dynamicznej rekrystalizacji Rysunek 4.7: Granica ziarna pomiędzy dwoma kryształami o kącie wzajemnej dezorientacji θ w płaszczyźnie prostopadłej do strony (wg [52]) dezorientacją granicy, opisywanej równaniem Shivindlermana (2.15): M(T, θ) = M(T )M(θ) (4.46) ( ) Qgb M(T ) = M m = M 0 exp (4.47) kt ( M(θ) = M m [1 exp B θ ) n ] (4.48) M(T, θ) = M 0 exp ( Qgb kt θ m ) [ ( 1 exp B θ ) n ] θ m (4.49) gdzie: Q gb energia (entalpia) aktywacji ruchliwości granicy ziarna, M 0 atermiczny współczynnik ruchliwości granicy ziarna, M m ruchliwość wysokokątowej granicy ziarna, k stała Boltzmanna, T temperatura w skali bezwzględnej [K]. Autor przyznaje, że w literaturze nie napotkał zależności określającej ruchliwość granicy ziarna w sposób wyrażony przez równanie (4.49). Zależność tą sformułowano na podstawie następującego rozumowania. Ruchliwość granicy uzależnia się od temperatury i członu atermicznego M 0, wprowadzanego poprzez iloczyn, np. równanie (2.13). Ruchliwość granicy wyraża się jako zależność od kąta dezorientacji granicy i członu niezależnego od orientacji M m poprzez iloczyn, np. równanie (2.15). Zatem człon niezależny od orientacji może być uzależniony od temperatury, a człon niezależny od temperatury wyrażony jako funkcja orientacji. Obydwie zależności przyjmują wówczas postać iloczynu, więc w wyniku (4.49) także jest iloczynem. Wedle wiedzy autora rozprawy, sformułowanie hipotezy o iloczynowej zależności (4.46) nie posiada bezpośredniego wsparcia doświadczalnego i zapewne wprowadza duże uproszczenia. Jednakże dostępne dane literaturowe świadczą o istnieniu zależności 69
82 4.2. Model CA dynamicznej rekrystalizacji ruchliwości granicy jednocześnie od temperatury i kąta dezorientacji, więc zależność taka powinna być w pewien sposób uwzględniona w opisywanym modelu. Wartości entalpii aktywacji Q gb oraz współczynnika M 0 dla różnych kątów dezorientacji, mierzone w bikryształach ultraczystego aluminium, można odnaleźć m. in. w pracach [142, 146, 147]. Wartości te podane są dla migracji granicy ziarna w spowodowanej naprężeniem lub krzywizną granicy. Prace te wskazują, że obydwa parametry równania (2.13) zależne są od orientacji. Na podstawie danych przedstawionych w wymienionych pracach oszacowano wartość Q gb dla granicy wysokokątowej rzędu 0.85 ev. W pracach tych wskazuje się także, że Q gb dla granic niskokątowych, a więc mniej ruchliwych, posiada wartość około 1.3 ev. Natomiast jako współczynnik M 0 przyjmuje się wartości rzędu 10 5 m 3 (sn) 1 i 10 2 m 3 (sn) 1 odpowiednio dla granic wysoko i niskokątowych. Raabe w pracy [105] poświęconej rekrystalizacji aluminium wykorzystał wartości M 0 = m 3 (sn) 1 oraz Q gb = 1.46 ev. Dla stali IF podczas rekrystalizacji statycznej przyjmuje się M 0 = m 3 (sn) 1 oraz Q gb = 3.9 ev [106]. Należy podkreślić, że parametry M 0 oraz Q gb dostępne w literaturze zazwyczaj odnoszą się do pierwiastków czystych. W przypadku roztworów stałych dane te są stosunkowo trudne do odnalezienia. Wynika to z ograniczeń w doświadczalnym pomiarze tych parametrów [52]. Alternatywnie w równaniu (4.49) można zastosować inną zależność typu Arrheniusa, np. równanie (2.12). Dla czystej miedzi w pracy [52] podano energię aktywacji ruchliwości granicy ziarna Q jako 123 kj/mol, a współczynnik ruchliwości granicy ziarna M 0 = 2.4 ms 1. Wartości tych współczynników zależne są od zakresu temperatury. Zauważalne są także różnice wartości w zależności od rodzaju doświadczenia, w jakim dokonywany był pomiar. Dla każdego sąsiada, przynależnego do innego ziarna, obliczana jest wartość M k (θ k ). Dla komórek sąsiednich, które przynależą do tego samego ziarna co komórka C, przyjmowana jest wartość 0, co zgodne jest z równaniem (4.46). Bazując na równaniach (2.16) oraz (2.17), podanych w rozdziale 2.4.4, wprowadzono do opisywanego modelu zależność energii granicy ziarna γ k od kąta dezorientacji θ. Energia granicy ziarna jest obliczana dla każdej komórki sąsiedniej, przynależnej do innego ziarna: ( ) θ γ k m θ γ k (θ) = m 1 ln θ k θ m : θk < θ m (4.50) γ m : θ k θ m W pracy [52] podano wartość energii wysokokątowej granicy ziarna γ m dla stali austenitycznej jako 0.76 Jm 2, natomiast dla miedzi Jm 2. Na rysunku 4.8 przedstawiono charakter zależności energii granicy ziarna, wy- 70
83 4.2. Model CA dynamicznej rekrystalizacji Rysunek 4.8: Zależność energii granicy ziarna γ (4.50) i ruchliwości M (4.48),(4.49) od kąta dezorientacji (wg [51]) rażonej równaniem (4.50), oraz ruchliwości obliczanej ze wzoru (4.48), od kąta dezorientacji. Na rysunku przyjęto θ m = rad. Wartości podane na wykresie mają charakter względny i reprezentują ułamek energii i ruchliwości granicy ziarna w stosunku do granicy wysokokątowej, o kącie dezorientacji powyżej θ m. Zarodkowanie DRX Występujące w literaturze metody opisu zarodkowania DRX, wykorzystywane w modelach opartych o CA, omówiono w rozdziale W niniejszej pracy przyjęto, że zarodkowanie nowych ziaren w trakcie dynamicznej rekrystalizacji zachodzi heterogenicznie, na granicach ziaren pierwotnych i wtórnych. Ogranicza to możliwe miejsca zarodkowania do komórek CA, które posiadają sąsiadów przynależnych do innych ziaren. Powstanie zarodka jest uzależnione od przekroczenia w komórce CA krytycznej gęstości dyslokacji ρ c. Zgodnie ze schematem przedstawionym na rysunku 4.6, wraz z utworzeniem w komórce CA zarodka, gęstość dyslokacji spada w niej do wartości ρ 0. W przeciwieństwie do szeregu prac wcześniejszych (m. in. [21, 22, 96, 136]), opracowane rozwiązanie nie wymaga obliczania prędkości zarodkowania i jawnego, pseudolosowego wyznaczania komórek CA mających stać się zarodkami. Wyeliminowanie tych sztucznych zabiegów jest możliwe dzięki wprowadzeniu opisanego w rozdziale algorytmu, zapewniającego niejednorodną gęstość dyslokacji w komórkach CA, oraz sąsiedztwa pseudo-heksagonalnego. Z faktu niejednorodności rozkładu ρ 71
84 4.2. Model CA dynamicznej rekrystalizacji w ziarnach wynika, że na granicy pomiędzy ziarnami także występują komórki CA o różnej gęstości dyslokacji. W związku z tym nie zachodzi sytuacja (lub zachodzi z bardzo małym prawdopodobieństwem), gdy wszystkie komórki na granicy spełniają warunek przekroczenia krytycznej gęstości dyslokacji. Dlatego w opisywanym modelu do utworzenia zarodka nowego ziarna wystarczające jest spełnienie kryterium przekroczenia krytycznej gęstości dyslokacji ρ c. Jest ona obliczana dla każdej z komórek sąsiednich przynależnych do innego ziarna. W obliczeniach wykorzystano odpowiednio dostosowane równanie (2.10), podane na stronie 28 i przyjmujące w opracowanym modelu postać: ( ) 20γk ε 1/3 ρ c [k] = (4.51) 3blM k τ 2 gdzie: ε prędkość odkształcenia, τ średnia energia na jednostkę długości linii dyslokacji, b wektor Burgersa, l średnia droga swobodna dyslokacji, M k, γ k odpowiednio ruchliwość i energia granicy ziarna względem komórki sąsiedniej o indeksie k. Średnia energia na jednostkę długości linii dyslokacji wyrażona jest wzorem [52]: τ = µb2 2 (4.52) Dla stali obliczono przybliżoną wartość τ = Jm 1, dla miedzi τ = Jm 1, oraz dla aluminium τ = Jm 1. Ponieważ część wyrazów występujących w równaniu (4.51) przyjmowana jest jako stała, możliwe jest zastąpienie ich jednym stałym parametrem C c. Krytyczna gęstość dyslokacji jest wówczas wyrażana następującym równaniem: ( ) γk ε 1/3 ρ c = C c (4.53) lm k ( ) 20 1/3 C c = (4.54) 3bτ 2 Równanie (2.10) wykorzystywane było także w cytowanych wcześniej pracach [21 23, 136], jednak jego zastosowanie wymagało uzupełnienia modelem wyznaczającym jako zarodki losowe komórki leżące na granicach ziaren. W niniejszej pracy nie ma potrzeby wprowadzania sztucznego, losowego wyznaczania zarodków. W omawianym modelu założono, że jako krytyczną gęstość dyslokacji, potrzebną do utworzenia zarodka, przyjmuje się minimalną wartość spośród ρ c [k]: ρ c = min ρ c[k] (4.55) k:c k O(C) 72
85 4.2. Model CA dynamicznej rekrystalizacji Analizując równanie (4.51) można zauważyć, że krytyczna gęstość dyslokacji jest pośrednio zależna od dwóch parametrów makroskopowych, jakim są prędkość odkształcenia i temperatura. Prędkość odkształcenia uwzględniana jest jawnie, natomiast temperatura pośrednio, przez zależność (4.47) wyrażającą ruchliwość granicy ziarna M k w funkcji T. Z kolei zależność od kąta dezorientacji granicy międzyziarnowej, będącego parametrem związanym ze skalą mikro, wynika z równań (4.48) i (4.50). Wartość stosunku γ k /M k, występującego w równaniu (4.51), odgrywa istotną rolę w obliczeniu krytycznej gęstości dyslokacji. Jego najmniejsza wartość w obrębie sąsiedztwa w dużym stopniu determinuje wartość ρ c. Kolejnym parametrem występującym w równaniu (4.51) jest średnia droga swobodna dyslokacji l. W szeregu prac przyjmowana jest jako rozmiar podziarna lub dyslokacyjnej struktury komórkowej. W niektórych pracach (np. [91, 120]) średnia droga swobodna dyslokacji wyrażana jest poprzez parametr Zenera-Hollomona. Zależność taka opisuje jednak rozmiar podziarna po procesie, nie uwzględniając ani czasu ani odkształcenia. W zakresie odkształceń odpowiadających ustalonemu płynięciu materiału (plateau na krzywej σ f ) rozmiar podziarna praktycznie nie zależy od odkształcenia [4], jednakże rozwój struktury podziarnowej następuje trakcie procesu. Z kolei w pracy [21] przyjęto l równe średniej wielkości ziarna, co wymagało znajomości stanu całego układu oraz á priori założenia końcowej wielkości ziarna. W modelu będącym przedmiotem niniejszej pracy nie operuje się bezpośrednio pojęciem podziarna. Model ten daje jednak możliwość oszacowania wielkości każdego ziarna z osobna w kolejnych chwilach czasu. Dzięki temu oszacowanie średniej drogi swobodnej dyslokacji może bazować na chwilowej wartości średnicy zastępczej D gr. Ponadto pożądane jest uzależnienie wartości l od historii procesu, a średnica zastępcza, obliczana indywidualnie dla każdego ziarna, jest jednym z parametrów, które zależne są od historii. Można zauważyć, że w przypadku ziaren powstających w trakcie DRX wartość l może być porównywalna z rozmiarem ziarna D gr. Powstanie struktury podziarnowej (dyslokacyjnej struktury komórkowej) w wyniku deformacji wymaga pewnego czasu i odkształcenia. W procesach, w których w wyniku DRX następuje duże rozdrobnienie ziarna, zarodkowanie jest intensywne, a rozrost ziaren ograniczony. W mikrostrukturze obecna jest więc duża liczba niewielkich, zrekrystalizowanych i w małym stopniu odkształconych ziaren. Dla takich warunków, gdy rozmiar zrekrystalizowanego ziarna jest niewielki, uzasadnione wydaje się przyjęcie l D gr, gdyż l jest ograniczone wielkością ziarna. Natomiast dla stosunkowo gruboziarnistej struktury początkowej założenie l D gr wymaga wprowadzenia korekty. W omawianym modelu przyjęto założenie, że dla ziaren pierwotnych średnia droga swobodna dys- 73
86 4.2. Model CA dynamicznej rekrystalizacji lokacji jest liniowo związana z rozmiarem ziarna, do którego przynależy komórka C. Równanie to ma postać: l = A 1 D gr (4.56) gdzie: A 1 współczynnik z przedziału (0, 1). Korekta ta nie jest jednak wprowadzana dla ziaren wtórnych, mimo, że w wyniku wzrostu mogą one przyjmować duże rozmiary oraz akumulować duże odkształcenia. Wraz z powstaniem zarodka nowego ziarna tworzone jest nowe dalekie sąsiedztwo. Zarodek otrzymuje orientację wygenerowaną pseudolosowo z zakresu [φ 1, φ 2 ], przedział ten przyjmowany jest jako [0, π]. Ponieważ dalszy rozrost zarodka uzależniony jest od jego korzystnego ulokowania, jedynie część z utworzonych zarodków jest zdolna do wzrostu. Rozrost ziarna Siła pędna pochodząca od różnicy gęstości dyslokacji pomiędzy materiałem odkształconym i zrekrystalizowanym jest wyrażana równaniem [4, 8, 52, 63]: P k = αµb 2 (ρ k ρ) = 2ατ ρ (4.57) gdzie: α współczynniki z przedziału [0.1, 1], Typowa wartość siły pędnej (4.57) wynosi około 10 7 Nm 2 [8]. Z kolei siła oddziałująca na granicę ziarna i powiązana z jej krzywizna wyrażana jest wzorem [8, 52, 63]: gdzie: r gr promień ziarna. P k = 2 γ k r gr (4.58) Siła oddziałująca na elementarną jednostkę powierzchni granicy ziarna S u powiązana jest zależnością F = P S u. Zastępując w równaniu (2.21) na stronie 32 promień ziarna przez średnicę ziarna otrzymano zależność, opisującą siłę pędną wzrostu ziarna w kierunku sąsiedniej komórki CA o indeksie k: F k = πd 2 grτ (ρ k ρ) 4πD gr γ k (4.59) Ważne jest właściwe zinterpretowanie siły pędnej w budowie reguł przejścia stanu komórek CA. Analizując kontekst wykorzystania równania (4.59) można stwierdzić, że używanie w opisie prezentowanego modelu pojęcia wzrostu ziarna może być nieco mylące. Zamiast tego zapewne lepiej byłoby używać komplementarnego pojęcia kurczenia się ziaren (ang. grain shrinkage). Reguła zmiany stanu automatu komórkowego opisuje bowiem proces odłączania się komórki od ziarna w przypadku 74
87 4.2. Model CA dynamicznej rekrystalizacji zaistnienia korzystniejszej konfiguracji gęstości dyslokacji po przyłączeniu do innego ziarna. Siła pędna (4.59) o wartości ujemnej powoduje przesunięcie frontu migracji granicy ziarna do wnętrza komórki CA. Siła pędna o wartości dodatniej powoduje przesunięcie frontu migracji granicy ziarna poza komórkę CA. Pomijając człon związany z energią granicy ziarna γ można stwierdzić, że przyłączenie komórki CA do sąsiedniego ziarna następuje pod warunkiem, że granica tamtego ziarna ma niższą gęstość dyslokacji. Z kolei wartość dodatnia siły pędnej wskazuje, że zmiana przyporządkowania do ziarna nie jest energetycznie korzystna, gdyż gęstość dyslokacji w komórce N (C)[k] jest wyższa. Według [4] składowa siły pędnej związana z energią granicy γ posiada relatywnie niewielką wartość w porównaniu ze składową pochodzącą od gęstości dyslokacji. Natomiast najsilniejsza składowa siły pędnej proporcjonalna jest do różnicy energii odkształcenia, czyli energii pól naprężeń sprężystych wokół dyslokacji i innych defektów sieciowych przed i za frontem rekrystalizacji. W modelach opartych o metodę automatów komórkowych utrudnione jest uwzględnienie zmiennej roli energii granicy ziaren, powiązanej z krzywizną granicy. Siła pochodząca od krzywizny granicy działa hamująco, gdy granica przemieszcza się w kierunku od środka krzywizny. W przypadku przeciwnym siła ta działa jako siła pędna [8]. Utrudnienie to wynika z ograniczeń metody pod względem analizy kształtu i zależności geometrycznych w stosunkowo rozległych obszarach siatki (takich jak dalekie sąsiedztwo). W modelu zakłada się, że wzrastające ziarna mają kształt globularny. Człon powiązany z energią granicy ziarna w równaniu (4.59) jest traktowany jako siła pędna, pochodząca od krzywizny granicy. W literaturze podaje się również inne siły pędne, działające na granice ziaren, jak również siły przeciwdziałające migracji granic [8, 52]. W omawianym modelu siły te są pomijane. Prędkość rozrostu ziarna w przyjętym rozwiązaniu zależna jest od ruchliwości M i siły pędnej P. Ze względu na zależności obydwu tych składowe od innych parametrów, prędkość rozrostu ziarna można wyrazić jako: v gb (T, θ, ρ) = M (T, θ) P (ρ, θ) (4.60) Całkowita prędkość ruchu granicy ziarna w komórce CA obliczana jest jako: v gb = 1 N N v gb [k] (4.61) k gdzie: N = O(C) moc zbioru O(C). 75
88 4.2. Model CA dynamicznej rekrystalizacji Przyrost ułamka rekrystalizacji w komórce wyrażony jest przez ułamek pola powierzchni komórki CA, na którym w wyniku ruchu granicy ziarna z prędkością v gb zaszedł proces rekrystalizacji: X rec = v gb (1 X) S u t (4.62) Wyznaczenie prędkości migracji granicy i przyrostu ułamka rekrystalizacji umożliwia określenie w której chwili czasowej nastąpi odłączenie komórki od ziarna. Natomiast wyznaczona w komórce CA prędkość ruchu granicy ziarna nie ma bezpośredniego wpływu na zmianę stanu komórek sąsiednich, co wynika z założeń metody automatów komórkowych. Zmienna stanu X kontroluje postęp rekrystalizacji wewnątrz komórki CA. Przyjmuje ona wartości z przedziału [0, 1]. Aktualizacja zmiennej X prowadzona jest w taki sposób, aby nie wykroczyć poza dopuszczalne wartości. W tym celu wprowadza się funkcję progową h o następującej postaci: Zmiana wartości X następuje w regule przejścia stanu i opisywana jest równaniem: X : 0 < X < 1 h(x) = 1: X 1 (4.63) X τ +1 = h(x τ + X rec ) (4.64) Osiągnięcie wartości X = 1 oznacza, że komórka w całości przyłączona została do innego ziarna. Wówczas wartość zmiennej X ustawiana jest ponownie na 0. Umożliwia to uwzględnienie w modelu wielokrotnego zajścia rekrystalizacji w komórkach CA. Inaczej mówiąc, wartość zmiennej stanu X 0 oznacza, że komórka CA znajduje się na froncie rekrystalizacji. Gęstość dyslokacji w komórce częściowo zrekrystalizowanej można obliczyć wykorzystując regułę dźwigni: ρ R = Xρ 0 + (1 X)ρ (4.65) Reguły przejścia stanu komórek CA zapis formalny Przedstawione powyżej rozważania zebrane zostały w postaci reguł przejścia stanu komórek CA. Reguły te opisują dynamikę systemu, a ich dobór i budowa przybliżają fizyczne zależności w układzie. Reguły te mają postać wyrażeń warunkowych w postaci: Jeżeli warunek wtedy: akcja. Aktualizowanie zmiennych stanu ozna- 76
89 4.2. Model CA dynamicznej rekrystalizacji czono strzałkami. Dla bardziej czytelnego przedstawienia działania reguł, zapis uzupełniono o elementy pseudokodu, opisującego niezbędne operacje obliczeniowe. ρ τ +1 ρ τ + ρ(n D (C), C) Jeżeli O(C) wtedy: Dla każdej komórki k w O(C) oblicz: θ k, M k, γ k, F k, v k Jeżeli v gb < 0 wtedy: X τ +1 h(x τ + X rec ) Jeżeli X τ +1 = 1 wtedy: ρ τ +1 ρ 0 x τ +1 0 Wyznacz j : v j = max v k I τ +1 I[j] Zakończ. Jeżeli ρ ρ c wtedy: ρ τ +1 ρ 0 X τ +1 0 I τ +1 nowy N D (C) Zakończ. Podane wyżej reguły przejścia stanu zapisano w sposób ułatwiający ich zrozumienie, który jednak nie jest optymalny z punktu widzenia implementacji numerycznej. Reguły przejścia automatu komórkowego wywoływane są w każdym kroku czasowym we wszystkich komórkach w siatce CA, a więc ogromną liczbę razy. Dla uzyskania jak najlepszej wydajności i poprawności numerycznej przeprowadzono w kodzie programu szereg zabiegów optymalizacyjnych. Wynikające z nich zmiany sprawiają na przykład, że niektóre operacje wykonywane są w innej kolejności. Jednakże niezależnie od implementacji programowej, logika reguł przejścia stanu w programie pozostaje taka sama jak w podanym wyżej pseudokodzie. Adaptacja długości kroku czasowego Ponieważ przyrost zmiennej stanu X, wyrażony równaniem (4.62), zależy od długości kroku czasowego, który może być á priori oszacowany jedynie zgrubnie, należy wziąć pod uwagę przypadki, gdy X rec lub X τ + X rec przyjmuje wartości powyżej jeden. 77
90 4.2. Model CA dynamicznej rekrystalizacji W tym celu wprowadzono w modelu algorytm korekty długości kroku czasowego symulacji CA. Algorytm ten powoduje skrócenie kroku czasowego w przypadku, gdy w dowolnej komórce CA przekroczone zostaje ograniczenie X τ + X rec > 1 + x p : t τ +1 = t τ (4.66) 1 + δ X u 1: u > 1 δ X = (4.67) 0: u 1 u = X τ + X cr rec x p (4.68) gdzie: δ X nadmiarowy przyrost X, Xrec cr krytyczny przyrost X rec odnotowany w całej siatce podczas kroku τ, x p maksymalny dopuszczalny przyrost nadmiarowy, przyjmowany jako arbitralna wartość z przedziału [0, 0.5]. Jako krytyczny przyrost Xrec cr przyjmowany jest maksymalny przyrost Xrec max, odnotowany w całej siatce w kroku τ. W opracowanym modelu przetestowano także zastosowanie jako X cr rec średniego przyrostu X rec w trakcie kroku czasowego, skutkujące łagodniejszą zmianę długości kroku t. Należy jednak zauważyć, że zastosowanie równania (4.66) stoi w częściowej sprzeczności z podstawowym założeniem metody automatów komórkowych, mówiącym o braku arbitra dysponującego wiedzą o stanie całej siatki. Używane jest jednak w celu poprawy stabilności numerycznej rozwiązania i może być traktowane jako zabieg techniczny. Gwarantuje także adaptację do zmieniających się warunków procesu, takich jak temperatura lub prędkość odkształcenia Tworzenie mikrostruktur początkowych Niezbędnym etapem do prowadzenia symulacji dynamicznej rekrystalizacji w oparciu o metodę automatów komórkowych jest utworzenie reprezentacji mikrostruktury początkowej. Wymaganie to jest powszechne we wszystkich metodach uwzględniających bezpośrednią reprezentację topologicznych zależności, występujących w mikrostrukturze, opisanych w rozdziale 2. Reprezentacja ta niekiedy nazywana jest w niniejszej rozprawie obrazem mikrostruktury. Termin ten jest wykorzystywany powszechnie w metaloznawstwie i zwykle rozumiany jest jako informacja o położeniu i wielkości ziaren w zgładzie. Określenie obraz mikrostruktury w kontekście niniejszej rozprawy jest używane w sensie nieco odmiennym niż w metaloznawstwie. Wynika to z możliwego w modelu CA reprezentowania w jednej siatce obliczeniowej różnych cech, opisujących mikrostrukturę, oraz relacji wiążących je ze sobą. Zatem obraz mikrostruktury w ujęciu omawianego 78
91 4.2. Model CA dynamicznej rekrystalizacji modelu zawiera jednocześnie informacje o przestrzennym rozkładzie cech, takich jak wielkość i orientacja ziaren lub gęstość dyslokacji. W obrazie tym mogą być także reprezentowane inne cechy elementów mikrostruktury, jak np. przynależność pewnych obszarów do frontów rekrystalizacji lub kolejnych cykli rekrystalizacji. Metody tworzenia reprezentacji mikrostruktur W dotychczasowych pracach dominującą metodą uzyskiwania początkowej reprezentacji mikrostruktury jest wygenerowanie jej za pomocą stosownego modelu symulacyjnego. Istnieją także podejścia wykorzystujące jako bazę dla symulacji dane doświadczalne [107]. Przeniesienie doświadczalnie uzyskanych obrazów mikrostruktury do modelu symulacyjnego wydaje się najkorzystniejszym wyborem. Pojawia się jednakże szereg utrudnień, czyniących przeniesienie danych, pochodzących z doświadczenia, do modelu symulacyjnego, zadaniem trudnym. Wśród tych niedogodności należy wymienić problemy kompletności i reprezentatywności danych pomiarowych, oraz zdolności modelu do wiarygodnego odtworzenia rzeczywistej mikrostruktury. Problem kompletności danych związany jest z faktem, że wykorzystywana w obliczeniach reprezentacja mikrostruktury wymaga określenia wszystkich rozważanych w modelu cech. W przypadku braku metody badawczej, udostępniającej dostatecznie szerokie spektrum danych pomiarowych, rozwiązaniem może być scalanie reprezentacji mikrostruktury z istniejących danych lub ograniczenie modelu do danych istniejących. Problem reprezentatywności polega na poprawnym wyborze takich obszarów mikrostruktury, które reprezentują cały modelowany układ. Zagadnienie to wydaje się rozwiązane przez istniejącą praktykę badań metalograficznych. Problem ten jednak powiązany jest z problemem kompletności danych pomiarowych w przypadku, gdy różne metody badawcze z przyczyn technicznych nie pozwalają na badanie tej samej próbki (lub tego samego jej obszaru). Metody badawcze, stosowane w metaloznawstwie, ujawniają w mikrostrukturze rzeczywistych materiałów szereg składników morfologicznych (np. wydzieleń faz), trudnych do uwzględnienia w modelu CA. Rozwiązaniem może być odpowiednie rozszerzenie modelu lub wyeliminowanie nieuwzględnianych składników z doświadczalnie uzyskanego opisu mikrostruktury. Pierwsze rozwiązanie może powodować trudności, wynikające z komplikacji modelu, rosnącej wraz z jego rozszerzaniem. Z kolei niejasnym pozostaje w jaki sposób eliminować nieuwzględniane przez model składniki mikrostruktury z danych doświadczalnych, nie wprowadzając przy tym przekłamań. 79
92 4.2. Model CA dynamicznej rekrystalizacji Biorąc pod uwagę sformułowane wyżej zastrzeżenia, atrakcyjnym wydaje się sposób alternatywny, bazujący na symulacyjnym generowaniu reprezentacji mikrostruktury, z uwzględnieniem dostępnych wyników doświadczalnych. Na podstawie ilościowego opisu mikrostruktury generowana jest jej reprezentacja. Jednocześnie reprezentacja ta jest bezpośrednio zgodna z wymaganą przez symulację rozważanego procesu lub zjawiska. Tym samym zapewniona jest adekwatność reprezentacji dla modelu, nie występują dane nadmiarowe oraz braki danych. Najpoważniejszą słabością tego podejścia jest utrata bezpośredniego przełożenia obrazów rzeczywistych (doświadczalnych) na reprezentację mikrostruktury wykorzystywaną przez model. Algorytm tworzenia mikrostruktury początkowej W niniejszej pracy wykorzystano metodę algorytmicznego generowania reprezentacji mikrostruktury początkowej. W rozwiązaniu zastosowano algorytm swobodnego rozrostu ziaren, zaimplementowany w sposób odpowiedni dla metody automatów komórkowych. Przyjęto siatkę obliczeniową, zawierającą komórki CA, z nałożonym periodycznym warunkiem brzegowym. W obliczeniach wykorzystano sąsiedztwo pseudo-heksagonalne, przedstawione w podrozdziale Wybór takiej metody tworzenia mikrostruktury początkowej umożliwia wprowadzenie pełnej zgodności reprezentacji z metodą symulacji DRX. W obu przypadkach wykorzystywane są te same struktury danych oraz duża część spośród algorytmów na nich działających. W szczególności, stan komórek CA i dalekiego sąsiedztwa zawiera takie same dane, odwzorowane na identycznych w obu przypadkach strukturach danych. Więcej informacji o wykorzystywanych rozwiązaniach programowych zamieszczono w dodatku A. Kluczowym elementem opracowanej metody tworzenia reprezentacji mikrostruktur jest algorytm rozmieszczenia zarodków w siatce CA. Przyjęto, że w chwili t = 0 cały obszar reprezentowany przez siatkę CA jest niepodzielony na ziarna. W chwili t = 0 dostarczane są do siatki położenia komórek, wyznaczonych na zarodki ziaren. Przyjęto, że liczba zarodków w poszczególnych podobszarach siatki może być różna. Zarodek otrzymuje orientację wygenerowaną pseudolosowo z zakresu [φ 1, φ 2 ], zazwyczaj przedział ten przyjmowany jest jako [0, π]. Stosowany generator liczb pseudolosowych przybliża jednostajny rozkład prawdopodobieństwa. Opracowany podprogram umożliwia także przyjęcie innego zakresu [φ 1, φ 2 ] oraz normalnego rozkładu prawdopodobieństwa. Siatka n m komórek dzielona jest na k l rozłącznych podobszarów. Każdy taki podobszar ma kształt prostokątny i obejmuje p i : i = 1,..., k komórek w kierunku zmian indeksu wierszy siatki oraz q j : j = 1,..., l w kierunku indeksu kolumn. 80
93 4.2. Model CA dynamicznej rekrystalizacji Z zasady zachowania rozłączności obszarów wynika, że k i p i = n oraz l i q i = m. Liczba podobszarów w siatce P wyrażona jest iloczynem P = kl. Generator obszarów umożliwia dobór szerokości p i oraz q j według jednego z trzech schematów: wszystkie szerokości p i oraz q j są jednakowe z dokładnością do 1. szerokości p i oraz q j zmieniają się liniowo, a więc p i+1 = A p + B p i dla każdego i : i p i < n p i+1 oraz q j+1 = A q + B q j dla każdego j : j q j < m q i+1. każda z szerokości p i oraz q j jest dobierana arbitralnie. Dla każdego obszaru (p i, q j ) wyznaczana jest liczba zarodków, pseudolosowo rozmieszczanych w tym obszarze. Liczba ta jest jednakowa dla wszystkich obszarów lub indywidualnie dobierana dla każdego obszaru. Schemat podziału siatki na jednakowej wielkości podobszary oraz przyporządkowanie do nich identycznej liczby zarodków spełnia założenia zarodkowania homogenicznego. W przypadku arbitralnego podziału siatki na obszary oraz arbitralnego wyznaczania liczby zarodków w każdym obszarze zarodkowanie może być uznane za heterogeniczne. Potencjalnie możliwa jest dowolna metoda podziału siatki na obszary oraz wyznaczania liczby zarodków. Natomiast ze względu na zadane periodyczne warunki brzegowe należy unikać stosowania dużych różnic gęstości zarodków w przylegających obszarach. Zarodki rozrastają się do momentu zderzenia z innymi wzrastającymi zarodkami. Przyjęto następującą regułę opisująca wzrost ziaren. Jeżeli komórka CA nie jest przypisana do ziarna oraz istnieje komórka w sąsiedztwie przyporządkowana do istniejącego ziarna, to komórka także zostaje przyłączona do tego ziarna. Tworzenie mikrostruktury początkowej na podstawie bitmapy Rzeczywiste obrazy mikrostruktury często odbiegają od wygenerowanych za pomocą symulacji swobodnego rozrostu ziarna. Dlatego opracowany został algorytm, pozwalający na wygenerowanie reprezentacji mikrostruktury w oparciu o dane doświadczalne. Źródłem danych mogą być badania metalograficzne, w tym mikroskopia świetlna lub EBSD. Wykorzystywane są dane, odwzorowujące obraz mikrostruktury za pomocą mapy bitowej. Oprócz obrazów pochodzących z pomiarów, możliwe jest także wprowadzenie bitmapy wygenerowanej w inny sposób (np. ręcznie sporządzonego rysunku). 81
94 4.3. Połączenie automatów komórkowych z MES W przypadku akwizycji danych z mikroskopu świetlnego należy uwzględnić problem kompletności danych pomiarowych, zasygnalizowany w podrozdziale 4.2.6, gdyż metoda ta nie udostępnia informacji o orientacji poszczególnych ziaren. Ponieważ prezentowany model wymaga przypisania orientacji do każdego ziarna, zastosowano uzupełnianie danych doświadczalnych, w oparciu o dwie alternatywne strategie: założenie, że każdemu ziarnu w mapie bitowej przypisywany jest znany kąt orientacji, orientacje ziaren generowane są losowo, z zadanym rozkładem (np. jednostajnym lub normalnym). 4.3 Połączenie automatów komórkowych z MES Model dynamicznej rekrystalizacji, opisany w rozdziale 4.2, połączono z rozwiązaniem problemu termomechanicznego, przedstawionego w rozdziale 4.1. Połączenie to opiera się na podobnych zasadach jak w przypadku modelu zmiennej wewnętrznej. Rolą modelu skali mikro, w tym wypadku bazującego na CA, jest dostarczenie dla MES wartości naprężenia uplastyczniającego, czyli własności materiału występującej w prawie plastycznego płynięcia Levy-Misesa (4.11). Rozwój zmiennej wewnętrznej, rozumianej jako stan zawarty w przestrzeni CA, jest powiązany z rozwiązaniem problemu termomechanicznego poprzez parametry wejściowe. Otrzymane w ten sposób sprzężenie zwrotne, uzyskiwane w każdym elemencie skończonym, przedstawiono schematycznie na rysunku 4.9. Zaznaczono na nim parametry przekazywane poprzez model pośredniczący oraz sprzężenie zwrotne pomiędzy odpowiedziami poszczególnych części systemu. Ponieważ naprężenie uplastyczniające jest jedynym parametrem materiałowym, występującym w równaniu (4.11), wygodnie jest wprowadzić pomiędzy symulacje CA i MES model pośredniczący. Model ten odpowiedzialny jest za dostarczenie do MES naprężenia uplastyczniającego, obliczonego na podstawie gęstości dyslokacji wyznaczonych symulacją CA, oraz za dostarczenie do właściwych siatek CA parametrów takich jak temperatura i prędkość odkształcenia, pochodzących z MES. Wśród funkcji spełnianych przez model pośredniczący znajdują się: odwzorowanie geometryczne punktów całkowania Gaussa w elementach skończonych na odpowiednie przestrzenie CA utworzenie przestrzeni CA na początku symulacji MES oraz zainicjalizowanie ich początkowym obrazem mikrostruktury, 82
95 4.3. Połączenie automatów komórkowych z MES Rysunek 4.9: Schemat połączenia symulacji CA i elementu skończonego w punktach całkowania Gaussa przeniesienie parametrów wejściowych symulacji skali mikro, takich jak T oraz ε z rozwiązania problemu termomechanicznego do odpowiedniej przestrzeni CA, obliczenie σ f na podstawie stanu odpowiedniej przestrzeni CA, interpolacja σ f pomiędzy krokami czasowymi rozwiązania quasi-stacjonarnego MES i krokami czasowymi CA. Pierwsza z wymienionych funkcji modelu pośredniczącego została zrealizowana przez zdefiniowanie funkcji odwzorowującej jednoznacznie numery elementów w siatce MES n EL i numery punktów całkowania na przestrzenie CA. Model pośredniczący odpowiada za utworzenie stosownych przestrzeni CA wraz z pierwszym do nich odwołaniem. Daje to możliwość przypisywania różnych reprezentacji mikrostruktury do różnych punktów całkowania. Na rysunku 4.10 przedstawiono schematycznie połączenie przestrzeni CA, zawierających reprezentacje mikrostruktur odmiennych pod względem wielkości ziarna, z elementami w siatce MES. Możliwe jest także np. przypisanie mniejszych siatek CA do obszarów, o których á priori wiadomo, że nie osiągają odkształcenia niezbędnego do zapoczątkowania DRX. W przypadku rozważanego problemu ściskania osiowosymetrycznego ta funkcjonalność modelu pośredniczącego nie wydaje się bardzo przydatna, jednak potencjalne możliwości przez nią stwarzane mogą skutkować znacznym skróceniem czasu obliczeń. Dysponując funkcją odwzorowującą punkt całkowania Gaussa na symulacje CA, możliwe jest uruchomienie każdej z nich dla zadanego kroku czasowego t MES, rozpoczynając od kroku czasowego t MES, z parametrami T i ε odpowiednimi dla danego punktu całkowania. Działanie to następuje wraz z żądaniem ze strony kodu 83
96 4.3. Połączenie automatów komórkowych z MES Rysunek 4.10: Ilustracja połączenia z elementami w siatce MES zróżnicowanych pod względem wielkości ziarna symulacji CA MES wyznaczenia naprężenia uplastyczniającego w chwili t MES + t MES : σ f = σ f (t, t, T, ε, ε, S(t, t, T, ε)) (4.69) Parametr S oznacza stan, zawarty w symulacji CA, obejmujący m.in. średnią gęstość dyslokacji w siatce CA ρ CA. Wartość σ f jest wyznaczana dla każdego punktu całkowania w pierwszej iteracji metody Newtona-Raphsona, rozwiązującej nieliniowy układ równań, wynikający z równania (4.7). Istotne jest, że w wykorzystywanym sformułowaniu sztywno-plastycznym wartości σ f są w kolejnych krokach metody Newtona-Raphsona przyjmowane jako stałe. Z kolei temperatura przyjmowana jest na podstawie rozwiązania problemu termicznego, przeprowadzonego w poprzednim kroku czasowym t MES. Naprężenie uplastyczniające jest wyznaczane w sposób podobny do podanego równaniem (2.9): σ f (t) = σ 0 + αµb ρ CA (4.70) gdzie: σ 0 naprężenie początkowe, α współczynnik, przyjmowany jako 0.5, µ moduł sprężystości poprzecznej, b wektor Burgersa, ρ CA średnia gęstość dyslokacji w siatce CA. Średnia gęstość dyslokacji w siatce CA jest wyznaczana za pomocą równania: ρ CA = 1 n m ρ R i,j (4.71) nm i=1 j=1 gdzie: ρ R i,j gęstość dyslokacji w komórce i, j, obliczona za pomocą równania (4.65), 84
97 4.3. Połączenie automatów komórkowych z MES n, m wymiary siatki CA. Przyrosty czasu rozwiązania skali makro t MES nie odpowiadają przyrostom czasu symulacji CA t CA. Zazwyczaj na krok t MES przypada kilkanaście lub kilkadziesiąt kroków czasowych t CA. Zadaniem modelu pośredniczącego jest interpolacja wartości naprężenia, otrzymywanych z równania (4.70) dla czasu t CA, w punktach czasowych t MES oraz t MES + t MES. Ponieważ przyrosty czasu w symulacji CA są zwykle niewielkie, zastosowano interpolację liniową pomiędzy rozwiązaniami w sąsiednich punktach czasowych. 85
98 Rozdział 5 Wyniki 5.1 Wpływ definicji sąsiedztwa na rozrost ziarna w ośrodku izotropowym W dotychczasowych pracach, podejmujących temat wpływu definicji sąsiedztwa, duży nacisk kładziono na kształt wzrastających ziaren, jaki przyjmują przed zderzeniem z innymi ziarnami. Na podstawie przeglądu literatury, przeprowadzonego w rozdziale 2.4.4, można stwierdzić, że najbardziej pożądane jest odtworzenie kształtu ziaren równoosiowych. Zatem kształt ziaren na początku wzrostu powinien być owalny lub zbliżony do globularnego. Jednakże standardowe definicje sąsiedztwa wprowadzają sztuczną anizotropię, powodującą rozwój ziaren o kształtach różniących się znacznie od obserwowanych w rzeczywistych materiałach. W rozdziale zaproponowano nową definicję sąsiedztwa, nazywanego pseudo- -heksagonalnym lub heksagonalnym losowo komutowanym. W celu zweryfikowania możliwości odtworzenia za jego pomocą globularnego kształtu ziaren przeprowadzono symulację CA swobodnego rozrostu ziaren w ośrodku izotropowym. Wykorzystany został zmodyfikowany algorytm swobodnego wzrostu ziarna, opisany w podrozdziale Modyfikacja algorytmu polegała na zastąpieniu modelu zarodkowania wyznaczeniem na początku symulacji pojedynczej komórki, położonej w środku siatki obliczeniowej i zmienieniu jej stanu na opowiadający zarodkowi ziarna. Następnie w kolejnych krokach czasowych prowadzano symulację swobodnego rozrostu ziarna. W obliczeniach wykorzystano siatkę komórek. Na rysunku 5.1a przedstawiono kształt ziarna w kroku czasowym τ = 85. Dla porównania wykonano analogiczne obliczenia i sporządzono rysunki kształtu ziarna w τ = 85 dla pięciu innych rodzajów sąsiedztwa: von Neumanna rysunek 5.1b, 86
99 5.2. Tworzenie początkowych obrazów mikrostruktury Moore a rysunek 5.1c heksagonalnego, z układem sąsiedztwa przedstawionym na rysunku 2.1c na stronie 13, rysunek 5.1d, heksagonalnego, z przyjęciem układu sąsiedztwa jak na rysunku 4.5a, rysunek 5.1e, heksagonalnego komutowanego, wykorzystywanego w pracach [17, 89] rysunek 5.1f. Pomimo, że żadne spośród ziaren, przedstawionych na rysunku 5.1 nie spełnia wymagania owalności, najbliższe pożądanego efektu są układy na rysunkach 5.1a oraz 5.1f. Sąsiedztwo zaproponowane w pracy [89] prowadzi do ośmiokątnego kształtu ziarna. Natomiast sąsiedztwo pseudo-heksagonalne, wprowadzone w rozdziale 4.2.3, skutkuje pojawieniem się wyraźnych zaokrągleń rozrastającego się ziarna. Powstawanie tych zaokrągleń jest zaletą definicji sąsiedztwa, zaproponowanej w niniejszej pracy, eliminuje bowiem ostre naroża ziaren, będące artefaktami wywodzącymi się ze standardowych rodzajów sąsiedztwa. Należy także uwzględnić, że promień sąsiedztwa pseudo-heksagonalnego pozostaje równy promieniowi sąsiedztwa Moore a. Przekłada się to bezpośrednio na czas obliczeń, gdyż w trakcie stosowania reguł przejścia stanu analizowana jest stosunkowo niewielka liczba komórek sąsiednich. Biorąc pod uwagę, że reguły przejścia stanu uruchamiane są w kolejnych krokach czasowych dla każdej komórki w siatce, wyznaczenie sąsiedztwa oraz przeanalizowanie stanu przynależnych do niego komórek posiada znaczący udział w całkowitym czasie wykonania symulacji. Dlatego utrzymanie niewielkiego promienia sąsiedztwa jest korzystne z punktu widzenia złożoności obliczeniowej. 5.2 Tworzenie początkowych obrazów mikrostruktury Przeprowadzenie symulacji DRX metodą automatów komórkowych wymaga wstępnego przygotowania obrazu mikrostruktury początkowej. Zastosowane zostały opisane w podrozdziale algorytmy, w tym symulacja swobodnego wzrostu ziarna oraz przetwarzanie zdjęć mikrostruktur, zapisanych w postaci map bitowych. Otrzymana jako rezultat reprezentacja mikrostruktury początkowej nie posiada jawnie zadanych wymiarów geometrycznych. Ziarna w siatce obliczeniowej są charakteryzowane bezpośrednio przez liczbę przynależnych komórek oraz wyznaczoną na tej 87
100 5.2. Tworzenie początkowych obrazów mikrostruktury (a) (b) (c) (d) (e) (f) Rysunek 5.1: Kształt wzrastającego ziarna otrzymany z wykorzystaniem różnych definicji sąsiedztwa: (a) pseudo-heksagonalnego, (b) von Neumanna, (c) Moore a, (d) heksagonalnego (rys. 2.1c), (e) heksagonalnego (rys. 4.5a), (f) heksagonalnego komutowanego. Skala na osiach wyraża numery komórek w siatce 88
101 5.2. Tworzenie początkowych obrazów mikrostruktury podstawie średnicę D p, wyrażoną równaniem (4.26). Powiązanie wygenerowanej mikrostruktury z wymiarami geometrycznymi następuje przez określenie powierzchni S u, jaką zajmuje pojedyncza komórka w siatce CA. Jednym z możliwych ilościowych wskaźników opisu wielkości ziarna jest względna wielkość ziarna, obliczana jako stosunek średnicy ziarna do średniej średnicy ziarna w siatce: D w = D p D p = D D (5.1) gdzie: D średnia średnica zastępcza ziarna. Wykresy częstości wystąpień klas wartości D/D ułatwiają analizę rozkładu wielkości ziarna w siatce obliczeniowej. Ilościowy opis postępu wzrostu ziaren w układzie wyrażony jest przez ułamek powierzchni, przypisanej do ziaren: X = p nm (5.2) gdzie: n, m liczba komórek CA na poziomym i pionowym boku siatki obliczeniowej, p liczba komórek CA przypisanych do ziaren Algorytm swobodnego wzrostu ziaren Algorytm swobodnego rozrostu ziaren, opisany w podrozdziale 4.2.6, jest podstawową metodą tworzenia początkowej reprezentacji mikrostruktury, używaną w niniejszej rozprawie. W celu przetestowania jego działania przeprowadzono obliczenia, stosując różne wielkości siatki i sposoby jej podziału, oraz różne liczby zarodków. Typowe zastosowanie algorytmu Na rysunku 5.2 przedstawiono przebieg tworzenia mikrostruktury za pomocą algorytmu swobodnego wzrostu ziaren. Wykorzystana została siatka CA komórek. Zastosowano podział siatki za pomocą 15 linii na każdym boku. Obrazy mikrostruktury w charakterystycznych punktach czasowych zaprezentowano na rysunkach 5.2a 5.2d. Podziałka na osiach wyraża numery komórek w siatce, natomiast skala kolorów oznacza kąt orientacji ziarna. Kolorem białym zaznaczono obszar nieprzypisany do ziaren. Ułamek X w funkcji czasu, wyrażonego w jednostkach umownych, przedstawiono na rysunku 5.2e. W początkowym etapie rozrostu ziaren (rysunek 5.2a) utrzymują one globularny kształt. W miarę wzrostu ziaren obserwowane są pomiędzy nimi zderzenia, co jest dobrze widoczne na rysunkach 5.2b 5.2c. Konsekwencją zderzenia wzrastających ziaren jest utworzenie między nimi nieruchomej granicy międzyziarnowej. Prowa- 89
102 5.2. Tworzenie początkowych obrazów mikrostruktury dzi to do lokalnego wyeliminowania niektórych kierunków wzrostu. Mikrostruktura, wyobrażona na rysunku 5.2b, odpowiada punktowi przegięcia na krzywej ułamka powierzchni przyporządkowanej do ziaren. Końcowy obraz mikrostruktury oraz odpowiadający mu rozkład wielkości względnej ziarna, przedstawiono na rysunkach 5.2d i 5.2f. Otrzymana mikrostruktura składa się z równomiernych ziaren, a rozkład wielkości jest zbliżony do normalnego. Dzięki zastosowaniu algorytmu podziału siatki, obserwowana jest stosunkowo niewielka liczba artefaktów, takich jak złącza wielokrotne. W otrzymanej reprezentacji mikrostruktury w przeważającej większości występują złącza potrójne. Wpływ podziału siatki na działanie algorytmu Opisany w rozdziale algorytm bazuje na podziale siatki obliczeniowej na podobszary rozłączne, poprzez określenie liczby linii podziału na każdym boku siatki. W każdym podobszarze zadawana jest liczba komórek, których stan jest losowo zmieniany w taki sposób, żeby reprezentowały zarodek ziarna. Zamiast liczby zarodków wygodniej jest posługiwać się pojęciem gęstości zarodkowania w siatce. Gęstość zarodkowania obliczano jako stosunek liczby zarodków n n, umieszczonych w siatce CA, do rozmiaru siatki obliczeniowej n m: d n = n n n m (5.3) W celu sprawdzenia właściwości algorytmu przeprowadzono obliczenia dla schematów podziału siatki obliczeniowej, podanych w tabeli 5.1. Wykorzystano siatkę obliczeniową komórek. Uzyskane w wyniku obliczeń obrazy mikrostruktury przedstawiono na rysunku 5.3, etykiety rysunków odpowiadają oznaczeniom podanym w pierwszej kolumnie tabeli 5.1. Schemat podziału wykorzystany w przypadkach (g) (i) sprowadza się do przeprowadzenia losowania położeń zarodków w całej siatce obliczeniowej. Najbardziej równomierny rozkład wielkości i kształtu ziarna uzyskano dla podziału siatki (a) (c). O ile wielkość ziarna jest parametrem wymiernym, to kształt ziaren trudno opisać jednoznacznie za pomocą wskaźnika liczbowego. Metalografia ilościowa dostarcza metod obliczeniowych, pozwalających na opisanie kształtu każdego ziarna, jednak dla potrzeb oceny mikrostruktur, uzyskanych w obliczeniach CA, wystarczająca jest analiza wizualna. Analiza ta wskazuje, że najwięcej ziaren równomiernych, pięciokątnych i sześciokątnych i zbliżonych do równoosiowych uzyskano dla podziału siatki na 100 podobszarów. Podział na mniejszą liczbę podobszarów prowadzi do zwiększania się liczby ziaren wydłużonych, trójkątnych oraz zawierają- 90
103 5.2. Tworzenie początkowych obrazów mikrostruktury (a) (b) (c) (d) (e) (f) Rysunek 5.2: Przebieg symulacji swobodnego wzrostu ziaren w wybranych krokach czasowych: (a) t = 1.8, (b) t = 3.2, (c) t = 3.8, (d) końcowy obraz mikrostruktury; skala na osiach numery komórek w siatce, skala kolorów kąt orientacji ziarna, kolor biały obszar nieprzypisany do ziaren; (e) ułamek powierzchni siatki, przypisany do ziaren; (f) rozkład względnej wielkości ziarna w mikrostrukturze finalnej, niebieską linią zaznaczono rozkład normalny 91
104 5.2. Tworzenie początkowych obrazów mikrostruktury Tabela 5.1: Schematy podziału siatki obliczeniowej na podobszary oraz gęstości zarodkowania, wykorzystane w testowaniu generatora mikrostruktur Oznaczenie Liczba Liczba Gęstość podziałów podobszarów P zarodkowania d n (a) E-03 (b) E-03 (c) E-03 (d) E-03 (e) E-03 (f) E-03 (g) E-03 (h) E-03 (i) E-03 cych obszary wklęsłe. Zmniejszanie liczby podziałów siatki sprzyja także uzyskaniu struktury niejednorodnej, zawierającej skupiska małych ziaren oraz ziarna rozrośnięte powyżej średniej. Na rysunku 5.4 przedstawiono rozkład względnej wielkości ziarna D w, dla czterech obrazów mikrostruktur, odpowiadających wierszom (a), (c), (g) oraz (i) w tabeli 5.1. Rozkłady dla schematu podziału siatki na 100 podobszarów (rysunki 5.4a i 5.4b) cechują się większym skupieniem wokół wartości średniej, oraz odchyleniem skośnym w kierunku ziaren większych od przeciętnego. Świadczy to o dużej jednorodności wielkości ziarna w obrazach mikrostruktury, generowanych z zastosowaniem podziału siatki na dużą liczbę podobszarów. Jednocześnie otrzymywane są także stosunkowo liczne ziarna duże, które jednak nie wykazują cech, charakterystycznych dla rozrostu anormalnego. Przyjęcie pojedynczego obszaru, w którym losowane są rozmieszczenia zarodków, prowadzi do zmniejszenia skupienia rozkładu wielkości ziarna wokół wartości średniej. Uzyskiwane rozkłady są bardziej zbliżone do normalnego. Spośród rozkładów przedstawionych na rysunku 5.4 jedynie 5.4d i 5.4c przedstawiają rozkład normalny, co sprawdzono za pomocą testu Shapiro-Wilka. Z drugiej strony, dla małej gęstości zarodkowania (rysunek 5.4a) uzyskiwana jest stosunkowo duża liczba ziaren o rozmiarze D, oraz mała liczba ziaren o rozmiarze średnim. Bimodalny rozkład, z minimum w okolicach wartości średniej, świadczy o niejednorodności wielkości ziarna w wygenerowanej mikrostrukturze. Przedstawione wyżej rozważania wskazują, że źródłem wyraźnych różnic w uzyskiwanych rozkładach wielkości ziarna oraz w kształcie ziaren jest zastosowany schemat podziału siatki na podobszary. Ponieważ losowanie położenia zarodków jest prowadzone oddzielnie dla każdego podobszaru, wprowadzana jest dodatkowa regularność ich rozmieszczenia. W każdym prostokącie, wyznaczonym liniami podzia- 92
105 5.2. Tworzenie początkowych obrazów mikrostruktury (a) (b) (c) (d) (e) (f) (g) (h) (i) Rysunek 5.3: Obrazy mikrostruktury, uzyskane dla schematów podziału siatki, odpowiadających podanym w tabeli 5.1: (a) (c) 100, (d) (f) 4, (g) (i) 1 podobszarów 93
106 5.2. Tworzenie początkowych obrazów mikrostruktury (a) P = 100, d n = 2.50E-03 (b) P = 100, d n = 7.50E-03 (c) P = 1, d n = 2.50E-03 (d) P = 1, d n = 7.50E-03 Rysunek 5.4: Rozkład względnej wielkości ziarna dla schematów podziału siatki CA i gęstości zarodkowania w siatce, wybranych z tabeli 5.1: (a) wiersz (a), (b) wiersz (c), (c) wiersz (g), (d) wiersz (i). Niebieską linią zaznaczono rozkład normalny 94
107 5.2. Tworzenie początkowych obrazów mikrostruktury Rysunek 5.5: Ułamek powierzchni przypisanej do ziaren, uzyskany z wykorzystaniem schematów podziału siatki obliczeniowej i gęstości zarodkowania, podanych w tabeli 5.1 łu siatki, umieszczana jest losowo jednakowa liczba zarodków. Zmniejsza to szansę przedwczesnego zderzenia wzrastających ziaren, przez co ich wzrost w części kierunków nie jest blokowany. Dowodem pośrednio potwierdzającym to wytłumaczenie jest przebieg krzywych, określających ułamek powierzchni siatki przypisanej do ziaren, w funkcji czasu. Na rysunku 5.5 przedstawiono ułamki powierzchni dla wszystkich schematów podziału siatki i gęstości zarodkowania, podanych w tabeli 5.1. Jak można się spodziewać, dla jednakowych gęstości zarodkowania obserwowane są zbliżone przebiegi wykresów ułamka X. Pojawiają się jednak różnice w zależności od liczby podobszarów w siatce. Dla każdej wartości parametru d n krzywa, opisująca schemat z podziałem na 100 podobszarów znajduje się na lewo od pozostałych dwóch. Świadczy to, że dla tego sposobu podziału siatki, wzrost ziaren jest najszybszy. Wolniejszy wzrost ziaren w pozostałych przypadkach wynika z blokowania wzrostu w części kierunków, będącego efektem zderzeń pomiędzy zarodkami na wczesnym etapie rozrostu. Efekt ten jest szczególnie widoczny przy dużej gęstości zarodkowania w końcowej części wykresów, dla X > 0.7. Algorytm swobodnego wzrostu ziaren podsumowanie Przedstawiony algorytm pozwala na tworzenie obrazów mikrostruktur dla siatek o niemal dowolnym rozmiarze, oraz z arbitralnie przyjętą liczbą ziaren. Utworzenie z jego pomocą początkowej reprezentacji mikrostruktury jest bardzo szybkie, co jest atutem rozwiązania. Poprzez dobór parametrów podziału siatki na podobszary oraz 95
108 5.2. Tworzenie początkowych obrazów mikrostruktury gęstości zarodkowania można wpływać na działanie algorytmu tworzenia nowych ziaren w siatce obliczeniowej. Dla podziału siatki na dużą liczbę podobszarów uzyskiwany jest zwarty rozkład wielkości ziarna wokół D/D = 1. Jednocześnie obserwowana jest również skośność tego rozkładu w stronę zwiększonego udziału ziaren o wielkości D/D > 1. Natomiast przy podziale siatki na niewielką liczbę podobszarów otrzymywany jest rozkład wielkości ziarna zbliżony do normalnego, oraz względnie duże nierównomierności ułożenia ziaren w siatce. Opracowany algorytm posiada jednak pewne ograniczenia. Pierwszym z nich jest uproszczony model wzrostu ziaren, zakładający zatrzymanie wzrostu ziarna przy zderzeniu z innym ziarnem. Drugim ograniczeniem jest wprowadzenie we wszystkich ziarnach jednakowej gęstości dyslokacji. Oznacza to, że obliczenia prowadzone są do osiągnięcia przypisania do ziaren wszystkich komórek w siatce CA, a nie do momentu uzyskania stanu równowagi. Pominięte są także zjawiska, przyczyniające się do zaniku małych ziaren oraz ziaren o małej liczbie kątów, w tym wpływ energii granicy ziaren. Nie uwzględniana jest również koalescencja ziaren o podobnej orientacji. Ponadto w mikrostrukturach, powstałych w drodze symulacji swobodnego rozrostu ziaren, uzyskiwane są liczne artefakty. Ich źródłem są anizotropia siatki oraz stosunkowo uproszczone reguły przejścia stanu komórek CA, opisujące rozrost ziaren. Przykładem artefaktu jest nadmierna liczność złączy poczwórnych i wielokrotnych, obserwowanych w wygenerowanych mikrostrukturach. Z przeprowadzonych przez autora doświadczeń numerycznych wynika, że występować mogą także inne artefakty, takie jak samopodobieństwo niektórych obszarów w siatce lub powtarzalność wzorców, np. kształtu ziaren. Efekt ten może być spowodowany podziałem siatki na zbyt dużą liczbę podobszarów, oraz słabą jakością generatora liczb pseudolosowych, zarządzającego rozmieszczaniem zarodków w siatce. Poruszone wyżej zagadnienia będą przedmiotem dalszych badań. W niniejszej rozprawie algorytm swobodnego rozrostu ziaren jest jedynie narzędziem pomocniczym, przygotowującym dane wejściowe, dlatego wprowadzenie uproszczeń wydaje się zasadne Przetwarzanie doświadczalnych obrazów mikrostruktury Opracowane oprogramowanie do symulacji DRX umożliwia importowanie zdjęć mikrostruktury, zapisanych w postaci mapy bitowej. Opis stosowanego algorytmu przedstawiono w podrozdziale Przygotowanie danych wejściowych wymaga zaznaczenia każdego ziarna na zdjęciu (a więc wszystkich punktów przynależnych do niego) odrębnym kolorem. Ponieważ dane doświadczalne zawierają często zaburzenia, 96
109 5.2. Tworzenie początkowych obrazów mikrostruktury (a) Obraz uzyskany z mikroskopii świetlnej (wg [5]) (b) Bitmapa wygenerowana programem Denoising Soft [112] (c) Zaimportowana reprezentacja mikrostruktury, gotowa do wykorzystania w symulacji DRX Rysunek 5.6: Kolejne etapy generowania reprezentacji mikrostruktury na podstawie danych z mikroskopii świetlnej niezbędne jest przeprowadzenie wstępnej obróbki zdjęć. Etap ten powinien nastąpić przez przekonwertowaniem zdjęć do formatu reprezentacji mikrostruktury używanego przez model symulacyjny CA. W analizie wstępnej obrazów, pochodzących z mikroskopii świetlnej, wykorzystano oprogramowanie Denoising Soft, opracowane w obecnej Katedrze Informatyki Stosowanej i Modelowania AGH przez Ł. Raucha i opisane w jego rozprawie doktorskiej [112]. Na rysunku 5.6 przedstawiono kolejne etapy przetwarzania danych. Wykorzystano zdjęcie zgładu próbki stopu Fe-30Ni (rysunek 5.6a), pochodzące z pracy [5]. Zdjęcie to zostało przetworzone programem Denoising Soft do postaci pokolorowanej mapy bitowej, zaprezentowanej na rysunku 5.6b. Następnie przekonwertowano ją do formatu reprezentacji danych, zgodnej z używaną w opracowanym w niniejszej pracy modelu CA. Przedstawiona na rysunku 5.6c mikrostruktura została uzupełniona o losowe orientacje ziaren, zaznaczone na rysunku za pomocą skali kolorów. Przyjęto zakres orientacji [0, π] oraz jednostajny rozkład prawdopodobieństwa. 97
110 5.2. Tworzenie początkowych obrazów mikrostruktury (a) Rozkład orientacji w ziarnach (b) Częstości wystąpień średnicy D/D. Niebieską linią zaznaczono rozkład normalny Rysunek 5.7: Rozkład klas orientacji i względnej wielkości ziarna w reprezentacji mikrostruktury na rysunku 5.6c Po zaimportowaniu obrazu mikrostruktury przeprowadzono prostą analizę statystyczną. Otrzymany rozkład orientacji w ziarnach przedstawiono na rysunku 5.7a. Rozkład ten jest w przybliżeniu jednostajny, co wynika z metody uzupełniania danych doświadczalnych losowo dobranymi kątami orientacji. Rozkład stosunku wielkości ziarna do wartości średniej D/D przedstawiono na rysunku 5.7b. Niebieską linią ciągłą zaznaczono przebieg rozkładu normalnego. Wykres 5.7b wskazuje, że w analizowanej mikrostrukturze rozkład wielkości ziarna jest daleki od normalnego. Duże odstępstwa od rozkładu normalnego obserwowane są dla kategorii ziaren bardzo dużych oraz małych i bardzo małych. Tworzenie reprezentacji mikrostruktury na podstawie zdjęć, pochodzących z mikroskopii świetlnej, w dużym stopniu zależy od jakości wstępnej obróbki zdjęcia. Szczególnie ważne jest poprawne oznaczenie granic międzyziarnowych, co dla zautomatyzowanych algorytmów rozpoznawania obrazów może przedstawiać trudności. Na rysunku 5.6a odnaleźć można granice ziaren, nie zidentyfikowane w bitmapie 5.6b. Powoduje to przeszacowanie udziału ziaren dużych w analizowanej mikrostrukturze. Rezultat ten zależy od metody przetwarzania danych źródłowych 5.6a i nie wynika ze stanu analizowanej mikrostruktury. Powstałe w efekcie tego rozbieżności przenoszą się na dalsze etapy obliczeń. Z tego powodu w dalszej części pracy, dotyczącej symulacji CA zjawiska DRX, wykorzystywane są obrazy mikrostruktury, wygenerowane za pomocą algorytmu swobodnego wzrostu ziarna. 98
111 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji 5.3 Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Stabilność obliczeń CA Przeprowadzone zostały obliczenia, mające na celu wykazanie czy średnia gęstość dyslokacji, pochodząca z obliczeń dokonywanych w modelu CA zgodna jest z rozwiązaniem analitycznym równania (4.29). Zgodność taka powinna zachodzić dla początkowych etapów odkształcenia, przed pojawieniem się pierwszych zarodków rekrystalizacji. W prezentowanych dalej obliczeniach dobrano parametry modelu w taki sposób, aby wykluczyć zajście DRX. Rozwiązanie analityczne wyrażono równaniem (4.32), opisującym rozwój gęstości dyslokacji przy założeniu mechanizmów umocnienia i dynamicznego zdrowienia, nie opisującym natomiast zachowania materiału w trakcie dynamicznej rekrystalizacji. Umożliwia to bezpośrednie porównanie wartości ρ uzyskanych z modelu CA i rozwiązania analitycznego (4.32). Część modelu CAFE, oparta o automaty komórkowe, bazuje na obliczeniach gęstości dyslokacji, jednak na podstawie tego parametru wyznaczane jest naprężenie uplastyczniające. Niewrażliwość σ f na długość kroku czasowego CA jest kluczowa dla działania całego modelu CAFE. Na rysunku 5.8 przedstawiono wartości naprężenia uplastyczniającego, obliczone z modelu CA na postawie wzoru (4.70), z przyjęciem różnych długości kroków czasowych symulacji CA. Rozwiązania te porównano z naprężeniem uplastyczniającym, wyliczonym ze wzoru (2.9) na stronie 10, dla gęstości dyslokacji otrzymanej z analitycznego równania (4.32). Uzyskane wyniki wskazują, że obliczana na podstawie symulacji CA średnia gęstość dyslokacji jest zgodna ilościowo z dostępnym rozwiązaniem analitycznym. Zmiana długości kroku czasowego nie wpływa znacząco na uzyskiwane średnie gęstości dyslokacji oraz wartości naprężenia uplastyczniającego, a także nie powoduje anomalii w rozwiązaniu. Można wnioskować, że opisany w rozdziale algorytm dystrybucji gęstości dyslokacji działa zgodnie z przyjętymi założeniami. Jednocześnie prowadzenie obliczeń rozwoju średniej gęstości dyslokacji na poziomie dalekiego sąsiedztwa nie narusza założeń metody automatów komórkowych Obliczenia krytycznej gęstości dyslokacji Na rysunku 5.9 przedstawiono porównanie średnich krytycznych gęstości dyslokacji ρ c, obliczonych z wykorzystaniem dwóch typów sąsiedztwa heksagonalnego: pseudo- -heksagonalnego i heksagonalnego o stałej topologii. Wszystkie parametry symulacji w obu przypadkach były identyczne. Parametry te zostały dobrane w taki sposób, 99
112 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Rysunek 5.8: Porównanie wartości naprężenia uplastyczniającego, uzyskanych z modelu CA na podstawie równania (4.70) oraz z równania (2.9) na podstawie analitycznego rozwiązania równania rozwoju gęstości dyslokacji (4.32): linia rozwiązanie analityczne, symbole rozwiązania uzyskane z modelu CA z przyjęciem różnych długości kroku czasowego aby wykluczyć zajście zarodkowania DRX. Uzyskane wyniki wskazują, że istnieje zależność ρ c od rodzaju sąsiedztwa. W wypadku sąsiedztwa pseudo-heksagonalnego w kolejnych krokach uwzględniane są różne liczby komórek, znajdujących się na granicach ziaren. Tym samym uzyskiwany jest losowy czynnik, wpływający na lokalne zróżnicowanie wartości ρ c. Pośrednio znajduje to odzwierciedlenie w wartości ρ c. Opracowane w niniejszej pracy sąsiedztwo pseudo-heksagonalne pozwala na wprowadzenie losowego czynnika w obliczeniach kluczowych dla zarodkowania. Przekroczenie krytycznej gęstości dyslokacji jest założonym w modelu warunkiem powstania nowego ziarna. Pseudolosowa dystrybucja gęstości dyslokacji jest drugim losowym czynnikiem, oddziałującym na przebieg zarodkowania. W obliczeniach ρ c nie jest wymagana wiedza o globalnym stanie układu, a probabilistyczne zachowanie wynika z czynnika losowego w definicji sąsiedztwa i w modelu rozwoju gęstości dyslokacji w komórkach CA. Tym samym zrealizowany został jeden z celów cząstkowych pracy, jakim jest wyeliminowanie konieczności globalnego wyznaczania komórek, które staną się zarodkami rekrystalizacji Rozrost zarodka w złączu potrójnym W trakcie dynamicznej rekrystalizacji procesy strukturalne zachodzą w ośrodku anizotropowym. Źródłem anizotropii jest m. in. obecność granic ziaren, niejednorodność 100
113 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Rysunek 5.9: Wpływ definicji sąsiedztwa na średnie krytyczne gęstości dyslokacji w siatce CA: sąsiedztwo heksagonalne losowo komutowane (symbole wypełnione) oraz heksagonalne o stałej topologii (symbole otwarte) gęstości dyslokacji, a także rozkład orientacji w materiale. Granice ziaren odgrywają w opracowanym modelu szczególną rolę, jako możliwe miejsca powstawania zarodków nowych ziaren. Opracowany model pozwala także na uwzględnienie wpływu dwóch ostatnich źródeł niejednorodności na prędkość wzrostu zrekrystalizowanego ziarna. Siła pędna wzrostu ziarna, wyrażona równaniem (4.59) lub (4.57), zależy od różnicy gęstości dyslokacji pomiędzy zrekrystalizowanym ziarnem i osnową. Z kolei ruchliwość granicy, opisana równaniem (4.48), zależna jest od kąta dezorientacji granicy międzyziarnowej. Zależność ruchliwości granicy od kąta dezorientacji przedstawiono na wykresie 4.8 na stronie 71. Możliwy wpływ niejednorodności pola temperatury jest pomijany w modelu, przez założenie stałej temperatury w całej siatce CA podczas pojedynczego kroku czasowego. Natomiast w kolejnych krokach czasowych temperatura może ulec zmianie, wpływając zarówno na ruchliwość granic ziaren, jak i na przyrost gęstości dyslokacji. W celu przetestowania działania modelu wzrostu ziaren w ośrodku anizotropowym przeprowadzono doświadczenie numeryczne, polegające na symulacji wzrostu zarodka, ulokowanego w złączu potrójnym. Spodziewanym wynikiem tego doświadczenia jest zróżnicowanie prędkości rozrostu zarodka w zależności od kąta dezorientacji. Przewidywany jest także wpływ niejednorodności gęstości dyslokacji w siatce obliczeniowej. Wynika ona z działania algorytmu rozwoju gęstości dyslokacji, opisanego w podrozdziale W obliczeniach założono utrzymanie stałej temperatury i prędkości odkształcenia. Układ próbki schematycznie przedstawiono na rysunku Zaznaczone na ry- 101
114 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Tabela 5.2: Układy kątów dezorientacji zarodka w złączu potrójnym względem osnowy Nr. θ 1, rad θ 2, rad θ 3, rad sunku kąty dezorientacji zarodka rekrystalizacji względem osnowy θ 1, θ 2, θ 3 wynikają z orientacji ziaren pierwotnych i zarodka rekrystalizacji. Obraz mikrostruktury początkowej wygenerowano ręcznie i zaimportowano do programu w postaci mapy bitowej. Utworzony zarodek składał się początkowo z pojedynczej komórki CA. Ponieważ algorytm importu umożliwia podanie orientacji dla każdego ziarna z osobna, możliwe jest więc pośrednio wprowadzenie kątów θ 1, θ 2, θ 3. W obliczeniach wykorzystano siatkę komórek. Rysunek 5.10: Układ kątów dezorientacji granic ziaren w domenie obliczeniowej z zarodkiem w złączu potrójnym. Kąty dezorientacji pomiędzy osnową i zarodkiem θ 1, θ 2, θ 3 zaznaczono kolorami Granice ziaren pierwotnych przyjęto jako nieruchome. Dla potrzeb doświadczenia, w regułach przejścia stanu komórek CA wyłączono regułę opisującą zarodkowanie, co zapobiega pojawianiu się nowych zarodków w trakcie symulacji. Pozostała część modelu CA nie została zmieniona i jest zgodna z opisem podanym w podrozdziale 4.2. Przeprowadzono obliczenia dla trzech różnych układów kątów dezorientacji θ 1, θ 2, θ 3, zestawionych w tabeli 5.2. Na rysunku 5.11 przedstawiono rozrost zarodka dla τ = 300 (rysunek 5.11b) oraz τ = 370 (rysunek 5.11b). Podziałka na osiach wyznacza współrzędne komórek CA w siatce. Linią ciągłą oznaczono położenie granic ziaren pierwotnych. Kolorowe punkty wyznaczają bieżącą granicę wzrastającego zarodka, a więc położenie frontu rekrystalizacji. Skala kolorów odpowiada wartości 102
115 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji zmiennej stanu X w komórkach CA, która reprezentuje lokalny ułamek rekrystalizacji. Zgodnie z regułami zmiany stanu, podanymi w podrozdziale 4.2.5, zarówno komórki przed jak i za frontem posiadają wartość X = 0. (a) (b) Rysunek 5.11: Rozrost zarodka w złączu potrójnym dla kątów dezorientacji podanych w tabeli 5.2, wiersz 1, w różnych krokach czasowych: (a) τ = 300, (b) τ = 370 Analiza rysunku 5.11 wskazuje, że granica wzrastającego zarodka przesuwa się wgłąb ziaren pierwotnych z różną prędkością. Wysokokątowa granica ziarna o θ 1 przesuwa się znacznie szybciej, niż granice o kącie dezorientacji θ 2 i θ 3. W przypadku obu granic niskokątowych obserwowane jest ich przesunięcie do wewnątrz ziaren pierwotnych, jednak migracja ta jest powolna. Wyraźne zakrzywienie granicy wysokokątowej, widoczne na rysunku 5.11b, jest efektem zastosowania sąsiedztwa pseudo-heksagonalnego. Ząbkowy charakter granicy wynika z niejednorodności gęstości dyslokacji w siatce, powodującej lokalny wzrost prędkości migracji granicy. Drugim czynnikiem może być niedeterministyczny układ sąsiedztwa, wprowadzający w pewnym stopniu sztuczną anizotropię. Warto podkreślić, że zakrzywienie granicy jest widoczne nawet na bardzo zgrubnej siatce CA komórek. Kąty dezorientacji, podane w tabeli 5.2, wiersz drugi, zostały dobrane w taki sposób, aby uzyskać dwie granice o podobnej ruchliwości, oraz bardziej mobilną granicę wysokokątową. Wyniki przeprowadzonych obliczeń symulacyjnych przedstawiono na rysunku Podobnie jak w poprzednio omawianym przypadku, rysunki 5.12a i 5.12b przedstawiają położenie granicy wzrastającego zarodka w krokach czasowych τ = 300 i τ = 370. Granice o kącie dezorientacji θ 1 i θ 2 przemieszczają się z podobną prędkością. Wzrost zarodka w kierunku wyższej dezorientacji θ 3 postępuje zdecydowanie szybciej. Przypadek przedstawiony w wierszu trzecim tabeli 5.2 odpowiada równoupraw- 103
116 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji (a) (b) Rysunek 5.12: Rozrost zarodka w złączu potrójnym dla kątów dezorientacji podanych w tabeli 5.2, wiersz 2, w różnych krokach czasowych: (a) τ = 300, (b) τ = 370 (a) (b) Rysunek 5.13: Rozrost zarodka w złączu potrójnym dla kątów dezorientacji podanych w tabeli 5.2, wiersz 3, w różnych krokach czasowych: (a) τ = 300, (b) τ =
117 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji nionemu wzrostowi do wnętrza wszystkich trzech ziaren osnowy, gdyż θ 1 = θ 2 = θ 3. Przewidywana zbliżona prędkość ruchu granicy zarodka we wszystkich kierunkach, oraz związany z tym globularny kształt wzrastającego ziarna znajdują potwierdzenie na rysunku Granice zarodków, przedstawione na rysunkach , posiadają załamania i wklęsłości, wynikające z anizotropii siatki i sąsiedztwa, jednak przede wszystkim z lokalnych niejednorodności gęstości dyslokacji w siatce. Prędkość wzrostu, kontrolowana przez zmienną stanu X w komórkach CA, uzależniona jest od siły pędnej, pochodzącej od lokalnej różnicy gęstości dyslokacji. Zatem w przypadku stosunkowo dużych niejednorodności ρ, także prędkość wzrostu może być lokalnie zróżnicowana. Znajduje to m. in. odbicie na rysunkach , w postaci niejednakowych wartości zmiennej X na frontach rekrystalizacji. W przypadku, gdy θ 1 = θ 2 = θ 3 (rysunek 5.13), lokalne niejednorodności gęstości dyslokacji stanowią w modelu jedyne źródło zróżnicowania prędkości wzrostu. Na rysunku 5.14 przedstawiono rozkład gęstości dyslokacji w siatce obliczeniowej, odpowiadające położeniom granic ziarna na rysunku Na rysunku tym widoczne są wyraźne strefy mniejszej gęstości dyslokacji, odpowiadające frontowi wzrostu zrekrystalizowanego ziarna. Obserwowane jest także stopniowe odbudowywanie się gęstości dyslokacji w obszarach, w których rekrystalizacja zaszła najwcześniej. Wzrost gęstości dyslokacji wynika z postępującego odkształcenia materiału. Taki efekt znajduje potwierdzenie we wcześniejszych pracach doświadczalnych i modelowych [52]. Na rysunku 5.15 przedstawiono schematyczny diagram gęstości dyslokacji na froncie DRX, zaczerpnięty z prac [4, 52, 124]. (a) (b) Rysunek 5.14: Rozkład gęstości dyslokacji w siatce obliczeniowej dla wzrostu zarodka w złączu potrójnym, odpowiadający położeniom granicy zarodka przedstawionym na rysunku
118 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Rysunek 5.15: Schematyczna ilustracja gęstości dyslokacji na froncie dynamicznej rekrystalizacji (wg [4, 52, 113, 124]) Kształt zrekrystalizowanego ziarna na rysunku 5.13 jest w przybliżeniu globularny. W porównaniu z kształtem ziarna, wzrastającego w otoczeniu izotropowym, przedstawionym na rysunku 5.1a na stronie 88, jest bardziej zbliżony do owalnego. Pomimo, że w obu przypadkach wykorzystywano ten sam typ sąsiedztwa, lepsze przybliżenie globularnego kształtu ziarna uzyskano na rysunku Wytłumaczeniem jest bardziej złożona budowa reguł przejścia stanu w symulacji DRX niż w prostym modelu wzrostu ziarna, wykorzystywanym w podrozdziale 5.1. Wzrost ziarna w modelu DRX uzależniony jest od obliczeń prędkości v gb oraz przyrostów zmiennej stanu X. Tymczasem symulacja swobodnego wzrostu ziarna wykorzystuje uproszczoną regułę, wymagającą do przyłączenia nowej komórki do ziarna jedynie obecności w sąsiedztwie innej komórki CA, już do niego przynależnej. Uzyskane wyniki wskazują, że model uwzględnia zróżnicowanie prędkości migracji granic ziarna w zależności od kąta dezorientacji. Uwzględniany jest także kierunkowy rozrost ziarna. Otrzymany wynik pośrednio tłumaczy zanikanie niekorzystnie usytuowanych zarodków. Z rysunku 4.8 na stronie 71 wynika, że ruchliwość granicy ziarna o kącie dezorientacji poniżej około 0.1 rad jest nieduża. W przypadku, gdy orientacja zarodka w niewielkim stopniu odbiega od orientacji osnowy (ziaren na granicach których zarodek się pojawił), jego wzrost zachodzi z bardzo małą prędkością. Pojawienie się w pobliżu innego zarodka, o bardziej korzystnej orientacji, spowoduje pochłonięcie zarodka ulokowanego niekorzystnie. Algorytm zarodkowania, wykorzystany w niniejszej pracy, zakłada losową orientację nowo powstałych ziaren, bez uwzględnienia orientacji osnowy. Dlatego część nowo utworzonych ziaren zanika z powodu braku możliwości rozrostu. 106
119 5.3. Sprawdzenie założeń modelu CA dynamicznej rekrystalizacji Przy założeniu losowego doboru orientacji zarodka, złącza potrójne są bardziej korzystne dla wzrostu zarodka zrekrystalizowanego ziarna. Wyższe jest prawdopodobieństwo, że istnieje korzystna do wzrostu dezorientacja względem osnowy, niż w przypadku zarodka utworzonego na granicy dwóch ziaren Zarodkowanie i rozrost zrekrystalizowanych ziaren Granice ziaren odgrywają w opisywanym modelu DRX szczególną rolę. W opisanych w podrozdziale regułach przejścia stanu komórek CA zakłada się, że granice ziaren są miejscem, w którym możliwe jest utworzenie zarodków nowych, zrekrystalizowanych ziaren. Zarodkowanie możliwe jest zarówno na granicach ziaren pierwotnych jak i wtórnych. Przeprowadzono obliczenia, mające na celu sprawdzenie działania modelu CA, opisujących zarodkowanie i późniejszy wzrost ziaren. W przeciwieństwie do przypadku opisanego w poprzednim paragrafie, wykorzystano pełny zestaw reguł przejścia stanu CA, opisany w podrozdziale Wymaganą do rozpoczęcia symulacji DRX reprezentację mikrostruktury początkowej wygenerowano za pomocą algorytmu swobodnego wzrostu ziarna, opisanego w podrozdziale Przyjęto rozdzielczość siatki obliczeniowej komórek. Obliczenia wykonano dla nominalnej temperatury 1000 C oraz prędkości odkształcenia 0.1 s 1. Na rysunku 5.16 przedstawiono obrazy mikrostruktury dla wybranych ułamków rekrystalizacji x rec. Ziarna zrekrystalizowane zaznaczono kolorem niebieskim. Obserwowane jest heterogeniczne zarodkowanie, przy czym liczba powstających zarodków jest zmienna w czasie. Charakter granicy ziarna, w szczególności kąt jej dezorientacji, wpływa na wartość lokalnie obliczonej krytycznej gęstości dyslokacji, wymaganej do utworzenia zarodka zrekrystalizowanego ziarna. W wyniku niedeterministycznego rozkładu gęstości dyslokacji w siatce obliczeniowej, możliwe jest wyeliminowanie jawnego wskazania liczby i położenia zarodków rekrystalizacji. Jak pokazano w podrozdziale 5.3.3, także rozrost powstałych zarodków jest zróżnicowany, w zależności od orientacji oraz lokalnej gęstości dyslokacji w osnowie. W szczególności, możliwe jest zablokowanie wzrostu niekorzystnie usytuowanych zarodków. Zderzenia wzrastających ziaren prowadzą do utworzenia granic międzyziarnowych o niewielkiej prędkości ruchu. Wynika to z małej wartości siły pędnej, gdyż fronty rozrostu zderzających się ziaren posiadają podobną gęstość dyslokacji ρ
120 5.4. Analiza jakościowa modelu CAFE (a) (b) (c) (d) (e) (f) Rysunek 5.16: Zarodkowanie i wzrost ziaren w trakcie DRX dla wybranych ułamków rekrystalizacji. Zarodki nowych ziaren zaznaczono kolorem niebieskim, skala na osiach oznacza numery komórek w siatce 5.4 Analiza jakościowa modelu CAFE Przeprowadzono szereg obliczeń, mających na celu sprawdzenie możliwości opracowanego modelu CAFE w zakresie przewidywania wpływu zmian zachodzących w mikrostrukturze na makroskopową odpowiedź modelu. Szczególną uwagę zwrócono na spójność powiązania pomiędzy wyjściami modelu, udostępniającymi opis różnorodnych zmian w mikrostrukturze, oraz oddziałujących na rozwiązanie makroskopowe. Obliczenia te mają charakter analizy jakościowej, dlatego nie zakładano konkretnego rodzaju materiału. Z przyjętych w modelu założeń i uproszczeń wynika, że rozważany materiał odkształca się przez poślizg, posiada losowy rozkład orientacji, a nowe ziarna przyjmują orientacje losowe. Podstawowym celem przeprowadzonej analizy jest ocena wzajemnego powiązania wybranych parametrów, opisujących w modelu mikrostrukturę. Kolejnym celem jest sprawdzenie, czy model jest w stanie odtworzyć pewną kategorię cech, znanych z literatury, takich jak jednopikowe i wielopikowe krzywe naprężenia uplastyczniającego, oraz czy spełnia kryterium struktu- 108
121 5.4. Analiza jakościowa modelu CAFE ralne, wiążące charakter krzywej σ f ze średnią wielkością ziarna. Kryterium strukturalne, wprowadzone i opisane przez Sakai m. in. w pracy [123], wskazuje, że dla jednopikowej krzywej naprężenia uplastyczniającego uzyskiwane jest ponad dwukrotne rozdrobnienie ziarna, zatem D 0 > 2D, gdzie D 0 i D są wielkościami ziarna przed i po odkształceniu. W przypadku przeciwnym, gdy D 0 < 2D, krzywa naprężenia uplastyczniającego zawiera wiele cyklicznych maksimów, natomiast mikrostruktura po procesie może zawierać ziarna większe od istniejących w mikrostrukturze pierwotnej. Wielopikowa krzywa naprężenia uplastyczniającego jest typowa dla materiałów takich jak miedź lub nikiel. Z kolei krzywe naprężenia uplastyczniającego dla stali austenitycznych zwykle zawierają pojedyncze, wyraźne maksimum, opisywane przez odkształcenie pikowe ε p i odpowiadające mu naprężenie pikowe σ p. Dla potrzeb przeprowadzenia analizy jakościowej, model DRX opisany w podrozdziale 4.2 uzupełniono o możliwość śledzenia wybranych zjawisk, zachodzących w komórkach CA. Dodano zmienne stanu, pozwalające na bardziej szczegółowy wgląd w zjawiska symulowane w modelu. Pierwsza ze zmiennych, L, zawiera informację o liczbie zmian przyporządkowania do ziarna, a więc liczbie cykli całkowitego zrekrystalizowania porcji materiału, reprezentowanej przez komórkę CA. Druga zmienna, oznaczana jako C, zawiera informację o liczbie porządkowej cyklu rekrystalizacji. Liczba ta umożliwia rozbicie całkowitego ułamka rekrystalizacji na ułamki cząstkowe, przynależne do cykli rekrystalizacji. Dla materiału przed rekrystalizacją zmienna C przyjmuje wartość 0. Każdy zarodek, pojawiający się w komórce CA osnowy, charakteryzowanej przez pewną wartość zmiennej C = C m, oznaczany jest wartością zmiennej C o jeden większą, tj. C = C m + 1. Każda komórka, która przyłączona zostaje do ziarna o zmiennej C = C g, także zostaje oznaczona wartością C g. W konsekwencji, zmienna stanu C reprezentuje przynależność do pokolenia ziaren, obecnych w mikrostrukturze. W badaniach doświadczalnych stosunkowo trudne jest zidentyfikowanie ziaren, przynależnych do poszczególnych cykli rekrystalizacji. Tym niemniej w niektórych materiałach daje się zaobserwować powstawanie tzw. struktury naszyjnikowej (rysunek 2.4 na stronie 19), będącej przykładem tworzenia się pokoleń ziaren w mikrostrukturze. W przypadku wielu materiałów podlegających dynamicznej rekrystalizacji, całkowity ułamek rekrystalizacji x rec, oznaczający ułamek objętości materiału zrekrystalizowanego, przyjmuje wartość równą jedności na stosunkowo wczesnym etapie odkształcenia. Opracowany model daje możliwość śledzenia kolejnych cykli rekrystalizacji także dla większych odkształceń. Dla każdej wartości zmiennej C możliwe jest obliczenie cząstkowego ułamka rekrystalizacji, przy czym ułamki te są addytywne. Zsumowanie ułamków, odpowiadających współistniejącym w materiale cyklom 109
122 5.4. Analiza jakościowa modelu CAFE rekrystalizacji, pozwala na obliczenie ułamka zastępczego x. Ułamek zastępczy pozwala na odzwierciedlenie wielokrotnego zrekrystalizowania całego materiału. Uzupełniony model dodatkowo daje możliwość śledzenia liczby komórek w których zachodzi zmiana stanu, wiążąca się z pojawieniem się nowego zarodka, oraz wynikająca ze zmiany przypisania do ziarna (dalekiego sąsiedztwa). Drugie z tych zdarzeń oznacza, że komórka przyłączona została do wzrastającego ziarna. Model daje możliwość zliczania zarówno łącznej liczby komórek, jak i prowadzenia zliczania w każdym kroku czasowym oddzielnie. Dla interpretacji przebiegu symulowanego procesu bardziej przydatne są jednak wartości chwilowe. Przeprowadzono obliczenia dla nominalnej temperatury próbki 1000 C oraz prędkości odkształcenia ε = 1 s 1. Symulację przeprowadzono do nominalnego odkształcenia Próbka przed odkształceniem posiadała wysokość h = 12 mm i średnicę d = 8 mm. Przyjęto współczynnik tarcia m = Jednopikowe i wielopikowe krzywe naprężenia uplastyczniającego uzyskano, dobierając wybrane parametry modelu. W obu przypadkach modyfikowano parametry odpowiadające za obliczenia krytycznej gęstości dyslokacji ρ c oraz gęstości dyslokacji w materiale zrekrystalizowanym ρ 0. Krzywą wielopikową uzyskano dla stosunkowo dużej wartości ρ c oraz niskiej wartości ρ 0. Natomiast krzywą z wyraźnym pikiem i stanem ustalonym otrzymano dla niższej wartości ρ c oraz dwukrotnie wyższej wartości ρ 0. Obliczenia przeprowadzono dwuetapowo. W pierwszym etapie dokonano obliczeń dla nominalnych wartości temperatury i prędkości odkształcenia, z wykorzystaniem metody CA. Wszelkie mapy mikrostruktury, wykresy ułamków rekrystalizacji oraz rozkłady wielkości ziarna, demonstrowane w dalszej części podrozdziału, pochodzą z obliczeń prowadzonych w tym etapie. Obliczenia za pomocą pełnego modelu CAFE zostały przeprowadzone w drugim etapie. Stwierdzono, że wyniki uzyskane w etapie pierwszym zbliżone są do wyników, uzyskanych w punktach Gaussa w elementach bliskich środka próbki. Otrzymane wyniki porównano z jakościowymi krzywymi naprężenia i ułamka rekrystalizacji, zaczerpniętymi z klasycznej pracy Lutona i Sellarsa [71]. Wybrane wykresy mają charakter modelowej idealizacji danych doświadczalnych, dlatego podobnie jak w pracy [71] na osiach odkształceń i naprężeń nie są podawane wartości Wielopikowa krzywa naprężenia uplastyczniającego Przed rozpoczęciem obliczeń wygenerowano za pomocą algorytmu swobodnego wzrostu ziarna obraz mikrostruktury początkowej, przedstawiony na rysunku 5.17a. Wykorzystano siatkę CA o rozmiarze komórek. We wszystkich punktach cał- 110
123 5.4. Analiza jakościowa modelu CAFE (a) (b) Rysunek 5.17: Uzyskany w obliczeniach CA obraz mikrostruktury dla wielopikowej krzywej σ f : (a) mikrostruktura początkowa, (b) reprezentatywna mikrostruktura końcowa kowania MES została zastosowana taka sama reprezentacja mikrostruktury. Reprezentatywny obraz mikrostruktury, uzyskany po zakończeniu odkształcenia w środku próbki, przedstawiono na rysunku 5.17b. Uzyskane z modelu cząstkowe ułamki rekrystalizacji, przynależne do kolejnych cykli, oraz odpowiadające im wartości naprężenia uplastyczniającego, przedstawiono na rysunku Linią przerywaną zaznaczono całkowity ułamek rekrystalizacji x rec. Obserwowane jest występowanie w materiale współistniejących cykli, oznaczonych na rysunku przez x C1,..., x C5. Każdy cykl, z wyjątkiem pierwszego, rozpoczyna się przy odkształceniu odpowiadającym punktowi przegięcia na krzywej ułamka rekrystalizacji, opisującej poprzedni cykl. Czerwonymi strzałkami zaznaczono przybliżone położenie punktów przecięcia się krzywych ułamków rekrystalizacji i opowiadające im punkty na krzywej naprężenia uplastyczniającego. Dla pierwszych trzech cykli zaobserwować można ich wyraźne powiązanie. Punkt przecięcia na krzywej ułamka rekrystalizacji przypada za pikiem na krzywej naprężenia. Wykresy ułamków rekrystalizacji posiadają kształt krzywych dzwonowych, o malejących w kolejnych cyklach wartościach maksymalnych oraz malejącym nachyleniu lewej strony krzywej. Wynika to z obecności kolejnych, konkurujących we wzroście, cykli rekrystalizacji. Korzystając z addytywności ułamków rekrystalizacji, przynależnych do współistniejących cykli, sporządzono wykres ułamka zastępczego, przedstawiony na rysunku 5.19a. Otrzymano ułamki rekrystalizacji oznaczone jako x A,..., x E. Można zauważyć, że punkty przecięcia wykresów ułamka rekrystalizacji, przynależnego do cykli, odpowiadają punktom przegięcia na krzywych ułamka zastępczego. Zaczerpnięty z pracy [71] wykres wyidealizowanego przebiegu naprężenia uplastyczniającego oraz ułamków rekrystalizacji przedstawiono na rysunku 5.19b. Wykres ten ilustruje koncepcję Lutona i Sellarsa, dotyczącą tworzenia się kolejnych cykli 111
124 5.4. Analiza jakościowa modelu CAFE Rysunek 5.18: Ułamki rekrystalizacji przynależne do kolejnych cykli rekrystalizacji i odpowiadający im wielopikowy wykres naprężenia uplastyczniającego. Strzałkami zaznaczono na krzywej σ f punkty przecięcia krzywych ułamków rekrystalizacji, pochodzących z kolejnych cykli. Linią przerywaną oznaczono całkowity ułamek rekrystalizacji x rec (a) (b) Rysunek 5.19: Naprężenie uplastyczniające oraz zastępczy ułamek rekrystalizacji: (a) uzyskany z modelu CAFE, (b) na podstawie pracy [71] (przypadek wielopikowej krzywej σ f ) 112
125 5.4. Analiza jakościowa modelu CAFE (a) (b) Rysunek 5.20: Mapy rozkładu w siatce CA: (a) przynależności do cyklu rekrystalizacji, liniami ciągłymi oznaczono granice ziaren, (b) gęstości dyslokacji rekrystalizacji wraz ze wzrostem odkształcenia. Oscylacje naprężenia uplastyczniającego, uzyskane z opracowanego modelu, posiadają mniejszą amplitudę oraz niższą regularność niż widoczne na rysunku 5.19b. Z doświadczenia autora wynika, że możliwe jest odtworzenie za pomocą opracowanego modelu krzywej naprężenia uplastyczniającego o regularnych oscylacjach. Jednakże przegląd danych literaturowych wskazuje, że w większości rzeczywistych materiałów, charakteryzujących się wielopikową krzywą σ f, pierwsze maksimum jest najbardziej wyraźne, pozostałe mają charakter oscylacji gasnących, o zmiennej amplitudzie i okresie. Oznaczone zostały charakterystyczne punkty na wykresach 5.19a oraz 5.19b, odpowiadające osiągnięciu odkształcenia pikowego oraz ułamka rekrystalizacji x rec = Odkształcenie pikowe na rysunku 5.19b osiągane jest wcześniej, jednak różnica jest niewielka. Ponadto odkształcenie pikowe na rysunku 5.19a przypada około ε = 0.2, co jest wartością stosunkowo często obserwowaną w badaniach doświadczalnych. W obu przypadkach wartość ułamka rekrystalizacji x rec = 0.98 uzyskano na początku drugiej oscylacji na krzywej σ f. Oscylacje na krzywej σ f powiązane są z przebiegiem krzywych ułamka x rec. Porównanie 5.19a oraz 5.19b wskazuje, że naprężenie σ f, uzyskane z modelu CAFE w kolejnych oscylacjach, posiada składowe, pochodzące z materiału umocnionego i zrekrystalizowanego. Dlatego nachylenie krzywych σ f w kolejnych cyklach na rysunku 5.19a jest mniejsze niż nachylenie na rysunku 5.19b. Wskazuje to, że uwzględnienie wpływu zmian zachodzących w mikrostrukturze, w tym rozdrobnienia ziarna i obecności współdziałających cykli rekrystalizacji, zmniejsza regularność oscylacji. Na rysunku 5.20 przedstawiono uzyskany dla ε = 0.7 rozkład przynależności do cyklu rekrystalizacji oraz rozkład gęstości dyslokacji w siatce obliczeniowej. Na rysunku 5.20a zaznaczono ciągłymi liniami kontury ziaren. Powstające skupiska zia- 113
126 5.4. Analiza jakościowa modelu CAFE Rysunek 5.21: Średnia wielkość ziarna dla wielopikowej krzywej naprężenia uplastyczniającego. Linią przerywaną zaznaczono D 0 /2 ren, przynależnych do tego samego cyklu rekrystalizacji i zaznaczające się najbardziej dla C = 4, mają źródło w blokowaniu wzrostu w kierunkach zajętych przez ziarna przynależne do tego samego cyklu. Rozrost jest blokowany, gdyż ziarna te posiadają podobną, niską gęstość dyslokacji (rysunek 5.20b). Widoczne na rysunku pozostałości materiału, przynależnego do cyklu C = 2, charakteryzują się najwyższą gęstością dyslokacji. Na mapie gęstości dyslokacji 5.20b wyraźnie zaznaczają się fronty rekrystalizacji, przy czym zaobserwować można zarówno pochłanianie materiału o C = 2 przez zrekrystalizowane ziarna o C = 3, jak i wzrost ziaren o C = 4 kosztem ziaren pochodzących z poprzedniego cyklu C = 3. Wykres średniej wielkości ziarna, obliczanej w trakcie symulacji CA, przedstawiono na rysunku Porównując wykresy 5.21 i 5.19a można zauważyć, że istnieje silne powiązanie pomiędzy pikami na krzywej σ f oraz D, szczególnie widoczne dla pierwszego maksimum na krzywej naprężenia uplastyczniającego. Na rysunku 5.21 zaznaczono krytyczną wartość D 0 /2, wynikającą z kryterium Sakai. Uzyskana w obliczeniach średnia wielkość ziarna we wszystkich punktach większa jest od wartości D 0 /2, co oznacza, że kryterium to jest spełnione. Ogólny trend spadku średniej wielkości ziarna, obserwowany na rysunku 5.21, pozornie wskazuje na postępujące rozdrobnienie ziarna. Tymczasem oscylacyjny charakter krzywej naprężenia uplastyczniającego często stowarzyszony jest z rozrostem ziarna [4]. Model CAFE daje możliwość przeanalizowania w trakcie odkształcenia w dowolnym punkcie całkowania Gaussa nie tylko średniej wielkości ziarna, ale także 114
127 5.4. Analiza jakościowa modelu CAFE rozkładu klas wielkości ziarna. Pozwala to na pełniejsze zobrazowanie zmian zachodzących w mikrostrukturze. Dla reprezentatywnego punktu, wykorzystywanego we wcześniejszej części podrozdziału, wykreślono rozkłady wielkości ziarna w wybranych odkształceniach (rysunek 5.22). Na rysunku 5.22d przedstawiono rozkład wielkości ziarna pod koniec odkształcenia. Uzyskana mikrostruktura zawiera dużą liczbę ziaren małych i średnich, jednakże obserwowane są także wystąpienia ziaren większych, niż w mikrostrukturze początkowej (rysunek 5.22a). Pojawienie się dużych ziaren w mikrostrukturze jest powiązane z końcem pierwszego piku na krzywej naprężenia uplastyczniającego, przedstawionej na rysunku 5.19a. Rozkład wielkości ziarna dla odpowiadającemu mu odkształcenia ε = 0.3 przedstawiono na rysunku 5.22b. Dla dalszego odkształcenia (rys. 5.22c obserwowany jest wzrost liczby małych i średnich ziaren, jednak w mikrostrukturze obecne są także duże ziarna. Kolejnym wnioskiem z łącznej analizy rysunków 5.22 i 5.19a jest, że w kolejnych cyklach rekrystalizacji duże ziarna są stale odbudowywane i pochłaniane przez kolejne wzrastające ziarna. Stan ten jest dynamiczny i powstaje w trakcie postępu DRX oraz w jego wyniku. Początek każdego cyklu jest poprzedzony wzrostem ziaren, powstałych w cyklu poprzednim. Uzyskane duże ziarna są niestabilne i zostają zastąpione w trakcie kolejnych cykli. Uzupełniony model pozwala na zliczanie w każdym kroku pojawiających się w siatce obliczeniowej zarodków oraz komórek, które zostały przyłączone do wzrastających ziaren. Na rysunku 5.23 przedstawiono porównanie liczby komórek-zarodków i komórek przyłączonych. Druga z tych wielkości pośrednio informuje o prędkości wzrostu ziaren. Liczba komórek przyłączanych dominuje co do wartości nad liczbą zarodków. Obserwowana jest zależność ujemnie skorelowana pomiędzy wzrostem ziaren i zarodkowaniem. Zarówno wzrost jak i zarodkowanie mają charakter wielopikowy, przy czym wykres liczby zarodków cechuje się mniejszą regularnością. Analizując łącznie wykres 5.23 oraz rysunek 5.18 można zauważyć, że minima i maksima na krzywej wyrażającej liczbę komórek przyłączanych następują z niewielkim przesunięciem w prawo względem odpowiednich ekstremów na krzywej naprężenia uplastyczniającego. Wskazuje to, że efekt szybkiego wzrostu zrekrystalizowanych ziaren oraz późniejszego zahamowania wzrostu przenosi się z opóźnieniem na uzyskiwaną wartość σ f. Według informacji podanych w pracy [4], występowanie kolejnych cykli na krzywej σ f powiązane jest z cykliczną zmianą prędkości wzrostu ziaren. Obecność widocznych na rysunku 5.23 wyraźnych oscylacji krzywej, wyobrażającej liczbę przyłączanych komórek, znajduje więc częściowe potwierdzenie w obserwacjach doświadczalnych. Opracowany model CA służy w MES do obliczania naprężenia uplastyczniają- 115
128 5.4. Analiza jakościowa modelu CAFE (a) (b) (c) (d) Rysunek 5.22: Rozkłady wielkości ziarna dla wielopikowej krzywej naprężenia uplastyczniającego w wybranych odkształceniach: (a) ε = 0, (b) ε = 0.3, (c) ε = 0.4, (d) ε =
129 5.4. Analiza jakościowa modelu CAFE Rysunek 5.23: Uzyskana w symulacji CA liczba zarodków i komórek przyłączonych do wzrastających ziaren w kolejnych krokach czasowych (przypadek wielopikowej krzywej σ f ) (a) (b) Rysunek 5.24: Wyniki makroskopowe rozwiązania CAFE: (a) porównanie naprężenia średniego, uzyskanego z rozwiązania CAFE i naprężenia uplastyczniającego, obliczanego metodą CA dla nominalnych warunków odkształcenia, (b) siła nacisku narzędzia, uzyskana z rozwiązania CAFE (przypadek wielopikowej krzywej σ f ) 117
130 5.4. Analiza jakościowa modelu CAFE cego, które może odbiegać od naprężeń średnich, obliczanych przez CAFE. Wyniki uzyskane z połączonego, wieloskalowego modelu CAFE zaprezentowano na rysunku Na rysunku 5.24a przedstawiono porównanie naprężeń średnich z MES i naprężenia uplastyczniającego, obliczanego dla stałej nominalnej temperatury i prędkości odkształcenia w pierwszym etapie obliczeń. Obserwowane odchylenia wynikają z pominięcia w działającej oddzielnie symulacji CA zmienności temperatury i prędkości odkształcenia w trakcie procesu. Uproszczenia tego nie wprowadza model CAFE. Wartości sił nacisku w zależności od przemieszczenia narzędzia d, otrzymane z modelu CAFE, przedstawiono na rysunku 5.24b. Przedstawione wyniki potwierdzają zdolność modelu do odtwarzania makroskopowego zachowania symulowanego układu Jednopikowa krzywa naprężenia uplastyczniającego W modelu skali mikro wykorzystano reprezentację mikrostruktury, wygenerowaną za pomocą algorytmu swobodnego wzrostu ziaren. Przyjęto siatkę obliczeniową komórek. Przeprowadzono symulację spęczania, z założeniem warunków podanych w podrozdziale 5.4. Na rysunku 5.25 przedstawiono ułamki rekrystalizacji, przynależne do kolejnych cykli rekrystalizacji. Krzywe x C1,..., x C14 otrzymano przez zliczanie komórek, posiadających odpowiednie wartości zmiennej C. Zaobserwować można pojawienie się ziaren przynależnych do drugiego cyklu w krótkim czasie po rozpoczęciu zarodkowania cyklu pierwszego. Wpływ rozpoczęcia cyklu C2 na przebieg krzywej x C1, a także rozpoczęcia cyklu C3 na poprzednio zachodzący proces rekrystalizacji, widoczny jest przez zmianę nachylenia krzywych x C1 i x C2, obserwowaną przy rozpoczęciu nowego cyklu. Wskazuje to na hamowanie wzrostu ziaren przez ziarna powstałe w kolejnych cyklach oraz na konkurencję pomiędzy procesami zarodkowania i wzrostu. Współzawodnictwo, zachodzące pomiędzy wieloma cyklami równocześnie, utrzymuje się do piątego cyklu i odkształcenia ε 0.4, powyżej którego w siatce obliczeniowej obserwowane są ziarna przynależne do trzech kolejnych cykli. Na rysunku 5.26a przestawiono obliczone przez model CA zastępcze ułamki rekrystalizacji oraz wykres naprężenia uplastyczniającego. Można zauważyć, że kolejne cykle, reprezentowane przez zastępcze ułamki rekrystalizacji, rozpoczynają się w pobliżu punktu przegięcia na krzywej opisującej cykl poprzedni. Widoczne jest więc nakładanie się kolejnych cykli rekrystalizacji, prowadzących do zajścia rekrystalizacji w całej objętości materiału, reprezentowanego przez siatkę CA. Dla porównania, na rysunku 5.26b przedstawiono krzywą naprężenia uplastyczniającego i wykres ułamków rekrystalizacji, zaczerpnięte z pracy [71]. W przypadku 118
131 5.4. Analiza jakościowa modelu CAFE Rysunek 5.25: Ułamki rekrystalizacji przynależne do kolejnych cykli rekrystalizacji dla jednopikowej krzywej naprężenia uplastyczniającego. Linią ciągłą oznaczono całkowity ułamek rekrystalizacji x rec (a) (b) Rysunek 5.26: Naprężenie uplastyczniające oraz zastępczy ułamek rekrystalizacji: (a) uzyskany z modelu CAFE, (b) na podstawie pracy [71] (przypadek jednopikowej krzywej σ f ) 119
132 5.4. Analiza jakościowa modelu CAFE wyników uzyskanych z modelu CAFE można wyraźnie zauważyć początek wpływu DRX na krzywą σ f, zaznaczony jako x rec = 0.05, który nie pokrywa się z odkształceniem ε p. Zgodnie z oczekiwaniami, rozpoczęcie rekrystalizacji nie znajduje natychmiastowego odbicia w naprężeniu uplastyczniającym. Zajście rekrystalizacji w niemal całym materiale, oznaczone na rysunkach 5.26a i 5.26b jako x rec = 0.98, przypada pod koniec piku na krzywej naprężenia uplastyczniającego. Stan ustalony na krzywej σ f w obu przypadkach składa się z oscylacji o niewielkiej amplitudzie, przy czym ich regularność jest mniejsza na rysunku 5.26a. Mniejsza jest także regularność wykresów ułamków rekrystalizacji, choć w obu przypadkach cykle rekrystalizacji nachodzą na poprzedzające, a rozpoczęcie każdego przypada w przybliżeniu w punkcie przegięcia poprzedniego. Przebieg zmian średniej wielkości ziarna w trakcie procesu przedstawiono na rysunku 5.27a. Uzyskana na końcu procesu wielkość ziarna jest mniejsza od wartości D 0 /2, zaznaczonej niebieską linią. Oznacza to, że dla jednopikowej krzywej naprężenia model CAFE poprawnie oddaje kryterium strukturalne Sakai. Ustalona wielkość ziarna, zbliżona do końcowej, uzyskiwana jest dla odkształcenia powyżej 0.4. Dla odkształceń od ε 0.1 do ε 0.25 zachodzi bardzo szybka zmiana wielkości ziarna. Dalsze odkształcenie do ε = 0.4 powoduje niewielki wzrost średniej wielkości ziarna, do wartości w przybliżeniu ustalonej. Wyraźne jest powiązanie pomiędzy ustaleniem wielkości ziarna i początkiem stanu ustalonego na krzywej naprężenia uplastyczniającego. Obserwowana na rysunku 5.25 regularność występowania kolejnych cykli powyżej ε = 0.4 oraz zmniejszenie efektu konkurencji między cyklami może wynikać z rozdrobnienia ziarna. Zmiany rozkładu wielkości ziarna w wybranych odkształceniach przedstawiono na rysunkach 5.27b f. W porównaniu z rozkładem wielkości ziarna w mikrostrukturze początkowej (rys. 5.27b), na rysunku 5.27c obserwowana jest duża liczba ziaren małych i bardzo małych, jednak ziarna duże i średnie pozostają obecne w mikrostrukturze. Oznacza to intensywne zarodkowanie oraz szybki wzrost nowych ziaren. W wyniku szybkiego zarodkowania i wzrostu duże ziarna w większości zanikają w miarę odkształcenia, co widoczne jest na rysunku 5.27d. Przy odkształceniu ε = 0.3 całość materiału uległa rekrystalizacji, oraz następuje duże rozdrobnienie ziarna w porównaniu z mikrostrukturą początkową. Rezultatem rozrostu zarodków jest rozbudowa ziaren i ustalenie wielkości ziarna dla odkształceń powyżej ε = 0.4 do finalnej mikrostruktury, przedstawionej na rysunku 5.27f. Z analizy rysunku 5.27a oraz porównania wykresów 5.27e i 5.27f można wnioskować, że uzyskana mikrostruktura końcowa zawiera ziarna większe, niż dla odkształcenia odpowiadającego końcowi piku na krzywej naprężenia uplastyczniającego. 120
133 5.4. Analiza jakościowa modelu CAFE (a) (b) (c) (d) (e) (f) Rysunek 5.27: Zmiana wielkości ziarna w trakcie odkształcenia dla jednopikowej krzywej naprężenia uplastyczniającego: (a) średnia wielkość ziarna; rozkłady wielkości ziarna przy wybranych odkształceniach: (b) ε = 0, (c) ε = 0.15, (d) ε = 0.2, (e) ε = 0.3, (f) ε =
134 5.4. Analiza jakościowa modelu CAFE Rysunek 5.28: Uzyskana w symulacji CA liczba zarodków i komórek przyłączonych do wzrastających ziaren w kolejnych krokach czasowych (przypadek jednopikowej krzywej σ f ) Na rysunku 5.28 przedstawiono porównanie liczby komórek-zarodków i komórek przyłączonych w kolejnych krokach podczas procesu. Najintensywniejsze zarodkowanie obserwowane jest dla odkształceń z zakresu ε (0.2, 0.25). Z kolei dla liczby komórek przyłączonych, informującej pośrednio o prędkości wzrostu, tendencja wzrostowa utrzymuje się do odkształcenia ε 0.35, po czym następują liczne i nieregularne oscylacje. Można jednak stwierdzić, że dla odkształceń powyżej ε = 0.4 liczba powstających zarodków oraz liczba komórek przyłączanych znajdują się w stanie dynamicznie ustalonym. W przeciwieństwie do analogicznego wykresu 5.23 na stronie 117, trudne jest odnalezienie wyraźnej korelacji pomiędzy liczbą zarodków i liczbą przyłączanych komórek. Naprężenia średnie, uzyskane z modelu CAFE, porównano z wykresem naprężenia uplastyczniającego, obliczonego dla warunków nominalnych procesu przez model CA (rysunek 5.29a). Na rysunku 5.29b przedstawiono wartości sił nacisku, uzyskanych na narzędziu w trakcie symulacji procesu. Otrzymany charakter wykresu siły spęczania zgodny jest ze znanym powszechnie z literatury, i uzyskiwanym doświadczalnie dla niektórych materiałów, podlegających DRX w trakcie odkształcenia na gorąco Podsumowanie Zaprezentowane działanie modelu CAFE wskazuje na jego duży potencjał w wyjaśnianiu mechanizmu zjawisk, składających się na proces dynamicznej rekrysta- 122
135 5.4. Analiza jakościowa modelu CAFE (a) (b) Rysunek 5.29: Wyniki makroskopowe rozwiązania CAFE: (a) porównanie naprężenia średniego, uzyskanego z rozwiązania CAFE i naprężenia uplastyczniającego, obliczanego metodą CA dla nominalnych warunków odkształcenia, (b) siła nacisku narzędzia, uzyskana z rozwiązania CAFE lizacji. Rozróżnialne są pojedyncze cykle dynamicznej rekrystalizacji, obserwować można także przemieszczanie się frontów rekrystalizacji w symulowanym materiale. Możliwe jest również analizowanie zmian rozkładu wielkości ziarna, która nie zawsze jest dobrze odzwierciedlana przez średni rozmiar ziarna. W porównaniu z modelami fenomenologicznymi, w których miarą postępu DRX jest ułamek rekrystalizacji, prezentowany model wprowadza znaczne usprawnienia. Ułamek objętości materiału zrekrystalizowanego osiąga wartość jedności dla stosunkowo niskich odkształceń, chociaż proces DRX zachodzi stale dla większych odkształceń. Cząstkowe i zastępcze ułamki rekrystalizacji, uzyskane z modelu CAFE, mogą służyć bardziej adekwatnemu opisowi zmian zachodzących w trakcie DRX. Należy także podkreślić, że obliczone przez model CAFE rozkłady wielkości ziarna i średnie wielkości ziarna wynikają bezpośrednio z dynamicznych zmian w mikrostrukturze, reprezentowanej w domenie obliczeniowej, a nie są uzyskiwane z zależności empirycznych lub półempirycznych. Uzyskane w wyniku obliczeń CAFE makroskopowe naprężenia średnie (rysunki 5.24 na stronie 117 i 5.29) są zbliżone do wartości σ f, otrzymanych z modelu CA. Jednak istniejące różnice wskazują, że pominięcie względnie dużej objętości próbki oraz oddziaływania warunków procesu w modelu CA ma wpływ na uzyskane wyniki. Źródła rozbieżności można upatrywać w niejednorodności pól odkształceń, prędkości odkształcenia, naprężenia i temperatury w próbce. Pełny model CAFE pozwala na symulację stosunkowo dużych próbek, uwzględniając lokalizację niejednorodności oraz ich wpływ na obliczone na podstawie modelu mikro naprężenie σ f. Uzyskane z modelu CAFE naprężenia średnie są wynikiem złożenia różnych zależności σ f, obli- 123
136 5.5. Weryfikacja modelu czanych przez model mikro w punktach całkowania Gaussa na podstawie lokalnych wartości temperatury i prędkości odkształcenia. We wcześniejszych pracach, np. [21, 22, 35, 57, 136], naprężenie σ f, uzyskane z modelu CA było traktowane jako porównywalne z doświadczalnymi. Wyniki uzyskane w niniejszej pracy wskazują, że wynik symulacji CA dla kilkudziesięciu lub kilkuset ziaren nie może być bezpośrednio odnoszony do danych doświadczalnych, pochodzących z odkształcenia próbki o co najmniej dwa rzędy wielkości większej. Przewidywane przez model skali mikro rozkłady wielkości ziarna obciążone są błędem systematycznym, powodującym przeszacowanie udziału ziaren bardzo małych. Wiąże się to bezpośrednio z założeniem dokonanym w modelu, że ziarno musi się składać z co najmniej jednej komórki CA. Podczas wzrostu ziaren w obliczeniach przyjmowane są wartości cząstkowe powierzchni, przypisanej do pojedynczej komórki (równanie (4.62)). Natomiast w algorytmie zarodkowania zakłada się, że komórki CA są niepodzielne. Oznacza to, że efekt przeszacowania udziału ziaren małych jest najbardziej widoczny w trakcie intensywnego zarodkowania. Kolejnym czynnikiem, sprzyjającym nasileniu się błędu, jest rzadka siatka obliczeniowa. W przypadku siatek gęstych, powierzchnia pojedynczej komórki CA może być porównywalna z rozmiarem korzystnie usytuowanego zarodka. Pomimo podanych wyżej zastrzeżeń, w obu przypadkach omawianych w rozdziałach i 5.4.2, uzyskano średnie wielkości ziarna zgodne z przewidywanymi przez kryterium Sakai. Można więc podsumować, że artefakt metody, prowadzący do przeszacowania udziału zarodków w strukturze, powinien być uwzględniany, jednak nie prowadzi do poważnego zaburzenia uzyskiwanych wyników. 5.5 Weryfikacja modelu Zastosowanie analizy odwrotnej do weryfikacji modelu CAFE Ze względu na stosunkowo niewielką dostępność w literaturze dokładnych wartości parametrów materiałowych, wykorzystywanych w opracowanym modelu CAFE, podjęto próbę ich identyfikacji za pomocą analizy odwrotnej (ang. inverse analysis), nazywanej też metodą inverse. Motywacją do zastosowania obliczeń odwrotnych jest także wprowadzenie w modelu szeregu parametrów, nie posiadających bezpośredniego znaczenia fizycznego, np. współczynników kontrolujących algorytm zarodkowania lub współczynnika proporcjonalności pomiędzy wielkością ziarna i średnią drogą swobodną dyslokacji. Do utworzenia punktu startowego, zawierającego przybliżenia 124
137 5.5. Weryfikacja modelu identyfikowanych parametrów modelu, wykorzystano dostępne dane pochodzące z literatury. W drodze obliczeń odwrotnych uzyskano parametry, dla których opracowany model w dobry sposób przybliża doświadczalnie obserwowane zachowanie materiału. Celem analizy odwrotnej jest wyznaczenie, na podstawie wyników otrzymanych doświadczalnie, wartości parametrów opisujących model rozważanego procesu oraz model warunków brzegowych, dających najlepszą zgodność między wynikami pomiarów i obliczeń. Zastosowana w rozprawie procedura analizy odwrotnej bazuje na wykorzystaniu technik optymalizacyjnych, rozwiązanie to opisano szczegółowo m. in. w pracach [32, 137, 139, 140]. W algorytmie obliczeń odwrotnych wyróżnić można trzy główne części: doświadczenie, którego wyniki są podstawą do budowy i obliczenia funkcji celu dla metody optymalizacji, rozwiązanie zadania bezpośredniego, symulującego doświadczenie, procedurę optymalizacyjną, pozwalającą na identyfikację poszukiwanych parametrów poprzez minimalizację zdefiniowanej funkcji celu. Wynik doświadczenia (procesu) F, oznaczany jako d e, zależny jest od znanych warunków procesu, takich jak temperatura lub prędkość odkształcenia, oraz od stanu materiału. Wynik rozwiązania zadania bezpośredniego, będącego symulacją procesu F, zapisać można jako: d c = F (X, P) (5.4) gdzie: X wektor parametrów modelu, symulującego proces F, P wektor warunków procesu. W przypadku analizy odwrotnej nieznany jest wektor parametrów procesu X, będący przedmiotem identyfikacji, natomiast znane są wektory P i d e. Procedura optymalizacyjna ma na celu zminimalizowanie funkcjonału błędu, zwykle zdefiniowanego jako odległość pomiędzy N wynikami doświadczenia i obliczeń symulujących doświadczenie: Ξ = N d e i d c i (5.5) i=0 Sposób prowadzenia obliczeń odwrotnych uzależniony jest w dużej mierze od rodzaju dostępnych danych pomiarowych oraz możliwych parametrów uzyskiwanych na wyjściach identyfikowanego modelu. Również konkretna postać funkcjonału celu Ξ w równaniu (5.5), służącego porównaniu danych doświadczalnych i obliczonych, zależna jest od rodzaju i reprezentacji danych. 125
138 5.5. Weryfikacja modelu W przeprowadzonych obliczeniach odwrotnych skorzystano z oprogramowania własnego, wykorzystywanego już we wcześniejszych pracach opublikowanych z udziałem autora, m. in. w [32, 137]. Program ten, o nazwie abaqopt, umożliwia rozwiązanie problemu odwrotnego, sformułowanego jako zadanie optymalizacji wielokryterialnej, za pomocą transformacji wektora kryteriów do skalarnej funkcji celu. Sformułowanie wielokryterialne jest bardzo ogólne, a jego przypadkiem szczególnym jest poszukiwanie minimum dla pojedynczego kryterium oceny rozwiązania. Inną zaletą wykorzystania sformułowania wielokryterialnego jest możliwość jawnego uwzględnienia i wykrywania współzależności pomiędzy kryteriami, w tym ewentualnych zależności konfliktowych. Szczegóły zastosowanego podejścia oraz elementy wykorzystywanego w nim aparatu matematycznego omówiono w pracy [37]. Dla każdej mierzonej cechy możliwe jest utworzenie oddzielnego kryterium oceny, a następnie zebranie zdefiniowanych kryteriów w wektor kryteriów Φ. Wektor ten tworzony jest na podstawie N doświadczeń (pomiarów), przeprowadzonych dla każdej z M próbek. Wszystkie składowe wektora kryteriów zależne są od wektora parametrów modelu procesu i warunków procesu. W dalszej części pracy przyjęto skrócony zapis φ j i (X, P) = φ j i. Wektor kryteriów przyjmuje postać: Φ(X, P) = { φ 1 1,..., φ N 1,..., φ 1 i,..., φ j i,... φ N i,..., φ 1 M,..., φ N M } (5.6) gdzie: i numer próbki, j numer doświadczenia. Program abaqopt pozwala na zastosowanie różnych strategii skalaryzacji wektora kryteriów (łączenia składowych φ j i w pojedynczą wartość skalarną) i wyznaczania funkcji celu Ξ, m. in. za pomocą średniej ważonej oraz tzw. strategii minimaks. Do poszukiwania minimum funkcji celu w programie wykorzystywana jest metoda sympleksów, możliwe jest także zastosowanie metod gradientowych i algorytmów ewolucyjnych. Jednocześnie z poszukiwaniem minimum funkcji celu prowadzona jest konstrukcja zbioru Pareto. Przeprowadzenie obliczeń odwrotnych dla wieloskalowego modelu CAFE wymaga wzięcia pod uwagę danych pomiarowych, opisujących mikrostrukturę odkształcanego materiału. Wskazane jest jak najszersze uwzględnienie tego opisu, stosownie do możliwości oferowanych przez model CAFE i dostępności danych doświadczalnych. Najbardziej elementarną charakterystyką mikrostruktury jest średnia wielkość ziarna. Wprowadzenie do metody obliczeń odwrotnych danych, opisujących stan materiału w skali mikro, rozszerza jej dotychczasowy algorytm, stosowany w identyfikacji parametrów krzywych płynięcia materiału. Schemat rozszerzonego algorytmu obliczeń odwrotnych, wyszczególniający najistotniejsze kroki procedury oraz wskazujący źródła danych, przedstawiono na rysunku Zgodnie z tym schematem propo- 126
139 5.5. Weryfikacja modelu Rysunek 5.30: Schemat rozszerzonego algorytmu obliczeń odwrotnych. Oznaczenia: prostokąty źródła danych, owale procesy przetwarzania danych, strzałki kierunek przepływu danych. Liczbami oznaczono kolejne kroki obliczeń odwrotnych. Prostokąty narysowane linią przerywaną zawierają objaśnienia nowane jest wykorzystanie trzech kolejnych kroków metody obliczeń odwrotnych, oznaczonych na rysunku owalami. W pierwszym i trzecim kroku wykorzystywane są dane o siłach zmierzonych na narzędziu. Z kolei w kroku drugim i trzecim identyfikacja parametrów modelu następuje w oparciu m. in. o dane opisujące mikrostrukturę, przede wszystkim pod kątem wielkości ziarna. Pierwszy etap obliczeń dostarcza zależność σ f od odkształcenia, zapisaną w postaci tabelarycznej, a prowadzony jest w sposób opisany w pracach [32, ]. Przeprowadzenie obliczeń odwrotnych dla modelu skali mikro bazuje na wyznaczonych na postawie doświadczenia naprężeniu uplastyczniającym oraz parametrach charakteryzujących mikrostrukturę. Wymagane w tym etapie σ f uzyskiwane jest na podstawie obliczeń odwrotnych, prowadzonych w etapie pierwszym, lub z danych literaturowych. W tym ostatnim przypadku należy zwrócić uwagę na sposób wyznaczania naprężenia uplastyczniającego w pracy źródłowej. Identyfikacja parametrów modelu skali mikro Jako podstawową cechę materiału, wyznaczaną na podstawie doświadczenia i którą powinien poprawnie odtwarzać model CA, przyjęto naprężenie uplastyczniające σ f. Średnia wielkość ziarna w próbce jest drugą cechą, mierzoną doświadczalnie i obliczaną przez model skali mikro. Bazując na porównaniu tych cech, pochodzących z pomiaru i obliczonych przez model, sformułowano następujące kryteria oceny 127
140 5.5. Weryfikacja modelu rozwiązania: φ 1 i = 1 ( ) N σf c j σ e 2 f j (5.7) N j=1 φ 2 Di c Di e i = Di e σ f e j (5.8) gdzie: i numer próbki, j numer punktu pomiarowego, N liczba punktów pomiarowych w doświadczeniu, σ f e naprężenie uplastyczniające, wyznaczone na podstawie doświadczenia, σ f c naprężenie uplastyczniające obliczone przez model CA, D e i średnia średnica ziarna uzyskana w doświadczeniu, D c i średnia średnica ziarna uzyskana w symulacji CA doświadczenia. Definicja kryterium oceny rozwiązania, powiązanego z wielkością ziarna, zależna jest od dostępnych danych doświadczalnych. Równanie (5.8) opisuje jedno z najprostszych kryteriów. Wprowadzenie podziału wielkości ziarna na klasy D j i zmierzenie dla każdej z nich częstości względnej występowania wielkości ziana, oznaczanej jako f j, pozwala na bardziej dokładną ocenę zgodności pomiędzy obliczoną i zmierzoną wielkością ziarna: φ 2 i = 1 ( M D e j fj e Djf c c ) 2 j (5.9) M Djf e j e j=1 gdzie: M liczba klas wielkości ziarna, D e j, D c j j-ta klasa wielkości ziarna, odpowiednio zmierzonego w doświadczeniu i obliczonego, f e j, f c j względna liczność wystąpień w j-tej klasie wielkości ziarna, odpowiednio uzyskana doświadczalnie i w drodze obliczeń CA. Parametry występujące w równaniu (4.29) na stronie 62 są kluczowe dla działania symulacji CA procesu dynamicznej rekrystalizacji. Możliwe jest ich przybliżone oszacowanie poprzez aproksymację równania (4.32) dla wartości ρ odpowiadających niewielkim odkształceniom (np. ε < 0.2ε p ), przy których dominującymi procesami w materiale są umocnienie i zdrowienie dynamiczne. Gęstość dyslokacji w materiale można wyliczyć, przekształcając równanie (4.70). Zarówno naprężenie uplastyczniające i średnica ziarna, uzyskane z modelu skali mikro, obliczane są dla nominalnych warunków procesu. Należy pamiętać, że σ f wyznaczone na podstawie standardowej próby plastometrycznej jest wynikiem otrzymanym dla stosunkowo dużej próbki. W rozdziale 5.4 wskazano, że naprężenia, wyznaczone z uwzględnieniem niejednorodności T, ε, σ i ε, obecnych w próbce, mogą odbiegać od obliczonych z przyjęciem warunków nominalnych. Dlatego wyznaczone 128
141 5.5. Weryfikacja modelu na tym etapie parametry modelu CA należy traktować z dużą dozą ostrożności, jako zgrubnie oszacowane. Identyfikacja parametrów modelu CAFE Wyznaczenia parametrów połączonego modelu wieloskalowego CAFE prowadzone jest na podstawie pochodzących z doświadczenia sił nacisku, zmierzonych na narzędziu, oraz wyników badań metalograficznych przeprowadzonych po zakończeniu spęczania. Ponownie zastosowano sformułowanie wielokryterialne, jednak w części związanej z ujęciem mechanicznym odkształcenia, jako wartości mierzone przyjęto siły nacisku w funkcji przemieszczenia narzędzia: φ 1 i = 1 ( N F c j F e ) 2 j (5.10) N j=1 gdzie: i numer próbki, j numer punktu pomiarowego, F e siła zmierzona, F c siła obliczona przez model CAFE, Kryterium powiązane z analizą stanu mikrostruktury w pojedynczym doświadczeniu można wyrazić za pomocą średniej wielkości ziarna w próbce: F e j φ 2 Di c Di e i = Di e (5.11) gdzie: i numer próbki, D e średnia średnica ziarna uzyskana w doświadczeniu, D c średnia średnica ziarna uzyskana w symulacji CAFE doświadczenia. Średnia średnica ziarna, otrzymana po zakończeniu symulacji CAFE procesu spęczania, obliczana jest jako średnia ze średnich wielkości ziarna, otrzymanych ze wszystkich symulacji CA prowadzonych w N G punktach całkowania Gaussa: D c = 1 N G N G D j (5.12) j=1 gdzie: D j średnia średnica zastępcza ziarna, obliczona w symulacji CA powiązanej z j-tym punktem całkowania Gaussa. Model CAFE umożliwia także obliczenie rozkładu wielkości ziarna w całej próbce lub w jej wybranych punktach. Zakładając, że pomiar częstości występowania klasy wielkości ziarna, uzyskany z badań metalograficznych, jest reprezentatywny dla całej próbki, można przeprowadzić porównanie rozkładu wielkości ziarna za pomocą równania (5.9). Niezbędne jest wówczas obliczenie fj c na podstawie wyniku symulacji CAFE, a więc biorąc pod uwagę reprezentacje mikrostruktury we wszystkich 129
142 5.5. Weryfikacja modelu siatkach CA, przyporządkowanych do punktów całkowania w MES. Wykorzystywana w równaniu (5.9) względna liczność wystąpień dla każdej klasy wielkości ziarna obliczana jest na zgodnie ze wzorem: f c j = N G kj i i=1 M N G kj i j=1 i=1 (5.13) gdzie: i indeks symulacji CA w punkcie całkowania w siatce MES, N G liczba symulacji CA, M liczba klas wielkości ziarna, kj i liczność bezwzględna wystąpień j-tej klasy wielkości ziarna w symulacji o indeksie i. Jako punkt startowy analizy odwrotnej modelu CAFE przyjmuje się wektor X o składowych oszacowanych w wyniku identyfikacji parametrów modelu skali mikro Weryfikacja danymi literaturowymi Miedź należy do grupy materiałów, w których dynamiczna rekrystalizacja zachodzi w stosunkowo szerokim zakresie temperatury. Uzyskiwane w próbach plastometrycznych wykresy naprężenia uplastyczniającego w zależności od warunków prowadzenia procesu mogą zawierać jedno lub wiele maksimów. Z tego względu materiał ten dobrze nadaje się do weryfikacji opracowanego modelu CAFE. Zaletą wykorzystania czystej miedzi jako materiału do weryfikacji modelu jest także stosunkowo dobra dostępność parametrów materiałowych. W przypadku pierwiastków czystych (lub z niewielkimi domieszkami) oszacowanie parametrów, istotnych dla modelu CA dynamicznej rekrystalizacji, takich jak ruchliwość i energia granicy ziarna lub gęstość dyslokacji w materiale zrekrystalizowanym, są dostępne w literaturze, np. w pracy [52]. Obszerne badania doświadczalne dla technicznie czystej miedzi przeprowadził w swojej rozprawie doktorskiej [26] Fernandez. Z pracy tej zaczerpnięto dla potrzeb oceny działania modelu wybrane wyniki pomiarów naprężenia uplastyczniającego oraz wielkości ziarna. Podany w dalszej części podrozdziału opis doświadczeń oraz ich wyniki pochodzą z pracy [26]. Z technicznie czystej miedzi rafinowanej, o składzie podanym w tabeli 5.3, wykonano próbki walcowe o wymiarach h = 15 mm, φ = 10 mm. W wyniku wyżarzania ujednolicającego, prowadzonego w temperaturze 950 C, uzyskano ziarno początkowe o przeciętnej średnicy zastępczej D 0 = 637 µm. Próbki spęczano w zadanej temperaturze i przy stałej prędkości odkształcenia. Spęczanie wykonano na elektromechanicznym urządzeniu Instron Jako smar pomiędzy próbką i narzędziem wykorzystano azotek boru. Po zakończeniu spęczania 130
143 5.5. Weryfikacja modelu Tabela 5.3: Skład chemiczny badanej miedzi rafinowanej o technicznej czystości 99.94% Cu, wyrażony w ppm (wg [26]) pierwiastek P Sn Pb Ni Ag S Fe Zn O Sb ppm pierwiastek As Te Cd Se Si Bi Co Mn Cr Mg ppm Tabela 5.4: Wybrane do analizy warunki procesu (temperatura T, prędkość odkształcenia ε) oraz średnica ziarna po zakończeniu procesu, uzyskane w doświadczeniu (wg [26]) T, C ε, s 1 D, µm próbki zamrażano, a następnie przeprowadzono badania metalograficzne. Szczegółowy opis przygotowania próbek oraz procedury doświadczalnej podano w pracy [26]. Wybrane do analizy w niniejszej pracy warunki procesu oraz uzyskane końcowe średnie rozmiary ziarna zestawiono w tabeli 5.4. Wyznaczone w doświadczeniu wykresy naprężenia uplastyczniającego dla wybranych warunków spęczania przedstawiono na rysunku Za pomocą algorytmu swobodnego wzrostu ziarna, opisanego w rozdziale 4.2.6, przygotowano początkową reprezentację mikrostruktury w siatce komórek CA. Korzystając z równania (4.27) obliczono powierzchnię pojedynczej komórki S u = m 2. W modelu CA ruchliwość granicy wysokokątowej (4.49) wyrażono za pomocą równania (2.12). Do wstępnego oszacowania parametrów równań (4.49) oraz (4.50) wykorzystano dane z pracy [52]. Energię aktywacji ruchliwości granicy ziarna Q przyjęto jako 123 kj/mol, a współczynnik ruchliwości granicy ziarna M 0 = m 3 (sn) 1. Energia wysokokątowej granicy ziarna została przyjęta jako γ m = Jm 2 [52]. Moduł sprężystości poprzecznej µ dla miedzi wynosi 63.4 GPa, długość wektora Burgersa b = nm. W obliczeniach odwrotnych jako dane doświadczalne wykorzystano uzyskane w doświadczeniu wartości naprężenia uplastyczniającego oraz średnie rozmiary ziarna po zakończeniu procesu. Wektor kryteriów oceny rozwiązania sformułowano zgodnie 131
144 5.5. Weryfikacja modelu (a) (b) (c) Rysunek 5.31: Naprężenia uzyskane w wyniku spęczania próbek walcowych, wykonanych z 99.94% Cu, przeprowadzonych w warunkach podanych w tabeli 5.4: (a) T = 750 C, (b) T = 850 C, (c) T = 950 C (wg [26]) Tabela 5.5: Wartości parametrów modelu CA dynamicznej rekrystalizacji, zidentyfikowane dla miedzi w drodze obliczeń odwrotnych k 1 k 2 m Q s, Jmol 1 x q ρ 0, m 2 M 0, m 3 (sn) 1 Q gb, Jmol 1 γ m, Jm 2 A 1 σ 0, Pa z równaniami (5.7) i (5.8): Φ(X, P) = { φ 1 1, φ 2 1,..., φ 1 i, φ 2 i,... φ 1 9, φ 2 9 } (5.14) Algorytm obliczeń odwrotnych uruchamiano wielokrotnie, przyjmując jako punkty startowe różne kombinacje parametrów modelu, w tym wartości losowe. Otrzymane w wyniku analizy odwrotnej parametry modelu CA dynamicznej rekrystalizacji zebrano w tabeli 5.5. Na rysunku 5.32 porównano krzywe naprężenia uplastyczniającego, obliczone modelem CA na podstawie zidentyfikowanych za pomocą metody inverse parametrów z danymi pochodzącymi z pracy [26]. Na rysunku zaznaczono wartości kryteriów optymalizacji, uzyskane dla zestawu parametrów modelu podanego w tabeli 5.5. Analogiczne oznaczenie zastosowano na rysunku 5.33, przedstawiającym porównanie średnich wielkości ziarna zmierzonych doświadczalnie i uzyskanych z modelu skali mikro. Dla większości z analizowanych krzywych naprężenia uplastyczniającego model CA jest w stanie poprawnie przewidzieć położenie pierwszego piku na krzywej naprężenia. Krzywe σ f uzyskane dla małych prędkości odkształce- 132
145 5.5. Weryfikacja modelu (a) (b) (c) Rysunek 5.32: Porównanie naprężenia uplastyczniającego, obliczonego przez model CA na podstawie zidentyfikowanych parametrów (σ c f, symbole otwarte) z naprężeniami wyznaczonymi doświadczalnie w pracy [26] (σ e f, symbole wypełnione): (a) T = 750 C, (b) T = 850 C, (c) T = 950 C. Dla każdej pary wykresów σ e f, σ c f na rysunku zaznaczono wartość kryterium optymalizacji φ 1 i, obliczonego na podstawie równania (5.7) nia składają się z co najmniej dwóch widocznych pików, co jest dobrze odtwarzane w wynikach obliczeń. W większości przypadków odtwarzany jest także oscylacyjny charakter krzywej σ f, chociaż np. dla T = 850 C i ε = 10 3 s 1 (rysunek 5.32b) na obliczonej krzywej σ f pojawiają się oscylacje, które na krzywej doświadczalnej są znacznie mniej intensywne. Z kryterium strukturalnego Sakai wynika, że rozdrobnienie ziarna do D < D 0 /2 pojawia się w przypadku jednopikowej charakterystyki krzywej σ f. Większość uzyskanych krzywych naprężenia uplastyczniającego zawiera drobne oscylacje wokół stanu w przybliżeniu ustalonego, pomimo występowania za pierwszym pikiem kolejnych maksimów. Dlatego na rysunku 5.33, na którym pokazano zależność końcowej wielkości ziarna od temperatury i odkształcenia, obserwowane jest duże rozdrobnienie ziarna. Wyjątkiem jest przypadek T = 950 C i ε = 0.1 s 1, w którym D > D 0 /2. Dla tych warunków odkształcenia na krzywej doświadczalnej obserwowane są jednak wyraźne oscylacje na krzywej σ f, z niewielką tendencją do ich wygaszania. Z kolei na krzywej σ f, uzyskanej z symulacji CA, oscylacje są słabiej zaznaczone i naprężenie uplastyczniające jest bardziej zbliżone do stanu ustalonego, a obliczona wielkość ziana jest mniejsza niż w doświadczeniu. Stosunkowo duże wartości kryteriów φ 1 9 i φ 1 7 są wynikiem niezgodności dla niewielkich odkształceń. Ponieważ równanie (5.7) wprowadza skalowanie składowych kryterium, duże błędy względne uzyskiwane dla ε < ε p, wpływają znacząco na całkowitą wartość kryterium. 133
146 5.5. Weryfikacja modelu Rysunek 5.33: Porównanie średniej wielkości ziarna zmierzonej po zakończeniu doświadczenia (symbole wypełnione) i uzyskanej z modelu CA na podstawie zidentyfikowanych parametrów (symbole otwarte). Dla każdej pary punktów D e, D c zaznaczono wartość kryterium optymalizacji φ 2 i, obliczonego zgodnie z równaniem (5.8) Opracowany model CA DRX stosunkowo dobrze przewiduje powiązanie krzywej naprężenia uplastyczniającego z wielkością ziarna, co obrazuje rysunek Tendencja zmiany wielkości ziarna wraz ze zmianą temperatury i prędkości odkształcenia jest podobna zarówno dla wyników obliczeń i doświadczenia. Charakterystyczne jest, że model CA systematycznie niedoszacowuje wielkość ziarna. Częściowo wynika to z przeszacowania udziału objętości materiału w składających się z pojedynczych komórek CA zarodkach i ziarnach złożonych z kilku komórek CA. Podobny problem zaobserwowano i przedyskutowano w rozdziale Zapewne wpływ mają także inne uproszczenia zakładane w modelu, w tym nieuwzględnienie tworzenia się struktury podziarnowej oraz innych procesów strukturalnych, takich jak bliźniakowanie. Jak wynika z tabeli 5.5, parametry związane z ruchliwością granicy zostały zmienione przez algorytm optymalizacyjny w kierunku zmniejszenia ruchliwości ziarna. Może to świadczyć o przeszacowaniu wartości tych parametrów startowych, zmierzonych dla ultraczystej miedzi, a zastosowanych do symulacji materiału zawierającego 0.05% pierwiastków domieszkowych. Z danych literaturowych wynika, że obecność nawet niewielkich domieszek innych pierwiastków może skutkować zmniejszeniem ruchliwości granic ziaren o 2 3 rzędy wielkości [52]. Uzyskane w wyniku działania algorytmu optymalizacyjnego zmniejszenie ruchliwości granic ziaren może wskazywać na wpływ obecności pierwiastków domieszkowym w badanym roztworze stałym. Wpływ ten zależy od powiązań pomiędzy pierwiastkami domieszkowymi, 134
147 5.5. Weryfikacja modelu a jego kierunek jest trudny do jednoznacznego przewidzenia [135]. Z drugiej strony, wprowadzenie korekty ruchliwości przez metodę optymalizacji może wynikać z prowadzenia trzech spośród procesów w stosunkowo wysokiej temperaturze 950 C, poza zakresem temperatur dla jakich w pracy [52] oszacowano parametry M 0 i Q. Uzyskana w optymalizacji wartość γ m znajduje się w przedziale (0.6, 0.8) Jm 2, co pozostaje w dobrej zgodności z danymi doświadczalnymi dla miedzi, podanymi w pracy [135]. (a) (b) (c) Rysunek 5.34: Siły nacisku w procesie spęczania próbek walcowych, wykonanych z 99.94% Cu, obliczone przez model CAFE na podstawie zidentyfikowanych parametrów modelu CA: (a) T = 750 C, (b) T = 850 C, (c) T = 950 C Wykorzystując otrzymane w drodze obliczeń odwrotnych parametry modelu CA dynamicznej rekrystalizacji, przeprowadzono symulacje CAFE dla warunków odkształcenia, podanych w tabeli 5.4. Na podstawie zdjęć próbek zamieszczonych w pracy [26] ilustrujących ich beczkowatość oraz własnego doświadczenia autora, założono współczynnik tarcia pomiędzy próbką i narzędziem jako m= 0.1. Otrzymane w wyniku obliczeń CAFE wykresy siły nacisku na narzędziu przedstawiono na rysunku Należy zaznaczyć, że uproszczenia przyjęte w modelu CA sprawiają, iż wartości jego parametrów uzyskane w drodze opisanych wyżej obliczeń odwrotnych nie powinny być traktowane jako rzeczywiste parametry opisujące materiał. W rozdziale wskazano, że porównywanie σ f wyznaczonego w próbie plastometrycznej z obliczanym przez model CA dla kilkuset ziaren, obarczone jest błędem, wynikającym m. in. z pominięcia niejednorodności warunków odkształcenia wewnątrz dużej próbki. Ze względu na brak stosownych danych doświadczalnych, w przepro- 135
148 5.5. Weryfikacja modelu wadzonych obliczeniach odwrotnych nie wprowadzono także bardziej złożonego opisu zmian zachodzących w mikrostrukturze oraz jej stanu. Zatem zastosowany algorytm obliczeń odwrotnych w omawianym przypadku powinien być traktowany jako narzędzie aproksymacji. Otrzymane parametry modelu CA skutkują jedynie dobrą zgodnością pomiędzy obliczonymi i zmierzonymi naprężeniami uplastyczniającymi i wielkościami ziarna. Ograniczenie to może jednak być przezwyciężone przez wykorzystanie w obliczeniach odwrotnych bardziej różnorodnych danych pomiarowych, opisujących mikroskopowe zachowanie materiału. Otrzymane rezultaty modelowania stanowią zatem przyczynek do dalszych badań, uwzględniających np. wynikową teksturę materiału oraz rozkład wielkości ziarna w próbce mierzonych na różnych etapach odkształcenia i w wielu wybranych punktach pomiarowych. Podsumowując można stwierdzić, że opracowany model dobrze oddaje powiązanie naprężenia uplastyczniającego z wielkością ziarna. Możliwe jest takie dobranie parametrów modelu CA, że uzyskiwana jest zadowalająca ilościowa zgodność wyników obliczeń z danymi doświadczalnymi Weryfikacja doświadczalna Przedstawione w poprzednim podrozdziale obliczenia przeprowadzono wykorzystując jako dane źródłowe krzywe naprężenia uplastyczniającego i średnią wielkość ziarna w próbce. Krzywe σ f wyznaczane metodami inżynierskimi obarczone są wpływem niejednorodności w objętości próbki temperatury, odkształcenia, umocnienia, prędkości odkształcenia oraz innych parametrów, oddziałujących na odkształcenie próbki [137, 139]. Z kolei oszacowanie rozmiaru ziarna przez wartość średnią także prowadzi do pominięcia różnorodności wielkości poszczególnych ziaren. W dalszej części rozdziału podjęto próbę częściowego wyeliminowania podanych wyżej ograniczeń. W tym celu wykorzystano przedstawiony na rysunku 5.30 na stronie 127 rozszerzony algorytm obliczeń odwrotnych. Dla zweryfikowania działania modelu CAFE przeprowadzono doświadczenia, polegające na ściskaniu na gorąco próbek walcowych, a następnie poddaniu ich analizie metalograficznej. Aby wyznaczyć początkową wielkość ziarna przeprowadzono także badania próbek poddanych wyżarzaniu ujednolicającemu. Doświadczenie Do badań wybrano stal z grupy bainitycznych o oznaczeniu 16NiCrMo13, której skład chemiczny podano w tabeli 5.6. Przygotowanie próbek oraz dalsze procedury badawcze, związane z wykonaniem doświadczeń, przeprowadzono w Instytucie Me- 136
149 5.5. Weryfikacja modelu Tabela 5.6: Skład chemiczny badanej stali 16NiCrMo13 wyrażony w procentach wagowych C Si Mn S P Ni Cr Mo Cu < (a) (b) Rysunek 5.35: Uzyskany w badaniach metalograficznych rozkład wielkości ziarna dla stali 16NiCrMo13: (a) próbka wyżarzona, (b) próbka odkształcona do ε = 0.4 talurgii Żelaza (IMŻ) w Gliwicach. Przygotowano próbki o wymiarach h = 12 mm, φ = 10 mm. Program badawczy obejmował spęczanie próbek do zadanego odkształcenia ε = 0.4 oraz ε = 1.0 na symulatorze termomechanicznym Gleeble Przeprowadzono doświadczenia dla szerokich zakresów temperatury i prędkości odkształcenia, spośród których wybrano do dalszej analizy T = 1150 C i ε = 0.1 s 1. Próbki nagrzewano do temperatury 1150 C z prędkością 3 Cs 1, wygrzewano w tej temperaturze przez 60 s, po czym spęczono do zadanego odkształcenia. Pomiędzy próbką i narzędziem zastosowano jako smar folię tantalową i grafitową. Proces prowadzono w atmosferze ochronnej argonu. Po zakończeniu spęczania próbki chłodzono wodą do temperatury pokojowej. Dla oddzielnej grupy próbek w analogicznych warunkach obróbki cieplnej przeprowadzono wyżarzanie bez odkształcenia. Próbki odkształcone do ε = 0.4 oraz pochodzące z wyżarzania poddano analizie metalograficznej z wykorzystaniem mikroskopii świetlnej. W wyniku wyznaczono średnie wielkości ziarna oraz zliczono występowanie ziaren przynależnych do różnych klas wielkości. Uzyskane względne częstości występowania f klas wielkości przestawiono na rysunku Wyznaczona średnia średnica zastępcza ziarna w próbce wyżarzonej wynosi µm, natomiast w próbce odkształconej µm, zatem obserwowane jest ponaddwukrotne rozdrobnienie ziarna. 137
150 5.5. Weryfikacja modelu Analiza odwrotna Bazując na zmierzonych w trakcie spęczania siłach w funkcji przemieszczenia narzędzia oraz wyznaczonych w badaniach metalograficznych rozkładach klas wielkości ziaren, przeprowadzono opisaną w podrozdziale analizę odwrotną (inverse). Procedurę obliczeń odwrotnych podzielono na trzy etapy: 1. identyfikację naprężenia uplastyczniającego na podstawie siły nacisku zmierzonej w próbie plastometrycznej, 2. identyfikację parametrów modelu CA na podstawie wyznaczonych w poprzednim etapie σ f oraz doświadczalnego rozkładu wielkości ziarna, 3. identyfikację parametrów pełnego modelu CAFE na podstawie zmierzonych w doświadczeniu sił oraz rozkładu wielkości ziarna. Uzyskane doświadczalnie wykresy sił zmierzonych na narzędziu w trakcie spęczania zostały wstępnie przetworzone za pomocą programu Opty axi, opracowanego w Katedrze Informatyki Stosowanej i Modelowania AGH. Program ten umożliwia obróbkę danych, zarejestrowanych przez oprogramowanie symulatora Gleeble 3800, w tym ich filtrację oraz eliminację szumu pomiarowego a także wycięcie właściwych przedziałów ze zbiorów danych pomiarowych. Wstępna analiza odwrotna wyznaczenie naprężenia uplastyczniającego W pierwszym etapie obliczeń wyznaczono krzywą naprężenia uplastyczniającego, bazując na sile spęczania zarejestrowanej w trakcie doświadczenia. Program symulacyjny MES comp axi, implementujący opisany w rozdziale 4.1 model termomechaniczny, udostępnia moduł obliczeń odwrotnych. Wykorzystywane w nim jest sformułowanie problemu odwrotnego jako zagadnienia optymalizacji. Zgodność sił uzyskanych doświadczalnie i obliczonych na podstawie identyfikowanego naprężenia uplastyczniającego jest podstawowym kryterium, używanym w budowie funkcji celu. Na podstawie zmierzonej beczkowatości próbki po spęczeniu wyznaczono współczynnik tarcia m = Szczegółowy opis algorytmu obliczeń odwrotnych, służącego identyfikacji naprężenia uplastyczniającego i współczynników modelu tarcia, podano m. in. w pracach [137, 139]. Na rysunku 5.36a przedstawiono wyznaczone w drodze obliczeń odwrotnych naprężenia uplastyczniające dla analizowanych warunków procesu. Porównanie sił spęczania, uzyskanych z symulacji MES wykorzystującej zidentyfikowaną krzywą σ f z siłami otrzymanymi doświadczalnie zamieszczono na rysunku 5.36b. Otrzymana 138
151 5.5. Weryfikacja modelu (a) (b) Rysunek 5.36: Wyniki pierwszego etapu obliczeń odwrotnych dla badanej stali: (a) wyznaczone naprężenie uplastyczniające σ f, (b) porównanie sił zmierzonych w doświadczeniu (symbole wypełnione) i obliczonych MES na podstawie wyznaczonego σ f (symbole otwarte), T = 1150 C, ε = 0.1 s 1 wysoka zgodność wyników doświadczenia i obliczeń wskazuje na poprawną identyfikację σ f w drodze obliczeń odwrotnych. Wykorzystanie na tym etapie metody inverse pozwala na wyznaczenie rzeczywistego naprężenia uplastyczniającego, w dużej mierze uniezależniając wynik od wymiarów próbki, warunków tarcia oraz wpływu niejednorodności ε, ε, σ i T w obszarze próbki. Analiza odwrotna modelu CA Bazując na otrzymanych krzywych naprężenia uplastyczniającego, w drugim etapie przeprowadzono wstępną identyfikację parametrów modelu skali mikro. Sformułowanie problemu odwrotnego jako zadania optymalizacji wielokryterialnej bazuje na wyodrębnieniu wyjść modelu, odpowiadających mierzonym doświadczalnie. W obliczeniach wykorzystano wektor kryteriów, zbudowany na podstawie krzywych naprężenia uplastyczniającego, uzyskanych w poprzednim etapie, oraz zmierzonych rozkładów klas wielkości ziarna. Dla wyników symulacji CA zdefiniowano dwa kryteria oceny rozwiązania, wyrażone równaniami (5.7) oraz (5.9). Pochodzące z poprzedniego kroku obliczeń odwrotnych naprężenie uplastyczniające wyznaczono dla odkształceń do ε 0.8, natomiast pomiar doświadczalny rozkładu wielkości ziarna prowadzono dla ε = 0.4. Z tego powodu w symulacji CA wywołanie procedury obliczającej rozkład wielkości ziarna przeprowadzano dla odkształcenia ε = 0.4. Za pomocą algorytmu swobodnego rozrostu ziarna wygenerowano początkową reprezentację mikrostruktury. Wykorzystano siatkę komórek CA. Uzyskany 139
152 5.5. Weryfikacja modelu Rysunek 5.37: Rozkład wielkości ziarna w początkowej reprezentacji mikrostruktury w modelu CA, wygenerowanej algorytmem swobodnego wzrostu ziarna rozkład wielkości ziarna przedstawiono na rysunku W porównaniu z rozkładem wielkości ziarna uzyskanym z badań metalograficznych, pominięta została ostatnia kategoria 340 µm, zdecydowanie odstająca od rozkładu dzwonowego. Analiza liczności bezwzględnej w danych doświadczalnych wskazuje bowiem, że ziarno o takim rozmiarze zarejestrowano tylko jedno, zatem obecność tej klasy wielkości może być incydentalna. Posługując się opisanym w podrozdziale programem abaqopt przeprowadzono obliczenia odwrotne, mające na celu wyznaczenie parametrów modelu CA dla warunków odkształcenia badanego materiału. Jako dane początkowe wykorzystano odnalezione w literaturze parametry dla stali IF podczas rekrystalizacji statycznej: M 0 = m 3 (sn) 1, Q gb = 3.9 ev oraz γ m = 0.79 Jm 2 [106]. W obliczeniach przyjęto µ = 79.3 GPa oraz b = nm. Na podstawie danych z pracy [91] przyjęto początkową wartość parametru Q s = Jmol 1. Algorytm obliczeń odwrotnych uruchomiano wielokrotnie, przyjmując różne warianty punktów startowych, w tym losowe. Ponieważ w wyniku obliczeń CA uzyskiwano wyraźne i systematyczne przeszacowanie udziału ziaren bardzo małych, prowadzące do uniewrażliwienia kryterium (5.9), zdecydowano się na wyłączenie z oceny trzech kategorii, odpowiadających najdrobniejszym ziarnom. Przesłanką do takiego działania jest z jednej strony sposób reprezentowania zarodków w modelu CA, powodujący przeszacowanie udziału ziaren bardzo małych, z drugiej zaś strony ograniczenie rozdzielczości metody badawczej, sprawiające, że część zarodków może nie być widoczna w obserwacji. Na rysunku 5.38 przedstawiono wyniki uzyskane z analizy odwrotnej modelu skali mikro. Dla zoptymalizowanych parametrów modelu poprawnie odtwarzana jest krzywa naprężenia uplastyczniającego (5.38a), zarówno ze względu na położenie piku na krzywej σ f oraz wartość naprężenia dla stanu ustalonego. Natomiast w przypad- 140
153 5.5. Weryfikacja modelu (a) (b) Rysunek 5.38: Wyniki obliczeń odwrotnych prowadzonych dla modelu CA DRX w stali: (a) porównanie naprężenia uplastyczniającego wyznaczonego metodą odwrotną (symbole wypełnione) i uzyskanego z obliczeń CA (symbole otwarte), (b) porównanie rozkładu wielkości ziarna w próbce wyznaczonego doświadczalnie (słupki czarne) i obliczonego modelem CA (słupki czerwone) ku rozkładu wielkości ziarna, przedstawionego na rysunku 5.38b, zauważyć można rozbieżności, szczególnie wyraźne dla klas wielkości odpowiadających ziarnom małym i bardzo małym, które jednak wyłączono z obliczania kryterium (5.9). Ilościowe niezgodności obserwowane są także dla ziaren większych od średniego. Natomiast trend, wskazujący na rozdrobnienie ziarna oraz przybliżone położenie maksimum w rozkładzie dzwonowym przewidywane są z zadowalającą dokładnością. Obliczenia odwrotne dla modelu CAFE Uzyskane w poprzednim etapie wartości parametrów modelu wykorzystano jako punkt startowy w obliczeniach odwrotnych modelu CAFE. Wektor Φ(φ 1, φ 2 ) kryteriów oceny rozwiązania skonstruowano na podstawie wzorów (5.10) oraz (5.9) i (5.13). Podobnie jak w poprzednim etapie obliczeń odwrotnych, z obliczania kryterium (5.9) wyłączono trzy klasy wielkości, odpowiadające najdrobniejszym ziarnom. Uzyskane w drodze obliczeń odwrotnych parametry modelu CAFE zebrano w tabeli 5.7. Na rysunku 5.39 przedstawiono porównanie wybranych wyjść modelu CAFE, obliczonych przy użyciu zidentyfikowanych parametrów, ze zmierzonymi w doświadczeniu. Siły spęczania otrzymane z rozwiązania CAFE pozostają w bardzo dobrej zgodności z wynikami doświadczenia (rysunek 5.39a). Natomiast przedstawiony na rysunku 5.39b obliczony rozkład wielkości ziarna w próbce wykazuje rozbieżności względem uzyskanych z analizy metalograficznej. Podobnie jak we wcześniejszym etapie obliczeń odwrotnych, udział ziaren małych jest przez model przeszacowany, jednakże dla środkowej części rozkładu obserwowana jest poprawa 141
154 5.5. Weryfikacja modelu Tabela 5.7: Wartości parametrów modelu CAFE, zidentyfikowane w drodze obliczeń odwrotnych dla stali 16NiCrMo13 k 1 k 2 m Q s, Jmol 1 x q ρ 0, m 2 M 0, m 3 (sn) 1 Q gb, ev γ m, Jm 2 A 1 σ 0, Pa (a) (b) Rysunek 5.39: Wyniki uzyskane z modelu CAFE na podstawie parametrów modelu CA, wyznaczonych w drodze obliczeń odwrotnych: (a) porównanie zmierzonych sił spęczania (symbole wypełnione) i uzyskanych z obliczeń CAFE (symbole otwarte), (b) porównanie rozkładu wielkości ziarna w próbce wyznaczonego doświadczalnie (słupki czarne) i obliczonego modelem CAFE (słupki czerwone) zgodności z doświadczeniem. Może to wynikać ze statystycznego zwiększenia liczności próby, gdyż w rozwiązaniu CAFE rozkład wielkości ziarna pochodzi z prawie czterystukrotnie większej liczby analizowanych ziaren. W uzyskanych w drodze obliczeń odwrotnych parametrach modelu CAFE obserwowana jest tendencja do zredukowania ruchliwości granic. Parametry dobrane przez algorytm optymalizacyjny w porównaniu ze znanymi z literatury dla stali IF skutkują zmniejszeniem ruchliwości granic o około rząd wielkości, do około Z drugiej strony uzyskiwane wartości ruchliwości są porównywalne z obliczonymi na podstawie parametrów podanych w pracy [113]: M 0 = m 3 (sn) 1 i Q = Jmol 1 dla stali austenitycznych. Stosunkowo niewielka wartość parametru x, związanego z algorytmem obliczania przyrostu gęstości dyslokacji w komórkach CA, wskazuje na duże zróżnicowanie ρ w siatce obliczeniowej. W efekcie statystycznie częściej pojawiają się duże wartości ρ na granicach ziaren, co skutkuje warunkami sprzyjającymi intensywnemu zarodkowaniu. 142
Modelowanie Wieloskalowe. Automaty Komórkowe w Inżynierii Materiałowej
 Modelowanie Wieloskalowe Automaty Komórkowe w Inżynierii Materiałowej Dr inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p.
Modelowanie Wieloskalowe Automaty Komórkowe w Inżynierii Materiałowej Dr inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p.
Modelowanie wieloskalowe. Automaty Komórkowe - podstawy
 Modelowanie wieloskalowe Automaty Komórkowe - podstawy Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p. 716 lmadej@agh.edu.pl
Modelowanie wieloskalowe Automaty Komórkowe - podstawy Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek B5 p. 716 lmadej@agh.edu.pl
Badanie mechanizmów rekrystalizacji w metalach
 Badanie mechanizmów rekrystalizacji w metalach Jacek Tarasiuk KFMS, 2007 dr Philippe Gerber, dr Krystian Piękoś prof. Krzysztof Wierzbanowski dr Brigitte Bacroix LPMTM, Univ. Paris XIII Plan referatu (1)
Badanie mechanizmów rekrystalizacji w metalach Jacek Tarasiuk KFMS, 2007 dr Philippe Gerber, dr Krystian Piękoś prof. Krzysztof Wierzbanowski dr Brigitte Bacroix LPMTM, Univ. Paris XIII Plan referatu (1)
OBRÓBKA PLASTYCZNA METALI
 OBRÓBKA PLASTYCZNA METALI Plastyczność: zdolność metali i stopów do trwałego odkształcania się bez naruszenia spójności Obróbka plastyczna: walcowanie, kucie, prasowanie, ciągnienie Produkty i półprodukty
OBRÓBKA PLASTYCZNA METALI Plastyczność: zdolność metali i stopów do trwałego odkształcania się bez naruszenia spójności Obróbka plastyczna: walcowanie, kucie, prasowanie, ciągnienie Produkty i półprodukty
Nauka o Materiałach. Wykład VIII. Odkształcenie materiałów właściwości sprężyste. Jerzy Lis
 Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
Nauka o Materiałach Wykład VIII Odkształcenie materiałów właściwości sprężyste Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Klasyfikacja reologiczna odkształcenia
17. 17. Modele materiałów
 7. MODELE MATERIAŁÓW 7. 7. Modele materiałów 7.. Wprowadzenie Podstawowym modelem w mechanice jest model ośrodka ciągłego. Przyjmuje się, że materia wypełnia przestrzeń w sposób ciągły. Możliwe jest wyznaczenie
7. MODELE MATERIAŁÓW 7. 7. Modele materiałów 7.. Wprowadzenie Podstawowym modelem w mechanice jest model ośrodka ciągłego. Przyjmuje się, że materia wypełnia przestrzeń w sposób ciągły. Możliwe jest wyznaczenie
ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE EFEKTÓW ROZDRABNIANIA POJEDYNCZYCH ZIAREN
 Akademia Górniczo Hutnicza im. Stanisława Staszica Wydział Górnictwa i Geoinżynierii Katedra Inżynierii Środowiska i Przeróbki Surowców Rozprawa doktorska ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE
Akademia Górniczo Hutnicza im. Stanisława Staszica Wydział Górnictwa i Geoinżynierii Katedra Inżynierii Środowiska i Przeróbki Surowców Rozprawa doktorska ANALIZA ROZDRABNIANIA WARSTWOWEGO NA PODSTAWIE
Narzędzia do geometrycznej charakteryzacji granic ziaren. K. Głowioski
 Narzędzia do geometrycznej charakteryzacji granic ziaren K. Głowioski Plan prezentacji Wprowadzenie do granic ziaren Cel badao Przykłady zastosowania rozwijanych metod i narzędzi: - Rozkłady granic i ich
Narzędzia do geometrycznej charakteryzacji granic ziaren K. Głowioski Plan prezentacji Wprowadzenie do granic ziaren Cel badao Przykłady zastosowania rozwijanych metod i narzędzi: - Rozkłady granic i ich
PODSTAWY SKRAWANIA MATERIAŁÓW KONSTRUKCYJNYCH
 WIT GRZESIK PODSTAWY SKRAWANIA MATERIAŁÓW KONSTRUKCYJNYCH Wydanie 3, zmienione i uaktualnione Wydawnictwo Naukowe PWN SA Warszawa 2018 Od Autora Wykaz ważniejszych oznaczeń i skrótów SPIS TREŚCI 1. OGÓLNA
WIT GRZESIK PODSTAWY SKRAWANIA MATERIAŁÓW KONSTRUKCYJNYCH Wydanie 3, zmienione i uaktualnione Wydawnictwo Naukowe PWN SA Warszawa 2018 Od Autora Wykaz ważniejszych oznaczeń i skrótów SPIS TREŚCI 1. OGÓLNA
Recenzja rozprawy doktorskiej mgr inż. Joanny Wróbel
 Prof. dr hab. inż. Tadeusz BURCZYŃSKI, czł. koresp. PAN Instytut Podstawowych Problemów Techniki PAN ul. A. Pawińskiego 5B 02-106 Warszawa e-mail: tburczynski@ippt.pan.pl Warszawa, 15.09.2017 Recenzja
Prof. dr hab. inż. Tadeusz BURCZYŃSKI, czł. koresp. PAN Instytut Podstawowych Problemów Techniki PAN ul. A. Pawińskiego 5B 02-106 Warszawa e-mail: tburczynski@ippt.pan.pl Warszawa, 15.09.2017 Recenzja
Charakterystyka mechaniczna cynku po dużych deformacjach plastycznych i jej interpretacja strukturalna
 AKADEMIA GÓRNICZO HUTNICZA im. Stanisława Staszica w Krakowie WYDZIAŁ METALI NIEŻELAZNYCH ROZPRAWA DOKTORSKA Charakterystyka mechaniczna cynku po dużych deformacjach plastycznych i jej interpretacja strukturalna
AKADEMIA GÓRNICZO HUTNICZA im. Stanisława Staszica w Krakowie WYDZIAŁ METALI NIEŻELAZNYCH ROZPRAWA DOKTORSKA Charakterystyka mechaniczna cynku po dużych deformacjach plastycznych i jej interpretacja strukturalna
Stochastic modelling of phase transformations using HPC infrastructure
 Stochastic modelling of phase transformations using HPC infrastructure (Stochastyczne modelowanie przemian fazowych z wykorzystaniem komputerów wysokiej wydajności) Daniel Bachniak, Łukasz Rauch, Danuta
Stochastic modelling of phase transformations using HPC infrastructure (Stochastyczne modelowanie przemian fazowych z wykorzystaniem komputerów wysokiej wydajności) Daniel Bachniak, Łukasz Rauch, Danuta
STATYCZNA PRÓBA ROZCIĄGANIA
 Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: STATYCZNA PRÓBA ROZCIĄGANIA oprac. dr inż. Jarosław Filipiak Cel ćwiczenia 1. Zapoznanie się ze sposobem przeprowadzania statycznej
Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: STATYCZNA PRÓBA ROZCIĄGANIA oprac. dr inż. Jarosław Filipiak Cel ćwiczenia 1. Zapoznanie się ze sposobem przeprowadzania statycznej
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów
 Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Nowoczesne narzędzia obliczeniowe do projektowania i optymalizacji kotłów Mateusz Szubel, Mariusz Filipowicz Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie AGH University of Science and
Defi f nicja n aprę r żeń
 Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Wytrzymałość materiałów Stany naprężeń i odkształceń 1 Definicja naprężeń Mamy bryłę materialną obciążoną układem sił (siły zewnętrzne, reakcje), będących w równowadze. Rozetniemy myślowo tę bryłę na dwie
Kształtowanie struktury i własności użytkowych umacnianej wydzieleniowo miedzi tytanowej. 7. Podsumowanie
 Kształtowanie struktury i własności użytkowych umacnianej wydzieleniowo miedzi tytanowej 7. Podsumowanie Praca wykazała, że mechanizm i kinetyka wydzielania w miedzi tytanowej typu CuTi4, jest bardzo złożona
Kształtowanie struktury i własności użytkowych umacnianej wydzieleniowo miedzi tytanowej 7. Podsumowanie Praca wykazała, że mechanizm i kinetyka wydzielania w miedzi tytanowej typu CuTi4, jest bardzo złożona
Przedmowa Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11
 Spis treœci Przedmowa... 9 Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11 1. Wstêp... 13 1.1. Rys historyczny... 14 1.2. Klasyfikacja automatów... 18 1.3. Automaty komórkowe a modelowanie
Spis treœci Przedmowa... 9 Czêœæ pierwsza. Podstawy frontalnych automatów komórkowych... 11 1. Wstêp... 13 1.1. Rys historyczny... 14 1.2. Klasyfikacja automatów... 18 1.3. Automaty komórkowe a modelowanie
Wykład IX: Odkształcenie materiałów - właściwości plastyczne
 Wykład IX: Odkształcenie materiałów - właściwości plastyczne JERZY LIS Wydział Inżynierii Materiałowej i Ceramiki Katedra Technologii Ceramiki i Materiałów Ogniotrwałych Treść wykładu: 1. Odkształcenie
Wykład IX: Odkształcenie materiałów - właściwości plastyczne JERZY LIS Wydział Inżynierii Materiałowej i Ceramiki Katedra Technologii Ceramiki i Materiałów Ogniotrwałych Treść wykładu: 1. Odkształcenie
Analiza stateczności zbocza
 Przewodnik Inżyniera Nr 25 Aktualizacja: 06/2017 Analiza stateczności zbocza Program: MES Plik powiązany: Demo_manual_25.gmk Celem niniejszego przewodnika jest analiza stateczności zbocza (wyznaczenie
Przewodnik Inżyniera Nr 25 Aktualizacja: 06/2017 Analiza stateczności zbocza Program: MES Plik powiązany: Demo_manual_25.gmk Celem niniejszego przewodnika jest analiza stateczności zbocza (wyznaczenie
Recenzja rozprawy doktorskiej mgra inż. Roberta Szymczyka. Analiza numeryczna zjawisk hartowania stali narzędziowych do pracy na gorąco
 Prof. dr hab. inż. Tadeusz BURCZYŃSKI, czł. koresp. PAN Instytut Podstawowych Problemów Techniki PAN ul. A. Pawińskiego 5B 02-106 Warszawa e-mail: tburczynski@ippt.pan.pl Warszawa, 20.09.2016 Recenzja
Prof. dr hab. inż. Tadeusz BURCZYŃSKI, czł. koresp. PAN Instytut Podstawowych Problemów Techniki PAN ul. A. Pawińskiego 5B 02-106 Warszawa e-mail: tburczynski@ippt.pan.pl Warszawa, 20.09.2016 Recenzja
Badanie materiałów polikrystalicznych w aspekcie optymalizacji ich własności
 WydziałFizyki i Informatyki Stosowanej Badanie materiałów polikrystalicznych w aspekcie optymalizacji ich własności dr inż. Sebastian Wroński Ośrodki współpracujące Modyfikacja własności poprzez: Deformacje
WydziałFizyki i Informatyki Stosowanej Badanie materiałów polikrystalicznych w aspekcie optymalizacji ich własności dr inż. Sebastian Wroński Ośrodki współpracujące Modyfikacja własności poprzez: Deformacje
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 02 Jarosław Miszczak IITiS PAN Gliwice 06/10/2016 1 / 31 Czego dowiedzieliśmy się na poprzednim wykładzie? 1... 2... 3... 2 / 31 1 2 3 3 / 31 to jeden z pierwszych
Obliczenia inspirowane Naturą Wykład 02 Jarosław Miszczak IITiS PAN Gliwice 06/10/2016 1 / 31 Czego dowiedzieliśmy się na poprzednim wykładzie? 1... 2... 3... 2 / 31 1 2 3 3 / 31 to jeden z pierwszych
Janusz Adamowski METODY OBLICZENIOWE FIZYKI Kwantowa wariacyjna metoda Monte Carlo. Problem własny dla stanu podstawowego układu N cząstek
 Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
Janusz Adamowski METODY OBLICZENIOWE FIZYKI 1 Rozdział 20 KWANTOWE METODY MONTE CARLO 20.1 Kwantowa wariacyjna metoda Monte Carlo Problem własny dla stanu podstawowego układu N cząstek (H E 0 )ψ 0 (r)
TEMAT PRACY DOKTORSKIEJ
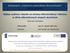 Krynica, 12.04.2013 Wpływ cyrkonu i skandu na zmiany mikrostruktury i tekstury w silnie odkształconych stopach aluminium ---------------------------------------------------------------------------- TEMAT
Krynica, 12.04.2013 Wpływ cyrkonu i skandu na zmiany mikrostruktury i tekstury w silnie odkształconych stopach aluminium ---------------------------------------------------------------------------- TEMAT
Projektowanie elementów z tworzyw sztucznych
 Projektowanie elementów z tworzyw sztucznych Wykorzystanie technik komputerowych w projektowaniu elementów z tworzyw sztucznych Tematyka wykładu Techniki komputerowe, Problemy występujące przy konstruowaniu
Projektowanie elementów z tworzyw sztucznych Wykorzystanie technik komputerowych w projektowaniu elementów z tworzyw sztucznych Tematyka wykładu Techniki komputerowe, Problemy występujące przy konstruowaniu
Zastosowanie symulacji Monte Carlo do zarządzania ryzykiem przedsięwzięcia z wykorzystaniem metod sieciowych PERT i CPM
 SZKOŁA GŁÓWNA HANDLOWA w Warszawie STUDIUM MAGISTERSKIE Kierunek: Metody ilościowe w ekonomii i systemy informacyjne Karol Walędzik Nr albumu: 26353 Zastosowanie symulacji Monte Carlo do zarządzania ryzykiem
SZKOŁA GŁÓWNA HANDLOWA w Warszawie STUDIUM MAGISTERSKIE Kierunek: Metody ilościowe w ekonomii i systemy informacyjne Karol Walędzik Nr albumu: 26353 Zastosowanie symulacji Monte Carlo do zarządzania ryzykiem
Laboratorium. Hydrostatyczne Układy Napędowe
 Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Laboratorium Hydrostatyczne Układy Napędowe Instrukcja do ćwiczenia nr Eksperymentalne wyznaczenie charakteru oporów w przewodach hydraulicznych opory liniowe Opracowanie: Z.Kudżma, P. Osiński J. Rutański,
Nauka o Materiałach. Wykład VI. Odkształcenie materiałów właściwości sprężyste i plastyczne. Jerzy Lis
 Nauka o Materiałach Wykład VI Odkształcenie materiałów właściwości sprężyste i plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Statyczna próba rozciągania.
Nauka o Materiałach Wykład VI Odkształcenie materiałów właściwości sprężyste i plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Właściwości materiałów -wprowadzenie 2. Statyczna próba rozciągania.
Nauka o Materiałach. Wykład IX. Odkształcenie materiałów właściwości plastyczne. Jerzy Lis
 Nauka o Materiałach Wykład IX Odkształcenie materiałów właściwości plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Odkształcenie plastyczne 2. Parametry makroskopowe 3. Granica plastyczności
Nauka o Materiałach Wykład IX Odkształcenie materiałów właściwości plastyczne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Odkształcenie plastyczne 2. Parametry makroskopowe 3. Granica plastyczności
WIELOSKALOWY NUMERYCZNY MODEL PRZEMIANY AUSTENIT FERRYT UWZGLĘDNIAJĄCY WPŁYW WYDZIELEŃ WĘGLIKOAZOTKÓW NIOBU
 Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Informatyki Stosowanej i Modelowania Rozprawa doktorska WIELOSKALOWY NUMERYCZNY MODEL PRZEMIANY
Akademia Górniczo-Hutnicza im. Stanisława Staszica Wydział Inżynierii Metali i Informatyki Przemysłowej Katedra Informatyki Stosowanej i Modelowania Rozprawa doktorska WIELOSKALOWY NUMERYCZNY MODEL PRZEMIANY
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ. Zmiany makroskopowe. Zmiany makroskopowe
 WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
KRYSTALIZACJA METALI I STOPÓW. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 KRYSTALIZACJA METALI I STOPÓW Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Krzepnięcie przemiana fazy ciekłej w fazę stałą Krystalizacja przemiana
KRYSTALIZACJA METALI I STOPÓW Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Krzepnięcie przemiana fazy ciekłej w fazę stałą Krystalizacja przemiana
Prognozowanie i Symulacje. Wykład I. Matematyczne metody prognozowania
 Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
Prognozowanie i Symulacje. Wykład I. e-mail:e.kozlovski@pollub.pl Spis treści Szeregi czasowe 1 Szeregi czasowe 2 3 Szeregi czasowe Definicja 1 Szereg czasowy jest to proces stochastyczny z czasem dyskretnym
KATEDRA WYTRZYMAŁOŚCI MATERIAŁÓW I METOD KOMPUTEROWYCH MECHANIKI. Wydział Mechaniczny Technologiczny POLITECHNIKA ŚLĄSKA W GLIWICACH
 KATEDRA WYTRZYMAŁOŚCI MATERIAŁÓW I METOD KOMPUTEROWYCH MECHANIKI Wydział Mechaniczny Technologiczny POLITECHNIKA ŚLĄSKA W GLIWICACH PRACA DYPLOMOWA MAGISTERSKA Obliczenie rozkładu temperatury generującego
KATEDRA WYTRZYMAŁOŚCI MATERIAŁÓW I METOD KOMPUTEROWYCH MECHANIKI Wydział Mechaniczny Technologiczny POLITECHNIKA ŚLĄSKA W GLIWICACH PRACA DYPLOMOWA MAGISTERSKA Obliczenie rozkładu temperatury generującego
Nauka o Materiałach Wykład II Monokryształy Jerzy Lis
 Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
Wykład II Monokryształy Jerzy Lis Treść wykładu: 1. Wstęp stan krystaliczny 2. Budowa kryształów - krystalografia 3. Budowa kryształów rzeczywistych defekty WPROWADZENIE Stan krystaliczny jest podstawową
CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ
 CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ Ciepło i temperatura Pojemność cieplna i ciepło właściwe Ciepło przemiany Przejścia między stanami Rozszerzalność cieplna Sprężystość ciał Prawo Hooke a Mechaniczne
CIEPLNE I MECHANICZNE WŁASNOŚCI CIAŁ Ciepło i temperatura Pojemność cieplna i ciepło właściwe Ciepło przemiany Przejścia między stanami Rozszerzalność cieplna Sprężystość ciał Prawo Hooke a Mechaniczne
Mechatronika i inteligentne systemy produkcyjne. Modelowanie systemów mechatronicznych Platformy przetwarzania danych
 Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Mechatronika i inteligentne systemy produkcyjne Modelowanie systemów mechatronicznych Platformy przetwarzania danych 1 Sterowanie procesem oparte na jego modelu u 1 (t) System rzeczywisty x(t) y(t) Tworzenie
Spis treści Przedmowa
 Spis treści Przedmowa 1. Wprowadzenie do problematyki konstruowania - Marek Dietrich (p. 1.1, 1.2), Włodzimierz Ozimowski (p. 1.3 -i-1.7), Jacek Stupnicki (p. l.8) 1.1. Proces konstruowania 1.2. Kryteria
Spis treści Przedmowa 1. Wprowadzenie do problematyki konstruowania - Marek Dietrich (p. 1.1, 1.2), Włodzimierz Ozimowski (p. 1.3 -i-1.7), Jacek Stupnicki (p. l.8) 1.1. Proces konstruowania 1.2. Kryteria
Technologie Materiałowe II Wykład 2 Technologia wyżarzania stali
 KATEDRA INŻYNIERII MATERIAŁOWEJ I SPAJANIA ZAKŁAD INŻYNIERII SPAJANIA Technologie Materiałowe II Wykład 2 Technologia wyżarzania stali dr hab. inż. Jerzy Łabanowski, prof.nadzw. PG Kierunek studiów: Inżynieria
KATEDRA INŻYNIERII MATERIAŁOWEJ I SPAJANIA ZAKŁAD INŻYNIERII SPAJANIA Technologie Materiałowe II Wykład 2 Technologia wyżarzania stali dr hab. inż. Jerzy Łabanowski, prof.nadzw. PG Kierunek studiów: Inżynieria
Spis treści. Przedmowa 11
 Podstawy konstrukcji maszyn. T. 1 / autorzy: Marek Dietrich, Stanisław Kocańda, Bohdan Korytkowski, Włodzimierz Ozimowski, Jacek Stupnicki, Tadeusz Szopa ; pod redakcją Marka Dietricha. wyd. 3, 2 dodr.
Podstawy konstrukcji maszyn. T. 1 / autorzy: Marek Dietrich, Stanisław Kocańda, Bohdan Korytkowski, Włodzimierz Ozimowski, Jacek Stupnicki, Tadeusz Szopa ; pod redakcją Marka Dietricha. wyd. 3, 2 dodr.
Summary in Polish. Fatimah Mohammed Furaiji. Application of Multi-Agent Based Simulation in Consumer Behaviour Modeling
 Summary in Polish Fatimah Mohammed Furaiji Application of Multi-Agent Based Simulation in Consumer Behaviour Modeling Zastosowanie symulacji wieloagentowej w modelowaniu zachowania konsumentów Streszczenie
Summary in Polish Fatimah Mohammed Furaiji Application of Multi-Agent Based Simulation in Consumer Behaviour Modeling Zastosowanie symulacji wieloagentowej w modelowaniu zachowania konsumentów Streszczenie
Metoda elementów skończonych
 Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
Metoda elementów skończonych Wraz z rozwojem elektronicznych maszyn obliczeniowych jakimi są komputery zaczęły pojawiać się różne numeryczne metody do obliczeń wytrzymałości różnych konstrukcji. Jedną
STRESZCZENIE. rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne.
 STRESZCZENIE rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne. Zasadniczym czynnikiem stanowiącym motywację dla podjętych w pracy rozważań
STRESZCZENIE rozprawy doktorskiej pt. Zmienne jakościowe w procesie wyceny wartości rynkowej nieruchomości. Ujęcie statystyczne. Zasadniczym czynnikiem stanowiącym motywację dla podjętych w pracy rozważań
9. PODSTAWY TEORII PLASTYCZNOŚCI
 9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
9. PODSTAWY TEORII PLASTYCZNOŚCI 1 9. 9. PODSTAWY TEORII PLASTYCZNOŚCI 9.1. Pierwsze kroki Do tej pory zajmowaliśmy się w analizie ciał i konstrukcji tylko analizą sprężystą. Nie zastanawialiśmy się, co
TEORIA PASMOWA CIAŁ STAŁYCH
 TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
TEORIA PASMOWA CIAŁ STAŁYCH Skolektywizowane elektrony w metalu Weźmy pod uwagę pewną ilość atomów jakiegoś metalu, np. sodu. Pojedynczy atom sodu zawiera 11 elektronów o konfiguracji 1s 2 2s 2 2p 6 3s
DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA
 71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
71 DYNAMIKA ŁUKU ZWARCIOWEGO PRZEMIESZCZAJĄCEGO SIĘ WZDŁUŻ SZYN ROZDZIELNIC WYSOKIEGO NAPIĘCIA dr hab. inż. Roman Partyka / Politechnika Gdańska mgr inż. Daniel Kowalak / Politechnika Gdańska 1. WSTĘP
Zastosowanie programu DICTRA do symulacji numerycznej przemian fazowych w stopach technicznych kontrolowanych procesem dyfuzji" Roman Kuziak
 Zastosowanie programu DICTRA do symulacji numerycznej przemian fazowych w stopach technicznych kontrolowanych procesem dyfuzji" Roman Kuziak Instytut Metalurgii Żelaza DICTRA jest pakietem komputerowym
Zastosowanie programu DICTRA do symulacji numerycznej przemian fazowych w stopach technicznych kontrolowanych procesem dyfuzji" Roman Kuziak Instytut Metalurgii Żelaza DICTRA jest pakietem komputerowym
SCENARIUSZ LEKCJI. TEMAT LEKCJI: Zastosowanie średnich w statystyce i matematyce. Podstawowe pojęcia statystyczne. Streszczenie.
 SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
SCENARIUSZ LEKCJI OPRACOWANY W RAMACH PROJEKTU: INFORMATYKA MÓJ SPOSÓB NA POZNANIE I OPISANIE ŚWIATA. PROGRAM NAUCZANIA INFORMATYKI Z ELEMENTAMI PRZEDMIOTÓW MATEMATYCZNO-PRZYRODNICZYCH Autorzy scenariusza:
STATYSTYKA MATEMATYCZNA WYKŁAD 4. WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X.
 STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
STATYSTYKA MATEMATYCZNA WYKŁAD 4 WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH X - cecha populacji, θ parametr rozkładu cechy X. Wysuwamy hipotezy: zerową (podstawową H ( θ = θ i alternatywną H, która ma jedną z
Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ.
 Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ. Jolanta Zimmerman 1. Wprowadzenie do metody elementów skończonych Działanie rzeczywistych
Materiały do laboratorium Przygotowanie Nowego Wyrobu dotyczące metody elementów skończonych (MES) Opracowała: dr inŝ. Jolanta Zimmerman 1. Wprowadzenie do metody elementów skończonych Działanie rzeczywistych
Wykład 2. Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova)
 Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Wykład 2 Przykład zastosowania teorii prawdopodobieństwa: procesy stochastyczne (Markova) 1. Procesy Markova: definicja 2. Równanie Chapmana-Kołmogorowa-Smoluchowskiego 3. Przykład dyfuzji w kapilarze
Recenzja Pracy Doktorskiej
 Politechnika Częstochowska Wydział Inżynierii Produkcji i Technologii Materiałów Instytut Inżynierii Materiałowej Dr hab. inż. Michał Szota, Prof. P.Cz. Częstochowa, 15.10.2014 roku Recenzja Pracy Doktorskiej
Politechnika Częstochowska Wydział Inżynierii Produkcji i Technologii Materiałów Instytut Inżynierii Materiałowej Dr hab. inż. Michał Szota, Prof. P.Cz. Częstochowa, 15.10.2014 roku Recenzja Pracy Doktorskiej
pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ
 Ćwiczenie audytoryjne pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ Autor: dr inż. Radosław Łyszkowski Warszawa, 2013r. Metoda elementów skończonych MES FEM - Finite Element Method przybliżona
Ćwiczenie audytoryjne pt.: KOMPUTEROWE WSPOMAGANIE PROCESÓW OBRÓBKI PLASTYCZNEJ Autor: dr inż. Radosław Łyszkowski Warszawa, 2013r. Metoda elementów skończonych MES FEM - Finite Element Method przybliżona
- prędkość masy wynikająca z innych procesów, np. adwekcji, naprężeń itd.
 4. Równania dyfuzji 4.1. Prawo zachowania masy cd. Równanie dyfuzji jest prostą konsekwencją prawa zachowania masy, a właściwie to jest to prawo zachowania masy zapisane dla procesu dyfuzji i uwzględniające
4. Równania dyfuzji 4.1. Prawo zachowania masy cd. Równanie dyfuzji jest prostą konsekwencją prawa zachowania masy, a właściwie to jest to prawo zachowania masy zapisane dla procesu dyfuzji i uwzględniające
Modelowanie Wieloskalowe. Automaty Komórkowe w Inżynierii Materiałowej
 Modelowanie Wieloskalowe Automaty Komórkowe w Inżynierii Materiałowej Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek
Modelowanie Wieloskalowe Automaty Komórkowe w Inżynierii Materiałowej Dr hab. inż. Łukasz Madej Katedra Informatyki Stosowanej i Modelowania Wydział Inżynierii Metali i Informatyki Przemysłowej Budynek
Zastosowanie MES do rozwiązania problemu ustalonego przepływu ciepła w obszarze 2D
 Równanie konstytutywne opisujące sposób w jaki ciepło przepływa w materiale o danych właściwościach, prawo Fouriera Macierz konstytutywna (właściwości) materiału Wektor gradientu temperatury Wektor strumienia
Równanie konstytutywne opisujące sposób w jaki ciepło przepływa w materiale o danych właściwościach, prawo Fouriera Macierz konstytutywna (właściwości) materiału Wektor gradientu temperatury Wektor strumienia
166 Wstęp do statystyki matematycznej
 166 Wstęp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwiązać nasz zasadniczy problem związany z identyfikacją cechy populacji generalnej
166 Wstęp do statystyki matematycznej Etap trzeci realizacji procesu analizy danych statystycznych w zasadzie powinien rozwiązać nasz zasadniczy problem związany z identyfikacją cechy populacji generalnej
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali. Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe
 Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
Technologie wytwarzania metali Odlewanie Metalurgia proszków Otrzymywanie monokryształów Otrzymywanie materiałów superczystych Techniki próżniowe KRYSTALIZACJA METALI I STOPÓW Krzepnięcie - przemiana fazy
STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH
 Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
Część. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH.. STATYKA Z UWZGLĘDNIENIEM DUŻYCH SIŁ OSIOWYCH Rozwiązując układy niewyznaczalne dowolnie obciążone, bardzo często pomijaliśmy wpływ sił normalnych i
Opis efektów kształcenia dla programu kształcenia (kierunkowe efekty kształcenia) WIEDZA. rozumie cywilizacyjne znaczenie matematyki i jej zastosowań
 TABELA ODNIESIEŃ EFEKTÓW KSZTAŁCENIA OKREŚLONYCH DLA PROGRAMU KSZTAŁCENIA DO EFEKTÓW KSZTAŁCENIA OKREŚLONYCH DLA OBSZARU KSZTAŁCENIA I PROFILU STUDIÓW PROGRAM KSZTAŁCENIA: POZIOM KSZTAŁCENIA: PROFIL KSZTAŁCENIA:
TABELA ODNIESIEŃ EFEKTÓW KSZTAŁCENIA OKREŚLONYCH DLA PROGRAMU KSZTAŁCENIA DO EFEKTÓW KSZTAŁCENIA OKREŚLONYCH DLA OBSZARU KSZTAŁCENIA I PROFILU STUDIÓW PROGRAM KSZTAŁCENIA: POZIOM KSZTAŁCENIA: PROFIL KSZTAŁCENIA:
Modelowanie i obliczenia techniczne. dr inż. Paweł Pełczyński
 Modelowanie i obliczenia techniczne dr inż. Paweł Pełczyński ppelczynski@swspiz.pl Literatura Z. Fortuna, B. Macukow, J. Wąsowski: Metody numeryczne, WNT Warszawa, 2005. J. Awrejcewicz: Matematyczne modelowanie
Modelowanie i obliczenia techniczne dr inż. Paweł Pełczyński ppelczynski@swspiz.pl Literatura Z. Fortuna, B. Macukow, J. Wąsowski: Metody numeryczne, WNT Warszawa, 2005. J. Awrejcewicz: Matematyczne modelowanie
PEŁZANIE WYBRANYCH ELEMENTÓW KONSTRUKCYJNYCH
 Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie PEŁZANIE WYBRANYCH ELEMENTÓW KONSTRUKCYJNYCH Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Reologia jest nauką,
Mechanika i wytrzymałość materiałów - instrukcja do ćwiczenia laboratoryjnego: Wprowadzenie PEŁZANIE WYBRANYCH ELEMENTÓW KONSTRUKCYJNYCH Opracowała: mgr inż. Magdalena Bartkowiak-Jowsa Reologia jest nauką,
Analiza współzależności zjawisk
 Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
Analiza współzależności zjawisk Informacje ogólne Jednostki tworzące zbiorowość statystyczną charakteryzowane są zazwyczaj za pomocą wielu cech zmiennych, które nierzadko pozostają ze sobą w pewnym związku.
[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)
![[ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia) [ P ] T PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES. [ u v u v u v ] T. wykład 4. Element trójkątny płaski stan (naprężenia lub odkształcenia)](/thumbs/88/115575588.jpg) PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
PODSTAWY I ZASTOSOWANIA INŻYNIERSKIE MES wykład 4 Element trójkątny płaski stan (naprężenia lub odkształcenia) Obszar zdyskretyzowany trójkątami U = [ u v u v u v ] T stopnie swobody elementu P = [ P ]
Zmęczenie Materiałów pod Kontrolą
 1 Zmęczenie Materiałów pod Kontrolą Wykład Nr 9 Wzrost pęknięć przy obciążeniach zmęczeniowych Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji http://zwmik.imir.agh.edu.pl
1 Zmęczenie Materiałów pod Kontrolą Wykład Nr 9 Wzrost pęknięć przy obciążeniach zmęczeniowych Wydział Inżynierii Mechanicznej i Robotyki Katedra Wytrzymałości, Zmęczenia Materiałów i Konstrukcji http://zwmik.imir.agh.edu.pl
Prawdopodobieństwo i statystyka
 Wykład XIV: Metody Monte Carlo 19 stycznia 2016 Przybliżone obliczanie całki oznaczonej Rozważmy całkowalną funkcję f : [0, 1] R. Chcemy znaleźć przybliżoną wartość liczbową całki 1 f (x) dx. 0 Jeden ze
Wykład XIV: Metody Monte Carlo 19 stycznia 2016 Przybliżone obliczanie całki oznaczonej Rozważmy całkowalną funkcję f : [0, 1] R. Chcemy znaleźć przybliżoną wartość liczbową całki 1 f (x) dx. 0 Jeden ze
Zagadnienia brzegowe dla równań eliptycznych
 Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
Temat 7 Zagadnienia brzegowe dla równań eliptycznych Rozważmy płaski obszar R 2 ograniczony krzywą. la równania Laplace a (Poissona) stawia się trzy podstawowe zagadnienia brzegowe. Zagadnienie irichleta
WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ MATERIAŁ. Właściwości materiałów. Właściwości materiałów
 WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ Właściwości materiałów O możliwości zastosowania danego materiału decydują jego właściwości użytkowe; Zachowanie się danego materiału w środowisku pracy to zaplanowana
WŁAŚCIWOŚCI MECHANICZNE SPRĘŻYSTOŚĆ Właściwości materiałów O możliwości zastosowania danego materiału decydują jego właściwości użytkowe; Zachowanie się danego materiału w środowisku pracy to zaplanowana
PRZEWODNIK PO PRZEDMIOCIE
 Nazwa przedmiotu: MODELOWANIE I SYMULACJA PROCESÓW WYTWARZANIA Modeling and Simulation of Manufacturing Processes Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy specjalności PSM Rodzaj zajęć: wykład,
Nazwa przedmiotu: MODELOWANIE I SYMULACJA PROCESÓW WYTWARZANIA Modeling and Simulation of Manufacturing Processes Kierunek: Mechatronika Rodzaj przedmiotu: obowiązkowy specjalności PSM Rodzaj zajęć: wykład,
8. PODSTAWY ANALIZY NIELINIOWEJ
 8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
8. PODSTAWY ANALIZY NIELINIOWEJ 1 8. 8. PODSTAWY ANALIZY NIELINIOWEJ 8.1. Wprowadzenie Zadania nieliniowe mają swoje zastosowanie na przykład w rozwiązywaniu cięgien. Przyczyny nieliniowości: 1) geometryczne:
INSTRUKCJA DO ĆWICZENIA NR 7
 KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
KATEDRA MECHANIKI STOSOWANEJ Wydział Mechaniczny POLITECHNIKA LUBELSKA INSTRUKCJA DO ĆWICZENIA NR 7 PRZEDMIOT TEMAT OPRACOWAŁ LABORATORIUM MODELOWANIA Przykładowe analizy danych: przebiegi czasowe, portrety
Układy stochastyczne
 Instytut Informatyki Uniwersytetu Śląskiego 21 stycznia 2009 Definicja Definicja Proces stochastyczny to funkcja losowa, czyli funkcja matematyczna, której wartości leżą w przestrzeni zdarzeń losowych.
Instytut Informatyki Uniwersytetu Śląskiego 21 stycznia 2009 Definicja Definicja Proces stochastyczny to funkcja losowa, czyli funkcja matematyczna, której wartości leżą w przestrzeni zdarzeń losowych.
Definicje i przykłady
 Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
Rozdział 1 Definicje i przykłady 1.1 Definicja równania różniczkowego 1.1 DEFINICJA. Równaniem różniczkowym zwyczajnym rzędu n nazywamy równanie F (t, x, ẋ, ẍ,..., x (n) ) = 0. (1.1) W równaniu tym t jest
METODY KOMPUTEROWE W MECHANICE
 METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
METODY KOMPUTEROWE W MECHANICE wykład dr inż. Paweł Stąpór laboratorium 15 g, projekt 15 g. dr inż. Paweł Stąpór dr inż. Sławomir Koczubiej Politechnika Świętokrzyska Wydział Zarządzania i Modelowania
WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA KOŁA NA ZMIANĘ SZTYWNOŚCI ZAZĘBIENIA
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2009 Seria: TRANSPORT z. 65 Nr kol. 1807 Tomasz FIGLUS, Piotr FOLĘGA, Piotr CZECH, Grzegorz WOJNAR WYKORZYSTANIE MES DO WYZNACZANIA WPŁYWU PĘKNIĘCIA W STOPIE ZĘBA
Testowanie hipotez statystycznych.
 Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Statystyka Wykład 10 Wrocław, 22 grudnia 2011 Testowanie hipotez statystycznych Definicja. Hipotezą statystyczną nazywamy stwierdzenie dotyczące parametrów populacji. Definicja. Dwie komplementarne w problemie
Sterowanie wielkością zamówienia w Excelu - cz. 3
 Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Sterowanie wielkością zamówienia w Excelu - cz. 3 21.06.2005 r. 4. Planowanie eksperymentów symulacyjnych Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji
Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych
 dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
dr Piotr Sulewski POMORSKA AKADEMIA PEDAGOGICZNA W SŁUPSKU KATEDRA INFORMATYKI I STATYSTYKI Porównanie generatorów liczb losowych wykorzystywanych w arkuszach kalkulacyjnych Wprowadzenie Obecnie bardzo
Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop
 Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop. 2015 Spis treści Przedmowa do wydania pierwszego 7 Przedmowa do wydania drugiego 9
Metoda elementów skończonych w mechanice konstrukcji / Gustaw Rakowski, Zbigniew Kacprzyk. wyd. 3 popr. Warszawa, cop. 2015 Spis treści Przedmowa do wydania pierwszego 7 Przedmowa do wydania drugiego 9
Naprężenia i odkształcenia spawalnicze
 Naprężenia i odkształcenia spawalnicze Cieplno-mechaniczne właściwości metali i stopów Parametrami, które określają stan mechaniczny metalu w różnych temperaturach, są: - moduł sprężystości podłużnej E,
Naprężenia i odkształcenia spawalnicze Cieplno-mechaniczne właściwości metali i stopów Parametrami, które określają stan mechaniczny metalu w różnych temperaturach, są: - moduł sprężystości podłużnej E,
Obliczenia inspirowane Naturą
 Obliczenia inspirowane Naturą Wykład 03 (uzupełnienie Wykładu 02) Jarosław Miszczak IITiS PAN Gliwice 31/03/2016 1 / 17 1 2 / 17 Dynamika populacji Równania Lotki-Voltery opisują model drapieżnik-ofiara.
Obliczenia inspirowane Naturą Wykład 03 (uzupełnienie Wykładu 02) Jarosław Miszczak IITiS PAN Gliwice 31/03/2016 1 / 17 1 2 / 17 Dynamika populacji Równania Lotki-Voltery opisują model drapieżnik-ofiara.
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory
 Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
Statystyka i opracowanie danych Podstawy wnioskowania statystycznego. Prawo wielkich liczb. Centralne twierdzenie graniczne. Estymacja i estymatory Dr Anna ADRIAN Paw B5, pok 407 adrian@tempus.metal.agh.edu.pl
POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA
 POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA Wykorzystanie pakietu MARC/MENTAT do modelowania naprężeń cieplnych Spis treści Pole temperatury Przykład
POLITECHNIKA ŚLĄSKA W GLIWICACH Wydział Mechaniczny Technologiczny PRACA DYPLOMOWA MAGISTERSKA Wykorzystanie pakietu MARC/MENTAT do modelowania naprężeń cieplnych Spis treści Pole temperatury Przykład
Analiza korespondencji
 Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Analiza korespondencji Kiedy stosujemy? 2 W wielu badaniach mamy do czynienia ze zmiennymi jakościowymi (nominalne i porządkowe) typu np.: płeć, wykształcenie, status palenia. Punktem wyjścia do analizy
Program MC. Obliczyć radialną funkcję korelacji. Zrobić jej wykres. Odczytać z wykresu wartość radialnej funkcji korelacji w punkcie r=
 Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
Program MC Napisać program symulujący twarde kule w zespole kanonicznym. Dla N > 100 twardych kul. Gęstość liczbowa 0.1 < N/V < 0.4. Zrobić obliczenia dla 2,3 różnych wartości gęstości. Obliczyć radialną
Zjawisko to umożliwia kształtowanie metali na drodze przeróbki plastycznej.
 ODKSZTAŁCENIE PLASTYCZNE, ZGNIOT I REKRYSTALIZACJA Zakres tematyczny 1 Odkształcenie materiałów metalicznych Materiały metaliczne są ciałami plastycznymi pod wpływem obciążenia, którego wartość przekracza
ODKSZTAŁCENIE PLASTYCZNE, ZGNIOT I REKRYSTALIZACJA Zakres tematyczny 1 Odkształcenie materiałów metalicznych Materiały metaliczne są ciałami plastycznymi pod wpływem obciążenia, którego wartość przekracza
Wstęp do równań różniczkowych
 Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Wstęp do równań różniczkowych
 Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Wstęp do równań różniczkowych Wykład 1 Lech Sławik Instytut Matematyki PK Literatura 1. Arnold W.I., Równania różniczkowe zwyczajne, PWN, Warszawa, 1975. 2. Matwiejew N.M., Metody całkowania równań różniczkowych
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne
 Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
Wykład 3 Zjawiska transportu Dyfuzja w gazie, przewodnictwo cieplne, lepkość gazu, przewodnictwo elektryczne W3. Zjawiska transportu Zjawiska transportu zachodzą gdy układ dąży do stanu równowagi. W zjawiskach
1. PODSTAWY TEORETYCZNE
 1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
1. PODSTAWY TEORETYCZNE 1 1. 1. PODSTAWY TEORETYCZNE 1.1. Wprowadzenie W pierwszym wykładzie przypomnimy podstawowe działania na macierzach. Niektóre z nich zostały opisane bardziej szczegółowo w innych
Nauka o Materiałach. Wykład XI. Właściwości cieplne. Jerzy Lis
 Nauka o Materiałach Wykład XI Właściwości cieplne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Stabilność termiczna materiałów 2. Pełzanie wysokotemperaturowe 3. Przewodnictwo cieplne 4. Rozszerzalność
Nauka o Materiałach Wykład XI Właściwości cieplne Jerzy Lis Nauka o Materiałach Treść wykładu: 1. Stabilność termiczna materiałów 2. Pełzanie wysokotemperaturowe 3. Przewodnictwo cieplne 4. Rozszerzalność
S O M SELF-ORGANIZING MAPS. Przemysław Szczepańczyk Łukasz Myszor
 S O M SELF-ORGANIZING MAPS Przemysław Szczepańczyk Łukasz Myszor Podstawy teoretyczne Map Samoorganizujących się stworzył prof. Teuvo Kohonen (1982 r.). SOM wywodzi się ze sztucznych sieci neuronowych.
S O M SELF-ORGANIZING MAPS Przemysław Szczepańczyk Łukasz Myszor Podstawy teoretyczne Map Samoorganizujących się stworzył prof. Teuvo Kohonen (1982 r.). SOM wywodzi się ze sztucznych sieci neuronowych.
Sieci obliczeniowe poprawny dobór i modelowanie
 Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
Sieci obliczeniowe poprawny dobór i modelowanie 1. Wstęp. Jednym z pierwszych, a zarazem najważniejszym krokiem podczas tworzenia symulacji CFD jest poprawne określenie rozdzielczości, wymiarów oraz ilości
PROJEKT METODA ELEMENTÓW SKOŃCZONYCH
 POLITECHNIKA POZNAŃSKA PROJEKT METODA ELEMENTÓW SKOŃCZONYCH Prowadzący: dr hab. Tomasz Stręk Wykonali: Kajetan Wilczyński Maciej Zybała Gabriel Pihan Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa
POLITECHNIKA POZNAŃSKA PROJEKT METODA ELEMENTÓW SKOŃCZONYCH Prowadzący: dr hab. Tomasz Stręk Wykonali: Kajetan Wilczyński Maciej Zybała Gabriel Pihan Wydział Budowy Maszyn i Zarządzania Mechanika i Budowa
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji
 Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
Weryfikacja hipotez statystycznych, parametryczne testy istotności w populacji Dr Joanna Banaś Zakład Badań Systemowych Instytut Sztucznej Inteligencji i Metod Matematycznych Wydział Informatyki Politechniki
MODELOWANIE OBCIĄŻEŃ ZIAREN AKTYWNYCH I SIŁ W PROCESIE SZLIFOWANIA
 Modelowanie obciążeń ziaren ściernych prof. dr hab. inż. Wojciech Kacalak, mgr inż. Filip Szafraniec Politechnika Koszalińska MODELOWANIE OBCIĄŻEŃ ZIAREN AKTYWNYCH I SIŁ W PROCESIE SZLIFOWANIA XXXVI NAUKOWA
Modelowanie obciążeń ziaren ściernych prof. dr hab. inż. Wojciech Kacalak, mgr inż. Filip Szafraniec Politechnika Koszalińska MODELOWANIE OBCIĄŻEŃ ZIAREN AKTYWNYCH I SIŁ W PROCESIE SZLIFOWANIA XXXVI NAUKOWA
Spis treści. Przedmowa... XI. Rozdział 1. Pomiar: jednostki miar... 1. Rozdział 2. Pomiar: liczby i obliczenia liczbowe... 16
 Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Spis treści Przedmowa.......................... XI Rozdział 1. Pomiar: jednostki miar................. 1 1.1. Wielkości fizyczne i pozafizyczne.................. 1 1.2. Spójne układy miar. Układ SI i jego
Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA
 Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA PRZEDMIOT: INŻYNIERIA WARSTWY WIERZCHNIEJ Temat ćwiczenia: Badanie prędkości zużycia materiałów
Zachodniopomorski Uniwersytet Technologiczny INSTYTUT INŻYNIERII MATERIAŁOWEJ ZAKŁAD METALOZNAWSTWA I ODLEWNICTWA PRZEDMIOT: INŻYNIERIA WARSTWY WIERZCHNIEJ Temat ćwiczenia: Badanie prędkości zużycia materiałów
AKADEMIA GÓRNICZO-HUTNICZA Wydział Matematyki Stosowanej ROZKŁAD NORMALNY ROZKŁAD GAUSSA
 AKADEMIA GÓRNICZO-HUTNICZA Wydział Matematyki Stosowanej KATEDRA MATEMATYKI TEMAT PRACY: ROZKŁAD NORMALNY ROZKŁAD GAUSSA AUTOR: BARBARA MARDOSZ Kraków, styczeń 2008 Spis treści 1 Wprowadzenie 2 2 Definicja
AKADEMIA GÓRNICZO-HUTNICZA Wydział Matematyki Stosowanej KATEDRA MATEMATYKI TEMAT PRACY: ROZKŁAD NORMALNY ROZKŁAD GAUSSA AUTOR: BARBARA MARDOSZ Kraków, styczeń 2008 Spis treści 1 Wprowadzenie 2 2 Definicja
