S. Baran - Podstawy fizyki materii skondensowanej Struktura krystaliczna. Struktura krystaliczna
|
|
|
- Helena Laskowska
- 9 lat temu
- Przeglądów:
Transkrypt
1 S. Baran - Podstawy fizyki materii skondensowanej Struktura krystaliczna Struktura krystaliczna
2 Kwarc (SiO2) (źródło: Wikipedia)
3 Piryt (FeS2) (źródło: Wikipedia)
4 Halit/Sól kamienna (NaCl) (źródło: Wikipedia)
5 Kryształy występują w formie wielościanów, zwykle pozlepianych ze sobą (polikryształ). Pojedynczy wielościan/ziarno polikryształu to monokryształ. Własności: - prawo Stensena/prawo Steno/prawo stałości kątów (1669 r.) kąty między tymi samymi ścianami, mierzone w jednakowych warunkach fizykochemicznych, są stałe i niezmienne w każdym krysztale tej samej substancji (kąt między ścianami, to kąt między normalnymi do nich). - XVIII w. - mineralodzy zauważyli, że wskaźniki opisujące kierunki płaszczyzn kryształu są liczbami całkowitymi - charakter wzrostu monokryształu sugeruje, że przyrasta on na skutek stopniowego dokładania identycznych elementów składowych - odkrycie dyfrakcji promieni X na kryształach (1912 r.) Max von Laue, W. Friedrich, P. Knipping (nagroda Nobla 1914 r. dla Maxa von Lauego) Wniosek: kryształy mają budowę periodyczną. Definicja kryształu (tradycyjna): Kryształ ciało stałe o periodycznym dalekozasięgowym uporządkowaniu elementów składowych (atomów, jonów, molekuł) struktura krystaliczna = sieć + baza (motyw)
6 źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 2, str. 18 Sieć krystaliczna zbiór punktów (węzłów) zdefiniowany przez podstawowe wektory translacji a1, a2, a3 takie, że ułożenie atomów wygląda identycznie z punktu r oraz r' = r + u1a1 + u2a2 + u3a3, u1,u2,u3 ℤ translacja sieci: T = u1a1 + u2a2 + u3a3, u1,u2,u3 ℤ sieć prymitywna (sieć Bravais'ego) jeśli dwa dowolne punkty, z których kryształ wygląda identycznie mogą być osiągnięte przez translację sieciową (podstawowe wektory translacji a1, a2, a3 są nazywane wówczas prymitywnymi) długości wektorów a1, a2, a3 to stałe sieci, a ich kierunki wyznaczają osie krystalograficzne
7 źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 5, str. 21 (prymitywna) komórka elementarna równoległościan zdefiniowany przez prymitywne wektory a1, a2, a3 (umowna) komórka elementarna równoległościan zdefiniowany przez wektory a1, a2, a3, które nie są prymitywne własności: V = a1 (a2 a3) - komórki el. poprzez translacje sieci wypełniają całą przestrzeń kryształu (bez przekrywania się) - (prymitywna) komórki el. ma najmniejszą możliwą objętość (przypada na nią 1 węzeł) baza atomowa (motyw) grupa atomów (jonów) związana z każdym węzłem sieci, przy czym jej struktura wewnętrzna i orientacja nie ulega zmianie (przy przejściu do kolejnego węzła) współrzędne j-tego atomu bazy w komórce elementarnej: rj = xja1 + yja2 + zja3, 0 xj,yj,zj 1 (xj,yj,zj współrzędne zredukowane)
8 komórka elementarna (definicja uogólniona) objętość, która po translacjach o wszystkie wektory sieci wypełnia całkowicie przestrzeń bez przekrywania się. komórka Wignera-Seitza (prymitywna, ma symetrię sieci) źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 6, str. 21 przykład: w sieci bcc komórka Wiegnera-Seitza to ośmiościan ścięty źródło: N. Ashcroft, N. Mermin, Fizyka..., rys. 4.15, str. 104
9 Grupa 1) A,B G: A B = C: C G 2) A,B,C G: (A B) C = A (B C) (łączność) 3) E G: A G: E A = A E = A (element neutralny) 4) A G B G: A B = B A = E (element przeciwny) grupa abelowa, gdy dodatkowo: A,B G: A B = B A (przemienność) izometria przekształcenie zachowujące odległość między punktami grupa punktowa sieci Bravais'ego zbiór zamkniętych (punktowych) izometrii przekształcających daną sieć w siebie (przynajmniej jeden punkt nie zmienia położenia) punktowe izometrie dozwolone dla sieci o symetrii translacyjnej proste elementy symetrii: 1) płaszczyzna symetrii - odbicie (oznaczenie: m) 2) oś symetrii - obrót o kąt 2 /n (oznaczenie: n) dopuszczalne n to 1, 2, 3, 4 i 6 3) inwersja (oznaczenie: 1) równoważna obrotowi o i odbiciu od pł. osi obrotu złożone elementy symetrii: 4) oś inwersyjna (oznaczenie: 1, 2, 3, 4 lub 6) złożenie odpowiedniego obrotu i inwersji względem punktu leżącego na osi obrotu 5) oś zwierciadlana (oznaczenie: m, 1, 6, 4 lub 3) złożenie odpowiedniego obrotu i odbicia od pł. osi obrotu (jest równoważna obrotowi inwersyjnemu o kąt różniący się o )
10 3-krotna oś inwersyjna źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.5, str. 38 przykład: sześcian ma tę samą grupę symetrii co ośmiościan foremny (oktaedr) źródło: N. Ashcroft, N. Mermin, Fizyka..., rys. 7.2, str. 149
11 7 układów krystalograficznych (istnieje tylko 7 różnych grup punktowych związanych z sieciami Bravais'ego) obiekty o symetriach grup punktowych sieci Bravais'ego wraz z parametrami komórek el. sieci = b,c = a,c = a,b Regularny a= b=c = = = 90 Tetragonalny a= b c = = = 90 Heksagonalny a= b c = = 90 ; = 120 Rombowy a b c = = = 90 Romboedryczny Jednoskośny Trójskośny (Trygonalny) a b c a b c a= b=c = = 90 = = 90 źródło: N. Ashcroft, N. Mermin, Fizyka..., rys. 7.3, str. 150
12 grupa przestrzenna sieci Bravais'ego zbiór izometrii przekształcających daną sieć w siebie twierdzenie: każde przekształcenie symetrii sieci Bravais'ego można złożyć z translacji o wektor sieci oraz izometrii z przynajmniej jednym stałym punktem sieci (dowód: N. Ashcroft, N. Mermin, Fizyka..., rozdz. 7) 14 sieci Bravais'ego wynik nietrywialny! Poprawny dowód podał w 1845 r. August Bravais. Wcześniej, w 1842 r., błędny wynik (15 sieci) Moritza Ludwiga Frankenheima.
13 14 sieci Bravais'ego układ regularny: a = b = c; = = = 90 sieć regularna prosta (prymitywna) sc = simple cubic przestrzennie centrowana bcc = body centered cubic powierzchniowo centrowana fcc = face centered cubic źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
14 14 sieci Bravais'ego układ tetragonalny: a = b c; = = = 90 sieć tetragonalna prosta (prymitywna) centrowana przestrzennie źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
15 14 sieci Bravais'ego układ rombowy: a b c; = = = 90 sieć rombowa prosta (prymitywna) o centrowanej podstawie centrowana przestrzennie źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36 centrowana powierzchniowo
16 14 sieci Bravais'ego układ heksagonalny: a = b c; = = 90 ; = 120 sieć heksagonalna źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
17 14 sieci Bravais'ego układ romboedryczny (trygonalny): a = b = c; = = < 120, 90 sieć romboedryczna (trygonalna) źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
18 14 sieci Bravais'ego układ jednoskośny: a b c; = = 90 sieć jednoskośna prosta (prymitywna) o centrowanej podstawie źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
19 14 sieci Bravais'ego układ trójskośny: a b c; sieć trójskośna źródło: H. Ibach, H. Lüth, Fizyka..., rys. 2.3, str. 36
20 14 sieci Bravais'ego zestawienie Układ Liczba sieci Krawędzie i kąty komórki umownej regularny 3 a = b = c; = = = 90 tetragonalny 2 a = b c; = = = 90 rombowy 4 a b c; = = = 90 heksagonalny 1 a = b c; = = 90 ; = 120 romboedryczny (trygonalny) jednoskośny 1 a = b = c; = = < 120, 90 2 a b c; = = 90 trójskośny 1 a b c;
21 14 sieci Bravais'ego Uwaga: w układach centrowanych wybiera się zwykle umowne komórki elementarne, które oddają symetrię sieci. Nie są to komórki prymitywne (zawierają więcej niż jeden węzeł sieci na komórkę)! Przykład: sieci bcc i fcc, dla których można wybrać romboedryczne komórki prymitywne. bcc fcc źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 12, 13, str. 27
22 230 grup przestrzennych Dotychczasowe rozważania dotyczące symetrii sieci Bravais'ego są również prawdziwe dla struktur krystalicznych gdzie baza ma symetrię sferyczną względem węzłów sieci. W ogólnym przypadku nie ma powodu, aby baza miała symetrię sferyczną. sieć Bravais'ego 7 układów krystalograficznych (7 grup punktowych sieci Bravais'ego) struktura krystaliczna 32 klasy symetrii (32 krystalograficzne grupy punktowe) 14 sieci Bravais'ego 230 grup przestrzennych (14 grup przestrzennych sieci Bravais'ego) (230 krystalograficznych grup przestrzennych) Krystalograficzne grupy przestrzenne są skatalogowane w Międzynarodowych tablicach krystalograficznych (International Tables for Crystallography).
23 230 grup przestrzennych Grupy przestrzenne mogą zawierać elementy nie dające się wyrazić jako złożenie translacji o wektor sieci oraz przekształcenia grupy punktowej. Żeby takie elementy mogły się pojawić musi zachodzić szczególna relacja między rozmiarami bazy, a rozmiarami komórki sieci Bravais'ego. oś śrubowa struktura krystaliczna przechodzi w siebie po translacji o wektor nie należący do sieci Bravais'ego, z następującym po niej obrotem wokół osi wyznaczonej przez wektor translacji. płaszczyzna poślizgu - struktura krystaliczna przechodzi w siebie po translacji o wektor nie należący do sieci Bravais'ego, z następującym po niej odbiciem w płaszczyźnie zawierającej dany wektor translacji. przykład: płaszczyzna poślizgu w strukturze hcp źródło: N. Ashcroft, N. Mermin, Fizyka..., rys. 7.8, str. 162
24 opis płaszczyzn w krysztale - wskaźniki Millera źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 15, str. 28 płaszczyzna krystalograficzna zawiera węzły sieci Niech x, y, z oznaczają współrzędne przecięcia osi krystalograficznych a1, a2, a3 w jednostkach stałych sieci. x, y, z 1/x, 1/y, 1/z h/n, k/n, l/n (hkl) h, k, l, N liczby całkowite Konwencje: - liczby ujemne zaznacza się kreską na górze, nie stosuje się przecinków - (hkl) może oznaczać pojedynczą pł. lub rodzinę płaszczyzn równoległych i równoodległych - jeśli pł. jest do którejś osi, to odpowiedni wskaźnik wynosi 0 - {hkl} oznacza zbiór płaszczyzn równoważnych ze względu na symetrię (np. {100} w układzie regularnym zawiera płaszczyzny (100), (010), (001), (100), (010), (001))
25 opis płaszczyzn w krysztale - wskaźniki Millera źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 16, str. 29 opis kierunków w krysztale [uvw] oznacza kierunek opisany wektorem ua1 + va2 + wa3, gdzie u, v, w są najmniejszymi liczbami całkowitymi pozostającymi w takim stosunku jak składowe wektora Konwencje: - liczby ujemne zaznacza się kreską na górze, nie stosuje się przecinków - <uvw> oznacza zbiór kierunków równoważnych ze względu na symetrię (np. <100> w układzie regularnym zawiera kierunki [100], [010], [001], [100], [010], [001])
26 Przegląd ważniejszych struktur krystalicznych liczba koordynacyjna liczba najbliższych sąsiadów (ang. nearest neighbors) gęstość upakowania - stosunek objętości kryształu zajętej przez atomy traktowane jako sztywne stykające się kule do objętości całkowitej. Przykładowe gęstości upakowania: fcc/hcp 0.74, bcc 0.68, sc 0.52, struktura diamentu 0.38.
27 struktura chlorku sodu (NaCl) sieć: fcc liczba atomów bazy: 2 liczba koordynacyjna: 6 Cl: 0,0,0; ½,½,0; ½,0,½; 0,½,½ Na: ½,½,½; 0,0,½; 0,½,0; ½,0,0 przykłady: NaCl, LiH, MgO, MnO, AgBr, PbS, KCl, KBr i in. (vide: N. Ashcroft, N. Mermin, Fizyka..., tab. 4.5, str. 111) źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 17, str. 30
28 struktura chlorku cezu (CsCl) sieć: sc liczba atomów bazy: 2 liczba koordynacyjna: 8 Cs: 0,0,0 Cl: ½,½,½ przykłady: CsCl, BeCu, AlNi, CuZn (mosiądz ), CuPd, AgMg, LiHg, NH4Cl, TlBr, TlI, TlCl. CsBr, CsI źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 20, str. 32
29 struktura heksagonalna gęstego upakowania (hcp hexagonal close-packed) sieć: heksagonalna liczba atomów bazy: 2 liczba koordynacyjna: 12 stosunek c/a dla idealnej struktury hcp: (w praktyce: ) współczynnik upakowania: 0.74 atomy: 0,0,0; 2/3,1/3,1/2 przykłady: He, Be, Mg, Ti, Zn, Cd, Co, Y, Zr, Gd, Lu i in. (vide: Ch. Kittel, Wstęp..., rozdz. 1, tab. 3, str. 39) źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 23, 22, str. 33
30 struktury gęstego upakowania: hcp i fcc źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 21, str. 33 ABABAB hcp ABCABC fcc w fcc krystalizują np.: Ne, Ar, Ni, Cu, Kr, Rh, Pd, Ag, Xe i in. (vide: Ch. Kittel, Wstęp..., rozdz. 1, tab. 3, str. 39) fcc liczba atomów bazy: 1 liczba koordynacyjna: 12 współczynnik upakowania: 0.74 źródło: N. Ashcroft, N. Mermin, Fizyka..., rys. 4.22, str. 110
31 sieć: fcc struktura diamentu liczba atomów bazy: 2 liczba koordynacyjna: 4 współczynnik upakowania: 0.34 atomy: 0,0,0; ¼,¼,¼ przykłady: C (diament), Si, Ge, -Sn (cyna szara) źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 24, 25, str. 35
32 sieć: fcc struktura blendy cynkowej (ZnS) liczba atomów bazy: 2 liczba koordynacyjna: 4 jest to pochodna struktury diamentu Zn: 0,0,0; 0,½,½; ½,0,½; ½,½,0 S: ¼,¼,¼; ¼,¾,¾; ¾,¼,¾; ¾,¾,¼ przykłady: CuF, SiC, CuCl, ZnS, AlP, GaP, ZnSe, GaAs, AlAs, CdS, InSb, AgI i in. jest to podstawowa struktura dla związków złożonych z atomów grup III i V (vide: N. Ashcroft, N. Mermin, Fizyka..., tab. 4.7, str. 112) źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, rys. 26, str. 36
33 Przegląd ważniejszych struktur krystalicznych 1 Å = m źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 1, tab. 3, str. 39
34 Skąd się bierze różnorodność struktur krystalicznych? - rodzaj wiązań chemicznych - kształt orbitali atomowych - uwzględnienie oddziaływań z drugimi/trzecimi/itd. najbliższymi sąsiadami - stosunek promieni atomowych/jonowych (w przypadku związków wieloskładnikowych)
35 Metody doświadczalne badania struktury kryształów - Badanie morfologii monokryształów określenie symetrii i relacji między stałymi sieci - Dyfrakcja (pr. X, n, e-) określenie symetrii, wartości parametrów sieci i położenia atomów w komórce elementarnej - Metody bezpośredniego obrazowania struktury atomowej (STM/AFM) określenie ułożenia atomów w warstwie powierzchniowej STM (Scanning Tunneling Microscope) Skaningowy mikroskop tunelowy tylko próbki metaliczne! AFM (Atomic Force Microscope) Mikroskop sił atomowych próbki dowolne źródło: Wikipedia
36 Metody doświadczalne badania struktury kryształów STM - przykład: powierzchnia (111) Ag źródło: S.G. García, D.R. Salinas, G. Staikov, Surface Science 576 (2005) 9 18
37 Podsumowanie - kryształy budowa periodyczna - struktura krystaliczna = sieć + baza - komórka elementarna (prymitywna, umowna, Wiegnera-Seitza) - sieć symetria translacyjna + izometrie punktowe (odbicie, obrót, inwersja, oś inwersyjna) - 7 układów krystalograficznych (regularny, tetragonalny, rombowy, heksagonalny, romboedryczny, jednoskośny, trójskośny) -14 sieci Bravais'ego - 32 klasy krystalograficzne, 230 grup przestrzennych - najważniejsze typy struktur: struktura chlorku sodu, struktura chlorku cezu, struktury gęstego upakowania hcp i fcc, struktura diamentu, struktura blendy cynkowej - metody doświadczalne badania struktury kryształów (badanie morfologii monokryształów, dyfrakcja, metody bezpośredniego obrazowania STM i AFM)
MATERIA. = m i liczby całkowite. ciała stałe. - kryształy - ciała bezpostaciowe (amorficzne) - ciecze KRYSZTAŁY. Periodyczność
 MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
MATERIA ciała stałe - kryształy - ciała bezpostaciowe (amorficzne) - ciecze - gazy KRYSZTAŁY Periodyczność Kryształ (idealny) struktura zbudowana z powtarzających się w przestrzeni periodycznie identycznych
Elementy teorii powierzchni metali
 Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
Prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład dla studentów fizyki Rok akademicki 2017/18 (30 godz.) Wykład 1 Plan wykładu Struktura periodyczna kryształów, sieć odwrotna Struktura
S 2, C 2h,D 2h,D 3d,D 4h, D 6h, O h
 Są tylko 32 grupy punktowe, które spełniają ten warunek, Można je pogrupować w 7 typów grup (spośród omówionych 12- tu), które spełniają powyższe własności S 2, C 2h,D 2h,D 3d,D 4h, D 6h, O h nazywają
Są tylko 32 grupy punktowe, które spełniają ten warunek, Można je pogrupować w 7 typów grup (spośród omówionych 12- tu), które spełniają powyższe własności S 2, C 2h,D 2h,D 3d,D 4h, D 6h, O h nazywają
STRUKTURA CIAŁA STAŁEGO
 STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
STRUKTURA CIAŁA STAŁEGO Podział ciał stałych Ciała - bezpostaciowe (amorficzne) Szkła, żywice, tłuszcze, niektóre proszki. Nie wykazują żadnych regularnych płaszczyzn ograniczających, nie można w nich
Wykład 5. Komórka elementarna. Sieci Bravais go
 Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Wykład 5 Komórka elementarna Sieci Bravais go Doskonały kryształ składa się z atomów jonów, cząsteczek) uporządkowanych w sieci krystalicznej opisanej przez trzy podstawowe wektory translacji a, b, c,
Aby opisać strukturę krystaliczną, konieczne jest określenie jej części składowych: sieci przestrzennej oraz bazy atomowej.
 2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
2. Podstawy krystalografii Podczas naszych zajęć skupimy się przede wszystkim na strukturach krystalicznych. Kryształem nazywamy (def. strukturalna) substancję stałą zbudowaną z atomów, jonów lub cząsteczek
STRUKTURA KRYSZTAŁÓW
 STRUKTURA KRYSZTAŁÓW Skala wielkości spotykanych w krystalografii: Średnica atomu wodoru: 10 Rozmiar komórki elementarnej: od kilku do kilkudziesięciu Å o D = 1*10 m = 1A 1 Struktura = sieć + baza atomowa
STRUKTURA KRYSZTAŁÓW Skala wielkości spotykanych w krystalografii: Średnica atomu wodoru: 10 Rozmiar komórki elementarnej: od kilku do kilkudziesięciu Å o D = 1*10 m = 1A 1 Struktura = sieć + baza atomowa
Krystalografia. Typowe struktury pierwiastków i związków chemicznych
 Krystalografia Typowe struktury pierwiastków i związków chemicznych Wiązania w kryształach jonowe silne, bezkierunkowe kowalencyjne silne, kierunkowe metaliczne słabe lub silne, bezkierunkowe van der Waalsa
Krystalografia Typowe struktury pierwiastków i związków chemicznych Wiązania w kryształach jonowe silne, bezkierunkowe kowalencyjne silne, kierunkowe metaliczne słabe lub silne, bezkierunkowe van der Waalsa
Wstęp do Optyki i Fizyki Materii Skondensowanej. Mateusz Goryca
 Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
Wstęp do Optyki i Fizyki Materii Skondensowanej Mateusz Goryca mgoryca@fuw.edu.pl Uniwersytet Warszawski 2015 Materia skondensowana OC 6 H 13 H 13 C 6 O OC 6 H 13 H 17 C 8 O H 17 C 8 O N N Cu O O H 21
BUDOWA KRYSTALICZNA CIAŁ STAŁYCH. Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale
 BUDOWA KRYSTALICZNA CIAŁ STAŁYCH Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale na: kryształy ciała o okresowym regularnym uporządkowaniu atomów, cząsteczek w całej swojej
BUDOWA KRYSTALICZNA CIAŁ STAŁYCH Stopień uporządkowania struktury wewnętrznej ciał stałych decyduje o ich podziale na: kryształy ciała o okresowym regularnym uporządkowaniu atomów, cząsteczek w całej swojej
Wykład 4: Struktura krystaliczna
 Wykład 4: Struktura krystaliczna Wg Blicharskiego, Wstęp do materiałoznawstwa http://webmineral.com/ Komórka elementarna Geometria komórki Dla zdefiniowania trójwymiarowej komórki elementarnej należy podać
Wykład 4: Struktura krystaliczna Wg Blicharskiego, Wstęp do materiałoznawstwa http://webmineral.com/ Komórka elementarna Geometria komórki Dla zdefiniowania trójwymiarowej komórki elementarnej należy podać
Rozwiązanie: Zadanie 2
 Podstawowe pojęcia. Definicja kryształu. Sieć przestrzenna i sieć krystaliczna. Osie krystalograficzne i jednostki osiowe. Ściana jednostkowa i stosunek osiowy. Położenie węzłów, prostych i płaszczyzn
Podstawowe pojęcia. Definicja kryształu. Sieć przestrzenna i sieć krystaliczna. Osie krystalograficzne i jednostki osiowe. Ściana jednostkowa i stosunek osiowy. Położenie węzłów, prostych i płaszczyzn
Fizyka Ciała Stałego
 Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
Wykład III Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć krystaliczną. Amorficzne, brak uporządkowania,
STRUKTURA KRYSTALICZNA
 PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
PODSTAWY KRYSTALOGRAFII Struktura krystaliczna Wektory translacji sieci Komórka elementarna Komórka elementarna Wignera-Seitza Jednostkowy element struktury Sieci Bravais go 2D Sieci przestrzenne Bravais
Układ regularny. Układ regularny. Możliwe elementy symetrii: Możliwe elementy symetrii: 3 osie 3- krotne. m płaszczyzny przekątne.
 Układ regularny Możliwe elementy symetrii: 3 osie 3- krotne m płaszczyzny równoległe do ścian m płaszczyzny przekątne 4 osie 4- krotne 2 osie 2- krotne Układ regularny Możliwe elementy symetrii: 3 osie
Układ regularny Możliwe elementy symetrii: 3 osie 3- krotne m płaszczyzny równoległe do ścian m płaszczyzny przekątne 4 osie 4- krotne 2 osie 2- krotne Układ regularny Możliwe elementy symetrii: 3 osie
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii. Laboratorium z Krystalografii. 2 godz. Komórki Bravais go
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Komórki Bravais go Cel ćwiczenia: kształtowanie umiejętności: przyporządkowywania komórek translacyjnych Bravais
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Komórki Bravais go Cel ćwiczenia: kształtowanie umiejętności: przyporządkowywania komórek translacyjnych Bravais
Elementy teorii powierzchni metali
 prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
prof. dr hab. Adam Kiejna Elementy teorii powierzchni metali Wykład 2 v.16 Sieci płaskie i struktura powierzchni 1 Typy sieci dwuwymiarowych (płaskich) Przecinając monokryształ wzdłuż jednej z płaszczyzn
Budowa ciał stałych. sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych
 Budowa ciał stałych sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych Ciała stałe to substancje o regularnej, przestrzennej budowie krystalicznej, czyli regularnym
Budowa ciał stałych sieć krystaliczna układy krystalograficzne sieć realna defekty wiązania w ciałach stałych Ciała stałe to substancje o regularnej, przestrzennej budowie krystalicznej, czyli regularnym
STRUKTURA MATERIAŁÓW
 STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
STRUKTURA MATERIAŁÓW ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY ATOMAMI Siły oddziaływania między atomami
Położenia, kierunki, płaszczyzny
 Położenia, kierunki, płaszczyzny Dalsze pojęcia Osie krystalograficzne; Parametry komórki elementarnej; Wskaźniki punktów kierunków i płaszczyzn; Osie krystalograficzne Osie krystalograficzne: układ osi
Położenia, kierunki, płaszczyzny Dalsze pojęcia Osie krystalograficzne; Parametry komórki elementarnej; Wskaźniki punktów kierunków i płaszczyzn; Osie krystalograficzne Osie krystalograficzne: układ osi
Rodzina i pas płaszczyzn sieciowych
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Rodzina i pas płaszczyzn sieciowych Cel ćwiczenia: kształtowanie umiejętności posługiwania się modelami komórek
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Rodzina i pas płaszczyzn sieciowych Cel ćwiczenia: kształtowanie umiejętności posługiwania się modelami komórek
Sieć przestrzenna. c r. b r. a r. komórka elementarna. r r
 Sieć przestrzenna c r b r r r u a r vb uvw = + + w c v a r komórka elementarna V = r r a ( b c) v Układy krystalograficzne (7) i Sieci Bravais (14) Triclinic (P) a b c, α β γ 90 ο Monoclinic (P) a b c,
Sieć przestrzenna c r b r r r u a r vb uvw = + + w c v a r komórka elementarna V = r r a ( b c) v Układy krystalograficzne (7) i Sieci Bravais (14) Triclinic (P) a b c, α β γ 90 ο Monoclinic (P) a b c,
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Sieć krystaliczna
 Wykład II Sieć krystaliczna Podstawowe definicje Wiele z pośród ciał stałych ma budowę krystaliczną. To znaczy, Ŝe atomy z których się składają ułoŝone są w określonym porządku. Porządek ten daje się stosunkowo
Wykład II Sieć krystaliczna Podstawowe definicje Wiele z pośród ciał stałych ma budowę krystaliczną. To znaczy, Ŝe atomy z których się składają ułoŝone są w określonym porządku. Porządek ten daje się stosunkowo
S. Baran - Podstawy fizyki materii skondensowanej Wiązania chemiczne w ciałach stałych. Wiązania chemiczne w ciałach stałych
 Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Wiązania chemiczne w ciałach stałych Wiązania chemiczne w ciałach stałych typ kowalencyjne jonowe metaliczne Van der Waalsa wodorowe siła* silne silne silne pochodzenie uwspólnienie e- (pary e-) przez
Fizyka Ciała Stałego. Struktura krystaliczna. Struktura amorficzna
 Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wykład II Struktura krystaliczna Fizyka Ciała Stałego Ciała stałe można podzielić na: Amorficzne, brak uporządkowania, np. szkła; Krystaliczne, o uporządkowanym ułożeniu atomów lub molekuł tworzącym sieć
Wstęp. Krystalografia geometryczna
 Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Wstęp Przedmiot badań krystalografii. Wprowadzenie do opisu struktury kryształów. Definicja sieci Bravais go i bazy atomowej, komórki prymitywnej i elementarnej. Podstawowe typy komórek elementarnych.
Podstawy krystalochemii pierwiastki
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Podstawy krystalochemii pierwiastki Cel ćwiczenia: określenie pełnej charakterystyki wybranych struktur pierwiastków
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Podstawy krystalochemii pierwiastki Cel ćwiczenia: określenie pełnej charakterystyki wybranych struktur pierwiastków
ROZDZIAŁ I. Symetria budowy kryształów
 ROZDZIAŁ I Symetria budowy kryształów I Ciała krystaliczne i amorficzne Każda substancja ciekła z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe Jednakże proces
ROZDZIAŁ I Symetria budowy kryształów I Ciała krystaliczne i amorficzne Każda substancja ciekła z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe Jednakże proces
Ciała stałe. Ciała krystaliczne. Ciała amorficzne. Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami.
 Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Ciała stałe Ciała krystaliczne Ciała amorficzne Bardzo często mamy do czynienia z ciałami polikrystalicznymi, rzadko monokryształami. r T = Kryształy rosną przez regularne powtarzanie się identycznych
Podstawowe pojęcia opisujące sieć przestrzenną
 Uniwersytet Śląski Instytut Chemii akład Krystalografii Laboratorium z Krystalografii 2 godz. Podstawowe pojęcia opisujące sieć przestrzenną Cel ćwiczenia: kształtowanie umiejętności posługiwania się modelami
Uniwersytet Śląski Instytut Chemii akład Krystalografii Laboratorium z Krystalografii 2 godz. Podstawowe pojęcia opisujące sieć przestrzenną Cel ćwiczenia: kształtowanie umiejętności posługiwania się modelami
Wiązania chemiczne. Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych. 5 typów wiązań
 Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Wiązania chemiczne Związek klasyfikacji ciał krystalicznych z charakterem wiązań atomowych 5 typów wiązań wodorowe A - H - A, jonowe ( np. KCl ) molekularne (pomiędzy atomami gazów szlachetnych i małymi
Układy krystalograficzne
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Układy krystalograficzne Cel ćwiczenia: kształtowanie umiejętności wyboru komórki elementarnej i przyporządkowywania
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii 2 godz. Układy krystalograficzne Cel ćwiczenia: kształtowanie umiejętności wyboru komórki elementarnej i przyporządkowywania
Opracowanie: mgr inż. Antoni Konitz, dr hab inż. Jarosław Chojnacki Politechnika Gdańska, Gdańsk 2007, 2016
 4. Stosowanie międzynarodowych symboli grup przestrzennych. Zamiana skróconych symboli Hermanna - Mauguina na symbole pełne. Określanie układu krystalograficznego, klasy krystalograficznej oraz operacji
4. Stosowanie międzynarodowych symboli grup przestrzennych. Zamiana skróconych symboli Hermanna - Mauguina na symbole pełne. Określanie układu krystalograficznego, klasy krystalograficznej oraz operacji
S. Baran - Podstawy fizyki materii skondensowanej Fonony. Fonony
 Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Fonony Drgania płaszczyzn sieciowych podłużne poprzeczne źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 4, rys. 2, 3, str. 118 Drgania płaszczyzn sieciowych Do opisu drgań sieci krystalicznej wystarczą
Zastosowanie teorii grup. Grupy symetrii w fizyce i chemii.
 Zastosowanie teorii grup Grupy symetrii w fizyce i chemii Katarzyna Kolonko Streszczenie Usystematyzowanie grup punktowych, omówienie ich na przykładzie molekuł Przedstawienie wkładu teorii grup w badanie
Zastosowanie teorii grup Grupy symetrii w fizyce i chemii Katarzyna Kolonko Streszczenie Usystematyzowanie grup punktowych, omówienie ich na przykładzie molekuł Przedstawienie wkładu teorii grup w badanie
Grupy przestrzenne i ich symbolika
 Grupy przestrzenne i ich symbolika Po co mi (chemikowi) znajomość symboli grup przestrzennych? Informacje zawarte w symbolu układ krystalograficzny obecność operacji symetrii punktowej (spektroskopia)
Grupy przestrzenne i ich symbolika Po co mi (chemikowi) znajomość symboli grup przestrzennych? Informacje zawarte w symbolu układ krystalograficzny obecność operacji symetrii punktowej (spektroskopia)
Wykład 5 Otwarte i wtórne operacje symetrii
 Wykład 5 Otwarte i wtórne operacje symetrii 1.Otwarty iloczyn operacji symetrii 2.Osie śrubowe i płaszczyzny poślizgu 3.Sieci Bravais a 4.Wtórne operacje symetrii Przekształecenia izometryczne Zamknięte
Wykład 5 Otwarte i wtórne operacje symetrii 1.Otwarty iloczyn operacji symetrii 2.Osie śrubowe i płaszczyzny poślizgu 3.Sieci Bravais a 4.Wtórne operacje symetrii Przekształecenia izometryczne Zamknięte
Krystalochemia białek 2016/2017
 Zestaw zadań 4. Grupy punktowe. Składanie elementów symetrii. Translacyjne elementy symetrii grupy punktowe, składanie elementów symetrii, translacyjne elementy symetrii: osie śrubowe, płaszczyzny ślizgowe
Zestaw zadań 4. Grupy punktowe. Składanie elementów symetrii. Translacyjne elementy symetrii grupy punktowe, składanie elementów symetrii, translacyjne elementy symetrii: osie śrubowe, płaszczyzny ślizgowe
STRUKTURA IDEALNYCH KRYSZTAŁÓW
 BUDOWA WEWNĘTRZNA MATERIAŁÓW METALICZNYCH Zakres tematyczny y 1 STRUKTURA IDEALNYCH KRYSZTAŁÓW 2 1 Sieć przestrzenna kryształu TRANSLACJA WĘZŁA TRANSLACJA PROSTEJ SIECIOWEJ TRANSLACJA PŁASZCZYZNY SIECIOWEJ
BUDOWA WEWNĘTRZNA MATERIAŁÓW METALICZNYCH Zakres tematyczny y 1 STRUKTURA IDEALNYCH KRYSZTAŁÓW 2 1 Sieć przestrzenna kryształu TRANSLACJA WĘZŁA TRANSLACJA PROSTEJ SIECIOWEJ TRANSLACJA PŁASZCZYZNY SIECIOWEJ
Tradycyjny podział stanów skupienia: fazy skondensowane
 Tradycyjny podział stanów skupienia: o o o stały (ciało stałe) zachowuje objętość i kształt ciekły (ciecz) zachowuje objętość, łatwo zmienia kształt gazowy (gaz) łatwo zmienia objętość i kształt lód woda
Tradycyjny podział stanów skupienia: o o o stały (ciało stałe) zachowuje objętość i kształt ciekły (ciecz) zachowuje objętość, łatwo zmienia kształt gazowy (gaz) łatwo zmienia objętość i kształt lód woda
Symetria w fizyce materii
 Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Symetria w fizyce materii - Przekształcenia symetrii w dwóch i trzech wymiarach - Wprowadzenie w teorię grup; grupy symetrii - Wprowadzenie w teorię reprezentacji grup - Teoria grup a mechanika kwantowa
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Wykład 1. Symetria Budowy Kryształów
 Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
Wykład Symetria Budowy Kryształów Ciała krystaliczne i amorficzne Każda substancja ciekła (z wyjątkiem helu) podczas oziębiania traci swoje własności ciekłe i przechodzi w ciało stałe. Jednakże proces
S. Baran - Podstawy fizyki materii skondensowanej Dyfrakcja na kryształach. Dyfrakcja na kryształach
 S. Baran - Podstawy fizyki materii skondensowanej Dyfrakcja na kryształach Dyfrakcja na kryształach Warunki dyfrakcji źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 2, rys. 6, str. 49 Konstrukcja Ewalda
S. Baran - Podstawy fizyki materii skondensowanej Dyfrakcja na kryształach Dyfrakcja na kryształach Warunki dyfrakcji źródło: Ch. Kittel Wstęp do fizyki..., rozdz. 2, rys. 6, str. 49 Konstrukcja Ewalda
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by Harcourt,
Metody badań monokryształów metoda Lauego
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40 006 Katowice, Tel. 0323591627 e-mail: joanna_palion@poczta.fm opracowanie: mgr Joanna Palion Gazda Laboratorium z Krystalografii
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40 006 Katowice, Tel. 0323591627 e-mail: joanna_palion@poczta.fm opracowanie: mgr Joanna Palion Gazda Laboratorium z Krystalografii
MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I. dr inż. Hanna Smoleńska
 MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I dr inż. Hanna Smoleńska Struktura materiałów UKŁAD ATOMÓW W PRZESTRZENI CIAŁA KRYSTALICZNE Układ atomów/cząstek (a/cz) w przestrzeni jest statystyczne
MATERIAŁOZNAWSTWO Wydział Mechaniczny, Mechatronika, sem. I dr inż. Hanna Smoleńska Struktura materiałów UKŁAD ATOMÓW W PRZESTRZENI CIAŁA KRYSTALICZNE Układ atomów/cząstek (a/cz) w przestrzeni jest statystyczne
Właściwości kryształów
 Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
Właściwości kryształów Związek pomiędzy właściwościami, strukturą, defektami struktury i wiązaniami chemicznymi Skład i struktura Skład materiału wpływa na wszystko, ale głównie na: właściwości fizyczne
3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów
 3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów Opracowanie: dr hab. inż. Jarosław Chojnacki, Politechnika Gdańska, Gdańsk 207 Każda
3. Operacje symetrii, macierze operacji symetrii. Grupy punktowe. Przypisywanie grupy punktowej dla zadanych obiektów Opracowanie: dr hab. inż. Jarosław Chojnacki, Politechnika Gdańska, Gdańsk 207 Każda
STRUKTURA MATERIAŁÓW. Opracowanie: Dr hab.inż. Joanna Hucińska
 STRUKTURA MATERIAŁÓW Opracowanie: Dr hab.inż. Joanna Hucińska ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY
STRUKTURA MATERIAŁÓW Opracowanie: Dr hab.inż. Joanna Hucińska ELEMENTY STRUKTURY MATERIAŁÓW 1. Wiązania miedzy atomami 2. Układ atomów w przestrzeni 3. Mikrostruktura 4. Makrostruktura 1. WIĄZANIA MIĘDZY
Struktura kryształów. Kittel, rozdz. 1 (Uwaga błędna terminologia!) Ashcroft, Mermin, rozdz.
 Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Struktur krysztłów http://www.uncp.edu/home/mcclurem/ptble/crbon.htm Kittel, rozdz. 1 (Uwg błędn terminologi!) Ashcroft, Mermin, rozdz. 4,7 1 Obserwowne włsności Ksztłt ogrniczony płszczyznmi. (1) Kierunki
Uniwersytet Śląski w Katowicach str. 1 Wydział
 Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy Sylabus modułu: Krystalografia (016) Nazwa wariantu modułu (opcjonalnie): _wariantu ( wariantu) 1. Informacje ogólne koordynator
Uniwersytet Śląski w Katowicach str. 1 Kierunek i poziom studiów: Chemia, pierwszy Sylabus modułu: Krystalografia (016) Nazwa wariantu modułu (opcjonalnie): _wariantu ( wariantu) 1. Informacje ogólne koordynator
Repeta z wykładu nr 3. Detekcja światła. Struktura krystaliczna. Plan na dzisiaj
 Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 3 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
NOWA STRONA INTERNETOWA PRZEDMIOTU: http://xrd.ceramika.agh.edu.pl/
 Wskaźnikowanie rentgenogramów i wyznaczanie parametrów sieciowych Wykład 8 1. Wskaźnikowanie rentgenogramów. 2. Metoda róŝnic wskaźnikowania rentgenogramów substancji z układu regularnego. 3. Metoda ilorazów
Wskaźnikowanie rentgenogramów i wyznaczanie parametrów sieciowych Wykład 8 1. Wskaźnikowanie rentgenogramów. 2. Metoda róŝnic wskaźnikowania rentgenogramów substancji z układu regularnego. 3. Metoda ilorazów
Chemia nieorganiczna. Copyright 2000 by Harcourt, Inc. All rights reserved.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Pierwiastki 1 1 H 3 Li 11
Stany skupienia materii
 Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Stany skupienia materii Ciała stałe - ustalony kształt i objętość - uporządkowanie dalekiego zasięgu - oddziaływania harmoniczne Ciecze -słabo ściśliwe - uporządkowanie bliskiego zasięgu -tworzą powierzchnię
Chemia nieorganiczna. Pierwiastki. niemetale Be. 27 Co. 28 Ni. 26 Fe. 29 Cu. 45 Rh. 44 Ru. 47 Ag. 46 Pd. 78 Pt. 76 Os.
 Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by arcourt,
Chemia nieorganiczna 1. Układ okresowy metale i niemetale 2. Oddziaływania inter- i intramolekularne 3. Ciała stałe rodzaje sieci krystalicznych 4. Przewodnictwo ciał stałych Copyright 2000 by arcourt,
Krystalografia i krystalochemia Wykład 15 Repetytorium
 Krystalografia i krystalochemia Wykład 15 Repetytorium 1. Czym zajmuje się krystalografia i krystalochemia? 2. Podsumowanie wiadomości z krystalografii geometrycznej. 3. Symbolika Kreutza-Zaremby oraz
Krystalografia i krystalochemia Wykład 15 Repetytorium 1. Czym zajmuje się krystalografia i krystalochemia? 2. Podsumowanie wiadomości z krystalografii geometrycznej. 3. Symbolika Kreutza-Zaremby oraz
Struktura energetyczna ciał stałych. Fizyka II, lato
 Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
Struktura energetyczna ciał stałych Fizyka II, lato 016 1 Stany związane Studnia potencjału o nieskończończonej głębokości jest idealizacją. W praktyce realizowalna jest skończona studnia, w której energia
Elementy symetrii makroskopowej.
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Elementy symetrii makroskopowej. 2 godz. Cel ćwiczenia: zapoznanie się z działaniem elementów symetrii makroskopowej
Wykład 9 Wprowadzenie do krystalochemii
 Wykład 9 Wprowadzenie do krystalochemii 1. Krystalografia a krystalochemia. 2. Prawa krystalochemii 3. Sieć krystaliczna i pozycje atomów 4. Bliskie i dalekie uporządkowanie. 5. Kryształ a cząsteczka.
Wykład 9 Wprowadzenie do krystalochemii 1. Krystalografia a krystalochemia. 2. Prawa krystalochemii 3. Sieć krystaliczna i pozycje atomów 4. Bliskie i dalekie uporządkowanie. 5. Kryształ a cząsteczka.
Struktura energetyczna ciał stałych. Fizyka II dla EiT oraz E, lato
 Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Struktura energetyczna ciał stałych Fizyka II dla EiT oraz E, lato 016 1 Struktura kryształu Doskonały kryształ składa się z uporządkowanych atomów w sieci krystalicznej, opisanej przez trzy podstawowe
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 08.06.017 Wydział Informatyki, Elektroniki i 1 Struktura
Rejestracja dyfraktogramów polikrystalicznych związków. Wskaźnikowanie dyfraktogramów i wyznaczanie typu komórki Bravais go.
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 133, 40006 Katowice tel. 0323591503, email: izajen@wp.pl opracowanie: dr hab. Izabela Jendrzejewska Laboratorium z Krystalografii
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 133, 40006 Katowice tel. 0323591503, email: izajen@wp.pl opracowanie: dr hab. Izabela Jendrzejewska Laboratorium z Krystalografii
Szkła. Forma i odlewy ze szkła kwarcowego wykonane w starożytnym Egipcie (około roku 2500 p.n.e.)
 Szkła metaliczne Szkła cdn.gemrockauctions.com/uploads/images/275000-279999/276152/276152_1338954219.jpg American Association for the Advancement of Science Grot ze szkła wulkanicznego obsydianu (epoka
Szkła metaliczne Szkła cdn.gemrockauctions.com/uploads/images/275000-279999/276152/276152_1338954219.jpg American Association for the Advancement of Science Grot ze szkła wulkanicznego obsydianu (epoka
Metody badań monokryształów metoda Lauego
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40 006 Katowice, Tel. 0323591627 e-mail: joanna_palion@poczta.fm opracowanie: mgr Joanna Palion Gazda Laboratorium z Krystalografii
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40 006 Katowice, Tel. 0323591627 e-mail: joanna_palion@poczta.fm opracowanie: mgr Joanna Palion Gazda Laboratorium z Krystalografii
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ Struktura kryształu Ciała stałe o budowie bezpostaciowej
KRYSTALOGRAFIA Studia pierwszego stopnia, stacjonarne II rok
 Akademia Górniczo-Hutnicza Wydział Odlewnictwa Katedra Inżynierii Stopów i Kompozytów Odlewanych Nr ćwiczenia: 1 Opracowała Temat: Cel ćwiczenia: Zakres wymaganego materiału Przebieg ćwiczenia Materiały
Akademia Górniczo-Hutnicza Wydział Odlewnictwa Katedra Inżynierii Stopów i Kompozytów Odlewanych Nr ćwiczenia: 1 Opracowała Temat: Cel ćwiczenia: Zakres wymaganego materiału Przebieg ćwiczenia Materiały
Dr inż. Zbigniew Szklarski
 Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Wykład : Ciało stałe Dr inż. Zbigniew Szklarski Katedra Elektroniki, paw. C-1, pok.31 szkla@agh.edu.pl http://layer.uci.agh.edu.pl/z.szklarski/ 19.06.018 Wydział Informatyki, Elektroniki i 1 Struktura
Proste struktury krystaliczne
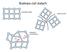 Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Budowa ciał stałych Proste struktury krystaliczne sc (simple cubic) bcc (body centered cubic) fcc (face centered cubic) np. Piryt FeSe 2 np. Żelazo, Wolfram np. Miedź, Aluminium Struktury krystaliczne
Model wiązania kowalencyjnego cząsteczka H 2
 Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
Model wiązania kowalencyjnego cząsteczka H 2 + Współrzędne elektronu i protonów Orbitale wiążący i antywiążący otrzymane jako kombinacje orbitali atomowych Orbital wiążący duża gęstość ładunku między jądrami
1. Elementy (abstrakcyjnej) teorii grup
 1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
1. Elementy (abstrakcyjnej) teorii grup Grupy symetrii def. Grupy Zbiór (skończony lub nieskończony) elementów {g} tworzy grupę gdy: - zdefiniowana operacja mnożenia (złożenia) g 1 g 2 = g 3 є G - (g 1
Arkusze zadań do ćwiczeń z podstaw fizyki ciała stałego Marek Izdebski
 Arkusze zadań do ćwiczeń z podstaw fizyki ciała stałego Marek Izdebski Spis treści Temat 1. Ciało stałe. Sieć krystaliczna doskonała. Symetrie kryształów.... 1 Temat. Sieć odwrotna. Kryształy rzeczywiste....
Arkusze zadań do ćwiczeń z podstaw fizyki ciała stałego Marek Izdebski Spis treści Temat 1. Ciało stałe. Sieć krystaliczna doskonała. Symetrie kryształów.... 1 Temat. Sieć odwrotna. Kryształy rzeczywiste....
Fizyka powierzchni. Dr Piotr Sitarek. Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska
 Fizyka powierzchni 1 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Fizyka powierzchni 1 Dr Piotr Sitarek Katedra Fizyki Doświadczalnej, Wydział Podstawowych Problemów Techniki, Politechnika Wrocławska Lista zagadnień Fizyka powierzchni i międzypowierzchni, struktura powierzchni
Wykład V Wiązanie kowalencyjne. Półprzewodniki
 Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
Wykład V Wiązanie kowalencyjne. Półprzewodniki Wiązanie kowalencyjne molekuła H 2 Tworzenie wiązania kowalencyjnego w molekule H 2 : elektron w jednym atomie przyciągany jest przez jądro drugiego. Wiązanie
4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH. Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu)
 4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Krzem, podstawowe parametry 1. Konfiguracja elektronowa:
4. STRUKTURA KRYSZTAŁÓW PÓŁPRZEWODNIKOWYCH Irena Zubel Wydział Elektroniki Mikrosystemów i Fotoniki Politechnika Wrocławska (na prawach rękopisu) Krzem, podstawowe parametry 1. Konfiguracja elektronowa:
Laboratorium z Krystalografii. 2 godz.
 Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
Uniwersytet Śląski - Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 132, 40-006 Katowice tel. 0323591627, e-mail: ewa.malicka@us.edu.pl opracowanie: dr Ewa Malicka Laboratorium z Krystalografii
Struktura elektronowa
 Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Struktura elektronowa Struktura elektronowa atomów układ okresowy pierwiastków: 1) elektrony w atomie zajmują poziomy energetyczne od dołu, inaczej niż te gołębie (w Australii, ale tam i tak chodzi się
Promieniowanie rentgenowskie. Podstawowe pojęcia krystalograficzne
 Promieniowanie rentgenowskie Podstawowe pojęcia krystalograficzne Krystalografia - podstawowe pojęcia Komórka elementarna (zasadnicza): najmniejszy, charakterystyczny fragment sieci przestrzennej (lub
Promieniowanie rentgenowskie Podstawowe pojęcia krystalograficzne Krystalografia - podstawowe pojęcia Komórka elementarna (zasadnicza): najmniejszy, charakterystyczny fragment sieci przestrzennej (lub
Rentgenografia - teorie dyfrakcji
 Rentgenografia - teorie dyfrakcji widmo promieniowania rentgenowskiego Widmo emisyjne promieniowania rentgenowskiego: -promieniowanie charakterystyczne -promieniowanie ciągłe (białe) Efekt naświetlenia
Rentgenografia - teorie dyfrakcji widmo promieniowania rentgenowskiego Widmo emisyjne promieniowania rentgenowskiego: -promieniowanie charakterystyczne -promieniowanie ciągłe (białe) Efekt naświetlenia
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ. Zmiany makroskopowe. Zmiany makroskopowe
 WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
WŁAŚCIWOŚCI MECHANICZNE PLASTYCZNOŚĆ Zmiany makroskopowe Zmiany makroskopowe R e = R 0.2 - umowna granica plastyczności (0.2% odkształcenia trwałego); R m - wytrzymałość na rozciąganie (plastyczne); 1
Krystalografia. Dyfrakcja na monokryształach. Analiza dyfraktogramów
 Krystalografia Dyfrakcja na monokryształach. Analiza dyfraktogramów Wyznaczanie struktury Pomiar obrazów dyfrakcyjnych Stworzenie modelu niezdeformowanej sieci odwrotnej refleksów Wybór komórki elementarnej
Krystalografia Dyfrakcja na monokryształach. Analiza dyfraktogramów Wyznaczanie struktury Pomiar obrazów dyfrakcyjnych Stworzenie modelu niezdeformowanej sieci odwrotnej refleksów Wybór komórki elementarnej
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Projekt współfinansowany z Europejskiego Funduszu Społecznego i BudŜetu Państwa. Krystalografia. Instrukcje do ćwiczeń laboratoryjnych
 Projekt współfinansowany z Europejskiego Funduszu Społecznego i BudŜetu Państwa Krystalografia Instrukcje do ćwiczeń laboratoryjnych Rok akademicki 2009/2010 SPIS TREŚCI WPROWADZENIE... 4 1. KRYSZTAŁY
Projekt współfinansowany z Europejskiego Funduszu Społecznego i BudŜetu Państwa Krystalografia Instrukcje do ćwiczeń laboratoryjnych Rok akademicki 2009/2010 SPIS TREŚCI WPROWADZENIE... 4 1. KRYSZTAŁY
= a (a c-c )x(3) 1/2. Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową
 Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Grafit i nanorurki węglowe Grafen sieć rombowa (heksagonalna) z bazą dwuatomową a 1 = a (a c-c )x(3) 1/ ( 3 a, ), ( 3 a a a = a, ) wektory bazowe sieci odwrotnej definiuje się inaczej niż w 3D musi zachodzić
Międzynarodowe Tablice Krystalograficzne (International Tables for Crystallography)
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Międzynarodowe Tablice Krystalograficzne (International Tables for Crystallography) 2 godz. Cel ćwiczenia: analiza
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii Laboratorium z Krystalografii Międzynarodowe Tablice Krystalograficzne (International Tables for Crystallography) 2 godz. Cel ćwiczenia: analiza
Klasyfikacja przemian fazowych
 Klasyfikacja przemian fazowych Faza- jednorodna pod względem własności część układu, oddzielona od pozostałej częsci układu powierzchnią graniczną, po której przekroczeniu własności zmieniaja się w sposób
Klasyfikacja przemian fazowych Faza- jednorodna pod względem własności część układu, oddzielona od pozostałej częsci układu powierzchnią graniczną, po której przekroczeniu własności zmieniaja się w sposób
Teoria pasmowa ciał stałych
 Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Teoria pasmowa ciał stałych Poziomy elektronowe atomów w cząsteczkach ulegają rozszczepieniu. W kryształach zjawisko to prowadzi do wytworzenia się pasm. Klasyfikacja ciał stałych na podstawie struktury
Prof. nzw. dr hab. Jarosław Mizera & dr inż. Joanna Zdunek
 Prof. nzw. dr hab. Jarosław Mizera & dr inż. Joanna Zdunek Krystalografia to nauka zajmująca się opisem i badaniem periodycznej budowy wewnętrznej materiałów krystalicznych oraz ich klasyfikacją. Plan
Prof. nzw. dr hab. Jarosław Mizera & dr inż. Joanna Zdunek Krystalografia to nauka zajmująca się opisem i badaniem periodycznej budowy wewnętrznej materiałów krystalicznych oraz ich klasyfikacją. Plan
Dyslokacje w kryształach. ach. Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska
 Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Dyslokacje w kryształach ach Keshra Sangwal Zakład Fizyki Stosowanej, Instytut Fizyki Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: Podstawowe pojęcie III. Własności mechaniczne kryształów
Dyslokacje w kryształach. ach. Keshra Sangwal, Politechnika Lubelska. Literatura
 Dyslokacje w kryształach ach Keshra Sangwal, Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: podstawowe pojęcie III. Własności mechaniczne kryształów IV. Źródła i rozmnażanie się dyslokacji
Dyslokacje w kryształach ach Keshra Sangwal, Politechnika Lubelska I. Wprowadzenie do defektów II. Dyslokacje: podstawowe pojęcie III. Własności mechaniczne kryształów IV. Źródła i rozmnażanie się dyslokacji
Inne koncepcje wiązań chemicznych. 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań?
 Inne koncepcje wiązań chemicznych 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań? Model VSEPR wiązanie pary elektronowe dzielone między atomy tworzące wiązanie.
Inne koncepcje wiązań chemicznych 1. Jak przewidywac strukturę cząsteczki? 2. Co to jest wiązanie? 3. Jakie są rodzaje wiązań? Model VSEPR wiązanie pary elektronowe dzielone między atomy tworzące wiązanie.
Konwersatorium 1. Zagadnienia na konwersatorium
 Konwersatorium 1 Zagadnienia na konwersatorium 1. Omów reguły zapełniania powłok elektronowych. 2. Podaj konfiguracje elektronowe dla atomów Cu, Ag, Au, Pd, Pt, Cr, Mo, W. 3. Wyjaśnij dlaczego występują
Konwersatorium 1 Zagadnienia na konwersatorium 1. Omów reguły zapełniania powłok elektronowych. 2. Podaj konfiguracje elektronowe dla atomów Cu, Ag, Au, Pd, Pt, Cr, Mo, W. 3. Wyjaśnij dlaczego występują
Natęż. ężenie refleksu dyfrakcyjnego
 Natęż ężenie refleksu dyfrakcyjnego Wskaźnikowanie dyfraktogramów 1. Natężenie refleksu dyfrakcyjnego - od czego i jak zależy 1. Wskaźnikowanie dyfraktogramów -metoda różnic 3. Wygaszenia systematyczne
Natęż ężenie refleksu dyfrakcyjnego Wskaźnikowanie dyfraktogramów 1. Natężenie refleksu dyfrakcyjnego - od czego i jak zależy 1. Wskaźnikowanie dyfraktogramów -metoda różnic 3. Wygaszenia systematyczne
SUROWCE I RECYKLING. Wykład 2
 SUROWCE I RECYKLING Wykład 2 Układ krystalograficzny grupuje kryształy o pewnych wspólnych cechach symetrii geometrycznej Postacie krystalograficzne Kryształy ograniczone ścianami jednoznacznymi stanowią
SUROWCE I RECYKLING Wykład 2 Układ krystalograficzny grupuje kryształy o pewnych wspólnych cechach symetrii geometrycznej Postacie krystalograficzne Kryształy ograniczone ścianami jednoznacznymi stanowią
Układ okresowy. Przewidywania teorii kwantowej
 Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
Przewidywania teorii kwantowej Chemia kwantowa - podsumowanie Cząstka w pudle Atom wodoru Równanie Schroedingera H ˆ = ˆ T e Hˆ = Tˆ e + Vˆ e j Chemia kwantowa - podsumowanie rozwiązanie Cząstka w pudle
WIĄZANIA. Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE
 WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
WIĄZANIA Co sprawia, że ciała stałe istnieją i są stabilne? PRZYCIĄGANIE ODPYCHANIE Przyciąganie Wynika z elektrostatycznego oddziaływania między elektronami a dodatnimi jądrami atomowymi. Może to być
Rejestracja dyfraktogramów polikrystalicznych związków. Wskaźnikowanie dyfraktogramów i wyznaczanie typu komórki Bravais go.
 Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 133, 40006 Katowice tel. 0323591503, email: izajen@wp.pl opracowanie: dr hab. Izabela Jendrzejewska Laboratorium z Krystalografii
Uniwersytet Śląski Instytut Chemii Zakład Krystalografii ul. Bankowa 14, pok. 133, 40006 Katowice tel. 0323591503, email: izajen@wp.pl opracowanie: dr hab. Izabela Jendrzejewska Laboratorium z Krystalografii
