Algorytmy i Struktury Danych.
|
|
|
- Aleksandra Zielińska
- 7 lat temu
- Przeglądów:
Transkrypt
1 Algorytmy i Struktury Dnyh. Gry. Drzwo rozpinj. Minimln rzwo rozpinj. Bożn Woźn-Szzśnik wozn@gmil.om Jn Długosz Univrsity, Poln Wykł 9 Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 1 / 4
2 Pln wykłu Drzwo rozpinj Algorytm Kruskl Algorytm Prim Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 / 4
3 Drzwo rozpinj gru Dinij Drzwm rozpinjym gru G nzywmy spójny i yklizny pogr gru G zwirjy wszystki jgo wirzhołki. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 3 / 4
4 Drzwo rozpinj gru Dinij Drzwm rozpinjym gru G nzywmy spójny i yklizny pogr gru G zwirjy wszystki jgo wirzhołki. Twirzni Kży gr spójny zwir rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 3 / 4
5 Drzwo rozpinj gru Dinij Drzwm rozpinjym gru G nzywmy spójny i yklizny pogr gru G zwirjy wszystki jgo wirzhołki. Twirzni Kży gr spójny zwir rzwo rozpinj. Twirzni W gri spójnym G = (V, E) krwęź E jst krwęzi ięi wty i tylko wty, gy nlży o kżgo rzw rozpinjgo gru G. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 3 / 4
6 Drzwo rozpinj gru Gnrowni rzw rozpinjgo ngo gru spójngo G możn rlizowć ior koljno krwęzi z pwnj listy i kptuj j po sprwzniu, zy ni tworz on yklu z otyhzs zkptownymi krwęzimi. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 4 / 4
7 Drzwo rozpinj gru Gnrowni rzw rozpinjgo ngo gru spójngo G możn rlizowć ior koljno krwęzi z pwnj listy i kptuj j po sprwzniu, zy ni tworz on yklu z otyhzs zkptownymi krwęzimi. Gnrowni wszystkih rzw rozpinjyh ngo gru jst złożon olizniowo, poniwż rzw rozpinjyh moż yć rzo użo. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 4 / 4
8 Drzwo rozpinj gru - przykł Pokżmy, ż gr tn zwir 8 różnyh rzw rozpinjyh. v4 v3 v Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 5 / 4
9 Drzwo rozpinj gru - przykł v4 v3 v Pokżmy, ż gr tn zwir 8 różnyh rzw rozpinjyh. Łtwo zuwżyć, ż kż rzwo rozpinj tgo gru m 3 krwęzi. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 5 / 4
10 Drzwo rozpinj gru - przykł v4 v3 v Pokżmy, ż gr tn zwir 8 różnyh rzw rozpinjyh. Łtwo zuwżyć, ż kż rzwo rozpinj tgo gru m 3 krwęzi. Uporzkujmy wszystki krwęzi gru, tworz listę krwęzi. Rozwżć ęzimy nstępuj listę krwęzi: (,,,, ). Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 5 / 4
11 Drzwo rozpinj gru - przykł v4 v3 v Pokżmy, ż gr tn zwir 8 różnyh rzw rozpinjyh. Łtwo zuwżyć, ż kż rzwo rozpinj tgo gru m 3 krwęzi. Uporzkujmy wszystki krwęzi gru, tworz listę krwęzi. Rozwżć ęzimy nstępuj listę krwęzi: (,,,, ). Kży poziór krwęzi ęzimy przstwić w posti listy uporzkownj, zgoni z porzkim w liśi krwęzi; Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 5 / 4
12 Drzwo rozpinj gru - przykł Do gnrowni wszystkih rzw rozpinjyh zstosujmy lgorytm z nwrotmi. (,,,, ) v4 v3 v Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
13 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Do gnrowni wszystkih rzw rozpinjyh zstosujmy lgorytm z nwrotmi. Zgoni z lgorytmm z nwrotmi, ęzimy tworzyć koljn listy. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
14 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Do gnrowni wszystkih rzw rozpinjyh zstosujmy lgorytm z nwrotmi. Zgoni z lgorytmm z nwrotmi, ęzimy tworzyć koljn listy. list zrwon oznz, ż krwęzi t zwirj ykl i trz się wyoć. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
15 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Do gnrowni wszystkih rzw rozpinjyh zstosujmy lgorytm z nwrotmi. Zgoni z lgorytmm z nwrotmi, ęzimy tworzyć koljn listy. list zrwon oznz, ż krwęzi t zwirj ykl i trz się wyoć. list pokrślon oznzj rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
16 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Do gnrowni wszystkih rzw rozpinjyh zstosujmy lgorytm z nwrotmi. Zgoni z lgorytmm z nwrotmi, ęzimy tworzyć koljn listy. list zrwon oznz, ż krwęzi t zwirj ykl i trz się wyoć. list pokrślon oznzj rzwo rozpinj. Listy (rzw) gnrown s w porzku lksykogriznym (ltyznym). Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
17 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 (), (), (, ), (,, ) Mmy pirwsz rzwo rozpinj. v Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 7 / 4
18 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v (), (), (, ), (,, ) Mmy pirwsz rzwo rozpinj. Usuwmy osttni krwęź z (,, ), ojmy koljn krwęź z listy i otrzymujmy: (,, ) - zwir ykl. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 7 / 4
19 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v (), (), (, ), (,, ) Mmy pirwsz rzwo rozpinj. Usuwmy osttni krwęź z (,, ), ojmy koljn krwęź z listy i otrzymujmy: (,, ) - zwir ykl. Usuwmy ztm i gnrujmy nstępn listę: (,, ) Otrzymliśmy rugi rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 7 / 4
20 Drzwo rozpinj gru - przykł Usuwmy krwęź, ni możmy (,,,, ) jnk kontynuowć o jst osttni krwęzi n liśi. v4 v3 v Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 8 / 4
21 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, ni możmy jnk kontynuowć o jst osttni krwęzi n liśi. Usuwmy koljn krwęź - i gnrujmy: (, ), (,, ). Mmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 8 / 4
22 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, ni możmy jnk kontynuowć o jst osttni krwęzi n liśi. Usuwmy koljn krwęź - i gnrujmy: (, ), (,, ). Mmy koljn rzwo rozpinj. Usuwmy osttni krwęź i kontynuujmy: (,, ). Znlźliśmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 8 / 4
23 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, nstępni krwęź, po zym gnrujmy koljno: (, ), (,, ). Mmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 9 / 4
24 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, nstępni krwęź, po zym gnrujmy koljno: (, ), (,, ). Mmy koljn rzwo rozpinj. Usuwmy krwęź, potm tworzymy now listę: (, ). Ni możmy jnk kontynuowć wię usuwmy krwęzi orz. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 9 / 4
25 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, nstępni krwęź, po zym gnrujmy koljno: (, ), (,, ). Mmy koljn rzwo rozpinj. Usuwmy krwęź, potm tworzymy now listę: (, ). Ni możmy jnk kontynuowć wię usuwmy krwęzi orz. Koljnymi utworzonymi listmi s wię: (), (, ), (,, ). Otrzymliśmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 9 / 4
26 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, l koljn list: (,, ) zwir ykl. Usuwmy wię koljno krwęź, potm i gnrujmy listy (, ) i (,, ). Znlźliśmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 10 / 4
27 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, l koljn list: (,, ) zwir ykl. Usuwmy wię koljno krwęź, potm i gnrujmy listy (, ) i (,, ). Znlźliśmy koljn rzwo rozpinj. Usuwmy koljno krwęzi i koljn list jst: (, ). Usuwmy, nstępni i tworzymy listy: (), (, ), (,, ). Mmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 10 / 4
28 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy krwęź, l koljn list: (,, ) zwir ykl. Usuwmy wię koljno krwęź, potm i gnrujmy listy (, ) i (,, ). Znlźliśmy koljn rzwo rozpinj. Usuwmy koljno krwęzi i koljn list jst: (, ). Usuwmy, nstępni i tworzymy listy: (), (, ), (,, ). Mmy koljn rzwo rozpinj. Usuwmy koljno i, nstępni gnrujmy ls (, ). Usuwmy, nstępni i gnrujmy koljn listy: (), (, ), (). Ni m już jnk więj rzw rozpinjyh. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 10 / 4
29 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy koljno krwęzi i, koljn list jst: (, ). Usuwmy, nstępni i tworzymy listy: (), (, ), (,, ). Mmy koljn rzwo rozpinj. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 11 / 4
30 Drzwo rozpinj gru - przykł (,,,, ) v4 v3 v Usuwmy koljno krwęzi i, koljn list jst: (, ). Usuwmy, nstępni i tworzymy listy: (), (, ), (,, ). Mmy koljn rzwo rozpinj. Usuwmy koljno i, nstępni gnrujmy ls (, ). Usuwmy, nstępni i gnrujmy koljn listy: (), (, ), (). Ni m już jnk więj rzw rozpinjyh. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 11 / 4
31 Drzwo rozpinj gru - przykł v4 v3 v Drzw rozpinj v4 v3 v4 v3 v4 v3 v4 v3 v v v v (,,) (,,) (,,) (,,) v4 v3 v4 v3 v4 v3 v4 v3 v v v v (,,) (,,) (,,) (,,) Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 1 / 4
32 Gnrowni rzw rozpinjyh gru - złożni Kżmu wirzhołkowi gru przyporzkujmy w tryuty: Korzn[r] - tzw. korzń rzw, w którym znjuj się wirzhołk r. Poprznik[v] - poprznik wirzhołk v n jynj śiż łz j v z korznim. Poprznik korzni jst niokrślony; w lgorytmh zkłmy, ż jst równy 0 lu NIL. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 13 / 4
33 Złożni - przykł i g j h k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 14 / 4
34 Złożni - przykł (g, ) (g, g) (g, ) i (g, g) (g, NIL) (g, g) (g, ) g (g, g) (g, ) j (g, g) h (g, ) k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 15 / 4
35 Gnrowni rzw rozpinjyh gru - i Pros gnrowni wszystkih rzw rozpinjyh wymg wóh oprji: Jżli koljn krwęź z listy ni zmyk yklu (jst zkptown), to oni jj powouj połzni wóh rzw T 1 i T w jno now rzwo T i w zwizku z tym nlży okonć opowinij zminy tykit wirzhołków T (Prour A i B). Po otrzymniu rzw rozpinjgo lu wyzrpniu się listy krwęzi w prosi gnrowni rzw, wykonujmy krok powrotu polgjy n wyrzuniu osttnio onj krwęzi. Powouj to rozii pwngo rzw T n w porzw T 1 i T (Prour C). Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 16 / 4
36 Prour A - psuoko Zmin tykit wirzhołków rzw T o korzniu r, po oprji zminy r n nowy korzń v. Algorytm NowyKorzń(v): 1: StryKorzn := Korzn[v] : i StryKorzn = v thn 3: rturn; 4: n i 5: := 0; v := v; 6: rpt 7: p := ; := v; v := Poprznik[]; Poprznik[] := p; 8: until = StryKorzn 9: or h w V o 10: i Korzn[w] = StryKorzn thn 11: Korzn[w] = v; 1: n i 13: n or Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 17 / 4
37 Prour A - przykł oprj zminy korzni g n nowy korzń i. (g, ) (g, g) (g, ) (g, ) (g, g) (g, ) i i (g, g) (g, NIL) (g, g) (g, ) (g, g) (g, NIL) (g, g) (g, ) g g (g, g) (g, ) (g, g) (g, ) j (g, g) h j (g, g) h (g, ) (g, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 18 / 4
38 Prour A - przykł,. zminimy skirowni krwęzi n śiż z g o i. zminimy rugi tykity wirzhołków ( i) tj śiżki. Etykity pozostłyh wirzhołków w rzwi T pozostj z zmin. (g, ) (g, g) (g, ) (g, ) (g, g) (g, ) i i (g, g) (g, NIL) (g, g) (g, ) (g, g) (g, ) (g, i) (g, ) g g (g, g) (g, ) (g, g) (g, ) j (g, g) h j (g, g) h (g, ) (g, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 19 / 4
39 Prour A - przykł,. Wszystki wirzhołki rzw T otrzymuj pirwsz tykitę (okrślj korzń) równ i, wirzhołk i ostj rug tykitę posti (i, NIL). (g, ) (g, g) (g, ) (i, ) (i, g) (i, NIL) i i (g, g) g (g, NIL) (g, g) (g, ) (i, g) g (i, ) (i, i) (i, ) j (g, g) (g, g) h (g, ) j (i, g) (i, g) h (i, ) (g, ) (i, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 0 / 4
40 Prour B - psuoko Zmini tykity wirzhołków wóh rzw T 1 i T, o korznih opowinio r1 i r, r1 < r, po oprji ih połzni przz oni krwęzi = (u, v), gzi u V(T 1), v V(T ). Algorytm DojKrwęź ( = (u, v)): 1: := Korzn[u]; v := Korzn[v]; : i v < thn 3: zmin(, v); zmin(u, v); 4: n i 5: NowyKorzn(v); 6: Poprznik[v] := u; 7: or h w V o 8: i Korzn[w] = v thn 9: Korzn[w] = ; 10: n i 11: n or Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 1 / 4
41 Prour B - Przykł Połzni wóh rzw T 1 i T, o korznih opowinio i m, przz oni krwęzi = (g, ), gzi g V(T 1), V(T ). (, ) (, NIL) (m, ) (m, NIL) (, ) (, NIL) (m, ) (m, NIL) i m i m (, g) (, ) (m, ) (m, m) (, g) (, ) (m, ) (m, m) g g (, g) (m, ) (, g) (m, ) j h j h (, g) (, ) (, g) (, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 / 4
42 Prour B - Przykł,. wirzhołkom w rzwi T zminimy rugi tykity tk jk przy zmini korzni z m n (Prour A); w rzwi T1 rugi tykity wirzhołków pozostj z zmin. (, ) (, NIL) (m, ) (m, NIL) (, ) (, NIL) (, ) (, ) i m i m (, g) (, ) (m, ) (m, m) (, g) (, ) (, NIL) (, ) g g (, g) (m, ) (, g) (, ) j h j h (, g) (, ) (, g) (, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 3 / 4
43 Prour B - Przykł,. wirzhołkowi jko rug tykitę przypisujmy g. wszystki wirzhołki rzw T otrzymuj pirwsz tykitę równ ; w rzwi T1 pirwsz tykity wirzhołków pozostj z zmin. (, ) (, NIL) (, ) (, ) (, ) (, NIL) (, ) (, ) i m i m (, g) (, ) (, NIL) (, ) (, g) (, ) (, g) (, ) g g (, g) (, ) (, g) (, ) j h j h (, g) (, ) (, g) (, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 4 / 4
44 Prour C - psuoko Zmini tykit wirzhołków rzw T o korzniu r po usunięiu z nigo krwęzi = (u, v), zyli roziiu T n w rzw T 1 i T, gzi u V(T 1), v V(T ) i r V(T 1). UWAGA! W nszym przypku zwsz usuwmy osttnio on krwęź, wię wirzhołk u jst wirzhołkim wiszym i po usunięiu krwęzi stni się rzwm trywilnym (jnowirzhołkowym). Ztm pros usunięi krwęzi polg jyni n zmini tryutów wirzhołk u. Rlizuj to lgorytm UsuńKrwęź. Algorytm UsuńKrwęź(=(u,v)): 1: i Poprznik[u] = v thn : zmin(u, v) 3: n i 4: Poprznik[v] := 0; 5: Korzn[v] = v; Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 5 / 4
45 Prour C - Przykł W rzwi T 1 oi tykity wirzhołków pozostj z zmin. Wirzhołkowi przypisujmy tykitę (, 0) (stj się korznim rzw T ). Drugi tykity pozostłyh wirzhołków w rzwi T pozostj z zmin, l otrzymuj pirwsz tykitę równ. (, ) (, NIL) (, ) (, ) (, ) (, NIL) (, ) (, ) i m i m (, g) (, ) (, g) (, ) (, g) (, ) (, NIL) (, ) g g (, g) (, ) (, g) (, ) j h j h (, g) (, ) (, g) (, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 6 / 4
46 Prour C - Przykł,. Usunięi krwęzi (g, ). (, ) (, NIL) (, ) (, ) (, ) (, NIL) (, ) (, ) i m i m (, g) (, ) (, NIL) (, ) (, g) (, ) (, NIL) (, ) g g (, g) (, ) (, g) (, ) j h j h (, g) (, ) (, g) (, ) k k Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 7 / 4
47 Algorytm gnrowni wszystkih rzw rozpinjyh gru Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 8 / 4
48 Znlźć wszystki rzw rozpięt gru v3 v4 g v5,,,,,, g,, g, g, g,,,,, g,,, g,, g, g,,,, g,, g, g,, g, g,, g, g, v,,,,, g,,, g,, g, g,,,, g,, g, g,,, g, g,, g, g,. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 9 / 4
49 Drzw rozpinj o minimlnj wz Jżli mmy o zynini z grm z wgmi, to njzęśij intrsuj ns znlzini rzw rozpinjgo o minimlnj wz, tzn., rzw z njmnijsz sum wg jgo krwęzi. Ay znlźć rzwo o żnyh włsnośih możn zstosowć w lgorytmy: Kruskl (lgorytm zhłnny) Prim (lgorytm njliższgo ssi). Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 30 / 4
50 Algorytmy Kruskl Algorytm jst oprty o mtoę zhłnn i polg n łzniu wilu porzw w jno z pomo krwęzi o njmnijszj wz. Wyirz krwęź (któr ni jst pętl) 1 tk, y wg tj krwęzi ył njmnijsz. Jżli krwęzi 1,,..., k zostły już wyrn, to z pozostłyh E \{ 1,,..., k } wyirz krwęź k+1 w tki sposó y: gr, który skł się tylko z krwęzi 1,,..., k, k+1 ył yklizny, orz wg krwęzi k+1 ył njmnijsz. Jśli ni możn wykonć kroku, to STOP. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 31 / 4
51 Algorytm Kruskl - Złożoność olizniow Algorytm możn pozilić n w tpy: w pirwszym tpi sortujmy krwęzi wług wg w zsi O(m log(m)). w rugim tpi uujmy rozpięt rzwo poprzz wyór njkrótszyh krwęzi z zioru krwęzi E(G); tn tp możn wykonć w zsi O(m log(n)). Sumryzny zs pry lgorytmu Kruskl wynosi: O(m log(n)) Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 3 / 4
52 Algorytm Kruskl - Przykł Po posortowniu krwęzi wg. wg otrzymujmy: =1, =, =, =, =3, =4, =6, =7, =8 Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 33 / 4
53 Algorytm Kruskl - Przykł Krok Krok Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 34 / 4
54 Algorytm Kruskl - Przykł Krok Krok 4 - slni Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 35 / 4
55 Algorytm Kruskl - Przykł Krok Minimln rzwo. 1 3 Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 36 / 4
56 Algorytm Prim Algorytm tn jst, pooni jk lgorytm Kruskl oprty o mtoę zhłnn. Buowę minimlngo rzw rozpinjgo zzynmy o owolngo wirzhołk, np. o pirwszgo. Dojmy wirzhołk o rzw, wszystki krwęzi inyntn umiszzmy n posortownj wg. wg liśi. Nstępni zjmujmy z listy pirwszy lmnt (o njmnijszj wz) i jżli wirzhołk, który łzy ni nlży o rzw, ojmy go o rzw n liśi znów umiszzmy wszystki krwęzi inyntn z wirzhołkim, który oliśmy. Jnym znim: zwsz ojmy o rzw krwęź o njmnijszj wz, osigln (w prziwiństwi o Kruskl) z jkigoś wirzhołk tgo rzw. Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 37 / 4
57 Algorytm Prim - Przykł Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 38 / 4
58 Algorytm Prim - Przykł Krok Krok Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 39 / 4
59 Algorytm Prim - Przykł Krok Krok Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 40 / 4
60 Algorytm Prim - Przykł Krok Minimln Drzwo 1 3 Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 41 / 4
61 Algorytm Prim Algorytm Kruskl - Przykł Minimln Drzwo wg. Algorytmu Kruskl. Minimln Drzwo wg. Algorytmu Prim Bożn Woźn-Szzśnik (AJD) Algorytmy i Struktury Dnyh. Wykł 9 4 / 4
Grafy hamiltonowskie, problem komiwojażera algorytm optymalny
 1 Grfy hmiltonowski, problm komiwojżr lgorytm optymlny Wykł oprcowny n postwi książki: M.M. Sysło, N.Do, J.S. Kowlik, Algorytmy optymlizcji yskrtnj z progrmmi w języku Pscl, Wywnictwo Nukow PWN, 1999 2
1 Grfy hmiltonowski, problm komiwojżr lgorytm optymlny Wykł oprcowny n postwi książki: M.M. Sysło, N.Do, J.S. Kowlik, Algorytmy optymlizcji yskrtnj z progrmmi w języku Pscl, Wywnictwo Nukow PWN, 1999 2
Prezentacja kierunków pracy naukowej
 Prznj kirunków pry nukowj Driusz Drniowski Kr Algorymów i Molowni Sysmów Polihnik Gńsk Kirunki wz Uporząkown kolorowni grów Szrgowni zń w śroowisku wiloprosorowym Wyszukiwni lmnów w zęśiowyh porząkh Przszukiwni
Prznj kirunków pry nukowj Driusz Drniowski Kr Algorymów i Molowni Sysmów Polihnik Gńsk Kirunki wz Uporząkown kolorowni grów Szrgowni zń w śroowisku wiloprosorowym Wyszukiwni lmnów w zęśiowyh porząkh Przszukiwni
Grafy hamiltonowskie, problem komiwojaera algorytm optymalny
 2 Grfy hmiltonowski, prolm komiwojr lgorytm optymlny 3 Grfy hmiltonowski Df. Cykl (rog) Hmilton jst to ykl (rog), w którym ky wirzhołk grfu wystpuj okłni rz. Grf jst hmiltonowski (półhmiltonowski), o il
2 Grfy hmiltonowski, prolm komiwojr lgorytm optymlny 3 Grfy hmiltonowski Df. Cykl (rog) Hmilton jst to ykl (rog), w którym ky wirzhołk grfu wystpuj okłni rz. Grf jst hmiltonowski (półhmiltonowski), o il
Algorytmy i Struktury Danych, Rozwiązania zadań z kolokwiów
 Algorytmy i Struktury Dnyh, Rozwiązni zń z kolokwiów 2017-11 1 Klsówk 2007 (1), zni 1 Opruj strukturę nyh, któr pozwl wykonywć nstępują oprj: Ini(k):: inijj struktury nyh i ustlni ługośi krotk liz łkowityh
Algorytmy i Struktury Dnyh, Rozwiązni zń z kolokwiów 2017-11 1 Klsówk 2007 (1), zni 1 Opruj strukturę nyh, któr pozwl wykonywć nstępują oprj: Ini(k):: inijj struktury nyh i ustlni ługośi krotk liz łkowityh
Instrukcje dotyczące systemu Windows w przypadku drukarki podłączonej lokalnie
 Stron 1 z 7 Połązni Instrukj otyzą systmu Winows w przypku rukrki połązonj loklni Uwg: Przy instlowniu rukrki połązonj loklni, jśli ysk CD-ROM Oprogrmowni i okumntj ni osługuj ngo systmu opryjngo, nlży
Stron 1 z 7 Połązni Instrukj otyzą systmu Winows w przypku rukrki połązonj loklni Uwg: Przy instlowniu rukrki połązonj loklni, jśli ysk CD-ROM Oprogrmowni i okumntj ni osługuj ngo systmu opryjngo, nlży
Klasa problemów #P. Paweł Gora 11/20/2008 1
 Kls prolmów #P Pwł Gor /2/28 Agn Prolmy klsy #P Prolmy #P-zupłn Przykł prolmu #PC: zlizni roszrzń liniowyh Przykłow lgorytmy zlizni rozszrzń liniowyh /2/28 2 Kls polmów #P Kls #P kls prolmów zlizni związnyh
Kls prolmów #P Pwł Gor /2/28 Agn Prolmy klsy #P Prolmy #P-zupłn Przykł prolmu #PC: zlizni roszrzń liniowyh Przykłow lgorytmy zlizni rozszrzń liniowyh /2/28 2 Kls polmów #P Kls #P kls prolmów zlizni związnyh
PROJEKT: Technologie multimedialne drogą do przyjaznej edukacji przyszłości realizowany w Szkole Podstawowej nr 11 w Będzinie
 Posumowni nkity wluyjnj l złonków Ry Pgogiznj po zkońzniu projktu Ersmus+: Thnologi multimiln rogą o przyjznj ukji przyszłośi. Ankit skłł się z 10 pytń, w tym jngo otwrtgo. Zostł przprowzon pozs szkolniowj
Posumowni nkity wluyjnj l złonków Ry Pgogiznj po zkońzniu projktu Ersmus+: Thnologi multimiln rogą o przyjznj ukji przyszłośi. Ankit skłł się z 10 pytń, w tym jngo otwrtgo. Zostł przprowzon pozs szkolniowj
Semantyka i Weryfikacja Programów - Laboratorium 2 Działania na ułamkach, krotki i rekordy
 Semntyk i Weryfikj Progrmów - Lortorium Dziłni n ułmkh, krotki i rekory Cz. I. Dziłni n ułmkh Prolem. Oprowć zestw funkji o ziłń rytmetyznyh n ułmkh zwykłyh posti q, gzie, są lizmi łkowitymi i 0. Rozwiąznie
Semntyk i Weryfikj Progrmów - Lortorium Dziłni n ułmkh, krotki i rekory Cz. I. Dziłni n ułmkh Prolem. Oprowć zestw funkji o ziłń rytmetyznyh n ułmkh zwykłyh posti q, gzie, są lizmi łkowitymi i 0. Rozwiąznie
ELEMENTY PROSTOKĄTNE Informacje techniczne 1 Kanały 2 Kolana 3 Trójniki 5 Odsadzki Czwórniki 7 Przejścia 8 ELEMENTY DACHOWE Podstawy dachowe 9
 ELEMENTY PROSTOKĄTNE nomcj tcniczn 1 Knły 2 Koln 3 Tójniki 5 Oszki Czwóniki 7 Pzjści 8 ELEMENTY DACHOWE Postwy cow 9 Wyzutni 11 Czpni powitz 13 Wywitzki 15 Koln czpn 15 NOX STANLESS STEEL 58-512 St Kminic
ELEMENTY PROSTOKĄTNE nomcj tcniczn 1 Knły 2 Koln 3 Tójniki 5 Oszki Czwóniki 7 Pzjści 8 ELEMENTY DACHOWE Postwy cow 9 Wyzutni 11 Czpni powitz 13 Wywitzki 15 Koln czpn 15 NOX STANLESS STEEL 58-512 St Kminic
Regionalne Koło Matematyczne
 Regionlne Koło Mtemtyzne Uniwersytet Mikołj Kopernik w Toruniu Wyził Mtemtyki i Informtyki http://www.mt.umk.pl/rkm/ List rozwiązń zń nr 8, grup zwnsown (3.03.200) O izometrih (..) Wektorem uporząkownej
Regionlne Koło Mtemtyzne Uniwersytet Mikołj Kopernik w Toruniu Wyził Mtemtyki i Informtyki http://www.mt.umk.pl/rkm/ List rozwiązń zń nr 8, grup zwnsown (3.03.200) O izometrih (..) Wektorem uporząkownej
Minimalizacja automatu
 Minimlizj utomtu Minimlizj utomtu to minimlizj lizy stnów. Jest to trnsformj utomtu o nej tliy przejśćwyjść n równowżny mu (po wzglęem przetwrzni sygnłów yfrowyh) utomt o mniejszej lizie stnów wewnętrznyh.
Minimlizj utomtu Minimlizj utomtu to minimlizj lizy stnów. Jest to trnsformj utomtu o nej tliy przejśćwyjść n równowżny mu (po wzglęem przetwrzni sygnłów yfrowyh) utomt o mniejszej lizie stnów wewnętrznyh.
1.1. Układy do zamiany kodów (dekodery, kodery, enkodery) i
 Ukły yrow (loizn) 1.1. Ukły o zminy koów (kory, kory, nkory) i Są to ukły kominyjn, zminiją sposó koowni lu przstwini ny yrowy. 1.1.1. kory kory to ukły kominyjn, zminiją n yrow, zpisn w owolnym kozi innym
Ukły yrow (loizn) 1.1. Ukły o zminy koów (kory, kory, nkory) i Są to ukły kominyjn, zminiją sposó koowni lu przstwini ny yrowy. 1.1.1. kory kory to ukły kominyjn, zminiją n yrow, zpisn w owolnym kozi innym
2. Regulamin uchwala Rada Nadzorcza na podstawie 69 Statutu Spółdzielni Mieszkaniowej Arka we Wrocławiu.
 Rgulmin rmontów orz wykorzystywni śroków z funuszu rmontowgo Spółzilni Miszkniowj Ark w Wrołwiu złąznik o uhwły 67/03 I Postnowini ogóln 1. Rgulmin okrśl oowiązki Spółzilni i jj Członków w zkrsi nprw wwnątrz
Rgulmin rmontów orz wykorzystywni śroków z funuszu rmontowgo Spółzilni Miszkniowj Ark w Wrołwiu złąznik o uhwły 67/03 I Postnowini ogóln 1. Rgulmin okrśl oowiązki Spółzilni i jj Członków w zkrsi nprw wwnątrz
ROZPORZĄDZENIE PARLAMENTU EUROPEJSKIEGO I RADY (WE) NR 1223/2009 z dnia 30 listopada 2009 r. dotyczące produktów kosmetycznych
 22.12.2009 Dzinnik Urzęowy Unii Europjskij L 342/59 ROZPORZĄDZENIE PARLAMENTU EUROPEJSKIEGO I RADY (WE) NR 1223/2009 z ni 30 listop 2009 r. otyzą prouktów kosmtyznyh (wrsj przksztłon) (Tkst mjąy znzni
22.12.2009 Dzinnik Urzęowy Unii Europjskij L 342/59 ROZPORZĄDZENIE PARLAMENTU EUROPEJSKIEGO I RADY (WE) NR 1223/2009 z ni 30 listop 2009 r. otyzą prouktów kosmtyznyh (wrsj przksztłon) (Tkst mjąy znzni
Ankieta absolwenta ANKIETA ABSOLWENTA. Losy zawodowe absolwentów PWSZ w Raciborzu
 24 mj 2012 r. Ankit solwnt Wyni I Sttus oowiązująy Symol Stron 1/5 ANKIETA ABSOLWENTA Losy zwoow solwntów PWSZ w Riorzu Dro Asolwntko, Droi Asolwni! HASŁO DO ANKIETY: Prosimy o okłn przzytni pytń i zznzni
24 mj 2012 r. Ankit solwnt Wyni I Sttus oowiązująy Symol Stron 1/5 ANKIETA ABSOLWENTA Losy zwoow solwntów PWSZ w Riorzu Dro Asolwntko, Droi Asolwni! HASŁO DO ANKIETY: Prosimy o okłn przzytni pytń i zznzni
PODSTAWY BAZ DANYCH Wykład 3 2. Pojęcie Relacyjnej Bazy Danych
 PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
PODSTAWY BAZ DANYCH Wykłd 3 2. Pojęcie Relcyjnej Bzy Dnych 2005/2006 Wykłd "Podstwy z dnych" 1 Rozkłdlno dlność schemtów w relcyjnych Przykłd. Relcj EGZ(U), U := { I, N, P, O }, gdzie I 10 10 11 N f f
Co można zrobić za pomocą maszyny Turinga? Wszystko! Maszyna Turinga potrafi rozwiązać każdy efektywnie rozwiązywalny problem algorytmiczny!
 TEZA CHURCHA-TURINGA Mzyn Turing: m końzenie wiele tnów zpiuje po jenym ymolu n liniowej tśmie Co możn zroić z pomoą mzyny Turing? Wzytko! Mzyn Turing potrfi rozwiązć kży efektywnie rozwiązywlny prolem
TEZA CHURCHA-TURINGA Mzyn Turing: m końzenie wiele tnów zpiuje po jenym ymolu n liniowej tśmie Co możn zroić z pomoą mzyny Turing? Wzytko! Mzyn Turing potrfi rozwiązć kży efektywnie rozwiązywlny prolem
G i m n a z j a l i s t ó w
 Ko³o Mtemtyzne G i m n z j l i s t ó w 1. Lizy,, spełniją wrunki: (1) ++ = 0, 1 () + + 1 + + 1 + = 1 4. Olizyć wrtość wyrżeni w = + + Rozwiąznie Stowrzyszenie n rzez Edukji Mtemtyznej Zestw 7 szkie rozwizń
Ko³o Mtemtyzne G i m n z j l i s t ó w 1. Lizy,, spełniją wrunki: (1) ++ = 0, 1 () + + 1 + + 1 + = 1 4. Olizyć wrtość wyrżeni w = + + Rozwiąznie Stowrzyszenie n rzez Edukji Mtemtyznej Zestw 7 szkie rozwizń
Podsumowanie wyników ankiet dotyczących żywienia w sklepikach szkolnych.
 Posumowni wyników nkit otyząyh żywini w sklpikh szkolnyh. 1.Czy jsz posiłki z stołówki szkolnj? )tk - )ni - )zsmi - 4 6 4 3 tk ni zsmi 1.Czy jsz posiłki z stołówki szkolnj? 2.Il śrnio spożywsz posiłków
Posumowni wyników nkit otyząyh żywini w sklpikh szkolnyh. 1.Czy jsz posiłki z stołówki szkolnj? )tk - )ni - )zsmi - 4 6 4 3 tk ni zsmi 1.Czy jsz posiłki z stołówki szkolnj? 2.Il śrnio spożywsz posiłków
5. WYKORZYSTANIE GRAFÓW PRZEPŁYWU SYGNAŁÓW DO BUDOWY MODELI MATEMATYCZNYCH
 5. Worzstni grów rzłwu sgnłu o uow moli mtmtznh 5. WYKORZYSTANIE RAFÓW PRZEPŁYWU SYNAŁÓW DO UDOWY MODELI MATEMATYCZNYCH 5.. Wrowzni o grów rzłwowh Njzęśij sotną ostią grizną ułów utomti są shmt struturln
5. Worzstni grów rzłwu sgnłu o uow moli mtmtznh 5. WYKORZYSTANIE RAFÓW PRZEPŁYWU SYNAŁÓW DO UDOWY MODELI MATEMATYCZNYCH 5.. Wrowzni o grów rzłwowh Njzęśij sotną ostią grizną ułów utomti są shmt struturln
Obozy Naukowe OMG poziom OMG Perzanowo
 Oozy Naukow OMG poziom OMG Przanowo 2014 1 Trśi zaań (poziom OMG) Pirwsz zawoy inywiualn 1. Dany jst trójkąt ABC, w którym
Oozy Naukow OMG poziom OMG Przanowo 2014 1 Trśi zaań (poziom OMG) Pirwsz zawoy inywiualn 1. Dany jst trójkąt ABC, w którym
Kolokwium II GRUPA A. Przy ka»dym z podpunktów wpisz, czy jest on prawdziwy (TAK) czy faªszywy (NIE).
 Mtmtyk dl Biologów Wrszw, 6 styzni 008. Imi i nzwisko:... nr indksu:... Kolokwium II GRUPA A Przy k»dym z podpunktów wpisz, zy jst on prwdziwy (TAK) zy fªszywy (NIE). 1. Przdstwiony n rysunku grf (wirzhoªki
Mtmtyk dl Biologów Wrszw, 6 styzni 008. Imi i nzwisko:... nr indksu:... Kolokwium II GRUPA A Przy k»dym z podpunktów wpisz, zy jst on prwdziwy (TAK) zy fªszywy (NIE). 1. Przdstwiony n rysunku grf (wirzhoªki
Stereochemia. Izomeria konformacyjna obrót wokół wiązania pojedynczego etan projekcja Newmana
 Uniwrsytt Jgilloński, Collgium Mdicum, Ktdr Chmii rgnicznj Strochmi Izomri konformcyjn obrót wokół wiązni pojdynczgo tn projkcj Nwmn konformcj: nprzminlgł nprzciwlgł kąt torsyjny w ukłdzi cztrch tomów
Uniwrsytt Jgilloński, Collgium Mdicum, Ktdr Chmii rgnicznj Strochmi Izomri konformcyjn obrót wokół wiązni pojdynczgo tn projkcj Nwmn konformcj: nprzminlgł nprzciwlgł kąt torsyjny w ukłdzi cztrch tomów
Załącznik nr 2 LISTA SPRAWDZAJĄCA DO WERYFIKACJI ADMINISTRACYJNEJ WNIOSKU O PŁATNOŚĆ
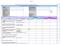 Minimlny zkrs pytń. List moż yć rozszrzn przz KK w zlżnośi o wymgń ngo progrmu EWT LISTA SPRAWDZAJĄCA DO WERYFIKACJI ADMINISTRACYJNEJ WNIOSKU O PŁATNOŚĆ lp. Nr projktu Tytuł projktu Nzw nfijnt Okrs rlizji
Minimlny zkrs pytń. List moż yć rozszrzn przz KK w zlżnośi o wymgń ngo progrmu EWT LISTA SPRAWDZAJĄCA DO WERYFIKACJI ADMINISTRACYJNEJ WNIOSKU O PŁATNOŚĆ lp. Nr projktu Tytuł projktu Nzw nfijnt Okrs rlizji
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 ĆWICZENIE 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ Opis kł pomirowego A) Wyzzie ogiskowej sozewki skpijąej z pomir oległośi przemiot i obrz o sozewki Szzególie proste, rówoześie
ĆWICZENIE 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ Opis kł pomirowego A) Wyzzie ogiskowej sozewki skpijąej z pomir oległośi przemiot i obrz o sozewki Szzególie proste, rówoześie
Ć W I C Z E N I E N R E-14
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
ZADANIE I OPIS PRZEDMIOTU ZAMÓWENIA SPECYFIKACJA TECHNICZNA (OPIS) OFEROWANEGO SPRZĘTU
 ZADANIE I OPIS PRZEDMIOTU ZAMÓWENIA SPECYFIKACJA TECHNICZNA (OPIS) OFEROWANEGO SPRZĘTU Nzw i rs Wykonwy:. I. Systm o ony i trningu koorynji nrwowo-mięśniowj i momntów sił mięśniowyh rozwijnyh w stwh końzyn
ZADANIE I OPIS PRZEDMIOTU ZAMÓWENIA SPECYFIKACJA TECHNICZNA (OPIS) OFEROWANEGO SPRZĘTU Nzw i rs Wykonwy:. I. Systm o ony i trningu koorynji nrwowo-mięśniowj i momntów sił mięśniowyh rozwijnyh w stwh końzyn
Materiały tylko do użytku wewnętrznego PZU SA. ankieta HOSPI
 Mtriły tylko o użytku wwnętrzngo PZU SA. nkit HOSPI Ankit l komórk lznitw stjonrngo w zkłzi opiki zrowotnj Ankit otyzy łąz wszystkih komórk orgnizyjnyh zkłu opiki zrowotnj związnyh z lznitwm stjonrnym,
Mtriły tylko o użytku wwnętrzngo PZU SA. nkit HOSPI Ankit l komórk lznitw stjonrngo w zkłzi opiki zrowotnj Ankit otyzy łąz wszystkih komórk orgnizyjnyh zkłu opiki zrowotnj związnyh z lznitwm stjonrnym,
Algebra Boola i podstawy systemów liczbowych. Ćwiczenia z Teorii Układów Logicznych, dr inż. Ernest Jamro. 1. System dwójkowy reprezentacja binarna
 lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
lger Bool i podstwy systemów liczowych. Ćwiczeni z Teorii Ukłdów Logicznych, dr inż. Ernest Jmro. System dwójkowy reprezentcj inrn Ukłdy logiczne operują tylko n dwóch stnch ozncznymi jko zero (stn npięci
2. Funktory TTL cz.2
 2. Funktory TTL z.2 1.2 Funktory z otwrtym kolektorem (O.. open olletor) ysunek poniżej przedstwi odnośny frgment płyty zołowej modelu. Shemt wewnętrzny pojedynzej rmki NAND z otwrtym kolektorem (O..)
2. Funktory TTL z.2 1.2 Funktory z otwrtym kolektorem (O.. open olletor) ysunek poniżej przedstwi odnośny frgment płyty zołowej modelu. Shemt wewnętrzny pojedynzej rmki NAND z otwrtym kolektorem (O..)
Wynik bezpośredniego spotkania między zainteresowanymi drużynami w przypadku 3 lub więcej drużyn tworzona jest małą tabele
 REGULAMIN I PRZEPISY GRY W PIŁKĘ NOŻNA OBOWIĄZUJĄCE PODCZAS V EDYCJI LIGI LET S MOVE WIOSNA 2013 Rozgrywk Lt s mov mją hrktr mtorsk tzn., h uzstnkm n mogą yć zwony zynn grjąy lu zgłoszn o rozgrywk płkrskh
REGULAMIN I PRZEPISY GRY W PIŁKĘ NOŻNA OBOWIĄZUJĄCE PODCZAS V EDYCJI LIGI LET S MOVE WIOSNA 2013 Rozgrywk Lt s mov mją hrktr mtorsk tzn., h uzstnkm n mogą yć zwony zynn grjąy lu zgłoszn o rozgrywk płkrskh
ANALIZA PRACY SYSTEMU ENERGETYCZNO-NAPĘDOWEGO STATKU TYPU OFFSHORE Z WYKORZYSTANIEM METODY DRZEW USZKODZEŃ
 MGR INŻ. LSZK CHYBOWSKI Politchnik Szczcińsk Wydził Mchniczny Studium Doktorncki ANALIZA PRACY SYSTMU NRGTYCZNO-NAPĘDOWGO STATKU TYPU OFFSHOR Z WYKORZYSTANIM MTODY DRZW USZKODZŃ STRSZCZNI W mtril przdstwiono
MGR INŻ. LSZK CHYBOWSKI Politchnik Szczcińsk Wydził Mchniczny Studium Doktorncki ANALIZA PRACY SYSTMU NRGTYCZNO-NAPĘDOWGO STATKU TYPU OFFSHOR Z WYKORZYSTANIM MTODY DRZW USZKODZŃ STRSZCZNI W mtril przdstwiono
Wyk lad 1 Podstawowe wiadomości o macierzach
 Wyk ld 1 Podstwowe widomości o mcierzch Oznczeni: N {1 2 3 } - zbiór liczb nturlnych N 0 {0 1 2 } R - ci lo liczb rzeczywistych n i 1 + 2 + + n i1 1 Określenie mcierzy Niech m i n bed dowolnymi liczbmi
Wyk ld 1 Podstwowe widomości o mcierzch Oznczeni: N {1 2 3 } - zbiór liczb nturlnych N 0 {0 1 2 } R - ci lo liczb rzeczywistych n i 1 + 2 + + n i1 1 Określenie mcierzy Niech m i n bed dowolnymi liczbmi
51. Ogólnopolski Konkurs Chemiczny im. A. Swinarskiego
 51. gólnopolski Konkurs Chmizny im. A. Swinrskigo Finł zęść tortyzn 27.03.2015 Przykłdowy shmt rozwiązni zdń i punktj Zdni A punkt Przykłdowy shmt odpowidzi Punktj I r = [Cu 2+ ][H ] 2 = 2,2 10-20 ph =
51. gólnopolski Konkurs Chmizny im. A. Swinrskigo Finł zęść tortyzn 27.03.2015 Przykłdowy shmt rozwiązni zdń i punktj Zdni A punkt Przykłdowy shmt odpowidzi Punktj I r = [Cu 2+ ][H ] 2 = 2,2 10-20 ph =
f(x)dx (1.7) b f(x)dx = F (x) = F (b) F (a) (1.2)
 Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Cłk oznczon Cłkę oznczoną będziemy zpisywli jko f(x)dx (.) z fnkcji f(x), któr jest ogrniczon w przedzile domkniętym [, b]. Jk obliczyć cłkę oznczoną? Obliczmy njpierw cłkę nieoznczoną z fnkcji f(x), co
Przykład 2.6. Przekrój złożony z trzech kształtowników walcowanych.
 Przkłd 6 Przkrój złożon z trzh ksztłtowników wlownh Polni: Wznzć główn ntrln momnt bzwłdnośi orz kirunki główn dl poniższgo przkroju złożongo z trzh ksztłtowników wlownh 0800 0 80800 Dn dotzą ksztłtowników
Przkłd 6 Przkrój złożon z trzh ksztłtowników wlownh Polni: Wznzć główn ntrln momnt bzwłdnośi orz kirunki główn dl poniższgo przkroju złożongo z trzh ksztłtowników wlownh 0800 0 80800 Dn dotzą ksztłtowników
Wykªad 8. Pochodna kierunkowa.
 Wykªd jest prowdzony w opriu o podr znik Anliz mtemtyzn 2. enije, twierdzeni, wzory M. Gewert i Z. Skozyls. Wykªd 8. ohodn kierunkow. enij Nieh funkj f b dzie okre±lon przynjmniej n otozeniu punktu (x
Wykªd jest prowdzony w opriu o podr znik Anliz mtemtyzn 2. enije, twierdzeni, wzory M. Gewert i Z. Skozyls. Wykªd 8. ohodn kierunkow. enij Nieh funkj f b dzie okre±lon przynjmniej n otozeniu punktu (x
Sieæ szpitalnych koordynatorów pobierania narz¹dów w Polsce w 2011 r.
 Siæ szpitlnyh poirni w ls w 2011 r. Do koñ 2011 roku stnowisko szpitlngo trnsplntyjngo powst³o ³¹zni w 186 szpitlh, unkjê p³ni³y 203 osoy. ltrnsplnt popis³ umowy ywilno-prwn z 200 mi w 184 szpitlh, w 2
Siæ szpitlnyh poirni w ls w 2011 r. Do koñ 2011 roku stnowisko szpitlngo trnsplntyjngo powst³o ³¹zni w 186 szpitlh, unkjê p³ni³y 203 osoy. ltrnsplnt popis³ umowy ywilno-prwn z 200 mi w 184 szpitlh, w 2
Automatyka i Robotyka Analiza Wykład 23 dr Adam Ćmiel
 Automty i ooty Aliz Wyłd dr Adm Ćmil mil@gh.du.pl SZEEGI POTĘGOWE iąg liz zspoloyh z z - szrg potęgowy, gdzi - iąg współzyiów szrgu, z C - środ, trum ustlo, z C - zmi. Dl dowolgo ustlogo z C szrg potęgowy
Automty i ooty Aliz Wyłd dr Adm Ćmil mil@gh.du.pl SZEEGI POTĘGOWE iąg liz zspoloyh z z - szrg potęgowy, gdzi - iąg współzyiów szrgu, z C - środ, trum ustlo, z C - zmi. Dl dowolgo ustlogo z C szrg potęgowy
Programy współbieżne
 Specyfikownie i weryfikownie Progrmy współieżne Mrek A. Bednrczyk, www.ipipn.gd.pl Litertur wiele prc dostępnych w Sieci np.: http://www.wikipedi.org/ Specyfikownie i weryfikcj progrmy współieżne PJP Prosty
Specyfikownie i weryfikownie Progrmy współieżne Mrek A. Bednrczyk, www.ipipn.gd.pl Litertur wiele prc dostępnych w Sieci np.: http://www.wikipedi.org/ Specyfikownie i weryfikcj progrmy współieżne PJP Prosty
Rys Wyrównanie spostrzeżeń zawarunkowanych jednakowo dokładnych C. KRAKOWIANY
 Rys. 9.. Wyrównnie spostrzeżeń zwrunkownyh jednkowo dokłdnyh C. KRAKOWIANY 9.9. Informje wstępne o krkowinh Krkowin jest zespołem liz rozmieszzonyh w prostokątnej teli o k kolumnh i w wierszh, dl którego
Rys. 9.. Wyrównnie spostrzeżeń zwrunkownyh jednkowo dokłdnyh C. KRAKOWIANY 9.9. Informje wstępne o krkowinh Krkowin jest zespołem liz rozmieszzonyh w prostokątnej teli o k kolumnh i w wierszh, dl którego
Gr. 100 i 125 mm INSTRUKCJA MONTA U KASETY. c f e. h g d. Systemy przesuwne do drzwi. System do œciany karton-gips
 Sstm przsuwn o rzwi INSTRUKCJA MONTA U KASETY Gr. 100 i 125 mm Sstm o œin krton-ips Zstwini poszzólnh lmntów h i m l ELEMENTY TYLKO DO KASET NA GR. 125 mm S³upki pionow kst 2 szt (komplt) i Klips s³u ¹
Sstm przsuwn o rzwi INSTRUKCJA MONTA U KASETY Gr. 100 i 125 mm Sstm o œin krton-ips Zstwini poszzólnh lmntów h i m l ELEMENTY TYLKO DO KASET NA GR. 125 mm S³upki pionow kst 2 szt (komplt) i Klips s³u ¹
NACIONALINIS EGZAMINŲ CENTRAS
 2016 NACIONALINIS EGZAMINŲ CENTRAS Imię, nzwisko Kls Ko uzni DIAGNOSTINIS MOKYMOSI PASIEKIMŲ VERTINIMAS CZYTANIE Weług M. Kepenienė Mingiusis krokoils, Vilnius: FOLIUM, 1998. Posłuhjie, o się przyrzyło
2016 NACIONALINIS EGZAMINŲ CENTRAS Imię, nzwisko Kls Ko uzni DIAGNOSTINIS MOKYMOSI PASIEKIMŲ VERTINIMAS CZYTANIE Weług M. Kepenienė Mingiusis krokoils, Vilnius: FOLIUM, 1998. Posłuhjie, o się przyrzyło
WYŻSZA SZKOŁA INFORMATYKI STOSOWANEJ I ZARZĄDZANIA
 DROGI i CYKLE HAMILTONA w grfh kierownh Dl grfu kierownego D = ( V, A ) rogą wierhołk 0 V o V nwm iąg (npremienn) wierhołków i łuków grfu: ( 0,,,,...,,, ), pełniją wrunek i = ( i, i ) l i =,..., rogę nwm
DROGI i CYKLE HAMILTONA w grfh kierownh Dl grfu kierownego D = ( V, A ) rogą wierhołk 0 V o V nwm iąg (npremienn) wierhołków i łuków grfu: ( 0,,,,...,,, ), pełniją wrunek i = ( i, i ) l i =,..., rogę nwm
Komisja Egzaminacyjna dla Aktuariuszy LIX Egzamin dla Aktuariuszy z 12 marca 2012 r. Część I Matematyka finansowa
 Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Mtemtyk finnsow 12.03.2012 r. Komisj Egzmincyjn dl Akturiuszy LIX Egzmin dl Akturiuszy z 12 mrc 2012 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 100 minut
Sieæ koordynatorów pobierania i przeszczepiania narz¹dów w Polsce w 2013 r.
 Siæ kooryntorów poirni i przszzpini nrz¹ów w Pols w 2013 r. N koni 2013 r. unkjê trnsplntyjngo p³ni³o w Pols ³¹zni 274 osoy. Njwiêksz¹ zœæ, 228 osó, stnowili szpitlni kooryntorzy poirni nrz¹ów. Kooryntorzy
Siæ kooryntorów poirni i przszzpini nrz¹ów w Pols w 2013 r. N koni 2013 r. unkjê trnsplntyjngo p³ni³o w Pols ³¹zni 274 osoy. Njwiêksz¹ zœæ, 228 osó, stnowili szpitlni kooryntorzy poirni nrz¹ów. Kooryntorzy
Środowisko życia i zdrowie - edukacja ekologiczna
 Zspół Szkół Mhniznyh Elktryznyh i Elktroniznyh mgr Grzgorz Gurzyński Śroowisko żyi i zrowi - ukj kologizn Projkt progrmu wyhowwzgo l wyhownków Intrntu ZSMEiE w Toruniu propgujągo ziłni prokologizn i zrowy
Zspół Szkół Mhniznyh Elktryznyh i Elktroniznyh mgr Grzgorz Gurzyński Śroowisko żyi i zrowi - ukj kologizn Projkt progrmu wyhowwzgo l wyhownków Intrntu ZSMEiE w Toruniu propgujągo ziłni prokologizn i zrowy
Przepisy Hokeja na Trawie Hala
 Przepisy Hokej n Trwie Hl Stn n 1 listop 2014 Tłumzenie: Anrzej Busz, Szymon Dolt 2 Spis treśi I Słownizek... 3 II Gr... 5 1 Boisko... 5 2 Skł rużyn... 5 3 Kpitnowie... 8 4 Uiór i wyposżenie zwonik...
Przepisy Hokej n Trwie Hl Stn n 1 listop 2014 Tłumzenie: Anrzej Busz, Szymon Dolt 2 Spis treśi I Słownizek... 3 II Gr... 5 1 Boisko... 5 2 Skł rużyn... 5 3 Kpitnowie... 8 4 Uiór i wyposżenie zwonik...
%%'!)%'targzip gunzipcompressuncompressdiffpatch* %!+%,-./! Nazwy programów, polece, katalogów, wyniki działania wydawanych polece.
 !" #!"#"$" % $%&%'( %%'!)%'trgzip gunzipomprssunomprssdiffpth* &$ #$"" " %!+%,-./! #"'% 0%%! +%%1'%! 23 23 () *"!#!! Czionk o stłj szrokoi Nzwy progrmów, pol, ktlogów, wyniki dziłni wydwnyh pol. Czionk
!" #!"#"$" % $%&%'( %%'!)%'trgzip gunzipomprssunomprssdiffpth* &$ #$"" " %!+%,-./! #"'% 0%%! +%%1'%! 23 23 () *"!#!! Czionk o stłj szrokoi Nzwy progrmów, pol, ktlogów, wyniki dziłni wydwnyh pol. Czionk
Autor prof. dr hab. inż. Marian Mokwa. Opiniodawca dr hab. inż. Jarosław Mirski, prof. nadzw.
 utor pro. r h. inż. Mrin Mokw Opiniow r h. inż. Jrosłw Mirski, pro. nzw. Rktor mrytoryzny r h. inż. Krzyszto Pulikowski, pro. UP Oprowni rkyjn mgr lżit Winirsk-Grosz Korkt r w Jworsk Łmni lin Gl Projkt
utor pro. r h. inż. Mrin Mokw Opiniow r h. inż. Jrosłw Mirski, pro. nzw. Rktor mrytoryzny r h. inż. Krzyszto Pulikowski, pro. UP Oprowni rkyjn mgr lżit Winirsk-Grosz Korkt r w Jworsk Łmni lin Gl Projkt
Arkusz 1 - karta pracy Całka oznaczona i jej zastosowania. Całka niewłaściwa
 Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Arkusz - krt prcy Cłk oznczon i jj zstosowni. Cłk niwłściw Zdni : Obliczyć nstępując cłki oznczon 5 d 5 d + 5 + 7 d Zuwżmy, ż d, Stąd d, + 5 + 7 d + ] 7 + + ln d cos sin d d ]. d + d 5, d + 5 + 7 7 7 d
Rozwiązania maj 2017r. Zadania zamknięte
 Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
Rozwiązni mj 2017r. Zdni zmknięte Zd 1. 5 16 5 2 5 2 Zd 2. 5 2 27 2 23 2 2 2 2 Zd 3. 2log 3 2log 5log 3 log 5 log 9 log 25log Zd. 120% 8910 1,2 8910 2,2 8910 $%, 050 Zd 5. Njłtwiej jest zuwżyć że dl 1
INSTRUKCJA. - Jak rozwiązywać zadania wysoko punktowane?
 INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
INSTRUKCJA - Jk rozwiązywć zdni wysoko punktowne? Mturzysto! Zdni wysoko punktowne to tkie, z które możesz zdobyć 4 lub więcej punktów. Zdni z dużą ilość punktów nie zwsze są trudniejsze, często ich punktcj
< f g = fg. f = e t f = e t. U nas: e t (α 1)t α 2 dt = 0 + (α 1)Γ(α 1)
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Algorytmy i struktury danych
 Cl ćwzn Alorytmy struktury ny Instytut Strown Systmów Inormtyzny Wyzł Elktrotnk, Inormtyk Tlkomunkj Unwrsytt Zlonoórsk Gry Ćwzn m n lu zpoznn stuntów z wyrnym znnm otyząym rów zrówno skrowny jk nskrowny.
Cl ćwzn Alorytmy struktury ny Instytut Strown Systmów Inormtyzny Wyzł Elktrotnk, Inormtyk Tlkomunkj Unwrsytt Zlonoórsk Gry Ćwzn m n lu zpoznn stuntów z wyrnym znnm otyząym rów zrówno skrowny jk nskrowny.
Egzamin dla Aktuariuszy z 15 marca 2010 r. Matematyka Finansowa
 Egzm dl Akturuszy z 5 mrc 0 r. Mtmtyk Fsow Zd Krok : Ay koc roku yło co jmj ml K mus spłć rówość: 000000 50 000 K 50 000 000000 K Krok : Lczymy st kot koc roku zkłdjąc, Ŝ koc roku mmy ml 000000 50 5000
Egzm dl Akturuszy z 5 mrc 0 r. Mtmtyk Fsow Zd Krok : Ay koc roku yło co jmj ml K mus spłć rówość: 000000 50 000 K 50 000 000000 K Krok : Lczymy st kot koc roku zkłdjąc, Ŝ koc roku mmy ml 000000 50 5000
KONKURS MATEMATYCZNY dla uczniów gimnazjów w roku szkolnym 2012/13. Propozycja punktowania rozwiązań zadań
 KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
KONKURS MATEMATYCZNY dl uczniów gimnzjów w roku szkolnym 0/ II etp zwodów (rejonowy) 0 listopd 0 r. Propozycj punktowni rozwiązń zdń Uwg: Z kżde poprwne rozwiąznie inne niż przewidzine w propozycji punktowni
WPŁYW DODATKU PRODUKTÓW Z AMARANTUSA NA CECHY TEKSTURY MIĘKISZU PIECZYWA
 At Agrophysi, 2008, 11(2), 499-508 WPŁYW DODATKU PRODUKTÓW Z AMARANTUSA NA CECHY TEKSTURY MIĘKISZU PIECZYWA Rnt RóŜyło, Jnusz Lskowski Ktr Eksplotji Mszyn Przmysłu SpoŜywzgo, Akmi Rolniz ul. Doświzln 44,
At Agrophysi, 2008, 11(2), 499-508 WPŁYW DODATKU PRODUKTÓW Z AMARANTUSA NA CECHY TEKSTURY MIĘKISZU PIECZYWA Rnt RóŜyło, Jnusz Lskowski Ktr Eksplotji Mszyn Przmysłu SpoŜywzgo, Akmi Rolniz ul. Doświzln 44,
WYZNACZNIKI. . Gdybyśmy rozważali układ dwóch równań liniowych, powiedzmy: Takie układy w matematyce nazywa się macierzami. Przyjmijmy definicję:
 YZNACZNIKI Do opisu pewnh oiektów nie wstrz użć liz. ie n przkłd, że do opisni sił nleż użć wektor. Sił to przeież nie tlko wielkość le i jej punkt przłożeni, zwrot orz kierunek dziłni. Zte jedną lizą
YZNACZNIKI Do opisu pewnh oiektów nie wstrz użć liz. ie n przkłd, że do opisni sił nleż użć wektor. Sił to przeież nie tlko wielkość le i jej punkt przłożeni, zwrot orz kierunek dziłni. Zte jedną lizą
Wkłady atramentowe dostarczone z urządzeniem. Płyta instalacyjna CD-ROM Płyta CD-ROM z dokumentacją
 Poręznik szykij osługi Zznij tutj MFC-J6510DW MFC-J6710DW Prz skonfigurownim urzązni zpoznj się z roszurą Bzpizństwo i zgoność z przpismi. Nstępni zpoznj się z ninijszym Poręznikim szykij osługi w lu przprowzni
Poręznik szykij osługi Zznij tutj MFC-J6510DW MFC-J6710DW Prz skonfigurownim urzązni zpoznj się z roszurą Bzpizństwo i zgoność z przpismi. Nstępni zpoznj się z ninijszym Poręznikim szykij osługi w lu przprowzni
N(0, 1) ) = φ( 0, 3) = 1 φ(0, 3) = 1 0, 6179 = 0, 3821 < t α 1 e t dt α > 0. f g = fg. f = e t f = e t. U nas: g = t α 1 g = (α 1)t α 2
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
4.5 Deterministyczne i zupełne automaty Moore a i Mealy ego
 4.5 Deterministyczne i zupełne utomty Moore i Mely ego Automty Moore i Mely ego ędziemy rozwżć tylko w rsji deterministycznej i zupełnej. W definicjch tych utomtów nie pojwi się pojęcie ów końcowych, z
4.5 Deterministyczne i zupełne utomty Moore i Mely ego Automty Moore i Mely ego ędziemy rozwżć tylko w rsji deterministycznej i zupełnej. W definicjch tych utomtów nie pojwi się pojęcie ów końcowych, z
Matematyka finansowa 10.03.2014 r. Komisja Egzaminacyjna dla Aktuariuszy. LXVI Egzamin dla Aktuariuszy z 10 marca 2014 r. Część I
 Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Mtemtyk finnsow.03.2014 r. Komisj Egzmincyjn dl Akturiuszy LXVI Egzmin dl Akturiuszy z mrc 2014 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoby egzminownej:... Czs egzminu: 0 minut 1 Mtemtyk
Wykład 2. Granice, ciągłość, pochodna funkcji i jej interpretacja geometryczna
 1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
1 Wykłd Grnice, ciągłość, pocodn unkcji i jej interpretcj geometryczn.1 Grnic unkcji. Grnic lewostronn i grnic prwostronn unkcji Deinicj.1 Mówimy, że liczb g jest grnicą lewostronną unkcji w punkcie =,
Metoda prądów obwodowych
 Metod prądów owodowyh Zmenmy wszystke rzezywste źródł prądowe n npęowe, Tworzymy kłd równń lnowyh opsjąyh poszzególne owody. Dowolną seć lnową skłdjąą sę z elementów skponyh możn opsć z pomoą kłd równń
Metod prądów owodowyh Zmenmy wszystke rzezywste źródł prądowe n npęowe, Tworzymy kłd równń lnowyh opsjąyh poszzególne owody. Dowolną seć lnową skłdjąą sę z elementów skponyh możn opsć z pomoą kłd równń
a a a ; ; ; (1.2) przez [ a ij ], czyli zbiór elementów w i-tym wierszu i w j-tej kolumnie. Wymiary ( n m) stanowią stopień macierzy.
![a a a ; ; ; (1.2) przez [ a ij ], czyli zbiór elementów w i-tym wierszu i w j-tej kolumnie. Wymiary ( n m) stanowią stopień macierzy. a a a ; ; ; (1.2) przez [ a ij ], czyli zbiór elementów w i-tym wierszu i w j-tej kolumnie. Wymiary ( n m) stanowią stopień macierzy.](/thumbs/65/52292306.jpg) . PODSWY LGEBY CIEZY.. Ukły równń liniowyh Ukł n równń o m niewiomyh x K x m m L L L L L x K x n nm m n możn zpisć w posti tli liz (mierzy): (.) x x x x x x x x x x zpisć w posti mierzowej. Wprowzją nstępująe
. PODSWY LGEBY CIEZY.. Ukły równń liniowyh Ukł n równń o m niewiomyh x K x m m L L L L L x K x n nm m n możn zpisć w posti tli liz (mierzy): (.) x x x x x x x x x x zpisć w posti mierzowej. Wprowzją nstępująe
RÓWNOWAGA CHEMICZNA. Reakcje chemiczne: nieodwracalne ( praktycznie nieodwracalne???) reakcje wybuchowe, np. wybuch nitrogliceryny: 2 C H 2
 RÓWNOWG CHEMICZN N O 4 NO Rekje hemizne: nieowrlne ( rktyznie nieowrlne???) rekje wyuhowe, n. wyuh nitroglieryny: C 3 H 5 N 3 O 9 6 CO + 3 N + 5 H O + / O rekje rozu romieniotwórzego, n. roz urnu gy jeen
RÓWNOWG CHEMICZN N O 4 NO Rekje hemizne: nieowrlne ( rktyznie nieowrlne???) rekje wyuhowe, n. wyuh nitroglieryny: C 3 H 5 N 3 O 9 6 CO + 3 N + 5 H O + / O rekje rozu romieniotwórzego, n. roz urnu gy jeen
4.3. Przekształcenia automatów skończonych
 4.3. Przeksztłceni utomtów skończonych Konstrukcj utomtu skończonego (niedeterministycznego) n podstwie wyrżeni regulrnego (lgorytm Thompson). Wejście: wyrżenie regulrne r nd lfetem T Wyjście : utomt skończony
4.3. Przeksztłceni utomtów skończonych Konstrukcj utomtu skończonego (niedeterministycznego) n podstwie wyrżeni regulrnego (lgorytm Thompson). Wejście: wyrżenie regulrne r nd lfetem T Wyjście : utomt skończony
Komisja Egzaminacyjna dla Aktuariuszy LII Egzamin dla Aktuariuszy z 15 marca 2010 r. Część I Matematyka finansowa
 Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
Mtemtyk finnsow 15.0.010 r. Komisj Egzmincyjn dl Akturiuszy LII Egzmin dl Akturiuszy z 15 mrc 010 r. Część I Mtemtyk finnsow WERSJA TESTU A Imię i nzwisko osoy egzminownej:... Czs egzminu: 100 minut 1
12. CZWÓRNIKI PARAMETRY ROBOCZE I FALOWE CZWÓRNIK U
 OBWODY SYGNAŁY Wykłd : Czwórniki prmtry robocz i flow. CWÓRN PARAMETRY ROBOCE FALOWE.. PARAMETRY ROBOCE Jżli do jdnych wrót czwórnik dołączono źródło wymuszń, ntomist drui wrot iążono dwójnikim bzźródłowym,
OBWODY SYGNAŁY Wykłd : Czwórniki prmtry robocz i flow. CWÓRN PARAMETRY ROBOCE FALOWE.. PARAMETRY ROBOCE Jżli do jdnych wrót czwórnik dołączono źródło wymuszń, ntomist drui wrot iążono dwójnikim bzźródłowym,
ANALIZA FOURIEROWSKA szybkie transformaty Fouriera
 AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
AALIZA FOURIEROWSKA szybi trasformaty Fourira dowola fuję priodyzą F( w zasi lub przstrzi (tx, ors T) moża przdstawić jao () F( b o + [ a si( + b os( ] gdzi π / T lub ω zauważmy, ż ω, jst ajiższą zęstośią
a) b) Rys. 6.1. Schemat ideowo-konstrukcyjny układu do przykładu 6.1 a) i jego schemat blokowy
 04 6. Ztoownie metod hemtów lokowh do nliz włśiwośi ukłdów utomtki Shemt lokow ukłdu utomtki jet formą zpiu mtemtznego modelu dnego ukłdu, n podtwie której, wkorztują zd przedtwione rozdzile 3.7, możn
04 6. Ztoownie metod hemtów lokowh do nliz włśiwośi ukłdów utomtki Shemt lokow ukłdu utomtki jet formą zpiu mtemtznego modelu dnego ukłdu, n podtwie której, wkorztują zd przedtwione rozdzile 3.7, możn
4.6. Gramatyki regularne
 4.6. Grmtyki regulrne G = < N,T,P,Z > jest grmtyką prwostronnie liniową, jeśli jej produkcje mją postć: ( i) U xv x T * U,V N ( ii) U x G = < N,T,P,Z > jest grmtyką prwostronnie regulrną, jeśli jej produkcje
4.6. Grmtyki regulrne G = < N,T,P,Z > jest grmtyką prwostronnie liniową, jeśli jej produkcje mją postć: ( i) U xv x T * U,V N ( ii) U x G = < N,T,P,Z > jest grmtyką prwostronnie regulrną, jeśli jej produkcje
 ć Ó Ł Ł ć Ę ć ć Ę Ę ć ż ć Ź Ę ć ć Ź Ę ż Ą ż ć ć ć ż ż ż ż ż Ś Ą ż Ś ć ć ź Ż Ę ż Ę Ó Ę ż Ź Ś Ź ć Ę Ę Ę ż ć Ż ć ć Ę ż Ę Ż Ś ć ć ż ć Ź ć Ą ć Ą ż ć Ę Ź ć ź ć Ę ć ć ż ć Ę ć ć ż ż Ę Ę ż Ś Ź Ę ż Ł Ś ż ć ź ż ć
ć Ó Ł Ł ć Ę ć ć Ę Ę ć ż ć Ź Ę ć ć Ź Ę ż Ą ż ć ć ć ż ż ż ż ż Ś Ą ż Ś ć ć ź Ż Ę ż Ę Ó Ę ż Ź Ś Ź ć Ę Ę Ę ż ć Ż ć ć Ę ż Ę Ż Ś ć ć ż ć Ź ć Ą ć Ą ż ć Ę Ź ć ź ć Ę ć ć ż ć Ę ć ć ż ż Ę Ę ż Ś Ź Ę ż Ł Ś ż ć ź ż ć
 Ś Ż Ś ń ć ć ć ć ć ć ć ń ń ć ź Ł Ł Ś ź ź ć ź ć Ę Ę Łź Ś Ę ń Ś ć ć ć ć ń ń ć ć ć ć Ś ć Ś Ł Ł Ś ć ź ć ć Ę ć ć ć ć ć ć Ę ź ń ź Ś Ł ć ć ć ź ć ć ć Ę ć ź ź ć Ś ć ć ć ć Ę ć ć ć Ł ń ć ć ć Ł ć ć ń ć ń ń ń ń ń ć
Ś Ż Ś ń ć ć ć ć ć ć ć ń ń ć ź Ł Ł Ś ź ź ć ź ć Ę Ę Łź Ś Ę ń Ś ć ć ć ć ń ń ć ć ć ć Ś ć Ś Ł Ł Ś ć ź ć ć Ę ć ć ć ć ć ć Ę ź ń ź Ś Ł ć ć ć ź ć ć ć Ę ć ź ź ć Ś ć ć ć ć Ę ć ć ć Ł ń ć ć ć Ł ć ć ń ć ń ń ń ń ń ć
Zadania. I. Podzielność liczb całkowitych
 Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Zdni I. Podzielność liczb cłkowitych. Pewn liczb sześciocyfrow kończy się cyfrą 5. Jeśli tę cyfrę przestwimy n miejsce pierwsze ze strony lewej to otrzymmy nową liczbę cztery rzy większą od poprzedniej.
Powiatowy Urząd Pracy ul. Andersa 2 59 220 Legnica MONITORING ZAWODÓW DEFICYTOWYCH I NADWYŻKOWYCH W POWIECIE LEGNICKIM W 2009 ROKU
 Powiatowy Urzą Pray ul. Anrsa 2 59 220 Lgnia MONITORING ZAWODÓW DEFICYTOWYCH I NADWYŻKOWYCH W POWIECIE LEGNICKIM W 2009 ROKU LIPIEC 2010 CZĘŚĆ II PROGNOSTYCZNA Źrółm inormaji w tj zęśi raportu są wyniki
Powiatowy Urzą Pray ul. Anrsa 2 59 220 Lgnia MONITORING ZAWODÓW DEFICYTOWYCH I NADWYŻKOWYCH W POWIECIE LEGNICKIM W 2009 ROKU LIPIEC 2010 CZĘŚĆ II PROGNOSTYCZNA Źrółm inormaji w tj zęśi raportu są wyniki
RBD Relacyjne Bazy Danych
 Wykłd 6 RBD Relcyjne Bzy Dnych Bzy Dnych - A. Dwid 2011 1 Bzy Dnych - A. Dwid 2011 2 Sum ziorów A i B Teori ziorów B A R = ) ( Iloczyn ziorów A i B ( ) B A R = Teori ziorów Różnic ziorów ( A) i B Iloczyn
Wykłd 6 RBD Relcyjne Bzy Dnych Bzy Dnych - A. Dwid 2011 1 Bzy Dnych - A. Dwid 2011 2 Sum ziorów A i B Teori ziorów B A R = ) ( Iloczyn ziorów A i B ( ) B A R = Teori ziorów Różnic ziorów ( A) i B Iloczyn
2 Criminal records. Vocabulary. burglary. Crimes. Criminals
 FR 2 C Vy G P P Vy C C P fi Sk R A W C C 1 Zjź z zę żzy yzy. Z y łóż zy ó łjąy zę (1 8). 1 k 2 4 y j y y z q y k q 5 6 7 8 4 Uzłj z (1 7) yz z ćzń 1, 2 j. y j. FR 1 T 2 T k M S. A k k. 4 I y k. 5 Ty k.
FR 2 C Vy G P P Vy C C P fi Sk R A W C C 1 Zjź z zę żzy yzy. Z y łóż zy ó łjąy zę (1 8). 1 k 2 4 y j y y z q y k q 5 6 7 8 4 Uzłj z (1 7) yz z ćzń 1, 2 j. y j. FR 1 T 2 T k M S. A k k. 4 I y k. 5 Ty k.
5. Zadania tekstowe.
 5. Zni tekstowe. Przykł. Kolrz połowę rogi pokonł ze śrenią prękością 0 km/, rugą połowę z prękością 50 km /. Wyzncz śrenią prękość kolrz n cłej trsie. nliz : pierwsz połow rogi rug połow rogi 0 km/ prękość
5. Zni tekstowe. Przykł. Kolrz połowę rogi pokonł ze śrenią prękością 0 km/, rugą połowę z prękością 50 km /. Wyzncz śrenią prękość kolrz n cłej trsie. nliz : pierwsz połow rogi rug połow rogi 0 km/ prękość
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego. best in training PRE TEST
 Projekt współfinnsowny przez Unię Europejską w rmh Europejskiego Funuszu Społeznego est in trining E-Pr@ownik ojrzłe kry społezeństw informyjnego n Mzowszu Numer Projektu: POKL.08.01.01-14-217/09 PRE TEST
Projekt współfinnsowny przez Unię Europejską w rmh Europejskiego Funuszu Społeznego est in trining E-Pr@ownik ojrzłe kry społezeństw informyjnego n Mzowszu Numer Projektu: POKL.08.01.01-14-217/09 PRE TEST
REGULAMIN PSKO 2016. I. Kryteria i wymagania dla zawodników Optimist PSKO. II. Mistrzostwa PSKO. III. Puchar Polski PSKO
 I. Krytria i wymagania dla zawodników Optimist PSKO 1. W rgatach PSKO mogą startować zawodnicy do lat 15 posiadający licncję sportową PZŻ, aktualn ubzpiczni OC i będący członkami PSKO, spłniający wymagania
I. Krytria i wymagania dla zawodników Optimist PSKO 1. W rgatach PSKO mogą startować zawodnicy do lat 15 posiadający licncję sportową PZŻ, aktualn ubzpiczni OC i będący członkami PSKO, spłniający wymagania
Wektor kolumnowy m wymiarowy macierz prostokątna o wymiarze n=1 Wektor wierszowy n wymiarowy macierz prostokątna o wymiarze m=1
 Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
Rchunek mcierzowy Mcierzą A nzywmy funkcję 2-zmiennych, któr prze liczb nturlnych (i,j) gdzie i = 1,2,3,4.,m; j = 1,2,3,4,n przyporządkowuje dokłdnie jeden element ij. 11 21 A = m1 12 22 m2 1n 2n mn Wymirem
POMIARY GPS/IMU, A WYZNACZANIE ELEMENTÓW ORIENTACJI ZEWNĘTRZNEJ
 162 nt Jędryczk POMIAY GPS/IMU, A WYZNACZANIE ELEMENTÓW OIENTACJI ZEWNĘTZNEJ Strszczni. Od kiku t prowdzon są dni nd wykorzystni nowych tchnik pomirowych tkich jk GPS czy IMU do wyznczni mntów orintcji
162 nt Jędryczk POMIAY GPS/IMU, A WYZNACZANIE ELEMENTÓW OIENTACJI ZEWNĘTZNEJ Strszczni. Od kiku t prowdzon są dni nd wykorzystni nowych tchnik pomirowych tkich jk GPS czy IMU do wyznczni mntów orintcji
Wykład 9: Różne rodzaje zbieżności ciągów zmiennych losowych. Prawa wielkich liczb.
 Rchuek prwopoobieństw MA1181 Wyził T, MS, rok k. 2013/14, sem. zimowy Wykłowc: r hb. A. Jurlewicz Wykł 9: Róże rozje zbieżości ciągów zmieych losowych. rw wielkich liczb. Zbieżość z prwopoobieństwem 1:
Rchuek prwopoobieństw MA1181 Wyził T, MS, rok k. 2013/14, sem. zimowy Wykłowc: r hb. A. Jurlewicz Wykł 9: Róże rozje zbieżości ciągów zmieych losowych. rw wielkich liczb. Zbieżość z prwopoobieństwem 1:
i na matematycznej wyspie materiały dla ucznia, pakiet 89, s. KARTA:... Z KLASY:...
 A@ i J@ś n mtemtycznej wyspie mteriły l uczni, pkiet 89, s. Eolonistyczn p Etemtyczn Strżk m Zzncz znkiem n obrzku te elementy, w których nzwie występuje głosk w. own ychzyczne ie W fi uktyccjzn E pls
A@ i J@ś n mtemtycznej wyspie mteriły l uczni, pkiet 89, s. Eolonistyczn p Etemtyczn Strżk m Zzncz znkiem n obrzku te elementy, w których nzwie występuje głosk w. own ychzyczne ie W fi uktyccjzn E pls
Mikroekonomia II. Teoria konsumenta - zadania dodatkowe. w której mamy 20 konsumentów, chcacych. kupić samochody, o 5 typach, charakteryzujacych
 Mikrokonomia II Toria konsumnta - zadania dodatkow 1. Rozważmy sytuacj w którj mamy 20 konsumntów, chcacych kupić samochody, o 5 typach, charaktryzujacych si różnymi cnami granicznymi. Poniższa tabla przdstawia
Mikrokonomia II Toria konsumnta - zadania dodatkow 1. Rozważmy sytuacj w którj mamy 20 konsumntów, chcacych kupić samochody, o 5 typach, charaktryzujacych si różnymi cnami granicznymi. Poniższa tabla przdstawia
Planimetria czworokąty
 Plnimetri czworokąty Emili Ruszczyk kl. II, I LO im. Stefn Żeromskiego w Ełku pod kierunkiem Grżyny iernot-lendo Klsyfikcj czworokątów zworokąty dzielą się n niewypukłe i wypukłe, wypukłe n trpezy i trpezoidy,
Plnimetri czworokąty Emili Ruszczyk kl. II, I LO im. Stefn Żeromskiego w Ełku pod kierunkiem Grżyny iernot-lendo Klsyfikcj czworokątów zworokąty dzielą się n niewypukłe i wypukłe, wypukłe n trpezy i trpezoidy,
Macierzy rzadkie symetryczne
 Mcierzy rzkie symetryczne Istnieje wielu problemów technicznych i nukowych, w których zstosownie formlizcji mtemtycznej oprowzi o ziłń n mcierzmi rzkimi symetrycznymi. To są zni mechniki, hyromechniki,
Mcierzy rzkie symetryczne Istnieje wielu problemów technicznych i nukowych, w których zstosownie formlizcji mtemtycznej oprowzi o ziłń n mcierzmi rzkimi symetrycznymi. To są zni mechniki, hyromechniki,
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Rachunek prawdopodobieństwa i statystyka matematyczna.
 Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Kombinowanie o nieskończoności. 4. Jak zmierzyć?
 Kombinownie o nieskończoności.. Jk zmierzyć? Projekt Mtemtyk dl ciekwych świt spisł: Michł Korch 9 kwietni 08 Trochę rzeczy z wykłdu Prezentcj multimediln do wykłdu. Nieskończone sumy Będzie nm się zdrzć
Kombinownie o nieskończoności.. Jk zmierzyć? Projekt Mtemtyk dl ciekwych świt spisł: Michł Korch 9 kwietni 08 Trochę rzeczy z wykłdu Prezentcj multimediln do wykłdu. Nieskończone sumy Będzie nm się zdrzć
H. Dąbrowski, W. Rożek Próbna matura, grudzień 2014 r. CKE poziom rozszerzony 1. Zadanie 15 różne sposoby jego rozwiązania
 H ąrowski, W Rożek Prón mtur, grudzień 014 r K poziom rozszerzony 1 Zdnie 15 różne sposoy jego rozwiązni Henryk ąrowski, Wldemr Rożek Zdnie 15 Punkt jest środkiem oku prostokąt, w którym Punkt leży n oku
H ąrowski, W Rożek Prón mtur, grudzień 014 r K poziom rozszerzony 1 Zdnie 15 różne sposoy jego rozwiązni Henryk ąrowski, Wldemr Rożek Zdnie 15 Punkt jest środkiem oku prostokąt, w którym Punkt leży n oku
Oddziaływania słabe. Bozony pośredniczące W i Z. Sprzężenia leptonowe. Sprzężenia kwarkowe - mieszanie kwarków. D. Kiełczewska, wykład 5
 Oziaływania słab Bozony pośrnizą i Z Sprzężnia lptonow Sprzężnia kwarkow - miszani kwarków Oziaływania słab ν + µ + ν ν + ν + µ µ µ ν µ µ ν µ µ ν ν µ µ + Z 0 - ν - ν Rakj z wymianą prąów nałaowanyh: CC
Oziaływania słab Bozony pośrnizą i Z Sprzężnia lptonow Sprzężnia kwarkow - miszani kwarków Oziaływania słab ν + µ + ν ν + ν + µ µ µ ν µ µ ν µ µ ν ν µ µ + Z 0 - ν - ν Rakj z wymianą prąów nałaowanyh: CC
69 b. 82a. 82b e f. d a g. 82b b 30 a a 97R 98R 98L
 200 80 280 WATERTEMP. E FUEL F 20 30 0012 10 50 0 60 0261 20 60 0 80 OIL 0 25 25 50 50 - + AMPERS GMC (CCKW-353) Clos Cin U.S. 2½ Ton Cro Truk 1/35 sl upt or Itlri mol ABER 35 059 WWW.ABER.NET.PL M in
200 80 280 WATERTEMP. E FUEL F 20 30 0012 10 50 0 60 0261 20 60 0 80 OIL 0 25 25 50 50 - + AMPERS GMC (CCKW-353) Clos Cin U.S. 2½ Ton Cro Truk 1/35 sl upt or Itlri mol ABER 35 059 WWW.ABER.NET.PL M in
Technika Cyfrowa 1. Wykład 5: Synteza automatów sekwencyjnych III UKŁADY SEKWENCYJNE C.D.
 JS TC III UKŁADY SEKWENCYJNE C.D. JS TC Tehnik Cyfrow Wykł 5: Syntez utomtów sekwenyjnyh r inż. Jrosłw Sugier Jroslw.Sugier@pwr.wro.pl IIAR, pok. 227 C-3 4 GRAF AUTOMATU, TABELE PRZEJŚĆ / WYJŚĆ Opis sekwenyjnego
JS TC III UKŁADY SEKWENCYJNE C.D. JS TC Tehnik Cyfrow Wykł 5: Syntez utomtów sekwenyjnyh r inż. Jrosłw Sugier Jroslw.Sugier@pwr.wro.pl IIAR, pok. 227 C-3 4 GRAF AUTOMATU, TABELE PRZEJŚĆ / WYJŚĆ Opis sekwenyjnego
Acta Agrophysica, 2013, 20(4), 633-649
 At Agrophysi, 2013, 20(4), 633-649 WPŁYW OPAKOWANIA NA JAKOŚĆ PRZECHOWYWANEGO PIECZYWA BEZGLUTENOWEGO Pulin Pjąk, Dri Kuzr, Trs Fortun Ktr Anlizy i Ony Jkośi Żywnośi, Wyził Thnologii Żywnośi, Uniwrsytt
At Agrophysi, 2013, 20(4), 633-649 WPŁYW OPAKOWANIA NA JAKOŚĆ PRZECHOWYWANEGO PIECZYWA BEZGLUTENOWEGO Pulin Pjąk, Dri Kuzr, Trs Fortun Ktr Anlizy i Ony Jkośi Żywnośi, Wyził Thnologii Żywnośi, Uniwrsytt
Instrukcje dla zawodników
 Płok, 12 mr 2016 r. Instrukje l zwoników Arkusze otwiermy n wyrźne poleenie komisji. Wszystkie poniższe instrukje zostną ozytne i wyjśnione. 1. Arkusz skł się z 3 zń. 2. Kże znie skł się z wprowzeni orz
Płok, 12 mr 2016 r. Instrukje l zwoników Arkusze otwiermy n wyrźne poleenie komisji. Wszystkie poniższe instrukje zostną ozytne i wyjśnione. 1. Arkusz skł się z 3 zń. 2. Kże znie skł się z wprowzeni orz


