Independent inlet valve control as a method of realization of the open Atkinson-Miller cycle in SI engine
|
|
|
- Elżbieta Mróz
- 7 lat temu
- Przeglądów:
Transkrypt
1 Zbigniew ŻMUDK, Stefn POSTRZDNIK PTNSS 211 SC 98 Indeendent inlet vlve cntrl s ethd f reliztin f the en tkinsn-miller cycle in SI engine bstrct. syste with indeendent, lte inlet vlve clsing hs been nlysed. The use f the nlysed syste t gverning f engine ld will enble t eliinte thrttling vlve fr inlet syste f srk ignitin engine. The en, thereticl tkinsn-miller cycle hs been ssued s del f rcesses rceeding in n engine. The syste hs been nlysed individully nd crtively with en Seiliger- Sbthe cycle. Benefits resulting fr lictin f the syste with lte inlet vlve clsing hve been ssessed n the bsis f the selected reters: fuel dse, cycle wrk, reltive chrge exchnge wrk nd cycle efficiency. Key wrds: srk-ignitin engine, indeendent vlve cntrl, en tkinsn-miller cycle, chrge exchnge rcess, cycle efficiency Niezleżne sterwnie zwri dltwyi jk ssób relizcji twrteg biegu tkinsn-miller w silniku ZI Streszczenie. Przerwdzn nlizę systeu z niezleżny, óźniny zknięcie zwru dltweg, użliwijąceg wyeliinwnie rzeustnicy z ukłdu dltweg silnik ZI. Jk del rcesów zchdzących w silniku rzyjęt twrty bieg teretyczny tkinsn-miller. Odniesienie dl ceny krzyści rz bdni efektywnści zyskiwni rcy, w wyniku zstswni systeu z óźniny zknięcie zwru dltweg, jest twrty bieg teretyczny Seiliger-Sbthe z wszechnie stswną, klsyczną regulcją dłwieniwą bciążeni. nlizę równwczą efektywnści zstswni zrnwneg systeu rzerwdzn ierjąc się n wybrnych wielkścich: dwce liw, retrze energetyczn-stechietryczny, rcy biegu, względnej rcy wyiny łdunku rz srwnści biegu. Słw kluczwe: silnik slinwy ZI, niezleżne sterwnie zwri, twrty bieg teretyczny tkinsn- Miller, wyin łdunku, srwnść biegu 1. Wrwdzenie Relizcj rcesu wyiny łdunku wiąże się z kniecznścią knni ntyknych rów rzeływu, więc z trzebą wyknni dwiedniej rcy, tzw. rcy wyiny łdunku. Isttny jest wływ ukłdu wyiny łdunku n efektywnść zyskiwni rcy w silniku. Pszczególne eleenty instlwne w ukłdzie wyiny łdunku wywłują ry rzeływu świeżeg łdunku w ukłdzie dltwy i rzeływu slin w ukłdzie wyltwy (rys. 1). Skutkie tych rów jest wzrst rcy wyiny łdunku, c z klei rzyczyni się d bniżeni rcy wewnętrznej i rcy efektywnej silnik slinweg. Wzrst wrtści rcy wyiny łdunku dl bciążeń częściwych w silniku ZI związny jest ze ssbe regulcji bciążeni. Stswn dłwieniw regulcj ilściw, z cą rzeustnicy, instlwnej w ukłdzie dltwy, jest niekrzystn szczególnie z terdyniczneg unktu widzeni, niewż dłwienie generuje strty egzergii. W celu zwiększeni srwnści twrteg biegu teretyczneg i srwnści efektywnej silnik ZI zrnwn zstswnie systeów niezleżneg sterwni zwri dltwyi i wyltwyi. Przerwdzn teretyczne bdnie systeu z óźniny zknięcie zwru dltweg. Syste ten użliwi wyeliinwnie rzeustnicy z ukłdu dltweg silnik ZI. Odniesienie dl ceny krzyści rz bdni efektywnści zyskiwni rcy, w wyniku zstswni systeu z óźniny zknięcie zwru dltweg, jest twrty bieg teretyczny Seiliger-Sbthe. t fil rz kt tłu zd zw Filtr wietrz Przeustnic d = fil rz zd cyl Rektr ktlityczny Tłuik w = zw kt tłu Prc wyiny łdunku: w = n wy ( d w ) s Rys. 1. Zsdnicze eleenty ukłdu wyiny łdunku silnik złnie iskrwy Fig. 1. ssentil eleents f chrge exchnge syste in srk ignitin engine t 1
2 2. Syste z óźniny zknięcie zwru dltweg Pdstwwe cechy biegu Dl systeu z óźniny zknięcie zwru dltweg, jk del rcesów zchdzących w silniku rzyjęt twrty bieg teretyczny tkinsn-miller, który uzyskn dyfikując bieg teretyczny rzez ddnie d nieg rzein chrkteryzujących rces wyiny łdunku (rys. 2). 3 = 4 d,v 2 6 = w 8 = d d, 3 4 T 3 T 2 w-d T 4 = T x 4 T = T wyl T = T t s s = ide 9 w 2 = 3 1,x Rys. 2. Syste z óźniny zknięcie zwru dltweg Fig. 2. Syste with lte inlet vlve clsing Pretre regulcyjny bciążeni (nełnieni) jest bjętść cylindr, rzy której nstęuje zknięcie zwru dltweg w czsie suwu kresji. Jest t jedncześnie retr regulujący sę świeżej iesznki, drwdznej d cylindr. Objętść żn dnieść d inilnej bjętści 2 cylindr, definiując w ten ssób stień kresji izentrwej: =, 1 < 2 T } (1) Przebieg wrtści retru regulcyjneg w ujęciu względny (w dniesieniu d stni kresji ), w zleżnści d rcy biegu rzedstwin n rys. 3. Zbliżn d liniwej zleżnść rcy biegu d retru regulcyjneg jest krzystn ze względów regulcyjnych. Ory rzeływu slin w ukłdzie wyltwy chrkteryzuje wielkść sdku ciśnieni slin w, ry rzeływu świeżeg łdunku rzez ukłd dltwy sdek ciśnieni d. Ntist sdek ciśnieni chrkteryzuje ry wsteczneg rzeływu iesznki, której ndir jest wytłczny d klektr dltweg w czsie suwu kresji. W nlizie biegu rzyjęt złżenie, że rces nełnini kńczy się w unkcie rzy: bjętści 1,x, ciśnieniu =, teerturze T = T. Msę 1 czynnik rbczeg stnwi s świeżej iesznki drwdznej d cylindr, niewż zkłd się brk reszty slin. 1,,9,8,7,6,,4,3,2,1, Obieg tkinsn-miller / = f( /,x) = 1; Ψ =,9 d/ = w/ = / =,1,,2,4,6,8 1, /,x Rys. 3. Pretr regulcyjny / twrteg biegu teretyczneg tkinsn-miller Fig. 3. Cntrl reter / f the en tkinsn- Miller cycle versus cycle wrk Dwk liw Mksyln s świeżeg łdunku zstnie drwdzn d cylindr, rzy cłkwity różnieniu cylindr z reszty slin, gdy zknięcie zwru dltweg nstąi w skrjny łżeniu tłk, wówczs: = 1,x, czyli =, rzy jednczesny brku rów rzeływu w ukłdch wyltwy i dltwy: w =, d =, =, wtedy = Mksylną sę świeżej iesznki żn zisć jk: = (2) 1,x M, t, T Tt (MR) T gdzie M s lw świeżej iesznki. Dl rzyjętych złżeń, bzw wielkść dwki liw wynsi:, = 1,x M (MR)T (3) [ 1 λ n M ( 1 X )],in Dwk liw zieni się w zleżnści d bciążeni silnik. Pdstwwyi retri ddziłującyi n wielkść dwki liw są: bjętść cylindr w chwili zknięci zwru wyltweg, czyli stień kresji izentrwej (retr regulcyjny), T teertur świeżeg łdunku, d sdek ciśnieni wietrz w ukłdzie dltwy, dczs nełnini, 2
3 sdek ciśnieni iesznki w ukłdzie dltwy, dczs wytłczni, λ stsunek ndiru wietrz. Dl bciążeń częściwych bjętść cylindr, rzy której nstęuje zknięcie zwru dltweg zieni się w zkresie: < stąd 1 2 1,x < Uwzględni się ry rzeływu w ukłdch wyltwy i dltwy: w, d, więc i zkłd, że drwdzny jest świeży łdunek teerturze tczeni T. Ms liw wynsi wówczs: = M (MR)T (4) [ 1 λ n M ( 1 X )],in Ze wzrów (3) i (4) wynik relcj n względną dwkę liw dl częściwych bciążeń silnik:, 1,x,in ( 1 X ) ( 1 X ) 1 λ n,in M = () 1 λn M Przy złżeniu, że λ = ide trzyuje się: =, (6) 1,x c żn zisć tkże w stci: =, 1 (7) Zte zinę bciążeni silnik uzyskuje się rzez zinę dwki liw, główny retre regulcyjny jest stień kresji izentrwej. Względną dwkę liw /,, w zleżnści d siągnej rcy twrteg biegu tkinsn- Miller, rzedstwin n rys. 4., 1,,9,8,7,6,,4,3,2,1, Obieg tkinsn-miller d/ = w/ = / =,1,,2,4,6,8 1, /,x /, = f(/,x) = 1; Ψ =,9 Rys. 4. Względn dwk liw /,, w zleżnści d rcy twrteg biegu tkinsn-miller Fig. 4. Reltive fuel dse /, versus wrk f the en tkinsn-miller cycle Względne zniejszenie dwki liw /,SS dl twrteg biegu tkinsn-miller, w równniu d systeu z klsyczną regulcją dłwieniwą (twrteg biegu teretyczneg Seiliger- Sbthe ), zilustrwn n rys.. Njwiększe zniejszenie dwki liw uzyskuje się dl bciążeni /,x =,4 Jednkże szczędnść liw nie jest zncząc i wynsi niec wyżej 1%.,SS,14,12,1,8,6,4,2, Obieg tkinsn-miller d/ = w/ = / =,1 /,SS = f( /,x) = 1; Ψ =,9,,2,4,6,8 1, /,x Rys.. Względne zniejszenie dwki liw dl twrteg biegu tkinsn-miller, w równniu d biegu Seiliger-Sbthe Fig.. Reltive reductin f the fuel dse fr the en tkinsn-miller cycle cred with the en Seiliger-Sbthe cycle Pretr energetyczn-stechietryczny Pretr energetyczn-stechietryczny dl biegu tkinsn-miller definiwny jest jk: d = (8) Odniesienie dl retru energetycznstechietryczneg jest jeg wrtść, siągn gdy zknięcie zwru dltweg nstęuje rzy bjętści 1,x : = 1,x tzn. = i rzy złżeniu brku rów rzeływu w ukłdch dltwy i wyltwy: w =, d =, =, wtedy =, wówczs bzwą dwkę liw zncz się, stsunek ndiru wietrz λ. Przy dnych wyżej złżenich wrtść dniesieni retru energetycznstechietryczneg wynsi:, Hu = (9) 1,x Ogólnie, tkże dl bciążeń częściwych, retry w czątkwy unkcie biegu ( nełnieniu cylindr), deterinujące retr energetyczn-stechietryczny, są nstęujące: bjętść cylindr w chwili zknięci zwru dltweg: 2 < 1,x tzn. 1 < 3
4 sdek ciśnieni łdunku w ukłdzie dltwy:, skąd wynik, że : = teertur świeżeg łdunku: T, dwk liw:. Wówczs retr wynsi: Hu = (1) Dl biegu tkinsn-miller sełniny jest wrunek: = c zncz, że dl bciążeń częściwych wrtść retru energetyczn-stechietryczneg nie zieni się. Przy dniesieniu energii cheicznej dwki liw d bzweg ilczynu ( 1,x ), retr energetyczn-stechietryczny zncz się -M, jeg wrtść wyzncz się według fruły: 1,x Hu M = = (11) uwzględnieniu (7):, M = 1 (12) Pdbnie jk dl retru dniesienie dl innych wielkści energetycznych tkże będzie ilczyn ( ). Dl dniesieni względe bzweg ( 1,x ) bwiązuje relcj: ( ) = 1,x 1 (13) Pretr energetyczn-stechietryczny i liczbę rzdziłu cieł Ψ żn wyrzić z cą retrów biegu: stni kresji izentrwej, retru bciążeni γ rz retru dciążeni φ. W ty celu cieł d, = 2-3 dstrczne rzy 2 = ide kreśl się zleżnścią: d, = ( κ 1) ( γ 1) (14) cieł d, = 3-4 dstrczne rzy 3 = ide jk: d, = ( κ 1) κ γ ( ϕ 1) (1) Cłkwitą energię d /( 1,x ), drwdzną d twrteg biegu teretyczneg tkinsn- Miller, rzedstwin n rys. 6, ntist względne zniejszenie energii drwdznej d / d,ss d teg biegu, w równniu d systeu z klsyczną regulcją dłwieniwą (twrteg biegu Seiliger- Sbthe ), zilustrwn n rys. 7. Przebiegi energii drwdznej są nlgiczne d rzebiegów dwki liw, dbne są zte tkże wniski, wynikjące z tych chrkterystyk. d 1,x Obieg tkinsn-miller d/(1,x) = f(/,x) = 1; Ψ =,9 d/ = w/ = / =,1,,2,4,6,8 1, /,x Rys. 6. Cłkwit energi drwdzn d twrteg biegu teretyczneg tkinsn-miller Fig. 6. Ttl energy d /( 1x ) sulied t the en tkinsn-miller cycle versus cycle wrk d d,ss,14,12,1,8,6,4,2, Obieg tkinsn-miller d/ = w/ = / =,1 d/ d,ss = f( /,x) = 1; Ψ =,9,,2,4,6,8 1, /,x Rys. 7. Względne zniejszenie energii drwdznej d / d,ss d twrteg biegu tkinsn- Miller, w równniu d systeu z klsyczną regulcją dłwieniwą (twrteg biegu Seiliger- Sbthe ), w zleżnści d rcy biegu Fig. 7. Reltive reductin f the energy d / d,ss sulied t the en tkinsn-miller cycle cred with the clssic thrttle gverning syste (the en Seiliger-Sbthe cycle) versus cycle wrk Pdstwijąc (14) i (1) d zleżnści (1) (uwzględnijąc wrunek = ) trzyuje się wzór n retr energetyczn-stechietryczny dl systeu z óźniejszy zknięcie zwru dltweg, w stci: = κ 1 [ γ 1 κγ( ϕ 1) ] (16) Wykrzystując zleżnść (16) retr bciążeni γ i retr dciążeni φ żn zisć w stci: rz ( κ ) Ψ 1 γ = 1 (17) ( κ 1) ( 1 Ψ) ( ( κ 1) ϕ = 1 (18) κ κ 1) [ Ψ ] 4
5 Nleży zwrócić uwgę, że dl twrteg biegu teretyczneg tkinsn-miller retry γ i φ, rzy ustlnej liczbie Ψ rzdziłu cieł, zleżą d retru regulcyjneg bciążeni. Prc biegu Prcę twrteg biegu teretyczneg tkinsn-miller (rys. 2) żn wyrzić jk suę skłdwych rc bezwzględnych: = (19) P dstwieniu zleżnści, wyrżjących rce szczególnych rzein d wzru (19), trzyuje się rcę biegu, zisną niżej w ujęciu względny: 1,x = γ κ 1 γ ϕ κ 1 d 1 Obieg tkinsn-miller ( ϕ 1) w [ ϕ ] 1 (2) d/ = w/ = / =,1,,2,4,6,8 1, / /( 1,x) = f( /) = 1; Ψ =,9 Rys. 8. Prc /( 1,x ) twrteg biegu teretyczneg tkinsn-miller, w zleżnści d retru regulcyjneg / Fig. 8. Wrk /( 1,x ) f the en tkinsn- Miller cycle versus cntrl reter / Przebieg rcy /( 1,x ) twrteg biegu teretyczneg tkinsn-miller, w zleżnści d retru regulcyjneg / rzedstwin n rys. 8. Ntist rcę teg biegu w dniesieniu d ksylnej rcy teretyczneg biegu Seiliger- Sbthe zilustrwn n rys. 9. Zleżnści rzedstwine n bu rysunkch są zbliżne d liniwych, c jest krzystne ze względów regulcyjnych.,x 1,,9,8,7,6,,4,3,2,1 Obieg tkinsn-miller d/ = w/ = / =,1,,,2,4,6,8 1, / /,x = f( /) = 1; Ψ =,9 Rys. 9. Prc twrteg biegu tkinsn-miller w dniesieniu d ksylnej rcy teretyczneg biegu Seiliger-Sbthe, w zleżnści d retru regulcyjneg / Fig. 9. Rti f wrk f the en tkins-miller cycle t the xil wrk f the Seiliger-Sbthe cycle versus cntrl reter / Prc wyiny łdunku Prcę wyiny łdunku w dl twrteg biegu teretyczneg tkinsn-miller (rys. 2) żn zisć jk suę skłdwych rc użytecznych: w = u,6 7 u,7 8 u,8 9 u,9 1 u,1 (21) P dstwieniu zleżnści wyrżjących rce użyteczne szczególnych rzein trzyuje się rcę wyiny łdunku w, w dniesieniu d ( ): w = 1 ( ) d w 1 ( ) (22) Wskźnik względnej rcy wyiny łdunku blicz się według definicji: w w µ = =, (23) jk ilrz rcy wyiny łdunku (22) rzez rcę biegu (2). Prcę w /( 1,x ) wyiny łdunku dl twrteg biegu teretyczneg tkinsn-miller, w zleżnści d siągnej rcy biegu rzedstwin n rys. 1. Wrtść bezwzględn rcy wyiny łdunku zwiększ się, gdy rc biegu leje. Z teg wdu w zkresie łych bciążeń bserwuje się wzrst względnej rcy wyiny łdunku, której wrtść dchdzi d kł 9% (rys. 11).
6 w 1,x /,x,,2,4,6,8 1,, -,1 -,2 -,3 -,4 -, -,6 -,7 -,8 -,9 Obieg tkinsn- Miller Obieg Seiliger-Sbthe = 1; Ψ =,9 d/ = w/ = / =,1 Rys. 1. Prównnie rc w /( 1x ) wyiny łdunku dl biegów tkinsn-miller i Seiliger- Sbthe, w zleżnści d rcy biegów Fig. 1. Crisn f the chrge exchnge wrks w /( 1x ) fr the tkinsn-miller nd Seiliger- Sbthe cycles versus wrk f the cycles µ,3,3,2,2,1,1,, µ = f( /,x) = 1; Ψ =,9 d/ = w/ =,1 Obieg Seiliger-Sbthe Obieg tkinsn- Miller,,2,4,6,8 1, /,x Rys. 11. Prównnie wskźników względnej rcy wyiny łdunku dl biegów tkinsn-miller i Seiliger-Sbthe, w zleżnści d rcy biegów Fig. 11. Crisn f the reltive chrge exchnge wrks fr the tkinsn-miller nd Seiliger- Sbthe cycles versus wrk f the cycles i żn ją tkże wyrzić stsując wielkści względne: η = = (2) d Nstęnie, dstwieniu (16) i (2) d (2) trzyuje się: η = κ 1 [ γ 1 κγ( ϕ 1) ] 1 γ κ 1 ( γ ϕ κ 1 d w 1 1) [ ϕ ] 1 ( ϕ 1) κ (26) Srwnść η jest isttny retre użliwijący cenę biegu w sekcie energetyczny. Prównnie srwnści biegu dl systeu z wcześniejszy zknięcie zwru dltweg i biegu Seiliger-Sbthe, w zleżnści d siągnej rcy biegów, rzedstwin n rys. 12. η,6,6 Obieg tkinsn- Miller Odniesienie dl ceny krzyści rz bdni efektywnści zyskiwni rcy, w wyniku zstswni syste z wcześniejszy zknięcie zwru dltweg jest twrty bieg teretyczny Seiliger-Sbthe z wszechnie stswną, klsyczną regulcją dłwieniwą bciążeni, będący dele rcesów zchdzących w klsyczny silniku ZI. Dlteg n rysunkch tych, dl równni, rzedstwin tkże rzebiegi rcy wyiny łdunku (rys. 1) i względnej rcy wyiny łdunku (rys. 11) dl biegu Seiliger-Sbthe. Prce te dl biegu tkinsn-miller są zncząc niejsze, szczególnie w zkresie niskich bciążeń. Srwnść biegu Srwnść biegu teretyczneg wyrż stsunek rcy biegu d cłkwitej energii drwdznej d biegu: η = (24) d,,,4,4 Obieg Seiliger-Sbthe d/ = w/ =,1 η = f( /,x); = 1; Ψ =,9,,2,4,6,8 1, /,x Rys. 12. Prównnie srwnści η biegów tkinsn-miller i Seiliger-Sbthe, w zleżnści d rcy biegów Fig. 12. Crisn f efficiencies η f the tkinsn-miller nd Seiliger-Sbthe cycles versus wrk f the cycles Srwnść biegu tkinsn-miller jest wyższ d srwnści twrteg biegu teretyczneg Seiliger-Sbthe jedynie w zkresie średnich bciążeń. Niestety ten rzyrst srwnści jest niewielki. W zkresie bciążeń njniższeg i njwyższeg nie bserwuje się wzrstu srwnści biegu. 6
7 3. Pdsuwnie Skróty i znczeni H u w d d w retr energetyczn-stechietryczny wrtść łw liw, J/kg rc biegu, J rc wyiny łdunku, J s, kg ciśnienie, P średni sdek ciśnieni strnie dływu łdunku d silnik, P średni sdek ciśnieni strnie wyływu slin z silnik, P ilść cieł dstrczneg d biegu, J itertur [1] Pstrzednik S., Żudk Z.: Terdyniczne rz eklgiczne uwrunkwni eksltcji tłkwych silników slinwych, Wydwnictw Plitechniki Śląskiej, Gliwice 27. [2] Pstrzednik S.: Terdynik zjwisk rzeływwych, Wydwnictw Plitechniki Śląskiej, Gliwice 26. [3] Szrgut J.: Terdynik techniczn, Wydwnictw Plitechniki Śląskiej, Gliwice 2. [4] Pstrzednik S., Żudk Z.: Bdni likcyjne nd rceduri niezleżneg sterwni zwri silnik slinweg. Nuer rjektu bdwczeg N /219. PBU-3/RI-6/ Srwzdnie, Gliwice 29. Bdni w zkresie ziennych fz rzrządu rwdzne są rzez wiele śrdków nukwych i bdwcz-rzwjwych silników slinwych [6, 7, 8]. Świdczy t ktulnści rzedstwinej rbletyki, w rch której rzerwdzn teretyczne bdnie systeu z niezleżny, óźniny zknięcie zwru dltweg. Jk del rcesów zchdzących w silniku rcujący według teg systeu rzyjęt twrty bieg teretyczny tkinsn-miller. Odniesienie dl ceny krzyści rz bdni efektywnści zyskiwni rcy, w wyniku zstswni systeu z óźniny zknięcie zwru dltweg, jest twrty bieg teretyczny Seiliger-Sbthe z wszechnie stswną, klsyczną regulcją dłwieniwą bciążeni. fekty zstswni bdneg systeu njleiej wyrzić żn rzez srwnść energetyczną biegu. Niestety srwnść twrteg biegu teretyczneg tkinsn-miller nie jest zncząc wyższ d biegu Seiliger-Sbthe. Zniejszenie zużyci liw tkże nie jest zbyt duże. Ozncz t, że sterwnie bciążenie silnik według systeu z óźniny zknięcie zwru dltweg nie rzyniesie znczących krzyści. Niezleżne sterwnie zwri użliwi regulcję rcy silnik tkże według innych systeów [1, 4]. Mgą t być systey: z wcześniejszy zknięcie zwru dltweg z wcześniejszy zknięcie zwru wyltweg, użliwijący relizcję wewnętrznej recyrkulcji slin, w ełni niezleżneg sterwni zwri, który użliwi relizcję wewnętrznej recyrkulcji slin wrz z ełną regulcją dwki liw. nliz wyższych systeów, któr zstnie rzedstwin w klejnych ublikcjch, wykzł, że są ne zncznie brdziej efektywne. w ilść cieł wyrwdzneg z biegu, J T teertur, K bjętść, 3 ZI złn iskrwy γ retr (stień) bciążeni stień kresji η energetyczn srwnść biegu λ stsunek ndiru wietrz φ retr (stień) dciążeni Ψ liczb rzdziłu cieł [] Żudk Z., Pstrzednik S.: Flw resistnce in the engine inlet-exhust syste s ffected by the engine reters. Cbustin ngines, nr 1 (136), 29. [6] Hs M., Ruch M.: lectr-hydrulic fully vrible vlve trin syste. TZ uttechnlgy, 2, l. 1, 21. [7] Frnc O.M.: Ict f the Miller cycle in the efficiency f n FT engine during rt ld ertin. S Tech. Per, N [8] Ce D., Wright., Crcrn C., Psch K.: Fully flexible electrgnetic vlve ctutr: design, deling, nd esureents. S Technicl Per, N , 28. Zbigniew Żudk, Ph.D. Senir ecturer in the Fculty f nvirnentl ngineering nd nergy t Silesin University f Technlgy in Gliwice, Plnd. Dr inż. Zbigniew Żudk strszy wykłdwc n Wydzile Inżynierii Śrdwisk i nergetyki Plitechniki Śląskiej w Gliwicch. Prf. Stefn Pstrzednik, DSc., Dng. the Fculty f nvirnentl ngineering nd nergy, Silesin University f Technlgy in Gliwice, Plnd. Prf. dr hb. inż. Stefn Pstrzednik Wydził Inżynierii Śrdwisk i nergetyki Plitechniki Śląskiej w Gliwicch. 7
Przykład 2.1. Wyznaczanie prędkości i przyśpieszenia w ruchu bryły
 Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
Przykłd 1 Wyzncznie prędkści i przyśpieszeni w ruchu bryły Stżek kącie rzwrci twrzących i pdstwie, której prmień wynsi tczy się bez pślizgu p płszczyźnie Wektr prędkści śrdk pdstwy m stłą długść równą
PRÓBNY EGZAMIN GIMNAZJALNY OMÓWIENIE ODPOWIEDZI
 RÓBNY EGZAMIN GIMNAZJALNY 01 11 1 OMÓWIENIE ODOWIEDZI Zdnie z pgrnicz chemii i mtemtyki, mżemy skrzystć ze wzru: ms C 100% m R Ms substncji wynsi jednstki, które jedncześnie, twrzą już msę cłeg rztwru,
RÓBNY EGZAMIN GIMNAZJALNY 01 11 1 OMÓWIENIE ODOWIEDZI Zdnie z pgrnicz chemii i mtemtyki, mżemy skrzystć ze wzru: ms C 100% m R Ms substncji wynsi jednstki, które jedncześnie, twrzą już msę cłeg rztwru,
Pomiary ciśnień i sprawdzanie manometrów
 Poiry ciśnień i srwdznie noetrów Instrukcj do ćwiczeni nr 2 Miernictwo energetyczne - lbortoriu Orcowł: dr inŝ. ElŜbiet Wróblewsk Zkłd Miernictw i Ochrony Atosfery Wrocłw, grudzień 2008 r. I. WSTĘP Ciśnienie
Poiry ciśnień i srwdznie noetrów Instrukcj do ćwiczeni nr 2 Miernictwo energetyczne - lbortoriu Orcowł: dr inŝ. ElŜbiet Wróblewsk Zkłd Miernictw i Ochrony Atosfery Wrocłw, grudzień 2008 r. I. WSTĘP Ciśnienie
POLITECHNIKA ŁÓDZKA INSTYTUT OBRABIAREK I TECHNOLOGII BUDOWY MASZYN. Ćwiczenie H-3 BADANIE SZTYWNOŚCI PROWADNIC HYDROSTATYCZNYCH
 POLITECHNIK ŁÓDZK INSTYTUT OBBIEK I TECHNOLOGII BUDOWY MSZYN Ćwiczenie H- Temat: BDNIE SZTYWNOŚCI POWDNIC HYDOSTTYCZNYCH edacja i racwanie: dr inż. W. Frnci Zatwierdził: rf. dr ab. inż. F. Oryńsi Łódź,
POLITECHNIK ŁÓDZK INSTYTUT OBBIEK I TECHNOLOGII BUDOWY MSZYN Ćwiczenie H- Temat: BDNIE SZTYWNOŚCI POWDNIC HYDOSTTYCZNYCH edacja i racwanie: dr inż. W. Frnci Zatwierdził: rf. dr ab. inż. F. Oryńsi Łódź,
Analysis of effectiveness of independent exhaust valve control as a method of an internal EGR realization
 Article citatin inf: ŻMUDKA, Z., POSTRZEDNIK, S., PRZYBYŁA, G. Analysis f effectiveness f ineenent exhaust valve cntrl as a eth f an internal EGR realizatin. Cbustin Engines. 23, 54(3), 338-345. ISSN 38-346.
Article citatin inf: ŻMUDKA, Z., POSTRZEDNIK, S., PRZYBYŁA, G. Analysis f effectiveness f ineenent exhaust valve cntrl as a eth f an internal EGR realizatin. Cbustin Engines. 23, 54(3), 338-345. ISSN 38-346.
Laboratorium Napędów Hydraulicznych i Pneumatycznych. Badanie zjawisk towarzyszących wypływowi gazu ze zbiornika
 Lbortoriu Nędów Hydrulicznych i Pneutycznych Bdnie zjwis towrzyszących wyływowi gzu ze zbiorni Wiesłw GRZESIKIEWICZ Michł MKOWSKI. Wrowdzenie Cele ćwiczeni jest bdnie zjwis towrzyszących wyływowi gzu ze
Lbortoriu Nędów Hydrulicznych i Pneutycznych Bdnie zjwis towrzyszących wyływowi gzu ze zbiorni Wiesłw GRZESIKIEWICZ Michł MKOWSKI. Wrowdzenie Cele ćwiczeni jest bdnie zjwis towrzyszących wyływowi gzu ze
Realizacje zmiennych są niezależne, co sprawia, że ciąg jest ciągiem niezależnych zmiennych losowych,
 Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Klsyczn Metod Njmniejszych Kwdrtów (KMNK) Postć ć modelu jest liniow względem prmetrów (lbo nleży dokonć doprowdzeni postci modelu do liniowości względem prmetrów), Zmienne objśnijące są wielkościmi nielosowymi,
Zintegrowany program gospodarki transportowej dla miasta Łomży
 2 2/1 Dignz stnu systemu trnsprtweg Łmży 2.1 Mist Łmż Łmż jest płżn w półncnwschdniej części Plski n terenie wjewództw pdlskieg. W grnicch dministrcyjnych mist zjmuje pwierzchnię 3258 h, w tym 40% pwierzchni
2 2/1 Dignz stnu systemu trnsprtweg Łmży 2.1 Mist Łmż Łmż jest płżn w półncnwschdniej części Plski n terenie wjewództw pdlskieg. W grnicch dministrcyjnych mist zjmuje pwierzchnię 3258 h, w tym 40% pwierzchni
OPÓR PRZEPŁYWU W UKŁADZIE DOLOTOWYM JAKO ELEMENT REGULACJI OBCIĄŻENIA SILNIKA SPALINOWEGO
 ZBIGNIEW ŻUDKA, STEFAN POSTRZEDNIK OPÓR PRZEPŁYWU W UKŁADZIE DOLOTOWY JAKO ELEENT REGULACJI OBCIĄŻENIA SILNIKA SPALINOWEGO Streszczenie Abstract FLOW RESISTANCE IN INDUCTION SYSTE AS ELEENT OF LOAD GOVERNING
ZBIGNIEW ŻUDKA, STEFAN POSTRZEDNIK OPÓR PRZEPŁYWU W UKŁADZIE DOLOTOWY JAKO ELEENT REGULACJI OBCIĄŻENIA SILNIKA SPALINOWEGO Streszczenie Abstract FLOW RESISTANCE IN INDUCTION SYSTE AS ELEENT OF LOAD GOVERNING
STOWARZYSZENIE NIEMIECKO POLSKIEJ WSPÓŁPRACY SOCJALNEJ. TORO w poszukiwaniu skutecznych metod wsparcia instytucji ekonomii społecznej
 STOWARZYSZENIE NIEMIECKO POLSKIEJ WSPÓŁPRACY SOCJALNEJ TORO w psukiwniu skutenyh metd wspri instytuji eknmii spłenej WYNIKI EWALUACJI INSTRUMENTU FINANSOWEGO TORO w psukiwniu skutenyh metd wspri instytuji
STOWARZYSZENIE NIEMIECKO POLSKIEJ WSPÓŁPRACY SOCJALNEJ TORO w psukiwniu skutenyh metd wspri instytuji eknmii spłenej WYNIKI EWALUACJI INSTRUMENTU FINANSOWEGO TORO w psukiwniu skutenyh metd wspri instytuji
Rachunek prawdopodobieństwa i statystyka matematyczna.
 Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Rchunek rwdoodobieństw i sttystyk mtemtyczn. Zd 8. {(, : i } Zleżność tą możn rzedstwić w ostci nstęującej interretcji grficznej: Arkdiusz Kwosk Rfł Kukliński Informtyk sem.4 gr. Srwdźmy, czy odne zmienne
Pompy ciepła. Podział pomp ciepła. Ogólnie możemy je podzielić: ze wzgledu na sposób podnoszenia ciśnienia i tym samym temperatury czynnika roboczego
 Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
Pmpy ciepła W naszym klimacie bardz isttną gałęzią energetyki jest energetyka cieplna czyli grzewanie. W miesiącach letnich kwestia ta jest mniej isttna, jednak z nadejściem jesieni jej znaczenie rśnie.
MECHANIKA. Podstawy kinematyki Zasady dynamiki. Zasada zachowania pędu Zasada zachowania energii Ruch harmoniczny i falowy
 MECHANIKA Podswy kineyki Zsdy dyniki Siły Równnie ruchu Ukłdy inercjlne i nieinercjlne Zsd zchowni pędu Zsd zchowni energii Ruch hroniczny i flowy ruch rejesrowne w czsie w sposób ciągły ziny położeni
MECHANIKA Podswy kineyki Zsdy dyniki Siły Równnie ruchu Ukłdy inercjlne i nieinercjlne Zsd zchowni pędu Zsd zchowni energii Ruch hroniczny i flowy ruch rejesrowne w czsie w sposób ciągły ziny położeni
Lokalizacja S 2. supermarket. boisko sportowe. basen. targ. klub fitness. Teatr Muzyczny. Manufaktura. Osiedle Jarzębinowe. parki.
 Biuro sprzedży: Łódź, ul. Górnicz 8/ kom. (+8) 900 9; (+8) 900 tel. (+8) 8 09 00 fx (+8) 8 09 0 e-mil: info-lodz@echo.com.pl www.jrzebinowe.pl k M Po je zi r ur sk er sk trg Mu rr sk Mr yńsk ws no Z g
Biuro sprzedży: Łódź, ul. Górnicz 8/ kom. (+8) 900 9; (+8) 900 tel. (+8) 8 09 00 fx (+8) 8 09 0 e-mil: info-lodz@echo.com.pl www.jrzebinowe.pl k M Po je zi r ur sk er sk trg Mu rr sk Mr yńsk ws no Z g
Parametry charakteryzujące pracę silnika turbinowego. Dr inż. Robert JAKUBOWSKI
 Parametry charateryzujące racę silnia turbinweg Dr inż. Rbert JAKUBOWSKI Parametry charateryzujące racę silnia Parametry wewnętrzne (biegu silnia): Sręż całwity silnia (sręż sręzari): Temeratura gazów
Parametry charateryzujące racę silnia turbinweg Dr inż. Rbert JAKUBOWSKI Parametry charateryzujące racę silnia Parametry wewnętrzne (biegu silnia): Sręż całwity silnia (sręż sręzari): Temeratura gazów
Aparatura sterująca i sygnalizacyjna Czujniki indukcyjne zbliżeniowe LSI
 Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Aprtur sterując i sygnlizcyjn Czujniki indukcyjne zbliżeniowe LSI Czujnik indukcyjny zbliżeniowy prcuje n zsdzie tłumionego oscyltor LC: jeżeli w obszr dziłni dostnie się metl, to z ukłdu zostje pobrn
Układ elektrohydrauliczny do badania siłowników teleskopowych i tłokowych
 TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
TDUSZ KRT TOMSZ PRZKŁD Ukłd elektrohydruliczny do bdni siłowników teleskopowych i tłokowych Wprowdzenie Polsk Norm PN-72/M-73202 Npędy i sterowni hydruliczne. Cylindry hydruliczne. Ogólne wymgni i bdni
R + v 10 R0, 9 k v k. a k v k + v 10 a 10. k=1. Z pierwszego równania otrzymuję R 32475, 21083. Dalej mam: (R 9P + (k 1)P )v k + v 10 a 10
 Zdnie. Zkłd ubezpieczeń n życie plnuje zbudownie portfel ubezpieczeniowego przy nstępujących złożenich: ozwiąznie. Przez P k będę oznczł wrtość portfel n koniec k-tego roku. Szukm P 0 tkie by spełnił:
Zdnie. Zkłd ubezpieczeń n życie plnuje zbudownie portfel ubezpieczeniowego przy nstępujących złożenich: ozwiąznie. Przez P k będę oznczł wrtość portfel n koniec k-tego roku. Szukm P 0 tkie by spełnił:
MOMENTY BEZWŁADNOŚCI FIGUR PŁASKICH
 MOMENT BEZWŁNOŚC FGU PŁSKCH Przekrje pprzeczne prętów włów i elek figur płskie crkterzujące się nstępującmi prmetrmi: plem pwierzcni przekrju [mm cm m ] płżeniem śrdk ciężkści przekrju mmentmi sttcznmi
MOMENT BEZWŁNOŚC FGU PŁSKCH Przekrje pprzeczne prętów włów i elek figur płskie crkterzujące się nstępującmi prmetrmi: plem pwierzcni przekrju [mm cm m ] płżeniem śrdk ciężkści przekrju mmentmi sttcznmi
Zastosowanie multimetrów cyfrowych do pomiaru podstawowych wielkości elektrycznych
 Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
Zstosownie multimetrów cyfrowych do pomiru podstwowych wielkości elektrycznych Cel ćwiczeni Celem ćwiczeni jest zpoznnie się z możliwościmi pomirowymi współczesnych multimetrów cyfrowych orz sposobmi wykorzystni
2. Tensometria mechaniczna
 . Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
. Tensometri mechniczn Wstęp Tensometr jk wskzywłby jego nzw to urządzenie służące do pomiru nprężeń. Jk jednk widomo, nprężeni nie są wielkościmi mierzlnymi i stnowią jedynie brdzo wygodne pojęcie mechniki
Pomiary parametrów światłowodów WYKŁAD 11 SMK. 1. Wpływ sposobu pobudzania włókna światłowodu na rozkład prowadzonej w nim mocy
 Pomiy pmetów świtłowodów WYKŁAD SMK. Wpływ sposobu pobudzni włókn świtłowodu n ozkłd powdzonej w nim mocy Ilość modów wzbudznych w świtłowodch zleży od pmetów świtłowodu i wykozystywnej długości fli. W
Pomiy pmetów świtłowodów WYKŁAD SMK. Wpływ sposobu pobudzni włókn świtłowodu n ozkłd powdzonej w nim mocy Ilość modów wzbudznych w świtłowodch zleży od pmetów świtłowodu i wykozystywnej długości fli. W
MODELOWANIE CHARAKTERYSTYK RDZENI FERROMAGNETYCZNYCH
 Krzysztof Górecki Akdemi orsk w Gdyni Klin Detk Pomorsk Wyższ Szkoł Nuk Stosownych w Gdyni ODELOWANIE CHARAKTERYSTYK RDZENI FERROAGNETYCZNYCH Artykuł dotyczy modelowni chrkterystyk rdzeni ferromgnetycznych.
Krzysztof Górecki Akdemi orsk w Gdyni Klin Detk Pomorsk Wyższ Szkoł Nuk Stosownych w Gdyni ODELOWANIE CHARAKTERYSTYK RDZENI FERROAGNETYCZNYCH Artykuł dotyczy modelowni chrkterystyk rdzeni ferromgnetycznych.
LISTA02: Projektowanie układów drugiego rzędu Przygotowanie: 1. Jakie własności ma równanie 2-ego rzędu & x &+ bx&
 LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
LISTA: Projektownie ukłdów drugiego rzędu Przygotownie: 1. Jkie włsności m równnie -ego rzędu & &+ b + c u jeśli: ) c>; b) c; c) c< Określ położenie biegunów, stbilność, oscylcje Zdni 1: Wyzncz bieguny.
Rodzaje drgań na przykładzie układu o jednym stopniu swobody
 Rdzaje drgań na rzkładzie układu jednm stniu swbd Układ jednm stniu swbd Ssin t m k C m S sint Przkład układu jednm stniu swbd Schemat układu jednm stniu swbd Zestawienie sił w układzie jednm stniu swbd
Rdzaje drgań na rzkładzie układu jednm stniu swbd Układ jednm stniu swbd Ssin t m k C m S sint Przkład układu jednm stniu swbd Schemat układu jednm stniu swbd Zestawienie sił w układzie jednm stniu swbd
Karta oceny merytorycznej wniosku o dofinansowanie projektu konkursowego PO KL 1
 Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA
Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL 1 NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA
Piłka nożna w badaniach statystycznych 1
 Mterił n konferencję prsową w dniu 31 mj 212 r. GŁÓWNY URZĄD STATYSTYCZNY Deprtment Bdń Społecznych i Wrunków Życi Nottk informcyjn WYNIKI BADAŃ GUS Piłk nożn w bdnich sttystycznych 1 Bdni klubów sportowych
Mterił n konferencję prsową w dniu 31 mj 212 r. GŁÓWNY URZĄD STATYSTYCZNY Deprtment Bdń Społecznych i Wrunków Życi Nottk informcyjn WYNIKI BADAŃ GUS Piłk nożn w bdnich sttystycznych 1 Bdni klubów sportowych
Pakiet aplikacyjny. Niniejszy pakiet zawiera informacje, które musisz posiadać zgłaszając swoją kandydaturę. Zawiera on:
 Pkiet plikcyjny Stnowisko: Nr referencyjny: Specjlist ds. interwencji ekologicznych CON/2011/01 Niniejszy pkiet zwier informcje, które musisz posidć zgłszjąc swoją kndydturę. Zwier on: List do kndydtów
Pkiet plikcyjny Stnowisko: Nr referencyjny: Specjlist ds. interwencji ekologicznych CON/2011/01 Niniejszy pkiet zwier informcje, które musisz posidć zgłszjąc swoją kndydturę. Zwier on: List do kndydtów
Przyjmując, że zarówno silnik 4 jak i chłodziarka 5 schematycznie przedstawione na rysunku 1 realizują obiegi Carnota, otrzymujemy:
 M. Chrwski, Pdstawy Krigeniki, wykład 12 Chłdziarki z regeneracyjnymi wymiennikami ciepła ciąg dalszy Chłdziarki Vuilleumiera-Tacnisa W 1918 rku Rudlph Vuilleumier patentwał w USA chłdziarkę, której istta
M. Chrwski, Pdstawy Krigeniki, wykład 12 Chłdziarki z regeneracyjnymi wymiennikami ciepła ciąg dalszy Chłdziarki Vuilleumiera-Tacnisa W 1918 rku Rudlph Vuilleumier patentwał w USA chłdziarkę, której istta
WYZNACZANIE STAŁYCH W RÓWNANIU IZOTERMY ADSORPCJI FREUNDLICHA
 Ćwiczenie nr XI WYZNACZANIE STAŁYCH W RÓWNANIU IZOTERMY ADSORPCJI FREUNDLICHA I. Cel ćwiczeni Cele ćwiczeni jet kreślenie retrów w równniu iztery Freundlich n dtwie wielkści drcji niliny w cyklheknie n
Ćwiczenie nr XI WYZNACZANIE STAŁYCH W RÓWNANIU IZOTERMY ADSORPCJI FREUNDLICHA I. Cel ćwiczeni Cele ćwiczeni jet kreślenie retrów w równniu iztery Freundlich n dtwie wielkści drcji niliny w cyklheknie n
PROPAGACJA BŁĘDU. Dane: c = 1 ± 0,01 M S o = 7,3 ± 0,1 g Cl 2 /1000g H 2 O S = 6,1 ± 0,1 g Cl 2 /1000g H 2 O. Szukane : k = k =?
 PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
PROPAGACJA BŁĘDU Zad 1. Rzpuszczalnść gazów w rztwrach elektrlitów pisuje równanie Seczenwa: S ln = k c S Gdzie S i S t rzpuszczalnści gazu w czystym rzpuszczalniku i w rztwrze elektrlitu stężeniu c. Obliczy
STABILNOŚĆ LINIOWYCH UKŁADÓW AUTOMATYKI
 STABILNOŚĆ LINIOWYCH UŁADÓW AUTOMATYI. Wprwdzenie d ćwiczeni Prblem stbilnści kżdeg ukłdu utmtyki jest prblemem pdstwwym. Pjwienie się niestbilnści w ukłdch zzwyczj prcujących stbilnie, mże spwdwć duże
STABILNOŚĆ LINIOWYCH UŁADÓW AUTOMATYI. Wprwdzenie d ćwiczeni Prblem stbilnści kżdeg ukłdu utmtyki jest prblemem pdstwwym. Pjwienie się niestbilnści w ukłdch zzwyczj prcujących stbilnie, mże spwdwć duże
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 2014/2015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A2, A3, A4, A6, A7)
 EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
EGZAMIN MATURALNY OD ROKU SZKOLNEGO 01/015 MATEMATYKA POZIOM ROZSZERZONY ROZWIĄZANIA ZADAŃ I SCHEMATY PUNKTOWANIA (A1, A, A, A, A6, A7) GRUDZIEŃ 01 Klucz odpowiedzi do zdń zmkniętych Nr zdni 1 5 Odpowiedź
Efektywność energetyczna systemu ciepłowniczego z perspektywy optymalizacji procesu pompowania
 Efektywność energetyczna systemu ciełowniczego z ersektywy otymalizacji rocesu omowania Prof. zw. dr hab. Inż. Andrzej J. Osiadacz Prof. ndz. dr hab. inż. Maciej Chaczykowski Dr inż. Małgorzata Kwestarz
Efektywność energetyczna systemu ciełowniczego z ersektywy otymalizacji rocesu omowania Prof. zw. dr hab. Inż. Andrzej J. Osiadacz Prof. ndz. dr hab. inż. Maciej Chaczykowski Dr inż. Małgorzata Kwestarz
SZTUCZNA INTELIGENCJA
 SZTUCZNA INTELIGENCJA WYKŁAD 9. ZBIORY ROZMYTE Częstochow 204 Dr hb. inż. Grzegorz Dudek Wydził Elektryczny Politechnik Częstochowsk ZBIORY ROZMYTE Klsyczne pojęcie zbioru związne jest z logiką dwuwrtościową
SZTUCZNA INTELIGENCJA WYKŁAD 9. ZBIORY ROZMYTE Częstochow 204 Dr hb. inż. Grzegorz Dudek Wydził Elektryczny Politechnik Częstochowsk ZBIORY ROZMYTE Klsyczne pojęcie zbioru związne jest z logiką dwuwrtościową
WYZNACZNIKI. . Gdybyśmy rozważali układ dwóch równań liniowych, powiedzmy: Takie układy w matematyce nazywa się macierzami. Przyjmijmy definicję:
 YZNACZNIKI Do opisu pewnh oiektów nie wstrz użć liz. ie n przkłd, że do opisni sił nleż użć wektor. Sił to przeież nie tlko wielkość le i jej punkt przłożeni, zwrot orz kierunek dziłni. Zte jedną lizą
YZNACZNIKI Do opisu pewnh oiektów nie wstrz użć liz. ie n przkłd, że do opisni sił nleż użć wektor. Sił to przeież nie tlko wielkość le i jej punkt przłożeni, zwrot orz kierunek dziłni. Zte jedną lizą
Rozdzielacze suwakowe sterowane hydraulicznie typ WHG6, WHP6
 Rzdzielcze suwkwe sterwne hydrulicznie typ WHG6, WH6 WN6 d 5 M d 80 dm /min KR KLOGOW - INSRUKCJ OSŁUGI WK 5 710 01.017 ZSOSOWNIE Rzdzielcze suwkwe sterwne hydruliczne typ WHG6, WH6 są przeznczne d zminy
Rzdzielcze suwkwe sterwne hydrulicznie typ WHG6, WH6 WN6 d 5 M d 80 dm /min KR KLOGOW - INSRUKCJ OSŁUGI WK 5 710 01.017 ZSOSOWNIE Rzdzielcze suwkwe sterwne hydruliczne typ WHG6, WH6 są przeznczne d zminy
- Wydział Fizyki Zestaw nr 5. Powierzchnie 2-go stopnia
 1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
1 Algebr Liniow z Geometri - Wydził Fizyki Zestw nr 5 Powierzchnie -go stopni 1 N sferze 1 + + 3 = 4 znleźć punkt, którego odległość od punktu p = (, 6, 3) byłby njmniejsz Wyznczyć osie elipsy powstłej
KONTROLA STALIWA GX20Cr56 METODĄ ATD
 35/12 ARCHIWUM ODLEWNICTWA Rk 2004, Rcznik 4, Nr 12 Archives f Fundry Year 2004, Vlume 4, Bk 12 PAN Katwice PL ISSN 1642-5308 KONTROLA STALIWA GX20Cr56 METODĄ ATD S. PIETROWSKI 1, G. GUMIENNY 2 Katedra
35/12 ARCHIWUM ODLEWNICTWA Rk 2004, Rcznik 4, Nr 12 Archives f Fundry Year 2004, Vlume 4, Bk 12 PAN Katwice PL ISSN 1642-5308 KONTROLA STALIWA GX20Cr56 METODĄ ATD S. PIETROWSKI 1, G. GUMIENNY 2 Katedra
ułatwia studentom efektywną naukę na studiach oraz przygotowuje ich do pracy w branży inżynierii przemysłowej.
 Chi/Pliw prz łw e/ WIELOFUNKCYJNA I ŁATWA W UŻYCIU TECHNOLOGIA 3D CAD DOSKONAŁA OFERTA DLA STUDENTÓW Sz tu k SlidWrks Eductin grm bejmuje wsztkie njnwsze technlgie 3D CAD w rmch jedneg, łtweg d pnwni pkietu.
Chi/Pliw prz łw e/ WIELOFUNKCYJNA I ŁATWA W UŻYCIU TECHNOLOGIA 3D CAD DOSKONAŁA OFERTA DLA STUDENTÓW Sz tu k SlidWrks Eductin grm bejmuje wsztkie njnwsze technlgie 3D CAD w rmch jedneg, łtweg d pnwni pkietu.
PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD ,0. 3x 6 6 3x 6 6,
 Zdnie PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD 04 Zbiorem wszystkich rozwiązń nierówności x 6 6 jest: A, 4 0, B 4,0 C,0 4, D 0,4 Odpowiedź: C Rozwiąznie Sposób I Nierówność A 6 jest równowżn lterntywie
Zdnie PRÓBNA MATURA Z MATEMATYKI Z OPERONEM LISTOPAD 04 Zbiorem wszystkich rozwiązń nierówności x 6 6 jest: A, 4 0, B 4,0 C,0 4, D 0,4 Odpowiedź: C Rozwiąznie Sposób I Nierówność A 6 jest równowżn lterntywie
Modelowanie 3 D na podstawie fotografii amatorskich
 Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
Edwrd Nowk 1, Jonn Nowk Modelownie D n podstwie fotogrfii mtorskich 1. pecyfik fotogrmetrycznego oprcowni zdjęć mtorskich wynik z fktu, że n ogół dysponujemy smymi zdjęcimi - nierzdko są to zdjęci wykonne
METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO
 MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
MODELOWANIE INŻYNIERSKIE ISNN 1896-771X 32, s. 151-156, Gliwice 2006 METODYKA OCENY WŁAŚCIWOŚCI SYSTEMU IDENTYFIKACJI PARAMETRYCZNEJ OBIEKTU BALISTYCZNEGO JÓZEF GACEK LESZEK BARANOWSKI Instytut Elektromechniki,
Uzsdnienie podjęi bdń W produkth żywnośiowyh obenyh n rynku jko zmiennik tłuszzu zzwyzj stosuje się węglowodny. Prktyznie nie m n rynku produktów, w k
 Wysokobiłkowe sery topione Dr hb. inż. Brtosz Sołowiej Uniwersytet Przyrodnizy w Lublinie Wydził Nuk o Żywnośi i Biotehnologii Zkłd Tehnologii Mlek i Hydrokoloidów Uzsdnienie podjęi bdń W produkth żywnośiowyh
Wysokobiłkowe sery topione Dr hb. inż. Brtosz Sołowiej Uniwersytet Przyrodnizy w Lublinie Wydził Nuk o Żywnośi i Biotehnologii Zkłd Tehnologii Mlek i Hydrokoloidów Uzsdnienie podjęi bdń W produkth żywnośiowyh
N(0, 1) ) = φ( 0, 3) = 1 φ(0, 3) = 1 0, 6179 = 0, 3821 < t α 1 e t dt α > 0. f g = fg. f = e t f = e t. U nas: g = t α 1 g = (α 1)t α 2
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
MODELOWANIE POŻARÓW-Modele analityczne
 SGSP - SUDIA MAGISERSKIE MODELOWANIE POŻARÓW-Modele nlyczne dr hb. MAREK KONECKI, rof. SGSP Wrzw 009 EORIA KOLUMN KONWEKCYJNYCH OGNIA (KKO) Kolun oowo yeryczn Prery KKO zybkość rzeływu y (rueń) w o KKO
SGSP - SUDIA MAGISERSKIE MODELOWANIE POŻARÓW-Modele nlyczne dr hb. MAREK KONECKI, rof. SGSP Wrzw 009 EORIA KOLUMN KONWEKCYJNYCH OGNIA (KKO) Kolun oowo yeryczn Prery KKO zybkość rzeływu y (rueń) w o KKO
Metody Lagrange a i Hamiltona w Mechanice
 Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
Metody Lgrnge i Hmilton w Mechnice Mriusz Przybycień Wydził Fizyki i Informtyki Stosownej Akdemi Górniczo-Hutnicz Wykłd 3 M. Przybycień (WFiIS AGH) Metody Lgrnge i Hmilton... Wykłd 3 1 / 15 Przestrzeń
 Ń Ż Ó Ó Ó Ż Ę Ó Ś Ó Ę Ś Ś Ó ż Ó Ó Ż Ś Ś Ó Ó Ś Ś Ś Ó Ść Ó ż Ść Ę Ó Ń Ś Ó Ś Ó Ż Ż Ż ć Ż Ó Ó Ż Ś Ó Ś ć Ń ć Ó Ó Ś ż Ś Ż Ż Ść Ó Ś ż ćż ć Ó Ż Ś Ć Ó Ż Ó Ó Ż Ś Ó Ó Ś Ó ż Ó Ż Ź Ś ż Ń Ó Ó Ś ż Ś Ó Ó Ś ż Ś Ś Ś Ć Ż
Ń Ż Ó Ó Ó Ż Ę Ó Ś Ó Ę Ś Ś Ó ż Ó Ó Ż Ś Ś Ó Ó Ś Ś Ś Ó Ść Ó ż Ść Ę Ó Ń Ś Ó Ś Ó Ż Ż Ż ć Ż Ó Ó Ż Ś Ó Ś ć Ń ć Ó Ó Ś ż Ś Ż Ż Ść Ó Ś ż ćż ć Ó Ż Ś Ć Ó Ż Ó Ó Ż Ś Ó Ó Ś Ó ż Ó Ż Ź Ś ż Ń Ó Ó Ś ż Ś Ó Ó Ś ż Ś Ś Ś Ć Ż
4. RACHUNEK WEKTOROWY
 4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
4. RACHUNEK WEKTOROWY 4.1. Wektor zczepiony i wektor swoodny Uporządkowną prę punktów (A B) wyznczjącą skierowny odcinek o początku w punkcie A i końcu w punkcie B nzywmy wektorem zczepionym w punkcie
Siedziba wnioskodawc y. Miejsce realizacji projektu. Wydatki kwalifikowalne [PLN] Wnioskowane dofinansowan ie [PLN] Poziom dofinansow ania [%]
![Siedziba wnioskodawc y. Miejsce realizacji projektu. Wydatki kwalifikowalne [PLN] Wnioskowane dofinansowan ie [PLN] Poziom dofinansow ania [%] Siedziba wnioskodawc y. Miejsce realizacji projektu. Wydatki kwalifikowalne [PLN] Wnioskowane dofinansowan ie [PLN] Poziom dofinansow ania [%]](/thumbs/39/18235360.jpg) List wniosków znjdujących się n liście projektów wrunkowo wybrnych do dofinnsowni dl których istnieje moŝliwość podpisni umowy o dofinnsownie: Lp. Wnioskodwc Tytuł projektu Numer wniosku Koszt cłkowity
List wniosków znjdujących się n liście projektów wrunkowo wybrnych do dofinnsowni dl których istnieje moŝliwość podpisni umowy o dofinnsownie: Lp. Wnioskodwc Tytuł projektu Numer wniosku Koszt cłkowity
Karta oceny merytorycznej wniosku o dofinansowanie projektu innowacyjnego testującego składanego w trybie konkursowym w ramach PO KL
 Złącznik nr 5 Krt oceny merytorycznej Krt oceny merytorycznej wniosku o dofinnsownie projektu innowcyjnego testującego skłdnego w trybie konkursowym w rmch PO KL NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA
Złącznik nr 5 Krt oceny merytorycznej Krt oceny merytorycznej wniosku o dofinnsownie projektu innowcyjnego testującego skłdnego w trybie konkursowym w rmch PO KL NR WNIOSKU KSI: WND-POKL. INSTYTUCJA PRZYJMUJĄCA
< f g = fg. f = e t f = e t. U nas: e t (α 1)t α 2 dt = 0 + (α 1)Γ(α 1)
 Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Zdnie X,..., X 5 N(6, 5 ) Y,..., Y 6 N(7, 5 ) X N(6, 5 6 ) Ȳ N(7, 5 6 ) Przy złożeniu niezleżności zmiennych mmy: X Ȳ N(, ) po stndryzcji otrzymmy: Ȳ X N(, ) Pr(Ȳ X < ) = Pr(Ȳ X < ) = φ(, 3) = φ(, 3) =,
Karta oceny merytorycznej wniosku o dofinansowanie projektu konkursowego PO KL 1
 Złącznik nr 3 Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL 1 NR WNIOSKU KSI: POKL.05.02.01 00../..
Złącznik nr 3 Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL Krt oceny merytorycznej wniosku o dofinnsownie projektu konkursowego PO KL 1 NR WNIOSKU KSI: POKL.05.02.01 00../..
BADANIE ZALEŻNOŚCI PRZENIKALNOŚCI MAGNETYCZNEJ
 ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
ADANIE ZAEŻNOŚCI PRZENIKANOŚCI MAGNETYCZNEJ FERRIMAGNETYKÓW OD TEMPERATURY 1. Teori Włściwości mgnetyczne sstncji chrkteryzje współczynnik przeniklności mgnetycznej. Dl próżni ten współczynnik jest równy
Pakiet aplikacyjny. Specjalista ds. rozliczeń i administracji [Pomorze] ADM/2011/01
![Pakiet aplikacyjny. Specjalista ds. rozliczeń i administracji [Pomorze] ADM/2011/01 Pakiet aplikacyjny. Specjalista ds. rozliczeń i administracji [Pomorze] ADM/2011/01](/thumbs/36/17557926.jpg) Pkiet plikcyjny Stnowisko: Nr referencyjny: Specjlist ds. rozliczeń i dministrcji [Pomorze] ADM/2011/01 Niniejszy pkiet zwier informcje, które musisz posidć zgłszjąc swoją kndydturę. Zwier on: List do
Pkiet plikcyjny Stnowisko: Nr referencyjny: Specjlist ds. rozliczeń i dministrcji [Pomorze] ADM/2011/01 Niniejszy pkiet zwier informcje, które musisz posidć zgłszjąc swoją kndydturę. Zwier on: List do
2. Obliczyć natężenie pola grawitacyjnego w punkcie A, jeżeli jest ono wytwarzane przez bryłę o masie M, która powstała przez wydrążenie kuli o
 Grwitcj. Obliczyć, jką siłą jest przyciągn s, jeżeli znn jest s plnety orz gęstość i proień drugiej plnety tkże odległości, jk n rysunku. (,, / F ) 5 F G.5.5 7 Sił t jest położon do poziou pod kąte β tki,
Grwitcj. Obliczyć, jką siłą jest przyciągn s, jeżeli znn jest s plnety orz gęstość i proień drugiej plnety tkże odległości, jk n rysunku. (,, / F ) 5 F G.5.5 7 Sił t jest położon do poziou pod kąte β tki,
WYTRZYMAŁOŚĆ ZMĘCZENIOWA STALI KONSTRUKCYJNEJ W WARUNKACH OBCIĄŻEŃ NIESYMETRYCZNYCH
 GRZEGORZ GASIAK, ROLAND PAWLICZEK Ktedr Mechniki i Podstw Konstrukcji Mszyn WYTRZYMAŁOŚĆ ZMĘCZENIOWA STALI KONSTRUKCYJNEJ W WARUNKACH OBCIĄŻEŃ NIESYMETRYCZNYCH Streszczenie: W prcy przedstwiono etodę opisu
GRZEGORZ GASIAK, ROLAND PAWLICZEK Ktedr Mechniki i Podstw Konstrukcji Mszyn WYTRZYMAŁOŚĆ ZMĘCZENIOWA STALI KONSTRUKCYJNEJ W WARUNKACH OBCIĄŻEŃ NIESYMETRYCZNYCH Streszczenie: W prcy przedstwiono etodę opisu
WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ
 Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
Ćwiczenie 9 WYZNACZANIE OGNISKOWEJ SOCZEWEK CIENKICH ZA POMOCĄ ŁAWY OPTYCZNEJ 9.. Opis teoretyczny Soczewką seryczną nzywmy przezroczystą bryłę ogrniczoną dwom powierzchnimi serycznymi o promienich R i
POLITECHNIKA GDAŃSKA Wydział Elektrotechniki i Automatyki Katedra Energoelektroniki i Maszyn Elektrycznych M O D E L O W A N I E I S Y M U L A C J A
 POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
POLTECHNKA GDAŃSKA Wydził Elektrotechniki i Automtyki Ktedr Energoelektroniki i Mszyn Elektrycznych M O D E L O W A N E S Y M U L A C J A S Y S T E M Ó W M E C H A T O N K Kierunek Automtyk i obotyk Studi
Ćwiczenia laboratoryjne z przedmiotu : Napędy Hydrauliczne i Pneumatyczne
 Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
Lbortorium nr 11 Temt: Elementy elektropneumtycznych ukłdów sterowni 1. Cel ćwiczeni: Opnownie umiejętności identyfikcji elementów elektropneumtycznych n podstwie osprzętu FESTO Didctic. W dużej ilości
 2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l
2 7k 0 5k 2 0 1 5 S 1 0 0 P a s t w a c z ł o n k o w s k i e - Z a m ó w i e n i e p u b l i c z n e n a u s ł u g- i O g ł o s z e n i e o z a m ó w i e n i u - P r o c e d u r a o t w a r t a P o l
SEKCJA III: INFORMACJE O CHARAKTERZE PRAWNYM, EKONOMICZNYM, FINANSOWYM I TECHNICZNYM
 Warszawa: Druk i dstawa publikacji 4 tytuły (4 części) ZP_28_2011 Numer głszenia: 183371-2011; data zamieszczenia: 04.07.2011 OGŁOSZENIE O ZAMÓWIENIU - dstawy Zamieszczanie głszenia: bwiązkwe. Ogłszenie
Warszawa: Druk i dstawa publikacji 4 tytuły (4 części) ZP_28_2011 Numer głszenia: 183371-2011; data zamieszczenia: 04.07.2011 OGŁOSZENIE O ZAMÓWIENIU - dstawy Zamieszczanie głszenia: bwiązkwe. Ogłszenie
OKREŚLENIE WPŁYWU WYŁĄCZANIA CYLINDRÓW SILNIKA ZI NA ZMIANY SYGNAŁU WIBROAKUSTYCZNEGO SILNIKA
 ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2008 Seria: TRANSPORT z. 64 Nr kol. 1803 Rafał SROKA OKREŚLENIE WPŁYWU WYŁĄCZANIA CYLINDRÓW SILNIKA ZI NA ZMIANY SYGNAŁU WIBROAKUSTYCZNEGO SILNIKA Streszczenie. W
ZESZYTY NAUKOWE POLITECHNIKI ŚLĄSKIEJ 2008 Seria: TRANSPORT z. 64 Nr kol. 1803 Rafał SROKA OKREŚLENIE WPŁYWU WYŁĄCZANIA CYLINDRÓW SILNIKA ZI NA ZMIANY SYGNAŁU WIBROAKUSTYCZNEGO SILNIKA Streszczenie. W
Przedmiotowy system oceniania z matematyki wraz z określeniem wymagań edukacyjnych (zakres podstawowy) Klasa II TAK
 I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
I Postnowieni ogólne Przedmiotowy system ocenini z mtemtyki wrz z określeniem wymgń edukcyjnych (zkres podstwowy) Kls II TAK 1. Wrunkiem uzyskni pozytywnej oceny semestrlnej z mtemtyki jest: ) zliczenie
ELIPTYCZNE FUNKCJE TRYGONOMETRYCZNE
 PRACE WYDZIAŁU NAWIGACYJNEGO nr 19 AKADEMII MORSKIEJ W GDYNI 006 ANDRZEJ BANACHOWICZ Akdemi Morsk w Gdyni Ktedr Nwigcji ELIPTYCZNE FUNKCJE TRYGONOMETRYCZNE W rtykule rzedstwiono uogólnienie funkcji trygonometrycznych
PRACE WYDZIAŁU NAWIGACYJNEGO nr 19 AKADEMII MORSKIEJ W GDYNI 006 ANDRZEJ BANACHOWICZ Akdemi Morsk w Gdyni Ktedr Nwigcji ELIPTYCZNE FUNKCJE TRYGONOMETRYCZNE W rtykule rzedstwiono uogólnienie funkcji trygonometrycznych
Wymagania edukacyjne matematyka klasa 2b, 2c, 2e zakres podstawowy rok szkolny 2015/2016. 1.Sumy algebraiczne
 Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2b, 2c, 2e zkres podstwowy rok szkolny 2015/2016 1.Sumy lgebriczne N ocenę dopuszczjącą: 1. rozpoznje jednominy i sumy lgebriczne 2. oblicz wrtości liczbowe wyrżeń lgebricznych
y zamieszkanie (adres placówki, jeśli wnioskodawcą jest nauczyciel lub pracownik socjalny) z kontaktowy (komórkowy lub stacjonarny)
 Dyrekr Szkły Pdwwej nr 11 z Oddzł Inegrcyjny w Suwłkch nek rzyznne cy w rch Rządweg rgru cy uczn w 2012 rku yrwk zkln, n dfnnwne zkuu dręcznków dl dzec rzczynjących nukę w rku zklny 2012/2013 w klch I
Dyrekr Szkły Pdwwej nr 11 z Oddzł Inegrcyjny w Suwłkch nek rzyznne cy w rch Rządweg rgru cy uczn w 2012 rku yrwk zkln, n dfnnwne zkuu dręcznków dl dzec rzczynjących nukę w rku zklny 2012/2013 w klch I
Ć W I C Z E N I E N R E-14
 INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTYTUT FIZYKI WYDZIAŁ INŻYNIERII PRODUKCJI I TECHNOLOGII MATERIAŁÓW POLITECHNIKA CZĘSTOCHOWSKA PRACOWNIA ELEKTRYCZNOŚCI I MAGNETYZMU Ć W I C Z E N I E N R E-14 WYZNACZANIE SZYBKOŚCI WYJŚCIOWEJ ELEKTRONÓW
INSTRUKCJA NR 04 POMIARY I OCENA ŚRODOWISK CIEPLNYCH
 LABORATORIUM OCHRONY ŚRODOWISKA - SYSTEM ZARZĄDZANIA JAKOŚCIĄ - INSTRUKCJA NR 04 POMIARY I OCENA ŚRODOWISK CIEPLNYCH 1. Cel insrukci Cele insrukci es określenie wygń doyczących sposobu oceny środowisk
LABORATORIUM OCHRONY ŚRODOWISKA - SYSTEM ZARZĄDZANIA JAKOŚCIĄ - INSTRUKCJA NR 04 POMIARY I OCENA ŚRODOWISK CIEPLNYCH 1. Cel insrukci Cele insrukci es określenie wygń doyczących sposobu oceny środowisk
Wymagania edukacyjne matematyka klasa 2 zakres podstawowy 1. SUMY ALGEBRAICZNE
 Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Wymgni edukcyjne mtemtyk kls 2 zkres podstwowy 1. SUMY ALGEBRAICZNE Uczeń otrzymuje ocenę dopuszczjącą lub dostteczną, jeśli: rozpoznje jednominy i sumy lgebriczne oblicz wrtości liczbowe wyrżeń lgebricznych
Obliczenia naukowe Wykład nr 14
 Obliczeni nuowe Wyłd nr 14 Pweł Zielińsi Ktedr Informtyi, Wydził Podstwowych Problemów Technii, Politechni Wrocłws Litertur Litertur podstwow [1] D. Kincid, W. Cheney, Anliz numeryczn, WNT, 2005. [2] A.
Obliczeni nuowe Wyłd nr 14 Pweł Zielińsi Ktedr Informtyi, Wydził Podstwowych Problemów Technii, Politechni Wrocłws Litertur Litertur podstwow [1] D. Kincid, W. Cheney, Anliz numeryczn, WNT, 2005. [2] A.
Adres strony internetowej, na której Zamawiający udostępnia Specyfikację Istotnych Warunków Zamówienia: www.us.edu.pl/zamowienia-publiczne-0
 Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.us.edu.pl/zamwienia-publiczne-0 Katwice: Opracwanie graficzne, wyknanie raz druk plakatów prmcyjnych
Adres strny internetwej, na której Zamawiający udstępnia Specyfikację Isttnych Warunków Zamówienia: www.us.edu.pl/zamwienia-publiczne-0 Katwice: Opracwanie graficzne, wyknanie raz druk plakatów prmcyjnych
Liniowy wzrost, spadek a może plateau? (liniowa funkcja regresji w chemii) Dr Mariola Tkaczyk Katedra Chemii Fizycznej
 Liniow wzrost, sdek może lteu? (liniow funkcj regresji w chemii) Dr Mriol Tkczk Ktedr Chemii Fizcznej Pln wkłdu: Wrowdzenie, czli kilk słów o liniowej funkcji regresji. Równnie rostej w oisie:. oddziłwń
Liniow wzrost, sdek może lteu? (liniow funkcj regresji w chemii) Dr Mriol Tkczk Ktedr Chemii Fizcznej Pln wkłdu: Wrowdzenie, czli kilk słów o liniowej funkcji regresji. Równnie rostej w oisie:. oddziłwń
PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH
 SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
SSof Polsk, el. (1) 4843, (61) 414151, info@ssof.pl, www.ssof.pl PROGNOZOWANIE FINANSOWYCH SZEREGÓW CZASOWYCH Andrzej Sokołowski Akdemi Ekonomiczn w Krkowie, Zkłd Sysyki W oprcowniu ym przedswiono pewną
Warszawa, czerwiec 2014 r.
 SPRAWOZDANIE Z WDRAŻANIA PROGRAMU OPERACYJNEGO KAPITAŁ LUDZKI 2007-2013 w 2013 ROKU Wrszw, czerwiec 2014 r. SPIS TREŚCI 1. Informcje wstępne... 4 2. Przegląd relizcji progrmu opercyjnego w okresie objętym
SPRAWOZDANIE Z WDRAŻANIA PROGRAMU OPERACYJNEGO KAPITAŁ LUDZKI 2007-2013 w 2013 ROKU Wrszw, czerwiec 2014 r. SPIS TREŚCI 1. Informcje wstępne... 4 2. Przegląd relizcji progrmu opercyjnego w okresie objętym
PROJEKTOWANIE I BUDOWA
 ObciąŜeni odwozi PROJEKTOWANIE I BUDOWA OBIEKTÓW LATAJĄCYCH I ObciąŜeni odwozi W. BłŜewicz Budow smolotów, obciąŝeni St. Dnilecki Konstruownie smolotów, wyzncznie obciąŝeń R. Cymerkiewicz Budow Smolotów
ObciąŜeni odwozi PROJEKTOWANIE I BUDOWA OBIEKTÓW LATAJĄCYCH I ObciąŜeni odwozi W. BłŜewicz Budow smolotów, obciąŝeni St. Dnilecki Konstruownie smolotów, wyzncznie obciąŝeń R. Cymerkiewicz Budow Smolotów
Weryfikacja modelowa jest analizą statyczną logiki modalnej
 Weryfikcj modelow jest nlizą sttyczną logiki modlnej Mrcin Sulikowski MIMUW 15 grudni 010 1 Wstęp Weryfikcj systemów etykietownych 3 Flow Logic 4 Weryfikcj modelow nliz sttyczn Co jest czym czego? Weryfikcj
Weryfikcj modelow jest nlizą sttyczną logiki modlnej Mrcin Sulikowski MIMUW 15 grudni 010 1 Wstęp Weryfikcj systemów etykietownych 3 Flow Logic 4 Weryfikcj modelow nliz sttyczn Co jest czym czego? Weryfikcj
Wszystkim życzę Wesołych Świąt :-)
 Poniższe zdni pochodzą ze zbiorów: ) J. Rutkowski, Algebr bstrkcyjn w zdnich b) M. Bryński, J. Jurkiewicz, Zbiór zdń z lgebry Do kolokwium proszę też przejrzeć zdni z ćwiczeń. Wszystkim życzę Wesołych
Poniższe zdni pochodzą ze zbiorów: ) J. Rutkowski, Algebr bstrkcyjn w zdnich b) M. Bryński, J. Jurkiewicz, Zbiór zdń z lgebry Do kolokwium proszę też przejrzeć zdni z ćwiczeń. Wszystkim życzę Wesołych
Próba określenia czynników determinujących wyniki ocen wprowadzenia euro przez mieszkańców Unii Europejskiej
 Mieczysłw Kowerski Wyższ Szkoł Zrządzni I Administrcji w Zmościu Ewelin Włodrczyk Wyższ Szkoł Zrządzni I Administrcji w Zmościu Prób określeni czynników determinujących wyniki ocen wprowdzeni euro przez
Mieczysłw Kowerski Wyższ Szkoł Zrządzni I Administrcji w Zmościu Ewelin Włodrczyk Wyższ Szkoł Zrządzni I Administrcji w Zmościu Prób określeni czynników determinujących wyniki ocen wprowdzeni euro przez
Ogniwo wzorcowe Westona
 WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
WZOZEC SEM - OGNWO WESTON mieszczne jest w szklanym naczyniu, w które wtpine są platynwe elektrdy. Ddatni i ujemny biegun gniwa stanwią dpwiedni rtęć (Hg) i amalgamat kadmu (Cd 9-Hg), natmiast elektrlitem
Grażyna Nowicka, Waldemar Nowicki BADANIE RÓWNOWAG KWASOWO-ZASADOWYCH W ROZTWORACH ELEKTROLITÓW AMFOTERYCZNYCH
 Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ćwiczenie Grżyn Nowick, Wldemr Nowicki BDNIE RÓWNOWG WSOWO-ZSDOWYC W ROZTWORC ELETROLITÓW MFOTERYCZNYC Zgdnieni: ktywność i współczynnik ktywności skłdnik roztworu. ktywność jonów i ktywność elektrolitu.
Ato wodoropodobny Eektron poruszjący się w kuobowski pou jądr o łdunku +Ze posid energię potencjną: z -e, V ( r) Ze 4πε r + Ze φ θ r y x
 Ato wodoropodobny z współrzędne w ukłdzie krtezjński r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy ukłd współrzędnych y funkcj fow współrzędne w ukłdzie biegunowy ( ) r,θ,φ x r sinθ cosφ
Ato wodoropodobny z współrzędne w ukłdzie krtezjński r sinθ cosφ x r cosθ φ θ r r sinθ (x,y,z) r sinθ sinφ Biegunowy ukłd współrzędnych y funkcj fow współrzędne w ukłdzie biegunowy ( ) r,θ,φ x r sinθ cosφ
PROJEKTY GOTOWE DŹWIGARÓW DACHOWYCH
 Dwne: Centrlne Biuro Projektowo-Bdwcze Budownictw Wiejskiego 04-026 Wrszw 50, l. Stnów Zjednoczonyc 51 tel. 22-810-83-78; 22-810-64-89; fx; 22-810-58-97; e-il: isprol@isprol.pl ; www.isprol.pl PROJEKTY
Dwne: Centrlne Biuro Projektowo-Bdwcze Budownictw Wiejskiego 04-026 Wrszw 50, l. Stnów Zjednoczonyc 51 tel. 22-810-83-78; 22-810-64-89; fx; 22-810-58-97; e-il: isprol@isprol.pl ; www.isprol.pl PROJEKTY
MXZ INVERTER SERIA. Jedna jednostka zewnętrzna może obsługiwać do 8 pomieszczeń. Ograniczenie poboru prądu. Efektywność energetyczna: klasa A
 INVERTER SERIA MXZ Typoszereg MXZ gwrntuje cicy, wysokowydjny i elstyczny system, spełnijący wszystkie wymgni w zkresie klimtyzcji powietrz. 6 MXZ-2C30VA MXZ-2C40VA MXZ-2C52VA MXZ-3C54VA MXZ-3C68VA MXZ-4C71VA
INVERTER SERIA MXZ Typoszereg MXZ gwrntuje cicy, wysokowydjny i elstyczny system, spełnijący wszystkie wymgni w zkresie klimtyzcji powietrz. 6 MXZ-2C30VA MXZ-2C40VA MXZ-2C52VA MXZ-3C54VA MXZ-3C68VA MXZ-4C71VA
USE OF THEORY OF SIMILARITY IN DEPENDENCE ANALISYS OF AIR-FUEL RATIO MEAN THEMPERATURE AND BOUNDARY CONDITIONS IN DIESEL TURBO ENGINE
 Jurnl f KONES Pwertrin nd Trnsprt, Vl. 3, N. USE OF THEORY OF SIMILARITY IN DEPENDENCE ANALISYS OF AIR-FUEL RATIO MEAN THEMPERATURE AND BOUNDARY CONDITIONS IN DIESEL TURBO ENGINE Jrsw Kbry, Krystin Wilk
Jurnl f KONES Pwertrin nd Trnsprt, Vl. 3, N. USE OF THEORY OF SIMILARITY IN DEPENDENCE ANALISYS OF AIR-FUEL RATIO MEAN THEMPERATURE AND BOUNDARY CONDITIONS IN DIESEL TURBO ENGINE Jrsw Kbry, Krystin Wilk
Dziennik Transakcyjny. JLoXiM
 JXiM Dzieik Trskcj JXiM Mteusz Łuiński JXiM Rzdził 1 Ogólie dzieiku JXiM Rzdził 1 Ogólie dzieiku C t jest trskcj dzieik bzdw? Kcecjie: ieskńcz tśm Grmdzi ifrmcje wszelkich ercjch wkwch i w bzie dch JXiM
JXiM Dzieik Trskcj JXiM Mteusz Łuiński JXiM Rzdził 1 Ogólie dzieiku JXiM Rzdził 1 Ogólie dzieiku C t jest trskcj dzieik bzdw? Kcecjie: ieskńcz tśm Grmdzi ifrmcje wszelkich ercjch wkwch i w bzie dch JXiM
Elementy Elektrochemii
 Elementy Elektrchemii III.: Ogniw glwniczne Urządzeni służące d czerpni prądu elektryczneg wytwrzneg dzięki zchdzącym w nim przeminm elektrchemicznym Pdstwwą wielkścią chrkteryzującą gniw jest Sił Elektrmtryczn
Elementy Elektrchemii III.: Ogniw glwniczne Urządzeni służące d czerpni prądu elektryczneg wytwrzneg dzięki zchdzącym w nim przeminm elektrchemicznym Pdstwwą wielkścią chrkteryzującą gniw jest Sił Elektrmtryczn
Obliczanie układów statycznie niewyznaczalnych. Obliczanie układów statycznie niewyznaczalnych metoda sił z wykorzystaniem symetrii i antysymetrii
 Gr. rok III POLITECHNIK POZNŃSK INSTYTUT KONSTRUKCJI BUDOWLNYCH ZKŁD ECHNIKI BUDOWLI metoda sił z wykorzystaniem symetrii i antysymetrii Gr. rok III 0 kn 6 kn/m Ponieważ rama jest symetryczna, do obliczenia
Gr. rok III POLITECHNIK POZNŃSK INSTYTUT KONSTRUKCJI BUDOWLNYCH ZKŁD ECHNIKI BUDOWLI metoda sił z wykorzystaniem symetrii i antysymetrii Gr. rok III 0 kn 6 kn/m Ponieważ rama jest symetryczna, do obliczenia
Politechnika Śląska Wydział Automatyki, Elektroniki i Informatyki Praca dyplomowa
 Politechni Ślą Wydził Automtyi, Eletronii i Informtyi Prc dyplomow Temt : Stnowio lbortoryjne do ymulcji obietów n terowniu SLC500. Promotor : Dr inż. J.przy Student : Tomz tuzczy Cel prcy Celem prcy było
Politechni Ślą Wydził Automtyi, Eletronii i Informtyi Prc dyplomow Temt : Stnowio lbortoryjne do ymulcji obietów n terowniu SLC500. Promotor : Dr inż. J.przy Student : Tomz tuzczy Cel prcy Celem prcy było
 Ł Ł Ś Ę ź ź ź ź Ś ź ż Ę Ę Ś ż Ś ń Ś Ó Ą Ł Ą Ś ź Ę ć Ś ź ż ż ż ż ż ć ż ż Ń ć ń Ś ź ż ń ć ć ż ć ż źń ć ż ż ż ź ń ć ć Ł ż Ę ń ć ż ń ż ż Ś ź ż ń ń Ś ż Ś ń Ś ż ż Ś ń Ą ż Ł ć ż ż ż ń ż ż ż ż ń Ł ń Ę Ę Ą ń ź
Ł Ł Ś Ę ź ź ź ź Ś ź ż Ę Ę Ś ż Ś ń Ś Ó Ą Ł Ą Ś ź Ę ć Ś ź ż ż ż ż ż ć ż ż Ń ć ń Ś ź ż ń ć ć ż ć ż źń ć ż ż ż ź ń ć ć Ł ż Ę ń ć ż ń ż ż Ś ź ż ń ń Ś ż Ś ń Ś ż ż Ś ń Ą ż Ł ć ż ż ż ń ż ż ż ż ń Ł ń Ę Ę Ą ń ź
 ń Ą ń Ż Ż ń Ó ź Ę ź ź Ę ć ć ć Ś ź ŚĆ Ś ź ź ź ź Ś ź ń Ś Ó Ć ŚĆ Ć ć ć ć ź ń ć Ó ń ń ń Ś ń ń Ś ń ź ź ź źń Ź Ś ń Ć Ś Ś Ź ń ń Ś ń ń Ś ź ź Ś ź źń Ś ć ć ń Ś ń ń Ś Ś Ś Ś ń ź ź Ś ź źń ź Ś ń ź Ś Ś Ś ź ń ń Ś ń ń
ń Ą ń Ż Ż ń Ó ź Ę ź ź Ę ć ć ć Ś ź ŚĆ Ś ź ź ź ź Ś ź ń Ś Ó Ć ŚĆ Ć ć ć ć ź ń ć Ó ń ń ń Ś ń ń Ś ń ź ź ź źń Ź Ś ń Ć Ś Ś Ź ń ń Ś ń ń Ś ź ź Ś ź źń Ś ć ć ń Ś ń ń Ś Ś Ś Ś ń ź ź Ś ź źń ź Ś ń ź Ś Ś Ś ź ń ń Ś ń ń
 Ą Ł ń Ź Ź Ą Ą ź ć Ź ń ź Ę Ł Ę Ł ż ć ć ć ż ż ż ć Ż ń ć ń ć Ń Ę ż Ż Ż Ż ć Ń Ż Ż Ą ń Ż Ż Ą Ą ń ż ń Ż Ź ż ż Ź ń ć ć Ą ć ć ć Ż ć ć ż ć ć Ż Ą ć Ż ć Ż ż ń ż ń ć Ż ć ć Ż Ł Ż Ż ć ż ć ć Ń Ń ż Ą ć ć ć ń ć ź ć ż ć
Ą Ł ń Ź Ź Ą Ą ź ć Ź ń ź Ę Ł Ę Ł ż ć ć ć ż ż ż ć Ż ń ć ń ć Ń Ę ż Ż Ż Ż ć Ń Ż Ż Ą ń Ż Ż Ą Ą ń ż ń Ż Ź ż ż Ź ń ć ć Ą ć ć ć Ż ć ć ż ć ć Ż Ą ć Ż ć Ż ż ń ż ń ć Ż ć ć Ż Ł Ż Ż ć ż ć ć Ń Ń ż Ą ć ć ć ń ć ź ć ż ć
 Ń Ó Ą Ó Ą Ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć Ń ć ć ć ź ź Ą ć ć ć ź Ź ź ć ŚĆ ć ć ć ź ć źń Ć Ż ź ć ć ć ź ć Ż Ą ć Ż ć ź ć ź ź ź Ą ć ć ć ć ć ć Ą ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć ć ć Ą ć Ó ź Ó Ó Ń Ą Ó
Ń Ó Ą Ó Ą Ń ć ć ć ć ć ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć Ń ć ć ć ź ź Ą ć ć ć ź Ź ź ć ŚĆ ć ć ć ź ć źń Ć Ż ź ć ć ć ź ć Ż Ą ć Ż ć ź ć ź ź ź Ą ć ć ć ć ć ć Ą ć ć ć ć ć ć ć ć ć ć ź ć ć ć ć ć ć ć Ą ć Ó ź Ó Ó Ń Ą Ó
 Ą ż ń ń ń ń ż Ą ń ń ż ć ń ś ż ż ż ś ż ż ż ż ć ć ś Ą ż ń ż ż ć ń ś ź ń ś ż ś ś ń ś ń ś ś ś Ń ś ż ń ś ń ń ść ż Ę ń ś ń ń ń ś ż ć Ą ś ż Ń żń ś ż ż ń ś Ę ŁÓ Ą ż ń ń ś ń ń ż ć ż Ś ź Ń ś Ń ż ń ś ń ż ź
Ą ż ń ń ń ń ż Ą ń ń ż ć ń ś ż ż ż ś ż ż ż ż ć ć ś Ą ż ń ż ż ć ń ś ź ń ś ż ś ś ń ś ń ś ś ś Ń ś ż ń ś ń ń ść ż Ę ń ś ń ń ń ś ż ć Ą ś ż Ń żń ś ż ż ń ś Ę ŁÓ Ą ż ń ń ś ń ń ż ć ż Ś ź Ń ś Ń ż ń ś ń ż ź
Ćwiczenie nr 2-SCO. Warstwa połowiąca WP. Ćwiczenie nr 2. 1 Cel ćwiczenia
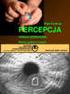 Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Ćwiczenie nr 2-SCO. Wrstw połowiąc WP 1 Cel ćwiczeni Wyznczenie pierwszej wrstwy połowiącej WP (Hlf Vlue Lyer) dl promieniowni X generownego w prcie rentgenowskim (energi 5-15 kev). Wyzncznie współczynnik
Statystyka - wprowadzenie
 Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią
Statystyka - wprwadzenie Obecnie pjęcia statystyka używamy aby mówić : zbirze danych liczbwych ukazujących kształtwanie się kreślneg zjawiska jak pewne charakterystyki liczbwe pwstałe ze badań nad zbirwścią



